2018届重庆中考复习:二次函数相关的最值问题练习(含答案)
中考数学《二次函数的最值》专项练习题及答案

中考数学《二次函数的最值》专项练习题及答案一、单选题1.定义:如果两个函数图象上至少存在一对点是关于原点对称的,我们则称这两个函数互为“守望函数”,这对点称为“守望点”.例如:点P(2,4)在函数y =x 2上,点 Q(−2,−4)在函数y =−2x −8上,点P 与点Q 关于原点对称,此时函数y =x 2和y =−2x −8互为“守望函数”,点P 与点Q 则为一对“守望点”.已知函数y =x 2+2x 和y =4x +n −2022互为“守望函数”,则n 的最大值为( ) A .2020B .2022C .2023D .40842.已知二次函数y=ax 2+2ax+3a 2+3(其中x 是自变量),当x ≥2时,y 随x 的增大而增大,且-2≤x ≤1时,y 的最大值为9,则a 的值为( ) A .1或B .- 或C .D .13.已知二次函数y =ax 2+bx −1(a ,b 是常数,a ≠0)的图象经过A(2,1),B(4,3),C(4,−1)三个点中的其中两个点.平移该函数的图象,使其顶点始终在直线y =x −1上,则平移后所得抛物线与y 轴交点纵坐标的( ) A .最大值为-1B .最小值为-1C .最大值为−12D .最小值为−124.二次函数y=ax 2+bx+c (a 、b 、c 为常数且a ≠0)中的x 与y 的部分对应值如下表:x ﹣3 ﹣2 ﹣1 0 1 2 3 4 5 y125﹣3﹣4﹣35121)二次函数y=ax 2+bx+c 有最小值,最小值为﹣3;2)当 −12<x <2 时,y <0;3)二次函数y=ax 2+bx+c 的图象与x 轴有两个交点,且它们分别在y 轴两侧.则其中正确结论的个数是( ) A .3B .2C .1D .05.已知二次函数 y =−(x −ℎ)2+4 (h 为常数),在自变量 x 的值满足 1≤x ≤4的情况下,与其对应的函数值 y 的最大值为0,则 h 的值为( ) A .和B . 和C .和D . 和6.经过点A (m ,n ),点B (m ﹣4,n )的抛物线y =x 2+2cx+c 与x 轴有两个公共点,与y 轴的交点在x 轴的上方,则当m >﹣12时,n 的取值范围是( )A .14<n <4B .12<n <2C .18<n <8D .14<n <27.二次函数y =x 2+2x -5有A .最大值-5B .最小值-5C .最大值-6D .最小值-68.①4的算术平方根是±2;②√2与-√8是同类二次根式;③点P (2,3)关于原点对称的点的坐标是(-2,-3); ④抛物线y=-12(x-3)2+1的顶点坐标是(3,1).其中正确的是( ) A .①②④B .①③C .②④D .②③④9.童装专卖店销售一种童装,已知这种童装每天所获得的利润y (元)与童装的销售单价x (元)之间满足关系式y=-x 2+50x+500,则要想每天获得最大利润,单价需为( ). A .25元B .20元C .30元D .40元10.已知二次函数y =ax 2+bx +c (a ,b ,c 是常数,a ≠0)的y 与x 的部分对应值如表:x ﹣5 ﹣4 ﹣2 0 2 y6﹣6﹣468,y 1),点(8,y 2)在二次函数图象上,则y 1<y 2;④方程ax 2+bx +c =﹣5有两个不相等的实数根.其中,正确结论的是( ) A .①②③B .①③④C .①②④D .②③④11.已知抛物线y=-2(x-3)2+5,则此抛物线( )A .开口向下,对称轴为直线x=-3B .顶点坐标为(-3,5)C .最小值为5D .当x >3时y 随x 的增大而减小12.如果抛物线 y =x 2−6x +c −2 的顶点到 x 轴的距离是3,那么 c 的值等于( )A .8B .14C .8或14D .-8或-14二、填空题13.二次函数y=2x 2﹣1,∵a= ,∴函数有最 值.14.公路上行驶的汽车急刹车时的行驶路程s (m )与时间t (s )的函数关系式为s=20t-5t 2,当遇到紧急情况时,司机急刹车,但由于惯性汽车要滑行 m 才能停下来.15.已知二次函数y = 12x ²+2若自变量x 的取值范围是-1≤x ≤2,则函数y 的取值范围是 .16.函数y =x 2−2x(0≤x ≤3)有最大值,也有最小值,则最小值是 . 17.若二次函数y =-x 2-4x +k 的最大值是9,则k = .18.当﹣2≤x≤1时,二次函数y=﹣(x﹣m)2+m2+1有最大值4,则实数m的范围是.三、综合题19.某农作物的生长率p与温度t ( C∘ )有如下关系:如图,当10≤t≤25 时可近似用函数p=150t−15刻画;当25≤t≤37 时可近似用函数p=−1160(t−ℎ)2+0.4刻画.(1)求ℎ的值.(2)按照经验,该作物提前上市的天数m (天)与生长率p满足函数关系,部分数据如下:生长率p0.20.250.30.35提前上市的天数m(天)051015②请用含t的代数式表示m③天气寒冷,大棚加温可改变农作物生长速度.在大棚恒温20℃时每天的成本为100元,该作物30天后上市时,根据市场调查:每提前一天上市售出(一次售完),销售额可增加600元.因此决定给大棚继续加温,但加温导致成本增加,估测加温到20≤t≤25时的成本为200元/天,但若加温到25<t≤37,由于要采用特殊方法,成本增加到400元/天,问加温到多少度时增加的利润最大?并说明理由。
初中数学二次函数的最值问题--练习题+答案

初中数学二次函数的最值问题--练习题+答案-CAL-FENGHAI-(2020YEAR-YICAI)_JINGBIAN二次函数的最值问题 二次函数2 (0)y ax bx c a =++≠是初中函数的主要内容,也是高中学习的重要基础.在初中阶段大家已经知道:二次函数在自变量x 取任意实数时的最值情况(当0a >时,函数在2b x a =-处取得最小值244ac b a -,无最大值;当0a <时,函数在2b x a=-处取得最大值244ac b a-,无最小值. 【例1】当22x -≤≤时,求函数223y x x =--的最大值和最小值.分析:作出函数在所给范围的及其对称轴的草图,观察图象的最高点和最低点,由此得到函数的最大值、最小值及函数取到最值时相应自变量x 的值.解:作出函数的图象.当1x =时,min 4y =-,当2x =-时,max 5y =.【例2】当12x ≤≤时,求函数21y x x =--+的最大值和最小值.解:作出函数的图象.当1x =时,min 1y =-,当2x =时,max 5y =-.由上述两例可以看到,二次函数在自变量x 的给定范围内,对应的图象是抛物线上的一段.那么最高点的纵坐标即为函数的最大值,最低点的纵坐标即为函数的最小值. 根据二次函数对称轴的位置,函数在所给自变量x 的范围的图象形状各异.下面给出一些常见情况:【例3】当0x ≥时,求函数(2)y x x =--的取值范围.解:作出函数2(2)2y x x x x =--=-在0x ≥内的图象.可以看出:当1x =时,min 1y =-,无最大值.所以,当0x ≥时,函数的取值范围是1y ≥-.【例4】当1t x t ≤≤+时,求函数21522y x x =--的最小值(其中t 为常数). 分析:由于x 所给的范围随着t 的变化而变化,所以需要比较对称轴与其范围的相对位置.解:函数21522y x x =--的对称轴为1x =.画出其草图. (1) 当对称轴在所给范围左侧.即1t >时: 当x t =时,2min 1522y t t =--; (2) 当对称轴在所给范围之间.即1101t t t ≤≤+⇒≤≤时:当1x =时,2min 1511322y =⨯--=-; (3) 当对称轴在所给范围右侧.即110t t +<⇒<时:当1x t =+时,22min 151(1)(1)3222y t t t =+-+-=-.综上所述:2213,023,0115,122t t y t t t t ⎧-<⎪⎪=-≤≤⎨⎪⎪-->⎩在实际生活中,我们也会遇到一些与二次函数有关的问题:【例5】某商场以每件30元的价格购进一种商品,试销中发现这种商品每天的销售量m (件)与每件的销售价x (元)满足一次函数1623,3054m x x =-≤≤.(1) 写出商场卖这种商品每天的销售利润y 与每件销售价x 之间的函数关系式;(2) 若商场要想每天获得最大销售利润,每件商品的售价定为多少最合适?最大销售利润为多少解:(1) 由已知得每件商品的销售利润为(30)x -元,那么m 件的销售利润为(30)y m x =-,又1623m x =-.2 (30)(1623)32524860,3054y x x x x x ∴=--=-+-≤≤(2) 由(1)知对称轴为42x =,位于x 的范围内,另抛物线开口向下 ∴当42x =时,2max 342252424860432y =-⨯+⨯-=∴当每件商品的售价定为42元时每天有最大销售利润,最大销售利润为432元.练习A 组1.抛物线2(4)23y x m x m =--+-,当m = _____ 时,图象的顶点在y 轴上;当m = _____ 时,图象的顶点在x 轴上;当m = _____ 时,图象过原点.2.用一长度为l 米的铁丝围成一个长方形或正方形,则其所围成的最大面积为 ________ .3.求下列二次函数的最值:(1) 2245y x x =-+; (2) (1)(2)y x x =-+.4.求二次函数2235y x x =-+在22x -≤≤上的最大值和最小值,并求对应的x 的值.5.对于函数2243y x x =+-,当0x ≤时,求y 的取值范围.6.求函数3y =7.已知关于x 的函数22(21)1y x t x t =+++-,当t 取何值时,y 的最小值为0?B 组1.已知关于x 的函数222y x ax =++在55x -≤≤上.(1) 当1a =-时,求函数的最大值和最小值;(2) 当a 为实数时,求函数的最大值.2.函数223y x x =++在0m x ≤≤上的最大值为3,最小值为2,求m 的取值范围.3.设0a >,当11x -≤≤时,函数21y x ax b =--++的最小值是4-,最大值是0,求,a b 的值.4.已知函数221y x ax =++在12x -≤≤上的最大值为4,求a 的值.5.求关于x 的二次函数221y x tx =-+在11x -≤≤上的最大值(t 为常数).答案解析A 组1.4 14或2,322.2216l m 3.(1) 有最小值3,无最大值;(2) 有最大值94,无最小值. 4.当34x =时,min 318y =;当2x =-时,max 19y =.5.5y ≥- 6.当56x =时,min 3y =-23x =或1时,max 3y =. 7.当54t =-时,min 0y =. B 组1.(1) 当1x =时,min 1y =;当5x =-时,max 37y =.(2) 当0a ≥时,max 2710y a =+;当0a <时,max 2710y a =-.2.21m -≤≤-. 3.2,2a b ==-.4.14a=-或1a=-.5.当0t≤时,max22y t=-,此时1x=;当0t>时,max 22y t=+,此时1x=-.。
中考数学《二次函数的最值》专项练习及答案

中考数学《二次函数的最值》专项练习及答案一、单选题1.如果抛物线y=x2−6x+c−2的顶点到x轴的距离是3,那么c的值等于()A.8B.14C.8或14D.-8或-142.已知二次函数y=ax2+2ax+3a2+3(其中x是自变量),当x≥2时,y随x的增大而增大,且-2≤x≤1时,y的最大值为9,则a的值为()A.1或B.- 或C.D.13.如图,已知点A(12,0),O为坐标原点,P是线段OA上任意一点(不含端点O,A),过P、O 两点的二次函数y1和过P、A两点的二次函数y2的图象开口均向下,它们的顶点分别为B、C,射线OB与AC相交于点D.当OD=AD=8时,这两个二次函数的最大值之和等于()A.5B.2√7C.8D.64.二次函数y=x2﹣2x﹣3,当m﹣2≤x≤m时的最大值为5,则m的值可能为()A.0或6B.4或﹣2C.0或4D.6或﹣25.我们定义一种新函数:形如y=|ax2+bx+c|(a≠0,b2−4ac>0)的函数叫做“鹊桥”函数.小丽同学画出了“鹊桥”函数y=|x2−2x−3|的图象(如图所示),并写出下列结论:①图象与坐标轴的交点为(−1,0),(3,0)和(0,3);②图象具有对称性,对称轴是直线x=1;③当−1≤x≤1或x≥3时,函数值y随x值的增大而增大;④当x=−1或x=3时,函数的最小值是0;⑤当x= 1时,函数的最大值是4,⑥若点P(a,b)在该图象上,则当b=2时,可以找到4个不同的点P.其中正确结论的个数是()A.6B.5C.4D.36.关于二次函数y=ax2+bx+c,自变量x与函数y的对应值如表,下列说法正确的是()x…﹣3﹣201…y…7﹣2﹣27…(0,2).图象的对称轴是直线x=1 C.y的最小值为-5D.图象与x轴有且只有一个交点7.二次函数y=ax2+bx+c的自变量x与函数y的对应值如下表:x…-5-4-3-2-10…y…40-2-204…A.抛物线的开口向下B.当x>-3时,y随x的增大而增大C.二次函数的最小值是-2D.抛物线的对称轴是直线x=-528.下列对抛物线y=−2(x−4)2+9性质的描写中,正确的是()A.开口向上B.对称轴是直线x=9C.顶点坐标是(﹣4,9)D.函数y有最大值9.二次函数y=(x﹣m)2﹣m2﹣1有最小值﹣4,则实数m的值可能是()A.﹣B.﹣3C.D.410.y=a(x−x1)(x−x2)+t(a>0),点(x0,y0)是函数图象上任意一点,()<−a4(x1−x2)2A.若t<0,则y>−a4(x1−x2)2B.若t≥0,则y≤−a4(x1−x2)2C.若t<0,则y≥−a4(x1−x2)2D.若t≥0,则y11.已知二次函数y=(x﹣h)2+1(h为常数),在自变量x的值满足1≤x≤3的情况下,与其对应的函数y的最小值为5,则h的值是()A.﹣1B.﹣1或5C.5D.﹣512.关于二次函数y=-x2+2x的最值,下列叙述正确的是()A.当x=2时,y有最小值0B.当x=2时,y有最大值0C.当x=1时,y有最小值1D.当x=1时,y有最大值1二、填空题13.如图,有长为24米的篱笆,一边利用墙(墙的最大可用长度为3米),围成一个由两个长方形组成的花圃,当花圃的边AB为米时,围成的花圃面积最大,最大面积为平方米.14.抛物线的y=(x﹣3)2﹣2的最小值为.15.飞机着陆后滑行的距离y(单位:m)关于滑行时间t(单位:s)的函数解析式是y=60t−62,飞机着陆至停下来共滑.5t16.如图所示,二次函数y=ax2+bx+c(a≠0,a,b,c为实数)的图象过点A(3,0),对称轴为直线x=1,给出以下结论:①abc<0;②3a+c=0;③ax2+bx≤a+ b;④若M(−0.5,y1)、N(3.5,y2)为函数图象上的两点,则y1<y2.其中正确的有.(填写序号即可)17.已知二次函数y=ax2+bx+c(a,b,c是常数,a≠0)的y与x的部分对应值如表:下列结论:①a>0;②当x=﹣2时,函数最小值为﹣6;③若点(﹣8,y1),点(8,y2)在二次函数图象上,则y1<y2;④方程ax2+bx+c=﹣5有两个不相等的实数根.其中,正确结论的序号是(把所有正确结论的序号都填上)x﹣5﹣4﹣202y60﹣6﹣461825元时,平均每天能售出8件,而当销售价每降低2元,平均每天能多售出4件,当每件的定价为元时,该服装店平均每天的销售利润最大.三、综合题19.已知二次函数y=−x2+4x+c.(1)该二次函数图象的对称轴是直线.(2)当4≤x≤6时,y的最大值是-3,求此二次函数解析式.20.已知函数y=-x2+bx+c(b,c为常数)的图象经过点(0,﹣3),(﹣6,﹣3).(1)求b,c的值.(2)当﹣4≤x≤0时,求y的最大值.(3)当m≤x≤0时,若y的最大值与最小值之和为2,求m的值.21.在一张足够大的纸板上截取一个面积为3600平方厘米的矩形纸板ABCD,如图1,再在矩形纸板的四个角上切去边长相等的小正方形,再把它的边沿虚线折起,做成一个无盖的长方体纸盒,底面为矩形EFGH,如图2.设小正方形的边长为x厘米.(1)当矩形纸板ABCD的一边长为90厘米时,求纸盒的侧面积的最大值;(2)当EH:EF=7:2,且侧面积与底面积之比为9:7时,求x的值.22.已知二次函数y=x2+bx+2b(b为常数).(1)若图象过(2,8),求函数的表达式.(2)在(1)的条件下,当−2≤x≤2时,求函数的最大值和最小值.(3)若函数图象不经过第三象限,求b的取值范围23.已知:如图,抛物线y=ax2+bx+c与坐标轴分别交于点A(0,6),B(6,0),C(−2,0),点P 是线段AB上方抛物线上的一个动点.(1)求抛物线的解析式;(2)当点P运动到什么位置时,△PAB的面积有最大值,面积最大值是多少?(3)已知抛物线的顶点为点D.点M是x轴上的一个动点,当点M的坐标为多少时,△ADM的周长最小?最小值是多少?24.如图,抛物线y=x2+bx−c与x轴交A(−1,0)、B(3,0)两点,直线l与抛物线交于A、C两点,其中C点的横坐标为2.(1)求抛物线及直线AC的函数表达式;(2)若P点是线段AC上的一个动点,过P点作y轴的平行线交抛物线于F点,求线段PF长度的最大值.参考答案1.【答案】C2.【答案】D3.【答案】B4.【答案】C5.【答案】B6.【答案】C7.【答案】D8.【答案】D9.【答案】A10.【答案】D11.【答案】B12.【答案】D13.【答案】7;2114.【答案】﹣215.【答案】750m16.【答案】①②③17.【答案】①③④18.【答案】2219.【答案】(1)x=2(2)y=−x2+4x−320.【答案】(1)解:把(0,-3),(-6,-3)代入y=−x2+bx+c 得b=-6,c=-3(2)解:∵y=−x2−6x−3=−(x+3)2+6又∵-4≤x≤0∴当x=-3时,y有最大值为6.(3)解:①当-3<m≤0时当x=0时,y有最小值为-3当x=m时,y有最大值为−m2−6m−3∴−m2−6m−3+(-3)=2∴m=-2或m=-4(舍去).②当m≤-3时当x =-3时y 有最大值为6 ∵y 的最大值与最小值之和为2 ∴y 最小值为-4 ∴−(m +3)2+6 =-4∴m = −3−√10 或m = −3+√10 (舍去). 综上所述,m =-2或 −3−√10 .21.【答案】(1)解:S 侧=2[x(90-2x)+x(40-2x)] =-8x 2+260x=-8(x - 654 )2+ 42252.∵-8<0,∴当x = 654 时,S 侧最大= 42252(2)解:设EF =2m ,则EH =7m则侧面积为2(7mx +2mx)=18mx ,底面积为7m·2m =14m 由题意,得18mx :14m =9:7,∴m =x . 则AD =7x +2x =9x ,AB =2x +2x =4x 由4x·9x =3600,且x >0 ∴x =1022.【答案】(1)解:∵图象经过点(2,8)∴8=4+2b +2b 解得b =1.∴此函数解析式为y =x 2+x +2.(2)解:y =x 2+x +2=(x +12)2+74.∵抛物线的开口向上∴当−2≤x ≤−12,y 随x 的增大而减小∴当x =−12时,y 的最小值为74当−12≤x ≤2时,y 随x 的增大而增大∴当x =2时y 的最大值为(2+12)2+74=8答:最小值74,最大值8.(3)解:∵图象不经过第三象限,且开口向上 ∴2b ≥0,即b ≥0∴对称轴直线x =−b2≤0,在y 轴左侧∴图象必在x 轴上方(包括x 轴)∴△=b2−8b≤0∴0≤b≤8.23.【答案】(1)解:∵抛物线y=ax2+bx+c与坐标轴分别交于点A(0,6),B(6,0)∴{c=636a+6b+c=0 4a−2b+c=0∴{c=6a=−12b=2∴抛物线的解析式为:y=−12x2+2x+6(2)解:设P点坐标为(x0,y0)∵点P是线段AB上方抛物线上的一个动点,A(0,6)∴0<x0<6过P点作x轴的垂线,与x轴交于点H,如图∵S四边形AOBP =S△PAB+S△AOB=S梯形AOHP+S△PHB∴12(6+y0)x0+12(6−x0)y0=S△PAB+12×6×6可得S△PAB=3x0+3y0−18∵y0=−12x02+2x0+6∴S△PAB=3x0+3(−12x02+2x0+6)−18,得∴S△PAB=−32x02+9x0=−32(x0−3)2+272∴当x0=3时,S△PAB面积最大为272(3)解:做出点A关于x轴的对称点A′,则A′(0,−6),设M点坐标为M(x1,0)根据对称性及两点间线段最短可知,当M 点刚好位于A ′D 与x 轴交点时,△ADM 的周长最小 ,且L △ADM =A ′D +AD∵ 抛物线解析式为y =−12x 2+2x +6=−12(x −2)2+8∴ D 点坐标为(2,8)设直线A ′D 解析式为y =kx +b∵A ′(0,−6),D(2,8) ,代入直线解析式得 {b =−68=2k +b ,得{b =−6k =7∴直线A ′D 解析式为y =7x −6 M 点为直线A ′D 与x 轴交点,则7x 1−6=0 ,得x 1=67∴M(67,0)∵ A ′(0,−6),A(0,6)∴L △ADM =A ′D +AD =√(0−2)2+(−6−8)2+√(0−2)2+(6−8)2=√4+196+√8=10√2+2√2=12√2∴当M 点坐标为M(67,0)时,△ADM 周长最小,最小值为12√2 24.【答案】(1)解:将A (﹣1,0),B (3,0)代入 y =x 2+bx −c得b=﹣2,c=3; ∴y =x 2−2x −3 .将C 点的横坐标x=2代入 y =x 2−2x −3 得y=-3 ∴C (2,-3);∴直线AC 的函数解析式是y=﹣x ﹣1(2)解:设P点的横坐标为x(﹣1≤x≤2)则P、E的坐标分别为:P(x,﹣x﹣1),E(x,x2−2x−3);∵P点在E点的上方,PE=(﹣x﹣1)﹣(y=x2−2x−3)= −x2+x+2∴当x= 12时,PE的最大值为94。
二次函数的最值问题(中考题)(含答案)

典型中考题(有关二次函数的最值)屠园实验 周前猛一、选择题1. 已知二次函数y=a (x-1)2+b 有最小值 –1,则a 与b 之间的大小关( )A. a<bB.a=b C a>b D 不能确定答案:C2.当-2≤x≤l 时,二次函数 y=-(x-m )2+m 2+1有最大值4,则实数m 的值为( )A 、-74 B 、 C 、 2或 D 2或或- 74答案:C∵当-2≤x≤l 时,二次函数 y=-(x-m )2+m 2+1有最大值4, ∴二次函数在-2≤x≤l 上可能的取值是x=-2或x=1或x=m.当x=-2时,由 y=-(x-m )2+m 2+1解得m= - 74 ,2765y x 416⎛⎫=-++ ⎪⎝⎭此时,它在-2≤x≤l 的最大值是6516,与题意不符. 当x=1时,由y=-(x-m )2+m 2+1解得m=2,此时y=-(x-2)2+5,它在-2≤x≤l 的最大值是4,与题意相符.当x= m 时,由 4=-(x-m )2+m 2+1解得m=当m=它在-2≤x≤l 的最大值是4,与题意相符;当,2≤x≤l 在x=1处取得,最大值小于4,与题意不符.综上所述,实数m 的值为2或. 故选C .3. 已知0≤x≤12,那么函数y=-2x 2+8x-6的最大值是( ) A -10.5 B.2 C . -2.5 D. -6答案:C解:∵y=-2x2+8x-6=-2(x-2)2+2.∴该抛物线的对称轴是x=2,且在x<2上y随x的增大而增大.又∵0≤x≤12,∴当x=12时,y取最大值,y最大=-2(12-2)2+2=-2.5.故选:C.4、已知关于x的函数.下列结论:①存在函数,其图像经过(1,0)点;②函数图像与坐标轴总有三个不同的交点;③当时,不是y随x的增大而增大就是y随x的增大而减小;④若函数有最大值,则最大值必为正数,若函数有最小值,则最小值必为负数。
真确的个数是()A,1个B、2个 C 3个D、4个答案:B分析:①将(1,0)点代入函数,解出k的值即可作出判断;②首先考虑,函数为一次函数的情况,从而可判断为假;③根据二次函数的增减性,即可作出判断;④当k=0时,函数为一次函数,无最大之和最小值,当k≠0时,函数为抛物线,求出顶点的纵坐标表达式,即可作出判断.解:①真,将(1,0)代入可得:2k-(4k+1)-k+1=0,解得:k=0.运用方程思想;②假,反例:k=0时,只有两个交点.运用举反例的方法;③假,如k=1,b5-=2a4,当x>1时,先减后增;运用举反例的方法;④真,当k=0时,函数无最大、最小值;k≠0时,y最=224ac-b24k+1=-4a8k,∴当k>0时,有最小值,最小值为负;当k<0时,有最大值,最大值为正.运用分类讨论思想.二、填空题:1、如图,已知;边长为4的正方形截去一角成为五边形ABCDE,其中AF=2,BF=l,在AB 上的一点P,使矩形PNDM有最大面积,则矩形PNDM的面积最大值是答案:122、已知直角三角形两直角边的和等于8,两直角边各为时,这个直角三角形的面积最大,最大面积是答案:4、4,8解:设直角三角形得一直角边为x,则,另一边长为8-x;设其面积为S.∴S= x·(8-x)(0<x<8). 配方得S=- (x2-8x)=- (x-4)2+8∴当x=4时,S最大=8.及两直角边长都为4时,此直角三角形的面积最大,最大面积为8.-≤≤的最大值与最小值分别是3、函数y=2(0x4)答案:2,0最小值为0,当4x-x2最大,即x=2最大为4,所以,当x=0时,y最大值为2,当x=2时,y取最小值为04、已知二次函数y=x2+2x+a (0≤x≤1)的最大值是3,那么a的值为答案:0解:二次函数y=x 2+2x+a 对称轴为x=-1,当0≤x ≤1时y 随x 的增大而增大,当x=1时最大值为3,代入y=x 2+2x+a 得a=0.5、如图,在△ABC 中,BC=5,AC=12,AB=13,在边AB 、AC 上分别取点D 、E ,使线段DE 将△ABC 分成面积相等的两部分,则这样线段的最小长度 .三、解答题:1某产品第一季度每件成本为50元,第二、第三季度每件产品平均降低成本的百分率为x⑴ 请用含x 的代数式表示第二季度每件产品的成本;⑵ 如果第三季度该产品每件成本比第一季度少9.5元,试求x 的值⑶ 该产品第二季度每件的销售价为60元,第三季度每件的销售价比第二季度有所下降,若下降的百分率与第二、第三季度每件产品平均降低成本的百分率相同,且第三季度每件产品的销售价不低于48元,设第三季度每件产品获得的利润为y 元,试求y 与x 的函数关系式,并利用函数图象与性质求y 的最大值(注:利润=销售价-成本)解:(1)()x -150 ⑵()5.9501502-=-x 解得1.0=x (3)(),48160≥-x 解得2.0≤x 而0 x ,∴2.00≤x而()()2150160x x y ---==1040502++-x x=()184.0502+--x ∵当4.0≤x 时,利用二次函数的增减性,y 随x 的增大而增大,而2.00≤x , ∴当2.0=x 时,y 最大值=18(元)说明:当自变量取值范围为体体实数时,二次函数在抛物线顶点取得最值,而当自变量取值范围为某一区间时,二次函数的最值应注意下列两种情形:若抛物线顶点在该区间内,顶点的纵坐标就是函数的最值。
最全二次函数区间的最值问题(中考数学必考题型)

二次函数的最值问题二次函数的最值问题,是每年中考的必考题,也是考试难点,经常出现在压轴题的位置,解决二次函数的最值问题,特别是含参数的二次函数,一定要考虑二次函数的三个要素:开口方向,对称轴,自变量的取值范围,对于二次函数能够分析出三要素,二次函数的问题就迎刃而解了。
例1.对于二次函数342+-=x x y(1)求它的最小值和最大值.(2)当1≤x ≤4时,求它的最小值和最大值.(3)当-2≤x ≤1时,求它的最小值和最大值.(4)二次函数的最值与哪些因素有关?对于给定的范围,最值可能出现在哪些位置?练习1.二次函数y =x 2+2x ﹣5有( )A .最大值﹣5B .最小值﹣5C .最大值﹣6D .最小值﹣6练习2.在二次函数y =x 2﹣2x ﹣3中,当0≤x ≤3时,y 的最大值和最小值分别是( )A .0,﹣4B .0,﹣3C .﹣3,﹣4D .0,0练习3若抛物线y =﹣x 2+4x +k 的最大值为3,则k = .练习4(多元消参,利用平方的性质确定自变量的取值范围)若实数a 、b 满足a +b 2=2,则a 2+5b 2的最小值为 .练习5如图,P 是抛物线y =x 2﹣2x ﹣3在第四象限的一点,过点P 分别向x 轴和y 轴作垂线,垂足分别为A 、B ,求四边形OAPB 周长的最大值及点P 的横坐标练习6.(回归教材)如图,一张正方形纸板的边长为8cm ,将它割去一个正方形,留下四个全等的直角三角形(图中阴影部分).设AE =BF =CG =DH =x (cm ),阴影部分的面积为y (cm 2).(1)求y 关于x 的函数解析式并写出x 的取值范围;(2)当x 取何值时,阴影部分的面积最大,最大面积是多少.一、对开口方向(二次项前面系数)进行讨论例2.当 41≤≤x 时,二次函数a ax ax y 342+-= 的最大值等于6.求二次项系数a 的值练习1已知二次函数y =mx 2+2mx ﹣1(m >0)的最小值为﹣5,则m 的值为( )A .﹣4B .﹣2C .2D .4练习2已知二次函数y =mx 2+(m 2﹣3)x +1,当x =﹣1时,y 取得最大值,则m = . 练习3已知二次函数y =mx 2+2mx +1(m ≠0)在﹣2≤x ≤2时有最小值﹣2,求m 的值二、对二次函数的对称轴的位置进行讨论例3.当 12≤≤x -时,二次函数a ax x y 342+-= 的最小值等于-1.求a 的值.变式1当﹣2≤x ≤1时,二次函数y =﹣(x ﹣m )2+m 2+1有最大值4,求实数m 的值.变式2当﹣1≤x ≤1时,函数y =﹣x 2﹣2mx +2n +1的最小值是﹣4,最大值是0,求m 、n 的值.三、对二次函数的x 取值范围进行讨论例4.当 2+≤≤a x a 时,二次函数a x x y 342+-= 的最大值等于-6.求a 的值.练习1.当a ﹣1≤x ≤a 时,函数y =x 2﹣2x +1的最小值为1,求a 的值.练习2.若t ≤x ≤t +2时,二次函数y =2x 2+4x +1的最大值为31,求t 的值练习3.已知二次函数y =﹣x 2+6x ﹣5.当t ≤x ≤t +3时,函数的最大值为m ,最小值为n ,若m ﹣n =3,求t 的值.练习4.设a ,b 是任意两个不等实数,我们规定:满足不等式a ≤x ≤b 的实数x 的所有取值的全体叫做闭区间,表示为[a ,b ].对于任何一个二次函数,它在给定的闭区间上都有最小值.求函数y =x 2﹣4x ﹣4在区间[t ﹣2,t ﹣1](t 为任意实数)上的最小值y min 的解析式.练习5.若关于x 的函数y ,当t ﹣≤x ≤t +时,函数y 的最大值为M ,最小值为N ,令函数h =,我们不妨把函数h 称之为函数y 的“共同体函数”.若函数y =﹣x 2+4x +k ,是否存在实数k ,使得函数y 的最大值等于函数y 的“共同体函数“h 的最小值.若存在,求出k 的值;若不存在,请说明理由.拓展:C 2的解析式为:y =a (x +2)2﹣3(a >0),当a ﹣4≤x ≤a ﹣2时,C 2的最大值与最小值的差为2a ,求a 的值.作业:1.矩形的周长等于40,则此矩形面积的最大值是2.若实数x ,y 满足x +y 2=3,设s =x 2+8y 2,则s 的取值范围是 .3.已知二次函数y =ax 2+4x +a ﹣1的最小值为2,则a 的值为 .4.已知实数满足x 2+3x ﹣y ﹣3=0,则x +y 的最小值是 .5.若二次函数y =﹣x 2+mx 在﹣2≤x ≤1时的最大值为5,则m 的值为6.当a ≤x ≤a +1时,函数y =x 2﹣2x +1的最小值为1,则a 的值为7.已知二次函数y =122+-ax ax ,当30≤≤x 时,y 的最大值为2,则a 的值为8.如图,在Rt △ABC 中,∠B =90°,AB =6cm ,BC =8cm ,点P 从A 点开始沿AB 边向点B 以1cm /s 的速度移动,点Q 从B 点开始沿BC 边向点C 以2cm /s 的速度移动,则P 、Q 分别从A 、B 同时出发,经过多少秒钟,使△PBQ 的面积最大.9.设a、b是任意两个不等实数,我们规定:满足不等式a≤x≤b的实数x的所有取值的全体叫做闭区间,表示为[a,b].对于一个函数,如果它的自变量x与函数值y满足:当m≤x≤n时,有m≤y≤n,我们就称此函数是闭区间[m,n]上的“闭函数”.若二次函数y=x2﹣x﹣是闭区间[a,b]上的“闭函数”,求实数a,b的值.10.抛物线y=x2+bx+3的对称轴为直线x=1.(1)b=;(2)若关于x的一元二次方程x2+bx+3﹣t=0(t为实数)在﹣1<x<4的范围内有实数根,则t的取值范围是.11.已知关于x的二次函数y1=x2+bx+c(实数b,c为常数).(1)若二次函数的图象经过点(0,4),对称轴为x=1,求此二次函数的表达式;(2)若b2﹣c=0,当b﹣3≤x≤b时,二次函数的最小值为21,求b的值;(3)记关于x的二次函数y2=2x2+x+m,若在(1)的条件下,当0≤x≤1时,总有y2≥y1,求实数m的最小值.12.已知抛物线y=﹣2x2+(b﹣2)x+(c﹣2020)(b,c为常数).(1)若抛物线的顶点坐标为(1,1),求b,c的值;(2)若抛物线上始终存在不重合的两点关于原点对称,求c的取值范围.(3)在(1)的条件下,存在正实数m,n(m<n),当m≤x≤n时,恰好,求m,n的值.。
中考数学总复习《二次函数的最值》练习题及答案
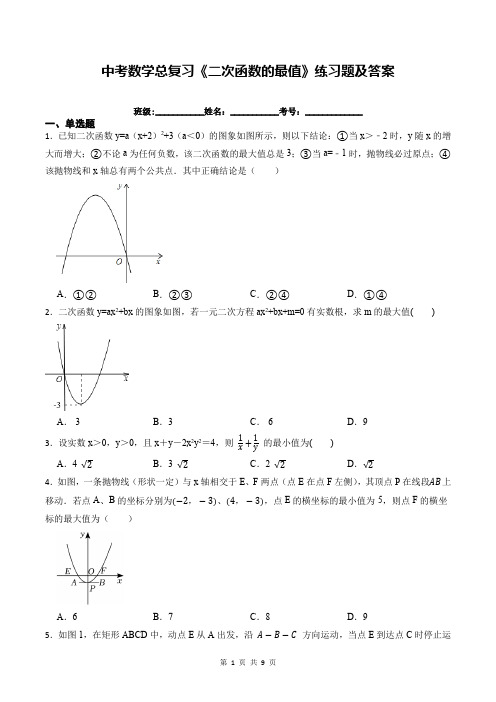
中考数学总复习《二次函数的最值》练习题及答案班级:___________姓名:___________考号:_____________一、单选题1.已知二次函数y=a(x+2)2+3(a<0)的图象如图所示,则以下结论:①当x>﹣2时,y随x的增大而增大;②不论a为任何负数,该二次函数的最大值总是3;③当a=﹣1时,抛物线必过原点;④该抛物线和x轴总有两个公共点.其中正确结论是()A.①②B.②③C.②④D.①④2.二次函数y=ax2+bx的图象如图,若一元二次方程ax2+bx+m=0有实数根,求m的最大值() A.-3B.3C.-6D.93.设实数x>0,y>0,且x+y-2x2y2=4,则1x+1y的最小值为()A.4 √2B.3 √2C.2 √2D.√24.如图,一条抛物线(形状一定)与x轴相交于E、F两点(点E在点F左侧),其顶点P在线段AB上移动.若点A、B的坐标分别为(−2,−3)、(4,−3),点E的横坐标的最小值为-5,则点F的横坐标的最大值为()A.6B.7C.8D.95.如图1,在矩形ABCD中,动点E从A出发,沿A−B−C方向运动,当点E到达点C时停止运动,过点E做FE⊥AE,交CD于F点,设点E运动路程为x,FC=y,如图2所表示的是y与x的函数关系的大致图象,当点E在BC上运动时,FC的最大长度是25,则矩形ABCD的面积是()A.235B.254C.6D.56.已知0≤x≤32,则函数y=x2+x+1()A.有最小值34,但无最大值B.有最小值34,有最大值1C.有最小值1,有最大值194D.无最小值,也无最大值7.已知二次函数y=ax2+bx+c(a,b,c是常数,a≠0)的y与x的部分对应值如表:x﹣5﹣4﹣202y60﹣6﹣46;③若点(﹣8,y1),点(8,y2)在二次函数图象上,则y1<y2;④方程ax2+bx+c=﹣5有两个不相等的实数根.其中,正确结论的是()A.①②③B.①③④C.①②④D.②③④8.已知二次函数y=ax2−2ax+a+2(a≠0),若−1≤x≤2时,函数的最大值与最小值的差为4,则a的值为()A.1B.-1C.±1D.无法确定9.如图,已知二次函数的图象(0≤x≤1+2 √2).关于该函数在所给自变量取值范围内,下列说法正确的是()A.有最小值﹣2,无最大值B.有最小值﹣2,有最大值﹣1.5C.有最小值﹣2,有最大值2D.有最小值﹣1.5,有最大值210.如图,Rt△ABC中,∠ACB=90°,AC=12BC=2点D是AB上一动点,连接CD,将线段CD绕点C逆时针旋转90°得到线段CE,连接DE,BE,当△BED面积最大时,AD的长为()A.2B.√5C.25√5D.4√5511.若二次函数y=﹣x2+mx在﹣1≤x≤2时的最大值为3,那么m的值是()A.﹣4或72B.﹣2 √3或72C.﹣4 或2 √3D.﹣2 √3或2 √3 12.若二次函数y=ax2+4x+a-1的最小值是2,则a的值为()A.4B.-1C.3D.4或-1二、填空题13.二次函数y=x2−2x+3的最小值是.14.当实数a满足2≤a≤5时,且代数式−a2+2ab−b2取最大值-1时,则b的值为.15.抛物线y=ax2+bx+c上部分点的横坐标x,纵坐标y的对应值如下表:x-2-1012y04664从上表可知,下列说法中正确的是.)①抛物线与x轴的一个交点为(3,0);②函数y=ax2+bx+c的最大值为6;②抛物线的对称轴是直线x=12;④在对称轴左侧,y随x增大而增大.16.二次函数y=﹣x2﹣4x+k的最大值是9,则k=.17.已知关于x的函数y=−x2−ax+1,当0≤x≤3时函数有最大值5,则a=.18.已知关于x的二次函数y=x2-2ax+3,当1≤x≤3时,函数有最小值2a,则a的值为.三、综合题19.已知抛物线y=ax2+bx+c与y轴交于点(0,3a),对称轴为x=1.(1)试用含a的代数式表示b、c.(2)当抛物线过点(2,3)时,求此抛物线的解析式.(3)求当b(c+6)取得最大值时的抛物线的顶点坐标.20.如图,正方形ABCD的边长为4,点G,H分别是BC、CD边上的点,直线GH与AB、AD的延长线相交于点E,F,连接AG、AH.(1)当BG=2,DH=3时,则GH:HF=,∠AGH=°;(2)若BG=3,DH=1,求DF、EG的长;(3)设BG=x,DH=y,若∠ABG∠∠FDH,求y与x之间的函数关系式,并求出y的取值范围.21.如图,抛物线y=12x2−32x−2与x轴交于A,B两点,与y轴交于点C,连接AC,BC,点M是线段BC下方抛物线上的任意一点,点M的横坐标为m,过点M画MN∠x轴于点N,交BC于点P.(1)填空:A(,),C(,);(2)探究∠ABC的外接圆圆心的位置,并求出圆心的坐标;(3)探究当m取何值时线段PM的长度取得最大值,最大值为多少?22.某商品现在的售价为每件50元,每天可卖出200件.市场调查反映:如调整价格,每涨价1元,每天要少卖出10件,已知商品的进价为每件40元,请你帮助分析,当每件商品涨价多少元时,可使每天的销售利润最大,最大利润是多少?设每件商品涨价x元,每天售出商品的利润为y元.(1)根据题意,填写下表:每件售价(元)505152……50+x每天售出商品的数量(件)200190……每天售出商品的利润(元)20002090……23.已知,一个铝合金窗框如图所示,所使用的铝合金材料长度为18m.设AB长为xm,窗户的总面积为Sm2.(1)求S关于x的函数表达式.(2)若AB的长不能低于2m,且AB<BC,求此时窗户总面积S的最大值和最小值.24.已知关于x的一元二次方程x2﹣(m+1)x+ 12(m2+1)=0有实数根.(1)求m的值;(2)先作y=x2﹣(m+1)x+ 12(m2+1)的图象关于x轴的对称图形,然后将所作图形向左平移3个单位长度,再向上平移2个单位长度,写出变化后图象的解析式;(3)在(2)的条件下,当直线y=2x+n(n≥m)与变化后的图象有公共点时,求n2﹣4n的最大值和最小值.参考答案1.【答案】C2.【答案】B3.【答案】A4.【答案】B5.【答案】B6.【答案】C7.【答案】B8.【答案】C9.【答案】C10.【答案】C11.【答案】C12.【答案】A13.【答案】214.【答案】1或615.【答案】①③④16.【答案】517.【答案】-418.【答案】119.【答案】(1)解:∵抛物线与y轴交于点(0,3a)∴c=3a∵对称轴为x=1∴x=−b2a=1∴b=−2a(2)解:∵抛物线过点(2,3)∴3=a×22+2(−2a)+3a∴a=1∴b=−2a=−2,c=3a=3∴抛物线为y=x2−2x+3(3)解:∵b(c+6)=−2a(3a+6)=−6a2−12a=−6(a+1)2+6∴当a=−1时,b(c+6)的最大值为6;∴抛物线y=−x2+2x−3=−(x−1)2−2故抛物线的顶点坐标为(1,−2)20.【答案】(1)1:3;90(2)解:∵正方形ABCD的边长为4,BG=3,DH=1∴CG=1,CH=3∵CG∠DF,CH∠BE∴∠CGH∠∠BGE∠∠DFH∴GCHC=BGBE=DFDH,即13=3BE=DF1解得BE=9,DF= 1 3∴Rt∠BEG中,EG= √BG2+BE2= √32+92=3 √10(3)解:∵正方形ABCD的边长为4,BG=x,DH=y ∴CG=4﹣x,CH=4﹣y由(1)可得,∠FDH∠∠GCH,而∠ABG∠∠FDH∴∠ABG∠∠GCH∴ABGC=BGCH,即44−x=x4−y∴y与x之间的函数关系式为:y= 14x2﹣x+4∵44−x=x4−y∴4﹣y= x(4−x)4=﹣14x2+x∴当x=﹣12×(−14)=2时,4﹣y有最大值,且最大值为﹣14×4+2=1∴0<4﹣y≤1解得3≤y<4.21.【答案】(1)-1;0;0;-2(2)解:|OA|=1,|OC|=2,|OB|=4∠AOC=∠COB=90°∴OAOC=OCOB=12∴∠AOC∠∠COB∴∠ACO=∠OBC∠ACO+∠OCB=90°∠OBC+∠OCB=90°=∠ACB∴Rt∠ACB的外接圆圆心为AB的中点∵A(-1,0)B(4,0)∴圆心的坐标( 32,0 ).(3)解:C (0,-2),B (4,0) 又∵直线BC 解析式y =12x −2 p(m ,12m −2) ,M (m , 12m 2−32m −2 )PM=( 12m −2 )-( 12m 2−32m −2 )PM =−12m 2+2m =−12(m −2)2+2 当m=2时,PM 最大值=2.22.【答案】(1)180;200﹣10x ;2160;(200﹣10x )(10+x )(2)解:y =(200﹣10x )(10+x )=﹣10x 2+100x+2000=﹣10(x ﹣5)2+2250 ∴当x =5时,y 取得最大值,此时y =2250即y =﹣10x 2+100x+2000,当每件商品涨价5元时,可使每天的销售利润最大,最大利润是2250元23.【答案】(1)解:∵AB=xm ,铝合金材料长为18m∴AD=BC=18−3x 2∴S =x·18−3x2=−32x 2+9x即S 与x 的函数表达式为:S =−32x 2+9x.(2)解:由题意得:2≤x <18−3x 2解得:2≤x <3.6∵S =−32x 2+9x =−32(x -3)2+272∵−32<0,对称轴是直线x =3,且2≤x <3.6∴当x =3时,S 取得最大值,此时S =272当x =2时,S 取得最小值,此时S =−32(2-3)2+272=12答:窗户总面积S 的最大值272m 2,最小值是12m 2.24.【答案】(1)解:对于一元二次方程x 2﹣(m+1)x+ 12(m 2+1)=0∠=(m+1)2﹣2(m 2+1)=﹣m 2+2m ﹣1=﹣(m ﹣1)2 ∵方程有实数根∴﹣(m﹣1)2≥0∴m=1.(2)解:由(1)可知y=x2﹣2x+1=(x﹣1)2图象如图所示:平移后的解析式为y=﹣(x+2)2+2=﹣x2﹣4x﹣2.(3)解:由{y=2x+ny=−x2−4x−2消去y得到x2+6x+n+2=0由题意∠≥0∴36﹣4n﹣8≥0∴n≤7∵n≤m,m=1∴1≤n≤7令y′=n2﹣4n=(n﹣2)2﹣4∴n=2时,y′的值最小,最小值为﹣4n=7时,y′的值最大,最大值为21∴n2﹣4n的最大值为21,最小值为﹣4.。
重庆中考二次函数最值复习

3. ③已知点 M(-2,3),连接 CM ,DM ,CD,求 S△CDM 的最大值及此时点 D 的坐标:
④过点 B 作 BE ∥ AC 交抛物线于点 E ,连接 AD,CD,AD 交直线 BE 于点 F ,求 S△CDF 的最大值 及此时点 D 的坐标:
AB= x1 - x2 = x2 - x1
例 1、如图 1,抛物线 y=-2x2+4x+6 与 x 轴交与点 A 和点 B,与 y 轴交于点 C, (1)点 A 坐标为 , ,点 B , ,点 C , ;直线 BC 的解析式; (2)如图 1 在直线 BC 上方的抛物线上有一点 P,过点 P 作 Y 轴的平行线交 BC 于点 Q,求线段 PQ 长的最大值,并求此时点 P 的坐标:
(1)连接 AD,CD. ①已知 S△ACD = S△ABC ,求点 D 的坐标:
②已知 S△ACD : S△ABC = 2:3,求点 D 的坐标;
③已 知 点 M( -2 ,3 ),连 接 CM ,DM ,CD ,已 知 S△CDM : S△ABC = 1 :2 ,求 点 D 的 坐 标 :
(2)过点 B 作 BE ∥ AC 交抛物线于点 E,连接 AD,CD,AD 交直线 BE 于点 F。
y
C
D
F H
G
AE
B
x
二次函数第二问解题模型
1. 例 1. 如图,在平面直角坐标系中,抛物线 y = ax2 + bx + c 分别交 x 轴于 A(-4,0),B(-1,0),交 y 轴于点 C(0,4). (1)求抛物线的解析式; (2)点 D 为抛物线上位于直线 AC 下方的一个动点 .
二次函数的最值问题举例附练习测试参考答案

二次函数的最值问题举例附练习测试参考答案 The pony was revised in January 2021二次函数的最值问题举例(附练习、答案) 二次函数2 (0)y ax bx c a =++≠是初中函数的主要内容,也是高中学习的重要基础.在初中阶段大家已经知道:二次函数在自变量x 取任意实数时的最值情况(当0a >时,函数在2b x a=-处取得最小值244ac b a -,无最大值;当0a <时,函数在2b x a=-处取得最大值244ac b a -,无最小值. 本节我们将在这个基础上继续学习当自变量x 在某个范围内取值时,函数的最值问题.同时还将学习二次函数的最值问题在实际生活中的简单应用.【例1】当22x -≤≤时,求函数223y x x =--的最大值和最小值.分析:作出函数在所给范围的及其对称轴的草图,观察图象的最高点和最低点,由此得到函数的最大值、最小值及函数取到最值时相应自变量x 的值.解:作出函数的图象.当1x =时,min 4y =-,当2x =-时,max 5y =. 12x ≤≤时,求函数21y x x =--+的最大值和最小值.【例2】当解:作出函数的图象.当1x =时,min 1y =-,当2x =时,max 5y =-.由上述两例可以看到,二次函数在自变量x 的给定范围内,对应的图象是抛物线上的一段.那么最高点的纵坐标即为函数的最大值,最低点的纵坐标即为函数的最小值.根据二次函数对称轴的位置,函数在所给自变量x 的范围的图象形状各异.下面给出一些常见情况:【例3】当0x ≥时,求函数(2)y x x =--的取值范围. 解:作出函数2(2)2y x x x x =--=-在0x ≥内的图象.可以看出:当1x =时,min 1y =-,无最大值.所以,当0x ≥时,函数的取值范围是1y ≥-.【例4】当1t x t ≤≤+时,求函数21522y x x =--的最小值(其中t 为常数). 分析:由于x 所给的范围随着t 的变化而变化,所以需要比较对称轴与其范围的相对位置.解:函数21522y x x =--的对称轴为1x =.画出其草图. (1)当对称轴在所给范围左侧.即1t >时: 当x t =时,2min 1522y t t =--; (2)当对称轴在所给范围之间.即1101t t t ≤≤+⇒≤≤时:当1x =时,2min 1511322y =⨯--=-; (3)当对称轴在所给范围右侧.即110t t +<⇒<时:当1x t =+时,22min 151(1)(1)3222y t t t =+-+-=-.综上所述:2213,023,0115,122t t y t t t t ⎧-<⎪⎪=-≤≤⎨⎪⎪-->⎩在实际生活中,我们也会遇到一些与二次函数有关的问题:【例5】某商场以每件30元的价格购进一种商品,试销中发现这种商品每天的销售量m (件)与每件的销售价x (元)满足一次函数1623,3054m x x =-≤≤.(1)写出商场卖这种商品每天的销售利润y 与每件销售价x 之间的函数关系式;(2)若商场要想每天获得最大销售利润,每件商品的售价定为多少最合适最大销售利润为多少解:(1)由已知得每件商品的销售利润为(30)x -元,那么m 件的销售利润为(30)y m x =-,又1623m x =-.(2)由(1)知对称轴为42x =,位于x 的范围内,另抛物线开口向下∴当42x =时,2max 342252424860432y =-⨯+⨯-=∴当每件商品的售价定为42元时每天有最大销售利润,最大销售利润为432元.A 组1.抛物线2(4)23y x m x m =--+-,当m =_____时,图象的顶点在y 轴上;当m =_____时,图象的顶点在x 轴上;当m =_____时,图象过原点.2.用一长度为l 米的铁丝围成一个长方形或正方形,则其所围成的最大面积为________.3.求下列二次函数的最值:(1)2245y x x =-+; (2)(1)(2)y x x =-+.4.求二次函数2235y x x =-+在22x -≤≤上的最大值和最小值,并求对应的x 的值.5.对于函数2243y x x =+-,当0x ≤时,求y 的取值范围.6.求函数3y =-7.已知关于x 的函数22(21)1y x t x t =+++-,当t 取何值时,y 的最小值为0?B 组1.已知关于x 的函数222y x ax =++在55x -≤≤上.(1)当1a =-时,求函数的最大值和最小值;(2)当a 为实数时,求函数的最大值. 2.函数223y x x =++在0m x ≤≤上的最大值为3,最小值为2,求m 的取值范围.3.设0a >,当11x -≤≤时,函数21y x ax b =--++的最小值是4-,最大值是0,求,a b的值.4.已知函数221y x ax=++在12x-≤≤上的最大值为4,求a的值.5.求关于x的二次函数221y x tx=-+在11x-≤≤上的最大值(t为常数).第五讲二次函数的最值问题答案A组1.414或2,3 22.22 16lm3.(1)有最小值3,无最大值;(2)有最大值94,无最小值.4.当34x=时,min318y=;当2x=-时,max19y=.5.5y≥-6.当56x=时,min3y=-23x=或1时,max3y=.7.当54t=-时,miny=.B组1.(1)当1x=时,min 1y=;当5x=-时,max 37y=.(2)当0a≥时,max 2710y a=+;当0a<时,max 2710y a=-.2.21m-≤≤-.3.2,2a b==-.4.14a=-或1a=-.5.当0t≤时,max 22y t=-,此时1x=;当0t>时,max 22y t=+,此时1x=-.。
中考数学题型专项训练:二次函数与最值问题(含答案)

二次函数与最值问题1.如图,二次函数y =-x 2+2(m -2)x +3的图象与x 、y 轴交于A 、B 、C 三点,其中A (3,0),抛物线的顶点为D . (Ⅰ)求m 的值及顶点D 的坐标;(Ⅱ)当a ≤x ≤b 时,函数y 的最小值为74,最大值为4,求a ,b 应满足的条件;(Ⅲ)在y 轴右侧的抛物线上是否存在点P ,使得△PDC 是等腰三角形如果存在,求出符合条件的点P 的坐标;如果不存在,请说明理由.解:(Ⅰ)把A (3,0)代入y =-x 2+2(m -2)x +3,得-9+6(m -2)+3=0, 解得m =3,则二次函数为y =-x 2+2x +3,∵y=-x2+2x+3=-(x-1)2+4, ∴顶点D 的坐标为(1,4);(Ⅱ)把y=74代入y=-x2+2x+3中,得74=-x2+2x+3,解得x1=-12,x2=25,又∵函数y的最大值为4,顶点D的坐标为(1,4), 结合图象知-12≤a≤1.当a=-12时,1≤b≤25,当-12<a≤1时,b=25;(Ⅲ)存在点P,使得△PDC是等腰三角形, 当x=0时,y=3,∴点C 坐标为(0,3).当△PDC 是等腰三角形时,分三种情况: ①如解图①,当DC =DP 时,由抛物线的对称性知由抛物线的对称性知::点P 与点C 关于抛物线的对称轴x =1对称,∴点P 坐标为(2,3);②如解图②,当PC =PD 时,则线段CD 的垂直平分线l 与抛物线的交点即为所求的点P ,过点D 作x 轴的平行线交y 轴于点H ,过点P 作PM ⊥y 轴于点M ,PN ⊥DH 的延长线于点N , ∵HD =HC =1,PC =PD ,∴HP 是线段CD 的垂直平分线. ∵HD =HC ,HP ⊥CD , ∴HP 平分∠MHN ,∵PM ⊥y 轴于点M ,PN ⊥HD 的延长线于点N , ∴PM =PN .设P (m ,-m 2+2m +3), 则m =4-(-m 2+2m +3),解得m =253±, ∴点P 的坐标为(253-,255+)(解图中未标记此点)或(253+,255-);③如解图③,当CD =CP 时,点P 在y 轴左侧,不符合题意.综上所述,所求点P 的坐标为(2,3)或(253-,255+)或(253+,255-).图① 图② 图③ 第1题解图2.已知抛物线y =ax 2+bx +c (a <0)过(m ,b ),(m +1,a )两点,(Ⅰ)若m =1,c =1,求抛物线的解析式;(Ⅱ)若b ≥a ,求m 的取值范围;(Ⅲ)当b ≥a ,m <0时,二次函数y =ax 2+bx +c 有最大值-2,求a 的最大值. 解:(Ⅰ)∵m =1,c =1,∴抛物线的解析式为y =ax 2+bx +1(a <0)过(1,b ),(2,a )两点,∴1421a b ba b a ++=ìí++=î, 解得11a b =-ìí=î,∴抛物线的解析式为y =-x 2+x +1; (Ⅱ)依题意得22am bm c b a m b m c a ì++=ïí①,由②-①得b=-am,∵b≥a,∴-am≥a,∵a<0,∴m≥-1;(Ⅲ) 由(Ⅱ)得b=-am,代入①得am2-am2+c=b,∴c=b=-am,∵b≥a,m<0,∴-1≤m<0,∵二次函数y=ax2+bx+c有最大值-2,∴244ac ba-=-2,∴8a=m2+4m,∴8a = (m +2)2-4, ∵-1≤m <0,∴-3≤(m +2)2-4<0,∴a ≤-83,∴a 的最大值为-83.3.平面直角坐标系xOy 中,抛物线y =mx 2-2m 2x +2交y 轴于A 点,交直线x =4于B 点.(Ⅰ)求抛物线的对称轴(用含m 的代数式表示); (Ⅱ)若AB ∥x 轴,求抛物线的解析式;(Ⅲ)若抛物线在A ,B 之间的部分任取一点P (x p ,y p ),一定满足y p ≤2,求m 的取值范围.解:(Ⅰ)由抛物线的对称轴公式可得x =2ba -=222m m--=m ,∴抛物线的对称轴为直线x=m;(Ⅱ)当x=0时,y=mx2-2m2x+2=2,∴点A(0,2).∵AB∥x轴,且点B在直线x=4上,∴点B(4,2),抛物线的对称轴为直线x=2,∴m=2,∴抛物线的解析式为y=2x2-8x+2;(Ⅲ)当m>0时,如解图①,∵A(0,2),∴要使0≤x p≤4时,始终满足y p≤2,只需使抛物线y=mx2-2m2x+2的对称轴与直线x=2重合或在直线x=2的右侧.∴m≥2;当m<0时,如解图②,m <0时,y p ≤2恒成立.综上所述,m 的取值范围为m <0或m ≥2.第3题解图4.已知抛物线y =ax 2+bx +c 的顶点为(2,5),且与y 轴交于点C (0,1).(Ⅰ)求抛物线的表达式;(Ⅱ)若-1≤x ≤3,试求y 的取值范围;(Ⅲ)若M (n 2-4n +6,y 1)和N (-n 2+n +74,y 2)是抛物线上的不重合的两点,试判断y 1与y 2的大小,并说明理由.解:(Ⅰ)∵抛物线y =ax 2+bx +c 的顶点为(2,5),∴设抛物线的表达式为:y=a(x-2)2+5, 把(0,1)代入得:a(0-2)2+5=1,a=-1,∴抛物线的表达式为:y=-(x-2)2+5=-x2+4x +1;(Ⅱ)∵抛物线的顶点为(2,5),a=-1,对称轴为直线x =2,且-1≤x ≤3,∴当x=-1时,y有最小值,最小值为y=-(-1-2)2+5=-4,当x=2时,y有最大值,最大值为y=5,∴y的取值范围是-4≤y≤5;(Ⅲ)∵n 2-4n+6=(n-2)2+2≥2,2,--n2+n+74=-(n-12)2+2≤2,∴点M在抛物线对称轴右侧,点N在抛物线对称轴左侧,∵N(-n2+n+74,y2),∴点N关于对称轴对称的点坐标为(n 2-n+94,y2), ∵在抛物线对称轴右侧,y随x的增大而减小,∴①当n2-4n+6>n2-n+94时,即n<45时,y1<y 2;②当n2-4n+6=n2-n+94时,即n=45时,y1=y2;③当n2-4n+6<n2-n+94时,即n>45时,y1>y2.5.已知抛物线y=ax2+bx+c与直线y=mx+n 相交于两点,这两点的坐标分别是(0,-12)和(m-b, m2-mb +n),其中 a,b,c,m,n为实数,且a,m不为0.(Ⅰ)求c的值;(Ⅱ)求证:抛物线y=ax2+bx+c与x 轴有两个交点; (Ⅲ)当-1≤x≤1时,设抛物线y=ax2+bx+c上与x轴距离最大的点为P(x0,y0),求这时|y0|的最小值.解:(Ⅰ)把点(0,-12)代入抛物线,得:c=-12;(Ⅱ)把点(0,-12)代入直线得:n=-12.把点(m-b,m2-mb+n)代入抛物线,得: a(m-b)2+b(m-b)+c =m2-mb+n∵c=n=-1 2,∴a(m-b)2+b(m-b)=m2-mb,am2-2abm+ab2+bm-b2-m2+mb=0, (a -1)m2-(a-1)1)•2•2bm+(a -1)b2=0, (a-1)(m2-2bm+b2)=0,(a-1)(m-b)2=0,若m -b =0,则(m -b ,m 2-mb +n )与(0,-12)重合,与题意不合, ∴a =1,∵抛物线y =ax 2+bx +c=x 2+bx -12,b 2-4ac =b 2-4×(-12)=b 2+2>0, ∴抛物线y =ax 2+bx +c 与x 轴有两个交点;(Ⅲ)y =x 2+bx -12,顶点(-2b ,-12-24b ),设抛物线y =x 2+bx -12在x 轴上方与x 轴距离最大的点的纵坐标为H ,在x 轴下方与x 轴距离最大的点的纵坐标为h , ①当-2b <-1时,即b >2时,在x 轴上方与x 轴距离最大的点是(1,y 0),∴|H |=y 0=12+b >52,在x 轴下方与x 轴距离最大的点是(-1,y 0),∴|h |=|y 0|=|12-b |=b -12>32,∴|H |>|h |,∴这时|y 0|的最小值大于52,②当-1≤-2b≤0时,即0≤b ≤2时,在x 轴上方与x 轴距离最大的点是(1,y 0),∴|H |=y 0=12+b ≥12,当b =0时等号成立, 在x 轴下方与x 轴距离最大的点是(-2b ,-12-24b ),∴|h |=|-1-2b |=2+2b ≥1,当b =0时等号成立,∴这时|y 0|的最小值等于12, ③当0<-2b≤1,即-2≤b <0时,在x 轴上方与x 轴距离最大的点是(-1,y 0), ∴|H |=y 0=|1+(-1)b -12|=|12-b |=12-b >12,在x 轴下方与x 轴距离最大的点是(-2b ,-12-24b ), ∴|h |=|y 0|=|-12-24b |=2+24b >12,∴这时|y 0|的最小值大于12;④当1<-2b时,即b <-2时,在x 轴上方与x 轴距离最大的点是(-1,y 0),∴|H|=12-b>52,在x轴下方与x轴距离最大的点是(1,y0),∴|h|=|12+b|=-(b+12)>32,∴|H|>|h|,∴这时|y0|的最小值大于52,综上所述:当b=0,x0=0时,这时|y0|取最小值为12.6.在平面直角坐标系中,直线l:y=x+3与x轴交于点A,抛物线C:y=x2+mx+n的图象经过点A.(Ⅰ)当m=4时,求n的值;(Ⅱ)设m=-2,当-3≤x≤0时,求二次函数y=x2+mx+n 的最小值;(Ⅲ)当-3≤x≤0时,若二次函数y=x2+mx+n时的最小值为-4,求m 、n 的值. 解:(Ⅰ)当y =x +3=0时,x =-3, ∴点A 的坐标为(-3,0).∵二次函数y =x 2+mx +n 的图象经过点A , ∴0=9-3m +n ,即n =3m -9, ∴当m =4时,n =3m -9=3; (Ⅱ)抛物线的对称轴为直线x =-2m,当m =-2时,对称轴为x =1,n =3m -9=-15, ∴当-3≤x ≤0时,y 随x 的增大而减小,∴当x =0时,二次函数y =x 2+mx +n 取得最小值,最小值为-15.(Ⅲ)①当对称轴-2m≤-3,即m ≥6时,在-3≤x ≤0范围内,y 随x 的增大而增大,当x =-3时,y 取得最小值0,不符合题意;②当-3<-2m <0,即0<m <6时,在-3≤x ≤0范围内,x =-2m 时,y取得最小值442m n -,∵二次函数最小值为-4, ∴244n m n -=493=0m n --+ìïíïî, 解得:2 3m n -ìíî==或1021m n ìíî==(舍去), ∴m =2,n =-3; ③当-2m ≥0,即m ≤0时,在-3≤x ≤0范围内,y 随x 的增大而减小,当x =0时,y 取最小值,即n =-4, ∴4930n m n --+ìïíïî==,解得:53m=4nì-ïíïî=(舍去).综上所述:m=2,n=-3.7.在平面直角坐标系中,抛物线y=x2-2x+c(c为常数)的对称轴为x=1.(Ⅰ)当c=-3时,点(x1,y1)在抛物线y=x2-2x+c上,求y1的最小值;(Ⅱ)若抛物线与x轴有两个交点,点A在点B左侧,且OA=12OB,求抛物线的解析式;(Ⅲ)当-1<x<0时,抛物线与x轴有且只有一个公共点,求c的取值范围.解:(Ⅰ)当c=-3时,抛物线为y=x 2-2x-3,∴抛物线开口向上,有最小值,∴y最小值=244ac ba-=2()(4324)1´´---=-4,∴y1的最小值为-4;(Ⅱ)抛物线与x轴有两个交点,①当点A、B都在原点的右侧时,如解图①,设A(m,0),∵OA=12OB,∴B(2m,0),∵二次函数y =x2-2x+c的对称轴为x=1,由抛物线的对称性得1-m=2m-1,解得m=2 3,∴A(23,0),∵点A在抛物线y=x2-2x+c上,∴0=49-43+c,解得c=89,此时抛物线的解析式为y=x2-2x+89;②当点A在原点的左侧,点B在原点的右侧时,如解图②, 设A(-n,0),∵OA=12OB,且点A 、B在原点的两侧,∴B(2n,0),由抛物线的对称性得n+1=2n -1,解得n=2,∴A(-2,0),∵点A在抛物线y =x2-2x+c上,∴0=4+4+c,解得c=-8,此时抛物线的解析式为y=x2-2x-8,综上,抛物线的解析式为y=x 2-2x+89或y=x2-2x-8;(Ⅲ)∵抛物线y =x2-2x+c与x轴有公共点,∴对于方程x2-2x+c=0,判别式b2-4ac=4-4c≥0, ∴c≤1.当x=-1时,y=3+c;当x=0时,y=c,∵抛物线的对称轴为x=1,且当-1<x<0时,抛物线与x 轴有且只有一个公共点,∴3+c>0且c<0,解得-3<c<0,综上,当-1<x<0时,抛物线与x轴有且只有一个公共点时,c的取值范围为-3<c<0.第7题解图8.已知抛物线 y=(m-1)x2+(m-2)x-1与x轴交于A、B 两点.(Ⅰ)求m的取值范围;(Ⅱ)若m <0,且点A 在点B 的左侧,OA :OB =3:1,试确定抛物线的解析式;(Ⅲ)设(Ⅱ)中抛物线与y 轴的交点为C ,过点C 作直线l ∥x 轴,将抛物线在y 轴右侧的部分沿直线l 翻折,抛物线的其余部分保持不变,得到一个新图象.当直线y =-x +b 与新图象只有一个公共点P (x 0,y 0)且 y 0≥-5时,求b 的取值范围.解:(Ⅰ)∵抛物线y =(m -1)x 2+(m -2)x -1与x 轴交于A 、B 两点,∴()210241)0(m m m -¹-+î-ìí>①②, 由①得m ≠1≠1, , 由②得m ≠0≠0,, ∴m 的取值范围是m ≠0且m ≠1;≠1;(Ⅱ)∵点A 、B 是抛物线y =(m -1)x 2+(m -2)x -1与x轴的交点,∴令y=0,即 (m-1)x2+(m-2)x-1=0.解得 x1=-1,x2=11m -.∵m<0,∴−1<11m-<0.∵点A在点B左侧,∴点A的坐标为(-1,0),点B的坐标为(11m-,0).∴OA=1,OB=11m-. ∵OA:OB=3:1,∴11m-=31.∴m=-2.∴抛物线的解析式为y=-3x2−4x−1.(Ⅲ)∵点C 是抛物线y =-3x 2−4x −1与y 轴的交点,∴点C 的坐标为(0,-1).依题意翻折后的图象如解图所示.令y =-5,即-3x 2−4x −1=- 5. 解得x 1=32,x 2=-2.∴新图象经过点D (-2,-5). 当直线y =-x +b 经过D 点时,可得b =-7. 当直线y =-x +b 经过C 点时,可得b =-1.当直线y =-x +b (b >−1)与函数y =-3x 2−4x −1的图象仅有一个公共点P (x 0,y 0)时,得-x 0+b =-3x 02−4x 0−1.整理得 3x 02+3x 0+b +1=0.由32-12(b +1)=-12b -3=0,得b =−14.结合图象可知,符合题意的b 的取值范围为-7≤b <-1或b>−1.4第8题解图9.如图,已知c<0,抛物线y=x2+bx+c与x轴交于A(x1,0),B(x2,0)两点(x2>x1),与y轴交于点C.(Ⅰ)若x2=1,BC=5,求函数y=x2+bx+c的最小值;(Ⅱ)过点A作AP⊥BC,垂足为P(点P在线段BC上),AP 交y轴于点M.若OA=2,求抛物线y=x2+bx+c顶点的纵OM坐标随横坐标变化的函数解析式,并直接写出自变量的取值范围.第9题图 解:(Ⅰ)∵x2=1, ∴OB=1,∵BC=5,∴OC=22BC OB-=2,∴C(0,-2),把B(1,0),C(0,-2)代入y=x2+bx+c,得:0=1+b-2, 解得:b=1,∴抛物线的解析式为:y=x2+x-2.转化为y=(x+12)2-94;∴函数y =x 2+bx +c 的最小值为-94;(Ⅱ)∵∠OAM +∠OBC =90°=90°,,∠OCB +∠OBC =90°=90°, , ∴∠OAM =∠OCB ,又∵∠AOM =∠BOC =90°=90°, , ∴△AOM ∽△COB , ∴OAOC OM OB =, ∴OC =OA OM•OB =2OB ,∵c <0,x 2>0,∴-c =2x 2,即x 2=-2c .∵x 22+bx 2+c =0,将x 2=-2c 代入化简得:c =2b -4.抛物线的解析式为:y =x 2+bx +c ,其顶点坐标为(-2b ,244c b -). 令x =-2b,则b =-2x .y =244c b -=c -24b =2b -4-24b =-4x -4-x 2,满足点P 在线段BC 上的x 最小取值,使P 、C 、M 重合, 此时C (0,c ),B (-2c ,0),A (2c ,0),根据根与系数的关系,对于x 2+bx +c =0, -b =-2c +2c =32c , 由c =2b -4,解得c =-1, 所以b =-32c =32,x =-2b=-34;所以自变量x 的取值范围x ≥-34∴顶点的纵坐标随横坐标变化的函数解析式为:y =-x 2-4x -4(x ≥-3).。
初中数学二次函数最值练习题(附答案)

初中数学二次函数最值练习题一、单选题1.二次函数245y x x -=+的最小值是( ) A.1-B.1C.3D.52.在平面直角坐标系中,对于二次函数2(2)1y x =-+,下列说法中错误的是( ) A.y 的最小值为1B.图象顶点坐标为(2,1),对称轴为直线2x =C.当2x <时,y 的值随x 值的增大而增大,当2x ≥时,y 的值随x 值的增大而减小D.它的图象可以由2y x =的图象向右平移2个单位长度,再向上平移1个单位长度得到3.将进货单价为70元的某种商品按零售价100元一个售出时,每天能卖出20个,若这种商品的零售价每降价1元,其日销量就增加1个,为了获取每日最大利润,则应降价( ) A.5元 B. 10元 C. 15元 D.20元4.当1a x a ≤≤+时,函数221y x x =-+的最小值为1,则a 的值为( ) A.-1 B.2 C.0或2 D.-1或2 5.当21x -≤≤时,二次函数22()1y x m m =--++有最大值4,则实数m 的值为( )A.74-或74- 6.已知二次函数2()1y x h =-+(h 为常数),在自变量x 的值满足13x 的情况下,与其对应的函数值y 的最小值为5,则h 的值为( )A.1或-5B.-1或5C.1或-3D.1或37.某二次函数,当自变量x 满足04x 时,对应的函数值y 满足02y ,则这个函数不可能是( ) A.21(2)2y x =- B.242y x x =-+ C.21(2)22y x =--+ D.2114y x x =-++ 8.在美化校园的活动中,某兴趣小组想借助如图所示的直角墙角(两边足够长),用28 m 长的篱笆围成一个矩形花园ABCD (篱笆只围,AB BC 两边),设m AB x =.若在点P 处有一棵树与墙,CD AD的距离分别是15 m 和6 m,要将这棵树围在花园内(含边界,不考虑树的粗细),则花园面积S 的最大值为( )A.2193mB.2194mC.2195mD.2196m9.已知二次函数22233y ax ax a =+++(其中x 是自变量),当2x ≥时,y 随x 的增大而增大,且21x -≤≤时,y 的最大值为9,则a 的值为( )A.1或-2B. D.110.已知二次函数2()y x h =--(h 为常数),当自变量x 的值满足25x ≤≤时,与其对应的函数值y 的最大值为1-,则h 的值为( ) A.3或6 B.1或6C.1或3D.4或6二、解答题11.2a b+≤(0,0)a b >>,当且仅当a b =时,等号成立,其中我们把2a b+叫作正数a b 、,a b 的几何平均数,其意义是两个正数的算术平均数不小于其几何平均数。
二次函数与最值问题练习题(含答案)

二次函数与最值 题集一、实际问题中的最值(1)(2)1.如图,某中学准备围建一个矩形苗圃,其中一边靠墙,另外三边用长为米的篱笆围成,若墙长为米,设这个苗圃垂直于墙的一边长为米.苗圃园若苗圃园的面积为平方米,求的值.若平行于墙的一边长不小于米,这个苗圃园的面积有最大值和最小值吗?如果有,求出最大值和最小值,如果没有,请说明理由.【答案】(1)(2).有,当时,取得最大值,最大值为.当时,取得最小值,最小值为.【解析】(1)(2)由题意,得:平行于墙的一边长为,根据题意,得:,解得:或,∵,∴.∴.∵矩形的面积,且,即,∴当时,取得最大值,最大值为.当时,取得最小值,最小值为.【标注】【知识点】二次函数的几何问题2.(1)(2)某校在基地参加社会实践活动中,基地计划新建一个矩形的生物园地,一边靠旧墙(墙的最大可用长度为米),另外三边用总长米的不锈钢栅栏围成,与墙平行的一边留一个宽为米的出入口.如图所示,设米.若这个生物园地的面积为平方米,求出与之间的函数关系式,并写出自变量的取值范围.当为多少米时,这个生物园地的面积最大,并求出这个最大面积.【答案】(1)(2).为米时面积最大,最大为平方米.【解析】(1)(2)由题意可知∴∴.当时有最大值平方米.故当为米时,生物园地面积最大,最大面积为平方米.【标注】【知识点】二次函数的几何问题3.某农场拟建两间矩形种牛饲养室,饲养室的一面靠现有墙(墙长),中间用一道墙隔开(如图),已知计划中的建筑材料可建围墙的总长为,设两饲养室合计长,总占地面积为.(1)(2)求关于的函数表达式和自变量的取值范围. 若要使两间饲养室占地总面积达到,则各道墙的长度为多少?占地总面积有可能达到吗?【答案】(1)(2)总占地面积为,.占地总面积达到时,道墙长分别为米、米或米、米;占地面积不可能达到平方米.【解析】(1)(2)∵围墙的总长为米,间饲养室合计长米,∴饲养室的宽米,∴总占地面积为,.当两间饲养室占地总面积达到平方米时,则,解得:或.答:各道墙长分别为米、米或米、米.当占地面积达到平方米时,则,方程的,所以此方程无解,所以占地面积不可能达到平方米.【标注】【知识点】根据条件列二次函数关系式(1)(2)4.某果园有颗橙子树,平均每颗树结个橙子,现准备多种一些橙子树以提高果园产量,但是如果多种树,那么树之间的距离和每一棵树所接受的阳光就会减少.根据经验估计,每多种一棵树,平均每棵树就会少结个橙子,假设果园多种了棵橙子树.直接写出平均每棵树结的橙子个数(个)与之间的关系.果园多种多少棵橙子树时,可使橙子的总产量最大?最大为多少个?【答案】(1)(2)().果园多种棵橙子树时,可使橙子的总产量最大,最大为个.【解析】(1)(2)平均每棵树结的橙子个数(个)与之间的关系为:().设果园多种棵橙子树时,可使橙子的总产量为,则,则果园多种棵橙子树时,可使橙子的总产量最大,最大为个.【标注】【知识点】二次函数的利润问题(1)(2)(3)5.已知某商品每件的成本为元,第天的售价和销量分别为元/件和件,设第天该商品的销售利润为元,请根据所给图象解决下列问题:求出与的函数关系式.问销售该商品第几天时,当天销售利润最大?最大利润是多少.该商品在销售过程中,共有多少天当天的销售利润不低于元.【答案】(1)(2)(3)当时,,当时,.该商品第天时,当天销售利润最大,最大利润是元.共天每天销售利润不低于元.【解析】(1)当时,设与的函数关系式为,∵当时,,当,,∴,解得:∴,∴当时,;当时,.(2)(3),∴当时取得最大值元;∵;∴当时,随的增大而减小,当时,,综上所述,该商品第天时,当天销售利润最大,最大利润是元.当时,,解得,因此利润不低于元的天数是,共天;当时,,解得,因此利润不低于元的天数是,共天,所以该商品在销售过程中,共天每天销售利润不低于元.【标注】【知识点】函数图象与实际问题最大(1)(2)(3)6.某商场将进价为元的冰箱以元售出,平均每天能售出台,为了配合国家“家电下乡”政策的实施,商场决定采取适当的降价措施.调查表明:这种冰箱的售价每降低元,平均每天就能多售出台.假设每台冰箱降价元,商场每天销售这种冰箱的利润是元,请写出与之间的函数表达式.(不要求写自变量的取值范围)商场要想在这种冰箱销售中每天盈利元,同时又要使百姓得到实惠,每台冰箱应降价多少元?每台冰箱降价多少元时,商场每天销售这种冰箱的利润最高?最高利润是多少?【答案】(1)(2)(3).每台冰箱应降价元.每台冰箱的售价降价元时,商场的利润最大,最大利润是元.【解析】(1)(2)根据题意,得,即.由题意,得.整理,得.解这个方程,得,.(3)要使百姓得到实惠,取.所以,每台冰箱应降价元.对于,当时,.所以,每台冰箱的售价降价元时,商场的利润最大,最大利润是元.【标注】【知识点】二次函数的利润问题最大值(1)(2)7.在新型城镇化型过程中,为推进节能减排,发展低碳经济,我市某公司以万元购得某项节能产品的生产技术后,再投入万元购买生产设备,进行该产品的生产加工.已知生产这种产品的成本价为每件元.经过市场调研发现,该产品的销售单价定在元到元之间较为合理,并且该产品的年销售量(万件)与销售单价(元)之间的函数关系式为:(年获利年销售收入生产成本投资成本)当销售单价定为元时,该产品的年销售量为多少万件?求该公司第一年的年获利(万元)与销售单价(元)之间的函数关系式,并说明投资的第一年,该公司是盈利还是亏损?若盈利,最大利润是多少?若亏损,最小亏损是多少?【答案】(1)(2)投资第一年,公司亏损,最少亏损万【解析】(1)(2)把代入,得(万件)当销售单价定为元时,该产品的年销售量为万件.①当时,故当时,最大为,即公司最少亏万.②当时,故当时,最大为,即公司最少亏万.综上,投资第一年,公司亏损,最少亏损万.【标注】【知识点】二次函数的利润问题二、几何问题中的最值(1)(2)1.已知,如图,抛物线与轴交于点,与轴交于,两点,点在点左侧.点的坐标为,.xyOxyO备用图求抛物线的解析式;若点是线段下方抛物线上的动点,求四边形面积的最大值.【答案】(1)(2)..【解析】(1)(2)∵∴∵∴∵过、∴解这个方程组,得∴抛物线的解析式为:.过点作轴分别交线段和轴于点、yOx在中,令得方程解这个方程,得,∴设直线的解析式为∴解这个方程组,得∴的解析式为:∵==设,当时,有最大值.此时四边形面积有最大值.【标注】【知识点】二次函数与面积四边形(1)(2)2.如图,二次函数的图象与轴交于点,,与轴交于点.xyO求二次函数表达式.若点是第一象限内的抛物线上的一个动点,且点的横坐标为,用含有的代数式表示的面积,并求出当为何值时,的面积最大,最大面积是多少?【答案】(1)(2).当时,的面积最大,最大面积是.【解析】(1)∵二次函数的图象与轴交于点,,∴二次函数的解析式为.(2)如图,连接,易得的解析式为.设点的坐标为,则点的坐标为,∴,,,当时,的面积最大,最大面积是.yO【标注】【知识点】二次函数与面积(1)(2)3.如图,已知经过原点的抛物线与轴的另一交点为,现将它向右平移()个单位,所得抛物线与轴交于、两点,与原抛物线交于点.求点的坐标,并判断存在时它的形状(不要求说理).在轴上是否存在两条相等的线段?若存在,请一一找出,并写出它们的长度(可用含的式子表示);若不存在,请说明理由.(3)设的面积为,求关于的关系式.【答案】(1)(2)(3)点的坐标为,是等腰三角形.存在,,..【解析】(1)(2)(3)令,得,.∴点的坐标为.是等腰三角形.存在.,.如图,当时,作轴于,设,∵,,∴.∴.∴.把代入,得.∵,∴.如图,当时,作轴于,设∵,,∴.∴.∴.把代入,得.∵,∴.综上可得:.【标注】【知识点】二次函数与面积(1)(2)4.已知抛物线与轴交于,两点,交轴于点,已知抛物线的对称轴为,点,点,为抛物线的顶点.求抛物线的解析式.在轴下方且在抛物线上有一动点,求四边形的面积最大值.【答案】(1)(2).【解析】(1)由、关于对称轴对称,对称轴为,点,得.将、、点的坐标代入函数解析式,得,解得.(2)故抛物线的解析式为.如图,过作轴于点,交于点.设,点坐标为,.,当时,.【标注】【知识点】二次函数与面积四边形最大(1)(2)(3)5.如图,二次函数(为非负整数)与轴交于、两点,与轴交于点.求抛物线的解析式.在直线上找一点,使的周长最小,并求出点的坐标.点在抛物线上,且在第二象限内,设点的横坐标为,问为何值时,四边形的面积最大?并求出这个最大面积.【答案】(1)(2)(3)时,四边形的面积最大,这个最大面积是.【解析】(1)(2)(3)由题意得,,解得:,∵是非负整数,∴或,当时,二次函数的解析式为,当时,二次函数的解析式为,∵图象与轴交于点和点,点、分别在原点的左、右两边,∴当时,二次函数的解析式为不符合题意,∴二次函数的解析式为.如图,作点关于的对称点连接交对称轴于点,.由得点坐标为.当时,.解得,,∴,.设的解析式为,图象过点,,得,解得,∴的解析式为,当时,,点坐标为 时,的周长最小.如图,设点坐标为(),作轴于点,由图可知:四边形梯形.因此时,四边形的面积最大,这个最大面积是.【标注】【知识点】二次函数与面积(1)(2)6.如图,已知抛物线经过,两点.x24y–22O 求该抛物线的解析式.在直线上方的该抛物线上是否存在一点,使得的面积最大?若存在,求出点的坐标及面积的最大值;若不存在,请说明理由.【答案】(1)(2).存在,,面积的最大值为.【解析】(1)(2)把,代入抛物线的解析式得:,解得:,则抛物线解析式为.存在,理由如下:设的横坐标为,则点的纵坐标为,过作轴的平行线交于,连接,,如图所示,x24y–22O 由题意可求得直线的解析式为,∴点的坐标为,∴,∴的面积,当时,,∴此时,面积的最大值为.【标注】【知识点】二次函数与面积最大(1)(2)(3)7.已知二次函数的图象和轴交于点、,与轴交于点,直线上方的抛物线上一动点,抛物线的顶点是点.图求直线的解析式.求面积的最大值及点的坐标.当的面积最大时,在直线上有一动点,使得的周长最小,求周长最小时点的坐标.图【答案】(1)(2)(3).,..【解析】(1)(2)(3)过抛物线上动点作轴的垂线,垂足是,线段交线段于,设,,,∵,∴当时,,此时.关于直线的对称点连接,∵,,∴,∴联立,解得,最大∴.【标注】【知识点】二次函数与动点问题(1)(2)(3)8.如图,抛物线与轴的两个交点分别为、,与轴交于点,顶点为,为线段的中点,的垂直平分线与轴、轴分别交于、.xyO 求抛物线的函数表达式,并写出顶点的坐标.在直线上是否存在一点,使周长最小,若存在,请求出最小周长和点的坐标;若不存在,请说明理由.若点在轴上方的抛物线上运动,当运动到什么位置时,面积最大?并求出最大面积.【答案】(1)(2)(3)抛物线的解析式为,顶点的坐标为.存在;的周长最小值为,.时,的面积最大,最大面积为.【解析】(1)(2)由题意,得,解得,,所以抛物线的解析式为,顶点的坐标为.设抛物线的对称轴与轴交于点,(3)∵垂直平分,∴关于直线的对称点为,连结交于于一点,xyO∴这一点为所求点,使最小,即最小为.而,∴的周长最小值为.设直线的解析式为,则,解得,,所以直线的解析式为.由于,,,得,所以,,.同理可求得直线的解析式为,联立直线与的方程,解得使的周长最小的点.设,.过作轴的垂线交于,xyO则,所以,即当时,的面积最大,最大面积为,此时.【标注】【知识点】二次函数的几何问题(1)(2)(3)9.如图,已知抛物线与一直线相交于、两点,与轴相交于点,其顶点为.求抛物线及直线的函数关系式.若是抛物线上位于直线上方的一个动点,求的面积的最大值及此时点的坐标.在对称轴上是否存在一点,使的周长最小.若存在,请求出点的坐标和周长的最小值;若不存在,请说明理由.备用图【答案】(1)(2);.;.(3)在对称轴上存在一点,使的周长最小,周长的最小值为.【解析】(1)(2)(3)将,代入,得:,解得:,∴抛物线的函数关系式为;设直线的函数关系式为,将,代入,得:,解得,∴直线的函数关系式为.过点作轴交轴于点,交直线于点,过点作轴交轴于点,如图所示.图设点的坐标为,则点的坐标为,点的坐标为,∴,,,∵点的坐标为,∴点的坐标为,∴,∴,∵,∴当时,的面积取最大值,最大值为,此时点的坐标为.当时,,∴点的坐标为,∵,∴抛物线的对称轴为直线,∵点的坐标为,∴点,关于抛物线的对称轴对称,令直线与抛物线的对称轴的交点为点,如图所示.图∵点,关于抛物线的对称轴对称,∴,∴,∴此时周长取最小值,当时,,∴此时点的坐标为,∵点的坐标为,点的坐标为,点的坐标为,∴,,∴,∴在对称轴上存在一点,使的周长最小,周长的最小值为.10.如图,已知抛物线经过、两点,与轴交于点.(1)(2)(3)求抛物线的解析式.点是对称轴上的一个动点,当的周长最小时,直接写出点的坐标和周长最小值.点为抛物线上一点,若,求出此时点的坐标.【答案】(1)(2)(3).点为,周长的最小值为.点的坐标为或或.【解析】(1)(2)(3)根据题意,将、代入抛物线,可得:,解得:,所以,抛物线为:.点为,周长的最小值为.∵抛物线为:,∴抛物线的对称轴为直线,点、关于直线对称,当的周长最小时,则需要最小,根据利用轴对称且最小值的方法,可知点是与对称轴的交点,令,则,所以,点坐标为,设为直线,把,代入直线解析式,可得:,解得:,所以,直线为,将代入,可得:,∴点为,此时,,,∴周长的最小值为:.∵,,∴,∵,,∴点的纵坐标为或,令,解得:,,∴点的坐标为:或,令,解得:,∴点的坐标为:.综上所述:点的坐标为:或或.【标注】【知识点】二次函数与轴对称问题。
二次函数最值问题解答题专项练习60题(有答案)

二次函数最值专项练习60题1.画出抛物线y=4(x﹣3)2+2的大致图象,写出它的最值和增减性.2.如图,二次函数y=ax2+bx+c的图象经过A(﹣1,0)、B(2,3)两点,求出此二次函数的解析式;并通过配方法求出此抛物线的对称轴和二次函数的最大值.3.已知二次函数y=x2﹣x﹣2及实数a>﹣2,求(1)函数在一2<x≤a的最小值;(2)函数在a≤x≤a+2的最小值.4.已知函数y=x2+2ax+a2﹣1在0≤x≤3范围内有最大值24最小值3,求实数a的值.5.我们知道任何实数的平方一定是一个非负数,即:(a+b)2≥0,且﹣(a+b)2≤0.据此,我们可以得到下面的推理:∵x2+2x+3=(x2+2x+1)+2=(x+1)2+2,而(x+1)2≥0∴(x+1)2+2≥2,故x2+2x+3的最小值是2.试根据以上方法判断代数式3y2﹣6y+11是否存在最大值或最小值?若有,请求出它的最大值或最小值.6.如图所示,已知平行四边形ABCD的周长为8cm,∠B=30°,若边长AB=x(cm).(1)写出▱ABCD的面积y(cm2)与x的函数关系式,并求自变量x的取值范围.(2)当x取什么值时,y的值最大?并求最大值.7.求函数y=2x2﹣ax+1当0≤x≤1时的最小值.8.已知m,n是关于x的方程x2﹣2ax+a+6=0的两实根,求y=(m﹣1)2+(n﹣1)2的最小值.9.当﹣1≤x≤2时,求函数y=f(x)=2x2﹣4ax+a2+2a+2的最小值,并求最小值为﹣1时,a的所有可能的值.10.已知二次函数y=x2﹣6x+m的最小值为1,求m的值.11.已知函数是关于x的二次函数.(1)求m的值;(2)当m取什么值时,此函数图象的顶点为最低点?(3)当m取什么值时,此函数图象的顶点为最高点?12.两个数的和为6,这两个数的积最大可以达到多少?利用图象描述乘积与因数之间的关系.13.将一条长为20cm的铁丝剪成两段,并以每一段铁丝的长度为周长各做一个正方形.这两个正方形面积之和有最值吗?如有,求出最值;如没有请说明理由.14.关于自变量x的二次函数y=x2﹣4ax+5a2﹣3a的最小值为m,且a满足不等式0≤a2﹣4a﹣2≤10,则m的最大值是多少?15.求函数的最小值.16.当﹣1≤x≤1时,函数y=﹣x2﹣ax+b+1(a>0)的最小值是﹣4,最大值是0,求a、b的值.17.已知a2+b2=1,,求a+b+ab的取值范围.18.如图,在矩形ABCD中,B(16,12),E、F分别是OC、BC上的动点,EC+CF=8.当F运动到什么位置时,△AEF的面积最小,最小为多少?19.如图;AC,BD是四边形ABCD的对角线,AC⊥BD于点O;(1)求证:S四边形ABCD=AC•BD;(2)若AC+BD=10,当AC,BD的长是多少时,四边形ABCD的面积最大?20.先画出函数图象,然后结合图象回答下列问题:(1)函数y=3x2的最小值是多少?(2)函数y=﹣3x2的最大值是多少?(3)怎样判断函数y=ax2有最大值或最小值?与同伴交流.21.将长为156cm的铁线剪成两段,每段都围成一个边长为整数(cm)的正方形,求这两个正方形面积和的最小值.22.已知函数y=(a+2)x2﹣2(a2﹣1)x+1,其中自变量x为正整数,a也是正整数,求x何值时,函数值最小.23.设实数a,b满足:3a2﹣10ab+8b2+5a﹣10b=0,求u=9a2+72b+2的最小值.24.若函数y=4x2﹣4ax+a2+1(0≤x≤2)的最小值为3,求a的值.25.说明:不论x取何值,代数式x2﹣5x+7的值总大于0.并尝试求出当x取何值时,代数式x2﹣5x+7的值最小?最小值是多少?26.求经过点A(0,2)、B(2,0)、C(﹣1,2)的抛物线的解析式,并求出其最大或最小值.27.如图,在△ABC中,∠A=90°,∠C=30°,AB=1,两个动点P,Q同时从A点出发,点P沿AC运动,点Q沿AB,BC运动,两点同时到达点C.(1)点Q的速度是点P速度的多少倍?(2)设AP=x,△APQ的面积是y,求y关于x的函数关系式,并写出x的取值范围,(3)求出y的最大值.28.已知二次函数y=x2与一次函数y=2x+1相交于A、B两点,点C是线段AB上一动点,点D是抛物线上一动点,且CD平行于y轴,求在移动过程中CD的最大值.29.代数式x2﹣3x﹣1有最大值或最小值吗?若有,请求出:当x取何值时,最大(小)值是多少?30.已知二次函数y=2x2﹣4ax+a2+2a+2(1)通过配方,求当x取何值时,y有最大或最小值,最大或最小值是多少?(2)当﹣1≤x≤2时,函数有最小值2.求a所有可能取的值.31.设函数y=|x2﹣x|+|x+1|,求﹣2≤x≤2时,y的最大值和最小值.32.求函数y=(k﹣1)x2﹣2(k﹣1)x﹣k的最值,其中k为常数且k≠1.33.已知函数y=﹣9x2﹣6ax+2a﹣a2,当时,y的最大值为﹣3,求a.34.求函数y=x2+5x+8的最小值.35.已知二次函数y=(3﹣k)x2+2,求:(1)当k为何值时,函数有最大值?最大值是多少?(2)当k为何值时,函数有最小值?最小值是多少?36.求关于x的二次函数y=x2﹣2tx+1在﹣1≤x≤1上的最大值(t为常数).37.已知二次函数y=﹣9x2﹣6ax﹣a2+2a有最大值﹣3,求实数a的值.38.(1)求函数y=|x2﹣4|﹣3x在区间﹣2≤x≤5中的最大值和最小值.(2)已知:|y|≤1,且2x+y=1,求2x2+16x+3y2的最小值.39.已知y=x2﹣2ax﹣3,﹣2≤x≤2.(1)求y的最小值;(2)求y的最大值.40.当|x+1|≤6时,求函数y=x|x|﹣2x+1的最大值?41.用长14m的篱笆围成如图所示的鸡舍,门MN宽2m,怎样设计才能使鸡舍的面积最大?42.如图所示,在直角梯形ABCD中,AB=2,P是边AB的中点,∠PDC=90°,问梯形ABCD面积的最小值是多少?43.有两条抛物线y=x2﹣3x,y=﹣x2+9,通过点P(t,0)且平行于y轴的直线,分别交这两条抛物线于点A和B,当t在0到3的范围内变化时,求线段AB的最大值.44.如图,半径为1的半圆内接等腰梯形,其下底是半圆的直径,试求:(1)它的周长y与腰长x之间的函数关系式,并求出自变量x的取值范围.(2)当腰长为何值时,周长有最大值?这个最大值为多少?45.已知点P,Q,R分别在△ABC的边AB,BC,CA上,且BP=PQ=QR=RC=1,求△ABC的面积的最大值.46.已知:0≤x≤1,函数的最小值为m,试求m的最大值.47.阅读下面的材料:小明在学习中遇到这样一个问题:若1≤x≤m,求二次函数y=x2﹣6x+7的最大值.他画图研究后发现,x=1和x=5时的函数值相等,于是他认为需要对m进行分类讨论.他的解答过程如下:∵二次函数y=x2﹣6x+7的对称轴为直线x=3,∴由对称性可知,x=1和x=5时的函数值相等.∴若1≤m<5,则x=1时,y的最大值为2;若m≥5,则x=m时,y的最大值为m2﹣6m+7.请你参考小明的思路,解答下列问题:(1)当﹣2≤x≤4时,二次函数y=2x2+4x+1的最大值为_________;(2)若p≤x≤2,求二次函数y=2x2+4x+1的最大值;(3)若t≤x≤t+2时,二次函数y=2x2+4x+1的最大值为31,则t的值为_________.48.如图,在矩形ABCD中,AB=6cm,BC=12cm,点P从点A出发,沿AB边向点B以1cm/s的速度移动,同时点Q从点B出发沿BC边向点C以2cm/s的速度移动,如果P,Q两点同时出发,分别到达B,C两点后就停止移动.(1)设运动开始后第t秒钟后,五边形APQCD的面积为Scm2,写出S与t的函数关系式,并指出自变量t的取值范围.(2)t为何值时,S最小?最小值是多少?49.已知二次函数y=x2与一次函数y=2x+1相交于A、B两点,点C是线段AB上一动点,点D是抛物线上一动点,且CD平行于y轴,求在移动过程中CD的最大值.50.如图,在△ABC中,∠A=90°,∠C=30°,AB=1,两个动点P,Q同时从A点出发,点P沿AC运动,点Q沿AB,BC运动,两点同时到达点C.(1)点Q的速度是点P速度的多少倍?(2)设AP=x,△APQ的面积是y,求y关于x的函数关系式,并写出x的取值范围,(3)求出y的最大值.51.一块三角形废料如图所示,∠A=30°,∠C=90°,BC=6.用这块废料剪出一个平行四边形AGEF,其中,点G,E,F分别在AB,BC,AC上.设CE=x(1)求x=2时,平行四边形AGEF的面积.(2)当x为何值时,平行四边形AGEF的面积最大?最大面积是多少?52.如图,在Rt△ABC中,∠ACB=90°,AB=10,BC=8,点D在BC上运动(不运动至B,C),DE∥AC,交AB 于E,设BD=x,△ADE的面积为y.(1)求y与x的函数关系式及自变量x的取值范围;(2)x为何值时,△ADE的面积最大?最大面积是多少?53.如图,将两张长为8,宽为2的矩形纸条交叉放置.(1)求证:重叠部分的图形是菱形;(2)求重叠部分图形的周长的最大值和最小值.(要求画图﹑推理﹑计算)54.如图,设点P是边长为a的正三角形ABC的边BC上一点,过点P作PQ⊥AB,垂足为Q,延长QP交AC的延长线于点R.当点P在何处时,△BPQ与△CPR的面积之和取最大(小)值?并求出最大(小)值.55.(2012•)当k分别取﹣1,1,2时,函数y=(k﹣1)x2﹣4x+5﹣k都有最大值吗?请写出你的判断,并说明理由;若有,请求出最大值.56.(2003•)二次函数y=x2+bx+c的图象与x轴交于A、B两点,与y轴交于C(0,3),若△ABC的面积为9,求此二次函数的最小值.57.(2013•南岗区一模)如图,在Rt△AOB中,∠AOB=90°,且AO=8,BO=6,P是线段AB上一个动点,PE⊥A0于E,PF⊥B0于F.设PE=x,矩形PFOE的面积为S(1)求出S与x的函数关系式;(2)当x为何值时,矩形PFOE的面积S最大?最大面积是多少?58.(2013•资阳)在关于x,y的二元一次方程组中.(1)若a=3.求方程组的解;(2)若S=a(3x+y),当a为何值时,S有最值.59.(2010•)如图,在△ABC中,∠C=90°,AC=4cm,BC=5cm,点D在BC上,且CD=3cm.动点P、Q分别从A、C两点同时出发,其中点P以1cm/s的速度沿AC向终点C移动;点Q以cm/s的速度沿CB向终点B移动.过P作PE∥CB交AD于点E,设动点的运动时间为x秒.(1)用含x的代数式表示EP;(2)当Q在线段CD上运动几秒时,四边形PEDQ是平行四边形;(3)当Q在线段BD(不包括点B、点D)上运动时,求四边形EPDQ面积的最大值.60.(2010•)如图,梯形ABCD中,AB∥DC,∠ABC=90°,∠A=45°.AB=30,BC=x,其中15<x<30.作DE⊥AB于点E,将△ADE沿直线DE折叠,点A落在F处,DF交BC于点G.(1)用含有x的代数式表示BF的长.(2)设四边形DEBG的面积为S,求S与x的函数关系式.(3)当x为何值时,S有最大值,并求出这个最大值.二次函数最值解答题60题参考答案:1.解:因为顶点坐标为(3,2),对称轴为x=3,与y轴交点为(0,38),因为△=144﹣4×2×19=144﹣152=﹣8<0,所以与x轴无交点.作图得:最值2.增减性:当x≥3时,y随x的增大而增大;当x≤3时,y随x的增大而减小2.解:由函数图象可得二次函数图象过点C(0,3),将A,B,两点代入函数解析式得解得:a=﹣1,b=2,c=3,可得二次函数解析式为:y=﹣x2+2x+3;配方得:y=﹣(x﹣1)2+4,∴对称轴x=1,最大值为43.解:二次函数y=x2﹣x﹣2=﹣的图象如图:顶点坐标为(,),(1)当﹣2<a<时,函数为减函数,最小值为当x=a时,y=a2﹣a﹣2.当a≥时,y min=﹣,(2)当a>﹣2,且a+2<,即:﹣2<a<﹣时,函数为减函数,最小值为:y x=a+2=(a+2)2﹣(a+2)﹣2,当a<≤a+2,即﹣≤a<时,函数的最小值为y=﹣4.解:配方y=(x+a)2﹣1,函数的对称轴为直线x=﹣a,顶点坐标为(﹣a,﹣1).①当0≤﹣a≤3即﹣3≤a≤0时,函数最小值为﹣1,不合题意;②当﹣a<0即a>0时,∵当x=3时,y有最大值;当x=0时,y有最小值,∴,解得a=2;③当﹣a>3即a<﹣3时,∵当x=3时,y有最小值;当x=0时,y有最大值,∴,解得a=﹣5.∴实数a的值为2或﹣55.解:原式=3(y﹣1)2+8,∵(y﹣1)2≥0,∴3(y﹣1)2+8≥8,∴有最小值,最小值为86.解:(1)过A作AE⊥BC于E,如图,∵∠B=30°,AB=x,∴AE=x,又∵平行四边形ABCD的周长为8cm,∴BC=4﹣x,∴y=AE•BC=x(4﹣x)=﹣x2+2x(0<x<4);(2)y=﹣x2+2x=﹣(x﹣2)2+2,∵a=﹣,∴当x=2时,y有最大值,其最大值为27.解:对称轴x=﹣=﹣=,①≤0,即a≤0时,0≤x≤1范围内,y随x的增大而增大,当x=0时,y最小,最小值y=2×02﹣a×0+1=1,②0<<1,即0<a<4时,当x=时有最小值,最小值y=2×()2﹣a×+1=1﹣,③≥1,即a≥4时,0≤x≤1范围内,y随x的增大而减小,当x=1时,y最小,最小值y=2×12﹣a×1+1=3﹣a,综上所述,a≤0时,最小值为1,0<a<4时,最小值为1﹣,a≥4时,最小值为3﹣a8.解:依题意△=4a2﹣4(a+6)≥0,即a2﹣a﹣6≥0,∴a≤﹣2或a≥3,(3分)由m+n=2a,mn=a+6,y=m2+n2﹣2(m+n)+2=(m+n)2﹣2mn﹣2(m+n)+2=4a2﹣6a﹣10,=4(a﹣)2﹣,∴a=3时,y的最小值为8.(12分)故y的最小值为89.解:对称轴x=﹣=﹣=a,①a≤﹣1时,﹣1≤x≤2范围内,y随x的增大而增大,当x=﹣1时,y最小,最小值y=2×(﹣1)2﹣4a×(﹣1)+a2+2a+2=a2+6a+4,②﹣1<a<2时,当x=a时,有最小值,最小值y=2×a2﹣4a×a+a2+2a+2=﹣a2+2a+2,③a≥2时,﹣1≤x≤2范围内,y随x的增大而减小,当x=2时,y最小,最小值y=2×22﹣4a×2+a2+2a+2=a2﹣6a+10,综上所述,a≤﹣1时,最小值为a2+6a+4,﹣1<a<2时,最小值为﹣a2+2a+2,a≥2时,最小值为a2﹣6a+10;∵最小值为﹣1,∴a2+6a+4=﹣1,整理得a2+6a+5=0,解得a1=﹣1,a2=﹣5,﹣a2+2a+2=﹣1,整理得,a2﹣2a﹣3=0,解得a3=﹣1,a4=3(舍去),a2﹣6a+10=﹣1,整理得,a2﹣6a+11=0,△=(﹣6)2﹣4×1×11=﹣8<0,方程无解,综上所述,a的所有可能值为﹣1、﹣510.解:根据抛物线顶点坐标公式得:=1,解得:m=1011.解:(1)根据二次函数的定义可知:m2+2m﹣6=2,m+2≠0,解得:m=2或﹣4.(2)当m=2时,抛物线的开口向上,有最小值,此函数图象的顶点为最低点;(3)当m=﹣4时,抛物线的开口向下,有最大值,此函数图象的顶点为最高点12.解:设两数为x、y,两数的积为s,根据题意列方程组得,,整理得,s=x(6﹣x)=﹣x2+6x,配方得,s=﹣(x﹣3)2+9,可见,s的最大值为9.如图:由于函数为抛物线,其与x轴的交点坐标为:(0,0),(6,0),顶点为(3,9),对称轴为直线x=3,画出函数图象13.解:设一段铁丝的长度为x,另一段为(20﹣x),则S=x2+(20﹣x)(20﹣x)=(x﹣10)2+12.5,∴由函数当x=10cm时,S最小,为12.5cm214.解:由0≤a2﹣4a﹣2≤0,解得:﹣2≤a≤2﹣或2+≤a≤6.由y=x2﹣4ax+5a2﹣3a可得y=(x﹣2a)2+a2﹣3a,则最小值m=a2﹣3a=(a﹣)2﹣,它的图象的对称轴为a=.在上述a的取值范围内的a值中6与的距离最大.∴a=6时,原函数的最小值m有最大值m=62﹣3×6=1815.解:根据x2﹣x﹣6≥0且x2﹣x﹣6≠6时,函数才有意义,解得:x≤﹣2且x≠﹣3或x≥3且x≠4,此时函数y=x2﹣4x﹣9,图象如图:在x≤﹣2且x≠﹣3或x≥3且x≠4的范围内可知,当x=3时,这个函数的最小值为﹣1216.解:由题意:对称轴为x=﹣.其次这是一个定区间(﹣1≤x≤1)动对称轴(x=﹣)的函数,所以需要对对称轴所在位置进行分类讨论.第一种情况:0<﹣≤1,不可能.因对称轴在区间内故函数最大值在x=﹣时取到,因对称轴在区间左半段故函数最小值在x=1时取到.联立x=﹣时y=﹣4与x=﹣1时y=0两个方程解得a=2±2,均不符合条件,故舍去.第二种情况,﹣<﹣1,即对称轴在区间外,此时a>2,在区间内函数单调递减,故x=﹣1时y=0,x=1时y=﹣4,解得a=2,b=﹣2,满足a>0的条件.解得:a=2,b=﹣217.解:∵a2+b2=(a+b)2﹣2ab,a2+b2=1,∴ab=,设a+b=t,则﹣≤t≤,∴y=a+b+ab=+a+b=(t2﹣1)+t=t2+t﹣=(t+1)2﹣1,∴t=﹣1时,y有最小值为﹣1,t=时,y有最大值,此时y=(+1)2﹣1=,∴﹣1≤y≤,即a+b+ab的取值范围为﹣1≤a+b+ab≤18.解:在矩形ABCD中,B(16,12),EC+CF=8;则AB=OC=16,BC=OA=12;设CF=x,则EC=8﹣x;S△AEF=S□ABCO﹣S△AOE﹣S△ABF﹣S△ECF=OA×OC﹣×OE×OA﹣×AB×BF﹣×CE×CF=12×16﹣×[16﹣(8﹣x)]×12﹣×16×(12﹣x)﹣×x×(8﹣x)=x2﹣2x+48=(x﹣2)2+46;因此,当x=2时,S△AEF取得最小值46.故当F运动到CF为2时,△AEF的面积最小,最小为4619.(1)证明:∵AC⊥BD,∴S四边形ABCD=S△ABC+S△ACD,=AC•OB+AC•OD,=AC(OB+OD)=AC•BD;(2)解:设AC=x,∵AC+BD=10,∴BD=10﹣x,∴四边形ABCD的面积=x(10﹣x)=﹣(x2﹣10x)=﹣(x﹣5)2+,∵﹣<0,∴当x=5时,四边形ABCD的面积有最大值,此时AC=5,BD=520.解:(1)根据图象得:它的最小值是0;(2)根据图象得:它的最大值是0;(3)当a>0时,y=ax2有最小值,当a<0时,y=ax2有最大值21.解:设其中一段铁丝的长度为xcm,另一段为(156﹣x)cm,则两个正方形面积和S=x2+(156﹣x)2=(x﹣78)2+761,∴由函数当x=78cm时,S最小,为761cm2.答:这两个正方形面积之和的最小值是761cm222.解:∵y=(a+2)x2﹣2(a2﹣1)x+1,∴y=(a+2)+1﹣,其对称轴为,因为a为正整数,故因,,因此,函数的最小值只能在x取a﹣2,a﹣1,时达到,(1)当a﹣1=时,a=1,此时,x=0使函数取得最小值,由于x是正整数,故应舍去;(2)a﹣2<<a﹣1时,即a>1时,由于x是正整数,而为小数,故x=不能达到最小值,当x=a﹣2时,y1=(a+2)(a﹣2)2﹣2(a2﹣1)(a﹣2)+1,当x=a﹣1时,y2=(a+2)(a﹣1)2﹣2(a2﹣1)(a﹣1)+1,又y1﹣y2=4﹣a,①当4﹣a>0时,即1<a<4且a为整数时,x取a﹣1,使y2为最小值;②当4﹣a=0时,即a=4时,有y1=y2,此时x取2或3;③当4﹣a<0时,即a>4且为整数时,x取a﹣2,使y1为最小值;综上,(其中a为整数)23.解:由3a2﹣10ab+8b2+5a﹣10b=0可得(a﹣2b)(3a﹣4b+5)=0,(6分)所以a﹣2b=0,或3a﹣4b+5=0.(8分)①当a﹣2b=0,即a=2b时,u=9a2+72b+2=36b2+72b+2=36(b+1)2﹣34,于是b=﹣1时,u的最小值为﹣34,此时a=﹣2,b=﹣1.(13分)②当3a﹣4b+5=0时,u=9a2+72b+2=16b2+32b+27=16(b+1)2+11,于是b=﹣1时,u的最小值为11,此时a=﹣3,b=﹣1.(18分)综上可知,u的最小值为﹣3424.解:∵y=4x2﹣4ax+a2+1(0≤x≤2),∴y=4+1,(1)当0≤≤2,即0≤a≤4时,最小值为1,不符合题意,舍去;(2)当<0即a<0时,令f(0)=3得:a2+1=3,解得:a=±,故a=﹣;(3)当>2即a>4时,令f(2)=3,即a2﹣8a+14=0,解得;a=4±,故a=4+;综上有;a=﹣或4+25.解:原式=(x)2+.∵(x)2≥0.∴原式>0恒成立;当x=时,原式有最小值为26.解:由题意设二次函数解析式为:y=ax2+bx+c,把A(0,2)、B(2,0)、C(﹣1,2)分别代入二次函数解析式,得:解得所以函数解析式为:y=﹣x2﹣x+2,配方得:y=﹣(x﹣)2+,所以二次函数有最大值且最大值为:27.解:(1)∵在△ABC中,∠A=90°,∠C=30°,AB=1,∴BC=2,AC=,而两个动点P,Q同时从A点出发,点P沿AC运动,点Q沿AB,BC运动,两点同时到达点C ∴Q的速度是P的速度的(2+1)÷=倍;(2)∵设AP=x,△APQ的面积是y,①当Q在AB上,即时,,②当Q在BC上,即时,,即:;(3)对于()当时,对于(≤x≤)当时,,∵,∴当时,.28.解:设C(m,2m+1),D(m,m2),则CD=2m+1﹣m2=﹣m2+2m+1=﹣(m﹣1)2+2,当m=1时,CD有最大值229.解:原式=(x﹣)2﹣,∴当x=时,原式有最小值为﹣30.解:(1)y=2x2﹣4ax+a2+2a+2,y=2(x﹣a)2﹣a2+2a+2,当x=a时,y有最小值为3﹣(a﹣1)2;(2)当﹣1≤x≤2时,3﹣(a﹣1)2=2,解得a=0或a=2,当x<﹣1时,则当x=﹣1时y=2,解得,当x>2时,则当x=2时y=2,解得a=4,所以:a=0或a=2或或a=431.解:(1)当1≤x≤2时,y=x2﹣x+x+1=x2+1,当x=1时取最小值为2,x=2时取最大值为5;(2)当﹣2≤x≤﹣1时,y=x2﹣2x﹣1=(x﹣1)2﹣2,当x=﹣1时,y取得最小值为2,当x=﹣2时,y取得最大值为7;(3)当﹣1≤x≤0时,y=x2﹣x+x+1=x2+1,当x=﹣1时,y取最大值为2,当x=0时,y取最小值为1;(4)当0≤x≤1时,y=x﹣x2+x+1=﹣(x﹣1)2+2,当x=1时y取最大值为2,当x=0时y取最小值为1;综上所述:y的最大值为7,最小值为132.解:∵y=(k﹣1)x2﹣2(k﹣1)x﹣k,=(k﹣1)(x﹣1)2﹣2k+1,∴当k>1时,函数有最小值为﹣2k+1,当k<1时,函数有最大值为﹣2k+133.解:(1)若,即﹣1≤a≤1,抛物线开口向下,当时,y最大值=2a,∵二次函数最大值﹣3,即与﹣1≤a≤1矛盾,舍去.(2)若当时,y随x增大而减小,当时,y最大值=﹣a2+4a﹣1,由又a>1,∴(3)若当时,y随x增大而增大,当时,y最大值=﹣a2﹣1,由又a<﹣1,∴综上所述,或34.最小值===.35.解:(1)3﹣k<0,即k>3时,函数有最大值2;(2)3﹣k>0,即k<3时,函数有最大小236.解:二次函数的对称轴为直线x=﹣=t,①﹣1≤t≤1时,x=t时,函数有最大值y=t2﹣2t•t+1=﹣t2+1,②t<﹣1时,x=1时,函数有最大值y=12﹣2t•1+1=﹣2t+2,③t>1时,x=﹣1时,函数有最大值y=(﹣1)2﹣2t•(﹣1)+1=2t+237.解:(1)若,即﹣1≤a≤1,抛物线开口向下,当时,y最大值=2a,∵二次函数最大值﹣3,即与﹣1≤a≤1矛盾,舍去.(2)若当时,y随x增大而减小,当时,y最大值=﹣a2+4a﹣1,由又a>1,∴(3)若当时,y随x增大而增大,当时,y最大值=﹣a2﹣1,由又a<﹣1,∴综上所述,或38.解:(1)若x2﹣4≥0,即|x|≥2,则y=x2﹣3x﹣4∴,若x2﹣4≤0,即|x|≤2,则y=﹣x2﹣3x+4∴,∴(2≤x≤5),当x=5时,y最大值=6;当x=2时,y最小值=﹣6,对(﹣2≤x≤2),当时,;x=2时,y最小值=﹣6,综上所述,x=2时,y最小值=﹣6;当时,;(2)由2x+y=1得,y=1﹣2x,由|y|≤1得﹣1≤x≤1故0≤x≤1,∴z为开口向上,对称轴为的抛物线,虽然有最小值,但不在0≤x≤1的范围内,因此不是所求的最值.又x=0时,z=3;x=1时,z=21.∴所求的最小值为339.解:对称轴为直线x=﹣=a,①a<﹣2时,x=﹣2时,y有最小值,最小值=(﹣2)2﹣2a×(﹣2)﹣3=4+4a﹣3=4a+1,x=2时,y有最大值,最大值=22﹣2a×2﹣3=4﹣4a﹣3=﹣4a+1;②﹣2≤a≤0时,x=a时y有最小值,最小值=a2﹣2a•a﹣3=﹣a2﹣3,x=2时,y有最大值,最大值=22﹣2a×2﹣3=4﹣4a﹣3=﹣4a+1;③0<a≤2时,x=a时y有最小值,最小值=a2﹣2a•a﹣3=﹣a2﹣3,x=﹣2时,y有最大值,最大值=(﹣2)2﹣2a×(﹣2)﹣3=4+4a﹣3=4a+1;④a>2时,x=2时,y有最小值,最小值=22﹣2a×2﹣3=4﹣4a﹣3=﹣4a+1,x=﹣2时,y有最大值,最大值=(﹣2)2﹣2a×(﹣2)﹣3=4+4a﹣3=4a+140.解:∵|x+1|≤6,解得:﹣7≤x≤5,∴当﹣7≤x<0时,y=﹣x2﹣2x+1=﹣(x+1)2+2,当x=﹣1时,取得最大值为2;当0≤x≤5时,y=x2﹣2x+1=(x﹣1)2,故当x=5时,y取得最大值为16.综合上述,原函数式最大值为1641.解:设鸡舍的长为x,则宽为(14﹣2x+2)=8﹣x,所以,鸡舍的面积=x(8﹣x)=﹣x2+8x=﹣(x﹣4)2+16,所以,当x=4,即长与宽都是4时,鸡舍的面积最大,最大值是16m2.答:鸡舍的长与宽都是4m时,鸡舍的面积最大42.解:设梯形上底为x,下底为y,∵AB=2,P是边AB的中点,∠PDC=90°,∴1+y2﹣(1+x2)=4+(y﹣x)2,解得:y=+x,梯形ABCD面积=×(x+y)×2=x+y=x+x+=2x+≥4=4,当x=时,即x=1,y=3时,梯形ABCD面积取得最小值为443.解:将直线x=t,代入y=x2﹣3x,y=﹣x2+9中,得A和B的纵坐标分别为t2﹣3t,﹣t2+9,∴AB=,∴当时,线段AB取得最大值44.解:(1)作OE⊥AD,DF⊥AO,垂足分别为E、F,由垂径定理可知AE=AD=x,易证Rt△ADF∽Rt△AOE,∴=,即=,解得AF=x2,∴CD=AB﹣2AF=2﹣x2,∴y=2x+2+2﹣x2=﹣x2+2x+4,∵OA=1,AF=x2,∴x2<1∴0<x<;(2)∵y=﹣x2+2x+4=﹣(x﹣1)2+5,∴x=1时,周长最大为545.解:由正弦定理得:BQ=2cosB,CQ=2cosC,由上可推出BC=2(cosB+cosC),AB=BC,AC=BC,∴S△ABC=×AB×AC×sinA,∵三边固定,当面积最大时,sinA=1,∠A=90°,又∠APR=∠ARP=∠QPR=∠QRP所以△APR相似于△QPR因为PR边公用,所以AP=AR=QP=QR=1AB=AC=2,∴S△ABC=×AB×AC×sinA=246.解:函数,∴y=+﹣,(1)当0≤≤1时,m=﹣,(2)当<0时,m=,(3)当>1时,m=1﹣a+,综上知:a=1时,m有最大值0.2547.解:(1)∵抛物线的对称轴为直线x=﹣1,∴当﹣2≤x≤4时,二次函数y=2x2+4x+1的最大值为:2×42+4×4+1=49;(2)∵二次函数y=2x2+4x+1的对称轴为直线x=﹣1,∴由对称性可知,当x=﹣4和x=2时函数值相等,∴若p≤﹣4,则当x=p时,y的最大值为2p2+4p+1,若﹣4<p≤2,则当x=2时,y的最大值为17;(3)t<﹣2时,最大值为:2t2+4t+1=31,整理得,t2+2t﹣15=0,解得t1=3(舍去),t2=﹣5,t≥﹣2时,最大值为:2(t+2)2+4(t+2)+1=31,整理得,(t+2)2+2(t+2)﹣15=0,解得t1=1,t2=﹣7(舍去),所以,t的值为1或﹣548.解:(1)第t秒钟时,AP=tcm,故PB=(6﹣t)cm,BQ=2tcm,故S△PBQ=•(6﹣t)•2t=﹣t2+6t∵S矩形ABCD=6×12=72.∴S=72﹣S△PBQ=t2﹣6t+72(0<t<6);(2)∵S=t2﹣6t+72=(t﹣3)2+63,∴当t=3秒时,S有最小值63cm249.解:设C(m,2m+1),D(m,m2),则CD=2m+1﹣m2=﹣m2+2m+1=﹣(m﹣1)2+2,当m=1时,CD有最大值250.解:(1)∵在△ABC中,∠A=90°,∠C=30°,AB=1,∴BC=2,AC=,而两个动点P,Q同时从A点出发,点P沿AC运动,点Q沿AB,BC运动,两点同时到达点C ∴Q的速度是P的速度的(2+1)÷=倍;(2)∵设AP=x,△APQ的面积是y,①当Q在AB上,即时,,②当Q在BC上,即时,,即:;(3)对于()当时,对于(≤x≤)当时,,∵,∴当时,51.解:设平行四边形AGEF的面积是S.∵四边形AGEF是平行四边形,∴EF∥AG;∵∠A=30°,∠C=90°,CE=x,BC=6,∴∠A=∠CFE=30°,∴CF=x,AC=6,∴AF=6﹣x;∴S=AF•CE=(6﹣x)x=﹣x2+6x,即S=﹣x2+6x;(1)当x=2时,S=﹣4+12=8,即S=8.答:平行四边形AGEF的面积为(平方单位)…4分(2)由S=﹣x2+6x,得,∴,∴当x=3时,平行四边形AGEF的面积最大,最大面积是(平方单位)…9分52.解:(1)在Rt△ABC中,AC==6,∴tanB=.∵DE∥AC,∴∠BDE=∠BCA=90°.∴DE=BD•tanB=x,CD=BC﹣BD=8﹣x.设△ADE中DE边上的高为h,∵DE∥AC,∴h=CD.∴y=DE•CD=•(8﹣x),即y=+3x.自变量x的取值范围是0<x<8;(2)x==4时,y最大==6.即当x=4时,△ADE的面积最大为653.(1)证明:过点A作AE⊥BC于E,AF⊥CD于F,∵两条纸条宽度相同(对边平行),∴AB∥CD,AD∥BC,AE=AF,∴四边形ABCD是平行四边形,∵S▱ABCD=BC•AE=CD•AF,又∵AE=AF,∴BC=CD,∴四边形ABCD是菱形;(2)解:当两张纸条如图所示放置时,菱形周长最大,设这时菱形的边长为xcm,由勾股定理:x2=(8﹣x)2+22,得:4x=17,即菱形的最大周长为17cm.当两张纸条如图所示放置时,即是正方形时取得最小值为:2×4=8.54.解:在Rt△BPQ中,设PB=x,由∠B=60°,得:BQ=,PQ=,从而有PC=CR=a﹣x,∴△BPQ与△CPR的面积之和为:S=x2+(a﹣x)2=(x﹣a)2+a2,∵0≤x≤a,∴当x=0时,S取最大值a2,当x=a时,S取最小值a255.解:k可取值﹣1,1,2(1)当k=1时,函数为y=﹣4x+4,是一次函数(直线),无最值;(2)当k=2时,函数为y=x2﹣4x+3,为二次函数.此函数开口向上,只有最小值而无最大值;(3)当k=﹣1时,函数为y=﹣2x2﹣4x+6,为二次函数.此函数开口向下,有最大值.因为y=﹣2x2﹣4x+6=﹣2(x+1)2+8,则当x=﹣1时,函数有最大值为856.解:设A(m,0),B(n,0),则m,n是方程x2+bx+c=0的两个根,∵y=x2+bx+c过点C(0,3),∴c=3,又∵S△ABC=|AB|•|OC|=|AB|•3=9,∴|AB|=6,∴|m﹣n|=6,即(m+n)2﹣4mn=36,而,∴b2﹣12=36,b=±4,∴y=x2±4x+3=(x±2)2﹣9,∴所求的最小值为﹣957.解:(1)在矩形PFOE中,OF=PE=x,∵AO=8,BO=6,∴tanB==,即=,解得PF=(6﹣x),∴矩形PFOE的面积为S=PE•PF=x•(6﹣x)=﹣x2+8x,即S=﹣x2+8x;(2)∵S=﹣x2+8x=﹣(x2﹣6x+9)+12=﹣(x﹣3)2+12,∴当x=3时,矩形PFOE的面积S最大,最大面积是1258.解:(1)当a=3时,方程组为,②×2得,4x﹣2y=2③,①+③得,5x=5,解得x=1,把x=1代入①得,1+2y=3,解得y=1,所以,方程组的解是;(2)方程组的两个方程相加得,3x+y=a+1,所以,S=a(3x+y)=a(a+1)=(a+)2﹣,所以,当a=﹣时,S有最小值﹣59.解:(1)∵PE∥CB,∴∠AEP=∠ADC,又∵∠EAP=∠DAC,∴△AEP∽△ADC,(2分)∴=,∴=,(3分)∴.(4分)(2)由四边形PEDQ1是平行四边形,可得EP=DQ1.(5分)即x=3﹣x,所以x=1.5.(6分)∵0<x<2.4(7分)∴当Q在线段CD上运动1.5秒时,四边形PEDQ是平行四边形.(8分)(3)S四边形EPDQ2=(x+x﹣3)•(4﹣x)(9分)=﹣x2+x﹣6=﹣(x﹣)2+,(10分)又∵2.4<x<4,(12分)∴当x=时,S取得最大值,最大值为60.解 :(1)由题意,得EF=AE=DE=BC=x ,AB=30, ∴BF=2x-30.(2)∵∠F=∠A=45°,∠CBF=∠ABC=90°, ∴∠BGF=∠F=45°.∴BG=BF=2x-30,∴S=S DEF △−S GBF △=21DE ²−21BF ² =21 x ²−21(2x −30)² =−23 x ²+60x −450. (3)S=−23 x ²+60x −450=−23 (x −20)²+150. ∵a =−23 <0,15<20<30, ∴当x=20时,S 有最大值,最大值为150。
中考数学总复习《二次函数的最值》练习题附带答案

中考数学总复习《二次函数的最值》练习题附带答案一、单选题(共12题;共24分)1.二次函数y=−(x−1)2+5,当m≤x≤n且mn<0时,y的最小值为2m,最大值为2n,则m+ n的值为()A.52B.2C.12D.322.已知二次函数y=(x-1)2-3,则此二次函数()A.有最大值1B.有最小值1C.有最大值-3D.有最小值-33.二次函数y=ax2+bx+c(a、b、c为常数且a≠0)中的x与y的部分对应值如下表:x﹣3﹣2﹣1012345y1250﹣3﹣4﹣30512⑴二次函数y=ax2+bx+c有最小值,最小值为﹣3;⑴当−12<x<2时,y<0;⑴二次函数y=ax2+bx+c的图象与x轴有两个交点,且它们分别在y轴两侧.则其中正确结论的个数是()A.3B.2C.1D.04.对于代数式x2-10x+24,下列说法:①它是二次三项式;②该代数式的值可能等于2017;③分解因式的结果是(x-4)(x-6);④该代数式的值可能小于-1.其中正确的有()A.1个B.2个C.3 个D.4个5.已知抛物线y=ax2+bx+c(b>a>0)与x轴最多有一个交点,现有以下四个结论:①该抛物线的对称轴在y轴左侧;②关于x的方程ax2+bx+c+2=0无实数根;③a﹣b+c≥0;④a+b+cb−a的最小值为3.其中,正确结论的个数为()A.1个B.2个C.3个D.4个6.已知非负数a,b,c满足a+b=3且c﹣3a=﹣6,设y=a2+b+c的最大值为m,最小值为n,则m ﹣n的值是()A.16B.15C.9D.77.由二次函数y=(x﹣1)2﹣3可知()A.图象开口向下B.对称轴是直线x=﹣1C.函数最小值是3D.顶点是(1,﹣3)8.抛物线y=x2,当﹣1≤x≤3时,y的取值范围是()A.﹣1≤y≤9B.0≤y≤9C.1≤y≤9D.﹣1≤y≤39.已知二次函数的图象(-0.7≤x≤2)如图所示。
中考数学总复习《二次函数的最值存在性问题》专题训练-附答案

中考数学总复习《二次函数的最值存在性问题》专题训练-附答案学校:___________班级:___________姓名:___________考号:___________ 1.如图,抛物线26(0)y ax x c a =-+≠与x 轴负半轴交于(5,0)A -,B 两点,与y 轴交于点(0,5)C -.(1)求抛物线的表达式;(2)若M 是直线AC 上方抛物线上一点,过点M 作MN AC ⊥交直线AC 于点N .设点M 的横坐标为m . ①若N 点与A 点重合,求M 的坐标;①请用含m 的代数式表示出线段MN 的长,并求出线段MN 的最大值.2.如图,在平面直角坐标系中,抛物线24y ax bx =++与x 轴分别交于()4,0A -,()2,0B 两点,与y 轴交于C 点.(1)求抛物线的解析式;(2)点P 为直线AC 上方抛物线上任意一点,过点P 作PD y ∥轴交直线AC 于点D ,过点D 作DH x ∥轴,交y 轴于点H ,求PD DH +的最大值及此时点P 的坐标;(3)将抛物线沿着水平方向向右平移2个单位长度得到新的抛物线,点E 为原抛物线与平移后的抛物线的交点,点M 为平移后的抛物线对称轴上一动点,点N 为坐标平面内一点,直接写出所有使得以点B ,E ,M ,N 为顶点的四边形是菱形的点N 的坐标,并把求其中一个点N 的坐标的求解过程写出来.3.如图,抛物线212y x mx n =-++与x 轴交于A 、B 两点,与y 轴交于点C ,抛物线的对称轴交x 轴于点D ,已知()1,0A -和()0,2C .(1)求抛物线的表达式; (2)求BDC 的面积;(3)线段BC 上有一动点P ,过点P 作y 轴的平行线,交抛物线于点Q ,求线段PQ 的最大值.4.如图,抛物线y =2ax bx c ++与x 轴交于A ,B 两点,点A 的坐标为()3,0-,与y 轴交于点C ,抛物线的对称轴是直线=1x -,连接BC ,AC .(1)用含a 的代数式求ABC S; (2)若6ABC S =,求抛物线的函数表达式;(3)在(2)的条件下,当11m x -≤≤-时,y 的最大值是2,求m 的值.5.如图,已知二次函数2y x bx c =-++经过A ,B 两点,BC x ⊥轴于点C ,且点()1,0A -,()2,0C 和AC=BC .(1)求抛物线的解析式;(2)点E 是AB 上方抛物线上的一个动点(不与A ,B 重合),求ABE S 的最大值以及此时E 点的坐标;(3)判断在抛物线的对称轴上是否存在点P ,使得ABP 是以AB 为腰的等腰三角形,如果存在,直接写出P 点的坐标,如果不存在,说明理由. 6.如图,点A 、B 在反比例函数()0,0k y k x x=>>的图像上,点(),2A m ,点B 的横坐标是4,过点B 作BC x ⊥轴于点C ,连接AC 、AB .(1)用含m 的式子表示BC ,则BC =______;(2)当04m <<时,求ABC 的面积S (用含m 的式子表示);(3)在(2)的条件下,当ABC 的面积S 最大时,求反比例函数k y x=的解析式. 7.如图,抛物线2y x bc c =-++与x 轴交于点(1,0)A -,(4,0)B 与y 轴交于点C ,连接BC ,点P 为线段CB 上一个动点(不与点C ,B 重合),过点P 作PQ y ∥轴交抛物线于点Q .(1)求抛物线的表达式和对称轴;(2)设P 的横坐标为t ,请用含t 的式子表示线段PQ 的长,并求出线段PQ 的最大值;(3)已知点M 是抛物线对称轴上的一个点,点N 是平面直角坐标系内一点,当线段PQ 取得最大值时,是否存在这样的点M ,N ,使得四边形PBMN 是菱形?若存在,请直接写出点M 的坐标;若不存在,请说明理由.8.如图,抛物线22y x x c =-++与x 轴交于A ,()1,0B -两点(点A 在点B 右侧),与y 轴交于点C .(1)求抛物线的解析式及顶点坐标. (2)设点(),P x y 为抛物线上一点,当1322x -≤≤时,点P 的纵坐标y 满足m y n ≤≤,求n m -的值. 9.如图,二次函数23y ax bx =+-的图像经过点()1,0A -,()3,0B 直线22y x =-与x 轴、y 轴交于点D ,E .(1)求该二次函数的解析式.(2)点M 为该二次函数图像上一动点.①若点M 在图像上的B ,C 两点之间,求DME 的面积的最大值.①若MED EDB ∠∠=,求点M 的坐标.10.已知抛物线2y ax bx c =++与x 轴交于()2,0A -、()6,0B 两点,与y 轴交于点()0,3C -.(1)求抛物线的表达式;(2)点P 为直线BC 下方的抛物线上一个动点,当PBC 面积最大时,求点P 的坐标;(3)点P 在直线BC 下方的抛物线上,连接AP 交BC 于点M ,当PM AM 最大时,求点P 的横坐标及PM AM的最大值. 11.如图,抛物线23y ax bx =++与x 轴交于A ,B 两点,且点B 的坐标为()20,,与y 轴交于点C ,抛物线对称轴为直线=1x -.连接AC BC ,,点P 是抛物线上在第二象限内的一个动点.过点P 作x 轴的垂线PH ,垂足为点H ,交AC 于点Q .过点P 作PG AC ⊥于点G .(1)求抛物线的解析式.(2)P 点在运动过程中线段PQ 有最大值吗?有求出最大值.(3)求PQG 周长的最大值及此时点P 的坐标.12.已知点()13A --,在直线2l y kx =-:上,点()1M m y ,是抛物线()2420y ax ax a =-+≠上一个动点.(1)如图,若抛物线与直线l 交于点A .①求a 和k 的值;①过点M 作y 轴的平行线交直线l 于点N ,当点M 在直线l 上方的抛物线上运动时,求线段MN 长度的最大值及此时点M 的坐标;(2)点()22B x y ,是抛物线与直线l 在第一象限内的交点,若12y y ≤接写出m 的取值范围.13.如图,抛物线2y x bx c =-++与x 轴交于A 、B 两点,与y 轴交于C 点,点A 的坐标为()3,0,点C 的坐标为()0,3.(1)求b 与c 的值;(2)求函数的最大值;(3)(),M m n 是抛物线上的任意一点,当74n ≥时,利用函数图像写出m 的取值范围. 14.综合与探究.如图,抛物线228=+-y x x 与x 轴交于A ,B 两点(点A 在点B 左侧),与y 轴交于点C .(1)求,,A B C 三点的坐标.(2)连接AC ,直线(40x m m =--<<)与抛物线交于点E ,与AC 交于点D ,m 为何值时线段DE 的长度最大,最大值是多少?(3)点M 在y 轴上,点N 在直线AC 上,点P 为抛物线对称轴上一点,是否存在点M 使得以C M N P 、、、为顶点的四边形是菱形?若存在,请直接写出点M 的坐标;若不存在,请说明理由.15.如图,抛物线2=23y x x --与x 轴交A 、B 两点(A 点在B 点左侧),直线l 与抛物线交于A 、C 两点,其中C 点的横坐标为2.(1)求A 、B 两点的坐标及直线AC 的函数表达式;(2)P 是线段AC 上的一个动点,过P 点作y 轴的平行线交抛物线于点E ,求线段PE 长度的最大值.参考答案:1.(1)265y x x =---(2)①(2,3)-;①当52m =-时,MN 最大,最大值为25282.(1)2142y x x =--+(2)92 53,2P ⎛⎫- ⎪⎝⎭ (3)()1,419-+或()1,419--或()3,19或()3,19-3.(1)213222y x x =-++; (2)52(3)2.4.(1)6ABC S a =△.(2)抛物线的函数表达式为223y x x =+-.(3)6m =-.5.(1)223y x x =-++;(2)278,E 的坐标为12,154⎛⎫ ⎪⎝⎭; (3)()1,14或 ()1,14-或 ()1,317+或 ()1,317-.6.(1)12m (2)214m m -+ (3)4y x=7.(1)234y x x =-++,直线32x =(2)24PQ t t =-+,最大值为4(3)3(2,7)2或3(2,7)2-) 8.(1)2(1)4y x =--+,顶点坐标为()14, (2)949.(1)2=23y x x --(2)①当2m =时,S 最大值52=;①点M 的坐标是11041022,39⎛⎫++- ⎪ ⎪⎝⎭或()12,2--10.(1)抛物线为:2134y x x =--; (2)153,4P ⎛⎫- ⎪⎝⎭ (3)此时P 的横坐标为:3,MP AM 有最大值916.11.(1)283384y x x =--+; (2)PQ 有最大值32; (3)185()2,3P -. 12.(1)①1,1a k =-=;①线段MN 长度的最大值为254,点M 的坐标为323()24, (2)0m ≤或4m ≥13.(1)2b = 3c =(2)4(3)1522m -≤≤14.(1)()()()4,0,2,0,0,8A B C --(2)2m =时,DE 最大为4(3)存在,()()()1234270,85,85,0,,0,124M M M M ⎛⎫=-+--=-- ⎪⎝⎭15.(1)()()1,0,3,0,1A B y x -=--(2)94。
(word完整版)年重庆中考数学总复习25题《二次函数》练习及答案
二次函数的综合运用此题主要针对中考26题压轴题此题分为三问(1)求函数解析式(二次函数解析式、一次函数解析式、反比例函数解析式);(2)求二次函数中的一些线段长度或某个四边形的面积;(3)求二次函数中某些动点坐标或轨迹。
解答题1、 (2013·重庆A卷25题) 如图,对称轴为直线x=-1的抛物线y=ax2+bx+c(a≠0)与x轴相交于A、B两点,其中点A的坐标为(-3,0).(1)求点B的坐标;(2)已知a=1,C为抛物线与y轴的交点.①若点P在抛物线上,且S△POC=4S△BOC.求点P的坐标;②设点Q是线段AC上的动点,作QD⊥x轴交抛物线于点D,求线段QD长度的最大值.2、(2013·重庆B卷25题)如图,已知正比例函数和反比例函数的图象都经过点A(3,3).(1)求正比例函数和反比例函数的解析式;(2)把直线OA向下平移后与反比例函数的图象交于点B(6,m),求m的值和这个一次函数的解析式;(3)第(2)问中的一次函数的图象与x轴、y轴分别交于C、D,求过A、B、D三点的二次函数的解析式;(4)在第(3)问的条件下,二次函数在第一象限的图象上是否存在点E ,使四边形OECD 的面积S1与四边形OABD 的面积S 满足:S1=S ?若存在,求点E 的坐标;若不存在,请说明理由.3、(2008•重庆)已知:如图,抛物线(a≠0)与y 轴交于点C (0,4),与x 轴交于点A 、B ,点A 的坐标为(4,0). (1)求该抛物线的解析式;(2)点Q 是线段AB 上的动点,过点Q 作QE ∥AC ,交BC 于点E ,连接CQ .当△CQE 的面积最大时,求点Q 的坐标;(3)若平行于x 轴的动直线l 与该抛物线交于点P ,与直线AC 交于点F ,点D 的坐标为(2,0).问:是否存在这样的直线l ,使得△ODF 是等腰三角形?若存在,请求出点P 的坐标;若不存在,请说明理由.2322y ax ax c =-+4、(2011•丹东)己知:二次函数(a≠0)与x 轴交于A 、B 两点(点A 在点B 的左侧),点A 、点B 的横坐标是一元二次方程x2-4x-12=0的两个根. (1)请直接写出点A 、点B 的坐标.(2)请求出该二次函数表达式及对称轴和顶点坐标.(3)如图1,在二次函数对称轴上是否存在点P ,使△APC 的周长最小,若存在,请求出点P 的坐标;若不存在,请说明理由.(4)如图2,连接AC 、BC ,点Q 是线段0B 上一个动点(点Q 不与点0、B 重合).过点Q 作QD ∥AC 交BC 于点D ,设Q 点坐标(m ,0),当△CDQ 面积S 最大时,求m 的值.26y ax bx =++5、如图,已知抛物线与x轴交于A,B两点,A在B的左侧,A坐标为(-1,0)与y轴交于点C(0,3)△ABC的面积为6.(1)求抛物线的解析式;(2)抛物线的对称轴与直线BC相交于点M,点N为x轴上一点,当以M,N,B为顶点的三角形与△ABC相似时,请你求出BN的长度;(3)设抛物线的顶点为D在线段BC上方的抛物线上是否存在点P使得△PDC是等腰三角形?若存在,求出符合条件的点P的坐标;若不存在,请说明理由.6、(2013•珠海)如图,在平面直角坐标系xOy中,矩形OABC的边OA、OC分别在y轴和x轴的正半轴上,且长分别为m、4m(m>0),D为边AB的中点,一抛物线l经过点A、D及点M(-1,-1-m).(1)求抛物线l的解析式(用含m的式子表示);(2)把△OAD沿直线OD折叠后点A落在点A′处,连接OA′并延长与线段BC的延长线交于点E,若抛物线l与线段CE相交,求实数m的取值范围;(3)在满足(2)的条件下,求出抛物线l顶点P到达最高位置时的坐标.7、(2013•舟山)如图,在平面直角坐标系xOy 中,抛物线的顶点为A ,与y轴的交点为B ,连结AB ,AC ⊥AB ,交y 轴于点C ,延长CA 到点D ,使AD=AC ,连结BD .作AE ∥x 轴,DE ∥y 轴.(1)当m=2时,求点B 的坐标; (2)求DE 的长?(3)①设点D 的坐标为(x ,y ),求y 关于x 的函数关系式?②过点D 作AB 的平行线,与第(3)①题确定的函数图象的另一个交点为P ,当m 为何值时,以,A ,B ,D ,P 为顶点的四边形是平行四边形?()221144y x m m m =--+。
2018年中考数学真题汇编:二次函数(含答案)

精选文档中考数学真题汇编 :二次函数一、选择题1.给出以下函数:① y=﹣ 3x+2;② y= ;③ y=2x2;④ y=3x,上述函数中切合条作“当 x>1 时,函数值 y 随自变量 x 增大而增大“的是()A. ①③B③④. C②④. D②③.【答案】 B2.如图 ,函数和( 是常数 ,且)在同一平面直角坐标系的图象可能是()A. B. C. D.【答案】 B3.对于二次函数,以下说法正确的选项是()A. 图像与轴的交点坐标为B. 图像的对称轴在轴的右边C. 当时,的值随值的增大而减小D. 的最小值为 -3【答案】 D4.二次函数的图像如下图,以下结论正确是( )A. B. C. D. 有两个不相等的实数根【答案】 C5.若抛物线与轴两个交点间的距离为2,称此抛物线为定弦抛物线,已知某定弦抛物线的对称轴为直线,将此抛物线向左平移 2 个单位,再向下平移 3 个单位,获得的抛物线过点 ( )【答案】 B6.若抛物线 y=x2+ax+b 与 x 轴两个交点间的距离为2,称此抛物线为定弦抛物线。
已知某定弦抛物线的对称轴为直线x=1,将此抛物线向左平移 2 个单位,再向下平移 3 个单位,获得的抛物线过点()A. (-3, -6)B.(-3, 0)C(. -3, -5) D.(-3, -1)【答案】 B7.已知学校航模组设计制作的火箭的升空高度h(m)与飞翔时间t( s)知足函数表达式h=﹣ t 2+ 24t +1.则以下说法中正确的选项是()A. 点火后 9s 和点火后13s 的升空高度同样B.点火后 24s 火箭落于地面C. 点火后 10s 的升空高度为139m D火.箭升空的最大高度为145m【答案】 D8.如图,若二次函数y=ax2 +bx+c( a≠0)图象的对称轴为 x=1,与 y 轴交于点 C,与 x 轴交于点A、点 B(﹣1,0),则①二次函数的最大值为a+b+c;② a﹣ b+c< 0;③ b2﹣4ac<0;④当 y>0 时,﹣ 1<x< 3,此中正确的个数是()A.1B.2C.3D.4【答案】 B9.如图是二次函数(,,是常数,)图象的一部分,与轴的交点在点和之间,对称轴是.对于以下说法:①;②;③;④(为实数);⑤当时,,此中正确的选项是()A. ①②④B. ①②⑤C. ②③④D. ③④⑤【答案】 A10.如图,二次函数y=ax2+bx 的图象张口向下,且经过第三象限的点P.若点 P 的横坐标为 -1,则一次函数y=(a-b) x+b 的图象大概是()A. B. C. D.【答案】 D11.四位同学在研究函数(b,c是常数)时,甲发现当时,函数有最小值;乙发现是方程的一个根;丙发现函数的最小值为3;丁发现当时,.已知这四位同学中只有一位发现的结论是错误的,则该同学是()A. 甲B.乙C.丙D.丁【答案】 B12.如下图 ,△ DEF中 ,∠ DEF=90°,∠ D=30°,DF=16,B是斜边 DF上一动点 ,过 B 作 AB⊥ DF 于 B,交边 DE(或边 EF) 于点 A,设 BD=x,△ABD 的面积为y,则 y 与 x 之间的函数图象大概为()A.(B.C.D(.【答案】 B二、填空题13.已知二次函数,当x>0时,y随x的增大而________(填“增大”或“减小”)14.右图是抛物线型拱桥,当拱顶离水面2m 时,水面宽4m,水面降落2m ,水面宽度增添________m。
中考复习专题二次函数分类讲解复习以及练习题含答案

1、二次函数的定义定义: y=ax2 + bx + c a 、 b 、 c 是常数, a ≠ 0 定义要点:①a ≠ 0 ②最高次数为2 ③代数式一定是整式练习:1、y=-x2,y=2x2-2/x,y=100-5 x2,y=3 x2-2x3+5,其中是二次函数的有____个;2.当m_______时,函数y=m+1χ - 2χ+1 是二次函数2、二次函数的图像及性质例2:已知二次函数1求抛物线开口方向,对称轴和顶点M 的坐标;2设抛物线与y 轴交于C 点,与x 轴交于A 、B 两点,求C,A,B 的坐标;抛物线 顶点坐标 对称轴 位置 开口方向 增减性 最值y=ax2+bx+ca>0y=ax 2+bx+ca<0由a,b 和c 的符号确定由a,b 和c 的符号确定 a>0,开口向上a<0,开口向下在对称轴的左侧,y 随着x 的增大而在对称轴的左侧,y 随着x 的增大而⎪⎪⎭⎫ ⎝⎛--a b ac a b 44,22⎪⎪⎭⎫ ⎝⎛--a b ac a b 44,22abx 2-=直线abx 2-=直线23212-+=x x y3x为何值时,y随的增大而减少,x为何值时,y有最大小值,这个最大小值是多少4x为何值时,y<0x为何值时,y>03、求抛物线解析式的三种方法1、一般式:已知抛物线上的三点,通常设解析式为________________y=ax2+bx+ca≠02,顶点式:已知抛物线顶点坐标h, k,通常设抛物线解析式为_______________求出表达式后化为一般形式.y=ax-h2+ka≠03,交点式:已知抛物线与x 轴的两个交点x1,0、x2,0,通常设解析式为_____________求出表达式后化为一般形式.y=ax-x1x-x2 a≠0练习:根据下列条件,求二次函数的解析式;1、图象经过0,0, 1,-2 , 2,3 三点;2、图象的顶点2,3, 且经过点3,1 ;3、图象经过0,0, 12,0 ,且最高点的纵坐标是3 ;例1已知二次函数y=ax2+bx+c的最大值是2,图象顶点在直线y=x+1上,并且图象经过点3,-6;求a、b、c;解:∵二次函数的最大值是2∴抛物线的顶点纵坐标为2又∵抛物线的顶点在直线y=x+1上∴当y=2时,x=1∴顶点坐标为 1 , 2∴设二次函数的解析式为y=ax-12+2又∵图象经过点3,-6∴-6=a 3-12+2 ∴a=-2∴二次函数的解析式为y=-2x-12+2即: y=-2x2+4x4、a,b,c符号的确定抛物线y=ax2+bx+c的符号问题:1a的符号:由抛物线的开口方向确定2C的符号:由抛物线与y轴的交点位置确定.3b的符号:由对称轴的位置确定4b2-4ac的符号:由抛物线与x轴的交点个数确定5a+b+c的符号:因为x=1时,y=a+b+c,所以a+b+c的符号由x=1时,对应的y值决定;当x=1时,y>0,则a+b+c>0当x=1时,y<0,则a+b+c<0当x=1时,y=0,则a+b+c=06a-b+c的符号:因为x=-1时,y=a-b+c,所以a-b+c的符号由x=-1时,对应的y值决定;当x=-1,y>0,则a-b+c>0当x=-1,y<0,则a-b+c<0当x=-1,y=0,则a-b+c=0练习1、二次函数y=ax2+bx+ca≠0的图象如图所示,则a、b、c的符号为A、a<0,b>0,c>0B、a<0,b>0,c<0C、a<0,b<0,c>0D、a<0,b<0,c<02、二次函数y=ax2+bx+ca≠0的图象如图所示,则a、b、c的符号为A、a>0,b>0,c=0B、a<0,b>0,c=0C、a<0,b<0,c<0D、a>0,b<0,c=03、二次函数y=ax2+bx+ca≠0的图象如图所示,则a、b、c 、△的符号为A、a>0,b=0,c>0,△>0B、a<0,b>0,c<0,△=0C、a>0,b=0,c<0,△>0D、a<0,b=0,c<0,△<0熟练掌握a,b, c,△与抛物线图象的关系上正、下负左同、右异4.抛物线y=ax2+bx+ca≠0的图象经过原点和二、三、四象限,判断a、b、c的符号情况:a 0,b 0,c 0.5.抛物线y=ax2+bx+ca≠0的图象经过原点,且它的顶点在第三象限,则a、b、c满足的条件是:a 0,b 0,c 0.6.二次函数y=ax2+bx+c中,如果a>0,b<0,c<0,那么这个二次函数图象的顶点必在第象限先根据题目的要求画出函数的草图,再根据图象以及性质确定结果数形结合的思想7.已知二次函数的图像如图所示,下列结论;⑴a+b+c=0 ⑵a-b+c﹥0 ⑶abc ﹥0 ⑷b=2a其中正确的结论的个数是A 1个B 2个C 3个D 4个要点:寻求思路时,要着重观察抛物线的开口方向,对称轴,顶点的位置,抛物线与x轴、y轴的交点的位置,注意运用数形结合的思想;5、抛物线的平移左加右减,上加下减 练习⑴二次函数y=2x2的图象向 平移 个单位可得到y=2x2-3的图象; 二次函数y=2x2的图象向 平移 个单位可得到y=2x-32的图象; ⑵二次函数y=2x2的图象先向 平移 个单位,再向 平移 个单位可得到函数y=2x+12+2的图象;引申:3由二次函数y=x2的图象经过如何平移可以得到函数y=x2-5x+6的图象.y=x2-5x+66二次函数与一元二次方程的关系一元二次方程根的情况与b2-4ac 的关系我们知道:代数式b2-4ac 对于方程的根起着关键的作用.二次函数y=ax2+bx +c 的图象和x 轴交点的横坐标,便是对应的一元二次方程ax2+bx +c=0的解;二次函数y=ax2+bx+c 的图象和x 轴交点有三种情况: 1有两个交点b2 – 4ac > 0 2有一个交点b2 – 4ac= 0 3没有交点 b2 – 4ac< 0若抛物线y=ax2+bx+c 与x 轴有交点,则b2 – 4ac ≥0例1如果关于x 的一元二次方程 x2-2x+m=0有两个相等的实数根,则m=____,此时抛物线 y=x2-2x+m 与x 轴有____个交点.2已知抛物线 y=x2 – 8x +c 的顶点在 x 轴上,则c=____.y=x 24125(2--=x y .2422,1aacb b x -±-=∴3一元二次方程 3 x2+x-10=0的两个根是x1= -2 ,x2=5/3, 那么二次函数y= 3 x2+x-10与x轴的交点坐标是____.7二次函数的综合运用1.已知抛物线y=ax2+bx+c与抛物线y=-x2-3x+7的形状相同,顶点在直线x=1上,且顶点到x轴的距离为5,请写出满足此条件的抛物线的解析式.解:抛物线y=ax2+bx+c与抛物线y=-x2-3x+7的形状相同a=1或-1又顶点在直线x=1上,且顶点到x轴的距离为5,顶点为1,5或1,-5所以其解析式为:1 y=x-12+52 y=x-12-53 y=-x-12+54 y=-x-12-5 展开成一般式即可.2.若a+b+c=0,a0,把抛物线y=ax2+bx+c 向下平移 4个单位,再向左平移5个单位所到的新抛物线的顶点是-2,0,求原抛物线的解析式. 分析:1由a+b+c=0可知,原抛物线的图象经过1,0 2 新抛物线向右平移5个单位, 再向上平移4个单位即得原抛物线练习题1.直线y =3 x -1与y =x -k 的交点在第四象限,则k 的范围是………………A k <31 B 31<k <1 C k >1 D k >1或k <1 提示由⎩⎨⎧-=-=k x y x y 13,解得⎪⎪⎩⎪⎪⎨⎧-=-=.23121k y k x 因点在第四象限,故21k ->0,231k -<0.∴ 31<k <1.答案B .点评本题应用了两函数图象交点坐标的求法,结合了不等式组的解法、象限内点的坐标符号特征等.2.二次函数y =ax 2+bx +c 的图象如图,则下列各式中成立的个数是…………1abc <0; 2a +b +c <0; 3a +c >b ; 4a <-2b . A1 B2 C3 D4 提示由图象知a <0,-ab2>0,故b >0,而c >0,则abc <0.当x =1时,y >0,即a +c -b >0;当x =-1时,y <0,即a +c -b <0. 答案B .点评本题要综合运用抛物线性质与解析式系数间的关系.因a <0,把4a <-2b 两边同除以a ,得1>-ab 2,即-a b 2<1,所以4是正确的;也可以根据对称轴在x =1的左侧,判断出-a b 2<1,两边同时乘a ,得a <-2b ,知4是正确的.3.若一元二次方程x 2-2 x -m =0无实数根,则一次函数y =m +1x +m -1的图象不经过………………………………………………………………………………… A 第一象限 B 第二象限 C 第三象限 D 第四象限提示由=4+4 m <0,得m +1<0,则m -1<0,直线过第二、三、四象限. 答案A .点评本题综合运用了一元二次方程根的判别式及一次函数图象的性质.注意,题中问的是一次函数图象不经过的象限.4.如图,已知A ,B 是反比例函数y =x2的图象上两点,设矩形APOQ 与矩形MONB 的面积为S 1,S 2,则……………………………………………………………… A S 1=S 2 B S 1>S 2 C S 1<S 2 D 上述A 、B 、C 都可能 提示因为S APOQ =|k |=2,S MONB =2,故S 1=S 2. 答案A .点评本题可以推广为:从双曲线上任意一点向两坐标轴引垂线,由这点及两个垂足和原点构成的矩形的面积都等于|k |.5.若点A 1,y 1,B 2,y 2,C ,y 3在反比例函数y =-xk 12+的图象上,则A y 1=y 2=y 3B y 1<y 2<y 3C y 1>y 2>y 3D y 1>y 3>y 2提示因-k 2+1<0,且-k 2+1=y 1=2 y 2=y 3,故y 1<y 2<y 3.或用图象法求解,因-k 2+1<0,且x 都大于0,取第四象限的一个分支,找到在y 轴负半轴上y 1,y 2,y 3 的相应位置即可判定. 答案B .点评本题是反比例函数图象的性质的应用,图象法是最常用的方法.在分析时应注意本题中的-k 2+1<0.6.直线y =ax +c 与抛物线y =ax 2+bx +c 在同一坐标系内大致的图象是……A B C D提示两个解析式的常数项都为c ,表明图象交于y 轴上的同一点,排除A,B .再从a 的大小去判断. 答案D .点评本题综合运用了一次函数、二次函数的性质.B 错误的原因是由抛物线开口向上,知a >0,此时直线必过第一、三象限.7.已知函数y =x 2-1840 x +1997与x 轴的交点是m ,0n ,0,则m 2-1841 m +1997n 2-1841 n +1997的值是…………………………………………… A1997 B1840 C1984 D1897提示抛物线与x 轴交于m ,0n ,0,则m ,n 是一元二次方程x 2-1840 x +1997=0的两个根.所以m 2-1840 m +1997=0,n 2-1840 n +1997=0,mn =1997.原式=m 2-1840 m +1997-mn 2-1840 n +1997-n =mn =1997. 答案A .点评本题揭示了二次函数与一元二次方程间的联系,应用了方程的根的定义、根与系数的关系等知识点,并要灵活地把所求代数式进行适当的变形. 8.某乡的粮食总产量为aa 为常数吨,设这个乡平均每人占有粮食为y 吨,人口数为x ,则y 与x 之间的函数关系为……………………………………………A B C D 提示粮食总产量一定,则人均占有粮食与人口数成反比,即y =xa.又因为人口数不为负数,故图象只能是第一象限内的一个分支. 答案D .点评本题考查反比例函数图象在实际问题中的应用.A 错在画出了x <0时的图象,而本题中x 不可能小于0. 二填空题每小题4分,共32分9.函数y =12-x +11-x 的自变量x 的取值范围是____________. 提示由2 x -1≥0,得x ≥21;又x -1≠0,x ≠1.综合可确定x 的取值范围.答案x ≥21,且x ≠1.10.若点Pa -b ,a 位于第二象限,那么点Qa +3,ab 位于第_______象限. 提示由题意得a >0,a -b <0,则b >0.故a +3>0,ab >0. 答案一.11.正比例函数y =kk +112--k k x 的图象过第________象限.提示由题意得k 2-k -1=1,解得k 1=2,k 2=-1舍去,则函数为y =6 x . 答案一、三.点评注意求出的k =-1使比例系数为0,应舍去.12.已知函数y =x 2-2m +4x +m 2-10与x 轴的两个交点间的距离为22,则m =___________.提示抛物线与x 轴两交点间距离可应用公式||a ∆来求.本题有∆=)10(4)42(22--+m m =5616+m =22,故m =-3. 答案-3.点评抛物线与x 轴两交点间距离的公式为||a ∆,它有着广泛的应用.13.反比例函数y =xk的图象过点Pm ,n ,其中m ,n 是一元二次方程x 2+kx +4=0的两个根,那么P 点坐标是_____________.提示Pm ,n 在双曲线上,则k =xy =mn ,又mn =4,故k =4. 答案-2,-2.点评本题是反比例函数、一元二次方程知识的综合应用.由题意得出k =mn =4是关键.14.若一次函数y =kx +b 的自变量x 的取值范围是-2≤x ≤6,相应函数值y 的范围是-11≤y ≤9,则函数解析式是___________.提示当k >0时,有⎩⎨⎧+=+-=-b k b k 69211,解得⎪⎩⎪⎨⎧-==.625b k当k <0时,有⎩⎨⎧+-=+=-b k b k 29611,解得⎪⎩⎪⎨⎧=-=.425b k答案y =25x -6或y =-25x +4.点评因k 是待定字母,而k 的不同取值,导致线段分布象限不一样,自变量的取值与函数取值的对应关系也就不同.故本例要分k >0时自变量最大值对应函数最大值,与k <0时自变量最大值对应函数最小值两种情形讨论. 15.公民的月收入超过800元时,超过部分须依法缴纳个人收入调节税,当超过部分不足500元时,税率即所纳税款占超过部分的百分数相同.某人本月收入1260元,纳税23元,由此可得所纳税款y 元与此人月收入x 元(800<x <1300)间的函数关系为____________. 提示因1260-800=460,46023=5%,故在800<x <1300时的税率为5%. 答案y =5%x -800.点评本题是与实际问题相关的函数关系式,解题时应注意并不是每个人月收入的全部都必须纳税,而是超过800元的部分才纳税,故列函数式时月收入x 须减去800. 16.某种火箭的飞机高度h 米与发射后飞行的时间t 秒之间的函数关系式是h =-10 t 2+20 t ,经过_________秒,火箭发射后又回到地面.提示火箭返回地面,即指飞行高度为0,则-10 t 2+20 t =0,故t =0或t =20. 答案20.点评注意:t =0应舍去的原因是此时火箭虽在地面,但未发射,而不是返回地面. 三解答题17.6分已知y =y 1+y 2,y 1 与x 成正比例,y 2 与x 成反比例,并且x =1时y =4,x =2时y =5,求当x =4时y 的值.解设y 1=k 1x ,y 2=xk 2,则y =k 1x +xk 2.把x =1时y =4,x =2时y =5分别代入上式,得⎪⎩⎪⎨⎧+=+=22542121k k k k ,解得∴ 函数解析式为y =2 x +x 2. 当x =4时,y =2×4+42=217.∴ 所求的y 值为217.点评本题考查用待定系数法求函数解析式.关键在于正确设出y 1,y 2 与x 的函数解析式.注意两个比例系数应分别用k 1,k 2 表示出来,而不能仅用一个k 值表示.18.6分若函数y =kx 2+2k +1x +k -1与x 轴只有一个交点,求k 的值. 提示本题要分k =0,k ≠0两种情况讨论.解当k =0时,y =2 x -1,是一次函数,此时,直线与x 轴必有一个交点.当k ≠0时,函数为二次函数,此时,=4k +12-4 kk -1=12 k +4=0.∴ k =-31. ∴ 所求的k 值为0或-31. 点评注意,当问题中未指明函数形式,而最高次项系数含字母时,要注意这个系数是否为0.函数图象与x 轴有一个交点包括两种情形:当函数是一次函数时,直线与x 轴必只有一个交点;当函数是二次函数时,在=0的条件下,图象与x 轴只有一个交点.19.8分已知正比例函数y =4 x ,反比例函数y =xk.1当k 为何值时,这两个函数的图象有两个交点k 为何值时,这两个函数的图象没有交点2这两个函数的图象能否只有一个交点若有,求出这个交点坐标;若没有,请说明理由. 解由y =4 x 和y =xk ,得 4 x 2-k =0,=16 k .1当>0,即k >0时,两函数图象有两个交点;当<0,即k <0时,两函数图象没有交点;2∵ 比例系数k ≠0,故≠0.∴ 两函数图象不可能只有一个交点.20.8分如图是某市一处十字路口立交桥的横断面在平面直角坐标系中的一个示意图,横断面的地平线为x 轴,横断面的对称轴为y 轴,桥拱的D ′GD 部分为一段抛物线,顶点G 的高度为8米,AD 和AD ′是两侧高为米的立柱,OA 和OA ′为两个方向的汽车通行区,宽都为15米,线段CD 和CD ′为两段对称的上桥斜坡,其坡度为1∶4.1求桥拱DGD ′所在抛物线的解析式及CC ′的长.2BE 和B ′E ′为支撑斜坡的立柱,其高都为4米,相应的AB 和A ′B ′为两个方向的行人及非机动车通行区,试求AB 和A ′B ′的宽.3按规定,汽车通过桥下时,载货最高处和桥拱之间的距离不可小于米,今有一大型运货汽车,装载上大型设备后,其宽为4米,车载大型设备的顶部与地面的距离为7米,它能否从OAOA ′安全通过请说明理由.分析欲求函数的解析式,关键是求出三个独立的点的坐标,然后由待定系数法求之.所以关键是由题中线段的长度计算出D 、G 、D ′的坐标,当然也可由对称轴x =0解之.至于求CC ′、AB 、A ′B ′的数值,则关键是由坡度的定义求解之;到底能否安全通过,则只需在抛物线的解析式中令x =4,求出相应的y 值,即可作出明确的判断.解1由题意和抛物线的对称轴是x =0,可设抛物线的解析式为y =ax 2+c .由题意得G 0,8,D 15,∴ ⎩⎨⎧=+=.5.52258c a c∴ ⎪⎩⎪⎨⎧=-=.8901c a∴ y =2901x -+8.又 AC AD =41且AD =, ∴ AC =×4=22米.∴ CC ′=2C =2×OA +AC =2×15+22=74米.∴ CC ′的长是74米.2∵ BC EB =41,BE =4, ∴ BC =16.∴ AB =AC -BC =22-16=6米.A ′B ′=AB =6米.3此大型货车可以从OAOA ′区域安全通过.在y =2901x -+8中,当x =4时,y =-901×16+8=45377,而 45377-7+=4519>0, ∴ 可以从OA 区域安全通过. 21.8分已知二次函数y =ax 2+bx +c 的图象抛物线G 经过-5,0,0,25,1,6三点,直线l 的解析式为y =2 x -3.1求抛物线G 的函数解析式;2求证抛物线G 与直线l 无公共点;3若与l 平行的直线y =2 x +m 与抛物线G 只有一个公共点P ,求P 点的坐标.分析1略;2要证抛物线G 与直线l 无公共点,就是要证G 与l 的解析式组成的方程无实数解;3直线y =2 x +m 与抛物线G 只有一个公共点,就是由它们的解析式组成的二元二次方程组有一个解,求出这组解,就得P 点的坐标.解1∵ 抛物线G 通过-5,0,0,25,1,6三点, ∴ ⎪⎪⎩⎪⎪⎨⎧++==--=cb ac c b a 6255250,解得 ⎪⎪⎩⎪⎪⎨⎧===.25321c b a∴ 抛物线G 的解析式为y =21x 2+3 x +25. 2由⎪⎩⎪⎨⎧++=-=25321322x x y x y , 消去y ,得21x 2+x +211=0, ∵ =12-4×21×211=-10<0, ∴ 方程无实根,即抛物线G 与直线l 无公共点.3由⎪⎩⎪⎨⎧++=+=2532122x x y m x y ,消去y ,得21x 2+x +25-m =0. ① ∵ 抛物线G 与直线y =2 x +m 只有一个公共点P ,∴ =12-4×21×25-m =0. 解得m =2. 把m =2代入方程①,解得x =-1. 把x =-1代入y =21x 2+3 x +25,得y =0. ∴ P -1,0.点评本题综合运用了二次函数解析式的求法.抛物线与直线的交点等知识,其关键是把函数问题灵活转化为方程知识求解.。
重庆市2018年中考数学题型复习 题型八 二次函数综合题 类型一 线段、周长最值问题练习

类型一线段、周长最值问题1. 如图,抛物线y=-x2-2x+3交x轴于A,C两点(点A在C的左边),抛物线交y轴于点B,点D是抛物线的顶点.(1)求线段AB的长;(2)点P是直线AB上方的抛物线上一点(不与A,B重合),过点P作x轴的垂线,交x轴于点H,交直线AB于点F,作PG⊥AB于点G,求出△PFG周长的最大值;2. 已知二次函数y=x2-x-2的图象和x轴相交于点A、B,与y轴交于点C,过直线BC的下方抛物线上一动点P作PQ∥AC交线段BC于点Q,再过P作PE⊥x轴于点E,交BC于点D.(1)求直线AC的解析式;(2)求△PQD周长的最大值;(3)当△PQD的周长最大值时,在y轴上有两个动点M、N(M在N的上方),若MN=1,求PN +MN+AM的最小值.第2题图3. (2017重庆大渡口二模)如图,抛物线y=x2-2x-3与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,该抛物线的顶点为D,对称轴交x轴于H.(1)求A、B两点的坐标;(2)设点P在x轴下方的抛物线上,当∠ABP=∠CDB时,求出点P的坐标;(3)以OB为边在第四象限内作等边△OBM,设点E为x轴正半轴上一动点(OE>OH),连接ME,把线段ME绕点M旋转60°得MF,求线段DF的长的最小值.第3题图4. (2017遵义改编)如图,抛物线y=ax2+bx-a-b(a<0,a、b为常数)与x轴交于A、C两点,与y 轴交于B 点,直线AB 的函数关系式为y =89x +163.(1)求该抛物线的函数关系式与C 点坐标;(2)已知点M (m ,0)是线段OA 上的一个动点,过点M 作x 轴的垂线l 分别与直线AB 和抛物线交于D 、E 两点.当△BDE 恰好是以DE 为底边的等腰三角形时,动点M 相应位置记为点M ′,将OM ′绕原点O 顺时针旋转得到ON (旋转角在0°到90°之间);ⅰ:探究:线段OB 上是否存在定点P (P 不与O 、B 重合),无论ON 如何旋转,NPNB始终保持不变,若存在,试求出P 点坐标;若不存在,请说明理由; ⅱ:试求出此旋转过程中,(NA +34NB )的最小值.第4题图5. (2016重庆渝中区校级二模)如图①,在平面直角坐标系中,已知抛物线y =-33x 2-3x +433交x 轴于A ,B 两点,交y 轴于点C ,抛物线上一点D 的横坐标为-5. (1)求直线BD 的解析式;(2)点E 是线段BD 上的动点,过点E 作x 轴的垂线交抛物线于点F ,当折线EF +BE 最大时,在对称轴上找一点P ,在y 轴上找一点Q ,连接QE 、OP 、PQ ,求OP +PQ +QE 的最小值; (3)如图②,连接BC ,把△OBC 沿x 轴翻折,翻折后的△OBC 记为△OBC ′,现将△OBC ′沿着x 轴平移,平移后△OBC ′记为△O ′B ′C ″,连接DO ′、C ″B ,记C ″B 与x 轴形成较小的夹角度数为α,当∠O ′DB =α时,求出此时C ″的坐标.第5题图6. (2017重庆西大附中月考)如图①,在平面直角坐标系中,抛物线y =ax 2+bx +43与x 轴交于A ,B 两点(点A 在点B 左侧),与y 轴交于点C ,抛物线的顶点为点D ,且B (33,0),对称轴为直线x =3,点E (23,0),连接CE 交对称轴于点F ,连接AF 交抛物线于点G .(1)求抛物线的解析式和直线CE 的解析式;(2)如图②,过E 作EP ⊥x 轴交抛物线于点P ,点Q 是线段BC 上一动点,当QG +45QB 最小时,线段MN 在线段CE 上移动,点M 在点N 上方,且MN =152,请求出四边形PQMN 周长最小时点N 的横坐标.第6题图答案1. 解:(1)抛物线y =-x 2-2x +3, 令y =0,则-x 2-2x +3=0,(x -1)(x +3)=0,x 1=1,x 2=-3,∵点A 在点C 的左边, ∴A (-3,0),C (1,0), 令x =0,得y =3,∴B (0,3), ∴AB =32+32=32, ∴线段AB 长为3 2.(2)由题意可知△PFG 是等腰直角三角形,设P (m ,-m 2-2m +3), ∴F (m ,m +3),∴PF =-m 2-2m +3-m -3=-m 2-3m ,∴PG =FG =22PF , △PFG 周长为:PG =FG +PF =PF +2PF =-m 2-3m +2(-m 2-3m )=-(2+1)(m +32)2+9(2+1)4, ∴△PFG 周长的最大值为9(2+1)4.2. 解:(1)令y =0,x 2-x -2=0 ∴x 1=-1,x 2=2, ∴A (-1,0),B (2,0), 令x =0,y =-2, ∴C (0,-2),设直线AC 的解析式为y =kx +b (k ≠0), ∵直线过点A 、C ,∴⎩⎪⎨⎪⎧0=-k +b b =-2,解得⎩⎪⎨⎪⎧k =-2b =-2, ∴直线AC 解析式为y =-2x -2; (2)∵BO =CO ,∠BOC =90°, ∴∠ABC =45°,∠ACO =∠EPQ , ∴tan ∠ACO =tan ∠EPQ =12,过Q 作PE 的垂线QH ,垂足是H .设QH =a ,PH =2a ,DH =a ,a +2a =PD ,a =13PD ,设P (m ,m 2-m -2),D (m ,m -2),C △PQD =PQ +QD +PD =(5+2+3)a =5+2+33PD , C △PQD =5+2+33PD =5+2+33(-m 2+2m )=-5+2+33(m -1)2+5+2+33, ∴当m =1时,C △PQD 最大=5+2+33,此时P (1,-2); (3)把点A 向下平移1个单位到点A ′,则A ′(-1,-1)连接A ′P , ∴AM +MN +PN 最小值=A ′P +MN =5+1.第2题解图① 第2题解图②3. 解:(1)y =x 2-2x -3=(x -3)(x +1),令y =0,解得x 1=-1,x 2=3,则A (-1,0),B (3,0);(2)过点P 作PQ ⊥x 轴于Q ,过点D 作DK ⊥y 轴于K ,如解图①,由C (0,-3),D (1,-4),得OC =OB =3,CK =DK =1,∴∠BCO =∠DCK =45°, ∵BC =32,CD =2,BD =25,∴BC 2+CD 2=BD 2,∴∠BCD =90°, 当∠ABP =∠CDB 时, 有Rt △PQB ∽Rt △BCD ,故PQ BQ =BC CD =322=3,即PQ =3BQ . 设P (x ,x 2-2x -3),则BQ =||3-x ,PQ =||x 2-2x -3.∵P 点在x 轴下方时, ∴-x 2+2x +3=3(3-x ),整理得x 2-5x +6=0,解得x 1=2,x 2=3(不合题意,舍去). 此时点P 的坐标为(2,-3).∴当∠ABP =∠CDB 时,P 的坐标为(2,-3).第3题解图①(3)易证△OME ≌△BMF ,故∠MBF =∠MOE =60°. 连接FB 并延长交抛物线对称轴于点G ,如解图②, ∴当DF ⊥BG 时,DF 取得最小值. ∵∠GBH =60°,∴∠G =30°, ∴HG =3BH =2 3.DF =12DG =2+3,∴线段DF 的长的最小值为2+ 3.第3题解图②4. 解:(1)在y =89x +163中,令x =0,则y =163,令y =0,则x =-6,∴B (0,163),A (-6,0),把B (0,163),A (-6,0)代入y =ax 2+bx -a -b 得⎩⎪⎨⎪⎧36a -6b -a -b =0-a -b =163,∴⎩⎪⎨⎪⎧a =-89b =-409,∴抛物线的函数关系式为y =-89x 2-409x +163,令y =0,则-89x 2-409x +163=0,∴x 1=-6,x 2=1, ∴C (1,0);(2)∵点M (m ,0),过点M 作x 轴的垂线l 分别与直线AB 和抛物线交于D 、E 两点,如解图①,∴D (m ,89m +163),当DE 为等腰三角形的底时,作BG ⊥DE 于G ,则EG =GD =12ED ,GM =OB =163,∵DM +DG =GM =OB ,∴89m +163+12(-89m 2-409m +163-89m -163)=163, 解得:m 1=-4,m 2=0(不合题意,舍去),∴当m =-4时,△BDE 恰好是以DE 为底边的等腰三角形;第4题解图①ⅰ:存在,∵ON =OM ′=4,OB =163,∵∠NOP =∠BON ,∴当△NOP ∽△BON 时,OP ON =NP NB =ON OB =34,∴NPNB不变, 即OP =34ON =34×4=3,∴P (0,3)ⅱ:如解图②,N 在以O 为圆心,4为半径的半圆上,由(ⅰ)知,NP NB =OP ON =34,∴NP =34NB ,∴(NA +34NB )的最小值=NA +NP ,∴此时N ,A ,P 三点共线,∴(NA +34NB )的最小值=32+62=3 5.第4题解图②5. 解:(1)令y =0,则-33x 2-3x +433=0,解得x =-4或1, ∴A (-4,0),B (1,0), 令x =0,则y =433,∴C (0,433),当x =-5时,y =-2533+53+433=-23,∴点D 坐标(-5,-23),设直线BD 解析式为y =kx +b ,则有⎩⎨⎧-5k +b =-23k +b =0,解得⎩⎪⎨⎪⎧k =33b =-33,∴直线BD 的解析式为y =33x -33. (2)如解图①中,设BD 交y 轴于K ,则K (0,-33),设E (m ,33m -33),则F (m ,-33m 2-3m +433),第5题解图①∴tan ∠ABD =33, ∴∠ABD =30°,∴EF +EB =-33m 2-3m +433-(33m -33)+2(33-33m )=-33(m +3)2+1633, ∴m =-3时,EF +EB 的值最大,此时点E 坐标(-3,-433),如解图②,作点E 关于y 轴的对称点N ,EM ⊥AB 于M ,连接MN ,交对称轴于P ,交y 轴于Q ,第5题解图②∵M 、O 关于对称轴对称,∴OP =PM ,E 、N 关于y 轴对称,∴QE =QN ,∴OP +PQ +QE =PM +PQ +QN ,∴当M 、N 、P 、Q 共线时,OP +PQ +QE 最小,最小值为MN 的长,在Rt △MNE 中,MN =EM 2+EN 2=(433)2+62=2933.∴OP +PQ +QE 的最小值为2933.(3)如解图③中,作O ′M ⊥BD 于M ,BD =(1+5)2+(23)2=43,设O ′B =a ,则O ′M =12a ,BM =32a ,DM =BD -BM =43-32a ,第5题解图③∵∠O ′DM =∠C ″BO ′,∠O ′MD =∠BO ′C ″=90°, ∴△O ′MD ∽△C ″O ′B , ∴O ′M O ′C ″=DM BO ′, ∴12a 433=43-32aa ,∴a 2+4a -32=0,解得a =4或-8(舍去), ∴C ″坐标为(-3,-433).6. 解:(1)由抛物线y =ax 2+bx +43的对称轴-b 2a = 3 ①,点E (23,0)在抛物线上,则(33)2a +33b +43=0 ②, 由①②解得⎩⎪⎨⎪⎧a =-439b =83,则抛物线的解析式为y =-439x 2+83x +43, 又点C (0,43),E (23,0), 设直线CE 的解析式为y =kx +m ,则⎩⎨⎧0+b =43,23k +b =0,解得⎩⎨⎧k =-2b =43,∴直线CE 的解析式为y =-2x +4 3. (2)由抛物线y =-439x 2+83x +43知,当x =23时,y =43, 则点P 的坐标为(23,43), 根据对称性得A (-3,0), 由y =-2x +43知,当x =3时,y =23,F (3,23), 直线AF 的解析式为:y =x +3,解方程组⎩⎪⎨⎪⎧y =-439x 2+83x +43y =x +3,解得⎩⎪⎨⎪⎧x =934y =1334,点G 的坐标为(934,1334).由sin ∠OBC =OC BC =4353=45,∴当QG ⊥x 轴时,QG +45QB 最小,∵直线BC 的解析式为y =-43x +43,∴当x =934时,y =3,∴点Q (934,3).如解图,过点P 作PK ∥MN ,取PK =MN =152, 则四边形PMNK 是平行四边形,∴四边形PQNM 的周长=PM +MN +NQ +PQ =NK +MN +NQ +PQ ,由于MN 、PQ 的值不变,所以只需NK +NQ 最短,所以作K 关于直线CE 的对称点K ′,连接K ′Q ,交CE 于N ,即当K ′、N 、Q 三点共线时,四边形PQNM 的周长最短.∵P 的坐标为(23,43),PK =152,PK ∥CE , ∴K 点横坐标x k =23+152cos ∠CEO =23+32=532, K 点纵坐标为y k =43-152sin ∠CEO =43-152×255=33,∴K (532,33),∵直线KK ′与直线CE 垂直, ∴设直线KK ′的解析式为y =12x +b ,则12×532+b =33,解得b =734, ∴直线KK ′为:y =12x +734,解方程组⎩⎪⎨⎪⎧y =12x +734y =-2x +43,得⎩⎪⎨⎪⎧x =9103y =1153,则KK ′与CE 交点坐标为(9310,1135),由对称特点可得K ′的横坐标为9310×2-532=-7310,K ′的纵坐标为1135×2-33=735, ∴K ′(-7310,735),由Q (934,3),设直线K ′Q 的解析式为y =kx +b ,则⎩⎪⎨⎪⎧-7310k +b =735934k +b =3,解得⎩⎪⎨⎪⎧k =-859b =77359,∴直线K ′Q 的解析式为y =-859x +77359,解方程组⎩⎪⎨⎪⎧y =-2x +43y =-859x +77359 ,解得x =1593110,则N 点的横坐标为1593110.第6题解图。
2018届重庆中考复习:二次函数相关的最值问题练习(含答案)

二次函数相关的最值问题例1. 如图,抛物线y=-x2-4x+5与x轴交于点A、B,与y轴交于点C,点D为抛物线的顶点.(1)求直线AC的解析式及顶点D的坐标;(2)若Q为抛物线对称轴上一动点,连接QA、QC,求|QA-QC|的最大值及此时点Q的坐标;(3)连接CD,点P是直线AC上方抛物线上一动点(不与点A、C重合),过P作PE∥x轴交直线AC于点E,作PF∥CD交直线AC于点F,当线段PE+PF取最大值时,求点P的坐标及线段EF的长;(4)在(3)问的条件下,将P 向下平移34个单位得到点H ,在抛物线对称轴上找一点L ,在y 轴上找一点K ,连接OL ,LK ,KH ,求线段OL +LK +KH L 的坐标;(5)在(3)问的条件下,将线段PE 沿着直线AC 的方向平移得到线段P′E′,连接DP′,BE ′,求DP′+P′E′+E′B 取最小值时点E′的坐标.针对训练1.如图,直线y=kx+b(k、b为常数)分别与x轴、y轴交于点A(-4,0)、B(0,3),抛物线y=-x2+2x+1与y轴交于点C.(1)求直线y=kx+b的解析式;(2)若点P(x,y)是抛物线y=-x2+2x+1上的任意一点,设点P到直线AB的距离为d,求d关于x的函数解析式,并求d取最小值时点P的坐标;(3)若点E在抛物线y=-x2+2x+1的对称轴上移动,点F在直线AB上移动,求CE+EF的最小值.2.如图①,已知抛物线y=-33x2+2 33x+3与x轴交于A,B两点(点A在点B的左侧),与y轴交于点C,点D是点C关于抛物线对称轴的对称点,连接CD,过点D作DH⊥x 轴于点H,过点A作AE⊥AC交DH的延长线于点E.(1)求线段DE的长度;(2)如图②,试在线段AE上找一点F,在线段DE上找一点P,且点M为线段PF上方抛物线上的一点,求当△CPF的周长最小时,△MPF面积的最大值是多少.3.如图,对称轴为直线x=2的抛物线经过A(-1,0),C(0,5)两点,与x轴另一交点为B.已知M(0,1),E(a,0),F(a+1,0),点P是第一象限内的抛物线上的动点.(1)求此抛物线的解析式;(2)若△PCM是以点P为顶点的等腰三角形,求a为何值时,四边形PMEF周长最小?说明理由.4.已知,如图,二次函数y=ax2+2ax-3a(a≠0)图象的顶点为H,与x轴交于A、B两点(B点在A点右侧),点H,B关于直线l:y=33x+3对称.(1)求A、B两点坐标,并证明点A在直线l上;(2)求二次函数的解析式;(3)过点B作直线BK∥AH交直线l于点K,M、N分别为直线AH和直线l上的两个动点,连接HN、NM、MK,求HN+NM+MK和的最小值.5.如图,在平面直角坐标系中,抛物线y =-12x 2+2x +3与x 轴交于A ,B 两点(点A 在点B 左侧),与y 轴交于点C ,连接BC ,过点A 作AD∥BC 交y 轴于点D.(1)求平行线AD 、BC 之间的距离;(2)点P 为线段BC 上方抛物线上的一动点,当△PCB 的面积最大时,Q 从点P 出发,先沿适当的路径运动到直线BC 上点M 处,再沿垂直于直线BC 的方向运动到直线AD 上的点N 处,最后沿适当的路径运动到点B 处停止.当点Q 的运动路径最短时,求点Q 经过的最短路径的长.6.如图,抛物线y=-34x2-94x+3 3交x轴于A、B两点,交y轴于点C,点Q为顶点,点D为点C关于对称轴的对称点.(1)求点D的坐标和tan∠ABC的值;(2)若点P是抛物线上位于点B、D之间的一个动点(不与B、D重合),在直线BC上有一动点E,在x轴上有一动点F.当四边形ABPD的面积最大时,一动点G从点P出发以每秒1个单位的速度沿P→E→F的路径运动到点F,再沿线段FA以每秒2个单位的速度运动到A 点后停止,当点F的坐标是多少时,动点G在运动过程中所用时间最少?二次函数相关的最值问题答案例1. 解:(1)∵y =-x 2-4x +5=-(x 2+4x )+5=-(x +2)2+9,∴D (-2,9).当x =0时,y =5,∴C (0,5).当y =0时,x 1=1,x 2=-5,∴A (-5,0),B (1,0),∴y AC =x +5;(2)因为点Q 在抛物线对称轴上,由抛物线对称性知QA =QB ,由C (0,5)和B (1,0)可求得y BC =-5x +5,根据三角形三边关系可知,当点Q ,C ,B 三点共线时,|QB -QC |最大,即|QA -QC |最大,可求直线y BC =-5x +5与抛物线对称轴交点Q 为(-2,15),此时|QA -QC |最大值=BC =26.解:(3)过P 作PQ ∥y 轴,交AC 于Q ,再作FM ⊥PQ 于M ,如图①,直线AC :y =x +5,设P (t ,-t 2-4t +5),Q (t ,t +5),∴PQ =(-t 2-4t +5)-(t +5)=-t 2-5t .∵∠PEF =∠CAO =45°,∴PE =PQ =-t 2-5t ,∵PF ∥CD ,∴k CD =-2=k PF ,∴tan ∠MPF =12,设FM =n =MQ ,则PM =2n ,PQ =3n ,PF =5n ,即PF =53PQ ,∴PE +PF =(3+5)n =(1+53)PQ , ∴当PQ 最大时,PE +PF 取最大值,而PQ =-t 2-5t =PE =-⎝ ⎛⎭⎪⎫t +522+254, 当t =-52时,PE +PF 取最大值, 此时P ⎝ ⎛⎭⎪⎫-52,354,EF =2PM =25 26.(4)如图②:在(3)问的条件下,P ⎝ ⎛⎭⎪⎫-52,354, ∴H ⎝ ⎛⎭⎪⎫-52,8,作H 关于y 轴的对称点H 1, 作O 关于抛物线对称轴对称点O 1,所以O 1(-4,0),H 1⎝ ⎛⎭⎪⎫52,8, 连接O 1H 1,则O 1H 1长即为OL +LK +KH 的最小值,直线O 1H 1:y =1613x +6413, ∴直线O 1H 1与抛物线对称轴交点即为L 点的位置,此时L ⎝⎛⎪⎫-2,3213OL +LK +KH 的最小值=O1H 1=5217;(5)在(3)问的条件下,P ′E ′=PE =254, 在线段PE 平移过程中,PE 即P′E′长度不变,将DP′沿P′E′向右平移PE 的长即254个单位,得到D′E′,如图③, 则四边形D′DP′E′为平行四边形,故DP′=D′E′,要使得DP′+P′E′+E′B 最小,即DP′+E′B 最小,即要使D′E′+E′B 最小,当D′,E ′,B 三点共线时,D ′E ′+E′B 最小,设D′B 与直线AC 交于点E″.由题意知D′⎝ ⎛⎭⎪⎫174,9,直线BD′:y =3613x -3613,∴E ″⎝ ⎛⎭⎪⎫10123,21623,即点E ′的坐标为(10123,21623). 针对训练:1. 解:(1)∵直线y =kx +b 经过A (-4,0)、B (0,3),∴⎩⎪⎨⎪⎧-4k +b =0,b =3,解得⎩⎪⎨⎪⎧k =34,b =3.∴y =34x +3.(2)过点P 作PH ⊥AB 于点H ,过点H 作x 轴的平行线MN ,分别过点A 、P 作MN 的垂线段,垂足分别为M 、N .设H (m ,34m +3),则M (-4,34m +3),N (x ,34m +3),P (x ,-x 2+2x +1). ∵PH ⊥AB ,∴∠PHN +∠AHM =90°,∵AM ⊥MN ,∴∠MAH +∠AHM =90°.∴∠MAH =∠PHN ,∵∠AMH =∠PNH =90°,∴△AMH ∽△HNP .∵MA ∥y 轴,∴△MAH ∽△OBA .∴△OBA ∽△NHP .∴NH 3=PN 4=PH 5. ∴x -m 3=(34m +3)-(-x 2+2x +1)4=d 5. 整理得:d =45x 2-x +85,所以当x =58时,d 取最小值,此时P (58,11964).(3)抛物线的对称轴为直线x =1,作点C 关于直线x =1的对称点C ′,过点C ′作C ′F ⊥AB 于F .过点F 作JK ∥x 轴,分别过点A 、C ′作AJ ⊥JK 于点J ,C ′K ⊥JK 于点K ,则C ′(2,1).设F (m ,34m +3), ∵C ′F ⊥AB ,∴∠AFJ +∠C ′FK =90°,∵C ′K ⊥JK ,∴∠C ′+∠C ′FK =90°, ∴∠C ′=∠AFJ ,∵∠J =∠K =90°,∴△AFJ ∽△FC ′K .∴AJ FK =JF C ′K ,∴34m +32-m =m +434m +2,解得m =825或m =-4(不符合题意,舍去)∴F (825,8125),∵C ′(2,1),∴FC ′=145. ∴CE +EF 的最小值=C ′F =145.2. 解:(1)对于抛物线y =-33x 2+2 33x +3, 令x =0,得y =3,即C (0,3),D (2,3),∴DH =3,令y =0,即-33x 2+2 33x +3=0,得x 1=-1,x 2=3, ∴A (-1,0),B (3,0),∵AE ⊥AC ,EH ⊥AH ,∴△ACO ∽△EAH ,∴OC AH =OA EH ,即33=1EH , 解得:EH =3,则DE =2 3;(2)如图②,找点C 关于DE 的对称点N (4,3),找点C 关于AE 的对称点G (-2,-3),连接GN ,交AE 于点F ,交DE 于点P ,即G 、F 、P 、N 四点共线时,△CPF 的周长=CF +PF +CP =GF +PF +PN 最小,直线GN 的解析式:y =33x -33;直线AE 的解析式:y =-33x -33;直线DE 的解析式:x =2.联立得:F (0,-33),P (2,33), 过点M 作y 轴的平行线交FH 于点Q ,设点M (m ,-33m 2+2 33m +3), 则Q (m ,33m -33)(0≤m ≤2); ∴S △MFP =S △MQF +S △MQP =12MQ ×2=MQ =-33m 2+33m +4 33, ∵对称轴为直线m =12,而0≤12≤2,抛物线开口向下, ∴m =12时,△MPF 的面积有最大值,为17 312.3. 解:(1)∵对称轴为直线x =2,∴设抛物线解析式为y =m ′(x -2)2+k .将A (-1,0),C (0,5)代入得:⎩⎪⎨⎪⎧9m ′+k =0,4m ′+k =5,解得⎩⎪⎨⎪⎧m ′=-1,k =9,∴y =-(x -2)2+9=-x 2+4x +5.(2)∵M (0,1),C (0,5),△PCM 是以点P 为顶点的等腰三角形,∴点P 的纵坐标为3.令y =-x 2+4x +5=3,解得x =2±6.∵点P 在第一象限,∴P (2+6,3).四边形PMEF 的四条边中,PM 、EF 长度固定,因此只要ME +PF 最小,则四边形PMEF 的周长最小.如图,将点M 向右平移1个单位长度(EF 的长度),得M 1(1,1);作点M 1关于x 轴的对称点M 2,则M 2(1,-1);连接PM 2,与x 轴交于F 点,此时ME +PF =PM 2最小.设直线PM 2的解析式为y =mx +n ,将P (2+6,3),M 2(1,-1)代入得:⎩⎨⎧(2+6)m +n =3,m +n =-1,解得:m =4 6-45,n =-4 6+15, ∴y =4 6-45x -4 6+15. 当y =0时,解得x =6+54.∴F (6+54,0). ∵a +1=6+54,∴a =6+14.∴a =6+14时, 四边形PMEF 周长最小.4. 解:(1)依题意,得ax 2+2ax -3a =0(a ≠0),解得x 1=-3,x 2=1,∵B 点在A 点右侧,∴A 点坐标为(-3,0),B 点坐标为(1,0),证明:∵直线l :y =33x +3, 当x =-3时,y =33×(-3)+3=0,∴点A 在直线l 上.(2)过顶点H 作HC ⊥AB 交AB 于C 点,∵点H 、B 关于过A 点的直线l :y =33x +3对称,∴AH =AB =4, 又∵点H 为抛物线顶点,则点H 在抛物线对称轴上,∴AH =BH =AB =4.在Rt △ACH 中,由勾股定理得CH =AH 2-AC 2=2 3,∴顶点H (-1,2 3),代入二次函数解析式,解得a =-32,∴二次函数解析式为y =-32x 2-3x +3 32.(3)直线AH 的解析式为y =3x +3 3,直线BK 的解析式为y =3x -3,由⎩⎪⎨⎪⎧y =33x +3,y =3x -3,解得⎩⎨⎧x =3,y =2 3, 即K (3,2 3),则BK =4,∵点H 、B 关于直线AK 对称,∴HN +MN 的最小值是MB ,过点K 作KD ⊥x 轴于D ,作点K 关于直线AH 的对称点Q ,连接QK ,交直线AH 于E ,则KE =KD =2 3,QM =MK ,QE =EK =2 3,AE ⊥QK ,∴BM +MK 的最小值是BQ ,即BQ 的长是HN +NM +MK 的最小值,∵BK ∥AH ,∴∠BKQ =∠HEQ =90°, 由勾股定理得QB =8,∴HN +NM +MK 的最小值为8.5. 解:(1)令y =0,即-12x 2+2x +3=0, 解得:x 1=-2,x 2=3 2,∴A (-2,0),B (3 2,0),∵当x =0时,y =3,∴C (0,3),在Rt △BOC 中,BO =3 2,CO =3,∴BC =3 3,∴sin ∠CBO =CO BC =33. 因为AD ∥BC ,∴sin ∠BAD =sin ∠CBO =33. 过B 作BH ⊥AD 于点H ,∴sin ∠BAD =BH AB=33,∴BH =4 63; ∴平行线AD 、BC 间的距离为436. (2)过P 作PQ ∥y 轴,交BC 于点Q ,设P (m ,-12m 2+2m +3),∵直线BC :y =-22x +3,∴Q (m ,-22m +3), ∴S △PCB =12·PQ ·(x B -x C )=3 22(-12m 2+3 22m ), 当m =3 22时,S △CPB 最大,此时,P (3 22,154). 取点B 关于AD 的对称点B ′,将B ′沿B ′B 方向平移4 63个单位长度得B ′′,此时B ′′与点H (5 23,-83)重合. 连接HP ,交BC 于点M ,点M 即为所求.∴(PM +NM +BN )最小=PH +MN =593712+4 63.6. 解:(1)令-34x 2-94x +3 3=0,解得x 1=-4 3,x 2=3,∴A (-4 3,0),B (3,0),在y =-34x 2-94x +3 3中,令x =0,则y =3 3, ∴C (0,3 3),∴OC =3 3,BO =3,在Rt △COB 中,∴tan ∠ABC =OC OB=3,由y =-34x 2-94x +3 3知,对称轴直线为x =-3 32,∴点D (-3 3,3 3);(2)由B (3,0),D (-3 3,3 3)可得直线BD 解析式:y =-34x +3 34, 过P 作PK ⊥x 轴交BD 于点K ,设P (m ,-34m 2-94m +3 3),则K (m ,-34m +3 34), S 四边形ABPD =S △ABD +S △PBD ,S △ABD 是定值,∴S 四边形ABPD 最大时,即S △PBD 最大. S △PBD =12(x B -x D )(y P -y K )=-32m 2-3 3m +272, 当m =-b 2a =-3时,S △PBD 最大,此时点P 坐标为(-3,9 32). 作点P (-3,9 32)关于直线BC 的对称点P ′(-310,24 35), 以A 为顶点,在x 轴下方作∠BAT =30°,过P ′作直线AT 的垂线分别交BC 、x 轴于点E 、F ,此时,点G 在运动过程中所用时间最少,点F 坐标为(-310-245,0).。
重庆初2018届中学考试数学压轴题——二次函数专题(无问题详解)

二次函数专项 1.如图1,在平面直角坐标系中,抛物线3332312++-=x x y 与x 轴交于A 、B 两点(点A 在点B 的左侧),与y 轴交于点C ,抛物线的顶点为点E.(1)判断△ABC 的形状,并说明理由;(2)经过B 、C 两点的直线交抛物线的对称轴于点D ,点P 为直线BC 上方抛物线上的一动点,当△PCD 的面积最大时,点Q 从点P 出发,先沿适当的路径运动到抛物线的对称轴上点M 处,再沿垂直于抛物线对称轴的方向运动到y 轴上的点N 处,最后沿适当的路径运动到点A 处停止.点Q 的运动路径最短时,求点N 的坐标及点Q 经过的最短路径的长;(3)如图2,平移抛物线,使抛物线的顶点E 在射线AE 上移动,点E 平移后的对应点为点/E ,点A 的对应点为/A .将△AOC 绕点O 顺时针旋转至11OC A ∆的位置,点A 、C 的对应点分别为点11、C A ,且点1A ,恰好落在AC 上,连接/1/1、E C A C ./1/E C A ∆是否能为等腰三角形?若能,请求出所有符合条件的点/E 的坐标;若不能,请说明理由.2.如图,在平面直角坐标系xoy 中, 23391644y x x =-++抛物线,分别交x 轴 于A 与B 点,交y 轴交于C 点,顶点为D ,连接AD 。
(1) 如图1, P 是抛物线的对称轴上的一点,当AP AD ⊥时,求P 的坐标。
(2) 在(1)的条件下,在直线AP 上方、对称轴右侧的抛物线上找一点Q ,过Q 作 QH x ⊥轴,交直线AP 于H,过Q 作,QE PH QHPE 交对称轴于E 当周长最大时,在抛物线的对称轴上找一点M ,使QM AM-最大,并求这个最大值及此时M 点的坐标。
(3)2BD DAB D A B D A B A '''''''∠∠∠如图:连接,把沿x 轴平移到,在平移过程中把绕旋转, D A B D '''∠使的一边始终经过点,另一边交直线DB 于R,是否存在这样的R 点,使DRA '∆ 为等腰三角形,若存在,求出BR 的长;若不存在,说明理由。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
二次函数相关的最值问题2例1.如图,抛物线y = —x —4x+ 5与x轴交于点A、B,与y轴交于点C,点D为抛物线的顶点. 求直线AC的解析式及顶点D的坐标;若Q为抛物线对称轴上一动点,连接QA QC求|QA—QC|的最大值及此时点Q的坐标;(3)连接CD点P是直线AC上方抛物线上一动点(不与点A、C重合),过P作PE//x轴交直线AC于点E,作PF//CD交直线AC于点F,当线段PE+ PF取最大值时,求点P的坐标及线段EF的长;⑷在⑶K,连接0L3问的条件下,将KH求线段(5)在⑶+ P' E'+ E 问的条件下,将线段PE沿着直线B取最小值时点E'的坐标.针对训练2 1 .如图,直线y= kx + b(k、b为常数)分别与x轴、y轴交于点A( —4, 0)、B(0 , 3),抛物线y=—x + 2x + 1与y 轴交于点C.⑴求直线y = kx + b的解析式;(2) 若点P(x , y)是抛物线y = —x2+ 2x+ 1上的任意一点,设点P到直线AB的距离为d,求d关于x 的函数解析式,并求d取最小值时点P的坐标;(3) 若点E在抛物线y = —x2+ 2x + 1的对称轴上移动,点F在直线AB上移动,求CE+ EF的最小值.2 .如图①,已知抛物线y =—身x2+ ^3~x + 3与x轴交于A, B两点(点A在点B的左侧),与y轴交于点C,点D是点C关于抛物线对称轴的对称点,连接CD过点D作DH Lx轴于点H,过点A作AEL AC 交DH的延长线于点E.⑴求线段DE的长度;(2)如图②,试在线段AE上找一点F,在线段DE上找一点P,且点M为线段PF上方抛物线上的一点,求当△ CPF的周长最小时,△ MPF面积的最大值是多少.① ②3.如图,对称轴为直线x= 2的抛物线经过A( —1, 0) , C(0, 5)两点,与x轴另一交点为B.已知M(0, 1), E(a,0),F(a + 1, 0),点P是第一象限内的抛物线上的动点.(1)求此抛物线的解析式;4. 已知,如图,二次函数y = ax2+ 2ax—3a(a丰0)图象的顶点为H,与x轴交于A B两点(B点在A点右侧),点H B关于直线I : y = #x + 3对称.(1) 求A、B两点坐标,并证明点A在直线I上;(2) 求二次函数的解析式;(3) 过点B作直线BK// AH交直线I于点K, M N分别为直线AH和直线I上的两个动点,连接HN NM MK求HW NW MK和的最小值.1 2 l5. 如图,在平面直角坐标系中,抛物线y= —2X + 2x + 3与x轴交于A, B两点(点A在点B左侧),与y轴交于点C,连接BC,过点A作AD// BC交y轴于点D.⑴求平行线AD BC之间的距离;(2)点P为线段BC上方抛物线上的一动点,当△ PCB的面积最大时,Q从点P出发,先沿适当的路径运动到直线BC上点M处,再沿垂直于直线BC的方向运动到直线AD上的点N处,最后沿适当的路径运动到点B处停止•当点Q的运动路径最短时,求点Q经过的最短路径的长.6. 如图,抛物线y= —fx2—9x + 3 3交x轴于A B两点,交y轴于点C,点Q为顶点,点D为点C关于对称轴的对称点.⑴求点D的坐标和tan / ABC的值;(2)若点P是抛物线上位于点B D之间的一个动点(不与B D重合),在直线BC上有一动点E,在x 轴上有一动点F.当四边形ABPD的面积最大时,一动点G从点P出发以每秒1个单位的速度沿iE^F的G 路径运动到点F,再沿线段FA以每秒2个单位的速度运动到在运动过程中所用时间最少?二次函数相关的最值问题答案2 2 2例 1.解:(1) T y = —x —4x + 5 =—(x + 4x) + 5 =—(x+ 2) + 9, •- D( —2, 9).当x = 0 时,y = 5,二qo , 5).当y = 0 时,X1= 1, x = —5,「. A—5, 0), B(1 , 0),• y AC= x + 5;(2)因为点Q在抛物线对称轴上,由抛物线对称性知QA= QB由C(0 , 5)和政1 , 0)可求得y BC=—5x + 5 ,根据三角形三边关系可知,当点Q, C, B三点共线时,| QE—QC最大,即| QA- QC最大,可求直线y BC=—5x+ 5与抛物线对称轴交点Q为(—2 , 15),此时| QA- QC最大值=BC= 26.解:(3)过P作PQ// y轴,交AC于Q 再作FML PQ于M如图①,直线AC y= x + 5,设P(t , —t2—4t + 5) , Qt, t + 5),• PQ= ( —t2—4t + 5) —(t + 5) = —t2—5t.•••/ PEF=Z CAO= 45°,「. PE= PQ=—t2—5t ,1■/ PF/ CD • k cD=—2 = k pF, • tan / MP= 2,设FM= n = MQ 贝卩PM= 2n, PQ= 3n, PF= 5n,即PF=^PQ • PE^ PF= (3 + 5)n= (1 +£)PQ•••当PQ最大时,P曰PF取最大值,而PQ=—t2—5t = PE=—t + 2 + 25,P曰PF取最大值,此时P - 2354,EF= 2PM k(4)如图②:在⑶ 问的条件下, 5 35 -2盲,••• H—2,8[,作H关于y轴的对称点H,作O关于抛物线对称轴对称点O,所以0( —4, 0),H 2,8,连接0H,贝U 0H长即为0』LK+ KH的最小值,直线0H: y = 16 64 —x亠13 十13,•直线0H与抛物线对称轴交点即为L点的位置,此时0L+ LK+ KH的最小值=0H= 討17;(5)在(3)问的条件下,P,E= PE= 25,⑵ 过点P 作PH L AB 于点H 过点H 作x 轴的平行线 MN 分别过点 A P 作MN 的垂线段,垂足分别为 M N⑶ 抛物线的对称轴为直线 x = 1,作点C 关于直线x = 1的对称点 C ,过点C'作C F 丄AB 于F .过点F 作JK// x 轴,分别过点 A 、C'作AJ L JK 于点J , C K 丄JK 于点K 则C (2 , 1).3 设 F (m 4m 1 3),•/ C F L AB •••/ AFJ+Z C FK= 90°,T C K 丄 JK ,「./ C'+/ C' FK= 90 ° ,•••/ C ,=Z AFJ,vZ J = Z K = 90°,.山 AF4A FC K37m* 3 , c 4 m * 4 82 — m =3 ,解得 m=亦或 m=- 4(不符合题意,舍去).;m * 2414,••<' (2 , 1),• FC = £1 C 曰EF 的最小值=C F =質5在线段PE 平移过程中,PE 即P' E'长度不变,D f将DP 沿P' E'向右平移 PE 的长即 单位,得到D E',如图③,则四边形D' DP E'为平行四边形, 故 DP = D' E',要使得 DP * P' E'+ E'B 最小,即 DP * E'B 最小, 即要使D' E'* E'B 最小,当D',E', B 三点共线时,D' E ' * E'B 最小, 设D' B 与直线AC 交于点E 〃.门7 、3636 由题意知D , 9,直线BD : y =-\ 101 ,即点E'的坐标为(灰 , 23••• E 〃 23, 针对训练:1. 解: 4216 23" 13'216 _2?)'/ f ,么 0B(1) •••直线 y = kx * b 经过 A - 4 , 0)、B (0 , 3), 3 k = 4,34•- y =4X * 3.••厂 4k * b = 0,解得]b = 3,[b = 3.3 33设 H (m 4m * 3),贝U M — 4, 3) , N (x , 4m * 3), P (x , - x 2+ 2x + 1).•/ PHLABPHN-Z AHI = 90° ,••• AM L MN MA *Z AHI = 90° .• Z MA ==Z PHN T Z AM =Z PN = 90° , •△ AMH^A HNP ••• MA/ y 轴,•△ MA HA OBANH PN PH• △ OBA^ NHP •H B 32(;m * 3)- (- x * 2x * 1)x - m 4d :5.A 4 2 8 57整理得:d = x - x*;,所以当x=:时,d 取最小值,此时 5 5 119 只8,丽).>X>?=-^+2^+1• AJ _ _J^ • F T CK • F (285,NE;O2.解:(1)对于抛物线 y =—fx 2 + + 3,令 x = 0,得 y = ^3,g 卩 qo ,西),D 2,护), • DH= 3, 令 y = 0,即一+ - x + 3 = 0,得 X 1=— 1 , X 2= 3 ,• A — 1, 0), B (3 , 0), v AE! AC EH! AH • △ AC®A EAH•匹O 即二=i AH EH 3 EH解得:EH= 3 ,则 DE= 2 3;⑵如图②,找点 C 关于DE 的对称点N(4,羽),找点C 关于AE 的对称点G — 2,—护), 连接GN 交AE 于点F ,交DE 于点P ,即G F 、P N 四点共线时,△ CPF 的周长=CF F PF + CP= GF F PF + PN 最小, 直线GN 的解析式:y =f x —电3;直线 AE 的解析式:y =过点M 作y 轴的平行线交 FH 于点Q 设点 Mm — fm + ^y^m F 3), 则 Qm fm-1x/3 2 V 3 4 \[3&MF = S ^MQF + S ^MQ = ~MQ< 2= MQ =—〒m + wm+ ~3^2 3 3 3 1 1•••对称轴为直线 m = 2,而O w 寸2,抛物线开口向下,• m= *时,△ MPF 的面积有最大值,为 —12*--3.解:(1) T 对称轴为直线 x = 2,「.设抛物线解析式为 9m+ k=0 解得 P=— J • y =— (x — 2)2 +9=— x 2+ 4x + 5.4m + k = 5 ,k = 9 ,2 ••• M 0 , 1) , C (0 , 5), △ PCM 是以点P 为顶点的等腰三角形,•••点P 的纵坐标为3.令y =— x 2 + 4x + 5= 3,解得x = 2± . 6. v 点P 在第一象限,二P (2 +'. 6, 3). 四边形PMEF 勺四条边中,PM EF 长度固定,因此只要 MB PF 最小,则四边形 PMEF 勺周长最小. 如图,将点M 向右平移1个单位长度(EF 的长度),得M (1 , 1); 作点M 关于x 轴的对称点M ,则M (1 , — 1);连接P 皿与x 轴交于F 点,此时 MEF PF = PM 最小.设直线PM 的解析式为y = mx+ n ,将P (2 + 6, 3) , M (1 , — 1)代入得:联立得:F (0,P (2 ,-fx —电3;直线DE 的解析式:x = 2.D 〒N将 A ( — 1 , 0) , C (0 , 5)代入得: < 2);5.解:⑴令 y = 0,即一夕2+〔 2x + 3= 0,解得:x i =— 2, X 2 = 3 厶 2,• A — 2, 0) , B (3 .2, 0) ,••当 x = 0 时,y = 3 , • C (0 , 3),在 Rt △ BOC 中, BO= 3 2 , CO= 3, • BC = 3 3 ,:(2+&) n = 3 ,n =— 1,46 — 4 4 6+ 1解得:m =, n = ----- :5 54 \IQ — 44 \[Q + 1• y =^^x —^^.当y = 0时,解得x =」+^. • H 亠6+5, 0).• a + 1=¥, • a =亍.• a =¥时, 4 4 4四边形PME 周长最小.y八c\AjO E ;/FM224.解:(1)依题意,得 ax + 2ax — 3a = 0(a z 0),解得 刘=—3 , X 2= 1 , • B 点在A 点右侧,二A 点坐标为(一3 , 0), B 点坐标为(1 , 0), 证明:••直线l : y =£x + 3 , 当 x =— 3 时,y =f x ( — 3) + 3= 0,•点 A 在直线 I 上. ⑵过顶点H 作HCL AB 交AB 于 C 点, ••点H 、B 关于过A 点的直线l : y = -3-x + 3对称,• AH = AB= 4 , 又••点H 为抛物线顶点,则点 H 在抛物线对称轴上, • AHh BHh AB= 4.在 Rt △ ACH 中, 由勾股定理得 c* ,A H — A C = 2 3, •顶点 H ( — 1 , 2 3), 代入二次函数解析式,解得 a =— -2,•二次函数解析式为 y =— -^x 2— 3x +宁(3)直线AH 的解析式为y = 3x + 3 "3, 直线BK 的解析式为y = .3x — ,3, 由+ ,3,x = 3, 解得1 厂 旳=2羽, y = ,3x — 3 , 即 K (3 , 2 3),贝U ••点H 、B 关于直线 过点K 作KDL x 轴于D,作点K 关于直线AH 的对称点Q 连接QK 交 直线AH 于E , 则 KE= KD= 2 3 , QM= MK QE= EK = 2 3 , AE ± QK • BW MK 的最小值是 BQ 即BQ 的长是HN^ NW MK 的最小值, • BK// AH BK(=Z HE = 90° , 由勾股定理得 QB= 8, • HN^ NW MK 的最小值为8.B2 4, AK 对称,••• HN^ MN 的最小值是MB y/\BD x5 ),••• sin / CB =务.因为 AD// BC •- sin Z BA*sin Z CB&-33.3 过 B 作 BHL AD 于点 H, • sin Z BAD=磐 飞3 , • BH= 6; AB 3 3•平行线AD BC 间的距离为4 品 ⑵过P 作PQ/ y 轴,交BC 于点Q, 设 P (m , — 1m i + 2n u 3), •••直线 BC y =— #x + 3, • Qn - #n u 3), 1 •- S\ PCB = 2 • PQ ・(X B — X C )=当m= —2-时,S\ CPB 最大,此时,R ”3.2-2m +才 3 ■ 2 15厂,T )- m ), 取点B 关于AD 的对称点B',将B'沿B' B 方向平移4■竿3个单位长度得B'',此时B''与点代5子,3—3)重合. 连接HP 交BC 于点M 点M 即为所求. •••( PMF NW BN 最小=PH+ M = 5937+^V 6 6.解:⑴令一#x 2— |x + 3 3= 0,解得 x i =— 4 3 X 2= 3 ,• A — 4 3, 0) , 0 3, 0),在y =—予2-条+ 3 3中,令x = 0,则y = 3 3, • C (0 , 3 3) , • OC= 3 3, BO= 3, 亠〜 OC 在 Rt △ COE 中, • tan Z AB(= 3, OB由y =— -^x 2 — 4x + 3 3知,对称轴直线为 x =— 3 2" •••点 D( — 3 .3, 3 3);3 y = —4x +⑵ 由耳3 , 0) , Q — 3 3 , 3 3)可得直线BD 解析式 过P 作PK 1 x 轴交BD 于点K ,设P (m —子用—9m+ 3 3),贝U K ( m S 四边形 ABPD = S\ ABD + S A PBD , S A ABD 是定值, • S 四边形 ABPD 最大时, 即 S A PBD 最大. ci3 2 厂 27 S A PBD = 2( X B — X D )( y p — yR =—尹―3 pnu-^ , 3 33—严于),当 m=— 2a =— .3时,S A PBD 最大,此时点 P 坐标为(—.3 , 9 2 3)- 作点 P (-& ,呼 )关于直线 BC 的对称点 P'(—计,24 ;3以A 为顶点,在x 轴下方作Z BAF 30 ° , 过P'作直线AT 的垂线分别交BC x 轴于点E 、F , 此时,点G 在运动过程中所用时间最少,一 小24点F 坐标为(一布—, 0) •5 ),。
