第二讲 溶液及胶体——拉乌尔定律、亨利定律
2.4 拉乌尔定律、亨利定律
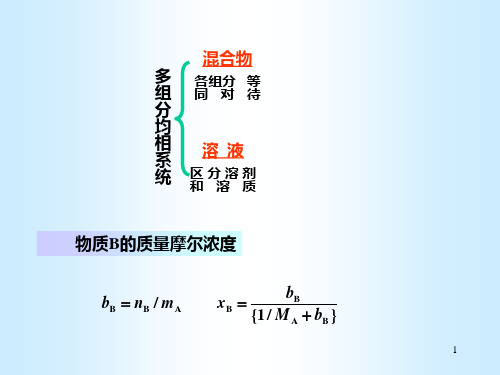
多 组
各组分 等 同对待
分
均
相 系
溶液
统
区分溶剂 和溶质
物质B的质量摩尔浓度
bB nB / mA
xB
{1 /
bB MA
bB }
1
§2-4 拉乌尔定律、亨利定律
1. 液态混合物和溶液的饱和蒸气 压
设由组分A, B, C……组成液态混 合物或溶液, T一定时, 达到气, 液两相 平衡.
此时, 气态混合物的总压力为p, 则 p 即为温度T下该液态混合物或溶液的 饱和蒸气压.
水(A)和乙酸乙酯(B)不完全混溶, 在37.55℃时两液相呈平衡.
一相中含质量分数为w(B) = 0.0675的酯, 另一相中含w(A) =
0.0379的水, 假定拉乌尔定律对每相中的溶剂都能适用, 已知
37.55℃时, 纯乙酸乙酯的蒸气压力是22.13kPa, 纯水的蒸气
压力是6.399kPa, 试计算:
ln p(s) 3133 27.650 11.99 p(s) 160.3k Pa Pa 200K / K
计算结果表明, 所给过程是恒温恒压不可逆相变化过程, 为
此可根据计算所得的液体及固体CO2在200 K的蒸气压数据, 设
计以下可逆过程进行计算:
8
s, 100kPa, 200K
s, 160.3kPa, 200K G2
(1)计算下述过程Gm :
CO2( s, 100kPa, 200K ) →CO2( l, 100kPa, 200K )
(2)判断在100 kPa下, CO2(l)能否稳定存在?
(1) 200 K时液体及固体CO2的饱和蒸气压:
ln p(l) 2013 22.405 12.34 p(l) 228.7kPa Pa 200K / K
拉乌尔定律和亨利定律的区别

拉乌尔定律和亨利定律的区别拉乌尔定律和亨利定律都是热力学中的重要定律,它们分别描述了气体和液体中溶解度与温度、压力之间的关系。
在研究物质的溶解度时,这两个定律都具有重要作用,但它们之间存在着一些明显的区别。
拉乌尔定律是描述气体溶解度与温度之间关系的定律。
它的基本表述是:在一定的压力下,气体的溶解度随着温度的升高而降低。
这个定律主要适用于理想气体,即气体分子之间不存在相互作用力的情况。
在实际情况下,气体分子之间会存在一定的相互作用力,因此拉乌尔定律只能作为近似计算的基础。
亨利定律则是描述气体或液体在溶剂中的溶解度与压力之间关系的定律。
它的基本表述是:在一定的温度下,气体或液体的溶解度随着压力的升高而增加。
这个定律适用于气体和液体的溶解度,但是在气体的溶解度计算中,由于气体分子之间的相互作用力较小,因此亨利定律通常更为准确。
在实际应用中,拉乌尔定律和亨利定律经常被用来计算化学反应中气体的溶解度。
例如,在某些化学反应中,气体的溶解度是反应速率的重要影响因素。
通过应用拉乌尔定律和亨利定律,我们可以计算出在不同温度和压力下气体的溶解度,从而更好地理解反应的动力学过程。
另一方面,拉乌尔定律和亨利定律在环境科学中也具有非常重要的应用。
例如,在海洋环境中,气体的溶解度对海洋生态系统和海洋化学循环过程具有重要影响。
通过应用这些定律,我们可以更好地理解海洋生态系统和化学循环的过程,预测海洋环境的变化和响应措施。
总之,拉乌尔定律和亨利定律都是热力学中非常重要的定律,它们分别描述了气体和液体中溶解度与温度、压力之间的关系。
尽管它们之间存在着一些区别,但在应用中它们经常被一起使用,以便更好地理解物质的溶解过程。
拉乌尔定律与亨利定律

PB = k X,B xB PB = kb,B bB PB = kC,B CB
+
应该注意,气体在液体里的分子状态应该相同 应该注意 气体在液体里的分子状态应该相同. 气体在液体里的分子状态应该相同
HCl ( g ) → H (aq ) + Cl (aq )
定律不适用
问题:对于 气体在H 的溶解 定律是否适用? 的溶解,定律是否适用 问题 对于CO2气体在 2O的溶解 定律是否适用 对于
课堂练习题P161,3-4 课堂练习题
提示: 提示
P=101325Pa(PN278%),有一个比例或者亨利系数 约 有一个比例或者亨利系数.约 有一个比例或者亨利系数 血液).不用 的系数。 为1.39× 10-5kg(N2)/kg(血液 不用 × 血液 不用P134例2的系数。 例 的系数 暂不考虑温度对系数的影响。 暂不考虑温度对系数的影响。即在体温时仍近似 用上面的系数。 用上面的系数。 压力增大, 溶解增加。 压力增大,N2溶解增加。 p = gh
ρ
必须考虑60m的水压;水柱高度与Pa的换算。 的水压;水柱高度与 的换算 的换算。 必须考虑 的水压 不要忘了水面上的压力. 不要忘了水面上的压力 或者直接计算压力增加值;因为必 气泡 V = 4 π r 3 或者直接计算压力增加值 因为必 3 须考虑常压时N 的残留即溶解。 须考虑常压时 2的残留即溶解。 另外, 的应用; 另外,PV=nRT的应用;P=101.325KPa 的应用
水的饱和蒸气压
10 C 1227.8 Pa 20 C 2337.8 Pa ° 30 C 4242.8 Pa
相对湿度(relative humidity)RH(% ) 相对湿度 20℃ ,空气中的 H2O为1568.9 Pa ℃ 空气中的 空气中的P RH=(1568.9/2337.8) ×100% =67.110 % 问题:相对湿度的可能的最大值与最小值分别是 问题 相对湿度的可能的最大值与最小值分别是? 相对湿度的可能的最大值与最小值分别是
物理化学2.3拉乌尔定律和亨利定律

pB T一定 (平衡)
xB
pB=kx,BxB
稀溶液的气、液平衡
kx,B 亨系数
pB=kx,BxB
kx,B 亨利系数 当溶质的组成标度用bB 表示时,亨利定律可表示成:
p B k b, B bB
注意:kx,B ,kb,B 的单位是不同的。
Pa
Pa/b
pB=kx,BxB
注意
亨利定律的适用条件及对象是稀溶液中的溶质,既 溶质分子B周围几乎全是溶剂A分子。
pA,p真B,p空C yA, yB, yC
T一定 (平衡)
xAA,,Bx,BC,x…C
多组分系统的气、液平衡
2. 拉乌尔定律
表述为:
平衡时,稀溶液中溶剂A在 气相中的蒸气分压等于同一 温度下,该纯溶剂的饱和蒸 气压p*A与该溶液中溶剂的摩 尔分数xA的乘积。
数学表达式为:
pA
p
* A
x
A
pA,pB1, yA, yB1, xA, xB1,
T一定 (平衡)
稀溶液的气、液平衡
注意
pA
p
* A
x
A
拉乌尔定律的适用条件及对象是:
稀溶液中的溶剂,既溶剂分子A 周围几乎全是 其它的A分子;
理想液态混合物中各组分。
3. 亨利定律
表述为:
一定温度下,稀溶液中挥发 性溶质B在平衡气相中的分压 力pB与该溶质B在平衡液相中 的摩尔分数xB成正比。
第二章 多组分系统热力学
《基础物理化学》 高等教育出版社,2011
§2.4 稀溶液的两个经验定律
—— 拉乌尔定律和亨利定律
1. 液态混合物和溶液的气、液平衡
设图中系统由组分A,B,C……组成液态混合物或溶液,
亨利定律与拉乌尔定律的区别和联系

亨利定律与拉乌尔定律的区别和联系
亨利定律和拉乌尔定律都是物理化学的基本定律,二者区别和联系如下:
区别:
适用范围:亨利定律适用于气体在溶液中的溶解度,而拉乌尔定律适用于难挥发非电解质稀溶液的蒸气压。
定律形式:亨利定律形式为p=kX(A),其中p为气体分压,k为亨利常数,X(A)为气体A在溶液中的摩尔分数。
拉乌尔定律形式为p(B)=p X(B)=p(1-X(A)),其中p为溶剂饱和蒸气压,X(B)为溶剂在溶液中的摩尔分数,X(A)为溶质在溶液中的摩尔分数。
应用领域:亨利定律主要用于气体在液体中的溶解度计算,而拉乌尔定律主要用于蒸馏和吸收等过程的计算。
联系:
亨利定律和拉乌尔定律都是溶液热力学的基本定律,对相平衡和溶液热力学函数的研究起指导作用。
在一定温度下,气体在溶液中的溶解度与该气体溶在溶液内的摩尔浓度成正比,这是亨利定律的核心内容,也是拉乌尔定律的一个重要应用。
总之,亨利定律和拉乌尔定律虽然有不同的适用范围和形式,但都是溶液热力学的基本定律,对相平衡和溶液热力学函数的研究起指导作用。
拉乌尔定律和亨利定律的适用范围为稀溶液

§ 3⋅7 稀溶液拉乌尔定律和亨利定律的适用范围为稀溶液,只要浓度足够稀(但确有某些溶液在相当浓的范围),溶剂符合拉乌尔定律,溶质符合亨利定律的溶液称为稀溶液。
一、各组分的化学势溶剂服从拉乌尔定律,气液平衡时液相中溶剂A 的化学势μA 与气相中A 的化学势μA g相等,此时气相中A 的分压p A 为溶剂的蒸汽压,有μμμμθθθθA A gA A A A A T RT p p T RT p x p ==+=+()ln /()ln /*=+μA A T p RT x *(.)ln (3—78)其中μμθθA A A T p T RTp p **(.)()/=+稀溶液中的溶剂与理想溶液中各组分有相同的化学势的表示式。
μA T p *(.)是T.p 时纯液体A 的化学势。
通常选择标准态的压力为p θ(101.325kPa),标准态化学势μθA T p *(.)与μA T p *(.)偏离不会很大。
稀溶液的溶质符合亨利定律,亨利定律有三种不同的表示式,稀溶液的溶质化学势亦有三种不同的表示式。
溶质在气液两相达到平衡,有μμμμθθθθB B gB B B x B T RT p p T RT k x p ==+=+()ln /()ln /=+μB B T p RT x *(.)ln (3—79)式中μμθθB B x T p T RT k p *(.)()ln /=+由式(3-79),当x B =1,即纯液体B 时,μμB B T p =*(,)。
但式中的μB T p *(,)并不是纯液体B 的化学势,因为当x B =1时,亨利定律已不适用,式(3-79)不能扩展应用在X B 接近于1的浓度范围。
μB T p *(.)是x B =1,满足亨利定律p B =k x x B 的假想态的化学势,即图(3.5)中R 点表示的状态。
x B =1,溶质已不服从亨利定律,故R 点是假设服从亨利定律,外推得到的假想态,此时溶质所处真实的状态在W 点处。
拉乌尔定律和亨利定律的适用范围为稀溶液

§ 3⋅7 稀溶液拉乌尔定律和亨利定律的适用范围为稀溶液,只要浓度足够稀(但确有某些溶液在相当浓的范围),溶剂符合拉乌尔定律,溶质符合亨利定律的溶液称为稀溶液。
一、各组分的化学势溶剂服从拉乌尔定律,气液平衡时液相中溶剂A 的化学势μA 与气相中A 的化学势μA g 相等,此时气相中A 的分压p A 为溶剂的蒸汽压,有μμμμθθθθA A g A A A A A T RT p p T RT p x p ==+=+()ln /()ln /*=+μA A T p RT x *(.)ln (3—78)其中μμθθA A A T p T RTp p **(.)()/=+稀溶液中的溶剂与理想溶液中各组分有相同的化学势的表示式。
μA T p *(.)是T.p 时纯液体A 的化学势。
通常选择标准态的压力为p θ(101.325kPa),标准态化学势μθA T p *(.)与μA T p *(.)偏离不会很大。
稀溶液的溶质符合亨利定律,亨利定律有三种不同的表示式,稀溶液的溶质化学势亦有三种不同的表示式。
溶质在气液两相达到平衡,有μμμμθθθθB B g B B B x B T RT p p T RT k x p ==+=+()ln /()ln /=+μB B T p RT x *(.)ln (3—79)式中μμθθB B x T p T RT k p *(.)()ln /=+由式(3-79),当x B =1,即纯液体B 时,μμB B T p =*(,)。
但式中的μB T p *(,)并不是纯液体B 的化学势,因为当x B =1时,亨利定律 已不适用,式(3-79)不能扩展应用在X B 接近于 1的浓度范围。
μB T p *(.)是x B =1,满足亨利 定律p B =k x x B 的假想态的化学势,即图(3.5) 中R 点表示的状态。
x B =1,溶质已不服从 亨利定律,故R 点是假设服从亨利定律,外 推得到的假想态,此时溶质所处真实的状态 在W 点处。
高中化学奥林匹克竞赛辅导讲座:第2讲《溶液》
高中化学奥林匹克竞赛辅导讲座第2讲溶液【竞赛要求】分散系。
胶体。
溶解度。
亨利定律。
稀溶液通性。
溶液浓度。
溶剂(包括混合溶剂)。
【知识梳理】一、分散系的基本概念及分类一种或几种物质以细小的粒子分散在另一种物质中所形成的体系称分散系。
被分散的物质称分散质,把分散质分开的物质称分散剂。
按照分散质粒子的大小,常把分散系分为三类,见表2-1。
*在体系中物理性质和化学性质完全相同的一部分称相。
分子分散系又称溶液,因此溶液是指分散质分子、离子或原子均匀地分散在分散剂中所得的分散系。
溶液可分为固态溶液(如某些合金)、气态溶液(如空气)和液态溶液。
最常见也是最重要的是液态溶液,特别是以水为溶剂的水溶液。
二、溶解度和饱和溶液1、溶解度在一定温度下的饱和溶液中,在一定量溶剂中溶解溶质的质量,叫做该物质在该温度下的溶解度。
易溶于水的固体的溶解度用100 g水中溶解溶质的质量(g)表示;一定温度下,难溶物质饱和溶液的“物质的量”浓度也常用来表示难溶物质的溶解度。
例如298 K氯化银的溶解度为1×10-5 mol·L-1。
2、饱和溶液在一定温度下,未溶解的溶质跟已溶解的溶质达到溶解平衡状态时的溶液称为饱和溶液。
在饱和溶液中,存在着下列量的关系:溶质的质量= 常数溶液的质量溶质的质量= 常数溶剂的质量3、溶解度与温度溶解平衡是一个动态平衡,其平衡移动的方向服从勒沙特列原理。
一个已经饱和的溶液,如果它的继续溶解过程是吸热的,升高温度时溶解度增大;如果它的继续溶解过程是放热的,升高温度时溶解度减小。
大多数固体物质的溶解度随温度的升高而增大。
气体物质的溶解度随着温度的升高而减小。
4、溶解度与压强固体或液体溶质的溶解度受压力的影响很小。
气体溶质的溶解度受压力影响很大。
对于溶解度很小,又不与水发生化学反应的气体,“在温度不变时,气体的溶解度和它的分压在一定范围内成正比”,这个定律叫亨利(Henry)定律。
其数学表达式是:C g = K g·p g (2-1)式中p g为液面上该气体的分压,C g为某气体在液体中的溶解度(其单位可用g·L-1、L(气)·L1 (水)、mol·L-1表示),K g称为亨利常数。
拉乌尔定律和亨利定律

91.3k Pa (1- 0.0120) KHx,B 0.0120
KHx,B 927k Pa
例2 97.11℃时,wB=0.0300的乙醇水溶液的蒸气总 压 为 101.325kPa , 纯 水 的 pA*=91.3kPa 。 设 可 看 作理想稀溶液,试求:xB=0.0200 时的蒸气总压 和气相组成。
利用吉布斯–杜亥姆方程证明,如果溶剂遵守拉乌 尔定律,溶质必定遵守亨利定律。
dfB fB dxB xB
ln{ fB} ln xB lnC
fB
CxB
xB ,
fB xB
C
实验事实告诉我们:对于溶质,下式成立
K Hx,B
lim
xB 0
fB xB
所以 C K Hx,B ,则
fB K Hx,B xB
(1y)A=0.2p0A0时 ,pA液x相A 的xA和蒸气总压。 9.96kPa 0.200 1.99kPa
pB pB xB pB (1 xA )
2.97kPa(1 0.200) 2.38kPa
p pA pB
1.99kPa 2.38kPa 4.37kPa
例1 苯(A)和甲苯(B)的混合物可看作理想混合物。
20℃ 时 它 们 的 饱 和 蒸 气 压 分 别 为 9.96kPa 和
2.97kPa。试计算:(1) xA=0.200 时,混合物中苯 和 甲 苯 的 分 压 和 蒸 气 总 压 ; (2) 当 蒸 气 的
(yA2=)0.200时y A,液pp相A 的 xpAA*和x蒸pA A*气x Ap总B* 压x B。
当压力较高,气相不能看作理想气体
路易斯–兰德尔规则
fi
f
* i
xi
fi pxii
拉乌尔定律和亨利定律

拉乌尔定律和亨利定律--溶液的蒸气压我们知道,液体可以蒸发成气体,气体也可以凝结为液体。
在一定的温度下,二者可以达成平衡,即液体的蒸发速度等于蒸气的凝结速度。
达到这种平衡时,蒸气有一定的压力,这个压力就叫做此液体的饱和蒸气压(简称蒸气压)。
蒸气压与温度有关,温度越高,分子具有的动能越大,蒸发速度越快,因而蒸气压越大。
溶液的蒸气压除与温度有关外,还与浓度有关。
拉乌尔定律和亨利定律所描述的就是溶液蒸气压和浓度之间的关系。
3.3.1 拉乌尔定律1887年法国物理学家拉乌尔(Raoult)在溶液蒸气压实验中总结出著名的拉乌尔定律。
拉乌尔定律指出:如果溶质是不挥发性的,即它的蒸气压极小,与溶剂相比可以忽略不计,则在一定的温度下,稀溶液的蒸气压等于纯溶剂的蒸气压与其克分子分数的乘积。
即式中p1--溶剂的蒸气压,溶质是不挥发性时,即为溶液的蒸气压;x1 ──溶液中溶剂的克分分数。
拉乌尔定律还可以表述为:在一定的温度下,当不挥发物质溶解在溶剂中时,溶液的蒸气压相对下降等于溶质的克分子分数。
即式中△p——溶液的蒸气压下降值;x2——溶质的克分子分数。
对于溶质是挥发性物质,它的蒸气压不能忽略时,拉乌尔定律仍然适用,但要注意此时p1是溶液中溶剂的蒸气压。
3.3.2 亨利定律亨利定律是1803年由亨利在对气体在液体中溶解度的实验研究中得出的。
亨利定律指出:在一定的温度下,气体在液体中的溶解度和该气体的平衡分压成正比。
即p2=k x x2 (3.22)式中x2 ──气体溶质在溶液中的克分子分数;p2──该气体的平衡分压;k x──常数。
亨利定律中的浓度单位除可用克分子分数外,也可用其他浓度单位表示,但是采用不同的单位时,常数k不同。
亨利定律可以推广到具有挥发性溶质溶于液体的稀溶液。
但是需要特别注意的是,亨利定律的应用是有条件的:只有当溶质在液相和在气相里都以相同的质点存在时亨利定律才适用。
由于气体在金属中往往以原子状态存在,因此气体在金属中的溶解往往不服从亨利定律。
拉乌尔定律与亨利定律课件

拉乌尔定律适用于不发生化学反 应的情况,而亨利定律可以应用
于化学反应和电离的情况。
两个定律的适用范 围
拉乌尔定律主要用于稀溶液中溶质分压的计算,是研究化学 反应中气体浓度的变化和反应速率的重要基础。
亨利定律主要用于气体在液体中的溶解度计算,以及工业生 产过程中的吸收、解吸等过程的设计和控制。
数据采集与处理
数据记录
记录实验过程中不同压力、温度 下的气体溶解度数据,以及对应 的实验条件。
数据处理
对采集到的数据进行整理、分析 和计算,提取有用的信息,如溶 解度常数、溶解度等。
数据分析与解 释
数据统计
对处理后的数据进行统计,计算 平均值、标准差等指标,评估数
据的可靠性和稳定性。
结果展示
通过图表、表格等方式展示数据 分析结果,对比拉乌尔定律和亨 利定律的符合程度,分析误差产
拉乌尔定律和亨利定律都是描述 气体溶质在液体中的溶解度的规
律。
两个定律都指出,气体的溶解度 与其分压成正比。
两个定律都适用于一定温度和压 力条件下,气体的溶解度与分压
之间的关系。
两个定律的不同之 处
拉乌尔定律适用于稀溶液,而亨 利定律适用于任何浓度的溶液。
拉乌尔定律中的比例系数是溶质 的摩尔溶解度,而亨利定律中的
即当气体的压力增加时,其溶解度也 会相应增加
亨利定律的应用场景
在化工生产中,常常需要将气体溶解在液体中,利用亨利定律可以指导生产过程 中的压力控制,以获得所需的溶解度和产品纯度
在环保领域,亨利定律可以用于计算气体在水中的溶解度,从而评估气体对水生 生态的影响
04
拉乌尔定律与亨利定律的比较
两个定律的相同之 处
拉乌尔定律和亨利定律的区别

拉乌尔定律和亨利定律的区别
拉乌尔定律和亨利定律是热力学中两个重要的定律,它们都与气体的性质有关,但是它们的研究对象和研究内容有所不同。
拉乌尔定律是指在一定温度下,气体的体积与压强成反比。
也就是说,当气体的压强增加时,它的体积会减小,反之亦然。
这个定律是由法国物理学家拉乌尔在19世纪初发现的,它适用于理想气体和实际气体。
理想气体是指分子之间没有相互作用力的气体,而实际气体则是指分子之间存在相互作用力的气体。
虽然实际气体的体积与压强的关系不是完全符合拉乌尔定律,但是在一定范围内,它仍然是适用的。
亨利定律则是指在一定温度下,气体溶解在液体中的浓度与气体的压强成正比。
也就是说,当气体的压强增加时,它在液体中的溶解度也会增加,反之亦然。
这个定律是由英国化学家亨利在18世纪末发现的,它适用于气体在液体中的溶解。
亨利定律的应用非常广泛,例如在饮料工业中,二氧化碳的溶解度与压强的关系就是根据亨利定律来计算的。
从以上的介绍可以看出,拉乌尔定律和亨利定律的研究对象和研究内容有所不同。
拉乌尔定律研究的是气体的体积与压强的关系,而亨利定律研究的是气体在液体中的溶解度与压强的关系。
虽然它们的研究对象不同,但是它们都是热力学中非常重要的定律,对于我们理解气体的性质和应用气体有很大的帮助。
拉乌尔定律和亨利定律PPT课件

拉乌尔定律和亨利定律是实验现象的总结,描述 了稀溶液溶剂和溶质的逸度与组成的关系。
1.拉乌尔定律(Raoult’s Law)
恒温下的稀溶液,溶剂的蒸气分压等于同 温度下纯溶剂的饱和蒸气压与溶液中溶剂 摩尔分数的乘积,即
pA pA xA
二元系
xA xB 1
pA pA pA xB
pB K Hb,BbB
可看作是一种虚拟的、具有无限稀释溶液性 质的bB=1mol·kg-1的溶液中溶质的蒸气压
pB K Hc,BcB
可看作是一种虚拟的、具有无限稀释溶液性 质的cB=1mol·dm-3的溶液中溶质的蒸气压
利用吉布斯–杜亥姆方程证明,如果溶剂遵守拉乌
尔定律,溶质必定遵守亨利定律。
利用吉布斯–杜亥姆方程证明,如果溶剂遵守拉乌 尔定律,溶质必定遵守亨利定律。
dfB fB dxB xB
ln{ fB} ln xB lnC
fB
CxB
xB ,
fB xB
C
实验事实告诉Байду номын сангаас们:对于溶质,下式成立
K Hx,B
lim
xB 0
fB xB
所以 C K Hx,B ,则
fB K Hx,B xB
xAdA xBdB 0
i i
(g) RT ln fi p
di RT dfi fi
xA dfA fA xB dfB fB 0
fA
f
A
xA
dfA fAdxA dfA fA dxA xA
xB dfB fB xA dfA fA xA dxA xA dxA dxB dfB fB dxB xB
1.拉乌尔定律(Raoult’s Law)
拉乌尔定律亨利定律

本章主要讨论液态旳非电解质溶液。 溶剂(solvent)和溶质(solute) 假如构成溶液旳物质有不同旳状态,一般将液态
物质称为溶剂,气态或固态物质称为溶质。 假如都是液态,则把含量多旳一种称为溶剂,含
量少旳称为溶质。
1
引言
混合物(mixture) 多组分均匀体系中,溶剂和溶质不加区别,各组
对理想稀溶液, 有 p = pA*xA + kx,B xB 先由上式计算97.11℃时乙醇溶在水中旳亨利系数, 即 101.3 kPa = 91.3 kPa(1-0.0300) + kx(乙醇)×0.0300
解得 kx(乙醇) = 425 kPa , 于是求得当x(乙醇) = 0.0200时 p(乙醇) = kx(乙醇)x(乙醇) = 425 kPa×0.0200 = 8.5 kPa p(水) = p*(水)x(水) = 91.30 kPa×(1-0.0200) = 89.5 kPa
0.0379旳水, 假定拉乌尔定律对每相中旳溶剂都能合用, 已知
37.55℃时, 纯乙酸乙酯旳蒸气压力是22.13kPa, 纯水旳蒸气压力
是6.399kPa, 试计算:
(1) 气相中酯和水蒸气旳分压;
(2) 总旳蒸气压力(忽视作为溶质时旳A和B旳气相压力).
(乙酸乙酯和水旳摩尔质量分别为88.10gmol1和18.02gmol1)
CB:摩尔浓度 mol/L kC,B单位:Pa .L.mol-1
pB kb,BbB
bB:质量摩尔浓度 mol/kg kb,B单位:Pa .kg.mol-1
7
亨利定律
亨利定律合用条件: (1)挥发性溶质,例如苯在水中溶解;O2、N2溶解于水中 (2)PB指旳是溶质在该溶液上方蒸汽中旳分压,假如同步 有多种挥发性溶质,则每一种均符合亨利定律。溶液约稀, 符合亨利定律越好
拉乌尔、亨利

1偏差的情况拉乌尔定律:在等温等压下,对溶液中组元i ,当其组元的浓度1i X →时,该组元在气相中的蒸气压i P 与其在溶液中的浓度i X 成线性关系。
数学描述为:其中,i P ----组元i 在气相中的蒸气压;;i P *----纯组元i 的蒸气压;i X ----组元i 在液相中的摩尔分数;"1i i X X ≤≤----组元i 服从拉乌尔定律的定义域。
亨利定律: 在等温等压下,对溶液中的组元i ,当其组元的浓度0(%0)i X or i →→时,该组元在气相中的蒸气压i P 与其在溶液中的浓度(%)i X or i 成线性关系。
数学描述为:或 其中,i P ----组元i 在气相中的蒸气压;,%,,H i i k k ----组元i 的浓度等于1或1%时,服从亨利定理的蒸气压;i X ,[]%i ----组元i 在液相中的摩尔分数或质量百分浓度;'0i i X X ≤≤,'0%%i i ≤≤----组元i 服从亨利定律的定义域。
2)掌握拉乌尔定律和亨利定律的区别与联系拉乌尔定律与亨利定律在以下方面有区别关于拉乌尔定律:● 是描述溶剂组元i 在液相中浓度与其在气相中的蒸气压的线性关系;在1i X −−→时,在定义域"1i i X X ≤≤成立;● 线性关系的斜率是纯溶剂i 的蒸气压;● 组元i 的浓度必须用摩尔分数。
而亨利定律:● 是描述溶质组元i 在液相中浓度与其在气相中的蒸气压的线性关系;在0i X −−→或%0i −−→时,在定义域'0i i X X ≤≤或'0%%i i ≤≤成立; ● 线性关系的斜率是从服从亨利定律的线性关系延长到1i X =的蒸气压(当浓度用摩尔分数,实际上是假想纯溶质i 的蒸气压)或从服从亨利定律的线性关系延长到%1i =的蒸气压(当浓度用质量百分浓度,实际上是假想%i 的蒸气压);● 组元i 的浓度可以用摩尔分数,也可以用质量百分浓度。
4.5_拉乌尔定律与亨利定律

§4.5 拉乌尔定律与亨利定律
本章讨论的溶液是指非电解质溶液。讨论的性质为它们 的蒸气压。
• 理想液态混合物中的任一组分(溶剂及溶质)的蒸气压和 理 想稀溶液中溶剂的蒸气压均可用拉乌尔定律描述。 • 理想稀溶液中挥发性溶质的蒸气压可用亨利定律描述。
pA pA pA pA xB ( xB 0)
pA 是加入溶质之后引起溶剂蒸气压的下降值。
拉乌尔定律最初是从含有不挥发性非电解质的 溶液中总结出来的,但后来进一步的实验证明,在含 有挥发性非电解质的稀薄溶液中,溶剂也遵守拉乌尔 定律。但由于在该情况下,溶液的蒸气压为溶剂与溶 质的蒸气压之和,因此溶液的蒸气压不一定低于同温 同压下纯溶剂的蒸气压用力不同于纯液体 B(若纯液体 B 存在)中的 B-B 间的作用力,所以亨利定律中的比例系数kx,B不 * 同于纯 B 的饱和蒸气压 pB
拉乌尔定律对于溶剂,及亨利定律对于挥发性溶质,仅对 于无限稀溶液,即理想稀溶液成立。
实际上在溶质摩尔分数近于 0 的很小范围内成立。若 A 与 B 性质相近,适用的范围还要宽些。
3 / 46.069g mol1 xB 3 / 46.069g mol1 97 / 18.015g mol1
0.01195
稀溶液的总蒸气压与各组分的摩尔分数的关系:
p pA pB p* A xA kx,B xB
将题给的 wB= 3% 的溶液的数据代入,求得:
例 4.4.1 在 97.11°C时,纯水(H2O)的饱和蒸气压为91.3 kPa。在此温度下,乙醇(C2H5OH)的质量分数为 3%的 乙醇水溶液上,蒸气总压为 101.325 kPa。 今有另一乙醇的摩尔分数为2%的乙醇水溶液,求此水溶 液在 97.11°C 下的蒸气总压。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
• 开启易拉罐后, 压力减小, CO2气体的溶解度随之减 小, 从液体中释放出来.
• 热玻棒插入碳酸饮料中, 亨利常数随之增大, CO2 5 气体从液体中释放出来 .
4. 亨利定律的其它形式 当溶质的组成用cB , bB 等表示时, 亨利定律可表示成:
pB kc ,B cB kb ,B bB k x ,B xB
注意 : k x ,B , kc ,B , kb ,B的 大小和单位都是不同的 .
5. 几点说明 • 同拉乌尔定律,亨利定律的应用条件与对象是稀溶液(严格 地说是理想稀溶液)中的溶质, 且溶质在两相中的分子形态必 须相同. (氯化氢、氨气溶于水不适用)
• 当有几种气体共存时, 每一种分别适用于亨利定律. • 亨利常数随温度升高而增大. • 亨利常数的大小和单位与采用的组成表示方式有关.
(2) p = pA + pB =(6.306 + 18.56)kPa = 24.86 kPa
3
另外若溶质和溶剂都有挥发性,溶液 仍为理想溶液,拉乌尔定律仍然适用, 可将分别求出溶质及溶剂的蒸气压
4
2. 亨利定律
实验表明:一定温度下, 稀溶液中挥发性溶质B在平衡气相中的 分压力pB与该溶质B在平衡液相中的摩尔分数xB成正比. 亨利定律: 气体的溶解度与气体的分压呈正比 pB = kx, BxB kx, B 亨利常数, 与T 及溶剂, 溶质的性质有 关
k x ,B
p
B
xB
101325Pa 3.61 10
5
2.81GPa
又
故
bB
k b ,B
4.490 10 2 dm 3 kg 1 22.4dm 3 mol 1
2.00 10 3 mol kg 1
pB 101325Pa 7 1 5 . 17 10 Pa kg mol bB 2.00 10 3 mol kg 1
(1) pA pB p* A xA
* pB xB
0.9325/18. 02 6.399kPa 6.306kPa 0.9325/ 18.02 0.0675/ 88.10 0.9621/88. 10 22.13kPa 18.56kPa 0.0379/ 18.02 0.9621/ 88.10
6
0℃, 101325Pa时, 氧气在水中的溶解度为4.490×102 dm3kg1, 试求0℃时, 氧气在水中的亨利系数kx,O和kb,O.
0℃ , 101325Pa 时, 氧气的摩尔体积为 22.4dm3· mol 1
4.490 10 2 dm 3 22.4dm 3 mol 1 xB 3.61 105 1000g 4.490 10 2 dm 3 18g mol 1 22.4dm3 mol 1
水溶液
• 溶液有电解质溶液和非电解质溶液之分。 • 非电解质溶液性质比电解质溶液的简单 些,故人们最先认识非电解质溶液的规 律。
非电解质溶液通性 (p299-305)
电解质溶液通性 (p305-307)
1
1. 拉乌尔定律
单位时间内由液面蒸发出的分子数和由 气相回到液体内的分子数相等时,气、液两 相处于平衡,这时的气体压强叫该溶液的饱 和蒸气压,简称蒸气压
T一定
实验得出:一定温度下, 稀溶液溶 剂的 p与 p*B , xB的关系: *
* pB
p pB xB
p
:表示溶剂在该温度下的饱和蒸汽压 :表示溶剂的物质的量分数 :表示溶液的压强
• 稀溶液溶剂的 PB 与xB关系
xB p
xB
拉乌尔定律的适用条件及对象:
理想溶液,但近似地适用于非电解质
稀溶液
2
水(A)和乙酸乙酯(B)不完全混溶, 在37.55℃时两液相呈平 衡. 一相中含质量分数为w(B) = 0.0675的酯, 另一相中含w(A) = 0.0379的水, 假定拉乌尔定律对每相中的溶剂都能适用, 已 知37.55℃时, 纯乙酸乙酯的蒸气压力是22.13kPa, 纯水的蒸 气压力是6.399kPa, 试计算: (1) 气相中酯和水蒸气的分压; (2) 总的蒸气压力(忽略作为溶质时的A和B的气相压力). (乙酸乙酯和水的摩尔质量分别为88.10gmol1和18.02gmol1)
