运动路径长度问题
动点问题中的最值、最短路径问题解析版
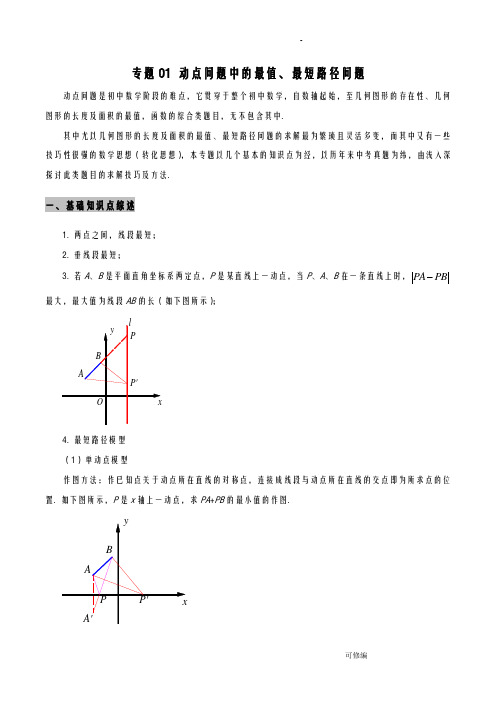
专题01 动点问题中的最值、最短路径问题动点问题是初中数学阶段的难点，它贯穿于整个初中数学，自数轴起始，至几何图形的存在性、几何图形的长度及面积的最值，函数的综合类题目，无不包含其中.其中尤以几何图形的长度及面积的最值、最短路径问题的求解最为繁琐且灵活多变，而其中又有一些技巧性很强的数学思想（转化思想），本专题以几个基本的知识点为经，以历年来中考真题为纬，由浅入深探讨此类题目的求解技巧及方法.一、基础知识点综述1. 两点之间，线段最短；2. 垂线段最短；3. 若A 、B 是平面直角坐标系两定点，P 是某直线上一动点，当P 、A 、B 在一条直线上时，PA PB 最大，最大值为线段AB 的长（如下图所示）；（1）单动点模型作图方法：作已知点关于动点所在直线的对称点，连接成线段与动点所在直线的交点即为所求点的位置. 如下图所示，P 是x 轴上一动点，求PA +PB 的最小值的作图.（2）双动点模型P是∠AOB一点，M、N分别是边OA、OB上动点，求作△PMN周长最小值.作图方法：作已知点P关于动点所在直线OA、OB的对称点P’、P’’，连接P’P’’与动点所在直线的交点M、N即为所求.OBPP'P''MN5. 二次函数的最大（小）值()2y a x h k=-+，当a>0时，y有最小值k；当a<0时，y有最大值k.二、主要思想方法利用勾股定理、三角函数、相似性质等转化为以上基本图形解答. （详见精品例题解析）三、精品例题解析例1. （2019·凉山州）如图，正方形ABCD中，AB=12，AE=3，点P在BC上运动（不与B、C重合），过点P作PQ⊥EP，交CD于点Q，则CQ的最大值为例2.（2019·凉山州）如图，已知A、B两点的坐标分别为（8,0），（0,8）. 点C、F分别是直线x=－5和x轴上的动点，CF=10，点D是线段CF的中点，连接AD交y轴于点E，当△ABE面积取最小值时，tan∠BAD=（）x y A B C F D EO x=-5A .817B . 717C . 49D . 59例3.（2019·）如图，矩形硬纸片ABCD 的顶点A 在y 轴的正半轴及原点上滑动，顶点B 在x 轴的正半轴及原点上滑动，点E 为AB 的中点，AB =24,BC =5,给出结论：①点A 从点O 出发，到点B 运动至点O 为止，点E 经过的路径长为12π；②△OAB 的面积的最大值为144；③当OD 最大时，点D 的坐标为)2626125,262625(，其中正确的结论是（填写序号）.例4.（2019·XX ）已知抛物线2y x bx c =-+（b 、c 为常数，b >0）经过点A (－1,0)，点M (m ,0)是x 轴正半轴上的动点，若点Q （1,2Q b y +22AM QM +332时，求b 的值.例5. （2019·）如图，一副含30°和45°角的三角板ABC 和EDF 拼合在个平面上，边AC 与EF 重合，12AC cm ．当点E 从点A 出发沿AC 方向滑动时，点F 同时从点C 出发沿射线BC 方向滑动．当点E 从点A 滑动到点C 时，点D 运动的路径长为cm ；连接BD ，则△ABD 的面积最大值为2cm ．例6. （2019·）如图，在菱形ABCD 中，连接BD 、AC 交于点O ，过点O 作OH ⊥BC 于点H ，以O 为圆心，OH 为半径的半圆交AC 于点M .（1）求证：DC 是圆O 的切线；（2）若AC =4MC ，且AC =8，求图中阴影部分面积；（3）在（2）的前提下，P 是线段BD 上的一动点，当PD 为何值时，PH +PM 的值最小，并求出最小值. ABC DH O M N专题01 动点问题中的最值、最短路径问题（解析）例1. （2019·凉山州）如图，正方形ABCD中，AB=12，AE=3，点P在BC上运动（不与B、C重合），过点P作PQ⊥EP，交CD于点Q，则CQ的最大值为【答案】4.【解析】解：∵PQ⊥EP，∴∠EPQ=90°，即∠EPB+∠QPC=90°，∵四边形ABCD是正方形，∴∠B=∠C=90°，∠EPB+∠BEP=90°，∴∠BEP=∠QPC，∴△BEP∽△CPQ，∴BE BP CP CQ=，∵AB=12，AE=3，∴BE=9，设CQ=y，BP=x，CP=12－x，（0<x<12）∴912xx y=-，即()()21216499x xy x-==--+，∴当x=6时，y有最大值为4，即CQ的最大值为4.【点睛】此题为“一线三直角模型”，解题方法为相似三角形性质求解，综合利用二次函数的性质求解最值问题.例2.（2019·）如图，已知A、B两点的坐标分别为（8,0），（0,8）. 点C、F分别是直线x=－5和x轴上的动点，CF=10，点D是线段CF的中点，连接AD交y轴于点E，当△ABE面积取最小值时，tan∠BAD=（）A . 817B . 717C . 49D . 59【答案】B .【解析】解：S △ABE =142BE OA BE ⨯⨯=,当BE 取最小值时，△ABE 面积为最小值.设x =－5与x 轴交于点G ，连接DG ，因为D 为CF 中点，△CFG 为直角三角形，所以DG =152CD =,∴D 点的运动轨迹为以G 为圆心，以5半径的圆上，如图所示 xyABD E O x=-5G由图可知：当AD 与圆G 相切时，BE 的长度最小，如下图，xyABD E O x=-5G H过点E 作EH ⊥AB 于H ，∵OG =5，OA =8，DG =5，在Rt △ADG 中，由勾股定理得：AD =12，△AOE ∽△ADG ， ∴AO AD OE DG =, 求得：OE =103， 由OB =OA=8，得：BE =143，∠B =45°，AB =82 ∴EH =BH =27223BE =,AH =AB -BH =1723， ∴tan ∠BAD =727317172EH AH ==, 故答案为B .【点睛】此题解题的关键是找到△ABE 面积最小时即是AD 与D 的远动轨迹圆相切的时刻. 进而构造以∠BAD 为角的直角三角形，利用勾股定理求出边长，代入三角函数定义求解.例3.（2019·）如图，矩形硬纸片ABCD 的顶点A 在y 轴的正半轴及原点上滑动，顶点B 在x 轴的正半轴及原点上滑动，点E 为AB 的中点，AB =24,BC =5,给出结论：①点A 从点O 出发，到点B 运动至点O 为止，点E 经过的路径长为12π；②△OAB 的面积的最大值为144；③当OD 最大时，点D 的坐标为)2626125,262625(，其中正确的结论是（填写序号）.【答案】②③.【解析】解：根据题意可知：OE =12AB =12,即E 的轨迹为以O 为圆心以12为半径的四分之一圆（第一象限的部分），根据弧长公式，得点E 的路径长为：9012180π⨯⨯=6π，故①错误； 因为AB =24,当斜边AB 上的高取最大值时，△OAB 的面积取最大值，点O 在以AB 为直径的圆上（圆心为E ），当OE ⊥AB 时，斜边AB 上的高最大， 所以△OAB 的面积取最大值为：124122⨯⨯=144，故②正确；连接OE 、DE ，得：OD ≤OE +DE ，当O 、E 、D 三点共线时取等号，即OD 的最大值为25，如图，过点D 作DF ⊥y 轴于F ，过点E 作EG ⊥y 轴于G ,25DF OD 即：1225EG DF =，512AF AD EG AE ==, 即：51125AF EG DF ==,设DF =x ，在Rt △ADF 中，由勾股定理得：221255x x ⎛⎫+= ⎪⎝⎭，解得：x =26，在Rt △ODF 中，由勾股定理得：OF =26，即点D 的坐标为)2626125,262625(，故③正确.综上所述，答案为：②③. 例4.（2019·XX ）已知抛物线2y x bx c =-+（b 、c 为常数，b >0）经过点A (－1,0)，点M (m ,0)是x 轴正半轴上的动点.若点Q （1,2Q b y +）在抛物线上，当22AM QM +的最小值为3324时，求b 的值. 【答案】见解析. 【解析】解：∵2y x bx c =-+经过点A (－1,0)，∴1+b +c =0，即21y x bx b =--- ∵点Q （1,2Q b y +）在抛物线2y x bx c =-+上， ∴324Q b y =--， 即13,224b Q b ⎛⎫+-- ⎪⎝⎭， ∵b >0，∴Q 点在第四象限，2222AM QM AM QM ⎛⎫+=+ ⎪⎝⎭所以只要构造出22AM QM ⎛⎫+ ⎪⎝⎭即可得到22AM QM +的最小值取N （1,0），连接AN ，过M 作MG ⊥AN 于G ，连接QM ，如图所示，△AGM 为等腰直角三角形，GM =22AM ，即当G 、M 、Q 三点共线时，GM +MQ 22QM +取最小值， 此时△MQH 为等腰直角三角形，∴QM=2QH=3224b⎛⎫+⎪⎝⎭，GM=22AM=()212m+∴()223332222=21222244bAM QM AM QM m⎛⎫⎡⎤⎛⎫+=++++=⎪⎢⎥⎪⎝⎭⎝⎭⎣⎦①∵QH=MH，∴324b+=12b m+-，解得：m=124b-②联立①②得：m=74，b=4.即当22AM QM+的最小值为3324时，b=4.【点睛】此题需要利用等腰直角三角形将22AM QM+转化为222AM QM⎛⎫+⎪⎝⎭，进而根据两点之间线段最短及等腰三角形性质求解.例5. （2019·）如图，一副含30°和45°角的三角板ABC和EDF拼合在个平面上，边AC与EF重合，12AC cm=．当点E从点A出发沿AC方向滑动时，点F同时从点C出发沿射线BC方向滑动．当点E从点A滑动到点C时，点D运动的路径长为cm；连接BD，则△ABD的面积最大值为2cm．【答案】24-1223623126；【解析】解：如图1所示，当E运动至E’，F滑动到F’时，DD'E'G图1过D ’作D ’G ⊥AC 于G ，D ’H ⊥BC 交BC 延长线于点H ，可得∠E ’D ’G =∠F ’D ’H ，D ’E ’=D ’F ’，∴Rt △E ’D ’G ≌Rt △F ’D ’H ，∴D ’G =G ’H ,∴D ’在∠ACH 的角平分线上，即C ，D ，D ’三点共线.通过分析可知，当D ’E ’⊥AC 时，DD ’的长度最大，随后返回初始D 点，如图2所示，D 点的运动路径为D →D ’→D ，行走路线长度为2DD ’；BD'图2∵∠BAC =30°，AC =12，DE =CD∴BC =CD =DE=由图知：四边形E ’CF ’D ’为正方形，CD ’=EF =12，∴DD ’=CD ’-CD =12-D 点运动路程为2DD ’=24-D'图3如图3所示，当点D 运动至D ’时，△ABD ’的面积最大，最大面积为：'''''''ABC AE D BD F E CF D S S S S ++-△△△正方形=(((211112222⨯+⨯--⨯+⨯=【点睛】准确利用全等、角平分线判定得到D 点的运动轨迹是关键，利用三角函数及勾股定理求解，计算较为繁琐，尤其是利用割补法求解三角形的面积时对学生计算能力要求较高，此题难度较大，新颖不失难度.例6. （2019·）如图，在菱形ABCD 中，连接BD 、AC 交于点O ，过点O 作OH ⊥BC 于点H ，以O 为圆心，OH 为半径的半圆交AC 于点M .（1）求证：DC 是圆O 的切线；（2）若AC =4MC ，且AC =8，求图中阴影部分面积；（3）在（2）的前提下，P 是线段BD 上的一动点，当PD 为何值时，PH +PM 的值最小，并求出最小值.BD【答案】见解析.【解析】（1）证明：过点O 作ON ⊥CD 于N ， AC 是菱形ABCD 的对角线，∴AC 平分∠BCD ，∵OH ⊥BC ，ON ⊥CD ，∴OH =ON ，又OH 为圆O 的半径，∴ON 为圆O 的半径，即CD 是圆O 的切线.（2）由题意知：OC =2MC =4，MC =OM =2，即OH =2，在Rt △OHC 中，OC =2OH ，可得：∠OCH =30°，∠COH =60°，由勾股定理得：CH==23OCH OMHS S S π-=-△阴影扇形（3）作点M 关于直线BD 的对称点M ’，连接M ’H 交BD 于点P ， 可知：PM =PM ’即PH +PM =PH +PM ’=HM ’，由两点之间线段最短，知此时PH +PM 最小， ∵OM ’=OM =OH ，∠MOH =60°，∴∠MM ’H =30°=∠HCM ，∴HM ’=HC=即PH +PM的最小值为在Rt △M ’PO 及Rt △COD 中，OP =OM ’ tan 30°=3，OD =OCtan 30°=3， 即PD =OP +OD=B D。
五年级奥数上第4讲环形路线
A
B
练习四：
有一个环形跑道，甲、乙两人分别从A、B两地出发，相向而行，乙的速度快于甲， 第一次相遇在距离A点100米处的C点，第二次相遇在距离B点200米处的地点，已知 A、B长是跑道总长的四分之一，请问跑道周长为多少米？
A C
B
D
挑战极限
例题五：
小鹿和小山羊在某个环形跑道上练习跑步项目，小鹿比小山羊稍快，如果从同一起 点出发背向而行，1小时后正好第5次相遇，如果从同一起点出发，同向而行，那么 经过1小时才第1次追上，请问小鹿和小山羊跑一圈各需要多长时间？ 【分析】题目中并没有告诉环形跑道的周长是多少，想一想跑道的周长是一个确定 的数吗？如果不是，那么周长的取值不同，对于结果有没有影响？
甲乙两人在一个周长为180米的圆形跑道上跑步甲每秒跑5米乙每秒跑4米如果两人从同一点同时出发反向跑步多少秒后第一次相遇再过多少秒两人第二次相遇在10有一个圆形跑道甲乙两人同时从同一点沿同一方向出发当甲跑完7圈到达出发点时恰好第二次追上乙如果甲的速度是14米每秒那么乙每秒跑多少米
第4讲
环形路线
• 行程问题专题
例题二：
有一个周长是40米的圆形水池，甲沿着水池散步，每秒钟走1米。乙沿着水池跑步， 每秒钟跑3.5米。甲、乙从同一地点同时出发，同向而行，当乙第8次追上甲时，他 还要跑多少米才能回到出发点？ 【分析】在环形路线上，快的每追上慢的一次就要多跑一圈，本题乙第8次追上甲 时，就比甲多跑了8圈，这时怎么确定两人的位置？
例题四：
如图甲、乙两人分别从一圆形场地的直径两端点A、B开始，同时匀速反向绕此圆形 路线运动。当乙走了100米以后，他们第一次相遇，在甲走完一周前60米处第二次 相遇，求此圆形场地的周长？ 【分析】题目中的已知条件很少，知道两个与路程有关的量，我们很难直接计算周 长，先画图分析一下运动过程，观察你所画出的示意图，题目给出的100米和60米 是图中的哪一段？如何利用这两段长度？
浅谈初中几何教学中常见的动点轨迹问题
浅谈初中几何教学中常见的动点轨迹问题作者：吕锦秀来源：《读写算》2020年第12期摘要在初中幾何教学中，动点轨迹问题向来是难点，也是学生在考试中的丢分点。
这是因为学生在解决该类问题时经常无从下手，无法发现动点轨迹中的动静结合关键节点，在问题求解过程中难以发现题目中的隐含条件。
所以本文结合实际教学问题，探讨了初中常见的动点轨迹难点问题，希望为学生破解知识点难题，培养从容应对的良好心态。
关键词动点轨迹问题;初中几何;解法探究;圆;平面直角坐标系中图分类号：G632 文献标识码：A 文章编号：1002-7661（2020）12-0190-01动点轨迹问题中是综合囊括了众多知识点内容的，它所表达的数学思想丰富，对数学思维的分析逻辑和推理过程都提出了较高要求，因此动点轨迹问题绝对是初中生学习数学的一大难点。
教师在教学过程中应该更多结合题目帮助学生把握动点轨迹问题相关细节，解决其中难点问题。
一、平面直角坐标系的动点轨迹问题（一）基本概述“平面直角坐标系”是初中数学中的关键知识点。
平面直角坐标系中是存在动点轨迹问题的，例如其坐标轴上的公共原点，包括平面直角坐标系中的都能衍生出动点轨迹问题。
为了帮助学生在未来的函数知识学习过程中打好基础，教师在“平面直角坐标系”教学中要把握先机，首先将动点轨迹问题引入到教学中，引导学生学好这部分知识内容。
（二）例题提出（三）例题解读（四）例题剖析具体来讲，该题目就涉及两个有关动点轨迹的小问题，且两个问题之间是存在相互递进发展关系的。
从第1问中的坐标点出发，求解四边形的最小值，这其实就是分析四边形的兑点对称性线段最值问题，阐释了“两点之间、线段最短”的数学定理。
结合上述定理就能直接求出线段最值问题;第2问是本题目解题最大难点，教师需要引导学生共同学习判断动点的运动轨迹究竟是什么。
这里需要考察的是学生的判断能力，要合理判断动点的运动轨迹，然后才能有效计算出它的运动路径长度。
（五）注意事项在上述题目求解过程中，需求解出四边形以及圆的运动路径、运动长度。
第2讲 空间几何体运动轨迹与长度问题(原卷版)
第2讲 空间几何体运动轨迹与长度问题一、单选题1．（2022·全国·高三专题练习（理））已知正方体ABCD A B C D ''''-的棱长为4，E ，F 分别为BB '，C D ''的中点，点P 在平面ABB A ''中，=PF N 在线段AE 上，则下列结论正确的个数是（ ）①点P 的轨迹长度为2π；①线段FP 的轨迹与平面A B CD ''的交线为圆弧；①NP ；①过A 、E 、F 作正方体的截面，则该截面的周长为103A ．4 B ．3 C ．2 D ．12．（2022·江西·模拟预测（理））已知正方体1111ABCD A B C D -的棱长为3，点P 在11A C B △的内部及其边界上运动，且DP =P 的轨迹长度为( )AB ．2πC ．D ．3π 3．（2022·河南河南·三模（理））已知正四棱柱1111ABCD A B C D -，2AB =，1AA a =，点M 为1CC 点的中点，点P 为上底面1111D C B A 上的动点，下列四个结论中正确的个数为（ ）①当a =P 位于上底面的中心时，四棱柱P ABCD -外接球的表面积为25π3； ①当2a =时，存在点P 满足4PA PM +=；①当2a =时，存在唯一的点P 满足90APM ∠=︒；①当2a =时，满足BP AM ⊥的点P ．A ．1B ．2C ．3D ．4 4．（2022·四川泸州·三模（理））已知三棱锥P ABC -的底面ABC 为等腰直角三角形，其顶点P 到底面ABC 的距离为3，体积为24，若该三棱锥的外接球O 的半径为5，则满足上述条件的顶点P 的轨迹长度为（ ）A ．6πB ．30πC ．(9π+D ．(6π+5．（2022·重庆·模拟预测）已知棱长为3的正四面体A BCD -，P 是空间内的任一动点，且满足2PA PD ≥，E 为AD 中点，过点D 的平面α∥平面BCE ，则平面α截动点P 的轨迹所形成的图形的面积为（ ）A ．πB ．2πC ．3πD ．4π6．（2022·浙江温州·高三开学考试）如图，正方体1AC ，P 为平面11B BD 内一动点，设二面角11A BD P --的大小为α，直线1A P 与平面11BD A 所成角的大小为β.若cos sin βα=，则点P 的轨迹是（ ）A ．圆B ．抛物线C ．椭圆D ．双曲线二、多选题 7．（2022·湖北·高一阶段练习）已知正方体1111ABCD A B C D -的棱长为2，E 为线段1AA 的中点，AP AB AD λμ=+，其中,[0,1]λμ∈，则下列选项正确的是（ ）A ．12μ=时，11A P ED ⊥B ．14λ=时，1B P PD +C ．1λμ+=时，直线1A P 与面11BDE D ．1λμ+=时，正方体被平面1PAD 截的图形最大面积是8．（2022·湖南岳阳·三模）如图，在直棱柱1111ABCD A B C D -中，各棱长均为2，π3ABC ∠=，则下列说法正确的是（ ）A ．三棱锥1A ABC -B ．异面直线1AB 与1BCC ．当点M 在棱1BB 上运动时，1MD MA +最小值为D ．N 是ABCD 所在平面上一动点，若N 到直线1AA 与BC 的距离相等，则N 的轨迹为抛物线9．（2022·广东·高二阶段练习）已知正方体1111ABCD A B C D -的棱长为2，点P 为正方形ABCD 所在平面内一动点，则下列命题正确的有（ ）A ．若点P 总满足11PD DC ⊥，则动点P 的轨迹是一条直线B ．若点P 到直线1BB 与到直线DC 的距离相等，则点P 的轨迹为抛物线C ．若点P 到直线1DD 的距离与到点C 的距离之和为2，则动点P 的轨迹是椭圆D ．若1D P 与AB 所成的角为π3，则点P 的轨迹为双曲线 10．（2022·江苏南通·模拟预测）设正方体ABCD —1111D C B A 的棱长为2，P 为底面正方形ABCD 内（含边界）的一动点，则（ ）A ．存在点P ，使得A 1P ∥平面11B CDB ．当PC PD ⊥时，|A 1P |2的最小值是10-C ．若1APC 的面积为1，则动点P 的轨迹是抛物线的一部分D ．若三棱锥P —111A B C 的外接球表面积为41π4，则动点P 的轨迹围成图形的面积为π11．（2022·山东·高一阶段练习）如图，在棱长为1111ABCD A B C D -中，点P 是平面11A BC 内一个动点，且满足15DP PB +=+ ） （参考数据：4sin 535︒=，3sin 375︒=）A ．1PB B D ⊥B ．点P 的轨迹是一个圆C ．直线1B P 与平面11A BC 所成角为53°D ．设直线1B P 与直线1AD 所成角为θ，则3790θ︒≤≤︒12．（2022·广东·佛山市南海区艺术高级中学模拟预测）如图，若正方体的棱长为1，点M 是正方体1111ABCD A B C D -的侧面11ADD A 上的一个动点（含边界），P 是棱1CC 的中点，则下列结论正确的是（ ）A ．沿正方体的表面从点A 到点PB ．若保持||PM =M 在侧面内运动路径的长度为3π C ．三棱锥1B C MD -的体积最大值为16 D ．若M 在平面11ADD A 内运动，且111MD B B D B ∠=∠，点M 的轨迹为抛物线13．（2022·广东佛山·高二期末）如图，在棱长为2的正方体1111ABCD A B C D -中，M 为1D D 的中点，连接BM ，设BM 的中点为E ，动点N 在底面正方形ABCD 内（含边界）运动，则下列结论中正确的是（ ）A ．存在无数个点N 满足0AN BM ⋅=B ．若2AN NC =，则1A ，E ，N 三点共线C ．若NB ND +=，则1A ND ．若MN 与平面ABCD 所成的角为3π，则点N 的轨迹为抛物线的一部分 14．（2022·全国·模拟预测）如图，点M 是棱长为1的正方体1111ABCD A B C D -中的侧面11ADD A 上的一个动点（包含边界），则下列结论正确的是（ ）A ．存在无数个点M 满足1CM AD ⊥B ．当点M 在棱1DD 上运动时，1||MA MB +1C ．在线段1AD 上存在点M ，使异面直线1B M 与CD 所成的角是30D ．满足1||2MD MD =的点M 的轨迹是一段圆弧15．（2022·福建·厦门一中高一阶段练习）如图，在棱长为2的正方体1111ABCD A B C D -中，O 为正方形ABCD 的中心，P 为棱1AA 上的动点.则下列说法正确的是（ ）A ．点P 为1AA 中点时，1PO DC ⊥B ．当P 点运动时，折线段1D P PC +长度的最小值是3C ．当P 点运动时，三棱锥1P BDC -外接球的球心总在直线1A C 上D ．当P 为1AA 的中点时，正方体表面到P 点距离为2的轨迹的总长度为43π⎛ ⎝16．（2022·山东聊城·三模）在直四棱柱1111ABCD A B C D -中，所有棱长均2，60BAD ∠=︒，P 为1CC 的中点，点Q 在四边形11DCC D 内（包括边界）运动，下列结论中正确的是（ ）A ．当点Q 在线段1CD 上运动时，四面体1A BPQ 的体积为定值B ．若AQ//平面1A BP ，则AQ 的最小值为5C ．若1A BQ △的外心为M ，则11A B AM ⋅为定值2D ．若1AQ =，则点Q 的轨迹长度为23π 17．（2022·全国·华中师大一附中模拟预测）如图，在四棱锥P -ABCD 中，底面ABCD 是边长为2的正方形，PA ⊥平面ABCD ，且2PA =．点E ，F ，G 分别为棱AB ，AD ，PC 的中点，下列说法正确的是（ ）A ．AG ⊥平面PBDB ．直线FG 和直线AC 所成的角为3π C ．过点E ，F ，G 的平面截四棱锥P -ABCD 所得的截面为五边形D ．当点T 在平面ABCD 内运动，且满足AGT △的面积为12时，动点T 的轨迹是圆 18．（2022·福建三明·模拟预测）已知棱长为4的正方体1111ABCD A B C D -中，14AM AB =，点P 在正方体的表面上运动，且总满足0MP MC ⋅=，则下列结论正确的是（ ） A ．点P 的轨迹所围成图形的面积为5 B ．点P 的轨迹过棱11A D 上靠近1A 的四等分点C ．点P 的轨迹上有且仅有两个点到点C 的距离为6D ．直线11B C 与直线MP 所成角的余弦值的最大值为3519．（2022·重庆巴蜀中学高一期中）在正方体1111ABCD A B C D -中，M ，N ，P 分别为棱111,,AB CC C D 的中点，动点Q ∈平面MNP ，2DQ AB ==，则（ ）A ．1AC MNB ．直线∥PQ 平面11A BCC ．正方体被平面MNP 截得的截面为正六边形D ．点Q 的轨迹长度为2π 20．（2022·云南·昭通市第一中学高一阶段练习）（多选）如图，若正方体的棱长为1，点M 是正方体1111ABCD A B C D -的侧面11ADD A 上的一个动点（含边界），P 是棱1CC 的中点，则下列结论正确的是（ ）A ．沿正方体的表面从点A 到点PB ．若保持PM M 在侧面内运动路径的长度为3π C ．三棱锥1B C MD -的体积最大值为16 D ．若点M 满足111MD B B D B ∠=∠，则点M 的轨迹为线段21．（2022·山东·模拟预测）如图，正方体1111ABCD A B C D -的棱长为2，点M 是其侧面11ADD A 上的一个动点（含边界），点P 是线段1CC 上的动点，则下列结论正确的是（ ）A ．存在点P ，M ，使得平面11B D M 与平面PBD 平行B ．存在点P ，M ，使得二面角--M DC P 大小为23π C．当P 为棱1CC 的中点且PM =M 的轨迹长度为23πD ．当M 为1A D 中点时，四棱锥M ABCD - 22．（2022·广东·三模）在正方体1111ABCD A B C D -中，1AB =，点P 满足1CP CD CC λμ=+，其中[][]0,1,0,1λμ∈∈，则下列结论正确的是（ ）A ．当1//B P 平面1A BD 时，1B P 可能垂直1CDB ．若1B P 与平面11CCD D 所成角为4π，则点P 的轨迹长度为2πC ．当λμ=时，1||DP A P +D．当1λ=时，正方体经过点1A ､P ､C 的截面面积的取值范围为 23．（2022·重庆巴蜀中学高三阶段练习）已知正四面体A BCD -的棱长为2，底面BCD 所在平面上一动点P 满足AP = ）A ．点PB ．直线AP 与底面BCD 所成角的正弦值为13C ．DPD ．直线AP 与直线CD 所成角的取值范围为ππ,32⎡⎤⎢⎥⎣⎦ 24．（2022·福建·莆田二中模拟预测）在棱长为1的正方体1111ABCD A B C D -中，点M 是11A D的中点，点P ，Q ，R 在底面四边形ABCD 内（包括边界），1PB ∥平面1MC D ，1D Q =，点R 到平面11ABB A 的距离等于它到点D 的距离，则（ ）A．点P B ．点Q 的轨迹的长度为4πC ．PQ 12D ．PR 25．（2022·全国·高三专题练习）如图，若正方体的棱长为1，点M 是正方体1111ABCD A B C D -的侧面11ADD A 上的一个动点（含边界），P 是棱1CC 的中点，则下列结论正确的是（ ）A ．沿正方体的表面从点A 到点PB ．若保持PM M 在侧面内运动路径的长度为π3C ．三棱锥1B C MD -的体积最大值为16D ．若M 在平面11ADD A 内运动，且111MD B B D B ∠=∠，点M 的轨迹为线段26．（2022·福建·厦门一中高二期中）在四棱锥P ABCD -中，底面ABCD 是边长为2的正方形，PA ⊥平面ABCD ，且2PA =.若点E ，F ，G 分别为棱AB ，AD ，PC 的中点，则（ ） A ．AG ⊥平面PBDB ．直线FG 和直线AB 所成的角为4π C ．当点T 在平面PBD 内，且2TA TG +=时，点T 的轨迹为一个椭圆D ．过点E ，F ，G 的平面与四棱锥P ABCD -表面交线的周长为27．（2022·全国·模拟预测）如图，在棱长为1的正方体1111ABCD A B C D -中，P 为棱1BB 的中点，Q 为正方形11BB C C 内一动点(含边界)，则下列说法中正确的是( )A ．若1D Q ∥平面1A PD ，则动点Q 的轨迹是一条线段B ．存在Q 点，使得1D Q ⊥平面1A PDC ．当且仅当Q 点落在棱1CC 上某点处时，三棱锥1Q A PD -的体积最大D ．若1D Q =Q 点的轨迹长度为428．（2022·湖南益阳·一模）已知正方体1111ABCD A B C D -的棱长为2，点E 、F 分别是棱AB 、11A B 的中点，点P 在四边形ABCD 内（包含边界）运动，则下列说法正确的是（ ） A ．若P 是线段BC 的中点，则平面1AB P ⊥平面DEFB ．若P 在线段AC 上，则异面直线1D P 与11A C 所成角的范围是ππ,42⎡⎤⎢⎥⎣⎦C．若1PD 平面11A C E ，则点PD ．若PF 平面11B CD ，则PF 长度的取值范围是 29．（2022·湖南·长沙市南雅中学高三阶段练习）已知正方体1111ABCD A B C D -的棱长为1，E 为线段1AA 的中点，AP AB AD λμ=+，其中,[0,1]λμ∈，则下列选项正确的是（ ） A ．12μ=时，11A P ED ⊥B ．14λ=时，1B P PD +C ．λμ=时，三棱锥1D EBP -的体积为定值D ．1λμ+=时，直线1A P 与面11B DE 30．（2022·湖北·襄阳五中模拟预测）如图，在棱长为1的正方体ABCD —111A B C D 中，E 为侧面11BCC B 的中心，F 是棱11C D 的中点，若点P 为线段1BD 上的动点，N 为ABCD 所在平面内的动点，则下列说法正确的是（ ）A ．PE ·PF 的最小值为148B ．若12BP PD =，则平面P AC 截正方体所得截面的面积为98C ．若1D N 与AB 所成的角为4π，则N 点的轨迹为双曲线的一部分 D ．若正方体绕1BD 旋转θ角度后与其自身重合，则θ的最小值是23π31．（2022·广东珠海·高三期末）如图，在直棱柱1111ABCD A B C D -中，各棱长均为2，3ABC π∠=，则下列说法正确的是（ ）A ．三棱锥1A ABC -外接球的表面积为283π B ．异面直线1AB 与1BC 所成角的余弦值为12C ．当点M 在棱1BB 上运动时，1MD MA +最小值为D ．N 是平面ABCD 上一动点，若N 到直线1AA 与BC 的距离相等，则N 的轨迹为抛物线 32．（2022·浙江杭州·高二阶段练习）如图，在正四棱柱ABCD －A 1B 1C 1D 1中，AB ＝3，1AA =P 是该正四棱柱表面或内部一点，直线PB ，PC 与底面ABCD 所成的角分别记为α，β，且sin β＝2sin α，记动点P 的轨迹与棱BC 的交点为Q ，则下列说法正确的是（ ）A ．Q 为BC 中点B ．线段P A 1长度的最小值为5C ．存在一点P ，使得PQ ①平面AB 1D 1D ．若P 在正四棱柱ABCD －A 1B 1C 1D 1表面，则点P 33．（2022·全国·高三专题练习）如图，若正方体的棱长为1，点M 是正方体1111ABCD A B C D -的侧面11ADD A 上的一个动点（含边界），P 是棱1CC 的中点，则下列结论正确的是（ ）A ．当M 为AD 中点时，三棱锥M -BDP 的体积为124B ．沿正方体的表面从点A 到点PC ．若保持PM =M 在侧面内运动路径的长度为3π D ．若M 在平面11ADD A 内运动，且111MD B B D B ∠=∠，点M 的轨迹为抛物线34．（2022·全国·高三专题练习）如图，已知直四棱柱ABCD -EFGH 的底面是边长为4的正方形，CG m =，点M 为CG 的中点，点P 为底面EFGH 上的动点，则（ ）A ．当4m =时，存在点P 满足8PA PM +=B ．当4m =时，存在唯一的点P 满足2APM π∠=C ．当4m =时，满足BP ①AM 的点P 的轨迹长度为D ．当m 时，满足2APM π∠=的点P35．（2022·浙江丽水·高二期末）如图，在正四棱柱1111ABCD A B C D -中，=3AB ，1AA =P 是该正四棱柱表面或内部一点，直线PB ，PC 与底面ABCD 所成的角分别记为,αβ，且sin 2sin βα=，记动点P 的轨迹与棱BC 的交点为Q ，则下列说法正确的是（ ）A ．Q 为BC 中点B ．线段1PA 长度的最小值为5C ．存在一点P ，使得//PQ 平面11AB DD ．若P 在正四棱柱1111ABCD A B C D -表面，则点P 36．（2022·江苏·扬州中学高三开学考试）如图，点P 是棱长为2的正方体1111ABCD A B C D -的表面上一个动点，则（ ）A ．当P 在平面11BCCB 上运动时，四棱锥11P AA D D -的体积不变B ．当P 在线段AC 上运动时，1D P 与11A C 所成角的取值范围是,62ππ⎡⎤⎢⎥⎣⎦C．当直线AP 与平面ABCD 所成的角为45°时，点P 的轨迹长度为π+D ．若F 是11A B 的中点，当P 在底面ABCD 上运动，且满足PF ∥平面11B CD 时，PF 长度的三、双空题37．（2022·山东潍坊·模拟预测）如图，将正四面体每条棱三等分，截去顶角所在的小正四面体，余下的多面体就成为一个半正多面体，亦称“阿基米德体”．点A ，B ，M 是该多面体的三个顶点，点N 是该多面体外接球表面上的动点，且总满足MN AB ⊥，若4AB =，则该多面体的表面积为______；点N 轨迹的长度为______．38．（2022·湖南·雅礼中学二模）已知菱形ABCD 的各边长为2,60D ∠=.如图所示，将ACB △沿AC 折起，使得点D 到达点S 的位置，连接SB ，得到三棱锥S ABC -，此时3SB =.则三棱锥S ABC -的体积为__________，E 是线段SA 的中点，点F 在三棱锥S ABC -的外接球上运动，且始终保持EF AC ⊥，则点F 的轨迹的周长为__________.39．（2022·浙江·1111ABCD A B C D -中，P 为侧面11BCC B 内的动点，且直线1A P 与AB 的夹角为30°，则点P 的轨迹长为___________；若点1A 与动点P 均在球O 表面上，球O 的表面积为___________．40．（2022·江苏无锡·高三期末）正四面体ABCD 的棱长为12，在平面BCD 内有一动点P ，且满足AP =则P 点的轨迹是__________；设直线AP 与直线BC 所成的角为θ，则cos θ的取值范围为__________.四、填空题41．（2022·广东·广州六中高二期中）在矩形ABCD 中，E 是AB 的中点，1,2AD AB ==，将ADE 沿DE 折起得到A DE '，设A C '的中点为M ，若将A DE '绕DE 旋转90，则在此过程中动点M 形成的轨迹长度为___________.42．（2022·全国·高三专题练习）在棱长为a 的正方体1111ABCD A B C D -中，M ，N 分别为1BD ，11B C 的中点，点P 在正方体表面上运动，且满足MP CN ⊥，点P 轨迹的长度是___________.43．（2022·湖北·黄冈中学二模）如图，棱长为1的正方体1111ABCD A B C D -，点P 沿正方形ABCD 按ABCDA 的方向作匀速运动，点Q 沿正方形11B C CB 按111B C CBB 的方向以同样的速度作匀速运动，且点,P Q 分别从点A 与点1B 同时出发，则PQ 的中点的轨迹所围成图形的面积大小是________.44．（2022·湖南师大附中三模）已知棱长为3的正四面体ABCD ，E 为AD 的中点，动点P 满足2PA PD =，平面α经过点D ，且平面//α平面BCE ，则平面α截点P 的轨迹所形成的图形的周长为_________.45．（2022·江西萍乡·三模（理））如图，在正方形ABCD 中，点M 是边CD 的中点，将ADM △沿AM 翻折到PAM △，连接,PB PC ，在ADM △翻折到PAM △的过程中，下列说法正确的是_________．（将正确说法的序号都写上）①点P 的轨迹为圆弧；①存在某一翻折位置，使得AM PB ⊥；①棱PB 的中点为E ，则CE 的长为定值；46．（2022·安徽·合肥一中模拟预测（文））如图，点M 是正方体1111ABCD A B C D -中的侧面11ADD A 内（包括边界）的一个动点，则下列命题正确的是___________(请填上所有正确命题的序号）．①满足1BM A D ⊥的点M 的轨迹是一条线段；①在线段1AD 上存在点M ，使异面直线1B M 与CD 所成的角是6π；①若正方体的棱长为1，三棱锥1B C MD -的体积最大值为13； ①存在无数个点M ，使得点M 到直线AD 和直线11C D 的距离相等． 47．（2022·河南·鹤壁高中模拟预测（文））如图，在棱长为1的正方体1111ABCD A B C D -中，P 为棱1BB 的中点，Q 为正方形11BB C C 内一动点（含边界），则下列说法中正确的是______．①若1//D Q 平面1A PD ，则动点Q 的轨迹是一条线段①存在Q 点，使得1D Q ⊥平面1A PD①当且仅当Q 点落在棱1CC 上某点处时，三棱锥1Q A PD -的体积最大①若1D Q =Q 48．（2022·北京·高三专题练习）如图，正方体ABCD －A 1B 1C 1D 1的棱长为2，点O 为底面ABCD 的中心，点P 在侧面BB 1C 1C 的边界及其内部运动.给出下列四个结论：①D 1O ①AC ；①存在一点P ，D 1O ①B 1P ；①若D 1O ①OP ，则①D 1C 1P①若P 到直线D 1C 1的距离与到点B 的距离相等，则P 的轨迹为抛物线的一部分. 其中所有正确结论的序号是_________________.49．（2022·四川南充·二模（理））已知正方体1111ABCD A B C D -的棱长为,M N 为体对角线1BD 的三等分点，动点P 在三角形1ACB 内，且三角形PMN 的面积PMN S =△P 的轨迹长度为___________. 50．（2022·宁夏·石嘴山市第三中学高三期末（理））如图正方体1111ABCD A B C D -的棱长为4，点M 是棱11A D 的中点，点P 在面ABCD 内（包含边界），且MP =则下列四个命题中：①点P 的轨迹的长度为2π①存在P ，使得1MP AC ⊥①直线MP 与平面11BDD B ①沿线段MP 的轨迹将正方体1111ABCD A B C D -切割成两部分，挖去体积较小部分，剩余部分几何体的表面积为881)+π其中正确命题的序号是___________.51．（2022·四川省叙永第一中学校模拟预测（文））正方体1111ABCD A B C D -棱长为3，点E 在边BC 上，且满足BE ＝2EC ，动点M 在正方体表面上运动，并且总保持1ME BD ⊥，则动点M 的轨迹的周长为__.52．（2022·青海·海东市教育研究室一模（理））已知P 为正方体1111ABCD A B C D -表面上的一动点，且满足,2PA AB =，则动点P 运动轨迹的周长为__________.。
中考数学重点难点专题练习-第12讲 运动路径长度问题
中考数学重点难点专题练习-第12讲运动路径长度问题想要对运动路径长度问题掌握得信手拈来，那么建议你对以下知识点进行提前学习会更好：1.《隐圆模型》2.《共顶点模型》-也可称“手拉手模型”3.《主从联动模型》-也可称“瓜豆原理模型”4.《旋转问题》—本系列的第二讲中所阐述的旋转相似模型此外，还需要明白的动点类型还有：5.线段垂直平分线——到线段两端点距离相等的动点一定在这条线段的垂直平分线上6.角平分线——到角两边距离相等的动点一定在这个角的角平分线上7.三角形中位线——动点到某条线的距离恒等于某平行线段的一半8.平行线分线段成比例——动点到某条线的距离与某平行线段成比例9.两平行线的性质——平行线间的距离，处处相等Ps强烈建议：如果您之前没有对上述模型进行过学习，建议您先到学科网搜索下载独家精品出版的：《中考数学几何模型能力提升篇》专题系列资料包，您一定可以大有提升！一、路径为圆弧型解题策略：①作出隐圆，找到圆心②作出半径，求出定长解题关键：通过《隐圆模型》中五种确定隐圆的基本条件作出隐圆，即可轻易得出结论.二、路径为直线型解题策略：①利用平行定距法或者角度固定法确定动点运动路径为直线型②确定动点的起点与终点，计算出路径长度即可解题关键：解题过程中常常出现中位线，平行线分线段成比例，相似证动角恒等于顶角等知识点三、路径为往返型解题策略：①通常为《主从联动模型》的衍生版②确定动点的起点与终点，感知运动过程中的变化③找出动点运动的最远点解题关键：解题过程中常常出现相似转线段长、《主从联动模型》中的滑动模型等【例题1】如图，等腰Rt△AOB中，∠AOB＝90°，OA＝，⊙O与AB相切，分别交OA、OB于N、M，以PB为直角边作等腰Rt△BPQ，点P在弧MN上由点M运动到点N，则点Q运动的路径长为（）A．B．C．D．【例题2】已知⊙O，AB是直径，AB＝4，弦CD⊥AB且过OB的中点，P是劣弧BC上一动点，DF垂直AP于F，则P从C运动到B的过程中，F运动的路径长度（）A．πB．C．πD．2【例题3】如图，⊙O的半径为1，弦AB＝1，点P为优弧AB上一动点，AC⊥AP交直线PB于点C，则△ABC的最大面积是．【例题4】如图，等腰Rt△ABC中，斜边AB的长为2，O为AB的中点，P为AC边上的动点，OQ⊥OP 交BC于点Q，M为PQ的中点，当点P从点A运动到点C时，点M所经过的路线长为（）A. B. C. 1 D. 2【例题5】已知：如图1，平面直角坐标系中，点A的坐标是（0，6），点B在x轴上，且∠BAO＝30°，点D是线段OA上的一点，以BD为边向下作等边△BDE．（1）如图2，当∠ODB＝45°时，求证：OE平分∠BED．（2）如图3，当点E落在y轴上时，求出点E的坐标．（3）利用图1探究并说理：点D在y轴上从点A向点O滑动的过程中，点E也会在一条直线上滑动；并直接写出点E运动路径的长度．【例题6】如图，Rt△ABC中，BC＝4，AC＝8，Rt△ABC的斜边在x轴的正半轴上，点A与原点重合，随着顶点A由O点出发沿y轴的正半轴方向滑动，点B也沿着x轴向点O滑动，直到与点O重合时运动结束．在这个运动过程中，点C运动的路径长是．【例题7】如图1，已知抛物线y＝x2+bx+c经过原点O，它的对称轴是直线x＝2，动点P从抛物线的顶点A 出发，在对称轴上以每秒1个单位的速度向上运动，设动点P运动的时间为t杪，连结OP并延长交抛物线于点B，连结OA，AB．（1）求抛物线的函数解析式；（2）当△AOB为直角三角形时，求t的值；（3）如图2，⊙M为△AOB的外接圆，在点P的运动过程中，点M也随之运动变化，请你探究：在1≤t≤5时，求点M经过的路径长度．【例题8】如图，OM⊥ON，A、B分别为射线OM、ON上两个动点，且OA+OB＝5，P为AB的中点．当B由点O向右移动时，点P移动的路径长为（）A．2 B．2C．D．5【例题9】如图1，在Rt△ABC中，∠C=90°，AC=6，BC=8，动点P从点A开始沿边AC向点C以1个单位长度的速度运动，动点Q从点C开始沿边CB向点B以每秒2个单位长度的速度运动，过点P作PD∥BC，交AB于点D，连接PQ分别从点A、C同时出发，当其中一点到达端点时，另一点也随之停止运动，设运动时间为t秒（t≥0），在整个运动过程中，求出线段PQ中点M所经过的路径长．【例题10】（1）如图1，已知AB=2，点D是等腰Rt△ABC斜边AC上一动点，以BD为一边向右下方作等边△BDE，当点D由点A运动到点C时，求点E运动的路径长；（2）如图2，已知AB=2，点D是等腰Rt△ABC斜边AC上一动点，以BD为一边向右下方作以E为直角顶点的等腰Rt△BDE，当点D由点A运动到点C时，求点E运动的路径长；（3）如图3，已知AB=2，点D是等腰Rt△ABC斜边AC上一动点，以BD为一边向右下方作以D为直角顶点的等腰Rt△BDE，当点D由点A运动到点C时，求点E运动的路径长；（4）如图4，已知AB=2，点D是等腰Rt△ABC斜边AC上一动点，以BD为一边向右下方作以D为直顶点的等腰△BDE，且∠BDE=120°，当点D由点A运动到点C时，求点E运动的路径长；【例题11】如图，已知扇形AOB中，OA=3，∠AOB=120°，C是在上的动点．以BC为边作正方形BCDE，当点C从点A移动至点B时，点D经过的路径长是________．1．如图，在等腰Rt△ABC中，AC＝BC＝，点P在以斜边AB为直径的半圆上，M为PC的中点，当点P沿半圆从点A运动至点B时，点M运动的路径长是．2．已知线段AB＝8，C、D是AB上两点，且AC＝2，BD＝4，P是线段CD上一动点，在AB同侧分别作等腰三角形APE和等腰三角形PBF，M为线段EF的中点，若∠AEP＝∠BFP，则当点P由点C移动到点D时，点M移动的路径长度为．3．已知线段AB＝10，P是线段AB上一动点，在AB同侧分别作等边三角形APE和等边三角形PBF，G为线段EF的中点，点P由点A移动到点B时，G点移动的路径长度为．4．如图，AB为⊙O的直径，AB＝3，弧AC的度数是60°，P为弧BC上一动点，延长AP到点Q，使AP•AQ ＝AB2．若点P由B运动到C，则点Q运动的路径长为．5．如图，矩形ABCD中，AB＝4，AD＝6，点E在边AD上，且AE:ED＝1:2．动点P 从点A出发，沿AB 运动到点B停止．过点E作EF⊥PE交射线BC于点F．设点M是线段EF的中点，则在点P运动的整个过程中，点M的运动路径长为________．6．等边三角形ABC的边长为2，在AC，BC边上各有一个动点E，F，满足AE＝CF，连接AF，BE相交于点P．（1）∠APB的度数；（2）当E从点A运动到点C时，试求点P经过的路径长；（3）连结CP，直接写出CP长度的最小值．7．如图，AB为半圆O的直径，AB=2，C，D为半圆上两个动点（D在C右侧），且满足∠COD=60°，连结AD，BC相交于点P若点C从A出发按顺时针方向运动，当点D与B重合时运动停止，则点P所经过的路径长为________．8．如图，A（﹣3，0），B（0，3），C（﹣1，4），P，C，M按逆时针顺序排列，动点P在线段AB上，∠C＝90°，∠CPM＝30°，请求出当P点从A运动到B点时，点M运动的路径时什么？并求出M点运动路径长度．9．如图，矩形ABCD中，AB＝6，BC＝6，动点P从点A出发，以每秒个单位长度的速度沿线段AD 运动，动点Q从点D出发，以每秒2个单位长度的速度沿折线段D﹣O﹣C运动，已知P、Q同时开始移动，当动点P到达D点时，P、Q同时停止运动．设运动时间为t秒．（1）当t＝1秒时，求动点P、Q之间的距离；（2）若动点P、Q之间的距离为4个单位长度，求t的值；（3）若线段PQ的中点为M，在整个运动过程中；直接写出点M运动路径的长度为．10．（2019秋•江岸区校级月考）如图，正△ABC中，AB＝2，AD⊥BC于D，P，Q分别是AB，BC上的动点，且PQ＝AD，点M在PQ的右上方且PM＝QM，∠M＝120°，当P从点A运动到点B时，M运动的路径长为．(看成固定三角板滑动处理/或反其道而行之)11．如图，在四边形ABCD中，∠C＝60°，∠A＝30°，CD＝BC．（1）求∠B+∠D的度数．（2）连接AC，探究AD，AB，AC三者之间的数量关系，并说明理由．（3）若BC＝2，点E在四边形ABCD内部运动，且满足DE2＝CE2+BE2，求点E运动路径的长度．12．已知在扇形AOB中，圆心角∠AOB＝120°，半径OA＝OB＝8．（1）如图1，过点O作OE⊥OB，交弧AB于点E，再过点E作EF⊥OA于点F，则FO的长是，∠FEO＝°；（2）如图2，设点P为弧AB上的动点，过点P作PM⊥OA于点M，PN⊥OB于点N，点M，N分别在半径OA，OB上，连接MN，则①求点P运动的路径长是多少？②MN的长度是否是定值？如果是，请求出这个定值；若不是，请说明理由；（3）在（2）中的条件下，若点D是△PMN的外心，直接写出点D运动的路经长．13．如图，AB为⊙O的直径，且AB＝4，点C在半圆上，OC⊥AB，垂足为点O，P为半圆上任意一点，过P点作PE⊥OC于点E，设△OPE的内心为M，连接OM、PM．（1）求∠OMP的度数；（2）当点P在半圆上从点B运动到点A时，求内心M所经过的路径长．14．（2019•兴化市模拟）正方形ABCD的边长为4，P为BC边上的动点，连接AP，作PQ⊥P A交CD边于点Q．当点P从B运动到C时，线段AQ的中点M所经过的路径长（）A．2 B．1 C．4 D．15．（2019•武汉模拟）如图，半径为2cm，圆心角为90°的扇形OAB的弧AB上有一运动的点P，从点P 向半径OA引垂线PH交OA于点H．设△OPH的内心为I，当点P在弧AB上从点A运动到点B时，内心I所经过的路径长为（）A．πB．πC．πD．π16．如图，BC是⊙O的直径，BC＝4，M、N是半圆上不与B、C重合的两点，且∠MON＝120°，△ABC的内心为E点，当点A在上从点M运动到点N时，点E运动的路径长是（）A．B．C．D．17．（2020•河北模拟）如图，在正方形ABCD中，AB＝1，P是边BC上的一个动点，由点B开始运动，运动到C停止．连接AP，以AP为直角边向右侧作等腰直角三角形，另一个顶点为Q．则点P从B运动到C的过程中，点Q的运动路径长为（）A．πB．C．D．118．无论a取什么实数，点P（a﹣1，2a﹣3）都在直线l上．Q（m，n）是直线l上的点，则（2m﹣n+3）2的值等于．19．如图，已知点C是以AB为直径的半圆的中点，D为弧AC上任意一点，过点C作CE⊥BD于点E，连接AE，若AB＝4，则AE的最小值为．20．如图，正方形OABC的边长为2，以O为圆心，EF为直径的半圆经过点A，连接AE，CF相交于点P，将正方形OABC从OA与OF重合的位置开始，绕着点O逆时针旋转90°，交点P运动的路径长是．21．如图，在平面直角坐标系中，点A（8，0），点P（0，m），将线段P A绕着点P逆时针旋转90°，得到线段PB，连接AB，OB，则BO+BA的最小值为．22．如图，P为边长为2的正方形ABCD的边BC上一动点，将线段DP绕P逆时针旋转90°得到线段PE （E为D的对应点），M为线段PE的中点，当点P从点C运动到点B的过程中，点M的运动路径长为____________.23．等边△ABC的边长为18，在AC，BC边上各取一点D，E，连接AE，BD相交于点P，若AE＝BD，当D从点A运动到点C时，点P所经过的路径长为．24．（2020•武汉模拟）如图，定直线l经过圆心O，P是半径OA上一动点，AC⊥l于点C，当半径OA绕着点O旋转时，总有OP＝OC，若OA绕点O旋转60°时，P、A两点的运动路径长的比值是．25．如图，已知正方形ABCD的边长为4，点P是AB边上一个动点，连接CP，过点P作PC的垂线交AD 于点E，以PE为边作正方形PEFG，顶点G在线段PC上，对角线EG、PF相交于点O．（1）若AP＝1，则AE＝；（2）①求证：点O一定在△APE的外接圆上；②当点P从点A运动到点B时，点O也随之运动，求点O经过的路径长；（3）在点P从点A到点B的运动过程中，△APE的外接圆的圆心也随之运动，求该圆心到AB边的距离的最大值．26．如图，正方形ABCD的边长为2，动点E从点A出发，沿边AB﹣BC向终点C运动，以DE为边作正方形DEFG（点D、E、F、G按顺时针方向排列）．设点E运动速度为每秒1个单位，运动的时间为x秒．（1）如图1，当点E在AB上时，求证：点G在直线BC上；（2）设正方形ABCD与正方形DEFG重叠部分的面积为S，求S与x之间的函数关系式；（3）直接写出整个运动过程中，点F经过的路径长．想要对运动路径长度问题掌握得信手拈来，那么建议你对以下知识点进行提前学习会更好：10.《隐圆模型》11.《共顶点模型》-也可称“手拉手模型”12.《主从联动模型》-也可称“瓜豆原理模型”13.《旋转问题》—本系列的第二讲中所阐述的旋转相似模型此外，还需要明白的动点类型还有：14.线段垂直平分线——到线段两端点距离相等的动点一定在这条线段的垂直平分线上15.角平分线——到角两边距离相等的动点一定在这个角的角平分线上16.三角形中位线——动点到某条线的距离恒等于某平行线段的一半17.平行线分线段成比例——动点到某条线的距离与某平行线段成比例18.两平行线的性质——平行线间的距离，处处相等Ps强烈建议：如果您之前没有对上述模型进行过学习，建议您先到学科网搜索下载独家精品出版的：《中考数学几何模型能力提升篇》专题系列资料包，您一定可以大有提升！一、路径为圆弧型解题策略：①作出隐圆，找到圆心②作出半径，求出定长解题关键：通过《隐圆模型》中五种确定隐圆的基本条件作出隐圆，即可轻易得出结论.二、路径为直线型解题策略：①利用平行定距法或者角度固定法确定动点运动路径为直线型②确定动点的起点与终点，计算出路径长度即可解题关键：解题过程中常常出现中位线，平行线分线段成比例，相似证动角恒等于顶角等知识点三、路径为往返型解题策略：①通常为《主从联动模型》的衍生版②确定动点的起点与终点，感知运动过程中的变化③找出动点运动的最远点解题关键：解题过程中常常出现相似转线段长、《主从联动模型》中的滑动模型等【例题1】如图，等腰Rt△AOB中，∠AOB＝90°，OA＝，⊙O与AB相切，分别交OA、OB于N、M，以PB为直角边作等腰Rt△BPQ，点P在弧MN上由点M运动到点N，则点Q运动的路径长为（）A．B．C．D．【分析】解题标签：《共顶点模型》中的旋转相似、《隐圆模型》中的动点定长模型、《主从联动模型》【解析】如图，连接OP，AQ，设⊙O与AB相切于C，连接OC，则OC⊥AB，∵OA＝OB，∠AOB＝90°，OB＝，∴AB＝2，OP＝OC＝AB＝，∵△ABO和△QBP均为等腰直角三角形，∴＝，∠ABO＝∠QBP＝45°，∴＝，∠ABQ＝∠OBP，∴△ABQ∽△OBP，∴∠BAQ＝∠BOP，＝，即＝，∴AQ＝，又∵点P在弧MN上由点M运动到点N，∴0°≤∠BOP≤90°，∴0°≤∠BAQ≤90°，∴点Q的运动轨迹为以A为圆心，AQ长为半径，圆心角为90°的扇形的圆弧，∴点Q运动的路径长为＝，故选：D．[本题用《主从联动模型》来接替会更快得到结果]【例题2】已知⊙O，AB是直径，AB＝4，弦CD⊥AB且过OB的中点，P是劣弧BC上一动点，DF垂直AP于F，则P从C运动到B的过程中，F运动的路径长度（）A．πB．C．πD．2【分析】解题标签：“定边对直角”确定隐圆模型【解析】作DQ⊥AC于Q，如图，当P点在C点时，F点与Q重合；当P点在B点时，F点与E点重合，∵∠AFD＝90°，∴点F在以AD为直径的圆上，∴点F运动的路径为，∵弦CD⊥AB且过OB的中点，∴OE＝OD，CE＝DE＝，AC＝AC＝2，∴∠DOE＝60°，∴∠DAC＝60°，∴△ACD为等边三角形，∴MQ和ME为中位线，∴MQ＝，∠QME＝60°，∴F运动的路径长度＝＝．故选：A．【例题3】如图，⊙O的半径为1，弦AB＝1，点P为优弧AB上一动点，AC⊥AP交直线PB于点C，则△ABC的最大面积是．【分析】解题标签：“定边对定角”确定隐圆模型【解析】连结OA、OB，作△ABC的外接圆D，如图1，∵OA＝OB＝1，AB＝1，∴△OAB为等边三角形，∴∠AOB＝60°，∴∠APB＝∠AOB＝30°，∵AC⊥AP，∴∠C＝60°，∵AB＝1，要使△ABC的最大面积，则点C到AB的距离最大，∵∠ACB＝60°，点C在⊙D上，∴∠ADB＝120°，如图2，当点C优弧AB的中点时，点C到AB的距离最大，此时△ABC为等边三角形，且面积为AB2＝，∴△ABC的最大面积为．故答案为：．【例题4】如图，等腰Rt△ABC中，斜边AB的长为2，O为AB的中点，P为AC边上的动点，OQ⊥OP 交BC于点Q，M为PQ的中点，当点P从点A运动到点C时，点M所经过的路线长为（）A. B. C. 1 D. 2【分析】解题标签：“线段垂直平分线”产生“平行定距型”【解析】连接OC，作PE⊥AB于E，MH⊥AB于H，QF⊥AB于F，如图，∵△ACB为到等腰直角三角形，∴AC=BC= AB= ，∠A=∠B=45°，∵O为AB的中点，∴OC⊥AB，OC平分∠ACB，OC=OA=OB=1，∴∠OCB=45°，∵∠POQ=90°，∠COA=90°，∴∠AOP=∠COQ，在Rt△AOP和△COQ中，∴Rt△AOP≌△COQ，∴AP=CQ，易得△APE和△BFQ都为等腰直角三角形，∴PE=22AP=22CQ，QF=22BQ，∴PE+QF=22（CQ+BQ）=22BC=2×22=1，∵M点为PQ的中点，∴MH为梯形PEFQ的中位线，∴MH=12（PE+QF）=12，即点M到AB的距离为12，而CO=1，∴点M的运动路线为△ABC的中位线，∴当点P从点A运动到点C时，点M所经过的路线长=12AB=1，故答案为：C．[或连接OM，CM，点M运动路径为线段OC中垂线]【例题5】已知：如图1，平面直角坐标系中，点A的坐标是（0，6），点B在x轴上，且∠BAO＝30°，点D是线段OA上的一点，以BD为边向下作等边△BDE．（1）如图2，当∠ODB＝45°时，求证：OE平分∠BED．（2）如图3，当点E落在y轴上时，求出点E的坐标．（3）利用图1探究并说理：点D在y轴上从点A向点O滑动的过程中，点E也会在一条直线上滑动；并直接写出点E运动路径的长度．【分析】解题标签：“共顶点模型”、“全等或相似转固定角度法确定动点的直线运动”【解析】（1）∵∠ODB＝45°，∠AOB＝90°，∴∠OBD＝∠ODB＝45°，∴OD＝OB，∵△BDE是等边三角形，∴DE＝BE，在△DOE和△BOE中，，∴△DOE≌△BOE（SSS），∴∠DEO＝∠BEO，即OE平分∠BED；（2）∵△BOE是等边三角形，∴∠EDB＝60°，∵OB⊥DE，设OD＝x，则OE＝x，∵∠BAO＝30°，∠AOB＝90°，∴∠DBO＝∠ABD＝∠BAO＝30°，∴BD＝2OD＝2x，AD＝BD＝2x，∵OA＝AD+OD＝3x＝6，解得，x＝2，∴E（0，﹣2）；（3）如图1，在x轴上取点C，使BC＝BA，连接CE，∵∠ABD+∠OBD＝∠CBE+∠OBD＝60°，∴∠ABD＝∠CBE，在△ABD和△CBE中，，∴△ABD≌△CBE（SAS），∴∠BCE＝∠BAO＝30°，∴当D在OA上滑动时，点E总在与x轴夹角为30°的直线CE上滑动，如图可知，点E运动路径的长度为6．【例题6】如图，Rt△ABC中，BC＝4，AC＝8，Rt△ABC的斜边在x轴的正半轴上，点A与原点重合，随着顶点A由O点出发沿y轴的正半轴方向滑动，点B也沿着x轴向点O滑动，直到与点O重合时运动结束．在这个运动过程中，点C运动的路径长是8﹣12．【分析】解题标签：“运动路径为来回型”【解析】①当A从O到现在的点A处时，如图2，此时C′A⊥y轴，点C运动的路径长是CC′的长，∴AC′＝OC＝8，∵AC′∥OB，∴∠AC′O＝∠COB，∴cos∠AC′O＝cos∠COB＝＝，∴＝，∴OC′＝4，∴CC′＝4﹣8；②当A再继续向上移动，直到点B与O重合时，如图3，此时点C运动的路径是从C′到C，长是CC′，CC′＝OC′﹣BC＝4﹣4，综上所述，点C运动的路径长是：4﹣8+4﹣4＝8﹣12；故答案为：8﹣12．【例题7】如图1，已知抛物线y＝x2+bx+c经过原点O，它的对称轴是直线x＝2，动点P从抛物线的顶点A 出发，在对称轴上以每秒1个单位的速度向上运动，设动点P运动的时间为t杪，连结OP并延长交抛物线于点B，连结OA，AB．（1）求抛物线的函数解析式；（2）当△AOB为直角三角形时，求t的值；（3）如图2，⊙M为△AOB的外接圆，在点P的运动过程中，点M也随之运动变化，请你探究：在1≤t≤5时，求点M经过的路径长度．【分析】解题标签：“运动路径为来回型”【解析】（1）∵抛物线y＝x2+bx+c经过原点O，且对称轴是直线x＝2，∴c＝0，﹣＝2，则b＝﹣4、c＝0，∴抛物线解析式为y＝x2﹣4x；（2）设点B（a，a2﹣4a），∵y＝x2﹣4x＝（x﹣2）2﹣4，∴点A（2，﹣4），则OA2＝22+42＝20、OB2＝a2+（a2﹣4a）2、AB2＝（a﹣2）2+（a2﹣4a+4）2，①若OB2＝OA2+AB2，则a2+（a2﹣4a）2＝20+（a﹣2）2+（a2﹣4a+4）2，解得a＝2（舍）或a＝，∴B（，﹣），则直线OB解析式为y＝﹣x，当x＝2时，y＝﹣3，即P（2，﹣3），∴t＝（﹣3+4）÷1＝1；②若AB2＝OA2+OB2，则（a﹣2）2+（a2﹣4a+4）2＝20+a2+（a2﹣4a）2，解得a＝0（舍）或a＝，∴B（，），则直线OB解析式为y＝x，当x＝2时，y＝1，即P（2，1），∴t＝[1﹣（﹣4）]÷1＝5；③若OA2＝AB2+OB2，则20＝（a﹣2）2+（a2﹣4a+4）2+a2+（a2﹣4a）2，整理，得：a3﹣8a2+21a﹣18＝0，a3﹣3a2﹣5a2+15a+6a﹣18＝0，a2（a﹣3）﹣5a（a﹣3）+6（a﹣3）＝0，（a﹣3）（a2﹣5a+6）＝0，（a﹣3）2（a﹣2）＝0，则a＝3或a＝2（舍），∴B（3，﹣3），∴直线OB解析式为y＝﹣x，当x＝2时，y＝﹣2，即P（2，﹣2），∴t＝[﹣2﹣（﹣4）]÷1＝2；综上，当△AOB为直角三角形时，t的值为1或2或5．（3）∵⊙M为△AOB的外接圆，∴点M在线段OA的中垂线上，∴当1≤t≤5时，点M的运动路径是在线段OA中垂线上的一条线段，当t＝1时，如图1，由（2）知∠OAB＝90°，∴此时Rt△OAB的外接圆圆心M是OB的中点，∵B（，﹣），∴M（，﹣）；当t＝5时，如图2，由（2）知，∠AOB＝90°，∴此时Rt△OAB的外接圆圆心M是AB的中点，∵B（，）、A（2，﹣4），∴M（，﹣）；当t＝2时，如图3，由（2）知，∠OBA＝90°，∴此时Rt△OAB的外接圆圆心M是OA的中点，∵A（2，﹣4），∴M（1，﹣2）；则点M经过的路径长度为＝．【例题8】如图，OM⊥ON，A、B分别为射线OM、ON上两个动点，且OA+OB＝5，P为AB的中点．当B由点O向右移动时，点P移动的路径长为（）A．2 B．2C．D．5【分析】解题标签：“利用解析法计算几何路径长”【解析】建立如图坐标系．设OB＝t，则OA＝5﹣t，∴B（t，0），A（0，5﹣t），∵AP＝PB，∴P（，），令x＝，y＝，消去t得到，y＝﹣x+（0≤x≤），∴点P的运动轨迹是线段HK，H（0，），K（，0），∴点P的运动路径的长为＝，故选：C．【例题9】如图1，在Rt△ABC中，∠C=90°，AC=6，BC=8，动点P从点A开始沿边AC向点C以1个单位长度的速度运动，动点Q从点C开始沿边CB向点B以每秒2个单位长度的速度运动，过点P作PD∥BC，交AB于点D，连接PQ分别从点A、C同时出发，当其中一点到达端点时，另一点也随之停止运动，设运动时间为t秒（t≥0），在整个运动过程中，求出线段PQ中点M所经过的路径长．【分析】解题标签：“利用解析法计算几何路径长”【解析】如图2，以C为原点，以AC所在的直线为x轴，建立平面直角坐标系．依题意，可知0≤t≤4，当t=0时，点M1的坐标为（3，0），当t=4时点M2的坐标为（1，4）．设直线M1M2的解析式为y=kx+b，∴，解得，∴直线M1M2的解析式为y=-2x+6．∵点Q（0，2t），P（6-t，0）∴在运动过程中，线段PQ中点M3的坐标（，t）．把x= 代入y=-2x+6得y=-2×+6=t，∴点M3在直线M1M2上．过点M2作M2N⊥x轴于点N，则M2N=4，M1N=2．∴M1M2=2∴线段PQ中点M所经过的路径长为2 单位长度．【例题10】（1）如图1，已知AB=2，点D是等腰Rt△ABC斜边AC上一动点，以BD为一边向右下方作等边△BDE，当点D由点A运动到点C时，求点E运动的路径长；（2）如图2，已知AB=2，点D是等腰Rt△ABC斜边AC上一动点，以BD为一边向右下方作以E为直角顶点的等腰Rt△BDE，当点D由点A运动到点C时，求点E运动的路径长；（3）如图3，已知AB=2，点D是等腰Rt△ABC斜边AC上一动点，以BD为一边向右下方作以D为直角顶点的等腰Rt△BDE，当点D由点A运动到点C时，求点E运动的路径长；（4）如图4，已知AB=2，点D是等腰Rt△ABC斜边AC上一动点，以BD为一边向右下方作以D为直顶点的等腰△BDE，且∠BDE=120°，当点D由点A运动到点C时，求点E运动的路径长；【分析】解题标签：“主从联动模型”【解析】22；2；4；26【例题11】如图，已知扇形AOB中，OA=3，∠AOB=120°，C是在上的动点．以BC为边作正方形BCDE，当点C从点A移动至点B时，点D经过的路径长是________．【分析】解题标签：“定边对定角”确定隐圆模型、主从联动模型【解析】如图所示，易得点D的运动轨迹的长为=2 π．1．如图，在等腰Rt△ABC中，AC＝BC＝，点P在以斜边AB为直径的半圆上，M为PC的中点，当点P沿半圆从点A运动至点B时，点M运动的路径长是．【解析】如图，连接OP，OC，取OC的中点K，连接MK．∵AC＝BC＝，∠ACB＝90°，∴AB＝＝2，∴OP＝AB＝1，∵CM＝MP，CK＝OK，∴MK＝OP＝，∴当点P沿半圆从点A运动至点B时，点M运动的路径是以K为圆心，长为半径的半圆，∴点M运动的路径长＝•2•π•＝，故答案为．2．已知线段AB＝8，C、D是AB上两点，且AC＝2，BD＝4，P是线段CD上一动点，在AB同侧分别作等腰三角形APE和等腰三角形PBF，M为线段EF的中点，若∠AEP＝∠BFP，则当点P由点C移动到点D时，点M移动的路径长度为4﹣3．【解析】如图，分别延长AE、BF交于点H．∵△APE和△PBF都是等腰三角形，且∠AEP＝∠BFP∵∠A＝∠FPB，∴AH∥PF，同理，BH∥PE，∴四边形EPFH为平行四边形，∴EF与HP互相平分．∵M为EF的中点，∴M为PH中点，即在P的运动过程中，M始终为PH的中点，所以M的运行轨迹为三角形HCD的中位线QN．∵CD＝AB﹣AC﹣BD＝8﹣6，∴QN＝CD＝4﹣3，即M的移动路径长为4﹣3．故答案是：4﹣3．3．已知线段AB＝10，P是线段AB上一动点，在AB同侧分别作等边三角形APE和等边三角形PBF，G为线段EF的中点，点P由点A移动到点B时，G点移动的路径长度为5．【解析】如图，分别延长AE、BF交于点H，∵∠A＝∠FPB＝60°，∴AH∥PF，∵∠B＝∠EP A＝60°，∴BH∥PE，∴四边形EPFH为平行四边形，∴EF与HP互相平分．∵G为EF的中点，∴G正好为PH中点，即在P的运动过程中，G始终为PH的中点，所以G的运行轨迹为△HAB的中位线MN．∴MN＝AB＝5，即G的移动路径长为5．故答案为：54．如图，AB为⊙O的直径，AB＝3，弧AC的度数是60°，P为弧BC上一动点，延长AP到点Q，使AP•AQ＝AB2．若点P由B运动到C，则点Q运动的路径长为3．【解析】连接BQ，如图，∵AB为⊙O的直径，∴∠APB＝90°，∵AP•AQ＝AB2．即＝，而∠BAP＝∠QAB，∴△ABP∽△AQB，∴∠ABQ＝∠APB＝90°，∴BQ为⊙O的切线，点Q运动的路径长为切线长，∵弧AC的度数是60°，∴∠AOC＝60°，∴∠OAC＝60°，当点P在C点时，∠BAQ＝60°，∴BQ＝AB＝3，即点P由B运动到C，则点Q运动的路径长为3．故答案为3．5．如图，矩形ABCD中，AB＝4，AD＝6，点E在边AD上，且AE:ED＝1:2．动点P 从点A出发，沿AB 运动到点B停止．过点E作EF⊥PE交射线BC于点F．设点M是线段EF的中点，则在点P运动的整个过程中，点M的运动路径长为________．【答案】4【解析】如图所示：过点M作GH⊥AD.∵AD∥CB，GH⊥AD，∴GH⊥BC.在△EGM和△FHM中，∴△EGM≌△FHM.∴MG=MH.∴点M的轨迹是一条平行于BC的线段当点P与A重合时,BF1=AE=2，当点P与点B重合时,∠F2+∠EBF1=90∘,∠BEF1+∠EBF1=90∘，∴∠F2=∠EBF1.∵∠EF1B=∠EF1F2，∴△EF1B∽△∠EF1F2.∴，即∴F1F2=8，∵M1M2是△EF1F2的中位线，∴M1M2= F1F2=4.故答案为：4.6．等边三角形ABC的边长为2，在AC，BC边上各有一个动点E，F，满足AE＝CF，连接AF，BE相交于点P．（1）∠APB的度数；（2）当E从点A运动到点C时，试求点P经过的路径长；（3）连结CP，直接写出CP长度的最小值．【解析】（1）∵△ABC为等边三角形，∴AB＝AC，∠C＝∠CAB＝60°，又∵AE＝CF，在△ABE和△CAF中，，∴△ABE≌△CAF（SAS），∴AF＝BE，∠ABE＝∠CAF．又∵∠APE＝∠BPF＝∠ABP+∠BAP，∴∠APE＝∠BAP+∠CAF＝60°．∴∠APB＝180°﹣∠APE＝120°．（2）如图1，∵AE＝CF，∴点P的路径是一段弧，由题目不难看出当E为AC的中点的时候，点P经过弧AB的中点，此时△ABP 为等腰三角形，且∠ABP＝∠BAP＝30°，∴∠AOB＝120°，又∵AB＝2，∴OA＝2，点P的路径是l＝＝＝；（3）如图2，∵AE＝CF，∴点P的路径是一段弧，∴当点E运动到AC的中点时，CP长度的最小，即点P为△ABC的中心，过B作BE′⊥AC于E′，∴PC＝BE′，∵△ABC是等边三角形，∴BE′＝BC＝3，∴PC＝2．∴CP长度的最小值是2．方法二：由图1可知，CP最小值等于CO减OA，OA就是那圆弧的半径，可得PC的最小值为2．7．如图，AB为半圆O的直径，AB=2，C，D为半圆上两个动点（D在C右侧），且满足∠COD=60°，连结AD，BC相交于点P若点C从A出发按顺时针方向运动，当点D与B重合时运动停止，则点P所经过的路径长为________．【答案】【解析】解：点C从点A运动到点D与点B从何时，AD与BC的相点P运动的轨迹是一条弧，C,D两点运动到恰好是半圆的三等分点时，AD与BC的相点P是弧的最高点，作AP,BP的中垂线，两线交于点E，点E是弧APB的圆心；由题意知：AD=BD，∠PAB=∠PBA=30°,连接AE,DE，根据圆的对称性得出A、O、E三点在同一直线上，易证△ADE是一个等边三角形，∠AED=60°,在Rt△ADO中，∠DOA=90°,∠PAB=30°,AO=1,故AD=,∴AE=AD=,弧APB的长度==。
2020年中考数学二轮核心考点讲解第12讲运动路径长度问题解析版
【中考数学二轮核心考点讲解】第12讲运动路径长度问题想要对运动路径长度问题掌握得信手拈来，那么建议你对以下知识点进行提前学习会更好：1.《隐圆模型》2.《共顶点模型》-也可称“手拉手模型”3.《主从联动模型》-也可称“瓜豆原理模型”4.《旋转问题》—本系列的第二讲中所阐述的旋转相似模型此外，还需要明白的动点类型还有：5.线段垂直平分线——到线段两端点距离相等的动点一定在这条线段的垂直平分线上6.角平分线——到角两边距离相等的动点一定在这个角的角平分线上7.三角形中位线——动点到某条线的距离恒等于某平行线段的一半8.平行线分线段成比例——动点到某条线的距离与某平行线段成比例9.两平行线的性质——平行线间的距离，处处相等一、路径为圆弧型解题策略：①作出隐圆，找到圆心②作出半径，求出定长解题关键：通过《隐圆模型》中五种确定隐圆的基本条件作出隐圆，即可轻易得出结论. 二、路径为直线型解题策略：①利用平行定距法或者角度固定法确定动点运动路径为直线型②确定动点的起点与终点，计算出路径长度即可解题关键：解题过程中常常出现中位线，平行线分线段成比例，相似证动角恒等于顶角等知识点三、路径为往返型解题策略：①通常为《主从联动模型》的衍生版②确定动点的起点与终点，感知运动过程中的变化③找出动点运动的最远点解题关键：解题过程中常常出现相似转线段长、《主从联动模型》中的滑动模型等【例题1】如图，等腰Rt△AOB中，∠AOB＝90°，OA＝，⊙O与AB相切，分别交OA、OB于N、M，以PB为直角边作等腰Rt△BPQ，点P在弧MN上由点M运动到点N，则点Q运动的路径长为（）A．B．C．D．【分析】解题标签：《共顶点模型》中的旋转相似、《隐圆模型》中的动点定长模型、《主从联动模型》【解析】如图，连接OP，AQ，设⊙O与AB相切于C，连接OC，则OC⊥AB，∵OA＝OB，∠AOB＝90°，OB＝，∴AB＝2，OP＝OC＝AB＝，∵△ABO和△QBP均为等腰直角三角形，∴＝，∠ABO＝∠QBP＝45°，∴＝，∠ABQ＝∠OBP，∴△ABQ∽△OBP，∴∠BAQ＝∠BOP，＝，即＝，∴AQ＝，又∵点P在弧MN上由点M运动到点N，∴0°≤∠BOP≤90°，∴0°≤∠BAQ≤90°，∴点Q的运动轨迹为以A为圆心，AQ长为半径，圆心角为90°的扇形的圆弧，∴点Q运动的路径长为＝，故选：D．[本题用《主从联动模型》来接替会更快得到结果]【例题2】已知⊙O，AB是直径，AB＝4，弦CD⊥AB且过OB的中点，P是劣弧BC上一动点，DF垂直AP于F，则P从C运动到B的过程中，F运动的路径长度（）A．πB．C．πD．2【分析】解题标签：“定边对直角”确定隐圆模型【解析】作DQ⊥AC于Q，如图，当P点在C点时，F点与Q重合；当P点在B点时，F点与E点重合，∵∠AFD＝90°，∴点F在以AD为直径的圆上，∴点F运动的路径为，∵弦CD⊥AB且过OB的中点，∴OE＝OD，CE＝DE＝，AC＝AC＝2，∴∠DOE＝60°，∴∠DAC＝60°，∴△ACD为等边三角形，∴MQ和ME为中位线，∴MQ＝，∠QME＝60°，∴F运动的路径长度＝＝．故选：A．【例题3】如图，⊙O的半径为1，弦AB＝1，点P为优弧AB上一动点，AC⊥AP交直线PB于点C，则△ABC的最大面积是．【分析】解题标签：“定边对定角”确定隐圆模型【解析】连结OA、OB，作△ABC的外接圆D，如图1，∵OA＝OB＝1，AB＝1，∴△OAB为等边三角形，∴∠AOB＝60°，∴∠APB＝∠AOB＝30°，∵AC⊥AP，∴∠C＝60°，∵AB＝1，要使△ABC的最大面积，则点C到AB的距离最大，∵∠ACB＝60°，点C在⊙D上，∴∠ADB＝120°，如图2，当点C优弧AB的中点时，点C到AB的距离最大，此时△ABC为等边三角形，且面积为AB2＝，∴△ABC的最大面积为．故答案为：．【例题4】如图，等腰Rt△ABC中，斜边AB的长为2，O为AB的中点，P为AC边上的动点，OQ⊥OP 交BC于点Q，M为PQ的中点，当点P从点A运动到点C时，点M所经过的路线长为（）A. B. C. 1 D. 2【分析】解题标签：“线段垂直平分线”产生“平行定距型”【解析】连接OC，作PE⊥AB于E，MH⊥AB于H，QF⊥AB于F，如图，∵△ACB为到等腰直角三角形，∴AC=BC= AB= ，∠A=∠B=45°，∵O为AB的中点，∴OC⊥AB，OC平分∠ACB，OC=OA=OB=1，∴∠OCB=45°，∵∠POQ=90°，∠COA=90°，∴∠AOP=∠COQ，在Rt△AOP和△COQ中，∴Rt△AOP≌△COQ，∴AP=CQ，易得△APE和△BFQ都为等腰直角三角形，∴PE=22AP=22CQ，QF=22BQ，∴PE+QF=22（CQ+BQ）=22BC=2×22=1，∵M点为PQ的中点，∴MH为梯形PEFQ的中位线，∴MH=12（PE+QF）=12，即点M到AB的距离为12，而CO=1，∴点M的运动路线为△ABC的中位线，∴当点P从点A运动到点C时，点M所经过的路线长=12AB=1，故答案为：C．[或连接OM，CM，点M运动路径为线段OC中垂线]【例题5】已知：如图1，平面直角坐标系中，点A的坐标是（0，6），点B在x轴上，且∠BAO＝30°，点D是线段OA上的一点，以BD为边向下作等边△BDE．（1）如图2，当∠ODB＝45°时，求证：OE平分∠BED．（2）如图3，当点E落在y轴上时，求出点E的坐标．（3）利用图1探究并说理：点D在y轴上从点A向点O滑动的过程中，点E也会在一条直线上滑动；并直接写出点E运动路径的长度．【分析】解题标签：“共顶点模型”、“全等或相似转固定角度法确定动点的直线运动”【解析】（1）∵∠ODB＝45°，∠AOB＝90°，∴∠OBD＝∠ODB＝45°，∴OD＝OB，∵△BDE是等边三角形，∴DE＝BE，在△DOE和△BOE中，，∴△DOE≌△BOE（SSS），∴∠DEO＝∠BEO，即OE平分∠BED；（2）∵△BOE是等边三角形，∴∠EDB＝60°，∵OB⊥DE，设OD＝x，则OE＝x，∵∠BAO＝30°，∠AOB＝90°，∴∠DBO＝∠ABD＝∠BAO＝30°，∴BD＝2OD＝2x，AD＝BD＝2x，∵OA＝AD+OD＝3x＝6，解得，x＝2，∴E（0，﹣2）；（3）如图1，在x轴上取点C，使BC＝BA，连接CE，∵∠ABD+∠OBD＝∠CBE+∠OBD＝60°，∴∠ABD＝∠CBE，在△ABD和△CBE中，，∴△ABD≌△CBE（SAS），∴∠BCE＝∠BAO＝30°，∴当D在OA上滑动时，点E总在与x轴夹角为30°的直线CE上滑动，如图可知，点E运动路径的长度为6．【例题6】如图，Rt△ABC中，BC＝4，AC＝8，Rt△ABC的斜边在x轴的正半轴上，点A与原点重合，随着顶点A由O点出发沿y轴的正半轴方向滑动，点B也沿着x轴向点O滑动，直到与点O重合时运动结束．在这个运动过程中，点C运动的路径长是8﹣12．【分析】解题标签：“运动路径为来回型”【解析】①当A从O到现在的点A处时，如图2，此时C′A⊥y轴，点C运动的路径长是CC′的长，∴AC′＝OC＝8，∵AC′∥OB，∴∠AC′O＝∠COB，∴cos∠AC′O＝cos∠COB＝＝，∴＝，∴OC′＝4，∴CC′＝4﹣8；②当A再继续向上移动，直到点B与O重合时，如图3，此时点C运动的路径是从C′到C，长是CC′，CC′＝OC′﹣BC＝4﹣4，综上所述，点C运动的路径长是：4﹣8+4﹣4＝8﹣12；故答案为：8﹣12．【例题7】如图1，已知抛物线y＝x2+bx+c经过原点O，它的对称轴是直线x＝2，动点P从抛物线的顶点A 出发，在对称轴上以每秒1个单位的速度向上运动，设动点P运动的时间为t杪，连结OP并延长交抛物线于点B，连结OA，AB．（1）求抛物线的函数解析式；（2）当△AOB为直角三角形时，求t的值；（3）如图2，⊙M为△AOB的外接圆，在点P的运动过程中，点M也随之运动变化，请你探究：在1≤t≤5时，求点M经过的路径长度．【分析】解题标签：“运动路径为来回型”【解析】（1）∵抛物线y＝x2+bx+c经过原点O，且对称轴是直线x＝2，∴c＝0，﹣＝2，则b＝﹣4、c＝0，∴抛物线解析式为y＝x2﹣4x；（2）设点B（a，a2﹣4a），∵y＝x2﹣4x＝（x﹣2）2﹣4，∴点A（2，﹣4），则OA2＝22+42＝20、OB2＝a2+（a2﹣4a）2、AB2＝（a﹣2）2+（a2﹣4a+4）2，①若OB2＝OA2+AB2，则a2+（a2﹣4a）2＝20+（a﹣2）2+（a2﹣4a+4）2，解得a＝2（舍）或a＝，∴B（，﹣），则直线OB解析式为y＝﹣x，当x＝2时，y＝﹣3，即P（2，﹣3），∴t＝（﹣3+4）÷1＝1；②若AB2＝OA2+OB2，则（a﹣2）2+（a2﹣4a+4）2＝20+a2+（a2﹣4a）2，解得a＝0（舍）或a＝，∴B（，），则直线OB解析式为y＝x，当x＝2时，y＝1，即P（2，1），∴t＝[1﹣（﹣4）]÷1＝5；③若OA2＝AB2+OB2，则20＝（a﹣2）2+（a2﹣4a+4）2+a2+（a2﹣4a）2，整理，得：a3﹣8a2+21a﹣18＝0，a3﹣3a2﹣5a2+15a+6a﹣18＝0，a2（a﹣3）﹣5a（a﹣3）+6（a﹣3）＝0，（a﹣3）（a2﹣5a+6）＝0，（a﹣3）2（a﹣2）＝0，则a＝3或a＝2（舍），∴B（3，﹣3），∴直线OB解析式为y＝﹣x，当x＝2时，y＝﹣2，即P（2，﹣2），∴t＝[﹣2﹣（﹣4）]÷1＝2；综上，当△AOB为直角三角形时，t的值为1或2或5．（3）∵⊙M为△AOB的外接圆，∴点M在线段OA的中垂线上，∴当1≤t≤5时，点M的运动路径是在线段OA中垂线上的一条线段，当t＝1时，如图1，由（2）知∠OAB＝90°，∴此时Rt△OAB的外接圆圆心M是OB的中点，∵B（，﹣），∴M（，﹣）；当t＝5时，如图2，由（2）知，∠AOB＝90°，∴此时Rt△OAB的外接圆圆心M是AB的中点，∵B（，）、A（2，﹣4），∴M（，﹣）；当t＝2时，如图3，由（2）知，∠OBA＝90°，∴此时Rt△OAB的外接圆圆心M是OA的中点，∵A（2，﹣4），∴M（1，﹣2）；则点M经过的路径长度为＝．【例题8】如图，OM⊥ON，A、B分别为射线OM、ON上两个动点，且OA+OB＝5，P为AB的中点．当B由点O向右移动时，点P移动的路径长为（）A．2B．2C．D．5【分析】解题标签：“利用解析法计算几何路径长”【解析】建立如图坐标系．设OB＝t，则OA＝5﹣t，∴B（t，0），A（0，5﹣t），∵AP＝PB，∴P（，），令x＝，y＝，消去t得到，y＝﹣x+（0≤x≤），∴点P的运动轨迹是线段HK，H（0，），K（，0），∴点P的运动路径的长为＝，故选：C．【例题9】如图1，在Rt△ABC中，∠C=90°，AC=6，BC=8，动点P从点A开始沿边AC向点C以1个单位长度的速度运动，动点Q从点C开始沿边CB向点B以每秒2个单位长度的速度运动，过点P作PD∥BC，交AB于点D，连接PQ分别从点A、C同时出发，当其中一点到达端点时，另一点也随之停止运动，设运动时间为t秒（t≥0），在整个运动过程中，求出线段PQ中点M所经过的路径长．【分析】解题标签：“利用解析法计算几何路径长”【解析】如图2，以C为原点，以AC所在的直线为x轴，建立平面直角坐标系．依题意，可知0≤t≤4，当t=0时，点M1的坐标为（3，0），当t=4时点M2的坐标为（1，4）．设直线M1M2的解析式为y=kx+b，∴，解得，∴直线M1M2的解析式为y=-2x+6．∵点Q（0，2t），P（6-t，0）∴在运动过程中，线段PQ中点M3的坐标（，t）．把x= 代入y=-2x+6得y=-2×+6=t，∴点M3在直线M1M2上．过点M2作M2N⊥x轴于点N，则M2N=4，M1N=2．∴M1M2=2∴线段PQ中点M所经过的路径长为2 单位长度．【例题10】（1）如图1，已知AB=2，点D是等腰Rt△ABC斜边AC上一动点，以BD为一边向右下方作等边△BDE，当点D由点A运动到点C时，求点E运动的路径长；（2）如图2，已知AB=2，点D是等腰Rt△ABC斜边AC上一动点，以BD为一边向右下方作以E为直角顶点的等腰Rt△BDE，当点D由点A运动到点C时，求点E运动的路径长；（3）如图3，已知AB=2，点D是等腰Rt△ABC斜边AC上一动点，以BD为一边向右下方作以D为直角顶点的等腰Rt△BDE，当点D由点A运动到点C时，求点E运动的路径长；（4）如图4，已知AB=2，点D是等腰Rt△ABC斜边AC上一动点，以BD为一边向右下方作以D为直顶点的等腰△BDE，且∠BDE=120°，当点D由点A运动到点C时，求点E运动的路径长；【分析】解题标签：“主从联动模型”【解析】22；2；4；26【例题11】如图，已知扇形AOB中，OA=3，∠AOB=120°，C是在上的动点．以BC为边作正方形BCDE，当点C从点A移动至点B时，点D经过的路径长是________．【分析】解题标签：“定边对定角”确定隐圆模型、主从联动模型【解析】如图所示，易得点D的运动轨迹的长为=2 π．1．如图，在等腰Rt△ABC中，AC＝BC＝，点P在以斜边AB为直径的半圆上，M为PC的中点，当点P沿半圆从点A运动至点B时，点M运动的路径长是．【解析】如图，连接OP，OC，取OC的中点K，连接MK．∵AC＝BC＝，∠ACB＝90°，∴AB＝＝2，∴OP＝AB＝1，∵CM＝MP，CK＝OK，∴MK＝OP＝，∴当点P沿半圆从点A运动至点B时，点M运动的路径是以K为圆心，长为半径的半圆，∴点M运动的路径长＝•2•π•＝，故答案为．2．已知线段AB＝8，C、D是AB上两点，且AC＝2，BD＝4，P是线段CD上一动点，在AB同侧分别作等腰三角形APE和等腰三角形PBF，M为线段EF的中点，若∠AEP＝∠BFP，则当点P由点C移动到点D时，点M移动的路径长度为4﹣3．【解析】如图，分别延长AE、BF交于点H．∵△APE和△PBF都是等腰三角形，且∠AEP＝∠BFP∵∠A＝∠FPB，∴AH∥PF，同理，BH∥PE，∴四边形EPFH为平行四边形，∴EF与HP互相平分．∵M为EF的中点，∴M为PH中点，即在P的运动过程中，M始终为PH的中点，所以M的运行轨迹为三角形HCD的中位线QN．∵CD＝AB﹣AC﹣BD＝8﹣6，∴QN＝CD＝4﹣3，即M的移动路径长为4﹣3．故答案是：4﹣3．3．已知线段AB＝10，P是线段AB上一动点，在AB同侧分别作等边三角形APE和等边三角形PBF，G为线段EF的中点，点P由点A移动到点B时，G点移动的路径长度为5．【解析】如图，分别延长AE、BF交于点H，∵∠A＝∠FPB＝60°，∴AH∥PF，∵∠B＝∠EP A＝60°，∴BH∥PE，∴四边形EPFH为平行四边形，∴EF与HP互相平分．∵G为EF的中点，∴G正好为PH中点，即在P的运动过程中，G始终为PH的中点，所以G的运行轨迹为△HAB的中位线MN．∴MN＝AB＝5，即G的移动路径长为5．故答案为：54．如图，AB为⊙O的直径，AB＝3，弧AC的度数是60°，P为弧BC上一动点，延长AP到点Q，使AP•AQ＝AB2．若点P由B运动到C，则点Q运动的路径长为3．【解析】连接BQ，如图，∵AB为⊙O的直径，∴∠APB＝90°，∵AP•AQ＝AB2．即＝，而∠BAP＝∠QAB，∴△ABP∽△AQB，∴∠ABQ＝∠APB＝90°，∴BQ为⊙O的切线，点Q运动的路径长为切线长，∵弧AC的度数是60°，∴∠AOC＝60°，∴∠OAC＝60°，当点P在C点时，∠BAQ＝60°，∴BQ＝AB＝3，即点P由B运动到C，则点Q运动的路径长为3．故答案为3．5．如图，矩形ABCD中，AB＝4，AD＝6，点E在边AD上，且AE:ED＝1:2．动点P 从点A出发，沿AB 运动到点B停止．过点E作EF⊥PE交射线BC于点F．设点M是线段EF的中点，则在点P运动的整个过程中，点M的运动路径长为________．【答案】4【解析】如图所示：过点M作GH⊥AD.∵AD∥CB，GH⊥AD，∴GH⊥BC.在△EGM和△FHM中，∴△EGM≌△FHM.∴MG=MH.∴点M的轨迹是一条平行于BC的线段当点P与A重合时,BF1=AE=2，当点P与点B重合时,∠F2+∠EBF1=90∘,∠BEF1+∠EBF1=90∘，∴∠F2=∠EBF1.∵∠EF1B=∠EF1F2，∴△EF1B∽△∠EF1F2.∴，即∴F1F2=8，∵M1M2是△EF1F2的中位线，∴M1M2= F1F2=4.故答案为：4.6．等边三角形ABC的边长为2，在AC，BC边上各有一个动点E，F，满足AE＝CF，连接AF，BE相交于点P．（1）∠APB的度数；（2）当E从点A运动到点C时，试求点P经过的路径长；（3）连结CP，直接写出CP长度的最小值．【解析】（1）∵△ABC为等边三角形，∴AB＝AC，∠C＝∠CAB＝60°，又∵AE＝CF，在△ABE和△CAF中，，∴△ABE≌△CAF（SAS），∴AF＝BE，∠ABE＝∠CAF．又∵∠APE＝∠BPF＝∠ABP+∠BAP，∴∠APE＝∠BAP+∠CAF＝60°．∴∠APB＝180°﹣∠APE＝120°．（2）如图1，∵AE＝CF，∴点P的路径是一段弧，由题目不难看出当E为AC的中点的时候，点P经过弧AB的中点，此时△ABP 为等腰三角形，且∠ABP＝∠BAP＝30°，∴∠AOB＝120°，又∵AB＝2，∴OA＝2，点P的路径是l＝＝＝；（3）如图2，∵AE＝CF，∴点P的路径是一段弧，∴当点E运动到AC的中点时，CP长度的最小，即点P为△ABC的中心，过B作BE′⊥AC于E′，∴PC＝BE′，∵△ABC是等边三角形，∴BE′＝BC＝3，∴PC＝2．∴CP长度的最小值是2．方法二：由图1可知，CP最小值等于CO减OA，OA就是那圆弧的半径，可得PC的最小值为2．7．如图，AB为半圆O的直径，AB=2，C，D为半圆上两个动点（D在C右侧），且满足∠COD=60°，连结AD，BC相交于点P若点C从A出发按顺时针方向运动，当点D与B重合时运动停止，则点P所经过的路径长为________．【答案】【解析】解：点C从点A运动到点D与点B从何时，AD与BC的相点P运动的轨迹是一条弧，C,D两点运动到恰好是半圆的三等分点时，AD与BC的相点P是弧的最高点，作AP,BP的中垂线，两线交于点E，点E是弧APB的圆心；由题意知：AD=BD，∠PAB=∠PBA=30°,连接AE,DE，根据圆的对称性得出A、O、E三点在同一直线上，易证△ADE是一个等边三角形，∠AED=60°,在Rt△ADO中，∠DOA=90°,∠PAB=30°,AO=1,故AD=,∴AE=AD=,弧APB的长度==。
中考数学：点动产生路径长问题
点动产生的路径长问题近几年中考，和我们同学做的中考模拟试卷中，不断的出现了因动点计算路径长问题，这种题型因为隐藏的比较深，从而难以发现，计算比较繁琐。
在填空题选择题中比较多。
只要同学们在做题的过程中发现是这种题型，那么点所经过的路径一般就是就是两种结果。
一是线段。
二是圆弧。
为什么呢？因为只有这两图形是可以计算路径长的。
其它图形我们目前能计算路径长吗。
哈哈，这样解释印象有没有很深。
下面我们来看看我们会碰到的几种题型。
题型1：简单的图形翻转问题。
解法：这种题型比较简单。
只要找出旋转圆心，旋转时圆的半径，还有圆心角就可以了，然后利用扇形的弧长计算公式来计算。
注意，如果是圆弧旋转的话，圆心的路径是直线。
例题1：一块等边三角形的木板，边长为1，现将木板沿水平线翻滚（如图），那么B点从开始至结束所走过的路径长度为___________试题分析：现将木板沿水平线翻滚， B点从开始至结束走过了4条弧，每条弧是一等边三角形的边为半径的扇形，圆心角为等边三角形的内角，所以 B点从开始至结束所走过的路程长度=4l=点评：本题考查扇形的弧长公式，关键是找出扇形的圆心角和半径，考查学生的空间想象能力例题2：矩形ABCD的边AB=8，AD=6，现将矩形ABCD放在直线l上且沿着l向右作无滑动地翻滚，当它翻滚至类似开始的位置A1B1C1D1时（如图所示），则顶点A所经过的路线长是例题3：将半径为1、圆心角为60°的扇形纸片AOB，在直线l上向右作无滑动的滚动至扇形A’O’B’处，则顶点O经过的路线长为。
例题4：如图，一个圆心角为270°，半径为2m的扇形工件，未搬动前如图所示，A，B两点触地放置，搬动时，先将扇形以B为圆心，作如图所示的无滑动翻转，再使它紧贴地面滚动，当A，B两点再次触地时停止，则圆心O所经过的路线长是m．（结果保留π）例题5：已知一个半圆形工件，未搬动前如图所示，直径平行于地面放置，搬动时为了保护圆弧部分不受损伤，先将半圆作如图所示的无滑动翻转，使它的直径紧贴地面，再将它沿地面平移50m，半圆的直径为4m，则圆心O所经过的路线长是 m。
蚂蚁最短路径问题的总结
蚂蚁最短路径问题的总结蚂蚁最短路径问题是指一群蚂蚁从一个起点出发，到达终点的过程中，所走的路线最短的问题。
这个问题在生活中有很多应用，比如在物流运输中，寻找最短路径可以节省时间和成本。
本文将对蚂蚁最短路径问题进行总结和分析。
一、问题描述假设有一条长度为 L 的木棍，上面有 n 只蚂蚁。
每只蚂蚁的速度相同，且只能向前爬行。
当两只蚂蚁相遇时，它们会掉头。
现在，我们把这些蚂蚁放在木棍的两端，让它们开始爬行。
问最终它们会在哪里相遇？二、问题分析1. 蚂蚁相遇的情况当两只蚂蚁相遇时，它们会掉头，相当于它们的速度变成了相反方向。
因此，我们可以把相向而行的两只蚂蚁看成是穿过了对方，继续向前爬行。
2. 蚂蚁相遇的时间由于蚂蚁的速度相同，因此它们相遇的时间是固定的。
假设蚂蚁的速度是 v，相遇的时间是 t，则两只蚂蚁之间的距离是 vt。
3. 最终相遇的位置由于我们无法确定蚂蚁的相对位置，因此我们无法确定它们最终相遇的位置。
但是，我们可以确定它们相遇的位置一定是在木棍的两端之间。
三、问题解决1. 排序法我们可以将蚂蚁按照它们的位置从左到右排序，然后让它们继续向前爬行。
当两只蚂蚁相遇时，它们会掉头，相当于它们的位置交换了。
因此，我们可以把相向而行的两只蚂蚁看成是穿过了对方，继续向前爬行。
2. 模拟法我们可以模拟每只蚂蚁的运动过程，直到它们相遇为止。
对于每只蚂蚁，我们可以记录它的位置、方向和状态。
当两只蚂蚁相遇时，它们会掉头，相当于它们的方向反转了。
因此，我们可以把相向而行的两只蚂蚁看成是穿过了对方，继续向前爬行。
3. 数学法我们可以通过数学公式来求解最终相遇的位置。
假设蚂蚁的数量为 n，速度为 v，木棍的长度为 L，则两只蚂蚁之间的距离是 vt。
因此，蚂蚁相遇的时间是 t=L/(2nv)。
当蚂蚁相遇时，它们的速度变成了相反方向，因此，它们会继续向前爬行，直到到达木棍的两端。
因此，最终相遇的位置一定是在木棍的两端之间。
四、应用实例蚂蚁最短路径问题在生活中有很多应用，比如在物流运输中，寻找最短路径可以节省时间和成本。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
硬核：狙击2020中考数学重点/难点/热点想要对运动路径长度问题掌握得信手拈来，那么建议你对以下知识点进行提前学习会更好：1.《隐圆模型》2.《共顶点模型》-也可称“手拉手模型”3.《主从联动模型》-也可称“瓜豆原理模型”4.《旋转问题》—本系列的第二讲中所阐述的旋转相似模型此外，还需要明白的动点类型还有：5.线段垂直平分线——到线段两端点距离相等的动点一定在这条线段的垂直平分线上6.角平分线——到角两边距离相等的动点一定在这个角的角平分线上7.三角形中位线——动点到某条线的距离恒等于某平行线段的一半8.平行线分线段成比例——动点到某条线的距离与某平行线段成比例9.两平行线的性质——平行线间的距离，处处相等一、路径为圆弧型解题策略：①作出隐圆，找到圆心②作出半径，求出定长解题关键：通过《隐圆模型》中五种确定隐圆的基本条件作出隐圆，即可轻易得出结论.二、路径为直线型解题策略：①利用平行定距法或者角度固定法确定动点运动路径为直线型②确定动点的起点与终点，计算出路径长度即可解题关键：解题过程中常常出现中位线，平行线分线段成比例，相似证动角恒等于顶角等知识点三、路径为往返型解题策略：①通常为《主从联动模型》的衍生版②确定动点的起点与终点，感知运动过程中的变化③找出动点运动的最远点解题关键：解题过程中常常出现相似转线段长、《主从联动模型》中的滑动模型等【例题1】如图，等腰Rt△AOB中，∠AOB＝90°，OA＝，⊙O与AB相切，分别交OA、OB于N、M，以PB为直角边作等腰Rt△BPQ，点P在弧MN上由点M运动到点N，则点Q运动的路径长为（）A．B．C．D．【例题2】已知⊙O，AB是直径，AB＝4，弦CD⊥AB且过OB的中点，P是劣弧BC上一动点，DF垂直AP于F，则P从C运动到B的过程中，F运动的路径长度（）A．πB．C．πD．2【例题3】如图，⊙O的半径为1，弦AB＝1，点P为优弧AB上一动点，AC⊥AP交直线PB于点C，则△ABC的最大面积是．【例题4】如图，等腰Rt△ABC中，斜边AB的长为2，O为AB的中点，P为AC边上的动点，OQ⊥OP 交BC于点Q，M为PQ的中点，当点P从点A运动到点C时，点M所经过的路线长为（）A. B. C.1 D.2【例题5】已知：如图1，平面直角坐标系中，点A的坐标是（0，6），点B在x轴上，且∠BAO＝30°，点D是线段OA上的一点，以BD为边向下作等边△BDE．（1）如图2，当∠ODB＝45°时，求证：OE平分∠BED．（2）如图3，当点E落在y轴上时，求出点E的坐标．（3）利用图1探究并说理：点D在y轴上从点A向点O滑动的过程中，点E也会在一条直线上滑动；并直接写出点E运动路径的长度．【例题6】如图，Rt△ABC中，BC＝4，AC＝8，Rt△ABC的斜边在x轴的正半轴上，点A与原点重合，随着顶点A由O点出发沿y轴的正半轴方向滑动，点B也沿着x轴向点O滑动，直到与点O重合时运动结束．在这个运动过程中，点C运动的路径长是．【例题7】如图1，已知抛物线y＝x2+bx+c经过原点O，它的对称轴是直线x＝2，动点P从抛物线的顶点A 出发，在对称轴上以每秒1个单位的速度向上运动，设动点P运动的时间为t杪，连结OP并延长交抛物线于点B，连结OA，AB．（1）求抛物线的函数解析式；（2）当△AOB为直角三角形时，求t的值；（3）如图2，⊙M为△AOB的外接圆，在点P的运动过程中，点M也随之运动变化，请你探究：在1≤t≤5时，求点M经过的路径长度．【例题8】如图，OM⊥ON，A、B分别为射线OM、ON上两个动点，且OA+OB＝5，P为AB的中点．当B由点O向右移动时，点P移动的路径长为（）A．2B．2C．D．5【例题9】如图1，在Rt△ABC中，∠C=90°，AC=6，BC=8，动点P从点A开始沿边AC向点C以1个单位长度的速度运动，动点Q从点C开始沿边CB向点B以每秒2个单位长度的速度运动，过点P作PD∥BC，交AB于点D，连接PQ分别从点A、C同时出发，当其中一点到达端点时，另一点也随之停止运动，设运动时间为t秒（t≥0），在整个运动过程中，求出线段PQ中点M所经过的路径长．【例题10】（1）如图1，已知AB=2，点D是等腰Rt△ABC斜边AC上一动点，以BD为一边向右下方作等边△BDE，当点D由点A运动到点C时，求点E运动的路径长；（2）如图2，已知AB=2，点D是等腰Rt△ABC斜边AC上一动点，以BD为一边向右下方作以E为直角顶点的等腰Rt△BDE，当点D由点A运动到点C时，求点E运动的路径长；（3）如图3，已知AB=2，点D是等腰Rt△ABC斜边AC上一动点，以BD为一边向右下方作以D为直角顶点的等腰Rt△BDE，当点D由点A运动到点C时，求点E运动的路径长；（4）如图4，已知AB=2，点D是等腰Rt△ABC斜边AC上一动点，以BD为一边向右下方作以D为直顶点的等腰△BDE，且∠BDE=120°，当点D由点A运动到点C时，求点E运动的路径长；【例题11】如图，已知扇形AOB中，OA=3，∠AOB=120°，C是在上的动点．以BC为边作正方形BCDE，当点C从点A移动至点B时，点D经过的路径长是________．1．如图，在等腰Rt△ABC中，AC＝BC＝，点P在以斜边AB为直径的半圆上，M为PC的中点，当点P沿半圆从点A运动至点B时，点M运动的路径长是．2．已知线段AB＝8，C、D是AB上两点，且AC＝2，BD＝4，P是线段CD上一动点，在AB同侧分别作等腰三角形APE和等腰三角形PBF，M为线段EF的中点，若∠AEP＝∠BFP，则当点P由点C移动到点D时，点M移动的路径长度为．3．已知线段AB＝10，P是线段AB上一动点，在AB同侧分别作等边三角形APE和等边三角形PBF，G为线段EF的中点，点P由点A移动到点B时，G点移动的路径长度为．4．如图，AB为⊙O的直径，AB＝3，弧AC的度数是60°，P为弧BC上一动点，延长AP到点Q，使AP•AQ ＝AB2．若点P由B运动到C，则点Q运动的路径长为．5．如图，矩形ABCD中，AB＝4，AD＝6，点E在边AD上，且AE:ED＝1:2．动点P从点A出发，沿AB 运动到点B停止．过点E作EF⊥PE交射线BC于点F．设点M是线段EF的中点，则在点P运动的整个过程中，点M的运动路径长为________．6．等边三角形ABC的边长为2，在AC，BC边上各有一个动点E，F，满足AE＝CF，连接AF，BE相交于点P．（1）∠APB的度数；（2）当E从点A运动到点C时，试求点P经过的路径长；（3）连结CP，直接写出CP长度的最小值．7．如图，AB为半圆O的直径，AB=2，C，D为半圆上两个动点（D在C右侧），且满足∠COD=60°，连结AD，BC相交于点P若点C从A出发按顺时针方向运动，当点D与B重合时运动停止，则点P所经过的路径长为________．8．如图，A（﹣3，0），B（0，3），C（﹣1，4），P，C，M按逆时针顺序排列，动点P在线段AB上，∠C ＝90°，∠CPM＝30°，请求出当P点从A运动到B点时，点M运动的路径时什么？并求出M点运动路径长度．9．如图，矩形ABCD中，AB＝6，BC＝6，动点P从点A出发，以每秒个单位长度的速度沿线段AD 运动，动点Q从点D出发，以每秒2个单位长度的速度沿折线段D﹣O﹣C运动，已知P、Q同时开始移动，当动点P到达D点时，P、Q同时停止运动．设运动时间为t秒．（1）当t＝1秒时，求动点P、Q之间的距离；（2）若动点P、Q之间的距离为4个单位长度，求t的值；（3）若线段PQ的中点为M，在整个运动过程中；直接写出点M运动路径的长度为．10．（2019秋•江岸区校级月考）如图，正△ABC中，AB＝2，AD⊥BC于D，P，Q分别是AB，BC上的动点，且PQ＝AD，点M在PQ的右上方且PM＝QM，∠M＝120°，当P从点A运动到点B时，M运动的路径长为．(看成固定三角板滑动处理/或反其道而行之)11．如图，在四边形ABCD中，∠C＝60°，∠A＝30°，CD＝BC．（1）求∠B+∠D的度数．（2）连接AC，探究AD，AB，AC三者之间的数量关系，并说明理由．（3）若BC＝2，点E在四边形ABCD内部运动，且满足DE2＝CE2+BE2，求点E运动路径的长度．12．已知在扇形AOB中，圆心角∠AOB＝120°，半径OA＝OB＝8．（1）如图1，过点O作OE⊥OB，交弧AB于点E，再过点E作EF⊥OA于点F，则FO的长是，∠FEO＝°；（2）如图2，设点P为弧AB上的动点，过点P作PM⊥OA于点M，PN⊥OB于点N，点M，N分别在半径OA，OB上，连接MN，则①求点P运动的路径长是多少？②MN的长度是否是定值？如果是，请求出这个定值；若不是，请说明理由；（3）在（2）中的条件下，若点D是△PMN的外心，直接写出点D运动的路经长．13．如图，AB为⊙O的直径，且AB＝4，点C在半圆上，OC⊥AB，垂足为点O，P为半圆上任意一点，过P点作PE⊥OC于点E，设△OPE的内心为M，连接OM、PM．（1）求∠OMP的度数；（2）当点P在半圆上从点B运动到点A时，求内心M所经过的路径长．14．（2019•兴化市模拟）正方形ABCD的边长为4，P为BC边上的动点，连接AP，作PQ⊥PA交CD边于点Q．当点P从B运动到C时，线段AQ的中点M所经过的路径长（）A．2B．1C．4D．15．（2019•武汉模拟）如图，半径为2cm，圆心角为90°的扇形OAB的弧AB上有一运动的点P，从点P 向半径OA引垂线PH交OA于点H．设△OPH的内心为I，当点P在弧AB上从点A运动到点B时，内心I所经过的路径长为（）A．πB．πC．πD．π16．如图，BC是⊙O的直径，BC＝4，M、N是半圆上不与B、C重合的两点，且∠MON＝120°，△ABC的内心为E点，当点A在上从点M运动到点N时，点E运动的路径长是（）A．B．C．D．17．（2020•河北模拟）如图，在正方形ABCD中，AB＝1，P是边BC上的一个动点，由点B开始运动，运动到C停止．连接AP，以AP为直角边向右侧作等腰直角三角形，另一个顶点为Q．则点P从B运动到C的过程中，点Q的运动路径长为（）A．πB．C．D．118．无论a取什么实数，点P（a﹣1，2a﹣3）都在直线l上．Q（m，n）是直线l上的点，则（2m﹣n+3）2的值等于．19．如图，已知点C是以AB为直径的半圆的中点，D为弧AC上任意一点，过点C作CE⊥BD于点E，连接AE，若AB＝4，则AE的最小值为．20．如图，正方形OABC的边长为2，以O为圆心，EF为直径的半圆经过点A，连接AE，CF相交于点P，将正方形OABC从OA与OF重合的位置开始，绕着点O逆时针旋转90°，交点P运动的路径长是．21．如图，在平面直角坐标系中，点A（8，0），点P（0，m），将线段PA绕着点P逆时针旋转90°，得到线段PB，连接AB，OB，则BO+BA的最小值为．22．如图，P为边长为2的正方形ABCD的边BC上一动点，将线段DP绕P逆时针旋转90°得到线段PE （E为D的对应点），M为线段PE的中点，当点P从点C运动到点B的过程中，点M的运动路径长为____________.23．等边△ABC的边长为18，在AC，BC边上各取一点D，E，连接AE，BD相交于点P，若AE＝BD，当D从点A运动到点C时，点P所经过的路径长为．24．（2020•武汉模拟）如图，定直线l经过圆心O，P是半径OA上一动点，AC⊥l于点C，当半径OA绕着点O旋转时，总有OP＝OC，若OA绕点O旋转60°时，P、A两点的运动路径长的比值是．25．如图，已知正方形ABCD的边长为4，点P是AB边上一个动点，连接CP，过点P作PC的垂线交AD 于点E，以PE为边作正方形PEFG，顶点G在线段PC上，对角线EG、PF相交于点O．（1）若AP＝1，则AE＝；（2）①求证：点O一定在△APE的外接圆上；②当点P从点A运动到点B时，点O也随之运动，求点O经过的路径长；（3）在点P从点A到点B的运动过程中，△APE的外接圆的圆心也随之运动，求该圆心到AB边的距离的最大值．26．如图，正方形ABCD的边长为2，动点E从点A出发，沿边AB﹣BC向终点C运动，以DE为边作正方形DEFG（点D、E、F、G按顺时针方向排列）．设点E运动速度为每秒1个单位，运动的时间为x秒．（1）如图1，当点E在AB上时，求证：点G在直线BC上；（2）设正方形ABCD与正方形DEFG重叠部分的面积为S，求S与x之间的函数关系式；（3）直接写出整个运动过程中，点F经过的路径长．。