计算方法(孙志忠)习题 第四章 插值法
数值方法课后习题答案

数值方法课后习题答案习题1:插值法给定一组数据点 \((x_1, y_1), (x_2, y_2), \ldots, (x_n, y_n)\),使用拉格朗日插值法构造一个多项式 \(P(x)\),使其通过所有给定的数据点。
答案:拉格朗日插值法的多项式 \(P(x)\) 可以表示为:\[ P(x) = \sum_{i=1}^{n} y_i \prod_{\substack{j=1 \\ j \neq i}}^{n} \frac{x - x_j}{x_i - x_j} \]习题2:数值积分使用梯形法则和辛普森法则分别计算定积分 \(\int_{0}^{1} x^2 dx\) 的近似值。
答案:- 梯形法则的近似值:\[ \text{Trapezoidal Rule} \approx \frac{h}{2}(y_0 + 2y_1 +2y_2 + \ldots + y_{n-1}) \]- 辛普森法则的近似值:\[ \text{Simpson's Rule} \approx \frac{h}{3}(y_0 + 4y_1 +2y_2 + 4y_3 + \ldots + y_{n-1}) \]习题3:微分方程数值解考虑常微分方程 \(y' = f(x, y)\),其中 \(f(x, y) = x^2 - y^2\),初始条件 \(y(0) = 1\)。
使用欧拉方法和改进的欧拉方法分别计算\(y(0.1)\) 的近似值。
答案:- 欧拉方法:\[ y_{n+1} = y_n + h \cdot f(x_n, y_n) \]- 改进的欧拉方法:\[ y_{n+1} = y_n + \frac{h}{2} \cdot (f(x_n, y_n) + f(x_{n+1}, y_{n+1})) \]习题4:线性方程组的数值解给定线性方程组 \(Ax = b\),其中 \(A\) 是一个 \(n \times n\)的矩阵,\(b\) 是一个 \(n \times 1\) 的向量。
计算方法习题集及实验指导书

《计算方法习题集及实验指导书》计算机科学与技术系檀明2008-02-10课程性质及目的要求(一)课程性质自计算机问世以来,科学计算一直是计算机应用的一个重要领域,数值计算方法是解决各种复杂的科学计算问题的理论与技术的基础。
《计算方法》课程讨论用于科学计算中的一些最基本、最常用的算法,不但具有数学的抽象性与严密的科学性的特点,而且具有应用的高度技术性的特点。
它对于培养从事计算机应用的科技人才有着重要的作用,是计算机应用专业(本科段)的一门重要的技术基础课程。
(二)目的要求通过本课程的学习和上机实验,了解用计算机解决科学计算问题的方法特点,掌握计算方法中的一些基本概念、基本公式和相应的算法流程,提高根据算法描述设计高级语言程序并进行验证的技能。
在学习过程中,应注重理解和应用,在搞清基本原理和基本概念的基础上,通过习题、编程和上机等环节,巩固和加深已学的内容,掌握重要的算法及其应用。
注重理论与算法的学习和应用相结合,强调编程及上机计算的技能培养,是本课程不同于一般数学课程的重要特点。
(三)学习方法指导1.循序渐进逐章学习本课程从第二章开始,每章都讨论一个大类的算法。
虽然各算法是相对独立的,但是也存在相互XXX与前后继承的关系。
前面的概念和算法学好了,后面的内容也就容易学,越学越感到容易。
前面的内容没有学好,后面就会感到难学,甚至会出现越来越感到困难、失去学习信心的情况。
2.稳扎稳打融会贯通学习要扎实、要讲求实效。
每一个重要的概念和公式,都会搞清楚,做到融会贯通。
只有这样,才能取得学习的学习效果。
3.多学练勤做习题教材及本习题集中的每一章都附有适量的习题,可以帮助考生巩固和加深理解所学的知识,提高解题能力。
因此,在学习过程中,应当适合习题进行思考,应当尽可能多做习题,遇到某些不会做的题,应三思之后再请老师给予提示。
4.抓住特点前后XXX 本课程只讲了五大类算法。
每类算法都是针对一类特定的计算问题,都有其自身的特点。
计算方法_课后习题答案

(4.5)(0.01172)
0.00879
(2)采用 Newton 插值多项式 y x N2(x) 根据题意作差商表:
i
xi
0
4
1
6.25
f (xi ) 2 2.5
一阶差商 2 9
2
9
3
2 11
二阶差商 4 495
N2 (7) 2 29 (7 4) ( 4 495) (7 4) (7 6.25) 2.6484848
1
e2
则根据二次Lagrange插值公式得:
L2 (x)
(x ( x0
x1)(x x2 ) x1)(x0 x2 )
y0
(x ( x1
x0 )(x x2 ) x0 )(x1 x2 )
y1
(x ( x2
x0 )(x x1) x0 )(x2 x1)
y2
2(x 1)(x 0.5) 2x(x 0.5)e1 4x(x 1)e0.5
8. 求作 f x xn1 关于节点 xi i 0,1, , n 的 Lagrange 插值多项式,并利用
插值余项定理证明
n
n
xin1li 0 1n xi
i0
i0
式中 li x 为关于节点 xi i 0,1, , n 的 Lagrange 插值基函数。
2 02 12 4 23 4 04 14 2 3
1 x2 3x 2 x 4 3x x2 6x 8 23 x x2 5x 4 1 x x2 3x 2
8
4
8
数值计算方法课后习题答案

第一章 绪论(12)1、设0>x ,x 的相对误差为δ,求x ln 的误差。
[解]设0*>x 为x 的近似值,则有相对误差为δε=)(*x r ,绝对误差为**)(x x δε=,从而x ln 的误差为δδεε=='=*****1)()(ln )(ln x x x x x , 相对误差为****ln ln )(ln )(ln x x x x rδεε==。
2、设x 的相对误差为2%,求n x 的相对误差。
[解]设*x 为x 的近似值,则有相对误差为%2)(*=x r ε,绝对误差为**%2)(x x =ε,从而nx 的误差为nn x x nxn x x n x x x **1***%2%2)()()()(ln *⋅=='=-=εε,相对误差为%2)()(ln )(ln ***n x x x nr==εε。
3、下列各数都是经过四舍五入得到的近似数,即误差不超过最后一位的半个单位,试指出它们是几位有效数字:1021.1*1=x ,031.0*2=x ,6.385*3=x ,430.56*4=x ,0.17*5⨯=x 。
[解]1021.1*1=x 有5位有效数字;0031.0*2=x 有2位有效数字;6.385*3=x 有4位有效数字;430.56*4=x 有5位有效数字;0.17*5⨯=x 有2位有效数字。
4、利用公式(3.3)求下列各近似值的误差限,其中*4*3*2*1,,,x x x x 均为第3题所给的数。
(1)*4*2*1x x x ++; [解]3334*4*2*11***4*2*1*1005.1102110211021)()()()()(----=⨯=⨯+⨯+⨯=++=⎪⎪⎭⎫ ⎝⎛∂∂=++∑x x x x x f x x x e nk k k εεεε;(2)*3*2*1x x x ;[解]52130996425.010********.2131001708255.01048488.2121059768.01021)031.01021.1(1021)6.3851021.1(1021)6.385031.0()()()()()()()()(3333334*3*2*1*2*3*1*1*3*21***3*2*1*=⨯=⨯+⨯+⨯=⨯⨯+⨯⨯+⨯⨯=++=⎪⎪⎭⎫⎝⎛∂∂=-------=∑x x x x x x x x x x x f x x x e n k k kεεεε;(3)*4*2/x x 。
计算方法与实习 第四版 (孙志忠 著) 东南大学出版社 课后答案

2
ww
w.
kh
da
w.
co
∗ − y | → ∞, 计算过程不稳定。 注 :此题中,|yn n
m
× 10−3 .
w.
n = 1, 2, · · ·
co m
e2 e2 r r = . 1 + er 1 − er
w.
课后答案网
aw . kh d
∗ − y | = 510 e ≤ n = 10时,|yn n 0
√ 计算到y100 , 若取 783 ≈ 27.982 (5位有效数字),试问计算到y100 将有多大误差? √ 答 :设x∗ = 783, x = 27.982, x∗ = x + e.
−2 ∗ = y∗ yn n−1 − 10 (x + e), yn = yn−1 − 10−2 x,
1 √ 783, 100
概率与数理统计 第二, C语言程序设计教程 第 西方经济学(微观部分) C语言程序设计教程 第 复变函数全解及导学[西 三版 (浙江大学 三版 (谭浩强 张 (高鸿业 著) 中 二版 (谭浩强 张 安交大 第四版]
社区服务
社区热点
进入社区
/
2009-10-15
ww
er − er = er −
e2 e e 1 r = . = e − = e − r r x∗ e+x 1 + er 1 + e1 r ·········
7. 设y0 = 28, 按递推公式
案 答
yn = yn−1 −
网 课 后
1 2
6. 机器数–略。
w. kh da
∗ −y |=e≤ n = 100时,|yn n
课后答案网
计算方法各章习题及答案

第二章数值分析4^92.1 已知多项式通过下列点:1 3答案:q(x) = p(x) -r(x) X5X4X3-3X 1 .2 22.2观测得到二次多项式2的值:表中p2(x)的某一个函数值有错误,试找出并校正它.答案:函数值表中p2(-1)错误,应有p2(-1) = 0 .2.3利用差分的性质证明12■ 22■川,n2=n(n ■ 1)(2n ■ 1)/6.2.4当用等距节点的分段二次插值多项式在区间[-1,1]近似函数e x时,使用多少个节点能够保证误差不超过丄10-6.2答案:需要143个插值节点.2.5 设被插值函数f (x) • C4[a,b] , H3h)(x)是f (x)关于等距节点b — aa ^Xo :::捲:::川:::x n=b的分段三次艾尔米特插值多项式,步长h .试估计n ||f(x)-H3h)(x)||::.答案:||住)-出5)仪川:乞令人4.384第三章函数逼近3.1求f(x)二sinx,x,[0,0.1]在空间门=span{1,x, x2}上最佳平方逼近多项式,并给出平方误差.答案:f (x) =sin X的二次最佳平方逼近多项式为sin x p2(x) = -0.832 440 7 105 1.000 999 1x - 0.024 985 1x2,二次最佳平方逼近的平方误差为20.12 12■ = 0 (sinx) - P 2(x))2dx =0.989 310 7 10•3.2确定参数a,b 和c ,使得积分1 ---------------------------2 1 I (a,b,c)[ax 2 bx c -1 -x 2]dx 取最小值.J 1 — x 2810答案:a, b = 0, c =3 二3 二3.3 求多项式f (x) =2x 4 x 3 5x 2 1在[-1,1]上的3次最佳一致逼近多项式p(x)-答案:f (x)的最佳一致逼近多项式为p(x) = X ’ 7x2 3.43.4用幕级数缩合方法,求 f(x)=e x (―1兰XW1)上的3次近似多项式 p 6,3(x),并估计 || f(X )-P 6,3(X )II ::.答案:p5,3(x) =0.994 574 65 + 0.997 395 83x+0.542 968 75x 2 十 0.177 083 33x 3, || f (x) - p 6,3 (x) |^<0.006 572 327 71 一3.5 求f (x) -e x ( -1乞x 乞1)上的关于权函数「(X )-的三次最佳平方逼近小-x 2多项式 Q(x),并估计误差 || f(x)-$(x)||2 和 || f(x)-S 3(x) ||::.答案:§3(x) =0.994 571 0.997 308x 0.542 991x 20.177 347x 3,|| f (x) -S 3(x) ||2 = 0.006 894 83, || f (x) - §3(x)||严 0.006 442 575.第四章数值积分与数值微分14.1用梯形公式、辛浦生公式和柯特斯公式分别计算积分 X n dx (n -1,2,3,4),并与精确值比较.答案:计算结果如下表所示I 2 0. 5 0. 333 333 0. 250 000 0. 208 333 I 30. 5 0. 333 333 0. 250 000 0. 200 000 精确值0. 50. 333 3330. 250 0000. 200 0004.2 确定下列求积公式中的待定参数,使得求积公式的代数精度尽量高,并指明所确定的求积公式具有的代数精度.h(])仁 f (x)dx 止 A_i f (-h) + A f (0) + A f (h)11 (2)J(x)dx: 3【f(-1) 2f(X i ) 3f(X 2)]hh2⑴ of(x)dxVf(O) f(h)「h[f g f(h)]答案:(1)具有三次代数精确度 (2)具有二次代数精确度 (3)具有三次代数精确度. 4.3 设h = % - X 0,确定求积公式r (x - x o ) f (x)dx = h 1 2[ Af (x o ) + Bf (x i )] + h 3[C 「(x o ) + Df^)] + R[ f ]xo中的待定参数 A, B,C, D ,使得该求积公式的代数精确度尽量高,并给出余项表达式.37 1 if 4)(叮)6答案:A = —, B— ,C —, D — , R[f]=— _) h ,其中 (x o ,xi).202030 20 14404.4设P 2(x)是以0,h,2h 为插值点的f(x)的二次插值多项式,用F 2(x)导出计算积分3h3 4 5If (x)dx 的数值积分公式I h ,并用台劳展开法证明:I - l h h f (0) O(h ).力83h3答案:I h P 2(x)dx h[ f(0) 3f (2h)].0 4(3)取7个节点处的函数值.1sin x4.6用变步长的复化梯形公式和变步长的复化辛浦生公式计算积分Idx .要x1o 1«求用事后误差估计法时,截断误不超过10和 10 .1(1) 运用复化梯形公式计算上述积分值,使其截断误差不超过丄10」. 2(2) 取同样的求积节点,改用复化辛浦生公式计算时,截断误差是多少?(3) 要求的截断误差不超过10“ ,若用复化辛浦生公式,应取多少个节点处的函数值? 答案:(1)只需n — 7.5,取9个节点,I : 0.9464.5 给定积分I 二1sin xdx|R n [f]耳一孟宀皿盂日中0.271估2 2答案:使用复化梯形公式时,I T^ 0.946满足精度要求;使用复化辛浦生公式时,I s4 =0.946 083满足精度要求.4.7 ( 1 )利用埃尔米特插值公式推导带有导数值的求积公式1 323 1 3>5.2用矩阵的直接三角分解法解方程组 广1 0 2 0、「5、0 10 1 X 2312 4 3X 3仃10 1 0 3丿 g<7;答案: &=2 , x 3 = 2 , x 2 = 1, X| = 1 .ba f(x)dx 二 其中余项为b —a(b 「a)2[f(a)f(b)] — ' 丿[f (b)-f (a)] R[f], 2 12R[f]=U 54!30 f ( 4()),(a,b).其中(2)利用上述公式推导带修正项的复化梯形求积公式h 2 f(x)dx :T^—[ f (X N ) - f (x 。
西北工业大学计算方法第四周作业答案第四章作业答案

4
3
12
1 x2 7 x 66
将 x 2 代入 L2 (x) ,得到 2 的近似值为 1.6667 。 2. 解:如果得到 x f 1( y) 的插值多项式,则该多项式的常数项就是 f (x) 0 的根的近似值,这种方
法被称为反插值法,利用上述数据,得到的反插值公式为:
x (y 1)(y 1) (1) (y 2)(y 1) 0
当 t [0,1] , max t(t 1) max t(1 t) max(t t2 ) ,当 t 1 , max t(t 1) 1 ,因此有
2
4
R 0.8415 h2 1 104
8
2
解得 h 0.0218 ,需要将区间至少 92 等分,总共 93 个节点。
5. 证明:基于 n 1个节点的不超过 n 次的 Lagrange 多项式为
)( x
2
)
1 24
cos( )x2 (x
)( x
2
)。
4. 解: 当 xi x xi1, (i 0,1, 2,, n 1) ,分段线性插值的截断误差公式为:
R
1 2!
f
(
)( x
xi
)( x
xi 1 )
R
1 2!
f
(
)( x
xi
)( x
xi 1 )
max
f ( )
1 2!
(
x
xi
)(
4 3
;
回代得到
p3 ( x)
2
x
1
4 3
(x
0)( x
)(x 2
)
。
化简得到
p3 ( x)
4 3
x3
计算方法的课后答案
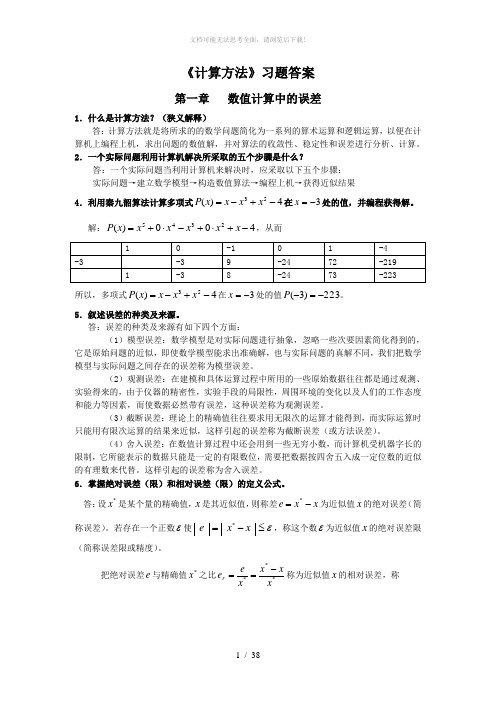
《计算方法》习题答案第一章 数值计算中的误差1.什么是计算方法?(狭义解释)答:计算方法就是将所求的的数学问题简化为一系列的算术运算和逻辑运算,以便在计算机上编程上机,求出问题的数值解,并对算法的收敛性、稳定性和误差进行分析、计算。
2.一个实际问题利用计算机解决所采取的五个步骤是什么?答:一个实际问题当利用计算机来解决时,应采取以下五个步骤: 实际问题→建立数学模型→构造数值算法→编程上机→获得近似结果 4.利用秦九韶算法计算多项式4)(53-+-=x x x x P 在3-=x 处的值,并编程获得解。
解:400)(2345-+⋅+-⋅+=x x x x x x P ,从而所以,多项式4)(53-+-=x x x x P 在3-=x 处的值223)3(-=-P 。
5.叙述误差的种类及来源。
答:误差的种类及来源有如下四个方面:(1)模型误差:数学模型是对实际问题进行抽象,忽略一些次要因素简化得到的,它是原始问题的近似,即使数学模型能求出准确解,也与实际问题的真解不同,我们把数学模型与实际问题之间存在的误差称为模型误差。
(2)观测误差:在建模和具体运算过程中所用的一些原始数据往往都是通过观测、实验得来的,由于仪器的精密性,实验手段的局限性,周围环境的变化以及人们的工作态度和能力等因素,而使数据必然带有误差,这种误差称为观测误差。
(3)截断误差:理论上的精确值往往要求用无限次的运算才能得到,而实际运算时只能用有限次运算的结果来近似,这样引起的误差称为截断误差(或方法误差)。
(4)舍入误差:在数值计算过程中还会用到一些无穷小数,而计算机受机器字长的限制,它所能表示的数据只能是一定的有限数位,需要把数据按四舍五入成一定位数的近似的有理数来代替。
这样引起的误差称为舍入误差。
6.掌握绝对误差(限)和相对误差(限)的定义公式。
答:设*x 是某个量的精确值,x 是其近似值,则称差x x e -=*为近似值x 的绝对误差(简称误差)。
计算方法试题集与答案(新)

1.*x 为精确值x 的近似值;()**x f y =为一元函数()x f y =1的近似值;()**,*y x f y =为二元函数()y x f y ,2=的近似值,请写出下面的公式:**e x x =-:***r x xe x -=()()()*'1**y f x x εε≈⋅ ()()()()'***1**r r x f x y x f x εε≈⋅()()()()()**,**,*2**f x y f x y y x y x yεεε∂∂≈⋅+⋅∂∂()()()()()****,***,**222r f x y e x f x y e y y x y y y ε∂∂≈⋅+⋅∂∂ 2、 计算方法实际计算时,对数据只能取有限位表示,这时所产生的误差叫 舍入误差 。
3、 分别用2.718281,2.718282作数e 的近似值,则其有效数字分别有6 位和7 1.73≈(三位有效数字)-211.73 10 2≤⨯。
4、 设121.216, 3.654x x ==均具有3位有效数字,则12x x 的相对误差限为 0.0055 。
5、 设121.216, 3.654x x ==均具有3位有效数字,则12x x +的误差限为 0.01 。
6、 已知近似值2.4560A x =是由真值T x 经四舍五入得到,则相对误差限为 0.0000204 .7、 递推公式,⎧⎪⎨⎪⎩0n n-1y y =10y -1,n =1,2,如果取0 1.41y =≈作计算,则计算到10y 时,误差为8110 2⨯;这个计算公式数值稳定不稳定 不稳定 . 8、 精确值 14159265.3*=π,则近似值141.3*1=π和1415.3*2=π分别有 3 位和 4 位有效数字。
9、 若*2.71828x e x =≈=,则x 有 6 位有效数字,其绝对误差限为1/2*10-5。
10、 设x*的相对误差为2%,求(x*)n的相对误差0.02n11、近似值*0.231x =关于真值229.0=x 有( 2 )位有效数字;12、计算方法主要研究( 截断 )误差和( 舍入 )误差;13、为了使计算 ()()2334610111y x x x =++---- 的乘除法次数尽量地少,应将该表达式改写为11,))64(3(10-=-++=x t t t t y ,为了减少舍入误差,应将表达式19992001-改写为199920012+。
计算方法 课后习题答案

0
1
2
4
1
9
23
3
解:
(1)Lagrange插值多项式
=
=
=
=
(2)Newton插值多项式
一阶差商
二阶差商
三阶差商
0
0
1
1
1
9
8
2
2
23
14
3
3
4
3
-10
由求解结果可知:
说明插值问题的解存在且唯一。
6.已知由数据 构造出的 插值多项式 的最高次项系数是6,试确定 。
解:因为第一列中10最大,因此把10作为列主元素
得到方程组
3。举例说明一个非奇异矩阵不一定存在LU分解。
例如:设
与题设相矛盾,所以一个非奇异矩阵不一定存在LU分解。
4。下列矩阵能否分解为LU(其中L为单位下三角矩阵,U为上三角矩阵)?若能分解,那么分解是否唯一?
解:
设 B可以进行LU分解,则B=
计算得
5。对下列给定的矩阵A作LU分解,并利用分解结果计算A-1。
解:
L= U=
由
6。用Doolittle分解法解方程组
解:A= =
其中L= U=
由Ly= 解得y=
由Ux=y,解得x=
7。用Crout分解法接方程组。
解:
由Ly=b= 得y=
由Ux=y= 得x=
8。用平方根法求解方程组
解:易知 是对称矩阵,可求得
注意到这里 是三重零点, 是单零点,故插值余项为
20.求作次数 的多项式 ,使满足条件
并列出插值余项。
98228-计算方法引论-第四章

计算方法引论:数值分析 误差插值法与数值微分 数据拟合法快速傅氏变换数值积分第四章快速傅氏变换•三角函数插值•三角插值函数的确定−DFT •FFT算法三角函数插值•已知f (x )在x l =2πl /N ,l =0,1,…,N -1上的值f l =f (x l ) ,l =0,1,…,N -1求满足即l =0,1,…,N -1(1)∑=-==Nj kxk c x 0i 1i ,e )(ϕ∑-===10/i 2e)(N k Nkl k l ll c f f x πϕ三角插值函数的确定−DFT•(1)的解k =0,1,…,N -1(2)(2)和(1)形式相似,分别称有限离散傅氏变换及其逆变换.∑-=-=1/i 2e1N l Nkl l k f Nc π正交性•记则•用e -2jlπi/N 乘(1)两边,对l 求和,交换求和次序,应用上边得到的正交性,就得到(2)式.1,,1,0,e e 1/i )1(2i/210-=⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=-N j f f f f N N j N j πj Nπϕ⎩⎨⎧≠====∑∑-=-=--kj kj N N l N l Nl k j Nkl N jl k j ,0,eee),(1010/i )2(i/2/i 2πππϕϕ向量表示•用向量记号(1)即∑∑-=-===11N j jj N k k k c c f ϕϕ∑-=-==1/i 2e1),(1)2(N l Nkl l k k k f Nf N c ,πϕϕ利用正交性乃得作内积与DFT 计算•记k =0,1,…,N -1(3)它代表(1)或(2).(3) 大体上要(复数)N 2个乘法和N 2个加法.但是注意到ω=e ±2πi /N 是N 次单位根,它的幂只有N 个值不同,即1,ω,ω2,…,ωN -1.因此,可用交换律、结合律化简,得到一个只需要N log 2N 个乘法和N log 2N 个加法的算法,FFT .∑∑-=-===101/i 2eN k N k lk l Nkl l k a a c ωπFFT:递推关系N =2m时FFT 可按奇偶项分成两个N /2的FFT 之和.∑∑∑∑-=-=+-=-=+++=+=12/012/02122212/012/0)12(12)2(2)()(N l N l lkl klkl N l N l kl l kl l k aa aa c ωωωωωk =0,1,…,N -1由ωN /2= -1可以对k =N /2,N /2+1,…,N -1采用下式计算12/,,2,1,)()(12/012/021222/2-=-=∑∑-=-=++N k aac N l N l lkl klk lk N ωωω•分而治之FFT:递归算法procedure fft(a,c,n,ω)if n=1c(0)=a(0)elsefor k=0,1,…,n/2-1 {数据奇偶拆分两组}u(k)=a(2k)s(k)=a(2k+1)endfft(u,v,n/2,ω2) {递归FFT调用}fft(s,t,n/2,ω2)for k=0,1,…,n/2-1c(k)=v(k)+ωk t(k) {合成结果数据}c(k+n/2)=v(k)-ωk t(k)endend二进制整数•以N =23=8为例,k,l ≤8•二进制表示k=k 222+k 121+k 020=(k 2k 1k 0)2l=l 222+l 121+l 020=(l 2l 1l 0)2不妨略去括号外下标2.•利用ωN =1可得•(3)可因此表示如次)()0()00(0120112k k k l k k l k l klωωωω=FFT:Cooley-Tukey (N =8))()0()00(1010101280012012001102012]))(([)(k k k l k k l k l l l l l lk l k l l l a a c k k k c ωωωω∑∑∑∑=======∑∑∑=======1)(0102210310)0(010101021)00(012001010120120001221011202)()()()()()()()(l k k k l l k k l l k l l k k Ak k k A l l kA l k k A l l l Al l k A l l l a l l l A ωωω(续)•可见所得A3要按二进制数按位反转的次序重排方得ck•归纳起来,整个过程分四步:由输入数据A0算A1,由A1算A2,由A2算A3,最后按位反转重排得到输出结果ck•还可利用ω0=1,ω4=-1再行简化.•下面整理的公式可供N=2m时编程参考.A 0 、A 1、A 2、A 3•A 1(0l 1l 0)=A 0(0l 1l 0)+A 0(1l 1l 0)A 1(1l 1l 0)=A 0(0l 1l 0)-A 0(1l 1l 0),l 0,l 1=0,1•A 2(k 00l 0)=A 1(k 00l 0)+A 1(k 01l 0)A 2(k 01l 0)=A 1(k 00l 0)-A 1(k 01l 0),k 0,l 0=0,1•A 3(k 0k 10)=A 2(k 0k 10)+A 2(k 0k 11)A 3(k 0k 11)=A 2(k 0k 10)-A 2(k 0k 11),k 0,k 1=0,1)00(0k ω)00(0k ω)0(01k k ω)0(01k k ω计算量与存储量•A1,A2,A3每个数组需复数乘法N/2次,加法N次,共乘法N/2log2N次,加法N log2N次.合计实数乘法2N log2N次,加法3N log2N次.•A1,A2,A3每个数组的分量皆可成对计算,只需几个辅助单元和一个数组A.注意,第二项中ω的幂正好是所算左端量二进下标从红字起往前读三位(前零计入)所表示的数.•N次单位根、二进制数按位反转另行安排.01•A(000)=A0(000)+A0(100)a0=a0+a4 1A1(100)=A0(000)-A0(100)a4=a0-a4 A1(001)=A0(001)+A0(101)a1=a1+a5 A1(101)=A0(001)-A0(101)a5=a1-a5 A1(010)=A0(010)+A0(110)a2=a2+a6 A1(110)=A0(010)-A0(110)a6=a2+a6 A1(011)=A0(011)+A0(111)a3=a3+a7 A1(111)=A0(011)-A0(111)a7=a3-a712•A(000)=A1(000)+A1(010)a0=a0+a22A2(010)=A1(000)-A1(010)a2=a0-a2A2(001)=A1(001)+A1(011)a1=a1+a3A2(011)=A1(001)-A1(011)a3=a1-a3A2(100)=A1(100)+A1(110)ω2a4=a4+a6ω2 A2(110)=A1(100)-A1(110)ω2a6=a4-a6ω2 A2(101)=A1(101)+A1(111)ω2a5=a5+a7ω2 A2(111)=A1(101)-A1(111)ω2a7=a5-a7ω223•A(000)=A2(000)+A2(001)a0=a0+a13A3(001)=A2(000)-A2(001)a1=a0-a1A3(010)=A2(010)+A2(011)ω2a2=a2+a3ω2 A3(011)=A2(010)-A2(011)ω2a3=a2-a3ω2 A3(100)=A2(100)+A2(101)ωa4=a4+a5ωA3(101)=A2(100)-A2(101)ωa5=a4-a5ωA3(110)=A2(110)+A2(111)ω3a6=a6+a7ω3 A3(111)=A2(110)-A2(111)ω3a7=a6-a7ω3按位反转重排•A(000)→c(000)a0→c0 3A3(001)→c(100)a1→c4 A3(010)→c(010)a2→c2 A3(011)→c(110)a3→c6 A3(100)→c(001)a4→c1 A3(101)→c(101)a5→c5 A3(110)→c(011)a6→c3 A3(111)→c(111)a7→c7FFT算法(先按位反转重排) a0→a0a0=a0+a1a0=a0+a2a0=a0+a4a4→a1a1=a0-a1a1=a1+a3ω2a1=a1+a5ωa2→a2a2=a2+a3a2=a0-a2a2=a2+a6ω2a6→a3a3=a2-a3a3=a1-a3ω2a3=a3+a7ω3a1→a4a4=a4+a5a4=a4+a6a4=a0-a4a5→a5a5=a4-a5a5=a5+a7ω2a5=a1-a5ωa3→a6a6=a6+a7a6=a4-a6a6=a2-a6ω2a7→a7a7=a6-a7a7=a5-a7ω2a7=a3-a7ω3FFT算法(续)•所得算法有其特点更易编程先按位反转重排,结果是自然顺序ω的幂递增规律明显每列成对分量间隔r按2的幂递增1,2,…,2m-1. r对分量成一组.共2m-j 组程序如右将原数据按逆序重排,仍记为a k.r = 1for j=1, 2, , mN p=2rθ = –2π/N p= –π/r,w p=exp(iθ)w = 1 初始化for s=0, 1, , r–1 逐对算for k=s,s+N p, , N–1 逐组算l = k + rd = w*a la k= a k +da l= a k –dendw=w*w pendr = N pend。
计算方法 课后习题答案

l0
(x ( x0
x1)(x x2 ) x1)(x0 x2 )
(x
1)( x 6
2)
l1
(x ( x1
x0 )(x x2 ) x0 )(x1 x2 )
(x
1)( x 2
2)
l2
(x ( x2
x0 )(x x1) x0 )(x2 x1)
L3 x 的最高次项系数是 6,试确定 y1 。
解: l0 (x)
x x1 x0 x1
x x2 x0 x2
x x3 x0 x3
x 0.5 0 0.5
x 1 0 1
x2 02
= x3
7 2
x2
7 2
x 1
l1 ( x)
x x0 x1 x0
1 8(x 0) 3(x 0)(x 1) 114 (x 0)(x 1)(x 2) 11 x3 45 x2 1 x 1
4 42
由求解结果可知: L3 (x) N3(x)
说明插值问题的解存在且唯一。
6. 已知由数据 (0, 0), (0.5, y1), (1,3)和(2, 2) 构造出的 Lagrange 插值多项式
2 02 12 4 23 4 04 14 2 3
1 x2 3x 2 x 4 3x x2 6x 8 23 x x2 5x 4 1 x x2 3x 2
8
4
8
11 x3 45 x2 1 x 1
y0
计算方法课后习题集规范标准答案

习 题 一3.已知函数y =4, 6.25,9x x x ===处的函数值,试通过一个二次插值函解:0120124, 6.25,9;2, 2.5,3y x x x y y y =======由题意 (1) 采用Lagrange插值多项式220()()j j j y L x l x y ==≈=∑27020112012010*********()|()()()()()()()()()()()()(7 6.25)(79)(74)(79)(74)(7 6.25)2 2.532.255 2.25 2.75 2.7552.6484848x y L x x x x x x x x x x x x x y y y x x x x x x x x x x x x ==≈------=++------------=⨯+⨯+⨯⨯-⨯⨯= 其误差为(3)25(3)25(3)2[4,9]2()(7)(74)(7 6.25)(79)3!3()83max |()|40.0117281|(7)|(4.5)(0.01172)0.008796f R f x x f x R ξ--=---==<∴<=又则(2)采用Newton插值多项式2()y N x =≈ 根据题意作差商表:224(7)2(74)()(74)(7 6.25) 2.64848489495N =+⨯-+-⨯-⨯-≈4. 设()()0,1,...,k f x x k n ==,试列出()f x 关于互异节点()0,1,...,i x i n =的Lagrange 插值多项式。
注意到:若1n +个节点()0,1,...,i x i n =互异,则对任意次数n ≤的多项式()f x ,它关于节点()0,1,...,i x i n =满足条件(),0,1,...,i i P x y i n ==的插值多项式()P x 就是它本身。
可见,当k n ≤时幂函数()(0,1,...,)kf x x k n ==关于1n +个节点()0,1,...,i x i n =的插值多项式就是它本身,故依Lagrange 公式有()00(),0,1,...,nn n k kk i j j j j j i j ii jx x x l x x x k n x x ===≠-=≡=-∑∑∏特别地,当0k =时,有()0001nn n ij j j i j ii jx x l x x x ===≠-=≡-∑∑∏而当1k =时有()000nnn ij j j j j i j ii jx x x l x x x x x ===≠⎛⎫- ⎪=≡ ⎪- ⎪⎝⎭∑∑∏ 5.依据下列函数表分别建立次数不超过3的Lagrange 插值多项式和Newton 插值多项式,并验证插值多项式的唯一性。
计算方法_课后习题答案

L3 x 的最高次项系数是 6,试确定 y1 。
解: l0 (x)
x x1 x0 x1
x x2 x0 x2
x x3 x0 x3
x 0.5 0 0.5
x 1 0 1
x2 02
= x3
7 2
x2
7 2
x 1
l1 ( x)
x x0 x1 x0
(2 2e1 4e0.5 )x2 (4e0.5 e1 3)x 1
2)根据Lagrange余项定理,其误差为
| R2 (x) ||
f
(3) ( 3!
)
21
(
x)
||
1 6
e
x(
x
1)(
x
0.5)
|
1 max | x(x 1)(x 0.5) |, (0,1) 6 0x1
x2 02
x4= 04
x3
7x2 14x 8 8
l1 ( x)
x x0 x1 x0
x x2 x1 x2
x x3 x1 x3
x0 1 0
x2 1 2
x4 1 4
=
x3
6x2 3
8x
l2 (x)
x x0 x2 x0
i j
而当 k 1时有
n
x jl j
j0
x
n
n
j0 i0 i j
x xi x j xi
x
j
计算方法

牛顿插值法在凸轮曲线修正设计中的应用作业人姓名:韩宇班级:090420学号:090420303摘要:利用牛顿插值法,提出了一种简单、实用的凸轮工作廓线的修正设计方法,只需通过对要进行修正的曲线附近的一些离散点的数据进行处理,就能实现对凸轮的局部工作廓线进行修正。
关键词:凸轮;曲线;修正;牛顿插值法。
Newton interpolation method on cam curvecorrection design applicationJob name :hanyuClass Student number:090420303Abstract : the use of Newton interpolation method, put forward a kind of simple, practical cam profile correction method, only need to be amended by the curve near Some discrete point data processing, we can achieve the cam profile correction of local work. Key words: cam; curve; correction; Newton interpolation method. 1 前言凸轮机构在高速包装机械设备中应用广泛,是一种不可缺少和替代的重要机构。
一般情况下,高速包装机械中凸轮工作廓线的设计多采用解析法,这样既保证了凸轮的运动特性,又便对凸轮机构进行运动学和动力学分析,因此这就使得在不同工况下,凸轮设计的解析方程式往往是不相同的。
这样虽然能保证凸轮的精度,但同时也对凸轮在实际使用中的修正提高了难度,因为只有建立新的解析方程式才能对凸轮进行修正,尤其是只需对凸轮局部曲线进行修正时,也要建立相应的解析方程,这样就使曲线修正的工作量大增,工作效率降低。
计算方法与实习 第四版 (孙志忠 著) 东南大学出版社 课后答案

f (0) = 1, f (1) < 0, f (ln 4) = 4 − 4 ln 4 < 0, f (2) < 0, f (3) > 0, 方程f (x) = 0存在两个根:
∗ x∗ 1 ∈ [0, 1], x2 ∈ [2, 3].
– 求根x∗ 1:
将方程f (x) = 0在区间[0, 1]改写成同解方程
∗ −2 ∗ −y ∴ yn n = yn−1 − yn−1 − 10 e ∗ −2 = yn −2 − yn−2 − 2 × 10 e = ··· ∗ − y − n × 10−2 e = y0 ∗ = 28). = −10−2 ne, (y0 = y0
ww
8. 序列{yn }满足递推关系 yn = 5yn−1 − 2, n = 1, 2, · · ·
ww
er − er = er −
e2 e e 1 r = . = e − = e − r r x∗ e+x 1 + er 1 + e1 r ·········
7. 设y0 = 28, 按递推公式
案 答
yn = yn−1 −
网 课 后
1 2
6. 机器数–略。
w. kh da
∗ −y |=e≤ n = 100时,|yn n
w.
kh
da
1 x 记ϕ(x) = 4 e ,则
w.
构造迭代格式
co
1 x = ex , x ∈ [0, 1] 4
m
co m
课后答案网
当x ∈ [0, 1]时,
所以此迭代格式对任意的x0 ∈ [0, 1]均收敛。
kh d
k xk 1 0.412180
取x0 = 0.5, 迭代得到
计算方法各章作业答案

计算方法作业第二章插值1.(1(2)用二次Lagrange插值多项式求当X=0.15时Y的近似值。
(3)写出余项R(x)=f(x)-Pn(x)的表达式。
解:(1)Pn (x) =knknkjj jkj yxxxx)(00∑∏=≠=--n=3P 3(x)=321321))()(())()((yxxxxxxxxxxxx------+13121132))()(())()((yxxxxxxxxxxxx------+23212231))()(())()((yxxxxxxxxxxxx------+32313321))()(())()((yxxxxxxxxxxxx------x 0=0.0 x1=0.1 x2=0.2 x3=0.3y 0=0.0000 y1=0.0998 y2=0.1987 y3=0.2955P 3(x)=0000.0)3.00.0)(2.00.0)(1.00.0()3.0)(2.0)(1.0(⨯------xxx+0998.0)3.01.0)(2.01.0)(0.01.0()3.0)(2.0)(0.0(⨯------xxx+1987.0)3.02.0)(1.02.0)(0.02.0()3.0)(1.0)(0.0(⨯------xxx+2955.0)2.03.0)(1.03.0)(0.03.0()2.0)(1.0)(0.0(⨯------xxx(2) y(0.15) = P2(0.15) = 0.1494(3)R(x) = f(x)-Pn (x)=)!1()()1(++nf nξnk0=∏(x - x k)=!4)(4ξf(x – 0.0) (x – 0.1)(x – 0.2)(x – 0.3)第三章 方程求根5.求解方程12-3x+2cosx=0的迭代法n n x x cos 3241+=+(1)证明对于任意的x 0€R 均有*lim x x n x =∞→ (x *为方程的根)(2)取x 0=4,用此迭代法求方程根的近似值,误差不超过10-3,列出各次的迭代值。
《计算方法》第四章 插值方法

Ln ( x) f ( xk ) l k ( x)
k 0
n
n
其中,
l k ( x)
j 0 j k
x xj x k x j (k 0,1,...n) .
20
构造插值多项式的方法:
(1) (2) 先求插值基函数. 构造插值多项式.
以下的问题:如何分析插值的余项?
21
例题 已知连续函数 f (x) 的函数表如下: x f (x) -1 0 1 2 -2 -2 1 2
Return
13
§4.2 拉格朗日多项式 /* Lagrange Polynomial */
1. 构造线性插值基函数的方法:
n=1 已知 x0 , x1 ; y0 , y1 ,求 L1(x) = a0 + a1 x 使得
L1 ( x0 ) y0 , L1 ( x1 ) y1
可见 L1(x) 是过 ( x0 , y0 ) 和 ( x1, y1 ) 两点的直线。
由 l k ( xk ) 1, 得:
1 A ( xk x0 ) ( xk xk 1 ) ( xk xk 1 ) ( xk xn )
l k ( x)
k = 0, 1 ,⋯, n .
( x x0 )( x xk 1 ) ( x xk 1 )( x xn ) , ( x k x0 )( xk xk 1 ) ( xk xk 1 )( xk xn )
18
一般情形
希望找到 li (x),i = 0, …, n 使得 li (xj) = ij ;然后令
Ln ( x ) f ( x k ) l k ( x ),则显然有 Pn(xi) = yi 。
k 0 n
计算方法及答案.docx

A. det A = 0B.detA k = 0(1 乞 k n)c. detA 0D. det A :: 0《计算方法》练习题一一、填空题1.理=3.14159…的近似值3.1428 ,准确数位是()。
2 .满足 f(a) = C, f(b) = d 的插值余项 R(X)=()。
3 .设{P k (x)}为勒让德多项式,则(F 2(χ), P 2(x)) - ( )o4 •乘幕法是求实方阵()特征值与特征向量的迭代法。
5 .欧拉法的绝对稳定实区间是()o6. e =2.71828…具有3位有效数字的近似值是( )。
7 .用辛卜生公式计算积分[fc ( ) oVHx8 .设A (kJ0 =(a (Z )第k 列主兀为a Pk J),则a (Pk A) =()10 •已知迭代法:X n 1 =(X n ), (n=0,1,…)收敛,则:(x)满足条件()。
、单选题1•已知近似数a,b,的误差限;(a), ;(b),则;(ab)=()。
A. E(a)E(b)B. E(a)+^(b)c. ag(a)+∣bw(b) D . a E (b)+'b w(a)2 .设 f(x) =X 2 X ,则 f[1,2,3]=()。
A.lB. 2C. 3D .4 3 . 设A =们 ,则化A 为对角阵的平面旋转 Q =().:1 3一ππππ A.—B .—C .—D .—23 464 . 若双点弦法收敛, 则双点弦法具有()敛速.A.线性B.超线性C.平方D .三次5 .改进欧拉法的局部截断误差阶是().A. o(h)Bo(h 2)C.o(h 3)D.o(h 4)6 .近似数 a = 20.47820 "0的误差限是()o1 一 c -51 _ -4 1__3 1 _ _2A. ×10B.×10 C.×10D . × 1022229 .已知贝TtJ 1 25 4_-7 .矩阵A满足(),则存在三角分解A=LR)&已知 X =(—1,3,-5)T ,则 X 1 =()。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
)
三、问答题 1、依据如下函数值表建立不超过三次的拉格朗日插值多项式及牛顿 插值多项式,并验证插值多项式的唯一性。
x
f ( x)
0 1
1 9
2 23
4 3
2、已知
x
f ( x)
0 1
2 -3
3 -4
5 2
写成f ( x)的3次Newton插值多项式N 3 (x)。
3、求三次多项式 P3 ( x ),使满足插值条件
第四章 插值法 一、填空题 1、拉格朗日插值基函数在节点上的取值是( ) 。
− 1,时 2 f ( x ) = 0, − 3,,则 4 f ( x ) 的二次插值多项式为 2、当 x = 1,
(
) 。
3、三次样条插值函数S ( x)满足:S ( x)在区间[a, b]内二阶连续可导, S ( xk ) = y ( , k = 0,1, 2,L, n, 且满足S ( x)在每个子区间[ xk , xk +1 ] k xk , yk已知)
x3 + 2 x + 1 − 1 ≤ x < 0 C、 f ( x ) = 3 2x + 2x +1 0 ≤ x ≤ 1
(2, 4), (3,1)点的分段线性插值函数P ( x ) = ( 2、 过(0,1),
3 x +1 0≤ x≤2 A、 2 − 3 x + 10 2 < x ≤ 3 3 x −1 0≤x≤2 C、 2 − 3 x + 10 2 < x ≤ 3
)
3 x +1 0≤ x≤2 B、 2 − 3 x 2 + 10 2 < x ≤ 3 3 x +1 0≤ x≤2 D、 2 − x + 4 2 < x ≤ 3
3 、 下列条件中,不是分段线性插值函数P(x)必须满足的条件为(
A、P ( xk ) = yk , ( k = 0,1,L , n) C、P ( x)在各子区间上是线性函数 B、P( x)在[ a, b]上连续 D、P ( x)在各节点处可导
)。
二、选择题 选择题 1、试判断下面的函数哪一个为三次样条函数?(
x2 x ≥ 0 A、 f ( x ) = sin x x < 0
)
0 −1 ≤ x < 0 B、 f ( x) = x3 0 ≤ x < 1 x 3 + ( x − 1) 2 1 ≤ x ≤ 2 D、 无
5、设f (0) = 0, f (1) = 16, f (2) = 46,则f [0,1] =(
f ( x)的二次牛顿插值多项式为 (
6 、 已 知 S ( x) =
a =(
2x 3 0 ≤ x ≤1 3 2 x + ax + bx + c 1 ≤ x ≤ 2
), b = (
), c ,b]上的一次(线性)插值函数(公式)L1 ( x) = ( ) , R1 ( x) = ( ) 。
函数f ( x) = ln( x + 2)在区间[0,上的线性插值函数 1] L1 ( x) = (
) ,其余项估计 R1 ( x ) ≤ ( ) 。 ) ,f [0,1, 2] =( ) 。 是三次样条函数,则 ) ,
