数学试题模板.doc
高中数学答题模板

一、选择填空题1.易错点归纳九大模块易混淆难记忆考点分析,如概率和频率概念混淆、数列求和公式记忆错误等,强化基础知识点记忆,避开因为知识点失误造成的客观性解题错误。
针对审题、解题思路不严谨如集合题型未考虑空集情况、函数问题未考虑定义域等主观性因素造成的失误进行专项训练。
2.答题方法选择题十大速解方法:排除法、增加条件法、以小见大法、极限法、关键点法、对称法、小结论法、归纳法、感觉法、分析选项法。
填空题四大速解方法:直接法、特殊化法、数形结合法、等价转化法。
二、解答题专题一、三角变换与三角函数的性质问题1.解题路线图①不同角化同角②降幂扩角③化f(x)=Asin(ωx+φ)+h④结合性质求解。
2.构建答题模板①化简:三角函数式的化简,一般化成y=Asin(ωx+φ)+h的形式,即化为“一角、一次、一函数”的形式。
②整体代换:将ωx+φ看作一个整体,利用y=sin x,y=cos x的性质确定条件。
③求解:利用ωx+φ的范围求条件解得函数y=Asin(ωx+φ)+h的性质,写出结果。
④反思:反思回顾,查看关键点,易错点,对结果进行估算,检查规范性。
专题二、解三角形问题1.解题路线图(1) ①化简变形;②用余弦定理转化为边的关系;③变形证明。
(2) ①用余弦定理表示角;②用基本不等式求范围;③确定角的取值范围。
2.构建答题模板①定条件:即确定三角形中的已知和所求,在图形中标注出来,然后确定转化的方向。
②定工具:即根据条件和所求,合理选择转化的工具,实施边角之间的互化。
③求结果。
④再反思:在实施边角互化的时候应注意转化的方向,一般有两种思路:一是全部转化为边之间的关系;二是全部转化为角之间的关系,然后进行恒等变形。
专题三、数列的通项、求和问题1.解题路线图①先求某一项,或者找到数列的关系式。
②求通项公式。
③求数列和通式。
2.构建答题模板①找递推:根据已知条件确定数列相邻两项之间的关系,即找数列的递推公式。
初中数学几何证明经典试题(含答案)【范本模板】
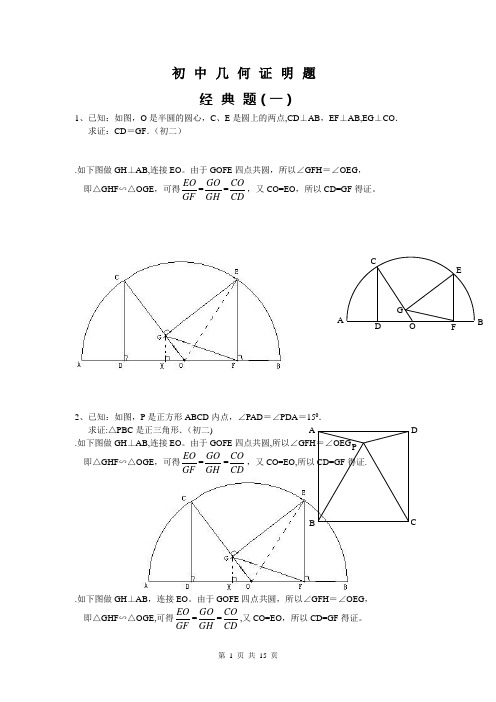
初中几何证明题经典题(一)1、已知:如图,O是半圆的圆心,C、E是圆上的两点,CD⊥AB,EF⊥AB,EG⊥CO.求证:CD=GF.(初二).如下图做GH⊥AB,连接EO。
由于GOFE四点共圆,所以∠GFH=∠OEG,即△GHF∽△OGE ,可得EOGF=GOGH=COCD,又CO=EO,所以CD=GF得证。
2、已知:如图,P是正方形ABCD内点,∠PAD=∠PDA=150.求证:△PBC是正三角形.(初二).如下图做GH⊥AB,连接EO。
由于GOFE四点共圆,所以∠GFH=∠OEG,即△GHF∽△OGE,可得EOGF=GOGH=COCD,又CO=EO,所以CD=GF得证..如下图做GH⊥AB,连接EO。
由于GOFE四点共圆,所以∠GFH=∠OEG,即△GHF∽△OGE,可得EOGF=GOGH=COCD,又CO=EO,所以CD=GF得证。
APCDBAFGCEBOD3、如图,已知四边形ABCD 、A 1B 1C 1D 1都是正方形,A 2、B 2、C 2、D 2分别是AA 1、BB 1、CC 1、DD 1的中点.求证:四边形A 2B 2C 2D 2是正方形.(初二)4、已知:如图,在四边形ABCD 中,AD =BC ,M 、N 分别是AB 、CD 的中点,AD 、BC的延长线交MN 于E 、F .求证:∠DEN =∠F .经典题(二)1、已知:△ABC 中,H 为垂心(各边高线的交点),O 为外心,且OM ⊥BC 于M . (1)求证:AH =2OM ; (2)若∠BAC =600,求证:AH =AO .(初二)D 2 C 2B 2 A 2D 1 C 1 B 1 C B DA A 1 A N FE CDMB · A HEOF2、设MN 是圆O 外一直线,过O 作OA ⊥MN 于A ,自A 引圆的两条直线,交圆于B 、C 及D 、E ,直线EB 及CD 分别交MN 于P 、Q . 求证:AP =AQ .(初二)3、如果上题把直线MN 由圆外平移至圆内,则由此可得以下命题:设MN 是圆O 的弦,过MN 的中点A 任作两弦BC 、DE,设CD 、EB 分别交MN 于P 、Q . 求证:AP =AQ .(初二)4、如图,分别以△ABC 的AC 和BC 为一边,在△ABC 的外侧作正方形ACDE 和正方形CBFG ,点P 是EF 的中点.求证:点P 到边AB 的距离等于AB 的一半.经典题(三)1、如图,四边形ABCD 为正方形,DE ∥AC ,AE =AC ,AE 与CD 相交于F .求证:CE =CF .(初二)2、如图,四边形ABCD 为正方形,DE ∥AC ,且CE =CA ,直线EC 交DA 延长线于F .求证:AE =AF .(初二)3、设P 是正方形ABCD 一边求证:PA =PF .(初二)4、如图,PC 切圆O 于C ,AC 为圆的直径,PEFB 、D .求证:AB =DC ,BC =AD.(初三)经典 1、已知:△ABC 是正三角形,P 是三角形内一点,PA =3,PB =4,PC 求:∠APB 的度数.(初二)2、设P 是平行四边形ABCD 内部的一点,且∠PBA =∠PDA . 求证:∠PAB =∠PCB .(初二)3、设ABCD 为圆内接凸四边形,求证:AB ·CD +AD ·BC =AC ·BD .(初三)4、平行四边形ABCD 中,设E 、F 分别是BC 、AB 上的一点,AE 与CF 相交于P,且 AE =CF .求证:∠DPA =∠DPC .(初二)经典难题(五)1、 设P 是边长为1的正△ABC 内任一点,L =PA +PB +PC ,求证:≤L <2.2、已知:P 是边长为1的正方形ABCD 内的一点,求PA +PB +PC 的最小值.3、P 为正方形ABCD 内的一点,并且PA =a ,PB =2a ,PC =3a ,求正方形的边长.C BD A F PD E CB A APCBACPDA CBPD4、如图,△ABC中,∠ABC=∠ACB=800,D、E分别是AB、AC上的点,∠DCA=300,∠EBA=200,求∠BED的度数.经典题(一)1.如下图做GH⊥AB,连接EO。
数学练习题模版

数学练习题模版数学练题模板题目一题目描述请解决以下问题:1. 计算2的平方根。
2. 计算5的立方根。
解答1. 2的平方根为1.414。
2. 5的立方根为1.710。
题目二题目描述已知一个等差数列的首项是3,公差是2。
请问数列的第10项是多少?解答我们可以使用等差数列的通项公式来解决这个问题。
设第n项为an,则通项公式为an = a1 + (n-1)d,其中a1为首项,d为公差。
根据题目的条件,a1 = 3,d = 2,n = 10。
代入公式,得到第10项为:a10 = 3 + (10-1)2 = 3 + 9 * 2 = 3 + 18 = 21。
题目三题目描述已知一个等比数列的首项是2,公比是3。
请计算前5项的和。
解答我们可以使用等比数列的前n项和公式来解决这个问题。
设前n项和为Sn,则前n项和公式为Sn = a1 * (1 - q^n) / (1 - q),其中a1为首项,q为公比。
根据题目的条件,a1 = 2,q = 3,n = 5。
代入公式,计算得到前5项的和为:S5 = 2 * (1 - 3^5) / (1 - 3) = 2 * (-242) / (-2) = -242。
题目四题目描述已知一条直线的方程为y = 2x + 3,请问该直线与x轴的交点坐标是什么?解答我们可以通过将y值置为0,解方程找到直线与x轴的交点坐标。
将方程中的y值置为0,得到:0 = 2x + 3将3移到等式左边,得到:2x = -3将方程两边都除以2,得到:x = -3/2所以该直线与x轴的交点坐标为(-3/2, 0)。
五年级数学上熟客模板

五年级数学上熟客模板
一、填空题
1. 一个正方形的边长是4厘米,它的周长是____厘米。
2. 一个长方形的长是8厘米,宽是5厘米,它的周长是____厘米。
3. 一个平行四边形的底是12厘米,高是8厘米,它的面积是____平方厘米。
4. 一个三角形的底是10厘米,高是6厘米,它的面积是____平方厘米。
5. 一个梯形的上底是7厘米,下底是11厘米,高是5厘米,它的面积是
____平方厘米。
二、选择题
1. 下列图形中,不是轴对称图形的是( )。
A. 等腰三角形
B. 长方形
C. 平行四边形
D. 等边三角形
2. 下列算式中,商最小的是( )。
A. 500÷2
B. 200÷5
C. 1000÷4
D. 400÷1
3. 下列算式中,积最大的是( )。
A. 3×0
B. 3×1
C. 3×2
D. 3×3
三、解答题
1. 一个正方形的周长是20厘米,求它的面积。
2. 一个三角形的底是15厘米,高是底的2倍,求它的面积。
第十二届全国大学生数学竞赛非数类试题

,1 = .y2 4第十二届全国大学生数学竞赛试题(非数学类)2020 年 11 月 28 号 9:00 - 11:30(模板制作者:八一与酸奶)考试形式: 闭卷 考试时间: 150 分钟 满分: 100 分一、填空题 ( 本题满分 30 分,每题 6 分)1. 极限 lim x →0 (x − sin x ) e −x 22. 设函数 f (x ) = (x + 1)n e −x 2,则 f (n )(−1) =.3. 设 y = f (x ) 是由方程 arctan x = ln ,x 2 + y 2 − 1 ln 2 +v 确定的隐函数,且满足 f (1) = 1,则曲线 y = f (x ) 在点 (1; 1) 处的切线方程为 .注 意 事 项考生在答题前请认真阅读本注意事项及各题答题要求1. 所有答题都须写在试卷密封线右边, 写在其他纸上一律无效.2. 密封线左边请勿答题, 密封线外不得有姓名及相关标记.3. 如答题空白不够, 可写在当页背面, 并标明题号.省市:学校:姓名:准考证号:装订线 内 不要答题∈ = :∫ d4. 已知+∞sin x x = v ,则∫ +∞ ∫ +∞ sin x s in (x + y ) d d y =x 2 0 0x (x + y ) 5. 设 f (x ); g (x ) 在 x = 0 的某一邻域 U 内有定义, 对任意 x U; f (x ) g (x ),且 lim f (x ) =x →0lim g (x ) = a > 0; 则x →0lim [f (x )]g (x ) − [g (x )]g (x )x →0 f (x ) − g (x )二、解答题 ( 本题满分 10 分)设数列 {a } 满足:a = 1,且 a=a n; n > 1: 求极限 lim n !ann +1(n + 1) (a n + 1)n →∞n x三、解答题( 本题满分8 分)设f(x)在[0;1]连续,f(x)在(0;1)内可导,且f(0)=0;f(1)=1,证明:(1) 存在x0∈ (0; 1),使得f (x0) = 3 −x0;(2) 存在‡; y ∈ (0; 1),且‡ y,使得[1 + f ′(‡)][1 + f ′(y)] = 4.. y已知 z = xf y x 四、解答题 (本题满分 12 分)Σ+ 2y ' . x Σ,其中 f ; ' 均为二次可微函数,则求(1) 求 @z ;@x @2z ; @x @y@2z 当 f = ',且@x @y|x =a = −by 2,求 f (y ).(2)计算x 2 + y 2 + z 2 = 8I =Γ.,3y − x . d x − 5z d z曲线 Γ :x 2 + y 2 = 2z,从 z 轴正向从坐标原点看去取逆时针方向.省市:学校: 姓名: 准考证号:装 订 线 内 不 要 答题I∑证明f (n ) =n m =1m cos2v n [x + 1] d xm等于 n 的所有因子 (包括 1 和 n 本身) 之和,其中 [x + 1] 表示不超过 x + 1 的最大整数,并计算 f (2021).∫∫ t∑− n →∞n =1 n pn设u n =1d n (n > 1) 0(1 + t 4)(1) 证明数列 {u n } 收敛,并求极限 lim u n ;(2) 证明级数 ∞ ( 1)n u n 条件收敛;n =1(3) 证明当 p > 1 时,级数∑∞u n收敛,并求级数∑∞u n 的和.n =1。
高考数学试卷模板及答案

一、选择题(本大题共10小题,每小题5分,共50分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
)1. 已知函数f(x) = 2x - 3,则f(2)的值为:A. 1B. 3C. 5D. 7答案:C2. 下列各数中,有理数是:A. √2B. πC. 1/3D. -√3答案:C3. 已知等差数列{an}的前三项分别为2,5,8,则该数列的公差为:A. 1B. 2C. 3D. 4答案:B4. 若log2x + log2(x + 2) = 3,则x的值为:A. 2B. 4C. 8D. 16答案:B5. 函数y = x^2 - 4x + 4的图像与x轴的交点个数为:A. 1B. 2C. 3D. 4答案:A6. 若sinA + sinB = 1,cosA + cosB = 1,则sin(A + B)的值为:A. 0B. 1C. -1D. 不确定答案:A7. 已知向量a = (2, 3),向量b = (3, 4),则向量a与向量b的夹角余弦值为:A. 1/2B. 1/√2C. √2/2D. 1答案:C8. 在△ABC中,角A、B、C的对边分别为a、b、c,若a^2 + b^2 = 2c^2,则△ABC为:A. 锐角三角形B. 直角三角形C. 钝角三角形D. 等腰三角形答案:B9. 已知函数y = ax^2 + bx + c的图像开口向上,且过点(1, 4),则a的取值范围为:A. a > 0B. a < 0C. a ≥ 0D. a ≤ 0答案:A10. 若log2x - log2(2x - 1) = 1,则x的值为:A. 2B. 4C. 8D. 16答案:B二、填空题(本大题共5小题,每小题5分,共25分。
)11. 已知等差数列{an}的首项为2,公差为3,则第10项a10的值为______。
答案:a10 = 2 + 9d = 2 + 9×3 = 2912. 函数y = log2x + 3的图像向右平移2个单位后,得到的函数解析式为______。
高考数学答题模板

高考数学答题模板
一、选择题
1. 易错点归纳:对于选择题,首先要避开常见的易错点和混淆点。
这些易错点可能包括概率与频率概念的混淆、数列求和公式的记忆错误等。
解决这些问题需要强化基础知识点记忆,理解每个概念和公式的具体含义和应用条件。
2. 答题方法:选择题有一些常用的速解方法,如排除法、增加条件法、以小见大法、极限法、关键点法、对称法、小结论法、归纳法、感觉法和分析选项法。
掌握这些方法可以大大提高解题速度和准确性。
二、填空题
1. 易错点归纳:填空题主要考察学生对基础知识的理解和应用能力,常见的失误可能包括审题不仔细、解题思路不严谨等。
例如,在集合题型中未考虑空集情况,在函数问题中未考虑定义域等。
2. 答题方法:对于填空题,有直接法、特殊化法、数形结合法和等价转化法等速解方法。
这些方法可以帮助学生在短时间内找到问题的突破口,提高解题效率。
三、解答题
1. 解题路线图:对于解答题,首先要明确解题的步骤和思路。
例如,三角变换与三角函数的性质问题,解题步骤可以归纳为:不同角化同角、降幂扩角、化f(x)=Asin(ωx+φ)+h形式,然后结合性质求解。
2. 构建答题模板:针对不同类型的题目,需要构建不同的答题模板。
例如,对于三角函数式,一般需要化简为y=Asin(ωx+φ)+h 的形式,即化为“一角、一次、一函数”的形式。
这样可以方便后续的计算和理解。
新高考数学试卷大致模板

一、试卷结构新高考数学试卷一般包括选择题、填空题、解答题三个部分,总分150分。
以下是试卷的大致模板:1. 选择题(共20题,每题3分,共60分)(1)选择题部分主要考察基础知识和基本技能,包括实数、代数式、函数、几何、概率统计等内容。
(2)选择题题型包括:单项选择题、多项选择题。
2. 填空题(共10题,每题5分,共50分)(1)填空题主要考察对基础知识的掌握程度,包括实数、代数式、函数、几何、概率统计等内容。
(2)填空题题型包括:填空题、计算题。
3. 解答题(共5题,每题20分,共100分)(1)解答题部分主要考察综合运用数学知识解决实际问题的能力。
(2)解答题题型包括:解答题、应用题、证明题。
二、试卷内容1. 选择题内容(1)实数:数的性质、实数运算、实数的大小比较等。
(2)代数式:代数式的化简、因式分解、二次根式等。
(3)函数:函数的定义、性质、图像、应用等。
(4)几何:平面几何、立体几何、解析几何等。
(5)概率统计:随机事件、概率、统计分布、统计推断等。
2. 填空题内容(1)实数:实数的运算、大小比较等。
(2)代数式:代数式的化简、因式分解、二次根式等。
(3)函数:函数的定义、性质、图像、应用等。
(4)几何:平面几何、立体几何、解析几何等。
(5)概率统计:随机事件、概率、统计分布、统计推断等。
3. 解答题内容(1)解答题:考察综合运用数学知识解决实际问题的能力。
(2)应用题:结合实际情境,考察学生的应用能力。
(3)证明题:考察学生的逻辑推理能力和证明能力。
三、试卷特点1. 注重基础知识的考察,体现数学学科的特点。
2. 考察学生的数学思维能力、运算能力和解决实际问题的能力。
3. 试题设计新颖,富有挑战性,有利于选拔优秀人才。
4. 试卷难度适中,既符合学生的认知水平,又具有一定的区分度。
四、注意事项1. 试卷在命题过程中,注意保持题目的科学性、严谨性、客观性和公正性。
2. 试题内容应与教材紧密结合,体现数学学科的核心素养。
初中数学试卷答题卡模板

一、试卷基本信息1. 试卷名称:初中数学模拟试题2. 试卷总分:100分3. 试题类型:选择题、填空题、解答题4. 答题时间:120分钟二、答题卡结构1. 个人信息区姓名:________班级:________学号:________2. 选择题答题区(1)选择题(每题2分,共20分)一、选择题(每题2分,共20分)1. 下列各数中,是整数的是()A. 3.14B. -0.5C. 2D. √22. 若a、b是实数,且a+b=0,则下列等式中正确的是()A. a=0,b≠0B. a≠0,b=0C. a=0,b=0D. a≠0,b≠03. 已知一个长方体的长、宽、高分别为a、b、c,则它的体积V=________。
()A. abcB. ab+cC. bc+aD. a+b+c4. 若x²=1,则x的值为()A. 1B. -1C. 1或-1D. 05. 下列各式中,是分式的是()A. 3/xB. x+1C. x²-1D. x³6. 已知一元二次方程x²-5x+6=0,则该方程的解为()A. x=2,x=3B. x=1,x=6C. x=2,x=6D. x=1,x=37. 下列函数中,是奇函数的是()A. y=x²B. y=x³C. y=x²+1D. y=x³+18. 若∠A、∠B、∠C是三角形ABC的内角,则下列不等式中正确的是()A. ∠A+∠B+∠C<180°B. ∠A+∠B+∠C=180°C. ∠A+∠B+∠C>180°D. ∠A+∠B+∠C=360°9. 下列各数中,是偶数的是()A. 3.14B. -0.5C. 2D. √210. 若x²=1,则x的值为()A. 1B. -1C. 1或-1D. 0(2)填空题(每题2分,共20分)一、填空题(每题2分,共20分)1. 若a、b是实数,且a+b=0,则a=________,b=________。
初中数学答题卡(模板)

初中数学答题卡(模板) XXX2015年九年级第一次月考数学一、选择题(共10小题,每小题4分,共40分)1.选出下列各组数中,互质的一组是()A。
12,16 B。
10,15 C。
8,9 D。
6,252.下列各数中,是偶数的是()A。
2/3 B。
1/5 C。
0.6 D。
0.753.若a∶b=3∶2,b∶c=4∶5,则a∶b∶c=()A。
6∶4∶5 B。
6∶8∶10 C。
3∶2∶5 D。
3∶4∶54.一件衣服原价为360元,现在打8折出售,则打折后的价格为()A。
288元 B。
320元 C。
324元 D。
336元5.下列各组数中,最大的一组是()A。
0.8、0.09、0.7、0.6 B。
0.8、0.7、0.6、0.5C。
0.8、0.09、0.7、0.05 D。
0.8、0.7、0.5、0.056.已知正比例函数y=kx的图象过点(2,4),则k的值为()A。
8 B。
2 C。
1 D。
0.57.已知函数y=2x-3,则当x=3时,y的值为()A。
3 B。
6 C。
-3 D。
-68.一条长为6m的绳子,从中间剪开,再把两段各分成相等的三段,则每段的长度为()A。
1m B。
2m C。
1.5m D。
3m9.直角三角形斜边长为10cm,其中一条直角边长为6cm,则另一条直角边长为()A。
8cm B。
9cm C。
12cm D。
15cm10.一块长方体木头,长为3dm,宽为2dm,高为4dm,则它的体积为()A。
24m³ B。
24dm³ C。
240dm³ D。
2400dm³二、填空题(共8小题,每小题4分,共32分)11.4.5×10³=________12.0.04÷0.2=________13.三个互不相等的整数,它们的平均数是15,这三个数的和是________14.一条河流宽80m,两岸各有一座灯塔,两座灯塔的距离为200m,从河流中心观察,两座灯塔的方向角分别为30°和45°,则两座灯塔的高度之差为________15.已知函数y=ax²+bx+c的图象过点(1,3),且在x=2处的函数值为5,则a+b+c的值为________16.已知等差数列{an}的公差为3,首项为4,则a10的值为________17.某工厂生产了1200个产品,其中次品占总数的10%,则合格品的数量为________18.一个三位数各位数字之和为9,且各位数字按从小到大排列,则这个三位数为________三、解答题(共7小题,共78分)19.下列各式中,哪些是恒等式?(写出所有正确答案)20.已知函数f(x)=x³-3x²+2x+1,g(x)=f(x)-2x+1,h(x)=f(x+1),求h(2)的值。
2019年山东省春季高考数学试题及答案【范本模板】

山东省2019年普通高校招生(春季)考试数学试题1.本试卷分卷一(选择题)和卷二(非选择题)两部分,满分120分,考试时间120分钟。
考生清在答题卡上答题,考试结束后,请将本试卷和答题卡一并交回。
2.本次考试允许使用函数型计算器,凡使用计算器的题目,除题目有具体要求外,最后结果精确到0。
01.卷一(选择题共60分)一、选择题(本大题20个小题,每小题3分,共60分.在每小题列出的四个选项中,只有一项符合题目要求,请将符合题目要求的选项字母代号选出.并填涂在答题卡上)1. 已知集合M={0,1},N={1,2},则M ∪N 等于( )A. {1}B. {0,2} C 。
{0,1,2} D. ∅ 2。
若实数a,b 满足ab>0,a+b 〉0,则下列选项正确的是( )A. a>0,b>0 B 。
a>0,b<0 C. a 〈0,b 〉0 D 。
a 〈0,b 〈03。
已知指数函数y=a x ,对数函数y=log b x 的图像如图所示,则下列关系式正确的是A. 0<a<b 〈1B 。
0〈a<1〈bC 。
0<b 〈1〈a D. a 〈0〈1〈b4。
已知函数f(x )=x 3+x ,若f(a)=2,则f(-a )的值是( )A 。
—2 B. 2 C. —10 D 。
10 5. 若等差数列{a n }的前7项和为70,则a 1+a 7等于( )A 。
5B 。
10 C. 15 D. 206。
如图所示,已知菱形ABCD 的边长是2,且∠DAB =60°,则AB AC ⋅ 的值是( ) A 。
4 B. 4+ C 。
6 D 。
4-y第3题 图B第6题 图7。
对于任意角α,β,“α=β"是“sin α=sin β”的( )A 。
充分不必要条件 B. 必要不充分条件 C 。
充要条件 D. 既不充分也不必要条件 8. 如图所示,直线l ⊥OP ,则直线l 的方程是( ) A 。
数学试卷分析模板初中生

一、试卷概述1. 试卷名称:______年级______学期数学期中/期末考试试卷2. 试卷总分:______分3. 考试时间:______分钟4. 试题类型:选择题、填空题、解答题二、试题分析1. 选择题分析(1)数量:______题(2)难度分布:简单题______题,中等题______题,难题______题(3)错题原因:______(分析学生错题的原因,如基础知识掌握不牢固、解题方法不当等)2. 填空题分析(1)数量:______题(2)难度分布:简单题______题,中等题______题,难题______题(3)错题原因:______(分析学生错题的原因)3. 解答题分析(1)数量:______题(2)难度分布:简单题______题,中等题______题,难题______题(3)错题原因:______(分析学生错题的原因)三、学生答题情况分析1. 答题速度(1)总体速度:______(分析学生答题速度是否合理)(2)错题耗时:______(分析学生错题耗时是否过多)2. 答题准确率(1)选择题准确率:______(分析学生选择题正确率)(2)填空题准确率:______(分析学生填空题正确率)(3)解答题准确率:______(分析学生解答题正确率)3. 答题规范性(1)书写规范:______(分析学生书写是否规范)(2)解题步骤:______(分析学生解题步骤是否完整)四、教学建议1. 针对错题原因,提出以下教学建议:(1)基础知识:加强基础知识教学,确保学生掌握相关概念、公式和定理。
(2)解题方法:引导学生掌握正确的解题方法,提高解题技巧。
(3)审题能力:培养学生的审题能力,使学生能够准确理解题意。
2. 针对答题速度,提出以下教学建议:(1)加强时间管理:教会学生合理安排答题时间,确保在规定时间内完成所有题目。
(2)提高答题速度:通过练习提高学生的答题速度,使学生能够在有限的时间内完成更多题目。
数学万能答题模板

数学万能答题模板在解答数学问题时,以下是一个通用的答题模板,可以帮助你组织思路并清晰地表达答案:1. 理解问题:首先,你需要明确问题的要求,理解题目的条件和目标。
2. 分析问题:分析问题中给出的信息,找出相关的数学概念和公式。
例如,如果问题是关于三角形的面积,你可能需要使用三角形的面积公式(面积 = 1/2 × 底× 高)。
3. 建立数学模型:根据问题的要求和已知的信息,建立数学方程或表达式。
例如,如果问题是关于两个数的和与积,你可以建立一个方程或表达式来表示这两个数的和与积。
4. 求解数学模型:使用数学方法来求解建立的数学模型。
这可能涉及到代数运算、方程求解、不等式求解等。
5. 验证答案:最后,你需要验证你的答案是否正确。
这可以通过重新检查你的计算过程、使用其他方法来求解问题,或者使用一些简单的测试样例来验证答案。
以下是一个具体的例子:题目:一个直角三角形的两条直角边分别为3和4,求这个直角三角形的斜边长度。
分析:这个问题涉及到勾股定理的应用。
勾股定理是一个关于直角三角形的基本定理,它告诉我们直角三角形的两条直角边的平方和等于斜边的平方。
建立数学模型:设直角三角形的斜边长度为c,根据勾股定理,我们有:3^2 + 4^2 = c^2求解数学模型:将数值代入公式中,得到:9 + 16 = c^2c^2 = 25c = 5验证答案:我们可以使用勾股定理的逆定理来验证答案是否正确。
如果三角形的三边满足勾股定理,那么这个三角形就是一个直角三角形。
由于3^2 + 4^2 = 5^2,所以这个三角形是一个直角三角形,斜边长度为5。
数学答题模板

模板 3 由数列的前 n 项和 Sn 与通项 an 的关系求通项 an
例 3 已知数列{an}的前 n 项和为 Sn,a1=1,an+1=2Sn+1 (n∈N*),等差数列{bn}中,bn>0 (n∈N*),且 b1+b2+b3= 15,又 a1+b1、a2+b2、a3+b3 成等比数列. (1)求数列{an}、{bn}的通项公式; (2)求数列{an·bn}的前 n 项和 Tn. 审 题 路 线 图 (1) an=Sn-Sn-1 (n≥2) → 消去Sn → 得an+1=3an → an=3n-1
在等差数列{bn}中,∵b1+b2+b3=15,∴b2=5.
如果适合,则统一“合写”;如果
又∵a1+b1、a2+b2、a3+b3 成等比数列,设等差数 不适合,则应分段表示.
列{bn}的公差为 d,则有(a1+b1)(a3+b3)=(a2+b2)2. 第四步:写出明确规范的答案.
∴(1+5-d)(9+5+d)=64,解得 d=-10 或
构建答题模板
模板4 立体几何中的基本关系与基本量问题
例4 如图所示,在四棱锥P—ABCD中, PD⊥平面ABCD,PD=DC=BC=1, AB=2,AB∥DC,∠BCD=90°. (1)求证:PC⊥BC; (2)求点A到平面PBC的距离. 审题路线图
规范解答示例
构建答题模板
(1)证明 ∵PD⊥平面ABCD,BC⊂平面ABCD,∴PD⊥BC. 第一步:根据条件
模板 2 与平面向量综合的三角函数问题 例 2 已知向量 a=(cos 32x,sin 32x),b=(-sin x2,-cos x2),
其中 x∈π2,π. (1)若|a+b|= 3,求 x 的值; (2)函数 f(x)=a·b+|a+b|2,若 c>f(x)恒成立,求实数 c 的取 值范围. 审题路线图 (1)|a+b|= 3→a2+2a·b+b2=3→三角方程 →求 x. (2)化 f(x)向量表示式为三角表示式→化简 f(x)=Asin(ωx+φ)+h→f(x)max→c>f(x)max.
初中中考数学试卷模板

一、试卷结构1. 总分:满分150分,考试时间120分钟。
2. 试卷内容:选择题、填空题、解答题。
3. 难度比例:选择题20%,填空题20%,解答题60%。
二、试卷内容(一)选择题(共30分,每题2分,共15题)1. 下列各数中,不是有理数的是()A. 0.1B. -2C. √4D. π2. 若a、b是方程2x-3=0的两个根,则a+b的值是()A. 1B. 3C. -1D. -33. 已知a=3,b=-2,则|a+b|的值是()A. 1B. 5C. 7D. -54. 下列图形中,是轴对称图形的是()A. 正方形B. 等边三角形C. 矩形D. 圆5. 已知一个等腰三角形的底边长为6cm,腰长为8cm,则该三角形的周长是()A. 20cmB. 22cmC. 24cmD. 26cm6. 下列函数中,是正比例函数的是()A. y=2x+3B. y=3x-2C. y=x/3D. y=3/x7. 若a、b、c是等差数列的前三项,且a+b+c=12,则b的值是()A. 3B. 4C. 5D. 68. 已知一次函数y=kx+b的图象经过点(1,2)和(-2,-6),则k和b的值分别是()A. 1,1B. 1,-1C. -1,1D. -1,-19. 下列各数中,不是实数的是()A. 0B. √(-1)C. √4D. π10. 若一个圆的半径为r,则该圆的周长是()A. 2πrB. πrC. 2rD. r11. 已知一次函数y=kx+b的图象经过点(0,1)和(2,3),则k和b的值分别是()A. 1,1B. 1,-1C. -1,1D. -1,-112. 下列各数中,不是有理数的是()A. 0.1B. -2C. √4D. π13. 若a、b是方程2x-3=0的两个根,则a+b的值是()A. 1B. 3C. -1D. -314. 已知a=3,b=-2,则|a+b|的值是()A. 1B. 5C. 7D. -515. 下列图形中,是轴对称图形的是()A. 正方形B. 等边三角形C. 矩形D. 圆(二)填空题(共30分,每题2分,共15题)1. 已知一个等腰三角形的底边长为6cm,腰长为8cm,则该三角形的周长是____cm。
工程数学期末考试试题与标准答案及评分标准模板

《工程数学》试题(A 卷)(考试时间: 90 分钟)一、选择题(共30分,共10小题,每小题3分)1.函数293x x xy -++=的定义域是( ). A.{}3|-≥x x ; B.{}3|≤x x ;C.{}33|≤≤-x x ; D .{}33|≤<-x x . 2.函数x y =在0=x 处( ) .A.连续且可导;B.不连续且不可导; C 不可导但连续;D.不连续但可导. 3.x x arctan lim +∞→=﹙ ).A.0;B.不存在 ;C. 2π-; D.2π. 4.若11,1,22()3,1,1,1x x f x x x ⎧+<⎪⎪==⎨⎪>⎪⎩,则1lim ()x f x →=( ). A.2; B. 1; C.1-; D.不存在. 5.函数11)(-=x x f 的水平渐近线是( ). A. 1=x ; B. 1-=y ; C. 0=x ; D. 0=y . 6.函数()y f x =在x 处可导是该点可微的( )条件.A.必要;B.充分;C.充要;D.无关.7.若),)(b a x f 在(内二阶可导,且0)(,0)(<''<'x f x f ,则在),(b a 内函数( ). A.单调减,凸函数; B. 单调增,凸函数; C. 单调减,凹函数; D. 单调增,凹函数.8.函数22,1(),1x x f x x x >⎧=⎨≤⎩,在点1x =处( ).A.不连续;B.连续;C. ()2f x '=可导且;D.无法判断. 9.设函数()f x ,()g x 在[,]a b 上连续,且()()f x g x ≥,则( ).A.()d ()d bbaaf x xg x x ≥⎰⎰ ; B.()d ()d bbaaf x xg x x ≤⎰⎰;C.()d ()d f x x g x x ≥⎰⎰ ; D.()d ()d f x x g x x ≤⎰⎰.10. 曲线x y x y ==与2所围成的平面图形绕x 轴旋转而成的旋转体的体积为( ).A. ⎰-124d )(x x x π; B. ⎰-142d )(x x x π;C.⎰-12d )(y y y π; D. ⎰-12d )(y y y π.二、填空题(共20分,共5小题,每小题4分)1.函数654)(22+--=x x x x f ,则2=x 是_______间断点,3=x 是 _______间断点.2. 复合而成和是由函数函数 e arcsin x y =. 3.点()1,0是曲线b ax x y +-=233 的拐点,则=a ______,=b ______. 4. 设 ()f x 的一个原函数为1x,则=)(x f . 5. ⎪⎩⎪⎨⎧==tty x 2ee,=x y d d __________.2.已知y x x y '+=求,cos sin 22.三、计算题(共42分,共6小题,每小题7分)1.求x x x2)51(lim +∞→ 2.已知y x x y '+=求,cos sin 22. 3. 已知.d ,2cos e 2y x y x 求= 4.求x x x d e 2⎰. 5.求⎰exdx x 1ln .6.求由曲线2,,1===x x y xy 围成的平面图形的面积. 四、证明题(共8分,共1小题,每小题8分)1.证明不等式()()0,1ln 1><+<+x x x xx.《工程数学》试题(B 卷)(考试时间: 90 分钟)一、选择题(共30分,共10小题,每小题3分)1.函数242y x x x-++=的定义域是( )..A {}2|-≥x x ; B.{}2|≤x x ;C.{}22|≤≤-x x ; D . {}22|≤<-x x2. 当0→x 时,下列变量为无穷小的是( )A.;cos x x B. ;sin xxC.;12-xD..sin 1x - 3.x x arctan lim ∞→=﹙ ﹚.A.0 ;B.不存在 ;C. —2π ; D.2π. 4.若⎩⎨⎧>-≤=1,21,)(2x x x x x f ,则1lim ()x f x →=( ).2;A .1;B .1;C - .;D 不存在5.函数xx f 1)(=的水平渐近线是( ). A. 1=x B. 1-=y C. 0=x D. 0=y6.函数()y f x =在x 处可导是该点连续的( )条件.;A 必要 .;B 充分 .;C 充要 .;D 无关7.若),)(b a x f 在(内二阶可导,且0)(,0)(///>>x f x f ,则在),(b a 内函数( ).A.单调减,凸函数B. 单调增,凸函数C. 单调减,凹函数D. 单调增,凹函数8.函数⎪⎩⎪⎨⎧>+≤=1,21211,)(2x x x x x f ,在点1x =处( )A.连续且可导;B.不连续且不可导; C 不可导但连续;D.不连续但可导.9.设函数()f x 在[,]a b 上连续,则( )dx x f dx x f A b ab a⎰⎰≤)()(. dx x f dx x f B bab a⎰⎰≥)()(.dx x f dx x f C b ab a⎰⎰=)()(. dx x f dx x f D bab a⎰⎰>)()(.10. 曲线12==x x y 与及x 轴所围成的平面图形绕x 轴旋转而成的旋转体的体积为( ) A. ⎰14dx x πB. ⎰102dx x π C. ⎰10ydy π D. ⎰12dy y π二、填空题(共20分,共5小题,每小题4分)1.函数231)(22+--=x x x x f ,则2=x 是_______间断点,1=x 是 _______间断点. 2. 复合而成和是由函数函数 sin x e y =. 3.点(1,3)是曲线y=23bx ax + 的拐点,则a=______,b=______. 4. 设 ()f x 的一个原函数为x sin ,则=)(x f .5. ⎩⎨⎧==3x bt y at ,=dxdy__________. 三、计算题(共42分,共6小题,每小题7分)1.x x x2)31(lim +∞→2.已知')),ln(ln(ln y x y 求=.3. 已知.dy ,2sin 求x x y =4.求dx xe x ⎰.5.求⎰-224dx x .6.求由曲线0,1,2===y x x y 围成的平面图形的面积.四、证明题(共8分,共1小题,每小题8分)1.证明:当x x x 211,0+>+>时一、单项选择题(共30分,共10小题,每小题3分)1、D2、C3、D4、B5、D6、C7、A8、A9、A 10、B 二、填空题(共20分,共5小题,每小题4分)1、可去(或者第一类);无穷(或者第二类)2、x u e y u arcsin ,==;3、a=0,b=1;4、21x-;5、t2e . 三、计算题(共42分,共6小题,每小题7分)1..7(5())5111(lim (3()5111(lim )51(lim 101051)51(102分)分)分)e x x xx x x x x x =+=+=+∞→∞→∞→ 2..7(sin 2cos sin 24()(sin )(sin sin 22'22''分)分)x x x x x x x x y -=-= 3..7()2sin 2(cos 23(2cos 2cos 222分)分)dx x x e x d e xde dy x x x -=+= 4. C e x d e dx e x dx xe x x x x +===⎰⎰⎰2222215)((213()(212'2分)分).(7分) 5.1ln ex xdx ⎰=211ln 2exdx ⎰(3分)=2221111111ln 2244ee x x x dx e x -⋅=+⎰(7分).6..72ln 235(|)ln 21(3()1(21221分)(分)分)-=-=-=⎰x x dx x x S 四、证明题(共8分,共1小题,每小题8分)1、证:令f(x)=ln(1+x), 在[]x 0,上连续,在(0,x )内可导, )(x f '=x11+,(2分) 由拉格朗日中值定理,在(0,x )内至少存在一点ξ,使得ξ+=-+-+110)01ln()x 1ln x ((4分) 有 ln(1+x)=ξ+1x ,又 0<x <ξ, 1<1+x +<1ξ, x xx x <+<+ξ11,(7分) 所以,x x xx<+<+)1ln(1 (8分)一、单项选择题(共30分,共10小题,每小题3分)1、D2、C3、B4、B5、D6、B7、D8、C9、A 10、A . 二、填空题(共20分,共5小题,每小题4分)1、无穷(或者第二类);可去(或者第一类)2、x u e y u sin ,==;3、29,23=-=b a ;4、x cos ;5、abt 23.三、计算题(共42分,共6小题,每小题7分)1..7(5())3111(lim (3()3111(lim )31(lim 6631)31(62分)分)分)e x x xx x x x x x =+=+=+∞→∞→∞→ 2..7(1ln 1)ln(ln 16()(ln ln 1)ln(ln 13())(ln(ln )ln(ln 1'''分)分)分)xx x x x x x x y ===3..7()2cos 22(sin 3(2sin 2sin 分)分)dx x x x x xd xdx dy +=+=4. .7(4()(''分)分)C e xe dx e x xe dx ex dx xe x x x x x x +-=-==⎰⎰⎰5.令2,2;0,0,cos 2sin 2π======t x t x tdt dx t x 当当则.(1分)⎰-224dx x =tdt ⎰202cos 4π(3分)=⎰+20)2cos 1(2πdt t (4分)=20|)2sin 21(2πt t +(6分)=π.(7分))6..7315(|313(10312分)(分)分)===⎰x dx x S 四、证明题(共8分,共1小题,每小题8分)1、证:令x x x f 211)(+-+=, )(x f '=02x1121>+-+x ,0>x (3分)0)0()(,0],0[)(=>>f x f x x x f 单调递增,在,(6分) ,0211)(>+-+=x x x f 即x x 211+>+.(8分)。
小学一年级下册数学期末测试卷【范本模板】

4个十和4个一2个百7个一
三、填一填
1. 3个一和7个十组成的数是()。
2. 99是()位数,它的十位上是(),个位上是()。
3。一个一个地数,59前面的数是( ),后面的数是(),和31相邻的数是( )和()。
4。比较大小
2772 9089 4个十40个一
36-630 58+1068-8 99+199-1
3。写出十位和个位数字相同的两位数:99、、、、、.
4.写出十位数字比个位数字多2的两位数:32、、、、、。
七、提问题
1、
(1)一共多少个?
(2)比多多少个?(3)和共多少个?
==
(4)哪两样水果合起来接近50个?
(1)一个洋娃娃比一个书包便宜多少元?(2)你喜欢哪两样东西?需要多少钱?
==
(3)用50元买这三件物品,够吗?
21、24、27、、、。
(10)最大的两位数是(),最小的两位数是(),最大的两位数比最小的两位数多().
六、列式计算。(8%)
一本书有86页,小明看了30页,小红比小明多看了8页。
(1)小红看了多少页?
(2)小明还剩)
一、口算。
34+5= 72+36= 65-41= 88-44=
70+9= 21-8= 66+6= 42-5=
17-9= 33+7= 34-8= 35+9=
28+4= 10+70= 79+10= 86-7=
90-60= 61+8= 49-20= 67+9=
35+50-8= 14+8-5= 45-5+30=
83-3-7= 65-40+8= 20+35-9=
66-8+4= 84-40+6= 19+9+7=
高中试题卷模板

高中试题卷模板高中数学试题卷一、选择题(每题3分,共30分)1. 已知函数f(x) = 2x^2 + 3x - 5,求f(-2)的值。
A. -27B. -19C. -11D. 112. 圆的方程为(x-1)^2 + (y-2)^2 = 25,求圆心坐标。
A. (1, 2)B. (-1, 2)C. (1, -2)D. (-1, -2)3. 已知等差数列的前三项分别为3, 5, 7,求第10项的值。
A. 17B. 19C. 21D. 23二、填空题(每题4分,共20分)4. 若sinα = 0.6,求cos^2α的值。
5. 一个直角三角形的两直角边分别为3和4,求斜边长。
三、解答题(共50分)6. 证明:若a, b, c是三角形的三边长,且满足a^2 + b^2 = c^2,则该三角形是直角三角形。
7. 已知函数g(x) = x^3 - 3x^2 + 2,求其导数g'(x)。
附加题(10分)8. 一个物体从静止开始,以加速度a = 2m/s^2做匀加速直线运动,求在第5秒时的速度。
注意事项:- 请在规定时间内完成试卷。
- 请在答题卡上作答。
- 请保持答题卡整洁,字迹清晰。
答题卡:选择题答案:1. ________2. ________3. ________填空题答案:4. ________5. ________解答题答案:6. ________7. ________ 附加题答案:8. ________ 祝考试顺利!。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
实践,小学科学教学的沃土
——浅谈小学科学教学在“做”字上下功夫摘要:20世纪初,陶行知先生提出了“教学做”合一的思想。
他认为,学校的教学过程包括教、学、做三个方面,它们不是三件事而是一件事,即在做上教,在做上学。
它主张以学生实践为最基本的教学方式,让学生在亲身实践中理解理论知识,再将知识运用到实践中去,在实践的过程中将所得的知识消化,即“实践、认识、再实践”。
在平时的小学科学教学中,坚持践行“教学做合一”的思想,在“做”字上下功夫。
这不仅强调了“以教师为主导,以学生为主体”的教学模式,更要求学生能积极主动地参与到课堂,自发的、有兴趣的一起实验、探索、思考,从而让学生的学习过程、获取知识的过程更深刻。
关键词:陶行知教学做合一实践过程
陶行知先生说:“要想教得好,学得好,就须做得好”。
践行“教学做合一”要以“做”为中心,“做”是学的中心也是教的中心,教与学在“做”中统一起来,这样的教才是真教,这样的学才是真学,正如行知先生说的:“先生拿做来教,乃是真教;学生拿做来学,乃是真学。
”那么,如何以行知先生的教育教学思想来指导我们的教学实践?如何在科学教学中协调好教学做合一?如何引导学生积极在“做”字上下功夫?本文就课堂教学中的案例来浅谈下如何在小学科学教学实践中在“做”字上下功夫。
一、在做中教:引导学生积极主动地学习
1、步步为营,下水实验不马虎
实验是小学科学实践的重要组成部分,教师的“下水实验”指科学老师在指导学生实验前,对课堂上学生要做的实验进行多次的预演或试验,从而为有效指导学生开展实验做好准备。
例如,第一年我执教六年级的《小苏打和白醋的变化》这一课时,因为临时有事未做下水实验就去上课了。
在做小苏打和白醋的混合实验时,没有拿药匙,有些小组是拍些小苏打到白醋那里的,还被学生嫌弃。
在做二氧化碳的灭火实验时,实验现象也不够明显,学生充满期待的眼神满是失望。
后来我重新备了这节课,自己再次去做二氧化碳的灭火实验,发现气体的量要多,不要让逃跑这样现象很明显。
教材上的观察、
实验活动,教师一定要在上课前亲自做一遍,才能保证课堂教学顺利实施。
顺利的实验开展、明显的实验现象都能激发学生极大的兴趣,引导他们积极主动地学习。
2、一心一意,演示实验讲到位
演示实验是小学科学实验中教师发挥引导作用的阵地和领域,学生在初识《科学》这门学科时充满了好奇,如果老师通过演示实验,将学生未知的景象展现给学生,这既能让学生获得生动的感性认知,又能调动学生的积极性,更好地提高课堂教学效率和教学质量。
如果教师不重视演示实验,敷衍了事,或用讲解代替实验,那么学生可能对科学会越来越不感兴趣。
例如,四年级学生在做食盐的蒸发实验前,教师应先演示一遍,边演示边讲解注意事项。
蒸发实验在初中的时候还会再做,可见有难度,而且酒精灯使用时的安全因素必须考虑在内。
我曾经听公开课时看到过酒精灯燃起来,为什么会发生这样的现象?我想,如果教师在探究实验时在演示下酒精灯的使用,可能学生在使用时就会注意。
学生在初识工具时也是一样的,量筒、温度计、弹簧测力计,这些如果教师没有示范过如何使用,甚至学生根本不会用,那么学生拿着工具进行探究根本就是无效的。
教师演示时,不仅为学生实验做了良好的指导,有时充满悬念的实验现象也会激发学生学习的兴趣。
二、在做中学:培养学生自主学习的能力
1、放开孩子,给他们自主探究的机会
孩子的天性是爱活动,强烈的好奇心促使他们什么都想自己去尝试,亲自动手“做”不仅能丰富学生的感性认识,还能帮助孩子建立清晰的表象,是理性认识的基础,因此,“在做中学”是孩子发现问题、分析问题和解决问题的一种重要方法。
教师要充分相信孩子,给他们自主的时间和空间去探索实践,不要一直牵着他走路,否则他一直不会自己走路。
放开孩子,即使摔倒在跌跌撞撞中他们能学会自己走路,教学也是如此。
在执教《电路》这一单元时,刚开始接触孩子们可能会觉得有些难,但是他们对于灯泡发亮充满了多大的兴趣。
这里可以以闯关的形式开展比赛,首先让学生利用小灯泡、电池和导线点亮小灯泡,再利用电池盒、灯座、开关等组装成简单电路,完成后再试着增加一个小灯泡,用开关控制灯泡的亮和灭,最后,棒的孩子完成上面的闯关后还可以想出其它的玩法。
提供材料,布置任务,放手让孩子自己去实践,这样的课堂既为学生创设了主动参
与的机会,也为学生提供了主动发展的空间。
2、花样实践,边看边学边思考
真正的学习不仅掌握书本的知识,真正的课堂也不局限于教室。
行知先生说过“生活即教育”。
三年级刚接触科学时,孩子们学的是植物和动物,没上课之前我发现那些平时爱跑来跑去的孩子很感兴趣,因为他们下课时见到过这些小动物,对它们熟悉,有兴趣去了解它们。
而我们班的一些成绩较好的女生反而不感兴趣,她们甚至连蜗牛、蚯蚓都没有见过。
最好的教材不是图片也不是视频,而是大自然,围绕学生的生活,以大自然为素材,以孩子熟悉的生活现象和周围的事物开展科学教育。
我放开孩子们,让他们边看边学边思考,这时我发现,刚接触科学的三年级小朋友,竟能像一个小科学家一样去实践探索。
给学生创设多样实践几乎,教师可以根据本校的情况灵活组织活动:如观看科教影片、参观科技馆所,再如,让学生设计科技板报。
老师指导学生做选题计划,并注意板报成果的积累。
还可以举办故事会、演讲会,可以与班会、其它学科活动联合起来搞。
还可以组织学生参观、调查、考察,可以有不同规模,可以集体也可以分组。
以实践活动的方式进行学习,总之,老师示范,坚持“在做上教”,通过多样的科技活动,有利于为学生创设心得学习环境,开拓新的学习途径,帮助学生走出书房,走向更广阔的知识天地。
三、坚持“教学做合一”,在“做”字上下功夫
1、让学生经历“做”的过程
“人有两个宝,双手和大脑,双手会做工,大脑会思考,用手又用脑,才能
有创造”。
在这首《手脑相长歌》里,我们知道手和脑是密不可分的,只有两者一起,才能发挥出最大的效果。
因此,动手动脑学科学对培养学生的思维能力显得尤其重要。
在去年的跟班研修中,我们执教的是四年级上册第三单元《声音》,我们先听张玲燕老师上了一节《听听声音》,在这课中有用不同的力敲击同一支音叉和用相同的力敲击大小音叉,倾听音叉发出的声音,找出不同点。
张老师大概花了10分钟时间让学生自己敲击音叉去倾听,但从学生的汇报来看,效果并不理想,音量的大小和音调的高低学生似乎弄混了。
课后,张老师说她知道学生没那么厉害,听不出来,但她就是要让学生经历这样一个实践的过程。
在接下来的几节课中,这个班的学生学的越来越好了,学生在运用多种感官参与活动时,进行观察、比较、分析,进而在实践中找到了规律,这班学生对音量和音调的认知不断加深。
2、让学生学会“做”中解决问题
“做”是孩子获取知识、解决实际问题的一种重要途径。
新课程在这方面为孩子们提供了大量的操作机会,通过观察、倾听、比较等方式来获取信息,解决问题。
在小学科学教学中有很多的探究活动,以“提出问题——提出假设——设计实验方案——进行实验——分析得出结论”这样的顺序展开。
以五年级下册《给冷水加热》一课为例,冷水袋为什么会在热水里浮起来?学生的猜测很多可能是体积变大,也可能是重要变轻。
根据提出的猜测进行实验设计,教师做好引导作用,选择合适的材料,使实验达到最优化。
进行实验时,学生惊奇地发现:试管放到热水里后,包在上面的气球皮鼓起来了;加热前后的试管放在天平两边仍平衡。
得出结论:加热后,冷水袋体积变大,质量不变。
在这个探究活动中,教师是引导者、合作者,而课堂的主角是学生,是他们在一步步的实验中找到了问题的答案。
得到的结论有什么用途?在举个例子,热水壶烧水时为什么会有个最大
容量?因为热水烧开后质量不变,体积会变大,可能存在溢水出来的危险。
这就是科学在生活中的应用,是我们解决问题的意义所在,这是一个实践、认识、再实践的过程。
实践是检验真理的唯一标准,实践是小学科学教学的沃土。
“教学做合一”是陶行知教学理论的精髓,是其生活教育理论的方法论,也是其教学论,它以实际生活为落脚点,突出“做”为中心。
行知先生说:“我们要能做,做的最高境界就是创造。
”教师最大的快乐是创造出值得自己崇拜的学生,作为一名人民教师,我们应当继承和发展陶行知先生的教育理论,不断丰富陶行知教育理论,在教育实践中灵活运用陶行知理论,使行知理论不断发扬光大。
