圆形截面钢筋混凝土偏压构件正截面抗压承载力计算系数
《公预规》提供的附录C表C.0.2“圆形截面钢筋混凝土偏压构件正截面抗压承载力计算系数”表

C.O.2沿用边均匀配筋的圆形截面钢筋混凝土偏心受压构件,其正截面抗压承载力可用查表法(表C.0.2)并按下列规定计算求得:1当对构件承载力进行复核验算时1)由本规范公式(5.3.9-1)和(5.3.9-2)解得轴向力的偏心距:'0'g cd sd cd sd Bf D f e r Af C f ρρ+=+(C.0.2-1)2)已知cd f 、'sd f 、ρ、r ,设定ξ值,查表C.0.2,将查得的系数A、B、C、D值代入公式(C.0.2-1)计算0e 值。
若此0e 值与实际计算偏心距/d d M N η相符(允许偏差在2%以内),则设定的ξ值为所求者;若不相符,重新设定ξ值,重复上述计算,直到相符为止;3)将最后确定的ξ相应的A、B、C、D值代入规范公式(5.3.9-1)或(5.3.9-2)进行构件正截面承载力的复核验算。
2当对构件进行配筋设计时1)由公式(C.0.2-1)变换得截面配筋率:0'cd sd o f Br Ae f Ce Dgr ρ−=•−(C.0.2-2)2)已知cd f 、'sd f 、0e 、r ,设定ξ值,查表C.0.2,将查得的系数A、B、C、D值代入公式( C.0.2-2)计算ρ值,计算时式中的0e 应乘以偏心距增大系数η;再再把ρ和A、C值直代入规范公式(5.3.9-1)算得轴向力值。
若此轴向力值与实际作用的轴向力设计值相符(允许偏差在2%以内),则该ξ值及依此计算的ρ值为所求者;若不相符,重新设定ξ值,重复上述计算,直至相符为止。
3)以最后确定的ρ值代入下列公式计算纵向钢筋截面面积:2s A r ρπ=(C.0.2-3)所得钢筋配筋率应符合最小配筋率的要求。
表C.O.2圆形截面钢筋混凝土偏压构件正截面抗压承载力计算系数ξA B C D ξA B C DξA B C D0.200.32440.2628-1.52961.4216 0.210.34810.2787-1.46761.4623 0.220.37230.2945-1.40741.5004 0.230.39690.3103-1.34861.5361 0.240.42190.3259-1.29111.5697 0.250.44730.3413-1.23481.6012 0.260.47310.3566-1.17961.6307 0.270.49920.3717-1.12541.6584 0.280.52580.3865-1.07201.6843 0.290.55260.4011-1.01941.7086 0.300.57980.4155-0.96751.7313 0.310.60730.4295-0.91631.7524 0.320.63510.4433-0.86561.7721 0.330.66310.4568-0.81541.7903 0.340.69150.4699-0.76571.8071 0.350.72010.4828-0.71651.8225 0.360.74890.4952-0.66761.8366 0.370.77800.5073-0.61901.8494 0.380.80740.5191-0.57071.8609 0.390.83690.5304-0.52271.8711 0.400.86670.5414-0.47491.8801 0.410.89660.5519-0.42731.8878 0.420.92680.5620-0.379818943 0.430.95710.5717-0.33231.8996 0.440.98760.5810-0.28501.9036 0.451.01820.5898-0.23771.9065 0.461.04900.5982-0.19031.9081 0.471.07990.6061-0.14291.9084 0.481.11100.6136-0.09541.9075 0.491.14220.6206-0.04781.9053 0.501.17350.6271-0.00001.9018 0.51 1.20490.63310.0480 1.8971 0.52 1.23640.63860.0963 1.8909 0.53 1.26800.64370.1450 1.8834 0.54 1.29960.64830.1941 1.8744 0.55 1.33140.65230.2436 1.8639 0.56 1.36320.65590.2937 1.8519 0.57 1.39500.65890.3444 1.8381 0.58 1.42690.66150.3960 1.8226 0.59 1.45890.66350.44851,8052 0.60 1.49080.66510.5021 1.78560.64 1.61880.66610.7373 1.67630.65 1.65080.66510.8080 1.63430.66 1.68270.66350.8766 1.59330.67 1.71470.66150.9430 1.55340.68 1.74660.6589 1.0071 1.51460.691.77840.6559 1.06921.47690.70 1.81020.6523 1.1294 1.44020.71 1.84200.6483 1.1876 1.40450.72 1.87360.6437 1.2440 1.36970.73 1.90520.6386 1.2987 1.33580.74 1.93670.6331 1.3517 1.30280.75 1.96810.6271 1.4030 1.27060.76 1.99940.6206 1.4529 1.23920.77 2.03060.6136 1.5013 1.20860.78 2.06170.6061 1.5482 1.17870.79 2.09260.5982 1.5938 1.14960.80 2.12340.5898 1.6381 1.12120.81 2.15400.5810 1.6811 1.09340.82 2.18450.5717 1.7228 1.06630.83 2.21480.5620 1.7635 1.03980.84 2.24500.5519 1.8029 1.01390.85 2.27490.5414 1.84130.98860.86 2.30470.5304 1.87860.96390.87 2.33420.5191 1.91490.93970.88 2.36360.5073 1.95030.91610.89 2.39270.4952 1.98460.89300.90 2.42150.4828 2.01810.87040.91 2.45010.4699 2.05070.84830.92 2.47850.4568 2.08240.82660.93 2.50650.4433 2.11320.80550.94 2.53430.4295 2.14330.78470.95 2.56180.4155 2.17260.76450.96 2.58900.4011 2.20120.74460.97 2.61580.3865 2.22900.72510.98 2.64240.3717 2.25610.70610.99 2.66850.3566 2.28250.68741.002.69430.3413 2.30820.66921.012.71120.3311 2.33330.65131.022.72770.3209 2.35780.63371.032.74400.3108 2.38170.61651.042.75980.3006 2.40490.59971.082.82000.26092.49240.53561.092.83410.25112.51290.52041.102.84800.24152.53300.50551.112.86150.23192.55250.49081.122.87470.22252.57160.47651.132.88760.21322.59020.46241.142.90010.20402.60840.44861.152.91230.19492.62610.43511.162.92420.18602.64340.42191.172.93570.17722.66030.40891.182.94690.16852.67670.39611.192.95780.16002.69280.38361.202.96840.15172.70850.37141.212.97870.14352.72380.35941.222.9886O.13552.73870.34761.232.99820.12772.75320.33611.243.00750.12012.76750.32481.253.01650.11262.78130.31371.263.02520.10532.79480.30281.273.03360.09822.80800.29221.283.04170.09142.82090.28181.293.04950.08472.83350.27151.303.05690.07822.84570.26151.313.06410.07192.85760.25171.323.07090.06592.86930.24211.333.07750.06002.88060.23271.343.08370.05442.89170.22351.353.08970.04902.90240.21451.363.09540.04392.91290.20571.373.10070.03892.92320.19701.383.10580.03432.93310.18861.393.11060.02982.94280.18031.403.11500.02562.95230.17221.413.11920.02172.96150.16431.423.12310.01802.97040.15661.433.12660.01462.97910.14911.443.12990.01152.98760.14171.453.13280.00862.99580.13451.463.13540.00613.00380.12751.473.13760.00393.01150.12061.483.13950.00213.01910.11400.61 1.52280.66610.5571 1.76360.62 1.55480.66660.6139 1.73870.63 1.58680.66660.6734 1.7103 1.05 2.77540.2906 2.42760.58321.06 2.79060.2806 2.44970.56701.07 2.80540.2707 2.47130.5512 1.49 3.14080.007 3.02640.10751.503.14160.00003.03340.10111.513.14160.00003.04030.09505.3.9沿周边均匀配置纵向钢筋的圆形截面钢筋混凝土偏心受压构件(图5.3.9),其正截面抗压承载力计算应符合下列规定:图5.3.9沿周边均匀配筋的圆形截面偏心受压构件计算22'0d cd sdN Ar f C r f γρ≤+(5.3.9-1)33'00d cd sd N e Br f D gr f γρ≤+(5.3.9-2)式中0e ——轴向力的偏心距,0/d d e M N =,应乘以偏心距增大系数η,η可按第5.3.10条的规定计算;A、B——有关混凝土承载力的计算系数,按附录C 的迭代法由表C.O.2查得;C、D——有关纵向钢筋承载力的计算系数,按附录C 的迭代法由表C.O.2查得;r ——圆形截面的半径;g ——纵向钢筋所在圆周的半径s r 与圆截面半径之比,/s g r r =;ρ——纵向钢筋配筋率,2/s A r ρπ=。
桩基强度验算
mm mm
mm mm mm 根
0 750
20 12 0 3768 0.002
先假定,求出e0后与实际比较,符合
混凝土轴心抗压强度设计值
钢筋抗拉强度设计值
fcd fsd′ Nd Md e0
Mpa Mpa KN KNm弯矩组合设计值 轴向力偏心距 桩基正截面抗压承载力设计荷载
0.00 0.00 合格
KNm 桩基强度验算结果
合格
先假定,求出e0后与实际比较,符合2%允许偏差则采用假定,不符则继续假定
e0
#DIV/0!
查表C.0.2
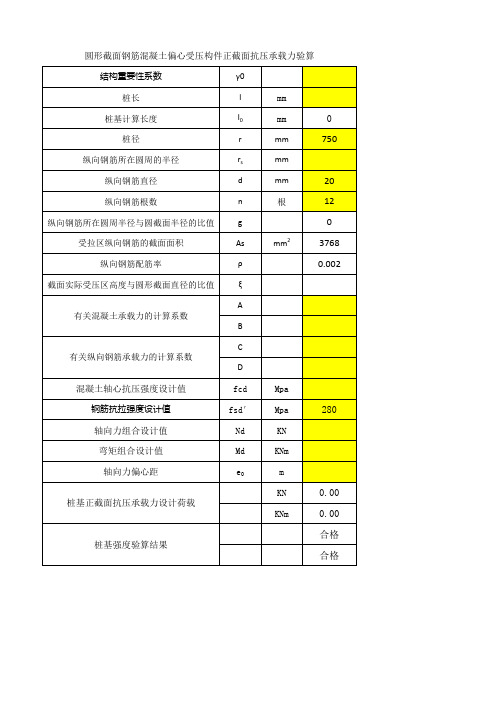
圆形截面钢筋混凝土偏心受压构件正截面抗压承载力验算
结构重要性系数 桩长 桩基计算长度 桩径 纵向钢筋所在圆周的半径 纵向钢筋直径 纵向钢筋根数 纵向钢筋所在圆周半径与圆截面半径的比值 受拉区纵向钢筋的截面面积 纵向钢筋配筋率 截面实际受压区高度与圆形截面直径的比值 有关混凝土承载力的计算系数 B C 有关纵向钢筋承载力的计算系数 D γ0 l l0 r rs d n g As ρ ξ A mm2
《公预规》提供的附录C表C.0.2“圆形截面钢筋混凝土偏压构件正截面抗压承载力计算系数”表

C.O.2沿用边均匀配筋的圆形截面钢筋混凝土偏心受压构件,其正截面抗压承载力可用查表法(表C.0.2)并按下列规定计算求得:1当对构件承载力进行复核验算时1)由本规范公式(5.3.9-1)和(5.3.9-2)解得轴向力的偏心距:'0'g cd sd cd sd Bf D f e r Af C f ρρ+=+(C.0.2-1)2)已知cd f 、'sd f 、ρ、r ,设定ξ值,查表C.0.2,将查得的系数A、B、C、D值代入公式(C.0.2-1)计算0e 值。
若此0e 值与实际计算偏心距/d d M N η相符(允许偏差在2%以内),则设定的ξ值为所求者;若不相符,重新设定ξ值,重复上述计算,直到相符为止;3)将最后确定的ξ相应的A、B、C、D值代入规范公式(5.3.9-1)或(5.3.9-2)进行构件正截面承载力的复核验算。
2当对构件进行配筋设计时1)由公式(C.0.2-1)变换得截面配筋率:0'cd sd o f Br Ae f Ce Dgr ρ−=•−(C.0.2-2)2)已知cd f 、'sd f 、0e 、r ,设定ξ值,查表C.0.2,将查得的系数A、B、C、D值代入公式( C.0.2-2)计算ρ值,计算时式中的0e 应乘以偏心距增大系数η;再再把ρ和A、C值直代入规范公式(5.3.9-1)算得轴向力值。
若此轴向力值与实际作用的轴向力设计值相符(允许偏差在2%以内),则该ξ值及依此计算的ρ值为所求者;若不相符,重新设定ξ值,重复上述计算,直至相符为止。
3)以最后确定的ρ值代入下列公式计算纵向钢筋截面面积:2s A r ρπ=(C.0.2-3)所得钢筋配筋率应符合最小配筋率的要求。
表C.O.2圆形截面钢筋混凝土偏压构件正截面抗压承载力计算系数ξA B C D ξA B C DξA B C D0.200.32440.2628-1.52961.4216 0.210.34810.2787-1.46761.4623 0.220.37230.2945-1.40741.5004 0.230.39690.3103-1.34861.5361 0.240.42190.3259-1.29111.5697 0.250.44730.3413-1.23481.6012 0.260.47310.3566-1.17961.6307 0.270.49920.3717-1.12541.6584 0.280.52580.3865-1.07201.6843 0.290.55260.4011-1.01941.7086 0.300.57980.4155-0.96751.7313 0.310.60730.4295-0.91631.7524 0.320.63510.4433-0.86561.7721 0.330.66310.4568-0.81541.7903 0.340.69150.4699-0.76571.8071 0.350.72010.4828-0.71651.8225 0.360.74890.4952-0.66761.8366 0.370.77800.5073-0.61901.8494 0.380.80740.5191-0.57071.8609 0.390.83690.5304-0.52271.8711 0.400.86670.5414-0.47491.8801 0.410.89660.5519-0.42731.8878 0.420.92680.5620-0.379818943 0.430.95710.5717-0.33231.8996 0.440.98760.5810-0.28501.9036 0.451.01820.5898-0.23771.9065 0.461.04900.5982-0.19031.9081 0.471.07990.6061-0.14291.9084 0.481.11100.6136-0.09541.9075 0.491.14220.6206-0.04781.9053 0.501.17350.6271-0.00001.9018 0.51 1.20490.63310.0480 1.8971 0.52 1.23640.63860.0963 1.8909 0.53 1.26800.64370.1450 1.8834 0.54 1.29960.64830.1941 1.8744 0.55 1.33140.65230.2436 1.8639 0.56 1.36320.65590.2937 1.8519 0.57 1.39500.65890.3444 1.8381 0.58 1.42690.66150.3960 1.8226 0.59 1.45890.66350.44851,8052 0.60 1.49080.66510.5021 1.78560.64 1.61880.66610.7373 1.67630.65 1.65080.66510.8080 1.63430.66 1.68270.66350.8766 1.59330.67 1.71470.66150.9430 1.55340.68 1.74660.6589 1.0071 1.51460.691.77840.6559 1.06921.47690.70 1.81020.6523 1.1294 1.44020.71 1.84200.6483 1.1876 1.40450.72 1.87360.6437 1.2440 1.36970.73 1.90520.6386 1.2987 1.33580.74 1.93670.6331 1.3517 1.30280.75 1.96810.6271 1.4030 1.27060.76 1.99940.6206 1.4529 1.23920.77 2.03060.6136 1.5013 1.20860.78 2.06170.6061 1.5482 1.17870.79 2.09260.5982 1.5938 1.14960.80 2.12340.5898 1.6381 1.12120.81 2.15400.5810 1.6811 1.09340.82 2.18450.5717 1.7228 1.06630.83 2.21480.5620 1.7635 1.03980.84 2.24500.5519 1.8029 1.01390.85 2.27490.5414 1.84130.98860.86 2.30470.5304 1.87860.96390.87 2.33420.5191 1.91490.93970.88 2.36360.5073 1.95030.91610.89 2.39270.4952 1.98460.89300.90 2.42150.4828 2.01810.87040.91 2.45010.4699 2.05070.84830.92 2.47850.4568 2.08240.82660.93 2.50650.4433 2.11320.80550.94 2.53430.4295 2.14330.78470.95 2.56180.4155 2.17260.76450.96 2.58900.4011 2.20120.74460.97 2.61580.3865 2.22900.72510.98 2.64240.3717 2.25610.70610.99 2.66850.3566 2.28250.68741.002.69430.3413 2.30820.66921.012.71120.3311 2.33330.65131.022.72770.3209 2.35780.63371.032.74400.3108 2.38170.61651.042.75980.3006 2.40490.59971.082.82000.26092.49240.53561.092.83410.25112.51290.52041.102.84800.24152.53300.50551.112.86150.23192.55250.49081.122.87470.22252.57160.47651.132.88760.21322.59020.46241.142.90010.20402.60840.44861.152.91230.19492.62610.43511.162.92420.18602.64340.42191.172.93570.17722.66030.40891.182.94690.16852.67670.39611.192.95780.16002.69280.38361.202.96840.15172.70850.37141.212.97870.14352.72380.35941.222.9886O.13552.73870.34761.232.99820.12772.75320.33611.243.00750.12012.76750.32481.253.01650.11262.78130.31371.263.02520.10532.79480.30281.273.03360.09822.80800.29221.283.04170.09142.82090.28181.293.04950.08472.83350.27151.303.05690.07822.84570.26151.313.06410.07192.85760.25171.323.07090.06592.86930.24211.333.07750.06002.88060.23271.343.08370.05442.89170.22351.353.08970.04902.90240.21451.363.09540.04392.91290.20571.373.10070.03892.92320.19701.383.10580.03432.93310.18861.393.11060.02982.94280.18031.403.11500.02562.95230.17221.413.11920.02172.96150.16431.423.12310.01802.97040.15661.433.12660.01462.97910.14911.443.12990.01152.98760.14171.453.13280.00862.99580.13451.463.13540.00613.00380.12751.473.13760.00393.01150.12061.483.13950.00213.01910.11400.61 1.52280.66610.5571 1.76360.62 1.55480.66660.6139 1.73870.63 1.58680.66660.6734 1.7103 1.05 2.77540.2906 2.42760.58321.06 2.79060.2806 2.44970.56701.07 2.80540.2707 2.47130.5512 1.49 3.14080.007 3.02640.10751.503.14160.00003.03340.10111.513.14160.00003.04030.09505.3.9沿周边均匀配置纵向钢筋的圆形截面钢筋混凝土偏心受压构件(图5.3.9),其正截面抗压承载力计算应符合下列规定:图5.3.9沿周边均匀配筋的圆形截面偏心受压构件计算22'0d cd sdN Ar f C r f γρ≤+(5.3.9-1)33'00d cd sd N e Br f D gr f γρ≤+(5.3.9-2)式中0e ——轴向力的偏心距,0/d d e M N =,应乘以偏心距增大系数η,η可按第5.3.10条的规定计算;A、B——有关混凝土承载力的计算系数,按附录C 的迭代法由表C.O.2查得;C、D——有关纵向钢筋承载力的计算系数,按附录C 的迭代法由表C.O.2查得;r ——圆形截面的半径;g ——纵向钢筋所在圆周的半径s r 与圆截面半径之比,/s g r r =;ρ——纵向钢筋配筋率,2/s A r ρπ=。
正截面承载力—受弯、受压、受拉

➢ 我国GBJ10-89规范取0=fcm=1.1fc;
➢ 我国DL/T5057-1996、JTJ267-98、GB50010-2002规范
取0=fc。
美国ACI 318—95、欧洲混凝土委员会模式规范
CEB —FIP 1990以及欧洲共同体委员会规范则以标
准圆柱体(150mm300mm)试件的抗压强度标准值
二、基本公式——对任意截面
1、截面的曲率 :
(a)
2、截面上的混凝土应变: 3、截面上的混凝土应力:
4、截面上的钢筋应力:
2
3
5、微元面积上混凝土压应力的合力:
dNi=ci.dAi=b(y).dy.ci(ci) 即:dNi = b(y).ci(ci).dy 6、平衡方程(b)、(c):
N 0 :
28
2、截面M-关系的计算
(a)
应
力钢理 、筋论 内,上 力的
(b)
的 分 布
混 凝 土 ,
—
弯 矩 曲 率
(c)
截 面 及 其 应
关 系 的 确 定
变 29
由上图,静力平衡条件得 :
(a) (b)
用数值计算时,沿高度把截面划分成若干条带,假 定条带上的应力是个常值,上式可近似写为:
力的影响不明显 ; 对0 大的超筋梁和小偏压柱,基本不变。
因此,有些规范把取为常数。 我国: 0=fc=0.67fcu; 美国ACI:0=/(2)=0.72/(2×0.425)fc=0.85 fc
11
❖1 关于混凝土抗压强度:
我国规范GBJl0—89、GB 50010-2002、水工混凝 土结构设计规范DL/T5057—1996、港工规范JTJ 267-98以及英国混凝土结构设计规范BS8110以标 准立方体试块(150mm×l50mm×l50mm)的抗压强 度标准值作为混凝土强度等级。
钢筋砼偏心受力构件承载力计算

Nu(kN)
1000 800 600 400 200
0
受压破坏
B
A
界限破坏
受拉破坏
10 20 30 40
利用M-N相关曲线寻找最不利内力:
• 作用在结构上的荷载往往有很多种,在结构设 计时应进行荷载组合;
• 在受压构件同一截面上可能会产生多组M、N 内力他们当中存在一组对该截面起控制作用;
• 这一组内力不容易凭直观多组M、N中挑选出 来,但利用N-M相关曲线的规律,可比较容易 地找到最不利内力组合
As先屈服,然后受压混凝土达到c,max,
As f y。
受拉破坏 (大偏心受
压破坏)
N
cmax1
cmax2
cu
ei N
ei N
sAs
f yAs
sAs
f yAs
(a) N
(b)
(c)
N的偏心较小一些或N的e0大,
然而As较多。 截面大部分受压
受
而少部分受拉,荷载增大沿构 件受拉边一定间隔将出现垂直
ei+ f = ei(1+ f / ei) = ei
=1 +f / ei
…7-6
––– 偏心距增大系数
ei N
af ei
f
N
图7-9
l
2 0
10
1
f
cu y
h0
规范采用了的界限状态为 依据,然后再加以修正
1 1
1 4 0 0 ei
(
l0 h
)2
1
2
h0
…7-7
式中: ei = e0+ ea
短柱 中长柱 细长柱
––– 材料破坏 ––– 失稳破坏
圆形截面钢筋混凝土偏心受压构件正截面承载力计算方法探讨_肖武

35 期
肖 武 , 等 :圆形截面 钢筋混凝土偏心受压构件正截面承载力计算方法探讨
88 7 9
图 1 圆形截面偏心受压 构件正截面承载力计算简图
2010 年 10月 9日收到 第一作者简介 :肖 武 (1976— ), 男 , 湖南益阳人 , 硕士 , 研究 方向 : 岩土工程及水电站工程设计 。 E-mail:xiaowuu@sohu.com。
表格对算例进行计算 , 并对各种计算方法的精度进 行分析对比 , 从而总结出一定的规律 , 为更方便 、有 效地进行圆截面承载力设计计算奠定一定的基础 。
1 圆形截面钢筋混凝土偏心受压构件承载 力计算原理及简化方法
1.1 圆形截面钢筋混凝土偏心受压构件承载力计 算原理
根据轴向力对截面形心的偏心距不同 , 圆形截 面偏心受压构件也会出现类 似于矩形截面那 样的 “受拉破坏 ”和 “受压破坏 ”两种破坏形态 。 但是 , 对 于钢筋沿周边均匀布置的圆形截面来说 , 构件破坏 时各根钢筋的应变是不 等的 , 应 力也不完全相同 , 随着轴向压力的偏心距的增加 , 构件的破坏由 “受 压破坏 ”向 “受拉破坏 ”的过渡基本上是连续的 。 沿 周边均匀配筋的圆形截面偏心受压构件 , 其正截面 强度计算的基本假定如下 :
规范 》(JTG D62— 2004)计算方法 《JTGD62— 2004》中基本采用了理论的推导公 式 , 只是对具体参数 进行了明确 , 如取受压混 凝土 等效矩形应力图形的应力集 度为混凝土轴心 抗压 强度设计值 , 即 Ra =fcd;混凝 土极限 压应变 εcu = 0.003 3;对 β的取值 , 当 ξ≤1时 , β =0.8;当 1 <ξ≤ 1.5时 , β =1.067 -0.267 ξ;对初始偏心距 ei, 仅考 虑了轴向压力对截面重心的偏心距 e0 , 未考虑附加 偏心距 ea, 即 ei =e0 ;对 g的取值 , 由于实际工程中 g 的变化不大 , 且通过计算可以发现 , g的稍许变化对 C、D的影响很小 , 对构件承载力 的影响更是有限 , 故 《JTGD62— 2004》中取 g=0.88进行计算 ;钢筋 屈服 应 变 取 常 用 钢 筋 的 平 均 值 , 即 f′sd /Es = 0.001 4, 从而使 A、B、C、D仅与 ξ有关 [ 2] 。 由此编 制了 A、B、C、D随 ξ变化的表格 。 1.3 《混凝土结构设计规范 》(GB 50010— 2002)及
轴心受力构件的截面承载力计算

l0/b=8~34
l0与构件两端支承条件有关:
两端铰支 l0= l,
两端固支 l0=0.5 l
一端固支一端铰支 l0=0.7 l
一端固支一端自由 l0=2 l
《规范》采用的ψ值根据长细比l0/b查表3-1
01
03
02
04
05
06
长细比l0/b的取值
实际结构中的端部支承条件并不好确定,《规范对排架柱、框架柱的计算长度做出了具体规定。
当柱截面短边大于400mm、且各边纵筋配置根数超过多于3根时,或当柱截面短边不大于400mm,但各边纵筋配置根数超过多于4根时,应设置复合箍筋。
对截面形状复杂的柱,不得采用具有内折角的箍筋 ?
1
2
3
4
5
四、箍 筋
内折角不应采用
内折角不应采用
复杂截面的箍筋形式
钢筋混凝土构件由两种材料组成,其中混凝土是非匀质材料,钢筋可不对称布置,故对钢筋混凝土构件,只有均匀受压(或受拉)的内合力与纵向外力在同一直线时为轴心受力,其余情况下均为偏心受力。在工程中,严格意义上轴心受压不存在,所谓的轴压构件或多或少的都存在偏心。
从经济、施工及受力性能方面考虑(施工布筋过多会影响混凝土的浇筑质量;配筋率过大易产生粘结裂缝,突然卸荷时混凝土易拉裂),全部纵筋配筋率不宜超过5%。全部纵向钢筋的配筋率按r =(A's+As)/A计算,一侧受压钢筋的配筋率按r '=A's/A计算,其中A为构件全截面面积。
三、纵向钢筋
1
柱中纵向受力钢筋的的直径d不宜小于12mm,且选配钢筋时宜根数少而粗,但对矩形截面根数不得少于4根,圆形截面根数不宜少于8根,不得少于6根,且应沿周边均匀布置。
偏心受压构件正截面承载力计算

这种破坏特点是受拉区、受压区的钢筋都能达到屈服,受压 区的混凝土也能达到极限压应变,如图8—3a 所示。
图8-3 受拉破坏和受压破坏时的截面应力
2、受压破坏:
当偏心距较小或很小时,或者虽然相对偏心距较大, 但此时配置了很多的受拉钢筋时,发生的破坏属小 偏压破坏。这种破坏特点是,靠近纵向力那一端的 钢筋能达到屈服,混凝土被压碎,而远离纵向力那 一端的钢筋不管是受拉还是受压,一般情况下达不 到屈服。如图8—3b 、c 所示
按这样求得的内力可直接用于截面设计不需要再乘系在生产和工作岗位上从事各种劳动的职工围绕企业的经营战略方针目标和现场存在的问题以改进质量降低消耗提高人的素质和经济效益为目的组织起来一矩形截面非对称配筋构件正截面承载力一偏心受压构件正截面承载力计算在生产和工作岗位上从事各种劳动的职工围绕企业的经营战略方针目标和现场存在的问题以改进质量降低消耗提高人的素质和经济效益为目的组织起来1基本计算公式及适用条件
h 0 ——纵向受压钢筋合力点到截面远边的距离;
2、垂直于弯矩作用平面的受压承载力验算
当轴向压力设计值N较大且弯矩作用平面内的偏心距较小 时,若垂直于弯矩作用平面的长细比较大或边长较小时,则 有可能由垂直于弯矩作用平面的轴心受压承载力起控制作用。 因此,《规范》规定:偏心受压构件除应计算弯矩作用平面 的受压承载力外,尚应按轴心受压构件验算垂直于弯矩作用 平面的受压承载力,此时,可不计入弯矩的作用,但应考虑 稳定系数的φ影响。
一规格的钢筋 。
因此在大偏心受压时,均有 fy As fy' As' 对于小偏压,由于一侧钢筋应力达不到屈服,情形则较为复杂。
1、截面选择
钢筋混凝土构件受压构件承载力计算

轴心受压、偏心受压和受弯构件截面极限应力状态
’
构件截面应力随偏心距变化
矩形截面偏心受压
偏
心 受
计算基本假定
重心轴
压 平截面假定
构
计算中和轴
件 不考虑混凝土的抗拉作用
正
实际中和轴
截 混凝土和钢筋的应力应变关系
面
承 受压区混凝土采用等效矩形应力图形。 载
力 x 2 a 时,受压钢筋达到抗压设计强度。
偏
心
受
N与M线性关系
压
N与M曲线关系
构
dN/dM=0
件
纵
向
弯
曲
的
影
响
短柱、长柱和细长柱 e0相同、长细比不同时Nu的变化
长细比增加,附加弯矩增大, 长柱承载力Nu降低。(同轴压)
偏
偏心距增大系数法是一个传统的方法,使
心
用方便,在大多数情况下具有足够的精度,至
受 压
今被各国规范所采用。
构
式(5-11)是由两端铰支、计算长度为l0 、
x) 2
f cbx f y As
KV
Vu
0.7 ftbh0
1.25 f yv
Asv s
h0
fy Asb sins
1.正截面承载力(N、M)
单
KN
Nu
fcbx
f
' y
As
s
As
向 偏
KNe
Nue
fcbx h0
x 2
f
' y
As'
算
推导
适筋、超筋、界限破坏时的截面平均应变图
钢筋混凝土偏心受力构件承载力计算

f y (h0 as' )
' 大
h 其中:e ei as' 2
③小偏心受压构件的配筋计算 I.受弯平面内的计算: 将б s的公式(6-14)代人式(6-12)及式(6-13),并将x代换为 x=ξ h0,则小偏心受压的基本公式为
(6-22)
(6-23) (6-24) 式(6-22)及式(6-23)中有三个未知 数ξ ,As及As’故不能得出唯一的 解、一般情况下As’无论拉压其应力 都达不到强度设计值,故配置数量 很多的钢筋是无意义的。故可取As =0.002bh,但考虑到在N较大而e0 较小的全截面受压情况下如附加偏 心
如图6-7所示,ab段表示大偏心受压时的M-N相 关曲线,为二次抛物线、随着轴向压力N的增大 截面能承担的弯矩也相应提高。 b点为受拉钢筋与受压混凝土同时达到其强 度值的界限状态。此时偏心受压构件承受的弯矩 M最大。 bc段表示小偏心受压时的M-N曲线,是一条 接近于直线的二次函数曲线。由曲线趋向可以看 出,在小偏心受压情况下,随着轴向压力的增大 截面所能承担的弯矩反而降低。
第六章 计算
本章的重点是:
钢筋混凝土偏心受力构件承载力
了解偏心受压构件的受力工作特性,熟悉两 种不同的受压破坏特性及由此划分成的两类受压 构件 掌握两类偏心受压构件的判别方法; 掌握两类偏心受压构件正截面承载力的计算 方法;
掌握偏心受压构件斜截面受剪承载力计算方
法。
§6.1
概述
结构构件的截面上受到轴力和弯矩的共同作用或受 到偏心力的作用时该结构构件称为偏心受压构件。 分为偏心受压构件和偏心受拉构件。 偏心受压构件又分为:单向偏心受压构件(图6-1a) 及双向偏心受压构件(图6-1b)。 偏心受拉构件在偏心拉力的作用下 是一种介于轴 心受拉构件与受弯构件之间的受力构件。承受节间荷载 的悬臂式桁架上弦(图6-2a)一般建筑工程及桥梁工程中 的双肢柱的受拉肢属于偏心受拉构件(图6-2b)。此外, 如图6-2c所示的矩形水池的池壁 其竖向截面同时承受轴 心拉力及平面外弯矩的作用故也属于偏心受拉构件。
现行规范钢筋混凝土偏压柱正截面承载力计算

摘 要:依据《混凝土结构设计规范》(GB50010-2002)和《混凝土结构设计规范》(GB50010-2010)给出的
钢筋混凝土偏心受压构件正截面承载力计算规定,结合本人教学中的体会,对计算中给出的二阶效应规定、控
制截面弯矩计算、以及需要注意的事项进行了说明,并结合矩形截面偏心受压构件对称配筋设计实例,灵活运
1偏压构件正截面承载力设计相关规定
偏压构件的正截面承载力设计涉及结构二阶效应的问题.结构二阶效应指除一阶以外在结构中的高 阶内力•建筑结构的二阶效应包括:重力二阶效应(P-J)和受压构件的挠曲效应(P-5)两部分些在结 构设计过程中,首先进行结构层面的内力计算,P-/二阶效应一般在结构整体分析已计算;而之后进行 构件层面的设计计算,则P*二阶效应一般会在构件设计层面中计算.
(1)在框架结构、剪力墙结构、框架-剪力墙结构及筒体结构中,当采用增大系数法近似计算结构
收稿日期:2021-01-17 基金项目:厦门理工学院教研教改项目(JG2018040);厦门理工学院校级精品线下课程建设项目([2020]16号) 作者简介:焦俊婷(1968-),女,河北保定人,教授,博士,主要研究方向:工程力学和混凝土结构.
范计算偏压构件正截面承载力设计时应注意新旧规范的不同之处,特别是在教学中,概念必须清晰,计
算过程时要注意:计算长度的取值、偏心距增大系数"与弯矩增大系数%的不同、偏心矩e的计算不
同、以及配筋计算结果好久有不同等.
参考文献: [1] 李新荣,秦文钺,白绍良.两端不等偏心距钢筋混凝土柱二阶效应试验研究[J].重庆建筑大学学报,2000(s22):41-46. [2] 魏巍.考虑非弹性及二阶效应特征的钢筋混凝土框架柱的强度问题与稳定问题[D].重庆:重庆建筑大学,2004. [3] 刘毅.钢筋混凝土结构二阶效应及设计方法的研究[D].重庆:重庆建筑大学,2007. [4] GB50010-2002.混凝土结构设计规范[S].北京:中国建筑工业出版社,2002. [5] GB50010-2010.混凝土结构设计规范[S].北京:中国建筑工业出版社,2010. [6] 韩丽婷,叶燕华.钢筋混凝土偏心受压构件正截面承载力计算的教学思考[J],东南大学学报:哲学社会科学版,2012(s2):
全混凝土结构设计规范附录
混凝土结构设计规范(附录)附录A钢筋的公称直径、公称截面面积及理论重量表AO1钢筋的公称直径、公称截面面积及理论重量表A.0.2钢绞线的公称直径、公称截面面积及理论重量表A.0.3钢丝的公称直径、公称截面面积及理论重量附录B近似计算偏压构件侧移二阶效应的增大系数法B.0.1在框架结构、剪力墙结构、框架-剪力墙结构及筒体结构中,当采用增大系数法近似计算结构因侧移产生的二阶效应(P—△效应)时,应对未考虑P-△效应的一阶弹性分析所得的柱、墙肢端弯矩和梁端弯矩以及层间位移分别按公式(Bo1-I)和公式(BO1—2)乘以增大系数ηs:[B.0.1-1]∆=3[B.0.1-2]式中:Ms——引起结构侧移的荷载或作用所产生的一阶弹性分析构件端弯矩设计值;Mns——不引起结构侧移荷载产生的一阶弹性分析构件端弯矩设计值;∆1——一阶弹性分析的层间位移;ηs——P-△效应增大系数,按第B.0.2条或第B.0.3条确定,其中,梁端ηs 取为相应节点处上、下柱端或上、下墙肢端ηs的平均值。
B.0.2在框架结构中,所计算楼层各柱的ηs可按下公式计算:式中:D——所计算楼层的侧向刚度。
在计算结构构件弯矩增大系数与计算结构位移增大系数时,应分别按本规范第B.0.5条的规定取用结构构件刚度;Nj——所计算楼层第j列柱轴力设计值;HO——所计算楼层的层高。
B.0.3剪力墙结构、框架-剪力墙结构、简体结构中的ηs可按下列公式计算:[B.0.3]式中:∑G——各楼层重力荷载设计值之和;EcJd——与所设计结构等效的竖向等截面悬臂受弯构件的弯曲刚度,可按该悬臂受弯构件与所设计结构在倒三角形分布水平荷载下顶点位移相等的原则计算。
在计算结构构件弯矩增大系数与计算结构位移增大系数时,应分别按本规范第B.0.5条规定取用结构构件刚度;H——结构总高度。
B.0.4排架结构柱考虑二阶效应的弯矩设计值可按下列公式计算:(B.0.4-2)(B.0.4-3)(B.0.4-4)式中:ζc——截面曲率修正系数;当Q>1.0时,取«=1.0。
混凝土正截面应力的计算详解
——轴向力对截面重心轴的偏心距, ;
——相应于轴向力的弯矩组合设计值;
——截面受压较大边边缘至受拉边或受压较小边纵向钢筋合力点的距离,
——偏心受压构件轴向力偏心距增大系数,按本规范第5.3.10条的规定计算。
截面受拉边或受压较小边纵向钢筋的应力和应按下列情况采用:
(2)当预应力钢筋的抗拉强度设计值 与表值不同时,其锚固长度应根据表值按强度比例增减。
5.2.1受弯构件的纵向受拉钢筋和截面受压区混凝土同时达到其强度设计值时,构件的正截面相对界限受压区高度 应按表5.2.1采用。
表5.2.1相对界限受压区高度
C50及以下
C55、C60
C65、C70
C75、C80
R235
、 ——受拉区、受压区纵向普通钢筋的截面面积;
、 ——受拉区、受压区纵向预应力钢筋的截面面积;
——矩形截面宽度或T形截面腹板厚度;
——截面有效高度,
——受拉区、受压区普通钢筋和预应力钢筋的合力点至受拉区边缘、受压区边缘的距离;
、 ——受压区普通钢筋合力点、预应力钢筋合力点至受压区边缘的距离;
——受压区预应力钢筋合力点处混凝土法向应力等于零时预应力钢筋的应力,先张法构件按本规范公式(6.1.5-2)计算;后张法构件按本规范公式(6.1.5-5)及第6.1.5条注2规定计算。
(5.3.1)
式中 ——轴向力组合设计值;
——轴压构件稳定系数,按表5.3.1采用;
——构件毛面面积,当纵向钢筋配筋率大于3%时,应改用
——全部纵向钢筋的截面面积
图5.3.1配有箍筋的构件混凝土轴心受压构件截面图
表5.3.1钢筋混凝土轴心受压构件的稳定系数
圆形截面钢筋混凝土偏心受压构件承载力的简化计算

T o n _ T o m
; n 1 T +
( s i n c r c  ̄ +s i n c r a t ) P r T{ c
( 2 )
其 中n : 1 T r O _ , t L , , m : , : 1 . 2 5 — 2 耵r L , c
c
式中, r 为圆形截面的半径 ; r 为纵向钢筋重心所在
图1 本文简化公式 采用的弯矩一 轴力
曲线上 的校 准点
收稿 日期 : 2 0 1 2  ̄5 — 1 0 作者简介 : 朱晓瑜( 1 9 8 9一) , 女, 河南 长葛人 , 硕士 , 研究方 向: 钢 管 钢筋混凝土承载力。
件之一 , 如 钢 筋混 凝 土 柱 、 钻 孔 灌 注桩 等 。因此 , 其
承载力计算非常重要 。现行 G B 5 0 0 1 0 -2 0 1 0 ( 混凝 土结构设计规范》 给出了圆形截面偏心受压钢筋
混 凝土 构件 正截 面 承 载 力 的 方 法 , 但 计 算公 式 比较
只与构件钢筋与混凝土的强度
图1 所示为钢筋混凝土偏心受压典型的弯矩一
轴力 (m —n) 曲线 , 其 中 A点表 示 构件 处 于轴 心 受
压状 态 , 即e i / r = 0时 1 7 , =i r t 。 ; B点 表 示 构件 处 于 纯
1 圆 形 截 面 偏 心 受 压 构 件 承 载 力 计 算公式
全 部纵 向钢 筋 的截 面 面积 ) ; O t 为 对 应 于 受 压 区 混
圆形受 压截 面构 件 是钢 筋混 凝土 结构 常用 的构
凝土截面面积的圆心角 ( t a d ) 与2 订的 比值 ; O t . 为纵
下部结构钻孔灌注桩、双柱式桥墩的计算

3.2 下部结构钻孔灌注桩、双柱式桥墩的计算3.2.1 设计资料1、设计标准及上部构造 设计荷载:公路-Ⅱ级; 桥面净空:净-8+2×1m ;标准跨径:13b L m ,梁长12.96m ; 上部构造:预应力简支空心板。
2、水文地质条件冲刷深度:最大冲刷线为河床线下6.88m 处;按无横桥向的水平力(漂流物、冲击力、水流压力等)计算。
3、材料钢筋:盖梁主筋用HRB335钢筋,其它均用R235钢筋 混凝土:盖梁、墩柱用C30,系梁及钻孔灌注桩用C25 4、桥墩尺寸图3-17:尺寸单位cm5、设计依据《公路桥涵地基与基础设计规范》(JTG D63-2007) 3.2.2 盖梁计算 (一)荷载计算1、上部结构永久荷载见表3-15:表3-152、盖梁自重及作用效应计算(1/2盖梁长度)图3-18表3-16:盖梁自重产生的弯矩、剪力效应计算1q +2q +3q +4q +5q =190.07KN 3、可变荷载计算(1)可变荷载横向分布系数计算:荷载对称布置时用杠杆法,非对称布置用偏心受压法。
○1公路-I 级 a 、单车列,对称布置(图3-19)时:图3-19b 、双车列,对称布置(图3-20)时:图3-20c 、单车列,非对称布置(图3-21)时:图3-21由()∑±=22/1a ea i i ηη,已知6=n ,185.3=e ,则460.02930.06199.42955.3185.3611=+=⨯+=η d 、双车列,非对称布置(图3-21)时: 已知:6=n ,635.1=e ,∑=99.4222a(2)按顺桥向可变荷载移动情况,求得支座可变荷载反力的最大值(图3-22)图3-22公路-I 级双孔布载单列车时: 双孔布载双列车时: 单孔布置单列车时: 单孔布载双列车时:(3)可变荷载横向分布后各梁支点反力(计算的一般公式为i i B R η=),见表3-17表3-17:各板支点反力计算(4)各板永久荷载、可变荷载反力组合:计算见表3-18,表中均取用各板的最大值,其中冲击系数为:表3-18:各板永久荷载、可变荷载基本组合计算表(单位:KN )4、双柱反力i G 计算(图3-23)所引起的各梁反力表3-19:图3-23:尺寸单位cm表3-19:双柱反力1G 计算由上表知应取组合○6控制设计,此时KN G G 07.277821== (二)内力计算1、恒载加活载作用下各截面的内力 (1)弯矩计算(图3-23)截面位置见图3-23,为求得最大弯矩值,支点负弯矩取用非对称布置时的数值,跨中弯矩取用对称布置时数值。
工程结构偏心受压构件正截面承载力计算(新规范)

161
积 As 和 As 。 解: (1)判别是否要考虑二阶效应
'
M 1 / M 2 200 / 250 0.8 0.9
N 1250 10 3 0.437 0.9 f c A 14.3 400 500 lc lc / i
34 12(
l I h 4000 lc / 12 c 12 27.71 A h 500 12
1 f c bx(ei 0.5h 0.5 x) f y As (ei 0.5h a) f y' As' (ei 0.5h a ' ) (5-45)
按式(5-45)求出 x 。若 x b h0 ,为大偏心受压,将 x 等数据代入式(5-22)便可算 得 N。若 x b h0 ,则为小偏心受压,将式(5-45)的 f y 改为 s 得:
处, r 、 r2 和 rs 按《规范》附录 E 第 E.0.3 条和第 E.0.4 条计算;
A ——构件截面面积。
排架结构柱的二阶效应应按《规范》第 5.3.4 条的规定计算。
5.5 非对称配筋矩形截面偏心受压构件正截面受压承载力计算方法
5.5.2 截面设计 可先初步判断构件的偏心类型:当 ei 0.3h0 时,先按大偏心受压计算,求出钢筋截 面面积和 x 后, 若 x xb , 说明原假定大偏心受压是正确的, 否则需按小偏心受压重新计算; 若 ei 0.3h0 ,则按小偏心受压设计。在所有情况下, As 和 As 均需满足最小配筋率要求,
lc ——构件的计算长度,可近似取偏心受压构件相应主轴方向上下支撑点之
间的距离;
i ——偏心方向的截面回转半径。
除排架结构柱外的其它偏心受压构件, 考虑轴向压力在挠曲杆件中产生的二阶效应后控 制截面弯矩设计值应按下列公式计算:
