圆的单元检测(三).doc

合集下载

人教版九年级上册数学《圆》单元综合检测(含答案)

人教版数学九年级上学期《圆》单元测试考试时间:100分钟;总分:120分一、单选题(每小题3分，共30分)1．(2019·全国初三课时练习)下列直线是圆的切线的是( )A．与圆有公共点的直线B．到圆心的距离等于半径的直线C．垂直于圆的半径的直线D．过圆直径外端点的直线2．(2019·全国初三课时练习)如图，PA、PB切⊙O于点A、B，PA=8，CD切⊙O于点E，交PA、PB于C、D两点，则△PCD的周长是( )A．8 B．18 C．16 D．143．(2019·台湾中考真题)如图，直角三角形ABC的内切圆分别与AB、BC相切于D点、E点，根据图中标示的长度与角度，求AD的长度为何？()A．32B．52C．43D．534．(2019·辽宁中考真题)如图，CB为⊙O的切线，点B为切点，CO的延长线交⊙O于点A，若∠A=25°，则∠C的度数是( )A.25°B.30°C.35°D.40°5．(2019·辽宁中考真题)如图，BC是O的直径，A，D是O上的两点，连接AB，AD，BD，若70ADB︒∠=，∠的度数是( )则ABCA．20︒B．70︒C．30︒D．90︒∆的内切圆的半径为( )6．(2019·湖南中考真题)如图，边长为23的等边ABCA．1 B．3C．2 D．237．(2019·山东初三期中)已知在△ABC中，∠ACB＝90°，AC＝6cm，BC＝8cm，CM是它的中线，以C为圆心，5cm为半径作⊙C，则点M与⊙C的位置关系为( )A.点M在⊙C上B.点M在⊙C内C.点M在⊙C外D.点M不在⊙C内8．(2018·浙江初三期中)如图:在⊙O中，AD平分圆周角∠BAC，AE⊥BC，∠BAC＝60°，∠OAD＝16°，求∠C的度数为()A.50°B.30°C.44°D.45°∠为() 9．如图，CA为O的切线，A为切点，点B在O上，如果55∠=，那么AOBCABA.55B.90C.110D.12010．(2018·杭州市下沙中学初三月考)如图，AC是⊙O的直径，弦BD⊥AO于E，连接BC，过点O作OF⊥BC 于F，若BD=8cm，AE=2cm．则OF的长度是( )A． 5B． 6C． 2.5D．3二、填空题(每小题4分，共24分)11．(2019·山东初三期中)如图CD是⊙O的直径，弦AB⊥CD于E，如果CD＝10，AB＝8，那么CE的长为_____．12．(2019·江阴市敔山湾实验学校初三期中)如图，△ABC内接于⊙O，OD⊥BC于D，∠A=50°，则∠OCD 的度数是_____°．13．(2019·无锡市硕放中学初三期中)如图，AB是⊙O的切线，点B为切点，若∠A=30°，则∠AOB=_________．14．(2019·浙江初三期中)已知在圆O中，AB是直径，点E和点D是圆O上的点，且∠EAB=45°，延长AE和BD相交于点C，连接BE和AD交于点F，BD=12，CD=8，则直径AB的长是_____．15．(2019·江苏初三期中)如图，A是半径为2的⊙O外的一点，OA＝4，AB切⊙O于点B，弦BC∥OA，连接AC，则图中阴影部分的面积为___________16．(2019·无锡市硕放中学初三期中)如图，Rt△ABC中，∠C=90°，AB=43，F是线段AC上一点，过点A的⊙F交AB于点D，E是线段BC上一点，且ED=EB，则EF的最小值为_______________.三、解答题一(每小题6分，共18分)17．(2018全国初三单元测试)已知:如图，在⊙O中，弦AB和CD相交，连接AC、BD，且AC＝BD．求证:AB＝CD．18．(2019·山东初三期中)已知AB，AC为弦，OM⊥AB于M，ON⊥AC于N，求证:MN∥BC且MN＝12 BC．19．(2019·江苏东绛实验学校初三期中)如图，AC是⊙O的直径，弦BD⊥AO于E，连接BC，过点O作OF⊥BC 于F，若BD＝16cm，AE＝4cm．(1)求⊙O的半径;(2)求OF的长．四、解答题二(每小题7分，共21分)20．(2018全国初三课时练习)如图，已知点O为等腰三角形ABC的底边AB的中点，以点O为圆心，AB 为直径的半圆分别交AC，BC于点D，E.求证:(1)∠AOE＝∠BOD;(2)AD BE.21．(2019·无锡市甘露学校初三期中)如图，AB＝AC，CD⊥AB于点D，点O是∠BAC的平分线上一点，⊙O与AB相切于点M，与CD相切于点N(1)求证:∠AOC＝135°;(2)若NC＝3，BC＝5DM的长．22．(2019·陕西延安职业技术学院附中初三期中)如图，在Rt ABC ∆中，90,BAC CD ∠=平分ACB ∠，交AB 于点D ，以点D 为圆心，DA 为半径的⨀D 与AB 相交于点E ．(1)判断直线BC 与⨀D 的位置关系，并证明你的结论;(2)若3,5AC BC ==，求BE 的长．五、解答题三(每小题9分，共27分)23．(2019·贵州中考真题)如图，AB 是⊙O 的直径，弦AC 与BD 交于点E ，且AC ＝BD ，连接AD ，BC ．(1)求证:△ADB ≌△BCA ;(2)若OD ⊥AC ，AB ＝4，求弦AC 的长;(3)在(2)的条件下，延长AB 至点P ，使BP ＝2，连接PC ．求证:PC 是⊙O 的切线．24．(2019广东中考真题)如图1，在ABC ∆中，AB AC =，O 是ABC ∆的外接圆，过点C 作BCD ACB ∠=∠交O 于点D ，连接AD 交BC 于点E ，延长DC 至点F ，使CF AC =，连接AF .(1)求证:ED EC =;(2)求证:AF 是O 的切线;(3)如图2，若点G 是ACD ∆的内心，25BC BE ⋅=，求BG 的长.25．(2016安徽初三月考)如图，⊙O 是△ABC 的外接圆，AC 是直径，过点O 作OD ⊥AB 于点D ，延长DO 交⊙O 于点P ，过点P 作PE ⊥AC 于点E ，作射线DE 交BC 的延长线于F 点，连接PF 。

数学九年级上册《圆》单元综合检测含答案

B.若有一点在圆外，则该点到圆心距离不小于
C.圆上任意两点之间的线段长度不大于
D.圆上任意两点之间的部分可以大于
8.已知⊙O和直线l相交，圆心到直线l的距离为10cm，则⊙O的半径可能为()．
A.10cmB.6cmC.12cmD.以上都不对
9.已知的半径为，点不在内，则点到圆心的距离满足()
详解】解:连接，，作于点，
∵ 的半径为，则的内接正八边形的中心角为: ，
∴ ，
∴ ，
∴ 正八边形，
故答案为．
【点睛】本题考查了正多边形和圆的知识，题目中没有作出边心距求面积是解答本题的亮点，难度一般．
15.正多边形的一个中心角为度，那么这个正多边形的一个内角等于________度．
三、解答题(本题共计 8 小题，共计60分，)
21.作一个圆，使它经过已知点和，并且圆心在已知直线上．
(1)当直线和相交时，可作几个？
(2)当直线和垂直但不经过的中点时，可作出几个？
(3)你还能提出不同于(1)，(2)的问题吗？
22.如图，过圆锥顶点和底面圆的圆心的平面截圆锥得截面，其中，是圆锥底面圆的直径，已知，，求截面的面积．
5. 如图，A、B、C是⊙O上的三点，且∠ABC=70°，则∠AOC的度数是( )
A. 35°B. 140°C. 70°D. 70°或140°
6.在⊙O中, 所对的圆心角为60°,半径为5cm,则的长为()
A. B. C. D.
7.关于半径为的圆，下列说法正确的是()
A.若有一点到圆心的距离为，则该点在圆外
A. 个B. 个C. 个D. 个
3.正六边形半径为，则它的边长、边心距、面积分别为()

数学九年级上册《圆》单元综合检测卷含答案

A. 米2B. 米2C. 米2D. 米2
4.如图，在矩形中，，，是以为直径的圆，则直线与的位置关系是()
A.相交B.相切C.相离D.无法确定
5.如图，是的直径，弦，，连接、，则的度数为()
A. B. C. D.
6.一个圆锥的侧面展开图是半径为的半圆，则该圆锥的高是()
A. B. C. D.
故选D．
【点睛】本题考查的是圆周角定理，熟知在同圆或等圆中，同弧或等弧所对的圆周角相等，都等于这条弧所对的圆心角的一半是解答此题的关键．
6.一个圆锥的侧面展开图是半径为的半圆，则该圆锥的高是()
A. B. C. D.
【答案】D
【解析】
【分析】
根据侧面展开图的弧长等于圆锥的底面周长，即可求得底面周长，进而即可求得底面的半径长，然后表示出圆锥的高即可．
【详解】连接DO，
∵CO=DO，
∴∠OCD=∠ODC=30°，
∴∠COD=120°，
∵AB是⊙O的直径，弦CD⊥AB，
∴∠BOC=60°，
∵CD=2 ，
∴CN= ，
∴CO=2，
∴扇形BOC的面积为: ，
故选A．
【点睛】此题主要考查了圆周角定理、垂径定理和扇形面积公式，关键是掌握垂直弦的直径平分这条弦，并且平分弦所对的两条弧．
∴∠．
【点睛】本题考查了垂径定理，解直角三角形，圆周角定理的应用，能求出∠BOC的度数是解此题的关键．
12.如图，是的直径，点、在上，，，则的度数()
A. B. C. D.
【答案】D
【解析】
【分析】
连接BC，由圆周角定理可知∠ACB=90°，由∠BOD=110°可得出∠AOD的度数，根据AC∥OD可知∠CAB=∠AOD，由直角三角形的性质可求出∠ABC的度数，再根据圆周角定理即可得出结论．

第三章《圆》单元测试(含答案)

单元测试(三)圆(时间：100分钟满分：120分)一、选择题(每小题3分，共30分)下列各小题均有四个答案，其中只有一个是正确的.1.已知⊙O的半径是5，直线l是⊙O的切线，则点O到直线l的距离是(C)A.2.5B.3C.5D.102.如图，在△ABC中，AB＝BC＝2，以AB为直径的⊙O与BC相切于点B，则AC等于(D)A. 2B. 3C.2 3D.2 23.如图，⊙O是△ABC的外接圆，连接OB，OC，若OB＝BC，则∠BAC等于(C)A.60°B.45°C.30°D.20°4.下列说法正确的是(B)A.三点确定一个圆B.经过圆心的直线是圆的对称轴C.和半径垂直的直线是圆的切线D.三角形的内心到三角形三个顶点距离相等5.如图，C，D是以线段AB为直径的⊙O上的两点，若CA＝CD，且∠ACD＝40°，则∠CAB ＝(B)A.10°B.20°C.30°D.40°6.如图，当圆形桥孔中的水面宽度AB为8米时，弧ACB恰为半圆.当水面上涨1米时，桥孔中的水面宽度A′B′为(D)A.15米B.4米C.217米D.215米7.如图，AB是⊙O的直径，P A切⊙O于点A，连接PO并延长交⊙O于点C，连接AC，AB ＝10，∠P＝30°，则AC的长度是(A)A.5 3B.5 2C.5D.5 28.如图，AP为⊙O的切线，P为切点，若∠A＝20°，C、D为圆周上的两点，且∠PDC＝60°，则∠OBC等于(B)A.55°B.65°C.70°D.75°9.如图，在△ABC中，∠A＝60°，BC＝6，它的周长为16.若⊙O与BC，AC，AB三边分别切于点E，F，D，则DF的长为(A)A.2B.3C.4D.610.如图，将正六边形ABCDEF放置在平面直角坐标系内，A(－2，0)，点B在原点，把正六边形ABCDEF沿x轴正半轴作无滑动的连续翻转，每次翻转60°，经过2 018次翻转之后，点C的坐标是(B)A .(4 038，0)B .(4 034，0)C .(4 038，3)D .(4 034，3)二、填空题(每小题3分，共15分)11.如图，在⊙O 中，已知∠AOB ＝120°，则∠ACB ＝60°.12.如图，在矩形ABCD 中，AB ＝3，AD ＝4，若以点A 为圆心，以4为半径作⊙A ，则点A ，点B ，点C ，点D 四点中在⊙A 外的是点C .13.如图，AB 是⊙O 的直径，C 、D 是⊙O 上的点，∠CDB ＝20°，过点C 作⊙O 的切线交AB 的延长线于点E ，则∠E ＝50°.14.如图，在△ABC 中，CA ＝CB ，∠ACB ＝90°，AB ＝22，点D 为AB 的中点，以点D 为圆心作圆心角为90°的扇形DEF ，点C 恰好在弧EF 上，则图中阴影部分的面积为π2－1(结果保留π).15.如图，半圆O 的半径为2，E 是半圆上的一点，将E 点对折到直径AB 上(EE ′⊥AB )，当被折的圆弧与直径AB 至少有一个交点时，则折痕的长度取值范围是三、解答题(本大题共8个小题，满分75分)16.(8分)如图，以正六边形ABCDEF 的边AB 为边，在内部作正方形ABMN ，连接M C.求∠BCM 的大小.解：∵六边形ABCDEF 为正六边形，∴∠ABC ＝120°，AB ＝B C. ∵四边形ABMN 为正方形，∴∠ABM ＝90°，AB ＝BM . ∴∠MBC ＝120°－90°＝30°，BM ＝B C. ∴∠BCM ＝∠BM C.∴∠BCM ＝12×(180°－30°)＝75°.17.(9分)如图，在⊙O 中，AB ︵＝AC ︵，∠ACB ＝60°，求证：∠AOB ＝∠BOC ＝∠AO C.证明：∵AB ︵＝AC ︵， ∴AB ＝A C.∴△ABC 是等腰三角形. ∵∠ACB ＝60°， ∴△ABC 是等边三角形. ∴AB ＝BC ＝A C.∴∠AOB ＝∠BOC ＝∠AO C.18.(9分)如图，在平面直角坐标系中，已知点A (1，3)、B (3，3)、C (4，2). (1)请在图中作出经过点A 、B 、C 三点的⊙M ，并写出圆心M 的坐标； (2)若D (1，4)，则直线BD 与⊙M 的位置关系是相切.解：如图所示，圆心M 的坐标为(2，1).19.(9分)如图，⊙O 的半径OD ⊥弦AB 于点C ，连接AO 并延长交⊙O 于点E ，连接E C.若AB ＝8，CD ＝2，求EC 的长.解：∵OD ⊥AB ，AB ＝8，∴AC ＝BC ＝12AB ＝4.设⊙O 的半径为r ，则OC ＝r －2.在Rt △AOC 中，OA 2＝AC 2＋OC 2，即r 2＝42＋(r －2)2，解得r ＝5.∴AE ＝2r ＝10. 连接BE .∵AE 是⊙O 的直径，∴∠ABE ＝90°.在Rt △ABE 中，∵AE ＝10，AB ＝8，∴BE ＝AE 2－AB 2＝102－82＝6. 在Rt △BCE 中，∵BE ＝6，BC ＝4， ∴CE ＝BE 2＋BC 2＝62＋42＝213.20.(9分)如图，在△ABC 中，以AB 为直径的⊙O 分别与BC ，AC 相交于点D ，E ，BD ＝CD ，过点D 作⊙O 的切线DF 交边AC 于点F . (1)求证：DF ⊥AC ；(2)若⊙O 的半径为5，∠CDF ＝30°，求BD ︵的长.(结果保留π)解：(1)证明：连接O D.∵DF 是⊙O 的切线，D 为切点，∴OD ⊥DF .∴∠ODF ＝90°. ∵BD ＝CD ，OB ＝OA ，∴OD 是△ABC 的中位线. ∴OD ∥A C.∴∠CFD ＝∠ODF ＝90°. ∴DF ⊥A C.(2)∵∠CDF ＝30°，∠ODF ＝90°， ∴∠ODB ＝180°－∠CDF －∠ODF ＝60°. ∵OB ＝OD ，∴△OBD 是等边三角形. ∴∠BOD ＝60°.∴l BD ︵＝60π×5180＝53π.21.(10分)如图，AB 是⊙O 的直径，点P 是AB 下方的半圆上不与点A ，B 重合的一个动点，点C 为AP 中点，延长CO 交⊙O 于点D ，连接AD ，过点D 作⊙O 的切线交PB 的廷长线于点E ，连接CE .(1)求证：△DAC ≌△ECP ； (2)填空：①当∠DAP ＝45°时，四边形DEPC 为正方形；②在点P 运动过程中，若⊙O 的半径为5，∠DCE ＝30°，则AD证明：∵DE 为切线， ∴OD ⊥DE .∴∠CDE ＝90°. ∵点C 为AP 的中点，∴DC ⊥AP .∴∠DCA ＝∠DCP ＝90°. ∵AB 是⊙O 直径， ∴∠APB ＝90°.∴四边形DEPC 为矩形.∴DC ＝EP .在△DAC 和△ECP 中，⎩⎪⎨⎪⎧AC ＝CP ，∠ACD ＝∠CPE ，DC ＝EP ，∴△DAC ≌△ECP (SAS ).22.(10分)如图，在平面直角坐标系xOy 中，以点O 为圆心的圆分别交x 轴的正半轴于点M ，交y 轴的正半轴于点N .劣弧MN ︵的长为65π，直线y ＝－43x ＋4与x 轴，y 轴分别交于点A ，B.(1)求证：直线AB 与⊙O 相切；(2)求图中所示的阴影部分的面积.(结果保留π)解：(1)证明：作OD ⊥AB 于D.∵劣弧MN ︵的长为65π，∴90π·OM 180＝6π5.解得OM ＝125.故⊙O 的半径为125.∵直线y ＝－43x ＋4与x 轴，y 轴分别交于点A ，B ，当y ＝0时，x ＝3；当x ＝0时，y ＝4，∴A (3，0)，B (0，4).∴OA ＝3，OB ＝4.∴AB ＝32＋42＝5. ∵S △AOB ＝12AB ·OD ＝12OA ·OB ，∴OD ＝OA·OB AB ＝125.∴OD 为⊙O 的半径. ∴直线AB 与⊙O 相切.(2)S 阴影＝S △AOB －S 扇形OMN ＝12×3×4－90π×（125）2360＝6－3625π.23.(11分)问题背景：如图1，在四边形ACBD 中，∠ACB ＝∠ADB ＝90°，AD ＝BD ，探究线段AC ，BC ，CD 之间的数量关系.小吴同学探究此问题的思路：将△BCD 绕点D 逆时针旋转90°到△AED 处，点B ，C 分别落在点A ，E 处(如图2)，易证点C ，A ，E 在同一条直线上，且△CDE 是等腰三角形，所以CE ＝2CD ，从而得出结论：AC ＋BC ＝2C D. 简单应用：(1)在图1中，若AC ＝2，BC ＝22，则CD ＝3；(2)如图3，AB 是⊙O 的直径，点C ，D 在⊙O 上，AD ︵＝BD ︵，若AB ＝13，BC ＝12，求CD 的长；(3)如图4，∠ACB ＝∠ADB ＝90°，AD ＝BD ，若AC ＝m ，BC ＝n (m ＜n )，求CD 的长.(用含m ，n 的代数式表示)图1 图2 图3 图4解：(2)连接AC ，BD ，AD ，∵AB 是⊙O 直径， ∴∠ADB ＝∠ACB ＝90°. ∴AC ＝AB 2－BC 2＝5. ∵AD ︵＝BD ︵， ∴AD ＝B D.将△BCD 绕点D 顺时针旋转90°到△AED ， ∴∠EAD ＝∠DB C. ∵∠DBC ＋∠DAC ＝180°， ∴∠EAD ＋∠DAC ＝180°. ∴E ，A ，C 三点共线. ∵BC ＝AE ，∴CE ＝AE ＋AC ＝BC ＋AC ＝17. ∵∠EDA ＝∠CDB ，∴∠EDA ＋∠ADC ＝∠CDB ＋∠ADC ，即∠EDC ＝∠ADB ＝90°.∵CD ＝ED ，∴△EDC 是等腰直角三角形. ∴CE ＝2C D. ∴CD ＝1722.(3)以AB 为直径作⊙O ，连接DO 并延长交⊙O 于点D 1，连接D 1A ，D 1B ，D 1C. 由(2)可知：AC ＋BC ＝2D 1C ， ∴D 1C ＝2（m ＋n ）2. 又∵D 1D 是⊙O 的直径， ∴∠DCD 1＝90°. ∵AC ＝m ，BC ＝n ，∴由勾股定理可求得：AB 2＝m 2＋n 2. ∴D 1D 2＝AB 2＝m 2＋n 2. ∵D 1C 2＋CD 2＝D 1D 2，∴CD 2＝m 2＋n 2－（m ＋n ）22＝（m －n ）22.∵m＜n，∴CD＝2（n－m）2.。

六上数学圆单元测试卷 (内含3套)

六年级上学期数学圆单元检测卷（一）班级：_____ 姓名：_____ 分数：_____一、填空题。

（共24分）1、画圆时，圆规两脚之间的距离为4cm，那么这个圆的直径是（）cm，周长是（）cm ，面积是（）平方厘米。

2、把一个圆平均分成若干份，可以拼成一个近似于平行四边形的图形，分得越小，拼成的图形就越（）平行四边形。

平行四边形的底相当于圆周长的（），高相当于（），所以圆的面积用字母表示是（）。

3、用一根长18.84dm的铁丝围成一个圆圈，所围成的圆圈的半径是（）dm，圆圈内的面积是（）平方分米。

4、大圆直径是小圆直径的3倍，大圆周长是小圆周长的（）倍，大圆的面积是小圆的面积的（）倍。

5、在一个长5厘米，宽3厘米的长方形中化一个最大的圆，这个圆的半径是（）厘米，面积是（）平方厘米。

6、把一块边长10分米的正方形铁片，剪成一个最大的圆形，这个圆的周长是（）。

7、用铁丝把2根横截面直径都是40厘米的圆木捆在一起，如果接头处铁丝长10厘米，那么捆一周至少需要（）厘米的铁丝。

8、用圆规画一个周长是37.68厘米的圆，圆规两脚之间的距离是（）厘米，所画的圆的面积是（）平方厘米9、一个圆平均分成若干等分，拼成一个近似的长方形，如果长方形的周长比圆的周长长4厘米，那么这个圆的面积是（）平方厘米，这个长方形的面积是（）平方厘米。

10、一辆自行车轮胎的外直径是80厘米，车轮每分钟转200周，这辆自行车每小时行（）千米。

11、在一个长为21分米，宽为6分米的长方形纸板上，想剪出半径为1.5分米的圆，最多可以剪（）个。

12、大圆半径是小圆半径的2倍，大圆面积比小圆面积多12平方厘米，小圆面积是（）平方厘米，大圆的面积是（）平方厘米。

二、判断题。

（10分）（）1、直径是半径的2倍，半径是直径的一半。

（）2、两端都在圆上并且经过圆心的线段是直径。

（）3、圆的对称轴就是直径所在的直线。

（）4、圆的周长是直径的3.14倍。

（）5、两条半径就是一条直径。

名师制作江苏省常州市武进区九年级数学上册第二章对称图形—圆章末单元测试题三(新版)苏科版.doc

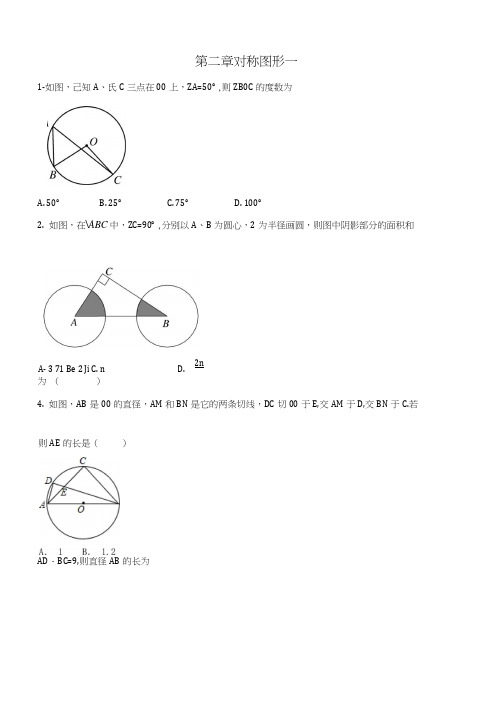
第二章对称图形一1-如图，己知A 、氏C 三点在00上，ZA=50° ,则ZB0C 的度数为A. 50°B. 25°C. 75°D. 100°2. 如图，在\ABC 中，ZC=90° ,分别以A 、B 为圆心，2为半径画圆，则图中阴影部分的面积和为（）4. 如图，AB 是00的直径，AM 和BN 是它的两条切线，DC 切00于E,交AM 于D,交BN 于C.若 AD ・BC=9,则直径AB的长为A- 3 71 Be 2 Ji C. n D.2n则AE 的长是（）A. 3^2B. 6C. 9D. V135. 如图，在正方形纸板上剪下一个扇形和圆，刚好能围成一个圆锥模型，设围成的圆锥底面半径为 r,母线长为R,则r 与R 之间的关系为（）33A. 3B. yjyC. —D.— 2 47. 图屮，EB 为半圆0的直径，点A 在EB 的延长线上，AD 切半圆0于点D, BC1AD 于点C, AB 二2,8. 如图所示，从00外一点力引圆的切线個切点为〃，连接M 并延长交圆于点C 连接处已知Z 力二26°,A. R 二2r B. 4R=9r C. R=3r D. R=4r6.如图，（DO 是的外接圆,连接创、0C, 00的半径広2, sinB^-,则弦化的长为（ 4半圆0的半径为2,则BC 的长为（）则ZACB的度数为（）A. 32°B. 30°C. 26°D. 13°9.如图，在AABC中，AB二8 cm, BCM cm, ZABC二30°,把AABC以点B为中心按逆时针方向旋转, 使点C旋转到AB边的延长线上的点C'处，那么AC边扫过的图形（图中阴影部分）面积是（）A. 20 n cm2B. （20 n +8） cm2C. 16 cm2D. （16 n+8） cm210.以下命题：①直径相等的圆是等圆；②长度相等弧是等弧；③相等的弦所对的弧也相等；④圆的对称轴是直径；⑤相等的圆周角所对的弧相等；其中正确的个数是（）A. 4B. 3C. 2D. 111.卞玄胡把圆的直径颁3和11两部分，弦和直渤咬成财角，则AB的长______________12._____________________________________________________________________ 如图，点A、B、C在半径为1的00±,亜的长为5兀，则ZACB的大小是 ____________________________13.如图，已知等腰△初C, ABBC,以肋为直径的圆交M于点〃，过点〃的00的切线交％于点14.如图，四边形ABCD内接于0（9, E为CQ的延长线上一点.若ZB = 110°,则ZADE的大小为15.如图，AB为＜30直径，BD切O0于B点，弦AC的延长线与BD交于D点，若AB二10, AC二8,则DC长为________ .16.已知00的周长为8^-cm,若P0=2cm,则点P在_________ ;若P0=4cm,则点P在_____ ;若P0=6cm,则点P在______ .17.用一张半径为9cm、圆心角为120°的扇形纸片，做成一个圆锥形冰淇淋的侧面（不计接缝），那么这个圆锥形冰淇淋的底面半径是cm.18.已知圆锥底面半径为5cm,高为12cm,则它的侧面展开图的面积是__________ cm2.19.如图，0 0鬼、血乞的外接圆，Z AOB=70°,则Z C为_____________ 度.20.如图是一个装有两个大小相同的球形礼品的包装盒，其中两个小球之间有个等腰三角形隔板，己知矩形长为45cm,宽为20cm,两圆与矩形的边以及等腰AABC的腰都相切，则所需的三角形隔板的底边AB长为__________21.在平面直角坐标系中，将某点（横坐标与纵坐标不相等）的横坐标与纵坐标互换后得到的点叫这个点的“互换点”，如（-3, 5）与（5, -3）是一对“互换点”.（1）以0为圆心，半径为5的圆上有无数对“互换点”，请写出一对符合条件的“互换点”；（2）点必斥是一对“互换点”，点肘的坐标为5, 〃），且5＞〃），OP经过点财，N.①点肘的坐标为(4, 0),求圆心"所在直线的表达式;②G)戶的半径为5,求ni~n的取值范围.22.(1)如图，在矩形ABCD中.点0在边AB上,ZA0C=ZB0D.求证：A0二0B.(2)如图，AB是OO的直径，PA与OO相切于点A, 0P与OO相交于点C,连接CB, Z0PA二40° , 23.如图，己知AABC, AC二3, BC二4, ZC二90°,以点C为圆心作(DC,半径为r.(1) 当r取什么值时，点A、B在OC外.(2)当r在什么范围时，点A在(DC内，点B在G)C外.24.如何在操场上・画一个半径为5m的圆，请说明你的理由？25.如图，在AABC中，过点A作AD丄BC,垂足为点D,以AD为半径的OA分别与边AC、AB交于点E和点F, DE〃AB,延长CA交OA于点G,连接BG.(1)求证：BG是OA的切线；(2)若ZACB=30° , AD=3,求图中阴影部分的面积.26.如图，四边形ABCD内接于＜30,点E在对角线AC上，EC二BC二DC.(1)若ZCBD二39°,求ZBAD 的度数;(2)求证：Z1=Z2.E27.如图，OO是△血〃的内切圆，切点分别为〃、E、F, ZB = 60° , ZC = 70°.(1)求Z〃仇•、的度数；(2)求Z竝尸的度数.答案:1. D试题分析：根据圆周角定理求解即可.TZA二50° ,・・・ZB0C二2ZA二100°・故选D.考点：圆周角定理.2. C.试题分析：先根据直角三角形的性质求出直角三角形两锐角的和，再根据扇形的面积公式进行计算即可.V A ABC 中，ZC=90° , .\ZA+ZB=90° ,•••两圆的半径都为2cm,•C_90X^X22_•• S -------------------- —71 ・360故选C.3. A分析利用圆周角性质和等腰三角形性质，确定AB为圆的直径，利用相似三角形的判定及性质，确定AADE和ABCE边长之间的关系，利用相似比求出线段AE的长度即可.详解：・・•等腰Rt.AABC, BCM,・・・AB为O0的直径,AC二4, AB二4*2AZD=90° ,4在RtAABD 中，AD二5, AB二4&,28・・・BD二5 ,VZD=ZC, ZDAC=ZCBE,AAADE^ABCE,4VAD： BC二6 4=1： 5,・••相似比为1： 5,设AE=x,・・・BE二5x,28ADE=5-5X,・・・CE=28-25x,VAC=4,・・・x+28-25x 二4,解得：x二1.故选：A.点拨：题目考查了圆的基本性质、等腰直角三角形性质、相似三角形的判定及应用等知识点，题目考查知识点较多，是一道综合性试题，题目难易稈度适屮，适合课后训练.4. B试题解析：如图，连接0C.TAM和BN是它的两条切线，・・・AM丄AB, BN±AB,・・・AM〃BN,.\ZADE+ZBCE=180°TDC 切00 于E,・・・Z0DE二丄ZADE, Z0CE= - ZBCE,2 2・・・Z0DE+Z0CE二90° ,:.ZD0C=90° ,.-.ZA0D+ZC0B=90° ,VZA0D+ZAD0-900 ,・・・ZA0D 二ZOCB,VZ0AD=Z0BC=90° ,AAAOD^ABCO,.AD AOA0A2=AD*BC=9,・・・0A二3,AAB=2*0A=6.故选B.点拨：本题考查切线的性质、平行线的性质、相似三角形的判定和性质等知识，解题的关键是正确寻找相似三角形，利用相似三角形性质解决问题，属于中考常考题型.5. D试题分析：求得侧而展开图的弧长，以及圆锥的底面周长，让它们相等即可求得r与RZ间的关系. 解：由题意得：90兀XR二2“,180解得：R=4r,故选D.6. A 延长外0交圆于点〃，连接A由圆周角定理，得：Z力炉90° ,3Rt'ADC中，s加片一，力彷2怡4, :.AgAD8 9 sin*3.故选A.7. B试题分析：连接0D. AD是切线，点D是切点，・・・BC丄AD,・・・Z0DA二ZACB二90° , BC〃0D.・・・AB=0B=2,则点B是AO的中点,1・・・BC二20D二1・故选B.8 A分析：连接0B,根据切线的性质和直角三角形的两锐角互余求得ZA0B二64°,再由等腰•三角形的性质可得ZC=Z0BC,根据三角形外角的性质即可求得Z/I必的度数.详解：连接0B,TAB与00相切于点B,A Z0BA=90° ,VZA=26° ,A ZA0B=90° -26° =64° ,V0B=0C,・・・ZC二ZOBC, ・・・ ZAOB二ZC+ZOBC二2ZC,.\ZC=32° .故选A.9. A因为△ ABC^AA Z BC,所以AC边扫过的图形屮阴影部分的面积是一个圆环的面积，即150n x (64 -16)360 二20兀cm?,故选人.10. D以下命题：①直径相等的圆是等圆，正确；②长度相等弧是等弧，错误，只有在同圆或等圆中长度相等的弧是等弧；③相等的弦所对的弧也相等，错误；④圆的对称轴是直径，错误，应该是直径所在的直线；⑤相等的圆周角所对的弧相等，错误；所以正确的只有1个，故选D.11.6^5 .试题分析：如图，过点0作0F丄AB于点F,设弦AB与直径CD相交于点E,连接0B,・.•分直径成3和11 两部分,ACD=14, A0C=-CD=7,二0E二0C - CE二4, V Z0EF=30° , A0F=-0E=2 (cm),BF= y/OB2-OF2 = 3A/5,AAB=2BF= 6^5 .故答案为：6^5 .12.36°试题解析：连结0A、0B.设ZA0B=n°・・・•心的长为2兀,An=40, •••ZAOB二40。

人教版数学九年级上册《圆》单元综合检测(附答案)

人教版数学九年级上学期《圆》单元测试（满分120分,考试用时120分钟）一、选择题（共 10 小题 ,每小题 3 分 ,共 30 分）1.在同圆或等圆中,如果弧AB的长度=弧CD的长度,则下列说法正确的个数是（）弧AB的度数等于弧CD的度数；所对的圆心角等于弧CD所对的圆心角；弧AB和弧CD是等弧；弧AB所对的弦的弦心距等于弧CD所对的弦的弦心距．A. 1个B. 2个C. 3个D. 4个2.、是直线上的两个不同的点,且,的半径为,下列叙述正确的是（）A. 点在外B. 点在外C. 直线与一定相切D. 若,则直线与相交3. 如图,已知⊙O的半径为5,点O到弦AB的距离为2,则⊙O上到弦AB所在直线的距离为3的点有（）A. 1个B. 2个C. 3个D. 4个4.如图,在中,已知,是圆周上的一点,则为（）A. B. C. D.5.如图,正六边形内接于圆,圆的半径为,则这个正六边形的边心距和的长分别为（）A. 、B. 、C. 、D. 、6.高速公路的隧道和桥梁最多．如图是一个隧道的横截面,若它的形状是以为圆心的圆的一部分,路面米,净高米,则此圆的半径A. 米B. 米C. 米D. 米7.已知和三点、、,的半径为,,,,经过这三点中的一点任意作直线总是与相交,这个点是（）A. B. C. D. 或8.如图,,是的直径,的半径为,,以为圆心,以为半径作,则与围成的新月形的面积为（）平方单位．A. B. C. D.9.如图,已知：是的直径,、是上的三等分点,,则是（）A. B. C. D.10.如图,点,,在上,点在圆外,则下列结论正确的是（）A. ∠C>∠DB. ∠C<∠DC. ∠C=∠DD. ∠C=2∠D二、填空题（共 10 小题 ,每小题 3 分 ,共 30 分）11.在,,,,点是的外心,现在以为圆心,分别以、、为半径作,则点与的位置关系分别是________．12.如下图,在以为圆心的两个同心圆中,大圆的弦交小圆于和两点,,,则长为________．13.已知：如图,为半的直径,、、为半圆弧上的点,,,则的度数为________度．14.如图,边长为的正方形的顶点、在一个半径为的圆上,顶点、在圆内,将正方形沿圆的内壁逆时针方向作无滑动的滚动．当点第一次落在圆上时,点运动的路径长为________．15.已知中,,,,直线过点且与平行,若以为轴将旋转一周,则所得的几何体的表面积为________．（不求近似值）16.如图,已知是的直径,为弦,度．过圆心作交于点,连接,则________度．17.如图,的边位于直线上,,,,若由现在的位置向右无滑动地旋转,当第次落在直线上时,点所经过的路线的长为________（结果用含有的式子表示）18.如图,圆柱底面半径为,高为,点、分别是圆柱两底面圆周上的点,且、在同一母线上,用一棉线从顺着圆柱侧面绕圈到,求棉线最短为________．19.以矩形的顶点为圆心作,要使、、三点中至少有一点在内,且至少有一点在外,如果,,则的半径的取值范围为________．20.如图,在中,是弦,,,那么圆心到的距离是________,弦的长是________．三、解答题（共 6 小题 ,每小题 10 分 ,共 60 分）21.一圆柱形排水管的截面如图所示,已知排水管的半径为,水面宽为．由于天气干燥,水管水面下降,此时排水管水面宽变为,求水面下降的高度．22.如图,在中,弦、于点,且．求证：．23.如图,在中,,,求分别以、、为圆心,以为半径画弧,三条弧与边所围成的阴影部分的面积．24.已知：如图,的外接圆,弦的长为,,求圆心到的距离．25.如图,已知为的直径,是弦,于,于,．求证：；求证：；若,,设,求值及阴影部分的面积．26.如图,内接于,,,．求的度数；将沿折叠为,将沿折叠为,延长和相交于点；求证：四边形是正方形；若,,求的长．参考答案一、选择题（共 10 小题 ,每小题 3 分 ,共 30 分）1.在同圆或等圆中,如果弧AB的长度=弧CD的长度,则下列说法正确的个数是（）弧AB的度数等于弧CD的度数；所对的圆心角等于弧CD所对的圆心角；弧AB和弧CD是等弧；弧AB所对的弦的弦心距等于弧CD所对的弦的弦心距．A. 1个B. 2个C. 3个D. 4个【答案】D【解析】【分析】由在同圆或等圆中,的长度=的长度,根据弧长公式得到它们所对的圆心角相等,再根据在同圆或等圆中,如果两个圆心角以及它们对应的两条弧、两条弦中有一组量相等,则另外两组量也对应相等,即可对选项进行判断．【详解】∵在同圆或等圆中,的长度=的长度,∴弧AB和弧CD所对的圆心角相等,∴的度数等于的度数；∴和是等弧；∴所对的弦的弦心距等于所对的弦的弦心距．故选D．【点睛】本题考查了在同圆或等圆中,如果两个圆心角以及它们对应的两条弧、两条弦中有一组量相等,则另外两组量也对应相等．在圆中经常利用此结论把圆心角、弧、弦之间进行转化．2.、是直线上的两个不同的点,且,的半径为,下列叙述正确的是（）A. 点在外B. 点在外C. 直线与一定相切D. 若,则直线与相交【答案】D【解析】【分析】由P、Q是直线l上的两个不同的点,且OP=5,⊙O的半径为5,可得点P在⊙O上,直线l与⊙O相切或相交；若OQ=5,则直线l与⊙O相交．【详解】∵OP=5,⊙O的半径为5,∴点P在⊙O上,故A错误；∵P是直线l上的点,∴直线l与⊙O相切或相交；∴若相切,则OQ＞5,且点Q在⊙O外；若相交,则点Q可能在⊙O上,⊙O外,⊙O内；故B、C错误．∴若OQ=5,则直线l与⊙O相交；故D正确．故选D．【点睛】此题考查了直线与圆的位置关系,注意掌握分类讨论思想的应用是解题关键.3. 如图,已知⊙O的半径为5,点O到弦AB的距离为2,则⊙O上到弦AB所在直线的距离为3的点有（）A. 1个B. 2个C. 3个D. 4个【答案】C【解析】考点：垂径定理；勾股定理．分析：根据垂径定理计算．解答：解：如图OD=OA=OB=5,OE⊥AB,OE=3,∴DE=OD-OE=5-3=2cm,∴点D是圆上到AB距离为2cm的点,∵OE=3cm＞2cm,∴在OD上截取OH=1cm,过点H作GF∥AB,交圆于点G,F两点,则有HE⊥AB,HE=OE-OH=2cm,即GF到AB的距离为2cm,∴点G,F也是圆上到AB距离为2cm的点．故选C．点评：本题利用了垂径定理求解,注意圆上的点到AB距离为2cm的点不唯一,有三个．4.如图,在中,已知,是圆周上的一点,则为（）A. B. C. D.【答案】B【解析】【分析】首先根据题画出图形,然后在优弧上取点D,连接AD,BD,根据圆周角的性质,即可求得∠ADB的度数,又由圆的内接四边形的性质,即可求得∠ACB的度数．【详解】如图：在优弧上取点D,连接AD,BD,∵∠AOB=100°,∴∠ADB=∠AOB=55°,∵四边形ADBC是⊙O的内接四边形,∴∠ADB+∠ACB=180°,∴∠ACB=125°．故选B．【点睛】此题考查了圆周角定理与圆的内接四边形的性质,根据题意作出图形,掌握数形结合思想的应用及圆周角定理是解题关键．5.如图,正六边形内接于圆,圆的半径为,则这个正六边形的边心距和的长分别为（）A. 、B. 、C. 、D. 、【答案】D【解析】试题解析：连接OC,OD,∵正六边形ABCDEF是圆的内接多边形,∴∠COD=60°,∵OC=OD,OM⊥CD,∴∠COM=30°,∵OC=6,∴OM=6cos30°=3,∴=2π故选D．考点：1.正多边形和圆；2.弧长的计算．6.高速公路的隧道和桥梁最多．如图是一个隧道的横截面,若它的形状是以为圆心的圆的一部分,路面米,净高米,则此圆的半径A. 米B. 米C. 米D. 米【答案】B【解析】【分析】根据垂径定理可知AD的长,设半径为r,利用勾股定理列方程求出r的值即可．【详解】∵CD⊥AB,∴由垂径定理得AD=6米,设圆的半径为r,则OD2+AD2=OA2,即（9-r）2+62=r2,解得r=米．故选B．【点睛】考查了垂径定理、勾股定理．根据题意构造一个由半径、半弦、弦心距组成的直角三角形进行计算是解题关键．7.已知和三点、、,的半径为,,,,经过这三点中的一点任意作直线总是与相交,这个点是（）A. B. C. D. 或【答案】A【解析】【分析】根据⊙O的半径为3,OP=2,OQ=3,OR=4,可以知道点P在圆内,点Q在圆上,点R在圆外,因而这三点中P的一点任意作直线总是与⊙O相交．【详解】∵的半径为,,,,∴Q点在圆上；R点在圆外；P点在圆内,∴经过P点任意作直线总是与⊙O相交．故选A．【点睛】本题考查了对点与圆的位置关系的判断．设点到圆心的距离为d,则当d=R时,点在圆上；当d＞R 时,点在圆外；当d＜R时,点在圆内．准确判断P、Q、R三点与⊙O的位置关系是解决本题的关键．8.如图,,是的直径,的半径为,,以为圆心,以为半径作,则与围成的新月形的面积为（）平方单位．A. B. C. D.【答案】B【解析】【分析】新月形ACED的面积是圆O半圆的面积-弓形CED的面积,弓形CED的面积又=扇形BCD面积-三角形BCD 的面积,然后依面积公式计算即可．【详解】∵OC=OB=R,,∴BC=R,）∴新月形ACED的面积=S半圆-（S扇形BCD-S△BCD=-（-)=R2．故选B．【点睛】本题的关键是看出：新月形ACED的面积是圆O半圆的面积-弓形CED的面积,然后逐一求面积即可．9.如图,已知：是的直径,、是上的三等分点,,则是（）A. B. C. D.【答案】C【解析】【分析】先求出∠BOE=120°,再运用“等弧对等角”即可解．【详解】∵∠AOE=60°,∴∠BOE=180°-∠AOE=120°,∴的度数是120°,∵C、D是上的三等分点,∴弧CD与弧ED的度数都是40度,∴∠COE=80°,故选：C.【点睛】本题主要考查圆周角定理：在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半．熟练掌握圆周角定理是解题关键.10.如图,点,,在上,点在圆外,则下列结论正确的是（）A. ∠C>∠DB. ∠C<∠DC. ∠C=∠DD. ∠C=2∠D【答案】A【解析】【分析】根据三角形外角的性质得到∠BEC＞∠BDC,根据圆周角定理得到∠BAC=∠BEC,得到答案【详解】如图：连接AE,∵∠BEA是△ADE的外角,∴∠BEA>∠D,∵∠C=∠BEA,∴∠C>∠D,故A选项正确,则B、C、错误,∵不确定D点的位置,∴∠C不一定等于2∠D,故D选项错误,故选A.【点睛】本题考查的是圆周角定理和三角形的外角的性质的应用,掌握同弧所对的圆周角相等和三角形的一个外角大于与它不相邻的任何一个内角是解题的关键．二、填空题（共 10 小题 ,每小题 3 分 ,共 30 分）11.在,,,,点是的外心,现在以为圆心,分别以、、为半径作,则点与的位置关系分别是________．【答案】圆外,圆上,圆内【解析】【分析】由点是的外心,可知O为△ABC的外接圆的圆心,因为∠C=90°,由圆周角定理可知AB为外接圆的直径,根据勾股定理可求出AB的长,根据直角三角形斜边中线等于斜边一半可知OC的长度,根据半径的长判断点C的位置即可.【详解】∵,点是的外心,∴AB为⊙O的直径,且O为AB中点,∵,,∴AB==5,∴OC=2.5,∵2.5>2；2.5=2.5； 2.5<3,∴以、、为半径作,则点与的位置关系分别是圆外、圆上、圆内.故答案为：圆外、圆上、圆内【点睛】本题考查了对点与圆的位置关系的判断．设点到圆心的距离为d,则当d=R时,点在圆上；当d＞R 时,点在圆外；当d＜R时,点在圆内．根据圆周角定理确定O点的位置是解题关键.12.如下图,在以为圆心的两个同心圆中,大圆的弦交小圆于和两点,,,则长为________．【答案】【解析】【分析】如图：作OE⊥AB于E,根据垂径定理可知CE=CD,AE=AB,根据AC=AE-CE求出AC的长即可.【详解】如图：作OE⊥AB于E,∴根据垂径定理得：CE=CD=3,AE=AB=5,∴AC=AE-CE=2.故答案为：2【点睛】本题考查了垂径定理：平分弦的直径平分这条弦,并且平分弦所对的两条弧,熟练掌握垂径定理是解题关键.13.已知：如图,为半的直径,、、为半圆弧上的点,,,则的度数为________度．【答案】【解析】【分析】根据同圆中,等弧所对的圆心角相等可知∠BOC的度数,即可求出∠AOC的度数.【详解】∵,∠BOE=55°,∴∠COD=∠DOE=∠BOE=55°,∴∠BOC=165°,∴∠AOC=180°-165°=15°,故答案为：15【点睛】本题考查圆周角定理,在同圆或等圆中,如果两个圆心角以及它们对应的两条弧、两条弦中有一组量相等,则另外两组量也对应相等．在圆中经常利用此结论把圆心角、弧、弦之间进行转化．14.如图,边长为的正方形的顶点、在一个半径为的圆上,顶点、在圆内,将正方形沿圆的内壁逆时针方向作无滑动的滚动．当点第一次落在圆上时,点运动的路径长为________．【答案】【解析】【分析】设圆心为O,连接AO,BO,AC,AE,易证三角形AOB是等边三角形,确定∠GFE=∠EAC=30°,再利用弧长公式计算即可．【详解】如图所示：设圆心为O,连接AO,BO,AC,AE,∵AB=,AO=BO=,∴AB=AO=BO,∴△AOB是等边三角形,∴∠AOB=∠OAB=60°同理：△FAO是等边三角形,∠FAB=2∠OAB=120°,∠DAF=120°-90°=30°,即旋转角为30°,∴∠EAC=30°,∠GFE=∠FAD=120°-90°=30°,∵AD=AB=,∴AC=2,∴当点C第一次落在圆上时,点C运动的路径长为=（）π；故答案为：（）π【点睛】本题考查了正方形的性质、旋转的性质、等边三角形的判定和性质、勾股定理的运用以及弧长公式的运用,题目的综合性较强,解题的关键是正确的求出旋转角的度数．15.已知中,,,,直线过点且与平行,若以为轴将旋转一周,则所得的几何体的表面积为________．（不求近似值）【答案】【解析】【分析】根据,,,可求出△ABC的其余边长,表面积为一个圆锥的侧面积+一个圆的底面积+圆柱的侧面积,按照公式计算即可.【详解】∵Rt△ABC中,∠C=90°,∠A=30°,AB=10,∴BC=5,AC=5,∴所得几何体的表面积为：π×5×10+π×52+2π×5×5=75π+50．故答案为75π+50．【点睛】考查圆锥的计算；画出相关图形,判断出表面积的组成是解决本题的关键．16.如图,已知是的直径,为弦,度．过圆心作交于点,连接,则________度．【答案】【解析】【分析】先根据直角三角形两锐角互余求出∠BOD,再根据圆周角定理∠DCB=∠BOD即可得答案.【详解】∵OD⊥BC交弧BC于点D,∠ABC=30°,∴∠BOD=90°-∠ABC=90°-30°=60°,∴∠DCB=∠BOD=30°．故答案为：30【点睛】本题主要考查圆周角定理,在同圆或等圆中同弧所对的圆周角的度数是圆心角的一半,熟练掌握圆周角定理是解题关键.17.如图,的边位于直线上,,,,若由现在的位置向右无滑动地旋转,当第次落在直线上时,点所经过的路线的长为________（结果用含有的式子表示）【答案】【解析】【分析】根据含30度的直角三角形三边的关系得到BC=1,AB=2BC=2,∠ABC=60°；点A先以B点为旋转中心,顺时针旋转120°到A1,再以点C1为旋转中心,顺时针旋转90°到A2,然后根据弧长公式计算两段弧长,从而得到点A第3次落在直线上时,点A所经过的路线的长．【详解】∵Rt△ABC中,AC=,∠ACB=90°,∠A=30°,∴BC=1,AB=2BC=2,∠ABC=60°；∵Rt△ABC由现在的位置向右无滑动的翻转,且点A第3次落在直线l上时,有3个的长,2个的长, ∴点A经过的路线长=×3+×2=(4+)π.故答案为：(4+)π.【点睛】本题考查了旋转的性质与弧长的计算,解题的关键是熟练的掌握旋转的性质与弧长的计算方法. 18.如图,圆柱底面半径为,高为,点、分别是圆柱两底面圆周上的点,且、在同一母线上,用一棉线从顺着圆柱侧面绕圈到,求棉线最短为________．【答案】【解析】【分析】将圆柱体展开,然后利用两点之间线段最短解答即可.【详解】圆柱体的展开图如图所示：用一棉线从A顺着圆柱侧面绕3圈到B的运动最短路线是：AC→CD→DB；即在圆柱体的展开图长方形中,将长方形平均分成3个小长方形,A沿着3个长方形的对角线运动到B的路线最短；∵圆柱底面半径为2cm,∴长方形的宽即是圆柱体的底面周长：2π×2=4πcm；又∵圆柱高为9πcm,∴小长方形的一条边长是3πcm；根据勾股定理求得AC=CD=DB=5πcm；∴AC+CD+DB=15πcm；故答案为：15π．【点睛】本题主要考查了圆柱的计算、平面展开--路径最短问题．圆柱的侧面展开图是一个长方形,此长方形的宽等于圆柱底面周长,长方形的长等于圆柱的高．本题就是把圆柱的侧面展开成长方形,“化曲面为平面”,用勾股定理解决．19.以矩形的顶点为圆心作,要使、、三点中至少有一点在内,且至少有一点在外,如果,,则的半径的取值范围为________．【答案】【解析】【分析】先求出矩形对角线的长,然后由B、C、D与⊙A的位置,确定⊙A的半径的取值范围．【详解】根据题意画出图形如下所示：∵AB=CD=5,AD=BC=12,∴AC=BD==13．∵B、C、D中至少有一个点在⊙A内,且至少有一个点在⊙A外,∴点B在⊙A内,点C在⊙A外．∴5＜r＜13．故答案是：5＜r＜13．【点睛】本题考查的是点与圆的位置关系,要确定点与圆的位置关系,主要根据点与圆心的距离与半径的大小关系来进行判断．当d＞r时,点在圆外；当d=r时,点在圆上；当d＜r时,点在圆内．20.如图,在中,是弦,,,那么圆心到的距离是________,弦的长是________．【答案】(1). (2).【解析】【分析】过O作OC⊥AB交AB于C点,根据垂径定理可知OC垂直平分AB,根据OA=OB,∠AOB=120°可求出∠OAB=30°,根据30°角所对直角边等于斜边一半即可求得圆心到的距离；根据勾股定理求出AC的长即可求出AB的长.【详解】过O作OC⊥AB交AB于C点,如图所示：由垂径定理可知,OC垂直平分AB,∵OA=OB,∠AOB=120°∴∠OAB=30°∴OC=OA=cm∴由勾股定理可得：AC= =cm∴AB=2AC=5cm.故答案为：；5；【点睛】本题考查垂径定理,垂直于弦的直径,平分弦且平分这条弦所对的两条弧,熟练掌握垂径定理是解题关键.三、解答题（共 6 小题 ,每小题 10 分 ,共 60 分）21.一圆柱形排水管的截面如图所示,已知排水管的半径为,水面宽为．由于天气干燥,水管水面下降,此时排水管水面宽变为,求水面下降的高度．【答案】水面下降了米．【解析】【分析】如图：过点O作ON⊥CD于N,交AB于M,先根据垂径定理求得AM、CN,然后根据勾股定理求出OM、ON的长,即可得出结论【详解】如图,下降后的水面宽CD为6m,连接OA,OC,过点O作ON⊥CD于N,交AB于M．∴∠ONC=90°．∵AB∥CD,∴∠OMA=∠ONC=90°．∵AB=8m,CD=6m,∴AM=AB=4,CN=CD=3,在Rt△OAM中,∵OA=5,∴OM==3．同理可得ON=4,∴MN=ON-OM=1（米）．答：水面下降了1米．【点睛】本题考查的是垂径定理的应用以及勾股定理的应用,熟知垂直于弦的直径平分弦,并且平分这条弦所对的两条弧是解答此题的关键．22.如图,在中,弦、于点,且．求证：．【答案】见解析【解析】【分析】根据,可证明,进而证明AC=BD,通过证明即可证明结论.【详解】∵,∴,,∴在与中,∵,∴,∴．【点睛】本题考查的是圆心角、弧、弦的关系及全等三角形的判定与性质,熟练掌握,圆心角、弧、弦的关系是解题关键.23.如图,在中,,,求分别以、、为圆心,以为半径画弧,三条弧与边所围成的阴影部分的面积．【答案】．【解析】【分析】由于三条弧所对的圆心角的和为180°,根据扇形的面积公式可计算出三个扇形的面积和,而三条弧与边AB 所围成的阴影部分的面积=S△ABC-三个扇形的面积和,再利用三角形的面积公式计算出△ABC的面积,然后代入即可得到答案．【详解】∵∠C=90°,CA=CB=2,∴AC=1,S△ABC==2,∵三条弧所对的圆心角的和为180°,三个扇形的面积和==,∴三条弧与边AB所围成的阴影部分的面积=S△ABC-三个扇形的面积和=2-,【点睛】本题考查扇形面积,熟练掌握面积公式并明确三条弧所对的圆心角的和为180°是解题关键.24.已知：如图,的外接圆,弦的长为,,求圆心到的距离．【答案】圆心到的距离为．【解析】【分析】连接,,过点作于点,根据圆周角定理可知∠BOC=60°,进而证明△OBC是等边三角形,根据垂径定理可知CD的长度,利用勾股定理求出OD的长即【详解】连接,,过点作于点,∵,∴．∵,∴是等边三角形,∴,∵OD⊥BC,∴CD=BC=2,∴=,即圆心到的距离为．【点睛】本题考查圆周角定理及垂径定理,在同圆中,同弧所对的圆周角的度数等于圆心角的一半,垂直于弦的直径,平分弦且平分这条弦所对的两条弧,熟练掌握定理是解题关键.25.如图,已知为的直径,是弦,于,于,．求证：；求证：；若,,设,求值及阴影部分的面积．【答案】（1）见解析；（2）见解析；（3）x=5,.【解析】【分析】（1）根据直径所对的圆周角是90°可知∠ACB=∠AFO=90°,由平行线判定定理即可证明OF//BC；（2）由可知∠CBE=∠FOA,利用,,即可证明；（3）在Rt△OCE中,利用勾股定理列方程即可求出x的值,根据OC=2OE可知∠OCE=30°,即可求出∠COD的度数,利用扇形面积及三角形面积公式求出阴影面积即可.【详解】证明：∵为的直径,∴又∵∴证明：∵∴∠CBE=∠FOA∵,,∴解：连接．设,∵∴．在中,,根据勾股定理可得：解得：,即,∵OC=5+5=10,∴OC=2OE,∴∠OCE=30°,∴,∴扇形的面积是：的面积是：∴阴影部分的面积是：．【点睛】本题考查圆周角定理、垂径定理及扇形面积,熟练掌握定理和公式是解题关键.26.如图,内接于,,,．求的度数；将沿折叠为,将沿折叠为,延长和相交于点；求证：四边形是正方形；若,,求的长．【答案】（1）；（2）见解析；（3）．【解析】【分析】（1）连接和,由OE=BC,可知OE=BE,进而可知∠OBE=45°,同理可证∠OCE=45°,即可证明∠BOC=90°,根据圆周角定理即可求得∠BAC的度数；（2）由折叠性质可知AG=AD=AF,∠AGH=∠AFH=90°,∠DAC=∠CAF,∠BAD=∠BAG,由∠BAD+∠DAC=45°,可证明∠GAF=90°,即可证明四边形AFHG 是正方形；（3）由折叠性质可知,；由（2）可知∠BHC=90°,设AD长为x,利用勾股定理列方程求出x的值即可得解.【详解】（1）连接和；∵,∴；∵,∴,∴；∵,∴；由折叠可知,,,,,∴；∴；∴四边形是正方形；解：由得,,,,；设的长为,则,．在中,,∴；解得,,（不合题意,舍去）；∴．【点睛】本题主要考查圆周角定理及折叠性质,在同圆中,同弧所对的圆周角的度数等于圆心角的一半；折叠后的图形与原图形全等,熟练掌握折叠的性质是解题关键.。

鲁教版(五四制)九年级数学下册《第三章圆》单元检测卷-带答案

鲁教版（五四制）九年级数学下册《第三章圆》单元检测卷-带答案（时间：90分钟满足：120分）一、选择题（每小题3分，共30分）1.下列说法：①直径是弦；②弦是直径；③半径相等的两个半圆是等弧；④长度相等的两条弧是等弧；⑤半圆是弧，但弧不一定是半圆.其中，说法正确的有（）A.1个B.2个C.3个D.4个2.如图，四边形ABCD内接于⊙O，若∠B=108°，则∠D的大小为（）A.54°B.62°C.72°D.82°题2 题3 题43.如图，在⊙O中，弦BC与半径OA相交于点D，连接AB，OC.若∠OAB=60°，∠ADC=85°，则∠OCB 的度数是（）A.25°B.27.5°C.30°D.35°4.如图，在5×5正方形网格中，一条圆弧经过A，B，C三点，那么这条圆弧所在圆的圆心是（）A.点PB.点QC.点MD.点R5.如图，⊙O的直径CD=20，AB是⊙O的弦，AB⊥CD，垂足为M，OM；OC=3:5，则AB的长为（）A.2√91B.16C.12D.8题5 题76.在Rt△ABC中，∠C=90°，∠B=30°，BC=4 cm，以点C为圆心，2 cm长为半径作圆，⊙C于AB的位置关系是（）A.相离B.相切C.相交D.相切或相交7.一把直尺、一个60°的直角三角板和光盘如图摆放，A为60°直角三角板的斜边与直尺的交点，AB=3，则光盘的直径是（）A.3B.3√3C.6D.6√38.如图，AB是圆锥的母线，BC为底面直径，已知BC=6 cm，圆锥的侧面积为15π cm2，则sin∠ABC的值为（）A.34 B.35C.45D.539.如图，四边形ABCD内接于⊙O，点I是△ABC的内心，∠AIC=124°，点E在AD的延长线上，则∠CDE 的度数为（）A.56°B.62°C.68°D.78°10.如图，在正方形ABCD中，AB=12，点E为BC的中点，以CD为直径作半圆CFD，点F为半圆的中点，连接AF，EF，图中阴影部分的面积是（）A.18+36πB.24+18πC.18+18πD.12+18π二、填空题（每小题4分，共24分）11.如图，AD是△ABC的外接圆⊙O的直径，若∠BCA=60°，则∠BAD= .题11 题1212.如图，在△ABC中，∠C=90°，AC=3，BC=4，则△ABC的内切圆半径r= .13.如图，工人师傅用扳手拧形状为正六边形的螺帽，现测得扳手的开口宽度b=3cm，则螺帽边长a= cm.题13题1414.工程上常用钢珠来测量零件上小孔的直径，假设钢珠的直径是12 mm，测得钢珠顶端离零件表面的距离为9 mm，如图所示，则这个小孔的直径AB= mm.15.如图，某数学兴趣小组将边长为5的正方形铁丝框ABCD变形为以点A为圆心，AB长为半径的扇形（忽略铁丝的粗细），则所得的扇形ABD的面积为 .16.如图，点A1的坐标为（2，0），过点A1作x轴的垂线交直线l：y=√3x于点B1，以原点O为圆心，OB1的长为半径画弧交x轴正半轴于点A2；再过点A2作x轴的垂线交直线l于点B2，以原点O为圆心，OB2的̂的长是 .长为半径画弧交x轴正半轴于点A3……按此作法进行下去，则A2024B2023三、解答题（共66分）̂上的一点（点P不与点D，E重合），求∠CPD 17.（10分）如图，正五边形ABCDE内接于⊙O，P为DE的余角的度数.18.（10分）如图,⊙0为锐角△ABC的外接圆，半径为5.(1)用尺规作图作出∠BAC 的平分线，并标出它与劣弧 BC的交点E.（保留作图痕迹，不写作法）(2)若(1)中的点E到弦BC 的距离为3, 求弦CE的长.19.（10分）如图，在△ABC中,∠ACB=90°, BO为△ABC 的角平分线，以点O为圆心，OC为半径作⊙, AD=2, 求BO的长.0,与线段AC交于点D.(1)求证：AB 为⊙0的切线.(2)若tan A=3420.(12分)如图,AB是⊙O的弦，C是⊙0外一点，OC⊥OA, CO交AB于点P，交⊙O于点D, 且CP=CB.(1)判断直线BC与⊙0的位置关系，并说明理由；(2)若∠A=30°, 0P=1,求图中阴影部分的面积.21.(12分)（威海中考）已知AB为⊙0的直径,AB=2,弦DE=1, 直线AD与BE相交于点C,弦DE在⊙0上运动且保持长度不变, ⊙0的切线DF交BC 于点F.(1)如图①，若 DE∥AB, 求证：CF=EF.(2)如图②,当点E运动至与点B重合时，试判断 CF与 BF是否相等，并说明理由.22.（12分）在古代，智慧的劳动人民已经会使用”石磨”，其原理为在磨盘的边缘连接一个固定长度的“连杆”，推动“连杯”带动磨盘转动，将粮食磨碎，物理学上称这种动力传输工具为“曲柄连杆机构”.小明受此启发设计了一个“双连杆机构”，设计图如图①，两个固定长度的“连杆”AP, BP的连接点P在⊙O上, 当点P在⊙0上转动时，带动点A, B 分别在射线OM, ON 上滑动, OM⊥ON.当AP与⊙0相切时，点B恰好落在⊙0上，如图②.请仅就图②的情形解答下列问题.（1）求证：∠PAO=2∠PBO.（2）若⊙O的半径为5，AP=203，求BP的长.参考答案一、选择题序号 1 2 3 4 5 6 7 8 9 10答案 C C D B B B D C C C二、填空题11. 30°；12. 1 ；13. √3；14. 6√3；15. 25 ；16. 22024π3；三、解答题17.54°.18.（2）√30.19.（2）3√5.20.（1）相切；（2）√32−π4.21.（1）连接OD，OE，△ODE为正三角形，△AOD和△BOE是正三角形，△CDE是正三角形；（2）此时BC为切线.22.（1）∠PAO=∠POD=2∠PBO.（2）AO=25，△AOP∽△OPD，OD=4，PD=3，CD=1，PC=√10，BP=3√10.3。

人教版小学六年级数学上学期第五单元《圆》单元检测题及答案(含三套题)

人教版小学六年级数学上学期第五单元《圆》单元检测题及答案（总分：100分时间：40分钟）一、填空。

（每空1分，共18分）1.圆有（）条直径，有（）条半径，在同一个圆中，半径r与直径d的关系可以表示为（），也可以表示为（）。

2.用圆规画圆，当圆规两脚间张开3cm时，画出的圆的周长是（）cm，面积是（）cm2。

3.一个圆的周长是9.42cm，它的半径是（）cm，若它的半径扩大到原来的3倍，则周长扩大到原来的（）倍，面积扩大到原来的（）倍。

4.半圆的半径为r，则半圆的周长可以表示为（），面积可以表示为（）。

5.自行车车轮转动一周前行12.56dm，那么车轮的半径为（）dm。

6.在一个长6cm，宽4cm的长方形中剪一个最大的半圆，则这个半圆的直径是（）cm。

7.圆形花坛的半径由3m增加到5m，花坛面积增加了（）m2。

8.一个环形大圆的直径是10cm，环宽是2cm，环形的周长是（）cm，面积是（）cm²。

9.一个圆可以分成（）个圆心角为60°的扇形。

10.运动场上，同学们拿着一条31.4m长的绳子，要想围出一个最大的圆形场地，这个圆形场地的面积是（）m²。

二、判断。

（对的在括号里画“√”，错的画“×”）（每题1分，共5分）1.圆的直径是它的半径的3.14倍。

（）2.大圆周长和直径的比值等于小圆周长和直径的比值。

（）3.因为圆周率是一个无限不循环小数，所以它不是一个固定的数值。

（）4.圆的对称轴有无数条，半圆的对称轴也有无数条。

（）5.甲乙两个圆的周长比是2∶9，则甲乙两圆的面积比是2∶9。

（）三、选择。

（2分×8＝16分）1.一个钟表的时针长8cm，从3点走到6点，针尖走过的路程为（）cm。

A.50.24B.25.12C.12.562.两个圆的周长相等，那么它们的面积（）。

A.相等B.不相等C.无法比较3.大圆的直径是小圆直径的2倍，那么大圆的面积是小圆面积的（）倍。

人教版数学九年级上册《圆》单元检测附答案

人教版数学九年级上学期《圆》单元测试（满分120分,考试用时120分钟）一．选择题（每小题3分,共36分）1.设⊙O的直径为12cm,点A在直线l上,若AO=6cm,则直线l与⊙O的位置关系是（）A. 相离B. 相切C. 相交或相切D. 以上都不对2.如图,CD是⊙O的弦,AB是⊙O的直径,AB⊥CD垂足为E,下列结论不一定成立的是（）A. B. C. EO=EB D. EC=ED3.钟面上的分针长为2cm,从8点到8点40,分针在钟面上扫过的面积是（）cm2．A. B. C. D.4.如图,在⊙O中,∠ABC=51°,则∠AOC等于（）A. 51°B. 80°C. 90°D. 102°5.已知点I为△ABC的内心,若∠A=40°,则∠BIC=（）A. 80°B. 110°C. 130°D. 140°6.如图,⊙O中,弦AB、CD相交于点P,∠A=35°,∠B=40°,则∠APD的大小是（）A. 45°B. 55°C. 65°D. 75°7.有一圆内接正八边形ABCDEFGH,若△ADE的面积为8,则正八边形ABCDEFGH的面积为（）A. 32B. 40C. 24D. 308.如图,⊙O的半径为3,四边形ABCD内接于⊙O,连接OB,OD．若∠BOD=∠BCD,则的度数为（）A. 60°B. 90°C. 120°D. 150°9.如图,AB是⊙O的直径,点C在AB的延长线上,CD与⊙O相切,切点为D,如果∠A＝28°,那么∠C为（）A. 28°B. 30°C. 34°D. 35°10.如图,AB是⊙O的直径,CD是⊙O的弦,连结AC、BC、BD、AD,若CD平分∠ACB,∠CBA=30°,BC=3,则AD的长为（）A. 3B. 6C. 4D. 311.如图,AD是半圆的直径,点C是弧BD的中点,∠BAD=70°,则∠ADC等于（）A. 50°B. 55°C. 65°D. 70°12.如图,AB是半圆O的直径,C、D两点在半圆上,CE⊥AB于E,DF⊥AB于F,点P是AB上的一个动点,已知AB=10,CE=4,DF=3,则PC+PD的最小值是（）A. 7B. 7C. 10D. 8二．填空题（每小题3分,共24分）13.如图,在Rt△ABC中,∠ACB=90°,AC=3,BC=4,以点C为圆心,CA为半径的圆与AB交于点D,则BD的长为_____．14.如图,在四边形ABCD中,AB=AD=5,BC=CD且BC＞AB,BD=8．当A,B,C,D四点在同一个圆上时,该圆的半径为_____．15.如图,PA、PB、DE切分别切⊙O于点A、B、C,若∠P=50°,则∠DOE=_____°．16.如图,已知直线y=与x轴、y轴分别交于A、B两点,P是以C（0,1）为圆心,1为半径的圆上一动点,连结PA、PB．则△PAB面积的最小值是_____．17.如图,在⊙O中,P为直径AB上的一点,过点P作弦MN,满足∠NPB＝45°,若AP＝2cm,BP＝6cm,则MN 的长是_____cm．18.如图,在矩形ABCD中,AB=6,AD=8,E是BC上的一动点（不与点B、C重合）．连接AE,过点D作DF⊥AE,垂足为F,则线段BF长的最小值为_____．19.如图,点A、B、C在⊙O上,∠O=44°,则∠C=_____°．20.如图,已知直线y=与x轴、y轴分别交于A、B两点,P是以C（0,2）为圆心,2为半径的圆上一动点,连结PA、PB．则△PAB面积的最小值是_____．三．解答题（每题10分,共60分）21.如图,AB是⊙O的直径,C是的中点,CE⊥AB于点E,BD交CE于点F．(1)求证：CF=BF；(2)若CD=5,AC=12,求⊙O的半径和CE的长．22.如图,四边形ABCD内接于⊙O,∠ABC=60°,BD平分∠ADC．(1)试说明△ABC是等边三角形；(2)若AD=2,DC=4,求四边形ABCD的面积．23.如图,AB是⊙O的直径,D、E为⊙O上位于AB异侧的两点,连接BD并延长至点C,使得CD=BD,连接AC交⊙O于点F连接AE、DE、DF．(1)证明：∠E=∠C；(2)若∠E=58°,求∠BDF的度数．24.如图所示,已知在△ABC中,∠B=90°,O是AB上一点,以O为圆心,OB为半径的圆与AB交于点E,与AC 切于点D．(1)求证：DE∥OC；(2)若AD=2,DC=3,且AD2=AE•AB,求的值．25.如图,在△ABC中,AB=AC．(1)如图1,若O为AB的中点,以O为圆心,OB为半径作⊙O交BC于点D,过D作DE⊥AC,垂足为E．①试说明：BD=CD；②判断直线DE与⊙O的位置关系,并说明理由．(2)如图2,若点O沿OB向点B移动,以O为圆心,以OB为半径作⊙O与AC相切于点F,与AB相交于点G,与BC相交于点D,DE⊥AC,垂足为E,已知⊙O的半径长为4,CE=2,求切线AF的长．26.如图,△ABC中,∠ACB=90°,⊙O是△ABC的内切圆,切点分别为D、E、F．连接DF并延长交BC的延长线于点G．(1)求证：AF=GC；(2)若BD=6,AD=4,求⊙O的半径；(3)在(2)的条件下,求图中由弧EF与线段CF、CE围成的阴影部分面积．参考答案一．选择题（每小题3分,共36分）1.设⊙O的直径为12cm,点A在直线l上,若AO=6cm,则直线l与⊙O的位置关系是（）A. 相离B. 相切C. 相交或相切D. 以上都不对【答案】C【解析】【分析】根据直线与圆的位置关系的判定方法,分OA⊥l和圆心O到直线l的距离小于AO两种情况判断即可解答. 【详解】已知⊙O的直径为12cm,则半径为6cm,又已知AO=6cm,所以AO为半径,则A在⊙O上．当AO⊥l时,有1个公共点,即相切．当圆心O到直线l的距离小于AO时,有2个公共点,即相交．故选C．【点睛】本题考查了直线与圆的位置关系,解决此类问题可通过比较圆心到直线距离d与圆半径大小关系完成判定．2.如图,CD是⊙O的弦,AB是⊙O的直径,AB⊥CD垂足为E,下列结论不一定成立的是（）A. B. C. EO=EB D. EC=ED【答案】C【解析】【分析】根据垂径定理解答即可.【详解】∵AB是直径,AB⊥CD,∴,,EC=DE,选项A,B,D正确,不能判断EO=EB,选项C错误.故选C．【点睛】本题考查了垂径定理,熟知垂直于弦的直径平分弦,并且平分弦所对的两条弧是解决问题的关键.3.钟面上的分针长为2cm,从8点到8点40,分针在钟面上扫过的面积是（）cm2．A. B. C. D.【答案】C【解析】【分析】分针1小时（60分钟）转1周,扫过的面积是一个圆的面积,40分钟分针扫过的面积是圆面积的,根据圆的面积公式s=πr2,把数据代入公式进行求解即可．【详解】依题意,得×π×22=π（cm2）；答：分针所扫过的面积是πcm2．故选C．【点睛】本题考查了扇形面积的计算和旋转的性质．解答本题的关键是明确分针的尖端40分钟扫过的面积是圆面积的．4.如图,在⊙O中,∠ABC=51°,则∠AOC等于（）A. 51°B. 80°C. 90°D. 102°【答案】D【解析】【分析】根据圆周角定理即可解答.【详解】由圆周角定理得,∠AOC=2∠ABC=102°,故选D．【点睛】本题考查了圆周角定理,熟知圆周角定理的内容是解决问题的关键.5.已知点I为△ABC的内心,若∠A=40°,则∠BIC=（）A. 80°B. 110°C. 130°D. 140°【答案】B【解析】【分析】根据三角形的内角和定理求得∠ABC+∠ACB=140°,由内心的定义可求得∠IBC+∠ICB=70°,再由三角形的内角和定理即可求得∠BIC的度数.【详解】∵∠A+∠ABC+∠ACB=180°,∠A=40°,∴∠ABC+∠ACB=140°,∵I是△ABC的内心,∴∠IBC=∠ABC,∠ICB=∠ACB,∴∠IBC+∠ICB=×140°=70°,∴∠BIC=180°﹣（∠IBC+∠ICB）=110°.故选B．【点睛】本题考查了三角形的内心,熟知三角形的内心是三角形三个角的角平分线的交点是解决问题的关键.6.如图,⊙O中,弦AB、CD相交于点P,∠A=35°,∠B=40°,则∠APD的大小是（）A. 45°B. 55°C. 65°D. 75°【答案】D【解析】【分析】根据等弧所对的圆周角相等可知∠B=∠C,故根据三角形的一个外角等于与它不相邻的两个内角和可以求出∠APD的大小.【详解】由于∠C和∠B所对应的弧都是,故∠C=∠B=40°,∴∠APD=∠C+∠A=75°,故答案选D.【点睛】本题主要考查了等弧所对应的圆周角相等以及三角形的外角等于与它不相邻的两个内角之和,灵活应用这些是解答本题的关键.7.有一圆内接正八边形ABCDEFGH,若△ADE的面积为8,则正八边形ABCDEFGH的面积为（）A. 32B. 40C. 24D. 30【答案】A【解析】【分析】取AE中点O,则点O为正八边形ABCDEFGH外接圆的圆心,连接OD,即可得△ODE的面积=×△ADE的面积,由此求得△ODE的面积,再由圆内接正八边形ABCDEFGH是由8个与△ODE全等的三角形构成,即可求得正八边形ABCDEFGH的面积.【详解】取AE中点O,则点O为正八边形ABCDEFGH外接圆的圆心,连接OD,∴△ODE的面积=×△ADE的面积=×8=4,圆内接正八边形ABCDEFGH是由8个与△ODE全等的三角形构成．则圆内接正八边形ABCDEFGH为8×4=32,故选A．【点睛】本题考查了正多边形和圆的知识,一般的,任何一个正n边形都有一个外接圆,分别经过各顶点的这些半径将这个正n边形分成n个全等的等腰三角形.8.如图,⊙O的半径为3,四边形ABCD内接于⊙O,连接OB,OD．若∠BOD=∠BCD,则的度数为（）A. 60°B. 90°C. 120°D. 150°【答案】C【解析】【分析】根据圆内接四边形的性质、圆周角定理即可求得∠A=60°,∠BOD=120°,由此即可求得的度数.【详解】∵四边形ABCD内接于⊙O,∴∠BCD+∠A=180°,∵∠BOD=2∠A,∠BOD=∠BCD,∴2∠A+∠A=180°,解得：∠A=60°,∴∠BOD=120°,∴的度数为120°故选C．【点睛】本题考查了圆内接四边形的性质及圆周角定理,正确求得∠BOD=120°是解决问题的关键.9.如图,AB是⊙O的直径,点C在AB的延长线上,CD与⊙O相切,切点为D,如果∠A＝28°,那么∠C为（）A. 28°B. 30°C. 34°D. 35°【答案】C【解析】【分析】连接OD,已知CD与⊙O相切,根据切线的性质定理可得∠ODC=90 °,由OA=OD,根据等腰三角形的性质可得∠A=∠ODA,由三角形外角的性质可得∠COD=∠A+∠ODA=2∠A=56°,由此即可求得∠C=34°.【详解】如图,连接OD,∵CD是⊙O的切线,∴OD⊥CD,即∠ODC=90 °,∵OA=OD,∴∠A=∠ODA,∴∠COD=∠A+∠ODA=2∠A=56°,∴∠C=90°﹣56°=34°,故选C．【点睛】本题考查了切线的性质定理、等腰三角形的性质及三角形外角的性质,熟练运用相关知识是解决问题的关键.10.如图,AB是⊙O的直径,CD是⊙O的弦,连结AC、BC、BD、AD,若CD平分∠ACB,∠CBA=30°,BC=3,则AD的长为（）A. 3B. 6C. 4D. 3【答案】B【解析】【分析】由直径所对的圆周角为直角可得∠ACB=∠ADB=90°,再利用特殊角的三角函数值求出AB的值,再根据等弧所对的弦相等结合勾股定理可得出结果.【详解】∵AB是⊙O的直径, ∴∠ACB=∠ADB=90°, ∵∠CBA=30°,BC=,∴AB==6,∵CD平分∠ACB,∴∠BCD=∠ACD, ∴AD=BD,∴AD=,∴2AD²=72, ∴AD=6.故选B.【点睛】本题考查了圆周角的性质,直径所对的圆周角为直角,在同圆或等圆中,相等的圆周角所对的弧相等,解题的关键是得出AD=BD.11.如图,AD是半圆的直径,点C是弧BD的中点,∠BAD=70°,则∠ADC等于（）A. 50°B. 55°C. 65°D. 70°【答案】B【解析】【分析】连接BD,根据直径所对的圆周角为直角可得∠ABD=90°,即可求得∠ADB=20°,再由圆内接四边形的对角互补可得∠C=110°,因,即可得BC=DC,根据等腰三角形的性质及三角形的内角和定理可得∠BDC=∠DBC=35°,由此即可得∠ADC=∠ADB+∠BDC=55°．【详解】解：连接BD,∵AD是半圆O的直径,∴∠ABD=90°,∵∠BAD=70°,∴∠C=110°,∠ADB=20°,∵,∴BC=DC,∴∠BDC=∠DBC=35°,∴∠ADC=∠ADB+∠BDC=55°．故选B．【点睛】本题考查了圆周角定理、圆内接四边形的对角互补、等腰三角形的性质及三角形的内角和定理等知识,熟练运用相关知识是解决问题的关键.12.如图,AB是半圆O的直径,C、D两点在半圆上,CE⊥AB于E,DF⊥AB于F,点P是AB上的一个动点,已知AB=10,CE=4,DF=3,则PC+PD的最小值是（）A. 7B. 7C. 10D. 8【答案】B【解析】【分析】作点C关于AB的对称点C′,连接C′D交AB于点P,则此时PC+PD最小,为C′D的长,求得C′D的长即可求得PC+PD的最小值.【详解】解：作点C关于AB的对称点C′,连接C′D交AB于点P,则此时PC+PD最小,连接OC,OD,由勾股定理得,OE==3,OF=4,∴EF=EO+OF=7,作C′H⊥DF交DF的延长线于H,则四边形EC′HF为矩形,∴FH=C′E=CE=4,C′H=EF=7,∴DH=DF+FH=7,∴PC+PD=C′D=.故选B．【点睛】本题考查了轴对称-线路最短的问题,确定使PC+PD的值最小时动点P的位置是解题的关键．二．填空题（每小题3分,共24分）13.如图,在Rt△ABC中,∠ACB=90°,AC=3,BC=4,以点C为圆心,CA为半径的圆与AB交于点D,则BD的长为_____．【答案】．【解析】【分析】先根据勾股定理求出AB的长,过C作CM⊥AB,交AB于点M,由垂径定理可知M为AD的中点,由三角形的面积可求出CM的长；再在Rt△ACM中,根据勾股定理可求出AM的长,然后再由AD=2AM即可得出结论.【详解】∵在Rt△ABC中,∠ACB=90°,AC=3,BC=4,∴过C作CM⊥AB,交AB于点M,如图所示,∵CM⊥AB,∴M为AD的中点,∵且AC=3,BC=4,AB=5,∴在Rt△ACM中,根据勾股定理得：AC2=AM2+CM2,即解得：∴故答案为：【点睛】考查勾股定理,垂径定理及推论,掌握垂径定理是解题的关键.注意辅助线的作法.14.如图,在四边形ABCD中,AB=AD=5,BC=CD且BC＞AB,BD=8．当A,B,C,D四点在同一个圆上时,该圆的半径为_____．【答案】【解析】【详解】如图,设AC交BD于点E,当A,B,C,D四点在同一个圆上时,∵AB=AD=5,CB=CD,∴AC垂直平分线段BD,AC为圆的直径,设该圆的半径为r,圆心为O．连接OD．∴BE=DE=4,AE==3,在Rt△ODE中,则有r2=（r﹣3）2+42,得r=．故答案为：．【点睛】本题考查了线段垂直平分线的性质、垂径定理及勾股定理,求得BE =4,AE=3是解决问题的关键.15.如图,PA、PB、DE切分别切⊙O于点A、B、C,若∠P=50°,则∠DOE=_____°．【答案】65【解析】【分析】连接OA、OC、OB,根据切线的性质定理可得∠DAO=∠EBO=90°,由是必须的内角和为360°可得∠P+∠AOB=180°,由此求得∠AOB=130°,由切线长定理可得∠AOD=∠DOC,∠COE=∠BOE,从而得∠DOE=∠AOB=65°.【详解】连接OA、OC、OB,∵OA⊥PA,OB⊥PB,OC⊥DE,∴∠DAO=∠EBO=90°,∴∠P+∠AOB=180°,∴∠AOB=180°﹣50°=130°；∵∠AOD=∠DOC,∠COE=∠BOE,∴∠DOE=∠AOB=×130°=65°．故答案为：65．【点睛】本题考查了切线的性质定理及切线长定理,求得∠AOB=130°是解决问题的关键.16.如图,已知直线y=与x轴、y轴分别交于A、B两点,P是以C（0,1）为圆心,1为半径的圆上一动点,连结PA、PB．则△PAB面积的最小值是_____．【答案】【解析】试题解析：∵直线与x轴、y轴分别交于两点,∴A点的坐标为(4,0),B点的坐标为(0,−3),∴OA=4,OB=3,过C作CM⊥AB于M,连接AC,MC的延长线交C于N,则由三角形面积公式得,圆C上点到直线的最小距离是∴△P AB面积的最小值是故答案为：17.如图,在⊙O中,P为直径AB上的一点,过点P作弦MN,满足∠NPB＝45°,若AP＝2cm,BP＝6cm,则MN 的长是_____cm．【答案】2【解析】【分析】作OH⊥MN于H,连接ON,由已知条件可得OA=OB=ON=4,OP =2,再求得OH=；在Rt△OHN中,利用勾股定理求得NH=,再利用垂径定理即可求得MNN=2cm.【详解】解：作OH⊥MN于H,连接ON,AB=AP+PB=8,∴OA=OB=ON=4,∴OP=OA﹣AP=2,∵∠NPB=45°,∴OH=OP=,在Rt△OHN中,NH=,∵OH⊥MN,∴MN=2HN=2（cm）,故答案为：2.【点睛】本题考查了垂径定理及勾股定理,根据题意作出辅助线,构造出直角三角形是解决问题的关键．18.如图,在矩形ABCD中,AB=6,AD=8,E是BC上的一动点（不与点B、C重合）．连接AE,过点D作DF⊥AE,垂足为F,则线段BF长的最小值为_____．【答案】2﹣4【解析】【分析】由∠AFD=90°可得点F的运动轨迹是以AD为直径的⊙O,连接OB,OF,根据勾股定理求得OB=2,由BF≥OB﹣OF即可求得BF的最小值为2﹣4.【详解】如图,∵AE⊥DF,∴∠AFD=90°,∴点F的运动轨迹是以AD为直径的⊙O,连接OB,OF．∵四边形ABCD是矩形,∴∠BAO=90°,∵AB=6,AO=4,∴OB==2,FO=AD=4,∵BF≥OB﹣OF,∴BF的最小值为2﹣4,故答案为2﹣4．【点睛】本题考查了圆周角定理的推论及勾股定理,明确点O、B、F在一条直线上时BF的值最小是解决问题的关键.19.如图,点A、B、C在⊙O上,∠O=44°,则∠C=_____°．【答案】22【解析】【分析】根据圆周角定理即可求解.【详解】由圆周角定理可得：∠C= ∠O=×44°=22°；故答案为：22；【点睛】本题考查了圆周角定理,熟练运用圆周角定理是解决本题的关键.20.如图,已知直线y=与x轴、y轴分别交于A、B两点,P是以C（0,2）为圆心,2为半径的圆上一动点,连结PA、PB．则△PAB面积的最小值是_____．【答案】5【解析】【分析】求出A、B的坐标,根据勾股定理求出AB,求出点C到AB的距离,即可求出圆C上点到AB的最小距离,根据面积公式求出即可．【详解】∵直线y=x﹣3与x轴、y轴分别交于A、B两点,∴A点的坐标为（4,0）,B点的坐标为（0,﹣3）,3x ﹣4y﹣12=0,即OA=4,OB=3,由勾股定理得：AB=5．过C作CM⊥AB于M,连接AC,则由三角形面积公式得：×AB×CM=×OA×OC+×OA×OB,∴5×CM=4×2+3×4,∴CM=4,∴圆C上点到直线y=x﹣3的最小距离是：4－2=2,∴△P AB面积的最小值是×5×2=5．故答案为：5．【点睛】本题考查了三角形的面积,点到直线的距离公式的应用,解答此题的关键是求出圆上的点到直线AB的最小距离．三．解答题（每题10分,共60分）21.如图,AB是⊙O的直径,C是的中点,CE⊥AB于点E,BD交CE于点F．(1)求证：CF=BF；(2)若CD=5,AC=12,求⊙O的半径和CE的长．【答案】(1)证明见解析；(2)CE=．【解析】【分析】（1）由AB是⊙O的直径,根据直径所对的圆周角是直角即可得∠ACB=90°,又由CE⊥AB,根据同角的余角相等可证得∠BCE =∠A,又由C是的中点,证得∠DBC =∠A,继而可证得CF﹦BF；（2）由C是的中点和CD=5可求得BC=5,利用勾股定理求得AB=13,即可求得⊙O的半径为6.5；在Rt△ACB中,利用三角形面积的两种表示方法即可求得EC的长.【详解】(1)∵AB是⊙O的直径,∴∠ACB=90°．∴∠A+∠ABC=90°．又∵CE⊥AB,∴∠CEB=90°．∴∠BCE+∠ABC=90°．∴∠BCE=∠A,∵C是的中点,∴=．∴∠DBC=∠A,∴∠DBC=∠BCE．∴CF=BF；(2)∵=,CD=5,∴BC=CD=5,∴AB==13,∴⊙O的半径为6.5,∵CE•AB=AC•BC,∴CE===．【点睛】本题考查了圆周角定理、勾股定理及直角三角形的面积求法,熟练运用相关知识是解决本题的关键.22.如图,四边形ABCD内接于⊙O,∠ABC=60°,BD平分∠ADC．(1)试说明△ABC是等边三角形；(2)若AD=2,DC=4,求四边形ABCD的面积．【答案】（1）见解析；（2）四边形ABCD的面积为.【解析】【分析】（1）据已知条件和圆周角定理即可得到结论;（2）过点A作AE⊥CD,过点B作BF⊥AC,得∠AED=90°,∠ADE=60°,∠DAE=30°,DE =1,,CE= 5,从而求出,再求出,即可求出结论.【详解】解:（1）∵ 四边形ABCD内接于⊙O∴∠ABC＋∠ADC=180°∵∠ABC=60°,∴∠ADC=120°∵ DB平分∠ADC,∴∠ADB=∠CDB=60°∴∠ACB=∠ADB=60°,∠BAC=∠CDB=60°∴∠ABC=∠BCA=∠BAC∴△ABC是等边三角形⑵ 过点A作AE⊥CD,垂足为点E；过点B作BF⊥AC,垂足为点F.∴∠AED=90°∵∠ADC=120°∴∠ADE=60°∴∠DAE=30°∴ DE==1,∵ CD=4∴ CE=CD＋DE=1＋4=5∴Rt△AEC中,∠AED=90°∴ AC=∵ △ABC是等边三角形∴ AB=BC=AC=∴ AF=FC=∴∴∴ 四边形ABCD的面积=.【点睛】本题考查勾股定理、圆周角定理、等边三角形的判定等知识,解题的关键是灵活运用所学知识解决问题,属于中考常考题型．23.如图,AB是⊙O的直径,D、E为⊙O上位于AB异侧的两点,连接BD并延长至点C,使得CD=BD,连接AC交⊙O于点F连接AE、DE、DF．(1)证明：∠E=∠C；(2)若∠E=58°,求∠BDF的度数．【答案】(1)证明见解析；(2)∠BDF=116°.【解析】【分析】(1)连接AD,已知AB是⊙O的直径,根据直径所对的圆周角是直角即可得∠ADB=90°,即AD⊥BC；由CD=BD 可得AD垂直平分BC,根据线段垂直平分线的性质可得AB=AC,所以∠B=∠C；根据同弧所对的圆周角相等可得∠B=∠E,由此即可证得∠E=∠C；（2）已知四边形AEDF是⊙O的内接四边形,根据圆内接四边形对角互补可得∠AFD=180°﹣∠E,由邻补角的定义可得∠CFD=180°﹣∠AFD,从而求得∠CFD=∠E=58°,再由∠BDF=∠C+∠CFD即可求得∠BDF的度数.【详解】(1)连接AD,∵AB是⊙O的直径,∴∠ADB=90°,即AD⊥BC,∵CD=BD,∴AD垂直平分BC,∴AB=AC,∴∠B=∠C,又∵∠B=∠E,∴∠E=∠C；(2)∵四边形AEDF是⊙O的内接四边形,∴∠AFD=180°﹣∠E,又∵∠CFD=180°﹣∠AFD,∴∠CFD=∠E=58°,又∵∠E=∠C=58°,∴∠BDF=∠C+∠CFD=116°.【点睛】本题考查了圆周角定理及圆内接四边形对角互补的性质,熟知圆周角定理及圆内接四边形对角互补的性质是解决问题的关键.24.如图所示,已知在△ABC中,∠B=90°,O是AB上一点,以O为圆心,OB为半径的圆与AB交于点E,与AC 切于点D．(1)求证：DE∥OC；(2)若AD=2,DC=3,且AD2=AE•AB,求的值．【答案】（1）证明见解析；（2） .【解析】试题分析：（1）首先连接OD,由在△ABC中,∠B=90°,以O为圆心,OB为半径的圆与AB交于点E,与AC切于点D,易证得Rt△ODC≌Rt△OBC（HL）,然后由等腰三角形与三角形外角的性质,证得∠OED=∠BOC,继而证得DE∥OC；（2）由AD、DC的长可得AC、BC的长,再根据勾股定理即可得AB的长,再根据AD2=AE•AB,从而可得AE的长,继而得到OB的长,问题得以解答.试题解析：（1）连接OD,∵AC切⊙O点D,∴OD⊥AC,∴∠ODC=∠B=90°,在Rt△OCD和Rt△OCB中, ,∴Rt△ODC≌Rt△OBC（HL）,∴∠DOC=∠BOC,∵OD=OE,∴∠ODE=∠OED,∵∠DOB=∠ODE+∠OED,∴∠BOC=∠OED,∴DE∥OC；（2）由AD=2,DC=3得：BC=3,AC=5,由勾股定理得AB= =4,又∵AD2=AE·AB,∴AE=1,∴BE=3,OB=BE=,∴=．【点睛】本题考查了切线的性质、全等三角形的判定与性质、勾股定理等．解题的关键是恰当添加辅助线,解题过程中要注意掌握数形结合思想的应用．25.如图,在△ABC中,AB=AC．(1)如图1,若O为AB的中点,以O为圆心,OB为半径作⊙O交BC于点D,过D作DE⊥AC,垂足为E．①试说明：BD=CD；②判断直线DE与⊙O的位置关系,并说明理由．(2)如图2,若点O沿OB向点B移动,以O为圆心,以OB为半径作⊙O与AC相切于点F,与AB相交于点G,与BC相交于点D,DE⊥AC,垂足为E,已知⊙O的半径长为4,CE=2,求切线AF的长．【答案】(1)①证明见解析；②直线DE与⊙O相切,理由见解析；(2)AF=3．【解析】【分析】（1）①连接AD,已知AB是⊙O的直径,根据直径所对的圆周角是直角即可得∠ADB=90°,即AD⊥BC；再由等腰三角形三线合一的性质即可证得结论；（2）直线DE与⊙O相切,连接OD,已知AB=AC、OB=OD,根据等腰三角形的性质可得∠ODB=∠B=∠C,即可判定OD∥BC,由DE⊥AC可得DE⊥OD,由此即可判定DE 与⊙O相切；（2）根据已知条件易证四边形ODEF是矩形,即可得OD=EF=4；设AF=x,则AB=AC=x+6,AO =x+2,在Rt△AOF中,利用勾股定理列出方程（x+2）2=x2+42,解方程求得x的值,即可求得AF的长.【详解】(1)①连接AD,∵AB为⊙O的直径,∴∠ADB=90°,即AD⊥BC,∵AB=AC,AD⊥BC,∴BD=CD；②直线DE与⊙O相切,理由：连接OD,∵AB=AC,OB=OD,∴∠ODB=∠B=∠C,∴OD∥BC,∵DE⊥AC,∴DE⊥OD,∴DE与⊙O相切；(2)由(1)同理得,DE与⊙O相切,连接OF,∵EF与⊙O相切,DE⊥AC,∴∠ODE=∠OFE=∠EDF=90°,即四边形ODEF是矩形,∴OD=EF=4,设AF=x,则AB=AC=x+6,AO=x+6﹣4=x+2,在Rt△AOF中,（x+2）2=x2+42,解得,x=3,即AF=3．【点睛】本题考查了切线的判定与性质,解决第（2）问构造直角三角形利用勾股定理作为相等关系列方程是解决问题的关键．26.如图,△ABC中,∠ACB=90°,⊙O是△ABC的内切圆,切点分别为D、E、F．连接DF并延长交BC的延长线于点G．(1)求证：AF=GC；(2)若BD=6,AD=4,求⊙O的半径；(3)在(2)的条件下,求图中由弧EF与线段CF、CE围成的阴影部分面积．【答案】（1）详见解析；（2）2；（3）4﹣π．【解析】【分析】（1）连接OD、OE、OF、OA,证明四边形OFCE为正方形,根据正方形的性质得到OF=CF,证明△GFC≌△AOF,根据全等三角形的性质证明结论；（2）根据切线长定理得到BE=BD=6,AF=AD=4,CF=CE,根据勾股定理列出方程,解方程即可；（3）根据正方形的面积公式和扇形面积公式计算．【详解】（1）证明：连接OD、OE、OF、OA,∵⊙O是△ABC的内切圆,切点分别为D、E、F,∴OE⊥BC,OF⊥AC,又∠ACB=90°,OE=OF,∴四边形OFCE为正方形,∴OF=CF,∵AF=AD,OF=OD,∴OA⊥DF,又∠AFD=∠GFC,∴∠G=∠OAF,在△GFC和△AOF中,,∴△GFC≌△AOF（AAS）,∴AF=GC；（2）解：由切线长定理得,BE=BD=6,AF=AD=4,CF=CE,则AB=AD+BD=10,由勾股定理得,AC2+BC2=AB2,即（4+CF）2+（6+CE）2=102,解得,CF=2,即⊙O的半径为2；（3）解：图中由弧EF与线段CF、CE围成的阴影部分面积=22﹣=4﹣π．【点睛】本题考查的是三角形的内切圆与内心,扇形面积计算,掌握切线长定理,扇形面积公式,全等三角形的判定和性质是解题的关键．。

2021-2022学年北师大版九年级数学下册第三章圆单元测试试题(含详细解析)

北师大版九年级数学下册第三章圆单元测试考试时间：90分钟；命题人：数学教研组考生注意：1、本卷分第I 卷（选择题）和第Ⅱ卷（非选择题）两部分，满分100分，考试时间90分钟2、答卷前，考生务必用0.5毫米黑色签字笔将自己的姓名、班级填写在试卷规定位置上3、答案必须写在试卷各个题目指定区域内相应的位置，如需改动，先划掉原来的答案，然后再写上新的答案；不准使用涂改液、胶带纸、修正带，不按以上要求作答的答案无效。

第I 卷（选择题 30分）一、单选题（10小题，每小题3分，共计30分）1、如图，O 中，90AOC ︒∠=，则ABC ∠等于（）A ．35︒B ．40︒C ．45︒D ．50︒2、如图，在圆内接五边形ABCDE 中，425C CDE E EAB ∠+∠+∠+∠=︒，则CDA ∠的度数为（）A ．75︒B ．65︒C ．55︒D ．45︒3、如图，AB 为O 的直径，C 、D 为O 上两点，30CDB ∠=︒，3BC =，则AB 的长度为（）A ．6B ．3C ．9D ．124、如图，点A ，B ，C 在O 上，OAB 是等边三角形，则ACB ∠的大小为（）A ．60°B ．40°C ．30°D ．20°5、如图，有一个弓形的暗礁区，弓形所含的圆周角50C ∠=︒，船在航行时，为保证不进入暗礁区，则船到两个灯塔A ，B 的张角ASB ∠应满足的条件是（）A ．sin sin 25ASB ∠>︒B ．sin sin50ASB ∠>︒C ．sin sin55ASB ∠>︒D ．cos cos50ASB ∠>︒6、下列说法正确的是（）A ．等弧所对的圆周角相等B ．平分弦的直径垂直于弦C ．相等的圆心角所对的弧相等D ．过弦的中点的直线必过圆心7、如图，ABC 中，90ACB ∠=︒，AC BC =，点D 是边AC 上一动点，连接BD ，以CD 为直径的圆交BD 于点E ．若AB 长为4，则线段AE 长的最小值为（）A 1B ．2C ．D 8、已知⊙O 的半径为5，若点P 在⊙O 内，则OP 的长可以是（）A ．4B ．5C ．6D ．79、如图，△ABC 内接于⊙O ，∠BAC ＝30°，BC ＝6，则⊙O 的直径等于（）A ．10B ．C ．D ．1210、小明设计了如图所示的树型图案，它是由4个正方形、8个等边三角形和5个扇形组成，其中正方形的边长、等边三角形的边长和扇形的半径均为3，则图中扇形的弧长总和为（）A．8πB．172πC．192πD．12π第Ⅱ卷（非选择题 70分）二、填空题（5小题，每小题4分，共计20分）1、如图，正六边形ABCDEF的边长为2，以A为圆心，AC的长为半径画弧，得EC，连接AC，AE，则图中阴影部分的面积为________．2、已知某扇形的半径为5cm，圆心角为120°，那么这个扇形的弧长为 _____cm．3、如图1所示的铝合金窗帘轨道可以直接弯曲制作成弧形．若制作一个圆心角为160°的圆弧形窗帘轨道（如图2）需用此材料800 mm，则此圆弧所在圆的半径为________mm．4、在Rt ABC 中，90BAC ∠=︒，4AC AB ==，D ，E 分别是AB ，AC 的中点，若等腰Rt ADE △绕点A 逆时针旋转，得到等腰11Rt AD E ，记直线1BD 与1CE 的交点为P ，则点P 到AB 所在直线的距离的最大值为________．5、如图，五边形ABCDE 是⊙O 的内接正五边形，则ODC ∠的度数是____．三、解答题（5小题，每小题10分，共计50分）1、已知：如图，ABC ∆中，AB AC =，以AB 为直径的O 交BC 于点P ，PD AC ⊥于点D ．（1）求证：PD 是O 的切线；（2）若120CAB ∠=︒，6AB =，求BC 的值．2、如图，AB 为⊙O 的切线，B 为切点，过点B 作BC ⊥OA ，垂足为点E ，交⊙O 于点C ，连接CO 并延长CO 与AB 的延长线交于点D ，连接AC ．（1）求证：AC 为⊙O 的切线；（2）若⊙O 半径为2，OD ＝4．求线段AD 的长．3、已知：如图，△ABC 为锐角三角形，AB ＝AC求作：一点P ，使得∠APC ＝∠BAC作法：①以点A 为圆心， AB 长为半径画圆；②以点B 为圆心，BC 长为半径画弧，交⊙A 于点C ，D 两点；③连接DA 并延长交⊙A 于点P点P即为所求（1）使用直尺和圆规，依作法补全图形（保留作图痕迹）；（2）完成下面的证明证明：连接PC，BD∵AB＝AC，∴点C在⊙A上∵BC＝BD，∴∠_________＝∠_________∠CAD∴∠BAC＝12∵点D，P在⊙A上，∴∠CPD＝1∠CAD（______________________）（填推理的依据）2∴∠APC＝∠BAC4、如图，在▱ABCD中，∠D＝60°，对角线AC⊥BC，⊙O经过点A、点B，与AC交于点M，连接AO并延长与⊙O交于点F，与CB的延长线交于点E，AB＝EB．（1）求证：EC是⊙O的切线；O的半径．（2）若AD＝5、如图，在△ABC中，∠C＝90°，点O为边BC上一点．以O为圆心，OC为半径的⊙O与边AB相切于点D．（1）尺规作图：画出⊙O，并标出点D（不写作法，保留作图痕迹）；（2）在（1）所作的图中，连接CD，若CD＝BD，且AC＝6．求劣弧CD的长．-参考答案-一、单选题1、C【分析】由题意直接根据圆周角定理进行分析即可得出答案.【详解】解：∵∠ABC和∠AOC是弧AC所对的圆周角和圆心角，90∠=，AOC︒∴∠ABC=1∠AOC=45︒.2故选：C.【点睛】本题考查圆周角定理，注意掌握同弧（等弧）所对的圆周角是圆心角的一半．2、B【分析】先利用多边的内角和得到540EAB B C CDE E ∠+∠+∠+∠+∠=︒，可计算出115B ∠=︒，然后根据圆内接四边形的性质求出CDA ∠的度数即可.【详解】解：∵五边形ABCDE 的内角和为()52180540-⨯︒=︒，∴540EAB B C CDE E ∠+∠+∠+∠+∠=︒，∵425EAB C CDE E ∠+∠+∠+∠=︒，∴540425115B ∠=︒-︒=︒，∵四边形ABCD 为O 的内接四边形，∴180B CDA ∠+∠=︒，∴18011565CDA ∠=︒-︒=︒.故选：B.【点睛】本题主要考查了多边形的内角和与圆内接四边形的性质，掌握圆内接四边形的性质是解答本题的关键.3、A【分析】连接AC ，利用直角三角形30°的性质求解即可．【详解】解：如图，连接AC ．∵AB是直径，∴∠ACB=90°，∵∠CAB=∠CDB=30°，∴AB=2BC=6，故选：A．【点睛】本题考查圆周角定理，含30°角的直角三角形的性质，解题的关键是学会添加常用辅助线，构造直角三角形解决问题．4、C【分析】由OAB∆为等边三角形，得：∠AOB=60°，再根据圆周角定理，即可求解．【详解】解：∵OAB∆为等边三角形，∴∠AOB=60°，∴ACB∠=12∠AOB =12×60°=30°．故选C．【点睛】本题主要考查圆周角定理，掌握同弧所对的圆周角是圆心角的一半是解题的关键．5、D【分析】本题利用了三角形外角与内角的关系和圆周角定理：在同圆或等圆中，同弧或等弧所对的圆周角相等，都等于这条弧所对的圆心角的一半．【详解】如图，AS交圆于点E，连接EB，由圆周角定理知，∠AEB=∠C=50°，而∠AEB是△SEB的一个外角，由∠AEB＞∠S，即当∠S＜50°时船不进入暗礁区．所以，两个灯塔的张角∠ASB应满足的条件是∠ASB＜50°．∴cos∠ASB＞cos50°，故选：D．【点睛】本题考查三角形的外角的性质，圆周角定理等知识，解题的关键是理解题意，灵活运用所学知识解决问题．6、A【分析】根据圆周角定理，垂径定理的推论，圆心角、弧、弦的关系，对称轴的定义逐项排查即可．【详解】解：A. 同弧或等弧所对的圆周角相等，所以A选项正确；B.平分弦（非直径）的直径垂直于弦，并且平分弦所对的弧，所以B选项错误；C 、在同圆和等圆中，相等的圆心角所对的弧相等，所对的弦相等，所以C 选项错误；D .圆是轴对称图形，任何一条直径所在的直线都是它的对称轴，所以D 选项错误.故选A.【点睛】本题主要考查了圆心角、弧、弦的关系,轴对称图形，垂径定理，圆周角定理等知识点．灵活运用相关知识成为解答本题的关键．7、D【分析】如图，连接,CE 由CD 为直径，证明E 在以BC 的中点O 为圆心，BC 为直径的O 上运动，连接,AO 交O 于点,E 则此时AEAO OE 最小，再利用锐角的正弦与勾股定理分别求解,AO OE ，即可得到答案.【详解】解：如图，连接,CE 由CD 为直径，90,CED BECE ∴在以BC 的中点O 为圆心，BC 为直径的O 上运动，连接,AO 交O 于点,E 则此时AE AO OE 最小，90ACB ∠=︒，AC BC =，4,AB =45,ABC BAC ∴∠=∠=︒AC BC AB OB OC OEsin4522,2,22AO22210,AE10 2.故选D【点睛】本题考查的是勾股定理的应用，圆外一点与圆的最短距离的理解，锐角的正弦的应用，掌握“圆外一点与圆的最短距离求解线段的最小值”是解本题的关键.8、A【分析】根据点与圆的位置关系可得5OP<，由此即可得出答案．【详解】解：O的半径为5，点P在O内，∴<，5OP观察四个选项可知，只有选项A符合，故选：A．【点睛】本题考查了点与圆的位置关系，熟练掌握点与圆的位置关系（圆内、圆上、圆外）是解题关键．9、D【分析】连接OB，OC，根据圆周角定理求出∠BOC的度数，再由OB=OC判断出△OBC是等边三角形，由此可得出结论．【详解】解：连接OB，OC，∵∠BAC=30°，∴∠BOC=60°．∵OB=OC，BC=6，∴△OBC是等边三角形，∴OB=BC=6．∴⊙O的直径等于12．故选：D．【点睛】本题考查的圆周角定理，根据题意作出辅助线，构造出等边三角形是解答此题的关键．10、C【分析】如图（见解析），先分别求出扇形①、②、③、④和⑤的圆心角的度数，再利用弧长公式即可得．【详解】解：如图，扇形①、③和⑤的圆心角的度数均为360906060150︒-︒-︒-︒=︒，扇形②和④的圆心角的度数均为180606060︒-︒-︒=︒，则图中扇形的弧长总和150********322 18018022πππππ⨯⨯⨯+⨯=+=，故选：C．【点睛】本题考查了求弧长，熟记弧长公式（180n r l π=，其中l 为弧长，n ︒为圆心角的度数，r 为扇形的半径）是解题关键．二、填空题1、2π【分析】由正六边形ABCDEF 的边长为2，可得AB =BC =2，∠ABC =∠BAF =120°，进而求出∠BAC =30°，∠CAE =60°，过B 作BH ⊥AC 于H ，由等腰三角形的性质和含30°直角三角形的性质得到AH =CH ，BH =1，在Rt △ABH 中，由勾股定理求得AH AC 分的面积【详解】解：∵正六边形ABCDEF 的边长为2，()6218021206AB BC ABC BAF -⨯︒∴==∠=∠==︒， =120°，∵∠ABC +∠BAC +∠BCA =180°，∴∠BAC =12（180°-∠ABC ）=12×（180°-120°）=30°，过B 作BH ⊥AC 于H ，∴AH =CH ，BH =12AB=12×2=1，在Rt △ABH 中， AH =22AB BH - =22231-=，∴AC =23 ，同理可证，∠EAF =30°，∴∠CAE =∠BAF -∠BAC -∠EAF =120°-30°-30°=60°，∴()260?232360CAE S ππ==扇形∴图中阴影部分的面积为2π，故答案为：2π．【点睛】本题考查的是正六边形的性质和扇形面积的计算、等腰三角形的性质、勾股定理，掌握扇形面积公式是解题的关键．2、103π 【分析】根据弧长公式代入求解即可．【详解】解：∵扇形的半径为5cm ，圆心角为120°，∴扇形的弧长＝120510=1803ππ︒⨯⨯︒．故答案为：103π．【点睛】此题考查了扇形的弧长公式，解题的关键是熟练掌握扇形的弧长公式：180n r π，其中n 是扇形圆心角的度数，r 是扇形的半径．3、900【分析】由弧长公式l =180n R π得到R 的方程，解方程即可．【详解】解：根据题意得，800π=160180R π，解得，R =900（mm ）．答：这段圆弧所在圆的半径R 是900 mm ．故答案是：900．【点睛】本题考查了弧长的计算公式：l =180n R π，其中l 表示弧长，n 表示弧所对的圆心角的度数．4、1##【分析】首先作PG ⊥AB ，交AB 所在直线于点G ，则D 1，E 1在以A 为圆心，AD 为半径的圆上，当BD 1所在直线与⊙A 相切时，直线BD 1与CE 1的交点P 到直线AB 的距离最大，此时四边形AD 1PE 1是正方形，进而求出PG 的长．【详解】解：如图，作PG ⊥AB ，交AB 所在直线于点G ，∵D 1，E 1在以A 为圆心，AD 为半径的圆上，当BD 1所在直线与⊙A 相切时，直线BD 1与CE 1的交点P 到直线AB 的距离最大，此时四边形AD 1PE 1是正方形，∵∠CAB =90°，AC =AB =4，D ，E 分别是AB ，AC 的中点，∴AD =AE 1=AD 1=PD 1=2，则BD1=故∠ABP =30°，则PB∴PG =12PB =1，故点P 到AB 所在直线的距离的最大值为：PG =1故答案为：1+【点睛】本题主要考查了旋转的性质以及等腰腰直角三角形的性质和勾股定理以及切线的性质等知识，根据题意得出PG 的最长时P 点的位置是解题关键．5、54︒【分析】根据圆内接正五边形的定义求出∠COD ，利用三角形内角和求出答案．【详解】解：∵五边形ABCDE 是⊙O 的内接正五边形，∴∠COD=360725︒=︒， ∵OC=OD ，∴ODC ∠=(180)5412COD ︒-∠=︒，故答案为：54︒．【点睛】此题考查了圆内接正五边形的性质，三角形内角和定理，同圆的半径相等的性质，熟记圆内接正五边形的性质是解题的关键．三、解答题1、（1）见解析；（2）BC =【分析】（1）根据等腰三角形的性质证得OPB C ∠=∠，进而证得OP ∥AC ，再根据平行线的性质和切线的判定即可证得结论；（2）连接AP ，根据圆周角定理和等腰三角形的性质可得90APB ∠=︒，BP CP =，30B ∠=︒，再根据含30°角的直角三角形性质求出BP 即可求解．【详解】（1）证明：AB AC =，B C ∴∠=∠，OP OB =，B OPB ∴∠=∠，OPB C ∴∠=∠，∴OP ∥AC ，PD AC ⊥，OP PD ∴⊥，又OP 是半径， PD ∴是O 的切线；（2）解：连接AP ，如图， AB 为直径，90APB ∴∠=︒，∵AB=AC ，∠CAB =120°， BP CP ∴=，(180120)230B ∠=-÷=︒，在Rt△APB 中，6AB =，30B ∠=︒， 132AP AB ∴==，BP ∴=2BC BP ∴==【点睛】本题考查等腰三角形的性质、平行线的判定与性质、切线的判定、圆周角定理、含30°角的直角三角形性质、三角形内角和定理，熟练掌握这些知识的联系与运用是解答的关键．2、（1）见解析；（2）【分析】（1）连接OB，证明△AOB≌△AOC（SSS），可得∠ACO＝∠ABO＝90°，即可证明AC为⊙O的切线；（2）在Rt△BOD中，勾股定理求得BD，根据sin D＝OBOD＝ACAD，代入数值即可求得答案【详解】解：（1）连接OB，∵AB是⊙O的切线，∴OB⊥AB，即∠ABO＝90°，∵BC是弦，OA⊥BC，∴CE＝BE，∴AC＝AB，在△AOB 和△AOC 中，AB AC AO AO BO CO =⎧⎪=⎨⎪=⎩， ∴△AOB ≌△AOC （SSS ），∴∠ACO ＝∠ABO ＝90°，即AC ⊥OC ，∴AC 是⊙O 的切线；（2）在Rt△BOD 中，由勾股定理得，BD∵sin D ＝OB OD ＝AC AD ，⊙O 半径为2，OD ＝4． ∴24解得AC ＝∴AD ＝BD +AB ＝【点睛】本题考查了切线的性质与判定，正弦的定义，三角形全等的性质与判定，勾股定理，掌握切线的性质与判定是解题的关键．3、（1）见解析；（2）BAC =BAD ，圆周角定理或同弧所对的圆周角等于它所对圆心角的一半【分析】（1）根据按步骤作图即可；（2）根据圆周角定理进行证明即可解：（1）如图所示，（2）证明：连接PC，BD∵AB＝AC，∴点C在⊙A上∵BC＝BD，∴∠BAC=∠BAD∠CAD∴∠BAC＝12∵点D，P在⊙A上，∠CAD（圆周角定理）（填推理的依据）∴∠CPD＝12∴∠APC＝∠BAC故答案为：BAC=BAD，圆周角定理或同弧所对的圆周角等于它所对圆心角的一半本题考查了尺规作图作圆，圆周角定理，掌握圆周角定理是解题的关键．4、（1）见详解；（2）4．【分析】（1）连接OB，根据平行四边形的性质得到∠ABC=∠D=60°，求得∠BAC=30°，根据等腰三角形的性质和三角形的外角的性质得到∠ABO=∠OAB=30°，于是得到结论；，过O作OH⊥AM于H，则四边形OBCH是矩形，解直角（2）根据平行四边形的性质得到BC=AD三角形即可得到结论．【详解】（1）证明：连接OB，∵四边形ABCD是平行四边形，∴∠ABC=∠D=60°，∵AC⊥BC，∴∠ACB=90°，∴∠BAC=30°，∵BE=AB，∴∠E=∠BAE，∵∠ABC=∠E+∠BAE=60°，∴∠E=∠BAE=30°，∵OA=OB，∴∠ABO=∠OAB=30°，∴∠OBC=30°+60°=90°，∴OB⊥CE，∴EC是⊙O的切线；（2）解：∵四边形ABCD 是平行四边形，∴BC =AD，过O 作OH ⊥AM 于H ，则四边形OBCH 是矩形，∴OH =BC∴OA =sin 60OH ︒=4， ∴ ⊙O 的半径为4．【点睛】本题考查了切线的判定，平行四边形的性质，矩形的判定和性质，正确的作出辅助线是解题的关键．5、（1）作图见解析；（2 【分析】（1）由于D 点为⊙O 的切点，即可得到OC =OD ，且OD ⊥AB ，则可确定O 点在∠A 的角平分线上，所以应先画出∠A 的角平分线，与BC 的交点即为O 点，再以O 为圆心，OC 为半径画出圆即可；（2）连接CD 和OD ，根据切线长定理，以及圆的基本性质，求出∠DCB 的度数，然后进一步求出∠COD 的度数，并结合三角函数求出OC 的长度，再运用弧长公式求解即可．【详解】解：（1）如图所示，先作∠A 的角平分线，交BC 于O 点，以O 为圆心，OC 为半径画出⊙O 即为所求；（2）如图所示，连接CD 和OD ，由题意，AD 为⊙O 的切线，∵OC⊥AC，且OC为半径，∴AC为⊙O的切线，∴AC=AD，∴∠ACD=∠ADC，∵CD=BD，∴∠B=∠DCB，∵∠ADC=∠B+∠BCD，∴∠ACD=∠ADC=2∠DCB，∵∠ACB=90°，∴∠ACD+∠DCB=90°，即：3∠DCB=90°，∴∠DCB=30°，∵OC=OD，∴∠DCB=∠ODC=30°，∴∠COD=180°-2×30°=120°，∵∠DCB=∠B=30°，∴在Rt△ABC中，∠BAC=60°，∵AO平分∠BAC，∴∠CAO=∠DAO=30°，∴在Rt△ACO中，tan6=∠==OC AC CAO∴CD==．【点睛】本题考查复杂作图-作圆，以及圆的基本性质和切线长定理等，掌握圆的基本性质，切线的性质以及灵活运用三角函数求解是解题关键．。

(必考题)初中数学九年级数学下册第三单元《圆》检测题(答案解析)(3)

一、选择题1．《九章算术》是我国古代数学成就的杰出代表，其中《方田》章给出计算弧田面积所用公式为：弧田面积＝12（弦×矢＋矢2），弧田（如图）是由圆弧和其所对的弦所围成，公式中“弦”指圆弧所对弦长AB ，“矢”等于半径长与圆心O 到弦的距离之差．在如图所示的弧田中，“弦”为8，“矢”为3，则cos ∠OAB ＝（）A ．35B ．2425C ．45D ．12252．如图，A B C D 、、、是O 上的点，180AOD BOC ∠+∠=︒．若2,6AD BC ==，则BOC ∆的面积为（）A ．3B ．6C ．9D ．123．已知△ABC 是半径为2的圆内接三角形，若BC =23，则∠A 的度数（） A ．30° B ．60° C ．120° D ．60°或120° 4．已知⊙O 的半径是一元二次方程2690x x -+=的解，且点O 到直线AB 的距离为2，则⊙O 与直线AB 的位置关系为( )A ．相交B ．相切C ．相离D ．无法确定 5．边长为2的正六边形的边心距为（） A ．1 B ．2 C ．3 D ．23 6．如图，已知⊙O 的直径8CD =，AB 是⊙O 的弦，AB CD ⊥，垂足为M ，2OM =，则AB 的长为（）A．2 B．23C．4 D．437．如图，P是正方形ABCD内的一点，将△ABP绕点B顺时针方向旋转到与△CBP'重合，若PB＝3，则点P经过的路径长度为（）A．23B．32C．32πD．34π8．如图，P是⊙O外一点，射线PA、PB分别切⊙O于点A、点B，CD切⊙O于点E，分别交PA、PB于点D、点C，若PB＝4，则△PCD的周长（）A．4 B．6 C．8 D．109．已知正六边形ABCDEF内接于O，若O的直径为2，则该正六边形的周长是（）A．12B．63C．6D．3310．往直径为26cm的圆柱形容器内装入一些水以后，截面如图所示，若水的最大深度为8cm，则水面AB的宽度为（）A．12cm B．18cm C．20cm D．24cm11．如图，由边长为1的小正方形构成的网格中，点A、B、C都在格点上，以AB为直径的圆经过点C、D，则cos∠ADC的值为（）A．21313B．1313C．31313D．2312．下列说法正确的是（）A．有一组邻边相等的平行四边形是菱形B．平分弦的直径垂直于弦C．两条边对应成比例且有一个内角相等的两个三角形相似D．对角线相等的四边形是矩形二、填空题13．如图，从点P引⊙O的切线PA，PB，切点分别为A，B，DE切⊙O于C，交PA，PB于D，E．若△PDE的周长为20cm，则PA＝______cm．14．如图，AB、CD是O的两条弦，连接AD、BC．若60BAD∠=︒，则BCD∠的度数为______度．15．如图，已知AB为O直径，若CD是O内接正n边形的一边，AD是O内接正()4n+边形的一边，BD AC=，则n=_____．16．如图，已知矩形ABCD中3AB=，4BC=，将三角板的直角顶点P放在矩形内，移动三角板保持两直角边分别经过点B、C，则PD的最小值为________．17．已知扇形的弧长为4π，半径为9，则此扇形的圆心角为_______度．18．如图，已知⊙O 的两条弦AC ，BD 相交于点E ，70A ∠=，50C ∠=，那么tan AEB ∠=___________．19．如图，在边长为2的正六边形ABCDEF 中，P 是ED 的中点，则AP =_______．20．如图，半圆O 的直径12,AB cm =弦6,AC cm AD =平分BAC ∠，则弧BD 的长为__.cm (结果用π表示)三、解答题21．如图，在Rt △ABC 中，∠ACB=90°，点D 在边AC 上，∠DBC=∠BAC ．O 经过A 、B 、D 三点．连接DO 并延长交O 于点E ，连接AE ，DE 与AB 交于点F ．（1）求证：CB 是O 的切线；（2）求证：AB=EB ；（3）若DF=3，EF=7，求BC 的长．22．在下列网格图中，每个小正方形的边长均为1个单位．Rt ABC 中，∠C ＝90°，AC ＝3，BC ＝4（1）试在图中作出ABC 绕A 顺时针方向旋转90°后的图形11AB C △；（2）求1BB 的长．23．如图，AB 为O 的直径，点C 为AB 上方的圆上一动点，过点C 作O 的切线l ，过点A 作直线l 的垂线AD ，交O 于点D ，连接OC ，CD ，BC ，BD ，且BD 与OC 交于点E ．（1）求证：CDE CBE ≅△△；（2）若6AB =，填空：①当CD 的长是________时，OBE △是等腰三角形；②当BC =________时，四边形OADC 为菱形．24．如图，将弧长为6π，圆心角为120°的扇形纸片AOB 围成圆锥形纸帽，使扇形的两条半径OA 与OB 重合（接缝粘连部分忽略不计），求圆锥的底面圆半径及圆锥的侧面积．25．如图，在平面直角坐标系中，正方形网格中每个小正方形的边长是一个单位长度，其中点B 的坐标为()2,1．（1）在平面直角坐标系中画出OAB ∆先向左平移4个单位长度，再向下平移3个单位长度后得到111O A B ∆．并写出点1B 的坐标．（2）在平面直角坐标系中画出OAB ∆绕点O 逆时针旋转90︒得到22OA B ∆，并求出旋转过程中线段OA 所扫过的面积（结果保留π）．26．如图，已知AB 是O 的直径，C ，D 是O 上的点，//OC BD ，交AD 于点E ，连结BC ．（1）求证：AE DE =；（2）若8AB =，30CBD ∠=︒，求图中阴影部分的面积．【参考答案】***试卷处理标记，请不要删除一、选择题1．B解析：B【分析】如图，作射线OH⊥AB于H．交圆弧于C，利用垂径定理以及勾股定理构建方程组求出OA，OH，利用余弦函数定义即可解决问题．【详解】解：如图，作OH⊥AB于H．交圆弧于C，由题意：AB＝8，HC=3，∴OA﹣OH＝3，∵OH⊥AB，OC为半径，∴AH＝BH＝1AB2=4，在Rt△OAH中由勾股定理得AH2＋OH2＝OA2，∴42＝（OA＋OH）（OA﹣OH），∴OA＋OH＝163，∴OA＝256，OH＝76，∴cos∠OAB＝AH424==25OA256，故选：B．【点睛】本题考查垂径定理与勾股定理，三角函数的定义，掌握垂径定理与勾股定理的条件与结论，三角函数的定义是解题关键．2．A解析：A【分析】作出辅助线延长BO 交O 于点E ，连接CE ，由此构建圆心角AOD COE ∠=∠，根据圆周角与弧长和弦长的关系得到2AD CE ==，再据此求出BEC △的面积，经由OB OE =即可求出BCE 的面积.【详解】解：如图延长BO 交O 于点E ，连接CE ，∵B O E 、、三点共线∴180COE BOC ∠+∠=︒，90BCE ∠=︒，∴CE BC ⊥，∵180AOD BOC ∠+∠=︒，∴AOD COE ∠=∠，∴AD CE =，∴2AD CE ==,∵6BC =， ∴1162622S BC CE ==⨯⨯=△BCE ， ∵OB OE =， ∴116322S S ==⨯=△BOC △BEC . 故选A.【点睛】本题主要考查圆心角所对弧、弦的关系，圆周角定理，关键在于作出OB 的延长线OE ，来构造出圆心角相等，以此来解决问题.3．D解析：D首先根据题意画出图形，然后由圆周角定理与含30°角的直角三角形的性质，求得答案．【详解】解：如图，作直径BD，连接CD，则∠BCD=90°，∵△ABC是半径为2的圆内接三角形，BC=23∴BD=4，∴22BD BC-，∴CD=12BD，∴∠CBD=30°，∴∠A=∠D=60°，∴∠A′=180°-∠A=120°，∴∠A的度数为：60°或120°．故选：D．【点睛】此题考查了圆周角定理与含30°角的直角三角形的性质．此题难度适中，注意掌握数形结合思想的应用．4．A解析：A【分析】解方程确定圆的半径为3，圆心距d=2,比较半径与圆心距的大小，根据法则判断即可.【详解】∵2690x x-+=，∴123x x==，∴圆的半径为3，∵点O到直线AB的距离为2，即d=2，∴d＜R，∴直线与圆相交，故选A.【点睛】本题考查了用半径、圆心距判定直线和圆的位置关系，熟练解方程，熟记d，R法则是解题的关键.5．C【分析】正六边形的边长与外接圆的半径相等，构建直角三角形，利用勾股定理即可求出．【详解】解：连接OA ，作OM ⊥AB ，垂足为M ，连接OB ，∵六边形ABCDEF 是正六边形∴△AOB 是等边三角形∴∠AOM =30°，AO =AB∵正六边形ABCDEF 的边长为2，∴AM =12AB =12×2=1，OA =2． ∴正六边形的边心距是OM 2222213OA AM -=-=故选：C ．【点睛】本题考查了正多边形的计算，正多边形的计算常用的方法是转化为直角三角形的计算． 6．D解析：D【分析】连接OB ，根据勾股定理计算BM=3AB=2BM 计算即可．【详解】连接OB ，∵直径8CD =，AB CD ⊥，2OM =∴22OB OM - =2242-=3根据垂径定理，得 AB=2BM=43故选D ．【点睛】本题考查了垂径定理，勾股定理，熟练掌握连接半径构造直角三角形，灵活运用垂径定理和勾股定理求解是解题的关键．7．C解析：C【分析】根据旋转的性质，可得BP′的长，∠PBP′的度数，得到P 点运动轨迹为四分之一圆，圆的半径为3，根据弧长公式即可求解．【详解】由旋转的性质，得BP′=BP=3，∠PBP′=∠ABC=90°，P 点运动轨迹为四分之一圆，圆的半径为3，∴弧PP ' =90331801802n r πππ⨯⨯== 故选C ．【点睛】此题考查旋转的性质、正方形的性质、弧长公式，重点是熟记弧长公式． 8．C解析：C【分析】由切线长定理可求得PA ＝PB ，BC ＝CE ，AD ＝ED ，则可求得答案．【详解】解：∵PA 、PB 分别切⊙O 于点A 、B ，CD 切⊙O 于点E ，∴PA ＝PB ＝4，BC ＝EC ，AD ＝ED ，∴PC+CD+PD ＝PC+CE+DE+PD ＝PC+BC+PD+AD ＝PB+PA ＝4+4＝8，即△PCD 的周长为8，故选：C ．【点睛】本题考查了切线长定理以及三角形的周长，熟练掌握切线长定理是解题的关键； 9．C解析：C【分析】如图，连接OA 、OB ，由正六边形ABCDEF 内接于O 可得∠AOB=60°，即可证明△AOB 是等边三角形，根据O 直径可得OA 的长，进而可得正六边形的周长．【详解】如图，连接OA、OB，∵O的直径为2，∴OA=1，∵正六边形ABCDEF内接于O，∴∠AOB=60°，∵OA=OB，∴△AOB是等边三角形，∴AB=OA=1，∴该正六边形的周长是1×6=6，故选：C．【点睛】本题考查正多边形和圆，正确得出∠AOB=60°是解题关键．10．D解析：D【分析】连接OB，过点O作OC⊥AB于点D，交圆O于点C，由题意可知CD为8，然后根据勾股定理求出BD的长，进而可得出AB的长．【详解】如图，连接OB，过点O作OC⊥AB于点D，交圆O于点C，则AB=2BD，∵圆的直径为26cm，∴圆的半径r=OB=13cm，由题意可知，CD=8cm，∴OD=13-8=5（cm），∴()221692512=-=-=，BD OB OD cm∴AB=24cm，故选：D．【点睛】本题考查了垂径定理的应用，过圆心向弦作垂线构造垂径定理是解题的关键． 11．C解析：C【分析】根据圆周角定理得到ADC ABC ∠=∠，再根据余弦的定义计算即可；【详解】由图可知ADC ABC ∠=∠，在Rt △ABC 中，2AC =，3BC =， ∴223213AB +=∴cos ∠ADC 3313cos 1313BC ABC AB =∠===；故答案选C ．【点睛】本题主要考查了圆周角定理、余弦定理、勾股定理，准确计算是解题的关键． 12．A解析：A【分析】根据菱形的判定定理、垂径定理的推论、相似三角形的判定定理、矩形的判定定理依次对选项进行判断即可．【详解】A ：根据菱形的判定定理可知，有一组邻边相等的平行四边形是菱形，故此选项符合题意；B ：根据垂径定理可知，平分弦的直径不一定垂直于弦，但垂直于弦的直径一定平分这条弦，故此选项不符合题意；C ：根据三角形相似的判定定理可知，两条边对应成比例且夹角相等的两个三角形相似，故此选项不符合题意；D ：对角线相等且平分的四边形是矩形，故此选项不符合题意；故选：A ．【点睛】本题考查矩形、菱形、相似三角形的判定定理及垂径定理的推论，掌握各判定定理是解题的关键．二、填空题13．10【分析】由于PAPBDE 都是⊙O 的切线可根据切线长定理将△PDE 的周长转化为切线PAPB 长的和【详解】解：∵PAPBDE 分别切⊙O 于ABC ∴PA=PBDA=DCEC=EB ；∴C △PDE=PD+D解析：10【分析】由于PA 、PB 、DE 都是⊙O 的切线，可根据切线长定理将△PDE 的周长转化为切线PA 、PB 长的和．【详解】解：∵PA 、PB 、DE 分别切⊙O 于A 、B 、C ，∴PA =PB ，DA =DC ，EC =EB ；∴C △PDE =PD +DE +PE =PD +DA +EB +PE =PA +PB =20；∴PA =PB =10，故答案为10．【点睛】此题主要考查的是切线长定理，能够发现△PDE 的周长和切线PA 、PB 长的关系是解答此题的关键．14．【分析】利用同圆中同弧上的圆周角相等求解即可【详解】∵∴故答案为：60°【点睛】本题考查了圆的基本性质熟练掌握性质并灵活运用是解题的关键解析：【分析】利用同圆中，同弧上的圆周角相等求解即可．【详解】∵BAD ∠=BCD ∠，60BAD ∠=︒∴60BCD ∠=︒，故答案为：60°．【点睛】本题考查了圆的基本性质，熟练掌握性质并灵活运用是解题的关键．15．【分析】连接ODOCBC 根据题意首先证明∠AOD=∠BOC 再根据题意分别用含n 的式子表示出∠AOD 和∠COD 建立关于n 的方程求解即可【详解】如图连接ODOCBC ∵AB 为直径∴∠ADB=∠BCA=90解析：4【分析】连接OD ，OC ，BC ，根据题意首先证明∠AOD=∠BOC ，再根据题意，分别用含n 的式子表示出∠AOD 和∠COD ，建立关于n 的方程求解即可．【详解】如图，连接OD ，OC ，BC ，∵AB 为直径，∴∠ADB=∠BCA=90°，又∵BD AC =，∴Rt △ABD ≌Rt △BAC （HL ），∴AD=BC ，∠AOD=∠BOC ，∵CD 是O 内接正n 边形的一边， ∴360COD n ︒∠=，同理：AD 是O 内接正()4n +边形的一边， ∴3604AOD BOC n ︒∠=∠=+，由180AOD BOC COD ∠+∠+∠=︒，得：36036021804n n︒︒⨯+=︒+，解得：4n =，或2n =-（不符合题意，舍去）经检验，4n =是原分式方程的解，故答案为：4．【点睛】本题主要考查了正多边形与圆，理解正多边形与圆的关系是解题关键．16．【分析】点P 的运动轨迹是以BC 为直径在矩形内的半圆圆心在线段BC 的中点处连接圆心和点D 交半圆于点P 则此时PD 最短利用勾股定理求出OD 的长再减去OP 的长即可【详解】由题意可得：点P 的运动轨迹是以BC 为 132【分析】点P的运动轨迹是以BC为直径，在矩形内的半圆，圆心在线段BC的中点处，连接圆心和点D，交半圆于点P，则此时PD最短，利用勾股定理求出OD的长，再减去OP的长即可【详解】由题意可得：点P的运动轨迹是以BC为直径，在矩形内的半圆，圆心在线段BC的中点处，设圆心为点O，如图：连接OD，交半圆与点P，则此时PD最短，4BC=∴圆的半径122OP OC BC===3AB DC==在Rt DCO中22222313OD DC OC+=+132PD OD OP∴=-=132．【点睛】本题考查了最值问题，矩形的性质，勾股定理，解题关键是能准确分析出点P的运动轨迹．17．80【分析】设此扇形的圆心角为x°代入弧长公式计算得到答案【详解】解：设此扇形的圆心角为x°由题意得解得x=80故答案为：80【点睛】本题考查的是弧长的计算掌握弧长的公式是解题的关键解析：80【分析】设此扇形的圆心角为x°，代入弧长公式计算，得到答案．【详解】解：设此扇形的圆心角为x°，由题意得，94 180xππ=，解得，x=80，故答案为：80．【点睛】本题考查的是弧长的计算，掌握弧长的公式180n r l π=是解题的关键． 18．【分析】求出∠AEB 的度数再求三角函数值即可【详解】解：∵∠B=∠C=50°∠A=70°∴∠AEB=180°-∠A-∠B=60°故答案为：【点睛】本题考查了圆周角的性质三角形内角和特殊角的三角函数值解析：3【分析】求出∠AEB 的度数，再求三角函数值即可．【详解】解：∵∠B=∠C=50°，∠A=70°，∴∠AEB=180°-∠A-∠B=60°，tan tan 603AEB ∠=︒=，故答案为：3．【点睛】本题考查了圆周角的性质，三角形内角和，特殊角的三角函数值，解题关键是灵活运用圆中角的关系，把已知条件集中在一个三角形中求角．19．【分析】连接AE 过点F 作FH ⊥AE 根据正六边形的内角和得出∠AFE ＝∠DEF ＝120°再根据等腰三角形的性质可得∠FAE ＝∠FEA ＝30°得出∠AEP ＝90°由直角三角形的性质和勾股定理求得FHAE解析：13【分析】连接AE ，过点F 作FH ⊥AE ，根据正六边形的内角和得出∠AFE ＝∠DEF ＝120°，再根据等腰三角形的性质可得∠FAE ＝∠FEA ＝30°，得出∠AEP ＝90°，由直角三角形的性质和勾股定理求得FH ，AE ，再利用勾股定理即可得出AP ．【详解】解：如图，连接AE ，过点F 作FH ⊥AE ，∵六边形ABCDEF 是正六边形，∴AB ＝BC ＝CD ＝DE ＝EF ＝AF ＝2，∠AFE ＝∠DEF ＝120°，∴∠FAE ＝∠FEA ＝30°，∴∠AEP ＝90°，∴FH ＝12AF ＝1， ∴AH ＝223AF FH -=，∴AE ＝2AH ＝23，∵P 是ED 的中点，∴EP ＝12DE ＝1， ∴AP ＝2212113AE EP +=+=．故答案为：13．【点睛】本题考查了正多边形、勾股定理及等腰三角形的性质等知识，掌握相关图形的性质并作辅助线构造出直角三角形是解题的关键．20．【分析】连接OCOD 可求得即△OAC 为等边三角形再根据角平分线的定义求得∠BAD=30°根据圆周角定理求得∠BOD=60°最后根据弧长公式计算即可【详解】解：如图连接OCOD ∵∴∴△OAC 为等边三角解析：2π【分析】连接OC ，OD ，可求得6AO OC AC cm ===，即△OAC 为等边三角形，再根据角平分线的定义求得∠BAD=30°，根据圆周角定理求得∠BOD=60°，最后根据弧长公式计算即可．【详解】解：如图，连接OC ，OD ，∵12,AB cm =6AC cm =，∴6OB AO OC AC cm ====，∴△OAC 为等边三角形，∠CAO=60°，∵AD 平分BAC ∠，∴1302BAD CAO ∠=∠=︒， ∴260BOD BAD ∠=∠=︒， ∴弧BD 的长=6062180ππ⋅=．故答案为：2π．【点睛】本题考查圆周角定理，等边三角形的性质和判定，弧长的计算．正确作出辅助线，得出△OAC为等边三角形，从而由边的关系求出角度是解题关键．三、解答题21．（1）见解析；（2）见解析；（3）57【分析】（1）连接OB，在⊙O中，由等腰三角形的性质∠ODB=∠OBD，由圆周角的性质得到∠DBC=∠BED，根据圆的切线的判定定理即可得结论；（2）由圆周角定理∠ABD=∠AED，根据平行线的判定定理得到AE∥BC，得到∠ABC=∠BAE，进而得到∠BEA=∠BAE，根据等腰三角形的判定即可证得结论；（3）延长BO交AE于H，由矩形的判定证得四边形ACBH是矩形，由垂径定理得到BC=AH=12AE，由已知可得直径DE=10，可得DO=EO=5，进而求出OF=2，根据相似三角形的判定的性质可求得AD，根据勾股定理求得AE，即可求得结果．【详解】（1）证明：连接OB=OA，在⊙O中，OB=OD，∠BAC=∠BED，∴∠ODB=∠OBD，∵∠DBC=∠BAC，∴∠DBC=∠BED，∵DE是⊙O的直径，∴∠DBE=90°，∴∠ODB+∠BED=90°，∴∠OBD+∠DBC=90°，∴OB⊥BC，∵OB是⊙O的半径，∴CB是⊙O的切线；（2）证明：在⊙O中，∠ABD=∠AED，由（1）得：∠DBC=∠BED，∴∠ABD+∠DBC=∠AED+∠BED，∴∠ABC=∠BEA，∵DE是⊙O的直径，∴∠EAC=90°，∵∠ACB=90°，∴∠EAC+∠ACB=180°，∴AE ∥BC ，∴∠ABC=∠BAE ，∴∠BEA=∠BAE ，∴AB=EB ；（3）解：延长BO 交AE 于H ，由∠HAC=∠ACB=∠OBC=90°，得四边形ACBH 是矩形，∴OH ⊥AE ，∴BC=AH=12AE ， ∵DF=3，EF=7，∴直径DE=10，即半径DO=EO=5，∴OF=2，∵OB ∥AC ，∴△OBF ~△DAF ， ∴OF OB DF AD =，即253AD=， ∴AD =152， ∴在Rt △ADE 中，AE 2257-DE AD =， ∴BC =AH =12AE 57= 【点睛】本题考查了切线的判定，相似三角形的判定和性质，平行线的判定和性质，勾股定理，矩形的判定和性质，正确的作出辅助线是解题的关键．22．（1）见解析；（2）52π．【分析】（1）根据△ABC 绕A 顺时针方向旋转90°，即可得到△AB 1C 1；（2）根据弧长计算公式，即可得出点B 运动路径的长．【详解】解：（1）如图所示，△AB 1C 1即为所求；（2）Rt ABC 中，∠C ＝90°，AC ＝3，BC ＝4 ∴2222AB AC BC 345=++=又∠BAB 1=90°，∴点B 的运动路径的长为：90551802ππ⨯=．【点睛】本题考查了利用旋转变换作图，熟练掌握网格结构准确找出对应点的位置是解题的关键． 23．（1）见解析；（2）①34π；②3【分析】（1）根据题意可证//OC AD ，OC BD ⊥，再结合垂径定理即可证明（2）①根据等腰三角形的性质，结合（1）得CD CB =根据等弦对等弧得CD BC =，再根据弧长公式求解即可；②根据菱形的性质即可求解【详解】解：（1）∵过点C 作O 的切线l ， ∴OC l ⊥，∵AD l ⊥，∴//OC AD ，∵AB 为O 的直径，点D 为AB 上方的圆上一点， ∴AD BD ⊥，∴BD OC ⊥90CED CEB ∴∠=∠=︒，∴点E 为BD 中点，∴BE DE =，∴在CDE △和CEB △中DB BE CED CEB CE CE =⎧⎪∠=∠⎨⎪=⎩∴()CDE CBE SAS ≅；（2）①若OBE △为等腰三角形，OC BD ⊥ ∴OBE △为等腰直角三角形∴45EOB EBO ∠=∠=︒CDE CBE ≅△△CD CB ∴=CD BC ∴=6345331801804AB OB n r BC πππ=∴=⨯∴=== 34CD π∴= ∴当34CD π=时OBE △为等腰三角形 ②若四边形OADC 为菱形132AO OC CD DA AB ∴===== CD BC =3BC ∴=∴当3BC =时OADC 为菱形【点睛】本题考查了切线的性质定理，平行线的判定，全等三角形的判定，等腰三角形的性质，菱形的性质，熟练掌握以上性质和定理是解题关键．24．圆锥的底面圆半径为3；圆锥的侧面积为27π．【分析】直接利用圆的周长公式即可求出圆的半径长，根据扇形的面积公式即可求出圆锥的侧面展开图的面积；【详解】设圆锥的底面圆的半径为r ，则2π6πr =，解得3r =，设扇形AOB 的半径为R ，则120π6π180R ⋅⋅=，解得9R =，∴圆锥的侧面积16π927π2=⨯⨯=．【点睛】本题考查了圆锥的展开图问题，正确以及圆的周长公式以及扇形面积公式是解题的关键； 25．（1）见详解；（2）134π，图形见详解【分析】（1）分别画出OAB ∆各个顶点的对应点，再顺次连接起来，即可；（2）分别画出OAB ∆各个顶点绕点O 逆时针旋转90︒后的对应点，再顺次连接起来，最后利用扇形的面积公式，即可求解．【详解】（1）111O A B ∆如图所示，点1B 的坐标为（-2，-2），（2）22OA B ∆如图所示，∵OA=2223=13+，∴线段OA 所扫过的面积=()29013360π⨯=134π，【点睛】本题主要考查平移和旋转变换以及扇形的面积公式，掌握扇形的面积公式，是解题的关键．26．（1）见解析；（2）16433π-【分析】（1）根据平行线的性质得出∠AEO=90°，再利用垂径定理证明即可．（2）根据S 阴=S 扇形OAD -S △ADO 计算即可．【详解】证明：（1）AB 是O 的直径，90ADB ∴∠=︒，//OC BD ，90AEO ADB ∴∠=∠=︒，即OC AD ⊥，AE DE ∴=；（2）连接CD ，OD ，//OC BD ，30OCB CBD ∴∠=∠=︒，OC OB =，30OCB OBC60AOC OCB OBC ∴∠=∠+∠=︒，260COD CBD ∠=∠=︒，120AOD ∴∠=︒，在直角三角形AOE 中，AO =4，∠BAD =30°，∴OE =2，AE 23=，∴43AD =，212041164324336023ADO OAD S S S ππ∆⋅⋅∴=-=-⨯⨯=-阴扇形．【点睛】本题考查扇形的面积公式，垂径定理，圆周角定理等知识，解题的关键是熟练掌握基本知识，属于中考常考题型．。

圆的基本性质单元测试卷(标准难度)(含答案)

浙教版初中数学九年级上册第三单元《圆的基本性质》单元测试卷考试范围：第三章；考试时间：120分钟；总分：120分学校:___________姓名：___________班级：___________考号：___________第I卷（选择题）一、选择题（本大题共12小题，共36分。

在每小题列出的选项中，选出符合题目的一项）1.若正多边形的内角和是540°，则该正多边形的一个外角为( )A. 45°B. 60°C. 72°D. 90°2.如图，已知BC是⊙O的直径，半径OA⊥BC，点D在劣弧AC上(不与点A，点C重合)，BD与OA交于点E.设∠AED=α，∠AOD=β，则( )A. 3α+β=180°B. 2α+β=180°C. 3α−β=90°D. 2α−β=90°3.如图，AB是半圆O的直径，以弦AC为折痕折叠AC⏜后，恰好经过点O，则∠AOC等于( )A. 120°B. 125°C. 130°D. 145°4.如图，在Rt△ABC中，∠ACB=90∘，∠A=60∘，AC=6，将△ABC绕点C按逆时针方向旋转得到△A′B′C，此时点A′恰好在AB边上，则点B′与点B之间的距离为( )A. 12B. 6C. 6√2D. 6√35. 在平面直角坐标系中，把点A(3,4)绕原点逆时针旋转90°，得到点B ，则点B 的坐标为( )A. (4,−3)B. (−4,3)C. (−3,4)D. (−3,−4)6. 如图，在⊙O 中，弦AB//CD ，OP ⊥CD ，OM =MN ，AB =18，CD =12，则⊙O 的半径为( )A. 4B. 4√2C. 4√6D. 4√37. 如图，将⊙O 沿AB 折叠后，圆弧恰好经过圆心，则AMB ⌢所对的圆心角等于( )A. 60°B. 90°C. 120°D. 150°8. 如图，在△ABC 中，∠C =90°，DE ⏜的度数为α，以点C 为圆心，BC 长为半径的圆交AB 于点D ，交AC 于点E ，则∠A 的度数为( )A. 45∘−12αB. 12αC. 45∘+12αD. 25∘+12α9. 如图，⊙O 是△ABC 的外接圆，∠BAC =60°，若⊙O 的半径OC 为2，则弦BC 的长为( ) A. 1B. √3C. 2D. 2√310.如图，四边形ABCD是半圆的内接四边形，AB是直径，DC⏜=CB⏜.若∠C=110°，则∠ABC的度数等于( )A. 55°B. 60°C. 65°D. 70°11.如上图，四边形ABCD是半圆的内接四边形，AB是直径，DC⌢=CB⌢.若∠C=110∘，则∠ABC的度数等于( )A. 55∘B. 60∘C. 65∘D. 70∘12.如图，在3×4的方格中，每个小方格都是边长为1的正方形，O，A，B分别是小正方形的顶点，则AB⏜的长度为( )A. πB. √2πC. 2πD. 4π第II卷（非选择题）二、填空题（本大题共4小题，共12分）13.根据“不在同一直线上的三点确定一个圆”，可以判断平面直角坐标系内的三个点A(3,0)、B(0,−4)、C(2,−3)______确定一个圆(填“能”或“不能”)．14.如图，在⊙A中，弦DE=6，∠BAC+∠EAD=180°，则点A到弦BC的距离等于_________．15.如图，四边形ABCD内接于⊙O，F是CD⏜上一点，且DF⏜=BC⏜，连接CF并延长交AD的延长线于点E，连接AC.若∠ABC=105∘，∠BAC=25∘，则∠E的度数为．16.如图，点A，B，C在⊙O上，四边形OABC是平行四边形，若对角线AC=2√3，则AC⏜的长为______．三、解答题（本大题共9小题，共72分。

人教版九年级上册数学《圆》单元综合检测题(带答案)

20.如图，点A，B，C，D在⊙O上，连结AB，CD，BD，若AB=CD．求证：∠ABD=∠CDB．
21.已知：如图，在中，，以为直径的交于点，过点作于点．求证：是的切线．
四、综合题（共6题；共56分）
22.已知在△ABC中，AB=AC，以AB为直径的⊙O分别交AC于D，BC于E，连接ED．
∴点P在圆外．
故选C．
【点睛】考查的是点与圆的位置关系，熟知设⊙O的半径为r，点P到圆心的距离OP=d，当d＜r时，点P在圆内是解答此题的关键．
3.如图，已知圆心角∠AOB=118°，则圆周角∠ACB=( )
A.59°B.118°C.121°D.125°
【答案】C
【解析】
【分析】
根据圆周角定理进行求解．一条弧所对的圆周角等于它所对的圆心角的一半．
A.3分米B.4分米C.5分米D.10分米
二、填空题（共6题；共6分）
13.如图，小明做实验时发现，当三角板中30°角的顶点A在⊙O上移动，三角板的两边与⊙O相交于点P、Q时，的长度不变．若⊙O的半径为9，则长为________.
14.如图，△ABC内接于⊙O，∠ACB=90°，∠ACB的角平分线交⊙O于D．若AC=6，BD=5 ，则BC的长为_____．
【答案】D
【解析】
【分析】
利用圆内接四边形的对角互补判断即可．
【详解】∵四边形ABCD内接于⊙O，
∴∠A+∠C=180°=∠B+∠D，
故选D．
【点睛】考查了圆内接四边形的性质，关键是根据内接四边形的对角互补的性质解答．
5.如图，Rt△ABC中，∠ACB=90°，CA=CB=2，以AB的中点D为圆心DC为半径，作圆心角为90°的扇形DEF，则图中阴影部分的面积为（）

浙教版九年级数学上册第三章《圆》单元测试卷(含答案)

浙教版九年级数学上册第三章《圆》单元测试卷（含答案）一选择题（每小题3分，共30分）1.下列命题中，假命题是（）A.两条弧的长度相等，它们是等弧B.等弧所对的圆周角相等C.直径所对的圆周角是直角D.一条弧所对的圆心角等于它所对圆周角的2倍.2．若圆的一条弦把圆分成度数的比为1 ：3的两段弧，则劣弧所对的圆周角等于（）A.45 °B.90°C.135°D.270°3.已知正六边形的周长是，则该正六边形的半径是（） A .6a B. 4a C. 2a D.4.如图1，圆与圆的位置关系是（）A.外离 B 相切 C.相交 D.内含图1 图25. 如图2，⊙A,⊙B,⊙C,⊙D,⊙E 的半径都是1，顺次连结这些圆心得到五边形ABCDE ，则图中的阴影部分面积之和为（）A. B. 32π C.2 D.52πππ6.过⊙O 内一点N 的最长弦为6，最短的弦长为4，那么ON 的长为（）7．若正三角形、正方形、正六边形的周长相等，它们的面积分别是，则下列关系成立的是（）A ．123S S S == B.123S S S <<C ． 123S S S >> D.231S S S >>8.平行四边形的四个顶点在同一个圆上，则该平行四边形一定是（）A.正方形 B 菱形 C.矩形 D.等腰梯形9.在半径等于的圆内有长为的弦，则此弦所对的圆周角为（）A.120° B .30°或120° C.60° D.60°或120°10.已知⊙O1、⊙O2、⊙O3两两外切，且半径分别为、、，则⊙O1 O2 O3的形状是（）A 锐角三角形 B.直角三角形 C 钝角三角形 D.等腰直角三角形.二、填空题（每小题3分，共30分）11.如图3，已知AB 为⊙O 的直径，，垂足为E ，由图你还能知道哪些正确的结论？请把它们一一写出来._____________.图3 图4 图5⊥D为垂足,且OD=10,则OD BC12.如图4，AB是⊙O的直径，C为圆上一点∠A=60°,,AB=_______,BC=_______.13.如图5,已知⊙O中,弧AB=弧BC,且弧AB：弧AMC=3:4,则______.14.如图6,在条件:①;②AC=AD=OA;③点E分别是AO、CD的中点；④，且中，能推出四边形OCAD是菱形的条件有_______个.图6 图715.为了改善市区人民的生活环境,某市建设污水管网工程,某圆柱型水管的直径为100cm,截面如图7所示,若管内的污水的面宽60=,则污水的最大深度为______.AB cm16. ⊙O的直径为11cm,圆心到一直线的距离为5cm,那么这条直线和圆的位置关系是_______;若圆心到一直线的距离为5.5cm,那么这条直线和圆的位置关系是_______;17. 若两圆相切,圆心距为8cm,其中一个圆的半径为12cm,则另一个圆的半径为_____.18.正五边形的一个中心角的度数是________,19.已知⊙O1和⊙O2的半径分别为2和3,如果它们既不相交又不相切,那么它们的圆心距d的取值范围是________.20.已知在同一平面内圆锥两母线在顶点处最大的夹角为,母线长为8,则圆锥的侧面积为______.三.解答题（共60分）21.（6分）如图8,已知中ABC,,AC=3,BC=4,已点C为圆心作⊙C,半径为.(1) 当取什么值时,点A、B在⊙C外？(2）当取什么值时,点A在⊙C内，点B在⊙C外？图822.（6分）如图9，两个同心圆，作一直线交大圆于A、B，交小圆于C、D，AC与BD有何关系？请说明理由.图923.（6分）如图10，PA、PB是⊙O的两条切线，A、B是切点，AC是⊙O的直径，∠BAC=35°，求∠p的度数.图1024.（8分）如图11，P是⊙O的直径AB上的一点，PC AB，PC交⊙O于C，∠OCP的平分线交⊙O于D，当点P在半径OA（不包括O点和A点）上移动时，试探究弧AD与弧BD的大小关系.图1125.（8分）.如图12，⊙O的半径OA=5，点C是弦AB上的一点，且OC AB，OC=BC.求AB 的长.图1226.（8分）如图13，⊙O的直径AB和弦CD相交于点E，已知AE=1，EB=5，∠DEB=60°，求CD的长.图1327.（8分）现有边长为a的正方形花布，问怎样剪裁，才能得到一个面积最大的正八边形花布来做一个形状为正八边形的风筝？28（10分）如图14，已知一底面半径为r，母线长为3r的圆锥，在地面圆周上有一蚂蚁位于A点，它从A点出发沿圆锥面爬行一周后又回到原出发点，请你给它指出一条爬行最短的路径，并求出最短路径的长.图14.备用题1.如图1，ABC中，AB=AC，BD是∠ABC的平分线，A、B、D三点的圆与BC相交于点E，你认为AD=CE吗？如果不能，请举反例；如果AD=CE，请说明理由.图12.如图2，在直角梯形ABCD中，AB∥CD，以AD为直径的圆切BC于E，谅解OB、OC，试探究OB与OC有何位置关系？图2答案一.1A 2A 3C 4A 5B 6C 7B 8C 9D 10B二.11.CE=DE ， AC AD =， BCBD =；12.40，13.144 ； 14. 4；15. 90；16.相交、相切；17. 4cm 或16cm ；18.72°； 19.5d >或01d ≤<； 20.32.π三.21，r< 3， 3<r<4；22. AC=BD. 理由：作OE AB ⊥于E ，（如图1）由垂径定理得AE=BE ，CE=DE ，所以AE-CE=BE-DE ，即AC=BD.（图1）图223. 因为∠BAC=35°，所以∠AOB=180°-35°×2=110°，因为PA 、PB 是的切线，所以∠PA0=∠PBO=90°，所以∠P=360°-∠PA0-∠PBO-∠AOB=70°.24.AD BD =.理由如图2，延长CP 交于E ，延长CO 交于F ，因为∠PCD=∠FCD，所以 DEDF = 因为直径AB CE ⊥，所以 AE AC= 因为 ∠A0C=∠BOF，所以 AC BF=，所以AE BF = ，所以 AE DE BF DF +=+，即 AD BD =.25. 因为OC AB ⊥，所以AC=BC ，又OC=BC ，所以OC=AC=BC设OC=AC=BC=，在Rt AOC 中，2225x x +=解得x =2AB x ==.26.作OF CD ⊥于F ，（如图3）则CF=EF ，连结DO ，在Rt OEF 中，∠OEF=∠DEB=60°，∠EOF=30°OE=OA-AE=13122AB AE -=-=，112122EF OE ==⨯=，所以,OF ===,所以DF ===所以2CD DF ==图3 图4 图527.如图4，将正方形花布的四个角各截去一个全等的直角三角形，设 DF=GC=，则 ,EF = 因为，EF=FG 2a x =-，解得x =的等腰直角三角形.28.圆锥的侧面展开图如图5所示，则线段的长为最短路径设扇形的圆心角为，则32180n r r ππ⋅=，解得120n =作，OC AA ⊥，60AOC ∠= ，30AOC ∠=因为OA=3r 所以32OC r =，由勾股定理求得AC =，所以AA =，即蚂蚁从A 点出发沿圆锥面爬行一周后又回到原出发点的最短路径长为.备用题.1.连结DE ，（如图6）因为BD 是ABC ∠的平分线，所以ABD EBD ∠=∠，所以AD=DE ，因为AB=AC ，所以ABC C ∠=∠，因为CDE ABC∠=∠所以C CDE ∠=∠，所以CE=DE ，所以AD=CE.图6 如图72. 连结OE ，（如图7）由切线性质及切线长定理可得：Rt AOB Rt EOB ≅ ， Rt COD Rt COE≅ 所以,AOB EOB COD COE∠=∠∠=∠ 所以111809022BOE COE AOD ∠+∠=∠=⨯=∠= ，所以OB OCBOC即90⊥.。

第3章圆的基本性质单元测试卷（含解析）

第三章圆的基本性质单元测试卷一．选择题（共10小题，满分20分，每小题2分）1．如图，四边形ABCD是⊙O的内接四边形，若∠B=80°，则∠ADC的度数是（）A．60°B．80°C．90°D．100°2．如图，等边△ABC内接于⊙O，动点P在劣弧AB上，且不与A、B重合，则∠BPC等于（）A．30°B．45°C．60 D．90°3．如图，张三同学把一个直角边长分别为3cm，4cm的直角三角形硬纸板，在桌面上翻滚（顺时针方向），顶点A的位置变化为A1⇒A2⇒A3，其中第二次翻滚时被桌面上一小木块挡住，使纸板一边A2C1与桌面所成的角恰好等于∠BAC，则A翻滚到A2位置时共走过的路程为（）A．8cm B．8πcm C．2cm D．4πcm4．用圆心角为60°，半径为24cm的扇形做成一个圆锥的侧面，那么这个圆锥底面的半径是（）A．4πcm B．8πcm C．4cm D．8cm5．已知点P是半径为5的⊙O内的一个定点，且OP=3，则过点P的所有弦中，弦长为整数的弦共有多少条（）A．2条B．3条C．4条D．5条6．如图，一个长方体盒子，BC=CD=8，AB=4，则沿盒子表面从A点到D点的最短路程是（）A．4B．4+4C．4+8 D．47．如图，点P在以AB为直径的半圆内，连接AP、BP，并延长分别交半圆于点C、D，连接AD、BC并延长交于点F，作直线PF，下列说法一定正确的是（）①AC垂直平分BF；②AC平分∠BAF；③FP⊥AB；④BD⊥AF．A．①③B．①④C．②④D．③④8．一个扇形的弧长是10πcm，面积是60πcm2，则此扇形的圆心角的度数是（）A．300°B．150°C．120°D．75°9．如图，AB是⊙O的直径，点C在⊙O上，弦BD平分∠ABC，则下列结论错误的是（）A．AD=DC B．C．∠ADB=∠ACB D．∠DAB=∠CBA10．如图，AB为⊙O的直径，作弦CD⊥AB，∠OCD的平分线交⊙O于点P，当点C在下半圆上移动时，（不与点A、B重合），下列关于点P描述正确的是（）A．到CD的距离保持不变B．到D点距离保持不变C．等分D．位置不变二．填空题（共10小题，满分30分，每小题3分）11．如图，点O是∠EPF的平分线上一点，⊙O和∠EPF的两边分别交于点A、B 和C、D，根据上述条件，可以推出．（要求：填写一个你认为正确的结论即可，不再标注其他字母，不写推理过程）12．把球放在长方体纸盒内，球的一部分露出盒外，其截面如图所示，已知EF=CD=4cm，则球的半径为cm．13．如图，以G（0，1）为圆心，半径为2的圆与x轴交于A、B两点，与y轴交于C，D两点，点E为⊙O上一动点，CF⊥AE于F，则弦AB的长度为；当点E在⊙O的运动过程中，线段FG的长度的最小值为．14．如图，已知A、C是半径为2的⊙O上的两动点，以AC为直角边在⊙O内作等腰Rt△ABC，∠C=90°．连接OB．则OB的最小值为．15．如图，在边长为1的小正方形网格中，△ABC的三个顶点都在格点上，将△ABC绕点B逆时针旋转90°得到△A′B′C′，则图中阴影部分图形的面积为．（结果保留π）．16．如图所示的扇形是一个圆锥的侧面展开图，若∠AOB=120°，弧AB的长为6πcm，则该圆锥的侧面积为．17．如图，矩形木块ABCD放置在直线L上，将其向右作无滑动的翻滚，直到被正方形PQRS挡住为止，已知AB=3，BC=4，BP=16，正方形木块PQRS边长为2，则点D经过的路线长为．18．如图，已知在扇形OAB中，∠AOB=90°，半径OA=10，正方形FCDE的四个顶点分别在和半径OA、OB上，则CD的长为．19．A、B两点在数轴上，点A所表示的实数是﹣3，⊙A的半径为2，⊙B的半径为3，若⊙B与⊙A相切，则点B所表示的实数是．20．如图，⊙O的直径AB为10cm，弦AC为6cm，∠ACB的平分线交AB于E，交⊙O于D．则弦AD的长是cm．三．解答题（共6小题，满分50分）21．（6分）如图，⊙O的直径EF为10cm，弦AB、CD分别为6cm、8cm，且AB ∥EF∥CD．求图中阴影部分面积之和．22．（8分）如图，AB是⊙O的直径，C是的中点，CE⊥AB，垂足为E，BD交CE于点F．（1）求证：CF=BF；（2）若AD=2，⊙O的半径为4，求BC的长．23．（8分）有一石拱桥的桥拱是圆弧形，如下图所示，正常水位下水面宽AB=60m，水面到拱项距离CD=18m，当洪水泛滥时，水面宽MN=32m时，高度为5m的船是否能通过该桥？请说明理由．24．（8分）如图，点A是半圆上的一个三等分点，点B是弧AN的中点，点P是直径MN上一个动点，圆O的半径为1，（1）找出当AP+BP能得到最小值时，点P的位置，并证明（2）求出AP+BP最小值．25．（8分）如图，AB为⊙O的直径，CD⊥AB于E，CO⊥AB于F，求证：AD=CD．26．（12分）已知AB是⊙O的直径，弦CD⊥AB于H，过CD延长线上一点E作⊙O的切线交AB的延长线于F，切点为G，连接AG交CD于K．（1）如图1，求证：KE=GE；（2）如图2，连接CABG，若∠FGB=∠ACH，求证：CA∥FE；（3）如图3，在（2）的条件下，连接CG交AB于点N，若sinE=，AK=，求CN的长．参考答案与试题解析一．选择题（共10小题，满分20分，每小题2分）1．解：∵四边形ABCD是⊙O的内接四边形，∴∠B+∠ADC=180°，又∠B=80°，∴∠ADC=100°，故选：D．2．解：∵△ABC为正三角形，∴∠A=60°，∴∠BPC=∠A=60°．故选：C．3．解：根据题意得：=4πcm，故选：D．4．解：根据扇形的弧长公式l===8π，设底面圆的半径是r，则8π=2πr∴r=4cm，这个圆锥底面的半径是4cm．故选：C．5．解：如图，过P作弦AB⊥OP，交⊙O于A、B，连接OA；Rt△OAP中，OP=3，OA=5；根据勾股定理，得AP=4；∴AB=2AP=8；故过点P的弦的长度都在8～10之间；因此弦长为8、9、10；当弦长为8、10时，过P点的弦分别为弦AB和过P点的直径，分别有一条；当弦长为9时，根据圆的对称性知，符合条件的弦应该有两条；故弦长为整数的弦共有4条．故选：C．6．解：如图，把正面和左面展开，形成一个平面，AD两点之间线段最短．即AD===4（cm）；如图，把正上面和上面展开，形成一个平面，AD两点之间线段最短．即AD===4（cm）．如图，把右面和上面展开，形成一个平面，AD两点之间线段最短．AD===4（cm），故从A点到D点的最短路程为：4cm．故选：D．7．证明：①∵AB为直径，∴∠ACB=90°，∴AC垂直BF，但不能得出AC平分BF，故①错误，②如图1，连结CD，∵AB为直径，∴∠ADB=90°，∴∠BDF=90°，假设AC平分∠BAF成立，则有DC=BC，∴在RT△FDB中，DC=BC=FC，∴AC⊥BF，且平分BF，∴AC垂直BF，但不能得出AC平分BF，与①中的AC垂直BF，但不能得出AC平分BF相矛盾，故②错误，③如图2：∵AB为直径，∴∠ACB=90°，∠ADB=90°，∴D、P、C、F四点共圆，∴∠CFP和∠CDB都对应，∴∠CFP=∠CDB，∵∠CDB=∠CAB，∴∠CFP=∠CAB，又∵∠FPC=∠APM，∴△AMP∽△FCP，∠ACF=90°，∴∠AMP=90°，∴FP⊥AB，故③正确，④∵AB为直径，∴∠ADB=90°，∴BD⊥AF．故④正确，综上所述只有③④正确．故选：D．8．解：∵一个扇形的弧长是10πcm，面积是60πcm2，∴S=Rl，即60π=×R×10π，解得：R=12，∴S=60π=，解得：n=150°，故选：B．9．解：∵弦BD平分∠ABC，∴∠DBC=∠ABD，∴=，AD=DC，故A、B正确；∵AB是⊙O的直径，∴∠ADB=∠ACB=90°，故C正确；∵无法确定∠DAB=∠CBA，故D错误，符合题意．故选：D．10．解：不发生变化．连接OP，∵OP=OC，∴∠P=∠OCP，∵∠OCP=∠DCP，∴∠P=∠DCP，∴CD∥OP，∵CD⊥AB，∴OP⊥AB，∴=，∴点P为的中点不变．故选：D．二．填空题（共10小题，满分30分，每小题3分）11．解：如图：作OM⊥AB，交AB于点M，ON⊥CD，交CD于点N，点O是∠EPF的平分线上一点，∴OM=ON，根据在同圆中两弦的弦心距相等，则弦长相等，知，AB=CD，故弧AB=弧CD．12．解：EF的中点M，作MN⊥AD于点M，取MN上的球心O，连接OF，∵四边形ABCD是矩形，∴∠C=∠D=90°，∴四边形CDMN是矩形，∴MN=CD=4，设OF=x，则ON=OF，∴OM=MN﹣ON=4﹣x，MF=2，在直角三角形OMF中，OM2+MF2=OF2即：（4﹣x）2+22=x2解得：x=2.5故答案为：2.513．解：作GM⊥AC于M，连接AG．∵GO⊥AB，∴OA=OB，在Rt△AGO中，∵AG=2，OG=1，∴AG=2OG，OA==，∴∠GAO=30°，AB=2AO=2，∴∠AGO=60°，∵GC=GA，∴∠GCA=∠GAC，∵∠AGO=∠GCA+∠GAC，∴∠GCA=∠GAC=30°，∴AC=2OA=2，MG=CG=1，∵∠AFC=90°，∴点F在以AC为直径的⊙M上，当点F在MG的延长线上时，FG的长最小，最小值=FM﹣GM=﹣1．故答案为2，﹣1．14．解：如图，作等腰直角三角形△OCO′，CO=CO′，∠OCO′=90°，∵AC=CB，∠ACB=∠OCO′，∴△ACO≌△BCO′，∴OA=O′B，∴当点C固定时，点B在以O′为圆心OA为半径的圆上运动，∴当O、B、O′共线时，OB的值最小，最小值=OO′﹣O′B=2﹣2．故答案为2﹣2．15．解：根据旋转的性质和勾股定理得到：A′B2=AB2=22+32=13．S阴影=﹣×2×3=．故答案是：．16．解：由题意得，=6π，解得，OA=9，∴该圆锥的侧面积=×6π×9=27π（cm2），故答案为：27πcm2．17．解：第一次旋转是以点C为圆心，CD为半径，旋转角度是90度，所以弧长==1.5π；第二次旋转是以点D为圆心，所以没有路程；第三次旋转是以点A为圆心，AD为半径，角度是90度，所以弧长==2π；第四次是以点B为圆心，BD为半径，角度是30度，所以弧长==π；所以点D经过的路线长=1.5π+2π+π=π．故答案为：π．18．解：过点O作OH⊥CF于点H，交DE于点K，连接OF，∵OH过圆心，∴CH=HF，∵四边形FCDE是正方形，∴OH⊥DE，DK=EK，∴△OEK是等腰直角三角形，OK=EK，设CD=x，则HK=x，HF=OK=EK=，在Rt△OHF中，OH2+HF2=OF2，即（x+）2+（）2=102，解得x=2．即CD的长为2．故答案为：2．19．解：设数轴上点B所表示的实数是b，如果⊙B与⊙A外切，则|b﹣（﹣3）|=2+3，即|b+3|=5，解得b=2或﹣8；如果⊙B与⊙A内切，则|b﹣（﹣3）|=3﹣2，即|b+3|=1，解得b=﹣2或﹣4．故答案为2或﹣8或﹣2或﹣4．20．解：连接BD，∵AB为⊙O的直径，∴∠BCA=90°，∵CD平分∠ACB，∴∠ACD=45°，∴∠ABD=45°，∴△ABD为等腰直角三角形，∴AD 2+BD 2=AB 2， ∵AB=10cm ，∴AD=5cm ．故答案为5．三．解答题（共6小题，满分50分）21．解：如图，作直径MN ，使MN ⊥EF 于O ，交AB 于G ，交CD 于H ；连接OA 、OB 、OC 、OD ；在Rt △OBG 中，BG=3cm ，OB=5cm ，因此OG=4cm ；同理：在Rt △OCH 中，CH=4cm ，OC=5cm ，因此OH=3cm ； sin ∠DOF==， sin ∠BOF==， sin ∠COE==， sin ∠AOE==，即∠DOF=∠AOM=∠COE=∠BOM ，∠CON=∠DON=∠AOE=∠BOF ，因此S 扇形OAE =S 扇形OBF =S 扇形CON =S 扇形ODN ∴S 阴影=S △ABE +S 弓形AMB +S △CDF +S 弓形CND =S △OAB +S 弓形AMB +S △OCD +S 弓形CND =S 扇形OAB +S 扇形OCN +S 扇形ODN =S 扇形OAB +S 扇形OAE +S 扇形OBF =S ⊙O =12.5πcm 2．故图中阴影部分面积之和为12.5πcm 2．22．（1）证明：延长CE交⊙O于点M，∵AB是⊙O的直径，CE⊥AB，∴=，∵C是的中点，∴=，∴=，∴∠BCM=∠CBD，∴CF=BF；（2）解：连接AC，∵AB是⊙O的直径，CE⊥AB，∴∠BEF=∠ADB=90°，∵∠ABD=∠FBE，∴Rt△ADB∽Rt△FEB，∴，∵AD=2，⊙O的半径为4，∴AB=8，∴，∴BF=4EF，又∵BF=CF，∴CF=4EF，利用勾股定理得：BE==EF，又∵∠ACB=∠CEB=90°，∠ABC=∠CBE，∴△EBC∽△ECA，∴，∴CE2=AE•BE，∴（CF+EF）2=（8﹣BE）•BE，∴25EF2=（8﹣EF）•EF，∴EF=，∴BC==2．23．解：不能通过．设OA=R，在Rt△AOC中，AC=30，CD=18，R2=302+（R﹣18）2，R2=900+R2﹣36R+324解得R=34m连接OM，在Rt△MOE中，ME=16，OE2=OM2﹣ME2即OE2=342﹣162=900，∴OE=30，∴DE=34﹣30=4，∴不能通过．（12分）24．（1）证明：过A作AA′⊥MN于E，连接BA′．∵MN过圆心O，∴AE=EA′，∴AP=PA′，即AP+BP=PA′+BP，根据两点间线段最短，当A′，P，B三点共线时，PA′+BP=BA'，AP+BP此时为最小值，∴P位于A′B与MN的交点处；（2）解：∵点A是半圆上的一个三等分点，∴∠AON=∠A'ON=60°，∵点B是弧AN的中点，∴=，∴∠BON=30°，∴∠BOA'=∠A'ON+∠BON=90°，∵OB=OA=1，∴BA′=，即AP+BP最小值为．25．证明：∵CD⊥AB，CO⊥AB，∴∠OEC=∠OFA=90°，AD=2AF，CD=2CE，在△OCE和△OAF中，，∴△OCE≌△OAF（AAS），∴CE=AF，∴AD=CD．26．（1）证明：连接OG．∵EF切⊙O于G，∴OG⊥EF，∴∠AGO+∠AGE=90°，∵CD⊥AB于H，∴∠AHD=90°，∴∠OAG=∠AKH=90°，∵OA=OG，∴∠AGO=∠OAG，∴∠AGE=∠AKH，∵∠EKG=∠AKH，∴∠EKG=∠AGE，∴KE=GE．（2）设∠FGB=α，∵AB是直径，∴∠AGB=90°，∴∠AGE=∠EKG=90°﹣α，∴∠E=180°﹣∠AGE﹣∠EKG=2α，∵∠FGB=∠ACH，∴∠ACH=2α，∴∠ACH=∠E，∴CA∥FE．（3）作NP⊥AC于P．∵∠ACH=∠E，∴sin∠E=sin∠ACH==，设AH=3a，AC=5a，则CH==4a，tan∠CAH==，∵CA∥FE，∴∠CAK=∠AGE，∵∠AGE=∠AKH，∴∠CAK=∠AKH，∴AC=CK=5a，HK=CK﹣CH=4a，tan∠AKH==3，AK==a，∵AK=，∴a=，∴a=1．AC=5，∵∠BHD=∠AGB=90°，∴∠BHD+∠AGB=180°，在四边形BGKH中，∠BHD+∠HKG+∠AGB+∠ABG=360°，∴∠ABG+∠HKG=180°，∵∠AKH+∠HKG=180°，∴∠AKH=∠ABG，∵∠ACN=∠ABG，∴∠AKH=∠ACN，∴tan∠AKH=tan∠ACN=3，∵NP⊥AC于P，∴∠APN=∠CPN=90°，在Rt△APN中，tan∠CAH==，设PN=12b，则AP=9b，在Rt△CPN中，tan∠ACN==3，∴CP=4b，∴AC=AP+CP=13b，∵AC=5，∴13b=5，∴b=，∴CN==4b=．。

《圆》单元检测

第9题图EOD C B A 第14题图第8题图第10题图思源学校第二十四章《圆》单元检测姓名：一．选择题（本大题共10个小题，每小题3分，共30分．） 1.下列说法正确的是（）A. 相等的圆心角所对的弧相等B.平分弦的直径垂直于弦C. 三角形有且仅有一个外接圆D. 圆的切线垂直于半径2.平面内，⊙O 的半径为1，点P 到O 的距离为2，过点P 可作⊙O 的切线条数为（） A ．0条 B ．1条 C ．2条 D ．无数条3.点P 在⊙O 内，OP ＝2cm ，若⊙O 的半径是3cm ，则过点P 的最短弦的长度为（） A. 1cm B. 2cm C. 5cm D. 25cm4.已知⊙O 的半径为10，弦AB ∥CD ，AB ＝12，CD ＝16，则AB 和CD 的距离为（）A ．2 B ．14 C ．2或14 D ．10或205.圆锥的底面半径r ＝6，高h ＝8，则圆锥的侧面积是（） A ．15π B ．30π C ．45π D ．60π6.如图，⊙O 的直径AB 垂直于弦CD ，垂足是点E ，∠CAO ＝22.5°， OC ＝6.则CD 的长为（） A ．26 B ．23 C ．6 D ．127.如图，△ABC 内接于圆O ，∠B ＝65°，∠C ＝70°，若BC ＝22，则BĈ的长为（） A.π B.π2 C.π2 D. π22 8.如图，P A 、PB 是⊙O 切线，A 、B 为切点，点C 在⊙O 上，且 ∠ACB ＝55°，则∠APB 等于（） A.55° B.70° C.110° D.125°9.如图，四边形ABCD 是菱形，⊙O 经过点A ，C ，D ，与BC 相交于点E ，连接AC ，AE ．若∠D ＝80°，则∠EAC 的度数为（） A. 20° B. 25° C. 30° D. 35°10.如图，在平面直角坐标系中，过格点A ，B ，C 作一圆弧，点B 与下列格点的连线中，能够与该圆弧相切的是（）A ．点(0，3)B ．点(2，3)C ．点(5，1)D ．点(6，1)二．填空题（本大题共6个小题，每小题3分，共18分） 11.一个正n 边形的中心角等于18°，那么n ＝________．12.沿一条母线将圆锥侧面剪开并展平，得到一个扇形，若圆锥的底面圆的半径r ＝2，扇形的圆心角θ＝120°，则该圆锥母线l 的长为．13.如图，矩形ABCD 中，AB=2√3，BC=4，以点A 为圆心，AD 长为半径画弧，交BC 于点E ，求图中阴影部分面积 .14.如图，等边三角形ABC 的边长为2，以A 为圆心，1为半径作圆分别交AB ，AC 边于D ，E ，再以点C 为圆心，CD 长为半径作圆交BC 边于F ，连接E ，F ，那么图中阴影部分的面积为 .15.如图，在平面直角坐标系中，⊙A 与y 轴相切于原点O ，平行于 x 轴的直线交⊙A 于M 、N 两点．若点M 的坐标是(－2，－1)，则点N 的坐标为 .16.如图，在Rt △AOB 中，OA ＝OB ＝24，⊙O 的半径为2，点P 是AB 边上的动点，过点P 作⊙O 的一条切线PQ （点Q 为切点），则线段PQ 长的最小值为．三．解答题（本大题共8个小题，共72分．） 17.(10分)如图，在直角坐标系中，A(0,4)，C(3,0).每个小正方形网格的顶点叫做格点，仅用无刻度直尺按要求作图，作图过程用虚线表示，作图结果用实线表示. ①画出线段AC 关于y 轴对称线段AB ，再画出将线段AB 绕点A 顺时针旋转90°后的线段AB 1. ②将线段CA 绕点C 顺时针旋转一个角，得线段CD,并使AD ∥x 轴，请画出线段CD. ③若直线l :y=kx 平分图中四边形ABCD 的面积，请画出直线l 图象. ④找一个格点F ，使CF ⊥AB.并直接写出点F 坐标 . ⑤求第①问旋转过程中，点B 所经过的路径长，线段AB 扫过区域的面积 . 18.(6分)如图，AB=AC ，以AB 为直径的⊙0交AC,BC 于E,D.连接BE.(1)求证:DE ̂=DB ̂. (2)如果BC=12,AB=10,求BE 的长.19.(7分)(教材P91习题16改编)如图,公路OM,ON 相交成30°角，沿公路OM 方向离O 点80m 处有一所学校A,当重型运输卡车P 沿道路ON 方向行驶时，在以点P 为圆心,50m 长为半径的圆形区域内都会受到卡车噪声的影响，且卡车与学校A 的距离越近噪声影响越大，若已知重型运输卡车P 沿道路ON 方向行驶的速度为18km/h. (1)求对学校A 的噪声影响最大时卡车P 与学校A 的距离.(2)求卡车P 沿道路ON 方向行驶一次给学校A 带来噪声影响的时间.第6题图第7题图第13题图第16题图第15题图20.（7分）(教材P102习题11改编)如图,直线AB，BC，CD分别与⊙0相切于E,F,G，且AB//CD，OB=6cm，OC=8cm.求:(1)∠BOC的度数; (2)BE+CG的长; (3)⊙0的半径.21.（8分）如图，AB，AC分别是∠O的直径和弦，OD∠AC于点D．过点A作∠O的切线与OD的延长线交于点P，PC，AB的延长线交于点F．(1)求证：PC是∠O的切线；(2)若∠ABC＝60°，AB＝10，求线段CF和PA的长．22.（8分）在Rt∠ABC中，∠ACB＝90°，BE平分∠ABC，D是边AB上一点，以BD为直径的∠O经过点E，且交BC于点F．(1)求证：AC是∠O的切线；(2)若CF＝2，CE＝4，求∠O的半径．23.（8分）如图，在Rt∠ABC中，∠ACB＝90°，D为AB的中点，以CD为直径的⊙O分别交AC，BC于点E，F两点，过点F作FG⊥AB 于点G．(1)试判断FG与⊙O的位置关系，并说明理由；(2)若AC＝3，CD＝2.5，求FG的长．24.(8分)如图,直线AB经过∠O上的点C.直线BO与∠O交于点F和点D，OA与∠O交于点E,与DC交于点G，OA=OB，CA=CB.(1)求证:AB是∠O的切线；(2)若FC//OA，CD=6，求图中阴影部分面积.25.（10分）阅读理解：“半圆（或直径）所对的圆周角是直角，90°的圆周角所对的弦是直径.”如图①.AB为定长线段，若线段AB外一点C与A、B两端所形成的张角为直角（即∠ACB=90°），则点C 在以AB为直径的圆上运动（不与A、B重合）。

人教版数学九年级上学期《圆》单元综合检测(附答案)

[答案]C
[解析]
[分析]
由条件可求得∠BOC=100°，可求得∠B A C= ∠BOC=50°，在劣弧B C上找点E,连接BE、CE,利用圆内接四边形的性质可求得∠BEC=130°，故弦B C所对的圆周角的度数为50°或130°.
[详解]连接OB，
∵OD⊥B C于D，∠OC D=40°，
∴∠DOC=50°，
∴∠APB=45°或135°．
故选C．
7.如图，A B是⊙O的直径，OD⊥A C于点D，B C=6Cm，则OD等于（）Cm．
A.2B.3C.4D.5
[答案]B
[解析]
[分析]
先由垂径定理得出点D为A C的中点，则OD为△A B C的中位线，再根据三角形的中位线定理，即可求出OD的长．
[详解]∵OD⊥A C，
(1)求证：B D平分∠A B C；
(2)当∠OD B=30°时，求证：B C=OD.
23.如图，在△A B C中，A B=A C，以A B为直径作圆O，分别交B C于点D，交C A的延长线于点E，过点D作DH⊥A C于点H，连接DE交线段OA于点F．
(1)求证：DH是圆O 切线；
(2)若，求证：A为EH的中点．
详解：连接OC.
则∠B A C=∠OC A=50°，
∴∠AOC=80°，
∴
故选D
点睛：此题考查了扇形的弧长公式的应用，连接OC，由等边对等角及三角形内角和定理得到∠AOC=80°是解题的关键.
3.如图，PA，PB分别与⊙O相切于点A，B，连接OP，则下列判断错误的是（）
A. ∠PAO=∠PBO=90°B. OP平分∠APB
九年级上册数学《圆》单元测试卷
[时间：90分钟分数：100分]