【湖北4月调考】2020年湖北省高三(4月)线上调研考试 数学(文)(高清含答案)
2020年湖北省高三(4月)线上调研考试文数
Ａ．２槡３＋２
Ｂ．槡３＋１
Ｃ．７槡３
Ｄ．７２槡３
２０２０年湖北省高三（４月）线上调研考试文科数学试卷 第 ２页（共 ５页）
１２．已知双曲线 Ｃ：ａｘ２２ －ｙ ｂ２ ２ ＝１（ａ＞０，ｂ＞０）的左右焦点分别为 Ｆ１，Ｆ２，过 Ｆ１的直线与 Ｃ的两 条渐近线分别交于 Ａ，Ｂ两点，若以 Ｆ１Ｆ２为直径的圆过点 Ｂ，且 Ａ为 Ｆ１Ｂ的中点，则双曲 线 Ｃ的离心率为
Ａ．±１
Ｂ．槡２
Ｃ．±槡２
Ｄ．槡２
{ －ｘ２＋ａｘ，ｘ≤１
１０．已知函数 ｆ（ｘ）＝ ３ａｘ－７，ｘ＞１ ，若存在 ｘ１，ｘ２∈Ｒ，且 ｘ１≠ｘ２，使得 ｆ（ｘ１）＝ｆ（ｘ２）成立，
则实数 ａ的取值范围是
Ａ．（－∞，３）
Ｂ．（－∞，３］
Ｃ．（－面四边 ＡＢＣＤ形中，∠ＡＢＣ＝１５０°，槡３ＡＢ＝２ＢＣ，ＡＣ＝槡１３，ＢＤ⊥ＡＢ，ＣＤ＝３，则四边形 ＡＢＣＤ的面积为
Ａ．槡３＋１
Ｂ．２
Ｃ．槡３
Ｄ．槡２
二、填空题：本大题共 ４小题，每小题 ５分，共 ２０分．
１３．设曲线 ｙ＝ｅｘ＋１上点 Ｐ处的切线平行于直线 ｘ－ｙ－１＝０，则点 Ｐ的坐标是
．
１４．已知 θ为锐角，且槡２ｓｉｎθｓｉｎ（θ＋π４）＝５ｃｏｓ２θ，则 ｔａｎθ＝
．
１５．已知 Ａ，Ｂ，Ｃ是球 Ｏ球面上的三点，ＡＣ＝ＢＣ＝６，ＡＢ＝６槡２，且四面体 ＯＡＢＣ的体积为
一、选择题：本大题共 １２小题，每小题 ５分，共 ６０分．在每小题给出的四个选项中，只有一项
是符合题目要求的． １．已知集合 Ａ＝｛ｘ｜ｘ２－４ｘ－５＜０｝，集合 Ｂ＝｛ｙ｜ｙ＞０｝，则 Ａ∩Ｂ＝
Ａ．｛ｘ｜０＜ｘ＜５｝ Ｂ．｛ｘ｜－５＜ｘ＜０｝ Ｃ．（－１，＋∞） Ｄ．｛ｘ｜－１＜ｘ≤１０｝
2020年湖北省武汉市武昌区四月调研数学试卷(文科)
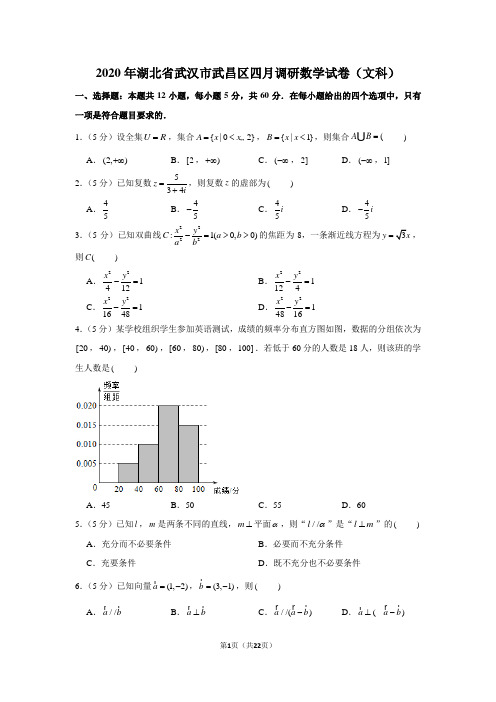
2020年湖北省武汉市武昌区四月调研数学试卷（文科）一、选择题：本题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的．1．（5分）设全集U R =，集合{|02}A x x =<…，{|1}B x x =<，则集合(A B =U ) A ．(2,)+∞ B ．[2，)+∞C ．(-∞，2]D ．(-∞，1]2．（5分）已知复数534z i =+，则复数z 的虚部为( ) A ．45B ．45-C ．45iD ．45i -3．（5分）已知双曲线2222:1(0,0)x y C a b a b-=>>的焦距为8，一条渐近线方程为3y x =，则(C )A ．221412x y -=B ．221124x y -=C ．2211648x y -=D ．2214816x y -=4．（5分）某学校组织学生参加英语测试，成绩的频率分布直方图如图，数据的分组依次为[20，40)，[40，60)，[60，80)，[80，100]．若低于60分的人数是18人，则该班的学生人数是( )A ．45B ．50C ．55D ．605．（5分）已知l ，m 是两条不同的直线，m ⊥平面α，则“//l α”是“l m ⊥”的( ) A ．充分而不必要条件 B ．必要而不充分条件C ．充要条件D ．既不充分也不必要条件6．（5分）已知向量(1,2)a =-r ，(3,1)b =-r ，则( ) A ．//a b r rB ．a b ⊥r rC ．//()a a b -r r rD ．(a ⊥r)a b -r r7．（5分）已知点(,8)m 在幂函数()(1)n f x m x =-的图象上，设()ma f n =，()b f ln π=，()c f n =，则( ) A ．b a c <<B ．a b c <<C ．b c a <<D ．a c b <<8．（5分）函数48||()x xln x x f x e e--=+的图象大致为( ) A ．B ．C ．D ．9．（5分）一艘海轮从A 处出发，以每小时24海里的速度沿南偏东40︒的方向直线航行，30分钟后到达B 处，在C 处有一座灯塔，海轮在A 处观察灯塔，其方向是南偏东70︒，在B 处观察灯塔，其方向是北偏东65︒，那么B ，C 两点间的距离是( )A ．62海里B ．63海里C ．82海里D ．83海里10．（5分）已知三棱锥P ABC -的顶点都在球O 的球面上，2PA =，14PB =，4AB =，10CA CB ==，面PAB ⊥面ABC ，则球O 的表面积为( )A ．103πB ．256πC ．409πD ．503π11．（5分）已知函数()sin()(0f x A x A ωϕ=+>，0ω>，0)2πϕ<<的部分图象如图所示，则3()(8f π= )A 26-B 26+ C 62- D 62+ 12．（5分）已知函数()f x 是定义域为R 的偶函数，且满足()f x f = (2)x -，当[0x ∈，1]时，()f x x =，则函数4()()12x F x f x x+=+-在区间[10-，9]上零点的个数为( ) A ．9 B ．10C ．18D ．20二、填空题：本题共4小题，每小题5分，共20分．13．（5分）直线10(0,0)mx ny m n --=>>过圆22:2210C x y x y +-+-=的圆心，则11m n+的最小值是 ．14．（5分）从分别写有1，2，3，4的4张卡片中随机抽取1张，放回后再随机抽取1张，则抽得的第一张卡片上的数不小于第二张卡片上的数的概率为 ． 15．（5分）给出以下式子：①tan 25tan353tan 25tan35︒+︒+︒︒； ②2(sin35cos25cos35cos65)︒︒+︒︒； ③1tan151tan15+︒-︒其中，结果为3的式子的序号是 ．16．（5分）已知椭圆2222:1(0)x y C a b a b+=>>的左、右焦点分别为1F ，2F ，椭圆的焦距为2c ，过C 外一点(,2)P c c 作线段1PF ，2PF 分别交椭圆C 于点A 、B ，若1||||PA AF =，则22||||PF BF = ． 三、解答题：共70分．解答应写出文字说明、证明过程或演算步骤．第17～21题为必考题，每个试题考生都必须作答．第22、23题为选考题，考生根据要求作答．（一）必考题：共60分．17．（12分）已知等差数列{}n a 的各项均为正数，n S 为等差数列{}n a 的前n 项和，11a =，4511a a =．（1）求数列{}n a 的通项n a ；（2）设3n n n b a =g，求数列{}n b 的前n 项和n T ． 18．（12分）如图，在三棱柱111ABC A B C -中，1A A ⊥平面ABC ，90ACB ∠=︒，11AC CB C C ===，M ，N 分别是AB ，1A C 的中点．（1）求证：直线MN ⊥平面1ACB ； （2）求点1C 到平面1B MC 的距离．19．（12分）某校共有学生2000人，其中男生900人，女生1100人，为了调查该校学生每周平均体育锻炼时间，采用分层抽样的方法收集该校100名学生每周平均体育锻炼时间（单位：小时）．（1）应抽查男生与女生各多少人？（2）根据收集100人的样本数据，得到学生每周平均体育锻炼时间的频率分布表：若在样本数据中有38名男学生平均每周课外体育锻炼时间超过2小时，请完成每周平均体育锻炼时间与性别的列联表，并判断是否有95%的把握认为“该校学生的每周平均体育锻炼时间与性别有关”？附：2K =．20．（12分）已知A 是抛物线2:2(0)E y px p =>上的一点，以点A 和点(2,0)B 为直径两端点的圆C 交直线1x =于M ，N 两点． （1）若||2MN =，求抛物线E 的方程；（2）若01p <<，抛物线E 与圆22(5)9x y -+=在x 轴上方的交点为P ，Q ，点G 为PQ 的中点，O 为坐标原点，求直线OG 斜率的取值范围． 21．（12分）已知函数2()(2)2f x x t x tlnx =+--+． （1）若2x =是()f x 的极值点，求()f x 的极大值； （2）求实数t 的范围，使得()2f x …恒成立．（二）选考题：共10分．请考生在第22、23题中任选一题作答．如果多做，则按所做的第一题计分．[选修4-4：坐标系与参数方程]22．（10分）在平面直角坐标系xOy 中，直线l的参数方程为2(1x t y ⎧=⎪⎪⎨⎪=⎪⎩为参数），以坐标原点O 为极点，x 轴的正半轴为极轴建立极坐标系，圆C 的极坐标方程为24cos 3ρρθ-=． （1）求直线l 的普通方程和圆C 的直角坐标方程；（2）直线l 与圆C 交于A ，B 两点，点(2,1)P ，求||||PA PB g 的值． [选修4-5：不等式选讲] 23．已知函数()||f x x a =-．（1）当1a =-时，求不等式()|21|1f x x +-…的解集；（2）若函数()()|3|g x f x x =-+的值域为A ，且[2-，1]A ⊆，求a 的取值范围．2020年湖北省武汉市武昌区四月调研数学试卷（文科）参考答案与试题解析一、选择题：本题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的．1．（5分）设全集U R =，集合{|02}A x x =<„，{|1}B x x =<，则集合(A B =U ) A ．(2,)+∞B ．[2，)+∞C ．(-∞，2]D ．(-∞，1]【解答】解：{|02}A x x =<Q „，{|1}B x x =<， {|2}A B x x ∴=U „，故选：C ．2．（5分）已知复数534z i=+，则复数z 的虚部为( ) A ．45B ．45-C ．45iD ．45i -【解答】解：55(34)3434(34)(34)55i z i i i i -===-++-， 则复数z 的虚部为45-．故选：B ．3．（5分）已知双曲线2222:1(0,0)x y C a b a b-=>>的焦距为8，一条渐近线方程为y =，则(C )A ．221412x y -=B ．221124x y -=C ．2211648x y -=D ．2214816x y -=【解答】解：由题意，28c =，则4c =，又ba，且222a b c +=， 解得24a =，212b =．∴双曲线C 的方程为221412x y -=．故选：A ．4．（5分）某学校组织学生参加英语测试，成绩的频率分布直方图如图，数据的分组依次为[20，40)，[40，60)，[60，80)，[80，100]．若低于60分的人数是18人，则该班的学生人数是( )A ．45B ．50C ．55D ．60【解答】解：根据频率分布直方图，得； 低于60分的频率是 (0.0050.010)200.30+⨯=，∴样本容量（即该班的学生人数）是18600.30=（人)． 故选：D ．5．（5分）已知l ，m 是两条不同的直线，m ⊥平面α，则“//l α”是“l m ⊥”的( ) A ．充分而不必要条件 B ．必要而不充分条件C ．充要条件D ．既不充分也不必要条件【解答】解：当m ⊥平面α时，若//l α”则“l m ⊥”成立，即充分性成立， 若l m ⊥，则//l α或l α⊂，即必要性不成立， 则“//l α”是“l m ⊥”充分不必要条件， 故选：A ．6．（5分）已知向量(1,2)a =-r ，(3,1)b =-r ，则( ) A ．//a b r rB ．a b ⊥r rC ．//()a a b -r r rD ．(a ⊥r)a b -r r【解答】解：Q 向量(1,2)a =-r，(3,1)b =-r ，∴a r 和b r 的坐标对应不成比例，故a r 、b r 不平行，故排除A ；显然，320a b =+≠r r g ，故a r、b r 不垂直，故排除B ；∴(2,1)a b -=--r r ，显然，a r 和a b -r r 的坐标对应不成比例，故a r 和a b -rr 不平行，故排除C ； ∴()220a a b -=-+=rr rg，故()a a b ⊥-rr r，故D 正确，故选：D ．7．（5分）已知点(,8)m 在幂函数()(1)n f x m x =-的图象上，设()ma f n =，()b f ln π=，()c f n =，则( ) A ．b a c <<B ．a b c <<C ．b c a <<D ．a c b <<【解答】解：由幂函数的定义可知，11m -=，2m ∴=，∴点(2,8)在幂函数()n f x x =上，28n ∴=，3n ∴=，∴幂函数解析式为3()f x x =，在R 上单调递增，Q23m n =，13ln π<<，3n =， ∴mln n nπ<<， a b c ∴<<，故选：B ．8．（5分）函数48||()x xln x x f x e e--=+的图象大致为( ) A ．B ．C ．D ．【解答】解：函数的定义域为{|2x R x ∈≠-且0x ≠且2}x ≠，448||8||()()xx x x ln x x x x f x f x e e e e---+--===++，则函数()f x 为偶函数，其图象关于y 轴对称，可排除BD ；当x →+∞时，48||0x x e e ln x x +>>->，则()0f x →且()0f x >，故排除C ．故选：A ．9．（5分）一艘海轮从A 处出发，以每小时24海里的速度沿南偏东40︒的方向直线航行，30分钟后到达B 处，在C 处有一座灯塔，海轮在A 处观察灯塔，其方向是南偏东70︒，在B 处观察灯塔，其方向是北偏东65︒，那么B ，C 两点间的距离是( )A ．62海里B ．63海里C ．82D ．83【解答】解：由题意可知：704030BAC ∠=︒-︒=︒．110ACD ∠=︒，1106545ACB ∴∠=︒-︒=︒，1803045105ABC ∴∠=︒-︒-︒=︒．又240.512AB =⨯=．在ABC ∆中，由正弦定理得sin 45sin30AB BC=︒︒， 122BC=，∴62BC = 故选：A ．10．（5分）已知三棱锥P ABC -的顶点都在球O 的球面上，2PA =14PB =4AB =，10CA CB ==PAB ⊥面ABC ，则球O 的表面积为( )A ．103πB ．256πC ．409πD ．503π【解答】解：如图；设AB 的中点为D ； 2PA Q ，14PB =4AB =，PAB ∴∆为直角三角形，且斜边为AB ，故其外接圆半径为：122r AB AD ===； 设外接球球心为O ；10CA CB ==Q PAB ⊥面ABC ，CD AB ∴⊥可得CD ⊥面PAB ；且226DC CA AD -=O ∴在CD 上；故有：222222(6)6AO OD AD R R r R =+⇒=+⇒；∴球O 的表面积为：225044(36R πππ=⨯=． 故选：D ．11．（5分）已知函数()sin()(0f x A x A ωϕ=+>，0ω>，0)2πϕ<<的部分图象如图所示，则3()(8f π= )A 26-B 26+ C 62- D 62+ 【解答】解：由图象可知1A =， Q32()4123T ππ=--，所以T π=，∴22Tπω==． ()sin(2)f x x ϕ∴=+，将(,1)12π代入得sin()16πϕ+=，∴2,62k k Z ππϕπ+=+∈，结合02πϕ<<，3πϕ∴=．∴()sin(2)3f x x π=+．∴33()sin()sin()sin sin()843121234f ππππππππ=+=+=-=-- 26(sincoscos sin )3434ππππ-=--=故选：A ．12．（5分）已知函数()f x 是定义域为R 的偶函数，且满足()f x f = (2)x -，当[0x ∈，1]时，()f x x =，则函数4()()12x F x f x x+=+-在区间[10-，9]上零点的个数为( ) A ．9 B ．10C ．18D ．20【解答】解：函数4()()12x F x f x x+=+-在区间[10-，9]上零点的个数等价于函数()f x 与4()12x g x x+=--图象在[9-，10]上交点的个数， 由()f x f = (2)x -，得函数()f x 图象关于1x =对称，()f x Q 为偶函数，取2x x =+，可得(2)()()f x f x f x +=-=，得函数周期为2．又Q 当[0x ∈，1]时，()f x x =，且()f x 为偶函数，∴当[1x ∈-，0]时，()f x x =-，4419()1221242x x g x x x x ++=-==+---， 作出函数()f x 与()g x 的图象如图：由图可知，两函数图象共10个交点， 即函数4()()12x F x f x x+=+-在区间[10-，9]上零点的个数为10． 故选：B ．二、填空题：本题共4小题，每小题5分，共20分．13．（5分）直线10(0,0)mx ny m n --=>>过圆22:2210C x y x y +-+-=的圆心，则11m n+的最小值是 4 ．【解答】解：10(0,0)mx ny m n --=>>Q 经过圆222210x y x y +-+-=的圆心(1,1)-，10m n ∴+-=，即1m n +=．∴1111()()2224m nm n m n m n n m +=++=+++=…，当且仅当12m n ==时取等号．∴则11m n+的最小值是4． 故答案为：4．14．（5分）从分别写有1，2，3，4的4张卡片中随机抽取1张，放回后再随机抽取1张，则抽得的第一张卡片上的数不小于第二张卡片上的数的概率为58． 【解答】解：从分别写有1，2，3，4的4张卡片中随机抽取1张，放回后再随机抽取1张，基本事件总数4416n =⨯=，抽得的第一张卡片上的数不小于第二张卡片上的数包含的基本事件有：(1,1)，(2,1)，(2,2)，(3,1)，(3,2)，(3,3)，(4,1)，(4,2)，(4,3)，(4,4)，共10个，则抽得的第一张卡片上的数不小于第二张卡片上的数的概率为105168p ==． 故答案为：58．15．（5分）给出以下式子：①tan 25tan3525tan35︒+︒+︒︒； ②2(sin35cos25cos35cos65)︒︒+︒︒； ③1tan151tan15+︒-︒的式子的序号是 ①②③ ． 【解答】解：①tan 25tan35tan 60tan(2535)1tan 25tan35︒+︒︒=︒+︒==-︒︒Qtan 25tan3525tan35︒+︒︒︒；tan 25tan 35)25tan 35=-︒︒︒︒，=，②2(sin35cos25cos35cos65)2(sin35cos25cos35sin 25)︒︒+︒︒=︒︒+︒︒，2sin 60=︒③1tan15tan 45tan15tan(4515)tan 601tan151tan 45tan 45+︒︒+︒==︒+︒=︒-︒-︒︒故答案为：①②③16．（5分）已知椭圆2222:1(0)x y C a b a b+=>>的左、右焦点分别为1F ，2F ，椭圆的焦距为2c ，过C 外一点(,2)P c c 作线段1PF ，2PF 分别交椭圆C 于点A 、B ，若1||||PA AF =，则22||||PF BF =【解答】解：因为1||||PA AF =，所以点A 是线段1PF 的中点， 又因为点O 为线段12F F 的中点，所以2//OA PF ，且2||2||PF OA =， 因为点(,2)P c c ，所以2PF x ⊥轴，则2||2PF c =，所以OA x ⊥轴，则点A 为椭圆上顶点， 所以||OA b =，则22b c =，所以b c =，a =，设(B c ，)(0)m m >，则222212c m c c +=，解得m =，所以2||BF =，则22||||PF BF ==故答案为：三、解答题：共70分．解答应写出文字说明、证明过程或演算步骤．第17～21题为必考题，每个试题考生都必须作答．第22、23题为选考题，考生根据要求作答．（一）必考题：共60分．17．（12分）已知等差数列{}n a 的各项均为正数，n S 为等差数列{}n a 的前n 项和，11a =，4511a a =．（1）求数列{}n a 的通项n a ；（2）设3n n n b a =g，求数列{}n b 的前n 项和n T ． 【解答】解：（1）由题意，设等差数列{}n a 的公差为(0)d d >，则 45(13)(14)11a a d d =++=，整理，得2127100d d +-=，解得54d =-（舍去），或23d =，2211(1)33n n a n +∴=+-=，*n N ∈． （2）由（1）知，12133(21)33n nn n n n b a n -+===+g g g ， 121123315373(21)3n n n T b b b b n -∴=+++⋯+=⨯+⨯+⨯+⋯++g ， 12133353(21)3(21)3n n n T n n -∴=⨯+⨯+⋯+-++g g ， 两式相减，可得：121231232323(21)3n n n T n --=⨯+⨯+⨯+⋯+-+g g 12132(333)(21)3n n n -=+⨯++⋯+-+g3332(21)313n n n -=+⨯-+-g23n n =-g ，3n n T n ∴=g ．18．（12分）如图，在三棱柱111ABC A B C -中，1A A ⊥平面ABC ，90ACB ∠=︒，11AC CB C C ===，M ，N 分别是AB ，1A C 的中点．（1）求证：直线MN ⊥平面1ACB ； （2）求点1C 到平面1B MC 的距离．【解答】解：（1）证明：连接1AC ，1BC ，则1N AC ∈且N 为1AC 的中点；M Q 是AB 的中点．所以：//MN BC ；1A A ⊥Q 平面ABC ，AC ⊂平面ABC ， 1A A AC ∴⊥，在三棱柱111ABC A B C -中，1//AA CC ， 1AC CC ∴⊥，90ACB ∠=︒Q ，1BC CC C =I ，BC ⊂平面11BB C C ，1CC ⊂平面11BB C C ，AC ∴⊥平面11BB C C ，BC ⊂平面11BB C C ，1AC BC ∴⊥；又1//MN BCAC MN ∴⊥，11CB C C ==Q ，∴四边形11BB C C 正方形，11BC B C ∴⊥，1MN B C ∴⊥，而1AC B C C =I ，且AC ⊂平面1ACB ，1CB ⊂平面1ACB ，MN ∴⊥平面1ACB ，（2）设1C 到平面1B CM 的距离为h ， 因为12MP =，1112B CC S =V ， 所以111111312M B CC B CC V S MP -==V g g ，因为2CM =，12B C =； 16B M =， 所以：11132B CM S CM B M ==V g ．19．（12分）某校共有学生2000人，其中男生900人，女生1100人，为了调查该校学生每周平均体育锻炼时间，采用分层抽样的方法收集该校100名学生每周平均体育锻炼时间（单位：小时）．（1）应抽查男生与女生各多少人？（2）根据收集100人的样本数据，得到学生每周平均体育锻炼时间的频率分布表： 时间（小时）[0，1](1，2](2，3](3，4](4，5](5，6]若在样本数据中有38名男学生平均每周课外体育锻炼时间超过2小时，请完成每周平均体育锻炼时间与性别的列联表，并判断是否有95%的把握认为“该校学生的每周平均体育锻炼时间与性别有关”？附：2()()()()K a b c d a c b d =++++．【解答】解：因为男生人数：女生人数900:11009:11==， 所以男生人数为91004520⨯=人，女生认识我1004555-=人， （2）由频率频率直方图可知学生每周平均体育锻炼时间超过2小时的人数为：(10.310.2510.1510.05)10075⨯+⨯+⨯+⨯⨯=人，每周平均体育锻炼时间超过2小时的女生人数为37人， 联表如下：因为2100(1838737) 3.892 3.84145552575K ⨯-⨯=≈>⨯⨯⨯，所以有95%的把握认为“该校学生的每周平均体育锻炼时间与性别有关．20．（12分）已知A 是抛物线2:2(0)E y px p =>上的一点，以点A 和点(2,0)B 为直径两端点的圆C 交直线1x =于M ，N 两点．（1）若||2MN =，求抛物线E 的方程；（2）若01p <<，抛物线E 与圆22(5)9x y -+=在x 轴上方的交点为P ，Q ，点G 为PQ 的中点，O 为坐标原点，求直线OG 斜率的取值范围．【解答】解：（1）设0(A x ，0)y 且202y px =，则圆心02(2x C +，0)2y，圆C 的直径||AB ， 圆心C 到直线1x =的距离002|1|||22x xd +=-=， 因为||2MN =，所以222||()()22MN AB d +=，即222000(2)144x x y -++=，2002y px =， 整理可得0(24)0p x -=，所以2p =， 所以抛物线的方程为：24y x =；（2）联立抛物线与圆的方程2222(5)9y pxx y ⎧=⎨-+=⎩整理可得22(5)160x p x --+=，△0>， 设1(P x ，1)y ，2(Q x ，2)y ，则122(5)x x p +=-，1216x x =，所以中点G 的横坐标5G x p =-，G y ==所以1)OGk P =<<，令5((4,5))t p t =-∈，则1111()54OG k t ==<<，解得0OG k <<，所以直线OG 斜率的取值范围． 21．（12分）已知函数2()(2)2f x x t x tlnx =+--+． （1）若2x =是()f x 的极值点，求()f x 的极大值； （2）求实数t 的范围，使得()2f x …恒成立． 【解答】解：（1）()22tf x x t x'=+--，0x >， 由题意可得，1(2)202f t '=+=，解可得4t =-，∴42(1)(2)()26x x f x x x x--'=-+=， 易得，当2x >，01x <<时，()0f x '>，函数单调递增，当12x <<时，()0f x '<，函数单调递减，故当1x =时，函数取得极大值f （1）3=-；（2）由2()(2)22f x x t x tlnx =+--+…在0x >时恒成立可得，2(2)0x t x tlnx +--…在0x >时恒成立，令2()(2)g x x t x tlnx =+--，则(1)(2)()22t x x t g x x t x x-+'=+--=， ()i 当0t …时，()g x 在(0,1)上单调递减，在(1,)+∞上单调递增， 所以()min g x g =（1）10t =-…，解可得1t …，()ii 当20t -<<时，()g x 在1(,1)2t -上单调递减，在1(0,)2t -，(1,)+∞上单调递增，此时g （1）11t =-<-不合题意，舍去；()iii 当2t =-时，22(1)()0x g x x-'=…，即()g x 在(0,)+∞上单调递增，此时g （1）3=-不合题意；()iv 当2t <-时，()g x 在1(1,)2t -上单调递减，在(0,1)，1(,)2t -+∞上单调递增，此时g （1）13t =-<-不合题意，综上，1t …时，()2f x …恒成立．（二）选考题：共10分．请考生在第22、23题中任选一题作答．如果多做，则按所做的第一题计分．[选修4-4：坐标系与参数方程]22．（10分）在平面直角坐标系xOy 中，直线l的参数方程为2(1x t y ⎧=⎪⎪⎨⎪=⎪⎩为参数），以坐标原点O 为极点，x 轴的正半轴为极轴建立极坐标系，圆C 的极坐标方程为24cos 3ρρθ-=． （1）求直线l 的普通方程和圆C 的直角坐标方程；（2）直线l 与圆C 交于A ，B 两点，点(2,1)P ，求||||PA PB g 的值．【解答】解：（1）直线l的参数方程为22(1x t y ⎧=+⎪⎪⎨⎪=⎪⎩为参数），转换为直角坐标方程为30x y +-=． 圆C 的极坐标方程为24cos 3ρρθ-=，转换为直角坐标方程为22430x y x +--=．（2）把直线l 的参数方程为2(1x t y ⎧=+⎪⎪⎨⎪=-⎪⎩为参数），代入圆的直角坐标方程22430x y x +--=，得到260t -=，所以12||||||6PA PB t t ==．[选修4-5：不等式选讲]23．已知函数()||f x x a =-．（1）当1a =-时，求不等式()|21|1f x x +-„的解集；（2）若函数()()|3|g x f x x =-+的值域为A ，且[2-，1]A ⊆，求a 的取值范围．【解答】解：（1）当1a =-时，()|1|f x x =+． ()|21|1f x x +-Q „，∴当1x -„时，原不等式可化为122x x ----„，1x ∴-„； 当112x -<<-时，原不等式可化为122x x +--„，1x ∴-„，此时不等式无解； 当12x -…时，原不等式可化为12x x +„，1x ∴…， 综上，原不等式的解集为{|1x x -„或1}x …．（2）当3a <-时，3,()23,33,3a x a g x x a a x a x +⎧⎪=-+<<-⎨⎪---⎩„…，∴函数()g x 的值域{|33}A x a x a =+--剟．[2-Q ，1]A ⊆，∴3231a a +-⎧⎨--⎩„…，5a ∴-„；当3a -…时，3,3()23,333,a x g x x a x a x a +-⎧⎪=-+-<<-⎨⎪--⎩„…， ∴函数()g x 的值域{|33}A x a x a =--+剟．[2-Q ，1]A ⊆，∴3231a a ---⎧⎨+⎩„…，1a ∴-…， 综上，a 的取值范围为(-∞，5][1--U ，)+∞．。
湖北省2020届高三4月调研考试数学试卷(文)有答案(精校版)
2019年湖北省高三四月调考文科数学第Ⅰ卷（选择题 共60分）一、选择题：本大题共12小题，每小题5分，共60分.在每个小题给出的四个选项中，有且只有一项符合题目要求.1.若复数1,z i z =+为z 的共轭复数，则z z ⋅= 2 D.2i2.设集合(){}(){}(),|,,,|1,,|11y U x y x R y R A x y y x B x y x ⎧⎫=∈∈==+==⎨⎬+⎩⎭，则U A C B =IA.(){}1,0- B. {}1- C. {}1,0- D.∅3.设等比数列{}n a 中，若22462,14a a a a =++=，则公比q = A.3 B. 3±2±4.已知点()()1,0,1,0A B -为双曲线()222210,0x y a b a b-=>>的左右顶点，点M 在双曲线上，ABM ∆为等腰三角形，且顶角为120o ，则该双曲线的标准方程为A. 2214y x -=B. 2212y x -=C.221x y -=D.2212y x -= 5.已知tan 52x π⎛⎫+= ⎪⎝⎭，则1sin cos x x =A. 265B. 265-C. 265±D.526-6. 设,,a b c r r r均为非零向量，则a c =r r 是a c b c ⋅=⋅r r r r 的A. 充分不必要条件B. 必要不充分条件C.充要条件D.既不充分也不必要条件7.已知圆22:4C x y +=，直线:l y x =，则圆C 上任取一点A 到直线l 的距离小于1的概率为 A.34 B. 23 C. 12 D.138. 已知函数()()cos 0,,2xx f x a R a e ωϕπωϕ+⎛⎫=><∈ ⎪⋅⎝⎭在区间[]3,3-上的图象如图所示，则a ω可取 A. 4π B. 2π C.π D.2π 9.执行如图所示的程序框图，若输出的值为5y =，则满足条件的实数x 的个数为 A. 4 B. 3 C. 2D. 110.网格纸上小正方形的边长为1，粗线画出的是某几何体的三视图，则该几何体的体积为 22D. 221+11.已知抛物线2:4C y x =的焦点为F,设过抛物线上一点P 处的切线为1l ，过点F且垂直于PF 的直线为2l ，则1l 与2l 交点Q 的横坐标为A. 34-B. 1-C. 43- D.不能确定 12. 已知实数,x y 满足()2221x y +-=223x y+的取值范围是A. 3,2⎤⎦B. []1,2C. (]0,2D. 3⎤⎥⎝⎦第Ⅱ卷（非选择题 共90分）二、填空题：本大题共4小题，每小题5分，共20分.13.已知正六棱锥S ABCDEF -的底面边长和高均为1，则异面直线SC 与DE 所成角的大小为为 .14. 已知函数()2143ln 2f x x x x =-+-在(),1t t +上存在极值点，则实数t 的取值范围是 . 15. 某单位植树节计划种杨树x 棵，柳树y 棵，若实数,x y 满足约束条件2527x y x y x ->⎧⎪-<⎨⎪<⎩，则该单位集合栽种这两种树的棵树最多为 .16. 已知数列{}n a 为等差数列，{}n b 为等比数列，且0,0n n a b >>，记数列{}n n a b ⋅的前n 项和为n S ，若()()111,131nn a b S n n N *===-⋅+∈，则数列25n n a b ⎧⎫-⎨⎬⎩⎭的最大项为第 项.三、解答题：本大题共6小题，共70分.解答应写出必要的文字说明或推理、验算过程. 17.（本题满分12分）在ABC ∆中，角A,B,C 的对边分别为,,a b c ，且cos .a C b= （1）求B ；（2）设CM 是角C 的平分线，且31,4CM a ==，求b .18.（本题满分12分）如图，长方体1111ABCD A B C D -中，点M 在棱1BB 上，两条直线,MA MC 与平面ABCD 所成角均为θ，AC 与BD 交于点O.（1）求证：AC OM ⊥； （2）当1112AB BM BB ===时，求点1D 到平面AMC 的距离.19.（本题满分12分）在某小学体育素质达标运动会上，对10名男生和10名女生在一分钟跳绳的次数进行统计，得到如下所示茎叶图:（1）已知男生组中数据的中位数为125，女生组数据的平均数为124，求,x y 的值；（2）从一分钟内跳绳次数不低于110次且不高于120次的学生中任取两名，求两名学生中至少有一名男生的概率.20.（本题满分12分）已知椭圆()2222:10x y E a b a b +=>>的长轴AB 为的长为6，离心率为1.3（1）求椭圆E 方程；（2）过椭圆E 的右焦点F 的直线与椭圆E 交于M,N 两点，记AMB ∆的面积为1S ，ANB ∆的面积为2S ，当12S S -取得最大值时，求12S S +的值.21.（本题满分12分）已知函数()214ln .xf x x-=（1）求函数()f x 的单调区间；（2）若对任意的121,,x x e ⎡⎫∈+∞⎪⎢⎣⎭，且12x x ≠，不等式()()12221212f x f x kx x x x -≤-⋅恒成立，求实数k 的取值范围.请考生在第22、23两题中任选一题作答，如果两题都做，则按照所做的第一题给分；作答时，请用2B 铅笔将答题卡上相应的题号涂黑。
湖北省宜昌市2020届高三年级4月线上统一调研考试 数学(文)(PDF版)
7
7
VN PCD
VDPCN
11 32
2 2
14 2 21 3 1 .
4 7 12
4
….……………….…...…..11 分
所以 PN 1 . PB 4
….…………………....…..12 分
19.（1）平均数 x (0.021 0.083 0.155 0.18 7 0.039 0.0311 0.0113) 2 6.
P(K 2 k0 )
k0
0.15 0.10 0.05 0.025 0.010 0.005 2.072 2.706 3.841 5.024 6.635 7.879
0.001 10.828
K
2
a
b
n ad bc2 c d a c
b
d
高三文数试卷 第 3页 共 4 页
20.（本题满分 12 分） 已知抛物线 C : x2 8y 和直线 l : y kx 2 ，直线 l 恒过圆 P 的圆心，且圆 P 上的点到直线 l 的最大距
3[sin( B C) sin B cosC] sin C sin B.
…………………………………….….….…….2 分
3 cosB sin C sin B sin C .
……………………………………….….…….4 分
在△ ABC 中， sin C 0,tan B 3. 又 0 B ,B .
3 （2）面积 S 1 acsin B 2 3 ac 8.
2
……………………………………….………..5 分 ……………………………………….….….….6 分
…………………….……..……….……….7 分
cosB a2 c2 b2 1 a2 c2 24 ac
湖南湖北四校2020届高三学情调研联考数学(文)试题及答案
湖南湖北四校2020届高三学情调研联考文科数学试题卷 考试时间：2020年4月24日本试卷共5页，满分150分，考试用时120分钟. 考生注意：1.答卷前，考生务必将自己的姓名和座位号填写在答题卡上.2.回答选择题时，选出每小题答案后，用铅笔把答题卡对应题目的答案标号涂黑.如需改动，用橡皮擦干净后，再选涂其他答案标号.回答非选择题时，将答案写在答题卡上.写在本试卷上无效.3.考试结束后，将本试卷和答题卡一并交回.祝考试顺利一、选择题：本题共12小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求的.1.已知集合{}04P x R x =∈≤≤，{}3Q x R x =∈<，则P Q =U （ ） A.[]3,4B.(]3,4-C.(],4-∞D.()3,-+∞2.x ，y 互为共轭复数，且()2346x y xyi i +-=-则x y +=（ ） A.2B.1C.22D.43.如图所示，三国时代数学家在《周脾算经》中利用弦图，给出了勾股定理的绝妙证明.图中包含四个全等的直角三角形及一个小正方形（阴影），设直角三角形有一个内角为30︒，若向弦图内随机抛掷200颗米粒（大小忽略不计，取3 1.732≈），则落在小正方形（阴影）内的米粒数大约为（ ）A.20B.27C.54D.644.如图，在ABC △中，点D 在线段BC 上，且3BD DC =，若AD AB AC λμ=+uuu v uu u v uuu v，则λμ=（ ）A.13B.12C.23D.25.已知定义在R 上的函数()21x mf x -=-（m 为实数）为偶函数，记()0.5log 3a f =，()2log 5b f =，()2c f m =+，则,,a b c 的大小关系为（ ）A.a b c <<B.c b a <<C.c a b <<D.a c b <<6.如图所示是某多面体的三视图，左上为正视图，右上为侧视图，左下为俯视图，且图中小方格单位长度为1，则该多面体的侧面最大面积为（ ）A.23B.6C.22D.27.已知双曲线()2222:10,0x y C a b a b -=>>的左，右焦点分别为()1,0F c -，()2,0F c ，又点23,2b N c a ⎛⎫- ⎪⎝⎭.若双曲线C 左支上的任意一点M 均满足24MF MN b +>，则双曲线C 的离心率的取值范围为（ ）A.1353⎛⎝B.)131,5,3⎛+∞ ⎝⎭UC.()513,+∞UD.5,138.为计算11111123499100S =-+-++-L ，设计了下面的程序框图，则在空白框中应填入（ ） A.1i i =+B.2i i =+C.3i i =+D.4i i =+9.已知ABC △的内角,,A B C 所对的边分别为,,a b c ，且3cos cos 5a Bb Ac -=，则()tan A B -的最大值为（ ）B.32C.3410.已知函数()()22π2sin cos sin 024r f x x x ωωωω⎛⎫=⋅-->⎪⎝⎭在区间2π5π,36⎡⎤-⎢⎥⎣⎦上是增函数，且在区间[]0,π上恰好取得一次最大值1，则w 的取值范围是（ ）A.30,5⎛⎤ ⎥⎝⎦B.13,25⎡⎤⎢⎥⎣⎦C.13,24⎡⎤⎢⎥⎣⎦D.15,22⎡⎫⎪⎢⎣⎭11.过双曲线()222210x y a b a b-=>>右焦点F 的直线交两渐近线于A 、B 两点，若0OA AB ⋅=uu r uu u r ，O 为坐标原点，且OAB △内切圆半径为12a ，则该双曲线的离心率为（ ）112.已知三棱锥P ABC -的四个顶点在球O 的球面上，PA PB PC ==，ABC △是边长为2的正三角形，,E F 分别是,PA AB 的中点，90CEF ∠=︒，则球O 的体积为（ ）A.B.C.二、填空题：本题共4小题，每小题5分，共20分. 13.命题“()00,x ∃∈+∞，00ln 1x x =-”的否定是. 14.观察分析下表中的数据：猜想一般凸多面体中,,F V E 所满足的等式是.15.设函数()()1xf x ex =-，函数()g x mx =，若对于任意的[]12,2x ∈-，总存在[]21,2x ∈，使得()()12f x g x >，则实数m 的取值范围是.16.某小商品生产厂家计划每天生产A 型、B 型、C 型三种小商品共100个，生产一个型小商品需5分钟，生产一个B 型小商品需7分钟，生产一个C 型小商品需4分钟，已知总生产时间不超过10小时.若生产一个A 型小商品可获利润8元，生产一个B 型小商品可获利润9元，生产一个C 型小商品可获利润6元.该厂家合理分配生产任务使每天的利润最大，则最大日利润是元.三、解答题：共70分.解答应写出文字说明、证明过程或演算步骤.第17~21题为必考题，每个试题考生都必须作答.第22、23题为选考题，考生根据要求作答. （一）必考题：60分.17.已知数列{}{},n n a b 满足：114a=，1n n a b +=，121n n n b b a +=-.（1）证明：11n b ⎧⎫⎨⎬-⎩⎭是等差数列，并求数列{}n b 的通项公式； （2）设1223341n n n S a a a a a a a a +=++++L ，求实数a 为何值时4n n aS b <恒成立.18.如图，ABCD 是边长为2的菱形，60DAB ∠=︒，EB ⊥平面ABCD ，FD ⊥平面ABCD ，24EB FD ==.（1）求证：EF AC ⊥； （2）求几何体EFABCD 的体积.19.在“挑战不可能”的电视节目上，甲、乙、丙三个人组成的解密团队参加一项解密挑战活动，规则是由密码专家给出题目，然后由3个人依次出场解密，每人限定时间是1分钟内，否则派下一个人.3个人中只要有一人解密正确，则认为该团队挑战成功，否则挑战失败.根据甲以往解密测试情况，抽取了甲100次的测试记录，绘制了如下的频率分布直方图.（1）若甲解密成功所需时间的中位数为47，求a 、b 的值，并求出甲在1分钟内解密成功的频率； （2）在“挑战不可能”节目上由于来自各方及自身的心理压力，甲，乙，丙解密成功的概率分别为()11911,2,31010n n n P P n --⎛⎫=+= ⎪⎝⎭，其中i P 表示第i 个出场选手解密成功的概率，并且1P 定义为甲抽样中解密成功的频率代替，各人是否解密成功相互独立. ①求该团队挑战成功的概率；②该团队以i P 从小到大的顺序按排甲、乙、丙三个人上场解密，求团队挑战成功所需派出的人数X 的可能值及其概率.20.如图，设抛物线()21:40C y mx m =->的准线l 与x 轴交于椭圆22222:1(0)x y C a b a b+=>>的右焦点21,F F 为2C 的左焦点.椭圆的离心率为12e =，抛物线1C 与椭圆2C 交于x 轴上方一点P ，连接1PF 并延长其交1C 于点Q ，M 为1C 上一动点，且在,P Q 之间移动.（1）当32a b+取最小值时，求1C 和2C 的方程； （2）若12PF F △的边长恰好是三个连续的自然数，当MPQ △面积取最大值时，求面积最大值以及此时直线MP 的方程. 21.已知函数()ln xf x a x e=+，其中a 为常数.（1）若直线2y x e=是曲线()y f x =的一条切线，求实数a 的值； （2）当1a =-时，若函数()()ln xg x f x b x=-+在[)1,+∞上有两个零点.求实数b 的取值范围.（二）选考题：共10分.请考生在第22、23题中任选一题作答，如果多做，则按所做的第一题计分. 22.[选修4—4：坐标系与参数方程]在平面直角坐标系xOy 中，直线l 的参数方程为21x ty t=--⎧⎨=+⎩，（t 为参数），曲线1:C y =以坐标原点为极点，x 轴正半轴为极轴建立极坐标系，曲线2C 的极坐标方程为π4ρα⎛⎫= ⎪⎝⎭-. （1）若直线l 与x ，y 轴的交点分别为,A B ，点P 在1C 上，求BA BP ⋅uu r uu r的取值范围；（2）若直线l 与2C 交于M N ,两点，点Q 的直角坐标为()2,1-，求QM QN -的值. 23.[选修4–5：不等式选讲]已知函数()223f x x x m =+++，R m ∈. （1）当2m =-时，求不等式()3f x ≤的解集； （2）若(),0x ∀∈-∞，都有()2f x x x≥+恒成立，求m 的取值范围.湖南湖北四校2020届高三学情调研联考文科数学试题卷参考答案及解析一、选择题：本题共12小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求的.1.B【解析】由题意得，[]0,4P =，()3,3Q =-，(]3,4P Q =-∴U ，故选B. 2.C 【解析】设x a bi =+，y a bi =-，代入得()()2222346a a bi i -+=-，所以()224a =，()2236a b +=，解得1a =，1b =，所以x y +=3.B 解析：设大正方体的边长为x ，12x x -，设落在小正方形内的米粒数大约为N ，则2212200x x N x ⎫-⎪⎝⎭=，解得：27N ≈. 4.A 【解析】()33134444AD AB BD AB BC AB AC AB AC AB =+=+=+-=+u u u r u u u r u u u r u u u u u r u u uu r u u u r u u u r u u u r r u u u r ，所以14λ=，34μ=，从而求得13λμ=.5.D 解析：Q 函数()f x 是偶函数，()()f x f x ∴=-在R 上恒成立，0m ∴=，∴当0x ≥时，易得()21x f x =-为增函数，()()0.52log 3log 3af f ∴==，，()2log5b f =，()2c f =，22log 32log 5<<Q，a c b ∴<<6.C 由三视图可知多面体是棱长为2的正方体中的三棱锥P ABC -， 故1AC =，2PA =，BC PC ==AB =PB =12112ABC PAC S S ∴==⨯⨯=△△，122PAB S =⨯⨯=△12PBC S =⨯=△，∴该多面体的侧面最大面积为.故选C.7.B 解析：双曲线C 左支上的任意一点M 均满足24MF MN b +>， 即()2min4MF MNb +>，又2 21232222b MF MN aMF MN a NF aa+≥++≥+=+2223244382ba b a b aba∴+>⇒+>34802b a ba b a⇒⋅+->⇒>或23ba<2221bea∴=+，5e>或131N<<8.B详解：由11111123499100S=-+-++-L得程序框图先对奇数项累加，偶数项累加，最后再相减.因此在空白框中应填入2i i=+，选B.9.C【解析】3cos cos5a Bb A c-=Q∴由正弦定理，得3sin cos sin cos sin5A B B A C-=，()()sin sinC A B C A Bπ=-+⇒=+Q，()3sin cos sin cos sin cos cos sin5A B B A A B A B∴-=+，整理，得sin cos4sin cosA B B A=，同除以cos cosA B，得tan4tanA B=，由此可得()2tan tan3tan3tan11tan tan14tan4tantanA B BA BA B B BB--===+++，AQ、B是三角形内角，且tan A与tan B同号，A∴、B都是锐角，即tan0A>，tan0B>，114tan4tan4tan tanB BB B+≥⋅=Q()33tan144tantanA BBB-=≤+，当且仅当14tantanBB=，即1tan2B=时，()tan A B-的最大值为34.10.B解析：2ππ2cos1cos1sin242xx xωωω⎛⎫⎛⎫-=+-=+⎪ ⎪⎝⎭⎝⎭Q，()()2sin1sin sin sinf x x x x xωωωω=+-=.令π2π2x kω=+可得π2π2kxωω=+，()f xQ在区间[]0,π上恰好取得一次最大值，π0π2ω∴≤≤解得12ω≥.令ππ2π2π22k x kω-+≤≤+，解得：π2ππ2π22k kxωωωω-+≤≤+，()f xQ在区间2π5π,36⎡⎤-⎢⎥⎣⎦上是增函数，2ππ325π365ωω⎧-≥-⎪⎪∴⎨⎪≤≤⎪⎩，解得35ω≤.综上，1325ω≤≤.故选：B.11.A解析：因为0a b>>，所以双曲线的渐近线如图所示，设内切圆圆心为M，则M在AOB∠平分线OF上，过点M分别作MN OA⊥于N，MT AB⊥于T，由FA OA⊥得四边形MTAN为正方形，由焦点到渐近线的距离为b得FA b=，又OF c=，所以OA a=，312NA MN a==-，所以332NO a=-，所以tan3MNbAOFa NO=∠==，得23213bea⎛⎫=+=⎪⎝⎭.故选A.12.D解析：方法一：本题也可用解三角形方法，达到求出棱长的目的.适合空间想象能力略差学生.设2PA PB PC x===，,E F分别为,PA AB中点，EF PB∴∥，且12EF PB x==，ABC△Q为边长为2的等边三角形，3CF∴=又90CEF∠=︒23CE x∴=-12AE PA x==AEC△中余弦定理()2243cos22x xEACx+--∠=⨯⨯，作PD AC⊥于D，PA PC=Q，DQ为AC中点，1cos2ADEACPA x∠==，2243142x xx x+-+∴=，2212x ∴+=，212x ∴=，2x =，PA PB PC ∴===2AB BC AC ===，,,PA PB PC∴两两垂直，2R ∴==2R ∴=，344338V R ππ∴==⨯=，故选D. 方法二：PA PB PC ==Q ，ABC △为边长为2的等边三角形，P ABC ∴-为正三棱锥，PB AC ∴⊥，又E ，F 分别为PA 、AB 中点，EF PB ∴∥，EF AC ∴⊥，又EF CE ⊥，CE AC C =I ，EF ∴⊥平面PAC ，PB ⊥平面PAC ，PAB ∴∠=90︒，PA PB PC ∴===，P ABC ∴-为正方体一部分，2R ==R =，34433V R ππ∴===，故选D. 二、填空题：本题共4小题，每小题5分，共20分. 13.()0,x ∀∈+∞，ln 1x x ≠- 14.2F V E +-=解析：凸多面体的面数为F .顶点数为V 和棱数为E ，①正方体：6F =，8V =，12E =，得86122F V E +-=+-=； ②三棱柱：5F =，6V =，9E =，得5692F V E +-=+-=； ③三棱锥：4F =，4V =，6E =，得4462F V E +-=+-=.根据以上几个例子，猜想：凸多面体的面数F .V 和棱数E 满足如下关系：2F V E +-= 再通过举四棱锥、六棱柱、…等等，发现上述公式都成立. 因此归纳出一般结论：2F V E +-= 故答案为：2F V E +-= 15.1,2⎛⎫-∞-⎪⎝⎭解析：()()1x f x e x =-Q ，()xf x xe '∴=，∴对于任意的[]2,2x ∈-，当[)2,0x ∈-时，()0f x '<，当(]0,2x ∈时，()0f x '>，即()f x 在[)2,0-上为减函数，在(]0,2上为增函数.0x ∴=为()f x 在[]2,2-上的极小值点，也是最小值点且最小值为[]2,2-，∴对于任意的[]12,2x ∈-，()1min 1f x =-，而总存在[]21,2x ∈，使得()()12f x g x >，()()12min min f x g x >.()g x mx =∵，∴①0m =时，()20g x =，不合题意，②0m >时，()[]22,2g x mx m m =∈，此时1m <-，不合题意，③0m <时，()[]222,g x mx m m =∈，()2min 2g x m ∴=，21m ∴<-，12m <-. 16.850【解析】依题意，每天生产的玩具A 型商品x 个、B 商品y 个、C 商品的个数等于：100x y --，所以每天的利润()89610023600T x y x y x y =++--=++.约束条件为：()*57410060010000,0,,x y x y x y x y x y N ++--≤⎧⎪--≥⎨⎪≥≥∈⎩，整理得*3200100,x y x y x y N ⎧+≤⎪+≤⎨⎪∈⎩.目标函数为23600T x y =++.如图所示，做出可行域.初始直线0:230l x y +=，平移初始直线经过点A 时，T 有最大值.由3200100x y x y +=⎧⎨+=⎩得5050x y =⎧⎨=⎩.最优解为()50,50A ，此时max 850T =（元）.即最大日利润是850元.三、解答题：共70分.解答应写出文字说明、证明过程或演算步骤.第17~21题为必考题，每个试题考生都必须作答.第22、23题为选考题，考生根据要求作答.17.（1）()()()111122n n n n n n n n b b b a a b b b +===-+--Q ，11112n nb b +∴-=--，12111111n n n n b b b b +-∴==-+---.∴数列11n b ⎧⎫⎨⎬-⎩⎭是以4-为首项，1-为公差的等差数列. ∴14(1)31n n n b =---=---，∴12133n n b n n +=-=++. （2）113n n a b n =-=+Q . ()()()12231111114556344444n n n n S a a a a a a n n n n +∴=++⋅⋅⋅+=++⋅⋅⋅=-=⨯⨯++++ ()()()()21368244334n n a n a n an n aS b n n n n -+--+∴-=-=++++.由条件可知()()213680a n a n -+--<恒成立即可满足条件，设()()()21328f n a n a n =-+--，当1a =时，()380f n n =--<恒成立，当1a >时，由二次函数的性质知不可能成立.当1a <时，对称轴3231102121a a a -⎛⎫-⋅=--< ⎪--⎝⎭，()f n 在[)1,+∞为单调递减函数. ()()()113684150f a a a =-+--=-<，154a ∴<，∴时4n aSb <恒成立.综上知：1a <时，4n aS b <恒成立. 18.【解析】（1）连接DB ，DF ⊥平面ABCD ，EB ⊥平面ABCD ，EB FD ∴∥，E ∴，F ，D ，B 四点共面，AC EB ∴⊥，设DB AC O =I ，ABCD Q 为菱形，AC DB ∴⊥.DB EB B =I ，AC ∴⊥平面EFDB ，EF ⊂Q 平面EFDB ，AC EF ∴⊥.（2）EB FD ∥Q ，EB BD ⊥，EFDB ∴为直角梯形，在菱形ABCD 中，60DAB ∠︒＝，2AB =，2BD =，3AO CO ==∴梯形EFDB 的面积()24262S +⨯==，AC ⊥Q 平面EFDB ，114333EFABCD C EFDB A EFDB V V V S AO S CO --∴==⨯+⨯=+. 19.解析：（1）甲解密成功所需时间的中位数为47，()0.0150.014550.03450.0447450.5b ∴⨯+⨯+⨯+⨯+⨯-=，解得0.026b =；0.0430.032550.010100.5a ∴⨯+⨯+⨯+⨯=，解得0.024a =；∴甲在1分钟内解密成功的频率是10.01100.9f =-⨯=（2）①由题意及（1）可知第一个出场选手解密成功的概率为10.9P =；第二个出场选手解密成功的概率为2910.910.911010P =⨯+⨯=， 第三个出场选手解密成功的概率为23910.920.9291010P ⎛⎫=+⨯= ⎪⎝⎭⨯， 所以该团队挑战成功的概率为0.90.10.910.10.090.9290.999361P =+⨯+⨯⨯=（或令“该团队挑战成功”的事件为A ，“挑战不成功”的事件为A ，()()()()10.910.9110.9290.10.090.0710.000639P A ⨯=---=⨯=，∴该团队挑战成功的概率为()()110.00016390.999361P A P A =-=-=②由①可知按i P 从小到大的顺序的概率分别1p ，2p ，3p ，根据题意知X 的取值为1，2，3；则()10.9P X ==，()()210.90.910.091P X ==-⨯=， ()()()310.910.910.10.090.009P X ==--=⨯=.20.（1）因为1,2c c m e a ===，则2,a m b ==，所以2a b +取最小值时1m =， 此时抛物线21:4C y x =-，此时22,3a b ==，所以椭圆2C 的方程为22143x y +=； （2）因为1,2c c m e a ===，则2,a m b ==，设椭圆的标准方程为2222143x y m m +=， ()()0011,,,P x y Q x y 由2222214334x y m m y mx ⎧+=⎪⎨⎪=-⎩得22316120x mx m --=，所以023x m =-或06x m =（舍去），代入抛物线方程得03y m =，即23m P ⎛- ⎝⎭， 于是153m PF =，21723m PF a PF =-=，12623m F F m ==，又12PF F △的边长恰好是三个连续的自然数，所以3m =.此时抛物线方程为212y x =-，()(13,0,F P --，则直线PQ的方程为)3y x =+.联立)2312y x y x⎧=+⎪⎨=-⎪⎩，得192x =-或12x =-（舍去），于是9,2Q ⎛-- ⎝.所以252PQ ==，设(()2,12t M t t ⎛⎫-∈- ⎪⎝⎭到直线PQ的距离为d，则2753022d t ⎛=⨯+- ⎝⎭，当t =max 752d ==，所以MPQ △的面积最大值为12522⨯=.此时:MP y =+.21.（1）函数()f x 的定义域为()0,+∞，()1a x ae f x e x ex+'=+=，曲线()y f x =在点()00,x y 处的切线方程为2y x e =.由题意得000012,2ln a e x e x x a x ee ⎧+=⎪⎪⎨⎪=+⎪⎩解得1a =，0x e =.所以a 的值为1. （2）当1a =-时，()ln xf x x e =-，则()11x e f x e x ex-'=-=，由()0f x '>，得x e >，由()0f x '<，得0x e <<，则()f x 有最小值为()0f e =，即()0f x ≥，所以()ln ln x x g x x b e x=--+，()0x >，由已知可得函数ln ln x x y x x e =+-的图象与直线y b =有两个交点， 设()()ln ln 0x x h x x x x e=+->，则()22211ln 1ln x ex e e x x h x x x e ex -+--'=+-=， 令()2ln x ex e e x x ϕ=+--，()222e ex e x x e x x x ϕ--'=--=， 由220ex e x --<，可知()0x ϕ'<，所以()x ϕ在()0,+∞上为减函数，由()0e ϕ=，得0x e <<时，()0x ϕ>，当x e >时，()0x ϕ<，即当0x e <<时，()0h x '>，当x e >时，()0h x '<，则函数()h x 在()0,e 上为增函数，在(),e +∞上为减函数，所以，函数()h x 在x e =处取得极大值()1h e e =， 又()11h e =-，()322331341h e e e e e=+-<-<-<-， 所以，当函数()g x 在[)1,+∞上有两个零点时，b 的取值范围是11b e e -≤<， 即11,b e e ⎡⎫∈-⎪⎢⎣⎭. 22.（1）由题意可知：直线l 的普通方程为10x y ++=，()1,0A ∴-，()0,1B -1C 的方程可化为()2210x y y +=≥，设点P 的坐标为()cos ,sin θθ，0θπ≤≤，cos sin 1114BA BP πθθθ⎛⎫⎡⎤∴⋅=-++=-+∈ ⎪⎣⎦⎝⎭uu r uu r（2）曲线2C 的直角坐标方程为：()()22228x y ++-=直线l的标准参数方程为212x m y m ⎧=-⎪⎪⎨⎪=+⎪⎩（m 为参数），代入2C得：270m -=设,M N 两点对应的参数分别为12,m m121270m m m m +=-<故12,m m异号12QM QN m m ∴-=+=23.答案：（1）当2m =-时，()()410322321023452x x f x x x x x x ⎧⎪+≥⎪⎪⎛⎫=++--<<⎨ ⎪⎝⎭⎪⎪⎛⎫--≤-⎪ ⎪⎝⎭⎩当4130x x +≤⎧⎨≥⎩解得102x ≤≤当30,132x -<<≤恒成立. 当45332x x --≤⎧⎪⎨≤-⎪⎩解得322x -≤≤-，此不等式的解集为12,2⎡⎤-⎢⎥⎣⎦. （2）()()43032233023432x m x f x x x m m x x m x ⎧⎪++≥⎪⎪⎛⎫=+++=+-<<⎨ ⎪⎝⎭⎪⎪⎛⎫--+≤-⎪ ⎪⎝⎭⎩， 当(),0x ∈-∞时，()33022233432m x f x x x m x m x ⎧⎛⎫+-<< ⎪⎪⎪⎝⎭=+++=⎨⎛⎫⎪--+≤- ⎪⎪⎝⎭⎩当302x -<<时，()3f x m =+，当()3,432x f x x m ≤-=--+单调递减， ()f x ∴的最小值为3m +设()()20g x x x x=+<当20,x x x ->-+≥-，当且仅当2x x -=-时，取等号2x x ∴+≤-即x =()g x取得最大值-.要使()2f x x x≥+恒成立，只需3m +≥-3m ≥-.。
2020年湖北省武汉市武昌区四月调研(文科)数学试卷 含解析
2020年四月调研（文科）数学试卷一、选择题（共12小题）.1．设全集U＝R，集合A＝{x|0＜x≤2}，B＝{x|x＜1}，则集合A∪B＝（）A．（2，+∞）B．[2，+∞）C．（﹣∞，2]D．（﹣∞，1]2．已知复数z＝，则复数z的虚部为（）A．B．C．i D．i3．已知双曲线C：＝1（a＞0，b＞0）的焦距为8，一条渐近线方程为y＝x，则C（）A．B．C．D．4．某学校组织学生参加英语测试，成绩的频率分布直方图如图，数据的分组依次为[20，40），[40，60），[60，80），[80，100]．若低于60分的人数是18人，则该班的学生人数是（）A．45B．50C．55D．605．已知l，m是两条不同的直线，m⊥平面α，则“l∥α”是“l⊥m”的（）A．充分而不必要条件B．必要而不充分条件C．充要条件D．既不充分也不必要条件6．已知向量＝（1，﹣2），＝（3，﹣1），则（）A．∥B．⊥C．∥（﹣）D．⊥（﹣）7．已知点（m，8）在幂函数f（x）＝（m﹣1）x n的图象上，设a＝f（），b＝f（lnπ），c＝f（n），则（）A．b＜a＜c B．a＜b＜c C．b＜c＜a D．a＜c＜b8．函数的图象大致为（）A．B．C．D．9．一艘海轮从A处出发，以每小时24海里的速度沿南偏东40°的方向直线航行，30分钟后到达B处，在C处有一座灯塔，海轮在A处观察灯塔，其方向是南偏东70°，在B 处观察灯塔，其方向是北偏东65°，那么B，C两点间的距离是（）A．6 海里B．6海里C．8海里D．8海里10．已知三棱锥P﹣ABC的顶点都在球O的球面上，PA＝，PB＝，AB＝4，CA＝CB＝，面PAB⊥面ABC，则球O的表面积为（）A．B．C．D．11．已知函数f（x）＝A sin（ωx+φ）（A＞0，ω＞0，0＜φ＜）的部分图象如图所示，则f（）＝（）A．B．C．D．12．已知函数f（x）是定义域为R的偶函数，且满足f（x）＝f（2﹣x），当x∈[0，1]时，f（x）＝x，则函数F（x）＝f（x）+在区间[﹣10，9]上零点的个数为（）A．9B．10C．18D．20二、填空题：本题共4小题，每小题5分，共20分．13．直线mx﹣ny﹣1＝0（m＞0，n＞0）过圆C：x2+y2﹣2x+2y﹣1＝0的圆心，则的最小值是．14．从分别写有1，2，3，4的4张卡片中随机抽取1张，放回后再随机抽取1张，则抽得的第一张卡片上的数不小于第二张卡片上的数的概率为．15．给出以下式子：①tan25°+tan35°+tan25°tan35°；②2（sin35°cos25°+cos35°cos65°）；③其中，结果为的式子的序号是．16．已知椭圆C：＝1（a＞b＞0）的左、右焦点分别为F1，F2，椭圆的焦距为2c，过C外一点P（c，2c）作线段PF1，PF2分别交椭圆C于点A、B，若|PA|＝|AF1|，则＝．三、解答题：共70分．解答应写出文字说明、证明过程或演算步骤．第17～21题为必考题，每个试题考生都必须作答．第22、23题为选考题，考生根据要求作答．（一）必考题：共60分．17．已知等差数列{a n}的各项均为正数，S n为等差数列{a n}的前n项和，a1＝1，a4a5＝11．（1）求数列{a n}的通项a n；（2）设b n＝a n⋅3n，求数列{b n}的前n项和T n．18．如图，在三棱柱ABC﹣A1B1C1中，A1A⊥平面ABC，∠ACB＝90°，AC＝CB＝C1C＝1，M，N分别是AB，A1C的中点．（1）求证：直线MN⊥平面ACB1；（2）求点C1到平面B1MC的距离．19．某校共有学生2000人，其中男生900人，女生1100人，为了调查该校学生每周平均体育锻炼时间，采用分层抽样的方法收集该校100名学生每周平均体育锻炼时间（单位：小时）．（1）应抽查男生与女生各多少人？（2）根据收集100人的样本数据，得到学生每周平均体育锻炼时间的频率分布表：时间（小时）[0，1]（1，2]（2，3]（3，4]（4，5]（5，6]频率0.050.200.300.250.150.05若在样本数据中有38名男学生平均每周课外体育锻炼时间超过2小时，请完成每周平均体育锻炼时间与性别的列联表，并判断是否有95%的把握认为“该校学生的每周平均体育锻炼时间与性别有关”？男生女生总计每周平均体育锻炼时间不超过2小时每周平均体育锻炼时间超过2小时总计附：K2＝．P（K2≥k0）0.1000.0500.0100.005k0 2.706 3.841 6.6357.87920．已知A是抛物线E：y2＝2px（p＞0）上的一点，以点A和点B（2，0）为直径两端点的圆C交直线x＝1于M，N两点．（1）若|MN|＝2，求抛物线E的方程；（2）若0＜p＜1，抛物线E与圆（x﹣5）2+y2＝9在x轴上方的交点为P，Q，点G为PQ的中点，O为坐标原点，求直线OG斜率的取值范围．21．已知函数f（x）＝x2+（t﹣2）x﹣tlnx+2．（1）若x＝2是f（x）的极值点，求f（x）的极大值；（2）求实数t的范围，使得f（x）≥2恒成立．（二）选考题：共10分．请考生在第22、23题中任选一题作答．如果多做，则按所做的第一题计分．[选修4-4：坐标系与参数方程]22．在平面直角坐标系xOy中，直线l的参数方程为（t为参数），以坐标原点O为极点，x轴的正半轴为极轴建立极坐标系，圆C的极坐标方程为ρ2﹣4ρcosθ＝3．（1）求直线l的普通方程和圆C的直角坐标方程；（2）直线l与圆C交于A，B两点，点P（2，1），求|PA|⋅|PB|的值．[选修4-5：不等式选讲]23．已知函数f（x）＝|x﹣a|．（1）当a＝﹣1时，求不等式f（x）≤|2x+1|﹣1的解集；（2）若函数g（x）＝f（x）﹣|x+3|的值域为A，且[﹣2，1]⊆A，求a的取值范围．参考答案一、选择题：本题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的．1．设全集U＝R，集合A＝{x|0＜x≤2}，B＝{x|x＜1}，则集合A∪B＝（）A．（2，+∞）B．[2，+∞）C．（﹣∞，2]D．（﹣∞，1]【分析】根据并集的定义进行求解．解：∵A＝{x|0＜x≤2}，B＝{x|x＜1}，∴A∪B＝{x|x≤2}，故选：C．2．已知复数z＝，则复数z的虚部为（）A．B．C．i D．i【分析】利用复数的运算法则、虚部的定义即可得出．解：z＝＝＝﹣i，则复数z的虚部为﹣．故选：B．3．已知双曲线C：＝1（a＞0，b＞0）的焦距为8，一条渐近线方程为y＝x，则C（）A．B．C．D．【分析】由题意求得c与的值，结合隐含条件列式求得a2，b2，则答案可求．解：由题意，2c＝8，则c＝4，又，且a2+b2＝c2，解得a2＝4，b2＝12．∴双曲线C的方程为．故选：A．4．某学校组织学生参加英语测试，成绩的频率分布直方图如图，数据的分组依次为[20，40），[40，60），[60，80），[80，100]．若低于60分的人数是18人，则该班的学生人数是（）A．45B．50C．55D．60【分析】根据频率分布直方图中频率＝小矩形的高×组距计算成绩低于60分的频率，再根据样本容量＝求出班级人数．解：根据频率分布直方图，得；低于60分的频率是（0.005+0.010）×20＝0.30，∴样本容量（即该班的学生人数）是＝60（人）．故选：D．5．已知l，m是两条不同的直线，m⊥平面α，则“l∥α”是“l⊥m”的（）A．充分而不必要条件B．必要而不充分条件C．充要条件D．既不充分也不必要条件【分析】根据充分条件和必要条件的定义，结合线面垂直的性质进行判断即可．解：当m⊥平面α时，若l∥α”则“l⊥m”成立，即充分性成立，若l⊥m，则l∥α或l⊂α，即必要性不成立，则“l∥α”是“l⊥m”充分不必要条件，故选：A．6．已知向量＝（1，﹣2），＝（3，﹣1），则（）A．∥B．⊥C．∥（﹣）D．⊥（﹣）【分析】由题意利用两个向量坐标形式的运算法则，两个向量平行、垂直的性质，得出结论．解：∵向量＝（1，﹣2），＝（3，﹣1），∴和的坐标对应不成比例，故、不平行，故排除A；显然，•＝3+2≠0，故、不垂直，故排除B；∴﹣＝（﹣2，﹣1），显然，和﹣的坐标对应不成比例，故和﹣不平行，故排除C；∴•（﹣）＝﹣2+2＝0，故⊥（﹣），故D正确，故选：D．7．已知点（m，8）在幂函数f（x）＝（m﹣1）x n的图象上，设a＝f（），b＝f（lnπ），c＝f（n），则（）A．b＜a＜c B．a＜b＜c C．b＜c＜a D．a＜c＜b【分析】先利用幂函数的定义求出m的值，得到幂函数解析式为f（x）＝x3，在R上单调递增，再利用幂函数f（x）的单调性，即可得到a，b，c的大小关系．解：由幂函数的定义可知，m﹣1＝1，∴m＝2，∴点（2，8）在幂函数f（x）＝x n上，∴2n＝8，∴n＝3，∴幂函数解析式为f（x）＝x3，在R上单调递增，∵＝，1＜lnπ＜3，n＝3，∴，∴a＜b＜c，故选：B．8．函数的图象大致为（）A．B．C．D．【分析】由函数的奇偶性可排除BD，由函数的趋近性可排除C，由此得出正确选项．解：函数的定义域为{x∈R|x≠﹣2且x≠0且x≠2}，，则函数f（x）为偶函数，其图象关于y轴对称，可排除BD；当x→+∞时，＞0，则f（x）→0且f（x）＞0，故排除C．故选：A．9．一艘海轮从A处出发，以每小时24海里的速度沿南偏东40°的方向直线航行，30分钟后到达B处，在C处有一座灯塔，海轮在A处观察灯塔，其方向是南偏东70°，在B处观察灯塔，其方向是北偏东65°，那么B，C两点间的距离是（）A．6 海里B．6海里C．8海里D．8海里【分析】先根据给的条件求出三角形ABC的三个内角，再结合AB可求，应用正弦定理即可求解．解：由题意可知：∠BAC＝70°﹣40°＝30°．∠ACD＝110°，∴∠ACB＝110°﹣65°＝45°，∴∠ABC＝180°﹣30°﹣45°＝105°．又AB＝24×0.5＝12．在△ABC中，由正弦定理得，即，∴．故选：A．10．已知三棱锥P﹣ABC的顶点都在球O的球面上，PA＝，PB＝，AB＝4，CA＝CB＝，面PAB⊥面ABC，则球O的表面积为（）A．B．C．D．【分析】由题意画出图形，找出△PAB外接圆的圆心及三棱锥P﹣BCD的外接球心为O，通过求解三角形求出三棱锥P﹣BCD的外接球的半径，则答案可求．解：如图；设AB的中点为D；∵PA＝，PB＝，AB＝4，∴△PAB为直角三角形，且斜边为AB，故其外接圆半径为：r＝AB＝AD＝2；设外接球球心为O；∵CA＝CB＝，面PAB⊥面ABC，∴CD⊥AB可得CD⊥面PAB；且DC＝＝．∴O在CD上；故有：AO2＝OD2+AD2⇒R2＝（﹣R）2+r2⇒R＝；∴球O的表面积为：4πR2＝4π×＝．故选：D．11．已知函数f（x）＝A sin（ωx+φ）（A＞0，ω＞0，0＜φ＜）的部分图象如图所示，则f（）＝（）A．B．C．D．【分析】先利用最高点纵坐标求出A，再根据求出周期，再将代入求出φ的值．最后将代入即可．解：由图象可知A＝1，∵，所以T＝π，∴．∴f（x）＝sin（2x+φ），将代入得φ）＝1，∴φ＝，结合0＜φ＜，∴φ＝．∴．∴＝﹣sin＝﹣＝．故选：A．12．已知函数f（x）是定义域为R的偶函数，且满足f（x）＝f（2﹣x），当x∈[0，1]时，f（x）＝x，则函数F（x）＝f（x）+在区间[﹣10，9]上零点的个数为（）A．9B．10C．18D．20【分析】由已知可得函数f（x）的周期与对称轴，函数F（x）＝f（x）+在区间[﹣10，9]上零点的个数等价于函数f（x）与g（x）＝﹣图象在[﹣9，10]上交点的个数，作出函数f（x）与g（x）的图象如图，数形结合即可得到答案．解：函数F（x）＝f（x）+在区间[﹣10，9]上零点的个数等价于函数f（x）与g （x）＝﹣图象在[﹣9，10]上交点的个数，由f（x）＝f（2﹣x），得函数f（x）图象关于x＝1对称，∵f（x）为偶函数，取x＝x+2，可得f（x+2）＝f（﹣x）＝f（x），得函数周期为2．又∵当x∈[0，1]时，f（x）＝x，且f（x）为偶函数，∴当x∈[﹣1，0]时，f（x）＝﹣x，g（x）＝﹣＝＝+，作出函数f（x）与g（x）的图象如图：由图可知，两函数图象共10个交点，即函数F（x）＝f（x）+在区间[﹣10，9]上零点的个数为10．故选：B．二、填空题：本题共4小题，每小题5分，共20分．13．直线mx﹣ny﹣1＝0（m＞0，n＞0）过圆C：x2+y2﹣2x+2y﹣1＝0的圆心，则的最小值是4．【分析】直线mx﹣ny﹣1＝0（m＞0，n＞0）经过圆x2+y2﹣2x+2y﹣1＝0的圆心（1，﹣1），可得m+n＝1，再利用“乘1法”和基本不等式的性质即可得出．解：∵mx﹣ny﹣1＝0（m＞0，n＞0）经过圆x2+y2﹣2x+2y﹣1＝0的圆心（1，﹣1），∴m+n﹣1＝0，即m+n＝1．∴＝（）（m+n）＝2++≥2+2＝4，当且仅当m＝n＝时取等号．∴则的最小值是4．故答案为：4．14．从分别写有1，2，3，4的4张卡片中随机抽取1张，放回后再随机抽取1张，则抽得的第一张卡片上的数不小于第二张卡片上的数的概率为．【分析】基本事件总数n＝4×4＝16，利用列举法求出抽得的第一张卡片上的数不小于第二张卡片上的数包含的基本事件有10个，由此能求出抽得的第一张卡片上的数不小于第二张卡片上的数的概率．解：从分别写有1，2，3，4的4张卡片中随机抽取1张，放回后再随机抽取1张，基本事件总数n＝4×4＝16，抽得的第一张卡片上的数不小于第二张卡片上的数包含的基本事件有：（1，1），（2，1），（2，2），（3，1），（3，2），（3，3），（4，1），（4，2），（4，3），（4，4），共10个，则抽得的第一张卡片上的数不小于第二张卡片上的数的概率为p＝＝．故答案为：．15．给出以下式子：①tan25°+tan35°+tan25°tan35°；②2（sin35°cos25°+cos35°cos65°）；③其中，结果为的式子的序号是①②③．【分析】由已知分别结合和差角的正切及正弦余弦公式进行化简即可求解．解：①∵tan60°＝tan（25°+35°）＝＝，tan25°+tan35°+tan25°tan35°；＝+tan25°tan35°，＝，②2（sin35°cos25°+cos35°cos65°）＝2（sin35°cos25°+cos35°sin25°），＝2sin60°＝；③＝＝tan（45°+15°）＝tan60°＝；故答案为：①②③16．已知椭圆C：＝1（a＞b＞0）的左、右焦点分别为F1，F2，椭圆的焦距为2c，过C外一点P（c，2c）作线段PF1，PF2分别交椭圆C于点A、B，若|PA|＝|AF1|，则＝2．【分析】根据条件可得判断OA∥PF2，且|PF2|＝2|OA|，从而得到点A为椭圆上顶点，则有b＝c，解出B的坐标即可得到比值．解：因为|PA|＝|AF1|，所以点A是线段PF1的中点，又因为点O为线段F1F2的中点，所以OA∥PF2，且|PF2|＝2|OA|，因为点P（c，2c），所以PF2⊥x轴，则|PF2|＝2c，所以OA⊥x轴，则点A为椭圆上顶点，所以|OA|＝b，则2b＝2c，所以b＝c，a＝＝c，设B（c，m）（m＞0），则，解得m＝c，所以|BF2|＝c，则＝＝2．故答案为：2．三、解答题：共70分．解答应写出文字说明、证明过程或演算步骤．第17～21题为必考题，每个试题考生都必须作答．第22、23题为选考题，考生根据要求作答．（一）必考题：共60分．17．已知等差数列{a n}的各项均为正数，S n为等差数列{a n}的前n项和，a1＝1，a4a5＝11．（1）求数列{a n}的通项a n；（2）设b n＝a n⋅3n，求数列{b n}的前n项和T n．【分析】本题第（1）题先设等差数列{a n}的公差为d（d＞0），然后根据等差数列的通项公式及已知条件可列出关于d的方程，解出d的值，即可得到数列{a n}的通项a n；第（2）题先根据第（1）题的结果计算出数列{b n}的通项公式，然后运用错位相减法计算前n项和T n．解：（1）由题意，设等差数列{a n}的公差为d（d＞0），则a4a5＝（1+3d）（1+4d）＝11，整理，得12d2+7d﹣10＝0，解得d＝﹣（舍去），或d＝，∴a n＝1+（n﹣1）＝，n∈N*．（2）由（1）知，b n＝a n⋅3n＝•3n＝（2n+1）•3n﹣1，∴T n＝b1+b2+b3+…+b n＝3×1+5×31+7×32+…+（2n+1）•3n﹣1，∴3T n＝3×31+5×32+…+（2n﹣1）•3n﹣1+（2n+1）•3n，两式相减，可得：﹣2T n＝3×1+2×31+2×32+…+2•3n﹣1﹣（2n+1）•3n＝3+2×（31+32+…+3n﹣1）﹣（2n+1）•3n＝3+2×﹣（2n+1）•3n＝﹣2n•3n，∴T n＝n•3n．18．如图，在三棱柱ABC﹣A1B1C1中，A1A⊥平面ABC，∠ACB＝90°，AC＝CB＝C1C＝1，M，N分别是AB，A1C的中点．（1）求证：直线MN⊥平面ACB1；（2）求点C1到平面B1MC的距离．【分析】（1）先利用已知条件证得AC⊥MN以及MN⊥B1C，进而得到MN⊥平面ACB1；（2）求出三角形的面积，利用体积公式求解即可．解：（1）证明：连接AC1，BC1，则N∈AC1且N为AC1的中点；∵M是AB的中点．所以：MN∥BC；∵A1A⊥平面ABC，AC⊂平面ABC，∴A1A⊥AC，在三棱柱ABC﹣A1B1C1中，AA1∥CC，∴AC⊥CC1，∵∠ACB＝90°，BC∩CC1＝C，BC⊂平面BB1C1C，CC1⊂平面BB1C1C，∴AC⊥平面BB1C1C，BC⊂平面BB1C1C，∴AC⊥BC1；又MN∥BC1∴AC⊥MN，∵CB＝C1C＝1，∴四边形BB1C1C正方形，∴BC1⊥B1C，∴MN⊥B1C，而AC∩B1C＝C，且AC⊂平面ACB1，CB1⊂平面ACB1，∴MN⊥平面ACB1，（2）设C1到平面B1CM的距离为h，因为MP＝，＝，所以•MP＝，因为CM＝，B1C＝；B1M＝，所以：＝CM•B1M＝．19．某校共有学生2000人，其中男生900人，女生1100人，为了调查该校学生每周平均体育锻炼时间，采用分层抽样的方法收集该校100名学生每周平均体育锻炼时间（单位：小时）．（1）应抽查男生与女生各多少人？（2）根据收集100人的样本数据，得到学生每周平均体育锻炼时间的频率分布表：时间（小时）[0，1]（1，2]（2，3]（3，4]（4，5]（5，6]频率0.050.200.300.250.150.05若在样本数据中有38名男学生平均每周课外体育锻炼时间超过2小时，请完成每周平均体育锻炼时间与性别的列联表，并判断是否有95%的把握认为“该校学生的每周平均体育锻炼时间与性别有关”？男生女生总计每周平均体育锻炼时间不超过2小时每周平均体育锻炼时间超过2小时总计附：K2＝．P（K2≥k0）0.1000.0500.0100.005k0 2.706 3.841 6.6357.879【分析】（1）根据人数比值，求出男生，女生人数，（2）填表，代入公式求值，比较，判断．解：因为男生人数：女生人数＝900：1100＝9：11，所以男生人数为，女生认识我100﹣45＝55人，（2）由频率频率直方图可知学生每周平均体育锻炼时间超过2小时的人数为：（1×0.3+1×0.25+1×0.15+1×0.05）×100＝75人，每周平均体育锻炼时间超过2小时的女生人数为37人，联表如下：男生女生总计每周平均体育锻炼时间不超过2小时71825每周平均体育锻炼时间超过2小时383775总计4555100因为≈3.892＞3.841，所以有95%的把握认为“该校学生的每周平均体育锻炼时间与性别有关．20．已知A是抛物线E：y2＝2px（p＞0）上的一点，以点A和点B（2，0）为直径两端点的圆C交直线x＝1于M，N两点．（1）若|MN|＝2，求抛物线E的方程；（2）若0＜p＜1，抛物线E与圆（x﹣5）2+y2＝9在x轴上方的交点为P，Q，点G为PQ的中点，O为坐标原点，求直线OG斜率的取值范围．【分析】（1）设A的坐标，由题意可得圆心C的坐标，求出C到直线x＝1的距离．由半个弦长，圆心到直线的距离及半径构成直角三角形可得p的值，进而求出抛物线的方程；（2）将抛物线的方程与圆的方程联立可得两根之和及两根之积，进而求出中点G的坐标，再求出直线OG的斜率的表达式，换元可得斜率的取值范围．解：（1）设A（x0，y0）且y02＝2px0，则圆心C（，），圆C的直径|AB|＝，圆心C到直线x＝1的距离d＝|﹣1|＝||，因为|MN|＝2，所以（）2+d2＝（）2，即1+＝，y02＝2px0，整理可得（2p﹣4）x0＝0，所以p＝2，所以抛物线的方程为：y2＝4x；（2）联立抛物线与圆的方程整理可得x2﹣2（5﹣p）x+16＝0，△＞0，设P（x1，y1），Q（x2，y2），则x1+x2＝2（5﹣p），x1x2＝16，所以中点G的横坐标x G＝5﹣p，y G＝（+）＝，所以k OG＝（0＜P＜1），令t＝5﹣p（t∈（4，5）），则k OG＝＝（），解得0＜k OG＜，所以直线OG斜率的取值范围（0，）．21．已知函数f（x）＝x2+（t﹣2）x﹣tlnx+2．（1）若x＝2是f（x）的极值点，求f（x）的极大值；（2）求实数t的范围，使得f（x）≥2恒成立．【分析】（1）先对函数求导，结合极值存在的条件可求t，然后结合导数可研究函数的单调性，进而可求极大值；（2）由已知代入可得，x2+（t﹣2）x﹣tlnx≥0在x＞0时恒成立，构造函数g（x）＝x2+（t﹣2）x﹣tlnx，结合导数及函数的性质可求．解：（1），x＞0，由题意可得，＝0，解可得t＝﹣4，∴＝，易得，当x＞2，0＜x＜1时，f′（x）＞0，函数单调递增，当1＜x＜2时，f′（x）＜0，函数单调递减，故当x＝1时，函数取得极大值f（1）＝﹣3；（2）由f（x）＝x2+（t﹣2）x﹣tlnx+2≥2在x＞0时恒成立可得，x2+（t﹣2）x﹣tlnx ≥0在x＞0时恒成立，令g（x）＝x2+（t﹣2）x﹣tlnx，则＝，（i）当t≥0时，g（x）在（0，1）上单调递减，在（1，+∞）上单调递增，所以g（x）min＝g（1）＝t﹣1≥0，解可得t≥1，（ii）当﹣2＜t＜0时，g（x）在（﹣）上单调递减，在（0，﹣），（1，+∞）上单调递增，此时g（1）＝t﹣1＜﹣1不合题意，舍去；（iii）当t＝﹣2时，g′（x）＝≥0，即g（x）在（0，+∞）上单调递增，此时g（1）＝﹣3不合题意；（iv）当t＜﹣2时，g（x）在（1，﹣）上单调递减，在（0，1），（﹣）上单调递增，此时g（1）＝t﹣1＜﹣3不合题意，综上，t≥1时，f（x）≥2恒成立．（二）选考题：共10分．请考生在第22、23题中任选一题作答．如果多做，则按所做的第一题计分．[选修4-4：坐标系与参数方程]22．在平面直角坐标系xOy中，直线l的参数方程为（t为参数），以坐标原点O为极点，x轴的正半轴为极轴建立极坐标系，圆C的极坐标方程为ρ2﹣4ρcosθ＝3．（1）求直线l的普通方程和圆C的直角坐标方程；（2）直线l与圆C交于A，B两点，点P（2，1），求|PA|⋅|PB|的值．【分析】（1）直接利用转换关系的应用，把参数方程极坐标方程和直角坐标方程之间进行转换．（2）利用一元二次方程根和系数关系式的应用求出结果．解：（1）直线l的参数方程为（t为参数），转换为直角坐标方程为x+y﹣3＝0．圆C的极坐标方程为ρ2﹣4ρcosθ＝3，转换为直角坐标方程为x2+y2﹣4x﹣3＝0．（2）把直线l的参数方程为（t为参数），代入圆的直角坐标方程x2+y2﹣4x﹣3＝0，得到，所以|PA||PB|＝|t1t2|＝6．[选修4-5：不等式选讲]23．已知函数f（x）＝|x﹣a|．（1）当a＝﹣1时，求不等式f（x）≤|2x+1|﹣1的解集；（2）若函数g（x）＝f（x）﹣|x+3|的值域为A，且[﹣2，1]⊆A，求a的取值范围．【分析】（1）将a＝﹣1代入f（x）中，然后由f（x）≤|2x+1|﹣1，利用零点分段法解不等式即可；（2）根据条件分a＜﹣3和a≥﹣3两种情况，由[﹣2，1]⊆A建立关于a的不等式，然后求出a的取值范围．解：（1）当a＝﹣1时，f（x）＝|x+1|．∵f（x）≤|2x+1|﹣1，∴当x≤﹣1时，原不等式可化为﹣x﹣1≤﹣2x﹣2，∴x≤﹣1；当时，原不等式可化为x+1≤﹣2x﹣2，∴x≤﹣1，此时不等式无解；当时，原不等式可化为x+1≤2x，∴x≥1，综上，原不等式的解集为{x|x≤﹣1或x≥1}．（2）当a＜﹣3时，，∴函数g（x）的值域A＝{x|3+a≤x≤﹣a﹣3}．∵[﹣2，1]⊆A，∴，∴a≤﹣5；当a≥﹣3时，，∴函数g（x）的值域A＝{x|﹣a﹣3≤x≤3+a}．∵[﹣2，1]⊆A，∴，∴a≥﹣1，综上，a的取值范围为（﹣∞，﹣5]∪[﹣1，+∞）．。
湖北省宜昌市2020届高三年级4月统一调研测试数学试题(文科)含答案
又菱形边长为 2， ABC 60，所以 BO 3, PO 1, PB 2 , CO 1, PC 2. ….………….......8 分
cosBPC 4 2 4 22 2
2 ,sin BPC 4
14 . 设 4
PN
PB
2 ，由VDPBC
VPDBC
得 D 到平面 PCB 的距离为 2 21 ，则 D 到平面 PNC 的距离也为 2 21 . ….………………….…...10 分
(a c)2 24 3ac 24 a c 4 3.
……………………………………….…….….11 分
△ ABC 的周长为 4 3 2 6.
………………………………………...…….….12 分
18.（1）由题意 PO 面ABCD,PO BD,
…………………………………..…………..…...2 分
短潜伏者 长潜伏者 合计
60 岁及以上
90
60 岁以下
140
合计
300
（3）研究发现，某药物对新冠病毒有一定的抑制作用，需要在抽取的 300 人中分层选取 7 位 60 岁以
下的患者做Ⅰ期临床试验，再从选取的 7 人中随机抽取两人做Ⅱ期临床试验，求两人中恰有 1 人为“长潜
伏者”的概率.
附表及公式：
A. (2, 2)
B. ( 2 5 , ) 5
C. ( 2 5 , 2 5 ) 55
D. ( 2 3 , 2 3 ) 55
8. 我国古代数学著作《九章算术》中有如下问题：“今有金箠，长五尺，斩本一尺，重四斤，斩末一尺，
重二斤．问次一尺各重几何？”意思是：“现有一根金杖，长 5 尺，一头粗，一头细．在粗的一端截下 1
P(K 2 k0 )
2020届湖北省宜昌市高三下学期4月统一调研考试数学(文)试卷及解析
2020届湖北省宜昌市高三下学期4月统一调研考试数学（文）试卷★祝考试顺利★(解析版)一、选择题1.已知集合{A x y ==,{}21,x B y y x R ==+∈,则A B =（） A. []1,3 B. [)1,+∞ C. [)1,3- D.[)3,+∞ 【答案】D【解析】求函数定义域得集合A ,求函数值域得集合B ,然后由交集的概念计算．【详解】由题意2{|230}{|1A x x x x x =--≥=≤-或3}x ≥,{|1}B y y =>, ∴{|3}x A B x =≥．故选：D ．2.复数z 满足()122i z i -=+,则z =（ ）A. 1i -B. 1i + 【答案】D【解析】 求出复数模22i +后由复数除法可求得z ．【详解】∵22i +==∴)1(1)(1)i z i i i +===--+．故选：D ．3.已知tan 2θ=-,3,22πθπ⎛⎫∈ ⎪⎝⎭,则cos θ=（ ）C. 5-D.5± 【答案】A【解析】 由tan 2θ=-可得sin 2cos θθ=-,然后结合22sin cos 1θθ+=可解出答案. 【详解】因为sin tan 2cos θθθ==-,所以sin 2cos θθ=- 因为22sin cos 1θθ+=,所以可得21cos 5θ= 因为3,22πθπ⎛⎫∈ ⎪⎝⎭,所以cos θ=5 故选：A4.设1312x ⎛⎫= ⎪⎝⎭,51log 6y =,14log 3z =,则（ ） A. x y z <<B. y z x <<C. z x y <<D. z y x <<【答案】B【解析】 与中间值0,－1比较后可得．【详解】1310()21<<,551log log 616=-<-,144log 3log 3(1,0)=-∈-,∴x z y >>． 故选：B ．5.运行如图所示的程序框图,则输出的结果为（ ）A. 0B. 1 3 D. 3【答案】C【解析】。
2020年湖北省高三4月线上调研考试语文参考答案及评分标准
2020年湖北省高三（4月）线上调研考试语文参考答案及评分标准1．D（并非所有的网络小说均是如此）2．A（“按照传承内容、传承现状的逻辑顺序展开”表述有误，文章首尾两段均属于网络文学在传承中的现状，开头侧重整体介绍网络文学的兴盛，末尾侧重强调其发展中的问题）3．C（“只要深入欣赏其中引人入胜的故事情节，就可以增长并丰富文化见识”的表述显得绝对）4．D（“1995年是中国儿童青少年身体素质最好的时候”表述有误，原文“如果在1995年那一年，你正处于7-18岁之间，那么恭喜你，你很可能曾是近30年来，身体素质最硬的一届中国少年”得不出这个结论）5．D（要提升学生的身体素质，除了把体育测试纳入考试评价体系，增加学生的体育活动时间，还需要减少不必要的课业负担，保障实施健康促进行动等）6．①学生意识层面，学生必须切实认识到体育课的重要性，保证体育课堂出勤率，保证锻炼时间。
②学校管理层面，开展科学体系的体育课程，加大对体育教师的培训力度，加强对学生的考核。
③政府管理层面，出台并落实相应的政策法规，坚决摒弃形式主义，确保体育教育取得实效。
不仅要完善学校的体育场地设施的配备，还要统筹好学科课程间的安排。
④社会观念层面，摒弃“分数思维”，避免体育教育功利化，真正涵养体育意识，长久提高体质。
（每点2分，任答三点给满分）7．D（“科技不会带给人类幸福，反而会增强人类的惰性，加速文明的衰亡”错误，文中可以看出，科技的发展给人类带来了便捷的生活，解决了许多难题，促进了社会的进步和发展，这当然会带给人类幸福）8．①科学性。
小说内容交织着科学事实和预见、想象，激发人们对宇宙、科技等的思考，开拓读者的创造性思维。
如文中的上帝经由外星飞船往来太空和地球，由反物质发动机推动的飞船可以进入光速飞行等超现实的存在。
②文学性。
小说在场景宏大震撼、想象奇幻之外，还注重在人物设置和情感描写等方面的细致刻画，体现出较强的文学思维。
如上帝与秋生一家离别之时和秋生在灿烂星空下的思索，都极具文学思维的细腻和真实。
【4月湖北宜昌一调文数】湖北省宜昌市2020届高三年级4月线上统一调研测试文科数学试题及答案解析(4.24)
97
M ，且 FM MP ，则直线 PF 的斜率为
.
高三文数试卷 第 2页 共 4 页
三、解答题：共 70 分. 解答应写出文字说明、证明过程或演算步骤. 第 17～21 题为必考题，每 个试题考生都必须作答. 第 22、23 题为选考题，考生根据要求作答.
（一）必考题：共 60 分. 17.（本题满分 12 分）
2
二、填空题：本大题共 4 小题，每小题 5 分，共 20 分. 请将答案填在答题卡对应题号的位置上. 填 错位置，书写不清，模棱两可均不得分.
13. 已知函数 f (x) 为 R 上的奇函数， x 0 时， f (x) x2 x ，则 f (2)
.
14.
若实数
x,
y
满足约束条件
xy
1 1
宜昌市 2020 届高三年级 4 月线上统一调研测试
数学试题（文科）
本试卷共 4 页，23 题（含选考题）. 全卷满分 150 分，考试时间 120 分钟.
一、选择题：本大题共 12 小题，每小题 5 分，共 60 分. 在每小题给出的四个选项中，只有一项是符合题 目要求的.
1. 已知集合 A {x y x2 2x 3}, B {y y 2x 1, x R}，则 A B
高三文数试卷 第 1页 共 4 页
尺，重 4 斤，在细的一端截下 1 尺，重 2 斤. 问依次每一尺各重多少斤？” 假定该金杖被截成长度相等
的若干段时，其重量从粗到细构成等差数列. 若将该金杖截成长度相等的 20 段，则中间两段的重量和为
A. 6 斤 5
B. 4 斤 3
C. 3 斤 2
9.
对于函数
Hale Waihona Puke log51 6，
湖北省宜昌市2020届高三年级4月模拟统一调研考试 数学(文)(含答案)
值范围.
高三文数试卷 第 4页 共 4 页
宜昌市 2020 届高三年级 4 月模拟统一调研测试
文科数学参考答案
命题：（秭归一中） 审题：（宜昌市一中）
菱形 ABCD 中，AC BD，又 PO AC O, 则 BD 面PAC， ………………………………...4 分
所以 BD PA；
……………………………………….….…….5 分
（2）因为 PO 面ABCD, 所以 PB 与平面 ABCD 所成角为 PBO 30 °， ……………...….…….6 分
(a c)2 24 3ac 24 a c 4 3.
……………………………………….…….….11 分
△ ABC 的周长为 4 3 2 6.
………………………………………...…….….12 分
18.（1）由题意 PO 面ABCD,PO BD,
…………………………………..…………..…...2 分
….…………………......…..2 分
“长潜伏者”即潜伏期时间不低于 6 天的频率为 0.5
所以 500 人中“长潜伏者”人数为 500 0.5 250 人.
….………..……..……………...…..4 分
（2）由题意补充的列联表如图：
短潜伏者
长潜伏者
合计
60 岁及以上
90
70
160
60 岁以下
宜昌市 2020 届高三年级 4 月模拟统一调研测试
数学试题（文科）
本试卷共 4 页，23 题（含选考题）. 全卷满分 150 分，考试时间 120 分钟.
2020年 湖北省高三(4月)线上调研考试 数学文
２０２０年湖北省高三（４月）线上调研考试文科数学试卷２０２０．４本试卷共５页，２３题（含选考题）。
全卷满分１５０分。
考试用时１２０分钟。
★祝考试顺利★注意事项：１．考试过程中，请考生自觉遵守考试纪律等相关规定，诚信应考，不得有作弊、泄露试题等行为。
请家长做好监考工作。
２．请确保网络环境、考试环境良好，备好答题所用的白纸和笔。
３．登录好分数ＡＰＰ，点击“作业测试”，进入对应考试科目。
“试卷”将根据考试时间准时显示。
开考后，考生首先在白纸上手写答题。
答题结束后，点击“填写答题卡”，进入到“在线答题卡”。
将事先准备好的答案，填写至在线答题卡上（选择题、多选题及判断题，直接在“在线答题卡”上勾选答案；主观题按照要求将手写的答案竖向拍照，并分别上传），然后点击“提交答题卡”完成提交。
答题卡上传提交后考试时间范围内还能继续提交覆盖，为了避免大家都在考试最后快结束的时间上传造成拥堵，建议提前上传。
备注：主观题要确保答案及照片清晰、干净、完整；为留取拍照时间，考试将延长１０分钟。
４．此次全省联考是检测复课前线上备考成效的一次重要考试，有利于调整和优化复课后备考策略，请考生和家长高度重视。
考试结束后，考试组织方将为所有考生免费提供《考试成绩和学情分析报告》。
请考生或家长及时扫描右方二维码，关注“育路通”微信公众号。
依次点击“高考测评—查看报告”，即可免费查询。
一、选择题：本大题共１２小题，每小题５分，共６０分．在每小题给出的四个选项中，只有一项是符合题目要求的．１．已知集合Ａ＝｛ｘ｜ｘ２－４ｘ－５＜０｝，集合Ｂ＝｛ｙ｜ｙ＞０｝，则Ａ∩Ｂ＝Ａ．｛ｘ｜０＜ｘ＜５｝Ｂ．｛ｘ｜－５＜ｘ＜０｝Ｃ．（－１，＋∞）Ｄ．｛ｘ｜－１＜ｘ≤１０｝２．已知ａ－ｉ３ｉ＝ｂ＋３ｉ（ａ，ｂ∈Ｒ），其中ｉ为虚数单位，则复数ｚ＝ａ－ｂｉ在复平面内对应的点在Ａ．第一象限Ｂ．第二象限Ｃ．第三象限Ｄ．第四象限３．已知ｘ＝２０．１，ｙ＝ｌｏｇ５２，ｚ＝ｌｏｇ０．５２，则Ａ．ｙ＜ｘ＜ｚＢ．ｙ＜ｚ＜ｘＣ．ｚ＜ｘ＜ｙＤ．ｚ＜ｙ＜ｘ４．已知平面向量ｍ，ｎ均为单位向量，若向量ｍ，ｎ的夹角为π３，则｜３ｍ＋４ｎ｜＝Ａ．３７Ｂ．２５Ｃ．３７Ｄ．５槡５．若不等式１ｘ＋１－１４ｘ≥ｍ（０，１４对ｘ∈）恒成立，则实数ｍ的最大值为Ａ．７Ｂ．８Ｃ．９Ｄ．１０２０２０年湖北省高三（４月）线上调研考试文科数学试卷第１页（共５页）６．某城市在进行创建文明城市的活动中，为了解居民对“创建文明城”的满意程度，组织居民给活动打分（分数为整数，满分１００分），从中随机抽取一个容量为１２０的样本，发现所给数据均在［４０，１００］内．现将这些分数分成以下６组并画出样本的频率分布直方图，但不小心污损了部分图形，如图所示．观察图形则下列说法中有错獉误獉Ａ．第三组的频数为１８人的是Ｂ．根据频率分布直方图估计众数为７５分Ｃ．根据频率分布直方图估计样本的平均数为７５分Ｄ．根据频率分布直方图估计样本的中位数为７５分７．我国著名数学家华罗庚先生曾说：“数缺形时少直观，形缺数时难入微，数形结合百般好，隔裂分家万事休．”在数学的学习和研究中，常用函数的图像研究函数的性质，也常用函数的解析式来琢磨函数的图像特征．如函数ｙ＝－２ｃｏｓｘ２＋ｃｏｓｘ＋１，ｘ∈［－π２，π２］的图象大致为８．函数ｆ（ｘ）＝槡３ｃｏｓ）＋ｃｏｓ（π＋２ｘ（２ｘ－π２）的单调增区间为Ａ．［－π６＋ｋπ，π３＋ｋπ［－π３＋ｋπ，π６＋ｋπ］，ｋ∈ＺＢ．］，ｋ∈ＺＣ．［－５１π２＋ｋπ，１π２＋ｋπ［－１π２＋ｋπ，５１π２＋ｋπ９．已知Ｆ是抛物线ｙ２＝４ｘ的焦点，过焦点Ｆ的直线ｌ交抛物线的准线于点Ｐ，点Ａ在抛物线上，且｜ＡＰ｜＝｜ＡＦ｜＝３，则直线ｌ的斜率为］，ｋ∈ＺＤ．］，ｋ∈ＺＡ．±１Ｂ．２Ｃ．±２Ｄ．２槡槡槡１０．已知函数ｆ（ｘ）＝－ｘ２＋ａｘ，ｘ≤１，若存在ｘ１，ｘ２∈Ｒ，且ｘ１≠ｘ２，使得ｆ（ｘ１）＝ｆ（ｘ２）成立，{ ＞１３ａｘ－７，ｘ则实数ａ的取值范围是Ａ．（－∞，３）Ｂ．（－∞，３］Ｃ．（－２，２）Ｄ．（－２，２］１１．平面四边ＡＢＣＤ形中，∠ＡＢＣ＝１５０°，槡３ＡＢ＝２ＢＣ，ＡＣ＝１３，ＢＤ⊥ＡＢ，ＣＤ＝３，则四边形槡ＡＢＣＤ的面积为７３Ａ．２３＋２Ｂ．３＋１Ｃ．７３Ｄ．槡２槡槡槡２０２０年湖北省高三（４月）线上调研考试文科数学试卷第２页（共５页）１２．已知双曲线Ｃ：ｘａ２－ｙ２２ｂ２＝１（ａ＞０，ｂ＞０）的左右焦点分别为Ｆ１，Ｆ２，过Ｆ１的直线与Ｃ的两条渐近线分别交于Ａ，Ｂ两点，若以Ｆ１Ｆ２为直径的圆过点Ｂ，且Ａ为Ｆ１Ｂ的中点，则双曲线Ｃ的离心率为Ａ．３＋１Ｂ．２Ｃ．３Ｄ．２槡槡槡二、填空题：本大题共４小题，每小题５分，共２０分．１３．设曲线ｙ＝ｅｘ＋１上点Ｐ处的切线平行于直线ｘ－ｙ－１＝０，则点Ｐ的坐标是．１４．已知θ为锐角，且槡２ｓｉｎθｓｉｎ（θ＋π４）＝５ｃｏｓ２θ，则ｔａｎθ＝．１５．已知Ａ，Ｂ，Ｃ是球Ｏ球面上的三点，ＡＣ＝ＢＣ＝６，ＡＢ＝６槡２，且四面体ＯＡＢＣ的体积为２４，则球Ｏ的表面积为．１６．自湖北爆发新型冠状病毒肺炎疫情以来，湖北某市医护人员和医疗、生活物资严重匮乏，全国各地纷纷驰援．某运输队接到从武汉送往该市物资的任务，该运输队有８辆载重为６ｔ的Ａ型卡车，６辆载重为１０ｔ的Ｂ型卡车，１０名驾驶员，要求此运输队每天至少运送２４０ｔ物资．已知每辆卡车每天往返的次数为Ａ型卡车５次，Ｂ型卡车４次，每辆卡车每天往返的成本Ａ型卡车１２００元，Ｂ型卡车１８００元，则每天派出运输队所花的成本最低为．三、解答题：共７０分．解答应写出文字说明、证明过程或演算步骤．第１７题～第２１题为必考题，每个试题考生都必须作答．第２２题～第２３题为选考题，考生根据要求作答．（一）必考题：共６０分．１７．（本小题满分１２分）已知函数ｆ（ｘ）＝ｌｏｇ３（ａｘ＋ｂ）的图像经过点Ａ（２，１）和Ｂ（５，２），ａｎ＝ａｎ＋ｂ（ｎ∈Ｎ（１）求｛ａｎ｝；）（２）设数列｛ａｎ｝的前ｎ项和为Ｓｎ，ｂｎ＝ｎ２（ｎ＋２）＋２槡ｎ，求｛ｂｎ｝的前ｎ项和Ｔｎ．Ｓ２０２０年湖北省高三（４月）线上调研考试文科数学试卷第３页（共５页）１８．（本小题满分１２分）２０２０年春节期间，新型冠状病毒（２０１９－ｎＣｏＶ）疫情牵动每一个中国人的心，危难时刻全国人民众志成城，共克时艰，为疫区助力．我国Ｓ省Ｑ市共１００家商家及个人为缓解湖北省抗疫消毒物资压力，募捐价值百万的物资对口输送湖北省Ｈ市．（１）现对１００家商家抽取５家，其中２家来自Ａ地，３家来自Ｂ地，从选中的这５家中，选出３家进行调研，求选出３家中１家来自Ａ地，２家来自Ｂ地的概率．（２）该市一商家考虑增加先进生产技术投入，该商家欲预测先进生产技术投入为４９千元的月产增量．现用以往的先进技术投入ｘｉ（千元）与月产增量ｙｉ（千件）（ｉ＝１，２，３，…，８）的数据绘制散点图，由散点图的样本点分布，可以认为样本点集中在曲线ｙ＝ａ＋ｂ槡ｘ的附，∑８）２＝２８９．９，∑８近，且ｘ珋＝４６．６，ｙ珋＝５６３，珋ｔ＝６．８（ｘｉ－ｘ珋（ｔｉ－珋ｔ）２＝１．６，ｉ＝１ｉ＝１∑槡ｉ，珋ｔ＝１８∑（ｘｉ－ｘ珋）（ｙｉ－ｙ珋（ｔｉ－珋ｔ）（ｙｉ－ｙ珋８）＝１４６９，∑８８）＝１０８．８，其中ｔｉ＝ｘｔｉ，根据ｉ＝１ｉ＝１ｉ＝１所给的统计量，求ｙ关于ｘ回归方程，并预测先进生产技术投入为４９千元时的月产增量．附：对于一组数据（ｕ１，ｖ１）（ｕ２，ｖ２），其回归直线ｖ＝α＋βｕ的斜率和截距的最小二乘法估计分别为β＾＝∑（ｕｉ－珔ｕ）（ｖｉ－珋ｖｎ，α＾＝珋ｖ－β＾珔ｕ．）ｉ＝１∑ｎ（ｕｉ－珔ｕ）２ｉ＝１１９．（本小题满分１２分）如图，在四棱锥Ｓ－ＡＢＣＤ中，侧面ＳＣＤ为钝角三角形且垂直于底面ＡＢＣＤ，ＣＤ＝ＳＤ，点Ｍ是ＳＡ的中点，ＡＤ∥ＢＣ，∠ＡＢＣ＝９０°（１）求证：平面ＭＢＤ⊥平面ＳＣＤ；，ＡＢ＝ＡＤ＝２１ＢＣ＝ａ．（２）若∠ＳＤＣ＝１２０°，求三棱锥Ｃ－ＭＢＤ的体积．２０．（本小题满分１２分）已知椭圆Ｃ：ｘａ２＋ｙ２２ｂ２＝１（ａ＞ｂ＞０）过点Ｅ（槡２，１），其左、右顶点分别为Ａ，Ｂ，左、右焦点为Ｆ１，Ｆ２，其中Ｆ１（－２，０）．槡（１）求椭圆Ｃ的方程；（２）设Ｍ（ｘ０，ｙ０）为椭圆Ｃ上异于Ａ，Ｂ两点的任意一点，ＭＮ⊥ＡＢ于点Ｎ，直线ｌ：ｘ０ｘ＋２ｙ０ｙ－４＝０，设过点Ａ且与ｘ轴垂直的直线与直线ｌ交于点Ｐ，证明：直线ＢＰ经过线段ＭＮ的中点．２０２０年湖北省高三（４月）线上调研考试文科数学试卷第４页（共５页）２１．（本小题满分１２分）已知函数ｆ（ｘ）＝ｘ２＋ａｃｏｓｘ（１）求函数ｆ（ｘ）的奇偶性，并证明当｜ａ｜≤２（２）当ａ＝π时，求ｆ（ｘ）的最小值；时函数ｆ（ｘ）只有一个极值点；（二）选考题：共１０分．请考生在２２，２３题中任选一题作答．如果多做，则按所做的第一题计分．作答时写清题号．２２．［选修４－４：坐标系与参数方程］（１０分）在平面直角坐标系ｘＯｙ中，曲线Ｃ１的参数方程为ｘ＝２＋２ｃｏｓθ{ θ（θ为参数），以原点为ｙ＝２ｓｉｎ极点，ｘ轴非负半轴为极轴，建立极坐标系，曲线Ｃ２的极坐标方程为ρ２＝１＋３４ｓｉｎ２α．（１）求曲线Ｃ１的极坐标方程以及曲线Ｃ２的直角坐标方程；（２）若直线ｌ：ｙ＝ｋｘ与曲线Ｃ１、曲线Ｃ２在第一象限交于Ｐ，Ｑ，且｜ＯＱ｜＝｜ＰＱ｜，点Ｍ的直角坐标为（１，０），求△ＰＭＱ的面积．２３．［选修４－５：不等式选讲］（１０分）已知实数ａ，ｂ满足ａ２＋ｂ２－ａｂ＝３．（１）求ａ－ｂ的取值范围；（２）若ａｂ＞０，求证：ａ１２＋ｂ１２＋３４≥ａ４ｂ．２０２０年湖北省高三（４月）线上调研考试文科数学试卷第５页（共５页）22020 年湖北省高三（4 月）线上调研考试数学（文科）参考答案及评分标准一、选择题1--12 ABDCC CBACA DB二、填空题13.（0,2）14. 5615. 13616.960011.解析：如图ABC 1500 3AB 2BC, AC 13, BD AB,CD 3在ABC 中，由余弦定理AC 2 AB 2 BC 2 2AB BCcos ABC3 3 3得13 AB 2 ( A B)2 2AB AB ()2 2 2所以AB 2 ，BC 3 ，由于DBC ABC ABD 1500 900 600 .在ABC 中，由余弦定理CD 2 BD 2 BC 2 2BD BC cos DBC 可得2 19 BD 3 2BD 3 ，所以BD 2 3 或 3 （舍），则四边形 ABCD 的面积2S1 1S S AB BDBD BC DBCsin ABD BCD2 2 122 23122333273212.方法一：由题意知F1A AB , F O F O ，故AOF 1 BF2O ，又由对称性知1 2AOF 1 BOF ，故BOF BF O2 ，所以2 2OB BF ，又F1B F B ，所以2 2OB OF 1 OF ，所以OBF 为等边三角形，即2 2BOF 2 60 ，则过第一、三象限的渐近线斜率 tan BOF 2 3k ，双曲线 C 的离心率为c ab2 11 k 2a22bm bm bm方法二：不妨设点B(m, )(m 0) ，故BF c m,, BF c m,1 2a a a1因为以b m2 2F1F 为直径的圆过点 B，所以0F1B F B ，从而m 2 c 2 0 ，解得m a2 22aa cb b故B(a,b) ，又 A 为F1B 的中点，故A , ，代入y x 可得2 2 a b b ac2 a 2解得c 2a ，故双曲线 C 的离心率为 2.16.解析：设每天派出 A 型卡车 x 辆，B 型卡车 y 辆，运输队所花成本为 z 元，则 0 x 8 0x 80 y 6 0 y 6x y 10 xy 106x 5 10y 4 240 3x 4y 24x, y N x, y N* *目标函数z 1200x1800y,画出满足条件的可行域,由图可知，当直线z 1200x1800y经过点 A 点（8,0）时使 z 取得最小值，即z min 1200818000 9600故每天只派 8 辆 A 型卡车运输，所花成本最低，最低成本为 9600 元.log (2ab)3 17.解：（1）由题意得log (5ab)312a，解得b2……………………4 分1所以a 2n 1,n N ……………………5 分*n（2）由（1）易知数列{a }为以 1 为首项，2 为公差的等差数列n所以n(n 1)S = n 2n2 ，……………………7 分n22 2 1 1所以S n nb 2 n 2 2 ……………………9 分n n n n n n n( 2) ( 2) 21 1 1 1 1 1 1 1 T 1n n n n n3 24 35 1 1 122(112)n22n 3 12n 1 ……………………12 分(n 1)(n 2) 218.（1）由题意可知，A 地 2 家分为A1, A2，B 地 3 家分为B B B1,2,3所有的情况为：(A , A , B ),(A , A , B ),(A , A , B ) ， (A , B , B ),(A , B , B ),(A ,B , B ) ，1 2 1 1 2 2 1 2 3 1 1 2 1 1 3 1 2 32(A , B , B ),(A , B , B ),(A , B , B ), (B , B , B ) ，共 10 种情况2 1 2 2 13 2 2 3 1 2 3其中 A 地 1 家，B 地 2 家的有 (A , B , B ),(A , B , B ),(A , B , B ) ，1 12 1 13 1 2 3(A , B , B ),(A , B , B ),(A , B , B ) 共有 6 种，所求的概率为2 1 2 2 13 2 2 36 3p . (6)分10 58 82 ，（2）由t 6.8, y 563,t t y y 108.8, t t 1.6i i ii 1 i 18t t y yi i108.8ˆ68，且a ˆ y bˆt 56368 6.8 100.6，bi 1有81.62t tii 1所以 y 关于 x 的回归方程为yˆ100.6 68 x ，当x 49时，年销售量 y 的预报值yˆ100.6 68 49 576.6 千件．所以预测先进养殖技术投入为 49 千元时的年收益增量为 576.6 千件．…………………12 分19.(1)证明：取 BC 中点 E，连接 DE，设 AB=AD=a,BC=2a,依题意得，四边形 ABED 为正方形，且有 BE=DE=CE=a, BD=CD= 2a ，BD2 CD2 BC2 , 则BD CD ，又平面SCD 底面 ABCD，平面SCD 底面 ABCD=CD,，BD 平面 SCD．平面 MBD⊥底面 ABCD ………………5 分(2)解：过点 S 作 CD 的垂线，交 CD 延长线于点 H，连接 AH，可证 DH 为斜线 SD 在底面 ABCD 内的射影，SDH 为斜线 SD 与底面 ABCD 所成的角，即SDH 60．由（1）得，SD CD 2a ，在Rt SHD 中，2a 6aSD 2a,HD ,SH ,2 2H6E∴M 到平面 ABCD 的距离d a .41 1 1 6 6三棱锥C MBD 的体积V V BD CD d 2a 2a a a3CMBD M BCD3 2 64 12………………………………12 分20.（1）由题意，2a EF EF ( 2 2)2 1 ( 2 2) 1 4123a 2,c 2,b 2故椭圆的方程为x y2 21 (4)分4 2（2）由（1）知A2, 0,B2, 0过点 A 且与x 轴垂直的直线的方程为 x 2 ，结合方程x2xx 2yy 4 0 ，得点P 2,y直线 PB 的斜率kx 2y x20 02 24yx 2则直线 PB 的方程为y x 20 .4yy因为 MN AB 于点 N ，所以N x0 ,0，线段 MN 的中点坐标为0 , 0x2令x 2 4x2x x ，得y x0 2 00 04y 4y0 0因为x02 2y02 4 ，所以yx 2y y2 2，0 0 04y 4y 20 0所以直线 PB 经过线段 MN 的中点yx,2. (12)分21.解：（1）由于f (x) = f (x) 函数f (x) 为偶函数………………2 分f (x) 2x a sin x, f (0) 0 ，故只需讨论x 0 时情况，x 0, 由三角函数性质知x sin x,2 a ,2x a sin x, f (x) 0 ，x 0时，f(x)单调递增，由偶函数性质知x 0 时，f(x)单调递减，故a 2 时函数 f（x）只有一个极小值点 x=0 ………………5 分（2）由（1）知只需求x 0,时f (x) 的最小值. f ' (x) 2x sin x ,当x0, 时，2设h(x) 2x sin x,h' (x) 2 cos x ，而h'(0) 0,h'( ) 0，2由零点存在性定理，存在唯一的x ，使得h'(x ) 00,0 02当x (0, 0 ), ' ( ) 0 ，h(x) 单减，当), ( ) 0x h x 0 ,x(x h' x2 ，h(x) 单增，40 (0, x0 ) x0(x , )2 2 ( ,)2h(x) - - 0 + +h(x) = f (x) h(x) 的极小0 减增0 +2x sin x值点f (x) 减拐点减极小值增所以 2f (x) f ( ) ……………12 分min2 422.解：依题意，曲线 1 :(x 2)2 y 2 4C ，即x 2 y 2 4x 0故 2 4 cos 0，即 4 cos……………………3 分因为24，故 2 3 2 sin 241 3sin2x2即x 2 4y 2 4，即 y 124……………………5 分（2）将代入0 24得，1 3sin22Q143sin2将代入 4cos得，0 P 4 cos由OQ PQ ，得162 ，即4 cos (7)分2PQ0 1 3sin22解得sin 2 ，则cos 20 03 1 3又0，故4 2 32Q ，P4cos4 332 1 3sin 3故PMQ 的面积1S PMQ S S OMsin 0OMP OMQ P Q2 122 336323……………………10 分23.解：（1）因为a 2b 2 ab 3 ，所以a 2 b 2 3 ab 2 ab ．①当ab 0 时，3 ab 2ab ，解得ab 3，即0 ab 3 ；5②当ab 0 时，3 ab 2ab ，解得ab 1，即1 ab 0 ，所以1 ab 3，则0 3 ab 4 ，2 2 2 23 2 3而 a b a b ab ab ab ab ，2所以0 a b 4 ，即 2 a b 2 ；………………5 分（2）由（1）知0 ab 3 ，因为1 1 3 4 a b 432 2a b 4 ab a b ab42 2 2 223 ab4 3 3 3 3 1 1 1 1 13 3 0a b ab 4 a b ab 4 a b ab 4 ab 22 2 2 2 2 2当且仅当ab 2 时取等号，所以1 1 3 4．………………10 分a b 4 ab2 26。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
Ａ．第三组的频数为 １８人
Ｂ．根据频率分布直方图估计众数为 ７５分
Ｃ．根据频率分布直方图估计样本的平均数为 ７５分
Ｄ．根据频率分布直方图估计样本的中位数为 ７５分
７．我国著名数学家华罗庚先生曾说：“数缺形时少直观，形缺数时难入微，数形结合百般好， 隔裂分家万事休．”在数学的学习和研究中，常用函数的图像研究函数的性质，也常用函 数的解析式来琢磨函数的图像特征．如函数 ｙ＝－２ｃｏｓ２ｘ＋ｃｏｓｘ＋１，ｘ∈［－π２，π２］的图象 大致为
Ａ．第一象限
Ｂ．第二象限
３．已知 ｘ＝２０．１，ｙ＝ｌｏｇ５２，ｚ＝ｌｏｇ０．５２，则
Ａ．ｙ＜ｘ＜ｚ
Ｂ．ｙ＜ｚ＜ｘ
Ｃ．第三象限 Ｃ．ｚ＜ｘ＜ｙ
Ｄ．第四象限 Ｄ．ｚ＜ｙ＜ｘ
４．已知平面向量 ｍ，ｎ均为单位向量，若向量 ｍ，ｎ的夹角为 π３，则 ｜３ｍ＋４ｎ｜＝
Ａ．３７
Ｂ．２５
Ｃ．槡３７
Ｄ．５
５．若不等式 １ｘ＋１－１４ｘ≥ｍ对 ｘ∈（０，１４）恒成立，则实数 ｍ的最大值为
８．函数 ｆ（ｘ）＝槡３ｃｏｓ（２ｘ－π２）＋ｃｏｓ（π＋２ｘ）的单调增区间为
Ａ．［－π６ ＋ｋπ，π３ ＋ｋπ］，ｋ∈Ｚ
Ｂ．［－π３ ＋ｋπ，π６ ＋ｋπ］，ｋ∈Ｚ
Ｃ．［－５１π２＋ｋπ，１π２＋ｋπ］，ｋ∈Ｚ
Ｄ．［－１π２＋ｋ４ｘ的焦点，过焦点 Ｆ的直线 ｌ交抛物线的准线于点 Ｐ，点 Ａ在抛物
２０２０年湖北省高三（４月）线上调研考试
文科数学试卷
２０２０．４
本试卷共 ５页，２３题（含选考题）。全卷满分 １５０分。考试用时 １２０分钟。
★祝考试顺利★
注意事项： １．考试过程中，请考生自觉遵守考试纪律等相关规定，诚信应考，不得有作弊、泄露试题等行为。请家
长做好监考工作。 ２．请确保网络环境、考试环境良好，备好答题所用的白纸和笔。 ３．登录好分数 ＡＰＰ，点击“作业测试”，进入对应考试科目。“试卷”将根据考试时间准时显示。开考
后，考生首先在白纸上手写答题。答题结束后，点击“填写答题卡”，进入到“在线答题卡”。将事先准备好 的答案，填写至在线答题卡上（选择题、多选题及判断题，直接在“在线答题卡”上勾选答案；主观题按照要 求将手写的答案竖向拍照，并分别上传），然后点击“提交答题卡”完成提交。答题卡上传提交后考试时间 范围内还能继续提交覆盖，为了避免大家都在考试最后快结束的时间上传造成拥堵，建议提前上传。
１１．平面四边 ＡＢＣＤ形中，∠ＡＢＣ＝１５０°，槡３ＡＢ＝２ＢＣ，ＡＣ＝槡１３，ＢＤ⊥ＡＢ，ＣＤ＝３，则四边形 ＡＢＣＤ的面积为
Ａ．２槡３＋２
Ｂ．槡３＋１
Ｃ．７槡３
Ｄ．７２槡３
２０２０年湖北省高三（４月）线上调研考试文科数学试卷 第 ２页（共 ５页）
１２．已知双曲线 Ｃ：ａｘ２２ －ｙ ｂ２ ２ ＝１（ａ＞０，ｂ＞０）的左右焦点分别为 Ｆ１，Ｆ２，过 Ｆ１的直线与 Ｃ的两 条渐近线分别交于 Ａ，Ｂ两点，若以 Ｆ１Ｆ２为直径的圆过点 Ｂ，且 Ａ为 Ｆ１Ｂ的中点，则双曲 线 Ｃ的离心率为
Ａ．７
Ｂ．８
Ｃ．９
Ｄ．１０
２０２０年湖北省高三（４月）线上调研考试文科数学试卷 第 １页（共 ５页）
６．某城市在进行创建文明城市的活动中，为了解居民对“创建文明城”的满意程度，组织居
民给活动打分（分数为整数，满分 １００分），从中随机抽取一个容量为 １２０的样本，发现所
给数据均在［４０，１００］内．现将这些分数分成以下 ６组并画出样本的频率分布直方图，但
线上，且 ｜ＡＰ｜＝｜ＡＦ｜＝３，则直线 ｌ的斜率为
Ａ．±１
Ｂ．槡２
Ｃ．±槡２
Ｄ.－槡２
{ １０．已知函数
ｆ（ｘ）＝
－ｘ２ ＋ａｘ，ｘ≤１ ，若存在
３ａｘ－７，ｘ＞１
ｘ１，ｘ２∈Ｒ，且
ｘ１≠ｘ２，使得
ｆ（ｘ）＝ｆ（ｘ）成立，
１
２
则实数 ａ的取值范围是
Ａ．（－∞，３）
Ｂ．（－∞，３］
Ｃ．（－２，２）
Ｄ．（－２，２］
送 ２４０ｔ物资．已知每辆卡车每天往返的次数为 Ａ型卡车 ５次，Ｂ型卡车 ４次，每辆卡车
每天往返的成本 Ａ型卡车 １２００元，Ｂ型卡车 １８００元，则每天派出运输队所花的成本最
低为
．
三、解答题：共 ７０分．解答应写出文字说明、证明过程或演算步骤．第 １７题 ～第 ２１题为必考 题，每个试题考生都必须作答．第 ２２题 ～第 ２３题为选考题，考生根据要求作答．
Ａ．槡３＋１
Ｂ．２
Ｃ．槡３
Ｄ．槡２
二、填空题：本大题共 ４小题，每小题 ５分，共 ２０分．
１３．设曲线 ｙ＝ｅｘ＋１上点 Ｐ处的切线平行于直线 ｘ－ｙ－１＝０，则点 Ｐ的坐标是
．
１４．已知 θ为锐角，且槡２ｓｉｎθｓｉｎ（θ＋π４）＝５ｃｏｓ２θ，则 ｔａｎθ＝
．
１５．已知 Ａ，Ｂ，Ｃ是球 Ｏ球面上的三点，ＡＣ＝ＢＣ＝６，ＡＢ＝６槡２，且四面体 ＯＡＢＣ的体积为
备注：主观题要确保答案及照片清晰、干净、完整；为留取拍照时间，考试将延长 １０分钟。 ４．此次全省联考是检测复课前线上备考成效的一次重要考试，有利于调整和优 化复课后备考策略，请考生和家长高度重视。考试结束后，考试组织方将为所有考生 免费提供《考试成绩和学情分析报告》。请考生或家长及时扫描右方二维码，关注“育 路通”微信公众号。依次点击“高考测评—查看报告”，即可免费查询。
一、选择题：本大题共 １２小题，每小题 ５分，共 ６０分．在每小题给出的四个选项中，只有一项
是符合题目要求的． １．已知集合 Ａ＝｛ｘ｜ｘ２－４ｘ－５＜０｝，集合 Ｂ＝｛ｙ｜ｙ＞０｝，则 Ａ∩Ｂ＝
Ａ．｛ｘ｜０＜ｘ＜５｝ Ｂ．｛ｘ｜－５＜ｘ＜０｝ Ｃ．（－１，＋∞） Ｄ．｛ｘ｜－１＜ｘ≤１０｝
２．已知ａ－ｉ３ｉ＝ｂ＋３ｉ（ａ，ｂ∈Ｒ），其中 ｉ为虚数单位，则复数 ｚ＝ａ－ｂｉ在复平面内对应的点在
２４，则球 Ｏ的表面积为
．
１６．自湖北爆发新型 冠 状 病 毒 肺 炎 疫 情 以 来，湖 北 某 市 医 护 人 员 和 医 疗、生 活 物 资 严 重 匮
乏，全国各地纷纷驰援．某运输队接到从武汉送往该市物资的任务，该运输队有 ８辆载重
为 ６ｔ的 Ａ型卡车，６辆载重为 １０ｔ的 Ｂ型卡车，１０名驾驶员，要求此运输队每天至少运