最新全等三角形平移、旋转翻折课件2

合集下载

全等三角形的基本模型复习正式经典ppt课件

“雪亮工程"是以区（县）、乡（镇）、村（社区）三级综治中心为指挥平台、以综治信息化为支撑、以网格化管理为基础、以公共安全视频监控联网应用为重点的“群众性治安防控工程” 。
模型三旋转型模型解读：将三角形绕着公共顶点旋转一定角度后，两个三角形能够完全重合，则称这两个三角形为旋转型三角形．识别旋转型三角形时，如图①，涉及对顶角相等；如图②，涉及等角加(减)公共角的条件．
“雪亮工程"是以区（县）、乡（镇）、村（社区）三级综治中心为指挥平台、以综治信息化为支撑、以网格化管理为基础、以公共安全视频监控联网应用为重点的“群众性治安防控工程” 。
解：∵AB⊥CD，∴∠EBC＝∠DBA＝90°.在 Rt△CEB 与 Rt△ADB 中 CBEE＝＝ABDD，，∴Rt△CEB≌Rt△ADB(HL)，∴∠C＝∠A，又∵∠C＋∠CEB＝ 90°，∠CEB＝∠AEF，∴∠A＋∠AEF＝90°，∴CF⊥AD
“雪亮工程"是以区（县）、乡（镇）、村（社区）三级综治中心为指挥平台、以综治信息化为支撑、以网格化管理为基础、以公共安全视频监控联网应用为重点的“群众性治安防控工程” 。
解：∵AD⊥AB，BE⊥AB，CD⊥CE，∴∠DAC＝∠CBE＝∠DCE＝90 °，又∵∠DCB＝∠D＋∠DAC＝∠DCE＋∠ECB，∴∠D＝∠ECB.在△ACD
“雪亮工程"是以区（县）、乡（镇）、村（社区）三级综治中心为指挥平台、以综治信息化为支撑、以网格化管理为基础、以公共安全视频监控联网应用为重点的“群众性治安防控工程” 。

12-1 全等三角形课件(共26张PPT)

时，对应的顶点放在对应的位置上.
知识梳理
例题 1：如图所示，△ ≌△ ，指出所有的对应边和对应角.
AB与DC，AC与DB，BC与CB是对应边；
∠ABC与∠DCB，∠A与∠D，∠ACB与∠DBC是对应角。
【解答】（1）已知△ABC≌△DCB，故公共边BC和CB
是对应边，它们所对的∠A和∠D是对应角，最短边
【结论】本题考查了全等三角形的性质及
比较角的大小，解题的关键是找到两全等
三角形的对应角、对应边.
80°
.
知识梳理
例题4：如图，将长方形ABCD沿AE折叠，使D点落在BC边上的F点处，
如果∠BAF = 60°，那么∠DAE= 15°
角
例题5：如图，△ ABC ≌△ ADE，则AB = AD ，∠E =
知识梳理
把两个全等的三角形重合到一起，重合的顶点叫做对应顶点，重合
的边叫做对应边，重合的角叫做对应角。例如，图中的△ 和△
全等，记作△ ≌ ，其中点和点，点和点，点
和点是对应顶点；和，和，和是对应边；∠和
∠，∠和∠，∠和∠是对应角.
∠BAE = 130°，∠BAD = 50°，则∠BAC=
。
80°
∠C
，若
知识梳理
例题6：如图，已知△ ABC ≌△ EBF，AB ⊥ CE，ED ⊥ AC，∠A = 24°，
则：（1）AB =
EB ，BC = BF ，∠C = 66 °，∠EFB = 66 °；
（2）若AB = 5cm，BC = 3cm，则AF = 2cm 。
AB和DC是对应边，它们所对的∠ACB和∠DBC是对应
角，余下的一对边和一对角分别是对应边和对应角.
（2）根据书写规范可知点A和点D，点B和点C，点C

1.4 全等三角形课件2024-2025学年浙教版数学八年级上册

∵AB=AC
∴点C与点B重合，即△ACD与△ABD重合
∴ △ABD≌△ACD （全等三角形的定义）
∴BD=CD=3 （全等三角形的对应边相等） ∠B=∠C=15°（全等三角形的对应角相等）
学以致用知识精练
例4：如图，△EFG≌△NMH，EF=2.1cm，EH=1.1cm，NH=3.3cm. （1）求线段NM及HG的长度；（2）写出一个图形中对应线段的数量或位置关系
A
G
图形语言B源自CEF文字语言
全等三角形的对应边相等，对应角相等
符号语言
∵△ABC≌△GEF ∴ AB=GE, BC=EF, AC=GF ∴ ∠A= ∠G, ∠B= ∠E, ∠C= ∠F
学以致用操作应用
例1：结合全等三角形填写对应边、对应角
A
A’
B
B’
C
C’
∵△___A_B_C___≌△_A__’B_’_C_’__
____F_G_=__M_H_____
E
EH=NG
EF//MN 解：F（G1/）/M∵H △EFG≌△NMH
∴MN=EF=2.1cm
H
1
M
EG=NH=3.3cm ∴HG=EG-EH=2.2cm
F
G2
N
总结展望
能够重合的两个图形
形状大小
特
全等图形
殊化
全等三角形
产生
图形的变换
平移翻折旋转
定义
∴ AC=__A_’_C_’_, BC=__B_’_C_’_, AB=__A_’B__’_
∠A=__∠__A_’_,∠B=∠__A_’_B_’_C,∠’ C=_∠__A_’_C_’B’
学以致用操作应用

第2讲.全等三角形辅助线--旋转与平移.

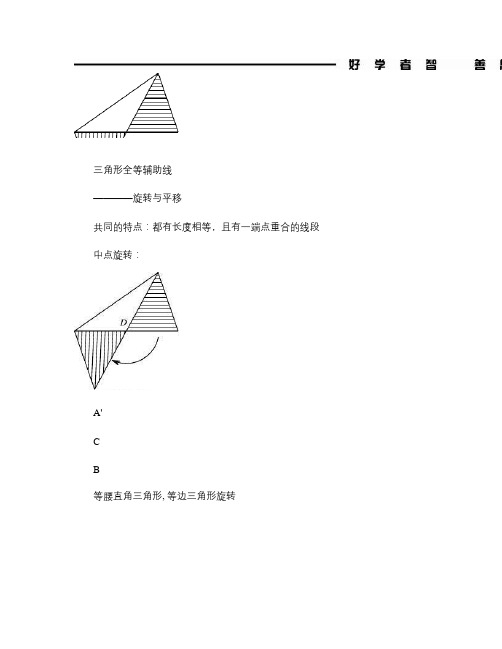
三角形全等辅助线————旋转与平移共同的特点：都有长度相等，且有一端点重合的线段中点旋转：A'CB等腰直角三角形, 等边三角形旋转CBAEBA正方形旋转FDCFEDCBA【精选例题】旋转中点类【例1】以ABC ∆的两边AB 、AC 为腰分别向外作等腰R t A B D ∆和等腰R t A C E ∆，90BAD CAE ∠=∠=︒连接DE ，M 、N 分别是BC 、DE 的中点．探究：AM 与DE 的位置关系及数量关系．（1）如图①当ABC ∆为直角三角形时，AM 与DE 的位置关系是；线段AM 与DE 的数量关系是；（2）将图①中的等腰Rt ABD ∆绕点A 沿逆时针方向旋转θ︒(090θ<< 后，如图②所示，（1）问中得到的两个结论是否发生改变？并说明理由．【例2】（顺义区2009一模第25题）已知：在Rt ABC ∆中，AB BC =，在Rt ADE ∆中，AD DE =，连结EC ，取EC 的中点M ，连结DM 和BM ．⑴若点D 在边AC 上，点E 在边AB 上且与点B 不重合，如图①，探索BM 、DM 的关系并给予证明；图1ABCDEM⑵如果将图①中的ADE ∆绕点A 逆时针旋转小于45︒的角，如图②，那么⑴中的结论是否仍成立？如果不成立，请举出反例；如果成立，请给予证明．图2MEDCBA【例3】在四边形ABCD 中，设M , N 分别为CD , AB 的中点，求证(12MN AD BC +≤，当且仅当AD BC ∥时等号成立．N MDCBA【例4】如图所示，在ABC ∆的AB 边上取两点E 、F ，使AE BF =，连接CE 、CF ，求证：AC BC +>EC FC +．CBA O E F对角互补类【例5】如图，90ABC ∠=︒，BD 为ABC ∠的角平分线，将一三角板的直角顶点固定在点D ，另外两边分别交AB ，BC 于E ，F 两点，证明：DE DF =EDAB C【例6】如图，120ABC ∠=︒，BD 为ABC ∠的角平分线，60DEF ∠=︒且角的两边分别交AB ，BC 于E ，F 两点，证明：DE DF =ABCD【例7】如图，在四边形ABCD 中，90ADC ABC ∠=∠=︒，AD CD =，DP AB ⊥于P ，若四边形ABCD的面积为18，求DP 的长．PDCBA【例8】直角三角形ABC 中9068A AB BC ∠=︒==，，；P 为BC 的中点，ABC ∆绕着点P 逆时针旋转90︒到DEF ∆，求重叠部分PQKR 的面积．【例9】已知，在四边形ABCD 中，90ABC ADC ∠=∠=︒，对角线AC 平分BAD ∠，在DA 的延长线上任取一点E ，连接EC ，作12ECF BCD ∠=∠，使CF 与AB 的延长线交于F ，连结EF ，请画出完整图形，探究：线段BF 、EF 、ED 之间具有怎样的数量关系，并说明理由DCBA【例10】（1）如图1，四边形ABCD 中，AB CB =，60ABC ∠=︒，120ADC ∠=︒，请你猜想线段DA 、DC 之和与线段BD 的数量关系，并证明你的结论；图1DBA（2）如图2，四边形ABCD 中，AB BC =，60ABC ∠=︒，若点P 为四边形ABCD 内一点，且120APD ∠=︒，请你猜想线段PA 、PD 、PC 之和与线段BD 的数量关系，并证明你的结论．P图2DC BA平移【例11】如图所示，在ABC ∆中，90B ∠=︒，M 为AB 上的一点，且AM BC =；N 为BC 上的一点，且CN BM =．连接AN 、CM 交于点P ，求证：45APM ∠=︒．PN M CBA【例12】 (07年北京中考如图，已知ABC ∆⑴请你在BC 边上分别取两点D 、E (BC 的中点除外，连结AD 、AE ，写出使此图中只存．．在两对．．．面积相等的三角形的相应条件，并表示出面积相等的三角形；CB A⑵请你根据使⑴成立的相应条件，证明AB AC AD AE +>+．⑴DE CB A【例13】如图14-1，ABC △的边BC 在直线l 上，AC BC ⊥，且AC BC =；EFP △的边FP 也在直线l 上，边EF 与边AC 重合，且EF FP =．（1）在图14-1中，请你通过观察、测量，猜想并写出AB 与AP 所满足的数量关系和位置关系；（2）将EFP △沿直线l 向左平移到图14-2的位置时，EP 交AC 于点Q ，连结AP ，BQ ．猜想并写出BQ 与AP 所满足的数量关系和位置关系，请证明你的猜想；（3）将EFP △沿直线l 向左平移到图14-3的位置时，EP 的延长线交AC 的延长线于点Q ，连结AP ，BQ ．你认为（2）中所猜想的BQ 与AP 的数量关系和位置关系还成立吗？若成立，给出证明；若不成立，请说明理由．A （E ）B C （F ） PlllB FC 图14-1图14-2图14-3平移加旋转【例14】如图，已知E 是正方形ABCD 的边AB 的中点，∠B 的外角∠CBG 的平分线BF 交DE 的垂线EF于F 。

三角形的翻折课件

三角形翻折是几何变换中的一种，它是指将三角形沿着一条直线进行折叠，使得两侧的图形完全重合。
在三角形翻折的过程中，图形的形状和大小不会发生变化，只是位置和方向可能会改变。
轴对称与中心对称
轴对称是指一个图形关于一条直线对称，折叠后两部分完全重合。
中心对称是指一个图形关于一个点对称，旋转180度后两部分完全重合。
等边三角形的翻折
等边三角形翻折后形成的三个直角三角形是全等的，因此可以通过翻折来证明等边三角形的性质。
翻折后形成的三个直角三角形可以通过勾股定理来证明其边长关系，从而证明等边三角形的性质。
一般三角形的翻折
一般三角形翻折后形成的两个直角三角形不一定是全等的，因此需要通过其他方法来证明其性质。
可以通过将一般三角形划分为几个小三角形，然后利用勾股定理来证明其边长关系，从而证明一般三角形的性质。
04
三角形翻折的解题策略
理解翻折的本质
翻折是一种几何变换，通过将一个平面图形沿着一条直线折叠，使图形的一部分与另一部分重合，从而得到一个新的图形。
在三角形翻折问题中，关键是要理解翻折的本质是图形的对称性，即图形经过翻折后，其对称轴两侧的部分是全等的。
高阶练习题与解析
题目5
将一个三角形进行多次翻折，每次翻折都使相邻两边中点连线与翻折线重合，求所有折痕的总长度。
解析
这道题需要运用三角形的中位线性质和翻折的性质，通过逐步推导和计算，求出所有折痕的总长度。
THANKS
感谢观看
基础练习题
题目1
将一个等边三角形进行翻折，使其一个顶点与相对边的中点重合，求折痕的长度。
题目2
将一个直角三角形进行翻折，使一条直角边与斜边的中点重合，求折痕的长度。

《全等三角形》数学教学PPT课件(6篇)

加深理解
E A
F
B
C
∆ABC ≌ ∆FDE
对应顶点对应顶点对应顶点对应角对应角对应角对应边对应边对应边
41
课堂测试 1.如果∆ABC≌ ∆ADC，AB=AD，∠B=70°, BC=3cm,那么∠D=___7_0,D°C=____3cm
D
课堂测试
2、若△AOC≌△BOD，对应边是应角是；
小组讨论完成
解：∵ △ABD ≌ △EBC，∴AB=EB，BD=BC, ∵BD=ED+EB ∴DE=BD-EB=BC-AB=5-3=2cm.
三、巩固练习
基础练习（教材第三十二页练习1-2题）
四、课堂小结，请大家回顾一下：
这节课你学到了什么？还有哪些疑惑？学生充分讨论回答。
点评梳理：
（1）全等三角形的概念及表示方法；（2）全等三角形的性质及应用。
思考
将两个全等三角形重合在一起，
重合的顶点叫对应顶点
A
D
重合的边叫对应边
重合的角叫对应角
根据动画效果，你能说出
这两个全等三角形的对应顶点、
B
CE
F 对应边、对应角各是什么吗？
36
全等三角形表示
如果两个三角形全等，那么该如何表示吗？
A
D
右图中的∆ABC和∆DEF全等
记作: ∆ABC ≌ ∆DEF
五、课后练习
1、教材第33-34页，1-6题。
第十二章全等三角形
12.1 全等三角形
人教版数学（初中）（八年级上）
Please Enter Your Detailed Text Here, The Content Should Be Concise And Clear, Concise And Concise Do Not Need Too Much Text

《全等三角形与实际问题——之平移、翻折、旋转》

课程名称：全等三角形与实际问题 ——之平移、翻折、旋转
全等三角形
性质：
判定：
全等三角形的对应S边S相S,等SA，S
全等三角形的对应A角S相A,等AA。S,HL
请同学们用课桌上的物品来进行
01 平移 02 翻折 03 旋转
折翻
Байду номын сангаас
全等三角形与实际应用
——之平移、旋转、翻折
全等三角形的实际应用
如图所示，已知线段BD和线段AE相交于点C，且C为这两条线段的中点，
E
全等三角形的实际应用
A
通过前两问的启发，你能“已知
A
三角形的一边和另一边的中线，
求第三边的范围吗？”
C D
B
倍长中线法
B
C
ED
请解决下列问题：在△ABC中，AD是BC边的中线， AD=3cm，AB=5cm，求AC的取值范围。
1＜AC＜11
小结
全等三角形是研究两个封闭图形之间关系的基本工具，同时也是移动图形位置的工具
全等三角形的实际应用
全等三角形的实际应用
如图所示，已知线段BD和线段AE相交于点C，且C为这两条线段的中点，
求证：AB=DE
△ABC≌△EDC
A
C D
B
E
全等三角形的实际应用
若点A与D点间的距离为200，且AC=120，其他条件不变，你能确定AB间的长度范围么？
40＜AB＜440
A
C D
B
在平面几何知识的应用中，若要证明线段相等或角的相等，或需要移动图形（元素）的位置
常要借助全等三角形的知识。
求证：AB=DE
△ABC≌△EDC
A

第十二章12.1全等三角形.1全等三角形课件ppt

1、有公共边
A
B
D
A
D B
A
D
B
C
CLeabharlann C2、有公共角、对顶角
D
A O
A
D
O
A
E
D
C B
C
B
C
B
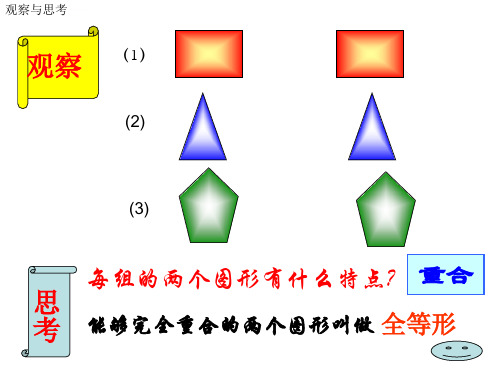
让我们记住找对应边、对应角的方法
活动5：展示才华认识到了贫困户贫困的根本原因，才能开始对症下药，然后药到病除。近年来国家对扶贫工作高度重视，已经展开了“精准扶贫”项目
A
填一填：
1、已知△ABC≌△ADE，
认识到了贫困户贫困的根本原因，才能开始对症下药，然后药到病除。近年来国家对扶贫工作高度重视，已经展开了“ 精准扶贫”项目
同一张底片洗出的照片
形状、大小相同的图形放在一起能够完全重合。能够完全重合的两个图形叫做全等形．
认识到了贫困户贫困的根本原因，才能开始对症下药，然后药到病除。近年来国家对扶贫工作高度重视，已经展开了“ 精准扶贫”项目
F
全等三角形的性质: 1、全等三角形的对应边相等,
2、全等三角形的对应角相等。 ∵△ABC≌△DEF （已知）
∴ AB=DE，BC=EF，AC=DF（全等三角形的对应边相等）
∠A=∠D,∠B=∠E,∠C=∠F（全等三角形的对应角相等）
例1
认识到了贫困户贫困的根本原因，才能开始对症下药，然后药到病除。近年来国家对扶贫工作高度重视，已经展开了“ 精准扶贫”项目
C
D
A
B
认识到了贫困户贫困的根本原因，才能开始对症下药，然后药到病除。近年来国家对扶贫工作高度重视，已经展开了“ 精准扶贫”项目

全等三角形平移、旋转翻折课件2

如果设BC交B'C'于点O，则变化更多.
C’
C
B’
图
图9
当点A是直角三角形的直角顶点时，点B、A、B’ 在同一条直线上， △CB’B是等腰三角形，如图10.
当点A是钝角顶点时，会有不同的翻折型全等三角形，如图11和图12
A
C
沿着经过三角形一边上的一点，且垂直于这条边的直线翻折
在锐角△ABC的一边上任取一点，过这点作这边的垂线，将△ABC沿着这条直线翻折得△A’B’C’，如图 13当这个点为这条边的中点时，得图14.当这个点为这条边的两个端点时，分别得图7和图9
或连接PD；
F
A
P
D
A P E E D
F
4、若看到正方形以及所要求证的等线段PB和PE 共端点，从而联想到旋转则可作PF⊥PC，交CB延长线于F；
B
C B C
或者作PF⊥PC，交CD延长线于F；
A P
D F E
G
B
H
C
B
C
1.若看到正方形的对角线 2、若看到正方形联想到平移，可联想到角平分线定理，则可过P作FG∥AD，交AB 则可作PH⊥BC，PF⊥DC，于G，交CD于F；垂足分别为H、F；
A P
D
A P E
D
E B C
B
F
C
3、若看到正方形的对角线想到角平分线的对称性，从而联想到翻折，则可截取 CF=CE，连接PF；
三角形全等的探究
30°
50° 可以发现给出两个条
③两边：
2cm 4cm 2cm 4cm
件时画出的三角形也
不能保证一定全等。
知识梳理:

初中数学《全等三角形》课件

2.能够完全重合的两个三角形叫全等三角形。
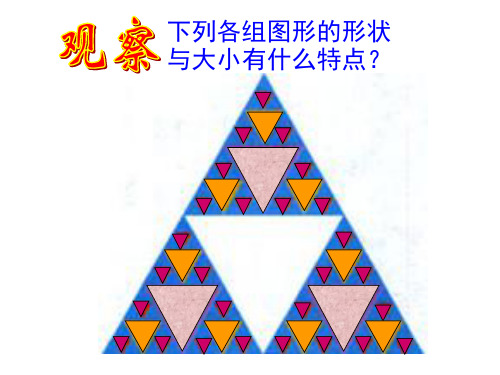
3.“全等”用符号≌“ ”来表示，读全作等于
4“.全等三角”形的对应边和对应角相等
5.书写全等式时要求把对应字母放在对应的位置上
先写出全等式，再指出它们的对应边和对应角
A ∵△ABC≌△FDE
E B
∴AB=FD,AC=FE,
BC=DE
∴∠A=∠F, ∠B=∠D, ∠ACB= ∠FED.
D
C
规律四：一对最长的边是对应边
一对最短的边是对应边
规律五：一对最大的角是对应角
F
一对最小的角是对应角
1.有公共边的，公共边一定是对应边。
∴BE=3cm,BD=5cm
如图, △EFG≌△NMH
E H
M
F
G
1、请找出对应边和对应角。
N
2、如果EF=2.1cm,EH=1.1cm,
HN=3.3cm, 求NM、HG的长.
解：∵△EFG ≌ △NMH ∴NM=EF=2.1,EG=HN=3.3
∴HG=EG-HG=3.3-1.1=2.2
△ABD≌△ACE，若∠ADB=100°，∠B=30°，说出△ACE中各角的大小？
形状相同
大小相同
两个图形全等，它们的形状一定相同，大小一定相等！
下列两三角形是怎样由一个三角形得到另一个三角形？它们有什么特点？
E
A PC M
D
A
BN
B
C
下列两三角形是怎样由一个三角形得到另一个三角形？它们有什么特点？
A
B
D
A
B
C
D
C
E
下列两三角形是怎样由一个三角形得到另一个三角形？它们有什么特点？

第6讲平移、旋转、翻折与三角形全等(讲义)

1 / 4图1NMEDCBA图2NMEDCBA第6讲平移、旋转、翻折与三角形全等一、专项练习【板块一】平移与全等问题1. 如图，已知△ABC(1)请你在BC 边上分别取两点D 、E (BC 的中点除外)，连接AD 、AE ，写出使此图中只存在两对．．．．．面积相等的三角形的相应条件，并表示出面积相等的三角形；(2)请你根据使(1)成立的相应条件，证明AB +AC ＞AD +AE ．【板块二】旋转与全等问题2. 在△ABC 中，∠ACB =90°,AC =BC ，直线MN 经过点C ，且AD ⊥MN 于D ，BE ⊥MN 于E .(1)当直线MN 绕点C 旋转到图1的位置时，求证：①△ADC ≌△CEB ；②DE =AD +BE ；(2)当直线MN 绕点C 旋转到图2的位置时，（1）中的结论还成立吗？若成立，请给出证明；若不成立，说明理由．2 / 4图1NM FEC BA图2NMCBA3. 如图1，点C 为线段AB 上一点，△ACM ，△CBN 是等边三角形，直线AN ，BM 分别交两三角形于点E 、F .连接EF . (1)求证：AN =BM ；(2)求证：△CEF 为等边三角形；(3)将△ACM 绕点C 按逆时针方向旋转90°，其他条件不变，在图2中补出符合要求的图形，并判断第（1）、（2）两小题的结论是否仍然成立（不要求证明）.3 / 4HF ED CBA4. 如图，EF 分别是正方形ABCD 的边BC 、CD 上的点，且∠EAF =45°，AH ⊥EF ，H 为垂足，求证：AH =AB ．【板块三】翻折与全等问题5. 如图①所示，OP 是∠MON 的平分线，请你利用该图形画一对以OP 所在直线为对称轴的全等三角形．请你参考这个作全等三角形的方法，解答下列问题：（1）如图②，在△ABC 中，∠ACB 是直角，∠B =60°，AD 、CE 分别是∠BAC 、∠BCA 的平分线，AD 、CE 相交于点F ．请你判断并写出FE 与FD 之间的数量关系．（2）如图③，在△ABC 中，如果∠ACB 不是直角，而（1）中的其他条件均不变，请问，你在（1）中得到的结论是否仍然成立？若成立，请证明；若不成立，请说明理由．6.已知△ABC，∠BAD=∠CAD，AB=2AC，AD=BD，求证：DC⊥AC．ACDB4/ 4。

《全等三角形》PPT优质课件

D A
O
C B
AD
O
B
C
A
B D
E C
A
E
D
B
C
1. 有公共边，则公共边为对应边； 2. 有公共角（对顶角），则公共角（对顶角）为对应角； 3.最大边与最大边（最小边与最小边）为对应边；
最大角与最大角（最小角与最小角）为对应角；
4. 对应角的对边为对应边；对应边的对角为对应角.
探究新知
找一找下列全等图形的对应元素？
A
D
A
2 B E CF
A
3 21 4
B E
CF
B
D CF
A
D
1
23 4
B
C
探究新知
全等的表示方法
“全等”用符号“≌”表示，读作“全等于”.
A
F
B
CD
E
△ABC≌△FDE
记两个三角形全等时，通常把表示对应顶点的字母写在对应的位置上.
探究新知
全等的性质
全等三角形的对应边相等，对应角相等.
A
D
B
C
E
∠A=∠F，∠B=∠D，∠C=∠E. （全等三角形对应角相等）
探究新知
素养考点 1 识别全等三角形的对应元素
例1 如图，若△BOD≌△COE，∠B＝∠C，指出这两个全等三角形的对应边；若△ADO≌△AEO，指出这两个三角形的对应角.
解：△BOD与△COE的对应边为： BO与CO，OD与OE，BD与CE； △ADO与△AEO的对应角为：
课堂检测
拼接的图形展示
课堂小结
全等三角形
定义能够完全重合的两个三角形叫做全等三角形
基本性质

全等三角形复习课件2_ppt

gxf
方法指引
证明两个三角形全等的基本思路：
（1）：已知两边----
找第三边 (SSS) 找夹角（SAS) 找是否有直角 (HL)
已知一边和它的邻角 (2):已知一边一角---
找这边的另一个邻角(ASA)
找这个角的另一个边(SAS) 找这边的对角 (AAS)
已知一边和它的对角
找一角(AAS) 已知角是直角，找一边(HL)
E
∵ △ABC和△ECD都是等边三角形
A
∴ AC=BC DC=EC ∠BCA=∠DCE=60°
∴ ∠BCA+∠ACE=∠DCE+ ∠ACE
B
D
即∠BCE=∠DCA
C
在△ACD和△BCE中
AC=BC ∠BCE=∠DCA DC=EC ∴ △ACD≌△BCE (SAS)
变式：以上条件不变，将
△ABC绕点C旋转一定角度（大于零度而小于六十度），以上的结论海成立吗？
∵BM是△ABC的角平分线,点P
在BM上,
A
ND
M
PF
∴PD=PE
B
E
C
(角平分线上的点到这个角的两边距离相等).
同理,PE=PF.
∴PD＝PE=PF.
即点P到三边AB、BC、CA的距离相等
gxf
3.如图，已知△ABC的外角∠CBD和 ∠BCE的平分线相交于点F，
求证：点F在∠DAE的平分线上．
证明：过点F作FG⊥AE于G，
gxf
三.练习：
1、如图：在△ABC中，∠C =900，AD 平分∠ BAC，DE⊥AB交AB于E， BC=30，BD：CD=3：2，则 DE= 12 。
c
D
A
B E

相关主题

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

绕着三角形一边上的一个点旋转180° 在△ABC的AC边上任取一点O
将△ABC绕着点O旋转180°，得△A’B’C’， △ABC与△A’B’C’或中心对称，如图31 当点O为AC边中点时，得图32，四边形ABCB’ 是平行四边形当点O在AC边的延长线上时，得图33
绕着平面内一个特殊点旋转绕着等边三角形的中心旋转120度
E
∴△ABC≌△DEF（SAS）
知识梳理:
三角形全等判定方法3
有两角和它们夹边对应相等的两个三角形全等(可以简写成“角边角”或“ASA”）。
用符号语言表达为：在△ABC和△DEF中
A
D
∠A=∠D （已知）
AB=DE（已知） ∠B=∠E（已知） B
CF E
∴ △ABC≌△DEF（ASA）
知识梳理: 三角形全等判定方法4
有两角和其中一个角的对边对应相等的两个三角形全等(可以简写成“角角边”或 “AAS”）。
在△ABC和△DEF中 ∠A=∠D （已知）
A
D
∠B=∠E （已知）
AC=DF （已知） B
CF
E
∴ △ABC≌△DEF（AAS）
知识梳理:
A
A
B
C
SSA不能
A
判定全等
B
C
D
B D
A
全等三角形的性质：
AB=AB'，B'C=BC'.
C
如果设BC交B'C'于点O，
则变化更多.
图9
当点A是直角三角形的直角顶点时，点B、A、B’ 在同一条直线上， △CB’B是等腰三角形，如图10. 当点A是钝角顶点时，会有不同的翻折型全等三角形，如图11和图12
A

沿着经过三角形一边上的一点，且垂直于这条边的直线翻折
全等三角形平移、旋转翻折课件2
知识梳理:
三角形全等的探究
1.只给一个条件(一组对应边相等或一组对应角相等).
①只给一条边：
②只给一个角：
可以发现只给一个
条件画出的三角形
不能保证一定全等
60°
60°
60°
知识梳理:
①一边一内角：
2.给出两个条件：
30° ②两内角：
30°
30°
三角形全等的探究
平移 B E CF
A
D
翻
旋
折
转
D
B
C
B
A EC
图3
A
B
B’图6
C’ B’
C
B C’
A
C’
C B’
图8
沿过一个顶点的
直线翻折
当点A是锐角三
角形的顶点时
图4
添加条件，可以变成很
图5 多题目。如图6，要证明
∠CBC'=∠C'B'C.
图7
可以加条件，
已知：AB=AB'，
AC=AC'.
也可以加条件，已知：
30°50° ③两边：
2cm 4cm
30° 50°
2cm 4cm
可以发现给出两个条件时画出的三角形也不能保证一定全等。
知识梳理: 注意：三两角个形三全角等形判全等定在方表法示1
简写三为边“对边应边相边时等”通的或常两把对“个对应SS应的三S顶位”角）点置形。的上全字。等母（写可在以
A
用符号语言表达为：
当∠BAC=60°时，△ABC绕着顶点 A旋转60°后，点C’在边AB上，如图26-1和图26-2 当∠BAC=120°时，△ABC绕着顶点A旋转60°后，点C、A、B’在同一条直线上，如图27-1和图27-2
旋转90度
△ABC为锐角三角形时，绕着顶点A旋转90度，得图28-1，联结BB’,CC’，则△ABB’与△ACC’是等腰直角三角形；常见的放置方向如图28-2 △ABC为直角三角形时，得图29和图30，与正方形相关
△ABD绕中心O旋转120°后，与△BCE重合，△ABD 与△BCE全等；图35中，△EBD与△DCF全等；图35中， △EBD与△DCF全等
绕着正方形的中心旋转90度
四边形ABDF是正方形，图 36中，△ABC绕中心O旋转 90°后，与△CBE与△EDG 全等；图38中，△ABC与 △BDE全等；图39中， △ABC与△BDE全等
当点A是直角三角形的直角顶点时，会有不同的旋转型全等三角形，如图21 至图23
旋转确定的角度
旋转60度
△ABC为锐角三角形时，绕着顶点A旋转60度，得图24-1，联结 BB’、CC’，则△ABB’与ACC’是等边三角形；常见的放置方向如图24-2 △ABC为钝角三角形时，得图 25-1和图25-2
再如图43，可以分解出五个常见的翻折型全等图形，如图43-1 至图43-5
如果能够掌握全等三角形的判定方法和这些常见的全等图形，那么判定两个三角形全等将会易如反掌
A P
B
D 已知：正方形ABCD,P为对角线AC上一点，PE⊥PB交线段CD于E. 求证：PB=PE.
平移型
将△ABC沿着边BC方向平移，得到△A’B’C’,如图40-1.将图40-1换个角度看，如图图40-2.继续将△ABC沿着边BC方向平移，使点B’与点C重合，得图41
在利用图形寻找全等三角形时，通常需要将图形换一个角度观察，从中找出常见的全等图形，如图19-1和图19-2，当图形比较复杂时，还可以将图形分解成几个常见的全等图形，如图42，可以分解出三个常见的旋转型全等图形，如图42-1至图42-3
在△ABC和△ DEF中
B
C
AB=DE
D
BC=EF
CA=FD
∴ △ABC ≌△ DEF（SSS） E
F
知识梳理: 三角形全等判定方法2
两边和它们的夹角对应相等的两个三角形
全等。(可以简写成“边角边”或“SAS”)
用符号语言表达为：在△ABC与△DEF中
A
D
AC=DF ∠C=∠F BC=EF
CF
B
在锐角△ABC的一边上任取一点，过这点作这边的垂线，将△ABC沿着这条直线翻折得△A’B’C’，如图 13当这个点为这条边的中点时，得图14.当这个点为这条边的两个端点时，分别得图7和图9
旋转型
绕着三角形一个顶点旋转旋转不确定的角度
锐角△ABC绕着顶点A 旋转一定的角度，得到 △AB’C’，如图16将 △ABC绕着点A顺时针旋转不同的角度可以得到不同的旋转型全等三角形，如图17至图20 其中，将图19-1换个方向看，得图19-2，这个图更常见。
全等三角形的对应边相等， B
C
对应角相等
D
E
F
如图： ∵ △ABC≌△DEF
∴A B=D E，A C=D F，BC= E F
（全等三角形的对应边相等）
∠A=∠D，∠B=∠E，∠C=∠F （全等三角形的对应角相等）
（16崇明二模）
一个三角形经过平移、翻折、旋转，前后的图形全等。常见的图形有： A D

最新全等三角形 平移、旋转翻折课件2