浙教版八年级三角形中几种模型

合集下载

全等三角形的重难点模型(八大题型)(原卷版)—八年级数学上册(浙教版)

全等三角形的重难点模型（八大题型）【题型01：平移型】【题型02：翻折型】【题型03：旋转型】【题型04：一线三等角型（三类型）】【题型05：手拉手模型（四大类型）】【题型06：半角模型】【题型07：对角互补模型】【题型08：平行+线段中点构造全等模型】【题型1 平移型】【方法技巧】【典例1】如图，点E，C在线段BF上，AB=DE，BE=CF，AC=DF．(1)求证：△ABC≌△DEF；(2)若∠B=45°，∠F=85°，求∠A的度数．【变式1-1】如图、点B、E、C、F在一条直线上AB=DE，AC=DF，BE=CF．(1)求证：∠A=∠D；(2)求证：AC∥DF．【变式1-2】如图，在△ABC和△DEF中，边AC，DE交于点H，AB∥DE，AB=DE，BC=EF．(1)若∠B=55°，∠ACB=100°，求∠CHE的度数；(2)求证：△ABC≌△DEF．【变式1-3】如图，点B、E、C、F在同一直线上，∠A=∠D=90°，BE=CF，AC=DF．求证：∠B=∠DEF．【题型2 翻折型】【方法技巧】【典例2】如图，AB=AD，CB⊥AB，CD⊥AD，垂足分别为B，D．(1)求证：△ABC≌△ADC；(2)若AB=4，CD=3，求四边形ABCD的面积．【变式2-1】如图，已知∠1=∠2，∠C=∠D，求证：AC=BD【变式2-2】如图，已知AD平分∠BAC，AB=AC．求证：△ABD≌△ACD．【变式2-3】如图，AB=AC，BO=CO，求证：∠ADC=∠AEB．【题型3 旋转型】【方法技巧】【典例3】如图，在△ABC和△AEF中，点E在BC边上，∠C＝∠F，AC＝AF，∠CAF＝∠BAE，EF与AC交于点G．（1）试说明：△ABC≌△AEF；（2）若∠B＝55°，∠C＝20°，求∠EAC的度数．【变式3-1】如图，点E在△ABC外部，点D在BC边上，若∠1＝∠2，∠E＝∠C，AE＝AC，求证：AB＝AD．【变式3-2】如图，点E在△ABC边AC上，AE＝BC，BC∥AD，∠BAC＝∠ADE．（1）求证：△ABC≌△DEA；（2）若∠CAD＝30°，求∠BCD的度数．【变式3-3】如图，在△ABC中，点D是BC的中点，E是AB边上一点，过点C作CF∥AB交ED的延长线于点F．求证：△BDE≌△CDF．【变式3-4】如图，∠ABC＝∠ADE，∠BAD＝∠CAE，AC＝AE，求证：△ABC≌△ADE．【题型4 一线三等角型】【方法技巧】模型一一线三垂直如图一，∠D=∠BCA=∠E=90°，BC=AC 。

三角形中的5种解题模型-2023年新八年级数学核心知识点与常见题型通关讲解练(浙教版)(解析版)

重难点：三角形中的5种解题模型【知识梳理】一、“8”字模型三角形三个内角的和等于180°对顶角相等二、飞镖模型三角形三个内角的和等于180°三角形的外角等子与它不相邻的两个内角的和.三、“A”字模型三角形三个内角的和等于180°四、“老鹰捉小鸡”模型三角形三个内角的和等于180°三角形的外角等于与它不相邻的两本内角的和.五、（双）角平分线模型1.双内角平分线2.双外角平分线3.内角平分线+外角平分线三角形三个内角的和等于180°三角形的外角等于与它不相邻的两本内角的和.【考点剖析】一、“8”字模型1．（2021秋•宁远县校级期中）如图所示，∠α的度数是（）A．10°B．20°C．30°D．40°【解答】解：∵∠A+∠B+∠AOB＝∠C+∠D+∠COD，∠AOB＝∠COD，∴∠A+∠B＝∠C+∠D∴30°+20°＝40°+α，∴α＝10°故选：A．2．（2022春•叙州区期末）如图，BP平分∠ABC交CD于点F，DP平分∠ADC交AB于点E，若∠A＝45°，∠P＝40°，则∠C的度数为（）A．30°B．35°C．40°D．45°【解答】解：∵∠A+∠ADG+∠AGD＝180°，∠ABC+∠C+∠BGC＝180°，∴∠A+∠ADG+∠AGD＝∠ABC+∠C+∠BGC．又∵∠AGD＝∠BGC，∴∠A+∠ADG＝∠C+∠GBC．同理可得，∠A+∠ADE＝∠P+∠PBE．∴∠A﹣∠P＝∠PBE﹣∠ADE．∵BP平分∠ABC交CD于点F，DP平分∠ADC交AB于点E，∴∠GBC＝2∠PBE，∠ADG＝2∠ADE．∴∠A﹣∠C＝2（∠A﹣∠P）．∴∠A+∠C＝2∠P．又∵∠A＝45°，∠P＝40°，∴∠C＝35°．故选：B．3．（2022春•靖江市校级月考）已知，如图，线段AD、CB相交于点O，连结AB、CD，∠DAB和∠BCD的平分线AP和CP相交于点P．试问∠P与∠D、∠B之间存在着怎样的数量关系，请说明理由．【解答】解：2∠P＝∠B+∠D，理由如下：如图，在△AOB和△COD中，∵∠AOB＝∠COD，∴∠OAB+∠B＝∠OCD+∠D，在△AEP和△CED中，∵∠AEP＝∠CED，∴∠1+∠P＝∠2+∠D，∵AP、CP分别是∠DAB和∠BCD的角平分线，∴2∠P﹣∠B＝2∠D﹣∠D，整理得，2∠P＝∠B+∠D．4．（2019春•邗江区校级月考）图1，线段AB、CD相交于点O，连接AD、CB，我们把形如图1的图形称之为“8字形”．如图2，在图1的条件下，∠DAB和∠BCD的平分线AP和CP相交于点P，并且与CD、AB分别相交于M、N．试解答下列问题：（1）在图1中，请直接写出∠A、∠B、∠C、∠D之间的数量关系：；（2）仔细观察，在图2中“8字形”的个数：个；（3）图2中，当∠D＝50度，∠B＝40度时，求∠P的度数．（4）图2中∠D和∠B为任意角时，其他条件不变，试问∠P与∠D、∠B之间存在着怎样的数量关系．（直接写出结果，不必证明）．【解答】解：（1）∵∠A+∠D+∠AOD＝∠C+∠B+∠BOC＝180°，∠AOD＝∠BOC，∴∠A+∠D＝∠C+∠B，故答案为：∠A+∠D＝∠C+∠B；（2）①线段AB、CD相交于点O8字形”；②线段AN、CM相交于点O，形成“8字形”；③线段AB、CP相交于点N，形成“8字形”；④线段AB、CM相交于点O，形成“8字形”；⑤线段AP、CD相交于点M，形成“8字形”；⑥线段AN、CD相交于点O，形成“8字形”；故“8字形”共有6个，故答案为：6（3）∠DAP+∠D＝∠P+∠DCP，①∠PCB+∠B＝∠PAB+∠P，②∵∠DAB和∠BCD的平分线AP和CP相交于点P，①+②得：∠DAP+∠D+∠PCB+∠B＝∠P+∠DCP+∠PAB+∠P，即2∠P＝∠D+∠B，又∵∠D＝50度，∠B＝40度，∴2∠P＝50°+40°，∴∠P＝45°；（4）关系：2∠P＝∠D+∠B．∠D+∠1＝∠P+∠3①∠B+∠4＝∠P+∠2②①+②得：∠D+∠1+∠4+∠B＝∠P+∠3+∠2+∠P，∵∠DAB和∠DCB的平分线AP和CP相交于点P，∴∠1＝∠2，∠3＝∠4∴2∠P＝∠D+∠B．二、飞镖模型1．（2021春•宝应县月考）如图，求证：∠BDC＝∠A+∠B+∠C．【解答】证明：作射线AD，如图，∵∠3＝∠B+∠1，∠4＝∠C+∠2，∴∠3+∠4＝∠B+∠C+∠1+∠2，2．（2020春•如东县期末）探究与发现：如图1所示的图形，像我们常见的学习用品﹣﹣圆规．我们不妨把这样图形叫做“规形图”，（1）观察“规形图”，试探究∠BDC与∠A、∠B、∠C之间的关系，并说明理由；（2）请你直接利用以上结论，解决以下三个问题：①如图2，把一块三角尺XYZ放置在△ABC上，使三角尺的两条直角边XY、XZ恰好经过点B、C，∠A＝54°，则∠ABX+∠ACX＝°；②如图3，DC平分∠ADB，EC平分∠AEB，若∠DAE＝α，∠DBE＝β，请直接写出∠DCE的度数（用含α和β的式子表示）；③如图4，∠ABD，∠ACD的12等分线相交于点G1、G2…、G11，若∠BDC＝115°，∠BG1C＝60°，求∠A的度数．【解答】解：（1）∠BDC＝∠A+∠B+∠C．理由：连接AD并延长到点E．∵∠BDE＝∠BAD+∠B，∠CDE＝∠CAD+∠C，∴∠BDE+∠CDE＝∠BAD+∠B+∠CAD+∠C，（2）①∵∠BXC＝∠ABX+∠ACX+∠A＝90°，∠A＝54°，∴∠ABX+∠ACX＝36°．故答案为36．②如图3中，设∠ADC＝∠CDB＝x，∠AEC＝∠CEB＝y，则有∠DCE＝x+y+α，β＝2x+2y+α，∴∠DCE＝．故答案为．③设∠ABD＝x°，∠ACD＝y°．由题意可得，解得∠A＝55°．3．（2020春•锡山区期中）探究与发现：如图1所示的图形，像我们常见的学习用品﹣﹣圆规．我们不妨把这样图形叫做“规形图”，那么在这一个简单的图形中，到底隐藏了哪些数学知识呢？下面就请你发挥你的聪明才智，解决以下问题：（1）观察“规形图”，试探究∠BDC与∠A、∠B、∠C之间的关系，并说明理由；（2①如图2，把一块三角尺XYZ放置在△ABC上，使三角尺的两条直角边XY、XZ恰好经过点B、C，若∠A＝50°，则∠ABX+∠ACX＝°；②如图3，DC平分∠ADB，EC平分∠AEB，若∠DAE＝50°，∠DBE＝130°，求∠DCE的度数；③如图4，∠ABD，∠ACD的10等分线相交于点G1、G2…、G9，若∠BDC＝140°，∠BG1C＝77°，求∠A的度数．【解答】解：（1）连接AD并延长至点F，且∠BDC＝∠BDF+∠CDF及∠BAC＝∠BAD+∠CAD；相加可得∠BDC＝∠BAC+∠B+∠C；（2）①由（1）的结论易得：∠ABX+∠ACX+∠A＝∠BXC，又因为∠A＝50°，∠BXC＝90°，所以∠ABX+∠ACX＝90°﹣50°＝40°；故答案为：40．②由（1）的结论易得∠DBE＝∠A+∠ADB+∠AEB，易得∠ADB+∠AEB＝80°；而∠DCE＝（∠ADB+∠AEB）+∠A，代入∠DAE＝50°，∠DBE＝130°，易得∠DCE＝90°；③∠BG1C＝（∠ABD+∠ACD）+∠A，∵∠BG1C＝77°，∴设∠A为x°，∵∠ABD+∠ACD＝140°﹣x°∴（140﹣x）+x＝77，14﹣x+x＝77，x＝70∴∠A为70°．题型三：“A”字模型1．（2022春•云龙区校级月考）已知如图，△ABC为直角三角形，∠C＝90°，若沿图中虚线剪去∠C，则∠1+∠2等于（）【解答】解：∵∠1、∠2是△CDE的外角，∴∠1＝∠4+∠C，∠2＝∠3+∠C，即∠1+∠2＝2∠C+（∠3+∠4），∵∠3+∠4＝180°﹣∠C＝90°，∴∠1+∠2＝2×90°+90°＝270°．故选：B．2．（2021春•东台市月考）如图，△ABC中，∠C＝75°，若沿图中虚线截去∠C，则∠1+∠2＝°．【解答】解：∵△ABC中，∠C＝75°，∴∠A+∠B＝180°﹣75°＝105°，∵∠1+∠2+∠A+∠B＝360°，∴∠1+∠2＝360°﹣105°＝255°．故答案为：255．3．（2020春•新野县期末）旧知新意：我们容易证明，三角形的一个外角等于与它不相邻的两个内角的和．那么，三角形的一个内角与它不相邻的两个外角的和之间存在怎样的数量关系呢？（1）如图1，∠DBC与∠ECB分别为△ABC的两个外角，试探究∠A与∠DBC+∠ECB之间存在怎样的数量关系？为什么？初步应用：（2）如图2，在△ABC纸片中剪去△CDE，得到四边形ABDE，∠1＝130°，则∠2﹣∠C＝；（3）小明联想到了曾经解决的一个问题：如图3，在△ABC中，BP、CP分别平分外角∠DBC、∠ECB，∠P与∠A有何数量关系？请利用上面的结论直接写出答案．拓展提升：（4）如图4，在四边形ABCD中，BP、CP分别平分外角∠EBC、∠FCB，∠P与∠A、∠D有何数量关系？为什么？（若需要利用上面的结论说明，可直接使用，不需说明理由．）【解答】解：（1）∠DBC+∠ECB＝180°﹣∠ABC+180°﹣∠ACB＝360°﹣（∠ABC+∠ACB）＝360°﹣（180°﹣∠A）＝180°+∠A；（2）∵∠1+∠2＝∠180°+∠C，∴130°+∠2＝180°+∠C，∴∠2﹣∠C＝50°；（3）∠DBC+∠ECB＝180°+∠A，∵BP、CP分别平分外角∠DBC、∠ECB，∴∠PBC+∠PCB＝（∠DBC+∠ECB）＝（180°+∠A），在△PBC中，∠P＝180°﹣（180°+∠A）＝90°﹣∠A；即∠P＝90°﹣∠A；故答案为：50°，∠P＝90°﹣∠A；（4）延长BA、CD于Q，则∠P＝90°﹣∠Q，∴∠Q＝180°﹣2∠P，∴∠BAD+∠CDA＝180°+∠Q＝180°+180°﹣2∠P＝360°﹣2∠P．题型四：“老鹰捉小鸡”模型1．（2022春•无锡期中）如图，把△ABC纸片沿DE折叠，当点A落在四边形BCED的外部时，则∠A与∠1和∠2之间有一种数量关系始终保持不变，请试着找一找这个规律，你发现的规律是（）A．2∠A＝∠1﹣∠2B．3∠A＝2（∠1﹣∠2）C．3∠A＝2∠1﹣∠2D．∠A＝∠1﹣∠2【解答】解：如图，由翻折的性质得，∠3＝∠A′DE，∠AED＝∠A′ED，∴∠3＝（180°﹣∠1），在△ADE中，∠AED＝180°﹣∠3A，∠CED＝∠3+∠A，∴∠A′ED＝∠CED+∠2＝∠3+∠A+∠2，∴180°﹣∠3﹣∠A＝∠3+∠A+∠2，整理得，2∠3+2∠A+∠2＝180°，∴2×（180°﹣∠1）+2∠A+∠2＝180°，∴2∠A＝∠1﹣∠2．故选：A．2．（2022春•洪泽区月考）如图，把△ABC纸片沿DE折叠，当点A落在四边形BCDE内部时，则∠A与∠1+∠2之间有一种数量关系始终保持不变，请试着找一找这个规律，这个规律是（）A．∠A＝∠1+∠2B．2∠A＝∠1+∠2C．3∠A＝2∠1+∠2D．3∠A＝2（∠1+∠2）【解答】解：∵在△ABC中，∠A+∠B+∠C＝180°①；在△ADE中∠A+∠ADE+∠AED＝180°②；在四边形BCDE中∠B+∠C+∠1+∠2+∠ADE+∠AED＝360°③；∴①+②﹣③得2∠A＝∠1+∠2．故选：B．3．（2021春•江都区校级期末）如图，三角形纸片ABC中∠A＝63°，∠B＝77°，将纸片一角折叠，使点C 落在△ABC的内部，若∠2＝50°，则∠1＝．【解答】解：设折痕为EF，连接CC′．∵∠2＝∠ECC′+∠EC′C，∠1＝∠FCC′+∠FC′C，∠ECF＝∠EC′F，∴∠1+∠2＝2∠ECF，∵∠C＝180°﹣∠A﹣∠B＝180°﹣63°﹣77°＝40°，∴∠1＝80°﹣50°＝30°，故答案为：30°．4．（2021春•南通期末）如图所示，把一个三角形纸片ABC的三个顶角向内折叠之后（3个顶点不重合），图中∠1+∠2+∠3+∠4+∠5+∠6＝°．【解答】解：由题意知，∠1+∠2+∠3+∠4+∠5+∠6＝720°﹣（∠B'FG+∠B'GF）﹣（∠C'HI+∠C'IH）﹣（∠A'DE+∠A'ED）＝720°﹣（180°﹣∠B'）﹣（180°﹣C'）＝（180°﹣A'）＝180°+（∠B'+∠C'+∠A'）又∵∠B＝∠B'，∠C＝∠C'，∠A＝∠A'，∠A+∠B+∠C＝180°，∴∠1+∠2+∠3+∠4+∠5+∠6＝360°．故答案为：360．5．（2019春•常熟市月考）将纸片△ABC沿DE折叠使点A落在A′处的位置．（1）如果A′落在四边形BCDE的内部（如图1），∠A′与∠1+∠2之间存在怎样的数量关系？并说明理由．（2）如果A′落在四边形BCDE的外部（如图2），这时∠A′与∠1、∠2之间又存在怎样的数量关系？并说明理由．【解答】解：（1）2∠A′＝∠1+∠2，理由沿DE折叠使点A落在A′处的位置，∴∠AED＝∠A′ED，∠ADE＝∠A′DE，∵∠AED+∠ADE＝180°﹣∠A，∠1+∠2＝180°+180°﹣2（∠AED+∠ADE），∴∠1+∠2＝360°﹣2（180°﹣∠A′）＝2∠A′；（2）2∠A′＝∠2﹣∠1，理由：∵沿DE折叠使点A落在A′处的位置，∴∠A＝∠A′，∵∠DME＝∠A′+∠1，∠2＝∠A+∠DME，∴∠2＝∠A+∠A′+∠1，即2∠A′＝∠2﹣∠1．【点评】本题考查了折叠的性质，三角形外角性质，三角形内角和定理的应用，主要考查学生运用定理进行推理和计算的能力．题型五：（双）角平分线模型1．（2022春•海州区校级期末）如图，将△ABC纸片沿DE折叠，使点A落在点A'处，且A'B平分∠ABC，A'C 平分∠ACB，若∠BA'C＝122°，则∠1+∠2的度数为（）A．116°B．100°C．128°D．120°【解答】解：∵△ABC纸片沿DE折叠，∴△AED≌△A′ED，∴∠ADE＝∠EDA′，∠AED＝∠DEA′，∴∠1+∠2＝180°﹣2∠ADE+180°﹣2∠AED＝180°﹣（∠ADE+∠AED）+180°﹣（∠ADE+∠AED）＝2∠A，∵A'B平分∠ABC，A'C平分∠ACB，∠BA'C＝122°，∴∠A'BC＝∠ABC，∠A'CB＝∠ACB，∴∠A'BC+∠A'CB＝180°﹣122°＝58°，∴∠ABC+∠ACB＝2（∠A'BC+∠A'CB）＝2×58°＝116°，∴∠A＝180°﹣116°＝64°，∴∠1+∠2＝2∠A＝2×64°＝128°，故选：C．2．（2022春•靖江市校级月考）如图，△ABC中，∠BAC＝50°，∠ABC的角平分线与∠ACB的角平分线交于点O．则∠BOC＝．【解答】解：∵∠BAC＝50°，∴∠ABC+∠ACB＝180°﹣50°＝130°，∵∠ABC的角平分线与∠ACB的角平分线交于点O，∴∠ABO＝∠OBC＝∠ABC，∠ACO＝∠OCB＝∠ACB，∴∠OBC+∠OCB＝∠ABC+∠ACB＝（∠ABC+∠ACB）＝×130°＝65°，∴∠BOC＝180°﹣∠OBC﹣∠OCB＝180°﹣65°＝115°，故答案为：115°．3．（2022春•丹徒区月考）在△ABC中，∠A＝40°：（1）如图（1）BO、CO是△ABC的内角角平分线，且相交于点O，求∠BOC；（2）如图（2）BO、CO是△ABC的外角角平分线，且相交于点O，求∠BOC；（3）如图（3）BO、CO分别是△ABC的一内角和一外角角平分线，且相交于点O，求∠BOC；（4）根据上述三问的结果，当∠A＝n时，分别可以得出∠BOC与∠A有怎样的数量关系（只需写出结论）．【解答】解：（1）∵∠BOC＝180°﹣∠OBC﹣∠OCB，∴2∠BOC＝360°﹣2∠OBC﹣2∠OCB，而BO平分∠ABC，CO平分∠ACB，∴∠ABC＝2∠OBC，∠ACB＝2∠OCB，∴2∠BOC＝360°﹣（∠ABC+∠ACB），∵∠ABC+∠ACB＝180°﹣∠A，∴2∠BOC＝180°+∠A，∴∠BOC＝90°+∠A．当∠A＝40°，∠BOC＝110°；（2）∠OBC＝（∠A+∠ACB），∠OCB＝（∠A+∠ABC），∠BOC＝180°﹣∠0BC﹣∠OCB，＝180°﹣（∠A+∠ACB）﹣（∠A+∠ABC），＝180°﹣∠A﹣（∠A+∠ABC+∠ACB），结论∠BOC＝90°﹣∠A．∠BOC＝90°﹣∠A．当∠A＝40°，∠BOC＝70°．（3）∵∠OCD＝∠BOC+∠OBC，∠ACD＝∠ABC+∠A，而BO平分∠ABC，CO平分∠ACD，∴∠ACD＝2∠OCD，∠ABC＝2∠OBC，∴2∠BOC+2∠OBC＝∠ABC+∠A，∴2∠BOC＝∠A，即∠BOC＝∠A．当∠A＝40°，∠BOC＝20°；（4）∠BOC＝90°+n；∠BOC＝90°﹣n；∠BOC＝n．【点评】本题考查了三角形的外角性质与内角和定理，熟记三角形的一个外角等于与它不相邻的两个内角的和是解题的关键．【过关检测】一、单选题 1．（2022秋·重庆渝北·八年级校考阶段练习）如图,将△ABC 沿着DE 翻折,使B 点与B'点重合,若∠1+∠2=80°,则∠B 的度数为（）A ．20°B ．30°C ．40°D ．50°【答案】C 【分析】由折叠的性质可知','BED B ED BDE B DE ∠=∠∠=∠,再利用平角的定义可求出BED BDE ∠+∠的度数，进而利用三角形内角和可求∠B 的度数.【详解】由折叠的性质可知','BED B ED BDE B DE ∠=∠∠=∠∵1'180,2'180BED B ED BDE B DE ∠+∠+∠=︒∠+∠+∠=︒∴11(36012)(36080)14022BED BDE ∠+∠=︒−∠−∠=⨯︒−︒=︒ ∴180()18014040B BED BDE ∠=︒−∠+∠=︒−︒=︒故选C【点睛】本题主要考查折叠的性质及三角形内角和定理，掌握折叠的性质及三角形内角和定理是解题的关键.2．（2023·全国·八年级假期作业）如图，AB 和CD 相交于点O ，∠A ＝∠C ，则下列结论中不能完全确定正确的是（）A ．∠B ＝∠DB ．∠1＝∠A ＋∠DC ．∠2＞∠D D ．∠C ＝∠D【答案】D【分析】利用三角形的外角性质，对顶角相等逐一判断即可．【详解】∵∠A ＋∠AOD ＋∠D ＝180°，∠C ＋∠COB ＋∠B ＝180°，∠A ＝∠C ，∠AOD ＝∠BOC ，∴∠B ＝∠D ，∵∠1＝∠2＝∠A ＋∠D ，∴∠2＞∠D ，故选项A ，B ，C 正确，故选D ．【点睛】本题考查了对顶角的性质，三角形外角的性质，熟练掌握并运用两条性质是解题的关键． 3．（2023·全国·八年级假期作业）如图，ABC 中，65A ∠=︒，直线DE 交AB 于点D ，交AC 于点E ，则BDE CED ∠+∠=（）．A ．180︒B ．215︒C ．235︒D ．245︒【答案】D 【分析】根据三角形内角和定理求出ADE AED ∠+∠，根据平角的概念计算即可．【详解】解：65A ∠=︒，18065115ADE AED ∴∠+∠=︒−︒=︒，360115245BDE CED ∴∠+∠=︒−︒=︒，故选：D ．【点睛】本题考查的是三角形内角和定理的应用，掌握三角形内角和等于180︒是解题的关键．4．（2023春·江苏镇江·七年级统考期中）在社会实践手工课上，小茗同学设计了一个形状如图所示的零件，如果52,25A B ︒︒∠=∠=，30,35,72C D E ︒︒︒∠=∠=∠=，那么F ∠的度数是（）．A ．72︒B ．70︒C ．65︒D ．60︒【答案】B【分析】延长BE 交CF 的延长线于O ，连接AO ，根据三角形内角和定理求出,BOC ∠再利用邻补角的性质求出DEO ∠，再根据四边形的内角和求出DFO ∠，根据邻补角的性质即可求出DFC ∠的度数．【详解】延长BE 交CF 的延长线于O ，连接AO ，如图，∵180,OAB B AOB ∠+∠+∠=︒∴180,AOB B OAB ∠=︒−∠−∠同理得180,AOC OAC C ∠=︒−∠−∠∵360,AOB AOC BOC ∠+∠+∠=︒∴360BOC AOB AOC ∠=︒−∠−∠360(180)(180)B OAB OAC C =︒−︒−∠−∠−−∠−∠107,B C BAC =∠+∠+∠=︒∵72,BED ∠=︒∴180108,DEO BED ∠=︒−∠=︒∴360DFO D DEO EOF ∠=︒−∠−∠−∠36035108107110,=︒−︒−︒−︒=︒∴180********DFC DFO ∠=︒−∠=︒−︒=︒,故选：B ．【点睛】本题考查三角形内角和定理，多边形内角和，三角形的外角的性质，邻补角的性质，解题关键是会添加辅助线，将已知条件联系起来进行求解．三角形外角的性质：三角形的一个外角等于与它不相邻的两个内角的和；邻补角性质：邻补角互补；多边形内角和：180(2)n ︒−．二、填空题 5．（2023·全国·八年级假期作业）如图是某建筑工地上的人字架，若1120∠=︒，那么32∠−∠的度数为．【答案】60︒【分析】根据平角的定义求出4∠，再利用三角形的外角的性质即可解决问题．【详解】解：如图14180∠+∠=︒，1120∠=︒，460∴∠=︒，324Ð=Ð+ÐQ ，32460∴∠−∠=∠=︒，故答案为：60︒．【点睛】本题考查三角形外角的性质、平角的性质等知识，解题的关键是熟练掌握基本知识，属于中考基础题．6．（2021·河北·统考中考真题）下图是可调躺椅示意图（数据如图），AE 与BD 的交点为C ，且A ∠，B ∠，E ∠保持不变．为了舒适，需调整D ∠的大小，使110EFD ∠=︒，则图中D ∠应（填“增加”或“减少”）度．【答案】减少 10【分析】先通过作辅助线利用三角形外角的性质得到∠EDF 与∠D 、∠E 、∠DCE 之间的关系，进行计算即可判断．【详解】解：∵∠A+∠B=50°+60°=110°，∴∠ACB=180°-110°=70°，∴∠DCE=70°，如图，连接CF 并延长，∴∠DFM=∠D+∠DCF=20°+∠DCF ，∠EFM=∠E+∠ECF=30°+∠ECF ，∴∠EFD=∠DFM+∠EFM=20°+∠DCF+30°+∠ECF=50°+∠DCE=50°+70°=120°，要使∠EFD=110°，则∠EFD 减少了10°，若只调整∠D 的大小，由∠EFD=∠DFM+∠EFM=∠D+∠DCF+∠E+∠ECF=∠D+∠E+∠ECD=∠D+30°+70°=∠ D+100°，因此应将∠D 减少10度；故答案为：①减少；②10．【点睛】本题考查了三角形外角的性质，同时涉及到了三角形的内角和与对顶角相等的知识；解决本题的关键是理解题意，读懂图形，找出图形中各角之间的关系以及牢记公式建立等式求出所需的角，本题蕴含了数形结合的思想方法． 7．（2022春·七年级单元测试）如图，把ABC 纸片沿DE 折叠，使点A 落在图中的A '处，若29A ∠=︒，90BDA ∠'=︒，则A EC ∠'的大小为．【答案】32︒/32度【分析】利用折叠性质得'45ADE A DE ∠=∠=︒，'AED A ED ∠=∠，再根据三角形外角性质得74CED ∠=︒，利用邻补角得到106AED ∠=︒，则'106A ED ∠=︒，然后利用''A EC A ED CED ∠=∠−∠进行计算即可．【详解】解：∵'90BDA ∠=︒，∴'90ADA ∠=︒，∵ABC 纸片沿DE 折叠，使点A 落在图中的A'处，∴'45ADE A DE ∠=∠=︒，'AED A ED ∠=∠，∵294574CED A ADE ∠=∠+∠=︒+︒=︒，∴106AED ∠=︒，∴'106A ED ∠=︒，∴''1067432A EC A ED CED ∠=∠−∠=︒−︒=︒．故答案为：32︒．【点睛】本题考查了折叠的性质，三角形外角的性质，三角形内角和定理等，理解题意，熟练掌握综合运用各个知识点是解题关键．七年级课时练习）如图，在ABC 中，【答案】61°【分析】先根据三角形的内角和定理和平角定义求得∠DAC+∠ACF 的度数，再根据角平分线的定义求得∠EAC+∠ECA 的度数，即可解答．【详解】解：∵∠B+∠BAC+∠BCA=180°，∠B=58°，∴∠BAC+∠BCA=180°﹣∠B=180°﹣58°=122°，∵∠BAC+∠DAC=180°，∠BCA+∠ACF=180°，∴∠DAC+∠ACF=360°﹣（∠BAC+∠BCA ）=360°﹣122°=238°，∵AE 平分∠DAC ，CE 平分∠ACF ，∴∠EAC=12∠DAC ，∠ECA=12∠ACF ，∴∠EAC+∠ECA =12（∠DAC+∠ACF ）=119°，∵∠EAC+∠ECA+∠AEC=180°，∴∠AEC=180°﹣（∠EAC+∠ECA ）=180°﹣119°=61°，故答案为：61°．【点睛】本题考查三角形的内角和定理、角平分线的定义、平角定义，熟练掌握三角形的内角和定理和角平分线的定义是解答的关键． 9．（2023春·山东泰安·七年级校考阶段练习）如图，在ABC 中，A α∠=，ABC ∠与ACD ∠的平分线交于点1A ，得1A ∠；1A BC ∠与1ACD ∠的平分线相交于点2A ，得2A ；L ；2019A BC ∠与2019A CD ∠的平分线相交于点2020A ，得2020A ∠，则2020A ∠= ．【答案】20202α【分析】结合题意，根据角平分线、三角形外角、三角形内角和的性质，得112A A ∠=∠，同理得212122A A α∠=∠=；再根据数字规律的性质分析，即可得到答案．【详解】根据题意，A α∠=，ABC ∠与ACD ∠的平分线交于点1A∴11118022A ABC ACB ACD ∠=︒−∠−∠−∠∵ACD A ABC ∠=∠+∠∴111802A ABC ACB A ∠=︒−∠−∠−∠∵180A ABC ACB ∠+∠+∠=︒∴112A A ∠=∠同理，得2121112222A A A α∠=∠=⨯∠=； 323111122222A A A α∠=∠=⨯⨯∠=；43411111222222A A A α∠=∠=⨯⨯⨯∠=；…1122n n n A A α−∠=∠= ∴202020202A α∠= 故答案为：20202α．【点睛】本题考查了三角形和数字规律的知识；解题的关键是熟练掌握三角形内角和、三角形外角、角平分线、数字规律的性质，从而完成求解．三、解答题 10．（2022秋·八年级课时练习）如图，ABC ∆中，(1)若ABC ∠、ACB ∠的三等分线交于点1O 、2O ，请用A ∠表示1BO C ∠、2BO C ∠；(2)若ABC ∠、ACB ∠的n 等分线交于点1O 、21n O O −⋅⋅⋅⋅⋅⋅（1O 、21n O O −⋅⋅⋅⋅⋅⋅依次从下到上），请用A ∠表示1BO C ∠，1n BO C −∠．【答案】(1)111203BO C A ∠=︒+∠，22603BO C A ∠=︒+∠，(2)()118011n BO C A n n ︒−∠=+∠，11801n n BO C A n n −︒−∠=+∠【分析】（1）根据三角形的内角和定理可得180ABC ACB A ∠+∠=︒−∠，再由ABC ∠、ACB ∠的三等分线交于点1O 、2O ，可得111(180),3O BC O CB A ∠+∠=︒−∠222(180),3O BC O CB A ∠+∠=︒−∠再根据三角形的内角和定理，即可求解；（2）根据三角形的内角和定理可得180ABC ACB A ∠+∠=︒−∠，再由ABC ∠、ACB ∠的n 等分线交于点1O 、21n O O −⋅⋅⋅⋅⋅⋅，可得111(180),O BC O CB A n ∠+∠=︒−∠111(180),n n n O BC O CB A n −−−∠+∠=︒−∠再根据三角形的内角和定理，即可求解．【详解】（1）解：∵180A ABC ACB ∠+∠+∠=︒，∴180ABC ACB A ∠+∠=︒−∠，∵ABC ∠、ACB ∠的三等分线交于点1O 、2O ，∴111(180),3O BC O CB A ∠+∠=︒−∠222(180),3O BC O CB A ∠+∠=︒−∠ ∴11111180()180(180)12033BO C O BC O CB A A ∠=︒−∠+∠=︒−︒−∠=︒+∠，22222180()180(180)6033BO C O BC O CB A A ∠=︒−∠+∠=︒−︒−∠=︒+∠；（2）解：∵180A ABC ACB ∠+∠+∠=︒，∴180ABC ACB A ∠+∠=︒−∠，∵ABC ∠、ACB ∠的n 等分线交于点1O 、21n O O −⋅⋅⋅⋅⋅⋅， ∴111(180),O BC O CB A n ∠+∠=︒−∠111(180),n n n O BC O CB A n −−−∠+∠=︒−∠∴()()111180111180180(180)n BO C O BC O CB A A n n n ︒−∠=︒−∠+∠=︒−︒−∠=+∠，()11111801180180(180)n n n n n BO C O BC O CB A A n n n −−−−︒−∠=︒−∠+∠=︒−︒−∠=+∠．【点睛】本题主要考查了有关角平分线三角形的内角和问题，熟练掌握三角形的内角和定理，并利用类比思想解答是解题的关键．）如图所示，在ABC 中，）如图所示，ABC 的外角平分线）如图所示，ABC 的内角平分线【答案】（1）见解析；（2）见解析；（3）见解析【详解】（1）设,ABO OBC x ACO BCO y ∠=∠=∠=∠=．由ABC 的内角和为180︒，得22180A x y ︒∠++=．①由BOC 的内角和为180︒，得180BOC x y ∠++=︒．②由②得180x y BOC +=−∠︒．③把③代入①，得()2180180A BOC ∠+−∠=︒︒，即2180BOC A ∠=︒+∠，即1902BOC A ∠=+∠︒（2）∵BD 、CD 为△ABC 两外角∠ABC 、∠ACB 的平分线，∴()()1122BCD A ABC DBC A ACB ∠=∠+∠∠=∠+∠、，由三角形内角和定理得，180BDC BCD DBC ∠=︒−∠−∠，=180°-12[∠A+（∠A+∠ABC+∠ACB ）]， =180°-12（∠A+180°）， =90°-12∠A ；（3）如图：∵BD 为△ABC 的角平分线，交AC 与点E ，CD 为△ABC 外角∠ACE 的平分线，两角平分线交于点D∴∠1=∠2，∠5=12（∠A+2∠1），∠3=∠4，在△ABE 中，∠A=180°-∠1-∠3∴∠1+∠3=180°-∠A①在△CDE 中，∠D=180°-∠4-∠5=180°-∠3-12（∠A+2∠1），即2∠D=360°-2∠3-∠A-2∠1=360°-2（∠1+∠3）-∠A②，把①代入②得∠D=12∠A ．【点睛】此题考查的是三角形内角与外角的关系，角平分线的性质，三角形内角和定理，属中学常规题． 12．（2023春·全国·七年级专题练习）如图，在△ABC 中，∠ABC 和∠ACB 的平分线相交于点P ．（1）若∠ABC +∠ACB ＝130°，求∠BPC 的度数．（2）当∠A 为多少度时，∠BPC ＝3∠A ？【答案】（1）115︒；（2）36A ∠=︒【分析】（1）根据角平分线的定义，求得PBC ∠，PCB ∠，再根据三角形内角和定理即可求得BPC ∠；（2）根据（1）的方法求得BPC ∠，再结合条件∠BPC ＝3∠A ，解方程即可求得∠A ．【详解】（1）PB 平分ABC ∠，PC 平分ACB ∠，11,22PBC ABC PCB ACB ∴∠=∠∠=∠，∠ABC+∠ACB ＝130°，1()652PBC PCB ABC ACB ∴∠+∠=∠+∠=︒，180()18065115BPC PBC PCB ∴∠=︒−∠+∠=︒−︒=︒，（2）PB 平分ABC ∠，PC 平分ACB ∠，11,22PBC ABC PCB ACB ∴∠=∠∠=∠，1()2PBC PCB ABC ACB ∴∠+∠=∠+∠，180ABC ACB A ∠+∠=︒−∠，1902PBC PCB A ∴∠+∠=︒−∠，180()BPC PBC PCB Ð=°-Ð+Ð1180(90)2A =︒−︒−∠1902A =+∠︒∠BPC ＝3∠A13902A A ∴∠=︒+∠，36A ∴∠=︒．【点睛】本题考查了与角平分线有关的角度计算，三角形内角和定理，掌握三角形内角和定理是解题的关键． 13．（2023·全国·八年级假期作业）如图所示，已知四边形ABDC ，求证BDC A B C ∠=∠+∠+∠．【答案】见解析【分析】方法1连接BC ，根据三角形内角和定理可得结果；方法2 作射线AD ，根据三角形的外角性质得到31B ∠=∠+∠，42C ∠=∠+∠，两式相加即可得到结论；方法3延长BD ，交AC 于点E ，两次运用三角形外角的性质即可得出结论．【详解】方法1如图所示，连接BC.在ABC 中，180A ABC ACB ∠+∠+∠=，即12180A ABD ACD ∠+∠+∠+∠+∠=.在BCD △中，12180BDC ∠+∠+∠=，++∴∠=∠∠∠；BDC A ABD ACD方法2如图所示，连接AD并延长.∠是ABD△的外角，3∴∠=∠∠.31+ABD∠=∠+∠.同理，42ACD∴∠+∠=∠+∠+∠+∠.3412ABD ACD∠=∠+∠+∠.即BDC A ABD ACD方法3如图所示，延长BD，交AC于点E.∠是ABE的外角，DEC∴∠=∠+∠.DEC A ABDBDC∠是DEC的外角，∴∠=∠+∠.BDC DEC ACDBDC A ABD ACD∴∠=∠+∠+∠.【点睛】本题考查了三角形的外角性质：解题的关键是知道三角形的任一外角等于与之不相邻的两内角的和．也考查了三角形内角和定理．14．（2023春·江苏·七年级专题练习）探究与发现：如图1所示的图形，像我们常见的学习用品——圆规．我们不妨把这样图形叫做“规形图”，那么在这一个简单的图形中，到底隐藏了哪些数学知识呢？下面就请你发挥你的聪明才智，解决以下问题：(1)观察“规形图”，试探究BDC ∠与A ∠、B ∠、C ∠之间的关系，并说明理由；(2)请你直接利用以上结论，解决以下三个问题：①如图2，把一块三角尺XYZ 放置在ABC 上，使三角尺的两条直角边XY 、XZ 恰好经过点B 、C ，若50A ∠=︒，则ABX ACX ∠+∠=_____°；②如图3，DC 平分ADB ∠，EC 平分AEB ∠，若50DAE ∠=︒，130DBE ∠=︒，则DCE ∠=______°； ③如图4，ABD ∠，ACD ∠的10等分线相交于点1G ，2G ，…，9G ，若140BDC ∠=︒，177BG C ∠=︒，求A ∠的度数．【答案】(1)=++BDC BAC B C ∠∠∠∠(2)①40，②90，③70°【分析】（1）根据题意观察图形连接AD 并延长至点F ，根据一个三角形的外角等于与它不相邻的两个内角的和即可证明；（2）①由（1）的结论可得ABX ACX A BXC ∠+∠+∠=∠，然后把50A ∠=︒，90BXC ∠=︒代入上式即可得到ABX ACX ∠+∠的值；②结合图形可得DBE DAE ADB AEB ∠=∠+∠+∠，代入50DAE ∠=︒，130DBE ∠=︒即可得到ADB AEB ∠+∠的值，再利用上面得出的结论可知()12DCE ADB AEB A ∠=∠+∠+∠，易得答案．③由②方法，进而可得答案．【详解】（1）=++BDC BAC B C ∠∠∠∠，理由如下：连接AD 并延长至点F ，由外角定理可得BDF BAD B ∠=∠+∠，CDF C CAD ∠=∠+∠，∵BDC BDF CDF ∠=∠+∠，∴BDC BAD B C CAD ∠=∠+∠+∠+∠，∵BAC BAD CAD ∠=∠+∠，∴=++BDC BAC B C ∠∠∠∠；（2）①由（1）的结论易得：ABX ACX A BXC ∠+∠+∠=∠，∵50A ∠=︒，90BXC ∠=︒，∴905040ABX ACX ∠+∠=︒−︒=︒，故答案是：40；②由（1）的结论易得=++DBE DAE ADB AEB ∠∠∠∠，DCE ADC AEC A ∠=∠∠∠＋＋，∵50DAE ∠=︒，130DBE ∠=︒，∴80ADB AEB ∠+∠=︒；∵DC 平分ADB ∠，EC 平分AEB ∠， ∴12ADC ADB ∠=∠，12AEC AEB ∠=∠， ∴()14050902DCE ADB AEB A ∠=∠+∠+∠=︒+︒=︒；③由②知，()1110BG C ABD ACD A ∠=∠+∠+∠， ∵177BG C ∠=︒，∴设A ∠为x ︒，∵140ABD ACD x ∠+∠=︒−︒， ∴()11407710x x −=+，∴70x =，∴A ∠为70°．故答案是：70°．【点睛】本题考查三角形外角的性质，三角形的内角和定理的应用，能求出BDC A B C ∠=∠+∠+∠是解答的关键，注意：三角形的内角和等于180°，三角形的一个外角等于和它不相邻的两个内角的和． 15．（2023·全国·八年级假期作业）如图，BP 平分ABC ∠，交CD 于点F ，DP 平分ADC ∠交AB 于点E ，AB 与CD 相交于点G ，42A ∠=︒．（1）若60ADC ∠=︒，求AEP ∠的度数；（2）若38C ∠=︒，求P ∠的度数．【答案】（1）72︒；（2）40︒．【分析】（1）根据角平分线的定义可得∠ADP=12ADC ∠ ，然后利用三角形外角的性质即可得解；（2）根据角平分线的定义可得∠ADP=∠PDF ，∠CBP=∠PBA ，再根据三角形的内角和定理可得∠A+∠ADP=∠P+∠ABP ，∠C+∠CBP=∠P+∠PDF ，所以∠A+∠C=2∠P ，即可得解．【详解】解：（1）∵DP 平分∠ADC ∴∠ADP=∠PDF=12ADC ∠，∵60ADC ∠=︒，∴30ADP ∠=︒，∴304272AEP ADP A ∠=∠+∠=︒+︒=︒；（2）∵BP 平分∠ABC ，DP 平分∠ADC ，∴∠ADP=∠PDF ，∠CBP=∠PBA ，∵∠A+∠ADP=∠P+∠ABP ，∠C+∠CBP=∠P+∠PDF ，∴∠A+∠C=2∠P ，∵∠A=42°，∠C=38°，∴∠P=12（38°+42°）=40°．【点睛】本题考查了三角形的内角和定理及三角形外角的性质，角平分线的定义，熟记定理并理解“8字形”的等式是解题的关键．16．（2023春·河北石家庄·七年级统考期末）如图①，在△ABC中，∠ABC与∠ACB的平分线相交于点P．(1)如果∠A＝70°，求∠BPC的度数；(2)如图②，作△ABC外角∠MBC，∠NCB的角平分线交于点Q，试探索∠Q，∠A之间的数量关系．(3)如图③，延长线段BP，QC交于点E，在△BQE中，存在一个内角等于另一个内角的3倍，求∠A的度数．【答案】(1)125︒(2)1902Q A ∠=︒−∠(3)∠A的度数是45︒或60︒或120︒或135︒【分析】（1）在△ABC中，根据三角形内角和定理求出∠ABC+∠ACB=110°，根据角平分线的定义得出∠PBC＝1 2∠ABC，∠PCB＝12∠ACB，求出∠PBC+∠PCB=55°，再在△BPC中，根据三角形内角和定理求出即可；（2）根据三角形外角性质得出∠MBC＝∠ACB+∠A，∠NCB＝∠ABC+∠A，求出∠MBC+∠NCB＝∠ACB+∠A+∠ABC+∠A＝180°+∠A，根据角平分线的定义得出QBC＝12∠MBC，∠QCB＝12∠NCB，求出∠QBC+∠QCB＝90°+12∠A，根据三角形内角和定理求出即可；（3）根据角平分线的定义得出∠ACF＝2∠BCF，∠ABC＝2∠EBC，根据三角形外角性质得出∠ECF＝∠EBC+∠E，求出∠A＝2∠E，求出∠EBQ=90°，分为四种情况：①∠EBQ＝3∠E＝90°，②∠EBQ＝3∠Q，③∠Q＝3∠E，④∠E ＝3∠Q，再求出答案即可【详解】（1）∵∠A＝70°，∴∠ABC+∠ACB＝180°﹣∠A＝110°，∵点P是∠ABC和∠ACB的角平分线的交点，∴∠PBC＝12∠ABC，∠PCB＝12∠ACB，∴∠PBC+∠PCB＝55°，∴∠BPC＝180°﹣（∠PBC+∠PCB）＝125°；（2）∵∠MBC＝∠ACB+∠A，∠NCB＝∠ABC+∠A，∴∠MBC+∠NCB＝∠ACB+∠A+∠ABC+∠A＝180°+∠A，∵点Q是∠MBC和∠NCB的角平分线的交点，∴∠QBC＝12∠MBC，∠QCB＝12∠NCB，∴∠QBC+∠QCB＝12（∠MBC+∠NCB）＝12（180°+∠A）＝90°+12∠A，∴∠Q＝180°﹣（∠QBC+∠QCB）＝180°﹣（90°+12∠A）＝90°﹣12∠A；（3）∵CQ为△ABC的外角∠NCB的角平分线，∴CE是△ABC的外角∠ACF的平分线，∴∠ACF＝2∠BCF，∵BE平分∠ABC，∴∠ABC＝2∠EBC，∵∠ECF＝∠EBC+∠E，∴2∠ECF＝2∠EBC+2∠E，即∠ACF＝∠BC+2∠E，∵∠ACF＝∠ABC+∠A，∴∠A＝2∠E，即∠E＝12∠A，∵∠EBQ＝∠EBC+∠CBQ＝12∠ABC+12∠MBC＝12（∠ABC+∠A+∠ACB）＝90°，如果△BQE中，存在一个内角等于另一个内角的3倍，那么分为四种情况：①∠EBQ＝3∠E＝90°，则∠E＝30°，∠A＝2∠E＝60°；②∠EBQ＝3∠Q，则∠Q＝30°，∠E＝60°，∠A＝2∠E＝120°；③∠Q＝3∠E，则∠E＝22.5°，∠A＝2∠E＝45°；④∠E＝3∠Q，则∠E＝67.5°，∠A＝2∠E＝135°，综合上述，∠A的度数是45°或60°或120°或135°．【点睛】本题考查了三角形的外角性质，三角形内角和定理，角平分线的定义等知识点，熟练掌握知识点及运用分类讨论思想是解题的关键．17．（2022秋·江西赣州·八年级校联考期中）如图，在△ABC中，(1)如果AB=4cm，AC=3cm，BC是能被3整除的的偶数，求这个三角形的周长．(2)如果BP、CP分别是∠ABC和∠ACB的角平分线．a、当∠A=45°时，求∠BPC的度数．b、当∠A=x°时，求∠BPC的度数．【答案】(1)13cm(2)a、112.5°；b、90°＋12x°【分析】（1）利用三角形的三边关系：两边之和大于第三边，两之差小于第三边，得出BC的取值范围为1＜BC＜7，再根据BC是能被3整除的偶数，得到BC=6 cm，再求出周长为13 cm．（2）利用三角形的内角和等于180°，先求出∠ABC+∠ACB，再利用角平分线平分角的知识，求出∠PBC+∠PCB，然后再一次用三角形内角和等于180°，求出∠BPC．【详解】（1）∵AB=4 cm，AC=3 cm∴1＜BC＜7∴BC=6 cm∴三角形的周长为：C△ABC=AB+AC+BC=4+3+6=13cm（2）a、当∠A=45°时，由三角形的内角和可知：∠ABC+∠ACB=180°−∠A=180°−45°=135°∵BP、CP分别是∠ABC和∠ACB的角平分线∴∠PBC=12∠ABC，∠PCB=12∠ACB∴∠PBC+∠PCB=12∠ABC+12∠ACB=12(∠ABC+∠ACB)=12×135°=67.5°∴∠BPC=180°− (∠PBC+∠PCB)=180°−67.5°=112.5°b、当∠A=x°时，由三角形的内角和可知：∠ABC+∠ACB=180°−∠A=180°− x°∵BP、CP分别是∠ABC和∠ACB的角平分线∴∠PBC=12∠ABC，∠PCB=12∠ACB∴∠PBC+∠PCB=12∠ABC+12∠ACB=12(∠ABC+∠ACB)=12×(180°− x°)=90°−12x°∴∠BPC=180°− (∠PBC+∠PCB)=180°−(90°−12x°)=90°＋12x°【点睛】本题考查有关三角形的知识．第一小问的解题关键是运用三角形的三边关系：两边之和大于第三边，两之差小于第三边进行解答；第二小问的解题关键是运用三角形的内角和等于180°，以及角平分线平分角的知识结合一起解答，在求角度时，有时不一定需要每个角都求出来，可以利用整体思想．【答案】（1）见解析；（2）26°；（3）()1902P B D ∠=︒+∠+∠；（4）()11802P B D ∠=︒−∠+∠【分析】（1）根据三角形的内角和等于180°和对顶角的性质即可得证；（2）设BAP PAD x ∠=∠=，BCP PCD y ∠=∠=，x ABC y P x P y ADC +∠=+∠⎧⎨+∠=+∠⎩解方程即可得到答案；（3）根据直线AP 平分BAD ∠，CP 平分BCD ∠的外角BCE ∠，得到1=2PAB PAD BAD ∠=∠∠，1=2PCB PCE PCD ∠=∠∠从而可以得到180°()2PAB PCB D B −∠+∠+∠=∠，再根据∠P+∠PAD=∠PCD+∠D ，∠BAD+∠B=∠BCD+∠D 得到=P B PAD PCB PAB PCB ∠−+=∠+∠∠∠∠即可求解；（4）连接PB ，PD 根据APB PBA PAB +∠+∠=∠ 180°，PCB PBC BPC +∠+∠=∠ 180°得到APC ABC PCB PAB ∠+∠+∠+=∠ 360°，同理得到：APC ADC PCD PAD ∠+∠+∠+=∠ 360°，再根据=PCE PCD ∠+∠180°，=PAB PAF +∠∠180°，FAP PAO ∠=∠，PCE PCB ∠=∠，即可求解.【详解】解：（1）A B AOB ∠+∠+∠=180°，C D COD ∠+∠+∠=180°，A B AOB C D COD ∴∠+∠+∠=∠+∠+∠．AOB COD ∠=∠，A B C D ∴∠+∠=∠+∠；（2）AP ，CP 分别平分BAD ∠，BCD ∠，设BAP PAD x ∠=∠=，BCP PCD y ∠=∠=，则有x ABC y P x P y ADC +∠=+∠⎧⎨+∠=+∠⎩，ABC P P ADC ∴∠−∠=∠−∠，()1122P ABC ADC ∴∠=∠+∠=（36°+16°）=26°（3）直线AP 平分BAD ∠，CP 平分BCD ∠的外角BCE ∠，1=2PAB PAD BAD ∴∠=∠∠，1=2PCB PCE BCE ∠=∠∠，∴2PAB B ∠+∠=180°-2PCB D ∠+∠，∴180°()2PAB PCB D B −∠+∠+∠=∠∵∠P+∠PAD=∠PCD+∠D ，∠BAD+∠B=∠BCD+∠D∴=P PAD BAD B PCD BCD ∠+−−−∠∠∠∠∠,P PAB B PCB ∴∠−∠−∠=∠∴P B PAB PCB ∠−=∠+∠∠∴180°()2P B D B−∠−∠+∠=∠，即P ∠=90°()12B D +∠+∠．（4）连接PB ，PD直线AP 平分BAD ∠的外角FAD ∠，CP 平分BCD ∠的外角BCE ∠， FAP PAO ∴∠=∠，PCE PCB ∠=∠，∵APB PBA PAB +∠+∠=∠180°，PCB PBC BPC +∠+∠=∠180° ∴APC ABC PCB PAB ∠+∠+∠+=∠360°同理得到：APC ADC PCD PAD ∠+∠+∠+=∠360°∴2APC ABC ADC PCB PAB PCD PAD ∠+∠+∠+∠++∠+=∠∠720°∴2APC ABC ADC PCE PAB PCD PAF ∠+∠+∠+∠++∠+=∠∠720°∵=PCE PCD ∠+∠180°，=PAB PAF +∠∠180°∴2APC ABC ADC ∠+∠+∠=360°，APC ∴∠=180°-()12ABC ADC ∠+∠【点睛】本题主要考查了角平分线的定义，三角形内角和定理，解题的关键在于能够熟练掌握相关知识进行求解.。

浙教版八年级数学上册全等三角形之手拉手模型、倍长中线-截长补短法

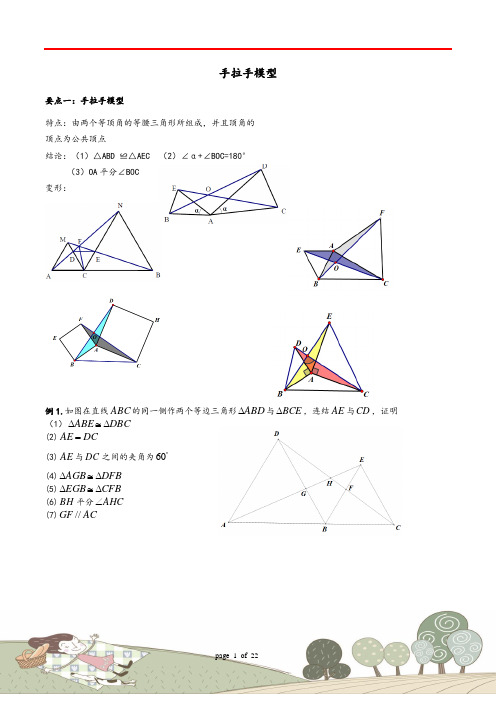
手拉手模型要点一：手拉手模型特点：由两个等顶角的等腰三角形所组成，并且顶角的顶点为公共顶点结论：（1）△ABD ≌△AEC （2）∠α+∠BOC=180° （3）OA 平分∠BOC 变形：例1.如图在直线ABC 的同一侧作两个等边三角形ABD ∆与BCE ∆，连结AE 与CD ，证明（1）DBC ABE ∆≅∆ (2)DC AE =(3)AE 与DC 之间的夹角为︒60 (4)DFB AGB ∆≅∆ (5)CFB EGB ∆≅∆ (6)BH 平分AHC ∠ (7)AC GF //变式精练1：如图两个等边三角形ABD ∆与BCE ∆，连结AE 与CD ，证明（1）DBC ABE ∆≅∆ （2）DC AE =（3）AE 与DC 之间的夹角为︒60（4）AE 与DC 的交点设为H ,BH 平分AHC ∠变式精练2：如图两个等边三角形ABD ∆与BCE ∆，连结AE 与CD ，证明（1）DBC ABE ∆≅∆ (2）DC AE =(3）AE 与DC 之间的夹角为︒60(4）AE 与DC 的交点设为H ,BH 平分AHC ∠例2：如图，两个正方形ABCD 与DEFG ,连结CE AG ,,二者相交于点H 问：（1）CDE ADG ∆≅∆是否成立？（2）AG 是否与CE 相等？（3）AG 与CE 之间的夹角为多少度？（4）HD 是否平分AHE ∠？例3：如图两个等腰直角三角形ADC 与EDG ，连结CE AG ,,二者相交于点H 问：（1）CDE ADG ∆≅∆是否成立？（2）AG 是否与CE 相等？（3）AG 与CE 之间的夹角为多少度？（4）HD 是否平分AHE ∠？例4：两个等腰三角形ABD ∆与BCE ∆，其中BD AB =,,EB CB =α=∠=∠CBE ABD ,连结AE 与CD ，问：（1）DBC ABE ∆≅∆是否成立？（2）AE 是否与CD 相等？（3）AE 与CD 之间的夹角为多少度？（4）HB 是否平分AHC ∠？例5：如图，点A. B. C 在同一条直线上，分别以AB 、BC 为边在直线AC 的同侧作等边三角形△ABD 、△BCE.连接AE 、DC ，AE 与DC 所在直线相交于F ，连接FB.判断线段FB 、FE 与FC 之间的数量关系，并证明你的结论。

浙教版数学八年级上册第一章三角形的初步认识《全等三角形经典模型总结》(无答案)

全等三角形相关模型总结一、角平分线模型(一）角平分线的性质模型辅助线：过点G作GE⊥射线ACA、例题1、如图，在△ABC中，∠C=90°，AD平分∠CAB，BC=6cm，BD=4cm，那么点D到直线AB 的距离是cm.2、如图，已知，∠1＝∠2，∠3＝∠4，求证：AP平分∠BAC.B、模型巩固1、如图，在四边形ABCD中，BC＞AB，AD＝CD，BD平分∠ABC，求证：∠A＋∠C＝180°.（二）角平分线＋垂线，等腰三角形必呈现A、例题辅助线：延长ED交射线OB于F 辅助线：过点E作EF∥射线OB 例1、如图，在△ABC中，∠ABC＝3∠C，AD是∠BAC的平分线，BE⊥AD于F .求证：1()2BE AC AB=-.例2、如图，在△ABC中，∠BAC的角平分线AD交BC于点D，且AB＝AD，作CM⊥AD交AD的延长线于M. 求证：1()2AM AB AC=+.（三）角分线，分两边，对称全等要记全两个图形飞辅助线都是在射线ON上取点B，使OB＝OA，从而使△OAC≌△OBC .A、例题1、如图，在△ABC中，∠BAC=60°，∠C=40°，AP平分∠BAC交BC于P，BQ平分∠ABC 交AC于Q，求证：AB＋BP＝BQ＋AQ .2、如图，在△ABC中，AD是∠BAC的外角平分线，P是AD上异于点A的任意一点，试比较PB＋PC与AB＋AC的大小，并说明理由.B、模型巩固1、在△ABC中，AB＞AC，AD是∠BAC的平分线，P是线段AD上任意一点（不与A重合）. 求证：AB－AC＞PB－PC .2、如图，△ABC中，AB＝AC，∠A＝100°，∠B的平分线交AC于D，求证：AD＋BD＝BC .3、如图，△ABC中，BC＝AC，∠C＝90°，∠A的平分线交BC于D，求证：AC＋CD＝AB .。

全等三角形中的常见压轴题五种模型全攻略—2023-2024学年八年级数学上册(浙教版)(解析版)

全等模型专题：全等三角形中的常见压轴题五种模型全攻略【考点导航】目录【典型例题】 (1)【解题模型一四边形中构造全等三角形解题】 ........................................................................................ 1 【解题模型二一线三等角模型】 ............................................................................................................... 8 【解题模型三三垂直模型】..................................................................................................................... 15 【解题模型四倍长中线模型】 ................................................................................................................. 22 【解题模型五旋转模型】 (28)【典型例题】【解题模型一四边形中构造全等三角形解题】例题：（2023春·广东梅州·八年级校联考开学考试）已知如图，四边形ABCD 中，AB BC =，AD CD =，求证：A C ∠=∠．【答案】见解析【分析】连接BD ，已知两边对应相等，加之一个公共边BD ，则可利用SSS 判定ABD CBD ≌△△，根据全等三角形的对应角相等即可证得．【详解】证明：连接BD ，AB CB =，BD BD =，AD CD =，SSS ABD CBD ∴≌（）． A C ∴∠=∠．【点睛】此题主要考查学生对全等三角形的判定方法的理解及运用，常用的判定方法有SSS ，SAS ，ASA ，HL 等．【变式训练】【答案】他的发现正确，理由见解析【分析】根据全等三角形的判定和性质直接证明即可．【详解】解：他的发现正确，理由如下：在ABD △与ACD 中，AB AC BD CD AD AD =⎧⎪=⎨⎪=⎩，∴ABD ACD △≌△，∴BAD CAD ∠=∠，ADB ADC ∠=∠，∴AD 不仅平分BAC ∠，且平分BDC ∠．【点睛】题目主要考查全等三角形的判定和性质，熟练掌握全等三角形的判定和性质是解题关键． 2．（2023秋·湖南常德·八年级统考期末）中国现役的第五代隐形战斗机歼−20的机翼如图，为适应空气动力的要求，两个翼角,A B ∠∠必须相等．(1)实际制造中，工作人员只需用刻度尺测量PA PB =，CA CB =就能满足要求，说明理由； (2)若30,40A P ∠=︒∠=︒，求ACB ∠的度数．【答案】(1)见解析 (2)100°【分析】（1）连接PC ，证明APC BPC ≌△△，即可解答．（2）由三角形的外角的性质即可解答．【详解】（1）证明：如图，连接PC ，在APC △和BPC △中，PA PB CA CB PC PC =⎧⎪=⎨⎪=⎩，∴APC BPC ≌△△（SSS ）, ∴A B ∠=∠．（2）∵APC BPC ≌△△，30,40A P ∠=︒∠=︒， ∴30A B ==︒∠∠，∵C C A B A E C B E =+∠∠∠，,,ACE APC A BCE BPC B ∠=∠+∠∠=∠+∠ ∴23040100ACB APC A BPC B A BPA B ∠=∠+∠+∠+∠=∠+∠+∠=⨯︒+︒=︒．【点睛】本题考查了三角形全等和外角的性质，掌握三角形全等是解题的关键．3.如图，在四边形ABCD 中，CB AB ⊥于点B ，CD AD ⊥于点D ，点E ，F 分别在AB ，AD 上，AE AF =，CE CF =．(1)若8AE =，6CD =，求四边形AECF 的面积；(2)猜想∠DAB ，∠ECF ，∠DFC 三者之间的数量关系，并证明你的猜想．【答案】(1)48(2)∠DAB ＋∠ECF ＝2∠DFC ，证明见解析【解析】【分析】（1）连接AC ，证明△ACE ≌△ACF ，则S △ACE ＝S △ACF ，根据三角形面积公式求得S △ACF 与S △ACE ，根据S 四边形AECF ＝S △ACF ＋S △ACE 求解即可；（2）由△ACE ≌△ACF 可得∠FCA ＝，∠FAC ＝∠EAC ，∠AFC ＝∠AEC ，根据垂直关系，以及三角形的外角性质可得∠DFC ＋∠BEC ＝∠FCA ＋∠FAC ＋∠ECA ＋∠EAC ＝∠DAB ＋∠ECF ．可得∠DAB ＋∠ECF ＝2∠DFC (1)解：连接AC ，如图，在△ACE 和△ACF 中AE AFCE CF AC AC =⎧⎪=⎨⎪=⎩∴△ACE ≌△ACF （SSS ）．∴S △ACE ＝S △ACF ，∠FAC ＝∠EAC ．∵CB⊥AB，CD⊥AD，∴CD＝CB＝6．∴S△ACF＝S△ACE＝12AE·CB＝12×8×6＝24．∴S四边形AECF＝S△ACF＋S△ACE＝24＋24＝48．(2)∠DAB＋∠ECF＝2∠DFC证明：∵△ACE ≌△ACF，∴∠FCA＝∠ECA，∠FAC＝∠EAC，∠AFC＝∠AEC．∵∠DFC与∠AFC互补，∠BEC与∠AEC互补，∴∠DFC＝∠BEC．∵∠DFC＝∠FCA＋∠FAC，∠BEC＝∠ECA＋∠EAC，∴∠DFC＋∠BEC＝∠FCA＋∠FAC＋∠ECA＋∠EAC＝∠DAB＋∠ECF．∴∠DAB＋∠ECF＝2∠DFC【点睛】本题考查了三角形全等的性质与判定，三角形的外角的性质，掌握三角形全等的性质与判定是解题的关键．4．在四边形ABDC中，AC=AB，DC=DB，∠CAB=60°，∠CDB=120°，E是AC上一点，F是AB延长线上一点，且CE=BF．(1)试说明：DE=DF：(2)在图中，若G在AB上且∠EDG=60°，试猜想CE，EG，BG之间的数量关系并证明所归纳结论．(3)若题中条件“∠CAB=60°，∠CDB=120°改为∠CAB=α，∠CDB=180°﹣α，G在AB上，∠EDG满足什么条件时，（2）中结论仍然成立？【答案】(1)见解析；(2)CE+BG=EG，理由见解析；(3)当∠EDG=90°-12α时，（2）中结论仍然成立．【解析】【分析】（1）首先判断出C DBF ∠=∠，然后根据全等三角形判定的方法，判断出ΔΔCDE BDF ≅，即可判断出DE DF =．（2）猜想CE 、EG 、BG 之间的数量关系为：CE BG EG +=．首先根据全等三角形判定的方法，判断出ABD ACD∆≅∆，即可判断出60BDA CDA ∠=∠=︒；然后根据60EDG ∠=︒，可得CDE ADG ∠=∠，ADE BDG ∠=∠，再根据CDE BDF ∠=∠，判断出EDG FDG ∠=∠，据此推得ΔΔDEG DFG ≅，所以EG FG =，最后根据CE BF =，判断出CE BG EG +=即可．（3）根据（2）的证明过程，要使CE BG EG +=仍然成立，则12EDG BDA CDA CDB ∠=∠=∠=∠，即11(180)9022EDG αα∠=︒−=︒−，据此解答即可．(1)证明：360CAB C CDB ABD ∠+∠+∠+∠=︒，60CAB ∠=︒，120CDB ∠=︒，36060120180C ABD ∴∠+∠=︒−︒−︒=︒，又180DBF ABD ∠+∠=︒，C DBF ∴∠=∠，在CDE ∆和BDF ∆中，CD BDC DBF CE BF =⎧⎪∠=∠⎨⎪=⎩ΔΔ()CDE BDF SAS ∴≅，DE DF ∴=．(2)解：如图，连接AD ，猜想CE 、EG 、BG 之间的数量关系为：CE BG EG +=．证明：在ABD ∆和ACD ∆中，AB AC BD CD AD AD =⎧⎪=⎨⎪=⎩，ΔΔ()ABD ACD SSS ∴≅，111206022BDA CDA CDB ∴∠=∠=∠=⨯︒=︒，又60EDG ∠=︒，CDE ADG ∴∠=∠，ADE BDG ∠=∠，由（1），可得ΔΔCDE BDF ≅，CDE BDF ∴∠=∠，60BDG BDF ∴∠+∠=︒，即60FDG ∠=︒，EDG FDG ∴∠=∠，在DEG ∆和DFG ∆中，DE DF EDG FDG DG DG =⎧⎪∠=∠⎨⎪=⎩ΔΔ()DEG DFG SAS ∴≅， EG FG ∴=，又CE BF =，FG BF BG =+，CE BG EG ∴+=；(3)解：要使CE BG EG +=仍然成立，则12EDG BDA CDA CDB ∠=∠=∠=∠，即11(180)9022EDG αα∠=︒−=︒−，∴当1902EDG α∠=︒−时，CE BG EG +=仍然成立．【点睛】本题综合考查了全等三角形的性质和判定，此题是一道综合性比较强的题目，有一定的难度，能根据题意推出规律是解此题的关键．【解题模型二一线三等角模型】例题：（2023春·七年级课时练习）【探究】如图①，点B 、C 在MAN ∠的边AM AN 、上，点E 、F 在MAN ∠内部的射线AD 上，12∠∠、分别是ABE 、CAF V 的外角．若AB AC =，12BAC ∠=∠=∠，求证：ABE CAF V V ≌．【应用】如图②，在等腰三角形ABC 中，AB AC =，AB BC >，点D 在边BC 上，2CD BD =，点E 、F 在线段AD 上，12BAC ∠=∠=∠，若ABC 的面积为9，则ABE 与CDF 的面积之和为．【答案】探究：见解析；应用：6【分析】探究：根据A BAE ABE ∠=∠∠，BAC CAF BAE ∠=∠+∠，得出ABE CAF ∠=∠，根据12∠=∠，得出AEB CFA ∠=∠，再根据AAS 证明即可；应用：根据全等三角形的性质得出：ABECAFSS=，进而得出CDFCAFACDSSS+=，根据2CD BD =，ABC的面积为9，得出263ACDABCSS ==，即可得出答案．【详解】探究证明：∵A BAE ABE ∠=∠+∠，BAC CAF BAE ∠=∠+∠，又∵1BAC ∠=∠， ∴ABE CAF ∠=∠， ∵12∠=∠， ∴AEB CFA ∠=∠，在ABE 和CAF V 中，AEB CFA ABE CAF AB AC ∠=∠⎧⎪∠=∠⎨⎪=⎩∴()AAS ABE CAF △≌△；应用解：∵ABE CAF V V ≌， ∴ABECAFS S=，∴CDFCAFACDSSS+=，∵2CD BD =，ABC 的面积为9， ∴263ACDABCSS ==，∴ABE 与CDF 的面积之和为6，故答案为：6．【点睛】本题考查全等三角形的判定与性质，掌握全等三角形的判定是解题的关键．【变式训练】≌ABF CAD ；，在ABC 中，．若ABC 的面积为与CDE 的面积之比．【答案】（1）证明见详解；（2）成立，证明见详解；（3）1:4【分析】（1）根据90BAC BFE CDE ∠=∠=∠=︒即可得到90BAF CAF ∠+∠=︒，90DCA CAF ∠+∠=︒，从而得到BAF DCA ∠=∠，即可得到证明；（2）根据BAC BFE CDE ∠=∠=∠得到BAF CAF DCA CAF ∠+∠=∠+∠，即可得到BAF DCA ∠=∠，即可得到证明；（3）根据ABC 的面积为15，2CE BE =，即可得到5ABE S =△，10AEC S =，结合2DE AD =可得103ADC S =△，203EDC S =，根据AB AC =，BAC BFE CDE ∠=∠=∠得到≌ABF CAD ，即可得到BEF S ，即可得到答案；【详解】（1）证明：∵90BAC BFE CDE ∠=∠=∠=︒，∴90BFA CDA ∠=∠=︒，90BAF CAF ∠+∠=︒，90DCA CAF ∠+∠=︒， ∴BAF DCA ∠=∠，在ABF △与CAD 中，∵BFA CDA BAF DCA AB AC ∠=∠⎧⎪∠=∠⎨⎪=⎩，∴(AAS)ABF CAD ≌；（2）解：成立，理由如下， ∵BAC BFE CDE ∠=∠=∠，∴BAF CAF DCA CAF ∠+∠=∠+∠，BFA CDA ∠=∠， ∴BAF DCA ∠=∠，在ABF △与CAD 中，∵BFA CDA BAF DCA AB AC ∠=∠⎧⎪∠=∠⎨⎪=⎩，∴(AAS)ABF CAD ≌；（3）解：∵ABC 的面积为15，2CE BE =， ∴5ABE S =△，10AECS=，∵2DE AD =， ∴103ADC S =△，203EDCS =，∵BAC BFE CDE ∠=∠=∠，∴BAF CAF DCA CAF ∠+∠=∠+∠，BFA CDA ∠=∠，∴BAF DCA ∠=∠，在ABF △与CAD 中，∵BFA CDA BAF DCA AB AC ∠=∠⎧⎪∠=∠⎨⎪=⎩，∴(AAS)ABF CAD ≌ ∴105533BEF S =−=， ∴520:1433BEF CDE S S ==::；【点睛】本题考查三角形全等的判定与性质及同高不同底三角形的面积，解题的关键是根据内外角关系得到三角形全等的条件．【答案】(1)①BE CF =；②180BCA α+∠=︒(2)EF BE AF =+【分析】（1）①由90BCA ∠=︒，90BEC CFA α∠=∠==︒，可得BCE CAF ∠=∠，从而可证BCE CAF ≌△△，故BE CF =；②添加180BCA α+∠=︒，可证明BCA BEF ∠=∠，则ACF CBE ∠=∠，根据AAS 可证明BCE CAF ≌△△，即可得证①中的结论仍然成立；（2）题干已知条件可证BCE CAF ≌△△，故BE CF =，EC FA =，从而可证明EF BE AF =+．【详解】（1）解：①BE CF =，理由如下：∵90BCA ∠=︒，∴90ACF BCE ∠+∠=︒，∵90BEC AFC α∠===∠︒，∴90ACF CAF ∠+∠=︒，∴BCE CAF ∠=∠，∵AC BC =，∴()AAS BCE CAF △≌△，∴BE CF =；②添加180BCA α+∠=︒，使①中的结论仍然成立，理由如下：∵BEC CFA α∠=∠=，∴180180BEF BEC α∠=︒−∠=︒−，∵BEF EBC BCE ∠=∠+∠，∴180EBC BCE α∠+∠=︒−，∵180BCA α+∠=︒，∴180BCA α∠=︒−，∴180BCA BCE ACF α∠=∠+∠=︒−，∴EBC ACF ∠=∠，∵AC BC =，BEC CFA α∠=∠=，∴()AAS BCE CAF △≌△，∴BE CF =；故答案为：180BCA α+∠=︒；（2）EF BE AF =+，理由如下：∵BCA α∠=，∴180180BCE FCA BCA α∠+∠=︒−∠=︒−，∵BEC α∠=，∴180180EBC BCE BEC α∠+∠=︒−∠=︒−，∴EBC FCA ∠=∠，∵AC BC =，BEC CFA α∠=∠=，∴()AAS BEC CFA △≌△，∴BE CF =，EC FA =，∴EF EC CF FA BE =+=+，即EF BE AF =+．【点睛】本题是三角形的综合题，主要考查全等三角形的性质与判定，熟练掌握全等三角形的性质与判定是解题的关键．3．在直线m 上依次取互不重合的三个点,,D A E ，在直线m 上方有AB AC =，且满足BDA AEC BAC α∠=∠=∠=．(1)如图1，当90α=︒时，猜想线段,,DE BD CE 之间的数量关系是____________；(2)如图2，当0180α<<︒时，问题（1）中结论是否仍然成立？如成立，请你给出证明；若不成立，请说明理由；(3)应用：如图3，在ABC 中，BAC ∠是钝角，AB AC =，,BAD CAE BDA AEC BAC ∠<∠∠=∠=∠，直线m 与CB 的延长线交于点F ，若3BC FB =，ABC 的面积是12，求FBD 与ACE 的面积之和．【答案】(1)DE ＝BD+CE(2)DE ＝BD+CE 仍然成立，理由见解析(3)△FBD 与△ACE 的面积之和为4【解析】【分析】（1）由∠BDA ＝∠BAC ＝∠AEC ＝90°得到∠BAD+∠EAC ＝∠BAD+∠DBA ＝90°，进而得到∠DBA ＝∠EAC ，然后结合AB＝AC得证△DBA≌△EAC，最后得到DE＝BD+CE；（2）由∠BDA＝∠BAC＝∠AEC＝α得到∠BAD+∠EAC＝∠BAD+∠DBA＝180°﹣α，进而得到∠DBA＝∠EAC，然后结合AB＝AC得证△DBA≌△EAC，最后得到DE＝BD+CE；（3）由∠BAD＞∠CAE，∠BDA＝∠AEC＝∠BAC，得出∠CAE＝∠ABD，由AAS证得△ADB≌△CAE，得出S△ABD ＝S△CEA，再由不同底等高的两个三角形的面积之比等于底的比，得出S△ABF即可得出结果．(1)解：DE＝BD+CE，理由如下，∵∠BDA＝∠BAC＝∠AEC＝90°，∴∠BAD+∠EAC＝∠BAD+∠DBA＝90°，∴∠DBA＝∠EAC，∵AB＝AC，∴△DBA≌△EAC（AAS），∴AD＝CE，BD＝AE，∴DE＝AD+AE＝BD+CE，故答案为：DE＝BD+CE．(2)DE＝BD+CE仍然成立，理由如下，∵∠BDA＝∠BAC＝∠AEC＝α，∴∠BAD+∠EAC＝∠BAD+∠DBA＝180°﹣α，∴∠DBA＝∠EAC，∵AB＝AC，∴△DBA≌△EAC（AAS），∴BD＝AE，AD＝CE，∴DE＝AD+AE＝BD+CE；(3)解：∵∠BAD＜∠CAE，∠BDA＝∠AEC＝∠BAC，∴∠CAE＝∠ABD，在△ABD和△CAE中，ABD CAEBDA CEAAB AC∠=∠⎧⎪∠=∠⎨⎪=⎩，∴△ABD≌△CAE（AAS），∴S△ABD＝S△CAE，设△ABC 的底边BC 上的高为h ，则△ABF 的底边BF 上的高为h ，∴S △ABC ＝12BC•h ＝12，S △ABF ＝12BF•h ，∵BC ＝3BF ，∴S △ABF ＝4，∵S △ABF ＝S △BDF+S △ABD ＝S △FBD+S △ACE ＝4，∴△FBD 与△ACE 的面积之和为4．【点睛】本题考查了全等三角形的判定与性质、直角三角形的性质，三角形的面积，解题的关键是熟练掌握全等三角形的判定与性质．【解题模型三三垂直模型】例题：（2023春·广东广州·九年级专题练习）如图，90,,ACB AC BC BE CE ∠=︒=⊥于E ，AD CE ⊥于D ，2.7cm, 1.8cm AD DE ==．(1)求证：ACD CBE ≌．(2)求BE 的长．【答案】(1)见解析；(2)0.9cm BE =．【分析】（1）由垂直得90ADC CEB ∠=∠=︒，求出ACD CBE ∠=∠，然后利用AAS 即可证明ACD CBE ≌；（2）根据全等三角形的性质可得 2.7cm CE AD ==，BE CD =，根据CD CE DE =−求出CD 即可得到BE 的长．【详解】（1）证明：∵AD CE ⊥，BE CE ⊥，∴90ADC CEB ∠=∠=︒，∵90ACB ∠=︒，∴90ACD ACB BCE BCE ∠=∠−∠=︒−∠，∵90CBE BCE ∠=︒−∠，∴ACD CBE ∠=∠，在ACD 与CBE △中，ADC CEB ACD CBE AC BC ∠=∠⎧⎪∠=∠⎨⎪=⎩， ∴()AAS ACD CBE ≌；（2）解：由（1）知，ACD CBE △△≌， ∴ 2.7cm CE AD ==，BE CD =，∵ 2.7 1.80.9cm CD CE DE =−=−=，∴0.9cm BE =．【点睛】本题考查了全等三角形的判定和性质，熟练掌握全等三角形的判定定理和全等三角形对应边相等的性质是解题的关键．【变式训练】 1．（2023春·河北邯郸·七年级校考阶段练习）已知：90ACB ∠=︒，AC BC =，AD CM ⊥，BE CM ⊥，垂足分别为D ，E ．在ACD 和CBE ∴ACD CBE ≌，（ CD BE =∵ACD CBE ≌，【答案】(1)①CBE ∠；同角的余角相等；ADC BEC ∠∠=，ACD CBE ∠=∠，AC BC =；AAS ；②AD CE =(2)不成立，DE BE AD −=，见解析【分析】（1）根据同角的余角相等，全等三形的判定方法角角边分析处理；（2）根据同角的余角相等，全等三形的判定方法角角边分析处理，注意观察图形，得出线段间的数量关系；【详解】（1）∵AD CM ⊥，BE CM ⊥，∴90ACB BEC ADC Ð=Ð=Ð=°，∴90ACD BCE ∠+∠=︒，90BCE CBE ∠+∠=︒，∴ACD ∠= CBE ∠ （同角的余角相等）在ACD 和CBE 中， ADC BEC ∠∠=，ACD CBE ∠=∠，AC BC = ，∴ACD CBE ≌，（ AAS ）∴CD BE =．②结论：AD BE DE =+．理由：∵ACD CBE ≌，∴ AD CE = ，∵CE CD DE BE DE =+=+，∴AD BE DE =+．（2）不成立，结论：DE BE AD −=．理由：∵AD CM ⊥，BE CM ⊥，∴90ACB BEC ADC Ð=Ð=Ð=°，∴90ACD BCE ∠+∠=︒，90BCE CBE ∠+∠=︒，∴ACD CBE ∠=∠在ACD 和CBE △中，ADC CEB ACD CBE AC CB ∠=∠⎧⎪∠=∠⎨⎪=⎩，∴ACD CBE △△≌，（AAS ）∴AD CE =，CD BE =，∴DE BE DE DC CE AD -=-==．【点睛】本题考查全等三角形的判定和性质，能够由图形的位置关系得出线段之间、角之间的数量关系是解题的关键．2．在△ABC 中，∠BAC =90°，AC=AB ，直线MN 经过点A ，且CD ⊥MN 于D ，BE ⊥MN 于E ．(1)当直线MN绕点A旋转到图1的位置时，EAB DAC∠+∠=度；(2)求证：DE=CD+BE；(3)当直线MN绕点A旋转到图2的位置时，试问DE、CD、BE具有怎样的等量关系？请写出这个等量关系，并加以证明．【答案】(1)90°(2)见解析(3)CD= BE + DE，证明见解析【解析】【分析】（1）由∠BAC=90°可直接得到EAB DAC∠+∠=90°；（2）由CD⊥MN，BE⊥MN，得∠ADC=∠BEA=∠BAC=90°，根据等角的余角相等得到∠DCA=∠EAB，根据AAS可证△DCA≌△EAB，所以AD=CE，DC=BE，即可得到DE = EA+AD = DC+BE．（3）同（2）易证△DCA≌△EAB，得到AD=CE，DC=BE，由图可知AE = AD +DE，所以CD= BE + DE．(1)∵∠BAC=90°∴∠EAB+∠DAC=180°-∠BAC=180°-90°=90°故答案为：90°．(2)证明：∵ CD⊥MN于D，BE⊥MN于E∴∠ADC=∠BEA=∠BAC=90°∵∠DAC+∠DCA=90°且∠DAC+∠EAB=90°∴∠DCA=∠EAB∵在△DCA和△EAB中90 ADC BEA DCA EABAC AB ︒⎧∠=∠=⎪∠=∠⎨⎪=⎩∴△DCA≌△EAB (AAS)∴ AD=BE且EA=DC由图可知：DE = EA+AD = DC+BE．(3)∵ CD⊥MN于D，BE⊥MN于E∴∠ADC=∠BEA=∠BAC=90°∵∠DAC+∠DCA=90°且∠DAC+∠EAB=90°∴∠DCA=∠EAB∵在△DCA和△EAB中90 ADC BEA DCA EABAC AB ︒⎧∠=∠=⎪∠=∠⎨⎪=⎩∴△DCA≌△EAB (AAS)∴ AD=BE且AE=CD由图可知：AE = AD +DE∴ CD= BE + DE．【点睛】本题考查了旋转的性质：旋转前后两图形全等，对应点到旋转中心的距离相等，对应点与旋转中心的连线段所夹的角等于旋转角，也考查了三角形全等的判定与性质．．如图，已知：在ABC中，）的位置时，求证：ADC CEB≅；【答案】（1）见解析；（2）见解析；（3）DE=BE-AD【分析】（1）由已知推出∠ADC=∠BEC=90°，因为∠ACD+∠BCE=90°，∠DAC+∠ACD=90°，推出∠DAC=∠BCE，根据AAS即可得到答案；（2）结论：DE=AD -BE ．与（1）证法类似可证出∠ACD=∠EBC ，能推出△ADC ≌△CEB ，得到AD=CE ，CD=BE ，即可得到答案．（3）结论：DE=BE -AD ．证明方法类似．【详解】解：（1）证明：如图1，∵AD ⊥DE ，BE ⊥DE ，∴∠ADC=∠BEC=90°，∵∠ACB=90°，∴∠ACD+∠BCE=90°，∠DAC+∠ACD=90°，∴∠DAC=∠BCE ，在△ADC 和△CEB 中，CDA BEC DAC ECBAC BC ∠=∠⎧⎪∠=∠⎨⎪=⎩，∴△ADC ≌△CEB （AAS ）；（2）如图2，∵BE ⊥EC ，AD ⊥CE ，∴∠ADC=∠BEC=90°，∴∠EBC+∠ECB=90°，∵∠ACB=90°，∴∠ECB+∠ACE=90°，∴∠ACD=∠EBC ，在△ADC 和△CEB 中，ACD CBE ADC BECAC BC ∠=∠⎧⎪∠=∠⎨⎪=⎩，∴△ADC ≌△CEB （AAS ），∴AD=CE ，CD=BE ，∴DE=EC -CD=AD -BE ．（3）DE=BE -AD ；如图3，∵∠ACB=90°，∴∠ACD+∠BCE=90°∵AD ⊥MN ，BE ⊥MN ，∴∠ADC=∠CEB=90°，∴∠ACD+∠DAC=90°，∴∠DAC=∠ECB ，在△ACD 和△CBE 中，ADC CEB DAC ECBAC BC ∠=∠⎧⎪∠=∠⎨⎪=⎩，∴△ACD ≌△CBE （AAS ），∴AD=CE ，CD=BE ，∴DE=CD -CE=BE -AD ．【点睛】本题主要考查了余角的性质，全等三角形的性质和判定等知识点，能根据已知证明△ACD ≌△CBE 是解此题的关键，题型较好，综合性比较强．【解题模型四倍长中线模型】八年级统考期中）如图，在ABC 中， (1)求BC 边的长的取值范围？(2)若AD 是ABC 的中线，求AD 【答案】(1)17BC <<(2)1722AD << 【分析】（1）根据三角形三边的关系求解即可；（2）延长AD 至E ，使AD DE =，连接BE ，证明ADC EDB V V ≌，得到AC BE =，由三角形三边关系得到17AE <<，则1722AD <<．【详解】（1）解：由三角形的三边关系可知：AC AB BC AC AB −<<+，∵34AB AC ==，，∴17BC <<；（2）解：延长AD 至E ，使AD DE =，连接BE ，在ABE 中，∵BD DC ADC BDE AD DE =∠=∠=，，，∴()SAS ADC EDB ≌△△，∴AC BE =，由三角形的三边关系：BE AB AE BE AB −<<+，∴17AE <<， ∴1722AD <<．【点睛】本题主要考查了三角形三边的关系，全等三角形的性质与判定，正确作出辅助线构造全等三角形是解题的关键．【变式训练】．如图，在ABC 中，【答案】(1)见解析(2)AC BE =，AC BE ∥(3)2AD BC =，证明见解析【分析】(1)根据三角形全等的判定定理SAS ，即可证得；(2)由ACD EBD △△≌，可得AC BE =，C EBC ∠=∠，据此即可解答；(3)根据三角形全等的判定定理SAS ，可证得BAC ABE ≌，据此即可解答．【详解】（1）证明：AD 是BC 边上的中线，BD CD ∴=，在ACD △与EBD △中AD ED ADC EDBBD CD =⎧⎪∠=∠⎨⎪=⎩，()SAS ACD EBD ∴≌；（2）解：ACD EBD ≌，AC BE ∴=，C EBC ∠=∠，∴∥AC BE ，故答案为：AC BE =，AC BE ∥；（3）解：2AD BC =证明：ACD EBD ≌，AC BE ∴=，C EBC ∠=∠，∴∥AC BE ，90BAC ∠=︒90BAC ABE ∴∠=∠=︒在BAC △和ABE △中，90AB BA BAC ABE AC BE =⎧⎪∠=∠=︒⎨⎪=⎩()SAS BAC ABE ∴≌， 2BC AE AD ∴==．【点睛】本题考查了全等三角形的判定与性质，平行线的判定与性质，熟练掌握和运用全等三角形的判定与性质是解决本题的关键． 2．（2023·全国·八年级假期作业）如图1，AD 为△ABC 的中线，延长AD 至E ，使DE ＝AD ．（1）试证明：△ACD ≌△EBD ；（2）用上述方法解答下列问题：如图2，AD 为△ABC 的中线，BMI 交AD 于C ，交AC 于M ，若AM ＝GM ，求证：BG ＝AC ．【答案】（1）详见解析；（2）详见解析．【分析】（1）根据中线的定义，即可得到BD ＝CD ，再根据SAS 即可判定△ACD ≌△EBD ．（2）延长AD 到F ，使AD ＝DF ，连接BF ，根据SAS 证△ADC ≌△FDB ，推出BF ＝AC ，∠CAD ＝∠F ，根据AM ＝GM ，推出∠CAD ＝∠AGM ＝∠BGF ，求出∠BGF ＝∠F ，根据等腰三角形的性质求出即可．【详解】（1）证明：∵AD 是△ABC 的中线，∴BD ＝CD ，在△ACD 和△EBD 中，CD BD ADC EDBAD ED =⎧⎪∠=∠⎨⎪=⎩，∴△ACD ≌△EBD （SAS ）．（2）证明：延长AD 到F ，使AD ＝DF ，连接BF ，∵AD 是△ABC 中线，∴BD ＝DC ，∵在△ADC 和△FDB 中BD DC ADC BDFAD DF =⎧⎪∠=∠⎨⎪=⎩，∴△ADC ≌△FDB （SAS ），∴BF ＝AC ，∠CAD ＝∠F ，∵AM ＝GM ，∴∠CAD ＝∠AGM ，∵∠AGM ＝∠BGF ，∴∠BGF ＝∠CAD ＝∠F ，∴BG ＝BF ＝AC ，即BG ＝AC ．【点睛】此题考查的是全等三角形的判定及性质，掌握倍长中线法构造全等三角形是解决此题的关键. 【探究与发现】（1）如图1，AD 是ABC 的中线，延长AD 至点E ，使ED AD =，连接【理解与应用】是DEF 的中线，若是ABC 的中线，【答案】（1）见解析；（2）14x <<；（3）见解析【分析】（1）根据全等三角形的判定即可得到结论；（2）延长EP 至点Q ，使PQ PE =，连接FQ ，根据全等三角形的性质得到3FQ DE ==，根据三角形的三边关系即可得到结论；（3）延长FD 至G ，使得GD DF =，连接BG ，EG ，结合前面的做题思路，利用三角形三边关系判断即可．【详解】（1）证明：CD BD =，ADC EDB ∠=∠，AD ED =，ACD EBD ∴≌，（2）14x <<；如图，延长EP 至点Q ，使PQ PE =，连接FQ ，在PDE ∆与PQF ∆中，PE PQ EPD QPFPD PF =⎧⎪∠=∠⎨⎪=⎩，PEP QFP ∴∆≅∆，3FQ DE ∴==，在EFQ ∆中，EF FQ QE EF FQ −<<+，即53253x −<<+，x ∴的取值范围是14x <<；故答案为：14x <<；（3）延长FD 至G ，使得GD =BG ，EG ，在DFC △和DGB 中，DF DG =，CDF BDG ∠=∠，DC DB =，(SAS)DFC DGB ∴≌，BG CF ∴=，在EDF 和EDG △中，DF DG =，90FDE GDE ∠=∠=︒，DE DE =，(SAS)EDF EDG ∴≌，EF EG ∴=，在BEG 中，两边之和大于第三边，BG BE EG ∴+>，又EF EG =，BG CF =，BE CF EF ∴+>【点睛】本题考查了全等三角形的判定和性质，三角形的中线的定义，三角形的三边关系，正确的作出图形是解题的关键．【解题模型五旋转模型】【答案】（1）见详解；（2）BD=CE，BD⊥CE；（3）902︒−【分析】（1）根据三角形全等的证明方法SAS证明两三角形全等即可；（2）由（1）△AEC≌△ADB可知CE=BD且CE⊥BD；利用角度的等量代换证明即可；（3）过A分别做AM⊥CE，AN⊥BD，易知AF平分∠DFC，进而可知∠CFA【详解】（1）∵∠CAB=∠EAD∴∠CAB+∠BAE=∠EAD+∠BAE，∴∠CAE=∠BAD，∵AB=AC，AE=AD在△AEC和△ADB中，AB ACCAE BAD AE AD=⎧⎪⎨⎪⎩∠=∠=∴△AEC≌△ADB（SAS）（2）CE=BD且CE⊥BD，证明如下：将直线CE与AB的交点记为点O，由（1）可知△AEC≌△ADB，∴ CE=BD，∠ACE=∠ABD，∵∠BOF=∠AOC，∠α=90°，∴∠BFO=∠CAB=∠α=90°，∴ CE⊥BD．（3）过A分别做AM⊥CE，AN⊥BD 由（1）知△AEC≌△ADB，∴两个三角形面积相等故AM·CE=AN·BD∴AM=AN∴AF平分∠DFC由（2）可知∠BFC=∠BAC=α∴∠DFC=180°-α∴∠CFA=12∠DFC=902α︒−【点睛】本题考查了全等三角形的证明，以及全等三角形性质的应用，正确掌握全等三角形的性质是解题的关键；【变式训练】 1．如图，在△ABC 中，AB ＝BC ，∠ABC ＝120°，点D 在边AC 上，且线段BD 绕着点B 按逆时针方向旋转120°能与BE 重合，点F 是ED 与AB 的交点．（1）求证：AE ＝CD ；（2）若∠DBC ＝45°，求∠BFE 的度数．【答案】（1）证明见解析；（2）∠BFE ＝105°．【分析】（1）根据旋转的性质证明△ABE ≌△CBD （SAS ），进而得证；（2）由（1）得出∠DBC=∠ABE=45°，BD=BE ，∠EBD=120°，最后根据三角形内角和定理进行求解即可．【详解】（1）证明：∵线段BD 绕着点B 按逆时针方向旋转120°能与BE 重合，∴BD ＝BE ，∠EBD ＝120°，∵AB ＝BC ，∠ABC ＝120°，∴∠ABD+∠DBC ＝∠ABD+∠ABE ＝120°，∴∠DBC ＝∠ABE ，∴△ABE ≌△CBD （SAS ），∴AE ＝CD ；（2）解：由（1）知∠DBC ＝∠ABE ＝45°，BD ＝BE ，∠EBD ＝120°，∴∠BED ＝∠BDE ＝12（180°﹣120°）＝30°，∴∠BFE ＝180°﹣∠BED ﹣∠ABE＝180°﹣30°﹣45°＝105°．【点睛】本题考查了旋转的性质，全等三角形的判定与性质，三角形内角和定理，利用旋转的性质证明是解题的关键．2．问题发现：如图1，已知C 为线段AB 上一点，分别以线段AC ，BC 为直角边作等腰直角三角形，=90ACD ∠︒，CA CD =，CB CE =，连接AE ，BD ，线段AE ，BD 之间的数量关系为______；位置关系为_______．拓展探究：如图2，把Rt ACD △绕点C 逆时针旋转，线段AE ，BD 交于点F ，则AE 与BD 之间的关系是否仍然成立？请说明理由．【答案】问题发现：AE BD =，AE BD ⊥；拓展探究：成立，理由见解析【分析】问题发现：根据题目条件证△ACE ≌△DCB ，再根据全等三角形的性质即可得出答案；拓展探究：用SAS 证ACE DCB ∆≅∆，根据全等三角形的性质即可证得．【详解】解：问题发现：延长BD ，交AE 于点F ，如图所示：∵90ACD ︒=∠，∴90ACE DCB ︒∠=∠=，又∵,CA CD CB CE ==,∴ACE DCB ∆≅∆（SAS ），,AE ED CAE CDB ∴=∠=∠， ∵90CDB CBD ︒∠+∠=，∴90CAE CBD ︒∠+∠=，∴90AFD ︒∠=，∴AF FB ⊥，AE BD ∴⊥，故答案为：AE BD =，AE BD ⊥；拓展探究：成立．理由如下：设CE 与BD 相交于点G ，如图1所示：∵90ACD BCE ︒∠=∠=，∴ACE BCD ∠=∠，又∵CB CE =，AC CD =，∴ACE DCB ∆≅∆（SAS ），∴AE BD =，AEC DBC ∠=∠，∵90CBD CGB ︒∠+∠=，∴90AEC EGF ︒∠+∠=， ∴90AFB ︒∠=，∴BD AE ⊥，即AE BD =，AE BD ⊥【点睛】本题考查全等三角形的判定和性质，三角形三边关系，手拉手模型，熟练掌握全等三角形的判定和手拉手模型是解决本题的关键． 3．（2023春·全国·七年级专题练习）在△ABC 中，∠BAC =90°，AC=AB ，直线MN 经过点A ，且CD ⊥MN 于D ，BE ⊥MN 于E ．(1)当直线MN绕点A旋转到图1的位置时，EAB DAC∠+∠=度；(2)求证：DE=CD+BE；(3)当直线MN绕点A旋转到图2的位置时，试问DE、CD、BE具有怎样的等量关系？请写出这个等量关系，并加以证明．【答案】(1)90°(2)见解析(3)CD= BE + DE，证明见解析【分析】（1）由∠BAC=90°可直接得到EAB DAC∠+∠=90°；（2）由CD⊥MN，BE⊥MN，得∠ADC=∠BEA=∠BAC=90°，根据等角的余角相等得到∠DCA=∠EAB，根据AAS可证△DCA≌△EAB，所以AD=CE，DC=BE，即可得到DE = EA+AD = DC+BE．（3）同（2）易证△DCA≌△EAB，得到AD=CE，DC=BE，由图可知AE = AD +DE，所以CD= BE + DE．【详解】（1）∵∠BAC=90°∴∠EAB+∠DAC=180°-∠BAC=180°-90°=90°故答案为：90°．（2）证明：∵ CD⊥MN于D，BE⊥MN于E∴∠ADC=∠BEA=∠BAC=90°∵∠DAC+∠DCA=90°且∠DAC+∠EAB=90°∴∠DCA=∠EAB∵在△DCA和△EAB中90 ADC BEA DCA EABAC AB ︒⎧∠=∠=⎪∠=∠⎨⎪=⎩∴△DCA≌△EAB (AAS)∴ AD=BE且EA=DC由图可知：DE = EA+AD = DC+BE．（3）∵ CD⊥MN于D，BE⊥MN于E ∴∠ADC=∠BEA=∠BAC=90°∵∠DAC+∠DCA=90°且∠DAC+∠EAB=90°∴∠DCA=∠EAB∵在△DCA 和△EAB 中90ADC BEA DCA EABAC AB ︒⎧∠=∠=⎪∠=∠⎨⎪=⎩∴△DCA ≌△EAB (AAS)∴ AD=BE 且AE=CD 由图可知：AE = AD +DE∴ CD= BE + DE ．【点睛】本题考查了旋转的性质：旋转前后两图形全等，对应点到旋转中心的距离相等，对应点与旋转中心的连线段所夹的角等于旋转角，也考查了三角形全等的判定与性质．八年级假期作业）在ABC 中， (1)【证明推断】求证：DN DM =；小明给出的思路：若要证明DN DM =，只需证明BDN △≌△你根据小明的思路完成证明过程；(2)【延伸发现】连接AE ，BF ，如图所示，求证：AE BF =；【答案】(1)见解析(2)见解析(3)AE BF ⊥，见解析【分析】（1）在ABC 中，根据点D 是BC 的中点，得出2AD BD BC==，由AD BC ⊥，DEF 是直角三角尺，得出90EDF ∠=︒，从而得到BDN ADM ∠=∠，在BDN 和ADM △中，立即证明全等，由性质即可解答DN DM =；（2）根据BDN ADM △≌△，得出BN AM =，BND AMD ∠=∠，DN DM =，从而得到BNF AME ∠=∠，由于DEF 是含45°直角三角尺，推出FN EM =，利用SAS 即可证明BNF 和AME △全等，从而求解；（3）猜想：AE BF ⊥，理由：根据BNF AME △≌△和90FDE ∠=︒，得出90AEM APD ∠+∠=︒，又根据APD FPQ ∠=∠，等量代换得到90FQP ∠=︒从而证明．【详解】（1）证明：在ABC 中，∵AB AC =，90BAC ∠=︒，∴45B C ∠==︒∠，又∵点D 是BC 的中点， ∴2AD BD BC ==，且AD BC ⊥，1452BAD CAD BAC ∠=∠=∠=︒∴90ADN BDN ∠+∠=︒，又∵DEF 是直角三角尺，∴90EDF ∠=︒，即90ADN ADM ∠+∠=︒，∴BDN ADM ∠=∠ 在BDN 和ADM △中45B DAM BD AD BDN ADM ∠=∠=︒⎧⎪=⎨⎪∠=∠⎩∴BDN ADM △≌△，∴DN DM =；（2）证明：∵BDN ADM △≌△∴BN AM =，BND AMD ∠=∠，DN DM =∴BNF AME ∠=∠，且由于DEF 是含45°直角三角尺，∴DF DE =，∴DF DN DE DM −=−即FN EM =在BNF 和AME △中BN AM BNF AMEFN EM =⎧⎪∠=∠⎨⎪=⎩∴BNF AME △≌△，∴AE BF =；（3）解：作图正确（如图所示）猜想：AE BF ⊥，理由如下：∵BNF AME △≌△，∴BFN AEM ∠=∠，∵90FDE ∠=︒，∴90AEM APD ∠+∠=︒又∵APD FPQ ∠=∠，∴90FPQ BFN ∠+∠=︒，∴90FQP ∠=︒，∴AE BF ⊥．【点睛】本题考查了旋转的性质、直角三角尺的特征、全等三角形的判定及性质，解题的关键是掌握三角形全等的判定及性质．。

初中数学《三角形中的经典模型》九大题型含解析

三角形中的经典模型【1A字模型 1【28字模型 3【3飞镖模型 6【4双垂直模型 9【5老鹰抓小鸡模型 15【6两内角角平分线模型 19【7两外角角平分线模型 21【8一内一外角角平分线模型 26【9三角形折叠模型 29知识点1：A字模型已知△ABC，AB至D，AC至E，∠1+∠2=∠A+180°【1A字模型1.(23-24八·全·专)如△ABC中∠A=65°，DE交AB于D，AC于E，∠BDE+∠CED=( )．A.180°B.215°C.235°D.245°【答案】D【分析】根据三角形内角和定理求出∠ADE+∠AED，根据平角的概念计算即可．【详解】解：∵∠A=65°，∴∠ADE+∠AED=180°-65°=115°，∴∠BDE+∠CED=360°-115°=245°，故选：D．【点睛】本题考查的是三角形内角和定理的应用，掌握三角形内角和等于180°是解题的关键．2.(23-24八年级·全国·专题练习)如图是某建筑工地上的人字架，若∠1=120°，那么∠3-∠2的度数为．【答案】60°【分析】根据平角的定义求出∠4，再利用三角形的外角的性质即可解决问题．【详解】解：如图∵∠1+∠4=180°，∠1=120°，∴∠4=60°，∵∠3=∠2+∠4，∴∠3-∠2=∠4=60°，故答案为：60°．【点睛】本题考查三角形外角的性质、平角的性质等知识，解题的关键是熟练掌握基本知识，属于中考基础题．3.(23-24八年级·河北沧州·期中)琪琪在操作课上将三角形剪掉一个角后得到四边形ABCD，则下列判断错误的是()A.变成四边形后对角线增加了两条B.变成四边形后内角和增加了360°C.外角和没有发生变化D.若剪掉的角的度数是60°，则∠1+∠2=240°【答案】B【分析】本题考查了多边形的对角线，内角和与外角和，三角形内角和定理，解题的关键是【详解】解：A、三角形没有对角线，变成四边形后对角线为两条，即增加了两条，故正确，不合题意；B、三角形内角和为180°，变成四边形后内角和为360°，增加了180°，故错误，不合题意；C、任意多边形的外角和是360°，故正确，不合题意；D、若剪掉的角的度数是60°，则∠A+∠B=120°，则∠1+∠2=360°-120°=240°，故正确，不合题意；故选：B．4.(23-24·浙江杭州·二模)将一把直尺与一块三角板在同一平面内按如图所示的方式放置，若∠1=130°，则∠2的度数为．【答案】40°/40度【分析】本题考查了平行线的性质，三角形的外角的性质，熟练掌握平行线的性质是解题的关键，根据平行线的性质可得∠FGH=∠1=130°，然后利用三角形外角的性质进行计算即可解答．【详解】解：如图：由题意得：AD∥BC，∴∠FGH=∠1=130°，∵∠FGH是△EFG的一个外角，∴∠FGH=∠2+∠E，∵∠E=90°，∴∠2=130°-90°=40°，故答案为：40°．知识点2：8字模型①已知AD，BC相交于O，则∠A+∠B=∠C+∠D②已知线段AP平分∠BAD，线段CP平分∠BCD，则∠P=12(∠B+∠D)【题型28字模型】5.(23-24八年级·浙江金华·期末)如图，BP平分∠ABC，交CD于点F，DP平分∠ADC交AB于点E，AB与CD相交于点G，∠A=42°．(1)若∠ADC=60°，求∠AEP的度数；(2)若∠C=38°，求∠P的度数．【答案】(1)72°；(2)40°．【分析】(1)根据角平分线的定义可得∠ADP=12∠ADC，然后利用三角形外角的性质即可得解；(2)根据角平分线的定义可得∠ADP=∠PDF，∠CBP=∠PBA，再根据三角形的内角和定理可得∠A+∠ADP=∠P+∠ABP，∠C+∠CBP=∠P+∠PDF，所以∠A+∠C=2∠P，即可得解．【详解】解：(1)∵DP平分∠ADC，∴∠ADP=∠PDF=12∠ADC，∵∠ADC=60°，∴∠ADP=30°，∴∠AEP=∠ADP+∠A=30°+42°=72°；(2)∵BP平分∠ABC，DP平分∠ADC，∴∠ADP=∠PDF，∠CBP=∠PBA，∵∠A+∠ADP=∠P+∠ABP，∠C+∠CBP=∠P+∠PDF，∴∠A+∠C=2∠P，∵∠A=42°，∠C=38°，∴∠P=12(38°+42°)=40°．【点睛】本题考查了三角形的内角和定理及三角形外角的性质，角平分线的定义，熟记定理并理解“8字形”的等式是解题的关键．6.(23-24八年级·河南漯河·期末)如图，AB和CD相交于点O，∠A=∠C，则下列结论中不能完全确定正确的是()A.∠B=∠DB.∠1=∠A+∠DC.∠2>∠DD.∠C=∠D【答案】D【分析】利用三角形的外角性质，对顶角相等逐一判断即可．【详解】∵∠A+∠AOD+∠D=180°，∠C+∠COB+∠B=180°，∠A=∠C，∠AOD=∠BOC，∴∠B=∠D，∵∠1=∠2=∠A+∠D，∴∠2>∠D，故选项A，B，C正确，故选D．【点睛】本题考查了对顶角的性质，三角形外角的性质，熟练掌握并运用两条性质是解题的关键．7.(23-24八年级·北京怀柔·期末)如图，在由线段AB,CD,DF,BF,CA组成的平面图形中，∠D=28°，则∠A+∠B+∠C+∠F的度数为( )．A.262°B.152°C.208°D.236°【答案】C【分析】如图标记∠1,∠2,∠3，然后利用三角形的外角性质得∠1=∠B+∠F=∠D+∠3，∠2=∠A+∠C，再利用∠2,∠3互为邻补角，即可得答案．【详解】解：如下图标记∠1,∠2,∠3，∵∠1=∠B+∠F=∠D+∠3，∵∠D=28°，∴∠3=∠B+∠F-28°，又∵∠2=∠A+∠C，∴∠2+∠3=∠A+∠C+∠B+∠F-28°，∵∠2+∠3=180°∴180°=∠A+∠C+∠B+∠F-28°，∴∠A+∠C+∠B+∠F=180°+28°=208°，故选C．【点睛】此题考查了三角形的外角性质与邻补角的意义，熟练掌握并灵活运用三角形的外角性质与邻补角的意义是解答此题的关键．8.(23-24八年级·全国·专题练习)如图，求∠A+∠B+∠C+∠D+∠E+∠F+∠G+∠H六个角的和．【答案】360°【分析】根据三角形内角和外角的性质可得：∠G+∠D=∠3，∠F+∠C=∠4，∠E+∠H=∠2，再根据三角形内角和定理可得答案．【详解】解：∵∠G+∠D=∠3，∠F+∠C=∠4，∠E+∠H=∠2，∴∠G+∠D+∠F+∠C+∠E+∠H=∠3+∠4+∠2，∵∠B+∠2+∠1=180°，∠3+∠5+∠A=180°，∴∠A+∠B+∠2+∠4+∠3=360°，∴∠A+∠B+∠C+∠D+∠E+∠F+∠G+∠H=360°．【点睛】此题主要考查了三角形内角与外角的性质，关键是掌握三角形的一个外角等于和它不相邻的两个内角的和．知识点3：飞镖模型①已知四边形ABCD，则∠C=∠A+∠B+∠D②已知四边形ABCD，线段BO平分∠ABC，线段OD平分∠ADC，则∠O=12(∠A+∠C)【题型3飞镖模型】9.(23-24·河北秦皇岛·一模)如图，用铁丝折成一个四边形ABCD(点C在直线BD的上方)，且∠A=70°，∠BCD=120°，若使∠ABC、∠ADC平分线的夹角∠E的度数为100°，可保持∠A不变，将∠BCD(填“增大”或“减小”)°．【答案】增大10【分析】利用三角形的外角性质先求得∠ABE+∠ADE=30°，根据角平分线的定义得到∠ABC+∠ADC= 60°，再利用三角形的外角性质求解即可．【详解】解：如图，连接AE并延长，连接AC并延长，∠BED=∠BEF+∠DEF=∠ABE+∠BAD+∠ADE=100°，∵∠BAD=70°，∴∠ABE+∠ADE=30°，∵BE，DE分别是∠ABC、∠ADC平分线，∴∠ABC+∠ADC=2(∠ABE+∠ADE)=60°，同上可得，∠BCD=∠BAD+∠ABC+∠ADC=130°，130°-120°=10°，∴∠BCD增大了10°．故答案为：增大，10．【点睛】本题考查了三角形的外角性质，三角形的内角和定理，角平分线的定义等知识，熟练运用题目中所给的结论是解题的关键．10.(23-24八年级·江苏苏州·阶段练习)在社会实践手工课上，小茗同学设计了如上图这样一个零件，如果∠A=52°，∠B=25°，∠C=30°，∠D=35°，∠E=72°，那么∠F=°．【答案】70【分析】延长BE、CF，交于点G，连接AG，根据三角形内角和定理和四边形的内角和为360°即可求解．【详解】解：延长BE、CF，交于点G，连接AG，如图，∴∠AGB=180°-∠B-∠BAG，∠AGC=180°-∠C-∠CAG，∴∠AGB+∠AGC=180°-∠B-∠BAG+180°-∠C-∠CAG=360°-∠B-∠C-∠BAC=253°，∴∠CGB=360°-∠AGB+∠AGC=107°．∵∠BED=72°，∴∠GED=108°，∴∠GFD=360°-∠GED-∠D-∠CGB=110°，∴∠CFD=70°．故答案为：70．【点睛】本题主要考查三角形内角和定理．正确的作出辅助线是解题关键．11.(23-24八年级·全国·专题练习)如图，若∠EOC=115°，则∠A+∠B+∠C+∠D+∠E+∠F=．【答案】230°【分析】根据三角形外角的性质，得到∠EOC=∠E+∠2=115°，∠2=∠D+∠C，∠EOC=∠1+∠F=115°，∠1=∠A+∠B，即可得到结论．【详解】解：如图∵∠EOC=∠E+∠2=115°，∠2=∠D+∠C，∴∠E+∠D+∠C=115°，∵∠EOC=∠1+∠F=115°，∠1=∠A+∠B，∴∠A+∠B+∠F=115°，∴∠A+∠B+∠C+∠D+∠E+∠F=230°，故答案为：230°．【点睛】本题主要考查三角形内角和定理和三角形外角的性质，解决本题的关键是要熟练掌握三角形外角性质．12.(23-24·河北邯郸·一模)嘉嘉在作业本上画了一个四边形，并标出部分数据(如图)，淇淇说，这四个数据中有一个是标错的；嘉嘉经过认真思考后，进行如下修改：若∠A，∠B，∠BCD保持不变，则将图中∠D(填“增大”或“减小”)度，淇淇说，“改得不错”．【答案】增大5【分析】连接BD，利用三角形的内角和计算即可．【详解】解：连接BD，∵∠CDB+∠CBD=180°-∠A-∠ABC-∠ADC∠CDB +∠CBD =180°-∠BCD∴∠A +∠ABC +∠ADC =∠BCD∵∠A =90°，∠ABC =25°，∠BCD =145°∴∠ADC =145°-25°-90°=30°∴30°-25°=5°故答案为：增大，5【点睛】本题主要考查三角形的内角和，添加辅助线利用三角形内角和计算是解决本题的关键．知识点4：双垂直模型已知∠B =∠D =∠ACE =90°.则∠BAC =∠DCE ，∠ACB =∠CED .【证明】∵∠B =∠D =∠ACE =90°；∴∠BAC +∠ACB =90°；又∠ECD +∠ACB =90°；∴∠BAC =∠DCE 同理,∠ACB +∠DCE =90°，且∠CED +∠DCE =90°；∴∠ACB =∠CED ，得证.【题型4双垂直模型】13.(23-24八年级·广东珠海·期末)如图1，AB ⊥BC 于点B ，CD ⊥BC 于点C ，点E 在线段BC 上，且AE ⊥DE ．(1)求证：∠EAB =∠CED ；(2)如图2，AF 、DF 分别平分∠BAE 和∠CDE ，则∠F 的度数是(直接写出答案即可)；(3)如图3，EH 平分∠CED ，EH 的反向延长线交∠BAE 的平分线AF 于点G ．求证：EG ⊥AF ．(提示：三角形内角和等于180°)【答案】(1)见解析；(2)45°；(3)见解析【分析】(1)利用同角的余角相等即可证明；(2)过点F 作FM ∥AB ，利用∠DFA =∠DFM +∠AFM =12∠CDE +12∠EAB =12(∠CDE +∠EAB )即可解决问题；(3)想办法证明∠EAG +∠AEG =90°即可解决问题.【详解】解：(1)∵AB ⊥BC ，CD ⊥BC ，∴∠B =∠C =90°，∴∠BAE +∠AEB =90°，∵AE ⊥DE ，∴∠AED =90°，∴∠AEB +∠CED =90°，∴∠BAE =∠CED ．(2)解：答案为45°；过点F 作FM ∥AB ，如图，∵AB ⊥BC ，CD ⊥BC ，∴∠B =∠C =90°，∴AB ∥CD ，∵∠C =90°，∴∠CED +∠CDE =90°，∵∠BAE =∠CED ，∴∠BAE +∠CDE =90°，∵AF 、DF 分别平分∠BAE 和∠CDE ，∴∠CDF =12∠CDE ，∠BAF =12∠BAE ，∴∠CDF +∠BAF =12(∠BAE +∠CDE )=45°，∵FM ∥AB ∥CD ，∴∠CDF =∠DFM ，∠BAF =∠AFM ，∴∠AFD =∠CDF +∠BAF =45°．(3)∵EH 平分∠CED ，∴∠CEH =12∠CED ，∴∠BEG =12∠CED ，∵AF 平分∠BAE ，∴∠BAG =12∠BAE ，∵∠BAE =∠CED ，∴∠BAG =∠BEG ，∵∠BAE +∠BEA =90°，∴∠BAG +∠GAE +∠AEB =90°，即∠GAE +∠AEB +∠BEG =90°，∴∠AGE =90°，∴EG ⊥AF ．【点睛】本题考查三角形内角和定理、平行线的性质、角平分线的定义等知识，解题的关键是学会添加常用辅助线，构造平行线解决问题，属于中考常考题型．14.(23-24八年级·陕西西安·期末)如图，在等腰Rt △ABC 中，∠ACB =90°，D 为BC 的中点，DE ⊥AB ，垂足为E ，过点B 作BF ∥AC 交DE 的延长线于点F ，连接CF ．(1)求证：AD⊥CF．(2)连接AF，试判断△ACF的形状，并说明理由．【答案】(1)见解析(2)△ACF为等腰直角三角形；理由见解析【分析】本题考查了全等三角形的判定和性质及等腰三角形性质和判定．(1)欲求证AD⊥CF，先证明∠CAG+∠ACG=90°，需证明∠CAG=∠BCF，利用三角形全等，易证．(2)要判断△ACF的形状，看其边有无关系．根据(1)的推导，易证CF=AF，从而判断其形状．【详解】(1)证明：在等腰直角△ABC中，∵∠ACB=90°，∴∠CBA=∠CAB=45°，∵DE⊥AB，∴∠DEB=90°，∴∠BDE=45°，∵BF∥AC，∴∠CBF=180°-∠ACB=90°，∴∠BFD=45°=∠BDE，∴BF=DB，又∵D为BC的中点，∴CD=DB，即BF=CD，在△CBF和△ACD中，BF=CD∠CBF=∠ACD=90°CB=AC，∴△CBF≌△ACD(SAS)．∴∠BCF=∠CAD．∵∠BCF+∠GCA=90°，∴∠CAD+∠GCA=90°，即AD⊥CF．(2)解：△ACF是等腰三角形，理由为：连接AF，如图所示，由(1)知：△CBF≌△ACD，∴CF=AD，∵△DBF是等腰直角三角形，且BE是∠DBF的平分线，∴BE垂直平分DF，∴AF=AD，∵CF=AD，∴CF=AF，∴△ACF是等腰三角形．15.(23-24八年级·山西晋中·期中)请把下面的证明过程补充完整如图，在△ABC中，∠ACB=90°,AE是角平分线，CD是高，AE、CD相交于点F，求证：CF=CE．证明：∵AE平分∠CAB(已知)，∴∠CAE=∠FAB(①)，∵∠ACE=90°(已知)，∴∠CAE+∠CEF=90°(②)，∵CD是△ABC的高(已知)，∴∠CDA=90°(三角形高的定义)，∴(③)，(直角三角形的两个锐角互余)，∴∠CEF=∠AFD(④)，∵∠CFE=∠AFD(⑤)，∴∠CFE=∠CEF(⑥)，∴CF=CE(⑦)．【答案】①角平分线的定义；②直角三角形的两锐角互余；③∠FAD+∠AFD=90°；④等角的余角相等；⑤对顶角相等；⑥等量代换；⑦等角对等边【分析】本题考查的是直角三角形的性质、角平分线的定义，等腰三角形的判定，掌握直角三角形的两锐角互余是解题的关键．根据角平分线的定义、直角三角形的性质、对顶角相等、等角对等边解答即可．【详解】证明：∵AE平分∠CAB(已知)，∴∠CAE=∠FAB(角平分线的定义)，∵∠ACE=90°(已知)，∴∠CAE+∠CEF=90°(直角三角形的两锐角互余)，∵CD是△ABC的高(已知)，∴∠CDA=90°(三角形高的定义)，∴∠FAD+∠AFD=90°(直角三角形的两锐角互余)，∴∠CEF=∠AFD(等角的余角相等)，∵∠CFE=∠AFD(对顶角相等)，∴∠CFE=∠CEF(等量代换)，∴CF=CE(等角对等边)．故答案为：角平分线的定义；直角三角形的两锐角互余；∠FAD+∠AFD=90°；等角的余角相等；对顶角相等；等量代换；等角对等边．16.(23-24八年级·江苏扬州·阶段练习)在Rt △ABC 中，∠CAB =90°，AB =AC ，点O 是BC 的中点，点P 是射线CB 上的一个动点(点P 不与点C 、O 、B 重合)，过点C 作CE ⊥AP 于点E ，过点B 作BF ⊥AP 于点F ，连接EO ，OF．(问题探究)如图1，当P 点在线段CO 上运动时，延长EO 交BF 于点G ．(1)求证：△AEC ≌△BFA ；(2)BG 与AF 的数量关系为：(直接写结论，不需说明理由)；(拓展延伸)(3)①如图2，当P 点在线段OB 上运动，EO 的延长线与BF 的延长线交于点G ，∠OFE 的大小是否变化？若不变，求出∠OFE 的度数；若变化，请说明理由；②当P 点在射线OB 上运动时，若AE =2，CE =6，直接写出△OEF 的面积，不需证明．【答案】(1)见解析；(2)BG =AF ；(3)①∠OFE 的大小不变，∠OFE =45°；②满足条件的△OEF 的面积为8或16【分析】(1)根据等角的余角相等得出∠CAE =∠ABF ，证明△AEC ≌△BFA AAS ；(2)证明△COE ≌△BOG AAS 得出CE =BG ，则CE =AF ，等量代换可得AF =BG ；(3)①证明△AEC ≌△BFA AAS ，进而证明∠CEO =∠BGO 证明△COE ≌△BOG AAS 得出∠EFO =12∠EFG =45°；②根据题意画出图形，分类讨论，根据三角形的面积公式，即可求解．【详解】(1)证明：如图1中，∵CE ⊥AE ，BF ⊥AE ，∴∠AEC =∠BFA =∠CAB =90°，∴∠CAE +∠BAF =90°，∠BAF +∠ABF =90°，∴∠CAE =∠ABF ，在△AEC 和△BFA 中，∠AEC =∠BFA∠CAE =∠ABF AC =BA，∴△AEC ≌△BFA AAS ；(2)解：结论：BG =AF ．理由：∵CE ⊥AE ，BF ⊥AE ，∴CE ∥BG ，∴∠CEO =∠BGO ，∵O 是BC 的中点，∴OC =OB ，在△COE 和△BOG 中，∠CEO =∠BGO∠AOE =∠BOG OC =OB，∴△COE ≌△BOG AAS ，∴CE =BG ，∵△AEC ≌△BFA ，∴CE =AF ，∴AF =BG ．故答案为：BG =AF ．(3)解：①如图2中，结论：∠OFE 的大小不变，∠OFE =45°．理由：∵CE ⊥AE ，BF ⊥AE ，∴∠AEC =∠BFA =∠CAB =90°，∴∠CAE +∠BAF =90°，∠BAF +∠ABF =90°，∴∠CAE =∠ABF ，在△AEC 和△BFA 中，∠AEC =∠BFA∠CAE =∠ABF AC =BA，∴△AEC ≌△BFA AAS ；∴CE =AF ，AE =BF ，∵CE ⊥AE ，BF ⊥AE ，∴CE ∥BG ，∴∠CEO =∠BGO ，∵O 是BC 的中点，∴OC =OB ，在△COE 和△BOG 中，∠CEO =∠BGO∠AOE =∠BOG OC =OB，∴△COE ≌△BOG AAS ，∴CE =BG ，OE =OG ，∴AF =BG ，∴EF =FG ，根据△EFO ≌△GFO SSS 可得：∠EFO =∠GFO∴∠EFO =12∠EFG =45°；②如图2中，当AE =2，CE=6时，EF =FG =6-2=4，∴S △EOF =12S △EFC =12×12×4×4=4如图3中，当AE =2，CE =6时，EF =FG =6+2=8，∴S △EOF =12S △EFG =12×12×8×8=16综上所述，满足条件的△OEF 的面积为8或16．【点睛】本题考查了全等三角形的证明与性质，等腰三角形的判定和性质，三角形的动点问题以及三角形求面积的问题，正确掌握知识点是解题的关键．知识点5：老鹰抓小鸡模型如图，∠A+∠O=∠1+∠2；口诀：腋下两角之和等于上下两角之和【题型5老鹰抓小鸡模型】17.(23-24八年级·江苏扬州·阶段练习)如图，把△ABC沿EF对折，叠合后的图形如图所示．若∠A=60°，∠1=95°，则∠2的度数为()A.24°B.35°C.30°D.25°【答案】D【分析】根据三角形内角和定理可得∠AEF+∠AFE=120°，再根据邻补角的性质可得∠FEB+∠EFC= 360°-120°=240°，再根据由折叠可得：∠B′EF+∠EFC′=∠FEB+∠EFC=240°，然后计算出∠1+∠2的度数，即可求得∠2的度数．【详解】∵∠A=60°，∴∠AEF+∠AFE=180°-60°=120°，∴∠FEB+∠EFC=360°-120°=240°，∵由折叠可得：∠B′EF+∠EFC′=∠FEB+∠EFC=240°，∴∠1+∠2=240°-120°=120°，∵∠1=95°，∴∠2=120°-95°=25°，故选D．【点睛】本题考查了三角形的内角和定理，翻折变换的性质，熟记定理及性质并准确识图是解题的关键．18.(23-24八年级·重庆渝北·阶段练习)如图，将△ABC沿着DE翻折，使B点与B 点重合，若∠1+∠2=80°，则∠B的度数为．【答案】40°/40度【分析】由翻折的性质可知，∠B=∠B ，∠BED=∠B ED，∠BDE=∠B DE，由∠BED+∠B ED+∠1= 180°，∠BDE+∠B DE+∠2=180°，∠1+∠2=80°，可得∠BED+∠BDE=140°，根据∠B=180°-∠BED+∠BDE，计算求解即可．【详解】解：由翻折的性质可知，∠B=∠B ，∠BED=∠B ED，∠BDE=∠B DE，∵∠BED+∠B ED+∠1=180°，∠BDE+∠B DE+∠2=180°，∠1+∠2=80°，∴∠BED+∠BDE=140°，∴∠B=180°-∠BED+∠BDE=40°，故答案为：40°．【点睛】本题考查了翻折的性质，三角形内角和定理．解题的关键在于对知识的熟练掌握与灵活运用．19.(23-24八年级·安徽铜陵·期中)如图，将△ABC纸片沿DE折叠，使点A落在点A′处，且A′B平分∠ABC，A′C平分∠ACB，若∠1+∠2=120°，则∠BA′C的度数为()A.120°B.110°C.100°D.90°【答案】A【详解】由∠BDE、∠CED是△ADE的两个外角知∠BDE=∠A+∠AED、∠CED=∠A+∠ADE，据此得∠BDE+∠CED=∠A+∠AED+∠A+∠ADE，推出∠1+∠2=2∠A得到∠A=60°，根据BA'平分∠ABC，CA'平分∠ACB知∠A'BC+∠A'CB=12(∠ABC+∠ACB)=90°-12∠A．利用∠BA'C=180°-(∠A'BC+∠A'CB)可得答案．解：∵∠BDE、∠CED是△ADE的两个外角，∴∠BDE=∠A+∠AED，∠CED=∠A+∠ADE，∴∠BDE+∠CED=∠A+∠AED+∠A+∠ADE，∴∠1+∠ADE+∠2+∠AED=2∠A+∠AED+∠ADE，即∠1+∠2=2∠A，∵∠1+∠2=120°，∴∠A=60°，∵BA'平分∠ABC，CA'平分∠ACB，∴∠A'BC+∠A'CB=12(∠ABC+∠ACB)=12(180°-∠A )=90°-12∠A ．∴∠BA 'C =180°-(∠A 'BC +∠A 'CB )，=180°-90°-12∠A =90°+12∠A =90°+12×60°=120°．故选：A ．【点睛】本题考查三角形的内角和定理、角平分线的定义、三角形的外角的性质等知识，解题的关键是灵活运用所学知识，属于中考常考题型．20.(23-24八年级·山东烟台·期中)折纸是我国一项古老的传统民间艺术，这项具有中国特色的传统文化在几何中可以得到新的解读．已知在△ABC 中，请根据题意，探索不同情境中∠1+∠2(或∠1-∠2)与∠A 的数量关系．(1)如图①，若∠A =80°，沿图中虚线DE 截去∠A ，则∠1+∠2=．(2)如图②，若∠A =80°，沿图中虚线DE 将∠A 翻折，使点A 落在BC 上的点A '处，则∠1+∠2=．(3)如图③，翻折后，点A 落在点A '处，若∠1+∠2=80°，求∠B +∠C 的度数(4)如图④，△ABC 纸片沿DE 折叠，使点A 落在点A '处，若∠1=80°，∠2=24°，求∠A 的度数．【答案】(1)260°(2)160°(3)∠B +∠C =140°(4)∠A =28°【分析】(1)根据三角形内角和定理得出∠B +∠C =180°-80°=100°，再由平角进行求解即可；(2)利用翻折的性质得出∠EDA '=∠ADE ，∠AED =∠DEA ',根据三角形内角和定理得出∠ADE +∠AED =100°，结合图形，由平角及各角之间的关系进行计算即可‘(3)连接AA ．根据三角形外角的性质得出∠1=∠DAA '+∠DA 'A ，∠2=∠EAA '+∠EA 'A ，然后利用各角之间的数量关系得出∠EAD =40°，再由三角形内角和定理即可求解；(4)设AB 与DA 交于点F ，根据三角形外角得出∠1=∠DFA +∠A ，∠DFA =∠A +∠2，再由折叠的性质得出∠A =∠A ，结合图形及各角之间的数量关系进行求解即可【详解】(1)解：∵∠A=80°，∴∠ADE+∠AED=180°-80°=100°，∴∠1+∠2=360°-∠ADE-∠AED=260°，故答案为：260°；(2)∵∠A=80°，∴∠ADE+∠AED=180°-80°=100°，∵翻折，∴∠EDA'=∠ADE，∠AED=∠DEA',∴∠ADA'+∠AEA'=2(∠ADE+∠AED)=200°，∴∠1+∠2=360°-(∠ADA'+∠AEA')=160°，故答案为：160°；(3)解：连接AA ．如图所示：∵∠1=∠DAA'+∠DA'A，∠2=∠EAA'+∠EA'A，∴∠1+∠2=∠DAA'+∠DA'A+∠EAA'+∠EA'A=∠EAD+∠EA'D，∵∠EAD=∠EA D，∴∠1+∠2=2∠EAD=80°，∴∠EAD=40°，∴∠B+∠C=180°-40°=140°．(4)解：如图，设AB与DA 交于点F，∵∠1=∠DFA+∠A，∠DFA=∠A +∠2，由折叠可得，∠A=∠A ，∴∠1=∠A+∠A +∠2=2∠A+∠2，又∵∠1=80°，∠2=24°，∴80°=2∠A+24°，∴∠A=28°．【点睛】题目主要考查三角形内角和定理及三角形外角的性质，平角的定义等，理解题意，作出相应辅助线求解是解题关键．知识点6：两内角角平分线模型在△ABC 中，BI 、CI 分别是∠ABC 和∠ACB 的角平分线，且相交于点I .则∠I =90°+12∠A【题型6两内角角平分线模型】21.(23-24八年级·河南信阳·开学考试)如图，AD ，CE 都是△ABC 的角平分线，且交于点O ，∠DAC =30°，∠ECA =35°，则∠ABO 的度数为．【答案】25°/25度【分析】本题考查了三角形内角和定理、角平分线，利用角平分线的定义结合三角形内角和定理找出∠ABO 的度数是解题的关键．根据角平分线的定义可得出∠BAC =60°、∠ACB =70°，结合三角形内角和可得出∠ABC =50°，由三角形的三条角平分线交于一点，可得出BO 平分∠ABC ，进而可得出∠ABO 的度数，此题得解．【详解】解：∵AD 平分∠BAC ，CE 平分∠ACB ，∠DAC =30°，∠ECA =35°，∴∠BAC =2∠DAC =60°，∠ACB =2∠ECA =70°，∴∠ABC =180°-∠BAC -∠ACB =50°．∵△ABC 的三条角平分线交于一点，∴BO 平分∠ABC ，∴∠ABO =12∠ABC =25°．故答案为：25°．22.(23-24八年级·全国·课后作业)如图，在△ABC 中，∠ABC 和∠ACB 的平分线BE ，CF 相交于点G ，若∠A =66°，则∠BGC 的度数为．【答案】123°/123度【分析】本题考查角平分线和三角形内角和定理，熟练利用角平分线的性质和三角形内角和定理找出题目中角的等量关系是解答本题的关键．由角平分线的性质可知∠GBC =12∠ABC ，∠GCB =12∠ACB ，再由三角形内角和定理可知∠BGC =180°-∠GBC +∠GCB ，即可求解．【详解】∵∠A =66°，∴∠ABC +∠ACB =180°-∠A =114°，∵BE 和CF 分别是∠ABC 和∠ACB 的平分线，∴∠GBC =12∠ABC ，∠GCB =12∠ACB ，∴∠BGC =180°-∠GBC +∠GCB =180°-12∠ABC +∠ACB =123°，故答案为：123°．23.(23-24八年级·河南信阳·开学考试)如图，在△ABC 中，AD 是BC 边上的高，AE ，BF 分别是∠BAC 和∠ABC 的角平分线，它们相交于点O ，∠AOB =125°．求∠CAD 的度数．【答案】∠CAD =20°．【分析】本题考查了角平分线的性质，三角形的内角和定理，以及余角的性质，解题的关键是熟练掌握所学的知识，正确求出∠C =70°，从而求出答案．根据角平分线的性质，由∠AOB =125°，得到∠CAB +∠CBA =110°，然后得到∠C ，由余角的性质，即可求出答案．【详解】解：∵AE ，BF 分别是∠BAC 和∠ABC 的角平分线，∴∠OAB =12∠BAC ，∠OBA =12∠ABC ．∴∠CAB +∠CBA =2(∠OAB +∠OBA )=2180°-∠AOB∵∠AOB =125°，∴∠CAB +∠CBA =110°，∴∠C =70°．∵AD 是BC 边上的高∴∠ADC =90°，∴∠CAD =20°．24.(23-24八年级·山东烟台·期末)如图，在△ABC 中，∠A =90°，BE ，CD 分别平分∠ABC 和∠ACB ，且相交于F ，EG ∥BC ，CG ⊥EG 于点G ，则下列结论：①∠CEG =2∠DCA ；②∠DFE =130°；③∠EFC =12∠G ：④∠ADC =∠GCD ；⑤△EGC 是等腰直角三角形，其中正确的结论是()A.①③④⑤B.①②③④C.①②③D.①③④【答案】D 【分析】本题主要考查了平行线的性质，角平分线的定义，三角形内角和定理，熟知平行线的性质，角平分线的定义是解题的关键．根据平行线的性质与角平分线的定义即可判断①；只需要证明∠ADC +∠ACD =90°，∠GCD +∠BCD =90°，即可判断④；根据角平分线的定义和三角形内角和定理先推出∠BFC=135°，即可判断②③；根据现有条件无法推出⑤．【详解】解：∵CD平分∠ACB，∴∠ACB=2∠DCA，∠ACD=∠BCD∵EG∥BC，∴∠CEG=∠ACB=2∠DCA，故①正确；∵∠A=90°，CG⊥EG，EG∥BC，∴∠ADC+∠ACD=90°，CG⊥BC，即∠BCG=90°，∴∠GCD+∠BCD=90°，又∵∠BCD=∠ACD，∴∠ADC=∠GDC，故④正确；∵∠A=90°，∴∠ABC+∠ACB=90°，∵BE，CD分别平分∠ABC，∠ACB，∴∠FBC=12∠ABC,∠FCB=12∠ACB，∴∠BFC=180°-∠FBC-∠FCB=180°-12(∠ACB+∠ABC)=135°，∴∠EFC=180°-∠BFC=45°，∵CG⊥EG∴∠G=90°，∴∠EFC=12∠G，故③正确；∵∠BFC=135°，∴∠DFE=∠BFC=135°，故②错误；∵∠G=90°∴△EGC是直角三角形，根据现有条件，无法推出CG=CE，即无法得到△EGC是等腰直角三角形，故⑤错误；∴正确的有①③④，故选：D．知识点7：两外角角平分线模型在△ABC中，BI、CI分别是△ABC的外角的角平分线，且相交于点O.则∠O=90°-12∠A.【证明】∵BO是∠EBC平分线，∴∠2=12∠EBC，∵CO是∠FCB平分线，∴∠5=12∠FCB由△BCO中内角和定理可知：∠O=180°-∠2-∠5=180°-12∠EBC-12∠FCB=180°-12(180°-∠ABC)-12(180°-∠ACB)=12(∠ABC+∠ACB)=12(180°-∠A)=∠O=90°-12∠A【题型7两外角角平分线模型】25.(23-24八年级·全国·专题练习)如图，在△ABC中，∠B=58°，三角形两外角的角平分线交于点E，则∠AEC=．【答案】61°【分析】先根据三角形的内角和定理和平角定义求得∠DAC+∠ACF的度数，再根据角平分线的定义求得∠EAC+∠ECA的度数，即可解答．【详解】解：∵∠B+∠BAC+∠BCA=180°，∠B=58°，∴∠BAC+∠BCA=180°-∠B=180°-58°=122°，∵∠BAC+∠DAC=180°，∠BCA+∠ACF=180°，∴∠DAC+∠ACF=360°-(∠BAC+∠BCA)=360°-122°=238°，∵AE平分∠DAC，CE平分∠ACF，∴∠EAC=12∠DAC，∠ECA=12∠ACF，∴∠EAC+∠ECA=12(∠DAC+∠ACF)=119°，∵∠EAC+∠ECA+∠AEC=180°，∴∠AEC=180°-(∠EAC+∠ECA)=180°-119°=61°，故答案为：61°．【点睛】本题考查三角形的内角和定理、角平分线的定义、平角定义，熟练掌握三角形的内角和定理和角平分线的定义是解答的关键．26.(23-24八年级·河南郑州·阶段练习)如图，G是ΔAFE两外角平分线的交点，P是ΔABC的两外角平分线的交点，F，C在AN上，又B，E在AM上；如果∠FGE=66°，那么∠P=度．【答案】66【分析】利用角平分线的定义和三角形、四边形的内角和可求得：∠G=180°-12×[360°-(180°-∠A)]=90°-1 2∠A，∠P=180°-12×[360°-(180°-∠A)]=90°-12∠A，所以∠P=∠FGE=66°．【详解】解：因为G是△AFE两外角平分线的交点，∴∠FGE=180°-12×[360°-(180°-∠A)]=90°-12∠A，∵P是△ABC两外角平分线的交点，∴∠P=180°-12×[360°-(180°-∠A)]=90°-12∠A，∴∠P=∠FGE=66°．故答案为：66．【点睛】本题考查了三角形内角和定理、角平分线的性质和三角形外角的性质，结合图形熟练运用定理和性质进行求解是解题的关键．27.(23-24八年级·山东聊城·期末)如图，在△ABC中，∠ABC，∠ACB的平分线交于点O，D是∠ACF与∠ABC平分线的交点，E是△ABC的两外角平分线的交点，若∠BOC=130°，则∠D的度数为()A.25°B.30°C.40°D.50°【答案】C【分析】根据角平分线的定义和平角定义可得∠OCD=∠ACO+∠ACD=90°，根据外角的性质可得∠BOC =∠OCD+∠D，继而即可求解．【详解】解：∵CO平分∠ACB，CD平分∠ABC的外角，∴∠ACO=12∠ACB，∠ACD=12∠ACF，∵∠ACB+∠ACF=180°，∴∠OCD=∠ACO+∠ACD=12∠ACB+∠ACF=90°，∴∠BOC=∠OCD+∠D，∴∠D=∠BOC-∠OCD=130°-90°=40°，故选择C．【点睛】本题考查角平分线的定义，平角定义，三角形的外角性质，解题的关键是根据角平分线定义和平角定义可得∠OCD=90°，根据外角的性质求得∠BOC=∠OCD+∠D．28.(23-24八年级·全国·课后作业)(分类讨论思想)△ABC的两外角平分线交于点F．(1)如图1，若∠A=30°，则∠BFC的度数为．(2)如图2，过点F作直线MN∥BC，分别交射线AB，AC于点M，N，若设∠MFB=α，∠NFC=β，则∠A与α+β的数量关系是．(3)在(2)的条件下，将直线MN绕点F转动．①如图3，当直线MN与线段BC没有交点时，试探索∠A与α，β之间的数量关系，并说明理由．②当直线MN 与线段BC 有交点时，试问①中∠A 与α，β之间的数量关系是否仍然成立？若成立，请说明理由；若不成立，请给出三者之间的数量关系．【答案】(1)75°(2)α+β-12∠A =90°(3)①α+β-12∠A =90°，见解析；②不成立，β-α-12∠A =90°或α-β-12∠A =90°【分析】(1)由三角形内角和定理可得∠ACB +∠ABC =180°-∠A ，从而可得∠CBD +∠BCE =180°+∠A ，再由角平分线的定义可得∠CBF +∠BCF =90°+12∠A ，最后由三角形内角和定理可得∠BFC =90°-12∠A ，进行计算即可；(2)由(1)可得由(1)可得∠BFC =90°-12∠A ，再由α+∠BFC +β=180°代入进行计算即可；(3)①根据(1)中的结论∠BFC =90°-12∠A ，以及平角的定义，即可得到答案；②分两种情况进行讨论：根据(1)中的结论∠BFC =90°-12∠A ，以及平角的定义，即可得到答案．【详解】(1)解：∵∠A +∠ACB +∠ABC =180°，∴∠ACB +∠ABC =180°-∠A ，∵∠ACB +∠BCE =180°，∠ABC +∠CBD =180°，∴∠CBD +∠BCE=180°-∠ABC +180-∠ACB=360°-∠ABC +∠ACB=360°-180°-∠A=180°+∠A ，∵BF 和CF 分别是∠DBC 和∠BCE 的平分线，∴∠CBF =12∠CBD ，∠BCF =12∠BCE ，∴∠CBF +∠BCF ，=12∠CBD +12∠BCE =12∠CBD +∠BCE =12×180°+∠A =90°+12∠A ，∵∠BFC +∠CBF +∠BCF =180°，∴∠BFC =180°-∠CBF +∠BCF =180°-90°+12∠A =90°-12∠A =75°，故答案为：75°；(2)解：α+β-12∠A =90°，由(1)可得∠BFC =90°-12∠A ，∵α+∠BFC +β=180°，∴α+β+90°-12∠A =180°，即α+β-12∠A =90°．(3)解：①当直线MN 与线段BC 没有交点时，α+β-12∠A =90°，理由如下：∵∠BFC =90°-12∠A ，∠MFB +∠NFC +∠BFC =180°，∴α+β+90°-12∠A =180°，即α+β-12∠A =90°；②当直线MN 与线段BC 有交点时，①中∠A 与α，β之间的数量关系不成立，需分两种情况讨论：a ．如图1，当M 在线段AB 上，N 在射线AC 上时，β-α-12∠A =90°，，∵∠BFC =90°-12∠A ，∠BFC -∠MFB +∠NFC =180°，∴90°-12∠A -α+β=180°，即β-α-12∠A =90°，b ．如图2，当M 在射线AB 上，N 在线段AC 上时，α-β-12∠A =90°，，∵∠BFC =90°-12∠A ，∠BFC -∠NFC +∠MFB =180°，∴90°-12∠A -β+α=180°，即α-β-12∠A =90°．【点睛】本题考查了三角形内角和定理、角平分线的定义、平角的定义等知识，熟练掌握以上知识点，采用分类讨论的思想解题，是解此题的关键．知识点8：一内一外角角平分线模型已知△ABC 中，BP 、CP 分别是△ABC 的内角和外角的角平分线，且相交于点P .则∠P =12∠A【证明】∵BP 是∠ABC 平分线，∴∠3=12∠ABC ∵CP 是∠ACE 平分线，∴∠1=12∠ACE 由△ABC 外角定理可知：∠ACE =∠ABC +∠A 即：2∠1=2∠3+∠A ⋯⋯①对①式两边同时除以2，得：∠1=∠3+12∠A⋯⋯②又在△BPC中由外角定理可知：∠1=∠3+∠P⋯⋯③比较②③式子可知：∠P=12∠A.【题型8一内一外角角平分线模型】29.(23-24八年级·江苏泰州·期末)如图，点B、C分别在AM、AN上运动(不与A重合)，CD是∠BCN的平分线，CD的反向延长线交∠ABC的平分线于点P．知道下列哪个条件①∠ABC+∠ACB；②∠A；③∠NCD -∠ABP；④∠ABC的值，不能求∠P大小的是()A.①B.②C.③D.④【答案】D【分析】本题考查三角形外角的性质与内角和定理，根据三角形外角的性质及角平分线的定义可得∠P=∠NCD-∠ABP，可判断③，再利用三角形外角的性质得到∠A=∠NCB-∠ABC，等量代换可判断②，根据三角形内角和定理及等量代换可判断①和④，即可求解．【详解】解：∵CD是∠BCN的平分线，CD的反向延长线交∠ABC的平分线于点P，∴∠NCD=∠BCD，∠ABP=∠CBP，∵∠P=∠DCB-∠CBP，∴∠P=∠NCD-∠ABP，∴③能求出∠P的大小；∵∠A=∠NCB-∠ABC=2∠NCD-∠ABP，∠P=∠NCD-∠ABP∴∠P=12∠A，∴②能求出∠P的大小；∵∠ABC+∠ACB=180°-∠A，∴∠A=180°-∠ABC+∠ACB∵∠P=12∠A，∴∠P=12180°-∠ABC+∠ACB=90°-12∠ABC+∠ACB，∴①能求出∠P的大小，④不能求出∠P的大小；故选：D．30.(23-24八年级·四川遂宁·开学考试)如图，点D为△ABC边BC的延长线上一点，若∠A:∠ABC=3:4，∠ACD=140°，∠ABC的角平分线与∠ACD的角平分线交于点M，则∠M=度．【答案】30【分析】本题考查了三角形的外角定理，与角平分线有关的计算．解题的关键是掌握三角形的一个外角等于与它不相邻的两个内角之和，以及角平分线的定义．先根据∠A:∠ABC=3:4，∠ACD=140°，求出∠ABC=80°，进而得出∠CBM=12∠ABC=40°,∠CDM=12∠ACD=70°，最后根据三角形的外角定理即可解答．【详解】解：∵∠ACD=140°，∴∠A+∠ABC=140°∵∠A:∠ABC=3:4，∴∠ABC=140°×43+4=80°，∵BM平分∠ABC，CM平分∠ACD，∴∠CBM=12∠ABC=40°,∠CDM=12∠ACD=70°，∴∠M=∠DCM-∠CBM=30°，故答案为：30．31.(23-24八年级·四川眉山·开学考试)如图，∠ABC=∠ACB，AD、BD、CD分别平分∠EAC、∠ABC和∠ACF．以下结论：①AD∥BC；②∠ACB=2∠ADB；③DB平分∠ADC；④∠ADC=90°-∠ABD．其中正确的结论有．(填序号)【答案】①②④【分析】证明∠EAD=∠DAC，由三角形外角得∠EAC=∠ACB+∠ABC，且∠ABC=∠ACB，得出∠EAD =∠ABC，再由平行线的判定即可判断出①是否正确；由AD∥BC，得出∠ADB=∠DBC，再由BD平分∠ABC，所以∠ABD=∠DBC，∠ABC=2∠ADB，进而可判断出②是否正确；假设DB平分∠ADC，推出与题干不符的结论，进而可判断出③是否正确，由∠ADC+∠CAD+∠ACD=180°，利用角的关系得∠ADC+∠CAD+∠ACD=∠ADC+2∠ABD+∠ADC=2∠ADC+2∠ABD=180°，进而可判断出④是否正确；【详解】解：①∵AD平分△ABC的外角∠EAC，∴∠EAD=∠DAC，∵∠EAC=∠ACB+∠ABC，且∠ABC=∠ACB，∴∠EAD=∠ABC，∴AD∥BC，故①正确；②由(1)可知AD∥BC，∴∠ADB=∠DBC，∵BD平分∠ABC，∴∠ABD=∠DBC，∴∠ABC=2∠ADB，∵∠ABC=∠ACB，∴∠ACB=2∠ADB，故②正确；③若DB 平分∠ADC ，∴∠ADB =∠CDB ，∵∠ADB =∠DBC =∠ABD ，∴∠ADB =∠DBC =∠ABD =∠CDB ，∴∠ABC =∠ADC ，与题干条件矛盾．故③错误.④在△ADC 中，∠ADC +∠CAD +∠ACD =180°，∵CD 平分△ABC 的外角∠ACF ，∴∠ACD =∠DCF ，∵AD ∥BC ，∴∠ADC =∠DCF ，∠ADB =∠DBC ，∠CAD =∠ACB ，∴∠ACD =∠ADC ，∠CAD =∠ACB =∠ABC =2∠ABD ，∴∠ADC +∠CAD +∠ACD =∠ADC +2∠ABD +∠ADC =2∠ADC +2∠ABD =180°，∴∠ADC +∠ABD =90°，∴∠ADC =90°-∠ABD ，故④正确；故答案为：①②④【点睛】此题考查三角形的外角性质，平行线的判定与性质，三角形的内角和定理的应用，解题关键在于掌握外角性质.32.(23-24八年级·河南开封·期末)如图，在△ABC 中，∠A =48°，△ABC 的内角∠ABC 与外角∠ACD 的平分线相交于点A 1，得到∠A 1；∠A 1BC 与∠A 1CD 的平分线相交于点A 2，得到∠A 2；⋯⋯按此规律继续下去，∠A n -1BC 与∠A n -1CD 的平分线相交于点A n ，要使∠A n 的度数为整数，则n 的最大值为()A.3B.4C.5D.6【答案】B 【分析】本题主要考查了三角形的内角和，三角形的外角定理，角平分线的定义，熟练掌握三角形内角和是解题的关键．先根据外角和定理得出∠ACD =∠ABC +∠A ，再根据题意总结出规律，∠A n =12n ∠A 即可得到答案．【详解】解：∵∠ACD 是△ABC 的一个外角，∴∠ACD =∠ABC +∠A ，∵△ABC 的内角∠ABC 与外角∠ACD 的平分线相交于点A 1，得到∠A 1；∠A 1BC 与∠A 1CD 的平分线相交于点A 2，∴∠A 1BC =12∠ABC ，∠A 1CA =12∠ACD ，∴∠A 1=180°-∠A 1BC -∠A 1CB=180°-12∠ABC -(∠ACB +∠A 1CA )=180°-12∠ABC -∠ACB -12∠ACD =180°-12∠ABC -∠ACB -12(∠ABC +∠A )。

三角形中几种常见模型

三角形中几种常见模型在数学的世界里，三角形是一个基础且重要的图形。

它不仅在几何领域中有着广泛的应用，在实际生活中也随处可见其身影。

接下来，咱们就一起来探讨一下三角形中几种常见的模型。

首先，咱们来说说“等腰三角形模型”。

等腰三角形，顾名思义，就是有两条边长度相等的三角形。

这两条相等的边被称为“腰”，另一条边则被称为“底边”。

等腰三角形有一个非常重要的性质，那就是“等边对等角”，也就是说，两条相等的边所对的角也是相等的。

同时，它的“三线合一”性质也很关键。

所谓“三线合一”，指的是等腰三角形顶角的平分线、底边上的中线以及底边上的高相互重合。

这个性质在解决很多与等腰三角形相关的问题时，都能发挥巨大的作用。

比如说，在一个等腰三角形 ABC 中，AB ＝ AC，如果已知顶角 A 的度数，那么通过“等边对等角”就能很容易求出底角 B 和 C 的度数。

又比如，如果知道底边 BC 的长度和底角 B 的度数，那么通过三角函数就能求出腰的长度。

接下来，再讲讲“等边三角形模型”。

等边三角形是一种特殊的等腰三角形，它的三条边长度都相等，三个角的度数也都是 60°。

由于其具有高度的对称性，所以在很多数学问题中，等边三角形往往能带来简洁而美妙的解法。

在计算等边三角形的面积时，我们可以使用公式：面积＝√3/4 ×边长²。

而且，等边三角形在镶嵌问题中也经常出现，因为它能够完美地拼接在一起，不留任何空隙。

然后，是“直角三角形模型”。

直角三角形有一个角是 90°，这个角所对的边被称为斜边，其余两条边被称为直角边。

直角三角形最著名的定理就是勾股定理：直角边 a、b 的平方和等于斜边 c 的平方，即 a²＋ b²＝ c²。

这个定理在解决直角三角形的边长计算问题时，简直是一把万能钥匙。

比如，已知一个直角三角形的两条直角边长度分别为 3 和 4，那么通过勾股定理就能迅速求出斜边的长度为 5。

初中数学三角形全等常用几何模型及构造方法大全初二

初二数学三角形全等常用几何模型及构造方法大全掌握它轻松搞定全等题！全等是初中数学中非常重要的内容，一般会在压轴题中进行考察，而掌握几何模型能够为考试节省不少时间，这次整理了常用的各大模型，一定要认真掌握~全等变换类型：（一）平移全等：平行等线段（平行四边形）（二）对称全等模型：角平分线或垂直或半角1：角平分线模型；2：对称半角模型；（三）旋转全等模型：相邻等线段绕公共顶点旋转1.旋转半角模型2.自旋转模型3.共旋转模型4.中点旋转如图，在△ABC的边上取两点D、E，且BD=CE，求证：AB+AC>AD+AE分析：将△ACE平移使EC与BD重合。

B\D，上方交点，左右两个三角形，两边和大于第三边！1：角平分线模型：说明：以角平分线为轴在角两边进行截长补短或者作边的垂线，形成对称全等。

两边进行边或者角的等量代换，产生联系。

垂直也可以做为轴进行对称全等。

2：对称半角模型说明：上图依次是45°、30°、 45+ °、对称（翻折）15°+30°直角三角形对称（翻折） 30+60+90直角三角形对称（翻折）翻折成正方形或者等腰直角三角形、等边三角形、对称全等。

1.半角：有一个角含1/2角及相邻线段2.自旋转：有一对相邻等线段，需要构造旋转全等3.共旋转：有两对相邻等线段，直接寻找旋转全等（共顶点）4.中点旋转：倍长中点相关线段转换成旋转全等问题（专题七）1、旋转半角模型说明：旋转半角的特征是相邻等线段所成角含一个二分之一角，通过旋转将另外两个和为二分之一的角拼接在一起，成对称全等。

2、自旋转模型构造方法：遇60度旋60度，造等边三角形遇90度旋90度，造等腰直角遇等腰旋顶点，造旋转全等遇中点旋180度，造中心对称3、共旋转模型说明：旋转中所成的全等三角形，第三边所成的角是一个经常考察的内容。

通过“8”字模型可以证明。

（接上------共旋转模型）模型变形说明：模型变形主要是两个正多边形或者等腰三角形的夹角的变化，另外是等腰直角三角形与正方形混用。

浙教版八年级三角形中几种模型

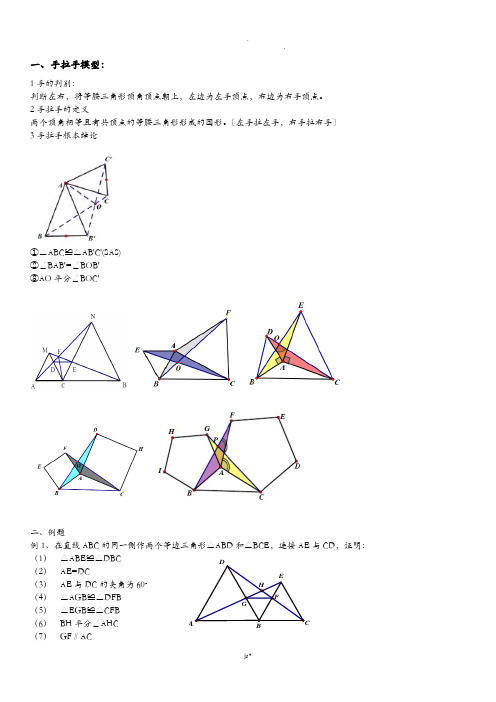
一、手拉手模型：1手的判别：判断左右，将等腰三角形顶角顶点朝上，左边为左手顶点，右边为右手顶点。

2手拉手的定义两个顶角相等且有共顶点的等腰三角形形成的图形。

〔左手拉左手，右手拉右手〕3手拉手根本结论①△ABC≌△AB'C'(SAS)②∠BAB'=∠BOB'③AO平分∠BOC'二、例题例1、在直线ABC的同一侧作两个等边三角形△ABD和△BCE，连接AE与CD，证明：（1）△ABE≌△DBC（2）AE=DC（3）AE与DC的夹角为60。

（4）△AGB≌△DFB （5）△EGB≌△CFB （6）BH平分∠AHC（7）GF∥ACHFGE D变式练习1、如果两个等边三角形△ABD 和△BCE ，连接AE 与CD ，证明：（1） △ABE ≌△DBC（2） AE=DC（3） AE 与DC 的夹角为60。

（4） AE 与DC 的交点设为H,BH 平分∠AHC变式练习2：如果两个等边三角形△ABD 和△BCE ，连接AE 与CD ，证明：（1） △ABE ≌△DBC（2） AE=DC（3） AE 与DC 的夹角为60。

〔4〕AE 与DC 的交点设为H,BH 平分∠AHC变式训练3：两个等腰三角形ABD 与BCE ，其中AB=BD,CB=EB,∠ABD=∠CBE=a连接AE 与CD.问〔1〕△ABE ≌△DBC 是否成立？〔2〕AE 是否与CD 相等？〔3〕AE 与CD 之间的夹角为多少度？〔4〕HB 是否平分∠AHC ？例2：如图，两个正方形ABCD 和DEFG ，连接AG 与CE ，二者相交于H 问：〔1〕△ADG ≌△CDE 是否成立？〔2〕AG 是否与CE 相等？〔3〕AG 与CE 之间的夹角为多少度？〔4〕HD 是否平分∠AHE ？例3：如图两个等腰直角三角形ADC 与EDG ，连接AG,CE,二者相交于H. 问〔1〕△ADG ≌△CDE 是否成立？〔2〕AG 是否与CE 相等？〔3〕AG 与CE 之间的夹角为多少度？〔4〕HD 是否平分∠AHE ？二、半角模型1、条件：.180210=+=γθβα且2、思路：①截长补短 ②旋转例1、在正方形ABCD 中，假设M 、N 分别在边BC 、CD 上移动，且满足MN=BM +DN ，求证：①.∠MAN=45 ②.ABC CMN 2=∆..③.AM、AN分别平分∠BMN和∠DNM.例2拓展：在正方形ABCD中，∠MAN=45，假设M、N分别在边CB、DC的延长线上移动，①.试探究线段MN、BM 、DN之间的数量关系.②.求证：AB=AH.例3.在四边形ABCD中，∠B+∠D=180，AB=AD，假设E、F分别在边BC、CD上，且满足EF=BE +DF.求证：.21BAD EAF∠=∠练习稳固1：〔1〕如图1，在正方形ABCD中，E、F分别是BC、CD上的点，且∠EAF＝45°，试判断BE、DF与EF 三条线段之间的数量关系，直接写出判断结果：；〔2〕如图2，假设把(1)问中的条件变为“在四边形ABCD 中，AB ＝AD ，∠B ＋∠D ＝180°，E 、F 分别是边BC 、CD 上的点，且∠EAF=21∠BAD 〞，那么〔1〕问中的结论是否仍然成立？假设成立，请给出证明，假设不成立，请说明理由；〔3〕在〔2〕问中，假设将△AE F 绕点A 逆时针旋转，当点分别E 、F 运动到BC 、CD 延长线上时，如图3所示，其它条件不变，那么〔1〕问中的结论是否发生变化？假设变化，请给出结论并予以证明..练习稳固2：：正方形ABCD 中，45MAN ∠=，绕点A 顺时针旋转，它的两边分别交CB 、DC 〔或它们的延长线〕于点M 、N ．〔1〕如图1，当MAN ∠绕点A 旋转到BM DN =时，有BM DN MN +=．当MAN ∠绕点A 旋转到BM DN ≠时，如图2，请问图1中的结论还是否成立？如果成立，请给予证明，如果不成立，请说明理由；〔2〕当MAN ∠绕点A 旋转到如图3的位置时，线段BM DN ，和MN 之间有怎样的等量关系？请写出你的猜测，并证明．NMDCBANMCDBANM D CBA练习稳固3：在等边ABC ∆的两边AB ，AC 所在直线上分别有两点M N D ，，为ABC ∆外一点，且60MDN ∠=︒，120BDC ∠=︒，BD CD =，探究：当点M N ，分别爱直线AB AC ，上移动时，BM BN MN ，，之间的数量关系及AMN ∆的周长Q 与等边ABC ∆的周长L 的关系．图①M ND CBA 图②MND CBAN图③MD CB A〔1〕如图①，当点M N ，在边AB AC ，上，且DM DN =时，BM NC MN ，，之间的数量关系式_________；此时QL=__________ 〔2〕如图②，当点M N ，在边AB AC ，上，且DM DN ≠时，猜测(1)问的两个结论还成立吗？写出你的猜测并加以证明；〔3〕如图③，当点M N ，分别在边AB CA ，的延长线上时，假设AN x =，那么Q =_________(用x L ，表示)练习稳固4：如图，在正方形ABCD 中，∠MAN =45°，连接BD 与AM ，AN 分别交于E 、F 两点。

浙教版八年级数学上册全等三角形之手拉手模型、倍长中线-截长补短法

手拉手模型要点一：手拉手模型特点：由两个等顶角的等腰三角形所组成，并且顶角的顶点为公共顶点结论：（1）△ABD≌△AEC（2）∠α+∠BOC=180°ABD BCE与AE与C D例1.如图在直线AB C的同一侧作两个等边三角形ABE DBC（1），连结，证明DC(2)AE(3)(4)(5)(6)B H 平分AHC (7)GFABD BCE与AE C D与变式精练1：如图两个等边三角形ABE DBCDC ，连结，证明（1）60（3）（4）AE与D C的交点设为H,BH 平分AH CABD BCE与AE C D与变式精练2：如图两个等边三角形ABE DBC证明（1），连结，DC(2）AE60AE(4）AE与D C的交点设为H,BH 平分AH C例 2：如图，两个正方形 AB C D 与 D EF G ,连结 AG ,CE,二者相交于点 HAD G CDE 问：（1）（2） A G 是否与C E 相等？（3） A G 与CE 之间的夹角为多少度？（4） H D 是否平分AHE是否成立？？例 3：如图两个等腰直角三角形 A D C 与 E D G ，连结 A G ,CE,二者相交于点 HAD G CDE 问：（1）（2） A G 是否与C E 相等？（3） A G 与CE 之间的夹角为多少度？（4） H D 是否平分AHE是否成立？？ABD BCE与AB B D CB E B,AB D C BE AE例4：两个等腰三角形问：（1），其中,,连结与C D，ABE DBC是否成立？（2）AE是否与C D相等？（3）AE与C D之间的夹角为多少度？（4）H B 是否平分AH C？例5：如图，点A.B.C在同一条直线上，分别以AB、BC为边在直线AC的同侧作等边三角形△ABD、△BCE.连接AE、DC，AE与DC所在直线相交于F，连接FB.判断线段FB、FE与FC之间的数量关系，并证明你的结论。

八年级上册数学三角形五种基本模型

八年级上册数学学科包含了各种重要概念和技能，其中三角形的五种基本模型是其中的重要一部分。

在本篇文章中，我们将深入探讨这五种基本模型，包括它们的性质、特点以及在实际问题中的应用。

通过对这些内容的深入讨论，我们可以更好地理解三角形的基本知识，并且可以在解决实际问题时更加灵活地应用这些知识。

让我们来回顾一下三角形的基本概念。

三角形是由三条边和三个角组成的多边形，其中最基本的三角形模型包括等边三角形、等腰三角形、直角三角形、普通三角形和直角等腰三角形。

这五种基本模型在数学中具有重要的地位，不仅在几何学中有着广泛的应用，而且在实际问题中也经常出现。

我们首先来讨论等边三角形。

等边三角形是指三条边长度均相等的三角形。

它有着特殊的性质，例如它的三个内角均相等，每个角都是60度，而且它的高度、中位线和重心重合于同一点。

在实际问题中，等边三角形常常出现在建筑、工程等领域中，例如在建筑设计中，我们常常会使用等边三角形来布局房屋的基础结构，利用它的稳定性来确保建筑物的安全性。

接下来，我们来讨论等腰三角形。

等腰三角形是指至少有两条边相等的三角形。

它也有着特殊的性质，例如它的两个底角相等，而顶角则不一定相等，而且它的高度、中位线和重心也有着特殊的关系。

在实际问题中，等腰三角形也经常出现，在日常生活中，我们可以用等腰三角形的性质来设计各种图案和装饰，从而增加空间的美感和艺术性。

第三个基本模型是直角三角形。

直角三角形是指其中一个角为90度的三角形。

它有着独特的性质，例如勾股定理的适用以及三条边的关系。

直角三角形在实际问题中有着广泛的应用，例如在测量、地理勘测和导航等领域中，我们常常会用到直角三角形的性质来解决实际问题。

接下来是普通三角形，即没有边相等的三角形。

普通三角形具有较为普遍的性质，例如它的三个内角的和为180度，而且它也有着丰富的性质和定理，如三角形内角和定理、外角定理等。

在实际问题中，普通三角形也经常出现，例如在地理测量、建筑设计和工程建设等领域中，我们经常需要利用普通三角形的性质来解决各种实际问题。

浙教版八年级上册 1.31三角形的中的模型

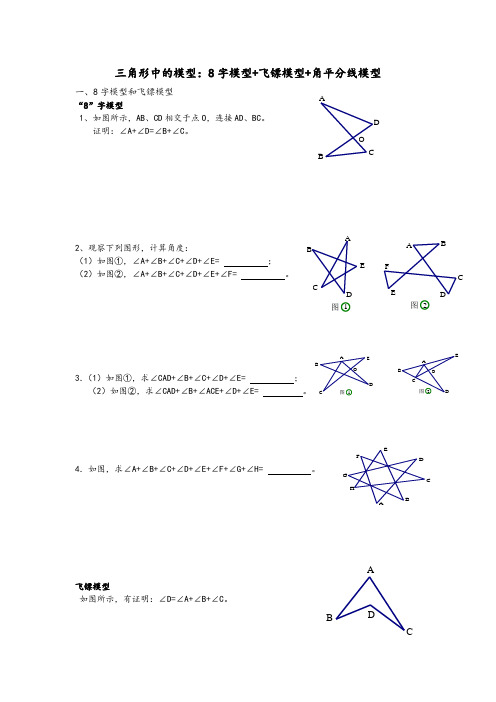
三角形中的模型：8字模型+飞镖模型+角平分线模型一、8字模型和飞镖模型 “8”字模型1、如图所示，AB 、CD 相交于点O ，连接AD 、BC 。

证明：∠A+∠D=∠B+∠C 。

2、观察下列图形，计算角度：（1）如图①，∠A+∠B+∠C+∠D+∠E= ；（2）如图②，∠A+∠B+∠C+∠D+∠E+∠F= 。

3．（1）如图①，求∠CAD+∠B+∠C+∠D+∠E= ；（2）如图②，求∠CAD+∠B+∠ACE+∠D+∠E= 。

4．如图，求∠A+∠B+∠C+∠D+∠E+∠F+∠G+∠H= 。

飞镖模型如图所示，有证明：∠D=∠A+∠B+∠C 。

图12图E A B C D E F DCBAO O 图12图E AB CD EDCBA HGEF DCBAD CB A OD C B A1、如下图，求α∠的度数．2、如图，求∠A+∠B+∠C+∠D+∠E+∠F= ；3、如下图，求A B C D ∠+∠+∠+∠= ．二、应用8字模型和飞镖模型1、如图所示，已知EGF BEG CFG ∠=∠+∠，试探索A B C D ∠+∠+∠+∠的度数．2、如下图，已知133α∠=︒，83β∠=︒，求A B C D ∠+∠+∠+∠= ．3、如图，点E 和D 分别在△ABC 的边BA 和CA 的延长线上，CF ，EF 分别平分∠ACB 和∠AED ．若∠B=70°，∠D=40°，求∠F 的度数．4、如图，BE ，CE 分别平分∠ABD ，∠ACD ，且交AC 于点M ，交BD 于点N ，试探究∠A ，∠D ，∠E 之间的数量关系，并说明理由．αDC BA 73︒30︒37︒120︒100︒DCBAO135E FDC B AD CBAβα5、如图，BP ，CP 分别平分ABD ∠，ACD ∠，求证：2A D P ∠+∠=∠．模型三：共顶点角平分线与高线夹角模型条件：△ABC 中，A H 是高、AD 是∠BAC 的角平分线。

浙教版初二(上)数学第三讲_全等三角形的相关模型

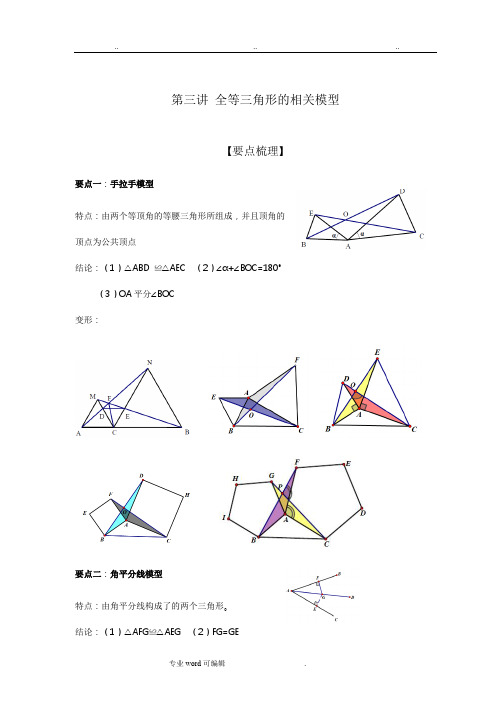
第三讲全等三角形的相关模型【要点梳理】要点一：手拉手模型特点：由两个等顶角的等腰三角形所组成，并且顶角的顶点为公共顶点结论：（1）△ABD ≌△AEC （2）∠α+∠BOC=180°（3）OA平分∠BOC变形：要点二：角平分线模型特点：由角平分线构成了的两个三角形。

结论：（1）△AFG≌△AEG （2）FG=GE变形：要点三：半角模型特点：结论：（1）MN=BM+DN （2）△CMN的周长=2AB （3）AM、AN分别平分∠BMN和∠DNM变形：要点四：等腰直角三角形模型1.在斜边上任取一点的旋转全等操作过程：（1）将△ABD逆时针旋转90°，使△ACM≌△ABD，从而推出△ADM为等腰直角三角形。

（2）过点C作BC⊥MC，连AM导出上述结论2.定点是斜边中点，动点在两直角边上滚动的旋转全等操作过程：连AD.（1）使BF=AE（或AF=CE），导出△BDF≌△ADE（2）使∠EDF+∠BAC=180°，导出△BDF≌△ADE3.将等腰直角三角形补全为正方形，如下图：要点五：双垂直模型特点：图形中包含两条垂线，且有一组边或角相等。

结论：若AD=BD,则BH=AC变形：∠1=∠2，则AE=AF ∠1=∠2，∠BAP=∠DAP，则AE=AF，AP⊥CF要点六：三垂直模型特点：图形中包含三条垂线，且有一组边。

结论：（1）△ABE≌△BCD （2）ED=AE-CD变形：要点七：全等三角形问题中常见的辅助线的作法1.遇到等腰三角形，可作底边上的高，利用“三线合一”的性质解题，思维模式是全等变换中的“对折”法构造全等三角形。

2.遇到三角形的中线，倍长中线，使延长线段与原中线长相等，构造全等三角形，利用的思维模式是全等变换中的“旋转”法构造全等三角形。

3.遇到角平分线：（1）可以自角平分线上的某一点向角的两边作垂线；（2）可以在角平分线上的一点作该角平分线的垂线与角的两边相交，形成一对全等三角形；（3）可以在该角的两边上，距离角的顶点相等长度的位置上截取二点，然后从这两点再向角平分线上的某点作边线，构造一对全等三角形。

全等模型：一线三等角(K字)2023-2024学年八年级数学上册常见几何模型解读(浙教版)解析版

全等模型--一线三等角（K 字）模型全等三角形在中考数学几何模块中占据着重要地位，也是学生必须掌握的一块内容，本专题就全等三角形中的重要模型（一线三等角（K 字）模型）进行梳理及对应试题分析，方便掌握。

模型1.一线三等角（K 型图）模型（同侧型）【模型解读】在某条直线上有三个角相等，利用平角为180°与三角形内角和为180°，证得两个三角形全等。

【常见模型及证法】同侧型一线三等角（常见）：锐角一线三等角直角一线三等角（“K 型图”）钝角一线三等角条件：A CED B ∠=∠=∠+ CE=DE证明思路：,A B C BED ∠=∠∠=∠+任一边相等BED ACE ⇒≅ ，已知：在ABC 中，【答案】（1）见解析；（2）成立，见解析【分析】（1）根据AAS 可证明ADB CEA ≌，可得AE BD AD CE ==，，可得DE BD CE =+．（2）由已知条件可知180BAD CAE α∠+∠=︒−，180DBA BAD α∠+∠=︒−，可得DBA CAE ∠=∠，结合条件可证明ADB CEA ≌，同（1）可得出结论．【详解】证明：（1）如图1，∵BD ⊥直线m ，CE ⊥直线m ，∴90BDA CEA ∠=∠=︒，∵90BAC ∠=︒，∴90BAD CAE ∠+∠=︒，∵90BAD ABD ∠+∠=︒，∴CAE ABD ∠=∠，在ADB 和CEA 中，BDA CEA CAE ABDAB AC ∠=∠⎧⎪∠=∠⎨⎪=⎩∴(AAS)ADB CEA ≌△△，∴AE BD AD CE ==，，∴DE AE AD BD CE =+=+；（2）如图2，∵BDA BAC α∠=∠=，∴180DBA BAD BAD CAE ∠∠∠∠α+=+=︒−，∴DBA CAE ∠=∠，在ADB 和CEA 中，BDA CEA CAE ABDAB AC ∠=∠⎧⎪∠=∠⎨⎪=⎩∴(AAS)ADB CEA ≌△△，∴AE BD AD CE ==，，∴DE AE AD BD CE =+=+．【点睛】本题主要考查了全等三角形的判定和性质，由条件证明三角形全等得到AE BD AD CE ==，是解题的关键．例2．（2023春·上海·七年级专题练习）在直线m 上依次取互不重合的三个点,,D A E ，在直线m 上方有AB AC =，且满足BDA AEC BAC α∠=∠=∠=．(1)如图1，当90α=︒时，猜想线段,,DE BD CE 之间的数量关系是____________；(2)如图2，当0180α<<︒时，问题（1）中结论是否仍然成立？如成立，请你给出证明；若不成立，请说明理由；(3)应用：如图3，在ABC 中，BAC ∠是钝角，AB AC =，,BAD CAE BDA AEC BAC ∠<∠∠=∠=∠，直线m 与CB 的延长线交于点F ，若3BC FB =，ABC 的面积是12，求FBD 与ACE △的面积之和．【答案】(1)DE ＝BD+CE(2)DE ＝BD+CE 仍然成立，理由见解析(3)△FBD 与△ACE 的面积之和为4【分析】（1）由∠BDA ＝∠BAC ＝∠AEC ＝90°得到∠BAD+∠EAC ＝∠BAD+∠DBA ＝90°，进而得到∠DBA ＝∠EAC ，然后结合AB ＝AC 得证△DBA ≌△EAC ，最后得到DE ＝BD+CE ；（2）由∠BDA ＝∠BAC ＝∠AEC ＝α得到∠BAD+∠EAC ＝∠BAD+∠DBA ＝180°﹣α，进而得到∠DBA ＝∠EAC ，然后结合AB ＝AC 得证△DBA ≌△EAC ，最后得到DE ＝BD+CE ；（3）由∠BAD ＞∠CAE ，∠BDA ＝∠AEC ＝∠BAC ，得出∠CAE ＝∠ABD ，由AAS 证得△ADB ≌△CAE ，得出S △ABD ＝S △CEA ，再由不同底等高的两个三角形的面积之比等于底的比，得出S △ABF 即可得出结果．【详解】（1）解：DE ＝BD+CE ∵∠BDA ＝∠BAC ＝∠AEC ＝90°，∴∠BAD+∠EAC ＝∠BAD+∠DBA ＝90°，∴∠DBA ＝∠EAC ，∵AB ＝AC ，∴△DBA ≌△EAC （AAS ），∴AD ＝CE ，BD ＝AE ，∴DE ＝AD+AE ＝BD+CE ，故答案为：DE ＝BD+CE ．（2）DE ＝BD+CE 仍然成立，理由如下，∵∠BDA ＝∠BAC ＝∠AEC ＝α，∴∠BAD+∠EAC ＝∠BAD+∠DBA ＝180°﹣α，∴∠DBA ＝∠EAC ，∵AB ＝AC ，∴△DBA ≌△EAC （AAS ），∴BD ＝AE ，AD ＝CE ，∴DE ＝AD+AE ＝BD+CE ；（3）解：∵∠BAD ＜∠CAE ，∠BDA ＝∠AEC ＝∠BAC ，∴∠CAE ＝∠ABD ，在△ABD 和△CAE 中，ABD CAE BDA CEA AB AC ∠=∠⎧⎪∠=∠⎨⎪=⎩，∴△ABD ≌△CAE （AAS ），∴S △ABD ＝S △CAE ，设△ABC 的底边BC 上的高为h ，则△ABF 的底边BF 上的高为h ，∴S △ABC ＝12BC•h ＝12，S △ABF ＝12BF•h ，∵BC ＝3BF ，∴S △ABF ＝4，∵S △ABF ＝S △BDF+S △ABD ＝S △FBD+S △ACE ＝4，∴△FBD 与△ACE 的面积之和为4．【点睛】本题考查了全等三角形的判定与性质、直角三角形的性质，三角形的面积，解题的关键是熟练掌握全等三角形的判定与性质．【答案】（1）△ACP 与△BPQ 全等，理由见解析；（2）PC ⊥PQ ，证明见解析；（3）存在，当t ＝1s ，x ＝2cm/s或t ＝94s ，x ＝289cm/s 时，△ACP 与△BPQ 全等．【分析】（1）利用SAS 定理证明ACP BPQ ∆≅∆；（2）根据全等三角形的性质判断线段PC 和线段PQ 的位置关系；（3）分ACP BPQ ∆≅∆，ACP BQP ∆≅∆两种情况，根据全等三角形的性质列式计算．【详解】（1）△ACP 与△BPQ 全等，理由如下：当t ＝1时，AP ＝BQ ＝2，则BP ＝9﹣2＝7，∴BP ＝AC ，又∵∠A ＝∠B ＝90°，在△ACP 和△BPQ 中，AP BQ A B CA PB =⎧⎪∠=∠⎨⎪=⎩，∴△ACP ≌△BPQ （SAS ）；（2）PC ⊥PQ ，证明：∵△ACP ≌△BPQ ，∴∠ACP ＝∠BPQ ，∴∠APC+∠BPQ ＝∠APC+∠ACP ＝90°．∴∠CPQ ＝90°，即线段PC 与线段PQ 垂直；（3）①若△ACP ≌△BPQ ，则AC ＝BP ，AP ＝BQ ，∴9﹣2t ＝7，解得，t ＝1（s ），则x ＝2（cm/s ）；②若△ACP ≌△BQP ，则AC ＝BQ ，AP ＝BP ，则2t ＝12×9，解得，t ＝94（s ），则x ＝7÷94＝289（cm/s ），故当t ＝1s ，x ＝2cm/s 或t ＝94s ，x ＝289cm/s 时，△ACP 与△BPQ 全等．【点睛】本题考查的是全等三角形的判定与性质，掌握全等三角形的判定定理和性质定理、注意分类讨论思想的灵活运用是解题的关键．例4．（2022·贵州铜仁·三模）（1）探索发现：如图1，已知Rt ABC 中，90ACB ∠=︒，AC BC =，直线l 过点C ，过点A 作AD l ⊥，过点B 作BE l ⊥，垂足分别为D 、E ．求证：CD BE =．（2）迁移应用：如图2，将一块等腰直角的三角板MON 放在平面直角坐标系内，三角板的一个锐角的顶点与坐标原点O 重合，另两个顶点均落在第一象限内，已知点N 的坐标为()4,2，求点M 的坐标．（3）拓展应用：如图3，在平面直角坐标系内，已知直线44y x =−+与y 轴交于点P ，与x 轴交于点Q ，将直线PQ 绕P 点沿逆时针方向旋转45︒后，所得的直线交x 轴于点R ．求点R 的坐标．【答案】（1）见详解；（2）点M 的坐标为（1，3）；（3）R （203，0）【分析】（1）先判断出∠ACB=∠ADC ，再判断出∠CAD=∠BCE ，进而判断出△ACD ≌△CBE ，即可得出结论；（2）过点M 作MF ⊥y 轴，垂足为F ，过点N 作NG ⊥MF ，判断出MF=NG ，OF=MG ，设M （m ，n ）列方程组求解，即可得出结论；（3）过点Q 作QS ⊥PQ ，交PR 于S ，过点S 作SH ⊥x 轴于H ，先求出OP=4，由y=0得x=1，进而得出Q （1，0），OQ=1，再判断出PQ=SQ ，即可判断出OH=5，SH=OQ=1，进而求出直线PR 的解析式，即可得出结论．【详解】（1）证明：∵∠ACB ＝90°，AD ⊥l ，∴∠ACB ＝∠ADC ．∵∠ACE ＝∠ADC+∠CAD ，∠ACE ＝∠ACB+∠BCE ，∴∠CAD ＝∠BCE ，∵∠ADC ＝∠CEB ＝90°，AC ＝BC ．∴△ACD ≌△CBE ，∴CD ＝BE ，（2）解：如图2，过点M 作MF ⊥y 轴，垂足为F ，过点N 作NG ⊥MF ，交FM 的延长线于G ，由已知得OM ＝ON ，且∠OMN ＝90°，∴由（1）得△OFM ≌△MGN ，∴MF ＝NG ，OF ＝MG ，设M （m ，n ），∴MF ＝m ，OF ＝n ，∴MG ＝n ，NG ＝m ，∵点N 的坐标为（4，2）∴42m n n m +=⎧⎨−=⎩解得13m n =⎧⎨=⎩∴点M 的坐标为（1，3）；（3）如图3，过点Q 作QS ⊥PQ ，交PR 于S ，过点S 作SH ⊥x 轴于H ，对于直线y ＝﹣4x+4，由x ＝0得y ＝4，∴P （0，4），∴OP ＝4，由y ＝0得x ＝1，∴Q （1，0），OQ ＝1，∵∠QPR ＝45°，∴∠PSQ ＝45°＝∠QPS ．∴PQ ＝SQ ．∴由（1）得SH ＝OQ ，QH ＝OP ．∴OH ＝OQ+QH ＝OQ+OP ＝4+1＝5，SH ＝OQ ＝1．∴S （5，1），设直线PR 为y ＝kx+b ，则451b k b =⎧⎨+=⎩，解得435b k =⎧⎪⎨=−⎪⎩．∴直线PR 为y ＝35-x+4．由y ＝0得，x ＝203，∴R （203，0）．【点睛】本题是一次函数综合题，主要考查了待定系数法，全等三角形的判定和性质，构造出全等三角形是解本题的关键．模型2.一线三等角（K 型图）模型（异侧型）【模型解读】在某条直线上有三个角相等，利用平角为180°与三角形内角和为180°，证得两个三角形全等。

浙教版八年级上册全等三角形的多种模型

OFECB A A F COBEDHABCDO EFG HDEC B A 全等三角形的多种模型题型一：手拉手模型“手拉手”数学模型：例1．如图，△ADC 与△EDC 都为等腰直角三角形，连接AG 、CE ，相交于点H ，问：（1）AG 与CE 是否相等？（2）AG 与CE 之间的夹角为多少度？例2．如图，直线AB 的同一侧作△ABD 和△BCE 都为等边三角形，连接AE 、CD ，二者交点为H 。

求证：（1）△ABE ≌△DBC ；（2）AE=DC ；（3）∠DHA=60°；（4）△AGB ≌△DFB ；（5）△EGB ≌△CFB ；（6）连接GF ，GF ∥AC ；（7）连接HB ，HB 平分∠AHC 。

例题精讲O H GA BC DO GFEC B A1.如图，等边三角形ABC ∆与等边DEC ∆共顶点于C 点．求证：AE BD =．2、如图，正方形BAFE 与正方形ACGD 共点于A ，连接BD 、CF ，求证：BD =CF 并求出∠DOH 的度数.3、如图，等边三角形ABE 与等边三角形AFC 共点于A ，连接BF 、CE ，求证：BF =CE 并求出∠EOB 的度数.4、如图，在△ABC 外面作正方形ABEF 与ACGH ，AD 为△ABC 的高，其反向延长线交FH 于M ，求证：(1)BH CF =;(2)MF MH =DECBA典题精练OHGDFECBA M EF HG D CBA题型二：垂直+角平分线模型模型介绍：(1)如图1：DA 平分∠EAF ，根据角平分线的性质，可得DE =DF ；DE ，DF 是两条常用的辅助线. (2)如图2：DA 平分∠EAF ，易得△ADF ≌△ADE ；DE 是一条常用的辅助线. (3)如图3：DA 平分∠EAF ，易得△ADF ≌△ADE ；这是角分线常构的一组全等.例1．如图，在△ABC 中，∠A =90°，AB =AC ，BD 是∠ABC 的平分线．求证：BC =AB +AD ．例2.在ABC △中，90∠=BAC °，⊥AD BC 于D ，BF 平分∠ABC 交AD 于E ，交AC 于F . 求证：AE=AF .1.如图，已知ABC △中，90ACB ∠=°，CD AB ⊥于D ，ABC ∠的角平分线BE 交CD 于G ，交AC 于E ，GF AB ∥交AC 于F ．求证：AF CG =．54321A BCDE F例题精讲典题精练54321G F E DC BA2、已知：如图，△ABC 中，∠ABC =45°，CD ⊥AB 于D ，BE 平分∠ABC ，且BE ⊥AC 于E ，与CD 相交于点F ，H 是BC 边的中点，连结DH 与BE 相交于点G 。

三角形中的八大经典模型(解析版)

三角形中的八大经典模型【八大题型】【题型1A字模型】【题型28字模型】【题型3双垂直模型】【题型4飞镖模型】【题型5风筝模型】【题型6两内角角平分线模型】【题型7两外角角平分线模型】【题型8内外角角平分线模型】【知识点1A字模型】【条件】△ADE与△ABC.【结论】∠AED+∠ADE=∠B+C.【证明】根据三角形内角和可得，∠AED+∠ADE=180°-∠A，∠B+C=180°-∠A，∴∠AED+∠ADE=∠B+C，得证.【题型1A字模型】1(2023春·湖北荆门·八年级校联考期末)如图，在△ABC中，∠C=70º，沿图中虚线截去∠C，则∠1+∠2 =()A.360ºB.250ºC.180ºD.140º【答案】B【分析】根据三角形内角和定理得出∠A+∠B=110°，进而利用四边形内角和定理得出答案．【详解】解：∵△ABC中，∠C=70°，∴∠A+∠B=180°-∠C，∴∠1+∠2=360°-110°=250°，故选：B．【点睛】本题主要考查了多边形内角和定理，根据题意得出∠A+∠B的度数是解题关键．1.(2023春·八年级单元测试)如图所示，∠DAE的两边上各有一点B,C，连接BC，求证∠DBC+∠ECB=180°+∠A．【答案】见解析【分析】根据三角形的外角等于与它不相邻的两个内角的和证明即可．【解析】解：∵∠DBC和∠ECB是△ABC的外角，∴∠DBC=∠A+∠ACB,∠ECB=∠A+∠ABC．又∵∠A+∠ABC+∠ACB=180°，∴∠DBC+∠ECB=∠A+∠ACB+∠ABC+∠A=180°+∠A．【点睛】本题主要考查三角形外角的性质，熟知三角形的外角等于与它不相邻的两个内角的和是解题的关键．2.(2023春•常州期中)如图，△ABC中，∠B=68°，∠A比∠C大28°，点D、E分别在AB、BC上．连接DE，∠DEB=42°．(1)求∠A的度数；(2)判断DE与AC之间的位置关系，并说明理由．【答案】(1)设∠C的度数为x，根据三角形的内角和列出方程解答即可；(2)根据平行线的判定解答即可．【解析】解：(1)设∠C的度数为x°，则∠A的度数为(x+28)°，△ABC中，∠A+∠B+∠C=180°，∠B=68°，可得：x+x+28+68=180，解得：x=42，所以∠C=42°，∠A=70°，(2)∵∠DEB=42°，∠C=42°，∴∠DEB=∠C，∴DE∥AC．3.(2023春·江苏泰州·八年级校联考期中)如图，已知∠A=40°，则∠1+∠2+∠3+∠4的度数为．【答案】280°【分析】根据三角形的内角和定理分别求得∠1+∠2，∠3+∠4，就可求得最后结果．【解析】∵∠A=40°，∴∠1+∠2=∠3+∠4=180°-∠A=140°，∴∠1+∠2+∠3+∠4=280°，故答案为280°．【点睛】本题考查了三角形内角和定理的运用，熟练掌握三角形内角和为180度是解题的关键．【知识点28字模型】【条件】AD、BC相交于点O.【结论】∠A+∠B=∠C+∠D.(上面两角之和等于下面两角之和)【证明】在△ABO中，由内角和定理：∠A+∠B+∠BOA=180°，在△CDO中，∠C+∠D+∠COD=180°，∴∠A+∠B+∠BOA=180°=∠C+∠D+∠COD，由对顶角相等：∠BOA=∠COD∴∠A+∠B=∠C+∠D，得证.【题型28字模型】1(2015-2016学年北京市怀柔区八年级上学期期末数学试卷(带解析))如图是由线段AB，CD，DF，BF，CA组成的平面图形，∠D=28°，则∠A+∠B+∠C+∠F的度数为()A.62°B.152°C.208°D.236°【答案】C【详解】∵如图可知∠BED=∠F+∠B，∠CGE=∠C+∠A，又∵∠BED=∠D+∠EGD，∴∠F+∠B=∠D+∠EGD，又∵∠CGE+∠EGD=180°，∴∠C+∠A+∠F+∠B-∠D=180°，又∵∠D=28°，∴∠A+∠B+∠C+∠F=180°+28°=208°，故选C．点睛：本题主要考查了三角形内角和定理即三角形外角与内角的关系，解答本题的关键是求出∠C+∠A +∠F+∠B-∠D=180°，此题难度不大．1.(2013-2014学年初中数学苏教版八年级上册第一章练习卷(带解析))如图，△ABC≌△ADE，且∠CAD=10°，∠B=∠D=25°，∠EAB=120°，求∠DFB和∠DGB的度数．【答案】90°；65°【分析】由ΔABC≅ΔADE，可得∠DAE=∠BAC=12(∠EAB-∠CAD)，根据三角形外角性质可得∠DFB=∠FAB+∠B，因为∠FAB=∠FAC+∠CAB，即可求得∠DFB的度数；根据三角形内角和定理可得∠DGB=∠DFB-∠D，即可得∠DGB的度数．【解析】解：∵ΔABC≅ΔADE，∴∠DAE=∠BAC=12(∠EAB-∠CAD)=12(120°-10°)=55°．∴∠DFB=∠FAB+∠B=∠FAC+∠CAB+∠B=10°+55°+25°=90°∠DGB=∠DFB-∠D=90°-25°=65°．综上所述：∠DFB=90°，∠DGB=65°．【点睛】本题主要考查三角形全等的性质，解题的关键是找到相应等量关系的角，做题时要结合图形进行思考．2.(2023·河北·统考中考真题)下图是可调躺椅示意图(数据如图)，AE与BD的交点为C，且∠A，∠B，∠E保持不变．为了舒适，需调整∠D的大小，使∠EFD=110°，则图中∠D应(填“增加”或“减少”)度．【答案】减少10【分析】先通过作辅助线利用三角形外角的性质得到∠EDF与∠D、∠E、∠DCE之间的关系，进行计算即可判断．【解析】解：∵∠A+∠B=50°+60°=110°，∴∠ACB=180°-110°=70°，∴∠DCE=70°，如图，连接CF并延长，∴∠DFM=∠D+∠DCF=20°+∠DCF，∠EFM=∠E+∠ECF=30°+∠ECF，∴∠EFD=∠DFM+∠EFM=20°+∠DCF+30°+∠ECF=50°+∠DCE=50°+70°=120°，要使∠EFD=110°，则∠EFD减少了10°，若只调整∠D的大小，由∠EFD=∠DFM+∠EFM=∠D+∠DCF+∠E+∠ECF=∠D+∠E+∠ECD=∠D+30°+70°=∠D+100°，因此应将∠D减少10度；故答案为：①减少；②10．【点睛】本题考查了三角形外角的性质，同时涉及到了三角形的内角和与对顶角相等的知识；解决本题的关键是理解题意，读懂图形，找出图形中各角之间的关系以及牢记公式建立等式求出所需的角，本题蕴含了数形结合的思想方法．3.(2023春·八年级期末)(1)如图①，求∠A+∠B+∠C+∠D+∠E+∠F的度数；(2)如图②，求∠A+∠B+∠C+∠D+∠E+∠F+∠G+∠H的度数；(3)如图③，求∠A+∠B+∠C+∠D+∠E+∠F+∠G的度数．【答案】(1)360°；(2)720°；(3)540°【分析】(1)连接AD，根据三角形的内角和定理得∠B+∠C=∠BAD+∠CDA，进而将问题转化为求四边形ADEF的内角和，(2)与(1)方法相同转化为求六边形ABCDEF的内角和，(3)使用上述方法，转化为求五边形ABCDE的内角和．【解析】解：(1)如图①，连接AD，由三角形的内角和定理得，∠B+∠C=∠BAD+∠CDA，∴∠BAF+∠B+∠C+∠CDE+∠E+∠F=∠BAF+∠BAD+∠CDA+∠D+∠E+∠F即四边形ADEF的内角和，四边形的内角和为360°，∴∠BAF+∠B+∠C+∠CDE+∠E+∠F=360°，(2)如图②，由(1)方法可得：∠BAH+∠B+∠C+∠D+∠E+∠EFG+∠G+∠H的度数等于六边形ABCDEF的内角和，∴∠BAH+∠B+∠C+∠D+∠E+∠EFG+∠G+∠H=(6-2)×180°=720°，(3)如图③，根据(1)的方法得，∠F+∠G=∠GAE+∠FEA，∠BAG+∠B+∠C+∠D+∠DEF+∠F+∠G的度数等于五边形ABCDE的内角和，∴∠BAG+∠B+∠C+∠D+∠DEF+∠F+∠G=(5-2)×180°=540°，【点睛】本题考查三角形的内角和、多边形的内角和的计算方法，适当的转化是解决问题的关键．【知识点3双垂直模型】【条件】∠B=∠D=∠ACE=90°.【结论】∠BAC=∠DCE，∠ACB=∠CED.【证明】∵∠B=∠D=∠ACE=90°；∴∠BAC+∠ACB=90°；又∠ECD+∠ACB=90°；∴∠BAC=∠DCE同理,∠ACB+∠DCE =90°，且∠CED+∠DCE =90°；∴∠ACB=∠CED，得证.【题型3双垂直模型】1(2023春·广东珠海·八年级校联考期末)如图1，线段AB⊥BC于点B，CD⊥BC于点C，点E在线段BC上，且AE⊥DE．(1)求证：∠EAB=∠CED；(2)如图2，AF、DF分别平分∠BAE和∠CDE，EH平分∠DEC交CD于点H，EH的反向延长线交AF于点G．①求证EG⊥AF；②求∠F的度数．【提示：三角形内角和等于180度】【答案】(1)证明见解析；(2)①证明见解析；②45°．【分析】(1)利用同角的余角相等即可证明；(2)①想办法证明∠EAG+∠AEG=90°即可解决问题；②利用∠DFA=∠DFM+∠AFM=12∠CDE+12∠EAB=12(∠CDE+∠EAB)即可解决问题.【详解】(1)∵AB⊥BC，∴∠EAB+∠AEB=90°，∵AE⊥ED，∴∠CED+∠AEB=90°，∴∠EAB=∠CED．(2)①∵AF平分∠BAE，∴∠EAG=12∠EAB，∵EH平分∠DEC，∴∠HED=12∠CED，∵∠EAB=∠CED，∴∠HED=∠EAG，∴∠HED+∠AEG=90°，∴∠EAG+∠AEG=90°，∴∠EGA=90°，∴EG⊥AF．②作FM∥CD，∵AB⊥BC，CD⊥BC，∴AB∥CD，∴FM∥AB，∴∠DFM=∠CDF=12∠CDE，∠AFM=∠FAB=12∠EAB，∵∠CDE+∠CED=90°，∴∠CDE+∠EAB=90°，∴∠DFA=∠DFM+∠AFM=12∠CDE+12∠EAB=12(∠CDE+∠EAB)=45°．【点睛】本题考查三角形内角和定理、平行线的性质、角平分线的定义等知识，解题的关键是学会添加常用辅助线，构造平行线解决问题，属于中考常考题型．1.(2023春·江苏泰州·八年级校考期中)如图，在△ABC中，∠ACB=90°，AE是角平分线，CD是高，AE、CD相交于点F，求证：∠CFE=∠CEF 请在以下的解题过程中的括号里填推理的理由．证明：∵AE平分∠CAB(已知)∴∠CAE=∠FAB()∵∠ACE=90°(已知)∴∠CAE+∠CEF=90°()∵CD是△ABC的高(已知)∴∠FDA=90°(三角形高的定义)∴∠FAB+∠AFD=90°(直角三角形的两锐角互余)∴∠CEF=∠AFD()∵∠CFE=∠AFD()∴∠CFE=∠CEF()【答案】角平分线的定义；直角三角形的两锐角互余；等角的余角相等；对顶角相等；等量代换【分析】根据角平分线的定义得到∠CAE=∠FAB，根据直角三角形两锐角互余得到∠CAE+∠CEF= 90°，∠FAB+∠AFD=90°，再利用等角的余角相等得到∠CEF=∠AFD，最后利用等量代换可得结果．【解析】解：证明：∵AE平分∠CAB(已知)∴∠CAE=∠FAB(角平分线的定义)∵∠ACE=90°(已知)∴∠CAE+∠CEF=90°(直角三角形的两锐角互余)∵CD是△ABC的高(已知)∴∠FDA=90°(三角形高的定义)∴∠FAB+∠AFD=90°(直角三角形的两锐角互余)∴∠CEF=∠AFD(等角的余角相等)∵∠CFE=∠AFD(对顶角相等)∴∠CFE=∠CEF(等量代换)故答案为：角平分线的定义；直角三角形的两锐角互余；等角的余角相等；对顶角相等；等量代换【点睛】本题考查的是三角形内角和定理，角平分线的定义，余角的性质，熟知三角形内角和是180°是解答此题的关键，此题难度不大．2.(2023春·山东青岛·八年级山东省青岛第五十九中学校考期中)如图，在等腰Rt△ABC中，∠ACB=90°，D为BC的中点，DE⊥AB，垂足为E，过点B作BF∥AC交DE的延长线于点F，连接CF交AD于点G．(1)判断△DBF的形状，并说明理由．(2)求证：AD⊥CF．【答案】(1)△DBF是等腰直角三角形，理由见解析；(2)证明见解析．【分析】(1)利用等腰Rt△ABC中，∠ACB=90°，证明∠CBA=∠CAB=45°，再利用BF∥AC得到∠ABF=∠CAB=45°，进一步得∠CBA+∠ABF=90°，利用DE⊥AB证明∠BDF=45°即可证明△DBF是等腰直角三角形；(2)欲求证AD⊥CF，先证明∠CAG+∠ACG=90°，需证明∠CAG=∠BCF，只要证明三角形全等，即可．【解析】(1)解：△DBF是等腰直角三角形，理由如下：∵等腰Rt△ABC中，∠ACB=90°，∴∠CBA=∠CAB=45°，∵BF∥AC，∴∠ABF=∠CAB=45°，∴∠CBA+∠ABF=90°，即∠DBF=90°，∵DE⊥AB，∠CBA=45°，∴∠BDF=45°，∴∠BFD=45°，∴△DBF是等腰直角三角形．(2)证明：在等腰直角三角形ABC中，∵∠ACB=90°，∴∠CBA=∠CAB=45°．又∵DE⊥AB，∴∠DEB=90°．∴∠BDE=45°．又∵BF∥AC，∴∠CBF=90°．∴∠BFD=45°=∠BDE．∴BF=DB．又∵D为BC的中点，∴CD=DB．∴BF=CD．在△CBF和△ACD中，BF=CD∠CBF=∠ACD CB=AC∴△CBF≌△ACD(SAS)．∴∠BCF=∠CAD．又∵∠BCF+∠GCA=90°，∴∠CAD+∠GCA=90°．∴∠AGC=90°，即AD⊥CF．【点睛】本题考查了三角形的综合问题，掌握全等三角形的性质以及判定定理、垂直的定义、等腰三角形的性质以及判定是解题的关键．3.(2023春·山东济南·八年级济南育英中学校联考期中)如图，△ABC中，∠B=90°，点D在射线BC上运动，DE⊥AD交射线AC于点E．(1)如图1，若∠BAC=60°，当AD平分∠BAC时，求∠EDC的度数；(2)如图2，当点D在线段BC上时，①判断∠EDC与∠BAD的数量关系并说明理由；②作EF⊥BC于F，∠BAD、∠DEF的角平分线相交于点G，随着点D的运动，∠G的度数会变化吗？如果不变，求出∠G的度数；如果变化，说明理由；(3)如图3，当点D在BC的延长线上时，作EF⊥BD于F，∠BAD的角平分线和∠DEF的角平分线的反向延长线相交于点G，∠G的度数会变化吗？如果不变，求出∠G的度数；如果变化，说明理由．【答案】(1)30°；(2)①∠EDC=∠BAD，理由见解析；②∠G的度数不变，理由见解析；(3)不变，45°.【分析】(1)先求出∠ACB=30°，再利用角平分线得出∠DAC=30°，即可得出∠ADC=120°即可得出结论；(2)①利用直角三角形的两锐角互余和等角的余角相等即可得出结论； ②先利用①的结论得出∠BAD+∠DEF=90°，进而得出∠DAG+∠DEG=45°，最后利用三角形的内角和即可得出结论；(3)利用三角形的外角和三角形的内角和即可得出结论．【解析】解：(1)在Rt△ABC中，∠BAC=60°，∴∠ACB=30°，∵AD平分∠BAC，∴∠DAC=12∠BAC=30°，∴∠ADC=120°，∵DE⊥AD，∴∠ADE=90°，∴∠EDC=∠ADC-∠ADE=30°；(2)①相等，在Rt△ABD中，∠BAD+∠ADB=90°，∵∠ADE=90°，∴∠EDC+∠ADB=90°，∴∠EDC=∠BAD；②∠G的度数不变，理由：∵EF⊥BC，∴∠EDF+∠DEF=90°，∵∠ADB+∠EDF=90°，∴∠ADB=∠DEF，∵∠BAD+∠ADB=90°，∴∠BAD+∠DEF=90°，∵∠BAD、∠DEF的角平分线相交于点G，∴∠DAG=12∠BAD，∠DEG=12∠DEF，∴∠DAG+∠DEG=12(∠BAD+∠DEF)=45°，∵∠DAE+∠DEA=90°，∴∠GAE+∠GEA=90°+45°=135°，∴∠G=45°；(3)∠G的度数不变化，理由：如图3，∵AD⊥DE，∴∠ADB+∠BDE=90°，∵EF⊥BD，∴∠DEF+∠BDE=90°，∴∠ADB=∠DEF，∵EM是∠DEF的角平分线，∴∠DEM=12∠DEF=12∠ADB，∵AG平分∠BAD，∴∠DAG=12∠BAD，延长DE交AG于N，∴∠AEN=∠ADE+∠DAE=90°+∠DAE，∴∠ENG=∠AEN+∠EAG=90°+∠DAE+∠EAG=90°+∠DAG=90°+12∠BAD，∴∠G=180°-(∠ENG+∠GEN)=180°-(∠ENG+∠DEM)，=180°-90°+12∠BAD+12∠ADB，=90°-12(∠BAD+∠ADB)=45°．【点睛】本题主要考查了角平分线的定义，直角三角形的性质，三角形的内角和和外角的性质，解(1)的关键是求出∠ADC=120°，解(2)的关键是求出∠DAG+∠DEG=45°，解(3)的关键是利用三角形的外角的性质．【知识点4飞镖模型】【条件】四边形ABDC如上左图所示.【结论】∠D=∠A+∠B+∠C.(凹四边形凹外角等于三个内角和)【证明】如上右图，连接AD并延长到E，则：∠BDC=∠BDE+∠CDE=(∠B+∠1)+(∠2+∠C)=∠B+∠BAC+∠C.本质为两个三角形外角和定理证明.【题型4飞镖模型】1(2023春·江苏镇江·八年级统考期中)在社会实践手工课上，小茗同学设计了一个形状如图所示的零件，如果∠A=52°,∠B=25°，∠C=30°,∠D=35°,∠E=72°，那么∠F的度数是( )．A.72°B.70°C.65°D.60°【答案】B【分析】延长BE交CF的延长线于O，连接AO，根据三角形内角和定理求出∠BOC,再利用邻补角的性质求出∠DEO，再根据四边形的内角和求出∠DFO，根据邻补角的性质即可求出∠DFC的度数．【详解】延长BE交CF的延长线于O，连接AO，如图，∵∠OAB+∠B+∠AOB=180°,∴∠AOB=180°-∠B-∠OAB,同理得∠AOC=180°-∠OAC-∠C,∵∠AOB+∠AOC+∠BOC=360°,∴∠BOC=360°-∠AOB-∠AOC=360°-(180°-∠B-∠OAB)-(180°-∠OAC-∠C)=∠B+∠C+∠BAC=107°,∵∠BED=72°,∴∠DEO=180°-∠BED=108°,∴∠DFO=360°-∠D-∠DEO-∠EOF=360°-35°-108°-107°=110°,∴∠DFC=180°-∠DFO=180°-110°=70°,故选：B．【点睛】本题考查三角形内角和定理，多边形内角和，三角形的外角的性质，邻补角的性质，解题关键是会添加辅助线，将已知条件联系起来进行求解．三角形外角的性质：三角形的一个外角等于与它不相邻的两个内角的和；邻补角性质：邻补角互补．1.(2023春·八年级期末)如图，已知在△ABC中，∠A=40°，现将一块直角三角板放在△ABC上，使三角板的两条直角边分别经过点B,C，直角顶点D落在△ABC的内部，则∠ABD+∠ACD=( )．A.90°B.60°C.50°D.40°【答案】C【分析】由三角形内角和定理可得∠ABC+∠ACB+∠A=180°，即∠ABC+∠ACB=180-∠A=140°，再说明∠DBC+∠DCB=90°，进而完成解答．【解析】解：∵在△ABC中，∠A=40°∴∠ABC+∠ACB=180-∠A=140°∵在△DBC中，∠BDC=90°∴∠DBC+∠DCB=180°-90°=90°∴∠ABD+∠ACD=40°-90°=50°故选C．【点睛】本题主要考查三角形内角和定理，灵活运用三角形内角和定理成为解答本题的关键．2.(2023·全国·八年级假期作业)如图所示，已知四边形ABDC，求证∠BDC=∠A+∠B+∠C．【答案】见解析【分析】方法1连接BC，根据三角形内角和定理可得结果；方法2作射线AD，根据三角形的外角性质得到∠3=∠B+∠1，∠4=∠C+∠2，两式相加即可得到结论；方法3延长BD，交AC于点E，两次运用三角形外角的性质即可得出结论．【解析】方法1如图所示，连接BC.在△ABC中，∠A+∠ABC+∠ACB=180°，即∠A+∠ABD+∠1+∠ACD+∠2=180°.在△BCD中，∵∠BDC+∠1+∠2=180°，∴∠BDC=∠A+∠ABD+∠ACD；方法2如图所示，连接AD并延长.∵∠3是△ABD的外角，∴∠3=∠1+∠ABD.同理，∠4=∠2+∠ACD.∴∠3+∠4=∠1+∠2+∠ABD+∠ACD.即∠BDC=∠A+∠ABD+∠ACD.方法3如图所示，延长BD，交AC于点E.∵∠DEC是△ABE的外角，∴∠DEC=∠A+∠ABD.∵∠BDC是△DEC的外角，∴∠BDC=∠DEC+∠ACD.∴∠BDC=∠A+∠ABD+∠ACD.【点睛】本题考查了三角形的外角性质：解题的关键是知道三角形的任一外角等于与之不相邻的两内角的和．也考查了三角形内角和定理．3.(2023春·福建南平·八年级统考期中)如图，若∠EOC=115°，则∠A+∠B+∠C+∠D+∠E+∠F=．【答案】【答案】230°【分析】根据三角形外角的性质，得到∠EOC=∠E+∠2=115°，∠2=∠D+∠C，∠EOC=∠1+∠F= 115°，∠1=∠A+∠B，即可得到结论．【解析】【详解】解：如图∵∠EOC=∠E+∠2=115°，∠2=∠D+∠C，∴∠E+∠D+∠C=115°，∵∠EOC=∠1+∠F=115°，∠1=∠A+∠B，∴∠A+∠B+∠F=115°，∴∠A+∠B+∠C+∠D+∠E+∠F=230°，故答案为：230°．【点睛】本题主要考查三角形内角和定理和三角形外角的性质，解决本题的关键是要熟练掌握三角形外角性质．【知识点5风筝模型】【条件】四边形ABPC，分别延长AB、AC于点D、E，如上左图所示.【结论】∠PBD+∠PCE=∠A+∠P.【证明】如上右图，连接AP，则：∠PBD=∠PAB+∠APB，∠PCE=∠PAC+∠APC，∴∠PBD+∠PCE=∠PAB+∠APB+∠PAC+∠APC=∠BAC+∠BPC，得证.【题型5风筝模型】1(2023春·重庆渝北·八年级校考期中)如图,将△ABC沿着DE翻折,使B点与B'点重合,若∠1+∠2= 80°,则∠B的度数为()A.20°B.30°C.40°D.50°【答案】C【分析】由折叠的性质可知∠BED=∠B'ED,∠BDE=∠B'DE,再利用平角的定义可求出∠BED+∠BDE的度数，进而利用三角形内角和可求∠B的度数.【详解】由折叠的性质可知∠BED=∠B'ED,∠BDE=∠B'DE∵∠1+∠BED+∠B'ED=180°,∠2+∠BDE+∠B'DE=180°∴∠BED+∠BDE=12(360°-∠1-∠2)=12×(360°-80°)=140°∴∠B=180°-(∠BED+∠BDE)=180°-140°=40°故选C【点睛】本题主要考查折叠的性质及三角形内角和定理，掌握折叠的性质及三角形内角和定理是解题的关键.1.(2023春·八年级期末)如图，把△ABC沿EF对折，叠合后的图形如图所示．若∠A=55°，∠1=95°，则∠2的度数为( )．A.14°B.15°C.28°D.30°【答案】B【分析】根据三角形内角和定理和平角定义证得∠FEB+∠EFC=360°-125°=235°，再根据折叠性质得出∠B′EF+∠EFC′=∠FEB+∠EFC=235°，进而求得∠1+∠2=110°即可求解．【解析】解：∵∠A=55°，∴∠AEF+∠AFE=180°-55°=125°，∴∠FEB+∠EFC=360°-125°=235°，由折叠可得：∠B′EF+∠EFC′=∠FEB+∠EFC=235°，∴∠1+∠2=235°-125°=110°，∵∠1=95°，∴∠2=110°-95°=15°，故选：B．【点睛】本题考查折叠性质、三角形的内角和定理、平角定义，熟练掌握折叠性质是解答的关键．2.(2023春·八年级期末)如图，三角形纸片ABC中，∠A=65°,∠B=75°，将∠C沿DE翻折，使点C落在△ABC外的点C 处．若∠1=20°，则∠2的度数为．【答案】100°【分析】根据三角形内角和定理求出∠C，根据折叠的性质求出∠C'，根据三角形的外角的性质计算，得到答案．【解析】解：∵∠A=65°，∠B=75°，∴∠C=180°-65°-75°=40°，由折叠的性质可知，∠C'=∠C=40°，∴∠3=∠1+∠C'=60°，∴∠2=∠C+∠3=100°，故答案是：100°．【点睛】本题考查的是三角形内角和定理、折叠的性质，掌握三角形内角和等于180°是解题的关键．3.(2023春·全国·八年级专题练习)如图，将△ABC纸片沿DE折叠，使点A落在点A'处，且A'B平分∠ABC，A'C平分∠ACB，若∠BA'C=120°，则∠1+∠2的度数为()A.90°B.100°C.110°D.120°【答案】D【分析】连接A'A，先求出∠BAC，再证明∠1+∠2=2∠BAC即可解决问题．【解析】解：如图，连接AA '，∵A 'B 平分∠ABC ，A 'C 平分∠ACB ，∴∠A 'BC =12∠ABC ，∠A 'CB =12∠ACB ，∵∠BA 'C =120°，∴∠A 'BC +∠A 'CB =180°-120°=60°，∴∠ABC +∠ACB =120°，∴∠BAC =180°-120°=60°，∵沿DE 折叠，∴∠DAA '=∠DA 'A ，∠EAA '=∠EA 'A ，∵∠1=∠DAA '+∠DA 'A =2∠DAA '，∠2=∠EAA '+∠EA 'A =2∠EAA '，∴∠1+∠2=2∠DAA '+2∠EAA '=2∠BAC =2×60°=120°，故选：D ．【点睛】本题考查了三角形内角和定理、角平分线定义、三角形外角的性质、折叠变换等知识，解题的关键是正确添加辅助线，灵活应用所学知识，属于中考常考题型．【知识点6两内角角平分线模型】【条件】△ABC 中，BI 、CI 分别是∠ABC 和∠ACB 的角平分线，且相交于点I .【结论】∠I =90°+12∠A 【证明】∵BI 是∠ABC 平分线，∴∠2=12∠ABC ∵CI 是∠ACB 平分线，∴∠3=12∠ACB 由A →B →I →C →A 的飞镖模型可知：∠I =∠A +∠2+∠3=∠A +12∠ABC +12∠ACB =∠A +12(180°−∠A )=90°+12∠A .【题型6两内角角平分线模型】1(2023春·江苏苏州·八年级期中)直线MN 与直线PQ 垂直相交于点O ，点A 在直线PQ 上运动，点B 在直线MN 上运动．(1)如图1，已知AE、BE分别是∠BAO和∠ABO角的平分线，点A、B在运动的过程中，∠AEB的大小是否会发生变化？若发生变化，请说明变化的情况；若不发生变化，试求出∠AEB的大小．(2)如图2，已知AB不平行CD，AD、BC分别是∠BAP和∠ABM的角平分线，又DE、CE分别是∠ADC和∠BCD的角平分线，点A、B在运动的过程中，∠CED的大小是否会发生变化？若发生变化，请说明理由；若不发生变化，试求出∠CED的度数．(3)如图3，延长BA至G，已知∠BAO、∠OAG的角平分线与∠BOQ的角平分线及反向延长线相交于E、F，在△AEF中，如果有一个角是另一个角的3倍，则∠ABO的度数为(直接写答案)【答案】(1)不发生变化，∠AEB=135°；(2)不发生变化，∠CED=67.5°；(3)60°或45°【分析】(1)根据直线MN与直线PQ垂直相交于O可知∠AOB=90°，再由AE、BE分别是∠BAO和∠ABO的角平分线得出∠BAE=12∠OAB，∠ABE=12∠ABO，由三角形内角和定理即可得出结论；(2)延长AD、BC交于点F，根据直线MN与直线PQ垂直相交于O可得出∠AOB=90°，进而得出∠OAB+∠OBA=90°，故∠PAB+∠MBA=270°，再由AD、BC分别是∠BAP和∠ABM的角平分线，可知∠BAD=12∠BAP，∠ABC=12∠ABM，由三角形内角和定理可知∠F=45°，再根据DE、CE分别是∠ADC和∠BCD的角平分线可知∠CDE+∠DCE=112.5°，进而得出结论；(3)由∠BAO与∠BOQ的角平分线相交于E可知∠EAO=12∠BAO，∠EOQ=12∠BOQ，进而得出∠E的度数，由AE、AF分别是∠BAO和∠OAG的角平分线可知∠EAF=90°，在△AEF中，由一个角是另一个角的3倍分四种情况进行分类讨论．【详解】解：(1)∠AEB的大小不变，∵直线MN与直线PQ垂直相交于O，∴∠AOB=90°，∴∠OAB+∠OBA=90°，∵AE、BE分别是∠BAO和∠ABO角的平分线，∴∠BAE=12∠OAB，∠ABE=12∠ABO，∴∠BAE+∠ABE=12(∠OAB+∠ABO)=45°，∴∠AEB=135°；(2)∠CED的大小不变．延长AD、BC交于点F．∵直线MN与直线PQ垂直相交于O，∴∠AOB=90°，∴∠OAB+∠OBA=90°，∴∠PAB +∠MBA =270°，∵AD 、BC 分别是∠BAP 和∠ABM 的角平分线，∴∠BAD =12∠BAP ，∠ABC =12∠ABM ，∴∠BAD +∠ABC =12(∠PAB +∠ABM )=135°，∴∠F =45°，∴∠FDC +∠FCD =135°，∴∠CDA +∠DCB =225°，∵DE 、CE 分别是∠ADC 和∠BCD 的角平分线，∴∠CDE +∠DCE =112.5°，∴∠CED =67.5°；(3)∵∠BAO 与∠BOQ 的角平分线相交于E ，∴∠EAO =12∠BAO ，∠EOQ =12∠BOQ ，∴∠E =∠EOQ -∠EAO =12(∠BOQ -∠BAO )=12∠ABO ，∵AE 、AF 分别是∠BAO 和∠OAG 的角平分线，∴∠EAF =90°．在△AEF 中，∵有一个角是另一个角的3倍，故有：①∠EAF =3∠E ，∠E =30°，∠ABO =60°；②∠EAF =3∠F ，∠E =60°，∠ABO =120°(舍弃)；③∠F =3∠E ，∠E =22.5°，∠ABO =45°；④∠E =3∠F ，∠E =67.5°，∠ABO =135°(舍弃)．∴∠ABO 为60°或45°．故答案为：60°或45°．【点睛】本题考查的是平行线的判定和性质，三角形内角和定理，熟知三角形内角和是180°是解答此题的关键．1.(2023春·全国·八年级专题练习)如图，BE 平分∠ABD ，CF 平分∠ACD ，BE 与CF 交于点G ，若∠BDC =140°，∠BGC =100°，则∠A =()A.80°B.75°C.60°D.45°【答案】C【分析】连接BC,先求解∠DBC+∠DCB, 再求解∠GBC+∠GCB, 可得∠GBD+∠GCD, 再利用角平分线的定义可得：∠ABD+∠ACD, 从而可得：∠ABC+∠ACB, 再利用三角形的内角和定理可得∠A的大小.【解析】解：连接BC, ∵∠BDC=140°,∴∠DBC+∠DCB=180°-140°=40°,∵∠BGC=100°,∴∠GBC+∠GCB=180°-100°=80°,∴∠GBD+∠GCD=∠GBC+∠GCB-∠DBC-∠DCB=40°,∵BE平分∠ABD，CF平分∠ACD，∴∠ABD+∠ACD=2(∠GBD+∠GCD)=80°,∴∠ABC+∠ACB=∠ABD+∠ACD+∠DBC+∠DCB=80°+40°=120°,∴∠A=180°-(∠ABC+∠ACB)=60°.故选：C.【点睛】本题考查的是三角形的内角和定理的应用，角平分线的定义，熟练利用三角形的内角和定理求解与之相关的角的大小是解题的关键.2.(2023春·全国·八年级专题练习)如图，在△ABC中，∠ABC和∠ACB的角平分线交于点O，延长BO与∠ACB的外角平分线交于点D，若∠BOC=130°，则∠D=【答案】40°【分析】根据角平分线的定义结合三角形外角的性质即可得到结论．【解析】解：∵∠ABC和∠ACB的角平分线交于点O，∴∠ACO=12∠ACB，∵CD平分∠ACE，∴∠ACD=12∠ACE，∵∠ACB+∠ACE=180°，∴∠OCD=∠ACO+∠ACD=12(∠ACB+∠ACE)=12×180°=90°，∵∠BOC=130°，∴∠D=∠BOC-∠OCD=130°-90°=40°，故答案为：40°．【点睛】本题考查了三角形的外角性质，角平分线的定义，熟练掌握相关性质和概念正确推理计算是解题的关键．3.(2023春·黑龙江哈尔滨·八年级校联考期末)如图1，点A、B分别在射线OM、ON上运动(不与点O重合)，AC、BC分别是∠BAO和∠ABO的角平分线，BC延长线交OM于点G．(1)若∠MON=60°，则∠ACG=；(直接写出答案)(2)若∠MON=n°，求出∠ACG的度数；(用含n的代数式表示)(3)如图2，若∠MON=80°，过点C作CF∥OA交AB于点F，求∠BGO与∠ACF的数量关系．【答案】(1)60°；(2)90°-12n°；(3)∠BGO-∠ACF=50°【分析】(1)根据三角形内角和定理求出∠BAO+∠ABO，根据角平分线的定义、三角形的外角性质计算，得到答案；(2)仿照(1)的解法解答；(3)根据平行线的性质得到∠ACF=∠CAG，根据(2)的结论解答．【解析】解：(1)∵∠MON=60°，∴∠BAO+∠ABO=120°，∵AC、BC分别是∠BAO和∠ABO的角平分线，∴∠CBA=12∠ABO，∠CAB=12∠BAO，∴∠CBA+∠CAB=12(∠ABO+∠BAO)=60°，∴∠ACG=∠CBA+∠CAB=60°，故答案为：60°；(2)∵∠MON=n°，∴∠BAO+∠ABO=180°-n°，∵AC、BC分别是∠BAO和∠ABO的角平分线，∴∠CBA=12∠ABO，∠CAB=12∠BAO，∴∠CBA+∠CAB=12(∠ABO+∠BAO)=90°-12n°，∴∠ACG=∠CBA+∠CAB=90°-12n°；(3)∵CF∥OA，∴∠ACF=∠CAG，∴∠BGO -∠ACF =∠BGO -∠CAG =∠ACG ，由(2)得：∠ACG =90°-12×80°=50°．∴∠BGO -∠ACF =50°．【点睛】本题考查的是角平分线的定义、平行线的性质、三角形的外角性质，掌握两直线平行、内错角相等是解题的关键．【知识点7两外角角平分线模型】【条件】△ABC 中，BI 、CI 分别是△ABC 的外角的角平分线，且相交于点O .【结论】∠O =90°−12∠A .【证明】∵BO 是∠EBC 平分线，∴∠2=12∠EBC ，∵CO 是∠FCB 平分线，∴∠5=12∠FCB 由△BCO 中内角和定理可知：∠O =180°-∠2-∠5=180°-12∠EBC -12∠FCB =180°-12(180°−∠ABC )-12(180°−∠ACB )=12(∠ABC +∠ACB )=12(180°−∠A )=∠O =90°−12∠A 【题型7两外角角平分线模型】1(2023春·江苏·八年级专题练习)【问题背景】(1)如图1的图形我们把它称为“8字形”，请说明∠A +∠B =∠C +∠D ；【简单应用】(2)如图2，AP 、CP 分别平分∠BAD ．∠BCD ，若∠ABC =46°，∠ADC =26°，求∠P 的度数；【问题探究】(3)如图3，直线AP 平分∠BAD 的外角∠FAD ，CP 平分∠BCD 的外角∠BCE ，若∠ABC =36°，∠ADC =16°，请猜想∠P 的度数，并说明理由．【拓展延伸】(4) ①在图4中，若设∠C =α，∠B =β，∠CAP =13∠CAB ，∠CDP =13∠CDB ，试问∠P 与∠C 、∠B 之间的数量关系为：(用α、β表示∠P )；②在图5中，AP 平分∠BAD ，CP 平分∠BCD 的外角∠BCE ，猜想∠P 与∠B 、∠D 的关系，直接写出结论．【答案】(1)见解析；(2)36°；(3)26°，理由见解析；(4)①∠P=2α+β3②∠P=180°+∠B+∠D2【分析】(1)根据三角形内角和定理即可证明；(2)直接利用(1)中的结论两次，两式相加，然后根据角平分线的性质求解即可；(3)由AP平分∠BAD的外角∠FAD，CP平分∠BCD的外角∠BCE，推出∠1=∠2，∠3=∠4，推出∠PAD=180°-∠2，∠PCD=180°-∠3，由∠P+(180°-∠1)=∠D+(180°-∠3)，∠P+∠1=∠B+∠4，推出2∠P=∠B+∠D，即可解决问题．(4)①同法利用(1)种的结论列出方程即可解决问题．②同法利用(1)种的结论列出方程即可解决问题．【详解】(1)在△AEB中，∠A+∠B+∠AEB=180°．在△CED中，∠C+∠D+∠CED=180°．∵∠AEB=∠CED，∴∠A+∠B=∠C+∠D；(2)由(1)得：∠1+∠B=∠3+∠P，∠4+∠D=∠2+∠P，∴∠1+∠B+∠4+∠D=∠3+∠P+∠2+∠P．∵∠1=∠2，∠3=∠4，∴2∠P=∠B+∠D=46°+26°=72°，∴∠P=36°．(3)∠P=26°，理由是：如图3：∵AP平分∠BAD的外角∠FAD，CP平分∠BCD的外角∠BCE，∴∠1=∠2，∠3=∠4，∴∠PAD=180°-∠2，∠PCD=180°-∠3．∵∠PAB=∠1，∠P+∠PAB=∠B+∠4，∴∠P+∠1=∠B+∠4．∵∠P+(180°-∠2)=∠D+(180°-∠3)，∴2∠P=∠B+∠D，∴∠P=12(∠B+∠D)=12×(36°+16°)=26°．(4)①设∠CAP=m，∠CDP=n，则∠CAB=3m，，∠CDB=3n，∴∠PAB=2m，∠PDB=2n．∵∠C+∠CAP=∠P+∠PDC，∠P+∠PAB=∠B+∠PDB，∵∠C=α，∠B=β，∴α+m=∠P+n，∠P+2m=β+2n，∴α-∠P=n-m，∠P-β=2n-2m=2(n-m)，∴2α+β=3∠P∴∠P=2α+β3．故答案为：∠P=2α+β3．②设∠BAP=x，∠PCE=y，则∠PAO=x，∠PCB=y．∵∠PAO+∠P=∠PCD+∠D，∠B+∠BAO=∠OCD+∠D，∴x+∠P=180°-y+∠D，∠B+2x=180°-2y+∠D，∴∠P=180°+∠B+∠D2．故答案为：∠P=180°+∠B+∠D2．【点睛】本题考查了三角形内角和，三角形的外角的性质、多边形的内角和等知识，解题的关键是学会用方程的思想思考几何问题，属于中考常考题型．1.(2023春·全国·八年级专题练习)如图，五边形ABCDE在∠BCD,∠EDC处的外角分别是∠FCD,∠GDC,CP,DP分别平分∠FCD和∠GDC且相交于点P．若∠A=160°,∠B=80°,∠E=90°，则∠CPD=．【答案】105°【分析】根据多边形内角和公式求出五边形的内角和，根据题意求出∠BCD+∠CDE的度数，从而求出∠PCD+∠PDC的度数，运用三角形内角和定理即可求出∠CPD的度数．【解析】解：∵∠A=160°，∠B=80°，∠E=90°，∴∠BCD+∠CDE=(5-2)×180°-160°-80°-90°=210°，∴∠PCD+∠PDC=12(180°×2-210°)=75°，在△CPD中，∠CPD=180°-(∠PCD+∠PDC)=180°-75°=105°，故答案为：105°．【点睛】本题主要考查多边形内角和公式，三角形内角和定理，以及外角的平分线，根据已知条件求出∠BCD+∠CDE的度数是解题的关键．2.(2023春·全国·八年级专题练习)如图，点P是ΔABC的外角∠BCE和∠CBF的角平分线交点，延长BP交AC于G，请写出∠A和∠CPG的数量关系.【答案】∠CPG=90°+12∠A【分析】先根据三角形外角的性质及角平分线的性质即可用含∠A的式子表示出∠CBP和∠BCP的和，再利用三角形外角的性质即可得到∠A和∠CPG的数量关系.【解析】解：∵∠ACB+∠ABC=180°-∠A,∴∠ECB+∠FBC=180°×2-(180°-∠A)=180°+∠A,∵点P是ΔABC的外角∠BCE和∠CBF的角平分线交点，∴∠CBP+∠BCP=12(180°+∠A)=90°+12∠A，又∵∠CPG=∠CBP+∠BCP，∴∠CPG=90°+12∠A.【点睛】本题考查了三角形内角和定理、三角形外角和的性质及角平分线的性质.熟练应用三角形外角的性质是解题的关键.3.(2023春·八年级期末)如图1，△ABC的外角平分线交于点F．(1)若∠A=40°，则∠F的度数为；(2)如图2，过点F作直线MN∥BC，交AB，AC延长线于点M，N，若设∠MFB=α，∠NFC=β，则∠A 与α+β的数量关系是；(3)在(2)的条件下，将直线MN绕点F转动．①如图3，当直线MN与线段BC没有交点时，试探索∠A与α，β之间的数量关系，并说明理由；②当直线MN与线段BC有交点时，试问①中∠A与α，β之间的数量关系是否仍然成立？若成立，请说明理由；若不成立，请给出三者之间的数量关系．【答案】(1)70°(2)α+β-12∠A=90° (3)①见解析 ②不成立；β-α-12∠A=90°或α-β-12∠A=90°【分析】(1)根据三角形内角和定理以及角平分线的定义，即可得到∠F的度数；(2)根据三角形内角和定理以及角平分线的定义，即可得到∠BFC的度数，再根据平行线的性质，即可得到∠A与α+β的数量关系；(3)①根据(2)中的结论∠BFC =90°-12∠A ，以及平角的定义，即可得到∠A 与α，β之间的数量关系；②分两种情况进行讨论，根据(2)中的结论∠BFC =90°-12∠A ，以及平角的定义，即可得到∠A 与α，β之间的数量关系．【解析】解：(1)如图1，∵∠A =40°，∴∠ABC +∠ACB =140°，∴∠DBC +∠ECB =360°-140°=220°，又∵△ABC 的外角平分线交于点F ，∴∠FBC +∠FCB =12(∠DBC +∠ECB )=12×220°=110°，∴△BCF 中，∠F =180°-110°=70°，故答案为：70°；(2)如图2，∵∠ABC +∠ACB =180°-∠A ，∴∠DBC +∠ECB =360°-(180°-∠A )=180°+∠A ，又∵△ABC 的外角平分线交于点F ，∴∠FBC +∠FCB =12(∠DBC +∠ECB )=12×(180°+∠A )=90°+12∠A ，∴△BCF 中，∠BFC =180°-90°+12∠A =90°-12∠A ，又∵∠MFB =α，∠NFC =β，MN ∥BC ，∴∠FBC =α，∠FCB =β，∵△BCF 中，∠FBC +∠FCB +∠BFC =180°，∴α+β+90°-12∠A =180°，即α+β-12∠A =90°，故答案为：α+β-12∠A =90°；(3)①α+β-12∠A =90°，理由如下：如图3，由(2)可得，∠BFC =90°-12∠A ，∵∠MFB +∠NFC +∠BFC =180°，∴α+β+90°-12∠A =180°，即α+β-12∠A =90°，②当直线MN 与线段BC 有交点时，①中∠A 与α，β之间的数量关系不成立．分两种情况：如图4，当M 在线段AB 上，N 在AC 延长线上时，由(2)可得，∠BFC =90°-12∠A ，∵∠BFC -∠MFB +∠NFC =180°，∴90°-12∠A -α+β=180°，即β-α-12∠A =90°；如图5，当M 在AB 的延长线上，N 在线段AC 上时，由(2)可得，∠BFC =90°-12∠A ，∵∠BFC -∠NFC +∠MFB =180°，∴90°-12∠A -β+α=180°，即α-β-12∠A =90°；综上所述，∠A 与α，β之间的数量关系为β-α-12∠A =90°或α-β-12∠A =90°．【点睛】此题主要考查三角形的角度求解与证明，解题的关键是根据题意分情况作图．【知识点8内外角角平分线模型】【条件】△ABC 中，BP 、CP 分别是△ABC 的内角和外角的角平分线，且相交于点P .【结论】∠P =12∠A 【证明】∵BP 是∠ABC 平分线，∴∠3=12∠ABC ∵CP 是∠ACE 平分线，∴∠1=12∠ACE 由△ABC 外角定理可知：∠ACE =∠ABC +∠A 即：2∠1=2∠3+∠A ⋯⋯①对①式两边同时除以2，得：∠1=∠3+12∠A ⋯⋯②又在△BPC 中由外角定理可知：∠1=∠3+∠P ⋯⋯③比较②③式子可知：∠P =12∠A .12(∠ABC +∠ACB )=12(180°−∠A )=∠O =90°−12∠A .【题型8内外角角平分线模型】1(2023春·八年级期末)如图，BA 1和CA 1分别是△ABC 的内角平分线和外角平分线，BA 2是∠A 1BD 的平分线，CA 2是∠A 1CD 的平分线，BA 3是∠A 2BD 的平分线，CA 3是∠A 2CD 的平分线，⋯⋯以此类推，若∠A =α，则∠A 2020=．【答案】α22020【分析】根据角平分线的定义可得∠A 1BC =12∠ABC ，∠A 1CD =12∠ACD ，再根据三角形的一个外角等于与它不相邻的两个内角的和可得∠ACD =∠A +∠ABC ，∠A 1CD =∠A 1BC +∠A 1，整理即可得解∠A 1=12∠A ，同理求出∠A 2，∠A 3，可以发现后一个角等于前一个角的12，根据此规律即可得解．【详解】∵A 1B 是∠ABC 的平分线，A 1C 是∠ACD 的平分线，∴∠A 1BC =12∠ABC ，∠A 1CD =12∠ACD ，又∵∠ACD =∠A +∠ABC ，∠A 1CD =∠A 1BC +∠A 1，∴12(∠A +∠ABC )=12∠ABC +∠A 1，∴∠A 1=12∠A ，∵∠A =α．∠A 1=12∠A =12α，同理可得∠A 2=12∠A 1=122α，根据规律推导，∴∠A 2020=α22020，故答案为α22020．【点睛】本题主要考查的是三角形外角性质，角平分线定理，熟知三角形的一个外角等于与它不相邻的两个内角的和的性质，角平分线的定义是解题的关键． 1.(2023春·八年级期末)如图，已知△ABC 的两条高BD 、CE 交于点F ，∠ABC 的平分线与。

初二数学三角形模型归纳

初二数学三角形模型归纳一、三角形的分类三角形根据边长和角度的不同可以分为不同的类型，常见的有等边三角形、等腰三角形、直角三角形、钝角三角形和锐角三角形等。

1. 等边三角形：三条边的边长相等，三个内角均为60度。

2. 等腰三角形：两边的边长相等，两个底角（底边两侧的角）也相等。

3. 直角三角形：其中一个内角为90度，被称为直角。

4. 钝角三角形：其中一个内角大于90度，被称为钝角。

5. 锐角三角形：三个内角均小于90度，被称为锐角。

二、三角形的性质三角形具有一些重要的性质，包括角度和边长的关系，以及三角形的外接圆和内切圆等。

1. 内角和定理：三角形的三个内角之和等于180度。

2. 外角和定理：三角形的一个内角和其对应的外角之和等于180度。

3. 角平分线定理：三角形的内角平分线上的点到对边的距离相等。

4. 三角形的外接圆：可以通过三角形的三个顶点构造一个唯一的外接圆，外接圆的圆心在三角形的外接圆心上。

5. 三角形的内切圆：可以通过三角形的三条边构造一个唯一的内切圆，内切圆的圆心在三角形的内切圆心上。

三、三角形的计算在初二数学中，我们还学习了一些与三角形相关的计算方法，包括三角形的面积、周长和三角形中的角度计算等。

1. 三角形的面积：可以通过底边和高来计算三角形的面积，公式为：面积 = 底边× 高÷ 2。

2. 三角形的周长：可以通过三条边的边长之和来计算三角形的周长。

3. 正弦定理：在任意三角形中，三条边的边长和对应的角度之间有一定的关系，可以使用正弦函数来计算。

4. 余弦定理：在任意三角形中，三条边的边长和对应的角度之间有一定的关系，可以使用余弦函数来计算。

四、应用举例三角形的知识在实际生活和工作中有很多应用，比如测量建筑物的高度、计算地图上两地之间的距离等。

下面举一个应用举例来说明三角形的实际应用。

假设有一栋高楼，我们想要知道它的高度，但是无法直接测量。

我们可以选择一个较平坦的地面上的位置，站立在那里，然后测量我们的位置到高楼的水平距离。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

一、手拉手模型：1手的判别：判断左右，将等腰三角形顶角顶点朝上，左边为左手顶点，右边为右手顶点。

2手拉手的定义两个顶角相等且有共顶点的等腰三角形形成的图形。

（左手拉左手，右手拉右手）3手拉手基本结论①△ABC≌△AB'C'(SAS)②∠BAB'=∠BOB'③AO平分∠BOC'二、例题例1、在直线ABC的同一侧作两个等边三角形△ABD和△BCE，连接AE与CD，证明：（1）△ABE≌△DBC（2）AE=DC（3）AE与DC的夹角为60。

（4）△AGB≌△DFB（5）△EGB≌△CFB（6）BH平分∠AHC（7）GF∥ACHFGED变式练习1、如果两个等边三角形△ABD 和△BCE ，连接AE 与CD ，证明：（1） △ABE ≌△DBC（2） AE=DC（3） AE 与DC 的夹角为60。

（4）AE 与DC 的交点设为H,BH 平分∠AHC变式训练3：两个等腰三角形ABD 与BCE ，其中AB=BD,CB=EB,∠ABD=∠CBE=a 连接AE 与CD. 问（1）△ABE ≌△DBC 是否成立？（2）AE 是否与CD 相等？（3）AE 与CD 之间的夹角为多少度？（4）HB 是否平分∠AHC ？例2：如图，两个正方形ABCD和DEFG，连接AG与CE，二者相交于H 问：（1）△ADG≌△CDE是否成立？（2）AG是否与CE相等？（3）AG与CE之间的夹角为多少度？（4）HD是否平分∠AHE？例3：如图两个等腰直角三角形ADC与EDG，连接AG,CE,二者相交于H. 问（1）△ADG≌△CDE是否成立？（2）AG是否与CE相等？（3）AG与CE之间的夹角为多少度？（4）HD是否平分∠AHE？二、半角模型1、条件：.18021=+=γθβα且2、思路：①截长补短②旋转例1、在正方形ABCD中，若M、N分别在边BC、CD上移动，且满足MN=BM +DN，求证：①.∠MAN=45②.AB CCMN2=∆③.AM、AN分别平分∠BMN和∠DNM.例2拓展：在正方形ABCD中，已知∠MAN=45，若M、N分别在边CB、DC的延长线上移动，①.试探究线段MN、BM 、DN之间的数量关系.②.求证：AB=AH.例3.在四边形ABCD中，∠B+∠D=180，AB=AD，若E、F分别在边BC、CD上，且满足EF=BE +DF.求证：.21BAD EAF∠=∠练习巩固1：（1）如图1，在正方形ABCD中，E、F分别是BC、CD上的点，且∠EAF＝45°，试判断BE、DF与EF 三条线段之间的数量关系，直接写出判断结果：；（2）如图2，若把(1)问中的条件变为“在四边形ABCD中，AB＝AD，∠B＋∠D＝180°，E、F分别是边BC、CD上的点，且∠EAF=21∠BAD”，则（1）问中的结论是否仍然成立？若成立，请给出证明，若不成立，请说明理由；（3）在（2）问中，若将△AE F 绕点A 逆时针旋转，当点分别E 、F 运动到BC 、CD 延长线上时，如图3所示，其它条件不变，则（1）问中的结论是否发生变化？若变化，请给出结论并予以证明..练习巩固2：已知：正方形ABCD 中，45MAN ∠=，绕点A 顺时针旋转，它的两边分别交CB 、DC （或它们的延长线）于点M 、N ．（1）如图1，当MAN ∠绕点A 旋转到BM DN =时，有BM DN MN +=．当MAN ∠ 绕点A 旋转到BM DN ≠时，如图2，请问图1中的结论还是否成立？如果成立，请给予证明，如果不成立，请说明理由；（2）当MAN ∠绕点A 旋转到如图3的位置时，线段BM DN ，和MN 之间有怎样的等量关系？请写出你的猜想，并证明．NMDCBANMCDBANM D CBA练习巩固3：在等边ABC ∆的两边AB ，AC 所在直线上分别有两点M N D ，，为ABC ∆外一点，且60MDN ∠=︒，120BDC ∠=︒，BD CD =，探究：当点M N ，分别爱直线AB AC ，上移动时，BM BN MN ，，之间的数量关系及AMN ∆的周长Q 与等边ABC ∆的周长L 的关系．图①M ND CBA 图②MND CBA N图③MD CBA（1）如图①，当点M N ，在边AB AC ，上，且DM DN =时，BM NC MN ，，之间的数量关系式_________；此时QL=__________ （2）如图②，当点M N ，在边AB AC ，上，且DM DN ≠时，猜想(1)问的两个结论还成立吗？写出你的猜想并加以证明；（3）如图③，当点M N ，分别在边AB CA ，的延长线上时，若AN x =，则Q =_________(用x L ，表示)练习巩固4：如图，已知在正方形ABCD 中，∠MAN =45°，连接BD 与AM ，AN 分别交于E 、F 两点。

求证：（1）MN=MB+DN ；（2）点A 到MN 的距离等于正方形的边长；（3）CMN 的周长等于正方形ABCD 边长的2倍；（4）=ABCD CMN S 2ABS MN；（5）若∠MAB =20°，求∠AMN ；（6）若()∠=ααMAB 045，求∠AMN ；（7）=+222EF EB DF ；（8）AEN 与AFM 是等腰三角形；（9）=AEF AMNS 1S2。

三、三垂直模型（一线三等角）（K型）1、常见的一线三垂直的模型。

例1：如图，正方形ABCD中，E、F分别为BC、CD上的点，且AE⊥BF，垂足为点G．求证：AE=BF．变式训练：等腰Rt△ABC中，AC=AB，∠BAC＝90°，点D是AC的中点，AF⊥BD于点E，交BC于点F，连接DF，求证：∠1=∠2。

例2：.如图，点P是正方形ABCD边AB上一点(不与点A．B重合)，连接PD并将线段PD绕点P顺时针方向旋转90°得到线段PE，PE交边BC于点F．连接BE、DF。

求证：∠ADP=∠EPB；求∠CBE的度数；N M O A BP2图4321A CP B D AB C图1A B D CP例3：等腰直角△ABC ，其中AB=AC ，∠BAC=90°，过B 、C 作经过A 点直线L 的垂线，垂足分别为M 、N ．（1）你能找到一对三角形的全等吗？并说明．（2）BM ，，MN 之间有何关系？若将直线l 旋转到如图2的位置，其他条件不变，那么上题的结论是否依旧成立？四、角平分线模型1、边垂直如图，P 是∠MON 的平分线上一点，过点P 作PA ⊥OM 于点A ，PB ⊥ON 于点B 。

结论：PB=PA 例1：（1）如图①，在△ABC 中，∠C=90°，AD 平分∠CAB ，BC=6，BD=4，那么点D 到直线AB 的距离是；（2）如图②，∠1=∠2，+∠3=∠4。

求证：AP 平分∠BAC 。

例2：如图，△ABC 的外角∠ACD 的平分线CP 与内角∠ABC 的平分线BP 交于点 P ，若∠BPC=40°，则∠CAP=。

A BDC P O N MB A图2D P AB C D C 1图P B A ABC DE DC BAA例3：．如图，在四边形ABCD 中，BC>AB ，AD=DC ，BD 平分∠ABC 。

求证：∠BAD+∠BCD=180°。

2、翻折全等（对称）如图，P 是∠MON 的平分线上一点，点A 是射线OM 上任意一点，在ON 上截取OB=OA ，连接PB 。

结论：△OPB ≌△OPA 。

例1：（1）如图①所示，在△ABC 中，AD 是△ABC 的外角平分线，P 是AD 上异于点A 的任意一点，试比较PB+PC 与AB+AC 的大小，并说明理由；（2）如图②所示， AD 是△ABC 的内角平分线，其他条件不变，试比较 PC-PB 与AC-AB 的大小，并说明理由。

例2：．已知，在△ABC 中，∠A=2∠B ，CD 是∠ACB 的平分线，AC=16，AD=8。

求线段BC的长。

例3：如图所示，在△ABC 中，∠A=100°，∠A=40°，BD 是∠ABC 的平分线，延长BD 至E ，DE=AD 。

求证：BC=AB+CE 。

例4：已知，在△ABC 中，AB=AC ，∠A=108°，BD 平分∠ABC 。

求证：BC=AB+CD 。

PO NMB AED C BA 21E D CBA3、角平分线+垂线→等腰（三线合一）如图，P 是∠MO 的平分线上一点，AP ⊥OP 于P 点，延长AP 于点B 。

结论：△AOB 是等腰三角形。

例1：如图，已知等腰直角三角形ABC 中，∠A=90°，AB=AC ，BD 平分∠ABC ， CE ⊥BD ，垂足为E 。

求证：BD=2CE 。

例2：如图，在△ABC 中，BE 是角平分线，AD ⊥BE ，垂足为D 。

求证：∠2=∠1+∠C 。

例3：（1）如图①，BD 、CE 分别是△ABC 的外角平分，过点A 作AD ⊥BD 、 AE ⊥CE ，垂足分别为D 、E ，连接DE 。

求证：(1)AB+AC+BC=MN（2）如图②，BD 、CE 分别是△ABC 的内角平分，其它条件不变。

上述结论是否成立？成立请说明理由，若不成立，那MN 与△ABC 三边又有怎样的数量关系？请写出你的猜想，并进行证明。

（3）如图③，BD 是△ABC 的内角平分，CE 是△ABC 的外角平分，其它条件不变。

MN 与△ABC 三边又有怎样的数量关系？请写出你的猜想，并进行证明。

11 / 11Q PO NMAEBCNMDAEB C4、角平分线+平行线→等腰（底角相等）如图，P是∠MO的平分线上一点，过点P作PQ∥ON，交OM于点Q。

结论：△POQ是等腰三角形。

例1：如图，在△ABC中，∠ABC、∠ACB 的平分线交于点E，过点E作EF∥BC，交AB于点M，交AC于点N。

若BM+=9，则线段MN的长为。

3．例2：如图，梯形ABCD中，AD∥BC，点E在CD上，且AE平分∠BAD，BE平分∠ABC。

求证：AD=AB-BC。

浙教版八年级三角形中几种模型

全等三角形的重难点模型(八大题型)(原卷版)—八年级数学上册(浙教版)

三角形中的5种解题模型-2023年新八年级数学核心知识点与常见题型通关讲解练(浙教版)(解析版)

浙教版八年级数学上册 全等三角形之手拉手模型、倍长中线-截长补短法

浙教版数学八年级上册第一章三角形的初步认识 《全等三角形经典模型总结》(无答案)

全等三角形中的常见压轴题五种模型全攻略—2023-2024学年八年级数学上册(浙教版)(解析版)

初中数学《三角形中的经典模型》九大题型含解析

三角形中几种常见模型

初中数学三角形全等常用几何模型及构造方法大全初二

浙教版八年级三角形中几种模型

浙教版八年级数学上册 全等三角形之手拉手模型、倍长中线-截长补短法

八年级上册数学三角形五种基本模型

浙教版八年级上册 1.31三角形的中的模型

浙教版初二(上)数学第三讲_全等三角形的相关模型

全等模型：一线三等角(K字)2023-2024学年八年级数学上册常见几何模型解读(浙教版)解析版

浙教版八年级上册 全等三角形的多种模型

三角形中的八大经典模型(解析版)

初二数学三角形模型归纳

浙教版八年级数学上册全等三角形之手拉手模型、倍长中线-截长补短法

浙教版数学八年级上册第一章三角形的初步认识《全等三角形经典模型总结》(无答案)

浙教版八年级数学上册全等三角形之手拉手模型、倍长中线-截长补短法

浙教版八年级上册全等三角形的多种模型