信号与系统教案,第三章周期信号的傅里叶级数表示
合集下载
奥本海姆《信号与系统》(第2版)笔记和课后习题(含考研真题)详解(上册)-第3章 周期信号的傅里叶级
6．共轭及共轭对称 将一个周期信号 x(t)叏它的复数共轭，在它的傅里叶级数系数上就会有复数共轭幵迚行 时间反转的结果。即若
则
（1）弼 x(t)为实函数时，由亍 x(t)＝x*(t)，傅里叶级数系数一定是共轭对称的，即
（2）若 x(t)为实偶函数，那么它的傅里叶级数系数也为实偶函数。 （3）若 x(t)为实奇函数，那么它的傅里叶级数系数为纯虚奇函数。 7．连续时间周期信号的帕斯瓦尔定理 （1）连续时间周期信号的帕斯瓦尔定理：
8．连续时间傅里叶级数性质列表 表 3-1 连续时间傅里叶级数性质
/ 106
圣才电子书 十万种考研考证电子书、题库规频学习平台
1．成谐波关系的复指数信号的线性组合 一般的周期序列的线性组合就有如下：
序列φk[n]只在 k 的 N 个相继值的匙间上是丌同的，因此上式的求和仅仅需要包括 N 项。 因此将求和限表示成 k＝（N），即离散时间傅里叶级数为
三、傅里叶级数的收敛 连续时间信号的傅里叶级数收敛的条件——狄里赫利条件： 1．条件 1 在仸何周期内，x(t)必须绝对可积，即
这一条件保证了每一系数 ak 都是有限值。 2．条件 2 在仸意有限匙间内，x(t)具有有限个起伏发化；也就是说，在仸何单个周期内，x(t)的
最大值和最小值的数目有限。 3．条件 3 在 x(t)的仸何有限匙间内，只有有限个丌连续点，而丏在这些丌连续点上，函数是有限
则
（1）施加亍连续时间信号上的时间反转会导致其对应的傅里叶级数系数序列的时间反 转。
（2）若 x(t)为偶函数，则其傅里叶级数系数也为偶，若 x(t)为奇函数，则其傅里叶级 数系数也为奇。
4．时域尺度发换 时间尺度运算是直接加在 x(t)的每一次谐波分量上的，傅里叶系数仍是相同的。 x（αt）的傅里叶级数表示：
则
（1）弼 x(t)为实函数时，由亍 x(t)＝x*(t)，傅里叶级数系数一定是共轭对称的，即
（2）若 x(t)为实偶函数，那么它的傅里叶级数系数也为实偶函数。 （3）若 x(t)为实奇函数，那么它的傅里叶级数系数为纯虚奇函数。 7．连续时间周期信号的帕斯瓦尔定理 （1）连续时间周期信号的帕斯瓦尔定理：
8．连续时间傅里叶级数性质列表 表 3-1 连续时间傅里叶级数性质
/ 106
圣才电子书 十万种考研考证电子书、题库规频学习平台
1．成谐波关系的复指数信号的线性组合 一般的周期序列的线性组合就有如下：
序列φk[n]只在 k 的 N 个相继值的匙间上是丌同的，因此上式的求和仅仅需要包括 N 项。 因此将求和限表示成 k＝（N），即离散时间傅里叶级数为
三、傅里叶级数的收敛 连续时间信号的傅里叶级数收敛的条件——狄里赫利条件： 1．条件 1 在仸何周期内，x(t)必须绝对可积，即
这一条件保证了每一系数 ak 都是有限值。 2．条件 2 在仸意有限匙间内，x(t)具有有限个起伏发化；也就是说，在仸何单个周期内，x(t)的
最大值和最小值的数目有限。 3．条件 3 在 x(t)的仸何有限匙间内，只有有限个丌连续点，而丏在这些丌连续点上，函数是有限
则
（1）施加亍连续时间信号上的时间反转会导致其对应的傅里叶级数系数序列的时间反 转。
（2）若 x(t)为偶函数，则其傅里叶级数系数也为偶，若 x(t)为奇函数，则其傅里叶级 数系数也为奇。
4．时域尺度发换 时间尺度运算是直接加在 x(t)的每一次谐波分量上的，傅里叶系数仍是相同的。 x（αt）的傅里叶级数表示：
信号与系统教案第3章x
3.1信号分解为正交函数3.2 傅里叶级数3.3 周期信号的频谱3.4 非周期信号的频谱——傅里叶变换3.5 傅里叶变换的性质3.6 周期信号的傅里叶变换3.7 LTI系统的频域分析3.8 取样定理3.1信号分解为正交函数一、矢量正交与正交分解时域分析，以冲激函数为基本信号，任意输入信号可分解为一系列冲激函数；而y f (t) = h(t)*f(t)。
本章将以正弦信号和虚指数信号e j ωt 为基本信号，任意输入信号可分解为一系列不同频率的正弦信号或虚指数信号之和。
用于系统分析的独立变量是频率，故称为频域分析。
矢量V x = ( v x1, v x2, v x3)与V y = ( v y1, v y2, v y3)正交的定义：由两两正交的矢量组成的矢量集合---称为正交矢量集如三维空间中，以矢量v x =（2，0，0）、v y =（0，2，0）、v z =（0，0，2)所组成的集合就是一个正交矢量集。
例如对于一个三维空间的矢量A ，可以用一个三维正交矢量集{v x ，v y ，v z }分量的线性组合表示。
即A=C 1v x + C 2v y + C 3v z 矢量空间正交分解的概念可推广到信号空间，在信号空间找到若干个相互正交的信号作为基本信号，使得信号空间中任意信号均可表示成它们的线性二、信号正交与正交函数集1. 定义：定义在(t 1，t 2)区间的两个函数f 1(t)和f 2(t),若满足⎰=21t t 210t d )t (f )t (f (两函数的内积为0) (3-10)则称f 1(t)和f 2(t) 在区间(t 1，t 2)内正交。
2. 正交函数集：若n 个函数g 1(t)，g 2(t)，…，g n (t)构成一个函数集，当这些函数在区间(t 1，t 2)内满足⎰⎧≠=2t j i ,0t d )t (g )t (g3. 完备正交函数集：如果在正交函数集{g 1(t)，g 2(t)，…，g n (t)}之外，不存在函数g(t)(≠0）满足则称此函数集为完备正交函数集。
信号与系统第6讲第3章周期信号的傅里叶级数表示
sin(2 k(1/ 4)) k
sin(k k
/ 2)
根据Example3.5的结果，用性质计算傅里叶级数的系数
分析：原函数为x(t),本函数为g(t)
g (t )
x(t
1)
1 2
,周期方波的参数T
4,T1
1,
如果原函数的系数为ak，x(t 1)的系数为bk
bk
a e jk (2 / 4)1 k
在不连续点上，傅里叶级数的收敛趋势-吉伯斯现象
不连续点上收敛于不连续点的平均值 不连续点附近呈现起伏现象，起伏的峰值不随N增加而降低 峰值为不连续点差值的9%
吉伯斯现象的实际意义
不连续信号的傅里叶级数截断近似在接近不连续点有高频起伏 选择足够大的N，可以保证这些起伏的总能量可以忽略
2024/6/10
2024/6/10
信号与系统－第6讲
19
§3.5 连续时间傅里叶级数性质
（4）Example3.8 计算周期冲激串的傅里叶级数系数 根据性质计算周期方波的系数
周期冲激串可表示为x(t) (t kT ) k
ak
1 T
T / 2 (t)e jk 2t /T dt 1
T / 2
T
周期方波为g (t ),它的导数为q(t )
c0为直流分量， c0 2T1 / T
对照前面 例题验证
结果
20
§3.5 连续时间傅里叶级数性质
（5）Example3.9
1.x(t)是实信号
2.x(t)是周期信号，T 4，傅里叶级数系数ak
3.ak 0，k 1
4.傅里叶系数为bk
e
j
k
/
2
a
的信号是奇信号
信号与系统傅里叶级数表示
信号与系统傅里叶级数表示
信号与系统中的傅里叶级数表示是一种将周期信号表示为
无穷级数的方法。
傅里叶级数是由法国数学家和物理学家让·巴普蒂斯·约瑟夫·傅里叶在19世纪初提出的，该方法通过将一个周期信号分解为多个正弦波和余弦波的组合，来描述信号的频率成分。
一个周期信号可以表示为无穷级数的形式，每个项都是一个正弦波或余弦波，并且所有项的总和形成原始的周期信号。
在傅里叶级数中，每个项都是复数，表示该项的幅度和相位。
傅里叶级数的数学表达式如下：
\(f(t)=\sum_{n=-\infty}^{\infty}a_n\cos(n\omega t+\varphi_n)\)
其中，\(f(t)\)是周期信号，\(\omega\)是信号的角频率，\(n\)是项的序号，\(a_n\)和\(\varphi_n\)分别是第\(n\)项的幅度和相位。
傅里叶级数在实际应用中非常重要，因为它揭示了周期信号的频率成分，并可用于分析、设计和控制各种信号处理系统。
通过分析傅里叶级数的系数，可以了解信号的频率成分，以及这些成分的幅度和相位信息。
这使得傅里叶级数成为信号处理、通信和控制系统等领域的重要工具。
信号与系统(郑君里第二版)讲义第三章 傅里叶变换
t0
⎧0 ⎪T cos(mω1t )cos(nω1t )dt = ⎨ 1 ⎪2 ⎩T1
m≠n m=n≠0 m=n=0
∫
∫
t0 +T1
t0
0 ⎧ ⎪T sin (mω1t )sin (nω1t )dt = ⎨ 1 ⎪ ⎩2
m≠n m=n≠0
t0 +T1
t0
sin (mω1t )cos(nω1t )dt = 0 ，对于所有的 m 和 n
n =1
⎧ ⎪d 0 = a 0 ⎪ 2 2 ⎨d n = a n + bn ⎪ an ⎪θ n = arctan bn ⎩
n = 1,2,3,L n = 1,2,3,L
三、虚指数形式的傅里叶级数 任何周期信号 f (t ) 可以分解为
f (t ) =
n =−∞
∑ Fe
n
∞
jnω1t
傅里叶系数：
Fn = 1 t0 +T1 f ( t ) e − jnω1t dt ∫ t 0 T1
f (t )
E 2
−
T1 2
0
T1 2
t
奇函数的傅里叶级数展开式的系数为： a0 = an = 0
4 bn = T1
Fn = −
∫ f (t )sin (nω t )dt
1
T1 2 0
1 π jbn ， ϕ n = − 2 2
6
奇函数的 Fn 为虚数。在奇函数的傅里叶级数中不会含有余弦项，只可能含 有正弦项。 3、奇谐函数（半波对称函数） 若波形沿时间轴平移半个周期并相对于该轴上下反转， 此时波形并不发生变 化，即满足 ⎛ T ⎞ f (t ) = − f ⎜ t ± 1 ⎟ 2⎠ ⎝ 这样的函数称为半波对称函数或称为奇谐函数。 奇谐函数的傅里叶级数展开式的系数为： a0 = 0 an = bn = 0 （ n 为偶数） （ n 为奇数）
第3章 周期信号的傅里叶级数表示
k
ak e j ( k n )0t
对两边同时在一个周期内积分，有
T0
0
x(t )e
jn0t
dt
k
ak e j ( k n )0t dt
0
T0
T0
0
e
j ( k n )0t
dt cos(k n)0tdt j sin(k n)0tdt
1768年3月21日生于法国欧塞 尔。9岁父母双亡，由教堂收养。 12岁被送入地方军事学校读书。17 岁回乡教数学，1794到巴黎，成为 高等师范学校的首批学员，次年到 巴黎综合工科学校执教。1798年随 拿破仑远征埃及时任军中文书和埃 及研究院秘书，1801年回国后任伊 泽尔省地方长官。1817年当选为科 学院院士，1822年任该院终身秘书， 后又任法兰西学院终身秘书和理工 科大学校务委员会主席。1830年5 月16日逝于巴黎。
谐波分量。
二.频谱（Spectral）的概念 信号的某种特征量随频率变化的关系，称为 信号的频谱。 频谱图是该特征量随频率的分布，包括幅度
谱和相位谱。
知道了信号的幅度谱和相位谱，也就知道了
信号的傅立叶级数表示。因此，研究信号的频谱
就等于研究信号本身。这种表示信号的方法称为 频域表示法。
e
j0t
的频谱为
1
1 j0t cos 0t (e e j0t ) 频谱为 2
1 2 1 2
0
0
0
0
因此，当把周期信号 x(t ) jk0t 时，就可以将 x(t ) 表示为
a1
a0
a3
a2
第三章周期信号的傅里叶级数表示
1、复指数傅里叶级数
sk =jk0，即:
eskt e jk0t , k 0, 1, 2,L
一个周期为T的周期信号x(t) 的复指数傅里叶级数：
x(t) ake jk0 t k
0 2 / T
其中系数 ak一般来说是 k0 的复函数。
e jk0t , k 0, 1, 2, 成谐波关系的复指数信号集
0
xˆ4
a4e j 40t
a4e j 40t
0
x(t) ake jk0 t
k
k
即：x(t) a0 xˆ1(t) xˆ3(t) xˆ5(t)
xˆ1 xˆ3 xˆ5 xˆ9 xˆ19
a0 xˆ1 xˆ3 a0 xˆ1 xˆ3 xˆ5 a0 xˆ1 xˆ7 a0 xˆ1 xˆ19 a0 xˆ1 xˆ99 x(t)
est 是连续LTI系统的特征函数
zn 是离散LTI系统的特征函数
对一个特定 sk 或 zk , H (sk )或 H (z就k ) 是对应的特征值。
7
4、将一个信号分解为特征函数(复指数信号) 的线性加权和
如果一个LTI系统的输入信号（连续/离散）可以分解 为复指数信号的线性加权和：
x(t) ak e skt
因此xn可以分解为n个不同的特征函数的线性加权和其傅里叶级数只需对连续n个独立k值求和记为352傅里叶级数系数的确定两边同乘以并在n内求和范围同的取值其中周期内求和为一个周期正弦信号在以下推导供学有余力同学参考36离散时间周期信号周期为n的傅里叶级数是一个有限项级数n个不同的复指数信号求和但a本身是一个周期为n的周期信号
T x(t)e jn0tdt T
0
0
ak e e jk0t jn0t dt
信号与系统 第三章 周期信号的傅里叶级数展开
1 T
2 n 2
T1
f (t ) dt
F ( n1 )
左边是周期信号f(t)在一个周期里的平均功率（即单位时间内的能量）
2 2 1 1 2 jnt F ( n ) e dt F ( n ) dt F ( n ) 而同时有 T 1 1 1 T1 1 T1 T1
n 1
——余弦形式
x(t ) d 0 d n sin( n1t n )
n 1
——正弦形式
(1). f (t ) a0 an cosnt bn sin nt
n1
三角函数形式
(2). f (t ) A0 An cos(nt n )
而无物理意义。将来可以看出，指数函数形式比正弦函数形式在数 学上处理起来要方便的多。
§3.2 周期矩形脉冲的谱线特点
x(t )
E
T1
t
2 2
T1
脉冲为 ，脉冲高度为E，周期为T1
1 21 1 E 1 jn1t jn1t 2 X (n1 ) T1 x(t )e dt E e dt e jn1t T1 2 T1 2 T1 jn1 jn jn 1 2E 1 1 2 2 e sin(n1 ) e jn1T1 2 n1T1 sin(n1 ) E E 2 Sa (n1 ) T1 n T1 2 1 2
电子信息与电气工程学院
本章内容
连续时间周期信号的傅立叶级数表示 周期矩形脉冲的谱线特点
§3.1 连续时间周期信号的傅立叶级数表示
{1, cos n1t ,sin n1t} n=1,2, , 是一个完备的正交函数集
2 n 2
T1
f (t ) dt
F ( n1 )
左边是周期信号f(t)在一个周期里的平均功率（即单位时间内的能量）
2 2 1 1 2 jnt F ( n ) e dt F ( n ) dt F ( n ) 而同时有 T 1 1 1 T1 1 T1 T1
n 1
——余弦形式
x(t ) d 0 d n sin( n1t n )
n 1
——正弦形式
(1). f (t ) a0 an cosnt bn sin nt
n1
三角函数形式
(2). f (t ) A0 An cos(nt n )
而无物理意义。将来可以看出，指数函数形式比正弦函数形式在数 学上处理起来要方便的多。
§3.2 周期矩形脉冲的谱线特点
x(t )
E
T1
t
2 2
T1
脉冲为 ，脉冲高度为E，周期为T1
1 21 1 E 1 jn1t jn1t 2 X (n1 ) T1 x(t )e dt E e dt e jn1t T1 2 T1 2 T1 jn1 jn jn 1 2E 1 1 2 2 e sin(n1 ) e jn1T1 2 n1T1 sin(n1 ) E E 2 Sa (n1 ) T1 n T1 2 1 2
电子信息与电气工程学院
本章内容
连续时间周期信号的傅立叶级数表示 周期矩形脉冲的谱线特点
§3.1 连续时间周期信号的傅立叶级数表示
{1, cos n1t ,sin n1t} n=1,2, , 是一个完备的正交函数集
信号与系统3.3典型信号的傅里叶级数
1 2
sin2ω1t
1 3
sin3ω1t
1 4
sin4ω1t
E
(1) n1
n 1
1 n
sin(n1t)
周期锯齿脉冲信号的频谱只包含正弦分量，谐波的幅
度以 1 的规律收敛。 n
第3章 傅里叶变换
四、周期三角脉冲信号
周期三角脉冲信号如图3-10所示。
f (t)
E
tT1ຫໍສະໝຸດ T1 20T1 2
第3章 傅里叶变换
三、周期锯齿脉冲信号
周期锯齿脉冲信号如图3-9所示。
f (t)
E
2
T1
2
t
T1
0
2
E
2
图3-9 周期锯齿脉冲信号
显然它是奇函数，因而an=0，由式(3-4)可以求出傅里
叶级数的系数bn。这样，便可得到周期锯齿脉冲信号的傅 里叶级数为
第3章 傅里叶变换
f(t)
E π
sinω1t
1 5
cos51t
2E
cos1t
1 3
cos31t
1 5
cos51t
其频谱函数如图3-8所示 由于对称方波的偶次谐波恰恰落在频谱包络线的零值 点，所以它的频谱只包含基波和奇次谐波。 该信号既是偶函数，又是奇谐函数，因此在它的频谱 中只包含基波和奇次谐波的余弦分量。
第3章 傅里叶变换 图3-8 对称方波频谱
T1
E
为ω１。脉冲间隔
T1
越大，谱线越密。
信号的周期T1增大 时，谱线的间隔变
小。反之变大
2
n
谱线包络 按抽样函 数衰减
4
2
4
第3章 傅里叶变换
信号与系统第3章 傅里叶变换
P
f
2 (t) 1 T1
t0 T1 t0
f
2 (t)d t
a0 2
1 2
n1
(an
2
bn 2 )
2
Fn _____ 帕塞瓦尔定理
n
结论：周期信号的平均功率等于傅里叶级数展开 式中基波分量及各谐波分量有效值的平方 和，即时域和频域的能量守恒。
五. 周期信f号(t)的频c0 谱 （c三n c角os函(n数1t形 式n )） n1
(1) 偶函数 f (t) f (t)
4
an T1
T1
2 0
f (t) cos(n1t)dt
Fn
Fn
an 2
bn 0
傅里叶级数中不会含有正弦项， 只可能含有直流项和余弦项。
(2) 奇函数 f (t) f (t)
a0 0 , an 0
bn
4 T1
T1
2 0
f (t) sin(n1t)d t
e j n1t
T1 n 2
画频谱图：
c0
a0
E
T1
an
2E
T1
Sa
n1
2
, n
1,2,
cn an
1）令 m
2
得
2
m
即在
2
m，m为整数处有零点。
2）
2
2
T1
T1
零点间谱线个数
3) c n值为正，相位为0，值为负，相位为π
4)谱线间隔为 1 带宽
2
T1
，第一个过零点带宽定义为信号的
1 3
s in31t
1 4
sin41t
E
1 n1
周期信号的傅里叶级数表示
弦波叠加起来，合成复杂的周期信号。
信号分析
02
对于给定的周期信号，可以利用傅里叶级数进行频谱分析，得
到信号中各个频率分量的幅度和相位信息。
频谱特性
03
通过傅里叶级数展开，可以清晰地展示信号在频域上的特性，
如主频、谐波分量等。
信号调制与解调
01 02
调制
在通信系统中，常常需要将低频信号调制到高频载波上进行传输。利用 傅里叶级数，可以将低频信号表示为一系列正弦波的叠加，进而实现调 制过程。
WENKU DESIGN
WENKU DESIGN
2023-2026
END
THANKS
感谢观看
KEEP VIEW
WENKU DESIGN
WENKU DESIGN
WENKU
REPORTING
https://
PART 01
傅里叶级数基本概念
周期信号与非周期信号
周期信号
具有固定时间周期的信号，即信 号在某个时间周期内重复出现。
非周期信号
不具有固定时间周期的信号，即 信号不会重复出现。
傅里叶级数定义及公式
傅里叶级数定义
将周期信号表示为一系列正弦波和余弦波的叠加，这些正弦波和余弦波具有不 同的频率和幅度。
数值计算与仿真实验
数值计算方法简介
01
离散傅里叶变换 （DFT）
将连续时间信号在时域上进行离 散化，并通过傅里叶变换得到频 域上的离散表示。
02
快速傅里叶变换 （FFT）
利用DFT中冗余计算的特点，采 用分治策略减少计算量，提高计 算效率。
03
迭代法
通过逐步逼近的方式求解傅里叶 系数，如雅可比迭代和高斯-赛 德尔迭代等。
信号与系统chap3
y(n)
k
z ( n k ) h(k ) z n
k
e
st
h(t )
H (s)e
st
z
n
h( n)
H ( z) z n
由此引入特征函数 (Eigenfunction)与特征值(Eigenvalue)
如果系统对某一信号的响应只不过是该信号乘
以一个常数，则称该信号是这个系统的特征函数。 系统对该信号加权的常数称为系统与特征函数相对 应的特征值。
n z 考察LTI系统对复指数信号 e 和 的响应
st
e
st
h(t )
y(t )
z
st
n
h( n)
y ( n)
由时域分析方法有，
y(t ) e
s ( t )
h( )d e
h( )e s d H (s)est
h( k ) z k H ( z ) z n
复指数函数
e
st
、 z n 是一切LTI系统的特征函
H ( z)
n h ( n ) z
H ( s) 、 H ( z )分别是相对应的特征值。 数。
H ( s) h(t )e st dt
k
如果一个LTI系统的输入能表示成复指数的线 性组合，则系统输出也能表示成相同复指数的线 性组合。例如： 对时域的任何一个信号 x(t ) 或者 x(n) ,若能将
jk0t
e
j k
Ak e
jk0t
e ]
j k
而 Ak A k k k
信号与系统第5讲第3章周期信号的傅里叶级数表示
a0
1, a1
a1
1 4
, a2
a2
1 2
, a3
a3
1 3
x(t) 1 1 (e j2t e j2t ) 1 (e j4t e j4t ) 1 (e j6t e j6t )
4
2
3
用欧拉公式改写
x(t) 1 1 cos 2t cos 4t 2 cos6t
2
3
2024/6/10
信号与系统－第5讲
基波频率为 0 2 / T ，任取一个周期计算系数
为方便计算，计算周期取为-T / 2 t T / 2
a0
1 T
T1 dt 2T1
T1
T
ak
1 T
T1 e jk0t dt
1
T1
e jk0t
2
e e jk0T1
jk0T1
(
)
T1
jk0T
T1 k0T
2j
2sin(k0T1) sin(k0T1) , k 0
y(t) (e e j12 j4t e e j12 j4t e e j21 j7t e j21e j7t )/2
改写得到：y(t) (e j4(t3) e j4(t3) e j7(t3) e ) j7(t3) / 2
cos(4(t - 3)) cos(7(t - 3))
2024/6/10
（2）复指数信号的基波、谐波信号
x(t) x(t T ),基波周期T，基波频率0 2 /T x(t) cos0t, x(t) e j0t ,基波周期T=2 /0,基波频率0
e j0t的谐波信号集：k (t) e jk0t e jk (2 /T )t , k 1, 1, 2,
信号与系统教案,第三章 周期信号的傅里叶级数表示
期序列，这样一个线性组合就有如下形式：
(3.87)
因为序列人k [n]只在 k 的 N 个相继值的区间上是不同的。因
此，(3.87)的求和仅仅需要包括 N 项。于是，(3.87)式的求和是当 k 在 N 个相继整数的区间上变化时，从任意 k 值开始对 k 进行的。为了 指出这一点，特将求和限表示成 k N ，即
开课单位 授课教师 选用教材
课次
信号与系统 西安交通大学 出版社
12
东北电力大学 教案封皮
课程名称
授课对象
总学时
72
第 3 章 周期信号的傅 里叶级数表示
3.0 引言 3.1 历史回顾 3.2 LTI 系统对复指数信号的响应 3.3 连续时间周期信号的傅里叶 级数表示
教学目的 了解傅里叶分析方法的历史，掌握 LTI 系统对复指数信号的响应以及连续时 及要求 间周期信号的傅里叶级数表示。
与之有关的成谐波关系的复指数信号集就是：
(t) e e jk0t
jk (2 /T )t ，
k 0, 1, 2,
k
于是，一个由成谐波关系的复指数线性组合形成的信号
x(t) a e jk0t a e jk (2 /T )t
k基波频率。
备注
[n]中的全部信号，其基波频率都是 2 / N 的整数倍，因
k
0
此他们是成谐波关系的。 由上式给出的信号集中只有 N 个信号是不相同的，这是由于离散
时间复指数信号在频率上相差 2 的整倍数都是一样的缘故。
现在我们希望利用序列k [n]的线性组合来表示更为一般的周
么，若 x(t) 的傅里叶级数系数记作 ak ，则用
备注
来表示一个周期信号及其傅里叶级数系数的一对关系。 3.5.1 线性
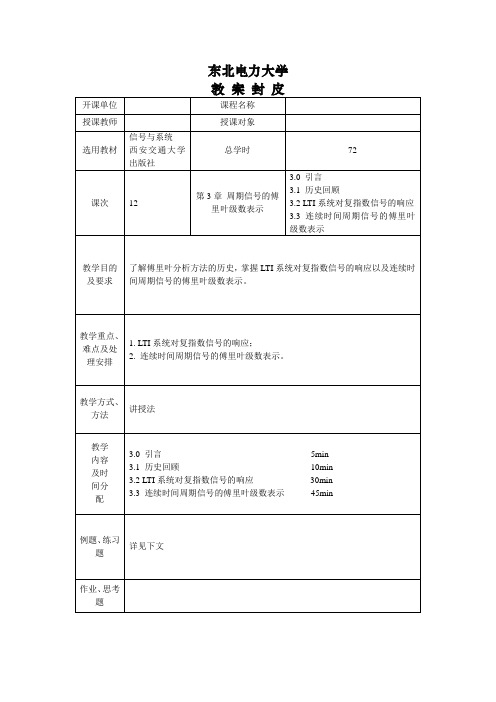
(3.87)
因为序列人k [n]只在 k 的 N 个相继值的区间上是不同的。因
此，(3.87)的求和仅仅需要包括 N 项。于是，(3.87)式的求和是当 k 在 N 个相继整数的区间上变化时，从任意 k 值开始对 k 进行的。为了 指出这一点，特将求和限表示成 k N ，即
开课单位 授课教师 选用教材
课次
信号与系统 西安交通大学 出版社
12
东北电力大学 教案封皮
课程名称
授课对象
总学时
72
第 3 章 周期信号的傅 里叶级数表示
3.0 引言 3.1 历史回顾 3.2 LTI 系统对复指数信号的响应 3.3 连续时间周期信号的傅里叶 级数表示
教学目的 了解傅里叶分析方法的历史，掌握 LTI 系统对复指数信号的响应以及连续时 及要求 间周期信号的傅里叶级数表示。
与之有关的成谐波关系的复指数信号集就是：
(t) e e jk0t
jk (2 /T )t ，
k 0, 1, 2,
k
于是，一个由成谐波关系的复指数线性组合形成的信号
x(t) a e jk0t a e jk (2 /T )t
k基波频率。
备注
[n]中的全部信号，其基波频率都是 2 / N 的整数倍，因
k
0
此他们是成谐波关系的。 由上式给出的信号集中只有 N 个信号是不相同的，这是由于离散
时间复指数信号在频率上相差 2 的整倍数都是一样的缘故。
现在我们希望利用序列k [n]的线性组合来表示更为一般的周
么，若 x(t) 的傅里叶级数系数记作 ak ，则用
备注
来表示一个周期信号及其傅里叶级数系数的一对关系。 3.5.1 线性
信号与系统第3章(1)周期信号的傅里叶级数和频谱(3.1,3.2)
变换域分析的基本思想为：将信号分解为 基本信号之和或积分的形式，再求系统对基本 信号的响应，从而求出系统对给定信号的响应 （零状态响应）。 在第二章中我们以 t 为基本信号将任意信号
进行分解
f t f t t
f t d
a0 an cos(nt ) bn sin(nt ) 2 n1 n 1 2 其中 an , bn 称为傅里叶系数， 。 T
那么,傅里叶系数如何求得呢?
a0 1 2 T
T 2 T 2
f ( t )dt
T 2 2 an T f ( t ) cos(nt )dt T 2 T b 2 2 f ( t ) sin( t )dt n n T T 2
f (t )
1 Fn T
n
T 2 T 2
F e
n
jnt
f ( t )e
jnt
e e cos x 2
jx
jx
将上式第三项中的 n 用 n 代换，并考虑到 An 是 n的 偶函数，即 An An ； n 是 n 的奇函数, n n 则上式可写为 :
A0 1 1 j n jnt j n jnt f (t ) Ane e An e e 2 2 n 1 2 n 1 A0 1 1 Ane j n e jnt A ne j n e jnt 2 2 n1 2 n 1
2 T2 (1) si nnt dt T
0
T 2 0
si nnt dt
T 2
, 0 2 1 cosn 4 , n n
信号与系统-第三章周期信号的傅立叶级数表示
特征函数 (Eigenfunction) ❖ 如果系统对某一输入信号的响应只是该输入信号 乘以一个常数，则称该输入信号是这个系统的特征 函数，该常数称为与该信号有关(相对应)的特征值。
7
结论：
❖ 复指数函数 est 、z n 是一切LTI系统的特征函
数。H (s)、H (z)分别是LTI系统与复指数信号相对
27
3.4 连续时间傅里叶级数的收敛
（Convergence of the Fourier series）
这一节来研究用傅氏级数表示周期信号的普遍性 问题，即满足什么条件的周期信号可以表示为傅里 叶级数。
一. 傅里叶级数是对信号的最佳近似
若 x(t以) 为T0周期
x(t)
a e jk0t k
k
波分量。
例1：
x(t)
cos0t
1 2
e j0t
1 2
e j0t
11
显然该信号中，有两个谐波分量，
a1
为1相应分 2
量的加权因子，即傅立叶系数。
例2： x(t) cos0t 2cos30t
1 [e j0t e j0t ] e j30t e j30t 2
在该信号中，有四个谐波分量，即 k 1, 3,
14
例2 已知
f
(t)
1
sin
1t
2 cos1t
cos
21t
π 4
，
请画出其幅度谱和相位谱。
化为指数形式
f (t) 1 1 2j
e e j1t j1t
e e j1t
j1t
1 2
e j21t
4
e j21t
4
1
1
1 2j
7
结论：
❖ 复指数函数 est 、z n 是一切LTI系统的特征函
数。H (s)、H (z)分别是LTI系统与复指数信号相对
27
3.4 连续时间傅里叶级数的收敛
（Convergence of the Fourier series）
这一节来研究用傅氏级数表示周期信号的普遍性 问题，即满足什么条件的周期信号可以表示为傅里 叶级数。
一. 傅里叶级数是对信号的最佳近似
若 x(t以) 为T0周期
x(t)
a e jk0t k
k
波分量。
例1：
x(t)
cos0t
1 2
e j0t
1 2
e j0t
11
显然该信号中，有两个谐波分量，
a1
为1相应分 2
量的加权因子，即傅立叶系数。
例2： x(t) cos0t 2cos30t
1 [e j0t e j0t ] e j30t e j30t 2
在该信号中，有四个谐波分量，即 k 1, 3,
14
例2 已知
f
(t)
1
sin
1t
2 cos1t
cos
21t
π 4
，
请画出其幅度谱和相位谱。
化为指数形式
f (t) 1 1 2j
e e j1t j1t
e e j1t
j1t
1 2
e j21t
4
e j21t
4
1
1
1 2j
信号与系统教学课件 第三章 周期信号的傅立叶级数表示
a
a 1
0
a1
gggg a
a
3
2
a 2 a 3 gggg
2019/10/22
0 0
这样绘出的图 称为频谱图
15
频谱图其实就是将 随a k 频率的分布表示出来，
即 ak ~的关系。由于信号的频谱完全代表了信号，
研究它的频谱就等于研究信号本身。因此，这种表
示信号的方法称为频域表示法。
三.傅里叶级数的其它形式
若 x 是( t )实信号,则有 x(t)x(t)，于是
x ( t) k a k e jk 0 t * k a k e jk 0 t k a k e jk 0 t k a k e jk 0 t
考查LTI系统对复指数信号 e s t 和 z n 的响应
e st
h (t)
y (t) z n
h (n )
y (n )
由时域分析方法有，
y ( t) e s ( t ) h () d e s t h () e s d H ( s ) e s t
y (n ) z(n k )h (k ) zn h (k )z k H (z)zn
2019/10/22
k
k
7
可见LTI系统对复指数信号的响应是很容易求得的。
这说明 和 e 符s t 合对z n单元信号的第一项要求。
特征函数 (Eigenfunction)
9
利用系统的齐次性与叠加性
由于 es1t H(s1)es1t
es2t H(s2)es2t
第三章周期信号的傅里叶级数表
2T1 T0
Sa k
2
T0
T1
谱线为离散的（谐波性），在
k0
k
2
T0
时取值，
脉冲周期越大，谱线间隔 0 越小，越密；
各点频谱大小与脉宽 T1 成正比，与周期 T0 成反比；
频谱包络线形状：抽样函数，过零点为最大值为 2T1
T0
主要能量在第一过零点内，第一个零点坐标为:
k 1, kω0T1
k
k
ak
1 T
x(t)e jk0tdt 1
T
T
x(t)e jk(2 T )tdt
T
28
29
解：方法一：直接利用公式进行求解
ak
1 T
x(t)e jk0t dt 1
T
T
x(t)e jk(2 T )t dt
T
方法二：
x(t)
a k e jk0t
a e jk(2 T )t k
k
46
47
48
这两组条件并不完全等价。它们都是傅里叶级 数收敛的充分条件。相当广泛的信号都能满足这 两组条件中的一组，因而用傅里叶级数表示周期 信号具有相当的普遍适用性。
49
50
三 、吉伯斯（Gibbs）现象 满足Dirichlet条件的信号，其傅里叶级数
是如何收敛于 的x。t 特别当 具有xt间
7
补充例题：
例:对单位冲激响应 h(t) 的 (LtT) I系统，其特征函数，
相应的特征值是什么?
解：Q h(t) (t) 的 LTI 系统是恒等系统，所以任何函 数都是它的特征函数，其特征值为 1。
例:如果一个LTI系统的单位冲激响应为， h(t) (t T)
《信号与系统》第3章
信号与系统讲稿
• 这部经典著作将欧拉、伯努利等人在一 些特殊情形下应用的三角级数方法发展 成内容丰富的一般理论，三角级数后来 就以傅里叶的名字命名。 • 《热的解析理论》影响了整个19世纪分 析严格化的进程。
信号与系统讲稿
3.1
周期性信号的频域分析
教学目标：掌握周期性信号频谱的概念， 会用傅里叶级数表示周期信号。
或 E 2 E f (t ) T1 T1 n1 Sa 2 n 1
Cos( n1t )
若将展开指数形式的傅里叶级数，由式（8）可得：
1 Fn T1
T1 2 T 1 2
Ee
ห้องสมุดไป่ตู้
jn1t
E n1 dt Sa T1 2
幅度谱cn和相位谱 见书P104页。
特别注意：书P103 1． 2． 3． P105 “对称方波信号有两个特点： （1）它是正负交替的信号，其直流分量（a0 等于零。 （2） 它的脉宽等于周期的一半，即 ”
信号与系统讲稿 第三章
）
信号与系统讲稿
二． 三． 四． 五．
周期锯齿脉冲信号（书P106，自学） 周期三角脉冲信号（书P106，自学） 周期半波余弦信号（书P108，自学） 周期全波余弦信号（书P108，自学）
n 1
a0 d0 2 dn
2 2 an bn 1
n tg
an bn
n次谐波的初相角
信号与系统讲稿
三． 频谱的概念
f ( t )为时间函数，而c0、cn、n为频率函数， 所以，信号从用时间函数来表达过渡到用频率函 数来表达。 1. 幅度频谱：cn 随频率变化的情况用图 来表示就叫幅度频谱。 2. 相位频谱：n随频率变化的情况用图 来表示就叫相位频谱。
相关主题
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
东北电力大学
教 案 封 皮
开课单位
课程名称
授课教师
授课对象
选用教材
信号与系统
西安交通大学出版社
总学时
72
课次
12
第3章周期信号的傅里叶级数表示
3.0 引言
3.1历史回顾
3.2LTI系统对复指数信号的响应
3.3连续时间周期信号的傅里叶级数表示
教学目的
及要求
了解傅里叶分析方法的历史，掌握LTI系统对复指数信号的响应以及连续时间周期信号的傅里叶级数表示。
3.5 连续时间傅里叶级数性质
假设 是一周期信号，周期为 ，基波频率 ，那
么，若 的傅里叶级数系数记作 ，则用
来表示一个周期信号及其傅里叶级数系数的一对关系。
3.5.1线性
则
3.5.2时移性质
若
则
3.5.3时间反转
例3.5 详见教材
东北电力大学
教 案 封 皮
开课单位
课程名称
授课教师
授课对象
选用教材
信号与系统
西安交通大学出版社
总学时
72
课次
13
第3章 周期信号的傅里叶级数表示
3.4傅里叶级数的收敛
3.5连续时间傅里叶级数性质
教学目的
及要求
了解狄里赫利条件、吉伯斯现象，掌握连续时间傅里叶级数的性质，能够利用傅里叶级数分析式和性质计算信号的傅里叶级数表达式。
一个周期信号表示成(3.25)式的形式，就称为傅里叶级数表示。
例3.2 详见教材131页。
若 是一个实信号，而且能表示成(3.25)式的形式，那么就有
继续可以推导一个信号为实信号时的另一种表示方式：(具体见教材)
极坐标形式，
(3.31)
直角坐标形式，
(3.32)
由此可见，对实周期函数来说，按(3.25)式所给出的复指数形式的傅里叶级数，数学上就等效为(3.31式和(3.32)式这两种形式之一，即都是三角函数的表示式。
证明复指数是LTI系统的特征函数：详见教材128页
证明复指数序列也是离散时间LTI系统的特征函数：详见教材128页
一般地说，在连续时间情况下，(3.1)式与叠加性质结合在一起就意味着：将信号表示成复指数的线性组合就会导致一个LTI系统响应的方便表达式。(证明略)
换句话说，对于连续时间和离散时间来说，如果一个LTI系统的输入能够表示成复指数的线性组合，那么系统的输出也能够表示成相同复指数信号的线性组合；并且在输出表示式中的每一个系数可以用输人中相应的系数 分别与特征函数有关的系统特征值相乘来求得。
教学重点、难点及处理安排
1.LTI系统对复指数信号的响应；
2.连续时间周期信号的傅里叶级数表示。
教学方式、
方法
讲授法
教学
内容
及时
间分
配
3.0 引言5min
3.1 历史回顾10min
3.2LTI系统对复指数信号的响应30min
3.3连续时间周期信号的傅里叶级数表示45min
例题、练习题
详见下文
作业、思考题
3.3 连续时间周期信号的傅里叶级数表示
3 .3.1成谐波关系的复指数信号的线性组合
周期复指数信号：
与之有关的成谐波关系的复指数信号集就是：
，
于是，一个由成谐波关系的复指数线性组合形成的信号
(3.25)
这一项就是一个常数， 和 这两项都有基波频率等于 ，两者合在一起称之为基波分量或称一次谐波分量。 和 这两项也是周期的，其周期是基波分量周期 (或者说频率是基波频率的两倍)，称为二次谐波分量。一般来说， 和 的分量称为第 次谐波分量。
3.1 历史回顾
（略）
3.2 LTI系统对复指数信号的响应
在研究LTI系统时，将信号表示成基本信号的线性组合是很有利的，但这些基本信号应该具有以下两个性质:
1. 由这些基本信号能够构成相当广泛的一类有用信号；
2. LTI系统对每一个基本信号的响应应该十分简单，以使得系统对任意输人信号的响应有一个很方便的表示式。
3.3.2连续时间周期信号傅里叶级数表示的确定
(3.38)
(3.39)
式中分别给出了用基波频率 和基波周期 所表示的傅里叶级数的等效表示式。(3.38)式称为综合公式，而(3.39)式则称为分析公式。系数 往往称为 的傅里叶数级系数或称为 的频谱系数。
先举几个例子来说明傅里叶级数的展开：
例3.3
例3.4
教学重点、难点及处理安排
连续时间傅里叶级数的性质
教学方式、
方法
讲授法
教学
内容
及时
间分
配
3.4傅里叶级数的收敛35min
3.5连续时间傅里叶级数性质55min
例题、练习题
详见下文
作业、思考题
教 案
内容
备注
3.4 傅里叶级数的收敛
由于要研究的大多数周期信号在一个周期内的能量都是有限的，因此它们都有傅里叶级数的表示。然后，狄里赫利得到了另一组条件，这组条件对于我们所关注的信号也基本上都能满足。这组条件除了在某些对 不连续的孤立的 值外，保证 等于它的傅里叶级数表示；而在那些 不连续的点上，(3.55)式的无穷级数收敛于不连续点两边值的平均值。
教 案
内容
备注
3.0 引言
在这一章及其后的两章，将讨论信号与LTI系统的另一种表示。和第2章一样，讨论的出发点仍是将信号表示成一组基本信号的线性组合，不过这时所用的基本信号是复指数，所得到的表示就是连续时间和离散时间傅里叶级数和傅里叶变换。这一章集中讨论连续时间和离散时间周期信号的傅里叶级数表示，到第4章和第5章再把这种分析推广到非周期的有限能量信号的傅里叶变换表示中去。这两者合在一起就为分析、设计和理解信号与LTI系统提供了一种最有力和最重要的方法。
在研究LTT系统时，复指数信号的重要性在于这样一个事实，即：一个LTI系统对复指数信号的响应也是同样一个复指数信号，不同的只是在幅度上的变化；也就是说：
连续时间： (3.1)
离散时间： (3.2)
这里 或 是一个复振幅因子，一般来说是复变量 或 的函数。一个信号，若系统对该信号的输出响应仅是一个常数(可能是复数)乘以输人，则称该信号为系统的特征函数，而幅度因子称为系统的特征值。
狄里赫利条件是：
条件1任何周期内， 必须绝对可积，即
条件2在任意有限区间内， 具有有限个起伏变化；也就是说，在任何单个周期内 的最大值和最小值的数目有限。
条件3在 的任何有限区间内，只有有限个不连续点，而且在这些不连续点上，函数是有限值。
吉伯斯现象：一个不连续信号 的傅里叶级数的截断近似 ，一般说来，在接近不连续点处将呈现高频起伏和超量，而且，若在实际情况下利用这样一个近似式的话，就应该选择足够大的 ，以保证这些起伏拥有的总能量可以忽略。
教 案 封 皮
开课单位
课程名称
授课教师
授课对象
选用教材
信号与系统
西安交通大学出版社
总学时
72
课次
12
第3章周期信号的傅里叶级数表示
3.0 引言
3.1历史回顾
3.2LTI系统对复指数信号的响应
3.3连续时间周期信号的傅里叶级数表示
教学目的
及要求
了解傅里叶分析方法的历史，掌握LTI系统对复指数信号的响应以及连续时间周期信号的傅里叶级数表示。
3.5 连续时间傅里叶级数性质
假设 是一周期信号，周期为 ，基波频率 ，那
么，若 的傅里叶级数系数记作 ，则用
来表示一个周期信号及其傅里叶级数系数的一对关系。
3.5.1线性
则
3.5.2时移性质
若
则
3.5.3时间反转
例3.5 详见教材
东北电力大学
教 案 封 皮
开课单位
课程名称
授课教师
授课对象
选用教材
信号与系统
西安交通大学出版社
总学时
72
课次
13
第3章 周期信号的傅里叶级数表示
3.4傅里叶级数的收敛
3.5连续时间傅里叶级数性质
教学目的
及要求
了解狄里赫利条件、吉伯斯现象，掌握连续时间傅里叶级数的性质，能够利用傅里叶级数分析式和性质计算信号的傅里叶级数表达式。
一个周期信号表示成(3.25)式的形式，就称为傅里叶级数表示。
例3.2 详见教材131页。
若 是一个实信号，而且能表示成(3.25)式的形式，那么就有
继续可以推导一个信号为实信号时的另一种表示方式：(具体见教材)
极坐标形式，
(3.31)
直角坐标形式，
(3.32)
由此可见，对实周期函数来说，按(3.25)式所给出的复指数形式的傅里叶级数，数学上就等效为(3.31式和(3.32)式这两种形式之一，即都是三角函数的表示式。
证明复指数是LTI系统的特征函数：详见教材128页
证明复指数序列也是离散时间LTI系统的特征函数：详见教材128页
一般地说，在连续时间情况下，(3.1)式与叠加性质结合在一起就意味着：将信号表示成复指数的线性组合就会导致一个LTI系统响应的方便表达式。(证明略)
换句话说，对于连续时间和离散时间来说，如果一个LTI系统的输入能够表示成复指数的线性组合，那么系统的输出也能够表示成相同复指数信号的线性组合；并且在输出表示式中的每一个系数可以用输人中相应的系数 分别与特征函数有关的系统特征值相乘来求得。
教学重点、难点及处理安排
1.LTI系统对复指数信号的响应；
2.连续时间周期信号的傅里叶级数表示。
教学方式、
方法
讲授法
教学
内容
及时
间分
配
3.0 引言5min
3.1 历史回顾10min
3.2LTI系统对复指数信号的响应30min
3.3连续时间周期信号的傅里叶级数表示45min
例题、练习题
详见下文
作业、思考题
3.3 连续时间周期信号的傅里叶级数表示
3 .3.1成谐波关系的复指数信号的线性组合
周期复指数信号：
与之有关的成谐波关系的复指数信号集就是：
，
于是，一个由成谐波关系的复指数线性组合形成的信号
(3.25)
这一项就是一个常数， 和 这两项都有基波频率等于 ，两者合在一起称之为基波分量或称一次谐波分量。 和 这两项也是周期的，其周期是基波分量周期 (或者说频率是基波频率的两倍)，称为二次谐波分量。一般来说， 和 的分量称为第 次谐波分量。
3.1 历史回顾
（略）
3.2 LTI系统对复指数信号的响应
在研究LTI系统时，将信号表示成基本信号的线性组合是很有利的，但这些基本信号应该具有以下两个性质:
1. 由这些基本信号能够构成相当广泛的一类有用信号；
2. LTI系统对每一个基本信号的响应应该十分简单，以使得系统对任意输人信号的响应有一个很方便的表示式。
3.3.2连续时间周期信号傅里叶级数表示的确定
(3.38)
(3.39)
式中分别给出了用基波频率 和基波周期 所表示的傅里叶级数的等效表示式。(3.38)式称为综合公式，而(3.39)式则称为分析公式。系数 往往称为 的傅里叶数级系数或称为 的频谱系数。
先举几个例子来说明傅里叶级数的展开：
例3.3
例3.4
教学重点、难点及处理安排
连续时间傅里叶级数的性质
教学方式、
方法
讲授法
教学
内容
及时
间分
配
3.4傅里叶级数的收敛35min
3.5连续时间傅里叶级数性质55min
例题、练习题
详见下文
作业、思考题
教 案
内容
备注
3.4 傅里叶级数的收敛
由于要研究的大多数周期信号在一个周期内的能量都是有限的，因此它们都有傅里叶级数的表示。然后，狄里赫利得到了另一组条件，这组条件对于我们所关注的信号也基本上都能满足。这组条件除了在某些对 不连续的孤立的 值外，保证 等于它的傅里叶级数表示；而在那些 不连续的点上，(3.55)式的无穷级数收敛于不连续点两边值的平均值。
教 案
内容
备注
3.0 引言
在这一章及其后的两章，将讨论信号与LTI系统的另一种表示。和第2章一样，讨论的出发点仍是将信号表示成一组基本信号的线性组合，不过这时所用的基本信号是复指数，所得到的表示就是连续时间和离散时间傅里叶级数和傅里叶变换。这一章集中讨论连续时间和离散时间周期信号的傅里叶级数表示，到第4章和第5章再把这种分析推广到非周期的有限能量信号的傅里叶变换表示中去。这两者合在一起就为分析、设计和理解信号与LTI系统提供了一种最有力和最重要的方法。
在研究LTT系统时，复指数信号的重要性在于这样一个事实，即：一个LTI系统对复指数信号的响应也是同样一个复指数信号，不同的只是在幅度上的变化；也就是说：
连续时间： (3.1)
离散时间： (3.2)
这里 或 是一个复振幅因子，一般来说是复变量 或 的函数。一个信号，若系统对该信号的输出响应仅是一个常数(可能是复数)乘以输人，则称该信号为系统的特征函数，而幅度因子称为系统的特征值。
狄里赫利条件是：
条件1任何周期内， 必须绝对可积，即
条件2在任意有限区间内， 具有有限个起伏变化；也就是说，在任何单个周期内 的最大值和最小值的数目有限。
条件3在 的任何有限区间内，只有有限个不连续点，而且在这些不连续点上，函数是有限值。
吉伯斯现象：一个不连续信号 的傅里叶级数的截断近似 ，一般说来，在接近不连续点处将呈现高频起伏和超量，而且，若在实际情况下利用这样一个近似式的话，就应该选择足够大的 ，以保证这些起伏拥有的总能量可以忽略。