三角函数——正弦余弦正切
三角函数公式(最全)

3a
cos3a =cos(2a+a) =cos^2acosa-sin^2asina =( 2cos^2a-1)cosa-2(1-cos^2a)cosa =4cos^3a3cosa
sin3 a =3sina-4sin^3a =4sina(3/4-sin^2a) =
4sina[( √3/2)-sina][( √3/2)+sina] =4sina(系
2 、商数关系
3 、平方关系 2
1、设 α为为任意角,终边相同的角的同一三角函数的值相等: 2、设 α为为任意角, π+ α与 α的三角函数值之间的关系: 3、设 α为为任意角, — α与α的三角函数值之间的关系: 4、设 α为为任意角, π—α与α的三角函数值之间的关系: 5、设 α为为任意角, 2π—α与α的三角函数值之间的关系:
x7/(2*4*6*7)
…… ∈],(x-1,1)
arctan x = x - x3/3 + x5/5 -
∈(- ∞,1…) , x
sinh x = x+x3/3!+x^/5!+
… +x2k-1/(2k-1)!+ ∈ R … , x
cosh x = 1+x2/2!+x^4/4!+
… +x2k/(2k)!+∈ R … , x
tan( α+β+γ)=(tan α+tan β+tan γ-tan α· tanβ· tanγ) ÷ (1tan α· tanβ-tan β· tanγ-tan γ· tanα)
5 、幂级数
c0+c1x+c2x2+...+cnxn+...=
正弦余弦正切公式

正弦余弦正切公式正弦、余弦、正切是三角函数中的基本函数,它们在数学和物理学中有着广泛的应用。
正弦函数描述了一个角的边与角度之间的关系,余弦函数描述了一个角的邻边与斜边之间的关系,而正切函数描述了一个角的对边与邻边之间的关系。
首先,我们来了解正弦函数。
正弦函数可表示为sin(x),其中x为角度。
在一个单位圆上,将角度x绘制到与x坐标轴的正向方向相同的地方,然后从原点向该点引出一条线段,这个线段就是角度为x的角的正弦值。
具体地表达为:sin(x) = y / r其中y表示角度为x的角所对边的长度,r表示单位圆的半径。
该公式说明了正弦函数是一个周期为360°(或2π弧度)的函数,其值在-1到1之间变化。
接下来,我们来看看余弦函数。
余弦函数可表示为cos(x),其中x 为角度。
同样地,在一个单位圆上,将角度x绘制到与x坐标轴的正向方向相同的地方,然后从原点向该点引出一条线段,这个线段就是角度为x 的角的余弦值。
具体地表达为:cos(x) = x / r其中x表示角度为x的角所邻边的长度,r表示单位圆的半径。
和正弦函数一样,余弦函数也是一个周期为360°(或2π弧度)的函数,其值在-1到1之间变化。
最后,我们来介绍正切函数。
正切函数可表示为tan(x),其中x为角度。
同样地,在一个单位圆上,将角度x绘制到与x坐标轴的正向方向相同的地方,然后从原点向该点引出一条线段,这个线段就是角度为x的角的正切值。
具体地表达为:tan(x) = y / x其中y表示角度为x的角所对边的长度,x表示角度为x的角所邻边的长度。
正切函数不像正弦和余弦函数那样具有周期性,它的值在整个数轴上变化。
除了在单位圆上的定义,这些三角函数还可以通过泰勒展开等方法来进行数值计算。
在泰勒展开中,正弦、余弦和正切函数都可以表示为无限级数的形式。
以正弦函数为例,其泰勒展开公式为:sin(x) = x - (x^3 / 3!) + (x^5 / 5!) - (x^7 / 7!) + ...其中^表示乘方运算,!表示阶乘运算。
余弦正弦正切大小关系

余弦正弦正切大小关系正弦余弦正切的关系:sinA/cosA=tanA,三角函数是基本初等函数之一,是以角度为自变量,角度对应任意角终边与单位圆交点坐标或其比值为因变量的函数。
也可以等价地用与单位圆有关的各种线段的长度来定义。
三角函数在研究三角形和圆等几何形状的性质时有重要作用,也是研究周期性现象的基础数学工具。
在数学分析中,三角函数也被定义为无穷级数或特定微分方程的解,允许它们的取值扩展到任意实数值,甚至是复数值。
正弦;在直角三角形中,任意一锐角∠a的对边与斜边的比叫做角a的正弦;余弦:在直角三角形中,任意一锐角∠a的邻边与斜边的比叫做角a的余弦;正切:在直角三角形中,任意一锐角∠a的对边与邻边的比叫做角a的正切;余切:在直角三角形中,任意一锐角∠a的邻边与对边的比叫做角a的余切。
关系:在直角三角形中,任意一个锐角的正弦值等于另一个锐角的余弦值;任意一个角的正弦值与余弦值的积为一。
正弦余弦正切余切九大关系公式:三角函数公式:正弦(sin):角α的对边比上斜边。
余弦(cos):角α的邻边比上斜边。
正切(tan):角α的对边比上邻边。
余切(cot):角α的邻边比上对边。
正割(sec):角α的斜边比上邻边。
余割(csc):角α的斜边比上对边。
同角三角函数:平方关系:sin^2(α)+cos^2(α)=1。
tan^2(α)+1=sec^2(α)。
cot^2(α)+1=csc^2(α)。
积的关系:sinα=tanαcosαcosα=cotαsinα。
tanα=sinαsecαcotα=cosαcscα。
secα=tanαcscαcscα=secαcotα。
正弦余弦正切函数

正切函数的图像没有水平渐近线,但在x=0处有垂直渐近线。
正切函数在x=0处取得极小值,无极大值。
图像形状
渐近线
极值点
应用领域
三种函数的比较
04
一个角的正弦等于它的对边与斜边的比。
定义的比较
正弦函数
一个角的余弦等于它的邻边与斜边的比。
余弦函数
一个角的正切等于它的对边与邻边的比。
正切函数
以原点为对称中心,左右对称,周期为2π,在区间[0,2π]上反复出现。
三角函数的起源与早期发展
现代发展
随着微积分和现代数学的发展,三角函数被广泛应用于各个领域,包括工程、物理、金融等。
应用领域
三角函数在求解振动问题、波动问题、电磁场问题等方面发挥了重要作用,同时也是处理信号和图像处理的重要工具之一。
三角函数的现代发展与应用
随着科技的不断进步,三角函数在大数据分析、人工智能、机器学习等领域的应用将更加广泛。
性质
图像特征与性质
物理
01
余弦函数在物理学中有广泛的应用,例如振动的描述、电磁波的传播、声音的波动等。
应用领域
工程
02
余弦函数也被广泛应用于工程领域,例如机械振动、结构设计、信号处理等。
数学
03
余弦函数是解决各种数学问题的基本工具之一,例如求解方程、优化问题、概率统计等。
正切函数
03
定义
周期性
正弦函数图像
以原点为对称中心,左右对称,周期为2π,在区间[0,2π]上反复出现。
余弦函数图像
在第一象限和第三象限以原点为对称中心,左右对称,周期为π,在区间[0,π/2]和[π/2,π]上反复出现。
正切函数图像
图像的比较
三角函数——正弦余弦正切

一、锐角三角函数——正弦、余弦、正切一、新课教学(一)、认识正弦、余弦、正切1、认识角的对边、邻边。
(2分钟)如图,在Rt △ABC 中,∠A 所对的边BC ,我们称为∠A 的对边;∠A 所在的直角边AC ,我们称为∠A 的邻边。
2、认识正弦、余弦、正切如图,在Rt △ABC 中,∠A 、∠B 、∠C 所对的边分别记为a 、b 、c 。
在Rt △ABC 中,∠C=90°,我们把锐角A 的对边与斜边的比叫做∠A 的正弦。
记作sinA 。
sinA =A a A c ∠=∠的对边的斜边、cosA=斜边邻边A ∠、tanA=对边邻边注意:1、sinA 不是 sin 与A 的乘积,而是一个整体; 2、正弦的三种表示方式:sinA 、sin56°、sin ∠DEF 3、sinA 是线段之间的一个比值;sinA 没有单位。
3、尝试练习:如图,在Rt △ABC 中,∠C=90°,求sinA 和tanB 的值.(二)探究:(1)一个锐角的正弦值与边的长短无关,与锐角的大小有关;锐角越大,正弦值越大,反之亦然。
(2)下面我们来验证一下吧!观察图中的Rt △AB 1C 1、Rt △AB 2C 2和Rt △AB 3C 3,它们之间有什么关系 分析:由图可知Rt △AB 1C 1∽Rt △AB 2C 2∽Rt △AB 3C 3,所以有:k AB C B AB C B AB C B ===333222111,即sinA=k 可见,在Rt △ABC 中,锐角A 的正弦值与边的长短无关,而与∠A 的度数大小有关。
也即是对于锐角A 的每一个确定的值,其对边与斜边的比值是惟一确定的.(1)CB 4319.3.2CB(三)例题教学:【例1】在△ABC中,∠C=90°.(1)若cosA=12,则tanB=______;(•2)•若cosA=45,则tanB=______.例2、在△ABC中,∠C为直角。
数学正切正弦余弦公式

数学正切正弦余弦公式
我们要了解数学中的正切、正弦和余弦公式。
首先,我们需要知道这些三角函数的基本定义。
正弦(sin)是直角三角形中,对边与斜边的比值。
余弦(cos)是直角三角形中,邻边与斜边的比值。
正切(tan)是直角三角形中,对边与邻边的比值。
正弦、余弦和正切之间的关系可以用以下公式表示:
1. 正弦的平方加上余弦的平方等于1,即:sin^2(θ) + cos^2(θ) = 1
2. 正切等于正弦除以余弦,即:tan(θ) = sin(θ) / cos(θ)
3. 正弦等于余切的倒数,即:sin(θ) = 1 / tan(θ)
4. 余弦等于正切的倒数,即:cos(θ) = 1 / tan(θ)
这些公式是三角函数的基础,它们在解决各种数学问题中非常有用。
正弦、余弦、正切:三角函数

正弦、余弦、正切:三角函数三角函数是数学中常见的函数,主要涉及正弦(sine)、余弦(cosine)和正切(tangent)三个函数。
这些函数在解决几何和物理问题中具有重要的应用。
本文将介绍正弦、余弦和正切函数的定义、性质以及在实际问题中的应用。
一、正弦函数(Sine Function)正弦函数是一个周期性函数,其定义如下:sin(x) = \frac{opposite}{hypotenuse} = \frac{y}{r}其中,x 是一个角度,y 是该角度对应的直角三角形中的对边,而 r 则是该直角三角形的斜边。
正弦函数的图像是一条连续的波浪线,其振幅为 1,周期为2π。
在数学和物理领域中,正弦函数常用于描述波动、周期性等现象。
二、余弦函数(Cosine Function)余弦函数也是一个周期性函数,其定义如下:cos(x) = \frac{adjacent}{hypotenuse} = \frac{x}{r}与正弦函数相似,x 为一个角度,而 r 是对应直角三角形的斜边,而 x 则是该直角三角形中的邻边。
余弦函数的图像是一条连续的波浪线,其振幅同样为 1,周期也为2π。
在几何和物理学中,余弦函数常用于描述旋转、震动等周期性现象。
三、正切函数(Tangent Function)正切函数是三角函数中的另一种常见形式,其定义如下:tan(x) = \frac{opposite}{adjacent} = \frac{y}{x}在直角三角形中,对于给定的角度 x,正切函数可用来表示直角三角形中对边与邻边的比值。
正切函数的图像是一条连续的波动曲线,没有周期性。
正切函数在几何和物理学中经常应用于描述斜率、角度等性质。
综上所述,正弦、余弦和正切是三角函数的重要组成部分。
它们在数学、几何学和物理学中都具有广泛的应用。
正弦函数描述了波动的特征,余弦函数则描述了旋转和震动的特征,而正切函数则描述了斜率和角度的特征。
三角函数公式(最全)
正弦定理变形可得:
五、其他公式
2、余弦定理
对于如图所示的边长为a、b、c而相应角为α、β、γ的△ABC, 有:
3、降幂公式
sin²α=[1-cos(2α)]/2 cos²α=[1+cos(2α)]/2 tan²α=[1-cos(2α)]/[1+cos(2α)]
4、三角和
sin(α+β+γ)=sinα·cosβ·cosγ+cosα·sinβ·cosγ+ cosα·cosβ·sinγ-sinα·sinβ·sinγ
ln(1+x)=x-x2/2+x3/3-…+(-1)k-1xk/k, x∈(-1,1)
sin x = x-x3/3!+x5/5!-…+(-1)k-1x2k-1/(2k-1)!+…, x∈R
cos x = 1-x2/2!+x4/4!-…+(-1)kx2k/(2k)!+…, x∈R
arcsin x = x + x3/(2*3) + (1*3)x5/(2*4*5) + (1*3*5)x7/(2* 4*6*7)…+(2k+1)!!*x2k+1/(2k!!*(2k+1))+…, x∈(-1,1)(!!表 示双阶乘)
1
一、定义公式
三角函数公式
锐角三角函数 任意角三角函数
正弦(sin) 余弦(cos) 正切(tan或tg) 余切(cot或ctg) 正割(sec) 余割(csc) 正弦(sin) 余弦(cos) 正切(tan或tg) 余切(cot或ctg) 正割(sec) 余割(csc)
1、倒数关系
二、函数关系
三角函数定理公式大全

三角函数定理公式大全在数学中,三角函数是一组基本的函数,用于描述角度和边长之间的关系。
三角函数定理是描述三角形中角度和边长之间的关系的公式集合。
三角函数定理被广泛应用于三角形的计算和解决各种实际问题。
在本篇文章中,我们将介绍三角函数的各种定理公式。
1. 正弦定理(Sine Rule):在任意三角形ABC中,边长a,b,c与对应的角A,B,C之间满足以下关系:a/sinA = b/sinB = c/sinC这意味着一个三角形的任意一边的长度与它所对应的角的正弦值成比例。
2. 余弦定理(Cosine Rule):在任意三角形ABC中,边长a,b,c与对应的角A,B,C之间满足以下关系:c² = a² + b² - 2ab*cosCb² = a² + c² - 2ac*cosBa² = b² + c² - 2bc*cosA这意味着一个三角形的任意一边的平方与其他两边的平方以及其夹角的余弦值有关。
3. 正切定理(Tangent Rule):在任意三角形ABC中,边长a,b,c与对应的角A,B,C之间满足以下关系:tanA = a/btanB = b/atanC = c/a这意味着一个三角形的任意一边的长度与其他两边的长度之间的比率与对应的角的正切值成比例。
4. 正割定理(Secant Rule):在任意三角形ABC中,边长a,b,c与对应的角A,B,C之间满足以下关系:secA = 1/cosAsecB = 1/cosBsecC = 1/cosC这意味着一个三角形的任意一边的长度与对应的角的余弦值的倒数成比例。
5. 余割定理(Cosecant Rule):在任意三角形ABC中,边长a,b,c与对应的角A,B,C之间满足以下关系:cosecA = 1/sinAcosecB = 1/sinBcosecC = 1/sinC这意味着一个三角形的任意一边的长度与对应的角的正弦值的倒数成比例。
常用正弦余弦正切值表

常用正弦余弦正切值表一、简介正弦、余弦和正切是三角函数中的重要概念之一。
它们在数学、物理和工程学中都有广泛的应用。
正弦、余弦和正切值表提供了这些三角函数在特定角度下的数值结果,使得计算和研究更加方便和高效。
二、正弦、余弦和正切的定义1. 正弦函数(Sine Function)正弦函数(简写为sin)表示一个角的对边与斜边的比值。
在一个直角三角形中,正弦值等于对边长度除以斜边长度。
正弦函数的取值范围介于-1和1之间。
2. 余弦函数(Cosine Function)余弦函数(简写为cos)表示一个角的邻边与斜边的比值。
在一个直角三角形中,余弦值等于邻边长度除以斜边长度。
余弦函数的取值范围同样介于-1和1之间。
3. 正切函数(Tangent Function)正切函数(简写为tan)表示一个角的对边与邻边的比值。
在一个直角三角形中,正切值等于对边长度除以邻边长度。
正切函数的取值范围是整个实数集合。
三、常用正弦、余弦和正切值表下面是常见角度(以度为单位)的正弦、余弦和正切值表:角度正弦值余弦值正切值0 0 1 030 0.5 √3/2 √3/345 √2/2 √2/2 160 √3/2 0.5 √390 1 0 无穷大(不存在)注意:表中的值都是取近似值,并非精确值。
在实际计算中,可以使用更高精度的值进行计算。
四、使用正弦、余弦和正切值表的示例以下是如何使用正弦、余弦和正切值表进行计算的示例:示例1:计算角度为60度的正弦、余弦和正切值。
根据表中的数值,我们可以得到角度为60度的正弦、余弦和正切值如下:正弦60度= √3/2余弦60度 = 0.5正切60度= √3示例2:计算角度为45度的余弦值。
根据表中的数值,我们可以得到角度为45度的余弦值为√2/2。
通过正弦、余弦和正切值表,我们可以快速地得到特定角度下的三角函数值,而无需进行复杂的计算。
这对于数学问题的解决、物体运动的描述以及工程设计中的角度处理都非常有用。
三角函数公式大全

三角函数公式大全本文主要介绍三角函数公式的大全,包括正弦、余弦、正切、余切、正割、余割、弧度制、角度制等,共计52个公式。
三角函数是初等数学中重要的一部分,以它为基础可以推导出很多数学公式,也是物理、化学等自然科学中常用的数学工具。
1、正弦(sin)与余弦(cos)的关系公式sin θ = cos(90° - θ)cos θ = sin(90° - θ)2、正弦(sin)与余切(ctg)的关系公式sin θ = 1 / ctg θctg θ = 1 / sin θ3、正弦(sin)与正割(sec)的关系公式sin θ = 1 / sec(90° - θ)sec θ = 1 / sin(90° - θ)4、余弦(cos)与正切(tan)的关系公式cos θ = 1 / tan(90° - θ)tan θ = 1 / cos(90° - θ)5、余弦(cos)与余切(cot)的关系公式cos θ = 1 / cot(90° - θ)cot θ = 1 / cos(90° - θ)6、余弦(cos)与余割(cosec)的关系公式c os θ = 1 / cosec(90° - θ)cosec θ = 1 / cos(90° - θ)7、正切(tan)与余切(cot)的关系公式tan θ = 1 / cot θcot θ = 1 / tan θ8、正切(tan)与正割(sec)的关系公式tan θ = 1 / sec(90° - θ)sec θ = 1 / cot(90° - θ)9、正切(tan)与余割(cosec)的关系公式tan θ = 1 / cosec(90° - θ)cosec θ = 1 / cot(90° - θ)10、余切(cot)与正割(sec)的关系公式cot θ = 1 / sec θsec θ = 1 / cot θ11、余切(cot)与余割(cosec)的关系公式cot θ = 1 / cosec(90° - θ)cosec θ = 1 / tan(90° - θ)12、正割(sec)与余割(cosec)的关系公式sec θ = 1 / cosec(90° - θ)cosec θ = 1 / sec(90° - θ)13、正弦(sin)的倒数公式sin(-θ) = -sin θsin(θ ± 360°) = sin θ14、余弦(cos)的倒数公式cos(-θ) = cos θcos(θ ± 360°) = cos θ15、正切(tan)的倒数公式tan(-θ) = -tan θtan(θ ± 180°) = tan θ16、余切(cot)的倒数公式cot(-θ) = -cot θcot(θ ± 180°) = cot θ17、正割(sec)的倒数公式sec(-θ) = sec θsec(θ ± 360°) = sec θ18、余割(cosec)的倒数公式cosec(-θ) = -cosec θcosec(θ ± 360°) = cosec θ19、正弦(sin)的平方公式sin² θ + cos² θ = 11 - sin² θ = cos² θsin² θ = 1 - cos² θ20、余弦(cos)的平方公式sin² θ + cos² θ = 11 - cos² θ = sin² θcos² θ = 1 - sin² θ21、正切(tan)的平方公式tan² θ + 1 = sec² θ1 + cot² θ = cosec² θtan² θ = sec² θ - 122、余切(cot)的平方公式cot² θ + 1 = cosec² θ1 + tan² θ = sec² θcot² θ = cosec² θ - 123、正弦(sin)的角和公式sin(A + B) = sin A cos B + cos A sin Bsin(A - B) = sin A cos B - cos A sin B 24、余弦(cos)的角和公式cos(A + B) = cos A cos B - sin A sin B cos(A - B) = cos A cos B + sin A sin B 25、正弦(sin)的二倍角公式sin 2A = 2 sin A cos A26、余弦(cos)的二倍角公式cos 2A = cos² A - sin² A27、正切(tan)的二倍角公式tan 2A = 2 tan A / (1 - tan² A)28、余切(cot)的二倍角公式cot 2A = (cot² A - 1) / 2 cot A29、正割(sec)的二倍角公式sec 2A = (sec² A + 1) / (2 sec A)30、余割(cosec)的二倍角公式cosec 2A = (cosec² A + 1) / (2 cosec A) 31、正弦(sin)的三倍角公式sin 3A = 3 sin A - 4 sin³ A32、余弦(cos)的三倍角公式cos 3A = 4 cos³ A - 3 cos A33、正切(tan)的三倍角公式tan 3A = (3 tan A - tan³ A) / (1 - 3 tan² A) 34、余切(cot)的三倍角公式cot 3A = (3 cot A - cot³ A) / (3 cot² A - 1) 35、正弦(sin)的四倍角公式sin 4A = 4 sin A cos A (2 cos² A - 1) 36、余弦(cos)的四倍角公式cos 4A = cos² 2A - sin² 2A37、正切(tan)的四倍角公式tan 4A = (4 tan A - 4 tan³ A) / (1 - 6 tan² A + tan⁴ A) 38、余切(cot)的四倍角公式cot 4A = (cot² 2A - 1) / 2 cot 2A39、正弦(sin)的半角公式sin (A/2) = ±√[(1 - cos A) / 2]40、余弦(cos)的半角公式cos (A/2) = ±√[(1 + cos A) / 2]41、正切(tan)的半角公式tan (A/2) = ±√[(1 - cos A) / (1 + cos A)]42、余切(cot)的半角公式cot (A/2) = ±√[(1 + cos A) / (1 - cos A)]43、正割(sec)的半角公式sec (A/2) = ±√[(1 + cos A) / (1 - cos A)]44、余割(cosec)的半角公式cosec (A/2) = ±√[(1 - cos A) / (1 + cos A)]45、正弦(sin)的万能公式a sin x +b cos x = √(a² + b²) sin(x + atan(b/a))46、余弦(cos)的万能公式a cos x -b sin x = √(a² + b²) cos(x + atan(b/a))47、正切(tan)的万能公式a tan x -b cot x = atan[(a sin x - b cos x)/(a cos x + b sin x)]48、余切(cot)的万能公式a cot x -b tan x = atan[(b sin x - a cos x)/(a sin x + b cos x)]49、正割(sec)的万能公式a sec x +b cosec x = 2 √(a² + b²) / [sin(2x + atan(b/a)) + sin(2x - atan(b/a))]50、余割(cosec)的万能公式a cosec x +b sec x = 2 √(a² + b²) / [sin(2x + atan(b/a)) - sin(2x - atan(b/a))]51、弧度制与角度制的转换公式弧度制 = 角度制× π / 180角度制 = 弧度制× 180 / π52、三角函数的图像正弦(sin)的图像:余弦(cos)的图像:正切(tan)的图像:余切(cot)的图像:正割(sec)的图像:余割(cosec)的图像:以上是三角函数公式的大全,通过掌握这些公式可以更深入地了解三角函数的性质和应用,有助于提高数学水平。
正弦余弦正切公式大全

正弦余弦正切公式大全正弦公式:正弦函数是指在直角三角形中,对于任意角度θ,对边与斜边的比值。
正弦函数使用sin(θ)表示,其中θ为角度。
正弦公式可以表示为:sin(θ) = 对边/斜边余弦公式:余弦函数是指在直角三角形中,对于任意角度θ,邻边与斜边的比值。
余弦函数使用cos(θ)表示,其中θ为角度。
余弦公式可以表示为:cos(θ) = 邻边/斜边正切公式:正切函数是指在直角三角形中,对于任意角度θ,对边与邻边的比值。
正切函数使用tan(θ)表示,其中θ为角度。
正切公式可以表示为:tan(θ) = 对边/邻边在直角三角形中,还有两个重要的三角函数:余切函数和正割函数。
余切公式:余切函数是指在直角三角形中,对于任意角度θ,邻边与对边的比值。
余切函数使用cot(θ)表示,其中θ为角度。
余切公式可以表示为:cot(θ) = 邻边/对边正割公式:正割函数是指在直角三角形中,对于任意角度θ,斜边与邻边的比值。
正割函数使用sec(θ)表示,其中θ为角度。
正割公式可以表示为:sec(θ) = 斜边/邻边除了以上基本的三角函数公式,还有一些重要的三角函数恒等式:1.和差公式:sin(A ± B) = sin(A)cos(B) ± cos(A)sin(B)cos(A ± B) = cos(A)cos(B) ∓ sin(A)sin(B)tan(A ± B) = (tan(A) ± tan(B))/(1 ∓ tan(A)tan(B))2.二倍角公式:sin(2A) = 2sin(A)cos(A)cos(2A) = cos^2(A) - sin^2(A)tan(2A) = 2tan(A)/(1 - tan^2(A))3.三倍角公式:sin(3A) = 3sin(A) - 4sin^3(A)cos(3A) = 4cos^3(A) -3cos(A)tan(3A) = (3tan(A) - tan^3(A))/(1 - 3tan^2(A))4.万能公式:sin^2(A) + cos^2(A) = 11 + tan^2(A) = sec^2(A)1 + cot^2(A) = csc^2(A)这些公式在解决三角函数的运算、证明、及物理模型等问题中起到非常关键的作用。
正弦余弦和正切之间的关系

正弦余弦和正切之间的关系正弦、余弦和正切是三角函数中最基本的三种函数,它们之间存在着密切的关系。
首先,我们来看它们的定义和计算方法。
正弦函数(sin)表示一个角的对边与斜边的比值,通常用a/h表示,其中a为对边,h为斜边。
余弦函数(cos)表示一个角的邻边与斜边的比值,通常用b/h表示,其中b为邻边。
正切函数(tan)表示一个角的对边与邻边的比值,通常用a/b表示。
这三个函数之间的关系可以通过三角恒等式来描述。
例如,tanθ = sinθ / cosθ,这意味着正切函数可以表示为正弦函数与余弦函数的比值。
另外,我们还可以通过sin²θ + cos²θ = 1这一三角恒等式得到sinθ与cosθ之间的关系,进而推导出tanθ与sinθ、cosθ之间的关系。
在三角函数的图像中,我们也可以清晰地看到它们之间的关系。
正弦函数的图像是一个周期性的波浪曲线,而余弦函数的图像则是正弦函数图像的相位延迟π/2。
正切函数的图像则是在余弦函数的零点处具有无穷大的间断点,这也反映了正切函数与正弦、余弦之间的关系。
除了上述数学关系和图像特点外,正弦、余弦和正切在实际问题中也有着丰富的应用。
在三角测量、物理学、工程学等领域,这三种函数经常被用来描述角度、振动、周期性变化等现象,它们之间的关系也为解决实际问题提供了重要的数学工具。
综上所述,正弦、余弦和正切之间存在着密切的数学关系,可以通过三角恒等式、图像特点和实际应用来全面理解它们之间的联系。
这些函数的相互关系不仅在数学领域具有重要意义,也在实际问题的求解中发挥着重要作用。
数学中的三角函数正弦余弦与正切的应用

数学中的三角函数正弦余弦与正切的应用在数学中,三角函数是一种基础的数学工具,常用于解决与角度和三角形相关的问题。
其中,正弦、余弦和正切是三角函数中最常见且广泛应用的三种。
它们在几何、物理、工程等领域中起到了重要的作用。
本文将介绍三角函数正弦、余弦和正切的定义、性质以及其在各个领域中的具体应用。
一、正弦函数的定义与性质在三角函数中,正弦函数(sin)是最基本且常见的函数之一。
它的定义如下:定义1:对于任意实数x,正弦函数sin(x)的值等于以x为角度的弧所对应的直角三角形中,斜边的长度与斜边所在直角的邻边的比值。
正弦函数的性质如下:性质1:正弦函数的周期为2π(或360°)。
即sin(x+2π) = sin(x),对于任意实数x。
性质2:正弦函数的取值范围为[-1,1]。
即-1≤ sin(x) ≤1,对于任意实数x。
正弦函数在几何、物理等领域中有许多应用。
1. 几何中的应用正弦函数在解决几何问题中起到了重要的作用,尤其是在三角形中。
其中,正弦定理是一项基于正弦函数的重要几何定理。
它可以用于计算三角形的边长或角度。
利用正弦函数,可以得到正弦定理的数学表达式如下:对于任意三角形ABC,边长分别为a, b, c,对应的角度分别为A, B, C,那么有:sin(A)/a = sin(B)/b = sin(C)/c根据这个定理,我们可以根据已知的两个边与它们夹角的关系,求解未知边长或角度。
2. 物理中的应用正弦函数在物理学中的应用非常广泛。
例如,振动和波动等现象均可以通过正弦函数进行描述和分析。
在简谐振动中,物体以正弦函数的形式来回振动。
振动的幅度、频率以及相位差等都可以通过正弦函数来表示。
在波动中,正弦函数也被广泛应用。
例如,声波、光波等均可以表示为正弦函数的形式。
通过正弦函数可以描述波的振幅、频率、波长等特征。
3. 工程中的应用正弦函数在工程领域中也有很多应用。
例如,在电工学中,交流电信号可以表示为正弦函数。
高中数学三角函数:正弦、余弦、正切

)ππk kpppxsin sin xp))x注意:正切函数在开区间(),22k k k Z p p p p æö-++Îç÷èø内都是增函数。
但要注意在整个定义域上不具有单调性。
(三)解题方法指导 函数函数 正弦函数正弦函数余弦函数余弦函数正切函数正切函数图象图象 定义域定义域 值域值域 周期周期 奇偶性奇偶性单调性单调性 增区间增区间减区间减区间 增区间增区间减区间减区间 增区间增区间减区间减区间 对称性对称性对称轴对称轴对称中心对称中心 对称轴对称轴对称中心对称中心 对称轴对称轴对称中心对称中心例1.用五点法画出函数)3πsin(+=x y 草图,并求出函数的周期,单调区间,对称轴,对称中心.草图,并求出函数的周期,单调区间,对称轴,对称中心.例2.求函数)6π2sin(2+=xy 在区间[0,2p ]上的值域.上的值域.例3.求下列函数的值域.求下列函数的值域. (1)y =sin 2x -cos x +2; (2)y =2sin x cos x -(sin x +cos x ).例4.求函数xxy cos 3sin 1--=的值域.的值域.三角函数图象几何性质xOyx =x1x =x 2x 4邻中心|x 3-x 4|= T /2邻渐近线|x 1-x 2|=T 无穷对称中心:由y =0或y 无意义确定x 3无对称轴任意一条y 轴的垂线与正切函数图象都相交,且相邻两交点的距离为一个周期!tan()y A x w j =+三角函数图象几何性质xOy x =x1x =x 2x 4邻中心|x 3-x 4|=T /2邻轴|x 1-x 2|=T /2无穷对称中心:由y =0确定无穷对称轴:由y =A 或-A 确定x 34T 邻中心轴相距sin()y A x w j =+3π+x0 2ππ2π3 2πx 3π- 6π 3π2 6π7 3π5 y0 1 0 -1 0 ,),6ππZ Î+k ),π7)sin()].2)]2,2].2].这是数形结合解题的一个典型问题. 这是数形结合解题的一个典型问题.。
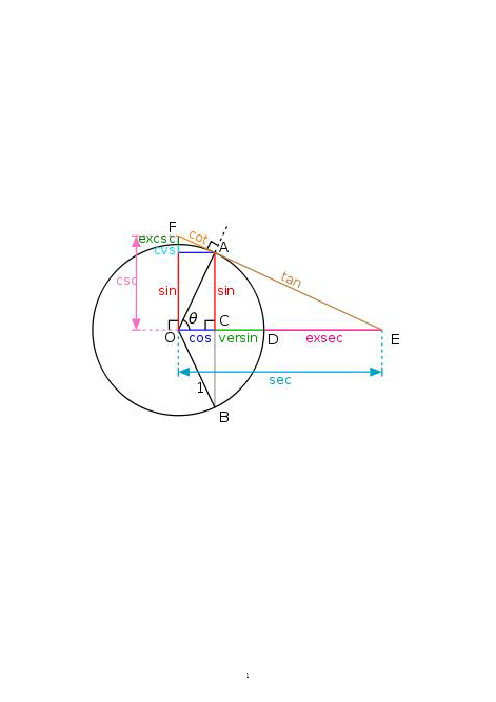
正弦、余弦、正切的定义正弦sinα=yr余弦cosα=(精)

正弦、余弦、正切的定义? 正弦:sinα =y/r 余弦:cosα=x/r 正切:tanα =y/x
交换三个比值的前后项是否可以得出三个 新的三角函数?
余切cotα=x/y,
正割secα=r/x , 余割cscα=r/y
设α是任意角,p(x,y)是角α终边上任 意一点,PO= x2 y2 =r(r>0),则把下面 六个函数
三角函数值在各象限的符号是怎样的?
y ++
Y>0 Y>0
x
-0 - Y<0 Y<0
sinα cscα
y
-
+
X<0 -0
X>0 x +
X<0 X>0
cosα sec α
y -+
X<0,y>0 X>0,y>0
x +0 -
X<0,y<0 X>0,y<0
tanα cotα
意为:第一象限各三角函数均为正,第二象限只有正弦及与正弦相关的余 割为正,其余均为负
R
|
k
2
,
k
Z
思考:余切、正割、余割函数定义域如何?
例2 求函数y=1/(1+sinx)的定义域。 解:∵1+sinx≠0, ∴ sinx≠-1
即角x的终边不能在y轴的负半轴上。 ∴x≠2kπ+3π/2,k∈Z, 故函数的定义域是 {x|x∈R,且x≠2kπ+3π/2,k∈Z}
⑷ tan11
3
sin 0
例4、已知角 满足 tan 0,问 是第几象限?
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一、锐角三角函数——正弦、余弦、正切
一、新课教学
(一)、认识正弦、余弦、正切
1、认识角的对边、邻边。
(2分钟)
如图,在Rt △ABC 中,∠A 所对的边BC ,我们称为∠A 的对边;∠A 所在的直角边AC ,我们称为∠A 的邻边。
2、认识正弦、余弦、正切
如图,在Rt △ABC 中,∠A 、∠B 、∠C 所对的边分别记为a 、b 、c 。
在Rt △ABC 中,∠C=90°,我们把锐角A 的对边与斜边的比叫做∠A 的正弦。
记作sinA 。
sinA =
A a A c ∠=∠的对边的斜边、cosA=斜边邻边A ∠、tanA=对边
邻边
注意:1、sinA 不是 sin 与A 的乘积,而是一个整体; 2、正弦的三种表示方式:sinA 、sin56°、sin ∠DEF 3、sinA 是线段之间的一个比值;sinA 没有单位。
3、尝试练习:
如图,在Rt △ABC 中,∠C=90°,求sinA 和tanB 的值.
(二)探究:(1)一个锐角的正弦值与边的长短无关,与锐角的大小有关;锐角越大,正弦值越大,反之亦然。
(2)下面我们来验证一下吧!
观察图中的Rt △AB 1C 1、Rt △AB 2C 2和Rt △AB 3C 3,它们之间有什么关系 分析:由图可知Rt △AB 1C 1∽Rt △AB 2C 2∽Rt △AB 3C 3,
所以有:
k AB C B AB C B AB C B ===3
3
3222111,即sinA=k 可见,在Rt △ABC 中,锐角A 的正弦值与边的长短无关,而与∠A 的度数大
小有关。
也即是对于锐角A 的每一个确定的值,其对边与斜边的比值是惟一确定的.
(1)
C
B 4319.3.2
C
B
(三)例题教学:
【例1】在△ABC中,∠C=90°.
(1)若cosA=1
2
,则tanB=______;(•2)•若cosA=
4
5
,则tanB=______.
例2、在△ABC中,∠C为直角。
(1)已知AC=3,AB=14,求sinA的值.
(2)已知sinB=
5
4,求sinA的值.
解:(1)如图,在Rt△ABC中,根据勾股定理可得:()5
3
142
2
=
-
=
BC,∴
14
70
14
5
sin=
=
=
AB
BC
A;
(2)∵sinB=
5
4
=
AB
AC,故设AC=4k,则AB=5k,根据勾股定理可得:BC=3k,所以:sinA=
5
3
小结:①求正弦值或运用正弦值求线段时,要根据正弦的概念,找准相应的边,不能张冠李戴.②正弦值只是一个比值,不能直接当作边长用。
锐角三角函数的定义和性质
【例3】(1)已知:cosα=
2
3
,则锐角α的取值范围是()
A.0°<α<30°B.45°<α<60°
C.30°<α<45°D.60°<α<90°
(2)(2006年潜江市)当45°<θ<90°时,下列各式中正确的是()
A.tanθ>cosθ>sinθB.sinθ>cosθ>tanθ
C.tanθ>sinθ>cosθD.cotθ>sinθ>cosθ
【例4】(1)如图,在Rt△ABC中,∠C=90°,AD是∠BAC∠的平分线,∠CAB=60°,•CD=3,BD=23,求AC,AB的长.
(2)(2005年黑龙江省)“曙光中学”有一块三角形状的花园ABC,•有人已经测出∠A=30°,AC=40米,BC=25米,你能求出这块花园的面积吗
(3)某片绿地形状如图所示,其中AB⊥BC,CD⊥AD,∠A=60°,AB=200m,CD=100m,•求AD、BC的长.
A
C
B
A
B
C
D
【点评】设法补成含60°的直角三角形再求解. 三、巩固练习:
1.﹙2006海南﹚三角形在正方形网格纸中的位置如图所示,则sin α的值是 。
A .4
3 B .3
4 C .53 D .5
4
2.(2005厦门市)如图,在直角△ABC 中,∠C =90o ,若AB =5,AC =4,则sinA =( )
A .35
B .45
C .34
D .43
3.﹙2006黑龙江﹚ 在△ABC 中,∠C=90°,BC=2,sinA=2
3,则边AC 的长是( ) A .13 B .3 C .4
3 D . 5
4.(2005年上海市)已知Rt △ABC 中,∠C=90°,AC=2,BC=3,那么下列各式中,正确的是( ) A .sinB=
23 B .cosB=23 C .tanB=23 D .tanB=3
2
5.点(-sin60°,cos60°)关于y 轴对称的点的坐标是( ) A .312) B .(312)C .(3-12)D .(-12,-32
) 6.﹙2006成都﹚如图,在Rt △ABC 中,∠ACB =90°,CD ⊥AB 于点D 。
已知AC= 5 ,BC=2,那么sin ∠ACD =( ) A 5
B .23
C 25
D 57.如图,已知AB 是⊙O 的直径,点C 、D 在⊙O 上,且AB =5,BC =3. 则sin ∠BAC= ;sin ∠ADC= .
8.(2005年沈阳市)在△ABC 中,AB=2,2,∠B=30°,则∠BAC 的度数是______. 9.计算2sin30°-2cos60°+tan45°=________.
10.(2005年辽宁省)在Rt △ABC 中,∠C=90°,AB=5,AC=3,则sinB=_____. 11.在△ABC 中,若2,7,AC=3,则cosA=________.
C
B A
12.在中,∠C =90°,a ,b ,c 分别是∠A 、∠B 、∠C 的对边,则有()
A .
B .
C .
D .
13. 在中,∠C =90°,如果那么的值为()
A .
B .
C .
D .
15.如图:P 是∠
的边OA 上一点,且P 点的坐标为(3,4), 则cos
=_____________.
在Rt △ABC 中,如果各边长度都扩大为原来的2倍,则锐角A 的正切值( ). A.扩大2倍 B.缩小2倍 C.扩大4倍 D.没有变化 16.(1)如图(1), 在中,
,
,
,求
的度数.
17.在△ABC 中,∠C=30°,∠BAC=105°,AD ⊥BC ,垂足为D ,AC=2cm ,求BC 的长.
18.在△ABC 中,∠A 、∠B 为锐角且sinA=1
2
,cosB=32,试判断△ABC 的形状
19.(2007)如图,A B ,两地之间有一座山,汽车原来从A 地到B 地须经C 地沿折线A C B --行驶,现开通隧道后,汽车直接沿直线AB 行驶.已知10km AC =,30A ∠=o
,45B ∠=o
,则隧道开通后,
汽车从A 地到B 地比原来少走多少千米(结果精确到0.1km )(参考数据:
2 1.41≈,
3 1.73≈)
20.(2006年金华市)如图所示,设A 城气象台测得台风中心在A•城正西方向600km 的B 处,正以每小时200km 的速度沿北偏东60°的BF 方向移动,距台风中心500km•的范围内是否受台风影响的区域. (1
)A 城是否受到这次台风的影响为什么
(2)若A 城受到这次台风的影响,那么A 城遭受这次台风的影响有多长时间
21.(2006重庆)如图,在梯形ABCD 中,AB 90︒
⑴求证:DC=BC ;
⑵E 是梯形内的一点,F 是梯形外的一点,且∠EDC=∠FBC ,DE=BF ,试判断△ECF 的形状,并证明你的结论;
⑶在⑵的条件下,当BE:CE=1:2,∠BEC=135︒
时,求sin ∠BFE 的值。
E
B
F
C
D
A。
