九年级上册数学第四章小结与复习重要知识点梳理与经典例题讲解(北师大版)
北师大版九年级数学上册《图形的相似》知识点归纳

北师大版九年级数学上册《图形的相似》知识点归纳北师大版九年级数学上册《图形的相似》知识点归纳第四章图形的相似一、成比例线段1、定义:(1)、线段比:如果选用一个长度单位量得两条线段AB、CD的长度分别是m,n,那么这两条线段的比就是它们长度的比,即AB:CD=m:n,或者写成AB/CD=m/n.(2)、成比例线段:四条线段a、b、c、d中,如果a与b的比等于c与d的比,即a/b=c/d,那么这四条线段a、b、c、d叫做成比例线段,简称比例线段。
2、定理:如果a/b=c/d==m/n(b+d++n≠0),那么(a+c+m)/(b+d++n)=a/b二、平行线分线段成比例1、两条直线被一组平行线所截,所得的对应线段成比例。
2、平行于三角形一边的直线与其他两边相交。
截得的线段成比例。
三、相似多边形定义:各角分别相等,各边成比例的两个多边形叫做相似多边形。
相似多边形对应边的比叫做相似比。
四、探索三角形相似的条件1、两角分别相等的两个三角形相似。
2、两边成比例且夹角相等的两个三角形相似。
3、三边成比例的两个三角形相似。
4、概念:一般地,点C把线段AB分成两条线段AC和BC,如果AC/AB=BC/AC,那么称线段AB被点C黄金分割,点C 叫做线段AB的黄金分割点,AC与AB的比叫做黄金比。
五、相似三角形判定定理的证明六、利用相似三角形测高1、利用阳光下的影子2、利用标杆3、利用镜子的反射七、相似三角形的性质1、相似三角形对应高的比、对应角平分线的比、对应中线的比等于相似比。
2、相似三角形的周长比等于相似比,面积比等于相似比的平方。
八、图形的位似定义:一般地,如果两个相似多边形任意一组对应顶点P、P1所在的直线都经过同一个点O,且有OP1=k*OP(k≠0),那么这样的两个多边形叫做位似多边形,点O叫做位似中心。
实际上,k就是这两个相似多边形的相似比。
北师大版数学九年级上册第四章 《图形的相似》重点题型归纳
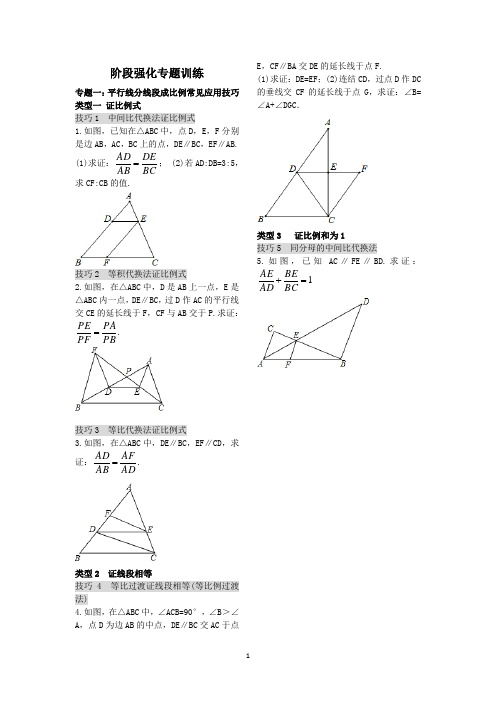
阶段强化专题训练专题一:平行线分线段成比例常见应用技巧 类型一 证比例式技巧1 中间比代换法证比例式1.如图,已知在△ABC 中,点D ,E ,F 分别是边AB ,AC ,BC 上的点,DE ∥BC ,EF ∥AB. (1)求证:BCDEAB AD =; (2)若AD:DB=3:5,求CF:CB 的值.技巧2 等积代换法证比例式2.如图,在△ABC 中,D 是AB 上一点,E 是△ABC 内一点,DE ∥BC ,过D 作AC 的平行线交CE 的延长线于F ,CF 与AB 交于P.求证:PBPAPF PE =.技巧3 等比代换法证比例式3.如图,在△ABC 中,DE ∥BC ,EF ∥CD ,求证:ADAFAB AD =.类型2 证线段相等技巧 4 等比过渡证线段相等(等比例过渡法)4.如图,在△ABC 中,∠ACB=90°,∠B >∠A ,点D 为边AB 的中点,DE ∥BC 交AC 于点E ,CF ∥BA 交DE 的延长线于点F.(1)求证:DE=EF ;(2)连结CD ,过点D 作DC 的垂线交CF 的延长线于点G ,求证:∠B=∠A+∠DGC .类型3 证比例和为1技巧5 同分母的中间比代换法5.如图,已知AC ∥FE ∥BD.求证:1=+BCBEAD AE专题二:证明相似三角形的方法名师点金要找三角形相似的条件,关键抓住以下几点:(1)已知角相等时,找两对对应角相等,若只能找到一对对应角相等,判断夹相等的角的两边是否对应成比例;(2)无法找到角相等时,判断三边是否对应成比例;(3)除此之外,也可考虑平行线分线段成比例定理及相似三角形的“传递性...”.方法1 利用边或角的关系判定两直角三角形相似1.下面关于直角三角形相似叙述错误的是( )A.有一锐角对应相等的两个直角三角形相似B.两直角边对应成比例的两个直角三角形相似C.有一条直角边相等的两个直角三角形相似D.两个等腰直角三角形相似2.如图,BC⊥AD,垂足为C,AD=6.4,CD=1.6,BC=9.3,CE=3.1.求证:△ABC∽△DEC.方法2 利用角判定两三角形相似3.如图,△ABC是等边三角形,CE是外角平分线,点D在AC上,连接BD并延长,与CE 交于点 E. (1)求证:△ABD∽△CED; (2)若AB=6,AD=2CD,求BE的长.方法3 利用边角判定两三角形相似4.如图,AB=3AC,BD=3AE,又BD∥AC,点B,A,E在同一条直线上.求证:△ABD∽△CAE. 方法4 利用三边判定两三角形相似5.如图,AD是△ABC的高,E,F分别是AB,AC的中点.求证:△DEF∽△ABC.专训三巧作平行线构造相似三角形名师点金:解题时,往往会遇到要证的问题与相似三角形联系不上或者说图中根本不存在相似三角形的情况,添加辅助线构造相似三角形是这类几何证明题的一种重要方法.常作的辅助线有以下几种:(1)由比例式作平行线;(2)有中点时,作中位线;(3)根据比例式,构造相似三角形.训练角度1 巧连线段的中点构造相似三角形1.如图,在△ABC中,E,F是边BC上的两个三等分点,D是AC的中点,BD分别交AE,AF于点P,Q,求BP:PQ:QD.训练角度 2 过顶点作平行线构造相似三角形2.如图,在△ABC中,AC=BC,F为底边AB 上一点,BF:AF=3:2,取CF的中点D,连接AD并延长交BC于点E,求BE:EC的值.3.如图,过△ABC的顶点C任作一直线,与边AB及中线AD分别交于点F和点E.求证:AE:ED=2AF:FB.训练角度 3 过一边上的点作平行线构造相似三角形4.如图,在△ABC中,AB>AC,在边AB上取一点D,在AC上取一点E,使AD=AE,直线DE和BC的延长线交于点P.求证: BP:CP=BD:EC.训练角度 4 过一点作平行线构造相似三角形5.如图,在△ABC中,点M为AC边的中点,点E为AB上一点,且AE=41AB,连接EM并延长交BC的延长线于点D.求证:BC=2CD. 作辅助线的方法一:作辅助线的方法二:作辅助线的方法三:作辅助线的方法四:全章整合提升密码专训一:证比例式或等积式的技巧 名师点金证比例式或等积式,若遇问题中无平行线或相似三角形时,则需构造平行线或相似三角形,得到等比例线段;若比例式或等积式中的线段分布在两个三角形或不在两个三角形中,可尝试证这两个三角形相似或先将它们转化到两个三角形中再证两三角形相似,若在两个明显不相似的三角形中,可运用中间比代换.技巧1 构造平行线法1.如图,在△ABC 中,D 为AB 的中点,DF 交AC 于点E ,交BC 的延长线于点F , 求证:AE ·CF =BF ·EC.2.如图,已知△ABC 的边AB 上有一点D ,边BC 的延长线上有一点E ,且AD =CE ,DE 交AC 于点F ,试证明:AB ·DF =BC ·EF.技巧2 三点找三角形相似法3.如图,在▱ABCD 中,E 是AB 延长线上的一点,DE 交BC 于F. 求证:DC AE =CF AD.4.如图,在△ABC 中,∠BAC =90°,M 为BC 的中点,DM ⊥BC 交CA 的延长线于D ,交AB于E.求证:AM 2=MD ·ME.技巧3 构造相似三角形法5.如图,在等边三角形ABC 中,点P 是BC 边上任意一点,AP 的垂直平分线分别交AB ,AC 于点M ,N. 求证:BP ·CP =BM ·CN.技巧4 等比过渡法6.如图,在△ABC 中,AB =AC ,DE ∥BC ,点F 在边AC 上,DF 与BE 相交于点G ,且∠EDF =∠ABE. 求证:(1)△DEF ∽△BDE ;(2)DG ·DF =DB ·EF.7.如图,CE 是Rt △ABC 斜边上的高,在EC 的延长线上任取一点P ,连接AP ,作BG ⊥AP于点G ,交CE 于点D. 求证:CE 2=DE ·PE.技巧5 两次相似法8.如图,在Rt △ABC 中,AD 是斜边BC 上的高,∠ABC 的平分线BE 交AC 于E ,交AD 于F. 求证:BF BE =ABBC.9.如图,在▱ABCD 中,AM ⊥BC ,AN ⊥CD ,垂足分别为M ,N.求证:(1)△AMB ∽△AND ;(2)AM AB =MNAC.技巧6 等积代换法10.如图,在△ABC 中,AD ⊥BC 于D ,DE ⊥AB 于E ,DF ⊥AC 于F.求证:AE AF =ACAB.技巧7 等线段代换法11.如图,等腰△ABC 中,AB =AC ,AD ⊥BC 于点D ,点P 是AD 上一点,CF ∥AB ,延长BP 交AC 于点E ,交CF 于点F ,求证:BP 2=PE ·PF.12.已知:如图,AD 平分∠BAC ,AD 的垂直平分线EP 交BC 的延长线于点P.求证:PD 2=PB ·PC.专训二 巧用“基本图形”探索相似条件 名师点金:几何图形大多数由基本图形复合而成,因此熟悉三角形相似的基本图形,有助于快速、准确地识别相似三角形,从而顺利找到解题思路和方法.相似三角形的四类结构图: 1.平行线型2.相交线型3.子母型4.旋转型训练角度1 平行线型1.如图,在△ABC 中,BE 平分∠ABC 交AC 于点E ,过点E 作ED ∥BC 交AB 于点D.(1)求证:AE ·BC =BD ·AC ; (2)如果S △ADE =3,S △BDE =2,DE =6,求BC 的长.训练角度2 相交线型2.如图,点D ,E 分别为△ABC 的边AC ,AB 上的点,BD ,CE 交于点O ,且EO BO =DOCO ,试问△ADE 与△ABC 相似吗?请说明理由.训练角度3 子母型3.如图,在△ABC 中,∠BAC =90°,AD ⊥BC 于点D ,E 为AC 的中点,ED 的延长线交AB 的延长线于点F.求证:AB AC =DFAF.训练角度4 旋转型 4.如图,已知∠DAB =∠EAC ,∠ADE =∠ABC.求证:(1)△ADE ∽△ABC ;(2)AD AE =BD CE.专训三 利用相似三角形巧证线段的数量和位置关系 名师点金:判断两线段之间的数量和位置关系是几何中的基本题型之一.由角的关系推出“平行或垂直”是判断位置关系的常用方法,由相似三角形推出“相等”是判断数量关系的常用方法.训练角度1 证明两线段的数量关系 类型1: 证明两线段的相等关系1.如图,已知在△ABC 中,DE ∥BC ,BE 与CD 交于点O ,直线AO 与BC 边交于点M ,与DE 交于点N. 求证:BM =MC.2.如图,一直线和△ABC 的边AB ,AC 分别交于点D ,E ,和BC 的延长线交于点F ,且AE:CE =BF:CF. 求证:AD =DB.类型2 证明两线段的倍分关系3.如图,在△ABC 中,BD ⊥AC 于点D ,CE ⊥AB 于点E ,∠A =60°,求证:DE =12BC.4.如图,AM 为△ABC 的角平分线,D 为AB 的中点,CE ∥AB ,CE 交DM 的延长线于E. 求证:AC =2CE.训练角度2 证明两线段的位置关系 类型1:证明两线段平行 5.如图,已知点D 为等腰直角三角形ABC 的斜边AB 上一点,连接CD ,DE ⊥CD ,DE =CD ,连接CE ,AE.求证:AE ∥BC.6.在△ABC 中,D ,E ,F 分别为BC ,AB ,AC 上的点,EF ∥BC ,DF ∥AB ,连接CE 和AD ,分别交DF ,EF 于点N ,M.(1)如图①,若E 为AB 的中点,图中与MN 平行的直线有哪几条?请证明你的结论; (2)如图②,若E 不为AB 的中点,写出与MN 平行的直线,并证明.类型2 证明两线垂直7.如图,在△ABC 中,D 是AB 上一点,且AC2=AB ·AD ,BC 2=BA ·BD ,求证:CD ⊥AB.8.如图,已知矩形ABCD ,AD =13AB ,点E ,F把AB 三等分,DF 交AC 于点G ,求证:EG ⊥DF.专训四巧用位似解三角形中的内接多边形问题名师点金位似图形是特殊位置的相似图形,它具有相似图形的所有性质,位似图形必须具备三个条件:(1)两个图形相似;(2)对应点的连线相交于一点;(3)对应边互相平行或在同一直线上.类型1 三角形的内接正三角形问题1.如图,用下面的方法可以画△AOB的内接等边三角形,阅读后证明相应问题.画法:①在△AOB内画等边三角形CDE,使点C在OA上,点D在OB上;②连接OE并延长,交AB于点E′,过点E′作E′C′∥EC,交OA于点C′,作E′D′∥ED,交OB于点D′;③连接C′D′,则△C′D′E′是△AOB的内接等边三角形.求证:△C′D′E′是等边三角形.类型2 三角形的内接矩形问题2.求作:内接于已知△ABC的矩形DEFG,使它的边EF在BC上,顶点D,G分别在AB,AC上,并且有DE∶EF=1∶2.类型 3 三角形的内接正形问题(方程思想)3.如图,△ABC 是一块锐角三角形余料,边BC=120mm ,高AD=80mm ,要把它加工成正方形零件,使正方形的一边QM 在BC上,其余两个顶点P ,N 分别在AB,AC上,则这个正方形零件的边长是多少?4.(1)如图①,在△ABC 中,点D ,E ,Q 分别在AB ,AC ,BC 上,且DE ∥BC ,AQ交DE 于点P.求证:DP:BQ=PE:QC.(2)在△ABC 中,∠BAC =90°,正方形DEFG 的四个顶点在△ABC 的边上,连接AG ,AF ,分别交DE 于M ,N 两点.①如图②,若AB=AC=1,直接写出MN的长;②如图③,求证:MN²=DM·EN.专训五: 图形的相似中的五种热门考点 名师点金:相似是初中数学的重要内容,也是中考重点考查内容之一,而对于成比例线段、相似三角形的判定与性质、位似图形等都是命题的热点.考点一: 比例线段及性质1.下列各组长度的线段,成比例线段的是( )A. 2 cm ,4 cm ,4 cm ,8 cmB. 2 cm ,4 cm ,6 cm ,8 cmC. 1 cm ,2 cm ,3 cm ,4 cmD. 2.1 cm ,3.1 cm ,4.3 cm ,5.2 cm2.若a 2=b 3=c 4=d 7≠0,则a +b +c +d c =________.3.如图,乐器上的一根弦AB =80 cm ,两个端点A ,B 固定在乐器板面上,支撑点C 是靠近点B 的黄金分割点,则支撑点C 到端点A 的距离约为________.(5≈2.236,结果精确到0.01)考点二: 平行线分线段成比例4.如图,若AB ∥CD ∥EF ,则下列结论中,与AD AF 相等的是( ) A.AB EF B.CD EF C.BO OE D.BC BE5.如图,在Rt △ABC 中,∠ACB =90°,∠ABC =60°,以AC 为边向三角形外作正方形ACDE ,连接BE 交AC 于F ,若BF = 3 cm ,则EF =________.6.如图,在△ABC 中,AM ∶MD =4∶1,BD ∶DC =2∶3,求AE ∶EC 的值.考点三 相似三角形的性质与判定7.已知△ABC ∽△DEF ,若△ABC 与△DEF 的相似比为3∶4,则△ABC 与△DEF 的面积之比为( ) A.4:3 B.3:4 C.16:9 D.9:168.在平行四边形ABCD 中,点E 在AD 上,且AE ∶ED =3∶1,CE 的延长线与BA 的延长线交于点F ,则S △AEF ∶S 四边形ABCE 为( ) A.3∶4 B.4∶3 C.7∶9 D.9∶79.若两个相似多边形的面积之比为1∶4,周长之差为6,则这两个相似多边形的周长分别是________.10.如图,△ABC 是直角三角形,∠ACB =90°,CD ⊥AB 于D ,E 是AC 的中点,ED 的延长线与CB 的延长线交于点F.(1)求证:FD 2=FB ·FC ; (2)若FB =5,BC =4,求FD 的长.11.如图,四边形ABCD 是正方形,BD 是对角线,BE 平分∠DBC 交DC 于点E ,点F 是BC 的延长线上一点,且CE =CF ,BE 的延长线交DF 于点M.(1)求证:BM ⊥DF ; (2)若正方形ABCD 的边长为2,求ME ·MB.考点四相似三角形的应用12.一天晚上,李明和张龙利用灯光下的影子长来测量一路灯的高度CD.如图,当李明走到点A处时,张龙测得李明直立时身高AM 与影子长AE正好相等;接着李明沿AC方向继续向前走,走到点B处时,李明直立时身高BN的影子恰好是线段AB,并测得AB=1.25 m,已知李明直立时的身高为1.75 m,求路灯的高度CD.(结果精确到0.1 m)13.某高中学校为高一新生设计的学生板凳的正面视图如图所示,其中BA=CD,BC=20 cm,BC,EF平行于地面AD且到地面AD的距离分别为40 cm,8 cm.为使板凳两腿底端A,D之间的距离为50 cm,那么横梁EF的长应为多少?(材质及其厚度等暂忽略不计)考点五图形的位似14.如图,已知正方形ABCD,以点A为位似中心,把正方形ABCD的各边缩小为原来的一半,得正方形A′B′C′D′,则点C′的坐标为________.15.如图,在6×8的网格图中,每个小正方形的边长均为1,点O和△ABC的顶点均在小正方形的顶点上.(1)以O为位似中心,在网格图中作△A′B′C′和△ABC位似,且相似比为1∶2;(2)连接(1)中的AA′,求四边形AA′C′C 的周长.(结果保留根号)专训六全章热门考点整合应用名师点金:本章主要内容为:平行线分线段成比例,相似三角形的判定及性质,位似图形及其画法等,涉及考点、考法较多,是中考的高频考点.其主要考点可概括为:3个概念、2个性质、1个判定、2个应用、1个作图、1个技巧.考点一:3个概念概念1:成比例线段1.下列各组线段,是成比例线段的是( )A.3cm,6cm,7cm,9cmB.2cm,5cm,0.6dm,8cmC.3cm,9cm,1.8dm,6cmD.1cm,2cm,3cm,4cm2.有一块三角形的草地,它的一条边长为25m,在图纸上,这条边的长为5cm,其他两条边的长都为4cm,则其他两边的实际长度都是________m.概念2:相似多边形3.如图,已知∠1′=∠1,∠2′=∠2,∠3′=∠3,∠4′=∠4,∠D′=∠D,试判断四边形A′B′C′D′与四边形ABCD是否相似,并说明理由.概念3:位似图形4.如图,在△ABC中,A,B两个顶点在x轴的上方,点C的坐标是(-1,0).以点C为位似中心,在x轴的下方作△ABC的位似图形,并把△ABC的边放大到原来的2倍,记所得的像是△A′B′C.设点B的对应点B′的坐标是(a,b),求点B的坐标.考点二: 2个性质性质1:平行线分线段成比例的性质5.如图,在Rt△ABC中,∠A=90°,AB=8,AC=6.若动点D从点B出发,沿线段BA运动到点A为止,运动速度为每秒2个单位长度.过点D作DE∥BC交AC于点E,设动点D运动的时间为x秒,AE的长为y.(1)求出y关于x的函数解析式,并写出自变量x的取值范围;(2)当x为何值时,△BDE的面积有最大值,最大值为多少?性质2:相似三角形的性质6.如图,已知D是BC边上的中点,且AD=AC,DE⊥BC,DE与BA相交于点E,EC 与AD相交于点F.(1)求证:△ABC∽△FCD;(2)若S△FCD=5,BC=10,求DE的长.考点三: 1个判定——相似三角形的判定7.如图,△ACB为等腰直角三角形,点D为斜边AB上一点,连接CD,DE⊥CD,DE=CD,连接AE,过C作CO⊥AB于O.求证:△ACE ∽△OCD.8.如图,在⊙O的内接△ABC中,∠ACB=90°,AC=2BC,过点C作AB的垂线l交⊙O 于另一点D,垂足为点E.设P是上异于点A,C的一个动点,射线AP交l于点F,连接PC 与PD,PD交AB于点G. (1)求证:△PAC∽△PDF; (2)若AB=5,弧AP=弧BP,求PD 的长.考点四: 2个应用应用1:测高的应用9.如图,在离某建筑物CE 4 m处有一棵树AB,在某时刻,1.2 m的竹竿FG垂直地面放置,影子GH长为2 m,此时树的影子有一部分落在地面上,还有一部分落在建筑物的墙上,墙上的影子CD高为2 m,那么这棵树的高度是多少?应用2:测宽的应用10.如图,一条小河的两岸有一段是平行的,在河的一岸每隔6 m有一棵树,在河的对岸每隔60 m有一根电线杆,在有树的一岸离岸边30 m处可看到对岸相邻的两根电线杆恰好被这岸的两棵树遮住,并且在这两棵树之间还有三棵树,求河的宽度.考点五: 1个作图——作一个图形的位似图形11.如图,在方格纸中(每个小方格的边长都是1个单位长度)有一点O和△ABC.请以点O 为位似中心,把△ABC缩小为原来的一半(不改变方向),画出△ABC的位似图形.考点六: 1个技巧——证明四条线段成比例的技巧12.如图,已知△ABC,∠BAC的平分线与∠DAC的平分线分别交BC及BC的延长线于点P,Q. (1)求∠PAQ的度数; (2)若点M为PQ的中点,求证:PM2=CM·BM.。
(北师大版数学)九上第1至4章知识点(再总结)

第一章 《特殊的平行四边形》一.知识点:平行四边形,菱形,矩形,正方形,各自的性质和判定(看笔记); (一)菱形:(1)有一个内角是60°(或120°),较短的对角线将菱形分成了两个等边三角形,较短的对角线等于边长,较长的对角线=边长的3倍;(2)菱形的对角线平分一组对角(即具有角平分线的性质),两条对角线分成的四个小直角三角形全等; (3)面积=底×高=21对角线乘积; (4)是轴对称图形(分别是两条对角线所在的直线),也是中心对称图形(对称中心为对角线的交点),过对称中心的任意一条直线都可以将它的面积平分; (5)两条宽度相等的矩形纸条重合,重合部分是菱形.(二)矩形(1)是轴对称图形(即过对边中点的直线)也是中心对称图形;两条对角线分成的四个三角形面积相等,而且是四个等腰三角形(注意:相对的两个等腰三角形全等);(2)直角三角形斜边的中线等于斜边的一半(特别重要,在等腰三角形,△的全等,△的相似中经常用到);例如:如图,AD 是△ABC 的高,E ,F 分别是AB ,AC 的中点.求证:△DEF ∽△ABC.提示:DE=21AB ,DF=21AC (直角三角形斜边的中线等于斜边的一半), EF=21BC(三角形的中位线性质),∴21===BC EF AC DF AB DE ,∴△DEF ∽△ABC(三边对应成比例的两个三角形相似)(三)正方形(1)四条对称轴,一个对称中心;对角线分成的四个三角形是全等的等腰直角三角形; (2)注意正方形在相似中的作用,利用勾股定理表示三角形的边经常用到.特别注意:如果要从对角线入手判定四边形是特殊的平行四边形,“互相平分”是前提,没有这个条件,添加其它再多的条件都是没有意义的;二.中点四边形:(只与原四边形的对角线“相等”还是“垂直”有关系,与互不互相平分无关)(1)对角线既不相等也不垂直的四边形的中点四边形是平行四边形(如:一般的四边形,平行四边形的中点四边形都是平行四边形);(2)对角线相等的四边形的中点四边形是菱形(如:矩形,等腰梯形它们的中点四边形都是菱形);(3)对角线垂直的四边形的中点四边形是矩形(如菱形,筝形它们的中点四边形都是矩形); (4)对角线既相等又垂直的四边形的中点四边形是正方形(如:正方形的中点四边形是正方形,当然还有其它满足条件的四边形);三.特殊三角形边的关系(1)30°,60°,90°的直角三角形:三边的比是:1:3:2; (2)45°,45°,90°的直角三角形:三边之比是:1:1:2; (3)30°,30°,120°的等腰三角形:三边之比为:1:1:3;(4) 边长为a 等等边三角形面积为:S=2a 43. 习题:如图,在四边形ABCD 中,AD ∥BC ,AD=4,BC=12,E 是BC 的中点,点P 以每秒1个单位长度的速度从点A 出发,沿AD 向点D 运动;点Q 同时以每秒2个单位长度的速度从点C 出发,沿CB 向点B 运动.点P 停止运动时,点Q 也随之停止运动.当运动时间为几秒时,以点P ,Q ,E ,D 为顶点的四边形是平行四边形.第二章 《一元二次方程方程》:一.判断是不是一元二次方程方程的标准:首先必须要把方程化成一般式,并且要化到最简[ax ²+bx+c=0(a ≠0)]再判断,关于谁的方程,谁就是未知数,其它的字母当做已知数对待,例如:a ²-a+x=0,是关于a 的一元二次方程,但不是关于x 的一元二次方程;其次,要满足“只有一个未知数,未知数的最高次数是2,化简后的二次项系数不为0的整式(分母中没有未知数,未知数不能在根号下)方程”这四个条件;只要有二次项[即ax ²(a ≠0)]就可以,可以没有一次项,也可以没有常数项,例如:x ²=0就是一元二次方程; 举例子:下列关于x 的方程是一元二次方程方程的有:(②、⑤)①ax ²=0;②x ²=1;③ax ²+bx+c=0;④(m ²-1)x ²+3x-5=0;⑤(m ²+1)x ²+3x-5=0;⑥2n ²-n+3x=0;⑦x1+x ²=2;⑧(x-2)²=x(x+1);⑨3x x 2+-=5. 分析:最容易错的是:①,③,④,⑥,⑧,其中①,③,④都是不能确定二次项系数不为0;⑥是关于n 的一元二次方程,不是关于x 的一元二次方程;⑧化简后没有二次项了.如果上面的题目改为“下列方程是一元二次方程的()”,那就只有②了,因为题目中没有说关于谁的一元二次方程,除了已知数外,其它的字母全是未知数,如⑤不止一个未知数.二.判断“二次项,二次项系数,一次项,一次项系数,常数项”时,必须在一般式[即ax ²+bx+c=0(a ≠0)]的形式下进行,判断时连同前面的符号一起看;三.解一元二次方程时,要把步骤写完整!!!①用配方法:注意书写步骤;弄清楚它与代数式配方的不同;(笔记中有,认真看看); ②用求根公式解:化成一般式,然后写出a ,b ,c ,判断△,再求解;③因式分解法:提公因式法;公式法[完全平方公式(有两个),平方差公式];十字相乘法;换元法[例如:(x-3)²+2(3-x)-3=0,那么原方程可化为:(x-3)²-2(x-3)-3=0,设t=x-3,则原方程变为:t ²-2t-3=0,解得:t=-1或t=3,即x-3=-1或x-3=3,解得:x ₁=2,x ₂=6]特别注意:x(x-1)=90,这种右边不为0的方程,不能直接分解因式,必须化成一般式再进行分解因式,上面的方程可化为:x ²-x-90=0,∴(x+9)(x-10)=0,解得:x ₁=-9,x ₂=10四. 根的判别式△=b ²-4ac特别注意:一元二次方程有实数根(或两个实数根),即△≥0;例如:方程(k+1)x ²-2kx+k-2=0有两个实数根,求k 的值;分析:因为有两个实数根,所以一定是一元二次方程,二次项系数k+1≠0,且△=(-2k)²-4(k+1)(k-2)≥0再例如:方程x ²-2kx+k ²-k+2=0有实数根,求k 的值.分析:和上一题比较,很容易发现,本题的方程本身就是一元二次方程,所以只需要保证△=(-2k)²-4×1×(k ²-k+2)≥0即可特别注意下面这道题:例如:方程(k+1)x ²-2kx+k-2=0有实数根,求k 的值;分析:因为题目说方程有实数根,而我们无法判断二次项系数等不等于0,如果二次项系数k+1=0即k=-1时,此时方程是一元一次方程:2x-3=0,显然有实数根,满足题意;当二次项系数k+1≠0时,此时方程是一元二次方程,要使方程有实数根,必须保证二次项系数k+1≠0,且△=(-2k)²-4(k+1)(k-2)≥0;最后再把两种情况综合起来,才是道题的完整解答!以上三个例子各有不同,解题时一定要看清楚!五. 根与系数的关系(韦达定理):【必须在一般式下进行,如果方程中除了未知数外还有其它字母,首先要保证△,有实数根(或两个实数根),即△≥0,有两个不相等的实数根即△>0】 若x ₁,x ₂是一元二次方程方程的ax ²+bx+c=0(a ≠0)的两个实数根,则:x ₁+x ₂=-b/a ;x ₁.x ₂=c/a ; 根与系数的关系的一些公式,一定要记住!!!①2122122212)(x x x x x x -+=+ ②21212111x x x x x x +=+ ③212212214)()(x x x x x x -+=-④21221214)(||x x x x x x -+=-六.应用题的各种类型:【看发的笔记】习题:某品牌童装进价为20元/件,如果以60元/件卖出,平均每天可售出20件.为了迎接“六一”儿童节,商场决定采取适当的降价措施,扩大销售量,增加盈利,减少库存.经市场调查发现,如果每件童装每降价4元,那么平均每天就可多售出8件.(1)要想平均每天在销售这种童装上盈利800元,那么每件童装应定价为多少元?(2)要想平均每天在销售这种童装上盈利最多,那么每件童装应降价多少元? 解:(1)设每件童装应定价为x 元,由题意,得: (x-20)(20+84x-60⨯)=800 整理,得:x ²-90x+1800=0 (x-30)(x-60)=0 解得:x=30或x=60因为商场决定采取适当的降价措施,扩大销售量,增加盈利,减少库存, 所以x=60.答:要想平均每天在销售这种童装上盈利800元,那么每件童装应定价为30元. (2)设每件童装应降价y 元,盈利为W 元,由题意,得: W=(60-20-y)(20+84y ⨯) =-2y ²+60y+800 =-2(y ²-30y)+800=-2(y ²-30y+15²-15²)+800 =-2(y-15)²+1250∵-2<0,∴当y=15时,W 最大,最大值为1250.答:要想平均每天在销售这种童装上盈利最多,那么每件童装应降价15元.第三章 《概率的进一步认识》一.列表法和画树状图分别适用范围:列表法:只适用于求两步实验的随机事件的概率;画树状图法:适用于求两步及两步以上的随机事件的概率;要求:必须是机会均等,计算时要不重复,不遗漏;特别注意:一次摸(或抽)两个,可以当做不放回:比如说:一次抽两张卡片,就可以当做先抽一张,不放回,在剩下的卡片中再抽一张,如果是列表的画,一定要把对角线上的情况划掉;注意书写格式:(概率题很简单,但有些同学由于不注意书写格式,导致丢分)解:由题意,可列表(或画树状图)如下:表格(或树状图)【略】由上表(或图)可知,共有…种等可能的情况,其中谁有…种情况,∴P₍₋₎=……,答:……二.用频率估计概率:当试验的次数足够大时,实验频率稳定在某一数值附近,此时,就可以用这个数值来估计随机事件发生的概率;注意:必须试验的次数足够大!第四章《图形的相似》考点一:1.线段的比(在同一单位长度下,比值无单位)2.成比例线段(四条,要讲顺序)3.比例的基本性质:(1)若a:b=c:d,则ad=bc;(2)若ad=bc(a,b,c,d都≠0),则a:b=c:d(当然还有其它的比例形式,如:a:c=b:d;d:c=b:a 等等)【注意:将积的形式拆成比例的形式时,如果先用前面的比后面的,=后面的比就要用后面的比前面的】【特例】比例中项:若a²=b.c,则a就叫做b与c的比例中项(即若a:b=c:a,则a叫做b与c的比例中项)4.合(分)比性质5.等比性质:如果b =d=f=…=n(b+d+f+…+n≠0),那么banfdbmeca=+⋯++++⋯+++.特别注意:若b+d+f+……+n=0时,则b=-(d+f+……+n),然后代入其中任何一个比例中求解;如果无法判断分母相加等不等于0时,要分=0和≠0两种情况考虑!考点二:平行线分线段成比例:1.定理:两条直线被一组平行线(不少于3条)所截,所得的对应线段成比例;【提示:所得的对应线段是斜着的线段,与平行的线段无关】注意:这里有许多组成比例线段,比的时候一定要注意先后顺序,而且这里比的线段都是斜着的,没有涉及平行的线段,如果要求平行的线段,可以过最上边的一个端点作其中一条直线的平行线,将图形分成一个平行四边形和一组相似三角形,再利用相似三角形对应边成比例求!例如:某高中学校为高一新生设计的学生板凳的正面视图如图所示,其中BA =CD ,BC =20 cm ,BC ,EF 平行于地面AD 且到地面AD 的距离分别为40 cm ,8 cm.为使板凳两腿底端A ,D 之间的距离为50 cm ,那么横梁EF 的长应为多少?(材质及其厚度等暂忽略不计)解:(如右上图)过点C 作CM ∥AB ,交EF 于点N ,交AD 于点M ,作CP ⊥AD ,分别交EF 、AD 于点Q 、P .由题意,得四边形ABCM 是平行四边形, ∴EN=AM=BC=20cm ,∴MD=AD-AM=50-20=30cm ,又由题意知CP=40cm ,PQ=8cm , ∴CQ=32cm . ∵EF ∥AD ,∴△CNF ∽△CMD .∴CP CQMD NF =(相似三角形的对应高之比等于相似比), 即403230=NF ,解得NF=24cm . ∴EF=EN+NF=20+24=44(cm ). 答:横梁EF 应为44cm .2.推论:平行于三角形一边的直线与其它两边相交,截得的对应线段成比例;【特别提醒:这里的对应线段成比例可以是斜着的对应线段成比例,也可以用三角形的对应边成比例(此时,斜着的边与平行的边就建立了联系)】如上图1(A 字型△相似),可以得出EC AE DB AD =,也可以得出BCDEAC AE AB AD ==. 考点三:多边形相似要证明多边形相似,既要证出对应边成比例,还证出对应角相等(缺一不可);【写相似时要把点对应准,否则比的时候就会出错】边数相等的正多边形一定相似;还要特别注意:折叠后的矩形与原矩形相似的题.考点四:相似三角形的判定:三个(AA ,SAS ,SSS),直角三角形相似的判定:(AA ,SAS ,SSS ,HL →即两个直角三角形的一条直角边和斜边对应成比例,则它们相似)特别注意:SAS 是两边对应成比例,夹角相等;证△相似时,首先考虑两角对应相等,行不通的话,再考虑其它两种方法; 可以用对应边比,也可以用同一个三角形的边比,这时要特别注意顺序; 以“∽”写出的不用分类讨论;用汉字“相似”写出的需分类讨论; 【写相似时要把点对应准】 大题常常需要用到多次相似.常见的相似图形: 1.平行线型2.相交线型3.子母型4.旋转型考点五:黄金分割 定义:一般地,点C 将线段AB 分成AC 和BC 两段(AC>BC),若AC:AB=BC:AC ,那么就把AC:AB 叫做黄金比,点C 叫做线段的黄金分割点,一条线段有两个黄金分割点。
2022年数学九上《第四章小结与复习》课件精品(新北师大版)

解:如下图.
y
A′
B′ O
C′ x
证明:∵△ABC是等边三角形,
∴∠BAC=∠ACB=60°,
∠ACF=120°.
∵CE是外角平分线,
∴∠ACE=60°,
B
∴∠BAC=∠ACE.
又∵∠ADB=∠CDE,
∴△ABD∽△CED.
A E
D CF
(2) 假设 AB = 6,AD = 2CD,求 BE 的长.
解:作 BM⊥AC 于点 M.
∵ AC=AB=6,
=120 mm,高 AD=80 mm,要把它加工成正方形
零件,使正方形的一边在 BC 上,其余两个顶点分
别在 AB、AC 上,这个正方形零件的边长是多少?
解:设正方形 EFHG 为加工成的
A
正方形零件,边 GH 在 BC 上,顶点 E、F 分别在AB、
EM F
AC上,△ABC 的高 AD 与边 EF 相交于点 M,设正方形的 B
面积 与 △DFA 的面积之比为 .
考点二 相似的应用
例3 如图,某一时刻一根 2 m 长的竹竿 EF 的影长 GE 为 1.2 m,此时,小红测得一棵被风吹斜的柏树 与地面成 30°角,树顶端 B 在地面上的影子点 D 与 B 到垂直地面的落点 C 的距离是 3.6 m,求树 AB 的长.
3.6m
5. 位似 (21) 性如质果:两位个似图图形形不上仅任相意似一,对而对且应对点应到顶位点似的中连心 的线距相离交之于比一等点于,位那似么比这;样对的应两线个段图平形行叫或做者位在 一似条图直形线,上这.个点叫做位似中心. (这时的相似 比也称为位似比)
(3) 位似性质的应用:能将一个图形放大或缩小.
要点梳理
北师版初三数学上册第四章相似图形知识点讲解

北师版初三数学上册第四章相似图形知识点讲解九年级(上)第四章图形的相似(1)形状相同的图形叫相似图形,在相似多边形中,最简单的是相似三角形. (2) 相似多边形:如果两个边数相同的多边形的对应角相等,对应边成比例,这两个多边形叫做相似多边形.相似多边形对应边长度的比叫做相似比.一.成比例线段(1)线段的比如果选用同一单位量得两条线段b a ,的长度分别为n m ,,那么就说这两条线段的比是nm b a =,或写成nm b a ::=.注:在求线段比时,线段单位要统一。
(2)成比例线段在四条线段d c b a ,,,中,如果b a 和的比等于d c 和的比,那么这四条线段d c b a ,,,叫做成比例线段,简称比例线段. 注:①比例线段是有顺序的,如果说a ,d c b ,,成比例,那么应得比例式为:b a =d c.②()a ca b c d b d==在比例式::中,a 、d 叫比例外项,b 、c 叫比例内项,如果b=c ,即 a b b d =::那么b 叫做a 、d 的比例中项, 此时有2b ad =。
③判断给定的四条线段是否成比例的方法:第一排:现将四条线段的长度统一单位,再按大小顺序排列好;第二算:分别算出前两条线的长度之比与后两条线段的长度之比;第三判:若两个比相等,则这四条线段是成比例线段,否则不是(3)比例的性质(注意性质立的条件:分母不能为0) 基本性质:① a:b=c:d 则有 ad=bc (两外项之积等于两内向之积); ② ②2::a b b c b a c =⇔=⋅.注:由一个比例式只可化成一个等积式,而一个等积式共可化成八个比例式,如bc ad =,除了可化为d c b a ::=,还可化为d b c a ::=,b a d c ::=,c a d b ::=,c d a b ::=,b d a c ::=,a b c d ::=,a c b d ::=.(2) 更比性质(交换比例的内项或外项):()()()a bc d a c d c b d b a d bc a ⎧=⎪⎪⎪=⇔=⎨⎪⎪=⎪⎩,交换内项,交换外项.同时交换内外项(3)合、分比性质:a c a b c d b d b d±±=⇔=. (4)等比性质:如果)0(≠++++====n f d b nmf e d c b a ,那么ban f d b m e c a =++++++++ .注:①此性质的证明运用了“设k 法”(即引入新的参数k )这样可以减少未知数的个数,这种方法是有关比例计算变形中一种常用方法.②应用等比性质时,要考虑到分母是否为零.③ 可利用分式性质将连等式的每一个比的前项与后项同时乘以一个数,再利用等比性质也成立.如:b a f d b e c a f e d c b a f e d c b a =+-+-⇒=--=⇒==32323322;其中032≠+-f d b . (4)比例题常用的方法有:比例合分比法,比例等比法,设参法,连等设k 法,消元法二,平行线分线段成比例(1)平行线分线段成比例定理:三条平行线截两条直线,所截得的对应线段成比例.已知AD ∥BE ∥CF,可得AB DE AB DE BC EF BC EF AB BCBC EF AC DF AB DE AC DF DE EF=====或或或或等. 注意:是所截的线段成比例,而跟平行线无关,所以比例线段中不可能有AD,BE,CF 的比例关系(2)黄金分割:把线段AB 分成两条线段)(,BC AC BC AC >,且使AC 是BC AB 和的比例中项,即2AC AB BC =⋅,叫做把线段AB 黄金分割,点C 叫做线段AB 的黄金分割点,其中AB AC 215-=≈0.618AB .即51AC BC AB AC -==简记为:51-长短==全长注:黄金三角形:顶角是360的等腰三角形。
北师版初三数学上册第四章相似图形知识点讲解

九年级(上)第四章图形的相像(1)形态一样的图形叫相像图形,在相像多边形中,最简洁的是相像三角形.(2) 相像多边形:假如两个边数一样的多边形的对应角相等,对应边成比例,这两个多边形叫做相像多 边形.相像多边形对应边长度的比叫做相像比.一.成比例线段(1)线段的比假如选用同一单位量得两条线段b a ,的长度分别为n m ,,那么就说这两条线段的比是nmb a =,或写成n m b a ::=.注:在求线段比时,线段单位要统一。
(2)成比例线段在四条线段d c b a ,,,中,假如b a 和的比等于d c 和的比,那么这四条线段d c b a ,,,叫做成比例线段,简称比例线段.注:①比例线段是有依次的,假如说a ,d c b ,,成比例,那么应得比例式为:b a =dc . ②()a ca b c d b d==在比例式::中,a 、d 叫比例外项,b 、c 叫比例内项,假如b=c ,即 a b bd =::那么b 叫做a 、d 的比例中项, 此时有2b ad =。
③推断给定的四条线段是否成比例的方法:第一排:现将四条线段的长度统一单位,再按大小依次排列好;第二算:分别算出前两条线的长度之比与后两条线段的长度之比;第三判:若两个比相等,则这四条线段是成比例线段,否则不是(3)比例的性质(留意性质立的条件:分母不能为0) 根本性质:① a:b=c:d 则有 ad=bc (两外项之积等于两内向之积);② ②2::a b b c b a c =⇔=⋅.注:由一个比例式只可化成一个等积式,而一个等积式共可化成八个比例式,如bc ad =,除了可化为d c b a ::=,还可化为d b c a ::=,b a d c ::=,c a d b ::=,c d a b ::=,b d a c ::=,a b c d ::=,a c b d ::=.(2) 更比性质(交换比例的内项或外项):()()()a bc d a c d cb d b ad bc a ⎧=⎪⎪⎪=⇔=⎨⎪⎪=⎪⎩,交换内项,交换外项.同时交换内外项(3)合、分比性质:a c abcd b d b d ±±=⇔=. (4)等比性质:假如)0(≠++++====n f d b nm f e d c b a ,那么b an f d b m e c a =++++++++ . 注:①此性质的证明运用了“设k 法”(即引入新的参数k )这样可以削减未知数的个数,这种方法是有关比例计算变形中一种常用方法.②应用等比性质时,要考虑到分母是否为零.③ 可利用分式性质将连等式的每一个比的前项与后项同时乘以一个数,再利用等比性质也成立.如:ba f db ec a f ed c b a fe d c b a =+-+-⇒=--=⇒==32323322;其中032≠+-f d b . (4)比例题常用的方法有:比例合分比法,比例等比法,设参法,连等设k 法,消元法二,平行线分线段成比例(1)平行线分线段成比例定理:三条平行线截两条直线,所截得的对应线段成比例已知AD ∥BE ∥CF,可得AB DE AB DE BC EF BC EF AB BCBC EF AC DF AB DE AC DF DE EF=====或或或或等. 留意:是所截的线段成比例,而跟平行线无关,所以比例线段中不行能 有AD,BE,CF 的比例关系(2)黄金分割:把线段AB 分成两条线段)(,BC AC BC AC >,且使AC 是BC AB 和的比例中项,即2AC AB BC =⋅,叫做把线段AB 黄金分割,点C 叫做线段AB 的黄金分割点,其中AB AC 215-=≈0.618AB .即12AC BC AB AC == 简记为:长短=全长注:黄金三角形:顶角是360的等腰三角形。
北师大版数学九年级上册第四章 回顾与思考-课件

回顾与思考
一、展现自我
二、巩固提升:
做一做:
1、四条线段a、b、c、d成比例,其中b=3cm, c=2cm,d=6cm,求线段a的长。
2、如果两个相似多边形面积的比为4︰9,那 么这两个相似多边形对应边的比是多少?
3、如图,将矩形ABCD沿两条较长边的中点的连线 对折,得到的矩形ADFE与矩形ABCD相似,确定矩 形ABCD长与宽的比。
•
知识源于悟
1、如图,DE∥BC,D是AB的中 A 点,DC、BE相交于点G。
求 (1) DE
BC
B
D
G
E
( 2) C GED
C
C GBC
知识源于悟
2、如图: DE∥BC,EF ∥AB,AE:EC=2:3, S △ABC=25,求S四边形BDEF
A
D
E
B
C
F
试一试:
1、在正方形方格中, △ABC的顶点A、B、C在
A
B D
F
E G
C
3、如图,BC与EF在一条直线上,AC//DF。将 图(2)中的三角形截去一块,使它变为与图 (1)相似的图形。
D
D
A
G
A
Q
B
CE
FB
CE P
F
三、课堂反馈:
1、如图,在
ABCD中,E是BC上一点,
BE:EC=1:2,AE与BD相交于F,则
BF:FD=___1_:_3__,S △ADF : S △EBF =__1_:_9__
单位正方形的顶点上 ,请在图中画一个
△A1B1C1 使 △ A1B1C1 ∽△ABC
C
(相似比不为1), 且点都在单位正方形
北师大版数学九年级上册第四章 本章小结与复习-课件

