第六章实数复习课件
合集下载
【新】人教版七年级数学下册第六章《 实数》复习公开课课件.ppt

第6章 实数的复习
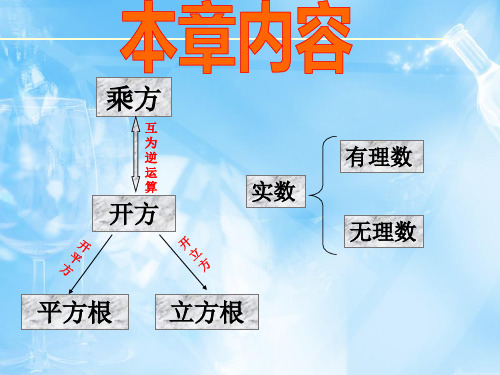
本章知识结 构图
乘 互为逆运算 开
方
方
开平方 开立方
算术平方根
平方根 立方根 负的平方根
有理数 无理数
实数
区别
你知道算术平方根、平方根、立方根联 系和区别吗?
算术平方根
平方根
立方根
表示方法
a的取值
正数
性
0
质
负数
开 方 是本身
a ≠ a
a≥ 0
a≥ 0
3a a是任何数
正数(一个) 互为相反数(两个) 正数(一个)
(略)
求商比较
同号正实数
对于同号正实数a、b, 若a∕b≧1,则a ≧b
(略)
计算近似值比较 含无理数的 牢牢记住
课本p72练习/2(2);课
实数
的近似值,直、接2计、算3比、较5。。。 本p87练习/6
实数的大小比较方法多种,要具体观察实数的特点,灵活选择最好的比较方法
学以致用
1.如图,数轴上点P表示的数可能是( B)
a2 a =
2 a
a
a a0 0 a0
a (a 0)
a0
3 a 3 a a为任何数
3 a 3 a a为任何数
已知 ao,求a2
3
a3的值
已m 知 n,求 ( m n) 23 ( nm ) 3的值
有限小数及无限循环小数整数
正整数 0
有理数
负整数
分数 正分数
实 数
负分数
正无理数
无理数
负无理数
自然数
2.如果3 2a1与3 8a互为相反数, 求a2 3a4的值。
3.当x 为任 意实 数 时3 , 3 x有 意义。
本章知识结 构图
乘 互为逆运算 开
方
方
开平方 开立方
算术平方根
平方根 立方根 负的平方根
有理数 无理数
实数
区别
你知道算术平方根、平方根、立方根联 系和区别吗?
算术平方根
平方根
立方根
表示方法
a的取值
正数
性
0
质
负数
开 方 是本身
a ≠ a
a≥ 0
a≥ 0
3a a是任何数
正数(一个) 互为相反数(两个) 正数(一个)
(略)
求商比较
同号正实数
对于同号正实数a、b, 若a∕b≧1,则a ≧b
(略)
计算近似值比较 含无理数的 牢牢记住
课本p72练习/2(2);课
实数
的近似值,直、接2计、算3比、较5。。。 本p87练习/6
实数的大小比较方法多种,要具体观察实数的特点,灵活选择最好的比较方法
学以致用
1.如图,数轴上点P表示的数可能是( B)
a2 a =
2 a
a
a a0 0 a0
a (a 0)
a0
3 a 3 a a为任何数
3 a 3 a a为任何数
已知 ao,求a2
3
a3的值
已m 知 n,求 ( m n) 23 ( nm ) 3的值
有限小数及无限循环小数整数
正整数 0
有理数
负整数
分数 正分数
实 数
负分数
正无理数
无理数
负无理数
自然数
2.如果3 2a1与3 8a互为相反数, 求a2 3a4的值。
3.当x 为任 意实 数 时3 , 3 x有 意义。
实数的复习课件(共38张PPT)

零
你知道算术平方根、平方根、立方根联系和区别吗?
算术平方根
平方根
立方根
表示方法
a 的取值
性 正数
0
质
负数
a
a
3a
a≥ 0
a≥ 0
a 是任何数
正数(一个) 互为相反数(两个) 正数(一个)
0
0
0
没有
没有
负数(一个)
开方
求一个数的平方根 求一个数的立方根 的运算叫开平方 的运算叫开立方
是本身
0,1
0
律
则3 5250的值是 17.38
1.已知 x 和 a 2 的和为0,则x的范围是为( B )
A.任意实数 B.非正实数 C .非负实数 D. 0
2.若- 3 m
=
7
3
8
,则m的值是
(B )
A 7
7 B
7
C
8
8
8
D
343 512
3. 若 (x 2)2 2 x成立,则x的取值范围是( A )
5.已知满足 3 a a 4 a ,求a的值
6、a、b互为相反数,c与d互为倒数,则a+1+b+
cd= 2
。
8、已知 a - 2 b 3 0,
则(a b)2 25 ;
9、计算: 1- x x 1 x2 1 0 ;
10、计算: 5 5 2 33
二.已知实数a、b、c,在数轴上的位置如下图所示, 试化简:
a
b0 c
(1) a2- |a-b|+|c-a|+ (b c)2
(2)|a+b-c|+|b-2c|+ (b a)2 -2 a2
你知道算术平方根、平方根、立方根联系和区别吗?
算术平方根
平方根
立方根
表示方法
a 的取值
性 正数
0
质
负数
a
a
3a
a≥ 0
a≥ 0
a 是任何数
正数(一个) 互为相反数(两个) 正数(一个)
0
0
0
没有
没有
负数(一个)
开方
求一个数的平方根 求一个数的立方根 的运算叫开平方 的运算叫开立方
是本身
0,1
0
律
则3 5250的值是 17.38
1.已知 x 和 a 2 的和为0,则x的范围是为( B )
A.任意实数 B.非正实数 C .非负实数 D. 0
2.若- 3 m
=
7
3
8
,则m的值是
(B )
A 7
7 B
7
C
8
8
8
D
343 512
3. 若 (x 2)2 2 x成立,则x的取值范围是( A )
5.已知满足 3 a a 4 a ,求a的值
6、a、b互为相反数,c与d互为倒数,则a+1+b+
cd= 2
。
8、已知 a - 2 b 3 0,
则(a b)2 25 ;
9、计算: 1- x x 1 x2 1 0 ;
10、计算: 5 5 2 33
二.已知实数a、b、c,在数轴上的位置如下图所示, 试化简:
a
b0 c
(1) a2- |a-b|+|c-a|+ (b c)2
(2)|a+b-c|+|b-2c|+ (b a)2 -2 a2
七年级下册数学第6章实数章节复习课件
比较大小
(1) 3 26 < 3; (2) 63 > -8; (3) 10 1 > 0.5;
4
掌 握
a
a2 a = 0
a 0 a 0
规 律
a (a 0)
a 2 a a 0
3 a3 a
3 a 3 a
3 -a 3 a
a为任何数
已知a o,求
a2
3
a3的值
0
已知m n,求 (m n)2 3(n m)3的值
这就是说,如果x 2 = a ,那么 x 就叫做 a 的平方根.
a的平方根记为± a
3.平方根的性质: 正数有2个平方根,它们互为相反数; 0的平方根是0; 负数没有平方根。
3.立方根的定义:
一般地,如果一个数的立方等于a,那 么这个数就叫做a的立方根,也叫做a的
三次方根.记作 3 .a
其中a是被开方数,3是根指数,符号 “3 ”读做“三次根号”.
平方根与立方根的概念错解剖析
1.36的平方根是6. 6
2.1 的算术平方根是± 1
1
4
22
3.0.01是0.1的平方根 0.1是0.01的平方根
3 4. 81的平方根是±9.
5.假设x2=9, 那么 x=3.
3
4 6. 16 =±4.
平方根与立方根的概念错解剖析
7.算术平方根等于本身的数是0. 0和1
a
分析:要化简|a-b|-|a+b|,需根据数轴上a、b 的位置判断a-b和a+b的符号 解:因为a>0,b<0,且∣a∣<∣b∣,所以a-b>0,a+b<0,
ba0 所以原式=〔a-b〕+〔a+b〕=a-b+a+b=2a
第六章 实数(复习课件)七年级数学下册(人教版)

举一反三
【7-2】如图,用两个边长为 18cm的小正方形纸片拼成一个大的正方形纸
片,沿着大正方形纸片的边的方向截出一个长方形纸片,能否使截得的长
方形纸片长宽之比为3:2,且面积为30cm2?请说明理由.
解:不能.理由如下:因为大正方形纸片的面
积为( 18)2+( 18)2=36(cm2) ,
高频考点
高频考点七 实数的综合运用
(3)如果2+ 5的整数部分是a,小数部分是b,求出a-b的值.
(3)因为 4< 5< 9,即2< 5<3,
所以4<2+ 5<5,
所以2+ 5的整数部分为4,小数部分为2+ 5-4= 5-2,即a=4,b= 5-2,
所以a-b=4-( 5-2)= 6- 5.
举一反三
【7-1】若 2的整数部分为x,小数部分为y,则 2x-y的值是( C )
A.2 2-2
B.2
C.1
D. 2
【7-2】如图,用两个边长为 18cm的小正方形纸片拼成一个大的正方形纸
片,沿着大正方形纸片的边的方向截出一个长方形纸片,能否使截得的长
方形纸片长宽之比为3:2,且面积为30cm2?请说明理由.
0
一个,为负数
3
a
可以为任何数
知识梳理
四、实数及其运算
有理数包括整数和分数,它们都可以写成有限小数或者无限循环小数的形
式.
5 3 27 11 9
, , , , .
2 5 4 9 11
5
2.5
2
3
0.6
5
27
6.75
4
.
11
第6章《实数》 小结与复习 人教版七年级数学下册课件(21张ppt)

(1) 25; (2) 6 1 ;(3) ( 10)2.
36
4
2. 求下列各数的立方根:
(1) 8 ;(2) 0.027;(3)1 7 .
125
8
解1题.答时案,:要(1注) 意56题;目(2)的要52;求(,3)是±求10平. 方根、立方根还是
求2算.答术案平:方(1根) ,52要;注(2意)0.所3;求(3结) 12果. 处理.
A. 1
B. 2
C. 3
D. 4
【注意】 3,, π 不属于分数而是无理数. 23
考点三 实数的估算与数轴的结合 【例3】(1) 20 位于相邻整数 4 和 5 之间.
(2) 实数 a,b 在数轴上的位置如图所示,化简
a b (b a)2 -2a .
a 0b
1. 实数与数轴上的点是一一对应的关系; 2. 在数轴上表示的数,右边的数总是比左边的数大.
深学细悟 请回顾、整理你曾在实数运算中出现的错误,通过错 题本等形式并尝试分类归纳,总结若干关于实数运算 的经验教训,并与其他同学分享. 错题本示例:
开立方运算时要注意小数点的变化规律,开立方是三 位与一位的关系,开平方是二位与一位的关系.
【例6】计算:
2 2
2 3
2 4
5 2 12
.
练一练
4. 用计算器计算:
(1) 7 π (精确到0.01);
(2) 6 π (精确到0.01);
答案:(1) 5.79; (2) 5.48.
练一练 5.(1) 2 2 的相反数是__2__2__,2 3 的相反数是_3____2_,
对实数进行分类不能只看表面形式,应先化简,再根据 结果去判断.
练一练 2.(1)在 23,0.618,π,3 8, 3 中,
第六章实数复习(公开课)ppt课件

在几何图形中,我们也需要使用在绘制函数图像时,我们需要使用实 数。例如,绘制一次函数、二次函数 、三角函数等图像时都需要用到实数 。
科学问题中的实数应用
物理测量
在物理学中,许多物理量都是用 实数来表示的。例如,物体的速 度、加速度、力等都需要用到实
总结词
实数减法的运算律
详细描述
实数减法具有一些重要的运算律,如差不变性质、减法结 合律和减法交换律等。这些运算律可以帮助我们简化复杂 的减法计算,提高计算的准确性和效率。
实数的乘法
总结词
实数乘法的定义与性质
详细描述
实数乘法是数学中的基本运算之一,它具有结合律、交换 律和分配律等性质。实数乘法可以用来解决许多实际问题 ,如计算面积、解决概率问题等。
根式的化简
化简根式是指将根式化简为一个最简 形式的过程。例如,√8=2√2,因为8 可以分解为4×2,而4的平方根是2, 所以√8=2√2。
Part
05
实数的应用
生活中的实数应用
长度测量
在日常生活中,我们经常需要测 量物体的长度、宽度和高度等, 这些都需要用到实数。例如,测 量房间的尺寸、家具的大小等。
总结词
实数乘法的几何意义
详细描述
实数乘法的几何意义可以理解为将数轴上的点进行拉伸或 压缩。在数轴上,一个数乘以另一个数的结果等于一个数 覆盖另一个数的长度。
总结词
实数乘法的运算律
详细描述
实数乘法具有结合律、交换律和分配律。结合律是指 (ab)c=a(bc);交换律是指ab=ba;分配律是指 a(b+c)=ab+ac。这些运算律可以帮助我们简化复杂的乘 法计算,提高计算的准确性和效率。
在数轴上进行乘法运算时,将数 轴上的每个点乘以一个正数或负 数,长度会相应地扩大或缩小。
人教版初中七年级(下册)数学《第六章实数复习课件 (1)》ppt课件

(X为任意实数) (X为任意实数)
1.说出下列各数的平方根和算术平方根:
(1)169 (2)0.16 ( 3 ) 2 1 4 8 和 8
13和13
0.4和0.4
25 5 5
(4)102 10和10 ( 5 ) 2 7 5 和 5
9 33
2.说出下列各数的立方根:
(1)-0.008 0 .2 (2)0.512 0 . 8
x2,y3
课后作业
•若 x3y2(z1)20,则
xyz_____. ___
, ,
2.下列数中是无理数的有_________.
3 5,
π, 4, ,
0,
0.1011010.
, 3.求下列数的绝对值和相反数.
5 - 2, 3 - 10.
4.求满足下列式子的 x的值.
(1)x2810;( 2) 25x2 36.
被开方数
平方根的定义
如果一个数X的平方等于a,即X2=a,那么这个数X 叫做a的平方根(二次方根)
a的平方根表示为 a 读作:正,负根号a
a
表示a的算术平方根
-a
表示a的算术平方根的相反数
a
表示a的平方根
x2 = a
X= a
求一个数a的平方根的运算叫做开平方
平方根的性质: 正数有2个平方根,它们互为相反数; 0的平方根是0; 负数没有平方根。
实数与 数轴上的点是一一对应的
在实数范围内,相反数、倒数、绝对值的意义
和有理数范围内的相反数、倒数、绝对值的意
义完全一样 在进行实数的运算时,有理数的运算法则及 运算性质同样适用。
有限小数及无限循环小数
正整数
整数
0
有理数
1.说出下列各数的平方根和算术平方根:
(1)169 (2)0.16 ( 3 ) 2 1 4 8 和 8
13和13
0.4和0.4
25 5 5
(4)102 10和10 ( 5 ) 2 7 5 和 5
9 33
2.说出下列各数的立方根:
(1)-0.008 0 .2 (2)0.512 0 . 8
x2,y3
课后作业
•若 x3y2(z1)20,则
xyz_____. ___
, ,
2.下列数中是无理数的有_________.
3 5,
π, 4, ,
0,
0.1011010.
, 3.求下列数的绝对值和相反数.
5 - 2, 3 - 10.
4.求满足下列式子的 x的值.
(1)x2810;( 2) 25x2 36.
被开方数
平方根的定义
如果一个数X的平方等于a,即X2=a,那么这个数X 叫做a的平方根(二次方根)
a的平方根表示为 a 读作:正,负根号a
a
表示a的算术平方根
-a
表示a的算术平方根的相反数
a
表示a的平方根
x2 = a
X= a
求一个数a的平方根的运算叫做开平方
平方根的性质: 正数有2个平方根,它们互为相反数; 0的平方根是0; 负数没有平方根。
实数与 数轴上的点是一一对应的
在实数范围内,相反数、倒数、绝对值的意义
和有理数范围内的相反数、倒数、绝对值的意
义完全一样 在进行实数的运算时,有理数的运算法则及 运算性质同样适用。
有限小数及无限循环小数
正整数
整数
0
有理数
第六章实数复习(公开课)ppt课件

19世纪
数学家逐步完善实数理论 ,形成了完备的实数体系 ,为数学分析、连续函数 等研究奠定了基础。
减法运算
总结词
减法运算的基本性质
详细描述
实数的减法运算可以转化为加法运算,即a-b=a+(-b)。
总结词
减法运算的运算律
详细描述
减法运算同样满足交换律和结合律,即a-b=b-a和(ab)-c=a-(b+c)。
总结词
减法运算的运算性质
详细描述
减法的可逆性也是减法的一个重要性质,每一个数都有 唯一的相反数;另外,0是减法的单位元,任何数与0 相减都等于它本身。
总结词
加法运算的运算律
详细描述
加法运算还有一些特殊的运算律,例如,任何数与0相加 都等于它本身,即a+0=a;相反数相加等于0,即a+(a)=0。
总结词
加法运算的运算性质
详细描述
加法运算还有一些重要的运算性质,例如,加法的可逆性 ,即每一个数都有加法逆元,与它相加等于0;加法的单 位元,即有一个特殊的数0,任何数与它相加都等于它本 身。
实数在几何学中有着广泛的应用,例如在计算长度 、面积和体积时,需要使用实数表示测量值。
函数定义域与值域
实数可以用来定义各种数学函数,包括代数函数、 三角函数、指数函数和对数函数等,同时函数的值 域也由实数构成。
数学分析基础
实数对于数学分析来说是必不可少的基础,极限、 连续性和可微性的定义都离不开实数。
在物理中的应用
80%
测量与计算
在物理学中,实数常被用于表示 和计算各种物理量,如长度、时 间、质量、电荷等。
100%
物理定律的数学表达
许多物理定律可以用实数表示的 数学公式来描述,例如牛顿第二 定律 F=ma。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
求一个数的平方根 的运算叫开平方
求一个数的立方根的运 算叫开立方
0
0,1,-1
典例剖析
【例1】1.求下列各数的平方根:
(1) 25 ; (2) 6 1 ; (3) (10)2 (1) 5 ; (2) 5 ; (3) 10.
36
4
6
2
2.求下列各数的立方根:
开 方
(1)
-
8 ;(2)0.027;(3)1125
第六章 实 数 复 习
授课教师: 科目:数 学 时间:2020年
1.知道平方根、立方根的概念,会进行开平方和开 立方运算,会求一个非负数的平方根、算术平方根; 2.知道实数的分类;会对实数准确分类; 3.知道实数的有关概念,会进行实数大小比较; 4.能够运用实数的有关知识解决问题。
乘 方 互为逆运算
被开方数 正数 负数 零
平方根 有两个互为相反数
无平方根 零
立方根 有一个,是正数 有一个,是负数
零
4 算术平方根、平方根、立方根
算术平方根
平方根
立方根
表示方法
a
Байду номын сангаас
a 的取值 a ≥ 0
性
正数(一个)
0
质
没有
开方
是本身
0,1
a
a≥ 0
互为相反数(两个)
0
3a a 是任何数
正数(一个)
0
没有
负数(一个)
正实数
实
正无理数 如:,5,3 4
数
0 负实数
负有理数
如:
6,
1 3
•
,0.3,
负无理数 如 : , 5,3 4
☆:分类可以有不同的方法,但要按同一标准,不重不漏。
9 实数的性质
7 实数的分类
1、按定义分类
有限小数或无限循环小数 整数 如: 3,0,5,9
有理数
实 数
分数
如:1
,
2
,0.
•
6,0.1
23
无理数 如:,3, 3 7,0.2929929992
(每两个2之间依次增加一个9)
无限不循环小数
8 实数的分类
2、按性质(或大小)分类:
正有理数
如
:6,
1 3
•
,0.3
典例剖析
不 要 搞 错 了
【例3】填空题
8是 64 的平方根 64的平方根是 ±8
64的值是 8
64的平方根是 8
64的立方根是 4
典例剖析
不 要 遗 漏
【例4】解下列方程:
x2 196
x 14
4x2 25
(x 2)2 3
9(3 y)2 4
x5 2
x 2 3或x 2 3
y 2 1 或y 3 2
2.0的平方根还是0.
3.负数没有平方根.
a2 a =
a 2 a
a a 0 0 a 0 a (a 0) a 0
3 立方根的性质
(1)立方根的特征
一个正数有一个正的立方根; 3 a3 a
一个负数有一个负的立方根,
零的立方根是零。
3
3
a
a
a为任何数 a为任何数
(2)平方根和立方根的异同点
【归纳拓展】被开方数的小数点每向右(或 左)移动两位,则它的算术平方根的小数点向右 (或左)移动一位.
典例剖析
【例8】:估计大小 (1) 10与 (2) 140与12 (3) 15 3 与 1
22
例:求 31的整数部分和小数部分 。
估
解: 31 的整数部分是 5
算
大
31的小数部分是 31 5
小
【归纳拓展】小数部分=原数-整数部分
思考:7 7的整数部分与小数部分 。
典例剖析
例:已知 x y 4 x 2y 5 0,求x、y的值。
解:由题意得
x y 4 0
x
2
y
5
0
非 负
解方程组得
x 3
y
1
性
【归纳拓展】我们已学习了3种非负数,即绝对值、
偶数次方、算术平方根。几个非负数的和为零,
规
【归纳拓展】开立方运算时要注意小数点的变
律
化规律,开立方是三位与一位的关系,开平方
是二位与一位的关系.
典例剖析
掌 握 规 律
【例7】填空题
1.若 12.5 3.535,1.25 1.118 那么 125 11. 8 ; 0.125 0.3 53 5 。
2.若已知 7.45 2.729,y 272.9; 那么y 74 500 。
3
3
当方程中出现平方时,若有解,一般都有两个解
典例剖析
解 方 程
【例5】解下列方程:
x3 8
x 2
2x3 128
x4
(y 3)3 125
y 2
2(7 x 2)3 125 0 x 1
3
当方程中出现立方时,一般都有一个解
典例剖析
【例6】已知
,
,
掌
,则
= 0.08138,
握
= 37.77 .
7 8
(1) 2 ; 5
(2) 0.3;
(3) 1 . 2
运
算
【归纳拓展】解题时,要注意题目的要求,是求平
方根、立方根还是求算术平方根.
典例剖析
平 方 根 性 质
【例2】下列说法正确的是 A. 16的平方根是 4
B. 6表示6的算术平方根的相反数
C.任何数都有平方根 D. a2一定没有平方根
a
表示a的算术平方根
-a
a
x2 = a
表示a的算术平方根的相反数
表示a的平方根
X= a
1 相关概念
4.立方根:一般地,如果 x3 a,那么 x 叫 a 的立方根 数 a的立方根用符号 3 a 表示。
5.开方: 求一个数的平方根(立方根)的运算,叫做开平方(开立方) 。
2 平方根的性质
平方根的性质: 1.正数有两个平方根,两个平方根互为相反数.
它们就同时为零,然后转化为方程(或方程组)
来解。
5 无理数的概念
请同学们用计算器计算,把下列有理数写成小数的形
●
式,你能发现什么?
3, 3 , 47 , 9 , 11 , 5 5 8 11 90 9
归纳:任何一个有理数都可以写成有限小数或无 限循环小数。(有理数的特征)
5 无理数的概念
☆归纳:它们是无限不循环小数,所以我们知道它们既不是整数, 也不是分数。 ●我们把这类无限不循环的小数叫做无理数。
、 如:2、 3 5、3 2、 、
0.1010010001 (每两个1之间依次增加一个 0)
6 无理数的特征
1.圆周率 及一些含有 的数
2
、 2 1
2.开方开不尽数 2 、3 5
3.有一定的规律,但不循环 的无限小数
注意:带根号的数 不一定是无理数
0.6363363336 (每两个6之间依次增加一个3)
开 方
开平方 开立方
平方根 立方根
算术平方根 负的平方根
实数
无理数 有理数
运算
1 相关概念
1.平方根:如果一个数X的平方等于a,即X2=a,那么 这个数X叫做a的平方根(二次方根)
a的平方根表示为 a 读作:正,负根号a
2.算术平方根:正数 a 的正的平方根也叫做 a 的算术平方根,
记作 a
3.表示意义:
