关于勾股定理及逆定理的综合应用课件
合集下载
勾股定理的逆定理-完整版课件
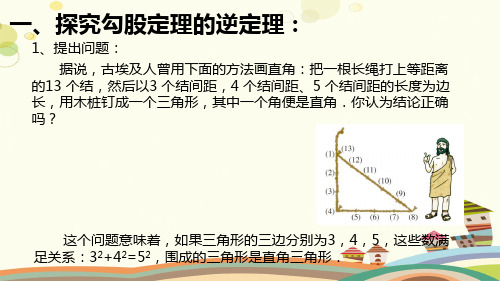
一、探究勾股定理的逆定理:
2、实验探究: (1)画一画:下列各组数中的两数平方和等于第三数的平方,分别以这些数 为边长画出三角形(单位:cm),它们是直角三角形吗? ① 2.5,6,6.5; ② 6,8,10. (2)量一量:用量角器分别测量上述各三角形的最大角的度数. (3)想一想:请判断这些三角形的形状,并提出猜想.
PQ=16×1.5=24,PR=12×1.5=18,QR=30. ∵24²+18²=30², 即PQ²+PR²=QR², ∴△PQR为直角三角形,即∠QPR=90°. ∵∠1=45°, ∴∠2=45°,即“海天”号沿西北方向航行.
练习4、如图,如图,南北向MN为我国领域,即MN以西为我国领海,以东 为公海.上午9时50分,我反走私A艇发现正东方向有一走私艇C以13海里/时的 速度偷偷向我领海开来,便立即通知正在MN线上巡逻的我国反走私艇B.已知 A、C两艇的距离是13海里,A、B两艇的距离是5海里;反走私艇B测得离C艇 的距离是12海里.若走私艇C的速度不变,最早会在什么时间进入我国领海?
2
2
∴BE= AB•BC60.
B
AC 13
.
在Rt△BCE中,由勾股定理得,
N
∴CE= BC 2BE 2 12 2(60 )2144
13 13
∴最早进入时间≈0.85小时=51分钟.
.
9时50分+51分=10时41分.
答:走私艇最早在10时41分进入我国领海.
五、课堂小结:
1、利用勾股定理的逆定理判定是否为直角三角形的一般步骤: ①确定最大边长c; ②计算a2+b2和c2的值, 若a2+b2=c2,则此三角形是直角三角形; 若a2+b2<c2,则此三角形是钝角三角形; 若a2+b2>c2,则此三角形是锐角三角形. 2、互逆命题表明两个命题在形式上的关系,将一个命题的题设和结论互换 即可得到它的逆命题,当原命题成立时,它的逆命题不一定成立,即互逆 的两个命题不一定同真或同假. 3、已知一三角形的三边的长度时,首先应对该三角形进行判断,判断最长 边的平方是否等于其余两边的平方和,如何满足这一条件则此三角形为直 角三角形.
《勾股定理的逆定理》勾股定理PPT精品课件

问题3 古埃及人用来画直角的三边满足这个等式吗?
∵32+42=52,∴满足.
猜想:
命题2:如果三角形的三边长a,b,c满足a2+b2=c2,那么这个三角形是直
角三角形。
这个命题和前面学的命题1(勾股定理)之间有什么关系吗?
1.题设和结论正好相反的两个命题,叫做互逆命题。
2.如果把其中一个命题叫做原命题,那么另一个命题叫做它的逆命题。
勾股定理的逆定理
1、理解勾股定理的逆定理。
2、了解逆命题的概念,知道原命题为真命题,它的逆命题不一
定为真命题。
3、应用勾股定理的逆定理解决实际问题。
学习目标
学习目标
1.理解勾股定理的逆定理及证明过程。
2.能简单的运用勾股定理的逆定理判定直角三角形。
3.利用勾股定理逆定理解决实际问题
重点
运用勾股定理的逆定理判定直角三角形。
命题2是正确的吗?你能试着证明吗?
利用勾股定理逆定理判断直角三角形
下面以a,b,c为边长的三角形是不是直角三角形?
1)a=15 ,b=8 ,c=17
2)a=13 ,b=14 ,c=15
解:∵152+82=289,172=289,
∴152+82=172,
根据勾股定理的逆定理,这个三角形是直角三角形。
∴∠QPR=90°。
P
由“远航”号沿东北方向航行可知,∠QPS=45°。 ∴∠RPS=45°,
即“海天”号沿西北方向航行。
E
利用勾股定理逆定理判断直角三角形
满足下列条件的△ABC不是直角三角形的是(
A.BC=1,AC=2,AB=
C.BC:AC:AB=3:4:5
)
B.BC=1,AC=2,AB=
∵32+42=52,∴满足.
猜想:
命题2:如果三角形的三边长a,b,c满足a2+b2=c2,那么这个三角形是直
角三角形。
这个命题和前面学的命题1(勾股定理)之间有什么关系吗?
1.题设和结论正好相反的两个命题,叫做互逆命题。
2.如果把其中一个命题叫做原命题,那么另一个命题叫做它的逆命题。
勾股定理的逆定理
1、理解勾股定理的逆定理。
2、了解逆命题的概念,知道原命题为真命题,它的逆命题不一
定为真命题。
3、应用勾股定理的逆定理解决实际问题。
学习目标
学习目标
1.理解勾股定理的逆定理及证明过程。
2.能简单的运用勾股定理的逆定理判定直角三角形。
3.利用勾股定理逆定理解决实际问题
重点
运用勾股定理的逆定理判定直角三角形。
命题2是正确的吗?你能试着证明吗?
利用勾股定理逆定理判断直角三角形
下面以a,b,c为边长的三角形是不是直角三角形?
1)a=15 ,b=8 ,c=17
2)a=13 ,b=14 ,c=15
解:∵152+82=289,172=289,
∴152+82=172,
根据勾股定理的逆定理,这个三角形是直角三角形。
∴∠QPR=90°。
P
由“远航”号沿东北方向航行可知,∠QPS=45°。 ∴∠RPS=45°,
即“海天”号沿西北方向航行。
E
利用勾股定理逆定理判断直角三角形
满足下列条件的△ABC不是直角三角形的是(
A.BC=1,AC=2,AB=
C.BC:AC:AB=3:4:5
)
B.BC=1,AC=2,AB=
勾股定理的逆定理课件

详细描述
在勾股定理的逆定理的证明中,反证 法是通过假设三角形不是直角三角形 ,然后利用勾股定理的逆定理推导出 矛盾的结论,从而证明三角形一定是 直角三角形。
证明方法二:直接证明法
总结词
直接证明法是一种直接根据已知 条件和定理,通过逻辑推理得到 结论的证明方法。
详细描述
在勾股定理的逆定理的证明中, 直接证明法是通过直接利用勾股 定理的条件和结论,推导出三角 形一定是直角三角形。
对于任意的整数a、b、c,都存在无穷多 个整数x、y、z,满足x²+y²=z²,且x、y 、z互质。
勾股定理的逆定理与欧几里得公设的关系
勾股定理的逆定理是 欧几里得公设的一个 推论。
勾股定理的逆定理证 明了欧几里得公设的 正确性。
欧几里得公设是勾股 定理逆定理的基础。
05 勾股定理的逆定理的挑战 和问题
勾股数的性质
唯一性
对于任何一个正整数n,都存在唯 一的一组整数a、b、c,满足 n=a²+b²=c²。
自然数性
勾股数的三边长可以都是自然数。
无穷多性
对于任意正整数n,都存在无穷多个 勾股数。
勾股数的扩展
广义勾股数
如果三个整数的平方和等于另一个整数 的平方,则这三个数被称为广义勾股数 。
VS
勾股数的组合
勾股定理的逆定理课件
目录
• 勾股定理的逆定理的概述 • 勾股定理的逆定理的证明 • 勾股定理的逆定理的应用 • 勾股定理的逆定理的扩展 • 勾股定理的逆定理的挑战和问题 • 勾股定理的逆定理的案例分析
01 勾股定理的逆定理的概述
什么是勾股定理的逆定理
勾股定理的逆定理定义
如果一个三角形的三条边满足两边的平方和等于第三边的平方,那么这个三角形 是直角三角形。
在勾股定理的逆定理的证明中,反证 法是通过假设三角形不是直角三角形 ,然后利用勾股定理的逆定理推导出 矛盾的结论,从而证明三角形一定是 直角三角形。
证明方法二:直接证明法
总结词
直接证明法是一种直接根据已知 条件和定理,通过逻辑推理得到 结论的证明方法。
详细描述
在勾股定理的逆定理的证明中, 直接证明法是通过直接利用勾股 定理的条件和结论,推导出三角 形一定是直角三角形。
对于任意的整数a、b、c,都存在无穷多 个整数x、y、z,满足x²+y²=z²,且x、y 、z互质。
勾股定理的逆定理与欧几里得公设的关系
勾股定理的逆定理是 欧几里得公设的一个 推论。
勾股定理的逆定理证 明了欧几里得公设的 正确性。
欧几里得公设是勾股 定理逆定理的基础。
05 勾股定理的逆定理的挑战 和问题
勾股数的性质
唯一性
对于任何一个正整数n,都存在唯 一的一组整数a、b、c,满足 n=a²+b²=c²。
自然数性
勾股数的三边长可以都是自然数。
无穷多性
对于任意正整数n,都存在无穷多个 勾股数。
勾股数的扩展
广义勾股数
如果三个整数的平方和等于另一个整数 的平方,则这三个数被称为广义勾股数 。
VS
勾股数的组合
勾股定理的逆定理课件
目录
• 勾股定理的逆定理的概述 • 勾股定理的逆定理的证明 • 勾股定理的逆定理的应用 • 勾股定理的逆定理的扩展 • 勾股定理的逆定理的挑战和问题 • 勾股定理的逆定理的案例分析
01 勾股定理的逆定理的概述
什么是勾股定理的逆定理
勾股定理的逆定理定义
如果一个三角形的三条边满足两边的平方和等于第三边的平方,那么这个三角形 是直角三角形。
八年级数学下册教学课件《勾股定理的逆定理的应用》

(2)a = 41 ,b = 4,c = 5;
∵b2 + c2 = 42 + 52 = 16 + 24 = 41,a2 = ( 41 )2 = 41, ∴b2 + c2 = a2.
由勾股定理的逆定理知这个三角形是直角三角形.
(3)a = 5 ,b = 1,c = 3 ;
4
4
∵b2 + c2 = 12 + ( 3 )2 = 1 + 9 = 25,a2 = ( 5 )2 = 25 ,
由勾股定理得:EF2 = EC2 + FC2 = 5x2,
B
E
C
AE2 = AB2 + BE2 = 20x2,AF2 = AD2 + DF2 = 25x2 = 25x2,
∴EF2 + AE2 = 25x2 = AF2.
由勾股定理的逆定理知,∠AEF = 90°.
拓广探索 【选自教材 P34】
7. 我们知道 3,4,5 是一组勾股数,那么 3k,4k,5k (k 是正整数)也是一组勾股数吗?一般地,如果 a,b, c 是一组勾股数,那么 ak,bk,ck(k 是正整数)也是 一组勾股数吗?
课堂小结
勾股理的 逆定理
判断一个三角形是不是直角三角形 判断航行方向 计算不规则四边形面积
综合运用 【选自教材 P34】
4. 在△ABC 中,AB =13,BC = 10,BC 边上的中线
AD =12. 求 AC.
解:在△ABD中,BD =
1 2
BC
=
5.
AD
=
12,AB
=
13.
∵BD2 + AD2 = 52 + 122 = 25 + 144 =169,
《勾股定理的逆定理》PPT免费课件(第2课时)

田的面积为( A )
A.7.5平方千米
B.15平方千米
C.75平方千米
D.750平方千米
课堂检测 基础巩固题
B
1.五根小木棒,其长度分别为7,15,20,24,25,现将他 们摆成两个直角三角形,其中摆放方法正确的是 ( D )
A.
B.
B
C.
D.
课堂检测
2.如图是医院、公园和超市的平面示意图,超市在医院的南偏东 25°的方向,且到医院的距离为300 m,公园到医院的距离为 400 m,若公园到超市的距离为500 m,则公园在医院的 ( B ) A.北偏东75°的方向上 B.北偏东65°的方向上 C.北偏东55°的方向上 D.无法确定
课堂检测
3.如图,某探险队的A组由驻地O点出发,以12km/h的速度前进,
同时,B组也由驻地O出发,以9km/h的速度向另一个方向前进,
2h后同时停下来,这时A,B两组相距30km.此时,A,B两组
行进的方向成直角吗?请说明理由.
解:∵出发2小时,A组行了12×2=24(km),
A
B组行了9×2=18(km),
Байду номын сангаас
巩固练习
解:由题意得,OB=12×1.5=18海里, OA=16×1.5=24海里, 又∵AB=30海里, ∴182+242=302,即OB2+OA2=AB2, ∴∠AOB=90°. ∵∠DOA=40°, ∴∠BOD=50°. 则另一艘舰艇的航行方向是北偏西50°.
探究新知
知识点 2 利用勾股定理的逆定理解答面积问题
应用 方法
航海问题
与勾股定理结合解决不规 则图形等问题
认真审题,画出符合题意的图 形,熟练运用勾股定理及其逆 定理来解决问题
勾股定理及其逆定理的运用课件

力。
通过学习勾股定理及其逆定理,学生可 以培养出严密的逻辑思维和推理能力, 为后续的数学、物理、工程等学科的学
习打下坚实的基础。
学生可以从中领悟到数学与实际生活的 紧密联系,激发对数学的兴趣和热爱,
提高自主学习和探索的能力。
对实际应用的展望和期待
随着科技的发展和实际问题的复杂化,勾股定理及其逆定理的应用前景 将更加广阔。
度。
物理学
在物理学中,勾股定理可以用来解 决与直角三角形相关的力和运动问 题,例如单摆的运动和受力分析。
航海学
在航海学中,勾股定理可以用来计 算船只的航行距离和方向,以确保 航行安全。
02
逆定理的的逆定理是指,如果一 个三角形的三边满足勾股定理的 条件,那么这个三角形一定是直 角三角形。
条件限制不同
勾股定理适用于所有直角 三角形,而逆定理只适用 于已知一边和与之相对的 角为直角的三角形。
证明方法不同
勾股定理可以通过相似三 角形或面积法证明,而逆 定理通常通过反证法证明 。
定理与逆定理的互补之处
勾股定理是逆定理的前提
01
只有当满足勾股定理的条件时,一个三角形才可能是直角三角
形。
逆定理是勾股定理的延伸
02
勾股定理的逆定理是勾股定理的 一个重要应用,它可以帮助我们 判断一个三角形是否为直角三角 形。
逆定理的证明方法
勾股定理的逆定理可以通过反证法进 行证明。
然后通过构造一个直角三角形与三角 形ABC全等,并利用勾股定理证明假 设不成立,从而得出三角形ABC是直 角三角形的结论。
首先假设一个三角形ABC的三边满足 a²+b²=c²,但角C不是直角。
勾股定理及其逆定理的运用ppt课件
目录
通过学习勾股定理及其逆定理,学生可 以培养出严密的逻辑思维和推理能力, 为后续的数学、物理、工程等学科的学
习打下坚实的基础。
学生可以从中领悟到数学与实际生活的 紧密联系,激发对数学的兴趣和热爱,
提高自主学习和探索的能力。
对实际应用的展望和期待
随着科技的发展和实际问题的复杂化,勾股定理及其逆定理的应用前景 将更加广阔。
度。
物理学
在物理学中,勾股定理可以用来解 决与直角三角形相关的力和运动问 题,例如单摆的运动和受力分析。
航海学
在航海学中,勾股定理可以用来计 算船只的航行距离和方向,以确保 航行安全。
02
逆定理的的逆定理是指,如果一 个三角形的三边满足勾股定理的 条件,那么这个三角形一定是直 角三角形。
条件限制不同
勾股定理适用于所有直角 三角形,而逆定理只适用 于已知一边和与之相对的 角为直角的三角形。
证明方法不同
勾股定理可以通过相似三 角形或面积法证明,而逆 定理通常通过反证法证明 。
定理与逆定理的互补之处
勾股定理是逆定理的前提
01
只有当满足勾股定理的条件时,一个三角形才可能是直角三角
形。
逆定理是勾股定理的延伸
02
勾股定理的逆定理是勾股定理的 一个重要应用,它可以帮助我们 判断一个三角形是否为直角三角 形。
逆定理的证明方法
勾股定理的逆定理可以通过反证法进 行证明。
然后通过构造一个直角三角形与三角 形ABC全等,并利用勾股定理证明假 设不成立,从而得出三角形ABC是直 角三角形的结论。
首先假设一个三角形ABC的三边满足 a²+b²=c²,但角C不是直角。
勾股定理及其逆定理的运用ppt课件
目录
《勾股定理的逆定理》数学教学PPT课件(5篇)

求证:△ ABC是直角三角形
证明:画一个△A′B′C′,
使∠
C′=900,
B′C′= a,
A'
A
B
b
b
a
C
B'
a
C'
在△ ABC和△ A′B′C′中
BC = a = B′C′,
CA = b = C′A′,
AB = c = A ′B′
C′A′=b
∵ ∠ C′=900
∴ A′B′ 2= a2+b2
∵ a2+b2=c2
c
b
C
作用:已知三角形的三边长,判断
这个三角形是否为直角三角形。
a
B
,
自主学习
例1:注意归纳例题的解题步骤和解题技巧!
已知三角形三条边的长度分别是:(1)1,
,
(2)2,3,4;
(3)3n,4n,5n(n > 0), 它们是否分别构成直角三角形?
解
(1)在 1, ,,
中,
)2 ,所以,边长为1,
(
∴S四边形ABCD=S△ABD+S△BCD
B
1
= -AB×AD+
2
1
= -×3×4+
2
1
-BD×CD
2
1
-×5×12
2
= 36
所以四边形ABCD的面积
为36.
C
知识升华
满足
a b的三个正整数,
c
2
称为勾股数组.
2
2
自主检测
1、满足________
勾股数组。
的三个____
__
正整数
如:
证明:画一个△A′B′C′,
使∠
C′=900,
B′C′= a,
A'
A
B
b
b
a
C
B'
a
C'
在△ ABC和△ A′B′C′中
BC = a = B′C′,
CA = b = C′A′,
AB = c = A ′B′
C′A′=b
∵ ∠ C′=900
∴ A′B′ 2= a2+b2
∵ a2+b2=c2
c
b
C
作用:已知三角形的三边长,判断
这个三角形是否为直角三角形。
a
B
,
自主学习
例1:注意归纳例题的解题步骤和解题技巧!
已知三角形三条边的长度分别是:(1)1,
,
(2)2,3,4;
(3)3n,4n,5n(n > 0), 它们是否分别构成直角三角形?
解
(1)在 1, ,,
中,
)2 ,所以,边长为1,
(
∴S四边形ABCD=S△ABD+S△BCD
B
1
= -AB×AD+
2
1
= -×3×4+
2
1
-BD×CD
2
1
-×5×12
2
= 36
所以四边形ABCD的面积
为36.
C
知识升华
满足
a b的三个正整数,
c
2
称为勾股数组.
2
2
自主检测
1、满足________
勾股数组。
的三个____
__
正整数
如:
八年级-人教版-数学-下册-第3课时-勾股定理及其逆定理的综合应用

再根据勾股定理的逆定理即可判断△ACD 的形状,从而可以求得
四边形 ABCD 的面积;
A
D
解:(1)连接 AC,
∵∠ABC=90°,AB=6,BC=8,
B
C
∴ AC AB2 BC2 62 82 10.
∵CD=10,AD=10 2 ,
∴CD2+AC2=102+102=200,AD2= 10 2 2=200,
(1)学校 C 会受噪声影响吗?为什么?
分析:(1)利用勾股定理的逆定理得出 C
△ABC 是直角三角形,然后利用三角形面积得出
B D
CD 的长,进而得出学校 C 是否会受噪声影响;
A
解:(1)学校 C 会受噪声影响. 理由:如图,过点 C 作 CD⊥AB 于 D, ∵AC=150 m,BC=200 m,AB=250 m,
岛,再从 B 岛沿 BM 方向航行 125 km 到达 C 岛,A 港到航线 BM
的最短距离是 60 km.
(1)若轮船速度为 25 km/h,求轮船从 C 岛沿 CA 方向返回
A 港所需的时间;
M
分析:(1)在 Rt△ABD 中,利用勾股定理
C
可求得 BD 的长度,则 CD=BC-BD;然后在
D
Rt△ACD 中,利用勾股定理可求得 AC 的长度,
∵拖拉机的行驶速度为 50 m/min,
∴100÷50=2(min), C
即拖拉机噪声影响该学校持续的时间有 2 min.
B
F D E A
例3 如图,在四边形ABCD中,∠ABC=90°,AB=6, BC=8,CD=10,AD=10 2.
(1)求四边形 ABCD 的面积.
分析:(1)连接 AC,然后根据勾股定理可以求得 AC 的长,
初中八年级数学课件 17.2.1勾股定理逆定理的应用

M
AE
C
B
CE=,
N
提高作业
4、已知 △ABC三角形的三边分别为 a,b,c 且a = m 2 - n2 ,b = 2mn,c = m 2 n2 (m > n,m,n是正整数), △ABC是直角三角形吗?说明理由。
分析:先来判断a,b,c三边哪条最长,可以 代m,n为满足条件的特殊值来试,m=5,n=4. 则a=9,b=40,c=41,c最大。 解:a2 b2 (m2 n2 )2 (2mn)2 (m2 n2 )2 c2
④ a=40, b=50, c=60
√ √
√
×
回顾与复习
2. 下列各命题都成立,写出它们的逆命题。这些逆命题成立吗?
① 同旁内角互补,两直线平行; ② 如果两个角是直角,那么它们相等; ③ 全等三角形的对应边相等; ④ 如果两个实数相等,那么它们的平方相等。
回顾与复习
3. 已知:如图,四边形ABCD中, ∠B=900,AB=3,BC=4,CD=12, AD=13,求四边形ABCD的面积?
∴△ABC是直角三角形
知道“远航”号沿东北方向航行, 能知道“海天”号沿哪个方向
航 解:行根吗据?题意,PQ=16×1.5=24; P分R析=:由12图×可1以.5看=到1,8由;于Q“R远=航”30号.
因为的航+向,已知,如果求出两艘船的航向所
N
S
Q
即=成,的角 ,就能知道“海天”号的航向了。
所以∠QPR=
由“远航”号沿东北方向航行可知:
求四边形ABCD的面积.
C
B
D
A
S四边形
提高作业
1.若△ABC的三边a、b、c,满足a:b:c=1:1: ,试判断△ABC的形状.
AE
C
B
CE=,
N
提高作业
4、已知 △ABC三角形的三边分别为 a,b,c 且a = m 2 - n2 ,b = 2mn,c = m 2 n2 (m > n,m,n是正整数), △ABC是直角三角形吗?说明理由。
分析:先来判断a,b,c三边哪条最长,可以 代m,n为满足条件的特殊值来试,m=5,n=4. 则a=9,b=40,c=41,c最大。 解:a2 b2 (m2 n2 )2 (2mn)2 (m2 n2 )2 c2
④ a=40, b=50, c=60
√ √
√
×
回顾与复习
2. 下列各命题都成立,写出它们的逆命题。这些逆命题成立吗?
① 同旁内角互补,两直线平行; ② 如果两个角是直角,那么它们相等; ③ 全等三角形的对应边相等; ④ 如果两个实数相等,那么它们的平方相等。
回顾与复习
3. 已知:如图,四边形ABCD中, ∠B=900,AB=3,BC=4,CD=12, AD=13,求四边形ABCD的面积?
∴△ABC是直角三角形
知道“远航”号沿东北方向航行, 能知道“海天”号沿哪个方向
航 解:行根吗据?题意,PQ=16×1.5=24; P分R析=:由12图×可1以.5看=到1,8由;于Q“R远=航”30号.
因为的航+向,已知,如果求出两艘船的航向所
N
S
Q
即=成,的角 ,就能知道“海天”号的航向了。
所以∠QPR=
由“远航”号沿东北方向航行可知:
求四边形ABCD的面积.
C
B
D
A
S四边形
提高作业
1.若△ABC的三边a、b、c,满足a:b:c=1:1: ,试判断△ABC的形状.
《勾股定理的逆定理》勾股定理PPT课件(第2课时)

13
4
12
┐
3
探究新知
解:连接BD 在Rt△ABD中
∵AB=3,AD=4 ∴BD= AB 2 AD 2 =5
在△BCD中 ∵CD=13 , BC=12
∴CD2=BC2+BD2
13
45
12
┐
3
∴△BCD是直角三角形 ∴∠DBC=90°
∴S四边形ABCD=S△ABD+S△BCD = 1×3×4+ 1×5×12=36
此时四边形ABCD 的面积是多少?
5、 已知a、b、c为△ABC的三边,且 满足 a2+b2+c2+338=10a+24b+26c. 试判断△ABC的形状.
思维训练
6、△ABC三边a,b,c为边向外作 正方形,正三角形,以三边为 直则径作是半直圆角,三若角S形1+吗S2=?S3成立,
C
S2
A
b
ca
能替工人师傅想办法完成任务吗?
9.三个半圆的面积分别为S1=3π, S2=4π,S3=7π,把三个半圆拼成如 右图所示的图形,则△ABC一定是
直角三角形吗?
B
C
D
B'
A'
A
B
勾股定理:
如果直角三角形的两直角边为a,b, 斜边长为c ,那么a2+b2=c2.
B
反过来,如果一个 a
c
三角形的三边长a、b、
(C)1:2:4; (D)1:3:5.
3. 三角形的三边分别是a、b、c, 且满足
(a+b)2-c2=2ab, 则此三角形是:( )
A. 直角三角形;
B. 是锐角三角形;
数学八年级下册勾股定理及其逆定理的综合应用PPT公开课

最短路程是多少? (π的值取3) (例如:方位角、测量物体等)
在波平如静的湖面上,有一朵美丽的红莲 ,它高出水面1米 ,一阵大风吹过,红莲被吹至一边,花朵齐及水面,如果知道红莲移动的水平距 离为2米 ,问这里水深多少? 飞机每时飞行多少千米?
4、结合方程,利用勾股定理列方程 当直角三角形只知道一边的长,以及另外
4、结合方程,利用勾股定理列方程 4、结合方程,利用勾股定理列方程
B
在波平如静的湖面上,有一朵美丽的红莲 ,它高出水面1米 ,一阵大风吹过,红莲被吹至一边,花朵齐及水面,如果知道红莲移动的水平距
离为2米 ,问这里水深多少?
有一个圆柱,它的高等于12厘米,底面半径等于3厘米,在圆柱下底面上的A点有一只蚂蚁,它想从点A爬到点B , 蚂蚁沿着圆柱侧面爬行的
最短路程是多少? (π的值取3)
蚂蚁爬行的最短路程是15厘米.
将AC折叠,使它落在AB上。
在波平如静的湖面上,有一朵美丽的红莲 ,它高出水面1米 ,一阵大风吹过,红莲被吹至一边,花朵齐及水面,如果知道红莲移动的水平距
离为2米 ,问这里水深多少?
4、结合方程,利用勾股定理列方程
4、结合方程,利用勾股定理列方程
程是多少? (π的值取3) 将AC折叠,使它落在AB上。
(例如:网格里的不规则线段、作垂线等) 则第三边长为多少?
问:他的解法对吗?为什么?
有一个圆柱,它的高等于12厘米,底面半径等于3厘米,在圆柱下底面上的A点有一只蚂蚁,它想从点A爬到点B , 蚂蚁沿着圆柱侧面爬行的
最短路程是多少? (π的值取3)
4000米 2、已知两边,求第三边 5000米 有一个圆柱,它的高等于12厘米,底面半径等于3厘米,在圆柱下底面上的A点有一只蚂蚁,它想从点A爬到点B , 蚂蚁沿着圆柱侧面爬行的
在波平如静的湖面上,有一朵美丽的红莲 ,它高出水面1米 ,一阵大风吹过,红莲被吹至一边,花朵齐及水面,如果知道红莲移动的水平距 离为2米 ,问这里水深多少? 飞机每时飞行多少千米?
4、结合方程,利用勾股定理列方程 当直角三角形只知道一边的长,以及另外
4、结合方程,利用勾股定理列方程 4、结合方程,利用勾股定理列方程
B
在波平如静的湖面上,有一朵美丽的红莲 ,它高出水面1米 ,一阵大风吹过,红莲被吹至一边,花朵齐及水面,如果知道红莲移动的水平距
离为2米 ,问这里水深多少?
有一个圆柱,它的高等于12厘米,底面半径等于3厘米,在圆柱下底面上的A点有一只蚂蚁,它想从点A爬到点B , 蚂蚁沿着圆柱侧面爬行的
最短路程是多少? (π的值取3)
蚂蚁爬行的最短路程是15厘米.
将AC折叠,使它落在AB上。
在波平如静的湖面上,有一朵美丽的红莲 ,它高出水面1米 ,一阵大风吹过,红莲被吹至一边,花朵齐及水面,如果知道红莲移动的水平距
离为2米 ,问这里水深多少?
4、结合方程,利用勾股定理列方程
4、结合方程,利用勾股定理列方程
程是多少? (π的值取3) 将AC折叠,使它落在AB上。
(例如:网格里的不规则线段、作垂线等) 则第三边长为多少?
问:他的解法对吗?为什么?
有一个圆柱,它的高等于12厘米,底面半径等于3厘米,在圆柱下底面上的A点有一只蚂蚁,它想从点A爬到点B , 蚂蚁沿着圆柱侧面爬行的
最短路程是多少? (π的值取3)
4000米 2、已知两边,求第三边 5000米 有一个圆柱,它的高等于12厘米,底面半径等于3厘米,在圆柱下底面上的A点有一只蚂蚁,它想从点A爬到点B , 蚂蚁沿着圆柱侧面爬行的
《勾股定理——勾股定理的逆定理》数学教学PPT课件(5篇)

判定一个三角形是直角三角形的方法
有一个角是直角的三角形是直角三角形.
角:
边:
如果三角形的三边长a,b,c满足 a2+b2=c2,那么这个三角形是直角三角形
再 见
1.直角三角形有哪些性质?
2.如何判断三角形是直角三角形?
古埃及人曾用下面的方法得到直角
按照这种做法真能得到一个直角三角形吗?
∴ ∠C= 900
已知:在△ABC中,AB=c BC=a CA=b 且a2+b2=c2
求证:△ ABC是直角三角形
证明:画一个△A’B’C’,使∠ C’=900,B’C’=a, C’A’=b
在△ ABC和△ A’B’C’中
∴ △ ABC是直角三角形(直角三角形的定义)
勾股定理的逆命题证明
例1 判断由a、b、c组成的三角形是不是直角三角形:(1) a=15 , b =8 , c=17
是
是
不是
是
∠ A=900
∠ B=900
∠ C=900
像25,20,15,能够成为直角三角形三条边长的三个正整数,称为勾股数.
例1: “远航”号、“海天”号轮船同时离开港口,各自沿一固定方向航行,“远航”号每小时航行16海里,“海天”号每小时航行12海里。它们离开港口一个半小时后相距30海里。如果知道“远航”号沿东北方向航行,能知道“海天”号沿哪个方向航行吗?
例题3:
如图,是一块四边形绿地示意图,其中AB长24米,BC长20米,CD长15米,DA长7米,∠ C=90度求:绿地ABCD的面积。
C
B
A
D
24
20
15
7
25
例2:如图,有一块地,已知,AD=4m,CD=3m,∠ADC=90°,AB=13m,BC=12m。求这块地的面积。
有一个角是直角的三角形是直角三角形.
角:
边:
如果三角形的三边长a,b,c满足 a2+b2=c2,那么这个三角形是直角三角形
再 见
1.直角三角形有哪些性质?
2.如何判断三角形是直角三角形?
古埃及人曾用下面的方法得到直角
按照这种做法真能得到一个直角三角形吗?
∴ ∠C= 900
已知:在△ABC中,AB=c BC=a CA=b 且a2+b2=c2
求证:△ ABC是直角三角形
证明:画一个△A’B’C’,使∠ C’=900,B’C’=a, C’A’=b
在△ ABC和△ A’B’C’中
∴ △ ABC是直角三角形(直角三角形的定义)
勾股定理的逆命题证明
例1 判断由a、b、c组成的三角形是不是直角三角形:(1) a=15 , b =8 , c=17
是
是
不是
是
∠ A=900
∠ B=900
∠ C=900
像25,20,15,能够成为直角三角形三条边长的三个正整数,称为勾股数.
例1: “远航”号、“海天”号轮船同时离开港口,各自沿一固定方向航行,“远航”号每小时航行16海里,“海天”号每小时航行12海里。它们离开港口一个半小时后相距30海里。如果知道“远航”号沿东北方向航行,能知道“海天”号沿哪个方向航行吗?
例题3:
如图,是一块四边形绿地示意图,其中AB长24米,BC长20米,CD长15米,DA长7米,∠ C=90度求:绿地ABCD的面积。
C
B
A
D
24
20
15
7
25
例2:如图,有一块地,已知,AD=4m,CD=3m,∠ADC=90°,AB=13m,BC=12m。求这块地的面积。
八年级数学勾股定理的逆定理课件-应用

人教版
第2课时勾股定理的逆定 理(二) —— 应用
(2)在图2中,画一个三边长分别为3,2, 13的三角形,一共可以画 16 个这样的三角形. 解析:如图2,一共可以画16个这样的三角形.
图2
数学
八年级 下册
人教版
第2课时勾股定理的逆定 理(二) —— 应用
10.在某小区在社区工作人员及社区居民的共同努力之下,
数学
八年级 下册
人教版
第2课时勾股定理的逆定 理(二) —— 应用
8.如图,明明在距离水面高度为5 m的岸边C处,用绳子拉船 靠岸,开始时绳子BC的长为13 m.若明明收绳6 m后,船到 达D处,则船向岸边A处移动了多少米?
数学
八年级 下册
人教版
第2课时勾股定理的逆定 理(二) —— 应用
解:∵开始时绳子BC的长为13 m,明明收绳6 m后,船到达D处,
数学
八年级 下册
人教版
第2课时勾股定理的逆定 理(二) —— 应用
知识点 勾股定理逆定理的应用 【例题】如图,甲船以5海里/时的速度离开港口O沿南偏东 30°方向航行,乙船同时同地沿某方向以12海里/时的速度 航行.已知它们离开港口2小时后分别到达B,A两点,且AB =26海里.你知道乙船是沿哪个方向航行的吗?
数学 人教版 八年级 下册
目 录
CONTENTS
数学
八年级 下册
人教版
第2课时勾股定理的逆定 理(二) —— 应用
第十七章 勾股定理
17.2 勾股定理的逆定理 第2课时勾股定理的逆定理(二) —— 应用
01 课标要求
02 基础梳理
03 典例探究
04 课时训练
数学
八年级 下册
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
例:折叠矩形ABCD的一边AD,点D落在
BC边上的点F处,已知AB=8CM,BC=10CM, 求 (1) CF ( 2) EC. (3) AE
10
D
A
8-X
8 10
E
8-X X
B
6
F4 C
正方体中的最值问
题
B
C
C
2a
B
a
A
A
结论5a: ,即由两个正个三级台阶,它的每一级的长、宽和 高分别等于5cm,3cm和1cm,A和B是这个台阶的两个 相对的端点,A点上有一只蚂蚁,想到B点去吃可口的 食物.请你想一想,这只蚂蚁从A点出发,沿着台阶面 爬到B点,最短线路是多少?
关于勾股定理及逆定理的综合 应用
例题评讲
例:如图,已知在正方形ABCD中,AE=EB,14 AF= AD.
求证:CE⊥EF
证明:连接CF,设AF=a,
a
3a
则DF=3a,AE=EB=2a,
2a
BC=CD=4a.
4a
2a
余下的部分请同学们完成。
4a
通过“角”来证
证明“垂直”的方 明
法
通过“边”来证
例题评讲
在直线l上依次摆放着五个正方形,如图所示,已知倾斜放置的
两个正方形的面积分别是3,5,正放置的三个正方形的面积依次
是 S1、S,则2、S3 S=1+_2_S__2+S3 8
分类思想
1.直角三角形中,已知两边长,但不能确 定是直角边、斜边时,应分类讨论。
2.当已知条件中没有给出图形时,应认真 读句画图,避免遗漏另一种情况。
A
5
A
3
1
5
C
12 B
∵ AB2=AC2+BC2=169,
∴ AB=13.
B
圆柱(锥)中的最值问题
例: 有一圆形油罐底面圆的周长为24m,高为6m, 一只老鼠从距底面1m的A处爬行到对角B处 吃食物,它爬行的最短路线长为多少?
B
C
B
A
A
分析:由于老鼠是沿着圆柱的
表面爬行的,故需把圆柱展开 成平面图形.根据两点之间线段 最短,可以发现A、B分别在 圆柱侧面展开图的宽1m处和 长24m的中点处,即AB长为最 短路线.(如图)
解:AC = 6 – 1 = 5 ,
BC
=
24
×
1 2
= 12,
由勾股定理得
AB2= AC2+ BC2=169, ∴AB=13(m) .
例:三角形ABC中,AB=10,AC=17,BC边 上的高线AD=8,求BC.
A
17
8 10
B
C
例:三角形ABC是等腰三角形AB=AC=13,
BC=10,将AB向AC方向对折,再将CD
折叠到CA边上,折痕为CE,求三角形
ACE的面积
A
A
A
12-x 8
12
13
x E x
D1 5
B D C D5 C D5 C
