平面汇交力系习题
平面汇交力系的平衡条件及例题

• 平面汇交力系平衡的充分与必要条件,也 平面汇交力系平衡的充分与必要条件,
可解析地表达为: 可解析地表达为:力系中各力在两个坐标 轴上投影的代数和分别为零。 轴上投影的代数和分别为零。
FR = ∑பைடு நூலகம்Fix + ∑ Fiy = 0 i =1 i =1
A
B
30 0
C
300
D
W
A
y
B
300
C
30 0
D
x
FCA FCB F
' T
300 300
C
W
FT
∑F
x
=0
0 ' T 0
FCB + FCA cos 30 + F cos 30 = 0
∑F
y
=0
0 ' T 0
FCA sin 30 − F sin 30 − FT = 0
FCA = 300kN
FCB = 346.4kN
n n 2 2
∑F
i =1
n
xi
=0
∑F
i =1
n
yi
=0
平面汇交力系应用举例
• 例3-2 小滑轮C铰接在三脚架ABC上,绳索 小滑轮C铰接在三脚架ABC上,绳索
绕过滑轮,一端连接在绞车上,另一端悬 挂重为W=100kN的重物。不计各构件的自 挂重为W=100kN的重物。不计各构件的自 重和滑轮的尺寸。试求AC和BC所受的力。 重和滑轮的尺寸。试求AC和BC所受的力。
§3-1-3平面汇交力系的平衡条件及应用
• 平面汇交力系平衡的充分和必要条件是: 平面汇交力系平衡的充分和必要条件是:
平面汇交力系习题知识分享
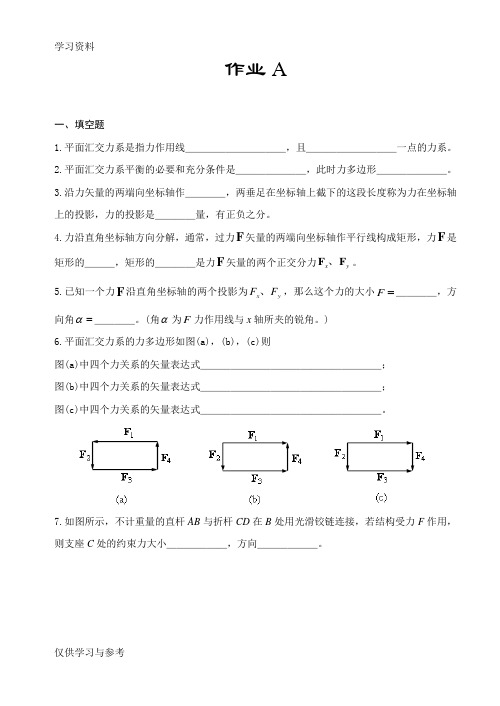
作业A一、填空题1.平面汇交力系是指力作用线__________,且_________一点的力系。
2.平面汇交力系平衡的必要和充分条件是_______,此时力多边形_______。
3.沿力矢量的两端向坐标轴作____,两垂足在坐标轴上截下的这段长度称为力在坐标轴上的投影,力的投影是____量,有正负之分。
4.力沿直角坐标轴方向分解,通常,过力F 矢量的两端向坐标轴作平行线构成矩形,力F 是矩形的___,矩形的____是力F 矢量的两个正交分力y x F F 、。
5.已知一个力F 沿直角坐标轴的两个投影为y x F F 、,那么这个力的大小=F ____,方向角=α____。
(角α为F 力作用线与x 轴所夹的锐角。
)6.平面汇交力系的力多边形如图(a),(b),(c)则图(a)中四个力关系的矢量表达式__________________; 图(b)中四个力关系的矢量表达式__________________; 图(c)中四个力关系的矢量表达式__________________。
7.如图所示,不计重量的直杆AB 与折杆CD 在B 处用光滑铰链连接,若结构受力F 作用,则支座C 处的约束力大小______,方向______。
(7题图) (8题图)8.如图所示,力F 在y x 、轴上投影x F =_____、y F =_____。
9.平面刚架在B 处受一水平力F 作用,如图所示,刚架自重不计,设F =20kN ,L =8m ,h =4m ,则求A 、D 处的约束反力,可以按以下步骤进行:(1)以刚架为研究对象,进行受力分析:请画出刚架的受力分析图(2)作用在刚架上的力(主动力和约束力)构成的力系属_____力系 (3)列出刚架的平衡方程(坐标如图)∑=0xF :_____________________; ∑=0yF:_____________________。
(4)解方程计算D A 、处的约束反力A F =______;D F =_______。
理论力学练习-2

第二章平面汇交力系与平面力偶系判断题:1.因为构成力偶的两个力满足F=F′,所以力偶的合力等于零。
()答案:×2.因为构成力偶的两个力满足F=F′,所以力偶在某轴上的投影不为零。
()答案:×3.力偶对其作用面内任一点之矩都等于力偶矩。
()答案:√4.力F在x轴方向的分力为零,则力F对坐标原点的力矩为零。
()答案:×5.力矩为零时表示力作用线通过矩心或力为零。
()答案:√6.平面汇交力系平衡时,力多边形各力应首尾相接,但在作图时力的顺序可以不同。
()答案:√7.一个力在任意轴上投影的大小一定小于或等于该力的模,而沿该轴的分力的大小则可能大于该力的模。
()答案:√8.力矩与力偶矩的单位相同,常用的单位为牛·米,千牛·米等。
()答案:√9.只要两个力大小相等、方向相反,该两力就组成一力偶。
()答案:×10.同一个平面内的两个力偶,只要它们的力偶矩相等,这两个力偶就一定等效。
()答案:√11.只要平面力偶的力偶矩保持不变,可将力偶的力和臂作相应的改变,而不影响其对刚体的效应。
()答案:√12.作用在刚体上的一个力,可以从原来的作用位置平行移动到该刚体内任意指定点,但必须附加一个力偶,附加力偶的矩等于原力对指定点的矩。
()答案:√13.某一平面力系,如其力多边形不封闭,则该力系一定有合力,合力作用线与简化中心的位置无关。
()答案:√14.平面任意力系,只要主矢R≠0,最后必可简化为一合力。
()答案:√15.平面力系向某点简化之主矢为零,主矩不为零。
则此力系可合成为一个合力偶,且此力系向任一点简化之主矩与简化中心的位置无关。
()答案:√16.若平面力系对一点的主矩为零,则此力系不可能合成为一个合力。
()答案:×17.当平面力系的主矢为零时,其主矩一定与简化中心的位置无关。
()答案:√18.在平面任意力系中,若其力多边形自行闭合,则力系平衡。
汇交力系例题
C
Y P TBD cos cos TBC cos cos 0
Z RA TBD sin TBC sin 0
联立解得
TBC 735 N
TBD 1094 N
RA 1500 N
p.4
例题
例题
例4.已知四根绳索AB、BC、BD、DE相互联接如图所示, DB保持水平,DE和BC分别与水平和铅垂线的夹角均
A
45o
0.8m
CB
0.4m
y
SC
A
45o C
RA
B x
E
P
EB BC 0.4m tg EB 0.4 1
AB 1.2 3 (2) 列出平衡方程;
X 0, RA cos Sc cos 45 0
Y 0,RA sin Sc sin 45 P 0
(3) 求未知力;
P
2
Sc sin 45 cos45tg
C EA
D
B -
y TDB D + x
y
TBE
TBC
B
TBD
x
P
TDA
P
SAB
解: (1) 研究D点,画受力图;
(2) 列出平衡方程并求解;
X 0,TDB cos( ) TDA cos( ) 0
Y 0,TDB sin( ) TDA sin( ) P 0
TDB
NA
O
O’与 O为矩形OAO’B的两个顶点,
O’ B
力的作用线既通过O’点也通过O点。
NB
由几何关系得
P A
90 2
NA
O
OA Lsin
p.6
例题
例题
例6. 铰接四连杆机构CABD的CD边固定。在铰链A上作用一 力Q,BAQ=45。在铰链B上作用一力R,ABR=30,
平面汇交力系答案

平面汇交力系答案【篇一:工程力学答案】1.作用在刚体上两个不在一直线上的汇交力f1和f2 ,可求得其合力r = f1 + f2 ,则其合力的大小 ( b;d )(a) 必有r = f1 + f2 ; (b) 不可能有r = f1 + f2 ; (c) 必有r f1、r f2 ;(d) 可能有r f1、r f2。
2. 以下四个图所示的力三角形,哪一个图表示力矢r是f1和f2两力矢的合力矢量 ( b )r f1 (a)f2r f1 (b)f2r f1 (c)f2r f1 (d)f23. 以下四个图所示的是一由f1 、f2 、f3 三个力所组成的平面汇交力系的力三角形,哪一个图表示此汇交力系是平衡的( a )f3 f1 (a)f2f3 f1 (b)f2f3 f1 (c)f2f3 f1 (d)f24.以下四种说法,哪一种是正确的( a) (a)力在平面内的投影是个矢量;(b)力对轴之矩等于力对任一点之矩的矢量在该轴上的投影;(c)力在平面内的投影是个代数量;(d)力偶对任一点o 之矩与该点在空间的位置有关。
5. 以下四种说法,哪些是正确的?( b ) (a) 力对点之矩的值与矩心的位置无关。
(b) 力偶对某点之矩的值与该点的位置无关。
(c) 力偶对物体的作用可以用一个力的作用来与它等效替换。
(d) 一个力偶不能与一个力相互平衡。
四、作图题(每图15分,共60分)画出下图中每个标注字符的物体的受力图和整体受力图。
题中未画重力的各物体的自重不计。
所有接触处均为光滑接触。
1213、平面力偶系合成的结果为一合力偶,此合力偶与各分力偶的代数和相等。
(√ ) 14、一个力和一个力偶可以合成一个力,反之,一个力也可分解为一个力和一个力偶。
(√ ) 15、力的平移定理只适用于刚体,而且也只能在同一个刚体上应用。
(√ )16、平面任意力系向作用面内任一点(简化中心)简化后,所得到的作用于简化中心的那一个力,一般说来不是原力系的合力。
自测题2 平面汇交力系与平面力偶系

图2-1F 1F 2 F 3F 1F 2F 3(a) (b)第二章 平面汇交力系与平面力偶系 自测题一、思考题1、图示两个力三角形中三个力的关系是否一样?其关系分别是什么?2、一平面力系(F 1,F 2,F 3,F 4,F 5)的五个力矢量组成图2-2所示的自行封闭的五边形。
请问:但该力系是否一定平衡?为什么?3、汇交于一点的三个平衡力,只要其中的两个力在同一直线上,则不共线的第三个力是否必定为零?为什么?二、判断题1、 合力一定比分力大。
( )2、作用在刚体上仅有两个力,且有F A + F B =0,则此刚体一定平衡。
( )3、凡是力偶都不能用一个力来平衡。
( )4、力偶系中的各力在任意轴上投影其代数各均等于零。
( )5、力偶对其作用面内任意点之矩都等于力偶矩。
( )6、作用在刚体上仅有两个力偶,力偶矩分别为M A 和M B ,且有M A + M B = 0,则该刚体一定平衡。
( )图2-2F 1F 2F 3F 4F 5图2-5图2-3A(a)A(b) A(c)图2-4三、填空题1. N 100=F ,方向如图示,若将F 沿图示y x ,方向分解,则x 方的向分力大小为____________N ,y 方向的分力大小为______________N 。
2、力偶对物体产生的运动效应是 。
(平移效应,转动效应) 四、作图题图示三个平衡机构,请画出在以下三种情况下A ,B 两处的约束力的方位和指向。
各杆自重不计。
五、计算题三铰拱AC 部分上作用有力偶,其力偶矩为M ,如图所示。
已知两个半拱的直角边成正比,即a :b =c :a ,略去三铰拱自身的重量。
求:A 和B 两点的约束力。
(a)图2-6B(b)六、图示(a),(b)两种情况,曲杆自重不计,其上作用一力偶矩为M 的力偶,比较两种情况下B 处的约束力是否相同?。
习题第3章答案
由平衡方程
,
,
,
得 ,
,
(c)解除题3-7图(c)所示梁的支座,代之以支座反力,作受力图(c1)
所示。
由平衡方程
,
,
,
得 ,
,
(d)解除题3-7图(d)所示梁的支座,代之以支座反力,作受力图(d1)
所示。
由平衡方程
,
,
,
得 ,
,
3-8试求题3-8图所示各梁的支座反力。
题3-8图
解:(a)解除题3-8图(a)所示悬臂梁的约束,代之以支座反力,作受力图(a1)
题3-6图
解:分别取杆AE和BD为研究对象,销子C作用于导槽的反力 因垂直于AE,因此决定了铰A处的反力 应于 等值、反向。杆BD上的反力 应于 等值、反向,铰B处的反力 应于 等值、反向,作杆AE和BD的受力图如题3-6图(b)和(c)所示。由题3-6图(a)中的几何关系,可得
由题3-6图(b)的平衡条件
,
,
得 (拉力)
3-2题3-2图(a)所示的电动机重 ,放在水平梁AC的中间,A和B为固定铰链,C为中间铰链。试求A点反力及杆BC所受的力。
题3-2图
解:解除题3-2图(a)所示电动机支架的支座,代之以约束反力,利用三力平衡汇交定理,作受力图如题3-2图(b)所示。由平衡方程
,
,
得
所以A点的反力为 ,杆BC为二力杆,B点受的力就是杆BC受的力,为 。
题3-5图
解:因杆AB是二力杆,所以杆AB俩端的铰A和B的约束力应沿杆的轴线方向,题3-5图(b)所示。因此,杆 和杆 的铰B和铰A处的约束反力的方向应如题3-5图(c)、(d)所示。因杆 和杆 的外力均为力偶,所以约束反力 及 分别应与 及 等值、反向,并有
平面汇交力系37习题

作业A一、填空题1、平面汇交力系就是指力作用线__________,且_________一点得力系。
2、平面汇交力系平衡得必要与充分条件就是_______,此时力多边形_______.3、沿力矢量得两端向坐标轴作____,两垂足在坐标轴上截下得这段长度称为力在坐标轴上得投影,力得投影就是____量,有正负之分。
4、力沿直角坐标轴方向分解,通常,过力矢量得两端向坐标轴作平行线构成矩形,力就是矩形得___,矩形得____就是力矢量得两个正交分力。
5、已知一个力沿直角坐标轴得两个投影为,那么这个力得大小____,方向角____。
(角为力作用线与x轴所夹得锐角.)6、平面汇交力系得力多边形如图(a),(b),(c)则图(a)中四个力关系得矢量表达式__________________;图(b)中四个力关系得矢量表达式__________________;图(c)中四个力关系得矢量表达式__________________。
7、如图所示,不计重量得直杆AB与折杆CD在B处用光滑铰链连接,若结构受力F作用,则支座C处得约束力大小______,方向______.(7题图) (8题图)8、如图所示,力在轴上投影=_____、=_____。
9、平面刚架在B处受一水平力F作用,如图所示,刚架自重不计,设F=20kN,L=8m,h=4m,则求A、D处得约束反力,可以按以下步骤进行:(1)以刚架为研究对象,进行受力分析:请画出刚架得受力分析图(2)作用在刚架上得力(主动力与约束力)构成得力系属_____力系(3)列出刚架得平衡方程(坐标如图):_____________________;:_____________________.(4)解方程计算处得约束反力=______;=_______.二、判断题( )1、平面汇交力系平衡时,力多边形中各力首尾相接,但在作力多边形时各力得顺序可以不同。
( )2、平面汇交力系平衡得几何条件就是力得多边形自行封闭.( )3、用解析法求平面汇交力系平衡问题时,所选取得两个轴必须相互垂直。
理论力学第二章课后习题答案

理论力学第二章课后习题答案·12·理论力系第2章平面汇交力系与平面力偶系一、是非题(恰当的在括号内踢“√”、错误的踢“×”)1.力在两同向平行轴上投影一定相等,两平行相等的力在同一轴上的投影一定相等。
2.用解析法求平面呈报力系的合力时,若挑选出相同的直角坐标轴,其税金的合力一定相同。
(√)3.在平面汇交力系的平衡方程中,两个投影轴一定要互相垂直。
(×)4.在维持力偶矩大小、转为维持不变的条件下,可以将例如图2.18(a)右图d处为平面力偶m移至例如图2.18(b)所示e处,而不改变整个结构的受力状态。
(×)(a)图2.185.如图2.19所示四连杆机构在力偶m1m2的作用下系统能保持平衡。
6.例如图2.20右图皮带传动,若仅就是包角发生变化,而其他条件均维持维持不变时,并使拎轮旋转的力矩不能发生改变。
(√图2.19图2.201.平面呈报力系的均衡的充要条件就是利用它们可以解言的约束反力。
2.三个力汇交于一点,但不共面,这三个力3.例如图2.21右图,杆ab蔡国用数等,在五个力促进作用下处在平衡状态。
则促进作用于点b的四个力的合力fr=f,方向沿4.如图2.22所示结构中,力p对点o的矩为plsin。
5.平面呈报力系中作力多边形的矢量规则为:各分力的矢量沿着环绕着力多边形边界的某一方向首尾相接,而合力矢量沿力多边形半封闭边的方向,由第一个分力的起点指向最后一个分力的终第面汇交力系与平面力偶图2.21图2.226.在直角坐标系中,力对坐标轴的投影与力沿坐标轴分解的分力的大小但在非直角坐标系中,力对坐标轴的投影与力沿坐标轴分解的分力的大小不相等。
1.例如图2.23右图的各图为平面呈报力系所作的力多边形,下面观点恰当的就是(c)。
(a)图(a)和图(b)就是平衡力系则(b)图(b)和图(c)就是平衡力系则(c)图(a)和图(c)就是平衡力系则(d)图(c)和图(d)就是平衡力系则f2f2f1(a)(b)(c)2.关于某一个力、分力与投影下面说法正确的是(b)。
工程力学 习题 第二部分 附答案
的矢量为:
FP
(
1 2
i
−
3 k); 2
∑ 力系的主矢 FR′ =
Fi
= 1− 2
2 (i
−
j)
主矩
i
j ki j
k
i jk
MO = a
−
2 2
FP
0
2 2
FP
= FPa ( 3i + 3 j + 2
由上知:
0+0 00
2k)
a
−1 2
FP
0+0 0
3 2
FP
−1 2
FP
0
3a
3 2
FP
FR′ ⋅ MO = (1 −
2
3
ABCF 的重力对点 C 之矩: bh × b × ρg 2
1 (a − b)h × 1 (a − b) × ρg = bh × b × ρg
2
3
2
b = 1 a = 0.366a 1+ 3
3-14 在图示变长为 a 的均质正方形薄板 ABCD 中挖去等腰三角形 EAB ,试求 E 点 y 坐 标的最大值 ymax ,使剩余薄板的重心仍在板内。
简化的最后结果。
解: q = γh ×1m = 78.4 kN m M O (F1) = F1a = 891kN ⋅ m
-2-
第 3 章 汇交力系
MO (F2 ) = −F2b = −297kN ⋅ m
水压力主矢大小: 1 qh = 313.6kN ,方向水平向右 2
水压力对 O 点主矩: − 1 qh × h = −836.3kN ⋅ m 23
解:椭圆的面积为: π ⋅ 3r ⋅ 7r = 7πr 2 ;形心坐标: (0,0) 3
力学平面力系习题

1.(10分)已知P=40kN,A、B、C三处都是铰接,杆的自重不计。求图示三角支架A、C铰的约束反力。
第1题图
2.(10分)图示各梁,不计梁的自重和摩擦。求各梁在荷载P作用下支座B的约束反力。
第2题图
3.(13分)结构如图所示,已知P=80kN,M=120kN·m,L=4m。求A、B支座的约束反力。
二、判断题(每题1分,共10分)
1.物体的平衡状态是指物体相对于地球保持静止的状态。()
2.作用力与反作用力总是一对等值、反向、共线的力。()
3.因作用力与反作用力大小相等,方向相反,且沿着同一直线,所以作用力与反作用力是一对平衡力。()
4.在同一平面内的两个力偶,只要力偶矩大小相是从第一个分力的________点,指向最后一个分力的________点。
5.平面一般力系向作用面内的任一点O简化,就分解成了________和________两个力系。
6.使物体产生运动或产生运动趋势的力称________________。
7.力垂直于某轴,则力在该轴上投影为________________。
A.充分条件B.必要条件C.充分必要条件D.无关系
3.只限制物体任何方向移动,不限制物体转动的支座称________支座。()
A.固定铰B.可动铰C.固定端D.光滑面
4.只限制物体垂直于支承面方向的移动,不限制物体向其他方向运动的支座称________支座。()
A.固定铰B.可动铰C.固定端D.光滑面
5.既限制物体任何方向运动,又限制物体转动的支座称________支座。()
A.固定铰B.可动铰C.固定端D.光滑面
6.平面汇交力系平衡的必要和充分条件是该力系的________为零。()
平面汇交力系习题
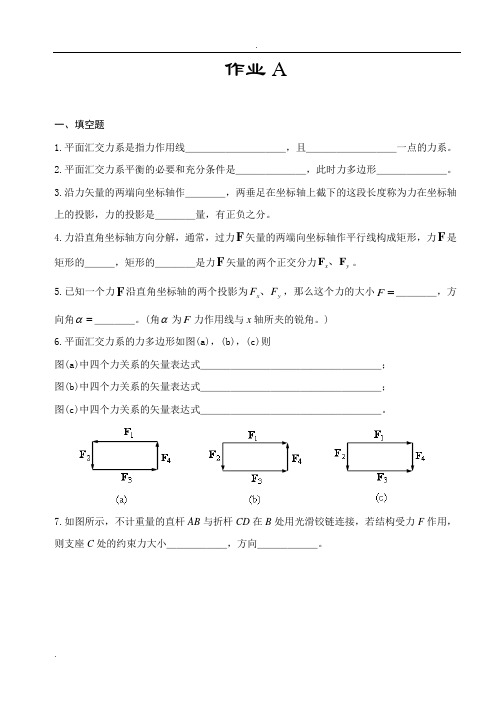
作业A一、填空题1.平面汇交力系是指力作用线__________,且_________一点的力系。
2.平面汇交力系平衡的必要和充分条件是_______,此时力多边形_______。
3.沿力矢量的两端向坐标轴作____,两垂足在坐标轴上截下的这段长度称为力在坐标轴上的投影,力的投影是____量,有正负之分。
4.力沿直角坐标轴方向分解,通常,过力F 矢量的两端向坐标轴作平行线构成矩形,力F 是矩形的___,矩形的____是力F 矢量的两个正交分力y x F F 、。
5.已知一个力F 沿直角坐标轴的两个投影为y x F F 、,那么这个力的大小=F ____,方向角=α____。
(角α为F 力作用线与x 轴所夹的锐角。
)6.平面汇交力系的力多边形如图(a),(b),(c)则图(a)中四个力关系的矢量表达式__________________; 图(b)中四个力关系的矢量表达式__________________; 图(c)中四个力关系的矢量表达式__________________。
7.如图所示,不计重量的直杆AB 与折杆CD 在B 处用光滑铰链连接,若结构受力F 作用,则支座C 处的约束力大小______,方向______。
(7题图) (8题图)8.如图所示,力F 在y x 、轴上投影x F =_____、y F =_____。
9.平面刚架在B 处受一水平力F 作用,如图所示,刚架自重不计,设F =20kN ,L =8m ,h =4m ,则求A 、D 处的约束反力,可以按以下步骤进行:(1)以刚架为研究对象,进行受力分析:请画出刚架的受力分析图(2)作用在刚架上的力(主动力和约束力)构成的力系属_____力系 (3)列出刚架的平衡方程(坐标如图)∑=0xF :_____________________; ∑=0yF:_____________________。
(4)解方程计算D A 、处的约束反力A F =______;D F =_______。
2第二章 力系的简化和平衡方程习题+答案

第二章力系的简化和平衡方程一、填空题1、在平面力系中,若各力的作用线全部,则称为平面汇交力系。
2、求多个汇交力的合力的几何法通常要采取连续运用力法则来求得。
3、求合力的力多边形法则是:将各分力矢首尾相接,形成一折线,连接其封闭边,这一从最先画的分力矢的始端指向最后面画的分力矢的的矢量,即为所求的合力矢。
4、平面汇交力系的合力作用线过力系的。
5、平面汇交力系平衡的几何条件为:力系中各力组成的力多边形。
6、平面汇交力系合成的结果是一个合力,这一个合力的作用线通过力系的汇交点,而合力的大小和方向等于力系各力的。
7、若平面汇交力系的力矢所构成的力多边形自行封闭,则表示该力系的等于零。
8、如果共面而不平行的三个力成平衡,则这三力必然要。
9、在平面直角坐标系内,将一个力可分解成为同一平面内的两个力,可见力的分力是量,而力在坐标轴上的投影是量。
10、合力在任一轴上的投影,等于各分力在轴上投影的代数和,这就是合力投影定理。
11、已知平面汇交力系合力R在直角坐标X、Y轴上的投影,利用合力R与轴所夹锐角a的正切来确定合力的方向,比用方向余弦更为简便,也即tg a= | Ry / Rx | 。
12、用解析法求解平衡问题时,只有当采用坐标系时,力沿某一坐标的分力的大小加上适当的正负号,才会等于该力在该轴上的投影。
13、当力与坐标轴垂直时,力在该坐标轴上的投影会值为;当力与坐标轴平行时,力在该坐标轴上的投影的值等于力的大小。
14、平面汇交力系的平衡方程是两个的方程,因此可以求解两个未知量。
15、一对等值、反向、不共线的平行力所组成的力系称为_____。
16、力偶中二力所在的平面称为______。
17、在力偶的作用面内,力偶对物体的作用效果应取决于组成力偶的反向平行力的大小、力偶臂的大小及力偶的______。
18、力偶无合力,力偶不能与一个_____等效,也不能用一个______来平衡.19、多轴钻床在水平工件上钻孔时,工件水平面上受到的是_____系的作用。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
作业A
一、填空题
1、平面汇交力系就是指力作用线__________,且_________一点的力系。
2、平面汇交力系平衡的必要与充分条件就是_______,此时力多边形_______。
3、沿力矢量的两端向坐标轴作____,两垂足在坐标轴上截下的这段长度称为力在坐标轴上的投影,力的投影就是____量,有正负之分。
4、力沿直角坐标轴方向分解,通常,过力F 矢量的两端向坐标轴作平行线构成矩形,力F 就是矩形的___,矩形的____就是力F 矢量的两个正交分力y x F F 、。
5、已知一个力F 沿直角坐标轴的两个投影为y x F F 、,那么这个力的大小=F ____,方向角=α____。
(角α为F 力作用线与x 轴所夹的锐角。
)
6、平面汇交力系的力多边形如图(a),(b),(c)则
图(a)中四个力关系的矢量表达式__________________;
图(b)中四个力关系的矢量表达式__________________;
图(c)中四个力关系的矢量表达式__________________。
7、如图所示,不计重量的直杆AB 与折杆CD 在B 处用光滑铰链连接,若结构受力F 作用,则支座C 处的约束力大小______,方向______。
(7题图) (8题图)
8、如图所示,力F 在y x 、轴上投影x F =_____、y F =_____。
9、平面刚架在B 处受一水平力F 作用,如图所示,刚架自重不计,设F =20kN ,L =8m ,h =4m ,则求
A 、D 处的约束反力,可以按以下步骤进行:
(1)以刚架为研究对象,进行受力分析:请画出刚架的受力分析图
(2)作用在刚架上的力(主动力与约束力)构成的力系属_____力系
(3)列出刚架的平衡方程(坐标如图)
∑=0x F
:_____________________; ∑=0y
F :_____________________。
(4)解方程计算D A 、处的约束反力
A F =______;D F =_______。
二、判断题
( )1、平面汇交力系平衡时,力多边形中各力首尾相接,但在作力多边形时各力的顺序可以不同。
( )2、平面汇交力系平衡的几何条件就是力的多边形自行封闭。
( )3、用解析法求平面汇交力系平衡问题时,所选取的两个轴必须相互垂直。
( )4、当平面汇交力系平衡时,选择几个投影轴就能列出几个独立的平衡方程。
三、选择题
1、汇交于O 点的平面汇交力系,其平衡方程式可表示为二力矩形式。
即∑=0)(i A M F ,∑=0)(i B M F 但必须(__)。
(A)A 、B 两点中有一点与O 点重合; (B)点O 不在A 、B 两点的连线上;
(C)点O 应在A 、B 两点的连线上; (D)不存在二力矩形式。
2、图示三铰刚架受力F 作用,则A 支座反力的大小为(__),B 支座反力的大小为(__)。
(A)2F ; (B)2F ; (C)F ; (D)F 2; (E)F 2。
四、计算题
1、铆接薄板在孔心A 、B 与C 处受三力作用,如图所示。
N F 1001=,沿铅直方向;N F 503=,沿水平方向,并通过A ;N F 502=,力的作用线也通过点A 。
求此力系的合力。
2、如图所示,平面汇交力系由321F F F 、、三个力组成,其中1F 沿水平方向作用,大小为20kN ,2F 与3F 大小相等且互相垂直。
设三力的合力R F 竖直向下,大小为15kN ,试求32F F 、的大小与方向。
3、图示液压夹紧机构中,D 为固定铰链,E C B 、、为活动铰链。
已知力F ,机构平衡时角度如图,求此时工件H 所受的压紧力。
作业B
一、填空题
1、平面汇交力系可简化为一个力,该力矢量等于力系中各力的___,作用线通过____。
2、平面汇交力系有___个独立平衡方程,即
∑=x F ____,∑=y F ____;可求解_____个未知量。
3、力沿直角坐标轴的分力就是___量,其大小与力在相应坐标轴上的投影的绝对值___。
4、已知合力R F 的投影∑=ix Rx F F ,∑=iy Ry F F ;那么合力的大小=R F _______,合力R F 的方向余弦cos α=_______。
(α为R F 与x 轴夹角)
5、某刚体受平面汇交力系作用,其力多边形分别如图(a)、(b)所示,则图___表示平衡力系;图___表示有合力,其合力=R F ______。
(a) (b)
6、两直角刚杆ABC 、DEF 在F 处铰接,支承如图。
若各杆重不计,则当垂直BC 边的力F 从B 点移动到C 点的过程中,A 处约束力的作用线与AB 方向的夹角从_______度变化到_______度。
(6题图) (7题图)
7、如图所示:力F 在η轴上的投影就是线段___,在ξ轴上的投影就是线段____;力F 在η轴上分力的大小就是线段____,在ξ轴上分力的大小就是线段_____。
二、判断题
( )1、两个力1F ,2F 在同一轴上的投影相等,则这两个力一定相等。
( )2、两个大小相等的力,在同一轴上的投影也相等。
( )3、某力在某轴上的投影为零,则该力不一定为零。
( )4、用解析法求平面汇交力系的平衡问题时,投影轴的方位不同,平衡方程的具体形式不同,但计算结果不变。
( )5、用几何法求平面汇交力系合力时,作图时画力的顺序可以不同,其合力不变。
三、选择题
1、平面汇交力系的独立平衡方程数目为(__)
(A)6; (B)4; (C)3; (D)2。
2、图示结构受力F 作用,杆重不计,则A 支座约束力的大小为(__)。
(A)2F ; (B)33F ; (C)F ; (D)0。
3、某力F 在某轴上的投影的绝对值等于该力的大小,则该力在另一任意与之共面的轴上的投影为:(__)。
(A)一定等于零; (B)不一定等于零;
(C)一定不等于零; (D)仍等于该力的大小。
四、计算题
1、如图,平面吊环上作用有四个力4321F F F F 、、、,它们汇交于圆环的中心。
其中kN F 101=,kN F 152=;kN F 83=;kN F 104=,试用解析法求其合力R F 。
2、构件ABCD 受重力W = 1kN 。
其中构件AB 与CD 在D 处铰接,B 、C 两点均为固定铰链支座。
如不计构件自重,试求构件CD 所受的力与支座B 处的约束反力。
3、圆柱O 重N G 1000=,半径m r 4.0=,放在斜面上用撑架支承如图;不计架重,求铰链
C A 、处反力。
4、电缆盘受重力W =20kN ,直径D =1、2m ,要越过h =0、2m 的台阶,如图所示。
试求作用的水平力F 应多大?若作用力F 方向可变,则求使缆盘能越过台阶的最小的力F 的大小与方向。
