立体几何证明方法汇总
立体几何所有的定理大总结(绝对全)

⽴体⼏何所有的定理⼤总结(绝对全)(⼆)异⾯直线所成⾓1.定义:不同在任何⼀个平⾯内的两条直线或既不平⾏也不相交的两条直线叫异⾯直线。
2.画法:借助辅助平⾯。
1.定义:对于异⾯直线a 和b ,在空间任取⼀点P ,过P 分别作a 和b 的平⾏线1a 和1b ,我们把1a 和1b 所成的锐⾓或者叫做异⾯直线a 和b 所成的⾓。
2.范围:(0°,90°】(★空间两条直线所成⾓范围:【0°,90°】)(三)线⾯⾓1.定义:当直线l 与平⾯α相交且不垂直时,叫做直线l 与平⾯α斜交,直线l 叫做平⾯α的斜线。
设直线l 与平⾯α斜交与点M ,过l 上任意点A ,做平⾯α的垂线,垂⾜为O ,把点O 叫做点A 在平⾯α上的射影,直线OM 叫做直线l 在平⾯α上的射影。
1.定义:把直线l 与其在平⾯α上的射影所成的锐⾓叫做直线l 和平⾯α所成的⾓。
2.范围【0°,90°】(★斜线与平⾯所成⾓范围:【0°,90°】)(三)⼆⾯⾓1.定义:(1)半平⾯:平⾯内的⼀条直线把这个平⾯分成两个部分,其中每⼀个部分叫做半平⾯。
(3)⼆⾯⾓的棱:这⼀条直线叫做⼆⾯⾓的棱。
(4)⼆⾯⾓的⾯:这两个半平⾯叫做⼆⾯⾓的⾯。
(5)⼆⾯⾓的平⾯⾓:以⼆⾯⾓的棱上任意⼀点为端点,在两个⾯内分别作垂直于棱的两条射线,这两条射线所成的⾓叫做⼆⾯⾓的平⾯⾓。
(6)直⼆⾯⾓:平⾯⾓是直⾓的⼆⾯⾓叫做直⼆⾯⾓。
1.定义:从⼀条直线出发的两个半平⾯所组成的图形叫做⼆⾯⾓。
2.表⽰:如下图,可记作α-AB-β或P-AB-Q3.范围为【0°,180°】(五)六种距离1.点到点的距离:两点之间的线段PQ 的长。
2.点到线的距离:过P 点作1PP ⊥l ,交l 于1P ,线段1PP 的长。
3.点到⾯的距离:过P 点作1PP ⊥α,交α于1P ,线段1PP 的长。
高考指南立体几何垂直证明的六大绝招秒懂

高考指南立体几何垂直证明的六大绝招秒懂!类型一AD⊥SC,求证:AD⊥面SBC证明:∵SA⊥面ABC ∴SA⊥BC又∠ACB=90°∴AC⊥BC又AC,SA⊆面SAC ∴BC ⊥面SAC∴BC⊥AD又AD⊥SC且BC,SC⊆面SBC∴AD⊥面SBC变式:如图,在三棱锥A-BCD中,AB⊥AD,BC⊥BD,平面ABD⊥平面BCD,求证:AD⊥AC类型二利用等腰三角形中线证垂直例题:在三棱锥P-ABC中,AC=BC,AP=BP,求证PC⊥AB证明:取AB的中点M,连接PM,CM∵AC=BC,M是AB的中点,∴AB⊥CM∵AP=BP,M是AB的中点,∴AB⊥PM∴AB⊥面PCM∴AB⊥PC变式:四棱锥P-ABCD,底面ABCD是正方形,PA=AD,求证面PAD⊥面PCD类型三利用勾股定理逆定理证垂直例题:如图,四棱锥P-ABCD的底面是边成为3的正方形,PA⊥CD,PA=4,PD=5,求证:PA⊥面ABCD证明:∵PA=4,AB=3,PD=5∴PA2+AB2=PD2,∴三角形PAD是直角三角形,∴PA⊥AD又PA ⊥CD,∴PA⊥面ABCD变式:如果,在三棱台ABC-DEF中,平面BDEF⊥平面ABC,∠ACB=90°,BE=EF=FC=1,BC=2,AC=3,求证:BF⊥面ACFD类型四利用三角形全等证垂直例题:如图,三棱锥P-ABC中,△PAB是等边三角形,∠PAC=∠PBC=90°,求证:AB⊥PC证明:取AB的中点M,连接CM,∵△PAB是等边三角形,∴PB=PA又PC=PC,∠PAC=∠PBC=90°∴△PBC≌△PAC,∴BC=AC∴△ACB是等腰三角形,M是AB的中点,∴CM⊥AB又在等边△PAB中,M是AB的中点,∴PM⊥AB∴AB⊥面PMC∴AB⊥PC变式:如图,在以A、B、C、D、E、F为顶点的五面体中,平面CDEF⊥平面ABCD,FC=FB,四边形ABCD为平行四边形,且∠BCD=45°,求证:CD⊥BF类型五利用平行关系证明垂直例题:如图四棱锥P-ABCD,底面是正方形,PA⊥底面ABCD,∠PDA=45°,E是棱AB的中点,求证:面PCE⊥面PCD证明:分别做PC,PD的中点M,N两点,连接EM,MN,NA∵MN为△PCD的中位线,∴MN∥CD且MN=1/2CD又∵E是AB的中点,∴AE∥CD且AE=1/2CD ∴四边形AEMN是平行四边形,则EM∥AN,∵PA⊥面ABCD,∴PA⊥AD,且∠PDA=45°,∴△PAD 是等腰直角三角形又N是PD中点,∴AN⊥PD∵四边ABCD是正方形,∴CD⊥AD,又PA⊥CD,∴CD⊥面PAD,∴CD⊥AN,又上面已求PD⊥AN,∴AN⊥面PCD又∵EM∥AN,∴EM⊥面PCD∵EM ⊂面PEC,∴面PEC⊥面PCD变式:如图1,在直角梯形ABCD中,AD∥BC,∠BAD=90°,AB=BC=1,AD=2,E是AD的中点,O是AC与BE的交点,将△ABE沿BE折起到△A1BE的位置,如图2,证明CD⊥面A1OC.类型六梯形,∠ABC=∠BCD=90°,AB=BC=PB=PC=2CD,侧面PBC⊥底面ABCD,证明:PA⊥BD。
立体几何常考定理的总结(八大定理)
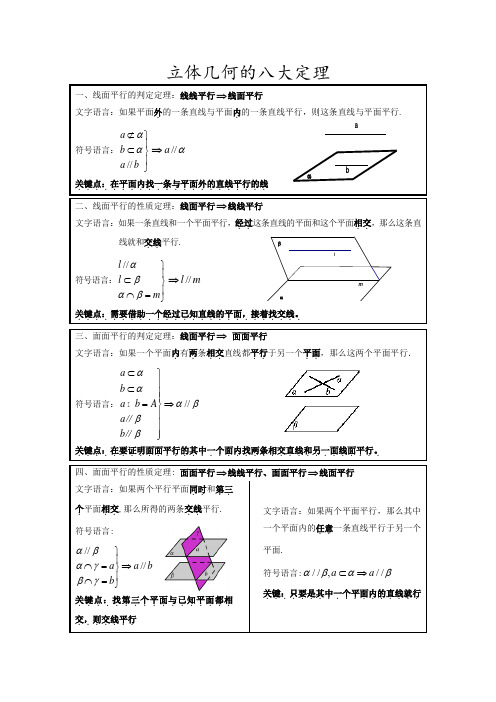
lmβααba立体几何的八大定理一、线面平行的判定定理:线线平行⇒线面平行文字语言:如果平面外.的一条直线与平面内.的一条直线平行,则这条直线与平面平行. 符号语言://a b a b αα⊄⎫⎪⊂⎬⎪⎭⇒//a α关键点:在平面内找一条与平面外的直线平行的线...................... 二、线面平行的性质定理:线面平行⇒线线平行文字语言:如果一条直线和一个平面平行,经过..这条直线的平面和这个平面相交..,那么这条直线就和交线..平行. 符号语言://l l m αβαβ⎫⎪⊂⎬⎪⋂=⎭⇒//l m关键点:需要借助一个经过已知直线的平面,接着找交线。
.......................... 三、面面平行的判定定理:线面平行⇒ 面面平行文字语言:如果一个平面内.有两.条相交..直线都平行..于另一个平面..,那么这两个平面平行. 符号语言://a b a b A a b αααβββ⊂⎫⎪⊂⎪⎪=⇒⎬⎪⎪⎪⎭∥∥ 关键点:在要证明面面平行的其中一个面内找两条相交直线和另一面线面平行。
................................... 四、面面平行的性质定理: 面面平行⇒线线平行、面面平行⇒线面平行 文字语言:如果两个平行平面同时..和第三..个.平面相交..,那么所得的两条交线..平行. 符号语言:////a a b b αβαγβγ⎫⎪⋂=⇒⎬⎪⋂=⎭关键点:找第三个平面与已知平面都相.................交,则交线平行.......文字语言:如果两个平面平行,那么其中一个平面内的任意..一条直线平行于另一个平面.符号语言://,//a a αβαβ⊂⇒ 关键:只要是其中一个平面内的直线就行..................nmAαaBA l βαaβα五、线面垂直的判定定理:线线垂直⇒线面垂直文字语言:如果一条直线和一个平面内.的两.条相交..直线垂直..,那么这条直线垂直于这个平面. 符号语言:,a ma n a m n A m n ααα⊥⎫⎪⊥⎪⇒⊥⎬⋂=⎪⎪⊂⊂⎭关键点:在平面内找两条相交直线与所要证的直线垂直........................ 六、线面垂直的性质定理:线面垂直⇒线线垂直文字语言:若一条直线垂直于一个平面,则这条直线垂直平面内的任意..一条直线. 符号语言:l l a a αα⊥⎫⇒⊥⎬⊂⎭关键点:往往线面垂直中的线线垂直需要用这个定理推出......................... 七、平面与平面垂直的判定定理:线面垂直⇒面面垂直文字语言:如果一个平面经过..另一个平面的一条垂线,则这两个平面互相垂直. (如果一条直线垂直于一个平面,并且有另一个平面经过这条直线,那么这两个平面垂直)符号表示:a a ααββ⊥⎫⇒⊥⎬⊂⎭关键点:....在需要证明的两个平面中找线面垂直................八、平面与平面垂直的性质定理:面面垂直⇒线面垂直文字语言:如果两个平面互相垂直,那么在一个平面内垂直..于它们的交线..的直线垂直于另一个平面.符号语言:l AB AB AB lαβαββα⊥⎫⎪=⎪⇒⊥⎬⊂⎪⎪⊥⎭关键点:先找交线,再在其中一个面内找与交线垂直的线。
立体几何平行证明题常见模型及方法

立体几何平行证明题常见模型及方法立体几何中的平行证明题常见的模型和方法有很多。
下面我将介绍一些常见的模型和方法,以帮助你更好地理解和应用立体几何的平行证明。
一、常见模型1.平面与平面的平行证明:常见的模型有两条平行线或两个平行四边形,通过证明平面与平面内对应的直线或四边形是平行的,即可得证。
2.直线与直线的平行证明:常见的模型有平行四边形和交叉角等,通过证明两直线间的对应角相等或同位角互补,即可得证。
3.平面与直线的平行证明:常见的模型有平行四边形的一对对角线、三角形的高、垂足、垂线等,通过证明直线与平面内的直线或线段互相垂直,即可得证。
4.空间中的平面与平面的平行证明:常见的模型有两个平行四边形的高度等、点到平面的垂直距离等,通过证明两个平面内的垂直线的相互平行性,即可得证。
二、常见方法1.剪影法:利用平行关系特殊的剪影形状进行证明。
例如,通过剪影的形状可以直观地判断两根线段平行。
2.联立法:通过建立适当的方程组,将待证的平行条件与已知条件进行联立,最终得到结论。
常见的方法有正投影、平行投影等。
3.直角法:利用直角关系进行证明。
通过找到合适的垂线、垂足等直角线段,可以推导出平行关系。
4.反证法:假设不平行,然后找到与之矛盾的证据,从而推出平行的结论。
5.三角形法:构造适当的三角形,通过三角形的性质和形状关系进行证明。
6.同增减法:通过分析多个角度相应的同增减性质,推导出平行的结论。
7.通道法:利用另一个已经知道的已知命题,构造合适的通道来推导出平行的结论。
以上仅是常见的模型和方法,实际的平行证明题在解题过程中可能会遇到各种不同的情况和策略。
解决此类问题的关键是要有良好的几何直观和分析能力,熟练掌握几何定理和性质,并能够合理运用不同的方法解决问题。
立体几何基本知识总结和线面垂直平行六种关系的证明方法

立体几何基本知识总结I. 基础知识要点 一、 平面.1. 经过不在同一条直线上的三点确定一个面.注:两两相交且不过同一点的四条直线必在同一平面内.2. 两个平面可将平面分成3或4部分.(①两个平面平行,②两个平面相交)3. 过三条互相平行的直线可以确定1或3个平面.(①三条直线在一个平面内平行,②三条直线不在一个平面内平行)[注]:三条直线可以确定三个平面,三条直线的公共点有0或1个. 4. 三个平面最多可把空间分成 8 部分.(X 、Y 、Z 三个方向) 二、 空间直线.1. 空间直线位置分三种:相交、平行、异面. 相交直线—共面有反且有一个公共点;平行直线—共面没有公共点;异面直线—不同在任一平面内[注]:①两条异面直线在同一平面内射影一定是相交的两条直线.(×)(可能两条直线平行,也可能是点和直线等) ②直线在平面外,指的位置关系:平行或相交③若直线a 、b 异面,a 平行于平面α,b 与α的关系是相交、平行、在平面α内. ④两条平行线在同一平面内的射影图形是一条直线或两条平行线或两点.⑤在平面内射影是直线的图形一定是直线.(×)(射影不一定只有直线,也可以是其他图形) ⑥在同一平面内的射影长相等,则斜线长相等.(×)(并非是从平面外一点..向这个平面所引的垂线段和斜线段) ⑦b a ,是夹在两平行平面间的线段,若b a =,则b a ,的位置关系为相交或平行或异面.2. 异面直线判定定理:过平面外一点与平面内一点的直线和平面内不经过该点的直线是异面直线.(不在任何一个平面内的两条直线)3. 平行公理:平行于同一条直线的两条直线互相平行.4. 等角定理:如果一个角的两边和另一个角的两边分别平行并且方向相同,那么这两个角相等(如下图). (二面角的取值范围[]180,0∈θ)(异面直线所成角(] 90,0∈θ)(斜线与平面成角()90,0∈θ)(直线与平面所成角[]90,0∈θ)(向量与向量所成角])180,0[ ∈θ推论:如果两条相交直线和另两条相交直线分别平行,那么这两组直线所成锐角(或直角)相等. 5. 两异面直线的距离:公垂线的长度.空间两条直线垂直的情况:相交(共面)垂直和异面垂直.21,l l 是异面直线,则过21,l l 外一点P ,过点P 且与21,l l 都平行平面有一个或没有,但与21,l l 距离相等的点在同一平面内. (1L 或2L 在这个做出的平面内不能叫1L 与2L 平行的平面) 三、 直线与平面平行、直线与平面垂直.1. 空间直线与平面位置分三种:相交、平行、在平面内.2. 直线与平面平行判定定理:如果平面外一条直线和这个平面内一条直线平行,那么这条直线和这个平面平行.(“线线平行,线面平行”)[注]:①直线a 与平面α内一条直线平行,则a ∥α. (×)(平面外一条直线) ②直线a 与平面α内一条直线相交,则a 与平面α相交. (×)(平面外一条直线)③若直线a 与平面α平行,则α内必存在无数条直线与a 平行. (√)(不是任意一条直线,可利用平行的传递性12方向相同12方向不相同证之)④两条平行线中一条平行于一个平面,那么另一条也平行于这个平面. (×)(可能在此平面内) ⑤平行于同一直线的两个平面平行.(×)(两个平面可能相交) ⑥平行于同一个平面的两直线平行.(×)(两直线可能相交或者异面) ⑦直线l 与平面α、β所成角相等,则α∥β.(×)(α、β可能相交)3. 直线和平面平行性质定理:如果一条直线和一个平面平行,经过这条直线的平面和这个平面相交,那么这条直线和交线平行.(“线面平行,线线平行”)4. 直线与平面垂直是指直线与平面任何一条直线垂直,过一点有且只有一条直线和一个平面垂直,过一点有且只有一个平面和一条直线垂直. ● 若PA ⊥α,a ⊥AO ,得a ⊥PO (三垂线定理),得不出α⊥PO . 因为a ⊥PO ,但PO 不垂直OA .●三垂线定理的逆定理亦成立.直线与平面垂直的判定定理一:如果一条直线和一个平面内的两条相交直线都垂直,那么这两条直线垂直于这个平面.(“线线垂直,线面垂直”)直线与平面垂直的判定定理二:如果平行线中一条直线垂直于一个平面,那么另一条也垂直于这个平面. 推论:如果两条直线同垂直于一个平面,那么这两条直线平行. [注]:①垂直于同一平面....的两个平面平行.(×)(可能相交,垂直于同一条直线.....的两个平面平行) ②垂直于同一直线的两个平面平行.(√)(一条直线垂直于平行的一个平面,必垂直于另一个平面)③垂直于同一平面的两条直线平行.(√) 5. ⑴垂线段和斜线段长定理:从平面外一点..向这个平面所引的垂线段和斜线段中,①射影相等的两条斜线段相等,射影较长的斜线段较长;②相等的斜线段的射影相等,较长的斜线段射影较长;③垂线段比任何一条斜线段短. [注]:垂线在平面的射影为一个点. [一条直线在平面内的射影是一条直线.(×)]⑵射影定理推论:如果一个角所在平面外一点到角的两边的距离相等,那么这点在平面内的射影在这个角的平分线上四、 平面平行与平面垂直.1. 空间两个平面的位置关系:相交、平行.2. 平面平行判定定理:如果一个平面内有两条相交直线都平行于另一个平面,哪么这两个平面平行.(“线面平行,面面平行”)推论:垂直于同一条直线的两个平面互相平行;平行于同一平面的两个平面平行. [注]:一平面间的任一直线平行于另一平面.3. 两个平面平行的性质定理:如果两个平面平行同时和第三个平面相交,那么它们交线平行.(“面面平行,线线平行”)4. 两个平面垂直性质判定一:两个平面所成的二面角是直二面角,则两个平面垂直.两个平面垂直性质判定二:如果一个平面与一条直线垂直,那么经过这条直线的平面垂直于这个平面.(“线面垂直,面面垂直”)注:如果两个二面角的平面对应平面互相垂直,则两个二面角没有什么关系.5. 两个平面垂直性质定理:如果两个平面垂直,那么在一个平面内垂直于它们交线的直线也垂直于另一个平面.推论:如果两个相交平面都垂直于第三平面,则它们交线垂直于第三平面.证明:如图,找O 作OA 、OB 分别垂直于21,l l ,因为ααββ⊥⊂⊥⊂OB PM OA PM ,,,则OB PM OA PM ⊥⊥,.6. 两异面直线任意两点间的距离公式:θcos 2222mn d n m l +++=(θ为锐角取加,θ为钝取减,综上,都POAaPαβθM AB O取加则必有⎥⎦⎤⎝⎛∈2,0πθ)7. ⑴最小角定理:21cos cos cos θθθ=(1θ为最小角,如图) ⑵最小角定理的应用(∠PBN 为最小角)简记为:成角比交线夹角一半大,且又比交线夹角补角一半长,一定有4条. 成角比交线夹角一半大,又比交线夹角补角小,一定有2条. 成角比交线夹角一半大,又与交线夹角相等,一定有3条或者2条. 成角比交线夹角一半小,又与交线夹角一半小,一定有1条或者没有. 五、 棱锥、棱柱. 1. 棱柱.⑴①直棱柱侧面积:Ch S =(C 为底面周长,h 是高)该公式是利用直棱柱的侧面展开图为矩形得出的. ②斜棱住侧面积:l C S 1=(1C 是斜棱柱直截面周长,l 是斜棱柱的侧棱长)该公式是利用斜棱柱的侧面展开图为平行四边形得出的.⑵{四棱柱}⊃{平行六面体}⊃{直平行六面体}⊃{长方体}⊃{正四棱柱}⊃{正方体}. {直四棱柱}⋂{平行六面体}={直平行六面体}.⑶棱柱具有的性质:①棱柱的各个侧面都是平行四边形,所有的侧棱都相等;直棱柱的各个侧面都是矩形........;正棱柱的各个侧面都是全.等的矩形..... ②棱柱的两个底面与平行于底面的截面是对应边互相平行的全等..多边形. ③过棱柱不相邻的两条侧棱的截面都是平行四边形.注:①棱柱有一个侧面和底面的一条边垂直可推测是直棱柱. (×) (直棱柱不能保证底面是钜形可如图) ②(直棱柱定义)棱柱有一条侧棱和底面垂直.⑷平行六面体:定理一:平行六面体的对角线交于一点.............,并且在交点处互相平分. [注]:四棱柱的对角线不一定相交于一点.定理二:长方体的一条对角线长的平方等于一个顶点上三条棱长的平方和.推论一:长方体一条对角线与同一个顶点的三条棱所成的角为γβα,,,则1cos cos cos 222=++γβα. 推论二:长方体一条对角线与同一个顶点的三各侧面所成的角为γβα,,,则2cos cos cos 222=++γβα. [注]:①有两个侧面是矩形的棱柱是直棱柱.(×)(斜四面体的两个平行的平面可以为矩形) ②各侧面都是正方形的棱柱一定是正棱柱.(×)(应是各侧面都是正方形的直.棱柱才行) ③对角面都是全等的矩形的直四棱柱一定是长方体.(×)(只能推出对角线相等,推不出底面为矩形)④棱柱成为直棱柱的一个必要不充分条件是棱柱有一条侧棱与底面的两条边垂直. (两条边可能相交,可能不相交,若两条边相交,则应是充要条件)2. 棱锥:棱锥是一个面为多边形,其余各面是有一个公共顶点的三角形. [注]:①一个棱锥可以四各面都为直角三角形.②一个棱柱可以分成等体积的三个三棱锥;所以棱柱棱柱3V Sh V ==.图1θθ1θ2图2⑴①正棱锥定义:底面是正多边形;顶点在底面的射影为底面的中心. [注]:i. 正四棱锥的各个侧面都是全等的等腰三角形.(不是等边三角形) ii. 正四面体是各棱相等,而正三棱锥是底面为正△侧棱与底棱不一定相等iii. 正棱锥定义的推论:若一个棱锥的各个侧面都是全等的等腰三角形(即侧棱相等);底面为正多边形. ②正棱锥的侧面积:'Ch 21S =(底面周长为C ,斜高为'h ) ③棱锥的侧面积与底面积的射影公式:αcos 底侧S S =(侧面与底面成的二面角为α)附: 以知c ⊥l ,b a =⋅αcos ,α为二面角b l a --.则l a S ⋅=211①,b l S ⋅=212②,b a =⋅αcos ③ ⇒①②③得αcos 底侧S S =. 注:S 为任意多边形的面积(可分别多个三角形的方法). ⑵棱锥具有的性质:①正棱锥各侧棱相等,各侧面都是全等的等腰三角形,各等腰三角形底边上的高相等(它叫做正棱锥的斜高). ②正棱锥的高、斜高和斜高在底面内的射影组成一个直角三角形,正棱锥的高、侧棱、侧棱在底面内的射影也组成一个直角三角形.⑶特殊棱锥的顶点在底面的射影位置:①棱锥的侧棱长均相等,则顶点在底面上的射影为底面多边形的外心.②棱锥的侧棱与底面所成的角均相等,则顶点在底面上的射影为底面多边形的外心. ③棱锥的各侧面与底面所成角均相等,则顶点在底面上的射影为底面多边形内心. ④棱锥的顶点到底面各边距离相等,则顶点在底面上的射影为底面多边形内心. ⑤三棱锥有两组对棱垂直,则顶点在底面的射影为三角形垂心. ⑥三棱锥的三条侧棱两两垂直,则顶点在底面上的射影为三角形的垂心.⑦每个四面体都有外接球,球心0是各条棱的中垂面的交点,此点到各顶点的距离等于球半径; ⑧每个四面体都有内切球,球心I 是四面体各个二面角的平分面的交点,到各面的距离等于半径.[注]:i. 各个侧面都是等腰三角形,且底面是正方形的棱锥是正四棱锥.(×)(各个侧面的等腰三角形不知是否全等)ii. 若一个三角锥,两条对角线互相垂直,则第三对角线必然垂直. 简证:A B ⊥CD ,AC ⊥BD ⇒ BC ⊥AD. 令b AC c AD a AB ===,,得c a c b AD BC c AD a b AB AC BC -=⋅⇒=-=-=,,已知()()0,0=-⋅=-⋅c a b b c a0=-⇒c b c a 则0=⋅AD BC .iii. 空间四边形OABC 且四边长相等,则顺次连结各边的中点的四边形一定是矩形. iv. 若是四边长与对角线分别相等,则顺次连结各边的中点的四边是一定是正方形. 简证:取AC 中点'O ,则⊥⇒⊥'⊥'AC AC O B AC o o ,平面=∠⇒⊥⇒'FGH BO AC B O O 90°易知EFGH 为平行四边形⇒EFGH 为长方形.若对角线等,则EFGH FG EF ⇒=为正方形. 3. 球:⑴球的截面是一个圆面. ①球的表面积公式:24R S π=. ②球的体积公式:334R V π=. l ab c FEH GBCDAO'⑵纬度、经度:①纬度:地球上一点P 的纬度是指经过P 点的球半径与赤道面所成的角的度数.②经度:地球上B A ,两点的经度差,是指分别经过这两点的经线与地轴所确定的二个半平面的二面角的度数,特别地,当经过点A 的经线是本初子午线时,这个二面角的度数就是B 点的经度. 附:①圆柱体积:h r V 2π=(r 为半径,h 为高) ②圆锥体积:h r V 231π=(r 为半径,h 为高) ③锥形体积:Sh V 31=(S 为底面积,h 为高) 4. ①内切球:当四面体为正四面体时,设边长为a ,a h 36=,243a S =底,243a S =侧 得a a a R R a R a a a 46342334/424331433643222=⋅==⇒⋅⋅+⋅=⋅. 注:球内切于四面体:h S R S 313R S 31V 底底侧ACD B ⋅=⋅+⋅⋅⋅=- ②外接球:球外接于正四面体,可如图建立关系式.构造以半径为斜边的直角三角形线面垂直平行六种关系的证明方法总结一、线线平行的证明方法:1、利用平行四边形。
立体几何线面平行证明

立体几何线面平行证明要证明两个线面平行,一般可以通过以下几种方法来进行证明:方法一:使用平行线的性质假设我们有线面A和线面B,要证明A和B平行,可以通过以下步骤进行证明:1.假设线面A和线面B不平行,即存在一条线a与线面A不平行,又与线面B相交于一点P。
2.假设在线面A上存在一点Q,它与直线a上相交于一点R。
3.由于线a与线面B相交于P,所以线段PR必然属于线面B。
4.由于线a与线面A相交于R,所以线段PR必然属于线面A。
5.由于线面A和线面B都包含线段PR,所以它们必然相交。
6.这与我们的假设相矛盾,因此假设不成立,即线面A和线面B是平行的。
方法二:使用支撑面的性质假设我们有线面A和线面B,要证明A和B平行,可以通过以下步骤进行证明:1.假设在线面A上存在一条直线a,它与线面B相交于一点P。
2.过直线a作平行于线面B的平面,该平面与线面A相交于线段QR。
3.由于直线a与线面B相交于点P,所以线段PR必然属于线面B。
4.由于平面上的任意两点可以确定一条直线,所以线段QR也属于线面B。
5.因此,线段QR同时属于线面A和线面B,所以它们不是平行的。
6.这与我们的假设相矛盾,因此假设不成立,即线面A和线面B是平行的。
方法三:使用平行四边形的性质假设我们有线面A和线面B,要证明A和B平行1.假设在线面A上存在一条直线a,它与线面B相交于一点P。
2.在线面A上选择一点Q,并通过P点作一条平行于线面A的直线b。
3.连接直线a和直线b,得到平行四边形PQRD。
4.由于平行四边形的特性,相邻两边平行且长度相等,所以线段PD也是平行于线面A的,并且它必然属于线面B。
5.因此,线段PD同时属于线面A和线面B,所以它们不是平行的。
6.这与我们的假设相矛盾,因此假设不成立,即线面A和线面B是平行的。
以上三种方法是一些常用的证明线面平行的方法,根据实际问题的具体情况,可以选择适合的方法进行证明。
立体几何常见证明方法

立体几何方法归纳小结一、线线平行的证明方法1、根据公理4,证明两直线都与第三条直线平行。
2、根据线面平行的性质定理,若直线a平行于平面A ,过a的平面B与平面A相交于b ,则a//b。
3、根据线面垂直的性质定理,若直线a与直线b都与平面A垂直,则a//b 。
4、根据面面平行的性质定理,若平面A//平面B,平面C与平面A和平面B的交线分别为直线a与直线b,则a//b 。
二、线面平行的证明方法1、根据线面平行的定义,证直线与平面没有公共点。
2、根据线面平行的判定定理,若平面A内存在一条直线b与平面外的直线a平行,则a//A 。
(用相似三角形或平行四边形)3、根据平面与平面平行的性质定理,若两平面平行,则一个平面内的任一直线与另一个平面平行。
三、面面平行的证明方法1、根据定义,若两平面没有公共点,则两平面平行。
2、根据两平面平行的判定定理,一个平面内有两相交直线与另一平面平行,则两平面平行。
或根据两平面平行的判定定理的推论,一平面内有两相交直线与另一平面内两相交直线平行,则两平面平行。
3、垂直同一直线的两平面平行。
4、平行同一平面的两平面平行。
四、两直线垂直的证明方法1、根据定义,证明两直线所成的角为90°2、一直线垂直于两平行直线中的一条,也垂直于另一条.3、一直线垂直于一个平面,则它垂直于平面内的所有直线.4、根据三垂线定理及逆定理,若平面内的直线垂直于平面的一条斜线(或斜线在平面内的射影),则它垂直于斜线在平面内的射影(或平面的斜线).五、线面垂直的证明方法1、根据定义,证明一直线与平面内的任一(所有)直线垂直,则直线垂直于平面.2、根据判定定理,一直线垂直于平面内的两相交直线,则直线垂直于平面.3、一直线垂直于两平行平面中的一个,也垂直于另一个.4、两平行直线中的一条垂直于一个平面,另一条也垂直于这个平面.5、根据两平面垂直的性质定理,两平面垂直,则一个平面内垂直于它们交线的直线垂直于另一个平面.六、面面垂直的证明方法1、根据面面垂直的定义,两平面相交所成的二面角为直二面角,则两平面垂直。
高中数学-立体几何位置关系-平行与垂直证明方法汇总

高中数学-立体几何位置关系-平行与垂直证明方法汇总(一)立体几何中平行问题证明直线和平面平行的方法有:①利用定义采用反证法;②平行判定定理;③利用面面平行,证线面平行。
主要方法是②、③两法在使用判定定理时关键是确定出面内的与面外直线平行的直线.常用具体方法:中位线和相似例1、P是平行四边形ABCD所在平面外一点,Q是PA的中点.求证:PC∥面BDQ.证明:如图,连结AC交BD于点O.∵ABCD是平行四边形,∴A O=O C.连结O Q,则O Q在平面BDQ内,且O Q是△APC的中位线,∴PC∥O Q.∵PC在平面BDQ外,∴PC∥平面BDQ.例2、在棱长为a的正方体ABCD-A1B1C1D1中,设M、N、E、F分别是棱A1B1、A1D1、C1D1、B1C1的中点.求证:(1)E、F、B、D四点共面;(2)面AMN∥面EFBD.证明:(1)分别连结B 1D 1、ED 、FB ,如图, 则由正方体性质得 B 1D 1∥BD. ∵E 、F 分别是D 1C 1和B 1C 1的中点, ∴EF ∥21B 1D 1.∴EF ∥21BD. ∴E 、F 、B 、D 对共面.(2)连结A 1C 1交MN 于P 点,交EF 于点Q ,连结AC 交BD 于点O ,分别连结PA 、Q O . ∵M 、N 为A 1B 1、A 1D 1的中点, ∴MN ∥EF ,EF ⊂面EFBD. ∴MN ∥面EFBD. ∵PQ ∥A O ,∴四边形PA O Q 为平行四边形. ∴PA ∥O Q.而O Q ⊂平面EFBD ,∴PA ∥面EFBD.且PA ∩MN=P ,PA 、MN ⊂面AMN , ∴平面AMN ∥平面EFBD.例3如图(1),在直角梯形P 1DCB 中,P 1D//BC ,CD ⊥P 1D ,且P 1D=8,BC=4,DC=46,A 是P 1D 的中点,沿AB 把平面P 1AB 折起到平面PAB 的位置(如图(2)),使二面角P —CD —B 成45°,设E 、F 分别是线段AB 、PD 的中点. 求证:AF//平面PEC ;证明:如图,设PC 中点为G ,连结FG ,则FG//CD//AE ,且FG=21CD=AE , ∴四边形AEGF 是平行四边形 ∴AF//EG ,又∵AF ⊄平面PEC ,EG ⊂平面PEC , ∴AF//平面PEC例4、 正方形ABCD 与正方形ABEF 所在平面相交于AB ,在AE 、BD 上各有一点P 、Q ,且AP=DQ.求证:PQ ∥面BCE.证法一:如图(1),作PM ∥AB 交BE 于M ,作QN ∥AB 交BC 于N,连接MN, 因为面ABCD ∩面ABEF=AB,则AE=DB. 又∵AP=DQ, ∴PE=QB.又∵PM ∥AB ∥QN, ∴AE PE AB PM =,BD BQDC QN =. ∴DCQNAB PM =. ∴PM ∥QN.四边形PMNQ 为平行四边形. ∴PQ ∥MN.又∵MN ⊂面BCE ,PQ ⊄面BCE , ∴PQ ∥面BCE.证法二:如图(2),连结AQ 并延长交BC 或BC 的延长线于点K ,连结EK. ∵AD ∥BC, ∴QKAQQB DQ =. 又∵正方形ABCD 与正方形ABEF 有公共边AB ,且AP=DQ ,∴PEAPQK AQ =.则PQ ∥EK. ∴EK ⊂面BCE ,PQ ⊄面BCE. ∴PQ ∥面BCE.例5、正方形ABCD 交正方形ABEF 于AB (如图所示)M 、N 在对角线AC 、FB 上且AM= FN 。
立体几何证明8条定理

直线与平面平行的判定定理与性质定理文字语言图形语言符号语言判定定理不在平面内的一条直线与此平面内的一条直线平行,则该直线与此平面平行(简记为线线平行⇒线面平行)⎭⎬⎫l⊄αa⊂αl∥a⇒l∥α性质定理一条直线与一个平面平行,则过这条直线的任一平面与此平面的交线与该直线平行(简记为线面平行⇒线线平行)⎭⎬⎫a∥αa⊂βα∩β=b⇒a∥b平面与平面平行的判定定理与性质定理文字语言图形语言符号语言判定定理一个平面内的两条相交直线与另一个平面平行,则这两个平面平行(简记为线面平行⇒面面平行)⎭⎪⎬⎪⎫a⊂αb⊂αa∩b=Pa∥βb∥β⇒α∥β性质定理如果两个平行平面同时和第三个平面相交,那么它们的交线平行⎭⎬⎫α∥βα∩γ=aβ∩γ=b⇒a∥b直线与平面垂直的判定定理及性质定理文字语言图形语言符号语言判定定理一条直线与平面内的两条相交直线都垂直,则该直线与此平面垂直⎭⎬⎫a,b⊂αa∩b=Ol⊥al⊥b⇒l⊥α性质定理垂直于同一个平面的两条直线平行⎭⎬⎫a⊥αb⊥α⇒a∥b平面与平面垂直的判定定理及性质定理文字语言图形语言符号语言判定定理一个平面过另一个平面的一条垂线,则这两个平面互相垂直⎭⎬⎫l⊂βl⊥α⇒α⊥β性质定理两个平面互相垂直,则一个平面内垂直于交线的直线垂直于另一个平面⎭⎬⎫α⊥βl⊂βα∩β=al⊥a⇒l⊥α。
立体几何证明定理及性质总结

一.直线和平面的三种位置关系:1。
线面平行2. 线面相交l符号表示:符号表示:3. 线在面内符号表示:二.平行关系:1.线线平行:方法一:用线面平行实现。
方法二:用面面平行实现.mlmll////⇒⎪⎭⎪⎬⎫=⋂⊂βαβαmlml////⇒⎪⎭⎪⎬⎫=⋂=⋂βγαγβα方法三:用线面垂直实现。
若αα⊥⊥ml,,则ml//。
2.线面平行:方法一:用线线平行实现。
ααα////llmml⇒⎪⎭⎪⎬⎫⊄⊂方法二:用面面平行实现.αββα////ll⇒⎭⎬⎫⊂3.面面平行:方法一:用线线平行实现. 方法二:用线面平行实现βααβ//',','//'//⇒⎪⎪⎭⎪⎪⎬⎫⊂⊂且相交且相交mlmlmmll。
βαβαα//,////⇒⎪⎭⎪⎬⎫⊂且相交mlml三.垂直关系:1. 线面垂直:方法一:用线线垂直实现。
方法二:用面面垂直实现。
αα⊥⇒⎪⎪⎭⎪⎪⎬⎫⊂=⋂⊥⊥lABACAABACABlACl,αββαβα⊥⇒⎪⎭⎪⎬⎫⊂⊥=⋂⊥llmlm,2。
面面垂直:l方法一:用线面垂直实现。
方法二:计算所成二面角为直角.βαβα⊥⇒⎭⎬⎫⊂⊥l l3. 线线垂直:方法一:用线面垂直实现.m l m l ⊥⇒⎭⎬⎫⊂⊥αα方法二:三垂线定理及其逆定理.PO l OA l PA l αα⊥⎫⎪⊥⇒⊥⎬⎪⊂⎭。
几何证明七种证明方法

几何证明七种证明方法1. 直接证明法直接证明法是几何证明中最基本的证明方法。
它是指通过已知命题的前提条件,推导出结论的证明过程。
这种方法常用于证明角度、线段、三角形及其性质等基本几何命题。
证明一个角等于另一个角时,可以使用直接证明法。
首先给定已知角,再通过几何定理或性质,推导出待证角等于已知角的过程,从而证明结论。
2. 反证法反证法是指假设命题的反命题为真,然后推导出与已知条件矛盾的结果,从而推翻假设,证明原命题为真的一种证明方法。
证明一个三角形为等腰三角形时,可以使用反证法。
假设这个三角形不是等腰三角形,那么它就不满足等腰三角形的性质,从而导致推导出与已知条件矛盾的结果,于是得出结论,该三角形是等腰三角形。
3. 归纳法归纳法是建立在归纳推理基础上的证明方法。
它是指通过证明某些基础情况成立,并证明当基础情况成立时,下一步情况也成立的方式,推导出全部情况都成立的结论。
证明一个多边形的内角和公式对于任意的n边形都成立时,可以使用归纳法。
先证明n=3时公式成立,再证明当n=k时公式成立,则根据归纳法可以得出,对于任意的n边形,公式都成立。
4. 数学归纳法数学归纳法是一种比普通归纳法更为严谨的证明方法。
它要求在归纳推理基础上,必须满足以下两个条件:(1)基础情况:证明当n等于某个正整数时,结论成立。
(2)归纳步骤:证明若当n等于k时结论成立,则当n等于k+1时结论也成立。
证明若干正整数的和大于等于它们的积时,可以使用数学归纳法。
首先证明当n=2时结论成立,即a1+a2>=2a1a2。
然后假设当n=k时结论成立,即a1+a2+...+ak>=ka1a2...ak。
再证明当n=k+1时结论也成立,即a1+a2+...+ak+ak+1>=(k+1)a1a2...akak+1,即得证。
5. 可逆推理法可逆推理法是一种利用“等价命题”的方法推导出结论的证明方法。
它是指若命题A等价于命题B,则命题B成立时命题A也成立。
立体几何证明方法总结及经典3例(推荐文档)

立体几何证明方法总结及典例例1:平行类证明 【平行类证明方法总结】 线线平行的证明方法:三线间平行的传递性,三角形中位线,平行四边形对边平行且相等,梯形的上下底平行,棱柱圆柱的侧棱平行且相等,两平行面被第三面所截交线平行,成比例(相似)证平行等等。
线面平行的证明方法:面外线与面内线平行,两面平行则面内一线与另面平行等等 面面平行的证明方法:面内相交线与另面平行则面面平行,三面间平行的传递性等等。
【例】正方形ABCD 与正方形ABEF 所在平面相交于AB ,在AE 、BD 上各有一点P 、Q ,且AP=DQ.求证:PQ ∥面BCE.证法一:如图(1),作PM ∥AB 交BE 于M , 作QN ∥AB 交BC 于N,连接MN, 因为面ABCD ∩面ABEF=AB, 则AE=DB. 又∵AP=DQ, ∴PE=QB.又∵PM ∥AB ∥QN, ∴AE PE AB PM =,BD BQDC QN =. ∴DCQNAB PM =. ∴PM ∥QN.四边形PMNQ 为平行四边形. ∴PQ ∥MN.又∵MN ⊂面BCE ,PQ ⊄面BCE , ∴PQ ∥面BCE. 证法二:如图(2),连结AQ 并延长交BC 或BC 的延长线于点K ,连结EK. ∵AD ∥BC, ∴QKAQQB DQ =. 又∵正方形ABCD 与正方形ABEF 有公共边AB ,且AP=DQ , ∴PEAPQK AQ =.则PQ ∥EK. ∴EK ⊂面BCE ,PQ ⊄面BCE. ∴PQ ∥面BCE. 例2:垂直类证明 【垂直类证明方法总结】证垂直的几种方法:勾股定理、等腰(边)三角形三线合一、菱形对角线、矩形(含正方形)、90o 、相似三角形(与直角三角形)、圆直径对的圆周角、平行线、射影定理(三垂线定理)、线面垂直、面面垂直等【例】如图所示,ABCD 为正方形,SA ⊥平面ABCD ,过A 且垂直于SC 的平面分别交SB SC SD ,,于E F G ,,.求证:AE SB ⊥,AG SD ⊥.证明:∵SA ⊥平面ABCD ,∴SA BC ⊥. ∵AB BC ⊥,∴BC ⊥平面SAB . 又∵AE ⊂平面SAB , ∴BC AE ⊥. ∵SC⊥平面AEFG ,∴SC AE ⊥.∴AE ⊥平面SBC . ∴AE SB ⊥. 同理证AG SD ⊥. 例3:向量法解立体几何类 【量法解立体几何类公式总结】 基本公式若),,(),,,(222111z y x b z y x a ==,则①212121z z y y x x b a ++=⋅;②222222212121||,||z y x b z y x a ++=++=;③212121z z y y x x b a ++=⋅④222222212121212121,cos z y x z y x z z y y x x b a ++⋅++++>=<夹角公式:.||||cos 2121n n n n ⋅⋅-=θ距离公式:||||||n n AB CD d ⋅== 【例】已知两个正四棱锥P -ABCD 与Q -ABCD 的高都为2,AB =4. (1)证明:PQ ⊥平面ABCD ;(2)求异面直线AQ 与PB 所成的角; (3)求点P 到面QAD 的距离.简解:(1)略;(2)由题设知,ABCD 是正方形,且AC ⊥BD .由(1),PQ ⊥平面ABCD ,故可分别以直线CA DB QP ,,为x ,y ,z 轴建立空间直角坐标系(如图1),易得(2202)(0222)AQ PB =--=-,,,,,,1cos 3AQ PB AQ PB AQ PB<>==,. 所求异面直线所成的角是1arccos3. (3)由(2)知,点(0220)(22220)(004)D AD PQ -=--=-,,,,,,,,设n =(x ,y ,z )是平面QAD 的一个法向量,则00AQ AD ⎧=⎪⎨=⎪⎩,,n n 得200x z x y ⎧+=⎪⎨+=⎪⎩,,取x =1,得(112)--,,n =.点P到平面QAD 的距离22PQ d==n n.立体几何证明经典习题平行题目1、P是平行四边形ABCD所在平面外一点,Q是PA的中点.求证:PC∥面BDQ.2、如图(1),在直角梯形P1DCB中,P1D//BC,CD⊥P1D,且P1D=8,BC=4,DC=46,A是P1D的中点,沿AB把平面P1AB折起到平面PAB的位置(如图(2)),使二面角P—CD—B成45°,设E、F分别是线段AB、PD的中点.求证:AF//平面PEC;垂直题目3、如图2,P是△ABC所在平面外的一点,且PA⊥平面ABC,平面PAC⊥平面PBC.求证:BC⊥平面PAC.4、如图2,在三棱锥A-BCD 中,BC =AC ,AD =BD ,作BE ⊥CD ,E为垂足,作AH ⊥BE 于H.求证:AH ⊥平面BCD向量法解立体几何题目5、在三棱柱ABC -A 1B 1C 1中,AB ⊥侧面BB 1C 1C ,E 为棱CC 1上异于C 、C 1的一点,EA ⊥EB 1.已知2AB =,BB 1=2,BC =1,∠BCC 1=3π.求二面角A -EB 1-A 1的平面角的正切值.立体几何证明经典习题答案1、证明:如图,连结AC 交BD 于点O . ∵ABCD 是平行四边形,∴A O =O C.连结O Q ,则O Q 在平面BDQ 内, 且O Q 是△APC 的中位线, ∴PC ∥O Q.∵PC 在平面BDQ 外, ∴PC ∥平面BDQ.2、证明:如图,设PC 中点为G ,连结FG ,则FG//CD//AE ,且FG=21CD=AE , ∴四边形AEGF 是平行四边形 ∴AF//EG ,又∵AF ⊄平面PEC ,EG ⊂平面PEC , ∴AF//平面PEC3、证明:在平面PAC 内作AD ⊥PC 交PC 于D . ∵平面PAC ⊥平面PBC ,且两平面交 于PC ,AD ⊂平面PAC ,且AD ⊥PC ,∴AD ⊥平面PBC . 又∵BC ⊂平面PBC , ∴AD ⊥BC .∵PA ⊥平面ABC ,BC ⊂平面ABC , ∴PA ⊥BC . ∵AD ∩PA =A , ∴BC ⊥平面PAC .4、证明:取AB 的中点F,连结CF ,DF . ∵ACBC =, ∴CFAB ⊥.∵AD BD =,(等腰三角形三线合一)∴DF AB ⊥. 又CFDF F =,∴AB ⊥平面CDF .∵CD ⊂平面CDF ,∴CD AB ⊥.又CD BE ⊥,BEAB B =,∴CD ⊥平面ABE ,CD AH ⊥.∵AH CD ⊥,AH BE ⊥,CD BE E =,∴ AH ⊥平面BCD .5、以B 为原点,分别以BB 1、BA 所在直线为y 轴、z 轴,过B 点垂直于平面AB 1的直线为x 轴建立空间直角坐标系. 由于BC =1,BB 1=2,AB =2,∠BCC 1=3π, ∴在三棱柱ABC -A 1B 1C 1中,有B (0,0,0)、A (0,0,2)、B 1(0,2,0)、31022c ⎛⎫-⎪ ⎪⎝⎭,,、133022C ⎛⎫ ⎪ ⎪⎝⎭,,.设302E a ⎛⎫ ⎪ ⎪⎝⎭,,且1322a -<<, 由EA ⊥EB 1,得10EA EB =,即3322022a a ⎛⎫⎛⎫---- ⎪ ⎪⎪ ⎪⎝⎭⎝⎭,,,, 233(2)2044a a a a =+-=-+=,∴13022a a ⎛⎫⎛⎫--= ⎪ ⎪⎝⎭⎝⎭, 即12a =或32a =(舍去).故31022E ⎛⎫ ⎪ ⎪⎝⎭,,. 由已知有1EA EB ⊥,111B A EB ⊥,故二面角A -EB 1-A 1的平面角θ的大小为向量11B A 与EA 的夹角.因11(002)B A BA ==,,,31222EA ⎛⎫=-- ⎪ ⎪⎝⎭,, 故11112cos 3EA B A EA B A θ==,即2tan 2θ=。
立体几何定理的推导与证明方法

立体几何定理的推导与证明方法一、概述立体几何是我们生活中常见的一种几何形式,它涉及到空间中的各种图形的性质和关系。
在立体几何中,有许多重要的定理和性质,这些定理和性质对于我们理解和应用立体几何至关重要。
在本文中,我们将探讨立体几何定理的推导和证明方法,希望能够为读者提供一些启发和帮助。
二、立体几何定理的推导方法1. 利用几何图形的性质在推导立体几何定理时,我们可以利用几何图形的性质来进行推导。
对于一个立体图形,我们可以利用它的各个面的性质和相互关系,来推导出一些定理和性质。
在推导过程中,我们可以通过作图和构造辅助线等方法,来帮助我们理解和推导定理。
2. 利用几何变换的性质在推导立体几何定理时,我们还可以利用几何变换的性质来进行推导。
我们可以通过平移、旋转、镜像等几何变换,来帮助我们理解和推导定理。
在推导过程中,我们可以通过构造适当的几何变换,来将一个复杂的问题转化为一个简单的问题,从而更容易理解和证明定理。
3. 利用解析几何的方法在推导立体几何定理时,我们还可以利用解析几何的方法来进行推导。
我们可以通过引入坐标系和方程等工具,来帮助我们理解和推导定理。
在推导过程中,我们可以通过求解方程组、计算向量等方法,来证明某个定理或性质的成立。
三、立体几何定理的证明方法1. 利用数学归纳法在证明立体几何定理时,我们可以利用数学归纳法来进行证明。
数学归纳法是一种常用的数学证明方法,它适用于形式化的推理过程。
通过证明基本情况成立,并假设某个结论对于一个整数成立,来证明该结论对于下一个整数也成立。
在证明立体几何定理时,我们可以通过数学归纳法来推导出某个定理的成立。
2. 利用反证法在证明立体几何定理时,我们可以利用反证法来进行证明。
反证法是一种常用的数学证明方法,它适用于证明某个命题的否定是否成立。
通过假设某个结论不成立,来推导出矛盾的结论,从而证明该结论的成立。
在证明立体几何定理时,我们可以通过反证法来证明某个定理的成立。
立体几何证明方法大全

一条直线垂直于三角形的 两条边.则垂直于第三边.
三垂线定理
三垂线定理 在平面内的一 条直线, 如果和这个平面的 一条斜线的射影垂直, 那么 它和这条斜线垂直
三垂线定理逆定 理
三垂线逆定理 在平面内的 一条直线, 如果和这个平面 的一条斜线垂直, 那么它和 这条斜线的射影垂直
3 线面平行判定定理
定理名称
(二)立体几何证明方法汇总 1、线线平行判定定理叙述
定义
一个平面内两条直线没 有公共点,则平行
平行公理
平行于同一条直线的两 条直线的两条直线平 行.
线面平行性质 定理
如果一条直线和一个平 面平行,经过这条直线 的平面和这个平面相 交,那么这条直线和交 线平行。
面面平行的性 质定理
公理 1
公理 1:如果一条直线上的两点在一 个平面内, 那么这条直线上的所有点 都在这个平面内。 (1)判定直线在平面内的依据 (2)判定点在平面内的方法 公理 3:如果两个平面有一个公共 点, 那它还有其它公共点, 这些公共 点的集合是一条直线 。 (1)判定两个平面相交的依据 (2)判定若干个点在两个相交平面 的交线上 公理 3:经过不在一条直线上的三 点,有且只有一个平面。 (1)确定 一个平面的依据 (2) 判定若干个点 共面的依据
5 面面平行的判定定理
定理名称
图形
用文字语言叙述
用符号语言叙述
定义
如果两个平面没有公共点,则两 个平面平行。
面面平行的 判定定理
如果一个平面内有两条相交直线 平行于另一个平面,那么这两个 平面平行
面面平行的 判定定理推 论
如果两个平面内两条相交直线平 行 于另 一个 平面 内两 条相 交直 线,则两个平面平行。
人教高中数学必修二1-2章立体几何证明题定理推论汇总

立体几何公理、定理推论汇总一、公理及其推论公理1 如果一条直线上的两点在一个平面内,那么这条直线上所有的点都在这个平面内。
符号语言:,,,A l B l A B l a a a ÎÎÎÎÞÌ作用:作用: ① 用来验证直线在平面内;用来验证直线在平面内;② 用来说明平面是无限延展的。
用来说明平面是无限延展的。
公理2 如果两个平面有一个公共点,那么它们还有其他公共点,且所有这些公共点的集合是一条过这个公共点的直线。
(那么它们有且只有一条通过这个公共点的公共直线)(那么它们有且只有一条通过这个公共点的公共直线)符号语言:P l P l a b a b ÎÞ=Î且作用:①作用:① 用来证明两个平面是相交关系;用来证明两个平面是相交关系;② 用来证明多点共线,多线共点。
用来证明多点共线,多线共点。
公理3 经过不在同一条直线上的三点,有且只有一个平面。
经过不在同一条直线上的三点,有且只有一个平面。
符号语言:,,,,A B C A B C Þ不共线确定一个平面推论1 经过一条直线和这条直线外的一点,有且只有一个平面。
经过一条直线和这条直线外的一点,有且只有一个平面。
符号语言:A a A a a a a ÏÞÎÌ有且只有一个平面,使,推论2 经过两条相交直线,有且只有一个平面。
经过两条相交直线,有且只有一个平面。
符号语言:a b P a b a a a Ç=ÞÌÌ有且只有一个平面,使,推论3 经过两条平行直线,有且只有一个平面。
经过两条平行直线,有且只有一个平面。
符号语言://a b a b a a a ÞÌÌ有且只有一个平面,使,公理3及其推论的作用:用来证明多点共面,多线共面。
及其推论的作用:用来证明多点共面,多线共面。
立体几何证明方法总结

、线线平行的证明方法1 、利用平行四边形。
2 、利用三角形或梯形的中位线。
3 、如果一条直线与一个平面平行,经过这条直线的平面与这个平面相交, 那么这条直线就与交线平行。
(线面平行的性质定理)4 、如果两个平行平面同时与第三个平面相交,那么它们的交线平行。
(面面平行的性质定理)5 、如果两条直线垂直于同一个平面,那么这两条直线平行。
(线面垂直的性质定理)6 、平行于同一条直线的两条直线平行。
7 、夹在两个平行平面之间的平行线段相等。
(需证明)二、线面平行的证明方法:1 、定义法:直线与平面没有公共点。
2 、如果平面外一条直线与这个平面内的一条直线平行,那么这条直线与这个平面平行。
(线面平行的判定定理)3 、两个平面平行,其中一个平面内的任何一条直线必平行于另一个平面。
三、面面平行的证明方法:1 、定义法:两平面没有公共点。
2 、如果一个平面内有两条相交直线都平行于另一个平面,那么这两个平面平行。
(面面平行的判定定理)3 、平行于同一平面的两个平面平行。
4 、经过平面外一点,有且只有一个平面与已知平面平行。
5 、垂直于同一直线的两个平面平行。
四、线线垂直的证明方法:1 、勾股定理。
2 、等腰三角形。
3 、菱形对角线。
圆所对的圆周角就是直角 点在线上的射影 。
如果一条直线与一个平面垂直 ,那么这条直线就与这个平面内任意的直线都垂直。
在平面内的一条直线 ,如果与这个平面一条斜线的射影垂直 ,那么它也与这条斜线垂直 。
(三垂线定理 ,需证明 ) 在平面内的一条直线 ,如果与这个平面一条斜线垂直 ,那么它也与这条斜线的射影垂直 。
(三垂线逆定理 ,需证 如果两条平行线中的一条垂直于一条直线 ,则另一条也垂直于这条直线 。
线面垂直的证明方法 :定义法 : 直线与平面内任意直线都垂直 。
点在面内的射影 。
如果一条直线与一个平面内的两条相交直线垂直 ,那么 这条直线垂直于这个平面 。
(线面垂直的判定定理 ) 如果两个平面互相垂直 ,那么在一个平面内垂直于它们 交线的直线垂直于另一个平面 。
立体几何知识归纳+典型例题+方法总结

立体几何知识归纳+典型例题+方法总结一、知识归纳1.平面平面的基本性质:掌握三个公理及推论,会说明共点、共线、共面问题.(1)证明点共线的问题,一般转化为证明这些点是某两个平面的公共点(依据:由点在线上,线在面内,推出点在面内),这样可根据公理2证明这些点都在这两个平面的公共直线上.(2)证明共点问题,一般是先证明两条直线交于一点,再证明这点在第三条直线上,而这一点是两个平面的公共点,这第三条直线是这两个平面的交线.(3)证共面问题一般先根据一部分条件确定一个平面,然后再证明其余的也在这个平面内,或者用同一法证明两平面重合.2. 空间直线(1)空间直线位置关系三种:相交、平行、异面. 相交直线:共面有且仅有一个公共点;平行直线:共面没有公共点;异面直线:不同在任一平面内,无公共点(2)平行公理:平行于同一条直线的两条直线互相平行.等角定理:如果一个角的两边和另一个角的两边分别平行并且方向相同,那么这两个角相等(如右图).(直线与直线所成角]90,0[︒︒∈θ)(向量与向量所成角])180,0[οο∈θ推论:如果两条相交直线和另两条相交直线分别平行,那么这两组直线所成锐角(或直角)相等.(3)两异面直线的距离:公垂线段的长度.空间两条直线垂直的情况:相交(共面)垂直和异面垂直.[注]:21,l l 是异面直线,则过21,l l 外一点P ,过点P 且与21,l l 都平行平面有一个或没有,但与21,l l 距离相等的点在同一平面内. (1L 或2L 在这个做出的平面内不能叫1L 与2L 平行的平面)3. 直线与平面平行、直线与平面垂直(1)空间直线与平面位置分三种:相交、平行、在平面内.(2)直线与平面平行判定定理:如果平面外一条直线和这个平面内一条直线平行,那么这条直线和这个平面平行.(“线线平行⇒线面平行”)(3)直线和平面平行性质定理:如果一条直线和一个平面平行,经过这条直线的平面和这个平面相交,那么这条直线和交线平行.(“线面平行⇒线线平行”)(4)直线与平面垂直是指直线与平面任何一条直线垂直,过一点有且只有一条直线和一个平面垂直,过一点有且只有一个平面和一条直线垂直. 若PA⊥α,a ⊥AO ,得a ⊥PO (三垂线定理),三垂线定理的逆定理亦成立.直线与平面垂直的判定定理一:如果一条直线和一个平面内的两条相PO A a交直线都垂直,那么这两条直线垂直于这个平面.(“线线垂直⇒线面垂直”)直线与平面垂直的判定定理二:如果平行线中一条直线垂直于一个平面,那么另一条也垂直于这个平面.性质:如果两条直线同垂直于一个平面,那么这两条直线平行.(5)a.垂线段和斜线段长定理:从平面外一点..向这个平面所引的垂线段和斜线段中,①射影相等的两条斜线段相等,射影较长的斜线段较长;②相等的斜线段的射影相等,较长的斜线段射影较长;③垂线段比任何一条斜线段短.b.射影定理推论:如果一个角所在平面外一点到角的两边的距离相等,那么这点在平面内的射影在这个角的平分线上.4. 平面平行与平面垂直(1)空间两个平面的位置关系:相交、平行.(2)平面平行判定定理:如果一个平面内有两条相交直线都平行于另一个平面,那么这两个平面平行.(“线面平行⇒面面平行”)推论:垂直于同一条直线的两个平面互相平行;平行于同一平面的两个平面平行.[注]:一平面内的任一直线平行于另一平面.(3)两个平面平行的性质定理:如果两个平面平行同时和第三个平面相交,那么它们交线平行.(“面面平行⇒线线平行”)(4两个平面垂直判定一:两个平面所成的二面角是直二面角,则两个平面垂直.两个平面垂直判定二:如果一条直线与一个平面垂直,那么经过这条直线的平面垂直于这个平面.(“线面垂直⇒面面垂直”)注:如果两个二面角的平面分别对应互相垂直,则两个二面角没有什么关系.(5)两个平面垂直性质定理:如果两个平面垂直,那么在一个平面内垂直于它们交线的直线也垂直于另一个平面.推论:如果两个相交平面都垂直于第三平面,则它们交线垂直于第三平面.简证:如图,在平面内过O 作OA 、OB 分别垂直于21,l l ,因为ααββ⊥⊂⊥⊂OB PM OA PM ,,,则OB PM OA PM ⊥⊥,.所以结论成立 b.最小角定理的应用(∠PBN 为最小角) 简记为:成角比交线夹角一半大,且又比交线夹角补角一半长,一定有4条.成角比交线夹角一半大,又比交线夹角补角小,一定有2条.成角比交线夹角一半大,又与交线夹角相等,一定有3条或者2条. 成角比交线夹角一半小,又与交线夹角一半小,一定有1条或者没有.5. 棱柱. 棱锥(1)棱柱a.①直棱柱侧面积:Ch S =(C 为底面周长,h 是高)该公式是利用直棱柱的侧面展开图为矩形得出的.②斜棱住侧面积:l C S 1=(1C 是斜棱柱直截面周长,l 是斜棱柱的侧棱长)该公式是利用斜棱柱的侧面展开图为平行四边形得出的.b.{四棱柱}⊃{平行六面体}⊃{直平行六面体}⊃{长方体}⊃{正四棱PαβθM A B O柱}⊃{正方体}.{直四棱柱}I {平行六面体}={直平行六面体}.c.棱柱具有的性质:①棱柱的各个侧面都是平行四边形,所有的侧棱都相等;直棱柱的各.个侧面都是矩形.......;正棱柱的各个侧面都是全等的矩形...... ②棱柱的两个底面与平行于底面的截面是对应边互相平行的全等..多边形.③过棱柱不相邻的两条侧棱的截面都是平行四边形.d.平行六面体:定理一:平行六面体的对角线交于一点.............,并且在交点处互相平分. [注]:四棱柱的对角线不一定相交于一点.定理二:长方体的一条对角线长的平方等于一个顶点上三条棱长的平方和.推论一:长方体一条对角线与同一个顶点的三条棱所成的角为γβα,,,则 1cos cos cos 222=++γβα.推论二:长方体一条对角线与同一个顶点的三各侧面所成的角为γβα,,,则2cos cos cos 222=++γβα. (2)棱锥:棱锥是一个面为多边形,其余各面是有一个公共顶点的三角形.[注]:①一个三棱锥四个面可以都为直角三角形.②一个棱柱可以分成等体积的三个三棱锥;所以棱柱棱柱3V S h V ==. a.①正棱锥定义:底面是正多边形;顶点在底面的射影为底面正多边形的中心.[注]:i. 正四棱锥的各个侧面都是全等的等腰三角形.(不是等边三角形)ii. 正四面体是各棱相等,而正三棱锥是底面为正三角形,侧棱与底棱不一定相等iii. 正棱锥定义的推论:若一个棱锥的各个侧面都是全等的等腰三角形(即侧棱相等);底面为正多边形. ②正棱锥的侧面积:'Ch 21S =(底面周长为C ,斜高为'h ) ③棱锥的侧面积与底面积的射影公式:αcos 底侧S S =(侧面与底面成的二面角为α) 附:以知c ⊥l ,b a =⋅αcos ,α为二面角b l a --.则l a S ⋅=211①,b l S ⋅=212②,b a =⋅αcos ③ ⇒①②③得αcos 底侧S S =.注:S 为任意多边形的面积(可分别求多个三角形面积和的方法). b.棱锥具有的性质:①正棱锥各侧棱相等,各侧面都是全等的等腰三角形,各等腰三角形底边上的高相等(它叫做正棱锥的斜高).②正棱锥的高、斜高和斜高在底面内的射影组成一个直角三角形,正棱锥的高、侧棱、侧棱在底面内的射影也组成一个直角三角形.c.特殊棱锥的顶点在底面的射影位置:①棱锥的侧棱长均相等,则顶点在底面上的射影为底面多边形的外心. ②棱锥的侧棱与底面所成的角均相等,则顶点在底面上的射影为底面多边形的外心. ③棱锥的各侧面与底面所成角均相等,则顶点在底面上的射影为底面l abc多边形内心.④棱锥的顶点到底面各边距离相等,则顶点在底面上的射影为底面多边形内心.⑤三棱锥有两组对棱垂直,则顶点在底面的射影为三角形垂心.⑥三棱锥的三条侧棱两两垂直,则顶点在底面上的射影为三角形的垂心.⑦每个四面体都有外接球,球心0是各条棱的中垂面的交点,此点到各顶点的距离等于球半径;⑧每个四面体都有内切球,球心I 是四面体各个二面角的平分面的交点,到各面的距离等于半径.(3)球:a.球的截面是一个圆面.①球的表面积公式:24R S π=.②球的体积公式:334R V π=. b.纬度、经度:①纬度:地球上一点P 的纬度是指经过P 点的球半径与赤道面所成的角的度数.②经度:地球上B A ,两点的经度差,是指分别经过这两点的经线与地轴所确定的二个半平面的二面角的度数,特别地,当经过点A 的经线是本初子午线时,这个二面角的度数就是B 点的经度.附:①圆柱体积:h r V 2π=(r 为半径,h 为高) ②圆锥体积:h r V 231π=(r 为半径,h 为高) ③锥体体积:Sh V 31=(S 为底面积,h 为高)(1). ①内切球:当四面体为正四面体时,设边长为a ,a h 36=,243a S =底,243a S =侧,得R a R a a a ⋅⋅+⋅=⋅2224331433643a a a R 46342334/42=⋅==⇒. 注:球内切于四面体:h S R S 313R S 31V 底底侧ACD B ⋅=⋅+⋅⋅⋅=-. ②外接球:球外接于正四面体,可如图建立关系式.6. 空间向量(1)a.共线向量:共线向量亦称平行向量,指空间向量的有向线段所在直线互相平行或重合.b.共线向量定理:对空间任意两个向量)0(≠a , ∥的充要条件是存在实数λ(具有唯一性),使b a λ=.c.共面向量:若向量a 使之平行于平面α或a 在α内,则a 与α的关系是平行,记作∥α.d.①共面向量定理:如果两个向量b a ,不共线,则向量与向量b a ,共面的充要条件是存在实数对x 、y 使y x +=.②空间任一点...O .和不共线三点......A .、.B .、.C .,则)1(=++++=z y x OC z OB y OA x OP 是PABC 四点共面的充要条件. (简证:→+==++--=AC z AB y AP OC z OB y OA z y OP )1(P 、A 、B 、C 四点共面)注:①②是证明四点共面的常用方法.(2)空间向量基本定理:如果三个向量....c b a ,,不共面...,那么对空间任一向量P ,存在一个唯一的有序实数组x 、y 、z ,使c z b y a x p ++=.推论:设O 、A 、B 、C 是不共面的四点,则对空间任一点P , 都存在唯一的有序实数组x 、y 、z 使 z y x ++=(这里隐含x+y+z≠1). O BDO R注:设四面体ABCD 的三条棱,,,,d AD c AC b AB ===其中Q 是△BCD 的重心, 则向量)(31c b a AQ ++=用MQ AM AQ +=即证.对空间任一点O 和不共线的三点A 、B 、C ,满足OP xOA yOB zOC =++u u u r u u u r u u u r u u u r , 则四点P 、A 、B 、C 是共面⇔1x y z ++=(3)a.空间向量的坐标:空间直角坐标系的x 轴是横轴(对应为横坐标),y 轴是纵轴(对应为纵坐标),z 轴是竖轴(对应为竖坐标). ①令=(a 1,a 2,a 3),),,(321b b b =,则),,(332211b a b a b a b a ±±±=+,))(,,(321R a a a a ∈=λλλλλ,332211b a b a b a b a ++=⋅ ,a ∥)(,,332211Rb a b a b a b ∈===⇔λλλλ332211b a b a b a ==⇔ 0332211=++⇔⊥b a b a b a .222321a a a ++==(向量模与向量之间的转化:a a =⇒•=空间两个向量的夹角公式232221232221332211||||,cos b b b a a a b a b a b a b a b a b a ++⋅++++=⋅•>=<ρρρρρρ(a =123(,,)a a a ,b =123(,,)b b b ). ②空间两点的距离公式:212212212)()()(z z y y x x d -+-+-=.b.法向量:若向量a 所在直线垂直于平面α,则称这个向量垂直于平面α,记作α⊥a ,如果α⊥a 那么向量a 叫做平面α的法向量.c.向量的常用方法:①利用法向量求点到面的距离定理:如图,设n 是平面α的法向量,AB 是平面α的一条射线,其中α∈A ,则点B 到平面α||n . ②异面直线间的距离d = (12,l l 是两异面直线,其公垂向量为n r ,C D 、分别是12,l l 上任一点,d 为12,l l 间的距离).③直线AB 与平面所成角的正弦值sin ||||AB m AB m β⋅=u u u r u r u u u r u r (m u r 为平面α的法向量). ④利用法向量求二面角的平面角定理:设21,n n 分别是二面角βα--l 中平面βα,的法向量,则21,n n 所成的角就是所求二面角的平面角或其补角大小(21,n n 方向相同,则为补角,21,n 反方,则为其夹角).d.证直线和平面平行定理:已知直线⊄a 平面α,α∈∈D C a B A ,,,,且C 、D 、E 三点不共线,则a ∥α的充要条件是存在有序实数对μλ,使μλ+=.(常设μλ+=求解μλ,若μλ,存在即证毕,若μλ,不存在,则直线AB 与平面相交).AB二、经典例题考点一 空间向量及其运算1. 已知,,A B C 三点不共线,对平面外任一点,满足条件122555OP OA OB OC =++u u u r u u u r u u u r u u u r , 试判断:点P 与,,A B C 是否一定共面?解析:要判断点P 与,,A B C 是否一定共面,即是要判断是否存在有序实数对,x y 使AP xAB y AC =+u u u r u u u r u u u r 或对空间任一点O ,有OP OA x AB y AC =++u u u r u u u r u u u r u u u r .答案:由题意:522OP OA OB OC =++u u u r u u u r u u u r u u u r ,∴()2()2()OP OA OB OP OC OP -=-+-u u u r u u u r u u u r u u u r u u u r u u u r ,∴22AP PB PC =+u u u r u u u r u u u r ,即22PA PB PC =--u u u r u u u r u u u r ,所以,点P 与,,A B C 共面.点评:在用共面向量定理及其推论的充要条件进行向量共面判断的时候,首先要选择恰当的充要条件形式,然后对照形式将已知条件进行转化运算.2.如图,已知矩形ABCD 和矩形ADEF 所在平面互相垂直,点M ,N 分别在对角线BD ,AE 上,且13BM BD =,13AN AE =.求证://MN 平面CDE .解析:要证明//MN 平面CDE ,只要证明向量NM u u u u r 可以用平面CDE 内的两个不共线的向量DE u u u r 和DC u u u r 线性表示. 答案:证明:如图,因为M 在BD 上,且13BM BD =, 所以111333MB DB DA AB ==+u u u r u u u r u u u r u u u r .同理1133AN AD DE =+u u u r u u u r u u u r , 又CD BA AB ==-u u u r u u u r u u u r ,所以MN MB BA AN =++u u u u r u u u r u u u r u u u r 1111()()3333DA AB BA AD DE =++++u u u r u u u r u u u r u u u r u u u r 2133BA DE =+u u u r u u u r 2133CD DE =+u u u r u u u r . 又CD uuu r 与DE u u u r 不共线,根据共面向量定理,可知MN u u u u r ,CD uuu r ,DE u u u r 共面.由于MN 不在平面CDE 内,所以//MN 平面CDE .点评:空间任意的两向量都是共面的.与空间的任两条直线不一定共面要区别开.考点二 证明空间线面平行与垂直3. 如图, 在直三棱柱ABC -A 1B 1C 1中,AC =3,BC =4,AA 1=4,点D 是AB 的中点, (I )求证:AC ⊥BC 1; (II )求证:AC 1//平面CDB 1;解析:(1)证明线线垂直方法有两类:一是通过三垂线定理或逆定理证明,二是通过线面垂直来证明线线垂直;(2)证明线面平行也有两类:一是通过线线平行得到线面平行,二是通过面面平行得到线面平行. 答案:解法一:(I )直三棱柱ABC -A 1B 1C 1,底面三边长AC =3,BC =4AB =5,∴ AC ⊥BC ,且BC 1在平面ABC 内的射影为BC ,∴ AC ⊥BC 1; (II )设CB 1与C 1B 的交点为E ,连结DE ,∵ D 是AB 的中点,E 是BC 1的中点,∴ DE//AC 1,∵ DE ⊂平面C D B 1,AC 1⊄平面C D B 1,∴ AC 1//平面C D B 1;解法二:∵直三棱柱ABC -A 1B 1C 1底面三边长AC =3,BC =4,AB =5,∴AC 、BC 、C 1C 两两垂直,如图,以C 为坐标原点,直线CA 、CB 、C 1C 分别为x 轴、y轴、z 轴,建立空间直角坐标系,则C (0,0,0),A (3,0,0),C 1(0,0,4),B (0,4,0),B 1(0,4,4),D (23,2,0) (1)∵AC =(-3,0,0),1BC =(0,-4,0),∴AC •1BC =0,∴AC ⊥BC 1. (2)设CB 1与C 1B 的交战为E ,则E (0,2,2).∵DE =(-23,0,2),1AC =(-3,0,4),∴121AC DE =,∴DE ∥AC 1.A B C A B C E x yz4. 如图所示,四棱锥P —ABCD 中,AB ⊥AD ,CD ⊥AD ,PA ⊥底面ABCD ,PA=AD=CD=2AB=2,M 为PC 的中点.(1)求证:BM ∥平面PAD ;(2)在侧面PAD 内找一点N ,使MN ⊥平面PBD ;(3)求直线PC 与平面PBD 所成角的正弦.解析:本小题考查直线与平面平行,直线与平面垂直,二面角等基础知识,考查空间想象能力和推理论证能力.答案:(1)ΘM 是PC 的中点,取PD 的中点E ,则 ME CD 21,又AB CD 21 ∴四边形ABME 为平行四边形∴BM ∥EA ,PAD BM 平面⊄,PAD EA 平面⊂∴BM ∥PAD 平面(2)以A 为原点,以AB 、AD 、AP 所在直线为x 轴、y 轴、z 轴建立空间直角坐标系,如图,则())0,0,1B ,()0,2,2C ,()0,2,0D ,()2,0,0P ,()1,1,1M ,()1,1,0E在平面PAD 内设()z y N ,,0,()1,1,1---=→--z y MN ,()2,0,1-=→--PB ,()0,2,1-=→--DB 由→--→--⊥PB MN ∴0221=+--=⋅→--→--z PB MN ∴21=z由→--→--⊥DB MN ∴0221=+--=⋅→--→--y DB MN ∴21=y∴⎪⎭⎫ ⎝⎛21,21,0N ∴N 是AE 的中点,此时BD MN P 平面⊥(3)设直线PC 与平面PBD 所成的角为θ()2,2,2-=→--PC ,⎪⎭⎫ ⎝⎛---=→--21,21,1MN ,设→--→--MN PC ,为α 3226322cos -=⋅-=⋅=→--→--→--→--MN PC MNPC α 32cos sin =-=αθ 故直线PC 与平面PBD 所成角的正弦为32解法二: (1)ΘM 是PC 的中点,取PD 的中点E ,则ME CD 21,又AB CD 21 ∴四边形ABME 为平行四边形∴BM ∥EA ,PAD BM 平面⊄PAD EA 平面⊂∴BM ∥PAD 平面(2)由(1)知ABME 为平行四边形ABCD PA 底面⊥∴AB PA ⊥,又AD AB ⊥∴PAD AB 平面⊥ 同理PAD CD 平面⊥,PAD 平面⊂AE∴A E A B ⊥ ∴AB ME 为矩形 CD ∥ME ,PD CD ⊥,又A E PD ⊥ ∴PD ⊥ME ∴ABME 平面⊥PD PBD PD 平面⊂∴ABME PBD 平面平面⊥ 作EB ⊥MF 故PBD 平面⊥MFMF 交AE 于N ,在矩形ABME 内,1==ME AB ,2=AE∴32=MF ,22=NE N 为AE 的中点 ∴当点N 为AE 的中点时,BD MN P 平面⊥(3)由(2)知MF 为点M 到平面PBD 的距离,MPF ∠为直线PC 与平面PBD 所成的角,设为θ,32sin ==MP MF θ ∴直线PC 与平面PBD 所成的角的正弦值为32点评:(1)证明线面平行只需证明直线与平面内一条直线平行即可;(2)求斜线与平面所成的角只需在斜线上找一点作已知平面的垂线,斜线和射影所成的角,即为所求角;(3)证明线面垂直只需证此直线与平面内两条相交直线垂直变可.这些从证法中都能十分明显地体现出来考点三 求空间图形中的角与距离根据定义找出或作出所求的角与距离,然后通过解三角形等方法求值,注意“作、证、算”的有机统一.解题时注意各种角的范围:异面直线所成角的范围是0°<θ≤90°,其方法是平移法和补形法;直线与平面所成角的范围是0°≤θ≤90°,其解法是作垂线、找射影;二面角0°≤θ≤180°,其方法是:①定义法;②三垂线定理及其逆定理;③垂面法 另外也可借助空间向量求这三种角的大小.5. 如图,四棱锥P ABCD -中,侧面PDC 是边长为2的正三角形,且与底面垂直,底面ABCD 是60ADC ∠=o 的菱形,M 为PB 的中点.(Ⅰ)求PA 与底面ABCD 所成角的大小;(Ⅱ)求证:PA ⊥平面CDM ;(Ⅲ)求二面角D MC B --的余弦值.解析:求线面角关键是作垂线,找射影,求异面直线所成的角采用平 移法 求二面角的大小也可应用面积射影法,比较好的方法是向量法答案:(I)取DC 的中点O ,由ΔPDC 是正三角形,有PO ⊥DC . 又∵平面PDC ⊥底面ABCD ,∴PO ⊥平面ABCD 于O .连结OA ,则OA 是PA 在底面上的射影.∴∠PAO 就是PA 与底面所成角.∵∠ADC =60°,由已知ΔPCD 和ΔACD 是全等的正三角形,从而求得OA =OP =3∴∠PAO =45°.∴PA 与底面ABCD 可成角的大小为45°.(II)由底面ABCD 为菱形且∠ADC =60°,DC =2,DO =1,有OA ⊥DC . 建立空间直角坐标系如图, 则(3,0,0),(0,0,3),(0,1,0)A P D -, (3,2,0),(0,1,0)B C .由M 为PB 中点,∴33(1,M . ∴33((3,0,3),DM PA ==u u u u r u u u r (0,2,0)DC =u u u r . ∴333203)0PA DM ⋅=⨯-=u u u r u u u u r ,03200(3)0PA DC ⋅=⨯+⨯-=u u u r u u u r .∴PA ⊥DM ,PA ⊥DC . ∴PA ⊥平面DMC .(III)33(),(3,1,0)CM CB ==u u u u r u u u r .令平面BMC 的法向量(,,)n x y z =r , 则0n CM ⋅=u u u u r r ,从而x +z =0; ……①, 0n CB ⋅=u u u r r 30x y +=. ……②由①、②,取x =−1,则3,1y z =. ∴可取(3,1)n=-r . 由(II)知平面CDM 的法向量可取(3,0,3)PA =u u u r , ∴2310cos ,||||56n PA n PA n PA ⋅-<>=⋅u u u r r u u u r r u u u r r 10法二:(Ⅰ)方法同上(Ⅱ)取AP 的中点N ,连接MN ,由(Ⅰ)知,在菱形ABCD 中,由于60ADC ∠=o ,则AO CD ⊥,又PO CD ⊥,则CD APO ⊥平面,即CD PA ⊥,又在PAB ∆中,中位线//MN 12AB ,1//2CO AB ,则//MN CO , 则四边形OCMN 为Y ,所以//MC ON ,在APO ∆中,AO PO =,则ON AP ⊥,故AP MC ⊥而MC CD C =I ,则PA MCD ⊥平面(Ⅲ)由(Ⅱ)知MC PAB ⊥平面,则NMB ∠为二面角D MC B --的平面角, 在Rt PAB ∆中,易得PA=PB ===,cos AB PBA PB ∠===,cos cos()5NMB PBA π∠=-∠=-故,所求二面角的余弦值为5-点评:本题主要考查异面直线所成的角、线面角及二面角的一般求法,综合性较强 用平移法求异面直线所成的角,利用三垂线定理求作二面角的平面角,是常用的方法.6. 如图,在长方体1111ABCD A B C D -中,11,2,AD AA AB ===点E 在线段AB 上. (Ⅰ)求异面直线1D E 与1A D 所成的角;(Ⅱ)若二面角1D EC D --的大小为45︒,求点B 到平面1D EC 的距离.解析:本题涉及立体几何线面关系的有关知识, 本题实质上求角度和距离,在求此类问题中,要将这些量归结到三角形中,最好是直角三角形,这样有利1D A B CD E 1A 1B 1C于问题的解决,此外用向量也是一种比较好的方法.答案:解法一:(Ⅰ)连结1AD .由已知,11AA D D 是正方形,有11AD A D ⊥.∵AB ⊥平面11AA D D ,∴1AD 是1D E 在平面11AA D D 内的射影.根据三垂线定理,11AD D E ⊥得,则异面直线1D E 与1A D 所成的角为90︒. 作DF CE ⊥,垂足为F ,连结1D F ,则1CE D F ⊥所以1DFD ∠为二面角1D EC D --的平面角,145DFD ∠=︒.于是111,DF DD D F ==易得Rt Rt BCE CDF ∆≅∆,所以2CE CD ==,又1BC =,所以BE =. 设点B 到平面1D EC 的距离为h .∵1,B CED D BCE V V --=即1111113232CE D F h BE BC DD ⋅⋅⋅=⋅⋅⋅,∴11CE D F h BE BC DD ⋅⋅=⋅⋅,即=,∴4h =.故点B 到平面1D EC 解法二:分别以1,,DA DB DD 为x 轴、y 轴、z 轴,建立空间直角坐标系.(Ⅰ)由1(1,0,1)A ,得1(1,0,1)DA =u u u u r设(1,,0)E a ,又1(0,0,1)D ,则1(1,,1)D E a =-u u u u r .∵111010DA D E ⋅=+-=u u u u r u u u u r ∴11DA D E ⊥u u u u r u u u u r则异面直线1D E 与1A D 所成的角为90︒.(Ⅱ)(0,0,1)=m 为面DEC 的法向量,设(,,)x y z =n 为面1CED 的法向量,则(,,)x y z =n|||cos ,|cos 45||||2⋅<>===︒=m n m n m n ∴222z x y =+. ①由(0,2,0)C ,得1(0,2,1)DC =-u u u u r ,则1D C ⊥u u u u r n ,即10DC ⋅=u u u u r n ∴20y z -= ② 由①、②,可取(3,1,2)=n 又(1,0,0)CB =u u u r ,所以点B 到平面1D EC 的距离||36422CB d ⋅===u u u r n |n |. 点评:立体几何的内容就是空间的判断、推理、证明、角度和距离、面积与体积的计算,这是立体几何的重点内容,本题实质上求角度和距离,在求此类问题中,尽量要将这些量归结于三角形中,最好是直角三角形,这样计算起来,比较简单,此外用向量也是一种比较好的方法,不过建系一定要恰当,这样坐标才比较容易写出来.考点四 探索性问题7. 如图所示:边长为2的正方形ABFC 和高为2的直角梯形ADEF 所在的平面互相垂直且DE=2,ED//AF 且∠DAF =90°.(1)求BD 和面BEF 所成的角的余弦;(2)线段EF 上是否存在点P 使过P 、A 、C 三点的平面和直线DB 垂直,若存在,求EP 与PF 的比值;若不存在,说明理由.解析:1.先假设存在,再去推理,下结论: 2.运用推理证明计算得出结论,或先利用条件特例得出结论,然后再根据条件给出证明或计算. 答案:(1)因为AC 、AD 、AB 两两垂直,建立如图坐标系,则B (2,0,0),D (0,0,2),E (1,1,2),F (2,2,0), 则)0,2,0(),2,1,1(),0,0,2(=-==BF BE DB设平面BEF 的法向量x z y x n -=则),,,(0,02==++y z y ,则可取)0,1,2(=n ,∴向量)1,0,2(=n DB 和所成角的余弦为1010)2(21220222222=-++-+⋅. 即BD 和面BEF 所成的角的余弦1010. (2)假设线段EF 上存在点P 使过P 、A 、C 三点的平面和直线DB 垂直,不妨设EP 与PF 的比值为m ,则P 点坐标为),12,121,121(m m m m m +++++ 则向量=),12,121,121(m m m m m +++++,向量=CP ),12,11,121(mm m m ++-++ 所以21,012)2(12101212==+-++++++m m m m m m 所以. 点评:本题考查了线线关系,线面关系及其相关计算,本题采用探索式、开放式设问方式,对学生灵活运用知识解题提出了较高要求.8. 如图,在三棱锥V ABC -中,VC ABC ⊥底面,AC BC ⊥,D 是AB 的中点,且AC BC a ==,π02VDC θθ⎛⎫=<< ⎪⎝⎭∠.(I )求证:平面VAB ⊥平面VCD ;(II )试确定角θ的值,使得直线BC 与平面VAB 所成的角为π6. 解析:本例可利用综合法证明求解,也可用向量法求解.答案:解法1:(Ⅰ)AC BC a ==∵,ACB ∴△是等腰三角形,又D 是AB 的中点,CD AB ⊥∴,又VC ⊥底面ABC .VC AB ⊥∴.于是AB ⊥平面VCD .又AB ⊂平面VAB ,∴平面VAB ⊥平面VCD .(Ⅱ) 过点C 在平面VCD 内作CH VD ⊥于H ,则由(Ⅰ)知CD ⊥平面VAB . 连接BH ,于是CBH ∠就是直线BC 与平面VAB 所成的角. 依题意π6CBH ∠=,所以在CHD Rt △中,sin 2CH a θ=; 在BHC Rt △中,πsin 62a CH a ==,sin θ=∴. π02θ<<∵,π4θ=∴. 故当π4θ=时,直线BC 与平面VAB 所成的角为π6.解法2:(Ⅰ)以CA CB CV ,,所在的直线分别为x 轴、y 轴、z 轴,建立如图所示的空间直角坐标系,则(000)(00)(00)000tan 222a a C A a B a D V a θ⎛⎫⎛⎫⎪ ⎪ ⎪⎝⎭⎝⎭,,,,,,,,,,,,,,,于是,tan 222a a VD θ⎛⎫=- ⎪ ⎪⎝⎭u u u r ,,,022a a CD ⎛⎫= ⎪⎝⎭u u u r ,,,(0)AB a a =-u u u r ,,. 从而2211(0)0002222a a ABCD a a a a ⎛⎫=-=-++= ⎪⎝⎭u u u r u u u r ,,,,··,即AB CD ⊥.同理2211(0)tan 02222a a AB VD a a a a θ⎛⎫=-=-++ ⎪ ⎪⎝⎭u u u r u u u r ,,,,··即AB VD ⊥.又CD VD D =I ,AB ⊥∴平面VCD . 又AB ⊂平面VAB .∴平面VAB ⊥平面VCD .(Ⅱ)设平面VAB 的一个法向量为()x y z =,,n ,则由00AB VD ==u u u r,··nn .得0tan 0222ax ay a a x y θ-+=⎧⎪⎨+-=⎪⎩,.可取(11)θ=n ,又(00)BC a =-u u u r,,,于是πsin 62BC BC θ===u u u r u u u r n n ··,即sin 2θ=π02θ<<∵,π4θ∴=. 故交π4θ=时,直线BC 与平面VAB 所成的角为π6.解法3:(Ⅰ)以点D 为原点,以DC DB ,所在的直线分别为x 轴、y 轴,建立如图所示的空间直角坐标系,则(000)000000222D A a B a C a ⎛⎫⎛⎫⎛⎫-- ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭,,,,,,,,,,,,0tan 22V a θ⎛⎫- ⎪ ⎪⎝⎭,,,于是0tan 22DV a a θ⎛⎫=- ⎪ ⎪⎝⎭u u u r ,,,002DC ⎛⎫=- ⎪ ⎪⎝⎭u u u r ,,,(00)AB =u u u r ,.从而(00)AB DC =u u u r u u u r ,·0002a ⎛⎫-= ⎪ ⎪⎝⎭,,·,即AB DC ⊥.同理(00)0tan 0AB DV θ⎛⎫== ⎪ ⎪⎝⎭u u u r u u u r ,,·,即AB DV ⊥. 又DC DV D =I , AB ⊥∴平面VCD . 又AB ⊂平面VAB , ∴平面VAB ⊥平面VCD .(Ⅱ)设平面VAB 的一个法向量为()x y z =,,n ,则由00AB DV ==u u u r u u u r ,··n n ,得2022tan 022ay ax az θ⎧=⎪⎨-+=⎪⎩,. 可取(tan 01)n θ=,,,又220BC a a ⎛⎫=-- ⎪ ⎪⎝⎭u u u r ,,, 于是22tan π22sin sin 61tan a BC BC a θθθ===+u u u r u u u r n n ···, 即πππsin 0224θθθ=<<,,∵∴=. 故角π4θ=时, 即直线BC 与平面VAB 所成角为π6.点评:证明两平面垂直一般用面面垂直的判定定理,求线面角一是找线在平面上的射影在直角三角形中求解,但运用更多的是建空间直角坐标系,利用向量法求解考点五 折叠、展开问题9.已知正方形ABCD E 、F 分别是AB 、CD 的中点,将ADE V 沿DE 折起,如图所示,记二面角A DE C --的大小为(0)θθπ<<(I) 证明//BF 平面ADE ;(II)若ACD V 为正三角形,试判断点A 在平面BCDE 内的射影G 是否在直线EF 上,证明你的结论,并求角θ的余弦值分析:充分发挥空间想像能力,重点抓住不变的位置和数量关系,借助模型图形得出结论,并给出证明.解: (I)证明:EF 分别为正方形ABCD 得边AB 、CD 的中点,ADBCVxyAEB CF DG∴EB//FD,且EB=FD,∴四边形EBFD 为平行四边形∴BF//ED.,EF AED BF AED ⊂⊄Q 平面而平面,∴//BF 平面ADE(II)如右图,点A 在平面BCDE 内的射影G 在直线EF 上,过点A 作AG 垂直于平面BCDE,垂足为G,连结GC,GDQ ∆ACD 为正三角形,∴AC=AD. ∴CG=GD. Q G在CD 的垂直平分线上, ∴点A 在平面BCDE 内的射影G 在直线EF 上,过G 作GH 垂直于ED 于H,连结AH,则AH DE ⊥,所以AHD ∠为二面角A-DE-C 的平面角 即G AH θ∠=.设原正方体的边长为2a,连结AF,在折后图的∆AEF中,EF=2AE=2a,即∆AEF 为直角三角形, AG EF AE AF ⋅=⋅.2AG a ∴=在Rt ∆ADE 中, AH DE AE AD ⋅=⋅AH ∴=.GH ∴=,1cos 4GH AH θ== 点评:在平面图形翻折成空间图形的这类折叠问题中,一般来说,位于同一平面内的几何元素相对位置和数量关系不变:位于两个不同平面内的元素,位置和数量关系要发生变化,翻折问题常用的添辅助线的方法是作棱的垂线.关键要抓不变的量.考点六 球体与多面体的组合问题10.设棱锥M-ABCD 的底面是正方形,且MA =MD ,MA ⊥AB ,如果ΔAMD 的面积为1,试求能够放入这个棱锥的最大球的半径.分析:关键是找出球心所在的三角形,求出内切圆半径. 解: ∵AB ⊥AD ,AB ⊥MA , ∴AB ⊥平面MAD ,由此,面MAD ⊥面AC.记E 是AD 的中点,从而ME ⊥AD. ∴ME ⊥平面AC ,ME ⊥EF.设球O 是与平面MAD 、平面AC 、平面MBC 都相切的球. 不妨设O ∈平面MEF ,于是O 是ΔMEF 的内心. 设球O 的半径为r ,则r =MFEM EF S MEF++△2设AD =EF =a,∵S ΔAMD =1. ∴ME =a 2.MF =22)2(aa +, r =22)2(22aa a a +++≤2222+=2-1. 当且仅当a =a2,即a =2时,等号成立.∴当AD =ME =2时,满足条件的球最大半径为2-1.点评:涉及球与棱柱、棱锥的切接问题时一般过球心及多面体中的特殊点或线作截面,把空间问题化归为平面问题,再利用平面几何知识寻找几何体中元素间的关系.注意多边形内切圆半径与面积和周长间的关系;多面体内切球半径与体积和表面积间的关系. 三、方法总结1.位置关系:(1)两条异面直线相互垂直证明方法:○1证明两条异面直线所成角为90º;○2证明两条异面直线的方向量相互垂直.(2)直线和平面相互平行证明方法:○1证明直线和这个平面内的一条直线相互平行;○2证明这条直线的方向向量和这个平面内的一个向量相互平行;○3证明这条直线的方向向量和这个平面的法向量相互垂直.(3)直线和平面垂直证明方法:○1证明直线和平面内两条相交直线都垂直,○2证明直线的方向量与这个平面内不共线的两个向量都垂直;○3证明直线的方向量与这个平面的法向量相互平行.(4)平面和平面相互垂直证明方法:○1证明这两个平面所成二面角的平面角为90º;○2证明一个平面内的一条直线垂直于另外一个平面;○3证明两个平面的法向量相互垂直.2.求距离:求距离的重点在点到平面的距离,直线到平面的距离和两个平面的距离可以转化成点到平面的距离,一个点到平面的距离也可以转化成另外一个点到这个平面的距离.(1)两条异面直线的距离。
立体几何证明方法汇总
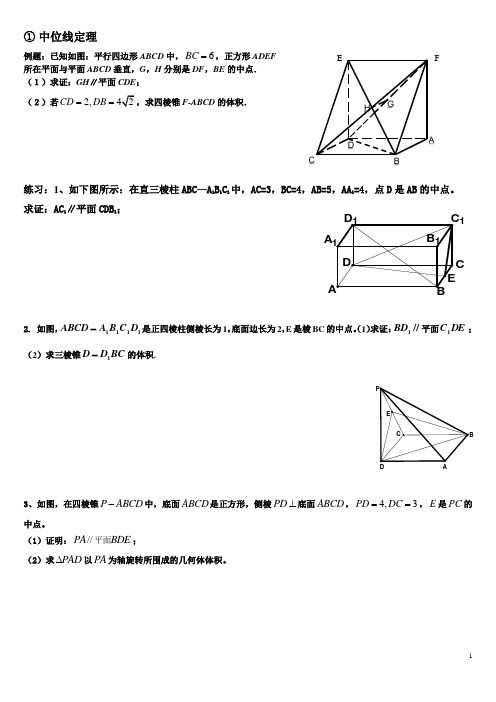
① 中位线定理例题:已知如图:平行四边形ABCD 中,6BC =,正方形ADEF 所在平面与平面ABCD 垂直,G ,H 分别是DF ,BE的中点. (1)求证:GH ∥平面CDE ;(2)若2,CD DB ==,求四棱锥F-ABCD 的体积.练习:1、如下图所示:在直三棱柱ABC —A 1B 1C 1中,AC=3,BC=4,AB=5,AA 1=4,点D 是AB 的中点。
求证:AC 1∥平面CDB 1;2. 如图,1111D C B A ABCD -是正四棱柱侧棱长为1,底面边长为2,E 是棱BC 的中点。
(1)求证://1BD 平面DE C 1;(2)求三棱锥BC D D 1-的体积.3、如图,在四棱锥P ABCD -中,底面ABCD 是正方形,侧棱PD ⊥底面ABCD ,4,3PD DC ==,E 是PC 的中点。
(1)证明://PA BDE 平面;(2)求PAD ∆以PA 为轴旋转所围成的几何体体积。
A 1C _ H_ G_ D_ A_ B_ CEFGPABCDFEA B C D EF例2、 如图, 在矩形ABCD 中,2AB BC = , ,P Q 分别为线段,AB CD 的中点, EP ⊥平面ABCD .求证: AQ ∥平面CEP ;(利用平行四边形)练习:①如图,PA 垂直于矩形ABCD 所在的平面,E 、F 分别是AB 、PD 的中点。
求证:AF ∥平面PCE ;②如图,已知P 是矩形ABCD 所在平面外一点,ABCD 平面PD ⊥,M ,N 分别是AB ,PC 中点。
求证://PAD MN 平面PABCDMN③ 如图,已知AB ⊥平面ACD ,DE//AB ,△ACD 是正三角形,AD = DE = 2AB ,且F 是CD 的中点.⑴求证:AF//平面BCE ;④、已知正方体ABCD-1111D C B A ,O 是底ABCD 对角线的交点.求证://1O C 面11AB D .D 1C 1B 1A 1A BCDEF③比例关系例题3、P 是平行四边形ABCD 平面外一点,M 、N 分别是PB 、BC 上的点,且NCBN PM BM =,求证:MN//平面PCD(利用比例关系)练习:如图,四边形ABCD 为正方形,⊥EA 平面ABCD ,//EF AB ,=4,=2,=1AB AE EF .(Ⅱ)若点M 在线段AC 上,且满足14CM CA =, 求证://EM 平面FBC ;④面面平行-线面平行例题4、如图,矩形ABCD 和梯形BEFC 所在平面互相垂直,BE//CF ,∠BCF=∠CEF=︒90,AD=3,EF=2。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
E BCD AP① 中位线定理例题:已知如图:平行四边形ABCD 中,6BC =,正方形ADEF 所在平面与平面ABCD 垂直,G ,H 分别是DF ,BE 的中点. (1)求证:GH ∥平面CDE ;(2)若2,42CD DB ==,求四棱锥F-ABCD 的体积.练习:1、如下图所示:在直三棱柱ABC —A 1B 1C 1中,AC=3,BC=4,AB=5,AA 1=4,点D 是AB 的中点。
求证:AC 1∥平面CDB 1;2. 如图,1111D C B A ABCD -是正四棱柱侧棱长为1,底面边长为2,E 是棱BC 的中点。
(1)求证://1BD 平面DE C 1;(2)求三棱锥BC D D 1-的体积.3、如图,在四棱锥P ABCD -中,底面ABCD 是正方形,侧棱PD ⊥底面ABCD ,4,3PD DC ==,E 是PC 的中点。
(1)证明://PA BDE 平面;(2)求PAD ∆以PA 为轴旋转所围成的几何体体积。
EA 1B 1C 1D 1DC B A_ H_ G_ D_ A_ B_ CEFGPABCDFEA B C D EF例2、 如图, 在矩形ABCD 中,2AB BC = , ,P Q 分别为线段,AB CD 的中点, EP ⊥平面ABCD .求证: AQ ∥平面CEP ;(利用平行四边形)练习:①如图,PA 垂直于矩形ABCD 所在的平面,E 、F 分别是AB 、PD 的中点。
求证:AF ∥平面PCE ;②如图,已知P 是矩形ABCD 所在平面外一点,ABCD 平面PD ⊥,M ,N 分别是AB ,PC 中点。
求证://PAD MN 平面PABCDMN③ 如图,已知AB ⊥平面ACD ,DE//AB ,△ACD 是正三角形,AD = DE = 2AB ,且F 是CD 的中点.⑴求证:AF//平面BCE ;④、已知正方体ABCD-1111D C B A ,O 是底ABCD 对角线的交点.求证://1O C 面11AB D .D 1C 1B 1A 1A BCDEF③比例关系例题3、P 是平行四边形ABCD 平面外一点,M 、N 分别是PB 、BC 上的点,且NCBN PM BM =,求证:MN//平面PCD(利用比例关系)练习:如图,四边形ABCD 为正方形,⊥EA 平面ABCD ,//EF AB ,=4,=2,=1AB AE EF .(Ⅱ)若点M 在线段AC 上,且满足14CM CA =, 求证://EM 平面FBC ;④面面平行-线面平行例题4、如图,矩形ABCD 和梯形BEFC 所在平面互相垂直,BE//CF ,∠BCF=∠CEF=︒90,AD=3,EF=2。
(Ⅰ)求证:平面ABE//平面CDF(II )求证:AE//平面DCF ;(利用面面平行-线面平行)练习:1、如图所示,四棱锥P ABCD -中,底面ABCD 为正方形,PD ⊥平面ABCD ,2PD AB ==,E ,F ,G 分别为PC 、PD 、BC 的中点.(1)求证:;EFG PA 面//; (2)求三棱锥P EFG -的体积. D ACBE F M1A 1C 1B EFGACBEBACNDFM2、如图,在直三棱柱111ABC A B C -中,090ACB ∠=,,,E F G 分别是11,,AA AC BB 的中点,且1CG C G ⊥.(Ⅰ)求证://CG BEF 平面;3、如图所示,正方形ADEF 与梯形ABCD 所在的平面互相垂直, ,//,22AD CD AB CD CD AB AD ⊥==. 在EC 上找一点M ,使得//BM 平面ADEF ,请确定M 点的位置,并给出证明.4、(2012山东文)如图,几何体E ABCD -是四棱锥,△ABD 为正三角形,,CB CD EC BD =⊥.(Ⅰ)求证:BE DE =;(Ⅱ)若∠120BCD =︒,M 为线段AE 的中点, 求证:DM ∥平面BEC .例题: 如图,已知四棱锥ABCD P -。
若底面ABCD 为平行四 边形,E 为PC 的中点,在DE 上取点F ,过AP 和点F 的平面与 平面BDE 的交线为FG ,求证:FG AP //。
证明:连AC 与BD ,设交点为O ,连OE 。
练习:1、如图,在四棱锥P ABCD -中,侧面PAD 是正三角形,且与底面ABCD 垂直,底面ABCD 是边长为2的菱形,60BAD ∠=︒,N 是PB 中点,过A 、N 、D 三点的平面交PC 于M .求证://AD MN ;2、(2012浙江高考)如图,在侧棱锥垂直底面的四棱锥ABCD-A 1B 1C 1D 1中,AD ∥BC ,AD ⊥AB ,AB=2。
AD=2,BC=4,AA 1=2,E 是DD 1的中点,F 是平面B 1C 1E 与直线AA 1的交点。
(1)证明:EF ∥A 1D 1;3.如图,四边形ABCD 是矩形,平面ABCD ⊥平面BCE ,BE ⊥EC. (1) 求证:平面AEC ⊥平面ABE ;(面面垂直性质) (2) 点F 在BE 上,若DE//平面ACF ,求BE BF 的值。
(线面平行的性质 21) DABC P MN例、如图,在正方体1111ABCD A B C D 中,E 、F 、G 分别是AB 、AD 、11C D 的中点.求证:平面1D EF ∥平面BDG .练习:如图所示,在正方体ABCD-1111D C B A 中,E 、F 、G 、H 分别是BC 、CC 1、C 1D 1、A 1A 的中点.求证:(1)EG ∥平面BB 1D 1D ;(2)平面BDF ∥平面B 1D 1H .例题:已知在正方体ABCD-1111D C B A 中,E,F 分别是1111A D D C 和上的点,点P 在正方体外,平面PEF 与正方体相交于AC ,求证:ABCD //平面EFABCDA1B1C1 D1ACBPACBDPM FE ABCD G①菱形的对角线互相垂直:例题。
已知E ,F 分别是正方形ABCD 边AD ,AB 的中点,EF 交AC 于M ,GC 垂直于ABCD 所在平面。
求证:EF ⊥平面GMC .练习:如图ABCD-1111D C B A 是底面为正方形的长方体,求证:(1)BD ⊥平面A ACC 1 (2)1AC BD ⊥②等腰三角形底边的中线垂直底边例1、 如图,在三棱锥P ABC -中,2AC BC ==,90ACB ∠=,AP BP AB ==,PC AC ⊥.求证:PC AB ⊥;练习:1、在三棱锥A-BCD 中,AB=AC,BD=DC,求证:AD BC ⊥ABCDABC D③圆的直径所对的圆周角为直角例题3、如图AB 是圆O 的直径,C 是圆周上异于A 、B 的任意一点,⊥PA 平面ABC ,(1)图中共有多少个直角三角形?(2)若PC AH ⊥,且AH 与PC 交于H ,求证:AH ⊥平面PBC.④利用勾股定理例4、在长方体1111D C B A ABCD -中,底面ABCD 是边长为1的正方形,侧棱21=AA ,E 是侧棱1BB 的中点。
求证:AE ⊥平面11A D E ;证明:1111D C B A ABCD - 为长方体,练习:如图,四棱锥P-ABCD 的底面是边长为1的正方形,2,1,==⊥PD PA CD PA ,求证:(1)⊥PA 平面ABCD(2)求四棱锥P-ABCD 的体积.⑤间接法,用线面垂直的性质定理(b l b b l ⊥⇒⊂⊥α,)例题:如图,四棱锥P-ABCD 中,底面ABCD 为平行四边形,︒=∠60DAB ,ABCD PD AD AB 底面⊥=,2,证明:BD PA ⊥;练习1:如图,在直三棱柱111ABC A B C -中,AC =3, BC =4,AB =5,14AA =,点D 是AB 的中点。
(Ⅰ)求证:1AC BC ⊥;D 1C 1B 1A 1EDCBABC DPA PACBHOa2aBD CAp练习2:如图,四边形ABCD为矩形,⊥BC平面ABE,F为CE上的点,且⊥BF平面ACE. 求证:BEAE⊥;证明:因为ABEBC平面⊥,ABEAE平面⊂,例1如图,AB是⊙O的直径,PA垂直⊙O所在的平面,C是圆上不同于A,B的任意一点,求证:平面PAC⊥平面PBC.练习1:如图,棱柱111ABC A B C-的侧面11BCC B是菱形,11B C A B⊥2、如图,在直三棱柱111ABC A B C-中,E、F分别是1A B、1A C的中点,点D在11B C上,11A DB C⊥。
求证:(1)EF∥平面ABC;(2)平面1A FD⊥平面11BB C C.3、如图, ABCD是正方形,SA⊥平面ABCD,BK⊥SC于K,连结DK,求证(1)平面SBC⊥平面KBDsACKDABCDEF例1:如图,在四棱锥P—ABCD中,侧面PAD⊥底面ABCD,侧棱PA=PD,O为AD中点.,求证:PO⊥平面ABCD;例2:如图,在四棱锥P ABCD-中,底面ABCD是060DAB∠=且边长为a的菱形,侧面PAD是等边三角形,且平面PAD垂直于底面ABCD.(1)若G为AD的中点,求证:BG⊥平面PAD;(2)求证:AD PB⊥;练习:1、如图AB是圆O的直径,C是圆周上异于A、B的任意一点,⊥PA平面ABC,(1)图中共有多少个直角三角形?(2)若PCAH⊥,且AH与PC交于H,求证:平面PAC⊥平面PBC.(3) AH⊥平面PBC 2、在四棱锥ABCDP-中,平面PAD⊥平面ABCD,AB=AD,∠BAD=60°,E、F分别是AP、AD的中点.求证:平面BEF⊥平面PAD3、如图,正方形ABCD所在平面与以AB为直径的半圆O所在平面ABEF互相垂直,P为半圆周上异于A,B两点的任一点,求证:○1直线AP⊥平面PBC。
②平面PBC⊥平面APCA BHOFEACDBPCF GB DE A C4、如图,三角形ABC 中,AC=BC=AB 22,ABED 是边长为a 的正方形,平面ABED ⊥底面ABC ,且,若G 、F 分别是EC 、BD 的中点,(Ⅰ)求证:GF//底面ABC ; (Ⅱ)求几何体ADEBC 的体积V 。
5、如图,AB C D ,,,为空间四点.在ABC △中, 22AB AC BC ===,.等边三角形ADB 以AB 为轴运动.(Ⅰ)当平面ADB ⊥平面ABC 时,求CD ;五、体积问题1. 如图,1111D C B A ABCD -是正四棱柱侧棱长为1,底面边长为2,E 是棱BC 的中点。
(1)求证://1BD 平面DE C 1; (2)求三棱锥BC D D 1-的体积.EA 1B 1C 1D 1D C B A DBACA 1B 1C 1D 1ABCDEABCDOP练习1:三棱锥P ABC -中,PAC ∆和PBC ∆都是边长为2的等边三角形,2AB =,O D 、分别是AB PB 、的中点.(1)求证://OD 平面PAC (2)求证:平面PAB ⊥平面ABC ; (3)求三棱锥A PBC -的体积.2、如图,长方体1111D C B A ABCD -中,11==AA AB ,2=AD ,E 是BC 的中点. (I)求证:平面AE A 1⊥平面DE D 1; (II)求三棱锥DE A A 1-的体积.3、如图,在四棱锥P-ABCD 中,,垂直于底面ABCD PD 底面ABCD 是直角梯形, ,90,//o BAD AB DC =∠且4222====PD DC AD AB (单位:cm ),E为PA的中点。
