多面体与旋转体习题

合集下载

高考数学多面体与旋转体选择题

高考数学多面体与旋转体选择题1. 下列关于多面体的说法正确的是：A. 所有多面体的对角线都是相交的B. 所有多面体的内角和都是360°C. 所有多面体的对角线都相交于一点D. 所有多面体的边数都大于22. 下列关于旋转体的说法正确的是：A. 所有旋转体的体积都是相等的B. 所有旋转体的表面积都是相等的C. 所有旋转体的轴都是垂直的D. 所有旋转体的中心都是对称的3. 下列哪个图形是旋转体？A. 圆锥B. 圆柱C. 圆台D. 球体4. 下列关于圆锥的说法正确的是：A. 圆锥的底面半径等于母线长B. 圆锥的底面半径小于母线长C. 圆锥的底面半径大于母线长D. 圆锥的底面半径与母线长无关5. 下列关于圆柱的说法正确的是：A. 圆柱的底面半径等于母线长B. 圆柱的底面半径小于母线长C. 圆柱的底面半径大于母线长D. 圆柱的底面半径与母线长无关6. 下列关于圆台的说法正确的是：A. 圆台的底面半径等于母线长B. 圆台的底面半径小于母线长C. 圆台的底面半径大于母线长D. 圆台的底面半径与母线长无关7. 下列关于球体的说法正确的是：A. 球体的直径等于半径的两倍B. 球体的直径小于半径的两倍C. 球体的直径大于半径的两倍D. 球体的直径与半径无关8. 下列哪个图形不是旋转体？A. 圆锥B. 圆柱C. 圆台D. 圆环9. 下列关于多面体的内角和的说法正确的是：A. 所有多面体的内角和都是360°B. 所有多面体的内角和都是480°C. 所有多面体的内角和都是540°D. 所有多面体的内角和都是600°10. 下列关于旋转体的体积的说法正确的是：A. 所有旋转体的体积都是相等的B. 所有旋转体的体积都与底面半径和高度有关C. 所有旋转体的体积都与底面半径无关D. 所有旋转体的体积都与高度无关11. 下列哪个图形是多面体？A. 圆锥B. 圆柱C. 圆台D. 球体12. 下列关于多面体的对角线说法正确的是：A. 所有多面体的对角线都是相交的B. 所有多面体的对角线都相交于一点C. 所有多面体的对角线都不相交D. 所有多面体的对角线都与顶点无关13. 下列关于旋转体的表面积的说法正确的是：A. 所有旋转体的表面积都是相等的B. 所有旋转体的表面积都与底面半径和高度有关C. 所有旋转体的表面积都与底面半径无关D. 所有旋转体的表面积都与高度无关14. 下列哪个图形是旋转体？A. 圆锥B. 圆柱C. 圆台D. 圆环15. 下列关于多面体的边数说法正确的是：A. 所有多面体的边数都大于2B. 所有多面体的边数都等于2C. 所有多面体的边数都小于2D. 所有多面体的边数都与顶点无关16. 下列关于旋转体的轴的说法正确的是：A. 所有旋转体的轴都是垂直的B. 所有旋转体的轴都与底面垂直C. 所有旋转体的轴都与高度垂直D. 所有旋转体的轴都与底面和高度无关17. 下列关于多面体的顶点说法正确的是：A. 所有多面体的顶点都位于对角线上B. 所有多面体的顶点都位于底面上C. 所有多面体的顶点都位于侧面D. 所有多面体的顶点都与对角线无关18. 下列关于旋转体的中心说法正确的是：A. 所有旋转体的中心都是对称的B. 所有旋转体的中心都与底面中心重合C. 所有旋转体的中心都与高度中心重合D. 所有旋转体的中心都与底面和高度无关19. 下列哪个图形是多面体？A. 圆锥B. 圆柱C. 圆台D. 球体20. 下列关于多面体的内角和的说法正确的是：A. 所有多面体的内角和都是360°B. 所有多面体的内角和都是480°C. 所有多面体的内角和都是540°D. 所有多面体的内角和都是600°21. 下列关于旋转体的体积的说法正确的是：A. 所有旋转体的体积都是相等的B. 所有旋转体的体积都与底面半径和高度有关C. 所有旋转体的体积都与底面半径无关D. 所有旋转体的体积都与高度无关22. 下列哪个图形是旋转体？A. 圆锥B. 圆柱C. 圆台D. 圆环23. 下列关于多面体的对角线说法正确的是：A. 所有多面体的对角线都是相交的B. 所有多面体的对角线都相交于一点C. 所有多面体的对角线都不相交D. 所有多面体的对角线都与顶点无关24. 下列关于旋转体的表面积的说法正确的是：A. 所有旋转体的表面积都是相等的B. 所有旋转体的表面积都与底面半径和高度有关C. 所有旋转体的表面积都与底面半径无关D. 所有旋转体的表面积都与高度无关25. 下列哪个图形是多面体？A. 圆锥B. 圆柱C. 圆台D. 球体26. 下列关于多面体的边数说法正确的是：A. 所有多面体的边数都大于2B. 所有多面体的边数都等于2C. 所有多面体的边数都小于2D. 所有多面体的边数都与顶点无关27. 下列关于旋转体的轴的说法正确的是：A. 所有旋转体的轴都是垂直的B. 所有旋转体的轴都与底面垂直C. 所有旋转体的轴都与高度垂直D. 所有旋转体的轴都与底面和高度无关28. 下列关于多面体的顶点说法正确的是：A. 所有多面体的顶点都位于对角线上B. 所有多面体的顶点都位于底面上C. 所有多面体的顶点都位于侧面D. 所有多面体的顶点都与对角线无关29. 下列关于旋转体的中心说法正确的是：A. 所有旋转体的中心都是对称的B. 所有旋转体的中心都与底面中心重合C. 所有旋转体的中心都与高度中心重合D. 所有旋转体的中心都与底面和高度无关30. 下列哪个图形是多面体？A. 圆锥B. 圆柱C. 圆台D. 球体31. 下列关于多面体的内角和的说法正确的是：A. 所有多面体的内角和都是360°B. 所有多面体的内角和都是480°C. 所有多面体的内角和都是540°D. 所有多面体的内角和都是600°32. 下列关于旋转体的体积的说法正确的是：A. 所有旋转体的体积都是相等的B. 所有旋转体的体积都与底面半径和高度有关C. 所有旋转体的体积都与底面半径无关D. 所有旋转体的体积都与高度无关33. 下列哪个图形是旋转体？A. 圆锥B. 圆柱C. 圆台D. 圆环34. 下列关于多面体的对角线说法正确的是：A. 所有多面体的对角线都是相交的B. 所有多面体的对角线都相交于一点C. 所有多面体的对角线都不相交D. 所有多面体的对角线都与顶点无关35. 下列关于旋转体的表面积的说法正确的是：A. 所有旋转体的表面积都是相等的B. 所有旋转体的表面积都与底面半径和高度有关C. 所有旋转体的表面积都与底面半径无关D. 所有旋转体的表面积都与高度无关36. 下列哪个图形是多面体？A. 圆锥B. 圆柱C. 圆台D. 球体37. 下列关于多面体的边数说法正确的是：A. 所有多面体的边数都大于2B. 所有多面体的边数都等于2C. 所有多面体的边数都小于2D. 所有多面体的边数都与顶点无关38. 下列关于旋转体的轴的说法正确的是：A. 所有旋转体的轴都是垂直的B. 所有旋转体的轴都与底面垂直C. 所有旋转体的轴都与高度垂直D. 所有旋转体的轴都与底面和高度无关39. 下列关于多面体的顶点说法正确的是：A. 所有多面体的顶点都位于对角线上B. 所有多面体的顶点都位于底面上C. 所有多面体的顶点都位于侧面D. 所有多面体的顶点都与对角线无关40. 下列关于旋转体的中心说法正确的是：A. 所有旋转体的中心都是对称的B. 所有旋转体的中心都与底面中心重合C. 所有旋转体的中心都与高度中心重合D. 所有旋转体的中心都与底面和高度无关41. 下列哪个图形是多面体？A. 圆锥B. 圆柱C. 圆台D. 球体42. 下列关于多面体的内角和的说法正确的是：A. 所有多面体的内角和都是360°B. 所有多面体的内角和都是480°C. 所有多面体的内角和都是540°D. 所有多面体的内角和都是600°43. 下列关于旋转体的体积的说法正确的是：A. 所有旋转体的体积都是相等的B. 所有旋转体的体积都与底面半径和高度有关C. 所有旋转体的体积都与底面半径无关D. 所有旋转体的体积都与高度无关44. 下列哪个图形是旋转体？A. 圆锥B. 圆柱C. 圆台D. 圆环45. 下列关于多面体的对角线说法正确的是：A. 所有多面体的对角线都是相交的B. 所有多面体的对角线都相交于一点C. 所有多面体的对角线都不相交D. 所有多面体的对角线都与顶点无关46. 下列关于旋转体的表面积的说法正确的是：A. 所有旋转体的表面积都是相等的B. 所有旋转体的表面积都与底面半径和高度有关C. 所有旋转体的表面积都与底面半径无关D. 所有旋转体的表面积都与高度无关47. 下列哪个图形是多面体？A. 圆锥B. 圆柱C. 圆台D. 球体48. 下列关于多面体的边数说法正确的是：A. 所有多面体的边数都大于2B. 所有多面体的边数都等于2C. 所有多面体的边数都小于2D. 所有多面体的边数都与顶点无关49. 下列关于旋转体的轴的说法正确的是：A. 所有旋转体的轴都是垂直的B. 所有旋转体的轴都与底面垂直C. 所有旋转体的轴都与高度垂直D. 所有旋转体的轴都与底面和高度无关50. 下列关于多面体的顶点说法正确的是：A. 所有多面体的顶点都位于对角线上B. 所有多面体的顶点都位于底面上C. 所有多面体的顶点都位于侧面D. 所有多面体的顶点都与对角线无关。

多面体和旋转体

多面体和旋转体【单项选择】１．如图，在多面体ABC-A 1B 1C 1中，AB>A 1B 1。

给出如下两个命题：甲：AB ∥A 1B 1，BC ∥B 1C 1；乙：多面体ABC-A1B 1C 1是棱台那么，命题甲是命题乙成立的( )。

A ．充分不必要条件B ．必要不充分条件C ．充分且必要条件D ．既不充分也不必要条件２．如图，圆台 OO' 中，轴截面 ABCD 垂直于轴截面 A'B'C'D'，且 OO'∶AB ∶CD = 1∶2∶4，则异面直线 B'D 与 AO' 所成角的余弦值是( )。

A ．63 B ．33 C ．32 D ．62３．如图，圆柱的高为 2m ，底面半径为 3m ，AE 和 DF 是两条母线，ABCD 为正方形，点 E 、F 、B 、C 在下底面圆周上，则以 A 、B 、C 、D 、E 、F 为顶点的多面体的体积是( )。

A ．165m3B ．85m3C ．5316m3 D ．538m3４．在等腰直角三角形 ABC 中，AC = BC = a ，O 为斜边 AB 的中点。

沿 OC 把 △BOC 折起，使 AB = a ，则三棱锥B-OAC 的体积是( )。

A ．243a 3B ．241a 3C ．121a 3 D ．242a 3５．一个正三棱台上、下底面的边长分别为 a 、b ，高为 h ，且侧面积等于两底面面积之和，则下列关系正确的是( )。

A ．h 1 = b a +1B ．h 1 = a 1 + b 1C ．a 1 = b 1 + h 1D ．b 1 = a1+ h 1６．母线长为 1 的圆锥体积最大时，其侧面展开图圆心角φ等于( )。

A ．322π B ．332π C ．2π D ．362π７．设正方体的全面积为24cm 2，一个球内切于该正方体，那么，这个球的体积是( )。

A ．6πcm 3B ．34πcm 3C ．38πcm 3 D ．332πcm 3８．设过长方体同一个顶点的三个面的对角线长分别是a 、b 、c ，那么这个长方体的对角线长是( )。

高考数学多面体与旋转体选择题

高考数学多面体与旋转体选择题1. 已知三棱锥S-ABC的底面ABC是边长为a的正三角形，高SD=2，点E、F、G分别是棱SA、SB、SC的中点，且EF=4，求三棱锥S-ABC 的体积。

2. 设四棱锥P-ABCD的底面ABCD是边长为a的正方形，侧棱PD=3，点E、F、G、H分别是棱PA、PB、PC、PD的中点，且EF=4，求四棱锥P-ABCD的体积。

3. 已知圆锥的底面半径为r，高为h，求圆锥的全面积。

4. 已知圆台的上下底面半径分别为r1和r2，高为h，求圆台的全面积。

5. 已知球体的直径为d，求球体的表面积。

6. 已知球的半径为r，求球的体积。

7. 已知球体的半径为r，求球体的表面积和体积。

8. 已知圆柱的底面半径为r，高为h，求圆柱的全面积。

9. 已知圆柱的底面半径为r，高为h，求圆柱的体积。

10. 已知圆柱的底面半径为r，高为h，求圆柱的表面积和体积。

11. 已知圆锥的底面半径为r，高为h，求圆锥的表面积。

12. 已知圆锥的底面半径为r，高为h，求圆锥的体积。

13. 已知圆锥的底面半径为r，高为h，求圆锥的表面积和体积。

14. 已知圆台的上下底面半径分别为r1和r2，高为h，求圆台的表面积。

15. 已知圆台的上下底面半径分别为r1和r2，高为h，求圆台的体积。

16. 已知圆台的上下底面半径分别为r1和r2，高为h，求圆台的表面积和体积。

17. 已知球的半径为r，求球的表面积和体积。

19. 已知球的半径为r，求球的表面积和体积。

20. 已知球的半径为r，求球的表面积和体积。

21. 已知球的半径为r，求球的表面积和体积。

22. 已知球的半径为r，求球的表面积和体积。

23. 已知球的半径为r，求球的表面积和体积。

24. 已知球的半径为r，求球的表面积和体积。

25. 已知球的半径为r，求球的表面积和体积。

26. 已知球的半径为r，求球的表面积和体积。

27. 已知球的半径为r，求球的表面积和体积。

多面体与旋转体的有关问题

如图, 分别是边长为2的正方形例2 如图 E, F分别是边长为的正方形分别是边长为的正方形ABCD的的的中点, 边BC, CD的中点沿图中虚线折起来它能围成怎的中点沿图中虚线折起来,它能围成怎样的几何体? 样的几何体
A D
F
D BO C
2 A
5 E
B
E
C
1
1
5
2
F
(1) 求它的体积和表面积求它的体积和表面积; (2) 求以求以AEF为底面的几何体的高为底面的几何体的高. 为底面的几何体的高 (3)求其外接球的半径求其外接球的半径r. 求其外接球的半径
6 6 r= a R= a 12 4
O H
A B
C
练习: 三棱锥A-BCD中, AB = CD = 6, 其余各棱练习三棱锥中的长多是5. 求三棱锥内切球的半径. 的长多是求三棱锥内切球的半径
5. 半球的半径为，一正方体的四个顶点在半半球的半径为R，球的底面上，另四个顶点在球面上，球的底面上，另四个顶点在球面上，求正方体的棱长. 的棱长
P E
P
F C E
C A B
A B
如图所示是一个奖杯的三视图，如图所示是一个奖杯的三视图，试根据奖杯的三视图计算它的表面积和体积
4
20
8 4
2
20 10
题组五:有关三视图问题题组五有关三视图问题
8 16
广东•理题如图6所示等腰△ 所示，例3（07广东理•题19 ）如图所示，等腰△ABC （广东的底边AB=6 6 ，高CD=3，点E是线段上异于是线段BD上异于的底边，是线段的动点.点在边上边上，点B、D的动点点F在BC边上，且EF⊥AB.现沿、的动点 ⊥ 现沿 EF将△BEF折起到△PEF的位置，使PE⊥AE。折起到△ 的位置，将折起到的位置 ⊥ 。表示四棱锥P 的体积。记BE＝x，V(x)表示四棱锥－ACFE的体积。＝，表示四棱锥的体积的表达式；（Ⅰ）求V(x)的表达式；的表达式为何值时，取得最大值？（Ⅱ）当x为何值时，V(x)取得最大值？为何值时取得最大值取得最大值时，（Ⅲ）当V(x)取得最大值时，求异面直线与PF 取得最大值时求异面直线AC与所成角的余弦值；所成角的余弦值；

立体几何测试题(多面体与旋转体)

立体几何测试题（多面体与旋转体）1、一个四棱柱是长方体的充要条件是（）A 、底面是矩形B 、侧面是正方形C 、侧面和底面都是矩形D 、侧面和底面都是正方形 2、长方体共顶点的三个面的面积分别是22cm ，62cm 和92cm ，那么这个长方体的体积为（）A 、633cmB 、363cmC 、73cmD 、83cm3、对角线长为d 的正方体的棱长为（）A 、d 31 B 、d 3 C 、d )13(- D 、d 33 4、长方体的12条棱的总长度为56m ，表面积为1122m ，那么长方体的对角线长为（）A 、143mB 、67mC 、212mD 、9m 5、如果直棱柱的底面是菱形，它的高是9cm ，它的两条对角线分别与底面成o 60角和o 45角，那么这个棱柱的体积是（） A 、323243cm B 、33243cm C 、323729cm D 、33729cm 6、在斜三棱柱中，各棱长都是a ，且有一组共顶点的三条棱两两夹角都等于60°，那么这个棱柱的全面积是（） A 、2233a B 、232a C 、2)13(a + D 、2)1233(a + 7、已知正六棱柱底面的边长和高都等于a ，那么最大对角截面的面积是（）A 、22aB 、23aC 、232aD 、223a8、三棱锥的三条侧棱两两互相垂直，各侧棱与底面所成的角彼此相等，那么顶点在底面的射影是底面三角形的（）A 、垂心但不是内心B 、内心但不是垂心C 、外心但不是重心D 、垂心又是重心9、三棱锥P-ABC 的侧棱两两互相垂直，且PA=1，PB=3，PC=6，那么∠ABC=（）A 、o 30B 、o 60C 、o 45D 、o 7510、如果正三棱锥的侧棱长为2a ，底面周长为9a ，那么这个棱锥的高为（） A 、 a B 、2a C 、a 23 D 、a 2311、已知三棱锥各侧面与底面所成二面角彼此相等，那么顶点在底面上的射影，一定是底面三角形的（） A 、内心 B 、外心 C 、垂心 D 、重心 12、一个棱锥被平行于底面的平面截成两部分，截面的面积恰好是棱锥底面面积的一半，那么截得的两部分的体积比为（） A 、21B 、41 C 、22 D 、42 13、正四棱锥底面边长为a ，侧棱长也是a ，那么它的体积是（）A 、363a B 、362a C 、333a D 、332a 14、沿长方体的三个面的对角线截去一个三棱锥，剩下的几何体的体积与原长方体体积之比是（）A 、1∶6B 、2∶3C 、1∶3D 、5∶6 15、球面面积膨胀为原来的3倍，那么体积变为原来的（） A 、9倍 B 、3倍 C 、33倍 D 、27倍 16、一个正方体的顶点都在球面上，它的棱长为4cm ，那么这个球的体积是（）A 、64cm 3B 、π332cm 3C 、π48cm 3D 、π3256cm 3 17、如果球的半径为41cm ，一个球的截面与球心的距离为9cm ，那么该棱截面面积是（）A 、π1600cm 2B 、π6724 2 cm 2C 、π81cm 2D 、π324cm 2 18、一圆柱的高为8cm ，底面半径为5cm ，一平面截该圆柱得到的截面是正方形，则这个截面与轴的距离是（） A 、4cm B 、3cm C 、2cm D 、1cm 19、已知圆柱的轴截面相邻边长之比是2∶3，侧面积是π24cm 2，则圆柱的体积是（）A 、π24cm 3B 、π36cm 3C 、π24cm 3或π36cm 3D 、π54cm 320、将半径为r 的圆形薄铁板沿三条半径裁成全等的三个扇形，做成三个圆锥筒（无底），则圆锥筒的高（不计接头）是（） A 、r 322 B 、r 223 C 、r 332 D 、r 22 21、圆锥的侧面母线长为3，侧面展开所成的扇形的中心角等于o 60，那么这个圆锥的底面积是（）A 、π4B 、π2C 、π41D 、π21 22、将一个半圆围成一个圆锥面，则该圆锥两条母线的夹角之最大值是（）A 、o 120B 、o 90C 、o 60D 、o 45 23、体积为8的正方体的外接球的体积为（） A 、π34 B 、π332 C 、π362 D 、π)13(4+ 24、下列命题中①底面边长都相等，侧棱也都相等的棱锥是正棱锥；②底面是正多边形，侧面是等腰三角形的棱锥是正棱锥；③底面是正多边形，侧面是全等的等腰三角形的棱锥是正棱锥；④底面边长都相等，侧面是全等的三角形的棱锥是正棱锥；⑤底面是正多边形，顶点的射影是底面的中心的棱锥是正棱锥；⑥侧棱都相等的棱锥是正棱锥；⑦侧面都是等腰三角形的棱锥是正棱锥；⑧侧棱与底面所成的角都相等的棱锥是正棱锥；⑨侧面与底面所成的角都相等的棱锥是正棱锥；⑩斜高都相等的棱锥是正棱锥；正确的是（）A 、①③⑤⑨⑩B 、②④⑤⑥C 、②③⑤⑦⑧D 、③⑤25、下列命题中①有两个面是互相平行的多边形，其余各面是平行四边形的多面体是棱柱；②有两个面是互相平行的多边形，其余各面每相邻两面的公共边互相平行的多面体是棱柱；③有两个面是互相平行的多边形，其余各面每相邻两面的公共边都等长的多面体是棱柱；④有两个面是互相平行的多边形，其余各面每相邻两面所成的二面角大小都相等的多面体是棱柱正确的是（）A 、①②③④B 、②④C 、②D 、②③④26、下列命题中①有一个侧面是矩形的棱柱是直棱柱；②有两个侧面是矩形的棱柱是直棱柱；③有两个相邻的侧面都是矩形的棱柱是直棱柱；④有一个侧面与底面垂直的棱柱是直棱柱；⑤有两个侧面与底面垂直的棱柱是直棱柱；⑥有两个相邻的侧面都与底面垂直的棱柱是直棱柱；正确的是（）A、①②③④B、③⑥C、②⑤⑥D、②③④⑤27、已知边长为3、4、5的直角三角形，分别以它的三条边为轴转一周，所得到的几何体的表面积之比是（）A、15∶10∶7B、18∶15∶7C、13∶12∶5D、25∶16∶928、把一个圆心角为120°的扇形卷成一个圆锥的侧面，则此圆锥底面圆的半径与这个圆锥的高之比是（）A、1∶4B、2∶2C、2∶3D、2∶429、把一个圆心角为α弧度（0＜α＜2π）的扇形卷成一个圆锥的侧面，则此圆锥底面圆的半径与这个圆锥的母线长之比是（）A、α∶π2B、α∶πC、α∶π2D、α∶π430、已知三棱锥各侧面与底面所成二面角彼此相等，那么顶点在底面上的射影，一定是底面三角形的（）A、内心B、外心C、垂心D、重心31、下列命题中①底面的边长都相等，侧面都是矩形的棱柱是正棱柱；②底面的边长都相等，侧面都是全等的矩形的棱柱是正棱柱；③底面是正多边形，侧面都是矩形的棱柱是正棱柱；④底面是正多边形，侧棱都相等的棱柱是正棱柱；⑤底面正多边形，侧棱与底面垂直的棱柱是正棱柱；正确的是（）A、①②③④⑤B、②⑤C、③⑤D、③④⑤32、正方体每条棱长都增加2cm，则它的体积就扩大到原来的8倍，那么正方体原来的棱长是（）A、1cmB、2cmC、1.5cmD、3cm33、圆柱的轴截面面积为S，则该圆柱的侧面积是（）Ａ、SπＢ、Sπ2Ｃ、Sπ21Ｄ、Sπ41二、填空题34、如果正方体的对角线长为34cm，则它的体积是____ ___ cm3；35、有两个面是的多边形，其余各面每都的多面体叫棱柱；36、与垂直的棱柱叫做直棱柱；的直棱柱叫正棱柱；37、有一个面是多边形，其余各面是的多面体叫做棱锥；38、正棱锥是指的棱锥；正棱锥斜高是指；39、用一个平行于底面的平面截棱锥，所得的截面与底面，截面面积与底面面积之比等于；40、如果两个锥体的底面积相等，高也相等，那么它们的体积。

多面体与旋转体高考题

第十章多面体与旋转体考试内容：棱柱(包括平行六面体).棱锥.棱台.多面体. 圆柱.圆锥.圆台.球.球冠.旋转体.体积的概念与体积公理.棱柱、圆柱的体积.棱锥、圆锥的体积.棱台、圆台的体积.球和球缺的体积.考试要求：(1)理解棱柱、棱锥、棱台、圆柱、圆锥、圆台、球及其有关概念和性质.(2)掌握直棱柱、正棱锥、正棱台和圆柱、圆锥、圆台、球的表面积和体积公式以及球冠的面积、球缺的体积公式(球缺体积公式不要求记忆)，并能运用这些公式进行计算.(3)了解多面体和旋转体的概念，能正确画出直棱柱、正棱锥、正棱台、圆柱、圆锥、圆台的直观图.(4)对于截面问题，只要求会解决与几种特殊的截面(棱柱、棱锥、棱台的对角面，棱柱的直截面，圆柱、圆锥、圆台的轴截面和平行于底面的截面，球的截面)以及已给出图形或它的全部顶点的其他截面的有关问题.一、选择题1. (85(1)3分)如果正方体ABCD －A ′B ′C ′D ′的棱长为a ，那么四面体A'－ABD 的体积是A.2a 3B.4a 3C.3a 3D.6a 32. (89(3)3分)如果圆锥的底半径为2，高为2，那么它的侧面积是 A.43π B.22π C.23π D.42π3. (89(8)3分)已知球的两个平行截面的面积分别为5π和8π，它们位于球心的同一侧，且相距为1，那么这个球的半径是 A.4 B.3 C.2 D.54. (90(3)3分)如果轴截面为正方形的圆柱的侧面积是S ，那么圆柱的体积等于 A.2S S B.πS 2S C.4SS D.πS 4S5. (90上海)设过长方体同一个顶点的三个面的对角线长分别为a ，b ，c ，那么这个长方体的对角线长为A.222222222222c b a 21D.)c b (a 31C.)c b (a 21B.c b a ++++++++ 6. (90广东)一个圆台的母线长是上下底面半径的等差中项，且侧面积为8πcm 2,那么母线长是 A.4cm B.22cm C.2cm D.2cm7. (91上海)设长方体对角线的长度是4，过每一顶点有两条棱与对角线的夹角都是60°，则此长方体的体积是 A.27332 B.82 C.83 D.1638. (91上海)设正方体的全面积为24cm 2,一个球内切于该正方体，那么这个球的体积是A.6πcm 3B.34πcm 3C.38πcm 3 D.332πcm 39. (91三南)设正六棱锥的底面边长为1，侧棱长为5，那么它的体积为A.63B.23C.33D.210. (91三南)体积相等的正方体、球、等边圆柱(即底面直径与母线相等的圆柱)的全面积分别为S 、S ′、S",那么它们的大小关系是 A.S ＜S ′＜S" B.S ＜S"＜S ′ C.S ′＜S"＜S D.S ′＜S ＜S"C DABD' A' B' C'11. (92(5)3分)已知轴截面是正方形的圆柱的高与球的直径相等，则圆柱的全面积与球的表面积的比是 A.6:5 B.5:4 C.4:3 D.3:2 12. (92(18)3分)长方体的全面积为11，十二条棱长之和为24，则这个长方体的一条对角线长为A.23B.14C.5D.6 13. (92上海)下列命题中的真命题是 A.各侧面都是矩形的棱柱是长方体B.有两个相邻侧面是矩形的棱柱是直棱柱C.各侧面都是等腰三角形的四棱锥是正四棱锥D.有两个面互相平行，其余四个面都是等腰梯形的六面体是正四棱台 14. (92三南)在长方体ABCD －A ′B ′C ′D ′中，若AB ＝BC ＝a ，AA ′＝2a ，那么A 点到直线A ′C 的距离等于A.362 a B.263 a C.323a D.36a15. (92三南)有一条半径为2的弧，度数是60°,它绕过弧中点的直径旋转得一个球冠，那么这个球冠的面积是A.4(2－3)πB.2(2－3)πC.43πD.23π 16. (92三南)若等边圆柱的体积是16πcm 2，则其底面半径为A.432cmB.4cmC.232cmD.2cm17. (93(3)3分)当圆锥的侧面积和底面积的比值是2时，圆锥的轴截面顶角是A.45°B.60°C.90°D.120° 18. (93(13)3分)若正棱锥的底面边长与侧棱长相等，则该棱锥一定不是．． A.三棱锥 B.四棱锥 C.五棱锥 D.六棱锥 19. (93(14)3分)如果圆柱轴截面的周长l 为定值，那么圆柱体积的最大值是A.3)61(πB.3)31(π C.3)41(π D.4π)41(320. (93上海)设有三个命题：甲：底面是平行四边形的四棱柱是平行六面体；乙：底面是矩形的平行六面体是长方体；丙：直四棱柱是平行六面体；以上命题中真命题的个数是： A.0 B.1 C.2 D.321. (94(7)4分)圆柱正六棱台的上、下底面边长分别为2和4，高为2，则其体积为 A.323 B.283 C.243 D.20322. (94(13)5分)圆柱过球面上A 、B 、C 三点的截面和球心的距离等于球半径的一半，且AB ＝BC ＝CA ＝2，则球面面积是 A.916π B.38π C.4π D.964π 23. (95(4)4分)正方体的全面积是a 2，它的顶点都在球面上，这个球的表面积是A.3a 2π B.2a 2π C.2πa 2 D.3πa 224. (95上海)设棱锥的底面面积为8cm 2，那么棱锥的中截面(过棱锥高的中点且平行于底面的截面)的面积是 A.4cm 2 B.22cm 2 C.2cm 2 D.2cm 225. (96(9)4分)将边长为a 的正方形ABCD 沿对角线AC 折起，使得BD ＝a ，则三棱锥D －ABC的体积为A.6a 3B.12a 3C.12a 33D.12a 2326. (96(14)5分)母线长为l 的圆锥体积最大时，其侧面展开图圆心角φ等于A.322π B.332π C.2π D.362π 27. (97(8)4分)长方体一个顶点上三条棱的长分别是3，4，5，且它的八个顶点都在同一个球面上，这个球的表面积是 A.202π B.252π C.50π D.200π28. (97(12)5分)圆台上、下底面积分别为π、4π，侧面积为6π，这个圆台的体积是A.332π B.23π C.637π D.337π 29. (98(8)4分)已知圆锥的全面积是底面积的3倍，那么该圆锥的侧面展开图扇形的圆心角为A.120°B.150°C.180°D.240° 30. (98(9)4分)如果棱台的两底面积分别为S ，S'，中截面积是S 0，那么A.2')('00SS S B S S S =+= C.2S 0＝S ＋S' D.S 02＝2SS' 31. (98(10)4分)向高为H 的水瓶中注水，注满为止，h 的函数关系的图像如图所示，那么水瓶的形状是 A. B. C. 32. (98(13)分)球面上有3个点，其中任意两点的球面距离都等于大圆周长的61，经过这3个点的小圆面积为4π，那么这个球的半径为A.43B.23C.2D.333. (99(7)4分)若干毫升水倒入底面半径为2cm 的圆柱形器皿中，量得水面的高度为6cm ，若将这些水倒入轴截面是正三角形的倒圆锥形器皿中，则水面的高度是 A.63cm B.6cm C.2318cm D.3312cm34. (99(10)4分)如图，在多面体ABCDEF 中，已知面ABCD 是边长为3的正方形，EF ∥AB ，EF＝23，EF 与面AC 的距离为2，则该多面体的体积为 A.29 B.5 C.6 D.215 35. (99(12)5分)如果圆台的上底面半径为5，下底面半径为R ，中截面把圆台分成上下两个圆台，它们的侧面积之比为1:2，那么R ＝ A.10 B.15 C.20 D.2536. (2000安徽(5)4分)一个圆锥的底面直径和高都同一个球的直径相等，那么圆锥与球的体积之比是 A.1:3 B.2:3 C.1:2 D.2:9 37. (2000⑶5分)一个长方体共一顶点的三个面的面积分别是6,3,2，这个长方体对角线的长是 A.23 B.32 C.6 D.638. (2000⑼5分)一个圆柱的侧面展开图是一个正方形，这个圆柱的全面积与侧面积的比是A.ππ221+B.ππ441+C.ππ21+D.ππ241+39. (2000⑿5分)如图，OA 是圆锥底面中心O 到母线的垂线，OA 绕轴旋转一周所得曲面将圆锥分成体积相等的两部分，则母线与轴的夹角为A.arccos 321 B.arccos 21C.arccos21D.arccos 42140. (2000上海(14)4分)设有不同的直线a 、b 和不同的平面α、β、γ，给出下列三个命题：⑴若a∥α，b∥α，则a∥b； ⑵若a∥α，a∥β，则α∥β； ⑶若α⊥γ，β⊥γ，则α∥β.其中正确命题的个数是 A.0 B.1 C.2 D.3 41. (2001(3)5分)若一个圆锥的轴截面是等边三角形，其面积为3，则这个圆锥的全面积是A ．6πB ．π33C ．3πD ．9π二、填空题1. (86(13)4分)在xoy 平面上，四边形ABCD 的四个顶点坐标依次为(0，0)，(1，0)，(2，1)，(0，3)，则这个四边形绕x 轴旋转一周所得到的几何体的体积为___________.2. (87(15)4分)一个正三棱台的下底和上底周长分别为30cm 和12cm ，而侧面积等于两底面积之差，则斜高为_________.注:满足条件“侧面积等于两底面积之差”的三棱台不存在，只有“压缩”成平面图形方可，而此时所求“斜高”实为内、外两正方形(上、下底)对应边的距离.3. (90(20)3分)如图，三棱柱ABC －A 1B 1C 1中，若E ，F 分别为AB ，AC 中点，平面EB 1C 1F 将三棱柱分成体积为V 1，V 2的两部分，那么V 1:V 2＝______.4. (90上海)已知圆锥的中截面周长为a,母线长为l ，则它的侧面积等于____ 5. (91(18)3分)已知正三棱台上底面边长为2，下底面边长为4，且侧棱与底面所成的角是45°，那么这个正三棱台的体积等于________.6. (91(20)3分)在球面上有四个点P 、A 、B 、C ，如果PA 、PB 、PC 两两互相垂直，且PA ＝PB ＝PC ＝a ，那么这个球面的面积是_________.7. (91上海)一个圆柱的底面直径和高都等于一个球的直径，则这个圆柱的体积与球的体积的比值为___________8. (91三南)在体积为V 的三棱柱ABC －A ′B ′C ′中，已知S 是侧棱CC ′上的一点，过点S 、A 、B 的截面截得的三棱锥的体积为V ′,那么过点S 、A ′、B ′的截面截得的三棱锥的体积为__________9. (91三南)已知圆台的上下底面半径分别为r 、2r ，侧面积等于上下底面面积之和，则圆台的高为__________10. (92上海)已知圆台下底面半径为8cm,高为6cm ，母线与底面成45°角，那么圆台的侧面积为_________(cm 2)(结果保留π) 11. 如(92上海)图，直平行六面体A ′C 的上底面ABCD 是菱形，∠BAD＝60°，侧面为正方形，E 、F 分别为A ′B ′、AA ′的中点，M 是AC 与BD 的交点，则EF 与B ′M 所成的角的大小为_________(用反三角函数表示) 12. (92三南)已知三棱锥A －BCD 的体积为V ，棱BC 的长为a ，面ABC 和面DBC 的面积分别为S 、S ′，设面ABC 和面DBC 所成二面角为α，则sin α＝_____________ 13. (93(20)4分)在半径为30m 的圆形广场上空，设置一个照明光源，射向地面的光成圆锥形，其轴截面顶角为120°，若要光源恰好照亮整个广场，其高度应为______(精确到0.1m) 14. (93上海)已知圆台的上下底半径分别是10cm 和20cm ，他的侧面展开后所得扇形的圆心角是180°,那么圆台的侧面积是______cm 2(保留π)15. (94(19)4分)设圆锥底面圆周上两点A 、B 间的距离为2，圆锥顶点到直线AB 的距离为3，AB 和圆锥轴的距离为1，则该圆锥的体积为________.16. (94上海)有一个实心圆锥体的零件，它的轴截面是边长为10cm 的等边三角形，现在要在它的整个表面镀上一层防腐材料，已知每平方厘米的工料价格是0.10元，则需要费用_____元17. (95(17)4分)已知圆台上、下底面圆周都在球面上，且下底面过球心，母线与底面所成的BACDD'C' B'A'M F E角为3π，则圆台的体积与球的体积之比为________. 18. (95上海)把圆心角为216°，半径为5分米的扇形铁皮焊成一个锥形容器(不计焊缝)，那么容器的容积是_________立方分米(结果保留两位小数)19. (96上海)如图，在正三角形ABC 中，E 、F 分别是AB 、AC 的中点，AD ⊥BC ，EH ⊥BC ，FG ⊥BC ，D 、H 、G 为垂足，若将正三角形ABC 绕AD 旋转一周所得的几何体的体积为V ，则其中由阴影部分所产生的旋转体的体积与V 的比值是___________ 20. (96上海)把半径为3cm ，中心角为π的扇形卷成一个圆锥形容器，这个容器的容积为_________cm 3(结果保留π)21. (97上海)设正四棱锥底面边长为4cm ，侧面和底面所成的二面角为60°，则这个棱锥的侧面积为___________cm 2 22. (98(18)4分)如图:在直四棱柱ABCD －A ′B ′C ′D ′中，当底面四边形ABCD 满足条件_______时，有A ′C ⊥B ′D ′.(注:填上你认为正确的一种条件即可，不必考虑所有可能的情形) 23. (99上海)若四面体各条棱长是1或2，且该四面体不是正四面体，则其体积的值是__________(只需写出一个可能的值)24. (2000安徽(16)4分)右图是一体积为72的正四面体，连结两个面的重心E 、F ，则线段EF 的长是_________.25. (2000安徽(18)4分)在空间，下列命题正确的是____________.(注：把你认为正确的命题的序号都填上)①如果两条直线a 、b 分别与直线l 平行，那么a ∥b②如果一条直线a 与平面β内的一条直线b 平行，那么a ∥β ③如果直线a 与平面β内的两条直线b 、c 都有垂直，那么a ⊥β ④如果平面β内的一条直线a 垂直平面γ，那么β⊥γ26. (2000⒃4分)如图，E 、F 分别为正方体的面ADD 1A 1、面BCC 1B 1的中心，则四边形BFD 1E 在该正方体的面上的射影可能是__________________.(要求：把可能的图的序号都．填上) 27. (2000上海(7)4分)命题A ：底面为正三角形，且顶点在底面的射影为底面中心的三棱锥是正三棱锥.命题A 的等价命题B 可以是：底面为正三角形，且_________的三棱锥是正三棱锥.28. (2001(13)4分)若一个圆锥的轴截面是等边三角形，其面积为3，则这个圆锥的侧面积是．29. (2001北京(13)4分)已知球内接正方体的表面积为S ，那么球体积等于__________。

多面体与旋转体习题

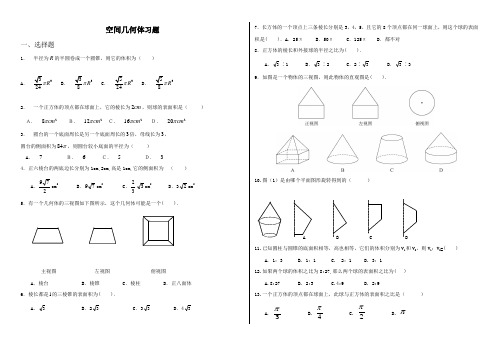
空间几何体习题一、选择题1．半径为R 的半圆卷成一个圆锥，则它的体积为（）A ． 3324R πB ． 338R πC ． 3524R πD ． 358R π 2．一个正方体的顶点都在球面上，它的棱长为2cm ，则球的表面积是（）Ａ． 28cm π Ｂ． 212cmπＣ． 216cmπＤ． 220cmπ3．圆台的一个底面周长是另一个底面周长的3倍，母线长为3，圆台的侧面积为84π，则圆台较小底面的半径为（） A ． 7 Ｂ． 6 Ｃ． 5 Ｄ． 34．正六棱台的两底边长分别为1cm,2cm,高是1cm,它的侧面积为（）A ．279cm 2B ．79cm 2C ．323cm 2D ．32cm 25．有一个几何体的三视图如下图所示，这个几何体可能是一个( )．主视图左视图俯视图 A ．棱台B ．棱锥C ．棱柱D ．正八面体6．棱长都是1的三棱锥的表面积为( )．A ．3B ．23C ．33D ．437．长方体的一个顶点上三条棱长分别是3，4，5，且它的8个顶点都在同一球面上，则这个球的表面积是( )．A ．25πB ．50πC ．125πD ．都不对8．正方体的棱长和外接球的半径之比为( )．A ．3∶1B ．3∶2C ．2∶3D ．3∶39．如图是一个物体的三视图，则此物体的直观图是( )．10.图（1）是由哪个平面图形旋转得到的（）A B C D11.已知圆柱与圆锥的底面积相等，高也相等，它们的体积分别为V 1和V 2，则V 1：V 2=( )A. 1：3B. 1：1C. 2：1D. 3：112.如果两个球的体积之比为8:27,那么两个球的表面积之比为( )A.8:27B. 2:3C.4:9D. 2:913.一个正方体的顶点都在球面上，此球与正方体的表面积之比是（）A.3πB.4πC.2πD.π二、填空题14．Rt ABC ∆中，3,4,5AB BC AC ===，将三角形绕直角边AB 旋转一周所成的几何体的体积为____________．15．一个长方体的长、宽、高之比为2：1：3，全面积为88cm 2，则它的体积为___________． 16．一个棱柱至少有______个面，面数最少的一个棱锥有________个顶点，顶点最少的一个棱台有________条侧棱．17．若三个球的表面积之比是1∶2∶3，则它们的体积之比是_____________．18．已知一个长方体共一顶点的三个面的面积分别是2、3、6，则这个长方体的对角线长是___________，它的体积为___________．19．一个直径为32厘米的圆柱形水桶中放入一个铁球，球全部没入水中后，水面升高9厘米则此球的半径为_________厘米．20.球的半径扩大为原来的2倍,它的体积扩大为原来的 _________ 倍.21.一个圆柱和一个圆锥的母线相等，底面半径也相等，则侧面积之比是_________.三、解答题22．已知圆台的上下底面半径分别是2,5,且侧面面积等于两底面面积之和,求该圆台的母线长.23．正四棱台的侧棱长为3cm ，两底面边长分别为1cm 和5cm ，求体积．24．如图，在四边形ABCD 中，∠DAB ＝90°，∠ADC ＝135°，AB ＝5，CD ＝22，AD ＝2，求四边形ABCD 绕AD 旋转一周所成几何体的表面积及体积．25．将圆心角为1200，面积为3π的扇形，作为圆锥的侧面，求圆锥的表面积和体积.26. （如图）在底半径为2母线长为4的圆锥中内接一个高为3的圆柱，求圆柱的表面积.。

多面体与旋转体

多面体与旋转体一、选择题（在每小题给出的四个选项中，只有一项是符合题目要求）（1）三条侧棱两两互相垂直，且侧棱与底面所成的角都相等是棱锥为正棱锥的（）（A）充分但非必要条件（B）必要但非充分条件（C）充要条件（D）非充分非必要条件（2）下列各图都是正方体，M、N、P、Q分别都是它们所在棱的中点，则M、N、P、Q 四点共面的是（）（A）（B）（C）（D）（3）正四棱锥每两条相邻侧棱所成的角都是，侧棱长为，则它的体积是（）（A）（B）（C）（D）（4）正三棱台的上、下底面边长及高，分别为1、2、2，则它的斜高是（）（A）（B）（C）（D）（5）正四棱台上、下底面边长分别为1，3，高为4，则侧棱与底面所成的角的正切值是（）（A）（B）2（C）2（D）4（6）两个平行于圆锥底面的平面将圆锥的高分成相等的三段，那么圆锥被分成的三部分的体积的比是（）（A）1∶2∶3（B）1∶7∶19（C）3∶4∶5（D）1∶9∶27（7）等边圆柱（轴截面是正方形）、球、正方体的体积相等，它们表面积的大小关系是（）（A）（B）（C）（D）（8）已知圆锥的母线长为8，底面积周长为，则它的体积是（）（A）（B）（C）（D）（9）若正三棱锥的底面边长为3，侧棱长为2，则这个正三棱锥的体积是（A）27/4（B）9/4（C）27/4（D）9/4（10）圆锥的高为1，底面半径为，则过圆锥顶点的截面面积的最大值为（A）1（B）2 （C）（D）2（11）如果圆锥的侧面积是全面积的3/4，则这个圆锥的侧面积展开图的中心角等于（A）Л/2（B）2Л/3（C）Л（D）3Л/2（12）三棱台的两底面对应边的比为1：2，过上底一边作平面平行于这边所对的侧棱，则这过平面截三棱台所成的两个几何体的体积之比是（A）1/2（B）2/3 （C）4/5（D）4/3二、填空题（13）正棱锥的一个侧面与底面所成的角是，底面积是Q，则它的侧面积__________ （14）截面是等边三角形的圆锥，它的侧面展开图扇形的圆心角的弧度数等于 .（15）三棱柱的体积是V，D、E分别在、上，线段DE经过矩形的中心，则四棱锥C-ABED 的体积是（16）已知母线长为10，底面半径为5的圆锥内有一球，球与圆锥的底面及圆锥的所有母线都相切，则球的体积是（17）P、Q是半径为R的球面上的两点，它们的球面距离是，则过P、Q的平面中，与球心的最大距离是三、解答题：（18）求棱长为的正方体的一个顶点A到平面的距离。

高考数学多面体与旋转体选择题

高考数学多面体与旋转体选择题1. 已知一个正四面体的一个顶点是平面ABC外的一点，且该顶点到平面ABC的距离为d，则该正四面体的外接球的半径R为：A. $\sqrt{3}d$B. $2\sqrt{3}d$C. $3d$D. $6d$2. 设E是正方体的一个顶点，F是正方体的一个对角线的中点，那么EF的长度是：A. 正方体棱长的$\sqrt{2}$倍B. 正方体棱长的$\sqrt{3}$倍C. 正方体棱长的2倍D. 正方体棱长的3倍3. 圆锥的母线与底面所成的角是：A. 45°B. 60°C. 90°D. 120°4. 圆台的上下底圆半径分别是3和1，高是4，那么圆台的体积是：A. $12\pi$B. $24\pi$C. $36\pi$D. $48\pi$5. 一个圆柱的侧面积是24π，底面半径是3，那么这个圆柱的高是：A. 2B. 3C. 4D. 66. 圆锥的底面半径是2，母线长是4，那么这个圆锥的体积是：A. $2\pi$B. $4\pi$C. $6\pi$D. $8\pi$7. 一个圆柱的底面半径和高分别是3和4，那么这个圆柱的侧面积是：B. $48\pi$C. $72\pi$D. $96\pi$8. 一个圆台的上下底圆半径分别是2和3，高是4，那么这个圆台的侧面积是：A. $24\pi$B. $48\pi$C. $72\pi$D. $96\pi$9. 一个圆锥的底面半径和高分别是2和4，那么这个圆锥的侧面积是：A. $12\pi$B. $24\pi$C. $36\pi$D. $48\pi$10. 一个圆柱的底面半径是2，高是4，那么这个圆柱的体积是：A. $8\pi$B. $16\pi$D. $32\pi$11. 一个圆台的上下底圆半径分别是2和3，高是4，那么这个圆台的体积是：A. $8\pi$B. $16\pi$C. $24\pi$D. $32\pi$12. 一个圆锥的底面半径和高分别是2和4，那么这个圆锥的体积是：A. $4\pi$B. $8\pi$C. $12\pi$D. $16\pi$13. 一个圆柱的底面半径是3，高是4，那么这个圆柱的侧面积是：A. $24\pi$B. $48\pi$C. $72\pi$14. 一个圆台的上下底圆半径分别是3和4，高是4，那么这个圆台的侧面积是：A. $24\pi$B. $48\pi$C. $72\pi$D. $96\pi$15. 一个圆锥的底面半径和高分别是3和4，那么这个圆锥的侧面积是：A. $12\pi$B. $24\pi$C. $36\pi$D. $48\pi$16. 一个圆柱的底面半径是4，高是4，那么这个圆柱的体积是：A. $16\pi$B. $32\pi$C. $48\pi$D. $64\pi$17. 一个圆台的上下底圆半径分别是4和5，高是4，那么这个圆台的体积是：A. $16\pi$B. $32\pi$C. $48\pi$D. $64\pi$18. 一个圆锥的底面半径和高分别是4和4，那么这个圆锥的体积是：A. $8\pi$B. $16\pi$C. $24\pi$D. $32\pi$19. 一个圆柱的底面半径是5，高是5，那么这个圆柱的侧面积是：A. $40\pi$B. $80\pi$C. $120\pi$D. $160\pi$20. 一个圆台的上下底圆半径分别是5和6，高是5，那么这个圆台的侧面积是：A. $40\pi$B. $80\pi$C. $120\pi$D. $160\pi$21. 一个圆锥的底面半径和高分别是5和5，那么这个圆锥的侧面积是：A. $20\pi$B. $40\pi$C. $60\pi$D. $80\pi$22. 一个圆柱的底面半径是6，高是6，那么这个圆柱的体积是：A. $24\pi$B. $48\pi$C. $72\pi$D. $96\pi$23. 一个圆台的上下底圆半径分别是6和7，高是6，那么这个圆台的体积是：A. $24\pi$C. $72\pi$D. $96\pi$24. 一个圆锥的底面半径和高分别是6和6，那么这个圆锥的体积是：A. $12\pi$B. $24\pi$C. $36\pi$D. $48\pi$25. 一个圆柱的底面半径是7，高是7，那么这个圆柱的侧面积是：A. $40\pi$B. $80\pi$C. $120\pi$D. $160\pi$26. 一个圆台的上下底圆半径分别是7和8，高是7，那么这个圆台的侧面积是：A. $40\pi$B. $80\pi$D. $160\pi$27. 一个圆锥的底面半径和高分别是7和7，那么这个圆锥的侧面积是：A. $20\pi$B. $40\pi$C. $60\pi$D. $80\pi$28. 一个圆柱的底面半径是8，高是8，那么这个圆柱的体积是：A. $24\pi$B. $48\pi$C. $72\pi$D. $96\pi$29. 一个圆台的上下底圆半径分别是8和9，高是8，那么这个圆台的体积是：A. $24\pi$B. $48\pi$C. $72\pi$D. $96\pi$30. 一个圆锥的底面半径和高分别是8和8，那么这个圆锥的体积是：A. $12\pi$B. $24\pi$C. $36\pi$D. $48\pi$31. 一个圆柱的底面半径是9，高是9，那么这个圆柱的侧面积是：A. $40\pi$B. $80\pi$C. $120\pi$D. $160\pi$32. 一个圆台的上下底圆半径分别是9和10，高是9，那么这个圆台的侧面积是：A. $40\pi$B. $80\pi$C. $120\pi$D. $160\pi$33. 一个圆锥的底面半径和高分别是9和9，那么这个圆锥的侧面积是：A. $20\pi$B. $40\pi$C. $60\pi$D. $80\pi$34. 一个圆柱的底面半径是10，高是10，那么这个圆柱的体积是：A. $24\pi$B. $48\pi$C. $72\pi$D. $96\pi$35. 一个圆台的上下底圆半径分别是10和11，高是10，那么这个圆台的体积是：A. $24\pi$B. $48\pi$C. $72\pi$D. $96\pi$36. 一个圆锥的底面半径和高分别是10和10，那么这个圆锥的体积是：A. $12\pi$B. $24\pi$C. $36\pi$D. $48\pi$37. 一个圆柱的底面半径是11，高是11，那么这个圆柱的侧面积是：A. $40\pi$B. $80\pi$C. $120\pi$D. $160\pi$38. 一个圆台的上下底圆半径分别是11和12，高是11，那么这个圆台的侧面积是：A. $40\pi$B. $80\pi$C. $120\pi$D. $160\pi$39. 一个圆锥的底面半径和高分别是11和11，那么这个圆锥的侧面积是：B. $40\pi$C. $60\pi$D. $80\pi$40. 一个圆柱的底面半径是12，高是12，那么这个圆柱的体积是：A. $24\pi$B. $48\pi$C. $72\pi$D. $96\pi$41. 一个圆台的上下底圆半径分别是12和13，高是12，那么这个圆台的体积是：A. $24\pi$B. $48\pi$C. $72\pi$D. $96\pi$42. 一个圆锥的底面半径和高分别是12和12，那么这个圆锥的体积是：A. $12\pi$C. $36\pi$D. $48\pi$43. 一个圆柱的底面半径是13，高是13，那么这个圆柱的侧面积是：A. $40\pi$B. $80\pi$C. $120\pi$D. $160\pi$44. 一个圆台的上下底圆半径分别是13和14，高是13，那么这个圆台的侧面积是：A. $40\pi$B. $80\pi$C. $120\pi$D. $160\pi$45. 一个圆锥的底面半径和高分别是13和13，那么这个圆锥的侧面积是：A. $20\pi$B. $40\pi$D. $80\pi$46. 一个圆柱的底面半径是14，高是14，那么这个圆柱的体积是：A. $24\pi$B. $48\pi$C. $72\pi$D. $96\pi$47. 一个圆台的上下底圆半径分别是14和15，高是14，那么这个圆台的体积是：A. $24\pi$B. $48\pi$C. $72\pi$D. $96\pi$48. 一个圆锥的底面半径和高分别是14和14，那么这个圆锥的体积是：A. $12\pi$B. $24\pi$C. $36\pi$49. 一个圆柱的底面半径是15，高是15，那么这个圆柱的侧面积是：A. $40\pi$B. $80\pi$C. $120\pi$D. $160\pi$50. 一个圆台的上下底圆半径分别是15和16，高是15，那么这个圆台的侧面积是：A. $40\pi$B. $80\pi$C. $120\pi$D. $160\pi$。

立体几何测试题(多面体与旋转体)

（多面体与旋转体）1、一个四棱柱是长方体的充要条件是（）A、底面是矩形B、侧面是正方形C、侧面和底面都是矩形D、侧面和底面都是正方形2、长方体共顶点的三个面的面积分别是2cm2，6cm2和9cm2,那么这个长方体的体积为（）A、3j6cm3B、6*3cm3C、7cm3D、8cm33、对角线长为d的正方体的棱长为（）A、1dB、忌C、（再€i）dD、申4、长方体的12条棱的总长度为56m，表面积为112m2，那么长方体的对角线长为（）A、3、14mB、7、.6mC、2*21mD、9m5、如果直棱柱的底面是菱形，它的高是9cm,它的两条对角线分别与底面成60。

角和45。

角，那么这个棱柱的体积是（）A>3v3a2B、2v'3a2C、（、.：3+1）a2D、（冬3+1）a27、已知正六棱柱底面的边长和高都等于a,那么最大对角截面的面积是（）A、2a2B、*3a28、三棱锥的三条侧棱两两互相垂直，各侧棱与底面所成的角彼此相等，那么顶点在底面的射影是底面三角形的A 、243打cm3B、243v'3cm3C、步cm32D、729,3cm36、在斜三棱柱中，各棱长都是a，且有一组共顶点的三条棱A、垂心但不是内心B、内心但不是垂心C、外心但不是重心D、垂心又是重心9、三棱锥P-ABC的侧棱两两互相垂直，且PA=1,PB^3，PC=.J6，那么Z ABC=（）A、30。

B、60。

C、45。

D、75。

10、如果正三棱锥的侧棱长为2a，底面周长为9a，那么这个棱锥的高为（）A、aB、2aC、aD、3a2211、已知三棱锥各侧面与底面所成二面角彼此相等，那么立体几何测试题两两夹角都等于60°，那么这个棱柱的全面积是（）B 、 a 3D 、角之最大值是（）顶点在底面上的射影，一定是底面三角形的（）A 、内心B 、外心C 、垂心D 、重心12、一个棱锥被平行于底面的平面截成两部分，截面的面积恰好是棱锥底面面积的一半，那么截得的两部分的体积比为（）那么该棱截面面积是（）A 、1600€cm 2B 、6724€2cm 2C 、81€cm 2D 、324€cm 218、一圆柱的高为8cm ，底面半径为5cm ,一平面截该圆柱得到的截面是正方形,则这个截面与轴的距离是（）A 、1B 、1C 、D 、竺242413、正四棱锥底面边长为a ,侧棱长也是a ,那么它的体积是（） A 、4cmB 、3cmC 、2cmD 、1cm19、已知圆柱的轴截面相邻边长之比是2：3,侧面积是24€cm 2,则圆柱的体积是（）A 、14、沿长方体的三个面的对角线截去一个三棱锥,剩下的几何体的体积与原长方体体积之比是（）A 、1：6B 、2：3C 、1：3D 、5：615、球面面积膨胀为原来的3倍,那么体积变为原来的（） A 、9倍B 、打倍C 、3•訂倍D 、27倍16、一个正方体的顶点都在球面上，它的棱长为4cm ，那么这 A 、24€cm 3B 、36€cm 3C 、24€cm 3或36€cm 3D 、54€cm 320、将半径为r 的圆形薄铁板沿三条半径裁成全等的三个扇形,做成三个圆锥筒（无底）,则圆锥筒的高（不计接头）是（）A 、土rB 、土2rC 、兰3rD 、2迈r323'21、圆锥的侧面母线长为3,侧面展开所成的扇形的中心角等于60o ,那么这个圆锥的底面积是（）A 、64cm 3B 、32^3兀cm 3C 、48兀cm 3D 、256^3兀cm 317、如果球的半径为41cm ,一个球的截面与球心的距离为9cm,个球的体积是（）A 、4€B 、2€ C 、1€ D 、1€22、将一个半圆围成一个圆锥面,则该圆锥两条母线的夹A、120oB、90oC、60oD、45o23、体积为8的正方体的外接球的体积为（）A、4^3兀B、2—兀C、2_6兀D、4（忖3+1）兀3324、下列命题中①底面边长都相等，侧棱也都相等的棱锥是正棱锥；②底面是正多边形，侧面是等腰三角形的棱锥是正棱锥；③底面是正多边形，侧面是全等的等腰三角形的棱锥是正棱锥;④底面边长都相等，侧面是全等的三角形的棱锥是正棱锥；⑤底面是正多边形，顶点的射影是底面的中心的棱锥是正棱锥;⑥侧棱都相等的棱锥是正棱锥；⑦侧面都是等腰三角形的棱锥是正棱锥；⑧侧棱与底面所成的角都相等的棱锥是正棱锥；⑨侧面与底面所成的角都相等的棱锥是正棱锥；⑩斜高都相等的棱锥是正棱锥；正确的是（）A、①③⑤⑨⑩B、②④⑤⑥C、②③⑤⑦⑧D、③⑤25、下列命题中①有两个面是互相平行的多边形，其余各面是平行四边形的多面体是棱柱；②有两个面是互相平行的多边形，其余各面每相邻两面的公共边互相平行的多面体是棱柱；③有两个面是互相平行的多边形，其余各面每相邻两面的公共边都等长的多面体是棱柱；④有两个面是互相平行的多边形，其余各面每相邻两面所成的二面角大小都相等的多面体是棱柱正确的是（）A、①②③④B、②④C、②D、②③④26、下列命题中①有一个侧面是矩形的棱柱是直棱柱；②有两个侧面是矩形的棱柱是直棱柱；③有两个相邻的侧面都是矩形的棱柱是直棱柱；④有一个侧面与底面垂直的棱柱是直棱柱；⑤有两个侧面与底面垂直的棱柱是直棱柱；⑥有两个相邻的侧面都与底面垂直的棱柱是直棱柱；正确的是（）A、①②③④B、③⑥C、②⑤⑥D、②③④⑤27、已知边长为3、4、5的直角三角形，分别以它的三条边为轴转一周，所得到的几何体的表面积之比是（）A、15：10：7B、18：15：7C、13：12：5D>25：16：928、把一个圆心角为120°的扇形卷成一个圆锥的侧面，则此圆锥底面圆的半径与这个圆锥的高之比是（）A、1：4B、迈:2C、迈:込D、迈:429、把一个圆心角为a弧度（0V a V2n）的扇形卷成一个圆锥的侧面，则此圆锥底面圆的半径与这个圆锥的母线长之比是（）A、a:2€B、a:兀C、a：\：2兀D、a：4兀30、已知三棱锥各侧面与底面所成二面角彼此相等，那么顶点在底面上的射影，一定是底面三角形的（）A、内心B、外心C、垂心D、重心31、下列命题中①底面的边长都相等，侧面都是矩形的棱柱是正棱柱；②底面的边长都相等，侧面都是全等的矩形的棱柱是正棱柱；③底面是正多边形，侧面都是矩形的棱柱是正棱柱；④底面是正多边形，侧棱都相等的棱柱是正棱柱；⑤底面正多边形，侧棱与底面垂直的棱柱是正棱柱；正确的是（）A、①②③④⑤B、②⑤C、③⑤D、③④⑤32、正方体每条棱长都增加2cm，则它的体积就扩大到原来的8倍，那么正方体原来的棱长是（）A、1cmB、2cmC、1.5cmD、3cm33、圆柱的轴截面面积为S，则该圆柱的侧面积是（）A、€SB、2€SC、1€SD、1€S24二、填空题34、如果正方体的对角线长为4j3cm，则它的体积是___cm3；35、有两个面是的多边形，其余各面每都的多面体叫棱柱；36、与_垂直的棱柱叫做直棱柱；的直棱柱叫正棱柱；37、有一个面是多边形，其余各面是的多面体叫做棱锥；38、正棱锥是指的棱锥；正棱锥斜高是扌旨;39、用一个平行于底面的平面截棱锥，所得的截面与底面_, 截面面积与底面面积之比等于；40、如果两个锥体的底面积相等，高也相等，那么它们的体积。

多面体与旋转体

多面体与旋转体11.（2001福建）设长方体的三条棱长分别为a 、b 、c ，若长方体所有棱的长度之和为24，一条对角线长度为5，体积为2，则a 1＋b 1＋c1等于___________. 【分析】:根据题意可得三个方程，从而求出a ，b ，c ，但计算量太大．若对a 1＋b 1＋c 1变形可得a 1＋b 1＋c 1＝abcca bc ab ++，故只需求出ab ＋bc ＋ca ，从而利用整体思想求解．【解】由题设，知⎪⎪⎩⎪⎪⎨⎧==++=++.2524)(4222abc c b a c b a∵ （a ＋b ＋c ）2＝a 2＋b 2＋c 2＋2（ab ＋bc ＋ca ），∴ 2)212(＝25＋2（ab ＋bc ＋ca ）， ∴ ab ＋bc ＋ac ＝211．从而a 1＋b 1＋c 1＝abc ca bc ab ++＝4112. 三棱锥的三条侧棱两两互相垂直，各侧棱与底面所成的角彼此相等，那么顶点在底面的射影是底面三角形的（）A 、垂心但不是内心B 、内心但不是垂心C 、外心但不是重心D 、垂心又是重心3. 一个棱锥被平行于底面的平面截成两部分，截面的面积恰好是棱锥底面面积的一半，那么截得的两部分的体积比为（）A 、21B 、41C 、22D 、424. 如图，以正四棱锥V-ABCD 底面中心O 为坐标原点建立空间直角坐标系O-xyz ，其中Ox ∥BC ，Oy ∥AB ，E 为VC 中点，正四棱锥底面边长为2a ，高为h ，求BE 与DE 所成角？解：以棱锥为载体，考查空间直角坐标系概念，空间点和向量的坐标表示，及两个向量夹角公式的计算方法，是近年高考新课程卷的命题趋势和发展方向．解：由题设得B （a ，a ，0），C （－a ，a ，0），D （－a ，－a ，0），E （22,2h a a ，-）由此得；⎪⎭⎫ ⎝⎛=⎪⎭⎫ ⎝⎛--=2,23,2,2,2,23h a a DE h a a BE ∴42322h a +-=⋅ ，221021h a +== ∴=,cos 2222222221061021423h a h a h a h a ++-=⎪⎭⎫ ⎝⎛++-=5. 已知长方体的对角线长为2cm ，则长方体全面积的最大值是____________?解：设长方体过同一顶点的三条棱长为a b c 、、则ab c 2224++= S ab ac bc a b a c b c a b c 全=++≤+++++=++=228222222222()()当且仅当ab c ==时取等号。

高考数学多面体与旋转体选择题

高考数学多面体与旋转体选择题1. 下列关于多面体的说法正确的是（）A. 棱柱的底面和顶面都是平行四边形B. 棱柱的底面和顶面是矩形时，其侧面都是矩形C. 圆柱的侧面展开图是矩形D. 圆柱的侧面展开图是梯形2. 已知长方体的长、宽、高分别为a、b、c，则该长方体的对角线长度d为（）A. $\sqrt{a^2 + b^2 + c^2}$B. $\sqrt{a^2 + b^2 - c^2}$C. $\sqrt{a^2 + b^2 + 2ac}$D. $\sqrt{a^2 + b^2 - 2ac}$3. 已知圆锥的底面半径为r，高为h，母线长为l，则该圆锥的体积V为（）A. $\frac{1}{3}\pi r^2h$B. $\frac{1}{3}\pi l^2h$C. $\frac{1}{3}\pi r^2l$D. $\frac{1}{3}\pi l^2r$4. 已知球的半径为R，则该球的表面积S为（）A. $4\pi R^2$B. $2\pi R^2$C. $4\pi R^3$D. $2\pi R^3$5. 已知圆台的上下底圆半径分别为r1和r2，高为h，则该圆台的体积V为（）A. $\pi (r1^2 + r2^2)h$B. $\pi (r1^2 - r2^2)h$C. $\pi (r1^2 + r2^2)^2$D. $\pi (r1^2 - r2^2)^2$6. 已知圆锥的底面半径为r，母线长为l，则该圆锥的侧面积S 为（）A. $\pi rl$B. $\pi l^2r$C. $\pi r^2l$D. $\pi l^2$7. 已知圆台的上下底圆半径分别为r1和r2，高为h，则该圆台的侧面积S为（）B. $\pi (r1^2 - r2^2)h$C. $\pi (r1^2 + r2^2)^2$D. $\pi (r1^2 - r2^2)^2$8. 已知球的半径为R，则该球的体积V为（）A. $\frac{4}{3}\pi R^3$B. $\frac{1}{3}\pi R^3$C. $\frac{4}{3}\pi R^2$D. $\frac{1}{3}\pi R^2$9. 已知圆锥的底面半径为r，高为h，则该圆锥的侧面积S为（）A. $\pi r^2h$B. $\pi rh^2$C. $\pi rl^2$D. $\pi l^2r$10. 已知圆台的上下底圆半径分别为r1和r2，高为h，则该圆台的侧面积S为（）A. $\pi (r1^2 + r2^2)h$B. $\pi (r1^2 - r2^2)h$C. $\pi (r1^2 + r2^2)^2$11. 已知球的半径为R，则该球的表面积S为（）A. $4\pi R^2$B. $2\pi R^2$C. $4\pi R^3$D. $2\pi R^3$12. 已知圆锥的底面半径为r，高为h，母线长为l，则该圆锥的体积V为（）A. $\frac{1}{3}\pi r^2h$B. $\frac{1}{3}\pi l^2h$C. $\frac{1}{3}\pi r^2l$D. $\frac{1}{3}\pi l^2r$13. 已知长方体的长、宽、高分别为a、b、c，则该长方体的对角线长度d为（）A. $\sqrt{a^2 + b^2 + c^2}$B. $\sqrt{a^2 + b^2 - c^2}$C. $\sqrt{a^2 + b^2 + 2ac}$D. $\sqrt{a^2 + b^2 - 2ac}$14. 已知圆台的上下底圆半径分别为r1和r2，高为h，则该圆台的体积V为（）A. $\pi (r1^2 + r2^2)h$B. $\pi (r1^2 - r2^2)h$C. $\pi (r1^2 + r2^2)^2$D. $\pi (r1^2 - r2^2)^2$15. 已知圆锥的底面半径为r，高为h，则该圆锥的侧面积S为（）A. $\pi r^2h$B. $\pi rh^2$C. $\pi rl^2$D. $\pi l^2r$16. 已知圆台的上下底圆半径分别为r1和r2，高为h，则该圆台的侧面积S为（）A. $\pi (r1^2 + r2^2)h$B. $\pi (r1^2 - r2^2)h$C. $\pi (r1^2 + r2^2)^2$D. $\pi (r1^2 - r2^2)^2$17. 已知球的半径为R，则该球的体积V为（）A. $\frac{4}{3}\pi R^3$B. $\frac{1}{3}\pi R^3$C. $\frac{4}{3}\pi R^2$D. $\frac{1}{3}\pi R^2$18. 已知圆锥的底面半径为r，高为h，母线长为l，则该圆锥的体积V为（）A. $\frac{1}{3}\pi r^2h$B. $\frac{1}{3}\pi l^2h$C. $\frac{1}{3}\pi r^2l$D. $\frac{1}{3}\pi l^2r$19. 已知长方体的长、宽、高分别为a、b、c，则该长方体的对角线长度d为（）A. $\sqrt{a^2 + b^2 + c^2}$B. $\sqrt{a^2 + b^2 - c^2}$C. $\sqrt{a^2 + b^2 + 2ac}$D. $\sqrt{a^2 + b^2 - 2ac}$20. 已知圆台的上下底圆半径分别为r1和r2，高为h，则该圆台的体积V为（）A. $\pi (r1^2 + r2^2)h$B. $\pi (r1^2 - r2^2)h$C. $\pi (r1^2 + r2^2)^2$D. $\pi (r1^2 - r2^2)^2$21. 已知圆锥的底面半径为r，高为h，则该圆锥的侧面积S为（）A. $\pi r^2h$B. $\pi rh^2$C. $\pi rl^2$D. $\pi l^2r$22. 已知圆台的上下底圆半径分别为r1和r2，高为h，则该圆台的侧面积S为（）A. $\pi (r1^2 + r2^2)h$B. $\pi (r1^2 - r2^2)h$C. $\pi (r1^2 + r2^2)^2$D. $\pi (r1^2 - r2^2)^2$23. 已知球的半径为R，则该球的体积V为（）A. $\frac{4}{3}\pi R^3$B. $\frac{1}{3}\pi R^3$C. $\frac{4}{3}\pi R^2$D. $\frac{1}{3}\pi R^2$24. 已知圆锥的底面半径为r，高为h，母线长为l，则该圆锥的体积V为（）A. $\frac{1}{3}\pi r^2h$B. $\frac{1}{3}\pi l^2h$C. $\frac{1}{3}\pi r^2l$D. $\frac{1}{3}\pi l^2r$25. 已知长方体的长、宽、高分别为a、b、c，则该长方体的对角线长度d为（）A. $\sqrt{a^2 + b^2 + c^2}$B. $\sqrt{a^2 + b^2 - c^2}$C. $\sqrt{a^2 + b^2 + 2ac}$D. $\sqrt{a^2 + b^2 - 2ac}$26. 已知圆台的上下底圆半径分别为r1和r2，高为h，则该圆台的体积V为（）A. $\pi (r1^2 + r2^2)h$B. $\pi (r1^2 - r2^2)h$C. $\pi (r1^2 + r2^2)^2$D. $\pi (r1^2 - r2^2)^2$27. 已知圆锥的底面半径为r，高为h，则该圆锥的侧面积S为（）A. $\pi r^2h$B. $\pi rh^2$C. $\pi rl^2$D. $\pi l^2r$28. 已知圆台的上下底圆半径分别为r1和r2，高为h，则该圆台的侧面积S为（）A. $\pi (r1^2 + r2^2)h$B. $\pi (r1^2 - r2^2)h$C. $\pi (r1^2 + r2^2)^2$D. $\pi (r1^2 - r2^2)^2$29. 已知球的半径为R，则该球的体积V为（）A. $\frac{4}{3}\pi R^3$B. $\frac{1}{3}\pi R^3$C. $\frac{4}{3}\pi R^2$D. $\frac{1}{3}\pi R^2$30. 已知圆锥的底面半径为r，高为h，母线长为l，则该圆锥的体积V为（）A. $\frac{1}{3}\pi r^2h$B. $\frac{1}{3}\pi l^2h$C. $\frac{1}{3}\pi r^2l$D. $\frac{1}{3}\pi l^2r$31. 已知长方体的长、宽、高分别为a、b、c，则该长方体的对角线长度d为（）A. $\sqrt{a^2 + b^2 + c^2}$B. $\sqrt{a^2 + b^2 - c^2}$C. $\sqrt{a^2 + b^2 + 2ac}$D. $\sqrt{a^2 + b^2 - 2ac}$32. 已知圆台的上下底圆半径分别为r1和r2，高为h，则该圆台的体积V为（）A. $\pi (r1^2 + r2^2)h$B. $\pi (r1^2 - r2^2)h$C. $\pi (r1^2 + r2^2)^2$D. $\pi (r1^2 - r2^2)^2$33. 已知圆锥的底面半径为r，高为h，则该圆锥的侧面积S为（）A. $\pi r^2h$B. $\pi rh^2$C. $\pi rl^2$D. $\pi l^2r$34. 已知圆台的上下底圆半径分别为r1和r2，高为h，则该圆台的侧面积S为（）A. $\pi (r1^2 + r2^2)h$B. $\pi (r1^2 - r2^2)h$C. $\pi (r1^2 + r2^2)^2$D. $\pi (r1^2 - r2^2)^2$35. 已知球的半径为R，则该球的体积V为（）A. $\frac{4}{3}\pi R^3$B. $\frac{1}{3}\pi R^3$C. $\frac{4}{3}\pi R^2$D. $\frac{1}{3}\pi R^2$36. 已知圆锥的底面半径为r，高为h，母线长为l，则该圆锥的体积V为（）A. $\frac{1}{3}\pi r^2h$B. $\frac{1}{3}\pi l^2h$C. $\frac{1}{3}\pi r^2l$D. $\frac{1}{3}\pi l^2r$37. 已知长方体的长、宽、高分别为a、b、c，则该长方体的对角线长度d为（）A. $\sqrt{a^2 + b^2 + c^2}$B. $\sqrt{a^2 + b^2 - c^2}$C. $\sqrt{a^2 + b^2 + 2ac}$D. $\sqrt{a^2 + b^2 - 2ac}$38. 已知圆台的上下底圆半径分别为r1和r2，高为h，则该圆台的体积V为（）A. $\pi (r1^2 + r2^2)h$B. $\pi (r1^2 - r2^2)h$C. $\pi (r1^2 + r2^2)^2$D. $\pi (r1^2 - r2^2)^2$39. 已知圆锥的底面半径为r，高为h，则该圆锥的侧面积S为（）A. $\pi r^2h$B. $\pi rh^2$C. $\pi rl^2$D. $\pi l^2r$40. 已知圆台的上下底圆半径分别为r1和r2，高为h，则该圆台的侧面积S为（）A. $\pi (r1^2 + r2^2)h$B. $\pi (r1^2 - r2^2)h$C. $\pi (r1^2 + r2^2)^2$D. $\pi (r1^2 - r2^2)^2$41. 已知球的半径为R，则该球的体积V为（）A. $\frac{4}{3}\pi R^3$B. $\frac{1}{3}\pi R^3$C. $\frac{4}{3}\pi R^2$D. $\frac{1}{3}\pi R^2$42. 已知圆锥的底面半径为r，高为h，母线长为l，则该圆锥的体积V为（）A. $\frac{1}{3}\pi r^2h$B. $\frac{1}{3}\pi l^2h$C. $\frac{1}{3}\pi r^2l$D. $\frac{1}{3}\pi l^2r$43. 已知长方体的长、宽、高分别为a、b、c，则该长方体的对角线长度d为（）A. $\sqrt{a^2 + b^2 + c^2}$B. $\sqrt{a^2 + b^2 - c^2}$C. $\sqrt{a^2 + b^2 + 2ac}$D. $\sqrt{a^2 + b^2 - 2ac}$44. 已知圆台的上下底圆半径分别为r1和r2，高为h，则该圆台的体积V为（）A. $\pi (r1^2 + r2^2)h$B. $\pi (r1^2 - r2^2)h$C. $\pi (r1^2 + r2^2)^2$D. $\pi (r1^2 - r2^2)^2$45. 已知圆锥的底面半径为r，高为h，则该圆锥的侧面积S为（）A. $\pi r^2h$B. $\pi rh^2$C. $\pi rl^2$D. $\pi l^2r$46. 已知圆台的上下底圆半径分别为r1和r2，高为h，则该圆台的侧面积S为（）A. $\pi (r1^2 + r2^2)h$B. $\pi (r1^2 - r2^2)h$C. $\pi (r1^2 + r2^2)^2$D. $\pi (r1^2 - r2^2)^2$47. 已知球的半径为R，则该球的体积V为（）A. $\frac{4}{3}\pi R^3$B. $\frac{1}{3}\pi R^3$C. $\frac{4}{3}\pi R^2$D. $\frac{1}{3}\pi R^2$48. 已知圆锥的底面半径为r，高为h，母线长为l，则该圆锥的体积V为（）A. $\frac{1}{3}\pi r^2h$B. $\frac{1}{3}\pi l^2h$C. $\frac{1}{3}\pi r^2l$D. $\frac{1}{3}\pi l^2r$49. 已知长方体的长、宽、高分别为a、b、c，则该长方体的对角线长度d为（）A. $\sqrt{a^2 + b^2 + c^2}$B. $\sqrt{a^2 + b^2 - c^2}$C. $\sqrt{a^2 + b^2 + 2ac}$D. $\sqrt{a^2 + b^2 - 2ac}$50. 已知圆台的上下底圆半径分别为r1和r2，高为h，则该圆台的体积V为（）A. $\pi (r1^2 + r2^2)h$B. $\pi (r1^2 - r2^2)h$C. $\pi (r1^2 + r2^2)^2$D. $\pi (r1^2 - r2^2)^2$。

多面体和旋转体(幼师)

睢县职教中心学前教育多面体和旋转体专项练习一、选择题1.侧面都是直角三角形的正三棱锥，其底面边长为，则该棱锥的全面积是（）2.侧棱长是的正三棱锥，其底面边长是，则棱锥的高是（）球的面积扩大到原来的倍，则球的体积扩大到原来的（）倍4.下面说法错误的是（）A.棱柱的侧面都是平行四边形B.直棱柱的侧面都是矩形C.棱柱的侧棱长不一定相等D.过棱柱的不相邻的两侧棱的截面都是平行四边形5.一个圆锥的轴截面为等边三角形且面积为，则圆锥的高为（）6.一个物体的下半部是圆柱，上半部是圆锥，圆锥的底面与圆柱的底面是半径相同的圆，已知圆柱的半径为，高度为，圆锥的母线长为，则该物体的表面积为（）7.如果一个三棱锥的三条侧棱相等，那么它的顶点在底面的射影是底面三角形的（）A.内心B.外心C.垂心D.重心8.正三棱柱的底面边长为,斜高为,则侧面积为（）9.一个边长为的正三角形，一其一条高为轴旋转一周所得旋转体的全面积为（）10.一个正四棱锥的底面边长为,高为，则体积为（）11．一个球的体积为，该球内切于一个正方体内，那么这个正方体的棱长为（）112.长方体一个顶点上的三条棱长分别为，则长方体的表面积为（）．13.若正三棱锥的侧棱与底面边长相等，则该棱锥侧棱与底面所成角的余弦值为（）已知圆柱底面周长为，高为，则轴截面的面积是（）已知圆锥的高为,轴截面是等边三角形，则轴截面的面积为（）过球面上任意两点的大圆（）A.有且只有一个B.有且只有两个C.有无穷多个D.有一个或无穷多个17.一个球的截面圆直径为，球心距为，则球的半径为（）18.如果棱柱的侧面是矩形，则这个棱柱一定是（）A.正棱柱B.直棱柱C.正方体D.长方体19.正四棱柱的底面边长和高都是，则其全面积为（）20.若正四棱柱的对角线和侧面所成的角为，底面边长为,则它的体积为（）21.圆锥的侧面展开图是扇形，且扇形的半径为，圆心角为，则圆锥的体积为（）二、填空题1.已知长方体的长是,宽是,高是,则对角线的长为：2.已知正六棱锥底面边长为，高为，则它的棱长为：3.已知正四棱柱底面边长为,高为,则它的侧面积为：全面积为：24.已知直棱柱底面是菱形，边长为,棱柱高为，则该四棱柱的体积为：5.在正三棱锥中，若底面边长为，侧棱长为，则其高为：侧棱与底面夹角为：侧面与底面所成角的正切值为：6.设正四棱锥底面边长为,高为,则其斜高为：侧面积为：7.用一个长,宽的矩形材料卷成圆柱，则圆柱的侧面积为：8.已知圆柱的高为,底面半径为,则它的侧面积为：体积为9.已知圆锥高为,轴截面是直角三角形，则它的底面半径为：母线长为：10.已知圆锥底面半径是,高为,则它的侧面积为：11.已知圆锥的轴截面是等边三角形，母线长为,则圆锥的体积为：12.已知球的大圆周长为,则这个球的表面积为：13.已知球的大圆面积为,则这个球的体积为：14.用一个平面截半径为的球，截面的面积为,则球心到截面的距离为：15.长方体的全面积为，各棱长总和是，则该长方体的对角线长为：16.圆柱的轴截面面积为，侧面积为:17.圆锥的底面面积为，母线与底面所成的角为，其体积为：18.一个圆锥底面积不变，高扩大为原来的倍，体积扩大为原来的倍19.若长方体的长、宽、高分别为、、，则对角线为：20.一个圆柱和圆锥的底面直径相等，圆锥的高是圆柱的倍，圆锥的体积是，则圆柱的体积为：21.正六棱柱的底面边长是，侧棱长也是，则它的体积是：22.已知正四棱柱的底面边长为,高为,则它的侧面积为：体积为：23.以直角边长为的等腰直角三角形一直角边为轴旋转一周，形成的圆锥的轴截面面积为：24.圆柱底面半径为，高为，其全面积为：25.三个球的半径之比为，那么最大球的表面积是其余两个球的表面积之和的倍26.正四面体的边长为，则其体积为：327.一个正方体的顶点都在这个球面上，它的棱长是,则这个球的体积为：28.火星的半径约等于地球半径的一半，则地球的体积是火星的倍29.将一个半径为的半圆卷成一个圆锥的侧面，则此圆锥的体积为：30.一个圆锥的轴截面是等边三角形，面积为，则它的高为：三、解答题1.已知正三棱锥的斜高等于，高等于，求它的全面积2.一个圆柱的侧面展开图是一个正方形，求这个圆柱的全面积与侧面积的比是多少？3．若圆锥的高等于底面直径，求它的侧面积与底面积的比4.在半径为的球内有一个截面，它的面积是，求球心到这个截面的距离5．已知正方体的对角线长为，求它的棱长6.已知圆锥的轴截面是直角三角形，求它的侧面积与底面积的比值7.已知圆柱的侧面展开图是边长为的正方形，求它的体积48.已知正三棱锥中，,斜高,求高和棱长9.已知圆锥的侧面展开图是一个半圆，求圆锥的母线与底面所成的角10.已知三棱锥的各顶点都在一个半径为的球面上，球心在上，底面,求球的体积和三棱锥的体积11.已知正四棱锥底面正方形的边长是，高与斜高的夹角为，求正四棱锥的侧面积，表面积和体积12.三棱锥的底面是直角三角形，斜边,求三棱锥的高5。

多面体与旋转体复习题61

61．棱柱、棱锥、棱台（2）一、典型例题1．在一张硬纸上挖去一个半径为3的圆洞，然后把此洞套在一个底面边长为4，高为6的正三棱锥上，并使纸面与锥底面平行，则能穿过这张纸面的棱锥的高的最大值是多少？[9/2] 2．在三棱台A 1B 1C 1－ABC 中，侧棱B 1B ⊥底面ABC ，∠ABC ＝∠AA 1C ＝90°，①求证：AA 1⊥A 1B 1；②若A 1B 1＝B 1C 1＝1，AB ＝2，求该棱台的侧面积。

[3+233]3．如图，斜三棱柱ABC －A 1B 1C 1的底面是边长为2的正三角形，顶点A 1在底面ABC 上射影O 是⊿ABC 的中心，AA 1与AB 的夹角是45°，①求证：AA 1⊥平面A 1BC ；②求此棱柱的侧面积。

[4+22]4．如图，正方体ABCD －A 1B 1C 1D 1中，EF 是异面直线AC 和A 1D的公垂线，求EF 和BD 1的关系。

[∥]5．直平行六面体的底面是菱形，过不相邻的两对侧棱的截面的面积是Q 1和Q 2，求它的侧面积。

[22221Q Q +]6．在三棱柱ABC －A 1B 1C 1中，AB ＝a 2，BC ＝CA ＝AA 1＝a ，A 1底面ABC 上的射影O 在AC 上，①求AB 与侧面AC 1所成的角；②若O 恰为AC 的中点，求此三棱柱的侧面积。

[45°、2)732(21a ++]7．正四棱锥侧棱和底面所成的角为α，相邻两侧面所成的二面角为b ，求证：cos β=2cos cos 22-αα。

沁园春·雪 <毛泽东>北国风光，千里冰封，万里雪飘。

望长城内外，惟余莽莽；大河上下，顿失滔滔。

山舞银蛇，原驰蜡象，欲与天公试比高。

须晴日，看红装素裹，分外妖娆。

江山如此多娇，引无数英雄竞折腰。

惜秦皇汉武，略输文采；唐宗宋祖，稍逊风骚。

一代天骄，成吉思汗，只识弯弓射大雕。

俱往矣，数风流人物，还看今朝。

沪教版(新教材)数学必修第三册第11章简单几何体11.1多面体与旋转体同步测试

沪教版（新教材）数学必修第三册第11章简单几何体11.1 多面体与旋转体同步测试共 19 题一、选择题1、由下列主体建筑物抽象得出的空间几何体中为旋转体的是（）A. B.C. D.2、一个几何体恰有6个顶点，则这个几何体可能是（）A.四棱柱B.四棱台C.五棱锥D.五棱台3、以下空间几何体是旋转体的是（）A.圆锥B.棱台C.正方体D.三棱锥4、如图，已知正方体的上、下底面的中心分别为、，将正方体绕直线旋转一周，其中由线段旋转所得图像是（）A. B.C. D.5、如图是一个简单多面体的表面展开图（沿图中虚线折叠即可还原），则这个多面体的顶点数为（）A.6B.7C.8D.96、如图，正方体的棱长为1，线段上有两个动点E､F，且.结出结论：①AC⊥BE；②EF平面ABCD；③三棱锥A-BEF的体积为定值；④的面积与△BEF的面积相等.其中正确的结论是（）A.①②③；B.①②④C.②③④D.①③④7、将选项中所示的三角形绕直线旋转一周，可以得到如图所示几何体的是哪一个三角形（）．A. B.C. D.8、一个棱锥被平行于底面的平面所截截面面积恰好是棱锥底面面积的一半，则截得的小棱锥与原棱锥的高之比是（）A. B.C. D.9、如图1所示，已知正方体面对角线长为a，沿阴影面将它切割成两块，拼成如图2所示的几何体，那么此几何体的表面积为（）A. B.C. D.10、如图所示的几何体，关于其结构特征，下列说法不正确的是A.该几何体是由两个同底的四棱锥组成的几何体B.该几何体有12条棱、6个顶点C.该几何体有8个面，并且各面均为三角形D.该几何体有9个面，其中一个面是四边形，其余均为三角形二、填空题11、一个几何体有6个顶点，则这个几何体可能是______棱柱．12、如图，第一排的图形绕虚线旋转一周能形成第二排中的某个几何体．请写出第一排、第二排中相应的图形的对应关系.A. B. C. D.（1）_____（2）_____（3）_____（4）_____13、一个简单多面体的面都是三角形，顶点数，则它的面数为__个．14、已知过球面上三点的截面到球心距离等于球半径的一半，且是边长为6的等边三角形，则球面面积为__________.15、一个圆台的母线长为20cm，母线与轴的夹角为30°，上底面半径为15cm，则下底面半径为___________.16、我国古代数学名著《九章算术》对立体几何也有深入的研究，从其中的一些数学用语可见，譬如“堑堵”意指底面为直角三角形，且侧棱垂直于底面的三棱柱，“阳马”指底面为矩形且有一侧棱垂直于底面的四棱锥.现有一如图所示的“堑堵”即三棱柱，其中，若，当“阳马”即四棱锥，体积最大时，“堑堵”即三棱柱的表面积为_______.三、综合题17、如图所示，图①是正方体木块，把它截去一块，可能得到的几何体有②③④⑤.（1）我们知道，正方体木块有8个顶点，12条棱、6个面，请你将②③④⑤中木块的顶点数、面数填入下表：图号顶点数棱数面数①8126②③④⑤（2）观察你填出的表格，归纳出上述各种木块的顶点数V、棱数E、面数F之间的关系．（3）看图⑥中正方体的切法，请验证你所得的数量关系是否正确.18、如图，以的一边AB所在直线为轴，其他三边旋转一周形成的面围成一个几何体，画出这个几何体的图形，并说出其中的简单几何体及有关的结构特征.19、已知长方体，其中，过三点的的平面截去长方体的一个角后，得到如图所示的几何体，这个几何体的体积为，求几何体的表面积.参考答案一、选择题1、【答案】B【解析】略2、【答案】C【解析】略3、【答案】A【解析】略4、【答案】D【解析】略5、【答案】B【解析】略6、【答案】A【解析】略7、【答案】B【解析】略8、【答案】C【解析】略9、【答案】B【解析】略10、【答案】D【解析】略二、填空题11、【答案】三【解析】略12、【答案】CBDA【解析】略13、【答案】8【解析】略14、【答案】64π【解析】略15、【答案】25cm【解析】略16、【答案】【解析】略三、综合题17、【答案】(1)略;(2) V+F- E=2 (3)略【解析】略18、【答案】略【解析】略19、【答案】36【解析】略3+22√2。

旋转体和多面体习题课

1．图1是由图2中的哪个平面图旋转而得到的 ( )2.如图，这是一个正方体的表面展开图，若把它再折回成正方体后，有下列命题：①点H 与点C 重合；②点D 与点M 与点R 重合；③点B 与点Q 重合；④点A 与点S 重合．其中正确命题的序号是．（注：把你认为正确的命题的序号都填上）3.一个正方体内接于一个球，过球心作一截面，则截面可能是下列图形中的 .4.圆台上底面半径为5 cm ，下底面半径为10 cm ，母线AB 长为20 cm ，A 在上底面上，B 在下底面上，从AB 的中点M 拉一根绳子绕圆台侧面一周转到B ，则绳子最短的长度为．5.两个完全相同的长方体的长、宽、高分别为5 cm 、4 cm 、3 cm ．把它们重叠在一起组成一个新长方体，在这些新长方体中，最长的对角线的长度是 ( ) A. 77cm B.27cm C.55cm D.210cm6．已知球的两个平行截面的面积分别为5π和8π，它们位于球心的同侧，且距离为1，求这个球的半径．7．将直角边长分别为x ，y 的直角三角形以斜边所在直线为轴旋转一周得一几何体．(1)求此几何体的体积表达式；(2)设此直角三角形的面积为12，求此几何体体积的最大值．8. 已知长方体的长、宽、高之比为4∶3∶12，对角线长为26cm, 则长、宽、高分别为多少？9. 棱台的上、下底面积分别是25和81，高为4，求截得这棱台的原棱锥的高10. 若棱长均相等的三棱锥叫正四面体，求棱长为a 的正四面体的高.11. 已知圆锥的轴截面等腰三角形的腰长为 5cm,,面积为12cm,求圆锥的底面半径.12.已知圆柱的底面半径为3cm,,轴截面面积为24cm,求圆柱的母线长.13.下列图形中，不是三棱柱的展开图（）14如图，长方体1111ABCD A BC D -中，交于顶点A 的三条棱长分别为3AD =，14AA =，5AB =，则从A 点沿表面到1C 的最短距离为（）Ａ．Ｃ．Ｄ．15.一个球与它的外切圆柱、外切等边圆锥的体积之比为（）Ａ．235∶∶ Ｂ．234∶∶ C ．358∶∶ D ．469∶∶16.一个球的半径为a ，放在墙角与两个墙角及地面都相切，那么球心与墙角顶点的距离是．17.用一个平面去截一个正方体，截法不同，所得截面的形状不一定相同，在各种截法中，边数最多的截面是（）Ａ．四边形Ｂ．五边形Ｃ．六边形Ｄ．八边形18.若一个棱锥的各棱长均相等，则该棱锥一定不是（）Ａ．三棱锥Ｂ．四棱锥Ｃ．五棱锥Ｄ．六棱锥。

多面体和旋转体练习2份

单元练习一选择题：1.过长方体任意一条棱的截面都是（）.（A）正方形（B）矩形（C）菱形（D）非平行四边形2.三棱锥底面是正三角形为三棱锥是正三棱锥的（）.（A）充分条件（B）必要条件（C）充要条件（D）非充分，且非必要条件3.直角三角形的两条直角边为3cm，4cm，以斜边所在直线为轴旋转，得旋转体的体积是（）.4.一个正方体所有的顶点都在球面上，如果这个球的体积是，那么正方体的棱长是（）.填空：5.直棱柱的侧棱长与它的高的关系是__________，它的侧面和经过不相邻的两条侧棱的截面都是__________形；6.圆柱的侧面展开图是一个边长为的正方形，则圆柱的全面积是__________，体积是_________；7.用半径为10，中心角为120°的扇形卷成圆锥筒，则它的容积是-____________；8.一球的截面面积为9，到球心的距离为4，则球的半径是_________________.9.已知：正三棱锥－，三条侧棱、、互相垂直，设侧棱与底面所成的角为.求证：10.求边长为的正方体－的顶点到平面的距离.11.棱锥底面是边长为2、8的矩形，它的侧面积为72，高经过底面对角线的交点，求它的体积.答案、提示和解答：1.B.2.B.3.C，4.A.5.相等，矩.6.7.，8.5.9.如图，侧棱与底面所成角为，为△的中心，为正三棱锥的高，则∠=.∵、、互相垂直，∴方法2：设正三棱锥底面边长为2，则=，在底面三角形中可求得10.如图，因为，，均为正方体侧面的对角线，所以即△为边长为的正三角形，设△的中心为，则为点到平面的距离.因为三棱锥－和三棱锥－体积相等，即11.如图，四棱锥－，=8，=2，设侧面△的高为, △的高为，由棱锥的侧面积为72，得8＋2=72, 4＋=36. （1）由棱锥的高过矩形的对角线的交点，即为棱锥的高，在△中得同理，在Rt△中，得（2）将（1）、（2）联立：由（1）得=36－4，代入（2），得得由于棱锥的高单元练习二选择题：1.一个棱锥被平行于底面的平面所截，若截面面积与底面面积之比为1：2，则此棱锥的一条侧棱被截面所分成的两段（自顶点至下）的比是（）.2.球面上两点的球面距离为5，过这两点的球半径成60°的角，则这球的半径为（）.3.将长、宽分别为2，4的矩形卷成圆柱筒（圆柱体的侧面），则这圆柱的体积为（）.4.若球的大圆面积扩大为原来的3倍，则它的体积扩大为原来的（）.填空：5.已知长方体的长、宽、高之比为4：3：12，对角线长为338，则它的长为_______.6.在正三棱锥中，若棱长都是，则它的全面积是_________.7.如果圆锥的底面半径为，高为2，则它的侧面积等于_______ .8.一个直角梯形，上、下底与不垂直于底面的腰长分别为3，6，5，将其以与底垂直的腰为旋转轴旋转一周，所得旋转体的侧面积为_______，体积为_______.9.已知球的两个平行截面的面积分别为5和8，它们位于球心的同一侧，且相距为1，那么这个球的半径为__________ .10.已知圆锥的侧面积是10，侧面展开图的扇形中心角是36°，则圆锥的全面积是___________.11.在直平行六面.12.已知是过圆锥顶点，且与底面斜交的截面，是底面圆的圆心（如图），若=20，=25，到的距离是15，求截面面积.13.一正方体内接于半径为的半球，它的四个顶点在半球的底面（大圆面）上，而另四个顶点在半球面上，求此正方体的体积.答案、提示和解答：1..2..3..4.5.8.6.7..8.45,84.9.3.10.11.11如图连结、则=5，=3，∠=60°，在△中，由余弦定理可得∴在得=7..12.作⊥，垂足为，则=15，为的中点，在△中，=－=25－15=20.=20连结，则⊥.在△中=＋=20＋15=625，=25.13.设过正方体对角面所作的截面如图所示.为面上的对角线，设正方体的棱长为，则为.为，=.由正方体的性质，可得得.。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

空间几何体习题
一、选择题
1．半径为R 的半圆卷成一个圆锥，则它的体积为（）
A ． 3324R π
B ． 338R π
C ． 3524R π
D ． 35
8
R π 2．一个正方体的顶点都在球面上，它的棱长为2cm ，则球的表面积是（）Ａ． 2
8cm π Ｂ． 2
12cm
π
Ｃ． 2
16cm
π
Ｄ． 220cm
π
3．圆台的一个底面周长是另一个底面周长的3倍，母线长为3，圆台的侧面积为84π，则圆台较小底面的半径为（） A ． 7 Ｂ． 6 Ｃ． 5 Ｄ． 3
4．正六棱台的两底边长分别为1cm,2cm,高是1cm,它的侧面积为（）
A ．2
79cm 2
B ．79cm 2
C ．
3
23cm 2
D ．32cm 2
5．有一个几何体的三视图如下图所示，这个几何体可能是一个( )．
主视图左视图俯视图 A ．棱台
B ．棱锥
C ．棱柱
D ．正八面体
6．棱长都是1的三棱锥的表面积为( )．
A ．3
B ．23
C ．33
D ．43
7．长方体的一个顶点上三条棱长分别是3，4，5，且它的8个顶点都在同一球面上，则这个球的表面积是( )．A ．25π
B ．50π
C ．125π
D ．都不对
8．正方体的棱长和外接球的半径之比为( )．
A ．3∶1
B ．3∶2
C ．2∶3
D ．3∶3
9．如图是一个物体的三视图，则此物体的直观图是( )．
10.图（1）是由哪个平面图形旋转得到的（）
A B C D
11.已知圆柱与圆锥的底面积相等，高也相等，它们的体积分别为V 1和V 2，则V 1：V 2=( )
A. 1：3
B. 1：1
C. 2：1
D. 3：1
12.如果两个球的体积之比为8:27,那么两个球的表面积之比为( )
A.8:27
B. 2:3
C.4:9
D. 2:9
13.一个正方体的顶点都在球面上，此球与正方体的表面积之比是（）
A.
3
π
B.
4
π
C.
2
π
D.
π
二、填空题
14．Rt ABC ∆中，3,4,5AB BC AC ===，将三角形绕直角边AB 旋转一周所成的几何体的体积为____________．
15．一个长方体的长、宽、高之比为2：1：3，全面积为88cm 2，则它的体积为___________． 16．一个棱柱至少有______个面，面数最少的一个棱锥有________个顶点，顶点最少的一个棱台有________条侧棱．
17．若三个球的表面积之比是1∶2∶3，则它们的体积之比是_____________．
18．已知一个长方体共一顶点的三个面的面积分别是2、3、6，则这个长方体的对角线长是___________，它的体积为___________．
19．一个直径为32厘米的圆柱形水桶中放入一个铁球，球全部没入水中后，水面升高9厘米则此球的半径为_________厘米．
20.球的半径扩大为原来的2倍,它的体积扩大为原来的 _________ 倍.
21.一个圆柱和一个圆锥的母线相等，底面半径也相等，则侧面积之比是_________.
三、解答题
22．已知圆台的上下底面半径分别是2,5,且侧面面积等于两底面面积之和,求该圆台的母线长.
23．正四棱台的侧棱长为3cm ，两底面边长分别为1cm 和5cm ，求体积．
24．如图，在四边形ABCD 中，∠DAB ＝90°，∠ADC ＝135°，AB ＝5，CD ＝22，AD ＝2，求四边形
ABCD 绕AD 旋转一周所成几何体的表面积及体积．
25．将圆心角为1200
，面积为3π的扇形，作为圆锥的侧面，求圆锥的表面积和体积.
26. （如图）在底半径为2母线长为4的圆锥中内接一个高为3的圆柱，求圆柱的表面积.。