多面体与旋转体复习题65
高考数学多面体与旋转体选择题

高考数学多面体与旋转体选择题1. 下列关于多面体的说法正确的是:A. 所有多面体的对角线都是相交的B. 所有多面体的内角和都是360°C. 所有多面体的对角线都相交于一点D. 所有多面体的边数都大于22. 下列关于旋转体的说法正确的是:A. 所有旋转体的体积都是相等的B. 所有旋转体的表面积都是相等的C. 所有旋转体的轴都是垂直的D. 所有旋转体的中心都是对称的3. 下列哪个图形是旋转体?A. 圆锥B. 圆柱C. 圆台D. 球体4. 下列关于圆锥的说法正确的是:A. 圆锥的底面半径等于母线长B. 圆锥的底面半径小于母线长C. 圆锥的底面半径大于母线长D. 圆锥的底面半径与母线长无关5. 下列关于圆柱的说法正确的是:A. 圆柱的底面半径等于母线长B. 圆柱的底面半径小于母线长C. 圆柱的底面半径大于母线长D. 圆柱的底面半径与母线长无关6. 下列关于圆台的说法正确的是:A. 圆台的底面半径等于母线长B. 圆台的底面半径小于母线长C. 圆台的底面半径大于母线长D. 圆台的底面半径与母线长无关7. 下列关于球体的说法正确的是:A. 球体的直径等于半径的两倍B. 球体的直径小于半径的两倍C. 球体的直径大于半径的两倍D. 球体的直径与半径无关8. 下列哪个图形不是旋转体?A. 圆锥B. 圆柱C. 圆台D. 圆环9. 下列关于多面体的内角和的说法正确的是:A. 所有多面体的内角和都是360°B. 所有多面体的内角和都是480°C. 所有多面体的内角和都是540°D. 所有多面体的内角和都是600°10. 下列关于旋转体的体积的说法正确的是:A. 所有旋转体的体积都是相等的B. 所有旋转体的体积都与底面半径和高度有关C. 所有旋转体的体积都与底面半径无关D. 所有旋转体的体积都与高度无关11. 下列哪个图形是多面体?A. 圆锥B. 圆柱C. 圆台D. 球体12. 下列关于多面体的对角线说法正确的是:A. 所有多面体的对角线都是相交的B. 所有多面体的对角线都相交于一点C. 所有多面体的对角线都不相交D. 所有多面体的对角线都与顶点无关13. 下列关于旋转体的表面积的说法正确的是:A. 所有旋转体的表面积都是相等的B. 所有旋转体的表面积都与底面半径和高度有关C. 所有旋转体的表面积都与底面半径无关D. 所有旋转体的表面积都与高度无关14. 下列哪个图形是旋转体?A. 圆锥B. 圆柱C. 圆台D. 圆环15. 下列关于多面体的边数说法正确的是:A. 所有多面体的边数都大于2B. 所有多面体的边数都等于2C. 所有多面体的边数都小于2D. 所有多面体的边数都与顶点无关16. 下列关于旋转体的轴的说法正确的是:A. 所有旋转体的轴都是垂直的B. 所有旋转体的轴都与底面垂直C. 所有旋转体的轴都与高度垂直D. 所有旋转体的轴都与底面和高度无关17. 下列关于多面体的顶点说法正确的是:A. 所有多面体的顶点都位于对角线上B. 所有多面体的顶点都位于底面上C. 所有多面体的顶点都位于侧面D. 所有多面体的顶点都与对角线无关18. 下列关于旋转体的中心说法正确的是:A. 所有旋转体的中心都是对称的B. 所有旋转体的中心都与底面中心重合C. 所有旋转体的中心都与高度中心重合D. 所有旋转体的中心都与底面和高度无关19. 下列哪个图形是多面体?A. 圆锥B. 圆柱C. 圆台D. 球体20. 下列关于多面体的内角和的说法正确的是:A. 所有多面体的内角和都是360°B. 所有多面体的内角和都是480°C. 所有多面体的内角和都是540°D. 所有多面体的内角和都是600°21. 下列关于旋转体的体积的说法正确的是:A. 所有旋转体的体积都是相等的B. 所有旋转体的体积都与底面半径和高度有关C. 所有旋转体的体积都与底面半径无关D. 所有旋转体的体积都与高度无关22. 下列哪个图形是旋转体?A. 圆锥B. 圆柱C. 圆台D. 圆环23. 下列关于多面体的对角线说法正确的是:A. 所有多面体的对角线都是相交的B. 所有多面体的对角线都相交于一点C. 所有多面体的对角线都不相交D. 所有多面体的对角线都与顶点无关24. 下列关于旋转体的表面积的说法正确的是:A. 所有旋转体的表面积都是相等的B. 所有旋转体的表面积都与底面半径和高度有关C. 所有旋转体的表面积都与底面半径无关D. 所有旋转体的表面积都与高度无关25. 下列哪个图形是多面体?A. 圆锥B. 圆柱C. 圆台D. 球体26. 下列关于多面体的边数说法正确的是:A. 所有多面体的边数都大于2B. 所有多面体的边数都等于2C. 所有多面体的边数都小于2D. 所有多面体的边数都与顶点无关27. 下列关于旋转体的轴的说法正确的是:A. 所有旋转体的轴都是垂直的B. 所有旋转体的轴都与底面垂直C. 所有旋转体的轴都与高度垂直D. 所有旋转体的轴都与底面和高度无关28. 下列关于多面体的顶点说法正确的是:A. 所有多面体的顶点都位于对角线上B. 所有多面体的顶点都位于底面上C. 所有多面体的顶点都位于侧面D. 所有多面体的顶点都与对角线无关29. 下列关于旋转体的中心说法正确的是:A. 所有旋转体的中心都是对称的B. 所有旋转体的中心都与底面中心重合C. 所有旋转体的中心都与高度中心重合D. 所有旋转体的中心都与底面和高度无关30. 下列哪个图形是多面体?A. 圆锥B. 圆柱C. 圆台D. 球体31. 下列关于多面体的内角和的说法正确的是:A. 所有多面体的内角和都是360°B. 所有多面体的内角和都是480°C. 所有多面体的内角和都是540°D. 所有多面体的内角和都是600°32. 下列关于旋转体的体积的说法正确的是:A. 所有旋转体的体积都是相等的B. 所有旋转体的体积都与底面半径和高度有关C. 所有旋转体的体积都与底面半径无关D. 所有旋转体的体积都与高度无关33. 下列哪个图形是旋转体?A. 圆锥B. 圆柱C. 圆台D. 圆环34. 下列关于多面体的对角线说法正确的是:A. 所有多面体的对角线都是相交的B. 所有多面体的对角线都相交于一点C. 所有多面体的对角线都不相交D. 所有多面体的对角线都与顶点无关35. 下列关于旋转体的表面积的说法正确的是:A. 所有旋转体的表面积都是相等的B. 所有旋转体的表面积都与底面半径和高度有关C. 所有旋转体的表面积都与底面半径无关D. 所有旋转体的表面积都与高度无关36. 下列哪个图形是多面体?A. 圆锥B. 圆柱C. 圆台D. 球体37. 下列关于多面体的边数说法正确的是:A. 所有多面体的边数都大于2B. 所有多面体的边数都等于2C. 所有多面体的边数都小于2D. 所有多面体的边数都与顶点无关38. 下列关于旋转体的轴的说法正确的是:A. 所有旋转体的轴都是垂直的B. 所有旋转体的轴都与底面垂直C. 所有旋转体的轴都与高度垂直D. 所有旋转体的轴都与底面和高度无关39. 下列关于多面体的顶点说法正确的是:A. 所有多面体的顶点都位于对角线上B. 所有多面体的顶点都位于底面上C. 所有多面体的顶点都位于侧面D. 所有多面体的顶点都与对角线无关40. 下列关于旋转体的中心说法正确的是:A. 所有旋转体的中心都是对称的B. 所有旋转体的中心都与底面中心重合C. 所有旋转体的中心都与高度中心重合D. 所有旋转体的中心都与底面和高度无关41. 下列哪个图形是多面体?A. 圆锥B. 圆柱C. 圆台D. 球体42. 下列关于多面体的内角和的说法正确的是:A. 所有多面体的内角和都是360°B. 所有多面体的内角和都是480°C. 所有多面体的内角和都是540°D. 所有多面体的内角和都是600°43. 下列关于旋转体的体积的说法正确的是:A. 所有旋转体的体积都是相等的B. 所有旋转体的体积都与底面半径和高度有关C. 所有旋转体的体积都与底面半径无关D. 所有旋转体的体积都与高度无关44. 下列哪个图形是旋转体?A. 圆锥B. 圆柱C. 圆台D. 圆环45. 下列关于多面体的对角线说法正确的是:A. 所有多面体的对角线都是相交的B. 所有多面体的对角线都相交于一点C. 所有多面体的对角线都不相交D. 所有多面体的对角线都与顶点无关46. 下列关于旋转体的表面积的说法正确的是:A. 所有旋转体的表面积都是相等的B. 所有旋转体的表面积都与底面半径和高度有关C. 所有旋转体的表面积都与底面半径无关D. 所有旋转体的表面积都与高度无关47. 下列哪个图形是多面体?A. 圆锥B. 圆柱C. 圆台D. 球体48. 下列关于多面体的边数说法正确的是:A. 所有多面体的边数都大于2B. 所有多面体的边数都等于2C. 所有多面体的边数都小于2D. 所有多面体的边数都与顶点无关49. 下列关于旋转体的轴的说法正确的是:A. 所有旋转体的轴都是垂直的B. 所有旋转体的轴都与底面垂直C. 所有旋转体的轴都与高度垂直D. 所有旋转体的轴都与底面和高度无关50. 下列关于多面体的顶点说法正确的是:A. 所有多面体的顶点都位于对角线上B. 所有多面体的顶点都位于底面上C. 所有多面体的顶点都位于侧面D. 所有多面体的顶点都与对角线无关。
高考数学多面体与旋转体选择题

高考数学多面体与旋转体选择题1. 已知三棱锥S-ABC的底面ABC是边长为a的正三角形,高SD=2,点E、F、G分别是棱SA、SB、SC的中点,且EF=4,求三棱锥S-ABC 的体积。
2. 设四棱锥P-ABCD的底面ABCD是边长为a的正方形,侧棱PD=3,点E、F、G、H分别是棱PA、PB、PC、PD的中点,且EF=4,求四棱锥P-ABCD的体积。
3. 已知圆锥的底面半径为r,高为h,求圆锥的全面积。
4. 已知圆台的上下底面半径分别为r1和r2,高为h,求圆台的全面积。
5. 已知球体的直径为d,求球体的表面积。
6. 已知球的半径为r,求球的体积。
7. 已知球体的半径为r,求球体的表面积和体积。
8. 已知圆柱的底面半径为r,高为h,求圆柱的全面积。
9. 已知圆柱的底面半径为r,高为h,求圆柱的体积。
10. 已知圆柱的底面半径为r,高为h,求圆柱的表面积和体积。
11. 已知圆锥的底面半径为r,高为h,求圆锥的表面积。
12. 已知圆锥的底面半径为r,高为h,求圆锥的体积。
13. 已知圆锥的底面半径为r,高为h,求圆锥的表面积和体积。
14. 已知圆台的上下底面半径分别为r1和r2,高为h,求圆台的表面积。
15. 已知圆台的上下底面半径分别为r1和r2,高为h,求圆台的体积。
16. 已知圆台的上下底面半径分别为r1和r2,高为h,求圆台的表面积和体积。
17. 已知球的半径为r,求球的表面积和体积。
19. 已知球的半径为r,求球的表面积和体积。
20. 已知球的半径为r,求球的表面积和体积。
21. 已知球的半径为r,求球的表面积和体积。
22. 已知球的半径为r,求球的表面积和体积。
23. 已知球的半径为r,求球的表面积和体积。
24. 已知球的半径为r,求球的表面积和体积。
25. 已知球的半径为r,求球的表面积和体积。
26. 已知球的半径为r,求球的表面积和体积。
27. 已知球的半径为r,求球的表面积和体积。
多面体与旋转体部分会考练习题(高三)

多面体与旋转体部分会考练习题一、选择题1、四棱柱成为长方体的一个充分必要条件是:它的( )A 、底面是矩形B 、侧面是正方形C 、侧面和底面都是矩形D 、侧面和底面都是正方形2、长方体共顶点的三个面的面积分别是22cm ,62cm 和92cm ,那么这个长方体的体积为( )A 、632cmB 、362cmC 、72cmD 、82cm3、对角线长d 为的正方体的棱长为( ) A 、d 31B 、d 3C 、 ()d 13- D 、d 33 4、长方体的12条棱的总长度为56m ,表面积为1122m ,那么长方体的对角线长为( ) A 、m 143 B 、m 67 C 、m 212 D 、m 95、如果直棱柱的底面是菱形,柱高9cm ,它的两条对角线分别与底面成060角和045角,那么这个棱柱的体积是( ) A 、323243cm B 、33243cm C 、323729cm D 、33729cm 6、在斜三棱柱中,各棱长都是a ,且有一组共顶点的三条棱两两夹角相等,那么这个棱柱的全面积是( ) A 、2233a B 、232a C 、()213a + D 、21233a ⎪⎪⎭⎫ ⎝⎛+7、已知正六棱柱底面的边长和柱高都等于a ,那么最大对角截面的面积是( )A 、22a B 、23a C 、232a D 、223a8、三棱锥的三条侧棱两两互相垂直,各侧棱与底面所成的角彼此相等,那么顶点在底面的射影是底面三角形的( )A 、垂心但不是内心B 、内心但不是垂心C 、外心但不是重心D 、垂心又是重心9、三棱锥P-ABC 的侧棱两两互相垂直,且PA=1,PB=3,PC=6,那么∠ABC=( )A 、030 B 、060 C 、045 D 、07510、如果正三棱锥的侧棱长为2a ,底面周长为9a ,那么这棱锥的高为( )A 、 aB 、2aC 、a 23 D 、a 23 11、已知三棱锥各侧面与底面所成二面角彼此相等,那么顶点在底面上的射影,一定是底面三角形的( )A 、 内心B 、外心C 、垂心D 、重心12、一个棱锥被平行于底面的平面截成两部分,截面的面积恰好是棱锥底面面积的一半,那么截得的两部分的体积比为( ) A 、21 B 、41C 、22D 、4213、正四棱锥底面边长为a ,侧棱长也是a ,那么过两相对侧棱的截面的面积是( ) A 、223a B 、2a C 、221a D 、231a14、平行六面体的各棱长都等于4,在共顶点A 的三条棱上分别取点P 、Q 、R ,使AP=1,AQ=2,AR=3,那么,三棱锥A —PQR 的体积与平行六面体的体积比为( )A 、与顶点A 的选择无关,都等于321B 、 与顶点A 的选择无关,都等于641C 、 与顶点A 的选择有关,等于321或641D 、与顶点A 的选择有关,等于161或32115、如果棱锥的底面积为4,那么该棱锥的中截面的面积是( )A 、 1B 、2C 、2D 、316、正四棱台上下底面边长分别为a 和2a ,斜高为a ,那么台高等于( )A 、aB 、a 23 C 、a 22 D 、a 4317、圆柱的轴截面的对角线为定值,为了使圆柱的侧面积最大,轴截面对角线与底所成的角之正切函数值应为( ) A 、3 B 、1 C 、33 D 、21 18、圆锥的侧面母线长为3,侧面展开所成的扇形的中心角等于060,那么这个圆锥的底面积是( )A 、π4B π2、C 、π21D 、π41219、将一个半圆围成一个圆锥面,则该圆锥两条母线的夹角之最大值是( )A 、0120 B 、090 C 、060 D 、045台的母线和底面成030,轴截面的面积为Q ,那么这个圆台的侧面积是( ) A 、Q 2π B 、Q π C 、Q π2 D 、Q π421、圆台上下底的半径分别为1和4,母线长为23,则圆台的体积为( ) A 、π15 B 、π21 C 、π25 D 、π22122、直角梯形以下底边所在直线为旋转轴旋转,那么其余各边旋转所生成的曲面围成的几何体可看成( )A 、 一个棱柱叠加一个棱锥B 、一个圆台叠加一个圆锥C 、一个圆柱叠加一个圆锥D 、一个棱台叠加一个圆锥23、体积为8的正方体的外接球的体积为( )A 、π34B 、π332C 、π362 D 、()π134+ 二、填空题24、如果正四棱柱对角线长为3.5cm ,侧面的一条对角线长为2.5cm ,那么这个棱柱的体积为________2cm ;25、棱锥的底面是边长为a 的正三角形,一个侧面垂直于底面,另外两个侧面和底面所成的二面角都等于θ,那么这个棱锥的侧面积是__________; 26、圆锥底面的半径为10cm ,轴截面是直角三角形,则圆锥的全面积是_______2cm ;27、圆台的高是8cm ,上底半径、下底半径和母线长三者的比1:4:5为,那么这个圆台轴截面的面积是__________2cm ;28、在面积为π26的球面内,作一个内接圆柱,柱的底面半径是柱高的31,那么样这 个圆柱的全面积是________;三、解答题29、三棱锥的一条侧棱长为4cm ,其余所有的棱长都等于3cm ,求该棱锥的体积。
立体几何测试题(多面体与旋转体)

立体几何测试题(多面体与旋转体)1、一个四棱柱是长方体的充要条件是( )A 、底面是矩形B 、侧面是正方形C 、侧面和底面都是矩形D 、侧面和底面都是正方形 2、长方体共顶点的三个面的面积分别是22cm ,62cm 和92cm ,那么这个长方体的体积为( )A 、633cmB 、363cmC 、73cmD 、83cm3、对角线长为d 的正方体的棱长为( )A 、d 31 B 、d 3 C 、d )13(- D 、d 33 4、长方体的12条棱的总长度为56m ,表面积为1122m ,那么长方体的对角线长为( )A 、143mB 、67mC 、212mD 、9m 5、如果直棱柱的底面是菱形,它的高是9cm ,它的两条对角线分别与底面成o 60角和o 45角,那么这个棱柱的体积是( ) A 、323243cm B 、33243cm C 、323729cm D 、33729cm 6、在斜三棱柱中,各棱长都是a ,且有一组共顶点的三条棱两两夹角都等于60°,那么这个棱柱的全面积是( ) A 、2233a B 、232a C 、2)13(a + D 、2)1233(a + 7、已知正六棱柱底面的边长和高都等于a ,那么最大对角截面的面积是( )A 、22aB 、23aC 、232aD 、223a8、三棱锥的三条侧棱两两互相垂直,各侧棱与底面所成的角彼此相等,那么顶点在底面的射影是底面三角形的( )A 、垂心但不是内心B 、内心但不是垂心C 、外心但不是重心D 、垂心又是重心9、三棱锥P-ABC 的侧棱两两互相垂直,且PA=1,PB=3,PC=6,那么∠ABC=( )A 、o 30B 、o 60C 、o 45D 、o 7510、如果正三棱锥的侧棱长为2a ,底面周长为9a ,那么这个棱锥的高为( ) A 、 a B 、2a C 、a 23 D 、a 2311、已知三棱锥各侧面与底面所成二面角彼此相等,那么顶点在底面上的射影,一定是底面三角形的( ) A 、 内心 B 、外心 C 、垂心 D 、重心 12、一个棱锥被平行于底面的平面截成两部分,截面的面积恰好是棱锥底面面积的一半,那么截得的两部分的体积比为( ) A 、21B 、41 C 、22 D 、42 13、正四棱锥底面边长为a ,侧棱长也是a ,那么它的体积是( )A 、363a B 、362a C 、333a D 、332a 14、沿长方体的三个面的对角线截去一个三棱锥,剩下的几何体的体积与原长方体体积之比是( )A 、1∶6B 、2∶3C 、1∶3D 、5∶6 15、球面面积膨胀为原来的3倍,那么体积变为原来的( ) A 、9倍 B 、3倍 C 、33倍 D 、27倍 16、一个正方体的顶点都在球面上,它的棱长为4cm ,那么这个球的体积是( )A 、64cm 3B 、π332cm 3C 、π48cm 3D 、π3256cm 3 17、如果球的半径为41cm ,一个球的截面与球心的距离为9cm ,那么该棱截面面积是( )A 、π1600cm 2B 、π6724 2 cm 2C 、π81cm 2D 、π324cm 2 18、一圆柱的高为8cm ,底面半径为5cm ,一平面截该圆柱得到的截面是正方形,则这个截面与轴的距离是( ) A 、4cm B 、3cm C 、2cm D 、1cm 19、已知圆柱的轴截面相邻边长之比是2∶3,侧面积是π24cm 2,则圆柱的体积是( )A 、π24cm 3B 、π36cm 3C 、π24cm 3或π36cm 3D 、π54cm 320、将半径为r 的圆形薄铁板沿三条半径裁成全等的三个扇形,做成三个圆锥筒(无底),则圆锥筒的高(不计接头)是( ) A 、r 322 B 、r 223 C 、r 332 D 、r 22 21、圆锥的侧面母线长为3,侧面展开所成的扇形的中心角等于o 60,那么这个圆锥的底面积是( )A 、π4B 、π2C 、π41D 、π21 22、将一个半圆围成一个圆锥面,则该圆锥两条母线的夹角之最大值是( )A 、o 120B 、o 90C 、o 60D 、o 45 23、体积为8的正方体的外接球的体积为( ) A 、π34 B 、π332 C 、π362 D 、π)13(4+ 24、下列命题中①底面边长都相等,侧棱也都相等的棱锥是正棱锥;②底面是正多边形,侧面是等腰三角形的棱锥是正棱锥;③底面是正多边形,侧面是全等的等腰三角形的棱锥是正棱锥;④底面边长都相等,侧面是全等的三角形的棱锥是正棱锥;⑤底面是正多边形,顶点的射影是底面的中心的棱锥是正棱锥;⑥侧棱都相等的棱锥是正棱锥;⑦侧面都是等腰三角形的棱锥是正棱锥;⑧侧棱与底面所成的角都相等的棱锥是正棱锥;⑨侧面与底面所成的角都相等的棱锥是正棱锥;⑩斜高都相等的棱锥是正棱锥;正确的是( )A 、①③⑤⑨⑩B 、②④⑤⑥C 、②③⑤⑦⑧D 、③⑤25、下列命题中①有两个面是互相平行的多边形,其余各面是平行四边形的多面体是棱柱;②有两个面是互相平行的多边形,其余各面每相邻两面的公共边互相平行的多面体是棱柱;③有两个面是互相平行的多边形,其余各面每相邻两面的公共边都等长的多面体是棱柱;④有两个面是互相平行的多边形,其余各面每相邻两面所成的二面角大小都相等的多面体是棱柱正确的是( )A 、①②③④B 、②④C 、②D 、②③④26、下列命题中①有一个侧面是矩形的棱柱是直棱柱;②有两个侧面是矩形的棱柱是直棱柱;③有两个相邻的侧面都是矩形的棱柱是直棱柱;④有一个侧面与底面垂直的棱柱是直棱柱;⑤有两个侧面与底面垂直的棱柱是直棱柱;⑥有两个相邻的侧面都与底面垂直的棱柱是直棱柱;正确的是( )A、①②③④B、③⑥C、②⑤⑥D、②③④⑤27、已知边长为3、4、5的直角三角形,分别以它的三条边为轴转一周,所得到的几何体的表面积之比是()A、15∶10∶7B、18∶15∶7C、13∶12∶5D、25∶16∶928、把一个圆心角为120°的扇形卷成一个圆锥的侧面,则此圆锥底面圆的半径与这个圆锥的高之比是()A、1∶4B、2∶2C、2∶3D、2∶429、把一个圆心角为α弧度(0<α<2π)的扇形卷成一个圆锥的侧面,则此圆锥底面圆的半径与这个圆锥的母线长之比是()A、α∶π2B、α∶πC、α∶π2D、α∶π430、已知三棱锥各侧面与底面所成二面角彼此相等,那么顶点在底面上的射影,一定是底面三角形的()A、内心B、外心C、垂心D、重心31、下列命题中①底面的边长都相等,侧面都是矩形的棱柱是正棱柱;②底面的边长都相等,侧面都是全等的矩形的棱柱是正棱柱;③底面是正多边形,侧面都是矩形的棱柱是正棱柱;④底面是正多边形,侧棱都相等的棱柱是正棱柱;⑤底面正多边形,侧棱与底面垂直的棱柱是正棱柱;正确的是()A、①②③④⑤B、②⑤C、③⑤D、③④⑤32、正方体每条棱长都增加2cm,则它的体积就扩大到原来的8倍,那么正方体原来的棱长是()A、1cmB、2cmC、1.5cmD、3cm33、圆柱的轴截面面积为S,则该圆柱的侧面积是()A、SπB、Sπ2C、Sπ21D、Sπ41二、填空题34、如果正方体的对角线长为34cm,则它的体积是____ ___ cm3;35、有两个面是的多边形,其余各面每都的多面体叫棱柱;36、与垂直的棱柱叫做直棱柱;的直棱柱叫正棱柱;37、有一个面是多边形,其余各面是的多面体叫做棱锥;38、正棱锥是指的棱锥;正棱锥斜高是指;39、用一个平行于底面的平面截棱锥,所得的截面与底面,截面面积与底面面积之比等于;40、如果两个锥体的底面积相等,高也相等,那么它们的体积。
多面体与旋转体例题精选

多面体与旋转体一、棱柱1、 由几个多边形围成的封闭的几何体叫做多面体。
2、 两个面互相平行,其余各面都是四边形,并且每相邻两个四边形的公共边都互相平行,由这些面围成的多面体叫做棱柱。
棱柱的互相平行的两个面叫做棱柱的底面,其余各面叫做棱柱的侧面,相邻的两个侧面的公共边叫做棱柱的侧棱,两个底面间的距离叫做棱柱的高。
棱柱的基本性质:(1) 棱柱的侧面都是平行四边形。
(2) 棱柱的两个底面及平行于底面的截面都是全等的多边形。
3、 侧棱与底面不垂直的的棱柱叫做斜棱柱。
侧棱与底面垂直的棱柱叫做直棱柱。
底面是正多边形的直棱柱叫做正棱柱。
性质:(1) 直棱柱侧面都是矩形。
(2) 直棱柱侧棱与高相等。
(3) 正棱柱的侧面都是全等的矩形。
4、 底面是平行四边形的棱柱叫做平行六面体。
底面是矩形的直棱柱是长方体。
长方体的对角线平方等于三边长的平方和。
5、 夹在两个平行平面间的两个几何体,如果被平行于这两个平面的任何平面所截得的两个截面的面积都相等,那么这两个几何体的体积相等。
6、 h V S =⋅棱柱底. 二、棱锥1、有一个面是多边形,其余各面是有一个公共顶点的三角形,由这些面所围成的多面体叫做棱锥。
棱锥的这个多边形的面叫做底面,其余各个三角形的面叫做侧面。
相邻的两个侧面的公共边叫做棱锥的侧棱。
各个侧面的公共顶点叫做棱锥的顶点,顶点到底面的距离叫做棱锥的高。
棱锥的基本性质:如果一个棱锥被平行于底面的一个平面所截,那么: (1) 侧棱和高被这个平面分成比例线段; (2) 截面和底面都是相似多边形;(3) 截面面积与底面面积之比,等于顶点到截面与顶点到底面的距离平方之比。
2、如果一个棱锥的底面是正多边形,且顶点在底面的射影是底面的中心,这个棱锥叫做正棱锥。
正棱锥的性质:(1) 各侧棱相等,各侧面都是全等的等腰三角形。
(2) 正棱锥的高、斜高和斜高在底面上的射影组成一个直角三角形。
正棱锥的高、侧棱和侧棱在底面上的射影也组成一个直角三角形。
多面体与旋转体习题
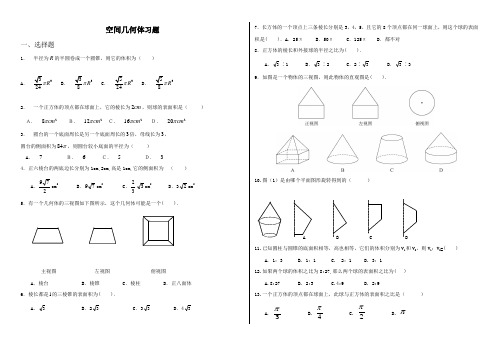
空间几何体习题一、选择题1. 半径为R 的半圆卷成一个圆锥,则它的体积为( )A . 3324R πB . 338R πC . 3524R πD . 358R π 2. 一个正方体的顶点都在球面上,它的棱长为2cm ,则球的表面积是( ) A. 28cm π B. 212cmπC. 216cmπD. 220cmπ3. 圆台的一个底面周长是另一个底面周长的3倍,母线长为3, 圆台的侧面积为84π,则圆台较小底面的半径为( ) A . 7 B. 6 C. 5 D. 34.正六棱台的两底边长分别为1cm,2cm,高是1cm,它的侧面积为 ( )A .279cm 2B .79cm 2C .323cm 2D .32cm 25.有一个几何体的三视图如下图所示,这个几何体可能是一个( ).主视图 左视图 俯视图 A .棱台B .棱锥C .棱柱D .正八面体6.棱长都是1的三棱锥的表面积为( ).A .3B .23C .33D .437.长方体的一个顶点上三条棱长分别是3,4,5,且它的8个顶点都在同一球面上,则这个球的表面积是( ).A .25πB .50πC .125πD .都不对8.正方体的棱长和外接球的半径之比为( ).A .3∶1B .3∶2C .2∶3D .3∶39.如图是一个物体的三视图,则此物体的直观图是( ).10.图(1)是由哪个平面图形旋转得到的( )A B C D11.已知圆柱与圆锥的底面积相等,高也相等,它们的体积分别为V 1和V 2,则V 1:V 2=( )A. 1:3B. 1:1C. 2:1D. 3:112.如果两个球的体积之比为8:27,那么两个球的表面积之比为( )A.8:27B. 2:3C.4:9D. 2:913.一个正方体的顶点都在球面上,此球与正方体的表面积之比是( )A.3πB.4πC.2πD.π二、填空题14.Rt ABC ∆中,3,4,5AB BC AC ===,将三角形绕直角边AB 旋转一周所成的几何体的体积为____________.15.一个长方体的长、宽、高之比为2:1:3,全面积为88cm 2,则它的体积为___________. 16.一个棱柱至少有______个面,面数最少的一个棱锥有________个顶点,顶点最少的一个棱台有________条侧棱.17.若三个球的表面积之比是1∶2∶3,则它们的体积之比是_____________.18.已知一个长方体共一顶点的三个面的面积分别是2、3、6,则这个长方体的对角线长是___________,它的体积为___________.19.一个直径为32厘米的圆柱形水桶中放入一个铁球,球全部没入水中后,水面升高9厘米则此球的半径为_________厘米.20.球的半径扩大为原来的2倍,它的体积扩大为原来的 _________ 倍.21.一个圆柱和一个圆锥的母线相等,底面半径也相等,则侧面积之比是_________.三、解答题22.已知圆台的上下底面半径分别是2,5,且侧面面积等于两底面面积之和,求该圆台的母线长.23.正四棱台的侧棱长为3cm ,两底面边长分别为1cm 和5cm ,求体积.24.如图,在四边形ABCD 中,∠DAB =90°,∠ADC =135°,AB =5,CD =22,AD =2,求四边形ABCD 绕AD 旋转一周所成几何体的表面积及体积.25.将圆心角为1200,面积为3π的扇形,作为圆锥的侧面,求圆锥的表面积和体积.26. (如图)在底半径为2母线长为4的圆锥中内接一个高为3的圆柱,求圆柱的表面积.。
多面体与旋转体

多面体与旋转体一、选择题(在每小题给出的四个选项中,只有一项是符合题目要求)(1)三条侧棱两两互相垂直,且侧棱与底面所成的角都相等是棱锥为正棱锥的()(A)充分但非必要条件(B)必要但非充分条件(C)充要条件(D)非充分非必要条件(2)下列各图都是正方体,M、N、P、Q分别都是它们所在棱的中点,则M、N、P、Q 四点共面的是()(A)(B)(C)(D)(3)正四棱锥每两条相邻侧棱所成的角都是,侧棱长为,则它的体积是()(A)(B)(C)(D)(4)正三棱台的上、下底面边长及高,分别为1、2、2,则它的斜高是()(A)(B)(C)(D)(5)正四棱台上、下底面边长分别为1,3,高为4,则侧棱与底面所成的角的正切值是()(A)(B)2(C)2(D)4(6)两个平行于圆锥底面的平面将圆锥的高分成相等的三段,那么圆锥被分成的三部分的体积的比是()(A)1∶2∶3(B)1∶7∶19(C)3∶4∶5(D)1∶9∶27(7)等边圆柱(轴截面是正方形)、球、正方体的体积相等,它们表面积的大小关系是()(A)(B)(C)(D)(8)已知圆锥的母线长为8,底面积周长为,则它的体积是()(A)(B)(C)(D)(9)若正三棱锥的底面边长为3,侧棱长为2,则这个正三棱锥的体积是(A)27/4(B)9/4(C)27/4(D)9/4(10)圆锥的高为1,底面半径为,则过圆锥顶点的截面面积的最大值为(A)1(B)2 (C)(D)2(11)如果圆锥的侧面积是全面积的3/4,则这个圆锥的侧面积展开图的中心角等于(A)Л/2(B)2Л/3(C)Л(D)3Л/2(12)三棱台的两底面对应边的比为1:2,过上底一边作平面平行于这边所对的侧棱,则这过平面截三棱台所成的两个几何体的体积之比是(A)1/2(B)2/3 (C)4/5(D)4/3二、填空题(13)正棱锥的一个侧面与底面所成的角是,底面积是Q,则它的侧面积__________ (14)截面是等边三角形的圆锥,它的侧面展开图扇形的圆心角的弧度数等于 .(15)三棱柱的体积是V,D、E分别在、上,线段DE经过矩形的中心,则四棱锥C-ABED 的体积是(16)已知母线长为10,底面半径为5的圆锥内有一球,球与圆锥的底面及圆锥的所有母线都相切,则球的体积是(17)P、Q是半径为R的球面上的两点,它们的球面距离是,则过P、Q的平面中,与球心的最大距离是三、解答题:(18)求棱长为的正方体的一个顶点A到平面的距离。
高考数学多面体与旋转体选择题

高考数学多面体与旋转体选择题1. 已知一个正四面体的一个顶点是平面ABC外的一点,且该顶点到平面ABC的距离为d,则该正四面体的外接球的半径R为:A. $\sqrt{3}d$B. $2\sqrt{3}d$C. $3d$D. $6d$2. 设E是正方体的一个顶点,F是正方体的一个对角线的中点,那么EF的长度是:A. 正方体棱长的$\sqrt{2}$倍B. 正方体棱长的$\sqrt{3}$倍C. 正方体棱长的2倍D. 正方体棱长的3倍3. 圆锥的母线与底面所成的角是:A. 45°B. 60°C. 90°D. 120°4. 圆台的上下底圆半径分别是3和1,高是4,那么圆台的体积是:A. $12\pi$B. $24\pi$C. $36\pi$D. $48\pi$5. 一个圆柱的侧面积是24π,底面半径是3,那么这个圆柱的高是:A. 2B. 3C. 4D. 66. 圆锥的底面半径是2,母线长是4,那么这个圆锥的体积是:A. $2\pi$B. $4\pi$C. $6\pi$D. $8\pi$7. 一个圆柱的底面半径和高分别是3和4,那么这个圆柱的侧面积是:B. $48\pi$C. $72\pi$D. $96\pi$8. 一个圆台的上下底圆半径分别是2和3,高是4,那么这个圆台的侧面积是:A. $24\pi$B. $48\pi$C. $72\pi$D. $96\pi$9. 一个圆锥的底面半径和高分别是2和4,那么这个圆锥的侧面积是:A. $12\pi$B. $24\pi$C. $36\pi$D. $48\pi$10. 一个圆柱的底面半径是2,高是4,那么这个圆柱的体积是:A. $8\pi$B. $16\pi$D. $32\pi$11. 一个圆台的上下底圆半径分别是2和3,高是4,那么这个圆台的体积是:A. $8\pi$B. $16\pi$C. $24\pi$D. $32\pi$12. 一个圆锥的底面半径和高分别是2和4,那么这个圆锥的体积是:A. $4\pi$B. $8\pi$C. $12\pi$D. $16\pi$13. 一个圆柱的底面半径是3,高是4,那么这个圆柱的侧面积是:A. $24\pi$B. $48\pi$C. $72\pi$14. 一个圆台的上下底圆半径分别是3和4,高是4,那么这个圆台的侧面积是:A. $24\pi$B. $48\pi$C. $72\pi$D. $96\pi$15. 一个圆锥的底面半径和高分别是3和4,那么这个圆锥的侧面积是:A. $12\pi$B. $24\pi$C. $36\pi$D. $48\pi$16. 一个圆柱的底面半径是4,高是4,那么这个圆柱的体积是:A. $16\pi$B. $32\pi$C. $48\pi$D. $64\pi$17. 一个圆台的上下底圆半径分别是4和5,高是4,那么这个圆台的体积是:A. $16\pi$B. $32\pi$C. $48\pi$D. $64\pi$18. 一个圆锥的底面半径和高分别是4和4,那么这个圆锥的体积是:A. $8\pi$B. $16\pi$C. $24\pi$D. $32\pi$19. 一个圆柱的底面半径是5,高是5,那么这个圆柱的侧面积是:A. $40\pi$B. $80\pi$C. $120\pi$D. $160\pi$20. 一个圆台的上下底圆半径分别是5和6,高是5,那么这个圆台的侧面积是:A. $40\pi$B. $80\pi$C. $120\pi$D. $160\pi$21. 一个圆锥的底面半径和高分别是5和5,那么这个圆锥的侧面积是:A. $20\pi$B. $40\pi$C. $60\pi$D. $80\pi$22. 一个圆柱的底面半径是6,高是6,那么这个圆柱的体积是:A. $24\pi$B. $48\pi$C. $72\pi$D. $96\pi$23. 一个圆台的上下底圆半径分别是6和7,高是6,那么这个圆台的体积是:A. $24\pi$C. $72\pi$D. $96\pi$24. 一个圆锥的底面半径和高分别是6和6,那么这个圆锥的体积是:A. $12\pi$B. $24\pi$C. $36\pi$D. $48\pi$25. 一个圆柱的底面半径是7,高是7,那么这个圆柱的侧面积是:A. $40\pi$B. $80\pi$C. $120\pi$D. $160\pi$26. 一个圆台的上下底圆半径分别是7和8,高是7,那么这个圆台的侧面积是:A. $40\pi$B. $80\pi$D. $160\pi$27. 一个圆锥的底面半径和高分别是7和7,那么这个圆锥的侧面积是:A. $20\pi$B. $40\pi$C. $60\pi$D. $80\pi$28. 一个圆柱的底面半径是8,高是8,那么这个圆柱的体积是:A. $24\pi$B. $48\pi$C. $72\pi$D. $96\pi$29. 一个圆台的上下底圆半径分别是8和9,高是8,那么这个圆台的体积是:A. $24\pi$B. $48\pi$C. $72\pi$D. $96\pi$30. 一个圆锥的底面半径和高分别是8和8,那么这个圆锥的体积是:A. $12\pi$B. $24\pi$C. $36\pi$D. $48\pi$31. 一个圆柱的底面半径是9,高是9,那么这个圆柱的侧面积是:A. $40\pi$B. $80\pi$C. $120\pi$D. $160\pi$32. 一个圆台的上下底圆半径分别是9和10,高是9,那么这个圆台的侧面积是:A. $40\pi$B. $80\pi$C. $120\pi$D. $160\pi$33. 一个圆锥的底面半径和高分别是9和9,那么这个圆锥的侧面积是:A. $20\pi$B. $40\pi$C. $60\pi$D. $80\pi$34. 一个圆柱的底面半径是10,高是10,那么这个圆柱的体积是:A. $24\pi$B. $48\pi$C. $72\pi$D. $96\pi$35. 一个圆台的上下底圆半径分别是10和11,高是10,那么这个圆台的体积是:A. $24\pi$B. $48\pi$C. $72\pi$D. $96\pi$36. 一个圆锥的底面半径和高分别是10和10,那么这个圆锥的体积是:A. $12\pi$B. $24\pi$C. $36\pi$D. $48\pi$37. 一个圆柱的底面半径是11,高是11,那么这个圆柱的侧面积是:A. $40\pi$B. $80\pi$C. $120\pi$D. $160\pi$38. 一个圆台的上下底圆半径分别是11和12,高是11,那么这个圆台的侧面积是:A. $40\pi$B. $80\pi$C. $120\pi$D. $160\pi$39. 一个圆锥的底面半径和高分别是11和11,那么这个圆锥的侧面积是:B. $40\pi$C. $60\pi$D. $80\pi$40. 一个圆柱的底面半径是12,高是12,那么这个圆柱的体积是:A. $24\pi$B. $48\pi$C. $72\pi$D. $96\pi$41. 一个圆台的上下底圆半径分别是12和13,高是12,那么这个圆台的体积是:A. $24\pi$B. $48\pi$C. $72\pi$D. $96\pi$42. 一个圆锥的底面半径和高分别是12和12,那么这个圆锥的体积是:A. $12\pi$C. $36\pi$D. $48\pi$43. 一个圆柱的底面半径是13,高是13,那么这个圆柱的侧面积是:A. $40\pi$B. $80\pi$C. $120\pi$D. $160\pi$44. 一个圆台的上下底圆半径分别是13和14,高是13,那么这个圆台的侧面积是:A. $40\pi$B. $80\pi$C. $120\pi$D. $160\pi$45. 一个圆锥的底面半径和高分别是13和13,那么这个圆锥的侧面积是:A. $20\pi$B. $40\pi$D. $80\pi$46. 一个圆柱的底面半径是14,高是14,那么这个圆柱的体积是:A. $24\pi$B. $48\pi$C. $72\pi$D. $96\pi$47. 一个圆台的上下底圆半径分别是14和15,高是14,那么这个圆台的体积是:A. $24\pi$B. $48\pi$C. $72\pi$D. $96\pi$48. 一个圆锥的底面半径和高分别是14和14,那么这个圆锥的体积是:A. $12\pi$B. $24\pi$C. $36\pi$49. 一个圆柱的底面半径是15,高是15,那么这个圆柱的侧面积是:A. $40\pi$B. $80\pi$C. $120\pi$D. $160\pi$50. 一个圆台的上下底圆半径分别是15和16,高是15,那么这个圆台的侧面积是:A. $40\pi$B. $80\pi$C. $120\pi$D. $160\pi$。
多面体和旋转体练习题

多面体和旋转体1、 下列命题中正确的命题序号为①棱长都相等的直四棱柱是正方体 ②侧面是全等的等边三角形的四棱锥是正四棱锥 ③侧棱两两垂直且侧棱长相等的三棱锥是争三棱锥 ④有两个侧面是矩形的棱柱是直棱柱 ⑤侧面是全等的等腰三角形的三棱锥是正三棱锥 ⑥直平行六面体是长方体2、 若正三棱锥的底面边长为3,且各侧棱与底面所成角为︒60,则此棱锥的体积为 侧面积为3、 四棱锥ABCD P -的底面是矩形,AP 垂直于底面,且3,4,1===BC AB AP ,则点P 到BD 的距离为4、 正四棱柱的对角线和侧面所成角为︒30,底面边长为a ,则其体积为5、 若正四棱锥的侧面积为3412,底面边长为6,则棱锥的高为6、 棱长为4的正方体1111D C B A ABCD -中,Q P ,是1CC 上两动点,且1=PQ ,则三棱锥AQD P -的体积为7、 一个棱锥被平行于底面的平面所截,若截面面积和底面面积之比为3:4,则棱锥被截面所截得的上下两部分的体积之比为8、 设P 是边长为a 的正三角形ABC 内的任意一点,由PAC PBC PAB ABC S S S S ∆∆∆∆++=可得P 到三角形三边的距离之和为a 23;类似地,在空间中,P 是边长为b 的正四面体BCD A -内的任意一点,由 可得P 到四面体四个面的距离之和为9、 圆锥的侧面展开图是一个半圆,则圆锥母线与底面所成角为 ;若其全面积为272cm π,圆锥体积为10、 斜边长为6的等腰直角三角形(及其内部)绕斜边所在直线旋转一周,形成一个几何体,该几何体的体积为11、 一个半径为1的球嵌在一个圆锥体内,且与该圆锥的侧面以及底部半径为2的大圆面均相切,则圆锥的侧面积为12、 地球半径为R ,在北纬︒45圈上有两点A 、B ,A 点的经度为东经︒115,B 点的经度为东经︒25,则A 、B 两地的球面距离为13、一个正方体的顶点都在球面上,它的棱长为2cm ,则球的表面积是 14、 用一张圆弧长为cm π12、半径是cm 10的扇形胶片制作一个圆锥体模型,这个圆锥体的体积等于15、 在底面是矩形的四棱锥ABCD P -中,⊥PA 平面2,1,===BC AB PA ABCD(1) 求PC 与平面PAD 所成角的大小(2) 若E 是PD 的中点,求异面直线AE 与PC 所成角的大小(3) 在BC 边上是否存在一点G ,使得D 点到平面PAG 的距离为2,若存在,求出BG 的值;若不存在,说明理由16、 圆柱的轴截面ABCD 为正方形,1,O O 分别为上、下底面的圆心,E 为上底面圆周上一点,已知︒=∠601E DO ,圆柱侧面积等于π16(1) 求圆柱的体积V (2)求异面直线BE 与DO 所成角的大小17、 过圆锥的顶点S 作截面SAB 与底面成︒60二面角,且B A ,分底面圆周为2:1两段弧,已知截面SAB 面积为324,(1)求圆锥的侧面积(2)求底面圆心到截面SAB 的距离。
立体几何测试题(多面体与旋转体)

(多面体与旋转体)1、一个四棱柱是长方体的充要条件是()A、底面是矩形B、侧面是正方形C、侧面和底面都是矩形D、侧面和底面都是正方形2、长方体共顶点的三个面的面积分别是2cm2,6cm2和9cm2,那么这个长方体的体积为()A、3j6cm3B、6*3cm3C、7cm3D、8cm33、对角线长为d的正方体的棱长为()A、1dB、忌C、(再€i)dD、申4、长方体的12条棱的总长度为56m,表面积为112m2,那么长方体的对角线长为()A、3、14mB、7、.6mC、2*21mD、9m5、如果直棱柱的底面是菱形,它的高是9cm,它的两条对角线分别与底面成60。
角和45。
角,那么这个棱柱的体积是()A>3v3a2B、2v'3a2C、(、.:3+1)a2D、(冬3+1)a27、已知正六棱柱底面的边长和高都等于a,那么最大对角截面的面积是()A、2a2B、*3a28、三棱锥的三条侧棱两两互相垂直,各侧棱与底面所成的角彼此相等,那么顶点在底面的射影是底面三角形的A 、243打cm3B、243v'3cm3C、步cm32D、729,3cm36、在斜三棱柱中,各棱长都是a,且有一组共顶点的三条棱A、垂心但不是内心B、内心但不是垂心C、外心但不是重心D、垂心又是重心9、三棱锥P-ABC的侧棱两两互相垂直,且PA=1,PB^3,PC=.J6,那么Z ABC=()A、30。
B、60。
C、45。
D、75。
10、如果正三棱锥的侧棱长为2a,底面周长为9a,那么这个棱锥的高为()A、aB、2aC、aD、3a2211、已知三棱锥各侧面与底面所成二面角彼此相等,那么立体几何测试题两两夹角都等于60°,那么这个棱柱的全面积是()B 、 a 3D 、角之最大值是()顶点在底面上的射影,一定是底面三角形的()A 、内心B 、外心C 、垂心D 、重心12、一个棱锥被平行于底面的平面截成两部分,截面的面积恰好是棱锥底面面积的一半,那么截得的两部分的体积比为() 那么该棱截面面积是()A 、1600€cm 2B 、6724€2cm 2C 、81€cm 2D 、324€cm 218、一圆柱的高为8cm ,底面半径为5cm ,一平面截该圆柱得到的截面是正方形,则这个截面与轴的距离是()A 、1B 、1C 、D 、竺242413、正四棱锥底面边长为a ,侧棱长也是a ,那么它的体积是() A 、4cmB 、3cmC 、2cmD 、1cm19、已知圆柱的轴截面相邻边长之比是2:3,侧面积是24€cm 2,则圆柱的体积是()A 、14、沿长方体的三个面的对角线截去一个三棱锥,剩下的几何体的体积与原长方体体积之比是()A 、1:6B 、2:3C 、1:3D 、5:615、球面面积膨胀为原来的3倍,那么体积变为原来的() A 、9倍B 、打倍C 、3•訂倍D 、27倍16、一个正方体的顶点都在球面上,它的棱长为4cm ,那么这 A 、24€cm 3B 、36€cm 3C 、24€cm 3或36€cm 3D 、54€cm 320、将半径为r 的圆形薄铁板沿三条半径裁成全等的三个扇形,做成三个圆锥筒(无底),则圆锥筒的高(不计接头)是()A 、土rB 、土2rC 、兰3rD 、2迈r323'21、圆锥的侧面母线长为3,侧面展开所成的扇形的中心角等于60o ,那么这个圆锥的底面积是()A 、64cm 3B 、32^3兀cm 3C 、48兀cm 3D 、256^3兀cm 317、如果球的半径为41cm ,一个球的截面与球心的距离为9cm,个球的体积是()A 、4€B 、2€ C 、1€ D 、1€22、将一个半圆围成一个圆锥面,则该圆锥两条母线的夹A、120oB、90oC、60oD、45o23、体积为8的正方体的外接球的体积为()A、4^3兀B、2—兀C、2_6兀D、4(忖3+1)兀3324、下列命题中①底面边长都相等,侧棱也都相等的棱锥是正棱锥;②底面是正多边形,侧面是等腰三角形的棱锥是正棱锥;③底面是正多边形,侧面是全等的等腰三角形的棱锥是正棱锥;④底面边长都相等,侧面是全等的三角形的棱锥是正棱锥;⑤底面是正多边形,顶点的射影是底面的中心的棱锥是正棱锥;⑥侧棱都相等的棱锥是正棱锥;⑦侧面都是等腰三角形的棱锥是正棱锥;⑧侧棱与底面所成的角都相等的棱锥是正棱锥;⑨侧面与底面所成的角都相等的棱锥是正棱锥;⑩斜高都相等的棱锥是正棱锥;正确的是()A、①③⑤⑨⑩B、②④⑤⑥C、②③⑤⑦⑧D、③⑤25、下列命题中①有两个面是互相平行的多边形,其余各面是平行四边形的多面体是棱柱;②有两个面是互相平行的多边形,其余各面每相邻两面的公共边互相平行的多面体是棱柱;③有两个面是互相平行的多边形,其余各面每相邻两面的公共边都等长的多面体是棱柱;④有两个面是互相平行的多边形,其余各面每相邻两面所成的二面角大小都相等的多面体是棱柱正确的是()A、①②③④B、②④C、②D、②③④26、下列命题中①有一个侧面是矩形的棱柱是直棱柱;②有两个侧面是矩形的棱柱是直棱柱;③有两个相邻的侧面都是矩形的棱柱是直棱柱;④有一个侧面与底面垂直的棱柱是直棱柱;⑤有两个侧面与底面垂直的棱柱是直棱柱;⑥有两个相邻的侧面都与底面垂直的棱柱是直棱柱;正确的是()A、①②③④B、③⑥C、②⑤⑥D、②③④⑤27、已知边长为3、4、5的直角三角形,分别以它的三条边为轴转一周,所得到的几何体的表面积之比是()A、15:10:7B、18:15:7C、13:12:5D>25:16:928、把一个圆心角为120°的扇形卷成一个圆锥的侧面,则此圆锥底面圆的半径与这个圆锥的高之比是()A、1:4B、迈:2C、迈:込D、迈:429、把一个圆心角为a弧度(0V a V2n)的扇形卷成一个圆锥的侧面,则此圆锥底面圆的半径与这个圆锥的母线长之比是()A、a:2€B、a:兀C、a:\:2兀D、a:4兀30、已知三棱锥各侧面与底面所成二面角彼此相等,那么顶点在底面上的射影,一定是底面三角形的()A、内心B、外心C、垂心D、重心31、下列命题中①底面的边长都相等,侧面都是矩形的棱柱是正棱柱;②底面的边长都相等,侧面都是全等的矩形的棱柱是正棱柱;③底面是正多边形,侧面都是矩形的棱柱是正棱柱;④底面是正多边形,侧棱都相等的棱柱是正棱柱;⑤底面正多边形,侧棱与底面垂直的棱柱是正棱柱;正确的是()A、①②③④⑤B、②⑤C、③⑤D、③④⑤32、正方体每条棱长都增加2cm,则它的体积就扩大到原来的8倍,那么正方体原来的棱长是()A、1cmB、2cmC、1.5cmD、3cm33、圆柱的轴截面面积为S,则该圆柱的侧面积是()A、€SB、2€SC、1€SD、1€S24二、填空题34、如果正方体的对角线长为4j3cm,则它的体积是___cm3;35、有两个面是的多边形,其余各面每都的多面体叫棱柱;36、与_垂直的棱柱叫做直棱柱;的直棱柱叫正棱柱;37、有一个面是多边形,其余各面是的多面体叫做棱锥;38、正棱锥是指的棱锥;正棱锥斜高是扌旨;39、用一个平行于底面的平面截棱锥,所得的截面与底面_, 截面面积与底面面积之比等于;40、如果两个锥体的底面积相等,高也相等,那么它们的体积。
春季20-高二数学基础版-多面体与旋转体-期末复习-课后作业学生版

一、填空题1、在空间中,若直线a 与b 无公共点,则直线,a b 的位值关系是________;2、若两个球的体积之比为8:27,则这两个球的表面积之比为____;3、若正方体''''ABCD A B C D -中,异面直线AC 和'BD 所成角的大小为_____;4、ABC ∆中,5,6,AB AC BC PA ===⊥平面ABC ,8PA =,则P 到BC 的距离是______5、若圆柱的轴截面面积为2,则其侧面积为___;6、正四棱锥底面边长为4,侧棱长为3,则其体积为_____;7、有一列正方体,它们的棱长组成以1位首项,12为公比的等比数列,设它们的体积依次为12,,,n V V V ,则()12lim n n V V V →∞+++=__________;8、已知ABC ∆,用斜二测画法作它的直观图'''A B C ∆,若'''A B C ∆是斜边平行于'x 铀的等腰直角三角形,则ABC ∆是________三角形(填“锐角”、“直角”、“钝角”).9、在北纬45°圈上有甲、乙两地,它们的经度差90°,则甲乙两地的球面距离与地球半多面体与旋转体径的比值为________;101的正方体截去四个角后得到,类比这种方法,一个相对棱长都相等的四面体ABCD ,其三组对棱长分别为AB CD AD BC AC BD ======_______;11、已知平面α截一球面得圆M ,过圆M 的圆心M 且与平面α呈45°二面角的平面β截该球面得圆N ,若球的半径为4,圆M 的面积为12π,则圆N 的面积为__________;12、如图,棱长为3的正方体的顶点A 在平面α上,三条棱,,AB AC AD 都在平面α的同侧,如顶点,B C 到平面α的距离分别为则顶点D 到平面α的距离为___________;二、选择题13、“直线l 垂直于ABC ∆的边,AB AC ’’是“直线l 垂直于ABC ∆的边BC ”的() A 、充分非必要条件 B 、必要非充分条件 C 、充要条件 D 、既不充分又不必要条件14、如果三棱锥S ABC -的底面不是等比三角形,网组对棱互相垂直,且顶点S 在底面的射影O 在ABC ∆内,那么O 是ABC ∆的()A 、外心B 、内心C 、垂心D 、重心15、底面是正三角形,且每个侧面是等腰三角形的三棱锥( ) A 、一定是正三棱锥 B 、一定是正四面体C 、不是斜三棱锥D 、可能是斜三棱锥16、在正方体1111ABCD A B C D -中,点P (异于点B )是棱长一点,则满足BP 与1AC ,所成的角为45°的点P 的个数为( )A 、0B 、3C 、4D 、6三、解答题:17、如图,在棱长为a 的正方体1111ABCD A B C D -中,E 是棱1DD 的中点. (1)求三棱锥1D A BE -的体积; (2)求异面直线BE 与1CC 所成角大小.18、如图,某甜品创作一种冰淇淋,其上半部分呈半球形,下半部分呈圆锥形,现把半径为10cm 的圆形蛋皮等分成5个扇形,用一个扇形蛋皮固成圆锥的侧面(蛋皮厚度忽略不计)。
高考数学多面体与旋转体选择题

高考数学多面体与旋转体选择题1. 下列关于多面体的说法正确的是()A. 棱柱的底面和顶面都是平行四边形B. 棱柱的底面和顶面是矩形时,其侧面都是矩形C. 圆柱的侧面展开图是矩形D. 圆柱的侧面展开图是梯形2. 已知长方体的长、宽、高分别为a、b、c,则该长方体的对角线长度d为()A. $\sqrt{a^2 + b^2 + c^2}$B. $\sqrt{a^2 + b^2 - c^2}$C. $\sqrt{a^2 + b^2 + 2ac}$D. $\sqrt{a^2 + b^2 - 2ac}$3. 已知圆锥的底面半径为r,高为h,母线长为l,则该圆锥的体积V为()A. $\frac{1}{3}\pi r^2h$B. $\frac{1}{3}\pi l^2h$C. $\frac{1}{3}\pi r^2l$D. $\frac{1}{3}\pi l^2r$4. 已知球的半径为R,则该球的表面积S为()A. $4\pi R^2$B. $2\pi R^2$C. $4\pi R^3$D. $2\pi R^3$5. 已知圆台的上下底圆半径分别为r1和r2,高为h,则该圆台的体积V为()A. $\pi (r1^2 + r2^2)h$B. $\pi (r1^2 - r2^2)h$C. $\pi (r1^2 + r2^2)^2$D. $\pi (r1^2 - r2^2)^2$6. 已知圆锥的底面半径为r,母线长为l,则该圆锥的侧面积S 为()A. $\pi rl$B. $\pi l^2r$C. $\pi r^2l$D. $\pi l^2$7. 已知圆台的上下底圆半径分别为r1和r2,高为h,则该圆台的侧面积S为()B. $\pi (r1^2 - r2^2)h$C. $\pi (r1^2 + r2^2)^2$D. $\pi (r1^2 - r2^2)^2$8. 已知球的半径为R,则该球的体积V为()A. $\frac{4}{3}\pi R^3$B. $\frac{1}{3}\pi R^3$C. $\frac{4}{3}\pi R^2$D. $\frac{1}{3}\pi R^2$9. 已知圆锥的底面半径为r,高为h,则该圆锥的侧面积S为()A. $\pi r^2h$B. $\pi rh^2$C. $\pi rl^2$D. $\pi l^2r$10. 已知圆台的上下底圆半径分别为r1和r2,高为h,则该圆台的侧面积S为()A. $\pi (r1^2 + r2^2)h$B. $\pi (r1^2 - r2^2)h$C. $\pi (r1^2 + r2^2)^2$11. 已知球的半径为R,则该球的表面积S为()A. $4\pi R^2$B. $2\pi R^2$C. $4\pi R^3$D. $2\pi R^3$12. 已知圆锥的底面半径为r,高为h,母线长为l,则该圆锥的体积V为()A. $\frac{1}{3}\pi r^2h$B. $\frac{1}{3}\pi l^2h$C. $\frac{1}{3}\pi r^2l$D. $\frac{1}{3}\pi l^2r$13. 已知长方体的长、宽、高分别为a、b、c,则该长方体的对角线长度d为()A. $\sqrt{a^2 + b^2 + c^2}$B. $\sqrt{a^2 + b^2 - c^2}$C. $\sqrt{a^2 + b^2 + 2ac}$D. $\sqrt{a^2 + b^2 - 2ac}$14. 已知圆台的上下底圆半径分别为r1和r2,高为h,则该圆台的体积V为()A. $\pi (r1^2 + r2^2)h$B. $\pi (r1^2 - r2^2)h$C. $\pi (r1^2 + r2^2)^2$D. $\pi (r1^2 - r2^2)^2$15. 已知圆锥的底面半径为r,高为h,则该圆锥的侧面积S为()A. $\pi r^2h$B. $\pi rh^2$C. $\pi rl^2$D. $\pi l^2r$16. 已知圆台的上下底圆半径分别为r1和r2,高为h,则该圆台的侧面积S为()A. $\pi (r1^2 + r2^2)h$B. $\pi (r1^2 - r2^2)h$C. $\pi (r1^2 + r2^2)^2$D. $\pi (r1^2 - r2^2)^2$17. 已知球的半径为R,则该球的体积V为()A. $\frac{4}{3}\pi R^3$B. $\frac{1}{3}\pi R^3$C. $\frac{4}{3}\pi R^2$D. $\frac{1}{3}\pi R^2$18. 已知圆锥的底面半径为r,高为h,母线长为l,则该圆锥的体积V为()A. $\frac{1}{3}\pi r^2h$B. $\frac{1}{3}\pi l^2h$C. $\frac{1}{3}\pi r^2l$D. $\frac{1}{3}\pi l^2r$19. 已知长方体的长、宽、高分别为a、b、c,则该长方体的对角线长度d为()A. $\sqrt{a^2 + b^2 + c^2}$B. $\sqrt{a^2 + b^2 - c^2}$C. $\sqrt{a^2 + b^2 + 2ac}$D. $\sqrt{a^2 + b^2 - 2ac}$20. 已知圆台的上下底圆半径分别为r1和r2,高为h,则该圆台的体积V为()A. $\pi (r1^2 + r2^2)h$B. $\pi (r1^2 - r2^2)h$C. $\pi (r1^2 + r2^2)^2$D. $\pi (r1^2 - r2^2)^2$21. 已知圆锥的底面半径为r,高为h,则该圆锥的侧面积S为()A. $\pi r^2h$B. $\pi rh^2$C. $\pi rl^2$D. $\pi l^2r$22. 已知圆台的上下底圆半径分别为r1和r2,高为h,则该圆台的侧面积S为()A. $\pi (r1^2 + r2^2)h$B. $\pi (r1^2 - r2^2)h$C. $\pi (r1^2 + r2^2)^2$D. $\pi (r1^2 - r2^2)^2$23. 已知球的半径为R,则该球的体积V为()A. $\frac{4}{3}\pi R^3$B. $\frac{1}{3}\pi R^3$C. $\frac{4}{3}\pi R^2$D. $\frac{1}{3}\pi R^2$24. 已知圆锥的底面半径为r,高为h,母线长为l,则该圆锥的体积V为()A. $\frac{1}{3}\pi r^2h$B. $\frac{1}{3}\pi l^2h$C. $\frac{1}{3}\pi r^2l$D. $\frac{1}{3}\pi l^2r$25. 已知长方体的长、宽、高分别为a、b、c,则该长方体的对角线长度d为()A. $\sqrt{a^2 + b^2 + c^2}$B. $\sqrt{a^2 + b^2 - c^2}$C. $\sqrt{a^2 + b^2 + 2ac}$D. $\sqrt{a^2 + b^2 - 2ac}$26. 已知圆台的上下底圆半径分别为r1和r2,高为h,则该圆台的体积V为()A. $\pi (r1^2 + r2^2)h$B. $\pi (r1^2 - r2^2)h$C. $\pi (r1^2 + r2^2)^2$D. $\pi (r1^2 - r2^2)^2$27. 已知圆锥的底面半径为r,高为h,则该圆锥的侧面积S为()A. $\pi r^2h$B. $\pi rh^2$C. $\pi rl^2$D. $\pi l^2r$28. 已知圆台的上下底圆半径分别为r1和r2,高为h,则该圆台的侧面积S为()A. $\pi (r1^2 + r2^2)h$B. $\pi (r1^2 - r2^2)h$C. $\pi (r1^2 + r2^2)^2$D. $\pi (r1^2 - r2^2)^2$29. 已知球的半径为R,则该球的体积V为()A. $\frac{4}{3}\pi R^3$B. $\frac{1}{3}\pi R^3$C. $\frac{4}{3}\pi R^2$D. $\frac{1}{3}\pi R^2$30. 已知圆锥的底面半径为r,高为h,母线长为l,则该圆锥的体积V为()A. $\frac{1}{3}\pi r^2h$B. $\frac{1}{3}\pi l^2h$C. $\frac{1}{3}\pi r^2l$D. $\frac{1}{3}\pi l^2r$31. 已知长方体的长、宽、高分别为a、b、c,则该长方体的对角线长度d为()A. $\sqrt{a^2 + b^2 + c^2}$B. $\sqrt{a^2 + b^2 - c^2}$C. $\sqrt{a^2 + b^2 + 2ac}$D. $\sqrt{a^2 + b^2 - 2ac}$32. 已知圆台的上下底圆半径分别为r1和r2,高为h,则该圆台的体积V为()A. $\pi (r1^2 + r2^2)h$B. $\pi (r1^2 - r2^2)h$C. $\pi (r1^2 + r2^2)^2$D. $\pi (r1^2 - r2^2)^2$33. 已知圆锥的底面半径为r,高为h,则该圆锥的侧面积S为()A. $\pi r^2h$B. $\pi rh^2$C. $\pi rl^2$D. $\pi l^2r$34. 已知圆台的上下底圆半径分别为r1和r2,高为h,则该圆台的侧面积S为()A. $\pi (r1^2 + r2^2)h$B. $\pi (r1^2 - r2^2)h$C. $\pi (r1^2 + r2^2)^2$D. $\pi (r1^2 - r2^2)^2$35. 已知球的半径为R,则该球的体积V为()A. $\frac{4}{3}\pi R^3$B. $\frac{1}{3}\pi R^3$C. $\frac{4}{3}\pi R^2$D. $\frac{1}{3}\pi R^2$36. 已知圆锥的底面半径为r,高为h,母线长为l,则该圆锥的体积V为()A. $\frac{1}{3}\pi r^2h$B. $\frac{1}{3}\pi l^2h$C. $\frac{1}{3}\pi r^2l$D. $\frac{1}{3}\pi l^2r$37. 已知长方体的长、宽、高分别为a、b、c,则该长方体的对角线长度d为()A. $\sqrt{a^2 + b^2 + c^2}$B. $\sqrt{a^2 + b^2 - c^2}$C. $\sqrt{a^2 + b^2 + 2ac}$D. $\sqrt{a^2 + b^2 - 2ac}$38. 已知圆台的上下底圆半径分别为r1和r2,高为h,则该圆台的体积V为()A. $\pi (r1^2 + r2^2)h$B. $\pi (r1^2 - r2^2)h$C. $\pi (r1^2 + r2^2)^2$D. $\pi (r1^2 - r2^2)^2$39. 已知圆锥的底面半径为r,高为h,则该圆锥的侧面积S为()A. $\pi r^2h$B. $\pi rh^2$C. $\pi rl^2$D. $\pi l^2r$40. 已知圆台的上下底圆半径分别为r1和r2,高为h,则该圆台的侧面积S为()A. $\pi (r1^2 + r2^2)h$B. $\pi (r1^2 - r2^2)h$C. $\pi (r1^2 + r2^2)^2$D. $\pi (r1^2 - r2^2)^2$41. 已知球的半径为R,则该球的体积V为()A. $\frac{4}{3}\pi R^3$B. $\frac{1}{3}\pi R^3$C. $\frac{4}{3}\pi R^2$D. $\frac{1}{3}\pi R^2$42. 已知圆锥的底面半径为r,高为h,母线长为l,则该圆锥的体积V为()A. $\frac{1}{3}\pi r^2h$B. $\frac{1}{3}\pi l^2h$C. $\frac{1}{3}\pi r^2l$D. $\frac{1}{3}\pi l^2r$43. 已知长方体的长、宽、高分别为a、b、c,则该长方体的对角线长度d为()A. $\sqrt{a^2 + b^2 + c^2}$B. $\sqrt{a^2 + b^2 - c^2}$C. $\sqrt{a^2 + b^2 + 2ac}$D. $\sqrt{a^2 + b^2 - 2ac}$44. 已知圆台的上下底圆半径分别为r1和r2,高为h,则该圆台的体积V为()A. $\pi (r1^2 + r2^2)h$B. $\pi (r1^2 - r2^2)h$C. $\pi (r1^2 + r2^2)^2$D. $\pi (r1^2 - r2^2)^2$45. 已知圆锥的底面半径为r,高为h,则该圆锥的侧面积S为()A. $\pi r^2h$B. $\pi rh^2$C. $\pi rl^2$D. $\pi l^2r$46. 已知圆台的上下底圆半径分别为r1和r2,高为h,则该圆台的侧面积S为()A. $\pi (r1^2 + r2^2)h$B. $\pi (r1^2 - r2^2)h$C. $\pi (r1^2 + r2^2)^2$D. $\pi (r1^2 - r2^2)^2$47. 已知球的半径为R,则该球的体积V为()A. $\frac{4}{3}\pi R^3$B. $\frac{1}{3}\pi R^3$C. $\frac{4}{3}\pi R^2$D. $\frac{1}{3}\pi R^2$48. 已知圆锥的底面半径为r,高为h,母线长为l,则该圆锥的体积V为()A. $\frac{1}{3}\pi r^2h$B. $\frac{1}{3}\pi l^2h$C. $\frac{1}{3}\pi r^2l$D. $\frac{1}{3}\pi l^2r$49. 已知长方体的长、宽、高分别为a、b、c,则该长方体的对角线长度d为()A. $\sqrt{a^2 + b^2 + c^2}$B. $\sqrt{a^2 + b^2 - c^2}$C. $\sqrt{a^2 + b^2 + 2ac}$D. $\sqrt{a^2 + b^2 - 2ac}$50. 已知圆台的上下底圆半径分别为r1和r2,高为h,则该圆台的体积V为()A. $\pi (r1^2 + r2^2)h$B. $\pi (r1^2 - r2^2)h$C. $\pi (r1^2 + r2^2)^2$D. $\pi (r1^2 - r2^2)^2$。
《高考研究系列》之多面体与旋转体-数学试题

《高考研究系列》之多面体与旋转体-数学试题考试内容:棱柱(包括平行六面体)。
棱锥。
棱台。
多面体。
圆柱。
圆锥。
圆台。
球。
球冠。
旋转体。
体积的概念与体积公理。
棱柱、圆柱的体积。
棱锥、圆锥的体积。
棱台、圆台的体积。
球和球缺的体积。
考试要求:(1)理解棱柱、棱锥、棱台、圆柱、圆锥、圆台、球及其有关概念和性质。
(2)掌握直棱柱、正棱锥、正棱台和圆柱、圆锥、圆台、球的表面积和体积公式以及球冠的面积、球缺的体积公式(球缺体积公式不要求记住),并能运用这些公式进行计算。
(3)了解多面体和旋转体的概念,能正确画出直棱柱、正棱锥、正棱台、圆柱、圆锥、圆台的直观图。
(4)对于截面问题,只要求会解决与几种特殊的截面(棱柱、棱锥、棱台的对角面,棱柱的直截面,圆柱、圆锥、圆台的轴截面和平行于底面的截面,球的截面)以及已给出图形或它的全部顶点的其他截面的有关问题。
一、选择题如果正方体ABCD-A’B’C’D’的棱长为a,那么四面体A‘-ABD的体积是()(85年(1)3分)(A)(B)(C)(D)如果圆锥的底半径为,高为2,那么它的侧面积是()(89年(3)3分)(A)4π(B)2π(C)2π(D)4π已知球的两个平行截面的面积分别为5π和8π,它们位于球心的同一侧,且相距为1,那么这个球的半径是()(89年(8)3分)(A)4(B)3(C)2(D)5如果轴截面为正方形的圆柱的侧面积是S,那么圆柱的体积等于()90年(3)3分)(A) (B)(C) (D)已知轴截面是正方形的圆柱的高与球的直径相等,则圆柱的全面积与球的表面积的比是()(92年(5)3分)(A)6:5 (B)5:4 (C)4:3 (D)3:2长方体的全面积为11,十二条棱长之和为24,则这个长方体的一条对角线长为()(92年(18)3分)(A)2 (B) (C)5(D)6当圆锥的侧面积和底面积的比值是时,圆锥的轴截面顶角是()(93年(3)3分)(A)45° (B)60° (C)90° (D)120°若正棱锥的底面边长与侧棱长相等,则该棱锥一定不是()(93年(13)3分)(A)三棱锥(B)四棱锥(C)五棱锥(D)六棱锥如果圆柱轴截面的周长l为定值,那么圆柱体积的最大值是()(93年(14)3分)(A)π(B)π(C)π(D)圆柱正六棱台的上、下底面边长分别为2和4,高为2,则其体积为()(94年(7)4分)(A)32(B)28(C)24(D)20圆柱过球面上A、B、C三点的截面和球心的距离等于球半径的一半,且AB=BC=CA=2,则球面面积是()(94年(13)5分)(A)π(B)π (C)4π (D)π正方体的全面积是a2,它的顶点都在球面上,这个球的表面积是()(95年(4)4分)(A)π(B)π(C)2πa2 (D)3πa2将边长为a的正方形ABCD沿对角线AC折起,使得BD=a,则三棱锥D-ABC的体积为( )(96年(9)4分)(A) (B) (C)(D)母线长为l的圆锥体积最大时,其侧面展开图圆心角φ等于()(96年(14)5分)(A)π (B)π(C)π(D)π长方体一个顶点上三条棱的长分别是3,4,5,且它的八个顶点都在同一个球面上,这个球的表面积是()(97年(8)4分)(A)20π (B)25π (C)50π (D)200π圆台上、下底面积分别为π、4π,侧面积为6π,这个圆台的体积是()(97年(12)5分)(A)<img width=31 height=40src="http://www.cb。
多面体和旋转体(附答案)

第八章多面体和旋转体一、考纲要求1.理解棱柱、棱锥、棱台、圆柱、圆台、球及其有关概念和性质.2.掌握直棱柱、正棱锥、正棱台和圆柱、圆锥、圆台、球的表面积和体积公式(球缺体积公式不要求记住),并能运用这些公式进行计算.3.了解多面体和旋转体的概念,能正确画出直棱柱、正棱住、正棱台、圆柱、圆锥、圆台的直观图.4.对于截面问题,只要求会解决与几种特殊的截面(棱柱、棱锥、棱台的对角面,棱柱的直截面,圆柱、圆锥、圆台的轴截面和平行于底面的截面,球的截面)以及已给出图形或它的全部顶点的其他截面的有关问题.二、知识结构1.几种常凸多面体间的关系2.棱柱、棱锥、棱台的基本概念和主要性质名称棱柱直棱柱正棱柱图形定义有两个面互相平行,而其余每相邻两个面的交线都互相平行的多面体侧棱垂直于底面的棱柱底面是正多边形的直棱柱侧棱平行且相等平行且相等平行且相等侧面的形状平行四边形矩形全等的矩形对角面平行四边形矩形矩形的形状平行于底面的截面的形状与底面全等的多边形与底面全等的多边形与底面全等的正多边形名称棱锥正棱锥棱台正棱台图形定义有一个面是多边形,其余各面是有一个公共顶点的三角形的多面体底面是正多边形,且顶点在底面的射影是底面的射影是底面和截面之间的部分用一个平行于棱锥底面的平面去截棱锥,底面和截面之间的部分由正棱锥截得的棱台侧棱相交于一点但不一定相等相交于一点且相等延长线交于一点相等且延长线交于一点侧面的形状三角形全等的等腰三角形梯形全等的等腰梯形对角面的形状三角形等腰三角形梯形等腰梯形平行于底的截面形状与底面相似的多边形与底面相似的正多边形与底面相似的多边形与底面相似的正多边形其他性质高过底面中心;侧棱与底面、侧面与底面、相邻两侧面所成角都相等两底中心连线即高;侧棱与底面、侧面与底面、相邻两侧面所成角都相等名称特殊性质平行六面体底面和侧面都是平行四边行;四条对角线交于一点,且被该点平分直平行六面体侧棱垂直于底面,各侧面都是矩形;四条对角线交于一点,且被该点平分长方体底面和侧面都是矩形;四条对角线相等,交于一点,且被该点平分正方体棱长都相等,各面都是正方形四条对角线相等,交于一点,且被该点平分4.面积和体积公式下表中S表示面积,c′、c分别表示上、下底面周长,h表斜高,h′表示斜高,l表示侧棱长 .名称侧面积(S侧) 全面积(S全) 体积(V) 棱棱柱直截面周长×l S侧+2S底S底·h=S直截面·l(1)全面积 S 全=3a 2;(2)体积 V=122a 3; (3)对棱中点连线段的长 d=22a ; (4)相邻两面所成的二面角 α=arccos31 (5)外接球半径 R=46a ; (6)内切球半径 r=126a. (7)正四面体内任意一点到四个面的距离之和为定值(等于正四面体的高). 6.旋转体 圆柱、圆锥、圆台、球的公式表中l 、h 分别表示母线、高,r 表示圆柱、圆锥与球冠的底半径,r 1、r 2分别表示圆台 上、下底面半径,R 表示半径. (2)圆锥、圆台某些数量关系②圆锥 圆锥轴截面两腰的夹角叫圆锥的顶角.②圆台 如图,圆台母线与下底面所成角为α,母线为l ,高为h ,上、下底面半径分别为r ′、r ,则h=lsin α r-r ′=lcos α.③球的截面 用一个平面去截一个球,截面是圆面.(1)过球心的截面截得的圆叫做球的大圆;不经过球心的截面截得的圆叫做球的小圆. (2)球心与截面圆圆心的连线垂直于截面.(3)球心和截面距离d,球半径R ,截面半径r 有关系:r=22d R .(3)球冠、球带和球缺①球缺 球面被平面所截得的一部分叫做球冠,截得的圆(圆周)叫做球冠的底,垂直于截面 的直径被截得的一段叫做相应球冠的高.球冠也可以看作一段圆弧绕经过它的一个端点的直径旋转一周所成的曲面. 球冠的面积公式 若球的半径为R ,球冠的高为h ,则S 球冠=2πRh其中h 表示球冠的高,R 是球冠所在的球的半径. ②球带 球面在两个平行截面之间的部分叫做球带.球带也可以看作一段圆弧绕它所在的半圆的直径旋转一周所成的曲面. 球带的面积公式 若球的半径为R ,球带的高为h ,则S 球带=2πRh③球缺 用一个平面截球体所得的部分叫做球缺,截面叫做球缺的底面,垂直于截面的直径 被截得的线段长叫做球缺的高.球缺的体积公式 若球的半径为R ,球缺的高h ,底面半径为r ,则V 球缺=31πh 2(3R-h)=61πh(3r 2+h 2)三、知识点、能力点提示 (一)多面体例1 如图,三棱柱ABC —A 1B 1C 1中,若E 、F 分别为AB 、AC 的中点,平面EB 1C 1将三棱柱分成体积为V 1、V 2的两部分,那么V 1∶V 2= .解:设三棱柱的高为h ,上下底的面积为S ,体积为V ,则V=V 1+V 2=Sh. ∵E 、F 分别为AB 、AC 的中点, ∴S △AEF =41S,V 1=31h(S+41S+41⋅S S)=127ShV 2=Sh-V 1=125Sh , ∴V 1∶V 2=7∶5.例2 一个长方体全面积是20cm 2,所有棱长的和是24cm ,求长方体的对角线长. 解:设长方体的长、宽、高、对角线长分别为xcm 、ycm 、zcm 、lcm 依题意得:⎩⎨⎧=++=++② ①24)(420)(2Z y x zx yz xy由②2得:x 2+y 2+z 2+2xy+2yz+2xz=36 ③由③-①得 x 2+y 2+z 2=16即l 2=16 ∵l=4(cm).例3 正四棱锥S-ABCD 中,高SO =26,两相邻侧面所成角为γ ,tg 3322=γ,(1)求侧棱与底面所成的角。
多面体和旋转体(幼师)

睢县职教中心学前教育多面体和旋转体专项练习一、选择题1.侧面都是直角三角形的正三棱锥,其底面边长为,则该棱锥的全面积是()2.侧棱长是的正三棱锥,其底面边长是,则棱锥的高是()球的面积扩大到原来的倍,则球的体积扩大到原来的()倍4.下面说法错误的是()A.棱柱的侧面都是平行四边形B.直棱柱的侧面都是矩形C.棱柱的侧棱长不一定相等D.过棱柱的不相邻的两侧棱的截面都是平行四边形5.一个圆锥的轴截面为等边三角形且面积为,则圆锥的高为()6.一个物体的下半部是圆柱,上半部是圆锥,圆锥的底面与圆柱的底面是半径相同的圆,已知圆柱的半径为,高度为,圆锥的母线长为,则该物体的表面积为()7.如果一个三棱锥的三条侧棱相等,那么它的顶点在底面的射影是底面三角形的()A.内心B.外心C.垂心D.重心8.正三棱柱的底面边长为,斜高为,则侧面积为()9.一个边长为的正三角形,一其一条高为轴旋转一周所得旋转体的全面积为()10.一个正四棱锥的底面边长为,高为,则体积为()11.一个球的体积为,该球内切于一个正方体内,那么这个正方体的棱长为()112.长方体一个顶点上的三条棱长分别为,则长方体的表面积为().13.若正三棱锥的侧棱与底面边长相等,则该棱锥侧棱与底面所成角的余弦值为()已知圆柱底面周长为,高为,则轴截面的面积是()已知圆锥的高为,轴截面是等边三角形,则轴截面的面积为()过球面上任意两点的大圆()A.有且只有一个B.有且只有两个C.有无穷多个D.有一个或无穷多个17.一个球的截面圆直径为,球心距为,则球的半径为()18.如果棱柱的侧面是矩形,则这个棱柱一定是()A.正棱柱B.直棱柱C.正方体D.长方体19.正四棱柱的底面边长和高都是,则其全面积为()20.若正四棱柱的对角线和侧面所成的角为,底面边长为,则它的体积为()21.圆锥的侧面展开图是扇形,且扇形的半径为,圆心角为,则圆锥的体积为()二、填空题1.已知长方体的长是,宽是,高是,则对角线的长为:2.已知正六棱锥底面边长为,高为,则它的棱长为:3.已知正四棱柱底面边长为,高为,则它的侧面积为:全面积为:24.已知直棱柱底面是菱形,边长为,棱柱高为,则该四棱柱的体积为:5.在正三棱锥中,若底面边长为,侧棱长为,则其高为:侧棱与底面夹角为:侧面与底面所成角的正切值为:6.设正四棱锥底面边长为,高为,则其斜高为:侧面积为:7.用一个长,宽的矩形材料卷成圆柱,则圆柱的侧面积为:8.已知圆柱的高为,底面半径为,则它的侧面积为:体积为9.已知圆锥高为,轴截面是直角三角形,则它的底面半径为:母线长为:10.已知圆锥底面半径是,高为,则它的侧面积为:11.已知圆锥的轴截面是等边三角形,母线长为,则圆锥的体积为:12.已知球的大圆周长为,则这个球的表面积为:13.已知球的大圆面积为,则这个球的体积为:14.用一个平面截半径为的球,截面的面积为,则球心到截面的距离为:15.长方体的全面积为,各棱长总和是,则该长方体的对角线长为:16.圆柱的轴截面面积为,侧面积为:17.圆锥的底面面积为,母线与底面所成的角为,其体积为:18.一个圆锥底面积不变,高扩大为原来的倍,体积扩大为原来的倍19.若长方体的长、宽、高分别为、、,则对角线为:20.一个圆柱和圆锥的底面直径相等,圆锥的高是圆柱的倍,圆锥的体积是,则圆柱的体积为:21.正六棱柱的底面边长是,侧棱长也是,则它的体积是:22.已知正四棱柱的底面边长为,高为,则它的侧面积为:体积为:23.以直角边长为的等腰直角三角形一直角边为轴旋转一周,形成的圆锥的轴截面面积为:24.圆柱底面半径为,高为,其全面积为:25.三个球的半径之比为,那么最大球的表面积是其余两个球的表面积之和的倍26.正四面体的边长为,则其体积为:327.一个正方体的顶点都在这个球面上,它的棱长是,则这个球的体积为:28.火星的半径约等于地球半径的一半,则地球的体积是火星的倍29.将一个半径为的半圆卷成一个圆锥的侧面,则此圆锥的体积为:30.一个圆锥的轴截面是等边三角形,面积为,则它的高为:三、解答题1.已知正三棱锥的斜高等于,高等于,求它的全面积2.一个圆柱的侧面展开图是一个正方形,求这个圆柱的全面积与侧面积的比是多少?3.若圆锥的高等于底面直径,求它的侧面积与底面积的比4.在半径为的球内有一个截面,它的面积是,求球心到这个截面的距离5.已知正方体的对角线长为,求它的棱长6.已知圆锥的轴截面是直角三角形,求它的侧面积与底面积的比值7.已知圆柱的侧面展开图是边长为的正方形,求它的体积48.已知正三棱锥中,,斜高,求高和棱长9.已知圆锥的侧面展开图是一个半圆,求圆锥的母线与底面所成的角10.已知三棱锥的各顶点都在一个半径为的球面上,球心在上,底面,求球的体积和三棱锥的体积11.已知正四棱锥底面正方形的边长是,高与斜高的夹角为,求正四棱锥的侧面积,表面积和体积12.三棱锥的底面是直角三角形,斜边,求三棱锥的高5。
多面体与旋转体复习题65

▁▂▃▄▅▆▇█▉▊▋▌精诚凝聚 =^_^= 成就梦想 ▁▂▃▄▅▆▇█▉▊▋▌▃ ▄ ▅ ▆ ▇ █ █ ■ ▓点亮心灯 ~~~///(^v^)\\\~~~ 照亮人生 ▃ ▄ ▅ ▆ ▇ █ █ ■ ▓ 65. 计算及其应用(1)一、典型例题1. 如图,直三棱柱ABC -A 1B 1C 1的侧面和底面边长都是a ,截面AB 1C 和截面A 1BC 1相交于DE ,求三棱锥B -B 1DE 的体积。
[3483a ] 2. 在边长为5+2的正方形ABCD 内,以A 为圆心画一个扇形,再画一个⊙O ,它在与BC 、CD 相切,切点为M 、N ,又与扇形的圆弧EF 相切于K 点,把扇形围成圆锥的侧面,⊙O 为圆锥的底面,求这个圆锥的体积。
[π3302] 3. 如图,已知在斜三棱柱ABC -A 1B 1C 1中,AC =BC ,D 为AB 的中点,平面A 1B 1C 1⊥平面ABB 1A 1,异面直线BC 1与AB 1互相垂直,①求证:AB 1⊥平面A 1CD ;②若CC 1与平面ABB 1A 1的距离为1,A 1C =37,AB 1=5,求三棱锥的体积。
[5/3]4. 直平行六面体,底面两邻边之和为a ,底面的锐角为30°,侧面积为S ,①求体积的最大值;②当体积最大时,底面是什么形状?[aS/16、菱形]5. 已知三棱锥A -BCD 的体积是V ,棱长BC =a ,面ABC 与面DBC 的面积分别是S 1和S 2,设面ABC 和面DBC 所成的二面角是α,求sin α。
[2123S S aV ] 6. 三棱锥S -ABC 中,各棱长都是2a ,棱SA 、SB 、SC 和AB 的中点分别为D 、E 、F 和G ,①求证:平面DEF ⊥平面EFG ;②求V G -DEF 。
[3122a ] 7. 已知三棱锥P -ABC 中,PA =a,PB=b,PC=c,侧棱PA 、PB 、PC 上各点A 1,B 1,C 1且PA 1=a 1,PB 1=b 1,PC 1=c 1,求证:111111c b a abc V V C B A P ABC P =--。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
65. 计算及其应用(1)
一、典型例题
1. 如图,直三棱柱ABC -A 1B 1C 1的侧面和底面边长都是a ,截面AB 1C 和截面A 1BC 1相交于
DE ,求三棱锥B -B 1DE 的体积。
[348
3a ] 2. 在边长为5+2的正方形ABCD 内,以A 为圆心画一个扇形,再画一个⊙O ,它在与BC 、
CD 相切,切点为M 、N ,又与扇形的圆弧EF 相切于K 点,把扇形围成圆锥的侧面,⊙O 为圆锥的底面,求这个圆锥的体积。
[π3
302] 3. 如图,已知在斜三棱柱ABC -A 1B 1C 1中,AC =BC ,D 为AB 的中点,平面A 1B 1C 1⊥平
面ABB 1A 1,异面直线BC 1与AB 1互相垂直,①求证:AB 1⊥平面A 1CD ;②若CC 1与平面ABB 1A 1的距离为1,A 1C =37,AB 1=5,求三棱锥的体积。
[5/3]
4. 直平行六面体,底面两邻边之和为a ,底面的锐角为30°,侧面积为S ,①求体积的最大
值;②当体积最大时,底面是什么形状?[aS/16、菱形]
5. 已知三棱锥A -BCD 的体积是V ,棱长BC =a ,面ABC 与面DBC 的面积分别是S 1和S 2,
设面ABC 和面DBC 所成的二面角是α,求sin α。
[2
123S S aV ] 6. 三棱锥S -ABC 中,各棱长都是2a ,棱SA 、SB 、SC 和AB 的中点分别为D 、E 、F 和G ,
①求证:平面DEF ⊥平面EFG ;②求V G -DEF 。
[312
2a ] 7. 已知三棱锥P -ABC 中,PA =a,PB=b,PC=c,侧棱PA 、PB 、PC 上各点A 1,B 1,C 1且PA 1
=a 1,PB 1=b 1,PC 1=c 1,求证:1
11111c b a abc V V C B A P ABC P =--。
