水力学-第六章管道
《管道水力学原理》课件
三. 沿程水头损失计算经验公式
1. 布拉休斯公式计算塑料管道沿程水头损失 多数塑料管道的流态属于紊流光滑区：
s——管道的比阻率或比阻抗
2. 哈森-威廉斯公式计算沿程水头损失 适于较大的管道(d≥5cm)，适中的流速（≤3m/s）
C——沿程摩擦系数
四. 局部水头损失计算
1.
计算原理
在管道系统中通常装有阀门、弯管、变截面管等局 部装置。流体流经这些局部装置时流速将重新分布， 流体质点与质点及与局部装置之间发生碰撞、产生 漩涡，使流体的流动受到阻碍，由于这种阻碍是发 生在局部的急变流动区段，所以称为局部阻力。流 体为克服局部阻力所损失的能量，称为局部损失。
根据水流的连续性原理，节点上流入 的能量与流出的能量相平衡。假定每 个喷头的流量都相等为q，则各段流量 依次为：
2 管道直径
确定喷灌系统中各级管道的直径 → 管网设计的主要 任务. (1)根据确定的管道材料和相应的管道规格标准，参考 各种管材和管径的适宜流速，初步拟定管道直径；
(2)通过水头损失计算校验初步拟定直径的合理性；
管道水力学原理
自然状况下：水往低处流
施压条件下：任何位置流动 能量高的位置→ 低
草坪的灌溉系统 — 压力灌溉系统 — 管壁摩擦 — 消耗压力水流能量 — 减少流动高度 了解管道消耗压力水流能量的规律 → 确定管道铺 设长度、断面尺寸、流量大小、管道提供压力范围
管道水流及其能量
一. 管道水流 在水力学中，指管道横断面为圆形、水完全充满管道 并具有一定压力的管道水流。 管道横断面上的平均流速：
一. 水头损失及分类
单位重量液体机械能的损失。 沿程水头损失 水流边界形状和大小沿程不 变，水流在长且直的流段中发生的 水头损失。hf表示。单位长度上损 失相等，与管道长度成正比。 局部水头损失 水流边界形状或大小沿流程 急剧变化所产生的水头损失。hj
水力学第六章课后习题答案
7.14虹吸管将A 池中的水输入B 池，已知长度1l =3m ，2l =5m ，直径d =75mm ，两池水面高差H =2m ，最大超高h =1.8m ，沿程摩阻系数λ=0.02，局部损失系数：进口a ζ=0.5，转弯b ζ=0.2，出口c ζ=1，试求流量及管道最大超高断面的真空度。
解： 以下游水面为基准面，从上池水面到下池水面列伯努利方程：22222350.7 1.00.0222220.0752v l v v v v H g d g g g gζλζζ+⎛⎫=+++=++⨯ ⎪⎝⎭b c 进∴ 3.20v ==（m/s ）23.200.07514.144Q vA π==⨯⨯=（L/s ）从C 过流断面到下池水面列伯努利方程：2222222C C C C Cp v l v v z g g d g gαλζρ++=+ 取1C α= ∵C v v =∴251.8 2.010.02 1.00.0752a C C V p p p vH g g g ρρ-⎛⎫==-=++-⨯- ⎪⎝⎭25 3.203.80.02 3.100.07529.807=-⨯⨯=⨯m答：流量14.14Q =L/s ，管道最大超高断面的真空度为3.10m 。
7.16水从密闭容器A ，沿直径d =25mm ，长l =10m 的管道流入容器B ，已知容器A 水面的相对压强1p =2at ，水面高1H =1m ，2H =5m ，沿程摩阻系数λ=0.025，局部损失系数：阀门v ζ=4.0，弯头b ζ=0.3，试求流量。
解： 以地面为基准面，从A 池面到B 池面列伯努利方程：222111222123222v b p v p v l v H H g g g g d g ααζζζζλρρ⎛⎫++=+++++++ ⎪⎝⎭进出取120v v ==；20p =；0.5ζ=进； 1.0ζ=出，则有121122100.5 1.0 4.030.30.0250.025p g H H g v ρ⎡⎤⎛⎫+-⎢⎥⎪⎝⎭⎢⎥=⎢⎥⎛⎫+++⨯+⨯ ⎪⎢⎥⎝⎭⎣⎦ ()122120516.4g ⨯+-⎡⎤=⎢⎥⎣⎦4.37=（m/s ）24.370.025 2.154Q vA π==⨯⨯=（l /s ）答：流量 2.15Q =l /7.17水车由一直径d =150mm ，长l =80m 的管道供水，该管道中有两个闸阀和4个90°弯头（λ=0.03，闸阀全开a ζ=0.12，弯头b ζ=0.48）。
水力学_第6章 有压管流
例.设有一倒虹吸管如图所示。上下游水位H=8m， 管长l=200m，管径d=0.5m，管壁为清洁水泥面，求 流量Q .
解：取上、下游液面， 列伯努利方程：
υ1≈υ2≈0
H=z1-z2=8m
查 表 取 ： 进 口 = 0.5,弯 头 = 0.1， = 1.0m m ，
运 动 粘 滞 系 数 1.306106m 2/sHhw8m=(dl
概念：
取水点至水泵进口的管道
水力计算目的：
确定水泵允许安装高度Hs
Hs hv(+dl )2g2
（2）压力水管（按长管计算）
概念： 水泵进口至提高液面的管道
水力计算目的：
确定水管的管径
d xQ0.8
X取0.8-1.2
（3）水泵装机容量
水泵扬程
Hp Zhw
水泵的有效功率 NpQpH /10 0 p(单 0 位 kW )：
根据管道布置与连接情况，管道可分为
简单管道
串联管道(pipe in series)
复杂管道
并联管道(pipe in parallel) 管 网(pipe networks)
枝状管网（branching pipe） 环状管网(looping pipe)
简单管道：指粗糙度相同没有分支的等管径管道， 复杂管道：指由两条以上有分支或粗糙度或管径不同管道组成的管系。
（ｃ）枝状管路：枝状管路起始点不同， 而汇合点相同。
（ｄ）网状管路：起始和汇合均不同的 不规则管路。
2、设计管路的目的
尽量减少动消耗，即能耗，节约能源，节约 原材料，降低成本。
为达到上述目的，需计算确定Q，尺寸（Ｌ、
d），损失hf。
有压管中的恒定流
有压管道 无压管道
水力学(闻德荪)习题答案第六章分析解析
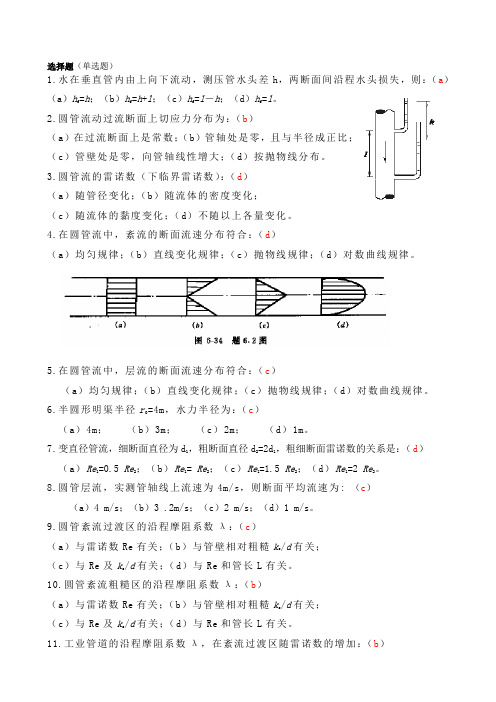
选择题（单选题）1.水在垂直管内由上向下流动，测压管水头差h，两断面间沿程水头损失，则：（a）（a）hf=h；（b）h f=h+l；（c）h f=l－h；（d）h f=l。
2.圆管流动过流断面上切应力分布为：（b）（a）在过流断面上是常数；（b）管轴处是零，且与半径成正比；（c）管壁处是零，向管轴线性增大；（d）按抛物线分布。
3.圆管流的雷诺数（下临界雷诺数）：（d）（a）随管径变化；（b）随流体的密度变化；（c）随流体的黏度变化；（d）不随以上各量变化。
4.在圆管流中，紊流的断面流速分布符合：（d）（a）均匀规律；（b）直线变化规律；（c）抛物线规律；（d）对数曲线规律。
5.在圆管流中，层流的断面流速分布符合：（c）（a）均匀规律；（b）直线变化规律；（c）抛物线规律；（d）对数曲线规律。
6.半圆形明渠半径r0=4m，水力半径为：（c）（a）4m；（b）3m；（c）2m；（d）1m。
7.变直径管流，细断面直径为d1，粗断面直径d2=2d1，粗细断面雷诺数的关系是：（d）（a）Re1=0.5 Re2；（b）Re1= Re2；（c）Re1=1.5 Re2；（d）Re1=2 Re2。
8.圆管层流，实测管轴线上流速为4m/s，则断面平均流速为: （c）（a）4 m/s；（b）3 .2m/s；（c）2 m/s；（d）1 m/s。
9.圆管紊流过渡区的沿程摩阻系数λ：（c）（a）与雷诺数Re有关；（b）与管壁相对粗糙k s/d有关；（c）与Re及k s/d有关；（d）与Re和管长L有关。
10.圆管紊流粗糙区的沿程摩阻系数λ：（b）（a）与雷诺数Re有关；（b）与管壁相对粗糙k s/d有关；（c）与Re及k s/d有关；（d）与Re和管长L有关。
11.工业管道的沿程摩阻系数λ，在紊流过渡区随雷诺数的增加：（b）（a ）增加；（b ）减小；（c ）不变；（d ）不定。
计算题【6.12】水管直径d =10cm ，管中流速v =1m/s ，水温为10℃，试判别流态。
水力学第六章 第三节 ppt
1
（1
6
）
＝56.7
0
n 0.014 4
0
l3
z
λ
＝8g C2
8 9.8 56.72
＝0.024
1
μc ( l
d
＝
1
＝0.571
i )
0.02435 0.5 2 0.365 1 1
Q c A 2gH 0.571 0.25 3.1412 19.6 1 1.985m3 / s
-
12
虹吸管中最大真空一般发生在管道最高位置。
上式表明：
水泵向单位重量液体所提供的机械能
将水流提高一个几何高度
克服全部水头损失
-
28
例题： 4-5 用离心泵将湖水抽到水池中去，流量为 0.2（m3/s），湖面高程为85.0m，水池水面高程为 105.0m，吸水管长度为10.0m，水泵的允许真空 hv = 4.5m，吸水管底阀的局部水头损失系数为2.5；弯 管的局部水头损失系数0.3，水泵入口前的渐变收缩 段局部水头损失系数为0.1；吸水管沿程水头损失系 数为0.022，压力管道采用铸铁管，其直径为500mm， 长度为1000m，n = 0.013。
NP
QHt 1000P
(kW)
式中，Ht 为水泵向单位液体所提供的机械能，称为水 泵的水头或者扬程（m）；
ηP 为水泵和动力机械的总效率。
-
27
0 0 0v02
2g
Ht＝z 0 hw14
Ht z hw14 z hw12 hw34
NP
QHt 1000P
(kW)
水泵的输入功率
-
8
例 有一渠道用两根直径为1.0m的混凝土虹吸管来跨 越山丘， 渠道上游水位为▽1＝100.0m，下游水位为▽2 ＝99.0m，虹吸管长度l1 = 8m l2= 15m；l3 = 15m，中间 有60°的折弯两个，每个弯头的局部水头损失系数为 0.365，若进口局部水头损失系数为0.5；出口局部水头 损失系数为1.0。试确定：
水力学_第6章 有压管流
真空区
对过流断面1-1、2-2 写伯努利方程，得
pa p2 v 2 0 0 hs hw12 g g 2 g hs hv
v 2
2g
hw12
0.5932 (7 0.464) 6.518 2 9.8
§9-1 简单短管中的恒定有压流
2.水泵
d2
4
d2
4
c 2 gH 0
c
1 l ( 2 ) d
管路流量系数
淹没出流
取0-0为基准面， 1-1与2-2为控制断面， 列伯努利方程：
pa 112 pa 22 2 H 0 hw g 2g g 2g
υ1≈υ2≈0
2 l H hw ( ) d 2g
hs
ξ2=0.55 1 l1=260m λ1=0.025 d=300mm ξ1=3.0
ξ3=0.17
2
ξ4=0.55 l2=40m λ2=0.025 d=300mm
hv = -p/=7
z=0.54
流速为
渠道
O
1
2
O
ξ5=1.0 集水池
Q 4 0.0419 v 0.593 m/s A 0.32
令H 0 H
112
2g
2 2 l H0 hw ( ) 2g 2g d 2g 2 22 2 22
2
1 l ( 2 ) d
1
2 gH 0
Q 2 A2
l ( 2 ) d
2 gH 0
剪应力与剪切应变率之间满足线性关系的流体 称为牛顿流体，而把不满足线性关系的流体称 为非牛顿流体。
水力学第六章讲义
第六章 流动阻力与能量损失本章首先讨论实际流体在运动过程中的能量损失的分类和计算公式，公式中损失系数的确定将是这一章主要的内容。
由于粘性的影响，实际流体的流动会呈现出两种不同的型态 — 层流和紊流，它们的流场结构和动力特性区别很大，必须加以判别，并分别研究。
由均匀流流动的特点，导出了均匀流的沿程损失与切应力之间的关系，圆管层流类似于均匀流，因此得到了圆管层流的沿程损失的计算方法。
由于在紊流流场中存在随机的脉动量，须对瞬时量取统计平均，分别讨论平均流动和脉动量。
紊流中切应力包含了粘性切应力和附加切应力（雷诺应力），采用混合长度理论建立起附加切应力与时均流速之间的关系。
本章还紊流运动中的局部水头损失的计算方法。
§6—1 流动阻力和能量损失的两种形式● 实际流体在渐变流段中流动，由流管壁面上粘性切应力形成的阻力称为沿程阻力或摩擦阻力。
在均匀流段上这种阻力是沿程不变的。
为克服沿程阻力形成的能量损失，称为沿程损失，沿程损失随着流程的增加而增加。
在均匀流段上每单位流程上的沿程损失是常数，沿程损失与流程长度呈正比例关系。
单位重量流体的沿程损失用 hf 表示，称为沿程水头损失。
计算公式为：gv d l h f 22λ= ● 在流管边壁沿程急剧变化，流速分布急剧调整的局部区段上，集中产生的流动阻力称为局部阻力。
由局部阻力引起的水头损失，称为局部水头损失，以 hj 表示，如管道进口、异径管、弯管、三通、阀门等各种管件处的水头损失，都是局部水头损失。
计算公式为：gv h j 22ζ= ● 若断面1至断面2的一段管路由若干段渐变流段组成，其间又有若干处局部损失，则这段管路的能量损失为所有沿程损失和局部损失的总和。
§6—2 流动的两种型态● 实际流体的流动会呈现出两种不同的型态：层流和紊流，它们的区别在于：流动过程中流体层之间是否发生混掺现象。
在紊流流动中存在随机的脉动量，而在层流流动中则没有。
● 1883年，雷诺试验表明：圆管中恒定流动的流态转化取决于雷诺数νvdR e =，d 是圆管直径，v 是断面平均流速，ν是流体的运动粘性系数。
第六章 有压管流
(6.16)
式中Ｋ为修正系数，且： (6.17)
(6.18)
二、串联管道
由直径不同的简单管道串联而成的管道为串联管道。
设串联管道中任一管段的直径为 ,管长为 ,流量为 ，管道来端由支管分出的流量为 ；如上图6-5所示，因串联管道的每一管道都是简单管道，都可用简单管道的水力计算公式，则：图6-5
例１：某渠道用直径 的钢筋混凝 虹吸管从河道引水灌溉，如上图所示，河道水位为120.00m，渠道水位为119.00m，虹吸管各段长度е１=10m，е2=6m,е3=12m,进口装滤水网，无底阀，ξ1=2.5,管的顶部有600的折角转弯两个，每个弯头ξ2=0.55。
求：（１）虹吸管的流量。
（２）当虹吸管内最大允许真空值 时，虹吸管的最大安装高度 。
§6－1简单短管中的恒定有压流
一、自由出流
图6-1
如图6-1所示，短管由三段管径不变的管道组成，以出口断面中心的水平面０－０为基准面，对渐变流断面１和２列出能量方程：
（6.1）
以总水头 代入上式得：
：式表明管道的总水头ＨＯ的一部分转换为出口的流速水头，另一部分则在流动过程中形成水头损失。上式中：
上式中的 是以达西一魏斯巴赫公式表示的，若 以谢才公式计算，其形式可作相应改变。将 代入 得：
也可算出各断面的测压管水头值，即可绘出管道的测压管水头线。
管道出口断面压强受到边界条件的控制。
由总水头线，测压管水头线和基准线三者的相互关系可以明确地表示出管道任一断面各种单位机械能量的大小。
四、短管水力计算举例（Ｐ河256）
：虹吸管的水力计算
虹吸管是指有一段管道高出上游液面，而出口低于上游液面的管道。
水泵装机容量就是水泵的动力机（如电动机）所具有的总动率，单位重量水体从水泵获得的能量为 ，则单位时间内重量为 的水流从水泵获得能量为 。 也为单位时间内水泵所做的有效功，称为水泵的有效功率，以 表示，即：
水力学第六章
虹吸管
虹吸管一部分管线高于上游自由水面。若在虹吸 管内造成真空，使作用在上游水面的大气压强与 虹吸管内的压强之间产生压差，则水流即能通过 虹吸管最高点流向下游。只要虹吸管内真空不被 破坏，就能持续输水。
2 60
0
60
0
1
hs
2
H
1
2 60
0
60
0
1
hs
2
H
1
最大允许真空度：虹吸管顶部的真空值不能太大， 当虹吸管内压强低于液体温度相应的汽化压强时， 液体将产生汽化，产生空化现象。 工程上虹吸管的最大允许真空度为7～8米水柱。
2
hw
1 4
0 .3 6 1 4 .0 7 1 4 .4 3 m
H z hw
1 4
2 0 1 4 .4 3 3 4 .4 3 m
(3)水泵的装机容量
N
QH
9 . 8 0 . 03 34 . 07 0 . 90 0 . 75
N
QH
η为电动机和水泵的总机械效率。
例6.3.2 吸水管和压水管均为铸铁管,粗糙系数n为 0.011，吸水管管径为200mm，吸水管长10m，进口有滤 水网并附有底阀,有一个900弯头，进口局部水头损失系 数为5.2，弯管处局部水头损失系数为1.10。压水管管 径为150mm，长度为500m，设有二个600弯头，每个弯头 局部损失系数为0.55；水塔水面与蓄水池水面高差z为 20m，水泵流量为30L/s，水泵最大允许真空值为6m，电 动机效率为0.9，水泵效率为0.75。 试确定： （1）水泵安装高度hs； （2）水泵扬程H； （3）水泵的装机容量N。 O
5 . 6 ( m)
水力学教程第6章
第六章明渠恒定均匀流人工渠道、天然河道以及未充满水流的管道等统称为明渠。
明渠流(OpenChannel Flow) 是一种具有自由表面的流动，自由表面上各点受当地大气压的作用，其相对压强为零，所以又称为无压流动。
与有压管流不同，重力是明渠流的主要动力，而压力是有压管流的主要动力。
明渠水流根据其水力要素是否随时间变化分为恒定流和非恒定流动。
明渠恒定流动又根据流线是否为平行直线分为均匀流和非均匀流。
明渠流动与有压管流的一个很大区别是：明渠流的自由表面会随着不同的水流条件和渠身条件而变动，形成各种流动状态和水面形态，在实际问题中，很难形成明渠均匀流。
但是，在实际应用中，如在铁路、公路、给排水和水利工程的沟渠中，其排水或输水能力的计算，常按明渠均匀流处理。
此外，明渠均匀流理论对于进一步研究明渠非均匀流也具有重要意义。
§6-1 概述1．明渠的分类由于过水断面形状、尺寸与底坡的变化对明渠水流运动有重要影响，因此在水力学中把明渠分为以下类型。
(1) 棱柱形渠道和非棱柱形渠道凡是断面形状及尺寸沿程不变的长直渠道，称为棱柱形渠道，否则为非棱柱形渠道。
前者的过水断面面积A仅随水深h变化，即A=f(h);后者的过水断面面积不仅随水深变化，而且还随着各断面的沿程位置而变化，即A=f(h, s) , s为过水断面距其起始断面的距离。
(2) 顺坡(正坡) 、平坡和逆坡(负坡)渠道明渠渠底线(即渠底与纵剖面的交线)上单位长度的渠底高程差，称为明渠的底坡(Bottom slope)，用i表示，如图6-1a，1-1和2-2两断面间，渠底线长度为A s,该两断面间渠底高程差为(a i-a2)= △ a,渠底线与水平线的夹角为B ,则底坡i 为。
(6-1-1)在水力学中，规定渠底高程顺水流下降的底坡为正，因此，以导数形式表示 时应为i=si n所以，在上述情况下，两断面间的距离△ s 可用水平距离△ l 代替，并且，过 水断面可以看作铅垂平面，水深 h 也可沿铅垂线方向量取。
水力学第六章
0
60
0
1
2
H
1
2 hs 60
0
60
0
1
2
H
1
最大允许真空度：虹吸管顶部的真空值不能太大， 最大允许真空度：虹吸管顶部的真空值不能太大， 当虹吸管内压强低于液体温度相应的汽化压强时， 当虹吸管内压强低于液体温度相应的汽化压强时， 液体将产生汽化，产生空化现象。 液体将产生汽化，产生空化现象。 工程上虹吸管的最大允许真空度为7 米水柱。 工程上虹吸管的最大允许真空度为7～8米水柱。 安装高度： 安装高度： 虹吸管管轴线的最高点到上游水面的 高差称虹吸管的安装高度。 高差称虹吸管的安装高度。
Σζ = ζ 阀 + ζ 弯 = 2.5 + 2 × 0.55 = 3.60
2 15 2.15 hs = 7.0 − 1 + 0.03 × + 3.60 × = 5.7m 0.5 2 × 9.8
说明：超过这个高度,最大真空度就要超过允许值, 说明：超过这个高度,最大真空度就要超过允许值, 水流的连续条件就受到破坏。 水流的连续条件就受到破坏。
（二） 离心水泵管路系统 由吸水管和压水管组成。 由吸水管和压水管组成 。 取水点到水泵进口断 之间的管路称为吸水管；水泵出口断面3 面2-2之间的管路称为吸水管；水泵出口断面33到水塔之间的管路称为压水管。水泵工作时， 到水塔之间的管路称为压水管。 水泵工作时， 必须在它的进口处形成一定真空， 必须在它的进口处形成一定真空 ， 水池的水在 大气压力作用下流向吸水管， 大气压力作用下流向吸水管 ， 流经水泵时从水 泵获得新的能量，然后沿压力水管流入水塔。 泵获得新的能量，然后沿压力水管流入水塔。
管路的分类 按沿程水头损失和局部水头损失在总水头损失中 所占的比重将管路分为长管和短管。 所占的比重将管路分为长管和短管。 长管： 长管：指管流的流速水头和局部水头损失的总和 与沿程水头损失比较起来很小，计算时流速水头 与沿程水头损失比较起来很小，计算时流速水头 和局部水头损失均可忽略。 和局部水头损失均可忽略。
水力学第6章有压管流
l1D1
H
B l2D2 C l3D3
q
Qt
Qp
作用水头为各段损失之和，即 q+0.45Qs 0.55Qs
6.3 管网水力计算基础
6.3.1 枝状管网 由多条串联而成的具有分支结构的管网系统称为枝状管网。 枝状管网节省材料、造价低，但供水的可靠性差。 枝状管网的计算 主要为以干管为主确 定作用水头与管径。 水源 干管指从水源到最远 点而且通过的流量为最大的管道部分。对水 头要求最高、通过流量最大的点称为控制点 。 于是，从水源到控制点的总水头可为：
6.2 长管的水力计算
6.2.1 简单管道 直径与流量沿程不变的管道为简单管道。
列1-2断面伯努利方程。 1
1
对于长管来说，局部水头
损失（包括流速水头）可忽略
H
2
不计，于是有 2
引入达西公式
式中 s = al 称为管道的阻抗，a 则称为比阻。于是 为简单管道按比阻计算的基本公式。
可按曼宁公式计算比阻。 在阻力平方区，根据曼宁公式可求得
由表6-1查得 D1= 450mm，a1= 0.123 s2/m6 D2= 400mm，a2= 0.230 s2/m6
于是
解得
l1= 1729 m， l2= 771 m
6.2.3 并联管道 两节点之间首尾并接两根以上的管道系统称为并联管道。
A、B 两点满足节点流量平衡
A：
B：
A
由于A、B两点为各管 Q1 段所共有， A、B两点的水
1
1
0
H
v
2
0
2
式中水头损失可表示为 解出流速
令 流量为
为短管管系流量系数
液体经短管流入液体为淹没出流。
水力学 有压管流测压管水头线的绘制
总水头线
测压管 水头线
2 2g
hj2 2
出水面
1
v
H2 v02≈0
0
２
1
(a)
v ②下游水池中渐变流断面2的 020，出口前后为突然扩
大的水流，总水头线下降，测压管水头线上升。
作图时，出口断面的局部水头损失集中绘在出口处，
即总水头线在此下降 hj 2 ，测压管水头线在此上升后与水面
相接，如图（b）所示
hj2
2 2g
测压管 水头线
1
v
0
02022 2g
2
出水面
H2 v02≠0
0
２
1
(b)
谢谢！
制作人 材料收集
测压管水பைடு நூலகம்线：
在管径不变的管段，流速水头相等，测压管水头线平行于总 水头线，从总水头线向下减去相应断面的流速水头值，便 可绘制出测压管水头线。（也可直接算出各断面的测压管 水头值）
Page 3
以图6.3为例，在绘制总水头线和测压管线时，有以下几种情况可作为 控制条件：
渐其变间流距⑴断为上面游 10水的0面2行；线近是流测速压水管头水头20线g02的起0始线，。则若总上水游头水线池绘（于或水水面库之）上中，
v 总水头线根据 02 的大小分为两种情况。
v ① 下 游 水 池 断 面 面 积 很 大 ， 渐 变
流断面2的 020，出口处
的 hj2
v2 2g
1.02 v2 g
， 正好等于
管道的流速水头，总水头线在出
口处突然下降 h j 2 ，然后连接于下 0
游水面线，测压管水头线直接接
到水面上，如图（a）所示
水力学 第六章第二节
水力学教程 第6章
第六章明渠恒定均匀流人工渠道、天然河道以及未充满水流的管道等统称为明渠。
明渠流(Open Channel Flow)是一种具有自由表面的流动，自由表面上各点受当地大气压的作用，其相对压强为零，所以又称为无压流动。
与有压管流不同，重力是明渠流的主要动力，而压力是有压管流的主要动力。
明渠水流根据其水力要素是否随时间变化分为恒定流和非恒定流动。
明渠恒定流动又根据流线是否为平行直线分为均匀流和非均匀流。
明渠流动与有压管流的一个很大区别是：明渠流的自由表面会随着不同的水流条件和渠身条件而变动，形成各种流动状态和水面形态，在实际问题中，很难形成明渠均匀流。
但是，在实际应用中，如在铁路、公路、给排水和水利工程的沟渠中，其排水或输水能力的计算，常按明渠均匀流处理。
此外，明渠均匀流理论对于进一步研究明渠非均匀流也具有重要意义。
§6-1 概述1．明渠的分类由于过水断面形状、尺寸与底坡的变化对明渠水流运动有重要影响，因此在水力学中把明渠分为以下类型。
(1)棱柱形渠道和非棱柱形渠道凡是断面形状及尺寸沿程不变的长直渠道，称为棱柱形渠道，否则为非棱柱形渠道。
前者的过水断面面积A仅随水深h变化，即A=f(h)；后者的过水断面面积不仅随水深变化，而且还随着各断面的沿程位置而变化，即A=f(h,s)，s为过水断面距其起始断面的距离。
(2)顺坡(正坡)、平坡和逆坡(负坡)渠道明渠渠底线(即渠底与纵剖面的交线)上单位长度的渠底高程差，称为明渠的底坡(Bottom slope)，用i表示，如图6-1a，1-1和2-2两断面间，渠底线长度为Δs，该两断面间渠底高程差为(a1-a2)=Δa，渠底线与水平线的夹角为θ，则底坡i为。
图6-1θsin 21=∆∆=∆-=sas a a i (6-1-1) 在水力学中，规定渠底高程顺水流下降的底坡为正，因此，以导数形式表示时应为dsdai -= (6-1-2) 当渠底坡较小时，例如i ＜0.1或θ＜6°时，因两断面间渠底线长度Δs ，与两断面间的水平距离Δl ，近似相等，Δs ≈Δl ，则由图6-1a 可知θtan =∆∆≈∆∆=la s a ii=sin θ≈tg θ (6-1-3) 所以，在上述情况下，两断面间的距离Δs 可用水平距离Δl 代替，并且，过水断面可以看作铅垂平面，水深h 也可沿铅垂线方向量取。
水力学-第六章管道
3．计算水泵装机容量N
水泵装机容量N：水泵的动力机(如电动机)所具有的总功率。
hp : 单位重量的水体从水泵获得的能量 有效功率 Np：单位时间 内重量为 gQ 的水流从水泵获得的 能量。 水泵总效率
N p gQhp
则
N p N
水泵装机容量为
gQhp N (kw) 1000 1000
2 1 1
Q Q1 Q2 ... Qn
6.3.4 沿程泄流管道 在工程中常有这样的情况，水在沿管轴方向
流动的同时，还从管侧壁上连续地有流量泄 出，这种管道称为沿程泄流管道。
如灌溉工程中的 人工降雨管道 或给水工程中 的滤池冲洗管
滴灌节水技术
农业滴灌技术
以 色 列 地 貌
以色列濒临东地中海,缺水少土,资源贫乏,沙漠荒山占了国 土的2/3,水资源仅16亿立方米,人均约250立方米水,不到全 球...― 以色列地处沙漠地带边缘,水资源匮乏。严重缺水使 以色列在农业方面形成了特有的滴灌节水技术。
12m。进口装滤水网，无底阀，ζ=2．5，管的顶部
有60度的折角转弯两个，每个弯头ζ=0.55。
求：(1)虹吸管的流量；(2)当虹吸管内最大允许真空值
为7.0m时，虹吸管的最大安装高度.
若绘制虹吸管的总水头线和测管水头线，其 测管水头线位于管轴线以下的区域，为真空 发生区。
(1)计算虹吸管的流量。 列断面1，3的能量方程或采用淹没出流
H H A HB
每段管道的水头差是相等
H H ... ... H
Q l K 2 Q2 2 l2 K2 2 Qn 2 ln Kn
2 1 2 1 1
水力学 第六章 有压管流
hp = z + hw
z 式中， 为提水高度； hw = hw1 − 2 + hw3 − 4 ，其中 hw1 − 2 为吸管中 式中， 为提水高度； 的水头损失， 为压水管中的水头上损失。 的水头损失，hw3 − 4 为压水管中的水头上损失。 由上式可得
hp = z + hw1 − 2 + hw3 − 4
2 αυ 0
H +0+
2 αυ 0
2g
= 0+0+
αυ 2
2g
+ hw
H为有效水头 为有效水头
2g
为行近水头
2 α 0υ 0
两者之和为总水头 将总水头 H 0 = H + 图6.1
2g
2
代
H 入上式，得：
0 =
α υ
2g
+ h w (6.1)
•
H 的一部分转换为出口的流速水头， 式（6.1）表明，管道的总水头 0 的一部分转换为出口的流速水头， ）表明， 另一部分在流动过程中转化为水头损失。 另一部分在流动过程中转化为水头损失。 式中
v
h
α υ2
测压管 水头线
j 2
2 α02υ02
2g
2g
2
出水面
1
v
0
H2 v02≠0
0
２
1
(b)
6.2.4 短管水力计算
• ⒈虹吸管的水力计算
见课本P149-151 见课本
⒉离心式水泵管道系统的水力计算
水泵水力计算主要是确定水泵扬程、水泵安装高度。 图见课本P 水泵水力计算主要是确定水泵扬程、水泵安装高度。（图见课本 151） ⑴计算水泵扬程 hp 单位重量的水体从水泵中获得的外加机械能， 单位重量的水体从水泵中获得的外加机械能，称为水泵的扬程 hp 取水池水面0-0为基准面，列断面1和4的能量方程，（忽略两个断面 取水池水面 为基准面，列断面 和 的能量方程，（忽略两个断面 为基准面 的能量方程，（ 的行近流速水头） 的行近流速水头）
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
新安汀水电站4号水轮机在1964年检查时，叶片空 蚀破坏面积达41321cm2：， 占 转轮叶片总面积的1／3，破坏最深处达30一33mm ，该电站另一台水轮机1972年7 月检查时发现，14个转轮叶片中有7个叶片因空蚀 破坏而穿孔。六朗洞水电站水轮机 在空蚀与泥沙磨蚀的作用下，某台水轮机曾发生 平均12天检修一次的情况。
6.2.2 管道动水压强的分布
----------总水头线和测管水头线的绘制
山东邹县电厂
华能海门电厂
华能电厂
盐城市城西水厂取水口
过滤池
在绘制总水头线和测管水头线时，有以下几 种情况可以作为控制条件：
(1) 上游水面线是测管水头线的起始线。 (2) 进口处有局部损失，集中绘在进口处，即总 水头线在此降落 (3) 出口为自由出流时，管道出口断面的压强为 零，测管水头线终止于出口断面中心 (4) 出口若为淹没出流，下游水面是测管水头线 的终止线
第6章 有压管流
供水管道破裂
6.1 概 述
1. 有压管道：整个断面均被液体充满没有自 由液
面、管壁处处受到水压力作用、管 中液体的动水相对压强不为零的管 道。 管中水流称为有压管流。
2. 管流: 无压管流→明渠 有压管流→满管液流，无自由液面
3. 短管、长管 v 短管: hj 和 2 g 与 hf 相比不能忽略， 须同时考虑 的管道。 2 v 长管： hf 起主要作用， hj和 可以忽 2g 略的管道。
列X方向的动量方程式
p1 A2 p2 A2 gA2 L cos Q(V2Байду номын сангаас V1 )
化简整理得：
p1 p2 v2 ( z1 ) ( z2 ) (v2 v1 ) g g g
p1 p ) ( z2 2 ) g g p p 若v2 0 ，v2 v1 , 则( z1 1 ) ( z2 2 ) g g 若v2 0 则 ( z1
0.0036
(2)列断面1，2的能量方程, 为厂保证虹吸管正常工作
，上游水面离虹吸管顶部的高度不得超过6．19m.
p2 v 2 0 0 0 hs hw g 2 g p2 l1 l2 hs ( 1 2 ) 6.19m g d
Np
6.3 长管的水力计算
6.3.1 简单管道的水力计算 直径不变没有分支的管道称为简单管道。是（长管）
中最基本的情形。
H
2 0v0
2g
0
v2 hw 2g
v2 H 0 hw 2g 2g
2 0v0
H hf
长管的水头H全部消耗于沿程水头损失hf上。
谢才公式计算：
淹没出流 v02 不为零测压管线的位置分析
对1-1、2-2断面列能量方程式
p1 1V12 p2 2V22 Z1 Z2 hw g 2g g 2g p1 p2 2V12 1V22 h j ( Z1 Z 2 ) ( )( ) g g 2g 2g
H Jl alQ sQ
2
2
l l 4 16 8l s al 2 2 2 2 5 2 2 4 K C RA d C d gd
上两式中S称为水管摩阻
比阻a、水管摩阻S与沿程水头损失系数λ 在分
区性质上一样
6.3.2 串联管道
串联管道: 由直径不同的简单管道串联而成的管道。
Q vA c A 2 gH 1 1 c l l1 l2 l3 d ( d ) 1 2 2 3
沿程水头损失系数的确定： 取 1.8mm , 则 1.8
d
假定紊流粗糙区即可查得，在校核
Q 0.352m3 / s
500
发明滴灌以后，以色列农业用水总量30年来一直稳定在13 亿立方米，而农业产出却翻了5番，以色列滴灌系统目前 已是第六代，如今，世界80多个国家使用以色列的滴灌技 术。
我国滴灌推广应用存在的若干问题浅析
1水价低廉的现实淡化了基层的节水意识 与传统漫灌相比，滴灌可以省水50%-80%，一亩漫灌的耗 水量能满足2-4亩滴灌用水。滴灌有效避免了输水过程损失 和深层渗漏损失，减少了地面蒸发和径流损失,几乎没有喷 灌和微喷灌出现的空中水分漂移，在北方特别是西北没有 灌溉就没有农业的干旱地区，推广滴灌的意义不言而喻。 但是，水价低廉的现实淡化了基层的节水意识 2 盲目追求低造价降低了滴灌工程应有的功能和质量 3 超小规模农村种植管理模式制约滴灌系统合理有效使用 4滴头堵塞一直困扰滴灌系统的正常应用 滴灌的滴头流道直径一般小于1mm，防堵塞一直是滴灌 面临的主要困难之一
0 0 0 hp z 0 0 hw hp z hw12 hw34
水泵扬程等于提水高度加上吸水管和压水管 的水头损失之和
2. 水泵安装高度 列1-2能量方程
p2 v 2 0 0 0 hs hw1 2 g 2 g p2 l v2 hs ( ) g d 2g l v2 hs hv ( ) d 2g
6.2.1 出流公式 –流量
1. 自由出流
总水头H0
H 0 H0
2 0v0
2g
00
v 2
2g
hw
H0 H
2 0v0
v 2
2g
2g
hf hj
l v v H0 2g d 2g 2g l v2 H 0 ( ) d 2g v 1 l d
l (3 ~ 4)d
液体经过管嘴并在出
口断面满管流出，称
管嘴出流。
孔口、管嘴出流的特点： 局部水头损失起主要作用，沿程水头损失可 以忽略不计。 6. 空化与空蚀
水轮机、水泵以及船舶螺旋桨推进器受到的空蚀破挥也比较严重。我 国水轮机通常 使用l一2年就要停机检修一次。某些水泵使用1000小时左右即出现严 重的空蚀，见 。船舶螺旋桨在使用一段时间后也因空蚀而效率大大降低。
02 v02 2
l v2 v2 l v2 H ( ) d 2g 2g d 2g
则
1 v l d Q vA c A 2 gH 2 gH c 2 gH
其中， c 为管道流量系数
总水头线总是沿程下降的，而测压管水头线沿程 可升可降。 在绘制总水头线时，局部水头损失可集中图示在 边界突然变化的断面上。
减蚀措施： 1 控制合理的边界轮廓线 从避免空蚀的角度看，边界轮廓最好能做到“平、直。 光”。从运转要求和施工水平看，这几乎是不可能际但应切 忌骤弯、急折、突缩或突扩。在边界不得已发生变化之处，应 注意流线化、椭圆化或圆角化；在局部凹凸不平整之处应修 成适当的平顺缓坡。 2.掺气 掺气的减蚀作用最早是在水轮机运转中发现的。当春、 夏季上游水库来水中含气较大时，水轮机空蚀损伤程度大为减 弱。后来用人工的方法在水轮机的空蚀区掺入气体发现空蚀 破坏也大为改善甚至消失。 3 在局部负压区设通气孔 在水流的局部负压区边界上设置通气孔，使与大气相连 可以有效地降低负压值并改善水流的流态。在我国的水工建 筑中，高压闸门后一般埋设有通气孔。对压力管道的收缩段、 转弯段以及其他可能产生负压的局部区域原则上均可埋没通 气孔，并宜埋设在负压区的略偏上游之处。若负压区随水流条 件作上下移动．则通气孔可埋设多处。
2 1 1
Q Q1 Q2 ... Qn
6.3.4 沿程泄流管道 在工程中常有这样的情况，水在沿管轴方向
流动的同时，还从管侧壁上连续地有流量泄 出，这种管道称为沿程泄流管道。
如灌溉工程中的 人工降雨管道 或给水工程中 的滤池冲洗管
滴灌节水技术
农业滴灌技术
以 色 列 地 貌
以色列濒临东地中海,缺水少土,资源贫乏,沙漠荒山占了国 土的2/3,水资源仅16亿立方米,人均约250立方米水,不到全 球...― 以色列地处沙漠地带边缘,水资源匮乏。严重缺水使 以色列在农业方面形成了特有的滴灌节水技术。
12m。进口装滤水网，无底阀，ζ=2．5，管的顶部
有60度的折角转弯两个，每个弯头ζ=0.55。
求：(1)虹吸管的流量；(2)当虹吸管内最大允许真空值
为7.0m时，虹吸管的最大安装高度.
若绘制虹吸管的总水头线和测管水头线，其 测管水头线位于管轴线以下的区域，为真空 发生区。
(1)计算虹吸管的流量。 列断面1，3的能量方程或采用淹没出流
v2 Q2 Q2 H hf 2 l 2 2 l 2 l C R C AR K 其中K CA R
给水工程中 ，
Q2 2 J 2 aQ l K 1 1 4 16 8 a 2 2 2 2 5 2 4 K C RA 8 g d d gd hf
a称为比阻。比阻的物理意义是：单位流量(Q=1)，通 过单位管长(l=1)所需要的水头。
为确保虹吸管正常工作，工程上常限制管 中的最大真空高度，不超过7m水柱。
虹吸应用：
例 6.2 水泵的水力计算
水泵的作用是增加水流能量，把水从低处引 向高处，图所示为装有水泵的供水系统。
计算内容： 1 水泵扬程hp； 2 水泵安装高度hs； 3 水泵装机容量N；
1．计算水泵扬程 单位重量的水体从水泵中获得的外加机械能， 称为水泵的扬程，如图所示。 取水池水面0—0为基准面，断面1和4列能 量方程
H H A HB
每段管道的水头差是相等
H H ... ... H
Q l K 2 Q2 2 l2 K2 2 Qn 2 ln Kn
2 1 2 1 1
H a1Q l 2 H a2Q2 l2 ... ... 2 H an Qn ln