第八章、分子轨道对称性守恒原理及应用—1
物理学中的对称性与守恒定律

物理学中的对称性与守恒定律对称性和守恒定律是物理学中的基本概念,它们在理解和解释自然界中各种物理现象和规律中起着重要作用。
本文将探讨物理学中的对称性和守恒定律,并探讨它们之间的密切关系。
一、对称性在物理学中的意义对称性是物理学中的重要概念,它描述了物理系统在某些变换下保持不变的性质。
在物理学中,对称性可以分为时空对称性和内禀对称性两种。
1. 时空对称性时空对称性是指物理系统在时空变换下保持不变。
在相对论物理学中,洛伦兹变换是描述时空变换的数学工具。
根据洛伦兹变换的不同类型,物理系统可以表现出平移对称性、旋转对称性和洛伦兹对称性等。
平移对称性是指物理系统在空间位置上的平移不会改变其物理性质。
例如,一个均匀介质中的物理规律在空间中的任何位置都是相同的。
旋转对称性是指物理系统在空间方向的旋转下保持不变。
例如,地球的自转周期不会影响物理规律的成立。
洛伦兹对称性是指物理系统在洛伦兹变换下保持不变,包括时间和空间的坐标变换。
相对论物理学中的基本原理就是洛伦兹对称性。
2. 内禀对称性内禀对称性是指物理系统在内部变换下保持不变。
在粒子物理学中,内禀对称性描述了粒子的基本性质。
例如,电荷共轭对称性指粒子与其反粒子具有相同的物理性质。
对称性在物理学中具有广泛的应用。
它不仅可以用于解释物理定律的成因,还可以帮助物理学家发现新的规律和预测新的物理现象。
二、守恒定律与对称性的关系守恒定律是物理学中的基本定律,描述了物理系统在某些变换下某个物理量保持不变的规律。
守恒定律与对称性之间存在着密切的关系。
以能量守恒定律为例,它描述了物理系统的能量在各种变换下保持不变。
能量守恒定律与时间平移对称性密切相关,即物理规律在时间上的平移不变性保证了能量守恒。
动量守恒定律是另一个重要的守恒定律,它描述了物理系统的总动量在某些变换下保持不变。
动量守恒定律与空间平移对称性密切相关,即物理规律在空间上的平移不变性保证了动量守恒。
角动量守恒定律和电荷守恒定律等也与对称性有着密切的联系。
分子轨道对称守恒原理

分子轨道对称守恒原理小资料:守恒原理的诞生。
分子轨道对称守恒原理认为:化学反应是分子轨道进行重新组合的过程,在一个协同反应中,分子轨道的对称性是守恒的,即反应物的分子轨道具有什么样的对称性,产物的分子轨道也应具有什么样的对称性,从原料到产物,分子轨道的对称性始终不变。
因为只有这样,才能用最低的能量形成反应中的过渡态。
因此,分子过渡的对称性控制着整个反应的进程。
能级相关理论:这种方法考虑了所有参与反应的分子轨道,强调了各分子轨道的对称性的分类,建立了反应物分子和产物分子轨道的能级之间相互转化的关系,分析协同反应进行的方式和条件,并且把能转化的能源(包括热能还是光能)定性地加以说明。
能级相关的方法及其应用:(1)画出反应物和产物分子的有关分子轨道,并按能级排列。
(2)选择一个适当的对称元素对反应物和产物分子的分子轨道进行分类,标上轨道的对称类型,而这个对称元素必须在整个反应过程中始终保持有效。
丁二烯顺旋环化反应只有C2轴始终保持有效,而其对旋环化反应,只有m1面才始终保持有效。
(3)用相关线将反应物和产物的分子轨道连接起来。
相连时,必须遵循2条原则:(a)对称守恒原则,即反应物和产物的分子轨道对称性要一致。
只能SS或AA相连,不能SA或AS相连,同时相连的分子轨道的能量要尽可能相近。
只有这样才符合分子轨道对称性守恒原理。
(b)不相交原则,是指对称性相同的两条相关线不能相互交叉。
即两条SS线或AA线不能相交,但SS连线和AA连线可以相交。
这一原则是根据量子力学原理确定的。
对称允许和对称禁阻:丁二烯加热顺旋环化的协同反应,在基态时,反应就可以进行,这种反应称为对称允许反应,反之,加热对旋环化反应,则称为对称禁阻反应。
这里的"允许"和"禁阻"只表示一个协同反应进程的难易程度。
分子轨道对称守恒原理

分子轨道对称守恒原理分子轨道对称守恒原理分子轨道对称守恒原理conservation of molecular orbital symmetry,principle of在协同反应中,反应循着保持分子轨道对称不变的方式进行。
若在协同反应过程中自始至终存在某种对称要素,反应物和产物的分子轨道都可以按这种对称操作分类,则反应物与产物的分子轨道对称性相合时反应就易于发生,而不相合时就难于发生。
单步骤的化学反应称为基元反应。
协同反应是这样一种基元反应,在其反应过程中所涉及的化学键的变动是协同一致地进行的。
一般说来,基元反应都是协同过程。
有机化学家R.B.伍德沃德首先从实验上总结了电环化、环加成、σ迁移、嵌入等周环协同反应的规律性,这些反应的共同特点是在加热和光照的作用下得到不同的立体异构物。
量子化学家R.霍夫曼从理论上对上述规律性进行分析。
1965年两人共同提出了分子轨道对称守恒原理。
这条原理可以用量子化学的能级相关理论,前线轨道理论或麦比乌斯结构理论加以阐明。
分子轨道对称守恒原理已推广到无机、催化、生化反应等许多重要领域,是微观化学反应动力学和量子化学应用的一个里程碑。
电环化反应含有k个π电子的线型共轭体系,在其末端生成一个单键的反应及其逆反应,称为电环化反应。
反应有对旋和顺旋两种情况,从而得到两种异构体(图1 )。
在对旋情况下,反应是以保持一个对称平面为特征;而顺旋过程始终具有一个二重对称轴。
以丁二烯转变为环丁烯为例。
丁二烯有4个π轨道:χ1、χ2、χ3、χ4 ,基态时χ和χ是占据的;环丁烯有一个占据的σ轨道和一个占据的π轨道,还有一个空的σ*轨道和一个空的π*轨道。
按能级相关理论,在对旋和顺旋反应过程中保持轨道的对称性,按不相交规则,即相同对称性的轨道在反应过程中不相交,图 2 是这两个过程的能级相关图。
在顺旋过程中,反应物和产物基态的分子轨道一一相连,因而在加热时丁二烯电环化反应只得到顺旋产物,与实验结果一致。
分子轨道的对称性和反应机理

乙烯加氢反应:
C2H4 H2 C2H6
G0:是热力学允许的反应 乙烯和氢的前线分子轨道:
对称性不匹配,反应很难进行。必须采用催化 剂才能使反应进行。
要想使反应进行,必须借助催化剂。工业上使用
Raney Ni(超细Ni粉) H2 首先吸附在 Ni 表面,Ni 的 d 电子流向 H2 的 1s* 轨道,使氢分子的LUMO变 成HOMO,使氢分子活化解离,就可以反应了。
光照时,电子激发,原来的 LUMO 将成为 HOMO,应分 析LUMO 的相位
例:丁二烯闭环 光照时,考虑LUMO
光照
ψ3
对旋才满足对称性要求
加热时,考虑HOMO 加热
ψ2
顺旋才满足对称性要求
例:己三烯与丁二烯相反,光照顺旋,加热对旋。
轨道形状可以根据 节面个数猜测!红 虚线为节面。
光照,顺旋
R
3 反应条件的判断
若反应物的成键分子轨道只与产物的成键轨道相关 联,则反应是对称性允许的。在这种情况下,反应 物处于基态就可直接转化为产物,活化能低,在加 热()条件下即可进行。 或表述成:反应物与产物的成键轨道中其对称轨道 数目相等,加热即可进行反应。
若反应物的部分成键轨道与产物的反键轨道关联,则 此反应是对称性禁阻的,在这种情况下,反应物必须 处在激发态才能转化为产物的基态,反应的活化能高, 光照才能使反应进行。 或表述成:反应物与产物的成键分子轨道中其对称轨 道数目不相等时,必须在光照下反应才能进行。
S
A
A
S
E
S
A
A
S
S
A
A
C2
S
光照,顺旋
A
A
S
A
A
S
分子轨道对称守恒原理

分子轨道对称守恒原理
分子轨道对称守恒原理是描述分子轨道形成和相互作用的基本规律。
在分子轨
道理论中,分子轨道对称性对于分子结构、光谱性质以及化学反应的理解都具有重要的意义。
本文将从分子轨道对称守恒原理的概念、原理和应用进行阐述。
首先,分子轨道对称守恒原理是指在分子形成过程中,分子轨道的对称性会保
持不变。
这意味着,如果原子轨道的对称性相同,它们将能够相互叠加形成对称性相同的分子轨道。
这一原理是基于量子力学的波函数叠加原理和对称性分析的基础上得出的。
其次,分子轨道对称守恒原理在分子结构和性质的理解中具有重要的作用。
通
过对分子轨道对称性的分析,可以预测分子的形状、键合方式以及分子的光谱性质。
例如,通过对称性分析可以确定分子中存在的π键和σ键的相对能量位置,从而解释分子的化学性质和反应活性。
另外,分子轨道对称守恒原理也在化学反应的研究中发挥着重要的作用。
在分
子轨道理论中,通过对称性分析可以预测分子间的相互作用方式,从而解释化学键的形成和断裂过程。
这对于设计新的催化剂、预测反应的活性以及理解反应机理都具有重要的意义。
总之,分子轨道对称守恒原理是分子轨道理论中的重要概念,它对于理解分子
结构、光谱性质以及化学反应具有重要的意义。
通过对分子轨道对称性的分析,可以预测分子的性质和行为,为理论化学和实验化学的发展提供了重要的指导。
希望本文对于分子轨道对称守恒原理的理解和应用能够有所帮助。
分子轨道的对称性和反应机理
(2)相互作用的HOMO和LUMO能量必须接近(约为6 eV);
+
(
* 2
p
)0
-
+
O2 HOMO
O2 LUMO
-
+
+
-
(
* 2
p
)1
+
-
(
* 2
p
)1
-
+
-
++
O2
+
--
N2
+
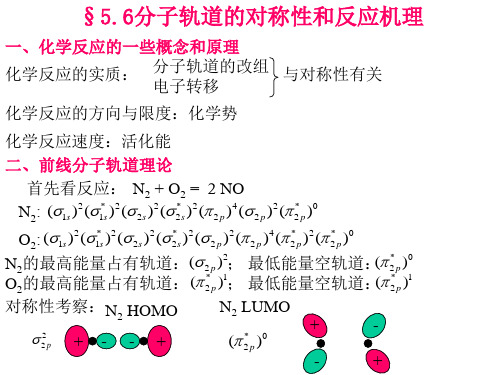
N2的LUMO和O2 的HOMO对称性匹配,但欲使反应进行,电 子需从电负性较高的O向电负性较低的N转移,而当O的电子向反键 轨道转移后,就会增强O2的化学键,反应很难进行。活化能很高。 这说明N2和O2能共存,而且NO也能分解。 前线轨道理论的基本要点:
)0
O2:
(1s
)2
(1*s
)2
(
2s
)2
(
* 2s
)2
(
2
p
)2
(
2
p
)4
(
* 2
p
)2
(
* 2
p
)0
N2的最高能量占有轨道:(
2
p
)2;
最低能量空轨道:(
* 2p
)0
O2的最高能量占有轨道:(
* 2p
)1;
分子轨道对称守恒

分子轨道对称守恒分子轨道对称守恒是化学中一个重要的概念,它对于分子的性质和反应有着重要的影响。
在本文中,我将详细介绍分子轨道对称守恒的概念、原理和应用。
分子轨道对称守恒是指在分子中,当分子发生对称性操作(如旋转、翻转)时,分子中的分子轨道的对称性保持不变。
这个概念可以用来预测分子的性质、解释分子的反应以及设计新的分子材料。
分子轨道对称守恒的原理可以通过对分子的对称性进行分析来理解。
分子的对称性由分子的几何结构决定,而分子的几何结构可以通过分子的轨道来描述。
分子轨道是分子中电子的运动状态,它们具有不同的对称性。
当分子发生对称性操作时,电子的运动状态会发生改变,但是分子轨道的对称性保持不变。
这是因为对称性操作不会改变分子的几何结构,而分子的几何结构决定了分子轨道的对称性。
分子轨道对称守恒在化学中有着广泛的应用。
首先,它可以用来预测分子的性质。
根据分子轨道的对称性,我们可以确定分子的电子结构和能级分布,从而预测分子的化学性质,如反应活性、化学稳定性等。
例如,具有对称轨道的分子通常具有较高的稳定性,而具有非对称轨道的分子通常具有较高的反应活性。
分子轨道对称守恒也可以用来解释分子的反应。
在化学反应中,分子的对称性可以发生改变,从而导致分子轨道的对称性发生改变。
根据分子轨道对称守恒原理,当反应发生时,只有那些保持分子轨道对称性的反应才是可能的。
这可以帮助我们理解为什么一些反应会发生,而另一些反应却不会发生。
分子轨道对称守恒还可以用来设计新的分子材料。
根据分子轨道的对称性,我们可以预测不同分子之间的相互作用,并设计出具有特定性质的分子材料。
例如,通过调控分子轨道的对称性,我们可以设计出具有特定光学、电学或磁学性质的分子材料。
这对于材料科学和纳米技术的发展具有重要的意义。
分子轨道对称守恒是化学中一个重要的概念,它对于分子的性质和反应有着重要的影响。
通过分子轨道对称守恒原理,我们可以预测分子的性质、解释分子的反应以及设计新的分子材料。
物理中的对称性与守恒定律

物理中的对称性与守恒定律在物理学中,对称性与守恒定律是两个非常重要的概念,它们贯穿于整个物理学的各个领域,为我们解释世界的运行规律提供了重要的理论支撑。
对称性和守恒定律之间存在着密切的联系,它们相辅相成,相互促进,共同构成了物理学中的基本框架。
本文将从对称性和守恒定律的基本概念入手,探讨它们在物理学中的重要作用以及彼此之间的内在联系。
## 对称性的基本概念对称性在物理学中是一个非常重要的概念,它指的是系统在某种变换下保持不变的性质。
具体来说,对称性可以分为空间对称性、时间对称性和内禀对称性等多种类型。
在物理学中,对称性通常表现为物理定律在某种变换下保持不变,这种不变性为我们揭示了自然界中隐藏的规律和对称性。
空间对称性是指系统在空间变换下保持不变的性质。
例如,一个物理系统在进行平移、旋转或镜像变换后仍保持不变,那么我们就说这个系统具有相应的空间对称性。
空间对称性的存在为我们提供了研究物理系统的重要线索,帮助我们揭示物质世界的奥秘。
时间对称性是指系统在时间变换下保持不变的性质。
在经典力学中,时间是一个普遍的参量,物理定律在时间平移下保持不变,这就是时间对称性。
时间对称性的存在为我们提供了研究物理系统随时间演化的重要线索,帮助我们理解自然界中的时间规律。
内禀对称性是指系统在内部变换下保持不变的性质。
例如,电荷守恒定律要求电荷在物理过程中保持不变,这就是内禀对称性的体现。
内禀对称性揭示了物理系统内部的稳定性和规律性,为我们理解微观世界提供了重要线索。
## 守恒定律的基本概念守恒定律是物理学中的另一个重要概念,它描述了系统某些物理量在时间演化过程中保持不变的规律。
根据不同的物理量和系统,可以得到不同的守恒定律,如能量守恒定律、动量守恒定律、角动量守恒定律等。
能量守恒定律是物理学中最基本的守恒定律之一,它表明一个封闭系统中能量的总量在时间演化过程中保持不变。
能量可以在不同形式之间转化,但总能量守恒。
能量守恒定律揭示了自然界中能量转化的规律,为我们研究能量转换和利用提供了基本原则。
分子轨道理论的发展及其应用

分子轨道理论的发展及其应用一、前言:分子轨道理论(MO理论)是处理双原子分子及多原子分子结构的一种有效的近似方法,是化学键理论的重要内容。
它与价键理论不同,后者着重于用原子轨道的重组杂化成键来理解化学,而前者则注重于分子轨道的认知,即认为分子中的电子围绕整个分子运动。
该理论注意了分子的整体性,因此较好地说明了多原子分子的结构。
目前,该理论在现代共价键理论中占有很重要的地位。
分子轨道理论描写单电子行为的波函数称轨道(或轨函),所对应的单电子能量称能级。
对于任何分子,如果求得了它的系列分子轨道和能级,就可以像讨论原子结构那样讨论分子结构,并联系到分子性质的系统解释。
有时,即便根据用粗糙的计算方案所得到的部分近似分子轨道和能级,也能分析出很有用处的定性结果。
二、分子轨道理论产生,分子轨道的含义,常用的构成分子轨道的方法:1、分子轨道理论产生:1926一1932年,在讨论分子(特别是双原子分子)光谱时,Mulliken和Hund分别对分子中的电子状态进行分类,得出选择分子中电子量子数的规律,提出了分子轨道理论.分子轨道理论认为,电子是在整个分子中运动,而不是定域化的.他们还提出能级相关图和成键、反键轨道等重要概念.1931一1933年,Huckel提出了一种简单的分子轨道理论(HMO),用以讨论共扼分子的性质,相当成功,是分子轨道理论的重大进展。
1951年,Roohtaan在Hartree一Fock方程的基础上,把分子轨道写成原子轨道的线性组合,得到TRoothaan方程,1950年Boys用Gauss函数研究原子轨道,解决了多中心积分的问题.从Hartree一Fock一Roohtaan方程出发,应用Gauss函数,是今天广为应用的自洽场分子轨道理论的基础,在量子化学的研究中占有重要地位。
1952年,福井谦一提出了前线轨道理论,用以讨论分子的化学活性和分子间的相互作用等,可以解释许多实验结果.1965年,Woodward和Hoffmann提出了分子轨道对称守恒原理,发展成为讨论基元化学反应可能性的重要规则,已成功地用于指导某些复杂有机化合物的合成.上述各个年代提出的基本理论和方法,是分子轨道理论发展过程中的几个里程碑。
分子轨道对称守恒原理

第13章 周 环 反 应
Pericyclic reaction
下页 退出
第13章 周 环 反 应
13.1 电环化反应 13.2 环加成反应 13.3 σ迁移反应
上页 下页 返回 退出
周环反应是指在反应过程中旧键的断裂和新键的 生成同时进行并且通过环状过渡态的协同反应.
周环反应特征:
一步反应,旧键的断裂和新键的生成是同时进 行的(协同反应)。
[小结] 环加成反应的立体选择性(同面-同面)
电子数
4n+2 4n
热反应
允许 禁阻
光反应
禁阻 允许
* 同面-异面加成的立体选择与同面-同面情况相反。
上页 下页 返回 退出
13.3 σ- 键迁移反应
定义:加热或光照下一个σ键上所连的氢原子或其 它基团通过一个同时连接的体系的两端的环状过 渡态而迁移的反应。
CH3
CH3
H
光照
CH3
CH3 顺旋
CH3 对 旋
CH3
H
上页 下页 返回 退出
13.1.2 含4n+2个π电子体系的电环化
反,顺,反-2,4,6-辛三烯的分子轨道图
上页 下页 返回 退出
基态时ψ3是HOMO,对旋轨道对称性允许:
H3C H H3C
对旋 H
+ CH3 H
H CH3
H CH3
CH3 H
sp3杂
p轨道
化轨
道
顺旋是指两个键 向同一方向旋转
上页 下页 返回 退出
p轨道
sp3杂 化轨 道
对旋是指两个键 向不同方向旋转
反应是顺旋还是对旋,取决于分子是基 态还是激发态时的HOMO轨道的对称性。
分子轨道的对称性

O
H
N
(2)共价键的方向性——决定分子的几何构型 根据最大重叠原理,在形成共价键时,原子间总是 尽可能的沿着原子轨道最大重叠的方向成键。电子云 重叠最大的方向即共价键的方向
7.3.3
分子轨道理论
顺磁性:受磁场所吸引, 0;
抗(反)磁性:被磁场所排斥, = 0;
1.物质的磁性
磁性
顺磁性
抗(反)磁性
2py 2pz 2px 2p 2py 2pz 2s
2s
2s
2s
N2 [(1s)2(*1s)2(2s)2(*2s)2(2py)2(2pz)2(2px)2]
N
N
4. 分子轨道电子排布式
N2分子的分子轨道电子排布式:
N2 [(1s)2(*1s)2(2s)2(*2s)2(2py)2(2pz)2(2px)2]
O O
O O
O2分子磁矩应为0 实验测定(O2)=2.83BM, O2中n=2,有两个未成对 电子。VB理论无法解释。 1932年前后,莫立根、洪特、伦纳德-琼斯等先后提 出分子轨道理论。
2. 分子轨道理论的基本要点 MO (molecular orbital)
(1)基本观点:把分子看成一个整体(如同原子结构中把 原子看成一个整体),通过分子中各原子互相对应(能量 相近或相同)的原子轨道(AO)重叠,组成若干分子轨道 (MO),而后电子依次填入MO中,电子属整个分子所有 (2)要点: •MO由AO组合而成,n个AO可组合得n个MO; b. 电子逐个填入MO中,填充规则与在AO中填充相同; 服从能量最低原理、泡利原理和洪特规则; c. AO组合成有效MO须符合:AO能量相近、最大重叠、 对称性相同,简称成键三 原则
《分子对称性》课件

05
分子对称性的实例分析
烷烃的分子对称性
烷烃的分子结构:由碳原子和氢原子组成,碳原子之间以单键相连
烷烃的对称性:烷烃分子具有对称性,可以划分为对称中心和旋转 对称轴 烷烃的对称性分类:根据对称性的不同,可以分为Cn、Dn、Cnv、 Dnh等类型
烷烃的对称性应用:在化学合成、药物设计等领域具有重要应用
添加 标题
杂环化合物的分子对称性:指杂环化合物 分子中存在的对称性关系
添加 标题
实例分析:苯环、吡啶环、嘧啶环等杂环 化合物的分子对称性
添加 标题
分子对称性的应用:在药物设计、材料科 学等领域具有重要应用
添加 标题
分子对称性的研究进展:近年来,杂环化 合物的分子对称性研究取得了重要进展, 为相关领域的发展提供了新的思路和方法。
对称操作和对称元素
对称操作:在空间中保持分子 不变的操作,如旋转、反射等
对称元素:在分子中保持不变 的元素,如原子、键等
对称性:分子在空间中的对称 性,如旋转对称、反射对称等
对称操作和对称元素的关系: 对称操作保持对称元素不变, 对称元素在空间中保持对称性
对称性的分类
对称性分为旋转对称性和反射 对称性
官能团
拉曼光谱(Raman):通 过拉曼光谱实验测定分子结
构中的振动模式
电子显微镜(EM):通过 电子显微镜实验测定分子结
构中的精细结构
对称性分析的方法
化学键对称性:研究分子中 化学键的对称性,如单键、 双键、三键等
空间对称性:研究分子在空 间中的对称性,如旋转对称、 反射对称等
电子对称性:研究分子中电 子的分布和对称性,如电子
对称性在化学反应中的应用主要体现在化学反应的预测、反应机理的解析、反应产物的 预测等方面。 对称性在化学反应中的应用还可以帮助科学家更好地理解化学反应的本质,为化学反应 的设计和优化提供指导。
对称性与守恒定律优秀课件

对称性与守恒定律
symmetry and conservation Lsw
一、问题的提出 我们已知: 牛力有局限性; 但, 又知: 由牛顿定律得出的动量守恒定律 和角动量守恒定律 却具有普遍性 这说明: 守恒定律超越力学理论 我们有理由提出问题: 守恒定律比力学理论具有更深厚的基础吗 ?
C
R
I I1
D
B
由 U AD 得出下式
2RI I1 RI1 R2I1 I
I1
ቤተ መጻሕፍቲ ባይዱ
3 5
I
RAB
U AB I
I1R I I1 2R
I
RAB
7 5
R
方便
五、对称性与守恒定律(简说〕 物理规律的某一种对称性(不变性〕 通常都属于一种守恒定律
由分析力学、量子力学 严格证明: 空间平移不变性 动量守恒定律 空间转动不变性 角动量守恒定律 时间平移不变性 能量守恒定律 等等
结果: 质点的轨道也一定在板面内
例3、已知:R1 求:R AB
I A I1
C
利用: 置换对称
节点电流关系
I I1
R
I I1
D
I1 B I
解 : 节 点 B 与 A 对称,设电流如图所示。
I I1 I I1
同样 节 点 D 与 C 对称,C D 的电流为
I1 I I1 2I1 I
I A I1
时间反演 (t -t)
相当于时间倒流 物理上:运动方向反向 即: 速度对时间反演变号
牛顿第二定律 对保守系统-时间反演不变 如 无阻尼的单摆
非保守系统 不具有时间 反演不变性
联合操作
武打片 动作的真实性
紧身衣
用前线轨道理论和分子轨道对称守恒原理

用前线轨道理论和分子轨道对称守恒原理分析乙烯环加成变为环丁烷孙娟湖北师范学院化学与环境工程系化教0202班435002摘要:本文在于利用前线轨道理论和分子轨道对称守恒原理对乙烯环加成变为环丁烷的反应条件及轨道叠加情况进行分析,为搞清一系列问题,本文对周环反应、分子轨道守恒理论、前线轨道理论进行了讨论,借以对乙烯环加成为环丁烷的情况进行理论阐述,并以此展开,讨论了诸多环加成的实例,以此完善相关学识。
关键词:前线轨道理论分子轨道对称守恒原理乙烯环加成环丁烷反应条件轨道叠加Analyzing How Ethylene Become Cyclobutane Through Cyclization By Frontline Molecule Orbital Theory and Symmetrical Conservation Principleof the Molecule TheorySun JuanChemistry and Environmental project Department of HuBei Normal University Chemistry educating Specialty Class0202HuBei Huang Shi 435002Abstract The purpose and scope of this paper is to explain how ethylene become cyclobutane through cycloaddition reaction this time ,I’ll chose Frontline Molecule Orbital Theory(FMO) and Symmetr ical Conservation Principle of the Molecule Theory to analyze how it reaction ,What are the essential conditions which needs and how the orbits overlap .In order to expound it clearly, I’ll introduce the accurate meanings of Cyclization Molecule Orbital T heory ,FMO and Symmetrical Conservation Principle of the Molecule Theory by definitions and illustrations, Furthermore, according these foundations, we can discuss the more instances with more complicated structure ,Thus we can master the knowledge perfectly.Keywords Frontline Molecule Orbital Theory(FMO) Symmetrical Conservation Principle of the Molecule Theory Ethylene cycloaddition reaction Cyclobutane the essential conditions orbits overlap分子成键的三大条件是:(1)、能量相近,(2)、轨道最大重叠,(3)、对称匹配。
物理中的对称性与守恒定律

物理中的对称性与守恒定律物理领域一直以来都是科学研究的重要组成部分,对称性与守恒定律则是物理学中的重要概念之一。
作为物理学家,我们需要深入了解和探讨对称性与守恒定律在自然界中的重要作用。
本文将重点围绕对称性与守恒定律展开讨论,并探索它们在现代物理学中的应用和意义。
对称性在物理学中的基本原理对称性是物理学中一个十分基础且关键的概念,它描述了一个系统在某种变换下保持不变的性质。
具体来说,对称性可以分为空间对称性、时间对称性和粒子对称性等多个方面。
在物理学中,对称性的存在往往伴随着一些守恒量的出现,例如动量守恒、能量守恒和角动量守恒等。
空间对称性空间对称性是指系统在空间平移、旋转、镜像变换等操作下保持不变。
其中,空间平移对称性导致了动量的守恒,空间旋转对称性导致了角动量的守恒,而空间镜像变换则涉及了手性对称性等重要概念。
时间对称性时间对称性是指系统在时间平移下保持不变。
这一原理引申出了能量守恒定律,即系统的能量在时间演化过程中保持不变。
粒子对称性粒子对称性描述了基本粒子在空间变换或相互作用下的特定行为。
例如,电荷共轭对称性、夸克色荷和强相互作用等都属于粒子对称性研究范畴。
守恒定律与理论物理守恒定律作为自然界普遍存在的规律,在现代物理学中起着举足轻重的作用。
其核心思想是:封闭系统中某个物理量的总量,在系统演化过程中保持不变。
能量守恒定律能量守恒定律是指封闭系统中能量总量保持不变。
这一定律深刻影响了热力学、光学、原子物理等多个领域的研究。
动量守恒定律动量守恒定律描述了封闭系统中动量总量保持不变。
无论是微观粒子碰撞问题还是宏观物体运动问题,动量守恒都是一个重要的约束条件。
角动量守恒定律角动量守恒定律则描述了封闭系统中角动量总量保持不变。
这一定律在描述自转、公转、陀螺运动等方面有着广泛应用。
对称性与守恒定律在物理学中的应用对称性与守恒定律作为物理学中重要的基本原理,渗透到了各个领域和层面。
从微观粒子到宏观世界,都能看到这些基本原理的影响。
5.6 分子轨道的对称性和反应机理

5.6 分子轨道的对称性和反应机理分子轨道的对称性对化学反应进行的难易程度及产物的构型和构象有决定的作用。
应用分子轨道对称性探讨反应机理,主要有福并谦一提出的前线轨道理论和Woodward和Hoffmann提出的分子轨道对称守恒原理。
5.6.1 有关化学反应的一些原理和概念化学反应的实质是分子轨道在化学反应过程中进行改组,在改组时涉及分子轨道的对称性。
1、加热反应(Δ),体系受热辐射影响,由于热辐射光子能量小,反应物分子不激发,一般处于基态情况下进行;2、光照反应(hυ),例如体系受紫外线照射,光子能量大,反应物常受激发而处于激发态。
3、催化剂,催化剂的作用为改变反应物的性质,或改变反应的途径。
5.6.2 前线轨道理论已填电子的能量最高的分子轨道称为最高占据轨道(HOMO),能量最低的空轨道称为最低空轨道(LUMO),这些轨道统称前线轨道。
前线轨道理论认为反应的条件和方式主要决定于前线轨道的对称性,其内容包括:(1)分子在反应过程中,分子轨道发生相互作用,优先起作用的是前线执道。
当反应的两个分子互相接近时,一个分子中的HOMO和另一个分子中的LUMO必须对称性合适,即按轨道正与正叠加、负与负叠加的方式相互接近所形成的过渡状态是活化能较低的状态,称为对称允许的状态。
(2)互相起作用的HOMO和LUMO能级高低必须接近(约6eV以内)。
(3)随着两个分子的HOMO与LUMO发生叠加,电子便从一个分子的HOMO转移到另一个分子的LUMO,电子的转移方向从电负性判断应该合理,电子的转移要和旧键的削霸相一致,不能发生矛盾。
例1、N2+O2=2NON2:1σg21σu21πu42σg21πgO2:σ2s2σ*2s2σ2pz2(π2px2π2py2)(π*2px1π*2py1)σ*2pzN2:HOMO:2σ2g LUMO:1πgO2:HOMO:(π*2px1π*2py1) LUMO:σ*2pzN2的LUMO:1πg和O2的HOMO:(π*2px1π*2py1)对称性是匹配的,但欲使反应进行,电子需从电负性较高的O向电负性较低的N转移,N2的HOMO:2σ2g 和O2的LUMO:σ*2pz能量相差很大对称性也不匹配,因此反应是很难进行的。
分子轨道对称守恒原理

分子轨道对称守恒原理分子轨道对称守恒原理是描述分子轨道对称性的重要原理,它对于理解分子结构和化学性质具有重要意义。
在分子轨道理论中,分子轨道对称守恒原理是指在分子中,如果一个分子轨道对于特定的对称操作(如旋转、反射等)保持不变,那么这个分子轨道在这个对称操作下是对称的。
在分子轨道理论中,分子轨道的对称性是由分子的对称元素(如旋转轴、反射面等)所决定的。
根据分子的对称元素的不同,分子轨道可以分为不同的对称类别,而每个对称类别中的分子轨道具有相同的对称性质。
这一原理在解释分子的光谱性质、化学键性质等方面具有重要的应用价值。
分子轨道对称守恒原理的具体应用可以通过分子轨道图谱来进行分析。
分子轨道图谱是描述分子轨道能级和对称性的图形表示,通过分子轨道图谱可以直观地了解分子轨道的对称性质和能级分布。
在分子轨道图谱中,对称轨道通常以不同的颜色或符号来表示,通过对称轨道的能级分布和对称性质可以进一步理解分子的结构和性质。
除了分子轨道图谱,分子轨道对称守恒原理还可以通过对称性适配原理来进行解释。
对称性适配原理是指在化学反应中,反应物和产物的分子轨道对称性必须适配才能发生有效的相互作用。
这一原理对于理解化学反应的速率和选择性具有重要的意义,通过对称性适配原理可以预测化学反应的发生性和产物的选择性。
总的来说,分子轨道对称守恒原理是分子轨道理论中的重要概念,它对于理解分子结构和化学性质具有重要的意义。
通过分子轨道对称守恒原理,可以更好地理解分子的光谱性质、化学键性质以及化学反应的速率和选择性。
因此,深入理解和应用分子轨道对称守恒原理对于化学领域的发展具有重要的意义。
第八章、分子轨道对称性守恒原理及应用—1

线型
非线型
Donor Acceptor
HOMO单侧 LUMO异侧
Donor
HOMO异侧
Acceptor LUMO单侧
总电子数=4
热允许
热禁阻
总电子数=6
总电子数=8
螯移变反应的规则:
热 —— 在线型螯移变反应中,若多烯为同面组分(端 基对旋),总电子数为4n+2是热允许的;若多烯为异 面组分(端基顺旋),总电子数为4n是热允许的。对于 非线型螯移变反应的热反应恰好相反。
2
光禁阻
+
LUMO HOMO
基态
[2+6]反应 —— 光-激发态-允许、热-基态-禁阻
LUMO
LUMO 4 [2+6]
[2+6] 热禁阻 热禁阻
HOMO
HOMO
3
3
基态
HOMO LUMO
基态
HOMO [2+6] 光允许
4
基态
HOMO
激发态
LUMO 光允许
[2+6] 光允许
3
激发态
在光化反应中 E 2 E1 E2 E3
(有一个电子被激发从E2跃迁到E3上)
丁二烯基态关环反应中E随 旋转角度φ而变化的曲线
丁二烯激发态关环反应中E 随旋转角度φ而变化的曲线
作 业 布 置
1)针对上三章(5-7章)相关知识点内容,8人一小组,每个人分别1篇文献 (共8篇,要有相关性、可成系统,且不可雷同)进行翻译打印装订(1个 小组装订为一册,装订册的第一页写上组内所有成员的姓名、学号,每篇 翻译文献(原文打印放前面、翻译文放在后面)的首页写上该翻译者的姓 名、学号),作为个人作业于下堂课上。电子版文件夹(英文文献+翻译 中文) 周六前发到李赢邮箱 995117229@(各人文件夹以人名学 号命名)。
对称守恒原理的应用

对称守恒原理的应用1. 引言对称守恒原理是自然科学中的一项基本原理。
它描述了物理系统在某些变换下的性质保持不变。
对称守恒原理在众多领域都有广泛的应用,本文将介绍对称守恒原理在粒子物理学、相对论、以及量子力学中的应用。
2. 对称守恒原理在粒子物理学中的应用对称守恒原理在粒子物理学中起到了重要的作用,它可以帮助研究人员理解粒子的性质和相互作用。
以下是对称守恒原理在粒子物理学中的一些具体应用:•电荷守恒:电荷是一种基本的物理量,根据对称守恒原理,电荷在物理过程中守恒不变。
这一原理在描述粒子间的强相互作用和电磁相互作用时起到了重要的作用。
•色守恒:色是一种衡量强相互作用的基本量子数。
根据对称守恒原理,色守恒要求在所有物理过程中,带色粒子的色荷总和保持不变。
这一原理在描述强子间的相互作用和强子的衰变过程中起到关键作用。
•轻子守恒:轻子守恒原理要求在所有物理过程中,轻子数(如电子数、中微子数等)守恒不变。
这一原理在解释核反应、粒子衰变等过程中发挥了重要作用。
3. 对称守恒原理在相对论中的应用相对论是研究高速运动物体行为的一门物理学理论。
对称守恒原理在相对论中起到了重要的作用,以下是对称守恒原理在相对论中的一些应用:•能量守恒:根据对称守恒原理,系统的能量在物理过程中保持不变。
能量转化、传递和守恒是相对论中的基本原理,也是许多相对论问题的关键。
•动量守恒:动量守恒原理要求在物理过程中,系统的总动量保持不变。
这一原理在解释高速运动物体的行为和相互作用时非常重要。
•质量守恒:质量守恒即质心守恒原理,对称守恒原理要求在物理过程中,系统的总质量保持不变。
这一原理在描述相对论性粒子产生和湮灭过程中发挥了重要作用。
4. 对称守恒原理在量子力学中的应用量子力学是描述微观粒子行为的物理理论,对称守恒原理在量子力学中也有广泛的应用,以下是一些例子:•自旋守恒:自旋是粒子的内禀角动量,守恒原理要求在量子力学过程中,自旋守恒不变。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2.环加成反应[HOMO+LUMO]
2.1. [2+4]反应 —— 光-激发态-禁阻、热-基态-允许
LUMO
HOMO
LUMO
[2+4]
热允许
HOMO
基态
基态
热-基态-允许
[2+4]反应 —— 光-激发态-禁阻、热-基态-允许
2
HOMO
激发态
3
光禁阻
+
LUMO
基态
光-激发态-禁阻
1
LUMO
激发态
1.
* ( A)
电环化反应
C2 C2
热允许、光禁阻
4 ( s)
*
( A)
4 ( s)
*
(s)
*
3
( A)
3 ( A)
( s)
( A)
2
(s)
( A)
2 (s)
σ (S)
1 ( A)
(s)
1
( A)
环丁烯
丁二烯
环丁烯
丁二烯
环丁烯的顺旋开环反应的 有关分子轨道及其对称性
A. O.能量相近
A.O.能量分离
分子轨道对称守恒规则 在化学反应中的应用
1.周环反应
4
6
5
3
4
2
3
2
1
1
丁二烯的分子轨道
己三烯的分子轨道
4
LUMO
基态
3
2
LUMO
1
激发态
丁二烯的分子轨道
6
LUMO
5
基态
4
3
LUMO
2
1
激发态
己三烯的分子轨道
一、电环化及其逆反应 反应物或产物中共轭 电子的数目是m
环丁烯的顺旋开环及其 逆反应的能级相关图
m
4 ( A)
m
* ( A)
热禁阻、光允许
( A)
*
-
对旋
4 ( A)
* ( A)
3 ( s)
* ( A)
3 ( s)
( s)
( s)
2 ( A)
2 ( A)
( s)
1 (s)
环丁烯
( s)
光允许、热禁阻 环丁烯
O HO
hv
+
O
4. 螯移变反应
Me Me
SO2
+
SO2
Me
Me
O
hv
CO
+CH2
CH CH
CH
CH
CH2
螯(移)变反应(Cheletropic Reaction) ——连接在同一原子上的两个σ键协同生成或断裂的反应
OMO
LUMO
Í ¬Ãæ 同面 Ö ×· é
HOMO
组分
LUMO
HOMO S
S
第八章、分子轨道对称性守恒原理 及应用
成键时,对称性匹配
A B
A B
A B
+
+
-
+ +
-
+ +
-
S S
A
Px Px
+ + + + + + B
S Px
B
A
-
-
Px Py
Px Pyz
A
对称性不匹配,不能成键
A
-
+ -
B
A
+ S Py
B
-
-
+ + -
B
Px Py
Px Pyz
环丁烯对旋开环生成丁二烯的能级相关图
m镜面
m镜面
* ( A)
* ( A)
4 ( A)
4 ( A)
( A)
*
* ( A)
3 ( s)
3 ( s)
( s)
( s)
2 ( A)
2 ( A)
( s)
( s)
1 (S )
1 (S )
环丁烯 丁二烯
0 r (1 cos )
cos E
0
0
r (1 cos ) 0 cos
E cos
=0
E
此行列式的四个解 E1 、 E2 、 E3 和 E4 是四个分子轨道的能量 E 2E1 2E2
E1 、 E2 随对旋时 角度变化,故 E 也随 变化
2
[3.3]
4
6 1
2
Cope重排
3
3
hv
T1
6
4 3
2
5
1
Ph
Ph CN 1 2
hv
CN 3 CN H 3C
3 2 CN H 1 H
H 3C
2 3 1 H D AcO H D
2 1 3 H AcO H
OCH 2CH
CH2
OH
克莱森重排
CH 2CH CH2
O
光- Fries重排
OH HO O HO OH
3. σ- 键迁移反应
C H D A B H D C
B
A
σ- 键迁移反应
5
LUMO
3
4
3
2
HOMO
2
1
1,3 -σ- 键迁移 1,5 -σ- 键迁移
1
具有构型翻转的σ- 键迁移反应 (原子团)
C
C
hv
C
HOMO
构型保持
C
C
C
HOMO
构型翻转
三、[ i + j ] σ- 键迁移反应
光允许、热禁阻 环丁烯 丁二烯
环丁烯开环生成丁二烯的状态相关图
环丁烯 顺旋
丁二烯
对旋 环丁烯
丁二烯
中国化学家对分子轨道对称守恒原理的贡献
2 1 3 4
唐敖庆院士
丁二烯
丁二烯对旋关环时的分子轨道 C11 C22 C33 C44
相应的久期行列式为
E cos
光 —— 光化学的螯移变反应与热化学的上述规则相反
实
例
Longuet-Higgins能级相关理论
1、能级相关图的构成
构成能级相关图的要点如下:
•
• • •
a) b)
确定反应过程中自始至终存在的对称元素
找出在反应过程中反应物与产物参与反应的分子轨道 根据对称元素确定参与反应的分子轨道的对称性——对称(S)或反称(A) 根据下列原则关联反应物与产物的相关分子轨道,构成能级相关图:
一一对应原则:反应体系的一个分子轨道只能与产物体系的一个分子轨道相关联,否 则可能违背泡利不相容原理 能量相近原则:在不违背轨道对称守恒及一一对应原则的条件下,尽量使能量相近的 轨道相关联
c)
不相交原则:对称性相同轨道的关联线不能相交,因为对称性相同的轨道会产生互相 排斥
•
根据得到的能级相关图,确定该反应在能量上是否有利。若能量有利,则反 应容易进行,是允许的反应;若能量不利,则该反应是禁阻的。
1 (s)
丁二烯
丁二烯
环丁烯的对旋开环反应的 有关分子轨道及其对称性
环丁烯的对旋开环及其 逆反应的能级相关图
2.
环加成反应
[2+2]加成反应
C + C + C C C C C C
x
y
z
对称元素 xy平面 yz平面
AA
热禁阻、光允许
1* 2 *
AA
* * * * 1 2
基态
LUMO
HOMO
热禁阻
[4+4]
HOMO
光允许 LUMO
基态 激发态
同面加成与异面加成
Supra
Supra
Supra
C
antara
C
antara
C
C
[2+2] 反应
LUMO 2
HOMO 1
2s+2s
2a+2a
加成反应的同侧进攻与异侧进攻
热-基态-禁阻
基态反应
HOMO
(激发态)
同面 2s +2s
状态相关理论简介
构成状态相关图的要点:
① 确定反应过程中自始至终存在的对称元素 ② 找出在反应过程中反应物与产物参与反应的分子轨道,根据对称元素确 定其对称性——对称(S)或反称(A) ③ 确定反应物与产物的基态、第一激发态和相应的高级激发态的状态及其 对称性。状态的对称性决定于相应轨道的对称性及其电子充填情况 ④ 依据不相交原则画出状态相关图,决定从反应物的初始状态到产物的相 关状态是否存在能垒,从而判定反应是否容易进行 (若不存在能垒,则 反应允许;若存在能垒,则反应禁阻)
含不对称碳基团的 键迁移反应 (热-基态) 4K 异面 + 构型保持 或 同面 + 构型翻转 hv 同面 + 构型保持 或 异面 + 构型翻转 4K+2 同面 + 构型保持 或 异面 + 构型翻转 hv 异面 + 构型保持 或 同面 + 构型翻转
[1.3]
3 2
4
1
5 6
hv
5
5
4
6 1
O
O
O
O
LUMO O
S O
丁二烯对旋成键 SO2 为同面组分 线型螯移变反应 4n+2, 热允许
丁二烯对旋成键 SO2 为异面组分 线型螯移变反应 4n+2, 热允许
