双曲线经典练习题总结(带答案)
双曲线专题经典练习及答案详解

双曲线专题一、学习目标:1.理解双曲线的定义;2.熟悉双曲线的简单几何性质;3.能根据双曲线的定义和几何性质解决简单实际题目.二、知识点梳理定 义1、到两个定点1F 与2F 的距离之差的绝对值等于定长(小于21F F )的点的轨迹2、到定点F 与到定直线l 的距离之比等于常数()1>e ee (>1)的点的轨迹标准方程-22a x 22b y =1()0,0>>b a -22a y 22bx =1()0,0>>b a 图 形性质范围a x ≥或a x -≤,R y ∈R x ∈,a y ≥或a y -≤对称性 对称轴: 坐标轴 ;对称中心: 原点渐近线x aby ±= x ba y ±= 顶点 坐标 ()0,1a A -,()0,2a A ()b B -,01,()b B ,02 ()a A -,01,()a A ,02()0,1b B -,()0,2b B焦点 ()0,1c F -,()0,2c F()c F -,01,()c F ,02轴 实轴21A A 的长为a 2 虚轴21B B 的长为b 2离心率1>=ace ,其中22b a c += 准线准线方程是c a x 2±=准线方程是ca y 2±=三、课堂练习1.椭圆x 24+y 2a 2=1与双曲线x 2a -y 22=1有相同的焦点,则a 的值是( )A.12 B .1或-2 C .1或12D .12.已知F 是双曲线x 24-y 212=1的左焦点,点A (1,4),P 是双曲线右支上的动点,则|PF |+|P A |的最小值为________.3.已知F 1,F 2分别为双曲线C :x 2-y 2=1的左、右焦点,点P 在C 上,∠F 1PF 2=60°,则|PF 1||PF 2|=( )A .2B .4C .6D .84.已知双曲线的两个焦点F 1(-10,0),F 2(10,0),M 是此双曲线上的一点,且MF 1→·MF 2→=0,|MF 1→|·|MF 2→|=2,则该双曲线的方程是( )A.x 29-y 2=1 B .x 2-y29=1C.x 23-y 27=1D.x 27-y 23=15.若F 1,F 2是双曲线8x 2-y 2=8的两焦点,点P 在该双曲线上,且△PF 1F 2是等腰三角形,则△PF 1F 2的周长为________.6.已知双曲线x 26-y 23=1的焦点为F 1,F 2,点M 在双曲线上,且MF 1⊥x 轴,则F 1到直线F 2M 的距离为( )A.365B.566C.65D.567.已知△ABC 的两个顶点A ,B 分别为椭圆x 2+5y 2=5的左焦点和右焦点,且三个内角A ,B ,C 满足关系式sin B -sin A =12sin C .(1)求线段AB 的长度; (2)求顶点C 的轨迹方程.8.双曲线C 的中点在原点,右焦点为F ⎝ ⎛⎭⎪⎫233,0,渐近线方程为y =±3x .(1)求双曲线C 的方程;(2)设直线L :y =kx +1与双曲线交于A ,B 两点,问:当k 为何值时,以AB 为直径的圆过原点?。
双曲线专题 (优秀经典练习题及答案详解)

双曲线专题一、学习目标:1.理解双曲线的定义;2.熟悉双曲线的简单几何性质;3.能根据双曲线的定义和几何性质解决简单实际题目.二、知识点梳理定 义1、到两个定点1F 与2F 的距离之差的绝对值等于定长(小于21F F )的点的轨迹2、到定点F 与到定直线l 的距离之比等于常数()1>e ee (>1)的点的轨迹标准方程-22a x 22b y =1()0,0>>b a -22a y 22bx =1()0,0>>b a 图 形性质范围a x ≥或a x -≤,R y ∈R x ∈,a y ≥或a y -≤对称性 对称轴: 坐标轴 ;对称中心: 原点渐近线x a by ±=x b a y ±=顶点 坐标 ()0,1a A -,()0,2a A ()b B -,01,()b B ,02 ()a A -,01,()a A ,02()0,1b B -,()0,2b B焦点 ()0,1c F -,()0,2c F()c F -,01,()c F ,02轴 实轴21A A 的长为a 2 虚轴21B B 的长为b 2离心率1>=ace ,其中22b a c += 准线准线方程是c a x 2±=准线方程是ca y 2±=三、课堂练习1、双曲线方程为2221x y -=,则它的右焦点坐标为( )A 、2,02⎛⎫ ⎪ ⎪⎝⎭B 、5,02⎛⎫⎪ ⎪⎝⎭C 、6,02⎛⎫⎪ ⎪⎝⎭D 、()3,01.解析:C2.设椭圆C 1的离心率为,焦点在x 轴上且长轴长为26,若曲线C 2上的点到椭圆C 1的两个焦点的距离的差的绝对值等于8,则曲线C 2的标准方程为( )A . ﹣=1B .﹣=1C .﹣=1D .﹣=12.解析A :在椭圆C 1中,由,得椭圆C 1的焦点为F 1(﹣5,0),F 2(5,0),曲线C 2是以F 1、F 2为焦点,实轴长为8的双曲线, 故C 2的标准方程为:﹣=1,故选A .3.已知F 1、F 2为双曲线C :x 2-y 2=2的左、右焦点,点P 在C 上,|PF 1|=2|PF 2|,则cos ∠F 1PF 2=( ) A.14 B.35 C.34 D.453.解析C :依题意得a =b =2,∴c =2. ∵|PF 1|=2|PF 2|,设|PF 2|=m ,则|PF 1|=2m .又|PF 1|-|PF 2|=22=m . ∴|PF 1|=42,|PF 2|=2 2. 又|F 1F 2|=4,∴cos ∠F 1PF 2=422+222-422×42×22=34.故选C.4.已知双曲线的两个焦点为F 1(﹣,0)、F 2(,0),P 是此双曲线上的一点,且PF 1⊥PF 2,|PF 1|•|PF 2|=2,则该双曲线的方程是( ) A.﹣=1 B.﹣=1 C.﹣y 2=1D.x 2﹣=14.解析C :解:设双曲线的方程为﹣=1. 由题意得||PF 1|﹣|PF 2||=2a ,|PF 1|2+|PF 2|2=(2)2=20.又∵|PF 1|•|PF 2|=2, ∴4a 2=20﹣2×2=16 ∴a 2=4,b 2=5﹣4=1.所以双曲线的方程为﹣y 2=1.故选C .5.已知双曲线C :x 2a 2-y 2b 2=1的焦距为10,点P (2,1)在C 的渐近线上,则C 的方程为( )A.x 220-y 25=1B.x 25-y 220=1C.x 280-y 220=1D.x 220-y 280=1 5.解析A :设焦距为2c ,则得c =5.点P (2,1)在双曲线的渐近线y =±ba x 上,得a =2b .结合c=5,得4b 2+b 2=25, 解得b 2=5,a 2=20,所以双曲线方程为x 220-y 25=1. 6.等轴双曲线C 的中心在原点,焦点在x 轴上,C 与抛物线y 2=16x 的准线交于A ,B 两点,|AB |=43,则C 的实轴长为( )A. 2 B .2 2 C .4 D .86.解析C :设等轴双曲线方程为x 2-y 2=a 2,根据题意,得抛物线的准线方程为x =-4,代入双曲线的方程得16-y 2=a 2,因为|AB |=43,所以16-(23)2=a 2,即a 2=4,所以2a =4,所以选C. 7.平面直角坐标系xOy 中,已知双曲线x 24-y 212=1上一点M 的横坐标为3,则点M 到此双曲线的右焦点的距离为________.7.解析:双曲线的右焦点(4,0),点M (3,15)或(3,-15),则点M 到此双曲线的右焦点的距离为4.8.以知F 是双曲线221412x y -=的左焦点,(1,4),A P 是双曲线右支上的动点,则PF PA + 的最小值为 。
双曲线经典练习题总结(带答案)

双曲线经典练习题总结(带答案)一、选择题1.以椭圆x 216+y 29=1的顶点为顶点,离心率为2的双曲线方程为( C )A .x 216-y 248=1B .y 29-x 227=1C .x 216-y 248=1或y 29-x 227=1D .以上都不对[解析] 当顶点为(±4,0)时,a =4,c =8,b =43,双曲线方程为x 216-y 248=1;当顶点为(0,±3)时,a =3,c =6,b =33,双曲线方程为y 29-x 227=1.2.双曲线2x 2-y 2=8的实轴长是( C ) A .2 B .22 C .4 D .42[解析] 双曲线2x 2-y 2=8化为标准形式为x 24-y 28=1,∴a =2,∴实轴长为2a =4.3.(全国Ⅱ文,5)若a >1,则双曲线x 2a 2-y 2=1的离心率的取值范围是( C )A .(2,+∞)B .(2,2 )C .(1,2)D .(1,2)[解析] 由题意得双曲线的离心率e =a 2+1a. ∴c 2=a 2+1a 2=1+1a2.∵a >1,∴0<1a 2<1,∴1<1+1a2<2,∴1<e < 2.故选C .4.(2018·全国Ⅲ文,10)已知双曲线C :x 2a 2-y 2b 2=1(a >0,b >0)的离心率为2,则点(4,0)到C的渐近线的距离为( D ) A .2 B .2 C .322D .22[解析] 由题意,得e =ca=2,c 2=a 2+b 2,得a 2=b 2.又因为a >0,b >0,所以a =b ,渐近线方程为x ±y =0,点(4,0)到渐近线的距离为42=22, 故选D .5.(2019·全国Ⅲ卷理,10)双曲线C :x 24-y 22=1的右焦点为F ,点P 在C 的一条渐近线上,O 为坐标原点,若|PO |=|PF |,则△PFO 的面积为( A ) A .324B .322C .22D .32[解析] 双曲线x 24-y 22=1的右焦点坐标为(6,0),一条渐近线的方程为y =22x ,不妨设点P 在第一象限,由于|PO |=|PF |,则点P 的横坐标为62,纵坐标为22×62=32,即△PFO 的底边长为6,高为32,所以它的面积为12×6×32=324.故选A . 6.若双曲线C :x 2a 2-y 2b 2=1(a >0,b >0)的一条渐近线被圆(x -2)2+y 2=4所截得的弦长为2,则C 的离心率为( A ) A .2 B .3 C .2D .233[解析] 设双曲线的一条渐近线方程为y =ba x ,圆的圆心为(2,0),半径为2,由弦长为2得出圆心到渐近线的距离为22-12= 3.根据点到直线的距离公式得2b a 2+b 2=3,解得b 2=3a 2. 所以C 的离心率e =ca =c 2a 2=1+b 2a2=2.故选A . 二、填空题7.(2019·江苏卷,7)在平面直角坐标系xOy 中,若双曲线x 2-y 2b 2=1(b >0)经过点(3,4),则该双曲线的渐近线方程是 [解析] 因为双曲线x 2-y 2b 2=1(b >0)经过点(3,4),所以9-16b 2=1(b >0),解得b =2,即双曲线方程为x 2-y 22=1,其渐近线方程为y =±2x .8.双曲线x 24+y 2k =1的离心率e ∈(1,2),则k 的取值范围是__-12<k <0__.[解析] 双曲线方程可变形为x 24-y 2-k =1,则a 2=4,b 2=-k ,c 2=4-k ,e =ca =4-k2.又因为e ∈(1,2),即1<4-k2<2,解得-12<k <0. 三、解答题9.(1)求与椭圆x 29+y 24=1有公共焦点,且离心率e =52的双曲线的方程;(2)求实轴长为12,离心率为54的双曲线的标准方程.[解析] (1)设双曲线的方程为x 29-λ-y 2λ-4=1(4<λ<9),则a 2=9-λ,b 2=λ-4,∴c 2=a 2+b 2=5,∵e =52,∴e 2=c 2a 2=59-λ=54,解得λ=5, ∴所求双曲线的方程为x 24-y 2=1.(2)由于无法确定双曲线的焦点在x 轴上还是在y 轴上,所以可设双曲线标准方程为x 2a 2-y 2b 2=1(a >0,b >0)或y 2a 2-x 2b 2=1(a >0,b >0).由题设知2a =12,c a =54且c 2=a 2+b 2,∴a =6,c =152,b 2=814.∴双曲线的标准方程为x 236-y 2814=1或y 236-x 2814=1.B 级 素养提升一、选择题1.如果椭圆x 2a 2+y 2b 2=1(a >b >0)的离心率为32,那么双曲线x 2a 2-y 2b 2=1的离心率为( A )A .52B .54C .2D .2[解析] 由已知椭圆的离心率为32,得a 2-b 2a 2=34,∴a 2=4b 2.∴a 2+b 2a 2=5b 24b 2=54.∴双曲线的离心率e =52. 2.双曲线x 2-y 2m =1的离心率大于2的充分必要条件是( C )A .m >12B .m ≥1C .m >1D .m >2[解析] 本题考查双曲线离心率的概念,充分必要条件的理解. 双曲线离心率e =1+m >2,所以m >1,选C .3.(多选题)已知M (x 0,y 0)是双曲线C :x 22-y 2=1上的一点,F 1、F 2是C 的两个焦点.若MF 1→·MF 2→<0,则y 0的取值可能是( BC ) A .-1 B .0 C .12D .1[解析] 由双曲线方程可知F 1(-3,0)、F 2(3,0), ∵MF 1→·MF 2→<0,∴(-3-x 0)(3-x 0)+(-y 0)(-y 0)<0, 即x 20+y 20-3<0,∴2+2y 20+y 20-3<0,y 20<13, ∴-33<y 0<33,故选BC . 4.(多选题)将离心率为e 1的双曲线C 1的实半轴长a 和虚半轴长b (a ≠b )同时增加m (m >0)个单位长度,得到离心率为e 2的双曲线C 2,则( BD ) A .对任意的a ,b ,e 1>e 2 B .当a <b 时,e 1>e 2 C .对任意的a ,b ,e 1<e 2 D .当a >b 时,e 1<e 2[解析] 由条件知e 21=c 2a 2=1+b 2a2,e 22=1+⎝ ⎛⎭⎪⎫b +m a +m 2,当a >b 时,b +m a +m >ba ,∴e 21<e 22.∴e 1<e 2.当a <b 时,b +m a +m <ba ,∴e 21>e 22.∴e 1>e 2.所以,当a >b 时,e 1<e 2;当a <b 时,e 1>e 2. 二、填空题5.(2019·课标全国Ⅰ理,16)已知双曲线C :x 2a 2-y 2b 2=1(a >0,b >0)的左、右焦点分别为F 1,F 2,过F 1的直线与C 的两条渐近线分别交于A ,B 两点.若F 1A →=AB →,F 1B →·F 2B →=0,则C 的离心率为__2__.[解析] 双曲线x 2a 2-y 2b 2=1(a >0,b >0)的渐近线方程为y =±ba x ,∵F 1B →·F 2B →=0,∴F 1B ⊥F 2B ,∴点B 在⊙O :x 2+y 2=c 2上,如图所示,不妨设点B 在第一象限,由⎩⎪⎨⎪⎧y =b ax x 2+y 2=c2a 2+b 2=c 2x >0,得点B (a ,b ),∵F 1A →=AB →,∴点A 为线段F 1B 的中点,∴A ⎝⎛⎭⎪⎫a -c 2,b 2,将其代入y =-b a x 得b 2=⎝⎛⎭⎫-b a ×a -c 2.解得c =2a ,故e =ca=2.6.已知双曲线x 29-y 2a =1的右焦点为(13,0),则该双曲线的渐近线方程为__y =±23x __.[解析] 由已知得9+a =13,即a =4,故所求双曲线的渐近线为y =±23x .三、解答题7.焦点在x 轴上的双曲线过点P (42,-3),且点Q (0,5)与两焦点的连线互相垂直,求此双曲线的标准方程.[解析] 因为双曲线焦点在x 轴上,所以设双曲线的标准方程为x 2a 2-y 2b 2=1(a >0,b >0),F 1(-c,0)、F 2(c,0).因为双曲线过点P (42,-3), 所以32a 2-9b2=1.①又因为点Q (0,5)与两焦点的连线互相垂直, 所以QF 1→·QF 2→=0,即-c 2+25=0. 所以c 2=25.② 又c 2=a 2+b 2,③所以由①②③可解得a 2=16或a 2=50(舍去). 所以b 2=9,所以所求的双曲线的标准方程是x 216-y 29=1. 8.(2020·云南元谋一中期中)双曲线x 2a 2-y 2b 2=1(a >0,b >0)的右焦点为F (c,0).(1)若双曲线的一条渐近线方程为y =x 且c =2,求双曲线的方程;(2)以原点O 为圆心,c 为半径作圆,该圆与双曲线在第一象限的交点为A ,过A 作圆的切线,其斜率为-3,求双曲线的离心率.[解析] (1)由题意,ba =1,c =2,a 2+b 2=c 2,∴a 2=b 2=2,∴双曲线方程为x 22-y 22=1.(2)由题意,设A (m ,n ),则k OA =33,从而n =33m ,m 2+n 2=c 2,∴A (32c ,c 2), 将A (32c ,c 2)代入双曲线x 2a 2-y 2b 2=1得:3c 24a 2-c 24b 2=1,∴c 2(3b 2-a 2)=4a 2b 2,且c 2=a 2+b 2,∴(a 2+b 2)(3b 2-a 2)=4a 2b 2, ∴3b 4-2a 2b 2-a 4=0,∴3(b a )4-2(ba )2-1=0,∴b 2a 2=1从而e 2=1+b 2a 2=2,∴e = 2.。
双曲线基础题(含答案)

双曲线基础题一、单选题1.已知动点(),P x y2=,则动点P 的轨迹是( )A .椭圆B .双曲线C .双曲线的左支D .双曲线的右支2.已知双曲线的两个焦点分别为()10,5F −,()20,5F ,双曲线上一点P 与1F ,2F 的距离差的绝对值等于6,则双曲线的标准方程为( )A .221916x y −=B .221169x y −=C .221916y x −=D .221169y x −=3.已知平面内两定点()13,0F −,()23,0F ,下列条件中满足动点P 的轨迹为双曲线的是( ) A .127PF PF −=± B .126PF PF −=± C .124PF PF −=±D .22126PF PF −=±4.已知双曲线22:1169x y C −=的两焦点分别为1F ,2F ,P 为双曲线上一点,若110PF =,则2PF =( ). A .16B .18C .4或16D .2或185.若双曲线22:1916x y E −=的左、右焦点分别为12,F F ,点P 在双曲线E 上,且13PF =,则2PF 等于( ) A .11B .9C .5D .36.设双曲线22:4640C x y −+=的焦点为12,F F ,点P 为C 上一点,16PF =,则2PF 为( ) A .22B .14C .10D .27.已知双曲线C :221169x y −=的左右焦点为1F ,2F ,点P 在双曲线C 的右支上,则21PF PF −=( ) A .-8B .8C .10D .8.若方程22122x y m m−=+−表示双曲线,则m 的取值范围是( )A .22m −<<B .2m >−C .0m ≥D .2m ≥9.已知方程22111x y k k−=+−表示双曲线,则实数k 的取值范围是( )A .(﹣1,1)B .(0,+∞)C .[0,+∞)D .(﹣∞,﹣1)∪(1,+∞) 10.双曲线mx 2+y 2=1的虚轴长是实轴长的2倍,则m 的值为( ) A .4B .-4C .-14D .1411.若方程22154x y m m +=−+表示的图形是双曲线,则m 的取值范围是( )A .m >5B .m <-4C .m <-4或m >5D .-4<m <512.“102a <<”是“方程22121x y a a+=−表示的曲线为双曲线”的( ) A .充分不必要条件 B .必要不充分条件 C .充要条件D .既不充分又不必要条件13.若双曲线221y x m−=的一个焦点为()3,0−,则m =( ). AB .18 C.D .814.椭圆22214x y a +=与双曲线22212x y a −=有相同的焦点,则=a ( )A .1−B .1C .1±D .215.若方程2244x ky k +=表示双曲线,则此双曲线的虚轴长等于( ) A.B.CD16.双曲线221916x y −=的左顶点与右焦点间的距离为( )A .2B .4C .5D .817.若椭圆22125x y m +=与双曲线221515x y −=的焦点相同,则m 的值为( )A .3±B .4C .6D .918.已知椭圆221(1)x y a a +=>和双曲线221(0)x y m m −=>有相同焦点,则( )A .2a m =+B .2m a =+C .222a m =+D .222m a =+19.与双曲线22154x y −=有公共焦点,且短轴长为2的椭圆方程为( )A .2212x y +=B .22154x y +=C .22110x y +=D .221134x y +=20.若椭圆22125x y m +=与双曲线221515x y −=的焦点相同,则m 的值为( )A .3B .6C .9D .1221.双曲线2214x y −=的一个焦点到一条渐近线的距离是( )AB .2 CD .122.等轴双曲线的一个焦点是()10,6F −,则其标准方程为( )A .2211818x y −=B .22199y x −=C .2211818y x −=D .22199x y −=23.等轴双曲线的两条渐近线的夹角大小为( ) A .π4B .π3C .π2D .2π324.双曲线22221(0,0)x y a b a b−=>>的一条渐近线方程为y x =,则此双曲线的离心率为( )A .2 BC .3 D25.等轴双曲线C :()222210,0x y a b a b−=>>焦距为4,则C 的一个顶点到一条渐近线的距离为( )A .1B .32C .2D .1226.双曲线2214y x −=的渐近线方程为( )A .12y x =± B .2y x =± C.y =D.2y x =±27.双曲线2228x y −=的渐近线方程是( )A .12y x =±B .2y x =± C.y = D.y x =28.已知双曲线()222:1016x y C b b−=>的焦距为10,则双曲线C 的渐近线方程为( )A .916y x =±B .169y x =±C .43y x =± D .34y x =?29.双曲线22221(0,0)x y a b a b −=>>A.y =B.y =C.2y x =±D.y x = 30.若直线31y x =−与双曲线22:1C x my −=的一条渐近线平行,则实数m 的值为( ) A .19B .9C .13D .331.双曲线22143x y −=的离心率是( )A .32B .54C2D .5232.若双曲线C 两条渐近线方程是y x =±,则双曲线C 的离心率是( ). ABC .2D33.已知直线20x y −=双曲线22221y xa b−=的一条渐近线,则双曲线的离心率为( )AB .2 CD34.已知双曲线22221x y a b−=(0a >,0b >)的一条渐近线的斜率为12,则该双曲线的离心率为( ) ABC .2D二、解答题35.求适合下列条件的双曲线的标准方程. (1)焦点在x轴上,a =A ()5,2−; (2)焦点在y 轴上,焦距是16,离心率43e =; (3)离心率e =M ()5,3−. 36.求适合下列条件的双曲线的标准方程: (1)经过点),()3,2; (2)焦点为()0,5−,()0,5,经过点⎝; (3)a b =,经过点()3,1−; (4)经过(3,−和9,54⎫⎛ ⎪⎝⎭两点.37.求满足下列条件的双曲线的标准方程:(1)焦点在x 轴上,离心率为53,两顶点间的距离为6;(2)以椭圆22159x y +=的焦点为顶点,顶点为焦点.38.求适合下列条件的曲线标准方程.(1)虚轴长为16的双曲线的标准方程; (2)过点()1,3P −的抛物线的标准方程.39.求双曲线22494x y −=−的顶点坐标、焦点坐标、实轴长、虚轴长、离心率和渐近线方程. 40.求下列双曲线的实轴和虚轴的长、离心率、焦点和顶点坐标、渐近线方程: (1)2277x y −=; (2)2228x y −=−. 41.根据下列条件,求双曲线的标准方程.(1)焦距为(-5,2),且焦点在x 轴上; (2)焦点为(0,-6),(0,6),且过点A (-5,6).42.m ,n 为何值时,方程221x y m n+=表示下列曲线:(1)圆; (2)椭圆; (3)双曲线?43.已知曲线C 的方程为22173x y m m−=−−,根据下列条件,求实数m 的取值范围:(1)曲线C 是椭圆; (2)曲线C 是双曲线.。
双曲线练习题及答案

运用双曲线的定义
例 1.若方程 x2 sin y 2 cos 1表示焦点在 y 轴上的双曲线,则角 所在象限是( )
A、第一象限
B、第二象限 C、第三象限 D、第四象限
练习 1.设双曲线 x2 y 2 1 上的点 P 到点 (5,0) 的距离为 15,则 P 点到 (5,0) 的距离是( ) 16 9
双曲线相关知识
双曲线的焦半径公式: 1:定义:双曲线上任意一点 P 与双曲线焦点的连线段,叫做双曲线的焦半径。 2.已知双曲线标准方程 x^2/a^2-y^2/b^2=1 点 P(x,y)在左支上 │PF1│=-(ex+a) ;│PF2│=-(ex-a) 点 P(x,y)在右支上 │PF1│=ex+a ;│PF2│=ex-a
A.7
B.23
C.5 或 23
D.7 或 23奎奎 奎奎奎 奎奎
例 2. 已知双曲线的两个焦点是椭圆 x 2 + 5y2 =1 的两个顶点,双曲线的两条准线分别通过椭圆的两个
10 32
焦点,则此双曲线的方程是( )。
(A) x 2 - y2 =1 (B) x 2 - y2 =1 (C) x 2 - y2 =1 (D) x 2 - y2 =1
课 1、[解析]设双曲线方程为 x2 4 y2 ,
当
0 时,化为
x2
y2
1, 2
5 10 20 , 4
4
当
0
时,化为
y2
y2
1 , 2
5 10 20 , 4
4
综上,双曲线方程为 x2 y2 1 或 y2 x2 1
ππ 3 3
π
双曲线练习题(含答案)

双曲线及其标准方程习题一、 单选题(每道小题 4分 共 56分 )1. 命题甲:动点P 到两定点A 、B 距离之差│|PA|-|PB|│=2a(a >0);命题乙; P 点轨迹是双曲线,则命题甲是命题乙的 [ ] A .充分非必要条件 B .必要非充分条件 C .充要条件 D .既非充分也非必要条件2.若双曲线的一个焦点是,,则等于 . . . .2kx ky =1(04)k [ ]A B C D 22---33258332583.点到点,与它关于原点的对称点的距离差的绝对值等于,则点的轨迹方程是 . .. .P (60)10P [ ]A y 11=1B y 25=1C y 6=1D y 25=12222-----x x x x 2222256125114.k 5+y 6k=1[ ]A B C D 2<是方程表示双曲线的 .既非充分又非必要条件 .充要条件.必要而非充分条件 .充分而非必要条件x k 25--5. 如果方程x 2sin α-y 2cos α=1表示焦点在y 轴上的双曲线,那么角α的终边在 [ ] A .第四象限 B .第三象限 C .第二象限 D .第一象限 6.下列曲线中的一个焦点在直线上的是 . .. .4x 5y +25=0[ ]A y 16=1B +y 16=1C x 16=1D +x 16=12222---x x y y 22229259257. 若a ·b <0,则ax 2-ay 2=b 所表示的曲线是 [ ] A .双曲线且焦点在x 轴上 B .双曲线且焦点在y 轴上 C .双曲线且焦点可能在x 轴上,也可能在y 轴上 D .椭圆 8.以椭圆的焦点为焦点,且过,点的双曲线方程为. .. .x x y y y 2222296109251150+y 25=1P(35)[ ]A y 10=1B x 6=1C x 3=1D x 2=122222----9.到椭圆的两焦点距离之差的绝对值等于椭圆短轴的点的轨迹方程是 . .. .x x x x x 2222225251697+y 9=1[ ]A y 9=1B y 9=1C y 7=1D y 9=122222----10.直线与坐标轴交两点,以坐标轴为对称轴,以其中一点为焦点且另一点为虚轴端点的双曲线的方程是 . .. .或2x 5y +20=0[ ]A y 16=1B y 84=1C y 84=1D y 84=1y 84=122222------x x x x x 2222284161001610011.以坐标轴为对称轴,过,点且与双曲线有相等焦距的双曲线方程是 .或 .或.或 .或A(34)y 20=1[ ]A y 20=1x 20=1B y 15=1x 15=1C y 20=1x 15=1D y 5=1x 10=1222222222x x y x y x y x y 22222222255510105102015---------12.与双曲线共焦点且过点,的双曲线方程是 . .. .x x x x x 2222215520916------y 10=1(34)[ ]A y 20=1B y 5=1C y 16=1D y 9=12222213. 已知ab <0,方程y=-2x +b 和bx 2+ay 2=ab 表示的曲线只可能是图中的 [ ]14.已知△一边的两个端点是、,另两边斜率的积是,那么顶点的轨迹方程是 . .. .ABC A(7,0)B(70)C [ ]A x +y =49B +x 49=1C =1D 5y 147=12222---,x 355147514749492222y y x二、 填空题(每道小题 4分 共 8分 )1.已知双曲线的焦距是,则的值等于 .x k 21+-y 5=18k 22.设双曲线,与恰是直线在轴与轴上的截距,那么双曲线的焦距等于 .x a 22--y b=1(a >0,b >0)a b 3x +5y 15=0x y 22双曲线的标准方程及其简单的几何性质1.平面内到两定点E 、F 的距离之差的绝对值等于|EF |的点的轨迹是( ) A .双曲线 B .一条直线 C .一条线段 D .两条射线 2.已知方程x 21+k -y 21-k =1表示双曲线,则k 的取值范围是( )A .-1<k <1B .k >0C .k ≥0D .k >1或k <-13.动圆与圆x 2+y 2=1和x 2+y 2-8x +12=0都相外切,则动圆圆心的轨迹为( ) A .双曲线的一支 B .圆 C .抛物线 D .双曲线4.以椭圆x 23+y 24=1的焦点为顶点,以这个椭圆的长轴的端点为焦点的双曲线方程是( )A.x 23-y 2=1 B .y 2-x 23=1 C.x 23-y 24=1D.y 23-x 24=1 5.“ab <0”是“曲线ax 2+by 2=1为双曲线”的( ) A .充分不必要条件 B .必要不充分条件 C .充要条件 D .既不充分也不必要条件6.已知双曲线的两个焦点为F 1(-5,0)、F 2(5,0),P 是此双曲线上的一点,且PF 1⊥PF 2, |PF 1|·|PF 2|=2,则该双曲线的方程是( ) A.x 22-y 23=1 B.x 23-y 22=1 C.x 24-y 2=1 D .x 2-y 24=17.已知点F 1(-4,0)和F 2(4,0),曲线上的动点P 到F 1、F 2距离之差为6,则曲线方程为( ) A.x 29-y 27=1 B.x 29-y 27=1(y >0) C.x 29-y 27=1或x 27-y 29=1 D.x 29-y 27=1(x >0) 8.已知双曲线的左、右焦点分别为F 1、F 2,在左支上过F 1的弦AB 的长为5,若2a =8,那么△ABF 2的周长是( ) A .16B .18C .21D .269.已知双曲线与椭圆x 29+y 225=1共焦点,它们的离心率之和为145,双曲线的方程是( )A.x 212-y 24=1B.x 24-y 212=1 C .-x 212+y 24=1 D .-x 24+y 212=1 10.焦点为(0,±6)且与双曲线x 22-y 2=1有相同渐近线的双曲线方程是( )A.x 212-y 224=1 B.y 212-x 224=1 C.y 224-x 212=1 D.x 224-y 212=111.若0<k <a ,则双曲线x 2a 2-k 2-y 2b 2+k 2=1与x 2a 2-y 2b 2=1有( )A .相同的实轴B .相同的虚轴C .相同的焦点D .相同的渐近线12.中心在坐标原点,离心率为53的双曲线的焦点在y 轴上,则它的渐近线方程为( )A .y =±54xB .y =±45xC .y =±43xD .y =±34x13.双曲线x 2b 2-y 2a 2=1的两条渐近线互相垂直,那么该双曲线的离心率为( )A .2B. 3C. 2D.3214.双曲线x 29-y 216=1的一个焦点到一条渐近线的距离等于( )A. 3 B .3 C .4 D .2二、填空题15.双曲线的焦点在x 轴上,且经过点M (3,2)、N (-2,-1),则双曲线标准方程是________. 16.过双曲线x 23-y 24=1的焦点且与x 轴垂直的弦的长度为________.17.如果椭圆x 24+y 2a 2=1与双曲线x 2a -y 22=1的焦点相同,那么a =________.18.双曲线x 24+y 2b =1的离心率e ∈(1,2),则b 的取值范围是________.19.椭圆x 24+y 2a 2=1与双曲线x 2a2-y 2=1焦点相同,则a =________.20.双曲线以椭圆x 29+y 225=1的焦点为焦点,它的离心率是椭圆离心率的2倍,求该双曲线的方程为________.双曲线及其标准方程习题答案一、单选题1. B2. C3. A4. D5. B6. C7. B8. B9. C 10. A 11. C 12. A 13. B 14. D 二、填空题1. 10 2.234双曲线的标准方程及其简单的几何性质(答案)1、[答案] D2、[答案] A [解析] 由题意得(1+k )(1-k )>0,∴(k -1)(k +1)<0,∴-1<k <1.3、[答案] A [解析] 设动圆半径为r ,圆心为O , x 2+y 2=1的圆心为O 1,圆x 2+y 2-8x +12=0的圆心为O 2,由题意得|OO 1|=r +1,|OO 2|=r +2, ∴|OO 2|-|OO 1|=r +2-r -1=1<|O 1O 2|=4, 由双曲线的定义知,动圆圆心O 的轨迹是双曲线的一支.4、[答案] B [解析] 由题意知双曲线的焦点在y 轴上,且a =1,c =2, ∴b 2=3,双曲线方程为y 2-x 23=1. 5、[答案] C [解析] ab <0⇒曲线ax 2+by 2=1是双曲线,曲线ax 2+by 2=1是双曲线⇒ab <0. 6、[答案] C [解析] ∵c =5,|PF 1|2+|PF 2|2=|F 1F 2|2=4c 2, ∴(|PF 1|-|PF 2|)2+2|PF 1|·|PF 2|=4c 2,∴4a 2=4c 2-4=16,∴a 2=4,b 2=1. 7、[答案] D [解析] 由双曲线的定义知,点P 的轨迹是以F 1、F 2为焦点, 实轴长为6的双曲线的右支,其方程为:x 29-y 27=1(x >0)8、[答案] D [解析] |AF 2|-|AF 1|=2a =8,|BF 2|-|BF 1|=2a =8, ∴|AF 2|+|BF 2|-(|AF 1|+|BF 1|)=16,∴|AF 2|+|BF 2|=16+5=21, ∴△ABF 2的周长为|AF 2|+|BF 2|+|AB |=21+5=26.9、[答案] C [解析] ∵椭圆x 29+y 225=1的焦点为(0,±4),离心率e =45,∴双曲线的焦点为(0,±4),离心率为145-45=105=2, ∴双曲线方程为:y 24-x 212=1.10、[答案] B [解析] 与双曲线x 22-y 2=1有共同渐近线的双曲线方程可设为x 22-y 2=λ(λ≠0),又因为双曲线的焦点在y 轴上, ∴方程可写为y 2-λ-x 2-2λ=1.又∵双曲线方程的焦点为(0,±6),∴-λ-2λ=36.∴λ=-12. ∴双曲线方程为y 212-x 224=1.11、[答案] C [解析] ∵0<k <a ,∴a 2-k 2>0.∴c 2=(a 2-k 2)+(b 2+k 2)=a 2+b 2.12、[答案] D [解析] ∵c a =53,∴c 2a 2=a 2+b 2a 2=259,∴b 2a 2=169,∴b a =43,∴a b =34.又∵双曲线的焦点在y 轴上,∴双曲线的渐近线方程为y =±a b x ,∴所求双曲线的渐近线方程为y =±34x .13、[答案] C [解析] 双曲线的两条渐近线互相垂直,则渐近线方程为:y =±x ,∴b a =1,∴b 2a 2=c 2-a 2a 2=1,∴c 2=2a 2,e =ca= 2. 14、[答案] C[解析] ∵焦点坐标为(±5,0),渐近线方程为y =±43x ,∴一个焦点(5,0)到渐近线y =43x 的距离为4.15、[答案] x 273-y 275=1 [解析] 设双曲线方程为:x 2a 2-y 2b 2=1(a >0,b >0)又点M (3,2)、N (-2,-1)在双曲线上,∴⎩⎨⎧ 9a 2-4b 2=14a 2-1b 2=1,∴⎩⎨⎧a 2=73b 2=75.16、[答案]833[解析] ∵a 2=3,b 2=4,∴c 2=7,∴c =7, 该弦所在直线方程为x =7,由⎩⎪⎨⎪⎧x =7x 23-y 24=1得y 2=163,∴|y |=433,弦长为833.17、[答案] 1 [解析] 由题意得a >0,且4-a 2=a +2,∴a =1.18、[答案] -12<b <0 [解析] ∵b <0,∴离心率e =4-b2∈(1,2),∴-12<b <0. 19、[答案]62 [解析] 由题意得4-a 2=a 2+1,∴2a 2=3,a =62. 焦点为(0,±4),离心率e =c a =45,∴双曲线的离心率e 1=2e =85,∴c 1a 1=4a 1=85,∴a 1=52,∴b 21=c 21-a 21=16-254=394,∴双曲线的方程为y 2254-x 2394=1.20、[答案]y2254-x2394=1 [解析]椭圆x29+y225=1中,a=5,b=3,c2=16,。
双曲线基础专项练习含解析

双曲线一、单选题(共29题;共58分)1.已知双曲线的焦距为,则的离心率为()A. B. C. D.2.已知,是双曲线的两个焦点,以线段为边作正,若边的中点在双曲线上,则双曲线的离心率为()A. B. C. D.3.双曲线的渐近线方程为()A. B. C. D.4.双曲线的一个焦点到一条渐近线的距离为()A. 4B.C. 2D.5.实轴长为的双曲线上恰有个不同的点满足,其中,分别是双曲线的左、右顶点.则的离心率的取值范围为()A. B. C. D.6.双曲线方程为x2-2y2=1,则它的左焦点的坐标为( )A. (-,0)B. (-,0)C. (-,0)D. (-,0)7.已知双曲线的离心率,且其右焦点,则双曲线的方程为()A. B. C. D.8.已知双曲线的渐近线为,实轴长为,则该双曲线的方程为()A. B. 或C. D. 或9.双曲线的焦点坐标是( )A. B. C. D.10.已知双曲线(a>0,b>0)的右焦点为F,若过点F且倾斜角为60°的直线l与双曲线的右支有且只有一个交点,则此双曲线的离心率e的取值范围是()A. B. (1,2), C. D.11.设F1,F2是双曲线的两个焦点,P在双曲线上,当△F1PF2的面积为时,的值为()A. 2B. 3C. 4D. 612.已知双曲线的左、右焦点为、,在双曲线上存在点P满足,则此双曲线的离心率e的取值范围是()A. B. C. D.13.设为双曲线的右焦点,过坐标原点的直线依次与双曲线的左.右支交于点,若,则该双曲线的离心率为()A. B. C. D.14.已知双曲线:的离心率为,则的渐近线方程为()A. B. C. D.15.双曲线C的对称轴与坐标轴重合,两个焦点分别为F1,F2,虚轴的一个端点为A,若△AF1F2是顶角为120°的等腰三角形,则双曲线C的渐近线方程为()A. B. 或 C. D. 或16.若双曲线的一条渐近线被圆所截得的弦长为2,则的离心率为()A. 2B.C.D.17.过点,且与双曲线有相同渐近线的双曲线的方程是()A. B. C. D.18.若双曲线的实轴长、虚轴长、焦距成等差数列,则双曲线的渐近线方程是()A. B. C. D.19.设、分别为双曲线的左、右顶点,、是双曲线上关于轴对称的不同两点,设直线、的斜率分别为、,若,则双曲线的离心率是()A. B. C. D.20.双曲线的焦点坐标为()A. B. C. D.21.双曲线的渐近线方程是()A. B. C. D.22.已知双曲线:(,)的左右顶点分别为,,点,若三角形为等腰直角三角形,则双曲线的离心率为()A. B. C. 2 D. 323.已知中心在原点,对称轴为坐标轴的双曲线的一条渐近线方程为,则该双曲线的离心率是()A. B. C. 或 D. 或24.若双曲线与直线无交点,则离心率的取值范围()A. B. C. D.25.若双曲线的离心率大于2,则该双曲线的虚轴长的取值范围是()A. B. C. D.26.已知点为双曲线上一点,则它的离心率为()A. B. C. D.27.设双曲线的一个焦点为F,虚轴的一个端点为B,焦点F到一条渐近线的距离为d,若,则双曲线离心率的取值范围是()A. B. C. D.28.设点是双曲线上的一点,分别是双曲线的左、右焦点,已知,且,则双曲线的一条渐近线方程是()A. B. C. D.29.以原点为中心,焦点在y轴上的双曲线C的一个焦点为,一个顶点为,则双曲线C的方程为()A. B. C. D.二、填空题(共12题;共13分)30.设为曲线上一点,,,若,则________.31.已知双曲线的离心率为2,则点到的渐近线的距离为________.32.若点在双曲线上,它的横坐标与双曲线的右焦点的横坐标相同,则点与双曲线的左焦点的距离为________33.双曲线上的一点到一个焦点的距离等于1,那么点到另一个焦点的距离为________.34.已知双曲线的离心率为2,过右焦点且垂直于轴的直线与双曲线交于两点. 设到双曲线的同一条渐近线的距离分别为和,且,则双曲线的方程为________.35.双曲线- =1的渐近线方程是________,实轴长为________.36.已知双曲线C的中心在原点,焦点在x轴上,其渐近线方程为2x±3y=0,焦距为2 ,则双曲线C的标准方程为________.37.双曲线的一个焦点是,一条渐近线是,那么双曲线的方程是________38.已知双曲线(,)满足,且双曲线的右焦点与抛物线的焦点重合,则该双曲线的方程为________.39.设是双曲线上一点,双曲线的一条渐近线方程为,分别是双曲线的左、右焦点,若,则的值为________.40.双曲线的其中一个焦点坐标为,则实数________.41.已知分别为双曲线的左、右焦点,过与双曲线的一条渐近线平行的直线交双曲线于点,若,则双曲线的离心率为________.三、解答题(共5题;共55分)42.已知双曲线的中心在原点,焦点在坐标轴上,离心率为,且过点.(1)求双曲线的方程;(2)若点在双曲线上,求的面积.43.已知双曲线与椭圆有相同焦点,且经过点(4,6).(1)求双曲线方程;(2)若双曲线的左,右焦点分别是F1,F2,试问在双曲线上是否存在点P,使得|PF1|=5|PF2|.请说明理由.44.已知双曲线:的实轴长为2.(1)若的一条渐近线方程为,求的值;(2)设、是的两个焦点,为上一点,且,的面积为9,求的标准方程.45.已知双曲线的中心在原点,焦点,在坐标轴上,离心率为,且过点.(1)求双曲线的方程;(2)若点在双曲线上,求证:;(3)求的面积.46.双曲线x2﹣=1(b>0)的左、右焦点分别为F1、F2,直线l过F2且与双曲线交于A、B两点.(1)若l的倾斜角为,△F1AB是等边三角形,求双曲线的渐近线方程;(2)设b= ,若l的斜率存在,M为AB的中点,且=0,求l的斜率.答案解析部分一、单选题1.【答案】C【考点】双曲线的简单性质【解析】【解答】依题意可知,所以,故,所以,故答案为:C.【分析】根据求得的值,进而求得双曲线离心率.2.【答案】C【考点】双曲线的简单性质【解析】【解答】依题意可知双曲线的焦点为,,,三角形高是,,边的中点,,代入双曲线方程得:,整理得:,,,整理得,求得,,.故答案为:C.【分析】先根据双曲线方程求得焦点坐标的表达式,进而可求得三角形的高,则点的坐标可得,进而求得边的中点的坐标,代入双曲线方程求得,和的关系式化简整理求得关于的方程求得.3.【答案】D【考点】双曲线的简单性质【解析】【解答】令,整理得,所以双曲线的渐近线方程为.故答案为:D【分析】令双曲线的为,从而得到方程,化简后即得渐近线方程.4.【答案】C【考点】双曲线的简单性质【解析】【解答】双曲线的,,,一个焦点设为,,一条渐近线设为,可得一个焦点到一条渐近线的距离为.故答案为:C.【分析】求得双曲线的,,,可设一个焦点和一条渐近线方程,由点到直线的距离公式,可得所求值.5.【答案】A【考点】双曲线的简单性质【解析】【解答】依题意可得,,,设,则由,得,整理得.由,得,因为双曲线上恰有个不同的点满足,所以方程有两不等实根,所以只需,解得,则.故答案为:A【分析】先由题意,得到,,,设,根据,得,再与双曲线联立,消去,得到,根据双曲线上存在个不同的点满足,得到只需,求出,进而可求出离心率的范围.6.【答案】C【考点】双曲线的标准方程【解析】【解答】由,可得,,由得,所以左焦点坐标为(-,0)故答案为:C【分析】将双曲线化成标准式,再结合双曲线的关系式求解7.【答案】B【考点】双曲线的标准方程【解析】【解答】由双曲线的离心率,且其右焦点为,可得,所以,所求双曲线的方程为,故答案为:B.【分析】由已知双曲线的离心率,右焦点为列式,得到,即可求出双曲线的标准方程.8.【答案】B【考点】双曲线的标准方程,双曲线的简单性质【解析】【解答】当双曲线的焦点在轴上时, ,又,即,所以,所求双曲线的方程为: ;当双曲线的焦点在轴上时, ,又,即,所以,所以所求双曲线的方程为: .所以所求双曲线方程为: 或.故答案为:.【分析】根据双曲线的焦点所在位置分两种情况讨论: 当双曲线的焦点在轴上时, ; 当双曲线的焦点在轴上时, ,结合可解得.9.【答案】D【考点】双曲线的简单性质【解析】【解答】由得,故,故焦点坐标为故答案为:D【分析】将化简成标准方程再进行焦点坐标运算即可.10.【答案】A【考点】双曲线的简单性质【解析】【解答】已知双曲线的右焦点为,若过点且倾斜角为的直线与双曲线的右支有且只有一个交点,则该直线的斜率的绝对值小于等于渐近线的斜率,,离心率,,故答案为:.【分析】若过点且倾斜角为的直线与双曲线的右支有且只有一个交点,则该直线的斜率的绝对值小于等于渐近线的斜率.根据这个结论可以求出双曲线离心率的取值范围.11.【答案】C【考点】双曲线的简单性质【解析】【解答】双曲线的两个焦点坐标为,设的坐标为,则△的面积为,,,代入双曲线方程解得,不妨取,,,故答案为:.【分析】求得双曲线的焦点坐标,利用△的面积为,确定的坐标,运用两点的距离公式,即可求得结论.12.【答案】B【考点】双曲线的应用【解析】【解答】因为为的边的中线,可知,双曲线上存在点满足,则,由,可知,则。
《双曲线》练习题经典(含答案)

《双曲线》练习题一. 选择题:1. 已知焦点在x 轴上的双曲线的渐近线方程是y=±4<则该双曲线的离心率是(A )2. 中心在原点,焦点在x 轴上的双曲线的实轴与虚轴相等,一个焦点到一条渐近线的距离为近,则双曲线方 程为(B )D."-讨1),且其两条渐近线的方程分别为2x+y=0和2x ・y=0,则双曲c-¥4=^<=i D •学辱十 224.已知椭圆2/ + 2沪=1 (a>b>0)与双曲线/ 一方2 =1有相同的焦点.则椭圆的离心率为(A )丄 鱼 心B.㊁C.飞一D. 丁2=一二1表示双曲线,且该双曲线两焦点间的距离为4,则n 的取值范围是(A ) 卅_ nB ・(-1, VI ) C. (0> 3) D ・(0, V3) 6•设双曲线笃-牛1 (0<a<b )的半焦距为c,直线1过(/ 0) (0, b )两点,已知原点到直线1的距2b 2禽为乎U 则双曲线的离心率为(A )A. 2B. V3C. V2D.色空37. 已知双曲线4~4=1的两条渐近线与以椭圆£+各=1的左焦点为圆心、半径为竽 的圆相切,则双曲 线的离心率为(A )A- i B - I c- J D . ?8. 双曲线虚轴的一个端点为",两个焦点为为、E, Z 斤莎=120° ,则双曲线的离心率为(B )f V"9. 已知双曲线一一 一 =1(加>0/>0)的一个焦点到一条渐近线的距离是2, 一个顶点到它的一条渐近线的m n距离为则m 等于(D )V13A. 9 B ・ 4 C ・ 2 D ・,310. 已知双曲线的两个焦点为尺(_ 顾,0)、E (何 0) , M 是此双曲线上的一点,且满足x" - y"=l B ・ x" - y"=2 C ・ x" - y"=V23.在平而直角坐标系中,双曲线C 过点P (b 线C 的标准方程为(42A. 225.已知方程今一 rn'+n A. ( - 1, 3)= OJ MF X N MF, \= 2,则该双曲线的方程是(A )■ ■ ■ ■ y yy—y = 1 B ・ x-—=l ——=1—y=l■11 •设凡 尺是双曲线/一計=1的两个焦点,尸是双曲线上的一点,且3 〃 =4|啟"则△彤E 的而枳等于 (c )A ・ 4、也B ・ 8、/5C. 24D ・ 4812.过双曲线y-/=8的左焦点片有一条弦尸0在左支上,若1PQ =7,匹是双曲线的右焦点,则△啟。
(2021年整理)《双曲线》练习题经典(含答案)

(完整)《双曲线》练习题经典(含答案)编辑整理:尊敬的读者朋友们:这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是任然希望((完整)《双曲线》练习题经典(含答案))的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈,这将是我们进步的源泉,前进的动力。
本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为(完整)《双曲线》练习题经典(含答案)的全部内容。
《双曲线》练习题一、选择题:1.已知焦点在x 轴上的双曲线的渐近线方程是y =±4x ,则该双曲线的离心率是( A )A.错误!B.错误!C.错误!D.错误!2.中心在原点,焦点在x 轴上的双曲线的实轴与虚轴相等,一个焦点到一条渐近线的距离为,则双曲线方程为( B )A .x 2﹣y 2=1 B .x 2﹣y 2=2C .x 2﹣y 2=D .x 2﹣y 2=3.在平面直角坐标系中,双曲线C 过点P(1,1),且其两条渐近线的方程分别为2x+y=0和2x ﹣y=0,则双曲线C 的标准方程为( B ) A .B .C .或D .4.已知椭圆222ax +222b y =1(a >b >0)与双曲线22ax -22b y =1有相同的焦点,则椭圆的离心率为( A )A .22 B .21C .66 D .365.已知方程﹣=1表示双曲线,且该双曲线两焦点间的距离为4,则n 的取值范围是( A ) A .(﹣1,3) B .(﹣1,) C .(0,3) D .(0,)6.设双曲线=1(0<a <b )的半焦距为c,直线l 过(a ,0)(0,b )两点,已知原点到直线l 的距离为,则双曲线的离心率为( A )A .2B .C .D .7.已知双曲线22219y x a-=的两条渐近线与以椭圆221259y x +=的左焦点为圆心、半径为165 的圆相切,则双曲线的离心率为( A ) A .54B .53C .43D .658.双曲线虚轴的一个端点为M ,两个焦点为F 1、F 2,∠F 1MF 2=120°,则双曲线的离心率为( B )A. 3 B 。
高考数学专题《双曲线》习题含答案解析

专题9.4 双曲线1.(2021·江苏高考真题)已知双曲线()222210,0x y a b a b-=>>的一条渐近线与直线230x y -+=平行,则该双曲线的离心率是( )ABC .2D【答案】D 【分析】写出渐近线,再利用斜率相等,进而得到离心率【详解】双曲线的渐近线为b y x a =±,易知by x a=与直线230x y -+=平行,所以=2b e a ⇒==故选:D.2.(2021·北京高考真题)若双曲线2222:1x y C a b-=离心率为2,过点,则该双曲线的程为()A .2221x y -=B .2213y x -=C .22531x y -=D .22126x y -=【答案】B 【分析】分析可得b =,再将点代入双曲线的方程,求出a 的值,即可得出双曲线的标准方程.【详解】2c e a == ,则2c a =,b =,则双曲线的方程为222213x y a a-=,将点的坐标代入双曲线的方程可得22223113a a a-==,解得1a =,故b ,因此,双曲线的方程为2213y x -=.故选:B3.(2021·山东高考真题)已知1F 是双曲线22221x y a b-=(0a >,0b >)的左焦点,点P 在双曲线上,直线1PF 与x 轴垂直,且1PF a =,那么双曲线的离心率是()练基础A B C .2D .3【答案】A 【分析】易得1F 的坐标为(),0c -,设P 点坐标为()0,c y -,求得20by a=,由1PF a =可得a b =,然后由a ,b ,c 的关系求得222c a =,最后求得离心率即可.【详解】1F 的坐标为(),0c -,设P 点坐标为()0,c y -,易得()22221c y a b--=,解得20b y a =,因为直线1PF 与x 轴垂直,且1PF a =,所以可得2b a a=,则22a b =,即a b =,所以22222c a b a =+=,离心率为e =故选:A .4.(2021·天津高考真题)已知双曲线22221(0,0)x y a b a b-=>>的右焦点与抛物线22(0)y px p =>的焦点重合,抛物线的准线交双曲线于A ,B 两点,交双曲线的渐近线于C 、D |AB .则双曲线的离心率为( )A B C .2D .3【答案】A 【分析】设公共焦点为(),0c ,进而可得准线为x c =-,代入双曲线及渐近线方程,结合线段长度比值可得2212a c =,再由双曲线离心率公式即可得解.【详解】设双曲线22221(0,0)x y a b a b-=>>与抛物线22(0)y px p =>的公共焦点为(),0c ,则抛物线22(0)y px p =>的准线为x c =-,令x c =-,则22221c y a b -=,解得2b y a =±,所以22bAB a=,又因为双曲线的渐近线方程为b y x a =±,所以2bcCD a=,所以2bc a =c =,所以222212a c b c =-=,所以双曲线的离心率ce a==故选:A.5.(2019·北京高考真题(文))已知双曲线2221x y a-=(a >0)a =( )AB .4C .2D .12【答案】D 【解析】∵双曲线的离心率ce a==,c = ,=,解得12a = ,故选D.6.(全国高考真题(文))双曲线2222:1(0,0)x y C a b a b -=>>的离心率为2,焦点到渐近线的,则C 的焦距等于( ).A.2B. C.4D.【答案】C 【解析】设双曲线的焦距为2c ,双曲线的渐进线方程为,由条件可知,,又,解得,故答案选C .7.(2017·天津高考真题(文))已知双曲线的左焦点为,点在双曲线的渐近线上,是边长为2的等边三角形(为原点),则双曲线的方程为( )A. B. C. D.【答案】D 【解析】22221(0,0)x y a b a b -=>>F A OAF △O 221412x y -=221124x y -=2213x y -=2213y x -=由题意结合双曲线的渐近线方程可得:,解得:,双曲线方程为:.本题选择D选项.8.(2021·全国高考真题(理))已知双曲线22:1(0)xC y mm-=>的一条渐近线为my+=,则C的焦距为_________.【答案】4【分析】将渐近线方程化成斜截式,得出,a b的关系,再结合双曲线中22,a b对应关系,联立求解m,再由关系式求得c,即可求解.【详解】my+=化简得y=,即ba,同时平方得2223ba m=,又双曲线中22,1a m b==,故231m m=,解得3,0m m==(舍去),2223142c a b c=+=+=⇒=,故焦距24c=.故答案为:4.9.(2019·江苏高考真题)在平面直角坐标系xOy中,若双曲线2221(0)yx bb-=>经过点(3,4),则该双曲线的渐近线方程是_____.【答案】y=.【解析】由已知得222431b-=,解得b=或b=,因为0b>,所以b=.因为1a=,所以双曲线的渐近线方程为y=.10.(2020·全国高考真题(文))设双曲线C:22221x ya b-= (a>0,b>0)的一条渐近线为y= 2222tan60cc a bba⎧⎪=⎪=+⎨⎪⎪==⎩221,3a b==2213yx-=x ,则C 的离心率为_________.【解析】由双曲线方程22221x y a b-=可得其焦点在x 轴上,因为其一条渐近线为y =,所以b a =c e a ===1.(2018·全国高考真题(理))设,是双曲线()的左、右焦点,是坐标原点.过作的一条渐近线的垂线,垂足为.若则的离心率为( )ABC .D【答案】B 【解析】由题可知在中,在中,故选B.2.(2020·云南文山·高三其他(理))已知双曲线2221(0)x y a a-=>上关于原点对称的两个点P ,Q ,右顶点为A ,线段AP 的中点为E ,直线QE 交x 轴于(1,0)M ,则双曲线的离心1F 2F 2222:1x y C a b-=O 2F C P 1PF =C222,PF b OF c==PO a∴=2Rt POF V 222cos P O PF b F OF c∠==12PF F △22221212212cos P O 2PF F F PF b F PF F F c+-∠==223bc a c=⇒=e ∴=练提升率为( )A B .C D 【答案】D 【解析】由已知得M 为APQ V 的重心,∴3||3a OM ==,又1b =,∴c ==,即c e a ==.故选:D.3.(2020·广东天河·华南师大附中高三月考(文))已知平行于x 轴的直线l 与双曲线C :()222210,0x y a b a b-=>>的两条渐近线分别交于P 、Q 两点,O 为坐标原点,若OPQ △为等边三角形,则双曲线C 的离心率为( )A .2B .C D 【答案】A 【解析】因为OPQ △为等边三角形,所以渐近线的倾斜角为3π,所以22,3,bb b a a=∴=∴=所以2222223,4,4,2c a a c a e e -=∴=∴=∴=.故选:A4.(2021·广东广州市·高三月考)已知1F ,2F 分别是双曲线C :2213xy -=的左、右焦点,点P 是其一条渐近线上一点,且以线段12F F 为直径的圆经过点P ,则点P 的横坐标为( )A .±1B .C .D .2±【答案】C 【分析】由题意可设00(,)P x ,根据圆的性质有120F P F P ⋅= ,利用向量垂直的坐标表示,列方程求0x 即可.【详解】由题设,渐近线为y =,可令00(,)P x x ,而1(2,0)F -,2(2,0)F ,∴100(2,)F P x x =+ ,200(2,)F P x =- ,又220120403x F P F P x ⋅=-+= ,∴0x =故选:C5.(2020·广西南宁三中其他(理))圆22:10160+-+=C x y y 上有且仅有两点到双曲线22221(0,0)x y a b a b -=>>的一条渐近线的距离为1,则该双曲线离心率的取值范围是( )A .B .55(,)32C .55(,42D .1)【答案】C 【解析】双曲线22221x y a b-=的一条渐近线为0bx ay -=,圆22:10160C x y y +-+=,圆心()0,5,半径3因为圆C 上有且仅有两点到0bx ay -=的距离为1,所以圆心()0,5到0bx ay -=的距离d 的范围为24d <<即24<<,而222+=a b c 所以524a c <<,即5542e <<故选C 项.6.【多选题】(2021·湖南高三)已知双曲线2222:1x y C a b-=(0a >,0b >)的左,右焦点为1F ,2F ,右顶点为A ,则下列结论中,正确的有( )A .若a b =,则CB .若以1F 为圆心,b 为半径作圆1F ,则圆1F 与C 的渐近线相切C .若P 为C 上不与顶点重合的一点,则12PF F △的内切圆圆心的横坐标x a =D .若M 为直线2a x c=(c =0的一点,则当M 的纵坐标为2MAF V 外接圆的面积最小【答案】ABD 【分析】由a b =,得到222a c =,利用离心率的定义,可判定A 正确;由双曲线的几何性质和点到直线的距离公式,可判定B 正确;由双曲线的定义和内心的性质,可判定C 不正确;由正弦定理得到2MAF V 外接圆的半径为222sin AF R AMF =∠,得出2sin AMF ∠最大时,R 最小,只需2tan AMF ∠最大,设2,a M t c ⎛⎫⎪⎝⎭,得到22tan tan()AMF NMF NMA ∠=∠-∠,结合基本不等式,可判定D 正确.【详解】对于A 中,因为a b =,所以222a c =,故C 的离心率ce a==A 正确;对于B 中,因为()1,0F c -到渐近线0bx ay -=的距离为d b ==,所以B 正确;对于C 中,设内切圆与12PF F △的边1221,,FF F P FP 分别切于点1,,A B C ,设切点1A (,0)x ,当点P 在双曲线的右支上时,可得121212PF PF PC CF PB BF CF BF -=+--=-1112A F A F =-()()22c x c x x a =+--==,解得x a =,当点P 在双曲线的左支上时,可得x a =-,所以12PF F △的内切圆圆心的横坐标x a =±,所以C 不正确;对于D 中,由正弦定理,可知2MAF V 外接圆的半径为222sin AF R AMF =∠,所以当2sin AMF ∠最大时,R 最小,因为2a a c<,所以2AMF ∠为锐角,故2sin AMF ∠最大,只需2tan AMF ∠最大.由对称性,不妨设2,a M t c ⎛⎫ ⎪⎝⎭(0t >),设直线2a x c =与x 轴的交点为N ,在直角2NMF △中,可得222=tan a c NF c NM t NMF -∠=,在直角NMA △中,可得2=tan a a NA c NM tMA N -∠=,又由22222222tan tan tan tan()1tan tan 1NMF NMA AMF NMF NMA NMF NMAa a c a c ct t a a c a c c t t--∠-∠∠=∠-∠==+∠∠--⨯+-⋅22()c a ab c a t c t-=≤-+当且仅当()22ab c a t c t -=,即t =2tan AMF ∠取最大值,由双曲线的对称性可知,当t =2tan AMF ∠也取得最大值,所以D 正确.故选:ABD .7.【多选题】(2021·重庆巴蜀中学高三月考)已知点Q 是圆M :()2224x y ++=上一动点,点()2,0N ,若线段NQ 的垂直平分线交直线MQ 于点P ,则下列结论正确的是( )A .点P 的轨迹是椭圆B .点P 的轨迹是双曲线C .当点P 满足PM PN ⊥时,PMN V 的面积3PMN S =△D .当点P 满足PM MN ⊥时,PMN V 的面积6PMN S =V 【答案】BCD 【分析】根据PM PN -的结果先判断出点P 的轨迹是双曲线,由此判断AB 选项;然后根据双曲线的定义以及垂直对应的勾股定理分别求解出PM PN ⋅的值,即可求解出PMN S △,据此可判断CD 选项.【详解】依题意,2MQ =,4MN =,因线段NQ 的垂直平分线交直线MQ 于点P ,于是得PQ PN =,当点P 在线段MQ 的延长线上时,2PM PN PM PQ MQ -=-==,当点P 在线段QM 的延长线上时,2PN PM PQ PM MQ -=-==,从而得24PM PN MN -=<=,由双曲线的定义知,点M 的轨迹是双曲线,故A 错,B 对;选项C ,点P 的轨迹方程为2213y x -=,当PM PN ⊥时,2222616PM PN PM PN PM PN MN ⎧-=⎪⇒⋅=⎨+==⎪⎩,所以132PMN S PM PN ==△,故C 对;选项D ,当PM MN ⊥时,2222316PM PN PM PN PM MN ⎧-=-⎪⇒=⎨-==⎪⎩,所以162PMN S PM MN ==△,故D 对,故选:BCD.8.(2021·全国高二课时练习)双曲线()22122:10,0x y C a b a b-=>>的焦距为4,且其渐近线与圆()222:21C x y -+=相切,则双曲线1C 的标准方程为______.【答案】2213x y -=【分析】根据焦距,可求得c 值,根据渐近线与圆2C 相切,可得圆心到直线的距离等于半径1,根据a ,b ,c 的关系,即可求得a ,b 值,即可得答案.【详解】因为双曲线()22122:10,0x y C a b a b-=>>的焦距为4,所以2c =.由双曲线1C 的两条渐近线b y x a=±与圆()222:21C x y -+=相切,可得1=又224a b +=,所以1b =,a =所以双曲线1C 的标准方程为2213x y -=.故答案为:2213x y -=9.(2021·全国高二单元测试)已知双曲线2213y x -=的左、右焦点分别为1F ,2F ,离心率为e ,若双曲线上一点P 使2160PF F ∠=︒,则221F P F F ⋅的值为______.【答案】3【分析】在12PF F △中,设2PF x =,则12PF x =+或12PF x =-.分别运用余弦定理可求得答案.【详解】解:由已知得2124F F c ==.在12PF F △中,设2PF x =,则12PF x =+或12PF x =-.当12PF x =+时,由余弦定理,得()222124242x x x +=+-⨯⨯,解得32x =,所以221314322F P F F ⋅=⨯⨯= .当12PF x =-时,由余弦定理,得()222124242x x x -=+-⨯⨯,无解.故2213F P F F ⋅=.故答案为:3.10.(2021·全国高二课时练习)如图,以AB 为直径的圆有一内接梯形ABCD ,且//AB CD .若双曲线1C 以A ,B 为焦点,且过C ,D 两点,则当梯形的周长最大时,双曲线1C 的离心率为______.1【分析】连接AC ,设BAC θ∠=,将梯形的周长表示成关于θ的函数,求出当30θ=︒时,l 有最大值,即可得到答案;【详解】连接AC ,设BAC θ∠=,2AB R c R ==,,作CE AB ⊥于点E ,则||2sin BC R θ=,()2||||cos 902sin EB BC R θθ=︒-=,所以2||24sin CD R R θ=-,梯形的周长221||2||||24sin 24sin 4sin 52l AB BC CD R R R R R R θθθ⎛⎫=++=++-=--+ ⎪⎝⎭.当1sin 2θ=,即30θ=︒时,l 有最大值5R ,这时,||BC R =,||AC =,1(||||)2a AC BC =-=,1=c e a .1+1. (2021·全国高考真题(理))已知12,F F 是双曲线C 的两个焦点,P 为C 上一点,且121260,3F PF PF PF ∠=︒=,则C 的离心率为( )ABCD【答案】A 【分析】根据双曲线的定义及条件,表示出12,PF PF ,结合余弦定理可得答案.【详解】因为213PF PF =,由双曲线的定义可得12222PF PF PF a -==,所以2PF a =,13PF a =;因为1260F PF ∠=︒,由余弦定理可得2224923cos 60c a a a a =+-⨯⋅⋅︒,整理可得2247c a =,所以22274a c e ==,即e =故选:A2.(2020·浙江省高考真题)已知点O (0,0),A (–2,0),B (2,0).设点P 满足|PA |–|PB |=2,且P 为函数y=|OP |=( )ABCD【答案】D 【解析】因为||||24PA PB -=<,所以点P 在以,A B 为焦点,实轴长为2,焦距为4的双曲线的右支上,由2,1c a ==可得,222413b c a=-=-=,即双曲线的右支方程为()22103y x x -=>,而点P还在函数y =练真题由()22103y x x y ⎧⎪⎨->==⎪⎩,解得x y ⎧=⎪⎪⎨⎪=⎪⎩,即OP ==.故选:D.3.(2019·全国高考真题(理))设F 为双曲线C :22221x y a b-=(a >0,b >0)的右焦点,O为坐标原点,以OF 为直径的圆与圆x 2+y 2=a 2交于P 、Q 两点.若|PQ |=|OF |,则C 的离心率为( )ABC .2D【答案】A 【解析】设PQ 与x 轴交于点A ,由对称性可知PQ x ⊥轴,又||PQ OF c == ,||,2cPA PA ∴=∴为以OF 为直径的圆的半径,A ∴为圆心||2c OA =.,22c c P ⎛⎫∴ ⎪⎝⎭,又P 点在圆222x y a +=上,22244c c a ∴+=,即22222,22c c a e a=∴==.e ∴=,故选A .4.(2019·全国高考真题(理))双曲线C :2242x y -=1的右焦点为F ,点P 在C的一条渐近线上,O 为坐标原点,若=PO PF ,则△PFO 的面积为( )A B C .D .【答案】A 【解析】由2,,,a b c ====.,P PO PF x =∴=,又P 在C 的一条渐近线上,不妨设为在y x =上,1122PFO P S OF y ∴=⋅==△,故选A .5. (2021·全国高考真题(文))双曲线22145x y -=的右焦点到直线280x y +-=的距离为________.【分析】先求出右焦点坐标,再利用点到直线的距离公式求解.【详解】由已知,3c ===,所以双曲线的右焦点为(3,0),所以右焦点(3,0)到直线280x y +-===.6.(2019·全国高考真题(理))已知双曲线C :22221(0,0)x y a b a b-=>>的左、右焦点分别为F 1,F 2,过F 1的直线与C 的两条渐近线分别交于A ,B 两点.若1F A AB = ,120F B F B ⋅=,则C 的离心率为____________.【答案】2.【解析】如图,由1,F A AB =得1.F A AB =又12,OF OF =得OA 是三角形12F F B 的中位线,即22//,2.BF OA BF OA =由120F B F B =g ,得121,,F B F B OA F A ⊥⊥则1OB OF =有1AOB AOF ∠=∠,又OA 与OB 都是渐近线,得21,BOF AOF ∠=∠又21BOF AOB AOF π∠+∠+∠=,得02160,BOF AOF BOA ∠=∠=∠=.又渐近线OB 的斜率为0tan 60ba==,所以该双曲线的离心率为2c e a ====.。
双曲线曲线练习题含答案

双曲线曲线练习题含答案1. 求下列双曲线的渐近线方程:(1)$ x^2-4y^2+8x-32=0 $(2)$ x^2-9y^2=81 $(3)$ x^2+4y^2+4x+16=0 $答案:(1)$ y=\frac{x+4}{2} $ 或$ y=\frac{1}{2}x-4 $ (斜渐近线)(2)$ x+3\sqrt{y^2+1}=0 $ 或 $ x-3\sqrt{y^2+1}=0 $ (与 $ y $ 轴垂直的渐近线)、$ y=-\frac{x}{9} $ (斜渐近线)(3)$ y=-1 $ 或 $ y=-\frac{(x+2)^2}{16} $ (与 $ y $ 轴平行的渐近线)2. 求双曲线 $ \frac{x^2}{9}-\frac{y^2}{16}=1 $ 的离心率和焦距长度。
答案:离心率为 $ \sqrt{1+\frac{b^2}{a^2}}=\frac{5}{3} $,焦距长度为 $ c=\sqrt{a^2+b^2}=5 $。
3. 求双曲线 $ \frac{x^2}{25}-\frac{y^2}{9}=1 $ 与直线$ y=\frac{3}{5}x-2 $ 的交点坐标。
答案:设交点坐标为 $ (x_0, y_0) $,则 $ \frac{x_0^2}{25}-\frac{(\frac{3x_0}{5}-2)^2}{9}=1 $,解得 $ x_0=\frac{50}{7} $ 或$ x_0=-\frac{50}{7} $,代入方程即可得到交点坐标。
4. 判断曲线 $ \frac{x^2}{4}-\frac{y^2}{16}=1 $ 是否关于直线$ y=-x $ 对称。
答案:首先求出曲线关于直线 $ y=-x $ 对称的公式为$ y=\frac{y_0}{x_0}x $,其中 $ (x_0,y_0) $ 是曲线上任意一点。
假设 $ A(a, b) $ 是曲线上的一点,则 $ B(-b,-a) $ 是曲线上的对称点。
双曲线经典练习题总结(带答案)

双曲线经典练习题总结(带答案)1.选择题1.以椭圆x^2/169 + y^2/64 = 1的顶点为顶点,离心率为2的双曲线方程为C,当顶点为(±4,0)时,a=4,c=8,b=√(a^2+c^2)=4√5,双曲线方程为x^2/16 - y^2/20 = 1;当顶点为(0,±3)时,a=3,c=6,b=√(a^2+c^2)=3√5,双曲线方程为y^2/9 - x^2/5 = 1,所以答案为C。
2.双曲线2x^2 - y^2 = 8化为标准形式为x^2/4 - y^2/8 = 1,所以实轴长为2a = 4,答案为C。
3.若a>1,则双曲线2x^2/a^2 - y^2 = 1的离心率的取值范围是C。
由双曲线方程得离心率e = √(a^2+1)/a,所以c^2 =a^2+b^2 = a^2(a^2+1)/(a^2-1),代入离心率公式得√(a^2+1)/a = 2,解得a = 2,所以答案为C。
4.已知双曲线C:2x^2/a^2 - 2y^2/b^2 = 1(a>0,b>0)的离心率为2,则点(4,0)到C的渐近线的距离为D。
由双曲线方程得离心率e = √(a^2+b^2)/a = 2,所以b^2 = 3a^2,又因为点(4,0)到渐近线的距离为c/a,所以c^2 = a^2+b^2 = 4a^2,代入双曲线方程得4x^2/a^2 - 2y^2/3a^2 = 1,化简得y^2 = 6x^2/5,所以渐近线方程为y = ±√(6/5)x,代入点(4,0)得距离为2√5,所以答案为D。
5.双曲线C:x^2/4 - y^2/16 = 1的右焦点坐标为F(6,0),一条渐近线的方程为y = x,设点P在第一象限,由于|PO| = |PF|,则点P的横坐标为4,纵坐标为3,所以△PFO的底边长为6,高为3,面积为9,所以答案为A。
6.若双曲线C:2x^2/a^2 - 2y^2/b^2 = 1(a>0,b>0)的一条渐近线被圆(x-2)^2 + y^2 = 4所截得的弦长为2,则b^2 = a^2-4,圆心为(2,0),半径为2,设截弦的两个交点为P和Q,则PQ = 2,所以PQ的中点M在圆上,即M为(5/2,±√(3)/2),所以PM = √(a^2-25/4)±√(3)/2,由于PM = PQ/2 = 1,所以(a^2-25/4)+(3/4) = 1,解得a = √(29)/2,所以答案为B。
双曲线的标准方程练习题及其答案

双曲线的标准方程1、过双曲线13422=-y x 的左焦点1F 的直线交双曲线的左支于N M 、两点,2F 为其右焦点,则MN NF MF -+22= 。
2、如图,已知定圆02410:221=+++x y x F ,定圆0910:222=+-+x y x F ,动圆M 与定圆21F F 、都外切,求动圆圆心M 的轨迹方程。
3、已知21F F 、是双曲线191622=-y x 的左、右焦点,PQ 是过1F 在左支上的弦,且PQ 的倾斜角为α,那么PQ QF PF -+22= 。
4、讨论192522=---ky k x 表示何种圆锥曲线,他们有何共同特征。
5、已知双曲线8822=-ky kx 的一个焦点为()3,0,则=k 。
6、已知方程12522=---k yk x 的图形是双曲线,则k 的取值范围是 。
7、已知双曲线过⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛-4,734523,221P P 、两点,求双曲线的标准方程。
8、在ABC ∆中,c b a ,,为其三边长,点()()0,10,1C B 、-,求满足A B C sin 21sin sin =-的顶点A 的轨迹方程,并画出图形。
9、P 为双曲线116922=-y x 的右支上一点,N M 、分别是圆()4522=++y x 和()1522=+-y x 上的点,则= 。
10、设P 为双曲线11222=-y x 上的一点,21F F 、为其两个焦点,若2:3:21=PF PF 。
则21F PF S ∆= 。
11、若21F F 、是双曲线116922=-y x 上的两个焦点,点P 在双曲线上,且3221=∙PF PF ,求21PF F ∠。
12、已知⊙();4252:22=++y x A ⊙();412:22=+-y x B ,动圆P 与⊙A 、⊙B 都外切;(1)、求动圆圆心P 的轨迹方程;并说明是什么曲线;(2)、若直线1+=kx y 与(1)中的曲线有两个不同的焦点21P P 、,求k 的取值范围。
高中数学双曲线习题及答案解析

双曲线习题练习及答案解析1、已知双曲线2222:1(0,0)x y C a b a b -=>>的一条渐近线方程为y x =,且与椭圆221123x y +=有公共焦点.则C 的方程为( )A .221810x y -=B .22145x y -=C .22154x y -=D .22143x y -=【答案】B 因为双曲线的一条渐近线方程为2y x =,则b a =.① 又因为椭圆221123x y +=与双曲线有公共焦点,双曲线的焦距26c =,即c =3,则a 2+b 2=c 2=9.②.由①②解得a =2,b =,则双曲线C 的方程为22145x y -=.故选:B.2已知双曲线22221x y a b-=(a 、b 均为正数)的两条渐近线与直线1x =-围成的三)A.B. C. D. 2【答案】D解:双曲线的渐近线为by x a=±,令1x =-,可得b y a=,不妨令1,b A a ⎛⎫- ⎪⎝⎭,1,b B a ⎛⎫-- ⎪⎝⎭,所以2b AB a =,所以12AOBA S AB x =⋅=AB ∴=,即2b a =b a =2c e a ===;故选:D3已知双曲线C 的中心为坐标原点,一条渐近线方程为2y x =,点()22,2P -在C 上,则C 的方程为A. 22124x y -=B. 221714x y -=C. 22142x y -=D. 221147y x -=【答案】B由于C 选项的中双曲线的渐近线方程为22y x =±,不符合题意,排除C 选项.将点()22,2P -代入A,B,D 三个选项,只有B 选项符合,故本题选B.4已知双曲线C :2218y x -=的左、右焦点分别为1F 、2F ,O 为坐标原点,点P在C 的一条渐近线上,若2OP PF =,则12PF F △的面积为 ( )A .B .C .D .【答案】C双曲线C :2218y x -=中,1(3,0)F -,2(3,0)F ,渐近线方程:y =±,因2OP PF =,则点P 在线段2OF 的中垂线:32x =上,则P 点纵坐标y 0有0||y =所以12PF F △面积121201||||2PF F SF F y =⋅=故选:C 5已知双曲线C :()22102y x m m m -=>+,则C 的离心率的取值范围为( )A .(B .()1,2C .)+∞D .()2,+∞【答案】C双曲线()22102y x m m m -=>+的离心率为e ===,因为0m >,所以e =>C的离心率的取值范围为)+∞.故选:C.6若双曲线2288ky x -=的焦距为6,则该双曲线的离心率为( )A.4B.32C. 3D.103因为2288ky x -=为双曲线,所以0k ≠,化为标准方程为:22181y x k -=. 由焦距为6可得:3c ==,解得:k =1.所以双曲线为22181y x -=.所以双曲线的离心率为4c e a ===.故选:A7已知1F ,2F 分别是双曲线22124y x -=的左,右焦点,若P 是双曲线左支上的点,且1248PF PF ⋅=.则12F PF △的面积为( ) A. 8B. 16C. 24D. 【答案】C 因为P 是双曲线左支上的点,所以2122PF PF a -==,22124100F F c ==. 在12F PF △中,()22221212121212121212cos 22cos F F PF PF PF PF F PF PF PF PF PF PF PF F PF=+-∠=-+-∠,即110049696cos F PF=+-∠,所以1cos 0F PF ∠=,12in 1s P F F =∠,故12F PF △的面积为121242PF PF ⋅=.故选:C .8已知双曲线()222:1016x y C a a -=>的一条渐近线方程为20x y -=,1F ,2F 分别是双曲线C 的左、右焦点,P 为双曲线C 上一点,若15PF =,则2PF = A.1B.9C.1或9D.3或93.B 由题意知42a=,所以2a =,所以c ==,所以152PF a c =<+=+,所以点Р在双曲线C 的左支上,所以214PF PF -=,所以29PF =.故选B9如图,F 1,F 2分别是双曲线22221x y a b-=(a >0,b >0)的两个焦点,以坐标原点O为圆心,|OF 1|为半径的圆与该双曲线左支交于A ,B 两点,若△F 2AB 是等边三角形,则双曲线的离心率为( )B. 211【答案】D 连接1AF ,依题意知:21AF =,12122c F F AF ==,所以21121)a AF AF AF =-=1c e a ===. 10已知双曲线22214x y b-=()0b >的左右焦点分别为1F 、2F ,过点2F 的直线交双曲线右支于A 、B 两点,若1ABF ∆是等腰三角形,且120A ∠=︒.则1ABF ∆的周长为( ) A.83+ B.)41C.83+ D.)22【答案】A双曲线的焦点在x 轴上,则2,24a a ==;设2||AF m =,由双曲线的定义可知:12||||24AF AF a m =+=+, 由题意可得:1222||||||||||AF AB AF BF m BF ==+=+, 据此可得:2||4BF =,又 ,∴12||2||8BF a BF =+=,1ABF 由正弦定理有:11||||sin120sin 30BF AF =︒︒,即11|||BF AF =所以8)m =+,解得:m =1ABF ∆的周长为: 11||||||AF BF AB ++=122(4)8162833m ++=+⨯=+故选:A11已知双曲线C :2218y x -=的左、右焦点分别为1F 、2F ,O 为坐标原点,点P在C 的一条渐近线上,若2OP PF =,则12PF F △的面积为 ( ) A.B.C. D.【答案】C双曲线C :2218y x -=中,1(3,0)F -,2(3,0)F,渐近线方程:y =±,因2OP PF =,则点P 在线段2OF 的中垂线:32x =上,则P 点纵坐标y 0有0||y = 所以12PF F △面积121201||||2PF F S F F y =⋅=故选:C12双曲线22221x y a b-=与22221x y a b -=-的离心率分别为12,e e ,则必有( )A. 12e e =B. 121e e ⋅=C.12111e e += D. 2212111e e += 【答案】D13多选以已知双曲线的虚轴为实轴、实轴为虚轴的双曲线叫做原双曲线的共轭双曲线,则以下说法,正确的有( ) A. 双曲线与它的共轭双曲线有相同的准线 B. 双曲线与它的共轭双曲线的焦距相等 C. 双曲线与它的共轭双曲线的离心率相等 D. 双曲线与它的共轭双曲线有相同的渐近线 【答案】BD由双曲线对称性不妨令双曲线C 的方程为:22221(0,0)x y a b a b-=>>,则其共轭双曲线C '的方程为22221y x b a-=,对于A ,双曲线C 的准线垂直于x 轴,双曲线C '的准线垂直于y 轴,A 不正确;对于B ,双曲线C 和双曲线C '的半焦距均为:c =,所以焦距相同,B 正确;对于C ,由B 选项知,双曲线C 的离心率为1ce a=,而双曲线C '的离心率为2c e b =,而a ,b 不一定等,C 不正确;对于D ,双曲线C 和双曲线C '的渐近线均为by x a=±,D 正确. 故选:BD13多选已知双曲线C :()222104x y b b-=>的离心率为72,1F ,2F 分别为C 的左右焦点,点P 在C 上,且26PF =,则( )A .7b =B .110PF =C .OP =D .122π3F PF ∠=【答案】BCD72=,可得b =A 不正确,而7c ==,因为27||6c PF =>=,所以点P 在C 的右支上,由双曲线的定义有:121||||||624PF PF PF a -=-==,解得1||10PF =,故选项B 正确,在12PF F △中,有2222221271076cos cos 02727OP OP POF POF OP OP +-+-∠+∠=+=⨯⨯⨯⨯,解得||OP =,22212106141cos 21062F PF +-∠==-⨯⨯,所以1223F PF π∠=,故选项C ,D 正确. 故选:BCD.多选若方程22151x y t t +=--所表示的曲线为C ,则下面四个命题中正确的是A .若1<t <5,则C 为椭图B .若t <1.则C 为双曲线 C .若C 为双曲线,则焦距为4D .若C 为焦点在y 轴上的椭圆,则3<t <5 【答案】BD 14多选已知双曲线C 1:)0,0(12222>>=-b a b y a x 的实轴长是2,右焦点与抛物线C 2:y 2=8x 的焦点F 重合,双曲线C 1与抛物线C 2交于A 、B 两点,则下列结论正确的是 ( ▲ )A .双曲线C 1的离心率为2 3B .抛物线C 2的准线方程是x =-2 C .双曲线C 1的渐近线方程为y =±3x D. |AF |+|BF |=320 【答案】BC【解析】由题意可知对于C 1:()0012222>>=-b a by a x ,,实轴长为2a =2,即a =1,而C 2:y 2=8x 的焦点F 为(2,0),所以c =2,则双曲线C 1的方程为1322=-yx ,则对于选项A ,双曲线C 1的离心率为212==a c ,所以选项A 错误;对于选项B ,抛物线C 2的准线方程是x =-2,所以选项B 正确;对于选项C ,双曲线C 1的渐近线方程为y =±abx =±3x ,所以选项C 正确;对于选项D ,由y 2=8x 与1322=-y x 联立可得A (3,62),B (3,62-),所以由抛物线的定义可得 |AF |+|BF |=10433=++=++p x x B A ,所以选项D 错误,综上答案选BC.14多选12,F F 分别是双曲线2221(0)y x b b-=>的左右焦点,过2F 作x 轴的垂线与双曲线交于,A B 两点,若1ABF 为正三角形,则( )A.b = B.C. 双曲线的焦距为D.1ABF 的面积为【答案】ABD在正三角形1ABF 中,由双曲线的对称性知,12F F AB ⊥,12||2||AF AF =, 由双曲线定义有:12||||2AF AF -=,因此,1||4AF =,2||2AF =,12||F F ==即半焦距c =b =,A 正确;双曲线的离心率1ce ==B 正确;双曲线的焦距12F F =C 不正确;1ABF 的面积为21||4AF =D 正确.故选:ABD15多选已知双曲线C 的左、右焦点分别为1F 、2F ,过2F 的直线与双曲线的右支交于A 、B 两点,若122||||2||AF BF AF ==,则( )A. 11AF B F AB ∠=∠B. 双曲线的离心率e =C. 直线的AB 斜率为±D. 原点O 在以2F 为圆心,2AF 为半径的圆上 【答案】ABC 如图:设122||||2||2(0)AF BF AF m m ===>,则22||||||3AB AF BF m =+=,由双曲线的定义知,12||||22AF AF m m a -=-=,即2m a =;12||||2BF BF a -=, 即1||22BF m a -=,∴1||3||BF m AB ==,即有11AF B F AB ∠=∠,故选项A 正确;由余弦定理知,在1ABF 中,22222211111||||||4991cos 2||||2233AF BF AB m m m AF B AF BF m m +-+-∠===⋅⋅,在△12AF F 中,22222212121112||||||441cos cos 2||||223AF AF F F m m c F AB AF B AF AF m m +-+-∠===∠=⋅⋅, 化简整理得,222121144c m a ==,∴离心率ce a ==,故选项B 正确; 在△21AF F中,2222222211134443cos 224m m c m m c m AF F c m cm -+--∠===⋅⋅,21sin AF F ∠==,∴212121sin tan cos AF F AF F AF F ∠∠==∠ ∴根据双曲线的对称性可知,直线AB的斜率为±,故选项C 正确; 若原点O 在以2F 为圆心,2AF 为半径的圆上,则2c m a ==,与3c a =不符,故选项D 错误.故选:ABC .16多选已知双曲线2222:1(0,0)x y C a b a b-=>>的右焦点为F,一条渐近线过点(,则下列结论正确的是( )A. 双曲线CB. 双曲线C 与双曲线22124y x -=有相同的渐近线C. 若F 到渐近线的距离为2,则双曲线C 的方程为22184x y -=D. 若直线2:a l x c=与渐近线围成的三角形面积为则焦距为【答案】BCD 渐近线的方程为by x a=±,因为一条渐近线过点(,故b a ⨯=a ===,故A 错误.又渐近线的方程为2y x =±,而双曲线22124y x -=的渐近线的方程为2y x =±, 故B 正确.若F 到渐近线的距离为2,则2b =,故a =C 的方程为22184x y -=,故C 正确. 直线2:a l x c =与渐近线的两个交点的坐标分别为:2,a ab c c ⎛⎫ ⎪⎝⎭及2,a ab cc ⎛⎫- ⎪⎝⎭,故2122a ab c c =⨯⨯⨯即23a b =,而a =,故b =,a =,所以23=,所以c =,故焦距为D 正确.故选:B CD.16多选已知点P 在双曲线221169x y -=上,1F ,2F 分别是左、右焦点,若12PF F △的面积为20,则下列判断正确的有( ) A. 点P 到x 轴的距离为203B. 12503PF PF += C. 12PF F △为钝角三角形 D. 123F PF π∠=【答案】BC由双曲线方程得4a =,3b =,则5c =,由△12PF F 的面积为20,得112||10||2022P P c y y ⨯⨯=⨯=,得||4P y =,即点P 到x 轴的距离为4,故A 错误, 将||4P y =代入双曲线方程得20||3P x =,根据对称性不妨设20(3P ,4),则213||3PF =, 由双曲线的定义知12||||28PF PF a -==,则11337||833PF =+=, 则12133750||||333PF PF +=+=,故B 正确,在△12PF F 中,113713||210||33PF c PF =>=>=, 则24012020553PF k -==>-,21PF F ∠为钝角,则△12PF F 为钝角三角形,故C 正确, 2222121212121212121337641002||||||(||||)2||||10033cos 13372||||2||||233PF PF F F PF PF PF PF F PF PF PF PF PF -+⨯⨯+--+-∠===⨯⨯3618911121337133729⨯=-=-≠⨯⨯⨯,则123F PF π∠=错误,故正确的是BC ,故选16双曲线:C 2214x y -=的渐近线方程为__________,设双曲线1:C 22221(0,0)x y a b a b -=>>经过点(4,1),且与双曲线C 具有相同渐近线,则双曲线1C 的标准方程为__________.【答案】12y x =± 221123y x -=【解析】(1)双曲线:C 2214x y -=的焦点在y 轴上,且1,2a b ==,渐近线方程为ay x b=±, 故渐近线方程为12y x =±;(2)由双曲线1C 与双曲线C 具有相同渐近线,可设221:4y C x λ-=,代入(4,1)有224134λλ-=⇒=-,故212:34x C y -=-,化简得221123y x -=.17已知O 为坐标原点,抛物线C :()220y px p =>的焦点为F ,P 为C 上一点,PF 与x 轴垂直,Q 为x 轴上一点,且PQ OP ⊥,若6FQ =,则PF =______. 【答案】3抛物线C :22y px = (0p >)的焦点,02p F ⎛⎫⎪⎝⎭,∵P 为C 上一点,PF 与x 轴垂直,所以P 的横坐标为2p ,代入抛物线方程求得P 的纵坐标为p ±,不妨设(,)2pP p , 因为Q 为x 轴上一点,且PQ OP ⊥,所以Q 在F 的右侧, 又||6FQ =,(6,0)2pQ +,(6,)PQ p =-,因为PQ OP ⊥,所以2602pPQ OP p ⋅=⨯-=, 0,3p p >∴=,所以PF =3故答案为△3.若双曲线1C :()2230y x λλ-=≠的右焦点与抛物线2C :28y x =的焦点重合,则实数λ=( ) A. 3±B.C. 3D. -3【答案】D双曲线1C 的右焦点与抛物线的焦点(2,0)重合,所以双曲线1C 方程化:()22103y x λλλ-=≠,再转化为:()22103x y λλλ-=<--,所以23a λ=-, 2b λ=-,所以222433c a b λλλ=+=--=-,所以c =2=平方得 3.λ=-故选:D.17设双曲线:的右焦点为,点,已知点在双曲线的左支上,若的周长的最小值是,则双曲线的标准方程是__________,此时,点的坐标为__________.【答案】【解析】如下图,设为双曲线的左焦点,连接,,则,,故的周长, 因为,所以的周长, 因为的周长的最小值是,,,所以,的方程为, 当的周长取最小值时,点在直线上,因为,,所以直线的方程为,联立,解得,或(舍去), 故的坐标为.故答案为:,.C 2221(0)y x b b-=>F ()0,Q b P CPQF △8C P 2214y x -=⎛⎫ ⎪ ⎪⎝⎭D C PD QD QD QF =2PFPD =+PQF△2l PQ PF QF PQ PD QD =++=+++PQ PD QD +≥=PQF△2l ≥PQF △82228,9c b +=+=22221cbab2b =c =C 2214y x -=PQF △P QD ()0,2Q ()D QD 25y x =+222514y x y x ⎧=+⎪⎪⎨⎪-=⎪⎩1x y ⎧=⎪⎨⎪=⎩4x y ⎧=⎪⎨=⎪⎩P 2⎛⎫- ⎪ ⎪⎝⎭2214y x -=,12⎛⎫- ⎪ ⎪⎝⎭18已知双曲线()221112211:10,0x y C a b a b -=>>与()222222222:10,0y x C a b a b -=>>有相同的渐近线,若1C 的离心率为2,则2C 的离心率为__________.双曲线()221112211:10,0x y C a b a b -=>>的渐近线方程为11b y x a =± ,()222222222:10,0y x C a b a b -=>>的渐近线方程为22a y x b =±,由题意可得1212b a a b =,由1C 的离心率为2得:22211121()b e a ==+ ,则222()3a b = , 所以设2C 的离心率为2e ,则22222141()133b e a =+=+=,故2=e ,故答案为:19知双曲线()222210,0x y a b a b-=>>,焦点()()()12,0,00F c F c c ->,,左顶点(),0A a -,若过左顶点A 的直线和圆22224a a x y ⎛⎫-+= ⎪⎝⎭相切,与双曲线在第一象限交于点P ,且2PF x ⊥轴,则直线的斜率是 _____, 双曲线的离心率是 _________. 【答案】如图,设圆22224a a x y ⎛⎫-+= ⎪⎝⎭的圆心为B ,则圆心坐标(,0)2a B ,半径为2a ,则32a AB =,设过左顶点A 的直线和圆22224a a x y ⎛⎫-+= ⎪⎝⎭相切于点C ,连接BC ,则2a BC =,所以AC ==,得tan aBC BAC AC ∠===;2PF x ⊥轴,由双曲线的通径可得,22b PF a=,又2AF a c =+,所以222tan PF AF b a BAC a c ∠===+,化简得24(40e -=,求解得e =.已知双曲线C :﹣y 2=1.(Ⅰ)求以C 的焦点为顶点、以C 的顶点为焦点的椭圆的标准方程; (Ⅱ)求与C 有公共的焦点,且过点(2,﹣)的双曲线的标准方程,并且求出这条双曲线的实轴长、焦距、离心率以及渐近线方程.解:(Ⅰ)双曲线C :﹣y 2=1的焦点为(±,0),顶点为(±2,0),设椭圆的标准方程为+=1(a >b >0),可得c =2,a =,b ==1,则椭圆的方程为+y 2=1;(Ⅱ)设所求双曲线的方程为﹣=1(m .n>0),由题意可得m 2+n 2=5,﹣=1,解得m =,n =,即所求双曲线的方程为﹣=1,则这条双曲线的实轴长为2、焦距为2、离心率为以及渐近线方程为y=±x .20已知双曲线C :﹣=1(a >0,b >0)与双曲线﹣=1有相同的渐近线,且经过点M (,﹣).(Ⅰ)求双曲线C 的方程;(Ⅱ)求双曲线C 的实轴长,离心率,焦点到渐近线的距离.:(Ⅰ)∵双曲线C 与双曲线﹣=1有相同的渐近线,∴设双曲线的方程为(λ≠0),代入M (,﹣).得λ=,故双曲线的方程为:.(Ⅱ)由方程得a =1,b =,c =,故离心率e =. 其渐近线方程为y =±x ;实轴长为2, 焦点坐标F (,0),解得到渐近线的距离为:=.21已知双曲线C :22221(0,0)x y a b a b-=>>,点)是双曲线的一个顶点.(1)求双曲线的方程;(2)经过双曲线右焦点2F 作倾斜角为30°的直线,直线与双曲线交于不同的两点A ,B ,求AB .(1)由题可得c a a ⎧=⎪⎨⎪=⎩3c =,b =,所以双曲线的方程为22136x y-=;(2)双曲线22136x y -=的右焦点为()23,0F所以经过双曲线右焦点2F 且倾斜角为30°的直线的方程为3)y x =-.联立221363)x y y x ⎧-=⎪⎪⎨⎪=-⎪⎩得256270x x +-=,设()11,A x y ,()22,B x y ,则1265x x +=-,12275x x =-.所以5AB ==. 22已知双曲线()2222:10,0x y C a b a b -=>>与双曲线22162y x -=的渐近线相同,且经过点()2,3.(1)求双曲线C 的方程;(2)已知双曲线C 的左右焦点分别为12,F F ,直线l 经过2F ,倾斜角为3,4l π与双曲线C 交于,A B 两点,求1F AB 的面积.(1)设所求双曲线C 方程为2262y x λ-=,代入点()2,3得:223262λ-=,即12λ=-, 所以双曲线C 方程为221622y x -=-,即2213y x -=.(2)由(1)知:()()122,0,2,0F F -,即直线AB 的方程为()2y x =--.设()()1122,,,A x y B x y ,联立()22213y x y x ⎧=--⎪⎨-=⎪⎩得22470x x +-=,满足>0∆且122x x +=-,1272x x =-,由弦长公式得12||AB x x =-=6==,点()12,0F -到直线:20AB x y +-=的距离d ===所以111622F ABS AB d =⋅=⋅⋅=。
双曲线练习题带答案,知识点总结(基础版)
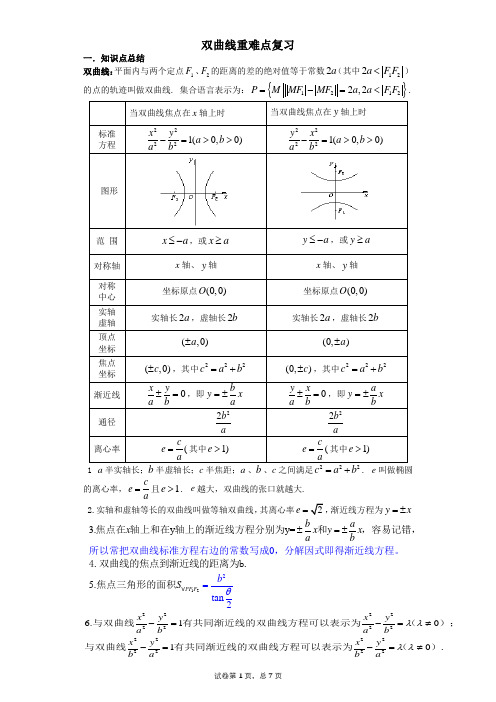
双曲线重难点复习一.知识点总结双曲线:平面内与两个定点1F 、2F 的距离的差的绝对值等于常数2a (其中122a F F <)1 a 半实轴长;b 半虚轴长;c 半焦距;a 、b 、c 之间满足c a b =+. e 叫做椭圆的离心率,ce a=且1e >.e 越大,双曲线的张口就越大.2.实轴和虚轴等长的双曲线叫做等轴双曲线,其离心率e =渐近线方程为y x =±3.y y=0b ax x y x a b±=±焦点在轴上和在轴上的渐近线方程分别为和,容所以常把双曲线标准方程右边的常数写成,分解因式即得渐近易记错,线方程。
4.双曲线的焦点到渐近线的距离为b.122ta 5n2.PF F S b θ= 焦点三角形的面积22222222222222226.1010x y x y a b a b x y x y b a b aλλλλ-=-=≠-=-=≠与双曲线有共同渐近线的双曲线方程可以表示为();与双曲线有共同渐近线的双曲线方程可以表示为().1.已知F 为双曲线C :116922=-y x 的左焦点,P ,Q 为C 上的点.若PQ 的长等于虚轴长的2倍,点A (5,0)在线段PQ 上,则△PQF 的周长为________. 442.已知双曲线22221(0)x y a b a b-=>>的焦距为20x y +=垂直,则双曲线的方程为A. 2214x y -=B. 2214y x -= C. 22331205x y -= D. 22331520x y -= 【答案】A【解析】由题可知2c =,则c =.渐近线方程为12y x =,则12b a =.又222c a b =+可得,224,1a b ==.所以双曲线的方程为2214x y -=;故本题答案选A .视频3.已知O 为坐标原点,设F 1,F 2分别是双曲线x 2−y 2=1的左、右焦点,点P 为双曲线左支上任一点,自点F 1作∠F 1PF 2的平分线的垂线,垂足为H ,则|OH |=( ) A. 1 B. 2 C. 4 D. 12【答案】A【解析】延长F 1H 交PF 2于点Q ,由角分线性质可知|PF 1|=|PQ |,根据双曲线的定义,||PF 1|−|PF 2||=2,从而|QF 2|=2,在ΔF 1QF 2中,OH 为其中位线,故|OH |=1.故选A.点睛:对于圆锥曲线问题,善用利用定义求解,注意数形结合,画出合理草图,巧妙转化.4.等轴双曲线C 的中心在原点,焦点在x 轴上,C 与抛物线y 2=16x 的准线交于A ,B 两点,||43AB =,则C 的实轴长为( ) A ..4 D .85.设双曲线22221(0,0)x y a b a b-=>>的左、右焦点分别为12F F A 、,是双曲线渐近线上的一点,212AF F F ⊥,原点O 到直线1AF 的距离为113OF ,则渐近线的斜率为(A (B (C )1或1-(D )2或2- D6.已知双曲线x 2-23y =1的左顶点为A 1,右焦点为F 2,P 为双曲线右支上一点,则1PA ·2PF的最小值为________.-27.已知双曲线E 的中心为原点,F (3,0)是E 的焦点,过F 的直线l 与E 相交于A ,B 两点,且AB 的中点为M (-12,-15),则E 的方程为( )A.x 23-y 26=1B.x 24-y 25=1C.x 26-y 23=1D.x 25-y 24=1 答案 B解析 由已知易得l 的斜率为k =k FM =1.设双曲线方程为x 2a 2-y 2b2=1(a >0,b >0),A (x 1,y 1),B (x 2,y 2),则有⎩⎨⎧x 21a 2-y 21b 2=1,x 22a 2-y 22b2=1,两式相减并结合x 1+x 2=-24,y 1+y 2=-30,得y 1-y 2x 1-x 2=4b 25a 2,从而4b 25a2=1,即4b 2=5a 2.又a 2+b 2=9,解得a 2=4,b 2=5,故选B. 8与双曲线622=-y x的左支交于不同的两点,()A .()11-, C【答案】C试题分析:联立方程2226y kx x y =+⎧⎨-=⎩得()2214100k x kx ---=…① 若直线y=kx+2与双曲线622=-y x 的左支交于不同的两点,则方程①有两个不等的负根k 9.经过双曲线4−y 2=1右焦点的直线与双曲线交于A ,B 两点,若 AB =4,则这样的直线的条数为( )A. 4条B. 3条C. 2条D. 1条 【答案】B【解析】由双曲线x 24−y 2=1,可得a =2,b =1,若AB 只与双曲线右支相交时,AB 的最小值距离是通径长度为2b 2a=1,∵AB =4>1,∴此时有两条直线符合条件;若AB 只与双曲线两支相交时,此时AB 的最小距离是实轴两顶点的即距离长度为2a =4,距离无最大值;∵AB =4,∴此时有1条直线符合条件;综上可得,共有3条直线符合条件,故选B.10.P 是双曲线C :x 2−y 2=2左支上一点,直线l 是双曲线C 的一条渐近线,P 在l 上的射影为Q ,F 2是双曲线C 的右焦点,则 PF 2 + PQ 的最小值为( ) A.22B. 2C. 3 2D. 2+22【答案】C【解析】由题知|PF 2|−|PF 1|=2a =2 2,则|PF 2|+|PQ |=|PF 1|+|PQ |+2 2,由对称性,当F 1,P ,Q 在同一直线上时|PF 1|+|PQ |最小,由渐近线方程y =x ,|F 1O |=2知|F 1Q |= 2 则|PF 2|+|PQ |的最小值为3 2.故本题答案选C .11.点P 是双曲线22221(0,0)x y a b a b -=>>上的点,12,F F 是其焦点,双曲线的离心率是54,且12•0PF PF = ,若12F PF ∆的面积是9,则a b +的值等于() A. 4 B. 7 C. 6 D. 5 【答案】B【解析】双曲线的离心率是5344c b a a ==⇒=,120PF PF ⋅=1212,PF PF PFF ∴⊥∴ 的面积121219182S PF PF PF PF =⋅=∴⋅=,. 在12PF F 中,由勾股定理可得222222*********||2?4369c PF PF PF PF PF PF a a b a =+=-+=+∴+=+(),,34b a ∴=∴=,,7a b ∴+=,故选 C .12.若双曲线C :x 2a2−y 2b 2=1(a >0,b >0)的一条渐近线被圆 x −2 2+y 2=4所截得的弦长为2,则C 的离心率为( ) A. 2 B. C. D. 2 33【答案】A【解析】由几何关系可得,双曲线x 2a 2−y 2b 2=1 a >0,b >0 的渐近线方程为bx ±ay =0,圆心 2,0 到渐近线距离为d = 2−12= 3,则点 2,0 到直线bx +ay =0的距离为d =22=2b c= 3,即4(c 2−a 2)c =3,整理可得c 2=4a 2,双曲线的离心率e = c 2a = 4=2.故选A .13.右焦点分别为12,F F ,过1F 作倾斜角为030的直线与y 轴和双曲线右支分别交于两点,若点A 平分1F B ,则该双曲线的离心率是()C. 2D.【答案】A14.右焦点分别为12,F F ,焦距为2(0)c c >,且120AOB ∠= ,其中O 为原点,则双曲线的离心率为()A. 2B. 【答案】C 【解析】如下图:,(0a >,0b >),过其左焦点F 作x 轴的垂线,交双曲两点,若双曲线的右顶点在以AB 为直径的圆内,则双曲线离心率的取值范围是()B. ()1,2C.D. ()2,+∞ 【答案】D【解析】AB 是双曲线通径,即2222a a cbc a +<=-,2220c ac a -->,即,故选D .16.设1F ,2F 分别为椭圆1C :221122111(0)x y a b a b +=>>与双曲线2C :222222221(0,0)x y a b a b -=>>的公共焦点,它们在第一象限内交于点M ,1290F MF ∠=︒,若椭圆的离心率134e =,则双曲线2C 的离心率2e 的值为()A. 92B. 2C. 32D. 54【答案】B【解析】设12,m MF n MF ==,所以1122122{{ 2m n a m a am n a n a a+==+∴-==-,由1290F MF ∠= 得()()()()222222212121222c m n a a a a a a =+=++-=+,222222212121222222121122a a a a c a a c c c e e +∴=+∴==+=+,1234e e =∴= 17.已知双曲线C :x 2a −y 2b =1(a >0,b >0),F 1,F 2分别为其左、右焦点,过F 1的直线l 与双曲线C 的左、右两支分别交于A ,B 两点,若|AB |:|BF 2|:|AF 2|=3:4:5,则双曲线C 的离心率为( )A. 2B. 4C. 13D. 15 【答案】A 【解析】∵|AB|:|BF 2|:|AF 2|=3:4:5,不妨令 AB =3, BF 2 =4,|AF 2|=5, ∵|AB |2+|BF 2|2=|AF 2|2 ,∴∠ABF 2=90∘又由双曲线的定义得:|BF 1|−|BF 2|=2a ,|AF 2|−|AF 1|=2a ∴|AF 1|+3−4=5−|AF 1|,∴|AF 1|=3 ,|BF 1|−|BF 2|=3+3−4=2a ,∴a =1在RtΔBF 1F 2 中,|F 1F 2|2=|BF 1|2+|BF 2|2=62+42=52, 又|F 1F 2|2=4c 2,∴4c 2=52,∴c = 13 所以双曲线的离心率e =c = 13 ,故选C.18.已知12,F F 是双曲线的左右焦点,过2F 作双曲线一条渐近线的垂线,垂足为点A ,交另一条渐近线于点B ,且则该双曲线的离心率为B. D. 2【答案】A则A. 19.已知F 为双曲线的左焦点,定点A 为双曲线虚轴的一个端点,过,F A 两点的直线与双曲线的一条渐近线在y 轴右侧的交点为B ,若3A B F A = ,则此双曲线的离心率为__________.【解析】F 为双曲线的左焦点,定点A 为双曲线虚轴的一个端点,。
《双曲线》练习题经典(含答案)

《双曲线》练习题一、选择题:1.已知焦点在x轴上的双曲线的渐近线方程是y=±4x,则该双曲线的离心率是(A)A.17B.15C.174 D.1542.中心在原点,焦点在x轴上的双曲线的实轴与虚轴相等,一个焦点到一条渐近线的距离为,则双曲线方程为(B)A.x2﹣y2=1 B.x2﹣y2=2 C.x2﹣y2=D.x2﹣y2=3.在平面直角坐标系中,双曲线C过点P(1,1),且其两条渐近线的方程分别为2x+y=0和2x﹣y=0,则双曲线C的标准方程为(B)A.B.C.或D.4.1(a>b>01有相同的焦点,则椭圆的离心率为( A )A B C D5.已知方程﹣=1表示双曲线,且该双曲线两焦点间的距离为4,则n的取值范围是(A)A.(﹣1,3)B.(﹣1,)C.(0,3)D.(0,)6.设双曲线=1(0<a<b)的半焦距为c,直线l过(a,0)(0,b)两点,已知原点到直线l的距离为,则双曲线的离心率为(A)A.2 B.C.D.7.已知双曲线22219y xa-=的两条渐近线与以椭圆221259yx+=的左焦点为圆心、半径为165的圆相切,则双曲线的离心率为( A )A.54B.53C.43D.658.双曲线虚轴的一个端点为M,两个焦点为F1、F2,∠F1MF2=120°,则双曲线的离心率为(B)A.3B.62 C.63 D.339.已知双曲线221(0,0)x ym nm n-=>>的一个焦点到一条渐近线的距离是2,一个顶点到它的一条渐近线的,则m等于( D )A.9 B.4 C.2 D.,310.已知双曲线的两个焦点为F 1(-10,0)、F 2(10,0),M 是此双曲线上的一点,且满足12120,||||2,MF MF MF MF ==则该双曲线的方程是( A )A.x 29-y 2=1 B .x 2-y 29=1 C.x 23-y 27=1D.x 27-y 23=1 11.设F 1,F 2是双曲线x 2-y 224=1的两个焦点,P 是双曲线上的一点,且3|PF 1|=4|PF 2|,则△PF 1F 2的面积等于( C )A .4 2B .83C .24D .4812.过双曲线x 2-y 2=8的左焦点F 1有一条弦PQ 在左支上,若|PQ |=7,F 2是双曲线的右焦点,则△PF 2Q 的周长是( C ) A .28 B .14-82 C .14+8 2D .8 213.已知双曲线﹣=1(b >0),以原点为圆心,双曲线的实半轴长为半径长的圆与双曲线的两条渐近线相交于A ,B ,C ,D 四点,四边形ABCD 的面积为2b ,则双曲线的方程为( D ) A .﹣=1B .﹣=1 C .﹣=1 D .﹣=114.设双曲线﹣=1(a >0,b >0)的左、右焦点分别为F 1,F 2,以F 2为圆心,|F 1F 2|为半径的圆与双曲线在第一、二象限内依次交于A ,B 两点,若3|F 1B |=|F 2A |,则该双曲线的离心率是( C ) A . B .C .D .215.过双曲线1222=-y x 的右焦点作直线l 交双曲线于A 、B 两点,若|AB|=4,则这样的直线共有( C )条。
双曲线基础练习题(后附答案)

双曲线基础练习题(后附答案)一、选择题(每题5分)1.已知a=3,c=5,并且焦点在x 轴上,则双曲线的标准程是( )A .116922=+y x B. 116922=-y x C. 116922=+-y x 1916.22=-y x D 2.已知,5,4==c b 并且焦点在y 轴上,则双曲线的标准方程是( )A .191622=-y x B. 191622=+-y x C.116922=+y x D.116922=-y x 3..双曲线191622=-y x 上P 点到左焦点的距离是6,则P 到右焦点的距离是( ) A. 12 B. 14 C. 16 D. 184..双曲线191622=-y x 的焦点坐标是 ( ) A. (5,0)、(-5,0)B. (0,5)、(0,-5) C. (0,5)、(5,0) D.(0,-5)、(-5,0)5、方程6)5()5(2222=++-+-y x y x 化简得:A .116922=-y x B. 191622=+-y x C.116922=+y x D. 191622=-y x 6.已知实轴长是6,焦距是10的双曲线的标准方程是( )A ..116922=-y x 和116922=+-y x B. 116922=-y x 和191622=+-y x C. 191622=-y x 和191622=+-y x D. 1162522=-y x 和1251622=+-y x 7.过点A (1,0)和B ()1,2的双曲线标准方程( )A .1222=-y xB .122=+-y xC .122=-y x D. 1222=+-y x 8.P 为双曲线191622=-y x 上一点,A 、B 为双曲线的左右焦点,且AP 垂直PB ,则三角形PAB 的面积为( ) A . 9 B . 18 C . 24 D . 369.双曲线191622=-y x 的顶点坐标是 ( ) A .(4,0)、(-4,0) B .(0,-4)、(0,4)C .(0,3)、(0,-3) D .(3,0)、(-3,0)10.已知双曲线21==e a ,且焦点在x 轴上,则双曲线的标准方程是( ) A .1222=-y x B .122=-y x C .122=+-y x D. 1222=+-y x11.双曲线191622=-y x 的的渐近线方程是( ) A . 034=±y x B .043=±y x C .0169=±y x D .0916=±y x12.已知双曲线的渐近线为043=±y x ,且焦距为10,则双曲线标准方程是( )A .116922=-y x B. 191622=+-y x C.116922=+y x D. 191622=-y x 二、填空题(每题5分共20分)13.已知双曲线虚轴长10,焦距是16,则双曲线的标准方程是________________.14.已知双曲线焦距是12,离心率等于2,则双曲线的标准方程是___________________.15.已知16522=++-t y t x 表示焦点在y 轴的双曲线的标准方程,t 的取值范围是___________. 16.椭圆C 以双曲线122=-y x 焦点为顶点,且以双曲线的顶点作为焦点,则椭圆的标准方程是___________________三、解答题 1. 求以椭圆18522=+y x 的焦点为顶点,且以椭圆的顶点为焦点的双曲线的方程。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
双曲线经典练习题总结(带答案)一、选择题1.以椭圆x 216+y 29=1的顶点为顶点,离心率为2的双曲线方程为( C )A .x 216-y 248=1B .y 29-x 227=1C .x 216-y 248=1或y 29-x 227=1D .以上都不对[解析] 当顶点为(±4,0)时,a =4,c =8,b =43,双曲线方程为x 216-y 248=1;当顶点为(0,±3)时,a =3,c =6,b =33,双曲线方程为y 29-x 227=1.2.双曲线2x 2-y 2=8的实轴长是( C ) A .2 B .22 C .4 D .42[解析] 双曲线2x 2-y 2=8化为标准形式为x 24-y 28=1,∴a =2,∴实轴长为2a =4.3.(全国Ⅱ文,5)若a >1,则双曲线x 2a 2-y 2=1的离心率的取值范围是( C )A .(2,+∞)B .(2,2 )C .(1,2)D .(1,2)[解析] 由题意得双曲线的离心率e =a 2+1a. ∴c 2=a 2+1a 2=1+1a2.∵a >1,∴0<1a 2<1,∴1<1+1a2<2,∴1<e < 2.故选C .4.(2018·全国Ⅲ文,10)已知双曲线C :x 2a 2-y 2b 2=1(a >0,b >0)的离心率为2,则点(4,0)到C的渐近线的距离为( D ) A .2 B .2 C .322D .22[解析] 由题意,得e =ca=2,c 2=a 2+b 2,得a 2=b 2.又因为a >0,b >0,所以a =b ,渐近线方程为x ±y =0,点(4,0)到渐近线的距离为42=22, 故选D .5.(2019·全国Ⅲ卷理,10)双曲线C :x 24-y 22=1的右焦点为F ,点P 在C 的一条渐近线上,O 为坐标原点,若|PO |=|PF |,则△PFO 的面积为( A ) A .324B .322C .22D .32[解析] 双曲线x 24-y 22=1的右焦点坐标为(6,0),一条渐近线的方程为y =22x ,不妨设点P 在第一象限,由于|PO |=|PF |,则点P 的横坐标为62,纵坐标为22×62=32,即△PFO 的底边长为6,高为32,所以它的面积为12×6×32=324.故选A . 6.若双曲线C :x 2a 2-y 2b 2=1(a >0,b >0)的一条渐近线被圆(x -2)2+y 2=4所截得的弦长为2,则C 的离心率为( A ) A .2 B .3 C .2D .233[解析] 设双曲线的一条渐近线方程为y =ba x ,圆的圆心为(2,0),半径为2,由弦长为2得出圆心到渐近线的距离为22-12= 3.根据点到直线的距离公式得2b a 2+b 2=3,解得b 2=3a 2. 所以C 的离心率e =ca =c 2a 2=1+b 2a2=2.故选A . 二、填空题7.(2019·江苏卷,7)在平面直角坐标系xOy 中,若双曲线x 2-y 2b 2=1(b >0)经过点(3,4),则该双曲线的渐近线方程是 [解析] 因为双曲线x 2-y 2b 2=1(b >0)经过点(3,4),所以9-16b 2=1(b >0),解得b =2,即双曲线方程为x 2-y 22=1,其渐近线方程为y =±2x .8.双曲线x 24+y 2k =1的离心率e ∈(1,2),则k 的取值范围是__-12<k <0__.[解析] 双曲线方程可变形为x 24-y 2-k =1,则a 2=4,b 2=-k ,c 2=4-k ,e =ca =4-k2.又因为e ∈(1,2),即1<4-k2<2,解得-12<k <0. 三、解答题9.(1)求与椭圆x 29+y 24=1有公共焦点,且离心率e =52的双曲线的方程;(2)求实轴长为12,离心率为54的双曲线的标准方程.[解析] (1)设双曲线的方程为x 29-λ-y 2λ-4=1(4<λ<9),则a 2=9-λ,b 2=λ-4,∴c 2=a 2+b 2=5,∵e =52,∴e 2=c 2a 2=59-λ=54,解得λ=5, ∴所求双曲线的方程为x 24-y 2=1.(2)由于无法确定双曲线的焦点在x 轴上还是在y 轴上,所以可设双曲线标准方程为x 2a 2-y 2b 2=1(a >0,b >0)或y 2a 2-x 2b 2=1(a >0,b >0).由题设知2a =12,c a =54且c 2=a 2+b 2,∴a =6,c =152,b 2=814.∴双曲线的标准方程为x 236-y 2814=1或y 236-x 2814=1.B 级 素养提升一、选择题1.如果椭圆x 2a 2+y 2b 2=1(a >b >0)的离心率为32,那么双曲线x 2a 2-y 2b 2=1的离心率为( A )A .52B .54C .2D .2[解析] 由已知椭圆的离心率为32,得a 2-b 2a 2=34,∴a 2=4b 2.∴a 2+b 2a 2=5b 24b 2=54.∴双曲线的离心率e =52. 2.双曲线x 2-y 2m =1的离心率大于2的充分必要条件是( C )A .m >12B .m ≥1C .m >1D .m >2[解析] 本题考查双曲线离心率的概念,充分必要条件的理解. 双曲线离心率e =1+m >2,所以m >1,选C .3.(多选题)已知M (x 0,y 0)是双曲线C :x 22-y 2=1上的一点,F 1、F 2是C 的两个焦点.若MF 1→·MF 2→<0,则y 0的取值可能是( BC ) A .-1 B .0 C .12D .1[解析] 由双曲线方程可知F 1(-3,0)、F 2(3,0), ∵MF 1→·MF 2→<0,∴(-3-x 0)(3-x 0)+(-y 0)(-y 0)<0, 即x 20+y 20-3<0,∴2+2y 20+y 20-3<0,y 20<13, ∴-33<y 0<33,故选BC . 4.(多选题)将离心率为e 1的双曲线C 1的实半轴长a 和虚半轴长b (a ≠b )同时增加m (m >0)个单位长度,得到离心率为e 2的双曲线C 2,则( BD ) A .对任意的a ,b ,e 1>e 2 B .当a <b 时,e 1>e 2 C .对任意的a ,b ,e 1<e 2 D .当a >b 时,e 1<e 2[解析] 由条件知e 21=c 2a 2=1+b 2a2,e 22=1+⎝ ⎛⎭⎪⎫b +m a +m 2,当a >b 时,b +m a +m >ba ,∴e 21<e 22.∴e 1<e 2.当a <b 时,b +m a +m <ba ,∴e 21>e 22.∴e 1>e 2.所以,当a >b 时,e 1<e 2;当a <b 时,e 1>e 2. 二、填空题5.(2019·课标全国Ⅰ理,16)已知双曲线C :x 2a 2-y 2b 2=1(a >0,b >0)的左、右焦点分别为F 1,F 2,过F 1的直线与C 的两条渐近线分别交于A ,B 两点.若F 1A →=AB →,F 1B →·F 2B →=0,则C 的离心率为__2__.[解析] 双曲线x 2a 2-y 2b 2=1(a >0,b >0)的渐近线方程为y =±ba x ,∵F 1B →·F 2B →=0,∴F 1B ⊥F 2B ,∴点B 在⊙O :x 2+y 2=c 2上,如图所示,不妨设点B 在第一象限,由⎩⎪⎨⎪⎧y =b ax x 2+y 2=c2a 2+b 2=c 2x >0,得点B (a ,b ),∵F 1A →=AB →,∴点A 为线段F 1B 的中点,∴A ⎝⎛⎭⎪⎫a -c 2,b 2,将其代入y =-b a x 得b 2=⎝⎛⎭⎫-b a ×a -c 2.解得c =2a ,故e =ca=2.6.已知双曲线x 29-y 2a =1的右焦点为(13,0),则该双曲线的渐近线方程为__y =±23x __.[解析] 由已知得9+a =13,即a =4,故所求双曲线的渐近线为y =±23x .三、解答题7.焦点在x 轴上的双曲线过点P (42,-3),且点Q (0,5)与两焦点的连线互相垂直,求此双曲线的标准方程.[解析] 因为双曲线焦点在x 轴上,所以设双曲线的标准方程为x 2a 2-y 2b 2=1(a >0,b >0),F 1(-c,0)、F 2(c,0).因为双曲线过点P (42,-3), 所以32a 2-9b2=1.①又因为点Q (0,5)与两焦点的连线互相垂直, 所以QF 1→·QF 2→=0,即-c 2+25=0. 所以c 2=25.② 又c 2=a 2+b 2,③所以由①②③可解得a 2=16或a 2=50(舍去). 所以b 2=9,所以所求的双曲线的标准方程是x 216-y 29=1. 8.(2020·云南元谋一中期中)双曲线x 2a 2-y 2b 2=1(a >0,b >0)的右焦点为F (c,0).(1)若双曲线的一条渐近线方程为y =x 且c =2,求双曲线的方程;(2)以原点O 为圆心,c 为半径作圆,该圆与双曲线在第一象限的交点为A ,过A 作圆的切线,其斜率为-3,求双曲线的离心率.[解析] (1)由题意,ba =1,c =2,a 2+b 2=c 2,∴a 2=b 2=2,∴双曲线方程为x 22-y 22=1.(2)由题意,设A (m ,n ),则k OA =33,从而n =33m ,m 2+n 2=c 2,∴A (32c ,c 2), 将A (32c ,c 2)代入双曲线x 2a 2-y 2b 2=1得:3c 24a 2-c 24b 2=1,∴c 2(3b 2-a 2)=4a 2b 2,且c 2=a 2+b 2,∴(a 2+b 2)(3b 2-a 2)=4a 2b 2, ∴3b 4-2a 2b 2-a 4=0,∴3(b a )4-2(ba )2-1=0,∴b 2a 2=1从而e 2=1+b 2a 2=2,∴e = 2.。
