离散数学自然推理系统p
论自然推理系统P的三种证明方法

论自然推理系统P的三种证明方法刘亚婷 兴义民族师范学院数学科学学院摘要:自然推理系统P是逻辑学中很好的一个推理规则,它可以用来解决日常生活、科学领域、社会活动等逻辑推理,它主要有三种证明方法:直接证明法、附加前提证明法和归谬证明法。
用这三种方法推出的结论,都是有效结论,当他的前提条件成立时,结论一定成立。
关键词:自然推理系统;证明;方法 中图分类号:O141 文献识别码:A 文章编号:1001-828X(2017)030-0389-02在数理逻辑中,最重要的就是用数学的方法研究推理。
所谓推理,就是通过一系列已知的命题公式,应用所给的推理规则推出命题公式的过程。
推理又分为公理推理和自然推理,在我们的日常生活中,经常用自然推理来解决一些实际问题。
自然推理是形式系统中的推理之一,我们常称为自然推理系统P。
现将自然推理系统P 定义如下:1.字母表(1)命题变项的符号: p, q, r, …(2) 联结词的符号: ┐,∧,∨, →, ↔(3)逗号与括号: ,, ( )2.合式公式(1) 单个的命题变项和命题常项是合式公式, 称作原子命题公式(2) 若A是合式公式,则 (A)也是合式公式(3) 若A, B是合式公式,则(AB), (AB),(AB), (AB)也是合式公式(4) 有限次地应用(1) --(3)组成的符号串也是合式公式3. 推理规则(1)前提引入: 在证明的任何步骤上都可引入已知前提;(2) 结论引入: 在证明的任何步骤上所得到的结论都可作为后续证明的前提。
(3) 置换规则:在证明的任何步骤上,命题公式都可以用与之等值的公式来置换。
(4)假言推理 (5)附加规则 (6)化简规则A→B A A∧B_ _A__ ∴A∨B ∴A∴ B(7)拒绝式 (8)假言三段论A→B A→B┐B B→C∴┐A ∴A→C(9)析取三段论 (10)构造性二难A∨B A→B┐B C→D∴ A A∨C∴B∨D(11)破坏性二难 (12)合取引入规则A→B AC→D B┐B∨┐D ∴A∧B∴┐A∨┐C那么如何在自然推理系统P中进行证明呢?步骤如下:(1)将原子命题符号化(2)将实际问题的前提A1, A2, …, A k写出来(3)将实际问题的结论B写出来(4)根据自然推理系统P中的推理规则进行判断在自然推理系统P中构造证明时,将形式构造成:前提:A1, A2, …, A k结论:B然后利用直接证明法、附加前提证明法和归谬证明法进行证明。
离散数学结构 第3章 命题逻辑的推理理论复习

第3章命题逻辑的推理理论主要内容1. 推理的形式结构:①推理的前提②推理的结论③推理正确④有效结论2. 判断推理是否正确的方法:①真值表法②等值演算法③主析取范式法3. 对于正确的推理,在自然推理系统P中构造证明4. ①自然推理系统P的定义②自然推理系统P的推理规则:前提引入规则、结论引入规则、置换规则、假言推理规则、附加规则、化简规则、拒取式规则、假言三段式规则、构造性二难规则、合取引入规则。
③附加前提证明法④归谬法学习要求1. 理解并记住推理的形式结构的三种等价形式,即①{A1,A2,…,A k}├B②A1∧A2∧…∧A k→B③前提与结论分开写:前提:A1,A2,…,A k结论:B在判断推理是否正确时,用②;在P系统中构造证明时用③。
2. 熟练掌握判断推理是否正确的三种方法(真值表法,等值演算法,主析取范式法)。
3. 牢记P系统中的各条推理规则。
4. 对于给定的正确推理,要求在P系统中给出严谨的证明序列。
5. 会用附加前提证明法和归谬法。
3.1 推理的形式结构定义3.1设A1,A2,…,A k和B都是命题公式,若对于A1,A2,…,A k和B中出现的命题变项的任意一组赋值,或者A1∧A2∧…∧A k为假,或者当A1∧A2∧…∧A k为真时,B也为真,则称由前提A1,A2,…,A k推出B的推理是有效的或正确的,并称B是有效结论。
二、有效推理的等价定理定理3.1命题公式A1,A2,…,A k推B的推理正确当且仅当(A1∧A2∧…∧A k )→B为重言式。
A k为假,或者A1∧A2∧…∧A k和B同时为真,这正符合定义3.1中推理正确的定义。
由此定理知,推理形式:前提:A1,A2,…,A k结论:B是有效的当且仅当(A1∧A2∧…∧A k)→B为重言式。
(A1∧A2∧…∧A k)→B称为上述推理的形式结构。
从而推理的有效性等价于它的形式结构为永真式。
于是,推理正确{A1,A2,…,A k} B可记为A1∧A2∧…∧A k B其中同一样是一种元语言符号,用来表示蕴涵式为重言式。
离散数学 命题逻辑推理

3.1 推理的形式结构
推理:从前提出发推导出结论思维过程, 前提 是已知的命题公式集合, 结论 是从前提出发应用推理规则推出的命题公式。 什么样的推理是正确的有效的? 定义3.1 设A1, A2, …, Ak, B为命题公式. 若对于每组赋值, A1A2… Ak 为假, 或当A1A2…Ak为真时B也为真, 则称由前提A1, A2, …, Ak推出结论B的推理是有效的或正 确的, 并称B是有效结论. 定理3.1 由命题公式A1, A2, …, Ak 推出B的推理正确当且仅当 A1A2…AkB为重言式 注意: 推理正确不能保证结论一定正确
10
推理规则
(4) 假言推理规则 AB A ∴B (6) 化简规则 AB ∴A (8) 假言三段论规则 AB BC ∴AC (5) 附加规则 A ∴AB (7) 拒取式规则 AB B ∴ A (9) 析取三段论规则 AB B ∴A
11
推理规则
(10) 构造性二难推理规则 AB CD AC ∴BD
7
推理定律——重言蕴涵式
用定义构造推理过程,需要一些有用的推理定律 1. A (AB) 附加律 2. (AB) A 化简律 3. (AB)A B 假言推理 4. (AB)B A 拒取式 5. (AB)B A 析取三段论 6. (AB)(BC) (AC) 假言三段论 7. (AB)(BC) (AC) 等价三段论 8. (AB)(CD)(AC) (BD) 构造性二难 (AB)(AB) B 构造性二难(特殊形式) 9. (AB)(CD)( BD) (AC) 破坏性二难 每个等值式可产生两个推理定律 如, 由AA可产生 AA 和 AA
0
1 1
0
0 1
1
0
不是重言式, 推理不正确
离散数学课件03命题逻辑的推理理论

③ p
④ q ⑤ q→r
Hale Waihona Puke ②化简②化简 ①③假言推理
⑥ r
⑦ r∨s ⑧ ┐r→s
④⑤假言推理
⑥附加 ⑦置换
例题
例3.4 在自然推理系统P中构造下面推理的证明: 若数a是实数,则它不是有理数就是无理数;若a不能表 示成分数,则它不是有理数;a是实数且它不能表示成分数。 所以a是无理数。 构造证明: (1)将简单命题符号化: 设 p:a是实数。 r:a是无理数。 (2)形式结构: 前提:p→(q∨r), ┐s→┐q, p∧┐s 结论:r q:a是有理数。 s:a能表示成分数。
若一个推理的形式结构与某条推理定律对应的蕴涵 式一致,则不用证明就可断定这个推理是正确的。
2.1节给出的24个等值式中的每一个都派生出两条推 理定律。例如双重否定律A A产生两条推理定 律A A和 AA。 由九条推理定律可以产生九条推理规则,它们构成了 推理系统中的推理规则。
–推理的形式结构 –自然推理系统P
本章与后续各章的关系
–本章是第五章的特殊情况和先行准备
3.1 推理的形式结构 3.2 自然推理系统P
本章小结
习题
作业
3.1 推理的形式结构
数理逻辑的主要任务是用数学的方法来研究数学中的 推理。 推理是指从前提出发推出结论的思维过程。
前提是已知命题公式集合。
(┐q∨p) ∨ q 1
推理定律--重言蕴含式
(1) A (A∨B) (2) (A∧B) A (3) (A→B)∧A B (4) (A→B)∧┐B ┐A 附加律 化简律 假言推理 拒取式
(5) (A∨B)∧┐B A
(6) (A→B) ∧ (B→C) (A→C) (7) (AB) ∧ (BC) (A C)
离 散 数 学

第一节等值式例6、求命题公式的主析取范式,主合取范式,成真赋值和成假赋值。
解:先求主析取范式故主合取范式为例6、求命题公式的主析取范式,主合取范式,成真赋值和成假赋值。
解:成真赋值为极小项角码对应的二进制数,即00,10,11。
成假赋值为极大项角码对应的二进制数,即01。
例7、设 (1) 求的真值表。
(2) 求的主析取范式、主合取范式。
解:例7、设 (2) 求的主析取范式、主合取范式。
解:例7、设 (2) 求的主析取范式、主合取范式。
解:例8、判断下列推理是否正确。
解:可用多种方法(如真值表法,等值演算法,主范式法)验证,并非重言式,故推理不正确。
(1) 前提:结论:,例8、判断下列推理是否正确。
(2) 如果今天是星期二,则<a name=baidusnap0></a>明天</B>是星期四。
今天是星期二,所以明天</B>是星期四。
以上推理即假言推理,所以是正确的。
解::明天</B>是星期四,:今天是星期二,前提:结论:,例9、写出对应下面推理的证明。
有红、黄、蓝、白四队参加足球联赛。
如果红队第三,则当黄队第二时,蓝队第四;或者白队不是第一,或者红队第三;事实上,黄队第二。
因此,如果白队第一,那么蓝队第四。
证明:设:红队第三,:黄队第二,:蓝队第四,:白队第一。
前提:结论:前提:结论:前提引入附加前提引入①②析取三段论前提引入④①③②⑤③④假言推理前提:结论:③④假言推理前提引入⑤⑥假言推理⑤⑦⑥由附加前提证明法知推理正确。
例10、一公安人员审查一件盗窃案,已知的事实如下: (1) 甲或乙盗窃了录音机; (2) 若甲盗窃了录音机,则作案时间不能发生在午夜前; (3) 若乙的证词正确,则午夜时屋里灯光未灭; (4) 若乙的证词不正确,则作案时间发生在午夜之前; (5) 午夜时屋里灯光灭了。
问是谁盗窃了录音机。
:乙盗窃了录音机,:作案时间发生在午夜前,:乙的证词正确,:午夜灯光未灭。
离散数学习题答案(耿素云屈婉玲)

(2)前提:
结论:
证明:用附加前提证明法。
①p附加前提引入
② ①附加
③ 前提引入
④ ②③假言推理
⑤s④化简
⑥ ⑤附加
⑦ 前提引入
⑧u⑥⑦假言推理
故推理正确。
16、在自然推理系统P中用归谬法证明下面推理:
(1)前提: , ,
结论:
证明:用归谬法
①p结论的否定引入
(2)反对称性:
(3)传递性:
综合(1)(2)(3)知T满足自反性、反对称性和传递性,故T为 上的偏序关系。
习题九及答案:(P179-180)
8、
(1)
(2) 。
解:(1)
(2)
11、
(3) ;
解:(3)由*运算的定义可知: ,
16、
习题十一及答案:(P218-219)
1、图11.11给出了6个偏序集的哈斯图。判断其中哪些是格。如果不是格,说明理由
则前提: , ,
结论:
证明:
① 前提引入
② ①化简
③ ①化简
④ 前提引入
⑤ ④UI规则
⑥ ②⑤假言推理
⑦ ③⑥合取引入
⑧ 前提引入
⑨ ⑧UI规则
⑩ ⑦⑨假言推理
习题七及答案:(P132-135)
22、给定 ,A上的关系 ,试
(1)画出R的关系图;
(2)说明R的性质。
解: (1)
● ●
● ●
(2)R的关系图中每个顶点都没有自环,所以R是反自反的,不是自反的;
(1)
解:原式
,此即主析取范式。
主析取范式中没出现的极小项为 , , ,所以主合取范式中含有三个极大项 , , ,故原式的主合取范式 。
离散数学---推理理论

实例分析
西 华 大 学 制 作
判断推理是否正确:张红不管有无空闲都不看电影。张红看了电影。所以张 红有空闲时间又没有空闲时间。 解:P:张红有空闲时间;Q:张红看电影 。 前提:A1=P∨ P→ Q A2=Q 结论:A=P∧ P 问题:该结论是否有效结论。(该推理是否正确)。
P 0 0 1 1
自然推理系统P
西 华 大 学 制 作
自然推理系统
特点:可以从任意给定的前提出发,
形式系统
应用系统中的推理进行推演,得到 的结论在系统中被认为是有效的。
公理系统
特点:只能从几个给定的公理出发, 应用系统中的推理规则进行推演,
得到的结论是系统中的定理。
自然推理系统P
自然推理系统P定义如下:
1.字母表
§1.6 推理理论
西 华 大 学 制 作
一、有效论证推理规则 二、基本蕴涵式 三、自然推理系统P 四、推理证明的方法
一、有效论证与推理规则
西 华 大 学 制 作
• 定义:A1∧A2∧…∧An→A,其为永真式,则称 前提A1,A2,…,An得到有效结论A;从前提公式得 到有效结论的过程称为正确推理。 • 若AB是永真式,则记为AB; • 若A→B是永真式,则记为AB。 • 前提一致和不一致: • 如果前提A1∧A2∧…∧An为可满足式,则 为前提A1,A2,…,An一致。
西 (1)命题常元,命题变元:P,Q,R,…,Pi,Qi,…,1,0(T,F) 华 大 (2)命题联结词:、∧、∨、→、 学 (3)括号:(,) 制 2.合式公式:(略) 作
3.推理规则:
(1).前提引入规则(P规则):在证明的任何步上,都可引入前 提; (2).结论引用规则(T规则):在证明的任何步上,所得的结论 都可作为证明得前提; (3).置换规则:在证明的任何步上,命题公式的任何子命题 公式都可以用与之等价的命题公式置换。 (4).永真蕴涵规则:使用基本蕴涵式,常常将条件用‘,’
离散复习题
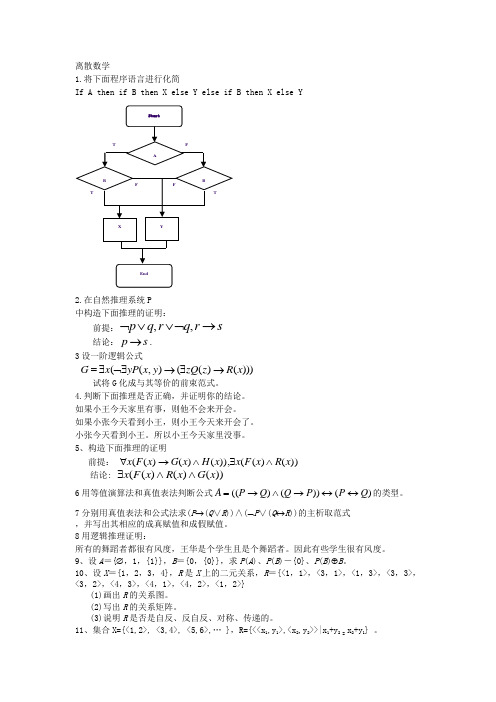
离散数学1.将下面程序语言进行化简If A then if B then X else Y else if B then X else Y2.在自然推理系统P中构造下面推理的证明:前提:,,p q r q rs ⌝∨∨⌝→ 结论:p s →.3设一阶逻辑公式((,)(()()))G x yP x y zQ z R x =∃⌝∃→∃→试将G 化成与其等价的前束范式。
4.判断下面推理是否正确,并证明你的结论。
如果小王今天家里有事,则他不会来开会。
如果小张今天看到小王,则小王今天来开会了。
小张今天看到小王。
所以小王今天家里没事。
5、构造下面推理的证明前提: ))()(()),()()((x R x F x x H x G x F x ∧∃∧→∀结论: ))()()((x G x R x F x ∧∧∃6用等值演算法和真值表法判断公式)())()((Q P P Q Q P A ↔↔→∧→=的类型。
7分别用真值表法和公式法求(P →(Q ∨R ))∧(⌝P ∨(Q ↔R ))的主析取范式,并写出其相应的成真赋值和成假赋值。
8用逻辑推理证明:所有的舞蹈者都很有风度,王华是个学生且是个舞蹈者。
因此有些学生很有风度。
9、设A ={∅,1,{1}},B ={0,{0}},求P (A )、P (B )-{0}、P (B )⊕B 。
10、设X ={1,2,3,4},R 是X 上的二元关系,R ={<1,1>,<3,1>,<1,3>,<3,3>,<3,2>,<4,3>,<4,1>,<4,2>,<1,2>}(1)画出R 的关系图。
(2)写出R 的关系矩阵。
(3)说明R 是否是自反、反自反、对称、传递的。
11、集合X={<1,2>, <3,4>, <5,6>,… },R={<<x 1,y 1>,<x 2,y 2>>|x 1+y 2 = x 2+y 1} 。
离散数学习题答案(耿素云屈婉玲)

离散数学习题答案习题二及答案:(P38)5、求下列公式的主析取式,并求成真赋值: (2)()()p q q r ⌝→∧∧ 解:原式()p q q r ⇔∨∧∧q r ⇔∧()p p q r ⇔⌝∨∧∧()()p q r p q r ⇔⌝∧∧∨∧∧37m m ⇔∨,此即公式的主析取式,所以成真赋值为011,111。
6、求下列公式的主合取式,并求成假赋值: (2)()()p q p r ∧∨⌝∨解:原式()()p p r p q r ⇔∨⌝∨∧⌝∨∨()p q r ⇔⌝∨∨4M ⇔,此即公式的主合取式,所以成假赋值为100。
7、求下列公式的主析取式,再用主析取式求主合取式: (1)()p q r ∧∨ 解:原式()(()())p q r r p p q q r ⇔∧∧⌝∨∨⌝∨∧⌝∨∧()()()()()()p q r p q r p q r p q r p q r p q r ⇔∧∧⌝∨∧∧∨⌝∧⌝∧∨⌝∧∧∨∧⌝∧∨∧∧ ()()()()()p q r p q r p q r p q r p q r ⇔⌝∧⌝∧∨⌝∧∧∨∧⌝∧∨∧∧⌝∨∧∧13567m m m m m ⇔∨∨∨∨,此即主析取式。
主析取式中没出现的极小项为0m ,2m ,4m ,所以主合取式中含有三个极大项0M ,2M ,4M ,故原式的主合取式024M M M ⇔∧∧。
9、用真值表法求下面公式的主析取式: (1)()()p q p r ∨∨⌝∧ 解:公式的真值表如下:由真值表可以看出成真赋值的情况有7种,此7种成真赋值所对应的极小项的析取即为主析取式,故主析取式1234567m m m m m m m ⇔∨∨∨∨∨∨习题三及答案:(P52-54)11、填充下面推理证明中没有写出的推理规则。
前提:,,,p q q r r s p ⌝∨⌝∨→结论:s 证明:① p 前提引入 ② p q ⌝∨ 前提引入 ③ q ①②析取三段论 ④q r ⌝∨ 前提引入⑤ r ③④析取三段论 ⑥ r s → 前提引入⑦ s ⑤⑥假言推理15、在自然推理系统P 中用附加前提法证明下面推理: (2)前提:()(),()p q r s s t u ∨→∧∨→ 结论:p u →证明:用附加前提证明法。
离散数学第三章 命题逻辑的推理理论

推理实例
例1 判断下面推理是否正确 (1) 若今天是 号,则明天是 号. 今天是 号. 所以 明天是 号. 若今天是1号 则明天是5号 今天是1号 所以, 明天是5号 (2) 若今天是 号,则明天是 号. 明天是 号. 所以 今天是 号. 若今天是1号 则明天是5号 明天是5号 所以, 今天是1号 解 设 p:今天是 号,q:明天是 号. :今天是1号 :明天是5号 → ∧ → (1) 推理的形式结构 (p→q)∧p→q 推理的形式结构: 用等值演算法 (p→q)∧p→q → ∧ → ⇔ ¬((¬p∨q)∧p)∨q ¬ ∨ ∧ ∨ ∨¬q∨ ⇔ ¬p∨¬ ∨q ⇔ 1 ∨¬ 由定理3.1可知推理正确 由定理 可知推理正确
19
练习1: 练习 :判断推理是否正确
1. 判断下面推理是否正确 判断下面推理是否正确: (1) 前提:¬p→q, ¬q 前提: → 结论: 结论:¬p ∧¬q→¬ 推理的形式结构: ¬ → ∧¬ →¬p 解 推理的形式结构 (¬p→q)∧¬ →¬ 方法一:等值演算法 方法一: (¬p→q)∧¬ →¬ ∧¬q→¬ ¬ → ∧¬ →¬p ∧¬q)∨¬ ⇔ ¬((p∨q)∧¬ ∨¬ ∨ ∧¬ ∨¬p ∧¬q)∨ ∨¬ ∨¬p ⇔ (¬p∧¬ ∨q∨¬ ¬ ∧¬ ∨¬p ⇔ ((¬p∨q)∧(¬q∨q))∨¬ ¬ ∨ ∧ ¬ ∨ ∨¬ ⇔ ¬p∨q ∨ 易知10是成假赋值,不是重言式,所以推理不正确 易知 是成假赋值,不是重言式,所以推理不正确. 是成假赋值
16
例4 前提:¬(p∧q)∨r, r→s, ¬s, p 前提: ∧ ∨ → 结论: 结论:¬q 证明 用归缪法 ①q 结论否定引入 ② r→s → 前提引入 ③ ¬s 前提引入 ②③拒取式 ④ ¬r ②③拒取式 ⑤ ¬(p∧q)∨r ∧ ∨ 前提引入 ④⑤析取三段论 ⑥ ¬(p∧q) ∧ ④⑤析取三段论 ∨¬q ⑦ ¬p∨¬ ∨¬ ⑥置换 ①⑦析取三段论 ⑧ ¬p ①⑦析取三段论 ⑨p 前提引入 ⑧⑨合取 ¬p∧p ∧ ⑧⑨合取
离散数学第三章习题详细答案
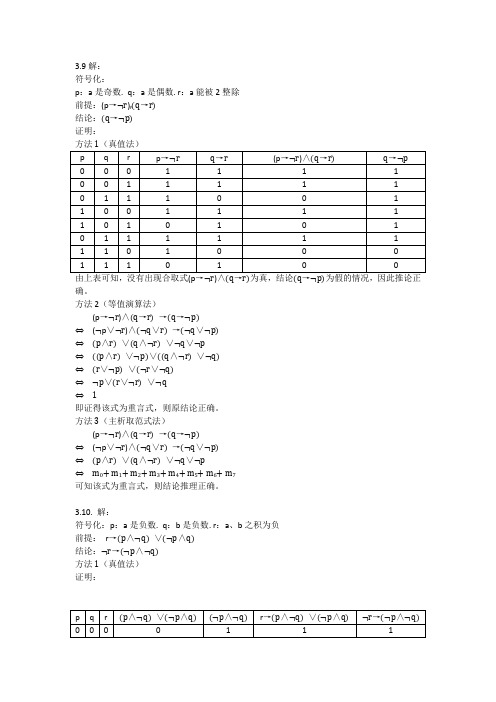
3.9解:符号化:p:a是奇数. q:a是偶数. r:a能被2整除前提:(p→¬r),(q→r)结论:(q→¬p)证明:确。
方法2(等值演算法)(p→¬r)∧(q→r)→(q→¬p)⇔(¬p∨¬r)∧(¬q∨r) →(¬q∨¬p)⇔(p∧r) ∨(q∧¬r) ∨¬q∨¬p⇔((p∧r) ∨¬p)∨((q∧¬r) ∨¬q)⇔(r∨¬p) ∨(¬r∨¬q)⇔¬p∨(r∨¬r) ∨¬q⇔ 1即证得该式为重言式,则原结论正确。
方法3(主析取范式法)(p→¬r)∧(q→r)→(q→¬p)⇔(¬p∨¬r)∧(¬q∨r) →(¬q∨¬p)⇔(p∧r) ∨(q∧¬r) ∨¬q∨¬p⇔m0+ m1+ m2+ m3+ m4+ m5+ m6+ m7可知该式为重言式,则结论推理正确。
3.10. 解:符号化:p:a是负数. q:b是负数. r:a、b之积为负前提:r→(p∧¬q) ∨(¬p∧q)结论:¬r→(¬p∧¬q)方法1(真值法)证明:不正确。
方法2(主析取范式法)证明:(r→(p∧¬q) ∨(¬p∧q))→(¬r→(¬p∧¬q))⇔¬ (¬r∨(p∧¬q) ∨(¬p∧q))∨(r∨(¬p∧¬q))⇔r∨(¬p∧¬q)⇔m0+m2+m4+m6+m7只含5个极小项,课件原始不是重言式,因此推理不正确3.11.填充下面推理证明中没有写出的推理规则。
离散数学1. (12)

(p→r)∧┐r→┐p
此形式结构为重言式,即
(p→r)∧┐r┐p
故推理正确。
(4)推理形式结构为
(p→q)∧┐p→┐q
此形式结构不是重言式,故推理不正确。
(5)推理形式结构为
p→(q∨r)
它不是重言式,故推理不正确。
(6)推理形式结构为
(p r)∧┐p→┐r
此形式结构为重言式,即
注意:有人说,前提中无s出现,结论却有s出现,所以推理不正确。此说法不对,
他忘了附加推理规则。(3)前提:┐p∨r,┐q源自s,p∧q;结论:r∧s证明:
①┐p∨r前提引入
②p∧q前提引入
③p②化简
④r①③析取三段论
⑤┐q∨s前提引入
⑥q②化简
⑦s⑤⑥析取三段论
⑧r∧s④⑦合取
(4)前提:p→(q→r),s→q,q;结论:s→r
结论:t→(r∨s)
答案2.
(1)证明:
①p→(q→r)前提引入
②p前提引入
③q→r①②假言推理
④q前提引入
⑤r③④假言推理
⑥r∨s⑤附加律
(2)证明:
①┐(q∧r)前提引入
②┐q∨┐r①置换
③r前提引入
④┐q②③析取三段论
⑤p→q前提引入
⑥┐p④⑤拒取式
(3)证明:
①p→q前提引入
②┐p∨q①置换
然后制作(*)的真值表,见下表
(*)的真值表
由于真值表的最后一列全为1,故(*)为重言式,因而推理正确。
方法二、等值演算法
(p→┐r)∧(q→r)→(q→┐r)
(┐p∨┐r)∧(┐q∨r)→(┐q∨┐p)(蕴涵等值式)
┐((┐p∨┐r)∧(┐q∨r))∨(┐q∨┐p)(蕴涵等值式)
离散数学答案 屈婉玲版 第二版 高等教育出版社课后答案之欧阳家百创编

离散数学答案屈婉玲版欧阳家百(2021.03.07)第二版高等教育出版社课后答案第一章部分课后习题参考答案16 设p、q的真值为0;r、s的真值为1,求下列各命题公式的真值。
(1)p∨(q∧r)⇔ 0∨(0∧1)⇔0(2)(p↔r)∧(﹁q∨s)⇔(0↔1)∧(1∨1)⇔0∧1⇔0.(3)(⌝p∧⌝q∧r)↔(p∧q∧﹁r)⇔(1∧1∧1)↔(0∧0∧0)⇔0(4)(⌝r∧s)→(p∧⌝q)⇔(0∧1)→(1∧0)⇔0→0⇔117.判断下面一段论述是否为真:“π是无理数。
并且,如果3是无理数,则2也是无理数。
另外6能被2整除,6才能被4整除。
”答:p: π是无理数 1q: 3是无理数 0r: 2是无理数 1s:6能被2整除 1t: 6能被4整除 0命题符号化为: p∧(q→r)∧(t→s)的真值为1,所以这一段的论述为真。
19.用真值表判断下列公式的类型:(4)(p→q) →(⌝q→⌝p)(5)(p∧r)↔(⌝p∧⌝q)(6)((p→q) ∧(q→r)) →(p→r)答:(4)p q p→q ⌝q ⌝p ⌝q→⌝p (p→q)→(⌝q→⌝p)0 0 1 1 1 1 10 1 1 0 1 1 11 0 0 1 0 0 11 1 1 0 0 1 1所以公式类型为永真式(5)公式类型为可满足式(方法如上例)(6)公式类型为永真式(方法如上例)第二章部分课后习题参考答案3.用等值演算法判断下列公式的类型,对不是重言式的可满足式,再用真值表法求出成真赋值.(1)⌝(p∧q→q)(2)(p→(p∨q))∨(p→r)(3)(p∨q)→(p∧r)答:(2)(p→(p∨q))∨(p→r)⇔(⌝p∨(p∨q))∨(⌝p∨r)⇔⌝p∨p∨q∨r⇔1所以公式类型为永真式(3)P q r p∨q p∧r (p∨q)→(p∧r)0 0 0 0 0 10 0 1 0 0 10 1 0 1 0 00 1 1 1 0 01 0 0 1 0 01 0 1 1 1 11 1 0 1 0 01 1 1 1 1 1所以公式类型为可满足式4.用等值演算法证明下面等值式:(2)(p→q)∧(p→r)⇔(p→(q∧r))(4)(p∧⌝q)∨(⌝p∧q)⇔(p∨q) ∧⌝(p∧q)证明(2)(p→q)∧(p→r)⇔ (⌝p∨q)∧(⌝p∨r)⇔⌝p∨(q∧r))⇔p→(q∧r)(4)(p∧⌝q)∨(⌝p∧q)⇔(p∨(⌝p∧q)) ∧(⌝q∨(⌝p∧q)⇔(p∨⌝p)∧(p∨q)∧(⌝q∨⌝p) ∧(⌝q∨q)⇔1∧(p∨q)∧⌝(p∧q)∧1⇔(p∨q)∧⌝(p∧q)5.求下列公式的主析取范式与主合取范式,并求成真赋值(1)(⌝p→q)→(⌝q∨p)(2)⌝(p→q)∧q∧r(3)(p∨(q∧r))→(p∨q∨r)解:(1)主析取范式(⌝p→q)→(⌝q∨p)⇔⌝(p∨q)∨(⌝q∨p)⇔(⌝p∧⌝q)∨(⌝q∨p)⇔ (⌝p∧⌝q)∨(⌝q∧p)∨(⌝q∧⌝p)∨(p∧q)∨(p∧⌝q)⇔(⌝p∧⌝q)∨(p∧⌝q)∨(p∧q)⇔∑(0,2,3)主合取范式:(⌝p→q)→(⌝q∨p)⇔⌝(p∨q)∨(⌝q∨p)⇔(⌝p∧⌝q)∨(⌝q∨p)⇔(⌝p∨(⌝q∨p))∧(⌝q∨(⌝q∨p))⇔1∧(p∨⌝q)⇔(p∨⌝q)⇔ M1⇔∏(1)(2) 主合取范式为:⌝(p→q)∧q∧r⇔⌝(⌝p∨q)∧q∧r⇔(p∧⌝q)∧q∧r⇔0所以该式为矛盾式.主合取范式为∏(0,1,2,3,4,5,6,7)矛盾式的主析取范式为 0(3)主合取范式为:(p∨(q∧r))→(p∨q∨r)⇔⌝(p∨(q∧r))→(p∨q∨r)⇔(⌝p∧(⌝q∨⌝r))∨(p∨q∨r)⇔(⌝p∨(p∨q∨r))∧((⌝q∨⌝r))∨(p∨q∨r))⇔1∧1⇔1所以该式为永真式.永真式的主合取范式为 1主析取范式为∑(0,1,2,3,4,5,6,7)第三章部分课后习题参考答案14.在自然推理系统P中构造下面推理的证明: (2)前提:p→q,⌝(q∧r),r结论:⌝p(4)前提:q→p,q↔s,s↔t,t∧r结论:p∧q证明:(2)①⌝(q∧r) 前提引入②⌝q∨⌝r ①置换③q→⌝r ②蕴含等值式④r 前提引入⑤⌝q ③④拒取式⑥p→q 前提引入⑦¬p(3)⑤⑥拒取式证明(4):①t∧r 前提引入②t ①化简律③q↔s 前提引入④s↔t 前提引入⑤q↔t ③④等价三段论⑥(q→t)∧(t→q) ⑤置换⑦(q→t)⑥化简⑧q ②⑥假言推理⑨q→p 前提引入⑩p ⑧⑨假言推理(11)p∧q ⑧⑩合取15在自然推理系统P中用附加前提法证明下面各推理:(1)前提:p→(q→r),s→p,q结论:s→r证明①s 附加前提引入②s→p 前提引入③p ①②假言推理④p→(q→r) 前提引入⑤q→r ③④假言推理⑥q 前提引入⑦r ⑤⑥假言推理16在自然推理系统P中用归谬法证明下面各推理:(1)前提:p→⌝q,⌝r∨q,r∧⌝s结论:⌝p证明:①p 结论的否定引入②p→﹁q 前提引入③﹁q ①②假言推理④¬r∨q 前提引入⑤¬r ④化简律⑥r∧¬s 前提引入⑦r ⑥化简律⑧r∧﹁r ⑤⑦合取由于最后一步r∧﹁r是矛盾式,所以推理正确.第四章部分课后习题参考答案3. 在一阶逻辑中将下面将下面命题符号化,并分别讨论个体域限制为(a),(b)条件时命题的真值:(1) 对于任意x,均有2=(x+)(x).(2) 存在x,使得x+5=9.其中(a)个体域为自然数集合.(b)个体域为实数集合.解:F(x):2=(x+)(x).G(x): x+5=9.(1)在两个个体域中都解释为)(x∀,在(a)中为假命题,xF在(b)中为真命题。
离散数学答案屈婉玲版第二版高等教育出版社课后答案

离散数学答案屈婉玲版第二版高等教育出版社课后答案第一章部分课后习题参考答案16 设p、q的真值为0;r、s的真值为1,求下列各命题公式的真值。
(1)p∨(q∧r)⇔ 0∨(0∧1) ⇔0(2)(p↔r)∧(﹁q∨s) ⇔(0↔1)∧(1∨1) ⇔0∧1⇔0.(3)(⌝p∧⌝q∧r)↔(p∧q∧﹁r) ⇔(1∧1∧1)↔ (0∧0∧0)⇔0(4)(⌝r∧s)→(p∧⌝q) ⇔(0∧1)→(1∧0) ⇔0→0⇔117.判断下面一段论述是否为真:“π是无理数。
并且,如果3是无理数,则2也是无理数。
另外6能被2整除,6才能被4整除。
”答:p: π是无理数 1q: 3是无理数 0r: 2是无理数 1s: 6能被2整除 1t: 6能被4整除 0命题符号化为: p∧(q→r)∧(t→s)的真值为1,所以这一段的论述为真。
19.用真值表判断下列公式的类型:(4)(p→q) →(⌝q→⌝p)(5)(p∧r) ↔(⌝p∧⌝q)(6)((p→q) ∧(q→r)) →(p→r)答:(4)p q p→q ⌝q ⌝p ⌝q→⌝p (p→q)→(⌝q→⌝p)0 0 1 1 1 1 10 1 1 0 1 1 11 0 0 1 0 0 11 1 1 0 0 1 1所以公式类型为永真式(5)公式类型为可满足式(方法如上例)(6)公式类型为永真式(方法如上例)第二章部分课后习题参考答案3.用等值演算法判断下列公式的类型,对不是重言式的可满足式,再用真值表法求出成真赋值.(1) ⌝(p∧q→q)(2)(p→(p∨q))∨(p→r)(3)(p∨q)→(p∧r)答:(2)(p→(p∨q))∨(p→r)⇔(⌝p∨(p∨q))∨(⌝p∨r)⇔⌝p∨p∨q∨r⇔1所以公式类型为永真式(3)P q r p∨q p∧r (p∨q)→(p∧r)0 0 0 0 0 10 0 1 0 0 10 1 0 1 0 00 1 1 1 0 01 0 0 1 0 01 0 1 1 1 11 1 0 1 0 01 1 1 1 1 1所以公式类型为可满足式4.用等值演算法证明下面等值式:(2)(p→q)∧(p→r)⇔(p→(q∧r))(4)(p∧⌝q)∨(⌝p∧q)⇔(p∨q) ∧⌝(p∧q)证明(2)(p→q)∧(p→r)⇔ (⌝p∨q)∧(⌝p∨r)⇔⌝p∨(q∧r))⇔p→(q∧r)(4)(p∧⌝q)∨(⌝p∧q)⇔(p∨(⌝p∧q)) ∧(⌝q∨(⌝p∧q)⇔(p∨⌝p)∧(p∨q)∧(⌝q∨⌝p) ∧(⌝q∨q)⇔1∧(p∨q)∧⌝(p∧q)∧1⇔(p∨q)∧⌝(p∧q)5.求下列公式的主析取范式与主合取范式,并求成真赋值(1)(⌝p→q)→(⌝q∨p)(2)⌝(p→q)∧q∧r(3)(p∨(q∧r))→(p∨q∨r)解:(1)主析取范式(⌝p →q)→(⌝q ∨p)⇔⌝(p ∨q)∨(⌝q ∨p)⇔(⌝p ∧⌝q)∨(⌝q ∨p)⇔ (⌝p ∧⌝q)∨(⌝q ∧p)∨(⌝q ∧⌝p)∨(p ∧q)∨(p ∧⌝q)⇔ (⌝p ∧⌝q)∨(p ∧⌝q)∨(p ∧q)⇔320m m m ∨∨⇔∑(0,2,3)主合取范式:(⌝p →q)→(⌝q ∨p)⇔⌝(p ∨q)∨(⌝q ∨p)⇔(⌝p ∧⌝q)∨(⌝q ∨p)⇔(⌝p ∨(⌝q ∨p))∧(⌝q ∨(⌝q ∨p))⇔1∧(p ∨⌝q)⇔(p ∨⌝q) ⇔ M 1⇔∏(1)(2) 主合取范式为:⌝(p →q)∧q ∧r ⇔⌝(⌝p ∨q)∧q ∧r⇔(p ∧⌝q)∧q ∧r ⇔0所以该式为矛盾式.主合取范式为∏(0,1,2,3,4,5,6,7)矛盾式的主析取范式为 0(3)主合取范式为:(p ∨(q ∧r))→(p ∨q ∨r)⇔⌝(p ∨(q ∧r))→(p ∨q ∨r)⇔(⌝p ∧(⌝q ∨⌝r))∨(p ∨q ∨r)⇔(⌝p ∨(p ∨q ∨r))∧((⌝q ∨⌝r))∨(p ∨q ∨r))⇔1∧1⇔1所以该式为永真式.永真式的主合取范式为 1主析取范式为∑(0,1,2,3,4,5,6,7)第三章部分课后习题参考答案14. 在自然推理系统P中构造下面推理的证明:(2)前提:p→q,⌝(q∧r),r结论:⌝p(4)前提:q→p,q↔s,s↔t,t∧r结论:p∧q证明:(2)①⌝(q∧r) 前提引入②⌝q∨⌝r ①置换③q→⌝r ②蕴含等值式④r 前提引入⑤⌝q ③④拒取式⑥p→q 前提引入⑦¬p(3)⑤⑥拒取式证明(4):①t∧r 前提引入②t ①化简律③q↔s 前提引入④s↔t 前提引入⑤q↔t ③④等价三段论⑥(q→t)∧(t→q) ⑤置换⑦(q→t)⑥化简⑧q ②⑥假言推理⑨q→p 前提引入⑩p ⑧⑨假言推理(11)p∧q ⑧⑩合取15在自然推理系统P中用附加前提法证明下面各推理:(1)前提:p→(q→r),s→p,q结论:s→r证明①s 附加前提引入②s→p 前提引入③p ①②假言推理④p→(q→r) 前提引入⑤q→r ③④假言推理⑥q 前提引入⑦r ⑤⑥假言推理16在自然推理系统P中用归谬法证明下面各推理:(1)前提:p→⌝q,⌝r∨q,r∧⌝s结论:⌝p证明:①p 结论的否定引入②p→﹁q 前提引入③﹁q ①②假言推理④¬r∨q 前提引入⑤¬r ④化简律⑥r∧¬s 前提引入⑦r ⑥化简律⑧r∧﹁r ⑤⑦合取由于最后一步r∧﹁r 是矛盾式,所以推理正确.第四章部分课后习题参考答案3. 在一阶逻辑中将下面将下面命题符号化,并分别讨论个体域限制为(a),(b)条件时命题的真值:(1) 对于任意x,均有2=(x+)(x).(2) 存在x,使得x+5=9.其中(a)个体域为自然数集合.(b)个体域为实数集合.解:F(x): 2=(x+)(x).G(x): x+5=9.(1)在两个个体域中都解释为)∀,在(a)中为假命题,在(b)中为真命题。
离散数学自然推理系统在计算机问题中的应用(一)

离散数学自然推理系统在计算机问题中的应用(一)离散数学自然推理系统在计算机问题中的应用应用一:证明算法的正确性离散数学自然推理系统在计算机科学中可以用来证明算法的正确性。
通过使用形式化的数学逻辑和推理规则,可以推导出算法在各种情况下的正确结果。
这有助于开发人员在实现算法之前,预先验证算法的逻辑和正确性,从而提高代码质量和减少错误。
应用二:谓词逻辑在数据库查询中的应用离散数学中的谓词逻辑可以用于数据库查询语言中,以支持高级的查询功能。
谓词逻辑可以描述对象之间的关系和约束条件,通过使用谓词逻辑,可以编写复杂的查询语句,从数据库中检索所需的数据。
这样,离散数学自然推理系统在数据库查询中的应用可以提高查询的灵活性和功能。
应用三:命题逻辑在形式化规约中的应用离散数学中的命题逻辑可以用于形式化规约的描述和验证。
通过使用命题逻辑,可以将复杂的规约问题转化为简单的逻辑表达式,进而验证规约的正确性和一致性。
这种使用离散数学自然推理系统的应用能够帮助开发人员更好地理解和分析规约问题,确保系统设计的正确性。
应用四:图论在网络流优化中的应用离散数学中的图论在计算机网络中有着广泛的应用。
特别是在网络流优化中,图论提供了强大的数学工具和算法。
通过应用图论中的最大流最小割定理以及相关算法,可以实现网络中的资源分配和传输优化,提高网络的吞吐量和效率。
应用五:布尔代数在数字电路设计中的应用离散数学中的布尔代数在数字电路设计中扮演着重要的角色。
通过使用布尔代数的逻辑运算和定理,可以分析、设计和优化数字电路的功能和性能,如门电路、计算机中央处理器等。
这种离散数学自然推理系统在数字电路设计中的应用,对于提高电子设备的性能和可靠性至关重要。
应用六:集合论在数据库和网络安全中的应用离散数学中的集合论在数据库和网络安全中有重要的应用。
通过使用集合论,可以描述和操作各种数据集合,并进行集合运算和关系判断。
这在数据库查询和数据分析中非常有用。
此外,在网络安全领域,集合论也被广泛应用于访问控制和安全策略的建模和验证。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
离散数学自然推理系统p
离散数学中的自然推理系统P是一种基于命题逻辑的证明系统。
该系统包含两个部分:公理和规则。
其中,公理是一些已经被证明的命题,而规则则是推导新命题的方法。
自然推理系统P包含以下规则:
1. 假言规则:如果已知命题A蕴含命题B,那么可以通过假定命题A成立,推导命题B成立。
2. 水平规则:如果已知命题A成立,同时已知命题A蕴含命题B,那么可以推导出命题B成立。
3. 消去规则:如果已知命题A蕴含命题B,且已知命题A或者命题非B成立,那么可以推导出命题非A或者命题B成立。
4. 拆分规则:如果已知命题A并且命题B成立,那么可以推导出命题A且命题B成立。
在自然推理系统P中,证明的过程是通过应用这些规则逐步推导出新的命题,直到能够得出所要证明的命题。
要注意的是,在每一步推导过程中都需要遵循推导规则,并保证逻辑上的正确性。
以上是对离散数学中自然推理系统P的简要介绍。
该证明系统在数学、计算机科学等领域有着广泛的应用。
