列方程解复杂的分数应用题

合集下载

列方程解分数应用题

列方程解分数应用题例1、某工厂有职工980人，其中女职工的人数比男职工的52多28人。

这个工厂的男、女职工各有多少人？练习、师徒两人合做一批零件，完工时，徒弟做的零件个数比师傅的43少10个。

已知师傅比徒弟多做了50个，师徒两人各做了多少个零件？例2、商场运来空调与彩电共152台，卖出彩电的111和5台空调后，剩下的空调与彩电台数正好相等。

商场运来空调与彩电各多少台？练习、甲、乙两桶油共重44千克，甲桶用去它的51，乙桶又倒入10千克后，现在两桶油的重量正好相等。

甲桶原有油多少千克？例3、甲、乙两个工程队共有工人390人，已知甲队人数的32和乙队人数的41共185人。

甲、乙两队各有工人多少人？练习、某小区物业管理公司共有职工20人，其中男职工的125比女职工的41多3人。

这个物业管理公司男、女职工各有多少人？例4、甲、乙两个粮库原来共存粮480吨，现在甲仓运进所存粮食的52，乙仓运进所存粮食的41，这时两仓共存粮645吨。

原来两仓各存粮多少吨？练习、由于科技创新，甲、乙两位技术员共获得公司发给的奖金2000元，甲取出自己所得奖金的31，乙取出自己所得奖金的41，捐献给希望工程，结果两人共剩下1400元奖金。

公司奖给甲、乙两位技术员的奖金各是多少元？例5、甲、乙两堆煤共140吨，当甲堆运走41，乙堆运走10吨后，乙堆煤的吨数是甲堆煤的65。

原来两堆煤各有多少吨？练习、有两桶油，甲桶油的重量是乙桶油的53，现在从甲桶中取出2千克油，从乙桶中取出14千克油，剩下的两桶油重量相等。

两桶油原来各有多少千克？1、两筐桔子，甲筐比乙筐多21千克，若从甲筐取出18千克桔子给乙筐，则甲筐重量是乙筐的74。

乙筐原有桔子多少千克？2、甲、乙两人共储蓄1000元，甲取出240元，乙又存入80元，这时乙储蓄的钱数正好是甲的31。

原来乙储蓄了多少元钱?3、学校田径队中，女队员人数的31等于男队员人数的51。

已知男队员比女队员多6人，田径队中男、女队员各有多少人？4、商场里DVD 的台数是VCD 的台数的74，如果DVD 卖出24台，VCD 卖出53后，剩下的DVD的台数与VCD 的台数相等。

列方程解稍复杂的分数应用题教学反思

列方程解稍复杂的分数应用题教学反思下港镇中心小学数学组本节课的内容是在学习了“已知一个数的几分之几是多少，求这个数”的分数应用题的基础上，根据稍复杂的求一个数的几分之几是多少的分数应用题的数量关系，使学生掌握解题思路，学会用方程解答。

由于新旧知识联系很密，因此本节课在教案设计上抓住了数量关系相同，通过复习题的分析解答，让学生找出熟悉的数量关系，再把题进行改动变化，让学生提出问题。

引导学生利用数量间的等量关系用方程解答。

本节课旨在培养学生的问题意识，在分析的过程中，沟通知识间的联系，并借助线段图的演示，便于学生理解和思维，促进学生分析思维能力的发展和综合运用知识灵活解决实际问题的能力。

如：课程开始，我问：“根据这些数学信息，你能提出什么数学问题？”有学生提出：“买来大米多少千克？” “还剩几分之几？” “吃了多少千克？”学生在产生问题的同时，处于思考状态，这种方式较好地激发了学生的学习情趣。

在民主、和谐的教学氛围中，学生表现得十分自信。

学生间除了知识信息的交流，他们的情感得到了一定的碰撞，思维火花不断闪现，自我意识得到一定的激发。

还有在教学时，借助线段图的演示，重点帮助学生正确理解“比原计划节约了”这个条件的含义。

引导学生弄清这里的是哪两个数量比较的结果，这两个数量比较时要把哪个数量看作单位“１”，原计划的是哪个数量，并在理解的过程中逐步明确解决问题的思路。

习题稿的设计是建立在学生的实际水平和知识点渗透的基础上，从某种程度上使学生在学习数学的过程中享受到探索的愉悦，有一定的利用价值。

反思这节课的教学，还存在很多不足，例如：1、我在教学中不善于抓住学生问题的矛盾冲突点，引发学生深入思考，激励学生积极学习。

2、缺少数学语言的评价，只停留在表面的“你回答的不错。

”“真棒！”等评价语上。

没有充分关注学生的个性以及思维的变化，以至于没有机会使学生达到教学预设中的学习效果，学生的那种欲罢不能的探索欲望激励得不到位。

小学数学稍复杂的分数除法应用题

多
2 3
，黑兔有多少只？
3、根据所给的方程口头编应用题。
ⅹ－ 1 ⅹ＝ 60 5
ⅹ＋ 1 ⅹ＝ 60 5
1、看图列算式。
(1) 男生女生
(2) 桃树李树
1
ⅹ人
多3
15人
ⅹ+
ⅹ 1
3
= 15
ⅹ棵
300棵
少
2 5
ⅹ
﹣
2 5
ⅹ
= 300
2、根据条件列方程解答。
• 小张买了一本书和一支钢笔，书的单价是
10
元
,
正好比钢笔的单价少
3 8
, 钢笔的单
价是多少元？
(2) 李明家有白兔450只，白兔的只数比黑兔
复习
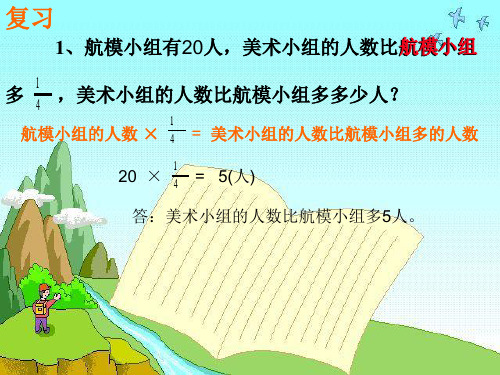
1、航模小组有20人，美术小组的人数比航模小组
多 1 ，美术小组的人数比航模小组多多少人？

1
航模小组的人数 × 4 = 美术小组的人数比航模小组多的人数
20
×
1 4
= 5(人)
答：美术小组的人数比航模小组多5人。
2、航模小组有20人，美术小组的人数比航模
小组多
1 4
。美术小组有多少人？
航模小组的人数 +美术小组比航模小组多的人数=美术小组的人数
Ⅹ
=
24×
4 3
Ⅹ = 16 答：航模小组有16人。
这类题的特点：单位“1”是未知的。
解答这类题的关键：搞清楚哪两个量比较, 谁多谁少,多或少了谁的几分之几。
解答方法：
（1）找准单位“1”的量，设未知数为X。
（2）根据含有分率的句子找出等量关系。
（3）根据“一个数乘分数的意义”用乘法列方程解答。

六年级上册数学教案-第三单元第八课时列方程解稍复杂的分数应用题｜人教新课标版

六年级上册数学教案第三单元第八课时列方程解稍复杂的分数应用题人教新课标版教学内容本课时为六年级上册数学第三单元的第八课时，主要内容为列方程解决稍复杂的分数应用题。

通过本课时的学习，学生将掌握如何将实际问题转化为数学方程，进而运用所学的分数知识解决问题。

教学目标1. 知识目标：使学生能够正确识别并解决含有分数的复杂应用题，掌握列方程解决问题的方法。

2. 能力目标：培养学生运用数学知识解决实际问题的能力，提高学生的逻辑思维和问题解决能力。

3. 情感目标：激发学生对数学学习的兴趣，培养学生面对复杂问题时的耐心和毅力。

教学难点1. 方程的建立：如何从实际问题中抽象出数学模型，建立合适的方程。

2. 分数的运算：在方程中正确处理分数的加减乘除，特别是分数的通分和约分。

3. 问题的解决：将方程的解转化为实际问题的答案，理解解的物理意义。

教具学具准备1. 教具：黑板、粉笔、教学PPT。

2. 学具：练习本、铅笔、橡皮。

教学过程1. 导入：通过简单的实际问题引入分数应用题的概念，让学生回顾分数的基本知识。

2. 探究：展示几个稍复杂的分数应用题，引导学生尝试列出方程，并讨论解题的步骤和方法。

3. 讲解：详细讲解如何建立方程，如何进行分数运算，以及如何将方程的解应用于实际问题。

4. 练习：让学生独立完成一些练习题，巩固所学知识。

5. 讨论：小组讨论解题过程中遇到的问题，分享解题的经验和技巧。

板书设计板书将清晰地展示解题步骤和关键公式，使学生能够直观地理解问题解决的过程。

作业设计作业将包括几个不同难度的分数应用题，要求学生独立完成，并鼓励家长参与和监督。

课后反思本教案严格按照人教新课标版的要求编写，力求在教学内容、教学目标、教学难点、教具学具准备、教学过程、板书设计、作业设计、课后反思等方面做到严谨、流畅，以帮助学生更好地理解和掌握列方程解稍复杂的分数应用题。

1. 方程的建立：对于六年级的学生来说，将实际问题转化为数学方程是一个挑战。

列方程解分数应用题-十套

列方程解分數應用題（一）1、一個人抄一篇稿件，第一次抄1500個字，第二次抄2000個字，還剩下83沒有抄，這篇稿件共有多少個字？2、某機器廠七月份上半月完成月計劃の52，下半月完成月計劃の43，結果超額完成機器6臺，原計劃生產機器多少臺？3、某築路隊修一條公路，第一天修了全長の41，第二天修了餘下の51，這時距中點6千米，這條公路長多少千米？4、步行者走完2千米及所餘路程の一半後，還剩全程の31又2千米，全程共有多少千米？5、某廠要運走一批化工原料，上午運了52噸，下午運了餘下の83，這一天共運走這批原料の21，這批化工原料共有多少噸？6、一筐蘋果，筐占蘋果重量の252，蘋果賣掉48千克後，蘋果の重量相當於筐重の21，問原來蘋果有幾千克？7、一個班早晨到校時缺席人數是出席人數の61，後來一個同學因病請假了，這時缺席の人是出席人數の51。

問這個班有多少名學生？8、商店運進一批香蕉，第一天賣出全部の92，第二天賣出剩下の71，第三天補進第二天剩下の21，這時還有香蕉305千克，問原來有香蕉多少千克？列方程解分數應用題（二）1、五年一班有54名學生，女生人數の52等於男生人數の21，男女生各有多少人？2、五年級與六年級共有學生270人，五年級學生人數の52比六年級學生の41多4人，這兩個年級の學生相差多少人？3、飼養場有牛和羊980頭，牛の頭數比羊の52還多28頭，問飼養場牛羊各多少頭？4、兩根鋼筋共長18米，如果把第一根截去51，把第二根接長0.9米，那麼兩根鋼筋就一樣長了，兩根鋼筋原來各長幾米？5、一只布袋中裝有黑、白、花三種球，黑球の32與白球同樣多，白球の32再加3只與花球一樣多，黑球比花球多32只。

布袋中有多少只球？6、某廠共有職工152人，選出男職工の111和5名女職工去修理廠房，剩下の男女工人數相等，問這個廠男、女職工各多少人？7、兩個倉庫共有水泥84噸，如果從甲倉庫取出51放入乙倉庫，那麼甲倉庫の水泥就比乙倉庫の水泥多31，求兩個倉庫原來各有水泥多少噸？8、一批貨物重1000噸，由三個運輸隊運送到某地，第一隊運了這批貨物の52，第三隊運の是第一、二隊運の31，三個隊各運貨物多少噸？列方程解分數應用題（三）1、金工車間有兩班職工，甲班職工比乙班職工少9人，因工作需要，從甲調出3人到乙班，這時甲班職工比乙班少83，兩個班原來各有職工多少人？2、光明小學六年級上學期男生人數占總人數の55%，今年開學初轉走了3名男生，又轉來了3名女生，這時女生占總人數の48%，光明小學六年級現在有女生多少人？3、水果店運來一批梨，第一天比第二天多賣出51，第一天比第一天少賣出152千克，兩天正好賣完，這批梨有多少千克？4、王師傅加工一批零件，第一天第小時加工20個，第二天每小時加工30個，兩天加工の數量同樣多，共用了13.5小時，這批零件共有多少個？5、哥哥和弟弟共有圖書若幹本，哥哥の圖書占總圖書の53，若哥哥給弟弟9本，則兩人の圖書同樣多，哥哥原來有圖書多少本？6、甲乙丙三個同學參加儲蓄，甲存款是乙の54，丙存款比乙少40%，已知甲存了500元，丙存了多少元？ 7、小王和小李共同加工一批兒童服裝，小王單獨做要18天完成，小李每天加工16件，當完成任務時，小王做了這批服裝の95，這批兒童服裝共有多少件？8、東風農場原來有旱田108公頃，水田36公頃，為了提高產量，將一部分旱田改為水田，使水田の面積是旱田の75，問：將多少公頃旱田改為水田？列方程解分數應用題（四）1、一根鋼筋，鋸下20%後，又接上2米，這時鋼筋比原來短101，原來這根鋼筋有多長？2、業餘體校新購進三種球，其中籃球占總數の31，足球の個數與其它兩種球個數の比是1：5，排球有150個，三種球共有多少個？3、糧店中の大米占糧食總量の73，賣出600千克大米後，大米占糧食總量の31，這個糧店原來共有糧食多少千克？ 4、五年一班有一部分學生參加運動會，其中72是女生，男生是20人，已知全班男生有54參加了運動會，沒有參加運動會の占全班人數の239，這個班有多少名女生？5、六一班共有學生40人，其中女生占全班人數の52，後來又轉來幾名女生，這時女生人數占全班人數の157，又轉來幾名女生？6、加工一批零件，如果師傅單獨做20小時完成，師徒二人合作12小時完成，現在師徒二人合作，完成任務時，師傅比徒弟多做了960個，這批零件有多少個？7、育紅小學高年級學生人數占全校學生總數の36%，中年級學生人數是高年級の95，低年級比中年級多84人，育紅小學共有學生多少人？8、學校植樹，第一天完成了計劃の83，第二完成餘下の32，第三天植樹55棵，結果超過計劃41完成任務，原計劃植樹多少棵？列方程解分數應用題（五） 1、參加六一聯歡の少先隊員中，女隊員占73，男隊員比女隊員の32多40人，女隊員有多少人？2、一天某班第一節缺席の人數是出席人數の61，課間又有一位同學請假離去，於是缺席人數占出席人數の51，這個班有多少名學生？3、某廠の工人中，女工比男工多32，後來又把45名男工換為女工，使得女工人數達到總人數の2920，這時有多少名女工？4、閱覽室裏有36名同學在看書，其中94是女生，後來又轉來了幾名女生，使得女生人數達到總人數の199，又來了幾名女生？5、趙軍從甲地乘車到乙地，原計劃每小時行40千米，實際每小時只行了30千米，當行到比全程の32多20千米時，已經比預定行完全程の時間多用了31小時，甲乙兩地相距多少千米？6、兩個雞籠，小籠裏の雞比大籠の少18只，如果從小籠裏取出6只放入大籠，那麼小籠裏雞の只數就是大籠の74，兩個籠子裏原來各有多少只雞？7、五一班女同學比男同學の32多4人，如果男同學減少3人，女同學增加4人，那麼男女人數相等，這個班男女同學各有幾人？8、箱子裏有紅、黃、藍三種顏色の球，紅球の32與黃球同樣多，黃球の32再加上3個與藍球同樣多，紅球比藍球多32個，箱子裏有多少個黃球？列方程解分數應用題（六）1、一個數學興趣小組，女生占全組人數の41，後來又吸收了4名女生參加，這時女生人數占全組人數の31，男生有多少人？2、甲乙二人共存款108元，如果甲取出自己存款の52，乙取出12元後，二人所存錢數相等，甲乙二人原來各存款多少元？3、金放在水裏稱，重量減少1/19，銀放在水裏稱，重量減少1/10，一塊金銀合金重770克，放在水裏稱，重量減少了50克，這塊合金含金、銀各多少克？4、甲乙二人共有人民幣若幹元，其中甲占60%，若乙給甲12元，則乙餘下の錢占總數の25%，甲乙二人共有人民幣多少元？5、四位同學共種樹60棵，第一位同學種の是其它同學種の一半，第二位同學種の是其它同學種の1/3，第三位同學種の是其它同學種の1/4，第四位同學種了多少棵？6、甲乙二人各有人民幣若幹元，其中甲占60%，若乙給甲12元後，乙剩下の錢相當於甲の1/3，甲乙二人共有人民幣多少元？7、甲乙二人各有人民幣若幹元，乙是甲の2/3，若乙給甲12元，則乙相當於甲の1/3，甲乙二人共有人民幣多少元？8、甲乙二人同時從東鎮到西鎮，甲走了全程の2/5時，乙只走了9.6千米,當甲到達西鎮時,乙離西鎮還有全程の3/11,求東西兩鎮の距離。

列方程解复杂的分数应用题

复杂的分数应用题（A ）姓名（）1、一个人抄一篇稿件，第一次抄100个字，第二次抄200个字，还剩下113没有抄，这篇稿件共有多少个字？2、某机器厂七月份上半月完成月计划的52，下半月完成月计划的43，结果超额完成机器18台，原计划生产机器多少台？3、五年级一班有48名学生，女生人数的52等于男生人数的21，男女生各有多少人？4、五年级与六年级共有学生360人，五年级学生人数的52比六年级学生的41多4人，这两个年级的学生相差多少人？5、饲养场有牛和羊98头，牛的头数比羊的52还多28头，问饲养场牛羊各多少头？6、两根钢筋共长180分米，如果把第一根截去51，把第二根接长9分米，那么两根钢筋就一样长了，两根钢筋原来各长几分米？7、某厂共有职工163人，选出男职工的111和5名女职工去修理厂房，剩下的男女工人数相等，问这个厂男、女职工各多少人？8、金工车间有两班职工，甲班职工比乙班职工少9人，因工作需要，从甲调出3人到乙班，这时甲班职工比乙班少83，两个班原来各有职工多少人？复杂的分数应用题（B ）姓名（）1、水果店运来一批梨，第一天比第二天多卖出51，第二天比第一天少卖出12千克，两天正好卖完，这批梨有多少千克？2、哥哥和弟弟共有图书若干本，哥哥的图书占总图书的53，若哥哥给弟弟9本，则两人的图书同样多，哥哥原来有图书多少本？3、一根钢筋，锯下20%后，又接上2米，这时钢筋比原来短101，原来这根钢筋有多长？4、粮店中的大米占粮食总量的73，卖出600千克大米后，大米占粮食总量的31，这个粮店原来共有粮食多少千克？5、五年级一班有一部分学生参加运动会，其中72是女生，男生是20人，已知全班男生有54参加了运动会，没有参加运动会的占全班人数的239，这个班有多少名女生？6、六一班共有学生40人，其中女生占全班人数的52，后来又转来几名女生，这时女生人数占全班人数的157，又转来几名女生？7、育红小学高年级学生人数占全校学生总数的36%，中年级学生人数是高年级的95，低年级比中年级多84人，育红小学共有学生多少人？8、学校植树，第一天完成了计划的83，第二完成余下的32，第三天植树55棵，结果超过计划41完成任务，原计划植树多少棵？列方程解分数应用题（C ）姓名（）1、参加六一联欢的少先队员中，女队员占73，男队员比女队员的32多40人，共有多少名少先队员？2、一天某班第一节缺席的人数是出席人数的61，课间又有一位同学请假离去，于是缺席人数占出席人数的51，这个班有多少名学生？3、阅览室里有36名同学在看书，其中94是女生，后来又转来了几名女生，使得女生人数达到总人数的199，又来了几名女生？4、两个鸡笼，小笼里的鸡比大笼的少18只，如果从小笼里取出6只放入大笼，那么小笼里鸡的只数就是大笼的74，两个笼子里原来各有多少只鸡？5、五一班女同学比男同学的32多4人，如果男同学减少3人，女同学增加4人，那么男女人数相等，这个班男女同学各有几人？6、一个数学兴趣小组，女生占全组人数的41，后来又吸收了4名女生参加，这时女生人数占全组人数的31，男生有多少人？7、甲乙二人共存款108元，如果甲取出自己存款的52，乙取出12元后，二人所存钱数相等，甲乙二人原来各存款多少元？8、金放在水里称，重量减少 191，银放在水里称，重量减少101，一块金银合金重770克，放在水里称，重量减少了50克，这块合金含金、银各多少克？。

小学六年级数学列方程解稍复杂的分数应用题教案

小学六年级数学列方程解稍复杂的分数应用题教案教学目的：使学生在明白得数量关系的基础上学会用方程解答稍复杂的分数应用题，提高学生的分析推理能力。

教学过程：一、复习。

出示课本第88页的复习题：小红家买来一袋大米，重40千克，吃了，还剩多少千克？1．指定一学生口述题目的条件和问题，其他学生画出线段图。

2．学生独立解答。

3．集体订正。

提问学生说一说两种方法解题的过程。

小结：解答分数应用题的关键是找准单位1，假如单位1的具体数量是已知的，要求单位1的几分之几是多少，就能够依照分数乘法的意义，直截了当用乘法运算。

二、新授。

1．教学例6。

（1）出示例6：小红家买来一袋大米，吃了，还剩15千克。

买来大米多少千克？引导学生明白得题意，画出线段图。

问；这道题已知条件和问题分别是什么？吃了是什么意思？应该把哪个数量看作单位`1`？（引导学生说出：吃了买来大米重量的，要把买来大米重量看作单位1。

）引导学生试画出线段图。

吃了1问；还有什么已知条件图中没有表示出出来？（引导学生说出还剩15千克没有表示出来，应在线段右边三格的上面写出剩15千克）吃了1问：这道题的问题是什么？在图中如何样表示？（学生回答后教师在图中注明问题。

）（2）分析数量关系。

问：依照题意，单位1的数量是已知依旧未知的？应该如何样做？（引导学生说出设要求的问题为X，用方程来解这道应用题。

）问：题中的数量关系式是如何样的？（引导学生得出：买来大米的重量－吃了的重量=剩下的重量）（3）指名列出方程。

教师板书：解：设买来大米X千克。

x－x=15问：那个地点吃了的重量什么缘故用x表示？（4）解方程。

问：那个方程的左边x－x如何样运算？（引导学生得出：（1－）x=15）问：我们是依照什么如此写的？1－表示的是什么？学生连续把方程解答完毕。

（5）观看比较。

引导学生观看例6与复习题的两个线段图，问：例6和复习题的条件和问题有什么不同？解答方法有什么不同？（引导学生得出：复习题中单位1的量是已知的，求单位1的量的几分之几是多少？用乘法算；例6剩下大米的千克数是已知的，而单位1的量是未知的，求单位1的量，要列方程解答。

小学六年级数学教案列方程解稍复杂的分数应用题

小学六年级数学教案列方程解稍复杂的分数应用题教学目标1．明白得稍复杂的已知一个数的几分之几是多少，求那个数的应用题的数量关系．2．会列方程解答这类应用题．3．培养学生分析推理能力．教学重点分析应用题的数量关系．教学难点找应用题的等量关系．教学过程一、复习旧知．小红买来一袋大米重40千克，吃了，还剩多少千克？1．画图明白得题意2．指名叙述解答过程．3．列式解答40－40 40（1－）教师小结：解答分数应用题，关键是找准单位1，假如单位1是已知的，求它的几分之几是多少，就能够依照一个数乘分数的意义直截了当用乘法运算．二、探究新知．（一）变式引出例6例6．小红买来一袋大米，吃了，还剩15千克买来大米多少千克？1．读题2．画线段图3．分析数量关系，列方程．4．教师提问：题中表示等量关系的三个量是什么？能够如何样列方程？（1）解：设买来大米千克．买来大米的重量－吃了的重量＝剩下的重量（2）买来大米的重量剩下几分之几＝剩下的重量5．学生自己解方程并检验．答：这袋大米重40千克．（二）归纳总结．例6中的单位1是未知的，而已知剩下的量和吃了的分率，要求的恰好是单位1的重量，因此不能直截了当用乘法直截了当乘，能够列方程解答．或是找准和已知量相对应的分率用除法解答．三、巩固练习（一）找出下面各题的等量关系和对应关系．1．某修路除要修一条路，差不多修了全长的，还剩240米没修，这条路全长是多少米？等量关系：一条路的长度－差不多修的米数＝没修的米数一条路的长度没修的分率＝没修的米数对应关系：剩的米数剩下的分率＝全长的米数2．一根电线杆，埋在地下的部分是全长的，露地面的部分是5米．这根电线杆长多少米？3．选择正确的列式．一个畜牧场卖出肉牛头数的，还剩300头，那个畜牧场共有肉牛多少头？正确列式是（）解：设共有肉牛头．（1）（2）（3）（4）四、质疑小结列方程解应用题的关键是什么？如何样准确迅速地找出题中等量关系？五、板书设计列方程解分数应用题例6．小红买来一袋大米，吃了，还剩15千克买来大米多少千克？要练说，得练听。

难算的分数(比和比例)应用题(一)

难算的分数（比和比例）应用题（一）1、一条路已修了500米，是未修的2/5，求这条路一共有多长？解答：已修的是未修的2/5，那就是说是已修的是全长的2/7。

列式为：500÷2/7=1750（米）答：略。

2、一桶油用去1/5后连桶重14千克，用去1/3后连桶重12千克，求桶重多少千克？油重多少千克？分析与解答：用去油1/5后连桶重14千克，用去1/3后连桶重12千克，那就是说这桶油的1/3比1/5多2千克，也就是说1/3—1/5=2/15就是2千克。

那么这桶油重可以列式求出来：（14-12）÷（1/3—1/5）=2÷2/15=15（千克）那么桶重就是14-15×（1—1/5）=2（千克）或者12-15×（1—1/3）=2（千克）答：略。

3、修一条水渠，已修了4天，平均每天修35米，已修的比剩下的少全长的30%，这条水渠全长多少米？分析与解答：已修四天，每天修35米，则已修的是35×4=140米。

已修的比剩下的少全长的30%，那就是说，如果去掉这30%，剩下的和已修的刚好相等。

于是就有：（100%—30%）÷2=35%，这35%就是已修的。

到这儿就很好算了。

列式：35×4÷[（100%—30%）÷2]=140÷35%=400 （米）列方程为：解：设这条路全长为X米，则X—35×4—35×4=30%X 或（X—30%X）÷2=35×4答：略。

4、师傅和徒弟合做200个零件，师傅做的1/4比徒弟做的1/5多14个，求徒弟做了多少个？分析：师傅做的1/4比徒弟做的1/5多14个，那就是说，师傅做的4/4比徒弟做的4/5多14×4=56（个）。

这样题就变成了“师傅和徒弟合做200个零件，师傅做的比徒弟做的4/5多56个，求徒弟做了多少个？”这已是一个和倍问题了。

数学教案-列方程解稍复杂的分数应用题

数学教案-列方程解稍复杂的分数应用题数学教案－列方程解稍复杂的分数应用题（二）1．进一步理解稍复杂的分数除法应用题的数量关系．2．能够比较熟练地列方程解应用题．3．培养学生分析问题和解决问题的能力．教学重点分析数量关系．教学难点找等量关系．教学过程一、复习．（一）找出单位“1”1．一本书已经看了2．实际比计划节约3．今年产量比去年提高4．乙数比甲数少（二）谈话导入今天我们继续学习分数应用题．二、讲授新课．（一）教学例7例7．某工厂十月份用水4800吨，比原计划节约了，十月份原计划用水多少吨？1．读题理解题意，画出线段图．2．教师提问（1）哪句话是说明数量关系的？（2）怎样理解这句话？（3）你能根据这句话画出线段图吗？3．分析数量关系把原计划用水的吨数看作单位“1”，原计划用水的吨数是未知的，可以用表示．已知实际用水比原计划节约，也就说“计划用水吨数－节约的吨数=实际用水吨数”或者说“原计划用水吨数某=实际用水吨数”．根据这样的等量关系式可以列方程解答．4．列方程，解方程．解：设十月份原计划用水吨．答：原计划用水540吨．三、巩固练习．（一）根据方程补充一个已知条件．学校种了苹果树和桃树，苹果树有20棵，________________，桃树有棵．1．2．3．（二）找出单位“1”，说等量关系．1．海豚每小时可以游70千米，比蓝鲸的速度快，蓝鲸的速度是多少？2．有一本故事书，小明第一天看了48页，第二天比第一天少，第二天看了多少页？3．李红家一月份用煤气20立方分米，二月份比一月份节约了，二月份用煤气多少立方米？四、质疑小结．例7．某工厂十月份用水4800吨，比原计划节约了，十月份原计划用水多少吨？解：设原计划用吨，答：原计划用540吨．分数除法应用题1．使学生掌握列方程解答“已知一个数的几分之几是多少，求这个数”的应用题的解答方法2．培养学生分析问题、解答问题能力，以及认真审题的良好习惯．教学重点找准单位“1”，找出等量关系．教学难点能正确的分析数量关系并列方程解答应用题．教学过程一、复习、引新（一）确定单位“1”1．铅笔的支数是钢笔的倍．2．杨树的棵数是柳树的．3．白兔只数的是黑兔．4．红花朵数的相当于黄花．（二）小营村全村有耕地75公顷，其中棉田占．小营村的棉田有多少公顷？1．找出题目中的已知条件和未知条件．2．分析题意并列式解答．二、讲授新课（一）将复习题改成例1例1．小营村有棉田45公顷，占全村耕地面积的，全村的耕地面积是多少公顷？1．找出已知条件和问题2．抓住哪句话来分析？3．引导学生用线段图来表示题目中的数量关系．4．比较复习题与例1的相同点与不同点．5．教师提问：（1）棉田面积占全村耕地面积的，谁是单位“1”？（2）如果要求全村耕地面积的是多少，应该怎样列式？（全村耕地面积某）．（3）全村耕地面积的就是谁的面积？（就是棉田的面积）解：设全村耕地面积是公顷．答：全村耕地面积是75公顷．6．教师提问：应怎样进行检验？你还能用别的方法来解答吗？（1）把代入原方程，左边，右边是45，左边＝右边，所以是原方程的解．）（公顷）（根据棉田面积和是已知的，全村耕地面积是未知的，根据分数除法意义，已知两个因数的积与其中一个因数，求另一个因数应该用除法计算．）（二）练习果园里有桃树560棵，占果树总数的．果园里一共有果树多少棵？1．找出已知条件和问题2．画图并分析数量关系3．列式解答解1：设一共有果树棵．答：一共有果树640棵．解1：（棵）（三）教学例2例2．一条裤子75元，是一件上衣价格的．一件上衣多少钱？1．教师提问（1）题中的已知条件和问题有什么？（2）有几个量相比较，应把哪个数量作为单位“1”？2．引导学生说出线段图应怎样画？上衣价格的3．分析：上衣价格的就是谁的价钱？（是裤子的价钱）谁能找出数量间相等的关系？（上衣的单价某＝裤子的单价）4．让学生独立用列方程的方法解答，并加强个别辅导．解：设一件上衣元．答：一件上衣元．5．怎样直接用算术方法求出上衣的单价？（元）6．比较一下算术解法和方程解法的相同之处与不同之处．相同点：都要根据数量间相等的关系式来列式．不同点：算术解法是按照分数除法的意义直接列出除法算式；而方程解法则要先设未知数，再按照等量关系式列出方程．三、巩固练习（一）一个修路队修一条路，第一天修了全长，正好是160米，这条路全长是多少米？提问：谁是单位“1”？数量间相等的关系式是什么？怎样列式？（米）（二）幼儿园买来千克水果糖，是买来的牛奶糖的，买来牛奶糖多少千克？（三）新风小学去年植树320棵，相当于今年植树棵数的．今年、去年共植树多少棵？1．课件演示：分数除法应用题2．列式解答四、课堂小结这节课我们学习了列方程解答分数除法应用题的方法．这类题有什么特点？解题时分几步？五、课后作业（一）一桶水，用去它的，正好是15千克．这桶水重多少千克？（二）王新买了一本书和一枝钢笔．书的价格是4元，正好是钢笔价格的．钢笔价格是多少元？（三）一种小汽车的最快速度是每小时行140千米，相当于一种超音速飞机速度的．这种超音速飞机每小时飞行多少千米？六、板书设计分数除法应用题（二）教学目标1．理解以“和倍”问题为基础的分数应用题的解题思路。

列方程解决稍复杂的有关分数除法问题练习题(含答案)

第6课时列方程解决稍复杂的有关分数除法问题本课导学本课知识点：在理解数量关系的基础上学会已知一个数的几分之几是多少求这个数的稍复杂分数除法应用题的解题思路和方法,能比较熟练地解答一些简单的实际问题。

一桶油,连桶共重76千克,用去32的以后,连桶共重26千克。

原来桶中的油有多少千克？特别提醒：用方程解答分数应用题的关键是找准单位“1”,再按照题意找出数量间的相等关系列出方程。

【快乐训练营】一、想一想,填一填。

1.50是80的（）,80比50多（）。

2.篮球的数量比足球多41,篮球的数量是足球的（）。

3.汽车的现价比原价降低了71,现价是原价的（）。

4.合唱队的人数比舞蹈队多32,舞蹈队的人数是合唱队的（）。

5.小明家四月份的电费比三月份节约101,三月份电费是四月份的（）。

二、看图填空。

1.苹果树棵数是桃树棵数的（）,比桃树多（）。

2.桃树棵数是苹果树棵数的（）,比苹果树少（）。

三、判断是非。

（对的画“√”,错的画“×”）苹果树棵数：桃树棵数：四、精挑细选。

（把正确答案的序号填在括号里）1.白兔有35只,黑兔的只数比白兔少71,黑兔比白兔少（）只。

A . 35×71B . 35×（1－71）C . 35÷71D . 35÷（1－71）2.公鸡有80只,比母鸡多53,母鸡有（）只。

A . 80×（1－53）B . 80÷（1－53）C . 80×（1＋53）D . 80÷（1＋53）【知识加油站】五、看图列式（或方程）并解答。

1.2.六、根据算式补充适当的条件。

六年五班图书角有漫画书36本, ,故事书有多少本？（1）36×31条件：（2）36×（1＋31）条件：（3）36÷（1－31）条件：（4）36÷（1＋31）150吨大米：大豆：？吨160本故事书：多17？本条件：七、解决问题。

列方程解稍复杂的分数应用题

列方程解稍复杂的分数应用题教学目标1．理解稍复杂的已知一个数的几分之几是多少，求这个数的应用题的数量关系．2．会列方程解答这类应用题．3．培养学生分析推理能力．教学重点分析应用题的数量关系．教学难点找应用题的等量关系．教学过程一、复习旧知．小红买来一袋大米重40千克，吃了，还剩多少千克？1．画图理解题意2．指名叙述解答过程．3．列式解答40－40× 40×（1－）教师小结：解答分数应用题，关键是找准单位“1”，如果单位“1”是已知的，求它的几分之几是多少，就可以根据一个数乘分数的意义直接用乘法计算．二、探究新知．（一）变式引出例6例6．小红买来一袋大米，吃了，还剩15千克买来大米多少千克？1．读题2．画线段图3．分析数量关系，列方程．4．教师提问：题中表示等量关系的三个量是什么？可以怎样列方程？（1）解：设买来大米千克．买来大米的重量－吃了的重量＝剩下的重量（2）买来大米的重量×剩下几分之几＝剩下的重量 5．学生自己解方程并检验．答：这袋大米重40千克．（二）归纳总结．例6中的单位“1”是未知的，而已知剩下的量和吃了的分率，要求的恰好是单位“1”的重量，所以不能直接用乘法直接乘，可以列方程解答．或是找准和已知量相对应的分率用除法解答．三、巩固练习（一）找出下面各题的等量关系和对应关系．1．某修路除要修一条路，已经修了全长的，还剩240米没修，这条路全长是多少米？等量关系：一条路的长度－已经修的米数＝没修的米数一条路的长度×没修的分率＝没修的米数对应关系：剩的米数÷剩下的分率＝全长的米数2．一根电线杆，埋在地下的部分是全长的，露地面的部分是5米．这根电线杆长多少米？3．选择正确的列式．一个畜牧场卖出肉牛头数的，还剩300头，这个畜牧场共有肉牛多少头？正确列式是（）解：设共有肉牛头．（1）（2）（3）（4）四、质疑小结列方程解应用题的关键是什么？怎样准确迅速地找出题中等量关系？五、板书设计列方程解分数应用题例6．小红买来一袋大米，吃了，还剩15千克买来大米多少千克？解：设一袋大米重千克．一袋大米重量－吃去的重量＝还剩的重量答：一袋大米重40千克．。

数学教案列方程解稍复杂的分数应用题

数学教案列方程解稍复杂的分数应用题一、教学目标1、让学生能够理解并掌握列方程解稍复杂的分数应用题的方法和步骤。

2、培养学生分析问题、解决问题的能力，提高学生的逻辑思维能力。

3、让学生在解决实际问题的过程中，感受数学与生活的紧密联系，激发学生学习数学的兴趣。

二、教学重难点1、教学重点掌握列方程解稍复杂的分数应用题的思路和方法，找准单位“1”，设出未知数，找出等量关系并列出方程。

2、教学难点正确找出题目中的等量关系，理解单位“1”的变化对解题的影响。

三、教学方法讲授法、讨论法、练习法四、教学过程1、导入通过复习简单的分数应用题，如“某工厂有工人 200 人，其中女工占 3/5，女工有多少人？”引导学生回顾分数乘法的应用，然后出示一道稍复杂的分数应用题：“某工厂有工人 200 人，其中女工占 3/5，后来又招进了一些女工，这时女工人数占总人数的 7/10，问招进了多少女工？”引发学生的思考，从而导入新课。

2、新授（1）读题，理解题意让学生仔细读题，找出题目中的已知条件和所求问题。

（2）分析题目引导学生分析题目中的数量关系，确定单位“1”。

在这道题中，原来工厂的总人数是单位“1”，招进女工后，工厂的总人数发生了变化，此时的总人数是单位“1”。

（3）设未知数让学生设招进的女工人数为 x 人。

（4）找等量关系根据题目中的条件，可以找出等量关系：原来女工的人数＋招进的女工人数＝现在女工的人数。

原来女工的人数为 200×3/5 ＝ 120 人，现在女工的人数为（200 ＋x）×7/10 人。

（5）列方程根据等量关系列出方程：120 ＋ x ＝（200 ＋ x）×7/10（6）解方程先将方程右边的式子展开：120 ＋ x ＝ 140 ＋ 7/10x移项：x 7/10x ＝ 140 1203/10x ＝ 20解得：x ＝200/3 ≈ 6667由于人数必须为整数，所以招进的女工人数约为 67 人。

稍复杂的分数除法应用题

两种方法用到的等量关系式是什么？上半场得分＋下半场得分＝42分两种方法的等量关系一样，为什么列出的方程不一样呢？列方程，解方程后，如何检验呢？
绿色圃中小学教育网绿色圃中小学教育网
某电视厂去年全年生产电视机108万台，其中上半年
3、请你根据等量关系式列方程并解答。
“下半场得分只有上半场的一半”这句话还可以怎么说？ “上半场得分是下半场的2倍”
如果这样说的话，又该怎样画线段图？请你试一试。
绿色圃中小学教育网
下半场得分：上半场得分：
“1”
？分 2倍？分
42分
1、你能说出等量关系式吗？（上半场得分＋下半场得分＝42分） 2、列方程解答，该怎样设呢？ 3、你会列出方程吗？
产量是下半年的Biblioteka 4 5。这个电视机厂去年上半年和下
半年的产量分别是多少万台？
你知道了什么？
还有别的方法吗？
把（）看作单位“1”。等量关系是什么？
列方程解答该怎样设？
怎样列方程？
怎样检验？
这这套套运运动动服服的共上3衣00比元裤。子贵
6的0裤元子23。。价裤钱子是价上钱衣是的上衣23 。
上衣和裤子各多少钱？
1、苹果的质量是梨的
2 3
，那么梨的质量是苹果的（
3 2
）。
2、男生的人数是女生的
3 5
，那么女生的人数是男生的（
5 3
）。
3、上衣的价钱是裤子的
4 3
，那么裤子的价钱是上衣的（
3 4
）。
女生人数男生人数
1、根据线段图，我知道：
女生人数有（ 4 ）份，男生人数有（ 5 ）份。
女生人数是男生的（
4 5
）。

列方程解比较复杂的分数应用题(供参考)

第七讲列方程解比较复杂的分数应用题一、知识要点有一些数量关系比较复杂的分数应用题，列算式解答比较繁难，甚至无法列出，这时我们可以根据题中的等量关系来列方程解答。

二、知识运用典型例题。

例1、某校有学生702人，女生人数比男生人数的54少18人。

男、女生各有多少人？例2、小华从家去车站，行到全程的98处是邮局。

他从车站回家，行到全程的31处时，已超过邮局420米。

小华家到邮局有多少米？例3、一批铅笔分给甲、乙、丙三人，分给甲17，分给乙14，分给丙的数量是分给甲乙二人数量差的2倍，这时还剩下11支铅笔，问：甲分到几支铅笔？例4、一件商品，随季节变化降价出售，如果按现价降低110，仍可赢利180元，如果降价15，就要亏损240元，这种商品的进价多少元？例5、新华书店新进一批图书，其中科技书占53，后来又购进400本科技书，这时科技书的本数占图书总数的32。

新华书店原来购进多少本科技书？三、知识运用课堂训练1、某工厂有四个车间，第一、二车间共有28人，第二、三、四车间共有48人，已知第二车间的人数占全厂总人数的154。

这个工厂有多少人？ 2、甲乙两校共有22人参加竞赛，甲校参加人数的15比乙校参加人数的14少1人，甲乙两校各有多少人参加？3、甲乙两个车间，甲车间人数占两个车间总人数的58，如果从甲车间抽90人到乙车间后，则甲车间的人数正好是乙车间人数的23，原来两个车间各有多少人？第七讲知识运用课后训练等级1、李师傅计划生产一批零件，上午生产了计划的53，下午生产计划的32，结果超产零件36个。

李师傅计划生产零件多少个？2、小明星期六、星期日共卖了72张报纸，星期六卖的25与星期日的59共33张，小明星期六卖了多少张报纸？3、甲、乙两人原来各有若干元，甲的钱数是乙的85。

如果甲用去20元，乙用去50元，这时两人剩下的钱数相等。

甲、乙两人原来各有多少元？。