稳恒电流和稳恒磁场1 恒定电流
大学物理磁学部分复习资料..

41 磁 学基本内容一、稳恒磁场 磁感应强度1. 稳恒磁场电流、运动电荷、永久磁体在周围空间激发磁场。
稳恒磁场是指不随时间变化的磁场。
稳恒电流激发的磁场是一种稳恒磁场。
2. 物质磁性的电本质无论是永磁体还是导线中的电流,它们的磁效应的根源都是电荷的运动。
因此,磁场是运动电荷的场。
3. 磁感应强度磁感应强度B是描述磁场的基本物理量,它的作用与E 在描述电场时的作用相当。
磁场对处于其中的载流导线、运动电荷、载流线圈、永久磁体有力及力矩的作用。
可以根据这些作用确定一点处磁场的强弱和方向——磁感应强度B。
带电q 的正点电荷在磁场中以速度v运动,若在某点不受磁力,则该点磁感应强度B 的方向必与电荷通过该点的速度v平行。
当该电荷以垂直于磁感应强度B 通过该点时受磁力⊥F ,则该点磁感应强度大小qvF B ⊥=,且⊥F ,v ,B两两互相垂直并构成右手系。
二、毕奥—萨伐尔定律 运动电荷的磁场1. 磁场的叠加原理空间一点的磁感强度等于各电流单独存在时在该点产生磁感应强度的矢量和:∑=ii B B 可推广为 ⎰=B d B42B d是电流强度有限而长度无限小的电流元l d I 或电流强度无限小而空间大小不是无限小的元电流的磁场。
上式中矢量号一般不能略去,只有当各电流产生磁场方向相同时,才能去掉矢量号。
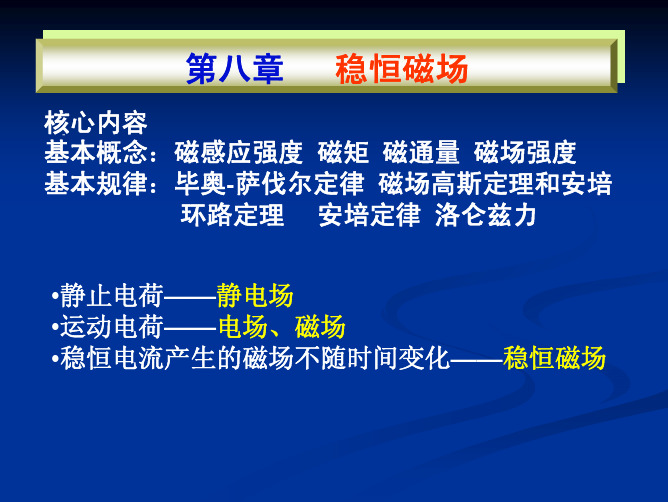
2. 毕奥—萨伐尔定律电流元l d I 在空间一点产生的磁场B d为: 304rr l d I B d πμ⨯= 大小: 02I sin(I ,r)dB 4r dl dl μπ∠=方向:B d 垂直于电流元l d I 与r 所形成的平面,且B d与l d I 、r构成右手螺旋。
3. 电流与运动电荷的关系导体中电荷定向运动形成电流,设导体截面积为S ,单位体积载流子数为n 。
每个载流子带电q ,定向运动速率为v ,则nqvS I =。
电量为q 的带电体作半径为R 、周期为T 的匀速圆周运动相当于半径为R 、电流强度T q I /=的圆电流,具有磁矩TqR I R p m 22ππ==。
稳恒磁场
二、电流的磁效应 二、电流的磁效应
I
S N •磁针和磁针 •在磁场 中运动的 电荷受到 的磁力 •磁铁与载流导 线的相互作用 S N S N
•电流的磁效应
I I
•载流导 线与载流 导线的相 互作用
三、磁场 三、磁场
1、概念
在运动电荷(或电流)周围空间存在的一种特殊形式的物质。
2、磁场的特性
•磁场对磁体、运动电荷或载流导 线有磁场力的作用; •载流导线在磁场中运动时,磁场 力要作功——磁场具有能量。
∧
Idl
r
R Idl’ θ
dB ⊥
dB dB//
P dB’
μ0 Idl sin(d l r ) μ0 Idl dB = = sin 90° 4π r2 4π r 2
分解 dB
dB ⊥ = dB cos θ
dB// = dB sin θ
电流对称
2
∫ dB
⊥
=0
μ0 I B = ∫ dB // = 4π
第八章 第八章
稳恒磁场 稳恒磁场
核心内容 基本概念:磁感应强度 磁矩 磁通量 磁场强度 基本规律:毕奥-萨伐尔定律 磁场高斯定理和安培 环路定理 安培定律 洛仑兹力 •静止电荷——静电场 •运动电荷——电场、磁场 •稳恒电流产生的磁场不随时间变化——稳恒磁场
一、电流 一、电流
8.1 电流 current
线圈所包围的面积
I
en
pm
其中 e n 与电流环绕方向符合右手螺旋法则
μ 0 IπR μ 0 pm B = (1)当x=0时,有 BO = = = 3 3 2( R 2 + x 2 ) 3 2 2R 2πR 2πR
2
μ0 I
大学物理 恒定电流稳恒磁场知识点总结

大学物理 恒定电流稳恒磁场知识点总结1. 电流强度和电流密度 电流强度:单位时间内通过导体截面的电荷量 (电流强度是标量,可正可负);电流密度:电流密度是矢量,其方向决定于该点的场强E 的方向(正电荷流动的方向),其大小等于通过该点并垂直于电流的单位截面的电流强度dQ I dt =, dIj e dS= , S I j dS =⎰⎰ 2. 电流的连续性方程和恒定电流条件 电流的连续性方程:流出闭合曲面的电流等于单位时间闭合曲面内电量增量的负值(其实质是电荷守恒定律)dqj dS dt=-⎰⎰ , ( j tρ∂∇=-∂ ); 恒定电流条件: 0j dS =⎰⎰ , ( 0j ∇= ) 3. 欧姆定律及其微分形式: UI R=, j E σ=, ,焦耳定律及其微分形式: 2Q A I Rt == 2p E σ= 4. 电动势的定义:单位正电荷沿闭合电路运行一周非静电力所作的功AK dl q ε+-==⎰ , K dl ε=⎰5. 磁感应强度:是描述磁场的物理量,是矢量,其大小为0sin FB q v θ=,式中F 是运动电荷0q 所受洛伦兹力,其方向由 0F q v B =⨯决定 磁感应线:为了形象地表示磁场在空间的分布,引入一族曲线,曲线的切向表示磁场的方向,密度是磁感应强度的大小;磁通量:sB dS φ=⎰⎰ (可形象地看成是穿过曲面磁感应线的条数)6.毕奥一萨伐尔定律: 034Idl r dB r μπ⨯=34L Idl rB r μπ⨯=⎰7.磁场的高斯定理和安培环路定理磁场的高斯定理: 0SB dS =⎰⎰、 ( 0B ∇= ) (表明磁场是无源场)安培环路定理:0i LiB dl I μ=∑⎰、LSB dl j dS =⎰⎰⎰ 、(0B j μ∇⨯=)(安培环路定理表明磁场是有旋场)8.安培定律: dF Idl B =⨯ 、L F Idl B =⨯⎰磁场对载流线圈的作用: M m B =⨯ (m 是载流线圈的磁矩m IS =)9.洛伦兹力:运动电荷所受磁场的作用力称为洛伦兹力f qv B =⨯带电粒子在匀强磁场中的运动:运动电荷在匀强磁场中作螺旋运动,运动半径为mv R qB⊥=、周期为 2m T qB π= 、螺距为 2mv h v T qB π==霍尔效应 : 12HIBV V K h-= 式中H K 称为霍尔系数,可正可负,为正时表明正电荷导电,为负时表明负电荷导电 1H K nq=10.磁化强度 磁场强度 磁化电流 磁介质中的安培环路定理mM τ∑=∆ 、 LL M dl I =∑⎰,内、n i M e =⨯, 0BH M μ=- 、m M H χ= 、 00m r B H H μχμμμ==(1+)H=、 0i LiH dl I =∑⎰、LSH dl j dS =⎰⎰⎰。
大学物理习题课-稳恒电流的稳恒磁场-2011.6.10

1 5
r r 向上, M垂直 B, 向上,
一根无限长的直圆柱形铜导线, 例5. 一根无限长的直圆柱形铜导线,外包一层相对磁导率为 µr的圆筒形磁介质,导线半径为 R1,磁介质的外半径为 R2。 的圆筒形磁介质, 导线内有电流通过, 磁介质内、 导线内有电流通过 , 求 : 磁介质内 、 外的磁场强度和磁感应 强度的分布
大学物理习题课
恒定电流的稳恒磁场
•
电流 电流密度 电动势
电流强度 电流密度
v v j = qnv
(S )
∆q dq I = lim = ∆t →0 ∆ t dt
v r 对任意曲面S: 对任意曲面 : I = ∫∫ j ⋅ dS
r I 是 j 的通量
v v dqin 电流的连续性方程 ∫∫S j ⋅ dS = − dt v v 电流稳恒条件 ∫∫ j ⋅ dS = 0
I
v × B 1
p -e 3r
用补偿法求p处的磁感应强度: 用补偿法求 处的磁感应强度: 处的磁感应强度
v v 根据 ∫ B⋅ dl = µ0 ∑Ii
L
v v
v • B2
δ
o`
v
得: B = 1
µ0δ r
6
B2 =
µ0δr
88
41µ0δr ∴B = B − B2 = 1 264
v v v v v fm = qv× B = −ev× B
计算得 方向: B = 5.0×10−16 (T) 方向:垂直于纸面向里
例2:空气中有一半径为 的“无限长”直圆柱金属导体,竖直 :空气中有一半径为r的 无限长”直圆柱金属导体, 的圆柱空洞, 线oo`为中心轴线 ,在圆柱体内挖一个直径为 r 的圆柱空洞, 为中心轴线 空洞侧面与oo`相切,在未挖洞部分通以均匀分布的电流I,方 空洞侧面与 相切,在未挖洞部分通以均匀分布的电流 , 相切 向沿oo`向下,如图所示。在距轴线 处有一电子 电量为-e) 处有一电子( 向沿 向下,如图所示。在距轴线3r处有一电子(电量为 ) 向下 o 沿平行于oo`轴方向 在中心轴线oo` 轴方向, 沿平行于 轴方向,在中心轴线 r/2
第十一章 电磁学 恒定磁场 Ma 2016

0 qnS d lv er dB 4 r2
d B 0 qv er B d N 4 r 2 方向根据右手螺旋法则, B 垂直 v 、 正, B 为 v r 的方向;q为负, B 与
q
+
r B
v
q-
q为 r组成的平面。 v r 相反。
μ0 I B (cos θ1 cos θ 2 ) 4πr0
0 π
2
I
无限长载流长直导线的磁场
θ1 θ2
μ0 I B 2πr0
注意用右手螺旋关系判断方向。 半无限长载流长直导线的磁场
1
r0
P
θ1 θ2
2 π
μ0 I B 4πr0
I
r0
P
大学物理 电磁学
2、载流圆线圈轴线上的磁场 真空中,半径为R的载流导线,通有电流I,称圆电流。求其 轴线上一点 P的磁感强度的方向和大小
1、5 点 : dB 0
7
6 5
Idl
R
×
× 3
3、7点 : dB
0 Idl 4 π R2
4
2、4、6、8 点 :
dB
0 Idl
4π R
2
sin 45
0
大学物理 电磁学
3. 毕—萨定律应用举例
dB 的方向均
沿x 轴负方向
(1) 载流长直导线的磁场
z
dz
解
2
dB
大学物理 电磁学
磁现象与电现象有没有联系?
静电场 ?
静止的电荷 运动的电荷
1820年奥斯特:发现电流的磁效应
N
稳恒电流的磁场

将线圈置于磁场中,当磁场发生变化时,线圈中产生感应电流,并 受到磁场的作用力而发生旋转,实现电磁驱动。
霍尔效应实验
将导体置于磁场中,当电流通过导体时,在导体两侧产生电势差, 这种现象称为霍尔效应,可用于测量磁场强度。
电磁感应现象实验
法拉第实验
通过在导线线圈中切割磁感线,发现导线中产生 感应电流,即电磁感应现象。
稳恒电流的磁场
https://
REPORTING
• 磁场和电流的关系 • 稳恒电流产生的磁场 • 磁场对稳恒电流的作用 • 稳恒电流的磁场应用 • 实验与观察
目录
PART 01
磁场和电流的关系
REPORTING
WENKU DESIGN
安培环路定律
安培环路定律是描述磁场和电流之间关系的物理定律,它指出磁场和电流之间的 关系是线性的,即磁场是由电流产生的,并且电流的存在会导致周围空间中磁场 的形成。
电流在磁场中的受力分析
02
根据左手定则,可以判断电流在磁场中受到的力的方向。
电磁感应
03
当导线在磁场中做切割磁感线运动时,导线中会产生感应电动
势,从而产生感应电流。
PART 03
磁场对稳恒电流的作用
REPORTING
WENKU DESIGN
洛伦兹力
定义
洛伦兹力是指带电粒子在磁场中 所受到的力,其大小与带电粒子 的电荷量、速度和磁感应强度有
磁场对电流的作用力
磁场对电流的作用力是指电流在磁场中受到的力,这个力的 大小和方向取决于电流和磁场的相互位置和方向。
磁场对电流的作用力遵循安培定律,其数学表达式为: F=IBLsinθ,其中F表示作用力,I表示电流,B表示磁场强度,L 表示导线长度,θ表示电流和磁场方向的夹角。
11-4 毕奥-萨伐尔定律
R
o * p
dx
x
x
++ ++++ ++ +++++ +
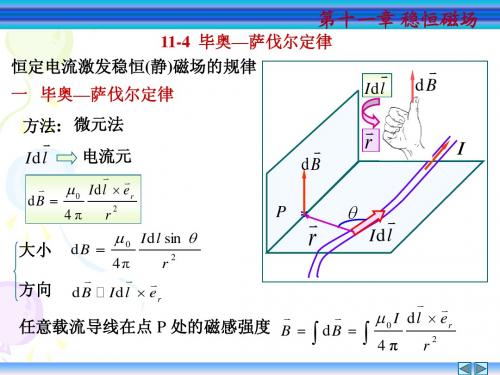
解 由圆形电流磁场公式
B=
µ 0 IR
2
2 2 3/ 2
(x + R ) 2
第十一章 稳恒磁场
β1
β
x1
o* p
β2
x2
++ + + + + + + + + + + + + +
x
dB =
µ0
2
(R + x
2
R In d x
2
2
)
3/ 2
, x 轴正向
B = µ 0 nI
或由 β1 = π , β 2 = 0 代入
B=
µ0nI
2
(cos β2 − cos β1 )
B
l − 2
π β1 = , β 2 = 0 2 1 B = µ 0 nI 2
µ0nI
l 2
1 µ 0 nI 2
O
x
第十一章 稳恒磁场 求无限长半圆筒轴上任意一点的磁感强度。 例5 求无限长半圆筒轴上任意一点的磁感强度。 y 解: 由对称性可知
σ R o
dI =
ω
σ 2 π rdr = σω rdr
o
R
B
I 解: 根据对称性分析
dB =
µ 0 Id l
4π r
2
x
B = Bx
第十一章 稳恒磁场
稳恒电流

S
稳恒电流:导体中各点的电流密度的大小和 方向不随时间变化。
电荷分布不 随时间变化
稳恒电流
稳恒电场
稳恒电流条件
S
j dS 0
单位时间从闭合面向外流出的电荷量等于单位 时间流进闭合面的电荷量。
9.1.3
欧姆定律的微分形式
一段均匀电路的 欧姆定律
U AB I R
l R S
电阻率(欧姆 米)
0
B
2 R x
2
0 IS
2 32
2当x R,即P点远离圆电流时,磁感应强度为
IS B 2x
0 3
(3)一段圆弧形载流导线在圆心处产生的磁感 应强度为
0 I 0 I B 2R 2 4R
定义:圆电流回路的磁矩
Pm ISn
S为线圈所围的面积
r
q
B
q, r
r
v
B
v
q
9.3
磁通量
恒定磁场的基本性质
dm B dS B cos dS
m
(S )
9.3.1 磁场的高斯定理
B dS
磁场高斯定理
B dS 0
S
磁场是一个无源场
9.3.2 安培环路定理
dq I I t dt
电流密度矢量
电流的方向:正电荷流 动的方向
电流在不均匀导体或大块导体中流动时, 导体中各点电流的分布不均匀。电流强度的描 述不再适用。
电流密度 矢量
dI j dS
dI
ds
ds
单位时间内通过垂直于电流方向单位面积的电量 方向: 该点电流的方向
第7章稳恒磁场

o
L
P
x
结论 任意平面载流导线在均匀磁场 中所受的力,与其始点和终点相同的载流 直导线所受的磁场力相同.
42
二 物理学 均匀磁场对载流线圈的作用力矩
将平面载流线圈放入均匀磁场中,
da边受到安培力大小:
Fda
Il
2
B
sin(
2
)
bc边受到安培力大小:
Fbc
Il 2 B
sin(
2
)
o
Fda
d
a
I
l1
qvB m v2 R
m qBR v
70 72 73 74 76
质谱仪的示意图
锗的质谱
30
物理学
霍耳效应
31
物理学
B
霍耳电压 Fm
UH
RH
IB d
b
d
vd+
+ ++
+q
+
- - - - - I
UH
Fe
qEH qvd B I qnvd S qnvdbd
EH vd B U H vd Bb
× ×
××0
粒子做匀速圆周运动
物理学
(3)
0与B成角
// 0 cos
0 sin
R m m0 sin
qB
qB
•
0 //
B
B
T 2R 2m qB
螺距 h : h //T 0 cos T 2m0 cos
qB
h //
0
q R
物理学
例题1 :请根据磁感应强度的方向规定,给 出下列情况运动电荷的受力方向:
B
c
en
第十一章 稳恒磁场

B d l 0
l
多电流情况
I1
I2
I3
B B1 B2 B3 B d l 0 ( I 2 I 3 )
l
l
以上结果对任意形状 的闭合回路(伸向无限远 的电流)均成立.
n B dl 0 Ii i 1
安培环路定理
的正负。
二、定理应用 1、螺线管内的磁场
解:对称性分析,选回路
(1)长直密绕螺线管内磁场
L.
M N +++ + + + ++++++ L O P
B
B d l B d l B d l B d l B d l
2
dB
0 Id l
r R x
2 2
2
B
0 IR
2
2 2 3
(x R )2 2
I
o
R
x
*
B
x
B
0 IR
2
2 2 3
(x R )2 2
N 0 IR
2 2 2 3
讨 论
1)若线圈有 N 匝
B
2)x 0 B 的方向不变( I 和 B 成右螺旋关系)
3)x
(x R )2 2
l MN NO OP PM
B MN 0nMNI
B 0 nI
(2)环形螺线管
解 1) 对称性分析;环内 B 线为同心圆,环外 B 为零.
l B d l 2π RB 0 NI 0 NI B 2π R
令 当
电流与磁场-稳恒电流的磁场

当导体中任意闭合曲面满足上式时,闭合曲面内没有电荷
被积累起来,此时通过导体截面的电流是恒定的——恒定 电流的条件。 1. 稳恒电流的电路必须是闭合的。
2.导体表面电流密度矢量无法向分量。
电阻率 欧姆定律的微分形式
一、电阻率
欧姆(Georg Simom Ohm,1787-1854)
德国物理学家,他从1825年开始研究导电学 问题,他利用电流的磁效应来测定通过导线 的电流,并采用验电器来测定电势差,在 1827年发现了以他名字命名的欧姆定律。 电流和电阻这两个术语也是由欧姆提出的。
2、电阻定律
对于粗细均匀的导体,当导体的材料与温度一定时,导 体的电阻与它的长度l 成正比,与它的横截面积S成反比
R l
S
:电阻率 =1/ :电导率
3、电阻与温度的关系
R
dl S
2 1 1 T2 T1
叫作电阻的温度系数,单位为K-1,与导体的材料有关。
电阻率的数量级:
4、应用:
纯金属:10-8W .m 合金:10-6W .m 半导体:10-5~10-6W .m 绝缘体:108~1017W .m
dS
dS
dI 1 dU dS
dl
U
dl
U+dU
dI 1 dU
dS dl
dU Edl
j E
j E / E
欧姆定律的微分形式: 通过导体中任一点的电流 密度,等于该点的场强与 导体的电阻率之比值
三、电流的功和功率
稳恒电流的情况下,在相同时间间隔
dt内,通过空间各点的电量 dq相同。
电场力对导线A、B内运动电荷做的功
一点的曲线数密度与该点的电流密 度的大小成正比
三、电流的连续性方程 恒定电流条件
大学物理电磁学 第11章 恒定磁场

四、毕-萨定律的应用
dB
0 4
Idl r r2
方法:
(1)将电流分解为无数个电流元
(2)由电流元求dB (据毕—萨定律)
(3)对dB积分求B = dB 矢量积分须化作分量积分去做
Bx dBx , By dBy , Bz dBz
例题1 直线电流在P点的磁场
2
解:
任取电流元 I dl
所有磁现象可归纳为:
运动电荷
运动电荷
载流导体
磁场
载流导体
磁体
磁体
磁场的宏观性质:对运动电荷(或电流)有力的 作用,磁场有能量
二、磁感应强度
B 1、磁场的描述:磁感应强度
方向: 磁针静止时,N极指向即B的正方向
S
N
2、B的大小:
以磁场对载流导线的作用为例
电流元所受到的磁场力
dF Idl sin
l
r
B
3)说明磁场为非保守场称为涡旋场
静电场是保守场、无旋场
二、简证(用特例说明安培环路定理的正确性)
(1)闭合路径L环绕电流
L在垂直于导线的平面内
B 0I 2 r
L
I d
o
B
r
dl
磁感线
(2)闭合路径L不包围电流
B dl1 dl2 L
P
·
I
d
o
dl2
dl1
L2
L1
磁感线
·
Q
三、运用安培环路定理求磁场 安培环路定理适用于任何形状恒定电流的载流体
P·
Idl r
B
dB
0 4
Idl r r2
B
dB
0 4
Idl r r2
大学物理 恒定磁场

11-1 恒定电流电流密度磁现象:我国是世界上最早发现和应用磁现象的国家之一,早在公元前300年久发现了磁铁矿石吸引铁的现象。
在11世纪,我国已制造出航海用的指南。
在1820年之前,人们对磁现象的研究仅局限于铁磁极间的相吸和排斥,而对磁与电两种现象的研究彼此独立,毫无关联。
1820年7月丹麦物理学家奥斯特发表了《电流对磁针作用的实验》,公布了他观察到的电流对磁针的作用,从此开创了磁电统一的新时代。
奥斯特的发现立即引起了法国数学家和物理学家安培的注意,他在短短的几个星期内对电流的磁效应作出了系列研究,发现不仅电流对磁针有作用,而且两个电流之间彼此也有作用,如图所示;位于磁铁附近的载流线圈也会受到力或力矩的作用而运动。
此外,他还发现若用铜线制成一个线圈,通电时其行为类似于一块磁铁。
这使他得出这样一个结论:天然磁性的产生也是由于磁体内部有电流流动。
每个磁性物质分子内部,都自然地包含一环形电流,称为分子电流,每个分子电流相当于一个极小的磁体,称为分子磁矩。
一般物体未被磁化时,单个分子磁矩取向杂乱无章,因而对外不显磁性;而在磁性物体内部,分子磁矩的取向至少未被完全抵消,因而导致磁铁之间有“磁力”相互作用。
1820年是人们对电磁现象的研究取得重大成果的一年。
人们发现,电荷的运动是一切磁现象的根源。
一方面,运动电荷在其周围空间激发磁场;另一方面,运动电荷在空间除受电场力作用之外,还受磁场力作用。
电磁现象是一个统一的整体,电学和磁学不再是两个分立的学科。
11-1 恒定电流电流密度如前所述,电荷的运动是一切磁现象的根源。
电荷的定向运动形成电流,称为传导电流;若电荷或宏观带电物体在空间作机械运动,形成的电流称为运流电流。
常见的电流是沿着一根导线流动的电流,其强弱用电流强度来描述,它等于单位时间通过某一截面的电量,方向与正电荷流动的方向相同,其数学表达式为dtdq I ,虽然我们规定了电流强度的方向,但电流强度I 是标量而不是矢量,因为电流的叠加服从代数加减法则,而不服从矢量叠加的平行四边形法则。
基础物理学 第5章 稳恒磁场

n 是载流子浓度;e 是载流子电荷量。
5.1.2 稳恒电场 欧姆定律
1. 稳恒电场 导体的电荷分布不随时间变化所激发的电场。
2020年3月18日星期三
吉林大学 物理教学中心
2. 欧姆定律
通过一段导体的电流与导体两端电压成正比
I
U R
-1 )。
(1)电阻与材料长度l成正比、横截面积S成反比;
线等于穿出r磁感r 应线,即
Ñ S B dS 0 (5.18)
此式称为磁场高斯定理,说明
r
磁场是无源场。
B
2020年3月18日星期三
吉林大学 物理教学中心
例 5.1 在通有电流 I 的无限长直导线旁有一矩形回路,且两者共
面。试计算通过该回路所包围面积的磁通量。
解 取直电流处为坐标原点,
向右为x轴,在S面内任一 点的磁感应强度为
有相互作用。
基本磁现象 磁悬浮
2020年3月18日星期三
吉林大学 物理教学中心
5.2.2 磁 场
磁场是一种特殊形态的物质。 对外表现:
(1)磁场对引入磁场中的运动电荷或载流导体
有磁力的作用;
(2)载流导体在磁场中移动时,磁场的作用力
对载流导体做功,可见,磁场具有能量。
这表明了磁场的物质性。
对磁现象的解释:
2020年3月18日星期三
吉林大学 物理教学中心
对不同的磁介质,磁导率量值为:
顺磁质: m 0,r 1 抗铁磁 磁质质::mm、0r,值很r 大1,是Hr 的非单值函数 真空中:m 0,r 1, 0
5.5.3 铁磁质
铁磁质
具有以下主要性质:
1. 磁导率大 铁磁质具有很大的磁导率。
2. 磁饱和现象
