第2章__正弦交流电路_习题参考答案[1]
《电工电子技术及应用》第二章-单相正弦交流电路习题

《学习指导与练习》上的题(P21)二、单项选择题1.两个正弦交流电流的解析式是i 1=2202sin(10πt+3π)A ,i 2=311sin(10πt -3π)A 。
在这两个式子中两个交流电流相同的量是( )。
【C 】 A. 最大值和初相位B. 有效值和初相位C. 最大值、有效值和周期D. 最大值、有效值、周期和初相位 2.对照明用交流电u=380sin(100πt -2π)V 的说法正确的是( )。
【A 】A. 1S 内交流电压有100次达到最大值B. 交流电的有效值为220VC. 初相位为π/2D. 1S 内交流电压有50次过零3.当两个同频率正弦量的初相位相等时,下列表述正确的是( )。
【D 】 A. 两个正弦量的最大值和有效值相等 B. 两个正弦量的计时起点一定相同C. 判断两个正弦量是否同时到达最大值和零值,还须由计时起点确定D. 两个正弦量同时到达最大值和零值4.在正弦量的有效值相量表示法中,下列说法正确的是( )。
【B 】 A. 相量的长度等于正弦量的最大值 B. 相量的长度等于正弦量的有效值 C. 相量与横轴的夹角等于正弦量的相位 D. 相量与横轴的夹角等于正弦量的初相位5.已知某交流电流,t=0时的瞬时值i 0=10A ,初相位ψ0=30°,则这个正弦交流电的有效值为( )。
【C 】 A. 20AB. 202AC. 14.14D. 10A6.电容器上标有“30μF ,600V ”的字样,600V 的电压是指( )。
【A 】 A. 额定电压B. 最小电压C. 正常工作时必须加的电压D. 交流电压有效值7.电感量一定的线圈,如果产生的自感电动势大,则反映该线圈中通过的电流( )。
【D 】 A. 数值大B. 变化量大C. 时间快D. 变化率大11.线圈电感的单位是( )。
【A 】 A.亨【利】B. 法【拉】C. 高【斯】D. 韦【伯】12.一个空心线圈,当通过它的电流为8A 时,电感为36mH ;若通过它的电流为4A 时,则( )。
大学物理学第2章正弦交流电路_02

解法2: 利用相量图分析求解
设 U AB为参考相量,
I1 10A
I2 100 5 5
2 2
j10Ω
I
I1
A
A
I 1 超前 U AB 90
10 2A,
I2
C1
B
5Ω j5Ω
V
画相量图如下:
I 2滞后UAB 45°
由相量图可求得: I =10 A
UL= I XL =100V U L超前I 90°
I1 Z2 j400 I 0.5 33 A Z1 Z 2 100 j200 j400
0.89 - 59.6 A
同理:
I
I2
Z1 I Z1 Z 2
100 j200 0.5 33 A 100 j200 j400 0.5 93.8 A
UL
I1 100 10
U
由相量图可求得: V =141V
45° I 45°
I2
U AB
10 2
2.5 正弦稳态电路的功率
2.5.1 功率
一、瞬时功率
I +
i = Im sinωt U u = Umsin (ωt + ) - p = u i = UmImsin(ωt + ) sinωt = U I cos + U I cos ( 2ωt + )
S =√P2 + Q2 = 190 V· A
例2 如图所示是测量电感线圈参数R和L的实验电路,已知电 压表的读数为50V,电流表的读数为1A,功率表的读数为30W, 电源的频率f=50Hz。试求R和L的值。 ﹡ I 解:根据图中3个仪表的读数, A W ﹡ + 可先求得线圈的阻抗 电 R 感 Z | Z | R jL V U 线 圈 L U | Z | 50 I 功率表读数表示线圈吸收的有功功率,故有 P UI cos 30W 30 arctan( ) 53.130 UI 从而求得
电工电子技术-第2章 正弦交流电路
•
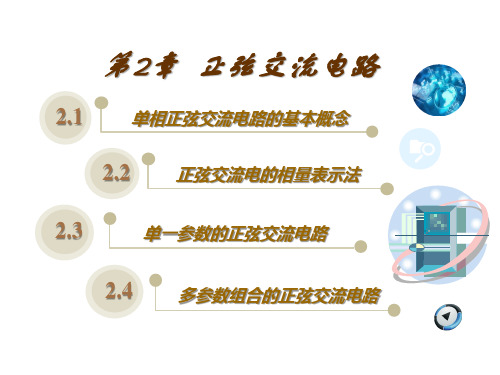
I m = 14.1∠36.9°A
其有效值相量为:I• = 10∠36.9°A
由于一个电路中各正弦量都是同频率的,所以相量只需 对应正弦量的两要素即可。即模值对应正弦量的最大值或 有效值,幅角对应正弦量的初相。
i u u、i 即时对应! R
电流、电压的瞬时值表达式
设 i Im sin t u、i 同相!
则 u ImR sin t Um sin t
u、i最大值或有效值之间符
合欧姆定律的数量关系。
Um ImR
或
U IR
•
相量关系式
•
I
U
U0
U
0 I0
RRR
相量图
U
I
(2)电阻元件上的功率关系
3
C -4
D
D 3 j4 第四象限 D 5 arctan 4
3
上式中的j 称为旋转因子,一个复数乘以j相当于在复
平面上逆时针旋转90°;除以j相当于在复平面上顺时针
旋转90°。
※数学课程中旋转因子是用i表示的,电学中为了区别 于电流而改为j。
正弦量的相量表示法
与正弦量相对应的复数形式的电压和电流称为相量。为
乘、除时用极坐标形式比较方便。
在复数运算当中,一定要根据复数所在象
限正确写出幅角的值。如:
+j
B4
A
A 3 j4 第一象限 A 553.1arctan 4 3
B 3 j4 第二象限 B 5180 arctan 4
-3 0
3
+1
3
电工电子技术第2章

第2章 正弦交流电路
在交流电路中,因各电流和电压多 +j A 为同一频率的正弦量,故可用有向线段 b r 来表示正弦量的最大值(有效值) Im 、 ψ Um(I、U)和初相ψ ,称为正弦量的相量。 O a +1 在正弦量的大写字母上打“•”表示,如 图2-5 有向线段的表示正弦量 幅值电流、电压相量用 I m、 m表示,有 U • U 效值电流、电压相量用 I 、 表示。将电 U • 路中各电压、电流的相量画在同一坐标 φ I ψ 中,这样的图形称为相量图。 ψ 同频率的u和i可用图2-6相量图表示。 图2-6 u和i的相量图 即 超前 Iφ°,I或 U滞后φ°。 U
第2章 正弦交流电路
2.1
正弦交流电的基本概念
正弦交流电压和电流的大小和方向都按正弦规律 作周期性变化,波形如图2-1a。
u U m s in ( t u ) i I m s in ( t i )
(2-1)
为便于分析,在电路中电压参考方向用“+”、“–” 标出,电流参考方向用实线箭头表示;电压、电流实 际方向用虚线箭头表示如图2-1b、c所示
第2章 正弦交流电路
u Im O φ Ψu Ψi i Um
u
i
t
T
图2-2 u和i相位不等的正弦量波形图
当φ=0º 时,称u、I同相;当φ=180º 时,称u比i反相; 当φ=±90º 时,称u与i正交 。 u i u i
u i
ui
u
i
t
u
i
O a) 同相
t O
b) 反相
O c)正交
t
图2-3 正弦量的同相、反相和正交
第2章 正弦交流电路
第2章 正弦交流电路

创新 求实 专注 自信
2.周期与频率
频率和周期之间满足如下关系:
1 f T
(2-3)
图2-2 交流电的周期和平均值
创新 求实 专注 自信
在汽车检测技术中,频率是一个重要参数, 如图 2-3 ( a )所示车速检测装置中,当自动 变速器输出轴转动时,安装在轴上的停止锁 止齿轮的凸齿交替靠近或离开车速传感器, 使感应线圈输出交流电压如图 2-3 ( b )所示。
创新 求实 专注 自信
可见,纯电容电路中,电容电压和电流 是同频率的正弦量,并且电流超前电压90°, 其有效值关系: (2-18) 式中,XC —电容的容抗,单位是欧姆 ()。 显然 1 1 XC ( 2-19 ) C 2 π fC
IC UC X C IC C
创新 求实 专注 自信
图2-3 车速检测
创新 求实 专注 自信
3.相位与初相
由正弦交流电的瞬时表达式(2-1)可知, 交流电在任一时刻的瞬时值取决于电角度 ( ),这个电角度称为交流电的相位。 交流电在t=0时所具有的相位称为初相, 用表示,单位是弧度或度,规定初相的绝对 值不超过π 弧度。 两同频率交流电的初相之差称为相位差, 即 (2-5)
2.3 RLC串联电路
2.3.1 电压和电流关系 2.3.2 电路的功率和能量转换
创新 求实 专注 自信
2.3.1 电压和电流关系
RLC串联电路如图2-12所示,取电压和电 流的参考方向一致。 为便于分析,电路中各量均采用相量表 示,各元件也采用相量化模型。
图2-12 RLC串联电路
创新 求实 专注 自信
2.2.1 纯电阻电路
1.电压和电流关系
图2-9(a)所示电路中,电压和电流的 参考方向一致,设电阻电压为
电工第2章 正弦交流电路

图2-2 正弦交流电波形图
2.1 正弦交流电量及基本概念
(1)最大值 又称为幅值,是正弦量的最大值,用带右下标m的大写 字母表示,如Im、Um、Em分别表示正弦电流、正弦电压、正弦电动 势的最大值。 (2)角频率ω 在单位时间内正弦量所经历的电角度,用ω表示,其单 位为弧度每秒(rad/s)。正弦交流电变化一次所需的时间,称为周期T, 其单位为秒(s),正弦量在单位时间内变化的次数,称为频率f, 其单位为赫[兹](Hz)。
图2-9 纯电阻电路
2.3 单一参数元件的正弦交流电路
(2) 有效值关系 由电流与电压的幅值关系Im= Um /R,两端同除 以 ,可得它们的有效值关系为U=IR (3) 相量关系 因为电流i和电压u均为同频率的正弦量。 相量形式为 2.电阻元件的功率 (1) 瞬时功率 在关联参考方向下,电阻元件的 瞬时功率(用小写字母p表示):
图2-4 两正弦量的同相与反相
2.1 正弦交流电量及基本概念
例2.1 已知正弦量u=220sin(314t + 30°)V, 试求正弦量的三要素、有效值及变化周期。 解:对照式(2-1),可知三要素:
2.1 正弦交流电量及基本概念
例2.2 已知正弦电压u和正弦电流i1、i2的瞬时表达式为u = 310sin(ωt -45°)V,,i2=28.2sin(ωt +45°)A,试以电压u为参考量重新写出u和 电流i1、i2的瞬时值表达式。 解:以电压u为参考量, 则电压u的表达式为 由于i1、i2与u的相位差为
2.2 正弦交流电的相量表示方法
2.2.2 正弦量的相量表示法 正弦量和相量是一一对应关系(注意:正弦量和相量不是相等
关系!)。在复平面中,例如相量可用长度为 ,与实轴正向的夹 角为ψ的矢量表示。这种表示相量的图形称为相量图。如图2-7所示
第二章 正弦交流电习题集

第二章正弦交流电一、填空1、已知u = 102sin(3140 t -240º)V ,则U m = V,U= V,ω=rad/s,f = Hz,T = s, Φ= 。
2、有一正弦交流电流:i(t)=5×1.414sin(1000t+300o)A,那么它的有效值为I= ,角频率ω= ,初相角Φi= 。
3、周期T=0.02s,振幅为50V、初相角为60º的正弦交流电压u的解析式为,其有效值。
4、用电流表测得一正弦交流电路中的电流为10A ,则其最大值为A。
5、在正弦交流电中完成一次周期性变化所用的时间叫。
6、正弦交流电1s内变化的次数叫做正弦交流电的。
7、周期、频率和角频率三者间满足的关系是。
8、描述正弦量的三要素是。
9、电容器的容抗与自身电容量之间是(正比或反比)关系,与信号频率之间是(正比或反比)关系。
10、下列属于直流电压范围的有(),属于交流电压范围的是()。
11、线圈的感抗与自身电感值之间是(正比或反比)关系,与信号频率之间是(正比或反比)关系。
12、在纯电阻电路中,功率因数为,感性负载电路中,功率因数介于与之间。
13、在R-L-C串联电路中,当X L>X C时,电路呈_ _性;当X L<X C时,电路呈_ 性;当X L=X C时,电路呈_ _性。
14、三相交流电相序正序为。
15、三相电源的连接方式有与两种,常采用方式供电。
16、根据电流对人体的伤害程度,触电可分为与两种。
18、当三相交流发电机作星形连接时,线路中存在着两种电压,一种是,它是与之间的电压。
另一种是,它是之间的电压。
这两种电压有效值之间的关系是。
19、对称三相电源星形连接时,U L= U P,线电压的相位超前于它所对应相电压的相位。
20、正序对称三相星形连接电源,若U VW,则U UV= V,U U= V,U W= V。
二、选择填空1、交流电流表在交流电路中的读数为()A、瞬时值B、平均值C、最大值D、有效值2、正弦交流电压u=100Sin(628t+60°)V,它的频率为()A、100HZB、50 HZC、60 HZD、628 HZ3、已知正弦交流电流i= 10T2sin(314t+25o)则频率为()A、50H ZB、220H ZC、314H ZD、1000H Z4、已知正弦交流电压u=220sin(314t-30o)则其角频率为()A、30B、220C、50D、100π5 、正弦交流电的有效值为10A,频率为50H Z,初相位为-30°,它的解析式为()A、i=10sin(314t+30°)AB、i=10sin(314t30°)AC、i=10sin(314t-30°)AD、i=10sin(50t+30°)A6、相量U=100e-j60°V的解析式为()A、u=100 2 sin(ωt-60°)VB、u=100sin(ωt-60°)VC、u=100sin(ωt+60°)VD、u=100 2 sin(ωt+60°)V7、关于正弦交流电相量的叙述中,()的说法不正确的。
电路 第二章 正弦交流电路(1)
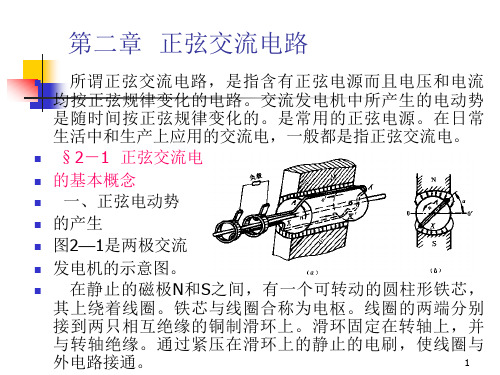
所以交流电的有效值就是与它热效应相等的直流电的数值, 它们之间的关系由焦耳-楞次定律确定。为了区别,交流电 流、电压和电动势的有效值分别用大写字母I、U、E表示。 设正弦电流i=Imsin(ωt+ψ),通过计算可知,正弦电流的有 效值是其最大值的1/√2倍,如图2—9(c)所示,即 I=Im/√2 =0.707Im (2—9) 同理,正弦电压和电动势的有效值分别为 U=Um/√2 ; E=Um/√2 在工程上,主要使用有效值,今后不加特别声明,交流电 的大小均指有效值。从交流电流表和电压表上读取的数值也 是有效值。电气设备所标明的交流电压、电流数值也都是有 效值。可以证明有效值为正弦量在一个周期内的方均根值, 即它不随时间变化,因此,和最大值比较,有效值更为实用。
15
相量也可以用复平面上的有向线段来表示。如图所示。这种 用来表示相量的图形,叫相量图,相量图与力学和物理学中 的向量图相似。但是,相量表示的是随时间作正弦变动的函 数,而向量指的是力、电 场强度等空间向量。 2 因为实际工程中,常采用正弦量的有效值,而且最大值与 有效值之间有着固定的 2关系,所以有效值相量应用较多。 它等于最大值相量除以 2 ,即 U=Um/ 2 同理 I=Im/ 2
上式表明,为了保证电动势的频率稳定,必须保 持发电机转速稳定。 周期T、频率f及角频率ω反映了正弦量随时间作 ω 周期性交变的快慢。各国在电力工业上所用交流 电的频率都规定了各自的标准。我国和有些国家 电力工业的标准频率为50Hz,称为工频。一般我 们讲交流电时,如果不加说明,指的就是50Hz的 工频。还有一些国家工频采用60Hz。
采用适当的磁极形状,使电枢表面的磁感应强度B 沿圆周按正弦规律分布,如图 (a)所示。由于铁芯 的磁导率远大于空气的磁导率,故磁力线的方向 与铁芯表面垂直。在磁极之间的分界面O~O',B= 0,称为磁中性面。在磁极的轴线上,磁感应强度 具有最大值Bm 。设线圈的一条有效边AA'(切割磁 力线的部分)和转轴所组成的平面,与磁中性面的 夹角为α,则AA'边所处位置的磁感应强度为(见图 2—2) B=Bmsinα 当电枢被原动机拖动,在磁场中以逆时 针方向作 等速旋转时,电枢线圈有效 边因切 割磁力线而产生感 应电动势。其表达式为 e=Emsinωt (2—1)
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第二章 正弦交流电路 习题参考答案一、填空题:1. 表征正弦交流电振荡幅度的量是它的 最大值 ;表征正弦交流电随时间变化快慢程度的量是 角频率ω ;表征正弦交流电起始位置时的量称为它的 初相 。
三者称为正弦量的 三要素 。
2. 电阻元件上任一瞬间的电压电流关系可表示为 u = iR ;电感元件上任由上述三个关系式可得, 电阻 元件为即时元件; 电感 和 电容 元件为动态元件。
3. 在RLC 串联电路中,已知电流为5A ,电阻为30Ω,感抗为40Ω,容抗为80Ω,那么电路的阻抗为 50Ω ,该电路为 容 性电路。
电路中吸收的有功功率为 750W ,吸收的无功功率又为 1000var 。
二、判断题:1. 正弦量的三要素是指最大值、角频率和相位。
(错)2. 电感元件的正弦交流电路中,消耗的有功功率等于零。
(对)3. 因为正弦量可以用相量来表示,所以说相量就是正弦量。
(错)4. 电压三角形是相量图,阻抗三角形也是相量图。
(错)5. 正弦交流电路的视在功率等于有功功率和无功功率之和。
(错)6. 一个实际的电感线圈,在任何情况下呈现的电特性都是感性。
(错)7. 串接在正弦交流电路中的功率表,测量的是交流电路的有功功率。
(错)8. 正弦交流电路的频率越高,阻抗越大;频率越低,阻抗越小。
(错)三、选择题:1. 某正弦电压有效值为380V ,频率为50Hz ,计时始数值等于380V ,其瞬时值表达式为( B )A 、t u 314sin 380=V ;B 、)45314sin(537︒+=t u V ;C 、)90314sin(380︒+=t u V 。
2. 一个电热器,接在10V 的直流电源上,产生的功率为P 。
把它改接在正弦交流电源上,使其产生的功率为P /2,则正弦交流电源电压的最大值为( D )A 、;B 、5V ;C 、14V ;D 、10V 。
3. 提高供电电路的功率因数,下列说法正确的是( D )A 、减少了用电设备中无用的无功功率;B 、减少了用电设备的有功功率,提高了电源设备的容量;C 、可以节省电能;D 、可提高电源设备的利用率并减小输电线路中的功率损耗。
4. 已知)90314sin(101︒+=t i A ,︒+=30628sin(102t i )A ,则( C ) A 、i 1超前i 260°; B 、i 1滞后i 260°; C 、相位差无法判断。
5. 电容元件的正弦交流电路中,电压有效值不变,频率增大时,电路中电流将( A )A 、增大;B 、减小;C 、不变。
6. 在RL 串联电路中,U R =16V ,U L =12V ,则总电压为( B ) A 、28V ; B 、20V ; C 、2V 。
7. RLC 串联电路在f 0时发生谐振,当频率增加到2f 0时,电路性质呈( B ) A 、电阻性; B 、电感性; C 、电容性。
8. 正弦交流电路的视在功率是表征该电路的( A )A 、电压有效值与电流有效值乘积;B 、平均功率;C 、瞬时功率最大值。
四、计算题把下列正弦量的时间函数用相量表示:(1) u =102sin314t 伏 (2) i =-5sin(314t -60º)安解:(1)U &=10/0º (V) (2)mI &=-5/-60º =5/180º-60º=5/120º (A) 已知工频正弦电压u ab 的最大值为311V ,初相位为-60°,其有效值为多少写出其瞬时值表达式;当t =时,U ab 的值为多少解:∵U U ab abm 2=∴有效值2203112121=⨯==U U abm ab (V) 瞬时值表达式为 ()︒-=60314sin 311t u ab (V) 当t =时,5.80)12sin(31130025.0100sin 311-=-=⎪⎭⎫⎝⎛-⨯⨯=πππU ab (V)用下列各式表示RC 串联电路中的电压、电流,哪些是对的,哪些是错的(1) i =Z u (2) I=CX R U + (3) I &= C j R U ω-& (4) I=Z U (5) U=U R +U C (6) U &=R U &+CU & (7)I &=-j C U ω& (8)I &= j C U ω& 解:在R 、C 串联电路中,总阻抗cjR X j R Z C ω1-=-= 而 X R Z C22+= ZU I &&= R I U R &&= X I U C &&= CR U U U &&&+= U U U C R 222+= 所以 (1)、(2)、(3)、(5)、(7)、(8)均是错的,(4)、(6)是对的。
图中,U 1=40V ,U 2=30V ,i =10sin314t A ,则U 为多少并写出其瞬时值表达式。
解:由电路图可知,电压u 1与电流i 同方向,而电压u 2超前电流i 90º,所以504030222221=+=+=U U U (V)∵电压u 超前电流i 的电度角︒===9.3643arctan arctan21U U ϕ ∴)9.364.31sin(250︒+=t u (V)图所示电路中,已知u =100sin(314t +30º)伏,i =(314t +º)安, i 2=10sin(314t +º)安,试求: i 1、Z 1、Z 2并说明Z 1、Z 2的性质,绘出相量图。
解:由题知,︒=7.19/36.22m I &(A) ︒=13.83/102m I &(A) ︒=30/100m U &(V) 所以︒-=-=87.6/2021mm m I I I &&&(A) 即()︒-=87.6314sin 201t i (A)∵︒=︒-︒==67.38/5067.8/230/10011m m I UZ &&(Ω)︒-=︒︒==13.53/1013.83/1030/10022m mI U Z &&(Ω) ∴Z 1为感性负载,Z 2为容性负载。
图所示电路中,X R =X L =R ,并已知电流表A 1的读数为3A ,试问A 2和A 3的读数为多少解:由图可以看出,电容与电感并联连接,由于电容电流落后两端电压900,而电感电流超前两端电压900,因为X R =X L ,所以通过电容的电流与通过电感的电流大小相等,方向相反,故而电流表A 2的读数为0A 。
由上分析可知,电压u 的有效值为3R ,故电感两端电压亦为3R 。
因为X L =R ,所以电流表A 3的读数为3A 。
有一R 、L 、C 串联的交流电路,已知R=X L =X C =10Ω,I=1A ,试求电压U 、U R 、U L 、U C 和电路总阻抗Z 。
解: 10110=⨯==RI U R (V) 10110=⨯==I X j U L L (V) 10110=⨯=-=I X j U C C (V) ∵10==-+=R X j X j R Z C L (Ω) ∴10110=⨯==I Z U (V)电路如图所示,已知ω=2rad/s ,求电路的总阻抗Z ab 。
解:∵ω=2rad/s∴2==L X L ω (Ω) 2ω1==CX C (Ω) ∴()j j j j j j j j j X j X j Z C L ab +=+-+-++=--++=-++=3)22)(22()22(42222422//22(Ω)电路如图所示,已知R =20Ω,RI &=10/0ºA ,X L =10Ω,1U &的有效值为200V ,求X C 。
解: 由题意可知:︒==0/20022I R U &&(V) CC C X jX U I ︒=-=90/2002&&(A) ∴︒+︒=+=0/1090/200CRC L X I I I &&&(A) ︒+︒=︒+︒⨯=⨯=90/100180/2000)0/1090/200(10CC L L L X X j I jX U &&(V) 10020002000/20090/100180/200021j X X U U U CC L +-=︒+︒+︒=+=&&&(V)又因U 1=200故有 22100)2000200(200+-=CX 221002002000200-±=-C X2.1732002000±=C X 2.1732002000±=C X 则得: X C =(Ω),或X C =(Ω)图所示电路中,u S =10sin314t V ,R 1=2Ω,R 2=1Ω,L =637mH ,C =637μF,求电流i 1, i 2和电压u c 。
解:ω=314rad/s200637314=⨯==L X L ω(Ω) 5106373141ω16=⨯⨯==-C X C (Ω) 13.5195151000))((221j j j jX jX R jX jX R Z C L C L -=+-=-+-+=(Ω)13.5211j Z R Z -=+=(Ω)︒=-︒==7.68/816.113.520/101j Z U I Sm m &&(A) ︒-=-⨯︒=⨯=3.21/32.9)13.5(7.68/816.111j Z I U m Cm &&(V) ︒=-︒-=-=7.68/86.153.21/32.92j jX U I C Cm m &&(A) 则 i 1=(314t +°)(A)i 2=(314t +°)(A) u c =°)(V)图所示电路中,已知电源电压U =12V ,ω=2000rad/s ,求电流I 、I 1。
解:当ω=2000rad/时s1105.020003=⨯⨯==-L X L ω(Ω)21025020001ω16=⨯⨯==-C X C (Ω)j j j jX R jX R Z C C -=--=--=1224)(221(Ω)21111=-++=++=j j Z jX R Z L (Ω) ︒=︒==0/620/12Z U I &&(A) ︒-=-⨯︒=⨯=45/49.8)1(0/61j Z I U C&&(V) ︒-=︒-==45/29.4245/49.821R U I C &&(A) 则 I =6(A) I 1=(A)图所示电路中,已知R 1=40Ω,X L =30Ω,R 2=60Ω,X c =60Ω,接至220V 的电源上.试求各支路电流及总的有功功率、无功功率和功率因数。
