典型题型之主题类探究题
2021年高考语文热点题型和提分秘籍专题24探究小说的主题和标题(含解析)

专题24 探究小说的主题和标题热点题型一探究标题意蕴例1、阅读下面的文字,完成后面的题目。
渡船王往渡船是水上的邮票。
涟河的东岸是家畜市场,一个叫红蜻蜓的女人在东岸的渡口开了个小卖部。
她在大堤上用木头搭了个小屋子,外间摆货,里间摆张小床。
红蜻蜓的小卖部前有一个水缸。
有人要喝水,红蜻蜓就一指小卖部前的水缸。
水缸里的水总是满的,是红蜻蜓一担一担从涟河挑上来的,碧清碧清的。
红蜻蜓每天起得很早。
起来第一件事就是去涟河里挑水,把水缸挑满了,她就站在窗前,朝对岸看。
她看着小谭先生走上大堤,小小的影子轻快地掠过一棵棵树,大树,小树。
小谭先生朝渡口走来,河风吹起他的衣角,显得很清瘦也很利落。
小谭先生上了渡船时,红蜻蜓的心会紧张,有时是因为浪太大,船晃得厉害;有时是因为小谭先生的目光朝着她的窗口。
小谭先生下了渡船,上了坡,一步一步走上来,红蜻蜓就笑微微的,好似小谭先生是奔她而来的。
但是,很快她又绝望了,小谭先生从她的小屋前经过,从来不看一下她的小屋。
她又转到另一个窗口,这下她只看到小谭先生的后背。
她想小谭先生要是回头看一下多好,但是他从来没回过头。
小谭先生是河西人,在河东的学校做民办老师。
红蜻蜓出嫁前,有个好姐妹给她和小谭先生牵过线。
当时,见面的地点就在渡口。
两个人都喜欢对方,但是,因家人的反对,没有成亲。
红蜻蜓早就结婚了,小谭先生还是单身。
那天,临散集时,红蜻蜓看见小谭先生牵着一头才成年的水牛往渡口走。
红蜻蜓想:小谭先生不教书了?下一个逢集,红蜻蜓又看见了小谭先生。
红蜻蜓问他:“你不教书了,老来集上?〞小谭先生说:“教呢,把牛牵来卖了。
〞红蜻蜓还想和他说说话,小谭先生已走了。
红蜻蜓感觉小谭先生瘦多了,头发也乱了,走路有些跌跌撞撞的。
红蜻蜓想刚买的牛又牵来卖,肯定是做贩牛的生意了,又教书又贩牛真是难为他了。
一天晚上,红蜻蜓已经睡了,听见敲门声。
拉开门,小谭先生一头就撞进来。
原来,小谭先生上回牵的牛让涟城北一个老头在宝滩买后,回去没两天就死了,媳妇和儿子一抱怨,老头喝药自尽了。
备战2025年中考语文答题技巧与模板构建(全国)题型11 概括、探究主旨(主题)(原卷版)

题型11概括、探究主旨(主题)类题型题型概述|模板构建|真题试炼模板01概括主旨1.这篇文章表达了什么主题?(八年级下册第3课《安塞腰鼓》教参【问题探究】第一题)2.(2022·湖北恩施·中考真题)阅读下面的小说,完成下面小题。
八千里的暖马海霞①他和她是中学同学,他高中毕业后参军到祖国的最北疆,她则在家乡当了一名民办教师。
那时,南方的冬天还不像现在这么冷,她从小没见过雪花,他来信说,他那里冬天都是千里冰封的景象。
她问他,冷不冷,是不是冬天得穿棉衣棉裤,外面还要罩个皮袍子,戴三大扇的狗皮帽子,然后狗拉雪撬,他们坐在雪橇上巡逻……②他回信说,不是的,没那么冷,感觉这里的冬天比南方还好过些,屋子里暖和,白天太阳好时,一点儿也感觉不到冷。
③她才不信呢,第二年的冬天,学校放假后,她打算去东北看他。
临走时,奶奶给她做了厚厚的棉衣棉裤,母亲给她买了件加长及踝的羽绒服,口罩、围巾、皮手套都准备妥当后,她坐上了北上的火车。
④刚下车,她就看到了他。
“怎么穿这么少?”她心疼地问他。
“你是不是把家里的衣服都穿上了?包裹得像个粽子。
”听他这样说完,她看了看自己,又看了看下车的旅客,还真没人比自己穿得多。
⑤“真该相信你的话,东北冬天里的冷只是个传说罢了。
”⑥“也不是,是爱的温度太高了,我们感觉不到严寒。
”他拉着她的手,幸福地说。
⑦从那以后,每年寒假她都会去东北看他,希望给他带去爱的温暖。
后来,他们结婚了,依然是两地分居。
她怀孕那年的寒假,她没有去他那里过年,他打电话说,等她生孩子时,他一定回来。
可就在孩子出生前一个月,他在一次救火行动中不幸牺牲了。
家人对她隐瞒了真相,骗她说他所在的部队接到了出国维和的任务,一年后任务结束再回来探亲。
⑧次年冬天,她和公婆还有一岁的儿子一起来到他牺牲的地方,她说他独自长眠在雪山下太冷了,她要去看他,陪他说说话……⑨以前他在世时,他们也是一年见一次,每年冬天都是他俩最期盼的日子,现在他不在了,每年寒假她还会领着儿子去看他。
河南数学中考题型汇总 几何探究题题型练习含答案

河南数学中考题型汇总几何探究题题型练习含答案类型 1 实践操作类探究题角度1 折叠类1.[2022河南]综合与实践综合与实践课上,老师让同学们以“矩形的折叠”为主题开展数学活动.(1)操作判断操作一:对折矩形纸片ABCD,使AD与BC重合,得到折痕EF,把纸片展平;操作二:在AD上选一点P,沿BP折叠,使点A落在矩形内部点M处,把纸片展平,连接PM,BM.根据以上操作,当点M在EF上时,写出图(1)中一个30°的角:.(2)迁移探究小华将矩形纸片换成正方形纸片,继续探究,过程如下.将正方形纸片ABCD按照(1)中的方式操作,并延长PM交CD于点Q,连接BQ.①如图(2),当点M在EF上时,∠MBQ= °,∠CBQ= °;②改变点P在AD上的位置(点P不与点A,D重合),如图(3),判断∠MBQ与∠CBQ的数量关系,并说明理由.(3)拓展应用在(2)的探究中,已知正方形纸片ABCD的边长为8 cm,当FQ=1 cm时,直接写出AP 的长.图(1)图(2)图(3)2.[2022河南省实验模拟]问题情境数学活动课上,同学们开展了以折叠为主题的探究活动,如图(1),已知矩形纸片ABCD(AD>AB),其中宽AB=8.动手实践(1)如图(1),威威同学将矩形纸片ABCD折叠,点A落在BC边上的点M处,折痕为BN,连接MN,然后将纸片展平,得到四边形ABMN,则折痕BN的长为;探究发现(2)如图(2),胜胜同学将图(1)中的四边形ABMN剪下,取AN边的中点E,将△ABE 沿BE折叠得到△A'BE,延长BA'交MN于点F.点Q为BM边的中点,点P是MN边上一动点,将△MQP沿PQ折叠,当点M的对应点M'落在线段BF上时,求此时tan∠PQM的值;反思提升(3)明明同学改变图(2)中点Q的位置,即点Q为BM边上一动点,点P仍是MN边上一动点,按照(2)中方式折叠△MQP,使点M'落在线段BF上,明明同学不断改变点Q 的位置,发现在某一位置∠QPM与(2)中的∠PQM相等,请直接写出此时BQ的长.图(1)图(2)备用图3.综合与实践——探究平行四边形折叠中的数学问题问题情境已知▱ABCD中,ÐA为锐角,AB<AD,点E,F分别是AB,CD边的中点,点G,H分别是AD,BC边上的点,分别沿EG和FH折叠▱ABCD,点A,C的对应点分别为点A',C'.操作分析(1)如图(1),点A'与点B重合,点C'与点D重合.①四边形BHDG 平行四边形(填“是”或“不是”).②当▱ABCD满足某个条件时,四边形BHDG能成为矩形.这个条件可以是.(2)点A',C'均落在▱ABCD内部(含边界),连接A'H,C'G,若AG=CH,则四边形A'HC'G是平行四边形吗?若是,请就图(2)进行证明;若不是,请说明理由.拓展探究(3)在(2)的条件下,若ÐA=60°,AD=2AB=8,且A'G与▱ABCD的一边平行,则此时四边形A'HC'G的面积为.图(1)图(2)备用图4.综合与实践数学活动课上,张老师找来若干张等宽的矩形纸条,让学生们进行折纸探究. (1)希望小组将如图(1)所示的矩形纸片ABCD沿过点A的直线折叠,使点D落在AB边上的点D'处,折痕为AE.填空:图(1)中四边形ADED'的形状是.(2)智慧小组准备了一张如图(2)所示的长、宽之比为3∶2的矩形纸片ABCD,用希望小组的方法折叠纸片,得到四边形ADED',接着沿过点B的直线折叠纸片,使点C落在ED'上的点M处,折痕为BF.求∠MBC的度数.(3)勤奋小组拿着一张如图(3)所示长为4,宽为2的矩形纸片ABCD,利用希望小组的方法折叠纸片,得到四边形ADED',在CE上取一点F(不与点C,E重合),沿BF 折叠△BCF,点C的对应点为N,射线FN交直线AB于点H.①HF与HB的数量关系为.②当射线FN经过△AED'的直角边的中点时,直接写出FC的长.图(1)图(2)图(3)5.综合与实践问题情境数学活动课上,老师让同学们以“矩形纸片的折叠”为主题,开展数学活动,如图(1),在矩形ABCD中,AB=8,BC=4.观察发现(1)如图(2),智慧小组连接对角线BD,将矩形纸片ABCD沿直线BD折叠,使点A落在点P的位置,PB交CD于点Q,连接AP.直接写出图中所有的等腰三角形:.(不再添加字母)探究证明(2)求实小组在智慧小组的启发下,又对矩形纸片ABCD进行了如下操作,并对其中所产生的问题进行了探究:如图(3),沿过点A的直线折叠,使点B的对应点F 落在CD上,折痕交BC于点E,过点F作FG∥BC交AE于点G,连接BG.①小组成员发现四边形BEFG是特殊四边形.请你判断四边形BEFG的形状,并说明理由.②小组成员通过计算求得四边形BEFG的面积.请你直接写出这个面积:.探索拓广(3)参照上面的探究方式,对图(1)进行一次折叠操作,使点B的对应点B'落在BD 的三等分点上,设折痕与AB交于点N.请直接写出BN的长.图(1)图(2)图(3)角度2 旋转类6.综合与实践——图形变换中的数学问题问题情境数学活动课上,老师出示了一个问题:如图(1),已知正方形ABCD、矩形BCEF,点E,F分别在边CD,AB上,且BF=k(3<k<5),BC=5.将矩形BCEF绕点B顺时针旋转得到矩形BGHK,点G,H,K分别是点C,E,F的对应点,如图(2).图(1)图(2)图(3)图(4)同学们通过小组合作,提出下列数学问题,请你解答.(1)在图(2)中,连接BE,BH,EH,CG,得到图(3),可以发现在旋转过程中存在一个三角形始终与△BCG相似,这个三角形是,它与△BCG的相似比为(用含k的式子表示).(2)如图(4),矩形BGHK的顶点K恰好落在正方形ABCD的对角线AC上,KH交DC 的延长线于点T.求证:BK=KT.(3)在旋转过程中,连接CH,CK.若k=23,则当CH=CK时,直接写出CK的长.备用图(1)备用图(2)角度3 平移类7.综合与实践问题背景如图(1),在矩形ABCD中,AB=10,BC=8,点E为边BC上一点,沿直线DE将矩形折叠,使点C落在AB边上的点C'处.问题解决(1)填空:AC'的长为.(2)如图(2),展开后,将△DC'E沿线段AB向右平移,使点C'的对应点与点B重合,得到△D'BE',D'E'与BC交于点F,D'B与DE交于点G.求EF的长.拓展探究(3)如图(3),在△DC'E沿射线AB向右平移的过程中,设点C'的对应点为C″,则当△D'C″E'在线段BC上截得的线段PQ(D'E',折线D'C″E'分别与BC交于点P,Q)的长度为2时,直接写出平移的距离.图(1)图(2)图(3)角度4 尺规作图类8.[2022南阳宛城区一调]下面是某数学兴趣小组探究用不同方法作线段AB的垂直平分线的讨论片段,请仔细阅读,并完成相应的任务.任务:(1)小明的作图依据是.(2)小军作图得到的直线CP是线段AB的垂直平分线吗?请判断并说明理由.(3)如图(3),已知△ABC中,CA=CB,∠ACB=30°,点D,E分别是射线CA,CB上的动点,且CD=CE,连接BD,AE,交点为P.当AB=6,∠PAB=45°时,请直接写出线段CD 的长.图(3)9.[2022开封二模]中华文明源远流长,图(1)是汉代数学家赵爽在注解《周髀算经》时给出的图形,人们称它为“赵爽弦图”.2002年北京国际数学家大会依据赵爽弦图制作了会标,该图由4个全等的直角三角形围成一个大正方形和中间一个小正方形,巧妙地证明了勾股定理.问题发现如图(1),若直角三角形的直角边BC=3,斜边AB=5,则中间小正方形的边长CD= ,连接BD,△ABD的面积为.知识迁移如图(2),P是正方形ABCD内一点,连接PA,PB,PC,当∠BPC=90°,BP=10时,△PAB的面积为.拓展延伸如图(3),已知∠MBN=90°,以点B为圆心,适当长为半径画弧,分别交射线BM,BN 于点A,C.(1)已知D为线段AB上一动点,连接CD,过点B作BE⊥CD,垂足为点E,在线段CE 上取一点F,使EF=BE,过点F作GF⊥CD交BC于点G,试判断BE,DE,GF这三条线段之间的数量关系,并说明理由.(2)在(1)的条件下,若D为射线BM上一动点,F为射线EC上一点,当AB=10,CF=2时,直接写出线段DE的长.图(1)图(2)图(3)备用图类型 2 阅读理解类探究题10.[2022许昌二模]问题情境数学课上,王老师出示了这样一个问题:如图(1),在矩形ABCD中,AD=2AB,点E是AB延长线上一点,且BE=AB,连接DE,交BC于点M,以DE为一边在DE的左下方作正方形DEFG,连接AM.试判断线段AM与DE的位置关系.探究展示小明发现,AM垂直平分DE,并展示了如下的证明方法:证明:∵BE=AB,∴AE=2AB.又∵AD=2AB,∴AD=AE.∵四边形ABCD是矩形,∴AD∥BC,∴.(平行线分线段成比例)∵BE=AB,∴EM=1,∴EM=DM,DM即AM是△ADE的边DE上的中线.又∵AD=AE,∴.(等腰三角形的“三线合一”)∴AM垂直平分DE.反思交流(1)请将上述证明过程补充完整;(2)小颖受到小明的启发,继续进行探究,如图(2),连接CE,以CE为一边在CE的左下方作正方形CEFG,发现点G在线段BC的垂直平分线上,请你给出证明;图(1)图(2)拓展应用(3)如图(3),连接CE,以CE为一边在CE的右上方作正方形CEFG,分别以点B,C 为圆心,m为半径作弧,两弧交于点M,连接MF.若MF=AB=1,请直接写出m的值.图(3)11.[2022商丘二模]如下是小明复习全等三角形时遇到的一个问题及由此引发的思考,请帮助小明完成以下学习任务.如图(1),OC平分∠AOB,点P在OC上,点M,N分别是OA,OB上的点,且OM=ON.求证:PM=PN.小明的思考:要证明PM=PN,只需证明△MOP≌△NOP即可.证明:如图(1),∵OC平分∠AOB,∴∠AOC=∠BOC.又∵OP=OP,OM=ON,∴△MOP≌△NOP,∴PM=PN.请仔细阅读并完成以下任务.(1)小明得出△MOP≌△NOP的依据是(填序号).①SSS ②SAS ③AAS ④ASA⑤HL(2)如图(2),在四边形ABCD中,AB=AD+BC,∠DAB的平分线和∠ABC的平分线交于CD边上的点P.求证:PC=PD.,当△PBC有一个内角是45°时,△PAD(3)在(2)的条件下,若AB=10,tan∠PAB=12的面积是.图(1)图(2)备用图(1)备用图(2)类型 3 类比、拓展探究题12.[2021湖北仙桃]已知△ABC和△DEC都为等腰三角形,AB=AC,DE=DC,∠BAC=∠EDC=n°.(1)当n=60时:①如图(1),当点D在AC上时,请直接写出BE与AD的数量关系:;②如图(2),当点D不在AC上时,判断线段BE与AD的数量关系,并说明理由.(2)当n=90时:①如图(3),探究线段BE 与AD 的数量关系,并说明理由; ②当BE ∥AC ,AB=3√2,AD=1时,请直接写出DC 的长.图(1) 图(2) 图(3)答案:1.(1)∠ABP ,∠PBM ,∠MBC 或∠BME (注:任意写出一个即可) (2)①15 15②∠MBQ=∠CBQ. 理由如下:∵四边形ABCD 是正方形,∴AB=BC ,∠A=∠C=90°. 由轴对称性质,得BM=AB ,∠BMP=∠A=90°,∴∠BMQ=90°=∠C ,BM=BC.又∵BQ 是公共边,∴Rt △MBQ ≌Rt △CBQ ,∴∠MBQ=∠CBQ.(3)4011 cm 或2413cm. 解法提示:由翻折的性质知AP=PM ,DF=CF=4. 由(2)可知,△MBQ ≌△CBQ ,∴MQ=CQ. 分两种情况讨论.①当点Q 在EF 下方时,如图(1),则MQ=CQ=4-1=3,DQ=4+1=5,PQ=AP+3,PD=8-AP. 由勾股定理,得PD 2+DQ 2=PQ 2,∴(8-AP )2+52=(AP+3)2,∴AP=4011.图(1)②当点Q 在EF 上方时,如图(2),则MQ=CQ=4+1=5,DQ=4-1=3,PQ=AP+5,PD=8-AP. 由勾股定理,得PD 2+DQ 2=PQ 2,∴(8-AP )2+32=(AP+5)2,∴AP=2413.图(2)综上所述,AP 的长为4011 cm 或2413cm. 2.(1)8√2(2)如图(1),连接MM'交PQ 于点O ,连接EF.图(1)由折叠的性质知,点O 为MM'的中点. 又∵点Q 为BM 边的中点,∴QO ∥BM',即QP ∥BF ,∴∠PQM=∠FBM.∵点E 是AN 边的中点,且将△ABE 沿BE 折叠得到△A'BE , ∴EN=EA',∠EA'F=∠N=90°. 又∵EF=EF ,∴Rt △NEF ≌Rt △A'EF. 设NF=x ,则A'F=x ,MF=8-x ,∴BF=BA'+A'F=BA+A'F=8+x.在Rt △BMF 中,由勾股定理,得BM 2+FM 2=BF 2, 即82+(8-x )2=(8+x )2,解得x=2,∴FM=6,∴tan ∠FBM=FM BM =68=34,∴tan ∠PQM=34. (3)BQ 的长为398. 解法提示:如图(2),连接MM'交PQ 于点G.图(2)由折叠的性质知,PQ 垂直平分MM',∴∠QPM+∠PMM'=90°.∵∠PMQ=90°,∴∠PMM'+∠M'MB=90°, ∴∠QPM=∠M'MB.由(2)知,(2)中∠PQM=∠M'BM. 又∵∠QPM 与(2)中的∠PQM 相等,∴∠M'BM=∠M'MB.过点M'作M'H ⊥BM 于点H ,则BH=MH=4,M'H BH =34, ∴M'H=3.设MQ=M'Q=a ,则HQ=4-a.在Rt △M'HQ 中,根据勾股定理,得M'H 2+HQ 2=M'Q 2, 即32+(4-a )2=a 2,解得a=258, ∴BQ=8-258=398. 3.(1)①是解法提示:∵四边形ABCD 是平行四边形,∴∠A=∠C ,∠ABC=∠ADC ,AD ∥BC. 如图(1),由折叠可知,∠A=∠1,∠C=∠2,图(1)∴∠1=∠2,∴∠ABC-∠1=∠ADC-∠2,即∠3=∠4. ∵AD ∥BC ,∴∠4+∠5=180°,∴∠3+∠5=180°, ∴BG ∥DH ,∴四边形BHDG 是平行四边形. ②∠A=45°(答案不唯一,正确即可) 解法提示:∵四边形BHDG 是矩形,∴∠BGD=90°,∴∠AGB=90°, 又由折叠可知,AG=A'G ,∴∠A=45°. (2)四边形A'HC'G 是平行四边形. 证明:如图(2),连接GH.图(2)∵四边形ABCD 是平行四边形, ∴∠A=∠C ,AB=CD ,AD ∥BC. ∵点E ,F 分别是AB ,CD 的中点,∴AE=12AB ,CF=12CD ,∴AE=CF. ∵AG=CH ,∴△AEG ≌△CFH , ∴∠1=∠3.由折叠可知,∠1=∠2,∠3=∠4,AG=A'G ,CH=C'H ,∴∠1=∠2=∠3=∠4,A'G=C'H. ∵AD ∥BC ,∴∠AGH=∠CHG ,∴∠5=∠6, ∴A'G ∥C'H ,∴四边形A'HC'G 是平行四边形. (3)2√3或4√3解法提示:当A'G ∥BC 时,如图(3),点A'落在AD 上,EG ⊥AD ,则A'G=AG=12AE=1,∴S 四边形A'HC'G =A'G ·AB sin 60°=1×4×√32=2√3.图(3)当A'G ∥AB 时,如图(4),则∠AGA'=120°,∴∠AGE=∠A'GE=60°,图(4)从而易得△AEG ,△A'EG ,△CHF ,△C'HF 均是等边三角形,EA'∥BC ,C'F ∥AD ,∴S 四边形A'HC'G =S ▱ABCD -4S △AEG -2S 四边形A'EBH=8×4×√32-4×√34×22-2×12×(2+6)×2×√32=4√3. 综上可知,四边形A'HC'G 的面积为2√3或4√3. 4.(1)正方形(2)由题意可知,AB∶AD=3∶2,∴设AD=2a ,AB=3a , ∴BM=BC=AD'=2a ,∴BD'=a ,∴sin ∠BMD'=a 2a =12,∴∠BMD'=30°.又ED'∥AD ∥BC ,∴∠MBC=∠BMD'=30°. (3)①HF=HB②FC 的长为3-√5或23. 解法提示:①∵DC ∥AB ,∴∠CFB=∠ABF. 由折叠可知∠CFB=∠NFB ,∴∠ABF=∠NFB ,∴HF=HB.②设FC=NF=x ,分两种情况讨论.a.当射线FN 经过AD'的中点时,点H 即为AD'的中点,如图(1),则HF=HB=3,∴HN=3-x.在Rt △HBN 中,由勾股定理,得HN 2+BN 2=HB 2,∴(3-x )2+22=32,解得x=3-√5(不合题意的值已舍去),∴FC=3-√5.图(1)b.当射线FN 经过ED'的中点P 时,如图(2), 易证△HD'P ≌△FEP ,∴HD'=EF=2-x ,∴HF=HB=2-x+2=4-x , ∴HN=4-x-x=4-2x.在Rt △HBN 中,由勾股定理,得BN 2+HN 2=HB 2,∴22+(4-2x )2=(4-x )2,解得x=23(不合题意的值已舍去),∴FC=23.图(2)综上可知,当射线FN 经过△AED'的直角边的中点时,FC 的长为3-√5或23. 5.(1)△ADP ,△ABP ,△BDQ (2)①四边形BEFG 是菱形. 理由如下:由折叠知∠BEG=∠FEG.∵FG ∥BC ,∴∠EGF=∠BEG , ∴∠EGF=∠FEG ,∴FG=FE. 又∵FE=BE ,∴FG=BE ,∴四边形BEFG 是平行四边形. 又∵FE=BE ,∴四边形BEFG 是菱形.②224-128√3解法提示:由折叠的性质知AF=AB=8.在Rt △ADF 中,由勾股定理得DF=√AF 2-AD 2=√82-42=4√3,∴CF=8-4√3. 设BE=y ,则EF=y ,CE=4-y.在Rt △CEF 中,由勾股定理得EF 2=CF 2+CE 2, 即y 2=(8-4√3)2+(4-y )2,解得y=16-8√3,∴S 四边形BEFG =BE ·CF=(16-8√3)×(8-4√3)=128-64√3-64√3+96=224-128√3.(3)BN 的长为103或53. 解法提示:分两种情况讨论.①当点B'落在离点D 较近的三等分点上时,如图(1),过点B'作B'H ⊥AB 于点H ,易知B'H=83,BH=163,B'N=BN ,∴HN=163-BN. 根据勾股定理,得B'H 2+HN 2=B'N 2,即(83)2+(163-BN )2=BN 2,∴BN=103.图(1) 图(2)②当点B'落在离点B 较近的三等分点上时,如图(2),同理可求得BN=53. 综上可知,BN 的长为103或53. 6.(1)△BEH√k 2+255(2)证明:如图(1),过点K 分别作KN ⊥BC 于点N ,KM ⊥CD 于点M , 则KN=KM ,∠MKN=90°=∠BKH ,∴∠TKM=∠BKN.又∠TMK=∠BNK=90°,∴△TMK ≌△BNK ,∴BK=KT.图(1)(3)CK 的长为√7或√67.解法提示:分如图(2)、图(3)所示的两种情况讨论,连接CG ,过点K 作KP ⊥BC ,垂足为点P.图(2)图(3)∵CK=CH ,∴∠CKH=∠CHK ,∴∠CKB=∠CHG. 又KB=HG ,∴△CKB ≌△CHG ,∴CG=CB=BG ,∴△CBG 是等边三角形, ∴∠CBG=60°. 图(2)中∠KBC=30°,∴KP=12KB=√3,BP=√32KB=3, ∴CP=2,∴CK=√(√3)2+22=√7. 图(3)中∠KBP=30°,∴KP=12KB=√3,BP=√32KB=3, ∴CP=8,∴CK=√(√3)2+82=√67. 综上可知,CK 的长为√7或√67. 7.(1)6(2)由(1)得AC'=6,∴BC'=AB -AC'=10-6=4.在Rt △BEC'中,设BE=x ,则EC'=EC=8-x ,根据勾股定理,得(8-x )2=x 2+42, 解得x=3,即BE=3,∴EC'=EC=5.连接EE',由平移可知,EE'=C'B=4,EE'∥AB ∥CD ,DE ∥D'E',∴△FEE'∽△FCD'∽△ECD , ∴EF∶EE'=EC∶DC=5∶10=1∶2, 又EE'=4,∴EF=2.(3)平移的距离为85或385. 解法提示:设平移的距离为x. 分两种情况讨论.①当点C″在BC 左侧时,如图(1),则BC″=4-x ,D'C=10-x ,∴CP=D'C ·tan ∠CD'P=D'C ·tan ∠CDE=510(10-x )=12(10-x ),BQ=BC″·tan ∠QC″B=BC″·tan ∠ADC'=68(4-x )=34(4-x ). 又CP+PQ+BQ=8,PQ=2,∴12(10-x )+2+34(4-x )=8,解得x=85.图(1) 图(2)②当点C″在BC 右侧时,如图(2),则BC″=x -4,D'C=10-x ,∴CP=D'C ·tan ∠CD'P=12(10-x ),BQ=BC″·tan ∠QC″B=BC″·tan ∠AC'D=43(x-4). 又CP+PQ+BQ=8,PQ=2,∴12(10-x )+2+43(x-4)=8,解得x=385.综上可知,平移的距离为85或385. 8.(1)等腰三角形的顶角平分线、底边上的高、底边上的中线互相重合 (2)是. 理由如下:由作图可知,CA=CB ,CD=CE. 又∵∠ACE=∠BCD ,∴△ACE ≌△BCD , ∴∠CAE=∠CBD. ∵CA=CB ,∴∠CAB=∠CBA , ∴∠PAB=∠PBA ,∴AP=BP ,∴直线CP 是线段AB 的垂直平分线. (3)线段CD 的长为√3+1或3√3+3. 解法提示:∵CD=CE ,∠C=∠C ,CA=CB ,∴△CAE ≌△CBD ,∴∠CAE=∠CBD. ∵CA=CB ,∠ACB=30°, ∴∠CAB=∠CBA=75°,∴∠PBA=∠PAB=45°,∴∠APB=90°, ∴PA=PB=√22AB=√3. 分两种情况讨论.①当点P 在AB 上方时,如图(1),图(1)则∠DAP=∠EBP=30°,∠APD=90°,∴DB=DC ,DP=√33AP=1,∴CD=DB=√3+1. ②当点P 在AB 下方时,如图(2), 则∠DAP=∠EBP=60°,∠APD=90°,∴∠ADP=30°,∴BD=BC,DP=√3AP=3,AD=2AP=2√3,∴BC=BD=√3+3,∴CD=CA+AD=CB+AD=√3+3+2√3=3√3+3.综上可知,线段CD的长为√3+1或3√3+3.图(2) 9.问题发现192知识迁移 5拓展延伸(1)BE=DE+GF.理由:如图(1),过点G作GH⊥BE于点H.图(1)∵BE⊥CD,GF⊥CD,∴∠HEF=∠EFG=∠EHG=90°,∴四边形EFGH为矩形,∴EH=GF,EF=GH.∵EF=BE,∴GH=BE.∵∠MBN=90°,∠BHG=90°,∴∠1+∠2=90°,∠2+∠3=90°,∴∠1=∠3.又∵∠BED=∠GHB=90°,BE=GH,∴△BDE≌△GBH(ASA),∴DE=BH,∴BE=BH+EH=DE+GF.(2)92或323. 解法提示:分两种情况讨论.①当点F 在线段EC 上时,如图(2).图(2)由(1)可得BE=DE+GF. 设BE=EF=m ,则EC=m+2.在Rt △BEC 中,根据勾股定理,得BE 2+CE 2=BC 2, 即m 2+(m+2)2=102,解得m=6(负值已舍),∴BE=EF=6.易证△CFG ∽△CEB ,∴CF CE =GF BE ,即22+6=GF 6, ∴GF=32,∴DE=BE -GF=6-32=92. ②当点F 在线段EC 的延长线上时,如图(3).图(3)同(1)中方法可得BE=DE-GF. 设BE=EF=n ,则EC=n-2.在Rt △BEC 中,根据勾股定理,得BE 2+CE 2=BC 2, 即n 2+(n-2)2=102,解得n=8(负值已舍),∴BE=EF=8.易证△CFG ∽△CEB ,∴CF CE =GF BE ,即28−2=GF 8, ∴GF=83,∴DE=BE+GF=8+83=323.10.(1)EM DM =EBAB AM ⊥DE(2)证明:如图(1),过点G 作GH ⊥BC 于点H.图(1)∵四边形ABCD 是矩形,点E 在AB 的延长线上, ∴∠CBE=∠GHC=90°,∴∠BCE+∠BEC=90°. ∵四边形CEFG 为正方形, ∴CG=CE ,∠GCE=90°,∴∠BCE+∠BCG=90°,∴∠BEC=∠BCG , ∴△GHC ≌△CBE ,∴HC=BE. ∵AD=BC=2AB ,BE=AB ,∴BC=2BE=2HC , ∴HC=BH ,∴GH 垂直平分BC , 即点G 在线段BC 的垂直平分线上. (3)√5或√17.解法提示:同(2)中思路可证得点F 在线段BC 的垂直平分线上.如图(2),过点F 作FN ⊥BC 于点N ,连接CF ,则CF=√2CE=√2×√22+12=√10,CN=1,∴NF=√(√10)2-12=3.图(2)由作图过程可知,点M 在线段BC 的垂直平分线上,故分两种情况讨论.①当点M 在点F 左侧时,如图(3),连接MC ,图(3)则NM=3-1=2,∴m=CM=√22+12=√5.②当点M在点F右侧时,如图(4),连接MC,图(4)则NM=3+1=4,∴m=CM=√42+12=√17.综上可知,m的值为√5或√17.11.(1)②(2)如图(1),在AB上取点E,使得AE=AD,连接PE.图(1)∵AP平分∠DAE,∴∠DAP=∠EAP.又∵AP=AP,AD=AE,∴△DAP≌△EAP,∴PD=PE.∵AD+BC=AB=AE+BE,AD=AE,∴BC=BE.∵BP平分∠CBE,∴∠CBP=∠EBP.又∵BP=BP,∴△EBP≌△CBP,∴PE=PC,∴PC=PD.(3)8或403解法提示:如图(1),由(2)可得△DAP ≌△EAP ,△EBP ≌△CBP ,∴∠DPA=∠EPA ,∠CPB=∠EPB ,∠D=∠AEP ,∠C=∠BEP. 又∵∠DPA+∠EPA+∠CPB+∠EPB=180°,∠AEP+∠BEP=180°,∴∠APB=∠EPA+∠EPB=90°,∠D+∠C=180°, ∴AD ∥BC.在Rt △PAB 中,tan ∠PAB=12,∠APB=90°, 故可设BP=x ,AP=2x ,∴AB=√x 2+(2x)2=√5x=10, 解得x=2√5,∴AP=4√5,sin ∠PAB=1√5. 易知∠PBC>45°,故分两种情况讨论.①当∠C=45°时,如图(2),图(2)过点P 作PM ⊥AD ,交AD 的延长线于点M ,则∠MDP=∠C=45°,∴MP=MD. 又∵tan ∠MAP=tan ∠PAB=12,∴AM=2MP , ∴AD=MD=MP=AP ·sin ∠MAP=4, ∴S △PAD =12×4×4=8. ②当∠BPC=45°时,如图(3),图(3)过点D 作DN ⊥AP 于点N ,则∠DPN=180°-45°-90°=45°,∴NP=ND.∵tan ∠DAP=tan ∠PAB=12,∴AN=2ND. 又∵AP=AN+NP ,∴4√5=2ND+ND ,∴ND=4√53,∴S △PAD =12×4√5×4√53=403. 综上可知,△PAD 的面积为8或403.12.(1)①BE=AD②BE=AD. 理由如下:当点D 不在AC 上时,∵∠ACB=∠ACD+∠DCB=60°,∠DCE=∠BCE+∠DCB=60°,∴∠ACD=∠BCE. 在△ACD 和△BCE中,{AC =BC,∠ACD =∠BCE,DC =EC,∴△ACD ≌△BCE ,∴AD=BE. (2)①BE=√2AD. 理由如下:当n=90时,在等腰直角三角形DEC 中,DC EC =sin 45°=√22, 在等腰直角三角形ABC 中,AC BC =sin 45°=√22.∵∠ACB=∠ACE+∠ECB=45°,∠DCE=∠ACE+∠DCA=45°,∴∠ECB=∠DCA. 在△DCA 和△ECB中,{DCEC=AC BC=√22,∠DCA =∠ECB,∴△DCA ∽△ECB ,∴AD BE =√22,∴BE=√2AD. ②5或√13.解法提示:当点D 在△ABC 外部时,设EC 与AB 交于点F ,如图(1)所示.图(1)∵AB=3√2,AD=1,由上可知:AC=AB=3√2,BE=√2AD=√2. 又∵BE ∥AC ,∴∠EBF=∠CAF=90°.而∠EFB=∠CFA ,∴△EFB ∽△CFA ,∴EF CF =BF AF =BE AC =√23√2=13,∴AF=3BF ,而AB=BF+AF=3√2,∴BF=14×3√2=3√24. 在Rt △EBF 中,EF=√EB 2+BF 2=(√2)2+(3√24)2=5√24. 又∵CF=3EF=3×5√24=15√24, ∴EC=EF+CF=5√24+15√24=5√2. 在等腰直角三角形DEC 中,DC=EC ·sin 45°=5√2×√22=5.当点D 在△ABC 内部时,设AB 延长线与CE 延长线交于点F ,如图(2),图(2)∵AB=3√2,AD=1,由上可知:AC=AB=3√2,BC=√2AB=6,BE=√2AD=√2. 又∵BE ∥AC ,∴△EFB ∽△CFA ,∴FB FA =BE AC =13, ∴BF=12AB=3√22,AF=AB+BF=3√2+3√22=9√22. 在Rt △ACF 中,CF=√AC 2+AF 2=3√262.CE=23CF=23×3√262=√26. 在等腰直角三角形DEC 中,DC=√22CE=√13. 综上所述,满足条件的CD 的值为5或√13.。
常见活动探究答题思路及举例

常见活动探究答题思路及举例1.题型特点实践与探究题是近几年中考中出现的一种新题型。
这种题型的出现是为了适应中考改革、发展形势的需要,适应新课标要求“培养学生的创新精神和实践能力,鼓励学生有自己的见解”而产生的。
这类试题主要有调查报告、活动设计、主题班会、演讲稿、发言提纲、撰写小论文等形式,具有设问发散性强、与学生和社会生活实际联系密切、答案倡导并鼓励多元化等特点。
对此类试题的一般性解答要求是:⑴首先要求学生积极参与活动与实践,熟悉和掌握各类实践活动的方法和程序。
⑵要具备较强的创新精神和实践能力,能独立思考、解决问题。
(3)要审明题意,按要求作答。
(4)要回归课本寻找知识的落脚点。
(5)设计的活动方案或步骤要切实可行,讲究实效、鼓励参与、有所创意、力求完美,具有较强的可操作性。
(6)注意答案内容的条理性、开放性和逻辑性。
2.题型及答题方法⑴调查报告类。
调查报告是人们对某一情况、事件、经验或问题,经过深入思致的调查研究而写成的文字材料。
它反映了人们通过调查研究找出的某些有规律性的东西,以及提出的相应措施和建议,是社会调查实践活动的成果。
学会撰写调查报告,有助于我们进一步认识社会、参与社会,把所学知识与社会实践结合起来,全面提高自身素质。
调查计划由下面几部分组成:(1)调查主题(2)调查的目的或意义(3)调查的时间、范围、参加对象(4)调查的准备、对象、方式(调查方法可采用问卷、访问、观察、座谈会等)。
(5)调查的内容等。
(6)结论和建议。
[例题]:我国拥有数量众多的江河湖泊,但我国却是一个严重缺水的国家。
结合你所在地区用水情况作一次居民生活用水状况的调查。
(1)列出调查题目(2)列出调查方案(目的、对象、内容或资料、途径或方法)(3)根据分析调查结果,提出建议。
[参考答案](1)题目:我市(县)居民用水状况及对策(2)a、目的:通过对居民生活用水状况的调查,了解供水情况及用水的浪费程度,分析原因,认识节水的紧迫性,增强全民节水意识。
小说阅读主题分析

文学类文本阅读之小说主题分析五、概括小说主题小说的主题是小说的灵魂,是作者的写作目的之所在,也是作品的价值意义之所在。
主题的深浅往往决定着作品价值的上下,因此,观赏小说必须观赏小说的主题。
小说主题高考设题方法有三类:概括、评价和探究。
对主题比拟单一的高考往往以概括的形式考查,对主题可以从不同角度挖掘的,往往以评价、探究的形式考查。
〔一〕常见题型:1、用自己的话概括作品的主题。
2、读了全文后,文章让你明白了什么道理。
3、本文对你有何启迪?谈谈你的一点体会。
4、结合全文主题,谈谈你对某一句话〔某一个问题〕的理解或看法。
〔二〕主题挖掘的根本途径:对主题的挖掘一般可从以下几方面:从小说的标题看、从作者背景看、从人物特征看、从情节开展看、从言语感情色彩看、从作者的思想倾向看。
对主题的概括常用这样一些根本术语:1、歌颂、赞扬、张扬什么。
2、挖苦、批判、揭露、责备什么。
3、揭示什么人生道理。
4、对什么现象的反思。
5、表达了什么感情。
〔三〕主题探究题分类与挖掘途径:〔1〕思想感情意蕴探究①通过形象来完成。
以小说主要人物的性格特点、道德风貌、品行等揭示人性中的真善美和假丑恶。
②通过叙事来完成。
用故事形式针砭时弊。
③通过手法(隐喻、象征等〕暗示。
通过寓言,寄寓人生哲理。
④通过环境描写,反映人物生存状的时代背景。
〔2〕思想意蕴、感情意蕴探究所谓思想意蕴,是指作品表现出的思想意义或价值,重在指文本给读者的思考和认识。
所谓感情意蕴,是指作品的感情意义或取向,就是作者的感情态度、喜怒褒贬等。
虽说二者有时在具体题目中有相通之处,但意蕴重在思想性、认识性,而感情是作者的倾向性,即他赞成什么,反对什么。
小说的思想、感情意蕴都是附着在小说的具体形象之中的,探究时特别要特长抓住小说中不同的人、事、物,再分析探究所附着的意蕴即可。
〔3〕启发(思考)类探究启发(思考)类探究题是近年新增的一种题型,这类题型有启发性,更简单让考生各抒己见,畅所欲言。
中考语文强化训练:语文综合运用题(题型+策略)

中考语文强化训练:语文综合运用题(题型+策略)语文综合运用的中考具体题型分类有:一、综合运用类二、实践探究类三、主题探讨类四、地方特色类五、图文结合类六、信息提取类七、关注时事类一、综合运用类例题:你班组织“毕业晚会”活动,你经历了下面一些事情,你是怎么解决的?1、班级征集晚会主题语,要求是简洁形象的一句话或一个短语。
你写的是什么?2、根据节目表,合唱《让我们荡起双桨》之后是舞蹈”友谊地久天长“,请你为连接这两个节目写几句串台词。
3、事后某同学为学校广播站写了一则消息,交稿前,她请你做些修改。
①为了活泼毕业班同学的课余生活,加强同学之间、师生之间的情感交流,九年级⑴班最近组织了毕业晚会。
②同学们踊跃参与、认真准备,各逞其能。
晚会内容丰富,形式多样,③有歌舞、朗诵、合唱、相声、小品等。
活动中,大家增进了友谊,展望了未来。
晚会过后,该班又精神饱满地投入到紧张的学习之中。
⑴句①中,有词语搭配不当,可将“____”一词改成“____”。
⑵句②中,有词语使用不当,应该为“____”。
⑶句③中,有词语并列不当,应删去“____”。
4、晚会后,你感到收获很大。
第二天上学路上,领班一位同学问你:”学习那么紧张,花那么多时间搞活动,划得来吗?“请你用一两句话得体地回答他的提问,表明你的看法。
解题指导这是一道语言综合运用题,兼容应用文、语病修改、语文活动等知识的应用与实践。
命题人做了一个精心的设计,把课堂中学习到的各种语文知识通过一次活动串联起来,各小题从不同的角度对学生的能力进行考察,而且题目与学生的实际结合非常紧密,使学生能够联系生活实际来思考和答题。
1、2题考察的是写广告、标语、解说词、拟对联、致欢迎词的能力。
3题考察的是修改病句的能力。
题4考察的口语交际能力。
二、实践探究类例题:每年的4月23日定为“世界图书和版权日”(也译为“世界读书日”、“世界书香日”),鼓励人们尤其是年轻人发现读书的乐趣,并以此对那些推动人类社会和文化进步的人们所做出的伟大贡献表示感谢和尊重。
高考小说意蕴主题探究题答题方法总结

小说意蕴解题方法意蕴探究题主要出现在江苏高考试题中,考察类型可以分为主题意蕴、句子意蕴、标题意蕴等。
意蕴指内容的深刻含义,须多角度、多层次思考,不可以停留在表面,应考虑作品的主旨意义,所以主题意蕴最具有代表性。
下面对这几类题型尤其是主题意蕴的探究做详细讲解。
一、标题意蕴其实直接考察标题意蕴的情况不算多,不过解读标题意蕴对于探究主旨、探究主题意蕴有一定帮助,如《药》《审丑》,所以也要稍加关注。
标题意蕴通常的解题思路有:1.标题的含义和手法,有无双关或比喻象征2.标题与环境、人物、主题的关系例:“审丑”作为小说的标题,意蕴丰富。
请结合全文谈谈你的理解。
参考答案:①标题一语双关(或反讽);(手法)②“审丑”是一种绘画原则,老人成为学生的审丑对象;(表层含义)③老人外貌丑陋,做人体模特被人们视为“丑”事,但这“丑”下面却隐藏着为孙子全力付出的淳朴心灵;(人物1)④小臭儿不孝,嫌弃爷爷,是真正的“丑”。
(人物2)补充:小说题目的考查类型及做题技巧1、小说标题的含意(双重或多重)①表面意义与真实意义。
②指代意义与比喻意义。
③一语双关,双层含义。
2、小说标题的用意(原因、作用、效果、好处)①点明时间地点,创设故事背景,渲染环境氛围。
②概括故事情节、暗示比喻象征、揭示小说主旨。
③结构线索,组织全文;寄托情感,深化主题。
④铺开情节,呼应细节;对比讽刺,强化效果。
3.标题是否可以替换①这个题目的优点(是否有助于突出XX形象、主题,是否是文章的线索或概括主要内容或制造悬念或讽刺或双关)。
②替代的题目有XX缺点。
二、句子意蕴通过江苏卷历年试题来看,考察结尾句意蕴的情况较多。
小说结尾据的意蕴,要结合小说内容,即情节、环境、人物、主旨来思考。
具体可参考下文对主题意蕴的讲解。
句子意蕴的答题思路1.句子的表层意思2.句子的深层意思(比喻义、象征义)3.情感意义4.主旨意义例:《安娜之死》15.请探究作品结尾画线句的意蕴。
(6分)一支蜡烛,她曾借着它的烛光浏览过充满了苦难、虚伪、悲哀和罪恶的书籍,比以往更加明亮地闪烁起来,为她照亮了以前笼罩在黑暗中的一切,哔剥响起来,开始昏暗下去,永远熄灭了。
探究主旨类题目解题技巧.

民族心理和人文精神的内涵。
(1)中华民族优秀传统: 一是团结统一的传统, 二是独立自主的传统, 三是爱好和平的传统, 四是自强不息的传统。 (2)中华民族的传统美德: 忠,尽己报国的责任; 孝,生生不息的爱心; 诚,求真务实的品质; 信,立身兴业的基点; 礼,人际文明的规范; 义,人间正道的向导; 廉,清白正气的根基; 耻,人之为人的底线。
(4)中华民族人文精神: 人生活在世界上面临的基本矛盾有三个: 人与自我的矛盾、人与社会的矛盾和人与自 然的矛盾. 人的价值可分为人的自我价值、人的社会价 值和人的自然价值。 人的自我价值在于人格; 人的社会价值在于对社会作出贡献; 人的自然价值在于促进人与自然的协调发展, 有益于自然生态的积极平衡。
人与自然
14.本文题为“江南无雪”,文中却用大量 篇幅写雪,请结合全文探究这样安排有哪 些意图。(6分)
14.①以昔日大雪反衬今日无雪,表现对环境恶化的忧虑 和希望环境早日改善的愿望。②以我童年赏雪和儿子童年无 雪可赏对照,希望孩子有快乐丰富的童年,能更好地认识自 然和人生。③以现实的无雪和想象中的夜饮赏雪映衬,表达 对人生美好情趣的渴望。(要求答出两点,一点3分。意思 对即可)
1.提出自己的看法
这种题型命题人往往要求考生结合作品谈谈自己的看法或见解。 不允许考生脱离文本海阔天空、信马由缰地随意发挥,一定 要与文本不即不离。 如:2008年高考广东卷《河的第三条岸》第18题:有人说, “河的第三条岸”在现实中并不存在,它象征着“父亲”超 越世俗的人生追求。如果这样,那么“我”对“父亲”的这 种追求持何种态度?请联系全文,谈谈你的看法。(6分) 此题“请联系全文,谈谈你的看法”的表述,可以赞同也可以 否定但无论怎样,都必须依据文本。 答案提示:如果说“河的第三条岸”是“父亲”超越世俗的人 生追求,“我”对“父亲”的这种追求既支持,但又害怕、 不理解。首先是支持,表现在乐意跟随父亲一起上船;在父 亲需要的时候帮助你“偷”食物;当全家人都走了我还在默 默地守护着父亲,说“无论何时,我会踏上你的船,顶上你 的位置。” 其次是不甚理解,少年的不理解,只为了追求而去,当父亲 接受你的提议后,我浑身战栗,害怕极了,甚至“发疯似的 逃掉”,把父亲看作是“另一个世界来的人”。
中考历史 中考题型专题探究 (四)探究题

(2)上述英雄人物参加这场战争主要是为了抵抗哪国的侵略?在他们身
上体现了怎样的精神?
国家:美国。精神:爱国主义精神;革命英雄 主义精神;革命忠诚精神;国际主义精神。 (其他符合题意的答案也可)
活动三:【理大事】
下表是对中国共产党百年历史中重大事件的梳理(部分)
时期
事件及意义
1921 年 7 月,①
请以《本草纲目》为例概述本草学入围的理由。
《本草纲目》收录多种药物、药方及多幅药物形 态图,对药物进行了新的分类,总结了我国古代 药物学成就,丰富了我国医药学宝库,在世界医 药史上占有重要的地位。
【探究二】科技改变世界 (2)1933 年,美国芝加哥举办的世博会对第二次工业革命的科技成果进行 了展示。请你列举一例当时的参观者可能看到的相关展品,并简要说明
重大事件,并简述其意义。
重大事件及意义:①中国共产党诞生。是中国 历史上开天辟地的大事,自从有了中国共产党, 中国革命的面貌焕然一新。②十一届三中全会 召开。是新中国成立以来党的历史上具有深远 意义的伟大转折,开启了改革开放和社会主义 现代化的伟大征程。(任选其一回答均可)
活动四:【悟党史】 习近平总书记强调,学习党史要做到学史明理、学史增信、学史崇德、 学史力行。 (4)结合中国共产党百年历程,概述党在中国近现代历史进程中发挥的重 要作用。
团结带领中国人民实现民族独立、人民解放; 团结带领全国各族人民走向国家富强、人民幸 福。(其他符合题意的答案也可)
【针对训练】 1.“中国梦”是中国人追求国家富强、民族复兴、人民幸福之梦。近代 以来,辈辈仁人志士,为追求“中国梦”而不懈努力,几多教训,几多 启示。请你结合所学完成探究问题。
【中体西用】
【历史情感的升华】
探究性试题的八种题型

探究性试题的八种题型1.观点式2008年海南(宁夏)卷的欧·享利《二十年以后》与夏东元《盛宣怀传》就已出现这种题型,2009年则增加到三套试卷,这里仅以辽宁卷为例,作重点分析。
2009年辽宁卷——贾平凹《遗璞》:小说最后描写了蛮儿一帮年轻人炸掉了遗璞,并用它去修水渠作者在结局上的这种处理是否合理?请结合小说具体内容,谈谈你的看法和理由这种题型的解答,无非是正反两个观点。
本题所考查的是“对作品进行个性化阅读和有创意的解读”的能力,能力层级为F级。
“对作品进行个性化阅读和有创意的解读”,首先必须明确:第一,探究类试题的内容是有疑难的,甚至是有争议的,即答题指向不是单一的而是多向的,不是单层次的而是多层次的。
第二,试题的答案不是唯一的,甚至不是规定的,目的在于考查考生“能否发现作品的丰富内涵和深层意义,是否对作品有独到的感受和创造性理解,是否具有批判质疑的能力等”。
第三,由于高考的选拔特点,试题将不可能是全开放的,即“一千个读者心目中的一千个哈姆莱特必须首先是哈姆莱特”,因此,试题应该是半开放的——多角度,但不是漫无边际。
观点式探究试题答题步骤:首先明确自已的观点,其次分别列出支持自身观点的事实依据,最后回归文本。
结合具体事例作合情合理的分析。
2009年辽宁卷——斯蒂芬·杰·古尔德《达尔文的拖延》:文中说:“疑惑和知识都应该坚持”这里的“疑惑”和“知识”有哪些含义?为什么说“都应该坚持”?请联系全文,谈淡你的理解和看法。
这一题考查的同样是“对作品进行个性化阅读和有创意的解读”的能力。
探究,是一个探索研究的过程,是一个“多方寻求答案,解决疑问”“探求事物的真相、性质、规律等”的学习、研究活动过程。
“对作品进行个性化阅读和有创意的解读”有两层含义:其一是“对作品进行个性化阅读”,其二是“对作品进行有创意的解读”。
前者侧重“个性化”,立足求异,展示对文本的不同解读:后者侧重“有创意”,立足求新,提出自己的新发现。
小说复习——探究标题意蕴

Ⅱ
抓住规律特点,多角度、深层次探究
一、题目让你探究什么——小说五个方向
尽管探究题要探究的方向(点)很多,但在小说中无非五个方
向:主题、人物、情节、环境和艺术特点。 2014年新课标全国卷Ⅰ《古渡头》的探究题指向小说的情节 安排, 2014 年新课标全国卷Ⅱ《鞋》则指向小说的特殊结 构——后记,2014年江苏、辽宁、浙江卷的探究题则指向小
(二)标题意蕴、作用探究 一是侧重内容的意蕴探究,二是不同标题的比较探究,
三是拟标题的意图。无论是哪种,都要关注两方面:一
命题者偏爱选择标题作为探究点。常见的探究题有三种:
是标题本身的内容、艺术特点;二是标题与文本的联系, 或多角度多层次切入。对于标题意蕴题,特别要关注表
层义、深层义、象征义或比喻义。
(三)病例剖析
现场答案1存在的问题: 提示该答案虽有三点,其实就一点,从人物形象角 度。这三点,①②两点重复,第③点探究缺乏文本 基础。 现场答案2存在的问题: 提示该答案能够从人物、情节、主旨等角度切入, 较好。只是第③点,它不属于马罗大叔烤包谷这一 内容中的,是针对全文内容而言的。
(四)实战演练
例题:2014年新课标全国卷Ⅰ小说《古渡头》探究题 作品为什么以渡夫的任情高歌为结尾?结合全文,谈谈你的看法。 答案 ①艺术结构上,通过突转产生戏剧性效果,最后以歌声结 尾,余韵悠长,耐人寻味;
②情感表现上,以渡夫的无表情代替哭泣,以任情高歌代替诉苦, 强化了表现苦难的力度; ③人物形象上,既表现渡夫的洒脱豪放,也反衬他的现实痛苦之 深,使渡夫的形象更加丰满; ④思想内容上,从批判社会现实的黑暗到表现渡夫追求自由生活 的信念,深化了作品的主题。
借鉴 “ 写法 ” 作审美探究。无论哪类探究,紧扣文本内容,结
七年级上学期题型训练05实践探究题(解析版)

题型训练05——实践探究题一、实践探究题1.人生梦想某校七年级(3)班以“编织人生梦想”为主题开展活动请你参与并完成任务。
(1)【设计问卷】设计关于“中学生梦想”的调查问卷,要做好以下四项工作:①搜集相关资料;①明确调查目的;①确定正式问卷;①设计具体问题。
请按照设计问卷的步骤把以上四项工作正确排序。
(写出序号即可)(2)【倡议梦想】调查结果显示,仅有1.76%的同学有十足的信心实现梦想,大部分同学不确定梦想能否实现。
因此,调查小组向全班同学提出倡议:有梦想,就有希望。
中学生要敢于“有梦”,勇于“追梦”,勤于“圆梦”。
中学生为什么要“编织人生梦想”?(3)请运用所学知识谈谈中学生应怎样“圆梦”。
(4)【实现梦想】我们要把实现个人梦、家庭梦融入国家梦、民族梦之中,用我们4亿多家庭、14亿多人民的智慧和力量汇聚起夺取新时代的磅礴力量。
材料表明实现中国梦必须怎么做?除此之外,还必须做些什么?【答案】(1)①→①→①→①(2)梦想是对未来美好生活的愿望,它能不断激发我们生命的热情和勇气,让生活更有色彩。
有梦想,就有希望。
梦想虽然总是和现实有一定距离,有时甚至不切实际,但是人类需要这样的梦想,因为有了这样的梦想,才能不断地进步和发展。
(3)①少年有梦,不应止于心动,更在于行动。
①努力,是梦想与现实之间的桥梁。
①努力,需要立志、坚持、方法。
①坚持梦想,将进取变成一种信念。
①实现梦想需要脚踏实地,落实到具体行动中。
(4)凝聚中国力量;走中国道路,弘扬中国精神。
【解析】(1)本题考查调查问卷的活动顺序。
调查首先要明确调查目的,然后搜集相关资料,设计好调查问题,最后确定正式问卷,顺序应该是①①①①。
(2)本题结合教材知识,从梦想的含义、梦想激发生命热情、有梦想就有希望、人类有梦想才能进步发展等方面作答。
(3)本题结合相关知识,从少年有梦,更在于行动;努力,是梦想与现实之间的桥梁;努力,需要立志、坚持、方法;实现梦想需要脚踏实地,落实到具体行动中作答。
中考数学题型归纳——探究题参考答案
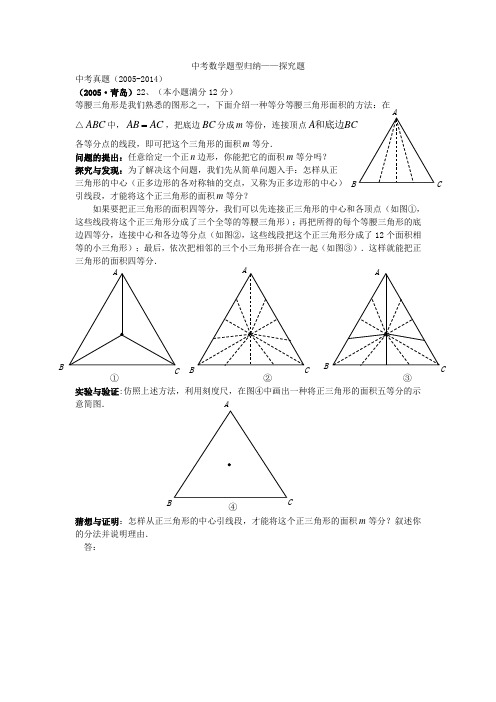
中考数学题型归纳——探究题中考真题(2005-2014)(2005·青岛)22、(本小题满分12分)等腰三角形是我们熟悉的图形之一,下面介绍一种等分等腰三角形面积的方法:在 △ABC 中,AB AC ,把底边BC 分成m 等份,连接顶点A和底边各等分点的线段,即可把这个三角形的面积m 等分.问题的提出:任意给定一个正n边形,你能把它的面积m 等分吗? 探究与发现:为了解决这个问题,我们先从简单问题入手:怎样从正 三角形的中心(正多边形的各对称轴的交点,又称为正多边形的中心) 引线段,才能将这个正三角形的面积m 等分?如果要把正三角形的面积四等分,我们可以先连接正三角形的中心和各顶点(如图①,这些线段将这个正三角形分成了三个全等的等腰三角形);再把所得的每个等腰三角形的底边四等分,连接中心和各边等分点(如图②,这些线段把这个正三角形分成了12个面积相等的小三角形);最后,依次把相邻的三个小三角形拼合在一起(如图③).这样就能把正三角形的面积四等分.① ② ③实验与验证:仿照上述方法,利用刻度尺,在图④中画出一种将正三角形的面积五等分的示意简图.猜想与证明:怎样从正三角形的中心引线段,才能将这个正三角形的面积m 等分?叙述你的分法并说明理由. 答:B CB ④ BBB拓展与延伸:怎样从正方形的中心引线段,才能将这个正方形的面积m 等分?(叙述分法即可,不需说明理由) 答:问题解决:怎样从正n 边形的中心引线段,才能将这个正n 边形的面积m 等分?(叙述分法即可,不需说明理由)答:22、(本小题满分12分)(1)实验与验证:图(略) ··················· 3分 (2)猜想与证明:先连接正三角形的中心和各顶点,再把所得的每个等腰三角形的底边m 等分,连接中心和各等分点,依次把相邻的三个小三角形拼合在一起,即可把正三角形的面积m 等分.······························ 5分 理由:正三角形被中心和各顶点连线分成三个全等的等腰三角形,所以这三个等腰三角形的底和高都相等;这个等腰三角形的底边被m 等分,所以所得到的每个小三角形的底和高都相等,即其面积都相等,因此,依次把相邻的三个小三角形拼合在一起合成的图形的面积也相等,即可把此正三角形的面积m 等分. ············· 8分(3)拓展与延伸:先连接正方形的中心和各顶点,再把所得的每个等腰三角形的底边m 等分,连接中心和各等分点,依次把相邻的四个小三角形拼合在一起,即可把正方形的面积m 等分.························· 10分 (4)问题解决:先连接正多边形的中心和各顶点,再把所得的每个等腰三角形的底边m 等分,连接中心和各等分点,依次把相邻的n 个小三角形拼合在一起,即可把正多边形的面积m 等分.······························· 12分A D BCA 34A 5 6(2006·青岛)23.(本小题满分 10 分)我国著名数学家华罗庚曾说过:“数缺形时少直观,形少数时难入微;数形结合百般好,隔离分家万事休”.数学中,数和形是两个最主要的研究对象,它们之间有着十分密切的联系,在一定条件下,数和形之间可以相互转化,相互渗透.数形结合的基本思想,就是在研究问题的过程中,注意把数和形结合起来考察,斟酌问题的具体情形,把图形性质的问题转化为数量关系的问题,或者把数量关系的问题转化为图形性质的问题,使复杂问题简单化,抽象问题具体化,化难为易,获得简便易行的成功方案.例如,求1+2+3+4+…+n的值,其中n是正整数.对于这个求和问题,如果采用纯代数的方法(首尾两头加),问题虽然可以解决,但在求和过程中,需对n的奇偶性进行讨论.如果采用数形结合的方法,即用图形的性质来说明数量关系的事实,那就非常的直观.现利用图形的性质来求1+2+3+4+…+n 的值,方案如下:如图,斜线左边的三角形图案是由上到下每层依次分别为1,2,3,…,n个小圆圈排列组成的.而组成整个三角形小圆圈的个数恰为所求式子1+2+3+4+…+n的值.为求式子的值,现把左边三角形倒放于斜线右边,与原三角形组成一个平行四边形.此时,组成平行四边形的小圆圈共有n行,每行有(n+1)个小圆圈,所以组成平行四边形小圆圈的总个数为n(n+1)个,因此,组成一个三角形小圆圈的个数为21)(+nn,即1+2+3+4+…+n=21)(+nn.(1)仿照上述数形结合的思想方法,设计相关图形,求1+3+5+7+…+(2n-1)的值,其中 n 是正整数.(要求:画出图形,并利用图形做必要的推理说明)(2)试设计另外一种图形,求1+3+5+7+…+(2n-1)的值,其中n是正整数.(要求:画出图形,并利用图形做必要的推理说明)23.(本小题满分10分)解:(1)………………………………………………………3′因为组成此平行四边形的小圆圈共有n 行,每行有[(2n -1)+1]个,即2n 个,所以组成此平行四边形的小圆圈共有(n×2n)个,即2n2个.∴1+3+5+7+…+(2n-1)=21 12〕)—〔(+⨯nn=n2.………………6′(2)…………………………………………………………………9′因为组成此正方形的小圆圈共有n 行,每行有n个,所以共有(n×n)个,即n2个.∴1+3+5+7+…+(2n-1)=n×n=n2.………………………………………10′(2007·青岛)23.(本小题满分10分)提出问题:如图①,在四边形ABCD中,P是AD边上任意一点,△PBC与△ABC和△DBC的面积之间有什么关系?探究发现:为了解决这个问题,我们可以先从一些简单的、特殊的情形入手:(1)当AP=12AD时(如图②):∵AP=12AD,△ABP和△ABD的高相等,∴S△ABP=12S△ABD .∵PD=AD-AP=12AD,△CDP和△CDA的高相等,∴S△CDP=12S△CDA .∴S△PBC =S四边形ABCD-S△ABP-S△CDP=S四边形ABCD-12S△ABD-12S△CDA=S四边形ABCD-12(S四边形ABCD-S△DBC)-12(S四边形ABCD-S△ABC)=12S△DBC+12S△ABC .(2)当AP=13AD时,探求S△PBC与S△ABC和S△DBC之间的关系,写出求解过程;解:(3)当AP=16AD时,S△PBC与S△ABC和S△DBC之间的关系式为:_____________________________________________________;(4)一般地,当AP=1nAD(n表示正整数)时,探求S△PBC与S△ABC和S△DBC之间的关系,写出求解过程;解:问题解决:当AP=mnAD(0≤mn≤1)时,S△PBC与S△ABC和S△DBC之间的关系式为:___________________________________________.解:(2)∵AP=AD,△ABP和△ABD的高相等,∴S△ABP=,又∵PD=AD-AP=AD,△CDP和△CDA的高相等,∴S△CDP=,∴ S△PBC=S四边形ABCD-S△ABP-S△CDP=S四边形ABCD-S△ABD-S△CDA=S四边形ABCD-(S四边形ABCD-S△DBC)-(S四边形ABCD-S△ABC)=S△DBC+S△ABC∴S△PBC=S△DBC+S△ABC;(3)S△PBC=S△DBC+S△ABC;(4)S△PBC=S△DBC+S△ABC;∵AP=AD,△ABP和△ABD的高相等,∴S△ABP=S△ABD又∵PD=AD-AP=AD ,△CDP 和△CDA 的高相等, ∴S △CDP =S △CDA , ∴S △PBC =S 四边形ABCD -S △ABP -S △CDP =S 四边形ABCD -S △ABD -S △CDA=S 四边形ABCD -(S 四边形ABCD -S △DBC )-(S 四边形ABCD -S △ABC ) =S △DBC +S △ABC , ∴S △PBC =S △DBC +S △ABC问题解决:S △PBC =S △DBC +S △ABC 。
强化主旨意识解答标题意蕴类探究题

可是,不知不觉中,那些被人遗忘了的种子,还是和千百年来 一样破土而出了。每天早上嫩绿的叶子上都会有珍珠一样的露水, 在晨风中把阳光变幻得五彩缤纷。这些种子们不知道,永远不会再 有人来伺候它们,收获它们了。从此往后,百亩园里将是炉火熊熊、 浓烟滚滚的另一番景象。
六安爷舍不得那些种子。他掐着指头计算着出苗的时间,到了 该间苗锄头遍的日子,六安爷就拄着锄头来到百亩园。一天三晌, 一晌不落。
栏目导航
☞解题思路示范 [典例 1] (2016·全国卷Ⅰ)阅读下面的文字,完成后面的题目。
锄 李锐 拄着锄把出村的时候又有人问:“六安爷,又去百亩园呀?” 倒拿着锄头的六安爷平静地笑笑:“是哩。” “咳呀,六安爷,后晌天气这么热,眼睛又不方便,快回家歇 歇吧六安爷!” 六安爷还是平静地笑笑:“我不是锄地,我是过瘾。”
栏目导航
☞分析命题角度
题干示例
审题定向
(1)(2018·江苏卷)小说叙述了小哥儿俩的日常故
事,请探究作者在其中所寄寓的情感态度。(《小 关 注 题 干 中 有 没 有
哥儿俩》)
“主旨”“主题”“创
作意图”“情感态度” (2)(2016·全国卷Ⅰ)“我不是锄地,我是过瘾”
和主旨句之类的词语和
这句话,既是理解六安爷的关键,也是理解小
3.“1 掌握”
掌握常用答题模板:总—分,即总说作品中流露出的思想意蕴 与情感意蕴,分点证明。
栏目导航
☞解题思路示范 [典例 2] (2018·江苏卷)阅读《小哥儿俩》(阅读文本见“第 3 讲 [典例]”),完成后面的题目。 小说叙述了小哥儿俩的日常故事,请探究作者在其中所寄寓的 情感态度。(6 分) [尝试解答]
栏目导航
答案: ①“锄”作为一种农具,象征六安爷的人生和精神; ②“锄”喻示劳动者与土地的亲密关系;③“锄”意味着传统的农 业生产和生活方式;④“锄”作为一种劳作行为,蕴含着六安爷对 土地的热爱,又暗含着他对土地的告别。
中考数学复习之项目式探究学习综合题-学生版

几何、函数与实际应用实际应用题一直以为是中考数学的热点题型,甚至可以说是必考题型.深圳中考数学对实际应用的考查尤其突出,此类题贴合实际,产生的问题源于生活,同时又与数学中的几何、函数结合.问题的解决一般需要用到几何知识和函数的相关知识.题目文字较多,对多数同学而言,难点在于文字的理解与问题的解决方法,文字的理解主要是了解实际问题,而解决方法则考查同学们的数学基本功底.例1(2023深圳中考21题)蔬菜大棚是一种具有出色的保温性能的框架覆膜结构,它出现使得人们可以吃到反季节蔬菜.一般蔬菜大棚使用竹结构或者钢结构的骨架,上面覆上一层或多层保温塑料膜,这样就形成了一个温室空间.如图1,某个温室大棚的横截面可以看作矩形ABCD 和抛物线AED 构成,其中AB =3m ,BC =4m ,取BC 中点O ,过点O 作线段BC 的垂直平分线OE 交抛物线AED 于点E ,若以O 点为原点,BC 所在直线为x 轴,OE 为y 轴建立如图所示平面直角坐标系.请回答下列问题:(1)如图2,抛物线AED 的顶点E (0,4),求抛物线的解析式;(2)如图3,为了保证蔬菜大棚的通风性,该大棚要安装两个正方形孔的排气装置LFGT ,SMNR ,若FL =NR =0.75m ,求两个正方形装置的间距GM 的长;(3)如图4,在某一时刻,太阳光线透过A 点恰好照射到C 点,此时大棚截面的阴影为CK ,求CK 的长.解:(1)∵AB =3m ,AD =BC =4m ,E (0,4),∴A (﹣2,3),B (﹣2,0),C (2,0),D (2,3),设抛物线表达式为y =ax 2+bx +c ,将A 、D 、E 三点坐标代入表达式,得4−2+=34+2+=3=4,解得=−14=0=4.∴抛物线表达式为=−142+4.(2)设G (﹣t ,3),则L (﹣t −34,3+34),∴3+34=−14(−−34)2+4,解得=14(负值舍去),∴GM =2t =12.(3)取最右侧光线与抛物线切点为F ,如图4,设直线AC 的解析式为y =kx +b ,∴−2+=32+=0,解得=−34=32,∴直线AC 的解析式为y =−34x +32,∵FK ∥AC ,设F :=−34+,∴=−34+=−142+4,得−142+34+4−=0,∴=(34)2−4×(−14)(4−p =0,解得m =7316,∴直线FK 的解析式为=−34+7316,令y =0,得x =7312,∴F =7312+2=9712.∴CK =BK ﹣BC =9712−4=4912例2(2024南山育才中考模拟)【项目式学习】项目主题:设计浇地窗的遮阳篷项目背景:小明家的窗户朝南,窗户的高度AB=2m ,为了遮挡太阳光,小明做了遮阳篷的设计方案,请根据不同的设计方案完成以下任务.方案1:直角形遮阳篷如图1:小明设计的第一个方案为直角遮阳篷BCD ,点C 在AB 的延长线上CD ⊥AC.(1)若BC=0.5m ,CD=1m ,则支撑杆BD=________m.(2)小明发现上述方案不能很好发挥遮阳作用,如图2,他观察到此地一年中的正午时刻,太阳光与地平面的最小夹角为α,最大夹角为β,小明查阅资料,计算出tanα=31,tanβ=34,为了让遮阳篷既能最大限度的使冬天温暖的阳光射入室内(太阳光与BD 平行),又能最大限度的遮挡夏天火热的阳光(太阳光与AD 平行),请求出图2中的BC 、CD 的长度.方案2:抛物线形遮阳篷(3)如图3,为了美观及实用性,小明在(2)的基础上将CD 边改为抛物线形可伸缩的遮阳篷(F 为抛物线的顶点,DF 段可伸缩),且∠CFD=90°,BC 、CD 的长保持不变,若以C 为原点,CD 方向为x 轴,BC 方向为y 轴,①求该二次函数的表达式;②若某时刻太阳光与水平地面夹角的正切值tan θ=32,使阳光最大限度的射入室内,求遮阳篷点D 上长升的高度的最小值(即点D'到CD 的距离)解:(1)由勾股定理直接计算BD=25(2)如图所示,设EF=m ,则AE=3m,DE=4m ,故2+m=4m 得m=32,故BC=32,CD=2m ;(3)①易知点F(1,1)设二次函数解析式为1)1(2+-=x a y ,将(0,0)代入得a=-1,故二次函数的解析式为xx y 22+-=②如图,设光线恰好经过点B ,与x 轴交于点I ,与抛物线交于点D,则易知BI 的解析式为3232-=x y ,与抛物线x x y 22+-=联立得x 1=9102+,x 2=9102-(舍去),此时y =92102-,故上升的最小高度为92102-全真模拟练习1.根据以下素材,探索完成任务如何探测弹射飞机的轨道设计素材1:图1是某科技兴趣小组的同学们制作出的一款弹射飞机,为验证飞机的一些性能,通过测试收集了飞机相对于出发点的飞行水平距离s与飞行时间t的函数关系式为:x=3t,飞行高度y(单位:m)随飞机时间t(单位:s)的变化满足二次函数关系,数据如表所示飞行时间t/s02468...飞行高度y/m010161816...素材2:图2是兴趣小组同学在室内操场的水平地面上设置一个高度可以变化的发射平台PQ,当弹射口高度变化时,飞机飞行的轨迹可视为抛物线上下平移得到,线段AB为飞机回收区域,已知AP=42m,AB=(182-24)m,问题解决任务1:确定函数表达式,求y关于t的函数表达式;任务2:探究飞行距离,当飞机落地(高度为0m)时,求飞机飞行的水平距离;任务3:确定弹射口高度,当飞机落到AB内(不包含端点A、B),求发射台弹射口高度(结果为整数)2.利用素材解决:《桥梁的设计》问题驱动某地欲修建一座搭桥,桥的底边两端间的水平宽AB=L,称跨度,桥面最高点到AB的距离CD=h 称拱高,拱桥的轮廓可以设计成是圆弧或抛物线型,若修建拱桥的距离L=32米,拱高h=8米.设计方案方案一方案二设计类型圆弧型抛物线型任务一设计成圆弧型,求该圆弧所在圆的半径设计成抛物线型,以AB所在直线为x轴,AB的垂直平分为y轴建立坐标系,求桥拱的函数表达式任务二如图,一艘船露出水面部分的横截面为矩形EFGH,测得EF=6.1米,EH=16米,请你通过计算说明货船能否分别顺利通过这两座桥梁.3.根据以下素材,探究完成任务设计求碗中面汤液面宽度的方案素材1图1是一个瓷碗,图2是其截面图,碗体DEC呈抛物线状(碗体厚度不计)碗高GF=7cm,碗底宽AB=3cm,当瓷碗中装满面汤时,液面宽CD=12cm,此时面汤最大深度EG=6cm.素材2如图3,把瓷碗绕点B缓缓倾斜倒出部分面汤,当点A离MN距离为1.8cm时停止任务1确定碗体形状在图2中建立合适的直角坐标系,求抛物线的表达式任务2拟定设计方案1根据图2位置,把碗中面汤喝掉一部分,当碗中液面高度(离桌面MN距离)为5cm时,求此时碗中液面宽度.任务3拟定设计方案2如图3,当碗停止倾斜时,求此时碗中液面宽度CH.4.九年级某班级同学进行项目式学习<项目式学习报告>如下:绿化带灌溉车的操作探究项目内容项目素材项目任务【项目一】明确灌溉方式如图1,灌溉车沿着平行于绿化带底部边线I的方向行驶,为绿化带浇水.喷水口H离地竖直高度为h(单位:m),灌溉车到l的距离OD长度为d(单位:m).“博学小组”经过实际测量,建立如下数学模型:如图2,可以把灌溉车喷出水的上、下边缘抽象为平面直角坐标系中两条抛物线的部分图象,下边缘抛物线是由上边缘抛物线向左平移得到;把绿化带横截面抽象为矩形DEFG,其水平宽度DE=3m,竖直高度EF=0.5m喷水口离开地面高h=1.5米,上边缘拋物线最高点离喷水口的水平距离为2m,高出喷水口0.5m.【任务一】结合图象和数据,请你求出灌溉车的最大射程OC的长度【项目二】提倡有效灌溉“笃志小组”实地调查发现:为了节约用水,进行有效灌溉,灌溉车在进行行业时,要保证喷出的水能浇灌到整个绿化带(上边缘抛物线不低于点F,点D不在下边缘抛物线内)【任务二】请你求出灌溉车有效灌溉时,灌溉车到绿化带底边缘的距离OD的取值范围.5.陕西饮食文化源远流长,“老碗面”是陕西地方特色美食之一.如图是从正面看到的一个“老碗”,其横截面可以近似的看成是如图(1)所示的以AB为直径的半圆O,MN为台面截线,半圆O与MN相切于点P,连结OP与CD相交于点 E.水面截线CD=63cm,MN//CD,AB=12cm.(1)如图(1)求水深EP;(2)将图(1)中的老碗先沿台面MN向左作无滑动的滚动到如图(2)的位置,使得A、C重合,求此时最高点B和最低点P之间的距离BP的长;(3)将碗从(2)中的位置开始向右边滚动到图(3)所示时停止,若此时∠BOP=75°,求滚动过程中圆心O运动的路径长.6.某厂家特制了一批高脚杯,分为男士杯和女士杯(如图1),相关信息如下:素材内容素材1如图1,这种高脚杯从下往上分为三部分:杯托,杯脚,杯体.杯托为一个圆,水平放置时候,杯脚经过杯托圆心,并垂直任意直径,杯体的水平横截面都为圆,这些圆的圆心都在杯脚所在直线上.素材2图2坐标系中,特制男士杯可以看作由线段AB,OC,抛物线DCE(实线部分),线段DF,线段EG绕y轴旋转形成的立体图形(不考虑杯子厚度,下同);特制女士杯可以看作由线段AB,OC,抛物线FCG(虚线部分)绕y轴旋转形成的立体图形.素材3已知,图2坐标系中,OC=5cm,记为C(0,5),D(−52,152),E(52,152),F(−52,15),G(52,15).根据以上素材内容,尝试求解以下问题:(1)求抛物线DCE和抛物线FCG的解析式;(2)当杯子水平放置及杯内液体静止时,若男士杯中的液体与女士杯中的液体深度均为4cm,求两者液体最上层表面圆面积之差;(结果保留π)(3)当杯子水平放置及杯内液体静止时,若男士杯中的液体与女士杯中的液体深度相等,两者液体最上层表面圆面积相差4πcm2,求杯中液体的深度.7.中新社上海3月21日电(记者缪璐)21日在上海举行的2023年全国跳水冠军赛女子单人10米跳台决赛中,陈芋汐以416.25分的总分夺得冠军,全红婵位列第二,掌敏洁获得铜牌.在精彩的比赛过程中,全红婵选择了一个极具难度的207C(向后翻腾三周半抱膝).如图2所示,建立平面直角坐标系xOy.如果她从点A(3,10)起跳后的运动路线可以看作抛物线的一部分,从起跳到入水的过程中,她的竖直高度y(单位:米)与水平距离x(单位:米)近似满足函数关系式y=a(x﹣h)2+k(a<0).(1)在平时训练完成一次跳水动作时,全红蝉的水平距离x与竖直高度y的几组数据如下:水平距离x/m03 3.54 4.5竖直高度y/m1010k10 6.25根据上述数据,直接写出k的值为,直接写出满足的函数关系式:;(2)比赛当天的某一次跳水中,全红婵的竖直高度y与水平距离x近似满足函数关系y=﹣5x2+40x﹣68,记她训练的入水点的水平距离为d1;比赛当天入水点的水平距离为d2,则d1d2(填“>”“=”或“<”);(3)在(2)的情况下,全红婵起跳后到达最高点B开始计时,若点B到水平面的距离为c,则她到水面的距离y与时间t之间近似满足y=﹣5t2+c,如果全红婵在达到最高点后需要1.6秒的时间才能完成极具难度的270C动作,请通过计算说明,她当天的比赛能否成功完成此动作?8.【发现问题】一天放学后,妈妈带小丽到面馆去吃牛肉面,爱思考的小丽仔细观察盛面的碗,如图1,她发现面碗的轴截面(不包含碗足部分)可以近似看成是抛物线的一部分.【提出问题】碗体(碗体的厚度忽略不计)上一点到碗底内部所在平面的距离y(cm)与这一点到碗的中轴线(面碗的上、下两个底面圆的圆心所在直线)m的距离x(cm)之间有怎样的函数关系?【分析问题】小丽从书包里拿出刻度尺、笔和本,向服务员借来一个空的面碗,把面碗正放在桌面上,对面碗进行了简单的测量,并根据测量数据画出面碗的轴截面,如图2,面碗的上口径AB=24cm,碗底直径CD=EF =6cm,面碗的边沿上一点B到桌面EF的距离BG=8cm,碗足高DF=1cm.小丽又进一步建立以CD 所在直线为x轴,以直线m为y轴的平面直角坐标系(如图3),从而求出y与x的关系式.【解决问题】(1)请你帮助小丽求出y与x的关系式;(2)小丽向空面碗中倒入一些水,当水面宽度为20cm时,求此时面碗中水的深度;(3)小丽将(2)中面碗中的水倾倒至如图4所示,水面刚好与BC重合,直接写出此时面碗中水的最大深度.如何调整蔬菜大棚的结构?素材1我国的大棚(如图1)种植技术已十分成熟,一块土地上有一个蔬菜大棚,其横截面顶部为抛物线型,大棚的一端固定在墙体OA上,另一端固定在墙体BC上,其横截面有2根支架DE,FG,相关数据如图2所示,其中DE=BC,OF=DF=BD.素材2已知大棚有200根长为DE的支架和200根长为FG的支架,为增加棚内空间,拟将图2中棚顶向上调整,支架总数不变,对应支架的长度变化如图3所示,调整后C与E上升相同的高度,增加的支架单价为60元/米(接口忽略不计),现有改造经费32000元.问题解决任务1确定大棚形状在图2中以点O为原点,OA所在直线为y轴建立平面直角坐标系,求抛物线的函数表达式.任务2尝试改造方案当CC′=1米,只考虑经费情况下,请通过计算说明能否完成改造.任务3拟定最优方案只考虑经费情况下,求出CC′的最大值.素材一太阳光线与地面的夹角叫做太阳高度角.冬至是北半球各地白昼时间最短、黑夜最长的一天;夏至是北半球各地黑夜时间最短、白昼最长的一天.设冬至这天正午时刻太阳高度角为α,夏至这天正午时刻太阳高度角为β.素材二厂家设计了可伸缩抛物线型遮阳棚,其侧面示意图如图1所示.曲线QM为遮阳棚,PQ 为遮阳棚安装在窗户上方的支架,PQ⊥QM,线段QM的长度称为遮阳棚的跨度.已知遮阳棚QM所在的抛物线与抛物线=−142的形状相同.素材三如图2,AB为小明家的朝南窗户,测得Ba=14,∠β=45°,窗户AB的高度为1.5米.为能最大限度地遮挡夏天炎热的阳光,又能最大限度地使冬天温暖的阳光射入室内,在安装遮阳棚时,需根据实际计算遮阳棚的跨度(QM的长).素材四春节前期,小明想在遮阳棚顶部挂一盏高为0.3米的灯笼(如图3).如图4,灯笼CD与窗户的水平距离为m米,灯笼的底端(点D)与窗户的上沿(点B)的铅垂高度为n米,灯笼顶端(点C)与悬挂点(点N)的距离为d米.解决问题任务1求小明家所需的遮阳棚的跨度QM.任务2当d=0.16时,求m的值.任务3现要求0.6≤m≤1.5且0.1≤n≤0.2,求d的取值范围.。
2025年中考化学总复习重难题型九 科学探究题

通电
2H2↑+O2↑
。
1
2
3
4
5
-3-
36.重难题型九
-4-
科学探究题
Ⅲ.探究影响电解水速率的因素
以收集20 mL氢气为标准,记录时间和收集氧气的体积,
实验数据如下表。
实验序号
①
②
③
④
⑤
NaOH溶液的温度/℃
15
15
15
30
45
外加电压/V
6
9
12
6
6
氧气/mL
9.9
10.0
9.5
9.6
9.7
汽车气缸工作时汽油以雾状喷出
(2)打火机中常用丁烷(C4H10)作燃料,请写出丁烷充分燃烧的化学方程
点燃
8CO2+10H2O
式: 2C4H10+13O2
。
1
2
3
4
5
-7-
36.重难题型九
-8-
科学探究题
【任务二】探究影响燃烧的因素
步骤Ⅰ:小组同学按如图1所示组装仪器,装入药品。
步骤Ⅱ:用凸透镜聚光对准燃烧匙中蜡烛的烛芯照射一
同浓度的NaOH溶液进行实验,测量收集20
mL氢气所需
_________________________________________________
的时间(与上一空对应,合理即可)
_________________________________________。
1
2
3
4
5
-6-
36.重难题型九
其他条件相同时,外
_________________________________________________
小说主旨

角度
文中对应的答案要点
文中对大乖、二乖的动作、语言等描写细致逼 真,二人可爱的形象在读者眼前活灵活现,这表 从人物 现了作者对儿童成长的关注 形象入 作者对“妈”的着墨虽然不多,但都是在关键 手 处,如“那野猫好像有了身子,不要太打狠了”, 大乖、二乖的快乐成长与母亲的关爱是分不开 的,这些反映了作者对母爱的颂扬
沉静的暮色中,百亩园显得寂寥、空旷。六安爷喜 欢这天地间昏暗的时辰,眼睛里边和眼睛外边的世界是 一样的。他知道自己正慢慢融入眼前这黑暗的世界里。
很多天以后,人们跟着推土机来到百亩园,无比惊讶 地发现,六安爷锄过的苗垅里,茁壮的禾苗均匀整齐,一 棵一棵蓬勃的庄稼全都充满了丰收的信心。没有人能相 信那是一个半瞎子锄过的地。于是人们想起六安爷说了 无数遍的话,六安爷总是平静固执地说,“我不是锄地, 我是过瘾。”
(2)参考答案:①小说起于祝福,结于祝福,中间一再写祝 福,情节的发展与祝福这一环境密切相关。②祝福作为 一个时间标志,把祥林嫂的人生悲剧串联起来,形成了清 答案 晰的发展脉络,起到线索的作用。③祥林嫂的悲剧遭遇 分析 是在祝福的欢乐气氛中展开的,鲜明的对照增加了祥林 嫂遭遇的悲剧性,深化了小说的主题。 答案分析:本题考查理解标题的作用,解答本题从情节、 环境和主题等角度思考,再找出对应内容进行分析。
第二步:分析标题的表层义 “锄”的表层义有两个:是一种农具,是一种劳作行 为。 第三步:分析标题的深层义 “锄”象征六安爷的人生和精神;喻示劳动者和土 地的亲密关系;意味着传统的农业生产和生活方式;蕴含 着六安爷对土地的热爱,又暗含着他对土地的告别。
(有删改)
小说以“锄”为标题,有什么寓意?请结合全文简要分析。 (6分) 答:___________________________________________ ______________________________________________
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
典型题型之主题类探究一、主题概括要点可从反映社会生活(现象)、揭示人性美丑、揭示哲理、表达情感等方面考虑。
二、提问模式1.直奔主题型。
一般是:直接问“主题是什么”;“探究文章的深刻(丰富)意蕴和作者的情感取向”;“探究文章的深刻(丰富)意蕴”;“探究作者的情感(情思)”。
需要说明的是:如果只问“深刻(丰富)意蕴”,也需要答作者情感;如果只问“情感”则需答对某现象、某人性、某哲理的情感;如果既问深刻意蕴也问情感取向,两者最好分开答。
2.小切口突破型。
主要是:标题含义及探究一句话(主题句)的意蕴。
答题时应围绕与标题或这句话相关的人物、事件探讨主题。
三、答题思路1.以小见大。
小说以小题材、小事件、或某个片段、平常现象反映大主题或深刻的道理。
答题时明确以小见大的写作方法,通过分析小说的事件,或揭露某种社会现象,或揭示人性美丑,或揭示深刻的哲理,或表达作者的情感。
2.多种对象或角度。
若小说出现的对象(人物、动物、环境等)比较多,经过分类后,分别探讨这些对象(或对象与对象间的关系)的特点,或通过他们揭示的现象、哲理,或表达的情感。
有时还要兼顾小说的情节。
而许多散文探讨主旨(或情感)时,一般按其行文思路,梳理对不同对象(或同一对象的不同方面)或不同事件的情感(或感悟)。
3.由浅入深。
若小说对象单一,往往先探讨小说人物特点,再进一步探讨其蕴含的精神(文化)或哲理。
而有一种散文文章本身的思路即由浅入深,探讨是则由物及人及精神(或哲理)。
4.物象类题目。
往往要考虑物象的象征(隐喻)内容、寄托的情感及揭示的主题。
四、典型题例★★★小说【主要立足于小说中的形象(人、物、环境),兼顾情节】(一)以小见大1.王安忆《洗澡》“‘洗澡’作为这篇小说构思的关键,有主题思想方面的考虑。
结合全文,试作分析。
”参考答案:小说通过写“他”是否给送货的小伙子洗澡和买水时内心激烈的斗争,塑造了精打细算斤斤计较典型的上海小男人形象【分析内容】。
以小见大【明确手法】,表现当代市民的凡俗人生,反映了人与人之间提防猜疑、缺乏信任的现实【反映的社会现象】,揭示了人性的复杂微妙【揭示的人性】,呼唤世人要洗去心灵的污浊,以一颗赤子之心对待他人【作者情感】。
2.莫泊桑《保护人》“小说以‘保护人’为题有主题思想方面的考虑,结合全文陈述你的观点。
”参考答案:启发读者理解小说的主题思想,使主题思想更加集中深刻:小说以小见大,揭露当时法国社会上层社会的不良风气和多种黑暗现实,讽刺官场中趋炎附势、官官相护、相互推诿的丑恶现象,揭示出一个道理:如果人家都寻求保护人,社会就会失去“保护“,体现了作者对社会公正的思考与追求。
(二)多种对象(角度)1.阿城《溜索》“本文写了驮队飞渡峡谷的故事,请探究其中的深刻意蕴和作者的情感取向。
”参考答案:深刻意蕴:(1)飞渡峡谷的情景(情节角度):表现人在自然面前接受挑战,战胜艰险【人性美】;(2)驮队的人际关系:体现团结协作,相互信任,关心爱护【人性美】;(3)动物形象:隐喻人应该像雄鹰飞翔、像骏马奔驰,而不是像牛那样软弱畏缩【哲理】;(4)“我”与领队的对照:表示人会在艰苦磨练中成长【哲理】。
情感取向:(1)骏马、雄鹰、高山峡谷:对雄奇险峻崇高的赞美;(2)领队、精瘦汉子:对乐观向上人生态度的赞美;(3)牛的恐惧、发抖:对平庸、畏难的厌弃。
(4)本文所写生存画面:张扬原始、野性的阳刚之美。
2.曾平《厂子》“本文写了坝坝村毁田建厂的故事,请探究其中的意蕴和作者的情感取向”参考答案:(1)意蕴:①大家毁田建厂:揭示急功近利、舍本逐末的现象;②王老板逐利损人:揭示见利忘义、缺失社会责任感的现象;③基层干部(村主任、乡长)重商轻农:揭示一味追求利益、政绩的现象。
(2)情感取向:①对村民的同情和批评;②对基层官员、商人的批判;③对美好环境逝去的叹惋。
(对以牺牲环境为代价发展经济的批判)(每点1分)3.刘建超《拐子李》“请结合小说内容,探究这篇小说的深刻意蕴”参考答案:(1)拐子李诊所的盛衰变化,以及老街人对拐子李态度的变化,揭示了当下社会人们在激烈的竞争中忘记了做人的根本【社会现象】,表达了对“诚信”(坚守本分)的呼唤【作者情感】。
(2)老街是一个特定的封闭的社会:固有的优越感、顽固的地域界限、品牌观念,同行的恶性竞争等,老街人优越感强、欺生,好事但不缺乏同情心。
作者对这种封闭、欺生作了批判【现象、人性兼情感】,揭示(呼吁)社会应走向开放、多元和包容【道理(情感)】。
4.《太阳·老人·少女》“请结合全文,探究这篇小说的丰富意蕴”参考答案:(1)写一位盲目老人从容安详地看落日,表现平凡人物内心的坚强【人性美】。
(2)写老人孤单寂寞的遭遇,针砭亲情的淡薄【社会现象兼情感】。
(3)写老人不幸的身世,控诉战争给人民精神造成的创伤【社会现象皆情感】。
(4)写少女与老人的邂逅,表现平凡生活对于人生和艺术的启迪【道理】。
(6分,答出任3点即可)5.《朋友》小说以“朋友”为题,试探究其深刻意蕴”注意:(此处深刻意蕴是指通过与“朋友”相关的人物与情节揭露社会现象、表达情感、反映人性、揭示哲理)参考答案:①亚当长期贫苦、孤独、寂寞,不被人关心,也没有朋友,反映了社会的人情冷漠;②在雷给予亚当关心帮助后,亚当敞开心扉对雷倾诉,表达了对朋友的渴望、友情的呼唤;③亚当没能从正常人那里得到温暖和帮助,却从被正常人认为的“精神病”人雷那里获得朋友般的关怀,到底谁正常谁不正常?在反讽中揭露了人性的扭曲。
(三)单一对象(角度)1.路翎《英雄的舞蹈》“探究题目中的“英雄”在小说中的多重含义”参考答案:(1)(浅层1)张小赖扮演的各种英雄人物;(2)(浅层2)与世俗文化(或“新潮文化”)作斗争的说书艺人张小赖的形象。
(3)(深层)对英雄崇拜的一种传统旧文化。
2.艾小羊《一个人的春天》“题目‘一个人的春天’的含义”参考答案:(1)(浅层)当时正是春天,方先生丧妻不久,孤身一人;(2)(深层)方先生关于妻子的美好追忆是属于他自己一个人的春天体验;(3)(深层)尽管方先生痛失爱妻,但他依然保持着对生活的热爱。
★★★散文【主要按行文思路梳理探讨】(一)多种对象(角度)1.王灏然《黄土招魂》“第⑦段开头说”再次游走于故乡的领地,我带着一种复杂的心情和沉重的思考”,请结合全文探究作者怀着怎样的复杂心情”参考答案:①对故乡亲附依傍和难以割舍的思念之情;(1段)②对黄土孕育了灿烂物质文明和精神文明的敬重、赞美和自豪之情;(2-6段)③对黄土领域失去了灵与肉的的失落和悲叹之情;(7段)④对我们“肤浅”的自责之情;(8、10段)⑤对黄土精神回归和重建精神家园的期盼之情。
(10段)2.朱以撒《在风中长大》“本文蕴含着作者丰富的情感,请予以探究”参考答案:①对朴素、简单的生活方式的留恋;②对温馨的童年生活的怀念;③对非自然的城市生活的排斥;④对大自然力量的敬畏;⑤对人类改造自然不自量力的批评;⑥对人类摆脱愚昧思维、认识上获得进步的欣慰。
3.贾平凹《壁画》“探究作者在文中寄寓的情思”参考答案:情:由对唐壁画的描写表达对热烈、外向、充满力量的盛唐精神的赞颂、向往、仰慕;由唐以后国力衰败表达对盛唐精神不再的叹惋;由对唐美人的描写表达对美的赞美和怜惜;思:表明美是禁锢不了的,是永恒的。
4.夏立君《一个人的仪式》本文以“一个人的仪式”为题,请探究其中蕴含的深意”注意:此处探讨围绕与“一个人的仪式”相关的人物与事件参考答案:①作者用“站好、垂手、阖眼、默哀”这样简单而肃穆的一个人的仪式,表达了对英雄行为的肯定、对英雄精神的赞扬;②寂静的墓园中只有作者进行着一个人的仪式,表达了作者为无人拜谒英雄而痛心、为人们漠视英雄而悲伤;③寂静的墓园中只有作者进行着一个人的仪式,表达了作者对当今人们追逐经济效益、追逐热闹的行为的否定和批判;④“一个人的仪式”引导读者去深入思考,如何准确公正地认识、评价特定时代的历史人物。
(二)由浅入深1.张笑天《上善若水》“请探究都江堰蕴含了“上善若水”的哪几层含意”参考答案:(1)以水比喻“上善”,即都江堰是上善之作【物】;修筑和维护都江堰的李冰及其后任可谓上善之人【人】;由此引申出做人要做上善之人,做事要做上善之事【道理】。
2.余秋雨《都江堰》“本文写了在都江堰水利工程前的所见所闻所感,请探究作者的创作意图”参考答案:①【物】歌颂都江堰,高度评价李冰从实践中总结治水经验的巨大作用,歌颂了古代水利科学的伟大成就;②【人】赞美李冰为民做实事的献身精神,充分肯定李冰为利民、富民,既做官又做水利专家的政治道路;③【精神】称颂李冰父子为民服务的伟大精神永世长存,并代代相传。
3.陈启文《天子坟》“探究“天子坟,原本就是一座山,一座不断长高的山”的几层含义。
参考答案:天子坟高大如山;神农氏所体现的民族精神厚重如山;这种精神在子孙后代心中传承,并不断发扬光大。
4.冯骥才《羌去何处》“请探究‘羌去何处’这个标题蕴含了哪几层深意”参考答案:(1)羌民族遭受巨大灾难后,如何重建家园、重返家园;(2)羌文化遭到毁坏后,如何将其修复、整理、保护和传承下去;(3)表达了作者对羌民生活、羌文化保护传承深深的思考和担忧之情。
★★★物象类题目的内涵1.《父亲的隔年花》“请探究小说以“父亲的隔年花”为题的深意”参考答案:①“隔年花”经历严寒的冬天隔年发芽盛开,隐喻了父子俩经历人生的严冬重新振作的经历;②“隔年花”代表了儿子的忏悔,在儿子的鼓励下,父亲走出了丧妻的阴影,儿子就是“父亲的隔年花”,“隔年花”包含着父子间的深情;③坚韧和真情使父子俩走出人生的严冬,“父亲的隔年花”形象地揭示了小说的主题。
2.《藏在草间》“‘藏在草间’作为标题,请探究它的丰富意蕴”参考答案:(1)乡村是藏在草里的,草给乡村以诗意,给生命以恩赐;农民是藏在草间,一辈子辛勤劳作在草间(乡村土地上),最终回归大自然“草间”。
(2)题目中草象征平凡朴素、默默奉献的品质,寄寓着对平凡朴素、默默奉献的草、农民乃至乡村的赞美。
(3)暗示美好的品德(世间万物)蕴藏在普通、平凡中的哲理(或)启示人们生命和生活的真谛藏在平凡中。
