利用辅助圆专题:如何做辅助圆,三种构造辅助圆解题的模型
浅谈构造辅助圆解决点的问题

浅谈构造辅助圆解决点的问题对于数学中较全面、有简易解题方法且不易看出知识点的题目,如果可以根据题干中的基本要素,结合到圆的相应理论,合适地画出辅助圆,一般可以变复杂为简单,变困难为基础,发现答题技巧,添加辅助圆的一般过程是:基于“圆的定义”添加辅助圆、通过“圆周角的性质”添加辅助圆、通过圆周角与圆内外角的联系添加辅助圆、基于“弦切角的模型”添加辅助圆、利用“圆幂定理”添加辅助圆、利用“判定四点共圆的理论”添加辅助圆、利用“两圆相切的定义”添加辅助圆、利用“托勒密理论”添加辅助圆。
标签:数学问题添加辅助圆基础题型从全国高中数学联赛与国际数学奥林匹克中涉及的相关题型来看,可以了解到,数学问题,作为竞赛中最常涉及的内容之一,在数学竞赛中,其地位是数一数二的。
对于一些较全面、有简易解题方法且不易看出知识点的题目而言,解题的人哪怕是在灵活运用所学知识与思维逻辑推算方面有着较强的能力,但是难免也会被此绊住脚步。
因此,解题者如果可以通过题干基本框架及特征,从而联系到圆的理论应用,合适地添加辅助圆,通常能够变复杂为简单,变困难为基础,从而发现答题的关键出口。
本篇文章的中心就是介绍如何利用添加辅助圆来达到解题目的。
在日常的教授课程中,老师们常会根据圆的性质来添加辅助圆,由此便将原有问题变成了辅助圆与直线的公共点的相应问题。
一、根据“在同一个圆内,若两弧相等,则两弧对的圆周角相等”添加辅助圆题1 如图所示,平行四边形ABCD中,E在AD,延长CE至F点,使得。
(1)证明:;(2)用做图工具在直线AD上取一点P,使∠CPB=∠PDC(作法不需写,保留作图印记)(1)由题目可知AD//BC,所以。
又,所以可以知道,由此可得。
(2)因为P在直线AD上,又AD//BC,所以。
若要得,就是要使得,从(1)可以知道条件,则只需,也就是和可以视为弧BC对应的圆周角,因此P 点为的外接圆和AD所相交的点。
解(1)省略。
(2)分别在边BF与BC上作垂直平分线,设两垂直平分线交于O点。
2020年中考数学专题突破6 辅助圆在解题中的应用

图②
微专题 辅助圆在解题中的应用 专题六 辅助圆在解题中的应用
针对训练 10. 如图,已知四边形ABCD. (1)如图①,在矩形ABCD中,请你在矩形ABCD的边上画出使∠APB=30°的所 有点P;
针对训练 7. 如图,已知矩形ABCD,请你在矩形ABCD的边上画出使∠BPC=90°的所有点P.
解:如解图,点P1、P2即为所求点.
第7题图
第7题解图
微专题 辅助圆在解题中的应用 专题六 辅助圆在解题中的应用
8. 如图,已知在Rt△ABC中,AC=5,BC=12,∠ACB=90°,P是边AB上的动
第3题图
微专题 辅助圆在解题中的应用 专题六 辅助圆在解题中的应用
4. 如图,在边长为2的菱形ABCD中,∠A=60°,M是AD边的中点,N是AB上一 个动点,将△AMN沿MN所在直线翻折得到△A′MN,连接A′C,则A′C长的最小值
为___7___1__.
第4题图
微专题 辅助圆在解题中的应用 专题六 辅助圆在解题中的应用
第12题图
专题六 辅助圆在解题中的应用
模型分析
模型六 四点共圆
(ⅰ) 如图①、②,Rt△ABC和Rt△ABD共斜边,取AB中点O,根据直角三角形斜边 中线等于斜边一半,可得:OC=OD=OA=OB,∴A、B、C、D四点共圆,共斜边 的两个直角三角形,同侧或异侧,都会得到四点共圆;四点共圆后可以根据圆周角定 理得到角度相等,完成角度等量关系的转化,是证明角度相等重要的途径之一.
辅助圆三大类

目标:解决中考填空压轴题,部分大题压轴 对象:中考尖子105/120,圆相关知识全部学完 三种圆: 一:圆定义(等线段,共端点)+例题1 二:三点共圆(定线段对定角度)+例题2 三:四点共圆(对角互补、同弦等角)+例题3、 例题4
前言: 辅助圆是一种思想,是一个 工具!不利用辅助圆我们照样可 以完成题目,但是利用辅助圆可 以使得我们更方便快捷解题!
辅助圆基本类型: 一、利用定义:等线段,共端 点
例题1:在边长为2的菱形中,∠A=60°,M是AD边上的 中点,N是AB边上的一个动点,将△AMN沿着MN所在直线 翻折,得到△A’MN,连接A’C,则A’C的最小值是多少?
辅助圆基本类型: 二、三点共圆:定线段对定角 度ቤተ መጻሕፍቲ ባይዱ
例题2:在△ABC中,∠C=45° ,AB=2,求△ABC,面积的最 大值.
辅助圆基本类型: 三、四点共圆:对角互补,同弦等 角
∠A+∠C=180°
∠D=∠C
例题3:如图,等边△PQR内接于正方形ABCD,其中,点 P、Q、R分别在边AD、AB、DC上,M是QR的中点,求证: 不论等边△PQR怎样运动,点M为不动点.
例题4:如图点E是正方形ABCD的边AB上的一点,过点E 做DE的垂线交∠ABC的外角平分线与点F; 求证:FE=DE
精心构造辅助圆,解决问题少困难

精心构造辅助圆 解决问题少困难圆是几何中具有美学价值的一种图形,不仅曲线光滑圆润,美丽迷人,是美好象征的化身,而且几何性质众多,在解决诸多数学问题中,显示出非常重要的作用,有圆的参与,将会使一个比较困难的问题简单起来,所以,在解决一些与圆有关的问题中,要深入挖掘圆的信息,精心构造辅助圆,利用圆的几何性质和圆的方程,发挥出圆的价值,让这些问题迎刃而解,实现“精心构造辅助圆,解决问题少困难”的理想目标.一、利用方程,构造圆在平面上涉及动点轨迹的问题中,直接求解问题比较困难时,可以先考虑建立直角坐标系,特别是有垂直条件与对称条件时,就更要考虑解析法,求出动点的轨迹方程,如果满足圆方程的结构特点,就可以构造圆,让圆的几何性质闪耀光彩,使问题得到解决.例1. (2016届北京西城期末理科)如图,正方形ABCD 的边长为6,点E ,F 分别在边AD ,BC 上,且2DE AE =,2CF BF =.如果对于常数λ,在正方形ABCD 的四条边上,有且只有6个不同的点P 使得=PE PF λ⋅成立,那么λ的取值范围是( )(A )(0,7)(B )(4,7)(C )(0,4)(D )(5,16)- 图1解:以D 为坐标原点,DC 所在直线建立直角坐标系,设点(,)P x y ,则点(0,4),(6,4)E F ,所以(0,4),=(6-x,4-y)PE x y PF =--,由=PE PF λ⋅得动点P 的轨迹方程是:22(3)(4)9x y λ-+-=+,所以动点P 的轨迹是一个以(3,4)为圆心, 9λ+为半径的圆,所以“在正方形ABCD 的四条边上,有且只有6个不同的点P 使得=PE PF λ⋅成立”等价于“圆与正方形四条边有且仅有6个不同交点”,当且仅当3913λ<+<,解得:04λ<<,所以选C.评析:通过解析法揭穿了动点P 的几何意义,为实现问题的转化起到了桥梁作用,通过几何背景的分析,抽象代数特征,促使问题圆满解决,其间,由代数方程,构造了一个圆,将原问题转化为直线与圆的位置关系讨论,从而建立起了不等式,实现了向量问题坐标化,几何问题代数化的转化目标.从而减少了解题的困难程度. 例2.直线:(2)l y k x =+与曲线2:465C y x x =----有且仅有两个不同公共点.求实数k 的取值范围.解:由曲线2:465C y x x =----的方程可以构造出半圆:22(3)(+4)4x y -+=且4y ≤-. E FD P C A BE FD P C A B x y 图2如图所示:要使直线l 与曲线C 有且仅有2个公共点,则需AB AC k k k <≤其中AB 为半圆的切线,(1,4)C -,半圆的圆心到直线:(2)l y k x =+的距离是2342202372,211k kd k k ++-±==⇒=+由图可知:20237=21AB k --,43AC k =- 所以实数k 的取值范围是202374(,]213--- 评析:解决本题的关键是由曲线C 的方程构造半圆,然后由图形抽象代数条件,完全回避了探究较复杂的一元二次方程在区间[1,5]上有两个不等实根的条件.所以在解决解析几何的问题时,一定要分析曲线方程的结构特点,抓住构造几何图形的机会,将会让图形闪耀光辉.相关问题:1.(2019届北京昌平区高三上期末理科)设点12,F F 分别为椭圆22:195x y C +=的左、右焦点,点P 是椭圆上任意一点,若使得12PF PF m ⋅=成立的点恰好是4个,则实数m 的值可以是( ) BA .B .C .5D .8 2.(2019届北京西城区高三上期末理科) 设双曲线22: 13y C x -=的左焦点为F ,右顶点为A . 若在双曲线C 上,有且只有2个不同的点P 使得=PF PA λ⋅成立,则实数λ的取值范围是____. (-2,0)二、利用定义,构造圆圆的定义是:在平面内到定点的距离等于定长的点的集合叫做圆.即动点满足一定点和一定长的轨迹可以生成圆,在解决问题的过程中,如能构造出这样的几何条件,就可以构造辅助圆,将原问题转化为圆的问题求解,可能使复杂问题简单化.例3. 设直线:,圆,若在圆C 上存在两点,在直线 上存在一点M ,使得,则的取值范围是( )A. [18,6]-B. [652,652]-+C. [16,4]-D. [652,652]---+解:考虑极端情形:当,MP MQ 是圆C 的切线时,如果此时的M 点轨迹与直线有公共点,那 么对于,MP MQ 不都是圆C 的切线时,都能在直线上存在符合条件的M 点.所以“在圆C 上存 在两点,在直线上存在一点M ,使得”等价于“当,MP MQ 是圆C 的切线时,M 点的轨迹与直线有公共点”.而当,MP MQ 是圆C 的切线时,易证:四边形MPCQ 是正方形,所 以MC 的长是定值2,且C 为定点,因此,动点M 的轨迹是以C 为圆心,2为半径的圆, C 123l 340x y a 22 (2)2C x y :,P Q l 90PMQ a l l ,P Q l 90PMQ l AD C B即M 点的轨迹方程是22(2)4x y -+=,直线2164a ≤⇒-≤≤,所以选C.评析:根据极端性原理,抓住几何条件构造点M 的圆轨迹是解决本题的关键,而构造圆的关键在于构造定值(即半径)与配套的定点(即圆心),所以在解决解析几何问题时,要时刻关注定值的出现于定点的出现,特别是在解决有关椭圆、双曲线问题中,要紧扣椭圆、双曲线定义,关注定值的相关信息与定点的相关信息.例4.过点(1,2)P --作圆22:(3)(4)1C x y -+-=的两切线,PA PB ,其中,,A B 为切点,求直线AB 的方程.解:由圆的切线性质可知:=PA PB ,所以由圆的定义可知:,A B 在以PA 为直径,P 为圆心的圆上,=PA PB =于是可得圆P 的方程:22(1)(2)52x y +++=,将圆C 的方程与圆P 的方程相减可得公共弦AB 所在的直线方程为:812710x y +-=评析:本题的解决中利用了等长线段构造辅助圆,从而出现了两圆公共弦的大好时机.具有一个公共定点的等长线段的另一个端点在一个圆上,这就是圆定义的灵活运用,在解决问题中要注意这些信息.相关问题:已知椭圆C: 22143x y +=的左右焦点分别是12,F F ,点P 是椭圆C 上的动点,N 是线段1F P 的延长线上一点,点M 是2NPF ∠的平分线上一点,且20PM F M ⋅=,直线:34150l x y --=与x 轴、y 轴交点分别为,A B ,求ABM ∆面积的最大值. 1258三、利用垂直,构造圆圆有一个重要性质是:直径上的圆周角是直角.反过来说,直角三角形的直角顶点在以斜边为直径,斜边中点为圆心的圆上,这显然是一个真命题.这也是构造辅助圆的依据,所以当垂直条件出现时,要注意辅助圆的构造,可能使原问题转化为圆的问题,从而获得解题思路. 例5. 已知圆和两点,,若圆上存在点,使得,则的最大值为( )A .7B .6C .5D .4解:由于,所以可以构造一个圆:点P 在以AB 为直径的圆上,记此圆为圆O ,点P 又在圆C 上,所以“圆上存在点,使得”等价于“圆O 与圆C 有公共点”, 所以1146m CO m m -≤≤+⇒≤≤,所以的最大值为6.选B.评析:从垂直条件出发,构造了一个辅助圆,实现了将原问题转化为两圆位置关系的转化目标,使问题轻松获解,其间表现出辅助圆的重要作用. l ()()22:341C x y -+-=(),0A m -()(),00B m m >C P 90APB ∠=m 90APB ∠=C P 90APB ∠=m例6.过点(0,4)P 的直线l 交椭圆22:14x C y +=于不同两点,A B (A 在PB 之间),O 为坐标原点.当90PAO ∠=,求直线l 的斜率.解:按照通常用到的方法,将直角用斜率之积为-1或用向量的数量积为0写出坐标关系,再用直线与曲线联立,出韦达定理,代入求值.但是在直角中不涉及,A B 两点坐标,只涉及A 点的坐标,所以直曲联立与韦达定理不好使.基于此,需要变换思路,由直角构造圆,点A 在PO 为直径的圆上,于是得到下列解法:设00(,)A x y ,则2200(2)4x y +-=,220044x y +=,消去0x 得:002,23y y ==-(舎),0x =l的斜率是24k -=24k -== 评析:由此题的解答可见:由垂直条件构造辅助圆是构造方程的主要依据,这种方法仅是直曲联立用韦达定理方法的补充,不能迷信它.比如将本题的条件90PAO ∠=改为90AOB ∠=,就没有必要构造辅助圆了,直接用斜率之积为-1或用向量的数量积为0,写出坐标关系,直曲联立出韦达定理,代入求值比较简单.相关问题:设点P 是双曲线22:1169x y C -=上一点,12,F F 是双曲线C 的左右焦点,且120PF PF ⋅=,求点P 到x 轴的距离. 95四、利用换元,构造圆由于圆的方程是特殊的二元二次方程,特殊性表现在两个方面:一是没有两元的交叉项,二是两元的二次项系数相等。
“构造辅助圆”在初中数学解题中的灵活运用

2023年9月下半月㊀解题研究㊀㊀㊀㊀构造辅助圆 在初中数学解题中的灵活运用◉吉林师范大学数学与计算机学院㊀王㊀雪㊀㊀摘要:在数学解题过程中,常规的解题思路并不能应对一些比较复杂的几何问题,这时候就需要转换思路,有时利用 圆 ,就可以有效解答一类问题.借助 辅助圆 将几何问题中分散的条件集中,有助于发现题目中的隐含条件,从而起到化繁为简的作用.本文中通过实例分析,帮助学生明确辅助圆的应用环境,以及针对不同题型如何构造辅助圆.关键词:辅助圆;初中数学;几何问题㊀㊀构造辅助圆 是指在原有的几何图形上,构建一个辅助圆,利用圆的特性来完成题目的解答.通过辅助圆的构造,能够将几何题目中较为繁杂的已知条件进行集中处理,同时能够发现几何图形中的隐藏条件,利用对这部分条件的分析,快速解决问题.本文中结合实例,帮助学生明确辅助圆的应用环境,以及针对不同题型如何构造辅助圆.1构造辅助圆 解决数学问题的应用现状目前初中生在解题的过程中,较少应用辅助圆,且应用效果不理想.在几何题的解答过程中,辅助线的应用是比较常见的,但是有部分题目通过辅助线来解答依旧存在难度,甚至需要多条辅助线才能完成,如果学生用这种方法应对选择题和填空题,就会浪费大量的时间.而应用辅助圆则可以为相关问题披上圆的外衣,这样就可以依据圆的性质进行解题,从根本上起到化繁为简的作用[1].2构造辅助圆 解决数学问题的实际案例2.1辅助圆在求线段长度的几何问题中的应用在解决求线段长度的几何问题中,通常是利用相同端点的线段构造辅助圆,以端点作为圆心,选取相等的线段作为半径或直径,完成辅助圆的构建后再利用圆的基本性质求解线段长度[2].例1㊀在四边形D C B E 中,点A 在B E 上,A E ʊC D ,A B =A C =A D =A E =5c m ,且B C =19c m ,求对角线B D 的长度.解析:由A E ʊC D ,得øB D C =øD B E .图1由A B =A C =A D =A E ,将点D ,C ,B ,E 视为圆上的点构建辅助圆,如图1.于是弦D E 与弦B C 的长度相等.又由B C =19c m ,得B C =D E =19c m .因为E B 为辅助圆的直径,所以øE D B =90ʎ.所以在R tәE D B 中,根据勾股定理可知,B D =E B 2-E D 2.又A B =5c m ,E B 为圆A 的直径,则E B =10c m .所以B D =102-(19)2=9(c m ).2.2辅助圆在求度数的几何问题中的应用在解决求度数的几何问题中,通常可以将公共点作为顶点,作三角形的外接圆.在构建辅助圆的过程中要将三角形与辅助圆建立明确的关系.图2例2㊀如图2所示,әA B C为等腰三角形,且A B =A C ,直线A P 为әA B C 外侧直线,点B 与点D 关于A P 轴对称.求证:ø1=ø2.证明:ȵ点B ,D 关于直线A P 对称,ʑ直线A P 为线段B D 的垂直平分线.ʑәA D B 为等腰三角形.图3ʑA D =A B =A C .故可以A C 为半径,点A 为圆心,构建如图3所示的辅助圆.ȵP 为B D 中点,且A P 为过点E 的直线,ʑәD E B 为等腰三角形.ʑD E =B E .ʑøE D B =øE B D .ʑø2=2øE D B .又ø1=2øC D B (同弧所对的圆心角是圆周角的2倍),ʑø1=ø2.2.3辅助圆在求图形面积问题中的应用在数学中考题中,涉及面积的题型也很多,当题目条件较多且分散的几何图形很难运用面积公式时,可以尝试构建辅助圆,利用圆的基本性质以及圆的面37Copyright ©博看网. All Rights Reserved.解题研究2023年9月下半月㊀㊀㊀积公式进行计算[3].例3㊀如图4,әA B C 为等边三角形,且A B =A D ,AH ʅC D 于点H ,且P C ʅBC ,C P 与AH 交于点P ,求证:S әA B C =34A PB D .图4㊀㊀㊀图5解析:依题意可知A B =A C =B C =A D ,构建以点A 为圆心,A B 为半径的圆,得到如图5所示的辅助圆.ȵәA B C 为等边三角形,ʑøB A C =øA C B =øA B C =60ʎ.ʑøB D C =12øB A C =30ʎ.又øB C P =90ʎ,øB C A =60ʎ,ʑøP C A =øC D B =30ʎ.ȵøC B D =12øC A D =øP A C ,ʑәB C D ʐәA P C .ʑB C ʒA P =B D ʒA C .又B C =A C ,ʑB C 2=A P ˑB D .ʑS әA B C =34A PB D .2.4辅助圆在求线段比或面积比问题中的应用图形中的某两条线段成比例或图形面积成比例这类题型是中考的难点和重点.利用辅助圆则可以结合圆的性质,通过圆中的线与角的关系进行求解.构建辅助圆时,要将有关线段置于辅助圆的关键位置,例如,可作为直径㊁半径或弧所对的弦.这样容易发现线段之间的关系,从而更加简便地进行解答[4].例4㊀在R t әA B C 中,A C =B C ,øA C B =90ʎ,P是C B 延长线上的一点,B P ʒB C =k ,已知0ɤk ɤ1,过点B 作A B 的垂线,过点P 作A P 的垂线,使两条垂线相交于点Q ,且A P =P Q ,连接A Q ,求әA B C 与әA P Q 的面积比.分析:根据已知条件分析,әA P Q 的面积较难求解,所以可以根据әA P Q 来构建辅助圆.解析:以A Q 为直径,A Q 的中点O 为圆心,构建如图6所示的辅助圆.ȵA P =P Q ,且øA P Q =90ʎ,ʑәA P Q 为等腰直角三角形.设B C =A C =m .图6ȵB P ʒB C =k ,ʑB P =k m ,P C =(k +1)m .ʑP A =m 2+[(k +1)m ]2=m k 2+2k +2.ʑS әA B C ʒS әA P Q=12A C 212P A 2=12m 212(k 2+2k +2)m 2=1ʒ(k 2+2k +2).2.5辅助圆在求线段极值问题中的应用辅助圆在求线段极值问题中有着广泛的应用,特别是在数学竞赛中经常遇到.例5㊀在边长为4的正方形A B C D 中,P 为对角线B D 上的一个动点,且与点B ,D 不重合,连接A P ,过B 作A P 的垂线,垂足为H ,连接DH ,求线段DH 的最小值.图7分析:由于无论点P 如何运动,A B 的长度都不会改变,因此可以A B 为直径,A B 的中点E 为圆心构建辅助圆,通过圆确定点H 的运动轨迹.解析:取A B 中点E ,连接D E ,构建如图7所示的几何图形,可得D E =(12A B )2+A D 2=42+22=25.当点H 与点M 重合时,线段DH 的长度最短,此时DH =DM =D E -M E =25-2.综上所述, 构造辅助圆 在初中数学解题中的广泛应用,不仅包含大量的几何问题,而且部分代数问题中也可使用.构建辅助圆时,要结合题目的具体情况,根据四点共圆的条件确定辅助圆.通过辅助圆在不同类型几何问题中的应用,明确构建辅助圆在初中数学解题中的可行性与实用性,通过辅助圆的灵活应用,提升学生的实际解题能力.参考文献:[1]刘怀权. 构造辅助圆 在初中数学解题中的应用[J ].数理天地(初中版),2022(12):21G22.[2]蒋天林.从江苏高考试题谈辅助圆在解题中的运用[J ].中学生数理化(高考使用),2020(5):11G12.[3]黄磊. 圆 来如此简单 辅助圆 构造的解题探究[J ].数理化解题研究,2021(14):10G11.[4]徐勤.辅助圆在中考数学试题中的应用[J ].科学大众:科学中考,2022(4):13G15.Z47Copyright ©博看网. All Rights Reserved.。
中考复习讲义:三种构造辅助圆解题的模型

中考热点:三种构造辅助圆解题的模型一、问题导读“圆”是一个完美的图形,在初中数学中具有丰富内容,其中大部分是与角度相关性质,如在圆周角中能轻易找到,等角和直角并与圆心角联系也比较紧密,通过在图形中构造辅助圆往往能获得意想不到的效果,如果题目中出现了以下条件:三点及三点以上到同一点距离相等,作辅助圆;同一侧有相等的角,或者需要构造出相等的角时,作辅助圆;若一个四边形的一组对角互补,则它的四个顶点共圆.在这些情况下,借助圆去解决一些问题都是非常好的一个选择,下面举例说明这三种构造辅助圆解题的模型应用。
二、典例精析类型1 根据共端点等线段模型,根据圆的定义构造圆1.如图,已知OA=OB=OC,且∠AOB=k∠BOC,则∠ACB是∠BAC的()A.k/2倍 B.k倍 C.2k D.1/k【分析】由OA=OB=OC,得到A,B,C在以O为圆心的同一个圆上,则∠AOB=2∠ACB,∠BOC=2∠BAC,而∠AOB=k∠BOC,即可得到∠ACB=k∠BAC.【解答】∵OA=OB=OC,∴A,B,C在以O为圆心的同一个圆上,如图,∴∠AOB=2∠ACB,∠BOC=2∠BAC,而∠AOB=k∠BOC,即2∠ACB=k2∠BAC,∴∠ACB=k∠BAC.故选:B.2.如图,在Rt△ABC中,∠C=90°,AC=6,BC=8,点F在边AC上,并且CF=2,点E 为边BC上的动点,将△CEF沿直线EF翻折,点C落在点P处,则点P到边AB距离的最小值是()A.1.5 B.1.2 C.2.4 D.以上都不对【分析】先依据勾股定理求得AB的长,然后依据翻折的性质可知PF=FC,故此点P在以F为圆心,以2为半径的圆上,依据垂线段最短可知当FP⊥AB时,点P到AB的距离最短,然后依据题意画出图形,最后,利用相似三角形的性质求解即可.【解答】如图所示:当PE∥AB.在Rt△ABC中,∵∠C=90°,AC=6,BC=8,∴由勾股定理可求得AB=10,由翻折的性质可知:PF=FC=2,∠FPE=∠C=90°.∵PE∥AB,∴∠PDB=90°.由垂线段最短可知此时FD有最小值.又∵FP为定值,∴PD有最小值.又∵∠A=∠A,∠ACB=∠ADF,∴△AFD∽△ABC.∴AF/AB=DF/BC,即4/10=DF/8,解得:DF=3.2.∴PD=DF﹣FP=3.2﹣2=1.2.故选:B.3.如图2所示,在凸四边形ABCD中,AB=BC=BD,∠ABC=80°,则∠ADC的度数为____度【解析】∵AB=BC=BD,得到A,C,D在以B为圆心的同一个圆上,∴∠ACD=1/2∠ABD, ∠DAC=1/2∠DBC,∵∠ABC=∠ABD +∠DBC =80°,∴∠ACD+∠DAC=1/2∠ABD+1/2∠DBC=1/2(∠ABD+∠DBC)= 1/2×80°=40°,∴∠ADC=180°﹣(∠DAC+∠ACD)=180°﹣40°=140°.故答案为:140.4. 如图,在四边形ABCD中,AB=AC=AD,若∠BAC=25°,∠CAD=75°,则∠BDC=度,∠DBC=_____度.【解析】法一:∵AB=AC=AD,∴点B,C,D在以A为圆心的圆上,∵∠BAC=25°,∴∠BDC=1/2∠BAC=12.5°,∵∠CAD=75°,∴∠DBC=1/2∠CAD=37.5°.故答案为:12.5,37.5.法二:∵AB=AC=AD,∴∠ADB=∠ABD,∠ACB=∠ABC,∠ADC=∠ACD,∵∠BAC=25°,∠CAD=75°,∴∠ACB=(180°﹣25°)÷2=77.5°,∠DAB=∠DAC+∠CAB=100°,∠ADC=∠ACD=(180°﹣75°)÷2=52.5°,∴∠ADB=(180°﹣100°)÷2=40°,∴∠BDC=∠ADC﹣∠ADB=52.5°﹣40°=12.5°,∠DCB=∠DCA+∠ACB=52.5°+77.5°=130°,∴∠DBC=180°﹣∠DCB﹣∠BDC=180°﹣130°﹣12.5°=37.5°.∴∠BDC=12.5°,∠DBC=37.5°.类型2 直角模型,依据直径所对的圆周角是直角,构造三角形的外接圆解题5. 如图所示,矩形ABCG与矩形CDEF全等,点BCD在一条直线上,∠APE的顶点P在线段BD上移动,使得∠APE为直角的点P的个数是_____个.【分析】∵∠APE的顶点P在线段BD上移动,且∠APE为直角,∴点P也在以AE为直径的⊙O的圆上运动;∴以AE为直径作⊙O,⊙O与BD的交点即为所求.【解答】∵点BCD在一条直线上,∠APE的顶点P在线段BD上移动,∠APE为直角,∴点P在以AE为直径的⊙O的圆上运动,∴点P就是⊙O与BD的交点,由图示知,BD与⊙O有2个交点.故答案为:2.【点评】本题主要考查了圆周角定理:直径所对的圆周角是直角.解答该题时,采用了“数形结合”的数学思想.6. 已知:如图,直尺的宽度为2,A、B两点在直尺的一条边上,AB=6,C、D两点在直尺的另一条边上.若∠ACB=∠ADB=90°,则C、D两点之间的距离为_____.【分析】由∠ACB=∠ADB=90°,根据90°的圆周角所对的弦是直径,可得A,B,C,D 在以AB为直径的圆上,C,D即是此圆与直尺的交点,设E为AB中点,可得EC是半径为3,然后作EF⊥CD交CD于F,根据垂径定理可得:CD=2CF,然后由勾股定理求得CF的长,继而求得答案.【解答】设E为AB中点,∵∠ACB=∠ADB=90°,∴A,B,C,D在以AB为直径的圆上,连接DE,CE,则CE=DE=1/2AB=3,作EF⊥CD交CD于F,∴CD=2CF,∵AB∥CD,∴EF=2,在Rt△CFE和Rt△DFE中,CF=√5,∴CD=2√5.故答案为:2√5.【点评】此题考查了圆周角定理,垂径定理以及勾股定理等知识.此题拿度适中,解题的关键是由∠ACB=∠ADB=90°,根据90°的圆周角所对的弦是直径,得到A,B,C,D 在以AB为直径的圆上.7. 已知Rt△ABC中,AC=5,BC=12,∠ACB=90°,P是AB边上的动点(与点A、B不重合),Q是BC边上的动点(与点B、C不重合)(1)如图,当PQ∥AC,且Q为BC的中点时,求线段CP的长;(2)当PQ与AC不平行时,△CPQ可能为直角三角形吗?若有可能,请求出线段CQ的长的取值范围;若不可能,请说明理由.【分析】(1)根据平行线等分线段定理得到点P是斜边的中点,再直角三角形斜边上的中线等于斜边的一半,要求线段CP的长,只需根据勾股定理求得AB的长.(2)若PQ与AC不平行,则要使△CPQ成为直角三角形.只需保证∠CPQ=90°.根据直径所对的圆周角是直角,则分析以CQ为直径的圆和斜边AB的公共点的情况:一是半圆和AB相切;二是半圆和AB相交.首先求得相切时CQ的值,即可进一步求得相交时CQ 的范围.【解答】(1)在Rt△ABC中∠ACB=90°,AC=5,BC=12,∴AB=13;∵Q是BC的中点,∴CQ=QB;又∵PQ∥AC,∴AP=PB,即P是AB的中点,∴Rt△ABC中,CP=13/2.(2)当AC与PQ不平行时,只有∠CPQ为直角,△CPQ才可能是直角三角形.以CQ为直径作半圆D,①当半圆D与AB相切时,设切点为M,连接DM,则DM⊥AB,且AC=AM=5,∴MB=AB﹣AM=13﹣5=8;设CD=x,则DM=x,DB=12﹣x;在Rt△DMB中,DB=DM+MB,即(12﹣x)=x+8,解之得x=10/3,∴CQ=2x=20/3;即当CQ=20/3且点P运动到切点M位置时,△CPQ为直角三角形.②当20/3<CQ<12时,半圆D与直线AB有两个交点,当点P运动到这两个交点的位置时,△CPQ为直角三角形③当0<CQ<20/3时,半圆D与直线AB相离,即点P在AB边上运动时,均在半圆D外,∠CPQ<90°,此时△CPQ不可能为直角三角形.∴当20/3≤CQ<12时,△CPQ可能为直角三角形.8.已知平面直角坐标系中两定点A(-1,0),B(4,0),抛物线y=ax+bx-2过点A,B,顶点为C,点P(m,n)为抛物线上一点,其中n<0.(1)求抛物线的解析式和顶点C的坐标;(2)当∠APB为钝角时,求m的取值范围.【分析】(1)利用待定系数法求出解析式,再利用x=0得出y的值即可得出C点坐标.(2)因为AB为直径,所以当抛物线上的点P在⊙C的内部时,满足∠APB为钝角,进而得出m的取值范围;]解:(1) (1)∵抛物线y=ax+bx﹣2(a≠0)过点A,B,∴a-b-2=0, 16a+4b-2=0,解得:a=1/2, b=-3/2,∴抛物线的解析式为:y=1/2x﹣3/2x﹣2,当x=0时,y=﹣2,∴C(0,﹣2);(2)∵A(-1,0),B(4,0),抛物线与y轴的交点D的坐标为(0,-2),如图,抛物线的对称轴与x轴的交点为M(3/2,0),∵AD=1+2=5,AB=(4+1) =25,BD=4+2=16+4=20,则AD+BD=AB,由勾股定理的逆定理,知△ABD是直角三角形,∠ADB=90°,以M为圆心,以MA为半径作圆,则☉M经过点D,则☉M内抛物线上的所有的点都可以是P点,且使∠APB为钝角,根据抛物线及圆的对称性,☉M与抛物线的另一个交点坐标为(3,-2),则满足条件的m的取值范围为:-1<m<0或3<m<4.类型3 四点共圆模型(1)若一个四边形的一组对角互补,则它的四个顶点共圆;(2)动点对定线段所张的角为定值.9. 如图2,在平面直角坐标系xOy中,点A的坐标为(0,m),点B的坐标为(0,n),其中m>n>0.点P为x轴正半轴上的一个动点,当∠APB达到最大时,直接写出此时点P的坐标________.【解析】当以AB为弦的圆与x轴正半轴相切时,对应的∠APB最大,根据垂径定理和勾股定理即可求解.当以AB为弦的圆与x轴正半轴相切时,作CD⊥y轴,连接CP、CB.∵A的坐标为(0,m),点B的坐标为(0,n),10. 在平面直角坐标系中,已知点A(4,0)、B(﹣6,0),点C是y轴上的一个动点,当∠BCA=45°时,点C的坐标为_____.【分析】如解答图所示,构造含有90°圆心角的⊙P,则⊙P与y轴的交点即为所求的点C.注意点C有两个.【解答】设线段BA的中点为E,∵点A(4,0)、B(﹣6,0),∴AB=10,E(﹣1,0).(1)如答图1所示,过点E在第二象限作EP⊥BA,且EP=1/2AB=5,则易知△PBA为等腰直角三角形,∠BPA=90°,PA=PB=5√2;以点P为圆心,PA(或PB)长为半径作⊙P,与y轴的正半轴交于点C,∵∠BCA为⊙P的圆周角,∴∠BCA=1/2∠BPA=45°,即则点C即为所求.过点P作PF⊥y轴于点F,则OF=PE=5,PF=1,在Rt△PFC中,PF=1,PC=5√2,由勾股定理得:CF=7,∴OC=OF+CF=5+7=12,∴点C坐标为(0,12);(2)如答图2所示,在第3象限可以参照(1)作同样操作,同理求得y轴负半轴上的点C坐标为(0,﹣12).综上所述,点C坐标为(0,12)或(0,﹣12).故答案为:(0,12)或(0,﹣12).【点评】本题难度较大.由45°的圆周角联想到90°的圆心角是解题的突破口,也是本题的难点所在.11. 已知△ABC是等腰直角三角形,AC=BC=2,D是边AB上一中点,将△CAD绕C逆时针向旋α得到△CEF,其点E是点A的对应点,点F是点D的对应点.DF与AE交于点M;当α从90°变化到180°时,点M运动的路径长为______.【分析】先证明A、D、M、C四点共圆,得到∠CMF=∠CAD=45°,即可推出点M在以AC 为直径的⊙O上,运动路径是弧CD,利用弧长公式即可解决问题.【解答】∵CA=CE,CD=CF,∴∠CAE=∠CEA,∠CDF=∠CFD∵∠ACD=∠ECF,∴∠ACE=∠DCF,∵2∠CAE+∠ACE=180°,2∠CDF+∠DCF=180°,∴∠CAE=∠CDF,∴A、D、M、C四点共圆,∴∠CMF=∠CAD=45°,∴∠CMD=180°﹣∠CMF=135°.(补充:不用四点共圆的方法:由△OAC∽△ODM,推出△AOD∽△COM,推出∠OCM=∠OAD,即可证明∠CMF=∠CDM+∠DCM=∠CAO+∠OAD=∠CAD=45°)∵O是AC中点,连接OD、CM.∵AD=DB,CA=CB,∴CD⊥AB,∴∠ADC=90°,∵A、D、M、C四点共圆,∴当α从90°变化到180°时,点M在以AC为直径的⊙O上,运动路径是弧CD,【点评】本题考查几何变换综合题、等腰直角三角形的性质、平行线的判定和性质、弧长公式、四点共圆等知识,解题的关键是发现A、D、M、C四点共圆,最后一个问题的关键,正确探究出点M的运动路径,记住弧长公式,属于中考压轴题.三、总结提升圆是我们初中阶段学习的唯一一个曲线图形,除了它本身的基本性质和计算常被考察到以外,还可以用作辅助线。
巧解初中几何问题——以构造辅助圆为例

2023年12月下半月㊀解法探究㊀㊀㊀㊀巧解初中几何问题以构造辅助圆为例◉江苏省靖江市外国语龙馨园学校㊀徐㊀乐㊀㊀圆是初中数学平面几何中非常重要的一个知识点,与初中数学中其他几何问题有着紧密的联系.所以在解决几何问题时,一些无法利用常规思路求解的综合问题可以尝试通过构造辅助圆的方式来解决.因此,在初中数学几何问题解题教学中,教会学生如何正确使用辅助圆来巧解几何问题是教师需要重点研究的问题.下面将通过例题对辅助圆的应用进行说明.1角的问题例1㊀在әA B C 中,A B =A C ,øA B C 的平分线交A C 于点D ,已知B C =B D +A D ,求øA 的度数.分析:根据题中所给已知条件,可以判定әA B C为等腰三角形,但是想要根据已知条件通过常规方式求øA 的度数存在一定困难.结合题中所给的角平分线,可以联想圆中共顶点的角的问题,作әA B D 的外图1接圆,与әA B C 的B C 边交于点E ,连接D E ,如图1.根据B D 是øA B C 的角平分线,可以知道A D =D E ,同时还能得到这个辅助圆为四边形A B E D 的外接圆.根据圆内接四边形的对角互补的性质可得øA B C =øE D C ,根据әA B C 为等腰三角形可知øA B C =øE D C =øC ,于是可得øB E D =2øC ,且әE D C 为等腰三角形.所以D E =C E ,则A D =D E =C E ,然后结合B C =B E +A D 得到B D =B E ,所以øB D E =øB E D =2øC .这样就可以在әB D E 中计算øC 的度数,即12øC +2øC +2øC =180ʎ,所以øC =40ʎ,最后计算得出øA =100ʎ.在初中数学几何问题中构造辅助线需要充分结合试题的情况来进行.本题中辅助圆的构造就是结合了本题所给定的角平分线的关系,根据相等的圆周角所对应的弧和弦长相等的性质来实现;然后通过辅助圆及相关线段关系来与相关角取得联系;最后利用三角形的性质求解.教师要对学生进行相应的引导,让学生掌握通过角的关系来构造辅助圆,进而借助辅助圆解决问题.2线段长度的问题图2例2㊀如图2所示,在R t әA B C中,A B ʅB C ,A B =6,B C =4,P 是R t әA B C 内部的一个动点,且满足øP A B =øP B C ,则线段C P 的最小值为(㊀㊀).A.32㊀㊀㊀㊀㊀㊀B .2C .81313D.121313图3分析:根据A B ʅB C 可以知道øA B C =90ʎ,结合øP A B =øP B C 可得到øA P B =90ʎ,所以әA B P 是直角三角形.根据直角三角形中斜边的中线等于斜边的一半以及圆的直径所对的圆周角是90ʎ,可知点P 在以A B 为直径的圆上.以A B 的中点O 为圆心,A B 为直径作圆,如图3所示.这样就可得到当P C 的值最小时,点P 正好在线段O C 上.因为A B =6,所以O B =3.在R t әO B C 中,B C =4,根据勾股定理得到O C =5,于是可求出P C 的最小值为2.所以正确答案是选项B .例2的解题关键是需要判断点P 的轨迹,首先根据试题中所给定的关系得到øA P B =90ʎ,结合直角三角形的性质和圆的性质很容易判断出点P 在以直线A B 为直径的圆上,然后就能够求解最小值.因此,在解题的过程中,只有认真分析题目条件,才能顺利找到解题思路.教师在进行解题教学时需要教会学生如何根据题目中所给定的已知条件来进行分析,从而找到解题思路.很多几何问题都是需要在解题的过程中才能够找到相应的解题思路,并不是通过对试题的观察就能得到解题思路的.因此结合已知条件来对试97解法探究2023年12月下半月㊀㊀㊀题中存在的关系进行分析,在解题的过程中发现解题思路,是解决问题最好的方式.教师需要引导学生先根据已知条件尝试找到解题的思路,进而解决问题.3三角形相似的问题例3㊀әA B C 中,A D 是øB A C 的外角平分线,交B C 的延长线于点D ,求证:B D D C =A BA C.分析:A B ,A C 是әA B C 的两条边,而B D ,D C则是线段B D 上的两条线段,根据所学的知识,要证明B D D C =A BA C ,线段成比例关系可以通过证明三角形相似来解决.因此需要将线段B A 延长至点F ,连接D F ,构建出әB A C ʐәB D F ,得到A B A C =B DD F,然后证明C D =D F 就可以了,从而将证明的关键转化为证明C D =D F .结合题意,øB A C 的外角平分线交B C的图4延长线于点D ,如图4,根据例题1中的方式构造әA C D 的外接圆,B A 的延长线与圆交于点F ,连接D F .根据圆的性质可以得到C D =D F ,通过相似三角形的证明就可以解决问题.几何问题中需要求证的结论存在线段比例关系或者线段等积关系时,都会涉及三角形相似或者全等的证明,通过构造圆为三角形相似或者全等提供条件,实现对问题的求解.在这个过程中,需要充分结合例题1和例题2中辅助圆构造的方式来找到相应的关系.4动点的问题图5例4㊀如图5所示,边长为3的等边三角形A B C ,D ,E 分别是B C ,A C 边上的两个动点,且B D =C E ,A D ,B E 交于点P ,求点P 的运动路径长和C P 的最小值.分析:首先需要对点P 的运动路径进行判定.根据等边三角形的相关性质和B D =C E 可以得到әA B D ɸәB C E ,这样就得到øC B E =øB A D ,然后通过øC B E +øA B P =60ʎ得到øB A P +øA B P =øA P E =60ʎ,于是øA P B =120ʎ.可以发现在点D 和点E 移动的过程中,øA P B =120ʎ是恒成立的,所以可以认为点P 在A B 为弦的圆上.假设弦A B 所在圆的圆心为O ,连接O P ,O A ,O B ,根据圆的性质㊁әA B C 的边长为3可计算出圆O 的半径O A =3,然后计算出点P 的运动路径长度为233π,C P 的最小值为3.解:由A B =B C ,øA B D =øB C E ,B D =C E 得әA B D ɸәB C E .由øC B E +øA B P =60ʎ,得øB A P +øA B P =øA P E =60ʎ.所以øA P B =120ʎ.故点P 的运动轨迹是以A B 为弦的圆上的一段弧.图6如图6所示,作әA B P 的外接圆,圆心为O ,连接O A ,O B ,O P ,O C .由O A =O B ,A C =B C ,得әA O C ɸәB O C .所以øO A C =øO B C ,øA C O =øB C O =12øA C B =30ʎ,øA O C =øB O C =12øA P B =60ʎ.故øO A C =90ʎ.根据勾股定理,可得O A =3,O C =23.所以,弦A B 所对的弧长为3ˑ23π=233π;当O ,P ,C 三点共线时,C P 最小,且最小值为3.在三角形的动点问题中,如果动点与一条线段所构成的角度固定,则说明这个动点的轨迹是以这个线段为弦的圆上的一段弧,通过这个关系可以构造辅助圆,然后利用圆的性质来求解问题.本题给定的是正三角形,当然不同的三角形中所呈现的关系可能会存在差别,但是本质没有变化.例如,在例题2中通过计算所得到的角度为90ʎ的特殊角,这个辅助圆的圆心就在直角三角形的斜边上.例4中这个角度为120ʎ,圆心在三角形的外部,通过辅助圆来充分利用圆的相关性质,能够更好地对问题进行求解,实现问题的解决.本文中对辅助圆在初中数学平面几何中的应用进行了总结,并通过相关例题对其用法进行了说明.在初中数学平面几何问题中巧用辅助圆能够优化试题解法,实现快速求解.因此,教师在解题教学的过程中需要对学生进行有效地引导,让学生掌握辅助圆的应用,从而提升解题能力;提升数学素养.Z08。
中考数学几何最值模型 专题03 辅助圆模型(学生版+解析版)

辅助圆模型模型讲解一、定点定长1、O为定点,OA=OB,且长度固定,那么O、A、B三点可以确定一个圆,动点P在圆弧AB上运动,如图所示,Q为圆外一定点,当P运动到OQ的连线上时,即:P落到P1处,O、P1、Q三点共线时,PQ最小。
二、定弦定角2、线段AB固定,Q为动点,且∠AQB为定值,那么Q、A、B三点可以确定一个圆,动点Q在圆弧AB上运动,如图所示,R为圆外一定点,当Q运动到OQ的连线上时,即:P落到P1处,O、P1、Q三点共线时,RQ最小。
方法点拨一、题型特征:①动点的运动轨迹为圆②圆外一点到圆上一点的距离最短:即圆外一点与圆心连线与圆的交点③常见确定圆的模型:定点定长、定弦定角。
二、模型本质:两点之间,线段最短。
例题演练1.如图,已知AB=AC=BD=6,AB⊥BD,E为BC的中点,则DE的最小值为()A.3﹣3B.3C.3﹣3D.2【解答】解:取AB的中点O,连接AE,OE,OD.∵AB=AC,BE=EC,∴AE⊥BC,∴∠AEB=90°,∵OA=OB,∴OE=AB=3,∵AB⊥BD,∴∠OBD=90°,∵OB=3,BD=6,∴OD===3,∵DE≥OD﹣OE,∴DE≥3﹣3,∴DE的最小值为3﹣3,故选:C.强化训练1.如图,矩形ABCD中,AB=3,BC=8,点P为矩形内一动点,且满足∠PBC =∠PCD,则线段PD的最小值为()A.5B.1C.2D.3 2.如图,在矩形ABCD中,AB=4,BC=6,E是矩形内部的一个动点,且AE ⊥BE,则线段CE的最小值为.3.如图,△ABC为等边三角形,AB=2.若P为△ABC内一动点,且满足∠P AB =∠ACP,则线段PB长度的最小值为.4.如图,在矩形ABCD中,AB=4,BC=6,E是平面内的一个动点,且满足∠AEB=90°,连接CE,则线段CE长的最大值为.5.如图1,P是⊙O外的一点,直线PO分别交⊙O于点A,B,则P A是点P 到⊙O上的点的最短距离.(1)探究一:如图2,在Rt△ABC中,∠ACB=90°,AC=BC=2,以BC为直径的半圆交AB于D,P是上的一个动点,连接AP,则AP的最小值是.(2)探究二:如图3,在边长为2的菱形ABCD中,∠A=60°,M是AD边的中点,N是AB边上一动点,将△AMN沿MN所在的直线翻折得到△A′MN,连接A′C,请求出A′C长度的最小值.(3)探究三,在正方形ABCD中,点E,F分别从D,C两点同时出发,以相同的速度在直线DC,CB上移动,连接AE和DF交于点P,由于点E,F的移动,使得点P也随之运动,若AD=4,试求出线段CP的最小值.1.如图,在边长为2的菱形ABCD中,∠A=60°,M是AD边的中点,N是AB边上的一动点,将△AMN沿MN所在直线翻折得到△A′MN,连接A′C,则A′C长度的最小值是.辅助圆模型模型讲解一、定点定长1、O为定点,OA=OB,且长度固定,那么O、A、B三点可以确定一个圆,动点P在圆弧AB上运动,如图所示,Q为圆外一定点,当P运动到OQ的连线上时,即:P落到P1处,O、P1、Q三点共线时,PQ最小。
最全最新初中数学竞赛专题讲解辅助圆

初中数学竞赛专题讲解辅助圆在处理平面几何中的许多问题时,常需要借助于圆的性质,问题才得以解决.而我们需要的圆并不存在(有时题设中没有涉及圆;有时虽然题设涉及圆,但是此圆并不是我们需要用的圆),这就需要我们利用已知条件,借助图形把需要的实际存在的圆找出来, 添补辅助圆的常见方法有:1.利用圆的定义添补辅助圆;2.作三角形的外接圆;3.运用四点共圆的判定方法: (1)若一个四边形的一组对角互补,则它的四个顶点共圆. (2)同底同侧张等角的三角形,各顶点共圆.(3)若四边形ABCD 的对角线相交于P ,且PA ·PC=PB ·PD ,则它的四个顶点共圆.(4)若四边形ABCD 的一组对边AB 、DC 的延长线相交于P ,且PA ·PB =PC ·PD ,则它的四个 顶点共圆.推论:同斜边的直角三角形顶点共圆(斜边就是圆的直径). 4.画出辅助圆就可以应用圆的有关性质.常用的有:① 同弧所对的圆周角相等.② 圆内接四边形对角互补,外角等于内对角. ③ 圆心角(圆周角)、弧、弦、弦心距的等量关系. ④ 圆中成比例线段定理:相交弦定理 ,切割线定理. 5.证明型如ab+cd=m 2常用切割线定理一、基础过关1.如图1,AB=AC=AD,如果∠DAC 是∠CAB 的K 倍(K 为实数).求:∠DBC 是∠BDC 的多少倍?2.△ABC 中,作BD ⊥AC 于D ,CE ⊥AB 于E ,连DE ,若∠ABC =45°, 求∠EDB 的度数。
A COD EB3.如图,B 是线段AC 的中点,过点C 的直线l 与AC 成60°的角,在直线l 上取一点P ,使得∠APB=30°,则满足条件的点P 的个数是( )(A)3个(B)2个 (C)1个 (D)不存在4.已知:如图,直尺的宽度为2,A 、B 两点在直尺的一条边上,AB=6,C 、D 两点在直尺的另一条边上.若∠ACB=∠ADB=90°,求则C 、D 两点之间的距离 .4.如图,矩形ABCG(AB<BC)与矩形CDEF 全等,点B 、C 、D 在同一条直线上,∠APE 的顶点P 在线段BD 上移动,使∠APE 为直角的点P的个数是 ( ) A.0 B.1 C.2 D.35.如图,点A 与点B 的坐标分别是(1,0),(5,0),点P 是该平面直角坐标系内的一个动点. (1)若点C 平面直角坐标系内的一个点,且△ABC 是等边三角形,则点C 的坐标是 ; (2)若点P 在y 轴上,且∠APB=30°,求满足条件的点P 的坐标;(3)当点P 在y 轴上移动时,∠APB 是否有最大值?若有,求点P 的坐标,并说明此时∠APB 最大的理由;若没有,也请说明理由.二、例题讲解1.根据圆的定义作辅助圆例1:如图,四边形ABCD 中,AB ∥CD ,AB =AC =AD =p ,BC =q ,求BD 的长.解析:以点A 为圆心、AB 为半径作⊙A .因为AB =AC =AD ,所以B 、C 、D 三点在⊙A 上.延长BA 交⊙A 于点E ,连结DE .因为DC ∥EB ,所以弧ED =弧BC ,所以ED =BC =q .在Rt △BDE 中,根据勾股定理,得BD =.例2:如图,PA =PB ,∠APB =2∠ACB ,AC 与PB 交于点D ,且PB =5,PD =3,求AD ·DC 的值.解析:以点P 为圆心、P B为半径的作⊙P .因为PA =PB ,∠APB =2∠ACB ,所以点A、B 、C在⊙P 上.此时⊙P 的直径BE =10,DE =8,DB =2, 由相交弦定理,得AD ·DC =DE ·DB =8216⨯=2.作三角形的外接圆例3:如图,D 、E 为△ABC 边BC 上的两点,且BD=CE ,∠BAD=∠CAE ,求证:AB=AC . 解析:作△ADE 的外接圆,分别交AB 、AC 于点M 、N ,连结MD 、NE .因为∠BAD =∠CAE ,所以∠BAD +∠DAE =∠CAE+∠DAE ,即∠NAD =∠MAE .因为∠BDM =∠MAE ,∠CEN =∠NAD ,所以∠BDM =∠CEN . 又BD =CE ,DM =EN ,所以△BDM ≌△CEN ,所以∠B =∠C ,即AB =AC .例4:如图,△ABC 中,BF 、CE 交于点D ,BD =CD ,∠BDE =∠A ,求证:BE =CF . 解析:作△ABC 的外接⊙O ,延长CE 交⊙O 于G ,连接BG .因为∠G =∠A ,∠BDE =∠A ,所以∠G =∠BDE ,所以BG=BD . 又BD =CD ,所以BG =CD.又因为∠G =∠CDF ,∠GBE =∠DCF ,所以△GBE ≌△DCF . 所以BE =CF .BC例5:如图,在△ABC 中,AB =AC ,∠BAC =100°,∠B 的平分线交AC 于D , 求证:BC =BD +AD .解析:作△ABD 的外接圆交BC 于E ,连结DE .因为BD 是∠ABC 的平分线,所以弧AD =弧DE ,所以AD =DE . 在△BDE 中,∠DBE =20°,∠BED =180°―100°=80°, 所以∠BDE =80°, 所以BE =BD .在△DEC 中,∠EDC =80°―40°=40°,所以EC =DE . 所以BC =BE +EC =BD +AD .3.结论类似于圆幂定理的形式时作辅助圆例6:如图,在△ABC 中,AB =AC =3,D 是边BC 上的一点,且A D=1,求BD ·DC 的值. 解析:以点A 为圆心、AB 为半径作⊙A ,交直线AD 于点E 、F ,则点C 在⊙A 上,DE =13-,DF =13+.由相交弦定理,得BD ·DC =DE ·DF =)13)(13(+-=2.例7:如图,在△ABC 中,∠DAB =∠C ,∠B 的平分线BN 交AD 于M .求证:(1)AM =AN ;(2)AB 2-AN 2=BM ·BN .解析:(1)略;(2)由(1),得AM =AN .以点A 为圆心、AM 为半径作⊙A ,交AB 于E ,交BA 的延长线于F ,则N 在⊙A 上,且AE =AF =AN .由割线定理,得BM ·BN =BE ·BF =(AB -AE)(AB +AF)=(AB ―AN)(AB +AN =AB 2-AN 2,即AB 2-AN 2=BM ·BN .4.探究动点对定线段所张的角时作辅助圆例8:如图,在直角梯形ABCD 中,AB ∥DC ,∠B =90°,设AB =a ,DC =b ,AD =c , 当a 、b 、c 之间满足什么关系时,在直线BC 上存在点P ,使AP ⊥PD ?解析:以AD 为直径作⊙O ,根据直径所对的圆周角是直角,当⊙O 与直线BC 有公共点(相切或相交)时,在直线BC 上存在点P ,使AP ⊥PD .因为⊙O 的半径r =22cAD =,圆心O 到直线BC 的距离d =22b a DC AB +=+. 所以,当d ≤r ,即a +b ≤c 时,在直线BC 上存在点P ,使AP ⊥PD .C例9:如图,在平面直角坐标系xOy 中,给定y 轴正半轴上的两点A (0,2)、B(0,8),试在x 轴正半轴上求一点C ,使∠ACB 取得最大值。
省时省力的辅助圆

2022年7月下半月㊀解法探究㊀㊀㊀㊀省时省力的辅助圆◉山东省滕州市滕南中学㊀郭效萍1引言圆是初中阶段学习的重要图形,它的一些性质,例如,同弧所对的圆周角相等,半圆所对的圆周角是直角,直径是圆中最长的弦等,给解决问题带来极大的方便.在解答有关几何问题时,并不是图形中出现圆才利用圆的性质,有时需要构造一个辅助圆,然后利用圆的性质解答,这是解决几何问题的基本方法之一.2利用圆的集合定义构造辅助圆从集合的角度定义:圆是平面内到定点距离等于定长的点的集合.根据这个定义可以得到,当几个点到同一点的距离相等时,则这几点一定在同一个圆上.这样构造辅助圆,解答时不仅能利用题中的已知条件,而且可以利用圆的一些性质.例1㊀如图1,在四边形A B C D 中,A B =A C =A D ,若øB AC =25ʎ,øC AD =75ʎ,分别求øB D C 和øD B C 的度数.图1㊀㊀㊀图2解法1:(普通方法)ȵA B =A C =A D ,ʑøA D B =øA B D ,㊀øA C B =øA B C ,㊀øA D C =øA C D .ȵøB A C =25ʎ,øC A D =75ʎ,ʑøA C B =(180ʎ-25ʎ)ː2=77.5ʎ,㊀øD A B =øD A C +øC A B =100ʎ,㊀øA D C =øA C D =(180ʎ-75ʎ)ː2=52.5ʎ.ʑøA D B =(180ʎ-100ʎ)ː2=40ʎ.ʑøB D C =øA D C -øA D B=52.5ʎ-40ʎ=12.5ʎ,㊀øD C B =øD C A +øA C B=52.5ʎ+77.5ʎ=130ʎ.ʑøD B C =180ʎ-øD C B -øB D C=180ʎ-130ʎ-12.5ʎ=37.5ʎ.解法2:(构造辅助圆的方法)由A B =A C =A D ,得点B ,C ,D 在以A 为圆心,以A D 为半径的圆上,如图2.由øB A C =25ʎ,得øB D C =12øB A C =12.5ʎ.由øC A D =75ʎ,得øD B C =12øC A D =37.5ʎ.点评:比较上面两种方法可以发现,构造辅助圆后,解决过程明显简洁.这里主要利用了圆周角定理及其推论:同弧所对的圆周角相等,等弧所对的圆周角也相等.这是因为这些圆周角都等于它所对的圆心角的一半.3利用圆周角定理的推论构造辅助圆因为90ʎ的圆周角所对的弦是直径,所以当直角三角形的斜边一定时,直角顶点一定在以斜边为直径的圆上运动.此时构造辅助圆,可以确定直角顶点的运动轨迹.例2㊀如图3所示,矩形A B C G (A B <B C )与矩形C D E F 全等,点B ,C ,D 在一条直线上,øA P E 的顶点P 在线段B D 上移动,使得øA P E 为直角的点P 的个数是.图3㊀㊀㊀图4解析:如图4所示,根据90ʎ的圆周角所对的弦是直径,当øA P E 为直角时,点P 应在以A E 为直径的☉O 上.又因为点B ,C ,D 在同一条直线上,øA P E的顶点P 在线段B D 上移动,所以点P 就是☉O 与B D 的交点.由图4可知,B D 与☉O 有2个交点.故答案为:2.点评:本题确定点的方法使用的是交轨法,即从每一个条件出发确定一个点的轨迹,两个点的轨迹的交点就是符合题意的点.本题两个点的轨迹分别是一条直线和一个圆.4利用一个角对定线段所张的角度为定值构造辅助圆㊀㊀当一个角对固定长度的线段所张开的角度为定值时,角的顶点的运动轨迹为一个圆,此时可以作辅助圆,这条定线段为辅助圆的弦,这个角为圆周角.此时可以利用圆的相关性质解答问题.例3㊀如图5,点A 与点B 的坐标分别是(1,0),(5,0),点P 是该直角坐标系内的一个动点.(1)使øA P B =30ʎ的点P 有个.(2)若点P 在y 轴上,且øA P B =30ʎ,求满足条件的点P 的坐标.57Copyright ©博看网. All Rights Reserved.解法探究2022年7月下半月㊀㊀㊀(3)当点P 在y 轴上移动时,øA P B 是否有最大值?若有,求点P 的坐标,并说明此时øA P B 最大的理由;若没有,请说明理由.图5㊀㊀㊀图6解析:(1)如图6,以A B 为边,在第一象限内作等边三角形A B C ,以点C 为圆心,A C 为半径作☉C ,交y 轴于点P 1,P 2.在优弧A P 1B 上任取一点P ,则øA P B =12øA C B =12ˑ60ʎ=30ʎ.所以使øA P B =30ʎ的点P 有无数个.(2)①当点P 在y 轴的正半轴上时,过点C 作C G ʅA B ,垂足为点G ,如图6.由点A (1,0),B (5,0),得O A =1,O B =5,则A B =4.由点C 为圆心,C G ʅA B ,得A G =B G =12A B =2.则O G =O A +A G =3.由әA B C 是等边三角形,得A C =B C =A B =4.则C G =A C 2-A G 2=42-22=23.于是点C 的坐标为(3,23).过点C 作C D 垂直于y 轴,垂足为点D ,连接C P 2,如图6.由点C (3,23),得C D =3,O D =23.由点P 1,P 2是☉C 与y 轴的交点,得øA P 1B =øA P 2B =30ʎ.由C P 2=C A =4,C D =3,得D P 2=42-32=7.由点C 为圆心,C D ʅP 1P 2,得P 1D =P 2D =7,从而P 2(0,23-7),P 1(0,23+7).②当点P 在y 轴的负半轴上时,同理可得:点P 3(0,-23-7),P 4(0,-23+7).综上所述,满足条件的点P 的坐标为(0,23-7),(0,23+7),(0,-23-7),(0,-23+7).图7(3)如图7,当过点A ,B 的☉E 与y 轴相切于点P 时,øA P B 最大.理由:可证øA P B =øA E H ,当øA P B 最大时,øA E H 最大.由s i n øA E H =2A E知,当A E最小即P E 最小时,øA E H 最大.所以当圆与y 轴相切时,øA P B 最大.①当点P 在y 轴的正半轴上时,连接E A ,作E H ʅx 轴,垂足为点H ,如图7.由☉E 与y 轴相切于点P ,得P E ʅO P .由E H ʅA B ,O P ʅO H ,得øE P O =øP O H =øE H O =90ʎ.则四边形O P E H 是矩形,O P =E H ,P E =O H =3,得E A =3.由øE HA =90ʎ,AH =2,E A =3,得E H =E A 2-AH 2=32-22=5,则O P =5,则点P (0,5).②当点P 在y 轴的负半轴上时也符合题意,此时点P (0,-5).综上所述,存在满足条件的点P ,其坐标为(0,5),(0,-5).点评:解答第(3)小题时,体现了转化的思想,即由øA P B 转化为øA E H ,由øA E H 转化为2A E,由2A E转化为A E ,再由A E 转化为P E ,由P E 转化为直线与圆相切.5利用作辅助圆求最值圆外一定点与圆上各点连接而成的所有线段中,有一条最短线段和最长线段,这两条线段都在过圆心与圆外一点的直线上,如图8所示,最长线段是P A ,最短线段是P B .利用这一点,可以求与圆有关的线段的最值.图8㊀图9㊀图10例4㊀如图9,R t әA B C 中,A B ʅB C ,A B =6,B C =4,P 是әA B C 内部的一个动点,且满足øP A B =øP B C ,则线段C P 长的最小值为.解析:如图10,由øA B C =90ʎ,得øA B P +øP B C =90ʎ.又øP A B =øP B C ,则øB A P +øA B P =90ʎ,即øA P B =90ʎ,则点P 在以A B 为直径的☉O 上.连接O C 交☉O 于点P ,此时P C 最小.在R t әB C O 中,øO B C =90ʎ,B C =4,O B =3,则O C =O B 2+B C 2=5,P C =O C -O P =5-3=2.因此P C 的最小值为2.点评:几何中求最值的情况包括:(1)利用轴对称求线段和的最小值;(2)利用勾股定理求曲面上或不同平面上两点之间的最短距离;(3)利用三角形相似解决系数不为1的线段和最小值问题;(4)利用直径是圆中最长的弦解决与圆有关的线段的最值.几何问题中作辅助线的方法比较多,如作垂线㊁平行线㊁连接㊁延长㊁倍长中线㊁旋转三角形等,但作辅助圆这种作铺助线的方法容易被忽略.上述四个实例分别从四个不同的角度阐释了在什么情况下需要作辅助圆,如何作辅助圆,作辅助圆后如何利用辅助圆,以期对学生突破几何学习有所帮助.W67Copyright ©博看网. All Rights Reserved.。
圆中的重要模型之辅助线模型(八大类)(解析版)

圆中的重要模型之辅助线模型(八大类)在平面几何中,与圆有关的许多题目需要添加辅助线来解决。
百思不得其解的题目,添上合适的辅助线,问题就会迎刃而解,思路畅通,从而有效地培养学生的创造性思维。
添加辅助线的方法有很多,本专题通过分析探索归纳八类圆中常见的辅助线的作法。
模型1、遇弦连半径(构造等腰三角形)【模型解读】已知AB 是⊙O 的一条弦,连接OA ,OB ,则∠A =∠B .在圆的相关题目中,不要忽略隐含的已知条件。
当我们要解决有关角度、长度问题时,通常可以连接半径构造等腰三角形,利用等腰三角形的性质、勾股定理及圆中的相关定理,还可连接圆周上一点和弦的两个端点,根据圆周角的性质可得相等的圆周角,解决角度或长度的计算问题1(2022·山东聊城·统考中考真题)如图,AB ,CD 是⊙O 的弦,延长AB ,CD 相交于点P .已知∠P =30°,∠AOC =80°,则BD 的度数是()A.30°B.25°C.20°D.10°【答案】C【分析】如图,连接OB ,OD ,AC ,先求解∠OAC +∠OCA =100°,再求解∠PAO +∠PCO =50°,从而可得∠BOA +∠COD =260°,再利用周角的含义可得∠BOD =360°-80°-260°=20°,从而可得答案.【详解】解:如图,连接OB ,OD ,AC ,∵∠AOC =80°,∴∠OAC +∠OCA =100°,∵∠P =30°,∴∠PAO +∠PCO =50°,∵OA =OB ,OC =OD ,∴∠OBA =∠OAB ,∠OCD =∠ODC ,∴∠OBA +∠ODC =50°,∴∠BOA +∠COD =260°,∴∠BOD =360°-80°-260°=20°.∴BD的度数20°.故选:C .【点睛】本题考查的是圆心角与弧的度数的关系,等腰三角形的性质,三角形的内角和定理的应用,掌握“圆心角与弧的度数的关系”是解本题的关键.2(2023•南召县中考模拟)如图,⊙O 的直径AB 与弦CD 的延长线交于点E ,若DE =OB ,∠AOC =84°,则∠E 等于()A.42°B.28°C.21°D.20°【分析】利用OB =DE ,OB =OD 得到DO =DE ,则∠E =∠DOE ,根据三角形外角性质得∠1=∠DOE+∠E ,所以∠1=2∠E ,同理得到∠AOC =∠C +∠E =3∠E ,然后利用∠E =13∠AOC 进行计算即可.【解答】解:连结OD ,如图,∵OB =DE ,OB =OD ,∴DO =DE ,∴∠E =∠DOE ,∵∠1=∠DOE +∠E ,∴∠1=2∠E ,而OC =OD ,∴∠C =∠1,∴∠C =2∠E ,∴∠AOC =∠C +∠E =3∠E ,∴∠E =13∠AOC =13×84°=28°.故选:B .【点评】本题考查了圆的认识:掌握与圆有关的概念(弦、直径、半径、弧、半圆、优弧、劣弧、等圆、等弧等).也考查了等腰三角形的性质.3(2023·江苏沭阳初三月考)如图,已知点C 是⊙O 的直径AB 上的一点,过点C 作弦DE ,使CD =CO .若AD 的度数为35°,则BE 的度数是.【答案】105°.【分析】连接OD 、OE ,根据圆心角、弧、弦的关系定理求出∠AOD =35°,根据等腰三角形的性质和三角形内角和定理计算即可.【解析】解:连接OD 、OE ,∵AD的度数为35°,∴∠AOD =35°,∵CD =CO ,∴∠ODC =∠AOD =35°,∵OD =OE ,∴∠ODC =∠E =35°,∴∠DOE =180°-∠ODC -∠E =180°-35°-35°=110°,∴∠AOE =∠DOE -∠AOD =110°-35°=75°,∴∠BOE =180°-∠AOE =180°-75°=105°,∴BE 的度数是105°.故答案为105°.【点睛】本题考查了圆心角、弧、弦的关系定理:在同圆和等圆中,相等的圆心角所对的弧相等,所对的弦也相等.4(2023年山东省淄博市中考数学真题)如图,△ABC是⊙O的内接三角形,AB=AC,∠BAC=120°,D 是BC边上一点,连接AD并延长交⊙O于点E.若AD=2,DE=3,则⊙O的半径为()A.10B.3210 C.210 D.310【答案】A【分析】连接OA,OC,CE, 根据等腰三角形的性质得到∠B=∠ACB=30°, 根据等边三角形的性质得到AC=OA,根据相似三角形的判定和性质即可得到结论.【详解】连接OA,OC,CE,∵AB=AC,∠BAC=120°,∴∠B=∠ACB=30°∴∠AOC=60°,∵OA=OC,∴△AOC是等边三角形,∴AC=OA,∵∠AEC=∠ACB=30°,∠CAD=∠EAC,∴△ACD∽△AEC,∴ACAD =AEAC,∴AC2=AD·AE,∵AD=2,DE=3,∴AC=AD×AE=2×2+3=10,∴OA=AC=10,即⊙O的半径为10,故选:A.【点睛】本题考查了圆周角定理,等腰三角形的性质,等边三角形的判定和性质,相似三角形的判定和性质,熟练掌握相似三角形的判定和性质度量是解题的关键.模型2、遇弦作弦心距(解决有关弦长的问题)【模型解读】已知AB是⊙O的一条弦,过点OE⊥AB,则AE=BE,OE2+AE2=OA2。
巧构辅助圆解题

巧构辅助圆解题就像在中国学习许多其他学科一样,学习数学也需要花费许多时间和精力。
当你被要求做题时,你需要仔细阅读题目,寻找陷阱,记住重点,然后确定最佳解决方案。
在只有少数几分钟可供学生考虑的情况下,学生可能会遇到困难。
为了帮助学生更好地解决这些难题,教师应该让学生使用一种被称为“巧构辅助圆解题”的方法。
此方法是由袁绍颖博士发明的,他历时十多年研究学习行为,终于开发出这个技术。
这种技术利用“巧构”的思维方式来解决问题。
巧构是一种在头脑中将复杂的问题进行拆分和归纳来有效解决问题的方法。
借助巧构辅助圆解题,老师可以教学生从多个视角来思考,进行思维分析和分层次分析,以及提出假设来帮助学生解决复杂的数学题。
通过分析题目和给出的数据,学生可以把握重点,找出问题的关键,从而快速而正确地完成题目。
几乎所有学习领域里都有“巧构辅助圆解题”,它们包括语文、物理、化学、历史等等,都可以通过这种方式实现学习效果。
为了让学生更容易掌握巧构辅助圆解题,教师可以使用图片、视频、文本等来帮助学生学习。
其中,图片能够把一个概念抽象化,让学生更容易理解;视频可以增强学习体验,提高学习兴趣;文字能够把概念分解成几个步骤,让学生更容易记住。
同时,教师可以在课堂上多给予学生实践性的机会,让他们利用自己的知识和思考能力探究解题方法,从而提高其解决题目的能力。
除此之外,教师还可以使用“巧构辅助圆解题”给学生布置作业,让他们在课下也能够准确地完成任务。
总之,“巧构辅助圆解题”能够帮助学生更好地理解学习过程,有助于提升解题能力和学习效率,增强学习兴趣,这是一种非常有效的学习策略。
只要教师能够恰当使用这门技术,学生就可以一路走来,完成数学题,提高素养和兴趣。
绝杀中考压轴题:“辅助圆模型”
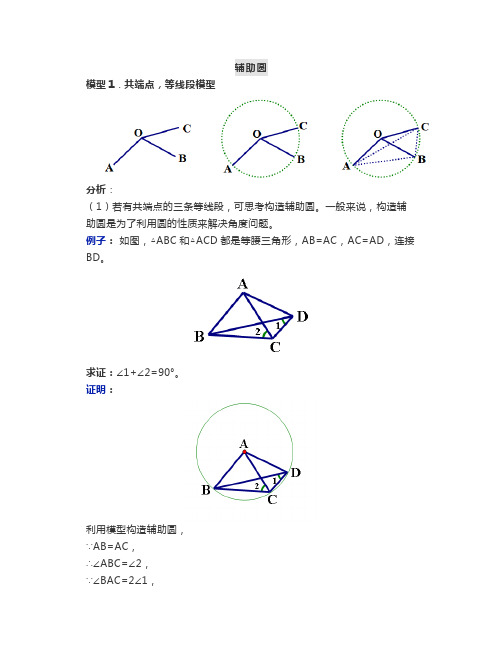
辅助圆模型1 . 共端点,等线段模型分析:(1)若有共端点的三条等线段,可思考构造辅助圆。
一般来说,构造辅助圆是为了利用圆的性质来解决角度问题。
例子:如图,△ABC和△ACD都是等腰三角形,AB=AC,AC=AD,连接BD。
求证:∠1+∠2=90°。
证明:利用模型构造辅助圆,∵AB=AC,∴∠ABC=∠2,∵∠BAC=2∠1,∴2∠2+2∠1=180°,∴∠1+∠2=90°。
方法二:利用模型构造辅助圆,延长CA交圆于点E,联结BE,∵CA是直径,∴∠EBC=90°。
∴∠E+∠2=90°,∵∠1=∠E,∴∠1+∠2=90°针对训练:如图,△ABC为等腰三角形,AB=AC,在△ABC的外侧作直线AP,点B与点D关于AP轴对称,连接BD、CD,CD与AP交于点E。
求证:∠1=∠2。
提示:可知AD=AB=AC,构造辅助圆可知关键的相等关系,∠1=2∠BDC,∠BDC=∠EBD,∠2=2∠BDC,∠1=∠2。
模型2. 直角三角形共斜边模型分析:共斜边的两个直角三角形,同侧或异侧,都有四点共圆,再根据圆周角定理得到角度相等,完成角度等量关系的代替,是证明角相等的思路之一。
例子:如图,AD、BE、CF为△ABC的三条高,H为垂心,求证:∠ADF=∠ADE。
证明:利用模型,可知B、C、E、F四点共圆,∴∠FBE=∠FCE,B、D、H、F四点共圆,∴∠ADF=∠FBE,D、C、E、H四点共圆,∴∠ADE=∠FCE,∴∠ADF=∠ADE。
针对训练:如图,已知△ABC中,AH是高,AT是角平分线,且TD⊥AB,TE⊥AC。
求:∠AHD=∠AHE。
提示:利用模型可知,A、D、T、E四点共圆,且AT为直径,联结OH,∵AH⊥BC,∴△ATH是直角三角形。
∴OH=1/2AT(O是AT中点),∴点H在圆上,∵AT是角平分线,TD⊥AB,TE⊥AC。
∴△ATD≌△ATE,∴AD=AE,∴∠AHD=∠AHE。
