薄膜干涉中的半波损失问题处理方法浅探
小议半波损失问题

小议半波损失问题作者:张石定;牛兴平来源:《价值工程》2010年第31期摘要: 从菲涅耳公式出发,讨论半波损失问题。
就前人发表的文章和教科书阐明该问题,以便更好的服务教学。
Abstract: Discussing the problems of Half-wave loss from Frenel's formula. According to the published articles and textbooks, we expound this problem to service teaching much better.关键词: 半波损失;菲涅耳公式;薄膜干涉Key words: Half-wave loss;Frenel's formula;interfence of thin film中图分类号:G42文献标识码:A文章编号:1006-4311(2010)31-0258-020引言在《大学物理》中数次提到“半波损失”问题。
主要是机械波的半波损失、电磁波包括光波反射时,在反射面处反射波相位突变。
但在《大学物理》教学中还有很多含糊之处,习惯于把半波损失简单表述为:“波(光)在空间传播时,由波(光)疏媒质到波(光)密媒质反射时有半波损失,反之则没有”;对于在薄膜上下表面,“当薄膜折射率与其上下方媒质的折射率关系是依次增大或减少(即n1>n2>n3)时没有半波损失,而当薄膜折射率同时大于或小于其上下方的媒质的折射率(即n1n3或n1>n2本文从菲涅耳公式出发,阐明半波损失问题。
和前人发表的文章、教科书内容相对照,使该问题更加明了。
1菲涅耳公式在波(光)传播过程中,E的方向不断变化,我们仅仅考虑反射、折射时刻的变化。
如右图1所示,入射光Ei 分解为Ei//和Ei⊥,反射光Er 分解为Er//和Er⊥,折(透)射光Et分解为Et//和Et⊥,两种介质的折射率分别为n1和n2。
薄膜干涉中半波损失问题的讨论

薄膜干涉中半波损失问题的讨论作者:喻国华来源:《物理教学探讨》2014年第10期摘要:半波损失的理论解释以及发生半波损失的条件就因为情况很多而难以理解,而几何光程差后面附加的λ/2(额外光程差)这一项理解起来也很困难,不同的教材对于它前面的“±”号的取法不同,这让笔者误以为无论取值正负对于结果都没有影响,但经过求证笔者才知道这是错误的,正负值的取法是因情况而定的。
本文将对半波损失的理论解释和发生以及附加光程差的具体表现形式进行分析讨论。
关键词:半波损失;薄膜干涉;额外光程差中图分类号:G633.7 文献标识码:A 文章编号:1003-6148(2014)10(S)-0039-31 引言在薄膜干涉中,半波损失和额外光程差占其中很大的成分,但是至今仍然没有文献系统的分析总结半波损失的发生条件以及额外光程差的计算问题,就算有也是粗略的概括下结论,没有对过程做过详细的介绍和推导。
在半波损失问题的讨论中,菲涅尔公式是最被常用的,也有少数人利用它做了一些有关半波损失的推导,本文将主要利用菲涅尔公式来总结半波损失发生过程和条件。
2 半波损失2.1 “半波损失”的理论解释“半波损失”,就是光在反射过程中产生了π相位差,使光在传播过程中多走或少走了半个波长,所以就发生半波损失。
2.2 “半波损失”发生与否的分析由maxcwell电磁场理论我们可以知道,在光的传播过程中,入射波、反射波、折射波的振幅矢量、、沿平行于入射面方向的分量和沿垂直于入射面方向的分量之间满足一种数学关系,也就是菲涅尔公式:E' E =-sin(i-r)sin(i+r)(1)E' E =-tan(i-r)tan(i+r)(2)E E =2sinr*cosi*sin(i+r)(3)E E =2sinr*cosi*sin(i+r)cos(i-r)(4)注释:其中i、r为入射角和折射角,E' 是反射波的振幅矢量垂直于入射面方向上的分量;E 表示入射波的振幅矢量垂直于入射面方向上的分量;E' 是反射波的振幅矢量平行于入射面方向上的分量;E 是折射波的振幅矢量平行于入射面方向上的分量。
薄膜干涉半波损失

薄膜干涉半波损失
薄膜干涉半波损失是指在光学薄膜中,由于光的干涉效应导致光波的相位差,进而引起光的强度损失。
这种损失通常是由于薄膜中反射和透射光之间的相位差所引起的,是光学薄膜制备和应用中需要注意的一个重要问题。
光学薄膜是指在光学器件中使用的非常薄的光学材料层,其厚度通常在几个波长范围内。
这些薄膜可以用于许多光学应用,如反射镜、透镜、光滤波器、光学波导和光学传感器等。
然而,在这些应用中,薄膜干涉半波损失可能会导致光学性能下降,影响器件的性能。
薄膜干涉半波损失的原因是光在薄膜内部发生的干涉效应。
光在薄膜中反射和透射时,会受到相位差的影响。
当光的波长和薄膜厚度相等时,反射光和透射光之间的相位差为半波长,这会导致光的强度损失。
这种损失可以通过调整薄膜的厚度、材料和设计来消除或减少。
在光学薄膜设计和制备中,薄膜干涉半波损失是需要考虑的一个重要问题。
为了减少这种损失,可以采用一些设计方法和制备技术。
例如,可以选择合适的材料和薄膜厚度,使得反射和透射光的相位差不是半波长。
此外,还可以采用多层薄膜结构,利用多层薄膜之间的相位差来减少半波损失。
在实际应用中,薄膜干涉半波损失可能会对器件的性能产生重要影响。
例如,在光学传感器中,由于薄膜干涉半波损失的影响,可能会导致传感器灵敏度下降。
因此,在设计和制备光学器件时,需要充分考虑薄膜干涉半波损失的影响,采取适当的措施来减少这种损失。
总之,薄膜干涉半波损失是光学薄膜制备和应用中需要注意的一个重要问题。
了解薄膜干涉半波损失的原因和影响,采取适当的设计和制备措施,可以减少或消除这种损失,提高光学器件的性能。
再论光波的半波损失

再论光波的半波损失作者:曹冬梅来源:《科学与财富》2011年第12期[摘要] 半波损失是大学物理中的重点和难点问题。
本文根据半波损失定义明确了其产生条件,重申了半波损失和附加光程差的区别与联系,最后结合薄膜干涉实例对附加光程差表达式作了针对性的分析。
[关键词] 半波损失薄膜干涉附加光程差引言半波损失问题是很久以来人们一直关注的问题,大量的文献从不同的角度对半波损失问题进行了探讨[1-3]。
由姚启钧原著的光学教材在提到半波损失对等倾干涉和等厚干涉反射光光程差的影响时,认为只要薄膜处于同一介质中,必然有额外光程差,我们在此取负号。
然而在等厚干涉一节的例1.2中却把附加光程差一项取为正号[4]。
在前一部分教材中“规定”附加光程差项取负号,而在例题运算中却取正号,附加光程差一项取正号和负号时有区别吗? 附加光程差与半波损失之间又有怎样的联系?1.半波损失半波损失,就是光在正入射或掠入射的情况下,从光疏(折射率相对小的)介质射向光密(折射率相对大的)介质被反射时,产生相位π的突变,相当于损失半个波长的光程,称为半波损失[5]。
当光从光疏介质射向光密介质,在垂直入射和掠入射时反射光有半波损失现象,我们可以由电磁场理论中的菲涅耳公式予以解释[4]。
当n1<n2时,无论一束光是垂直入射还是掠入射,在介质界面附近反射光矢量的振动方向都与入射光矢量的振动方向相反,都将出现光矢量在同一点相位突变的情形,即有半波损失发生。
那么对于斜入射,反射光矢量的垂直分量与入射光矢量的垂直分量的振动方向始终相反,但是,平行分量的方向之间却成一定的角度,此时比较它们的相位是没有绝对意义的。
故一般描述为“光从光疏介质入射到光密介质反射时具有半波损失”,这样很容易理解为:不管入射角为多少,只要光从光疏介质入射到光密介质,反射光矢量与入射光矢量就有相位突变π,相当于反射时产生了半波损失,似乎半波损失产生条件与入射角无关。
事实上半波损失的产生,不仅取决于界面两侧介质的折射率,还取决于入射角的大小[6]。
薄膜干涉中的半波损失与薄膜厚度

薄膜干涉中的半波损失与薄膜厚度张厚石摘要本文阐述了薄膜干涉中增透膜的增透过程,指出了学生在知识整理中因忽视半波损失而对皂液薄膜厚度产生的错误认识,分析了学生学习中容易出现错误的原因,提出在教学中值得注意的问题.学生在对水波干涉、光的双缝干涉及薄膜干涉学习后,知识体系在学生的头脑中已初步形成.然而在对知识进行整理和再认识的过程中,自然会遇到许多问题,如皂液薄膜干涉中的薄膜厚度问题,干涉中的能量传递问题等.在解决薄膜厚度问题时,无法回避“半波损失”的概念,所谓光波的半波损失是指:当光波被光密介质反射时,反射波的相位要发生π的突变.一、增透膜中的半波损失如图1所示为增透膜示意图,其中n0、n1、n2分别表示空气、膜层和玻璃的折射率.当入射光线S A入射到薄膜时,由于光线在膜内的多次反射,将分裂成功率递减的1、2、3…等各条反射光线和Ⅰ、Ⅱ、Ⅲ…等各条透射光线.若薄膜上下两面互相平行,则反射光线和透射光线将组成两平行光线组.图11.反射光组中的半波损失对增透膜而言n0<n1<n2(如空气的折射率n0=1,MgF2的折射率n1=1.38,冕牌玻璃的折射率n2=1.52),光线在由空气进入薄膜(光线由光疏到光密介质),和由薄膜进入玻璃时,上下两面反射均出现半波损失,即产生相位π的突变.因此,反射光组1、2、3…中由于反射引起的相位差为零.如果相邻两反射光互相抵消,则有光程差Δ=2dn1cosγ=(k+(1/2))λ0,其中λ0为光在空气中的波长,d为薄膜的厚度,γ为光在薄膜中的折射角,k=0,1,2,3….当光线SA正射薄膜时,γ=0,则Δ=2dn1=(k+(1/2))λ0,n1d=(k+(1/2))λ0/2,又n1=λ0/λ1,所以薄膜厚度为d=((2k+1)/4)λ1,当k=0时,d=λ1/4,即增透膜薄膜厚度为入射光在薄膜中波长的1/4.2.透射光组中的半波损失由于反射光组1、2、3…的互相抵消,就大大减少了反射光组的能量.同样因为n0<n1<n2,所以光在薄膜中连续两次反射时,只在薄膜下表面出现半波损失,产生相位π的突变.直接由薄膜下表面透射的光(如光线Ⅰ)与在薄膜中连续两次反射后再透射的光(如光线Ⅱ),由于反射引起的相位差为π,同理可知在透射光组Ⅰ、Ⅱ、Ⅲ…中相邻两透射光线由于反射引起的相位差均为π.当反射光线1、2、3…互相抵消时,透射光线Ⅰ、Ⅱ、Ⅲ…中相邻的两透射光线的光程差也为(光线正射时):Δ=2dn1,再加上相位差π或附加光程差±λ0/2(在此可取+λ0/2),所以相邻的两透射光线将是互相加强,从而使透射光的能量也得以加强.在增透膜实现增透的过程中不难发现:反射光组1、2、3…的互相抵消与透射光组Ⅰ、Ⅱ、Ⅲ…的互相加强形成了互补效应,体现出干涉效果只是将能量重新分配,而总能量仍然守恒.二、皂液薄膜干涉中的半波损失1.学生理解上的偏差“增透膜”是“薄膜干涉”知识的应用,学生在学完增透膜的内容后,对薄膜干涉现象的认识将会出现反复.在增透膜的增透过程中,“当薄膜的厚度是入射光在薄膜中波长的1/4时,在薄膜的两个面上反射的光,光程差恰好等于半个波长,因而互相抵消.”[1]在前面“双缝干涉”的学习中,我们知道:“在屏上距两个狭缝的光程差是半个波长的奇数倍处出现暗条纹.”[2]根据如图2所示的皂液薄膜干涉模型,学生在判断出现暗纹处的薄膜厚度d时,依据上述两种情形的结论认为:当皂液薄膜前后两表面反射回来的两反射光的光程差Δ=(k+(1/2))λ时(其中λ为光在皂液中的波长,k=0、1、2、3……),两反射光也互相抵消,从而得出“当薄膜厚度d=((2k+1)/4)λ处(如图2所示),两反射光互相抵消,形成暗条纹”这一错误结论.图22.引起学生理解偏差的原因(1)“相干”过程不清造成这一错误的原因之一是:学生缺乏一定的知识基础,没有考虑到薄膜反射中的半波损失问题.由于皂液薄膜的两侧均是空气,光在经过皂液薄膜前一面反射时会出现半波损失,产生的相位差为π,而经过皂液薄膜后一面反射时不会出现半波损失,当皂液薄膜厚度恰好为d=((2k+1)/4)λ时,两反射光的光程差虽为半个波长的奇数倍,但加上由于皂液薄膜一面反射时产生的相位差π或附加光程差±λ/2,恰使两反射光互相加强,形成亮条纹(“空气薄膜”干涉中也存在类似问题).比较“皂液薄膜”与“增透膜”相干的过程,可以看出:由于光线在MgF2薄膜前后两面反射均出现半波损失,因而反射引起的相位差为零.而光线在皂液薄膜前后两面反射时只在前一面出现半波损失,反射引起的相位差为π.虽然薄膜厚度均为1/4个波长的奇数倍,但现象却是一个互相抵消,一个互相加强,结果截然相反,这一点在教学中应引起广大师生的注意.(2)教材的误导造成学生认识上错误的另一原因是:教材在前后处理“双缝干涉”和“增透膜”的机理中,引入了“光程差”的概念,对相干问题加以量化处理,两次涉及出现暗纹的条件,强化了“光程差为半个波长的奇数倍”这一条件,而在“皂液薄膜干涉”及“空气薄膜干涉”中却回避了“光程差”的问题.然而学生在知识的整理及再认识过程中,考虑到皂液薄膜的厚度与暗亮条纹间的关系问题,是学生实施思维迁移的必然,而迁移的结果却导致了认识上的错误.究其原因,教科书在编写上有不妥之处,既然在“皂液薄膜干涉”中由于半波损失而回避了光程差及薄膜厚度问题,那么在“增透膜”中也应回避此类问题,这样才能保证教材前后的连续性和完整性,才能有利于学生系统地把握知识,更有利于学生思维的正向迁移.参考文献1 人民教育出版社物理室.高级中学课本,物理(第二册).人民教育出版社,19952 张阜权,孙荣山,唐伟国.光学.北京师范大学出版社,19853 孙自文.增透膜教学要讲清四点.中学物理教学参考,2000(4)4 彭生标.剖析肥皂膜成像分析的一种错误.中学物理,2000(10)来自: 中基网>>教学科研。
半波损失

§12.2分振幅的干涉(一) 薄膜反射光的干涉如(图12.2a ),一束平面光在透明薄膜上下两表面反射成两束光,让它们叠加在一起(例如用透镜会聚在一起)时,可满足相干条件。
它们的光程差L ∆可计算如下:()AE n BC AB n L 12-+=∆321n n n <<或321n n n >> (12.2.1)()212λ+-+=∆AE n BC AB n L 321n n n ><或321n n n <> (12.2.2)半波损失的情况比较复杂,本教材只按正入射和掠入射的情况列式1[1]。
如果折射率321n n n <<,则薄膜上下两表面的反射光都有半波损失;如果折射率321n n n >>,则上下两表面的反射光都没有半波损失。
因此,在(12.2.1)式中对这两种情况计算光程差时,都不计半波损失。
如果折射率321n n n ><或321n n n <>,则薄膜上下表面的两反射光中,一个有半波损失,另一个没有半波损失。
因此,在(12.2.2)式中计算这两种情况的光程差时,都应计算半波损失。
在(图12.2a )中,入射光对上表面的入射角与折射角为i 与r 。
由于C 与A 两点很靠近,此处薄膜上下表面可近似看成是平行的,因此,此光束对下表面的入射角可用r 表示。
设此处的薄膜厚度为e ,则可用e 、i 、r 诸量表示(12.2.1)式的光程差L ∆。
计算如下:r e BC AB cos ==,etgr AC 2=,i etgr i AC AE sin 2sin ==。
∴ ()i r n n r e i e t g r n r e n L s i n s i n c o s 2s i n 2c o s 22212-=-=∆。
将折射定律表式r n i n sin sin 21=代入上式,消去i sin 或r cos 得:()r en r n n r e L cos 2sin cos 22212=-=∆ (12.2.3) i n n r n n r n r n 2212222222222sin sin sin 1cos -=-=-= (12.2.4)将(12.2.3)式代入(12.2.1)及(12.2.2)式,并参考(12.1.18)式,可写出薄膜干涉(12.2.5) (12.2.6) 由于薄膜厚度e 不为负值或零,故k 与k '1[1] 赵凯华、钟锡华《光学》上册256页,1984年版。
薄膜的半波损失

薄膜的半波损失是指光线在通过薄膜时,由于反射和透射而损失了大约一半的光强。
这个现象是由于光在介质界面上发生反射和透射时的折射和干涉效应引起的。
薄膜的半波损失可以通过薄膜的折射率和入射角来计算。
一般来说,当光线从一个介质进入到折射率较高的薄膜中,然后再从薄膜出射到另一个介质时,会发生反射和透射。
在某些特定的入射角下,反射波和透射波之间的干涉会导致光强的减少,这就是半波损失发生的地方。
半波损失的计算涉及到薄膜的光学性质、波长以及入射角等因素。
一般来说,当薄膜的厚度等于光的波长的一半时,半波损失最显著。
这是因为在这种情况下,反射波和透射波之间的干涉效应最强烈。
半波损失可以通过精确的计算来确定,通常需要使用薄膜的光学常数(折射率和消光系数)以及入射角等信息。
这种计算通常在光学设计和薄膜涂层工程中用于优化薄膜的性能,以减小光信号的损失。
要进行半波损失的详细计算,通常需要使用光学模拟软件或咨询专业的光学工程师。
基于薄膜干涉研究[论文]
![基于薄膜干涉研究[论文]](https://img.taocdn.com/s3/m/19615a4c69eae009581bec7c.png)
基于薄膜干涉的研究摘要:光学薄膜是现代光学仪器和光学器件的重要组成部分,它在各类光学系统中的应用极为广泛。
传统的光学薄膜是以光的干涉为基础,并以此设计和制备增透膜、高反膜、滤光膜、分光膜、偏振及消振膜。
本文根据薄膜干涉的基本原理,阐述了半波损失的条件和薄膜厚度的选取。
关键词:光学薄膜薄膜干涉薄膜厚度随着现代科学技术特别是激光技术和信息光学的发展,光学薄膜不仅用于纯光学器件,在光通讯、光电探测器、化学及生物传感器、纳米器件等领域也有广泛的应用。
传统的光学薄膜是以光的干涉为基础,并以此设计和制备增透膜、高反膜、滤光膜、分光膜等。
薄膜的光学特性(折射率和厚度)是至关重要的参量。
本文主要依据薄膜干涉的原理,根据不同的应用要求,研究薄膜的光学性质。
一、薄膜干涉的基本原理光学薄膜是现代光学仪器和光学器件的重要组成部分,它通过在光学玻璃、光学塑料、光纤、晶体等各种材料的表面镀制一层或多层薄膜,基于薄膜内光的干涉效应来改变透射光或反射光的强度、偏振状态和相位变化。
光学薄膜具有良好的牢固性和光学稳定性,且质量极轻,成本相对较低,因此光学薄膜在各类光学系统中应用极为广泛。
薄膜干涉:一列光波照射到透明薄膜上,从膜的前、后表面分别被反射形成两列相干光波,这两列相干光波在叠加后产生干涉。
对于前、后表面不平行的楔形薄膜来说,凡是薄膜厚度相等的一些相邻位置,光的干涉效果相同而形成一条同种情况(譬如光振动加强)的干涉条纹(亮纹)。
随着薄膜厚度的逐渐变化,干涉效果出现周期性变化,一般在薄膜上形成明暗交替相间的干涉条纹图样,称为等厚薄膜干涉。
设基片的折射率为n■,介质膜的折射率为n■,介质膜上方空间的折射率为n■,n■>n■,cd⊥ad。
(如左图所示)二、半波损失设基片的折射率为n■,介质膜的折射率为n■,介质膜上方空间的折射率为n■(如右图所示),取介质膜的光学厚度n■·d=λ/4。
判断有无半波损失,根据具体情况而定:①当n■n■n■或n■>n■n■>n■时,在入射点a处,反射光束无半波损失,b点无半波损失,所以也不需要加■;综③和④所述,当n■n■>n■时,因薄膜上下表面的光学性质相同,上下表面的反射光没有附加光程差,两反射光的光程差δ=■,两反射光干涉相消,增加了投射光的能量,这种薄膜被称为增透膜。
薄膜干涉现象中值得探讨和澄清的几个问题
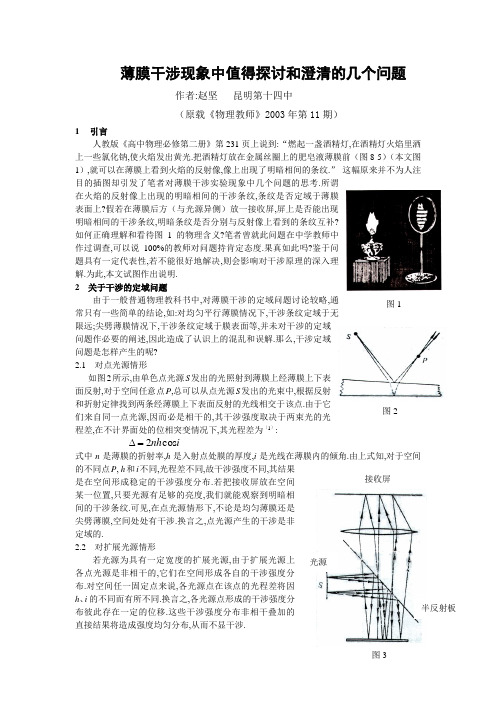
薄膜干涉现象中值得探讨和澄清的几个问题作者:赵坚 昆明第十四中(原载《物理教师》2003年第11期)1 引言人教版《高中物理必修第二册》第231页上说到:“燃起一盏酒精灯,在酒精灯火焰里洒上一些氯化钠,使火焰发出黄光.把酒精灯放在金属丝圈上的肥皂液薄膜前(图8-5)(本文图1),就可以在薄膜上看到火焰的反射像,像上出现了明暗相间的条纹.” 这幅原来并不为人注目的插图却引发了笔者对薄膜干涉实验现象中几个问题的思考.所谓在火焰的反射像上出现的明暗相间的干涉条纹,条纹是否定域于薄膜表面上?假若在薄膜后方(与光源异侧)放一接收屏,屏上是否能出现明暗相间的干涉条纹,明暗条纹是否分别与反射像上看到的条纹互补?如何正确理解和看待图1的物理含义?笔者曾就此问题在中学教师中作过调查,可以说100%的教师对问题持肯定态度.果真如此吗?鉴于问题具有一定代表性,若不能很好地解决,则会影响对干涉原理的深入理解.为此,本文试图作出说明.2 关于干涉的定域问题由于一般普通物理教科书中,对薄膜干涉的定域问题讨论较略,通常只有一些简单的结论,如:对均匀平行薄膜情况下,干涉条纹定域于无限远;尖劈薄膜情况下,干涉条纹定域于膜表面等,并未对干涉的定域问题作必要的阐述,因此造成了认识上的混乱和误解.那么,干涉定域问题是怎样产生的呢?2.1 对点光源情形如图2所示,由单色点光源S 发出的光照射到薄膜上经薄膜上下表面反射,对于空间任意点P ,总可以从点光源S 发出的光束中,根据反射和折射定律找到两条经薄膜上下表面反射的光线相交于该点.由于它们来自同一点光源,因而必是相干的,其干涉强度取决于两束光的光程差,在不计界面处的位相突变情况下,其光程差为〔1〕:i nh cos 2=∆式中n 是薄膜的折射率,h 是入射点处膜的厚度,i 是光线在薄膜内的倾角.由上式知,对于空间的不同点P , h 和i 不同,光程差不同,故干涉强度不同,其结果是在空间形成稳定的干涉强度分布.若把接收屏放在空间某一位置,只要光源有足够的亮度,我们就能观察到明暗相间的干涉条纹.可见,在点光源情形下,不论是均匀薄膜还是尖劈薄膜,空间处处有干涉.换言之,点光源产生的干涉是非定域的.2.2 对扩展光源情形若光源为具有一定宽度的扩展光源,由于扩展光源上各点光源是非相干的,它们在空间形成各自的干涉强度分布.对空间任一固定点来说,各光源点在该点的光程差将因h 、i 的不同而有所不同.换言之,各光源点形成的干涉强度分布彼此存在一定的位移.这些干涉强度分布非相干叠加的直接结果将造成强度均匀分布,从而不显干涉.然而,借助仪器我们有可能在空间找到某些特定的区域,上述非相干迭加不致造成强度均匀分布,从而使我们得到强弱相间的分布,此时我们说干涉条纹定域于这些区域.如:利用如图3所示的装置,在透镜焦面上观察.从扩展光源上每一点发出的光,经薄膜上下表面反射,在透镜的焦面上形成干涉条纹.从图中可见,扩展光源上不同光源点发出的光束中,只有彼此平行的光线经过薄膜上下表面反射后仍维持平行,最后经透镜才会聚于焦面上的同一点.而对应于同一方向的光线入射到薄膜的入射倾角相同,故光程差相同,扩展光源上各光源点在透镜焦面上形成的干涉条纹彼此是明纹与明纹重叠,暗纹与暗纹重叠.这也就是通常所说的,均匀薄膜情况下干涉条纹定域于无限远.由此可见,薄膜干涉产生的定域问题,实质是来源于采用了扩展光源的缘故.通常,当扩展光源不太小时,对于厚度均匀的薄膜(图4a ),无穷远为薄膜的定域中心;对于厚度不均匀的薄膜,随着上下表面交棱的方位不同,同一入射线的两反射线或交于薄膜前(图4b ),或延长线交于薄膜之后(图4c ),其定域中心并不在薄膜的表面上.正是由于扩展光源产生的薄膜干涉定域中心在无限远或膜的近旁,因此不能用放置接收屏的方法来观察干涉条纹.常用的观察方法是用透镜成像于屏上观察(如图3),用显微镜或人眼直接观察(如图5).用透镜成像观察要求透镜和接收屏的位置放置正确,只要确实是把薄膜干涉的定域中心层成像于接收屏上,就可以在接收屏上观察到较为清晰的干涉条纹.用人眼直接观察时,由于眼的瞳孔比透镜的孔径小得多,它限制了进入瞳孔的光束,如图5(a ),也就是说用人眼直接观察时,扩展光源的有效宽度比起用透镜来观察要小得多,这样干涉条纹的亮度固然要减弱,但干涉条纹的定域深度增加,同时人眼可以随意调焦,这样容易捕捉到干涉条纹.3 问题解答由于图1实验采用的光源为扩展光源,因此所谓“可以在薄膜上看到火焰的反射像,像上出现了明暗相间的条纹”,实质上明暗相间的条纹并非定域于薄膜上,而是定域于薄膜表面附近旁(如图4b 或c )的区域内,且由扩展光源上的各光源点形成的干涉强度分布,彼此并不处在同一焦面上.因此我们不可能采用放一接收屏的方法而在接收屏上观察到任何干涉条纹.当然,也不会出现在薄膜后方(与光源异侧)放一接收屏,屏上出现明暗相间的干涉条纹,且明暗条纹分别与反射像上看到的条纹互补的现象. 对于前述《高中物理必修第二册》上的图8-5(本文图1),实质是酒精灯火焰的反射像和从薄膜上下表面反射的光线,经照相机透镜会聚成像于平面底片上并重叠在一起的结果(人眼直接进行观察的情形与此类似),这也正好是容易产生误解的根源.值得提及的是,虽然人教社新版的《全日制普通高级中学教科书(试验本)物理第四册》第62页图20-9,此处已将图8-5改成绘制的插图,.但我们认为这样做仍不易说明问题.为了避免出现不必要的误会,笔者建议教材此处采用类似本文图3的装置(在要求不太高时,图中的半反射板可以不要)或许更容易说明问题的实质.致谢:作者感谢北京大学物理系赵凯华和陈熙谋先生的悉心指导以及进行的有益讨论.参考文献1 赵凯华,钟锡华.光学.上册.北京:北京大学出版社,2872 母国光,战元龄.光学.北京:高等教育出版社,19783 姚启钧.光学教程.华东师大《光学》教材编写组改编. 北京:高等教育出版社,1981英文题目Clarifying several questions arising from film interference。
半波损失

半波损失光在被反射过程中,如果反射光在离开反射点时的振动方向对入射光到达入射点时的振动方向恰好相反,这种现象叫做半波损失。
从波动理论知道,波的振动方向相反相当于波多走(或少走)了半个波长的光程。
入射光在光疏媒质中前进,遇到光密媒质界面时,在掠射或垂直入射2种情况下,在反射过程中产生半波损失,这只是对光的电场强度矢量的振动而言。
如果入射光在光密媒质中前进,遇到光疏媒质的界面时,不产生半波损失。
不论是掠射或垂直入射,折射光的振动方向相对于入射光的振动方向,永远不发生半波损失。
我们生活一个光的世界里,人们无法想象,如果没有光,世界将会是什么样子?!正是由于光以及与光有关的物理现象的存在,才组成了我们这个丰富多彩的世界。
光的干涉现象是有关光的现象中的很重要的一部分,而只要涉及到光的干涉现象,半波损失就是一个不得不考虑的问题。
光在不同介质表面反射时,在入射点处,反射光相对于入射光来说,可能存在半波损失,半波损失可以通过直观的实验现象——干涉花样——来得到验证。
半波损失理论在实践生活中有很重要的应用,如:检查光学元件的表面,光学元件的表面镀膜、测量长度的微小变化以及在工程技术方面有广泛的应用。
半波损失的原因在洛埃镜实验中,如果将屏幕挪进与洛埃镜相接触。
接触处两束相干波的波程差为零,但实验发现接触处不是明条纹,而是暗条纹。
这一事实说明洛埃镜实验中,光线自空气射向平面镜并在平面镜上反射后有了量值为∏的位相突变,这也相当于光程差突变了半个波长。
光在发射时为什么会产生半波损失呢?这是和光的电磁本性有关的,可通过菲涅耳公式来解释。
在任何时刻,我们都可以把入射波、反射波和折射波的电矢量分成两个分量,一个平行入射面,另一个垂直入射面。
有关各量的平行分量和垂直分量依次用指标p和s表示。
以i1、i1´ 和i2分别表示入射角、反射角和折射角,它们确定了各波的传播方向。
以A1、A1´、A2来依次表示入射波、反射波和折射波的电矢量的振幅,它们的分量相应就是Ap1、Ap1´、Ap2和As1、As1´、As2。
薄膜干涉的若干问题探讨

自我评价的学习.自主学习强调个体学习的主动眭,
是区别于被动学习、机械学习的一种学习方式.可 见,自主学习具有以下几个特征.
第一,学习者参与确认对自己有意义的学习目 标,自己制定学习进度.选择学习方法.
万方数据
图1
用钠光或激光垂直照射平凸透镜时,平凸透镜 两表面反射光的光程差为对应玻璃厚度的2倍,由 于钠光的相干长度大约为3 cm,而激光的相干长度 竟是15 km,所以不能看到平凸透镜两表面反射的 钠光的干涉条纹,但能看到激光的干涉条纹.
2 问题2:肥皂膜和增透膜的干涉结果为何不同
在增透膜干涉中,当薄膜厚度是入射光在薄膜
增透膜干涉情况与肥皂膜不同,例如摄影机镜 头上的增透膜由氟化镁制成,其折射率为1.38,比 空气的折射率大,比玻璃折射率(n=1.52)小.射向 增透膜前后表面的光都是由光疏介质射向光密介 质,前后表面的反射都存在“半波损失”,并未给两反 射光间增加新的光程差.因此在增透膜厚度为膜中
1
波长÷处,增透膜干涉出现了暗条纹. 叶 1 由以上分析可知,同为厚度是光波波长{的肥
图3
万方数据
如果用扩展光源照射薄膜,扩展光源可看成是
由连续分布的无数的点光源组成,这些点光源是非
相干的,空间某一点的光强是这些点光源各自产生
的干涉光强之和,没有固定的光强度的相长和相消
现象.如果在干涉场中该点放一接收屏,光源上各点
在接收屏上各自生成一组干涉条纹,由于各点光源 位置不同,它们产生的干涉图样彼此错开,使得可见
4 问题4:薄膜干涉图样能用光屏接收吗
如果用点光源照射薄膜,它发出的光经薄膜的
半波损失(仅供借鉴)
e
ek ek+1
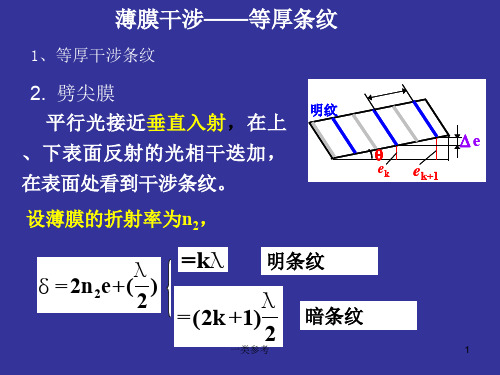
设薄膜的折射率为n2,
λ =kλ 明条纹
δ = 2n2e+( 2 )
λ
=(2k +1)
暗条纹
2
一类参考
1
3.干涉条纹分布的特点:
(1). 当有半波损失时,在劈棱 纹, 否则为一亮纹;
e 处 0为暗
(2). 干涉条纹是平行于棱边的 直条纹
(3). 相邻明(暗)纹间距L:
L 明纹 暗纹Байду номын сангаас
增透膜是使膜上下两表面 的反射光满足减弱条件。
2n2d cosr 2
(2k 1)
2
(k 1,2) 减弱
一类参考
32
例:为增强照相机镜头的透射光,往往在镜头
(n3=1.52)上镀一层 MgF2 薄膜(n2=1.38),使对 人眼和感光底片最敏感的黄绿光 = 555 nm 反射最小,
Lsin ek1 ek 2n2
劈棱
e
ek ek+1
L ≈ (适于平行光垂直入射) 2n2 sin 2n2
只有在 很小的劈尖上,才能看到干涉条纹
一类参考
2
(4) 当某种原因引起膜的等厚线发生变化时,将 引起条纹作相应地移动。
A.膜厚增加
B.膜厚减薄
等厚线
等厚线
corekrk?牛顿环仪19一类参考当用平行单色光垂直照射到牛顿环仪上时一部分光线在空气层的下表面反射一部分光线在空气层的上表面反射这两部分光有光程差它们在平凸透镜的凸面附近相遇而发生干涉
薄膜干涉——等厚条纹
1、等厚干涉条纹
2. 劈尖膜 平行光接近垂直入射,在上
浅谈薄膜干涉现象中的几个问题

光的干涉现象
光的干涉是指两个或多个相干 光波的叠加产生明暗相间的条
纹的现象。
干涉条纹的形成是光波动原理 的表现之一,可以用来研究光 的波动性质和检测微小的位移
。
在薄膜干涉中,光的干涉现象 通常表现为薄膜表面反射光和 透射光形成的明暗相间的干涉
条纹。
薄膜干涉中的光波动
当光照射到薄膜上时,一部分 光会发生反射,一部分光会透 射过去。
实验操作流程
清洁薄膜表面
确保薄膜表面无灰尘、污垢等杂质,以保 证干涉条纹的清晰度。
调整光源
调整光源的位置和角度,以获得最佳的干 涉条纹。
安置光学元件
将光学元件按照实验设计要求安置,确保 光路的正确性。
观察干涉条纹
通过观察干涉条纹的变化,记录并分析实 验数据。
数据处理与分析
条纹间距的测量
通过测量相邻干涉条纹之 间的距离,计算出薄膜的 厚度。
通过调整薄膜的厚度和选择合适的材料可以减小色散的影响。
采用光学仪器如棱镜、光栅等可以实现对不同波长光的分离和重新组合,从而消除色散现 象。
通过计算机模拟和算法也可以实现对干涉条纹的修正和分析,以得到更准确的实验结果。
05
薄膜干涉现象中的稳定性 问题
稳定性问题的定义
薄膜干涉现象中的稳定性问题指的是在实验过程中,干涉条纹的清晰度和重复性是否能够保持恒定。
光吸收与薄膜的材质、厚度以及入射光的波长和偏振状态等 有关。不同材质的薄膜对不同波长的光具有不同的吸收率, 因此会影响薄膜干涉的颜色和强度。
光散射
光散射是指光在传播过程中遇到微观颗粒或分子时,发生 方向改变的现象。在薄膜干涉中,光在经过薄膜时,会受 到薄膜中不均匀分布的微小颗粒或分子的散射,导致光的 传播方向发生变化。
《薄膜干涉》 讲义

《薄膜干涉》讲义一、什么是薄膜干涉当一束光照射到薄膜上时,一部分光会在薄膜的上表面反射,另一部分光会穿过薄膜,在薄膜的下表面反射。
这两束反射光如果满足一定的条件,就会发生干涉现象,这就是薄膜干涉。
薄膜干涉在日常生活中并不罕见,比如我们看到肥皂泡表面的彩色条纹,或者雨天马路上油膜呈现的色彩,都是薄膜干涉的结果。
二、薄膜干涉的原理要理解薄膜干涉,首先得明白光的波动性。
光具有波的特性,就像水波一样,当两列波相遇时,如果它们的频率相同、相位差恒定、振动方向相同,就会发生干涉现象。
在薄膜中,由于上下表面反射的光来自同一光源,所以频率相同。
而它们经过的路程不同,会导致相位差的产生。
具体来说,设薄膜的厚度为 d,入射光的波长为λ,折射率为 n。
对于在薄膜上表面反射的光,其光程为 2nd;对于在薄膜下表面反射的光,由于在穿过薄膜时会有半波损失(即相位突变π),其光程为 2nd +λ/2。
当这两束光的光程差等于波长的整数倍时,就会发生相长干涉,出现亮条纹;当光程差等于半波长的奇数倍时,就会发生相消干涉,出现暗条纹。
三、薄膜干涉的条件并不是所有的薄膜都能产生明显的干涉现象。
为了能清晰地观察到薄膜干涉,需要满足一定的条件。
首先,薄膜的厚度要足够小,通常在微米甚至纳米级别。
这样才能保证两束反射光的光程差在光的波长范围内,从而产生明显的干涉条纹。
其次,薄膜的折射率要适中。
如果折射率过大或过小,都会导致反射光的强度过弱,难以观察到干涉现象。
此外,入射光的单色性要好。
也就是说,光源发出的光波长要尽量单一,这样才能保证干涉条纹的清晰和稳定。
四、薄膜干涉的应用薄膜干涉在科学技术和日常生活中有许多重要的应用。
1、光学仪器中的增透膜和增反膜在光学仪器中,为了减少反射光的损失,提高透光率,可以在镜头表面镀上一层厚度适当的增透膜。
增透膜的原理就是利用薄膜干涉,使反射光发生相消干涉,从而减少反射光的强度,增加透射光的强度。
相反,如果需要增加反射光的强度,比如在激光谐振腔中,可以镀上增反膜,使反射光发生相长干涉,从而提高反射率。
对半波损失问题的两点讨论

若r / >n , , 此 时 因全发 射 , 则 由后文 图 5 ( b ) 知, 反 射光 相 对于 入射 光仍 有半 波损 失. 3 )斜入 射 时 , 虽然 E 和 E 仍 在 一条 直线 上 , 但E 。 和E , 振 动不 在一 条 直线上 , 使 得 总 光矢 量E。
关键词: 半 波损 失 ; 反射 光的相位 变化 ; 薄 膜干 涉
中 图分 类 号 : 0 4— 4 文献标识码 : A 文章 编 号 : 1 0 0 9— 7 9 0 2 ( 2 0 1 5 ) 0 6— 0 0 3 4— 0 3
1 半 波损 失 的产 生 条 件
光 在介 质表 面反射 时 , 相 位突变 了 订, 相 当于光
( b ) n l > 2
图 2 正 入 射 时反 射 光 的振 动 分 量 方 向
间坐标 取 向如 图 1所示.
若t / , 。 >凡 2 , 则 r 口 <0 , > 0, 其 含 义是 E 。 与规
定 取 向相反 , E 与规 定 取 向相 同 , 反 射 光 的 实 际光 矢 量如 图 2 ( b ) 所 示. 此 时 入射 光 的光 矢量 E 和反 射 光 的 光矢 量 E 方 向相同, 说 明 反 射 光相 对 于 入
计 算 2和 3之 间 的相 位 差要 多添 加 , 相 当于 在光
程差 △ 中加上 或减 去半个 波 长.
根据 1 . 3 ) 斜 入射 情 况 的分析 结 果 , 我 们 知道 当
图 3 掠 入 射 时 反 射 光 的振 动 方 向
光斜 入射 在界 面上 时 , 说 反 射 光 相 对 于入 射 光 有 半
向光密 介质 反 射 时会 有 半 波 损 失 ” , 一 些 教 学 指 导 书 中也 采 用 了类 似 的 表 述 , 其 实 这 种 表 述 是 不 严
薄膜干涉半波损失判断

薄膜干涉半波损失判断
薄膜干涉半波损失判断是一种光学现象,它发生在光线穿过薄膜时。
半波损失是由于光线在薄膜内部反射和透射时产生的相位差造成的。
当光的波长和薄膜厚度相等时,反射光和透射光之间的相位差为半波长,从而导致干涉现象。
在这种情况下,薄膜干涉中的半波损失会发生。
半波损失的判断方法如下:
1.光从光疏介质射向光密介质时,若发生正入射(入射角趋近于0),则反射光存在半波损失。
光从光密介质射向光疏介质时,反射光和透射光均无半波损失。
2.可以通过菲涅尔公式来判断半波损失。
菲涅尔公式描述了光在两种介质之间传播时的反射和透射现象。
当光从光疏介质射向光密介质时,若折射率差值较大,相位差接近半波长,则半波损失明显。
3.薄膜干涉中的半波损失与薄膜的厚度有关。
当薄膜厚度为光波长的奇数倍时,反射光和透射光之间的相位差为半波长,从而产生半波损失。
4.可以通过构建薄膜干涉模型来判断半波损失。
例如,可以研究空气中的楔形肥皂膜上的薄膜干涉现象。
当光从空气(光疏介质)射向肥皂膜(光密介质)时,若入射角为0,则反射光存在半波损失。
综上所述,薄膜干涉中的半波损失判断主要取决于光从哪种介质射向另一种介质、入射角的大小、折射率的变化以及薄膜的厚度。
在实际应用中,半波损失的判断有助于分析薄膜干涉现象,优化光学器件的性能。
半波损失与增透膜原理

半波损失与增透膜原理这是2010年10月在仪器信息网上由版主祥子发起的一个讨论,我参与讨论,但总觉得还不够深入。
转载到这里,希望和更多的同行讨论这个问题。
关于半波损失或者相位突变,版主的论述比较详细,转载如下(略有编辑),并提出我的问题(红色字体部分):增透膜中的半波损失一。
基本概念图1所示为增透膜示意图,其中n0、n1、n2分别表示空气、膜层和玻璃的折射率,如空气的折射率n0=1,MgF2的折射率n1=1.38,冕牌玻璃的折射率n2=1.52。
n0相对于n1就是光疏介质,n1相对于n2就是光疏介质。
当入射光线SA从no射入n1时,在no和n1的界面反射,由于n0<n1,在n0和n1界面发生半波损失。
A。
所谓“半波损失",就是当光从折射率小的光疏介质射向折射率大的光密介质时,在入射点,反射光相对于入射光有相位突变π,即在入射点反射光与入射光的相位差为π,由于相位差π与光程差λ /2相对应,它相当于反射光多走了半个波长λ /2的光程,故这种相位突变π的现象叫做半波损失。
问题1:这是经典的理论。
为什么光从光疏介质入射到光密介质时,反射光相对于入射光会产生半个波长的变化这种半波突变的机理是什么B。
半波损失仅存在于当光从光疏介质射向光密介质时的反射光中,折射光没有半波损失。
当光从光密介质射向光疏介质时,反射光也没有半波损失。
以图1为例,光从n1射向n0,在n0和n1界面上,反射光没有半波损失。
半波损失概念为什么很重要,是因为“它相当于反射光多走了半个波长λ /2的光程”,这是因为在光的干涉研究中,两个光线的光程不同,干涉的效果不同。
以图1为例,因为光线1,2,3都在某个界面有半波损失,所以,在考虑光线1,2,3之间的干涉时,它们的光程都要再加上半个波长。
问题2:为何在光密介质到光疏介质的反射过程与光透射过程中没有波长或者相位变化在优酷网上,有个演示半波损失的例子:二。
增透膜中的半波损失1.反射光组中的半波损失对增透膜而言n0<n1<n2(如空气的折射率n0=1,MgF2的折射率n1=1.38,冕牌玻璃的折射率n2=1.52),光线在由空气进入薄膜(光线由光疏到光密介质),和由薄膜进入玻璃时,上下两面反射均出现半波损失,即产生相位π的突变.因此,反射光组1、2、3…中由于反射引起的相位差为零.如果相邻两反射光互相减弱。
两反射光均有半波损失

山东农业大学应用物理系
例 在迈克耳孙干涉仪的两臂中,分别插入l=10.0cm 长的玻璃管, 其中一个抽成真空,另一个储有压强为1.013×105Pa的空气, 用以测定空气的折射率n 。设所用光波波长为546nm,实验时, 向真空玻璃管中逐渐充入空气,直至压强达到1.013×105Pa 。 在此过程中,观察到107.2条干涉条纹的移动 求 空气的折射率n 。 解 设玻璃管充入空气前,两相干光之间的光程差为 Δ1 ,充 入空气后两相干光的光程差为Δ2 ,根据题意,有
山东农业大学应用物理系
(1) 干涉仪结构
M1 M'2
S
G1
G2
L
M2
P
山东农业大学应用物理系
(2) 工作原理 光束 1 和 2 发生干涉,光程差:
d
M2 M1
1G
1
2d (无半波损失)
或
G2
2
2d
2
(有半波损失)
S
加强
L P
2d k
2d (2k 1 )
山东农业大学应用物理系
劈尖干涉的应用:
(1)可测量小角度、小位移、微小直径、波长等
↑
条纹变密; ↑ 条纹变密
n
(2) 检测表面不平整度
等厚条纹 平晶
d
待测工件
山东农业大学应用物理系
2、牛顿环 (1)牛顿环实验装置及光路
T L M
S
A B
山东农业大学应用物理系
(2)干涉条纹
〔
2d 2 (2k 1)
考虑半波损失,实际光程差为: 2k k 1,2, 明纹 2 2 2 2 2e n2 n1 sin i 2k 1) 2 ( k 0, 1,2, 暗纹 2
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
薄膜干涉中的半波损失问题处理方法浅探
作者:徐铁刚
来源:《中学物理·高中》2015年第11期
高中物理课中讲述肥皂膜、牛顿环、增透膜、增反膜等薄膜干涉问题时,经常遇到是否要考虑半波损失的问题.顾及到中学生难以理解,中学教材回避了半波损失问题.不少老师讲到这里时,往往对在什么情况下有半波损失,以及如何做到既不出现知识性错误,又不至于让学生越听越糊涂,感觉难以把握.[JP3]笔者拟从自己的教学实践出发,谈谈在处理这一问题的粗浅做法.
按照波动光学的理论,光从光疏介质射向光密介质时,若正入射(入射角趋近于0°),其反射光有π的相位突变,对应有半波损失;光从光密介质进光疏介质时其反射光无相位突变,对应无半波损失;在任何情况下透射光都无相位突变,对应无半波损失.据此,笔者编了句口诀:“疏进密,反有失;密进疏,均无辜”.意即光从光疏介质正射入光密介质时,只有反射光有半波损失,光从光密介质射向光疏介质时,其反射光、透射光都没有半波损失.根据上述理论和口诀,对常见薄膜干涉建立如下四种模型:如图1所示,有三层介质,其绝对折射率(以下简称[JP3]为折射率)分别n1、n和n2,光趋近于垂直入射,可分别讨论如下.
1 应考虑半波损失的两种情况
(1) n1n2(疏密疏型),空气中的楔形肥皂膜上出现的薄膜干涉就是这种情况.如图2所示,光在界面1(疏进密)反射光a有π的相位突变,在界面2(密进疏)反射光b无相位突变.此时a、b光程差应附加π的相位突变,即有半波损失.
(2) n1>n
在上述两种情况下,反射光a、b中一条有半波损失,另一条无半波损失.考虑到半波损失后,膜上出现亮纹的条件为光程差等于光在介质中半波长的奇数倍,膜厚应为介质中[SX
(]1[]4[SX)]波长的奇数倍,即d=(2k+1)[SX(]λ[]4[SX)],(其中k=0,1,2,…),出现暗纹的条件为光程差等于光在介质中波长的整数倍,膜厚应为[SX(]1[]2[SX)]介质中波长的整数倍,即d=[SX(]kλ[]2[SX)],(其中k=1,2,…).
在实际中人们经常关心的只是条纹的相对变动,只关心相邻两条纹处膜厚的差值,即相邻明条纹上的光程差等于一个波长,因此相邻条纹对应的厚度差为介质中波长的一半,很少需要知道膜的厚度具体值.因此在中学物理教学中可回避讨论膜的厚度,只需指出:出现亮条纹是两条反射光线干涉加强,暗条纹是两条反射光线干涉减弱,两相邻亮(暗)纹处肥皂膜的厚度差为[SX(]1[]2[SX)]介质中波长.
2 不要考虑半波损失的两种情况
(1) n1
(2) n1>n>n2(折射率递减型).如图6所示,在界面1、2反射的光线a、b均属于密进疏型,均无相位突变.此种情况下a、b两反射光无相位突变,无需计算半波损失,结果与前述n1
综上所述,笔者利用口诀“疏进密,反有失;密进疏,均无辜”,能快速的理清薄膜干涉中的半波损失问题,即:光在1、2两介面反射时,折射率“先增后减”和“先减后增”两种情况,两反射光要附加半波损失,折射率“递增”和“递减”两种情况下,两反射光无需附加半波损失.。
