初中数学反比例函数动点问题.pdf
2024年九年级数学中考复习——反比例函数-动态几何问题(含答案)

2024年九年级数学中考复习——反比例函数-动态几何问题1.如图,在矩形ABCD 中,已知点A (2,1),且AB =4,AD =3,把矩形ABCD 的内部及边上,横、纵坐标均为整数的点称为靓点,反比例函数y=(x >0)的图象为曲线L .(1)若曲线L 过AB 的中点.①求k 的值.②求该曲线L 下方(包括边界)的靓点坐标.(2)若分布在曲线L 上方与下方的靓点个数相同,求k 的取值范围.2.如图,在平面直角坐标系中,一次函数 与反比例函数 相交于点 ,与 轴相交于点 ,点 的横坐标为-2.(1)求 的值;(2)直接写出当 且 时, 的取值范围;(3)设点 是直线AB 上的一点,过点 作 轴,交反比例函数 的图象于点 .若以A ,O ,M ,N 为顶点的四边形为平行四边形,求点 的坐标.k x12y x =-+2(0)k y x x=<B x A B k 0x <12y y <x M M //MN x 2(0)k y x x=<N M3.如图,在平面直角坐标系中,OA ⊥OB ,AB ⊥x 轴于点C ,点A (,1)在反比例函数y = 的图象上.(1)求反比例函数y = 的表达式; (2)在x 轴上是否存在一点P ,使得S △AOP =S △AOB ,若存在,求所有符合条件点P 的坐标;若不存在,简述你的理由.4.如图,点 , 在 轴上,以 为边的正方形 在 轴上方,点 的坐标为 ,反比例函数 的图象经过 的中点 , 是 上的一个动点,将 沿 所在直线折叠得到 .(1)求反比例函数 的表达式; (2)若点 落在 轴上,求线段 的长及点 的坐标.k x k x12A B x AB ABCD x C (14),(0)k y k x=≠CD E F AD DEF EF GEF (0)k y k x=≠G y OG F5.如图,已知反比例函数y=(x >0)的图象经过点A (4,2),过A 作AC ⊥y 轴于点C .点B 为反比例函数图象上的一动点,过点B 作BD ⊥x 轴于点D ,连接AD .直线BC 与x 轴的负半轴交于点E .(1)求k 的值;(2)连接CD ,求△ACD 的面积;(3)若BD =3OC ,求四边形ACED 的面积.6.已知:如图1,点是反比例函数图象上的一点.(1)求的值和直线的解析式;(2)如图2,将反比例函数的图象绕原点逆时针旋转后,与轴交于点,求线段的长度;(3)如图3,将直线绕原点逆时针旋转,与反比例函数的图象交于点,求点的坐标.k x(4)A n ,8(0)y x x=>n OA 8(0)y x x =>O 45︒y M OM OA O 45︒8(0)y x x=>B B7.已知:反比例函数的图像过点A ( , ),B ( , )且 (1)求m 的值;(2)点C 在x 轴上,且 ,求C 点的坐标;(3)点Q 是第一象限内反比例函数图象上的动点,且在直线AB 的右侧,设直线QA ,QB 与y 轴分别交于点E 、D ,试判断DE 的长度是否变化,若变化请说明理由,若不变,请求出长度.8.规定:在平面直角坐标系中,横坐标与纵坐标均为整数的点,叫做整点,点,在反比例函数的图象上;(1)m= ;(2)已知,过点、D 点作直线交双曲线于E 点,连接OB ,若阴影区域(不包括边界)内有4个整点,求b 的取值范围.m y x =1x 121m --2x 45m-120x x +=16ABC s ∆=()22A ,()1B m ,()0k y x x=>0b >()40C b -,()0b ,()0k y x x=>9.已知,矩形OCBA 在平面直角坐标系中的位置如图所示,点C 在x 轴的正半轴上,点A 在y 轴的正半轴上,已知点B 坐标为(3,6),反比例函数的图象经过AB 的中点D ,且与BC 交于点E ,顺次连接O ,D ,E .(1)求m 的值及点E 的坐标;(2)点M 为y 轴正半轴上一点,若△MBO 的面积等于△ODE 的面积,求点M 的坐标;(3)平面直角坐标系中是否存在一点N ,使得O ,D ,E ,N 四点顺次连接构成平行四边形?若存在,请直接写出N 的坐标;若不存在,请说明理由.10.如图,点P 为函数与函数图象的交点,点P 的纵坐标为4,轴,垂足为点B .(1)求m 的值;(2)点M 是函数图象上一动点,过点M 作于点D ,若,求点M的坐标.m y x=1y x =+()0m y x x=>PB x ⊥()0m y x x =>MD BP ⊥12tan PMD ∠=11.如图,在平面直角坐标系中,直线与轴、轴分别交于点、,与双曲线交于点,直线分别与直线和双曲线交于点、.(1)求和的值;(2)当点在线段上时,如果,求的值;(3)点是轴上一点,如果四边形是菱形,求点的坐标.12.如图,等边和等边的一边都在x 轴上,双曲线经过的中点C 和的中点D .已知等边的边长为4.(1)求k 的值;(2)求等边的边长;(3)将等边绕点A 任意旋转,得到等边,P 是的中点(如图2所示),连结,直接写出的最大值.xOy 34l y x b =+:x y A B x k H y =:922P ⎛⎫ ⎪⎝⎭,x m =H E D k b E AB ED BO =m C y BCDE C OAB AEF ()0k y k x=>OB AE OAB AEF AEF AE F '' E F ''BP BP13.如图,点A 、B 是反比例函数y = 的图象上的两个动点,过A 、B 分别作AC ⊥x 轴、BD ⊥x 轴,分别交反比例函数y =- 的图象于点C 、D ,四边形ACBD 是平行四边形. (1)若点A 的横坐标为-4.①直接写出线段AC 的长度;②求出点B 的坐标;(2)当点A 、B 不断运动时,下列关于□ACBD 的结论:①□ACBD 可能是矩形;②□ACBD 可能是菱形;③□ACBD 可能是正方形;④□ACBD 的周长始终不变;⑤□ACBD 的面积始终不变.其中所有正确结论的序号是 .8x2x14.在平面直角坐标系 中,正比例函数 与反比例函数 的图象相交于点 与点Q . (1)求点Q 的坐标;(2)若存在点 ,使得 ,求c 的值; (3)过点 平行于x 轴的直线,分别与第一象限内的正比例函数 、反比例函数数 的图象相交于点 、点 ,当 时,请直接写出a 的取值范围.15.在平面直角坐标系中,直线y=x+2与x 轴交于点A ,与y 轴交于点B ,并与反比例函数y=(k≠0)的图象在第一象限相交于点C ,且点B 是AC 的中点xOy ()1110y k x k =≠()2220k y k x=≠(11)P ,(0)C c ,2PQC S = (0)M a ,()1110y k x k =≠()2220k y k x =≠()11A x y ,()22B x y ,1252x x +≤kx(1)如图1,求反比例函数y=(k≠0)的解析式;(2)如图2,若矩形FEHG 的顶点E 在直线AB 上,顶点F 在点C 右侧的反比例函数y=(k≠0)图象上,顶点H ,G 在x 轴上,且EF=4.①求点F 的坐标;②若点M 是反比例函数的图象第一象限上的动点,且在点F 的左侧,连结MG ,并在MG 左侧作正方形GMNP .当顶点N 或顶点P 恰好落在直线AB 上,直接写出对应的点M 的横坐标.16.如图,动点P 在函数y (x >0)的图象上,过点P 分别作x 轴和y 轴的平行线,交函数y 的图象于点A 、B ,连接AB 、OA 、OB .设点P 横坐标为a .(1)直接写出点P 、A 、B 的坐标(用a 的代数式表示);(2)点P 在运动的过程中,△AOB 的面积是否为定值?若是,求出此定值;若不是,请说明理由;(3)在平面内有一点Q (,1),且点Q 始终在△PAB 的内部(不包含边),求a 的取值范围.k xk x 3x =1x =-1317.如图1,一次函数y =kx ﹣3(k≠0)的图象与y 轴交于点B ,与反比例函数y=(x >0)的图象交于点A (8,1).(1)求出一次函数与反比例函数的解析式;(2)点C 是线段AB 上一点(不与A ,B 重合),过点C 作y 轴的平行线与该反比例函数的图象交于点D ,连接OC ,OD ,AD ,当CD 等于6时,求点C 的坐标和△ACD 的面积;(3)在(2)的前提下,将△OCD 沿射线BA 方向平移一定的距离后,得到△O'CD',若点O 的对应点O'恰好落在该反比例函数图象上(如图2),求出点O',D'的坐标.18.如图1所示,已知 图象上一点 轴于点 ,点 ,动点 是 轴正半轴点 上方的点,动点 在射线AP 上,过点 作AB 的垂线,交射线AP 于点 ,交直线MN 于点 ,连结AQ ,取AQ 的中点 . m x6(0)y x x=>P PA x ⊥,(0)A a ,(0)(0)B b b >,M y B N B D Q C(1)如图2,连结BP ,求 的面积;(2)当点 在线段BD 上时,若四边形BQNC 是菱形,面积为 .①求此时点Q ,P 的坐标;②此时在y 轴上找到一点E ,求使|EQ-EP|最大时的点E 的坐标.19.已知反比例函数y=的图象经过点A (6,1).(1)求该反比例函数的表达式;(2)如图,在反比例函数y=在第一象限的图象上点A 的左侧取点C ,过点A 作x 轴的垂线交x 轴于点H ,过点C 作y 轴的垂线CE ,垂足为点E ,交直线AH 于点D .①过点A 、点C 分别作y 轴、x 轴的垂线,两条垂线相交于点B ,求证:O 、B 、D 三点共线;②若AC=2CO ,求证:∠OCE=3∠CDO .PAB Q k xk x20.如图,一次函数与反比例函数的图象交于点和,与y 轴交于点C .(1) , ;(2)过点A 作轴于点D ,点P 是反比例函数在第一象限的图象上一点,设直线与线段交于点E ,当时,求点P 的坐标.(3)点M 是坐标轴上的一个动点,点N 是平面内的任意一点,当四边形是矩形时,求出点M 的坐标.21.如图1,将函数的图象T 1向左平移4个单位得到函数的图象T 2,T 2与y 轴交于点.(1)若,求k 的值(2)如图2,B 为x 轴正半轴上一点,以AB 为边,向上作正方形ABCD ,若D 、C 恰好落在T 1上,线段BC 与T 2相交于点E①求正方形ABCD 的面积;②直接写出点E 的坐标.114y k x =+22k y x=()2A m ,()62B --,1k =2k =AD x ⊥OP AD Δ41ODE ODAC S S =四边形::ABMN ()0k y x x =>()44k y x x =>-+()0A a ,3a =22.如图1,直线的图像与x 轴、y 轴分别交于A 、B 两点,点D 是线段AB 上一点,过D 点分别作OA 、OB 的垂线,垂足分别是C 、E ,矩形OCDE 的面积为4,且.(1)求D 点坐标;(2)将矩形OCDE 以1个单位/秒的速度向右平移,平移后记为矩形MNPQ ,记平移时间为t 秒.①如图2,当矩形MNPQ 的面积被直线AB 平分时,求t 的值;②如图3,当矩形MNPQ 的边与反比例函数的图像有两个交点,记为T 、K ,若直线TK 把矩形面积分成1:7两部分,请直接写出t 的值.23.如图1,在平面直角坐标系中,点,点,直线与反比例函数的图象在第一象限相交于点,26y x =-+CD DE >12y x=()40A -,()04B ,AB ()0k y k x=≠()6C a ,(1)求反比例函数的解析式;(2)如图2,点是反比例函数图象上一点,连接,试问在x 轴上是否存在一点D ,使的面积与的面积相等,若存在,请求点D 的坐标;若不存在,请说明理由;(3)新定义:如图3,在平面内,如果三角形的一边等于另一边的3倍,这两条边中较长的边称为“麒麟边”,两条边所夹的角称为“麒麟角”,则称该三角形为“麒麟三角形”,如图所示,在平面直角坐标系中,为“麒麟三角形”, 为“麒麟边”, 为“麒麟角”,其中A ,B 两点在反比例函数 图象上,且A 点横坐标为,点C 坐标为,当为直角三角形时,求n 的值.24.如图1,已知点A (a ,0),B (0,b ),且a 、b 满足 +(a +b +3)2=0,平等四边形ABCD的边AD 与y 轴交于点E ,且E 为AD 中点,双曲线y =经过C 、D 两点. (1)a = ,b = ;(2)求D 点的坐标;(3)点P 在双曲线y = 上,点Q 在y 轴上,若以点A 、B 、P 、Q 为顶点的四边形是平行四边形,试求满足要求的所有点Q 的坐标;(4)以线段AB 为对角线作正方形AFBH (如图3),点T 是边AF 上一动点,M 是HT 的中点,MN ⊥HT ,交AB 于N ,当T 在AF 上运动时, 的值是否发生改变?若改变,求出其变化范围;若()6E m ,()0k y k x=≠CE AE ,ACD ACE ABC AB BAC ∠n y x=1-()02,ABC k x k xMN HT不改变,请求出其值,并给出你的证明.25.在平面直角坐标系中,已知点,点.(1)若将沿轴向右平移个单位,此时点恰好落在反比例函数的图象上,求的值;(2)若绕点按逆时针方向旋转度.①当时,点恰好落在反比例函数图象上,求的值;②问点能否同时落在(1)中的反比例函数的图象上?若能,直接写出的值;若不能,请说明理由.26.如图,已知直线与双曲线交第一象限于点.(1)求点的坐标和反比例函数的解析式;(2)将点绕点逆时针旋转至点,求直线的函数解析式;(3)在(2)的条件下,若点C 是射线上的一个动点,过点作轴的平行线,交双曲线xOy ()A -()60B -,OAB x m A y =m OAB O α()0α180<<α30= B k y x=k A B ,α2y x =(0)k y k x=≠(4)A m ,A O A 90︒B OB OB C y的图像于点,交轴于点,且,求点的坐标.27.如图,一次函数的图象与反比例函数的图象交于点,与y 轴交于点B .(1)求a ,k 的值;(2)直线CD 过点A ,与反比例函数图象交于点C ,与x 轴交于点D ,AC =AD ,连接CB .①求△ABC 的面积;②点P 在反比例函数的图象上,点Q 在x 轴上,若以点A ,B ,P ,Q 为顶点的四边形是平行四边形,请求出所有符合条件的点P 坐标.28.如图1,反比例函数与一次函数的图象交于两点,已知.(1)求反比例函数和一次函数的表达式;(2)一次函数的图象与轴交于点,点(未在图中画出)是反比例函数图象上的一个动点,若,求点的坐标:(0)k y k x=≠D x E 23DCO DEO S S = ::C 112y x =+()0k y x x =>()3A a ,k y x=y x b =+A B ,()23B ,y x b =+x C D 3OCD S = D(3)若点是坐标轴上一点,点是平面内一点,是否存在点,使得四边形是矩形?若存在,请求出所有符合条件的点的坐标;若不存在,请说明理由.29.如图,已知直线y=-2x 与双曲线y=(k<0)上交于A 、B 两点,且点A 的纵坐标为-2 (1)求k 的值;(2)若双曲线y= (k<0)上一点C 的纵坐标为 ,求△BOC 的面积;(3)若A 、B 、P 、Q 为顶点组成的四边形为正方形,直接写出过点P 的反比例函数解析式。
专题. 反比例函数(动点问题)(基础篇)(专项练习)八年级数学下册基础知识专项讲练(苏科版)

专题11.29反比例函数(动点问题)(基础篇)(专项练习)一、单选题1.如图,点A 是反比例函数4y x=-图象上的一个动点,过点A 作AB ⊥x 轴,AC ⊥y轴,垂足分别为B ,C ,则矩形ABOC 的面积为()A .-4B .2C .4D .82.如图,在平面直角坐标系中,矩形ABCD 的边BC 在x 轴上,点D 的坐标为(-2,6),点B 是动点,反比例函数(0)ky x x=<经过点D ,若AC 的延长线交y 轴于点E ,连接BE ,则△BCE 的面积为()A .6B .5C .3D .73.如图,点A 是双曲线y =6x是在第一象限上的一动点,连接AO 并延长交另一分支于点B ,以AB 为斜边作等腰Rt △ABC ,点C 在第二象限,随着点A 的运动,点C 的位置也不断的变化,但始终在一函数图象上运动,则这个函数的解析式为()A .13y x=-B .3y x =-C .16y x=-D .6y x=-4.一次函数(0)y kx b k =+≠的图像经过点(1,4)A --,(2,2)B 两点,P 为反比例函数kby x=图像上的一个动点,O 为坐标原点,过P 作y 轴的垂线,垂足为C ,则PCO △的面积为()A .2B .4C .8D .不确定5.如图,在平面直角坐标系中,点A 是x 轴正半轴上的一个定点,点P 是函数()0,0ky k x x=>>的图象上的一个动点,PB y ⊥轴于点B .当点P 的纵坐标逐渐增大时,四边形OAPB 的面积的变化为()A .不变B .逐渐增大C .逐渐减小D .先增大后减小6.如图,已知A (1,a ),B (b ,1)为反比例函数y =2x图象上y 的两点,动点P 在x 轴正半轴上运动,当线段AP 与线段BP 之和最小时,则点P 的坐标是()A .(35,0)B .(1,0)C .(53,0)D .(2,0)7.反比例函数4y x =和6y x =在第一象限的图象如图所示,点A 在函数6y x=图象上,点B 在函数4y x=图象上,AB ∥y 轴,点C 是y 轴上的一个动点,则△ABC 的面积为()A .1B .2C .3D .48.如图,在平面直角坐标系xoy 中,矩形OABC 的边OA 、OC 分别在x 轴和y 轴上,8OA =,6OC =,点D 是BC 边上一动点,过点D 的反比例函数(0)k y x x=>与边AB 交于点E .若将DBE ∆沿DE 折叠,点B 的对应点F 恰好落在对角线AC 上.则反比例函数的解析式是()A .6y x=B .12y x=C .24y x=D .36y x=9.如图,在平面直角坐标系中,点A 是函数()0k y x x=>在第一象限内图象上一动点,过点A 分别作AB x ⊥轴于点B AC y ⊥、轴于点C ,AB AC 、分别交函数()10y x x=>的图象于点E F 、,连接OE OF 、.当点A 的纵坐标逐渐增大时,四边形OFAE 的面积()A .不变B .逐渐变大C .逐渐变小D .先变大后变小10.如图,已知点A 是双曲线y =2x在第一象限的分支上的一个动点,连接AO 并延长交另一分支于点B ,过点A 作y 轴的垂线,过点B 作x 轴的垂线,两垂线交于点C ,随着点A 的运动,点C 的位置也随之变化.设点C 的坐标为(m ,n),则m ,n 满足的关系式为()A .n =-2mB .n =-2mC .n =-4mD .n =-4m二、填空题11.如图,已知点A 是双曲线2y x=在第一象限的分支上的一个动点,连接AO 并延长交另一分支于点B ,过点A 作y 轴的垂线,过点B 作x 轴的垂线,两垂线交于点C ,随着点A 的运动,点C 的位置也随之变化,设点C 的坐标为(),m n ,则m ,n 满足的关系式为______.12.如图,已知点A 是反比例函数()40y x x=>图象上的动点,AB x ∥轴,AC y ∥轴,分别交反比例函数1y x=(0x >)的图象于点B 、C ,交坐标轴于点E 、D ,连接BC .则ABC 的面积是______.13.如图,A 、B 是函数6y x=上两点,P 为一动点,作PB y ∥轴,PA x ∥轴,若2BOP S =△,则ABP S =△______.14.如图,在平面直角坐标系中,已知第一象限上的点A (m ,n )是双曲线ky x=上的动点,过点A 作AM ∥y 轴交x 轴于点M ,过点N (0,2n )作NB ∥x 轴交双曲线于点B ,交直线AM 于点C ,若四边形OACB 的面积为4,则k 的值为________.15.如图,在平面直角坐标系xOy 中,点A 为反比例函数y =-4x(x >0)的图象上一动点,AB ⊥y 轴,垂足为B ,以AB 为边作正方形ABCD ,其中CD 在AB 上方,连接OA ,则OA 2-OC 2=_______.16.反比例函数2y x=和3y x =在第一象限的图象如图所示,点A 在函数3y x =的图象上,点B 在函数2y x=的图象上,点C 是y 轴上一个动点,若AB y ∥轴,则ABC 的面积是______.17.如图,点A 是反比例函数2y x =-在第二象限内图像上一点,点B 是反比例函数4y x=在第一象限内图像上一点,且AB x ∥轴,C 为x 轴上动点,连接CA 、CB ,则CAB △的面积是___________.18.如图,平行于x 轴的直线分别交反比例函数2(0)y x x =>和4(0)y x x=-<的图像于点A 和点B ,点C 是x 轴上的动点,则ABC 的面积为__________.19.如图,已知点A 是反比例函数y =6xOA ,3为长,OA 为宽作矩形AOCB ,且点C 在第四象限,随着点A 的运动,点C 也随之运动,但点C 始终在反比例函数y =kx的图象上,则k 的值为________.20.如图,□OABC 的顶点A 的坐标为()2,0,,B C 在第一象限反比例函数1k y x=和22ky x =的图象分别经过,C B 两点,延长BC 交y 轴于点D .设P 是反比例函数1k y x=图象上的动点,若POA ∆的面积是PCD ∆面积的2倍,POD ∆的面积等于28k -,则k 的值为________.三、解答题21.在矩形AOBC 中,4OB =,3OA =分别以OB 、OA 在直线为x 轴和y 轴,建立如图所示的平面直角坐标系.F 是边BC 上的一个动点(不与B 、C 合),过点F 的反比例函数(0)ky k x=>的图像与AC 边交于点E .(1)求证:AOE △与BOF 的面积相等;(2)记OEF ECF S S S =- ,求当k 为何值时,S 有最大值,最大值是多少?22.如图,点(,2)A a 在反比例函数4y x=的图象上,AB x 轴,且交y 轴于点C ,交反比例函数ky x=的图象于点B ,已知2AC BC =.(1)求反比例函数ky x=的解析式;(2)点D 为反比例函数ky x=图象上一动点,连接AD 交y 轴于点E ,当E 为AD 中点时,求OAD △的面积.23.如图,在平面直角坐标系中,直线y =k 1x +b 与反比例函数y =2k x的图象交于A 、B 两点,已知A (1,2),B (m ,1).(1)求m 的值及直线AB 的解析式;(2)若点P 是直线AB 上的一动点,将直线AB 向下平移n 个单位长度(0<n <3),平移后直线与x 轴、y 轴分别交于点D 、E ,当△PED 的面积为1时,求n 的值.24.直线y kx b =+与反比例函数8(0)y x x=>的图象分别交于点A (m ,4)和点B (8,n ),与坐标轴分别交于点C 和点D .(1)求直线AB 的解析式;(2)观察图象,当0x >时,直接写出8kx b x+>的解集;(3)若点P 是x 轴上一动点,当△ADP 的面积是6时,求出P 点的坐标.25.已知,如图,正比例函数y =ax 的图象与反比例函数图象交于A 点(3,2),(1)试确定上述正比例函数和反比例函数的表达式.(2)根据图象回答:在第一象限内,当反比例函数值大于正比例函数值时x 的取值范围?(3)M (m ,n )是反比例函数上一动点,其中0大于m 小于3,过点M 作直线MN 平行x 轴,交y 轴于点B .过点A 作直线AC 平行y 轴,交x 轴于点C ,交直线MB 于点D .当四边形OADM 的面积为6时,请判断线段BM 与DM 的大小关系,并说明理由.26.已知:在矩形AOBC 中,4,3OB OA ==.分别以,OB OA 所在直线为x 轴和y 轴,建立如图所示的平面直角坐标系,F 是边BC 上的一个动点(不与B ,C 重合),过F 点的反比例函数(0)ky k x=>的图象与AC 边交于点E .(1)记OEF ECF S S S =- ,当S 取得最大值时,求k 的值;(2)在(1)的条件下,若直线EF 与x 轴、y 轴分别交于点,M N ,求EM FN ⋅的值.参考答案1.C【分析】根据反比函数的几何意义,可得矩形ABOC 的面积等于比例系数的绝对值,即可求解.解:∵点A 是反比例函数4y x=-图象上的一个动点,过点A 作AB ⊥x 轴,AC ⊥y 轴,∴矩形ABOC 的面积44-=.故选:C .【点拨】本题主要考查了反比函数的几何意义,熟练掌握本题主要考查了反比例函数()0ky k x=≠中k 的几何意义,即过双曲线上任意一点引x 轴、y 轴垂线,所得矩形面积等于k 是解题的关键.2.A【分析】依据点D 的坐标为(-2,6),CD ⊥CO ,即可得出CO=2,CD=6=AB ,进而得到CO×AB=12,再根据BC AB OC EO=,可得BC•EO=AB•CO=12,进而得到△BCE 的面积1BC OE 62=⨯⨯=.解:∵点D 的坐标为(-2,6),CD ⊥CO ,∴CO=2,CD=6=AB ,∴CO×AB=12,∵AB ∥OE ,∴BC AB OC EO=,即BC•EO=AB•CO=12,∴△BCE 的面积1BC OE 62=⨯⨯=【点拨】本题主要考查了反比例函数系数k 的几何意义,矩形的性质以及平行线分线段成比例定理的综合应用.解题的关键是将△BCE 的面积与点D 的坐标联系在一起,体现了数形结合的思想方法.3.D【分析】连接OC ,作CD ⊥x 轴于D ,AE ⊥x 轴于E ,利用反比例函数的性质和等腰直角三角形的性质,根据“AAS”可判定△COD ≌△OAE ,设A 点坐标为(a ,6a ),得出OD =AE =6a,CD =OE =a ,最后根据反比例函数图象上点C 的坐标特征确定函数解析式.解:如图,连接OC ,作CD ⊥x 轴于D ,AE ⊥x 轴于E ,∵A 点、B 点是正比例函数图象与双曲线y =6x的交点,∴点A 与点B 关于原点对称,∴OA =OB ,∵△ABC 为等腰直角三角形,∴OC =OA ,OC ⊥OA ,∴∠DOC +∠AOE =90°,∵∠DOC +∠DCO =90°,∴∠DCO =∠AOE ,∴△COD ≌△OAE (AAS ),设A 点坐标为(a ,6a ),得出OD =AE =6a ,CD =OE =a ,∴C 点坐标为(-6a ,a ),∵-6a•a =-6,∴点C 在反比例函数y =-6x 图象上.故选:D .【点拨】本题主要考查了用待定系数法求反比例函数的解析式,解题时需要综合运用反比例函数图象上点的坐标特征、等腰直角三角形的性质.判定三角形全等是解决问题的关键环节.4.A【分析】由一次函数图像上的两个点(1,4)A --,(2,2)B ,可确定一次函数中的参数k 、b 的值,从而确定反比例函数的关系式,再根据反比例函数k 的几何意义直接求解.解:把点(1,4)A --,(2,2)B 代入(0)y kx b k =+≠得:422k b k b -=-+⎧⎨=+⎩,解得:22k b =⎧⎨=-⎩,所以反比例函数表达式为4y x-=,根据题意可得:1|4|22PCO S =⨯-= .故选:A .【点拨】本题考查了反比例函数k 的几何意义、一次函数关系式的确定,熟练掌握反比例函数k 的几何意义是解题的关键.5.B【分析】连接OP ,根据反比例函数的比例系数的几何意义,可得2BOP k S =V ,再由四边形OAPB 的面积等于p 12BOP AOP k S S y OA x +=+´V V ,即可求解.解:如图,连接OP ,∵PB ⊥y 轴,∴2BOP k S =V ,∵四边形OAPB 的面积等于p 12BOP AOP k S S y OA x +=+´V V ,∵点A 是x 轴正半轴上的一个定点,点P 的纵坐标逐渐增大∴四边形OAPB 的面积随点P 的纵坐标的增大而增大.故选:B【点拨】本题主要考查了反比例函数的比例系数的几何意义,利用数形结合思想解答是解题的关键.6.C【分析】先求出A ,B 的坐标,然后作B 点关于x 轴的对称点B ′,连接AB ′交x 轴即为P ,此时PA +PB 最小,最小值为AB ′的长,然后求出直线AB ′的解析式,求出其与x 轴的交点坐标即可.解:把A (1,a ),B (b ,1)代y =2x得a =2,b =2,则A 点坐标为(1,2),B 点坐标为(2,1),作B 点关于x 轴的对称点B ′,连接AB ′交x 轴即为P ,此时PA +PB 最小,最小值为AB ′的长,∵B点坐标为(2,1),∴B′点坐标为(2,﹣1),设直线AB′的解析式为y=kx+b,∴2 21 k bk b+=⎧⎨+=-⎩解得35 kb=-⎧⎨=⎩∴直线AB′的解析式为y=﹣3x+5,令y=0,则﹣3x+5=0,∴x=5 3,∴P的坐标为(53,0),故选C.【点拨】本题主要考查了反比例函数与一次函数的综合,解题的关键在于能够熟练掌握相关知识进行求解.7.A【分析】连接OA、OB,延长AB,交x轴于D,如图,利用三角形面积公式得到S△OAB=S△ABC,再根据反比例函数的比例系数k的几何意义得到S△OAD=3,S△OBD=2,即可求得S△OAB=S△OAD-S△OBD=1.解:连结OA、OB,延长AB,交x轴于D,如图,∵AB ∥y 轴,∴AD ⊥x 轴,OC ∥AB ,∴S △OAB =S △ABC ,而S △OAD =12×6=3,S △OBD =12×4=2,∴S △OAB =S △OAD ﹣S △OBD =1,∴S △ABC =1,故选:A .【点拨】本题考查了反比例函数的比例系数k 的几何意义:在反比例函数k y x=图象中任取一点,过这一个点向x 轴和y 轴分别作垂线,与坐标轴围成的矩形的面积是定值|k|.8.C 【分析】设,4,6,46K K D E ⎛⎫⎛⎫ ⎪ ⎪⎝⎭⎝⎭,求得DC=4K ,AE=6K ,得到DB=6-4K ,BE=4-6K ,根据三角函数的定义得到tan ∠BAC=tan ∠BED ,根据平行线的判定定理得到DE ∥AC,连接BF ,根据折叠的性质得到BH=FH ,根据平行线分线段成比例得到AE=BE=2,于是得到结论.解:∵四边形OABC 是矩形,OA=6,OC=4,∴BC=OA=6,AB=OC=4,∴()6,4B ,设,4,6,46K K D E ⎛⎫⎛⎫ ⎪ ⎪⎝⎭⎝⎭,∴DC=4K ,AE=6K ,∴DB=6-4K ,BE=4-6K ,∴tan ∠BED=BD BE =634246K K -=-,∵tan ∠BAC=6342BC AB ==,∴tan ∠BAC=tan ∠BED ,∴∠BED=∠BAC,∴DE ∥AC,连接BF,∵将△DBE 沿DE 折叠,点B 的对应点F 正好落在对角线AC 上,∴BH=FH ,∴AE=BE=2,∴26k=,∴k=12.∴反比例函数的解析式12y x=.故选C.【点拨】本题主要考查反比例函数的图像性质,结合了矩形的性质和翻转折叠的知识点.9.A【分析】根据反比例函数系数k 的几何意义得出矩形ACOB 的面积为k ,BOE S COF S = 12=,则四边形OFAE 的面积为定值1k -.解:∵点A 是函数(0k y x x=>)在第一象限内图象上,过点A 分别作AB ⊥x 轴于点B ,AC ⊥y 轴于点C ,∴矩形ACOB 的面积为k ,∵点E 、F 在函数1y x =的图象上,∴BOE S COF S = 12=,∴四边形OFAE 的面积11122k k =--=-,故四边形OFAE 的面积为定值1k -,保持不变,故选:A .【点拨】本题考查了反比例函数中系数k 的几何意义,根据反比例函数系数k 的几何意义可求出四边形和三角形的面积是解题的关键.10.B解:首先根据点C 的坐标为(m ,n ),分别求出点A 为(2n ,n ),点B 的坐标为(-2n ,-n ),根据图像知B 、C 的横坐标相同,可得-2n=m.故选B .【点拨】此题主要考查了反比例函数的图像上的点的坐标特点,解答此题的关键是要明确:①图像上的点(x ,y)的横纵坐标的积是定值k ,即xy=k ;②双曲线是关于原点对称的,两个分支上的点也是关于原点对称;③在坐标系的图像上任取一点,过这个点向x 轴、y 轴分别作垂线.与坐标轴围成的矩形的面积是一个定值|k|.11.2mn =-【分析】首先根据点C 的坐标为(,)m n ,分别求出点A 的坐标、点B 的坐标;然后根据点B 和点C 的横坐标相同,求出m ,n 满足的关系式即可.解:由反比例函数的性质可知,A 点和B 点关于原点对称,点C 的坐标为(,)m n ,∴点A 的坐标为2(n ,)n ,∴点B 的坐标为2(n -,)n -,根据图象可知,B 点和C 点的横坐标相同,2m n ∴-=,即2n m=-.故答案为:2mn =-.【点拨】此题主要考查了反比例函数的图象上点的坐标的特征,要熟练掌握,解答此题的关键是要明确:①图象上的点(,)x y 的横纵坐标的积是定值k ,即xy k =;②双曲线是关于原点对称的,两个分支上的点也是关于原点对称;③在xk 图象中任取一点,过这一个点向x 轴和y 轴分别作垂线,与坐标轴围成的矩形的面积是定值||k .12.98##1.125【分析】设点A 的坐标为4,a a ⎛⎫ ⎪⎝⎭,可得点B 的坐标为4,4a a ⎛⎫ ⎪⎝⎭,点C 的坐标为1,a a ⎛⎫ ⎪⎝⎭,AB AC ⊥,从而得到33,4AB a AC a==,即可求解.解:设点A 的坐标为4,a a ⎛⎫ ⎪⎝⎭,∵AB x ∥轴,AC y ∥轴,分别交反比例函数1y x=(0x >)的图象于点B 、C ,∴点B 的坐标为4,4a a ⎛⎫ ⎪⎝⎭,点C 的坐标为1,a a ⎛⎫ ⎪⎝⎭,AB AC ⊥,∴33,4AB a AC a==,∴ABC 的面积是113392248AB AC a a ⨯⨯=⨯⨯=.故答案为:98【点拨】本题主要考查了反比例函数图象上点的坐标特征,三角形的面积,熟练掌握反比例函数图象上点的坐标特征是解题的关键.13.4【分析】设6,A m m ⎛⎫ ⎪⎝⎭、6,B n n ⎛⎫ ⎪⎝⎭,根据2BOP S =△找到m 、n 之间的关系,最后表述出ABP S △,整体代入求值即可.解:设6,A m m ⎛⎫ ⎪⎝⎭、6,B n n ⎛⎫ ⎪⎝⎭,∴6,P n m ⎛⎫ ⎪⎝⎭∴66PB n m=-,PA m n =-,∴1662()2BOP S n n m==⋅-△,整理得3m n =,∴1166166(()()(3)42223ABP PA PB m n n nS n n m n =⋅=-⋅-=-⋅-=△,故答案为:4.【点拨】本题考查的是反比例函数的性质、三角形面积公式,掌握反比例函数图象上点的坐标特征是解本题的关键.14.4【分析】根据反比例函数系数k 的几何意义得到S △AOM =S △BON 12=k ,列方程即可得到结论.解:∵NB ∥x 轴,AM ∥y 轴,∴四边形OMCN是矩形,∵点A、点B在双曲线上,∴S△AOM=S△BON12=k,∵四边形OACB的面积为4,∴12k12+k+4=m•2n,∵点A(m,n),∴mn=k,∴k=4,故答案为:4.【点拨】本题考查了反比例函数系数k的几何意义,矩形和三角形的面积的矩形,正确的识别图形是解题的关键.15.8【分析】利用反比例函数系数k的几何意义、正方形的性质以及勾股定理即可求得OA2-OC2=8.解:正方形ABCD中,BC=AB,∴OC=BC-OB=AB-OB,∵点A为反比例函数y=-4x(x>0)的图象上一动点,AB⊥y轴,垂足为B,∴AB•OB=4,OA2=AB2+OB2,∴OA2-OC2=AB2+OB2-(AB-OB)2=2AB•OB=2×4=8,故答案为:8.【点拨】本题考查了正方形的性质,勾股定理的应用以及反比例函数系数k的几何意义,得出OC=BC-OB=AB-OB,AB•OB=4,OA2=AB2+OB2是解题的关键.16.12##0.5【分析】设A(m,3m),B(m,2m),则AB=3m-2m,△ABC的高为m,根据三角形面积公式计算即可得答案.解:∵A、B分别为3yx=、2yx=图象上的点,AB//y轴,∴设A(m,3m),B(m,2m),∴S△ABC=12(3m-2m)m=12,故答案为:12【点拨】本题考查反比例函数图象上点的坐标特征,熟知反比例函数图象上点的坐标都满足反比例函数的解析式是解题关键.17.3【分析】连接OA ,OB ,设AB 与y 轴交于点D ,由AB x ∥轴,可得OAB ABC S S =△△,又由反比例函数系数k 的几何意义可知,212OAD S ==△,422OBD S ==△,进而可得OAB 的面积,由此可得出结论.解:如图,连接OA ,OB ,设AB 与y 轴交于点D ,∵AB x ∥轴,∴OAB ABC S S =△△,∵点A 是反比例函数2y x =-在第二象限内图像上一点,点B 是反比例函数4y x =在第一象限内图像上一点,∴212OAD S ==△,422OBD S ==△,∴3OAB OAD OBD S S S =+=△△△,∴3ABC OAB S S ==△△.故答案为:3.【点拨】本题考查了反比例函数的比例系数k 的几何意义:在反比例函数k y x=图像中任取一点,过这一个点向x 轴和y 轴分别作垂线,与坐标轴围成的矩形的面积是定值k .18.3【分析】根据反比例函数图象上点的坐标特征设点A (a ,2a ),代入4y x=-中求出点B 坐标,再利用三角形面积公式计算.解:设点A 的坐标为(a ,2a ),将y =2a 代入4y x=-中,得:2x a =-,∴点B 的坐标为(2a -,2a ),∴△ABC 的面积为()1222a a a ⨯⨯--⎡⎤⎣⎦=3,故答案为:3.【点拨】此题主要考查了反比例函数系数k 的几何意义,以及图象上点的特点,求解函数问题的关键是要确定相应点坐标,表示出相应线段长度即可求解问题.19.【分析】设A (a ,b ),则A ,C 作AE ⊥x 轴于E ,CF ⊥x 轴于F ,根据相似三角形的判定证得△AOE ∽△COF ,由相似三角形的性质得到,,则.解:设A(a,b),∴OE=a ,AE=b ,∵在反比例函数y=x图象上,∴分别过A ,C 作AE ⊥x 轴于E ,CF ⊥x 轴于F ,∵矩形AOCB ,∴∠AOE+∠COF=90°,∴∠OAE=∠COF=90°−∠AOE ,∴△AOE ∽△OCF ,∵,∴OCOA =OF AE =CF OE ∴,∵C 在反比例函数y=k x的图象上,且点C 在第四象限,∴k=−OF ⋅.【点拨】本题考查反比例函数图象上点的坐标特征和矩形的性质,解题的关键是掌握反比例函数图象上点的坐标特征和矩形的性质.20.6.4【分析】根据题意求得CD =BC =2,即可求得OD =2k ,由△POA 的面积是△PCD 面积的2倍,得出x P =3,根据△POD 的面积等于2k ﹣8,列出关于k 的方程,解方程即可求得.解:∵▱OABC 的顶点A 的坐标为(2,0),∴BD ∥x 轴,OA =BC =2,∵反比例函数1k y x=和22k y x =的图象分别经过C ,B 两点,∴DC•OD =k ,BD•OD =2k ,∴BD =2CD ,∴CD =BC =2,BD =4,∴C (2,2k ),B (4,2k ),∴OD =2k ,∵△POA 的面积是△PCD 面积的2倍,∴y P =2323k k ⨯=,∴x P =3kk =3,∵△POD 的面积等于2k ﹣8,∴12OD•x P =2k ﹣8,即122k ⨯×3=2k ﹣8,解得k =6.4,故答案为6.4.【点拨】本题考查反比例函数系数k 的几何意义,平行四边形的性质,反比例图象上点的坐标特征,求得P 的横坐标是解题的关键.21.(1)证明过程见详解;(2)当6k =时,S 有最大面积,最大面积为3【分析】(1)设11(,)E x y ,22(,)F x y ,根据点E ,F 在反比例函数图像上,则可求出11x y k =,22x y k =,且11112AOE S S x y ==△,22212BOF S S x y ==△,由此即可求证;(2)确定,33k E ⎛⎫ ⎪⎝⎭,4,4k F ⎛⎫ ⎪⎝⎭,11432234ECF k k S EC CF ⎛⎫⎛⎫==-- ⎪⎪⎝⎭⎝⎭ △,EOF AOE BOF ECF AOBC S S S S S =--- 矩形,将OEF ECF S S S =- 转化为含有k 的一元二次方程方程,根据一元二次方程的顶点式即可求解.解:(1)证明:设11(,)E x y ,22(,)F x y ,AOE △的面积为1S ,BOF 的面积为2S ,∵11(,)E x y ,22(,)F x y 都在反比例函数(0)k y k x =>的图像上,∴11k y x =,22k y x =,则11x y k =,22x y k =,∴1111122AOE S S x y k ===△,2221122BOF S S x y k ===△,∴12AOE BOF S S k ==△△.(2)解:根据题意可知,,33k E ⎛⎫ ⎪⎝⎭,4,4k F ⎛⎫ ⎪⎝⎭,∴11432234ECF k k S EC CF ⎛⎫⎛⎫==-- ⎪⎪⎝⎭⎝⎭△,∴EOF AOE BOF ECF AOBC S S S S S =--- 矩形,即S 121222EOF ECF ECF k k S k S =---=--△△△,∴112212243234OEF ECF ECF k k S S S k S k ⎛⎫⎛⎫=-=--=--⨯-- ⎪⎪⎝⎭⎝⎭△△△,即2211(6)31212S k k k =-+=--+,∴当6k =时,S 有最大面积,最大面积为3.【点拨】本题主要考查矩形的性质,反比函数与几何的综合问题,掌握反比例函数图形的性质,矩形的性质是解题的关键.22.(1)2y x=-;(2)3【分析】(1)把点A 坐标代入反比例函数4y x =求得点A 坐标,根据AC =2BC 求出点B 的坐标,然后把点B 的坐标代入k y x =中求得k 的值,即可求出k y x=的解析式.(2)设2,D n n -⎛⎫ ⎪⎝⎭.根据AD 的中点E 在y 轴上求出点D 和点E 坐标,然后根据三角形面积公式求解即可.(1)解:∵点(,2)A a 在反比例函数4y x=的图象上,∴42a =.∴a =2.∴(2,2)A .∵AB x 轴,且交y 轴于点C ,∴2AC =.∵2AC BC =,∴1BC =.∴(1,2)B -.∴把点B 坐标代入k y x=得21k =-.∴2k =-.∴该反比例函数的解析式为2y x =-.(2)解:设2,D n n -⎛⎫ ⎪⎝⎭.∵(2,2)A ,点E 为AD 的中点,∴21,2n n E n +-⎛⎫ ⎪⎝⎭.∵点E 在y 轴上,∴20n n+=.∴2n =-.∴(2,1)-D ,30,2E ⎛⎫ ⎪⎝⎭.∴32OE =.∴1322OEA A S OE x =⋅=△,1322OED D S OE x =⋅=△.∴3OE OAD OED A S S S =+=△△△.∴△OAD 的面积为3.【点拨】本题考查根据函数值求自变量,待定系数法求反比例函数解析式,中点坐标,熟练掌握这些知识点是解题关键.23.(1)m =2;3y x =-+;(2)n =2或1.【分析】(1)求出点A 、B 的坐标,即可求解;(2)△PED 的面积S =S 四边形PDOE -S △ODE =1,即可求解.(1)解:反比例函数y =2k x 的图象过点A ,则k 2=1×2=2,故反比例函数的表达式为:y =2x;点B (m ,1)在该函数上,故m ×1=2,解得:m =2,故点B (2,1);将点A 、B 的坐标代入一次函数表达式得:11212k b k b +=⎧⎨+=⎩,解得113k b =-⎧⎨=⎩,故一次函数的表达式为y =-x +3;(2)解:连接PO ,设点P (m ,3-m ),平移后直线的表达式为:y =-x +3-n ,令x =0,则y =3-n ,令y =0,则x =3-n ,即点D 、E 的坐标分别为(3-n ,0)、(0,3-n ),即OD =OE =3-n ,△PED 的面积=S 四边形PDOE -S △ODE =S △OPD +S △OPE -S △OED =12×OD ×xP +12×OE ×yP -12×OD ×OE =12×(3-n )(3-m +m )−12(3-n )2=1,整理得:n 2-3n +2=0,解得:n =2或1.【点拨】本题考查了反比例函数与一次函数的交点,当有两个函数的时候,着重使用一次函数,体现了方程思想,综合性较强.24.(1)152y x =-+;(2)28x <<;(3)点P 的坐标为()7,0或()13,0【分析】(1)根据反比例函数上的点的特点求得,m n 的值进而求得点,A B 的坐标,待定系数法求直线解析式即可;(2)根据反比例函数和直线在第一象限的图象直接求得直线在双曲线上方时,x 的取值范围即可;(3)根据(1)的解析式求得点D 的坐标,设P 点坐标为(),0a ,则10PD a =-,根据三角形面积公式求解即可,进而解绝对值方程求得a 的值,即可求得点P 的坐标.解:(1) 点(),4A m 和点()8,B n 在8y x=图象上,824m ∴==,818n ==,即()2,4A ,()8,1B 把()2,4A ,()8,1B 两点代入y kx b =+中得4218k b k b =+⎧⎨=+⎩解得:125k b ⎧=-⎪⎨⎪=⎩,所以直线AB 的解析式为:152y x =-+(2)由图象可得,当0x >时,8kx b x+>的解集为28x <<(3)由(1)得直线AB 的解析式为152y x =-+,当0y =时,10x =,D ∴点坐标为()10,0设P 点坐标为(),0a ,则10PD a=- ADP 的面积是612∴×4×PD =6 ∴PD =3103a ∴-=解得7a =或13∴P 的坐标为()7,0或()13,0因此,点P 的坐标为()7,0或()13,0时, ADP 的面积是6.【点拨】本题考查了反比例函数与一次函数结合,一次函数与坐标轴交点问题,一次函数与坐标轴围成的面积问题,掌握一次函数与反比例函数的图象与性质是解题的关键.25.(1)6y x =,23y x =;(2)03x <<;(3)理由见分析【分析】(1)把A 点坐标分别代入两函数解析式可求得a 和k 的值,可求得两函数的解析式;(2)由反比例函数的图象在正比例函数图象的下方可求得对应的x 的取值范围;(3)用M 点的坐标可表示矩形OCDB 的面积和△OBM 的面积,从而可表示出四边形OADM 的面积,可得到方程,可求得M 点的坐标,从而可证明结论.解:(1)∵将()3,2A 分别代入k y x =,y ax =中,得23k =,32a =,∴6k =,23a =,∴反比例函数的表达式为:6y x =,正比例函数的表达式为23y x =.(2)∵()3,2A 观察图象,得在第一象限内,当03x <<时,反比例函数的值大于正比例函数的值;(3)BM DM=理由:∵//MN x 轴,//AC y 轴,∴四边形OCDB 是平行四边形,∵x 轴y ⊥轴,∴OCDB 是矩形.∵M 和A 都在双曲线6y x=上,∴6BM OB ⨯=,6OC AC ⨯=,∴132OMB OAC S S k ==⨯= ,又∵6OADM S =四边形,∴33612OMB OAC OBDC OADM S S S S =++=++= 矩形四边形,即12OC OB ⋅=,∵3OC =,∴4OB =,即4n =∴632m n ==,∴32MB =,33322MD =-=,∴MB MD =.【点拨】本题为反比例函数的综合应用,涉及知识点有待定系数法、函数与不等式、矩形及三角形的面积和数形结合思想等.在(2)中注意数形结合的应用,在(3)中用M 的坐标表示出四边形OADM 的面积是解题的关键.26.(1)6;(2)25【分析】(1)由条件可分别表示出E 、F 的坐标,用k 可表示出S ,再根据函数的性质可求得其最大值,及取得最大值时的k 的值;(2)求得E 、F 的坐标,即可求得EC =2,CF =32,根据勾股定求得EF =52,设∠CEF =α,即可求得sin α=35,cos α=45,进而解直角三角形求得EM =3sin α,FN =4cos α,从而求得EM•FN 的值.解:(1)∵OB =4,OA =3,且E 、F 为反比例函数图象上的两点,∴E ,F 两点坐标分别为E (3k ,3),F (4,4k ),如图,连接OE 、OF,∴S △ECF =12(4−3k )(3−4k ),∴S △EOF =S 矩形AOBC −S △AOE −S △BOF −S △ECF =3×4−12×3k ×3−12×4×4k −S △ECF ,∴S △EOF =12−k−S △ECF ,∴S =S △OEF −S △ECF =12−k−2S △ECF =12−k−2×12(4−3k )(3−4k ),∴S =−112k 2+k .当k =161212-=⎛⎫⨯- ⎪⎝⎭时,S 有最大值,即S 取得最大值时k =6.(2)∵k =6,∴E (2,3),F (4,32),∴EC =2,FC =32,EF =52,设∠CEF =α,则sin α=332552=,cos α=24552=,∴EM•FN =3425sin cos αα⋅=.【点拨】本题主要考查反比例函数k 的意义及二次函数的性质,解直角三角形等,掌握反比例函数图象上点的坐标满足k =xy 是解题的关键.。
反比例函数(面积、动点)专项训练一 第1课时(解析版)

【热身训练】要求:快速完成!并写出方法小结或感悟!1.已知两点P 1(x 1,y 1)、P 2(x 2,y 2)在反比例函数3y x=的图象上,当021>>x x 时,下列结论正确的是A .120y y <<B .210y y <<C .120y y <<D .210y y <<答案:A解析:反比例函数3y x=的图象在一、三象限,在每一个象限内,y 随x 的增大而减小,所以,当021>>x x 时,有120y y <<2.(2013•铁岭)如图,点P 是正比例函数y=x 与反比例函数y=在第一象限内的交点,PA ⊥OP 交x 轴于点A ,△POA 的面积为2,则k的值是 . =y=S =k=1((3.(2013•淄博)如图,矩形AOBC 的面积为4,反比例函数的图象的一支经过矩形对角线的交点P ,则该反比例函数的解析式是 。
矩形×(矩形.((交于点A,与反比例函数在第一象限内的图象相交于点B(m,2).(1)求反比例函数的关系式;(2)将直线y=x﹣2向上平移后与反比例函数图象在第一象限内交于点C,且△ABC的面积为18,求平移后的直线的函数关系式.5.(2013•十堰)如图,已知正比例函数y=2x和反比例函数的图象交于点A(m,﹣2).(1)求反比例函数的解析式;(2)观察图象,直接写出正比例函数值大于反比例函数值时自变量x的取值范围;(3)若双曲线上点C(2,n)沿OA方向平移个单位长度得到点B,判断四边形OABC 的形状并证明你的结论.y=(,判断出四边形(上,;OA==CB=y==【问题解决】例.如图,已知四边形ABCD 是平行四边形,BC =2AB ,A ,B两点的坐标分别是(-1,0),(0,2),C ,D 两点在反比例函数)0(<=x x k y 的图象上,则k 的值等于 . 答案:-12 解析:如图,过C 、D 两点作x 轴的垂线,垂足为F 、G ,CG 交AD于M 点,过D 点作DH ⊥CG ,垂足为H ,∵CD ∥AB ,CD=AB ,∴△CDH ≌△ABO (AAS ),∴DH=AO=1,CH=OB=2,设C (m ,n ),D (m -1,n -2),则mn =(m -1)(n -2)=k ,解得n=2-2m ,BC AB BC =2AB , 解得:m =-2,n =6,所以,k =mn =-122.(2013•莆田)如图,直线l :y=x+1与x 轴、y 轴分别交于A 、B 两点,点C 与原点O 关于直线l 对称.反比例函数y=的图象经过点C ,点P 在反比例函数图象上且位于C 点左侧,过点P 作x 轴、y 轴的垂线分别交直线l 于M 、N 两点.(1)求反比例函数的解析式;(2)求AN•BM的值.求得:得:,即;,﹣﹣AN=(﹣),﹣(﹣且DM⊥DN.作MF⊥AB于点F,NE⊥AB于点E.(1)特殊验证:如图1,若AC=BC,且D为AB中点,求证:DM=DN,AE=DF;(2)拓展探究:若AC≠BC.①如图2,若D为AB中点,(1)中的两个结论有一个仍成立,请指出并加以证明;②如图3,若BD=kAD,条件中“点M在BC边上”改为“点M在线段CB的延长线上”,其它条件不变,请探究AE与DF的数量关系并加以证明.,即,即,,∴;,∴,∴,即由①同理可得:又∵。
(word完整版)初中数学反比例函数知识点及经典例题,文档

反比率函数一、基础知识1. 定义:一般地,形如 yk〔 k 为常数, k o 〕的函数称为反比率函数。
ykxx还可以够写成 y kx 12. 反比率函数剖析式的特色:⑴等号左边是函数 y ,等号右边是一个分式。
分子是不为零的常数 k 〔也叫做比率系数 k 〕,分母中含有自变量 x ,且指数为 1. ⑵比率系数 k 0⑶自变量 x 的取值为所有非零实数。
⑷函数 y 的取值是所有非零实数。
3. 反比率函数的图像⑴图像的画法:描点法① 列表〔应以 O 为中心,沿 O 的两边分别取三对或以上互为相反的数〕 ② 描点〔有小到大的序次〕③ 连线〔从左到右圆滑的曲线〕 ⑵反比率函数的图像是双曲线,yk〔 k 为常数, k 0 〕中自变量 x 0 ,x函数值 y0 ,所以双曲线是不经过原点, 断开的两个分支, 延伸局部逐渐凑近坐标轴,但是永远不与坐标轴订交。
⑶反比率函数的图像是是轴对称图形〔对称轴是y x 或 y x 〕。
⑷反比率函数 yk〔 k 0 〕中比率系数 k 的几何意义是:过双曲线 ykxx〔 k 0 〕上任意引 x 轴 y 轴的垂线,所得矩形面积为 k 。
4.反比率函数性质以下表:k 的取值 图像所在象限函数的增减性ko 一、三象限在每个象限内, y 值随 x 的增大而减小ko二、四象限在每个象限内, y 值随 x 的增大而增大5. 反比率函数剖析式确实定:利用待定系数法〔只需一对对应值或图像上一个点的坐标即可求出 k 〕6.“反比率关系〞与“反比率函数〞 :成反比率的关系式不用然是反比率函数 ,但是反比率函数 y k中的两个变量必成反比率关系。
x7. 反比率函数的应用二、例题【例 1】若是函数 y kx2k2k 2的图像是双曲线,且在第二,四象限内,那么的值是多少?【剖析】有函数图像为双曲线那么此函数为反比率函数y k,〔 k0〕即y kx1 x(k 0 〕又在第二,四象限内,那么 k 0能够求出的值【答案】由反比率函数的定义,得:2k 2k21解得 k1或 k12 k0k0k1k1时函数 y kx2 k2k 2为 y1x【例 2】在反比率函数 y 1 的图像上有三点x1, y1, x2, y2, x3, y3。
初中数学反比例函数及动点问题专题讲解及练习

(K>0)考点二、反比例函数的性质1.2.形状反比例函数的图象是由两支双曲线组成的.因此称反比例函数的图象为双曲线;3.位置当k>0时,两支双曲线分别位于第一,三象限内;当k<0时,两支双曲线分别位于第二,四象限内;4.增减性反比例函数的图象,当k>0时,在每一象限内,y随x的增大而减小; 当k<0时,在每一象限内,y随x的增大而增大.5.图象的发展趋势反比例函数的图象无限接近于x,y轴,但永远达不到x,y轴,画图象时,要体现出这个特点.6.对称性反比例函数的图象是关于原点成中心对称的图形.7.任意一组变量的乘积是一个定值,即xy=k.温馨提示:反比例函数的涉及内容1.ⅰ当路程s 一定时,时间t 与速度v的函数关系t=s/v2.ⅱ当矩形面积S一定时,长a与宽b的函数关系a=s/b3.ⅲ当三角形面积S 一定时,三角形的底边y 与高x的函数关系y=2s/x动点问题(重点)所谓“动点型问题”是指题设图形中存在一个或多个动点,它们在线段、射线或弧线上运动的一类开放性题目.解决这类问题的关键是动中求静,灵活运用有关数学知识解决问题。
“动点型问题”题型繁多、题意创新,考察学生的分析问题、解决问题的能力,内容包括空间观念、应用意识、推理能力等,是近几年中考题的热点和难点。
解决动点问题的关键是“动中求静”。
从变换的角度和运动变化来研究三角形、四边形、函数图像等图形,通过“对称、动点的运动”等研究手段和方法,来探索与发现图形性质及图形变化,在解题过程中渗透空间观念和合情推理。
在动点的运动过程中观察图形的变化情况,理解图形在不同位置的情况,做好计算推理的过程。
在变化中找到不变的性质是解决数学“动点”探究题的基本思路,这也是动态几何数学问题中最核心的数学本质。
考点一:建立动点问题的函数解析式(或函数图像)函数揭示了运动变化过程中量与量之间的变化规律,是初中数学的重要内容。
动点问题反映的是一种函数思想,由于某一个点或某图形的有条件地运动变化,引起未知量与已知量间的一种变化关系,这种变化关系就是动点问题中的函数关系。
反比例函数与动点问题

Q( , 一 2 ) 或 (一 , 2 ) . Βιβλιοθήκη z ・’,
.
当 = 时 , , , = 一 ; 当 = 一 孚 日 寸 ' y =
・ . .
・ . .
P ( 孚 , 一 叫 一 T , .
.
②若 LO P Q=LA B O, 则△ P Q O ' - " AB O A .
求 出 点 Q 的 坐标 , 如果不存在 , 请 说 明理 由. 解
・ .
( 1 ) ‘ . ‘ Y=k x过 (一1 , 2 ) , . ‘ . k =一 2 , 即Y = 一2 x .
解由 尸 点 在 反 比 例 函 数 y = 一 ÷ 的 图 像 上 可 设 P ( , y ) .
2
升 ( 甘肃省陇 南市武都 区滨 江学校 , 甘肃 陇 南 7 4 6 0 0 0 )
【 基金项 目】 甘肃省 “ 十三五 ” 教 育科学规 划 2 0 1 6年度
《 初 中数 学 动 点 问题 分 析 研 究》课 题 ( 课题立 项号: G s
[ 2 0 1 6 ] G H B 0 6 5 3 ) 成果.
数 y = 与 反 比 例 函 数 y = 詈图 像 上 的 一
个 交 点.
一
( 1 ) 求这 两个函数的解析式 ;
A 一 1 一
图 2
中 0( 0 , 0 ) , A( 0 , 2 ) , ( 1 , 0 ) , 点 P是 反
1
比例 函数 Y=一 图像 上的一个动点 , 过 点 P作 P Q上 轴, 垂足 为 Q, 若 以点 0,
‘
‘ , , = 詈 且 过 ( 一 1 , 2 ) , . ‘ = 一 2 , 即 , , = 一 2 .
专题66 反比例函数中的动点最值问题(解析版)-中考数学解题大招复习讲义

例题精讲【例1】.如图,直线与x轴、y轴分别交于点A和点B,点C、D分别为线段AB、OB的中点,点P为OA上一动点,PC+PD值最小时点P的坐标为________解:当x=0时,y=×0+4=4,∴点B的坐标为(0,4);当y=0时,x+4=0,解得:x=﹣6,∴点A的坐标为(﹣6,0).∵点C、D分别为线段AB、OB的中点,∴点C的坐标为(﹣3,2),点D坐标为(0,2).作点C关于x轴的对称点C′,连接C′D交x轴于点P,此时PC+PD的值最小,如图所示.∵点C的坐标为(﹣3,2),∴点C′的坐标为(﹣3,﹣2).设直线C′D的解析式为y=kx+b(k≠0),将C′(﹣3,﹣2),D(0,2)代入y=kx+b得:,解得:,∴直线C′D的解析式为y=x+2.当y=0时,x+2=0,解得:x=﹣,∴点P的坐标为(﹣,0),即点P的坐标为(﹣1.5,0).变式训练【变1-1】.如图,在平面直角坐标系中,点A是x轴正半轴上的一个定点,点P是双曲线y=(x>0)上的一个动点,PB⊥y轴于点B,当点P的横坐标逐渐增大时,四边形OAPB 的面积将会()A.逐渐增大B.不变C.逐渐减小D.先增大后减小解:设点P的坐标为(x,),∵PB⊥y轴于点B,点A是x轴正半轴上的一个定点,∴四边形OAPB是个直角梯形,∴四边形OAPB的面积=(PB+AO)•BO=(x+AO)•=+=+•,∵AO是定值,∴四边形OAPB的面积是个减函数,即点P的横坐标逐渐增大时四边形OAPB的面积逐渐减小.故选:C.【变1-2】.如图,一次函数y=2x与反比例函数y=(k>0)的图象交于A,B两点,点M在以C(2,0)为圆心,半径为1的⊙C上,N是AM的中点,已知ON长的最大值为,则k的值是.解:方法一、联立,∴,∴,∴A(),B(),∴A与B关于原点O对称,∴O是线段AB的中点,∵N是线段AM的中点,连接BM,则ON∥BM,且ON=,∵ON的最大值为,∴BM的最大值为3,∵M在⊙C上运动,∴当B,C,M三点共线时,BM最大,此时BC=BM﹣CM=2,∴(,∴k=0或,∵k>0,∴,方法二、设点B(a,2a),∵一次函数y=2x与反比例函数y=(k>0)的图象交于A,B两点,∴A与B关于原点O对称,∴O是线段AB的中点,∵N是线段AM的中点,连接BM,则ON∥BM,且ON=,∵ON的最大值为,∴BM的最大值为3,∵M在⊙C上运动,∴当B,C,M三点共线时,BM最大,此时BC=BM﹣CM=2,∴=2,∴a1=或a2=0(不合题意舍去),∴点B(,),∴k=,故答案为:.【例2】.如图,在平面直角坐标系中,反比例函数y=(x>0)的图象与边长是6的正方形OABC的两边AB,BC分别相交于M,N两点.△OMN的面积为10.若动点P在x 轴上,则PM+PN的最小值是2.解:∵正方形OABC 的边长是6,∴点M 的横坐标和点N 的纵坐标为6,∴M (6,),N (,6),∴BN =6﹣,BM =6﹣,∵△OMN 的面积为10,∴6×6﹣×6×﹣×6×﹣×(6﹣)2=10,∴k =24,∴M (6,4),N (4,6),作M 关于x 轴的对称点M ′,连接NM ′交x 轴于P ,则NM ′的长=PM +PN 的最小值,∵AM =AM ′=4,∴BM ′=10,BN =2,∴NM ′===2,故答案为2.变式训练【变2-1】.已知在平面直角坐标系中有两点A (0,1),B (﹣1,0),动点P 在反比例函数y =的图象上运动,当线段PA 与线段PB 之差的绝对值最大时,点P 的坐标为(1,2)或(﹣2,﹣1).解:如图,设直线AB的解析式为y=kx+b,将A(0,1)、B(﹣1,0)代入,得:,解得:,∴直线AB的解析式为y=x+1,直线AB与双曲线y=的交点即为所求点P,此时|PA﹣PB|=AB,即线段PA与线段PB 之差的绝对值取得最大值,由可得或,∴点P的坐标为(1,2)或(﹣2,﹣1),故答案为:(1,2)或(﹣2,﹣1).【变2-2】.如图,一次函数y1=mx+n(m≠0)的图象与双曲线y2=(k≠0)相交于A(﹣1,2)和B(2,b)两点,与y轴交于点C,与x轴交于点D.(1)求双曲线的解析式;(2)经研究发现:在y轴负半轴上存在若干个点P,使得△CPB为等腰三角形.请直接写出P点所有可能的坐标.解:(1)∵点A(﹣1,2)在双曲线y2=(k≠0)上,∴k=﹣1×2=﹣2,∴反比例函数解析式为y2=﹣,(2)∵点B在双曲线y2=﹣上,∴2b=﹣2,∴b=﹣1,∴B(2,﹣1),将点A(﹣1,2),B(2,1)代入一次函数y1=mx+n(m≠0)中,得,∴,∴一次函数的解析式为y=﹣x+1;令x=0,则y=1,∴C(0,1),设P(0,p)(p<0),∵B(2,﹣1),∴BC==2,BP=,CP=1﹣p,∵△CPB为等腰三角形,∴①当BC=BP时,2=,∴p=1(舍)或p=﹣3,∴P(0,﹣3),②当BC=CP时,2=1﹣p,∴p=1﹣2,∴P(0,1﹣2),③当BP=CP时,=1﹣p,∴p=﹣1,∴P(0,﹣1),故满足条件的点P的坐标为(0,﹣3)或(0,1﹣2)或(0,﹣1).1.如图,点N是反比例函数y=(x>0)图象上的一个动点,过点N作MN∥x轴,交直线y=﹣2x+4于点M,则△OMN面积的最小值是()A.1B.2C.3D.4解:设点N的坐标为(,m),则点M的坐标为(2﹣m,m)(m>0),∴MN=﹣(2﹣m)=m+﹣2,=MN•m=m2﹣m+3=(m﹣2)2+2,∴S△OMN∴当m=2时,△OMN面积最小,最小值为2.故选:B.2.如图,在△ABC中,AB=AC=a,∠BAC=18°,动点P、Q分别在直线BC上运动,且始终保持∠PAQ=99°.设BP=x,CQ=y,则y与x之间的函数关系用图象大致可以表示为()A.B.C.D.解:∵AB=AC=a,∠BAC=18°,∴∠ABC=∠ACB=(180°﹣18°)=81°,∴∠ABC=∠APB+∠PAB=81°,∵∠PAQ=99°,∠BAC=18°,∴∠PAB+∠QAC=99°﹣18°=81°,∴∠APB=∠QAC,同理可得∠PAB=∠AQC,∴△APB∽△QAC,∴=,即=,整理得,y=,∵x、y都是边的长度,是正数,∴y与x之间的函数关系用图象表示是反比例函数在第一象限内的部分,纵观各选项,只有A符合.故选:A.3.如图,已知A、B是反比例函数y=(k>0,x>0)图象上的两点,BC∥x轴,交y轴于点C,动点P从坐标原点O出发,沿O→A→B→C匀速运动,终点为C,过点P作PM ⊥x轴,PN⊥y轴,垂足分别为M、N.设四边形OMPN的面积为S,点P运动的时间为t,则S关于t的函数图象大致为()A.B.C.D.解:①点P在AB上运动时,此时四边形OMPN的面积S=K,保持不变,故排除B、D;②点P在BC上运动时,设路线O→A→B→C的总路程为l,点P的速度为a,则S=OC×CP=OC×(l﹣at),因为l,OC,a均是常数,所以S与t成一次函数关系.故排除C.故选:A.4.已知点A是双曲线y=在第一象限上的一动点,连接AO并延长交另一分支于点B,以AB为一边作等边△ABC.随着点A的运动,点C的位置也不断变化,但始终在一个函数的图象上运动,则这个函数的表达式为y=﹣.解:设A(a,),∵点A与点B关于原点对称,∴OA=OB,∵△ABC为等边三角形,∴AB⊥OC,OC=AO,∵AO=,∴CO=,过点C作CD⊥x轴于点D,则可得∠AOD=∠OCD(都是∠COD的余角),设点C的坐标为(x,y),则tan∠AOD=tan∠OCD,即=,解得:y=﹣a2x,在Rt△COD中,CD2+OD2=OC2,即y2+x2=3a2+,将y=﹣a2x代入,(a4+1)x2=3×可得:x2=,故x=,y=﹣a2x=﹣a,则xy=﹣3,故可得:y=﹣(x>0).故答案为:y=﹣(x>0).5.如图,点P是双曲线C:y=(x>0)上的一点,过点P作x轴的垂线交直线AB:y=x﹣2于点Q,连接OP,OQ.当点P在曲线C上运动,且点P在Q的上方时,△POQ面积的最大值是3.解:∵PQ⊥x轴,∴设P(x,),则Q(x,x﹣2),∴PQ=﹣x+2,=(﹣+2)•x=﹣(x﹣2)2+3,∴S△POQ∵﹣<0,∴△POQ面积有最大值,最大值是3,故答案为3.6.如图,直线AB与x轴交于点A(1,0),与y轴交于点B(0,2),将线段AB绕点A顺时针旋转90°得到线段AC,反比例函数y=(k≠0,x>0)的图象经过点C.已知点P是反比例函数y=(k≠0,x>0)图象上的一个动点,则点P到直线AB距离最短时的坐标为(,).解:(1)设直线AB的解析式为y=ax+b,将点A(1,0),点B(0,2)代入得,解得,∴直线AB为y=﹣2x+2;∵过点C作CD⊥x轴,∵线段AB绕点A顺时针旋转90°得到线段AC,∴△ABO≌△CAD(AAS),∴AD=OB=2,CD=OA=1,∴C(3,1),∴k=3,∴y=;设与AB平行的直线y=﹣2x+h,联立﹣2x+h=,∴﹣2x2+hx﹣3=0,当△=h2﹣24=0时,h=2或﹣2(舍弃),此时点P到直线AB距离最短,解方程﹣2x2+2x﹣3=0得x==,∴P(,),故答案为P(,).7.如图,在平面直角坐标系中,点A,B在反比例函数y=(k≠0)的图象上运动,且始终保持线段AB=4的长度不变.M为线段AB的中点,连接OM.则线段OM长度的最小值是(用含k的代数式表示).解:如图,因为反比例函数关于直线y=x对称,观察图象可知:当线段AB与直线y=x 垂直时,垂足为M,此时AM=BM,OM的值最小,∵M为线段AB的中点,∴OA=OB,∵点A,B在反比例函数y=(k≠0)的图象上,∴点A与点B关于直线y=x对称,∵AB=4,∴可以假设A(m,),则B(m+4,﹣4),∴(m+4)(﹣4)=k,整理得k=m2+4m,∴A(m,m+4),B(m+4,m),∴M(m+2,m+2),∴OM===,∴OM的最小值为.故答案为.8.如图,点A是反比例函数y=在第一象限的图象上的一点,过点A作AB⊥y轴于点B.连接AO,以点A为圆心,分别以AB,AO为半径作直角扇形BAC和OAD,并连接CD,则阴影部分面积的最小值是2π+2.解:如图,过点D作DE垂直于CA的延长线于点E,则∠AED=90°,由题意可知,AB=AC,AO=AD,∠BAC=∠DAO=90°,∵AB⊥y轴,∴∠ABO=90°,∴∠BAO+∠OAE=90°,∠DAE+∠OAE=90°,∴∠BAO=∠DAE,∴△BAO≌△EAD(AAS),∴DE=OB.∵点A是反比例函数y=在第一象限的图象上的一点,∴OB•AB=4,∴S△AOB=OB•AB=2,∴S△ACD=AC•DE=OB•AB=2,∴S阴影=S△ACD+S扇形OAD=2+=2+∵(AB﹣OB)2≥0,∴AB2﹣2AB•OB+OB2≥0,∴AB2+OB2≥2AB•OB,∴S阴影≥2+×2AB•OB=2+2π.故答案为:2+2π.9.如图,点A是反比例函数y=(k>0)图象第一象限上一点,过点A作AB⊥x轴于B 点,以AB为直径的圆恰好与y轴相切,交反比例函数图象于点C,在AB的左侧半圆上有一动点D,连接CD交AB于点E.记△BDE的面积为S1,△ACE的面积为S2,连接BC,△ACB是等腰直角三角形,则若S1﹣S2的值最大为1,则k的值为4+4.解:如图连接BC、O′C,作CH⊥x轴于H.由题意⊙O′与反比例函数图象均关于直线y=x对称,∴点A、C关于直线y=x对称,设A(m,2m)则C(2m,m),∴BO′=CH=m,BO′∥CH,∴四边形BHCO′是平行四边形,∵BH=CH,∠BHC=90°,∴四边形BHCO′是正方形.∴∠ABC=45°,∴△ACB是等腰直角三角形,∵S1﹣S2=S△DBC﹣S△ACB,△ABC的面积是定值,∴△DBC的面积最大时,S1﹣S2的值最大,∴当DO′⊥BC时,△DBC的面积最大,∴m•(m+m)﹣•2m•m=1,∴m2=2(+1),∵k=2m2,∴k=4+4,故答案为:等腰直角三角形,4+4.10.如图,正比例函数y=x的图象与反比例函数y=(k≠0)在第一象限的图象交于A 点,过A点作x轴的垂线,垂足为M,已知△OAM的面积为1.(1)求反比例函数的解析式;(2)如果B为反比例函数在第一象限图象上的点(点B与点A不重合),且B点的横坐标为1,P为x轴上一点,求使PA+PB的值最小时点P的坐标.解:(1)设A点的坐标为(a,b),则由,得ab=2=k,∴反比例函数的解析式为;(2)由条件知:两函数的交点为,解得:,,∴A点坐标为:(2,1),作出A点关于x轴对称点C点,连接BC,P点即是所求则点C(2,﹣1),∵B(1,2),设直线BC的解析式为:y=kx b,解得:,∴直线BC的解析式为:y=﹣3x+5,当y=0时,x=,∴点P(,0).11.如图,正比例函数y=2x的图象与反比例函数y=的图象交于A、B两点,过点A作AC垂直x轴于点C,连接BC,若△ABC面积为2.(1)求k的值(2)x轴上是否存在一点D,使△ABD是以AB为斜边的直角三角形?若存在,求出点D的坐标,若不存在,说明理由.解:(1)∵反比例函数与正比例函数的图象相交于A、B两点,∴A、B两点关于原点对称,∴OA=OB,∴△BOC的面积=△AOC的面积=2÷2=1,又∵A是反比例函数y=图象上的点,且AC⊥x轴于点C,∴△AOC的面积=|k|,∴|k|=1,∵k>0,∴k=2.故这个反比例函数的解析式为y=;(2)x轴上存在一点D,使△ABD为直角三角形.将y=2x与y=联立成方程组得:,解得:,,∴A(1,2),B(﹣1,﹣2),∵△ABD是以AB为斜边的直角三角形∴∠ADB=90°,如图3,∵O为线段AB的中点,∴OD=AB=OA,∵A(1,2),∴OC=1,AC=2,由勾股定理得:OA==,∴OD=,∴D(,0).根据对称性,当D为直角顶点,且D在x轴负半轴时,D(﹣,0).故x轴上存在一点D,使△ABD以AB为斜边的直角三角形,点D的坐标为(,0)或(﹣,0).12.如图,一次函数y=x+2的图象与反比例函数y=的图象交于点A(1,a),B两点.(1)求反比例函数的解析式及点B的坐标;(2)在x轴上找一点C,使|CA﹣CB|的值最大,求满足条件的点C的坐标及△ABC的面积.解:(1)∵直线y=x+2经过点A(1,a),∴a=3,∵反比例函数y=经过A(1,3),∴k=3,∴y=,由,解得或,∴B(﹣3,﹣1).(2)作点B关于x轴的对称点B′,连接AB′,延长AB′交x轴于点C,点C即为所求;∵A(1,3),B′(﹣3,1),∴直线AB′的解析式为y=x+,∴C(﹣5,0),=S△CBB′+S△BB′A=×2×2+×2×4=6.∴S△ABC13.如图,一次函数y=2x﹣3的图象与反比例函数y=的图象相交于点A(﹣1,n),B 两点.(1)求反比例函数的解析式与点B的坐标;(2)连接AO、BO,求△AOB的面积;(3)点D是反比例函数图象上的一点,当∠BAD=90°时,求点D的坐标.解:(1)∵点A(﹣1,n)在一次函数y=2x﹣3的图象上,∴n=﹣5,∴点A(﹣1,﹣5),∵点A(﹣1,﹣5)在反比例函数的图象上,∴k=﹣1×(﹣5)=5,∴;联立,解得:,,∴点;(2)设y=2x﹣3与y轴的交点为点E,则点E(0,﹣3),∴OE=3,=S△AOE+S△BOE=×3×1+×3×=;∴S△AOB(3)设点,如图,分别过点D,B作y轴的平行线DM,BN,过点A作MN⊥DM于M,交BN于N,则MN⊥BN,∴∠M=∠N=90°,∴∠DAM+∠ADM=90°,∵∠BAD=90°,∴∠BAN+∠DAM=90°,∴∠BAN=∠ADM,∴△BAN∽△ADM,∴=,即=,解得:a1=﹣10,a2=﹣1(舍),∴.14.如图,直线y=2x+3与y轴交于A点,与反比例函数y=(x>0)的图象交于点B,过点B作BC⊥x轴于点C,且C点的坐标为(1,0).(1)求反比例函数的解析式;(2)点D(a,1)是反比例函数y=(x>0)图象上的点,在x轴上是否存在点P,使得PB+PD最小?若存在,求出点P的坐标;若不存在,请说明理由.解:(1)∵BC⊥x轴于点C,且C点的坐标为(1,0),∴在直线y=2x+3中,当x=1时,y=2+3=5,∴点B的坐标为(1,5),又∵点B(1,5)在反比例函数y=上,∴k=1×5=5,∴反比例函数的解析式为:y=;(2)将点D(a,1)代入y=,得:a=5,∴点D坐标为(5,1)设点D(5,1)关于x轴的对称点为D′(5,﹣1),过点B(1,5)、点D′(5,﹣1)的直线解析式为:y=kx+b,可得:,解得:,∴直线BD′的解析式为:y=﹣x+,根据题意知,直线BD′与x轴的交点即为所求点P,当y=0时,得:﹣x+=0,解得:x=,故点P的坐标为(,0).15.如图,在矩形OABC中,OA=3,OC=2,F是AB上的一个动点(F不与A,B重合),过点F的反比例函数y=(x>0)的图象与BC边交于点E.(1)当F为AB的中点时,求该反比例函数的解析式和点E的坐标.(2)设过(1)中的直线EF的解析式为y=ax+b,直接写出不等式ax+b<的解集.(3)当k为何值时,△AEF的面积最大,最大面积是多少?解:(1)∵四边形OABC为矩形,OA=3,OC=2,∴AB=2,BC=3,∵F为AB的中点,∴点F坐标为(3,1),∵点F在反比例函数y=(x>0)的图象上,∴k=3×1=3,∴反比例函数解析式为y=,∵点E在BC上,∴E点纵坐标为2,在y=中,令y=2,可求x=,∴E点坐标为(,2);(2)不等式ax+b<的解集即直线在反比例函数下方时对应的自变量的取值范围,由(1)可知点E、F两点的横坐标分别为、3,∴不等式ax+b<的解集为:0<x<或x>3;(3)由题意可知点E的纵坐标为为2,点F的横坐标为3,且E、F在反比例函数y=(x>0)的图象上,∴可设E(,2),F(3,),∴AF=,CE=,∴BE=BC﹣CE=3﹣,=AF•BE=••(3﹣)=﹣k2+=﹣(k﹣3)2+,∴S△AEF∵﹣<0,是关于k的开口向下的抛物线,∴S△AEF有最大值,最大值为,∴当k=3时,S△AEF即当k的值为3时,△AEF的面积最大,最大面积为.16.如图,直线OA:y=x的图象与反比例函数y=(k≠0)在第一象限的图象交于A 点,过A点作轴的垂线,垂足为M,已知△OAM的面积为1.(1)求反比例函数的解析式;(2)如果B为反比例函数在第一象限图象上的点(点B与点A不重合),且B点的横坐标为1,在x轴上求一点P,使PA+PB最小.解:(1)设点A的坐标为(a,b),则,解得:k=2.∴反比例函数的解析式为y=.(2)联立直线OA和反比例函数解析式得:,解得:.∴点A的坐标为(2,1).设A点关于x轴的对称点为C,则C点的坐标为(2,﹣1),连接BC较x轴于点P,点P即为所求.如图所示.设直线BC的解析式为y=mx+n,由题意可得:B点的坐标为(1,2),∴,解得:.∴BC的解析式为y=﹣3x+5.当y=0时,0=﹣3x+5,解得:x=.∴P点的坐标为(,0).17.已知:如图,一次函数y=﹣2x+10的图象与反比例函数y=的图象相交于A、B两点(A在B的右侧),点A横坐标为4.(1)求反比例函数解析式及点B的坐标;(2)观察图象,直接写出关于x的不等式﹣2x+10﹣>0的解集;(3)反比例函数图象的另一支上是否存在一点P,使△PAB是以AB为直角边的直角三角形?若存在,求出所有符合条件的点P的坐标;若不存在,请说明理由.解:(1)把x=4代入y=﹣2x+10得y=2,∴A(4,2),把A(4,2)代入y=,得k=4×2=8.∴反比例函数的解析式为y=,解方程组,得,或,∴点B的坐标为(1,8);(2)观察图象得,关于x的不等式﹣2x+10﹣>0的解集为:1<x<4或x<0;(3)存在,理由:①若∠BAP=90°,过点A作AH⊥OE于H,设AP与x轴的交点为M,如图1,对于y=﹣2x+10,当y=0时,﹣2x+10=0,解得x=5,∴点E(5,0),OE=5.∵A(4,2),∴OH=4,AH=2,∴HE=5﹣4=1.∵AH⊥OE,∴∠AHM=∠AHE=90°.又∵∠BAP=90°,∴∠AME+∠AEM=90°,∠AME+∠MAH=90°,∴∠MAH=∠AEM,∴△AHM∽△EHA,∴,即,∴MH=4,∴M(0,0),可设直线AP的解析式为y=mx,则有4m=2,解得m=,∴直线AP的解析式为y=x,解方程组,得,,∴点P的坐标为(﹣4,﹣2).②若∠ABP=90°,同理可得:点P的坐标为(﹣16,﹣).综上所述:符合条件的点P的坐标为(﹣4,﹣2)、(﹣16,﹣).18.反比例函数(k为常数.且k≠0)的图象经过点A(1,3),B(3,m).(1)求反比例函数的解析式及B点的坐标;(2)在x轴上找一点P,使PA+PB的值最小,①求满足条件的点P的坐标;②求△PAB的面积.解:(1)把A(1,3)代入y=得,k=3,∴反比例函数的关系式为:y=;把B(3,m)代入y=得,m=1,∴点B的坐标为(3,1);(2)①如图所示,作点B关于x轴的对称点B′,则B′(3,﹣1),连接AB′交x轴于点P,此时PA+PB最小.设直线AB′的关系式为y=kx+b,把A(1,3),B′(3,﹣1)代入得,,解得,,∴直线AB′的关系式为y=﹣2x+5,当y=0时,x=,即:P(,0),也就是,OP=,②S△P AB=S梯形ABNM﹣S△AMP﹣S△BPN=(1+3)×2﹣(﹣1)×3﹣(3﹣)×1=.19.如图,一次函数y=﹣x+4的图象与反比例y=(k为常数,且k≠0)的图象交于A (1,a),B两点.(1)求反比例函数的表达式及点B的坐标;(2)①在x轴上找一点P,使PA+PB的值最小,求满足条件的点P的坐标;②在x轴上找一点M,使|MA﹣MB|的值为最大,直接写出M点的坐标.解:(1)把点A(1,a)代入一次函数y=﹣x+4,得a=3,∴A(1,3),把点A(1,3)代入反比例y=,得k=3,∴反比例函数的表达式y=,解得或,故B(3,1).(2)作点B关于x轴的对称点D,连接AD,交x轴于点P,此时PA+PB的值最小∴D(3,﹣1)设直线AD的解析式为y=mx+n,则,解得,∴直线AD的解析式为y=﹣2x+5,令y=0,则x=,∴P点坐标为(,0);(3)直线y=﹣x+4与x轴的交点即为M点,此时|MA﹣MB|的值为最大,令y=0,则x=4,∴M点的坐标为(4,0).20.如图,四边形ABCD是正方形,点A的坐标是(0,1),点B的坐标是(0,﹣2),反比例函数y=的图象经过点C,一次函数y=ax+b的图象经过A、C两点,两函数图象的另一个交点E的坐标是(m,3).(1)分别求出一次函数与反比例函数的解析式.(2)求出m的值,并根据图象回答:当x为何值时,一次函数的值大于反比例函数的值.(3)若点P是反比例函数图象上的一点,△AOP的面积恰好等于正方形ABCD的面积,求点P坐标.解:(1)∵点A的坐标为(0,1),点B的坐标为(0,﹣2),∴AB=1+2=3,∵四边形ABCD为正方形,∴BC=AB=3,∴C(3,﹣2),把C(3,﹣2)代入y=,得k=3×(﹣2)=﹣6,∴反比例函数解析式为y=﹣;把C(3,﹣2),A(0,1)代入y=ax+b,得,解得,∴一次函数解析式为y=﹣x+1;(2)∵反比例函数y=﹣的图象过点E(m,3),∴m=﹣2,∴E点的坐标为(﹣2,3);由图象可知,当x<﹣2或0<x<3时,一次函数落在反比例函数图象上方,即当x<﹣2或0<x<3时,一次函数的值大于反比例函数的值;(3)设P(t,﹣),∵△AOP的面积恰好等于正方形ABCD的面积,∴×1×|t|=3×3,解得t=18或t=﹣18,∴P点坐标为(18,﹣)或(﹣18,).21.如图,点A是反比例函数y=(x>0)的图象上的一个动点,AC⊥x轴于点C;E是线段AC的中点,过点E作AC的垂线,与y轴和反比例函数的图象分别交于点B、D两点;连接AB、BC、CD、DA.设点A的横坐标为m.(1)求点D的坐标(用含有m的代数式表示);(2)判断四边形ABCD的形状,并说明理由;(3)当m为何值时,四边形ABCD是正方形?并求出此时AD所在直线的解析式.解:(1)∵点A的横坐标为m,∴点A的纵坐标为,∵E是AC的中点,AC⊥x轴,∴E(m,),∵BD⊥AC,AC⊥x轴,∴BD∥x轴,∴点B,E,D的纵坐标相等,为,∴点D的横坐标为2m,∴D(2m,);(2)四边形ABCD是菱形,∵B(0,),E(m,),D(2m,),∴EB=ED=m,∵AE=EC,∴四边形ABCD是平行四边形,∵BD⊥AC,∴平行四边形ABCD是菱形;(3)∵平行四边形ABCD是菱形,∴当AC=BD时,四边形ABCD是正方形,∴2m=,∴m=2,或m=﹣2(舍),∴A(2,4),D(4,2),设直线AD的解析式为y=kx+b,∴,∴,∴直线AD解析式为y=﹣x+6,∴当m=2时,四边形ABCD是正方形,此时直线AD解析式为y=﹣x+6.22.如图,一次函数y=﹣x+2的图象与两坐标轴分别交于A,B两点,与反比例函数y=交于点C、D,且点C坐标为(﹣2,m).(1)求反比例函数的解析式;(2)若点M在y轴正半轴上,且与点B,C构成以BC为腰的等腰三角形,求点M的坐标.(3)点P在第二象限的反比例函数图象上,若tan∠OCP=3,求点P的坐标.解:(1)∵点C(﹣2,m)在一次函数y=﹣x+2的图象上,∴m=﹣(﹣2)+2,解得:m=4,∴C(﹣2,4),将C(﹣2,4)代入y=,得k=﹣8,∴反比例函数为y=﹣;(2)如图1,过点C作CH⊥y轴于H,在直线y=﹣x+2中,当x=0时,则y=2,∴B(0,2),由(1)知,C(﹣2,4),∴BC==2,当BM=BC=2时,OM=2+2,∴M(0,2+2),当BC=MC时,点C在BM的垂直平分线,∴M(0,6),综上所述,点M的坐标为(0,2+2)或(0,6)(3)作OQ⊥PC于Q,过Q作HG⊥x轴于G,CH∥x轴,交HG于H,则△CHQ∽△QGO,∴,∵tan∠OCP=3,∴,设CH=x,则GQ=3x,HQ=4﹣3x,∴OG=3HQ=12﹣9x=x+2,解得x=1,∴Q(﹣3,3),∴直线CQ的解析式为y=x+6,∴x+6=﹣,解得x1=﹣2,x2=﹣4,∵点P与C不重合,∴P(﹣4,2).。
专题18 反比例函数中动点问题及图形存在性探究(解析版)

= =⎩5k+b=0⎪⎪4⎪b=-15专题18反比例函数中动点问题及图形存在性探究1.(2019·山东泰安中考)已知一次函数y=kx+b的图象与反比例函数y=mx的图象交于点A,与x轴交于点B(5,0),若OB=AB,且△SOAB 15 2.(1)求反比例函数与一次函数的解析式;(2)若点P为x轴上一点,且△ABP是等腰三角形,求点P的坐标.【答案】见解析.【解析】解:(1)如图,过点A作AD⊥x轴于点D,∵B(5,0),OB=AB,且△SOAB 15 2,∴115⨯5⨯AD=,即AD=3,22在△R t ABD中,由勾股定理得:BD=∴A点坐标为(9,3),AB2-AD2=4,∵反比例函数y=mx的图象过点A,∴m=27,将(9,3),(5,0)代入y=kx+b得:⎧9k+b=3⎨⎧3k=,解得:⎨⎪⎩4y=2的图象上,AC⊥x轴于点E,BD⊥x轴于点F,AC=2,BD=4,EF=3,则k2﹣k1=.,,即一次函数解析式为:y=31527x-,反比例函数解析式为:y=44x;(2)由题意知,AB=5,①当AB=BP时,BP=5,即P点坐标为(0,0)或(10,0),②当AB=AP时,由AD=3知,BP=4,即点P与点B关于点D对称,即P点坐标为(13,0),③当AP=BP时,即P在线段AB的垂直平分线上,设P(m,0),则AP2=(9-m)2+9,BP2=(5-m)2,∴(9-m)2+9=(5-m)2解得:m=658,即P点坐标为(658,0),综上所述,满足题意的P点坐标为:(0,0),(10,0),(13,0),(658,0).k2.(2019·四川达州中考)如图,A、B两点在反比例函数y=1的图象上,C、D两点在反比例函数xkx【答案】4.【解析】解:设A(a,k k k k1),C(a,2)B(b,1),D(b,2)a ab bk k则CA=2﹣1=2,a ak-k k-k即21=2,得a=21,a2k-k k-k同理:BD=12=4,得b=1b4又∵a﹣b=32,∴k-k(x<0)的图象上,则tan∠BAO的值为k-k21-1242=3,解得:k2﹣k1=4.故答案为:4.3.(2019·山东枣庄中考)如图,在平面直角坐标系中,等腰直角三角形A BC的顶点A、B分别在x 轴、y轴的正半轴上,∠ABC=90°,CA⊥x轴,点C在函数y=()kx(x>0)的图象上,若AB=1,则k的值为A.1B.22C.2D.2【答案】A.【解析】解:过点C作CD⊥y轴于D,如图所示,∵CA⊥x轴,∴∠ACO=90°,∴四边形OACD是矩形,∵AB=BC=1,∴S四边形OACD=2△SABC=1,即k=1,故答案为:A.4.(2019·山东潍坊中考)如图,△R t AOB中,∠AOB=90°,顶点A,B分别在反比例函数y=-5>0)与y=x.1x(x(x >0)与 y = (x <0)的图象上,,△S AOC = , =【答案】 5 .【解析】解:过 A 作 AC ⊥x 轴于 C ,过 B 作 BD ⊥x 轴于 D ,则∠BDO =∠ACO =90°,∵点 A ,B 分别在反比例函数 y =1 -5x x∴△S BDO5 1 22∵∠AOB =90°,∴∠BOD +∠DBO =∠BOD +∠AOC =90°,∴∠DBO =∠AOC ,∴△BDO ∽△OCA ,S∴ V BOD =SV AOC(OB )2 (OA )2= 5 ,∴ OB OA= 5 ,∴tan ∠BAO = OB OA= 5 ,故答案为: 5 .合,顶点A,B恰好分别落在函数y=-15.(2019·甘肃陇南中考)如图,已知反比例函数y=kx(k≠0)的图象与一次函数y=-x+b的图象在第一象限交于A(1,3),B(3,1)两点(1)求反比例函数和一次函数的表达式;(2)已知点P(a,0)(a>0),过点P作平行于y轴的直线,在第一象限内交一次函数y=-x+b的图象于点M,交反比例函数y=k上的图象于点N.若PM>PN,结合函数图象直接写出a的取值范围.x【答案】见解析.【解析】解:(1)∵反比例函数y=两点,代入可得:k=3,b=4,kx的图象与一次函数y=-x+b的图象交于A(1,3),B(3,1)即反比例函数和一次函数的表达式分别为y=3x,y=-x+4;(2)由图象可得:当1<a<3时,PM>PN.6.(2019·湖北咸宁中考)在平面直角坐标系中,将一块直角三角板如图放置,直角顶点与原点O重4(x<0),y=(x>0)的图象上,则sin∠ABO的值为()x x(A)13355(B)(C)(D)345【答案】D.【解析】解:过A作AC⊥x轴于C,过B作BD⊥x轴于D,如图所示,设 A ( x ,- ),B ( x , ),x2 x x y 轴的正半轴上,∠ABC =90°,CA ⊥x 轴,点 C 在函数 y = (x >0)的图象上,若 AB =1,则 k 的值为()2C .2∴△AOC ∽△OBD ,∴ OA AC OC = =OB OD BD,1 4 1 121 -OA x - x ∴ = 1 = 1 ,OB x4 22可得: (x x1 2)2 = 4 ,∵ x x <0,1 2∴ x x =-2,1 2即 OA 1 = ,OB 2设 OA =k ,则 OB =2k ,由勾股定理得:AB = 5 k ,在 △R t AOB 中,sin ∠ABO = OA k 5= = ,AB 5k 5故答案为:D .7.(2019·山东枣庄中考)如图,在平面直角坐标系中,等腰直角三角形 ABC 的顶点 A 、B 分别在 x 轴、kxA .1【答案】A .B . 2D .2∴点C的坐标为(,2),∵点C在函数y=的图象上,x+k1+⎪∴C(m+n,0),D(0,k⎛1+⎪),∴△SODM=1n×k +⎪=,△S OCA=(m+n)×=,【解析】解:∵由题意知,∠ABC=90°,CA⊥x轴,AB=1,∴∠BAC=∠BAO=45°,∴OA=OB=22,AC=2,22kx∴k=2×2=1,2故答案为:A.8.(2019·湖南长沙中考)如图,函数y=kx(k为常数,k>0)的图象与过原点的O的直线相交于A,B两点,点M是第一象限内双曲线上的动点(点M在点A的左侧),直线AM分别交x轴,y轴于C,D两点,连接BM分别交x轴,y轴于点E,△F.现有以下四个结论:①ODM与△OCA的面积相等;②若BM⊥AM于点M,则∠MBA=30°;③若M点的横坐标为1,△OAM为等边三角形,则k=2+3;④若MF==2MA.其中正确的结论的序号是.25MB,则MD【答案】①③④.【解析】解:①设点A(m,kmk),M(n,),n则直线AC的解析式为y=﹣k⎛1⎫,mn⎝m n⎭⎝m1⎫n⎭2⎛11⎫k(m+n)1k k(m+n)⎝m n⎭2m2m2m∴△ODM与△OCA的面积相等,故①正确;∵反比例函数与正比例函数关于原点对称,∴O是AB的中点,∵BM⊥AM,∴OM=OA,∴k=mn,∴A(m,n),M(n,m),∴AM=2(n﹣m),OM=m2+n2,∴AM不一定等于OM,即∠BAM不一定是60°,∴∠MBA不一定是30°.故②错误,∵M点的横坐标为1,设M(1,△k),OAM为等边三角形,∴OA=OM=AM,∴1+k2=m2+k2 m2,∴m=k,∵OM=AM,∴(1﹣m)2+=1+k2,∴k2﹣4k+1=0,∴k=2±3,∵m>1,∴k=2+3,故③正确,如图,作MK∥OD交OA于K,y∵OF∥MK,∴FM OK2==,BM KB5OK2∴=,OB3∵OA=OB,∴OK=2,AK∵KM∥OD,∴DM OK==2,AM AK∴DM=2AM,故④正确.故答案为:①③④.9.(2019·湖北荆门中考)如图,在平面直角坐标系中,函数=k(k>0,x>0)的图象与等边三角形OABx的边O A,AB分别交于点M,N,且O M=2MA,若AB=3,那么点N的横坐标为.【答案】3+5.2【解析】解:由题意知,OA=OB=AB=3,∵OM=2MA,∠AOM=∠A=∠ABO=60°,∴OM=2,AM=1,则M点横坐标为1,纵坐标为3,解得:x=或x=(∵N在M的左侧,而<2,舍去),3+510.(2019·河南开封二模)如图,在平面直角坐标系xOy中,已知正比例函数y=﹣2x的图象与反比例函数y2=的图象交于A(﹣1,n),B两点.把A(﹣1,2)代入y=,可得k=﹣2,∴k=3,设N点坐标为(x,3),x过N作NH⊥x轴于H,则NH=3BH,∴3x=3(3-x),3+53-53-5222故答案为:.21kx(1)求出反比例函数的解析式及点B的坐标;(2)观察图象,请直接写出满足y≤2的取值范围;(3)点P是第四象限内反比例函数的图象上一点,若△POB的面积为1,请直接写出点P的横坐标.【答案】见解析.【解析】解:(1)把A(﹣1,n)代入y=﹣2x,得n=2,∴A(﹣1,2),kx∴反比例函数的表达式为 y =﹣ ,△S POB =1,m ),则×(2+ m )(m ﹣1)=1 或 (2+ m )(1﹣m )=1, 2 或 2 (舍), 2 或2 x ∵点 B 与点 A 关于原点对称,∴B (1,﹣2).(2)∵A (﹣1,2),∴y ≤2 的取值范围是:x <﹣1 或 x >0;(3)作 BM ⊥x 轴于 M ,PN ⊥x 轴于 N ,∵S = 梯形 MBPN设 P (m ,﹣ 2 1 2 2 1 2 2 整理得,m 2﹣m ﹣1=0 或 m 2+m +1=0,解得 m = 1 + 51 - 52 (舍)或 5 - 12 或 - 5 - 1 ∴P 点的横坐标为 1 + 5 5 -12 .。
反比例函数图象上的动点问题

反比例函数图像上的动点问题——反比例函数复习一、开门见山揭示课题二、复习过程演绎(一)问题1教学出示右图:如图,坐标系内有一点A(2,4),有一反比例函数图像经过A点。
则它的函数关系式是什么?(学生口答)变:过A作AD⊥x轴于D,连结OA,则S△AOD=___.学生口答。
(预设两种:S△AOD=12OD×AD=4, S△AOD=12×8)师:你是怎么知道的?总结:①把点的坐标转化为线段的长,往往是解决直角坐标系中有关图形计算的手段(预设1);变1:若C是图像上的一个动点,也构造这样的直角三角形COF,则面积为多少?你的理由?S△AOD=12︳k︳(根据学生回答,引出C为动点)师:提问:连结AC,在这个图形中,你还能找出其他面积相等的部分吗?(学生在工作单上试做)学生回答:(1)S△AOM =S梯MDFC;S△AOC =S△ADFC板书(移动几何画板观看)变2:若C点坐标为(4,2),求S△AOC生说师写过程(板书转化思想)变3:S△AOC=6,求C点坐标学生试做。
优生板演。
毕。
师:请大家仔细看黑板上同学所做题目。
请给与评价。
有哪些地方值得你欣赏的?哪些地方你觉得要修正的?(老师根据学生所言,共同规范书写过程)板书分类思想阶段评价(二)出示问题2变4:延长AO交图像于点B,则B点坐标为多少?(口答)师:你的理由?(中心对称图形)延长CO、AO交图像的另一分支于点E、B,连结AF、BF,四边形AEBC是什么4)特殊四边形?理由?提问:四边形AEBC变5:点C求此时点C的坐标;有可能是菱形吗?你有理由吗?三、总结:谈谈本节课的收获。
“两种解题方法:求面积,一般性图形。
初中数学反比例函数动点问题

反比例函数 ---动点、面积专项
k旳图象在第一象限旳分支上有一点A(3,4),P为x轴正半轴上旳1.反比例函数y=
x
一种动点,(1)求反比例函数解析式. (2)当P在什么位置时,△OPA为直角三角形,求出此时P点旳坐标.
2、如图,M点是正比例函数y=kx和反比例函数旳图象旳一种交点.
(1)求这两个函数旳解析式;
(2)在反比例函数旳图象上取一点P,过点P做PA垂直于x轴,垂足为A,点Q 是直线MO上一点,QB垂直于y轴,垂足为B,直线MO上与否存在这样旳点Q,使得△OBQ旳面积是△OPA旳面积旳2倍?如果存在,祈求出点Q旳坐标,如果不存在,请阐明理由.
3、如图1,已知正比例函数和反比例函数旳图象都通过点M(﹣2,﹣1),且P(﹣1,﹣2)为双曲线上旳一点,Q为坐标平面上一动点,PA垂直于x轴,QB垂直于y轴,垂足分别是A、B.
(1)写出正比例函数和反比例函数旳关系式;
(2)当点Q在直线MO上运动时,直线MO上与否存在这样旳点Q,使得△OBQ与△OAP面积相等如果存在,祈求出点旳坐标,如果不存在,请阐明理由;
(3)如图2,当点Q在第一象限中旳双曲线上运动时,作以OP、OQ为邻边旳平行四边形OPCQ,求平行四边形OPCQ周长旳最小值.。
中考数学反比例函数的综合热点考点难点及详细答案

中考数学反比例函数的综合热点考点难点及详细答案一、反比例函数1.如图,反比例函数y= 的图象经过点A(﹣1,4),直线y=﹣x+b(b≠0)与双曲线y= 在第二、四象限分别相交于P,Q两点,与x轴、y轴分别相交于C,D两点.(1)求k的值;(2)当b=﹣2时,求△OCD的面积;(3)连接OQ,是否存在实数b,使得S△ODQ=S△OCD?若存在,请求出b的值;若不存在,请说明理由.【答案】(1)解:∵反比例函数y= 的图象经过点A(﹣1,4),∴k=﹣1×4=﹣4;(2)解:当b=﹣2时,直线解析式为y=﹣x﹣2,∵y=0时,﹣x﹣2=0,解得x=﹣2,∴C(﹣2,0),∵当x=0时,y=﹣x﹣2=﹣2,∴D(0,﹣2),∴S△OCD= ×2×2=2(3)解:存在.当y=0时,﹣x+b=0,解得x=b,则C(b,0),∵S△ODQ=S△OCD,∴点Q和点C到OD的距离相等,而Q点在第四象限,∴Q的横坐标为﹣b,当x=﹣b时,y=﹣x+b=2b,则Q(﹣b,2b),∵点Q在反比例函数y=﹣的图象上,∴﹣b•2b=﹣4,解得b=﹣或b= (舍去),∴b的值为﹣.【解析】【分析】(1)根据反比例函数的图象上点的坐标特征易得k=﹣4;(2)当b=﹣2时,直线解析式为y=﹣x﹣2,则利用坐标轴上点的坐标特征可求出C(﹣2,0),D(0,﹣2),然后根据三角形面积公式求解;(3)先表示出C(b,0),根据三角形面积公式,由于S△ODQ=S△OCD,所以点Q和点C到OD的距离相等,则Q的横坐标为(﹣b,0),利用直线解析式可得到Q(﹣b,2b),再根据反比例函数的图象上点的坐标特征得到﹣b•2b=﹣4,然后解方程即可得到满足条件的b的值.2.如图,一次函数y=kx+b(k<0)与反比例函数y= 的图象相交于A、B两点,一次函数的图象与y轴相交于点C,已知点A(4,1)(1)求反比例函数的解析式;(2)连接OB(O是坐标原点),若△BOC的面积为3,求该一次函数的解析式.【答案】(1)解:∵点A(4,1)在反比例函数y= 的图象上,∴m=4×1=4,∴反比例函数的解析式为y=(2)解:∵点B在反比例函数y= 的图象上,∴设点B的坐标为(n,).将y=kx+b代入y= 中,得:kx+b= ,整理得:kx2+bx﹣4=0,∴4n=﹣,即nk=﹣1①.令y=kx+b中x=0,则y=b,即点C的坐标为(0,b),∴S△BOC= bn=3,∴bn=6②.∵点A(4,1)在一次函数y=kx+b的图象上,∴1=4k+b③.联立①②③成方程组,即,解得:,∴该一次函数的解析式为y=﹣x+3【解析】【分析】(1)由点A的坐标结合反比例函数系数k的几何意义,即可求出m的值;(2)设点B的坐标为(n,),将一次函数解析式代入反比例函数解析式中,利用根与系数的关系可找出n、k的关系,由三角形的面积公式可表示出来b、n的关系,再由点A在一次函数图象上,可找出k、b的关系,联立3个等式为方程组,解方程组即可得出结论.3.已知反比例函数y= 的图象经过点A(﹣,1).(1)试确定此反比例函数的解析式;(2)点O是坐标原点,将线段OA绕O点顺时针旋转30°得到线段OB.判断点B是否在此反比例函数的图象上,并说明理由;(3)已知点P(m, m+6)也在此反比例函数的图象上(其中m<0),过P点作x轴的垂线,交x轴于点M.若线段PM上存在一点Q,使得△OQM的面积是,设Q点的纵坐标为n,求n2﹣2 n+9的值.【答案】(1)解:由题意得1= ,解得k=﹣,∴反比例函数的解析式为y=﹣(2)解:过点A作x轴的垂线交x轴于点C.在Rt△AOC中,OC= ,AC=1,∴OA= =2,∠AOC=30°,∵将线段OA绕O点顺时针旋转30°得到线段OB,∴∠AOB=30°,OB=OA=2,∴∠BOC=60°.过点B作x轴的垂线交x轴于点D.在Rt△BOD中,BD=OB•sin∠BOD= ,OD= OB=1,∴B点坐标为(﹣1,),将x=﹣1代入y=﹣中,得y= ,∴点B(﹣1,)在反比例函数y=﹣的图象上(3)解:由y=﹣得xy=﹣,∵点P(m, m+6)在反比例函数y=﹣的图象上,其中m<0,∴m( m+6)=﹣,∴m2+2 m+1=0,∵PQ⊥x轴,∴Q点的坐标为(m,n).∵△OQM的面积是,∴OM•Q M= ,∵m<0,∴mn=﹣1,∴m2n2+2 mn2+n2=0,∴n2﹣2 n=﹣1,∴n2﹣2 n+9=8.【解析】【分析】(1)由于反比例函数y= 的图象经过点A(﹣,1),运用待定系数法即可求出此反比例函数的解析式;(2)首先由点A的坐标,可求出OA的长度,∠AOC的大小,然后根据旋转的性质得出∠AOB=30°,OB=OA,再求出点B的坐标,进而判断点B是否在此反比例函数的图象上;(3)把点P(m, m+6)代入反比例函数的解析式,得到关于m的一元二次方程;根据题意,可得Q点的坐标为(m,n),再由△OQM的面积是,根据三角形的面积公式及m<0,得出mn的值,最后将所求的代数式变形,把mn的值代入,即可求出n2﹣2 n+9的值.4.心理学家研究发现,一般情况下,一节课40分钟中,学生的注意力随教师讲课的变化而变化.开始上课时,学生的注意力逐步增强,中间有一段时间学生的注意力保持较为理想的稳定状态,随后学生的注意力开始分散.经过实验分析可知,学生的注意力指标数y 随时间x(分钟)的变化规律如下图所示(其中AB、BC分别为线段,CD为双曲线的一部分):(1)开始上课后第五分钟时与第三十分钟时相比较,何时学生的注意力更集中?(2)一道数学竞赛题,需要讲19分钟,为了效果较好,要求学生的注意力指标数最低达到36,那么经过适当安排,老师能否在学生注意力达到所需的状态下讲解完这道题目?【答案】(1)解:设线段AB所在的直线的解析式为y1=k1x+20,把B(10,40)代入得,k1=2,∴y1=2x+20.设C、D所在双曲线的解析式为y2= ,把C(25,40)代入得,k2=1000,∴当x1=5时,y1=2×5+20=30,当,∴y1<y2∴第30分钟注意力更集中.(2)解:令y1=36,∴36=2x+20,∴x1=8令y2=36,∴,∴∵27.8﹣8=19.8>19,∴经过适当安排,老师能在学生注意力达到所需的状态下讲解完这道题目.【解析】【分析】(1)根据一次函数和反比例函数的应用,用待定系数法求出线段AB所在的直线的解析式,和C、D所在双曲线的解析式;把x1=5时和进行比较得到y1<y2,得出第30分钟注意力更集中;(2)当y1=36时,得到x1=8,当y2=36,得到,由27.8﹣8=19.8>19,所以经过适当安排,老师能在学生注意力达到所需的状态下讲解完这道题目.5.一次函数y=ax+b(a≠0)的图象与反比例函数y= (k≠0)的图象相交于A,B两点,与y轴交于点C,与x轴交于点D,点D的坐标为(﹣1,0),点A的横坐标是1,tan∠CDO=2.过点B作BH⊥y轴交y轴于H,连接AH.(1)求一次函数和反比例函数的解析式;(2)求△ABH面积.【答案】(1)解:∵点D的坐标为(﹣1,0),tan∠CDO=2,∴CO=2,即C(0,2),把C(0,2),D(﹣1,0)代入y=ax+b可得,,解得,∴一次函数解析式为y=2x+2,∵点A的横坐标是1,∴当x=1时,y=4,即A(1,4),把A(1,4)代入反比例函数y= ,可得k=4,∴反比例函数解析式为y=(2)解:解方程组,可得或,∴B(﹣2,﹣2),又∵A(1,4),BH⊥y轴,∴△ABH面积= ×2×(4+2)=6.【解析】【分析】(1)先由tan∠CDO=2可求出C坐标,再把D点坐标代入直线解析式,可求出一次函数解析式,再由直线解析式求出A坐标,代入双曲线解析式,可求出双曲线解析式;(2)△ABH面积可以BH为底,高=y A-y B=4-(-2)=6.6.如图1,已知一次函数y=ax+2与x轴、y轴分别交于点A,B,反比例函数y= 经过点M.(1)若M是线段AB上的一个动点(不与点A、B重合).当a=﹣3时,设点M的横坐标为m,求k与m之间的函数关系式.(2)当一次函数y=ax+2的图象与反比例函数y= 的图象有唯一公共点M,且OM= ,求a的值.(3)当a=﹣2时,将Rt△AOB在第一象限内沿直线y=x平移个单位长度得到Rt△A′O′B′,如图2,M是Rt△A′O′B′斜边上的一个动点,求k的取值范围.【答案】(1)解:当a=﹣3时,y=﹣3x+2,当y=0时,﹣3x+2=0,x= ,∵点M的横坐标为m,且M是线段AB上的一个动点(不与点A、B重合),∴0<m<,,DANG则,﹣3x+2= ,当x=m时,﹣3m+2= ,∴k=﹣3m2+2m(0<m<)(2)解:由题意得:,ax+2= ,ax2+2x﹣k=0,∵直线y=ax+2(a≠0)与双曲线y= 有唯一公共点M时,∴△=4+4ak=0,ak=﹣1,∴k=﹣,则,解得:,∵OM= ,∴12+(﹣)2=()2,a=±(3)解:当a=﹣2时,y=﹣2x+2,∴点A的坐标为(1,0),点B的坐标为(0,2),∵将Rt△AOB在第一象限内沿直线y=x平移个单位得到Rt△A′O′B′,∴A′(2,1),B′(1,3),点M是Rt△A′O′B′斜边上一动点,当点M′与A′重合时,k=2,当点M′与B′重合时,k=3,∴k的取值范围是2≤k≤3【解析】【分析】(1)当a=﹣3时,直线解析式为y=﹣3x+2,求出A点的横坐标,由于点M的横坐标为m,且M是线段AB上的一个动点(不与点A、B重合)从而得到m的取值范围,由﹣3x+2= ,由X=m得k=﹣3m2+2m(0<m<);(2)由ax+2= 得ax2+2x﹣k=0,直线y=ax+2(a≠0)与双曲线y= 有唯一公共点M时,△=4+4ak=0,ak=﹣1,由勾股定理即可;(3)当a=﹣2时,y=﹣2x+2,从而求出A、B两点的坐标,由平移的知识知A′,B′点的坐标,从而得到k的取值范围。
专题. 反比例函数(动点问题)(巩固篇)(专项练习)八年级数学下册基础知识专项讲练(苏科版)

专题11.30反比例函数(动点问题)(巩固篇)(专项练习)一、单选题1.如图,点M 是反比例函数y =4x(x <0)图象上一点,MN ⊥y 轴于点N .若P 为x 轴上的一个动点,则△MNP 的面积为()A .2B .4C .6D .无法确定2.如图,点A 是双曲线3y x =在第一象限上的一个动点,连接AO 并延长交另一分支于点B ,以AB 为边作等边△ABC ,点C 在第四象限.下列结论:①连接OC ,则AB OC ⊥;②点C 在函数()90y x x =->上运动.则()A .①对②错B .①错②对C .①②都对D .①②都错3.如图,过双曲线(0)ky x x =>上的动点A 作AB x ⊥轴于点B ,P 是直线AB 上的点,且满足2AP AB =,过点P 作x 轴的平行线交此双曲线于点C .如果APC △的面积为8,则k 的值为()A .10B .8C .16D .124.如图,矩形OABC 的顶点О与坐标原点重合,边OA ,OC 分别落在x 轴和y 轴上,点B 的坐标为()42,,点D 是边BC 上一动点,函数()0ky x x=>的图像经过点D ,且与边AB 交于点E ,连接OB 、OD .若线段OB 平分AOD ∠,则点E 的纵坐标为()A .12B .34C .1D .325.如图,A 、B 是函数y =12x上两点,P 为一动点,作PB ∥y 轴,PA ∥x 轴.若S △BOP =3.6,则S △ABP =()A .3.6B .4.8C .5.4D .66.如图,在平面直角坐标系中,A (8,0),点B 为一次函数y x =图像上的动点,以OB 为边作正方形OBCD ,当AB 最小时,点D 恰好落在反比例函数k y x =的图像上,则k =()A .-9B .-12C .-16D .-257.如图,线段AB 是直线y =x +1的一部分,其中点A 在y 轴上,点B 横坐标为2,曲线BC 是双曲线k y x=(0k ≠)的一部分,由点C 开始不断重复“A−B−C”的过程,形成一组波浪线,点P(2019,m )与Q(2025,n )均在该波浪线上,G 为x 轴上一动点,则△PQG 周长的最小值为()A .16B .6+C .6+D .98.如图,将边长为10的正三角形OAB 放置于平面直角坐标系xOy 中,C 是AB 边上的动点(不与端点A ,B 重合),作CD ⊥OB 于点D ,若点C ,D 都在双曲线y =k x上(k >0,x >0),则k 的值为()A .B .C .9D .9.如图,已知点A 是直线y=x 与反比例函数y=(k >0,x >0)的交点,B 是y=图象上的另一点,BC ∥x 轴,交y 轴于点C .动点P 从坐标原点O 出发,沿O→A→B→C (图中“→”所示路线)匀速运动,终点为C ,过点P 作PM ⊥x 轴,PN ⊥y 轴,垂足分别为M ,N .设四边形OMPN 的面积为S ,P 点运动时间为t ,则S 关于t 的函数图象大致为()A .B .C .D .10.如图,反比例函数2y x =和正比例函数12y x =的图象交于点M ,N ,动点(),0P m 在x 轴上.若PMN 为直角三角形,则m 的值为()A .2m =5B .52m =52C .2m =±或52D .52m =±或5二、填空题11.如图,点()2,2A -在反比例函数k y x=的图象上,点M 在x 轴的正半轴上,点N 在y 轴的负半轴上,且5OM ON ==.点(),P x y 是线段MN 上一动点,过点A 和P 分别作x 轴的垂线,垂足为点D 和E ,连接OA 、OP .当OAD OPE S S < 时,x 的取值范围是________.12.如图,已知点A 是反比例函数3y x=-(0x <)的图像上的一个动点,连接OA ,若将线段OA 绕点O 顺时针旋转90°得到线段OB ,则点B 所在反比例图像的函数关系式是____.13.如图,点A 是双曲线4y x=在第一象限上的一动点,连接AO 并延长交另一分支于点B ,以AB 为斜边作等腰Rt △ABC ,点C 在第二象限,随着点A 的运动,点C 的位置也不断的变化,但始终在一函数图象上运动,则这个函数的解析式为_____.14.如图,A 、B 是函数y =12x图象上两点,P 为一动点.作PB ∥y 轴.PA ∥x 轴,下列说法中:①AOP BOP ≌△△;②AOP BOP S S =;③若OA =OB ,则OP 平分∠AOB ;④若4BOP S =,则16ABP S =.正确的序号是___.15.如图,点A 为反比例函数k y x=图象上的一点,过点A 作AB ⊥y 轴于B ,点C 为x 轴上的一个动点,△ABC 的面积为3,则k 的值为________.16.如图,点A 、B 是反比例函数y 12x =图象上的两个动点,过点A 、B 分别作AC ⊥x 轴、BD ⊥x 轴,分别交反比例函数y 3x=-图象于点C 、D ,得四边形ACBD 是平行四边形.当点A 、B 不断运动时,现有以,结论:①▱ACBD 可能是菱形;②▱ACBD 不可能是矩形;③▱ACBD 可能是正方形;④▱ACBD 不可能是正方形.其中正确的是_____.(写出所有正确结论的序号)17.如图,函数112y x =+与函数(0)k y x x =>图像的交于点P ,点P 的纵坐标为4,PB x ⊥轴,垂足为点B ,点M 是函数(0)ky x x =>图像上一动点(不与P 点重合),过点M 作MD AP⊥于点D ,若45PMD ∠=︒,点M 的坐标是________.18.如图,点A 是反比例函数()280y x x=>的图象上的一动点,过点A 分别作x 轴、y 轴的平行线,与反比例函数1k y x=(0k ≠,0x >)的图象交于点B 、点C ,连接OB ,OC .若四边形OBAC 的面积为5,则k =________.三、解答题19.如图,一次函数114y k x =+与反比例函数22k y x=的图象交于点()2,A m 和()6,2B --,与y 轴交于点C .(1)1k =,2k =;(2)过点A 作AD x ⊥轴于点D ,点P 是反比例函数在第一象限的图象上一点,设直线OP与线段AD 交于点E ,当:4:1ODE ODAC S S ∆=四边形时,求点P 的坐标.(3)点M 是坐标轴上的一个动点,点N 是平面内的任意一点,当四边形ABMN 是矩形时,求出点M 的坐标.20.如图,反比例函数1k y x=的图像与一次函数2y mx n =+的图像相交于(),1A a -,()1,3B -两点.(1)求反比例函数和一次函数的解析式;(2)点P 在线段AB 上,且:1:2AOP BOP S S = ,直接写出点P 的坐标;(3)设直线AB 交y 轴于点C ,点(),0N t 是x 轴正半轴上的一个动点,过点N 作NM x ⊥轴交反比例函数1k y x=的图像于点M ,连接CN ,OM .若S 四边形COMN >3,直接写出t 的取值范围.21.如图,在平面直角坐标系中,直线y x =与反比例函数图象交于点(),A a a ,点1,22B a a ⎛⎫ ⎪⎝⎭为反比例函数()0k y x x =>图象上的点,连接OB ,AB ,且AOB S ∆为3.(1)求反比例函数的解析式;(2)点P 为y 轴上一动点,当ABP 的周长最小时,直接写出点P 的坐标.22.一次函数2y x =--的图象与反比例函数k y x=的图象相交于()3,A m -,(),3B n -两点.(1)求这个反比例函数的解析式;(2)根据图象写出使一次函数值不大于反比例函数值的x 的取值范围.(3)若动点E 在y 轴上,且6EBA S =△,求动点E 的坐标.23.如图,一次函数()110y k x b k =+≠的图象与反比例函数()220k y k x=≠的图象交于点()14A ,,()4B n -,两点.(1)求一次函数和反比例函数的表达式;(2)连接AO 并延长交双曲线于点C ,点D 为y 轴上一动点,点E 为直线AB 上一动点,连接CD ,DE ,求当CD DE +最小时点D 的坐标;24.如图,点A 在反比例函数(00)m y m x x =>>,的图像上,点A 的纵坐标为3.过点A 作x 轴的平行线交反比例函数(0)n y n m x x=>>,的图像于点C .点P 为线段AC 上一动点,过点P 作AC 的垂线,分别交反比例函数m y x =和n y x =的图像于点B ,D .(1)当416m n ==,时,①若点P 的横坐标为4(如图1),求直线AB 的函数表达式;②若点P 是AC 的中点(如图2),试判断四边形ABCD 的形状,并说明理由;(2)四边形ABCD 能否成为正方形?若能,求此时m ,n 之间的数量关系;若不能,说明理由.参考答案1.A 【分析】根据1()2MNP P M S MN y y ∆=⋅-求解.解:设点M 坐标为(,)a b ,点M 在反比例函数图象上,4ab ∴=,111()()()2222MNP P M S MN y y a b ab ∆∴=⋅-=⨯--==.故选:A .【点拨】本题考查反比例函数系数k 的几何意义,解题关键是掌握xy k =,掌握坐标系内求图形面积的方法.2.C【分析】设点A 的坐标为(a ,3a),连接OC ,则OC ⊥AB ,表示出OC ,过点C 作CD ⊥x 轴于点D ,设出点C 坐标,在Rt △OCD 中,利用勾股定理可得出x 2的值,进而得出结论.解:如图,设A (a ,3a ),点C 始终在双曲线()0k y x x=->上运动,∵点A 与点B 关于原点对称,∴OA =OB ,∵△ABC 为等边三角形,∴AB ⊥OC ,OC,∵AO =∴CO 过点C 作CD ⊥x 轴于点D ,则可得∠AOD =∠OCD (都是∠COD 的余角),设点C 的坐标为(x ,y ),则tan ∠AOD =tan ∠OCD ,即3x a a y =-,解得23a y x =-.在Rt △COD 中,CD 2+OD 2=OC 2,即2222273y x a a +=+,将23a y x =-代入,可得:2227x a =,故23a x y x ==-=,则xy =-9,即k =-9,所以,点C 在函数()90y x x=->上运动.所以,①②都对,故选:C .【点拨】本题考查的是反比例函数图象上点的坐标特点,熟知反比例函数图象上各点的坐标一定适合此函数的解析式是解答此题的关键.3.D【分析】设AB =a ,则PB =3a ,从而得到B kx a =,3C k x a =,根据矩形的性质,得到PC =AD =BE =B C x x -,利用三角形面积为载体建立等式计算即可.解:设AB =a ,则PB =3a ,过点C 作CE ⊥x 轴,垂足为E ,过点A 作AD ∥x 轴,交CE 于点D ,则四边形APCD 是矩形,四边形BPCE 是矩形,∴CE =PB =3a ,∵点A 、点C 都在函数(0)k y x x =>的图像上,∴A B k x x a==,3C k x a =,根据矩形的性质,得到PC =AD =BE =B C x x -=3kk a a -,∵APC △的面积为8,∴1(2823kk a a a-⨯=,解得k =12,故选D .【点拨】本题考查了反比例函数的图像及其性质,矩形的判定和性质,三角形面积计算,熟练掌握反比例函数的性质是解题的关键.4.B【分析】先根据矩形的性质,角平分线定义得出DBO DOB ∠=∠,然后根据等腰三角形的判定得出BD OD =,在Rt COD 中根据勾股定理可求出CD ,从而求出点D 的坐标,根据待定系数法求出反比例函数解析式,最后把4x =代入求解即可.解:解∶∵OB 平分AOD ∠,∴AOB DOB ∠=∠,∵四边形ABCD 是矩形,()42B ,,∴BC OA ∥,4BC AO ==,2==OC AB ,90BCO ∠=︒,∴DBO AOB ∠=∠,∴DBO DOB ∠=∠,∴BD OD =,设BD OD a ==,则4CD BC BD a =-=-,在Rt COD 中,222CO CD OD +=,∴()22242a a -+=,解得52a =,∴32CD =,∴3,22D ⎛⎫ ⎪⎝⎭,∴3232k =⨯=,∴3y x =,当4x =时,34y =,∴点E 的纵坐标为34.故选:B .【点拨】本题考查了矩形的性质,等腰三角形的判定,勾股定理,待定系数法等知识,正确求出点D 的坐标是解题的关键.5.C【分析】延长BP ,交x 轴于点C ,由题意可设点1212,,,A a B b a b ⎛⎫⎛⎫ ⎪ ⎪⎝⎭⎝⎭,则有1212,,AP a b BP OC b b a=-=-=,然后由S △BOP =3.6可进行求解问题.解:延长BP ,交x 轴于点C ,如图所示:∵PB ∥y 轴,PA ∥x 轴,∴AP BP ⊥,BC x ⊥轴,由题意可设点1212,,,A a B b a b ⎛⎫⎛⎫ ⎪ ⎪⎝⎭⎝⎭,则有1212,,AP a b BP OC b b a =-=-=,∵S △BOP =3.6,∴1 3.62BP OC ⋅=,即12127.2b b a ⎛⎫-= ⎪⎝⎭,解得:25b a =,∴()111212130123 5.42225APB S AP BP a b a b a a a ⎛⎫⎛⎫=⋅=--=⨯-⨯= ⎪ ⎪⎝⎭⎝⎭ ;故选C .【点拨】本题主要考查反比例函数与几何的综合,熟练掌握反比例函数的性质及几何意义是解题的关键.6.C【分析】根据垂线段最短可得,当AB 垂直直线y x =时AB 最短,此时△AOB 是等腰直角三角形,易求OB =42D 作DE ⊥x 轴于点E ,知△DEO 为等腰直角三角形,求出DE ,OE 的长即可得到结论.解:根据垂线段最短可得,当AB 垂直直线y x =时AB 最短,∵∠AOB =45°∴∠BAO =45°∴△AOB 是等腰直角三角形,∵点A 的坐标为(8,0)∴OA =8∴42BO BA ==∵四边形OBCD 是正方形,∴90DO BO DOB ==∠=︒∴45DOC BOC ∠=∠=︒过点D 作DE ⊥x 轴于点E ,∴45ODE DOE ∠=∠=︒∴△DEO 为等腰直角三角形,∴4DE OE ==∵点D 在第二象限,∴D (-4,4)又点D 在反比例函数k y x=的图像上∴(4)416k =-⨯=-故选:C .【点拨】本题考查了最短路径问题、待定系数法求函数解析式、正方形的性质等知识,解答此题的关键是正确求出点D 的坐标.7.B【分析】由点B 在直线y=x+1上,点B 横坐标为2,可求纵坐标,确定点B 的坐标,进而求出反比例函数的关系式,再确定点C 的坐标,由点C 开始不断重复“A-B-C”的过程,可以推断点P (2019,m )与Q (2025,n )具体所在的位置,再依据对称,求线段的和最小的方法求出答案.解:当x=2时,y=x+1=2+1=3,∴B (2,3)∵B (2,3)在双曲线k y x =上,∴k=6把x=6代入6y x=得:y=1,∴C (6,1)∵2019÷6=336……3,2025÷6=337……3,∴点P 落在第337个“A-B-C”的P 处,而点Q 落在第338个“A-B-C”的Q 处,示意如图:把3x =代入6,y x =2,y ∴=∴P (2019,2),Q (2025,2),PQG 周长的最小,PQ=6定值,∴只要GP+GQ 最小即可,过Q 作QH x ⊥轴,使Q,H 关于x 轴对称,连接HP 交x 轴于,G ()2025,2,H ∴-6,4,PQ QH ∴==由勾股定理得:PH =∴PQG 周长的最小值为PQ+GP+GQ=6PH PQ +=+故选B .【点拨】考查反比例函数、一次函数的图象和性质,轴对称性质的应用,根据规律推断出点P 、Q 的位置,找出点G 的位置,依据勾股定理求出线段的长,是解决问题的关键.8.D【分析】根据等边三角形的性质表示出D ,C 点坐标,进而利用反比例函数图象上点的坐标特征得出答案.解:过点D 作DE ⊥x 轴于点E ,过C 作CF ⊥x 轴于点F ,如图所示.可得:∠ODE =30°,∠BCD =30°,设OE =a ,则OD =2a ,DE a ,∴BD =OB ﹣OD =10﹣2a ,BC =2BD =20﹣4a ,AC =AB ﹣BC =4a ﹣10,∴AF =12AC =2a ﹣5,CF AF 2a ﹣5),OF =OA ﹣AF =15﹣2a ,∴点D (a a ),点C [15﹣2a 2a ﹣5)].∵点C 、D 都在双曲线y =k x 上(k >0,x >0),∴a a =(15﹣2a )2a ﹣5),解得:a =3或a =5.当a =5时,DO =OB ,AC =AB ,点C 、D 与点B 重合,不符合题意,∴a =5舍去.∴点D (3,∴k =故选D .【点拨】本题考查了反比例函数图象上点的坐标特征以及等边三角形的性质,解题的关键是找出点D 、C 的坐标.9.B解:设点P 的运动速度为v ,①由于点A 在直线y=x 上,故点P 在OA 上时,四边形OMPN 为正方形,四边形OMPN 的面积S=(vt )2,②点P 在反比例函数图象AB 时,由反比例函数系数几何意义,四边形OMPN 的面积S=k ;③点P 在BC 段时,设点P 到点C 的总路程为a ,则四边形OMPN 的面积=OC•(a ﹣vt )=﹣2OC v ⋅t+2OC a ⋅,只有B 选项图形符合.故选B .考点:动点问题的函数图象.10.D 【分析】联立方程组212y x y x ⎧=⎪⎪⎨⎪=⎪⎩并求解,得到(2,1),(2,1)M N --,由两点间距离公式求出,,PM PN MN 的长,再分90,90,90PMN PNM MPN ∠=︒∠=︒∠=︒三种情况依据勾股定理列出方程求解即可解:联立方程组得212y x y x ⎧=⎪⎪⎨⎪=⎪⎩,解得,21x y =-⎧⎨=-⎩或21x y =⎧⎨=⎩,(2,1),(2,1)M N ∴--∵(),0P m ∴[][]2222(2)0(1)45,PN m m m =--+--=++222(22)(11)20,MN =--+--=2222(2)(01)45,PM m m m =-+-=-+①若90PNM ∠=︒时,则有222PN MN PM +=,22452045m m m m ∴+++=-+,5,2m \=-②若90MPN ∠=︒时,则有222PM PN MN +=,22454520.m m m m ∴-++++=,m ∴=③若90PMN ∠=︒时,则有222PM MN PN +=,22452045m m m m ∴-++=++,52m ∴=;综上所述,m 的值为52±或故选:D .【点拨】本题考查了一次函数与反比例函数的交点问题,正确进行分类讨论是解题的关键.11.14x <<【分析】先求出反比例函数的解析式,再求出线段MN 的解析式,最后联立两个解析式求出B 和C 两个点的坐标,再根据k 的几何意义,确定P 点位置,即可得到相应的x 的取值范围.解:∵点()2,2A -∴()224k =⨯-=-,所以反比例函数的解析式为:4y x=-,因为5OM ON ==,∴()()5,0,0,5M N -,设线段MN 解析式为:()05y px q x =+≤≤,∴505p q q +=⎧⎨=-⎩,∴15p q =⎧⎨=-⎩,∴线段MN 解析式为:()505y x x =-≤≤,联立以上两个解析式得:54y x y x =-⎧⎪⎨=-⎪⎩,解得:14x y =⎧⎨=-⎩或41x y =⎧⎨=-⎩,经检验,符合题意;由图可知,两个函数的图像交点分别为点B 和点C ,∴()1,4B -,()4,1C -,∵OAD OPE S S < ,∴P 点应位于B 和C 两点之间,∴14x <<,故答案为:14x <<.【点拨】本题涉及到了动点问题,考查了反比例函数的图像与性质、k 的几何意义、待定系数法等内容,解决本题的关键是牢记反比例函数的图像与性质,理解k 的几何意义,以及能联立两个函数的解析式求交点坐标等,本题蕴含了数形结合的思想方法等.12.3y x=【分析】如图,设A (m ,n ),过A 作AC ⊥x 轴于C ,过B 作BD ⊥x 轴于D ,得到AC =n ,OC =-m ,根据反比例函数图象上点的坐标特征可得3=-mn ,根据平角的定义及角的和差关系可得∠OAC =∠BOD ,根据旋转的性质可得OB =OA ,利用AAS 可证明△ACO ≌△ODB ,根据全等三角形的性质得到AC =OD =n ,CO =BD =-m ,可得点B 坐标,利用待定系数法即可得答案.解:如图,设A (m ,n ),过A 作AC ⊥x 轴于C ,过B 作BD ⊥x 轴于D ,∵点A 是反比例函数3y x=-(0x <)的图像上的一个动点,∴3=-mn ,AC =n ,OC =-m ,∵将线段OA 绕点O 顺时针旋转90°得到线段OB ,∴∠AOB =90°,OA =OB ,∴∠OAC +∠AOC =∠BOD +∠AOC =90°,∴∠OAC =∠BOD ,在△ACO 和△ODB 中,ACO BDO OAC BOD OA OB ∠=⎧⎪∠=∠⎨⎪=⎩,∴△ACO ≌△ODB ,∴AC =OD =n ,CO =BD =-m ,∴B (n ,-m ),设过点B 的反比例函数的解析式为k y x=,∴3k mn =-=,∴点B 所在反比例图像的函数关系式为3y x =,故答案为:3y x=【点拨】本题考查了坐标与图形变化-旋转,反比例函数图形上点的坐标特征,待定系数法求反比例函数的解析式,全等三角形的判定和性质,正确的作出辅助线是解题的关键.13.y =-4x【分析】连结OC ,作CD ⊥x 轴于D ,AE ⊥x 轴于E ,如图,设A 点坐标为4,a a骣琪琪桫,再证明△COD ≌△OAE (AAS ),表示C 点坐标为4,a a骣琪-琪桫,从而可得答案.解:连结OC ,作CD ⊥x 轴于D ,AE ⊥x 轴于E ,如图,设A 点坐标为4,a a骣琪琪桫,∵A 点、B 点是正比例函数图象与双曲线4y x =的交点,∴点A 与点B 关于原点对称,∴OA =OB∵△ABC 为等腰直角三角形,∴OC =OA ,OC ⊥OA ,∴∠DOC +∠AOE =90°,∵∠DOC +∠DCO =90°,∴∠DCO =∠AOE ,∵在△COD 和△OAE 中CDO OEA DCO EOA CO OAìÐ=ÐïïÐ=Ðíï=ïî∴△COD ≌△OAE (AAS ),∴OD =AE =4a,CD =OE =a ,∴C 点坐标为4,a a骣琪-琪桫,∵44a a -=-g ,∴点C 在反比例函数4y x =-图象上.故答案为:4y x=-【点拨】本题考查的是等腰直角三角形的性质,三角形全等的判定与性质,反比例函数的图象与性质,利用三角形的全等确定C 的坐标是解本题的关键.14.②③##③②【分析】由点P 是动点,可判断出①错误,设出点P 的坐标,求出AP 、BP 的长,再利用三角形面积公式计算即可判断出②;利用角平分线定理的逆定理可判断③;先求出矩形OMPN 的面积为4,进而得出mn =4,最后用三角形的面积公式解答即可.解:∵点P 是动点,∴BP 与AP 不一定相等,∴BOP △与AOP 不一定全等,故①不正确;设P (m ,n ),∵BP ∥y 轴,∴B (m ,12m ),A (12n ,n )∴AP =|12n-m |∴S △AOP =12·|12n-m |n =12|12-mn |同理:S △BOP =12·|12m -n |m =12|12-mn |∴S △AOP =S △BOP ;故②正确;如图1,过点P 作PF ⊥OA 于F ,PE ⊥OB 于E ,∴BOP S =12OB ·PE ,AOP S =12OA ·PF∵BOP AOP S S = ,∴OB ·PE =OA ·PF∵OA =OB ,∴PE =PF ,∵PE ⊥OB ,PF ⊥OA∴OP 是∠AOB 的平分线,故③正确;如图2,延长BP 交x 轴于N ,延长AP 交轴于M ,∵AM ⊥y 轴,BN ⊥x 轴,∴四边形OMPN 是矩形,∵点A ,B 在双曲线y =12x 上,∴6AMO ONB S S == ,∵4BOP S = ,∴2PMO PNO S S == ,∴S 矩形OMPN =4,∴mn =4,∴m =4n ∴12|3|2||BP n n n n m=-=-=,8||12AP m n n =-=∴1182||822||APBS AP BP n n ∆=⨯=⨯⨯=故④不正确;故答案为②③.【点拨】本题属于反比例函数与几何综合题,主要考查了反比例函数的性质、三角形面积公式、角平分线定理逆定理、矩形的判定和性质等知识点,正确作出辅助线并灵活应用所学知识是解答本题的关键.15.6【分析】连接OA ,可得S △ABO =S △ABC =3,根据反比例函数k 的几何意义,可求出k 的值.解:连接OA ,∵AB ⊥y 轴,∴AB ∥x 轴,∴S △ABO =S △ABC =3,即:12|k |=3,∴k =6或k =-6,∵在第二象限,∴k =-6,故答案为:-6.【点拨】考查反比例函数的图象和性质,理解反比例函数k 的几何意义以及同底等高的三角形的面积相等,是解决问题的前提.16.①②④【分析】设A(a,12a),B(b,12b),则C(a,-3a),D(b,-3b),由平行四边形的性质AC=BD列出方程求得a、b的关系,进而得B、C的坐标,根据坐标可以判断BC不与x轴平行,从而判断AC与BD垂直,进而判断③错误;②④正确;根据随着|a|不断变小,AC越来越大,BC越来越小,可以判断AC有可能与BC相等,进而判断①的正误.解:设A(a,12a),B(b,12b),则C(a,-3a),D(b,-3b),∵AC=BD,∴-15a=15b,∴a=-b,∴yC=-3a=3b≠yB=12b,∴BC不与x轴平行,∴AC与BC不可能垂直,∴▱ACBD不可能是矩形,▱ACBD不可能是正方形.故③错误;②④正确;∵随着|a|不断变小,AC越来越大,BC越来越小,∴AC有可能与BC相等,故①正确;故答案为①②④.【点拨】本题主要考查了反比例函数的图象与性质,平行四边形的性质,菱形的判定,矩形、正方形的判定,解题的关键是由平行四边形的对边相等,得出a、b的关系.17.(12,2)【分析】过点D作GH⊥PB,交BP的延长线于G,作MH⊥HG于H,证得△PGD≅△DHM(AAS),得PG=DH,DG=MH,设D(m,112m ),表示出点M的坐标,从而得出m的方程,解方程即可.解:过点D作GH⊥PB,交BP的延长线于G,作MH⊥HG于H,如图所示,∵△PMD 是等腰直角三角形,∴PD =DM ,∵∠PDG +∠MDH =90°,∠PDG +∠DPG =90°,∴∠DPG =∠MDH ,∵∠G =∠H ,∴△PGD ≅△DHM (AAS),∴PG =DH ,DG =MH ,∵点P 的纵坐标为4,∴将y =4代入112y x =+,得x =6,∴P 点坐标为(6,4),将P (6,4),代入(0)k y x x =>,得:k =24,∴反比例函数解析式为:24(0)y x x=>设D (m ,112m +),∴DG =m -6,PG =132m -,∴MH =m -6,DH =132m -,∴M (332m -,172m -),∵点M 在反比例24y x=的图象上,∴31372422m m ⎛⎫⎛⎫--= ⎪ ⎪⎝⎭⎝⎭ ,解得16m =,210m =,当m =6时,M (6,4)(舍去),当m =10时,M (12,2),故答案为:(12,2).【点拨】本题是反比例函数与一次函数图象的交点问题,主要考查了函数图象上点的坐标的特征,等腰直角三角形的性质,全等三角形的判定与性质,构造全等三角形表示出点M 的坐标是解题的关键.18.3【分析】延长,AB AC 分别交y 轴,x 轴于点,E D ,易得四边形OBAC 的面积等于8k -,即可得解.解:延长,AB AC 分别交y 轴,x 轴于点,E D ,∵AB x 轴,AC y 轴,则:四边形AEOD 为矩形,,OBE ODC 为直角三角形,∵点A 在反比例函数()280y x x=>的图象上,点B 、点C 在反比例函数1k y x =(0k ≠,0x >)上,∴8AEOD S =矩形,2OBE ODC k S S ==,∴四边形OBAC 的面积85OBE ODC AEOD S S S k =--=-= 矩形,∴3k =;故答案为:3.【点拨】本题考查一直图形面积求k 值.熟练掌握k 值的几何意义,是解题的关键.19.(1)1,12;(2)⎝;(3)()0,8-或()8,0-.【分析】(1)根据点B 的坐标,利用待定系数法即可求出1k 、2k 的值;(2)根据一次函数图象上点的坐标特征求出点A 、C 的坐标,根据梯形的面积公式求出ODAC S 四边形的值,进而即可得出ODE S ∆的值,结合三角形的面积公式即可得出点E 的坐标,利用待定系数法即可求出直线OP 的解析式,再联立直线OP 与双曲线的解析式成方程组,通过解方程组求出点P 的坐标;(3)过点B 作直线12M M AB ⊥交x 轴于点2M 交y 轴于点1M ,作出符合题意的图形,利用待定系数法求出直线12M M 的解析式,再求出1M 、2M 的坐标即可.(1)解:将点()6,2B --代入114y k x =+,1264k -=-+,解得:11k =,故一次函数的解析式为;14y x =+,将点()6,2B --代入22k y x =,226k -=-,解得:212k =,故反比例函数的解析式为12y x =;故答案为:1,12(2)解:依照题意,画出图形,如图所示.当2x =时,246m =+=,∴点A 的坐标为()2,6;当0x =时,14044y x =+=+=,∴点C 的坐标为()0,4,∵()114621022()ODAC S OC AD OD =+⋅=⨯+⨯=四边形,:4:1ODE ODAC S S ∆=四边形,∴111210224ODE S OD DE DE =⋅=⨯=⨯ ,∴52DE =,即点E 的坐标为52,2⎛⎫ ⎪⎝⎭,设直线OP 的解析式为y kx =,将点52,2E ⎛⎫ ⎪⎝⎭代入y kx =,得522k =,解得:54k =,∴直线OP 的解析式为54y x =,联立得1254y x y x ⎧=⎪⎪⎨⎪=⎪⎩,解得:11x y ⎧⎪⎨⎪⎩22x y ⎧=⎪⎨⎪=⎩,∵点P 在第一象限,∴点P的坐标为⎝;(3)解:过点B 作直线12M M AB ⊥交x 轴于点2M 交y 轴于点1M ,依照题意画出图形,如图所示.则1290CBM CBM ∠=∠=︒时,四边形11ABM N 与22ABM N 是满足题意的矩形,∵直线AB 的解析式为4y x =+,∴可设直线12M M 的解析式为y x b =-+,把点()6,2B --代入y x b =-+得到26b -=+,解得8b =-,直线12M M 的解析式为8y x =--,当0x =时,8088y x =--=-=-,当0y =时,08x =--,解得8x =-,∴()10,8M -,()28,0M -,故点M 的坐标为()0,8-或()8,0-.【点拨】本题考查了待定系数法求出一次函数及反比例函数解析式、一次函数图象上点的坐标特征、梯形(三角形)的面积公式、矩形的性质,解题的关键是根据题意画出图形,作出辅助线.20.(1)反比例函数的解析式为3y x-=,一次函数解析式为2y x =-+;(2)点P 的坐标为(53,13);(3)t >32【分析】(1)将点B ,点A 坐标代入反比例函数的解析式,可求a 和k 的值,利用待定系数法可求一次函数解析式;(2)连接OA ,OB ,OP ,求得OC 的长,根据AOB AOC BOC S S S =+ ,:1:2AOP BOP S S = ,求得BOP BOC POC S S S =+ 进而求得点P 的坐标;(3)先求出点C 坐标,由面积关系可求解.解:(1)∵反比例函数k y x=的图像与一次函数y mx n =+的图像相交于(),1A a -,()1,3B -两点,∴()131k a =-⨯=⨯-,∴3,3k a =-=,∴点()3,1A -,∴反比例函数的解析式为3y x-=,由题意可得:313m n m n =-+⎧⎨-=+⎩,解得:12m n =-⎧⎨=⎩,∴一次函数解析式为2y x =-+;(2)连接OA ,OB ,OP ,令0x =代入22y x =-+,解得22y =,∴一次函数与y 轴的交点C 坐标为()0,2,∴2OC =,∵点P 在线段AB 上,∴设点P 为(),2m m -+,∵点A ()3,1-,点B ()1,3-,∴4AOB AOC BOC S S S =+= ,∵:1:2AOP BOP S S = ,∴2833BOP AOB S S == ,∵1BOP BOC POC S S S m =+=+ ,∴813m +=,解得53m =,∴123m -+=,∴点P 的坐标为51,33⎛⎫ ⎪⎝⎭;(3)∵直线AB 交y 轴于点C ,∴点C ()0,2,∴31222OMN OCN COMN S S S t =+=+⨯⨯ 四边形,∵3COMN S >四边形,∴312322t +⨯⨯>,∴32t >.【点评】本题考查了反比例函数与一次函数的交点问题,利用待定系数法求解析式,反比例函数的性质等知识,求出两个解析式是解题的关键.21.(1)4y x =;(2)100,3P ⎛⎫ ⎪⎝⎭.【分析】(1)先求出直线OA 的解析式为y x =,直线OB 的解析式为4y x =,过点A作AC x ∥轴,交OB 于C ,在求出1,4C a a ⎛⎫ ⎪⎝⎭,进而得出1344AC a a a =-=,根据21313324244AOB AOC ABC S S S a a a a a =+=⨯⨯+⨯⨯= ,再根据面积即可得出a 的值,求出()2,2A ,即可得出答案;(2)根据(1)可得:()2,2A ,()1,4B ,由于点D 与点A 关于y 轴对称,可知当PA PB +的值最小,即B ,P ,D 三点在同一直线上时ABP 的周长最小,求出直线BD 的解析式为21033y x =+,即可得出答案.(1)解:∵设直线OA 的解析式为1y k x =,将(),A a a 代入,得出:11k =,∴直线OA 的解析式为y x =,设直线OB 的解析式为2y k x =,将1,22B a a ⎛⎫ ⎪⎝⎭代入,得出:24k =,∴直线OB 的解析式为4y x =,过点A 作AC x ∥轴,交OB 于C ,∵(),A a a ,∴点C 的纵坐标为a ,∵点C 在直线OB 上,∴点c 的横坐标为:14a ,∴1,4C a a ⎛⎫ ⎪⎝⎭,∴1344AC a a a =-=,∴21313324244AOB AOC ABC S S S a a a a a =+=⨯⨯+⨯⨯= ,∴2334a =,解得:12a =,22a =-(舍去),∴()2,2A ,∴224k =⨯=,∴反比例函数的解析式为:4y x=;(2)解:根据(1)可得:()2,2A ,()1,4B ,∵点D 与点A 关于y 轴对称,∴PA PD =,∴AB PA PB AB PD PB ++=++,∵AB 为定值,∴当PA PB +的值最小,即B ,P ,D 三点在同一直线上时ABP 的周长最小,∴()2,2D -,设直线BD 的解析式为y ax b =+,将()1,4B ,()2,2D -,代入得:422a b a b +=⎧⎨-+=⎩,解得:23103a b ⎧=⎪⎪⎨⎪=⎪⎩,∴直线BD 的解析式为21033y x =+,当0x =时,103y =,∴100,3P ⎛⎫ ⎪⎝⎭.【点拨】本题考查反比例函数与一次函数,轴对称的性质,正确得出反比例函数解析式是解题的关键.22.(1)3y x=-;(2)-<3≤0x 或1x ≥;(3)()0,5-或()0,1【分析】(1)将点A 坐标代入直线表达式,求出m ,得到具体坐标,再将点A 坐标代入反比例函数表达式,求出k 值可;(2)求出点B 坐标,结合图像可得结果;(3)设点E 坐标为()0,a ,求出直线AB 与y 轴交点F 的坐标,再根据6EBA S =△,列出方程,解之可得.(1)解:将()3,A m -代入2y x =--得:()321m =---=,∴()3,1A -,代入k y x=中,得:()313k =-⨯=-,∴3y x=-;(2)将(),3B n -代入2y x =--中,得32n -=--,解得:1n =,∴()1,3B -,由图像可知:当一次函数图像在反比例函数图像下方时,对应的x 为-<3≤0x 或1x >,∴使一次函数值不大于反比例函数值的x 的取值范围是-<3≤0x 或1x ≥.(3)设点E 坐标为()0,a ,直线AB 与y 轴交于点F ,在2y x =--中,令0x =,则=2y -,∴()0,2F -,∵6EBA S =△,∴()162B A EF x x ⨯⨯-=,即12462a ⨯--⨯=,解得:5a =-或1a =,∴点E 的坐标为()0,5-或()0,1.【点拨】本题考查了一次函数与反比例函数交点问题,用待定系数法确定反比例函数的解析式;要能够熟练掌握待定系数法,学会表示交点形成的三角形面积是解题的关键.23.(1)一次函数解析式为3y x =+,反比例函数解析式为4y x=;(2)()03D -,【分析】(1)先把点A 坐标代入反比例函数解析式中求出反比例函数解析式,进而求出点B 的坐标,再把A 、B 的坐标代入一次函数解析式中求出一次函数解析式即可;(2)设直线AB 与x 轴,y 轴分别交于N ,M ,作点C 关于y 轴的对称点H ,连接CH 交y 轴于G ,连接HD ,推出当H D E 、、三点共线且HD AB ⊥时,HD DE +最小,即CD DE +最小;求出()()3003N M -,,,,进而证明45OMN ONM ∠=∠=︒,即可退出45GHD GDH =︒=∠∠,得到DG HG =;由对称性可知()14C --,,则()14H -,,由此求出3OD =,则()03D -,.(1)解:把()14A ,代入到反比例函数()220k y k x=≠中得:241k =,∴24k =,∴反比例函数解析式为4y x =,把()4B n -,代入到()4B n -,4y x=中得:414n ==--,∴()41B --,;把()14A ,,()41B --,代入到一次函数()110y k x b k =+≠中得:11441k b k b +=⎧⎨-+=-⎩,∴113k b =⎧⎨=⎩,∴一次函数解析式为3y x =+;(2)解:设直线AB 与x 轴,y 轴分别交于N ,M ,作点C 关于y 轴的对称点H ,连接CH 交y 轴于G ,连接HD ,∴CD HD =,∴CD DE HD DE +=+,∴当H D E 、、三点共线且HD AB ⊥时,HD DE +最小,即CD DE +最小;在3y x =+中,令0x =,则3y =,令0y =,则3x =-,∴()()3003N M -,,,,∴3OM ON ==,∴45OMN ONM ∠=∠=︒,∴45GDH EDM ==︒∠∠,∴45GHD GDH =︒=∠∠,∴DG HG =;由对称性可知()14C --,,∴()14H -,,∴41OG DG HG ===,,∴3OD =,∴()03D -,.【点拨】本题主要考查了一次函数与反比例函数综合,轴对称最短路径问题,等腰直角三角形的性质与判定,正确作出辅助线确定当H D E 、、三点共线且HD AB ⊥时,HD DE+最小,即CD DE +最小是解题的关键.24.(1)①直线AB 的解析式为344y x =-+;②四边形ABCD 是菱形,理由见分析;(2)四边形ABCD 能成为正方形,9m n +=.【分析】(1)①先确定出点A ,B 坐标,再利用待定系数法即可得出结论;②先确定出点D 坐标,进而确定出点P 坐标,进而求出PD PB ,,即可得出结论;(2)先确定出33m A ⎛⎫ ⎪⎝⎭,,33n C ⎛⎫ ⎪⎝⎭,进而求出点P 的坐标,再求出B ,D 坐标,最后用BD AC =,即可得出结论.(1)解:①∵4m =,∴反比例函数为4y x=,当4x =时,1y =,∴()41B ,,当3y =时,∴43x =,∴43x =,∴433A ⎛⎫ ⎪⎝⎭,设直线AB 的解析式为y kx b =+,∴43341k b k b ⎧+=⎪⎨⎪+=⎩,解得344k b ⎧=-⎪⎨⎪=⎩,∴直线AB 的解析式为344y x =-+;②四边形ABCD 是菱形,理由如下:由①知,433A ⎛⎫ ⎪⎝⎭,∵AC x ∥轴,∴1633C ⎛⎫ ⎪⎝⎭,,∵点P 是线段AC 的中点,∴1033P ⎛⎫ ⎪⎝⎭,,当103x =时,由4y x =得,65y =,由16y x =得,245y =,∴56359PB =-=,355249PD =-=,∴PB PD =,∵PA PC =,∴四边形ABCD 为平行四边形,∵BD AC ⊥,∴四边形ABCD 是菱形;(2)解:四边形ABCD 能是正方形,理由:当四边形ABCD 是正方形,记AC BD ,的交点为P ,P 为AC 的中点,∴BD AC =,当3y =时,由m y x =得,3m x =,由n y x=得,3n x =,∴33m A ⎛⎫ ⎪⎝⎭,,33n C ⎛⎫ ⎪⎝⎭,∴36m n P +⎛⎫ ⎪⎝⎭,∴66m n m B m n +⎛⎫ +⎝⎭,,66m n n D m n +⎛⎫ ⎪+⎝⎭,,∵BD AC =,∴6633n m n m m n m n -=-++,∴18m n +=.【点拨】此题是反比例函数综合题,主要考查了待定系数法,平行四边形的判定,菱形的判定和性质,正方形的性质,判断出四边形ABCD 是平行四边形是解本题的关键.。
二轮复习:反比例中的动点问题 适合初三学霸的压轴复习题精编版
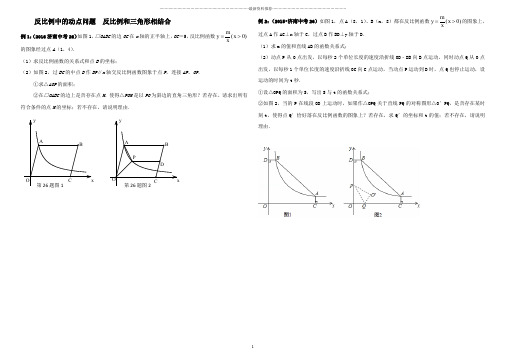
反比例中的动点问题 反比例和三角形相结合例1:(2016济南中考26)如图1,□OABC 的边OC 在x 轴的正半轴上,OC =5,反比例函数)0(>=x xmy 的图象经过点A (1,4).(1)求反比例函数的关系式和点B 的坐标;(2)如图2,过BC 的中点D 作DP ∥x 轴交反比例函数图象于点P ,连接AP 、OP .①求△AOP 的面积;②在□OABC 的边上是否存在点M ,使得△POM 是以PO 为斜边的直角三角形?若存在,请求出所有符合条件的点M 的坐标;若不存在,请说明理由.例2:(2015•济南中考26)如图1,点A (8,1)、B (n ,8)都在反比例函数)0(>=x xmy 的图象上,过点A 作AC ⊥x 轴于C ,过点B 作BD ⊥y 轴于D . (1)求m 的值和直线AB 的函数关系式;(2)动点P 从O 点出发,以每秒2个单位长度的速度沿折线OD ﹣DB 向B 点运动,同时动点Q 从O 点出发,以每秒1个单位长度的速度沿折线OC 向C 点运动,当动点P 运动到D 时,点Q 也停止运动,设运动的时间为t 秒.①设△OPQ 的面积为S ,写出S 与t 的函数关系式;②如图2,当的P 在线段OD 上运动时,如果作△OPQ 关于直线PQ 的对称图形△O ′PQ ,是否存在某时刻t ,使得点Q ′恰好落在反比例函数的图象上?若存在,求Q ′的坐标和t 的值;若不存在,请说明理由.例3:(2014济南中考26)如图1,反比例函数)0(>=x xky 的图象经过点A (2,1),射线AB 与反比例函数图象交于另一点B (1,a ),射线AC 与y 轴交于点C ,∠BAC=75°,AD ⊥y 轴,垂足为D . (1)求k 的值;(2)求tan ∠DAC 的值及直线AC 的解析式;(3)如图2,M 是线段AC 上方反比例函数图象上一动点,过M 作直线l ⊥x 轴,与AC 相交于点N ,连接CM ,求△CMN 面积的最大值.练习1:已知:一次函数y =﹣2x +10的图象与反比例函数y =(k >0)的图象相交于A ,B 两点(A 在B 的右侧).(1)当A (4,2)时,求反比例函数的解析式及B 点的坐标;(2)在(1)的条件下,反比例函数图象的另一支上是否存在一点P ,使△PAB 是以AB 为直角边的直角三角形?若存在,求出所有符合条件的点P 的坐标;若不存在,请说明理由.(3)当A (a ,﹣2a +10),B (b ,﹣2b +10)时,直线OA 与此反比例函数图象的另一支交于另一点C ,连接BC 交y 轴于点D .若=,求△ABC 的面积.练习2:如图1,已知直线y=x+3与x轴交于点A,与y轴交于点B,将直线在x轴下方的部分沿x轴翻折,得到一个新函数的图象(图中的“V形折线”).(1)类比研究函数图象的方法,请列举新函数的两条性质,并求新函数的解析式;(2)如图2,双曲线y=与新函数的图象交于点C(1,a),点D是线段AC上一动点(不包括端点),过点D作x轴的平行线,与新函数图象交于另一点E,与双曲线交于点P.①试求△PAD的面积的最大值;②探索:在点D运动的过程中,四边形PAEC能否为平行四边形?若能,求出此时点D的坐标;若不能,请说明理由.练习3:如图,已知点A(4,0),B(0,4),把一个直角三角尺DEF放在△OAB内,使其斜边FD 在线段AB上,三角尺可沿着线段AB上下滑动.其中∠EFD=30°,ED=2,点G为边FD的中点.(1)求直线AB的解析式;(2)如图1,当点D与点A重合时,求经过点G的反比例函数y=(k≠0)的解析式;(3)在三角尺滑动的过程中,经过点G的反比例函数的图象能否同时经过点F?如果能,求出此时反比例函数的解析式;如果不能,说明理由.练习4:如图,直线y=ax+1与x轴、y轴分别相交于A、B两点,与双曲线y=(x>0)相交于点P,PC⊥x轴于点C,且PC=2,点A的坐标为(﹣2,0).(1)求双曲线的解析式;(2)若点Q为双曲线上点P右侧的一点,且QH⊥x轴于H,当以点Q、C、H为顶点的三角形与△AOB 相似时,求点Q的坐标.。
八年级数学下册11反比例函数反比例函数与动点与面积有关培优训练试题

反比例函数与动点P 与面积相关例1、反比例函数y=的图象经过点A〔﹣,1〕.〔1〕试确定此反比例函数的解析式;〔2〕点O是坐标原点,将线段OA绕O点顺时针旋转30°得到线段OB.判断点B是否在此反比例函数的图象上,并说明理由;〔3〕点P〔m,m+6〕也在此反比例函数的图象上〔其中m<0〕,过P点作x轴的垂线,交x 轴于点M.假设线段PM上存在一点Q,使得△OQM的面积是,设Q点的纵坐标为n,求n2﹣2n+9的值.2、:反比例函数经过点B〔1,1〕.〔1〕求该反比例函数解析式;〔2〕连接OB,再把点A〔2,0〕与点B连接,将△OAB绕点O按顺时针方向旋转135°得到△OA′B′,写出A′B′的中点P的坐标,试判断点P是否在此双曲线上,并说明理由;〔3〕假设该反比例函数图象上有一点F〔m,〕〔其中m>0〕,在线段OF上任取一点E,设E 点的纵坐标为n,过F点作FM⊥x轴于点M,连接EM,使△OEM的面积是,求代数式的值.3、如图,M点是正比例函数y=kx和反比例函数的图象的一个交点.〔1〕求这两个函数的解析式;〔2〕在反比例函数的图象上取一点P,过点P做PA垂直于x轴,垂足为A,点Q是直线MO 上一点,QB垂直于y轴,垂足为B,直线MO上是否存在这样的点Q,使得△OBQ的面积是△OPA的面积的2倍?假如存在,恳求出点Q的坐标,假如不存在,请说明理由.4、如图,:一次函数:y=﹣x+4的图象与反比例函数:〔x>0〕的图象分别交于A、B两点,点M是一次函数图象在第一象限局部上的任意一点,过M分别向x轴、y轴作垂线,垂足分别为M1、M2,设矩形MM1OM2的面积为S1;点N为反比例函数图象上任意一点,过N分别向x 轴、y轴作垂线,垂足分别为N1、N2,设矩形NN1ON2的面积为S2;〔1〕假设设点M的坐标为〔x,y〕,请写出S1关于x的函数表达式,并求x取何值时,S1的最大值;〔2〕观察图形,通过确定x的取值,试比拟S1、S2的大小.5、如图,正比例函数和反比例函数的图象都经过点M〔﹣2,﹣1〕,且P〔﹣1,﹣2〕为双曲线上的一点,Q为坐标平面上一动点,PA垂直于x轴,QB垂直于y轴,垂足分别是A、B.〔1〕写出正比例函数和反比例函数的关系式;〔2〕当点Q在直线MO上运动时,直线MO上是否存在这样的点Q,使得△OBQ与△OAP面积相等?假如存在,恳求出点的坐标,假如不存在,请说明理由.6、如图1,正比例函数和反比例函数的图象都经过点M〔﹣2,﹣1〕,且P〔﹣1,﹣2〕为双曲线上的一点,Q为坐标平面上一动点,PA垂直于x轴,QB垂直于y轴,垂足分别是A、B.〔1〕写出正比例函数和反比例函数的关系式;〔2〕当点Q在直线MO上运动时,直线MO上是否存在这样的点Q,使得△OBQ与△OAP面积相等假如存在,恳求出点的坐标,假如不存在,请说明理由;〔3〕如图2,当点Q在第一象限中的双曲线上运动时,作以OP、OQ为邻边的平行四边形OPCQ,求平行四边形OPCQ周长的最小值.7、如图,点P〔a,b〕和点Q〔c,d〕是反比例函数y=图象上第一象限内的两个动点〔a<b,a≠c〕,且始终有OP=OQ.〔1〕求证:a=d,b=c;〔2〕P1是点P关于y轴的对称点,Q1是点Q关于x轴的对称点,连接P1Q1分别交OP、OQ于点M、N.①求证:PQ ∥P 1Q 1;②求四边形PQNM 的面积S 能否等于?假设能,求出点P 的坐标;假设不能,请说明理由.反比例函数进步练习1、如图:P 是反比例函数x ky =图象上的一点,由P 分别向x 轴和y 轴引垂线,阴影局部面积为3,求函数的表达式。
中考数学常考易错点:34《反比例函数》.pdf

【例 3】 (2014·四川南充)如图,一次函数 y1=kx+b 的图象与反比例函数 y2=的图象相交于点 A(2,5)和点 B,
与 y 轴相交于点 C(0,7).
(1)求这两个函数的解析式;
(2)当 x 取何值时,y1<y2.
【解析】 (1)将点 C、点 A 的坐标代入一次函数解析式可得 k,b 的值,将点 A 的坐标代入反比例函数解析式 可得 m 的值,继而可得两函数解析式; (2)寻找满足使一次函数图象在反比例函数图象下面的 x 的取值范围.
三、 解答题
9 / 13
更多资料请扫描右边二维码
(1)求 k 的值及点 E 的坐标; (2)若点 F 是边上一点,且△FCB∽△DBE,求直线 FB 的解析式.
(第 6 题)
7. (2014·江苏大丰模拟)如图,一次函数 y=kx+b 的图象与反比例函数 (1)试确定上述反比例函数和一次函数的关系式; (2)求△AOB 的面积.
B. y2>y1>y3
C. y1>y3>y2
D. y3>y2>y1
的图象上,则 y1,y2,y3
(第 1 题)
(第 2 题)
8 / 13
更多资料请扫描右边二维码
2. (2014 · 山 东 济 南 二 模 ) 如 图 , 过 x 轴 正 半 轴 上 的 任 意 一 点 P, 作 y 轴 的 平 行 线 , 分 别 与 反 比 例 函 数
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
反比例函数 ---动点、面积专题
1.反比例函数y =x
k 的图象在第一象限的分支上有一点A (3,4),P 为x 轴正半轴上的一个动点,(1)求反比例函数解析式. (2)当P 在什么位置时,△OPA 为直角三角形,求出此时P 点的坐标.
2、如图,M 点是正比例函数y=kx 和反比例函数
的图象的一个交点. (1)求这两个函数的解析式;
(2)在反比例函数的图象上取一点P ,过点P 做PA 垂直于x 轴,垂足为A ,点Q 是直线MO 上一点,QB 垂直于y 轴,垂足为B ,直线MO 上是否存在这样的点Q ,使得△OBQ 的面积是△OPA 的面积的2倍?如果存在,请求出点Q 的坐标,如果不存在,请说明理由.
3、如图1,已知正比例函数和反比例函数的图象都经过点M(﹣2,﹣1),且P(﹣1,﹣2)为双曲线上的一点,Q为坐标平面上一动点,PA垂直于x轴,QB垂直于y轴,垂足分别是A、B.
(1)写出正比例函数和反比例函数的关系式;
(2)当点Q在直线MO上运动时,直线MO上是否存在这样的点Q,使得△OBQ与△OAP面积相等如果存在,请求出点的坐标,如果不存在,请说明理由;
(3)如图2,当点Q在第一象限中的双曲线上运动时,作以OP、OQ为邻边的平行四边形OPCQ,求平行四边形OPCQ 周长的最小值.。
