水位的变化优质课件PPT

合集下载

2.7水位的变化

姓名身高身高与平均身高的差小明 159 －1 ＋2 0 小彬小丽小亮小颖小山 154 ＋3 165
(2)谁最高谁最低谁最高? 谁最低? 谁最高 (3)最高与最矮的学生身高相差多少最高与最矮的学生身高相差多少? 最高与最矮的学生身高相差多少
2.小明的父亲上星期六买进某公司股票1000股，每股27元，下表为本周内每日该股票的涨跌情况（单位：元）
点拨：收益＝卖出所得－买入所花，点拨：收益＝卖出所得－买入所花，这只是应得收益，这只是应得收益，实际上还要除去买入和卖出时所花的手续费和交易税，入和卖出时所花的手续费和交易税，剩下的才是真正的收益．剩下的才是真正的收益．注意题目中成交额”，的“成交额，这是每次交易成功时的成交额这是每次交易成功时的款项，故每次的成交额都不同．款项，故每次的成交额都不同．
方法二: 对水位变化的数据求和方法二 +0.2 + (+0.81) + (-0.35) + (+0.03) + (+0.28) + (-0.36) + (-0.01) = 0.60(米) 米
星期水位变化（米）
一
＋0.20
二
＋0.81
三
－0.35
四
＋0.03
五六
＋0.28 －0.36
日
－0.01
星期一二三四五六
每股张跌
+4
+4.5
—1
-2.5
-6
+2
⑴星期三收盘时，每股是多少元？ ⑵本周内最高价是每股多少元？最低每股多少元？ ⑶已知小明父亲买进股票时付了1.5‰的手续费，卖出时需付成交额1.5‰的手续费和1‰的交易税，如果他在周六收盘前将全部股票卖出，他的收益情况如何？

《水位的变化》课件

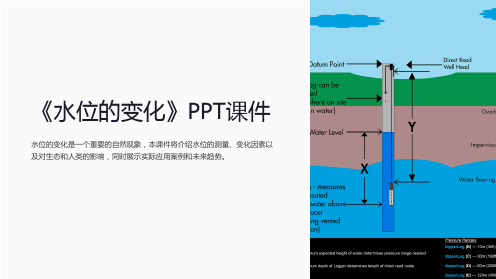
水位的测量
传感器
使用水位传感器进行直接测量。
浮子和刻度尺
压力传பைடு நூலகம்器
通过浮子和刻度尺测量间接水位。通过压力变化计算水位。
水位的变化因素
降雨
降雨是影响水位变化的重要因素。大量降雨可以导致水位上升，引发洪水。
蒸发
蒸发是水位下降的主要原因之一，当蒸发速度大于补充速度时水位会下降。
河流和湖泊水位变化
洪水防治的方法
堤坝
建造堤坝以防止洪水涌入低洼地区。
河道整治
通过加宽和加深河道来提高水流量和水位的容纳能力。
早期预警
建立有效的洪水预警系统，提前通知公众并采取行动。
水位变化的图表表示
折线图
用折线图直观显示水位的变化趋势。
柱状图
用柱状图比较不同时间段的水位数据。
地图
在地图上用色块显示不同地区的水位情况。
《水位的变化》PPT课件
水位的变化是一个重要的自然现象，本课件将介绍水位的测量、变化因素以及对生态和人类的影响，同时展示实际应用案例和未来趋势。
什么是水位？
定义
水位指的是水面相对于某个基准面的高度。
重要性
水位的变化对自然系统和人类社会都具有重大意义。
影响因素
水位受降雨、蒸发、河流和湖泊水位变化等多个因素影响。
洪水可能促使鱼类等生物迁移，寻找更适宜的生存条件。
河岸侵蚀
洪水会加剧河岸的侵蚀，对附近的土地造成损害。
洪水对人类的影响
1
财产损失
洪水可能导致房屋和财产的损坏，给人们造成巨大经济负担。
2
生命安全
洪水会威胁人们的生命安全，造成伤亡和失踪。
3

鄱阳湖水位变化

1.4 季节入湖总水量变化特征
1.4.1 1—3 月入湖总水量变化特征鄱阳湖 1959—2009 年 1—3 月入湖总水量年代距平见表 2．从表中可以看出，20 世纪 80、90 年代入湖总水量距平为正，说明其间入湖总水量偏多，但是距平百分率只有 0.08%和0.030%，表明入湖总水量接近正常值，增长趋势缓和。虽然，20 世纪 60、70 年代和 21 世纪初入湖总水量距平为负，说明其间入湖总水量偏少，并且目前处于湖总水量偏少时期。但是，从它们的距平百分率看，入湖总水量接近正常值。

但无论是年最高水位、年最低水位，还是年平均水位，进入21世纪以来均呈下降趋势，相对于55年的总体（直线）趋势而言，以年最高水位的下降最剧烈，其次是年最低水位，年平均水位的下降相对较为平缓。值得注意的是，近20年来星子站最高、最低、平均水位均呈显著下降变化趋势，大洪水明显减少、严重枯水明显增多，水情朝偏枯方向快速发展。近9年（2000～2008年）来鄱阳湖枯水位有下降且维持时间延长的趋势，尤其是自2003年以来，鄱阳湖枯水位连创新低，枯水期不断延长。
1.1资料与方法
1.1.1资料
资料简介

采用鄱阳湖1959—2009年日入湖总水量序列资料，经过统计分析，分别得到年入湖总水量序列和月入湖总水量序列和 1月—3 月和4月—6 月和7 月—9 月和10 月—12 月，4个季节入湖总水量序列。为了反映年入湖总水量的总体趋势，应用 MannKendal秩相关检验和5点滑动平均对其变化趋势进行分析。为研究方便，对基本资料进行距平处理，然后对相应的距平值进行莫莱( Morlet) 连续小波变换，分析鄱阳湖入湖总水量的周期规律。
1.4.2 4—6 月入湖总水量变化特征由表 2 可以得出，20 世纪 70、90 年代入湖总水量距平为正，说明其间入湖总水量偏多，而 20 世纪 60、80 年代和 21 世纪初入湖总水量距平为负，说明其间入湖总水量偏少，且目前处于入湖总水量偏少期; 但是它们的距平百分比都很小，表明入湖总水量与正常值相接近． 1.4.3 7—9 月入湖总水量变化特征由表 2 可知，20 世纪 60—80 年代入湖总水量距平为负，说明其间入湖总水量偏少，20 世纪末和 21 世纪初入湖总水量距平为正，说明其间入湖总水量偏多，且目前处于入湖总水量偏多期; 除 20 世纪 60 年代和 90 年代的距平百分比相对较大，其它年代距平百分比绝对值仅为 0.07%，都基本上接近正常值． 1.4.4 10—12 月入湖总水量变化特征由表 2 可知，20 世纪 60 年代的入湖总水量距平为负，说明其间入湖总水量偏少，其它年代的入湖总水量距平值均为正，说明其间入湖总水量偏多，目前处于入湖总水量偏多期; 距平百分率较小，表明入湖总水量接近正常值，但从 20 世纪 80 年代以来，入湖总水量年代距平百分比有逐渐增大的趋势．

七年级数学课件-水位的变化

随堂小练 1．吴明发高烧住院，医院给他开了药并挂了吊瓶，护士每隔 1 小时给他测一次体温，及时了解他的好转情况，测得体温的变化数据如下表：
时间 7：00 8：00 9：00 10：00 11：00 12：00 13：00 14：00 15：00 体温变化＋0.2 －1.0 －0.8 －1.0 －0.6 ＋0.4 －0.2 －0.2 －0.0
图7
蜗牛是否爬出井口【例题】一口井，水面比井口低 3 米，一只蜗牛从水面沿着井壁往井口爬，第一次往上爬了 0.5 米后又往后滑了 0.1 米；第二次往上爬了 0.42 米，却又下滑了 0.15 米；第三次往上爬了 0.7 米，却下滑了 0.15 米；第四次往上爬了 0.75 米，却下滑了 0.1 米；第五次往上爬了 0.55 米，没有下滑；第六次往上爬了 0.48 米．问蜗牛有没有爬出井口？
7 水位的变化
水位变化图表 “水位的变化”之类的问题是典型的利用有理数加减混合运算来解决的实际问题．要理解在水位变化表下面标明的 “注”或“注意”的含义： (1)正号表示水位比前一天上升，负号表示水位比前一天下降，参考对象是前一天的水位； (2)正号表示比某一参考水位上升，负号表示比某一参考水位下降，参考对象是某一具体参考水位值．
折线统计图(难点) 根据相关数据，在图中标出能反映这些数据特征的点，然后再按照事物发展的一种趋势，将标出的点连成折线，这样就得到了各种折线统计图．
随堂小练 2．武警某部近期要检查官兵的 100 米短跑训练情况，规定及格的成绩是 15 秒．战士张文虎每天坚持锻炼，并记录了一周内的成绩变化情况，如下表：
℃
(注：(1)人的正常体温是 37 ℃；(2)病人早晨 6：00 时住院时测得的体温是 40.2 ℃；(3)正数表示比前 1 小时高，负数表示比前 1 小时低．)

教科版三年级上册科学《水到哪里去了》PPT说课教学课件

什么叫蒸发？
在常温下，水会慢慢变成水蒸气散发到空中，这种现象叫做蒸发。
举例说生活中哪些是水蒸发现象?
• 鱼缸里的水慢慢减少了，这是为什么呢？。
衣服晾起来慢慢变干了，这是怎么回事？
请问：蒸发还会出现什么现象呢？
体验
当小水珠滴在你的手背上时，你有什么感觉？为什么会有凉的感觉？说明温度怎样？那么热量被谁带走了？
蒸发是水从液体变成气体的现象，在这个变化过程中要吸收周围热量。
看谁说的多！
举例生活中蒸发过程中吸热的现象，看哪一组写的多？
炎热的夏天在地面上洒些水会有凉爽的感觉
城市的洒水车帮城市降温。
实验要求：
• 1.请各组介绍一下本组的实验材料。 • 2.用火烤时，不要离得太近，以免伤到手。 • 3.不要把水弄到桌面上。 • 4.做完实验，填好实验记录表,整理好实验
第一单元水
1.水到哪里去了
水有哪些特点？
讨论：说一说你认为水到哪里去了？
实验一：观察两杯水一段时间后的水位变化
对比实验
相同条件：
1.水量相同 2.都做好标记 3.同时放在同一位置
不同条件：
一个用塑料薄膜盖好，一个不盖
一天一夜后
我发现：没有盖料薄膜的杯子里的水都“跑”到空气中了，而盖了塑料薄膜的杯子里的水在跑出去的过程中被拦住了。
无色无味透明会流动无固定形状
气态看不见摸不着没有固定体积较轻
讨论：白汽是水蒸气吗？提示：水蒸气是看不见的
小水滴水蒸气
水壶冒出来的白汽不是水蒸气。因为水蒸气的微粒太小，我们无法看见，而白汽能够看到所以它不是水蒸气而是雾状的小水滴。
水到哪里去了
黑板上的字怎么不见了？水跑到哪里去了？水变成什么物质跑掉了？

水位的变化

解法提示:
把往上爬的距离用正数表示,下滑的距离用负数表示. 根据题意,蜗牛每次上爬和下滑的情况可用下表表示:
时间第一次第二次第三次第四次第五次第六次
上爬/米 +0.5 +0.42 +0.7 +0.75 +0.55 +0.48
下滑/米－0.1 －0.15 －0.15 －0.1
0
(3)完成下面的本周水位记录表:
星期
一二三四五六日
水位记录/米 33.6 34.41 34.06 34.09 34.37 34.01 34.00
星期
一二三四五六日
水位记录/米 0.20 1.01 0.66 0.69 0.97 0.61 0.60
星期
一二三四五六日
水位记录/米 33.6 34.41 34.06 34.09 34.37 34.01 34.00
水位变化/米 +0.20 1.01 0.66 0.69 0.97 0.61 0.60
注:正号表示水位比周末上升,负号表示水位比周末下降
ቤተ መጻሕፍቲ ባይዱ
水位/米 1.2 1.0
(4)以警戒水位为0点, 用折线统计图表示本周的水位情况.
0.8
0.6
0.4
0.2
星期
0
日一二三四五六日
练习
光明中学初一(1)班学生的平均身高是160厘米. (1)下表给出了该班6名同学的身高情况(单位:厘米). 试完成下表:
姓名
小明小彬小丽小亮小颖小山
身高
159
154
165
身高与平均身高的差－1 ＋2 0
＋3
(2)谁最高? 谁最低?
(3)最高与最矮的学生身高相差多少?

北师大版数学七年级上册《2.6水位的变化》优课件

水位的变化
最高水位:75.30
警戒水位:73.40 平均水位:62.60 最低水位:51.50
流花河水位
75.30 73.40 62.60 51.50
流花河一周内水位变化情况
星期一二三四五六日
水位变化 +0.20 +0.81 -0.35 +0.03 +0.28 -0.36 -0.01
上周日
星期一二三四五六日
见课本44页
1.已知上周五股市指数以1570点报收，
本周的跌涨如下（“+”表示比前一天涨， “—”表示比前一天跌），本周三的指数为（）
A.1555点 B .1582点 C .1620点 D.1525点
星期
一二三四五
股指变化点 +20 -35 +27 -15 -25
3.小明的爸爸星期五买进股票2000股，
每股10.2元，第二周星期一到星期五
该股票涨跌（收盘）情况如下：
星期一二三四五
每股涨 +0.4 +0.45 -0.1 -0.25 -0.4
跌/元
（1）星期四收盘时每股多少元？（2）本周最高价是每股多少元？
4.三峡水库大坝修建以后，长江水位随着水库的蓄水而升高，2003 年6月13日蓄水到135米，以135米为准，高于的记为正，蓄水前，蓄满水的水位分别记为：-69、40，则蓄水前水位高米，蓄满水
与警 0.20 1.01 0.66 0.69 0.97 0.61 0.60
戒位距离水位 73.60 74.41 74.06 74.09 74.37 74.01 74.00 记录
2.以警戒水位为0点，用折线统计图表示本周的水位变化情况。

水位的变化课件(“表示”相关文档)共7张

图7
降，参考对象是前一天的水位；时测得的体温是 40. 时测得的体温是 40. (2)请用折线统计图表示张文虎一周内的成绩变化情况．时测得的体温是 40. 运算来解决的实际问题．要理解在水位变化表下面标明的 (2)病人早晨 6：00 时住院运算来解决的实际问题．要理解在水位变化表下面标明的降，参考对象是前一天的水位；根据题意，蜗牛每次上爬和下滑的情况可用下表表示： “注”或“注意”的含义：位下降，参考对象是某一具体参考水位值． (2)病人早晨 6：00 时住院时测得的体温是 40. 降，参考对象是前一天的水位； (2)以及格成绩为基数，折线统计图如图 7.
解：把往上爬的距离用正数表示，下滑的距离用负数表示．
根据题意，蜗牛每次上爬和下滑的情况可用下表表示：
时间第一次第二次第三次第四次第五次第六次上爬/米＋0.5 ＋0.42 ＋0.7 ＋0.75 ＋0.55 ＋0.48 下滑/米－0.1 －0.15 －0.15 －0.1 0
蜗牛爬六次的总路程为 0.5－0.1＋0.42－0.15＋0.7－0.15＋ 0.75－0.1＋0.55＋0.48＝2.9<3，
7 水位的变化
水位变化图表 “水位的变化”之类的问题是典型的利用有理数加减混合
运算来解决的实际问题．要理解在水位变化表下面标明的
“注”或“注意”的含义：
(1)正号表示水位比前一天上升，负号表示水位比前一天下降，参考对象是前一天的水位；
(2)正号表示比某一参考水位上升，负号表示比某一参考水位下降，参考对象是开了药并挂了吊瓶，护士每隔 1 小时给他测一次体温，及时了解他的好转情况，测得体温
的变化数据如下表：
时间 7：00 8：00 9：00 10：00 11：00 12：00 13：00 14：00 15：00

27水位的变化

姓名小明小彬小丽小亮小颖小山
身高 159
154
165
身高与 -1 +2 0
+3
平均身
高差值
（1）谁最高？谁最矮？（2）最高和最矮的学生身高相差多少？
练习一： 9.11事故后，美国股市出现狂跌，股市指数一度跌到历史最低点，后经政府宏观调控，稍有反弹，下表是某周的股市指数升跌情况，+号表示指数比头一天上升，-号表示指数比头一天下跌：
星期一二三四五六日水位 +0.20 +0.81 -0.35 +0.03 +0.28 -0.36 -0.01 变化
(1)请你估算一下，本周哪天长江的水位最高？哪一天长江的水位最低？它们位于警戒水位之上还是之下？ ( 2)与上周末相比，本周末长江水位是上升了还是下降了? (3)完成下面的水位记录表：
时间星期一星期二星期三星期四星期五
升跌情况 +100点 -50点 +60点 +20点 -70点
(1）本周内哪天股市指数最高？哪天股市指数最低？（2）本周五的股市指数比上周五的股市指数高还是低？（3）若将上周五的股市指数记为0点，请你画出本周的股市指数折线图。
练习二：试一试：
象下图那样，把16个球围成一圈排列着，并编上从1到16的号码，从第一个球顺时针前进3个球就到第4个球，像这样，从第一个球顺时针前进 328个，再从那里逆时针前进485个，然后又接着沿顺时针前进136个，这时到第几个球的位置？
15 16 1
14
2
13
3
12
4
11
5
10
6
987
小结：这节课，我们通过实例看到了有理数加减混合运算在现实生活中的应用，还复习了折线统计图的制作过程，希望同学们日后可以学以致用。

初中数学人教版九年级上册探究3“水位变化”

宽度为__4___m？水面宽度减少(_2__6__4_) m？
→↑
3m
2 6m
你能总结吗？
通过刚才的学习，你能总结出用二次函数知识解决抛物线问题的一般步骤吗？
审题，弄清已知和未知(审) 建立适当的直角坐标（建）合理的设出二次函数解析式（设）求出二次函数解析式（求）
利用解析式求解（解）得出实际问题的答案（答）
检验
的答案
作业
1、课本52页第3题
2、设计方案：某建筑公司需在两山之间的峡谷上架设一座公路桥，桥下是一条宽 100m的河流，河面距所要架设的公路桥的高度是50m，根据各方面的条件分析，专家认为抛物线型桥是最好的选择。按照专家的建议，你设计一座跨峡谷的公路桥。
教师寄语数学来源于生活,服务于生活,把我们所学知识运用到生活中去.
内，与水平桥面相交于A、B两点，桥拱最
高点C到AB的距离为9m,AB=36m,D、E为桥拱
底部的两点，且DE AB，点E到直线AB的距
离为7m,则DE的长为_4__8_m。
y
C
X
A
B
D
E
(3)一位运动员在距篮下4m处跳起投篮,篮球运行的路线是抛物线,当球运行的水平距离为2.5m时, 达到最大高度3.5m,然后准确落入篮圈,已知篮圈中心到地面的距离为3.05m. ①建立如图所示的直角坐标系,求抛物线的解析式
纵坐标为 y 3
当y 3时，x 6
你还有别的方法吗？
y
2
0
X 4y
2
0
X
4
y
2
0 x
4y
2
0
4
X
y
2
0
4
y

水位为什么会升高的教学课件

水位升高的重要性
水位升高是水文循环和水量平衡的重要组成部分，对于水资源的合理利用和保护具有重要意义。
水位升高可能会导致自然生态系统的改变，影响生物多样性，同时也会对社会经济产生深远影响。因此，对水位升高进行监测、预测和管理是十分必要的。
02
水位升高的原因分析
降雨量增加
总结词
降雨量增加是导致水位上升的直接原因之一。
地下水位上升是水位上升的另一个重要原因。
VS
详细描述
地下水位上升可能是由于地下水补给不足或者过度开采地下水引起的，这会导致地下水的水位上升，进而使地表水位上升。
蒸发量增加
总结词
蒸发量增加也是导致水位上升的原因之一。
详细描述
蒸发量增加会导致地表水的水量减少，而地下水的水量也会受到影响，进而使水位上升。此外，蒸发还会使水中的盐分等物质浓缩，导致水质变差。
详细描述
降雨量增加会导致地表水和地下水的水量增加，进而使水位上升。
地表径流变化
总结词
地表径流变化是指水流路径和流量的变化，也是导致水位上升的原因之一。
详细描述
地表径流变化可能是由于地形、地貌、土壤类型和气候等因素的变化引起的，这些因素会影响水流的路径和流量，从而导致水位上升。
地下水位上升
总结词
水位为什么会升高的教学课件
2023-10-28
目录
• 水位升高的现象和定义 • 水位升高的原因分析 • 水位升高对环境和人类的影响 • 水位升高的预防和解决方案 • 水位升高研究的意义和价值
01
水位升高的现象和定义
水位升高的定义
水位升高是指水位在垂直方向上的增加，通常以相对于基准面的高度变化来衡量。
水位升高会导致农田被淹没，农民需要投入更多的时间和金钱来应对这种情况，从而增加了农业成本。

鄂教版小学科学三上《11水位为什么会升高》PPT课件

研究的物体水
受热受热方法出现的现象放入热水中水位升高
受冷受冷的方法出现的现象放入冷水中水位下降
油
放入热水中水位升高放入水中水位下降
空气
放入热水中气球鼓起放入冷水中水位萎缩
硬币
用火烧
穿不过两钉浸入冷水穿过两钉之间之间
上面这些物体在受热时体积就会变大，受冷时体积就会缩小，这种现象就叫做热胀冷缩。生活中有很多热胀冷缩的现象，请看下面的图片：
鄂教版科学小学三年级上册
请同学们回忆一下，在烧开水的这个实验过程中我们会观察到那些现象呢？
水温升高、水面逐渐上升、水底渐渐冒泡、加热到一定时候睡眠冒白气、水沸腾一会儿、水变少
水位为什么会升高呢？为什么呢？
我也不知道为什么？但是我们可以用以下器材来做实验找到答案：
我们的实验做完啦！我们还填写了如下的实验报告，小朋友们有我们做的好吗？
你还知道生活中哪些热胀冷缩的例子呢？和大家一起分享分享吧！！！
把整个瓶盖浸在热水里泡一会？
如何打开瓶盖？
我什么时候才能吃到羊
啊？
小羊们果然聪明！！！

初中人教版数学课件-223实际问题与二次函数(3)水位变化问题

想一想
如图，隧道的截面由抛物线和长方形构成，长方形的长是8m，宽是2m，抛物线可以用 y 1 x2 4 表示.
4
（1）一辆货运卡车高4m，宽2m，它能通过该隧道吗？
（2）如果该隧道内设双行道，那么这辆货运卡车是否可以通过？
（1）卡车可以通过.
3
提示：当x=±1时，y =3.75, 3.75
解：
3 1 x2 2
x2 6
解得 x1 6, x2 6
水面的宽度 2x 2 6 m
水面下降1cm，水面宽度增加___2___6____4__m.
探究3：
图中是抛物线形拱桥，当水面在 l 时，拱顶离水面2m，水
面宽4m，水面下降1m时，水面宽度增加了多少？
y （2，2）我们来比较一下
解法三:如图所示,以抛物线和水面的两个交点的连线为x
轴，以其中的一个交点(如左边的点)为原点，建立平面
直角坐标系.
此时,抛物线的顶点为(2,2) ∴可设这条抛物线所表示
的二次函数的解析式为:
y a( x 2 )2 2
∵抛物线过点(0,0)
0 a ( 2 )2 2
a 0.5
∴这条抛物线所表示的二次函数为:
做一做如图建立如下直角坐标系可设这条抛物线表示的二次函数为y =ax2 .
由抛物线经过点（2，－2），可得
2 a 22, a 1
1
2
-2 -1 -1
12
这条抛物线表示的二次函数为
-2 -3
y 1 x2
2
做一做
当水面下降1m时，水面的纵坐标为y = －3. 请你根据上面的函数表达式求出这时的水面宽度．
y
（0，0）
o
x