生活中的立体图形 含答案
(最新)北师大版七年级数学上册《生活中的立体图形》试卷(附答案)

第1页 共4页
11.将下列几何体分类,柱体有: ,锥体有 (填序号) ;
12.长方体由_______________个面_______________条棱_______________个顶点;
13.半圆面绕直径旋转一周形成__________;
4. 围成几何体的侧面中,至少有一个是曲面的是______________;(举一例)
5. 正方体有_____个顶点,经过每个顶点有_________条棱,这些棱都____________;
6. 圆柱、圆锥、球的共同点是_____________________________;
7.线,说明了______________,时钟秒针旋转时,形成一个圆面,这说明了_______________,三角板绕它的一条直角边旋转一周,形成一个圆锥体,这说明了___________________;
8. 圆可以分割成_____ 个扇形,每个扇形都是由___________________;
9. 从一个七边形的某个顶点出发,分别连结这个点与其余各顶点,可以把七边形分割成__________个三角形;
10.在乒乓球、橄榄球、足球、羽毛球、冰球中,是球体的有 ;
《生活中的立体图形》试卷
第1.1.1课时家庭作业 (生活中的立体图形1) 姓名 学习目标:
1.经历从现实世界中抽象出几何图表的过程,感受图形世界的丰富多彩。
2.在具体情境中认识圆柱、圆锥、正方体、长方体、棱柱、棱台、球,并能用自已的语言描述它们的某些特征。
一.填空题:
1.立体图形的各个面都是__________的面,这样的立体图形称为多面体.;
2.图形是由________,_________,________构成的;
生活中的立体图形含答案

1.生活中的立体图形一.选择题1.观察下图,请把左边的图形绕着给定的直线旋转一周后可能形成的几何体选出来( )2.下列说法错误的是( )A.长方体、正方体都是棱柱B.三棱柱的侧面是三角形C.直六棱柱有六个侧面、侧面为长方形D.球体的三种视图均为同样大小的图形3.从多边形一条边上的一点(不是顶点)发出发,连接各个顶点得到2003个三角形,则这个多边形的边数为 ( )A.2001B.2005C.2004D.20064.如图所示立体图形,是由____个面组成,面与面相交成____条线( )A.3,6B.4,5C.4,6D.5,7第4题 第5题5.如图,在一个棱长为6cm 的正方体上摆放另一个正方体,使得上面正方体的四个顶点恰好均落在下面正方体的四条棱上,则上面正方体体积的可能值有( )A .1个B .2个C .3个D .无数个二.填空题1.如图所示的几何体是由一个正方体截去41后而形成的,这个几何体是由( )个面围成的,其中正方形有( )个,长方形有( )个.第1题2.用一长20cm ,宽8cm 的纸片卷成(无重合部分)一个高为8cm 的圆柱,那么这个圆柱的底面圆的半径是( ),圆柱的体积是( )。
3.如图所示的几何体是由若干个棱长为1的正方体堆放而成的,则这个几何体的体积是( )。
第3题 第4题4.将棱长为1cm 的正方体组成如图所示的几何体,那么这个几何体的表面积是( )。
5.如图,观察由棱长为1的小立方体摆成的图形,寻找规律:如图①中; 共有1个小立方体,其中1个看得见,0个看不见;如图②中;把共有8个小立方体,其中7个看得见,1个看不见;如图③中;共有27个小立方体,其中19个看得见,8个看不见;……,则第⑥个图中,看得见的小立方体有______________个。
三.解答题1.在正方体的六个面上分别涂上红、黄、蓝、白、黑、绿六种颜色,现有涂色方式完全相同的四个正方体,如图拼成一个长方体,请判断涂红、黄、白三种颜色的对面分别涂着哪一种颜色?2.如图,已知一个正方体的六个面上分别写着六个连续的整数,且每两个相对面上的两个数的和都相等,图中所能看到的数是16,19和20,求这6个整数的和.答案一选择题1.D2.B3.B4.C5.D 解析:因为上面正方体的棱长不确定,所以根据正方体体积公式可知,上面正方体体积的可能值有无数个. 二填空题1.8,2,42.π10,π800 3.6 4.362cm 5.125 三解答题1.绿 蓝 黑(分析:红不与蓝、白、黄、黑相对,所以红与绿相对;黄不与白、黑、绿、红相对,黄必与蓝相对;剩下黑与白相对。
2024~2025学年七年级数学上册1.1生活中的立体图形第二课时课后练「含答案」

1.一个多面体有7个面,10个顶点,则它的棱数只能是()A.11B.13C.15D.172.中国扇文化有着深厚的文化底蕴;历来中国有“制扇王国”之称.如图,打开折扇时,随着扇骨的移动形成一个扇面,这种现象可以用数学原理解释为()A.点动成线B.线动成面C.面动成体D.两点确定一条直线3.下面现象说明“线动成面”的是( )A.天空划过一道流星B.扔一块小石子,石子在空中飞行的路线C.旋转一扇门,门在空中运动的痕迹D.汽车雨刷在挡风玻璃上面画出的痕迹4.下列图形旋转一周,能得到如图几何体的是()A.B.C.D.5.如图,将下面的平面图形绕直线l旋转一周,得到的立体图形是( )A.B.C.D.6.将如图所示的长方形绕它的对角线所在直线旋转一周,形成的几何体是()A.B.C.D.7.一个七棱柱一共有条棱,有面,有个顶点.8.一个七棱柱有个面.9.(1)一张纸对折后,纸上会留下一道折痕,用数学知识可解释为;(2)夏夜,天上飞逝的流星形成一道亮光,用数学知识可解释为;(3)黑板擦在黑板上擦出一片干净的区域,用数学知识可解释为;(4)长方形绕它的一边在的直线旋转,形成一个圆柱,用数学知识可解释为.【分析】本题考查的是立体图形的基本知识,解题的关键是熟练掌握几何体的基本概念,根据多面体的顶点数+面数-棱数=2,即可解答.【详解】解:Q多面体有7个面,10个顶点,\棱数为:107215+-=,故选:C.2.B【分析】本题考查了线、面的关系,根据题意,结合线动成面的数学原理:某一条线在运动过程中留下的运动轨迹会组成一个平面图形,这个平面图形就是一个面,即可得出答案.熟练掌握线动成面的数学原理是解本题的关键.【详解】解:打开折扇时,随着扇骨的移动形成一个扇面,这种现象可以用数学原理解释为线动成面,故选:B.3.D【分析】本题考查了点、线、面、体.根据点、线、面、体之间的关系对各选项分析判断后利用排除法求解.【详解】解:A、天空划过一道流星,说明“点动成线”,本选项不符合题意;B、扔一块小石子,石子在空中飞行的路线,说明“点动成线”,本选项不符合题意;C、旋转一扇门,门在空中运动的痕迹,说明“面动成体”,本选项不符合题意;D、汽车雨刷在挡风玻璃上面画出的痕迹,说明“线动成面”,本选项符合题意.故选:D.4.A【分析】根据面动成体,判断出各个选项旋转得到的立体图,即可得出结论.【详解】A.旋转一周可得本题的几何体,故选项正确,符合题意;B.旋转一周为两个圆锥结合体,故选项错误,不符合题意;C.旋转一周为圆锥和圆柱的结合体,故选项错误,不符合题意;D.旋转一周为两个圆锥和一个圆柱的结合体,故选项错误,不符合题意;故选:A.【点睛】此题考查了面动成体,解题的关键是要有空间想象能力,熟悉并判断出旋转后的立体图形.【分析】根据面动成体,梯形绕下底边旋转是圆锥加圆柱,可得答案.【详解】面动成体,直角三角形绕直角边旋转一周可得圆锥,长方形绕一边旋转一周可得圆柱,那么所求的图形是下面是圆锥,上面是圆柱的组合图形.故选D.【点睛】此题考查点、线、面、体的问题,解决本题的关键是得到所求的平面图形是得到几何体的主视图的被纵向分成的一半.6.B【分析】根据矩形角度和顶点观察,绕对角线可得答案.【详解】解:通过观察可知,B图形的构造满足旋转结果.故选:B.【点睛】本题主要考查旋转的性质,认真观察旋转中心和线段、角度的特点是解题的关键.7.21 9 14【分析】本题考查了认识立体图形,是基础题,熟记棱柱的结构并以及七棱柱的特点是解题的关键.根据七棱柱的特点填空.【详解】解:一个七棱柱共有21条棱,9个面,14个顶点.故答案为:21,9,14.8.9【分析】本题考查了棱柱的面,一个七棱柱是由两个七边形的底面和7个四边形的侧面组成,根据其特征进行填空即可.【详解】解:一个七棱柱有9个面,故答案为:9.9.面与面相交得到线点动成线线动成面面动成体【分析】题目考查了点、线、面之间的动态关系,理解生活中的点、线、面关系是解题的关键.【详解】(1)一张纸对折后,纸上会留下一道折痕,用数学知识可解释为面与面相交得到线;故答案为:面与面相交得到线(2)夏夜,天上飞逝的流星形成一道亮光,用数学知识可解释为点动成线;故答案为:点动成线(3)黑板擦在黑板上擦出一片干净的区域,用数学知识可解释为线动成面;故答案为:线动成面(4)长方形绕它的一边所在的直线旋转,形成一个圆柱,用数学知识可解释为面动成体.故答案为:面动成体。
北师大数学七年级上册第一单元《丰富的图形世界1.1生活中的立体图形2

。
【解析】笔尖在纸上快速滑动写出了一个又一个字,这说明了 点动成线;风扇的扇叶旋转时,看起来像一个整体的圆面,这说 明线动成面. 答案:点动成线 线动成面 点动成线
5.有一同学手拿一枚硬币,将其立在桌面上用力一转,
它形成的是一个
体,由此说明
.
【解析】硬币立在桌面上用力一转,它形成的是一个球体;从运动的观点可知,这种 现象说明面动成体. 答案:球 面动成体
【总结提升】点、线、面、体之间的关系
题组二:几何体的形成 1.(2012·娄底中考)如图,长方形绕它的一条边MN 所在的直线旋转一周形.
2.如图,把一个圆绕虚线旋转一周,得到的几何体是( )
【解析】选B.A是长方形绕虚线旋转一周,得到的几何体,B是 一个圆绕虚线旋转一周,得到的几何体,C是一个直角梯形绕 长底边旋转一周,得到的几何体,D是半圆绕直径旋转一周,得 到的几何体.
做一做:如图,第二行的图形围绕红线旋转一周, 便能形成第一行的某个几何体,用线连一连.
知识点 2 几何体的形成 【例2】观察如图所示的图形,把左边的图形绕着给 定的直线旋转一周后可能形成的立体图形是( )
【思路点拨】本题考查学生立体图形的空间想象能力及分析问 题的能力,根据面动成体的原理以及空间想象力即可得解. 【自主解答】选D.由图形可以看出,左边的长方形的竖直的两 个边与已知的直线平行,因而这两条边旋转形成两个柱形表面, 因而旋转一周后可能形成的立体图形是一个管状的物体.
3.如图是由哪个平面图形旋转得到的( )
【解析】选A.图中所给的几何体是由上部的圆锥和下部的圆台 组合而成的,故轴截面的上部是直角三角形,下部为直角梯形.
4.笔尖在纸上快速滑动写出了一个又一个字,这说明了
;风扇的扇叶旋转时,看起来像一个整体的圆面,
生活中的立体图形课后题(题目+答案)

【采分点】面的个数(4分)
【采分点】判断平曲面(2分)
【题干】2.你认为生活中有哪些几何体可以由平面图形旋转而得到?你能想象它们是由什么平面图形旋转而成的吗?举例说明.
【答案】比如:篮球是由圆旋转而成;圆锥形的沙堆是由三角形旋转而成;水杯是由四边形旋转而成的;易拉罐是由矩形旋转而成的;.
【答案】(1)圆柱体和长方体(2)圆柱体(3)圆柱体和圆锥(4)长方体和球
【采分点】每幅图(1.5分)
【题干】6.圆柱和棱柱有很多相同点,下面的这个几何体也有这样的相同点吗?
【答案】有,上下底面相同且平行;侧面展开是矩形.
【采分点】有(2分)
【采分点】相同点(4分)
【大题】习题1.2(每小题6分)
【题干】1.图中的棱柱,圆锥分别是由几个面围成的?他们分别是平的还是曲的?
【采分点】正确举例3个(6分)
【题干】3.下列几何体可以由平面图形绕其中一条直线旋转一周得到吗?
【答案】(1)(3)(4)可以由平面图形绕其中一条直线旋转一周得到
【采分点】(1)(3)(4)(6分)
【小题】(2)这个六棱柱的所有侧面的面积之和是多少?
【答案】侧面积之和:5×4×6=120cm2
【采分点】120cm2(4分)
【问答题】
【题干】3.将下列几何体分类,并说明理由.
正方体长方体球圆柱圆锥四棱柱三棱柱
【答案】这些几何体分别是正方体、长方体、球、圆柱、圆锥、四棱柱、三棱柱
可以分为柱体、锥体、球体三类;
【综合题】
【题干】2.一个六棱柱模型如图所示,它的底面边长都是5cm,侧棱长4cm观察这个模型,回答下列问题:
01-第一章1生活中的立体图形 (3)

1生活中的立体图形测试时间:30分钟一、选择题1.下列几何体中,属于棱柱的有( )A.3个B.4个C.5个D.6个答案 A 根据棱柱的概念,有两个面互相平行,其余各面都是平行四边形,并且每相邻两个四边形的公共边都互相平行,由这些面所围成的多面体叫做棱柱,因此长方体、四棱柱、三棱柱属于棱柱.2.下面几何体中,全是由曲面围成的是( )A.圆柱B.圆锥C.球D.正方体答案 C 圆柱的上下底面是平的面,圆锥的底面是平的面,正方体的六个面都是平的面.故选C.3.下列说法中,不正确的是( )A.棱锥的侧面都是三角形B.棱柱的上下底面一样大C.正方体、长方体都是棱柱D.四棱锥与四棱柱的棱数一样多答案 D 根据我们所熟悉的几何体,A、B、C选项均正确,四棱锥有8条棱,而四棱柱有12条棱,D选项错误,故选D.4.不透明袋子中装有一个几何体模型,两位同学摸该模型并描述它的特征.甲同学:它有2个面是三角形;乙同学:它有9条棱,该模型的形状所对应的立体图形可能是( )A.三棱柱B.四棱柱C.三棱锥D.四棱锥答案 A 根据该模型有两个三角形的面,且有9条棱,可知该模型是三棱柱.四棱柱没有三角形的面,三棱锥有四个三角形的面,四棱锥有四个三角形的面.5.如图,一个正方形绕它的对角线所在直线旋转,则其旋转一周后得到的几何体为( )答案 C 正方形绕它的对角线所在直线旋转,可看做两个直角三角形各自绕着它们的斜边所在直线旋转,旋转后得到的几何体应该是两个圆锥体的组合图形,故选C.二、填空题6.分别写出下列各立体图形的名称:①②③答案①圆锥②五棱柱③三棱锥解析根据几何体的形状,可知①是圆锥,②是五棱柱,③是三棱锥.7.雨滴从空中落下、流星从空中划过,这些现象给我们以的形象;汽车的雨刷摆动、将教室前的投影幕展开,这些现象给我们以的形象;硬币在桌面上快速旋转、向玻璃杯中注水水面的上升,这些现象给我们以的形象.答案点动成线;线动成面;面动成体8.若一个棱柱有10个顶点,那么它共有条棱.答案15解析因为这个棱柱有10个顶点,所以它是五棱柱,上下两个底面共有10条棱,侧面有5条棱,所以它共有15条棱.故答案为15.9.用五个面围成的几何体可能是.答案四棱锥或三棱柱解析四棱锥是由4个侧面和1个底面围成的,三棱柱是由3个侧面和2个底面围成的.故用五个面围成的几何体可能是四棱锥或三棱柱.三、解答题10.在日常生活中,我们看到的物体,如①易拉罐;②饮水机;③金字塔;④自来水管;⑤八角亭;⑥西红柿;⑦小喇叭;⑧气球;⑨课本等.你能指出这些物体和什么立体图形类似吗?解析类似于圆柱体的有:①易拉罐、④自来水管;类似于圆锥体的有:⑦小喇叭;类似于长方体的有:②饮水机、⑨课本;类似于棱锥体的有:③金字塔、⑤八角亭;类似于球体的有:⑥西红柿、⑧气球.11.观察如图所示的直四棱柱.(1)它有几个面?几个底面?底面与侧面分别是什么图形?(2)侧面的个数与底面多边形的边数有什么关系?(3)若底面的周长为20 cm,侧棱长为8 cm,则它的侧面积为多少?解析(1)它有6个面,2个底面,底面是梯形,侧面是长方形.(2)侧面的个数与底面多边形的边数相等,都为4.(3)它的侧面积为20×8=160 cm2.。
生活中的立体图形_第一课时

生活中的立体图形
北京天安门
北京天坛
发神 射舟 场六 景号
生活中的立体图形
(4)在上图中找出与球类似的几何体? 答:墙上挂着的足球与地球类似。
生活中的立体图形
(1)上图中哪些物体的形状与长方体、正方体类似? 答:文具盒、书与长方体类似;魔方与正方体类似。
生活中的立体图形
(2)上图中哪些物体的形状与圆柱、圆锥类似? 答:笛子、水杯与圆柱类似;小丑帽与圆锥类似。
1、棱柱的上、下两底 认识棱柱 面平行且形状相同, 大小一样; 底面 2、棱柱的侧面形状都 是平行四边形; 侧棱 侧面 3、棱柱的侧棱的长度 都相等。 4、侧面的个数和底面 图形的边数相等.
根据底面图形的边数可将棱柱分类:
三棱柱
四棱柱
五棱柱
六棱柱
棱柱
面的个数
三棱柱
四棱柱 五棱柱 六棱柱
5
6 7 8
篮球
这更没问题:
篮球
球
生活中还有哪些物体是球体?
月饼包装盒
你肯定错不了:
月饼包 装盒
棱柱
生活中还有哪些物体是棱柱体?
常见的几何体
长方体 正方体
棱柱
圆柱
圆锥
球体
圆柱的特征: 1、圆柱的上、下两 底面平行且形状都 是圆形,大小一样;
2、圆柱的侧面都 是曲面,展开后为 长方形;
认识圆柱
底 面
侧面
棱柱的特征:
愿同学们运用今天学到的几何体 的知识去妆点自己;妆点你的空间; 妆点那属于你的世界。
愿在不久的将来,在世界知名的 某一场所,能看到出自你的手的几何 体。
生活中的立体图形
(3)在上图中找出与笔筒类似的物体。 答:书架上的棱柱与笔筒类似。
《生活中的立体图形》典型例题-掌门1对1
\
生活中的立体图形典型例题-掌门1对1
知识点1 正确识别球体、柱体与锥体三大类
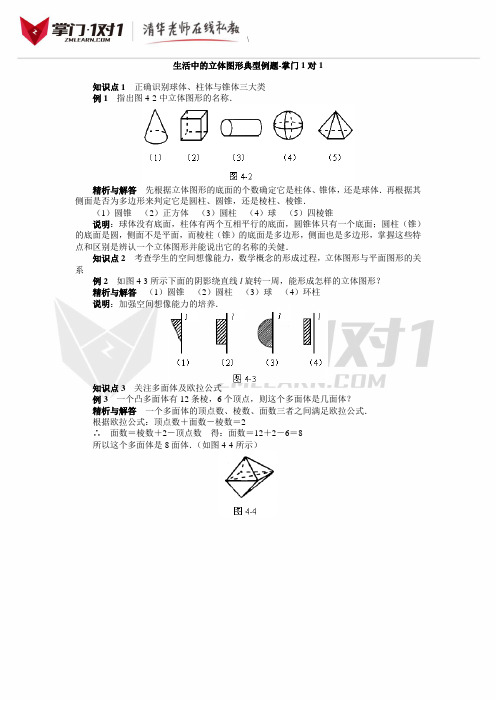
例1指出图4-2中立体图形的名称.
精析与解答先根据立体图形的底面的个数确定它是柱体、锥体,还是球体.再根据其侧面是否为多边形来判定它是圆柱、圆锥,还是棱柱、棱锥.
(1)圆锥(2)正方体(3)圆柱(4)球(5)四棱锥
说明:球体没有底面,柱体有两个互相平行的底面,圆锥体只有一个底面;圆柱(锥)的底面是圆,侧面不是平面,而棱柱(锥)的底面是多边形,侧面也是多边形,掌握这些特点和区别是辨认一个立体图形并能说出它的名称的关健.
知识点2 考查学生的空间想像能力,数学概念的形成过程,立体图形与平面图形的关系
例2 如图4-3所示下面的阴影绕直线l旋转一周,能形成怎样的立体图形?
精析与解答(1)圆锥(2)圆柱(3)球(4)环柱
说明:加强空间想像能力的培养.
知识点3关注多面体及欧拉公式
例3一个凸多面体有12条棱,6个顶点,则这个多面体是几面体?
精析与解答一个多面体的顶点数、棱数、面数三者之间满足欧拉公式.
根据欧拉公式:顶点数+面数-棱数=2
∴面数=棱数+2-顶点数得:面数=12+2-6=8
所以这个多面体是8面体.(如图4-4所示)。
北师版七年级上1.1生活中的立体图形同步习题有答案和解析
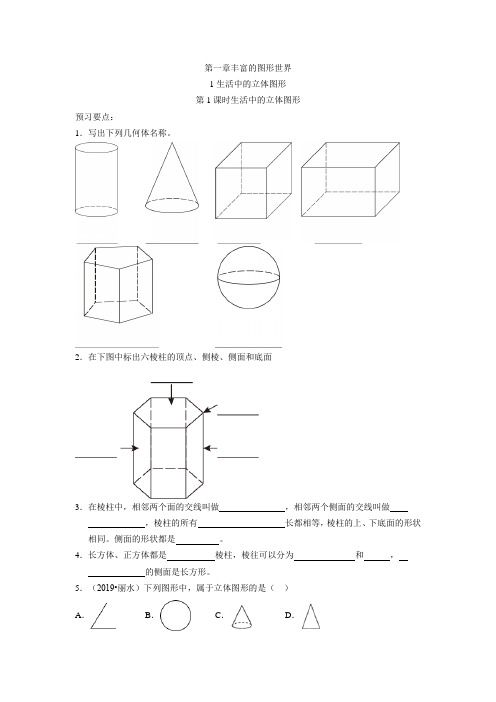
第一章丰富的图形世界1生活中的立体图形第1课时生活中的立体图形预习要点:1.写出下列几何体名称。
2.在下图中标出六棱柱的顶点、侧棱、侧面和底面3.在棱柱中,相邻两个面的交线叫做,相邻两个侧面的交线叫做,棱柱的所有长都相等,棱柱的上、下底面的形状相同。
侧面的形状都是。
4.长方体、正方体都是棱柱,棱往可以分为和,的侧面是长方形。
5.(2019•丽水)下列图形中,属于立体图形的是()A.B.C.D.6.下列说法正确的是()①教科书是长方形;②教科书是长方体,也是棱柱;③教科书的表面是长方形.A.①②B.①③C.②③D.①②③7.埃及金字塔类似于几何体()A.圆锥B.圆柱C.棱锥D.棱柱8.在下列立体图形中,只要两个面就能围成的是()A.长方体B.圆柱体C.圆锥体D.球9.六棱柱有面.10.在正方体、长方体、球、圆柱、圆锥、三棱柱这些几何体中,不属于柱体的有,属于四棱柱的有.11.若一直棱柱有10个顶点,那么它共有条棱.同步小题12道一.选择题1.下列几何图形是立体图形的是()A.扇形B.长方形C.正方体D.圆2.下面的几何体中,属于棱柱的有()A.1个B.2个C.3个D.4个3.下列物体的形状类似于球的是()A.乒乓球B.羽毛球C.茶杯D.白织灯泡4.下列几何图形中,属于圆锥的是()A.B.C.D.5.三棱柱的顶点个数是()A.3 B.4 C.5 D.66.下列说法不正确的是()A.长方体与正方体都有六个面B.圆锥的底面是圆C.棱柱的上下底面是完全相同的图形D.五棱柱有五个面,五条棱二.填空题7.下列图形中,是柱体的有.(填序号)8.如果一个六棱柱的一条侧棱长为5cm,那么所有侧棱之和为.9.一个棱柱的棱数恰是其面数的2倍,则这个棱柱的顶点个数是.10.若一个直棱柱共有12个顶点,所有侧棱长的和等于60,则每条侧棱的长为.三.解答题11.将下列几何体与它的名称连接起来.12.如图,一个正五棱柱的底面边长为2cm,高为4cm.(1)这个棱柱共有多少个面?计算它的侧面积;(2)这个棱柱共有多少个顶点?有多少条棱?(3)试用含有n的代数式表示n棱柱的顶点数、面数与棱的条数.第2课时图形变换预习要点:1.图形是由点、线、面构成的。
1.1 生活中的立体图形 (2)

本节目标
1 整理你所学过认识立体图形与平面图形的有关知识; 2 知道点、线、面、体是构成几何图形的元素; 3 进一步认识点、线、面、体的几何特征;
4 知道点、线、面、体之间的关系.
回顾与思考
1. 观察下面的长方体,它有几个面?面与面相交的地方形成了几条棱?棱和棱相交成 几个顶点?
说一说
如下图,围成这些立体图形的各个面中,哪些面是平的?哪些面是曲的?
新课讲解
观察长方体、圆柱、棱锥等熟悉的几何体模型,结合下列问题小组
合作探究:
(1) 面和面相交的地方形成了什么?它们有什么不同吗? (2) 线和线相交处又形成了什么?它们有什么不同吗?
新课讲解
长方体 6 个面相交成的
12 条线是直的.
答案:16 cm3 或 32 cm3 .
本节总结
再见
做一做 如下图,上面的平面图形绕轴旋转一周,可以得到下面的立体图形, 把有对应关系的平面图形与立体图形连接起来.
课堂练习
1. 围成圆柱体的面有
A. 1个
B. 2个
C
()
C. 3个
D. 多于3个
2. 下列说法:①平面上的线都是直线;②曲面上的线都是曲线;③
两条线相交只能得到一个交点;④两个面相交只能得到一条直线,
不正确的有
A
()
A. 4个
B. 3个
C. 2个
D. 1个
课堂练习
3. 笔尖在纸上快速滑动写出了一个又一个字这说明了__点__动__成__线__;自 行车车轮旋转时,看起来像一个整体的圆面,这说明了_线__动__成__面__; 直角三角形绕它的直角边旋转一周,形成了一圆锥体,这 说明了 _____面__动__成. 体 4. 如图:三棱锥有__4个面,它们相交形成了__6条棱, 这些棱相交形成了_4_个点.
北师大版七年级数学上册 1 1 生活中的立体图形同步练习(Word版含答案)

北师大版七年级上 1.1 生活中的立体图形一、选择题(共10小题)1. 如图所示,几何体的主视图是( )A. B.C. D.2. 图中几何体的俯视图是( )A. B.C. D.3. 用4个小立方体搭成如图摆放的几何体,下面视图是几何体主视图的是( )A. B.C. D.4. 如图,由三个小立方体搭成的几何体的俯视图是( )A. B.C. D.5. 如图是某物体的三视图,则这个物体的形状是( )A. 四面体B. 直三棱柱C. 直四棱柱D. 直五棱柱6. 如图是一个几何体的三视图,则该几何体的展开图可以是( )A. B.C. D.7. 如图,立体图形由小正方体组成,这个立体图形有小正方体( )A. 9个B. 10个C. 11个D. 12个8. 将如图所示的直角梯形绕直线l旋转一周,得到的立体图形是( )A. B.C. D.9. 下列四个图形中是正方体的平面展开图的是( )A. B.C. D.10. 已知一个圆柱的侧面展开图为如图所示的矩形,则其底面圆的面积为( )A. πB. 4πC. π或4πD. 2π或4π二、填空题(共5小题)11. 下列图形中,是平面图形的有,是立体图形的有.12. 如图所示,将图沿实线折起来得到一个正方体,那么“5”的对面是(填编号).13. 有底面为正方形的直四棱柱容器A和圆柱形容器B,容器材质相同,厚度忽略不计.如果它们的主视图是完全相同的矩形,那么将B容器盛满水,全部倒入A容器,则结果是.(填“溢出”“刚好装满”“未装满”)14. 如图,已知某几何体的三视图,则这个几何体是.15. 在市委、市政府的领导下,全市人民齐心协力,努力将我市创建为“全国文明城市”,为此学生小红特制了一个正方体玩具,其展开图如图所示,则原正方体中与“文”字所对的面上标的字应是.三、解答题(共5小题)16. 将图①的正方体切去一块,不同的切法可以得到图②−⑤的几何体,它们各有多少个面?多少条棱?多少个顶点?17. 如图所示是由几个小正方块所组成的几何体俯视图,小正方形中的数字表示在该位置小正方块的个数,请你画出这个几何体的正视图和左视图.18. 如图是一个食品包装盒的表面展开图.(1)请写出这个包装盒的多面体形状的名称.(2)请根据图中所标的尺寸,计算这个多面体的表面积和体积.19. 如图所示是n个小正方体搭成的几何体的俯视图,请分别画出它的主视图和左视图.20. 如图中的一些积木是由16块棱长为2cm的正方体堆成的,它的表面积是多少平方厘米?答案1. A2. D3. C4. A5. B6. A7. C8. C【解析】图是一个直角梯形,上底短,下底长,绕对称轴旋转后上底形成的圆小于下底形成的圆, 因此得到的立体图形应该是一个圆台.9. B10. C【解析】题意可知,圆柱底面圆的周长为 4π 或 2π,∴ 圆柱底面圆的半径为 2 或 1,∴ 圆柱底面圆的面积为 4π 或 π.11. ①②④⑤⑥⑧,③⑦⑨【解析】根据平面图形和立体图形的区别,进行辨别即可.12. 113. 未装满14. 四棱锥15. 城16. 图形面(个)棱(条)顶点(个)②71510③7149④7138⑤712717. 如图所示:18. (1)长方体.(2)表面积是4ab+2b2,体积是ab2.19. 如图所示:20. 上面和下面的面积为2×9×(2×2)=72(cm2);前面和后面的面积为2×7×(2×2)=56(cm2);两个侧面的面积为2×8×(2×2)=64(cm2);中间缺口处还有2个面,其面积为2×(2×2)=8(cm2).因为72+56+64+8=200(cm2),所以这个几何体的表面积为200cm2.。
七年级数学生活中的立体图形(含答案)

1.1生活中的立体图形一、选择题1.长方体属于( )A.棱锥B.棱柱C.圆柱D.以上都不对2.下列几何体中(如图)属于棱锥的是( )(1) (2) (3) (4) (5) (6)A.(1)(5)B.(1)C.(1)(5)(6)D.(5)(6)3.下列所讲述的物体,_______与圆锥的形状类似( )A.香烟盒B.铅笔C.西瓜D.烟囱帽4. 如图7所示立体图形,是由____个面组成,面与面相交成____条线( )A.3,6B.4,5C.4,6D.5,7(7) (8) (9)二、填空题5.面与面相交成_____________,线与线相交成___________.6.机器零件中的六角螺母,圆筒形的易拉罐、足球、火柴盒、铅垂体中,•类似于棱柱的物体有________,•类似于球体的物体有_________,••类似于圆锥的物体有________,类似于圆柱的物体有__________.7. 如图8的棱柱有_______个顶点,有_______条线,有________个面,经过每个顶点有________条边.8. 如图9所示图形绕图示的虚线旋转一周,(1)能形成________,•(•2)•能形成_________,(3)能形成_________.三、解答题:9. 如图中的立体图形分别是由几个面围成的,它们是平面还是曲面.10.将下图中的几何体分类,并说明理由.11.在圆柱、圆锥、正方体、长方体、各类棱柱和球这些几何体中,•表面都是平的有哪些?表面只有一个面的有哪些?表面有两个面的有哪些?表面有三个面的有哪些?表面有五个面的有哪些?12.你能想像用4个面构成的几何体吗?它的每个面是什么图形?•它有几个顶点?你能从生活中环境中找到类似的几何体吗?13.大家都知道,一只足球是用黑白两种颜色皮缝制成的,黑皮是正五边形,白皮是正六边形,如图,其中黑皮有12块,问白皮有多少块?答案一、1.B 2.B 3.D 4.C二、5.线,点6.火柴盒;六角螺母;足球;铅垂体;易拉罐7.10;15;7;38.圆柱;圆锥;球三、9.(1)是一个面围成的,它是曲面.(2)是六个平面围成的(3)•是由一个曲面和一个平面围成的(4)是由三个平面和一个曲面围成的;10.1.分类标准1:•按柱、锥、球划分①、②、④、⑤、⑦、⑧为柱体⑥为锥体③为球体分类标准2:按围成的面是曲面还是平面分①、②、④、⑦、⑧各面为平面③、⑤、⑥为一类,围成的面中至少有一个为曲面.11.表面都是平面的有:正方体、•长方体、各类型棱柱表面只有一个面的有:球表面有两个面的有:圆锥 •表面有三个面的有:圆柱表面有五个面的有:三棱柱12.能.用4个面构成的几何体是四面体,每个面是三角形它有四个顶点.13.因为每块白皮有三条边与黑皮缝在一块,即每三条黑皮的边确定一块白皮,•而每块黑皮有五条边,十二块黑皮有5×12=60(条边)所以白皮有60÷3=20块.。
北师大版七年级数学上册《1.1生活中的立体图形》同步测试题及答案

北师大版七年级数学上册《1.1生活中的立体图形》同步测试题及答案学校:___________班级:___________姓名:___________考号:___________一、单选题1.下列立体图形中,是圆锥的是()A.B.C.D.2.下列图形中是多面体的有()A.(1)(2)(4)B.(2)(4)(6)C.(2)(5)(6)D.(1)(3)(5)3.子弹从枪膛中射出去的轨迹像是一条线,这个现象可以用数学知识解释为()A.点动成线B.线动成面C.面动成体D.以上都不对4.一个印有“你要探索数学”字样的立方体纸盒表面展开图如图1所示,若立方体纸盒是按图2展开,则印有“索”字在几号正方形内()A.①B.①C.①D.①5.几何图形都是由点、线、面、体组成的,点动成线,线动成面,面动成体,下列生活现象中可以反映“线动成面”的是()A.笔尖在纸上移动划过的痕迹B.长方形绕一边旋转一周形成的几何体C.流星划过夜空留下的尾巴D.汽车雨刷的转动扫过的区域6.如图,下列图形中属于棱柱的有()A.2B.3C.4D.57.夜晚时,我们看到的流星划过属于()A.点动成线B.线动成面C.面动成体D.以上答案都不对8.一个直角三角形绕它的一边所在直线旋转一周所得到的几何体一定是()A.圆锥B.圆柱C.圆锥或圆柱D.以上都不对9.观察下面四个图形是圆锥的是()A.B.C.D.10.在①球体;①柱体;①锥体;①棱柱;①棱锥中,必是多面体的是() A.①~①B.①①C.①D.①①11.一个棱柱有18条棱,那么它的底面一定是()A.五边形B.六边形C.十边形D.十五边形12.将下列平面图形绕轴旋转一周,可得到图中所示的立体图形的是().A.B.C.D.二、填空题13.一个正方体有个面,条棱,个顶点.14.今年十一国庆节当晚,香港以“富兴百业贺国庆,盈聚慧城耀香江”为主题,在维多利亚港举行国庆烟花汇演,庆祝中华人民共和国成立74周年.绚烂的焰火可以看成由点运动形成的,这个现象说明.15.如果长方形的长和宽分别为6和4,那么以长方形的一边为轴旋转一周所得的几何体的体积为(结果保留 ).16.如图的几何体有个面,条棱,个顶点,它是由简单的几何体和组成的.17.如图,有一个盛有水的正方体玻璃容器,从内部量得它的棱长为30 cm,容器内的水深为8 cm.现把一块长,宽,高分别为15 cm,10 cm,10 cm的长方体实心铁块平放进玻璃容器中,容器内的水将升高cm.三、解答题18.小明学习了“面动成体”之后,他用一个边长为6cm、8cm和10cm的直角三角形,绕其中一条边旋转一周,得到了一个几何体.请计算出几何体的体积.(锥体体积=13底面积×高)19.请把下图中的平面图形与其绕所画直线旋转一周之后形成的立体图形用线连接起来.20.将一个长方形分别沿它的长和宽所在的直线旋转一周,回答下列问题:(1)旋转后将得到什么几何体?(2)若长方形的长和宽分别为6cm和4cm,求旋转后两个几何体的体积.(结果保留π)21.请你观察下列几种简单多面体模型,解答下列问题:多面体面数(F)棱数(E)四面体46长方体612正八面体8(1)计算长方体棱数,可依据长方体有6个面,每个面均为四边形即有4条棱,得出总棱数为12;请你猜想多面体面数、形状、棱长之间的数量关系,完成以下计算:①如图所示,正八面体的每一个面都是三角形,则正八面体有__________条棱;①正十二面体的每一个面都是正五边形,则它共有__________条棱;(2)如下图,一种足球(可视作简单32面多面体)是由32块黑白相间的牛皮缝制而成,黑皮为正五边形,白皮为正六边形,且边长相等,已知图中足球有90条棱;某体育公司采购630张牛皮用于生产这种足球,已知一张牛皮可用于制作30个正五边形或者制作20个正六边形,要使裁剪后的五边形和六边形恰好配套,应怎样计划用料才能制作尽可能多的足球?22.十八世纪瑞士数学家欧拉证明了简单多面体中顶点数(V)、面数(F)、棱数(E)之间存在的一个有趣的关系式,被称为欧拉公式.请你观察下列几种简单多面体模型,解答下列问题:(1)根据上面多面体模型,完成表格中的空格:多面体顶点数(V)面数(F)棱数(E)四面体44①长方体8612正八面体①812正十二面体201230(2)你发现顶点数(V)、面数(F)、棱数(E)之间存在的关系式是.(3)一个多面体的面数与顶点数相同,且有12条棱,则这个多面体的面数是.23.18世纪瑞士数学家欧拉证明了简单多面体中顶点数(V)、面数(F)、棱数(E)之间存在的一个有趣的关系式,被称为欧拉公式.请你观察下列几种简单多面体模型,解答下列问题.(1)根据上面的多面体模型,直接写出表格中的m,n的值,则m=______,n=______.多面体顶点数(V)面数(F)棱数(E)四面体446长方体m612正八面体n812正十二面体201230(2)你发现顶点数(V)、面数(F)、棱数(E)之间存在的关系式是_______.(3)一个多面体的面数等于顶点数,且这个多面体有30条棱,求这个多面体的面数.参考答案1.A【分析】本题考查常见的几何体.熟记常见的几何体,是解题的关键.根据圆锥的特征,进行判断即可.【详解】解:A、是圆锥,符合题意;B、是球体,不符合题意;C、是圆柱体,不符合题意;D、是长方体,不符合题意;故选:A.2.B【分析】多面体指四个或四个以上多边形所围成的立体.【详解】解:(1)圆锥有2个面,一个曲面,一个平面,不是多面体;(2)正方体有6个面,故是多面体;(3)圆柱有3个面,一个曲面两个平面,不是多面体;(4)三棱锥有4个面,故是多面体;(5)球有1个曲面,不是多面体;(6)三棱柱有5个面,故是多面体.故是多面体的有(2)(4)(6)故选:B.【点睛】本题考查多面体的定义,关键点在于:多面体指四个或四个以上多边形所围成的立体.3.A【分析】根据“点动成线”的概念直接回答即可.【详解】解:子弹从枪膛中射出去的轨迹可以看作点动成线的实际应用;故选A【点睛】此题考查了点、线、面、体,正确理解点线面体的概念是解题的关键.4.A【详解】试题分析:正方体的表面展开图的特征:相对面展开后间隔一个正方形.由图可得印有“索”字在①号正方形内,故选A.考点:正方体的表面展开图点评:本题属于基础应用题,只需学生熟练掌握正方体的表面展开图的特征,即可完成.5.D【分析】根据点动成线,线动成面,面动成体即可一一判定.【详解】解:A.笔尖在纸上移动划过的痕迹,反映的是“点动成线”,故不符合题意;B.长方形绕一边旋转一周形成的几何体,反映的是“面动成体”,故不符合题意;C.流星划过夜空留下的尾巴,反映的是“点动成线”,故不符合题意;D.汽车雨刷的转动扫过的区域,反映的是“线动成面”,故符合题意.故选:D【点睛】本题考查了点动成线,线动成面,面动成体,理解和掌握点动成线,线动成面,面动成体是解决本题的关键.6.B【分析】根据有两个面互相平行,其余各面都是四边形,并且每相邻两个四边形的公共边都互相平行,由这些面所围成的多面体叫做棱柱,由此可选出答案.【详解】解:根据棱柱的定义可得①符合棱柱定义的有第一、二、四个几何体都是棱柱,共3个,其余都不是棱柱.故选①B.【点睛】本题考查棱柱的定义,属于基础题,掌握基本的概念是关键.7.A【分析】把流星视为点,流星的轨迹是一条线,符合点动成线的原理.【详解】①把流星视为点,流星的轨迹是一条线,符合点动成线的原理①选A.【点睛】本题考查了点动成线的原理,正确理解题意是解题的关键.8.D【分析】此题考查面与体的关系,正确理解面与体的关系是解题的关键.由平面图形绕某条直线旋转一周可得到体,据此依次判断.【详解】解:将直角三角形绕一边所在的直线旋转一周形成的几何体不一定是圆锥,以斜边所在的直线为轴旋转一周所得到的几何体是两个圆锥组成的组合体,不是圆锥故选:D9.C【分析】根据圆锥的定义:圆锥面和一个截它的平面(满足交线为圆)组成的空间几何图形叫圆锥,进行判断即可.【详解】解:A、不是圆锥,故错误;B、不是圆锥,故错误;C、是圆锥,故正确;D、不是圆锥,故错误;故选C.【点睛】本题主要考查了圆锥的定义,解题的关键在于能够熟练掌握圆锥的定义.10.D【详解】解:①球体只有一个曲面,故球体不是多面体;①柱体,圆柱有三个面,故柱体不一定是多面体;①锥体,圆锥有两个面,故锥体不一定是多面体;①棱柱至少有两个底面,三个侧面,故棱柱是多面体;①棱锥至少有一个底面,三个侧面,故棱锥是多面体.故选D.11.B【分析】根据题意利用n棱柱中棱的条数为3n,由棱的总条数为18,进行计算即可求出答案.【详解】解:n棱柱有3n条棱,又18÷3=6,因此底面是六边形.故选:B.【点睛】本题考查认识立体图形,熟练掌握棱柱的顶点、面数和棱的条数是正确判断的前提.12.B【分析】根据点动成线,线动成面,面动成体进行判断即可.【详解】解:绕轴旋转一周,可得到图中所示的立体图形的是:故选:B.【点睛】此题主要考查了点、线、面、体,关键是掌握面动成体.点、线、面、体的运动组成了多姿多彩的图形世界.13.612 8【分析】根据正方体的特征:正方体有6个面、12条棱、8个顶点,每个面都是正方形,而且面积相等,每条棱的长度都相等,正方体是特殊的长方体.据此解答.【详解】解:正方体有6个面,有12条棱,有8个顶点,一个正方体所有面的大小相等;每条棱长度都相等;故答案为6,12,8.【点睛】本题考查正方体,解题关键是理解并掌握正方体的特征.14.点动成线【分析】根据点,线,面,体的关系得出答案.【详解】绚烂的烟花可以看成由点运动形成的,这个现象说明了点动成线.故答案为:点动成线.15.96π或144π【分析】由题意易得可分两种情况进行求解,即①若以长方体的长为轴,旋转一周,则得到高为6,底面半径为4的圆柱,①若以长方体的宽4为轴,旋转一周,则得到高为4,底面半径为6的圆柱;然后进行求解即可.【详解】解:①若以长方体的长为轴,旋转一周,则得到高为6,底面半径为4的圆柱,其体积为24696ππ⨯⨯=;①若以长方体的宽4为轴,旋转一周,则得到高为4,底面半径为6的圆柱,其体积为264144ππ⨯⨯=.故答案为:96π或144π.【点睛】本题主要考查几何初步,关键是由平面图形得到几何体,进而求解即可.16.9 16 9 四棱锥四棱柱【详解】观察这个几何体可知,它有9个面,16条棱,9个顶点,它是由简单的几何体四棱锥和四棱柱组成的.17.315或1【分析】根据题意列出式子,进行计算即可【详解】解:设长方体浸入水面的高度为xcm,则水面升高了(x-8)cm 当以15 cm,10 cm为底面积浸入水中时:30308+1510x=3030x⨯⨯⨯⨯解得:3 x=95故水面升高了:339-8=155(cm)当以10 cm,10 cm为底面积浸入水中时:30308+1010x=3030x⨯⨯⨯⨯解得:x=9故水面升高了:9-8=1(cm)故答案为:315或1【点睛】此题主要考查了有理数乘除的应用,根据题意得出式子进行计算是解题关键.18.几何体的体积为:96πcm3或128πcm3或76.8πcm3.【分析】根据三角形旋转是圆锥,可得几何体;根据圆锥的体积公式,分类讨论可得答案.【详解】解:以8cm为轴,得:以8cm为轴体积为13×π×62×8=96π(cm3);以6cm为轴,得:以6cm为轴的体积为13×π×82×6=128π(cm3);以10cm为轴,得以10cm 为轴的体积为13×π(245)2×10=76.8π(cm 3). 故几何体的体积为:96πcm 3或128πcm 3或76.8πcm 3.【点睛】本题考查了点线面体,利用三角形旋转是圆锥是解题关键.19.见解析【分析】本题考查了点线面体,熟记各种图形旋转得出的立体图形是解题关键.直角三角形绕直角边旋转一周得到的立体图形是圆锥,长方形绕一边旋转一周得到的立体图形是圆柱,直角梯形绕如图所示的一边旋转一周得到的立体图形是圆台,半圆绕直径旋转一周得到的立体图形是球.【详解】解:如图所示:20.(1)圆柱(2)396cm π 3144cm π【分析】(1)根据平面图形中矩形旋转一周可得到圆柱求解即可;(2)根据绕长方形的长旋转一周得到圆柱的高为6cm ,圆柱底面半径为4cm ;绕长方形的宽旋转一周得到的圆柱的高为4cm ,底面半径为6cm ,分别利用圆柱的体积公式求解即可.【详解】(1)解:由题意可得,旋转后将得到圆柱答:旋转后将得到的几何体是圆柱;(2)解:由题意可得,绕长方形的长旋转一周得到圆柱的高为6cm ,圆柱底面半径为4cm①236496V cm ππ=⨯⨯=圆柱绕长方形的宽旋转一周得到的圆柱的高为4cm ,底面半径为6cm①2246144V cm ππ=⨯⨯=圆柱答:旋转后两个几何体的体积分别为396cm π 3144cm π.21.(1)12;30(2)用于制作30个正五边形的牛皮共180张,用于制作20个正六边形的牛皮共450张.【分析】本题考查了几何体中点、棱、面之间的关系以及二元一次方程组的应用与整除问题,解题的关键是审清题意.(1)根据每一个面有三条棱,每二个面共用一条棱即可求解,即:棱数=面数32⨯÷.(2)设一个足球有黑皮x 块,白皮y 块,根据二个面共用一条棱,结合题意可列方程组,求得每个足球黑皮块数与白皮块数;然后再设用于制作正五边形的需要m 张,用于制作正六边形的需要n 张,依据题意建立方程组,求得m 与n 的最大整数值,并检验是否符合题意即可得到答案.【详解】(1)解:①正八面体的每一个面都是三角形,则每一个面有三条棱,故八个面共有2438=⨯条棱,但每两个面共用一条棱,因此正八面体棱数是:24212÷=(条).①根据①的思路可知,正十二面体共有棱数:125302⨯=(条). 故答案为:12;30.(2)设一个足球有黑皮x 块,白皮y 块,根据题意得: 5690232x y x y +=⨯⎧⎨+=⎩,解得:1220x y =⎧⎨=⎩ 设630张牛皮中,用于制作正五边形的需要m 张,用于制作正六边形的需要n 张,依据题意得:63030201220m n m n +≤⎧⎪⎨=⎪⎩,解得:180450m n ≤⎧⎨≤⎩(m 、n 为整数) m 、n 取最大的整数并经过检验知,180,450m n ==正好符合题意①最多制作2045020n =(个)足球,且正好将630张牛皮全部用完. 答:用于制作30个正五边形的牛皮共180张,用于制作20个正六边形的牛皮共450张.22.(1)6,6;(2)V+F -E=2;(3)7.【分析】(1)观察图形即可得出结论;(2)观察可得:顶点数+面数-棱数=2;(3)代入(2)中的式子即可得到面数【详解】解:(1)观察图形,四面体的棱数为6;正八面体的顶点数为6;多面体顶点数(V)面数(F)棱数(E)四面体446长方体8612正八面体6812正十二面体201230(2)观察表格可以看出:顶点数+面数-棱数=2,关系式为:V+F-E=2;(3)由题意得:F+F-12=2,解得F=7.故答案为:(1)6,6;(2)V+F-E=2;(3)7.【点睛】本题考查多面体的顶点数,面数,棱数之间的关系及灵活运用.23.(1)8;6(2)V+F-E=2(3)这个多面体的面数为16【分析】(1)观察图形即可得出结论;(2)观察可得:顶点数+面数-棱数=2;(3)将所给数据代入(2)中的式子即可得到面数.【详解】(1)解:观察图形,长方体的定点数为8;正八面体的顶点数为6;多面体顶点数(V)面数(F)棱数(E)四面体446长方体8612正八面体6812正十二面体201230故答案为:8;6;(2)解:观察表格可以看出:顶点数+面数-棱数=2,关系式为:V+F-E=2;(3)解:由题意得:F+F-30=2解得F=16①这个多面体的面数为16.【点睛】本题主要考查多面体的顶点数,面数,棱数之间的关系及灵活运用,正确理解题意是解题的关键.。
北师大版七年级数学上册第一章 1、生活中的立体图形(练习题及答案)

1.生涯中蕴含着大量的几何图形,这些几何图形可以抽象为几何体.罕有的几何体有().().().().().和()等.2.几何图形包含立体图形和(),几何图形是由().().()构成.面有平面和(),面不分厚薄;线有直线和(),线不分粗细.面与面订交得到(),线与线订交得到(),点不分大小.3.从活动的角度看,点动成(),线动成(),面动成().(例如,把笔尖看做一个点,笔尖在纸上移动就能形成一条线,即点动成线.点动成线的实例还有:流星划过天空.粉笔在黑板上划动.保龄球滚动过的路线等.钟表的分针扭转一周形成一个圆面,即线动成面.线动成面的实例还有:汽车上的雨刷扫过玻璃窗.用刷子涂油漆等.长方形绕它的一边扭转一周就能形成一个圆柱,即面动成体.面动成体的实例还有:以三角形的一边为轴扭转一周形成的几何体等)4.如图所示的立体图形,是由()个面构成的,个中有()个平面,有()个曲面;面与面订交成()条线,个中曲线有()条.5.立体图形的辨认.几何图形的特点:(1)圆柱:两个底面是(),正面是().如().()等.(2)圆锥:底面是(),正面是(),像锥子.如().()等.(3)长方体:有6个面,底面是(),相对的两个面平行且().如().()等.(4)正方体:6个面是大小完整雷同的().如().()等.(5)棱柱:所有()都相等,底面是(),上.下底面的(),正面的外形都是().(6)球:由一个()构成,圆圆的.如足球.乒乓球等.(7)棱锥:一个面是多边形,其余各面是一个有公共极点的().多边形的面称为棱锥的(),其余各面称为棱锥的().依据()可将棱锥分为三棱锥.四棱锥……谈重点从哪几个方面熟悉几何体的特点①有几个面围成,是平面照样曲面;②有无极点,有几个极点;③正面是平面照样曲面;④底面是什么外形,是多边形照样圆,有几个底面等.6.请在每个几何体下面写出它们的名称.7.如图,鄙人面四个物体中,最接近圆柱的是( ).8.几何体的分类(1)几何体按柱.锥.球的特点分为:(2)按围成的面分为:9.在粉笔盒.三棱镜.乒乓球.易拉罐瓶.书本.热水瓶胆等物体中,外形相似于棱柱的有( ).A.1个B.2个C.3个D.4个10.将下列几何体分类,并解释来由.11.几何体的形成(1)长方形绕其一边地点直线扭转一周得到();(2)直角三角形绕其一条直角边地点直线扭转一周得到();(3)半圆绕其直径地点直线扭转一周得到().扭转体的形成①平面图形扭转会形成();②平面图形绕某一向线扭转一周才可以形成();③由平面图形扭转而得到的几何体有:().().()以及().12.我们曾学过圆柱的体积盘算公式:V=Sh=πR2h(R是圆柱底面半径,h为圆柱的高),现有一个长方形,长为2 cm,宽为1 cm,以它的一边地点的直线为轴扭转一周,得到的几何体的体积是若干?13.典题精讲如图所示的立体图形,是由________个面构成的,面与面订交成________条线.14.变式练习下图是把一圆柱体纵向切开后的图形.问:图中有几个面,有几个面是平的?有几个面曲直的?有几条线?它们是直的照样曲的?线与线订交成若干点?15.写出图1-1-4中所示立体图形的名称.16.绿色通道:分类是数学进修中一种很主要的思惟办法,应留意的是:按统一尺度区分.变式练习下面图形中,属于立体图形的有()①正方形②圆③球④棱柱⑤圆锥⑥六边形A.①③④B.②④⑤C.③④⑤D.③④⑤⑥答案:1. 长方体.正方体.圆柱.圆锥.球棱柱2. 平面图形点.线.面;曲面曲线线点3.线面体4.4 3 1 6 25.(1)等圆曲面(2)圆曲面 (3)长方形完整雷同(4)正方形(5)侧棱长多边形外形雷同平行四边形(6)曲面(7)三角形底面正面底面的边数6.三棱柱圆柱长方体圆锥四棱柱正方体球7.C解析:圆柱是“直”的,与弯管B有显著差别;D中的饮料瓶的盖确切可以算作是圆柱,但它在该物中只占很小的一部分,该物体从整体上讲更接近于棱柱;A中烟囱高低粗细不合,不是圆柱,故应消除A,B,D;作为柱体的本质特点之一是“粗细”处处雷同,而与高.矮(长.短)无关,C中玩具硬币尽管扁一些,但是最接近圆柱,所以应选C. 8.略9. C解析:粉笔盒.三棱镜.书本可以算作棱柱,乒乓球是球体,易拉罐瓶是圆柱,热水瓶胆既不是棱柱,也不是圆柱和球体.故答案选C.10.剖析:分类时,先肯定分类尺度.分类尺度不合,所属类别也不合,同时应留意分类要不重不漏.解:(1)按柱.锥.球划分:①②④⑤为一类,它们都是柱体;③⑦为一类,它们都是锥体;⑥为一类,它是球体.(2)按围成几何体的面是平面或曲面分:①④⑤⑦为一类,它们是多面体;②③⑥为一类,它们是扭转体.(3)按几何体有无极点分:①③④⑤⑦为一类,它们都有极点;②⑥为一类,它们都无极点.11.圆柱圆锥球体几何体几何体圆柱.圆锥.球以及它们的组合体.12.剖析:问题中的几何体可由两种方法扭转得到.一种是绕这个长方形的长地点的直线扭转,另一种是绕这个长方形的宽地点的直线扭转,其成果不合,留意不要漏解.解:(1)当以长方形的宽地点的直线为轴扭转时,如图(1)所示,得到的圆柱的底面半径为 2 cm,高为 1 cm.,所以,其体积是V1=π×22×1=4π(cm3)(2)当以长方形的长地点的直线为轴扭转时,如图(2)所示,得到的圆柱的底面半径为 1 cm,高为 2 cm,所以,其体积是V2=π×12×2=2π(cm3)所以,得到的几何体的体积是4π cm3或2π cm313.解析:任何图形都是由点.线.面构成的.点.线.面的变更构成了不合的图形.在数面时可先数底面,再数正面;数线时,可先数底面与正面的订交线.答案:4 614.图中有4个面,3个面是平面,1个正面曲直面;有6条线,4条是直的,2条曲直的;线与线订交成4个点.15.解析:分解各类几何体的特点,卖力地不雅察并给出断定.答案:(1)四棱柱;(2)圆柱;(3)长方体;(4)圆锥;(5)正方体;(6)棱锥.16.答案:C。
1 生活中的立体图形同步练习含答案

第一章丰富的图形世界1 生活中的立体图形A基础知识训练1.(2016•丽水中考)下列图形中,属于立体图形的是()2.(2016•滨湖中学月考)下列说法正确的是()①教科书是长方形;②教科书是长方体,也是棱柱;③教科书的表面是长方形.A.①②B.①③C.②③D.①②③3. (2016•阴平中学月考)如图所示为8个立体图形.其中,是柱体的序号为;是锥体的序号为;是球的序号为.4.如图,在长方体ABCD-EFGH中,与平面ADHE垂直的棱共有条.5.(2016•枣庄实验期中)汽车的雨刷把玻璃上的雨水刷干净,是运用了的原理.6.如图,把下列物体和与其相似的图形连接起来.B基本技能训练1(2016•台儿庄39中模拟)下面图形中为圆柱的是()2.(2016•龙口期中)若一个棱柱有10个顶点,则下列说法正确的是()A.这个棱柱有4个侧面B.这个棱柱有5条侧棱C.这个棱柱的底面是十边形D.这个棱柱是一个十棱柱3.(2015•本溪二模)将如图所示的几何图形,绕直线l旋转一周得到的立体图形()4.硬币在桌面上快速地转动时,看上去象球,这说明了.5.(2016•枣庄十五中月考)如图:将一个长方形形沿它的长或宽所在的直线l旋转一周,回答下列问题:(1)得到什么几何体?(2)长方形的长和宽边分别为6厘米和4厘米,分别绕它的长或宽所在直线旋转一周,得到不同的几何体,它们的体积分别为多少?(结果保留π)6.(2016•丹东七中月考)已知一个长方体的长为4cm,宽为3cm,高为5cm,请求出:(1)长方体所有棱长的和.(2)长方体的表面积.7.(能力提升题)将一个正方体木块涂成红色,然后如图把它的棱三等分,再沿等分线把正方体切开,可以得到27个小正方体.观察并回答下列问题:(1)其中三面涂色的小正方体有个,两面涂色的小正方体有个,各面都没有涂色的小正方体有个;(2)如果将这个正方体的棱n等分,所得的小正方体中三面涂色的有个,各面都没有涂色的有个;(3)如果要得到各面都没有涂色的小正方体100个,那么至少应该将此正方体的棱等分.附答案:1.1生活中的立体图形A基础知识训练1.【解析】选C.A、角是平面图形,故A错误;B、圆是平面图形,故B错误;C、圆锥是立体图形,故C正确;D、三角形是平面图形,故D错误.2.【解析】选C.因为教科书是一个空间实物体,是长方体所以不能说它是一个长方形,因为有两个面互相平行,其余各面都是四边形,并且每相邻两个四边形的公共边都互相平行,由这些面所围成的多面体叫做棱柱所以它是棱柱.教科书的表面是一个长方形.3.【解析】是柱体的序号为①②⑤⑦⑧;是锥体的序号为④⑥;是球的序号为③.答案:①②⑤⑦⑧,④⑥,③.4.【解析】与平面ADHE垂直的棱有:AB,DC,HG,EF.共4条.答案:45.【解析】汽车的雨刷把玻璃上的雨水刷干净,是运用了线动成面的原理,答案:线动成面.6.【解析】如图:B基本技能训练1.【解析】选D.由圆柱的特征可知,D是圆柱.2.【解析】选B.一个棱柱有10个顶点,则它是五棱柱,五棱柱有5个侧面,有5条侧棱,底面是五边形.3.【解析】选C.绕直线l旋转一周,可以得到的圆台.4.【解析】硬币在桌面上快速地转动时,看上去象球,这说明了面动成体.答案:面动成体.5.解:(1)得到的图形是圆柱形;(2)绕宽旋转得到的圆柱的底面半径为6cm,高为4cm,体积=π×62×4=144πcm3;绕长旋转得到的圆柱底面半径为4cm,高为6cm,体积=π×42×6=96πcm3.6.解:长方体的长、宽、高分别为4cm,3cm,5cm,(1)这个长方体的棱长总和为4×(4+3+5)=48cm,(2)长方体的表面积为:2×(4×3+4×5+3×5)=2×47=94cm2.7. 解:(1)把正方体的棱三等分,然后沿等分线把正方体切开,得到27个小正方体.观察其中三面被涂色的有8个,两面涂色的有12个;各面都没有涂色的有1个,故答案为:8,12,1;(2)根据正方体的棱三等分时三面被涂色的有8个,有1个是各个面都没有涂色的,正方体的棱四等分时三面被涂色的有8个,有8个是各个面都没有涂色的,所以正方体的棱n等分时三面被涂色的有8个,有(n-2)3个是各个面都没有涂色的,故答案为:8,(n-2)3;(3)由(2)得将这个正方体的棱n等分,有(n-2)3个是各个面都没有涂色的,所以(n-2)3=100,解得6<n<7,∴至少应该将此正方体的棱7等分,故答案为:7.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
A B C
D 1.生活中的立体图形
一.选择题
1.观察下图,请把左边的图形绕着给定的直线旋转一周后可能形成的几何体选出来( )
2.下列说法错误的是( )
A.长方体、正方体都是棱柱
B.三棱柱的侧面是三角形
C.直六棱柱有六个侧面、侧面为长方形
D.球体的三种视图均为同样大小的图形
3.从多边形一条边上的一点(不是顶点)发出发,连接各个顶点得到2003个
三角形,则这个多边形的边数为 ( )
A.2001
B.2005
C.2004
D.2006
4.如图所示立体图形,是由____个面组成,面与面相交成____条线( )
A.3,6
B.4,5
C.4,6
D.5,7
第4题 第5题
5.如图,在一个棱长为6cm 的正方体上摆放另一个正方体,使得上面正方体的四个顶点恰好均落在下面正方体的四条棱上,则上面正方体体积的可能值有( )
A .1个
B .2个
C .3个
D .无数个
二.填空题
1.如图所示的几何体是由一个正方体截去4
1后而形成的,这个几何体是由( )个面围成的,其中正方形有( )个,长方形有( )个.
第1题
2.用一长20cm,宽8cm的纸片卷成(无重合部分)一个高为8cm的圆柱,那么这个圆柱的底面圆的半径是(),圆柱的体积是()。
3.如图所示的几何体是由若干个棱长为1的正方体堆放而成的,则这个几何体的体积是()。
第3题第4题
4.将棱长为1cm的正方体组成如图所示的几何体,那么这个几何体的表面积是()。
5.如图,观察由棱长为1的小立方体摆成的图形,寻找规律:如图①中; 共有1个小立方体,其中1个看得见,0个看不见;如图②中;把共有8个小立方体,其中7个看得见,1个看不见;如图③中;共有27个小立方体,其中19个看得见,8个看不见;……,则第⑥个图中,看得见的小立方体有______________个。
三.解答题
1.在正方体的六个面上分别涂上红、黄、蓝、白、黑、绿六种颜色,现有涂色方式完全相同的四个正方体,如图拼成一个长方体,请判断涂红、黄、白三种颜色的对面分别涂着哪一种颜色?
2.如图,已知一个正方体的六个面上分别写着六个连续的整数,且每两个相对面上的两个数的和都相等,图中所能看到的数是16,19和20,求这6个整数的和.
答案
一选择题
1.D
2.B
3.B
4.C
5.D 解析:因为上面正方体的棱长不确定,所以根据正方体体积公式可知,上面正方体体积的可能值有无数个.
二填空题
1.8,2,4
2.π10,π
800 3.6 4.362cm 5.125 三解答题
1.绿 蓝 黑(分析:红不与蓝、白、黄、黑相对,所以红与绿相对;黄不与白、黑、绿、红相对,黄必与蓝相对;剩下黑与白相对。
)
2.111 因为六个面上是连续的六个整数,而已知有16、19、20,所以有两种可能16、17、18、19、20、21或15、16、17、。
