2019年全国各地中考数学真题汇编:图形的相似(含答案)
2019年中考数学试题汇编:相似形选择题部分(解析版)

1. (2019年四川内江市)如图,将△ ABC 沿着过BC 的中点D 的直线折叠,使点 B 落在AC 边上的B i 处,称为第一次操作,折痕DE 到AC 的距离为h 仁还原纸片后,再将△ BDE沿着过BD 的中点D i 的直线折叠,使点 B 落在DE 边上的B 2处, 痕D i E i 到AC 的距离记为h 2;按上述方法不断操作下去……经过第 D n -i E n -i ,到AC 的距离记为h n .若h i = i ,则h n 的值为(h 4、h 5、……h n ,再对h n 进行计算变形即可.【解答】解:••• D 是BC 的中点,折痕 DE 到AC 的距离为 •••点B 到DE 的距离=h i = i ,•••D i 是BD 的中点,折痕 D i E i 到AC 的距离记为h 2, •••点 B 到 D i E i 的距离=h 2= i^h i = i+ ,22同理:h 3= h 2+—h i=i+ 1 + 丄,42 4h 4=h 3+ h i = i+-!-+—+—:: ::-:;.i+l +l +l + + 1 2 1 hn = i+_ —+ +__+••• + ------- = 2 — --------2 4 8211-1 2n_1故选:C .【点评】考查图形变化规律的问题,首先根据变化求出第一个、第二个、第三个……发 现规律得出一般性的结论.2. (20i9 年四川内江市)如图,在△ ABC 中,DE // BC , AD = 9, DB = 3, CE = 2,贝U AC 的 长为()A . 6B . 7C . 8D . 9【分析】利用平行线分线段成比例定理得到二=「,利用比例性质求出AE ,然后计算 AE+EC 即可.【解答】解:• DE // BC ,称为第二次操作,折 n 次操作后得到折痕A . i+— 2n_1B . 1 + 2nC . 2 - 尹1【分析】根据相似三角形的性质,对应高的比对于相似比,得出 D . 2 -2nh 2 = -L ,依次得出h 3、 ::hiAD = AE 即9 = AEDB 丽’3~••• AE= 6,•. AC= AE+ EC= 6+2 = 8.故选:C.【点评】本题考查了平行线分线段成比例:三条平行线截两条直线,所得的对应线段成比例.3. (2019年广西玉林市)如图,AB // EF // DC , AD // BC, EF与AC交于点G,则是相似三角形共有()A . 3对B . 5对C. 6对 D . 8对【分析】图中三角形有:△ AEG ,△ ADC , CFG , △ CBA,因为AB // EF // DC , AD // BC,所以△ AEGADC s CFGCBA,有 6 种组合【解答】解:图中三角形有:△ AEG,^ ADC , CFG , △ CBA ,T AB// EF // DC , AD // BC• △AEG s^ ADC s CFGCBA共有 6 个组合分别为:AEGADC , △ AEG s CFG , △ AEGCBA, △ ADC s CFG , △ ADC CBA , CFG CBA故选:C.【点评】本题主要考查相似三角形的判定.4. (2019年内蒙古赤峰市)如图,D、E分别是△ ABC边AB , AC上的点,/ ADE = /ACB , 若AD = 2 , AB= 6 , AC= 4,贝U AE 的长是()A . 1B . 2 C. 3 D. 4【分析】证明△ ADE ACB,根据相似三角形的性质列出比例式,计算即可.【解答】解:•••/ ADE = / ACB ,Z A=Z A,• △ ADEACB ,.AD AE 0n2 AE-- = ,即__= ,AC AB 4 6解得,AE = 3,故选:C.【点评】本题考查的是相似三角形的判定和性质,掌握相似三角形的判定定理和性质定理是解题的关键.5. (2019年海南省)如图,在Rt△ ABC中,/ C= 90°, AB= 5, BC = 4.点P是边AC上一动点,过点P作PQ // AB交BC于点Q, D为线段PQ的中点,当BD平分/ ABC时,PQ // AB ,• / ABD = Z BDQ ,又/ ABD = Z QBD , • / QBD = Z BDQ , -QB = QD , • QP =2QB , PQ / AB ,• △ CPQ s^ CAB ,CP^Q = PQ:=7T =7T 解得,CP ==,13AP = CA - CP = ,13故选:B .【点评】本题考查的是相似三角形的判定和性质,掌握相似三角形的判定定理和性质定 理是解题的关键.6. (2019年黑龙江省哈尔滨市)如图,在?ABCD 中,点E 在对角线AB 于点M , EN // AB ,交AD 于点N ,则下列式子一定正确的是(D【分析】根据平行四边形的性质以及相似三角形的性质. 【解答】解:•••在?ABCD 中,EM // AD.易证四边形AMEN 为平行四边形15 13AC ,根据角平分线的定义、平行线的性质得到/C .13【分析】根据勾股定理求出BDQ ,得到QB = QD ,根据相似三角形的性质列出比例式,计算即可. 【解答】解:•••/ C = 90°, AB = 5, BC = 4,D .二13QBD = Z2QBBD 上,EM // AD ,交)Alt NE A ------- = ----- .-'i rir. Alt ANB =B .「’ MBC BEC . - r.riD .「厂BE EM)•••易证△ BEM s\ BAD S \ END、' =亠=-,A 项错误BM BN BE=—,B 项错误AD=丄_=二_, C 项错误ME BE=二_=上_, D 项正确ME ME故选:D .【点评】此题主要考查相似三角形的性质及平行四边形的性质,本题关键是要懂得找相 似三角形,利用相似三角形的性质求解.7. (2019年黑龙江省鸡西市)如图,在平行四边形ABCD 中,/ BAC = 90°, AB = AC ,过点A 作边BC 的垂线AF 交DC 的延长线于点 E ,点F 是垂足,连接 BE 、DF , DF 交AC 于点O .则下列结论: ①四边形ABEC 是正方形;②CO : BE = 1: 3;③DE =「BC ; ④S 四边形OCEF = Ss OD ,正确的个数是()A . 1B . 2C . 3D . 4【分析】①先证明厶ABF ◎△ ECF ,得AB = EC ,再得四边形ABEC 为平行四边形,进而 由/BAC = 90。
2019年中考数学真题分类汇编——专题14:图形的相似

“兵”所在位置的格点构成的三角形相似
A.①处
B.②处
C.③处
D.④处
【答案】B
11.(2019 安徽)如图,在 Rt△ABC 中,∠ACB=90°,AC=6,BC=12,点 D 在边 BC 上,点 E 在线段 AD 上,
EF⊥AC 于点 F,EG⊥EF 交 AB 于点 G.若 EF=EG,则 CD 的长为
的长是
A.1 【答案】C
B.2
C.3
D.4
9.(2019 重庆)如图,△ABO∽△CDO,若 BO=6,DO=3,CD=2,则 AB 的长是
A.2
B.3
C.4
D.5
【答案】C
10.(2019 连云港)在如图所示的象棋盘(各个小正方形的边长均相等)中,根据“马走日”的规则,“马”
应落在下列哪个位置处,能使“马”、“车”、“炮”所在位置的格点构成的三角形与“帅”、“相”、
16
【答案】
5 AB
20.(2019 河池)如图,以点 O 为位似中心,将△OAB 放大后得到△OCD,OA=2,AC=3,则 =__________. CD
2
【答案】
5 21.(2019 淮安)如图,l1∥l2∥l3,直线 a、b 与 l1、l2、l3 分别相交于点 A、B、C 和点 D、E、F.若 AB=3,
2019 年中考数学真题分类训练——专题十四:图形的相似 一、选择题 1.(2019 邵阳)如图,以点 O 为位似中心,把△ABC 放大为原图形的 2 倍得到△A′B′C′,以下说法中 错误的是
A.△ABC∽△A′B′C′
B.点 C、点 O、点 C′三点在同一直线上
C.AO∶AA′=1∶2
D.AB∥A′B′
2019年中考数学真题汇编----图形的相似与位似(含解析)

2019年中考数学真题汇编----图形的相似与位似一.选择题1. (2019•浙江杭州•3分)如图,在△ABC中,点D,E分别在AB和AC上,DE∥BC,M为BC边上一点(不与点B,C重合),连接AM交DE于点N,则( )A.=B.=C.=D.=【分析】先证明△ADN∽△ABM得到=,再证明△ANE∽△AMC得到=,则=,从而可对各选项进行判断.【解答】解:∵DN∥BM,∴△ADN∽△ABM,∴=,∵NE∥MC,∴△ANE∽△AMC,∴=,∴=.故选:C.【点评】本题考查了相似三角形的判定与性质:三在判定两个三角形相似时,应注意利用图形中已有的公共角、公共边等隐含条件,以充分发挥基本图形的作用,寻找相似三角形的一般方法是通过作平行线构造相似三角形;灵活运用相似三角形的性质表示线段之间的关系.2. (2019•广西贺州•3分)如图,在△ABC中,D,E分别是AB,AC边上的点,DE∥BC,若AD=2,AB=3,DE=4,则BC等于( )A.5B.6C.7D.8【分析】由平行线得出△ADE∽△ABC,得出对应边成比例=,即可得出结果.【解答】解:∵DE∥BC,∴△ADE∽△ABC,∴=,即=,解得:BC=6,故选:B.【点评】本题考查了相似三角形的判定与性质;证明三角形相似得出对应边成比例是解题的关键.3. (2019•甘肃省庆阳市•3分)如图,将图形用放大镜放大,应该属于( )A.平移变换B.相似变换C.旋转变换D.对称变换【分析】根据放大镜成像的特点,结合各变换的特点即可得出答案.【解答】解:根据相似图形的定义知,用放大镜将图形放大,属于图形的形状相同,大小不相同,所以属于相似变换.故选:B.【点评】本题考查的是相似形的识别,关键要联系图形,根据相似图形的定义得出.二.填空题1. (2019•江苏无锡•2分)如图,在△ABC中,AC:BC:AB=5:12:13,⊙O在△ABC内自由移动,若⊙O的半径为1,且圆心O在△ABC内所能到达的区域的面积为,则△ABC的周长为 25 .【分析】如图,由题意点O所能到达的区域是△EFG,连接AE,延长AE交BC于H,作HM⊥AB于M,EK⊥AC于K,作FJ⊥AC于J.利用相似三角形的性质以及三角形的面积公式求出EF,再证明△HAC≌△HAM(AAS),推出AM=AC=5m,CH=HM,BM=8m,设CH=HM=x,在Rt△BHM中,则有x2+(8m)2=(12m图x)2,推出x=m,由EK∥CH,推出=,推出=,可得AK=,求出AC即可解决问题.【解答】解:如图,由题意点O所能到达的区域是△EFG,连接AE,延长AE交BC于H,作HM⊥AB于M,EK⊥AC于K,作FJ⊥AC于J.∵EG∥AB,EF∥AC,FG∥BC,∴∠EGF=∠ABC,∠FEG=∠CAB,∴△EFG∽△ACB,∴EF:FG:EG=AC:BC:AB=5:12:13,设EF=5k,FG=12k,∵×5k×12k=,∴k=或图(舍弃),∴EF=,∵四边形EKJF是矩形,∴KJ=EF=,设AC=5m,BC=12m,AB=13m,∵∠ACH=∠AMH=90°,∠HAC=∠HAM,AH=AH,∴△HAC≌△HAM(AAS),∴AM=AC=5m,CH=HM,BM=8m,设CH=HM=x,在Rt△BHM中,则有x2+(8m)2=(12m图x)2,∴x=m,∵EK∥CH,∴=,∴=,∴AK=,∴AC=AK+KJ+CJ=++1=,∴BC=××12=10,AB=××13=,∴△ABC的周长=AC+BC+AB=+10+=25,故答案为25.【点评】本题考查动点问题,轨迹,相似三角形的判定和性质,全等三角形的判定和性质,解直角三角形等知识,解题的关键是理解题意,学会添加常用辅助线,构造相似三角形解决问题,属于中考填空题中的压轴题.2. (2019•江苏无锡•2分)如图,在△ABC中,AB=AC=5,BC=4,D为边AB上一动点(B点除外),以CD为一边作正方形CDEF,连接BE,则△BDE面积的最大值为 8 .【分析】过点C作CG⊥BA于点G,作EH⊥AB于点H,作AM⊥BC于点M.由AB=AC=5,BC=4,得到BM=CM=2,易证△AMB∽△CGB,求得GB=8,设BD =x,则DG=8图x,易证△EDH≌△DCG,EH=DG=8图x,所以S△BDE===,当x=4时,△BDE面积的最大值为8.【解答】解:过点C作CG⊥BA于点G,作EH⊥AB于点H,作AM⊥BC于点M.∵AB=AC=5,BC=4,∴BM=CM=2,易证△AMB∽△CGB,∴,即∴GB=8,设BD=x,则DG=8图x,易证△EDH≌△DCG(AAS),∴EH=DG=8图x,∴S△BDE===,当x=4时,△BDE面积的最大值为8.故答案为8.【点评】本题考查了正方形,熟练运用正方形的性质与相似三角形的判定与性质以及全等三角形的判定与性质是解题的关键.3. (2019•江苏扬州•3分)如图,在△ABC 中,AB =5,AC =4,若进行一下操作,在边BC 上从左到右一次取点D 1、D 2、D 3、D 4…;过点D 1作AB 、AC 的平行线分别交于AC 、AB 与点E 1、F 1;过点D 2作AB 、AC 的平行线分别交于AC 、AB 于点E 2、F 2;过点D 3作AB 、AC 的平行线分别交于AC 、AB 于点E 3、F 3…,则4(D 1E 1+D 2E 2+…+D 2019E 2019)+5(D 1F 1+D 2F 2+…+D 2019F 2019)= 40380 .【考点】:相似三角形,比例性质【解析】:∵D 1E 1∥AB D 1F 1∥AC ∴CB CD AB E D 111=BCBD AC F D 11=∵AB =5 AC =4∴CB CD E D 1115=BCBD F D 114=∴14511111==+=+BCBCBC BD CB CD F D E D ∴4D 1E +5D 1F =20有2019组,即2019×20=40380【答案】:403804. (2019•江西•3分)在平面直角坐标系中,A ,B ,C 三点的坐标分别为(4,0), (4,4),(0,4),点P 在x 轴上,点D 在直线AB 上,DA =1, CP ⊥DP 于点P ,则点P 的坐标为P (2,0), P (,0), P (,0) .x图2图1解析:设P (m ,0)如图1,∠CPD=90°,△OCP∽△PAD∴即:∴m=2 ∴P(2,0)如图2,∠CPD=90°,△OCP∽△APD ∴即:∴m=∴P(,0)P(,0)综上分析可知:P(2,0),P(,0),P(,0)5. (2019•浙江杭州•4分)如图,把某矩形纸片ABCD沿EF,GH折叠(点E,H在AD边上,点F,G在BC边上),使点B和点C落在AD边上同一点P处,A点的对称点为A′点,D点的对称点为D′点,若∠FPG=90°,△A′EP的面积为4,△D′PH的面积为1,则矩形ABCD的面积等于 2(5+3) .【分析】设AB=CD=x,由翻折可知:PA′=AB=x,PD′=CD=x,因为△A′EP的面积为4,△D′PH的面积为1,推出A′E=4D′H,设D′H=a,则A′E=4a,由△A′EP∽△D′PH,推出=,推出=,可得x=2a,再利用三角形的面积公式求出a即可解决问题.【解答】解:∵四边形ABC是矩形,∴AB=CD,AD=BC,设AB=CD=x,由翻折可知:PA′=AB=x,PD′=CD=x,∵△A′EP的面积为4,△D′PH的面积为1,∴A′E=4D′H,设D′H=a,则A′E=4a,∵△A′EP∽△D′PH,∴=,∴x2=4a2,∴x=2a或图2a(舍弃),∴PA′=PD′=2a,∵•a•2a=1,∴a=1,∴x=2,∴AB=CD=2,PE==2,PH==,∴AD=4+2++1=5+3,∴矩形ABCD的面积=2(5+3).故答案为2(5+3)【点评】本题考查翻折变换,矩形的性质,勾股定理,相似三角形的判定和性质等知识,解题的关键是学会利用参数解决问题,属于中考填空题中的压轴题.6.(2019•四川自贡•4分)如图,在Rt△ABC中,∠ACB=90°,AB=10,BC=6,CD∥AB,∠ABC的平分线BD交AC于点E,DE= .【分析】由CD∥AB,∠D=∠ABE,∠D=∠CBE,所以CD=BC=6,再证明△AEB∽△CED,根据相似比求出DE的长.【解答】解:∵∠ACB=90°,AB=10,BC=6,∴AC=8,∵BD平分∠ABC,∴∠ABE=∠CDE,∵CD∥AB,∴∠D =∠CBE ,∴CD =BC =6,∴△AEB ∽△CED ,∴,∴CE =AC =×8=3,BE =,DE =BE =×=,故答案为.【点评】本题考查了相似三角形,熟练掌握相似三角形的判定与性质以及勾股定理是解题的关键.7.(2019•天津•3分)如图,正方形纸片ABCD 的边长为12,E 是边CD 上一点,连接AE ,折叠该纸片,使点A 落在AE 上的G 点,并使折痕经过点B ,得到折痕BF ,点F 在AD 上,若DE =5,则GE 的长为.【答案】1349【解析】因为四边形ABCD 是正方形,易得△AFB ≌△DEA ,∴AF =DE =5,则BF =13.又易知△AFH ∽△BFA ,所以,即AH =,∴AH =2AH =,∴由勾股定理BF AF BA AH136013120得AE =13,∴GE =AE -AG =13498.(2019•河南•3分)如图,在矩形ABCD 中,AB =1,BC =a ,点E 在边BC 上,且BE =a.连接AE,将△ABE沿AE折叠,若点B的对应点B′落在矩形ABCD的边上,则a 的值为 或 .【分析】分两种情况:①点B′落在AD边上,根据矩形与折叠的性质易得AB=BE,即可求出a的值;②点B′落在CD边上,证明△ADB′∽△B′CE,根据相似三角形对应边成比例即可求出a的值.【解答】解:分两种情况:①当点B′落在AD边上时,如图1.∵四边形ABCD是矩形,∴∠BAD=∠B=90°,∵将△ABE沿AE折叠,点B的对应点B′落在AD边上,∴∠BAE=∠B′AE=∠BAD=45°,∴AB=BE,∴a=1,∴a=;②当点B′落在CD边上时,如图2.∵四边形ABCD是矩形,∴∠BAD=∠B=∠C=∠D=90°,AD=BC=a.∵将△ABE沿AE折叠,点B的对应点B′落在CD边上,∴∠B=∠AB′E=90°,AB=AB′=1,EB=EB′=a,∴DB′==,EC=BC图BE=a图a=a.在△ADB′与△B′CE中,,∴△ADB′∽△B′CE,∴=,即=,解得a1=,a2=0(舍去).综上,所求a的值为或.故答案为或.【点评】本题考查了折叠的性质:折叠是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等.也考查了矩形的性质,勾股定理,相似三角形的判定与性质.进行分类讨论与数形结合是解题的关键.9.10.三.解答题1. (2019•江苏宿迁•12分)如图①,在钝角△ABC中,∠ABC=30°,AC=4,点D为边AB中点,点E为边BC中点,将△BDE绕点B逆时针方向旋转α度(0≤α≤180).(1)如图②,当0<α<180时,连接AD、CE.求证:△BDA∽△BEC;(2)如图③,直线CE、AD交于点G.在旋转过程中,∠AGC的大小是否发生变化?如变化,请说明理由;如不变,请求出这个角的度数;(3)将△BDE从图①位置绕点B逆时针方向旋转180°,求点G的运动路程.【分析】(1)如图①利用三角形的中位线定理,推出DE∥AC,可得=,在图②中,利用两边成比例夹角相等证明三角形细相似即可.(2)利用相似三角形的性质证明即可.(3)点G的运动路程,是图③图1中的的长的两倍,求出圆心角,半径,利用弧长公式计算即可.【解答】解:(1)如图②中,由图①,∵点D为边AB中点,点E为边BC中点,∴DE∥AC,∴=,∴=,∵∠DBE=∠ABC,∴∠DBA=∠EBC,∴△DBA∽△EBC.(2)∠AGC的大小不发生变化,∠AGC=30°.理由:如图③中,设AB交CG于点O.∵△DBA∽△EBC,∴∠DAB=∠ECB,∵∠DAB+∠AOG+∠G=180°,∠ECB+∠COB+∠ABC=180°,∠AOG=∠COB,∴∠G=∠ABC=30°.(3)如图③图1中.设AB的中点为K,连接DK,以AC为边向右作等边△ACO,连接OG,OB.以O为圆心,OA为半径作⊙O,∵∠AGC=30°,∠AOC=60°,∴∠AGC=∠AOC,∴点G在⊙O上运动,以B为圆心,BD为半径作⊙B,当直线与⊙B相切时,BD⊥AD,∴∠ADB=90°,∵BK=AK,∴DK=BK=AK,∵BD=BK,∴BD=DK=BK,∴△BDK是等边三角形,∴∠DBK=60°,∴∠DAB=30°,∴∠DOG=2∠DAB=60°,∴的长==,观察图象可知,点G的运动路程是的长的两倍=.【点评】本题属于相似形综合题,考查了相似三角形的判定和性质,弧长公式,等边三角形的判定和性质,圆周角定理等知识,解题的关键是正确寻找相似三角形解决问题,学会正确寻找点的运动轨迹,属于中考压轴题.2. (2019•江西•9分)数学活动课上,张老师引导同学进行如下研究:如图1,将长为12cm的铅笔AB斜靠在垂直于水平桌面AE的直尺FO的边沿上,一端A 固定在桌面上,图2是示意图活动一如图3,将铅笔AB绕端点A顺时针旋转,AB与OF交于点D,当旋转至水平位置时铅笔AB的中点C与点O重合。
2019年中考数学真题分类训练——专题14:图形的相似
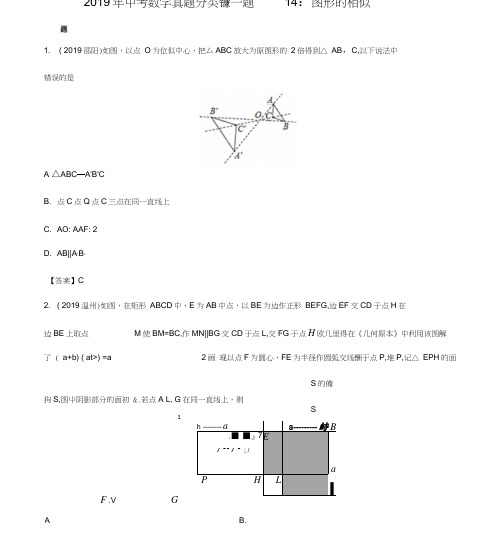
2019年中考数学真题分类镰一题14:图形的相似AB.1. ( 2019邵阳)如图,以点 O 为位似中心,把厶ABC 放大为原图形的 2倍得到△ AB ,C,以下说法中错误的是A △ABC —A'B'CB. 点C 点Q 点C 三点在同一直线上C. AO: AAF: 2D. AB||A ,B ,【答案】C2. ( 2019温州)如图,在矩形 ABCD 中,E 为AB 中点,以BE 为边作正形 BEFG,边EF 交CD 于点H 在M 使BM=BC,作MN||BG 交CD 于点L,交FG 于点H 欧几里得在《几何原本》中利用该图解了 ( a+b) ( at>) =a2画 现以点F 为圆心,FE 为半径作圆弧交线酬于点P,堆P,记△ EPH 的面S 的備狗S,图屮阴影部分的面初 &.若点A L, G 在同一直线上,则S2h --------aa --------- 峙B.■ ■』7 E/ •• / • ;/aPHLLF .VG边BE 上取点AD AN A ——=——AN AE c DN NE • W = MC【答案】C5. (2019玉林)如图,AB || EF|| DC, AD || BC, EF 与AC 交于点G 则是相似三角形共有c .42D. V2【答案】C3. (2019淄博)如图,在厶 ABC 中,AC=2, BC=4, D 为BC 边上的一点,且z CAD=zB.若AADC 的面积为a,则AABD 的面积为A 2a C. 3a【答案】C4. (2019杭州)如图,在△ ABC 中, 重合),连接AM 交DE 于点N,则点D E 分别在AB 和AC 上,DE : BC, M 为BC上一点(不与点 B, CBD MN B.MN CEDNNED.MC BMA 3 时 5 SI 6E )j 8 对【答案】C6. ( 2019常德)如图,在等腰三角形△ ABC 中,AB=AC,图屮所有三角形均相似,其中最小的三角形面积为A ABC 的面积张,则四边形DBCE 的面积是BCA 20B. 22C. 24D. 26【答案】DE, 贝ij BE: EC=【答案】B8. ( 2019 赤峰)如图, Q E 分别是△ ABC 边 AB, AC ±的点,z ADE —ACB,若 AD=2, AB=6, AC=4,贝ij AE的长是B. 2C. 3D. 4【答案】C7.(2019凉山)如图,在公ABC 屮, D 在AC 边上,AD: DC=1: 2, O 是BD 的屮点,连杞并延长陋于A 1: 2B. 1: 3D. 2: 3C. 1: 49. ( 2019 重庆)如图,△ ABO —CDO,若 BO=6, DO=3, CD=2,風B 的长是【答案】BBC =12. ( 2019 兰州)已知△ ABC -AB=8, AB 二6,则B. 3D. 5【答案】C10. (2019连云港)在如图所示的象楫(各个小正方形的边长均相筹 4 根据吗走于 的规则吗"应落在下列哪个位置处,能使"马气"车气 訣矿所在位置的格点构成的三角形与勿巾气纺T 、 “兵"所在位置的格点构成的三角形相似A ①处 B.②处D.④处【答案】B11. ( 2019 安徽)如图,在 RfABC 屮,z ACB=90°, AC 二 6, BC=12,点D 在边BC 上,点EF 丄AC 于点F, EG±EF 交AB 于点G 若EF=EG, OD 的长为A 3.6B. 4C. 4.8DC. 4 C.③处BCA 2B. 4C. 3D. 163丁【答案】B13. ( 2019常州)若公ABC 〜△A'BC,相似比为2,则△ ABC 与A /XBC 的周长的比为 A 2: 1B. 1: 2C. 4: 1D. 1: 4【答案】B 二、填空题14. ( 2019吉林)在某一时刻,测得一枫妁8 m 的竹竿的影长3师,同时同地测得一栋楼的影长为 90 m,则这栋楼的腐 __________ m.【答案】5415. (2019台州)如图,直綢II2III3, A B, C 分别逍线,丨2,丨3上的动点,接AB, BC, AC,线D.设直线,I2Z 间的距斷n 直线,IsZ 间的距离n,若zABC=90。
2019年中考数学真题分类汇编第二期专题26图形的相似与位似试题含解析

=S=S2019年中考数学真题分类汇编图形的相似与位似一.选择题1.(2019·湖北随州·3分)如图,平行于BC的直线DE把△ABC分成面积相等的两部分,则的值为()A.1B.C.1D.【分析】由DE∥BC可得出△ADE∽△ABC,利用相似三角形的性质结合△SADE四边形BCED,可得出=,结合BD=AB﹣AD即可求出的值,此题得解.【解答】解:∵DE∥BC,∴∠ADE=∠B,∠AED=∠C,∴△ADE∽△ABC,∴()2=△∵S ADE四边形BCED,.∴=,∴===﹣1.故选:C.【点评】本题考查了相似三角形的判定与性质,牢记相似三角形的面积比等于相似比的平方是解题的关键.2.(2019江苏宿迁3分)如图,菱形A BCD的对角线AC.BD相交于点O,点E为边CD的中点,若菱形ABCD的周长为16,∠BAD=60°,则△OCE的面积是()A. B.2 C. D.4【答案】A【分析】根据菱形的性质得菱形边长为4,AC⊥BD,由一个角是60度的等腰三角形是等边三角形得△ABD是等边三角形;在△R t AOD中,根据勾股定理得AO=2,AC=2AO=4,根据三角形面积公式得△SACD=OD·AC=4,根据中位线定理得OE∥AD,根据相似三角形的面积比等于相似比继而可求出△OCE的面积.【详解】∵菱形ABCD的周长为16,∴菱形ABCD的边长为4,∵∠BAD=60°,∴△ABD是等边三角形,又∵O是菱形对角线AC.BD的交点,∴AC⊥BD,在△R t AOD中,∴AO=,∴AC=2AO=4,∴S△ACD=OD·AC=×2×4=4,又∵O、E分别是中点,∴OE∥AD,∴△COE∽△CAD,∴,∴,△∴SCOE=S△CAD=×4=,故选A.【点睛】本题考查了相似三角形的判定与性质,等边三角形的判定与性质,勾股定理,菱形的性质,结合图形熟练应用相关性质是解题的关键.3.(2019•江苏无锡•3分)如图,已知点E是矩形ABCD的对角线AC上的一动点,正方形EFGH 的顶点G、H都在边AD上,若AB=3,BC=4,则tan∠AFE的值()A.等于C.等于B.等于D.随点E位置的变化而变化【分析】根据题意推知EF∥AD,由该平行线的性质推知△AEH∽△ACD,结合该相似三角形的对应边成比例和锐角三角函数的定义解答.【解答】解:∵EF∥AD,∴∠AFE=∠FAG,∴△AEH∽△ACD,∴设EH=3x,AH=4x,∴HG=GF=3x,==.∴tan∠AFE=tan∠FAG===.故选:A.【点评】考查了正方形的性质,矩形的性质以及解直角三角形,此题将求∠AFE的正切值转化为求∠FAG的正切值来解答的.5.2019•内蒙古包头市•3分)如图,在四边形ABCD中,BD平分∠ABC,∠BAD=∠BDC=90°,E 为BC的中点,AE与BD相交于点F.若BC=4,∠CBD=30°,则DF的长为()A.B.C.D.【分析】先利用含30度角的直角三角形的性质求出BD,再利用直角三角形的性质求出DE=BE=2,即:∠BDE=∠ABD,进而判断出DE∥AB,再求出AB=3,即可得出结论.【解答】解:如图,在Rt△BDC中,BC=4,∠DBC=30°,∴BD=2,连接DE,∵∠BDC=90°,点D是BC中点,∴DE=BE=CE BC=2,∵∠DCB=30°,∴∠BDE=∠DBC=30°,∵BD平分∠ABC,∴∠ABD=∠DBC,∴∠ABD=∠BDE,∴DE∥AB,∴△DEF∽△BAF,∴,在Rt△ABD中,∠ABD=30°,BD=2∴AB=3,,∴∴,,3∴DF= BD= ×2故选:D .= ,【点评】此题主要考查了含 30 度角的直角三角形的性质,相似三角形的判定和性质,角平分线的定义,判断出 DE∥是解本题的关键.6. (2019•达州•3 分)如图,E ,F 是平行四边形 ABCD 对角线 AC 上两点,AE=CF= AC .连接DE ,DF 并延长,分别交 AB ,BC 于点 G ,H ,连接 GH ,则的值为( )A .B .C .D .1【分析】首先证明 AG :AB=CH :BC=1: ,推出 GH ∥△B C ,推出 BGH ∽△BAC ,可得 = =()2=( )2= , = ,由此即可解决问题.【解答】解:∵四边形 ABCD 是平行四边形∴AD=BC ,DC=AB ,∵AC=CA ,∴△ADC ≌△CBA ,∴△S A DC △=SABC,∵AE=CF= AC ,AG ∥CD ,CH ∥AD ,∴AG :DC=AE :CE=1:3,CH :AD=CF :AF=1:3,∴AG :AB=CH :BC=1:3,∴GH ∥BC ,∴△BGH ∽△BAC ,∴= =( )2=( )2= ,∵= ,∴= × = ,故选:C .【点评】本题考查平行四边形的性质、相似三角形的判定和性质、全等三角形的判定和性质、等高模型等知识,解题的关键是灵活运用所学知识解决问题,属于中考选择题中的压轴题.7. (2019•乌鲁木齐•4 分)如图,在 ABCD 中,E 是 AB 的中点,EC 交 BD 于点 △F ,则 BEF 与△DCB 的面积比为()A .B .C .D .【分析】根据平行四边形的性质得出 AB=CD ,AB ∥△C D ,根据相似三角形的判定得出 BEF ∽△DCF ,根据相似三角形的性质和三角形面积公式求出即可.【解答】解:∵四边形 ABCD 是平行四边形,E 为 AB 的中点,∴AB=DC=2BE ,AB ∥CD ,∴△BEF ∽△DCF ,∴= = ,∴DF=2BF ,=( )2= ,∴= ,∴△S B EF = △S D CF ,△S D CB = △S D CF ,∴ = = ,故选:D .【点评】本题考查了相似三角形的性质和判定和平行四边形的性质,能熟 记相似三角形的性质是解此题的关键.8. (2019•杭州•3 分)如图,在△ABC 中,点 D 在 AB 边上,DE ∥BC ,与边 AC 交于点 E ,连结△BE ,记 ADE ,△BCE 的面积分别为 S 1 , S 2 , ()A.若 ,则B.若,则C.若 ,则D.若,则【答案】D【考点】三角形的面积,平行线分线段成比例【 解 析 】【 解 答 】 解 : 如 图 , 过 点 D 作 DF ⊥ AC 于 点 F , 过 点 B 作 BM ⊥ AC 于 点M∴DF ∥BM ,设 DF=h 1 , BM=h 2∴∵DE ∥BC∴∴∵若∴设=k <0.5(0<k <0.5)∴AE=AC ∙k ,CE=AC-AE=AC (1-k),h 1=h 2k∵S 1=AE ∙h 1=AC ∙k ∙h 1 , S 2=CE ∙h 2=AC (1-k )h 2( (∴3S 1=k 2ACh 2 , 2S 2=(1-K ) ACh 2∵0<k <0.5∴k 2<(1-K )∴3S 1<2S 2 故答案为:D【分析】过点 D 作 DF ⊥AC 于点 F ,过点 B 作 BM ⊥AC 于点 M ,可得出 DF ∥BM ,设 DF=h 1 ,BM=h 2 ,再根据 DE ∥BC ,可证得,若 ,设=k <0.5(0<k <0.5),再分别求出 3S 1 和 2S 2, 根据 k 的取值范围,即可得出答案。
(word完整版)2019年全国中考数学真题分类汇编24:相似、位似及其应用

相似、位似及其应用一、选择题1.(2019·苏州)如图,在△ABC 中,点D 为BC 边上的一点.且AD =AB =2,AD ⊥AB ,过点D 作DE ⊥AD ,DE 交AC 于点F .若DE =1,则△ABC 的面积为( ) A .B .4C .D .8【答案】B【解析】∵AB ⊥AD ,AD ⊥DE ,∴∠BAD =∠ADE =90°,∴DE ∥AB ,∴∠CED =∠CAB ,∵∠C =∠C ,∴△CED ∽△CAB ,∵DE =1,AB =2,即DE ∶AB =1∶2,∴S △DEC ∶S △ACB =1∶4,∴S四边形ABDE ∶S △ACB =3∶4,∵S 四边形ABDE =S △ABD +S △ADE 12=⨯2×212+⨯2×1=2+1=3,∴S △ACB =4,故选B . 2.(2019·杭州)如图,在△ABC 中,点D ,E 分别在AB 和AC 边上,DE ∥BC ,M 为BC 边上一点(不与点B ,C 重合)连接AM 交DE 干点N ,则( ) A.AD AN AN AE = B. BD MN MN CE = C. DN NE BM MC = D. DN NE MC BM=【答案】CB【解析】根据DE ∥BC ,可得△ADN ∽△ABM 与△ANE ∽△AMC ,再应用相似三角形的性质可得结论.∵DN ∥BM ,∴△ADN ∽△ABM ,∴DN AN BM AM =,∵NE ∥MC ,∴△ANE ∽△AMC ,∴NE AN MC AM =,∴DN NE BM MC=.故选C .3.(2019·常德)如图,在等腰三角形△ABC 中,AB =AC ,图中所有三角形均相似,其中最小的三角形的面积为1,△ABC 的面积为42,则四边形DBCE 的面积是( )A .20B .22C .24D .26【答案】D【解析】∵图中所有三角形均相似,其中最小的三角形的面积为1,△ABC 的面积为42,∴最小的三角形与△ABCADE ∽△ABC ,∴ADE ABC S S V V =2DE BC ⎛⎫ ⎪⎝⎭,∵DE BC =4ADE ABC S S V V =1642=821, ∴S △ADE =821×42=16,∴四边形DBCE 的面积=S △ABC -S △ADE =26,故选项D 正确. 4.(2019·陇南)如图,将图形用放大镜放大,应该属于( )A .平移变换B .相似变换C .旋转变换D .对称变换【答案】B【解析】由图可知,放大前与放大后图形是相似的,故选:B .5. (2019·枣庄)如图,将△ABC 沿BC 边上的中线AD 平移到△A'B'C'的位置,已知△ABC 的面积为16,阴影部分三角形的面积为9,若AA'=1,则A'D 等于A.2B.3C.4D.32【答案】B【解析】由平移可得,△ABC ∽△A'MN,设相似比为k,∵S △ABC =16,S △A'MN =9,∴k 2=16:9,∴k =4:3,因为AD 和A'D分别为两个三角形的中线,∴AD:A'D =k =4:3,∵AD =AA'+A'D,∴AA':A'D =1:3,∵AA'=1,则A'D =3,故选B.6.(2019·淄博)如图,在△ABC 中,AC =2,BC =4,D 为BC 边上的一点,且∠CAD =∠B. 若△ADC 的面积为a ,则△ABD 的面积为()B。
2019年中考数学专题《图形的相似》复习试卷含答案解析

2019年中考数学专题复习卷: 图形的相似一、选择题1.已知,下列变形错误的是()A. B.C.D.【答案】B【解析】由得,3a=2b,A. 由得,所以变形正确,故不符合题意;B. 由得3a=2b,所以变形错误,故符合题意;C. 由可得,所以变形正确,故不符合题意;D.3a=2b变形正确,故不符合题意.故答案为:B.【分析】根据已知比例式可得出3a=2b,再根据比例的基本性质对各选项逐一判断即可。
2.如图,已知直线a∥b∥c,直线m分别交直线a、b、c于点A,B,C,直线n分别交直线a、b、c于点D,E,F,若, ,则的值应该()A. 等于B. 大于C. 小于D. 不能确定【答案】B【解析】:如图,过点A作AN∥DF,交BE于点M,交CF于点N∵a∥b∥c∴AD=ME=NF=4(平行线中的平行线段相等)∵AC=AB+BC=2+4=6∴设MB=x,CN=3x∴BE=x+4,CF=3x+4∵∵x>0∴故答案为:B【分析】过点A作AN∥DF,交BE于点M,交CF于点N,根据已知及平行线中的平行线段相等,可得出AD=ME=NF=4,再根据平行线分线段成比例得出BM和CN的关系,设MB=x,CN=3x,分别表示出BE、CF,再求出它们的比,利用求差法比较大小,即可求解。
3.在平面直角坐标系中,线段AB两个端点的坐标分别为A(6,8),B(10,2),若以原点O为位似中心,在第一象限内将线段AB缩短为原来的后得到线段CD,则点A的对应点C的坐标为()A. (5,1)B. (4,3) C. (3,4) D. (1,5)【答案】C【解析】:∵以原点O为位似中心,在第一象限内将线段AB缩小为原来的后得到线段CD,∴端点C的横坐标和纵坐标都变为A点的横坐标和纵坐标的一半,又∵A(6,8),∴端点C的坐标为(3,4).故答案为:C.【分析】根据位似图形的性质,位似图形上一个点的坐标等于原图形上对应点的横纵坐标分别乘以位似比,或位似比的相反数。
2019年全国各地中考数学试题分类汇编(第一期) 专题26 图形的相似与位似(含解析)

图形的相似与位似一.选择题1. (2019•浙江绍兴•4分)如图1,长、宽均为3,高为8的长方体容器,放置在水平桌面上,里面盛有水,水面高为6,绕底面一棱进行旋转倾斜后,水面恰好触到容器口边缘,图2是此时的示意图,则图2中水面高度为()A.B.C.D.【分析】设DE=x,则AD=8﹣x,由长方体容器内水的体积得出方程,解方程求出DE,再由勾股定理求出CD,过点C作CF⊥BG于F,由△CDE∽△BCF的比例线段求得结果即可.【解答】解:过点C作CF⊥BG于F,如图所示:设DE=x,则AD=8﹣x,根据题意得:(8﹣x+8)×3×3=3×3×6,解得:x=4,∴DE=4,∵∠E=90°,由勾股定理得:CD=,∵∠BCE=∠DCF=90°,∴∠DCE=∠BCF,∵∠DEC=∠BFC=90°,∴△CDE∽△BCF,∴,即,∴CF=.故选:A.【点评】本题考查了勾股定理的应用、长方体的体积、梯形的面积的计算方法;熟练掌握勾股定理,由长方体容器内水的体积得出方程是解决问题的关键.www .czsx .com .cn2. (2019•江苏苏州•3分)如图,在ABC V 中,点D 为BC 边上的一点,且2AD AB ==,AD AB ⊥,过点D 作DE AD ⊥,DE 交AC 于点E ,若1DE =,则ABC V 的面积为()A.B .4C. D .8DABC【分析】考察相似三角形的判定和性质、等腰直角三角形的高,中等题型 【解答】AB AD DE AD ∴⊥⊥, 90BAD ADE ∴∠=∠=o //AB DE ∴易证CDE CBA V :V 12DC DE BC BA ∴== 即12DC BD DC =+由题得BD =∴解得DC =ABC V11422ABC S BC ∴=⨯⨯=V故选B3 (2019•湖南邵阳•3分)如图,以点O 为位似中心,把△ABC 放大为原图形的2倍得到△A ′B ′C ′,以下说法中错误的是( )A.△ABC∽△A′B′C′B.点C.点O、点C′三点在同一直线上C.AO:AA′=1:2D.AB∥A′B′【分析】直接利用位似图形的性质进而分别分析得出答案.【解答】解:∵以点O为位似中心,把△ABC放大为原图形的2倍得到△A′B′C′,∴△ABC∽△A′B′C′,点C.点O、点C′三点在同一直线上,AB∥A′B′,AO:OA′=1:2,故选项C错误,符合题意.故选:C.【点评】此题主要考查了位似变换,正确把握位似图形的性质是解题关键.4.(2019,山东枣庄,3分)如图,将△ABC沿BC边上的中线AD平移到△A′B′C′的位置.已知△ABC的面积为16,阴影部分三角形的面积9.若AA′=1,则A′D等于()A.2 B.3 C.4 D.【分析】由S△ABC=16.S△A′EF=9且AD为BC边的中线知S△A′DE=S△A′EF=,S△ABD =S△ABC=8,根据△DA′E∽△DAB知()2=,据此求解可得.【解答】解:∵S△ABC=16.S△A′EF=9,且AD为BC边的中线,∴S △A ′DE =S △A ′EF =,S △ABD =S △ABC =8, ∵将△ABC 沿BC 边上的中线AD 平移得到△A 'B 'C ', ∴A ′E ∥AB , ∴△DA ′E ∽△DAB ,则()2=,即()2=,解得A ′D =3或A ′D =﹣(舍), 故选:B .【点评】本题主要平移的性质,解题的关键是熟练掌握平移变换的性质与三角形中线的性质、相似三角形的判定与性质等知识点.5.( 2019甘肃省兰州市) (4分)已知△ABC ∽△A ′B ′C ′, AB =8,A ’B ’=6, 则''C B BC = ( )A. 2 .B.34 . C. 3 . D. 916. 【答案】B .【考点】相似三角形的性质. 【考察能力】运算求解能力. 【难度】容易【解析】∵△ABC ∽△A ′B ′C ′,∴''B A AB =''CB BC又∵AB =8,A ’B ’=6, ∴''C B BC =34. 故选B.6.(2019甘肃省陇南市)(3分)如图,将图形用放大镜放大,应该属于( )A .平移变换B .相似变换C .旋转变换D .对称变换【分析】根据放大镜成像的特点,结合各变换的特点即可得出答案.【解答】解:根据相似图形的定义知,用放大镜将图形放大,属于图形的形状相同,大小不相同,所以属于相似变换.故选:B.【点评】本题考查的是相似形的识别,关键要联系图形,根据相似图形的定义得出.7.(2019,四川巴中,4分)如图▱ABCD,F为BC中点,延长AD至E,使DE:AD=1:3,连结EF交DC于点G,则S△DEG:S△CFG=()A.2:3 B.3:2 C.9:4 D.4:9【分析】先设出DE=x,进而得出AD=3x,再用平行四边形的性质得出BC=3x,进而求出CF,最后用相似三角形的性质即可得出结论.【解答】解:设DE=x,∵DE:AD=1:3,∴AD=3x,∵四边形ABCD是平行四边形,∴AD∥BC,BC=AD=3x,∵点F是BC的中点,∴CF=BC=x,∵AD∥BC,∴△DEG∽△CFG,∴=()2=()2=,故选:D.【点评】此题主要考查了相似三角形的判定和性质,平行四边形的性质,中点的定义,表示出CF是解本题的关键.8.(2019,山东淄博,4分)如图,在△ABC中,AC=2,BC=4,D为BC边上的一点,且∠CAD=∠B.若△ADC的面积为a,则△ABD的面积为()A.2a B.a C.3a D.a【分析】证明△ACD∽△BCA,根据相似三角形的性质求出△BCA的面积为4a,计算即可.【解答】解:∵∠CAD=∠B,∠ACD=∠BCA,∴△ACD∽△BCA,∴=()2,即=,解得,△BCA的面积为4a,∴△ABD的面积为:4a﹣a=3a,故选:C.【点评】本题考查的是相似三角形的判定和性质,掌握相似三角形的面积比等于相似比的平方是解题的关键.9 (2019•江苏连云港•3分)在如图所示的象棋盘(各个小正方形的边长均相等)中,根据“马走日”的规则,“马”应落在下列哪个位置处,能使“马”、“车”、“炮”所在位置的格点构成的三角形与“帅”、“相”、“兵”所在位置的格点构成的三角形相似()A.①处B.②处C.③处D.④处【分析】确定“帅”、“相”、“兵”所在位置的格点构成的三角形的三边的长,然后利用相似三角形的对应边的比相等确定第三个顶点的位置即可.【解答】解:帅”、“相”、“兵”所在位置的格点构成的三角形的三边的长分别为2.2、4;“车”、“炮”之间的距离为1,“炮”②之间的距离为,“车”②之间的距离为2,∵==,∴马应该落在②的位置,故选:B.【点评】本题考查了相似三角形的知识,解题的关键是利用勾股定理求得三角形的各边的长,难度不大.10. 2019•甘肃武威•3分)如图,将图形用放大镜放大,应该属于()A.平移变换B.相似变换C.旋转变换D.对称变换【分析】根据放大镜成像的特点,结合各变换的特点即可得出答案.【解答】解:根据相似图形的定义知,用放大镜将图形放大,属于图形的形状相同,大小不相同,所以属于相似变换.故选:B.【点评】本题考查的是相似形的识别,关键要联系图形,根据相似图形的定义得出.11 (2019•广西贵港•3分)如图,在△ABC中,点D,E分别在AB,AC边上,DE∥BC,∠ACD=∠B,若AD=2BD,BC=6,则线段CD的长为()A.2B.3C.2D.5【分析】设AD=2x,BD=x,所以AB=3x,易证△ADE∽△ABC,利用相似三角形的性质可求出DE的长度,以及,再证明△ADE∽△ACD,利用相似三角形的性质即可求出得出=,从而可求出CD的长度.【解答】解:设AD=2x,BD=x,∴AB=3x,∵DE∥BC,∴△ADE∽△ABC,∴=,∴=,∴DE=4,=,∵∠ACD=∠B,∠ADE=∠B,∴∠ADE=∠ACD,∵∠A=∠A,∴△ADE∽△ACD,∴=,设AE=2y,AC=3y,∴=,∴AD=y,∴=,∴CD=2,故选:C.【点评】本题考查相似三角形,解题的关键是熟练运用相似三角形的性质与判定,本题属于中等题型.12. (2019•湖北十堰•3分)如图,平面直角坐标系中,A(﹣8,0),B(﹣8,4),C(0,4),反比例函数y=的图象分别与线段AB,BC交于点D,E,连接DE.若点B关于DE的对称点恰好在OA上,则k=()A.﹣20 B.﹣16 C.﹣12 D.﹣8【分析】根据A(﹣8,0),B(﹣8,4),C(0,4),可得矩形的长和宽,易知点D的横坐标,E的纵坐标,由反比例函数的关系式,可用含有k的代数式表示另外一个坐标,由三角形相似和对称,可用求出AF的长,然后把问题转化到三角形ADF中,由勾股定理建立方程求出k的值.【解答】解:过点E作EG⊥OA,垂足为G,设点B关于DE的对称点为F,连接DF、EF、BF,如图所示:则△BDE≌△FDE,∴BD=FD,BE=FE,∠DFE=∠DBE=90°易证△ADF∽△GFE∴,∵A(﹣8,0),B(﹣8,4),C(0,4),∴AB=OC=EG=4,OA=BC=8,∵D.E在反比例函数y=的图象上,∴E(,4)、D(﹣8,)∴OG=EC=,AD=﹣,∴BD=4+,BE=8+∴,∴AF=,在Rt△ADF中,由勾股定理:AD2+AF2=DF2即:(﹣)2+22=(4+)2解得:k=﹣12故选:C.【点评】此题综合利用轴对称的性质,相似三角形的性质,勾股定理以及反比例函数的图象和性质等知识,发现BD与BE的比是1:2是解题的关键.13. (2019•湖北天门•3分)如图,AB为⊙O的直径,BC为⊙O的切线,弦AD∥OC,直线CD交BA的延长线于点E,连接B D.下列结论:①CD是⊙O的切线;②CO⊥DB;③△EDA∽△EBD;④ED•BC=BO•BE.其中正确结论的个数有()A.4个B.3个C.2个D.1个【分析】由切线的性质得∠CBO=90°,首先连接OD,易证得△COD≌△COB(SAS),然后由全等三角形的对应角相等,求得∠CDO=90°,即可证得直线CD是⊙O的切线,根据全等三角形的性质得到CD=CB,根据线段垂直平分线的判定定理得到即CO⊥DB,故②正确;根据余角的性质得到∠ADE=∠BDO,等量代换得到∠EDA=∠DBE,根据相似三角形的判定定理得到△EDA∽△EBD,故③正确;根据相似三角形的性质得到,于是得到ED•BC=BO•BE,故④正确.【解答】解:连结DO.∵AB为⊙O的直径,BC为⊙O的切线,∴∠CBO=90°,∵AD∥OC,∴∠DAO=∠COB,∠ADO=∠CO D.又∵OA=OD,∴∠DAO=∠ADO,∴∠COD=∠CO B.在△COD和△COB中,,∴△COD≌△COB(SAS),∴∠CDO=∠CBO=90°.又∵点D在⊙O上,∴CD是⊙O的切线;故①正确,∵△COD≌△COB,∴CD=CB,∵OD=OB,∴CO垂直平分DB,即CO⊥DB,故②正确;∵AB为⊙O的直径,DC为⊙O的切线,∴∠EDO=∠ADB=90°,∴∠EDA+∠ADO=∠BDO+∠ADO=90°,∴∠ADE=∠BDO,∵OD=OB,∴∠ODB=∠OBD,∴∠EDA=∠DBE,∵∠E=∠E,∴△EDA∽△EBD,故③正确;∵∠EDO=∠EBC=90°,∠E=∠E,∴△EOD∽△ECB,∴,∵OD=OB,∴ED•BC=BO•BE,故④正确;故选:A.【点评】本题主要考查了切线的判定、全等三角形的判定与性质以及相似三角形的判定与性质,注意掌握辅助线的作法,注意数形结合思想的应用是解答此题的关键.二.填空题1.(2019▪广西池河▪3分)如图,以点O为位似中心,将△OAB放大后得到△OCD,OA=2,AC=3,则=.【分析】直接利用位似图形的性质进而分析得出答案.【解答】解:∵以点O为位似中心,将△OAB放大后得到△OCD,OA=2,AC=3,∴===.故答案为:.【点评】此题主要考查了位似变换,正确得出对应边的比值是解题关键.2. (2019•湖南长沙•3分)如图,函数y=(k为常数,k>0)的图象与过原点的O的直线相交于A,B两点,点M是第一象限内双曲线上的动点(点M在点A的左侧),直线AM分别交x轴,y轴于C,D两点,连接BM分别交x轴,y轴于点E,F.现有以下四个结论:①△ODM与△OCA的面积相等;②若BM⊥AM于点M,则∠MBA=30°;③若M点的横坐标为1,△OAM为等边三角形,则k=2+;④若MF=MB,则MD=2M A.其中正确的结论的序号是①③④.(只填序号)【分析】①设点A(m,),M(n,),构建一次函数求出C,D坐标,利用三角形的面积公式计算即可判断.②△OMA不一定是等边三角形,故结论不一定成立.③设M(1,k),由△OAM为等边三角形,推出OA=OM=AM,可得1+k2=m2+,推出m=k,根据OM=AM,构建方程求出k即可判断.④如图,作MK∥OD交OA于K.利用平行线分线段成比例定理解决问题即可.【解答】解:①设点A(m,),M(n,),则直线AC的解析式为y=﹣x++,∴C(m+n,0),D(0,),∴S△ODM=n×=,S△OCA=(m+n)×=,∴△ODM与△OCA的面积相等,故①正确;∵反比例函数与正比例函数关于原点对称,∴O是AB的中点,∵BM⊥AM,∴OM=OA,∴k=mn,∴A(m,n),M(n,m),∴AM=(n﹣m),OM=,∴AM不一定等于OM,∴∠BAM不一定是60°,∴∠MBA不一定是30°.故②错误,∵M点的横坐标为1,∴可以假设M(1,k),∵△OAM为等边三角形,∴OA=OM=AM,1+k2=m2+,∴m=k,∵OM=AM,∴(1﹣m)2+=1+k2,∴k2﹣4k+1=0,∴k=2,∵m>1,∴k=2+,故③正确,如图,作MK∥OD交OA于K.∵OF∥MK,∴==,∴=,∵OA=OB,∴=,∴=,∵KM∥OD,∴==2,∴DM=2AM,故④正确.故答案为①③④.【点评】本题考查反比例函数与一次函数的交点问题,三角形的面积,平行线分线段成比例定理等知识,解题的关键是学会利用参数解决问题,学会构造平行线,利用平行线分线段成比例定理解决问题,属于中考填空题中的压轴题.3. (2019•湖南岳阳•4分)如图,AB为⊙O的直径,点P为AB延长线上的一点,过点P作⊙O的切线PE,切点为M,过A.B两点分别作PE的垂线A C.BD,垂足分别为C.D,连接AM,则下列结论正确的是①②④.(写出所有正确结论的序号)①AM平分∠CAB;②AM2=AC•AB;③若AB=4,∠APE=30°,则的长为;④若AC=3,BD=1,则有CM=DM=.【分析】连接OM,可证OM∥AC,得出∠CAM=∠AMO,由OA=OM可得∠OAM=∠AMO,故①正确;证明△ACM∽△AMB,则可得出②正确;求出∠MOP=60°,OB=2,则用弧长公式可求出的长为,故③错误;由BD∥AC可得PB=,则PB=OB=OA,得出∠OPM=30°,则PM=2,可得出CM=DM=DP=,故④正确.【解答】解:连接OM,∵PE为⊙O的切线,∴OM⊥PC,∵AC⊥PC,∴OM∥AC,∴∠CAM=∠AMO,∵OA=OM,∠OAM=∠AMO,∴∠CAM=∠OAM,即AM平分∠CAB,故①正确;∵AB为⊙O的直径,∴∠AMB=90°,∵∠CAM=∠MAB,∠ACM=∠AMB,∴△ACM∽△AMB,∴,∴AM2=AC•AB,故②正确;∵∠APE=30°,∴∠MOP=∠OMP﹣∠APE=90°﹣30°=60°,∵AB=4,∴OB=2,∴的长为,故③错误;∵BD⊥PC,AC⊥PC,∴BD∥AC,∴,∴PB=,∴,BD=,∴PB=OB=OA,∴在Rt△OMP中,OM==2,∴∠OPM=30°,∴PM=2,∴CM=DM=DP=,故④正确.故答案为:①②④.【点评】本题考查圆知识的综合应用,涉及切线的性质,圆周角定理,相似三角形的判定和性质、弧长公式、含30度直角三角形的性质等知识,解题的关键是灵活运用这些知识解决问题.4.(2019▪贵州毕节▪3分)如图,在一块斜边长30cm的直角三角形木板(Rt△ACB)上截取一个正方形CDEF,点D在边BC上,点E在斜边AB上,点F在边AC上,若AF:AC =1:3,则这块木板截取正方形CDEF后,剩余部分的面积为()A.100cm2B.150cm2C.170cm2D.200cm2【分析】设AF=x,根据正方形的性质用x表示出EF、CF,证明△AEF∽△ABC,根据相似三角形的性质求出BC,根据勾股定理列式求出x,根据三角形的面积公式、正方形的面积公式计算即可.【解答】解:设AF=x,则AC=3x,∵四边形CDEF为正方形,∴EF=CF=2x,EF∥BC,∴△AEF∽△ABC,∴==,∴BC=6x,在Rt△ABC中,AB2=AC2+BC2,即302=(3x)2+(6x)2,解得,x=2,∴AC=6,BC=12,∴剩余部分的面积=×12×6﹣4×4=100(cm2),故选:A.【点评】本题考查的是相似三角形的应用、正方形的性质,掌握相似三角形的判定定理和性质定理是解题的关键.5.(2019▪黑龙江哈尔滨▪3分)如图,在▱ABCD中,点E在对角线BD上,EM∥AD,交AB于点M,EN∥AB,交AD于点N,则下列式子一定正确的是()A.=B.=C.=D.=【分析】根据平行四边形的性质以及相似三角形的性质.【解答】解:∵在▱ABCD中,EM∥AD∴易证四边形AMEN为平行四边形∴易证△BEM∽△BAD∽△END∴==,A项错误=,B项错误==,C项错误==,D项正确故选:D.【点评】此题主要考查相似三角形的性质及平行四边形的性质,本题关键是要懂得找相似三角形,利用相似三角形的性质求解.6.(2019•浙江宁波•4分)如图,Rt△ABC中,∠C=90°,AC=12,点D在边BC上,CD=5,BD=13.点P是线段AD上一动点,当半径为6的⊙P与△ABC的一边相切时,AP的长为 6.5或3.【分析】根据勾股定理得到AB==6,AD==13,当⊙P于BC相切时,点P到BC的距离=6,过P作PH⊥BC于H,则PH=6,当⊙P于AB 相切时,点P到AB的距离=6,根据相似三角形的性质即可得到结论.【解答】解:∵在Rt△ABC中,∠C=90°,AC=12,BD+CD=18,∴AB==6,在Rt△ADC中,∠C=90°,AC=12,CD=5,∴AD==13,当⊙P于BC相切时,点P到BC的距离=6,过P作PH⊥BC于H,则PH=6,∵∠C=90°,∴AC⊥BC,∴PH∥AC,∴△DPH∽△DAC,∴,∴=,∴PD=6.5,∴AP=6.5;当⊙P于AB相切时,点P到AB的距离=6,过P作PG⊥AB于G,则PG=6,∵AD=BD=13,∴∠P AG=∠B,∵∠AGP=∠C=90°,∴△AGP∽△BCA,∴,∴=,∴AP=3,∵CD=5<6,∴半径为6的⊙P不与△ABC的AC边相切,综上所述,AP的长为6.5或3,故答案为:6.5或3.【点评】本题考查了切线的判定和性质,勾股定理,相似三角形的判定和性质,熟练正确切线的性质是解题的关键.7.(2019•浙江衢州•4分)如图,在平面直角坐标系中,O为坐标原点,ABCD的边AB 在x轴上,顶点D在y轴的正半轴上,点C在第一象限,将△AOD沿y轴翻折,使点A落在x轴上的点E处,点B恰好为OE的中点,DE与BC交于点F。
2019年中考数学真题分类专项训练--图形的相似

2019年中考数学真题分类专项训练--图形的相似一、选择题1.(2019邵阳)如图,以点O 为位似中心,把△ABC 放大为原图形的2倍得到△A ′B ′C ′,以下说法中错误的是A .△ABC ∽△A ′B ′C ′B .点C 、点O 、点C ′三点在同一直线上 C .AO ∶AA ′=1∶2D .AB ∥A ′B ′ 【答案】C2.(2019温州)如图,在矩形ABCD 中,E 为AB 中点,以BE 为边作正方形BEFG ,边EF 交CD 于点H ,在边BE 上取点M 使BM =BC ,作MN ∥BG 交CD 于点L ,交FG 于点N ,欧几里得在《几何原本》中利用该图解释了(a +b )(a ﹣b )=a 2﹣b 2,现以点F 为圆心,FE 为半径作圆弧交线段DH 于点P ,连结EP ,记△EPH 的面积为S 1,图中阴影部分的面积为S 2.若点A ,L ,G 在同一直线上,则12S S 的值为A.2B.3C D【答案】C3.(2019淄博)如图,在△ABC中,AC=2,BC=4,D为BC边上的一点,且∠CAD=∠B.若△ADC的面积为a,则△ABD的面积为A.2a B.5 2 aC.3a D.7 2 a【答案】C4.(2019杭州)如图,在△ABC中,点D,E分别在AB和AC上,DE∥BC,M为BC边上一点(不与点B,C 重合),连接AM交DE于点N,则A.AD ANAN AE=B.BD MNMN CE=C.DN NEBM MC=D.DN NEMC BM=【答案】C5.(2019玉林)如图,AB∥EF∥DC,AD∥BC,EF与AC交于点G,则是相似三角形共有A.3对B.5对C.6对D.8对【答案】C6.(2019常德)如图,在等腰三角形△ABC中,AB=AC,图中所有三角形均相似,其中最小的三角形面积为1,△ABC的面积为42,则四边形DBCE的面积是A.20 B.22 C.24 D.26【答案】D7.(2019凉山)如图,在△ABC中,D在AC边上,AD∶DC=1∶2,O是BD的中点,连接AO并延长交BC于E,则BE∶EC=A.1∶2 B.1∶3 C.1∶4 D.2∶3【答案】B8.(2019赤峰)如图,D、E分别是△ABC边AB,AC上的点,∠ADE=∠ACB,若AD=2,AB=6,AC=4,则AE 的长是A.1 B.2 C.3 D.4【答案】C9.(2019重庆)如图,△ABO∽△CDO,若BO=6,DO=3,CD=2,则AB的长是A.2 B.3 C.4 D.5【答案】C10.(2019连云港)在如图所示的象棋盘(各个小正方形的边长均相等)中,根据“马走日”的规则,“马”应落在下列哪个位置处,能使“马”、“车”、“炮”所在位置的格点构成的三角形与“帅”、“相”、“兵”所在位置的格点构成的三角形相似A.①处B.②处C.③处D.④处【答案】B11.(2019安徽)如图,在Rt△ABC中,∠ACB=90°,AC=6,BC=12,点D在边BC上,点E在线段AD上,EF⊥AC于点F,EG⊥EF交AB于点G.若EF=EG,则CD的长为A.3.6 B.4 C.4.8 D.5【答案】B12.(2019兰州)已知△ABC∽△A'B'C',AB=8,A'B'=6,则BCB'C'=A.2 B.43C.3 D.169【答案】B13.(2019常州)若△ABC~△A′B'C′,相似比为1∶2,则△ABC与△A'B′C'的周长的比为A.2∶1 B.1∶2 C.4∶1 D.1∶4【答案】B二、填空题14.(2019吉林)在某一时刻,测得一根高为1.8 m的竹竿的影长为3 m,同时同地测得一栋楼的影长为90 m,则这栋楼的高度为__________m.【答案】5415.(2019台州)如图,直线l1∥l2∥l3,A,B,C分别为直线l1,l2,l3上的动点,连接AB,BC,AC,线段AC交直线l2于点D.设直线l1,l2之间的距离为m,直线l2,l3之间的距离为n,若∠ABC=90°,BD=4,且23mn,则m+n的最大值为__________.【答案】25 316.(2019南京)如图,在△ABC中,BC的垂直平分线MN交AB于点D,CD平分∠AC B.若AD=2,BD=3,则AC的长__________.17.(2019)烟台)如图,在直角坐标系中,每个小正方形的边长均为1个单位长度,△ABO的顶点坐标分别为A(-2,-1),B(-2,-3),O(0,0),△A1B1O1的顶点坐标分别为A1(1,-1),B1(1,-5),O1(5,1),△ABO与△A1B1O1是以点P为位似中心的位似图形,则P点的坐标为__________.【答案】(-5,-1)18.(2019)本溪)在平面直角坐标系中,点A,B的坐标分别是A(4,2),B(5,0),以点O为位似中心,相似比为12,把△ABO缩小,得到△A1B1O,则点A的对应点A1的坐标为__________.【答案】(2,1)或(-2,-1)19.(2019宜宾)如图,已知直角△ABC中,CD是斜边AB上的高,AC=4,BC=3,则AD=__________.【答案】16 520.(2019河池)如图,以点O为位似中心,将△OAB放大后得到△OCD,OA=2,AC=3,则ABCD=__________.【答案】2 521.(2019淮安)如图,l1∥l2∥l3,直线a、b与l1、l2、l3分别相交于点A、B、C和点D、E、F.若AB=3,DE=2,BC=6,则EF=__________.【答案】4三、解答题22.(2019福建)已知△ABC和点A',如图.(1)以点A'为一个顶点作△A'B'C',使△A'B'C'∽△ABC,且△A'B'C'的面积等于△ABC面积的4倍;(要求:尺规作图,不写作法,保留作图痕迹)(2)设D、E、F分别是△ABC三边AB、BC、AC的中点,D'、E'、F'分别是你所作的△A'B'C'三边A'B'、B'C'、C'A'的中点,求证:△DEF∽△D'E'F'.解:(1)作线段A'C'=2AC、A'B'=2AB、B'C'=2BC,得△A'B'C'即可所求.∵A 'C '=2AC 、A 'B '=2AB 、B 'C '=2BC ,∴△ABC ∽△A ′B ′C ′,∴2()4A B C'ABC ''S A B''S AB==△△.(2)如图,∵D 、E 、F 分别是△ABC 三边AB 、BC 、AC 的中点, ∴111222DE BC DF AC EF AB ===,,, ∴△DEF ∽△ABC同理:△D 'E 'F '∽△A 'B 'C ', 由(1)可知:△ABC ∽△A ′B ′C ′, ∴△DEF ∽△D 'E 'F '.23.(2019绍兴)如图,矩形ABCD 中,AB =a ,BC =b ,点M ,N 分别在边AB ,CD 上,点E ,F 分别在边BC ,AD 上,MN ,EF 交于点P ,记k =MN :EF .(1)若a :b 的值为1,当MN ⊥EF 时,求k 的值.(2)若a :b 的值为12,求k 的最大值和最小值. (3)若k 的值为3,当点N 是矩形的顶点,∠MPE =60°,MP =EF =3PE 时,求a :b 的值.解:(1)如图1中,作FH⊥BC于H,MQ⊥CD于Q,设EF交MN于点O.∵四边形ABCD是正方形,∴FH=AB,MQ=BC,∵AB=CB,∴FH=MQ,∵EF⊥MN,∴∠EON=90°,∵∠ECN=90°,∴∠MNQ+∠CEO=180°,∠FEH+∠CEO=180°,∴∠FEH=∠MNQ,∵∠EHF=∠MQN=90°,∴△FHE≌△MQN(ASA),∴MN=EF,∴k=MN:EF=1.(2)∵a:b=1:2,∴b=2a,由题意:2a≤MN≤,a≤EF≤,∴当MN的长取最大时,EF取最短,此时k当MN的长取最短时,EF的值取最大,此时k.(3)连接FN,ME.∵k=3,MP=EF=3PE,∴MN EFPM PE==3,∴PN PFPM PE==2, ∴△PNF ∽△PME ,∴NF PNME PM==2,ME ∥NF , 设PE =2m ,则PF =4m ,MP =6m ,NP =12m ,①如图2中,当点N 与点D 重合时,点M 恰好与点B 重合.过点F 作FH ⊥BD 于点H .∵∠MPE =∠FPH =60°,∴PH =2m ,FH m ,DH =10m ,∴a AB FHb AD HD ===.②如图3中,当点N 与点C 重合,过点E 作EH ⊥MN 于点H .则PH =m ,HE =,∴HC =PH +PC =13m ,∴tan ∠HCE MB HE BC HC ===∵ME ∥FC ,∴∠MEB =∠FCB =∠CFD , ∵∠B =∠D ,∴△MEB ∽△CFD ,∴CD FC MB ME ==2,∴213a CD MBb BC BC ===,综上所述,a :b24.(2019凉山)如图,∠ABD=∠BCD=90°,DB平分∠ADC,过点B作BM∥CD交AD于M.连接CM交DB 于N.(1)求证:BD2=AD·CD;(2)若CD=6,AD=8,求MN的长.解:(1)证明:∵DB平分∠ADC,∴∠ADB=∠CDB,且∠ABD=∠BCD=90°,∴△ABD∽△BCD,∴AD BD BD CD,∴BD2=AD·CD.(2)∵BM∥CD,∴∠MBD=∠BDC,∴∠ADB=∠MBD,且∠ABD=90°,∴BM=MD,∠MAB=∠MBA,∴BM=MD=AM=4,∵BD2=AD·CD,且CD=6,AD=8,∴BD2=48,∴BC2=BD2-CD2=12,∴MC2=MB2+BC2=28,∴MC=,∵BM∥CD,∴△MNB∽△CND,∴23BM MN CD CN ==,且MC =,∴MN . 25.(2019舟山)小波在复习时,遇到一个课本上的问题,温故后进行了操作、推理与拓展.(1)温故:如图1,在△ABC 中,AD ⊥BC 于点D ,正方形PQMN 的边QM 在BC 上,顶点P ,N 分别在AB ,AC 上,若BC =a ,AD =h ,求正方形PQMN 的边长(用a ,h 表示). (2)操作:如何画出这个正方形PQMN 呢?如图2,小波画出了图1的△ABC ,然后按数学家波利亚在《怎样解题》中的方法进行操作:先在AB 上任取一点P ',画正方形P 'Q 'M 'N ',使点Q ',M '在BC 边上,点N '在△ABC 内,然后连结BN ',并延长交AC 于点N ,画NM ⊥BC 于点M ,NP ⊥NM 交AB 于点P ,PQ ⊥BC 于点Q ,得到四边形PQMN . (3)推理:证明图2中的四边形PQMN 是正方形.(4)拓展:小波把图2中的线段BN 称为“波利亚线”,在该线上截取NE =NM ,连结EQ ,EM (如图3),当∠QEM =90°时,求“波利亚线”BN 的长(用a ,h 表示). 请帮助小波解决“温故”、“推理”、“拓展”中的问题.解:(1)证明:如图1,由正方形PQMN 得PN ∥BC ,∴△APN ∽△ABC ,∴NP AE BC AD =,即PN h PNa h-=, 解得PN aha h=+.(3)证明:由画法得,∠QMN=∠PNM=∠POM=90°,∴四边形PQMN为矩形,∵N'M'⊥BC,NM⊥BC,∴NM'∥NM,∴△BN'M'∽△BNM,∴N'M'BN'NM BN=,同理可得=N'P'BN'NP BN,∴N'M'P'N' NM PN=.∵N′M′=P′N′,∴NM=PN,∴四边形PQMN为正方形.(4)如图2,过点N作NR⊥ME于点R.∵NE=NM,∴∠NEM=∠NME,∴ER=RM=12 EM,又∵∠EQM+∠EMQ=∠EMQ+∠EMN=90°,∴∠EQM=∠EMN.又∠QEM=∠NRM=90°,NM=QM,∴△EQM≌△RMN(AAS),∴EQ=RM,∴EQ=12 EM,∵∠QEM=90°,∴∠BEQ+∠NEM=90°,∴∠BEQ=∠EMB,又∵∠EBM=∠QBE,∴△BEQ∽△BME,∴1=2 BQ BE EQBE BM EM==.设BQ=x,则BE=2x,BM=4x,∴QM=BM–BQ=3x=MN=NE,∴BN=BE+NE=5x,∴BN=53NM=533aha h+.26.(2019巴中)△ABC在边长为1的正方形网格中如图所示.①以点C为位似中心,作出△ABC的位似图形△A1B1C,使其位似比为1∶2.且△A1B1C位于点C的异侧,并表示出A1的坐标.②作出△ABC绕点C顺时针旋转90°后的图形△A2B2C.③在②的条件下求出点B经过的路径长.解:①如图,△A 1B 1C 为所作,点A 1的坐标为(3,-3). ②如图,△A 2B 2C 为所作.③OB =点B 经过的路径长=90ππ1802⋅=.27.(2019衢州)如图,在Rt △AB C 中,∠C =90°,AC =6,∠BAC =60°,AD 平分∠BAC 交BC 于点D ,过点D 作DE ∥AC 交AB 于点E ,点M 是线段AD 上的动点,连结BM 并延长分别交DE ,AC 于点F 、G .(1)求CD 的长.(2)若点M 是线段AD 的中点,求EFDF的值. (3)请问当DM 的长满足什么条件时,在线段DE 上恰好只有一点P ,使得∠CPG =60°? 解:(1)∵AD 平分∠BAC ,∠BAC =60°, ∴∠DAC 12=∠BAC =30°,在Rt △ADC 中,DC =AC •tan30°=6=(2)由题意易知:BC ,BD ∵DE ∥AC ,∴∠EDA =∠DAC ,∠DFM =∠AGM , ∵AM =DM ,∴△DFM ≌△AGM (ASA ),∴DF =AG , 由DE ∥AC ,得△BFE ∽△BGA , ∴EF BE BDAG AB BC==,∴23EF EF BD DF AG BC ====. (3)∵∠CPG =60°,过C ,P ,G 作外接圆,圆心为Q , ∴△CQG 是顶角为120°的等腰三角形.①当⊙Q 与DE 相切时,如图1,过点Q 作QH ⊥AC 于H ,并延长HQ 与DE 交于点P .连结QC ,QG .设⊙Q 的半径QP =r .则QH 12=r ,r 12+r解得r 3=,∴CG 3==4,AG =2, 易知△DFM ∽△AGM ,可得43DM DF AM AG ==,∴DM 47=,∴DM 7=. ②当⊙Q 经过点E 时,如图2,过点C 作CK ⊥AB ,垂足为K ,设⊙Q 的半径QC =QE =r .则QK r .在Rt △EQK 中,12+(r )2=r 2,解得r =,∴CG 143==,易知△DFM ∽△AGM ,可得DM 5=.③当⊙Q 经过点D 时,如图3中,此时点M 与点G 重合,且恰好在点A 处,可得DM∴综上所述,当DM 7=或5DM ≤P 只有一个. 28.(2019荆门)如图,为了测量一栋楼的高度OE ,小明同学先在操场上A 处放一面镜子,向后退到B 处,恰好在镜子中看到楼的顶部E;再将镜子放到C处,然后后退到D处,恰好再次在镜子中看到楼的顶部E (O,A,B,C,D在同一条直线上),测得AC=2 m,BD=2.1 m,如果小明眼睛距地面髙度BF,DG为1.6 m,试确定楼的高度OE.解:如图,设E关于O的对称点为M,由光的反射定律知,延长GC、FA相交于点M,连接GF并延长交OE 于点H,∵GF∥AC,∴△MAC∽△MFG,∴AC MA MO FG MF MH==,即:AC OE OE OEBD MH MO OH OE BF ===++,∴21.62.1OEOE=+,∴OE=32,答:楼的高度OE为32米.29.(2019安徽)如图,Rt△ABC中,∠ACB=90°,AC=BC,P为△ABC内部一点,且∠APB=∠BPC=135°.(1)求证:△PAB∽△PBC;(2)求证:PA=2PC;(3)若点P到三角形的边AB,BC,CA的距离分别为h1,h2,h3,求证h12=h2·h3.证明:(1)∵∠ACB =90°,AB =BC , ∴∠ABC =45°=∠PBA +∠PBC ,又∠APB =135°,∴∠PAB +∠PBA =45°, ∴∠PBC =∠PAB ,又∵∠APB =∠BPC =135°, ∴△PAB ∽△PBC .(2)∵△PAB ∽△PBC ,∴PA PB ABPB PC BC ==,在Rt △ABC 中,AB =AC ,∴ABBC=∴PB PA ==,,∴PA =2PC .(3)如图,过点P 作PD ⊥BC ,PE ⊥AC 交BC 、AC 于点D ,E ,∴PF =h 1,PD =h 2,PE =h 3,∵∠CPB +∠APB =135°+135°=270°, ∴∠APC =90°,∴∠EAP +∠ACP =90°,又∵∠ACB =∠ACP +∠PCD =90°, ∴∠EAP =∠PCD , ∴Rt △AEP ∽Rt △CDP ,∴2PE APDP PC==,即322h h =,∴h 3=2h 2,∵△PAB ∽△PBC,∴12h AB h BC==,∴12h =,∴2212222322h h h h h h ==⋅=.即h 12=h 2·h 3.30.(2019长沙)根据相似多边形的定义,我们把四个角分别相等,四条边成比例的两个凸四边形叫做相似四边形.相似四边形对应边的比叫做相似比.(1)某同学在探究相似四边形的判定时,得到如下三个命题,请判断它们是否正确(直接在横线上填写“真”或“假”).①四条边成比例的两个凸四边形相似;(__________命题) ②三个角分别相等的两个凸四边形相似;(__________命题) ③两个大小不同的正方形相似.(__________命题)(2)如图1,在四边形ABCD 和四边形A 1B 1C 1D 1中,∠ABC =∠A 1B 1C 1,∠BCD =∠B 1C 1D 1,1111AB BC A B B C ==11CDC D .求证:四边形ABCD 与四边形A 1B 1C 1D 1相似.(3)如图2,四边形ABCD 中,AB ∥CD ,AC 与BD 相交于点O ,过点O 作EF ∥AB 分别交AD ,BC 于点E ,F .记四边形ABFE 的面积为S 1,四边形EFCD 的面积为S 2,若四边形ABFE 与四边形EFCD 相似,求21S S 的值.解:(1)①四条边成比例的两个凸四边形相似,是假命题,角不一定相等. ②三个角分别相等的两个凸四边形相似,是假命题,边不一定成比例.③两个大小不同的正方形相似.是真命题.故答案为:假,假,真.(2)证明:如图1中,连接BD ,B 1D 1.∵∠BCD =∠B 1C 1D 1,且1111BC CD B C C D =, ∴△BCD ∽△B 1C 1D 1,∴∠CDB =∠C 1D 1B 1,∠C 1B 1D 1=∠CBD , ∵111111AB BC CD A B B C C D ==,∴1111BD AB B D A B =, ∵∠ABC =∠A 1B 1C 1,∴∠ABD =∠A 1B 1D 1,∴△ABD ∽△A 1B 1D 1, ∴1111AD AB A D A B =,∠A =∠A 1,∠ADB =∠A 1D 1B 1,∴11111111AB BC CD AD A B B C C D A D ===,∠ADC =∠A 1D 1C 1,∠A =∠A 1,∠ABC =∠A 1B 1C 1,∠BCD =∠B 1C 1D 1, ∴四边形ABCD 与四边形A 1B 1C 1D 1相似.(3)证明:∵四边形ABCD 与四边形EFCD 相似. ∴DE EF AE AB=, ∵EF =OE +OF ,∴DE OE OF AE AB +=, ∵EF ∥AB ∥CD , ∴DE OE DE OC OF AD AB AD AB AB =-=,,∴DE DE OE OF AD AD AB AB +=+,∴2DE DE AD AE =, ∵AD =DE +AE , ∴21DE AE AE=+, ∴2AE =DE +AE ,∴AE =DE ,∴12S S =1.。
全国各地2019年中考数学真题分类解析汇编 27图形的相似与位似

图形的相似与位似一、选择题1. ( 2018•安徽省,第9题4分)如图,矩形ABCD中,AB=3,BC=4,动点P从A点出发,按A→B→C的方向在AB和BC上移动,记PA=x,点D到直线PA的距离为y,则y关于x的函数图象大致是()A.B.C.D.考点:动点问题的函数图象.分析:①点P在AB上时,点D到AP的距离为AD的长度,②点P在BC上时,根据同角的余角相等求出∠APB=∠PAD,再利用相似三角形的列出比例式整理得到y与x的关系式,从而得解.解答:解:①点P在AB上时,0≤x≤3,点D到AP的距离为AD的长度,是定值4;②点P在BC上时,3<x≤5,∵∠APB+∠BAP=90°,∠PAD+∠BAP=90°,∴∠APB=∠PAD,又∵∠B=∠DEA=90°,∴△ABP∽△DEA,∴=,即=,∴y=,纵观各选项,只有B选项图形符合.故选B.点评:本题考查了动点问题函数图象,主要利用了相似三角形的判定与性质,难点在于根据点P的位置分两种情况讨论.2. (2018•广西玉林市、防城港市,第7题3分)△ABC与△A′B′C′是位似图形,且△ABC与△A′B′C′的位似比是1:2,已知△ABC的面积是3,则△A′B′C′的面积是()A.3 B.6 C.9 D.12考点:位似变换.分析:利用位似图形的面积比等于位似比的平方,进而得出答案.解答:解:∵△ABC与△A′B′C′是位似图形,且△ABC与△A′B′C′的位似比是1:2,△ABC的面积是3,∴△ABC与△A′B′C′的面积比为:1:4,则△A′B′C′的面积是:12.故选:D.点评:此题主要考查了位似图形的性质,利用位似图形的面积比等于位似比的平方得出是解题关键.3.(2019年天津市,第8题3分)如图,在▱ABCD中,点E是边AD的中点,EC交对角线BD于点F,则EF:FC 等于()A.3:2 B.3:1 C.1:1 D. 1:2考点:平行四边形的性质;相似三角形的判定与性质.分析:根据题意得出△DEF∽△BCF,进而得出=,利用点E是边AD的中点得出答案即可.解答:解:∵▱ABCD,故AD∥BC,∴△DEF∽△BCF,∴=,∵点E是边AD的中点,∴AE=DE=AD,∴=.故选:D.点评:此题主要考查了平行四边形的性质以及相似三角形的判定与性质等知识,得出△DEF∽△BCF是解题关键.4.(2018•毕节地区,第12题3分)如图,△ABC中,AE交BC于点D,∠C=∠E,AD:DE=3:5,AE=8,BD=4,则DC的长等于()A.B.C. D.考点:相似三角形的判定与性质分析:根据已知条件得出△ADC∽△BDE,然后依据对应边成比例即可求得.解答:解:∵∠C=∠E,∠ADC=∠BDE,△ADC∽△BDE,∴=,又∵AD:DE=3:5,AE=8,∴AD=3,DE=5,∵BD=4,∴=,∴DC=,故应选A.点评:本题考查了相似三角形的判定和性质:对应角相等的三角形是相似三角形,相似三角形对应边成比例.5.(2018•武汉,第6题3分)如图,线段AB两个端点的坐标分别为A(6,6),B(8,2),以原点O为位似中心,在第一象限内将线段AB缩小为原来的后得到线段CD,则端点C的坐标为()A.(3,3) B.(4,3) C.(3,1) D.(4,1)考点:位似变换;坐标与图形性质分析:利用位似图形的性质结合两图形的位似比进而得出C点坐标.解答:解:∵线段AB的两个端点坐标分别为A(6,6),B(8,2),以原点O为位似中心,在第一象限内将线段AB缩小为原来的后得到线段CD,∴端点C的坐标为:(3,3).故选:A.点评:此题主要考查了位似图形的性质,利用两图形的位似比得出对应点横纵坐标关系是解题关键.6. (2019年江苏南京,第3题,2分)若△ABC∽△A′B′C′,相似比为1:2,则△ABC与△A′B′C′的面积的比为()A.1:2 B.2:1 C.1:4 D.4:1考点:相似三角形的性质分析:根据相似三角形面积的比等于相似比的平方计算即可得解.解答:∵△ABC∽△A′B′C′,相似比为1:2,∴△ABC与△A′B′C′的面积的比为1:4.故选C.点评:本题考查了相似三角形的性质,熟记相似三角形面积的比等于相似比的平方是解题的关键.7. (2019年江苏南京,第6题,2分)如图,在矩形AOBC中,点A的坐标是(﹣2,1),点C的纵坐标是4,则B、C两点的坐标分别是()(第2题图)A.(,3)、(﹣,4)B.(,3)、(﹣,4)C.(,)、(﹣,4)D.(,)、(﹣,4)考点:矩形的性质、全等三角形的判定与性质以及相似三角形的判定与性质。
2019全国各地中考数学试题分考点解析汇编图形的相似与位似

第28章图形的相似与位似一、选择题1.(2019浙江金华,9,3分)如图,西安路与南京路平行,并且与八一街垂直,曙光路与环城路垂直.如果小明站在南京路与八一街的交叉口,准备去书店,按图中的街道行走,最近的路程约为()A.600mB.500mC.400mD.300m北环城路曙光路西安路南京路书店八一街400m400m300m【答案】B2.(2019安徽,9,4分)如图,四边形ABCD中,∠BAD=∠ADC=90°,AB=AD=22,CD=2,点P在四边形ABCD的边上.若P到BD的距离为32,则点P的个数为()A.1 B.2 C.3 D.4【答案】B3. (2019广东东莞,31,3分)将左下图中的箭头缩小到原来的12,得到的图形是()【答案】A4. (2019浙江省,6,3分)如图,直角三角形纸片的两直角边长分别为6、8,按如图那样折叠,使点A 与点B 重合,折痕为DE ,则S △BCE :S △BDE 等于( ) A . 2:5 B .14:25 C .16:25 D . 4:21【答案】B5. (2019浙江台州,5,4分)若两个相似三角形的面积之比为1:4,则它们的周长之比为( ) A . 1:2 B . 1:4 C . 1:5 D . 1:16 【答案】A6. (2019浙江省嘉兴,7,4分)如图,边长为4的等边△ABC 中,DE 为中位线,则四边形BCED 的面积为( ) (A )32(B )33(C )34(D )36【答案】B7. (2019浙江丽水,9,3分)如图,西安路与南京路平行,并且与八一街垂直,曙光路与环城路垂直.如果小明站在南京路与八一街的交叉口,准备去书店,按图中的街道行走,最近的路程约为( )(第7题)A BCD EA .600mB .500mC .400mD .300m【答案】B8. (2019台湾台北,26)图(十)为一ABC ∆,其中D 、E 两点分别在AB 、AC 上,且AD=31,DB =29,AE =30,EC =32。
2019年全国各地中考数学真题分类解析汇编:27 图形的相似与位似

图形的相似与位似一、选择题1. (2019•安徽省,第9题4分)如图,矩形ABCD中,AB=3,BC=4,动点P从A点出发,按A→B→C的方向在AB和BC上移动,记P A=x,点D到直线P A的距离为y,则y关于x 的函数图象大致是()A.B.C.D.考点:动点问题的函数图象.分析:①点P在AB上时,点D到AP的距离为AD的长度,②点P在BC上时,根据同角的余角相等求出∠APB=∠P AD,再利用相似三角形的列出比例式整理得到y与x的关系式,从而得解.解答:解:①点P在AB上时,0≤x≤3,点D到AP的距离为AD的长度,是定值4;②点P在BC上时,3<x≤5,∵∠APB+∠BAP=90°,∠P AD+∠BAP=90°,∴∠APB=∠P AD,又∵∠B=∠DEA=90°,∴△ABP∽△DEA,∴=,即=,∴y=,纵观各选项,只有B选项图形符合.故选B.点评:本题考查了动点问题函数图象,主要利用了相似三角形的判定与性质,难点在于根据点P的位置分两种情况讨论.2. (2019•广西玉林市、防城港市,第7题3分)△ABC与△A′B′C′是位似图形,且△ABC 与△A′B′C′的位似比是1:2,已知△ABC的面积是3,则△A′B′C′的面积是()A.3 B.6 C.9 D.12考点:位似变换.分析:利用位似图形的面积比等于位似比的平方,进而得出答案.解答:解:∵△ABC与△A′B′C′是位似图形,且△ABC与△A′B′C′的位似比是1:2,△ABC 的面积是3,∴△ABC与△A′B′C′的面积比为:1:4,则△A′B′C′的面积是:12.故选:D.点评:此题主要考查了位似图形的性质,利用位似图形的面积比等于位似比的平方得出是解题关键.3.(2019年天津市,第8题3分)如图,在▱ABCD中,点E是边AD的中点,EC交对角线BD于点F,则EF:FC等于()A.3:2 B.3:1 C.1:1 D. 1:2考点:平行四边形的性质;相似三角形的判定与性质.分析:根据题意得出△DEF∽△BCF,进而得出=,利用点E是边AD的中点得出答案即可.解答:解:∵▱ABCD,故AD∥BC,∴△DEF∽△BCF,∴=,∵点E是边AD的中点,∴AE=DE=AD,∴=.故选:D.点评:此题主要考查了平行四边形的性质以及相似三角形的判定与性质等知识,得出△DEF∽△BCF是解题关键.4.(2019•毕节地区,第12题3分)如图,△ABC中,AE交BC于点D,∠C=∠E,AD:DE=3:5,AE=8,BD=4,则DC的长等于()A.B.C.D.考点:相似三角形的判定与性质分析:根据已知条件得出△ADC∽△BDE,然后依据对应边成比例即可求得.解答:解:∵∠C=∠E,∠ADC=∠BDE,△ADC∽△BDE,∴=,又∵AD:DE=3:5,AE=8,∴AD=3,DE=5,∵BD=4,∴=,∴DC=,故应选A.点评:本题考查了相似三角形的判定和性质:对应角相等的三角形是相似三角形,相似三角形对应边成比例.5.(2019•武汉,第6题3分)如图,线段AB两个端点的坐标分别为A(6,6),B(8,2),以原点O为位似中心,在第一象限内将线段AB缩小为原来的后得到线段CD,则端点C 的坐标为()A.(3,3)B.(4,3)C.(3,1)D.(4,1)考点:位似变换;坐标与图形性质分析:利用位似图形的性质结合两图形的位似比进而得出C点坐标.解答:解:∵线段AB的两个端点坐标分别为A(6,6),B(8,2),以原点O为位似中心,在第一象限内将线段AB缩小为原来的后得到线段CD,∴端点C的坐标为:(3,3).故选:A.点评:此题主要考查了位似图形的性质,利用两图形的位似比得出对应点横纵坐标关系是解题关键.6. (2019年江苏南京,第3题,2分)若△ABC∽△A′B′C′,相似比为1:2,则△ABC与△A′B′C′的面积的比为()A.1:2 B.2:1 C.1:4 D.4:1 考点:相似三角形的性质分析:根据相似三角形面积的比等于相似比的平方计算即可得解.解答:∵△ABC∽△A′B′C′,相似比为1:2,∴△ABC与△A′B′C′的面积的比为1:4.故选C.点评:本题考查了相似三角形的性质,熟记相似三角形面积的比等于相似比的平方是解题的关键.7. (2019年江苏南京,第6题,2分)如图,在矩形AOBC中,点A的坐标是(﹣2,1),点C的纵坐标是4,则B、C两点的坐标分别是()(第2题图)A.(,3)、(﹣,4)B.(,3)、(﹣,4)C.(,)、(﹣,4)D.(,)、(﹣,4)考点:矩形的性质、全等三角形的判定与性质以及相似三角形的判定与性质。
2019年中考数学真题汇编 图形的相似

中考数学真题汇编:图形的相似一、选择题1.已知,下列变形错误的是()A. B.C.D.【答案】B2.已知与相似,且相似比为,则与的面积比()A. B.C.D.【答案】D3.要制作两个形状相同的三角形框架,其中一个三角形的三边长分别为,和,另一个三角形的最短边长为2.5 cm,则它的最长边为()A. 3cmB. 4cmC. 4.5cmD. 5cm【答案】C4.在平面直角坐标系中,线段AB两个端点的坐标分别为A(6,8),B(10,2),若以原点O为位似中心,在第一象限内将线段AB缩短为原来的后得到线段CD,则点A的对应点C的坐标为()A. (5,1)B. (4,3) C. (3,4) D. (1,5)【答案】C5.如图,△ACB 和△ECD 都是等腰直角三角形,CA=CB ,CE=CD ,△ACB 的顶点A 在△ECD 的斜边DE 上,若AE=,AD=,则两个三角形重叠部分的面积为( )A. B. C. D.【答案】D6.在平面直角坐标系中,点是线段上一点,以原点 为位似中心把放大到原来的两倍,则点 的对应点的坐标为( )A.B. 或C.D.或【答案】B 7.如图,点 在线段 上,在的同侧作等腰和等腰, 与、分别交于点 、.对于下列结论:①;②;③.其中正确的是( )∵∠BEA=∠CDA ∠PME=∠AMD∴P 、E 、D 、A 四点共圆 ∴∠APD=AED=90°∵∠CAE=180°-∠BAC-∠EAD=90° ∴△CAP ∽△CMA ∴AC 2=CP•CM ∵AC=AB∴2CB 2=CP•CM所以③正确A. ①②③B. ①C. ①②D. ②③【答案】A8.如图,将沿边上的中线平移到的位置,已知的面积为9,阴影部分三角形的面积为4.若,则等于()A. 2B. 3C.D.【答案】A9.学校门口的栏杆如图所示,栏杆从水平位置绕点旋转到位置,已知,,垂足分别为,,,,,则栏杆端应下降的垂直距离为( )A. B.C.D.【答案】C10.如图,在△ABC中,点D在AB边上,DE∥BC,与边AC交于点E,连结BE,记△ADE,△BCE的面积分别为S1, S2,()A. 若,则B. 若,则C. 若,则D. 若,则【答案】D11.如图,菱形ABCD的对角线AC、BD相交于点O,点E为边CD的中点,若菱形ABCD的周长为16,∠BAD =60°,则△OCE的面积是()。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
数学精品复习资料中考数学真题汇编:图形的相似一、选择题1.已知,下列变形错误的是()A. B. C. D.【答案】B2.已知与相似,且相似比为,则与的面积比()A. B. C. D.【答案】D3.要制作两个形状相同的三角形框架,其中一个三角形的三边长分别为,和,另一个三角形的最短边长为2.5 cm,则它的最长边为()A. 3cmB. 4cmC. 4.5cmD. 5cm【答案】C4.在平面直角坐标系中,线段AB两个端点的坐标分别为A(6,8),B(10,2),若以原点O为位似中心,在第一象限内将线段AB缩短为原来的后得到线段CD,则点A的对应点C的坐标为()A. (5,1)B. (4,3)C. (3,4)D. (1,5)【答案】C5.如图,△ACB和△ECD都是等腰直角三角形,CA=CB,CE=CD,△ACB的顶点A在△ECD的斜边DE上,若AE= ,AD= ,则两个三角形重叠部分的面积为()A. B. C. D.【答案】D6.在平面直角坐标系中,点是线段上一点,以原点为位似中心把放大到原来的两倍,则点的对应点的坐标为( )A. B. 或 C. D. 或【答案】B7.如图,点在线段上,在的同侧作等腰和等腰,与、分别交于点、.对于下列结论:①;②;③.其中正确的是()∵∠BEA=∠CDA∠PME=∠AMD∴P、E、D、A四点共圆∴∠APD=AED=90°∵∠CAE=180°-∠BAC-∠EAD=90°∴△CAP∽△CMA∴AC2=CP•CM∵AC= AB∴2CB2=CP•CM所以③正确A. ①②③B. ①C. ①②D. ②③【答案】A8.如图,将沿边上的中线平移到的位置,已知的面积为9,阴影部分三角形的面积为4.若,则等于()A. 2B. 3C.D.【答案】A9.学校门口的栏杆如图所示,栏杆从水平位置绕点旋转到位置,已知,,垂足分别为,,,,,则栏杆端应下降的垂直距离为( )A. B. C. D.【答案】C10.如图,在△ABC中,点D在AB边上,DE∥BC,与边AC交于点E,连结BE,记△ADE,△BCE的面积分别为S1,S2,()A. 若,则B. 若,则C. 若,则D. 若,则【答案】D11.如图,菱形ABCD的对角线AC、BD相交于点O,点E为边CD的中点,若菱形ABCD的周长为16,∠BAD=60°,则△OCE的面积是()。
A. B. 2 C. D. 4【答案】A12.如图,已知AB是的直径,点P在BA的延长线上,PD与相切于点D,过点B作PD的垂线交PD的延长线于点C,若的半径为4,,则PA的长为()A. 4B.C. 3D. 2.5【答案】A二、填空题13.如图,△ABC中,点D、E分别在AB、AC上,DE∥BC,AD:DB=1:2,则△ADE与△ABC的面积的比为________.【答案】1:914.如图,在边长为1的小正方形网格中,点A、B、C、D都在这些小正方形的顶点上,AB、CD相交于点O,则tan∠AOD=________.【答案】215.矩形ABCD中,AB=6,BC=8.点P在矩形ABCD的内部,点E在边BC上,满足△PBE∽△DBC,若△APD 是等腰三角形,则PE的长为数________.【答案】3或1.216.如图,在矩形ABCD中,AB=2,BC=4,点E、F分别在BC、CD上,若AE= ,∠EAF=45°,则AF的长为________.【答案】17.如图,E、F、G、H分别为矩形ABCD的边AB、BC、CD、DA的中点,连接AC、HE、EC、GA、GF,已知AG⊥GF,AC=,则AB的长为________.【答案】218.在Rt△ABC中∠C=90°,AD平分∠CAB,BE平分∠CBA,AD、BE相交于点F,且AF=4,EF= ,则AC=________.【答案】19.如图,在矩形中,,点为线段上的动点,将沿折叠,使点落在矩形内点处.下列结论正确的是________. (写出所有正确结论的序号)①当为线段中点时,;②当为线段中点时,;③当三点共线时,;④当三点共线时,.【答案】①③④20.如图,在△ABC中,AC=3,BC=4,若AC,BC边上的中线BE,AD垂直相交于点O,则AB=________.【答案】三、解答题21.为了测量竖直旗杆AB的高度,某综合实践小组在地面D处竖直放置标杆CD,并在地面上水平放置个平面镜E,使得B,E,D在同一水平线上,如图所示.该小组在标杆的F处通过平面镜E恰好观测到旗杆顶A(此时∠AEB=∠FED).在F处测得旗杆顶A的仰角为39.3°,平面镜E的俯角为45°,FD=1.8米,问旗杆AB 的高度约为多少米? (结果保留整数)(参考数据:tan39.3°≈0.82,tan84.3°≈10.02)【答案】解:如图,∵FM//BD,∴∠FED=∠MFE=45°,∵∠DEF=∠BEA,∴∠AEB=45°,∴∠FEA=90°,∵∠FDE=∠ABE=90°,∴△FDE∽△ABE,∴,在Rt△FEA中,∠AFE=∠MFE+∠MFA=45°+39.3°=84.3°,tan84.3°= ,∴,∴AB=1.8×10.02≈18,答:旗杆AB高约18米.22.如图,在正方形ABCD中,点G在边BC上(不与点B,C重合),连接AG,作DE⊥AG,于点E,BF⊥AG于点F,设。
(1)求证:AE=BF;(2)连接BE,DF,设∠EDF= ,∠EBF= 求证:(3)设线段AG与对角线BD交于点H,△AHD和四边形CDHG的面积分别为S1和S2,求的最大值.【答案】(1)因为四边形ABCD是正方形,所以∠BAF+∠EAD=90°,又因为DE⊥AG,所以∠EAD+∠ADE=90°,所以∠ADE=∠BAF,又因为BF⊥AG,所以∠DEA=∠AFB=90°,又因为AD=AB所以Rt△DAE≌Rt△ABF,所以AE=BF(2)易知Rt△BFG∽Rt△DEA,所以在Rt△DEF和Rt△BEF中,tanα= ,tanβ=所以kta nβ= = = = =tanα所以(3)设正方形ABCD的边长为1,则BG=k,所以△ABG的面积等于k因为△ABD的面积等于又因为=k,所以S1=所以S2=1- k- =所以=-k2+k+1= ≤因为0<k<1,所以当k= ,即点G为BC中点时,有最大值23.如图,以的直角边为直径作交斜边于点,过圆心作,交于点,连接.(1)判断与的位置关系并说明理由;(2)求证:;(3)若,,求的长.【答案】(1)解:DE是圆O的切线证明:连接OD∵OE∥AC∴∠1=∠3,∠2=∠A∵OA=OD∴∠1=∠A∴∠2=∠3在△BOE和△DOE中OE=OD,∠2=∠3,OE=OE∴△BOE≌△DOE(SAS)∴∠ODE=∠OBE=90°∴OD⊥DE∴DE是圆O的切线(2)解:证明:连接BD∵AB是直径∴∠BDC=∠ADB=∠ABC=90°∵OE∥AC,O是AB的中点∴OE是△ABC的中位线∴AC=2OE∵∠BDC=∠ABC,∠C=∠C∴△ABC∽△BDC∴∴BC2=2CD•OE∵BC=2DE,∴(2DE)2=2CD•OE∴(3)解:∵设:BD=4x,CD=3x∵在△BDC中,,∴BC=2DE=5∴(4x)2+(3x)2=25解之:x=1,x=-1(舍去)∴BD=4∵∠ABD=∠C∴AD=BD•tan∠ABD=24.若一个三角形一条边的平方等于另两条边的乘积,我们把这个三角形叫做比例三角形.(1)已知△ABC是比例三角形,AB=2,BC=3.请直接写出所有满足条件的AC的长;(2)如图1,在四边形ABCD中,AD∥BC,对角线BD平分∠ABC,∠BAC=∠ADC.求证:△ABC是比例三角形;(3)如图2,在(2)的条件下,当∠ADC=90°时,求的值。
【答案】(1)或或.(2)证明:∵AD∥BC,∴∠ACB =∠CAD,又∵∠BAC=∠ADC,∴△ABC∽△DCA,∴= ,即CA2=BC·AD,又∵AD∥BC,∴∠ADB=∠CBD,∵BD平分∠ABC,∴∠ABD=∠CBD,∴∠ADB=∠ABD,∴AB=AD,∴CA2=BC·AB,∴△ABC是比例三角形.(3)解:如图,过点A作AH⊥BD于点H,∵AB=AD,∴BH= BD,∴AD∥BC,∠ADC=90°,∴∠BHA=∠BCD=90°,又∵∠ABH=∠DBC,∴△ABH∽△DBC,∴= ,∴AB·BC=DB·BH,∴AB·BC= BD2,又∵AB·BC=AC2,∴BD2=AC2,∴= .。
