八年级数学上册等腰梯形的性质及证明(人教版)
教
学
过
程
证明：如图，过点D作DE∥AB,交BC于点E。
∴∠B=∠DEC
∵AD∥BC
∴AB=DE
又∵AB=DC
∴DE=DC
∴∠DEC=∠C
∴∠B=∠C
问题五：上述证明中的辅助线是如何将问题转化的？(教师引导学生总结。)
第一种添加辅助线的方法：
1．可理解为将梯形转化为平行四边形和等腰三角形来研究。
等腰梯形的性质及证明
课题
等腰梯形的性质及证明
教
材
简
介
等腰梯形与直角梯形是并列的梯形，梯形与平行四边形又是并列的四边形。等腰梯形的性质是梯形问题的重点，深刻的理解等腰梯形的性质，有助于知识的内化，有助于形成知识系统，有助于发展学生的数学思维。
教
学
目
标
1.使学生掌握等腰梯形的性质定理及证明。
2.使学生理解适当的添加辅助线是解决问题的关键。
第二是使发散的思维转ቤተ መጻሕፍቲ ባይዱ聚拢。
巩固练习的实质是等腰梯形的判定定理的证明。因为其证明与性质定理的证明类似，引用它可以促使知识的正迁移，使知识与技能及时得到巩固和深化。其次是为下节判定定理的教学打下伏笔。
总结的目的是为了突出规律，使学生掌握解决问题的一般性的方法。
三、分析探索、寻求证明：
已知：如图，在梯形ABCD中，AD∥BC,AB=DC
求证：∠B=∠C
启发与思考：
问题一：证明两角相等通常采用什么办法？
创设问题情境，鼓励学生讨论中的三个问题由教学多媒体集成。
1.是起到创设问题情景的作用。
2.是为了引入新课。
分组讨论，进行问题类比是为学生创造合作的学习环境，提供探索问题的方法。并使学生在类比中产生直觉思维（建立猜想）。
3．等腰梯形与等腰三角形比较，等腰梯形有什么性质？（猜想）
（板书课题：等腰梯形的性质定理及证明）
二、问题类比，提出猜想：
将学生分组，讨论上述第三个问题。很快得出一个猜想（命题）：
命题：等腰梯形在同一底上的两个角相等。
（学生对命题的叙述不一定准确，教师引导学生得出叙述准确的命题，并提出应对命题的正确性加以证明。）
B C
启发与思考：
1．是不是可以类比性质定理的方法进行证明？
2．都有什么方法？（重点突出如何添加辅助线）
学生很容易将性质定理证明的方法迁移到此题，会得出许多证法。除此以外，可以引导学生如下图的方法添加辅助线进行证明。E
证明可由学生完成。
A D
证明略
B C
五、总结规律，促使知识内化：
a)注意“转化”的数学思想，并能够应用它。
问题三：怎样转化？
(添加辅助线。)
问题四：怎样添加辅助线？可以将问题转化为大家熟悉的图形，并利用已知图形的性质及已知条件进行证明和研究。
这个问题是教学中的难点和关键，为突破这个教学难点，教学中必须注意引导学生联系问题一中所提到的方案，即添加辅助线后能将梯形问题转化为问题一中所涉及的已知（熟悉的）图形，或者是转化后能将分散的、没有联系的条件聚拢到一起，建立直接联系。并利用已知图形的性质及已知条件进行证明。
启发与思考中设计了五个问题，旨在引导学生应用正确的方法证明猜想；并引导学生在对问题探索过程中发现规律、总结规律；第三是引导学生在探索过程中养成良好的思维习惯和思维方法；第四是使学生的直觉思维（猜想、感性的）上升为形象思维(正确、理性的)。
其中问题一是引导学生运用分析法（执果索因）探索证明方法，并使学生领会这一常用的数学方法。
在实际教学中，估计学生可以很容易的填出（一）中的前两种、(二)中的第一种，其它情况可由教师引导填出。
教学中一定要注意添加辅助线是关键，要注意学生的思维过程，引导学生克服思维障碍。
引出辅助线后，证明比较简单，可由小组推荐代表到黑板板演，比一比那个组的证法最规范。
下面的证明是针对第一种情况第一个图的证明，其它情况的证明略。
问题二是使学生重温“转化”这一重要的数学思想；使学生的探索在正确的思想指导下进行；并且可以自然的引出下面的问题。
问题三是引导学生发现解决“转化”的途径和方法。
问题四是一个开放性的问题，同时是教学中的难点和关键，所以提出这个问题是必然的。
第二是通过对这个开放性的问题的探索，可以很好的培养学生的发散思维，可以很好的培养学生的数学能力。
教学中将学生分组讨论，并证明。
可能的添法：
(一)、过梯形的顶点作腰的平行线，将梯形转化为一个平行四边形和一个三角形。如图所示:
ADA D
C
BEC B E C
A D E E A D
B C B C
(二)、过上底的端点作下底的垂线或过下底的端点作上底延长线的垂线。如图所示：
A D E A D F
B E F C B C
教
学
过
程
（可能的答案：1.证明所在的两三角形全等。
2.证明是等腰三角形。
3．证角平分线，等等。）
依据学生的回答，让学生观察图形，发现可能采用的证法与所给的已知条件相距甚远。因此，引出新的问题：
问题二：对于研究新问题（未知的、复杂的问题），通常采用什么数学思想解决？
(回答是肯定的：“转化”的思想。也就是将未知的转化为已知的，将复杂的图形转化为熟悉的基本图形进行研究。)
3.使学生理解几何问题中转化的数学思想。
教学重点：
等腰梯形的性质。
教学难点：
1．等腰梯形的性质。2.添加辅助线进行问题的转化。
教学关键：
准确（适当）地添加辅助线。
教学方法：
启发引导探索发现
教学用具：
教学多媒体
教学内容
设计意图
教
学
过
程
一、创设问题情境，鼓励学生讨论:
1．什么是等腰三角形？有什么性质？
2．什么是等腰梯形？
2．可理解为将梯形的一腰平移，使这个腰与另一个腰产生直接联系（构成等腰三角形）。
这两种方法均可用问题一中的2进行证明。
第二种添加辅助线的方法：
可理解为构造两个三角形，并证明这两个三角形全等，从而使问题得证。
四、巩固练习，促进知识正迁移：
已知：如图，梯形ABCD, A D
AD∥BC,∠B=∠C
求证：AB=CD
b)注意研究梯形问题中常见的添加辅助线的一般规律。（问题四及练习中的方法。）
c)注意学会分析问题、解决问题的一般性方法。
六、作业：
a)阅读教材。
总结在梯形问题中常用的转化方法。（即怎样添加辅助线，为什么这样添加？）
形问题常用的添加辅助线的规律，并使学生形成研究梯形问题的基本技能。
问题五是使学生理解添加辅助线的实质，并引导学生总结在一般情况下添加辅助线的规律，促使知识内化，从而使学生在探索中获得的认识上升为理性认识。
人教版八年级数学讲义梯形及等腰梯形(含解析)(2020年最新)
第19讲梯形及等腰梯形知识定位讲解用时：3分钟A、适用范围：人教版初二，基础较好；B、知识点概述：本讲义主要用于人教版初二新课，本节课我们要学习梯形及等腰梯形。
梯形和等腰梯形属于四边形章节，选择填空中会涉及到，也经常出现在几何大题中，是中考考查范围内的一个重要知识点，熟练掌握一般梯形、直角梯形和等腰梯形及它们的性质和判定，灵活运用并处理含梯形的综合类型题目.知识梳理讲解用时：20分钟梯形的认识1、定义：一组对边平行而另一组对边不平行的四边形叫做梯形（概念记清楚哦）一般梯形梯形标注：梯形是特殊的四边形，有且只有一组对边平行哦梯形的分类2、梯形的分类：一般梯形、特殊梯形（直角梯形、等腰梯形）直角梯形：有一个角是直角的梯形叫做直角梯形等腰梯形：两腰相等的梯形叫做等腰梯形直角梯形等腰梯形AB//CD AB//CDAD≠BC AD=BCAD⊥CD AD不平行BC梯形的中位线3、梯形的中位线：连接梯形两腰上的中点的线段叫做梯形的中位线. 梯形中位线定理：梯形的中位线平行于两底，并且等于两底和的一半你知道怎么证明吗？EF//AB//CDEF=12（AB+CD）等腰梯形的性质和判定1、等腰梯形的性质定理性质定理1：等腰梯形同一底边上的两个角相等性质定理2：等腰梯形的两条对角线相等性质3：等腰梯形既是轴对称图形，只有一条对称轴（底边的垂直平分线）∠A=∠B AC=BD 虚线为等腰梯形的对称轴∠C=∠D2、等腰梯形的判定定理判定定理1：同一底边上两个内角相等的梯形是等腰梯形判定定理2：对角线相等的梯形是等腰梯形判定3：利用定义课堂精讲精练【例题1】已知，在梯形ABCD中，AD∥BC，AD=4，AB=CD=6，∠B=60°，那么下底BC的长为．【答案】10【解析】首先过A作AE∥DC交BC与E，可以证明四边形ADCE是平行四边形，进而得到CE=AD=4，再证明△ABE是等边三角形，进而得到BE=AB=6，从而得到答案．解：如图，过A作AE∥DC交BC与E，∵AD∥BC，∴四边形AECD是平行四边形，∴AD=EC=4，AE=CD，∵AB=CD=6，∴AE=AB=6，∵∠B=60°，∴△ABE是等边三角形，∴BE=AB=6，∴BC=6+4=10．故答案为：10．讲解用时：3分钟解题思路：此题主要考查了梯形，关键是掌握梯形中的重要辅助线，过一个顶点作一腰的平行线得到一个平行四边形．教学建议：利用梯形的知识作辅助线构造出平行四边形和等边三角形.难度： 3 适应场景：当堂例题例题来源：普陀区期中年份：2017【练习1.1】如图，已知在梯形ABCD中，AD∥BC，∠B=30°，∠C=75°，AD=2，BC=7，那么AB= ．【答案】5【解析】过点D作DE∥AB交BC于E，根据平行线的性质，得∠DEC=∠B=30°，根据三角形的内角和定理，得∠EDC=75°，再根据等角对等边，得DE=CE．根据两组对边分别平行，知四边形ABED是平行四边形，则AB=DE=CE=7﹣2=5，从而求解．解：过点D作DE∥AB交BC于E，∴∠DEC=∠B=30°．又∵∠C=75°，∴∠CDE=75°．∴DE=CE．∵AD∥BC，DE∥AB，∴四边形ABED是平行四边形．∴AD=BE=2．﹣BE=BC﹣AD=7﹣2=5．∴AB=DE=CE=BC故答案为：5．讲解用时：3分钟解题思路：此题综合考查了平行四边形的判定及性质、平行线的性质、等角对等边的性质，解题的关键是作平行线构造平行四边形．教学建议：利用梯形的知识作辅助线构造出平行四边形进行求解.难度： 3 适应场景：当堂练习例题来源：潍坊三模年份：2016【例题2】如图，在梯形ABCD中，AB∥CD，∠ABC=90°，如果AB=5，BC=4，CD=3，那么AD= ．【答案】2【解析】试题分析：过点D作DE⊥AB于点E，后根据勾股定理即可得出答案．解：过点D作DE⊥AB于点E，如下图所示：则DE=BC=4，AE=AB﹣EB=AB﹣DC=2，AD==2．故答案为：2．讲解用时：3分钟解题思路：本题考查了梯形及勾股定理的知识，难度不大，属于基础题．教学建议：利用梯形和勾股定理的知识进行求解.难度： 3 适应场景：当堂例题例题来源：普陀区期末年份：2016【练习2.1】如图，已知梯形ABCD中，AD∥BC，E为AB中点，DE⊥EC．求证：（1）DE平分∠ADC；（2）AD+BC=DC．【答案】（1）DE平分∠ADC；（2）AD+BC=DC【解析】试题分析：（1）延长DE交CB的延长线于F，可证得△AED≌△BEF，根据三线合一的性质可得出CD=CF，推出∠CDF=∠F，由∠ADF=∠F即可证明；（2）由△AED≌△BEF，根据三线合一的性质可得出CD=CF，进而利用等线段的代换可证得结论；证明：（1）延长DE交CB的延长线于F，∵AD∥CF，∴∠A=∠ABF，∠ADE=∠F．在△AED与△BEF中，，∴△AED≌△BEF，∴AD=BF，DE=EF，∵CE⊥DF，∴∠CDF=∠F，∵AD∥CF，∴∠ADE=∠F，∴∠ADE=∠CDF，∴ED平分∠ADC．（2）∵△AED≌△BEF，∴AD=BF，DE=EF，∵CE⊥DF，∴CD=CF=BC+BF，∴AD+BC=DC．讲解用时：4分钟解题思路：本题考查梯形、全等三角形的判定和性质、线段的垂直平分线的性质等知识，解题的关键是因为点E是中点，所以应该联想到构造全等三角形，这是经常用到的解题思路，同学们要注意掌握．教学建议：学会运用梯形、全等三角形的判定和性质、线段垂直平分线的性质进行解题.难度： 4 适应场景：当堂练习例题来源：松江区期末年份：2017【例题3】如图，梯形ABCD中，AD∥BC，对角线BD与中位线EF交于点G，若AD=2，EF=5，那么FG= ．【答案】4【解析】试题分析：根据梯形中位线性质得出EF∥AD∥BC，推出DG=BG，则EG 是△ABD的中位线，即可求得EG的长，则FG即可求得．解：∵EF是梯形ABCD的中位线，∴EF∥AD∥BC，∴DG=BG，∴EG=AD=×2=1，∴FG=EF﹣EG=5﹣1=4．故答案是：4．讲解用时：3分钟解题思路：本题考查了梯形的中位线，三角形的中位线的应用，主要考查学生的推理能力和计算能力．教学建议：熟练掌握梯形的中位线、三角形的中位线知识并灵活运用.难度： 3 适应场景：当堂例题例题来源：无年份：2018【练习3.1】边长为8的正方形ABCD中，E、F是边AD、AB的中点，连接CE，取CE中点G，那么FG= ．【答案】6【解析】试题分析：根据题意，正方形ABCD的边长为8，E边AD的中点，可得出AE、BC的长；又由点F、G分别是AB、CE的中点，根据梯形的中位线定理，可得出FG的长；解：如图，∵正方形ABCD的边长为8，E、F是边AD、AB的中点，∴AE=4，BC=8，又∵点G是CE的中点，∴FG为梯形ABCE的中位线，∴EF==×（4+8）=6．故答案为：6．讲解用时：3分钟解题思路：本题主要考查了梯形的中位线定理，熟练掌握梯形的中位线定理：梯形的中位线平行于两底，并且等于两底和的一半．教学建议：学会应用梯形的中位线定理.难度： 3 适应场景：当堂练习例题来源：无年份：2018【例题4】在梯形ABCD中．AB∥CD，EF为中位线，则△AEF的面积与梯形ABCD的面积之比是．【答案】1：4【解析】试题分析：过A作AG⊥BC于G，交EF于H，再根据梯形的中位线定理及面积公式解答即可．解：过A作AG⊥BC于G，交EF于H，∵EF是梯形ABCD的中位线，∴AD+BC=2EF，AG=2AH，设△AEF的面积为xcm2，即EF?AH=xcm2，∴EF?AH=2xcm2，∴S梯形ABCD=（AD+BC）？AG=×2EF×2AH=2EF?AH=2×2xcm2=4xcm2．∴△AEF的面积与梯形ABCD的面积之比为：1：4．故答案为：1：4．讲解用时：3分钟解题思路：本题考查了梯形的中位线定理，比较简单，注意掌握梯形的中位线定理即是梯形的中位线等于上下底和的一半．教学建议：学会应用梯形的中位线定理.难度： 3 适应场景：当堂例题例题来源：六安期末年份：2013【练习4.1】在梯形ABCD中，AD∥BC，E、F分别是边AB、CD的中点．如果AD=5，EF=11，那么BC= ．【答案】17【解析】试题分析：根据梯形中位线定理“梯形的中位线长是上下底和的一半”，进行计算．解：根据梯形中位线定理，得EF=（AD+BC），则BC=2EF﹣AD=2×11﹣5=17．讲解用时：2分钟解题思路：考查了梯形的中位线定理．教学建议：熟练掌握并应用梯形的中位线定理.难度： 2 适应场景：当堂练习例题来源：无年份：2018【例题5】已知：如图，在梯形ABCD中，DC∥AB，AD=BC=2，BD平分∠ABC，∠A=60°．求：梯形ABCD的周长．【答案】10【解析】试题分析：由等腰梯形的性质得出∴∠ABC=∠A=60°．周长∠ABD=∠CBD=30°，∠ADB=90°，由直角三角形的性质得出AD=AB．AB=2AD=4．证出∠CDB=∠CBD．得出CD=BC=2．即可求出梯形ABCD的周长．解：在梯形ABCD中，∵DC∥AB，AD=BC=2，∠A=60°．∴∠ABC=∠A=60°．∵BD平分∠ABC，∴∠ABD=∠CBD=30°，∴∠ADB=90°，∴AD=AB．∴AB=2AD=4．又 DC∥AB，∴∠CDB=∠ABD，又∠ABD=∠CBD，∴∠CDB=∠CBD．∴CD=BC=2．．∴梯形ABCD的周长=AB+BC+CD+AD=4+2+2+2=10讲解用时：3分钟解题思路：本题主要考查对等腰梯形的性质，平行线的性质，等腰三角形的性质，角平分线的性质等知识点的理解和掌握，能求出DC=BC是解此题的关键．教学建议：掌握等腰梯形的性质和判定并灵活运用.难度： 3 适应场景：当堂例题例题来源：无年份：2018【练习5.1】已知：如图，在梯形ABCD中，DC∥AB，AD=BC=2，∠A=60°，对角线BD平分∠ABC．（1）求对角线BD的长；（2）求梯形ABCD的面积．【答案】（1）2√3；（2）3√3【解析】试题分析：（1）根据等腰梯形的同一底上的两个底角相等，即可求得∠B的度数，根据三角形的内角和定理证明△ABD是直角三角形，利用直角三角形的性质以及勾股定理即可求解；（2）过点D、C分别作DH⊥AB，CG⊥AB，垂足为点H、G，在直角△ADB中求得DH和AH的长，则AB即可求得，然后利用梯形的面积公式求解．解：（1）∵DC∥AB，AD=BC，∴∠A=∠ABC．∵BD平分∠ABC，∠A=60°，∴∠ABD=∠ABC=30°．∴∠ADB=90°．∵AD=2，∴AB=2AD=4．∴BD=．（2）过点D、C分别作DH⊥AB，CG⊥AB，垂足为点H、G．∵DC∥AB，BD平分∠ABC，∴∠CDB=∠ABD=∠CBD．∵BC=2，∴DC=BC=2．在RT△ADH和RT△BCG中，，∴RT△ADH≌RT△BCG．∴AH=BG．∵∠A=60°，∴∠ADH=30°．∴AH=AD=1，DH=．∵DC=HG=2，∴AB=4．∴．讲解用时：3分钟解题思路：本题主要考查对等腰梯形的性质，平行线的性质，等腰三角形的性质，角平分线的性质等知识点的理解和掌握，能求出DC=BC是解此题的关键．教学建议：掌握等腰梯形的性质并灵活应用.难度： 4 适应场景：当堂练习例题来源：无年份：2018【例题6】如图，在等腰梯形ABCD中，DC∥AB，AD=BC=2，BD平分∠ABC．∠A=60°，求对角线BD的长和梯形ABCD的面积．【答案】3√3【解析】根据等腰梯形的同一底上的两个底角相等，即可求得∠B的度数，根据三角形的内角和定理证明△ABD是直角三角形，利用直角三角形的性质以及勾股定理即可求解，过点D、C分别作DH⊥AB，CG⊥AB，垂足为点H、G，在直角△ADB中求得DH和AH的长，则AB即可求得，然后利用梯形的面积公式求解．解：∵DC∥AB，AD=BC，∴∠A=∠ABC．∵BD平分∠ABC，∠A=60°，∴∠ABD=∠ABC=30°．∴∠ADB=90°．∵AD=2，∴AB=2AD=4．∴BD=．过点D、C分别作DH⊥AB，CG⊥AB，垂足为点H、G．∵DC∥AB，BD平分∠ABC，∴∠CDB=∠ABD=∠CBD．∵BC=2，∴DC=BC=2．在Rt△ADH和Rt△BCG中，，∴Rt△ADH≌Rt△BCG．∴AH=BG．∵∠A=60°，∴∠ADH=30°．∴AH=AD=1，DH=．∵DC=HG=2，∴AB=4．∴梯形ABCD的面积=．讲解用时：4分钟解题思路：本题主要考查对等腰梯形的性质，平行线的性质，等腰三角形的性质，角平分线的性质等知识点的理解和掌握，能求出DC=BC是解此题的关键．教学建议：熟练地运用等腰梯形、平行线、等腰三角形的性质进行解题.难度： 4 适应场景：当堂例题例题来源：无年份：2018【练习6.1】已知：如图，等腰梯形ABCD的中位线EF的长为6cm，对角线BD平分∠ADC，下底BC的长比等腰梯形的周长小20cm，求上底AD的长．【答案】4cm【解析】试题分析：由等腰梯形的性质得出AB=DC，AD∥BC，得出∠ADB=∠CBD，，由已知再由已知条件得出BC=DC=AB，由梯形中位线定理得出AD+BC=2EF=12cm条件求出BC，即可得出AD的长．解：∵四边形ABCD是等腰梯形，∴AB=DC，AD∥BC，∴∠ADB=∠CBD，∵BD平分∠ADC，∴∠ADB=∠CDB，∴∠CBD=∠CDB，∴BC=DC=AB，∵EF是等腰梯形的中位线，，∴AD+BC=2EF=12cm∵下底BC的长比等腰梯形的周长小20cm，﹣20，∴BC=AB+BC+CD+AD即BC=AB+DC﹣8，∴BC=8cm，∴AD=4cm．讲解用时：3分钟解题思路：本题考查了等腰梯形的性质、等腰三角形的判定、梯形中位线定理；熟练掌握等腰梯形的性质，并能进行推理论证与计算是解决问题的关键．教学建议：利用等腰梯形、等腰三角形的判定、梯形中位线等知识点进行解题.难度： 3 适应场景：当堂练习例题来源：无年份：2018【例题7】已知：如图，在等腰梯形ABCD中，AD∥BC，AB=DC，点E为边BC上一点，且AE=DC．（1）求证：四边形AECD是平行四边形；（2）当∠B=2∠DCA时，求证：四边形AECD是菱形．【答案】（1）四边形AECD是平行四边形；（2）四边形AECD是菱形【解析】试题分析：（1）由等腰梯形的性质（等腰梯形同一底上的角相等），可得∠B=∠DCB，又由等腰三角形的性质（等边对等角）证得∠DCB=∠AEB，即可得AE∥DC，则四边形AECD为平行四边形；（2）根据平行线的性质，易得∠EAC=∠DCA，又由已知，由等量代换即可证得∠EAC=∠ECA，根据等角对等边，即可得AE=CE，则四边形AECD为菱形．证明：（1）∵在等腰梯形ABCD中，AD∥BC，AB=DC，∴∠B=∠DCB，∵AE=DC，∴AE=AB，∴∠B=∠AEB，∴∠DCB=∠AEB，∴AE∥DC，∴四边形AECD为平行四边形；（2）∵AE∥DC，∴∠EAC=∠DCA，∵∠B=2∠DCA，∠B=∠DCB，∴∠DCB=2∠DCA，∴∠ECA=∠DCA，∴∠EAC=∠ECA，∴AE=CE，∵四边形AECD为平行四边形，∴四边形AECD为菱形．讲解用时：3分钟解题思路：此题考查了等腰梯形的性质、平行四边形的判定、菱形的判定以及等腰三角形的判定与性质．解题的关键是仔细识图，应用数形结合思想解答．教学建议：利用等腰梯形、平行四边形的判定、菱形的判定等知识点进行解题.难度： 3 适应场景：当堂例题例题来源：连云港校级模拟年份：2010【练习7.1】如图，在梯形ABCD中，AD∥BC，BA=AD=DC，点E在边CB的延长线上，并且BE=AD，点F在边BC上．（1）求证：AC=AE；（2）如果∠AFB=2∠AEF，求证：四边形AFCD是菱形．【答案】（1）AC=AE；（2）四边形AFCD是菱形【解析】试题分析：（1）由已知条件可判定四边形ABCD是等腰梯形，利用等腰梯形的性质以及给出的条件利用SAS可判定△ABE≌△ADC，从而可证得结论；，所以四边形AFCD是菱形．（2）由（1）和外角和定理可证得AD=DC=AF=CF证明：（1）∵AD∥BC，BA=AD=DC，∴梯形ABCD是等腰梯形，∴∠ABC=∠DCE，∵∠ABE+∠ABC=180°，∠DCE+∠D=180°，∴∠D=∠ABE，又∵BE=AD，∴△ABE≌△ADC，∴AC=AE．（2）∵∠AFB=∠CAF+∠FCA，∠AFB=2∠E，∴2∠E=∠CAF+∠FCA，∵∠E=∠DAC=∠DCA，又∵AD∥BC，∴∠DAC=∠FCA，，∴AD=DC=AF=CF∴四边形AFCD是菱形．讲解用时：3分钟解题思路：此题主要考查等腰梯形的性质及全等三角形的判定方法的综合运用，难度较大，解答此类综合题目还需从基本做起，掌握一些基本性质是解答此类题目必备的．教学建议：利用等腰梯形的性质、全等三角形的判定等知识点进行解题.难度：4 适应场景：当堂练习例题来源：无年份：2018课后作业【作业1】如果梯形的中位线长为6，一条底边长为8，那么另一条底边长等于．【答案】4【解析】只需根据梯形的中位线定理“梯形的中位线等于两底和的一半”，进行计算．解：根据梯形的中位线定理，得另一底边长=中位线×2﹣一底边长=2×6﹣8=4．故答案为：4难度：2 适应场景：练习题例题来源：金山区二模年份：2018【作业2】如图，等腰梯形ABCD的面积为144，AD∥BC，AB=DC，且AC⊥BD．求等腰梯形ABCD的高．【答案】12【解析】过点D 分别作DE∥AC与BC的延长线交于点E，DF⊥BC，垂足为点F，将等腰梯形的面积转化为△DBE的面积，从而求得三角形的高即可得到等腰梯形的高．解：过点D 分别作DE∥AC与BC的延长线交于点E，DF⊥BC，垂足为点F．∵AD∥BC，∴四边形ACED是平行四边形．∴AD=CE，AC=DE．又∵四边形ABCD是等腰梯形，∴AC=BD．∴BD=DE．∴BF=FE．∵AC⊥BD，∴∠BGC=∠BDE=90°．∴．又∵AB=CD，∴△ADB≌△CED．∴S△BED=S梯形ABCD=144，∵BE?DF=144，∴×2DF2=144∴等腰梯形ABCD的高等于12．难度： 3 适应场景：练习题例题来源：普陀区期末年份：2014【作业3】如图，在等腰梯形ABCD中，AB∥DC，AC、BD是对角线，△ABD≌△ABE．求证：四边形AEBC是平行四边形．【答案】四边形AEBC是平行四边形【解析】根据等腰梯形的对角线相等，易得AC=BD，又由△ABD≌△ABE，易得AD=AE，BD=BE，则可证得AE=BC，AC=BE，根据有两组对边分别相等的四边形是平行四边形，可证得四边形AEBC是平行四边形．证明：∵四边形ABCD是等腰梯形，∴AD=BC，AC=BD，又∵△ABD≌△ABE，∴AD=AE，BD=BE，∴AE=BC，AC=BE，∴四边形AEBC是平行四边形．难度： 3 适应场景：练习题例题来源：香坊区期末年份：2011。
【数学课件】等腰梯形的性质定理和判定定理及其证明
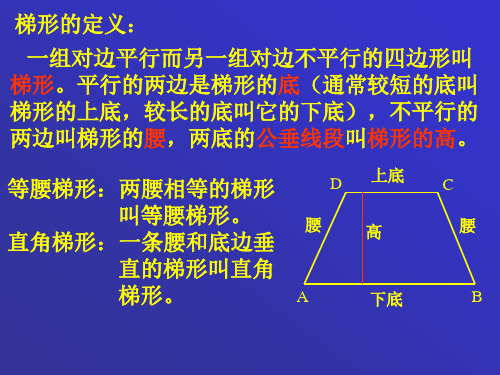
延长梯形的两交于一点，得到两个三 角形。如果是等腰梯形，则得到分别以梯 形两底为底的等腰三角形。
1、做老师的只要有一次向学生撒谎撒漏了底，就可能使他的全部教育成果从此为之毁灭。——卢梭 2、教育人就是要形成人的性格。——欧文 3、自我教育需要有非常重要而强有力的促进因素——自尊心、自我尊重感、上进心。——苏霍姆林斯基 4、追求理想是一个人进行自我教育的最初的动力，而没有自我教育就不能想象会有完美的精神生活。我认为，教会学生自己教育自己，这是一种 最高级的技巧和艺术。——苏霍姆林斯基 5、没有时间教育儿子——就意味着没有时间做人。——（前苏联）苏霍姆林斯基 6、教育不是注满一桶水，而且点燃一把火。——叶芝 7、教育技巧的全部奥秘也就在于如何爱护儿童。——苏霍姆林斯基 8、教育的根是苦的，但其果实是甜的。——亚里士多德 9、教育的目的，是替年轻人的终生自修作准备。——R.M.H. 10、教育的目的在于能让青年人毕生进行自我教育。——哈钦斯 11、教育的实质正是在于克服自己身上的动物本能和发展人所特有的全部本性。——（前苏联）苏霍姆林斯基 12、教育的唯一工作与全部工作可以总结在这一概念之中——道德。——赫尔巴特 13、教育儿童通过周围世界的美，人的关系的美而看到的精神的高尚、善良和诚实，并在此基础上在自己身上确立美的品质。——苏霍姆林斯基 14、教育不在于使人知其所未知，而在于按其所未行而行。——园斯金 15、教育工作中的百分之一的废品，就会使国家遭受严重的损失。——马卡连柯 16、教育技巧的全部诀窍就在于抓住儿童的这种上进心，这种道德上的自勉。要是儿童自己不求上进，不知自勉，任何教育者就都不能在他的身 上培养出好的品质。可是只有在集体和教师首先看到儿童优点的那些地方，儿童才会产生上进心。——苏霍姆林斯基 17、教育能开拓人的智力。——贺拉斯 18、作为一个父亲，最大的乐趣就在于：在其有生之年，能够根据自己走过的路来启发教育子女。——蒙田 19、教育上的水是什么就是情，就是爱。教育没有了情爱，就成了无水的池，任你四方形也罢、圆形也罢，总逃不出一个空虚。班主任广博的爱 心就是流淌在班级之池中的水，时刻滋润着学生的心田。——夏丐尊 20、教育不能创造什么，但它能启发儿童创造力以从事于创造工作。——陶行知
2020年寒假八年级数学课程第八讲 梯形
第八讲梯形第一部分知识梳理一、梯形的性质和判定1．梯形有关概念：一组对边平行而另一组对边______的四边形叫做梯形，梯形中平行的两边叫做底，按______分别叫做上底、下底(与位置无关)，梯形中不平行的两边叫做______，两底间的______叫做梯形的高．一腰垂直于底边的梯形叫做______；两腰______的梯形叫做等腰梯形．2．等腰梯形的性质：等腰梯形中______的两个角相等，两腰______，两对角线______，等腰梯形是轴对称图形，只有一条对称轴，______就是它的对称轴．3．等腰梯形的判定：______的梯形是等腰梯形；同一底上的两个角______的梯形是等腰梯形．第二部分例题与解题思路方法归纳类型一梯形的面积【例题1】如图，点C是线段AB上的一个动点，△ACD和△BCE是在AB同侧的两个等边三角形，DM，EN分别是△ACD和△BCE的高，点C在线段AB上沿着从点A向点B的方向移动（不与点A，B重合），连接DE，得到四边形DMNE．这个四边形的面积变化情况为（）A、逐渐增大B、逐渐减小C、始终不变D、先增大后变小〖选题意图〗考查等边三角形的性质和梯形的面积公式．〖解题思路〗易得此四边形为直角梯形，AB的长度一定，那么直角梯形的高为AB的长度的一半，上下底的和也一定，所以面积不变．〖参考答案〗解：当点C在线段AB上沿着从点A向点B的方向移动时，设两个等边三角形的边长分别为a，b，根据等边三角形的性质，等边△ACD和△BCE的高DM和EN的和不会改变，即DM+EN=MC+CN=AC+CB=AB，而且MN的长度也不会改变，即MN=AC+CB=AB．∴四边形DMNE 面积= AB 2， ∴面积不会改变．故选C ．【课堂训练题】1．某校研究性学习小组在研究列车的行驶速度时，得到一个数学问题．如图，若v 是关于t 的函数，图象为折线O ﹣A ﹣B ﹣C ，其中A （t 1，350），B （t 2，350），C （，0），四边形OABC 的面积为70，则t 2﹣t 1=（ ）A ．B ．C ．D ．〖参考答案〗解：根据题意得， （AB+）×350=70，解之得，AB= ；读图可知，t 2﹣t 1=AB=．故选B ． 2．如图为菱形ABCD 与正方形EFGH 的重迭情形，其中E 在CD 上，AD 与GH 相交于I点，且AD ∥HE ．若∠A=60°，且AB=7，DE=4，HE=5，则梯形HEDI 的面积为（ ）A ．6B ．8C ．10﹣2D ．10+2〖参考答案〗解：四边形ABCD 为菱形且∠A=60°⇒∠ADE=180°﹣60°=120°，又AD ∥HE ⇒∠DEH=180°﹣120°=60°，作DM ⊥HE 于M 点，则△DEM 为30°﹣60°﹣90°的三角形，又DE=4⇒EM=2，DM=2 ，且四边形EFGH 为正方形⇒∠H=∠I=90°，即四边形IDMH 为矩形⇒ID=HM=5﹣2=3，梯形HEDI 面积=（ ）=8 ． 故选B ．类型二梯形的中位线相关【例题2】如图，已知梯形ABCD，AD∥BC，AD=DC=4，BC=8，点N在BC上，CN=2，E是AB中点，在AC上找一点M使EM+MN的值最小，此时其最小值一定等于（）A．6 B．8C．4 D．4〖选题意图〗解决此题的关键是确定点M的位置．如果在直线的同侧有两个点，要在直线上找一点到两个点的距离之和最短，方法是找其中一个点关于直线的对称点，连接该点和另一个点，与直线的交点即为到两个点的距离之和最小的点的位置．〖解题思路〗此题关键是确定M的位置，将EM、MN转化到一条直线上，就可求出其和最小值．〖参考答案〗解：作N点关于AC的对称点N’，连接N’E交AC于M∴∠DAC=∠ACB，∠DAC=∠DCA，∴∠ACB=∠DCA，∵点N关于AC对称点N′在CD上，CN=CN′=2又∵DC=4∴EN’为等腰梯形的中线∴EN′=（AD+BC）=6，∴EM+MN最小值为：EN′=6故选A【课堂训练题】1．如图所示，DE是△ABC的中位线，FG为梯形BCED的中位线，若BC=8，则FG等于（）A．2cm B．3cmC．4cm D．6cm〖参考答案〗解：∵DE是△ABC的中位线，∴DE=BC=×8=4；∵FG为梯形BCED的中位线，∴FG=（DE+BC）=（4+8）=6．故选D．2．如图，在梯形ABCD中，AB∥CD，AB=3CD，对角线AC、BD交于点O，中位线EF 与AC、BD分别交于M、N两点，则图中阴影部分的面积是梯形ABCD面积的（）A．B．C．D．〖参考答案〗解：过点D作DQ⊥AB，交EF于一点W，∵EF是梯形的中位线，∴EF∥CD∥AB，DW=WQ，∴AM=CM，BN=DN．∴EM=CD，NF=CD．∴EM=NF，∵AB=3CD，设CD=x，∴AB=3x，EF=2x，∴MN=EF﹣（EM+FN）=x，∴S△AME+S△BFN=×EM×WQ+×FN×WQ=（EM+FN）QW=x•QW，S梯形ABFE=（EF+AB）×WQ=QW，S△DOC+S△OMN=CD×DW=xQW，S梯形FECD=（EF+CD）×DW=xQW，∴梯形ABCD面积=xQW+xQW=4xQW，图中阴影部分的面积=x•QW+xQW=xQW，∴图中阴影部分的面积是梯形ABCD面积的：=．故选：C．类型三角度的相关问题【例题3】如图，在梯形ABCD中，AB∥CD，AD=DC，求证：AC是∠DAB的平分线．〖选题意图〗本题考查了梯形的定义、平行线的性质及等腰三角形的性质，难度较小，是一道不错的证明题．〖解题思路〗利用梯形的一组对边平行可以得到内错角相等，然后利用等边对等角得到两个角相等，从而得到两个角相等，证得结论．〖参考答案〗解：∵AB ∥CD ，∴∠CAB=∠DCA ．∵AD=DC ，∴∠DAC=∠DCA ．∴∠DAC=∠CAB ，即AC 是∠DAB 的角平分线．【课堂训练题】1．在梯形ABCD 中，DC ∥AB ，AD ＝BC ，∠A ＝60°，BD ⊥AD .求∠DBC 和∠C 的大小.〖参考答案〗如图1，梯形ABCD 中，因为DC ∥AB ，∠A ＝60°，所以∠ADC ＝120°，又因为BD ⊥AD ，所以∠ADB ＝90°，即∠ABD ＝30°，而AD ＝BC ，所以∠ABC ＝60°，∠C ＝∠ADC ＝120°，所以∠DBC ＝30°.2．已知：如图，在直角梯形ABCD 中，AD ∥BC ，∠ABC=90°．点E 是DC 的中点，过点E 作DC 的垂线交AB 于点P ，交CB 的延长线于点M ．点F 在线段ME 上，且满足CF=AD ，MF=MA ．（1）若∠MFC=120°，求证：AM=2MB ；（2）求证：∠MPB=90°﹣∠FCM ．〖参考答案〗证明：（1）连接MD ，∵点E 是DC 的中点，ME ⊥DC ，∴MD=MC ，A D C B又∵AD=CF，MF=MA，∴△AMD≌△FMC，∴∠MAD=∠MFC=120°，∵AD∥BC，∠ABC=90°，∴∠BAD=90°，∴∠MAB=30°，在Rt△AMB中，∠MAB=30°，∴BM=AM，即AM=2BM；（2）∵△AMD≌△FMC，∴∠ADM=∠FCM，∵AD∥BC，∴∠ADM=∠CMD∴∠CMD=∠FCM，∵MD=MC，ME⊥DC，∴∠DME=∠CME=∠CMD，∴∠CME=∠FCM，在Rt△MBP中，∠MPB=90°﹣∠CME=90°﹣∠FCM．类型四求线段的长的问题【例题4】如图，在梯形ABCD中，AD∥BC，延长CB到点E，使BE=AD，连接DE交AB于点M．（1）求证：△AMD≌△BME；（2）若N是CD的中点，且MN=5，BE=2，求BC的长．〖选题意图〗本题考查了全等三角形的判断及三角形中位线定理的应用，熟记其性质、定理是证明、解答的基础．〖解题思路〗（1）找出全等的条件：BE=AD ，∠A=∠ABE ，∠E=∠ADE ，即可证明；（2）首先证得MN 是三角形的中位线，根据MN= （BE+BC ），又BE=2，即可求得． 〖参考答案〗证明：（1）∵AD ∥BC ，∴∠A=MBE ，∠ADM=∠E ，在△AMD 和△BME 中，，∴△AMD ≌△BME ；（2）∵△AMD ≌△BME ，∴MD=ME ，ND=NC ，∴MN= EC ，∴EC=2MN=2×5=10，∴BC=EC ﹣EB=10﹣2=8．【课堂训练题】1．如图，已知梯形ABCD ，上底AD ＝12，下底BC ＝28，EF ∥AB 分别交AD 、BC 于点E 、F ，且将梯形分成面积相等的两部分.试求BF 的长.〖参考答案〗设BF ＝x ，则FC ＝28－x.又设AD 与BC 间的距离为h ，即梯形和平行四边形ABFE 的BF 边上的高为h.在梯形ABCD 中，因为AD ∥BC ，EF ∥AB ，所以四边形ABFE 是平行四边形，所以AE ＝BF ＝x ，DE ＝12－x.因为平行四边形ABFE 的面积＝BE×h ，梯形EFCD 的面积＝12(DE+FC)×h ， 所以x×h ＝12[(12－x)+(28－x)]×h ，解得x ＝10， 答 BF 的长为10.2．如图，在直角梯形ABCD 中，AB ∥CD ，AD ⊥DC ，AB=BC ，且AE ⊥BC ．（1）求证：AD=AE ； D A FB C E（2）若AD=8，DC=4，求AB 的长．〖参考答案〗解：（1）连接AC ，∵AB ∥CD ，∴∠ACD=∠BAC ，∵AB=BC ，∴∠ACB=∠BAC ，∴∠ACD=∠ACB ，∵AD ⊥DC ，AE ⊥BC ，∴∠D=∠AEC=90°，∵AC=AC ，∴， ∴△ADC ≌△AEC ，（AAS ）∴AD=AE ；（2）由（1）知：AD=AE ，DC=EC ，设AB=x ，则BE=x ﹣4，AE=8，在Rt △ABE 中∠AEB=90°，由勾股定理得：82+（x ﹣4）2=x 2，解得：x=10，∴AB=10． 类型五 线段的和差问题【例题5】已知：等腰梯形ABCD 中，AD ∥BC ，MN 是中位线交AC 于P ，AC 平分∠BCD ，MP=12，PN=8，求：梯形ABCD 的周长．〖选题意图〗此题主要考查梯形、三角形中位线的性质和角平分线的定义，难度中等．〖解题思路〗由三角形中位线性质可求得上底为16，下底为24，再由角平分线和平行的性质，可求得腰长和上底相等，据此求解．〖参考答案〗解：∵AD∥BC，MN是中位线交AC于P，∴MP是△ABC的中位线，PN是△ACD的中位线，∠1=∠3，∵MP=12，PN=8，∴BC=2MP=24，AD=2PN=16，∵AC平分∠BCD，∴∠1=∠2，∴∠2=∠3，∴AD=CD=16，∴AB=CD=16，∴梯形ABCD的周长为：16×3+24=72．【课堂训练题】1．如图所示．△ABC外一条直线l，D，E，F分别是三边的中点，AA1，FF1，DD1，EE1都垂直l于A1，F1，D1，E1．求证：AA1+EE1=FF1+DD1．〖参考答案〗证明：连接EF，EA，ED．由中位线定理知，EF∥AD，DE∥AF，∴ADEF是平行四边形，∴对角线AE，DF互相平分，设它们交于O，作OO1⊥l于O1，则OO1是梯形AA1E1E及FF1D1D的公共中位线，∴（AA1+EE1）=（FF1+DD1）=OO1，即AA1+EE1=FF1+DD1．2．如图，过线段AB的两个端点作射线AM、BN，使AM∥BN，按下列要求画图并回答：（1）画∠MAB、∠NBA的平分线交于E，∠AEB是什么角？（2）过点E作一直线交AM于D，交BN于C，观察线段DE、CE，你有何发现？（3）无论DC的两端点在AM、BN如何移动，只要DC经过点E，AD+BC的值是否有变化？并说明理由．〖参考答案〗解：（1）∵AM∥BN，∴∠MAB+∠ABN=180°，又AE，BE分别为∠MAB、∠NBA的平分线，∴∠1+∠3=（∠MAB+∠ABN）=90°，∴∠AEB=180°﹣∠1﹣∠3=90°，即∠AEB为直角；（2）过E点作辅助线EF使其平行于AM，如图则EF∥AD∥BC，∴∠AEF=∠4，∠BEF=∠2，∵∠3=∠4，∠1=∠2，∴∠AEF=∠3，∠BEF=∠1，∴AF=FE=FB，∴F为AB的中点，又EF∥AD∥BC，根据平行线等分线段定理得到E为DC中点，∴ED=EC；（3）由（2）中结论可知，无论DC的两端点在AM、BN如何移动，只要DC经过点E，总满足EF为梯形ABCD中位线的条件，所以总有AD+BC=2EF=AB．类型六等腰梯形的判定【例题6】（2011•百色）已知矩形ABCD的对角线相交于点O，M、N分别是OD、OC上异于O、C、D的点．（1）请你在下列条件①DM=CN，②OM=ON，③MN是△OCD的中位线，④MN∥AB中任选一个添加条件（或添加一个你认为更满意的其他条件），使四边形ABNM为等腰梯形，你添加的条件是．（2）添加条件后，请证明四边形ABNM是等腰梯形．〖选题意图〗本题主要考查了等腰梯形的判定，难度中等，注意灵活运用全等三角形的判定与性质、矩形的性质和平行线分线段成比例的关系．〖解题思路〗（1）从4个条件中任选一个即可，可以添加的条件为①．（2）先根据SAS证明△AND≌△BCN，所以可得AM=BN，有矩形的对角线相等且平分，可得OD=OC即OM=ON，从而知，根据平行线分线段成比例，所以MN∥CD ∥AB，且MN≠AB，即四边形ABNM是等腰梯形．〖参考答案〗解：（1）选择①DM=CN；（2）证明：∵AD=BC，∠ADM=∠BCN，DM=CN∴△AND≌△BCN，∴AM=BN，由OD=OC知OM=ON，∴∴MN∥CD∥AB，且MN≠AB∴四边形ABNM是等腰梯形．【课堂训练题】1．如图，在四边形ABCD中，AD＜BC，对角线AC、BD相交于O点，AC=BD，∠ACB=∠DBC．（1）求证：四边形ABCD为等腰梯形．（2）若E为AB上一点，延长DC至F，使CF=BE，连接EF交BC于G，请判断G点是否为EF中点，并说明理由．〖参考答案〗证明：（1）∵∠ACB=∠DBC，∴OB=OC∵AC=BD，∴OA=OD，∴∠OAD=∠ODA∵∠DOC=∠OAD+∠ODA=∠OBC+∠OCB∴2∠OAD=2∠OCB，∴∠OAD=∠OCB∴AD∥BC∵AD＜BC∴四边形ABCD为梯形．在△ABC和△DCB中：AC=BD，∠ACB=∠DBC，CB=BC．∴△ABC≌△DCB∴AB=CD∴四边形ABCD为等腰梯形．（2）点G是EF中点理由：过E作EH∥CD交BC于H．∴∠EHB=∠DCB，∠EHG=∠GOF∵梯形ABCD为等腰梯形∴∠EBH=∠DCB，∴EB=EH∵EB=CF，∴EH=CF在△EHG和△FGC中：∠EHG=∠FCG∠EGH=∠FGCEH=CF∴△EHG≌△FGC∴EG=FG即G为EF中点．2．如图，在梯形ABCD中，AB∥DC，DB平分∠ADC，过点A作AE∥BD，交CD的延长线于点E，且∠C=2∠E．（1）求证：梯形ABCD是等腰梯形；（2）若∠BDC=30°，AD=5，求CD的长．〖参考答案〗证明：（1）∵AE∥BD，∴∠E=∠BDC．∵DB平分∠ADC，∴∠ADC=2∠BDC．又∵∠C=2∠E，∴∠ADC=∠BCD．∴梯形ABCD是等腰梯形．（2）由第（1）问，得∠C=2∠E=2∠BDC=60°，且BC=AD=5，∵在△BCD中，∠C=60°，∠BDC=30°，∴∠DBC=90°．∴DC=2BC=10．第三部分课后自我检测试卷A类试题：1．我们学习了四边形和一些特殊的四边形，如图表示了在某种条件下它们之间的关系．如果①，②两个条件分别是：①两组对边分别平行；②有且只有一组对边平行．那么请你对标上的其他6个数字序号写出相对应的条件．2．如图，在正六边形ABCDEF中，对角线AE与BF相交于点M，BD与CE相交于点N．（1）观察图形，写出图中两个不同形状的特殊四边形；（2）选择（1）中的一个结论加以证明．3．在▱ABCD中，AC是一条对角线，∠B=∠CAD，延长BC至点E，使CE=BC，连接DE．（1）求证：四边形ABED是等腰梯形；（2）若AB=AD=4，求梯形ABED的面积．4．如图，在梯形ABCD中，DC∥AB，AD=BC，BD平分∠ABC，∠A=60°．过点D作DE ⊥AB，过点C作CF⊥BD，垂足分别为E、F，连接EF，求证：△DEF为等边三角形．5．已知，如图，MN是▱ABCD外的一条直线，AA′、BB′、CC′、DD′都垂直于MN，A′、B′、C′、D′为垂足．求证：AA′+CC′=BB′+DD′．B类试题：6．如图，在直角梯形ABCD中，AD∥BC，BC⊥CD，∠B=60°，BC=2AD，E、F分别为AB、BC的中点．（1）求证：四边形AFCD是矩形；（2）求证：DE⊥EF．7．在直角梯形ABCD中，AB∥DC，AB⊥BC，∠A=60°，AB=2CD，E、F分别为AB、AD的中点，连接EF、EC、BF、CF．（1）判断四边形AECD的形状（不证明）；（2）在不添加其它条件下，写出图中一对全等的三角形，用符号“≌”表示，并证明；（3）若CD=2，求四边形BCFE的面积．8．如图：E在线段CD上，EA、EB分别平分∠DAB和∠CBA，∠AEB=90°，设AD=x，BC=y，且（x﹣3）2+|y﹣4|=0．（1）求AD和BC的长；（2）你认为AD和BC还有什么关系？并验证你的结论；（3）你能求出AB的长度吗？若能，请写出推理过程；若不能，请说明理由．C类试题：9．如图所示，在梯形ABCD中，AD∥BC，AB=AD，∠BAD的平分线AE交BC于点E，连接DE．（1）求证：四边形ABED是菱形；（2）若∠ABC=60°，CE=2BE，试判断△CDE的形状，并说明理由．10．如图，在四边形ABCD中，AD∥BC，AE、BF分别平分∠DAB和∠ABC，交CD于点E、F，AE、BF相交于点M．（1）求证：AE⊥BF；（2）求证：点M在AB、CD边中点的连线上．课后自我检测试卷参考答案A类试题：1．解：③﹣﹣相邻两边垂直；④﹣﹣相邻两边相等；⑤﹣﹣相邻两边相等；⑥﹣﹣相邻两边垂直；⑦﹣﹣两腰相等；⑧﹣﹣一条腰垂直于底边．2．解：（1）矩形ABDE，矩形BCEF；或菱形BNEM；或直角梯形BDEM，AENB等．（2）选择ABDE是矩形．证明：∵ABCDEF是正六边形，∴∠AFE=∠FAB=120°，∴∠EAF=30°，∴∠EAB=∠FAB﹣∠FAE=90°．同理可证∠ABD=∠BDE=90°．∴四边形ABDE是矩形．选择四边形BNEM是菱形．证明：同理可证：∠FBC=∠ECB=90°，∠EAB=∠ABD=90°，∴BM∥NE，BN∥ME．∴四边形BNEM是平行四边形．∵BC=DE，∠CBD=∠DEN=30°，∠BNC=∠END，∴△BCN≌△EDN．∴BN=NE．∴四边形BNEM是菱形．选择四边形BCEM是直角梯形．证明：同理可证：BM∥CE，∠FBC=90°，又由BC与ME不平行，得四边形BCEM是直角梯形．3．（1）证明：∵在□ABCD中，AD∥BC，∴∠CAD=∠ACB．∵∠B=∠CAD，∴∠ACB=∠B．∴AB=AC．∵AB∥CD，∴∠B=∠DCE．又∵BC=CE，∴△ABC≌△DCE（SAS）．∴AC=DE=AB．∵AD∥BE，∴为等腰梯形．（2）解：∵四边形ABCD为平行四边形，∴AD=BC=CE=4．∴△ABC为等边三角形．∴梯形高=三角形高=2．∴S=（4+8）×2×=12．4．证明：∵DC∥AB，AD=BC，∠A=60°，∴∠A=∠ABC=60°，∵BD平分∠ABC，∴∠ABD=∠CBD=∠ABC=30°，∵DC∥AB，∴∠BDC=∠ABD=30°，∴∠CBD=∠CDB，∴CB=CD，∵CF⊥BD，∴F为BD的中点，∵DE⊥AB，∴DF=BF=EF，由∠ABD=30°，得∠BDE=60°，∴△DEF为等边三角形．5．证明：连接AC，BD交于O，过O作OO′⊥MN垂足为O′根据平行四边形的性质知OO′同为梯形BB′D′D与梯形AA′C′C的中位线得AA′+CC′=BB′+DD′．B类试题：6．证明：（1）∵F为BC的中点，∴BF=CF=BC，∵BC=2AD，即AD=BC，∴AD=CF，∵AD∥BC，∴四边形AFCD是平行四边形，∵BC⊥CD，∴∠C=90°，∴▱AFCD是矩形；（2）∵四边形AFCD是矩形，∴∠AFB=∠FAD=90°，∵∠B=60°，∴∠BAF=30°，∴∠EAD=∠EAF+∠FAD=120°，∵E是AB的中点，∴BE=AE=EF=AB，∴△BEF是等边三角形，∴∠BEF=60°，BE=BF=AE，∵AD=BF，∴AE=AD，∴∠AED=∠ADE=﹣=30°，∴∠DEF=180°﹣∠AED﹣∠BF=180°﹣30°﹣60°=90°．∴DE⊥EF．7．解：（1）平行四边形；（2）△BEF≌△FDC或（△AFB≌△EBC≌△EFC）证明：连接DE，∵AB=2CD，E为AB中点，∴DC=EB，又∵DC∥EB，∴四边形BCDE是平行四边形，∵AB⊥BC，∴四边形BCDE为矩形，∴∠AED=90°，Rt△ABF中，∠A=60°，F为AD中点，∴AE=AD=AF=FD，∴△AEF为等边三角形，∴∠BEF=180°﹣60°=120°，而∠FDC=120°，在△BEF和△FDC中DC=BE，∠CDA=∠FEB=120°，DF=EF，∴△BEF≌△FDC（SAS）．（其他情况证明略）（3）若CD=2，则AD=4，DE=BC=2，∴S△ECF=S AECD=CD•DE=×2×2=2，S△CBE=BE•BC=×2×2=2，∴S四边形BCFE=S△ECF+S△EBC=2+2=4．8．解：（1）∵AD=x，BC=y，且（x﹣3）2+|y﹣4|=0，∴AD=3，BC=4．（2）AD∥BC，∵在△AEB中，∠AEB=90°，∴∠EAB+∠EBA=90°，又∵EA、EB分别平分∠DAB和∠CBA，∴∠DAB+∠ABC=180°．∴AD∥BC．（3）能．如图，过E作EF∥AD，交AB于F，则∠DAE=∠AEF，∠EBC=∠BEF，∵EA、EB分别平分∠DAB和∠CBA，∴∠EAF=∠AEF，∠EBF=∠BEF，∴AF=EF=FB，又∵EF∥AD∥BC，∴EF是梯形ABCD的中位线，∴EF=，∴AB=7．C类试题：9．（1）证明：如图，∵AE平分∠BAD，∴∠1=∠2，∵AB=AD，AE=AE，∴△BAE≌△DAE，∴BE=DE，∴∠2=∠3=∠1，∴AB=BE，∴AB=BE=DE=AD，∴四边形ABED是菱形．（2）解：△CDE是直角三角形．如图，过点D作DF∥AE交BC于点F，则四边形AEFD是平行四边形，∴DF=AE，AD=EF=BE，∵CE=2BE，∴BE=EF=FC，∴DE=EF，又∵∠ABC=60°，AB∥DE，∴∠DEF=60°，∴△DEF是等边三角形，∴DF=EF=FC，∴△CDE是直角三角形．10．（1）证明：如图，∵AE、BF分别平分∠DAB和∠ABC，∴∠1=∠2，∠3=∠4，∵AD∥BC，∴∠DAB+∠CBA=180°，即（∠1+∠2）+（∠3+∠4）=180°，2∠2+2∠3=180°，∴∠2+∠3=90°，而∠2+∠3+∠AMB=180°，∴∠AMB=90°，即AE⊥BF；（2）证明：如图，设AB、CD的中点分别为G、H，连接MG，∵M为Rt△ABM斜边AB的中点，∴MG=AG=GB，又∵∠1=∠2，∴∠1=∠5，∴GM∥AD．∵AD∥BC，∴四边形ABCD是以AD、BC为底的梯形，又G、H分别为两腰AB、DC的中点，由梯形中位线定理可知，GH∥AD，而证得GM∥AD，根据平行公理可知，过点G与AD平行的直线只有一条，∴M点在GH上，即M点在AB、CD边中点的连线上．。
八年级数学等腰梯形的性质2
斯就是遥远的北方的一个国家。他在那里执行任务，但是因为你家祖先在那里不适应气候，很快就病倒了。病了还不算可怜，可怜的是他 因为只懂我们现在说的中原话，不会讲也听不懂那边的俄语，就没有办法和当地人进行交流，也没有办法买药治病。于是病就一直没有好 转。傅元甲老前辈也不能一直因为生病而不去完成任务，于是他就带病继续奔波。”说了这么一大段，先喝一口茶水。边喝边瞅了一下那 两妞，发现她们已经开始根据我的牛皮在自己脑中飞速的想象着情节发展，那傻傻的听书人的表情真逗。“咳咳，我继续说。傅老前辈一 路向北的走着，在一间名叫九龙冰室的客栈停了下了，因为他实在太累了，而且还带病在身，即使再能打也只是空有一身武术。他刚走进 客栈，就遇到了有几个本地人在闹事，客栈老板是个女子，名字好像叫伊莎贝拉。当时店里的小二都被闹事的人打伤了，他们还打算欺负 客栈的女主子。傅老前辈当然抱打不平，上前去教训了那些闹事的人渣！”我越讲越激动，连忙又喝了几口水。“闹事的人也不是无名小 辈，他们也有相当的功夫，傅老前辈虽然身怀中原绝世武术，但是面对俄罗斯的奇特功夫，再加上他有恙在身，勉强只能招架着。这时候， 门外突然杀进来一男子，三下五除二就把贼人给打倒了。但是由于傅老前辈带病出战，动了真气，加之被贼人武功所伤，也最后支撑不住 倒了下去。”缓一会儿吧，说的好累。“然后呢？然后呢？”大和小琴迫不及待地向我问来。“然后啊，就是”没等我继续接着吹牛皮吹 下去，门外突然闯进一个人来。我乍眼一看，居然是翠大娘。翠大娘来得匆匆，也不看我在那里坐着喝茶，就往大那走去，关心地问道， “您没事吧？刚听到您大声叫唤，是怎么了吗？”什么？！刚听到？我讲书都讲了一大段了，你这才来，还装着时事发之后第一时间冲过 来的？你也太会演戏了吧，翠大娘！我心中有无限的鄙视了这个丫环主管。大貌似听我讲故事听得很来趣，一时被翠大娘打断了，明显有 点不高兴。但是翠大娘毕竟是自己的长辈，也不好不回她。“翠大娘，让你担心了。我只是不小心磕了一下，现在已经好了。”咦！想不 到大帮我瞒着事情的真相，看来大已经在偏袒我了。可能是想把故事给听完吧。听完大的说词之后，翠大娘把目光投向我这，蓦地发现我 坐着并且在悠闲地喝着茶，顿时气不打一处来，对我吼道，“是谁叫你坐下来的？谁叫你用这里的杯子喝茶的？”我一听，知道出事了， 连忙站起来，弓着身子退到门角处等着被骂。翠大娘刚想破口大骂，谁知道外头传来呼唤声，翠大娘应了一声之后，回头对我说，“把你 留在这里肯定会跟我们添麻烦，你跟我出来。”说罢，转身就走出去了。我也伸了伸身子，准备跟着
八年级数学上册 第十一章 梯形知识点总结 (新版)新人教版
八年级数学上册第十一章梯形知识点总
结 (新版)新人教版
1. 梯形的定义
梯形是指有两条平行边的四边形。
其中，较长的两边叫做上底和下底，两条连接上底和下底的斜边叫做腰，而两条腰的交点叫做顶点。
2. 梯形的分类
根据上底和下底的长度关系，梯形可以分为以下几类：
- 等腰梯形：上底和下底长度相等的梯形。
- 直角梯形：腰和底边之间有直角的梯形。
- 一般梯形：除了等腰梯形和直角梯形以外的其他梯形。
3. 梯形的性质
- 梯形的对边平行：一条边和与之不共顶点的另一条边平行。
- 梯形的底角和顶角互补：底边的两个邻角和顶边的两个邻角互补，即它们的和为180度。
- 等腰梯形的性质：等腰梯形的底角相等，顶角相等，且底边中点连线与顶边中点连线平行。
4. 梯形的面积计算
梯形的面积可以用以下公式计算：
面积 = [(上底 + 下底) ×高] ÷ 2
5. 梯形的周长计算
梯形的周长可以用以下公式计算：
周长 = 上底 + 下底 + 两条腰的长度
以上是八年级数学上册第十一章梯形的基本知识点总结，希望对您的研究有所帮助！。
八年级数学等腰梯形的性质
思
考
1、用一块面积为800 cm 2 的等腰
梯形彩纸做风筝 ，为牢固起见，
用竹条作梯形的对角线，对角
线恰好互相垂直，那么至少需 要竹条 80 cm
A
D
解: ∵四边形ABCD是等腰梯形
∴设AC=BD=x
B
C
又∵AC⊥BD
∴ 1 x 2 = 800
2
解得：x=40
∴至少需要竹条 80 cm
“横断面”的概念
3
S2
5
4
D、S1 ＝ S2
7
练习二
3、如图：若a=4 , b=6 , c=7 ,d=3 , 以它们为边作梯形，其中a∥b , 你认为这样的梯形能作出吗？
若能请作出图形，若不能，
Aa D
c
d
请说明 解: 这样的梯形不能作出
B
Hb C
过A点作AH∥CD 交BC于H点,得到 AHCD
∴AH=CD=d=3 , AD=HC= a = 4
A、m>h B、m<h C、m=h D、不能确定 B 解：
D
h
EC H
2 1 2 1 2 1
∟
过D作DH∥AC交BC 延长线于H点 ∴ BD＝DH
∵AC⊥BD
又过D作DE ⊥ BH于E点
∴BD ⊥ DH
∴ DE＝ BH
又∵ AD ∥ BH ， DH ∥ AC ∴四边形ACHD是平行四边形
＝ （BC＋CH）
“横断面”的概念
梯形的性质应用1
横断面
梯形的性思质应用考
2、河流的一个横断面，如图，根据下表中的测量数据计算断面面积
离河一岸的距离（m） 0 2 3 5 9 11
水 深（m）
人教版八年级数学上册说课稿13.3等腰三角形
人教版八年级数学上册说课稿13.3 等腰三角形一. 教材分析等腰三角形是八年级数学上册第十三章《三角形》的一个小节，本节内容主要让学生掌握等腰三角形的性质，并能运用等腰三角形的性质解决一些实际问题。
在教材中，通过引入等腰三角形的定义，让学生通过观察、操作、猜想、验证等方法，探究等腰三角形的性质，从而培养学生的动手操作能力和探究能力。
二. 学情分析学生在学习本节内容前，已经学习了三角形的概念、性质和分类，对三角形有了一定的了解。
但等腰三角形作为一种特殊的三角形，学生可能还比较陌生。
因此，在教学过程中，我将会引导学生运用已学的知识，通过观察、操作、猜想、验证等方法，探究等腰三角形的性质，从而加深学生对三角形知识的理解。
三. 说教学目标1.知识与技能目标：让学生掌握等腰三角形的性质，并能运用等腰三角形的性质解决一些实际问题。
2.过程与方法目标：通过观察、操作、猜想、验证等方法，培养学生的动手操作能力和探究能力。
3.情感态度与价值观目标：让学生在探究等腰三角形性质的过程中，体验到数学的乐趣，增强对数学的兴趣。
四. 说教学重难点1.教学重点：等腰三角形的性质。
2.教学难点：如何引导学生运用已学的知识，通过观察、操作、猜想、验证等方法，探究等腰三角形的性质。
五. 说教学方法与手段1.教学方法：采用问题驱动法、探究法、小组合作法等。
2.教学手段：多媒体课件、几何画板、实物模型等。
六. 说教学过程1.导入新课：通过复习三角形的相关知识，引出等腰三角形的概念。
2.探究等腰三角形的性质：（1）让学生观察等腰三角形的模型，引导学生发现等腰三角形的两腰相等。
（2）让学生用几何画板画出一个等腰三角形，并测量其角度，引导学生发现等腰三角形的底角相等。
（3）让学生分组讨论，总结等腰三角形的性质，并展示成果。
3.验证等腰三角形的性质：（1）让学生运用已学的知识，通过观察、操作、猜想、验证等方法，探究等腰三角形的性质。
（2）教师引导学生进行总结，得出等腰三角形的性质。
说课稿人教版数学八年级上册《等腰三角形》
《等腰三角形》各位评委老师：大家好！我是应聘初中数学01号考生，今天我抽到的说课题目是等腰三角形。
下面我将从说教材、说学情、说教法、说学法、说教学程序和板书设计这六个方面展开。
接下来开始我的说课。
一、说教材等腰三角形是人教版八年级上册第十二章第三节《等腰三角形》第一课时。
本节内容学习是在理解了轴对称以及了解了全等三角形的判定的基础上实行的所以具有一定的知识积累，。
通过对本节内容等腰三角形的“等边对等角”和“等腰三角形的三线合一”的性质等知识的学习。
为今后学习等边三角形和等腰梯形等知识打下基础，所以本节课无论是在本章教学中，还是初中数学教学中都占有非常重要的位置。
基于以上对教材地位和作用的分析，依照《新课程标准》的教学要求，结合教材和学生的年龄特点，确定本节课的三维教学目标如下：知识技能：能够探究，归纳，验证等腰三角形的性质，并学会应用等腰三角形的性质。
过程与方法：通过实践，观察，证明等腰三角形的性质，发展学生合情推理水平和演绎推理水平。
通过观察等腰三角形的对称性，培养学生观察，分析，归纳问题的水平。
情感、态度与价值观：引导学生对图像的观察，发现，激发学生的好奇心和求知欲，并在使用数学知识解答问题的活动中获取成功的喜悦，建立学习的自信心。
通过对数学课程标准理解及对教材分析的基础上，在新课改理念的指导下，我确立了如下教学重点、难点重点：掌握等腰三角形的性质并能使用该性质解决一些实际问题。
难点：理解等腰三角形性质的证明的过程。
二、说学情现代教育理论强调：“任何教学活动都必须以满足学习者的需要为出发点和落脚点。
”新课程标准也强调“数学教育要面向全体学生”，接下来我对学情实行分析。
这是八年级的课程，处在该年级的学生在生理上的特点是，学生的思维逐步由具体形象思维向抽象逻辑思维转变，观察水平，抽象水平和想象水平也随着迅速度完成长。
通过前面的学习，学生已具备一些分析问题、解决问题的水平，这些都是我在教学中较为注意的地方。
八年级数学上册等腰梯形的性质及证明(人教版)
其中问题一是引导学生运用分析法（执果索因）探索证明方法，并使学生领会这一常用的数学方法。
在实际教学中，估计学生可以很容易的填出（一）中的前两种、(二)中的第一种，其它情况可由教师引导填出。
教学中一定要注意添加辅助线是关键，要注意学生的思维过程，引导学生克服思维障碍。
引出辅助线后，证明比较简单，可由小组推荐代表到黑板板演，比一比那个组的证法最规范。
下面的证明是针对第一种情况第一个图的证明，其它情况的证明略。
三、分析探索、寻求证明：
已知：如图，在梯形ABCD中，AD∥BC,AB=DC
求证：∠B=∠C
启发与思考：
问题一：证明两角相等通常采用什么办法？
创设问题情境，鼓励学生讨论中的三个问题由教学多媒体集成。
1.是起到创设问题情景的作用。
2.是为了引入新课。
分组讨论，进行问题类比是为学生创造合作的学习环境，提供探索问题的方法。并使学生在类比中产生直觉思维（建立猜想）。
3.使学生理解几何问题中转化的数学思想。
教学重点：
等腰梯形的性质。
教学难点：
1．等腰梯形的性质。2.添加辅助线进行问题的转化。
教学关键：
准确（适当）地添加辅助线。
教学方法：
启发引导探索发现
教学用具：
教学多媒体
教学内容
设计意图
教
学
过
程
一、创设问题情境，鼓励学生讨论:
1．什么是等腰三角形？有什么性质？
八年级数学等腰梯形的性质
在地理测量中，等腰梯形可用于测量 地形高度、计算面积等，其简单的几 何形状能够方便测量和计算。
06 总结与展望
对等腰梯形性质的总结
等腰梯形的定义：等腰梯形是一组对 边平行且另一组对边相等的四边形。
等腰梯形的性质
等腰梯形的两腰相等。
等腰梯形同一底上的两个内角相等。 等腰梯形的对角线相等。
等腰梯形是轴对称图形，对称轴是上下底中 点的连线所在直线(过两底中点的直线）。
在土地测量中，等腰梯形可以 用来表示某块土地的形状，通 过计算其面积可以确定土地的 面积和价值等信息。
05 等腰梯形在生活中的应用
建筑领域中的应用
建筑设计
等腰梯形可用于建筑设计中的门 窗、楼梯、走廊等部分，其对称 性和稳定性使得建筑物更加美观 和实用。
桥梁设计
在桥梁设计中，等腰梯形可用于 桥墩、桥台等部分，其结构稳定 性能够增强桥梁的承重能力和安 全性。
等腰梯形的上下底边平行，因此 同旁内角互补，即相邻两个内角
的度数之和为180度。
03 等腰梯形的判定方法
通过边长判定等腰梯形
两条腰相等
两条对角线相等
在等腰梯形中，两条腰的长度是相等 的，这是判定等腰梯形的基本条件。
在等腰梯形中，两条对角线的长度也 是相等的。
上底和下底平行
等腰梯形的上底和下底必须是平行的， 这也是等腰梯形的一个重要特征。
该公式是计算等腰梯形面积的基本方 法，适用于所有已知上底、下底和高 的情况。
面积计算方法的推导过程
推导等腰梯形面积的计算方法，可以 通过将等腰梯形划分为两个等高的直 角三角形和一个矩形来进行。
然后，根据三角形和矩形的面积计算 公式，可以分别求出两个直角三角形 的面积和矩形的面积。