应力莫尔圆应力平衡微分方程

合集下载

02讲-应力与平衡、位移与应变 PPT

用转轴公式能求得斜面上的正应力和剪应力。
王正伟
主应力
Principal Stress
对于给定的应力状态，若改变斜面方向，则斜面应力的大小和方向都会发生改变，因此是否存在一个面，使得只存在正应力而无剪应力？
() g
x xy xz
xy y
yz
xz yz 0 z
1、2、3
、2、3
王正伟
主应力的性质 Principal Stress
在笛卡尔坐标系中，用六个平行于坐标面的截面在一点周围截取一个正六面体微元。正六面体的六个面法向矢量与坐标轴平行，同向的三个面称之为正面，反向的三个面称之为负面。将作用在正面上的应力矢量沿坐标轴方向分解。
1 xxi xy j xzk
2 yxi yy j yzk
3 zxi zy j zzk
王正伟
外力、载荷 Load
面力是作用在物体表面上的外力。
p lim F S 0 S
体积力是作用在物体内部体积上的外力。
F f lim
V 0 V
王正伟
应力矢量(应力) Stress Vector
应力矢量(应力)
( )
lim S0
F S
若取 S 为变形前面元的初始面积，则上式给出工程应力，亦称名义应力，常用于小变形情况。对于大变形问题，应取 S 为变形后面元的实际面积，称真实应力，简称真应力, 也称柯西应力。
四面体体积为：
V 1dhdS 3
王正伟
斜面应力公式 Cauchy Formula
四面体平衡条件为：
(1) dS1 (2) dS2 (3) dS3
()
dS
f
(1dhdS) 3
0

应力莫尔圆

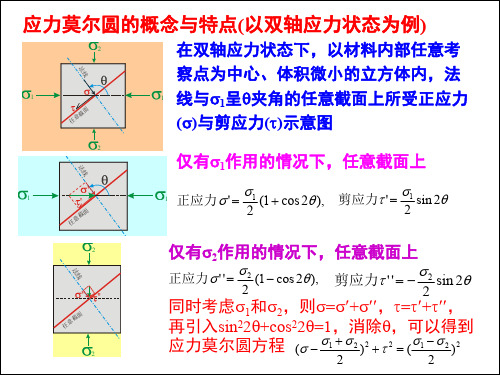
（，）分别代表法线与最大主应力轴1呈夹角的那个截面上所受到的正
N力与剪应力。
平面应力状态的应力莫尔圆
应力莫尔圆的概念与特点(以双轴应力状态为例)
1．双轴应力状态的特点
（1）剪应力互等定律：两个相互垂直的截面上受到的剪应力大小相等，符号相反；
（2）两个相互垂直的截面上受到的正应力之和不变，
(

1

2
)2

2

(
1
2
)2
2
2
应力莫尔圆的概念与特点(以双轴应力状态为例)
以横坐标代表正应力，纵坐标代表剪应力，建立
－坐标系，一点的应力状态在该坐标系中可以表
示为一个圆的方程
(

1
2
)2

2

(
1
2
)2
2
2
这个圆就是该点的应力莫尔圆，圆上某点的坐标
T A( , )
应力莫尔圆的概念与特点以双轴应力状态为例在双轴应力状态下以材料内部任意考察点为中心体积微小的立方体内法呈夹角的任意截面上所受正应力与剪应力示意图作用的情况下任意截面上同时考虑21消除可以得到应力莫尔圆方程应力莫尔圆的概念与特点以双轴应力状态为例以横坐标代表正应力纵坐标代表剪应力建立坐标系一点的应力状态在该坐标系中可以表示为一个圆的方程平面应力状态的应力莫尔圆这个圆就是该点的应力莫分别代表法线与最大主应力轴呈夹角的那个截面上所受到的正应力与剪应力
2
2
法线
2
'' ''
面截意任
2
仅有2作用的情况下，任意截面上
正应力 ' ' 2 (1 cos 2 ), 2

第1章应力分析及应力平衡微分方程

沈阳工业大学
1.1.1 应力
一，连续介质模型
连续介质是一种理论模型．该模型认为物质连续地分布在物体所占有的空间之内．要研究物体的宏观机械运动，可以取连续介质的质点，实际上是物质的微块，它的尺度与所研究的宏观尺度相比充分小，这样在微块内，每一个物理量都可以看作均匀分布的常量．而数学上把这微块当作一个点来处理．另一方面，又要求这微块的尺度与分子运动的尺度足够大，使微块包含大量分子，从而对分子的运动作统计平均．以得到表征宏观现象的物理量．因此对微块要求宏观小，微观大．
第1章应力分析
沈阳工业大学
第 1 章应力分析
1.1 点的应力状态 1.2特殊应力状态 1.3应力平衡微分方程
沈阳工业大学
1.1 点的应力状态
1.1 .1应力 1.1.2 点的应力状态 1.1.3主应力及应力张量不变量 1.1.4主切应力和最大切应力 1.1.5应力偏张量和应力球张量 1.1.6八面体应力和等效应力 1.1.7应力莫尔圆
沈阳工业大学
1.1.1 应力
一，外力(Load)
塑性成型是利用金属的塑性，在外力的作用下使其成型的一种方法．作用于金属的外力可以分两类：一类是作用于金属表面上的力，称为面力，它可以是集中力也可以是分布力，一般由加工设备和模具提供；另一类是作用于金属物体每个质点上的力，称为体积力．如重力、磁力、惯性力等等。
Ｆ１
沈阳工业大学
1.1.1 应力
应力Sｎ是内力的集度
内力和应力均为矢量
应力的单位： 1Pa=1N/m2=1.0197Kgf/mm2
1MPa=106N/m2
应力是某点A的坐标的函数，即
受力体内不同点的应力不同。
应力是某点A在坐标系中的方向Ｆ３Ｆ２

第1章应力分析及应力平衡微分方程

，可以把σij（Stress tensor ）分解成与体积变化有关的量和形状变化有关的量。前者称为应力球张量
(Spherical stress tensor) ，后者称为应力偏张量
(Deviatoric stress tensor) 。设σm为平均应力，则有
m
1 3
(
x
y
z)
按照应力叠加原理，σij具有可分解性。因此有
整理后可得S：zdA xzdAx yzdAy zdAz
求和约定：全应力：
Sx xl yxm zxn S y xyl ym zyn Sz xzl yzm zn
S j ijli
S2
S
2 x
Sy2
Sz2
很重要！（１－１）
（１－２）
沈阳工业大学
1.1.２点的应力状态
由于微元体处于静力平衡状态，所以，绕其各轴的合力矩为零，因此可以得到
xy= yx, yz= zy zx= xz 称为剪应变互等定律
沈阳工业大学
1.1.２点的应力状态
一，一点的应力状态：是指通过变形体内某点的单元体所有截面上的应力的有无、大小、方向等情况。
一点的应力状态的描述
（１）数值表达：x=50MPa，xz=35MPa （２）图示表达：在单元体的三个正交面上标
第1章应力分析
沈阳工业大学
第 1 章应力分析
1.1 点的应力状态 1.2特殊应力状态 1.3应力平衡微分方程
沈阳工业大学
1.1 点的应力状态
1.1 .1应力 1.1.2 点的应力状态 1.1.3主应力及应力张量不变量 1.1.4主切应力和最大切应力 1.1.5应力偏张量和应力球张量 1.1.6八面体应力和等效应力 1.1.7应力莫尔圆

3-1-4 应力分析_应力莫尔圆及应力平衡微分方程

10 3 10
l1=
10 1
m2= 10
最大切应力τmax=500MPa
金属塑性成形原理
解析法验证：
2 3 0
三个不变量： J1 x y z 4
J2
(x y
yz
zx )
2 xy
2 yz
2 zx
21
ij 3
0
6 0(100MPa) 0 0
J3
x
y z
2 xy
yz zx
( x
金属塑性成形原理
练习题1：应用莫尔圆分析单向拉伸时的各横截面上的应力变化状态。
y B（ σy＝40 τyx＝0 ） θ
τ C (0,20)
2θ
A
A
（ σx＝0 τxy＝0 ）
Bσ
(40,0)
x
当2θ＝90°（θ＝45°）时，截面的剪切力达到最大值20MPa
金属塑性成形原理
练习题2：物体中某点为平面应力状态，应力张量为：
试利用莫尔圆图解主应力,主方向和最大切应力
τ
τmax (0,5)
2 3 0
ij 3 6 0(100MPa)
0 0 0
2α2
B(6,3)
σ2 (-3,0) 2β2
A(-2,-3) σ2＝－3
2α1 σ1(7,0)
O(2,0) D
σ
2β1 σ1＝7
OD的长度＝1/2（6+2）＝4；R＝5；
y
B
以应力主轴为坐标轴，作一斜微分面，其方向
余弦为l，m，n，则有 :
金属塑性成形原理
l2 m2 n2 1
S1 1 l S2 2 m S3 3 n S 2 S12 S22 S32 12l 2 22m2 32n2

金属塑性成形原理期末复习

（2）变形时的外部条件，如变形温度、变形速度、应力状态等。
塑性指标：拉伸率δ和断面收缩率Ψ。概念：金属在破坏前产生的最大
变形程度，即极限变形量。
H0 - Hk
塑性指标ε= ------------- ×100%（压缩法）
H0
塑性指标衡量金属塑性高低的指标。塑性状态图及其应用概念：表示金属塑性指标与变形温度及加载方式的关系曲线图形，简称塑性图。应用：合理选择加工方法
静态回复动态回复——主要通过位错的攀移、交滑移来实现。 2.再结晶
静态再结晶：利用金属变形余热发生动态再结晶：热塑性变形过程中发生亚动态再结晶：动态再结晶晶粒在热变形停止后的长大过程 (二)热塑性变形后金属组织和性能的变化 1.改善铸造组织，锻合内部缺陷 2.形成纤维组织 3 产生带状组织超塑性的分类：恒温超塑性或第一类超塑性。
提高塑性的主要途径有以下几个方面： (1)控制化学成分、改善组织结构，提高材料的成分和组织的均匀性； (2)采用合适的变形温度—速度制度； (3)选用三向压应力较强的变形过程，减小变形的不均匀性，尽量造成均匀的变形状态； (4)避免加热和加工时周围介质的不良影响
第二节金属的流动及其影响因素
第三节金属塑性成形中的摩擦和润滑
几个基本概念弹性(Elasticity)：卸载后变形可以恢复特性，可逆性。塑性(Plasticity)：固体金属在外力作用下能稳定地产生永久变形而不破坏其完整性的能力屈服(Yielding)：开始产生塑性变形的临界状态损伤(Damage)：材料内部缺陷产生及发展的过程断裂(Fracture)：宏观裂纹产生、扩展到变形体破断的过程
一般讲，如果变形速度大，有没有足够时间完成塑性变形，金属的变形抗力会提高，塑性降低。变形速度对塑性的影响概括为变形速度的增大，金属和合金的变形抗力提高；随变形速度提高，塑性变化的一般趋势如图；变形速度对锻压工艺也有广泛的影响。

莫尔应力圆公式推导

莫尔应力圆公式推导莫尔应力圆是材料力学和土力学中一个非常重要的概念，对于理解材料或土体在复杂应力状态下的强度和变形特性具有关键作用。

接下来咱们就一起好好推导一下这个莫尔应力圆公式。

先来说说啥是莫尔应力圆。

想象一下，咱们有一个物体，它内部各个点都受到不同方向和大小的力，这些力综合起来就形成了复杂的应力状态。

莫尔应力圆就是一种能把这种复杂应力状态直观表示出来的工具。

咱从最基础的开始，假设一个平面内有两个互相垂直的主应力，分别是σ₁和σ₃（σ₁ > σ₃）。

还有一个与主应力方向夹角为α 的斜截面上的正应力σ 和剪应力τ 。

根据应力平衡原理，能得到正应力σ 的表达式：σ = (σ₁ + σ₃) / 2 + (σ₁ - σ₃) / 2 × cos 2α 。

剪应力τ 的表达式是：τ = (σ₁ - σ₃) / 2 × sin 2α 。

为了方便推导莫尔应力圆，咱们把上面两个式子变形一下。

令 x =σ ，y = τ 。

先把正应力的式子变形：σ - (σ₁ + σ₃) / 2 = (σ₁ - σ₃) / 2 × cos 2α 。

然后两边平方：[σ - (σ₁ + σ₃) / 2]² = [(σ₁ - σ₃) / 2 × cos 2α]² 。

再把剪应力的式子变形：τ / [(σ₁ - σ₃) / 2] = sin 2α 。

两边平方：τ² / [(σ₁ - σ₃)² / 4] = sin² 2α 。

因为cos² 2α + sin² 2α = 1 ，所以把上面两个平方后的式子相加：[σ - (σ₁ + σ₃) / 2]² + τ² / [(σ₁ - σ₃)² / 4] = 1 。

整理一下，就得到了莫尔应力圆的方程：(x - (σ₁ + σ₃) / 2)² + y² = [(σ₁ - σ₃) / 2]²。

2-弹塑性力学-应力分析

第二章应力分析 (Stress Analysis)
应力的坐标变换(例题讲解) 应力的坐标变换(例题讲解)*
实际应用:晶体取向, 实际应用:晶体取向,织构分析等
应力莫尔圆**: 应力莫尔圆 :
二维应力莫尔圆与三维应力莫尔圆掌握如何画,如何分析(工程力学已学,看书) 掌握如何画,如何分析(工程力学已学,看书)
不计体力) (不计体力)
物理意义:表示变形体内无限相邻两质点的点的应力状态的关系. 物理意义:表示变形体内无限相邻两质点的点的应力状态的关系. 对弹性变形和塑性变形均适用. 对弹性变形和塑性变形均适用.
第二章应力分析 (Stress Analysis)
推导原理:
– 静力平衡条件: 静力平衡条件: –
第二章应力分析 (Stress Analysis)
八面体应力的求解思路: 八面体应力的求解思路:
σij (i, j = x, y, z) →σ1,σ2 ,σ3 →σ8,τ8
↓→I1,I2 →↑
因为
2 2 τ8 = (I1 3I2 ) 3
第二章应力分析 (Stress Analysis)
等效应力( 2.6 等效应力(equivalent stress) )
通常规定: 通常规定:
σ1 ≥ σ 2 ≥ σ3
τ max = σ1 σ 3
2
则有最大剪应力:
或者: 或者: 其中: 其中: 且有:
τ max = max{ 12 , τ 23 , τ31 } τ τ12 = ± σ1 σ 2
2 ,τ 23 = ±
σ 2 σ 3
2
,τ31 = ±
σ3 σ1
2
τ12 +τ 23 +τ31 = 0

材料成型原理——主切应力及八面体应力

+σ3 )2 2 +σ1 )2 2
+τ 2 +τ 2
=
l
2
(σ1
−
σ
2
)(σ1
−
σ
3
)
+
σ (
2
− 2
σ
3
)2
=
m2
(σ
2
−
σ
3
)(σ
2
−
σ1)
+
σ (
3
− 2
σ1
)2
⎫ ⎪ ⎪ ⎪ ⎬ ⎪
(σ
−
σ1
+σ2 2
)2
+τ
2
=
n2 (σ 3
− σ1)(σ 3
−σ2)
+
(σ1
−σ2 2
)2
⎪ ⎪⎭
1圆外 2圆内 3圆外
第十一章应力与应变理论
第三讲主切应力及八面体应力
阎昱
一、主切应力
1. 复习主应力、主平面的概念
z 主平面： τ = 0 的微分面 z 主应力：主平面上作用的正应力
z 主切应力平面：切应力τ达到极值的微分面
z 主切应力：主切应力平面上作用的切应力
一、主切应力
求解切应力极值
l = 0, m = ±1 2 , n = ±1 2
四、应力平衡微分方程
一点的应力状态
各点的应力变化关系？
应力是坐标的连续函数，即 σij = f (x, y, z)
在直角坐标系中，点Q (x,y,z)的应力状态为σij。
无限邻近处点Q′((x+dx),(y+dy),(z+dz))的应力状态为

02讲-应力与平衡、位移与应变

2022/2/8
王正伟 13601363209
9
斜面应力公式 Cauchy Formula
四面体平衡条件为：
(1) dS1 (2) dS2 (3) dS3
()
dS
f
(1dhdS) 3
0
1 xi xy j xzk 2 yxi y j yzk 3 zxi zy j zk
刚体位移和变形是同时出现的，在弹性力学中我们忽略刚体运动对物体的影响，仅考虑变形。
2022/2/8
王正伟 13601363209
23
位移的描述 Characterization of Displacement
拉格朗日坐标系其坐标系是放在所描述的物
体上随着物体一起运动。拉格朗日描述法以物体变形前的初始构形为参照构
1 xxi xy j xzk
2 yxi yy j yzk
3 zxi zy j zzk
xx yx
xy yy
xz yz
zx zy zz
王正伟 13601363209
6
面力、应力矢量与应力状态辨析
相同点：量纲相同；内力与应力的数学定义相同。
S 0
F S
若取 S 为变形前面元的初始面积，则上式给出工程应力，亦称名义应力，常用于小变形情况。对于大变形问题，应取 S 为变形后面元的实际面积，称真实应力，简称真应力, 也称柯西应力。
2022/2/8
王正伟 13601363209
4
应力矢量(应力) Stress Vector
下图为低碳钢轴向拉伸变形情况，前两个图为小变形情况，应力计算采用工程应力，第三个真实截面面积相比于初始情况变化剧烈，因而必须采用真实应力来描述。在以后的讨论中主要研究小变形问题，因而应力计算上为工程应力。

摩尔应力圆公式

摩尔应力圆公式好的，以下是为您生成的文章：咱来聊聊这个摩尔应力圆公式。

你说这玩意儿，乍一听好像挺复杂，其实啊，要是把它掰开了揉碎了，也没那么吓人。

我记得有一次，我给学生们讲这个摩尔应力圆公式的时候，那场面可有意思了。

有个小同学，瞪着一双大眼睛，满脸写着“这是啥呀，老师你饶了我吧”。

我就笑了笑，跟他们说：“别慌，咱们一步一步来。

”这摩尔应力圆公式啊，就像是一个神秘的宝藏地图，能帮我们找到材料内部应力的秘密。

它的表达式是这样的：（σ₁ - σ₃）/ 2 乘以 sin2α 加上σₘ = （σ₁+ σ₃）/ 2 。

这里面的σ₁、σ₃分别代表最大主应力和最小主应力，α 呢，是某个平面与最大主应力平面的夹角，σₘ 就是这个平面上的正应力。

咱就拿盖房子打个比方。

你想啊，房子的大梁得承受多大的力啊。

要是不搞清楚这些应力，万一哪天大梁咔嚓一下断了，那可不得了。

这时候，摩尔应力圆公式就派上用场了。

通过这个公式，我们能算出不同方向上的应力大小，看看大梁在哪个地方受力最大，哪个地方又比较轻松，然后就能针对性地加强或者优化设计。

还有一次，我带着学生们去工地参观。

看到那些工人师傅在搭建脚手架，我就问学生们：“你们想想，这脚手架上的钢管，它受到的力能用摩尔应力圆公式来分析不？”学生们一下子来了精神，七嘴八舌地讨论起来。

有个聪明的小家伙还真说对了，他说可以把钢管看成一个受力的单元，然后通过测量和计算，就能用这个公式算出应力情况，确保脚手架的安全。

其实啊，在我们的生活中，很多地方都能用到这个摩尔应力圆公式。

比如说桥梁的设计，道路的铺设，甚至是你坐的椅子、用的桌子，都离不开对材料应力的考虑。

学习摩尔应力圆公式，就像是掌握了一把打开材料世界大门的钥匙。

刚开始的时候，可能会觉得有点晕头转向，但只要多琢磨，多练习，你就会发现，它其实没那么难。

就像骑自行车，一开始摇摇晃晃，但一旦掌握了平衡，就能自由自在地骑行了。

所以啊，同学们，别被这个公式吓到，只要用心去学，它就是我们解决问题的好帮手。

应力状态几何描述(莫尔圆)

2
) 2 xy
2
圆心
(
1 + 2
2
1 0 0 0 0 ij 2 0 0 3
, 0)
半径
1 2
2
应力状态的几何描述
圆心半径
(
x + y
2
, 0)
(
x y
2
) 2 xy
2
圆心
(
2 + 3
2
1 0 0 0 0 ij 2 0 0 3
应力状态的几何描述
y
B
圆心
(
x y
2
,0)
x

N
半径
(
x y
2
) 2 xy
2
xy
yx
A
y
x
1 0 0 0 0 ij 2 0 0 3
应力状态的几何描述
圆心半径
(
x + y
2
, 0)
(
x y
2
主方向：
1 1 2 xy tg 2 x y
应力状态的几何描述
1 x y x y xy 2 2 2 2 3 0
2
9
1、已知 3 0
3 1 0
0 0 0
求主应力
1 9 1 9 1 2 2 10 3 = 0 2 2 2 3 0
应力状态的几何描述
1、平面应力状态的分析
x xy 0 0 yx y 0 0 0
则AB方向余弦：

2.3应力莫尔圆、应力平衡微分方程

yzxzcossinsincoscossincossinxyyxcossincossin主应力主应力1与x轴之间的夹角从某一平面顺逆转的任意斜面上应力在莫尔圆上对应的是从相应的坐标点顺逆时旋对于三向应力状态设变形体中某点的三个主应力为三个圆的半径分别等于三个主切应力三个圆的方程为每一个圆分别表示某方向余弦为零的斜面上的正每一个圆分别表示某方向余弦为零的斜面上的正应力和切应力的变化规律
( x y ) sin cos xy (sin 2 cos 2 ) sin 2 xy cos 2 2 S xl S y m x cos2 y sin 2 2 xy sin cos

x y
ij
10
0
10
ij 4 1
0 0
0 4
1）画出该点的应力单元体； 2）求出该点的应力张量不变量、主应力、主方向、主切应力、最大切应力、等效应力、应力偏张量及应力球张量。 3）画出该点的应力莫尔圆，并将应力单元体的微分面分别标注在应力莫尔圆上。
ij xi 0
应力平衡微分方程
轴对称问题的平衡微分方程
z
dq

dq
rz rz dz dr r rq rq dr r
dr dz
r
q
q r r
q
r
rz
zr
dr
q z
o
y
z
q

z
r
r dr r
q
x
r
应力平衡微分方程
轴对称问题的平衡微分方程
xz xz dx x
xy
xy x dx
y

应力分析之应力平衡微分方程

应力平衡微分方程
单元体六个面上的应力分量图
z
zx dz z
zx
z dz z zy zy dz z
yx y yz
dz Q
xz
xy
x
Q’ yz dy yz
y
xz xz dx x
xy
xy x dx
r dr r
o
y

x
r
应力平衡微分方程
轴对称问题的平衡微分方程
r 1 r zr r fr 0 r r z r
r 1 z 2 r f 0 r r z r rz 1 z z rz fz 0 r r z r
应力平衡微分方程
轴对称问题的平衡微分方程由于子午面在变形过程中始终不会扭曲，轴对称状态具有以下特点： 1）在θ面上没有剪应力，即r θ ＝ θ r ＝0， θ 是一个主应力； 2）各应力分量与θ坐标无关，对θ的偏导数都为零。因此有
r zr r fr 0 r z r
x fx 0 x y yx
yx x
y
xy
y
fx fy
y
yx
y y dy
dy
xy x

y y
yx y
dx
fy 0
x
x x dx x
xy
xy x
应力平衡微分方程
轴对称应力状态在塑性成形中经常遇到旋转体。当旋转体承受的外力为对称于旋转轴的分布力而且没有周向力时，则物体内的质点就处于轴对称应力状态。此时，旋转体的每个子午面都始终保持平面，而且各子午面之间的夹角始终不变。用圆柱坐标表示的单元体应力状态为：

应力莫尔圆公式推导

应力莫尔圆公式推导应力莫尔圆公式是应用于材料力学领域的一种重要公式，它描述了应力状态下的主应力和主应力方向之间的关系。

应力莫尔圆公式的推导是基于材料的应力变形关系和平衡条件的基础上进行的。

我们需要了解一些基本概念。

在材料力学中，应力是指单位面积上的力。

应力分为正应力和剪应力两种，正应力是垂直于某个截面的力在该截面上的投影与该截面的面积之比，剪应力是相邻两个平行截面上的力之间的比值。

根据应力分析的原理，我们可以得到应力莫尔圆公式。

设某一平面上的正应力为σ，剪应力为τ，该平面的方向与x轴的夹角为θ。

根据三角函数的性质，可以得到该平面上的应力分量为σx = σcos^2θ，σy = σsin^2θ，τxy = σsinθcosθ。

根据平衡条件，我们可以得到该平面上的剪应力方向与主应力方向之间的关系。

设该平面上的剪应力方向与x轴的夹角为α，则有τxy = τcos(α - θ)。

根据三角函数的性质，我们可以得到τxy = (σx - σy)sinαcosθ - τ(cos^2θ - si n^2θ)cosα。

根据应力分量的定义，我们可以得到σx - σy = σ(cos^2θ - sin^2θ)。

将其代入上式，得到τxy = 2σsinαcosθ。

这是应力莫尔圆公式的一般形式。

根据应力莫尔圆公式，我们可以得到一些重要的结论。

首先，当剪应力为零时，应力莫尔圆退化为一个圆心在主应力方向上的圆。

其次，当剪应力不为零时，应力莫尔圆的圆心不在主应力方向上，而是偏离主应力方向一定角度。

最后，当剪应力方向与主应力方向重合时，应力莫尔圆退化为一个直线。

应力莫尔圆公式的推导过程相对简单明了，但其应用却非常广泛。

通过应力莫尔圆公式，我们可以对材料在复杂应力状态下的应力进行准确的分析和计算，进而指导工程实践中的设计和施工。

应力莫尔圆公式是材料力学中的重要工具，它描述了应力状态下的主应力和主应力方向之间的关系。

通过对应力莫尔圆公式的推导和分析，我们可以更好地理解和应用这一公式，为工程实践提供准确的力学分析依据。

莫尔圆应力分析.

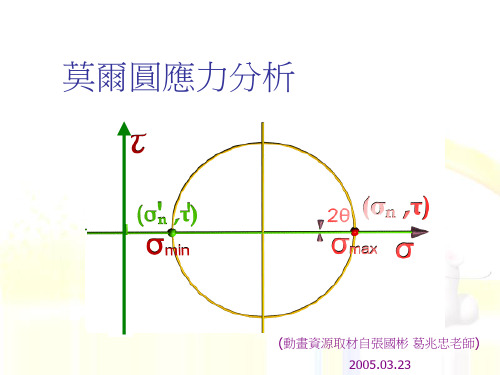
A
σn=1/2(σx+σy)+1/2(σx-σy) cos2θ-τxysin2θ
=1/2(50+(-10))+1/2(50-(-10)) cos2x30°-40sin2x30°
=0.359(kg/cm2) τ=1/2(σx-σy)sin2θ+ τxysin2θ
=1/2(50-(-10)) sin2x30°-40sin2x30°
雙軸應力狀態
正負符號判斷
+
-
雙軸應力—垂直面
最大正交應力 σ1=σx σ2 =σy 最大剪應力 τ=1/2(σx-σy)
雙軸應力分析
破壞面上正交應力 σθ =1/2(σx+σy)+1/2(σx-σy)cos2θ 破壞面上剪應力 τθ =1/2(σx-σy)sin2θ
雙軸應力---斜截面
最大正交應力 θ=0° σmax=1/2(σx+σy)+1/2(σx-σy)cos0°
1000kg
1000kg
莫尔圆解
σx=1000/(4x5)=50
圆心坐标=1/2(50+0)=25 (σ,τ)=(25,0)
半径 r=1/2(50 - 0)=25
1. σθ=25 (kg/cm2) τθ=25 (kg/cm2)
2. σ1=50(kg/cm2) σ2=0(kg/cm2) τmax=25(kg/cm2)
應力分析
單軸應力雙軸應力平面應力純剪應力
1.在斜面：σ=σxcos2θ，τ=σxsinθcosθ。 2.45°面：σave== τmax=σx/2(平均正交應力等於最大剪應力)
1.σx與σy稱為主應力(principal stress)，其作用面稱為主平面 (pnincipal plane)，主平面上之剪應力為零。

应力莫尔圆的相关理论

2
) + τα = (
2 2
σ x −σ y
2
,
)
2
2 +τx
变化时, 当斜截面随方位角 α 变化时其上的应力
在 α
σ
τα
σ - τ 直角坐标系内的轨迹是一个圆 ,圆心位于横坐标轴圆心位于横坐标轴 ( σ 轴 )上,离原点的距离为上离原点的距离为
半径为
σx +σ y
2 或称为莫尔圆。此圆习惯上称为应力圆 , 或称为莫尔圆。
应力莫尔圆的相关理论
一、应力圆的概念
σα =
由
σ x +σ y σ x −σ y
+ 2
τα =
2 σ x −σ y 2
cos2α − τ x sin2α
sin2α + τ x cos2α
削去α得到
(σ α −
σx +σ y
2
) + τα = (
2 2
σ x −σ y
2
)
2
2 +τx
(σ α −
σx +σ y
τ D1
σy τy
σx
o σx B1 σ
σx τx
τy σy
τx
τ
σy τy
(b)
D1
σx τx
τy σy
σx τx
o
B2
B1 σ
σy
D2 σx
量取 OB2=σy , B2D2= τy , 得D2 点
τ 连接D 连接 1D2两点的直线与
(b)
轴相交于C σ 轴相交于点, 以C为为圆心, 圆心 CD1或CD2为半径 o 作圆 σy D2 σx B2 C B1 σ D1

应力莫尔圆求主应力

要使用应力莫尔圆来求主应力，我们首先需要理解莫尔圆是什么。

在材料力学中，莫尔圆表示的是在某一点上，应力与应变之间的关系。

对于各向同性的材料，三个主应力和主应变在莫尔圆上都有对应的点。

首先，我们需要知道三个方向的应变：ε1，ε2和ε3。

这些应变可以通过实验测量得到，或者通过其他方式计算。

接下来，我们需要知道三个方向的应力：σ1，σ2和σ3。

这些应力也可以通过实验测量得到，或者通过其他方式计算。

有了这些数据后，我们可以根据胡克定律（Hooke's Law）来建立方程组：
ε1 = α1 * σ1
ε2 = α2 * σ2
ε3 = α3 * σ3
其中，α1，α2和α3是材料的弹性常数。

然后，我们可以使用这三个方程来解出α1，α2和α3。

有了这三个弹性常数后，我们就可以求出主应力了。

具体来说，我们可以使用以下公式来求主应力：
σ1 = α1 * ε1
σ2 = α2 * ε2
σ3 = α3 * ε3
这三个公式可以帮助我们找到三个方向的应力，其中最大的那个就是主应力。

需要注意的是，这个方法只适用于各向同性的材料。

对于各向异性的材料，这个方法可能不适用。