广东省惠州市2021届高三上学期第一次调研数学试题

合集下载

难点5 溶液稀释与酸碱中和滴定曲线分析-2021年高考化学专练 (原卷版)

难点5 溶液稀释与酸碱中和滴定曲线分析【命题规律】本专题为高考热点。

主要考查溶液稀释图像、酸碱中和滴定图像的分析。

考查的核心素养以宏观辨识和微观探析、变化观念和平衡思想为主。

【备考建议】2021年高考备考时，应关注多曲线酸碱中和滴定图像分析。

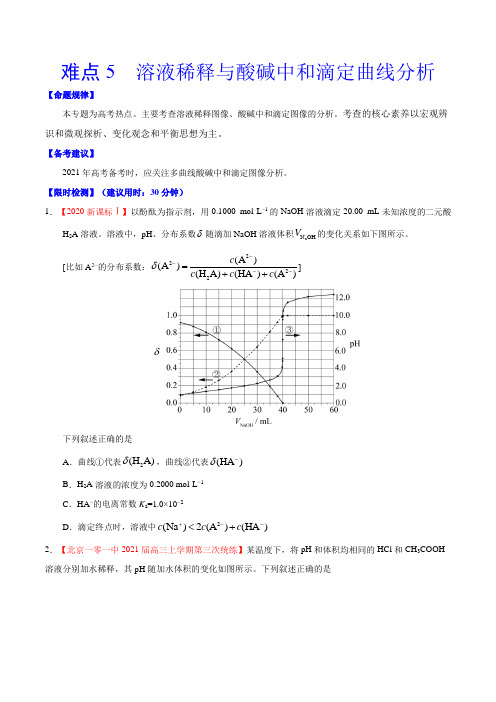
【限时检测】（建议用时：30分钟）1．【2020新课标Ⅰ】以酚酞为指示剂，用0.1000 mol·L −1的NaOH 溶液滴定20.00 mL 未知浓度的二元酸H 2A 溶液。

溶液中，pH 、分布系数δ随滴加NaOH 溶液体积a N OH V 的变化关系如下图所示。

[比如A 2−的分布系数：2222(A )(A )(H A)(HA )(A )c c c c δ----=++]下列叙述正确的是A ．曲线①代表2(H A)δ，曲线②代表(HA )δ-B ．H 2A 溶液的浓度为0.2000 mol·L −1C ．HA −的电离常数K a =1.0×10−2D ．滴定终点时，溶液中2(Na )2(A )(HA )c c c +--<+2．【北京一零一中2021届高三上学期第三次统练】某温度下，将pH 和体积均相同的HCl 和CH 3COOH 溶液分别加水稀释，其pH 随加水体积的变化如图所示。

下列叙述正确的是A．曲线II代表HCl的稀释过程B．溶液中水的电离程度：b点＞c点C．从b点到d点，溶液中-+33c(CH COO)c(H)c(CH COOH)⨯保持不变D．该温度下，b点K w的数值比e点大3．【广东省惠州市2021届高三上学期第一次调研】25℃时，向10mL0.01mol/LNaCN溶液中逐滴滴加10mL0.01mol/L的盐酸，其pH变化曲线如图所示。

下列溶液中的关系一定正确的是(忽略体积微小变化)A．a点溶液的pH≥12B．b点的溶液：c(CN－)＞c(HCN)C．c点的溶液：c(CN－)＋c(HCN)＋c(Cl－)＝0.01mol/LD．pH＝7的溶液：c(Na+)＋c(H+)＝c(Cl－)＋c(CN－)4．【湖南省永州市2021届高三第一次模拟】已知：p[()c HXc(X)－]＝－lg[()c HXc(X)－]。

专题13 利用导数解决函数的极值、最值-学会解题之高三数学万能解题模板(2021版)【原卷版】

学习界的专题13 利用导数解决函数的极值、最值【高考地位】导数在研究函数的极值与最值问题是高考的必考的重点内容，已由解决函数、数列、不等式问题的辅助工具上升为解决问题的必不可少的工具，特别是利用导数来解决函数的极值与最值、零点的个数等问题，在高考中以各种题型中均出现，对于导数问题中求参数的取值范围是近几年高考中出现频率较高的一类问题，其试题难度考查较大.类型一利用导数研究函数的极值例1 已知函数f (x) =+ ln x ，求函数f (x)的极值.x【变式演练1】（极值概念）【西藏日喀则市拉孜高级中学2020 届月考】下列说法正确的是（）A.当f '(x0 ) = 0 时，则f (x0 ) 为f (x) 的极大值B.当f '(x0 ) = 0 时，则f (x0 ) 为f (x) 的极小值C.当f '(x0 ) = 0 时，则f (x0 ) 为f (x) 的极值D.当f (x0 ) 为f (x) 的极值且f '(x0 ) 存在时，则有f '(x0 ) = 0【变式演练2】（图像与极值）【百师联盟2020 届高三考前预测诊断联考全国卷1】如图为定义在R 上的函数f (x)=ax3 +bx2 +cx +d (a ≠ 0)的图象，则关于它的导函数y =f '(x)的说法错误的是（）A．f '(x)存在对称轴B．f '(x)的单调递减区间为⎛-∞,1 ⎫2 ⎪ ⎝⎭C．f '(x)在(1, +∞)上单调递增D．f '(x)存在极大值【变式演练3】（解析式中不含参的极值）【江苏省南通市2020 届高三下学期高考考前模拟卷】已知函数f (x)=(ax2 +x +1)e x ，其中e是自然对数的底数，a ∈R .（1）当a = 2 时，求f (x )的极值；（2）写出函数f (x )的单调增区间；（3）当a = 0 时，在y 轴上是否存在点P，过点P 恰能作函数f (x)图象的两条切线？若存在，求出所有这样的点；若不存在，请说明理由.【变式演练4】（解析式中含参数的极值）【四川省德阳市2020 届高三高考数学（理科）三诊】已知函数f (x )=ax - 2 ln x - 2 ，g (x )=axe x - 4x ．（1）求函数f (x )的极值；（2）当a > 0 时，证明：g (x )- 2 (ln x -x +1)≥ 2 (ln a - ln 2 )．【变式演练5】（由极值求参数范围）【黑龙江省哈尔滨一中2020 届高三高考数学（理科）一模】已知函数学习界的007f ( x ) = x ln x -1 (m + 1) x2 - x 有两个极值点，则实数m 的取值范围为（）2A ． ⎛ - 1 , 0⎫B ． ⎛-1, 1 -1⎫C ． ⎛ -∞, 1 -1⎫ ）D ． (-1, +∞)e ⎪ e⎪ e⎪ ⎝ ⎭ ⎝⎭⎝⎭【变式演练 6】（由极值求其他）【四川省江油中学 2020-2021 学年高三上学期开学考试】已知函数f ( x ) = 1x 3 + ax 2 + bx (a , b ∈ R ) 在 x = -3 处取得极大值为 9.3（1）求 a ， b 的值；（2）求函数 f (x ) 在区间[-4, 4] 上的最大值与最小值.类型二求函数在闭区间上的最值万能模板内容使用场景一般函数类型解题模板第一步求出函数 f (x ) 在开区间(a , b ) 内所有极值点；第二步计算函数 f (x ) 在极值点和端点的函数值；第三步比较其大小关系，其中最大的一个为最大值，最小的一个为最小值.例 2 【河南省天一大联考 2020 届高三阶段性测试】已知函数 f ( x ) = ln x - x ， g ( x ) = ax 2+ 2x (a < 0) .（1）求函数 f( x ) 在⎡1 , e ⎤上的最值； ⎢⎣ e ⎥⎦（2）求函数 h( x ) = f (x ) + g (x ) 的极值点.【变式演练 7】（极值与最值关系）【安徽省皖江联盟 2019-2020 学年高三上学期 12 月联考】已知函数 f ( x ) 在区间(a , b ) 上可导，则“函数 f ( x ) 在区间(a , b ) 上有最小值”是“存在 x 0 ∈(a ,b ) ，满足 f '(x 0 ) = 0 ”的⎨ 1 （）A ．充分不必要条件B ．必要不充分条件C ．充要条件D ．既不充分也不必要条件【变式演练 8】（由最值求参数范围）【湖北省武汉市 2020 届高三下学期六月模拟】若函数⎧a ln x - x 2 - 2 (x > 0 )f ( x ) = ⎪x + + a (x < 0) 的最大值为 f (-1) ，则实数a 的取值范围为（）⎩⎪ xA ． ⎡⎣0, 2e 2 ⎤⎦B ． ⎡⎣0, 2e 3⎤⎦C ． (0, 2e 2⎤⎦D ． (0, 2e 3⎤⎦【变式演练 9】（不含参数最值）【安徽省江淮十校 2020-2021 学年高三上学期第一次联考】已知函数f (x ) = cos 2 x s in 2x ，若存在实数 M ，对任意 x 1 , x 2 ∈R 都有 f ( x 1 ) - f (x 2 ) ≤ M 成立.则 M 的最小值为（）A.3 38B.32C.3 3 4D.2 3 3【变式演练 10】（含参最值）【重庆市经开礼嘉中学 2020 届高三下学期期中】已知函数f (x ) = (x - a - 1)e x -1 - 1x 2 + ax , x > 02（1）若 f (x ) 为单调增函数，求实数 a 的值；（2）若函数 f (x ) 无最小值，求整数 a 的最小值与最大值之和.【高考再现】1.【2018 年全国普通高等学校招生统一考试数学（江苏卷）】若函数 ƒ(x ) = 䂸x 3 — t x 䂸 + 1(t C R )在(t h + œ) 内有且只有一个零点，则 ƒ(x )在[ — 1h 1]上的最大值与最小值的和为．2【. 2018 年全国普通高等学校招生统一考试理科数学（新课标 I 卷）】已知函数 ƒ x = 䂸sinx + sin 䂸x ，则 ƒ x的最小值是．3. 【2020 年高考全国Ⅱ卷理数 21】已知函数 f (x ) = sin 2x sin 2x ．3 381 2 n （1）讨论 f ( x ) 在区间(0,π) 的单调性；（2）证明： f (x ) ≤ ；（3）设 n ∈ N *，证明： sin 2x sin 22x sin 24x sin 22nx ≤ 3 ． 4n4. 【2020 年高考天津卷 20】已知函数 f (x ) = x3+ k ln x (k ∈ R ) ， f ' (x ) 为 f ( x ) 的导函数．（Ⅰ）当 k = 6 时，（i ）求曲线 y = f ( x ) 在点(1, f (1)) 处的切线方程；（ii ）求函数 g (x ) = f (x ) - f '(x ) + 9的单调区间和极值；x（Ⅱ）当 k - 3 时，求证：对任意的 x , x ∈[1, +∞) ，且 x> x ，有 f '( x ) + f ' (x ) > f (x 1 )- f (x 2 ) ． 1 2 1 2 2x - x 1 25. 【2018 年全国卷Ⅲ理数】已知函数 ƒ x = 䂸+ x + tx 䂸 ln 1 + x — 䂸x ．（1）若 t = t ，证明：当— 1 ǹ x ǹ t 时，ƒ x ǹ t ；当 x Σ t 时，ƒ x Σ t ；（2）若 x = t 是 ƒ x 的极大值点，求 t ．6. 【2018 年全国普通高等学校招生统一考试文科】设函数 ƒ(x ) = [tx 䂸 — (3t + 1)x + 3t + 䂸]e x .（Ⅰ）若曲线 y = ƒ(x )在点(䂸h ƒ(䂸))处的切线斜率为 0，求 a ；（Ⅱ）若 ƒ(x)在 x = 1 处取得极小值，求 a 的取值范围.7. 【2018 年全国普通高等学校招生统一考试文科数学（天津卷）】设函数 ƒ(x )=(x — t 1)(x — t 䂸)(x — t 3)，其中t 1h t 䂸h t 3 C R ,且t 1h t 䂸h t 3是公差为 d 的等差数列.（I ）若t 䂸 = t h d = 1h 求曲线 y = ƒ(x )在点(t h ƒ(t ))处的切线方程；（II ）若 d = 3，求 ƒ(x)的极值；4 4 （III ）若曲线 y = ƒ(x) 与直线 y =— (x — t 䂸) — 6 3有三个互异的公共点，求d 的取值范围.【反馈练习】1.【2020 届高三 6 月质量检测巩固卷数学（文科）】若函数 f ( x ) = e x (-x 2 + 2x + a )在区间(a , a +1) 上存在最大值，则实数a 的取值范围为（）⎛ -1 A ．, -1 + 5 ⎫ B ． (-1, 2)2 2 ⎪ ⎝ ⎭⎛ -1 C ． 2 ⎫ , 2⎪⎛ -1 D ．2⎫, -1⎪ ⎝ ⎭⎝⎭2. 【黑龙江省大庆市第四中学 2020 届高三下学期第四次检测】若函数 f (x ) = ae x- 1在其定义域上只有 3x个极值点，则实数a 的取值范围（）⎛ e 2 ⎫⎛ e 2 ⎫ A ． -∞, - ⎪ (1, +∞)⎝⎭ B ． -∞, - ⎪⎝⎭C ． ⎛-e , -1 ⎫ (1, +∞)D ． ⎛-∞, - 1 ⎫4e 2 ⎪ e ⎪ ⎝ ⎭⎝ ⎭xx2 x3. 【湖北省金字三角 2020 届高三下学期高考模拟】已知函数 f ( x ) = e + - ln x 的极值点为1 ，函数 2g ( x ) = e x + x - 2 的零点为 x ，函数 h ( x ) = ln x的最大值为x ，则（） 2 2x 3A. x 1 > x 2 > x 3B. x 2 > x 1 > x 3C. x 3 > x 1 > x 2D. x 3 > x 2 > x 14. 【湖北省宜昌一中、龙泉中学 2020 届高三下学期 6 月联考】已知函数（ff (e ) = 1，当 x ＞0 时，下列说法正确的是（）ex ）满足 x 2 f '(x ) + 2xf (x ) = 1+ ln x ，① f (x ) 只有一个零点；② f (x ) 有两个零点；- 5 + 5 - 5③ f (x) 有一个极小值点；④ f (x) 有一个极大值点A．①③B．①④C．②③D．②④5.【山东省潍坊市2020届高三6月高考模拟】已知函数f(x)的导函数f'(x)=x4(x-1)3(x-2)2(x-3)，则下列结论正确的是（）A．f (x)在x = 0 处有极大值B．f (x )在x = 2 处有极小值C. f (x)在[1, 3]上单调递减D．f (x )至少有3 个零点6.【云南省曲靖市2020 届高三年级第二次教学质量监测】已知实数a, b 满足0 ≤a ≤1，0 ≤b ≤ 1 ，则函数f (x)=x3 -ax2 +b2 x +1 存在极值的概率为（）A．1B．3C．16 6 3D.37.【云南省红河自治州2019-2020 学年高三第二次高中毕业生复习统一检测】下列关于三次函数f ( x) =ax3 +bx2 +cx +d (a ≠ 0) ( x ∈R) 叙述正确的是（）①函数f (x) 的图象一定是中心对称图形；②函数f (x) 可能只有一个极值点；③当x ≠-b时，f (x) 在x =x 处的切线与函数y = f (x) 的图象有且仅有两个交点；0 3a 0④当x ≠-b时，则过点(x, f (x))的切线可能有一条或者三条．0 3a 0 0A．①③B．②③C．①④D．②④8.【2020 届江西省分宜中学高三上学期第一次段考】已知e 为自然对数的底数，设函数f (x)=1 x2 -ax +b ln x 存在极大值点x ，且对于a 的任意可能取值，恒有极大值f (x )< 0 ,则下列结论2 0 0bb ( ) 中正确的是()A. 存在 x 0= ,使得f (x 0 ) < - 12eB. 存在 x 0= ，使得f (x 0 ) > -e 2C.b 的最大值为e 3D.b 的最大值为 2e 2ax 2⎛ 1 , 3⎫9. 【四川省内江市 2020 届高三下学期第三次模拟考试】函数f （x ）＝ 2+（1﹣2a ）x ﹣2ln x 在区间 2 ⎪⎝ ⎭内有极小值，则 a 的取值范围是（）A ． ⎛ -2, -1 ⎫B ． ⎛-2, -1 ⎫3 ⎪2 ⎪ ⎝ ⎭⎝ ⎭C ． ⎛ -2, - 1 ⎫ ⋃⎛ - 1 , +∞⎫D ． ⎛ -2, - 1 ⎫ ⋃ ⎛ - 1 , +∞ ⎫ 3 ⎪ 3 ⎪ 2 ⎪ 2 ⎪ ⎝ ⎭ ⎝ ⎭⎝ ⎭ ⎝ ⎭10.【河北省衡水中学 2019-2020 学年高三下学期期中】已知函数 f (x ) =(x2- a )2- 3 x 2 -1 - b ，当时（从①②③④中选出一个作为条件），函数有 .（从⑤⑥⑦⑧中选出相应的作为结论，只填出一．组．即可）1 3 5 9① a ≤ - ② < a < ③ a = 1 ，-2 < b < 0 ④ a = 1 ，- < b < -2 或b = 0 ⑤4 个极小值点⑥1 个极小值点2 2 2 4⑦6 个零点⑧4 个零点1. 【福建省漳州市 2020 届高三高考数学（文科）三模】已知函数 f (x ) = ( x + 3) e x- 2m ， m ∈ R .（1）若 m = 3，求 f ( x ) 的最值；2（2）若当 x ≥ 0 时， f (x - 2) + 2m ≥ 1 mx 2+ 2x +1 ，求 m 的取值范围.e 212. 【安徽省合肥七中、三十二中、五中、肥西农兴中学 2020 届高三高考数学（文科）最后一卷】已知函数 f (x ) = 1 x 2- 2x + a ln x ， a > 1 . 2e（1）讨论 f( x ) 的单调性；（2）若f (x )存在两个极值点x1 、x2 ，求f (x1 )+f (x2 )的取值范围.13.【2020 届安徽省芜湖市高三下学期教育教学质量监测】已知函数f (x)=ae x + 2e -x+(a - 2 )x .（1）若y =f (x )存在极值，求实数 a 的取值范围；（2）设1 ≤a ≤ 2 ，设g (x)= f (x)-(a + 2)cos x 是定义在⎛-∞,π ⎤上的函数.2 ⎥⎝⎦（ⅰ）证明：y =g'(x )在⎛-∞,π ⎤上为单调递增函数( g'(x)是y =g (x )的导函数)；2 ⎥⎝⎦ （ⅱ）讨论y =g (x )的零点个数.14.【广东省惠州市2021 届高三上学期第一次调研】已知函数f (x) =x- ln(ax) ．a（1）若a > 0 ，求f (x) 的极值；（2）若e x ln x +mx 2 +(1 -e x )x +m ≤ 0 ，求正实数m 的取值范围．15.【北京五中2020 届高三（4 月份）高考数学模拟】设函数f（x）＝me x﹣x2+3，其中m∈R.（1）如果f（x）同时满足下面三个条件中的两个：①f（x）是偶函数；②m＝1；③f（x）在（0，1）单调递减.指出这两个条件，并求函数h（x）＝xf（x）的极值；（2）若函数f（x）在区间[﹣2，4]上有三个零点，求m 的取值范围.16.【辽宁省锦州市渤大附中、育明高中2021 届高三上学期第一次联考】已知函数f (x) =ae x - cos x -x(a ∈R).（1）若 a = 1 ，证明：f (x) ≥ 0 ；（2）若f (x) 在(0,π) 上有两个极值点，求实数 a 的取值范围.17.【西南地区名师联盟2020 届高三入学调研考试】已知函数f (x)=1x3 +bx2 +cx ，b 、c 为常数，且3学习界的007- 1< b < 1， f '(1) = 0 . 2（1）证明： -3 < c < 0 ；（2）若 x 是函数 y = f (x ) - cx 的一个极值点，试比较 f ( x - 4) 与 f (-3) 的大小. 0218.【山东省威海荣成市 2020 届高三上学期期中】某水产养殖公司在一片海域上进行海洋牧场生态养殖，如图所示，它的边界由圆O 的一段圆弧 PMQ （ M 为此圆弧的中点）和线段 PQ 构成.已知圆O 的半径为12 千米， M 到 PQ 的距离为16 千米.现规划在此海域内修建两个生态养殖区域，养殖区域 R 1 为矩形 ABCD ，养殖区域 R 2 为 A M B ，且 A , B 均在圆弧上，C ,D 均在线段 PQ 上，设∠AOM =α.（Ⅰ）用α分别表示矩形 ABCD 和 A M B 的面积，并确定cos α的范围；（Ⅱ）根据海域环境和养殖条件，养殖公司决定在 R 1 内养殖鱼类，在 R 2 内养殖贝类，且养殖鱼类与贝类单位面积的年产值比为3 : 2 .求当α为何值时，能使年总产值最大.19.【江苏省南通市 2020 届高三下学期高考考前模拟卷】已知函数 f (x ) = ( x - a ) e x + b (a , b ∈ R ) ．（1）讨论函数 f( x ) 的单调性；（2）对给定的 a ，函数 f( x ) 有零点，求b 的取值范围；（3）当 a = 2 ， b = 0 时， F (x ) = f ( x ) - x + ln x ，记 y = F ( x ) 在区间⎛ 1 ,1⎫上的最大值为 m ，且4 ⎪ ⎝ ⎭m ∈[n, n + 1), n ∈Z ，求n 的值．20.【陕西省西安中学2020-2021 学年高三上学期第一次月考】已知函数f ( x) =x -1 -a ln x ．（1）当 a = 1 时，求f(x)的最小值；（2）设m 为整数，且对于任意正整数n ，(1+1)(1+1) ⋅⋅⋅ (1+1) <m ，求m 的最小值．2 22 2n。

广东省惠州市2021届高三第一次调研考测试数学(含答案)

惠州市 2021 届高三第一次调研考试试题数学
全卷满分 150 分，时间 120 分钟．
2020.07
注意事项：
1．答题前，考生务必将自己的姓名、准考证号、座位号、学校、班级等考生信息填写在答题卡上。
2．作答单项及多项选择题时，选出每个小题答案后，用 2B 铅笔把答题卡上对应题目的答案信息点涂黑。
如需改动，用橡皮擦干净后，再选涂其它答案，写在本试卷上无效。
3．非选择题必须用黑色字迹签字笔作答，答案必须写在答题卡各题指定的位置上，写在本试卷上无效。
一、单项选择题：本题共 10 小题，每小题满分 5 分，共 50 分。
在每小题给出的四个选项中，只有一项符合题目要求，选对得 5 分，选错得 0 分。
1．设集合
，集合
,则
（）.
A．
B．
C．
D．
2．复数满足
，其中为虚数单位，则复数=（）.
“女子织布”问题：某女子善于织布，一天比一天织得快，且每日增加的数量相同。已知第一日织布 5 尺，
30 日共织布 390 尺，则该女子织布每日增加（）尺.
A． B． C． 8．函数
D．的部分图象的大致形状是（）.
A
BC
D
1
9．根据中央关于精准脱贫的要求，某市某农业经济部⻔随机派遣甲、乙等共 4 位专家对 3 个县区进行调研，每个县区至少派 1 位专家，则甲、乙两位专家派遣至同一县区的概率为（）.
（i）采取逐一化验，求所需化验次数的分布列及数学期望；（ii）采取平均分组混合化验（每组血液份数相同），求不同分组方法所需化验次数的数学期望。你认为选择哪种化验方案更合理？请说明理由。
22．（本小题满分 12 分）
已知函数

{高中试卷}广东省2021年上学期惠州市高三数学第一次调研考试试题答案[仅供参考]

20XX年高中测试高中试题试卷科目：年级：考点：监考老师：日期：广东省2021年上学期惠州市高三数学第一次调研考试试题答案一、单项选择题：本题共10小题，每小题满分5分，共50分。

1.【解析】由题意可得{}32<<=x x M ，{}0>=x x N ，所以=N M {}0x x >，故选A ．2.【解析】11i z i i-+==+，故选C ． 3.【解析】91)32(21sin 212cos )2cos(22=⨯-=-==-ααα，故选A ． 4.【解析】由已知得120431-=∴=⨯+⨯=⋅k k ，，故选B ． 5.【解析】连接1CB ，则11//DA CB ，可知1ACB ∆是正三角形，213cos ,cos 1=>=<∴πAC DA ，故选C ． 6.【解析】由题知双曲线的一条渐近线方程为12y x =-，则21-=-a b ，411222222=-=-=∴e a a c a b ， 25=∴e ，故选D ． 7.【解析】由题意可知该女子每日织布数呈等差数列，设为{}n a ，首项51=a ，39030=S ，可得39022930305=⨯+⨯d ，解之得2916=d ，故选B ． 8.【解析】由)(cos )cos()(x f x x x x x f -=-=--=-，所以()f x 为奇函数，排除A ，C ；因为()f x 的大于0的零点中，最小值为2π；又因为06cos 6)6(>=πππf ，故选D ．9.【解析】先从4个专家中选2个出来，看成1个专家有624=C 种选法，再将捆绑后的专家分别派到3 个县区，共有633=A 种分法，故总共有3666=⨯种派法。

其中甲、乙两位专家派遣至同一县区有633=A 种，其概率为61366=. 故选A ． 10.【解析】由“局部奇函数”可得：22422342230x x x x m m m m ---⋅+-+-⋅+-=，整理可得：()()244222260x x x x m m --+-++-=，考虑到()244222x x x x --+=+-，从而可将22x x -+视为整体，方程转化为：()()2222222280x x x x m m --+-++-=，利用换元设22x x t -=+（2t ≥），则问题转化为只需让方程222280t mt m -+-=存在大于等于2的解即可，故分一个解和两个解来进行分类讨论。

惠州市2021届高三第--次调研考试试题

惠州市2021届高三第--次调研考试试题生物一、单项选择题《下面每个小题只有一个选项符合题意，多选错选均不给分，每小题4分，10小题共40分)1、下列有关细胞内物质的叙述，错误的是A.蛋白质、多糖的单体均以碳链为基本骨架B.高温使蛋白质分子的空间结构变得伸展松散而发生变性C.核酸和蛋白质的组成元素中均有C、H、0、N元素D.生物体内的糖类绝大多数以单糖形式存在2、下列有关ATP和酶的叙述，正确的是A.细胞正常的生命活动离不开酶和ATPB.蛋白酶和ATP的组成元素中都含有P元素C.酶的催化必然伴随ATP的供能D. ATP 的合成和水解都离不开同一种酶的催化3、研究发现，冬小麦在秋冬受低温袭击时，呼吸速率先升高后降低;持续的冷害使根生长迟缓，吸收能力下降，但细胞内可溶性糖的含量有明显的提高。

下列推断不合理的是A.冷害初期呼吸作用增强，有利于抵御寒冷B.持缕低温使线粒体内氧化酶活性减弱，影响可溶性糖合成淀粉C.低温时细胞液浓度上升，自由水含量相对较少。

有利于适应低温环境D.低温使根细胞呼吸臧弱，使根细胞吸收矿质营养能力下降4.小鼠睾丸中存在间质细胞和实质细胞，实质细胞就是精原细胞，间质细胞是为实质细胞提供营养物质和相关激素的细胞。

科学家用显微镜观察从睾丸中所取的部分组织，下列有关说法正确的是A.实质细胞和间质细胞因细胞核内的遗传物质不同而功能不同B.间质细胞产生的激素不需要通过体液运输即可到达靶细胞C.观察到染色体条数最多的细胞不含姐妹染色单体D.显微镜下能看到染色体的细胞最多含两条性染色体5.下列有关生物学原理在生产生活中的运用，错误的是A.大量使用青霉素类抗生素来治疗病毒性感冒B.儿童口服“脊髓灰质炎疫苗糖丸”预防小儿麻痹症C.治疗糖尿病的胰岛素只能注射不能口服D.给持续高热不退的新冠病人用湿毛巾醮冷水或酒精擦拭额头、腋窝等处物理辅助降温6.某雌雄异株二倍体植物的花色由位于常染色体上三个复等位基因A1、A2和A3控制，且A1、A2和A3中任何两个基因组合在一起，各基因都能正常表达，如图表示基因对花色的控制关系，下列说法正确的是A.花色的表达体现了基因通过控制酶的合成来直接控制生物性状B.白花植株的基因型只有A2A2和A3A3两种C.若橙色和紫色植株杂交，后代同时出现四种花色D.白花植株与红花植株杂交后代均为红花7.小王和小张准备结婚，下列关于坊间流传的一些优生学的说法他们应该采纳的是A.适龄生育的意思是生育年龄既不能太小也不能太大B.色盲男性只要与色觉正常的女性结婚，婚后胎儿不必进行产前基因诊断C.有精神病史的人禁止结婚D.既然“婚前检查”已经不再是强制要求，所以能省尽量省去这一个环节8.感染赤霉菌的水稻植株会出现疯长现象，科学家推测可能是赤霉菌产生了某种物质所致。

广东省惠州市2021届高三理综第一次调研考试试题(1)

惠州市2021届高三第一次调研考试理科综合生物试题1.以下样本与菲林试剂水浴加热后不产生砖红色沉淀的是( )A．发芽小麦研磨液40℃恒温10min以后的上清液B．煮沸的苹果提取液C．煮沸的蔗糖溶液D．糖尿病人的尿液2.以下关于酒精的应用正确的选项是A．组织培育时用70%的酒精给外植体消毒B．DNA的粗提取实验顶用95%的冷酒精溶解DNAC．色素提取时用70%的酒精溶解色素D．细胞工程顶用酒精诱导动物细胞融合3.以下应用实例与原理匹配不准确的是应用实例原理A预防接种免疫学原理B目的基因检测分子杂交C生产香蕉组培苗细胞全能性D细胞代谢产物工厂化生产细胞全能性4.依照下面的人体神经元结构模式图，分析以下表达中不正确的选项是：( ) A．将④中的物质释放到⑤中的方式是主动运输B．假设刺激A点，电流计B将显现2次偏转C．假设①中含有一致病基因（不考虑突变），那么该致病基因来自其外祖母D．抑制该细胞的呼吸作用，将会阻碍神经兴奋的传导5. 以下与植物生长素（生长素类似物）的生理作用没有直接关系的是A．摘除棉花的顶芽，增进侧芽的生长发育B．扦插时，保留芽或幼叶的插条容易成活C．将成熟的木瓜放入未熟的的柿子中，有利于柿子成熟D．在没有受粉的雌蕊柱头上喷洒必然浓度的2,4-D溶液，取得无籽果实6．下图为某家族单基因遗传病系谱图（不考虑突变与互换，涂黑为患者），以下说法错误的是A．此病为常染色体显性遗传病B．五、6均为杂合子C．8号是纯合子的概率为1/4D．7号与9号均为纯合子24 ．用等体积的三个玻璃瓶甲、乙、丙，同时从某水池水深0.5m处的同一名置取满水样，当即测定甲瓶中的氧气含量，并将乙、丙瓶密封后沉回原处。

一日夜后掏出玻璃瓶，别离测定两瓶中的氧气含量，结果如下（不考虑化能合成作用）。

有关分析合理的是透光玻璃瓶甲透光玻璃瓶乙不透光玻璃瓶丙4.9mg5.6mg 3.8mgA．丙瓶中浮游植物的细胞产生[H]的场所是线粒体内膜B．在一昼夜内，丙瓶生物细胞呼吸消耗的氧气量约为1.lmgC．在一日夜后，乙瓶水样的pH 比丙瓶的低D．在一昼夜内，乙瓶中生产者实际光合作用制造的氧气量约为1.8mg25. 以下实验结果与真实结果相较必然偏大的是A．用稀释涂布平板法计算某土壤中微生物的数量B．调查白化病发病率时以患者家系为调查对象C．标志重捕时部份标志物的脱落D．显微镜下计数酵母菌数量时只统计计数室方格内的菌体26．（16分）图甲是某种细胞结构的模式图，图乙是图甲的局部放大。

2023 届广东省惠州市高三第一次调研考试数学参考答案

2023届广东省惠州市高三第一次调研考试数学参考答案1．【答案】C 【解析】集合{|0}A x x =>，则{|0}A x x =R ≤ ，集合{|21}B x x =-<≤，所以(){|20}A B x x =-<R ≤ ．故选：C ． 2．【答案】D【解析】22log 3log 21a =>= ，1133log 2log 10b =<=，0.102210c -=<<=，a c b ∴>>．3．【答案】C【解析】6x ⎛ ⎝的展开式的通项公式为36216C (2)rr r r T x -+=⋅-⋅，令3602r -=，求得4r =，可得展开式中的常数项为4462C 240⋅=，故选：C ．4．【答案】A 【解析】∵向量2)a =，12e ⎛= ⎝⎭，a e ⋅=+=∴向量a 在向量e上的投影向量为：a e e e⋅⋅=．故选：A ．5．【答案】A 【解析】20212024a a > ，420202020a q a q ∴>，又20200a >，4q q ∴>，2(1)(1)0q q q q ∴-++>， (1)0q q ∴->，解得01q <<，∴等比数列{}n a 是单调递减数列，20222023a a ∴>．反之，由20222023a a >，即2320202020a q a q >，又20200a >，1q ∴>，1q ∴<且0q ≠，等比数列{}n a 是单调递减数列或摆动数列，不一定得出20212024a a >，∴ “20212024a a >”是“20222023a a >”的充分不必要条件，故选：A ． 6．【答案】B【解析】由圆的标准方程可得圆心为(1,2)--半径为2r =，由于圆C 关于直线20ax by ++=对称，所以直线10ax by ++=过圆22(1)(2)4x y +++=的圆心，即210a b --+=，21(0,0)a b a b +=>>，121222(2)559b a a b a b a b a b ⎛⎫+=++=+++= ⎪⎝⎭≥，当且仅当22b a a b =，即31a b ==时等号成立．故选：B ．7．【答案】A ．【解析】定义域{|0}x x ≠，排除CD ，由55e e (5)05f --=>排除B ，所以选A ．8．【答案】C【解析】在事件1A 发生的条件下，乙罐中有5红2白7个球，则25127C 10(|)C 21P B A ==，A 正确；在事件2A 发生的条件下，乙罐中有4红3白7个球，则1143227C C 124(|)C 217P C A ===，B 正确；因15()8P A =，23()8P A =，110(|)21P B A =，24227C 6(|)C 21P B A ==．则11225103617()()(|)()(|)82182142P B P A P B A P A P B A =+=⨯+⨯=，C 不正确；因212(|)21P C A =，1152127C C 10(|)C 42P C A ==，则112251031243()()(|)()(|)82182184P C P A P C A P A P C A =+=⨯+⨯=，D 正确． 9．【答案】AC【解析】由折线图知，小组A 打分的9个分值排序为：42，45，46，47，47，47，50，50，55，小组B 打分的9个分值排序为：36，55，58，62，66，68，68，70，75；对于A ：小组A 打分的分值的众数为47，故选项A 正确；对于B ：小组B 打分的分值第80百分位数为980%7.2⨯=，所以应排序第8，所以小组B 打分的分值第80百分位数为70，故选项B 不正确；对于C ：小组A 打分的分值比较均匀，即对同一个选手水平对评估相对波动较小，故小组A 更像是由专业人士组成，故选项C 正确；对于D ：小组A 打分的分值的均值约47.7，小组B 打分的分值均值为62，根据数据对离散程度可知小组B 的方差较大，选项D 不正确；10．【答案】AB 【解析】因为121n n a a +=+，得112(1)n n a a ++=+，所以数列{1}n a +是等比数列，B 正确；又11a =，则111(1)22n n n a a -+=+⋅=，所以21n n a =-，所以C 错误；则33217a =-=，A 正确；所以12(12)2212n n n S n n +-=-=---，所以D 错误，故选AB ．11．【答案】AC 【解析】()f x 的对称中心即为()f x 的零点，则2sin()03f ππ⎛⎫-=-= ⎪⎝⎭，所以A 正确；当50,12x π⎡⎤∈⎢⎥⎣⎦时，2,332x πππ⎡⎤-∈-⎢⎥⎣⎦，sin y x =在,32ππ⎡⎤-⎢⎥⎣⎦单调递增，所以B 错误； ()f x 在对称轴处取到最值，1132sin 2122f ππ⎛⎫==-⎪⎝⎭，所以C 正确；将函数()f x 的图象沿x 轴向左平移4π个单位长度得到2sin 22sin 2436y x x πππ⎡⎤⎛⎫⎛⎫=+-=+ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦，所以D 错误，故选AC ．12．【答案】BCD 【解析】对于A ，易知MN 与1BD 为异面直线，所以M ，N ，B ，1D 不可能四点共面，故A 错误；对于B ，连接1CD ，CP ，易得1//MN CD ，所以1PD C ∠为异面直线1PD 与MN 所成角，设2AB =，则1CD =，1D P =，3PC =，所以1cos PD C ∠==，所以异面直线1PD 与MN ，故B 正确；对于C ，连接1A B ，1A M ，易得1//A B MN ，所以平面BMN 截正方体所得的截面为梯形1MNBA ，故C 正确；对于D ，易得1//D P BN ，因为1D P ⊄平面MNB ，MN ⊂平面MNB ，所以1//D P 平面MNB ，所以11111122323P MNB D MNB B MND V V V ---===⨯⨯⨯⨯=，故D 正确．故选BCD ．13．【解析】z =．14．【解析】设经过点P 的终边角度为(02π)αα<<，根据题意，利用任意角的三角函数的定义，得：1cos 2α=-，sin α=2π3α=，cos s πco 3π3a α⎛⎫∴=-= ⎪⎝⎭，sin sin 3π3πb α⎛⎫=-= ⎪⎝⎭，12π1cos sin sin sin 3323πππ23ab ∴====．15．【答案】DM PC ⊥（或BM PC ⊥，OM PC ⊥等，答案不唯一）【解析】由ABCD 为菱形，则AC BD ⊥，PA ⊥ 平面ABCD ，PA BD ∴⊥，BD ∴⊥平面PAC ，BD PC ∴⊥，面PCD 为固定平面，面DMB 为运动平面，且运动平面中的固定直线BD PC ⊥，所以只需在运动平面中增加一条与DB 相交且垂直于PC 的直线即可满足面DMB ⊥面PCD ，故填DM PC ⊥，BM PC ⊥，OM PC ⊥，等，都满足要求． 16．【答案】4，4k <【解析】如图所示，过点Q 作拋物线准线的垂线QE ，垂足为点E ，设PFO θ∠=，则θ为锐角，设抛物线28y x =的准线与x 轴的交点为M ，则4MF =，由抛物线的定义可知QF QE =，4cos cos MF PF θθ==，cos QE QF PQ PF QFθ==-，所以1cos cos PF QF θθ+=，当点P的坐标为(-时，12PF ==，则1cos 3MF PF θ==，此时1cos ()4cos PF d P FQθθ+===；当点(2,)(0)P t t ->时，若4()0d P PF k -->恒成立，则4()k d P PF <-，4(1cos )44()4cos cos d P PF θθθ+-=-=，4k ∴<．17．【解析】（1）选①②时：由12n n a a +-=可知数列{}n a 是以公差2d =的等差数列，·········1 分又55a =得51(51)a a d =+-⨯，（2分）得13a =-， ···········································3分故32(1)n a n =-+-，即*25()N n a n n =-∈．·····························································4分选②③时：由12n n a a +-=可知数列{}n a 是以公差2d =的等差数列，·································1分由24S =- 可知124a a +=-，即1224a +=-．（2分）得13a =-，··································3分故32(1)n a n =-+-，即*25()N n a n n =-∈．······························································4分【备注】选①③这两个条件无法确定数列，不给分． (2) 111111(25)(23)22523n n n b a a n n n n +⎛⎫===- ⎪⋅-⋅---⎝⎭，············································2分11111111123111132523n T n n ⎡⎤⎛⎫⎛⎫⎛⎫⎛⎫=-+-+-+⋯+- ⎪ ⎪ ⎪ ⎪⎢⎥-----⎝⎭⎝⎭⎝⎭⎝⎭⎣⎦．··································4分 1112323n ⎛⎫=-- ⎪-⎝⎭（5分）11646n =---．所以69n n T n =-+ ·······································6分 18．【解析】方法1：（1）1121()3333AD AB BD AB BC AB AC AB AB AC =+=+=+-=+．··························2分222221421=++233999AD AB AC AB AB AC AC ⎛⎫=⨯⋅+ ⎪⎝⎭··················································4分224217=1+213cos120+3=9999⨯⨯⨯⨯︒⨯，（6分）故AD ．·······································7分PQME（2）cos AD AC DAC AD AC ⋅=⋅∠（1分）22122AB AC AC AB AC AC ⎛⎫+⋅⋅+ ⎪== ···········3分221113()3⨯⨯⨯-+⨯（4分）=···································································5分方法2：（1）在ABC △中，22222+2cos 13213cos12013BC AB AC AB AC BAC =-⋅∠=+-⨯⨯︒=，（1分）所以BC =，222cos 2AB BC AC ABC AB BC +-==⋅∠·····················3分==．····································································································4分在ABD △中，222+2cos AD AB BD AB BD ABD =-⋅∠2131+219=-⨯··········5分 79=，（6分）故AD =·······················································································7分（2）由（1）可得：2222223cos =2AC AD DC DAC AC AD+-+-===⋅∠．19．【解析】（1）由题22⨯列联表为兴趣较大兴趣一般合计男生 35 15 50 女生 30 20 50 合计6535100零假设为0H ：学生对课后延时服务的兴趣与性别无关，····················································1分根据列联表计算得：22()()()()()n ad bc a c b d a b c d χ-=++++······················································2分2100(700450)1001.0996535505091-==≈⨯⨯⨯，（3分）0.1002.706α<=．···········································4分根据小概率值0.100α=的独立性检验，没有充分的证据推断0H 不成立，因此认为学生对课后延时服务的兴趣与性别无关．····························································5分（2）由样本可知，分层抽样得到5名女生中，有3名兴趣较大，2名兴趣一般．····················1分ξ可能的取值为0,1,2，······························································································2分3335C 1(0)C 10P ξ===，213235C C 6(1)C 10P ξ⋅===，123235C C 3(3)C 10P ξ⋅===．························4分【任意一个正确得1分，全部正确得2分】所以ξ的分布列为分所以期望为：163()012101010E x =⨯+⨯+⨯（6分）65=．···············································7分 20．【解析】（1）证明：取PC 的中点F ，连接EF ，BF ．因为AE 是等边ADP △的中线，所以AE PD ⊥．···························································1分因为E 是棱PD 的中点，F 为PC 的中点，所以//EF CD ，且12EF CD =．······················2分因为//AB CD ，12AB CD =，所以//EF AB ，且EF AB =，所以四边形ABFE 是平行四边形，所以//AE BF ．·························································3分因为BC BP =，F 为PC 的中点，所以BF PC ⊥，从而AE PC ⊥．································4分又PC PD P = ，且PC ⊂平面PCD ，PD ⊂平面PCD ，【注：无本行三个条件扣1分】所以AE ⊥平面PCD ．······························································································5分（2）【解法1】由（1）知AE CD ⊥，又AD CD ⊥，AD AE A = ，且AD、AE ⊂平面ADP ，所以CD ⊥平面ADP ，从而EF ⊥平面ADP ．以E 为坐标原点，,,EP EA EF的方向分别为,,x y z 轴的正方向，建立如图所示的空间直角坐标系E xyz -．··························································1分则P ，(0,2)B ，(4)C -，所以(2)PB =-，(4)PC =-．···························································2分设平面PBC 的法向量为(,,)m x y z =，由00PB m PC m ⎧⋅=⎪⎨⋅=⎪⎩，得2040z z ⎧-++=⎪⎨-+=⎪⎩，······························································3分令1x =，则0y =，z =，所以m =．·························································4分又平面PAD 的一个法向量为(0,0,1)n =，·····································································5分所以cos ,m n m n m n⋅〈〉===⋅···········································································6分即平面PBC 与平面PAD ．······························································7分21．【解析】（1）由已知得12c a =，所以22222131124b c a a ⎛⎫=-=-= ⎪⎝⎭，·································1分又点31,2⎛⎫-⎪⎝⎭在该椭圆上，所以221914a b +=，（2分）所以24a =，23b =，·······················3分所以椭圆C 的标准方程为22143x y +=．·········································································4分（2）由于BN 的斜率为k ，设直线BN 的方程为(2)y k x =-，·········································1分22(2)143y k x x y =-⎧⎪⎨+=⎪⎩，整理得2222(43)1616120k x k x k +-+-=，············································2分所以22161243B N k x x k -=+，所以228643N k x k -=+，从而21243N k y k =-+，即2228612,4343k k N k k ⎛⎫-- ⎪++⎝⎭，（3分）同理可得：由于AM 的斜率为3k ，则直线AM 的方程为3(2)y k x =+，联立方程组223(2)143y k x x y =+⎧⎪⎨+=⎪⎩，可得2222(363)144144120k x k x k +++-=，即2222(121)484840k x k x k +++-=，所以22484121A M k x x k -=+，所以22242121M k x k -+=+，从而212121M k y k =+，即22224212,121121k k M k k ⎛⎫-+ ⎪++⎝⎭，························4分当12k ≠±时，22222221212412143412428612143MN k k k k k k k k k k k ⎛⎫-- ⎪++⎝⎭==-+⎛⎫-+--- ⎪++⎝⎭，············································5分所以直线MN 为222212486434143k k k y x k k k ⎛⎫---=- ⎪+-++⎝⎭，整理得24(1)41ky x k =+-+，············6分即直线MN 过定点(1,0)P -，当M N x x =，即12k =±时，直线MN 的方程为1x =-，也过点(1,0)P -，··························7分综上可得，直线MN 过定点(1,0)P -．··········································································8分22．【解析】（1）由题得11()22(1)2e e x x x f x ax a x a -⎛⎫'=+-=-- ⎪⎝⎭．·································1分① 当0a ≤时，120ex a -<，令()0f x '=则1x =，故当(,1)x ∈-∞时，()0f x '>，()f x 单调递增；当(1,)x ∈+∞时，()0f x '<，()f x 单调递减；·······························································2分 ② 当0a >时，令()0f x '=则11x =，2ln 2x a =-，当ln 21a -<，即12ea >时，当(,ln 2)x a ∈-∞-和(1,)+∞时，()0f x '>，()f x 单调递增；当(ln 2,1)x a ∈-时，()0f x '<，()f x 单调递减；··························································3分当ln 21a -=，即12ea =时，()0f x '≥，()f x 在R 上单调递增；····································4分当ln 21a ->，即102ea <<时，当(,1)x ∈-∞和(ln 2,)a -+∞时，()0f x '>，()f x 单调递增；当(1,ln 2)x a ∈-时，()0f x '<，()f x 单调递减；··························································5分综上所述，当0a ≤时，()f x 在(,1)-∞上单调递增，在(1,)+∞上单调递减；当102ea <<时，()f x 在(,1)-∞和(ln 2,)a -+∞上单调递增，在(1,ln 2)a -上单调递减；当12e a =时，()f x 在R 上单调递增；当12ea >时，()f x 在(,ln 2)a -∞-和(1,)+∞上单调递增，在(ln 2,1)a -上单调递减．··········6分（2）由题，即证3ln 2243e x x ax a x ++<+，[1,0)a ∈-，即233ln 22e 2x x x ax a x ⎛⎫++<+ ⎪⎝⎭，得232(ln )e 2x x ax ax x x +-<-．·················································································1分由（1）可得当[1,0)a ∈-时2()2ex x f x ax ax =+-，()f x 在(,1)-∞上单调递增，在(1,)+∞上单调递减．························································2分故21111221e e e ex x ax ax a a a +-+-=-+≤≤，当且可当1x =时取等号．·························3分设3()(ln )2h x x x =-，则3(1)()2x h x x-'=，故在(0,1)上()0h x '<，()h x 单调递减；在(1,)+∞上()0h x '>，()h x 单调递增．········································································································4分故3()(1)2h x h =≥，即33(ln )22x x -≥，·····································································5分故213321(ln )e e 22x x ax ax x x +-+<-≤≤，故232(ln )e 2x x ax ax x x +-<-，即得证．·······6分。

惠州市2025届高三第一次调研考试试题含答案

惠州市2025届高三第一次调研考试试题本试卷共8页，23小题考试时间：150分钟满分：150分注意事项：1．答卷前，考生务必将自己所在的县（区）、学校、班级、姓名、考场号、座位号和考生号填写在答题卡上，将条形码横贴在每张答题卡右上角“条形码粘贴处”。

2．作答选择题时，选出每小题答案后，用2B铅笔在答题卡上将对应题目选项的答案信息点涂黑；如需改动，用橡皮擦干净后，再选涂其他答案。

答案不能答在试卷上。

3．非选择题必须用黑色字迹的钢笔或签字笔作答，答案必须写在答题卡各题目指定区域内相应位置上；如需改动，先画掉原来的答案，然后再写上新答案；不准使用铅笔和涂改液。

不按以上要求作答无效。

4．考生必须保证答题卡的整洁。

考试结束后，将答题卡交回。

一、现代文阅读（35分）（一）现代文阅读I（本题共5小题，19分）阅读下面的文字，完成1～5题。

材料一：由于每个物种都有按照几何级数过度繁殖的趋向，而且各个物种中变异了的后代，可以通过其习性及构造的多样化去占据自然条件下多种多样的生活场所，以满足数量不断增加的需要，所以自然选择的结果就更倾向于保存物种中那些最为歧异的后代。

这样，在长期连续的变异过程中，同一物种的不同变种间细微的特征差异趋于增大，并成为同一属内不同物种间较大的特征差异。

新的改良变种必将替代旧的、少有改良的中间变种，并使其绝灭；这样，物种在很大程度上就成为确定的、界限分明的自然群体了。

每一纲中凡是属于较大种群中的优势物种，它更能产生新的优势类型，其结果必然是每一个大的种群在规模上更趋于增大，同时性状分异也就更大。

由于地球上的生存空间有限，不可能允许所有的种群都扩大规模，其结果就是优势类型在竞争中打败了较不占优势的类型。

这使大类群在规模上不断扩大，性状分异更趋明显，并不可避免地导致大量物种的绝灭；这就可以解释为什么仅有极少数大纲在竞争中自始至终占据着优势，而其中所有的生物类型都可以排列成许多大小不一的次一级生物群。

高三数学上学期第一次月考试题文扫描试题

HY中学2021届高三数学上学期第一次月考试题文〔扫描版〕创作人：历恰面日期：2020年1月1日一中第一期联考文科数学答案命题、审题组老师杨昆华彭力杨仕华王佳文张波毛孝宗丁茵易孝荣江明李春宣一、选择题题号 1 2 3 4 5 6 7 8 9 10 11 12 答案BCBCDADDCAAB1. 解析：由题意，因为集合{}1>=x x A ，所以=B A {}31<<x x ，选B ． 2. 解析：因为2i 12i i i)i)(1(1i)i(1i 1i 2+=-=-+-=+，选C ． 3. 解析：18=0.4540，选B ． 4. 解析：由得54)cos(-=--αβα，即54cos )cos(-==-ββ，又πβ（∈，）23π，所以0sin <β，且53cos 1sin 2-=--=ββ，选C ．5. 解析：在长、宽、高分别为2，1，1的长方体中截得该三棱锥A DBC -，那么最长棱为2222116AB =++=，选D ．6. 解析：对于B ，函数的周期是π，不是π4；对于C ，函数在3π=x 时不取最值；对于D ，当∈x 65(π-，)6π时，34(32ππ-∈+x ，）32π，函数不是单调递增，选A ． 7. 解析：因为()()11f x f x -=+，所以()f x 的图象关于直线1x =对称，选D ．8. 解析：由垂径定理可知直线CM 的斜率为2-，所以直线CM 的方程是)2(21--=+x y ，即032=-+y x ，选D ．9. 解析：设外接球的半径为R ，因为PA ⊥平面ABC ，所以BC PA ⊥，又BC AB ⊥，所以BC PB ⊥，设PC 的中点为O ，易知：OA OB OC OP ===，故O 为四面体P ABC -的外接球的球心，又2PA AB BC ===，所以22AC =，23PC =，半径3R =，四面体P ABC -的外接球的外表积为()24312ππ=，选C ．10. 解析：由()y f x =,()01f =-排除B ，()f x 是偶函数排除C,()20f =和()40f =排除D ，选A ．11. 解析：由题设得3=ab，2)(12=+=a b e ，所以b e a +2362322323322=≥+=+=aa a a ，选A ． 12. 解析：由余弦定理及22b ac a -=得，22222cos b a c ac B a ac =+-=+，所以有2cos c a B a =+，因此sin 2sin cos sin C A B A =+，故有()sin 2sin cos sin A B A B A +=+，即()sin sin A B A =-，因为三角形ABC 为锐角三角形，所以A B A =-，即2B A =，所以022A π<<，所以04A π<<，又3B A A +=，所以32A ππ<<，所以63A ππ<<，综上,64A ππ⎛⎫∈ ⎪⎝⎭，所以()sin sin 22cos 2,3sin sin B At A A A===∈，选B ．二、填空题13. 解析：由22a b a b -=+解得0a b ⋅=，所以向量a 与b 夹角为90︒． 14. 解析：N=126+146+96+136=288⨯⨯⨯⨯．15. 解析：由图知，直线4z y x =-过()1,0时，4y x -有最小值1-. 16. 解析：由得()()22log 1933f x x x -=+++，所以()()6f x f x +-=，因为2lg 3⎛⎫ ⎪⎝⎭与3lg 2⎛⎫⎪⎝⎭互为相反数，所以23lg lg 632f f ⎛⎫⎛⎫+= ⎪ ⎪⎝⎭⎝⎭，所以3lg 22f ⎛⎫=- ⎪⎝⎭．三、解答题〔一〕必考题17. 解：〔1〕证明：设1122n n nn a a d ---=那么122n n n a a d --= 所以1122n n n a a d ++-=,11122222n n n n n n a a da a d++--==-所以}{12n na a +-是首项为4,公比为2的等比数列. ………6分〔2〕因为{}2n n a 是等差数列，所以1221122=-=a a d ,所以11(1)22n n a a n d =+-⨯ , 所以1()22nn a n =-所以123113531222...()2()222222n n n S n n -=⨯+⨯+⨯++-+-① 2311333222...()2()22222n n n S n n +=⨯+⨯++-+-②由①-②得23111=2+2+2...2()222n n n S n +-⨯++-- 13=(n-)232n n S ++． ………12分18. 解：〔1〕选派B 同学参加比拟适宜．理由如下：1(7580808385909295)858A x =+++++++=，1(7879818284889395)858B x =+++++++=，22222221[(7885)(7985)(8185)(8285)(8485)(8885)8B S =-+-+-+-+-+-+22(9385)(9585)]35.5-+-=，22222221[(7585)(8085)(8085)(8385)(8585)(9085)8A S =-+-+-+-+-+-+22(9285)(9585)]41-+-=，从A B x x =，22B A S S <可以看出：A ，B 两位同学的平均程度一样而B 的成绩较稳定，所以选派B 参加比拟适宜． ………7分〔2〕任选派两人有(,)A B ，(,)A C ，(,)A D ，(,)A E ，(,)B C ，(,)B D ，(,)B E ，(,)C D ，(,)C E ，(,)D E 一共10种情况；所以A ，B ，C 三人中至多有一人参加英语口语竞赛有7种情况；所以710P =． ………12分19. 解：〔1〕在直角梯形ABCD 中，2BC AD AB ⋅=，即AB ADBC AB=，因为90DAB PBC ∠=∠=, 所以tan AB ACB BC ∠=，tan ADABD AB∠=，所以ABD ACB ∠=∠，又因为90ACB BAC ∠+∠=，所以90ABD BAC ∠+∠=，即AC BD ⊥图2的四棱锥1P ABCD -中，1P A AB ⊥，由题知1P A AD ⊥，那么1P A ⊥平面ABCD ，所以1BD P A ⊥，又1P AAC A =所以BD ⊥平面1P AC . ………6分(2)在图1中，因为AB =,1AD =，2BC AD AB ⋅=，所以3BC =因为PAD ∆∽PBC ∆，所以13PA AD PA PB BC ==⇒=，即1P A = 由〔1〕知1P A ⊥平面ABCD ，那么1C P BD V -1P CBD V -=1P CBD V -=111111133332324CBD S P A BC AB P A ∆⋅⋅=⨯⋅⋅=⨯⨯=. ………12分20. 解：〔1〕由椭圆定义知，224AF BF AB a ，又222AF BF AB ，得43ABa ，l 的方程为y x c ，其中22c a b .设11(,)A x y ，22(,)B x y ，将y x c 代入22221x y a b 得，2222222()2()0a b x a cx a c b . 那么212222-a c x x a b ，2221222)a cb x x a b （.因为直线AB 的倾斜角为4π，所以212122()4ABx x x x ，由43AB a 得，222443a ab a b ，即222a b .所以C的离心率2222c a b e a a. ………6分 (2) 设AB 的中点为0,0()N x y ，由〔1〕知，2120222--23x x a c c x a b ，003cy x c .由PA PB 得，PN 的斜率为-1，即001-1y x ，解得，3c ，32a ，3b .所以椭圆C 的方程为221189x y . ………12分21. 解：〔1〕()f x 的定义域为(,)-∞+∞,因为()e x f x a '=+，由(0)0f '=，得1a =-, 所以()e 2x f x x =--，由()e 10x f x '=->得0x >，由()e 10x f x '=-<得0x <，所以()f x 的单调递增区间为(0,)+∞，单调递减区间为(,0)-∞. ………6分 (2) 因为0x >,所以()e 1e 1xxm x -<+可化为e 1e 1x x x m +<-，令e 1()e 1x x x F x +=-，那么()2e (e 2)()e 1x x x x F x --'=-，由〔1〕得()e 2x f x x =--在(0,)+∞上单调递增，而(1)e 30f =-<,2(2)e 40f =->,所以()f x 在(1,2)上存在唯一的0x ，使0()0f x =，所以()F x 在0(0,)x 上单调递减，在0(,)x +∞上单调递增，所以0()F x 是()F x 00e 20x x --=得00e 2x x =+，所以00000000e 1(2)1()11e 1x x x x x F x x x +++===++-，又因为012x <<，所以02()3F x <<，所以[]max 2m =. ………12分〔二〕选考题：第22、23题中任选一题做答。

惠州市2021届高三第一次调研考试参考答案

惠州市2021届高三第一次调研考试参考答案【阅读理解】21-23. BDA 24-26. BCA 27-30. DCBD【七选五】31-35. CGFEA【完形填空】36-40. BABCD 41-45. CABDD 46-50. CABDC 51-55. AACBD【语法填空】56. trends 57. have chosen 58. stressful 59. higher 60. are convinced 61. an 62. eating 63. to 64. to produce 65. if【概要写作】Possible version 1:Physical exercise plays a significant role in teenagers’ fitness. Teenagers are advised to identify their fitness level to design a health programme.(要点1) “Overweight”, “inactive” and “active” are the three levels of fitness that urge one to change his lifestyle. (要点2) In addition to calorie-burning exercises that overweight teenagers should do, inactive and active teenagers are advised to exercise more due to their strong bodies.(要点3) Furthermore, intensive exercise is vital to injury-prevention while body-strengthening exercises help build up one’s physical strength.(要点4)(79 words) Possible version 2:Physical exercise is beneficial to teenagers’ health. Teenagers are advised to figure out their fitness level and make a plan to keep fit. (要点1) There are three levels of physical states, namely “Overweight”, “Inactive” and “Active”, which urge a change of lifestyle. (要点2) According to different fitness levels, experts suggest teenagers do calorie-burning exercises, bending and stretching exercises. (要点3) Besides, intensive exercise and body-strengthening exercises are recommended to avoid injuries and build up one’s strength. (要点4)(73 words)【概要写作】各档次的给分范围和要求（总分15分）：【应用文写作】Possible version 1:Dear David,What a pity to hear that you have to cancel your visit to China this summer because of the worldwide epidemic!To make up for it, I strongly recommend that you watch the series “Visiting China Online”. For one thing, combining different experiences of tourists and daily lives of average people, the series of short films provide you with a comprehensive glimpse into China, which will definitely enhance your understanding of China. For another, with various elements about China included in it, the program presents abundant Chinese culture, ranging from festivals, customs to legends, like a feast to your eyes.However, if you decide to visit China in person next year, it’s my great honor to be your partner and guide. Looking forward to your coming.Yours,Li HuaPossible version 2:Dear David,I’m sorry to hear that you can’t come to China this summer due to the worldwide spread of COVID-19. However, an online tourism promotional activity “Visiting China Online” may offer you a chance to experience the charm of China at home.Without leaving home, you can have a good look of China’s most beautiful scenery and varied cultures through a series of short films. The most famous mountains, rivers and lakes as well as all kinds of landscape will surely attract your eyes. Besides, the ancient towns will bring you to understand more about Chinese history and cultures. If you are interested in traditional handicrafts and Chinese cuisine, there are also some DIY activities introduced in the series.China is a place worth a visit. I’d like to be your guide if you come next year. Looking forward to your coming.Yours,Li Hua。

广东省惠州市2021届高三第一次调研考试数学

惠州市2021届高三数学第一次调研考试试题全卷满分150分，时间120分钟．注意事项：1．答题前，考生务必将自己的姓名、准考证号、座位号、学校、班级等考生信息填写在答题卡上。

2．作答单项及多项选择题时，选出每个小题答案后，用2B 铅笔把答题卡上对应题目的答案信息点涂黑。

如需改动，用橡皮擦干净后，再选涂其它答案，写在本试卷上无效。

3．非选择题必须用黑色字迹签字笔作答，答案必须写在答题卡各题指定的位置上，写在本试卷上无效。

一、单项选择题：本题共10小题，每小题满分5分，共50分。

在每小题给出的四个选项中，只有一项符合题目要求，选对得5分，选错得0分。

1．设集合2{|560}M x x x =-+<，集合{}0N x x =>, 则=N M （）.A ．{}0x x > B ．{|3}x x < C ．{|2}x x < D ．{}23x x <<2．复数z 满足(1)=1i z i +⋅-+，其中i 为虚数单位，则复数z =（）.A ．1i +B ．1i -C ．iD ．i - 3．已知2sin 3α=，则()cos 2α-=（）.A ．19 B ．19-C D ．3-4．已知向量(),3k =a ，向量()1,4=b ，若⊥a b ，则实数k =（）.A ．12B ．12-C ．43 D ．43- 5．已知正方体1111ABCD A B C D -的棱长为1，则直线1DA 与直线AC 所成角的余弦值为（）.A ．12-B ．2C ．12D ．26．已知双曲线22221(0,0)x y a b a b-=>>的一条渐近线平行于直线:250l x y ++=，则双曲线的离心率为（）.A ．12BCD7．《张丘建算经》是我国北魏时期大数学家张丘建所著，约成书于公元466-485年间。

其中记载着这么一道“女子织布”问题：某女子善于织布，一天比一天织得快，且每日增加的数量相同。

2025届广东省惠州市高三上学期第一次调研考试物理试题(原卷版)

惠州市2025届高三第一次调研考试物理本试卷共8页，15小题，满分100分。

考试用时75分钟。

注意事项：1.答卷前，考生务必用黑色字迹钢笔或签字笔将自己的姓名、考生号、考场号和座位号填写在答题卡上。

将条形码横贴在答题卡右上角“条形码粘贴处”。

2.作答选择题时，选出每小题答案后，用2B 铅笔把答题卡上对应题目选项的答案信息点涂黑；如需改动，用橡皮擦干净后，再选涂其他答案，答案不能答在试卷上。

3.非选择题必须用黑色字迹钢笔或签字笔作答，答案必须写在答题卡各题目指定区域内相应位置上；如需改动，先划掉原来的答案，然后再写上新的答案；不准使用铅笔和涂改液。

不按以上要求作答的答案无效。

4.考生必须保持答题卡的整洁。

考试结束后，将答题卡交回。

一、单项选择题：本题共7小题，每小题4分，共28分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

1. 2019年，中国科学院物理研究所陈立泉院士带领团队研发出某新能源固态电池，该电池在能量密度、功率密度和安全性等均达到世界第一，功率密度，指的是电池放电时单位质量单位时间输出的能量，功率密度用国际单位制的基本单位符号表示正确的是（）A W/kg B. J/kg C. m 2/s 2 D. m 2/s 32. 如图（a ）所示，2023年杭州亚运会田径赛场上，工作人员利用电子狗捡铁饼和标枪，这在世界上尚属首次。

电子狗在一次捡铁饼的过程，速度时间图像如图（b ）所示，其中2~10s 为曲线，其余为直线。

下列说法正确的是（）A. 2~10s 时间内，电子狗做匀加速直线运动B. 0~10s 时间内，电子狗的平均速度大小为3m/sC. 16s 时，电子狗距离出发点最远D. 12s 时，电子狗开始反向运动3. 目前很多课室里的黑板都采用铁质材料制成，用磁性材料做的黑板擦可以吸附在黑板上，如图所示，下.列关于黑板擦受力说法正确的是（）A. 黑板擦与黑板间存三对作用力与反作用力B. 黑板擦一共受到3个力的作用C. 黑板擦受到磁吸引力大于黑板对它的弹力D. 黑板对黑板擦的作用力为零4. 某款天花板消防自动感温喷淋头如图（a ）所示，当室内达到一定温度时，感温玻璃球自动爆开，喷淋开始启动达到自动喷水灭火的目的。

广东省惠州市2021届高三生物高考一模试卷

广东省惠州市2021届高三生物高考一模试卷一、单选题1. ( 2分) “人是铁，饭是钢，一顿不吃饿得慌（心跳加快）”，下列说法错误的是（）A. “饿”是一种感觉，产生于大脑皮层的相应中枢B. “慌（心跳加快）”是机体在能量供应不足时的一种保护反应C. 吃饭时口腔分泌的唾液淀粉酶，可将淀粉水解成还原糖D. 细胞吸收的葡萄糖直接进入线粒体彻底氧化分解供能2. ( 2分) 下列相关显微观察类实验（实验材料、实验试剂等）叙述，正确的是（）A. 观察线粒体和观察DNA，RNA在细胞中的分布均可使用人口腔上皮细胞B. 洋葱鳞片叶的内外表皮均可发生质壁分离且均能作为此实验的材料C. 脂肪酶的化学本质可通过滴加苏丹Ⅲ显橘黄色来鉴定D. 细胞膜具有选择透过性，因此健那绿染液不能通过活细胞膜3. ( 2分) 幽门螺杆菌（简称Hp）感染是导致胃病或胃癌的重要原因之一，14C呼气检测是目前检查Hp的主要方法之一。

受检者口服特殊的尿素[14CO(NH2)2]胶囊（人体胃内含普通尿素），胃内Hp产生的高活性尿素酶（哺乳动物细胞中不存在尿素酶）催化尿素迅速水解成NH3和14CO2，收集呼气标本并测量14CO2，便可判断有无Hp的感染。

以下说法错误的是（）A. NH3呈碱性、中和胃酸，是Hp能在胃内强酸性环境下存活的重要原因之一B. 该检测方法证明了Hp能通过呼吸系统传染，所以Hp感染患者要佩戴口罩C. 胃中的14CO2需吸收入血，经血液循环运输、最终经肺以14CO2形式呼出D. 人体细胞中不存在尿素酶是该检测方法具有可信性的一个重要依据4. ( 2分) 研究人员为确定决定糖酵解（葡萄糖分解为丙酮酸）酶的基因，从一只健康小鼠的6个不同组织中收集样本，并测量出了每种组织细胞内6种基因表达出的mRNA的含量，结果如下图，下列观点或结论错误的是（）A. 同一基因在不同细胞中表达的程度可能不一样B. 同一细胞中不同基因表达的程度可能不一样C. 不同细胞mRNA种类不同的根本原因是它们的基因不同D. 基因G最有可能是决定糖酵解酶的基因5. ( 2分) 已知某二倍体亲本植株Aa，Aa自交得到F1。

广东省三校(广州真光中学、深圳市第二中学、珠海市第二中学)2021届高三数学上学期第一次联考试题理

广东省三校（广州真光中学、深圳市第二中学、珠海市第二中学）2021届高三数学上学期第一次联考试题理本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分．满分150分．考试时间120分钟．第Ⅰ卷(选择题共60分)一、选择题：本大题共12小题，每小题5分，满分60分．在每小题给出的四个选项中，只有一项符合要求．1．已知集合A ＝{x ｜lg(2)y x =-}，B ＝{2|30x x x -≤}，则A ∩B ＝.A. {x ｜0＜x ＜2}B. {x ｜0≤x ＜2}C. {x ｜2＜x ＜3}D. {x ｜2＜x ≤3} 2．若复数z 的共轭复数满足()112i Z i -=-+,则||Z =.A.2 B.32C.10D.123．下列有关命题的说法错误的是.A. 若“p q ∨”为假命题，则p 、q 均为假命题；B. 若αβ、是两个不同平面，m α⊥,m β⊂，则 αβ⊥；C. “1sin =2x ”的必要不充分条件是“=6x π”；D. 若命题p ：200,0x R x ∃∈≥，则命题：2:,0P x R x ⌝∀∈<；4．已知某离散型随机变量X 的分布列为X 0 1 2 3P827 49m127则X 的数学期望()E X =.A ．23B ．1C ．32D ．25．已知向量a 、b 均为非零向量，则a 、b 的夹角为.A ．6π B ．3π C ．32π D ．65π6．若1cos =86πα⎛⎫- ⎪⎝⎭，则3cos 24πα⎛⎫+⎪⎝⎭的值为. A. 1718B. 1718-C. 1819D. 1819-7．若直线()m n +2=0m>0n>0x y +、截得圆()()2231=1x y +++的弦长为2，则13m n+的最小值为. A. 4B. 12C. 16D. 68．设抛物线C ：y 2=4x 的焦点为F ，过点（–2，0）且斜率为23的直线与C 交于M ，N 两点，则FM FN ⋅=. A ．5B ．6C ．7D ．89．已知定义在R 上的偶函数()()3sin()cos()(0,),0f x x x ωϕωϕϕπω=+-+∈>对任意x ∈R 都有()02f x f x π⎛⎫++= ⎪⎝⎭，当ω取最小值时，6f π⎛⎫⎪⎝⎭的值为. A.13 C.12D.3210．在如图直二面角ABDC 中，△ABD 、△CBD 均是以BD 为斜边的等腰直角三角形，取AD 的中点E ，将△ABE 沿BE 翻折到△A 1BE ，在△ABE 的翻折过程中，下列不可能成立的是.A ．BC 与平面A 1BE 内某直线平行B ．CD ∥平面A 1BEC ．BC 与平面A 1BE 内某直线垂直D ．BC ⊥A 1B11．定义12nnp p p ++⋅⋅⋅+为n 个正数12n p p p ⋅⋅⋅、、、的“均倒数”，若已知正整数数列{}n a的前n 项的“均倒数”为121n +，又1=4n n a b +，则12231011111=b b b b b b ++⋅⋅⋅+. A.111 B. 112 C. 1011 D. 1112 12．已知函数()2x mf x xe mx =-+在(0,)+∞上有两个零点，则m 的取值范围是. A. (0,)e B. (0,2)eC. (,)e +∞D. (2,)e +∞第II 卷（非选择题共90分）本卷包括必考题和选考题两部分．第13-21题为必考题，每个试题考生都必须作答，第22-23题为选考题，考生根据要求作答．二、填空题:本大题共4小题,每小题5分,共20分13．设,x y 满足约束条件12314y x y x y ≥-⎧⎪-≥⎨⎪+≤⎩，则4z x y =+的最大值为；14．若3()nx x-的展开式中各项系数之和为32，则展开式中x 的系数为；15．已知点P 在双曲线()2222=10x y a b a b->>0,上，PF x ⊥轴(其中F 为双曲线的右焦点)，点P 到该双曲线的两条渐近线的距离之比为13，则该双曲线的离心率为；16．已知三棱锥P ABC -的所有顶点都在球O 的球面上，PA ABC ⊥平面，==2AB AC ， ∠BAC =120。

2021年10月广东省普通高中2022届高三上学期10月阶段性质量检测数学试卷及答案

2021年10月广东省普通高中2022届高三上学期10月阶段性质量检测数学试卷★祝考试顺利★(含答案)本试卷分选择题和非选择题两部分。

满分150分,考试时间120分钟。

本卷命题范围：集合、常用逻辑用语、函数与导数、三角函数与解三角形,解答题高考范围。

一、选择题：本题共8小题,每小题5分,共40分。

在每小题给出的四个选项中,只有一项是符合题目要求的。

1.已知全集U ＝{x|－1≤x ≤5,x ∈Z},集合A ＝{0,1,2,3,4},B ＝{－1,0,1,2},则A ∩(∁U B)＝A.{0,1,2}B.{1,2}C.{3,4}D.{3,4,5}2.设命题p ：∃n ∈N *,n 2＋2n>3,则命题p 的否定是A.∃n ∉N *,n 2＋2n>3B.∃n ∈N *,n 2＋2n ≤3C.∀n ∈N *,n 2＋2n ≤3D.∀n ∈N *,n 2＋2n>33.函数f(x)＝1x＋4x 在[1,2)上的值域是 A.[5,172) B[4,172) C.(0,172) D.[5,＋∞) 4.已知sinθ－2cosθ＝0,θ∈(0,2π),则cos sin 2sin2θθθ--5.若1和2是函数f(x)＝4lnx ＋ax 2＋bx 的两个极值点,则log 2(2a －b)＝A.－3B.－2C.2D.36.已知函数f(x)＝lnx ＋ax 在函数g(x)＝x 2－2x ＋b 的递增区间上也单调递增,则实数a 的取值范围是A.(－∞,－1]B.[0,＋∞)C.(－∞,－1]∪[0,＋∞)D.(－1,0]7.在△ABC 中,内角A 、B 、C 所对的边分别为a 、b 、c,则“acosA ＝bcosB ”是“△ABC 是以A 、B 为底角的等腰三角形”的A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件8.若对任意的x 2,x 2∈(m,＋∞),且x 1<x 2,都有122121x lnx x lnx x x --<2,则m 的最小值是(注：e ＝2.71828…为自然对数的底数) A.1e B.e C.1 D.3e二、选择题：本题共4小题,每小题5分,共20分。

广东省惠州市2021届高三第一次模拟考试数学试题 PDF版含答案详解

1024，则
t
=
．
数学试题
第 3 页，共 5 页
16．已知函数 f (x) = ln x ，关于 x 的不等式 f (x)2 − a f (x) 0 只有 1 个整数解，
x
则实数 a 的取值范围是
．
四、解答题：本题共 6 小题，共 70 分．解答应写出文字说明、证明过程或演算步骤．
17．（本小题满分 10 分）
学家帕普斯在他的著作《数学汇篇》中，完善了欧几里得关于圆锥曲线的统一定义，并对
这一定义进行了证明。他指出，到定点的距离与到定直线的距离的比是常数 e 的点的轨迹
叫做圆锥曲线；当 0 e 1时，轨迹为椭圆；当 e = 1时，轨迹为抛物线；当 e 1时，轨
( ) 迹为双曲线。现有方程 m x2 + y2 + 2y +1 = ( x − 2y + 3)2 表示的曲线是双曲线，则 m 的
i ，所以 z
的的虚部是
1，故选
A．
2．【解析】由图可知，阴影部分为 B ( U A) ，故选 B．
3．【解析】圆心 (a,0) 到直线 x y 1 0 的距离 d a 1 ，r 2 ，直线与圆有公共点，则有 d r ， 2
即 a 1 2 ，解得 3 a 1 ，且 [3,1] [3,) ；所以，“ a 3 ”是“直线 y x 1 与圆 2
C．必要不充分
D．既不充分也不必要
4. 某工厂利用随机数表对生产的 50 个零件进行抽样测试，先将 50 个零件进行编号，编号
分别为 01，02，…，50，从中抽取 5 个样本，下面提供随机数表的第 1 行到第 2 行： 66 67 40 37 14 64 05 71 11 05 65 09 95 86 68 76 83 20 37 90 57 16 03 11 63 14 90 84 45 21 75 73 88 05 90 52 23 59 43 10

广东省惠州市2024-2025学年高三上学期第二次调研考试数学含解析

惠州市2025届高三第二次调研考试试题数学全卷满分150分，时间120分钟．2024.10注意事项：1答题前，考生务必将自己的姓名、准考证号、座位号、学校、班级等考生信息填写在答题卡上．2．作答单项及多项选择题时，选出每个小题答案后，用2B铅笔把答题卡上对应题目的答案信息点涂黑如需改动，用橡皮擦干净后，再选涂其它答案，写在本试卷上无效．3非选择题必须用黑色字迹签字笔作答，答案必须写在答题卡各题指定的位置上，写在本试卷上无效一、单项选择题：本题共8小题，每小题满分5分，共40分．在每小题给出的四个选项中，只有一项符合题目要求，选对得5分，选错得0分l已知集合A={�2�x<5}，集合B={xl x2-4x<O}，则A^B=( ）A.(o,s)B.[2,4) c.(4,5) o.(-00,O)u[2,+oo)2已知复数z满足z2+l = 0,则lz+ll=( )A.3B.2C.l D．五3已知等差数列{a,,}前9项的和为27，如＝8，则a.oo= ()A.100B.99C.98 0.974在正方体ABCD-'4iB1Cp1中，棱BC,A戊的中点分别为E,F，则直线E F与平面ABBA所成角的正弦值为（）石 B. 森2石 D. 痀5已知向凳a,b满足：a=(✓3,1)，叫＝石，（兹－b ）·6=3，则向豐6在向榄五上的投影向榄为（）A胃气）B[竿i)C［告）叶亨订6已知函数f(x)=log2厅－2ax),aeR,则“a:s;O"是“函数f(x)在(1，七吩上单调递增＂的（）A充分不必要条件B必要不充分条件C充要条件D既不充分也不必要条件7已知“水滴＂的表面是一个由圆锥的侧面和部分球面（常称为“球冠”)所围成的几何体如图所示，将“水滴＂的轴截面看成由线段AB,AC 和优弧BC所围成的平面图形，其中点B,C 所在直线与水平面平行，AB和AC与圆弧相切已知“水滴＂的“竖直高度”与“水平宽度”(“水平宽度”指的是平行千水4平面的直线截轴截面所得线段的长度的最大值）的比值为－，则sin乙BAC=<A3416 24A.-B .- C.—D .—55252538在统计某学校所有选择理科和文科的学生数据中，发现理科生多千文科生，女生多千男生，则关千本次学生样本的数据中，结论一定成立的是（）A理科男生多千文科女生B文科女生多千文科男生C理科女生多干文科男生D理科女生多于理科男生二、多选题：本题共3小题，每小题6分，共18分．在每小题给出的四个选项中，有多项符合题目要求全部选对的得6分，部分选对的得部分分，有选错的得0分9某公司为保证产品生产质量，连续10天监测某种新产品生产线的次品件数，得到关千每天出现的次品的件数的一组样本数据：3,4, 3, 1,5, 3, 2,5, 1, 3则关千这组数据的结论正确的是（）A极经是4B众数小千平均数c ．方差是2D数据的第80百分位数为4.510函数f (x) =A sin (cvx+ <p)(A> O,a> > 0树<§）的部分图象如图所示，现将f(x )的图象向左平移巴6个单位长度，得到函数g(x)的图象，则下列结论正确的是(2亡7兀X12兀A.<p =－一6B.(i)=2c ．函数）1= xf (x ＋王）是奇函数12 D.g (x )=2c os （2x -¾)II 如图，心形曲线L:x 2+(y -|入扩＝1与Y 轴交于A ,B 两点，点P 是L 上的一个动点，则（）ypXBA点［孚叩11(-1,1.）均在L 上B.IO月的最大值和最小值之和为3C 点P 的纵坐标的最大值为J5D.I PAl+IPB 怍2石三、填空题：本题共3小题，每小题5分，共15分．12．在（x+1)5的二项展开式中，各项的系数和为13椭圆于fi =l (a >b>O )的左、右顶点分别是A 、B ，左、右焦点分别是R 、F2，若I A F.I ,I F.Fzl,IF.纠成等比数列，则此椭圆的离心率e=.14若关千X的方程ln(ax4)＝[二了有实根，则a江护的最小值为四、解答题：本题共5小题，共77分解答应写出必要的文字说明、证明过程或演算步骤15（本题满分13分）已知函数f(x)=�X 2一x-2ln x(l)求曲线y=f(x)在点(l,f(1)）处的切线方程：(2)求函数f(x)在区间[1,e]上的晟小值16（木题满分15分）如图，四棱锥P-ABCD中，PA J_底面ABCD,AB II CD,AD=CD=l.乙BAD=120'，乙ACB=90°.D C(l)求证：BC上平面PAC:(2)若PA＝石，求平面PCD与平面PCA夹角的余弦值l7 （本题满分15分）已知双曲线C:x2-y2=l及直线l:y＝虹－1(])若l与C有两个不同的交点，求实数K的取值范围：(2)若l与C交千A,B两点，O是坐标原点，且t:.OAB的面积为J5，求实数K的值18（本题满分17分）记t:,.ABC的内角A,B,C的对边分别为a,b,c,已知a<b<c且tanA,tanB, t anC均为整数(I)求tanA,tanB, t anC的值，(2)设AC的中点为D,求乙CDB的余弦值19（本题满分17分）若数列{a,,}(1 s n s k, n E N*, k EN*）满足a,，叶0,1}，则称数列{a,,｝为K项0-1数列，由所有k项0-1数列组成集合M ks4)时，a,,=0,求数列{(-l)飞，｝的所有(])若伈｝是12项0-1数列，当且仅当n=3p(p E N*,p项的和；(2)从梊合M人．中仔意取出两个数列｛动，｛丸｝，记X=区|a,－b/|i=I＠求随机变量X的分布列，并证明：E(X)＞一：k2＠若用某软件产生k(k2'.:2)项0-1数列，记事件A =“第一次产生数字1"'B=“第二次产生数字l"'且0<P(A ) <1,0<P (B) <l若P(BIA)<P(B区），比较P(Al B)与P(AI B )的大小惠州市2025届高三第二次调研考试试题高三数学参考答案与评分细则一、单项选择题：本题共8小题，每小题满分5分，共40分．题号2345 678答案BDc BAADcl 【解析】因为B ={xl O < x <4}，所以A nB={xl 2�x<4}故选：B 2【解析】因为z 2+l=O,即z 2= -1,所以z ＝土，所以卜＋11=11士11=f言75了＝J5故选：D.的公妇为d，由已知得：｛9a, +36d =273【解析】设等劳数列{a ,,}，解得a,= -1, cl = 1,a, +9d =8所以a 100=a , + 99d = -1 + 99 = 98故选：C.4【解析】连接FB ，在正方体ABCD -f\B ,C 1D 1中，BC..l 平面A BB A ，棱BC 的中点为E,则BE..l 平面A BB I A ，而BFc 平面A BB A ，故BE..l BF,则乙EFB 即为迎线EF 与平面A BB I A 所成角，设正方体棱长为2,则BE=l,BF=.JB I F 2+B阻＝j了I ＝心，BE1✓6则EF =✓BF 2+BE 2＝拆，故sin乙E FB =－－＝－－＝一－故选：BEF拆6A lni ,DI L ,“K ,＇,'…,'} ，夕,j A5【解析】由例＝石，（2ii-b)·b =3,得2li·b -lbi 2=2li·b -2=3,即a 6=－525由已知得la:1=2,所以向摄6在向量a上的投影向量为彗向＝＼卢＝｀石，l)＝厂产，i)故选：A .as l6【解析】若函数f(x)在（l，切）上单调递增，则｛，解得a5-，Il-2a之02所以“a�O"是＂函数f(x)在(1.冲~)上单调递增”的充分不必要条件．故选：A7【解析】设优弧BC 所在圆的圆心为O,半径为R,连接OA ,OB ,OC 易知“水滴＂的＂竖直商度”为OA +R, OA +R 45 “水平宽度”为2R,由题意知＝一，解得OA=－R 因为AB 与圆弧相切千点B ,2R 3 3OB R 3 所以B 在Rt 心ABO 中，sin乙BAO =—=—=－冗OA 5 :::...R5，又乙BAO e l 0，一，（』4所以COS乙BAO=.Jl-sm 汔BAO ＝一，由对称性知，5乙BAO ＝乙CA O,则乙BAC=2乙BAO,3 4 24所以sin 乙BAC=2sin 乙BAOcos 乙BA0=2x-=-x-=—故选：D.5 5 258【解析】根据已知条件设理科女生有x 1人，理科男生有X 2人：文科女生有）'1人，文科男生有）5人；根据题意可知：X 1 + X 2 > Y i + Y 2'X i +Y i > X 2 + Y 2'根据同向不等式可加的性质有：X 1 + X 2 + X 1 + Y 1 > Y 1 + Y 2 + X 2 + Y 2'即X 1> Y 2，所以理科女生多千文科男生，C正确其他选项没有足够证据论证故选：C .二、多项选择题：本题共3小题，每小题满分6分，共18分．在每小题给出的四个选项中，有多项符合题目要求全部选对得6分，部分选对得部分分，有选错的得0分．题号I 9 I 10 I 11全部正确选项I A D I ABO I ACD9【解析】数据从小到大排列为：1,1, 2, 3, 3, 3, 3, 4, 5, 5对千A,该组数据的极差为5-1=4,故A正确：对于B,众数为3,平均数为lx2+2+3x4+4+5x210=3,两者相等，故B错误；对干C,方差为而伈－3)2x2+(2-3)2xl+(3-3)2x4+(4-3)2xl+(S-3)2x2] = 1.8,故C错误，对千D,10x80%=8,这组数据的第80百分位数为第8个数和第9个数的平均数4.5,故D正确故选：AD.10【解析】由图像可知：f(x)ma x = 2, A= 2:又f(0)=2s叩＝－l,故sinrp＝一L，又lrp|＜巴，所以rp＝－巴，所以A项正确，2 2 6已知f（气＝2sin（五0－勹＝0,由五点作图法可知：卫坛－巴＝亢，解得：OJ=2'所以B项正l2 12 6 l2 6确；故f(x) =2sin（三）则xj.（咕）＝2xsin2x设h(x)=xf.（咕）＝2xsin2x则h(-x)= 2(-x)sin(-2x) =2.xsin2x= h(x)，所以函数y=.-1;小号）是偶函数，故C项错误g(x)=f(x十艺）＝2s i n[2(x+：)－去］＝2s i n(2x＋艺）＝2c o s[�-(2x＋艺）］=2cos甘－2x)=2cos（三），所以D项正确故选：ABD.五II【解析】A选项，经验算，点(—,0和(-1,1)的坐标满足曲线L的方程x2 +(y-lxl)2 =L所以` o)和(-l,l）均在L上故2A项：确B 选项，I OP l ＝心三了，因为曲线L:x江(y-I 入扩＝l 关千Y 轴对称，当x 以0时，x 2 +(y-x)2 =l,设x=cos0, y-x= s in0,0e[－豆］，2 2.l+co s20 所以IOPl 2=.,\,:2+y 2=cos 20+(cos0+sin0)2 =l+�+sin20 23 1 3森l =-＋sin20+－cos20=－＋—sin (20 + rp ),其中tanrp ＝一，2 22 22 所以OP l min =[工石－�,10P 1m ax =[工石＋12 2 2 2 2 2，所以10月的最大值和最小值之和为石，故B项错误；C 选项，因为曲线L:x 2+(y -l x 忙＝1关千Y 轴对称，当x习0时，x 2+(y-x)2 =I ,则(y-x)2 =1-.,\,，2，所以y =x 土』7了因求，占P 的纵坐标的最大值，故取y =x+.[i':了，2又y 2=(x ＋石二了）＝1+2x../I 二了＝1+2[x.了7平1+.,\,;2+(l －入＂2)=2（当且仅当x 2＝上时等号2成立），所以y�.,fi ，故C项正确；x -D 选项，IPA I +I P B� 2✓3等价千点P 在椭圆上－＋—＝1内（包含椭圆），由B 项可知，即满足：322(cos0+sin0)2 +3cos 20 � 6,即2(l+sin20)+3(1+cos20)�6，整理得：23 4sin20 + 3cos20 � 5,即5sin(20+/3）�5'其中其中tan/3＝－，即sin(20+/3）�l 恒成立，则故D4项正确故选：A BD .三、填空题：本题共3小题，每小题5分，共15分．12.32五5314.e i12.【解析】当x =l 时，二项式展升式各项的系数和为25=32故答案为：3213【解析】由题意知I Mi l =a-c,I F;Fz l =2c,IF;科＝c+a,且三者成等比数列，则IFiFi l 2= IAF;I .I F;BIl石石即4c 2= (c-a )(c +a )= c 2 -a 2,所以e 2=－，所以e =—故答案为：—－55514【解析】设方程ln （釭＋勹＝k的实根为X。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

广东省惠州市2021届高三上学期第一次调研数学试
题
学校_________ 班级__________ 姓名__________ 学号__________
一、单选题
1. 设集合，集合，则（）A．B．
C．D．
2. 复数满足，其中为虚数单位，则复数=（）A．B．C．D．
3. 已知，则的值为（）
A．B．C．D．
4. 已知向量，向量，若，则实数（）
A．B．
C．D．
5. 已知正方体的棱长为1，则直线与直线所成角的余弦值为（）
A．B．C．D．
6. 已知双曲线的一条渐近线平行于直线，
则双曲线的离心率为（）
A．B．C．D．
7. 《张丘建算经》是我国北魏时期大数学家张丘建所著，约成书于公元466-485年间．其中记载着这么一道“女子织布”问题：某女子善于织布，一天比一天织得快，且每日增加的数量相同．已知第一日织布5尺，30日共织布390尺，则该女子织布每日增加（）尺
A．B．C．D．
8. 函数的部分图象的大致形状是（）
A．B．
D．
C．
9. 根据党中央关于“精准”脱贫的要求，我市某农业经济部门派四位专家对三个县区进行调研，每个县区至少派一位专家，则甲，乙两位专家派遣至同一县区的概率为（）
A．B．C．D．
10. 若在定义域内存在实数，满足，则称为“有点奇函数”，若为定义域上的“有点奇函数”，则实数
的取值范围是（）．
A．B．
C．D．
二、多选题
11. 下列说法中正确的有（）
A ．不等式恒成立
B．存在a ，使得不等式成立
D．若正实数x，y 满足，则C ．若，则
12. 在空间中，已知a，b 是两条不同的直线，，是两个不同的平面，则下列选项中正确的是（）
A ．若，且，，，则
B ．若，且，，则
C．若a与b 相交，且，，则与相交
D ．若，且，，则
三、填空题
13. 函数在点处的切线方程为______．
14. 二项式的展开式中的系数是_________．
15. 若抛物线y2=4x上的点M到焦点的距离为10，则M到y轴的距离是
_______．
四、双空题
16. 已知△ABC，AB=AC=4，BC=2．点D为AB延长线上一点，BD=2，连结CD，则△BDC的面积是______，cos∠BDC=_______．
五、解答题
17. 已知等差数列的公差，若，且，，成等比数列. （1）求数列的通项公式；
（2）设，求数列的前项和.
18. 在中，角的对边分别为，且
．
（1）求角的值；
（2）若，的面积为，求的周长．
19. 如图，底面是边长为1的正方形，平面，
，与平面所成角为60°.
（1）求证：平面；
（2）求二面角的余弦值.
20. 已知椭圆（）的一个焦点为，且该椭圆经
过点．
（1）求椭圆的方程；
（2）过点作直线与椭圆交于不同的两点、，试问在轴上是否存在
定点使得直线与直线恰关于轴对称？若存在，求出点的坐标；若不存在，说明理由．
21. 已知6名某疾病病毒密切接触者中有1名感染病毒，其余5名健康，需要通过化验血液来确定感染者．血液化验结果呈阳性的即为感染者，呈阴性即为健康．
（1）若从这6名密切接触者中随机抽取3名，求抽到感染者的概率；
（2）血液化验确定感染者的方法有：①逐一化验；②平均分组混合化验：先将血液样本平均分成若干组，对组内血液混合化验，若化验结果呈阴性，则该组血液不含病毒；若化验结果呈阳性，则对该组的备份血液逐一化验，直至确定感染者．
（i）采取逐一化验，求所需化验次数的分布列及数学期望；
（ii）采取平均分组混合化验（每组血液份数相同），求不同分组方法所需化验次数的数学期望．你认为选择哪种化验方案更合理？请说明理由．
22. 已知函数．
（1）若，求的极值；
（2）若，求正实数的取值范围．。