无刻度直尺作图(一)

合集下载

掌握无刻度直尺在几何作图中的应用技巧

掌握无刻度直尺在几何作图中的应用技巧直尺是几何学中常用的工具之一，用于绘制直线和测量长度。

无刻度直尺是一种没有刻度的直尺，可以准确地划线和测量，但需要掌握一些技巧才能正确使用。

掌握无刻度直尺在几何作图中的应用技巧对于学习几何学和解决几何问题非常重要。

本文将介绍几种常见的无刻度直尺的应用技巧。

一、使用无刻度直尺绘制直线无刻度直尺没有刻度，但我们可以利用直角来绘制垂直或水平的直线。

首先，将直尺的一边与绘图纸上的一条直线对齐，并确定直尺的一端与绘图纸上的一个点相切。

然后，将另一边轻轻地与直尺上的直角对齐，并保持直尺与绘图纸保持紧密接触。

这样，我们就可以绘制一条垂直或水平的直线。

二、使用无刻度直尺绘制等边三角形等边三角形的三条边长度相等。

使用无刻度直尺绘制等边三角形的关键是确定等边三角形的边长。

首先，选择无刻度直尺上的一个固定长度，将直尺的一端放置在绘图纸上的一个点上。

然后，保持直尺与绘图纸保持紧密接触，将直尺转动至一个合适的角度，使直尺的另一端与绘图纸上的一点相切。

这样，我们就可以绘制等边三角形的一条边。

接下来，使用相同的方法绘制另外两条边，确保它们的长度与第一条边相等即可。

三、使用无刻度直尺绘制角度使用无刻度直尺绘制角度需要注意的是，无刻度直尺上没有刻度，无法准确测量角度的大小。

因此，我们需要通过其他的方法来绘制所需的角度。

一种常用的方法是使用三角板或者其他角度工具来辅助绘制。

首先，确定要绘制的角度的大小，并选择一个合适的角度工具。

将角度工具的一边对齐于绘图纸上的一条直线，并确保角度工具上的角度大小与要绘制的角度相等。

然后，将无刻度直尺的一边与角度工具的另一边对齐，并保持直尺与绘图纸保持紧密接触。

这样，我们就可以在绘图纸上绘制出所需的角度。

四、使用无刻度直尺测量线段长度无刻度直尺没有刻度，无法直接测量线段的长度。

但我们可以通过比较两条线段的长度来大致测量线段的长度。

使用无刻度直尺测量线段长度的关键是选择一个已知长度的线段作为基准。

2025年中考数学总复习第一部分考点精讲第七章图形变化微专题(十五)无刻度直尺作图

2025版
数学
甘肃专版
解：(1)如图①,点F即为所求. (2)如图②,点G即为所求. (3)如图③,点H,H′即为所求.
2025版
数学
甘肃专版
【方法归纳】三角形中,已知两边中点： (1)画第三边中点时,一般运用“三角形三条中线交于一点”； (2)画某条中位线的中点时,先确定该中位线对应的底边中线,根据相似三角形的性质,由底边中线与中位线的交点确定中点； (3)一般地,已知中位线,可由中位线直接得到比例为1∶2的线段,由中位线的性质可构造全等三角形,得到相等线段,也可由相似三角形的性质得到1∶3,1∶4的线段.
2025版
数学
甘肃专版
【方法归纳】特殊四边形中,已知一边中点,由对称性画出其他三边的中点；将特殊四边形的四个中点呈“十字相连”,得到四个与原四边形相似的小的四边形,继续作这些小四边形的中点并呈“十字相连”,得到一个网格,每一个中点均是网格的格点,且该网格具有该特殊四边形的一切性质.
2025版
AC与网格线的交点.先将点B绕
点E旋转180°得到点F,画出点F,
再在AC上画点G,使DG∥BC；
(2)在图②中,P是边AB上一点,∠BAC＝α.先将AB绕点A逆时针旋转2α,得到线
段AH,画出线段AH,再画点Q,使P,Q两点关于直线AC对称.
2025版
解：(1)作图如图①所示. (2)作图如图②所示.
2025版
数学
甘肃专版
解：(1)如图①,AP即为所求. (2)如图②,AG即为所求.
2025版
数学
甘肃专版
5.(2022·武汉)如图是由小正方形组成的9×6网格,每个小正方形的顶点叫做格点.
△ABC的三个顶点都是格点.仅用无刻度的直尺在给定网格中完成画图,画图过

巧用无刻度直尺作图几例

二、用无刻度直尺同时平分平行四边形和圆的面积
例２如图２，己知：ＱＯ位于平行四边
形ＡＢＣＤ内，用无刻度直尺将ＱＯ和平行
四边形ＡＢＣＤ的面积同时平分．
【作法】
１．连结对角Ｃ、ＢＤ，其交点为０；
Ｂ
２．过０和０用无刻度直尺作直线Ｚ交
·
．
．
／４ＣＢ：／＿＿ＡＤＢ：９０”，￣［ＩＡＤ上ＰＢ，ＢＣ３ＰＡ．＿
· 点为 △ＡＰＢ的垂心．
．
．
‘
．
．
ＰＨＬＡＢ．
从以上几例可以看出，用无刻度直尺作一类特殊要求的几
何图形，就是根据己给命题内含的特殊性，再根据几何公理，即
经过两点有且只有一条直线而作出的，这就需要我们对问题有
．．
又·．·ｏ０．既是轴对称图形又是中心对称图形，而直线Ｚ又过圆心０，
· 直线Ｚ平分ｏ０的面积．
．
．
故直线Ｚ同时平分ｏ０和平行四边形ＡＢＣＤ的面积．
三、用无刻度直尺作已知直线的垂线
例３如图３，己知：点Ｊｐ为半ｏＤ外的一点，用无刻度直尺过点Ｐ作ＡＢ
一、用无刻度直尺将三角形面积三等分例１如图１，己知：点Ｇ为ＡＡＢＣ的重心，用无刻度直尺将其面积三等分．【作法】分别过Ａ、Ｇ；Ｂ、Ｇ；Ｃ、Ｇ用无刻度直尺作直线ｚ、ｚ、ｚ交ＢＣ、、于Ｄ、、Ｆ，则Ｚ、ｆ１、Ｚ将 △ＡＢＣ的面积三等分．证明：设ＡＢＧＣ和ＡＡＢＣ的高为ｈ、ｈ，在ＡＢＧＣ和ＡＡＢＣ中，

人教版九上数学第二十三章方法技巧旋转作图(二)无刻度直尺作图

人教版九上数学第二十三章方法技巧旋转作图（二）无刻度直尺作
图
1.已知平行四边形ABCD，请用无刻度直尺完成下列作图（保留作图痕迹）．
(1) 如图1，点E是平行四边形ABCD的边AB上的点，在CD边上找一点F，使得CF=
AE；
(2) 如图2，点P是平行四边形ABCD内部的点，过点P作直线l，使得直线l平分四边形
ABCD的面积；
(3) 如图3，点E为BC上一点，且CE=CD，作∠ABC的平分线BP．
2.已知矩形ABCD，请用无刻度直尺完成下列作图（保留作图痕迹）．
(1) 如图1，在矩形ABCD内部找一点O，使得OA=OB=OC=OD；
(2) 如图2，点E为AD边上一点，DE=2AE，在BC上画一点F，使BF=2CF；
(3) 如图3，点P为CD的中点．
①画出矩形的一条对称轴；
②画出PC的中点Q．
3.已知菱形ABCD，请用无刻度直尺完成下列作图（保留作图痕迹）
(1) 如图1，P是BC的中点，画出AD的中点H；
(2) 如图2，E是对角线BD上的一点，在BD上找点F，使DF=BE．
4.已知正方形ABCD，请用无刻度直尺完成下列作图（保留作图痕迹）．
(1) 如图1，E是BC的中点，作BF∥DE交AD于点F；
(2) 如图2，E是CD边上一点，将△ADE绕点A顺时针旋转90∘，画出旋转后的△ABF．
答案
1. 【答案】
(1)
(2)
(3)
2. 【答案】
(1)
(2)
(3)
3. 【答案】
(1)
(2)
4. 【答案】
(1)
(2)。

中考数学压轴题之无刻度直尺作图技巧分类详解

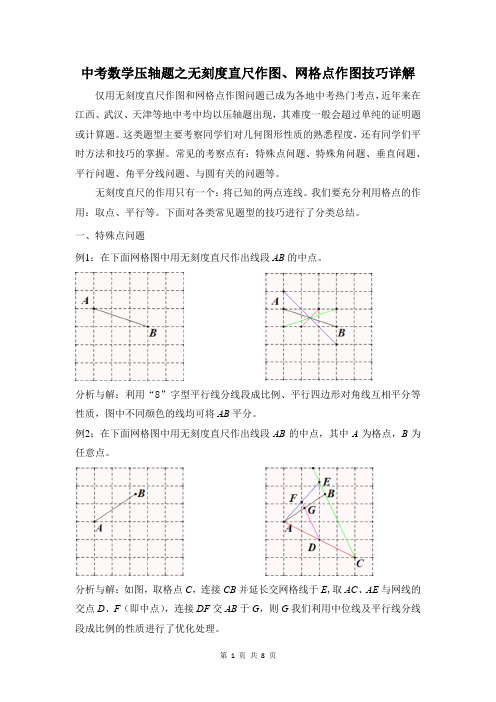
中考数学压轴题之无刻度直尺作图、网格点作图技巧详解仅用无刻度直尺作图和网格点作图问题已成为各地中考热门考点，近年来在江西、武汉、天津等地中考中均以压轴题出现，其难度一般会超过单纯的证明题或计算题。

这类题型主要考察同学们对几何图形性质的熟悉程度，还有同学们平时方法和技巧的掌握。

常见的考察点有：特殊点问题、特殊角问题、垂直问题、平行问题、角平分线问题、与圆有关的问题等。

无刻度直尺的作用只有一个：将已知的两点连线。

我们要充分利用格点的作用：取点、平行等。

下面对各类常见题型的技巧进行了分类总结。

一、特殊点问题例1：在下面网格图中用无刻度直尺作出线段AB的中点。

分析与解：利用“8”字型平行线分线段成比例、平行四边形对角线互相平分等性质，图中不同颜色的线均可将AB平分。

例2：在下面网格图中用无刻度直尺作出线段AB的中点，其中A为格点，B为任意点。

分析与解：如图，取格点C，连接CB并延长交网格线于E,取AC、AE与网线的交点D、F（即中点），连接DF交AB于G，则G我们利用中位线及平行线分线段成比例的性质进行了优化处理。

例3：在下面网格图中，在线段AB 上找一点C ，使AB AC 31=。

方法1方法2 方法3分析与解：方法1和方法2都利用了网格线平行的性质，通过“8”字型模型，构造1：2的相似比例，从而将线段AB 分为1：2两段。

方法3利用了重心的性质，AB 和EF 为BED ∆的两条中线，所以C 为BED ∆的重心。

二、特殊角问题例4：在下面网格图中找格点C ，使O BAC 45=∠。

分析与解：利用“12345”模型，即若βα、均为锐角，且31tan ,21tan ==βα，则O 45=+βα。

例5：如下图，利用无刻度直尺在线段MN 上找一点Q ，使O AQB 45=∠。

分析与解：O AQB 45=∠，典型定弦定角问题。

注意到O AMB 90=∠，所以点Q 在以M 为圆心，MA 长为半径的圆上，故2=MQ 。

2022-2023学年人教版九年级上册数学期中复习之作图专题练习

期中复习之作图题模块一：无刻度直尺作图1.如图，在下列10×10的网格中，横、纵坐标均为整数的点叫做格点，例如A（2,1），B（5,4），C（1,8）都是格点。

（1）直接写出△ABC的形状；（2）要求在下图中仅用无刻度的直尺作图：将△ABC绕点A顺时针旋转角度a得到△AB1C1,a=∠BAC，其中B,C的对应点分别为B1,C1,操作如下：第一步：找一个格点D，连接AD，使∠DAB=∠CAB；第二步：找两个格点C1,E,连接C1E交AD于点B1;第三步：连接AC1,则△AB1C1即为作出的图形。

请你按步骤完成作图，并直接写出D，C1,E三点的坐标。

2.如图，在△ABC中，∠B=90°，点D为边AC的中点，请按下列要求用无刻度的直尺作图，并解决问题：（1）作点D关于BC的对称点O；（2）在（1）的条件下，将△ABC绕点O顺时针旋转90°，画出旋转后的△EFG（其中A,B,C三点旋转后的对应点分别是E,F,G）。

3.如图，在正方形网格中，△ABC的顶点在格点上，请仅用无刻度直尺完成以下作图．（1）在图1中，作△ABC关于点O对称的△A1B1C1；（2）在图2中，作△ABC绕点A顺时针旋转90°后得到的△AB2C2．4.如图，在正方形网格中，△ABC的顶点在格点上．请仅用无刻度直尺完成以下作图（保留作图痕迹）．（1）在图1中，作△ABC关于点O对称的△A'B'C'；（2）在图2中，作△ABC绕点A顺时针旋转一定角度后，顶点仍在格点上的△AB'C'．5.如图AB是半圆的直径，图1中，点C在半圆外；图2中，点C在半圆内，请仅用无刻度的直尺按要求画图．（1）在图1中，画出△ABC的三条高的交点；（2）在图2中，画出△ABC中AB边上的高．模块二：网格作图10 的网格中的位置如图所示1.⊿ABC与点O在10（1）画出⊿ABC绕点O逆时针旋转90°后的图形；（2）若⊙M能盖住⊿ABC，则⊙M的半径最小值为 .2.如图，ABC ∆的顶点坐标分别为(0,1)A ，(3,3)B ，(1,3)C ．（1）画出ABC ∆关于点O 的中心对称的△111A B C ．（2）画出ABC ∆绕点O 顺时针旋转90︒后的222A B C ．（3）求（2）中线段BC 扫过的面积．3.如图所示，正方形网格中，ABC ∆为格点三角形（即三角形的顶点都在格点上）．（1）把ABC ∆沿BA 方向平移后，点A 移到点1A ，在网格中画出平移后得到的△111A B C ；（2）把△111A B C 绕点1A 按逆时针方向旋转90︒，在网格中画出旋转后的△122A B C ；（3）如果网格中小正方形的边长为1，求点B 经过（1）、（2）变换的路径总长．4.如图，在边长为1的小正方形组成的网格中，△AOB 的三个顶点均在格点上，点A 、B 的坐标分别为 A （﹣2，3）、B （﹣3，1）．（1）画出坐标轴，画出△AOB 绕点O 顺时针旋转90°后的△A 1OB 1；（2）点A 1的坐标为；（3）四边形AOA 1B 1的面积为．5.如图，边长为1的方格纸中建立直角坐标系，△OAB旋转得到△OA'B′，观察图形并回答问题：（1）请将作图过程补充完整；并说明△OAB是如何旋转得到△OA'B'．（2）填空：△OAA′的形状是．模块三：非网格作旋转图形1.如图，菱形ABCD和Rt△ABE，∠AEB=90°，将△ABE绕点O旋转180°得到△CDF。

2020年无锡中考初三数学第二轮专题复习：仅用无刻度直尺作图 1

无锡市**实验学校初三数学(2017级) 日期：2020−5−21 讲义编号： < >初三数学第二轮专题复习：仅用无刻度直尺作图1班级：________ 学生：______________姓名：______________一、格点作图例1：如图1是边长为1的小正方形网格，请用无刻度的直尺在图中作图：（1）画线段AB ＝17，使得点A ，B 均落在格点上；（2）在线段AB 上画出点P ，使AP ＝2173，并说明理由．CBA练一练：如图2是边长为1的小正方形网格，请用无刻度的直尺在图中画线段AP ＝5267．（1）过点C 画直线CD ，使CD ∥AB ，过点C 画直线CF ，使CF ⊥AB ；（2）画线段AB 的垂直平分线MN ．例3：如图4，A ，O ，B 均为格点，请用无刻度的直尺作出∠CAB 的平分线。

CBACB ACBA图4 图5 图6练一练：在6×6的正方形网格中，点A 、B 、C 均在格点上，请仅用无刻度的直尺画图：（1）在图5中找出∆ABC 的重心G ．（2）在图6中找出∆ABC 的外心O ．练一练：如图7，A 、B 、C 、D 均在正方形网格的格点上，D 是边AB 上一点，请用无刻度的直尺在△ABC 的边BC 上找一点E ，使得△BDE ∽△BAC 相似。

图7D CBA思考题：如图8，A、B、C均在正方形网格的格点上，用无刻度的直尺，在线段AC上找一点D，使得AB2＝AD•AC。

OA图8 图9例4：如图9，点A、B、O均为6×6的正方形格点图中的格点．（1）tan∠AOB＝；（2）请用无刻度的直尺画出∠COB，使得tan∠COB＝23．例5：如图10，在10×10的正方形格点图中，点A、B、C均在格点上，请仅用无刻度的直尺：（1）画出∆ABD，使得∆ABD与∆ABC关于AB对称；（2）画出∆ACE，使得∆ACE与∆ACB关于AC对称；图10 图11 图12 练一练：如图11，点A，B，C是边长为1的正方形网格中的格点，点P，Q分别为线段AB，AC上的动点．请仅用无刻度的直尺，画出当PC＋PQ取得最小值时的线段PC、PQ．例6：如图12，点A、B、C均为6×8的正方形格点图中的格点．请用无刻度的直尺，画出一个以AB为一边的矩形ABMN，使矩形ABMN的面积等于△ABC的面积．练一练：如图13，点A、B、C均为8×9的正方形格点图中的格点．请用无刻度的直尺，在△ABC的内部有一点P，满足S△P AB：S△PBC：S△PCA＝1：2：3，并简要说明点P的位置是如何找到的（不要求证明）．- 2 -- 2 -。

无刻度直尺作图专题

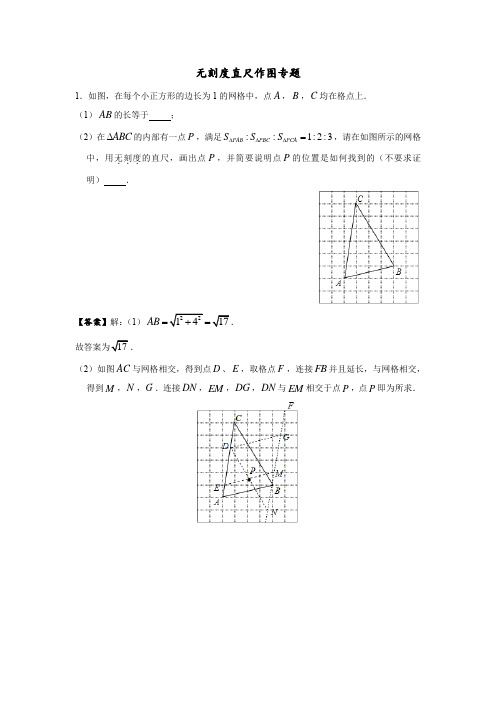
无刻度直尺作图专题1．如图，在每个小正方形的边长为1的网格中，点A ，B ，C 均在格点上．（1）AB 的长等于；（2）在ABC ∆的内部有一点P ，满足::1:2:3PAB PBC PCA S S S ∆∆∆=，请在如图所示的网格中，用无刻度．．．的直尺，画出点P ，并简要说明点P 的位置是如何找到的（不要求证明）．【答案】解：（1）AB =．（2）如图AC 与网格相交，得到点D 、E ，取格点F ，连接FB 并且延长，与网格相交，得到M ，N ，G ．连接DN ，EM ，DG ，DN 与EM 相交于点P ，点P 即为所求．2．如图，六个完全相同的小长方形拼成了一个大长方形，AB是其中一个小长方形的对角线，请在大长方形中完成下列画图，要求：①仅用无刻度直尺，②保留必要的画图痕迹．（1）在图1中画出一个45︒角，使点A或点B是这个角的顶点，且AB为这个角的一边；（2）在图2中画出线段AB的垂直平分线．【答案】解：（1）如图所示，45∠=︒．(AB、AC是小长方形的对角线）．ABC（2）线段AB的垂直平分线如图所示，3．如图，已知正七边形ABCDEFG，请仅用无刻度的直尺，分别按下列要求画图．（1）在图1中，画出一个以AB为边的平行四边形；（2）在图2中，画出一个以AF为边的菱形．【答案】解：（1）连接AF、BE、CG，CG交AF于M，交BE于N．四边形ABNM是平行四边形．（2）连接AF、DF，延长DC交AB的延长线于M，四边形AFDM是菱形．4．如图，在四边形ABCD中，//AB CD=，E为AB的中点，请仅用无刻度的直AB CD，2尺分别按下列要求画图（保留画图痕迹）．（1）在图1中，画出ABD∆的BD边上的中线；（2）在图2中，若BA BD∆的AD边上的高．=，画出ABD【答案】解：（1）如图1所示，AF即为所求：（2）如图2所示，BH即为所求．5．在ABC=，点A在以BC为直径的半圆内．请仅用无刻度的直尺分别按下列∆中，AB AC要求画图（保留画图痕迹）．（1）在图1中作弦EF，使//EF BC；（2）在图2中以BC为边作一个45︒的圆周角．【答案】解：（1）如图1，EF为所作；（2）如图2，DBC∠为所作．6．如图，在正方形网格中，ABC∆的顶点在格点上．请仅用无刻度直尺完成以下作图（保留作图痕迹）．'''；（1）在图1中，作ABC∆关于点O对称的△A B C（2）在图2中，作ABC∆绕点A顺时针旋转一定角度后，顶点仍在格点上的△AB C''．'''即为所求．【答案】解：（1）如图1中，△A B C（2）如图2中，△AB C''即为所求．。

掌握无刻度直尺在几何作图中的方法与技巧

掌握无刻度直尺在几何作图中的方法与技巧直尺作为几何作图的基本工具之一，在绘制线段、角度等几何图形的过程中起到重要作用。

传统的刻度直尺在一些情况下可能不够精确，而无刻度直尺则可以克服这一限制，能够更加准确地绘制图形。

本文将介绍无刻度直尺在几何作图中的方法与技巧，帮助读者掌握这一重要工具的使用。

一、无刻度直尺简介无刻度直尺，又称为不透明直尺或者不透明尺，是一种没有刻度且不透明的直尺。

它通常由透明或半透明材料制成，边缘呈直线状，并且具备一定的刚性。

由于无刻度直尺没有刻度标记，所以无法直接读取长度，但是可以用来测量、绘制线段、角度等几何图形。

二、使用无刻度直尺作图的方法1. 绘制直线要绘制一条直线，首先需要选择两个明确的点作为起点和终点。

将无刻度直尺平放在绘图纸上，将起点和终点对准无刻度直尺的边缘上，并且保持直尺的位置不变，然后用一支铅笔或者细线笔沿着直尺的边缘缓慢滑动，从而绘制出一条直线。

2. 绘制平行线若要绘制与已有直线平行的直线，可以利用无刻度直尺的边缘作为导向。

首先，将直尺平放在已有直线上，调整角度，使直尺与直线边缘平行。

然后，在直尺的边缘上选择一个点作为起点，然后保持直尺不动，沿着边缘绘制出一条平行线。

3. 绘制垂直线绘制与已有直线垂直的直线时，同样可以利用无刻度直尺的边缘作为导向。

将直尺平放在已有直线上，调整角度，使直尺与直线边缘垂直。

然后，在直尺的边缘上选择一个点作为起点，保持直尺不动，沿着边缘绘制出一条垂直线。

4. 绘制角度使用无刻度直尺绘制角度时，需要首先确定一个顶点，然后将直尺放置在该顶点上，并且调整角度。

接下来，在直尺的边缘上选择两个点，作为角度的两条边，保持直尺的位置不变，沿着边缘绘制出所需的角度。

三、无刻度直尺在几何作图中的技巧1. 使用透明胶带或者可移动标记由于无刻度直尺没有刻度标记，有时可能难以准确测量和标记长度。

此时，可以使用透明胶带或者可移动标记来辅助测量和标记。

将透明胶带粘贴在直尺边缘，标出所需长度，或者使用可移动标记夹在直尺上，便于测量和标记长度。

九年级数学上册第24章无刻度直尺作图——画内心

（九年义务教育九年级上册二十四章圆作图题）
（九年义务教育九年级上册二十四章圆作图题）
三角形角平分线的交点
（九年义务教育九年级上册二十四章圆作图题）
三角形角平分线的交点
（九年义务教育九年级上册二十四章圆作图题）
三角形角平分线的交点
E
（九年义务教育九年级上册二十四章圆作图题）
三角形角平分线的交点
（九年义务教育九年级上册二十四章圆作图题）
（九年义务教育九年级上册二十四章圆作图题）
三角形角平分线的交点
弧BE=弧CE E
AE是△ABC的一条角平分线 F
（九年义务教育九年级上册二十四章圆作图题）
三角形角平分线的交点
弧BE=弧CE E
AE是△ABC的一条角平分线 F
（九年义务教育九年级上册二十四章圆作图题）
三角形角平分线的交点
弧BE=弧CE E
AE是△ABC的一条角平分线 BF也是△ABC的一条角平分线 F
（九年义务教育九年级上册二十四章圆作图题）
三角形角平分线的交点
P 弧E=弧CE
E
AE是△ABC的一条角平分线 BF也是△ABC的一条角平分线 F
（九年义务教育九年级上册二十四章圆作图题）
三角形角平分线的交点
P 弧BE=弧CE
E
AE是△ABC的一条角平分线 BF也是△ABC的一条角平分线 F AE、BF相交于P点，是所求内心。
弧BE=弧CE E
（九年义务教育九年级上册二十四章圆作图题）
三角形角平分线的交点
弧BE=弧CE E
（九年义务教育九年级上册二十四章圆作图题）
三角形角平分线的交点
弧BE=弧CE E
AE是△ABC的一条角平分线
（九年义务教育九年级上册二十四章圆作图题）

专题2：无刻度的直尺作图(一)-人教版九年级数学中考复习专题练

中考复习专题2：无刻度的直尺作图（一）1.如图，点A（3，1），B（9，7），C为AB中点，点D（8，0）．（1）将线段AD绕点A逆时针旋转90°得到线段AP，画出线段AP的位置，并直接写出的值；（2）将点B绕点C逆时针旋转180°，用直尺或圆规画出点B所经过的路径L；（3）延长AP交（2）中路径L于点E，用无刻度的直尺在（2）中的路径上找点F，使EF∥AB，保留作图痕迹．【解答】解：（1）如图所示，线段AP即为所求，∵AP＝＝，PB＝＝，∴＝1；（2）如图所示，半圆即为路径L；（3）如图所示，EF即为所求．2.如图，在下列10×10的网格中，横、纵坐标均为整点的数叫做格点，例如A（﹣2，﹣2）、B（5，﹣3）、C（1，1）都是格点．（1）∠ACB的大小为90°．（2）要求在图中仅用无刻度的直尺作图：以A为中心，取旋转角等于∠BAC．把△ABC逆时针旋转，得到△AB1C1，其中点C和点B的对应点分别为点C1和点B1，操作步骤如下：第一步：延长AC到格点B1，使得AB1＝AB．第二步：延长BC到格点E，使得CE＝CB，连接AE．第三步：取格点F，连接FB1交AE于点C1，则△AB1C1即为所求．请你按步骤完成作图，并直接写出B1．【解答】解：（1）观察图象可知∠ACB＝90°．故答案为90°．（2）如图，△AB1C1即为所求．其中点B1坐标为（3，3）．3.如图，由边长为1的小正方形构成的网格中，每个小正方形的顶点叫做格点，△ABC的顶点在格点上．（1）直接写出△ABC的面积为；（2）请用无刻度的直尺画出将CB绕C点顺时针旋转α（α＝2∠BAC）角后得到的线段CD，并写出点D的坐标为；（3）若一个多边形各点都不在⊙M外，则称⊙M全覆盖这个5多边形，已知点E（6，5），⊙M全覆盖四边形ABCE，则⊙M的直径最小为．【解答】解：（1）S△ABC＝×5×4＝10．故答案为10．（2）如图，AB＝＝5，BC＝5，∴AB＝CB，∴∠BAC＝∠ACB，∵∠BCD＝∠ACB+∠ACD＝∠BAC+∠ACD＝2∠BAC，∴∠ACD＝∠BAC，∴AB∥CD，点D即为所求，D（9，5）．（3）如图，作出△ABC，△ACE，△ABE，△ECB的外接圆可知：△BCE的外接圆⊙M全覆盖四边形ABCE，且⊙M的直径最小，直径＝BE＝＝故答案为．4.如图，在下列的网格中，横、纵坐标均为整点的数叫做格点，例如A（3，0）、B（0，4）、C（4，2）都是格点．（1）直接写出△ABC的形状；（2）要求在上图中仅用无刻度的直尺作图：将△ABC绕点B逆时针旋转得到△A1BC1，旋转角＝2∠ABC，请你完成作图；（3）在网格中找一个格点G，使得C1G⊥AB，并直接写出G点坐标．【解答】解：如图所示：（1）△ABC的形状为：直角三角形；（2）将△ABC绕点B逆时针旋转得到△A1BC1，旋转角＝2∠ABC；（3）在网格中找一个格点G，使得C1G⊥AB，G点坐标为（0，3）．5.如图，在边长为1的正方形网格中，已知A（0，0），B（8，6），C（8，0），要求用无刻度直尺作图，画出△ABC的内心．（1）在AC上找一格点D，使得BD平分∠ABC，则D（5，0）；（2）在BD上找一格点I使得CI平分∠ACB，则I点即为△ABC的内心，I（6，2）；（3）直接写出△ABC内切圆半径为2．【解答】解：如图，（1）在AC上找一格点D，使得BD平分∠ABC，则D（5，0）；（2）在BD上找一格点I使得CI平分∠ACB，则I点即为△ABC的内心，I（6，2）；（3）∵I点为△ABC的内心，∴I到三角形三边的距离为△ABC内切圆半径，∴IE＝IF＝2，即为△ABC内切圆半径．故答案为：5，0；6，2；2．6.坐标为整数的点叫格点，如图，已知A（-3，0）、B（-3，4）和原点都是格点，在如图6×9的网格中使用无刻度的直尺按要求作图．（1）找格点C，连BC，使BC与OA的交点就是OA的中点，画出图形直接写出C点坐标．（2）按以下方法可以作出∠AOB的平分线．第一步：找格点D，使OD=OB；第二步：找格点E，使DE⊥OB交AB于F；第三步：连OF，则OF是∠AOB的平分线；请你按步骤完成作图，并写出D、E三点的坐标．【解答】（1）如图1所示，取格点C（0，-4），连接BC与OA的交点就是AC的中点D，根据四边形ABOC 是平行四边形，对角线互相平分可得；（2）如图2，点D（0，-5），E（-1，3）．7.（1）如图1，方格纸中的每个小方格都是边长为1个单位的正方形，△ABC的顶点以及点O均在格点上．①直接写出AB的长为；②画出以AC为边，O为对角线交点的平行四边形ACA1C1；（2）如图2，画出一个以DF为对角线，面积为6的矩形DEFG，且D和E均在格点上（D、E、F、G按顺时针方向排列）；（3）如图3，正方形ABCD中，E为BC上一点，在线段AB上找一点F，使得BF=BE．（要求用无刻度的直尺画图，不准用圆规，不写作法，保留画图痕迹）【解答】（1）①AB=13；②如图1所示：（2）如图2所示：DF==25，矩形两边长为2，32，（3）如图3所示：8.如图，方格纸中每个小正方形的边长均为1，线段AB的两个端点在小正方形的顶点上．（1）在图1中画一个以AB为边的平行四边形ABCD，点C、D在小正方形的顶点上，且平行四边形ABCD的面积为15．（2）在图2中画一个以AB为边的菱形ABEF（不是正方形），点E、F在小正方形的顶点上，请直接写出菱形ABEF的面积．【解答】（1）如图1中，平行四边形ABCD即为所求．（2）如图2中，菱形ABEF即为所求，菱形ABEF的面积=8．9.如图，在7×7正方形网格中的每个小正方形边长都为1个单位长度，我们把每个小正方形的顶点称为格点，点A、B、C都为格点，且点A（1，2），请分别仅用一把无刻度的直尺画图；（1）过点C画一条线段AB的平行线段CD，直接写出格点D的坐标；（2）过点C画一条线段AB的垂直线段CE，直接写出格点E的坐标；（3）作∠DCE的角平分线CF，直接写出格点F的坐标；（4）作∠ABM，使∠ABM=45°，直接写出格点M的坐标；【解答】如图：根据画图可知：（1）D（6，2）；（2）E（3-3）；（3）F（7，-2）；（4）M（2，-2）．。

仅用无刻度的直尺作图题1

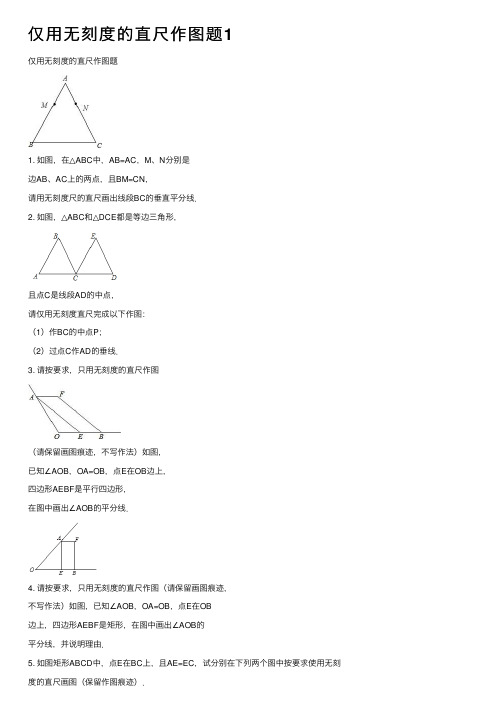
仅⽤⽆刻度的直尺作图题1仅⽤⽆刻度的直尺作图题1. 如图，在△ABC中，AB=AC，M、N分别是边AB、AC上的两点，且BM=CN，请⽤⽆刻度尺的直尺画出线段BC的垂直平分线．2. 如图，△ABC和△DCE都是等边三⾓形，且点C是线段AD的中点，请仅⽤⽆刻度直尺完成以下作图：（1）作BC的中点P；（2）过点C作AD的垂线．3. 请按要求，只⽤⽆刻度的直尺作图（请保留画图痕迹，不写作法）如图，已知∠AOB，OA=OB，点E在OB边上，四边形AEBF是平⾏四边形，在图中画出∠AOB的平分线．4. 请按要求，只⽤⽆刻度的直尺作图（请保留画图痕迹，不写作法）如图，已知∠AOB，OA=OB，点E在OB边上，四边形AEBF是矩形，在图中画出∠AOB的平分线，并说明理由．5. 如图矩形ABCD中，点E在BC上，且AE=EC，试分别在下列两个图中按要求使⽤⽆刻度的直尺画图（保留作图痕迹）．（1）在图1中，画出∠DAE的平分线；（2）在图2中，画出∠AEC的平分线．6. 如图，请仅⽤⽆刻度的直尺按下列要求画图：（1）如图1，在△ABC中，AB=AC，M、N分别是边AB、AC上的两点，且BM=CN，请画出线段BC的垂直平分线；（2）如图2，在菱形ABCD中，∠B=60°，E是AB边的中点，请画出线段BC的垂直平分线．图1 图2图1 图28. 如图，在正⽅形ABCD中，点M是BC边上任意⼀点，请你仅⽤⽆刻度直尺、⽤连线的⽅法，分别在图（1）、图（2）中按要求作图（保留作图痕迹，不写作法）．（1）在图（1）中，在AB边上求作⼀点N，连接CN，使CN=AM；（2）在图（2）中，在AD边上求作⼀点Q，连接CQ，使CQ∥AM．9. 如图，在矩形ABCD中，点E为AD的中点，请只⽤⽆刻度的直尺作图（1）如图1，在BC上找点F，使点F是BC的中点；（2）如图2，在AC上取两点P，Q，使P，Q是AC的三等分点．10. 请仅⽤⽆刻度的直尺在下列图1和图2中按要求画菱形．（1）图1是矩形ABCD，E，F分别是AB和AD的中点，以EF为边画⼀个菱形；（2）图2是正⽅形ABCD，E是对⾓线BD上任意⼀点（BE＞DE），以AE为边画⼀个菱形．11. 如图，将线段AB 放在边长为1的⼩正⽅形⽹格，点A 点B 均落在格点上，12. 如图AB 是半圆的直径，图1中，点C 在半圆外；图2中，点C 在半圆内，请仅⽤⽆刻度的直尺按要求画图．（1）在图1中，画出△ABC 的三条⾼的交点；（2）在图2中，画出△ABC 中AB 边上的⾼．13. 请仅⽤⽆刻度的直尺画图：（1）如图1，△ABC 与△ADE 是圆内接三⾓形，AB=AD ，AE=AC ，画出圆的⼀条直径．（2）如图2，AB，CD 是圆的两条弦，AB=CD 且不相互平⾏，画出圆的⼀条直径．C B A C B A 图1 图214. 作图题：在⊙O 中，点D 是劣弧AB 的中点，仅⽤⽆刻度的直尺画线的⽅法，按要求完下列作图：在图（1）中作出∠C 的平分线；在图（2）中画⼀条弦，平分△ABC 的⾯积．15. 如图，△ABC 是⊙O 的内接三⾓形，请仅⽤⽆刻度的直尺在下列图形中按要求画图．（1）在图1中，已知 OD ⊥BC 于点 D ，画出∠A 的⾓平分线；（2）在图2中，已知 OE ⊥AB 于点 E ，OF ⊥AC 于点 F ，画出∠A 的⾓平分线．16. 如图，点A 、B 在⊙O 上，点O 是⊙O 的圆⼼，请你只⽤⽆刻度的直尺，分别画出图①和图②中∠A 的余⾓．①图①中，点C 在⊙O 上；②图②中，点C 在⊙O 内．图1 图217. 等腰△ABC 中，AB=AC ，以AB 为直径作圆交BC 于点D ，请仅⽤⽆刻度的直尺，根据下列条件分别在图1、图2中画⼀条弦，使这条弦的长度等于弦BD ．（保留作图痕迹，不写作法）（1）如图1，∠A ＜90°；（2）如图2，∠A ＞90°．18. 在如图的正⽅形⽹格中，点O 在格点上，⊙O 的半径与⼩正⽅形的边长相等，请利⽤⽆刻度的直尺完成作图:在图（1）中画出⼀个45°的圆周⾓;在图（2）中画出⼀个22.5°的圆周⾓．19. 仅⽤⽆刻度的直尺过点C 作出圆的切线（保留作图痕迹，并简要的写出作图过程）．D C B A 图2图1 D C B A。

数学复习：无刻度直尺作图

数学复习：无刻度直尺作图1．（1）如图1，在△ABC 中，D 是BC 边上的一点，以AD 为直径作半圆O ，半圆O 经过点C ．若△ABC 的面积为10，请仅用无刻度的直尺作一个三角形，使所作三角形的面积等于5（2）如图2，在△ABC 中，DE ∥BF ，EF ∥AB ，若△ABC 的面积为10，请仅用无刻度的直尺作一个三角形，使所作三角形的面积等于52．在图1，图2中，点E 是ABCD 边AD 上的中点，请仅用无刻度直尺按要求画图，（保留作图痕迹）（1）在图1中，以BC 为边作三角形，使其面积等于ABCD 的面积；（2）在图2中，以BE ，ED 为邻边作四边形，使其面积等于ABCD 面积的一半．3．如图是由2个全等的正方形错位叠放组成的图形，请仅用没有刻度的直尺按要求完成下列作图．（1）在图1中画一个平行四边形（要求所画出的平行四边形不是矩形）；（2）在图2中画一个菱形（要求所画出的菱形不是正方形）．4．如图是由6个形状、大小完全相同的小矩形组成的大矩形，其中小矩形的长为2，宽为1，请用无刻度的直尺在矩形中完成以下作图（保留作图痕迹，不写作法）．（1）在图1中，画出一个面积为5的正方形；（2）在图2中，画出一个面积为4的非特殊的平行四边形．5．如图，四边形ABCD是平行四边形，AD与圆相切，请在下图中，仅用无刻度的直尺按要求画图．（1）如图①，若BC是圆的直径，画出平行四边形ABCD的边CD上的高；（2）如图②，若CD与圆相切，画出平行四边形ABCD的边AD上的高CE；（3）如图③，若CD与圆相切，画出平行四边形ABCD的边BC上的高AF．6．如图，在正方形ABCD中，请仅用无刻度直尺按下列要求作图（保留作图痕迹，不写作法）．（1）在图①中，将线段AB绕点O逆时针旋转一定角度，使点A与点B重合，点B与点C 重合，作出点O的位置．（2）在图②中，E为AB的中点，将△ABD绕点D逆时针旋转某个角度，得到△CFD，使DA与DC重合，作出△CFD．7．如图，在平面直角坐标系中，A ，B 是双曲线(0)k y k x=≠上的两点，请仅用无刻度的直尺完成下列作图（保留作图痕迹）．（1）在图1中画出一条与AB 相等的线段；（2）在图2中画出一个菱形．8．如图，AB 是O 中不过圆心的一条弦，请仅用无刻度的直尺，分别按下列要求画图．（1）在图1中画出一条弦CD 使//CD AB ；（2）在图2中，M 是AB 下方O 上的一点，以点A ，M 为顶点画一个直角三角形，使其第三个顶点也落在O 上，并使该直角三角形的一个内角与ABM ∠相等．数学复习：无刻度直尺作图答案1．（1）如图1，在△ABC 中，D 是BC 边上的一点，以AD 为直径作半圆O ，半圆O 经过点C ．若△ABC 的面积为10，请仅用无刻度的直尺作一个三角形，使所作三角形的面积等于5（2）如图2，在△ABC 中，DE ∥BF ，EF ∥AB ，若△ABC 的面积为10，请仅用无刻度的直尺作一个三角形，使所作三角形的面积等于5【答案】（1）由O 是AD 的中点，则连接OC ，BO ，可得出12OCD ACD S S ∆∆=，12BOD ABD S S ∆∆=，从而有12BCO ABC S S ∆∆=；（2）连接BE ，DF 交于点P ，根据平行四边形的性质可得出P 为BE 的中点，进而12AEP ABE S S ∆∆=，12PEC BCE S S ∆∆=，从而有12APC ABC S S ∆∆=．解：（1）如图，连接BO ，OC ，OCB ∆即为所求；（2）如图，连接BE ，DF 交于点P ，连接AP ，CP ，则APC ∆即为所求．此题主要考查了复杂作图，利用三角形的中线平分面积的性质，以及平行四边形的性质是解答此题的关键．2．在图1，图2中，点E 是ABCD 边AD 上的中点，请仅用无刻度直尺按要求画图，（保留作图痕迹）（1）在图1中，以BC 为边作三角形，使其面积等于ABCD 的面积；（2）在图2中，以BE ，ED 为邻边作四边形，使其面积等于ABCD 面积的一半．【答案】（1）连接CE 并延长，交BA 的延长线于点P ，根据()APE DCE ASA ≅ 可得PBC ABCD S S = ；（2）连接平行四边形的对角线，交于点O ，可得BO=DO ，再连接EO 并延长，交BC 于点F ，根据()BOF DOE ASA ≅ ，可得EO=FO ,连接DF ，即可得到平行四边形BEDF 面积等于ABCD 面积的一半．（1）连接CE 并延长，交BA 的延长线于点P ，APE V 即为所求的以BC 为边所作的三角形；（2）连接平行四边形的对角线，交于点O ，连接EO 并延长，交BC 于点F ，连接DF ，平行四边形BEFD 就是以BE ，ED 为邻边所求作的四边形．本题考查尺规作图，涉及平行四边形的性质、全等三角形的判定与性质、平行线的性质等知识，是重要考点，难度较易，掌握相关知识是解题关键．3．如图是由2个全等的正方形错位叠放组成的图形，请仅用没有刻度的直尺按要求完成下列作图．（1）在图1中画一个平行四边形（要求所画出的平行四边形不是矩形）；（2）在图2中画一个菱形（要求所画出的菱形不是正方形）．【答案】（1）利用平行四边形的性质结合矩形的性质得出即可；（2）利用菱形的性质结合矩形的性质得出符合题意的答案．解：（1）图1中平行四边形ABCD 为所求；（2）图2中菱形ABCD 为所求．此题主要考查了应用设计与作图，正确掌握矩形与菱形的性质是解题关键．4．如图是由6个形状、大小完全相同的小矩形组成的大矩形，其中小矩形的长为2，宽为1，请用无刻度的直尺在矩形中完成以下作图（保留作图痕迹，不写作法）．（1）在图1中，画出一个面积为5的正方形；（2）在图2中，画出一个面积为4的非特殊的平行四边形．【答案】（1）直接利用正方形的判定方法得出答案；（2）直接利用平行四边形的判定方法得出答案．（1）如图正方形ABCD；（2）如图平行四边形EFGH．此题考查应用设计与作图，正确掌握平行四边形以及正方形的判定方法是解题关键．5．如图，四边形ABCD是平行四边形，AD与圆相切，请在下图中，仅用无刻度的直尺按要求画图．（1）如图①，若BC是圆的直径，画出平行四边形ABCD的边CD上的高；（2）如图②，若CD与圆相切，画出平行四边形ABCD的边AD上的高CE；（3）如图③，若CD与圆相切，画出平行四边形ABCD的边BC上的高AF．【答案】（1）连接AC，利用圆周角定理得到∠BAC＝90°，再根据平行四边形的性质和平行线的性质得到∠ACD＝90°，即AC⊥CD；（2）连接BD交圆于P，连接CP，延长CP交AD于E，利用切线长定理得到DA＝DC，四边形ABCD为菱形，则BD垂直平分AC，所以BP为直角，则∠BCP＝90°，根据平行线的性质得到∠CEA＝90°，所以CE⊥AD；（3）连接BD交圆于P，交AC于Q，连接CP，延长CP交AD于E，连接EQ交BC于F，连接AF，易证明四边形AECP为矩形，则AF⊥BC．解：（1）如图①所示，AC为所求的高；（2）如图②所示，CE为所求的高；（3）如图③所示，AF为所求的高．．本题考查了作图-复杂作图：复杂作图是在五种基本作图的基础上进行作图，一般是结合了几何图形的性质和基本作图的方法，解决此类题目的关键是熟悉基本几何图形的性质，结合几何图形的基本性质把复杂作图拆解成基本作图，逐步操作，也考查了平行四边形的性质、圆周角定理和切线的性质．6．如图，在正方形ABCD中，请仅用无刻度直尺按下列要求作图（保留作图痕迹，不写作法）．（1）在图①中，将线段AB绕点O逆时针旋转一定角度，使点A与点B重合，点B与点C 重合，作出点O的位置．（2）在图②中，E为AB的中点，将△ABD绕点D逆时针旋转某个角度，得到△CFD，使DA与DC重合，作出△CFD．【答案】（1）作正方形的对角线，对角线交点即为所求；（2）先找到对角线交点O ，再连接EO 并延长EO 交CD 于H ，连接AH ，并延长交BC 延长线于F ，连接DF ，△CFD 即为所求．解：（1）如图所示，点O 即为所求．（2）如图所示，△CFD 即为所求．本题主要考查作图-旋转变换，熟悉相关性质是解题的关键．7．如图，在平面直角坐标系中，A ，B 是双曲线(0)k y k x=≠上的两点，请仅用无刻度的直尺完成下列作图（保留作图痕迹）．（1）在图1中画出一条与AB 相等的线段；（2）在图2中画出一个菱形．【答案】（1）利用平分线四边形的性质作CD=AB 即可；（2）利用平行四边形一组平行线与两轴的交点来作，再证明菱形即可．解：(1)如图1，连结AO 并延长交反比例函数图像交于D ,连结BO 并延长交反比例函数图像交于C ,连结AC 、CD 、BD ，∵反比例函数为中心对称图形，∴OA =OD ，OC =OB ，∴四边形ABDC 为平行四边形，∴CD =AB ，∴CD即为所求；（2）线段AB 与CD 交两坐标轴与M 、N 、P 、Q ，则MNPQ 为所求如图2，∵四边形ABDC 为平行四边形，∴AB ∥CD ，即AN ∥DQ ，OA =OD ，∴∠NAO =∠QDO ，∠ANO =∠DQO ，在△AON 和△DOQ 中，NAO QDO ANO DQO OA OD ∠=∠⎧⎪∠=∠⎨⎪=⎩，∴△AON ≌△DOQ （AAS ），∴ON=OQ ，在Rt △NMO 和Rt △QPO 中，MNO PQO ON OQ NOM QOP ∠=∠⎧⎪=⎨⎪∠=∠⎩，∴Rt △NMO ≌Rt △QPO （ASA ），∴OM =OP ，∴四边形MNPQ 为平行四边形，∵QP ⊥NQ ，∴四边形MNPQ为菱形，方法二连结AN 与DQ ，延长AC 交两轴与M 、Q ，延长BD 交两轴于P 、N ，则MNPQ 为所求∵四边形ABDC 为平行四边形，∴AC ∥BD ，即AQ ∥DN ，OA =OD ，∴∠DNO =∠AQO ，在△AOQ 和△DON 中，AQO DNO AOQ DON OA OD ∠=∠⎧⎪∠=∠⎨⎪=⎩，∴△AON ≌△DOQ （AAS ），∴ON =OQ ，在Rt △NPO 和Rt △QMO 中，PNO MQO ON OQ NOP QOM ∠=∠⎧⎪=⎨⎪∠=∠⎩，∴Rt △NPO ≌Rt △QMO （ASA ），∴OP =OM ，∴四边形MNPQ 为平行四边形，∵QP ⊥NQ ，∴四边形MNPQ 为菱形，菱形MNPQ 即为所求．本题考查尺规作图，以及证明平行四边形与菱形，反比例函数的性质，三角形全等的判定与性质，平行四边形的性质，掌握尺规作图，以及证明平行四边形与菱形，反比例函数的性质，三角形全等的判定与性质，平行四边形的性质是解题关键8．如图，AB 是O 中不过圆心的一条弦，请仅用无刻度的直尺，分别按下列要求画图．（1）在图1中画出一条弦CD 使//CD AB ；（2）在图2中，M 是AB 下方O 上的一点，以点A ，M 为顶点画一个直角三角形，使其第三个顶点也落在O 上，并使该直角三角形的一个内角与ABM 相等．【答案】（1）分别连接AO 、BO 并延长交⊙O 于点D 、C ，连接CD 即可；（2）连接AM ，若以A 为直角顶点，则连接MO 并延长交⊙O 于点E ，连接AE 即可；若以M 点为直角顶点，则连接AO 并延长交⊙O 于点F ，连接MF 即可．解：（1）如图所示，CD 即为所求．（2）如图所示，AME △或AMF 即为所求．本题作图题，考查了直径所对圆周角是直角，同弧（等弧）圆周角相等，三角形全等的判定与性质，平行线的判定等知识，注意题目要求是仅用无刻度的直尺画图，关键是灵活运用圆的相关知识解决问题．。