2019-2020年高三综合练习(一)理科数学
2019-2020年高三一模试题及答案(数学理)

2019-2020 年高三一模试题及答案(数学理) 本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分 . 共 150 分 .考试时间 120 分钟. 注意事项:1 .答卷前,考生务必用 2B 铅笔和 0.5 毫米黑色签字笔(中性笔)将姓名、准考证号、 考试科目、试卷类型填涂在答题卡规定的位置上.2 .第Ⅰ卷每小题选出答案后,用 2B 铅笔把答题卡上对应的答案标号涂黑;如需改动, 用橡皮擦干净后,再选涂其他答案标号.答案不能答在试题卷上.3 .第Ⅱ卷必须用 0.5 毫米黑色签字笔(中性笔)作答,答案必须写在答题卡各题目指定 区域内相应的位置,不能写在试题卷上;如需改动,先划掉原来的答案,然后再写上新的答 案;不准使用涂改液、胶带纸、修正带.不按以上要求作答的答案无效.第Ⅰ卷(选择题 共 60 分)、选择题:本大题共 12 小题.每小题 5 分,共 60 分.在每小题给出的四个选 项中,只有一项是符合题目要求的.3.设 p 和 q 是两个简单命题,若 p 是 q 的充分不必要条件,则 p 是 q 的A. 充分不必要条件B. 必要不充分条件C. 充要条件D. 既不充分也不必要条件 4.计算机执行下面的程序段后,输出的结果是a1 b3 a a b b a bPRINT a,b A . 1 3B.41C . 0 0D .6025 .若 a sin xdx ,2b1cosxdx ,则 a 与 b 的关系是A . a bB . abC . a bD . a b 06.圆 x 2 y 2 2x 2y 1 0上的点到直线 x y 2 的距离的最大值是1. 复数1 3i(i 为虚数单位 )等于A .1B . 112.若集合 A {y|y x 3, 1 x 1} , C . i D . iB {x y 1 x} ,则 A BA .,1B . [ 1,1]C .D .{1}A . 2 B. 1 2 C . 2 D. 1 2 227.已知抛物线 x 2 ay 的焦点恰好为双曲线 y 2 x 2 2的上焦点,则 a 的值为A .1B . 4C .8D .168.将奇函数 f(x) Asin( x )(A 0, 0,) 的图象向左平移个单位得到2 2 6的图象关于原点对称,则 的值可以为A . 2B . 3C .4D .69.已知28 xy1(x 0,y 0) ,则x y 的最小值为A . 12B . 14C .16D . 18xx10 .过原点的直线与函数 y 2x 的图像交于 A,B 两点,过B 作 y 轴的垂线交于函数 y 4x 的图像于点 C ,若直线AC 平行于 y 轴,则点 A 的坐标是A . (1,2) 1B . (2,4)C .( , 2)D . (0,1)211 .在数列 {a n }中,a n 1 a n a ( n N , a 为常数),若平面上的三个不共线的非零向量OA,OB,OC 满足 OC a 1OA a 2010OB ,三点 A,B,C 共线且该直线不过 O 点,则 S 2010 等12.平面 外有两条直线 m 和n ,如果 m 和 n 在平面 内的射影分别是直线 m 1和直线 n 1,给出下列四个命题: ① m 1 ⊥ n 1 m ⊥ n ; ② m ⊥ n m 1 ⊥ n 1 ;第Ⅱ卷(非选择题 共 90 分)、填空题:本大题共 4 小题,每小题 4 分,共 16分.1n13 .若 (x)n 展开式中第 2 项与第 6项的系数相同,那么展开式的中间一项的系数 x14 .已知区域 {(x,y)|x y 10,x 0,y 0},A {(x,y)|x y 0,x 5,y 0} ,若于A . 1005B . 1006C . 2010D . 2012③ m 1与 n 1相交 m 与 n 相交或重合; 其中不.正.确.的命题个数是A.1B. 2④ m 1 与 n 1 平行 m 与 n 平行或重合;C. 3D. 4向区域上随机投1个点,则这个点落入区域A 的概率P A ;15 .关于x 的不等式|x 2| |x 1| 5的解集为;log2x (x 0)16 .已知函数 f (x) 3x 2(x 0),且关于x 的方程f(x) x a 0有且只有一个实根,则实数a 的范围是.三、解答题:本大题共 6 小题,共74分,解答时应写出必要的文字说明、证明过程或演算步骤.17 .(本小题满分12 分)已知向量m ( 3sin2x t,cosx) ,n (1,2 cosx) ,设函数f (x) m n.1(Ⅰ)若cos(2x ) ,且m n ,求实数t 的值;323(Ⅱ)在ABC 中,a,b,c 分别是角A,B,C 的对边,若f (A) 3,b 1,且ABC 的面积为3, 2实数t 1,求边长a的值.18 .(本小题满分12 分)某商场准备在国庆节期间举行促销活动,根据市场调查,该商场决定从2 种服装商品, 2 种家电商品, 3种日用商品中,选出3种商品进行促销活动.(Ⅰ)试求选出的3 种商品中至多有一种是家电商品的概率;(Ⅱ )商场对选出的某商品采用的促销方案是有奖销售,即在该商品现价的基础上将价格提高x 元,同时,若顾客购买该商品,则允许有3次抽奖的机会,若中奖,则每次中奖都获得数额为40元1的奖券.假设顾客每次抽奖时获奖的概率都是,若使促销方案对商场有利,则x 最少为多少2元?19. ( 本题满分共12 分) 下图分别为三棱锥S ABC 的直观图与三视图,在直观图中,SA SC ,M、N 分别为AB、SB的中点.(Ⅰ)求证:AC SB;(Ⅱ)求二面角M NC B 的余弦值.侧视图20. (本题满分共12 分)已知各项均为正数的数列a n 满足a n21 2a n2 a n a n 1,且a2 a4 2a3 4,其中n N . (Ⅰ )求数列a n 的通项公式;2 T n 1 12 2log2 b n 1 2 (Ⅱ)设数列b n 的前n项和为T n,令b n a n2,其中n N ,试比较n 1与 2 n1 n n n n4T n 2log2 b n 1 的大小, 并加以证明.21. (本题满分12 分)12 2 已知定义在正实数集上的函数f(x) x22ex, g(x) 3e2ln xb(其中e为常数,e 2.71828 ) ,若这两个函数的图象有公共点,且在该点处的切线相同.(Ⅰ)求实数b 的值;(Ⅱ)当x 1,e 时,2(f(x) 2ex) a2(2g(x) e2) (a 2)x恒成立,求实数a的取值范e 6e围.22. (本题满分14 分)22已知椭圆C: x2y2 1(a b 0)的左右两焦点分别为F1,F2,P是椭圆C上的一点,且ab在x轴的上方,H 是PF1上一点,若PF2 F1F2 0,OH PF1 0,OH OF1 ,11 , (其中O 为坐标原点) .32(Ⅰ)求椭圆C 离心率e的最大值;2(Ⅱ)如果离心率e取(Ⅰ)中求得的最大值, 已知b2 2,点M( 1,0),设Q 是椭圆C 上的一点,过Q、M 两点的直线l交y轴于点N,若NQ 2QM , 求直线l的方程.38分青岛市高三教学质量统一检测一、选择题: CBBBA 二、填空题: 本大题共 BCDDA 本大题共 13 .20 14 . 三、解答题(共 74 分).17 .(本小题满分 12 分) 数学试题(理科)答案12 小题,每小题 5 分,共 60 分. AD 4 小题,每小题 4 分,共 16 分 1 4 15 .( 3,2) 16 .(1, ) 解: ( Ⅰ )由题意得 m n ( 3 sin2x t) 2cos 2 x 2sin(2x ) t 1 0 6 3分所以 t 2sin(2x ) 1 2cos(2x ) 1 2 63 6分(Ⅱ)由(Ⅰ )知 f (x) 2sin(2x ) t 1 2sin(2x ) 2 由题意得 f (A) 2sin(2A ) 2 3 1 所以 sin(2A ) 13 5 因为 0 A , 2A ,所以 2A 6 6 6 6 6 8分 2010.313 解得 A 3 3 1 3因为 ABC 的面积为 ,所以 bcsin A,bc 2即c 22210 分由余弦定理得 a b 2 c 2 2bc cos A 12 分18 .(本小题满分 12 分) 3解: (Ⅰ)选出 3种商品一共有 C 7 种选法 , 选出的 3 种商品中至多有一种是家电商品有 ⋯⋯ 2 分 C 53 C 21C 52种. ⋯⋯C 3 C 1C 2 6 所以至多有一种是家电商品的概率为 P C5 C 32C5 6.⋯⋯ C737 ⋯⋯(Ⅱ)奖券总额是一随机变量 ,设为 ,可能值为 0, 40, 80, 120. P0 C 30 14分 5分6分1 3 12 2 8, P 40 C31 1 132 2 8 7分10 分P 80 C 32 3P 120 C 33211 21 1 3 , 228 1 3 1 0 12284080120P133 1 88 881 33 1 所以 EX 0 40 80 120 60.8 888所以 x 60 ,因此要使促销方案对商场有利,则 x 最少为 60元.19.( 本题满分 12 分 )解: 由题意知 : SA SC 2 3,侧面 SAC 底面 ABC ,(Ⅱ) 如图所示建立空间直角坐标系 O xyz ,则 A(2,0,0),B(0,2 3,0),C( 2,0,0),S(0,0,2 2),M (1, 3,0), N (0, 3, 2).AC ( 4,0,0), SB (0,2 3, 2 2) .CM (3, 3,0), MN ( 1,0, 2).设n (x, y, z)为平面 CMN 的一个法向量 ,n CM 3x 3y 0 ,取 z 1, 得 x 2,y 6 . n MN x 2z 0 所以 n ( 2, 6,1) 又由上可得 CB (2,2 3,0),CN (2, 3, 2). 设 m (a,b,c)为平面 NBC 的法向量 ,m CB 2a 2 3b 0 ,得 a 2c 0,m CN 2a 3b 2c 0 令 c 1 ,则 m ( 2, 6 ,1)39分10 12 分底面 ABC 为正三角形2分(Ⅰ) 取 AC 的中点 O ,连结 OS,OB .因为 SA SC,AB BC , 所以 AC SO,AC OB . 所以 AC 平面 OSB .所以AC SB4分6分8分①当 n 1时, 7 40 7 3 1 1 4 ,上面不等式显然成立;②假设当 n k 时,不等式 7 4k 1 3k 1成立⋯⋯⋯⋯ 9 分 当 n k 1 时,7 4k 4 7 4k 1 4(3k 1) 12k 4 3k 4 3(k 1) 1 综上①②对任意的 n N 均有 7 4n 1 3n 1 ⋯⋯⋯⋯ 11 分m n 2 2 1 33 所以 cos n,m所以|m||n|3 33 11 33 所以二面角 M NC B 的余弦值为 33 . 11 12 分20.( 本题满分 12 分 ) 22 解:(Ⅰ)因为 a n 1 2a n a n a n 1,即(a n1 a n )(2a n a n 1) 0 又 a n 0,所以有 2a n a n 1 0,所以 2a n a n 1 所以数列 a n 是公比为 2的等比数列⋯⋯⋯⋯ 2 分 由 a 2 a 4 2a 3 4得 2a 1 8a 1 8a 1 4,解得 a 1 2 故数列 a n 的通项公式为 a n 2n (n N )⋯⋯⋯⋯ 4分 (Ⅱ) 因 b n a n 2 4 ,所以 b 1 4, n 1 4 b n 即数列 b n 是首项为 4,公比是 4 的等比数列 4n所以 T n (4 n 1) 3 6分 则T n 1 12 4n 18 4T n 4(4n 1) 13 n 41 2log 2b n 1 2 4n 6又 2log 2 b n 1 4n 1 7 1 4n 1 T n 1 12 2log 2 b n 1 2 4T n 3 2log 2 b n 1 4n 1 4n 14(3n 1 7 4n 1)(4n 1)(4n 1)猜想: 7 4n 1 3n 18分9分又 4n 1 0,4n 1 01 2 2x 0 2ex 0 3e ln x 02x 0x 0 0 2 e解得:b⋯⋯⋯⋯⋯⋯⋯⋯⋯ 5 分22 2e (Ⅱ)由(Ⅰ)知, g(x) 3e 2 ln x 2所以 2( f (x) 2ex) a 2 (2g(x) e 2) x 2 aln x6e 2即 a ( x ln x) x 2 2x (1)当 x [ ,1) 时, ln x 0 , x ln x 0 e当 x 1,e 时, lnx 1 x ,且等号不能同时成立, x ln x 0x 2 2x 1所以,则由(1)式可得 a在 ,e 上恒成立⋯⋯⋯⋯⋯⋯⋯⋯ 7 分x ln x ex 2 2x1 设 F(x) , x ,ex ln xe又 F (x) (x 1)(x 2 22ln x )⋯⋯⋯⋯⋯⋯⋯⋯(x ln x)2T n 1 12 4T n2log 2 b n 1 2 2log 2 b n 1所以对任意的 n N 均有 T n 1 12 2log 2 b n 1 24T n2log 2 b n 112 分21.( 本题满分 12 分 ) 解:(Ⅰ) f ( x) x 2e , g ( x) 3e2x1分设函数 f(x) 1 x 2 2ex 与 g (x)23e ln x b的图象有公共点为(x 0,y 0)由题意得 x 0 2e3e 23分1 2 16分令 F (x) 0 得: x 1 又 ln x 1, x 2 2ln x 0 F (x) 0 ;当 x 1,e 时, F (x) 0;1所以, F(x) 在[ ,1)上为减函数, F(x) 在 1,e 上为增函数 e 又 F(1) 1 2e 0 F(e) e 2ee e(e 1) e 1故 F(x)max F(e) e e 12ee122.( 本题满分 14 分 )则有 F 1OH 与 F 1PF 2 相似设 F 1( c,0),F 2(c,0),c 0, P(c,y 1)所以实数 a 的取值范围是 e 2ee112 分22 c y 1 则有 2 1 a b 2 1, 解得 y 1 b 2 a 所以 PF 2 b 2 y 1 根据椭圆的定义得 : F 1P 2a PF 2 2a b2a4分b 2 2a 2 b 2 ,即a b22a所以 e 22c2 12 ab 22a所以,当 x 1,1 时, e11 分解 :(Ⅰ)由题意知 PF 2 F 1F 2,OHPF 1所以OH PF 2OF 1 F 1P2分2 1 1 1在 [ , ] 上是单调减函数 13 2 1 2 1当时, e 2取最大值32设Q (x 1,y 1),由于 NQ 2QM ,所以有 (x 1,y 1 k) 2( 1C ( 3)又 Q 是椭圆 C 上的一点 , 则 34解得 k 4所以直线 l 的方程为 4x y 4 0或 4xy 4 02kx13,y1 3 12显然 e 2 所以椭圆 C 离心率 e 的最大值是8分2(Ⅱ)由(Ⅰ )知c 2b212 aa2 1 21 a2 2,解得a 4所以此时椭圆 2C 的方程为 y14210 分由题意知直线 l 的斜率存在 ,故设其斜率为 k , 则其方程为 y k(x 1),N(0,k)x 1, y 1)(3)1 31 214 分。
2019-2020年高三数学第一次统一考试试题 理(含解析)

2019-2020年高三数学第一次统一考试试题 理(含解析)【试卷综析】试题在重视基础,突出能力,体现课改,着眼稳定,实现了新课标高考数学试题与老高考试题的尝试性对接.纵观新课标高考数学试题,体现数学本质,凸显数学思想,强化思维量,控制运算量,突出综合性,无论是在试卷的结构安排方面,还是试题背景的设计方面以全新的面貌来诠释新课改的理念.【题文】一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.【题文】 l.集合 {}{}{}1,2,3,4,5,1,2,3,|,A B C z z xy x A y B ====∈∈且,则集合C 中的元素个数为A.3 B .4 C .11 D .12【知识点】集合中元素的特征:确定性,互异性,无序性. A1 【答案】【解析】C 解析:{1,2,3,4,5,6,8,9,10,12,15}C =,故选C. 【思路点拨】利用已知求得集合C 即可.【题文】 2.已知i 为虚数单位,复数123,12z ai z i =-=+,若12z z 复平面内对应的点在第四象限,则实数a 的取值范围为 A. {}|6a a <- B . 3|62a a ⎧⎫-<<⎨⎬⎩⎭ C .3|2a a ⎧⎫<⎨⎬⎩⎭ D . 3|62a a a ⎧⎫<->⎨⎬⎩⎭或 【知识点】复数的运算;复数的几何意义. L4 【答案】【解析】B 解析:12z z ()()()()312332612121255ai i ai a a i i i i ----+===-++-,因为12zz 复平面内对应的点在第四象限,所以32036602a a a ->⎧⇒-<<⎨+>⎩,故选 B.【思路点拨】先把复数z 化为最简形式,在利用复数的几何意义求解.【题文】3.已知θ为第二象限角, sin ,cos θθ是关于x 的方程22x R)∈的两根,则 sin -cos θθ的等于 A .12+ B .12C ..【知识点】已知三角函数式的值,求另一个三角函数式的值. C7 【答案】【解析】A解析:由已知得1sin cos 2θθ+=2sin cos 2θθ⇒=-又θ为第二象限角,所以sin -cos θθ==12+,故选 A.【思路点拨】由已知得1sin cos 2θθ-+=2sin cos 2θθ⇒=-,又θ为第二象限角,所以sin -cos θθ==12+. 【题文】4.下面四个推导过程符合演绎推理三段论形式且推理正确的是A .大前提:无限不循环小数是无理数;小前提:π丌是无理数;结论:π是无限不循环小数B .大前提:无限不循环小数是无理数;小前提: π是无限不循环小数;结论: π是无理数C.大前提:π是无限不循环小数;小前提:无限不循环小数是无理数;结论: π是无理数D.大前提: π是无限不循环小数;小前提: π是无理数;结论:无限不循环小数是无理数 【知识点】演绎推理的定义及特点. M1【答案】【解析】B 解析:A :小前提不正确;C 、D 都不是由一般性命题到特殊性命题的推理,所以A 、C 、D 都不正确,只有B 正确,故选 B.【思路点拨】演绎推理是由一般性命题到特殊性命题的推理,及其推理的一般模式---“三段论”,由三段论的含义得出正确选项.【题文】5.某几何体的三视图如图所示,图中三个正方形的边长均为2,则该几何体的体积为 A .38 B . 82π- C . 43π D . 283π-【知识点】几何体的三视图;几何体的结构. G1 G2【答案】【解析】D 解析:由三视图可知此几何体是:棱长为2 的正方体挖去了一个圆锥而形成的新几何体,其体积为3212212833ππ-⨯⨯⨯=-,故选 D.【思路点拨】由几何体的三视图得此几何体的结构,从而求得此几何体的体积.【题文】6.已知 ()f x 是定义在R 上的偶函数,且()f x 在(],0-∞上单调递增,设333(sin )(cos ),(tan )555a fb fc f πππ===,则a,b,c 的大小关系是,A .a<b<cB .b<a<cC .c<a<bD .a<c<b【知识点】函数奇偶性,单调性的应用. B3 B4【答案】【解析】C 解析:∵()f x 是定义在R 上的偶函数,且()f x 在(],0-∞上单调递增, ∴()f x 在[)0,+∞上单调递减,且22coscos 55b f f ππ⎛⎫⎛⎫=-= ⎪⎪⎝⎭⎝⎭, 22tantan 55c f f ππ⎛⎫⎛⎫=-= ⎪⎪⎝⎭⎝⎭,又∵2sin 5a f π⎛⎫=⎪⎝⎭,且2220cos sin tan 555πππ<<<,∴ c<a<b ,故选 C.【思路点拨】由已知得函数()f x 在[)0,+∞上单调递减,而2sin5a f π⎛⎫= ⎪⎝⎭, 22coscos 55b f f ππ⎛⎫⎛⎫=-= ⎪⎪⎝⎭⎝⎭,22tan tan 55c f f ππ⎛⎫⎛⎫=-=⎪⎪⎝⎭⎝⎭,所以只需比较 222cos,sin ,tan555πππ的大小关系即可. 【题文】7.执行如图的程序,则输出的结果等于 A .9950 B .200101 C .14950 D . 15050【知识点】对程序框图描述意义的理解. L1【答案】【解析】A 解析:根据框图中的循环结构知,此程序是求下式的值:1111136104950T =+++++222222612209900=+++++1111212233499100⎛⎫=++++⎪⨯⨯⨯⨯⎝⎭1111111212233499100⎛⎫=-+-+-++- ⎪⎝⎭1992110050⎛⎫=-=⎪⎝⎭,故选A. 【思路点拨】由程序框图得其描述的算法意义.【题文】 8.在△ABC 中,D 为AC 的中点,3BC BE =,BD 与 AE 交于点F ,若 AF AE λ=,则实数λ的值为 A .12 B . 23 C . 34 D . 45【知识点】平面向量的线性运算. F1 【答案】【解析】C 解析:作EFAC 交BD 于G ,因为13BE BC =,所以13EG DC =,因为 D 为AC 的中点,所以13EG AD =,所以1334EF AF AE FA =⇒=,故选C.【思路点拨】画出几何图形,利用平行线分线段成比例定理求得结论.【题文】9.设 12,F F 分别为双曲线 221x y -=的左,右焦点,P 是双曲线上在x 轴上方的点, 1F PF ∠为直角,则 12sin PF F ∠的所有可能取值之和为A .83B .2C .D .2【知识点】双曲线的性质. H6【答案】【解析】D 解析:设P 是第一象限点,且12,PF m PF n ==,则222181m n m m n n ⎧-==⎧⎪⇒⎨⎨+==⎩⎪⎩,所以所求= 2m n c +==,故选 D. 【思路点拨】根据双曲线的定义及勾股定理,求得P 到两焦点的距离,这两距离和与焦距的比值为所求. 【题文】10.曲线 1(0)y x x=>在点 00(,)P x y 处的切线为 l .若直线l 与x ,y 轴的交点分别为A ,B ,则△OAB 的 周长的最小值为A. 4+5+ 【知识点】导数的几何意义;基本不等式求最值. B11 E6 【答案】【解析】A 解析:∵21y x '=-,∴00201:()l y y x x x -=--即20020x x y x +-=, 可得A(02x ,0),B(0,02x ),∴△OAB的周长00224l x x =+≥+当01x =时等号成立.故选 A.【思路点拨】由导数的几何意义得直线l 的方程,从而求得A 、B 的坐标,进而用0x 表示△OAB 的周长,再用基本不等式求得周长的最小值.【题文】11.若直线(31)(1)660x y λλλ++-+-= 与不等式组 70,310,350.x y x y x y +-<⎧⎪-+<⎨⎪-->⎩,表示的平 面区域有公共点,则实数λ的取值范围是 A . 13(,)(9,)7-∞-+∞ B . 13(,1)(9,)7-+∞ C .(1,9) D . 13(,)7-∞-【知识点】简单的线性规划. E5【答案】【解析】A 解析:画出可行域,求得可行域的三个顶点A(2,1),B(5,2),C(3,4) 而直线(31)(1)660x y λλλ++-+-=恒过定点P(0,-6),且斜率为311λλ+-,因为 7810,,253PA PB PC k k k ===,所以由8317512λλ+<<-得λ∈13(,)(9,)7-∞-+∞,故选A.【思路点拨】:画出可行域,求得可行域的三个顶点, 确定直线过定点P(0,-6),求得直线PA 、PB 、PC 的斜率,其中最小值85,最大值72,则由8317512λλ+<<-得λ的取值范围. 【题文】12.在平面直角坐标系中,点P 是直线 1:2l x =-上一动点,点 1(,0)2F ,点Q 为PF 的 中点,点M 满MQ ⊥PF ,且 ()MP OF R λλ=∈.过点M 作圆 22(3)2x y -+= 的切线,切点分别为S ,T ,则 ST 的最小值为A .. C . 72 D. 52【知识点】曲线与方程;距离最值问题. H9 【答案】【解析】A 解析:设M(x,y),1(,2)2P b -,则Q(0,b),由QM ⊥FP 得 (,)(1,2)02()0x y b b x b y b -⋅-=⇒-+-=.由()MP OF R λλ=∈得y=2b,所以点M 的轨迹方程为22y x =,M 到圆心距离=,易知当d 去最小ST 取最小值,此时MT ==,由三角形面积公式得:11222ST ST ==故选A. 【思路点拨】先求得点M 的轨迹方程22y x =,分析可知当M 到圆心距离最小时ST 最小,所以求M 到圆心距离d 得最小值,再用三角形面积公式求得ST 的最小值. 【题文】二、填空题:本大题共4小题,每小题5分,共20分. 【题文】13.设随机变量 2(,)N ξμσ,且 (1)(1),(2)0.3P P P ξξξ<-=>>=,则(20)P ξ-<<= _____________.【知识点】正态分布的意义. I3【答案】【解析】0.2 解析:因为(1)(1)P P ξξ<-=>,所以正态分布曲线关于y 轴对称, 又因为(2)0.3P ξ>=,所以(20)P ξ-<<=120.30.22-⨯=【思路点拨】根据正态分布的性质求解.【题文】14.若正四梭锥P- ABCD 的底面边长及高均为2,刚此四棱锥内切球的表面积为_______.【知识点】组合体的意义;几何体的结构. G1【答案】【解析】2(3π- 解析:根据题意得正四梭锥的底面面积为4,一个侧面面积为R ,则由等体积法得,()111442332R R =⨯⨯⇒=,所以球的表面积为2(3π.【思路点拨】由等体积法求得此四棱锥内切球的半径,再由球的表面积公式求得结论. 【题文】15.将函数 ()sin()223y sin x x ωωπ=+的图象向右平移3π个单位,所得图象关于y轴对称,则正数 ω的最小值为________.【知识点】sin()y A x ωϕ=+的图像与性质. C4 【答案】【解析】 1 解析:函数()sin()223y sin x x ωωπ=+=1sin()sin()cos()2222x x x ωωω⎛⎫+ ⎪ ⎪⎝⎭=21sin ()sin()cos()2222x x x ωωω+=11sin()264x πω-+,向右平移3π个单位后为: 1111sin[()]sin 23642364y x x πππωπωω⎡⎤⎛⎫=--+=-++ ⎪⎢⎥⎝⎭⎣⎦,这时图像关于y 轴对称,所以31362k k πωπππω+=+⇒=+,k Z ∈,所以正数 ω的最小值为1.【思路点拨】先利用两角和与差的三角函数,二倍角公式,把已知函数化为: y=11sin()264x πω-+,再由其平移后关于y 轴对称得31k ω=+,k Z ∈,所以正数 ω的最小值为1.【题文】 16.在△ABC 中,角A ,B ,C 的对边分别是a ,b ,c ,若b=l ,a= 2c ,则当C 取最大值时,△ABC 的面积为________.【知识点】余弦定理;三角形的面积公式. C8【答案】解析:当C 取最大值时,cosC 最小,由22223111cos 3244a b c c C c ab c c +-+⎛⎫===+≥⎪⎝⎭得,当且仅当c= 3时C 最大,且此时sinC=12,所以△ABC的面积为111sin 21222ab C c =⨯⨯⨯=【思路点拨】由余弦定理求得C 最大的条件,再由三角形面积公式求解.【题文】三、解答题:本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.【题文】17.(本小题满分10分) 已知 {}{},n n a b 均为等差数列,前n 项和分别为 ,n n S T .(1)若平面内三个不共线向量 ,,OA OB OC 满足 315OC a OA a OB =+,且A ,B ,C 三点共线.是否存在正整数n ,使 n S 为定值?若存在,请求出此定值;若不存在,请说明理由。
2019-2020年高三统一质量检测理科数学试题及详细解析

2019-2020年高三统一质量检测理科数学试题及详细解析一、选择题:本大题共12小题.每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1. 已知实数集R ,集合集合,则 A.B. C. D.1. B 【解析】.2. 已知函数,则A .B .C .D . 2.B 【解析】3. 某个小区住户共户,为调查小区居民的月份用水量,用分层抽样的方法抽取了户进行调查,得到本月的用水量(单位:m 3)的频率分布直方图如图所示,则小区内用水量超过m 3的住户的户数为 A. B. C. D.3.C 【解析】以为样本容量可计算出超过用水量的户数为所以可估算户居民超过用水量的户数.4. 设为两个不同的平面,、为两条不同的直线,且,有两个命题::若,则;:若,则;那么 A .“或”是假命题 B .“且”是真命题 C .“非或” 是假命题 D .“非且”是真命题 4.D 【解析】是假命题,是真命题,所以D 正确.5. 运行如右图所示的程序框图,则输出的值为 A. B. C. D. 5.B 【解析】6. 的展开式中的系数为 A. B. C. D.6.B 【解析】()()66621661221rrr r r rr r T C x C x x ---+⎛⎫=-=⋅⋅- ⎪⎝⎭, 所以()2262642422366212240.T C x C x x --=⋅⋅-=⋅=7. 直线与抛物线所围成封闭图形的面积是 A . B . C .D .7.C 【解析】联立方程求得交点分别为所以阴影部分的面积为()()321140324210124.233S x dx -=⨯⨯+-+=-=⎰8. 将函数的图象上所有点的横坐标伸长到原来的倍(纵坐标不变),再将所得图象向左平移个单位,则所得函数图象对应的解析式为 A. B. C. D. 8.D 【解析】sin()sin()sin 33336111sin .222y x y x y x x πππππ=-→=-→=+-⎡⎤⎛⎫⎛⎫=- ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦9. 已知函数的图象如右图所示,则函数的图象可能为9.B 【解析】由图象可知,所以为增函数,B 符合.10. 已知圆的圆心为抛物线的焦点,且与直线相切,则该圆的方程为 A. B. C. D.10.C 【解析】抛物线的焦点为,则所以圆的方程为. 11. 已知,且,则的最小值为A. B. C. D.11.C 【解析】142114424a b ab ab ab b a +===+≥ 12. 设与是定义在同一区间上的两个函数,若函数在上有两个不同的零点,则称和在上是“关联函数”,区间称为“关联区间”.若与在上是“关联函数”,则的取值范围为A. B. C. D.12.A 【解析】为开口向上的抛物线,是斜率的直线,可先求出与相切时的值. 由得切点为,此时,因此的图象与的图象有两个交点只需将向上平移即可。
2020届高三毕业班第一次综合质量检测数学(理)试题—附答案

5.
已知函数
f
(
x)
1
x x
2
sin x ,则函数 y
f (x) 的图像大致为
A.
B.
C.
D.
6.从区间 0,1随机抽取 2n 个数 x1, x2 ,, xn , y1, y2 ,, yn ,组成坐标平面上的 n 个点
(x1, y1 ) ,(x2 , y2 ) ,… (xn , yn ) ,其中到原点距离小于1的点有 m 个,用随机模拟的
A.20100
B.20200
C.40200
D.40400
12.在棱长为 4 的正方体 ABCD A1B1C1D1 中, E, F 分别为 AA1, BC 的中点,点 M 在
棱 B1C1 上, B1M
1 4
B1C1
,若平面
FEM
交
A1B1 于点 N
,四棱锥 N
BDD1B1 的五
个顶点都在球 O 的球面上,则球 O 半径为
A(3, 0, 0) , B(0, 3, 0) , S(0, 3 , 3 3 ) , C(1,0,0) , 22
上.
(1)求曲线 C 的普通方程及直线 l 的直角坐标方程. (2)求△PAB 面积的最大值.
23.(本小题满分 10 分)选修 4-5:不等式选讲
已知函数 f (x) | 2x t | ,若 f (x) 1的解集为 (1,0) . (1)求 t 并解不等式 f (x) x 2 ; (2)已知: a,b R ,若 f (x) 2a b | 2x 2 | ,对一切实数 x 都成立, 求证: a 2b 1 .
3
2
根据所给数据用事件发生的频率来估计相应事件发生的概率,估计该顾客支付的平均费用
2019-2020学年第一学期高三综合测试理科数学参考答案
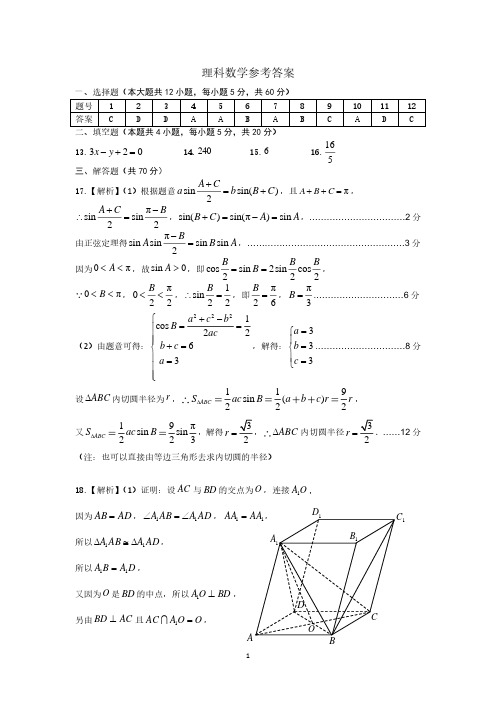
理科数学参考答案二、填空题(本题共4小题,每小题5分,共20分)13.023=+-y x 14.240 15.6 16.516三、解答题(共70分) 17.【解析】(1)根据题意sinsin()2A Ca b B C +=+,且πA B C ++=, πsinsin22A C B+-∴=,sin()sin(π)sin B C A A +=-=,……………………………2分 由正弦定理得πsin sin sin sin 2BA B A -=,………………………………………………3分因为0πA <<,故sin 0A >,即cos sin 2sin cos 222B B BB ==,0πB <<,π022B <<,1sin 22B ∴=,即π26B =,π3B =.…………………………6分(2)由题意可得:2221cos 2263a cb B ac b c a ⎧+-==⎪⎪⎪+=⎨⎪=⎪⎪⎩,解得:333a b c =⎧⎪=⎨⎪=⎩.…………………………8分设ABC ∆内切圆半径为r ,119sin ()222ABCS ac B a b c rr ∆, 又19πsin sin 223ABCS ac B ∆,解得2r =,ABC ∆内切圆半径2r =.……12分 (注:也可以直接由等边三角形去求内切圆的半径)18.【解析】(1)证明:设AC 与BD 的交点为O ,连接O A 1, 因为AD AB =,AD A AB A 11∠=∠,11AA AA =, 所以AD A AB A 11∆≅∆, 所以D A B A 11=,又因为O 是BD 的中点,所以BD O A ⊥1, 另由AC BD ⊥且O O A AC =1 ,ABC1C D1A 1B 1D O所以⊥BD 平面AC A 1,而⊂BD 平面BD A 1,所以平面⊥AC A 1平面BD A 1.……………………………………6分(2)(法一)连接1OC ,由(1)知⊥BD 平面AC A 1, 所以O BC 1∠为直线1BC 与平面AC A 1所成的角θ, 因为2111==C B BB ,︒=∠12011C BB , 所以321=BC ,又因为︒=∠60BAD ,所以1=OB ,所以63sin 1==BC OB θ.……………………………………………………………………12分 (法二)过O 作直线⊥OZ 平面ABCD , 分别以OB 、OC 、OZ 为x 、y 、z 轴, 建立如图所示空间直角坐标系, 依题意,得)0,3,0(-A ,)362,33,0(1-A ,)0,0,1(B ,)0,3,0(C ,)362,335,0(1C , 所以)362,332,0(1-=,)0,32,0(=,)362,335,1(1-=BC , 设平面AC A 1的法向量为),,(z y x n =,所以⎪⎩⎪⎨⎧==-0320362332y z y ,令1=x ,则0==z y ,即)0,0,1(=, 所以631321sin =⨯==θ, 即直线1BC 与平面AC A 1所成的角θ的正弦值为63.…………………………………12分A1ABC1C D1A 1B 1D O19.【解析】(1)须抛掷两次才能获得大奖的所有可能情况如下:)2,2(,)7,2(,)1,3(,)6,3(,)4,5(,)11,5(,)3,6(,)10,6(,)2,7(,)9,7(,)1,8(,)8,8(, )6,10(,)5,11(,)4,12(,共15种情况.……………………………………………………6分(2)依题意得ξ的取值为48,360,1440,3240,5760, 则121)360(==ξP ,7271442121)1440(=+==ξP ,811446121)3240(=+==ξP , 1447)5760(==ξP ,4831)48(==ξP , 所以ξ的分布列为:所以311717483601440324057608864812728144E ξ=⨯+⨯+⨯+⨯+⨯=(元). ……………………………………………………………………12分20.【解析】(1)(1)因为1e )(+-='x mx f x,0x =是()f x 的极值点, 所以010e )0(0=+-='m f ,解得1=m ,即11e )(+-='x x f x , 又因为x y e =与11+-=x y 在),1(+∞-上单调递增, 所以当01<<-x 时,0)(<'x f ;当0>x 时,0)(>'x f ,即)(x f 在)0,1(-上单调递减,在),0(+∞上单调递增.……………………………………6分 (2)因为当4=m 时,14e )(+-='x x f x在),1(+∞-上单调递增, 因为034e )0(0<-=-='f ,02e 24e )1(1>-=-='f , 所以存在)1,0(0∈x ,使得0)(0='x f ,即)(x f 在),0(0x 上单调递减,在),(0+∞x 上单调递增,另由0e )0(0>=f ,016ln lne ln24e )1(e 1<-=-=f ,而03ln 4e )2(2>⋅-=f , 所存在)1,0(1∈x ,)2,1(2∈x ,使得0)()(21==x f x f ,即)(x f 有且仅有两个不同的零点.…………………………………………………………12分21.【解析】(1)因为212F F PF ⊥,所以设),(0y c P ,代入22221x y a b+=中解得a b y 20±=,即),(2a b c P ±,而)0,(1c F -,所以43)(212222222±=-⨯±=-±=±=±=a c c a ac c a acbc a b k ..………………5分 (2)当||m b ≥时,P Q 、两点在椭圆C 的同侧,易知PNM QNM ∠≠∠,故||m b <, 因为222a b c =+且12c a =,故2a c =,b =, 设椭圆C 为2223412x y c +=,11(,)P x y ,22(,)Q x y ,联立方程组2223412x y c y kx m ⎧+=⎨=+⎩,化简得2222(34)8(412)0k x kmx m c +++-=,所以122834kmx x k +=-+,2212241234m c x x k -=+,又1212,PN QN y n y nk k x x --==,根据PNM QNM ∠=∠,易得0PN QN k k +=, 于是12120y n y n x x --+=,故211212()()0x y n x y n x x -+-=,即2112()()0x y n x y n -+-=, 故211212()()()0x kx m x kx m n x x +++-+=,化得12122()()0kx x m n x x +-+=,化简得222241282()03434m c kmk m n k k-⨯--⨯=++, 因为0≠k ,所以上式化简得222(3)()0,3m c m n m mn c ---⨯==,综上,可知满足条件的点N 是存在的,且2mn b =...………………………………………………………12分22.【解析】(1)由θcos a a x =-,θsin a y =,两边平方得222)(a y a x =+-, 故曲线1C 的普通方程为222)(a y a x =+-, 又由22y x +=ρ,x =θρcos ,代入2cos =-θρρ得222+=+x y x ,当2-≥x 时两边平方,并整理得442+=x y ,故曲线2C 的直角坐标方程为442+=x y .…………………………………………………6分 (2)联立1C 与2C 的方程得04)24(2=+-+x a x , 因为0>a ,要使1C 与2C 有且仅有四个公共点, 则方程04)24(2=+-+x a x 有两个大于0的正根,所以⎪⎩⎪⎨⎧>--=∆>--16)24(02242a a,解得⎩⎨⎧>>,4,2a a ,即a 的取值范围为),4(+∞.……………10分23.【解析】(1)由⎪⎩⎪⎨⎧>-≤<≤-=5,8253 ,23,28)(x x x x x x f 得)(x f 的最小值2=m .…………………5分(2)由(1)知2422=+b a ,因为abb a b a 441)21(222++=+, 所以)441()4(21441222222ab b a b a ab b a ++⨯+⨯=++)2444(212222++++⨯=a b b a a b b a , 因为2442222≥+a b b a ,44a bb a+≥(当且仅当a b 2=时取等号), 所以2121()(242)42a b +≥⨯++=(当且仅当a b 2=时取等号), 即122a b+≥(当且仅当a b 2=时取等号), 当a b 2=,2422=+b a 时,解得1=a ,2=b , 即122a b+≥(当且仅当1=a ,2=b 时取等号).……………………………………10分。
2019-2020年高三统一考试(数学)理科.doc

2019-2020年高三统一考试(数学)理科本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分。
共150分,测试时间120分钟。
第Ⅰ卷(选择题,共60分)注意事项:1.答第Ⅰ卷前,考生务必将自己的姓名、准考证号、考试科目用铅笔涂写在答题卡上。
2.选择题为四选一题目,每小题选出答案后,用铅笔把答题卡上对应题目的答案标号 涂黑。
如需改动,用橡皮擦干净后,再选涂其它答案。
不能答在测试卷上。
一、选择题:本大题共12小题,每小题5分;共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.若集合=⋂-==<--=P M x y y P x x x M 那么},1|{},032|{2( )A .(0,3)B .)3,0[C .)3,1[D .),1[+∞-2.已知复数21211,2z z z i z i z ⋅=-=+=,则在复平面上对应的点位于 ( )A .第一象限B .第二象限C .第三象限D .第四象限3.在等比数列{a n }中,==+=⋅>+16614411715,6a a a a a a a a n n ,则,且 ( )A .32B .23 C .61-D .65-4.对于平面α和共面的直线m 、n ,下列命题 中是真命题的是 ( ) A .若m ⊥α,m ⊥n ,则n//α B .若m//α,n//α,则m//n C .若m ⊂α,n//α,则m//n D .若m 、n 与α所成的角相等,则m//n 5.若平面向量a =(1,-2)与b 的夹角是180°且|b |=35,则b 等于 ( )A .(-3,6)B .(3,-6)C .(6,-3)D .(-6,3)6.如图,一个空间几何体的主视图,左视图、储视图为全等的等腰直角三角形,如果直角三角形的直 角边长为1,那么这几何体的体积为 ( ) A .1 B .21C .31D .617.若圆C 1:1)1()1(:1)()(222222=++++=-+-y x C b b y a x 与圆的交点连线平分圆C 2周长,则实数a 、b 应满足的关系式是( )A .02222=+++b a aB .06222=---b a aC .022222=++++b a b aD .0322222=--+-b a b a8.下列四个命题,其中正确的是( )A .函数),(cos ∞-∞=在x y 内是减函数B .函数|)22sin(|π+=x y 的最小正周期是πC .函数]472,2[cos ππππ++=k k x y 在区间 )(Z k ∈上是增函数D .函数)4tan(π+=x y 是奇函数9.如图,该程序运行后输出的结果为( ) A .7 B .15C .31D .6310.正四棱锥S —ABCD 底面边长为2,高为2,E 是边BC 的中点,动点P 在表面上运动,并且总保持PE ⊥AC 则动点P 的轨迹的周长为( )A .22+B .32+C .62+D .262+11.过抛物线y 2=2px (p>0)的焦点F 斜率为34的直线交抛物于A 、B 两点,若)1(>=λλ,则λ的值为( )A .5B .4C .34D .2512.定义在R 上的函数2)1(),)(()()()(=∈+=+f R y x y f x f y x f x f ,且,满足,那么下面四个式子①)1()1(2)1(nf f f +++ ; ②]2)1([+n n f ;③)1(+n n ;④).1()1(f n n +其中*))(()2()1(N n n f f f ∈+++ 相等的是( )A .①③B .①②C .①②③④D .①②③9题图第Ⅱ卷(非选择题 共90分)注意事项:1.第Ⅱ卷共6页,用钢笔或蓝圆珠笔直接写在试题卷中。
2019-2020年高三测试(一)数学(理)试题含答案

2019-2020 年高三测试(一)数学(理)试题含答案123456781. 已知向量p (2, 3),q (x,6),且p/ /q,则|p+q| 的值为A .5 B.13 C.5 D .132. 为了在一条河上建一座桥,施工前在河两岸打上两个桥位桩A,B (如图),要测算A, B两点的距离,测量人员在岸边定出基线BC ,测得BC 50m,ABC 105, BCA 45 ,就可以计算出A,B两点的距离为()A.50 2 m B .50 3 m C .25 2 m D. 25 2m2223.“ a b ”是“直线y x 2与圆x a 2 x b 2 2相切”A .充分不必要条件B .必要不充分条 C.充要条件4.设a n 是公差不为 0的等差数列,a1 2且a1,a3,a6成等比数列,则a n 的前n项和S n=n 27n n25n2n 3n2A.B.C. D .n n44 33 242 5.若抛物线y24x的焦点与椭22xy 的左焦点重合,则m 的值为()A. - 1m 73B.1C.-2 D . 22 26.已知三条不重合的直线 m、 n、 l,两个不重合的平面, ,有下列命题①若l // ,m// ,且// ,则l //m ②若l ,m ,且l //m,则//③若m ,n ,m/ / ,n// ,则//④若, m,n ,n m,则n 其中真命题的个数是D .既不充分也不必要条件2x7. 已知曲线 y 3ln x 的一条切线的斜率为4A .4B .3C .21,则切点的横坐标为A .3 B.2 C.1 D.228. 已知双曲线 a x 2 b y2 1的一个焦点与抛物线 于 5 ,则该双曲线的方程为10.直线 y kx b 与曲线 y x 3 ax 1相切于点( 2, 3),则 b 的值为 2y 2=1 的渐近线与圆 (x 2)2y 23 相切,则此双曲线的离心率 b2⋯,根据以上式子可以猜想:1 1 1 ... 22 3220112三、解答题1)求sinA 的值;(2)若b 2, ABC 的面积 S ABC 3,求 a 的值。
2019-2020年高三教学质量检测(一模)数学(理)试题 含答案

2019-2020年高三教学质量检测(一模)数学(理)试题 含答案一、选择题(本大题共12个小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的)1、已知集合{1,0,1},{||10}A B x x =-=+>,那么A .B .C .D .2、已知复数,则A .B .1C .D .-13、沿一个正方体三个面的对角线截得的几何体如图所示,则该几何体的左视图为4、已知程序框图如图所示,则该程序框图的功能是A .求的值B .求的值C .求的值D .求的值5、已知平面向量满足11,(2)()2a b a b a b ==+-=-, 则与与的夹角为A .B .C .D .6、在正项等比数列中,232629log log log 3a a a ++=,则的值是A .16B .8C .4D .27、在二项式的展开式中,含的项的系数为A .-10B .10C .-5D .58、某城市对机动车单双号限行进行了调查,在参加调查的2548名有车人中有1560名持反对意见,2452名无车人中有1200名持反对意见,在运用这些数据说明“拥有车辆”与“反对机动车单双号限行”是否有关系时,用什么方法最有说服力A .平均数与方差B .回归直线方程C .独立性检验D .概率9、焦点在y 轴上的双曲线G 的下焦点为F ,上顶点为A ,若线段FA 的中垂线与双曲线G 有公共点,则双曲线G 的离心率的取值范围是( )A .B .C .D .10、已知()[)[]211,010,1x x f x x x ⎧+∈-⎪=⎨+∈⎪⎩,则下列函数的图象正确的是A .的图象B .的图象C .的图象D .的图象11、若直线20(0,0)ax by a b -+=>>过圆22:2410C x y x y ++-+=的圆心,则的最小值为( )A .B .C .D .12、定义域为R 的偶函数满足对任意,有,且当时,,若函数在上恰有三个零点,则的取值范围是( )A .B .C .D .第Ⅱ卷二、填空题:本大题共4小题,每小题5分,共20分,把答案填在答题卷的横线上。
2019-2020年高三综合练习数学理科试题(一)

2019-2020年高三综合练习数学理科试题(一)一、选择题:本大题共8小题。
每小题5分,共40分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.设为两个非空实数集合,定义集合,若,,则中元素的个数为 ( )A . 9B . 8C . 7D . 6 2.设3.02131)21(,31log ,2log ===c b a ,则大小关系为( ) A . B .C .D . 3.已知向量与的夹角为,则等于( )A .5B .4C .3D .1 4.向量, ,,为了得到函数的图象,可将函数的图象( )A .向右平移个单位长度B .向右平移个单位长度C .向左平移个单位长度D .向左平移个单位长度5.等比数列中,,=4,函数()128()()()f x x x a x a x a =---,则( )A .B .C .D .6. 函数()⎩⎨⎧≥-<+-=,0,1,0,1x x x x x f 则不等式的解集是 ( )A .B .C .D .7.函数与有相同的定义域,且都不是常值函数,对于定义域内的任何, 有,,且当时,,则的奇偶性为( )A .奇函数非偶函数B .偶函数非奇函数C .既是奇函数又是偶函数D .非奇非偶函数8.设非空集合满足:当,给出如下三个命题:①若;②若③若;其中正确的命题的个数为( )A .0个B .1个C .2个D .3个二、填空题:本大题共6小题,每小题5分,共30分。
把答案填在题中横线上。
9.若数列满足(,为常数),则称数列为调和数列.记数列1652021,200,}1{x x x x x x n+=+++则且为调和数列 = . 10.若等边的边长为,平面内一点满足,则=_________.11.已知变量满足4335251x y x y x -≤-⎧⎪+≤⎨⎪≥⎩,设, 若当取得最大值时对应的点有无数个,则值为 .12.在△中,内角的对边分别是,若,,则A 角大小为. 13.若某空间几何体的三视图如图所示,则该几何体的体积为 .14已知是定义在上不恒为零的函数,对于任意的,都有成立.数列满足,且.则数列的通项公式__________________ .三、解答题:本大题共6小题,共80分。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2019-2020年高三综合练习(一)理科数学高三数学(理科)学校 ______________ 班级 _________________ 姓名 _______________ 考号 _____________ 本试卷分第I 卷和第n 卷两部分,第I 卷1至2页,第n 卷3至5页,共150分。
考试时长120分钟。
考生务必将答案答在答题卡上,在试卷上作答无效。
考试结束后,将本试卷和答题卡 一并交回。
第I 卷(选择题共40分)一、本大题共8小题,每小题5分,共40分。
在每小题列出的四个选项中,选出符合题目要求的一项。
(1 )已知全集U ={1,2,3,4},集合A={1,2},那么集合$A 为(A) {3}(B) {3,4} (C) {1,2} (D) {2,3}【答案】BA 二{1,2},所以 e u A={3,4},选 B.(2)已知ABCD 为平行四边形,若向量7B”,忑二b ,则向量BC 为 (A) a-b (B) a + b (C) b-a(D) -a - b【答案】C*叮】因为BC = A A -AB ‘所以BC=b-a ‘选c.2 2(3)已知圆的丿丿悝为(x -1) (y-2) =4,那么该圆圆心到直线距离为(B) ff x = t + 3(t 为参数)的y 二11r =2,直线方程为x ・y ・2 = 0,所以圆心到直线的距离为d12 2 3>112渥选C.(4)某游戏规则如下:随机地往半径为 1的圆内投掷飞标,若飞标到圆心的距离大于 1成绩为及格;若飞标到圆心的距离小于 一,则成绩为优秀;若飞标到圆心的距离大于 1丄,则2【答案】c【「卅.1】圆心坐标为(1,2),半径1且小于一,则成绩为良好, 2那么在所有投掷到圆内的飞标中得到成绩为良好的概率为a A aiq nJ = 2 2nd =2n ,所以b n = log 2 a n = log 22n = n ,为等差数列。
所以数列 的前10项和为池亠一亠=55,选C.222(6)已知R (・c,0) , F2 (C ,0)分别是双曲线G :笃…每二12 0,b0)的两个焦点,双a b曲线G 和圆C2: x 2&的一个交点为P ,且2 PFF A PFFi ,那么双曲线G的离心率为(A)丄 (B) ( C) 2( D) '、3 12【答案】D【「*叮】因为圆的半径为C,所以三角形PF1F2为直角三角形,又2 PF1F2M/PF2F1 ,所以/PF I F 2 =§ » 所以丨 PF2 = c, PR = . 3c 。
又 PF Ai - PF2 =・ 3c - c = 2a ,即 c 2 3 1,选 D. a .3 -1(7) 已知定义在R 上的函数f (x)的对称轴为x=・3,且当x_-3时,f (x)=旷・3 •若函 数f (x)在区间(k-1,k) ( k-Z )上有零点,贝Uk 的值为 (A) 2 或・7( B) 2 或 -8 (C)1 或-7 (D) 1 或・8【答案】A(C)- 4(D)・16【答案】A*T I 】到圆心的距离大于-且小于■的圆环面积为42二 r) 2 .二(\2=3 二,所以所有2 4 16投掷到圆内的飞标中得到成绩为良好的概率为3一兀16 嗚,选(5)已知数列{a.}中,耳=2,am -2a n 等于(A )130 (B )120【答案】Cbn =log 2a n ,那么数列{0}的前10项和(C) 55(D )50堆门】由%1-2务二0得a. 1=2%,所以数列 {a n }为公比数列‘公比q=2,所以【卅・1】当X__3时,由f (x) =2X —3=0,解得x=log 23,因为1乞log 23乞2,即函数的零点所在的区间为(1,2),所以k = 2<>又函数矢于x ・_3对称,所以另外一个零点在区间(_8,_7),此时k = _7,所以选A.(8)已知向量OA ,WB ,O 是坐标原点,若天B = kOA ,且TB 方向是沿oA 的方向绕着A 点按逆时针方向旋转二角得到的,则称OA 经过一次(v,k)变换得到TB •现有向量OA=(1,1)经过一次⑺,可变换后得到TA- TA 经过一次(鮎k2)变换后得到 AA 2,…,如此下去,后A 二经过一次(片,心)变换后得到石An.设A=Ai= (x,y), 1 1盯,人j ,贝【I 八%等于【答案】B解析】根据题意,日丨二丄二1判二小二丄,所以一次(o1, k1)变换就是将向2cosE cos1得,且■■x* = cosi —s in1一,所以,即向量「逆时针旋转1弧v* = si n1 +cos1得到向量a 二(cosi - sinl, sin 1+cosl),再将◎的模长度伸长为原来的 ......... 倍,COS1得至 U .、「二…(cosi ・ si nl, sin 1+cosl) = (1 一二」一、二」・・+1) 1 cosi cosi cosi.设向量逆时针旋转1弧度,所得的向量为 1= (x‘,y‘)(C) 2sin[2・G 丿“」〕1 1 sin 1sinsin p2 2n 2COS 侶一(;尸j ]1sin 1si n sin(B)1 n_/ 2si n[2_(?)n 」] 1 1 coslcos COS—JTT 222cos[2 —QU(D )COS1 COSMOS22一*量「逆时针旋转1弧度,再将长度伸长为原来的1 _______________ •一*一倍,即「「由「,逆时针旋转1弧度而COSlL则有cosi sinlsin1x = 1 -cos1,由此可得 y ・ x=Sm! sini' cosi+1y . 1COSI_( 1 —三—:”cosi2s in[2n=l 时 ---2cos[2 一纣]时 2 1 sinlsin 刁川 sin 尹n=l 11 n _L2cos[2 七)U 时 2......1 1coslcos COS-A 2n综王所述,可密只有B 项符合题意2cos1sini ,与计算结果不相等,故°不正确; 2cos1詬二S 与计算结果不相等,故D 不正确故选:B第H 卷(共110分)二、填空题:本大题共6小题, 每小题5分,共30分。
(9) 复数z =(2 -i)i 的虚部是亠【答案】21琳门】z =(2-i)i = 2i-i 2 =1 • 2i ,所以复数的虚部为 2.对于n=l 2sin [2 一([)2]时2—11如込2川cos 尹 •,与计算结果相等,故B 正确; COSI 因此当n=l 时,''」+1),即cosi对于=2,与计算结果不相等,故 A 不正确;sin1对于C,(10) (x21 22)6的展开式中x3的系数是一.【答案】160sinlsinsin 卫222I 卅1】展开式的通项公式为Tk严Ck(x2)6和)k=CkX巩2k,由12-3k=3,解x得k =3,所以T4 =C: x3 23 =160x3,所以x3的系数是160。
(11)如图是甲、乙两名同学进入高中以来5次体育测试成绩的茎叶图,则甲5次测试成绩的甲乙6 93 02 80 1平均数是,乙5次测试成绩的平均数与中位数之差是【答案】84 2【.「斗叮】甲的测试成绩的平均数是80 ±(-43 4 7 10) =84,51均数是80 (-1 28 11)=84,乙的测试成绩的中位数为82,所以乙5次测试成绩的平' 5均数与中位数之差是84 -82 = 2 o/“'力口冈・口in PA 匕南 C 炯4T1工 A ,半仅 CC CD ,OC =1 , OP =2 »贝I] PA = , PB =【答案】、3 、、3I 猝叮】连结OA、则0 A = 0C = 1,所以PA二..OP?匚0A? 「牡乎OC _ OP , ZOCB =ZOAB , 所以OBC ”ABP “PABPB 二PA「3. 〜(13)有甲、乙、丙在内的6个人排成一排照相,其中甲和乙必须相邻,丙不排在两头,则这样的排法共有 _______________ 种.【答案】144【厂堆厂I】把甲和乙看做一个元素,则有A?A2,若丙排在两头,此时有2A4A2,所以满足乙的测试成绩的平AC交PO于B ,若条件的排法有AjA2-2A4A| -144 O(14)数列{不}的各项排成如图所示的三角形形状,其中每一行比上一行增加两项'若a n=a n(a=O),则位于第10行的第8列的项a i fl3务尙at a a等于一,a^3在图中位于一・(填第几行的第几列) ................................【答案】a89第45行的第77列[G5U解析】因为第n行的最后一项为a n2,所以第9行的最后一项为asi,所以第10行的第8列的项为asi &=as9 =a89。
因为2013 =442• 77,所以比0)3在图中位于第45行的第77列。
三、解答题:本大题共6小题,共80分。
解答应写出文字说明,演算步骤或证明过程。
(15) (本小题共13分)在厶ABC中,三个内角A,B,C的对边分别为a,b,c,且bsi nA二3acos B .(i)求角B ;(n)若b=2、.3,求ac的最大值.(16) (本小题共14分)如图,已知ACDE是直角梯形,且ED//AC,平面ACD E平面ABC ,1NBAC =NACD =90* AB = AC = AE =2 ED AB p 毎BC :小|:山2 ,小'•(i)求证:DP 〃平面EAB ;(n)求平面EBD与平面ABC所成锐二面角大小的余弦值.(17) (本小题共13分)某班联欢会举行抽奖活动,现有六张分别标有 1 , 2, 3, 4 , 5, 6六个数字的形状相同的卡片,其中标有偶数数字的卡片是有奖卡片,且奖品个数与卡片上所标数字相同,游戏规则如下:每人每次不放回抽取一张,抽取两次(I)求所得奖品个数达到最大时的概率;(n)记奖品个数为随机变量X,求X的分布列及数学期望・(18) (本小题共14分)已知函数f(X" (xax a)e A ,( a为常数,e为自然对数的底).(I)当a = 0 时,求f (2);(n)若f (x)在x = 0时取得极小值,试确定a的取值范围;(川)在(口)的条件下,设由 f (x)的极大值构成的函数为g(a),将a换元为x,试判断曲线y二g(x)是否能与直线3x_2y-m = 0( m为确定的常数)相切,并说明理由.(19) (本小题共13分)22 1已知椭圆c :/ y =1 (ab 0)的两个焦点分别为F-已,离心率为一,过F的C : 2 .2 9直线I与椭圆C交于M , N两点,且△ MNF2的周长为8 •(I)求椭圆C的方程;(n)过原点O的两条互相垂直的射线与椭圆C分别交于A , B两点,证明:点O到直线AB的距离为定值,并求出这个定值.(20) (本小题共13分)设A是由n个有序实数构成的一个数组,记作:A= (a,aJILaJI|耳).其中a,(i =1,2,川,n)称为数组A的“元” ,i称为a,的下标•如果数组S中的每个“元”都是来自数组A中不同下标的“元”,则称S为A的子数组•定义两个数组A(ai,a2A l3a n), B =(3心川1,0啲矢系数为C(A,B)二aba?b2川务①.(I)若A =(-2,2), B =(-1,1,2,3),设S是B的含有两个“元”的子数组,求C(A, S)的最大值;,B=(0, a,b,c),且a2+b +2 =1, S 为B 的含有三个“元” 的子数组,求C(A,S)的最大值;(川)若数组A二(印42电)中的“元”满足詁・込 a?Ji •设数组B m(m=1,2,3,||),n)含有四个“兀”,且‘ bm 4A m,求A与Bm的所有含有三个“元”的子数组的尖系数C(A,B m)(m二1,2,3,(1)山)的最大值.北京市东城区2012-2013学年度第二学期高三综合练习(一)数学参考答案(理科)、选择题(本大题共8小题,每小题5分,共40分)(1) B (2) C (3) C (4) A(5) C (6) D (7) A (8) B、填空题(本大题共6小题,每小题5分,共30分)(9) 2 (10) 160 (11) 84 2(n)若力=(12) .3 .3 (13) 144 (14)衣9第45行的第77列注:两个空的填空题第一个空填对得3分,第二个空填对得2分.三、解答题(本大题共6小题,共80分)(15)(共13 分)解:(I)因为bsi nA = .. 3acosB ,由正弦定理可得sin B sin A二3sin AcosB,因为在△ ABC中,sin A = 0 ,所以tanB = 3.又0 :: B ::二所以B .3(n)由余弦定理b?二a2• c2 -2accosB ,因为B,八2.3,3所以12 = a? • &「ac.因为a2• c2 _ 2ac ,所以ac <12.当且仅当a二c = 2八3时,ac取得最大值12.(16)(共14 分)证明⑴取AB的中点F,连结PF, EF.因为P是BC的中占,1 所以FP//AC , FP AC2 ■1 1因为ED //AC,且ED AB AC ,2 2所以ED// FP,且ED =FP ,所以四边形EFPD是平行四边形.所以DP// EF .因为EF平面EAB , DP :二平面EAB ,所以DP 〃平面EAB .(n)因为・BAC = 90,平面EACD _平面ABC ,所以以点A为原点‘直线AB为X轴,直线AC为y轴,建立如图所示的空间直角坐标系A _xyz ,则z 轴在平面EACD 内.由已知可得 A(0,0,0) , B(2,0,0) , E(0,1,、,3) , D(0,2,、、3)・所以 EB =(2, -1A ,3),ED =(0,1,0),设平面EBD 的法向量为门=(x , y , z ). 丄 n EB =0 , 由n ED =0.所以 2x -y i 、3z=o ,[y =0・取 z=2 ,所以 n 二(、30,2).又因为平面ABC 的一个法向量为即平面EBD 与平面ABC 所成锐二面角大小的余弦值为乙7 .7 (17)(共 13 分)(I )由题意可知所得奖品个数最大为10,概率为:_A|丄 P-Ae 2 15(n)X 的可能取值是:0,2,4,6,8,10 X 0 2 4 6 8 10 p1 1 r 1 4 1 1555151515111411所以EX =02 4 6 8104 .5 55151515(⑻(共 14分)解:(I )当a =0 时,f (x) = x 2e :f (x) = 2xe* _x 2e* = xe=(2 _x).所以 f (2) =0 .(n)f(x) =(2x a)e» -e 亠(x 2ax a)二 e A [-x 2 (2 _a)x]zi-e Ax[x -(2 -a)]. 令 f (x) = 0,得 x=0 或 x=2-a .当2 _a =0,艮卩a =2时,f(x)二・x 2e 公< 0恒成立,此时f(x)在区间(」:,・::)上单调递减,没有极小值;m 二(0,0,1).所以cos c n , m x n||m|2眉7~当2 —a 0,即a : : : 2 时,若x : : : 0 ,则f (x) : : : 0 .若0 ::: x : : : 2_a,贝【J f (x) .0 .所以x = 0是函数f (x)的极小值点.当2・a : : : 0,即a.2时,若X0 ,则f (x) : : : 0 .若2 — a : : : x : : : 0,则f (x) . 0 .此时x = 0是函数f (x)的极大值点.综上所述,使函数f (x)在x = 0时取得极小值的a的取值范围是a:::2 .(川)由(n)知当a ::: 2,且x .2 - a 时,f (x) : : : 0 ,因此x = 2-a是f (x)的极大值点,极大值为 f (2・a) = (4 -a)e aA .所以g(x)二(4 -x)e x °(x : : 2).g (x) = -e XA e x,(4 ・x)二(3 -x)e x,.令h(x) =(3-x)e x, (x : : 2).则h(x)=(2-x)e x, 0恒成立,即h(x)在区间(』,2)上是增函数.所以当x :: 2 时,h(x) :: h(2)二(3 -2)e2,n 1,即恒有g (x)::: 1 .(19)(共13 分)解(1)由题意知,4a=8,所以a =2.1因为e =—2222b a ...c- 2 3所以2 2 1 -e:a a 4所以b2 =3 .22(II)矗攣擊缪齬褊拿不存在’皿时可设A(Xo,Xo) , B(X O AX O).又A, B两点在椭圆C上,2212估…0X0 212所以一一=1 ,Xo4 3 7当直线AB 的斜率存在时,设直线AB 的方程为y = kx • m .y = kx m,22消去y 得x_.y_, i 4 3(3 4k 2)x 2 8kmx 4m 2-12=0.由已知・:o .设 A(Xi,vi . B (Xa, V2).所以 xix 2 ・ y,y2 =0.所以 NX2 (k A m)(kx 2 m) = 0.即(k 2 1)为 x km(xi X2) m A 0.整理得7m 2=12(k 21),满足丄.0.(20)(共 13 分)解:(I)依据题意'当S=(,3)时,C(A,S)取得最大值为2.(n)①当0是S 中的“元”时,由于A 的三个“元”都相等及B 中a,b,c 三个称性,可以只计算C(A,S) 3(a b)的最大值,其中a 2 b 2 c A1 .3由(a b)2 =a 2 b 2 2ab A 2(a 2b?)空 2(a? b 2 c 2) =2 ,所以x ・i X 2 =8km 3 4k 2NX? 4時・123 4k 28k 计 3 4k 2-m 2的对所以点o 到直线AB 的距离d 二所以点O 到直线AB 的距离得-i.2 - 8 ■ b -2 .当且仅当C = o ,且a=b =—2-H^t ,a b 达到最大值・、2 ,②当o 不是S 中的“元”时,计算C (代S)3(a b c)的最大值,3由于 a 2 b 2 c 2 =1,所以(a b c)2 = a 2 b 2 c 2 2ab 2ac 2bc.乞 3(a 2 b 2 c 2)二3 ,当且仅当a=b =c 时,等号成立.即当a=b=c 3时,a b c 取得最大值、、3,此时C( A, S)3 (a ■ b c) =1 .3 3综上所述,c (代S)的最大值为1. (川)因为 Bm = (bm1, bm2 , "3 , *4)满足bm22 bm32 - bm4A ITI .3于是 C (代 S) (a b)=363由bmi, bm2, bm3,bm4矢系的对称性,只需考(bm2,也也)与(印盘厶)的矢系数的情况.f (bm4 )2i 当bmi=O时,有(肓)Vm 」Vma? •噎a2 b2 b2兰m + m + 也a2 •皿m-2 2 2al a?? a3?.唸]bk 1 匪2m丄丄汀22a2 二-?3.maibm2« a2bm3 ■ aabm4 的最大值为―m •当£ =0 时,恥2*32*42m , 得4A2 ■ a2bms. aabnu 最大值小于■- m .所以C(A,Bm)的最大值为m (m =1,2,3,川,n).。
