传输矩阵在物理学
传递函数阵

传递函数阵传递函数矩阵指的是在多输入、多输出线性时不变系统下,将系统各个输入与各个输出之间的关系统一表示为矩阵的形式。
该矩阵被称为传递函数矩阵。
系统的物理特性可以用数学模型来描述,通常采用微分方程的形式来表示。
而当系统具有多个输入和多个输出时,为了方便描述,我们可以采用矩阵的形式表示系统的状态,即将状态向量、输入向量和输出向量都表示为矩阵的形式:$$\mathbf{x} = \begin{bmatrix} x_1 \\ x_2 \\ \vdots \\ x_n \end{bmatrix} , \quad\mathbf{u} = \begin{bmatrix} u_1 \\ u_2 \\ \vdots \\ u_m \end{bmatrix} , \quad\mathbf{y} = \begin{bmatrix} y_1 \\ y_2 \\ \vdots \\ y_p \end{bmatrix}$$其中$\mathbf{x}$表示状态量矩阵,$\mathbf{u}$表示输入量矩阵,$\mathbf{y}$表示输出量矩阵。
$n, m, p$分别表示状态量、输入量和输出量的个数。
在线性时不变系统中,系统的状态方程可用矩阵形式表示:$$\begin{aligned}\dot{\mathbf{x}} &= \mathbf{Ax}+\mathbf{Bu} \\\mathbf{y} &= \mathbf{Cx}+\mathbf{Du}\end{aligned}$$我们可以根据线性时不变系统的传输特性,将输入矩阵$\mathbf{B}$和直流增益矩阵$\mathbf{D}$组成一个$m\times p$的矩阵,称为传递函数矩阵$\mathbf{G}(s)$:其中,$\mathbf{G}_{ij}(s)$表示第$i$个输入对第$j$个输出的传递函数。
传递函数矩阵$\mathbf{G}(s)$反映了系统各个输入与各个输出之间的传递特性。
传输矩阵方法

(b ) ky kx ky kx ky kx
图1.Dirac点K 附近波矢圆上单层(左),双层(中)和三层(右)石墨烯 的赝自旋矢量旋转图.图中单层赝自旋旋转一次,双层赝自旋旋转 两次而三层旋转三次.第一行表示导带中赝自旋矢量,第二行表示 价带中赝自旋矢量,其方向正好与导带中的方向相反.
2 2
假定势垒边缘相当陡峭且在晶格尺度上光滑,则不引起 能 谷 间 散 射,那 么 我 们 只 需 研 究 一 个 能 谷K 的 散 射. 由 于 势 函 数 与 坐 标y 无 关,则 粒 子 的 波 函 数 可 写 为ψ (r ) = ψ (x)eiky y .二维矩阵表示中, 对无势垒区域的波函数的x分 量满足本征值方程 2 0 (kx − iky )2 ψ1 (x) ψ1 (x) =E − 2m (kx + iky )2 0 ψ2 (x) ψ2 (x) (5) 这里E 是费米能.式(5)可写为下面的两个微分方程 d + ky dx d − ky dx 由(6)(7)消去ψ2 (x)有 d2 2 − ky dx2
其中nJ = −(cos(Jφ), sin(Jφ))表示赝自旋极化轴,在二维 波矢平面上的极化角φ = arctan(ky /kx ),波矢k与动量p与 的 关 系 为p = k.赝 自 旋 矢 量σ = (σx , σy )是 两 维 泡 利 矩 阵.在 上 面 的 表 示 中, J 表 示 石 墨 烯 的 层 数,也 叫 手 性 自由度,它联系各层的电子密度,比如对单层J = 1,对双 层J = 2,等等.
以后的研究进一步指出J 可表示赝自旋在倒空间的缠 绕数.这里赝自旋矢量描述粒子两分量波函数的相对相 位,J 表示当电子波矢绕狄拉克点作一次完全旋转时赝自旋 矢量经历的旋转次数.正如图1所示,在k空间对单层石墨烯 它是厄米和么正算符,本征值为±1.不存在质量项时,螺旋 当波矢绕Dirac点K 旋转一周,赝自旋矢量的方向σ 也旋转 1
矩阵在生活中的应用

矩阵在生活中的应用
矩阵是数学中一个重要的概念,它在生活中有着广泛的应用。
从科学到工程,
从经济到医学,矩阵都扮演着重要的角色。
在科学领域,矩阵被广泛应用于物理学、化学等学科中。
在物理学中,矩阵被
用来描述物体的运动和变形,例如在力学中,矩阵可以表示物体受力的情况,从而帮助科学家们分析物体的运动规律。
在化学中,矩阵被用来描述化学反应的过程,从而帮助化学家们预测反应的结果。
在工程领域,矩阵被广泛应用于控制系统、通信系统等领域。
在控制系统中,
矩阵被用来描述系统的状态和控制输入之间的关系,从而帮助工程师们设计出高效的控制系统。
在通信系统中,矩阵被用来描述信号的传输和处理过程,从而帮助工程师们设计出高效的通信系统。
在经济领域,矩阵被广泛应用于金融、市场分析等领域。
在金融中,矩阵被用
来描述资产的收益和风险之间的关系,从而帮助金融分析师们进行投资决策。
在市场分析中,矩阵被用来描述市场数据之间的关系,从而帮助市场分析师们预测市场走势。
在医学领域,矩阵被广泛应用于医学影像处理、生物信息学等领域。
在医学影
像处理中,矩阵被用来描述医学影像的特征,从而帮助医生们进行疾病诊断。
在生物信息学中,矩阵被用来描述生物数据之间的关系,从而帮助生物学家们研究生物信息。
总的来说,矩阵在生活中有着广泛的应用,它不仅帮助科学家们研究自然规律,还帮助工程师们设计出高效的系统,帮助金融分析师们进行投资决策,帮助医生们诊断疾病。
可以说,矩阵已经成为了现代社会不可或缺的数学工具之一。
一维光子晶体中电磁场传播规律的转移矩阵理论

方法得 到 了周期 性光子晶体介质 中的 电磁场传输特性 , 计算 了电磁 场在一维光子 晶体 中的透射 率和反射 率, 为 计 算和 分析 究一维光子晶体的传输特性提供 了依据.
关键词 : 光 子 晶体 ; 传输矩阵 ; 透射 率 ; 反 射 率 中图分类号 : O 4 3 1 . 2 收 稿 日期 : 2 0 1 5— 0 5~1 0 文献 标 识 码 : A 文章 编 号 : 1 6 7 4—1 3 3 1 ( 2 0 1 5 ) 0 3— 0 0 4 0— 0 6
思想 是将 研究 体 系划分 为 多层 , 把 Ma x w e l l 方 程离 散化 , 通 过 边界 条 件将 各 层 中 的 电磁 场 , 用 一 个传 输 矩 阵联 系起 来 . 然后 依据 初始 条件 , 从第 一 层开始 逐 层计算 各 层 电磁 场 的分 布规 律 , 最 后得 出电磁 场 在 整个 介质 体 系 中的分 布特 性 J . 转 移 矩 阵法 因其 具 有 计 算 简 单 、 精确度高等特点 , 受 到 了研 究 人 员 的广 泛
关 注.
本文 采用 M a x w e l l 电磁场 理论 , 推导 了平 面 电磁 场 在 均 匀各 向 同性 介 质 中传 播 的波 动 方 程 , 利 用 转
移矩 阵方 法得 到 了周期 性光 子 晶体介 质 中电磁 场 的传播 特性 , 计 算 了 电场 在一 维光 子 晶体 中的透 射 率 和 反射 率 .
在 电子 能带计 算 中则 是必须 要 考虑 的. 计 算光 子 晶体 中电 磁波 传 播 特性 的常 用方 法 , 主要 有 时 域 有 限差
分法 、 多 重散 射法 、 平 面波展 开法 和转 移矩 阵法 等 . 其 中转 移 矩 阵 法 又称 为 特 征矩 阵法 或 传输 矩 阵法 , 其
波干涉和波衍射的传输线矩阵(TLM)法模拟

现象 关 键词
TLM
法
,
数值 模拟
,
干涉
,
衍射
.
在 研究光的干 涉和 衍 射 现 象 中采 用 标量波的近似具有 广泛 的 代表意 义
,
.
标量波近似
,
就是把 光 波当作标量波处理 只考虑光波电磁场 的一个横 向分量 随着研究的深入 人们 发现 干 涉 和 衍射 现象是所有波 动 过程 (从 电磁波 到 声波 ) 都具有 的属 性 对 于波 的 干涉
e
劝1 )
(m (二
=
1 4
,
)
(5 ) (6 )
A A
’
、
V
2 该
,
=
A
Z
s
i
.
n
r (2 7
,
2 /入 + 叻 )
,
=
1 4)
,
(万1
.
川
(
,
2
川 是双 缝所对应 的 节点 坐 标
.
Al
和
A Z 劝1
2 二 和 劝 可 以 相 同 也可 以 不 同
边 界 的其余 节 点 电压为零
L 3
采样信号 采样 屏 上 的 节 点 的 时域响应为
、、 n
e
,
、
a n 、
1
r
,
.
,
合理 的计算结构 对 于 各种边界 的模 拟 (包括反射边界 能 够反 映实 际 情 况 合适 的 激励模 型
.
,
、
吸 收 边界
,
,
[ ] 以及 黑体 边界等 l)
.
,
本文研 究 了如何 用
多体系统传递矩阵法及其应用

多体系统传递矩阵法及其应用多体系统是由许多互相作用的体组成的复杂体系,如分子、原子、晶体等。
传递矩阵法是一种处理多体系统的方法,它能够高效地计算多体系统在空间中的相互作用关系,是现代物理学研究中不可或缺的重要手段。
传递矩阵法最早应用于固体物理领域中的声子传输问题。
其基本思想是通过计算相邻体间的相互作用关系,得出整个体系中体与体之间的传递矩阵。
具体来说,传递矩阵法假设每个体以弹性球体为模型,并将每个弹性球体中储存的平面波能量互相传递,形成整个体系中的传递矩阵。
这种方法在研究固体中光声声子的传输、声子光子的散射等问题中具有重要的应用价值。
除了固体物理领域,传递矩阵法还广泛应用于原子、分子的电子结构计算以及化学反应机理的模拟等领域。
计算和分析分子/团簇数据在化学特异性中的作用是大量分子和聚集体计算化学和物理学领域的重要问题。
基于传递矩阵法可以对分子结构、物理特性以及从催化到切削的各种机械和电子反应进行分析和预测。
在实际应用中,传递矩阵法的计算和建模过程也面临着许多挑战,如有限的计算能力、模型精度等问题。
为了解决这些问题,一些改进的传递矩阵法,如多重散射和Greens函数方法等也被提出,以提高计算精度和效率。
同时,也有越来越多的科研工作者尝试将传递矩
阵法与机器学习等前沿技术相结合,从而拓展传递矩阵法的应用范围和精度,实现更加智能化的计算和数据分析。
总之,传递矩阵法在物理、化学、材料学、和计算机科学等领域都扮演着重要的角色。
通过该方法,我们可以更加深入地理解多体系统内部的相互作用关系,进而更好地预测和优化系统的性质和行为,为理论和实践应用提供了新的思路和创新性解决方案。
矩阵的迹的几何意义

此外,在图像处理和计算机图形学中,矩阵的迹也有重要的几何意义。例如,在计算机图形学中,为了将3D物体投影到2D平面上,可以使用投影矩阵。投影矩阵的迹给出了投影后的图像在平面上的缩放比例。这个比例可以用来调整3D物体在2D场景中的大小。
矩阵的迹的几何意义
矩阵的迹是指矩阵对角线上元素的和。它在计算线性变换的特征值、进行迹变幻等许多应用中起着重要的作用。在几何学和物理学中,矩阵的迹有着深刻的几何意义。
首先,我们来看一个二维空间中的刚体变换。刚体变换是指保持空间中所有点的相对位置和角度不变的变换。在二维空间中,刚体变换可以表示为二阶矩阵。对于一个二维矩阵A来说,它的迹tr(A)表示了刚体变换在平面上的平移和旋转。具体来说,tr(A)表示了刚体变A是一个二维刚体变换矩阵,那么A可以写成如下形式:
A = [cosθ -sinθ]
[sinθ cosθ]
其中,θ表示旋转角度。我们来看一下tr(A)的几何意义。根据定义,tr(A) = cosθ + cosθ = 2cosθ,即tr(A)等于旋转角度的余弦值的两倍。
我们知道,余弦值的范围在[-1,1]之间。当θ = 0°时,即没有旋转,tr(A) = 2;当θ = 180°时,即旋转180度,tr(A) = -2;当θ = 90°或θ = -90°时,即旋转90度或-90度,tr(A) = 0。可以看出,tr(A)的绝对值表示了旋转的强度,tr(A)的正负表示了旋转的方向。
总而言之,矩阵的迹在几何学和物理学中具有重要的意义。它可以表示刚体变换的平移和旋转,在量子力学中给出能量的总和,在光学中表示光线传输的强度,在计算机图形学中表示物体的缩放比例,等等。通过理解和利用矩阵的迹的几何意义,我们可以更好地了解和应用线性代数在实际问题中的应用。
传输矩阵法在大学物理波动光学教学中的应用

Abstract In the teaching of wave optics in college physics,the optical path difference is main- ly described for the superposition interference of multiple beams,which is not conducive to the intuitive reflection of the optical characteristics of the optical system.How to more intui- tively reflect the propagation properties of electromagnetic waves in multi-layered media is of great significance for understanding the basic concepts of physics,cultivating studentsinno- vative ability and the ability of“learning for application”.The propagation of electromagnetic wave in multi-layered homogeneous medium is studied based on optical transmission matrix. Through the establishment of the interface matrix and the propagation matrix,the total trans- fer matrix of the multi-layered medium system is derived.Then the reflection coefficient and transmission coefficient of the system can be obtained.In this paper,through two practical ca- ses of reflecting film and distributed Bragg reflector(DBR),combined with the idea of trans- mission matrix and MATLAB programming,the propagation properties of electromagnetic wave on the interface of multi-layered media and the properties of optical system are visually demonstrated from the perspective of reflectivity and transmittance. Key words coherent superposition of electromagnetic wave;transmission matrix;high-reflec- tion coating;distributed Bragg reflector(DBR);Matlab
(整理)传输矩阵法.
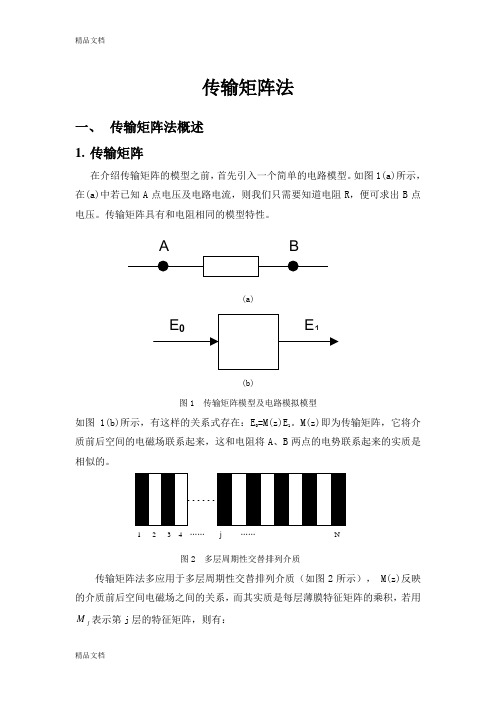
传输矩阵法一、 传输矩阵法概述 1. 传输矩阵在介绍传输矩阵的模型之前,首先引入一个简单的电路模型。
如图1(a)所示, 在(a)中若已知A 点电压及电路电流,则我们只需要知道电阻R ,便可求出B 点电压。
传输矩阵具有和电阻相同的模型特性。
(a)(b)图1 传输矩阵模型及电路模拟模型如图1(b)所示,有这样的关系式存在:E 0=M(z)E 1。
M(z)即为传输矩阵,它将介质前后空间的电磁场联系起来,这和电阻将A 、B 两点的电势联系起来的实质是相似的。
图2 多层周期性交替排列介质传输矩阵法多应用于多层周期性交替排列介质(如图2所示), M(z)反映的介质前后空间电磁场之间的关系,而其实质是每层薄膜特征矩阵的乘积,若用j M 表示第j 层的特征矩阵,则有:1 2 3 4 …… j …… N(1)其中, (2)j δ为相位厚度,有 (3)如公式(2)所示,j M 的表示为一个2×2的矩阵形式,其中每个矩阵元都没有任何实际物理意义,它只是一个计算结果,其推导过程将在第二部分给出。
2. 传输矩阵法在了解了传输矩阵的基础上,下面将介绍传输矩阵法的定义:传输矩阵法是将磁场在实空间的格点位置展开,将麦克斯韦方程组化成传输矩阵形式,变成本征值求解问题。
从其定义可以看出,传输矩阵法的实质就是将麦克斯韦方程转化为传输矩阵,也就是传输矩阵法的建模过程,具体如下:利用麦克斯韦方程组求解两个紧邻层面上的电场和磁场,从而可以得到传输矩阵,然后将单层结论推广到整个介质空间,由此即可计算出整个多层介质的透射系数和反射系数。
传输矩阵法的特点:矩阵元少(4个),运算量小,速度快;关键:求解矩阵元;适用介质:多层周期性交替排列介质。
二、 传输矩阵的基础理论——薄膜光学理论 1.麦克斯韦方程组麦克斯韦方程组由四个场量:D 、E 、B 、H ,两个源量:J 、ρ以及反映它们之间关系的方程组成。
而且由媒质方程中的参数ε、μ、σ反映介质对电磁场的影响。
基于传输矩阵法的多层介质膜反射特性研究

第39卷第8期大 学 物 理Vol.39No.82020年8月COLLEGE PHYSICSAug.2020收稿日期:2019-11-01;修回日期:2020-01-07 基金项目:2019年校级教育教学改革研究项目(精品课程建设专项)(2019JG0840K)、教育部高等学校电子信息类专业教学指导委员会光电信息科学与工程专业教学指导分委员会2019年教育教学研究项目资助 作者简介:马海霞(1976—),女,山东兖州人,南京航空航天大学理学院副教授,博士,主要从事大学物理教学和纳米光子学研究工作.基于传输矩阵法的多层介质膜反射特性研究马海霞,武艳军,王吉明,路元刚,杨雁南(南京航空航天大学理学院,江苏南京 211106)摘要:薄膜干涉是大学物理波动光学教学的重要内容,也是薄膜光学的理论基础.薄膜干涉的一个重要应用是用于设计减反膜和高反膜.本文基于传输矩阵法,定量计算了多层介质膜的反射率.以BK7玻璃为例,无镀膜时在可见光范围内,其反射率约为4%.利用薄膜的相消干涉可以减少表面的反射率.镀一层减反膜时,对设计波长550nm其反射率下降为1.3%,一旦偏离设计波长减反效果变差;镀两层减反膜时,在470nm~670nm范围内,减反效果明显改善,反射率均低于1.3%.利用薄膜的相长干涉可以增加表面的反射率.以熔石英为例,镀一层薄膜时,对设计波长1500nm其反射率可由未镀膜时的3.3%提高到30%;镀七组薄膜时在1360nm~1660nm范围内其反射率均可达99%以上.通过这些定量计算,让学生更加深刻地理解所学理论知识在实际中的应用,培养工程意识,提高学习兴趣.关键词:薄膜干涉;传输矩阵法;减反膜;高反膜中图分类号:O436.1 文献标识码:A 文章编号:1000 0712(2020)08 0025 06【DOI】10.16854/j.cnki.1000 0712.190500光波经薄膜两表面反射后相互叠加形成的薄膜干涉既是日常生活中常见的光学现象,也是光学器件设计中需要考虑的一个重要环节.利用薄膜干涉原理,可以对光学材料表面的反射或透射特性进行调控,因此该方面的知识一直是大学物理教学中的重要内容.为了使学生更好地理解掌握该部分的理论知识,有多位学者对此开展了深入细致的教学研究.王文梁利用Macleod软件分析了楔形薄膜分振幅干涉的相长和相消的情形,以及薄膜干涉位相突变的情况[1];刘萍讨论了薄膜干涉中条纹形状、条纹分布、薄膜干涉中相干光束个数等问题[2].薄膜干涉的一个重要应用是用于设计减反膜和高反膜.针对学生学习过程中的一些疑惑,本文在大学物理的层面上,利用传输矩阵法以常用材料BK7玻璃和硅片为例,计算了没有镀膜时材料表面的反射率,镀一层、两层减反膜,以及多层高反膜时的反射率,并考虑了不同入射角以及不同入射波长时的反射情况,让学生更加深刻地理解薄膜干涉在实际中的应用,培养学生的工程意识.本文的研究结果有益于加深学生对薄膜干涉知识的理解,同时巩固电磁学知识,通过对大学物理知识适当的拓展,提高学习者的兴趣.1 传输矩阵法在薄膜干涉中的应用传输矩阵法是用矩阵的形式来描述电磁波在多层介质中的传播情况,在每一层介质传播过程中的运动规律满足Maxwell方程组,层与层之间满足电磁场边界条件,该方法是光学薄膜计算与设计中常用和有效的方法[3].图1表示由N个相邻的均匀介质层构成的多层介质,边界为介电常数为εa和εb的介质,第n层介质位置位于zn~zn+1,介电常数为εn.对于垂直于入射面的线偏振光(s波),它在第n层介质中的矩阵Mns可以表示为Mns=cosδnqn-1sinδn-qnsinδncosδn(1)其中,qn=(ω2/c2)(εn-εasin2θa槡),δn=qn(zn+1-zn),qn表示第n层介质中波矢垂直于分界面的法向分量,ω代表圆频率,c为光速,电磁波从介电常数为εa的介质入射,θa为入射角;经过N层介质后,从介电常数为εb的介质出射,δn表示电磁波从zn到zn+1传播时相位的增量.这样我们可以写出每一层介质的矩阵,M1s,M2s,……,MNs,对于整个多层介质而言,s波的矩阵Ms可以表示为Ms=m11sm12sm21sm22s=MNsM(N-1)s…Mns…M2sM1s (2)26 大 学 物 理 第39卷这样电磁波经过多层介质时,反射率Rs、透射率Ts可以表示为Rs=(qaqbm12s+m21s)2+(qbm11s-qam22s)2(qaqbm12s-m21s)2+(qbm11s+qam22s)2(3)Ts=4qaqb(qaqbm12s-m21s)2+(qbm11s+qam22s)2(4)其中,qa,qb表示入射和出射介质中波矢垂直于分界面的法向分量,它们可以分别表示为qa=(ω2/c2)(εa-εasin2θa槡)qb=(ω2/c2)(εb-εasin2θa槡)对于在入射面内的线偏振光(p波),它在第n层介质层中的矩阵不同,其Mnp可以表示为:Mnp=cosδnQn-1sinδn-Qnsinδncosδn(5)其中,Qn=qn/εn.同理我们可以写出p波在每一层介质的矩阵,M1p,M2p,……,MNp,对于整个多层介质而言,p波的矩阵Mp可以表示为Mp=m11pm12pm21pm22p=MNpM(N-1)p…Mnp…M2pM1p(6)p波的反射率Rp以及透射率Tp可以表示为Rp=(QaQbm12p+m21p)2+(Qbm11p-Qam22p)2(QaQbm12p-m21p)2+(Qbm11p+Qam22p)2(7)Tp=4QaQb(QaQbm12p-m21p)2+(Qbm11p+Qam22p)2(8)基于传输矩阵法,我们可以获得每一层介质中的振幅,求出入射电磁场经过多层介质后总的反射率,透射率.图1 由N个相邻的均匀介质层构成的多层介质2 结果与分析2.1 无镀膜时材料表面的反射菲涅耳公式可以计算两种介质分界面入射光的反射率和透射率[4],解释光的反射与折射的起偏及半波损失问题等.在垂直入射时,自然光由空气入射到某一介质时,介质的折射率越大,其反射率就越大.图2(a)表示BK7玻璃表面在波长为550nm的入射光下,s波、p波以及自然光在不同入射角下的反射率.BK7玻璃的折射率取自文献[5].在可见光光谱内,它的折射率约为1.52.在垂直入射时,其反射率大概为4%.当入射角小于10度时,s波和p波反射率近似相等;一旦入射角增大,s波和p波表现出不一样的行为;p波在入射角约为57°时发生布儒斯特现象,这时它的反射率为0,全部透射;随着入射角的进一步增大,s波和p波的反射率迅速增加;掠入射时几乎全部反射.对于入射自然光的情况,自然光可以看成具有一切可能振动方向的光波的总和,对所有可能的方位角取值所对应的反射率取平均,可以得到自然光反射率.由于色散现象,当入射光波长改变时,玻璃的折射率亦发生改变.玻璃材料的折射率随波长的增加,折射率会逐渐减小.入射光垂直入射时,BK7玻璃随着入射波长的改变其反射率如图2(b)所示,随着入射光波长的增大,其反射率略微减小.在整个可见光光谱内,BK7玻璃表面的反射率变化不大,都可以近似为4%.波长为550nm的单色光以不同入射角入射时的反射率.Rs代表s分量,Rp代表p分量,R代表自然光;垂直入射时不同入射光波长的反射率图2 不镀膜时BK7玻璃表面的反射率.第8期马海霞,等:基于传输矩阵法的多层介质膜反射特性研究27 玻璃分成2大类:冕牌玻璃和火石玻璃.冕牌玻璃的特点是低折射率、低色散,火石玻璃的特点是高折射率、高色散.火石玻璃的折射率略高,反射率也略高,一般在5%左右.因此在粗略估计光学系统的光能损失时,冕牌玻璃反射率可以按照4%计算,火石玻璃反射率按照5%计算.对于硅片,在可见光区域,在波长550nm附近,折射率大概为4.1[6],而且存在吸收现象,它的反射率要远大于玻璃.硅表面的反射情况如图3所示,在垂直入射时,在550nm的入射光下,它的反射率大概为37%,入射角在约为76°发生布儒斯特现象.垂直入射时,随着入射光波长的增加,其反射率下降比玻璃明显,反射率从48%变化到32%.波长为550nm的单色光以不同入射角入射时的反射率.Rs代表s分量,Rp代表p分量,R代表自然光;垂直入射时不同入射光波下的反射率图3 不镀膜时硅片表面的反射率由此可见,在垂直入射时材料表面都存在菲涅尔反射,当反射面增多时,其反射光能的损失也增多.以BK7玻璃为例,如果透镜的个数为3个透镜,一共6个和空气的接触面,反射能损失就达到22%;而更复杂的系统,透镜的个数更多,反射损失就相当可观了.为了减少入射光能在透镜玻璃表面上反射时所引起的损失,常常通过镀膜的方式,利用薄膜干涉减少反射损失,这就是减反膜.2.2 单层减反膜最简单的是单层减反膜,在光垂直入射时,它的光学厚度为波长的四分之一,减反原理在大学物理教学中讲述,在这儿不再赘述.对于均匀的折射率为ns的材料,对于光学厚度为(1/4)λ(λ为波长)的减反膜,其薄膜的折射率要满足式(9)时,其反射率才会降为0[7].n=nsn槡env(9)其中nenv表示周围环境的折射率.对于光伏产业中常用的硅而言,在550nm的入射光下,需要镀一层厚度为68nm、折射率为2.02的薄膜,就可以使得反射率在该波长下降为0.Si3N4材料的折射率接近2.02[8],在光学厚度为四分之一波长时,在垂直入射时,对于不同波长的入射光其反射率如图4(a)所示.在波长为550nm时反射率接近零,入射波长一旦垂直入射时不同入射波长下的反射率波长550nm单色光入射时,不同入射角下的反射率图4 硅片表面镀单层Si3N4薄膜时的反射率偏离550nm,其反射率将增加,在整个可见光光谱内,其反射率平均约为5.3%.图4(b)给出了不同入28 大 学 物 理 第39卷射角下的反射率.单层(1/4)λ减反膜的最大问题是它只是在特定的波长和角度下才能够达到减反的目的,一旦入射角增大,比如掠入射时,减反效果消失.由等倾干涉的知识易知,当入射角改变时,经薄膜的上下表面反射后产生的一对相干光束的光程差发生改变,不能满足相消干涉的条件而导致反射率增加.实际上,对于很多低折射率衬底材料很难发现合适的单层(1/4)λ的减反膜材料.例如,对于玻璃材料BK7,其折射率为1.52,根据式(9)其镀膜材料的折射率应该为1.23.在自然界中,这样的材料不存在,因此,我们只能采用一些折射率接近这个数值的薄膜材料尽量地降低反射率.对于BK7玻璃,常用的镀膜材料如MgF2,它的折射率约为1.38,它的反射率如图5(a)所示.由于薄膜的相消干涉,在特定波长下它的反射率会降低,但不会到零.镀一层厚度为99.6nm的MgF2薄膜,在550nm左右获得的最低反射率为1.3%.波长一旦偏离550nm减反效果将变差.图5(b)给出了不同入射角下的反射率.一旦入射角偏离垂直入射,其反射率会逐渐增大,到了掠入射时完全失去减反效果.单层膜的这种性质限制了它的使用.垂直入射时不同入射波长下的反射率波长550nm单色光入射时,不同入射角下的反射率图5 BK7玻璃表面镀单层MgF2薄膜时的反射率2.3 双层减反膜为了获得更好的减反效果,可以采用双层膜或多层膜,本文以双层膜为例.对于双层膜的情况,首先在衬底上沉积一层高折射率材料薄膜,紧接着沉积折射率较低的材料如MgF2,这是最靠近空气的一层薄膜.双层膜可以采用光学厚度为(1/4)λ~(1/4)λ膜系或者(1/2)λ~(1/4)λ膜系,不论哪种膜系,只有在特定的高折射率薄膜下才能在某一些波长下反射率为0.对于常用的薄膜组合ZnS/MgF2,采用(1/2)λ~(1/4)λ膜系时其反射率曲线如图6所示,反射率曲线有两个谷值,分别在波长为489nm和627nm.图6中,BK7玻璃为衬底,ZnS薄膜和MgF2薄膜,厚度分别为118nm和99.6nm,折射率分别为2.33和1.38.和单层减反膜相比,利用双层薄膜可以在一个比较宽的波带内获得优良的减反效果,在470nm~670nm范围内,其反射率均低于1.3%.双层膜的优点是在可见光范围的中段有更低的反射率,缺点在于在红,蓝端的反射率上升过快,采用3层膜可以进一步拓宽带宽,并且获得更低的反射率[9].图6 BK7衬底镀ZnS薄膜和MgF2薄膜时的反射率2.4 高反膜采用薄膜干涉可以使得某种单色光干涉相消,也可以利用类似的方法,来加强某一特定单色光的反射强度,这就是高反膜,可用于激光器的谐振腔腔镜或者制作各种干涉滤色片.以熔石英为例,在其表面镀一层光学厚度为(1/4)λ(波长为1500nm)的Nb2O5薄膜后,反射率曲线如图7(a)所示,对波长为1500nm的入射光其反射率可由未镀膜时的3.3%提高到30%以上.如果要进一步提高反射率,可采用多层膜.我们在熔石英玻璃表面交替镀高折射率的Nb2O5薄膜(折射率约为2.237)和低折射率的SiO2薄膜(折射率约为1.44),最后再镀一层高折射率薄第8期马海霞,等:基于传输矩阵法的多层介质膜反射特性研究29 膜,采用光学厚度为(1/4)λ的膜系,即SiO2薄膜的厚度为260nm,Nb2O5薄膜的厚度为168nm,示意图如图7(b)所示.高折射率薄膜和低折射率薄膜合称为1组,图7(c)给出了镀不同组数薄膜时的反射率.从图7(c)可以看出,镀到七组薄膜时,其反射率在1360nm~1660nm波长范围内均可达99%以上.如果要获得更高的反射率,还需增加镀膜组数.镀单层Nb2O5薄膜时的反射率镀多层高反膜时的示意图镀不同组数的高低折射率薄膜时的反射率图7 熔石英表面镀高反膜时的反射率TFCalc是一款光学薄膜设计和分析的通用工具,可以分析设计多层薄膜,可以计算反射率、透过率、吸收率、光密度、颜色、亮度等.为保证计算结果的正确性,本文所有的计算结果都经过TFCalc3.5验证,计算结果完全一致.3 结论本文采用传输矩阵法计算了常规材料表面镀不同减反膜、高反膜时的反射率.得到的结论如下:1)在可见光范围内,玻璃表面没有镀膜时,光近垂直入射时反射率约4%~5%,硅片表面的反射率高达38%;大角度掠入射时反射率趋于1;2)通过镀单层光学厚度为四分之一波长的减反膜时,对设计波长550nm其反射率下降为1.3%,但对偏离设计波长的其它光波反射率改善较小;镀两层减反膜时,在470nm~670nm范围内,其反射率都有明显改善,均低于1.3%;3)对于高反膜,以熔石英为例,镀一层薄膜时,对设计波长1500nm其反射率可由未镀膜时的3.3%提高到30%;如果要达到高反的目的,通常需要交替镀高低折射率薄膜,镀七组薄膜时,在1360nm~1660nm波长范围内其反射率均可达99%以上.通过这些定量计算,让学生更加深入具体地了解薄膜干涉在实际中的应用,进一步激发学习兴趣.参考文献:[1] 王文梁,戎晓红,陈华英.基于Macleod软件的分振幅薄膜干涉仿真教学[J].大学物理,2018,37(11):24 27,51.[2] 刘萍,苏亚凤,方爱平.浅谈薄膜干涉现象中的几个问题[J].物理与工程,2017,27(1):47 49,54.[3] LeknerJ.Theoryofreflection:reflectionandtransmissionofelectromagnetic,particleandacousticwaves[M].secondedition,springerseriesonatomic,optical,andplasmaphysics,SpringerChamHeidelbergNewYorkDordrechtLondon SpringerInternationalPublishingSwitzerland,2016.[4] 郁道银,谭恒英.工程光学[M].4版,北京:机械工业出版社,2015.[5] SCHOTTZemaxcatalog2017-01-20b(obtainedfromhttp://www.schott.com).[6] AspnesDE,StudnaAA.DielectricfunctionsandopticalparametersofSi,Ge,GaP,GaAs,GaSb,InP,InAs,andInSbfrom1.5to6.0eV[J].PhysRevB,1983,27:985 1009.[7] HedayatiMK,ElbahriM.Antireflectivecoatings:con30大 学 物 理 第39卷ventionalstackinglayersandultrathinplasmonicmetasurfaces,amini-review[J].Materials,2016,9:497.[8] PalikED,Handbookofopticalconstantsofsolids[M].AcademicPress,SanDiego,California,1998.[9] CoxJT,HassG.Triple-layerantireflectioncoatingsonglassforthevisibleandnearinfrared[J].JournaloftheOpticalSocietyofAmerica,1962,52(9):965 969.ReflectioncharacteristicsofmultilayerdielectricfilmbasedontransfermatrixmethodMAHai xia,WUYan jun,WANGJi ming,LUYuan gang,YANGYan nan(DepartmentofAppliedPhysics,NanjingUniversityofAeronauticsandAstronautics,Nanjing,Jiangsu211106,China)Abstract:ThinfilminterferenceisanimportantcontentintheteachingofwaveopticsinUniversityPhysics,anditisalsothetheoreticalbasisofthinfilmoptics.Oneofthemostimportantapplicationsofthinfilminterferenceistodesignantireflectionandhighreflectioncoatings.Reflectanceofmultilayerdielectricfilmisquantitativelycal culatedbasedontransfermatrixmethodinthemanuscript.ThereflectanceoftheoneBK7glasssurfacewithoutcoatingsisabout4%overthevisiblespectrum;Lowreflectancecanbeobtainedbydestructiveinterferenceofthethinfilm.Thereflectanceofsingleantireflectioncoatingonglassdecreasesto1.3%atthedesignedwavelength,550nm.However,performanceofsuchquarter-wavecoatingsfallsoffwhendeviatingfromthedesignedwavelength.Thereflectanceofdoubleantireflectioncoatingsonglassmaintainslowreflectance,lessthan1.3%,overthe470~670nmwavelengthrange.Onthecontrary,highreflectancecanbeobtainedbyconstructiveinterferenceofthethinfilm.Thereflectanceoffusedquartzcanbeincreasedfrom3.3%forthebaresurfaceto30%forthesinglelayerhighreflectioncoatingatthedesignedwavelength,1500nm.Thereflectanceofthesevengroupsoffilmscanreachmorethan99%overthe1360~1660nmwavelengthrange.Throughthesequantitativecalculations,studentscanhaveadeeperunderstandingoftheapplicationoftheoreticalknowledgeinpractice,cultivatetheirengineeringawarenessandenhancetheirinterestinlearning.Keywords:thinfilminterference;transfermatrixmethod;anti-reflectioncoating;highreflectioncoating(上接6页)ComparinganalyticsolutionofthemagneticfieldofringcurrentwithitsnumericalintegrationandtheirvisualizationZHOUQun yi1,MOYun fei2,HOUZhao yang3,ZHOULi li4(1.CollegeofTianhe,GuangdongPolytechnicNormalUniversity,Guangzhou,Guangdong510540,China;2.SchoolofElectronicInformationandElectricalEngineering,ChangshaUniversity,Changsha,Hunan410022,China;3.SchoolofScience,Chang’anUniversity,Xi’an,Shaanxi710064,China;4.DepartmentofInformationEngineering,GannanMedicalUniversity,Ganzhou,Jiangxi341000,China)Abstract:Theintegralformulasofmagneticfieldofringcurrentarederivedinthedimensionlessforms.Themagneticfieldiscalculatedbythenumericalintegration,anditsspatialdistributionisvisualizedbymeansofMAT LAB.Theanalyticsolutionsofthemagneticfieldofringcurrentarealsoderived,anditsvalidityisverifiedaccord ingtotheirgraph.Keywords:ringcurrent;magneticfield;numericalintegration;dimensionlessdiagram。
数学理论在物理学中的应用

数学理论在物理学中的应用数学作为一门学科,不仅仅是一些数字、符号和公式的堆积,更是一种独立的思维方式和理论体系。
在物理学中,数学的应用是十分广泛的,很多物理学的定律和规律都与数学理论密切相关。
在本文中,将介绍数学在物理学中的应用。
一、微积分在物理学中的应用微积分是数学中的一门重要课程,它主要研究函数的极限、导数和积分等相关概念。
微积分在物理学中的应用非常广泛,例如利用微积分可以求解物理学中的速度、加速度、力、功、热等物理量,同时还可以描述物理学中的变化和过程等。
二、矩阵论在物理学中的应用矩阵论是线性代数的一个分支,它用于研究矩阵的性质和运算等。
在物理学中,矩阵论的应用也非常广泛,例如使用矩阵运算可以描述光的偏振、音波的传输、电子的自旋、薛定谔方程等等。
三、群论在物理学中的应用群论是一种数学分支,它主要研究代数结构和空间变换等。
在物理学中,群论被广泛应用于描述物质和粒子的对称性和相互作用等。
例如,使用群论可以解释磁性、红外光谱、核子相互作用等等。
四、拓扑学在物理学中的应用拓扑学是数学中的一个分支,它主要研究空间形态和连接性等相关概念。
在物理学中,拓扑学的应用也非常广泛。
例如,拓扑能帮助我们理解和探究材料的表面导电性和表面色彩、超导现象等。
五、几何学在物理学中的应用几何学是数学中的一门重要课程,它主要研究空间、形体和位置等概念。
在物理学中,几何学的应用也非常广泛。
例如,在相对论中几何学可以用于描述时空的曲率和引力等。
六、运筹学在物理学中的应用运筹学是数学中的一门研究方法学,它主要研究决策、优化和规划等相关问题。
在物理学中,运筹学的应用也非常广泛。
例如,利用运筹学可以优化粒子反应堆的燃料设计、太阳能电池板的安置和设计等等。
综上所述,数学理论在物理学中的应用非常广泛和重要。
物理学是一门实验科学,但是,实验结果必须有数学理论的支持才能变得准确有力。
因此,深入了解数学理论,提高数学运算能力,对于从事物理学研究的人来说,显得尤为必要。
一位光子晶体的计算

一维光子晶体的研究方法----传输矩阵法1:绪论1.1:光子晶体研究的意义在以前对半导体材料的研究导致一场轰轰烈烈的电子工业革命,我们的科技水平有了突飞猛进的发展,并为此进入了计算机和信息为标准的信息时代。
在过去的几十年里,半导体技术正向高速,高集成化方向发展。
但这也引发了一系列的问题,比如电路中能量损失过大,导致集成体发热。
此外,由于高速处理对信号器件中的延迟提出更高的要求,半导体器件的能力已经基本达到了极限,为此科学家们把目光从电子转向广光子。
这是因为光子有着电子所不具备的优势:1.极高的信息容量和效率。
2.极快的响应速度。
3.极强的互连能力和并行能力。
4.极大地存储能力。
5.光子间的相互作用很弱,可极大地降级能力损失。
但是与集成电路相比,科学家们设想能像集成电路一样制造出集成光路,在集成光路中,光子在其中起着电子的作用,全光通过。
光子计算机将成为未来的光子产业,集成光路类似于电子产业中半导体的作用,光子产业中也存在着向集成电路的器件一样的集成光路——光子晶体,光子晶体的研究不仅仅是光通讯领域内的问题,同时也对其他相关产业将产生巨大的影响。
1.2:光子晶体的概念及应用光子晶体是八十年代未提出的新概念和新材料,迄今取得了较快的发展,光子晶体不仅具有理论价值,更具有非常广阔的应用前景,这个领域已经成为国际学术界的研究热点。
控制光子是人们长期以来的梦想,光子晶体能帮助人们实现这一梦想。
1987年Yablonol itch在讨论如何控制自发辐射和 John 在讨论光子局域化时各自独立的提出了光子晶体的概念。
他们所讨论问题的共同实质是周期性电介质材料中光传播的特性,根据固体电子能带理论,晶体内部原子呈周期性排列,库仑场的叠加产生周期性势场,当电子在其中运动时受到周期性势场的布格拉散射而形成的能带结构,带与带之间有带隙,称为禁带。
能量落在禁带中的电子波不能传播。
与此相仿,当电磁波在周期性电介质结构材料中传播时由于受到调制而形成能带结构——光子能带结构,其带隙称为光带隙(PBG:photonic band gap)。
传输矩阵法
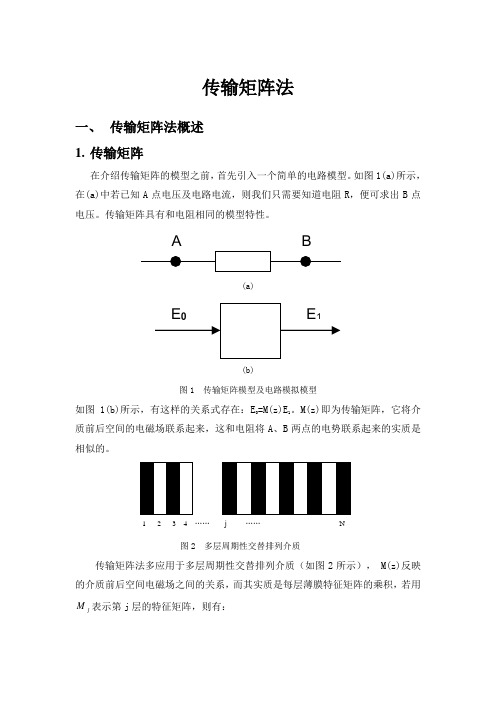
传输矩阵法一、 传输矩阵法概述 1. 传输矩阵在介绍传输矩阵的模型之前,首先引入一个简单的电路模型。
如图1(a)所示, 在(a)中若已知A 点电压及电路电流,则我们只需要知道电阻R ,便可求出B 点电压。
传输矩阵具有和电阻相同的模型特性。
(a)(b)图1 传输矩阵模型及电路模拟模型如图1(b)所示,有这样的关系式存在:E 0=M(z)E 1。
M(z)即为传输矩阵,它将介质前后空间的电磁场联系起来,这和电阻将A 、B 两点的电势联系起来的实质是相似的。
图2 多层周期性交替排列介质传输矩阵法多应用于多层周期性交替排列介质(如图2所示), M(z)反映的介质前后空间电磁场之间的关系,而其实质是每层薄膜特征矩阵的乘积,若用j M 表示第j 层的特征矩阵,则有:1 2 3 4 …… j …… N(1)其中, (2)j δ为相位厚度,有 (3)如公式(2)所示,j M 的表示为一个2×2的矩阵形式,其中每个矩阵元都没有任何实际物理意义,它只是一个计算结果,其推导过程将在第二部分给出。
2. 传输矩阵法在了解了传输矩阵的基础上,下面将介绍传输矩阵法的定义:传输矩阵法是将磁场在实空间的格点位置展开,将麦克斯韦方程组化成传输矩阵形式,变成本征值求解问题。
从其定义可以看出,传输矩阵法的实质就是将麦克斯韦方程转化为传输矩阵,也就是传输矩阵法的建模过程,具体如下:利用麦克斯韦方程组求解两个紧邻层面上的电场和磁场,从而可以得到传输矩阵,然后将单层结论推广到整个介质空间,由此即可计算出整个多层介质的透射系数和反射系数。
传输矩阵法的特点:矩阵元少(4个),运算量小,速度快;关键:求解矩阵元;适用介质:多层周期性交替排列介质。
二、 传输矩阵的基础理论——薄膜光学理论 1.麦克斯韦方程组麦克斯韦方程组由四个场量:D 、E 、B 、H ,两个源量:J 、ρ以及反映它们之间关系的方程组成。
而且由媒质方程中的参数ε、μ、σ反映介质对电磁场的影响。
矩阵代数在物理学中的运用

矩阵代数在物理学中的运用矩阵代数是数学中的一个重要分支,它在各个领域中都有广泛的应用,尤其在物理学中。
物理学是研究自然界中各种现象和规律的科学,而矩阵代数则为物理学提供了一种强大的工具,用于描述和解决各种物理问题。
首先,矩阵代数在量子力学中起到了重要的作用。
量子力学是描述微观世界中粒子行为的理论,而矩阵代数则是量子力学的基础。
在量子力学中,物理量的测量结果可以用矩阵表示,而矩阵的乘法和加法运算则对应了物理量的组合和相加。
通过矩阵的运算,我们可以计算出各种物理量的期望值和变化规律,从而更好地理解和解释量子力学中的现象。
其次,矩阵代数在电磁学中也有广泛的应用。
电磁学是研究电荷和电磁场相互作用的学科,而矩阵代数可以用来描述电磁场的传播和变化。
例如,在电磁波的传播过程中,可以用矩阵表示电磁场在不同介质中的传输关系,通过矩阵的运算,可以计算出电磁波的传播速度和传播方向。
此外,矩阵代数还可以用来描述电磁场的极化和散射现象,通过矩阵的运算,可以计算出电磁场的偏振状态和散射角度,从而更好地理解和解释电磁学中的现象。
再次,矩阵代数在力学中也有重要的应用。
力学是研究物体运动和力的学科,而矩阵代数可以用来描述物体的运动和力的作用。
例如,在刚体运动中,可以用矩阵表示刚体的旋转和平移变换,通过矩阵的运算,可以计算出刚体的角速度和线速度。
此外,矩阵代数还可以用来描述物体之间的相互作用和力的传递,通过矩阵的运算,可以计算出物体之间的力和加速度,从而更好地理解和解释力学中的现象。
最后,矩阵代数在统计物理学中也有重要的应用。
统计物理学是研究大量粒子的集体行为的学科,而矩阵代数可以用来描述粒子的分布和相互作用。
例如,在热力学中,可以用矩阵表示粒子的状态和能量,通过矩阵的运算,可以计算出粒子的平均能量和熵。
此外,矩阵代数还可以用来描述粒子之间的相互作用和相变现象,通过矩阵的运算,可以计算出粒子之间的相互作用能和相变温度,从而更好地理解和解释统计物理学中的现象。
杨振宁对物理学的贡献

杨振宁对物理学的贡献
1 引言
杨振宁,著名科学家、原中科院物理所所长,1937年出生于上海,是当今世界重要的理论物理学家。
杨振宁以自己出色的学术成就,为
一生献身于物理学研究,影响了一代物理学家,颇受人们的尊敬与赞誉。
2 杨振宁的贡献
杨振宁在国际上享有盛名,并受到许多国家和刊物给予大量荣誉,他主要贡献:
(1)杨振宁对量子场论思想的发展作出了重要贡献。
他在量子场
论中运用改变量子系统的方法,提出了“传输矩阵”的概念,推出了
影响函数经典化,并将改变量子系统的方法用来研究实际问题,为量
子力学在高能物理研究和超导物理研究中的应用提供了坚实的理论基础。
(2)杨振宁还提出了量子介质的新概念,以及费米子的分解和殊
途同归的理论,把粒子之间的相互作用建立起更强有力的理论框架,
从而给出了一套完整、一致、重要的理论基础。
(3)杨振宁针对弱相互作用和核反应发展出了弱中性形式因子理论,对特殊相对论模型也有不少贡献,提出量子调和外场理论,和康
拉德-路德维希反应放大效应等等,这些重要的理论预言及其有效地描
述了宇宙中物质的微观结构。
3 总结
由此可见,杨振宁以出色的学术成就,为一生献身于物理学研究,为物理学作出了巨大的贡献,他的成就对物理学有着深远影响,受到
后人钦佩。
光线传输矩阵技术在光学成像中的应用

光线传输矩阵技术在光学成像中的应用光学成像是现代科技领域中一个重要的研究方向,其在医学、工业、科研等领域都有广泛的应用。
但是光学成像技术受到像散、畸变、干扰等因素的影响,也将限制成像效果和质量。
随着科技的不断进步,人们逐渐发现使用光线传输矩阵技术在光学成像中的应用将能有效地解决这些问题。
光线传输矩阵技术,简称RTM技术,是在传递光线过程中,将入射光线和出射光线之间存在的映射关系表示出来的一种数学方法。
RTM技术可用来进行光线传输过程的模拟,在光学成像、光学通信、光学传感器等方面都有广泛的应用。
在光学成像方面,RTM技术被用于消除光比较散的影响。
因为当光线经过多次反射、散射、透射后,其会发生散射,从而导致成像不清晰,影响成像效果。
但是,使用RTM技术,可以通过纠正光线传输矩阵,来减少或消除散射的影响。
以医学成像为例,医学成像中常用CT、MRI等成像方法,但以上方法在成像出来后,容易出现散射、噪点等。
通过RTM技术,可以提高成像的分辨率和对比度,消除噪点等干扰,从而更准确地捕捉病变区域的信息,提高医学成像的诊断准确性。
此外,RTM技术还可以用于光学通信和光学传感器领域。
因为在光学通信和传感器中,光线会受到环境因素和设备对光线的影响,从而导致数据传输不稳定,精度不高等问题。
通过RTM技术,可以对信道进行模拟分析,修复信道传输矩阵,从而提高数据传输的稳定性和准确性。
然而,RTM技术也面临一些挑战和限制。
首先,RTM技术需要大量计算资源和算法支持,才能在实际应用中发挥作用。
其次,RTM技术对于光源和探测器的空间位置相对稳定,对于光传输环境的变化较为敏感。
因此,当物体的位置发生改变或对环境变化进行成像时,需要重新对光线传输矩阵进行修复和校正。
总的来说,随着物理学、数学等学科的不断发展和深入研究,RTM技术将会得到更完善的发展和应用。
其在光学成像、光学通信、光学传感器等领域的重要性和应用前景将会更加广阔。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
传输矩阵在物理学中的前沿应用
2013261021 李霄强
传输矩阵在物理学中的前沿应用
2013261021 李霄强
传输矩阵法(TMM) 就是将麦克斯韦方程组转换为传输矩阵的形式, 应用传输矩阵进行分析的方法。
为了了解传输矩阵的前沿应用,我查找并阅读了几篇关于传输矩阵应用的文献,这些都是使用传输矩阵解决问题。
列如《传输矩阵法在行波管内部反射引起的增益波动计算中的应用》、《光纤光栅法布里-珀罗腔的V-I传输矩阵法研究》及《用传输矩阵法研究微波波段准一维同轴光子晶体能隙结构》。
在《传输矩阵法在行波管内部反射引起的增益波动计算中的应用》一文中,研究者分析了由于行波管慢波结构制造误差引入的多个不连续点对小信号增益的影响. 行波管内部反射对增益波动的影响, 须采用考虑反射波的四阶模型进行分析, 用传输矩阵法对节点处的自左至右入射和自右至左入射两种散射类型建立传输矩阵, 研究在不同空间电荷参量下, 慢波电路的单个反射节点以及慢波电路的皮尔斯速度参量b 和增益参量C 的多个随机分布不连续性对行波管小信号增益的影响。
即通过传输矩阵可以将一个层面上的电磁波幅值与紧邻的另一个层面的电磁波幅值联系起来,如果知道了第一段入射波分布, 就可以利用传输矩阵法计算最后一段电磁波分布,将第一段电磁波幅值与最后一段电磁波幅值联系起来, 通过求解边界条件, 就可以求任一段电磁波幅值,也可以求出行波管的增益。
在《光纤光栅法布里-珀罗腔的V-I传输矩阵法研究》中,研究者要进行光纤光栅法布里-珀罗腔反射光谱特性的分析,由于目前对于结构简单的光栅构成的法布里-珀罗腔的特性分析多采用偶合模理论。
但对于复杂结构的光栅,由于难以得到解析解,一般采用四阶的龙格-库塔方法进行数值求解或采用多层膜法进行分析计算。
这两种方法都可以保证分析精度,但求解速度较慢。
要快速实时获得光器件、光通信系统以及光传感系统的特性,由于庞大的运算量而引起耗费时间过长成为突出问题。
研究者将V-I传输矩阵法用于光纤光栅法布里-珀罗腔反射光谱特性的分析,并建立了V-I传输矩阵模型。
V-I传输矩阵法是2003年Capmany 基于多层膜方法提出的用于计算光纤光栅反射谱特性的方法,采用该模型对三种不同结构的光纤光栅法布里-珀罗腔在不同参数下的光谱特性进行分析,并与传统多层膜法的分析结果相比较,表明V-I传输矩阵法能够在保证分析精度的前提下大大节省运算时间。
而且实验结果表明,V-I传输矩阵法对光纤光栅法布里-珀罗腔特性的分析结果比耦合模法更准确。
这表明,传输矩阵法将会推动对级联光纤光栅、多法布里-珀罗腔级联的理论研究,并进一步发挥更大的作用。
在《用传输矩阵法研究微波波段准一维同轴光子晶体能隙结构》一文中,作者使用ABCD 传输矩阵传输线等效模型和布洛赫周期性边界条件分析计算了同轴准一维光子晶体中具有明显的光子带隙,而且计算结果与实验测试结果能很好地吻合。
该文章中,作者写出了运用ABCD矩阵的详细过程。
即利用ABCD传输矩阵与周期性边界条件分析输入变量和输出变量之间存在的关系,得到计算结果。
传输矩阵方法作为一种时域的数值方法,可以克服一般的频域分析方法所难以克服的问题,即(1)由于频域分析方法基于叠加原理,故而很难处理非线性问题。
(2)不能处理具有时变特性的结构和介质的场问题。
(3)由于一般的频域分析方法都要进行空间的傅里叶变换,故而很难处理具有复杂的,不规则的结构和边界的场问题。
传输矩阵方法也具有以下优点:(1)传输矩阵方法避免了求解复杂的方程组,因而不存在收敛与否,稳定与否和有无奇异解的问题。
(2)物理概念清晰,非常便于计算机程序实现,而且程序的通用性很强。
不同的结构、不同的介质只需改变相应的数据文件就可以计算。
(3)可以用于分析高频(几十GHz到几百GHz的频率)、高速微波和数字电路的特性。
正是由于传输矩阵方法具有上述诸多优点,使得他一出现,就引起很大的反响。
众多学者教授对其表现出很大热情,是的传输矩阵方法经过二十余年的发展,得以不断完善提高,同时其应用范围也不断扩大。
传输矩阵方法传统的应用领域有:
1、矩形波导的二维散射问题
2、二维本征值问题
3、三维本征位和混合场问题
而正在发展的应用领域有
1、运用传输矩阵法对一阶比例方程组和非线性常微分方程组进行求解
2、有源器件特性的模拟,包括半导体中电子的漂移,扩散和复合效应的模拟
3、半导体激光器及光通信系统的模拟
4、声学、电磁场、遥感及高温超导等方面
传输矩阵方法之所以得到迅速的发展的一个很重要的原因便是受益于计算机技术的发展。
可以说没有计算机技术的发展和推广应用,就没有传输矩阵方法的发展。
而未来的传输矩阵也必将与计算机技术紧密结合并长足发展!。
