2019-2020学年人教版a版数学高一必修1模块综合检测-附解析
2019-2020学年高一数学人教A版必修一检测:模块综合评价(二)Word版含解析

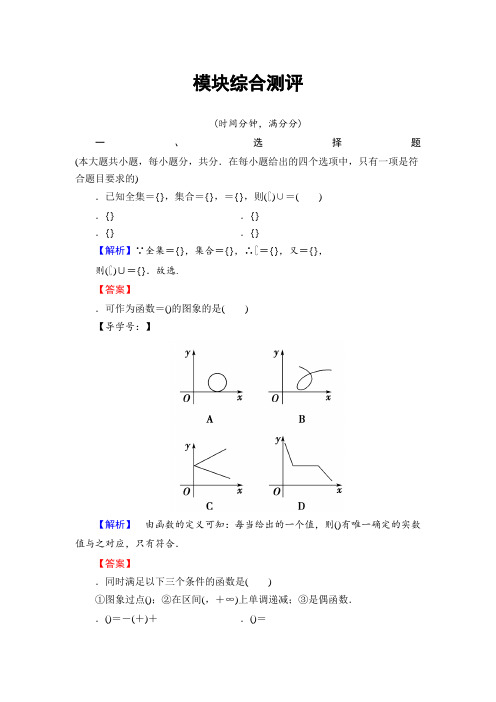
模块综合评价(二)(时间:120分钟满分:150分)一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项符合题目要求)1.已知集合A={2,3,4,5},B={3,5,6},全集U={1,2,3,4,5,6 },则A∩(?U B)=( )A.{1,3} B.{2,4} C.{1,6} D.{3,5}解析:因为?U B={1,2,4},所以A∩(?U B)={2,4}.答案:B2.集合(x,y)x+y=52x-y=1=( )A.{2,3} B.{x=2,y=3} C.{(2,3)} D.(2,3)解析:本题中的元素是点,故答案是{(2,3)}.答案:C3.设函数f(x)=|x-1|-2,|x|≤1,11+x2,|x|>1,则f f12等于( )A.12 B.2541C.-95 D.413解析:f f 12=f-32=413.答案:D4.函数f(x)=|log0.5x|-12x的零点个数为( )A.1 B.2 C.3 D.4解析:在同一坐标系中作出函数y=|log0.5x|与y=12x的图象,可知这两个图象有两个交点,所以函数f(x)=|log0.5x|-12x有两个零点.答案:B5.函数y=log12(4x-x2)的值域是( )A.[-2,+∞) B.RC.[0,+∞) D.(0,4]解析:令t=4x-x2,画出t=4x-x2(t>0)的图象如图所示,则0<t≤4,所以y=log12t∈[-2,+∞).答案:A6.已知f(x)为定义在R上的奇函数,在区间(-∞,0)内有1005个零点,则函数f(x)在R上的零点个数为( )A.2 009 B.2 010 C.2 011 D.2 012解析:定义在R上的奇函数f(x)满足f(0)=0,图象自身关于原点对称,所以零点的个数为2×1 005+1=2 011.答案:C7.已知集合A={x|x-2≤0,x∈N},B={x|x≤2,x∈Z},则满足条件A? C?B的集合C的个数为( )A.5 B.4 C.3 D.2解析:A={x|x-2≤0,x∈N}={0,1,2},B={x|x≤2,x∈Z}={0,1,2,3,4},若A?C?B,则集合C可以是{0,1,2},{0,1,2,3},{0,1,2,4},{0,1,2,3,4},共4个.答案:B8.已知a =243,b =425,c =2513,则()A .b<a<cB .a<b<cC .b<c<aD .c<a<b 解析:因为a =243,b =425=245,由函数y =2x 在R 上为增函数知b<a ;又因为a =243=423,c =2513=523,由函数y =x 23在(0,+∞)上为增函数知a<c.综上得b<a<c.故选A.答案:A9.已知奇函数f(x)在区间[-b ,-a]上单调递减,且f(x)>0.若0<a<b ,则|f(x)|在区间[a ,b]上() A .单调递减B .单调递增C .先增后减D .先减后增解析:利用奇函数的对称性可知,函数f(x)在区间[a ,b]上单调递减,且f(x)<0,则|f(x)|在区间[a ,b]上单调递增.答案:B10.若函数f(x)=log a (x +b)(其中a ,b 为常数)的图象如图所示,则函数g (x)=a x +b 的大致图象是( )A B。
2019-2020学年人教A版高中数学必修1 章末综合质量检测卷(二) Word版含答案

姓名,年级:时间:章末综合质量检测卷(二)(时间:120分钟满分:150分)一、选择题(本题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的)1.若a<错误!,则化简错误!的结果是( )A。
2a-1 B.-错误!C.1-2a D.-错误!解析:选C 因为a<错误!,所以2a-1〈0。
于是,原式=错误!=错误!.2.函数y=错误!+lg(5-3x)的定义域是()A.错误!B.错误!C.错误!D.错误!解析:选C 由函数的解析式得:错误!即错误!所以1≤x<错误!。
3.已知log2m=2.016,log2n=1。
016,则错误!等于( )A.2 B.错误!C.10 D.错误!解析:选B 因为log2m=2。
016,log2n=1。
016,所以m=22。
016,n=21。
016,所以错误!=错误!=错误!。
4.下列函数中,满足“f(x+y)=f(x)f(y)”的单调递增函数是( )A.f(x)=x3B.f(x)=3xC.f(x)=x错误!D.f(x)=错误!x解析:选B 对于选项A,f(x+y)=(x+y)3≠f(x)·f(y)=x3y3,排除A;对于选项B,f(x+y)=3x+y=3x·3y=f(x)f(y),且f(x)=3x在其定义域内是单调增函数,B正确;对于选项C,f(x+y)=x+y≠f(x)f(y)=x错误!y错误!=错误!,排除C;对于选项D,f(x+y)=错误!x+y=错误!x错误!y=f(x)f(y),但f(x)=错误!x在其定义域内是减函数,排除D.故选B。
5.已知f(x)是函数y=log2x的反函数,则y=f(1-x)的图象是()解析:选C 函数y=log2x的反函数为y=2x,故f(x)=2x,于是f(1-x)=21-x=错误!x-1,此函数在R上为减函数,其图象过点(0,2),所以选项C中的图象符合要求.6.已知x=log23-log2错误!,y=log0。
20192020高中数学 模块综合测评A含解析新人教A版必修1

模块综合测评〔A〕(时间:120分钟总分值:150分)一、选择题(本大题共12小题,每题5分,共60分)1.(2021全国1高考,理2)集合A={x|x2-x-2>0},那么?RA=( )A.{x|-1<x<2}B.{x|-1≤x≤2}C.{x|x<-1}∪{x|x>2}D.{x|x≤-1}∪{x|x≥2}解析解一元二次不等式x2-x-2>0,可得x<-1或x>2,那么A={x|x<-1或x>2}, 所以?RA={x|-1≤x≤2}.答案B2.函数y=的定义域为( )A. B.C. D.(-∞,2)解析要使函数有意义,那么解得<x<2,即函数的定义域为,应选B.答案B3.函数f(x)为奇函数,且在(0,+∞)上单调递增,那么以下结论正确的选项是( )A.函数|f(x)|为偶函数,且在(-∞,0)上单调递增B.函数|f(x)|为奇函数,且在(-∞,0)上单调递增C.函数f(|x|)为奇函数,且在(0,+∞)上单调递增D.函数f(|x|)为偶函数,且在(0,+∞)上单调递增解析函数f(x)为奇函数,且在(0,+∞)上单调递增,不妨令f(x)=x,那么|f(x)|=|x|,f(|x|)=|x|;∴函数|f(x)|为偶函数,且在(-∞,0)上单调递减,∴命题A,B错误;函数f(|x|)为偶函数,且在(0,+∞)上单调递增,∴命题C错误、D正确.应选D.答案D4.与函数y=10lg(x-1)相等的函数是( )A.y=x-1B.y=|x-1|C.y=D.y=解析y=10lg(x-1)=x-1(x>1),应选C.答案C5.假设a=22.5,b=lo2.5,c=,那么a,b,c之间的大小关系是( )A.c>b>aB.c>a>bC.a>c>bD.b>a>c解析a=22.5>22=4,b=lo2.5<lo1=0,c==1,又c=>0,所以a>c>b,应选C.答案C6.假设关于x的方程x2-x-m=0在[-1,1]上有解,那么m的取值范围是( )≤m≤1 ≥-≤1 ≤m≤2解析关于x的方程x2-x-m=0在[-1,1]上有解等价于求函数m=x2-x在x∈[-1,1]上的值域, 因为函数m=x2-x在-1,上递减,在,1上递增,所以当x=时,函数取得最小值-,当x=-1时,函数取得最大值2,故实数m的取值范围是-,2.答案D7.假设定义运算a*b为:a*b=如1*2=1,那么函数f(x)=2x*2-x的值域为( )B.(0,1]C.(0,+∞)D.[1,+∞)解析f(x)=2x*2-x=∴f(x)在区间(-∞,0]上是增函数,在区间(0,+∞)上是减函数,∴0<f(x)≤1.答案B8.设f(x)为定义在R上的奇函数,当x≥0时,f(x)=2x+2x+b(b为常数),那么f(-1)=( )解析∵f(x)是R上的奇函数,∴f(0)=0.当x≥0时,f(x)=2x+2x+b,∴20+b=0,b=-1.当x≥0时,f(x)=2x+2x-1.∴f(1)=21+2×1-1=3.∵f(x)是定义在R上的奇函数,∴f(-1)=-f(1)=-3.答案A9.函数f(x)=lg(|x|-1)的大致图象是( )解析由f(x)=lg(|x|-1),知x>1或x<-1.排除C,D.当x>1时,f(x)=lg(x-1)在区间(1,+∞)上为增函数.应选B.答案B10.衣柜里的樟脑丸随着时间挥发而体积缩小,刚放进的新丸的体积为a,经过t天后体积V与天数t的关系式为V=a·e-kt.新丸经过50天后,体积变为a.假设一个新丸体积变为a,那么需经过的天数为( )解析由得a=a·e-50k,即e-50k=.∴a=·a=(e-50k·a=e-75k·a,∴t=75.答案C11.函数f(x)=假设函数f(x)在R上有两个不同的零点,那么a的取值范围是( )A.[-1,+∞)B.(-1,+∞)C.[-1,0)D.(-1,0)解析当x>0时,由f(x)=0,即2x-1=0,解得x=.故由题意可得当x≤0时,令f(x)=0,即ex+a=0有一个解.所以a=-ex,而x≤0,所以0<ex≤e0=1,所以a=-ex∈[-1,0).应选C.答案C≥(x-1)lg 3对任意的x∈(-∞,1]恒成立,那么a的取值范围是( )A.(-∞,0]B.(-∞,1]C.[0,+∞)D.[1,+∞)解析由lg≥lg 3(x-1),得≥3(x-1),1+2x+(1-a)3x≥3x,1+2x≥a·3x,即≥a对任意的x∈(-∞,1]恒成立.设f(x)=(x∈(-∞,1]),那么f(x)min=f(1)==1,∴a≤1.答案B二、填空题(本大题共4小题,每题5分,共20分)13.log28+lg 0.01+ln+lg+2lg 2-= .?解析log28+lg 0.01+ln+lg+2lg 2-=3-2+×3+1-2=2.答案214.函数f(x)=lo(x2-2x-3)的单调递增区间为.?解析函数f(x)的定义域为{x|x>3或x<-1}.令t=x2-2x-3,那么y=lot.因为y=lot在区间(0,+∞)上单调递减,t=x2-2x-3在区间(-∞,-1)上单调递减,在区间(3,+∞)上单调递增,故所求函数的单调递增区间为(-∞,-1).答案(-∞,-1)15.函数f(x)=假设函数g(x)=f(x)-m有三个零点,那么实数m的取值范围为.?解析如图,作出函数f(x)=的图象,作出直线y=m.由图可知,该函数的图象与直线y=m有三个交点时,需m∈(0,1),此时函数g(x)=f(x)-m有三个零点.答案(0,1)16.函数y=lg(3-4x+x2)的定义域为M,当x∈M时,那么f(x)=2x+2-3×4x的最大值为.?解析函数y=lg(3-4x+x2)的定义域为M,∴3-4x+x2>0,即(x-1)(x-3)>0,解得M={x|x>3或x<1}.∴f(x)=2x+2-3×4x,令2x=t,那么0<t<2或t>8,∴f(t)=-3t2+t+2=-3.当t=时,f(t)取最大值,f(x)max=f.答案三、解答题(本大题共6小题,共70分.解容许写出文字说明、证明过程或演算步骤)17.(本小题总分值10分)设U=R,A={x|2x-3≤1},B={x|2<x<5},C={x|a≤x≤a+1}(a为实数).(1)求A∩B;(2)假设B∪C=B,求a的取值范围.解(1)∵2x-3≤1,∴x≤3.∴A∩B={x|2<x≤3}.(2)由B∪C=B,得C?B.∴即2<a<4.18.(本小题总分值12分)函数f(x)=log2(x+3)-2x3+4x的图象在[-2,5]内是连续不断的,对应值表如下:x -2 -1 0 1 2 3 4 5f(x) a -1 b -227(1)计算上述表格中的对应值a和b.(2)从上述对应值表中,可以发现函数f(x)在哪几个区间内有零点?说明理由.解(1)由题意可知a=f(-2)=log2(-2+3)-2×(-2)3+4×(-2)=0+16-8=8,b=f(1)=log24-2+4=4.(2)∵f(-2)f(-1)<0,f(-1)f(0)<0,f(1)f(2)<0,∴函数f(x)分别在区间(-2,-1),(-1,0),(1,2)内有零点.19.(本小题总分值12分)(2021徐汇区校级期末)函数f(x)=x2-3x+m,且f(-1)=5.(1)求不等式f(x)>-1的解集;(2)求函数f(x)在区间[-2,4]上的最值.解(1)由f(-1)=1+3+m=5,解得m=1,∴f(x)=x2-3x+1.由f(x)>-1得x2-3x+2>0,解得x<1或x>2,∴f(x)>-1的解集为{x|x<1或x>2}.(2)∵f(x)=x2-3x+1=x-2-,且,所以当x=时,f(x)min=-;当x=-2时,f(x)max=f(-2)=11.20.(本小题总分值12分)函数f(x)=lg(m,n∈R,m>0)的图象关于原点对称.(1)求m,n的值;(2)假设函数h(x)=f(2x)-lg在(0,1)内存在零点,求实数b的取值范围.解(1)函数f(x)=lg(m,n∈R,m>0)的图象关于原点对称,所以f(-x)+f(x)=0,所以lg+lg=0,所以=1,即=0.所以解得(2)由h(x)=f(2x)-lg=lg-lg=lg,由题设知h(x)=0在(0,1)内有解,即方程2x-1=b-(2x)2-2x 在(0,1)内有解.b=(2x)2+2x+1-1=(2x+1)2-2在(0,1)内递增,得2<b<7.所以当2<b<7时,函数h(x)=f(2x)-lg在(0,1)内存在零点.21.(本小题总分值12分)某上市股票在30天内每股的交易价格P(单位:元)与时间t(单位:天)组成有序数对(t,P),点(t,P)落在图中的两条线段上,该股票在30天内的日交易量Q(单位:万股)与时间t(单位:天)的局部数据如表所示:第t天 4 10 16 22Q/万股36 30 24 18(1)根据提供的图象,写出该种股票每股交易价格P与时间t所满足的函数关系式;(2)根据表中数据求出日交易量Q与时间t的一次函数关系式;(3)在(2)的结论下,用y表示该股票日交易额(单位:万元),写出y关于t的函数关系式,并求在这30天中第几天日交易额最大?最大值是多少?解(1)P=(t∈N*).(2)设Q=at+b(a≠0,a,b为常数),把(4,36),(10,30)代入,得解得所以日交易量Q与时间t的一次函数关系式为Q=-t+40,0<t≤30,t∈N*.(3)由(1)(2)可得y=(t∈N*),即y=(t∈N*).当0<t≤20时,y有最大值ymax=125万元,此时t=15;当20<t≤30时,y随t的增大而减小,ymax<(20-60)2-40=120(万元).所以在30天中的第15天日交易额最大,且最大值125万元.22.(本小题总分值12分)函数f(x)=,且f(1)=3.(1)求函数f(x)在(-∞,0)上的单调区间,并给出证明.(2)设关于x的方程f(x)=x+b的两根分别为x1,x2,试问是否存在实数m,使得不等式m2+tm+1≥|x1-x2|对任意的b∈[2, ]及t∈[-1,1]恒成立?假设存在,求出m的取值范围;假设不存在,说明理由.解(1)∵f(1)=3,∴a=1,∴f(x)=.任取x1,x2∈(-∞,0),且x1<x2<0,那么f(x2)-f(x1)=2x2+=(x2-x1).①当x1<x2≤-时,x1x2>,∴2->0.又x2-x1>0,∴f(x2)-f(x1)>0,∴f(x2)>f(x1),∴f(x)在上单调递增.②当-<x1<x2<0时,0<x1x2<,∴2-<0.又x2-x1>0,∴f(x2)-f(x1)<0,∴f(x2)<f(x1),∴f(x)在上单调递减.∴f(x)在(-∞,0)上的单调递增区间为,单调递减区间为. (2)存在实数m.∵f(x)=x+b,∴x2-bx+1=0,|x1-x2|=.又2≤b≤,∴0≤|x1-x2|≤3.故只需当t∈[-1,1],使m2+tm+1≥3恒成立,记g(t)=mt+m2-2,只需∴∴m≤-2或m≥2.故存在实数m符合题意,其取值范围是(-∞,-2]∪[2,+∞).。
2019-2020学年新教材人教A版数学必修第一册综合质量检测 Word版含解析

综合质量检测本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.满分150分.考试时间120分钟.第Ⅰ卷(选择题 共60分)一、选择题(本大题共12个小题,每小题5分,共60分,在每小题给出的四个选项中只有一个是符合题目要求的)1.全集U =R ,A ={x |x <-3,或x ≥2},B ={x |-1<x <5},则集合{x |-1<x <2}是( )A .(∁U A )∪(∁UB ) B .∁U (A ∪B )C .(∁U A )∩BD .A ∩B[解析] 由题意知,∁U A =[-3,2),又因为B =(-1,5),所以(∁U A )∩B =(-1,2).故选C.[答案] C2.函数f (x )=x 2x 2-1+lg(10-x )的定义域为( )A .RB .[1,10]C .(-∞,-1)∪(1,10)D .(1,10)[解析]要使函数f (x )有意义,需使⎩⎨⎧x 2-1>0,10-x >0,解得x <-1或1<x <10.故选C.[答案] C3.已知f (x )=x 2-ax 在[0,1]上是单调函数,则实数a 的取值范围是( )A .(-∞,0]B .[1,+∞)C .[2,+∞)D .(-∞,0]∪[2,+∞)[解析] 函数f (x )=x 2-ax 图象的对称轴为直线x =a2,根据二次函数的性质可知a 2≤0或a2≥1,解得a ≤0或a ≥2.故选D.[答案] D4.下列函数是偶函数且值域为[0,+∞)的是( ) ①y =|x |;②y =x 3;③y =2|x |;④y =x 2+|x |. A .①② B .②③ C .①④ D .③④[解析] 对于①,y =|x |是偶函数,且值域为[0,+∞);对于②,y =x 3是奇函数;对于③,y =2|x |是偶函数,但值域为[1,+∞);对于④,y =x 2+|x |是偶函数,且值域为[0,+∞),所以符合题意的有①④,故选C.[答案] C5.已知a =log 20.2,b =20.2,c =0.20.3,则( ) A .a <b <c B .a <c <b C .c <a <bD .b <c <a[解析] a =log 20.2<log 21=0,b =20.2>20=1,0<c =0.20.3<0.20=1,即0<c <1,则a <c <b .故选B.[答案] B6.若sin α>0且tan α<0,则α2的终边在( ) A .第一象限 B .第二象限C .第一象限或第三象限D .第三象限或第四象限 [解析] 因为sin α>0且tan α<0, 所以α位于第二象限. 所以π2+2k π<α<2k π+π,k ∈Z ,则π4+k π<α2<k π+π2,k ∈Z .当k 为奇数时α2是第三象限的角,当k 为偶数时α2是第一象限的角, 所以角α2的终边在第一象限或第三象限.选C. [答案] C7.函数y =sin(ωx +φ)(x ∈R ,且ω>0,0≤φ<2π)的部分图象如右图所示,则( )A .ω=π2,φ=π4 B .ω=π3,φ=π6 C .ω=π4,φ=π4 D .ω=π4,φ=5π4[解析] ∵T =4×2=8,∴ω=π4. 又∵π4×1+φ=π2,∴φ=π4. [答案] C8.函数f (x )=2sin x -sin2x 在[0,2π]的零点个数为( ) A .2 B .3 C .4 D .5[解析] 由f (x )=2sin x -sin2x =2sin x -2sin x cos x =2sin x (1-cos x )=0,得sin x =0或cos x =1,∵x ∈[0,2π],∴x =0、π或2π,∴f (x )在[0,2π]的零点个数是3.[答案] B9.已知lg a +lg b =0,函数f (x )=a x 与函数g (x )=-log b x 的图象可能是( )[解析] ∵lg a +lg b =0,∴ab =1,则b =1a ,从而g (x )=-logb x =log a x ,故g (x )与f (x )=a x 互为反函数,图象关于直线y =x 对称.故选B.[答案] B10.若α∈⎝ ⎛⎭⎪⎫π2,π,且sin α=45,则sin ⎝ ⎛⎭⎪⎫α+π4-22cos(π-α)等于( )A.225 B .-25 C.25 D .-225 [解析] sin ⎝⎛⎭⎪⎫α+π4-22cos(π-α) =22sin α+22cos α+22cos α=22sin α+2cos α.∵sin α=45,α∈⎝ ⎛⎭⎪⎫π2,π,∴cos α=-35.∴22sin α+2cos α=22×45-2×35=-25. [答案] B11.设函数f (x )=sin(ωx +φ)+cos(ωx +φ)⎝ ⎛⎭⎪⎫ω>0,|φ|<π2的最小正周期为π,且f (-x )=f (x ),则( )A .f (x )在⎝⎛⎭⎪⎫0,π2单调递减 B .f (x )在⎝ ⎛⎭⎪⎫π4,3π4单调递减C .f (x )在⎝⎛⎭⎪⎫0,π2单调递增D .f (x )在⎝ ⎛⎭⎪⎫π4,3π4单调递增[解析] y =sin(ωx +φ)+cos(ωx +φ)=2sin ⎝⎛⎭⎪⎫ωx +φ+π4,由最小正周期为π得ω=2,又由f (-x )=f (x )可知f (x )为偶函数,由|φ|<π2可得φ=π4,所以y =2cos2x 在⎝ ⎛⎭⎪⎫0,π2单调递减. [答案] A12.将函数f (x )=23cos 2x -2sin x cos x -3的图象向左平移t (t >0)个单位,所得图象对应的函数为奇函数,则t 的最小值为( )A.2π3B.π3C.π2D.π6[解析] 将函数f (x )=23cos 2x -2sin x cos x -3=3cos2x -sin2x =2cos ⎝ ⎛⎭⎪⎫2x +π6的图象向左平移t (t >0)个单位,可得y =2cos ⎝ ⎛⎭⎪⎫2x +2t +π6的图象.由于所得图象对应的函数为奇函数,则2t +π6=k π+π2,k ∈Z ,则t 的最小值为π6.故选D.[答案] D第Ⅱ卷(非选择题 共90分)二、填空题(本大题共4个小题,每小题5分,共20分,把正确答案填在题中横线上)14.函数f (x )=⎩⎪⎨⎪⎧x 2-1,x ≤0,x -2+ln x ,x >0的零点个数为________.[解析]令f (x )=0,得到⎩⎨⎧x 2-1=0,x ≤0,解得x =-1;或⎩⎨⎧x -2+ln x =0,x >0,在同一个直角坐标系中画出y =2-x 和y =ln x 的图象,观察交点个数,如图所示.函数y =2-x 和y =ln x ,x >0在同一个直角坐标系中交点个数是1,所以函数f (x )在x <0时的零点有一个,在x >0时零点有一个,所以f (x )的零点个数为2.[答案] 215.若函数f (x )=⎩⎪⎨⎪⎧3x ,x ≤0,-2-x,x >0,则函数y =f [f (x )]的值域是________.[解析] 当x ≤0时,f (x )=3x ∈(0,1],∴y =f [f (x )]=f (3x )=-2-3x∈⎝⎛⎦⎥⎤-1,-12;当x >0时,f (x )=-2-x ∈(-1,0),y =f [f (x )] =f (-2-x )=3-2-x ∈⎝⎛⎭⎪⎫13,1. 综上所述,y =f [f (x )]的值域是 ⎝ ⎛⎦⎥⎤-1,-12∪⎝ ⎛⎭⎪⎫13,1.[答案] ⎝ ⎛⎦⎥⎤-1,-12∪⎝ ⎛⎭⎪⎫13,116.关于函数f (x )=cos ⎝ ⎛⎭⎪⎫2x -π3+cos ⎝ ⎛⎭⎪⎫2x +π6,给出下列命题:①f (x )的最大值为2; ②f (x )的最小正周期是π;③f (x )在区间⎣⎢⎡⎦⎥⎤π24,13π24上是减函数;④将函数y =2cos2x 的图象向右平移π24个单位长度后,与函数y =f (x )的图象重合.其中正确命题的序号是________.[解析] f (x )=cos ⎝⎛⎭⎪⎫2x -π3+cos ⎝⎛⎭⎪⎫2x +π6=cos ⎝⎛⎭⎪⎫2x -π3+sin ⎣⎢⎡⎦⎥⎤π2-⎝ ⎛⎭⎪⎫2x +π6=cos ⎝ ⎛⎭⎪⎫2x -π3-sin ⎝ ⎛⎭⎪⎫2x -π3=2 ⎣⎢⎡⎦⎥⎤22cos ⎝ ⎛⎭⎪⎫2x -π3-22sin ⎝ ⎛⎭⎪⎫2x -π3=2cos ⎝ ⎛⎭⎪⎫2x -π3+π4=2cos ⎝ ⎛⎭⎪⎫2x -π12,∴函数f (x )的最大值为2,最小正周期为π,故①②正确;又当x ∈⎣⎢⎡⎦⎥⎤π24,13π24时,2x -π12∈[0,π],∴函数f (x )在⎣⎢⎡⎦⎥⎤π24,13π24上是减函数,故③正确;由④得y =2cos ⎣⎢⎡⎦⎥⎤2⎝ ⎛⎭⎪⎫x -π24=2cos ⎝ ⎛⎭⎪⎫2x -π12,故④正确.[答案] ①②③④三、解答题(本大题共6个大题,共70分,解答应写出文字说明,证明过程或演算步骤)18.(本小题满分12分)已知函数f (x )=2cos x ·sin ⎝ ⎛⎭⎪⎫x +π3-3sin 2x+sin x cos x .(1)当x ∈⎣⎢⎡⎦⎥⎤0,π2时,求f (x )的值域;(2)用“五点法”在下图中作出y =f (x )在闭区间⎣⎢⎡⎦⎥⎤-π6,5π6上的简图.[解] f (x )=2cos x ·sin ⎝ ⎛⎭⎪⎫x +π3-3sin 2x +sin x cos x=2cos x ⎝ ⎛⎭⎪⎫sin x cos π3+cos x sin π3-3sin 2x +sin x cos x =sin2x +3cos2x =2sin ⎝⎛⎭⎪⎫2x +π3.(1)∵x ∈⎣⎢⎡⎦⎥⎤0,π2,∴π3≤2x +π3≤4π3, ∴-32≤sin ⎝ ⎛⎭⎪⎫2x +π3≤1,∴当x ∈⎣⎢⎡⎦⎥⎤0,π2时,f (x )的值域为[-3,2]. (2)由T =2π2,得最小正周期T =π,列表:x -π6 π12 π3 7π12 5π6 2x +π3 0 π2 π 3π2 2π 2sin ⎝ ⎛⎭⎪⎫2x +π32-2图象如图所示.19.(本小题满分12分) 已知A (cos α,sin α),B (cos β,sin β),其中α,β为锐角,且|AB |=105.(1)求cos(α-β)的值; (2)若cos α=35,求cos β的值. [解] (1)由|AB |=105, 得(cos α-cos β)2+(sin α-sin β)2=105,∴2-2(cos αcos β+sin αsin β)=25, ∴cos(α-β)=45.(2)∵cos α=35,cos(α-β)=45,α,β为锐角, ∴sin α=45,sin(α-β)=±35. 当sin(α-β)=35时,cos β=cos[α-(α-β)]=cos αcos(α-β)+sin αsin(α-β)=2425. 当sin(α-β)=-35时, cos β=cos[α-(α-β)]=cos αcos(α-β)+sin αsin(α-β)=0. ∵β为锐角,∴cos β=2425.20.(本小题满分12分)已知函数f (x )是定义在区间[-1,1]上的奇函数,对于任意的m ,n ∈[-1,1]有f (m )+f (n )m +n>0(m +n ≠0).(1)判断函数f (x )的单调性; (2)解不等式f ⎝ ⎛⎭⎪⎫x +12<f (1-x ).[解] (1)设x 1=m ,x 2=-n ,由已知可得f (x 1)-f (x 2)x 1-x 2>0,不妨设x 1<x 2,则f (x 1)<f (x 2),由函数单调性的定义可得函数f (x )在区间[-1,1]上是增函数.(2)由(1)知函数在区间[-1,1]上是增函数.又由f ⎝ ⎛⎭⎪⎫x +12<f (1-x ),得⎩⎪⎨⎪⎧-1≤x +12≤1,-1≤1-x ≤1,x +12<1-x ,解得0≤x <14.所以不等式f ⎝ ⎛⎭⎪⎫x +12<f (1-x )的解集为⎩⎨⎧⎭⎬⎫x |0≤x <14.21.(本小题满分12分)某村电费收取有以下两种方案供用户选择:方案一:每户每月收管理费2元,月用电不超过30度时,每度0.5元,超过30度时,超过部分按每度0.6元收取.方案二:不收管理费,每度0.58元.(1)求方案一收费L (x )(单位:元)与用电量x (单位:度)间的函数关系;(2)老王家九月份按方案一交费35元,问老王家该月用电多少度?(3)老王家月用电量在什么范围时,选择方案一比选择方案二更好?[解] (1)当0≤x ≤30时,L (x )=2+0.5x ;当x >30时,L (x )=2+30×0.5+(x -30)×0.6=0.6x -1,∴L (x )=⎩⎨⎧2+0.5x ,0≤x ≤30,0.6x -1,x >30.(注:x 也可不取0)(2)当0≤x ≤30时,令L (x )=2+0.5x =35得x =66,舍去; 当x >30时,由L (x )=0.6x -1=35得x =60,∴老王家该月用电60度.(3)设按方案二收费为F (x )元,则F (x )=0.58x . 当0≤x ≤30时,由L (x )<F (x ),得2+0.5x <0.58x , 解得x >25,∴25<x ≤30;当x >30时,由L (x )<F (x ),得0.6x -1<0.58x , 解得x <50,∴30<x <50. 综上,25<x <50.故老王家月用电量在25度到50度范围内(不含25度、50度)时,选择方案一比方案二更好.22.(本小题满分12分)已知函数f (x )=A sin(ωx +φ)+B (A >0,ω>0)的一系列对应值如表:(1)(2)根据(1)的结果,若函数y =f (kx )(k >0)的周期为2π3,当x ∈⎣⎢⎡⎦⎥⎤0,π3时,方程f (kx )=m 恰有两个不同的解,求实数m 的取值范围.[解] (1)设f (x )的最小正周期为T ,则T =11π6-⎝ ⎛⎭⎪⎫-π6=2π,由T =2πω,得ω=1,又⎩⎨⎧B +A =3,B -A =-1,解得⎩⎨⎧A =2,B =1,令ω·5π6+φ=π2+2k π,k ∈Z ,即5π6+φ=π2+2k π,k ∈Z ,取φ=-π3, 所以f (x )=2sin ⎝ ⎛⎭⎪⎫x -π3+1. (2)因为函数y =f (kx )=2sin ⎝ ⎛⎭⎪⎫kx -π3+1的周期为2π3,又k >0,所以k =3.令t =3x -π3,因为x ∈⎣⎢⎡⎦⎥⎤0,π3,所以t ∈⎣⎢⎡⎦⎥⎤-π3,2π3,如图,sin t =s 在⎣⎢⎡⎦⎥⎤-π3,2π3上有两个不同的解,则s ∈⎣⎢⎡⎭⎪⎫32,1,所以方程f (kx )=m 在x ∈⎣⎢⎡⎦⎥⎤0,π3时恰好有两个不同的解,则m ∈[3+1,3),即实数m 的取值范围是[3+1,3).。
2019_2020学年高中数学模块综合测试新人教A版必修1

模块综合测试时间:120分钟 分值:150分第Ⅰ卷(选择题,共60分)一、选择题(每小题5分,共60分)1.设全集U ={1,2,3,4,5},集合A ={1,2,3},B ={2,3,4},则下列结论中正确的是( D ) A .A ⊆BB .A ∩B ={2}C .A ∪B ={1,2,3,4,5}D .A ∩(∁U B )={1}解析:A 显然错误;A ∩B ={2,3},B 错;A ∪B ={1,2,3,4},C 错.故选D.2.已知集合A ={x |y =1-x 2,x ∈Z },B ={y |y =x 2+1,x ∈A },则A ∩B 为( B ) A .∅ B .{1} C .[0,+∞)D .{(0,1)}解析:由1-x 2≥0,得-1≤x ≤1, ∵x ∈Z ,∴A ={-1,0,1}.当x ∈A 时,y =x 2+1∈{2,1},即B ={1,2}, ∴A ∩B ={1}.3.下列函数中,定义域是R 且为增函数的是( B ) A .y =e -xB .y =x 3C .y =ln xD .y =|x |解析:A 项,函数y =e -x为R 上的减函数;B 项,函数y =x 3为R 上的增函数;C 项,函数y =ln x 为(0,+∞)上的增函数;D 项,函数y =|x |在(-∞,0)上为减函数,在(0,+∞)上为增函数.故只有B 项符合题意,故选B.4.已知函数f (x )=⎩⎨⎧x ,x ≥2,3-x ,x <2.则f (f (-1))的值为( D )A .-1B .0C .1D .2解析:由题意,得f (-1)=4,f (f (-1))=f (4)=4=2.故选D.5.函数f (x )=e x-1x的零点所在的区间是( B )A.⎝ ⎛⎭⎪⎫0,12B.⎝ ⎛⎭⎪⎫12,1C.⎝ ⎛⎭⎪⎫1,32 D.⎝ ⎛⎭⎪⎫32,2 解析:∵f ⎝ ⎛⎭⎪⎫12=e 12 -2<0,f (1)=e -1>0,f ⎝ ⎛⎭⎪⎫12·f (1)<0,∴函数f (x )=e x-1x 的零点所在的区间是⎝ ⎛⎭⎪⎫12,1.6.已知a >b ,函数f (x )=(x -a )(x -b )的图象如图,则函数g (x )=log a (x +b )的图象可能为( C )解析:由图象及函数f (x )得a >1>b >0,g (x )即由y =log a x 向左平移b 个单位得到,与C 图象符合,故选C.7.实数a =0.22,b =log 2 0.2,c =(2)0.2的大小关系正确的是( C ) A .a <c <b B .a <b <c C .b <a <cD .b <c <a解析:根据指数函数和对数函数的性质,知b =log 20.2<0<a =0.22<1<c =(2)0.2. 8.函数f (x )是定义在R 上的奇函数,当x ≥0时,f (x )为减函数,且f (-1)=1,若f (x -2)≥-1,则x 的取值范围是( A )A .(-∞,3]B .(-∞,1]C .[3,+∞)D .[1,+∞)解析:函数f (x )是定义在R 上的奇函数,且是[0,+∞)上的减函数,故函数f (x )在R 上单调递减.又f (-1)=1,所以f (1)=-1,因此f (x -2)≥-1⇔f (x -2)≥f (1)⇔x -2≤1⇔x ≤3,所以x 的取值范围是(-∞,3],故选A.9.已知函数y =f (x )是偶函数,且函数y =f (x -2)在区间[0,2]上是单调减函数,则( C )A .f (-1)<f (2)<f (0)B .f (-1)<f (0)<f (2)C .f (0)<f (-1)<f (2)D .f (2)<f (-1)<f (0)解析:函数y =f (x -2)的图象是由函数y =f (x )的图象向右平移2个单位长度得到的, ∵y =f (x -2)在区间[0,2]上是减函数, ∴y =f (x )在区间[-2,0]上是减函数, ∴f (-2)>f (-1)>f (0).∵f (x )为偶函数,∴f (0)<f (-1)<f (2).10.已知函数f (x )=⎩⎪⎨⎪⎧-x 2+2ax ,x ≤1,(2a -1)x -3a +6,x >1,若f (x )在(-∞,+∞)上是增函数,则实数a 的取值范围是( D )A.⎝ ⎛⎦⎥⎤12,1B.⎝ ⎛⎭⎪⎫12,+∞ C .[1,+∞)D .[1,2]解析:由f (x )在(-∞,1]上单调递增得a ≥1. 由f (x )在(1,+∞)上单调递增得2a -1>0, 解得a >12.由f (x )在(-∞,+∞)上单调递增,所以-12+2a ×1≤(2a -1)×1-3a +6,即a ≤2. 综上,a 的取值范围为1≤a ≤2.故选D.11.已知函数f (x )=⎩⎪⎨⎪⎧kx +2,x ≤0,ln x ,x >0,若k >0,则函数y =|f (x )|-1的零点个数是( D )A .1B .2C .3D .4解析:由题意若k >0,函数y =|f (x )|-1的零点个数等价于y =|f (x )|与y =1交点的个数,作出示意图,易知y =|f (x )|与y =1交点的个数为4,故函数y =|f (x )|-1有4个零点.12.某商场宣传在节假日对顾客购物实行一定的优惠,商场规定:①如一次购物不超过200元,不予以折扣;②如一次购物超过200元,但不超过500元,按标价予以九折优惠;③如一次购物超过500元的,其中500元给予九折优惠,超过500元的给予八五折优惠. 某人两次去购物,分别付款176元和432元,如果他只去一次购买同样的商品,则应付款( C )A .608元B .574.1元C .582.6元D .456.8元解析:由题意得购物付款432元,实际标价为432×109=480元,如果一次购买标价176+480=656元的商品应付款500×0.9+156×0.85=582.6元.故选C.第Ⅱ卷(非选择题,共90分)二、填空题(每小题5分,共20分)13.设P 、Q 是两个非空集合,定义集合间的一种运算“⊙”:P ⊙Q ={x |x ∈P ∪Q ,且x ∉P ∩Q },如果P ={y |y =4-x 2},Q ={y |y =4x,x >0},则P ⊙Q =[0,1]∪(2,+∞).解析:P =[0,2],Q =(1,+∞), ∴P ⊙Q =[0,1]∪(2,+∞).14.设函数f (x )=⎩⎪⎨⎪⎧e x,x ≤1,f (x -1),x >1,则f (ln3)=3,e.解析:f (ln3)=f (ln3-1)=e(ln3-1)=e ln3·e -1=3e.15.已知函数f (x )=lg(2x-b )(b 为常数),若x ∈[1,+∞)时,f (x )≥0恒成立,则b 的取值范围是(-∞,1].解析:∵要使f (x )=lg(2x-b )在x ∈[1,+∞)上,恒有f (x )≥0,∴有2x-b ≥1在x ∈[1,+∞)上恒成立,即2x ≥b +1恒成立.又∵指数函数g (x )=2x在定义域上是增函数,∴只要2≥b +1成立即可,解得b ≤1.16.设a 、b 、c 均为正实数,且⎝ ⎛⎭⎪⎫12a =log 12 a ,⎝ ⎛⎭⎪⎫12b =log 2b,2c=log 12c ,则a 、b 、c 的大小关系为c <a <b .解析:由y =⎝ ⎛⎭⎪⎫12x 与y =log 2x 函数图象交点的横坐标大于1,即得b >1;由y =⎝ ⎛⎭⎪⎫12x与y =log 12 x 交点横纵坐标均在区间(0,1)内,即0<a <1,且0<log 12 a <1,即log 12 1<log 12 a <log 1212,得12<a <1,同理得0<c <12,综上得c <a <b . 三、解答题(写出必要的计算步骤,只写最后结果不得分,共70分)17.(10分)设全集是实数集R ,集合A ={x |y =log a (x -1)+3-x },B ={x |2x+m ≤0}. (1)当m =-4时,求A ∩B 和A ∪B ; (2)若(∁R A )∩B =B ,求实数m 的取值范围.解:(1)由⎩⎪⎨⎪⎧x -1>0,3-x ≥0,得1<x ≤3,即集合A =(1,3];由2x-4≤0,得2x≤22,x ≤2,即集合B =(-∞,2]. 故A ∩B =(1,2],A ∪B =(-∞,3]. (2)∁R A ={x |x >3,或x ≤1}. ∵(∁R A )∩B =B ,∴B ⊆∁R A .①若B =∅,则m ≥0;②若B ≠∅,则m <0, ∴2x ≤-m ,∴x ≤log 2(-m ). ∵B ⊆∁R A ,∴log 2(-m )≤1,即log 2(-m )≤log 22,因此0<-m ≤2,-2≤m <0. 综上所述,实数m 的取值范围是[-2,+∞). 18.(12分)已知函数f (x )=1-2x2x +1.(1)判断函数f (x )的奇偶性并证明;(2)当x ∈(1,+∞)时,求函数f (x )的值域. 解:(1)函数f (x )是奇函数,f (-x )=1-2-x2-x +1=1-12x 12x +1=2x -11+2x =-f (x ).所以f (x )是奇函数.(2)令2x=t ,则g (t )=1-t t +1=-1+2t +1.因为x ∈(1,+∞),所以t >2, 因此t +1>3,0<2t +1<23.所以-1<g (t )<-13, 所以f (x )的值域是⎝⎛⎭⎪⎫-1,-13.19.(12分)已知函数f (x )是定义在区间[-1,1]上的奇函数,对于任意的m ,n ∈[-1,1]有f (m )+f (n )m +n>0(m +n ≠0).(1)判断函数f (x )的单调性;(2)解不等式f ⎝ ⎛⎭⎪⎫x +12<f (1-x ). 解:(1)设x 1=m ,x 2=-n ,由已知可得f (x 1)-f (x 2)x 1-x 2>0,不妨设x 1<x 2,则f (x 1)<f (x 2),由函数单调性的定义可得函数f (x )在区间[-1,1]上是增函数.(2)由(1)知函数在区间[-1,1]上是增函数.又由f ⎝ ⎛⎭⎪⎫x +12<f (1-x ),得⎩⎪⎨⎪⎧-1≤x +12≤1,-1≤1-x ≤1,x +12<1-x ,解得0≤x <14.所以不等式f ⎝ ⎛⎭⎪⎫x +12<f (1-x )的解集为 {x |0≤x <14}.20.(12分)已知函数f (x )=⎩⎪⎨⎪⎧x -2x ,x >12,x 2+2x +a -1,x ≤12.(1)若a =1,求函数f (x )的零点;(2)若函数f (x )在[-1,+∞)上为增函数,求a 的取值范围.解:(1)当a =1时,由x >12,x -2x =0,得x =2,由x ≤12,x 2+2x =0,得x 1=0,x 2=-2,所以f (x )的零点为2,0,-2.(2)显然,函数g (x )=x -2x 在区间⎣⎢⎡⎭⎪⎫12,+∞上是增函数,且g ⎝ ⎛⎭⎪⎫12=-72; 函数h (x )=x 2+2x +a -1在区间⎣⎢⎡⎦⎥⎤-1,12上也是增函数,且h ⎝ ⎛⎭⎪⎫12=a +14.故若函数f (x )在[-1,+∞)上为增函数,则a +14≤-72,解得a ≤-154,故a 的取值范围为⎝⎛⎦⎥⎤-∞,-154.21.(12分)已知y =f (x )是定义在R 上的偶函数,当x ≥0时,f (x )是二次函数,其图象与x 轴交于A (1,0)、B (3,0),与y 轴交于C (0,6).(1)求y =f (x )(x ∈R )的解析式;(2)若方程f (x )-2a +2=0有四个不同的实数根,试求a 的取值范围. 解:(1)依题意可设,当x ≥0时,f (x )=a (x -1)(x -3). 由f (0)=6,得3a =6,所以a =2,此时f (x )=2(x -1)(x -3)=2x 2-8x +6(x ≥0). 当x <0时,-x >0, 则f (-x )=2x 2+8x +6. 又因为f (x )是偶函数, 所以f (-x )=f (x ),所以f (x )=2x 2+8x +6(x <0).所以f (x )=⎩⎪⎨⎪⎧2x 2-8x +6,x ≥0,2x 2+8x +6,x <0.(2)依题意f (x )=2a -2有四个不同实数根,即y =f (x )与y =2a -2在同一坐标系中的图象有四个不同的交点.如图可知只需满足条件-2<2a -2<6,所以0<a<4,即实数a的取值范围是(0,4).22.(12分)一片森林原面积为a,计划每年砍伐一些树,且每年砍伐面积的百分比相等,计划砍伐到面积一半时,所用时间是10年,为保护生态环境,森林面积至少要保留原面积的1 4,已知到今年为止,森林剩余面积为原来的22.(1)求每年砍伐面积的百分比;(2)到今年为止,该森林已砍伐了多少年?(3)求今后最多能砍伐多少年?解:(1)设每年砍伐面积的百分比为x(0<x<1).则a(1-x)10=12a,即(1-x)10=12,解得x=1-⎝⎛⎭⎪⎫12110.(2)设到今年为止,该森林已砍伐了n年,则a(1-x)n=22a,即⎝⎛⎭⎪⎫12n10=⎝⎛⎭⎪⎫1212,n10=12,n=5.故到今年为止,该森林已砍伐了5年.(3)设从今年开始,以后砍伐了n年,则n年后剩余面积为22a(1-x)n,令22a(1-x)n≥14a,即(1-x)n≥24,⎝⎛⎭⎪⎫12n10≥⎝⎛⎭⎪⎫1232,n10≤32,n≤15.故今后最多还能砍伐15年.。
20192020学年人教版A版高中数学必修一模块综合检测一Word版含解析

模块综合检测〔一〕(时间120 分钟,总分值150 分)一、选择题(本大题共12小题,每题4分,共48分)2+1,x∈A},那么A∩B为( ) 1.会集A={x |y=1-x2,x∈Z} ,B={ y|y=xA.?B.{1}C.[0,+∞) D.{(0,1)}剖析:选 B 由1-x2≥0 得,-1≤x≤1,∵x∈Z ,∴A={-1,0,1}.当x∈A 时,y=x2+1∈{2,1},即B={1,2},∴A∩B={1}.x+3x的零点所在的一个区间是( )2.函数f(x)=2A.(-2,-1) B.(-1,0)C.(0,1) D.(1,2)剖析:选 B ∵f (x)=2x+3x,∴f(-1)=-5<0,f(0)=1>0,应选B.23.假设函数f(x)=错误!那么f(log43)=( )1 3 A.1 4 B.C.3 D.4剖析:选 C ∵log43∈(0,1),∴f(log43)=4 log 3 =3,应选 C.44.高为H、满缸水量为V的鱼缸的轴截面以以下图,其底部碰了一个小洞,满缸水从洞中流出,假设鱼缸水深为h时水的体积为v,那么函数v=f(h)的大体图象是( )剖析:选 B 水流速度恒定,开始鱼缸中水的高度下降快,逐渐越来越慢,到达中间,尔后高度下降又越来越快,故消除选项A,C,D,选 B.5.实数a=2,b=log 2,c=( 2)的大小关系正确的选项是( ) A.a<c<b B.a<b<cC.b<a<c D.b<c<a剖析:选 C 依照指数函数和对数函数的性质,b=log 20.2<0< a=2<1< c=( 2).6.设α∈{-1,1,12,3},那么使函数y=xα的定义域为R且为奇函数的所有α的值为( )α的定义域为R且为奇函数的所有α的值为( )A.1,3 B.-1,1C.-1,3 D.-1,1,3-1=1剖析:选 A 当α=-1 时,y=x ,定义域不是R;x当α=1,3 时,满足题意;当α=12时,定义域为[0,+∞).7.函数y=f(x)是R上的偶函数,且在(-∞,0]上是增函数,假设f(a)≤f(2),那么实数a的取值范围是( ) A.(-∞,2]B.[-2,+∞)C.[-2,2]D.(-∞,-2]∪[2,+∞)剖析:选 D ∵y=f(x)是偶函数,且在(-∞,0]上是增函数,∴y=f (x)在[0,+∞)上是减函数,由f( a)≤f(2),得f(| a|)≤f(2).∴|a|≥2,得a≤- 2 或a≥2.8.函数f(x)=4x+ 1的图象( ) 2xA.关于原点对称B.关于y=x对称C.关于x轴对称D.关于y轴对称剖析:选 D ∵f(x)=4x+ 1=2x+2-x,x+2-x,2x∴f(-x)= 2-x+2x=f(x).∴f(x)为偶函数.1 9.函数f(x)=log x,那么方程2 12|x |=|f(x)|的实根个数是( )A.1 B. 2 C.3 D.2 006剖析:选 B 在同一平面直角坐标系中作出函数y=12 |x |及y=|log12x|的图象如图,易得B.10.定义在R上的偶函数f(x)在[0,+∞)上递加,且f 13 =0,那么满足f(log18x)>0的x的取值范围是( )12A.(0,+∞) B. 0,∪(2,+∞)18 C. 0,∪12,2 D. 0,12剖析:选B 由题意知f(x)=f(-x)=f(|x|),所以f(|log18 x|)>f13 ,由于f(x)在[0,+∞)上递加,所以|log18 x|>1 1,解得0<x<或x>2.3 211.函数f(x)=|log3x|,0<x≤9,-x+11,x>9,假设a,b,c均不相等,且f(a)=f( b)=f( c),那么abc的取值范围是( )A.(0,9) B.(2,9)C.(9,11) D.(2,11)剖析:选C 作出f(x)的图象,可知f(x)在(0,1)上是减函数,在(1,9)上是增函数,在(9,+∞)上是减函数.∵a,b,c 互不相等,且f(a)=f(b)=f( c),且f(1)=0,∴不如设a<b<c,那么0<a<1<b<9<c<11,又∵f(a)=f (b),∴-log3a=log3b,∴ab=1,∴abc=c∈(9,11),应选C.12.某商店迎来店庆,为了吸引顾客,采用“满一百送二十,连环送〞的酬宾促销方式,即顾客在店内花销满100元(能够是现金,也能够是奖励券或二者合计),就送20元奖励券;满200元,就送40元奖励券;满300元,就送60元奖励券⋯⋯当日花销最多的一位顾客共花现金70040元,若是依照酬宾促销方式,他最多能获取优惠( )A.17 000元B.17 540元C.17 500元D.17 580元剖析:选C这位顾客花的70 000 元可得奖励券700×20=14 000(元),只有这位顾客连续把奖励券消费掉,才能获取最多优惠,当他把14 000 元奖励券花销掉可得140×20=2 800(元)奖励券,再花销又可获取28×20=560(元)奖励券,560 元花销再加上先前70 040 中的40 元共花销600 元应得奖励券6×20=120(元),120 元奖励券花销时又得20 元奖励券.所以他总合会获取14 000+2 800+560+120+20=17 500(元)优惠.二、填空题(本大题共6小题,每题5分,共30分)2+3,g(x+1)=f(x),那么g(3)=________.13.设f( x)=2x剖析:∵g(x+1)=f(x)=2x2+3∴g(3)=f(2)=2×22+3=11.答案:111,那么f(x)=________,g(x)=________. 14.设f( x)为奇函数,g( x)为偶函数,又f(x)+g(x)=x- 1剖析:∵f( x)为奇函数,∴f(-x)=-f( x),g(x)为偶函数,∴g(-x)=g(x).又∵f(x)+g(x )=1,①x-1∴f(-x)+g(-x)=1-x- 1即-f(x)+g(x )=错误!②1①+②得2g(x)=- x- 11 2=,x+1 x2-1∴g(x )=1. x2-1①-②得2f(x)=1 1+=x-1 x+12x,x2-1∴f(x)=x. x2-1答案:xx2-11x2-115.设P,Q是两个非空会集,定义会集间的一种运算“⊙〞:P ⊙Q={ x|x ∈P ∪Q,且x ?x,x>0},那么P⊙Q=________.P∩Q},若是P={ y|y=4-x2},Q={ y|y= 4剖析:P=[0,2],Q=(1,+∞),∴P⊙Q=[0,1]∪(2,+∞).答案:[0,1]∪(2,+∞)16.函数f (x)=2x+1,x<1,x2+ax,x≥1,假设f( f(0))=4a,那么实数a等于________.剖析:∵0<1,∴f(0)=20+1=2. ∵2>1,∴f(2)=4+2a,∴f(f(0))=f(2)=4+2a=4a,∴a=2.答案: 217.如图是偶函数y=f(x)的局部图象,依照图象所给信息,有以下结论:①函数必然有最小值;②f(-1)-f(2)>0;③f(-1)-f(2)=0;④f(-1)-f(2)<0;⑤f(-1)+f(2)>0.其中正确的结论有________(填序号).剖析:由于所给图象为函数的局部图象,所以不能够确定函数必然有最小值;由图象知函数y=f(x)在区间[1,3]上是增函数,那么f(1)-f(2)<0.又∵函数y=f(x)是偶函数,∴f(-1)=f(1),∴f(-1)-f(2)<0.∵f(-1)=f(1)>0,f(2)>0 ,∴f(-1)+f(2)>0.答案:④⑤x-b)( b为常数),假设x ∈18.函数f (x)=lg(2[1,+∞)时,f (x)≥0恒成立,那么b的取值范围是________.剖析:∵要使f(x)=lg(2x-b)在x∈[1,+∞)上,恒有f(x)≥0,∴有2x-b≥1 在x∈[1,+∞)上恒成立,即 2x≥b+1 恒成立.又∵指数函数g(x)=2x在定义域上是增函数.∴只要2≥b+1 成马上可,解得b≤1.答案:(-∞,1]三、解答题(本大题共6小题,共72分.解答时应写出文字说明、证明过程或运算步骤.)19.(12分)全集为实数集R,会集A={ x|y=x-1+3-x},B={ x|log2x>1}.(1)求A∩B,(?R B)∪A;(2)会集C={ x|1<x<a},假设C?A,求实数a的取值范围.解:(1)由得A={ x|1≤x≤3},B={ x|log2x>1}={ x|x>2},所以A∩B={x|2<x≤3},(?R B)∪A={ x|x≤2}∪{ x|1≤x≤3}={ x|x≤3}.(2)①当a≤1 时,C=?,此时C?A;②当a>1 时,假设C?A,那么1<a≤3.综合①②,可得 a 的取值范围是(-∞,3].x+2,x≤-1,x2,-1<x<2,20.(12分)函数f(x)=2x,x≥2.(1)求f[ f( 3)]的值;(2)假设f( a)=3,求a的值.解:(1)∵-1< 3<2,∴f( 3)=( 3) 2=3.而3≥2,∴f[f ( 3)]=f (3)=2×3=6.(2)当a≤-1 时,f(a)=a+2,又f(a)=3,∴a=1(舍去);当-1<a<2 时,f(a)=a2,又f(a)=3,∴a=±3,其中负值舍去,∴a=3;当a≥2 时,f(a)=2a,又f(a)=3,3∴a=(舍去).综上所述,a=3.21+2x+4xa,且当x∈(-∞,1]时,f(x)有意义,求实数a的取值范围.21.(12分)设f( x)=lg3解:当x∈(-∞,1]时,f(x)有意义,须1+2x+4x a>0 恒成立,也就是a>-x+4x a>0 恒成立,也就是a>-12x+14x (x≤1)恒成立.令u(x)=-12 x+14 x .∵u( x)=-12x+14x 在(-∞,1]上是增函数,∴当x=1 时,[u(x)]max=-3 4.3于是可知,当a>-时,满足题意,43即 a 的取值范围为-,+∞.422.(12分)设函数f(x)的定义域为(-3,3),满足f(-x)=-f(x),且对任意x,y,都有f(x)-f(y)=f (x-y),当x<0时,f(x)>0,f(1)=-2.(1)求f(2)的值;(2)判断f(x)的单调性,并证明;(3)假设函数g(x)=f(x-1)+f(3-2x),求不等式g(x)≤0的解集.解:(1)在f(x)-f(y)=f (x-y)中,令x=2,y=1,代入得:f(2)-f (1)=f(1),所以f(2)=2f(1) =-4.(2) f(x)在(-3,3)上单调递减.证明以下:设-3< x1<x2<3,那么x1-x2<0,所以f( x1)-f(x2)=f(x1-x2)>0,即f( x1)> f(x2),所以f(x)在(-3,3)上单调递减.(3)由g(x)≤0 得f(x-1)+f(3-2x)≤0,所以f( x-1)≤-f(3-2x).又f( x)满足f(-x)=-f(x),所以f( x-1)≤f(2x-3),又f( x)在(-3,3)上单调递减,-3<x-1<3,-3<2x-3<3,所以解得0<x≤2,x-1≥2-x 3,故不等式g(x)≤0 的解集是(0,2].23.(12分)设函数y=f(x)的定义域为R,并且满足f( x+y)=f(x)+f(y),f 13 =1,当x>0时,f(x)>0.(1)求f(0)的值;(2)判断函数的奇偶性;(3)若是f(x)+f(2+x)<2,求x的取值范围.解:(1)令x=y=0,那么f(0)=f(0)+f(0),∴f(0)=0.(2)令y=-x,得f(0) =f(x)+f(-x)=0,∴f(-x)=-f(x),故函数f(x)是R 上的奇函数.(3)任取x1,x2∈R,x1<x2,那么x2-x1>0.∵f(x2)-f(x1)=f( x2-x1+x1)-f(x1)=f(x2-x1)+f( x1)-f(x1)=f(x2-x1)>0,∴f(x1)< f(x2).故f( x)是R 上的增函数.∵ f 13 =1,∴ f 23 = f13+13 =f13 +f13 =2,∴f(x)+f(2+x)=f[x+(2+x)]=f(2x+2)< f 23 .又由y=f(x)是定义在R 上的增函数,2 2得2x+2< ,解之得x<-.3 3故x∈-∞,-2 3 .24.(12分)为了保护环境,睁开低碳经济,某单位在国家科研部门的支持下,进行技术攻关,采用新工艺,把二氧化碳转变成一种可利用的产品.该单位每个月办理二氧化碳最少为400吨,最多为600吨,月办理本钱y(元)与月办理量x(吨)之间的函数关系可近似表示为y=122-200x+80x000,且每办理1吨二氧化碳获取可利用的化工产品价值为100元.(1)假设该单位每个月本钱支出不高出105 000元,求月办理量x的取值范围.(2)该单位每个月能否盈利?若是盈利,求出最大利润;若是不盈利,那么国家最少需要补贴多少元才能使该单位不损失?解:(1)设月办理量为x 吨,那么每个月办理x 吨二氧化碳可获化工产品价值为100x 元,那么每个月本钱支出 f (x) 为12-200x+80 000-100x,x∈[400,600].f(x)=2x假设f( x)≤105 000,即122-300x-25 000≤0,x即(x-300)2≤140 000,∴300-100 14≤x≤100 14+300.∵100 14+300≈674>600,且x∈[400,600],∴该单位每个月本钱支出不高出105 000 元时,月办理量x 的取值范围是{x|400≤x≤600}.(2) f(x)=122-300x+80 000 x=12-600x+90 000)+35 000 (x2=12+35 000,x∈[400,600],(x-300)2∵12+35 000>0,(x-300)2∴该单位不盈利.由二次函数性质适合x=400 时,f( x)获取最小值.f(x)min=12+35 000=40 000. 2(400-300)∴国家最少需要补贴40 000 元才能使该单位不损失.。
2019-2020学年高一数学人教A版必修1练习:模块综合测评(B) Word版含解析

模块综合测评(B )(时间:120分钟 满分:150分)一、选择题(本大题共12小题,每小题5分,共60分)1.已知集合U={1,3,5,7,9},A={1,5,7},则∁U A=( )A.{1,3}B.{3,7,9}C.{3,5,9}D.{3,9}U={1,3,5,7,9},A={1,5,7},∴∁U A={3,9}.2.已知函数f (x )=,则函数的定义域为( )x -2·x +5A.{x|x ≥-2} B.{x|x ≥-5}C.{x|x ≤5}D.{x|x ≥2}f (x )得{x -2≥0,x +5≥0,即{x ≥2,x ≥-5,∴x ≥2.故选D .3.若log 2a<log 2b<0,则( )A.0<b<a<1 B.0<a<b<1C.b>a>1 D.a>b>1log 2a<log 2b<0得log 2a<log 2b<log 21,得0<a<b<1.故选B .4.下列函数中,既是偶函数又在(0,+∞)上单调递增的函数是( )A.y=x 3 B.y=|x|+1C.y=-x 2+1 D.y=2-|x|A 中y=x 3是奇函数;选项C 中y=-x 2+1在(0,+∞)上单调递减;选项D 中y=2-|x|在(0,+∞)上单调递减.故选B .5.计算+lg -lg 5的结果为( )3log 3212A.2 B.1C.3D.-1+lg -lg 5=2-(lg 2+lg 5)=2-1=1.故选B .log 32126.已知二次函数f (x )=ax 2+bx+c (x ∈R )的部分对应值及符号如下表:x-3-2-101234y+m --5-5-n+则可判断方程ax 2+bx+c=0的两个根所在的区间是( )A.(-3,-1)和(-1,1)B.(-1,1)和(1,2)C.(-3,-1)和(2,4)D.(-∞,-3)和(4,+∞).7.函数f (x )=若f (a )>f (-a ),则实数a 的取值范围是( ){log 2x ,x >0,log 12(-x ),x <0,A.(-1,0)∪(0,1)B.(-∞,-1)∪(1,+∞)C.(-1,0)∪(1,+∞)D.(-∞,-1)∪(0,1)a>0时,-a<0,若f (a )>f (-a ),则log 2a>lo [-(-a )],即log 2a>lo a ,此时a>1;当a<0时,-a>0,若f (a )>f (-a ),g 12g 12则lo (-a )>log 2(-a ),此时0<-a<1,-1<a<0.g 128.(2018天山区校级期中)当x ≤1时,函数y=4x -2x+1+2的值域为( )A.[1,+∞) B.[2,+∞)C.[1,2)D.[1,2]4x -2x+1+2=(2x )2-2×2x +2=(2x -1)2+1.设t=2x ,∵x ≤1,∴0<t ≤2,则函数等价为y=(t-1)2+1.∵0<t ≤2,∴1≤y ≤2,即函数的值域为[1,2].9.若方程2ax 2-x-1=0在x ∈(0,1)内含有一个解,则a 的取值范围是( )A.a>1 B.a<-1C.-1<a<1D.0≤a<1f (x )=2ax 2-x-1,因为f (x )=0在(0,1)内恰有一解,所以f (0)·f (1)<0,即(-1)·(2a-2)<0,得a>1.10.函数y=lo (6+x-x 2)的单调增区间是( )g 12A.(-∞,12]B.(-2,12]C.[12,+∞)D.[12,3),需6+x-x 2>0,解得-2<x<3,故函数的定义域是(-2,3).令t=-x 2+x+6=-,(x -12)2+254则函数t 在上单调递减,[12,3)所以函数y=lo (6+x-x 2)在上单调递增.g 12[12,3)11.(2018全国3高考,理7)函数y=-x 4+x 2+2的图象大致为( )x=0时,y=2>0,排除A,B;当x=时,y=-+2>2.排除C .故选D .12(12)4+(12)212.2016年在云南昭通举行的翼装飞行世界杯总决赛中,某翼人空中高速飞行,如图反映了他从某时刻开始的15分钟内的速度v (x )与时间x 的关系,若定义“速度差函数”u (x )为时间段[0,x ]内的最大速度与最小速度的差,则u (x )的图象是( ),当x ∈[0,6]时,翼人做匀加速运动,v (x )=80+x ,“速度差函数”u (x )=x.403403当x ∈[6,10]时,翼人做匀减速运动,速度v (x )从160开始下降,一直降到80,u (x )=160-80=80.当x ∈[10,12]时,翼人做匀减速运动,v (x )从80开始下降,v (x )=180-10x ,u (x )=160-(180-10x )=10x-20.当x ∈[12,15]时,翼人做匀加速运动,“速度差函数”u (x )=160-60=100,结合所给的图象,故选D .二、填空题(本大题共4小题,每小题5分,共20分)13.已知A={y|y=3x },B={x|y=ln(2-x )},则A ∩B= .{y|y=3x }=(0,+∞),B={x|y=ln(2-x )}=(-∞,2),则A ∩B=(0,2).14.若函数f (x )=,x ∈(-∞,b )∪(b+2,+∞)是奇函数,则a+b= .x +a2x2-1函数f (x )在区间(-∞,b )∪(b+2,+∞)上是奇函数,∴b+b+2=0,得b=-1.∴函数f (x )在区间(-∞,-1)∪(1,+∞)上是奇函数,∴f (-2)=-f (2),即=-,-2+a2×(-2)2-12+a2×22-1解之得a=0,∴a+b=-1.115.(2018浙江高考,15)已知λ∈R ,函数f (x )=当λ=2时,不等式f (x )<0的解集是 .{x -4,x ≥λ,x 2-4x +3,x <λ.若函数f (x )恰有2个零点,则λ的取值范围是 .λ=2时,f (x )={x -4,x ≥2,x 2-4x +3,x <2.当x ≥2时,f (x )=x-4<0,解得x<4,∴2≤x<4.当x<2时,f (x )=x 2-4x+3<0,解得1<x<3,∴1<x<2.综上可知,1<x<4,即f (x )≤0的解集为(1,4).分别画出y 1=x-4和y 2=x 2-4x+3的图象如图,由函数f (x )恰有2个零点,结合图象可知1<λ≤3或λ>4.故λ的取值范围为(1,3]∪(4,+∞). (1,3]∪(4,+∞)16.已知定义域为R 的奇函数f (x )在(0,+∞)上是增函数,且f=0,则不等式f (log 4x )>0的解集是 .(-12)R 的奇函数f (x )在(0,+∞)上是增函数,且f =0,(-12)可得f (x )在(-∞,0)上是增函数,且f=-f =0,(12)(-12)当log 4x>0即x>1,f (log 4x )>0即为log 4x>,解得x>2;12当log 4x<0即0<x<1,f (log 4x )>0即为log 4x>-,解得<x<1.1212综上可得,原不等式的解集为∪(2,+∞).(12,1)∪(2,+∞)(12,1)三、解答题(本大题共6小题,共70分.解答应写出文字说明,证明过程或演算步骤)17.(本小题满分10分)已知集合A={x|y=},B={x|x<-4或x>2}.m +1-x (1)若m=-2,求A ∩(∁R B );(2)若A ∪B=B ,求实数m 的取值范围.m=-2,A={x|y=}={x|x ≤-1},∁R B={x|-4≤x ≤2},m +1-x ∴A ∩(∁R B )={x|-4≤x ≤-1}.(2)若A ∪B=B ,则A ⊆B.∵A={x|x ≤1+m },B={x|x<-4或x>2},∴1+m<-4,∴m<-5.18.(本小题满分12分)已知=4,求的值.x 12+x -12x +x -1+4x 2+x -2-200=4,∴x+2+x -1=16.x 12+x -12∴x+x -1=14.∴x 2+2+x -2=196,即x 2+x -2=194.∴原式==-3.14+4194-20019.(本小题满分12分)已知幂函数f (x )=x (3-k )k (k ∈Z )在(0,+∞)上为增函数,(1)求实数k 的值,并写出相应的函数f (x )的解析式;(2)若函数g (x )=mf (x )+mx+1在区间[0,1]上的最大值为5,求出m 的值.已知幂函数f (x )=x (3-k )k (k ∈Z )在(0,+∞)上为增函数,故k (3-k )>0,解得0<k<3.∵k ∈Z ,∴k=1或k=2.当k=1或k=2时,f (x )=x 2满足题意.∴f (x )=x 2.(2)∵f (x )=x 2,∴g (x )=mx 2+mx+1.当m=0时,g (x )=1不合题意;当m ≠0时,函数g (x )的对称轴为直线x=-,12函数g (x )在[0,1]上是单调函数,有{m <0,g (0)=5,或{m >0,g (1)=5,解得m=2.20.(本小题满分12分)已知函数f (x )=log 4(4x -1).(1)求函数f (x )的定义域;(2)讨论函数f (x )的单调性;(3)求函数f (x )在区间上的值域.[12,2]由4x -1>0,得x>0,所以函数f (x )的定义域是(0,+∞).(2)函数f (x )在(0,+∞)上单调递增,证明如下:设0<x 1<x 2,则f (x 1)-f (x 2)=log 4(-1)-log 4(-1)=log 4.4x14x24x 1-14x 2-1∵0<x 1<x 2,∴1<,0<-1<-1.4x 1<4x 24x 14x2∴0<<1,即log 4<0.4x 1-14x 2-14x 1-14x 2-1∴f (x 1)<f (x 2),函数f (x )在(0,+∞)上单调递增.(3)∵函数f (x )在区间上单调递增,[12,2]∴最小值为log 4(-1)=log 41=0,412最大值为log 4(42-1)=log 415.∴函数f (x )在区间上的值域为[0,log 415].[12,2]21.(本小题满分12分)某厂生产某种零件,每个零件的成本为40元,出厂单价定为60元,该厂为鼓励销售商订购,决定当一次订购量超过100个时,每多订购一个,订购的全部零件的出厂单价就降低0.02元,实际出厂单价不低于51元.(1)当一次订购量为多少个时,零件的实际出厂单价恰降为51元?(2)设一次订购量为x 个,零件的实际出厂单价为P 元,写出函数P=f (x )的解析式.(3)当销售商一次订购500个零件时,该厂获得的利润是多少元?如果订购1 000个利润又是多少元?(工厂售出一个零件的利润=实际出厂单价-成本)设每个零件的实际出厂单价恰好降为51元时,一次订购量为x 0个,则x 0=100+=550(个).60-510.02(2)当0<x ≤100时,P=60;当100<x<550时,P=60-0.02(x-100)=62-;x50当x ≥550时,P=51,∴P=f (x )={60(0<x ≤100),62-x50(100<x <550),x ∈N ,51(x ≥550).(3)设销售商一次订购量为x 时,工厂获得的利润为L 元,则有L=(P-40)x={20x (0<x ≤100),22x -x250(100<x <550),x ∈N ,11x (x ≥550),当x=500时,L=6 000元;当x=1 000时,L=11 000元.22.(本小题满分12分)已知指数函数y=g (x )满足:g (3)=27,定义域为R 的函数f (x )=是奇函数.n -g (x )m +3g (x )(1)确定函数y=g (x ),y=f (x )的解析式;(2)若函数h (x )=kx-g (x )在(0,1)上有零点,求k 的取值范围;(3)若对任意的t ∈(1,4),不等式f (2t-3)+f (t-k )>0恒成立,求实数k 的取值范围.设函数g (x )=a x (a>0且a ≠1),则a 3=27,∴a=3.∴g (x )=3x .∴f (x )=.n -3xm +3x +1∵f (x )是定义域为R 的奇函数,∴f (0)=0,即=0⇒n=1.n -12+m ∴f (x )=.1-3x3x +1+m 又f (-1)=-f (1),∴=-⇒m=3.1-13m +11-39+m ∴f (x )=.1-3x3+3x +1(2)由(1)知g (x )=3x ,又因h (x )=kx-g (x )在(0,1)上有零点,从而h (0)·h (1)<0,即(0-1)·(k-3)<0,∴k-3>0,∴k>3.∴k 的取值范围为(3,+∞).(3)由(1)知函数f (x )==-=-,1-3x3+3x +113·3x -13x+113+23·13x +1∴f (x )在R 上为减函数.又∵f (x )是奇函数,f (2t-3)+f (t-k )>0,∴f (2t-3)>-f (t-k )=f (k-t ).因f (x )为减函数,由上式得2t-3<k-t ,即对一切t ∈(1,4),有3t-3<k 恒成立.令m (t )=3t-3,t ∈[1,4],易知m (t )在[1,4]上递增,所以m (t )max =3×4-3=9,∴k ≥9,即实数k 的取值范围为[9,+∞).。
2019_2020学年高中数学模块综合检测含解析新人教A版必修1

模块综合检测(时间:120分钟 满分:150分)一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.设全集U={x|x<6,且x ∈N *},集合A={1,3},B={3,5},则∁U (A ∪B )等于( ) A.{1,4}B.{1,5}C.{2,4}D.{2,5}解析:由已知可得U={1,2,3,4,5},A ∪B={1,3,5},故∁U (A ∪B )={2,4}. 答案:C2.函数y=-1+l og 14x (x ≥4)的值域是( )A.(-∞,-2]B.(-∞,0]C.[-2,+∞)D.[2,+∞)解析:∵函数y=-1+l og 14x 在[4,+∞)上单调递减,∴y ≤-1+l og 144=−2,∴所求函数的值域为(-∞,-2].答案:A3.函数y =√3x -1+1x -1的定义域为( ) A.(-∞,0] B.[1,+∞) C.[0,1)D.[0,1)∪(1,+∞)解析:函数有意义时{3x -1≥0,x -1≠0,解得x ≥0,且x ≠1.故函数定义域为[0,1)∪(1,+∞).答案:D4.下列函数中,在区间(0,+∞)内是增函数的是()A.y=x2-2xB.y=(12)x C.x=logπx D.x=x-12解析:对于A,函数y=x2-2x在区间(0,1)内递减,在(1,+∞)内递增,故A不正确,B,D在(0,+∞)内为减函数;对于C,因为π>1,所以y=logπx在(0,+∞)内为增函数.答案:C5.函数f(x)=e x−1x的零点所在的区间是()A.(0,12)B.(12,1)C.(1,32)D.(32,2)解析:∵x(12)=e12−2<0,x(1)=e−1>0,∴x(12)·f(1)<0,∴函数f(x)=e x−1x的零点所在的区间是(12,1).答案:B6.设a=70.3,b=0.37,c=log70.3,则a,b,c的大小关系是()A.a<b<cB.c<b<aC.c<a<bD.b<c<a解析:∵a=70.3>1,0<b=0.37<1,c=log70.3<0,∴c<b<a.答案:B7.已知函数f(x)是定义在R上的偶函数,当x<0时,y=f(x)是减函数,若|x1|<|x2|,则()A.f(x1)-f(x2)<0B.f(x1)-f(x2)>0C.f(x1)+f(x2)<0D.f(x1)+f(x2)>0解析:∵f(x)是定义在R上的偶函数,∴f (x )的图象关于y 轴对称.又当x<0时,y=f (x )是减函数,∴当x>0时,y=f (x )是增函数. ∴当|x 1|<|x 2|时,f (|x 1|)<f (|x 2|),即f (x 1)<f (x 2),即f (x 1)-f (x 2)<0. 答案:A8.已知一次函数f (x )=kx+b 的图象过第一、第二、第三象限,且f (f (x ))=9x+8,则f (2)等于( ) A.-10B.-4C.2D.8解析:∵f (x )=kx+b ,∴f (f (x ))=k (kx+b )+b=k 2x+kb+b.又f (f (x ))=9x+8,∴{x 2=9,xx +x =8,解得{x =3,x =2或{x =-3,x =-4.∴f (x )=3x+2或f (x )=-3x-4.又f (x )的图象过第一、二、三象限,∴f (x )=3x+2,∴f (2)=8.答案:D9.已知函数f (x )=log a (2x+b-1)(a>0,且a ≠1)的图象如图所示,则a ,b 满足的关系是( )A.0<a-1<b<1B.0<b<a-1<1C.0<b-1<a<1D.0<a-1<b-1<1解析:由题图,可知函数f(x)在R上单调递增,故a>1.函数图象与y轴的交点坐标为(0,log a b),由题图可知-1<log a b<0,得a-1<b<1.综上,0<a-1<b<1,选A.答案:A10.给出下列集合A到集合B的几种对应:其中,是从A到B的映射的有()A.①②B.①②③C.①②④D.①②③④解析:根据映射的定义知,③中集合A中的元素a对应集合B中的两个元素x,y,则此对应不是映射;④中集合A中的元素b在集合B中没有对应元素,则此对应也不是映射.仅有①②符合映射的定义,故①②是映射.答案:A11.某企业去年销售收入1 000万元,年成本为生产成本500万元与年广告成本200万元两部分.若年利润必须按p%纳税,且年广告费超出年销售收入2%的部分也按p%纳税,其他不纳税.已知该企业去年共纳税120万元,则税率p%为()A.10%B.12%C.25%D.40%解析:利润300万元,纳税300·p%万元,年广告费超出年销售收入2%的部分为200-1000×2%=180(万元),纳税180·p %万元, 共纳税300·p %+180·p %=120(万元), 故p %=25%. 答案:C12.如果函数f (x )对其定义域内的任意两个实数x 1,x 2都满足不等式x (x 1+x 22)<x (x 1)+x (x 2)2,那么称函数x (x )在定义域上具有性质x .给出函数:①x =√x ;②x =x 2;③x =2x ;④x =log 2x .其中具有性质x 的是( ) A.①②B.②③C.③④D.①④解析:分别画出它们的图象,可知函数y =√x 与函数y=log 2x 满足x (x 1+x 22)>x (x 1)+x (x 2)2;函数y=x 2与函数y=2x满足x (x 1+x 22)<x (x 1)+x (x 2)2.答案:B二、填空题(本大题共4小题,每小题5分,共20分.把答案填在题中的横线上)13.若幂函数f (x )的图象过点(3,√274),则x (x )的解析式是____________________.解析:设f (x )=x α,则由已知得3α=√274=334,∴α=34,∴x (x )=x 34.答案:f (x )=x 3414.已知f (x )={x 2+1,x ≤0,-2x ,x >0,则x (x (1))=___________________.解析:∵f (1)=-2,∴f (f (1))=f (-2)=(-2)2+1=5.答案:515.已知函数f (x )是定义在R 上的奇函数,并且当x ∈(0,+∞)时,f (x )=1+ln x ,则当x<0时,f (x )= . 解析:设t<0,则-t>0.∵当x ∈(0,+∞)时,f (x )=1+ln x , ∴f (-t )=1+ln(-t ).又f (x )是定义在R 上的奇函数,∴-f (t )=1+ln(-t ),∴f (t )=-1-ln(-t ). ∴当x<0时,f (x )=-1-ln(-x ).答案:-1-ln(-x )16.已知函数f (x )={log 2x ,x >0,3x ,x ≤0,且函数x (x )=x (x )+x −x 有且只有一个零点,则实数x 的取值范围是___________________.解析:由题意可画出函数f (x )={log 2x ,x >0,3x ,x ≤0的图象,如图所示,函数h (x )=f (x )+x-a 有且只有一个零点,即y=f (x )的图象与y=a-x 的图象有且只有一个交点,显然当a>1时满足条件.答案:(1,+∞)三、解答题(本大题共6小题,共70分.解答时应写出文字说明、证明过程或演算步骤)17.(10分)计算下列各式的值:(1)2-12√2√2-1√(1-√5)0;(2)log 3√27+lg 25+lg 4+7log 72+(−9.8)0. 解:(1)原式=2-12√2√2-1−√1=2-12+2-12+√2+1−1=2×2-12+√2=√2+√2=2√2.(2)原式=log 3332+lg 100+2+1=32+2+2+1=132.18.(12分)设全集是实数集R ,集合A={x|y=log a (x-1)+√3-x },x ={x |2x +x ≤0}. (1)当m=-4时,求A ∩B 和A ∪B ; (2)若(∁R A )∩B=B ,求实数m 的取值范围.解:(1)由{x -1>0,3-x ≥0,得1<x ≤3,即集合A=(1,3];由2x-4≤0,得2x≤22,x ≤2, 即集合B=(-∞,2].故A ∩B=(1,2],A ∪B=(-∞,3]. (2)由(1)得∁R A={x|x>3,或x ≤1}.∵(∁R A )∩B=B ,∴B ⊆∁R A. ①若B=⌀,则m ≥0;②若B ≠⌀,则m<0,∴2x ≤-m.∴x ≤log 2(-m ). ∵B ⊆∁R A ,∴log 2(-m )≤1,即log 2(-m )≤log 22,因此0<-m ≤2,-2≤m<0.综上所述,实数m 的取值范围是[-2,+∞).19.(12分)某化工厂引进一条先进生产线生产某种化工产品,其生产的总成本y (单位:万元)与年产量x (单位:吨)之间的函数解析式可以近似地表示为y =x 25−48x +8 000,已知此生产线年产量最大为210吨.(1)求年产量为多少吨时,其生产的总成本最低?最低成本是多少?(2)如果每吨产品平均出厂价为40万元,那么当年产量为多少吨时,可以获得最大利润?最大利润是多少?解:(1)由y =x 25−48x +8000=15(x −120)2+5120(0≤x ≤210),所以当年产量为120吨时,其生产的总成本最低,最低成本为5120万元. (2)设该工厂年获得总利润为f (x )万元,则f (x )=40x-y=40x −x 25+48x −8000=−x 25+88x −8000=−15(x −220)2+1680(0≤x ≤210).因为f (x )在区间[0,210]上是增函数,所以当x=210时,f (x )有最大值为−15(210−220)2+1680=1660.故当年产量为210吨时,可获得最大利润1660万元.20.(12分)已知函数f (x )是定义在区间[-1,1]上的奇函数,若当x ,y ∈[-1,1],x+y ≠0时,有(x+y )·[f (x )+f (y )]>0. (1)比较x (12)与x (13)的大小;(2)判断f (x )的单调性,并加以证明; (3)解不等式x (x +12)<x (1−2x ).解:(1)令x =12,x =−13,因为12+(-13)≠0, 由[12+(-13)][x (12)+x (-13)]>0,得x (12)>−x (-13),所以x (12)>x (13).(2)f (x )在区间[-1,1]上是增函数.证明如下:在区间[-1,1]上任取x 1,x 2,且x 1<x 2,则x 2-x 1>0.由题意(x 2-x 1)[f (x 2)+f (-x 1)]>0, 因为f (x )为奇函数, 所以(x 2-x 1)[f (x 2)-f (x 1)]>0. 所以f (x 2)-f (x 1)>0,即f (x 2)>f (x 1). 所以f (x )在区间[-1,1]上是增函数. (3)由(2)知,f (x )在区间[-1,1]上是增函数, 所以{-1≤x +12≤1,-1≤1-2x ≤1,x +12<1-2x ,解得0≤x <16.即不等式x (x +12)<x (1−2x )的解集为[0,16).21.(12分)设f (x )=l og 121-xxx -1为奇函数,x 为常数.(1)求a 的值;(2)证明f (x )在区间(1,+∞)内单调递增;(3)若对于区间[3,4]上的每一个x 的值,不等式f (x )>(12)x+m 恒成立,求实数m 的取值范围.解:(1)∵f (-x )=-f (x ),∴lo g 121+xx-1-x=-lo g 121-xxx -1=lo g 12x -11-xx .∴1+xx -x -1=x -11-xx ,即(1+ax )(1-ax )=-(x+1)(x-1),∴a=-1.(2)由(1)可知f (x )=lo g 12x +1x -1. 任取x 1>x 2>1,则f (x 1)-f (x 2)=lo g 12x 1+1x 1-1-lo g 12x 2+1x 2-1=lo g 12(x 1+1)(x 2-1)(x 1-1)(x 2+1).由x 1>x 2>1易知(x 1+1)(x 2-1)>0,(x 1-1)·(x 2+1)>0,现比较(x 1+1)(x 2-1)(x 1-1)(x 2+1)与1的大小.(x 1+1)(x 2-1)(x 1-1)(x 2+1)-1=(x 1+1)(x 2-1)-(x 1-1)(x 2+1)(x 1-1)(x 2+1)=2(x 2-x 1)(x 1-1)(x 2+1)<0, 所以0<(x 1+1)(x 2-1)(x 1-1)(x 2+1)<1,lo g 12(x 1+1)(x 2-1)(x 1-1)(x 2+1)>0,即f (x 1)>f (x 2).故f (x )在区间(1,+∞)内单调递增. (3)设g (x )=lo g 12x +1x -1−(12)x,则g (x )在区间[3,4]上为增函数.∴g (x )>m 对x ∈[3,4]恒成立,∴m<g (3)=-98.∴实数m 的取值范围是m<-98.22.(12分)(1)当m 为何值时,f (x )=x 2+2mx+3m+4.①有且仅有1个零点? ②有2个零点,且均比-1大?(2)若函数F (x )=|4x-x 2|+a 有4个零点,求实数a 的取值范围. 解:(1)①若函数f (x )=x 2+2mx+3m+4有且仅有1个零点,则等价于Δ=4m 2-4(3m+4)=0,即4m 2-12m-16=0,即m 2-3m-4=0,解得m=4或m=-1. ②设2个零点分别为x 1,x 2,且x 1>-1,x 2>-1,x 1≠x 2,则x 1+x 2=-2m ,x 1·x 2=3m+4,故只需{x =4x 2-4(3x +4)>0,(x 1+1)+(x 2+1)>0,(x 1+1)(x 2+1)>0⇔{x 2-3x -4>0,-2x +2>0,3x +4+(-2x )+1>0⇔{x <-1或x >4,x <1,x >-5.故m 的取值范围是-5<m<-1.(2)F (x )=|4x-x 2|+a 有4个零点,即|4x-x 2|+a=0有4个实数根,即|4x-x 2|=-a 有4个实数根.令g (x )=|4x-x 2|,h (x )=-a.在同一坐标系中作出g (x )和h (x )的图象,如图所示.由图象可知要使|4x-x 2|=-a 有4个实数根,则需g (x )的图象与h (x )的图象有4个交点, 故0<-a<4,即-4<a<0.所以实数a 的取值范围为-4<a<0.。
2019-2020学年人教A版高中数学必修一模块综合检测(二) Word版含解析

模块综合检测(二)(时间90分钟,满分120分)一、选择题(本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.如图,AB ∥EM ∥DC ,AE =ED ,EF ∥BC ,EF =12 cm ,则BC 的长为( )A .6 cmB .12 cmC .18 cmD .24 cm解析:选D 根据AE =ED ,AB ∥EM ∥DC ,有BM =MC . 又EF ∥BC ,所以EF =MC ,于是EF =12BC .2.在▱ABCD 中,E 是AD 的中点,AC ,BD 交于O ,则与△ABE 面积相等的三角形有( )A .5个B .6个C .7个D .8个解析:选C利用三角形面积公式,等底等高的两个三角形面积相等,再利用平行四边形的面积为中介,建立面积相等关系.3.在正方形ABCD 中,点E 在AB 边上,且AE ∶EB =2∶1,AF ⊥DE 于G ,交BC 于F ,则△AEG 的面积与四边形BEGF 的面积比为( )A .1∶2B .1∶4C .4∶9D .2∶3解析:选C 易证△ABF ≌△DAE .故知BF =AE . 因为AE ∶EB =2∶1,故可设AE =2x ,EB =x , 则AB =3x ,BF =2x .由勾股定理得AF =错误!=错误!x . 易证△AEG ∽△ABF .可得S △AEG ∶S △ABF =AE 2∶AF 2=(2x )2∶(13x )2=4∶13.可得S △AEG ∶S 四边形BEGF =4∶9.4.在梯形ABCD 中,AD∥BC (其中BC >AD )E ,F 分别是AB ,DC 的中点,连接EF ,且EF 交BD 于G ,交AC 于H ,则GH 等于( )A .ADB.12(AD +BC )C .BCD.12(BC -AD )解析:选D 结合平行线等分线段定理及梯形中位线定理可解决此问题.5.如图,在梯形ABCD 中,AD ∥BC ,∠BAD =135°,以A 为圆心,AB 为半径,作⊙A 交AD ,BC 于E ,F 两点,并交BA 延长线于G ,则BF 的度数是( )A .45°B .60°C .90°D .135°解析:选C ¼BF的度数等于圆心角∠BAF 的度数. 由题意知∠B =45°,所以∠BAF =180°-2∠B .6.在△ABC 中,点D ,E 分别在AB ,AC 上,下列条件中,不能判定DE ∥BC 的是( ) A .AD =5,AB =8,AE =10,AC =16 B .BD =1,AD =3,CE =2,AE =6 C .AB =7,BD =4,AE =4,EC =3 D .AB =AC =9,AD =AE =8解析:选C 对应线段必须成比例,才能断定DE 和BC 是平行关系,显然C 中的条件不成比例.7.如图,PA 是⊙O 的切线,A 为切点,PC 是⊙O 的割线,且PB =12BC ,则PAPB等于( )A .2 B.12C.3 D .1解析:选C 利用切割线定理得PA 2=PB ·PC =3PB 2, 则PA PB=3.8.D 、E 、F 是△ABC 的三边中点,设△DEF 的面积为4,△ABC 的周长为9,则△DEF 的周长与△ABC 的面积分别是( )A.92,16 B .9,4 C.92,8 D.94,16解析:选A 如右图,D 、E 、F 分别为△ABC 三边中点.∴EF 綊12BC ,∴△AEF ∽△ABC ,且EFBC =12.∴l△DEF l△ABC =EF BC =12, 又∵l △ABC =9,∴l △DEF =92.又∵S△DEFS△ABC =EF2BC2=14,又∵S △DEF =4, ∴S △ABC =16.9.如图,已知在△ABC 中,AD∶DC =1∶2,E 为BD 的中点,AE 延长线交BC 于F ,则BF ∶FC 等于( )A .1∶5B .1∶4C .1∶3D .1∶2解析:选C 过D 作DG 平行于AF ,交BC 于点G ,再根据平行线分线段成比例定理即可解决.10.如图,四边形ABCD 内接于⊙O ,BC 是直径,AD =DC ,∠ADB =20°,则∠ACB ,∠DBC 分别为( )A .15°与30°B .20°与35°C .20°与40°D .30°与35°解析:选B ∵∠ADB =20°, ∴∠ACB =∠ADB =20°. 又∵BC 为⊙O 的直径,∴¼ADC 的度数为180°-40°=140°. ∵D 为¼AC 的中点, ∴»CD的度数为70°, ∴∠DBC =70°2=35°.二、填空题(本大题共4小题,每小题5分,共20分.把答案填写在题中的横线上)11.(湖北高考)如图,点D 在⊙O 的弦AB 上移动,AB =4,连接OD ,过点D 作OD 的垂线交⊙O 于点C ,则CD 的最大值为________.解析:由题意知CD 2=OC 2-OD 2,OC 是半径,所以当OD 的值最小时,DC 最大,易知D 为AB 的中点时,DB =DC =2最大.答案:212.如图,在Rt △ABC 中,∠C=90°,以BC为直径作半圆交AB于D,过D作半圆的切线交AC于E,若AD=2,DB=4,则DE=________.解析:由切割线定理得:AC2=AD·AB=2×6=12.所以AC=23.连接CD,可证:EC=ED,∠A=∠EDA.所以AE=ED,所以ED=AE=EC=12AC=3.答案:313.如图所示,圆O的直径AB=6,C为圆周上一点,BC=3,过C作圆的切线l,过A作l的垂线AD,AD 分别与直线l、圆交于点D、E,则∠DAC=________,线段AE的长为________.解析:因为AB为⊙O的直径,所以∠ACB=90°.又因为AB=6,BC=3,所以∠CAB=30°.又∠DCA=90°-30°=60°,而AD⊥DC,所以∠DAC=30°,即可得出¼AE=»BC=»EC.所以AE=BC=3.答案:30° 314.如图,△ABC是圆O的内接三角形,PA是圆O的切线,A为切点,PB交AC于点E,交圆O于点D,若PE=PA,∠ABC=60°,且PD=1,BD=8,则AC=________.解析:因为PA是圆O的切线,所以∠CAP=∠ABC=60°.又PE=PA,所以△PAE为等边三角形.由切割线定理得PA2=PD·PB=1×9=9,所以PA=3,所以PA=PE=AE=3,ED =PE -PD =3-1=2, BE =BD -ED =8-2=6. 由相交弦定理得AE ·EC =BE ·ED . 所以EC =BE·ED AE =6×23=4,所以AC =AE +EC =3+4=7. 答案:7三、解答题(本大题共4个小题,共50分.解答应写出必要的文字说明、证明过程或演算步骤)15.(本小题满分12分)如图,已知在梯形ABCD 中,AD ∥BC ,E 是CD 的中点,EF ∥BC 交AB 于F ,FG ∥BD 交AD 于G .求证:AG =DG .证明:∵AD ∥EF ∥BC ,E 是CD 的中点,∴F 是AB 的中点. 又∵FG ∥BD ,∴G 是AD 的中点.∴AG =DG .16.(本小题满分12分)(江苏高考)如图,AB 和BC 分别与圆O 相切于点D ,C ,AC 经过圆心O ,且BC =2OC .求证:AC =2AD .证明:连接OD .因为AB 和BC 分别与圆O 相切于点D ,C , 所以∠ADO =∠ACB =90°.又因为∠A =∠A , 所以Rt △ADO ∽Rt △ACB . 所以BCOD =ACAD .又BC =2OC =2OD , 故AC =2AD .17.(本小题满分12分)如图所示,两圆内切于点T ,大圆的弦AB 切小圆于点C .TA ,TB 与小圆分别相交于点E ,F .FE 的延长线交两圆的公切线TP 于点P .求证:(1) »CE=»CF ; (2)AC ·PF =BC ·PT .证明:(1)设小圆的圆心为点O ,连接OC .∵AB切小圆于点C,∴OC⊥AB. ∵∠1=∠3=∠2,∴EF∥AB,∴OC⊥EF,∴»CE=»CF.(2)∵EF∥AB,∴AEBF=ATBT=TETF.∵AB切小圆于点C,∴AC2=AE·AT,BC2=BF·BT.∴AC2BC2=AE·ATBF·BT=TE2TF2,ACBC=TETF.∵PT是公切线,∴∠PTF=90°,∵TF是⊙O的直径,∴TE⊥PF,△PTF∽△TEF,∴PTPF=TETF,∴ACBC=PTPF,∴AC·PF=BC·PT.18.(本小题满分14分)如图,在矩形ABCD中,以A为圆心,AD为半径的圆交AC,AB于M,E.CE的延长线交⊙A于F,CM=2,AB=4.(1)求⊙A的半径;(2)求CE的长和△AFC的面积.解:(1)∵四边形ABCD为矩形,AB=4,∴CD=4.在Rt△ACD中,AC2=CD2+AD2,∴(2+AD)2=42+AD2.解得:AD=3,即⊙A的半径为3.(2)过点A作AG⊥EF于点G,∵BC=3,BE=AB-AE=4-3=1,∴CE=BC2+BE2=32+12=10.∵∠ADC=90°,∴CD 为⊙A 的切线, ∴CE ·CF =CD 2, ∴CF =CD2CE =4210=8510.又∠B =∠AGE =90°,∠BEC =∠GEA , ∴△BCE ∽△GAE ,∴BCAG =CE AE 即3AG =103.∴AG =91010, ∴S △AFC =12CF ·AG =12×8510×91010=365.。
2019_2020学年高中数学模块综合检测(含解析)新人教A版选修1_1

模块综合检测[学生用书P145(单独成册)] (时间:120分钟,满分:150分)一、选择题:本题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的.1.“(2x -1)x =0”是“x =0”的( ) A .充分不必要条件 B .必要不充分条件 C .充分必要条件D .既不充分也不必要条件解析:选B.由(2x -1)x =0可得x =12或x =0.因为“x =12或x =0”是“x =0”的必要不充分条件,所以“(2x -1)x =0”是“x =0”的必要不充分条件.2.设a ,b ∈R ,则“(a -b )a 2<0”是“a <b ”的( ) A .充分不必要条件 B .充要条件 C .必要不充分条件 D .既不充分也不必要条件解析:选A.由(a -b )a 2<0可知a 2≠0,则一定有a -b <0,即a <b ;但是a <b 即a -b <0时,有可能a =0,所以(a -b )a 2<0不一定成立,故“(a -b )a 2<0”是“a <b ”的充分不必要条件,选A.3.下列命题中是假命题的是( )A .∀x ∈⎝⎛⎭⎪⎫0,π2,x >sin xB .∃x 0∈R ,sin x 0+cos x 0=2C .∀x ∈R ,3x>0 D .∃x 0∈R ,lg x 0=0解析:选B.因为sin x 0+cos x 0=2sin ⎝ ⎛⎭⎪⎫x 0+π4≤2,所以B 错误,选B.4.与双曲线y 25-x 2=1共焦点,且过点(1,2)的椭圆的标准方程为( )A.x 28+y 22=1 B .x 210+y 24=1C.y 28+x 22=1 D .y 210+x 24=1解析:选C.由题知,焦点在y 轴上,排除A ,B ,将(1,2)代入C ,D 可得C 正确,故选C.5.函数f (x )=x -e x+2的单调增区间为( ) A .(0,+∞) B .(-∞,0) C .(-∞,1)D .(1,+∞)解析:选B.因为f ′(x )=1-e x(x ∈R ),所以f ′(x )>0的解集为{x |x <0},所以函数f (x )的单调增区间为(-∞,0),故选B.6.若椭圆x 2a 2+y 2b 2=1(a >b >0)的离心率为32,则双曲线x 2a 2-y 2b2=1的渐近线方程为( )A .y =±12xB .y =±2xC .y =±4xD .y =±14x解析:选A.由椭圆的离心率e =c a =32,可知c 2a 2=a 2-b 2a 2=34,所以b a =12,故双曲线x 2a 2-y 2b2=1的渐近线方程为y =±12x .7.已知命题p :若方程ax 2+x -1=0有实数解,则a ≥-14且a ≠0;命题q :函数y =x2-2x 在[0,3]上的最大值与最小值之和为2.则下列为真命题的是( )A .p 且qB .p 且﹁qC .p 或﹁qD .p 或q解析:选D.由于a =0时,方程ax 2+x -1=0有实数解x =1,故p 是假命题;函数y =x 2-2x 在[0,3]上的最小值为-1,最大值为3,最大值与最小值之和为2,故q 是真命题,在四个选项中,只有p 或q 是真命题.8.若命题“∃x 0∈R ,使x 20+(a -1)x 0+1<0”是假命题,则实数a 的取值范围为( ) A .1≤a ≤3 B .-1≤a ≤3 C .-3≤a ≤3D .-1≤a ≤1解析:选B.根据题意可得∀x ∈R ,都有x 2+(a -1)x +1≥0,所以Δ=(a -1)2-4≤0, 所以-1≤a ≤3.9.设斜率为2的直线l 过抛物线y 2=ax (a ≠0)的焦点F ,且和y 轴交于点A ,若△OAF (O 为坐标原点)的面积为4,则抛物线的方程为( )A .y 2=±4x B .y 2=±8x C .y 2=4xD .y 2=8x解析:选B.由已知可得,抛物线的焦点坐标为⎝ ⎛⎭⎪⎫a4,0.又直线l 的斜率为2,故直线l 的方程为y =2⎝ ⎛⎭⎪⎫x -a 4,则|OA |=|a |2,故S △OAF =12·|a |4·|a |2=4,解得a =±8,故抛物线的方程为y 2=±8x .10.已知函数f (x )=x 3-px 2-qx 的图象与x 轴切于点(1,0),则f (x )的极值为( ) A .极大值为427,极小值为0B .极大值为0,极小值为-427C .极小值为-527,极大值为0D .极小值为0,极大值为527解析:选A.f ′(x )=3x 2-2px -q (x ∈R ),由题可得f ′(1)=0,f (1)=0,解得p =2,q =-1,故f ′(x )=3x 2-4x +1.令f ′(x )>0,解得x <13或x >1,令f ′(x )<0,解得13<x <1,所以f (x )极大=f ⎝ ⎛⎭⎪⎫13=427,f (x )极小=f (1)=0.11.P 是长轴在x 轴上的椭圆x 2a 2+y 2b2=1(a >b >0)上的点,F 1,F 2分别为椭圆的两个焦点,椭圆的半焦距为c ,则|PF 1|·|PF 2|的最大值与最小值之差一定是( )A .1B .a 2C .b 2D .c 2解析:选D.由椭圆的几何性质得a -c ≤|PF 1|≤a +c ,|PF 1|+|PF 2|=2a ,所以|PF 1|·|PF 2|≤⎝ ⎛⎭⎪⎫|PF 1|+|PF 2|22=a 2,当且仅当|PF 1|=|PF 2|时取等号. |PF 1|·|PF 2|=|PF 1|·(2a -|PF 1|)=-|PF 1|2+2a |PF 1|=-(|PF 1|-a )2+a 2≥-c 2+a 2=b 2,所以|PF 1|·|PF 2|的最大值与最小值之差为a 2-b 2=c 2.12.设函数f (x )=ax 2+bx +c (a ,b ,c ∈R ).若x =-1为函数f (x )e x的一个极值点,则下列图象不可能为y =f (x )的图象的是( )解析:选D.[f (x )e x]′=[ax 2+(2a +b )x +b +c ]e x ,由x =-1为函数f (x )e x的一个极值点,易得a =c .选项A ,B 中,对称轴x =-b2a=-1,所以b =2a ,所以f (x )=a (x +1)2,当a 大于0时,与A 中图象相符,当a <0时,与B 中图象相符;选项C 中,对称轴x =-b2a>0,且开口向下,所以a <0,b >0,所以f (-1)=2a -b <0,与图象相符;选项D 中,对称轴x =-b2a<-1,且开口向上,所以a >0,b >2a ,所以f (-1)=2a -b <0,与图象不相符,故选D. 二、填空题:本题共4小题,每小题5分.13.已知函数y =ln(x -4)的定义域为A ,集合B ={x |x >a }.若x ∈A 是x ∈B 的充分不必要条件,则实数a 的取值范围为________.解析:要使函数y =ln(x -4)有意义,则x -4>0,即x >4,即A ={x |x >4}.由x ∈A 是x ∈B 的充分不必要条件,得AB ,则a <4.答案:(-∞,4)14.已知双曲线x 2a 2-y 2b2=1(a >0,b >0)的一条渐近线平行于直线l :y =2x +10,双曲线的一个焦点在直线l 上,则双曲线的方程为________.解析:由已知得b a=2,所以b =2a .在y =2x +10中令y =0得x =-5,故c =5,从而a 2+b 2=5a 2=c 2=25,所以a 2=5,b 2=20,所以双曲线的方程为x 25-y 220=1.答案:x 25-y 220=115.已知下列命题:①“x =2”是“x 2-4x +4=0”的必要不充分条件;②“圆心到直线的距离等于半径”是“这条直线为圆的切线”的充要条件; ③“sin α=sin β”是“α=β”的充要条件; ④“ab ≠0”是“a ≠0”的充分不必要条件. 其中为真命题的是________(填序号).解析:x =2是x 2-4x +4=0的充要条件,①为假命题;②为真命题;③“sin α=sin β”是“α=β”的必要不充分条件,③为假命题;ab ≠0⇒a ≠0,但a ≠0⇒/ ab ≠0,则④为真命题.故填②④.答案:②④16.已知椭圆C :x 22+y 2=1的焦点为F (1,0),直线l :x =2,点A ∈l ,线段AF 交C 于点B ,若FA →=3FB →,则|AF →|=________.解析:设A (2,t ),B (x ,y ),又F (1,0), 所以FA →=(1,t ),FB →=(x -1,y ), 由FA →=3FB →得1=3(x -1),t =3y , 解得x =43,又B 在椭圆C 上,所以⎝ ⎛⎭⎪⎫4322+y 2=1,即y 2=1-89=19. 又t =3y ,所以t 2=9y 2=1, 故|AF →|=|FA →|=12+t 2= 2. 答案: 2三、解答题:解答应写出文字说明、证明过程或演算步骤.17.(本小题满分10分)已知命题p :方程x 22+y 2m=1表示焦点在y 轴上的椭圆;命题q :∀x ∈R ,4x 2-4mx +4m -3≥0.若(﹁p )∧q 为真,求m 的取值范围.解:p 真时,m >2.q 真时,4x 2-4mx +4m -3≥0在R 上恒成立.Δ=16m 2-16(4m -3)≤0, 解得1≤m ≤3.因为(﹁p )∧q 为真,所以p 假,q 真.所以⎩⎪⎨⎪⎧m ≤2,1≤m ≤3,即1≤m ≤2.所以所求m 的取值范围为[1,2].18.(本小题满分12分)已知抛物线C :x 2=2py (p >0)上一点M (m ,4)到其焦点的距离为5.(1)求抛物线C 的方程;(2)若过点M 的双曲线y 2a 2-x 2b2=1(a >0,b >0)的一个顶点为抛物线C 的焦点,求该双曲线的渐近线方程.解:(1)由抛物线的定义可得4+p2=5,解得p =2,所以抛物线C 的方程为x 2=4y . (2)把M (m ,4)代入x 2=4y 可得m =±4, 所以M 点的坐标为(±4,4), 因为抛物线x 2=4y 的焦点为(0,1), 所以a =1,所以双曲线的方程为y 2-x 2b2=1(b >0),代入M (±4,4)得b 2=1615,b =415,所以双曲线的渐近线方程为y =±1415x , 即为y =±154x . 19.(本小题满分12分)已知函数f (x )=12ax 2+2x -ln x .(1)当a =0时,求f (x )的极值;(2)若f (x )在区间⎣⎢⎡⎦⎥⎤13,2上是增函数,求实数a 的取值范围. 解:(1)由题意知函数f (x )的定义域为(0,+∞). 当a =0时,f (x )=2x -ln x ,则f ′(x )=2-1x,令f ′(x )=0,得x =12.当x 变化时,f ′(x ),f (x )的变化情况如下表:所以当x =12时,f (x )取极小值1+ln 2,f (x )无极大值.(2)已知f (x )=12ax 2+2x -ln x ,且x >0,所以f ′(x )=ax +2-1x =ax 2+2x -1x.若a =0,由f ′(x )>0,x >0得x >12,显然不合题意.若a ≠0,因为f (x )在区间⎣⎢⎡⎦⎥⎤13,2上是增函数, 所以f ′(x )≥0对任意的x ∈⎣⎢⎡⎦⎥⎤13,2恒成立,即不等式ax 2+2x -1≥0对任意的x ∈⎣⎢⎡⎦⎥⎤13,2恒成立,即a ≥1-2x x 2=1x 2-2x =⎝ ⎛⎭⎪⎫1x -12-1在⎣⎢⎡⎦⎥⎤13,2上恒成立,故a ≥⎣⎢⎡⎦⎥⎤⎝ ⎛⎭⎪⎫1x -12-1max,x ∈⎣⎢⎡⎦⎥⎤13,2.而当x =13时,⎝ ⎛⎭⎪⎫1x -12-1取得最大值3,所以实数a 的取值范围为a ≥3.20.(本小题满分12分)已知椭圆C :x 2+2y 2=4. (1)求椭圆C 的离心率;(2)设O 为原点,若点A 在直线y =2上,点B 在椭圆C 上,且OA ⊥OB ,求线段AB 长度的最小值.解:(1)由题意,得椭圆C 的标准方程为x 24+y 22=1,所以a 2=4,b 2=2,从而c 2=a 2-b 2=2. 因此a =2,c = 2. 故椭圆C 的离心率e =c a =22. (2)设点A ,B 的坐标分别为(t ,2),(x 0,y 0),其中x 0≠0. 因为OA ⊥OB ,所以OA →·OB →=0, 即tx 0+2y 0=0,解得t =-2y 0x 0.又x 20+2y 20=4,所以|AB |2=(x 0-t )2+(y 0-2)2=⎝⎛⎭⎪⎫x 0+2y 0x 02+(y 0-2)2=x 20+y 20+4y 20x 20+4=x 2+4-x 202+2(4-x 20)x 20+4=x 202+8x 20+4(0<x 20≤4). 因为x 202+8x 20≥4(0<x 20≤4),当且仅当x 20=4时等号成立,所以|AB |2≥8.故线段AB 长度的最小值为2 2.21.(本小题满分12分)已知椭圆E :x 2a 2+y 2b 2=1(a >b >0)过点(0,1),且离心率为32.(1)求椭圆E 的标准方程;(2)设直线l :y =12x +m 与椭圆E 交于A ,C 两点,以AC 为对角线作正方形ABCD ,记直线l 与x 轴的交点为N ,求证|BN |为定值.解:(1)由题意,可知椭圆的焦点在x 轴上,且b =1,由椭圆的离心率e =ca=1-b 2a 2=32,得a =2, 所以椭圆E 的标准方程为x 24+y 2=1. (2)证明:设A (x 1,y 1),C (x 2,y 2),线段AC 的中点为M , 由⎩⎪⎨⎪⎧y =12x +m x 24+y 2=1,整理得x 2+2mx +2m 2-2=0,由Δ=(2m )2-4(2m 2-2)=8-4m 2>0, 解得-2<m <2,则x 1+x 2=-2m ,x 1x 2=2m 2-2,y 1+y 2=12(x 1+x 2)+2m =m ,则M ⎝⎛⎭⎪⎫-m ,12m . |AC |=1+k 2·|x 1-x 2|=1+k 2·(x 1+x 2)2-4x 1x 2=1+⎝ ⎛⎭⎪⎫122·4m 2-4×(2m 2-2)=10-5m 2. 由l 与x 轴的交点N (-2m ,0),得|MN |=(-m +2m )2+⎝ ⎛⎭⎪⎫12m 2=54m 2. 所以|BN |2=|BM |2+|MN |2=14|AC |2+|MN |2=52.所以|BN |为定值.22.(本小题满分12分)已知函数f (x )=a ln x +1x(a >0).(1)求函数f (x )的单调区间和极值;(2)已知对任意的x >0,ax (2-ln x )≤1恒成立,求实数a 的取值范围.解:由题意知函数的定义域为{x |x >0},f ′(x )=a x -1x2(a >0).(1)由f ′(x )>0解得x >1a,所以函数f (x )的单调递增区间是⎝ ⎛⎭⎪⎫1a,+∞;由f ′(x )<0解得x <1a,所以函数f (x )的单调递减区间是⎝⎛⎭⎪⎫0,1a .所以当x =1a时,函数f (x )有极小值f ⎝ ⎛⎭⎪⎫1a =a ln 1a+a =a -a ln a ,无极大值.(2)设g (x )=ax (2-ln x )=2ax -ax ln x , 则函数g (x )的定义域为(0,+∞).g ′(x )=2a -⎝ ⎛⎭⎪⎫ax ·1x +a ln x =a -a ln x .由g ′(x )=0,解得x =e.由a >0可知,当x ∈(0,e)时,g ′(x )>0,函数g (x )单调递增; 当x ∈(e ,+∞)时,g ′(x )<0,函数g (x )单调递减. 所以函数g (x )的最大值即g (x )的极大值g (e)=a e.要使不等式ax (2-ln x )≤1恒成立,只需[g (x )]max ≤1,即a e ≤1, 解得a ≤1e.又a >0,所以0<a ≤1e.故实数a 的取值范围为⎝ ⎛⎦⎥⎤0,1e .。
2019-2020学年高中人教版数学a版高一必修1(45分钟课时作业与单元测试卷):模块综合检测_word版含解析

模块综合检测时间:120分钟 分值:150分一、选择题:本大题共12题,每题5分,共60分.在下列各题的四个选项中,只有一个选项是符合题目要求的.1.已知集合A ={x |0<log 4x <1},B ={x |x ≤2},则A ∩B 等于( ) A .(0,1) B .(0,2] C .(1,2) D .(1,2] 答案:D解析:A ={x |0<log 4x <1}={x |1<x <4},B ={x |x ≤2} 所以A ∩B ={x |1<x ≤2}2.如果幂函数f (x )=x α的图象经过点(3,33),则f (8)的值等于( )A.22B.24C.34 D.32 答案:B解析:由3α=33得α=-12,故f (8)=812-=24.3.函数y =lg x +1x -1的定义域是( )A .(-1,+∞)B .[-1,+∞)C .(-1,1)∪(1,+∞)D .[-1,1)∪(1,+∞) 答案:C解析:要使函数有意义,需⎩⎪⎨⎪⎧x +1>0x -1≠1,解得x >-1且x ≠1.∴函数定义域为(-1,1)∪(1,+∞).4.设f (x )=⎩⎪⎨⎪⎧2e x -1,x <2,log 3x 2-1,x ≥2,)则f [f (2)]的值为( )A .0B .1C .2D .3 答案:C解析:f [f (2)]=f (1)=2,故选C.5.函数y =x 2+x (-1≤x ≤3)的值域是( )A .[0,12]B .[-14,12]C .[-12,12]D .[34,12]答案:B解析:画出函数y =x 2+x (-1≤x ≤3)的图象,由图象得值域是[-14,12],故选B.6.函数f (x )=⎩⎪⎨⎪⎧x 2+2x -3,x ≤0,lg x -1,x >0的所有零点之和为( )A .7B .5C .4D .3 答案:A解析:当x ≤0时,令x 2+2x -3=0,解得x =-3;当x >0时,令lg x -1=0解得x =10,所以已知函数所有零点之和为-3+10=7.7.三个数20.3,0.32,log 0.32的大小顺序是( )A .log 0.32<20.3<0.32B .20.3<0.32<log 0.32C .log 0.32>20.3>0.32D .20.3>0.32>log 0.32 答案:D解析:∵20.3>20=1,0<0.32<1,log 0.32<log 0.32<log 0.31=0,∴20.3>0.32>log 0.32.8.函数f (x )=lg(21-x+a )是奇函数,则实数a 等于( )A .-3B .-1C .1D .-1或1 答案:B解析:(法一)f (-x )=lg(21+x+a )=-f (x ),∴f (-x )+f (x )=0,即lg[(21+x +a )(21-x+a )]=0,∴a =-1.(法二)由f (0)=0得a =-1.9.某种生物的繁殖数量y (只)与时间x (年)之间的关系式为y =a log 2(x +1),设这种生物第一年有100只,则第7年它们发展到( )A .300只B .400只C .500只D .600只 答案:A解析:由题意得100=a log 2(1+1),∴a =100,∴第7年时,y =100log 2(7+1)=300.10.函数f (x )=x (x 2-1)的大致图象是( )答案:A解析:∵f (-x )=(-x )[(-x )2-1]=-x (x 2-1)=-f (x )∴y =x (x 2-1)为奇函数,排除C 、D.又0<x <1时,y <0.故选A. 11.已知f (x )是R 上的偶函数,且满足f (x +4)=f (x ),当x ∈(0,2)时,f (x )=x +1,则f (3)等于( ) A .2 B .-2 C .1 D .-1 答案:A解析:由条件知f (3)=f (-1+4)=f (-1).又因为f (-1)=f (1),当x ∈(0,2)时,f (x )=x +1,所以f (1)=2.所以f (3)=f (-1)=f (1)=2.12.函数f (x )=⎩⎪⎨⎪⎧a x x <1,a -3x +4a x ≥1满足对任意x 1≠x 2,都有f x 1-f x 2x 1-x 2<0成立,则a 的取值范围是( )A .(0,34)B .(0,34]C .(0,1)D .[3,+∞) 答案:B解析:由题意知f (x )在R 上是减函数,∴0<a <1,又a -3+4a ≤a,4a ≤3,a ≤34,∴0<a ≤34.二、填空题:本大题共4小题,每小题5分,共20分.把答案填在题中横线上.13.已知函数f (x )对任意x ,y ∈R ,都有f (x +y )=f (x )+f (y ),且f (2)=4,则f (-1)等于________. 答案:-2解析:由题意得f (0)=f (0)+f (0) ∴f (0)=0.又f (x -x )=f (x )+f (-x )=0 ∴f (x )为奇函数. f (2)=f (1)+f (1)=4∴f (1)=2,则f (-1)=-2.14.若函数f (x )=log a (x +1)(a >0,且a ≠1)的定义域和值域都是[0,1],则a 的值是________. 答案:2解析:∵0≤x ≤1,∴1≤x +1≤2,又函数f (x )值域[0,1],∴a >1,∴f (1)=log a (1+1)=1,∴a =2.15.对于任意实数a 、b ,定义min{a ,b }=⎩⎪⎨⎪⎧a ,a ≤bb ,a >b .设函数f (x )=-x +3,g (x )=log 2x ,则函数h (x )=min{f (x ),g (x )}的最大值是________.答案:1解析:依题意,h (x )=⎩⎪⎨⎪⎧log 2x 0<x ≤2-x +3x >2,结合图象,易知h (x )的最大值为1.16.已知y =f (x )+x 是偶函数,且f (2)=lg32+log 416+6lg 12+lg 15,若g (x )=f (x )+1,则g (-2)=________.答案:6解析:f (2)=lg32+log 416+6lg 12+lg 15=5lg2+2-6lg2-lg5=2-(lg2+lg5)=2-1=1,因为y =f (x )+x 是偶函数,所以f (-x )-x =f (x )+x ,所以f (-x )=f (x )+2x , 所以g (-2)=f (-2)+1=f (2)+2×2+1=6.三、解答题:本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤. 17.(10分)求下列各式的值:(1)1.513-×⎝ ⎛⎭⎪⎫-760+80.25×42+(32× 3)6-;(2)2log 32-log 3329+log 38-552log 3.解:(1)原式=⎝ ⎛⎭⎪⎫2313×1+(23)14×214+(213)6×(312)6-[⎝ ⎛⎭⎪⎫2323]12=⎝ ⎛⎭⎪⎫2313+(23×2) 14+22×33-⎝ ⎛⎭⎪⎫2313 =2+4×27=110.(2)原式=2log 32-(log 325-log 332)+log 323-5log 59 =2log 32-5log 32+2log 33+3log 32-9 =2-9=-7.18.(12分)已知集合A ={x |x 2+ax -6=0},B ={x |x 2+bx +c =0},且A ≠B ,A ∪B ={-2,3},A ∩B ={-2},求a ,b ,c 的值.解:∵A ∩B ={-2},∴-2∈A 且-2∈B ,将-2代入方程:x 2+ax -6=0中,得a =-1,从而A ={-2,3}.将-2代入方程x 2+bx +c =0,得2b -c =4. ∵A ∪B ={-2,3},∴A ∪B =A ,∴B ⊆A . ∵A ≠B ,∴B ={-2}.∴方程 x 2+bx +c =0的判别式Δ=b 2-4c =0,∴⎩⎪⎨⎪⎧2b -c =4, ①b 2-4c =0, ②由①得c =2b -4,代入②整理得:(b -4)2=0, ∴b =4,c =4.19.(12分)函数y =lg(3-4x +x 2)的定义域为M ,x ∈M 时,求f (x )=2x +2-3×4x的最大值.解:要使函数y =lg(3-4x +x 2)有意义,需3-4x +x 2>0,解得x <1或x >3.设t =2x,则0<t <2或t >8,f (x )=g (t )=4t -3t 2(0<t <2或t >8).而g (t )=4t -3t 2=-3(t -23)2+43,所以当0<t <2,t =23时,g (t )取最大值43.当t >8时,g (t )是减函数,所以g (t )<g (8)=-160.总之,t =23时,g (t )最大为43,即f (x )=2x +2-3×4x的最大值为43.20.(12分)某商店将进货价每个10元的商品按每个18元售出时,每天可卖出60个.商店经理到市场上做了一番调查后发现,若将这种商品的售价(在每个18元的基础上)每提高1元,则日销售量就减少5个;若将这种商品的售价(在每个18元的基础上)每降低1元,则日销售就增加10个.为了每日获得最大利润,此商品的售价应定为每个多少元?解:设此商品每个售价为x 元时,每日利润为y 元.当18≤x <30时,有y =[60-5(x -18)](x -10)=-5(x -20)2+500. 即在商品提价时,当x =20时,每日利润y 最大,最大利润是500元.当10<x <18时,有y =[60+10(18-x )](x -10)=-10(x -17)2+490, 即在商品降价时,当x =17时,每日利润y 最大,最大利润是490元. 因为500>490,所以此商品的售价应定为每个20元.21.(12分)已知函数f (x )=a log 2x -b log 13x ,其中常数a ,b 满足ab ≠0.(1)若a >0,b >0,证明函数f (x )在定义域内为增函数;(2)若a =ln(m 2+2m +3),b =ln10,解不等式f (3x -1)≤f (x +3).解:f (x )=a log 2x -b log 13x =a log 2x +b log 3x ,其定义域为(0,+∞).(1)任取x 1,x 2∈(0,+∞),x 1<x 2,则f (x 1)-f (x 2)=a log 2x 1+b log 3x 1-(a log 2x 2+b log 3x 2)=a (log 2x 1-log 2x 2)+b (log 3x 1-log 3x 2). ∵0<x 1<x 2且y =log 2x 和y =log 3x 在(0,+∞)上为增函数,。
2019秋高中数学 模块综合评价(一)(含解析)新人教A版必修1.doc

模块综合评价(一)(时间:120分钟 满分:150分)一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.若a >b ,则下列正确的是( ) A .a 2> b 2B .ac > bcC .ac 2> bc 2D .a -c > b -c解析:A 选项不正确,因为若a =0,b =-1,则不成立;B 选项不正确,c ≤0时不成立;C 选项不正确,c =0时不成立;D 选项正确,因为不等式的两边加上或者减去同一个数,不等号的方向不变.答案:D2.在△ABC 中,A =60°,a =43,b =42,则B 等于( ) A .45°或135° B .135° C .45°D .30°解析:因为A =60°,a =43,b =42, 由正弦定理a sin A =bsin B,得sin B =b sin Aa=42×3243=22. 因为a >b ,所以A >B , 所以B =45°. 答案:C3.数列1,-3,5,-7,9,…的一个通项公式为( ) A .a n =2n -1 B .a n =(-1)n +1(2n -1)C .a n =(-1)n(2n -1) D .a n =(-1)n(2n +1)解析:将a 1=1,a 2=-3,a 3=5,a 4=-7,a 5=9代入各选项中的通项公式验证,可知B 选项正确.答案:B4.若集合M ={x |x 2>4},N =⎩⎨⎧⎭⎬⎫x ⎪⎪⎪3-x x +1>0,则M ∩N =( ) A .{x |x <-2}B .{x |2<x <3}C .{x |x <-2或x >3}D .{x |x >3}解析:由x 2>4,得x <-2或x >2, 所以M ={x |x 2>4}={x |x <-2或x >2}. 又3-xx +1>0,得-1<x <3, 所以N ={x |-1<x <3};所以M ∩N ={x |x <-2或x >2}∩{x |-1<x <3}={x |2<x <3}. 答案:B5.下列各函数中,最小值为2的是( ) A .y =x +1xB .y =sin x +1sin x ,x ∈⎝⎛⎭⎪⎫0,π2C .y =x 2+3x 2+2D .y =x -2x +3解析:A 中,当x <0时,y <0,不合题意;B 中,y =sin x +1sin x ≥2,等号成立时,sinx =1sin x ,即sin x =1,与x ∈⎝ ⎛⎭⎪⎫0,π2矛盾;C 中,y =x 2+3x 2+2=x 2+2+1x 2+2≥2,等号成立时,x 2+2=1x 2+2,得x 2=-1,不合题意;D 中,y =(x -1)2+2≥2.答案:D6.在△ABC 中,角A ,B ,C 所对的边分别是a ,b ,c ,若a cos B =b cos A ,则△ABC 是( )A .等腰三角形B .直角三角形C .等腰直角三角形D .等腰或直角三角形解析:因为a sin A =bsin B =2R ,即a =2R sin A ,b =2R sin B ,所以a cos B =b cos A 变形得:sin A cos B =sin B cos A , 整理得:sin A cos B -cos A sin B =sin(A -B )=0. 又A 和B 都为三角形的内角, 所以A -B =0,即A =B ,则△ABC 为等腰三角形. 答案:A7.若实数x ,y 满足⎩⎪⎨⎪⎧x ≤2,y ≤3,x +y ≥1,则S =2x +y -1的最大值为( )A .6B .4C .3D .2解析:作出不等式组对应的平面区域(如图阴影部分),由图可知,当目标函数过图中点(2,3)时取得最大值6.答案:A8.公差不为零的等差数列{a n }的前n 项和为S n ,若a 4是a 3与a 7的等比中项,S 8=32,则S 10等于( )A .18B .24C .60D .90解析:因为a 4是a 3与a 7的等比中项,所以a 24=a 3a 7, 即(a 1+3d )2=(a 1+2d )(a 1+6d ),整理得2a 1+3d =0.① 又因为S 8=8a 1+562d =32,整理得2a 1+7d =8.②由①②联立,解得d =2,a 1=-3, 所以S 10=10a 1+902d =60.答案:C9.在坐标平面内,不等式组⎩⎪⎨⎪⎧y ≥x -1,y ≤-3|x |+1所表示的平面区域的面积为( )A. 2B.32C.322D .2解析:该不等式组所表示的平面区域是如图所示的阴影部分,可求得A (0,1),B (0,-1),C ⎝ ⎛⎭⎪⎫12,-12,D (-1,-2),所以S △ACD =S △ABD +S △ABC =12·|AB |·|x D |+12|AB |·|x C |=32.答案:B10.已知数列{a n }满足:a 1=2,a n +1=3a n +2,则{a n }的通项公式为( ) A .a n =2n -1 B .a n =3n-1 C .a n =22n -1D .a n =6n -4解析:a n +1=3a n +2⇒a n +1+1=3(a n +1)⇒a n +1+1a n +1=3. 所以数列{a n +1}是以首项为a 1+1=3,公比为3的等比数列.所以a n +1=3×3n -1=3n,所以a n =3n-1.答案:B11.一轮船从A 点沿北偏东70°的方向行驶10海里至海岛B ,又从B 沿北偏东10°的方向行驶10海里至海岛C ,若此轮船从A 点直接沿直线行驶至海岛C ,则此船沿________方向行驶________海里至海岛C .( )A .北偏东50°;10 2B .北偏东40°;10 3C .北偏东30°;10 3D .北偏东20°;10 2解析:由已知得在△ABC 中,∠ABC =180°-70°+10°=120°,AB =BC =10,故∠BAC =30°,所以从A 到C 的航向为北偏东70°-30°=40°,由余弦定理得AC 2=AB 2+BC 2-2AB ·BC cos ∠ABC =102+102-2×10×10×⎝ ⎛⎭⎪⎫-12=300,所以AC =10 3.答案:B12.在△ABC 中,内角A ,B ,C 所对的边分别是a ,b ,c ,若a =4,A =π3,则该三角形面积的最大值是( )A .2 2B .3 3C .4 3D .4 2解析:a 2=b 2+c 2-2bc cos A ≥2bc -bc =bc ,即bc ≤16,当且仅当b =c =4时取等号, 所以S △ABC =12bc sin A ≤12×16×sin π3=8×32=4 3.答案:C二、填空题(本大题共4小题,每小题5分,共20分.把答案填在题中横线上) 13.若△ABC 的内角A 满足sin 2A =23,则sin A +cos A =________.解析:由sin 2A =2sin A cos A >0,可知A 是锐角,所以sin A +cos A >0,又(sin A +cos A )2=1+sin 2A =53,所以sin A +cos A =153. 答案:15314.已知a <b ∈R ,且ab =50,则|a +2b |的最小值为________.解析:因为ab =50>0,所以a 、b 同号,从而|a +2b |=|a |+2|b |≥2|a |·|2b |=22·|ab |=20,其中“=”成立的条件是⎩⎪⎨⎪⎧a =10,b =5.或⎩⎪⎨⎪⎧a =-10,b =-5. 又因为a <b ∈R ,所以a =-10,b =-5. 所以|a +2b |的最小值为20. 答案:2015.不等式组⎩⎪⎨⎪⎧y ≤-x +2,y ≤x -1,y ≥0所表示的平面区域的面积为________.解析:作出不等式组对应的区域为△BCD ,由题意知x B =1,x C =2.由⎩⎪⎨⎪⎧y =-x +2,y =x -1,得y D=12, 所以S △BCD =12×(x C -x B )×12=14.答案:1416.对于使-x 2+2x ≤M 成立的所有常数M 中,我们把M 的最小值1叫做-x 2+2x 的上确界,则函数y =2-3x -4x(x >0)的上确界为________.解析:因为x >0,所以3x +4x≥23x ·4x =43(当且仅当⎩⎪⎨⎪⎧3x =4x ,x >0,即x =233时取等号).所以y =2-3x -4x=2-⎝ ⎛⎭⎪⎫3x +4x ≤2-43,当且仅当x =233时取等号.故y 的上确界为2-4 3.答案:2-4 3三、解答题(本大题共6小题,共70分.解答应写出必要的文字说明、证明过程或演算步骤)17.(本小题满分10分)已知实数a >0,解关于x 的不等式a (x -1)x -3>1.解:原不等式可转化为[(a -1)x -(a -3)](x -3)>0. 因为a -3a -1-3=a -3-3a +3a -1=-2aa -1,且a >0, 所以当0<a <1时,a -1<0,-2a a -1>0,即a -3a -1-3>0, 所以原不等式的解集为⎩⎨⎧⎭⎬⎫x ⎪⎪⎪3<x <a -3a -1. 当a =1时,原不等式的解集为{x |x >3}.当a >1时,a -1>0,-2a a -1<0,即a -3a -1-3<0,原不等式的解集为⎩⎨⎧⎭⎬⎫x ⎪⎪⎪x >3或x <a -3a -1. 18.(本小题满分12分)已知数列{a n }是公差为2的等差数列,它的前n 项和为S n ,且a 1+1,a 3+1,a 7+1成等比数列.(1)求{a n }的通项公式;(2)求数列⎩⎨⎧⎭⎬⎫1S n 的前n 项和T n .解:(1)由题意,得a 3+1=a 1+5,a 7+1=a 1+13,所以由(a 3+1)2=(a 1+1)·(a 7+1)得(a 1+5)2=(a 1+1)·(a 1+13), 解得a 1=3,所以a n =3+2(n -1), 即a n =2n +1.(2)由(1)知a n =2n +1,则S n =n (n +2),1S n =12⎝ ⎛⎭⎪⎫1n -1n +2,T n =12⎝ ⎛⎭⎪⎫1-13+12-14+13-15+…+1n -1n +2=12⎝ ⎛⎭⎪⎫1+12-1n +1-1n +2=34-2n +32(n +1)(n +2). 19.(本小题满分12分)小王在年初用50万元购买一辆大货车,第一年因缴纳各种费用需支出6万元,从第二年起,每年都比上一年增加支出2万元,假定该车每年的运输收入均为25万元.小王在该车运输累计收入超过总支出后,考虑将大货车作为二手车出售,若该车在第x 年年底出售,其销售价格为25-x 万元(国家规定大货车的报废年限为10年).(1)大货车运输到第几年年底,该车运输累计收入超过总支出?(2)在第几年年底将大货车出售,能使小王获得的年平均利润最大(利润=累计收入+销售收入-总支出)?解:(1)设大货车到第x 年年底的运输累计收入与总支出的差为y 万元, 则y =25x -⎣⎢⎡⎦⎥⎤6x +x (x -1)2·2-50,(0<x ≤10,x ∈N),即y =-x 2+20x -50,(0<x ≤10,x ∈N),由-x 2+20x -50>0,解得10-52<x <10+52, 而2<10-52<3,故从第3年开始运输累计收入超过总支出. (2)因为利润=累计收入+销售收入-总支出. 所以销售二手货车后,小王的年平均利润为y -=1x [y +(25-x )]=1x (-x 2+19x -25)=19-⎝⎛⎭⎪⎫x +25x ,而19-⎝⎛⎭⎪⎫x +25x ≤19-2x ·25x=9,当且仅当x =5时取得等号.即小王应当在第5年年底将大货车出售,才能使年平均利润最大.20.(本小题满分12分)在△ABC 中,内角A ,B ,C 所对的边分别为a ,b ,c ,且满足(2a -c )cos B =b cos C .(1)求内角B 的大小;(2)设m =(sin A ,cos 2A ),n =(4k ,1)(k >1),m·n 的最大值为5,求k 的值. 解:(1)由正弦定理及(2a -c )cos B =b cos C ,得 (2sin A -sin C )cos B =sin B cos C ,整理得2sin A cos B =sin B cos C +sin C cos B =sin(B +C )=sin A , 因为A ∈(0,π),所以sin A ≠0,故cos B =12,所以B =π3.(2)m·n =4k sin A +cos 2A =-2sin 2A +4k sin A +1,其中A ∈⎝⎛⎭⎪⎫0,2π3,设sin A =t ,t ∈(0,1], 则m·n =-2t 2+4kt +1=-2(t -k )2+1+2k 2. 由于k >1,故当t =1时,m·n 取得最大值. 由题意得-2+4k +1=5,解得k =32.21.(本小题满分12分)已知x ,f (x )2,3(x ≥0)成等差数列.又数列{a n }(a n >0)中,a 1=3 ,此数列的前n 项的和S n (n ∈N *)对所有大于1的正整数n 都有S n =f (S n -1).(1)求数列{a n }的第n +1项; (2)若b n 是1a n +1,1a n的等比中项,且T n 为{b n }的前n 项和,求T n .解:因为x ,f (x )2,3(x ≥0)成等差数列,所以f (x )2×2=x + 3.所以f (x )=(x +3)2. 因为S n =f (S n -1)(n ≥2), 所以S n =f (S n -1)=(S n -1+3)2. 所以S n =S n -1+3,S n -S n -1= 3. 所以{S n }是以3为公差的等差数列. 因为a 1=3,所以S 1=a 1=3.所以S n =S 1+(n -1)3=3+3n -3=3n . 所以S n =3n 2(n ∈N *).所以a n +1=S n +1-S n =3(n +1)2-3n 2=6n +3. (2)因为数列b n 是1a n +1,1a n的等比中项,所以(b n )2=1a n +1·1a n,所以b n =1a n +1a n=13(2n +1)·3(2n -1)=118(12n -1-12n +1).所以T n =b 1+b 2+…+b n =118[⎝ ⎛⎭⎪⎫1-13+⎝ ⎛⎭⎪⎫13-15+…+⎝ ⎛⎭⎪⎫12n -1-12n +1]=118⎝ ⎛⎭⎪⎫1-12n +1=n9(2n +1).22.(本小题满分12分)在△ABC 中,角A ,B ,C 所对的边分别为a ,b ,c ,且a 2-(b-c )2=(2-3)bc ,sin A sin B =cos 2C2.(1)求角B 的大小;(2)若等差数列{a n }的公差不为零,且a 1cos 2B =1,a 2,a 4,a 8是等比数列,求数列⎩⎨⎧⎭⎬⎫4a n a n +1的前n 项和S n .解:(1)由a 2-(b -c )2=(2-3)bc ,得a 2-b 2-c 2=-3bc ,所以cos A =b 2+c 2-a 22bc =32.因为0<A <π,所以A =π6.所以由sin A sin B =cos 2C2,得12sin B =1+cos C 2, 所以sin B =1+cos C ,所以cos C <0,则C ∈⎝ ⎛⎭⎪⎫π2,π.又因为B +C =π-A =56π,所以sin ⎝ ⎛⎭⎪⎫56π-C =1+cos C , 所以cos ⎝⎛⎭⎪⎫C +π3=-1.解得C =23π.故B =π-A -C =π6.(2)设数列{a n }的公差为d .由已知得a 1=1cos 2B =2.因为a 2,a 4,a 8是等比数列,所以a 24=a 2·a 8, 所以(a 1+3d )2=(a 1+d )(a 1+7d ), 整理,得d (d -2)=0.又因为d ≠0,所以d =2,所以a n =2n , 所以4a n a n +1=1n (n +1)=1n -1n +1,所以S n =⎝ ⎛⎭⎪⎫1-12+⎝ ⎛⎭⎪⎫12-13+⎝ ⎛⎭⎪⎫13-14+…+⎝ ⎛⎭⎪⎫1n -1n +1=1-1n +1=n n +1.。
2019-2020年高中数学模块综合评价(一)新人教版必修

2019-2020年高中数学模块综合评价(一)新人教版必修一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项符合题目要求)1.已知集合M ={x |0<x <3},N ={x |1<x <4},则M ∩N =( ) A .{x |1<x <3} B .{x |0<x <4} C .{x |3<x <4}D .{x |0<x <1}解析:M ∩N ={x |0<x <3}∩{x |1<x <4}= {x |1<x <3}. 答案:A2.设集合A ={x |1<x <2},B ={x |x <a }.若A ⊆B ,则a 的范围是( ) A .a ≥1 B .a ≤1 C .a ≥2D .a ≤2解析:在数轴上作出两个集合所在的区间,可知满足A ⊆B 的a ≥2. 答案:C3.已知幂函数f (x )=x a的图象过点(4,2),若f (m )=3,则实数m 的值为( ) A. 3 B .± 3 C .±9 D .9 解析:依题意有2=4a,得a =12,所以f (x )=x 12,当f (m )=m 12=3时,m =9. 答案:D4.设a =log 123,b =⎝ ⎛⎭⎪⎫130.2,c =213,则( ) A .a <b <c B .c <b <a C .c <a <bD .b <a <c解析:数形结合,画出三个函数的图象. 由图象可知a <0,0<b <1,c >1,因此a <b <c . 答案:A5.已知A ∩{-1,0,1}={0,1},且A ∪{-2,0,2}={-2,0,1,2},则满足上述条件的集合A 共有( )A .2个B .4个C .6个D .8个 解析:因为A ∩{-1,0,1}={0,1}, 所以0,1∈A 且-1∉A .又因为A∪{-2,0,2}={-2,0,1,2},所以1∈A且至多-2,0,2∈A.故0,1∈A 且至多-2,2∈A,所以满足条件的A只能为{0,1},{0,1,-2},{0,1,2},{0,1,2,-2},共有4个.答案:B6.已知集合A={x|y=x+1},B={y|y=x2+1},则A∩B=( )A.∅B.[-1,1]C.[-1,+∞) D.[1,+∞)解析:A={x|y=x+1}={x|x≥-1},B={y|y=x2+1}={y|y≥1}.所以A∩B=[1,+∞).答案:D7.设f(x)是R上的偶函数,且在(0,+∞)上是减函数,若x1<0,x1+x2>0,则( ) A.f(-x1)>f(-x2)B.f(-x1)=f(-x2)C.f(-x1)<f(-x2)D.f(-x1)与f(-x2)大小不确定解析:由x1<0,x1+x2>0得x2>-x1>0,又f(x)是R上的偶函数,且在(0,+∞)上是减函数,所以f(-x2)=f(x2)<f(-x1).答案:A8.已知函数f(x)的单调递增区间是(-2,3),则y=f(x+5)的单调递增区间是( ) A.(3,8) B.(-7,-2)C.(-2,3) D.(0,5)解析:因为f(x)的单调递增区间是(-2,3),则f(x+5)的单调递增区间满足-2<x+5<3,即-7<x<-2.答案:B9.若x∈[0,1],则函数y=x+2-1-x的值域是( )A.[2-1,3-1] B.[1,3]C.[2-1,3] D.[0,2-1]解析:该函数为增函数.自变量最小时,函数值最小;自变量最大时,函数值最大.故y min=2-1,y max= 3.答案:C10.设二次函数f(x)=x2-x+a(a>0).若f(m)<0,则f(m-1)的值为( )A .正数B .负数C .非负数D .正数、负数和零都有可能解析:二次函数f (x )=x 2-x +a (a >0)的对称轴是x =12,且f (0)=f (1)=a >0.因为f (m )<0,所以m -1<0,所以f (m -1)>0. 答案:A11.已知函数在f (x )=⎩⎪⎨⎪⎧x 2-ax +5,x <1,1+1x,x ≥1在R 上单调,则实数a 的取值范围为( )A .(-∞,2]B .[2,+∞)C .[4,+∞)D .[2,4]解析:当x ≥1时,f (x )=1+1x为减函数,所以f (x )在R 上应为单调递减函数,要求当x <1时,f (x )=x 2-ax +5为减函数,所以a2≥1,即a ≥2,并且满足当x =1时,f (x )=1+1x的函数值不大于x =1时,f (x )=x 2-ax+5的函数值,即1-a +5≥2,解得a ≤4,所以实数a 的取值范围[2,4]. 答案:D12.设方程3-x =|lg x |的两个根分别为x 1,x 2,则( ) A .x 1x 2<0 B .x 1x 2=1 C .x 1x 2>1D .0<x 1x 2<1解析:由题意知,当x >1时,3-x 1=lg x 1,当0<x <1时,3-x 2=-lg x 2且3-x 1<3-x 2.故3-x 1-3+x 2=lg x 1+lg x 2=lg(x 1x 2)<0,所以0<x 1x 2<1.答案:D二、填空题(本大题共4小题,每小题5分,共20分.把答案填在题中横线上) 13.已知定义在R 上的奇函数f (x ),当x >0时,f (x )=12x +1,则当x <0时,f (x )=________.解析:设x <0,则-x >0,所以f (-x )=12-x +1,所以f (-x )=-12-x +1=-2x1+2x .答案:-2x1+2x14.已知函数f (x )=b -2x2x +1为定义是区间[-2a ,3a -1]上的奇函数,则a +b =________.解析:因为函数f (x )=b -2x2x+1为定义是区间[-2a ,3a -1]上的奇函数,所以-2a +3a-1=0,所以a =1.又f (0)=b -2020+1=b -12=0,所以b =1.故a +b =2.答案:215.若函数f (x )=|4x -x 2|-a 的零点个数为3,则a =________.解析:作出g (x )=|4x -x 2|的图象(图略),g (x )的零点为0和4.由图象可知,将g (x )的图象向下平移4个单位时,满足题意,所以a =4.答案:416.给定集合A ,若对于任意a ,b ∈A ,有a +b ∈A ,且a -b ∈A ,则称集合A 为闭集合,给出如下四个结论:①集合A ={0}为闭集合;②集合A ={-4,-2,0,2,4}为闭集合; ③集合A ={n |n =3k ,k ∈Z}为闭集合; ④若集合A 1、A 2为闭集合,则A 1∪A 2为闭集合. 其中所有正确结论的序号是________.解析:对于①集合A ={0},满足条件,所以A ={0}是闭集;对于集合②A ={-4,-2,0,2,4},应为4-(-4)=8∉A ,所以A ={-4,-2,0,2,4}不是闭集;对于③A ={n |n =3k ,k ∈Z},集合中的元素是3的倍数,因为任何两个3的倍数的和与差都是3的倍数,所以A ={n |n =3k ,k ∈Z}是闭集;对于④,若集合A 1、A 2为闭集合,则A 1∪A 2不一定为闭集合.如A 1={n |n =2k ,k ∈Z}是闭集,A 2={n |n =3k ,k ∈Z}为闭集合,但A 1∪A 2不是闭集,应为2+3∈(A 1∪A 2).所以正确结论为①③.答案:①③三、解答题(本大题共6小题,共70分.解答应写出文字说明,证明过程或演算步骤) 17.(本小题满分10分)已知函数f (x )=2x -1x,其定义域为{x |x ≠0}.(1)用单调性的定义证明函数f (x )在区间(0,+∞)上为增函数;(2)利用(1)所得到的结论,求函数f (x )在区间[1,2]上的最大值与最小值. (1)证明:设x 1,x 2∈(0,+∞),且x 1<x 2,则x 2-x 1>0,f (x 2)-f (x 1)=2x 2-1x 2-2x 1-1x 1=x 2-x 1x 1x 2.因为x 1<x 2,所以x 2-x 1>0, 又因为x 1,x 2∈(0,+∞), 所以x 2x 1>0,f (x 2)-f (x 1)>0.故f (x )=2x -1x在区间(0,+∞)上为增函数.(2)解:因为f (x )=2x -1x在区间(0,+∞)上为增函数,所以f (x )min =f (1)=2-11=1,f (x )max =f (2)=2×2-12=32. 18.(本小题满分12分)已知x 1,x 2是方程x 2-2(m -1)x +m +1=0的两个不等实根,且y =x 21+x 22,求y =f (m )的表达式及值域.解:由Δ=4(m -1)2-4(m +1)>0, 解得m >3或m <0.由韦达定理可得x 2+x 1=2(m -1),x 2x 1=m +1.故y =x 21+x 22=(x 1+x 2)2-2x 1x 2=4(m -1)2-2(m +1)=4m 2-10m +2(m >3或m <0).因为f (m )=4m 2-10m +2=4⎝ ⎛⎭⎪⎫m -542-174,所以f (m )的值域为(2,+∞).19.(本小题满分12分)已知函数f (x )=x m-4x,且f (4)=3.(1)求m 的值;(2)证明f (x )的奇偶性;(3)若不等式f (x )-a >0在区间[1,+∞)上恒成立,求实数a 的取值范围. (1)解:因为f (4)=3,所以4m-43=3,所以m =1.(2)证明:由(1)知f (x )=x -4x,其定义域为{x |x ≠0},关于原点对称.又f (-x )=-x -4-x =-⎝ ⎛⎭⎪⎫x -4x =-f (x ),所以f (x )是奇函数. (3)解:因为y =x ,y =-1x在区间[1,+∞)上都是增函数,所以f (x )在区间[1,+∞)上为增函数,所以f (x )≥f (1)=-3.因为不等式f (x )-a >0在区间[1,+∞)上恒成立,即不等式a <f (x )在区间[1,+∞)上恒成立,所以a <-3,故实数a 的取值范围是(-∞,-3).20.(本小题满分12分)求函数f (x )=x 2+2x +a -1在区间⎝ ⎛⎦⎥⎤-∞,12上的零点.解:Δ=4-4(a -1)=8-4a . 当Δ<0,即a >2时,f (x )无零点. 当Δ=0,即a =2时,f (x )有一个零点-1.当Δ>0且f ⎝ ⎛⎭⎪⎫12<0, 即⎩⎪⎨⎪⎧8-4a >0,14+1+a -1<0,a <-14时,f (x )仅有一个零点:-1-2-a .当Δ>0且f ⎝ ⎛⎭⎪⎫12≥0, 即⎩⎪⎨⎪⎧8-4a >0,14+1+a -1≥0⇒-14≤a <2时,f (x )有两个零点:x =-2±8-4a2=-1±2-a .综上所述,当a >2时,f (x )无零点; 当a =2时,f (x )有一个零点-1;当-14≤a <2时,f (x )有两个零点:-1±2-a ;当a <-14时,f (x )有一个零点:-1-2-a .21.(本小题满分12分)“活水围网”养鱼技术具有养殖密度高、经济效益好的特点.研究表明:“活水围网”养鱼时,某种鱼在一定的条件下,每尾鱼的平均生长速度v (单位:千克/年)是养殖密度x (单位:尾/立方米)的函数.当x 不超过4(尾/立方米)时,v 的值为2(千克/年);当4≤x ≤20时,v 是x 的一次函数;当x 达到20(尾/立方米)时,因缺氧等原因,v 的值为0(千克/年).(1)当0<x ≤20时,求函数v (x )的表达式;(2)当养殖密度x 为多大时,鱼的年生长量(单位:千克/立方米)f (x )=x ·v (x )可以达到最大,并求出最大值.解:(1)由题意:当0<x ≤4时,v (x )=2 当4<x ≤20时,设v (x )=ax +b , 显然该函数在[4,20]是减函数, 由已知得⎩⎪⎨⎪⎧20a +b =0,4a +b =2,解得⎩⎪⎨⎪⎧a =-18,b =52.故函数v (x )=⎩⎪⎨⎪⎧2,0<x ≤4,x ∈N *,-18x +52,4≤x ≤20,x ∈N *.(2)依题意并由(1)可得f (x )=⎩⎪⎨⎪⎧2x ,0<x ≤4,x ∈N *,-18x 2+52x ,4≤x ≤20,x ∈N *. 当0≤x ≤4时,f (x )为增函数, 故f max (x )=f (4)=4×2=8;当4≤x ≤20时,f (x )=-18x 2+52x =-18(x 2-20x )=-18(x -10)2+10028,f max (x )=f (10)=12.5.所以,当0<x ≤20时,f (x )的最大值为12.5.当养殖密度为10尾/立方米时,鱼的年生长量可以达到最大,最大值约为12.5千克/立方米.22.(本小题满分12分)已知奇函数f (x )=m -g (x )1+g (x )的定义域为R ,其中g (x )为指数函数,且过定点(2,9).(1)求函数f (x )的解析式;(2)若对任意的t ∈[0,5],不等式f (t 2+2t +k )+f (-2t 2+2t -5)>0恒成立,求实数k 的取值范围.解:(1)设g (x )=a x(a >0,且a ≠1)),则a 2=9, 所以a =-3 (舍去)或a =3, 所以g (x )=3x,f (x )=m -3x1+3x .又f (x )为奇函数,且定义域为R , 所以f (0)=0,即m -301+30=0,所以m =1,所以f (x )=1-3x 1+3x .(2)设x 1<x 2,则f (x 1)-f (x 2)=1-3x 11+3x 1-1-3x 21+3x 2=2(3x 2-3x 1)(1+3x 1)(1+3x 2).因为x 1<x 2,所以3x 2-3x 1>0, 所以2(3x 2-3x 1)(1+3x 1)(1+3x 2)>0,所以f (x 1)-f (x 2)>0,即f (x 1)>f (x 2), 所以函数f (x )在R 上单调递减. 要使对任意的t ∈[0,5],f (t 2+2t +k )+f (-2t 2+2t -5)>0恒成立,即对任意的t ∈[0,5],f (t 2+2t +k )>-f (-2t 2+2t -5)恒成立.因为f (x )为奇函数,所以f (t 2+2t +k )>f (2t 2-2t +5)恒成立. 又因为函数f (x )在R 上单调递减,所以对任意的t ∈[0,5],t 2+2t +k <2t 2-2t +5恒成立, 即对任意的t ∈[0,5],k <t 2-4t +5=(t -2)2+1恒成立. 而当t ∈[0,5]时,1≤(t -2)2+1≤10,所以k <1.2019-2020年高中数学模块综合评价(二)新人教版必修一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项符合题目要求)1.已知集合A ={2,3,4,5},B ={3,5,6},全集U ={1,2,3,4,5,6},则A ∩(∁U B )=( )A .{1,3}B .{2,4}C .{1,6}D .{3,5} 解析:因为∁U B ={1,2,4},所以A ∩(∁U B )={2,4}. 答案:B2.集合⎩⎪⎨⎪⎧(x ,y )⎪⎪⎪⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x +y =52x -y =1=( ) A .{2,3} B .{x =2,y =3} C .{(2,3)}D .(2,3)解析:本题中的元素是点,故答案是{(2,3)}. 答案:C3.设函数f (x )=⎩⎪⎨⎪⎧|x -1|-2,|x |≤1,11+x 2,|x |>1,则f ⎝ ⎛⎭⎪⎫f ⎝ ⎛⎭⎪⎫12等于( )A.12B.2541 C .-95 D.413解析:f ⎝ ⎛⎭⎪⎫f ⎝ ⎛⎭⎪⎫12=f ⎝ ⎛⎭⎪⎫-32=413.答案:D4.函数f (x )=|log 0.5x |-12x 的零点个数为( )A .1B .2C .3D .4解析:在同一坐标系中作出函数y =|log 0.5x |与y =12x 的图象,可知这两个图象有两个交点,所以函数f (x )=|log 0.5x |-12x 有两个零点.答案:B5.函数y =log 12(4x -x 2)的值域是( )A .[-2,+∞)B .RC .[0,+∞)D .(0,4]解析:令t =4x -x 2,画出t =4x -x 2(t >0)的图象如图所示, 则0<t ≤4,所以y =log 12t ∈[-2,+∞).答案:A6.已知f (x )为定义在R 上的奇函数,在区间(-∞,0)内有1 005个零点,则函数f (x )在R 上的零点个数为( )A .2 009B .2 010C .2 011D .2 012解析:定义在R 上的奇函数f (x )满足f (0)=0,图象自身关于原点对称,所以零点的个数为2×1 005+1=2 011.答案:C7.已知集合A ={x |x -2≤0,x ∈N},B ={x |x ≤2,x ∈Z},则满足条件A ⊆C ⊆B 的集合C 的个数为( )A .5B .4C .3D .2解析:A ={x |x -2≤0,x ∈N}={0,1,2},B ={x |x ≤2,x ∈Z}={0,1,2,3,4},若A ⊆C ⊆B ,则集合C 可以是{0,1,2},{0,1,2,3},{0,1,2,4},{0,1,2,3,4},共4个.答案:B8.已知函数f (x +1)是偶函数,当x ∈(-∞,1]时,函数f (x )单调递减,设a =f ⎝ ⎛⎭⎪⎫-12,b =f (-1),c =f (2),则a ,b ,c 的大小关系为( )A .c <a <bB .a <b <cC .a <c <bD .c <b <a解析:因为函数f (x +1)是偶函数,所以函数f (x )图象的对称轴为x =1,所以c =f (2)=f (0),因为f (x )在(-∞,1)上单调递减,所以f (-1)>f ⎝ ⎛⎭⎪⎫-12>f (0),即b >a >c . 答案:A9.已知奇函数f (x )在区间[-b ,-a ]上单调递减,且f (x )>0.若0<a <b ,则|f (x )|在区间[a ,b ]上( )A .单调递减B .单调递增C .先增后减D .先减后增解析:利用奇函数的对称性可知,函数f (x )在区间[a ,b ]上单调递减,且f (x )<0,则|f (x )|在区间[a ,b ]上单调递增.答案:B10.若函数f (x )=log a (x +b )(其中a ,b 为常数)的图象如图所示,则函数g (x )=a x+b 的大致图象是( )A BC D解析:根据题中的图象可知,0<a <1,0<b <1.根据指数函数的性质可知,选项D 符合题意.答案:D11.设函数y =x 3与y =⎝ ⎛⎭⎪⎫12x -2的图象的交点为(x 0,y 0),则x 0所在的区间是( )A .(3,4)B .(2,3)C .(1,2)D .(0,1)解析:函数y =x 3与y =⎝ ⎛⎭⎪⎫12x -2的图象的交点的横坐标x 0即函数f (x )=x 3-⎝ ⎛⎭⎪⎫12x -2的零点.当x =1,f (x )=x 3-⎝ ⎛⎭⎪⎫12x -2<0;当x =2时,f (x )=x 3-⎝ ⎛⎭⎪⎫12x -2>0,即f (1)f (2)<0,又因为f (x )=x 3-⎝ ⎛⎭⎪⎫12x -2为连续函数,故函数f (x )=x 3-⎝ ⎛⎭⎪⎫12x -2的零点一定在区间(1,2)内.答案:C12.已知x 1,x 2是二次方程f (x )=0的两个不同实根,x 3,x 4是二次方程g (x )=0的两个不同实根.若g (x 1)g (x 2)<0,则( )A .x 1,x 2介于x 3和x 4之间B .x 3,x 4介于x 1和x 2之间C .x 1与x 2相邻,x 3与x 4相邻D .x 1,x 2与x 3,x 4相间排列解析:画图可知x 3,x 4中有一个在x 1,x 2之间,故x 1,x 2与x 3,x 4相间排列. 答案:D二、填空题(本大题共4小题,每小题5分,共20分.把答案填在题中横线上)13.设f (x )=⎩⎪⎨⎪⎧2-x,x ∈(-∞,1],log 81x ,x ∈(1,+∞),则满足f (x )=14的x 值为________.解析:令2-x =14,则2-x =2-2,所以x =2,不满足x ∈(-∞,1];令log 81x =14,则x =8114=3,满足x ∈(1,+∞).综上知,x =3.答案:314.若a =⎝ ⎛⎭⎪⎫1223,b =⎝ ⎛⎭⎪⎫1523,c =⎝ ⎛⎭⎪⎫1213,则a ,b ,c 的大小关系是________(请用“<”号连接).解析:因为函数f (x )=x 23在区间(0,+∞)上单调递增,所以⎝ ⎛⎭⎪⎫1223>⎝ ⎛⎭⎪⎫1523.又f (x )=⎝ ⎛⎭⎪⎫12x 在定义域是减函数,所以⎝ ⎛⎭⎪⎫1223<⎝ ⎛⎭⎪⎫1213.故b <a <c .答案:b <a <c15.设集合A ={-1,3,2m -1},B ={3,m 2}.若A ∩B =B ,则实数m 的值为________. 解析:因为A ∩B =B ,所以B ⊆A ,所以m 2=2m -1,解得m =1. 答案:116.下列命题中:①若集合A ={x |kx 2+4x +4=0}中只有一个元素,则k =1;②已知函数y =f (3x)的定义域为[-1,1],则函数y =f (x )的定义域为(-∞,0]; ③函数y =11-x在(-∞,0)上是增函数; ④方程2|x |=log 2(x +2)+1的实根的个数是2.所有正确命题的序号是________(请将所有正确命题的序号都填上)解析:对于①,k =0也符合题意;对于②,y =f (x )的定义域应该是[3-1,3];对于③,画出y =11-x 的图象,或利用定义可判定y =11-x 在(-∞,0)上是增函数;对于④在同一坐标系中做出y =2|x |,y =log 2(x +2)+1的图象,由图可知有两个交点.故方程的实根的个数为2.答案:③④三、解答题(本大题共6小题,共70分.解答应写出文字说明,证明过程或演算步骤) 17.(本小题满分10分)已知全集U =R ,集合A ={x |-7≤2x -1≤7},B ={x |m -1≤x ≤3m -2}.(1)当m =3时,求A ∩B 与A ∪(∁U B ); (2)若A ∩B =B ,求实数m 的取值范围. 解:易得A ={x |-3≤x ≤4}. (1)当m =3时,B ={x |2≤x ≤7}, ∁U B ={x |x <2或x >7}.故A ∩B =[2,4],A ∪(∁U B )=(-∞,4]∪(7,+∞). (2)因为A ∩B =B ,所以B ⊆A . 当B =∅时,m -1>3m -2,所以m <12;当B ≠∅,即m ≥12时,m -1≥-3,且3m -2≤4,所以-2≤m ≤2,所以12≤m ≤2.综上所述,m ≤2.18.(本小题满分12分)已知函数f (x )是定义在R 上的偶函数,当x ≥0时,f (x )=2x-x 2.(1)求函数f (x )的解析式,并画出函数f (x )的图象; (2)根据图象写出单调区间和值域.解:(1)设x <0,则-x >0,因为函数f (x )是定义在R 上的偶函数, 所以f (x )=f (-x )=2(-x )-(-x )2=-x 2-2x ,所以f (x )=⎩⎪⎨⎪⎧2x -x 2,x ≥0,-x 2-2x ,x <0.图象如图所示:(2)由图可知,函数的单调递增区间为:(-∞,-1)和(0,1);单调递减区间为:(-1,0)和(1,+∞).值域为(-∞,1].19.(本小题满分12分)已知二次函数f (x )的图象过点(0,3),它的图象的对称轴为x =2,且f (x )的两个零点的平方和为10,求f (x )的解析式.解:设f (x )=ax 2+bx +c (a ≠0), 由题意知,c =3,-b2a=2.设x 1,x 2是方程ax 2+bx +c =0的两根, 则x 1+x 2=-b a ,x 1x 2=c a.因为x 21+x 22=10,所以(x 1+x 2)2-2x 1x 2=10,即⎝ ⎛⎭⎪⎫-b a 2-2c a =10,所以(-4)2-6a =10, 所以a =1,b =-4. 所以f (x )=x 2-4x +3.20.(本小题满分12分)某商场在促销期间规定:商场内所有商品按标价的80%出售,同时,当顾客在该商场内消费满一定金额后,按如下方案获得相应金额的奖券:商品,消费金额为320元,可获得的优惠额为(400-320)+30=110(元).设购买商品得到的优惠率=购买商品获得的优惠额/商品的标价.(1)若购买一件标价为1 000元的商品,顾客得到的优惠额是多少元?(2)对于标价在[500,800]元内的商品,顾客购买标价为多少元的商品,可以得到不小于13的优惠率? 解:(1)顾客得到的优惠额为1 000×(1-0.8)+130=330(元). (2)设商品的标价为x 元,则500≤x ≤800,消费额400≤0.8x ≤640. 当消费额在[400,500)元内时,优惠率为0.2x +60x,所以⎩⎪⎨⎪⎧400≤0.8x <500,0.2x +60x ≥13.该不等式组无解.当消费额在[500,640]元内时,优惠率为0.2x +100x,所以⎩⎪⎨⎪⎧500≤0.8x ≤640,0.2x +100x ≥13,解得625≤x ≤750.故当顾客购买标价在[625,750]元内的商品时,可以得到不小于13的优惠率.21.(本小题满分12分)已知函数f (x )=log 9(9-x+1)+kx (k ∈R)是偶函数. (1)求k 的值;(2)若函数y =f (x )的图象与直线y =12x +b 没有交点,求b 的取值范围.解:(1)因为f (x )为偶函数, 所以对任意x ∈R,f (x )=f (-x ),即log 9(9x +1)-kx =log 9(9x+1)+kx 对于任意的x ∈R 恒成立,故2kx =log 9(9-x+1)-log 9(9x+1)=log 99x+19x -log 9(9x+1)=-x 恒成立.又x 不恒为零,所以k =-12.(2)由题意知,方程log 9(9x +1)-12x =12x +b 无解,即方程log 9(9x+1)-x =b 无解.令g (x )=log 9(9x+1)-x ,则函数y =g (x )的图象与直线y =b 无交点.易知g (x )=log 99x+19x =log 9⎝ ⎛⎭⎪⎫1+19, 任取x 1,x 2∈R ,且x 1<x 2, 则0<9x 1<9x 2,从而19x 1>19x 2,于是log 9⎝ ⎛⎭⎪⎫1+19x 1>log 9⎝ ⎛⎭⎪⎫1+19x 2, 即g (x 1)>g (x 2),故g (x )在R 上是减函数. 因为1+19x >1,所以g (x )=log 9⎝ ⎛⎭⎪⎫1+19x >0. 故b 的取值范围是(-∞,0].22.(本小题满分12分)已知函数f (x )=1-42a x +a (a >0,a ≠1)且f (0)=0.(1)求a 的值;(2)若函数g (x )=(2x+1)·f (x )+k 有零点,求实数k 的取值范围; (3)当x ∈(0,1)时,f (x )>m ·2x-2恒成立,求实数m 的取值范围. 解:(1)由f (0)=0得1-42a 0+a =0,即a +2=4,解得a =2.(2)函数g (x )=(2x +1)·f (x )+k 有零点⇔方程2x-1+k =0有解, 即k =1-2x有解,因为1-2x∈(-∞,1),所以k ∈(-∞,1). (3)由f (x )>m 2x -2得m (2x )2+(m -3)2x-1<0, 令t =2x,因为x ∈(0,1),所以t ∈(1,2),即f (x )>m 2x -2⇔mt 2+(m -3)t -1<0对于t ∈(1,2)恒成立. 设g (t )=mt 2+(m -3)t -1, ①当m <0时,m -3<0,所以g (t )=mt 2+(m -3)t -1<0在(1,2)上恒成立. 此时m <0符合题意.②当m =0时,g (t )=-3t -1<0在(1,2)上恒成立,所以m =0符合题意. ③当m >0时,只需⎩⎪⎨⎪⎧g (1)≤0,g (2)≤0,⇒⎩⎪⎨⎪⎧m +(m -3)-1≤0,4m +2(m -3)-1≤0,⇒m ≤76,此时0<m ≤76.综上知:m 的取值范围是⎝ ⎛⎦⎥⎤-∞,76.。
2019_2020学年高中数学学期综合测评新人教A版必修1

学期综合测评本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.满分150分,考试时间120分钟.第Ⅰ卷(选择题,共60分)一、选择题(本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的)1.已知全集U ={0,1,2,3,4},集合A ={1,2,3},B ={2,4},则(∁U A )∪B 为( ) A .{1,2,4} B .{4} C .{0,2,4} D .{0,2,3,4}答案 C解析 (∁U A )∪B ={0,4}∪{2,4}={0,2,4}.2.函数f (x )=x 2x -1+lg (10-x )的定义域为( )A .RB .[1,10]C .(-∞,-1)∪(1,10)D .(1,10)答案 D解析 由题意得⎩⎪⎨⎪⎧x -1>0,10-x >0,解得1<x <10.3.已知f (x )=x 2-ax 在[0,1]上是单调函数,则实数a 的取值范围是( ) A .(-∞,0] B .[1,+∞)C .[2,+∞)D .(-∞,0]∪[2,+∞)答案 D解析 函数图象的对称轴为直线x =a 2,根据二次函数的性质可知a 2≤0或a2≥1,解得a ≤0或a ≥2.4.已知函数f (2x)的定义域为[-1,1],则函数f (log 2x )的定义域为( ) A .[-1,1] B.⎣⎢⎡⎦⎥⎤12,2C .[2,2]D .[2,4]答案 D解析 ∵x ∈[-1,1],∴2x∈[2-1,2],即2x∈⎣⎢⎡⎦⎥⎤12,2.要使函数f (log 2x )有意义,须使12≤log 2x ≤2,即2≤x ≤4,故选D.5.下列函数是偶函数且值域为[0,+∞)的是( )①y=|x|;②y=x3;③y=2|x|;④y=x2+|x|.A.①②B.②③C.①④D.③④答案 C解析①y=|x|是偶函数且值域为[0,+∞);②y=x3是奇函数;③y=2|x|是偶函数但值域为[1,+∞);④y=x2+|x|是偶函数且值域为[0,+∞).故符合题意的有①④.故选C.6.函数f(x)=ln x+3x-11在以下哪个区间内一定有零点( )A.(0,1) B.(1,2)C.(2,3) D.(3,4)答案 D解析因为f(x)的图象是一条连续不断的曲线,且f(3)=ln 3+3×3-11=ln 3-2<0,f(4)=ln 4+3×4-11=ln 4+1>0,所以f(3)·f(4)<0,故f(x)在区间(3,4)内一定有零点,选D.7.设f(x)是R上的偶函数,且在(0,+∞)上是减函数,若x1<0,x1+x2>0,则( ) A.f(-x1)>f(-x2)B.f(-x1)=f(-x2)C.f(-x1)<f(-x2)D.f(-x1)与f(-x2)大小不确定答案 A解析因为f(x)是R上的偶函数,且在(0,+∞)上是减函数,所以f(x)在(-∞,0)上是增函数,因为x1<0,x1+x2>0,所以有-x2<x1<0,所以f(x1)>f(-x2),由偶函数的性质可得f(x1)=f(-x1),所以有f(-x1)>f(-x2),故选A.8.已知函数f(x)=(x-a)(x-b)(其中a>b)的图象如图所示,则函数g(x)=a x+b的图象是( )答案 A解析 由二次函数的图象可知:0<a <1,b <-1,所以函数g (x )=a x+b 的图象如选项A 所示.9.下列函数f (x )与g (x )是相同函数的是( ) A .f (x )=x -2;g (x )=x -1B .f (x )=x 2-1x -1;g (x )=x +1C .f (x )=lg (x +1)+lg (x -1);g (x )=lg (x 2-1) D .f (x )=e x +1·ex -1;g (x )=e 2x答案 D解析 对于A ,f (x )=x -2=|x -1|,g (x )=x -1,解析式不同;对于B ,f (x )=x 2-1x -1,x ≠1,g (x )=x +1,x ∈R ,定义域不同;对于C ,f (x )=lg (x +1)+lg (x -1),x >1,g (x )=lg (x 2-1),x >1或x <-1,定义域不同;对于D ,f (x )和g (x )的定义域均为R ,且解析式相同,故选D.10.方程log 2x +log 2(x -1)=1的解集为M ,方程22x +1-9·2x+4=0的解集为N ,那么M 与N 的关系是( )A .M =NB .M NC .N MD .M ∩N =∅答案 B解析 log 2x +log 2(x -1)=1⇒log 2[x (x -1)]=log 22⇒x (x -1)=2,解得x =2或x =-1.又x >1,所以 x =2,即M ={2}.22x +1-9·2x +4=0⇒2·(2x )2-9·2x +4=0,解得2x。
高一数学人教A版必修1模块综合测评 Word版含解析
模块综合测评(时间分钟,满分分)一、选择题(本大题共小题,每小题分,共分.在每小题给出的四个选项中,只有一项是符合题目要求的).已知全集={},集合={},={},则(∁)∪=( ).{} .{}.{} .{}【解析】∵全集={},集合={},∴∁={},又={},则(∁)∪={}.故选.【答案】.可作为函数=()的图象的是( )【导学号:】【解析】由函数的定义可知:每当给出的一个值,则()有唯一确定的实数值与之对应,只有符合.【答案】.同时满足以下三个条件的函数是( )①图象过点();②在区间(,+∞)上单调递减;③是偶函数..()=-(+)+.()=.()=.()=-【解析】.若()=-(+)+,则函数关于=-对称,不是偶函数,不满足条件③..若()=,在区间(,+∞)上单调递增,不满足条件②..若()=,则三个条件都满足..若()=-,则()无意义,不满足条件①.故选.【答案】.与函数=有相同图象的一个函数是( ).=-.=.=-.=【解析】要使函数解析式有意义,则≤,即函数=的定义域为(-∞,],故===-,又因为函数=-的定义域也为(-∞,],故函数=与函数=-表示同一个函数,则他们有相同的图象,故选.【答案】.函数()=-+的零点所在区间是( ).()【解析】∵函数()=-+,∴=-,()=,∴()<,故连续函数()的零点所在区间是,故选.【答案】.幂函数=()的图象经过点,则满足()=的的值是( )【导学号:】.-..-【解析】设幂函数为=α,因为图象过点,所以有-=(-)α,解得α=-,所以幂函数解析式为=-,由()=,得-=,所以=.【答案】.函数()=+ (+)的定义域为( )。
2019-2020学年新教材高中数学 模块质量检测(含解析)新人教A版必修第一册

模块质量检测一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.已知集合A ={x|x<3},B ={x|2x>4},则A∩B=( )A .∅B .{x|0<x<3}C .{x|1<x<3}D .{x|2<x<3}解析:依据函数y =2x是增函数,可得B ={x|2x>4}={x|x>2},则A∩B={x|2<x<3}. 答案:D2.对于实数x ,y ,若p :x +y≠4,q :x≠3或y≠1,则p 是q 的( )A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件解析:考虑该命题的逆否命题.綈q :x =3且y =1,綈p :x +y =4,显然綈q ⇒綈p ,但綈p⇒綈q ,所以綈q 是綈p 的充分不必要条件,则p 是q 的充分不必要条件.答案:A3.函数y =1-x22x 2-3x -2的定义域为( )A .(-∞,1]B .[-1,1]C .[1,2)∪(2,+∞)D .⎣⎢⎡⎭⎪⎫-1,-12∪⎝ ⎛⎦⎥⎤-12,1解析:由函数y =1-x22x 2-3x -2得⎩⎪⎨⎪⎧1-x 2≥0,2x 2-3x -2≠0,解得⎩⎪⎨⎪⎧-1≤x≤1,x≠2且x≠-12,即-1≤x≤1且x≠-12,所以所求函数的定义域为⎣⎢⎡⎭⎪⎫-1,-12∪⎝ ⎛⎦⎥⎤-12,1. 答案:D4.已知0<a<b ,且a +b =1,则下列不等式中正确的是( )A .log 2a>0B .2a -b <12C .log 2a +log 2b<-2D .2+a b b a ⎛⎫ ⎪⎝⎭<12解析:特殊值法,令a =13,b =23代入检验只有C 正确,故选C .答案:C5.关于x 的不等式ax -b<0的解集是(1,+∞),则关于x 的不等式(ax +b)(x -3)>0的解集是( )A .(-∞,-1)∪(3,+∞)B .(1,3)C .(-1,3)D .(-∞,1)∪(3,+∞)解析:关于x 的不等式ax -b<0的解集是(1,+∞),即不等式ax<b 的解集是(1,+∞),∴a=b<0,∴不等式(ax +b)·(x-3)>0可化为(x +1)(x -3)<0,解得-1<x<3,∴所求解集为(-1,3).答案:C6.已知sin α-cos α=2,α∈(0,π),则sin 2α=( )A .-1B .-22C .22D .1 解析:∵(sin α-cos α)2=2, ∴2sin αcos α=-1,即sin 2α=-1. 答案:A7.设函数f(x)=⎩⎪⎨⎪⎧21-x, x≤1,1-log 2x ,x>1,则满足f(x)≤2的x 的取值范围是( )A .[-1,2]B .[0,2]C .[1,+∞)D .[0,+∞)解析:原不等式可化为⎩⎪⎨⎪⎧x≤121-x≤2或⎩⎪⎨⎪⎧x>11-log 2x≤2,解得0≤x≤1或x>1,即x≥0, 所以x 的取值范围是[0,+∞)故选D . 答案:D8.若sin (α+β)=12,sin (α-β)=13,则tan (π-α)tan (-β)=( )A .5B .-1C .6D .16解析:sin (α+β)=sin αcos β+cos αsin β=12,sin (α-β)=sin αcos β-cos αsin β=13,两式作和得sin αcos β=512, 两式作差得cos αsin β=112, 则tan (π-α)tan (-β)=-tan α-tan β=sin αcos βcos αsin β=512112=5.故选A . 答案:A9.已知函数f(x)的图象向左平移1个单位后关于y 轴对称,当x 2>x 1>1时,[f(x 2)-f(x 1)]·(x 2-x 1)<0恒成立,设a =f ⎝ ⎛⎭⎪⎫-12,b =f(2),c =f(3),则a ,b ,c 的大小关系为( )A .c>a>bB .c>b>aC .a>c>bD .b>a>c解析:根据已知可得函数f(x)的图象关于直线x =1对称,且在(1,+∞)上是减函数,因为a =f ⎝ ⎛⎭⎪⎫-12=f(52),且2<52<3,所以b>a>c. 答案:D10.(23cos 20°-tan 70°)cos 10°=( )A .12 B .32C .1D . 3解析:(23cos 20°-tan 70°)cos 10°=⎝⎛⎭⎪⎫23cos 20°-sin 70°cos 70°cos 10°=23cos 20°cos 70°-sin 70°cos 70°·cos 10°=23cos 20°sin 20°-sin 70°cos 70°·cos 10°=3sin 40°-sin (30°+40°)cos 70°·cos 10°=3sin 40°-12cos 40°-32sin 40°cos 70°·cos 10°=32sin 40°-12cos 40°cos 70°·cos 10°=sin 10°cos 70°×cos 10°=12×sin 20°sin 20°=12.答案:A11.函数f(x)=12ln x +x -1x-2的零点所在的区间是( )A .⎝ ⎛⎭⎪⎫1e ,1 B .(1,2)C .(2,e )D .(e,3)解析:因为f ⎝ ⎛⎭⎪⎫1e =-12+1e -e -2<0,f(1)=-2<0,f(2)=12ln 2-12<0,f(e )=12+e -1e-2>0,所以f(2)f(e )<0,所以函数f(x)=12ln x +x -1x -2的零点所在区间是(2,e ).答案:C12.f(x)是定义在(0,+∞)上的单调增函数,满足f(xy)=f(x)+f(y),f(3)=1,当f(x)+f(x -8)≤2时,x 的取值范围是( )A .(8,+∞)B .(8,9]C .[8,9]D .(0,8)解析:∵f(9)=f(3)+f(3)=2, ∴不等式f(x)+f(x -8)≤2可化为 f(x(x -8))≤f(9), ∵⎩⎪⎨⎪⎧x (x -8)≤9x>0x -8>0,解得8<x≤9,∴x 的取值范围是(8,9],故选B . 答案:B二、填空题(本大题共4小题,每小题5分,共20分.请把正确答案填在题中横线上) 13.命题∃x∈R ,x 2-2x >0的否定是________.解析:存在量词命题的否定是全称量词命题,即∀x ∈R ,x 2-2x ≤0. 答案:∀x ∈R ,x 2-2x ≤014.如图所示的是2018年福建省某市某天中6时至14时的温度变化曲线,其近似满足函数y =A sin(ωx +φ)+b ⎝ ⎛⎭⎪⎫其中π2<φ<π的半个周期的图象,与图中曲线对应的函数的解析式是________.解析:从6~14时的图象是函数y =A sin(ωx +φ)+b 的半个周期的图象,∴振幅A =12×(30-10)=10,b =12×(30+10)=20,∵周期T =2×(14-6)=16,∴2πω=16,∴ω=π8,∴y =10sin ⎝ ⎛⎭⎪⎫π8x +φ+20.将x =6,y =10代入上式,得10sin ⎝ ⎛⎭⎪⎫π8×6+φ+20=10,即sin ⎝⎛⎭⎪⎫3π4+φ=-1,由于π2<φ<π,可得φ=3π4.综上,所求解析式为y =10sin ⎝ ⎛⎭⎪⎫π8x +3π4+20,x ∈[6,14].答案:y =10sin ⎝⎛⎭⎪⎫π8x +3π4+20,x ∈[6,14]15.若对任意x >0,xx 2+3x +1≤a 恒成立,则a 的取值范围是________.解析:因为对任意x >0,xx 2+3x +1≤a 恒成立,所以对x ∈(0,+∞),a ≥⎝ ⎛⎭⎪⎫x x 2+3x +1max,而对x ∈(0,+∞),x x 2+3x +1=1x +1x+3≤12x ·1x+3=15, 当且仅当x =1x 时等号成立,∴a ≥15.答案:⎣⎢⎡⎭⎪⎫15,+∞ 16.已知a >0,函数f (x )=⎩⎪⎨⎪⎧x 2+2ax +a ,x ≤0,-x 2+2ax -2a ,x >0.若关于x 的方程f (x )=ax 恰有2个互异的实数解,则a 的取值范围是________.解析:设函数g (x )=f (x )-ax ,则g (x )=⎩⎪⎨⎪⎧x 2+ax +a ,x ≤0,-x 2+ax -2a ,x >0,即g (x )=⎩⎪⎨⎪⎧⎝ ⎛⎭⎪⎫x +a 22+a -a 24,x ≤0,-⎝ ⎛⎭⎪⎫x -a 22+a24-2a ,x >0.依题意得,函数g (x )恰有两个零点,即函数g (x )与x 轴有两个交点.又因为a >0,所以⎩⎪⎨⎪⎧ a >0,g ⎝ ⎛⎭⎪⎫-a 2>0,g ⎝ ⎛⎭⎪⎫a 2>0,或⎩⎪⎨⎪⎧ a >0,g ⎝ ⎛⎭⎪⎫-a 2<0,g ⎝ ⎛⎭⎪⎫a 2<0,或⎩⎪⎨⎪⎧ a >0,g ⎝ ⎛⎭⎪⎫-a 2=0,g ⎝ ⎛⎭⎪⎫a 2=0,所以⎩⎪⎨⎪⎧ a >0,a -a 24>0,a 24-2a >0,或⎩⎪⎨⎪⎧ a >0,a -a 24<0,a 24-2a <0,或⎩⎪⎨⎪⎧a >0,a -a 24=0,a 24-2a =0,解得4<a <8.所以a 的取值范围为(4,8). 答案:(4,8)三、解答题(本大题共6小题,共70分.解答时应写出必要的文字说明、证明过程或演算步骤)17.(10分)已知P ={x |x 2-8x -20≤0},非空集合S ={x |1-m ≤x ≤1+m }.若x ∈P 是x ∈S 的必要条件,求m 的取值范围.解析:由x 2-8x -20≤0,得-2≤x ≤10, ∴P ={x |-2≤x ≤10},由x ∈P 是x ∈S 的必要条件,知S ⊆P . 则⎩⎪⎨⎪⎧1-m ≤1+m ,1-m ≥-2,1+m ≤10,∴0≤m ≤3.∴当0≤m ≤3时,x ∈P 是x ∈S 的必要条件,即所求m 的取值范围是[0,3]. 18.(12分)已知函数f (x )=ax 2+bx +c (a ≠0),满足f (0)=2,f (x +1)-f (x )=2x -1.(1)求函数f (x )的解析式; (2)求函数f (x )的单调区间;(3)当x ∈[-1,2]时,求函数的最大值和最小值. 解析:(1)由f (0)=2,得c =2, 又f (x +1)-f (x )=2x -1, 得2ax +a +b =2x -1,故⎩⎪⎨⎪⎧2a =2,a +b =-1,解得:a =1,b =-2.所以f (x )=x 2-2x +2.(2)f (x )=x 2-2x +2=(x -1)2+1函数,图象的对称轴为x =1,且开口向上, 所以f (x )单调递增区间为(1,+∞),单调递减区间为(-∞,1). (3)f (x )=x 2-2x +2=(x -1)2+1, 对称轴为x =1∈[-1,2], 故f min (x )=f (1)=1, 又f (-1)=5,f (2)=2, 所以f max (x )=f (-1)=5.19.(12分)函数f (x )=A sin ⎝ ⎛⎭⎪⎫ωx -π6+1(A >0,ω>0)的最大值为3,其图象相邻两条对称轴之间的距离为π2.(1)求函数f (x )的解析式和当x ∈[0,π]时f (x )的单调减区间.(2)设α∈⎝ ⎛⎭⎪⎫0,π2,则f ⎝ ⎛⎭⎪⎫α2=2,求α的值.解析:(1)因为函数f (x )的最大值是3, 所以A +1=3,即A =2.因为函数图象的相邻两条对称轴之间的距离为π2,所以最小正周期T =π,所以ω=2. 所以f (x )=2sin ⎝⎛⎭⎪⎫2x -π6+1. 令π2+2k π≤2x -π6≤3π2+2k π,k ∈Z , 即π3+k π≤x ≤5π6+k π,k ∈Z , 因为x ∈[0,π],所以f (x )的单调减区间为⎣⎢⎡⎦⎥⎤π3,5π6.(2)因为f ⎝ ⎛⎭⎪⎫α2=2sin ⎝⎛⎭⎪⎫α-π6+1=2,即sin ⎝⎛⎭⎪⎫α-π6=12, 因为0<α<π2,所以-π6<α-π6<π3,所以α-π6=π6,所以α=π3.20.(12分)设定义在[-2,2]上的奇函数f (x )在区间[0,2]上单调递减,若f (m )+f (m -1)>0,求实数m 的取值范围.解析:由f (m )+f (m -1)>0,得f (m )>-f (m -1),即f (1-m )<f (m ).又因为f (x )在[0,2]上单调递减且f (x )在[-2,2]上为奇函数,所以f (x )在[-2,2]上为减函数.所以1-m >m ,又-2≤m -1≤2,-2≤m ≤2, 所以解得-1≤m <12.故m 的取值范围是⎣⎢⎡⎭⎪⎫-1,12. 21.(12分)提高过江大桥的车辆通行能力可改善整个城市的交通状况.在一般情况下,大桥上的车流速度v (单位:千米/小时)是车流密度x (单位:辆/千米)的函数.当桥上的车流密度达到200辆/千米时,造成堵塞,此时车流速度为0千米/小时;当车流密度不超过20辆/千米时,车流速度为60千米/小时,研究表明:当20≤x ≤200时,车流速度v 是车流密度x 的一次函数.(1)当0≤x ≤200时,求函数v (x )的表达式;(2)当车流密度x 为多大时,车流量(单位时间内通过桥上某观测点的车辆数,单位:辆/小时)f (x )=x ·v (x )可以达到最大,并求出最大值.(精确到1辆/小时)解析:(1)由题意可知当0≤x ≤20时,v (x )=60;当20≤x ≤200时,设v (x )=ax +b ,显然v (x )=ax +b 在[20,200]上是减函数,由已知得⎩⎪⎨⎪⎧200a +b =0,20a +b =60,解得⎩⎪⎨⎪⎧a =-13,b =2003,故函数v (x )的表达式为v (x )=⎩⎪⎨⎪⎧60,0≤x <20,13(200-x ),20≤x ≤200.(2)依题意并由(1)可得f (x )=⎩⎪⎨⎪⎧60x ,0≤x <20,13x (200-x ),20≤x ≤200,当0≤x ≤20时,f (x )为增函数,故当x =20时,其最大值为60×20=1 200;当20≤x ≤200时, f (x )=13x (200-x )≤13⎣⎢⎡⎦⎥⎤x +(200-x )22=10 0003,当且仅当x =200-x ,即x =100时,等号成立,所以,当x =100时,f (x )在区间[20,200]上取得最大值10 0003.综上,当x =100时,f (x )在区间[0,200]上取得最大值10 0003≈3 333, 即当车流密度为100辆/千米时,车流量可以达到最大,最大值约3 333辆/小时. 22.(12分)设函数f (x )=3sin x cos x +cos 2x +a . (1)写出函数f (x )的最小正周期及单调递减区间.(2)当x ∈⎣⎢⎡⎦⎥⎤-π6,π3时,函数f (x )的最大值与最小值的和为32,求a 的值. 解析:(1)f (x )=32sin 2x +1+cos 2x 2+a =sin ⎝⎛⎭⎪⎫2x +π6+12+a , 函数f (x )的最小正周期T =2π2=π, 令2k π+π2≤2x +π6≤2k π+3π2,k ∈Z ,所以k π+π6≤x ≤k π+2π3,k ∈Z ,所以函数f (x )的单调递减区间是⎣⎢⎡⎦⎥⎤k π+π6,k π+2π3,k ∈Z .(2)由x ∈⎣⎢⎡⎦⎥⎤-π6,π3得-π6≤2x +π6≤5π6,所以-12≤sin ⎝ ⎛⎭⎪⎫2x +π6≤1,所以当2x +π6=-π6,即x =-π6时,f (x )min =a ,当2x +π6=π2,即x =π6时,f (x )max =32+a ,由题意得32+a +a =32,解得a =0.。
2019-2020学年人教A版数学必修一作业:模块综合测评A.doc

必修一模块综合测评(A)一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.如果A={x|x>—1},那么( )A. OGAB. {0}eAC. 0EAD. {0}GA答案D解+析VOeA, .-.{0}£A.2.若集合A={y|y = 2x, x£R}, B = {y|y=x2, xWR},贝0( )A. AGBB. A BC. A=BD. AHB = 0答案A解+析VxeR, .-.y=2x>0,即A={y|y>0}.又B = {y|y=x2, x eR} = {y|y>0}, /.AC;B.3.已知f(苏一l) = 2x+3, f(m) = 6,则m 等于( )A—丄B丄A. 4-3 3C2 D- _2答案A解+析令*x—l=t,则x=2t+2,所以f(t)=2X(2t+2)+3=4t+7.令4m+7=6,得m =—£4.设2a=5b=m,且扌+*=2,则m等于( )A.V1OB. 10C. 20D. 100答案A解+析由2a=5b=m 得a=log2m, b=log5m, /. =log m2+log m5=log m 10.T*+¥=2, log m10=2, .°.m2=10, m=V10.5.设函数f(x)满足:①y=f(x+l)是偶函数;②在[1, +8)上为增函数,则f( —1)与f(2)的大小关系是()A. f(-l)>f(2)B. f(-l)<f(2)C. f(—l)=f(2)D.无法确定答案A解+析由y=f(x+l)是偶函数,得到y=f(x)的图象关于直线x=l对称;—l) = f(3).又f(x)在[1, +8)上为单调增函数,.•.f(3)>f(2),即f(-l)>f(2).6.已知a=帧,b = 203, c = 0.3°'2,则a, b, c三者的大小关系是( )A. b>c>aB. b>a>cC. a>b>cD. c>b>a答案A解+析因为a=Q5^=0.3°'v0.3°2=cv0.3°=l,而b=20,3>2°=l,所以b>c>a.7.函数f(x)=log3x-8+2x的零点一定位于区间( )A. (5, 6)B. (3, 4)C・(2, 3) D・(1, 2)答案B解+析f(3) = log33 — 8+2X3 = — lvO, f(4) = log34—8 + 2X4=log34>0.又f(x)在(0, +°°)上为增函数,所以其零点一定位于区间(3, 4).8.已知函数f(x)=a x+log a x(a>0且aHl)在[1, 2]上的最大值与最小值之和为log a2+6,贝!J a 的值为()A丄B 1A.? 口.4C. 2D. 4答案C解+析依题意,函数f(x)=a x+log a x(a>0且aHl)在[1, 2]上具有单调性,因此a+a2+log a2 =loga2+6,解得a—2.9.函数y=|lg(x+l)|的图象是()答案A解+析将y=lgx的图象向左平移一个单位,然后把x轴下方的部分关于x轴对称到上方, 就得到y=|lg(x +1)|的图象.4X—b10.若函数f(x)=lg(10x+l)+ax是偶函数,g(x)=十是奇函数,则a+b的值是() A.* B. 1C. -+D. -1答案A解+析Vf(x)是偶函数,・・・f(—x) = f(x),_ 1 + IO*即lg(10_x+ l)_ax=lg ]0X _ax=lg(l(T+ l)-(a+ l)x=lg(10x+ l)+ax, •°.a= —(a+1), .・.a=—又g(x)是奇函数, .•.g(—x)=—g(x), 即2_x—^7=—2X+^-, .'.b=l, .・.a+b=£.11.设函数f(x)定义在实数集上,f(2-x)=f(x),且当x$l时,f(x)=lnx,则有( )A. f(|)<f(2)<f(|)B. f(|)<f(2)<f(|)C. f(|)<f(|)<f(2)D. f(2)<f(|)<f(|)答案C2—x ~x解+析由f(2—x)=f(x)知f(x)的图象关于直线x= —=1对称,又当x21时,f(x)=lnx,所以离对称轴x=l距离大的X的函数值大,V |2-1|> |-1 > |-1 , .-.f(|)<f(|)<f(2).12•函数f(x)= Ji x+log2x的零点所在区间为()A. [0, |]B. [|, |]C. [|,D. [|, 1]答案C解+析在其定义域(0, +8)上是单调递增函数,而在四个选项中,只有f(|).f(|)<0, 函数f(x)的零点所在区间为百,*],故选C.二、填空题(本大题共4小题,每小题5分,共20分.把答案填在横线上)13.已知f(x5)=lgx,则f(2)= __________ .答案|lg2「丄] ]解+析令x5=t,则x=t5./.f(t)=^lgt, .°.f(2)=mg2.14.函数y=f(x)是定义域为R的奇函数,当x<0时,f(x)=x3+2x-l,贝0 x>0时函数的解+析式f(x) = ________ .答案X3-2_X+1解+析Vf(x)是R 上的奇函数,.•.当x>0 时,f(x)=—f(—x)= — [(—xf + 2-x—l] = x3—2「x+1.15.若幕函数f(x)的图象过点(3,折),则f(x)的解+析式是____________ .3答案f(x)=x Z解+析设f(x) = x n,则有3n=^/27,即3n = 34, 即f(x) = x4.16.已知关于x的函数y=loga(2—ax)在[0, 1]上是减函数,则a的取值范围是___________ •答案(1,2)解+析依题意,a>0且a^l, /.2—ax在[0, 1]上是减函数,fa>l,即当x=l时,2—ax的值最小,又V2—ax为真数,・・・| 解得l<a<2.[2-a>0,三、解答题(本大题共6小题,共70分)7 丄77 117.(10分)(1)计算:(2赏+趣5)°+(詡一亍(2)角军方程:log3(6x-9)=3.解+析⑴原式= (y)2+(lg5)°+ [(|)3]-|=|+1 +1=4.(2)由方程log3(6x-9)=3 得6X-9=33=27,:.6X=36=62,■'■x=2.经检验,x=2是原方程的解.18.(12分)已知函数f(x)=、yiog* (x—1)的定义域为集合A,函数g(x)=3m-2x-x2-l的值域为集合B,且AUB=B,求实数m的取值范围. 解+析由题意得A={x|l<xW2},B=(-l, -l+31+m].由AUB = B,得AGB,即一l+3i+m±2,即31+m^3, 所以m±0.19.(12 分)已知函数f(x)=-3x2+2x-m+l.a+1 ^+T,设X1,X2^R,则f(xi)—f(x)—a+1X2+Ia+1Xi+ 1(a+1) (xi—X2) (xi +1)⑴当a=l时,f(x) = l x+r 设0W<X2W3,(1)当m为何值时,函数有两个零点,一个零点,无零点;(2)若函数恰有一个零点在原点处,求m的值.解+析⑴函数有两个零点,则对应方程一3x?+2x—m+l= 0有两个根,易知△>(),即△ =4+12(l-m)>0,4 4 4可解得m<§; A = 0,可解得m=亍;A<0,可解得m>亍4 4 , . . 4故m<§时,函数有两个零点;m=§时,函数有一个零点;m>§时,函数无零点.(2)因为0是对应方程的根,有1— m=0,可解得m=l.20.(12分)A, B两城相距100 km,在两地之间距A城x km处的D地建一核电站给A、B 两城供电.为保证城市安全,核电站与城市的距离不得少于10km.已知供电费用与供电距离的平方和供电量之积成正比,比例系数入=0.25.设A城供电量为20亿度/月,B城为10亿度/月.⑴求x的范围;⑵把月供电总费用y表示成x的函数;(3)核电站建在距A城多远的地方,才能使供电费用最小?解+析(l)x的取值范围为[10, 90],(2)y=0.25 X 20x2+0.25 X 10(100-x)2=5X2+|(100-X)2(10^X^90).(3)y=5x2+|(100-x)2=yx2一500x+25 00015 100,, , 50 000=-(x-—)2+^-.当时,y最小.故当核电站距A城晋km时,才能使供电费用最小.21.(12分)设函数f(x)=*^,其中aeR⑴若a=l, f(x)的定义域为区间[0, 3],求f(x)的最大值和最小值;(2)若f(x)的定义域为区间(0, +8),求a的取值范围,使f(x)在定义域内是单调减函数.ax—1 a (x+1) —a—1f(x)=i+r=^+i =(xMO), (x<0) .fx<l,当迪时'有Ul-lo ga2, xMl,x<l+log a5.2 (xi—x2)则f(X1)-f(x2)=(X1 + 1)(X2+1),又xi—x2<0, xi + l>0, /.f(xi) —f(x2)<0, .•.f(xi)<f(x2)..・.f(x)在[0, 3]上是增函数,f(X)max = f(3)= 1 £=*,(2)设xi>x2>0,则xi—x2>0, xi +1>0, x2 +1>0. 若使f(X)在(0, +8)上是减函数,只要f(xj —f(X2)<0,十(a+1) (xi—X2).而f(xi)-f(X2)= a + 1)(恋+1),•■-当a+l<0,即a<—1 时,有f(xi)—f(x2)<0, .°.f(xi)<f(X2), 当a<—1时,f(x)在定义域(0,十8)内是单调减函数.22.(12分)已知f(x)是定义在R上的奇函数,当x$0时,f(x)=aX—l.其中a>0且aHl. ⑴求f(2)+f(-2)的值;(2)求f(x)的解+析式;(3)解关于x的不等式一l<f(x—1)<4,结果用集合或区间表示.解+析(l)Tf(x)是奇函数,/.f(-2)=-f(2),即f(2)+f(-2)=0.(2)当x<0 时,一x>0, .•.f(—x)=a「x—l.由f(x)是奇函数,有f(—X)=—f(x),•.* f(—x)=a %—1, f(x) =—a x+ l(x<0).[a x—1・••所求的解+析式为f(x)=| _x , 1[ — a 十l(3)不等式等价于Jx-l<0, Jx—1$0,[—1<—a_x+l + l<4:^[—l<a x_l—1<4.x—1<0, Jx—120,-3<a^x+l<2,或[0<a x_l<5.注意此时log a2>0, log a5>0,可得此时不等式的解集为(l~log a2, l+log a5).同理可得,当Ovavl时,不等式的解集为R.综上所述,当a>l时,不等式的解集为(l-log a2, l+log a5);当Ovavl时,不等式的解集为R.。
2019-2020学年高中数学人教A版必修一模块质量检测 含解析

一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.设全集为R ,集合A ={x |0<x <2},B ={x |x ≥1},则A ∩(∁R B )=( A .{x |0<x ≤1} B .{x |0<x <1} C .{x |1≤x <2} D .{x |0<x <2}解析:因为B ={x |x ≥1},所以∁R B ={x |x <1},因为A ={x |0<x <2},所以∩(∁R B )={x |0<x <1}.答案:B2.函数f (x )=x 2x -1+lg(10-x )的定义域为( )A .RB .[1,10]C .(-∞,-1)∪(1,10)D .(1,10)解析:由题意得⎩⎪⎨⎪⎧x -1>0,10-x >0,解得1<x <10.解析:因为f (-2)=4-6<0,f (-1)=2-3<0,f (0)=1>0,f (1)=5>0,10>0,所以f (x )在区间(-1,0)上存在零点. 答案:B6.若集合A ={y |y =lg x },B ={x |y =x },则集合A ∩B =( ) A .(0,+∞) B .[0,+∞) C .(1,+∞) D .∅解析:集合A ={y |y =lg x }=R ,B ={x |y =x }={x |x ≥0},所以A ∩B ,+∞).答案:B7.函数y =⎝ ⎛⎭⎪⎫1322x x-+的单调递增区间是( )A .(-∞,1)B .(0,1)C .(1,2)D .(1,+∞)解析:函数t =-x 2+2x 的单调递增区间为(1,+∞),又y = ⎛⎪⎫13t 为减函-∞,-1)∪(0,1)根据已知条件画出函数f(x)的图象如图所示.的取值范围为(-∞,--x|的图象是()|1-x|可由下列变换得到:y=log故选D.e x,x≤0,g(x)=f(x)+x+a.若ln x,x>0,).[0,+∞).[1,+∞)x)+x+a存在2个零点,即关于个不同的实根,即函数f(x)的图象与直线y=-x 与函数f(x)的图象,如图所示,由图可知,-a ≤1,解得a ≥-1,故选C. 答案:C二、填空题(本大题共4小题,每小题5分,共20分.请把正确答案填在题中横线上)13.设g (x )=⎩⎪⎨⎪⎧e x ,x ≤0,ln x ,x >0,则g ⎝ ⎛⎭⎪⎫g ⎝ ⎛⎭⎪⎫12=________.解析:∵g ⎝ ⎛⎭⎪⎫12=ln 12<0,∴g ⎝ ⎛⎭⎪⎫g ⎝ ⎛⎭⎪⎫12=e 1ln2=12.答案:12 14.设x 0是方程ln x +x =4的解,且x 0∈(k ,k +1),k ∈Z ,则k =________. 解析:令f (x )=ln x +x -4,且f (x )在(0,+∞)上递增,答案:3三、解答题(本大题共6小题,共70分.解答时应写出必要的文字说明、证明过程或演算步骤)17.(10分)已知全集为R ,集合A ={x |y =lg x +2-x },B ⎭⎬⎫14<2x -a ≤8. (1)当a =0时,求(∁R A )∩B ;(2)若A ∪B =B ,求实数a 的取值范围.解析:(1)由已知得A ={x |0<x ≤2},当a =0时,B =⎩⎨⎧⎭⎬⎫x ⎪⎪⎪14<2x ≤8 ={x |-2<x ≤3},所以∁R A ={x |x ≤0或x >2},所以(∁R A )∩B ={x |x ≤0或x >2}∩{x |-2<x ≤3}3=-14+2+2=154.19.(12分)已知函数f (x )=⎩⎪⎨⎪⎧3-x 2,x ∈[-1,2],x -3,x ∈(2,5].(1)在直角坐标系内画出f (x )的图象; (2)写出f (x )的单调递增区间.解析:(1)函数f (x )的图象如下图所示:(2)函数f (x )的单调递增区间为[-1,0]和[2,5].20.(12分)已知函数f (x )是定义在R 上的偶函数,f (0)=0,当x >0时,=log x .的解析式;解得2=1或2=-2(舍去).所以x=0,所以函数f(x)的零点为x=0.(2)若f(x)有零点,则方程2a·4x-2x-1=0有解.于是2a=2x+14x=⎝⎛⎭⎪⎫12x+⎝⎛⎭⎪⎫14x=⎣⎢⎡⎦⎥⎤⎝⎛⎭⎪⎫12x+122-14.因为⎝⎛⎭⎪⎫12x>0,所以2a>14-14=a>0.22.(12分)辽宁号航母纪念章从2012年10月5日起开始上市.通过市场调查,得到该纪念章每1枚的市场价y(单位:元)与上市时间x(单位:天的数据如下:上市时间x/天41036市场价y/元905190(1)根据上表数据结合散点图,从下列函数中选取一个恰当的函数描述辽宁号航母纪念章的市场价y与上市时间x的变化关系并说明理由:①y=2画出散点图,如图的增加,y的值先减后增,而所给的三个函数中显然都是单调函数,不满足题意,所以应选,(36,90)代入y=ax2+bx+,所以当x=20时,y有最小值y min=26.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2
8.函数
f
(x)=
lg( 1-
x+
a)是奇函数,则实数
a 等于 (
)
A .- 3 B.- 1 C. 1 D .- 1 或 1
答案: B
2 解析: (法一 )f (- x)= lg(1+x+ a)=- f(x),
-
-
2
2
∴ f(-x)+ f(x)= 0,即 lg[(1+ x+ a)(1-x+ a)]=0,
解:要使函数 y= lg(3- 4x+ x2)有意义, 需 3- 4x+ x2> 0,解得 x<1 或 x>3.设 t= 2x,则 0< t< 2 或 t> 8,
24
2
4
f (x)= g(t )=4t- 3t2(0<t < 2 或 t> 8).而 g(t)= 4t- 3t2=- 3(t- )2+ ,所以当 0< t<2,t= 时, g(t)取最大值 .
-
-
上做了一番调查后发现,若将这种商品的售价
(在每个 18 元的基础上 )每提高 1 元,则日销售量就减少 5 个;
若将这种商品的售价 (在每个 18 元的基础上 )每降低 1 元,则日销售就增加 10 个.为了每日获得最大利润,
此商品的售价应定为每个多少元? 解: 设此商品每个售价为 x 元时,每日利润为 y 元. 当 18 ≤x<30 时,有 y=[60- 5(x- 18)](x-10)=- 5(x- 20)2+ 500. 即在商品提价时,当 x= 20 时,每日利润 y 最大,最大利润是 500 元. 当 10< x<18 时,有 y= [60+ 10(18- x)](x- 10)=- 10(x-17)2+ 490,
1 解: f (x)= alog2x-blog3x= alog2x+ blog3x,其定义域为 (0,+∞ ) .
(1)任取 x1, x2∈ (0,+∞ ) ,x1< x2,则 f(x1)- f(x2)= alog2x1+ blog3x1- (alog2x2+ blog3x2)= a(log2x1- log2x2)+ b(log3x1- log3x2). ∵ 0< x1< x2 且 y= log2x 和 y= log3x 在 (0,+∞ ) 上为增函数, ∴ log2x1< log2x2,log3x1< log3x2, 当 a> 0, b> 0 时, a(log2x1- log2x2)< 0, b(log3x1- log3x2)< 0, ∴ f(x1)- f (x2)< 0,即 f (x1)<f (x2),函数 f(x)在 (0,+∞ ) 上为增函数. (2)∵a= ln(m2+ 2m+ 3)= ln[( m+ 1)2+ 2] ≥ ln2 l>n1= 0, b= ln10> ln1= 0, ∴由 (1)可知函数 f (x)在(0,+∞ ) 上为增函数,
)
A . log0.32< 20.3< 0.32 B. 20.3< 0.32<log0.32 C. log0.32> 20.3>0.32
D . 20.3>0.32> log0.32
答案: D
解析: ∵ 20.3> 20= 1,0< 0.32< 1, log0.32< log0.32< log0.31=0,∴ 20.3> 0.32>log0.32.
解析: 由题意得 100= alog2(1+ 1),∴ a=100,∴第 7 年时, y= 100log2(7+ 1)= 300. 10.函数 f(x)= x(x2- 1)的大致图象是 ( )
答案: A 解析: ∵ f(- x)= (- x)[(- x)2- 1]=- x(x2- 1)=- f(x) ∴ y= x(x2- 1)为奇函数,排除 C、 D.又 0< x<1 时, y<0. 故选 A. 11.已知 f(x)是 R 上的偶函数,且满足 f (x+ 4)= f(x),当 x∈ (0,2)时, f(x)= x+1,则 f (3)等于 ( ) A . 2 B.- 2 C. 1 D.- 1 答案: A 解析: 由条件知 f (3)= f (- 1+4)= f(- 1).又因为 f (- 1)= f (1),当 x∈ (0,2)时, f(x)= x+ 1,所以 f (1)= 2. 所以 f (3)= f(- 1)= f(1)= 2.
= 2+ 4× 27 =110. (2)原式= 2log32- (log325- log332)+ log323- 5log59 = 2log32- 5log32+2log33+ 3log32- 9 = 2- 9=- 7. 18.(12 分)已知集合 A= { x| x2+ ax- 6= 0} , B= { x| x2+bx+ c= 0} ,且 A≠B, A∪ B= { - 2,3} ,A∩ B=
,结合图象,易知 h(x)的最大值为 1.
11 16.已知 y= f (x)+ x 是偶函数,且 f(2)= lg32+ log416+ 6lg2+ lg5,若 g(x)=f (x)+ 1,则 g(-2)= ________.
答案: 6 11
解析: f(2)= lg32+ log416+ 6lg2+ lg5= 5lg2+ 2- 6lg2-lg5= 2- (lg2+ lg5)= 2- 1=1,
因为 y= f (x)+ x 是偶函数,所以 f(- x)- x=f (x)+ x,所以 f (- x)= f (x)+2x,
所以 g(- 2)= f(- 2)+ 1= f(2)+ 2× 2+1= 6.
三、解答题:本大题共 6 小题,共 70 分.解答应写出文字说明、证明过程或演算步骤.
17. (10 分 )求下列各式的值:
33
3
3
2
4
当 t> 8 时, g(t)是减函数,所以 g(t )< g(8)=- 160.总之, t= 时, g(t)最大为 ,即 f(x)= 2x+2- 3×4x 的最大值
3
3
4
为
. 3
20. (12 分 )某商店将进货价每个 10 元的商品按每个 18 元售出时,每天可卖出 60 个.商店经理到市场
二、填空题:本大题共 4 小题,每小题 5 分,共 20 分.把答案填在题中横线上. 13.已知函数 f(x)对任意 x, y∈R,都有 f(x+ y)= f (x)+f(y),且 f (2)= 4,则 f(-1)等于 ________. 答案: - 2 解析: 由题意得 f (0)= f(0)+ f(0) ∴ f(0)= 0. 又 f (x- x)= f(x)+f (- x)= 0 ∴ f(x)为奇函数. f(2)= f(1)+ f (1)=4 ∴ f(1)= 2,则 f(- 1)=- 2. 14.若函数 f(x)= loga(x+1)(a>0 ,且 a≠ 1) 的定义域和值域都是 [0,1],则 a 的值是 ________. 答案: 2 解析: ∵ 0≤x≤ 1,∴ 1≤x+ 1≤ 2,又函数 f (x)值域 [0,1],∴ a>1 ,∴ f (1)= loga(1+ 1)=1,∴ a= 2.
ax x< , 12.函数 f(x)=
a- x+ 4a x
f x1 - f x2
满足对任意 x1≠ x2,都有
x1- x2
< 0 成立,则 a 的
取值范围是 ( )
3
3
A .(0,4)
B
.(0,
] 4
C. (0,1) D . [3,+∞)
答案: B
-
-
3
3
解析: 由题意知 f (x)在 R 上是减函数,∴ 0< a< 1,又 a- 3+ 4a≤ a,4a≤ 3,a≤ 4,∴ 0<a≤4.
∵ A≠ B,∴ B= { - 2} . ∴方程 x2+ bx+ c= 0 的判别式 Δ= b2-4c= 0,
2b- c= 4, ① ∴
b2- 4c= 0, ②
由①得 c= 2b- 4,代入②整理得: (b- 4)2= 0,
∴ b= 4, c= 4. 19. (12 分 )函数 y= lg(3-4x+ x2)的定义域为 M, x∈ M 时,求 f(x)= 2x+ 2- 3×4x 的最大值.
-
模块综合检测 时间: 120 分钟 分值: 150 分
一、选择题:本大题共 12 题,每题 5 分,共 60 分.在下列各题的四个选项中,只有一个选项是符合题
目要求的.
1.已知集合 A= { x|0<log 4x<1} , B={ x| x≤ 2} ,则 A∩ B 等于 ( )
A .(0,1)
B.(0,2]
即在商品降价时,当 x= 17 时,每日利润 y 最大,最大利润是 490 元.
因为 500>490,所以此商品的售价应定为每个 20 元.
1
21. (12 分 )已知函数
f
(x)
=
alog
2x-
blog
x,其中常数 3
a,b 满足 ab≠ 0.
(1)若 a> 0, b> 0,证明函数 f (x)在定义域内为增函数; (2)若 a= ln(m2+ 2m+ 3), b= ln10,解不等式 f(3x- 1) ≤f(x+ 3).
C. (1,2)
D .(1,2]
答案: D
解析: A= { x|0<log 4x<1} = { x|1< x<4} , B={ x| x≤ 2} 所以 A∩ B={ x|1< x≤ 2}
3 2.如果幂函数 f(x)= xα的图象经过点 (3, ),则 f (8)的值等于 ( )
3
2
2
A.
B.
2
4
3
3
5.函数 y= x2+ x(- 1≤x≤ 3) 的值域是( )
A .[0,12]
1 B.[-4, 12]
1
3
C. [- 2, 12] D. [4, 12]
