一元二次不等式解法

合集下载

一元二次不等式公式解法

一元二次不等式公式解法一元二次不等式是指类似于ax+bx+c>0的不等式，其中a、b、c 为实数且a≠0。

解一元二次不等式的方法可以分为以下两种公式解法：1.配方法当a>0时，我们可以通过配方法将一元二次不等式转化为(x+m)+n>0的形式。

具体步骤如下：①将一元二次不等式转化为ax+bx+c≥0的形式。

②将a提出来，得到a(x+bx/a+c/a)≥0。

③将b/a的一半平方再减去c/a，得到(b/2a)-c/a=m，其中m为实数。

④将式子转化为a[(x+b/2a)-(b/2a)+c/a]≥0。

⑤将式子化简，得到(x+b/2a)+(4ac-b)/4a>0。

⑥将4ac-b表示为n，得到(x+b/2a)+n/4a>0。

⑦由于a>0，所以n>0，而完全平方数加上正数大于0，所以(x+b/2a)+n/4a>0，即(x+m)+n>0。

2.因式分解法当a<0时，我们可以通过因式分解法将一元二次不等式转化为(ax+b)(x+c)<0或(ax+b)(x+c)>0的形式。

具体步骤如下：①将一元二次不等式转化为ax+bx+c≤0或ax+bx+c≥0的形式。

②将a提出来，得到a(x+bx/a+c/a)≤0或a(x+bx/a+c/a)≥0。

③将x+bx/a+c/a表示为(x+d)(x+e)的形式，其中d、e为实数。

④当a<0时，(x+d)(x+e)>0；当a>0时，(x+d)(x+e)<0。

⑤当a<0时，解(x+d)(x+e)>0的方法为：找出实数d、e的大小关系，将实数轴分为三段，判断每一段上的符号，最后得到不等式的解集；当a>0时，解(x+d)(x+e)<0的方法为：找出实数d、e的大小关系，将实数轴分为三段，判断每一段上的符号，最后得到不等式的解集。

以上就是一元二次不等式的两种公式解法。

需要注意的是，在解一元二次不等式时，我们需要根据a的正负性和不等式的形式来选择不同的解法。

一元二次不等式的解法

一元二次不等式的解法在数学中，一元二次不等式是指形如ax^2+bx+c>0或ax^2+bx+c<0的二次不等式。

解一元二次不等式的方法可以通过图像法、代入法和判别法来实现。

本文将介绍这三种解法，并通过实例来说明其具体步骤。

图像法图像法是解一元二次不等式最直观的方法之一，它通过绘制一元二次函数的图像来找到不等式的解集。

下面以一元二次不等式x^2-4x+3>0为例来说明图像法的解题步骤：首先，将不等式转化为方程x^2-4x+3=0，求出方程的根。

我们可以通过求解x的一元二次方程来得到根，即使用求根公式x = (-b±√(b^2-4ac))/(2a)。

将方程x^2-4x+3=0代入求根公式中，得到x=1和x=3。

其次，在数轴上绘制一元二次函数y=x^2-4x+3的图像。

根据函数的开口方向和图像的凹凸性，我们可以确定函数在x<1和x>3的区间上为正值，即图像在该区间上位于x轴之上。

最后，根据不等式的正号，我们可以得出一元二次不等式x^2-4x+3>0的解集为x<1或x>3。

代入法代入法是通过代入特定的数值来判断一元二次不等式的真假。

下面以一元二次不等式x^2-4x+3>0为例来说明代入法的解题步骤：首先，将不等式转化为方程x^2-4x+3=0，求出方程的根。

我们可以使用同样的方法得到x=1和x=3。

其次，选择一些特定的数值，代入一元二次不等式中，判断不等式的真假。

例如，选择x=0、x=2和x=4来代入不等式。

计算得到代入x=0时，不等式为3>0，代入x=2时，不等式为-1>0，代入x=4时，不等式为3>0。

根据计算结果，我们可以确定不等式在x<1和x>3的区间上为真。

最后，根据不等式的真假，我们可以得出一元二次不等式x^2-4x+3>0的解集为x<1或x>3。

判别法判别法是解一元二次不等式的一种常用方法，它利用一元二次不等式的判别式来确定不等式的解集。

一元二次不等式的解法

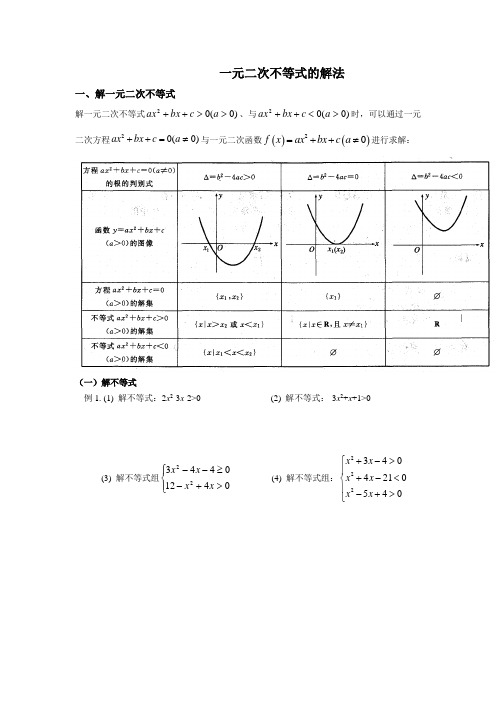
一元二次不等式的解法一、解一元二次不等式解一元二次不等式)0(02>>++a c bx ax 、与)0(02><++a c bx ax 时，可以通过一元二次方程20(0)ax bx c a ++=≠与一元二次函数()()20f x ax bx c a =++≠进行求解：（一）解不等式例1. (1) 解不等式：2x 2-3x -2>0 (2) 解不等式：-3x 2+x +1>0(3) 解不等式组⎪⎩⎪⎨⎧>+-≥--0412044322x x x x (4) 解不等式组：2223404210540x x x x x x ⎧+->⎪+-<⎨⎪-+>⎩（二）已知不等式的解集，写不等式例2. (1) 写出一个一元二次不等式，使它的解集()1,3-.(2) 已知219990ax x b -+>的解集是()3,1--，求不等式219990ax x b ++>的解集.(3) 不等式组⎪⎩⎪⎨⎧<+++>--05)25(20222a x a x x x 的整数解值只有2-，求实数a 的范围.二、一元二次方程根的分布例3. 若一元二次方程0)1(2)1(2=-++-m x m x m 有两个正根，求m 的取值范围.例4.⑴ 已知方程032222=-++m mx x 有一根大于2，另一根比2小，求m 的取值范围.⑵ 已知方程012)2(2=-+-+m x m x 有一实根在()0,1内，求m 的取值范围.⑶ 已知方程012)2(2=-+-+m x m x 只有较大实根在()0,1内，求实数m 的取值范围⑷ 若方程0)2(2=-++k x k x 的两实根均在区间（1-、1）内，求k 的取值范围.⑸ 若方程012)2(2=-+-+k x k x 的两根中，一根在()0,1内，另一根在()1,2内，求k 的取值范围.⑹ 已知关于x 的方程062)1(22=-++--m m mx x m 的两根为βα、且满足βα<<<10，求m 的取值范围.（三）含参数一元二次不等式例5. 当k 为何值时，不等式010)5()5(2>+----k x k x k ，对一切实数都成立.例6. 关于x 的不等式0622<+++m m mx x 的解集包含区间（1，2）时，求实数m 的范围.例7. 设集合{}{}034,0107222<+-=<++=a ax x x B x x x A ，并且B A ⊆，求实数a 的范围.例8. 解关于x 的不等式032>--a ax x .例9. 解关于x 的不等式02)2(2>--+x m mx .例10. (1) 设不等式02>++c bx ax 的解集为βαβα<<<<0},{x x ，试求不等式02<++a bx cx 的解集.(2) 已知关于x 的不等式20ax bx c -+>的解集为（1，2），解关于x 的不等式20cx bx a -+>.(3) 已知关于x 的不等式0k x b x a x c++<++的解集为（-2，-1）∪（2，3），解关于x 的 1011kx bx ax cx -+<--.(4) 已知不等式223()0x a a x a -++<的解集为{|33}x x <<，求实数a 的取值情况；(5) 已知不等式223()0x a a x a -++<在{|33}x x <<内恒成立，求实数a 的取值情况．(6) 已知集合]2,21[=P ，}022|{2>+-=x ax x Q ．① 若∅≠Q P ，求实数a 的取值范围；② 若方程0222=--x ax 在]2,21[内有解，求实数a 的取值范围．(7) k 为何值时，不等式13642222<++++x x k kx x 恒成立例11. 已知2()2(2)4f x x a x =+-+，（1）如果对一切x R ∈，()0f x >恒成立，求实数a 的取值范围；（2）如果对[3,1]x ∈-，()0f x >恒成立，求实数a 的取值范围．例12. 设不等式x 2－2ax +a +2≤0的解集为M ，如果M ⊆［1，4］，求实数a 的取值范围.例13. 若不等式2x －1＞m （x 2－1）对满足|m |≤2的所有m 都成立，求x 的取值范围.例14. 设c bx ax x f ++=2)(，若27)1(=f ，问是否存在R c b a ∈,,，使得不等式212+x 2322)(2++≤≤x x x f 对一切实数x 都成立，证明你的结论.。

一元二次不等式全部解法

一元二次不等式全部解法一元二次不等式是指形如ax^2 + bx + c > 0或ax^2 + bx + c < 0的不等式，其中a、b、c是已知实数且a ≠ 0。

要求解一元二次不等式，我们需要找到其解集，即使不等式成立的x的取值范围。

下面将介绍几种解一元二次不等式的方法。

方法一：图像法通过绘制二次函数的图像，我们可以直观地观察到不等式的解集。

以ax^2 + bx + c > 0为例，我们可以绘制出函数y = ax^2 + bx + c的图像，然后观察函数图像在x轴上的位置。

如果函数图像位于x轴上方，则不等式成立的x的取值范围为图像所在的区间；如果函数图像位于x轴下方，则不等式不成立的x的取值范围为图像所在的区间。

方法二：因式分解法对于一元二次不等式ax^2 + bx + c > 0，我们可以先通过因式分解将其转化为(ax + m)(ax + n) > 0的形式，其中m、n是已知实数。

然后根据乘积大于零的性质，我们可以得到两个因子同时大于零或同时小于零时不等式成立。

因此，我们需要解以下两个不等式：ax + m > 0和ax + n > 0，得到的解集再取交集，即为原不等式的解集。

方法三：配方法对于一元二次不等式ax^2 + bx + c > 0，我们可以通过配方法将其转化为完全平方的形式。

具体步骤如下：1. 将不等式移项，得到ax^2 + bx + c = 0的形式。

2. 根据二次方程的求根公式，求得方程的两个根x1和x2。

3. 根据二次函数的性质，我们可以得到该二次函数在x1和x2之间变号。

即对于ax^2 + bx + c > 0来说，当x在x1和x2之间时，不等式成立。

方法四：求解判别式对于一元二次不等式ax^2 + bx + c > 0，我们可以先求解对应的二次方程ax^2 + bx + c = 0的判别式Δ=b^2-4ac。

根据判别式的值，我们可以得到不等式的解集：1. 当Δ>0时，二次方程有两个不相等的实根x1和x2，此时不等式成立的x的取值范围为x<x1或x>x2。

一元二次不等式方程的解法

一元二次不等式方程的解法含有一个未知数且未知数的最高次数为2次的的不等式叫做一元二次不等式，它的一般形式是ax2+bx+c>0或ax2+bx+c<0(a不等于0),其中ax2+bx+c实数域上的二次三项式。

一元二次不等式的解法有哪几种?1、公式法可以解所有的一元二次方程，公式法不能解没有实数根的方程(也就是b²-4ac<0的方程)。

求根公式： x=-b±√(b2-4ac)/2a。

2、配方法比较简单：首先将方程二次项系数a化为1，然后把常数项移到等号的右边，最后后在等号两边同时加上一次项系数绝对值一半的平方。

3、数轴穿根：用穿根法解高次不等式时，就是先把不等式一端化为零，再对另一端分解因式，并求出它的零点，把这些零点标在数轴上，再用一条光滑的曲线，从x轴的右端上方起，依次穿过这些零点，大于零的不等式的解对应这曲线在x轴上方部分的实数x的值的集合，小于零的则相反。

这种方法叫做序轴穿根法，又叫“穿根法”。

口诀是“从右到左，从上到下，奇穿偶不穿。

”4、一元二次不等式也可通过一元二次函数图象进行求解。

通过看图象可知，二次函数图象与X轴的两个交点，然后根据题中所需求"<0"或">0"而推出答案。

求一元二次不等式的解集实际上是将这个一元二次不等式的所有项移到不等式一侧并进行因式分解分类讨论求出解集。

解一元二次不等式，可将一元二次方程不等式转化成二次函数的形式，求出函数与X轴的交点，将一元二次不等式，二次函数，一元二次方程联系起来，并利用图象法进行解题，使得问题简化。

等式的基本性质：1、等式两边同时加(或减)同一个数或同一个代数式，所得的结果仍是等式。

用字母表示为：若a=b，c为一个数或一个代数式。

2、等式的两边同时乘或除以同一个不为0的数,所得的结果仍是等式。

用字母表示为：若a=b，c为一个数或一个代数式(不为0)。

3、不等式的两边同时加上(或减去)同一个数(或式子)，不等号的方向不变;4、不等式的两边同时乘(或除以)同一个正数，不等号的方向不变;5、不等式的两边同时乘(或除以)同一个负数，不等号的方向变。

一元二次不等式6种解法大全

一元二次不等式6种解法大全一元二次不等式是指形如ax²+bx+c>0或ax²+bx+c≥0的二次不等式，其中a、b、c为实数，a≠0。

这种不等式的解法有很多种，下面我将介绍其中的六种解法。

解法一：使用因式分解法。

对于形如(ax+b)(cx+d)>0或(ax+b)(cx+d)≥0的一元二次不等式，可以尝试将其因式分解为两个一次因式相乘的形式，然后根据不等式的性质讨论各个因式的取值范围，从而求得不等式的解。

解法二：使用它的图像解法。

将一元二次不等式对应的二次函数的图像画出来，然后根据图像的特点来确定使得函数大于0（或大于等于0）的x的取值范围，即为不等式的解。

解法三：使用开平方法。

对于形如x²+a≥0或x²+a>0的一元二次不等式，可以通过开平方的方法来求解。

首先将不等式移到一边，得到一个完全平方的形式，然后对不等式两边同时开平方，得到关于x的两个二次方程，根据二次方程的性质来求解。

解法四：使用代数求解法。

对于一元二次不等式ax²+bx+c>0或ax²+bx+c≥0，可以将其转化为一个关于x的二次方程ax²+bx+c=0的解的范围问题。

求得这个二次方程的解，然后根据这些解的范围来确定不等式的解。

解法五：使用数轴法。

将一元二次不等式对应的二次函数的图像画在数轴上，然后根据函数的凸性来确定函数取正值的x的取值范围，即为不等式的解。

解法六：使用区间法。

将一元二次不等式移项，化成形如ax²+bx+c<0或ax²+bx+c≤0的不等式，然后求出二次函数的零点，并根据二次函数的凸性来确定函数小于0（或小于等于0）的x的取值范围，即为不等式的解。

以上是关于一元二次不等式的六种解法，每种解法都有其独特的思路和方法。

在实际的解题过程中，可以根据具体的题目情况选择合适的解法来求解，以提高解题效率和准确性。

一元二次不等式的解法

一元二次不等式的解法一元二次不等式是由一个二次方程构成的数学不等式，其形式通常为 ax^2 + bx + c > 0 或 ax^2 + bx + c < 0。

解一元二次不等式需要运用一些特定的方法和原理，下面将介绍一些常用的解法。

1. 图像法图像法是一种直观的解一元二次不等式的方法。

首先，我们可以将不等式的左边化简成一个二次函数的形式，例如将 ax^2 + bx + c > 0 转化为 y = ax^2 + bx + c 的图像。

然后，通过观察图像的形状和位置，确定不等式的解集。

对于一元二次不等式 ax^2 + bx + c > 0，可以按照以下步骤使用图像法解答：a) 计算二次函数的顶点坐标 (-b/(2a), f(-b/(2a)))，其中 f(x) = ax^2 + bx + c。

b) 如果 a > 0，表示二次函数开口向上，则解集为顶点坐标的右侧部分。

如果 a < 0，表示二次函数开口向下，则解集为顶点坐标的左侧部分。

c) 如果二次函数与 x 轴有交点，则解集还包括这些交点。

举例说明：假设要解一元二次不等式 x^2 + 4x + 3 > 0。

a) 通过计算，可得到顶点坐标为 (-2, -1)。

b) 由于 a > 0，解集为顶点坐标的右侧部分。

c) 二次函数与 x 轴的交点为 (-3, 0) 和 (-1, 0)。

因此，解集为 (-∞, -3) ∪ (-1, +∞)。

2. 因式分解法对于一元二次不等式，我们可以先将其因式分解为二次方程的形式，然后再解这个二次方程。

具体步骤如下：a) 将不等式左边移项，将其写成一个完全平方的形式，例如 a(x -r)(x - s) > 0 或 a(x - r)(x - s) < 0，其中 r 和 s 是待定系数。

b) 将方程 a(x - r)(x - s) = 0 求解，得到方程的根（解），记作 x = r和 x = s。

一元二次不等式6种解法大全

一元二次不等式6种解法大全
一元二次不等式有多种解法，以下是一些常见的解法：
1. 图像法：将一元二次不等式转化为图像，通过观察图像的变化来确定解的范围。

首先，将不等式转化为等式，再画出对应的抛物线图像，然后根据不等式的符号确定解的范围。

2. 因式分解法：将一元二次不等式进行因式分解，得到一个或多个一次因子和一个二次因子。

然后，根据这些因子的正负确定不等式的解。

3. 求导法：对一元二次不等式两边同时求导数，得到一个一次方程。

然后，通过解这个一次方程得到不等式的解。

4. 完全平方式：将一元二次不等式进行变形，使其成为完全平方式。

然后，通过对方程两边取平方根，得到不等式的解。

5. 化简法：将一元二次不等式进行化简，整理为一个或多个一次项和一个常数项的形式。

然后，根据这些项的符号确定不等式的解。

6. 区间法：将一元二次不等式转化为一个或多个区间，并确定每个区间内的解的情况。

然后，将这些区间的解合并，得到不等式的解集。

以上是一些常见的一元二次不等式的解法，具体使用哪种解法取决于不等式的形式和题目要求。

在解题过程中，可以根据需要选择适合的方法进行求解。

一元二次不等式的解法

一元二次不等式的解法一元二次不等式是指一个未知数的二次函数与一个数之间的关系式，其形式为ax² + bx + c > 0或ax² + bx + c < 0。

解一元二次不等式的关键是找到其解集，即满足不等式的所有实数解。

本文将介绍两种常用的一元二次不等式的解法：图像法和区间法。

一、图像法1. 将一元二次不等式的左边移至右边，得到一个一元二次函数的对称形式。

例如，将ax² + bx + c > 0移至右边，得到ax² + bx + c = 0。

2. 绘制出对应一元二次函数的图像，并标出顶点。

对于一元二次函数y = ax² + bx + c，其图像是一个抛物线。

顶点的横坐标为-x₀ = -b/2a，纵坐标为y₀ = f(-x₀) = f(-b/2a)。

3. 根据一元二次不等式的符号确定解集。

若a > 0，表示抛物线开口向上，此时对应不等式的解集是(x < x₀) ∪ (x > x₁)。

若a < 0，表示抛物线开口向下，此时对应不等式的解集是(x₀ < x < x₁)。

二、区间法1. 将一元二次不等式的左边移至右边，得到一个一元二次函数的对称形式。

例如，将ax² + bx + c > 0移至右边，得到ax² + bx + c = 0。

2. 求出一元二次函数的判别式Δ = b² - 4ac的值，并根据Δ的正负确定解集。

若Δ > 0，则对应不等式的解集是(-∞, x₁) ∪ (x₂, +∞)。

若Δ = 0，则对应不等式的解集是(-∞, x) ∪ (x, +∞)。

若Δ < 0，则对应不等式的解集为空集。

需要注意的是，使用图像法和区间法时必须要了解一元二次函数的图像特征和判别式的意义。

另外，在求解过程中，可以运用一些常用的数学知识，如因数分解、配方法等，以便更快地得到解集。

一元二次不等式解法

④求对应方程根：即 ax2 bx c 0的解可以因式分解，也可以用求根公式：
b b 2 4ac b b 2 4ac x1 , x2 2a 2a
⑤得出不等式的解：
不等式是“>”号，解为：x>x ₁或x<x ₂ 口诀为“取两边”
不等式是“<”号，解为：x₂<x<x₁ 口诀为“取中间”。 ⑥不等式是“>”号，解为R，不等式是“<”号，解为∅
b b 2 4ac 5 25 24 x1 1 2a 2
b b 2 4ac 5 - 25 （ 24） x2 6 2a 2
⑤得不等式的解，不等式中是“>”号口诀为“取两边”即：x>x ₁或x<x ₂ 所以此不等式的解为：｛x |x>1或x<-6 ｝用区间表示为（- ∞ ，－6） ∪（1，+ ∞）
例： x 2 4 x 3 0
解：△＝16-12＝4>0 解方程 x 2 4 x 3 0
（x 3)(x 1) 0 x1 3, x2 1
所以此不等式的解为：x 1或x 3
， 3 1 ，用区间表示为：
b b 2 4ac 4 - 16 12 x2 3 2a 2
⑤得不等式的解，不等式中是“<”号口诀为“取中间”即： x₂<x<x₁ 所以此不等式的解为：｛x |-3<x<-1｝用区间表示为（- 3 ，－1）
例：（ 1 x)(4 x) 0
2 x 3x 4 0 ①化成一般式：二次项系数a=-1，即a<0 2 ②化正得同解不等式： x 3x 4 0 ③计算△， △＝b ²-4ac＝9-（-16）＝25>0 2 x 3x 4 0 的根 ④求对应方程用求根公式得：

一元二次不等式的解法

一元二次不等式的解法一元二次不等式是指包含一个未知数的二次函数不等式，其解的范围通常是实数集合中的某个区间。

解决一元二次不等式问题需要运用一些基本的数学原理和方法。

本文将介绍几种常见的一元二次不等式的解法。

1. 图形法解一元二次不等式图形法是解决一元二次不等式的一种直观方法。

我们可以通过绘制一元二次函数的图像来观察其解的范围。

具体步骤如下：1）将一元二次不等式转化为二次函数的形式，确保不等式的右边为0；2）绘制该二次函数的图像，并标出函数图像上的关键点，如顶点、交点等；3）根据函数图像的特征，确定不等式的解的范围。

2. 因式分解法解一元二次不等式因式分解法是解决一元二次不等式的常用方法之一。

通过将不等式转化为因式的形式，可以更方便地确定解的范围。

具体步骤如下：1）将一元二次不等式转化为二次函数的形式，确保不等式的右边为0；2）将二次函数因式分解为一元一次函数的乘积，得到因式表达式；3）根据因式表达式的性质，确定不等式的解的范围。

3. 完全平方式解一元二次不等式完全平方式也是解决一元二次不等式的一种常用方法。

通过完全平方式，可以将不等式转化为平方形式，从而更容易确定解的范围。

具体步骤如下：1）将一元二次不等式转化为二次函数的形式，确保不等式的右边为0；2）将一元二次函数利用完全平方式转化为平方（二次）表达式；3）根据平方表达式的性质，确定不等式的解的范围。

4. 配方法解一元二次不等式配方法是解决一元二次不等式的另一种有效方法。

通过进行配方法，可以将一元二次不等式转化为二次函数的平方差形式，从而简化求解过程。

具体步骤如下：1）将一元二次不等式转化为二次函数的形式，确保不等式的右边为0；2）运用配方法，将二次函数转化为平方差的形式；3）根据平方差的性质，确定不等式的解的范围。

综上所述，一元二次不等式的解法包括图形法、因式分解法、完全平方式和配方法等多种方法。

在具体解题过程中，可以根据实际情况选择合适的解法。

一元二次不等式的解法

一元二次不等式的解法一元二次不等式是指只含有一个未知数的二次不等式，通常形式为ax^2+bx+c>0或ax^2+bx+c<0，其中a、b、c为实数，且a ≠ 0。

解一元二次不等式的方法主要有以下几种：图像法、代数法和判别法。

一、图像法1. 绘制一元二次函数的图像：根据不等式的形式，确定二次函数的开口方向（a的正负），以及顶点的横坐标、纵坐标（b和c的值）。

2. 根据不等式的符号（大于或小于），确定图像与x轴的关系，即求解函数值大于0或小于0的区间。

3. 根据求解得到的区间，直观地表示出不等式的解集。

二、代数法1. 化简一元二次不等式：通过合并同类项、配方等方法，将二次不等式化简为标准形式，即ax^2+bx+c>0或ax^2+bx+c<0。

2. 求解方程：将不等式转化为等式，即ax^2+bx+c=0，并求解得出方程的根。

3. 利用根的性质：通过根的位置和值的正负判断方程在不等式中的取值情况，从而确定不等式的解集。

三、判别法1. 计算判别式：根据二次不等式的形式，计算出判别式Δ=b^2-4ac。

2. 根据判别式的值判断解集：a) 当Δ>0时，二次不等式有两个不同的实数根，根据系数的正负关系，可得出不等式的解集；b) 当Δ=0时，二次不等式有且仅有一个实数根，根据系数的正负关系，可得出不等式的解集；c) 当Δ<0时，二次不等式没有实数根，根据系数的正负关系，可得出不等式的解集。

综上所述，一元二次不等式的解法包括图像法、代数法和判别法。

根据具体情况，选择合适的方法求解可以快速得到一元二次不等式的解集。

通过掌握这些解法，我们能够更加灵活地处理和求解各种形式的一元二次不等式，提高数学问题的解决能力。

一元二次不等式的解法全面版

际上就是二次函数 ya2xb xc(a0)
与x轴交点的横坐标。
下面我们来研究如何应用二次函数的图象来解一元二次不等式。
首先，我们可以把任何一个一元二次不等式转化为下列四种形式中的一种：
(1 )a2x b xc0(a0) (2)a2x b xc0(a0) (3)a2x b xc0(a0) (4)a2x b xc0(a0)
一元二次不等式的解法（一）
y
o
x
问题：
（1）如何解一元二次方程 a2xb xc0(a0) （2）二次函数ya2xb xc(a0)的图象是
什么曲线？（3）一元二次方程 a2xb xc0(a0) 的
解与二次函数ya2xb xc(a0)的图象有什么联系？
一元二次方程a2xb xc0(a0)的解实
下面我们一起来完成下表：
△＝b2－4ac f(x)＞0的解集 f(x)＜0的解集 f(x) ≥0的解集 f(x) ≤0的解集
△＞0
△＝0
xxx2或 xx1
xR
x

b 2a
xx1xx2
xxx2或 xx1 R
xx1xx2
x
x

b 2a
小结：
（1）根据数形结合的思想，利用二次函数的图象解二次不等式。
（2）根据分类讨论的思想，正确选定分类标准，解含参数的不等式。
同学们再见！
只要我们坚持了，就没有克服不了的困难。或许，为了将来，为了自己的发展，我们会把一件事情想得非常透彻，对自己越来越严，要求越来越高，对任何机会都不曾错过，其目的也只不过是不让自己随时陷入逆境与失去那种面对困难不曾屈服的精神。但有时，“千里之行，始于足下。”我们更需要用时间持久的用心去做一件事情，让自己其中那小小的浅浅的进步，来击破打破突破自己那本以为可以高枕无忧十分舒适的区域，强迫逼迫自己一刻不停的马不停蹄的一直向前走，向前看，向前进。所有的未来，都是靠脚步去丈量。没有走，怎么知道，不可能；没有去努力，又怎么知道不能实现？幸福都是奋斗出来的。那不如，生活中、工作中，就让这“幸福都是奋斗出来的”完完全全彻彻底底的渗入我们的心灵，着心、心平气和的去体验、去察觉这一种灵魂深处的安详，侧耳聆听这仅属于我们自己生命最原始最动人的节奏。但，这种聆听，它绝不是仅限于、执着于 “我”，而是观察一种生命状态能够扩展和超脱到什么程度，也就是那“幸福都是奋斗出来的”深处又会是如何？生命不止，奋斗不息！又或者，对于很多优秀的人来说，我们奋斗了一辈子，拼搏了一辈子，也只是人家的起点。可是，这微不足道的进步，对于我们来说，却是幸福的，也是知足的，因为我们清清楚楚的知道自己需要的是什么，隐隐约约的感觉到自己的人生正把握在自己手中，并且这一切还是通过我们自己勤勤恳恳努力，去积极争取的!“宝剑锋从磨砺出，梅花香自苦寒来。”当我们坦然接受这人生的终局，或许，这无所皈依的心灵就有了归宿，这生命中觅寻处那真正的幸福、真正的清香也就从此真正的灿烂了我们的人生。一生有多少属于我们的时光？陌上的花，落了又开了，开了又落了。无数个岁月就这样在悄无声息的时光里静静的流逝。童年的玩伴，曾经的天真，只能在梦里回味，每回梦醒时分，总是多了很多伤感。不知不觉中，走过了青春年少，走过了人世间风风雨雨。爱过了，恨过了，哭过了，笑过了，才渐渐明白，酸甜苦辣咸才是人生的真味！生老病死是自然规律。所以，面对生活中经历的一切顺境和逆境都学会了坦然承受，面对突然而至的灾难多了一份从容和冷静。这世上没有什么不能承受的，只要你有足够的坚强！这世上没有什么不能放下的，只要你有足够的胸襟！一生有多少属于我们的时光？当你为今天的落日而感伤流泪的时候，你也将错过了明日的旭日东升；当你为过去的遗憾郁郁寡欢，患得患失的时候，你也将忽略了沿途美丽的风景，淡漠了对未来美好生活的憧憬。没有十全十美的生活，没有一帆风顺的旅途。波平浪静的人生太乏味，抑郁忧伤的人生少欢乐，风雨过后的彩虹最绚丽，历经磨砺的生命才丰盈而深刻。见过了各样的人生：有的轻浮，有的踏实；有的喧哗，有的落寞；有的激扬，有的低回。肉体凡胎的我们之所以苦恼或喜悦，大都是缘于生活里的际遇沉浮，走不出个人心里的藩篱。也许我们能挺得过物质生活的匮乏，却不能抵挡住内心的种种纠结。其实幸福和欢乐大多时候是对人对事对生活的一种态度，一花一世界，一树一菩提，就是一粒小小的沙子，也有自己精彩的乾坤。如果想到我们终有一天会灰飞烟灭，一切象风一样无影亦无踪，还去争个什么？还去抱怨什么？还要烦恼什么？未曾生我谁是我？生我之时我是谁？长大成人方是我，合眼朦胧又是谁？一生真的没有多少时光，何必要和生活过不去，和自己过不去呢。你在与不在，太阳每天都会照常升起；你愁与不愁，生活都将要继续。时

一元二次次不等式解法

一元二次次不等式解法一、一元二次不等式的基本形式一元二次不等式的一般形式为ax^2+bx + c>0或ax^2+bx + c<0（a≠0），例如x^2-2x - 3>0， - x^2+3x+4<0等。

二、一元二次不等式的解法步骤（以ax^2+bx + c>0为例，a> 0）1. 将不等式化为标准形式- 确保二次项系数a>0。

如果原不等式是ax^2+bx + c<0且a<0，则先将不等式两边同时乘以-1，改变不等号方向，化为-ax^2-bx - c>0，此时二次项系数变为正数。

2. 求解对应的一元二次方程ax^2+bx + c = 0的根- 对于一元二次方程ax^2+bx + c = 0（a≠0），根据求根公式x=frac{-b±√(b^2)-4ac}{2a}求出方程的根x_{1},x_{2}（假设x_{1}<x_{2}）。

- 例如对于方程x^2-2x - 3 = 0，其中a = 1，b=-2，c=-3，根据求根公式x=frac{2±√((-2)^2)-4×1×(-3)}{2×1}=(2±√(16))/(2)，解得x_{1}=-1，x_{2}=3。

3. 根据二次函数y = ax^2+bx + c的图象确定不等式的解集- 因为a>0，二次函数y = ax^2+bx + c的图象开口向上。

- 当ax^2+bx + c>0时，不等式的解集为x<x_{1}或x>x_{2}；对于x^2-2x - 3>0，其解集为x < - 1或x>3。

- 当ax^2+bx + c<0时，不等式的解集为x_{1}<x<x_{2}；例如对于x^2-2x - 3<0，其解集为-1<x<3。

三、特殊情况1. 判别式Δ=b^2-4ac = 0时- 对于方程ax^2+bx + c = 0，此时方程有且仅有一个根x =-(b)/(2a)。

一元二次不等式的解法

一元二次不等式的解法一元二次不等式是指形式为ax^2 + bx + c > 0 (或ax^2 + bx + c < 0)的不等式，其中a、b、c为实数，且a ≠ 0。

要解一元二次不等式，需要通过一系列的步骤来确定其解集。

步骤一：将一元二次不等式的左边转化为一个二次函数f(x)。

根据一元二次不等式的形式，我们可以将其左边的项看作是二次函数f(x) = ax^2 + bx + c。

这个二次函数的图像可能是一个抛物线开口向上，也可能是开口向下。

步骤二：求出二次函数f(x)的零点。

为了求出二次函数f(x)的零点，我们需要将其转化为标准形式。

标准形式是指f(x) = a(x - h)^2 + k，其中(h, k)为抛物线的顶点坐标。

步骤三：根据二次函数f(x)的开口方向，确定一元二次不等式的解集。

如果二次函数f(x)开口向上，即a > 0，那么一元二次不等式的解集是抛物线上方的区域。

如果二次函数f(x)开口向下，即a < 0，那么一元二次不等式的解集是抛物线下方的区域。

步骤四：根据一元二次不等式的形式，找出它的解集。

通过分析图像和零点，我们可以进一步确定一元二次不等式的解集。

例如，考虑不等式x^2 - 3x + 2 > 0。

首先，我们将不等式左边的项转化为二次函数f(x) = x^2 - 3x + 2，然后求出其零点。

将f(x)转化为标准形式可以得到f(x) = (x - 1)(x - 2)，则它的零点是x = 1和x = 2。

这意味着抛物线与x轴相交于点(1, 0)和(2, 0)。

由于a = 1 > 0，我们知道抛物线开口向上。

因此，不等式的解集是抛物线上方的区域。

我们可以通过测试f(x)在零点以及零点左右的取值来进一步确定解集。

当x < 1时，抛物线在x轴上方，因此f(x) > 0；当1 < x < 2时，抛物线在x轴下方，因此f(x) < 0；当x > 2时，抛物线再次在x轴上方，因此f(x) > 0。

一元二次不等式的解法

一元二次不等式的解法引言一元二次不等式是数学中常见的一类问题，解决一元二次不等式可以帮助我们确定变量的取值范围，进而解决实际问题。

本文将介绍一元二次不等式的解法，包括代入法、求值法以及图像法。

代入法代入法是解决一元二次不等式的一种常用方法。

该方法的基本思想是通过逐个地代入可能的解，从而找到满足不等式的解。

以一元二次不等式x2−5x+6<0为例，我们可以通过代入法来解决。

首先，我们需要找到该不等式的零点，即x2−5x+6=0。

解这个方程可以得到x=2和x=3两个解。

接下来，我们选择代入两个解的中间值x=2.5，代入原来的不等式，即(2.5)2−5(2.5)+6<0。

计算得到2.5<0，不满足该不等式。

然后，我们选择代入两个解的两边值x=2，代入原来的不等式，即(2)2−5(2)+6<0。

计算得到2>0，也不满足该不等式。

最后，我们选择代入两个解的另一边值x=3，代入原来的不等式，即(3)2−5(3)+6<0。

计算得到3<0，符合该不等式。

因此，根据代入法，我们可以得出不等式x2−5x+6<0的解为2<x<3。

求值法求值法是解决一元二次不等式的另一种常用方法。

该方法的基本思想是通过判断不等式在每个可能的解点的取值情况，从而找到满足不等式的解。

以一元二次不等式x2−4x−5>0为例，我们可以通过求值法来解决。

首先，我们需要找到该不等式的零点，即x2−4x−5=0。

解这个方程可以得到x=−1和x=5两个解。

接下来，我们选择零点的两边值x=−2，代入原来的不等式，即(−2)2−4(−2)−5>0。

计算得到15>0，满足该不等式。

然后，我们选择零点的两边值x=0，代入原来的不等式，即(0)2−4(0)−5>0。

计算得到−5>0，不满足该不等式。

最后，我们选择零点的两边值x=6，代入原来的不等式，即(6)2−4(6)−5>0。

一元二次不等式的解法

一元二次不等式的解法一元二次不等式是数学中常见的一种不等式类型，涉及到一个未知数的平方，通常可以表示为ax^2 + bx + c < 0，其中a、b、c为已知常数，x为未知数。

解决一元二次不等式的关键在于找到其解集，即满足不等式的x的取值范围。

本文将介绍两种常用的解法：因式分解法和判别式法。

一、因式分解法因式分解法是解决一元二次不等式的常用方法之一。

其主要思路是将不等式左侧转化为一个或多个二次因子的乘积，并通过每个因子的正负确定不等式的取值范围。

例如，对于不等式x^2 - 5x + 6 \geq 0，可以通过因式分解将其转化为(x - 2)(x - 3) \geq 0。

根据因子的正负确定不等式的解集。

由于(x -2)(x - 3)为两个因子的乘积，因此只有在这两个因子同时为非负或同时为非正的情况下，不等式才成立。

首先考虑(x - 2) \geq 0，解得x \geq 2；然后考虑(x - 3) \geq 0，解得x \geq 3。

因此，不等式的解集为x \geq 3。

二、判别式法判别式法是解决一元二次不等式的另一种常用方法。

其基本思想是通过求解一元二次不等式对应二次方程的判别式来确定不等式的解集。

对于一元二次不等式ax^2 + bx + c < 0，首先计算其对应的二次方程的判别式，记作\Delta = b^2 - 4ac。

若\Delta > 0，则二次方程有两个不相等的实数解，此时不等式的解集为x < \frac{-b-\sqrt{\Delta}}{2a} 或 \frac{-b+\sqrt{\Delta}}{2a} < x。

若\Delta = 0，则二次方程有两个相等的实数解，此时不等式的解集为x = \frac{-b}{2a}。

若\Delta < 0，则二次方程无实数解，此时不等式无解。

举个例子，考虑不等式x^2 - x - 6 > 0。

计算其对应的二次方程的判别式：\Delta = (-1)^2 - 4 \cdot 1 \cdot (-6) = 25。

一元二次不等式的解法

要使 B ⊆ A，则 a ∈ [1, 4 ]。
6. A = x | x 2 + 4 x + p < 0 , B = x | x 2 − x − 2 > 0 ，满足 A ⊆ B，
解：B = {x | x < −1 或 x > 2} ① A = ∅，则 ∆ = 16 − 4 p ≤ 0 ⇒ p ≥ 4。
一元二次不等式的解法
1. 一元二次不等式：
ax 2 + bx + c > 0 或 ax 2 + bx + c < 0 (a ≠ 0)
2. 区间
闭区间：闭区间：开区间：开区间：
[a , b] = {x | a ≤ x ≤ b} (a , b) = {x | a < x < b}

R = (−∞ , + ∞)
解：a = 2 + 3 = 5 , − b = 2 × 3 = 6 ⇒ b = −6
1 1 不等式 bx − ax − 1 > 0 为 − 6 x − 5 x − 1 > 0，解为 − < x < − 。 2 3 推广：若不等式 ax 2 + bx + c > 0 的解集为 (α , β )，其中 0 < α < β ，
的根的判别式不等式的解集
△ = b 2 − 4ac = 0 △ = b 2 − 4ac < 0
ax 2 + bx + c > （a > 0）(−∞, x1 ) ∪ ( x2 ,+∞) (−∞, x0 ) ∪ ( x0 ,+∞) 0
不等式的解集不等式
R R
ax 2 + bx + c ≥ （a > 0）(−∞, x1 ] ∪[ x2 ,+∞) 0

一元二次不等式解法步骤

一元二次不等式解法步骤【原创实用版】目录一、一元二次不等式的基本概念二、一元二次不等式的解法步骤1.确定二次项系数2.计算根的判别式3.判断根的情况4.求解一元二次不等式正文一、一元二次不等式的基本概念一元二次不等式是指形如 ax+bx+c>0（a≠0）的不等式，其中 a、b、c 为常数，x 为未知数。

一元二次不等式的解集为使不等式成立的 x 的取值范围。

二、一元二次不等式的解法步骤1.确定二次项系数在给定的一元二次不等式中，二次项系数为 a。

注意，a 必须不等于0，否则不等式将不再是一元二次不等式。

2.计算根的判别式根的判别式，也称为德尔塔（Δ），计算公式为：Δ=b-4ac。

根据Δ的值，我们可以判断方程的根的情况。

3.判断根的情况根据Δ的值，我们可以将一元二次不等式的根的情况分为以下三种：（1）Δ>0：方程有两个不相等的实根，即一元二次不等式有两个解。

（2）Δ=0：方程有两个相等的实根，即一元二次不等式有一个解。

（3）Δ<0：方程无实根，即一元二次不等式无解。

4.求解一元二次不等式根据根的情况，我们可以采用以下方法求解一元二次不等式：（1）当Δ>0 时，设方程的两个实根为 x1 和 x2，且 x1<x2。

那么，一元二次不等式的解集为{x|x<x1 或 x>x2}。

（2）当Δ=0 时，设方程的两个实根为 x1 和 x2，且 x1=x2。

那么，一元二次不等式的解集为{x|x≠x1}。

（3）当Δ<0 时，方程无实根，一元二次不等式无解。

综上所述，我们可以通过以上步骤求解一元二次不等式，并得到其解集。