第一讲 合(1和2)
张松老师《精神分析》讲课笔记1-2课

张松老师《精神分析讲座》听课笔记(1~2课)第一讲什么是精神分析Ⅰ本讲课内容提要一、精神分析的研究对象二、精神分析的两大魅力1、精神分析的魅力之一是这把刀能深入到人的内心底层2、精神分析另外一个魅力是它的辩证性三、精分是什么?1、对精分的态度2、精神分析的本土化3、怎样学习精神分析?4、对精神分析学派治疗取向的简短评论四、精神分析的历史——驱力理论;客体;自体心理学Ⅱ具体授课内容一、精神分析的研究对象“精神分析”如果对这个词做自由联想会想到什么?头脑中的意象是什么?从学员反馈的情况来看,学员的理性反映比较多。
张老师的内容——中德培训、武汉中德医院、施其嘉的大烟斗、椅子、老外来培训的情景。
精神分析研究对象是潜意识。
潜意识对来访者来“内心深处”、“心劲”、“心理能量”可能比较容易被接受。
潜意识内容有:情结和症结。
它们的关系是:情结:一般是比较美好的。
女生喜欢一类男孩,是因为喜欢父亲的情结的体现。
症结:一般是压抑的内心冲突。
一般是一堆、一大束。
对症结的比喻:放在地下室的包、长了一个包刺。
神经症的症结特点是:被打碎的结,弥散性的。
如何来理解症结:第一,不被觉察、被意识排斥第二,痛苦的经历,不想被知道,被压抑在内心深处。
如何来识别症结:一般的来说,来访者在谈话时,咨询要仔细观察,一般不要打断。
当来访者诉说过程中,发生了:语速的改变、表情的改变、流眼泪、突改话题,这些都是识别创伤和症结的标志。
一个比喻:症结有了,冒出了,杀毒软件就开始运行,机器运行速度就会缓慢。
个案:一女生,2~4岁父母为了要第二个小孩子,把她送到姑姑家。
在咨询前5、6次,只要谈到父亲,就会流眼泪。
精神分析就是研究我们不能意识到潜意识。
给来访者做精神分析,就是让来访者进行自我探索,觉察自己所不知道的潜意识。
二、精神分析是什么?第一,从临床来看,精神分析是观察学。
所谓的观察学,即把我们所观察的东西告诉知病人。
这种观察看我们内心的感受来实现的。
第一讲讲道的重要观念

第一讲:讲道的重要观念本课程分下列几个部分:一、讲道到和讲道的人。
二、讲道和读经。
三、讲道和信息的结构。
首先分享几个讲道的观念:(一)讲道是宣扬那已经完成上帝话语。
一定要讲圣经,以圣经为素材与根基,不可增加或减少甚么。
要忠心的解释神的话语。
(二)讲道是上帝对人讲话。
讲道的职分非常重要,要看重它。
我们代表上帝,把祂的话语告诉祂的百姓。
我们倚靠神而讲道,因为我们是蒙召的人,上帝呼召我们讲道。
我们要先用神的话来造就自己,然后靠圣灵所加的力量,忠心的传讲给别人。
(三)基督教不祇是一个系统的神学思想,而且是一种生活方式。
讲道不可只有神学思想,并且一定要有生活的应用。
听者必须要知道如何将这一篇道运用在他们的生活当中。
只有上帝的话语才能改变人的生命。
没有应用的讲道不是讲道。
(四)讲道是见证过去发生的历史事实。
我们知道所讲的事情是实在的,知道福音改变人心是实在的,就更有确据的传讲。
讲道的人是一个见证人。
(五)每次讲道必需发问以下三个问题。
1)我是否有传讲耶稣?2)我的讲道是否有救赎性成份?3)我是否忠于该段经文?第二讲:讲道为首的生活习惯如果确定要为你一生积存讲道材料,这是传道面临的主要问题,因此传道人需要养成一种生活习惯,使你一生都不缺乏讲道材料。
(一)不断为预备讲道而读经。
三种读经1.灵修的读经,用神的话来洁净我们的生命。
2.熟读全本圣经,逐卷研读,为要讲全备的道。
3.为讲道而读经,看弟兄姊妹的需要挑出经文讲道。
(二)养成祷告的习惯。
1.反省讲道与自己生命关系:求上帝先对我讲话。
2.为听道弟兄姊妹祷告,求上帝借着所讲的道改变他们。
(三)过着一个实践圣经教导的生活。
遇到生活的每一件事,首先想到圣经是如何教导。
(四)学习如何将理想实践化。
将一些奥秘,难懂的事情,深入浅出,教导会众如何实现出来。
(五)养成有系统性,结构性的逻辑生活习惯。
(六)不断的读书,增广见闻。
加深讲道的深度。
第三讲:讲道的重要性讲道是事奉最重要工作,为什么?假如牧者不真实地相信讲道的重要,他的事奉不过是一位从事宗教工作者。
幼儿园数学教案_学习1和2

幼儿园数学教案:学习1和2教案标题:幼儿园数学——学习1和2一、教学目标:1. 让孩子们认识并能识别数字1和2。
2. 培养孩子们的数数能力和初步的计数概念。
3. 通过实践活动,提升孩子们的观察力和动手能力。
4. 初步理解1和2的含义,如“一个”和“两个”。
二、教学内容:1. 认识数字1和2的形状和写法。
2. 学习用手指表示1和2。
3. 进行与1和2相关的实物计数活动。
4. 理解“一个”和“两个”的概念。
三、教学准备:1. 数字卡片1和2。
2. 各种实物,如水果、玩具等,数量分别为1个和2个。
3. 白板和白板笔。
4. 计数游戏材料。
四、教学过程:1. 引入:展示数字卡片1和2,引导孩子们认识它们的形状和名称。
2. 讲解:通过手指演示,让孩子们理解1和2的含义,并尝试自己用手指表示。
3. 实践活动:分发实物,让孩子们进行计数活动,理解“一个”和“两个”的概念。
4. 游戏环节:设计简单的计数游戏,如找一找教室里有多少个“1”和“2”,或者将物品分成“1”和“2”的两组等。
5. 回顾总结:带领孩子们一起回顾今天学到的知识,确认他们是否能正确识别和理解1和2。
五、教学延伸:在日常生活中,鼓励孩子们寻找和识别与1和2相关的事物,如一个苹果、两个香蕉等,进一步巩固他们的学习。
六、教学总结:本次课程,孩子们成功地认识了数字1和2,能够用手指表示并进行简单的计数活动。
他们对“一个”和“两个”的概念有了初步的理解。
在接下来的学习中,我们将继续深化他们的计数能力和数字认知。
七、教学评估:1. 观察孩子们在课堂上的参与度和反应,了解他们对1和2的理解程度。
2. 设计简单的测试或游戏,如请孩子们指出哪些物品的数量是1或2,以此评估他们的学习效果。
3. 鼓励家长在家中进行复习和实践,反馈孩子们在家中的表现,作为教学效果的参考。
教育管理原理-第一讲-(第1-2章)练习题

教育管理原理-第一讲-(第1-2章)练习题1.管理具有两重性,即() [单选题] *A.文化性与非文化性的统一B.经济性与非经济性的统一C.非政治性与政治性的统一(正确答案)D.一般性和特殊性的统一2. 年中国设立了学部,后改称教育部。
() [单选题] *A.1949B.2000C.1905(正确答案)D.19103.日本的中小学设立“教员意见登记簿”,鼓励教员对学校管理工作提出意见,到期末,须对教员的意见给予答复,意见采纳了的要予以表扬,未被采纳的要说明原因。
这反映了教育管理发展趋势的() [单选题] *A.民主化(正确答案)B.科学化C.均权化D.专业化4.教育管理的特殊规律包括()①教育管理活动的规律②教育管理体制的规律③教育管理机制的规律④教育管理观念的规律 [单选题] *A.①②③B.②③④C.①②④D.①②③④(正确答案)5.学科体系包括() [单选题] *A.一门学科和学科群B.著作体系和著作层次体系C.著作体系和教材体系(正确答案)D.著作层次体系和教材层次体系6.现代教育管理学的两大源流是()①德国的行政学②美国的行政学③法国的行政学④中国的行政学 [单选题] *A.①②(正确答案)B.②③C.①④D.③④7.人际关系理论,是等在霍桑工厂里通过实验而创立的理论。
() [单选题] *A.梅奥和雷斯利斯伯格(正确答案)B.卡伯利和梅奥C.泰勒和雷斯利斯伯格D.巴纳德和西蒙8.教育管理学在我国作为独立形态的学科始于() [单选题] *A.中华人民共和国成立B.改革开放C.19世纪初D.19世纪末20世纪初(正确答案)9.库恩提出了的概念,不主张用数学概念来阐述理论,而是借助历史材料来构建理论() [单选题] *A.变式B.范式(正确答案)C.实证主义D.思辨哲学10.管理具有两重性,其中,管理与生产力和社会化大生产相联系的属性我们称之为() [单选题] *A.非政治性(正确答案)B.政治性C.经济性D.复杂性11.目前在美国的各大学普遍设有教育管理专业,培养教育管理方面的专业人员。
组合计数1 教师版 (1)

第一讲 组合计数(1)本讲概述组合数学是竞赛中最重要的一个板块,也是变化最多,最灵活,难以掌握,至今还没有一个系统体系的学科.解决竞赛中的组合数学问题,往往不需要太多专门的知识,而是要求深刻的洞察能力和强大的化归、转化能力.所谓“得组合者得天下”,在联赛一二试乃至冬令营、集训队、IMO 中,最后的胜者往往是成功完成组合问题的同学.因此,学习组合数学对于竞赛获奖以及数学能力的培养都有着十分重要的意义.从本讲开始,我们将用七讲来对组合数学做一个大致的勾勒.通过这七讲的学习,达到以下目的:1、掌握联赛一二试组合问题的特点与解法;2、对组合数学这门学科有一个初步的认识,为进一步学习打下基础;3、了解部分冬令营级别组合问题的难度与解题模式.七讲内容分别为:一、组合计数(1) 比高考略难的基本计数问题 二、组合计数(2) 需要较多技巧的专门计数问题 三、组合恒等式 较为重要和有趣味的组合恒等式 四、抽屉原理与存在性问题 五、容斥原理与极端性原理六、染色问题与操作问题 七、组合数学综合问题本讲中,假定各位同学已经大致学完了高考难度的排列组合模块内容,对加法原理、乘法原理等有一定的理解并能完成相关的问题.教师备注:本讲可与下一讲打通讲述,也可本讲专门讲常规的枚举、基本的组合问题,下一讲专门讲述一些较为高级的技巧.首先给出一些相关的基本知识: 1、 加法原理与乘法原理加法原理:完成一件事的方法可分成n 个互不相交的类,在第1类到第n 类分别有12,,...,n m m m 种方法,则总共完成这件事有121...nin i mm m m ==+++∑种方法.应用加法原理的关键在于通过适当的分类,使得每一类都相对易于计数.乘法原理:完成一件事的方法有n 个步骤,,在第1步到第n 步分别有12,,...,n m m m 种方法,则总共完成这件事有121...nini m m m m ==∏ 种方法. 应用乘法原理的关键在于通过适当的分步,使得每一步都相对易于计数.由上可见,加法原理与乘法原理也是化归思想的应用,通过这两个原理以及它们的组合,可以将一个复杂的组合计数问题分解成若干个便于计数的小问题.2、 无重排列与组合阶乘:定义 !(1)(2)...21n n n n =⋅-⋅-⋅⋅⋅,读作n 的阶乘无重排列:从n 个不同元素中任取m 个不同元素排成一列,不同的排列种数称为排列数,记为mn A (部分书中记为m n P ),由乘法原理得到!(1)...(1)()!m n n A n n n m n m ==⋅-⋅⋅⋅-+-无重组合:从n 个不同元素中任取m 个元素并为一组,不同的组合种数称为组合数,记为mn C ,其公式为(1)...(1)!!!()!!mmn nA n n n m n C m m n m m ⋅-⋅⋅⋅-+===- 3、 可重排列与组合(仅给出结论,请自证之)可重排列:从n 个不同元素中可重复地任取m 个元素排成一列,不同的排列种数有mn 种; 有限个重复元素的全排列:设n 个元素由k 个不同元素12,,...,k a a a 组成,分别有12,,...,k n n n 个(12...k n n n n +++=),那么这n 个元素的全排列数为12!!!...!k n n n n ⋅⋅⋅可重组合:从n 个不同元素中,任意可重复地选取m 个元素,称为n 个不同元素中取m 个元素的可重组合,其种数为1mn m C +-4、 圆排列(仅给出结论,请自证之)在n 个不同元素中,每次取出m 个元素排在一个圆环上,叫做一个圆排列(或叫环状排列).圆排列有三个特点:(i )无头无尾;(ii )按照同一方向转换后仍是同一排列;(iii )两个圆排列只有在元素不同或者元素虽然相同,但元素之间的顺序不同,才是不同的圆排列.在},,,,{321n a a a a A =的n 个元素中,每次取出m 个不同的元素进行圆排列,圆排列数为mn A m.例题精讲板块一 利用加法、乘法原理以及枚举方法计数联赛一试的填空题中出现的计数问题有接近一半的问题不需要用到很高深的技巧,而是直接利用最基本的加法、乘法原理,以及枚举方法来计数.这主要是考虑到有一部分参加联赛的同学并未经过专业的竞赛训练.虽然如此,这部分计数问题枚举起来往往分类复杂,需要小心仔细.从往年的联赛试题来看,枚举法解决计数问题是最主要的题型之一,其难点在于做到“不重不漏”,这是加法原理的一个简单的应用.枚举过程中,采用恰当的分类、分步形式,往往会收到化难为易的效果.【例1】 (高考难度的热身问题)(1)等腰三角形的三边均为正整数.它们周长不大于10.这样不同的三角形的种数为A .8B .9C .10D .1l(2)有两排座位,前排11个座位,后排12个座位,现安排2人就座,规定前排中间的3个座位不能坐,并且这2人不左右相邻,那么不同排法的种数是 A.234 B .346 C. 350 D .363 【解析】 (1)设三边为x,y ,z ,则x+y+z ≤10,由三边关系共有(1,1,1),(1,2,2),(1,3,3),(1,4,4),(2,2,2),(2,2,3),(2,3,3),(2,4,4),(3,3,3),(3,3,4)共10种.(2)B 前排中间的3个座位不能坐,有排法220A ,其中相邻的分三类,在前排的其中的4个座位有322A ;则符合条件的排法种数中2222222201133A A A A ---=346,故选B (这是正难则反的思想,从总体中除去不符合要求的) 另解:分三类:①两人坐在前排,按要求有4·6+4·5=44种坐法.②两人坐在后排,按要求有:211A =110种坐法.③两人分别坐在前后排,有8×12×2=192种∴共有346种排法.【例2】 (1)有多少个能被3整除而又含有数字6的五位数?(2)集合{1,2,...,100}的子集中共有多少个至少包含一个奇数?【解析】 (1)按照上题正难则反的思想,可以先找出所有的五位数,共有90000个,其中可被3整除的有30000个,下面研究这30000个数中不含数字6的数,最高位有8种选择,千、百、十位各有9种选择,个位数除不能为6外,还应满足恰各位数之和可被3整除,这恰有3种选择,例如当前四位除以3余2时,个位应为1,4,7之一;故能被3整除且不含数字6的有8999317496⨯⨯⨯⨯=个,故所求五位数有30000-17496=12504个(2)显然全部子集数为1002个,不包含任何奇数的子集即{2,4,6,...,98,100}的子集共有502个,故所求子集个数为1005022-个.(思考:请用最简洁的方法确定为何n 元集合子集数为2n个)【例3】 设ABCDEF 为正六边形,一只青蛙开始在顶点A 处,它每次可随意地跳到相邻两顶点之一.若在5次之内跳到D 点,则停止跳动;若5次之内不能到达D 点,则跳完5次也停止跳动,那么这只青蛙从开始到停止,可能出现的不同跳法共 种【解析】 这是标准的联赛风格的枚举问题,所谓杀鸡焉用牛刀,用递归方法来解这类问题就太麻烦了.显然青蛙不能跳1,2,4次到达D 点,于是青蛙的跳法只有以下两种: (1)青蛙跳3次后到达D 点,有2种跳法; (2)青蛙跳5次后停止,跳3次有322-种,后两次有22种,共计24种; 所以,合计有26种跳法注 本题为1997年联赛试题【例4】 从给定的六种不同颜色中选用若干种颜色,将一个正方体的六个面染色,每面恰染一种颜色,每两个具有公共棱的面染成不同的颜色。
1_第一讲_基础知识

D B
+ v DS -
+ -
G
vGS
S
v DS
vGS
+ +
G D
B S
n+
n+
p-
耗尽层
15
(2)当VGS>0,VGB>0,VDS=0
衬底中的电子受到吸引,向衬 底表面运动;空穴受到排斥,向 衬底内部运动。向上运动的电子 与表面的空穴复合,形成了一层 耗尽层,形成一个栅极指向衬底 的垂直电场EV 。
=1/Ron
深线性区等 效电阻
29
(四)IV特性总结
截止区: VGS VTH 深线性区: 线性区: VDS VGS VTH 饱和区:
ID 0
I D n Cox
I D nCox
W VGS VTH VDS L
ID
1 W 2 nCox VGS VTH 2 L
模拟CMOS集成电路设计
Design of Analog CMOS Integrated Circuit
Institute of VLSI Design, Hefei U.of Tech
第一讲 基础知识
1
1.1 概 述
2
1、为什么需要模拟集成电路?
(1)为什么需要模拟电路
自然界的信 号大多是模 拟信号
8
仿真验证电路性能
修改电路参数、拓扑
版图设计
版图参数提取
测试方案设计
工 艺
芯片制造
测试与分析
单元库
系统要求
综合
系统设计和 功能划分
系 统 及 功 能 级 设 计
门级仿真
第一讲 聚合方法(3逐步聚合反应)

← ←
三级反应 二级反应
3.1 自催化体系
通式 R=
羧基既是反应官能团 ,又是催化剂 设开始时 C=[COOH]=[OH]
记C0为t=0的羧基或羟基浓度 (C为 t时刻的) 忽略移去水使体积减少:
积分
C=C0(1-P)
讨 论:
1. 数据处理:
a. 以
1 (1 P ) 2 ~t,
X ~t,亦即
kc: 该化学反应速度常数 则:生成物的形成速率:
ka kc d [ P] [ A][ B] dt kb kc
① 扩散速率远大于反应速率,kb
>>
kc
d [ p] k a k c [ A][ B] dt kb
②反应速率远大于扩散速率,kc
>>
kb
d [ p] ka [ A][ B] dt
COOH参加反应的几率 则1-P就是此时刻一个给定的COOH还没参加
反应的几率
聚酰胺化反应的过程
分子式
O
存在的结构 反应了的 单元数 COOH数 1 2 3 4 x 0 1 2 3 x-1
若端基从-NH2 开始,则有(x-1)个反应了的 COOH基和一个未反应的COOH基作尾端基
则: 1 个COOH反应掉的几率: P x-1个COOH连续反应掉的几率: Px-1 1 个COOH未反应掉的几率: 1-P
3. P≥0.80时,积分动力学表达式与实验值符合得很好
3.2 外加酸催化体系
通式
外加强酸催化剂
kcat[H+]>>k3[COOH],k3[COOH]可忽略
[H+]不变, 令k2=kcat [H+] 二级反应,将其积分可得
讨 论:
第一讲 集合的概念与运算技巧

解答启迪:∵A∩B={2,5},∴ 3-2 2- +7=5,由此求得 =2或 =±1. A={2,4,5},集合B中的元素是什么,它是否满足元素的互异性,有待于进一步考查.
∴M∩N={y|y≥1}∩{y|y∈R}={y|y≥1},∴应选D.
点评:①本题求M∩N,经常发生解方程组
从而选B的错误,这是由于在集合概念的理解上,仅注意了构成集合元素的共同属性,而忽视了集合的元素是什么.事实上M、N的元素是数而不是点,因此M、N是数集而不是点集.②集合是由元素构成的,认识集合要从认识元素开始,要注意区分{x|y=x2+1}、{y|y=x2+1,x∈R}、{(x,y)|y=x2+1,x∈R},这三个集合是不同的.
思路启迪:本题用推理的方法求解不如先画出文氏图,用填图的方法来得简捷,由图不难看出.
解:A={1,3,5,7},B={2,3,4,6,8}.
例17.集合A={x|x2+5x-6≤0},B={x|x2+3x>0},求A∪B和A∩B.
解:∵ A={x|x2-5x-6≤0}={x|-6≤x≤1},
当 =1时, 2-2 +2=1,与元素的互异性相违背,故应舍去 =12,5}相矛盾,故又舍去 =-1.
当 =2时,A={2,4,5},B={1,3,2,5,25},此时A∩B={2,5},满足题设.
故 =2为所求.
例6. 已知集合A={ , +b, +2b},B={ , c, c2}.若A=B,则c的值是______.
∴c2-2c+1=0,即c=1,但c=1时,B中的三元素又相同,此时无解.
第一讲 集合

第一讲准确把握集合与逻辑用语中的概念1. 重视集合元素的互异性在解题中的作用例1 设集合A={1,3,a},B={1,a2-a+1},求AUB.解:(1)如果a2-a+1=3,则a=-1或a=2.由集合元素的互异性知在集合A中a≠ 1且a≠ 3.在集合B中a2-a+1≠ 1,即a≠ O且a≠ 1.AB={-1,1,3}或者是AUB={1,2,3}.(2)如果a2-a+1=a,则a=1.但这不符合集合元素的互异性,应舍去.(3)如果a≠ 1,a≠ 3,a≠ 0,a≠ -1,a≠ -2,则AUB={1,3,a,a2-a+1}.例2 已知集合A={3,3+m,3+ 5m},B={3,3p,3p2},且A=B,求m,p的值.先看错解的过程错解:由A=B,得或( Ⅱ)故; , .评注:事实上,当m=0,p=1时,集合A={3,3,3}和集合B={3,3,3}显然不符合元素的互异性,应当舍去.正解答案为:或.2. 忽视空集是任何一个集合的子集,往往发生解题错误空集是任何一个集合的子集,是任何一个非空集合的真子集.在解答某些关于集合A 是集合B的子集这类问题时,往往因为忽视空集的重要性而造成解题失误.例 3 已知集合A={x|x2+(p+2)x+1=0,x∈ R}且A∩ R+= Φ,则实数p的集合是( ).A.{p|p≥ -2}B.{p|p≥ 0}C.{p|-4<p<0}D.{p|p>-4}解:(1)A≠Φ时,A∩ R+=Φ表示方程x2+(p+2)x+1=0有实数解,且为非正实数.根据判别式和韦达定理,得到{△=(p+2)2-4≥ 0,p+2≥ 0.∴p≥ 0.(2)A= Φ时,显然A∩ R+= Φ,它表示方程没有实数解.∴△=(p+2)2-4<0.∴-4<p<0.综上得到{p>-4},应选D.例 4 设集合A={x|x2-3x+2=O},集合B={x|x2-ax+2=0},若A∪ B=A,求实数a 的值所组成的集合.解:易知A={1,2},由A∪B=A,有B A.(1)若B=A,显然a=3.(2)若B A,则分两种情况讨论.①B中只含一个元素1或2.由△=a2-8=0,得a=± 2;当a=± 2时,x=或x=-.但B={}或B={-}都不符合 B A,应该舍去.②B= Φ,此时方程x2-x+2=0没有实数根,由△=a2-8<0,得-2 <a<2 .综上知,若A∪B=A,则由a值组成的集合是:{a|-2 <a<2 }∪{a|a=3}3. 在研究两个集合的关系时,“集合相等”至关重要例 5 集合P,Q,M 满足P∩ Q=P,Q∩ M=Q,则集合P,M的关系为( ).A. P MB.P MC.P MD.P M解:(1)当集合P,Q,M不相等时,如图(1)所示:有P M.(2)当集合P=Q=M时,如图(2)所示:所以得到P=M.综上所述,∴P M.应当选C.例 6 已知集合M,N及全集U,则M N是M∩ C U N= Φ的( ).A.充分非必要条件B.必要非充分条件C.充要条件D.既非充分又非必要条件解:如图可知M N是M∩C U N= Φ的充分条件.M∩ C U N= Φ时则有M N或M=N两种可能.∴M N是M∩ C U N= Φ的充分非必要条件. ∴应选A.4. 弄懂集合语言的含义。
第一讲 化学反应(讲义)

第一讲化学反应1.把铜粉放入装有浓氨水的试管中,塞紧试管塞,振荡后发现试管塞越来越紧,且溶液逐渐变为浅黄色(近乎无色)溶液A,打开试管塞后,溶液迅速变为蓝色溶液B。
试回答下列问题:(1)写出上述变化的化学方程式。
(2)试从结构上解释:A为何为无色,B为何为蓝色?(3)上述反应有何用途?(4)若将铜粉换成氧化亚铜,重复上述实验,现象是否一样?2.将NH4Cl溶液用盐酸调制成pH=4的溶液,然后进行电解,发现制成了一种常见的二元化合物A,用空气把气体产物带出电解槽即得到较为纯净的A。
A是一种挥发性的易爆炸的浓稠液体,沸点只有700C,其结构与NH3相似。
(1)试确定A,写出生成A的离子方程式。
(2)比较A和NH3的极性大小。
(3)将A与NaClO2按物质的量之比1∶6混合,可得到一种绿色环保的消毒剂B以及能使湿润的红色石蕊试纸变蓝的气体C。
A的消毒效果是同质量的Cl2的2.63倍。
试写出其反应的离子方程式。
(4)已知A中两元素的电负性相同。
试设计一个试验确定A中哪一种元素带部分正电荷,哪一种元素带部分负电荷?简述其实验步骤。
3.某固体化合物,一经撞击就发生分解,产生大量气体(所得气体均为单质),所以该化合物应用于汽车安全装置中。
经测此化合物只有N、H两种元素组成,其中含N质量分数为93.29%。
(1)试写出此化合物的结构式,每100g此化合物,受撞击后可生成多少升的气体(在298K、120Kpa的条件下)(2)在特定条件下,K2CrO4与H2O2发生氧化还原反应,生成化合物A,A中含有Cr17.49%,K39.46%,请写出A的化学式,指出A中Cr的氧化数,A在化学性质上最大的特点为是什么?请写出K2CrO4与H2O2反应的离子方程式4.氰氨化钙(CaCN2)是一种多用途的有机肥料,它很容易用廉价的普通化学品如CaCO3来生产,CaCO3热分解产生白色固体X A和无色气体X B,后者不支持燃烧。
用碳还原X A生产灰色固体X C和气体X D,X C和X D能进一步氧化,X C与氮反应,最终生成CaCN2。
线性代数讲座_1,2章

IO
P T A* A A 0
Q A T A1 b A 0
Q可逆 Q 0 T A1 b 0 T A1 b
例4. 设
A, B 均为 2 阶矩阵, 若
A
2,
B
3,
O
则
B
A O
*
=
A
O 2A*
3B*
O
B
O 3A*
2B*
O
C
O 2B*
3A*
a122
a123
3a121 1
a11 3 3
例3. 设 A 为 n 阶可逆矩阵, α 为 n 维列向量, b 为常数, 记
I O A
P
T
A*
A
,
Q
T
b
.
(1) 计算并化简 PQ. (2) 证明矩阵 Q可逆 T A1 b.
分析:
I O A
PQ
T
A*
A
标准方法: 利用行列式性质直接计算:
A 2B 1, 2, 3, 1 23, 1, 2, 2
1 23 , 2 21 , 3 22 , 1 22
A 2B 1 23 , 2 21, 3 22 , 1
1 23 , 2 21 , 3 22 , 22
1 2 0 0
按第一行(列)展开, 直接求得;
(3) 三线型:
按第一行(列)或最后一行(列)展开, 得
递推关系式, 解递推关系式;
(4) “爪”型(箭型) 行列式: 用中间的“爪”消去某条 “爪”;
(5) 计算某行(列)元的(代数)余子式的线性组合:
构造“新行列式”;
知识点2: 行列式计算
(6) 抽象行列式 |A| = |α, β, γ|的计算:
(复习指导)第一章第一讲 集合的概念与运算含答案

第一章集合与常用逻辑用语第一讲集合的概念与运算知识梳理·双基自测ZHI SHI SHU LI SHUANG JI ZI CE知识梳理知识点一集合的基本概念一组对象的总体构成一个集合.(1)集合中元素的三大特征:确定性、互异性、无序性.(2)集合中元素与集合的关系:对于元素a与集合A,a∈A或a∉A,二者必居其一.(3)常见集合的符号表示.数集自然数集正整数集整数集有理数集实数集符号N N*Z Q R(4)集合的表示法:列举法、描述法、Venn图法、区间表示法.(5)集合的分类:集合按元素个数的多少分为有限集、无限集,有限集常用列举法表示,无限集常用描述法表示.知识点二集合之间的基本关系关系定义表示相等集合A与集合B中的所有元素都相同A=B子集A中的任意一个元素都是B中的元素A⊆B真子集A是B的子集,且B中至少有一个元素不属于A A B注意:(1)空集用∅表示.(2)若集合A中含有n个元素,则其子集个数为2n,真子集个数为2n-1,非空真子集的个数为2n-2.(3)空集是任何集合的子集,是任何非空集合的真子集.(4)若A⊆B,B⊆C,则A⊆C.知识点三集合的基本运算符号语言交集A∩B 并集A∪B 补集∁U A图形语言意义A∩B={x|x∈A且x∈B}A∪B={x|x∈A或x∈B}∁U A={x|x∈U且x∉A}重要结论1.A∩A=A,A∩∅=∅.2.A∪A=A,A∪∅=A.3.A∩(∁U A)=∅,A∪(∁U A)=U,∁U(∁U A)=A.4.A⊆B⇔A∩B=A⇔A∪B=B⇔∁U A⊇∁U B⇔A∩(∁U B)=∅.双基自测题组一走出误区1.判断下列结论是否正确(请在括号中打“√”或“×”)(1)集合A中含有三个元素0,1,x,且x2∈A,则实数x的值为1或-1或0.(×)(2){x|y=x2}={y|y=x2}={(x,y)|y=x2}.(×)(3)方程x -2 022+(y+2 023)2=0的解集为{2 022,-2 023}.(×)(4)若A∩B=A∩C,则B=C.(×)(5)设U=R,A={x|lg x<1},则∁U A={x|lg x≥1}={x|x≥10}.(×)题组二走进教材2.(必修1P 5B1改编)若集合P={x∈N|x≤ 2 022},a=45,则(D)A.a∈P B.{a}∈PC.{a}⊆P D.a∉P[解析]452=2 025>2 022,∴a∉P,故选D.3.(必修1P7T3(2)改编)若A={x|x=4k-1,k∈Z},B={x=2k-1,k∈Z},则集合A与B 的关系是(B)A.A=B B.A BC.A B D.B⊆A[解析]因为集合B={x|x=2k-1,k∈Z},A={x|x=4k-1,k∈Z}={x|x=2(2k)-1,k∈Z},集合B表示2与整数的积减1的集合,集合A表示2与偶数的积减1的集合,所以A B,故选B.题组三走向高考4.(2020·新高考Ⅱ,1,5分)设集合A={2,3,5,7},B={1,2,3,5,8},则A∩B =(C)A.{1,8} B.{2,5}C.{2,3,5} D.{1,2,3,5,7,8}[解析]∵A={2,3,5,7},B={1,2,3,5,8},∴A∩B={2,3,5},故选C.5.(2020·新高考Ⅰ,1,5分)设集合A ={x |1≤x ≤3},B ={x |2<x <4},则A ∪B =( C ) A .{x |2<x ≤3} B .{x |2≤x ≤3} C .{x |1≤x <4}D .{x |1<x <4}[解析] 已知A ={x |1≤x ≤3},B ={x |2<x <4},在数轴上表示出两个集合,由图易知A ∪B ={x |1≤x <4}.故选C .6.(2020·天津,1,5分)设全集U ={-3,-2,-1,0,1,2,3},集合A ={-1,0,1,2},B ={-3,0,2,3},则A ∩(∁U B )=( C )A .{-3,3}B .{0,2}C .{-1,1}D .{-3,-2,-1,1,3}[解析] 因为U ={-3,-2,-1,0,1,2,3},B ={-3,0,2,3},所以∁U B ={-2,-1,1},又A ={-1,0,1,2},所以A ∩(∁U B )={-1,1},故选C .考点突破·互动探究KAO DIAN TU PO HU DONG TAN JIU 考点一 集合的基本概念——自主练透例1 (1)(多选题)已知集合A ={x |x =3k +1,k ∈Z },则下列表示正确的是( ABD )A .-2∈AB .2 022∉AC .3k 2+1∉AD .-35∈A(2)已知集合A ={0,1,2},则集合B ={(x ,y )|x ≥y ,x ∈A ,y ∈A }中元素的个数是( C ) A .1 B .3 C .6D .9(3)已知集合A ={a +2,(a +1)2,a 2+3a +3},若1∈A ,则2 020a 的值为1;若1∉A ,则a 不可能取得的值为-2,-1,0,-1+52,-1-52.[解析] (1)当-2=3k +1时,k =-1∈Z ,故A 正确;当2 022=3k +1时,k =67323∉Z ,故B 正确;∵k ∈Z ,∴k 2∈Z ,显然3k 2+1∈A ,当-35=3k +1时,k =-12∈Z ,故D 正确.故选A 、B 、D .(2)当x =0时,y =0;当x =1时,y =0或y =1; 当x =2时,y =0,1,2.故集合B ={(0,0),(1,0),(1,1),(2,0),(2,1),(2,2)}, 即集合B 中有6个元素.(3)若a +2=1,则a =-1,A ={1,0,1},不合题意;若(a +1)2=1,则a =0或-2,当a =0时,A ={2,1,3},当a =-2时,A ={0,1,1},不合题意;若a 2+3a +3=1,则a =-1或-2,显然都不合题意;因此a =0,所以2 0200=1.∵1∉A ,∴a +2≠1,∴a ≠-1;(a +1)2≠1,解得a ≠0,-2;a 2+3a +3≠1解得a ≠-1,-2.又∵a +2、(a +1)2、a 2+3a +3互不相等,∴a +2≠(a +1)2得a ≠-1±52;a +2≠a 2+3a+3得a ≠-1;(a +1)2≠a 2+3a +3得a ≠-2;综上a 的值不可以为-2,-1,0,-1+52,-1-52.名师点拨 MING SHI DIAN BO(1)用描述法表示集合,首先要搞清楚集合中代表元素的含义,再看元素的限制条件,明白集合的类型,是数集、点集还是其他类型的集合.(2)集合中元素的互异性常常容易忽略,特别是含有字母的集合,在求出字母的值后,要注意检验集合中元素是否满足互异性.分类讨论的思想方法常用于解决集合问题.考点二 集合之间的基本关系——师生共研例2 (1)(2021·新高考八省联考)已知M ,N 均为R 的子集,且∁R M ⊆N ,则M ∪(∁R N )=( B )A .∅B .MC .ND .R(2)(多选题)已知集合A =⎩⎨⎧⎭⎬⎫-13,12,B ={x |ax +1=0},且B ⊆A ,则实数a 的可能取值为( BCD )A .-3B .-2C .0D .3(3)设集合M =⎩⎨⎧⎭⎬⎫x |x =k 3+16,k ∈Z ,N =⎩⎨⎧⎭⎬⎫x ⎪⎪x =k 6+23,k ∈Z ,则下面正确的是( B ) A .M =N B .MNC .NMD .M ∩N =∅[解析] (1)如图,∁R M ⊆N ,显然(∁R N )⊆M ,∴M ∪(∁R N )=M ,故选B .(2)本题考查集合之间的关系.由题知B ⊆A ,B ={x |ax +1=0},所以B =⎩⎨⎧⎭⎬⎫-13,⎩⎨⎧⎭⎬⎫12,∅.当B =⎩⎨⎧⎭⎬⎫-13时,-13a +1=0,解得a =3;当B =⎩⎨⎧⎭⎬⎫12时,12a +1=0,解得a =-2;当B =∅时,a =0.综上可得实数a 的可能取值为3,0,-2,故选B 、C 、D .(3)解法一:(列举法),由题意知 M =⎩⎨⎧⎭⎬⎫…,-12,-16,16,12,56,76,…N =⎩⎨⎧⎭⎬⎫…,-16,0,16,13,12,23,56,…显然M N ,故选B .解法二:(描述法) M =⎩⎨⎧⎭⎬⎫x |x =2k +16,k ∈Z ,N =⎩⎨⎧⎭⎬⎫x |x =k +46,k ∈Z∵2k +1表示所有奇数,而k +4表示所有整数(k ∈Z ) ∴MN ,故选B .名师点拨 MING SHI DIAN BO 判断集合间关系的3种方法 列举法根据题中限定条件把集合元素表示出来,然后比较集合元素的异同,从而找出集合之间的关系.(如第(3)题解法一)结构法从元素的结构特点入手,结合通分、化简、变形等技巧,从元素结构上找差异进行判断.(如第(3)题解法二)数轴法在同一个数轴上表示出两个集合,比较端点之间的大小关系,从而确定集合与集合之间的关系.(1)集合M =⎩⎨⎧⎭⎬⎫x |x =n 2+1,n ∈Z ,N =⎩⎨⎧⎭⎬⎫y |y =m +12,m ∈Z ,则两集合M ,N 的关系为( D )A .M ∩N =∅B .M =NC .M ⊆ND .N ⊆M(2)(多选题)(2020·湖南长郡中学模拟改编)已知集合M ={y |y =x -|x |,x ∈R },N =⎩⎨⎧⎭⎬⎫y |y =⎝⎛⎭⎫12x ,x ∈R ,则下列结论不正确的是( ABD ) A .M =N B .N ⊆M C .M =∁R ND .(∁R N )∩M =∅(3)已知集合A ={x ∈R |x 2-3x +2=0},B ={x ∈N |0<x <5},则满足条件A ⊆C ⊆B 的集合C 的个数为4.(4)已知集合A ={x |x 2-2 023x +2 022<0},B ={x |x <a },若A ⊆B ,则实数a 的取值范围是[2_022,+∞).[解析] (1)由题意,对于集合M ,当n 为偶数时,设n =2k (k ∈Z ),则x =k +1(k ∈Z ),当n 为奇数时,设n =2k +1(k ∈Z ),则x =k +1+12(k ∈Z ),∴N ⊆M ,故选D .(2)由题意得y =x -|x |=⎩⎪⎨⎪⎧0,x ≥0,2x ,x <0,∴M =(-∞,0],N =(0,+∞),∴M =∁R N .故选A 、B 、D . (3)由题意可得,A ={1,2},B ={1,2,3,4}.又∵A ⊆C ⊆B ,∴C ={1,2}或{1,2,3}或{1,2,4}或{1,2,3,4},∴有4个. (4)由x 2-2 023x +2 022<0,解得1<x <2 022, 故A ={x |1<x <2 022}.又B ={x |x <a },A ⊆B ,如图所示,可得a ≥2 022.考点三 集合的基本运算——多维探究 角度1 集合的运算例3 (1)(2020·课标Ⅱ)已知集合U ={-2,-1,0,1,2,3},A ={-1,0,1},B ={1,2},则∁U (A ∪B )=( A )A .{-2,3}B .{-2,2,3}C .{-2,-1,0,3}D .{-2,-1,0,2,3}(2)(2020·课标Ⅱ)已知集合A ={x ||x |<3,x ∈Z },B ={x ||x |>1,x ∈Z },则A ∩B =( D ) A .∅B .{-3,-2,2,3}C .{-2,0,2}D .{-2,2}(3)(2021·浙江杭州模拟)已知全集U =R ,集合A ={x |x 2-3x +2<0},集合B = {x |log 3(x +1) <1},则A ∪B =(-1,2),( ∁R A )∩B =(-1,1].[解析] (1)∵A ={-1,0,1},B ={1,2},∴A ∪B ={-1,0,1,2},又∵集合U ={-2,-1,0,1,2,3},∴∁U (A ∪B )={-2,3}.故选A .(2)由已知得A ={x |-3<x <3,x ∈Z }={-2,-1,0,1,2},B ={x |x <-1或x >1,x ∈Z },∴A ∩B ={-2,2}.故选D .(3)依题意可知,A ={x |1<x <2},B ={x |0<x +1<3}={x |-1<x <2},所以A ∪B =(-1,2),∁R A ={x |x ≤1或x ≥2},所以(∁R A )∩B =(-1,1].角度2 利用集合的运算求参数例4 (1)已知集合A ={x |x 2-3x <0),B ={1,a },且A ∩B 有4个子集,则实数a的取值范围是( B )A .(0,3)B .(0,1)∪(1,3)C .(0,1)D .(-∞,1)∪(3,+∞)(2)已知集合A ={x |-2≤x ≤5},B ={x |m +1≤x ≤2m -1}≠∅,若A ∩B =B ,则实数m 的取值范围为[2,3].[解析] (1)因为A ∩B 有4个子集,所以A ∩B 中有2个不同的元素,所以a ∈A ,所以a 2-3a <0,解得0<a <3.又a ≠1,所以实数a 的取值范围是(0,1)∪(1,3),故选B .(2)由A ∩B =B 知,B ⊆A .又B ≠∅,则⎩⎪⎨⎪⎧2m -1≥m +1,m +1≥-2,2m -1≤5.解得2≤m ≤3,则实数m 的取值范围为[2,3].[引申1]本例(2)中若B ={x |m +1≤x ≤2m -1}情况又如何? [解析] 应对B =∅和B ≠∅进行分类. ①若B =∅,则2m -1<m +1,此时m <2. ②若B ≠∅,由例得2≤m ≤3.由①②可得,符合题意的实数m 的取值范围为(-∞,3].[引申2]本例(2)中是否存在实数m ,使A ∪B =B ?若存在,求实数m 的取值范围;若不存在,请说明理由.[解析] 由A ∪B =B ,即A ⊆B 得⎩⎪⎨⎪⎧m +1≤-2,2m -1≥5,即⎩⎪⎨⎪⎧m ≤-3,m ≥3,不等式组无解,故不存在实数m ,使A ∪B =B . [引申3]本例(2)中,若B ={x |m +1≤x ≤1-2m },AB ,则m 的取值范围为(-∞,-3].[解析] 由题意可知⎩⎪⎨⎪⎧m +1≤-2,1-2m ≥5,解得m ≤-3.名师点拨 MING SHI DIAN BO集合的基本运算的关注点1.集合是由元素组成的,从研究集合中元素的构成入手是解决集合运算问题的前提. 2.有些集合是可以化简的,先化简再研究其关系并进行运算,可使问题简单明了,易于解决.3.注意数形结合思想的应用,常用的数形结合形式有数轴、坐标系和Venn 图. 4.根据集合运算结果求参数,先把符号语言译成文字语言,然后应用数形结合求解. 〔变式训练2〕(1)(角度1)(2020·北京,1,4分)已知集合A ={-1,0,1,2},B ={x |0<x <3},则A ∩B =( D )A .{-1,0,1}B .{0,1}C .{-1,1,2}D .{1,2}(2)(角度1)设全集U =R ,集合A ={x |0≤x ≤2},B ={y |1≤y ≤3},则(∁U A )∪B =( D ) A .(2,3] B .(-∞,1]∪(2,+∞) C .[1,2)D .(-∞,0)∪[1,+∞)(3)(角度2)已知集合A ={x |x <a },B ={x |x 2-3x +2<0},若A ∩B =B ,则实数a 的取值范围是( D )A .a <1B .a ≤1C .a >2D .a ≥2[解析] (1)集合A 与集合B 的公共元素为1,2,由交集的定义知A ∩B ={1,2},故选D . (2)∁U A ={x |x <0或x >2},则(∁U A )∪B ={x |x <0或x ≥1},故选D .(3)集合B ={x |x 2-3x +2<0}={x |1<x <2},由A ∩B =B 可得B ⊆A ,作出数轴如图,可知a ≥2.名师讲坛·素养提升MING SHI JIANG TAN SU YANG TI SHENG集合中的新定义问题例5 定义集合的商集运算为A B =⎩⎨⎧⎭⎬⎫x ⎪⎪x =m n ,m ∈A ,n ∈B ,已知集合A ={2,4,6},B =⎩⎨⎧⎭⎬⎫x ⎪⎪x =k 2-1,k ∈A ,则集合⎝⎛⎭⎫B A ∪B 中的元素个数为( B ) A .6 B .7 C .8D .9[解析] 由题意知,B ={0,1,2},B A =⎩⎨⎧⎭⎬⎫0,16,14,13,12,1,则⎝⎛⎭⎫B A ∪B =⎩⎨⎧⎭⎬⎫0,16,14,13,12,1,2,共有7个元素.名师点拨 MING SHI DIAN BO集合新定义问题的“3定”(1)定元素:确定已知集合中所含的元素,利用列举法写出所有元素.(2)定运算:根据要求及新定义运算,将所求解集合的运算问题转化为集合的交集、并集与补集的基本运算问题,或转化为数的有关运算问题.(3)定结果:根据定义的运算进行求解,利用列举法或描述法写出所求集合中的所有元素. 〔变式训练3〕(2021·江西九江联)设A ,B 是非空集合,定义A ⊗B ={x |x ∈(A ∪B )且x ∉(A ∩B )}.已知M ={y |y =-x 2+2x ,0<x <2},N ={y |y =2x -1,x >0},则M ⊗N =⎝⎛⎦⎤0,12∪(1,+∞) [解析] M ={y |y =-x 2+2x ,0<x <2}=(0,1],N ={y |y =2x -1,x >0}=⎝⎛⎭⎫12,+∞,则M ∪N =(0,+∞),M ∩N =⎝⎛⎦⎤12,1,所以M ⊗N =⎝⎛⎦⎤0,12∪(1,+∞).。
人教版九年级数学上册 第一讲 一元二次方程 讲义

第一讲 一元二次方程知识点1.一元二次方程的判断标准:(1)方程是_____方程(2)只有___个未知数(一元)(3)未知数的最高次数是____(二次) 三个条件同时满足的方程就是一元二次方程练习A :1、下面关于x 的方程中:①ax 2+bx+c=0;②3x 2-2x=1;③x+3=;④x 2-y=0;④(x+1)2= x 2-1.一元二次方程的个数是 . 2、若方程kx 2+x=3x 2+1是一元二次方程,则k 的取值范围是_________. 3、若关于x 的方程05122=+-+-x k x k是一元二次方程,则k 的取值范围是_________.4、若方程(m-1)x |m|+1-2x=4是一元二次方程,则m=______. 知识点 2.一元二次方程一般形式及有关概念一元二次方程的一般形式______________________,其中_______是二次项,______为二次项系数,_______是一次项,_______为一次项系数,______为常数项。
注意:二次项、二次项系数、一次项、一次项系数、常数项都包括前面的符号练习B:1、将一元二次方程3x(x-1)=5(x+2)化成一般形式为_____________,其中二次项系数 a=________,一次项系数b=__________,常数项c=__________ 知识点3.完全平方式练习C:1、说明代数式2241x x --总大于224x x -- 2、已知110a a +=求1a a-的值.3、若x 2+mx+9是一个完全平方式,则m= , 若x 2+6x+m 2是一个完全平方式,则m 的值是 。
若942++kx x 是完全平方式,则k = 。
知识点4.整体运算练习D: 1、已知x 2+3x+5的值为11,则代数式3x 2+9x+12的值为 2、已知实数x 满足210x x +-=则代数式2337x x ++的值为____________ 知识点5.方程的解练习E :1、已知关于x 的方程x 2+3x+k 2=0的一个根是x=-1,则k=___________. 2、求以12x 1x 3=-=-,为两根的关于x 的一元二次方程 。
学习1和2

练习:《装糖果》《找盖子》 1
作业:《发水果》《发糖果》 1
小朋友现在有几个苹果,请找出卡片数字1,你找的和老师的一样吗?数字1的 背面是1点数,小朋友想想数字1像什么?
2
摘一个梨,引导幼儿比较苹果和梨子谁多谁少,引导幼儿说出一样多。 再摘一个梨,现在有几个梨,一起数一数,可以用数字几表示?
2Hale Waihona Puke 12像鸭子水中游。
小朋友现在有几个梨子,现在有几个梨,一起数一数,请找出卡片数字2,你 找的和老师的一样吗?数字2的背面是2点数,小朋友想想数字2像什么?
学习 和
会手口一致点数2以内的实物并说出总数。 认读数字1和2,理解数字的意义。 能进行2以内的按物取物,按物取数、按数取物。
果园里的水果丰收啦!请小朋友看看有哪些水果?
1
杨美美摘了几颗苹果?可以用数字几表示?不管苹果是大的、小的,还是红色、绿色、黄色,只要是一个苹果就 可以用数字1表示
1
1
1像铅笔写写字
高考专题复习—集合与常用逻辑用语 第一讲+第二讲(解析版)
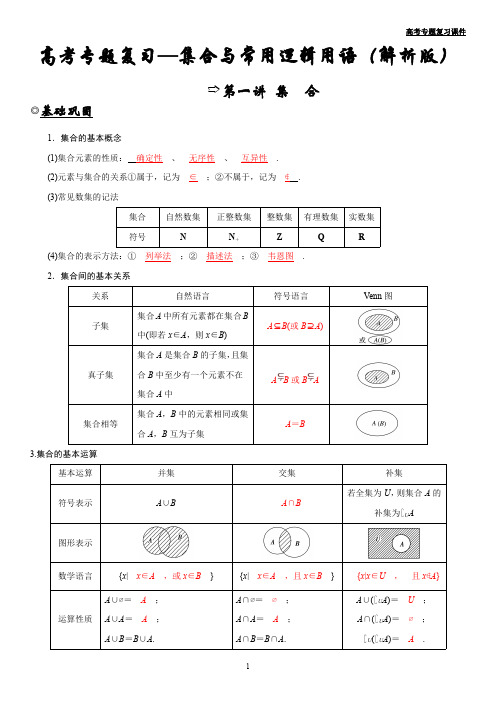
高考专题复习—集合与常用逻辑用语(解析版)➱第一讲集合◎基础巩固1.集合的基本概念(1)集合元素的性质:确定性、无序性、互异性.(2)元素与集合的关系①属于,记为∈;②不属于,记为∉.(3)常见数集的记法集合自然数集正整数集整数集有理数集实数集符号N N +Z Q R(4)集合的表示方法:①列举法;②描述法;③韦恩图.2.集合间的基本关系关系自然语言符号语言Venn 图子集集合A 中所有元素都在集合B 中(即若x ∈A ,则x ∈B )A ⊆B(或B⊇A )真子集集合A 是集合B 的子集,且集合B 中至少有一个元素不在集合A 中A B 或B A集合相等集合A ,B 中的元素相同或集合A ,B 互为子集A =B3.集合的基本运算基本运算并集交集补集符号表示A ∪BA ∩B若全集为U ,则集合A 的补集为∁U A图形表示数学语言{x |x ∈A ,或x ∈B }{x |x ∈A,且x ∈B }{x |x ∈U ,且x ∉A }运算性质A ∪∅=A ;A ∪A =A;A ∪B =B ∪A .A ∩∅=∅;A ∩A =A;A ∩B =B ∩A .A ∪(∁U A )=U ;A ∩(∁U A )=∅;∁U (∁U A )=A.1.A∪B=A⇔B⊆A,A∩B=A⇔A⊆B.2.若集合A中含有n个元素,则它的子集个数为2n,真子集个数为2n-1,非空真子集个数为2n-2.[思考辨析]判断下列说法是否正确,正确的在它后面的括号里打“√”,错误的打“×”.(1)∅={0}.()(2)空集是任何集合的子集,两元素集合是三元素集合的子集.()(3)a在集合A中,可用符号表示为a⊆A.()(4)N⊆N+⊆Z.()(5)若A={x|y=x2},B={(x,y)|y=x2},则A∩B={x|x∈R}.()答案:(1)×(2)×(3)×(4)×(5)×[小题查验]1.若集合A={x∈N|x≤10},a=22,则下列结论正确的是()A.{a}⊆A B.a⊆AC.{a}∈A D.a∉A解析:D[由题意知A={0,1,2,3},由a=22,知a∉A.]2.已知集合A={1,2,3,4},B={2,4,6,8},则A∩B中元素的个数为()A.1B.2C.3D.4解析:B[由题意可得:A∩B={2,4},故选B.]3.已知全集U={1,2,3,4,5},A={1,2,4},B={2,5},则(∁U A)∪B=()A.{3,4,5}B.{2,3,5}C.{5}D.{3}解析:B[因为U={1,2,3,4,5},A={1,2,4},所以∁U A={3,5},又B={2,5},所以(∁U A)∪B={2,3,5}.] 4.已知集合A={x|x2-2x+a>0},且1∉A,则实数a的取值范围是________.解析:∵1∉{x|x2-2x+a>0},∴1∈{x|x2-2x+a≤0},即1-2+a≤0,∴a≤1.答案:(-∞,1]5.(教材改编)已知全集U={1,2,3,4,5,6,7},A={2,4,5},B={1,3,5,7},则A∩(∁U B)=___________________.答案:{2,4}◎考点探究考点一集合的基本概念(自主练透)[题组集训]1.已知集合A ={(x ,y )|x 2+y 2≤3,x ∈Z ,y ∈Z },则A 中元素的个数为()A .9B .8C .5D .4解析:A[∵x 2+y 2≤3,∴x 2≤3,∵x ∈Z ,∴x =-1,0,1,当x =-1时,y =-1,0,1;当x =0时,y =-1,0,1;当x =1时,y =-1,0,1;所以共有9个,选A.]2.若集合A ={x ∈R |ax 2-3x +2=0}中只有一个元素,则a =()A.92B.98C .0D .0或98解析:D[若集合A 中只有一个元素,则方程ax 2-3x +2=0只有一个实根或有两个相等实根.当a =0时,x =23,符合题意;当a ≠0时,由Δ=(-3)2-8a =0,得a =98,所以a 的取值为0或98.]3.已知集合A ={m +2,2m 2+m },若3∈A ,则m 的值为________.解析:因为3∈A ,所以m +2=3或2m 2+m =3.当m +2=3,即m =1时,2m 2+m =3,此时集合A 中有重复元素3,所以m =1不符合题意,舍去.当2m 2+m =3时,解得m =-32或m =1(舍去),此时当m =-32时,m +2=12≠3符合题意.所以m =-32.答案:-324.已知集合M ={1,m },N ={n ,log 2n },若M =N ,则(m -n )2019=________.解析:由M =N =1,2n =m =m ,2n =1,=0,=12,=2.∴(m -n )2019=-1或0.答案:-1或01.研究集合问题,一定要抓住元素,看元素应满足的属性,对于含有字母的集合,在求出字母的值后,要注意检验集合的元素是否满足互异性.2.对于集合相等首先要分析已知元素与另一个集合中哪一个元素相等,分几种情况列出方程(组)进行求解,要注意检验是否满足互异性.考点二集合间的基本关系(师生共研)[典例](1)已知集合A ={x |ax =1},B ={x |x 2-1=0},若A ⊆B ,则a 的取值构成的集合是()A .{-1}B .{1}C .{-1,1}D .{-1,0,1}(2)已知集合A ={x |-2≤x ≤7},B ={x |m +1<x <2m -1},若B ⊆A ,则实数m 的取值范围是________.[解析](1)由题意,得B ={-1,1},因为A ⊆B ,所以当A =∅时,a =0;当A ={-1}时,a =-1;当A ={1}时,a =1.又A 中至多有一个元素,所以a 的取值构成的集合是{-1,0,1}.故选D.(2)当B =∅时,有m +1≥2m -1,则m ≤2.当B ≠∅时,若B ⊆A ,如图.+1≥-2m -1≤7+1<2m -1,解得2<m ≤4.综上,m 的取值范围为m ≤4.[答案](1)D (2){m |m ≤4}[互动探究]本例(1)中若A ={x |ax >1(a ≠0)},B ={x |x 2-1>0},其它条件不变,则a 的取值范围是________.解析:由题意,得B ={x |x >1,或x <-1},对于集合A ,①当a >0时,A |x >1a因为A ⊆B ,所以1a ≥1.又a >0,所以0<a ≤1.②当a <0时,A |x <1a因为A ⊆B ,所以1a ≤-1,又a <0,所以-1≤a <0,综上所述,0<a ≤1,或-1≤a <0.答案:[-1,0)∪(0,1]由集合的关系求参数的关键点由两集合的关系求参数,其关键是将两集合的关系转化为元素间的关系,进而转化为参数满足的关系,解决这类问题常常要合理利用数轴、Venn 图帮助分析,而且常要对参数进行讨论,注意区间端点的取舍.提醒:解决两个集合的包含关系时,要注意空集的情况.[跟踪训练](1)若集合A ={x |ax 2+ax +1=0}的子集只有两个,则实数a =________.解析:∵集合A 的子集只有两个,∴A 中只有一个元素,即方程ax 2+ax +1=0只有一个根.当a =0时方程无解.当a ≠0时,Δ=a 2-4a =0,∴a =4.故a =4.答案:4(2)已知集合A ={x |log 2x ≤2},B =(-∞,a ),若A ⊆B ,则实数a 的取值范围是(c ,+∞),其中c =________.解析:由log 2x ≤2,得0<x ≤4,即A ={x |0<x ≤4},而B =(-∞,a ).由于A ⊆B ,如图所示,则a >4,即c =4.答案:4考点三集合的基本运算(多维探究)[命题角度1]求交集、并集1.(文科)已知集合A ={0,2},B ={-2,-1,0,1,2},则A ∩B =()A .{0,2}B .{1,2}C .{0}D .{-2,-1,0,1,2}解析:A[根据集合交集中元素的特征,可以求得A ∩B ={0,2},故选A.]2.(文科)已知集合A ={x |x <2},B ={x |3-2x >0},则()A .A ∩B |x B .A ∩B =∅C .A ∪B |xD .A ∪B =R解析:A[由3-2x >0得x <32,所以A ∩B ={x |x <2}|x |x ,故选A.][命题角度2]集合的交、并、补的综合运算3.(文科)设集合A ={1,2,3,4,5,6},B ={x |2<x <5},则A ∩(∁R B )等于()A .{2,3,4,5}B .{1,2,5,6}C .{3,4}D .{1,6}解析:B[因为∁R B ={x |x ≤2,或x ≥5},A ={1,2,3,4,5,6};所以A ∩(∁R B )={1,2,5,6}.][命题角度3]利用集合的基本运算求参数的取值(范围)4.设集合A ={1,2,4},B ={x |x 2-4x +m =0}.若A ∩B ={1},则B =()A .{1,-3}B .{1,0}C .{1,3}D .{1,5}解析:C[由题意知x =1是方程x 2-4x +m =0的解,代入解得m =3,所以x 2-4x +3=0,解得x =1或x =3,从而B ={1,3}.]5.已知集合A ={x |x ≤a },B ={x |1≤x ≤2},且A ∪∁R B =R ,则实数a 的取值范围是________.解析:∁R B ={x |x <1,或x >2},要使A ∪(∁R B )=R ,则a ≥2.答案:[2,+∞)解集合运算问题应注意以下三点(1)看元素组成.集合是由元素组成的,从研究集合中元素的构成入手是解决集合运算问题的关键.(2)对集合化简.有些集合是可以化简的,先化简再研究其关系并进行运算,可使问题简单明了、易于解决.(3)注意数形结合思想的应用,常用的数形结合形式有数轴、坐标系和韦恩(Venn)图.提醒:Venn图图示法和数轴图示法是进行集合交、并、补运算的常用方法,其中运用数轴图示法要特别注意端点是实心还是空心.考点四集合的新定义问题(师生共研)数学抽象——集合新定义中的核心素养以集合为背景的新定义问题常以“问题”为核心,以“探究”为途径,以“发现”为目的,这类试题只是以集合为依托,考查考生对新概念的理解,充分体现了核心素养中的数学抽象.[典例]设A是自然数集的一个非空子集,对于k∈A,如果k2∉A,且k∉A,那么k是A的一个“酷元”,给定S={x∈N|y=lg(36-x2)},设M⊆S,集合M中有两个元素,且这两个元素都是M的“酷元”,那么这样的集合M有()A.3个B.4个C.5个D.6个[解析]C[由36-x2>0可解得-6<x<6,又x∈N,故x可取0,1,2,3,4,5,故S={0,1,2,3,4,5}.由题意可知:集合M不能含有0,1,且不能同时含有2,4.故集合M可以是{2,3}、{2,5}、{3,5}、{3,4}、{4,5}.]解决以集合为背景的新定义问题,要抓住两点:(1)紧扣新定义.首先分析新定义的特点,把新定义所叙述的问题的本质弄清楚,应用到具体的解题过程之中.(2)用好集合的性质.解题时要善于从试题中发现可以使用集合性质的一些因素.[跟踪训练]定义一种新的集合运算△:A△B={x|x∈A,且x∉B}.若集合A={x|x2-4x+3<0},B={x|2≤x≤4},则按运算△,B△A等于()A.{x|3<x≤4}B.{x|3≤x≤4}C.{x|3<x<4}D.{x|2≤x≤4}解析:B[A={x|1<x<3},B={x|2≤x≤4},由题意知,B△A={x|x∈B,且x∉A}={x|3≤x≤4}.]◎课时作业[基础训练组]1.已知集合A ={1,3,5,7},B ={2,3,4,5},则A ∩B =()A .{3}B .{5}C .{3,5}D .{1,2,3,4,5,7}解析:C[A ={1,3,5,7},B ={2,3,4,5},∴A ∩B ={3,5},故选C.]2.集合P ={x |0≤x <3},M ={x ||x |≤3},则P ∩M =()A .{1,2}B .{0,1,2}C .{x |0≤x <3}D .{x |0≤x ≤3}解析:C[集合P ={x |0≤x <3},M ={x ||x |≤3}={x |-3≤x ≤3},则P ∩M ={x |0≤x <3}.]3.如图,I 为全集,M 、P 、S 是I 的三个子集,则阴影部分所表示的集合是()A .(M ∩P )∩SB .(M ∩P )∪SC .(M ∩P )∩∁I SD .(M ∩P )∪∁I S解析:C [图中的阴影部分是M ∩P 的子集,不属于集合S ,属于集合S 的补集的子集,即是∁I S 的子集,则阴影部分所表示的集合是(M ∩P )∩∁I S .故选C.]4.满足{2018}⊆A {2018,2019,2020}的集合A 的个数为()A .1B .2C .3D .4解析:C[满足{2018}⊆A{2018,2019,2020}的集合A 可得:A ={2018},{2018,2019},{2018,2020}.因此满足的集合A 的个数为3.]5.已知集合P ={x |x 2≤1},M ={a }.若P ∪M =P ,则a 的取值范围是()A .(-∞,-1]B .[1,+∞)C .[-1,1]D .(-∞,-1]∪[1,+∞)解析:C[因为P ∪M =P ,所以M ⊆P ,即a ∈P ,得a 2≤1,解得-1≤a ≤1,所以a 的取值范围是[-1,1].]6.已知集合A ={y |y =x 2-1},B ={x |y =lg(x -2x 2)},则∁R (A ∩B )=()A.0B .(-∞,0)∪12,+∞D .(-∞,0]∪12,+∞解析:D[A ={y |y =x 2-1}=[0,+∞),B ={x |y =lg(x -2x 2)}A ∩B所以∁R (A ∩B )=(-∞,0]∪12,+7.已知A =[1,+∞),B ∈R |12a ≤x ≤2a -A ∩B ≠∅,则实数a 的取值范围是()A .[1,+∞) B.12,1 C.23,+∞D .(1,+∞)解析:A[因为A ∩B ≠∅a -1≥1,a -1≥12a ,解得a ≥1,故选A.]8.函数y =x -2与y =ln(1-x )的定义域分别为M ,N ,则M ∪N =()A .(1,2]B .[1,2]C .(-∞,1]∪[2,+∞)D .(-∞,1)∪[2,+∞)解析:D[使x -2有意义的实数x 应满足x -2≥0,∴x ≥2,∴M =[2,+∞),y =ln(1-x )中x 应满足1-x>0,∴x <1,∴N =(-∞,1),所以M ∪N =(-∞,1)∪[2,+∞),故选D.]9.已知集合A ={(x ,y )|x ,y ∈R ,x 2+y 2=1},B ={(x ,y )|x ,y ∈R ,y =4x 2-1},则A ∩B 的元素个数是________.解析:集合A 是以原点为圆心,半径等于1的圆周上的点的集合,集合B 是抛物线y =4x 2-1上的点的集合,观察图像可知,抛物线与圆有3个交点,因此A ∩B 中含有3个元素.答案:310.已知集合A ={x |4≤2x ≤16},B =[a ,b ],若A ⊆B ,则实数a -b 的取值范围是________.解析:集合A ={x |4≤2x ≤16}={x |22≤2x ≤24}={x |2≤x ≤4}=[2,4],因为A ⊆B ,所以a ≤2,b ≥4,所以a -b ≤2-4=-2,即实数a -b 的取值范围是(-∞,-2].答案:(-∞,-2]11.对于集合M 、N ,定义M -N ={x |x ∈M ,且x ∉N },M ⊕N =(M -N )∪(N -M ).设A ={y |y =3x ,x ∈R },B ={y |y =-(x -1)2+2,x ∈R },则A ⊕B =________.解析:由题意得A ={y |y =3x ,x ∈R }={y |y >0},B ={y |y =-(x -1)2+2,x ∈R }={y |y ≤2},故A -B ={y |y >2},B -A ={y |y ≤0},所以A ⊕B ={y |y ≤0,或y >2}.答案:(-∞,0]∪(2,+∞)12.若A ={x |ax 2-ax +1≤0,x ∈R }=∅,则a 的取值范围是________.解析:∵A ={x |ax 2-ax +1≤0,x ∈R }=∅,∴a =0>0=(-a )2-4a <0,解得0≤a <4.∴a 的取值范围是[0,4).[能力提升组]13.集合U =R ,A ={x |x 2-x -2<0},B ={x |y =ln(1-x )},则图中阴影部分所表示的集合是()A .{x |x ≥1}B .{x |1≤x <2}C .{x |0<x ≤1}D .{x |x ≤1}解析:B [易知A =(-1,2),B =(-∞,1),∴∁U B =[1,+∞),A ∩(∁U B )=[1,2).因此阴影部分表示的集合为A ∩(∁U B )={x |1≤x <2}.]14.设P ,Q 为两个非空实数集合,定义集合P *Q ={z |z =a ÷b ,a ∈P ,b ∈Q },若P ={-1,0,1},Q ={-2,2},则集合P *Q 中元素的个数是()A .2B .3C .4D .5解析:B[当a =0时,无论b 取何值,z =a ÷b =0;当a =-1,b =-2时,z =(-1)÷(-2)=12;当a =-1,b =2时,z =(-1)÷2=-12;当a =1,b =-2时,z =1÷(-2)=-12;当a =1,b =2时,z =1÷2=12.故P *Q ,12,-3个元素.]15.若集合A={x|(a-1)x2+3x-2=0,x∈R}有且仅有两个子集,则实数a的值为________.解析:由题意知,方程(a-1)x2+3x-2=0,x∈R,有一个根,∴当a=1时满足题意,当a≠1时,Δ=0,即9+8(a-1)=0,解得a=-18.答案:1或-1816.某班共有学生40名,在乒乓球、篮球、排球三项运动中每人至少会其中的一项,有些人会其中的两项,没有人三项均会.若该班18人不会打乒乓球,24人不会打篮球,16人不会打排球,则该班会其中两项运动的学生人数是________.解析:设同时会打乒乓球和篮球的学生有x人,同时会打乒乓球和排球的学生有y人,同时会打排球和篮球的学生有z人,∵该班18人不会打乒乓球,24人不会打篮球,16人不会打排球,∴该班会打乒乓球或篮球的学生有24人,会打乒乓球或排球的学生有16人,会打篮球或打排球有22人,∴x+y+z=24+16+22-40=22.∴该班会其中两项运动的学生人数是22.答案:22➱第二讲命题、充分条件与必要条件◎基础巩固1.命题的概念可以判断真假、用文字或符号表述的语句叫作命题.其中判断为真的语句叫真命题,判断为假的语句叫假命题.2.四种命题及其关系3.四种命题的真假关系(1)两个命题互为逆否命题,它们有相同的真假性;(2)两个命题互为逆命题或互为否命题,它们的真假性没有关系.4.充分条件与必要条件(1)如果p⇒q,则p是q的充分条件,q是p的必要条件.(2)如果p⇒q,q⇒p,则p是q的充要条件.1.互为逆否的两个命题具有相同的真假性,互逆的或互否的两个命题真假性没有关系.2.若p是q的充分(必要)条件,q是r的充分(必要)条件,则p是r的充分(必要)条件,即“p⇒q且q⇒r”⇒“p⇒r”(“p⇐q且q⇐r”⇒“p⇐r”).[思考辨析]判断下列说法是否正确,正确的在它后面的括号里打“√”,错误的打“×”.(1)若原命题为真,则这个命题的否命题、逆命题、逆否命题中至少有一个为真.()(2)若p是q成立的充分条件,则q是p成立的必要条件.()(3)若p是q成立的充要条件,则可记为p⇔q.()(4)命题“若p,则q”的否命题是“若p,则q”.()答案:(1)√(2)√(3)√(4)×[小题查验]1.“x=1”是“x2-2x+1=0”的()A.充要条件B.充分不必要条件C.必要不充分条件D.既不充分也不必要条件解析:A[因为x2-2x+1=0有两个相等的实数根为x=1,所以“x=1”是“x2-2x+1=0”的充要条件.] 2.给出命题:“若实数x,y满足x2+y2=0,则x=y=0”,在它的逆命题、否命题、逆否命题中,真命题的个数是()A.0个B.1个C.2个D.3个解析:D[原命题显然正确,其逆命题为:若x=y=0,则x2+y2=0,显然也是真命题,由四种命题之间的关系知,其否命题、逆否命题也都是真命题.故选D.]3.“a=1”是“直线ax+y+1=0与直线(a+2)x-3y-2=0垂直”的()A.充要条件B.充分不必要条件C.必要不充分条件D.既不充分也不必要条件解析:B[直线ax+y+1=0与直线(a+2)x-3y-2=0垂直的充要条件为a(a+2)+1×(-3)=0,解得a=14.(教材改编)已知命题:若m>0,则方程x2+x-m=0有实数根.则其逆否命题为_________.答案:若方程x2+x-m=0无实根,则m≤05.下列命题:①若ac2>bc2,则a>b;②若sinα=sinβ,则α=β;③“实数a=0”是“直线x-2ay=1和直线2x-2ay=1平行”的充要条件;④若f(x)=log2x,则f(|x|)是偶函数.其中正确命题的序号是________.解析:对于①,∵ac2>bc2,∴c2>0,∴a>b正确;对于②,sin30°=sin150°⇒/30°=150°,所以②错误;对于③,l1∥l2⇔A1B2=A2B1,即-2a=-4a⇒a=0且A1C2≠A2C1,所以③正确;④显然正确.答案:①③④◎考点探究考点一命题的四种形式及其关系(自主练透)[题组集训]1.命题p:若a>b,则a-1>b-1,则命题p的否命题为()A.若a>b,则a-1≤b-1B.若a≥b,则a-1<b-1C.若a≤b,则a-1≤b-1D.若a<b,则a-1<b-1解析:C[根据否命题的定义:若原命题为:若p,则q,否命题为:若非p,则非q.∵原命题为:若a>b,则a-1>b-1,∴否命题为:若a≤b,则a-1≤b-1,故选C.]2.命题“若x2+3x-4=0,则x=4”的逆否命题及其真假性为()A.“若x=4,则x2+3x-4=0”为真命题B.“若x≠4,则x2+3x-4≠0”为真命题C.“若x≠4,则x2+3x-4≠0”为假命题D.“若x=4,则x2+3x-4=0”为假命题解析:C[根据逆否命题的定义可以排除A,D,因为x2+3x-4=0,所以x=4或-1,故选C.]3.以下关于命题的说法正确的有________(填写所有正确命题的序号).①“若log2a>0,则函数f(x)=log a x(a>0,a≠1)在其定义域内是减函数”是真命题;②命题“若a=0,则ab=0”的否命题是“若a≠0,则ab≠0”;③命题“若x,y都是偶数,则x+y也是偶数”的逆命题为真命题;④命题“若a∈M,则b∉M”与命题“若b∈M,则a∉M”等价.解析:对于①,若log2a>0=log21,则a>1,所以函数f(x)=log a x在其定义域内是增函数,故①不正确;对于②,依据一个命题的否命题的定义可知,该说法正确;对于③,原命题的逆命题是“若x+y是偶数,则x、y都是偶数”,是假命题,如1+3=4是偶数,但3和1均为奇数,故③不正确;对于④,不难看出,命题“若a∈M,则b∉M”与命题“若b∈M,则a∉M”是互为逆否命题,因此二者等价,所以④正确.综上可知正确的说法有②④.1.由原命题写出其他三种命题,关键要分清原命题的条件和结论,将条件与结论互换即得逆命题,将条件与结论同时否定即得否命题,将条件与结论互换的同时进行否定即得逆否命题.提醒:当一个命题有大前提而要写出其他三种命题时,必须保留大前提,也就是大前提不动.2.命题真假的判断方法(1)联系已有的数学公式、定理、结论进行正面直接判断.(2)利用原命题和其逆否命题的等价关系进行判断.考点二充分、必要条件的判断与应用(多维探究)[命题角度1]充分、必要条件的判定1.设p∶0<x<1,q∶2x≥1,则p是q的()A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件解析:A[q∶2x≥1,解得x≥0.又p∶0<x<1,则p是q的充分不必要条件.]2.函数f(x)在x=x0处导数存在,若p∶f′(x0)=0,q∶x=x0是f(x)的极值点,则()A.p是q的充分必要条件B.p是q的充分条件,但不是q的必要条件C.p是q的必要条件,但不是q的充分条件D.p既不是q的充分条件,也不是q的必要条件解析:C[函数在x=x0处有导数且导数为0,x=x0未必是函数的极值点,还要看函数在这一点左右两边的导数的符号,若符号一致,则不是极值点;反之,若x=x0为函数的极值点,则函数在x=x0处的导数一定为0,所以p是q的必要不充分条件.]3.已知向量a=(-2,m),b m∈R,则“a⊥(a+2b)”是“m=2”的()A.充要条件B.必要不充分条件C.充分不必要条件D.既不充分也不必要条件解析:B[∵a=(-2,m),b m∈R,∴a+2b=(4,2m)若a⊥(2a+2b),则-8+2m2=0,解得m=±2,故“a⊥(a+2b)”是“m=2”的必要不充分条件.]命题的充分、必要条件的判断方法(1)定义法:直接判断若p则q、若q则p的真假.(2)等价法:利用A⇒B与非B⇒非A,B⇒A与非A⇒非B,A⇔B与非B⇔非A的等价关系,对于条件或结论是否定式的命题,一般运用等价法.(3)利用集合间的包含关系判断:若A⊆B,则A是B的充分条件或B是A的必要条件;若A=B,则A是B的充要条件.[命题角度2]利用充要条件求参数的取值(范围)逻辑推理——充分、必要条件关系中的核心素养充分、必要条件问题中常涉及参数取值(范围)问题,直接解决较为困难,先用等价转化思想,将复杂、生疏的问题转化为简单、熟悉的问题来解决,充分体现“逻辑推理”的核心素养.4.已知p:-2≤x≤10,q:(x-a)(x-a-1)>0,若p是q成立的充分不必要条件,则实数a的取值范围是______.[破题关键点]若p是q成立的充分不必要条件,则{x|-2≤x≤10} {x|x>a+1,或x<a},即转化为相对应的集合间的基本关系来求实数a的取值范围.解析:由(x-a)(x-a-1)>0,得x>a+1或x<a,由题意,得{x|-2≤x≤10} {x|x>a+1,或x<a},所以a+1<-2或a>10,即a<-3或a>10.答案:(-∞,-3)∪(10,+∞)[互动探究]本例中,若p:-2<x<10,q:(x-a)(x-a-1)≥0,其他条件不变,则a的取值范围是______.解析:由(x-a)(x-a-1)≥0,得x≥a+1或x≤a,由题意得{x|-2<x<10} {x|x≥a+1,或x≤a}.所以a+1≤-2,或a≥10,即a≤-3,或a≥10.答案:(-∞,-3]∪[10,+∞)(1)解决此类问题一般是把充分条件、必要条件或充要条件转化为集合之间的关系,然后根据集合之间的关系列出关于参数的不等式求解.(2)注意利用转化的方法理解充分必要条件:若非p是非q的充分不必要(必要不充分、充要)条件,则p是q的必要不充分(充分不必要、充要)条件.◎课时作业[基础训练组]1.命题“若a 2+b 2=0,a ,b ∈R ,则a =b =0”的逆否命题是()A .若a ≠b ≠0,a ,b ∈R ,则a 2+b 2=0B .若a =b ≠0,a ,b ∈R ,则a 2+b 2≠0C .若a ≠0且b ≠0,a ,b ∈R ,则a 2+b 2≠0D .若a ≠0或b ≠0,a ,b ∈R ,则a 2+b 2≠0解析:D[写逆否命题只要交换命题的条件与结论,并分别否定条件与结论即可.]2.设a ∈R ,则“a >3”是“函数y =log a (x -1)在定义域上为增函数”的()A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件解析:A[因为函数y =log a (x -1)在定义域(1,+∞)上为增函数,所以a >1,因此“a >3”是“函数y =log a (x -1)在定义域上为增函数”的充分不必要条件.]3.“m =1”是“圆C 1:x 2+y 2+3x +4y +m =0与圆C 2“x 2+y 2=4的相交弦长为23”的()A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件解析:A[由题意知圆C 1与圆C 2的公共弦所在的直线是3x +4y +m +4=0,故(0,0)到3x +4y +m +4=0的距离d=|m +4|5=4-3=1,即|m +4|=5,解得m =1或m =-9.故m =1是m =1或m =-9的充分不必要条件,故选A.4.已知条件p :|x -4|≤6,条件q :x ≤1+m ,若p 是q 的充分不必要条件,则m 的取值范围是()A .(-∞,-1]B .(-∞,9]C .[1,9]D .[9,+∞)解析:D[由|x -4|≤6,解得-2≤x ≤10,即p :-2≤x ≤10;又q :x ≤1+m ,若p 是q 的充分不必要条件,则1+m ≥10,解得m ≥9.故选D.]5.若x >m 是x 2-3x +2<0的必要不充分条件,则实数m 的取值范围是()A .[1,+∞)B .(-∞,2]C .(-∞,1]D .[2,+∞)解析:C[由x 2-3x +2<0得1<x <2,若x >m 是x 2-3x +2<0的必要不充分条件,则m ≤1,即实数m 的取值范围是(-∞,1].]6.a 2+b 2=1是a sin θ+b cos θ≤1恒成立的()A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件解析:A[因为a sin θ+b cos θ=a 2+b 2sin (θ+φ)≤a 2+b 2,所以由a 2+b 2=1可推得a sin θ+b cos θ≤1恒成立.反之,取a =2,b =0,θ=30°,满足a sin θ+b cos θ≤1,但不满足a 2+b 2=1,即由a sin θ+b cos θ≤1推不出a 2+b 2=1,故a 2+b 2=1是a sin θ+b cos θ≤1恒成立的充分不必要条件.故选A.]7.“m >1”是“函数f (x )=3x +m -33在区间[1,+∞)无零点”的()A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件解析:A[因为函数f (x )=3x +m -33在区间[1,+∞)上单调递增且无零点,所以f (1)=31+m -33>0,即m +1>32,解得m >12,故“m >1”是“函数f (x )=3x +m -33在区间[1,+∞)无零点的充分不必要条件,故选A.]8.设等比数列{a n }的公比为q ,前n 项和为S n .给出命题s :若|q |=2,则S 6=7S 2,则在命题s 的逆命题、否命题、逆否命题中,错误命题的个数是()A .3B .2C .1D .0解析:B[若|q |=2,则q 2=2,S 6=a 1(1-q 6)1-q =a 1(1-q 2)(1+q 2+q 4)1-q =7·a 1(1-q 2)1-q=7S 2,所以原命题为真,从而逆否命题为真;而当S 6=7S 2时,显然q ≠1,这时a 1(1-q 6)1-q =7·a 1(1-q 2)1-q ,解得q =-1或|q |=2,因此,逆命题为假,否命题为假,故错误命题的个数为2.]9.《左传·僖公十四年》有记载:“皮之不存,毛将焉附?”这句话的意思是说皮都没有了,毛往哪里依附呢?比喻事物失去了借以生存的基础,就不能存在.皮之不存,毛将焉附?则“有毛”是“有皮”的_______条件(将正确的序号填入空格处).①充分条件②必要条件③充要条件④既不充分也不必要条件解析:由题意知“无皮”⇒“无毛”,所以“有毛”⇒“有皮”即“有毛”是“有皮”的充分条件.答案:①10.在△ABC 中,角A ,B ,C 所对应的边分别为a ,b ,c ,则“a ≤b ”是“sin A ≤sin B ”的__________条件.解析:由正弦定理,得a sin A =bsin B,故a ≤b ⇔sin A ≤sin B.答案:充要11.若“x >a ”是“x 2-5x +6≥0”成立的充分不必要条件,则实数a 的取值范围是_________.解析:由x 2-5x +6≥0得x ≥3或x ≤2,若“x >a ”是“x 2-5x +6≥0”成立的充分不必要条件,则a ≥3,即实数a 的取值范围是[3,+∞).答案:[3,+∞)12.已知条件p :2x 2-3x +1≤0,条件q :x 2-(2a +1)x +a (a +1)≤0.若非p 是非q 的必要不充分条件,则实数a 的取值范围是________.解析:由2x 2-3x +1≤0,得12≤x ≤1,∴命题p |12≤x ≤由x 2-(2a +1)x +a (a +1)≤0,得a ≤x ≤a +1,∴命题q 为{x |a ≤x ≤a +1}.非p 对应的集合A |x >1或x q 对应的集合B ={x |x >a +1或x <a }.∵非p 是非q 的必要不充分条件,∴a +1≥1且a ≤12,∴0≤a ≤12,即实数a 的取值范围是0,12.答案:0,12[能力提升组]13祖暅原理:“幂势既同,则积不容异”.它是中国古代一个涉及几何体体积的问题,意思是两个同高的几何体,如果在等高处的截面积恒相等,那么体积相等.设A ,B 为两个同高的几何体,p :A ,B 的体积不相等,q :A ,B 在等高处的截面积不恒相等,根据祖暅原理可知,p 是q 的()A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件解析:A[设命题a :“若p ,则q ”,可知命题a 是祖暅原理的逆否命题,则a 是真命题.故p 是q 的充分条件.设命题b :“若q ,则p ”,若A 比B 在某些等高处的截面积小一些,在另一些等高处的截面积大一些,且大的总量与小的总量相抵,则它们的体积还是一样的.所以命题b 是假命题,即p 不是q 的必要条件.综上所述,p 是q 的充分不必要条件.故选A.]14.已知条件p :4x -1≤-1,条件q :x 2+x <a 2-a ,且非q 的一个充分不必要条件是非p ,则a 的取值范围是()A.-2,-12B.12,2C .[-1,2],12∪[2,+∞)解析:C [由4x -1≤-1,移项得4x -1+1≤0,通分得x +3x -1≤0,解得-3≤x <1;由x 2+x <a 2-a ,得x 2+x -a 2+a <0.由非q 的一个充分不必要条件是非p ,可知非p 是非q 的充分不必要条件,即p 是q 的必要不充分条件,即条件q 对应的x 取值集合是条件p 对应的x 取值集合的真子集.设f (x )=x 2+x -a 2+a -3)=-a 2+a +6≥0,1)=-a 2+a +2≥0,2<a <31≤a ≤2∴-1≤a ≤2,故选C.]15.给出下列命题:①“数列{a n }为等比数列”是“数列{a n a n +1}为等比数列”的充分不必要条件;②“a =2”是“函数f (x )=|x -a |在区间[2,+∞)上为增函数”的充要条件;③“m =3”是“直线(m +3)x +my -2=0与直线mx -6y +5=0互相垂直”的充要条件;④设a ,b ,c 分别是△ABC 三个内角A ,B ,C 所对的边,若a =1,b =3,则“A =30°”是“B =60°”的必要不充分条件.其中真命题的序号是________.解析:对于①,当数列{a n }为等比数列时,易知数列{a n a n +1}是等比数列,但当数列{a n a n +1}为等比数列时,数列{a n }未必是等比数列,如数列1,3,2,6,4,12,8显然不是等比数列,而相应的数列3,6,12,24,48,96是等比数列,因此①正确;对于②,当a ≤2时,函数f (x )=|x -a |在区间[2,+∞)上是增函数,因此②不正确;对于③,当m =3时,相应的两条直线互相垂直,反之,这两条直线垂直时,不一定有m =3,也可能m =0.因此③不正确;对于④,由题意得b a =sin B sin A =3,若B =60°,则sin A =12,注意到b >a ,故A =30°,反之,当A =30°时,有sin B =32,由于b >a ,所以B =60°或B =120°,因此④正确.综上所述,真命题的序号是①④.答案:①④16.设命题p :2x -1x -1<0,命题q ∶x 2-(2a +1)x +a (a +1)≤0,若p 是q 的充分不必要条件,则实数a 的取值范围是________.解析:2x -1x -1<0⇒(2x -1)(x -1)<0⇒12<x <1,x 2-(2a +1)x +a (a +1)≤0⇒a ≤x ≤a +1.[a ,a +1].≤12,+1≥1,解得0≤a ≤12.答案:0,12。
高中数学必修一第一讲集合

升高一数学精选精讲第一讲A A =∅=∅ B A ⊆A A = A ∅=B A ⊇()U A =∅ð 2()U A U =ð()()()U U A B A B =痧?()()()U U A B A B =痧?NM.B)=(∪(; (2)B)=(((A A求且A 求(B)={1,5},((课后测试卷考试说明:1、本试卷完成时间为 分钟;2、本试卷满分为 100 分;3、考试中考生必须遵守考试规则,独立完成;4、考生草稿纸要求规范使用,考试结束后上交。
一、选择题(每小题4分,共48分)1.设A={x|x ≤4}, )(A ){a} A (B )a ⊆A (C ){a}∈A (D )a ∉A 2.若{1,2} A ⊆{1,2,3,4,5},则集合A 的个数是( )(A )8 (B )7 (C )4 (D )33.下面表示同一集合的是( )(A )M={(1,2)},N={(2,1)} (B )M={1,2},N={(1,2)} (C )M=Φ,N={Φ} (D )M={x|2210}x x -+=,N={1}4.若P ⊆U ,Q ⊆U ,且x ∈C U (P ∩Q ),则( )(A )x ∉P 且x ∉Q (B )x ∉P 或x ∉Q (C )x ∈C U (P ∪Q) (D )x ∈C U P 5. 若M ⊆U ,N ⊆U ,且M ⊆N ,则( )(A )M ∩N=N (B )M ∪N=M (C )C U N ⊆C U M (D )C U M ⊆C U N 6.已知集合M={y|y=-x 2+1,x ∈R},N={y|y=x 2,x ∈R},全集I=R ,则M ∪N 等于( )(A ){(x,y)|x=1,,}22y x y R ±=∈ (B ){(x,y)|x 1,,}22y x y R ≠±≠∈(C ){y|y ≤0,或y ≥1} (D ){y|y<0, 或y>1}7.50名学生参加跳远和铅球两项测试,跳远和铅球测试成绩分别及格40人和31人,两项测试均不及格的有4人,则两项测试成≠ ≠绩都及格的人数是( )(A )35 (B )25 (C )28 (D )15 8.设x,y ∈R,A={}(,)x y y x =,B= {}(,)1y x y x=,则A 、B 间的关系为( )(A )AB (B )BA (C )A=B (D )A ∩B=Φ9. 设全集为R ,若M={}1x x ≥ ,N= {}05x x ≤<,则(C U M )∪(C U N )是( )(A ){}0x x ≥ (B ) {}15x x x <≥或 (C ){}15x x x ≤>或 (D ) {}05x x x <≥或10.已知集合{|31,},{|32,}M x x m m Z N y y n n Z ==+∈==+∈,若00,,x M y N ∈∈ 则00y x 与集合,M N 的关系是 ( )(A )00y x M ∈但N ∉(B )00y x N ∈但M ∉(C )00y x M ∉且N ∉(D )00y x M ∈且N ∈ 11.集合U ,M ,N ,P 如图所示,则图中阴影部分所表示的集合是( ) (A )M ∩(N ∪P ) (B )M ∩C U (N ∪P ) (C )M ∪C U (N ∩P ) (D )M ∪C U (N ∪P ) 12.设I 为全集,A ⊆I,B A,则下列结论错误的是( )(A )C I AC I B (B )A ∩B=B (C )A ∩C I B =Φ (D ) C I A ∩B=Φ二、填空题(每题3分,共12分)13.已知x ∈{1,2,x 2},则实数x=__________.14.已知集合M={a,0},N={1,2},且M ∩N={1},那么M ∪N 的真子集有 个. 15.已知A={-1,2,3,4};B={y|y=x 2-2x+2,x ∈A},若用列举法表示集合B ,则B= . 16.设{}1,2,3,4I =,A 与B 是I 的子集,若{}2,3A B =,则称(,)A B 为一个“理想配集”,那么符合此条件的“理想配集”的个数是 .(规定(,)A B 与(,)B A 是两个不同的“理想配集”) 三、解答题(40分)17.(5分)已知全集U={0,1,2,…,9},若(C U A)∩(C U B)={0,4,5},A ∩(C U B)={1,2,8},A ∩B={9}, 试求A ∪B .18.(6分)设全集U=R,集合A={}14x x -<<,B={}1,y y x x A =+∈,试求C U B, A ∪B, A ∩B,A ∩(C U B), ( C U A) ∩(C U B). 19.(6分)设集合A={x|2x 2+3px+2=0};B={x|2x 2+x+q=0},其中p ,q ,x ∈R ,当A ∩B={}12时,求p 的值和A ∪B .20.(7分)设集合A={2(,)462x y y x x a=++,B={}(,)2x y y x a =+,问:(1) a 为何值时,集合A ∩B 有两个元素; (2) a 为何值时,集合A ∩B 至多有一个元素.21.(7分)已知集合A={}1234,,,a a a a ,B={}22221234,,,a a a a ,其中1234,,,a a a a 均为正整数,且1234a a a a <<<,A ∩B={a 1,a 4},a 1+a 4=10, A ∪B 的所有元素之和为124,求集合A 和B .22.(7分)已知集合A={x|x 2-3x+2=0},B={x|x 2-ax+3a -5},若A ∩B=B ,求实数a 的值.。
有线数字电视讲座第一讲-数字电视广播系统-2信源编码

《中国有线电视》2004(03/04)CHINA CABLE TELEVISION・实用连载・有线数字电视讲座第一讲数字电视广播系统(2)数字电视的信源编码□冯传岗,宋茜(泰州市广播电视局,江苏泰州225321)中图分类号:TN949.197 文献标识码:E 文章编号:1007-7022(2004)03-0132-13(上接第01期)1 数字压缩编码技术概述1.1 数字压缩的必要性数字信号有很多优点,但当模拟信号数字化后其频带将大大加宽,1路6MHz带宽的普通电视信号数字化后,其数码速率将高达167Mb/s,这对存储器容量要求很大,占有的带宽将达80MHz左右,这样将使数字信号失去实用价值。
数字压缩技术很好地解决了上述困难,信号压缩后所占用的频带大大低于原模拟信号的频带,因此说,数字压缩编码技术是使数字信号走向实用化的关键技术之一。
表4列出了各种应用的码率。
1.2 图像压缩编码的可能性从信息论观点来看,图像作为一个信源,描述信源的数据是信息量(信源熵)和信息冗余量之和。
信息冗余量有许多种,如空间冗余、时间冗余、结构冗余、知识冗余、视觉冗余等,数据压缩实质上是减少这些冗余量,由此可见冗余量减少可以减少数据量而不减少信源的信息量。
从数学上讲,图像可以看作一个多维函数,压缩描述这个函数的数据量实质是减少其相关性。
在一些情况下,允许图像有一定的失真,而并不妨碍图像的实际应用,那么数据量压缩的可能性就更大了。
视频图像存在3种冗余信息:相邻像素间相关带来的空间冗余度,帧间相关产生的时间冗余度,不能被视觉感知的心理———视觉冗余度。
消除这些冗余度,可在满足质量要求的情况下,实现图像信息的压缩。
1.3 图像压缩编码方法的分类编码压缩方法很多,从不同的角度出发有不同的分类方法,如,从信息论角度出发可分为2大类。
1.3.1 冗余度压缩方法。
也称无损压缩、信息保持编码或熵编码,具体讲就是解码图像与压缩编码前的图像严格相同没有失真,从数学上讲是一种可逆运算。
高中数学第一讲二平行线分线段成比例定理学案含解析新人教A版选修

AD AF AF ∴ DC= FB= DE , A 正确. CE DE BF CB= AB =AB , B 正确. CD CE CE AD = EB= DF , C 正确. 2.已知线段 a,m, n 且 ax= mn,求作 x,图中作法正确的是 ( )
an 解析:选 C 因为 ax= mn,所以 m= x,故选 C.
3.如图,在△ ACE 中, B,D 分别在 AC,AE 上,下列推理不.正确的 是( )
AB BD A. BD∥ CE? AC= CE
AD BD B.BD ∥ CE? AE = CE
AB AD C. BD ∥CE? BC= DE
AB BD D . BD ∥CE? BC= CE
FC EF ∴ AB= AE .
FG EF ∵ FG∥ AD ,∴ AD = AE .
FC FG ∴ AB= AD .
∵ AB= AD .
∴ FC=FG .
4.如图,在 ? ABCD 中, E 是 AB 延长线上一点, DE 交 AC
于点 G,交 BC 于点 F. 求证: (1)DG 2= GE· GF;
马鸣风萧萧整理
》》》》》》》》》积一时之跬步 臻千里之遥程《 《《《《《《《《《《《
2.如图,已知 AE ∥ CF∥ DG,AB∶ BC∶CD = 1∶ 2∶ 3,CF= 12 cm,
求 AE, DG 的长.
AE AB
解:∵
AE ∥
CF,∴
CF=
. BC
AB ∴ AE= BC· CF.
∵ AB∶ BC= 1∶ 2, CF=12 cm,
AE 2
∵
EB=
, 3
微机原理及应用习题库硬件应用设计题(1)

微机原理及应用微型计算机系统概述第一讲和第二讲0.20.81画出微型计算机应用硬件基本组成框图。
微机原理及应用变量及伪指令第18讲0.80.810设变量var1的逻辑地址为0100:0000,画出下列语句定义的变量的存储分配图。
VAR1 DB 12H,0A5H,18+20,50/3,0,-1VAR2 DW 12H,0VAR3 DD 12345678HVAR4 DB ‘ABC’DW ‘AB’VAR5 DB ?,?VAR6 DB 4 DUP(0FFH,?)VAR7 DB 3 DUP(55H, 2 DUP(77H))微机原理及应用 总线结构与时序 第42~44讲 0.8 0.88CPU 执行一条指令的时间称为指令周期。
画出一个基本总线周期时序。
CLK微机原理及应用总线结构与时序第42~44讲0.80.810利用74LS373数据锁存器设计系统地址总线A19~A形成电路。
解:根据AD15~AD、A19/S6、A18/S5、A17/S4、A16/S3和ALE信号功能以及74LS373芯片引脚功能,设计的系统地址总线A19~A形成电路如下图所示。
微机原理及应用总线结构与时序第42~44讲0.80.810利用74LS245数据双向缓冲器设计系统数据总线D15~D0形成电路。
解:根据AD15~AD0、DEN和R/DT信号功能以及74LS245芯片引脚功能,设计的系统数据总线D15~D0形成电路如下图所示。
15 ~ D 87 ~ D 0微机原理及应用 总线结构与时序 第42~44讲 0.80.8 10画出8086CPU 工作在最小方式时的系统总线读时序图。
A 19/S 6 ~ A 16S 3AD 15 ~ AD 0ALE M/IO 地址,BHE 输出地址输出数据输入状态输出BHE/S 7低为I/O 读,高为存储器读RD微机原理及应用 总线结构与时序 第42~44讲 0.8 0.810画出8086CPU 工作在最小方式时的系统总线写时序图。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
高中数学第一讲 集合(一)1.理解集合的概念,知道常用数集的概念及其记法,会判断一组对象是否构成集合。
2.理解元素与集合的“属于”关系,会判断某一个元素属于或不属于某一个集合,了解数集的记法,掌握元素的特征,理解列举法和描述法的意义。
3理解子集、真子集概念,会判断和证明两个集合包4.会判断简单集合的相等关系⑴结合集合的图形表示,理解交集与并集的概念;⑵掌握交集和并集的表示法,会求两个集合的交集和并集。
二.重点知识分析: 1.集合的基本概念及表示方法。
2.交集和并集的概念,集合的交、并的性质。
3.子集的概念、真子集的概念。
三.难点知识分析: 1.运用集合的两种常用表示方法——列举法与描述法,正确表示。
2.元素与子集、属于与包含间区别、描述法给定集合的运算。
3.交集和并集的概念、符号之间的区别与联系。
4.集合的交、并的性质。
三.知识要点精讲 1.集合的概念 ⑴集合:某些指定的对象集在一起就形成一个集合。
⑵元素:集合中每个对象叫做这个集合的元素。
2.集合元素的性质:元素具有确定性、互异性、无序性。
◆确定性 我们把研究的对象统称为元素,把一些元素组成的总体叫做集合。
集合是一个“整体”,构成集合的对象必须是“确定的”。
怎样理解集合的“确定的”性呢?其中“确定”是指构成集合的对象具有非常明确的特征,这个特征不能是模棱两可的,通过这个特征,我们能很容易判断一个元素是否是这个集合的元素。
例1判断下列对象能否构成集合。
1.某校的年轻教师 2.某校大于50岁的教师 3.某校的女教师◆互异性 集合中的元素是互不相同的,不能重复出现。
通俗地讲就是一个集合中不存在相同的元素,每个元素都是独一无二的。
例2 已知{}12,12-∈a a ,则a = .◆无序性 集合中的元素是没有顺序的。
这个是从集合表示方法的角度来强调的。
比如{1,2}和{2,1}其实表示的是同一个集合。
元素前后顺序的不同并不影响相同集合的判断。
注意:数列的表示从外观看象集合的列举法表示,但是数列中元素的顺序不同,他所表示的数列也不一样。
例3 (湖北高考)设P 、Q 为两个非空数集,定义集合P+Q={}Q b P a b a ∈∈+,|,若P={}5,2,0,Q={}6,2,1,则P+Q 中元素的个数是( ) A.9 B.8 C.7 D.62.集合的分类及表示方法⑴集合通常用大写拉丁字母A 、B 、C ……表示,元素通常用小写拉丁字母a 、b 、c ……表示。
这只是一个约定俗成,使用的时候便于区分。
⑵常见数集的表示:自然数集,即非负整数集,记作N ;(注:包括“0”) 正整数集,记作N + 或者N *;(注:不包括“0”) 整数集,记作Z ;有理数集,记作Q ; 实数集,记作R ; 复数集,记作C。
⑶集合的分类:集合可以根据它含元素的个数分为“有限集”和“无限集”⑷集合的表示方法有自然语言法、列举法、描述法,还有图像法。
◇自然语言法就是用文字叙述的形式描述集合的方法。
使用此方法要注意叙述清楚即可。
如“由所有正方形构成的集合”、“大于2且小于10的奇数构成的集合”都是用自然语言表示的。
◇列举法就是将集合中的元素一一列举说明来表示集合。
比如{2,3,4,5}、{a ,b ,c ,d}。
注意元素之间用“,”分隔开。
◇描述法就是通过将集合中元素的范围和共同特征描述出来,以此方法表示集合。
用符号来表示就是{x ∈A|P (x )},其中x 表示集合中的代表元,A 指的是代表元x 的范围, P (x )表示代表元x 的共同特征,“|”表示将代表元与其特征分隔开来,使得意思明确。
注意:①写清楚集合中的代表元的代号,如集合{x ∈R|x<1}不能写成{x<1};②集合与代表元素所采用的字母符号无关,如集合{x ∈R|x<1}也可以写成 {y ∈R|y<1},还可以写成{a ∈R|a<1},都是一样的集合; ③准确使用“且”和“或”;④集合中不能出现未被说明的符号,如{x ∈Z|x=2k}中的k 未被说明,故此集合元素是不明确的;⑤描述的内容应该都要写进集合符号内,如{x ∈Z|x=2k},k ∈Z 不符合要求,应该写成{x ∈Z|x=2k ,k ∈Z};⑥有时联系上下文,元素的范围x ∈R 是明确的,则x ∈R 可以省略。
几种特殊数集的范围和意义需要牢记,经常会应用到。
注意区分下面集合中的元素所表示的含义:⑴集合(){,|x y y =中的元素是()x y ,,这个集合表示二元方程y =的解集,或者理解为曲线y =上的点组成的点集;⑵集合{x |y =中的元素是x ,这个集合表示函数y =x 的取值范围,即表示函数的定义域;⑶集合{y |y =中的元素是y ,这个集合表示函数y =y 的取值范围,即表示函数的值域;⑷集合{y =中的元素只有一个(方程y =),它是用列举法表示的单元素集合.◇还有其他的一些表示方法,这里介绍一个常用的方法就是维恩图,也叫文氏图,用于显示元素集合重叠区域的图示。
上图中圆圈A 内表示集合A ,圆圈A以外的元素都不属于集合A,同时我们还可以看出A是B的子集。
在解题中使用维恩图的方式比较直观,往往更易理解。
注:维恩图的应用往往起到帮助理解的作用。
在集合类题目的求解中,特别是集合应用题中,往往数形结合的方法比较简易快捷的得到结果。
例4 向50名学生调查对A 、B 两件事的态度,有如下结果:赞成A 的人是全体人数的53,其余的不赞成;赞成B 的比赞成A 的多3人,其余的不赞成;另外,对A 、B 都不赞成的学生比对A 、B 都赞成的学生数的31多1人。
问:对A 、B 都赞成的学生和都不赞成的学生各有多少人?3.集合与元素的关系元素与集合有属于和不属于两种关系。
如果a 是集合A 的元素,则a ∈A ;如果a 不是集合A 的元素,则a 不属于A ,记作a ∉A 。
注意a 与{a}的区别,a 表示一个元素,而{a}表示一个集合,两者是属于的关系,如0∈{0}。
4.集合与集合的关系如果集合A 的任何一个元素都是集合B 的元素,我们就说集合A 包含于集合B ,或称集合B 包含集合A ,记作A 包含于B 。
这时,我们也说集合A 是集合B 的子集。
任何一个集合是它本身的子集,注意不要漏掉。
如果A 包含于B ,且A ≠B ,则集合A 是集合B 的真子集。
如果A 包含B ,B 包含C ,则A 包含C 。
(注:包含具有“传递性”)只要构成两个集合的元素是一样的,我们就称这两个集合是相等的。
5.空集的特性不含任何元素的集合叫做空集,记作∅。
∅是任何集合的子集,是任何非空集合的真子集。
∅只有一个子集,即它本身。
注意∅与{∅}的区别,∅是不含任何元素的集合,{∅}是指以空集为元素的集合,已经成为非空集合了。
顾名思义,空集就是什么都没有的集合。
可以这么理解,空口袋也是口袋啊。
第二讲 集合(二)例5 判断正误{}∅∈∅( ) {}∅⊆∅( ) {}{}0,,∅∅∈∅( ) 6.有限集合的子集个数由n 个元素构成的集合有2n 个子集、2n -1个真子集、2n -1个非空子集、2n -2个非空真子集。
例6.已知集合A ={1,2,3,4},那么A 的真子集的个数是( )A .15B .16C .3D .47.运算关系(交、并、补)◇由所有属于集合A 或属于集合B 的元素组成的集合,称为集合A 与集合B 的并集,记作A∪B,读作“A 并B ”,即A∪B={x|x ∈A ,或x ∈B}。
“或”的意思是指两者满足其一即可,当然都满足也是可以的。
在写并集时要注意元素的互异性,两个集合的公共元素只能出现一次。
比如A={1,2,3},B={1,2,4},则A∪B={1,2,3,4},而不能写成A∪B={1,1,2,2,3,4}。
并集就是把两个集合中的元素合在一起,去掉重复的,然后放进一个集合里。
◇由所有属于集合A且属于集合B的元素组成的集合,称为集合A与集合B的交集,记作A∩B,读作“A交B”。
即A∩B={x|x ∈A ,且x ∈B}。
“且”的意思是指两者必须都满足,缺一不可。
另外要注意“所有”,不能漏掉一些元素。
交集就是两个集合中相同的元素全部挑出来,组成一个新集合。
◇如果一个集合含有我们所要研究的每个集合的全部元素,这个集合就可以看作一个全集,全集通常用U 表示。
全集是一个相对的概念。
设U是一个全集,A 是U的一个子集,由U中所有不属于A 的元素组成的集合,叫做U中子集A 的补集(或余集),记作C UA 。
补集是相对于全集而存在的,在研究补集之前必须先明确全集。
补集就是互补的集合。
通俗理解就是一个全集,一刀切两半,这样分开后的两个集合就是互补了,而且一个元素在一个集合中,那么肯定不在另一个集合里。
从符号的角度来看,若x ∈U,则x ∈A 和x ∈C UA 二者必居其一。
2. 运算性质⑴C UU=∅,C U∅=U,C U(C UA )=A,A∪C UA =U,A∩C UA =∅;若A包含于B,则C UA 包含C UB;反之,若C UA 包含C UB,则A包含于B; 若A=B,则C UA =C UB;反之,若C UA =C UB,则A=B ; C U(A ∩B )=C UA ∪C UB ,C U(A ∪B )=C UA ∩C UB ; 注: 希望你能全部理解掌握!!! ⑵对于任意两个集合A 、B ,都有:A B B A Y Y = B A A Y ⊆ B A B Y ⊆ A B A ⊆I B B A ⊆I 注: 并集越并越大,交集越交越小分配律,结合律:A∩(B∩C)=(A∩B)∩C; A∪(B∪C)=(A∪B)∪C; A∩(B∪C)=(A∩B)∪(A∩C); A∪(B∩C)=(A∪B)∩(A∪C)。
9. 德摩根定律计算集合元素个数公式设有限集A、B、C,card (A )表示集合A 的元素个数,则 (1)card (A∪B)=card (A)+card (B)-card (A∩B).(2)card (A∪B∪C)=card (A)+card (B)+card (C)-card (A∩B)-card (B∩C)-card (C∩A)+card (A∩B∩C)题型一:考查集合的概念与性质1、下列命题真命题的个数有( )⑴集合{}的正有理数小于1是一个有限集; ⑵集合{}1|2-=x y y 与集合(){}1|,2-=x y y x 是同一个集合; ⑶由1,32,64,|-32|,0.5这些数组成的集合有5个元素; ⑷集合(){}R y x xy y x ∈≤,,0|,是指第二和第四象限内的点集。
2、已知x 、y 、z 为非零实数,代数式xyzxyz z z y y x x +++的值所组成的集合为M ,则下列判断正确的是( )A 、M ∉0B 、M ∈2C 、M ∉-4D 、M ∈43、设a ,b ,c 为实数,))(()(2c bx x a x x f +++=,)1)(1()(2+++=bx cx ax x g 。
