三角形证明题集锦ppt课件
合集下载
三角形全等判定复习ppt课件
N 明方法与前题基本相同,只
须证明⊿ABN≌⊿BCM
A
C
B
变式4:如图,⊿ABD,⊿ACE都是正三角形, 求证CD=BE
D
A
E
B
C
分析:此题实质上是把题目中的条件B,A,C三点改为 不共线,证明方法与前题基本相同.
变式6:如图,分别以⊿ABC的边AB,AC为一边 画正方形AEDB和正方形ACFG,连结CE,BG.
求证BG=CE
E
分析:此题是把两个三
角形改成两个正方形而
D
A
G 以,证法类同
FBBiblioteka C小结:1.证明两个三角形全等,要结合题目的条件 和结论,选择恰当的判定方法
2.全等三角形,是证明两条线段或两个角相 等的重要方法之一,证明时
①要观察待证的线段或角,在哪两个可能全等的三 角形中。
②分析要证两个三角形全等,已有什么条件,还缺 什么条件。
AB=CB
A
AD=CD
BD=BD
_
=
P
∴ △ABD≌△CBD(SSS)
B
D
∴∠ABD=∠CBD
_
=
在△ABP和△CBP中
C
AB=BC
∠ABP=∠CBP
BP=BP
∴ △ABP ≌ △CBP(SAS)
∴PA=PC
例4。已知:如图AB=AE,∠B=∠E,BC=ED AF⊥CD 求证:点F是CD的中点
分析:要证CF=DF可以考虑CF 、 DF所在的两个三角形全等,为此可 添加辅助线构建三角形全等 ,如何 添加辅助线呢?
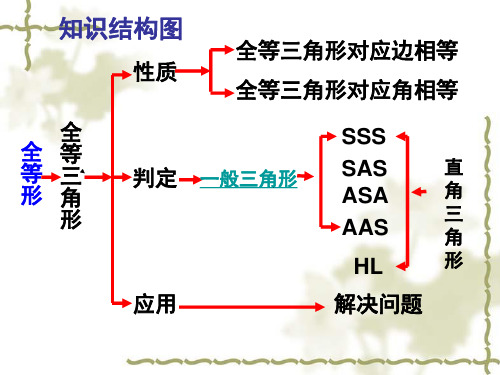
知识结构图
性质
全等三角形对应边相等 全等三角形对应角相等
全 全等 等三 形角
形
《直角三角形》三角形的证明PPT(第1课时)

ห้องสมุดไป่ตู้
例1 已知:Rt△ABC和Rt△A′B′C′,∠C=∠C′=90°,BC=B′C′,BD、B′D′分别是AC、A′C′边 上的中线且BD=B′D′ (如图). 求证: Rt△ABC≌CORt△A′B′C′. 证明:在Rt△BDC和Rt△B′D′C′中, ∵BD=B′D′,BC=B′C′, ∴Rt△BDC≌Rt△B′D′C′ (HL定理). CD=C'D'. 又∵AC=2CD,A′C′=2C′D′,∴AC=A′C′. ∴在Rt△ABC和Rt△A 'B 'C '中, ∵BC=B′C ′,∠C=∠C ′ =90°,AC=A′ C ′ , ∴Rt△ABC≌CORt△A′B′C′(SAS)
跟踪检测
1.如图,一张长方形纸片,剪去部分后得到一个三角形,则图中∠1+∠2的度 数是( C) A.30° B.60° C.90° D.120° 2.由下列 条件不能判定△ABC是直角三角形的是(C ) A.∠A=37°,∠C=53° B.∠A=34°,∠B=56° C.∠B=42°,∠C=38° D.∠A=72°,∠B=18° 3.如图,点D在△ABC的边AC上,将△ABC沿BD翻折后,点A恰好与点C重 合.若BC=5,CD=3,则BD的长为(D ) A.1 B.2 C.3 D.4
(4)∠A=∠A′,∠B=∠B′ (×)
(5)AC=A′C′,AB=A′B′ (HL)
活动探究
活动1:如图,两角及其中一角的对边对应相等的两个三角形全等(AAS); 那么, “两边及其中一边的对角对应相等的两个三角形全等”吗?.
观察下列演示,你有什么发现?
A
B
C
归纳
两边及其中一边的对角对应相等的两个三角形不 一定全等.
例1 已知:Rt△ABC和Rt△A′B′C′,∠C=∠C′=90°,BC=B′C′,BD、B′D′分别是AC、A′C′边 上的中线且BD=B′D′ (如图). 求证: Rt△ABC≌CORt△A′B′C′. 证明:在Rt△BDC和Rt△B′D′C′中, ∵BD=B′D′,BC=B′C′, ∴Rt△BDC≌Rt△B′D′C′ (HL定理). CD=C'D'. 又∵AC=2CD,A′C′=2C′D′,∴AC=A′C′. ∴在Rt△ABC和Rt△A 'B 'C '中, ∵BC=B′C ′,∠C=∠C ′ =90°,AC=A′ C ′ , ∴Rt△ABC≌CORt△A′B′C′(SAS)
跟踪检测
1.如图,一张长方形纸片,剪去部分后得到一个三角形,则图中∠1+∠2的度 数是( C) A.30° B.60° C.90° D.120° 2.由下列 条件不能判定△ABC是直角三角形的是(C ) A.∠A=37°,∠C=53° B.∠A=34°,∠B=56° C.∠B=42°,∠C=38° D.∠A=72°,∠B=18° 3.如图,点D在△ABC的边AC上,将△ABC沿BD翻折后,点A恰好与点C重 合.若BC=5,CD=3,则BD的长为(D ) A.1 B.2 C.3 D.4
(4)∠A=∠A′,∠B=∠B′ (×)
(5)AC=A′C′,AB=A′B′ (HL)
活动探究
活动1:如图,两角及其中一角的对边对应相等的两个三角形全等(AAS); 那么, “两边及其中一边的对角对应相等的两个三角形全等”吗?.
观察下列演示,你有什么发现?
A
B
C
归纳
两边及其中一边的对角对应相等的两个三角形不 一定全等.
三角形内角和定理的证明证明教学PPT课件

15、最终你相信什么就能成为什么。因为世界上最可怕的二个词,一个叫执着,一个叫认真,认真的人改变自己,执着的人改变命运。只要在路上,就没有到不了的地方。 16、你若坚持,定会发光,时间是所向披靡的武器,它能集腋成裘,也能聚沙成塔,将人生的不可能都变成可能。 17、人生,就要活得漂亮,走得铿锵。自己不奋斗,终归是摆设。无论你是谁,宁可做拼搏的失败者
1 2 1800 BDC(等式性质).
BDC BAC ABD ACD(等量代换).
即BDC BAC B C.
1、快乐总和宽厚的人相伴,财富总与诚信的人相伴,聪明总与高尚的人相伴,魅力总与幽默的人相伴,健康总与阔达的人相伴。 2、人生就有许多这样的奇迹,看似比登天还难的事,有时轻而易举就可以做到,其中的差别就在于非凡的信念。
A
M
B
N
C
F
D
练一练
A
1、 如图,已知AD是△ABD
34
和△ACD的公共边.求证:
∠BDC=∠BAC+∠B+∠C
12
B
D
证法一:
∵在△ABD中, ∠1=180°-∠B-∠3,
C
在△ADC中, ∠2=180°-∠C-∠4(三角形内角和定理),
又∵∠BDC=360°-∠1-∠2(周角定义)
∴∠ BDC =360°-( 180°-∠B-∠3 )-( 180°-∠C-∠4 )
= ∠B+∠C+∠3+∠4.
又 ∵ ∠BAC = ∠3+∠4,
∴ ∠ BDC = ∠B+∠C+ ∠BAC (等量代换)
A
证法二:
连接BC.
B
1
D
2
C
在ABC中,BAC ABD ACD 1 2 1800,
1 2 1800 BDC(等式性质).
BDC BAC ABD ACD(等量代换).
即BDC BAC B C.
1、快乐总和宽厚的人相伴,财富总与诚信的人相伴,聪明总与高尚的人相伴,魅力总与幽默的人相伴,健康总与阔达的人相伴。 2、人生就有许多这样的奇迹,看似比登天还难的事,有时轻而易举就可以做到,其中的差别就在于非凡的信念。
A
M
B
N
C
F
D
练一练
A
1、 如图,已知AD是△ABD
34
和△ACD的公共边.求证:
∠BDC=∠BAC+∠B+∠C
12
B
D
证法一:
∵在△ABD中, ∠1=180°-∠B-∠3,
C
在△ADC中, ∠2=180°-∠C-∠4(三角形内角和定理),
又∵∠BDC=360°-∠1-∠2(周角定义)
∴∠ BDC =360°-( 180°-∠B-∠3 )-( 180°-∠C-∠4 )
= ∠B+∠C+∠3+∠4.
又 ∵ ∠BAC = ∠3+∠4,
∴ ∠ BDC = ∠B+∠C+ ∠BAC (等量代换)
A
证法二:
连接BC.
B
1
D
2
C
在ABC中,BAC ABD ACD 1 2 1800,
三角形全等的证明ppt课件

∴AC=AD .
讲解新课
例2、已知:点D在AB上,点E在AC上,BE和CD交于 O点,AB=AC,∠B=∠C. 求证:BD=CE
证明:在△ABE和△ACD中 ∠A= ∠A
AB=AC
∠B=∠C
∴ △ABE≌△ACD (ASA)
∴AD=AE
∵AB=AC
∴BD=CE
.
课
堂 如图,要证明△ACE≌ △BDF,根据给定的条件
E
的条件,不难发现图3是由图2平移而得。 利用AE=CF,可得:AF=CE
证明:∵AD∥BC(已知)
F
B
C
图3
∴∠A=∠C(两直线平行,内错角相等)
又 AE=CF
∴AE+EF=CF+EF(等式性质)
即AF=CE 在△AFD 和△CEB 中
AD=CB(已知)
问:若求证∠D=∠B ,
如何证明?
∠A=∠C(已证)
∴ ∠B=∠D(全等三角形对应角相等)
D C
.
小结:四边形问题转化为三角形 问题解决。
问:此题添加辅助线,若连结BD行吗?A 在原有条件下,还能推出什么结论?
B
答:∠ABC=∠ADC,AB∥CD,AD∥BC
.
D C
归纳:二个三角形全等的判定方法
对应 相等 的元
素
两边一角 两角一边
两边及其 两边及其 两角及其 两角及其
写为“ASA”)
.
讲解新课:
例1、已知:如图,∠DAB=∠CAB,∠C=∠D 求证:AC=AD 证明:∵ ∠DAB=∠CAB,∠C=∠D
∴∠ABD=∠ACD (三角形内角和定理) 在△ACB和△ADB中
∠DAB=∠CAB AB=AB (共用边) ∠ABD=∠ACD
讲解新课
例2、已知:点D在AB上,点E在AC上,BE和CD交于 O点,AB=AC,∠B=∠C. 求证:BD=CE
证明:在△ABE和△ACD中 ∠A= ∠A
AB=AC
∠B=∠C
∴ △ABE≌△ACD (ASA)
∴AD=AE
∵AB=AC
∴BD=CE
.
课
堂 如图,要证明△ACE≌ △BDF,根据给定的条件
E
的条件,不难发现图3是由图2平移而得。 利用AE=CF,可得:AF=CE
证明:∵AD∥BC(已知)
F
B
C
图3
∴∠A=∠C(两直线平行,内错角相等)
又 AE=CF
∴AE+EF=CF+EF(等式性质)
即AF=CE 在△AFD 和△CEB 中
AD=CB(已知)
问:若求证∠D=∠B ,
如何证明?
∠A=∠C(已证)
∴ ∠B=∠D(全等三角形对应角相等)
D C
.
小结:四边形问题转化为三角形 问题解决。
问:此题添加辅助线,若连结BD行吗?A 在原有条件下,还能推出什么结论?
B
答:∠ABC=∠ADC,AB∥CD,AD∥BC
.
D C
归纳:二个三角形全等的判定方法
对应 相等 的元
素
两边一角 两角一边
两边及其 两边及其 两角及其 两角及其
写为“ASA”)
.
讲解新课:
例1、已知:如图,∠DAB=∠CAB,∠C=∠D 求证:AC=AD 证明:∵ ∠DAB=∠CAB,∠C=∠D
∴∠ABD=∠ACD (三角形内角和定理) 在△ACB和△ADB中
∠DAB=∠CAB AB=AB (共用边) ∠ABD=∠ACD
三角形内角和定理证明ppt课件

(1) ∠ACD是△ABC的
CD
(2)∵∠ +∠ ∠ +∠
∴∠ = ∠
+∠ =180°(三角形三个内角的和等于180° )
=180°(平角的定义)
+∠
(
)
推论:三角形的一个外角等于与它不相邻的两个内角的和.
公理、定理及由它们直接推出来的 结论(推论),以后可以直接运用. 9
练一练:
已知:如图,AD是△ABC的角平分线,E是BC延长 线上一点,∠EAC=∠B,求证:∠ADE=∠DAE
B
∠A+∠B+∠AOB=180°(三角形三个内角的和等于180°)
O
∴∠A+∠B=180°-∠AOB
在⊿COD中 同理可得
∠C+∠D=180°-∠COD
∵∠AOB与∠COD是对顶角
C
D
∴∠AOB=∠COD
∴∠A+∠B=∠C+∠D( 等量代换)
8
A
议一议:
B
如图所示:把△ABC的边BC延长,得到∠ACD.
∠2= ∠B(两直线平行,同位角相等)
∵∠1+∠2+∠ACB=180°(平角的定义)
∴ ∠A+∠B+∠ACB=180°(等量代换).
1
2 C
辅助线
D
6
A
E
你还有什么
不同的方法?
B
P
AC
Q
B
H
C
B
A
E
C
7
试一试:
已知:如图,AC、BD相交于点O, 求证:∠A+∠B=∠C+∠D.
A 证明:
在⊿AOB中
CD
(2)∵∠ +∠ ∠ +∠
∴∠ = ∠
+∠ =180°(三角形三个内角的和等于180° )
=180°(平角的定义)
+∠
(
)
推论:三角形的一个外角等于与它不相邻的两个内角的和.
公理、定理及由它们直接推出来的 结论(推论),以后可以直接运用. 9
练一练:
已知:如图,AD是△ABC的角平分线,E是BC延长 线上一点,∠EAC=∠B,求证:∠ADE=∠DAE
B
∠A+∠B+∠AOB=180°(三角形三个内角的和等于180°)
O
∴∠A+∠B=180°-∠AOB
在⊿COD中 同理可得
∠C+∠D=180°-∠COD
∵∠AOB与∠COD是对顶角
C
D
∴∠AOB=∠COD
∴∠A+∠B=∠C+∠D( 等量代换)
8
A
议一议:
B
如图所示:把△ABC的边BC延长,得到∠ACD.
∠2= ∠B(两直线平行,同位角相等)
∵∠1+∠2+∠ACB=180°(平角的定义)
∴ ∠A+∠B+∠ACB=180°(等量代换).
1
2 C
辅助线
D
6
A
E
你还有什么
不同的方法?
B
P
AC
Q
B
H
C
B
A
E
C
7
试一试:
已知:如图,AC、BD相交于点O, 求证:∠A+∠B=∠C+∠D.
A 证明:
在⊿AOB中
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
10
例3(6分题) :如图,已知∠B=∠C=90°,M是BC的中点,DM平分∠ADC。求证:AD =AB+CD
11
练4(6分题) :如图,已知在△ABC中,AB=CD,∠BDA=∠BAD,AE为△ABD的BD边 上的中线,求证:AC=2AE
12
练2 (6分题) :如图,已知AB∥CD,AD与BC相交于F,BE平分∠ABC,E为AD的中 点,问:AB、BC和CD三条线段之间有什么数量关系,并给出证明(如有需要可直接运 用下面的定理:在一个三角形中,如果有两个角相等,那么它们所对的边也相等——简 写成“等角对等边”)。
8
例1(6分题):如图,已知∠B=∠C=90°,M是BC的中点,DM平分∠ADC。 (1)若连接AM,则AM是否平分∠BAD?请你证明你的结论。 (2)DM与AM有怎样的位置关系?请说明理由。 (3)求证:AD=AB+CD
9
练2(6分题) :如图,AB∥CD,DE平分∠ADC,AE平分∠BAD,求证:AD=AB+CD
△MBO, ∴ON=OM,∠AON=∠BOM,∵AC=AB,O是BC的中点, ∴AO⊥BC,即∠BOM+∠AOM=90°, ∴∠AON+∠AOM=90°,即∠NOM=90°, ∴△OMN是等腰直角三角形.
6. 延长CD到F,使DF=BC,连结EF ∵AE=BD ∴AE=CF ∵△ABC为正三角形 ∴BE=BF ∠B=60° ∴△EBF为=等 边三角形 ∴角F=60° EF=EB 在△EBC和△EFD中 EB=EF(已证) ∠B=∠F(已证) BC=DF(已作) ∴△EBC≌△EFD(SAS) ∴EC=ED
13
例3(9分题):如图,已知在有公共顶点的△OAB和△OCD中,OA=OB,OC=OD,且 ∠AOB=∠COD。 (1)求证:CA=BD (2)若将△OCD绕点O沿着逆时针方向旋转,当旋转到A、C、D在同一条直线上时,问(1)
。 中的结论是否仍然成立?如果结论成立,请证明;如果不成立,请说明理由
4.∵BP CD分别平分角∠ABC和∠ACB∴∠DBP=∠PBC∠ECP=∠PCB∵DE∥BC∴∠DPB=∠PBC∠EPC=∠ PCB ∴DP=DP EP=EC ∴DE-DP=DE-DB=EP=EC∴DE-DB=EC
5.(1)因为直角三角形的斜边中点是三角形的外心,所以 O到△ABC的三个顶点A、B、C距离相等; (2)△OMN是等腰直角三角形。证明:连接OA,如图,∵AC=AB,∠BAC=90°, ∴OA=OB,OA平分∠BAC, ∠B=45°,∴∠NAO=45°, ∴∠NAO=∠B,在△NAO和△MBO 中, AN=BM ,∠NAO=∠B ,AO=BO ,∴△NAO≌
6
7、如图,等腰三角形ABC中,AB=AC,∠A=90°,BD平分∠ABC, DE⊥BC且BC=10,求△DCE的周长。
7
几何证明习题答案
1. 连接AD,由△ABC为等腰直角三角形可得AD垂直AC,且AD=BD,∠DAQ=∠DBR=45度,又由平行关系得,四边形RPQA为 矩形,所以AQ=RP,△BRP也是等腰直角三角行,即BR=PR,所以AQ=BR由边角边,△BRD全等于△AQD,所以 ∠BDR=∠ADQ,DR=DQ,∠RDQ=∠RDA+∠ADQ=∠RDA+∠BDR=90度,所以△RDQ是等腰RT△。 2. 作AG平分∠BAC交BD于G∵∠BAC=90° ∴∠CAG= ∠BAG=45°∵∠BAC=90° AC=AB
A
DP
E
B 图⑴ C
4
5、在Rt△ABC中,AB=AC,∠BAC=90°,O为BC的中点。 (1)写出点O到△ABC的三个顶点A、B、C的距离的大小关系(不要求证明);
(2)如果点M、N分别在线段AB、AC上移动,在移动中保持AN=BM,请判断△OMN的形 状,并证明你的结论。
C N
O
AM
B
5
6、如图,△ABC为等边三角形,延长BC到D,延长BA到E,AE=BD, 连结EC、ED,求证:CE=DE
7. ∵DE⊥BC∴∠DEB=90∵BD平分∠ABC在直角三角形ABD和直角三角形DBE中 ∠A=∠DEB BD=BD ∠ABD=∠DBE ∴直角三角形ABD全等直角三角形DBE ∴BE=AB AD=DE ∵AB=AC
∴BE+CE=AC+CE △DCE=CE+DE+CD=CE+AD+CD=CE+CA=BE+CE=10
A
D E
B
F
C
A
D E
B
F
C
2
3、已知:在⊿ABC中BD、CE是高,在BD、CE或其延长线上分别截取BM=AC、CN=AB, 求证:MA⊥NA。
N
A
E D
M
B
C
3
4、已知:如图(1),在△ABC中,BP、CP分别平分∠ABC和∠ACB,DE过点P交AB于 D,交AC于E,且DE∥BC.求证:DE-DB=EC.
∴∠C=∠ABC=45°∴∠C=∠BAG ∵AE⊥BD ∴∠ABE+∠BAE=90° ∵∠CAF+∠BAE=90° ∠CAF=∠ABE∵ AC=AB ∴△ACF ≌△BAG∴CF=AG ∵∠C=∠DAG =45° CD=AD∴△CDF ≌△ADG ∴∠CDF=∠ADB 3. 易证△ABM≌△NAC.∠NAM=∠NAE+∠BAM=∠NAE+ANE=90°
14
练4 (9分压轴题) :如图①,OP是∠MON的平分线,请你利用该图形画一对以OP所在直线为对 称轴的全等三角形。请你参考这个做全等三角形的方法,解答下列问题(1)如图②,在△ABC中, ∠ACB是直角,∠B=60°,AD、CE分别是∠BAC、∠BCA的平分线,AD、CE相交于点F。请你 写出FE与FD之间的数量关系。(2)如图③,在△ABC中,如果∠ACB不是直角,而(1)中的其 它条件不变。请问:你在(1)中的结论是否仍然成立?若成立,请给予证明;若不成立,请说明 理由。(3)你还能得出什么结论?请给出证明。
八年级数学(上)几何证明练习题
1、已知:在⊿ABC中,∠A=90度,AB=AC,在BC上任取一点P,作PQ∥AB交AC于 Q,作PR∥CA交BA于R,D是BC的中点,求证:⊿RDQ是等腰直角三角形。
A
Q
R
C
BPD1来自2、已知:在⊿ABC中,∠A=900,AB=AC,D是AC的中点,AE⊥BD,AE延长线交BC于 F,求证:∠ADB=∠FDC。
例3(6分题) :如图,已知∠B=∠C=90°,M是BC的中点,DM平分∠ADC。求证:AD =AB+CD
11
练4(6分题) :如图,已知在△ABC中,AB=CD,∠BDA=∠BAD,AE为△ABD的BD边 上的中线,求证:AC=2AE
12
练2 (6分题) :如图,已知AB∥CD,AD与BC相交于F,BE平分∠ABC,E为AD的中 点,问:AB、BC和CD三条线段之间有什么数量关系,并给出证明(如有需要可直接运 用下面的定理:在一个三角形中,如果有两个角相等,那么它们所对的边也相等——简 写成“等角对等边”)。
8
例1(6分题):如图,已知∠B=∠C=90°,M是BC的中点,DM平分∠ADC。 (1)若连接AM,则AM是否平分∠BAD?请你证明你的结论。 (2)DM与AM有怎样的位置关系?请说明理由。 (3)求证:AD=AB+CD
9
练2(6分题) :如图,AB∥CD,DE平分∠ADC,AE平分∠BAD,求证:AD=AB+CD
△MBO, ∴ON=OM,∠AON=∠BOM,∵AC=AB,O是BC的中点, ∴AO⊥BC,即∠BOM+∠AOM=90°, ∴∠AON+∠AOM=90°,即∠NOM=90°, ∴△OMN是等腰直角三角形.
6. 延长CD到F,使DF=BC,连结EF ∵AE=BD ∴AE=CF ∵△ABC为正三角形 ∴BE=BF ∠B=60° ∴△EBF为=等 边三角形 ∴角F=60° EF=EB 在△EBC和△EFD中 EB=EF(已证) ∠B=∠F(已证) BC=DF(已作) ∴△EBC≌△EFD(SAS) ∴EC=ED
13
例3(9分题):如图,已知在有公共顶点的△OAB和△OCD中,OA=OB,OC=OD,且 ∠AOB=∠COD。 (1)求证:CA=BD (2)若将△OCD绕点O沿着逆时针方向旋转,当旋转到A、C、D在同一条直线上时,问(1)
。 中的结论是否仍然成立?如果结论成立,请证明;如果不成立,请说明理由
4.∵BP CD分别平分角∠ABC和∠ACB∴∠DBP=∠PBC∠ECP=∠PCB∵DE∥BC∴∠DPB=∠PBC∠EPC=∠ PCB ∴DP=DP EP=EC ∴DE-DP=DE-DB=EP=EC∴DE-DB=EC
5.(1)因为直角三角形的斜边中点是三角形的外心,所以 O到△ABC的三个顶点A、B、C距离相等; (2)△OMN是等腰直角三角形。证明:连接OA,如图,∵AC=AB,∠BAC=90°, ∴OA=OB,OA平分∠BAC, ∠B=45°,∴∠NAO=45°, ∴∠NAO=∠B,在△NAO和△MBO 中, AN=BM ,∠NAO=∠B ,AO=BO ,∴△NAO≌
6
7、如图,等腰三角形ABC中,AB=AC,∠A=90°,BD平分∠ABC, DE⊥BC且BC=10,求△DCE的周长。
7
几何证明习题答案
1. 连接AD,由△ABC为等腰直角三角形可得AD垂直AC,且AD=BD,∠DAQ=∠DBR=45度,又由平行关系得,四边形RPQA为 矩形,所以AQ=RP,△BRP也是等腰直角三角行,即BR=PR,所以AQ=BR由边角边,△BRD全等于△AQD,所以 ∠BDR=∠ADQ,DR=DQ,∠RDQ=∠RDA+∠ADQ=∠RDA+∠BDR=90度,所以△RDQ是等腰RT△。 2. 作AG平分∠BAC交BD于G∵∠BAC=90° ∴∠CAG= ∠BAG=45°∵∠BAC=90° AC=AB
A
DP
E
B 图⑴ C
4
5、在Rt△ABC中,AB=AC,∠BAC=90°,O为BC的中点。 (1)写出点O到△ABC的三个顶点A、B、C的距离的大小关系(不要求证明);
(2)如果点M、N分别在线段AB、AC上移动,在移动中保持AN=BM,请判断△OMN的形 状,并证明你的结论。
C N
O
AM
B
5
6、如图,△ABC为等边三角形,延长BC到D,延长BA到E,AE=BD, 连结EC、ED,求证:CE=DE
7. ∵DE⊥BC∴∠DEB=90∵BD平分∠ABC在直角三角形ABD和直角三角形DBE中 ∠A=∠DEB BD=BD ∠ABD=∠DBE ∴直角三角形ABD全等直角三角形DBE ∴BE=AB AD=DE ∵AB=AC
∴BE+CE=AC+CE △DCE=CE+DE+CD=CE+AD+CD=CE+CA=BE+CE=10
A
D E
B
F
C
A
D E
B
F
C
2
3、已知:在⊿ABC中BD、CE是高,在BD、CE或其延长线上分别截取BM=AC、CN=AB, 求证:MA⊥NA。
N
A
E D
M
B
C
3
4、已知:如图(1),在△ABC中,BP、CP分别平分∠ABC和∠ACB,DE过点P交AB于 D,交AC于E,且DE∥BC.求证:DE-DB=EC.
∴∠C=∠ABC=45°∴∠C=∠BAG ∵AE⊥BD ∴∠ABE+∠BAE=90° ∵∠CAF+∠BAE=90° ∠CAF=∠ABE∵ AC=AB ∴△ACF ≌△BAG∴CF=AG ∵∠C=∠DAG =45° CD=AD∴△CDF ≌△ADG ∴∠CDF=∠ADB 3. 易证△ABM≌△NAC.∠NAM=∠NAE+∠BAM=∠NAE+ANE=90°
14
练4 (9分压轴题) :如图①,OP是∠MON的平分线,请你利用该图形画一对以OP所在直线为对 称轴的全等三角形。请你参考这个做全等三角形的方法,解答下列问题(1)如图②,在△ABC中, ∠ACB是直角,∠B=60°,AD、CE分别是∠BAC、∠BCA的平分线,AD、CE相交于点F。请你 写出FE与FD之间的数量关系。(2)如图③,在△ABC中,如果∠ACB不是直角,而(1)中的其 它条件不变。请问:你在(1)中的结论是否仍然成立?若成立,请给予证明;若不成立,请说明 理由。(3)你还能得出什么结论?请给出证明。
八年级数学(上)几何证明练习题
1、已知:在⊿ABC中,∠A=90度,AB=AC,在BC上任取一点P,作PQ∥AB交AC于 Q,作PR∥CA交BA于R,D是BC的中点,求证:⊿RDQ是等腰直角三角形。
A
Q
R
C
BPD1来自2、已知:在⊿ABC中,∠A=900,AB=AC,D是AC的中点,AE⊥BD,AE延长线交BC于 F,求证:∠ADB=∠FDC。
