新人教版八年级数学《全等三角形基础证明题》练习
人教版八年级数学上册第十二章全等三角形证明方法归纳及典型例题

全等三角形的证明全等三角形的性质:对应角相等,对应边相等,对应边上的中线相等,对应边上的高相等,对应角的角平分线相等,面积相等.寻找对应边和对应角,常用到以下方法:(1)全等三角形对应角所对的边是对应边,两个对应角所夹的边是对应边.(2)全等三角形对应边所对的角是对应角,两条对应边所夹的角是对应角.(3)有公共边的,公共边常是对应边.(4)有公共角的,公共角常是对应角.(5)有对顶角的,对顶角常是对应角.(6)两个全等的不等边三角形中一对最长边(或最大角)是对应边(或对应角),一对最短边(或最小角)是对应边(或对应角).要想正确地表示两个三角形全等,找出对应的元素是关键.全等三角形的判定方法:(1)边角边定理(SAS):两边和它们的夹角对应相等的两个三角形全等.(2)角边角定理(ASA):两角和它们的夹边对应相等的两个三角形全等.(3)边边边定理(SSS):三边对应相等的两个三角形全等.(4)角角边定理(AAS):两个角和其中一个角的对边对应相等的两个三角形全等.(5)斜边、直角边定理(HL):斜边和一条直角边对应相等的两个直角三角形全等.全等三角形的应用:运用三角形全等可以证明线段相等、角相等、两直线垂直等问题,在证明的过程中,注意有时会添加辅助线.拓展关键点:能通过判定两个三角形全等进而证明两条线段间的位置关系和大小关系.而证明两条线段或两个角的和、差、倍、分相等是几何证明的基础.专题1、常见辅助线的做法典型例题找全等三角形的方法:(1)可以从结论出发,寻找要证明的相等的两条线段(或两个角)分别在哪两个可能全等的三角形中;(2)可以从已知条件出发,看已知条件可以确定哪两个三角形全等;(3)可从条件和结论综合考虑,看它们能确定哪两个三角形全等;(4)若上述方法均不可行,可考虑添加辅助线,构造全等三角形。
三角形中常见辅助线的作法:①延长中线构造全等三角形;②利用翻折,构造全等三角形;③引平行线构造全等三角形;④作连线构造等腰三角形。
新人教版初中数学八年级数学上册第二单元《全等三角形》测试卷(含答案解析)(4)
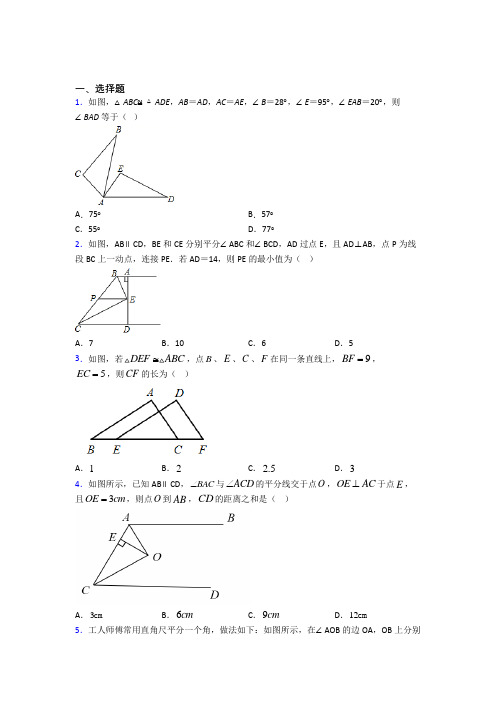
一、选择题1.如图,△ABC ≌△ADE ,AB =AD ,AC =AE ,∠B =28︒,∠E =95︒,∠EAB =20︒,则∠BAD 等于( )A .75︒B .57︒C .55︒D .77︒2.如图,AB ∥CD ,BE 和CE 分别平分∠ABC 和∠BCD ,AD 过点E ,且AD ⊥AB ,点P 为线段BC 上一动点,连接PE .若AD =14,则PE 的最小值为( )A .7B .10C .6D .53.如图,若DEF ABC ≅,点B 、E 、C 、F 在同一条直线上,9BF =,5EC =,则CF 的长为( )A .1B .2C .2.5D .34.如图所示,已知AB ∥CD ,BAC ∠与ACD ∠的平分线交于点O ,OE AC ⊥于点E ,且3OE cm =,则点O 到AB ,CD 的距离之和是( )A .3cmB .6cmC .9cmD .12cm5.工人师傅常用直角尺平分一个角,做法如下:如图所示,在∠AOB 的边OA ,OB 上分别取OM =ON ,移动直角尺,使直角尺两边相同的刻度分别与M ,N 重合(即CM =CN ).此时过直角尺顶点C 的射线OC 即是∠AOB 的平分线.这种做法的道理是( )A .HLB .SASC .SSSD .ASA6.下列四个命题中,真命题是( )A .如果 ab =0,那么a =0B .面积相等的三角形是全等三角形C .直角三角形的两个锐角互余D .不是对顶角的两个角不相等7.如图,在ABC 中,90C ∠=︒,AD 是BAC ∠的角平分线,E 是边AB 上一点,若6CD =,则DE 的长可以是( )A .1B .3C .5D .78.如图,AB BC ⊥,CD BC ⊥,AC BD =,则能证明ABC DCB ≅的判定法是( )A .SASB .AASC .SSSD .HL9.如图,OB 平分∠MON ,A 为OB 的中点,AE ⊥ON ,EA=3,D 为OM 上的一个动点,C 是DA 延长线与BC 的交点,BC //OM ,则CD 的最小值是( )A .6B .8C .10D .1210.如图,AC 与DB 相交于E ,且BE CE =,如果添加一个条件还不能判定ABE △≌DCE ,则添加的这个条件是( ).A .AC DB =B .A D ∠=∠C .B C ∠=∠D .AB DC = 11.如图,C 是∠AOB 的平分线上一点,添加下列条件不能判定△AOC ≌△BOC 的是( )A .OA =OB B .AC =BC C .∠A =∠BD .∠1=∠2 12.下列说法正确的是 ( )A .一直角边对应相等的两个直角三角形全等B .斜边相等的两个直角三角形全等C .斜边相等的两个等腰直角三角形全等D .一边长相等的两个等腰直角三角形全等二、填空题13.如图,已知四边形,90,3,4,5,ABCD B AB BC AC ︒∠====180BAD CAD ︒∠+∠=,180BCD ACD ︒∠+∠=,则四边形ABCD 的面积是_________.14.如图,AOP BOP ∠=∠,PD OA ⊥,C 是OB 上的动点,连接PC ,若4PD =,则PC 的最小值为_________.15.如图,△ABC ≌△DEF ,由图中提供的信息,可得∠D =__________°.16.如图,AB ,CD 交于点O ,AD ∥BC .请你添加一个条件_____,使得△AOD ≌△BOC .17.如图,四边形ABDC 中,对角线AD 平分BAC ∠,136ACD ∠=︒,44BCD ∠=︒,则ADB ∠的度数为_____18.如图,OM 平分∠POQ ,MA ⊥OP ,MB ⊥OQ ,垂足为A ,B ,S △AOM =8cm 2,OA=4cm ,则MB=___.19.如图,已知AB AC =,D 为BAC ∠的角平分线上面一点,连接BD ,CD ;如图,已知AB AC =,D 、E 为BAC ∠的角平分线上面两点,连接BD ,CD ,BE ,CE ;如图,已知AB AC =,D 、E 、F 为BAC ∠的角平分线上面三点,连接BD ,CD ,BE ,CE ,BF ,CF ;…,依此规律,第n 个图形中有全等三角形的对数是______.20.如图,在ABC 中,AB AC =,BD CD =,点E ,F 是AD 上的任意两点、若8BC =,6AD =,则图中阴影部分的面积为__________.三、解答题21.如图,已知A ABC ∠=∠,D CBD ∠=∠,ABD CBD ∠=∠,点E 在BC 的延长线上.求证:CD 平分ACE ∠.22.在ABC 中,AD 是ABC 的高,30B,52C ︒∠=(1)尺规作图:作ABC 的角平分线AE(2)求DAE ∠的大小.23.已知:如图,BAD CAE ∠=∠,AB AD =,AC AE =.(1)求证:ABC ADE △≌△.(2)若42,86B C ∠=︒∠=︒,求DAE ∠的度数.24.如图,点D ,E 分别在AB 和AC 上,DE//BC ,点F 是AD 上一点,FE 的延长线交BC 延长线BH 于点G .(1)若∠DBE =40°,∠EBC =35°,求∠BDE 的度数;(2)求证:∠EGH >∠ADE ;(3)若点E 是AC 和FG 的中点,△AFE 与△CEG 全等吗?请说明理由.25.已知:在△ABC 中,AC =BC ,∠ACB =90°,点D 是AB 的中点,点E 是AB 边上一点.(1)直线BF垂直CE于点F,交CD于点G(如图1),求证:AE=CG;(2)直线AH垂直于CE,垂足为H,交CD的延长线于点M(如图2),找出图中与BE相等的线段,并说明理由.26.(1)问题背景:如图1:在四边形ABCD中,AB=AD,∠BAD=120°,∠B=∠ADC=90°,E、F分别是BC,CD上的点且∠EAF=60°,探究图中线段BE、EF、FD之间的数量关系.小王同学探究此问题的方法是,延长FD到点G.使DG=BE.连结AG,先证明ABE≌ADG,再证明AEF≌AGF,可得出结论,他的结论应是______________;(2)探索延伸:如图2,若在四边形ABCD中,AB=AD,∠B+∠D=180°.E,F分别是BC,CD上的点,且∠EAF12∠BAD,上述结论是否仍然成立,并说明理由;(3)实际应用:如图3,在某次军事演习中,舰艇甲在指挥中心(O处)北偏西30°的A 处,舰艇乙在指挥中心南偏东70°的B处,并且两舰艇到指挥中心的距离相等,接到行动指令后,舰艇甲向正东方向以45海里/小时的速度前进,同时舰艇乙沿北偏东50°的方向以60海里/小时的速度前进,2小时后,指挥中心观测到甲、乙两地分别到达E、F处,且两舰艇之间的夹角为70°,试求此时两舰艇之间的距离.【参考答案】***试卷处理标记,请不要删除一、选择题1.D解析:D【分析】先根据全等三角形的对应角相等得出∠B=∠D=28°,再由三角形内角和为180°,求出∠DAE=57°,然后根据∠BAD=∠DAE+∠EAB即可得出∠BAD的度数.【详解】解:∵△ABC≌△ADE,∴∠B=∠D=28°,又∵∠D+∠E+∠DAE=180°,∠E=95°,∴∠DAE=180°-28°-95°=57°,∵∠EAB=20°,∴∠BAD=∠DAE+∠EAB=77°.故选:D.【点睛】本题考查了全等三角形的性质,三角形内角和定理,比较简单.由全等三角形的对应角相等得出∠B=∠D=28°是解题的关键.2.A解析:A【分析】当EP⊥BC时,EP最短,根据角平分线的性质,可知EP=EA=ED=12AD,由AD=14,求出即可.【详解】解:当EP⊥BC时,EP最短,∵AB∥CD,AD⊥AB,∴AD⊥CD,∵BE平分∠ABC,AE⊥AB,EP⊥BC,∴EP=EA,同理,EP=ED,此时,EP=12AD=12×14=7,故选A.【点睛】本题考查了角平分线的性质和垂线段最短,熟练找到P点位置并应用角平分线性质求EP是解题关键.3.B解析:B【分析】根据全等三角形的对应边相等得到BE=CF,计算即可.【详解】解:∵△DEF≌△ABC,∴BC=EF,∴BE+EC=CF+EC,∴BE=CF,又∵BF=BE+EC+CF=9,EC=5∵CF=12(BF-EC)=12(9-5)=2.故选:B.【点睛】本题考查了全等三角形的性质,掌握全等三角形的对应边相等、全等三角形的对应角相等是解题的关键.4.B解析:B【分析】过点O作MN,MN⊥AB于M,证明MN⊥CD,则MN的长度是AB和CD之间的距离;然后根据角平分线的性质,分别求出OM、ON的长度,再把它们求和即可.【详解】如图,过点O作MN,MN⊥AB于M,交CD于N,∵AB∥CD,∴MN⊥CD,∵AO是∠BAC的平分线,OM⊥AB,OE⊥AC,OE=3cm,∴OM=OE=3cm,∵CO是∠ACD的平分线,OE⊥AC,ON⊥CD,∴ON=OE=3cm,∴MN=OM+ON=6cm,即AB与CD之间的距离是6cm,故选B【点睛】此题主要考查角平分线的性质和平行线之间的距离,解答此题的关键是要明确:①角的平分线上的点到角的两边的距离相等,②从一条平行线上的任意一点到另一条直线作垂线,垂线段的长度叫两条平行线之间的距离,③平行线间的距离处处相等.5.C解析:C【分析】根据题中的已知条件确定有三组边对应相等,由此证明△OMC ≌△ONC(SSS),即可得到结论.【详解】在△OMC 和△ONC 中,OM ON CM CN OC OC =⎧⎪=⎨⎪=⎩, ∴△OMC ≌△ONC(SSS),∴∠MOC=∠NOC ,∴射线OC 即是∠AOB 的平分线,故选:C.【点睛】此题考查了全等三角形的判定及性质,比较简单,注意利用了三边对应相等,熟记三角形全等的判定定理并解决问题是解题的关键.6.C解析:C【分析】根据有理数的乘法、全等三角形的概念、直角三角形的性质、对顶角的概念判断即可.【详解】解:A 、如果 ab =0,那么a =0或b =0或a 、b 同时为0,本选项说法是假命题,不符合题意;B 、面积相等的三角形不一定全等,本选项说法是假命题,不符合题意;C 、直角三角形的两个锐角互余,本选项说法是真命题,符合题意;D 、不是对顶角的两个角可能相等,本选项说法是假命题,不符合题意;故选:C .【点睛】本题考查的是命题的真假判断,正确的命题叫真命题,错误的命题叫做假命题,判断命题的真假关键是要熟悉课本中的性质定理.7.D解析:D【分析】过点D 作DF AB ⊥于点F ,根据角平分线的性质定理得6CD DF ==,而DE 的长一定是大于等于点D 到AB 的距离也就是DF 的长,即可得出结果.【详解】解:如图,过点D 作DF AB ⊥于点F ,∵AD 平分BAC ∠,DF AB ⊥,90C ∠=︒,∴6CD DF ==,∵DE DF ≥,∴6DE ≥,则只有D 选项符合.故选:D .【点睛】本题考查角平分线的性质,解题的关键是掌握角平分线的性质定理.8.D解析:D【分析】直接证明全等三角形,即可确定判断方法.【详解】解:∵AB BC ⊥,CD BC ⊥,∴ABC 与△DCB 均为直角三角形,又AC DB =,BC CB =, ∴()ABC DCB HL ≅,故选:D.【点睛】本题考查全等三角形的判定定理,属于基础题.9.A解析:A【分析】根据两条平行线之间的距离可知当CD ⊥OM 时,CD 取最小值,先利用角平分线的性质得出AD =AE =3,利用全等三角形的判定和性质得出AC =AD =AE =3,进而解答即可.【详解】解:由题意得,当CD ⊥OM 时,CD 取最小值,∵OB 平分∠MON ,AE ⊥ON 于点E ,CD ⊥OM ,∴AD =AE =3,∵BC ∥OM ,∴∠DOA =∠B ,∵A 为OB 中点,∴AB =AO ,在△ADO 与△ABC 中B DOA AB AO BAC DAO ∠=∠⎧⎪=⎨⎪∠=∠⎩,∴△ADO ≌△ABC (SAS ),∴AC =AD =3,∴336CD AC AD =+=+=,故选A .【点睛】此题考查角平分线的性质、全等三角形的判定和性质、平行线之间的距离,关键是利用全等三角形的判定和性质得出AC =AD =AE =3.10.D解析:D【分析】根据全等三角形的判定定理,对每个选项分别分析、解答出即可.【详解】根据题意:BE=CE ,∠AEB=∠DEC ,∴只需要添加对顶角的邻边,即AE=DE (由AC=BD 也可以得到),或任意一组对应角,即∠A=∠D ,∠B=∠C ,∴选项A 、B 、C 可以判定,选项D 不能判定,故选:D .【点睛】此题考查全等三角形的判定定理,熟记判定定理并熟练应用是解题的关键.11.B解析:B【分析】根据题意可以得到∠AOC=∠BOC ,OC=OC ,然后即可判断各个选项中条件是否能判定△AOC ≌△BOC ,从而可以解答本题.【详解】解:由已知可得,∠AOC=∠BOC ,OC=OC ,∴若添加条件OA=OB ,则△AOC ≌△BOC (SAS ),故选项A 不符合题意;若添加条件AC=BC ,则无法判断△AOC ≌△BOC ,故选项B 符合题意;若添加条件∠A=∠B ,则△AOC ≌△BOC (AAS ),故选项C 不符合题意;若添加条件∠1=∠2,则∠ACO=∠BCO ,则△AOC ≌△BOC (ASA ),故选项D 不符合题意;故选:B .【点睛】本题考查全等三角形的判定,解答本题的关键是明确题意,利用数形结合的思想解答. 12.C解析:C【分析】根据全等三角形的判定定理:SSS、SAS、ASA、AAS、HL定理针对四个选项分别进行判断即可.【详解】A. 一直角边对应相等的两个直角三角形不一定全等,还要知道它的边或角才能证明,故此选项错误;B. 斜边相等的两个直角三角形不一定全等,还要知道它的边或角才能证明,故此选项错误;C. 斜边相等的两个等腰直角三角形全等,对应角相等,根据AAS即可证明全等,故此选项正确;D. 一边长相等的两个等腰直角三角形不一定全等,必须说明是对应边相等,故此选项错误.故选:C.【点睛】本题考查了全等三角形的判定,掌握证明三角形全等的条件尤其是必须含有边这个条件是解题的关键.二、填空题13.21【分析】如图作DHBA交BA的延长线于H作DFBC的延长线于F作DEAC于E首先证明利用面积法求出DE即可解决问题【详解】解:作DHBA交BA的延长线于H作DFBC的延长线于F作DEAC于E设则解析:21【分析】如图,作DH⊥BA交BA的延长线于H,作DF⊥BC的延长线于F,作DE⊥AC于E,首先==,利用面积法求出DE,即可解决问题.证明DH DE DF【详解】解:作DH⊥BA交BA的延长线于H,作DF⊥BC的延长线于F,作DE⊥AC于E,∠+∠=︒∠+∠=︒,180,180BAD CAD BAD DAH∴∠=∠,CAD DAH180,180BCD ACD BCD DCF ∠+∠=︒∠+∠=︒,ACD DCF ∴∠=∠,,,DH BH DE AC DF BF ⊥⊥⊥,DH DE DF ∴==,设DH DE DF x ===, 则有:11112222AB DH BC DF AB BC AC DE ⋅⋅+⋅⋅=⋅⋅+⋅⋅, ∴34125x x x +=+,6x ∴=,∴S 四边形ABCD=11113456212222AB CB AC DE ⋅+⋅=⨯⨯+⨯⨯=. 故答案为:21.【点睛】本题考查了角平分线的性质、三角形的面积等知识,解题的关键是学会利用参数构建方程解决问题,属于中考常考题型. 14.4【分析】当PC 垂直于OB 时PC 最小根据角平分线的性质可求最小值【详解】解:当PC ⊥OB 时PC 最小∵PC ⊥OB ∴PC=PD=4故答案为:4【点睛】本题考查了垂线段最短和角平分线的性质能够根据垂线段最解析:4【分析】当PC 垂直于OB 时,PC 最小,根据角平分线的性质可求最小值.【详解】解:当PC ⊥OB 时,PC 最小,∵AOP BOP ∠=∠,PD OA ⊥,PC ⊥OB ,∴PC=PD=4,故答案为:4.【点睛】本题考查了垂线段最短和角平分线的性质,能够根据垂线段最短的性质判断出点C 的位置,并根据角平分线的性质得出PC=PD 是根关键.15.【分析】先根据三角形的内角和定理求出∠A 的度数再利用全等三角形的性质求出答案即可【详解】∵∠A+∠B+∠C=∴∠A=-∠B-∠C=∵△ABC ≌△DEF ∴∠D=∠A=故答案为:【点睛】此题考查全等三角 解析:70︒【分析】先根据三角形的内角和定理求出∠A 的度数,再利用全等三角形的性质求出答案即可【详解】∵∠A+∠B+∠C=180︒,∴∠A=180︒-∠B-∠C=180506070︒-︒-︒=︒,∵△ABC ≌△DEF ,∴∠D=∠A=70︒,故答案为:70︒【点睛】此题考查全等三角形的性质:全等三角形的对应角相等,对应边相等,以及三角形的内角和定理.16.OA =OB (答案不唯一)【分析】由AD ∥BC 可得∠A =∠B ∠C =∠D 然后根据全等三角形的判定方法添加条件即可【详解】解:添加的条件是OA =OB 理由如下:∵AD ∥BC ∴∠A =∠B ∠C =∠D 在△AOD 和解析:OA =OB (答案不唯一)【分析】由AD ∥BC 可得∠A =∠B ,∠C =∠D ,然后根据全等三角形的判定方法添加条件即可.【详解】解:添加的条件是OA =OB ,理由如下:∵AD ∥BC ,∴∠A =∠B ,∠C =∠D在△AOD 和△BOC 中A B AO BO AOD BOC ∠=∠⎧⎪=⎨⎪∠=∠⎩∴△AOD ≌△BOC (ASA ).故答案为:OA =OB (答案不唯一).【点睛】本题主要考查了全等三角形的判定定理和平行线的性质,掌握全等三角形的判定定理的内容是解答本题的关键.17.【分析】先添加辅助线过点作交的延长线于点过点作交的延长线于点过点作于点根据角平分线的判定性质定义以及三角形外角的性质邻补角的定义角的和差等可求得【详解】解:过点作交的延长线于点过点作交的延长线于点过 解析:46︒【分析】先添加辅助线“过点D 作DE AB ⊥交AB 的延长线于点E ,过点D 作DF AC ⊥交AC 的延长线于点F ,过点D 作DG BC ⊥于点G ”,根据角平分线的判定、性质、定义以及三角形外角的性质、邻补角的定义、角的和差等可求得()1462ADB CBE BAC ∠=∠-∠=︒. 【详解】 解:过点D 作DE AB ⊥交AB 的延长线于点E ,过点D 作DF AC ⊥交AC 的延长线于点F ,过点D 作DG BC ⊥于点G ,如图:∵AD 平分BAC ∠,DE AB ⊥,DF AC ⊥ ∴12BAD BAC ∠=∠,DE DF = ∵136ACD ∠=︒ ∴18044DCF ACD ∠=︒-∠=︒∵44BCD ∠=︒,92ACB ACD BCD ∠=∠-∠=︒∴CD 平分BCF ∠∵DF AC ⊥,DG BC ⊥∴DF DG =∴DE DG =∵DE AB ⊥,DG BC ⊥∴BD 平分CBE ∠ ∴12DBE CBE ∠=∠ ∴ADB DBE BAD ∠=∠-∠1122CBE BAC =∠-∠ ()12CBE BAC =∠-∠ 12BCA =∠ 46=︒.故答案是:46︒【点睛】本题考查了角平分线的判定、性质、定义以及三角形外角的性质、邻补角的定义、角的和差等,熟练掌握相关知识点是解题的关键.18.4cm 【分析】根据求得AM 的长度利用角平分线上的点到角两边的距离相等即可求解【详解】解:解得∵OM 平分∠POQ ∴故答案为:4cm 【点睛】本题考查角平分线的性质掌握角平分线上的点到角两边的距离相等是解解析:4cm【分析】 根据12AOM SOA AM =⋅求得AM 的长度,利用角平分线上的点到角两边的距离相等即可求解.【详解】 解:114822AOM S OA AM AM =⋅=⨯=, 解得4cm AM =,∵OM 平分∠POQ ,∴4cm MB AM ==,故答案为:4cm .【点睛】本题考查角平分线的性质,掌握角平分线上的点到角两边的距离相等是解题的关键. 19.【分析】根据图形得出当有1点D 时有1对全等三角形;当有2点DE 时有3对全等三角形;当有3点DEF 时有6对全等三角形;根据以上结果得出当有n 个点时图中有个全等三角形即可【详解】解:当有1点D 时有1对全 解析:)(12n n +【分析】根据图形得出当有1点D 时,有1对全等三角形;当有2点D 、E 时,有3对全等三角形;当有3点D 、E 、F 时,有6对全等三角形;根据以上结果得出当有n 个点时,图中有)(12n n +个全等三角形即可.【详解】解:当有1点D 时,有1对全等三角形;当有2点D 、E 时,有3对全等三角形;当有3点D 、E 、F 时,有6对全等三角形;当有4点时,有10个全等三角形;…当有n 个点时,图中有)(12n n +个全等三角形.故答案为:)(12n n +.【点睛】 本题考查了对全等三角形的应用,关键是根据已知图形得出规律,题目比较典型,但有一定的难度.20.12【分析】利用SSS 证明△ADC ≌△ADB 可得△ABD 的面积=△ACD 的面积通过拼接可得阴影部分的面积=△ABD 的面积再利用三角形的面积公式可求解【详解】解:∵AB=ACBD=CDAD=AD ∴△A解析:12【分析】利用SSS 证明△ADC ≌△ADB ,可得△ABD 的面积=△ACD 的面积,通过拼接可得阴影部分的面积=△ABD 的面积,再利用三角形的面积公式可求解.【详解】解:∵AB=AC ,BD=CD ,AD=AD ,∴△ADC ≌△ADB (SSS ),∴S △ADC =S △ADB ,∵BC=8,∴BD=4,∵AB=AC ,BD=DC ,∴AD ⊥BC ,∴EB=EC ,FB=FC ,∵EF=EF ,∴△BEF ≌△CEF (SSS )∴S △BEF =S △CEF ,∵AD=6,∴S 阴影=S △ADB =12BD•AD =12×4×6=12. 故答案为:12.【点睛】本题考查了全等三角形的性质与判定,三角形的面积,理解S 阴影=S △ADB 是解题的关键.三、解答题21.见解析【分析】根据题意,先证明//AB CD ,然后由平行线的性质以及等量代换,得到ACD DCE ∠=∠,即可得到结论成立.【详解】证明:D CBD ∠=∠,ABD CBD ∠=∠,D ABD ∴∠=∠,//AB CD ∴ABC DCE ∴∠=∠,A ACD ∠=∠又A ABC ∠=∠,ACD DCE ∴∠=∠,CD ∴平分ACE ∠.【点睛】本题考查了平行线的判定和性质,角平分线的判定,解题的关键是掌握所学的知识,正确得到//AB CD .22.(1)作图见解析;(2)11【分析】(1)以任意长度为半径,点A 为圆心画圆弧,分别交AB 、AC 于点M 、N ;再分别以点M 、N 为圆心,大于2MN 的长度为半径画圆弧并相交于点K ,连接AK ,AK 交BC 于点E ,即可得到答案; (2)结合题意,根据三角形内角和定理,得BAC ∠;再根据角平分线性质得EAC ∠;结合AD 是ABC 的高,根据直角三角形两锐角互余的性质计算得DAC ∠;最后通过DAE EAC DAC ∠=∠-∠的关系计算完成求解.【详解】(1)作图如下:AE 即为ABC 的角平分线;(2)∵30B ,52C ︒∠=∴180180305298BAC B C ∠=-∠-∠=--=∵AE 为BAC ∠的角平分线∴492BAC EAC ∠∠== ∵AD 是ABC 的高 ∴90ADC ∠=∴90905238DAC C ∠=-∠=-=∴493811DAE EAC DAC ∠=∠-∠=-=.【点睛】本题考查了角平分线、三角形内角和、直角三角形两锐角互余、三角形高的知识;解题的关键是熟练掌握角平分线、三角形内角和、直角三角形两锐角互余的性质,从而完成求解.23.(1)详见解析;(2)52︒【分析】(1)先证明∠BAC=∠DAE ,即可根据SAS 证得结论;(2)根据三角形内角和定理求出∠BAC 的度数,再根据全等三角形的性质得到答案.【详解】(1)∵∠BAD=∠CAE ,∴∠BAD+∠DAC=∠CAE+∠DAC .即∠BAC=∠DAE .在△ABC 和△ADE 中AB AD BAC DAE AC AE =⎧⎪∠=∠⎨⎪=⎩, ∴ABC ADE △≌△;(2)∵42,86B C ∠=︒∠=︒,∴18052BAC B C ∠=︒-∠-∠=︒.∵ABC ADE △≌△,∴52DAE BAC ∠=∠=︒.【点睛】此题考查全等三角形的判定及性质,三角形内角和定理,熟记三角形全等的判定定理是解题的关键.24.(1)∠BDE =105°;(2)见解析;(3)全等,理由见解析.【分析】(1)根据平行线的性质得出∠DEB=∠EBC=35°,再根据三角形的内角和定理即可得到结论;(2)根据三角形的外角性质得出∠EGH >∠ABC ,又根据平行线的性质得出∠ABC=∠ADE ,即可得出答案;(3)根据全等三角形判定的“SAS”定理即可得到结论.【详解】(1)解:∵DE//BC ,∠EBC =35°,∴∠DEB =∠EBC =35°,又∵∠BDE+∠DEB+∠DBE =180°,∠DBE =40°,∴∠BDE =105°;(2)证明:∵∠EGH 是△FBG 的外角,∴∠EGH >∠ABC ,又∵DE//BC ,∴∠ABC =∠ADE ,∴∠EGH >∠ADE ;(3)全等.证明:E 是AC 和FG 的中点,∴AE =CE ,FE =GE ,在△AFE 和△CEG 中,AE CE AEF CEG FE GE =⎧⎪∠=∠⎨⎪=⎩,∴△AFE ≌△CGE (SAS ).【点睛】本题考查了三角形的外角性质,平行线的性质的应用,全等三角形的判定,三角形内角和定理,能运用三角形外角性质进行推理是解此题的关键.25.(1)证明见详解;(2)BE=CM ,证明见详解;【分析】(1)首先根据点D 是AB 的中点,∠ACB=90° ,可得出∠ACD=∠BCD=45°,判断出△AEC ≌△CGB ,即可得出AE=CG ;(2)根据垂直的定义得出∠CMA+∠MCH=90°,∠BEC+∠MCH=90°,再根据AC=BC ,∠ACM=∠CBE=45°,得出△BCE ≌△CAM ,进而证明出BE=CM ;【详解】(1)∵点D 是AB 的中点,AC=BC ,∠ACB=90°,∴ CD ⊥AB ,∠ACD=∠BCD=45°,∴ ∠CAD=∠CBD=45°,∴∠CAE=∠BCG ,又∵BF ⊥CE ,∴∠CBG+∠BCF=90°,又∵∠ACE+∠BCF=90°,∴∠ACE=∠CBG ,在△AEC 和△CGB 中,⎧⎪⎨⎪⎩∠CAE=∠BCG AC=BC∠ACE=∠CBG ∴△AEC ≌△CGB(ASA),∴AE=CG ;(2)BE=CM ,∵CH ⊥HM ,CD ⊥ED ,∴∠CMA+∠MCH=90°,∠BEC+∠MCH=90°,∴∠CMA=∠BEC ,又∵∠ACM=∠CBE=45°,在△BCE 和△CAM 中,⎧⎪⎨⎪⎩∠BEC=∠CMA ∠CBE=∠ACM BC=AC , ∴△BCE ≌△CAM(AAS),∴ BE=CM .【点睛】本题主要考查了全等三角形的性质与判定,掌握全等三角形的判定方法(即SSS 、SAS 、ASA 、AAS )和全等三角形的性质是解题的关键;26.(1)EF =BE +DF ;(2)结论EF =BE +DF 仍然成立;(3)此时两舰艇之间的距离是210海里【分析】(1)延长FD 到点G ,使DG=BE .连结AG ,即可证明ABE ≌ADG ,可得AE=AG ,再证明AEF ≌AGF ,可得EF=FG ,即可解题; (2)延长FD 到点G ,使DG=BE .连结AG ,即可证明ABE ≌ADG ,可得AE=AG ,再证明AEF ≌AGF ,可得EF=FG ,即可解题; (3)连接EF ,延长AE 、BF 相交于点C ,然后与(2)同理可证.【详解】解:(1)EF =BE +DF ,证明如下: 在ABE 和ADG 中, DG BE B ADG AB AD =⎧⎪∠=∠⎨⎪=⎩, ∴ABE ≌ADG (SAS ),∴AE =AG ,∠BAE =∠DAG ,∵∠EAF 12=∠BAD , ∴∠GAF =∠DAG +∠DAF =∠BAE +∠DAF =∠BAD ﹣∠EAF =∠EAF ,∴∠EAF =∠GAF , 在AEF 和GAF 中,AE AG EAF GAF AF AF =⎧⎪∠=∠⎨⎪=⎩, ∴AEF ≌AGF (SAS ),∴EF =FG ,∵FG =DG +DF =BE +DF ,∴EF =BE +DF ;故答案为 EF =BE +DF .(2)结论EF =BE +DF 仍然成立;理由:延长FD 到点G .使DG =BE .连结AG ,如图2,在ABE 和ADG 中,DG BE B ADG AB AD =⎧⎪∠=∠⎨⎪=⎩, ∴ABE ≌ADG (SAS ),∴AE =AG ,∠BAE =∠DAG ,∵∠EAF 12=∠BAD , ∴∠GAF =∠DAG +∠DAF =∠BAE +∠DAF =∠BAD ﹣∠EAF =∠EAF , ∴∠EAF =∠GAF ,在AEF 和GAF 中,AE AG EAF GAF AF AF =⎧⎪∠=∠⎨⎪=⎩,∴AEF ≌AGF (SAS ),∴EF =FG ,∵FG =DG +DF =BE +DF ,∴EF =BE +DF ;(3)如图3,连接EF ,延长AE 、BF 相交于点C ,∵∠AOB =30°+90°+(90°﹣70°)=140°,∠EOF =70°,∴∠EOF 12=∠AOB , 又∵OA =OB ,∠OAC +∠OBC =(90°﹣30°)+(70°+50°)=180°,∴符合探索延伸中的条件,∴结论EF=AE+BF成立,即EF=2×(45+60)=210(海里).答:此时两舰艇之间的距离是210海里.【点睛】本题考查了全等三角形的判定以及全等三角形对应边相等的性质,本题中求证△AEF≌△AGF是解题的关键.。
人教版八年级数学上册三角形全等的证明培优综合训练(含答案)

人教版八年级数学上册三角形全等的证明培优综合训练(含答案)考点1 利用SSS求证三角形全等1.如图,点B,F,C,E在同一条直线上,点A,D在直线BC的异侧,AB=DE,AC=DF,BF=EC.(1)求证:△ABC≌△DEF;(2)若∠BFD=150°,求∠ACB的度数.2.如图,C是AB的中点,AD=CE,CD=BE.求证:(1)△DCA≌△EBC;(2)AD//CE.3.已知:如图,已知线段AB、CD相交于点O、AD、CB的延长线交于点E、OA=OC、EA=EC,求证:∠A=∠C、考点2 利用SAS求证三角形全等4.如图,在△ABC和△DEF中,点B、F、C、E在同一直线上,AB=DE,BF=CE,AB‖DE,求证:△ABC≅△DEF.5.在△ABC中,AD为边BC上的中线,延长AD到点E,使DE=AD,连接BE.△ABC的面积与△ABE的面积相等吗?说明理由6.两组邻边分别相等的四边形我们称它为筝形,如图,在筝形ABCD中,AB=AD,BC =DC,AC,BD相交于点O.(1)求证:①△ABC≌△ADC;②OB=OD,AC⊥BD;(2)如果AC=6,BD=4,求筝形ABCD的面积.考点3 利用AAS 或ASA 求证三角形全等7.已知:在ABC 中,90BAC ∠=︒,AB AC =,直线m 经过点A ,BD ⊥直线m ,CE ⊥直线m ,垂足分别为点D 、E .(1)证明:BDA AEC ≌;(2)3BD =,4CE =,求DE 的长.8.如图,已知AD 为ABC ∆的中线,延长AD ,分别过点B ,C 作BE AD ⊥,CF AD ⊥.求证:BED CFD ∆≅∆.9.如右图,已知,90AB AC BAC BE CE =∠=︒,⊥于点E ,延长BE CA 、相交于点F ,求证:ADC AFB ≌10.如图,已知E 、F 在AC 上,AD //CB ,且∠D=∠B ,AE=CF .求证:DF=BE .考点4 利用HL 求证三角形全等11.在ABC 中,AB CB =,90ABC ∠=︒,F 为AB 延长线上一点,点E 在BC 上,且AE CF =.(1)求证:ABE CBF ≌;(2)若30CAE ∠=︒,求ACF ∠度数.12.如图,已知AE =DE ,AB ⊥BC ,DC ⊥BC ,且AB =EC .求证:BC =AB +DC .13.如图,已知AC平分∠BAD,CE⊥AB于E,CF⊥AD于F,且BC=CD.(1)证明:Rt△BCE≌Rt△DCF;(2)若AB=21,AD=9,求AE的长.14.如图:AD是ABC的高,E为AC上一点,BE交AD于F,且有BF=AC,FD=CD、求 .证:BE AC考点5 全等三角形综合15.已知点P为∠EAF平分线上一点,PB⊥AE于B,PC⊥AF于C,点M、N分别是射线AE、AF上的点,(1)如图1,当点M在线段AB上,点N在线段AC的延长线上,且PM=PN,求证:BM=CN;(2)在(1)的条件下,直接写出线段AM、CN与AC之间的数量关系_______.(3)如图2,当点M在线段AB的延长线上,点N在线段AC上时,∠MAN+MPN=180°,若AC:PC=2:1,PC=4,求四边形ANPM的面积.16.如图,在平面直角坐标系中,A、B坐标为(6,0)、(0,6),P为线段AB上的一点.(1)如图1,若P为AB的中点,点M、N分别是OA、OB边上的动点,且保持AM=ON,则在点M、N运动的过程中,探究线段PM、PN之间的位置关系与数量关系,并说明理由.(2)如图2,若P为线段AB上异于A、B的任意一点,过B点作BD⊥OP,交OP、OA分别于F、D两点,E为OA上一点,且∠PEA=∠BDO,试判断线段OD与AE的数量关系,并说明理由.答案1.解:(1)证明:BF EC =∵,BF FC EC FC ∴+=+,BC EF ∴=,在ABC ∆和DEF ∆中,AB DE AC DF BC EF =⎧⎪=⎨⎪=⎩,()ABC DEF SSS ≅∆∆∴;(2)150BFD ∠=︒,180BFD DFE ∠+∠=︒, 30DFE ∴∠=︒,由(1)知,ABC DEF ∆≅∆,ACB DFE ∴∠=∠,30ACB ∴∠=︒.2.(1)证明:点C 是AB 的中点,AC BC ∴=;在DCA ∆与EBC ∆中,AD CE CD BE AC BC =⎧⎪=⎨⎪=⎩,()DCA EBC SSS ∴∆≅∆,(2)证明:DCA EBC ∆≅∆,A BCE ∴∠=∠,//AD CE ∴.3.如图,连结OE在、OEA 和、OEC 中OA OC EA EC OE OE =⎧⎪=⎨⎪=⎩、、OEA、、OEC (SSS )、、A =、C (全等三角形的对应角相等)4.∵BF=CE ,∴BF+FC=CE+FC ,即BC=EF .∵AB ∥DE ,∴∠B=∠E .在△ABC 和△DEF 中AB DE B E BC EF =⎧⎪∠=∠⎨⎪=⎩∴△ABC ≌△DEF (SAS )5.△ABC 与△ABE 的面积相等.理由:∵AD 为边BC 上的中线,∴BD=CD ,在△BDE 和△CAD 中,BD DC BDE CDA DE AD =⎧⎪∠=∠⎨⎪=⎩,∴△BDE ≌△CAD、SAS、,BDE ABD CAD ABD S S S S +=+,即△ABC 与△ABE 的面积相等.6.(1)证明:①在△ABC 和△ADC 中,AB=AD ,BC=DC ,AC=AC ,∴△ABC ≌△ADC (SSS ).②∵△ABC ≌△ADC ,∴∠BAO=∠DAO.∵AB=AD ,∠BAO=∠DAO ,OA=OA ,∴△ABO ≌△ADO (SAS ).∴OB=OD ,AC ⊥BD.(2)筝形ABCD 的面积=△ABC 的面积+△ACD 的面积=12×AC×BO+12×AC×DO=12×AC×(BO+DO)=12×AC×BD=12×6×4=12. 7.(1)证明:∵BD m ⊥,CE m ⊥,∴90ADB CEA ∠=∠=︒,∴90ABD BAD ∠+∠=︒,∵AB AC ⊥,∴90BAD CAE ∠+∠=︒,∴ABD CAE ∠=∠,在BDA 和AEC 中,90ADB CEA ABD CAEAB AC ∠=∠=︒⎧⎪∠=∠⎨⎪=⎩, ∴()BDA AEC AAS ≅;(2)∵BDA AEC ≅△△,∴BD AE =,AD CE =,∴7DE DA AE BD CE =+=+=.8.证明:∵AD 是△ABC 的中线,∴ BD =CD ,∵ BE ⊥AD ,CF ⊥AD ,∴∠E =∠CFD =90°在Rt △BDE 和Rt △CDF 中,90BDE CDF E CFD BD CD ∠=∠⎧⎪∠=∠=⎨⎪=⎩,∴ Rt △BDE ≌Rt △CDF (AA S )9.、、BAC=90°,、、BAF=180°-、BAC=90°,、、BAF=、CAD ,、F+、ABF=90°,∵CE ⊥BE ,、、CEF=90°,、、F+、ACD=90°,、、ABF=、ACD ,在、ADC 和、AFB 中,BAF CAD AC ABACD ABF ∠=∠⎧⎪=⎨⎪∠=∠⎩, 、、ADC ≌、AFB (ASA ).10.解:证明:∵AE=CF ,∴AE -EF=CF -EF即AF=CE ,∵AD ∥CB ,∴∠A=∠C ,在△ADF 和△CBE 中,A C AF CE DB ∠=∠⎧⎪=⎨⎪∠=∠⎩,∴△ADF ≌△CBE (ASA ),∴DF=BE .11.(1)证明:∵∠ABC=90°,∴∠CBF=∠ABE=90°,在Rt △ABE 和Rt △CBF 中,AE CF AB BC=⎧⎨=⎩, ∴Rt △ABE ≌Rt △CBF (HL );(2)解:∵AB=BC ,∠ABC=90°,∴∠CAB=∠ACB=45°,又∵∠BAE=∠CAB -∠CAE=45°-30°=15°,由(1)知:Rt △ABE ≌Rt △CBF ,∴∠BCF=∠BAE=15°,∴∠ACF=∠BCF+∠ACB=15°+45°=60°.12.∵AB ⊥BC ,DC ⊥BC ,∴∠B=∠C=90°,在Rt △AEB 和Rt △EDC 中,AB EC AE DE =⎧⎨=⎩, ∴Rt △AEB ≌Rt △EDC (HL ),∴DC=BE ,∵BC=BE+CE ,∴AB+DC=BC .13.(1)∵AC 平分∠BAD ,CE ⊥AB 于E ,CF ⊥AD 于F , ∴CF=CE ,∠DFC=∠BEC=90°,在Rt △BCE 和Rt △DCF 中,CE CF BC CD =⎧⎨=⎩, ∴Rt △BCE ≌Rt △DCF (HL );(2)∵AC 平分∠BAD ,CE ⊥AB 于E ,CF ⊥AD 于F , ∴CF=CE ,∠CFA=∠CEA=90°,在Rt △AFC 和Rt △AEC 中,CF CE AC AC =⎧⎨=⎩,∴Rt △AFC ≌Rt △AEC (HL ),∴AF=AE ,由(1)知Rt △BCE ≌Rt △DCF ,则BE=DF ,∵AB=21,AD=9,∴AB=AE+EB=AF+EB=AD+DF+ DF =AD+2DF=9+2DF=21, 解得,DF=6,∴AE=AF=AD+DF=9+6=15,即AE 的长是15.14.证明: ∵AD ⊥BC ,∴∠BDF =∠ADC =90°.又∵BF =AC ,FD =CD ,∴△RtADC ≌Rt △BDF (HL ).∴∠EBC =∠DAC .又∵∠DAC +∠ACD =90°,∴∠EBC +∠ACD =90°.∴BE ⊥AC .15.(1)证明:点P 为EAF ∠平分线上一点,PB AE ⊥于B ,PC AF ⊥于C , PB PC ∴=,在Rt PBM ∆和Rt PCN ∆中,PB PC PM PN =⎧⎨=⎩, Rt PBM Rt PCN ∴∆≅∆,BM CN ∴=;(2)AM CN AC +=,理由如下:在Rt PBA ∆和Rt PCA ∆中,PB PC AP AP =⎧⎨=⎩, Rt PBA Rt PCA ∴∆≅∆,AB AC ∴=,AM CN AM BM AB AC ∴+=+==,故答案为:AM CN AC +=;(3):2:1AC PC =,4PC =,8AC ∴=,PB AE ⊥,PC AF ⊥,90ABP ACP ∴∠=∠=︒,180MAN BPC ∴∠+∠=︒,又180MAN MPN ∠+∠=︒, MPB NPC ∴∠=∠,在PBM ∆和PCN ∆中,BPM CPN PB PCPBM PCN ∠=∠⎧⎪=⎨⎪∠=∠⎩, PBM PCN ∴∆≅∆,∴四边形ANPM 的面积=四边形ABPC 的面积1842322=⨯⨯⨯=. 16.解:(1)结论:PM =PN ,PM ⊥PN .理由如下:如图1中,连接OP .∵A 、B 坐标为(6,0)、(0,6),∴OB =OA =6,∠AOB =90°,∵P为AB的中点,∴OP=12AB=PB=P A,OP⊥AB,∠PON=∠P AM=45°,∴∠OP A=90°,在△PON和△P AM中,ON AMPON PAMOP AP=⎧⎪∠=∠⎨⎪=⎩,∴△PON≌△P AM(SAS),∴PN=PM,∠OPN=∠APM,∴∠NPM=∠OP A=90°,∴PM⊥PN,PM=PN.(2)结论:OD=AE.理由如下:如图2中,作AG⊥x轴交OP的延长线于G.∵BD⊥OP,∴∠OAG=∠BOD=∠OFD=90°,∴∠ODF+∠AOG=90°,∠ODF+∠OBD=90°,∴∠AOG=∠DBO,∵OB=OA,∴△DBO≌△GOA,∴OD=AG,∠BDO=∠G,∵∠BDO=∠PEA,∴∠G=∠AEP,在△P AE和△P AG中,AEP GPAE PAGAP AP∠=∠⎧⎪∠=∠⎨⎪=⎩,∴△P AE≌△P AG(AAS),∴AE=AG,∴OD=AE.。
完整版)全等三角形基础练习证明题

完整版)全等三角形基础练习证明题1.已知三角形ABC中,AD为中线,BE⊥AD,CF⊥AD,证明BE=CF。
2.已知四边形ACBD中,AC=BD,AE=CF,BE=DF,证明AE∥CF。
3.已知四边形ABCD中,AB=CD,BE=DF,AE=CF,证明AB∥CD。
4.已知四边形ABCD中,AB=CD,AD=CB,证明AB∥CD。
5.已知两个三角形中,∠BAC=∠DAE,∠1=∠2,BD=CE,证明三角形ABD≌三角形ACE。
6.已知四边形ABED中,CD∥AB,DF∥EB,DF=EB,证明AF=CE。
7.已知四边形BEFC中,BE=CF,AB=CD,∠B=∠C,证明AF=DE。
8.已知四边形ABED中,AD=CB,∠A=∠C,AE=CF,证明EB∥DF。
9.已知三角形ABC中,M为AB的中点,∠1=∠2,MC=MD,证明∠C=∠D。
10.已知四边形ABFE和CDFE中,AE=DF,BF=CE,AE∥DF,证明AB=CD。
11.已知四边形ABCD中,∠1=∠2,∠3=∠4,证明AC=AD。
12.已知四边形ABCD中,∠E=∠F,∠1=∠2,AB=CD,证明AE=DF。
13.已知四边形ABCDEF中,ED⊥AB,EF⊥BC,BD=EF,证明BM=ME。
14.已知三角形ABC中,高AD与BE相交于点H,且AD=BD,证明三角形BHD≌三角形ACD。
15.已知四边形ABCDE中,∠A=∠D,AC∥FD,AC=FD,证明AB∥DE。
16.已知三角形ABC和三角形ADE中,AC=AB,AE=AD,∠1=∠2,证明∠3=∠4.17.已知三角形ABC和三角形DEF中,EF∥BC,AF=CD,AB⊥BC,DE⊥EF,证明三角形ABC≌三角形DEF。
18.已知四边形ABED中,AD=AE,∠B=∠C,证明AC=AB。
19.已知三角形ABC中,AD⊥BC,BD=CD,证明AB=AC。
20.已知三角形ABC和三角形BAD中,∠1=∠2,BC=AD,证明三角形ABC≌三角形BAD。
最新人教版八年级数学上册第12章 全等三角形 基础训练题(合集)(含答案)

最新人教版八年级数学上册基础训练题第十二章全等三角形12.1 全等三角形1.下列说法中,不正确的是()A.形状相同的两个图形是全等形B.大小不同的两个图形不是全等形C.形状、大小都相同的两个三角形是全等三角形D.能够完全重合的两个图形是全等形2.如图所示,△ABD△△BAC,B,C和A,D分别是对应顶点,如果AB=4 cm,BD=3 cm,AD=5 cm,那么BC的长是()A.5 cm B.4 cm C.3 cm D.无法确定3.如图所示,△ABC△△ADC,△ABC=70°,则△ADC的度数是()A.70° B.45° C.30° D.35°4.如图所示,若△ABC△△DBE,那么图中相等的角有()A.1对B.2对C.3对D.4对5.如图所示,若△ABC△△DEF,那么图中相等的线段有()A.1组B.2组C.3组D.4组6.(1)已知如图,△ABE△△ACD,△1=△2,△B=△C,指出其他的对应边和对应角.(2)由对应边找对应角,由对应角找对应边有什么规律?7.已知等腰△ABC的周长为18 cm,BC=8 cm,若△ABC△△A′B′C′,则△A′B′C′中一定有一条边等于()A.7 cm B.2 cm或7 cm C.5 cm D.2 cm或5 cm8.下图所示是用七巧板拼成的一艘帆船,其中全等的三角形共有__________对.9.如图所示,△ADF△△CBE,且点E,B,D,F在一条直线上.判断AD与BC的位置关系,并加以说明.10.下图是把4×4的正方形方格图形沿方格线分割成两个全等图形,请在下列三个4×4的正方形方格中,沿方格线分别画出三种不同的分法,把图形分割成两个全等图形。
11.如图,△ABC△△ADE,且△CAD=10°,△B=△D=25°,△EAB=120°,求△DFB和△DGB的度数.参考答案:1.A2.A3.A4.D5.D6.解:(1)AB与AC,AE与AD,BE与CD是对应边,△BAE与△CAD是对应角.(2)对应边所对的角是对应角,对应边所夹的角是对应角,对应角所对的边是对应边,对应角所夹的边是对应边.7.D8.29.解:AD与BC的关系是AD△BC.理由如下:因为△ADF△△CBE,所以△1=△2,△F=△E,点E,B,D,F在一条直线上,所以△3=△1+△F,△4=△2+△E,即△3=△4,所以AD△BC.10.解:如图.答案不唯一.11.解:△△ABC△△ADE,△11()(12010)5522DAE BAC EAB CAD∠=∠=∠-∠=︒-︒=︒.△△DFB=△FAB+△B=△FAC+△CAB+△B=10°+55°+25°=90°,△DGB=△DFB-△D=90°-25°=65°.第十二章全等三角形12.2 三角形全等的判定1.如图,在△ABC中,AB=AC,BE=CE,则直接利用“SSS”可判定() A.△ABD△△ACDB.△BDE△△CDEC.△ABE△△ACED.以上都不对2.如图,在△ABC和△DEF中,AB=DE,△B=△DEF,请你再补充一个条件,能直接运用“SAS”判定△ABC△△DEF,则这个条件是()A.△ACB=△DEFB.BE=CFC.AC=DFD.△A=△F3.如图,请看以下两个推理过程:△△△D=△B,△E=△C,DE=BC,△△ADE△△ABC(AAS);△△△DAE=△BAC,△E=△C,DE=BC,△△ADE△△ABC(AAS).则以下判断正确的(包括判定三角形全等的依据)是()A.△对△错B.△错△对C.△△都对D.△△都错4.如图是跷跷板的示意图,支柱OC与地面垂直,点O是横板AB的中点,AB可以绕着点O上下转动,当A端落地时,△OAC=20°,横板上下可转动的最大角(即△A′OA)是()A.80° B.60° C.40° D.20°5.如图,在△ABC中,D是BC边上的中点,△BDE=△CDF,请你添加一个条件,使DE=DF成立.你添加的条件是__________.(不再添加辅助线和字母)6.如图是一个三角形测平架,已知AB=AC,在BC的中点D挂一个重锤DE,让其自然下垂,调整架身,使点A恰好在重锤线上,这时AD和BC的位置关系为__________.7.如图,AC△BD,垂足为点B,点E为BD上一点,BC=BE,△C=△AEB,AB=6 cm,则图中长度为6 cm的线段还有__________.8.如图,为了固定门框,木匠师傅把两根同样长的木条BE,CF两端分别固定在门框上,且AB=CD,则木条与门框围成的两个三角形(图中阴影部分)__________全等(填“一定”、“不一定”或“一定不”).9.如图,A,B,C三点在同一条直线上,△A=△C=90°,AB=CD,请添加一个适当的条件__________,使得△EAB△△BCD.10.在Rt△ABC中,△ACB=90°,BC=2 cm,CD△AB,在AC上取一点E,使EC=BC,过点E作EF△AC交CD的延长线于点F,若EF=5 cm,则AE=__________ cm.11.如图,D是△ABC的边AB上一点,E是AC的中点,过点C作CF△AB,交DE的延长线于点F.求证:AD=CF.12.如图,点F,B,E,C在同一直线上,并且BF=CE,△ABC=△DEF.能否由上面的已知条件证明△ABC△△DEF?如果能,请给出证明;如果不能,请从下列三个条件中选择一个合适的条件,添加到已知条件中,使△ABC△△DEF,并给出证明.提供的三个条件是:△AB=DE;△AC=DF;△AC△DF.13.如图,在△ABC中,AB=AC,DE是过点A的直线,BD△DE于点D,CE△DE于点E,AD=CE.(1)若BC在DE的同侧(如图△).求证:AB△AC.(2)若BC在DE的两侧(如图△),其他条件不变,(1)中的结论还成立吗?若成立,请予证明;若不成立请说明理由.参考答案 1-4 C 2.B 3.B 4.C5.AB =AC 或△B =△C 或△BED =△CFD 或△AED =△AFD. 6.垂直 7.BD 8.一定9.AE =CB(或EB =BD 或△EBD =90°或△E =△DBC 等) 10.311.证明:△E 是AC 的中点, △AE =CE. △CF△AB ,△△A =△ECF ,△ADE =△F. 在△ADE 与△CFE 中,ADE F A ECF AE CE ∠=∠⎧⎪∠=∠⎨⎪=⎩,,,△△ADE△△CFE(AAS). △AD =CF12.解:由前面的已知条件不能证明△ABC△△DEF.需要再添加条件△时: 证明: △BF =CE , △EF =BC ,△△ABC =△DEF ,AB =DE , △△ABC△△DEF(SAS). 添加条件△时,△AC△DF , △△ACB =△DFE , △△ABC△△DEF(ASA).13.(1)证明:△BD△DE ,CE△DE ,△△ADB =△CEA =90°,△BAD +△ABD =90° 在Rt△ADB 和Rt△CEA 中,AB AC AD EC =⎧⎨=⎩,,△Rt△ADB△Rt△CEA(HL) △△ABD =△CAE. △△BAD +△CAE =90°△△BAC =180°-(△BAD +△CAE)=90°, △AB△AC(2)解:仍有AB△AC 证明:△BD△DE ,CE△DE△△ADB =△CEA =90°,△BAD +△ABD =90° 在Rt△ADB 和Rt△CEA 中AB CA AD CE =⎧⎨=⎩,,△Rt△ADB△Rt△CEA(HL). △△ABD =△CAE. △△BAD +△CAE =90° △△BAC =90° △AB△AC.第十二章全等三角形12.3 角的平分线的性质1.作△AOB的平分线OC,合理的顺序是()△作射线OC;△以O为圆心,适当长为半径画弧,交OA于D,交OB于E;△分别以D,E为圆心,大于12DE的长为半径画弧,两弧在△AOB内交于点C.A.△△△ B.△△△ C.△△△ D.△△△2.三角形中到三边距离相等的点是()A.三条边的垂直平分线的交点B.三条高的交点C.三条中线的交点D.三条内角平分线的交点3.如图,△1=△2,PD△OA,PE△OB,垂足分别为D,E,下列结论错误的是() A.PD=PEB.OD=OEC.△DPO=△EPOD.PD=OD4.如图,在△ABC中,△ACB=90°,BE平分△ABC,DE△AB于点D,如果AC=3 cm,那么AE+DE等于()A.2 cm B.3 cm C.4 cm D.5 cm5.△ABC中,△C=90°,点O为△ABC三条角平分线的交点,OD△BC于D,OE△AC 于E,OF△AB于F,且AB=10 cm,BC=8 cm,AC=6 cm,则点O到三边AB,AC,BC的距离为()A.2 cm,2 cm,2 cm B.3 cm,3 cm,3 cmC.4 cm,4 cm,4 cm D.2 cm,3 cm,5 cm6.如图所示,△AOB=60°,CD△OA于点D,CE△OB于点E,且CD=CE,则△DCO=__________.7.在△ABC中,△C=90°,AD平分△BAC交BC于D,若BC=32,且BD△CD=9△7,则D到AB的距离为__________.8.点O是△ABC内一点,且点O到三边的距离相等,△A=60°,则△BOC的度数为__________.9.如图,BN是△ABC的平分线,P在BN上,D,E分别在AB,BC上,△BDP+△BEP =180°,且△BDP,△BEP都不是直角.求证:PD=PE.10.如图,在△ABC中,△C=90°,AD平分△BAC,DE△AB于点E,点F在AC上,BD=DF.(1)求证:CF=EB;(2)请你判断AE,AF与BE的大小关系,并说明理由.参考答案1.C2.D3.D4.B5.B6.60°7.148.120°9.证明:过点P 分别作PF△AB 于F ,PG△BC 于G , △BN 是△ABC 的平分线△PF =PG.又△△BDP +△BEP =180°,△PEG +△BEP =180°, △△BDP =△PEG.在△PFD 和△PGE 中,FDP GEP PFD PGE PF PG ∠=∠⎧⎪∠=∠⎨⎪=⎩,,,△△PFD△△PGE(AAS),△PD =PE.10.(1)证明:△△C =90°△DC△AC△AD 平分△BAC ,DE△AB△DC =DE ,△DEB =△C =90°在Rt△DCF 与Rt△DEB 中,DF DB DC DE =⎧⎨=⎩,,△Rt△DCF△Rt△DEB(H L),△CF=EB.(2)解:AE=AF+BE.理由如下:△AD平分△BAC,△△CAD=△EAD,又△△C=△DEA=90°,△△ACD△△AED(AAS),△AC=AE,由(1)知BE=CF△AC=AF+CF=AF+BE,即A E=AF+BE.。
人教版八年级数学上册第十二章全等三角形证明方法归纳及典型例题

全等三角形的证明全等三角形的性质:对应角相等,对应边相等,对应边上的中线相等,对应边上的高相等,对应角的角平分线相等,面积相等.寻找对应边和对应角,常用到以下方法:(1)全等三角形对应角所对的边是对应边,两个对应角所夹的边是对应边.(2)全等三角形对应边所对的角是对应角,两条对应边所夹的角是对应角.(3)有公共边的,公共边常是对应边.(4)有公共角的,公共角常是对应角.(5)有对顶角的,对顶角常是对应角.(6)两个全等的不等边三角形中一对最长边(或最大角)是对应边(或对应角),一对最短边(或最小角)是对应边(或对应角).要想正确地表示两个三角形全等,找出对应的元素是关键.全等三角形的判定方法:(1)边角边定理(SAS):两边和它们的夹角对应相等的两个三角形全等.(2)角边角定理(ASA):两角和它们的夹边对应相等的两个三角形全等.(3)边边边定理(SSS):三边对应相等的两个三角形全等.(4)角角边定理(AAS):两个角和其中一个角的对边对应相等的两个三角形全等.(5)斜边、直角边定理(HL):斜边和一条直角边对应相等的两个直角三角形全等.全等三角形的应用:运用三角形全等可以证明线段相等、角相等、两直线垂直等问题,在证明的过程中,注意有时会添加辅助线.拓展关键点:能通过判定两个三角形全等进而证明两条线段间的位置关系和大小关系.而证明两条线段或两个角的和、差、倍、分相等是几何证明的基础.专题1、常见辅助线的做法典型例题找全等三角形的方法:(1)可以从结论出发,寻找要证明的相等的两条线段(或两个角)分别在哪两个可能全等的三角形中;(2)可以从已知条件出发,看已知条件可以确定哪两个三角形全等;(3)可从条件和结论综合考虑,看它们能确定哪两个三角形全等;(4)若上述方法均不可行,可考虑添加辅助线,构造全等三角形。
三角形中常见辅助线的作法:①延长中线构造全等三角形;②利用翻折,构造全等三角形;③引平行线构造全等三角形;④作连线构造等腰三角形。
(必考题)初中八年级数学上册第十二章《全等三角形》经典练习题(答案解析)

一、选择题1.如图,在ABC 中,8AB AC ==厘米,6BC =厘米,点D 为AB 的中点.如果点P 在线段BC 上以3厘米/秒的速度由B 点向C 点运动,同时,点Q 在线段CA 上,由C 点向A 点运动,为了使BPD CPQ △≌△,点Q 的运动速度应为( )A .1厘米/秒B .2厘米/秒C .3厘米/秒D .4厘米/秒D解析:D【分析】 根据三角形全等的性质与路程、速度、时间的关系式求解.【详解】解:设△BPD ≌△CPQ 时运动时间为t ,点Q 的运动速度为v ,则由题意得:BP CP BD CQ =⎧⎨=⎩, 即3634t t vt =-⎧⎨=⎩, 解之得:14t v =⎧⎨=⎩, ∴点Q 的运动速度为4厘米/秒,故选D .【点睛】本题考查三角形全等的综合应用,熟练掌握三角形全等的判定与性质、路程、速度、时间的关系式及方程的思想方法是解题关键.2.如图,在ABC 中,ABC 的面积为10,4AB =,BD 平分ABC ∠,E 、F 分别为BC 、BD 上的动点,则CF EF +的最小值是( )A .2B .3C .4D .5D解析:D【分析】 过点C 作CM AB ⊥于点M ,交BD 于点'F ,过点'F 作''F E BC ⊥于'E ,则CM 即为CF EF +的最小值,再根据三角形的面积公式求出CM 的长,即为CF EF +的最小值.【详解】解:过点C 作CM AB ⊥于点M ,交BD 于点'F ,过点'F 作''F E BC ⊥于'E ,BD 平分ABC ∠,'MF AB ⊥于点M ,''F E BC ⊥于'E ,'''MF F E ∴=,'''''CM CF MF CF E F ∴=+=+的最小值.三角形ABC 的面积为10,4AB =, ∴14102CM ⨯⋅=,21054CM ⨯∴==. 即CF EF +的最小值为5,故选:D .【点睛】本题考查的是轴对称-最短路线问题,根据题意作出辅助线是解题的关键.3.如图,若DEF ABC ≅,点B 、E 、C 、F 在同一条直线上,9BF =,5EC =,则CF 的长为( )A .1B .2C .2.5D .3B解析:B【分析】 根据全等三角形的对应边相等得到BE=CF ,计算即可.【详解】解:∵△DEF ≌△ABC ,∴BC=EF ,∴BE+EC=CF+EC ,∴BE=CF ,又∵BF=BE+EC+CF=9,EC=5∵CF=12(BF-EC)=12(9-5)=2. 故选:B .【点睛】本题考查了全等三角形的性质,掌握全等三角形的对应边相等、全等三角形的对应角相等是解题的关键.4.如图,AB 是线段CD 的垂直平分线,则图中全等三角形的对数有( )A .2对B .3对C .4对D .5对B解析:B【分析】 根据线段垂直平分线的性质得到,AC=AD ,BC=BD ,OC=OD ,然后根据”HL”可判断Rt △AOC ≌Rt △AOD ,Rt △BOC ≌Rt △BOD ;根据“SSS”可判断△ABC ≌△ABD .【详解】解:∵AB 是线段CD 的垂直平分线,∴AC=AD ,BC=BD ,OC=OD ,∴Rt △AOC ≌Rt △AOD (HL ),Rt △BOC ≌Rt △BOD (HL ),△ABC ≌△ABD (SSS ). 故选:B .【点睛】本题考查了全等三角形的判定与性质:判定三角形全等的方法有“SSS”、“SAS”、“ASA”、“AAS”“HL”;全等三角形的对应边相等.也考查了线段垂直平分线的性质.5.如图所示,已知AB ∥CD ,BAC ∠与ACD ∠的平分线交于点O ,OE AC ⊥于点E ,且3OE cm =,则点O 到AB ,CD 的距离之和是( )A .3cmB .6cmC .9cmD .12cm B解析:B【分析】 过点O 作MN ,MN ⊥AB 于M ,证明MN ⊥CD ,则MN 的长度是AB 和CD 之间的距离;然后根据角平分线的性质,分别求出OM 、ON 的长度,再把它们求和即可.【详解】如图,过点O 作MN ,MN ⊥AB 于M ,交CD 于N ,∵AB ∥CD ,∴MN ⊥CD ,∵AO 是∠BAC 的平分线,OM ⊥AB ,OE ⊥AC ,OE =3cm ,∴OM =OE =3cm ,∵CO 是∠ACD 的平分线,OE ⊥AC ,ON ⊥CD ,∴ON =OE =3cm ,∴MN =OM +ON =6cm ,即AB 与CD 之间的距离是6cm ,故选B【点睛】此题主要考查角平分线的性质和平行线之间的距离,解答此题的关键是要明确:①角的平分线上的点到角的两边的距离相等,②从一条平行线上的任意一点到另一条直线作垂线,垂线段的长度叫两条平行线之间的距离,③平行线间的距离处处相等.6.如图,AD 平分BAC ∠交BC 于点D ,DE AB ⊥于点E ,DF AC ⊥于点F ,若ABC S 12=,DF 2=,AC 3=,则AB 的长是 ( )A .2B .4C .7D .9D解析:D【分析】 求出DE 的值,代入面积公式得出关于AB 的方程,求出即可.【详解】解:∵AD 平分∠BAC ,DE ⊥AB ,DF ⊥AC ,∴DE=DF=2,∵S △ABC =S △ABD +S △ACD ,∴12=12×AB×DE+12×AC×DF , ∴24=AB×2+3×2,∴AB=9,故选:D .【点睛】本题考查了角平分线性质,三角形的面积的应用,注意:角平分线上的点到角两边的距离相等.7.如图,ABC 和DEF 中,∠A=∠D ,∠C=∠F ,要使ABC DEF ≅,还需增加的条件是( )A .AB=EFB .AC=DFC .∠B=∠ED .CB=DE B解析:B【分析】 根据AAS 定理或ASA 定理即可得.【详解】在ABC 和DEF 中,,A C F D ∠∠∠=∠=,∴要使ABC DEF ≅,只需增加一组对应边相等即可,即需增加的条件是AB DE =或AC DF =或BC EF =,观察四个选项可知,只有选项B 符合,故选:B .【点睛】本题考查了三角形全等的判定定理,熟练掌握三角形全等的判定定理是解题关键. 8.到ABC 的三条边距离相等的点是ABC 的( )A.三条中线的交点B.三条边的垂直平分线的交点C.三条高的交点D.三条角平分线的交点D解析:D【分析】由于角平分线上的点到角的两边的距离相等,而已知一点到ABC的三条边距离相等,那么这样的点在这个三角形的三条角平分线上,由此即可作出选择.【详解】解:∵到ABC的三条边距离相等,角平分线上的点到角的两边的距离相等,∴这点在这个三角形三条角平分线上,即这点是三条角平分线的交点,故选:D.【点睛】此题主要考查了三角形的角平分线的性质:三条角平分线交于一点,并且这一点到三边的距离相等.9.如图,OB平分∠MON,A为OB的中点,AE⊥ON,EA=3,D为OM上的一个动点,C 是DA延长线与BC的交点,BC//OM,则CD的最小值是()A.6 B.8 C.10 D.12A解析:A【分析】根据两条平行线之间的距离可知当CD⊥OM时,CD取最小值,先利用角平分线的性质得出AD=AE=3,利用全等三角形的判定和性质得出AC=AD=AE=3,进而解答即可.【详解】解:由题意得,当CD⊥OM时,CD取最小值,∵OB平分∠MON,AE⊥ON于点E,CD⊥OM,∴AD=AE=3,∵BC∥OM,∴∠DOA=∠B,∵A为OB中点,∴AB=AO,在△ADO与△ABC中B DOAAB AOBAC DAO∠=∠⎧⎪=⎨⎪∠=∠⎩,∴△ADO ≌△ABC (SAS ),∴AC =AD =3,∴336CD AC AD =+=+=,故选A .【点睛】此题考查角平分线的性质、全等三角形的判定和性质、平行线之间的距离,关键是利用全等三角形的判定和性质得出AC =AD =AE =3.10.如图,AB =AC ,点D 、E 分别是AB 、AC 上一点,AD =AE ,BE 、CD 相交于点M .若∠BAC =70°,∠C =30°,则∠BMD 的大小为( )A .50°B .65°C .70°D .80°A解析:A【分析】 根据题意可证明ABE ACD ≅,即得到B C ∠=∠.再利用三角形外角的性质,可求出DME ∠,继而求出BMD ∠.【详解】根据题意ABE ACD ≅(SAS ),∴30B C ∠=∠=︒∵DME B BDC ∠=∠+∠,BDC C A ∠=∠+∠∴307030130DME B A C ∠=∠+∠+∠=︒+︒+︒=︒∴180********BMD DME ∠=︒-∠=︒-︒=︒故选A .【点睛】本题考查三角形全等的判定和性质,三角形外角的性质.利用三角形外角的性质求出DME B A C ∠=∠+∠+∠是解答本题的关键.二、填空题11.如图,四边形ABCD 中,180B D ∠+∠=︒,AC 平分DAB ∠,CM AB ⊥于点M ,若4cm AM =, 2.5cm BC =,则四边形ABCD 的周长为______cm .13【分析】过点C 作CN ⊥AD 交AD 延长线于点N 由角平分线的性质得到CN=CM 然后证明△CDN ≌△CBM 得到DN=BMCD=CB=25然后求出AN=AM=4则AD=4DN 即可求出四边形的周长【详解】解析:13【分析】过点C 作CN ⊥AD ,交AD 延长线于点N ,由角平分线的性质,得到CN=CM ,然后证明△CDN ≌△CBM ,得到DN=BM ,CD=CB=2.5,然后求出AN=AM=4,则AD=4-DN ,即可求出四边形的周长.【详解】解:根据题意,过点C 作CN ⊥AD ,交AD 延长线于点N ,如图:∵CM AB ⊥,CN ⊥AD ,∴∠N=∠CMB=90°,∵180B ADC ∠+∠=︒,180CDN ADC ∠+∠=︒,∴B CDN ∠=∠,∵AC 平分DAB ∠,∴CN=CM ,∴△CDN ≌△CBM ,∴DN=BM ,CD=CB=2.5,∵AC=AC ,∠N=∠CMA=90°,∴△ACN ≌△ACM (HL ),∴AN=AM=4,∴AD=4-DN ,∴AB=4+BM=4+DN ,∴四边形ABCD 的周长为:4 2.5 2.5413AD DC CB AB DN DN +++=-++++=;故答案为:13.【点睛】本题考查了角平分线的性质,全等三角形的判定和性质,解题的关键是利用所学的知识,正确得到AD=4-DN ,AB=4+DN .12.如图,点C 在AOB ∠的平分线上,CD OA ⊥于点D ,且2CD =,如果E 是射线OB上一点,那么CE 长度的最小值是___________.2【分析】根据垂线段最短及角平分线的性质定理求解【详解】解:如图由垂线段最短定理可知:当CE ⊥OB 时CE 的长度最小∵点C 在∠AOB 的平分线上CD ⊥OA ∴CE=CD=2故答案为2【点睛】本题是基础题目解析:2【分析】根据垂线段最短及角平分线的性质定理求解 .【详解】解:如图,由垂线段最短定理可知:当CE ⊥OB 时,CE 的长度最小,∵点C 在 ∠AOB 的平分线上,CD ⊥OA ,∴CE=CD=2,故答案为2 .【点睛】本题是基础题目,熟练掌握垂线段最短及角平分线的性质定理是解题关键.13.如图(1),已知AB AC =,D 为BAC ∠的角平分线上一点,连接BD ,CD ;如图(2),已知AB AC =,D ,E 为BAC ∠的角平分线上两点,连接BD ,CD ,BE ,CE ;如图(3),已知AB AC =,D ,E ,F 为BAC ∠的角平分线上三点,连接BD ,CD ,BE ,CE ,BF ,CF ;……,依此规律,第7个图形中有全等三角形的对数是________.28【分析】设第n 个图形中有an (n 为正整数)对全等三角形根据各图形中全等三角形对数的变化可找出变化规律an=(n 为正整数)再代入n=7即可求出结论【详解】解:设第n 个图形中有an (n 为正整数)对全解析:28【分析】设第n 个图形中有a n (n 为正整数)对全等三角形,根据各图形中全等三角形对数的变化可找出变化规律“a n =(1)2n n +(n 为正整数)”,再代入n=7即可求出结论. 【详解】解:设第n 个图形中有a n (n 为正整数)对全等三角形.∵点E 在∠BAC 的平分线上∴∠BAD=∠CAD 在△ABD 和△ACD 中,AB AC BAD CAD AD AD =⎧⎪∠=∠⎨⎪=⎩,∴△ABD ≌△ACD (SAS ),∴a 1=1;同理,可得:a 2=3=1+2,a 3=6=1+2+3,a 4=10=1+2+3+4,…,∴a n =1+2+3+…+n=(1)2n n +(n 为正整数), ∴a 7=7(71)282⨯+=. 故答案为:28.【点睛】本题考查了全等三角形的判定以及规律型:图形的变化类,根据各图形中全等三角形对数的变化,找出变化规律“a n =(1)2n n +(n 为正整数)”是解题的关键. 14.如图,在ABC 中,C 90∠=,A ∠、B ∠的平分线交于O ,OD AB ⊥于D .若AC 3=,BC 4=,AB 5=,则AD =________.【分析】根据三角形角平分线的交点到边的距离相等再利用三角形面积公式解答即可【详解】解:过作于于∵的平分线交于于∴∵∴四边形是正方形∴∵的面积即解得:∴∴在与中∴∴故答案为:【点睛】本题考查了角平分线解析:2【分析】根据三角形角平分线的交点到边的距离相等,再利用三角形面积公式解答即可.【详解】解:过O 作OE AC ⊥于E ,OF BC ⊥于F ,∵A ∠、B ∠的平分线交于O ,OD AB ⊥于D ,∴OD OE OF ==.∵C 90∠=,∴四边形ECFO 是正方形,∴OE OF CE CF ===.∵ABC 的面积1111AC BC AB OD AC OE BC OF 2222=⋅=⋅+⋅+⋅, 即()1134OE 34522⨯⨯=⨯++,解得:1OE =,∴CE OE 1==,∴AE AC CE 2=-=.在Rt AEO 与Rt ADO 中,AO AO OE OD =⎧⎨=⎩,∴Rt AEO Rt ADO ≅,∴AD AE 2==.故答案为:2.【点睛】本题考查了角平分线的性质,全等三角形的判定和性质,正确作出辅助线是解题的关键. 15.如图,线段AB ,CD 相交于点O ,AO=BO ,添加一个条件, 能使AOC BOD ≅,所添加的条件的是___________________________.或或或【分析】先根据对顶角相等可得再根据三角形全等的判定定理即可得【详解】由对顶角相等得:当时由定理可证当时由定理可证当时由定理可证当时则由定理可证故答案为:或或或【点睛】本题考查了对顶角相等三角形解析:CO DO =或A B ∠=∠或C D ∠=∠或//AC BD【分析】先根据对顶角相等可得AOC BOD ∠=∠,再根据三角形全等的判定定理即可得.【详解】由对顶角相等得:AOC BOD ∠=∠,AO BO =,∴当CO DO =时,由SAS 定理可证AOC BOD ≅,当A B ∠=∠时,由ASA 定理可证AOC BOD ≅,当C D ∠=∠时,由AAS 定理可证AOC BOD ≅,当//AC BD 时,则A B ∠=∠,由ASA 定理可证AOC BOD ≅,故答案为:CO DO =或A B ∠=∠或C D ∠=∠或//AC BD .【点睛】本题考查了对顶角相等、三角形全等的判定定理等知识点,熟练掌握三角形全等的判定定理是解题关键.16.在ABC 中,48ABC ︒∠=,点D 在BC 边上,且满足18,BAD DC AB ︒∠==,则CAD ∠=________度.66【分析】在线段CD 上取点E 使CE=BD 再证明△ADB ≅△AEC 即可求出【详解】在线段DC 取点ECE=BD 连接AE ∵CE=BD ∴BE=CD ∵AB=CD ∴AB=BE ∠BAE=∠BEA=(180°-4解析:66【分析】在线段CD 上取点E 使CE =BD ,再证明△ADB ≅△AEC 即可求出. 【详解】在线段DC 取点E ,CE =BD ,连接AE ,∵CE =BD ,∴BE =CD ,∵AB =CD ,∴AB =BE ,∠BAE =∠BEA =(180°-48°)÷2=66°,∴∠DAE =48° ,∠AED =66°,∴△ADB ≅△AEC ,∴∠BAD =∠CAE =18°,∴∠CAD =∠DAE +∠CAE =66°.故答案为:66.【点睛】本题考察了全等三角形的证明和三角形内角和定理,解题的关键是做出辅助线找到全等三角形.17.如图,ABC 的面积为215cm ,以顶点A 为圆心,适当长为半径画弧,分别交AC ,AB 于点M ,N ,再分别以点M ,N 为圆心,大于12MN 的长为半径画弧,两弧交于点P ,作射线AP ,过点C 作CD AP ⊥于点D ,连接DB ,则DAB 的面积是______2cm .【分析】如图延长CD 交AB 于E 由题意得AP平分∠CAB 证明△ADC ≌△ADE 得到CD=DE 由此得到推出即可得到答案【详解】如图延长CD 交AB 于E 由题意得AP 平分∠CAB ∴∠CAD=∠EAD ∵CD ⊥A 解析:152【分析】如图,延长CD 交AB 于E ,由题意得AP 平分∠CAB ,证明△ADC ≌△ADE ,得到CD=DE ,由此得到,ACD ADE BCD BED SS S S ==,推出ACD BCD ADE BED S S S S +=+,即可得到答案.【详解】如图,延长CD 交AB 于E ,由题意得AP 平分∠CAB ,∴∠CAD=∠EAD,∵CD ⊥AD ,∴∠ADC=∠ADE ,∵AD=AD ,∴△ADC ≌△ADE ,∴CD=DE ,∴,ACD ADE BCD BED SS S S ==, ∴ACD BCD ADE BED SS S S +=+, ∴12ABD ADE BED ABC S S S S =+==152, 故答案为:152. .【点睛】此题考查三角形角平分线的作图方法,全等三角形的判定及性质,证出CD=DE 得到,ACD ADE BCD BED S S S S ==是解此题的关键.18.如图所示,己知ABC ∆的周长是22,,OB OC 分别平分ABC ∠和ACB OD BC D ∠⊥,于,且3OD =,则ABC ∆的面积是__________.【分析】连接OA 过O 作OE ⊥AB 于EOF ⊥AC 于F 根据角平分线上的点到角的两边的距离相等可得点O 到ABACBC 的距离都相等(即OE =OD =OF )从而可得到△ABC 的面积等于周长的一半乘以3代入求出即 解析:33【分析】连接OA ,过O 作OE ⊥AB 于E ,OF ⊥AC 于F ,根据角平分线上的点到角的两边的距离相等可得点O 到AB 、AC 、BC 的距离都相等(即OE =OD =OF ),从而可得到△ABC 的面积等于周长的一半乘以3,代入求出即可.【详解】解:如图,连接OA ,过O 作OE ⊥AB 于E ,OF ⊥AC 于F ,∵OB 、OC 分别平分∠ABC 和∠ACB ,OD ⊥BC 于D∴OE=OF=OD=3,∵△ABC的周长是22,∴S△ABC=12×AB×OE+12×BC×OD+12×AC×OF=12×(AB+BC+AC)×3=12×22×3=33.故答案为:33.【点睛】本题考查了角平分线的性质和三角形的面积求法,熟知角平分线的性质,并根据题意合理添加辅助线是解题关键.19.如图,OM平分∠POQ,MA⊥OP,MB⊥OQ,垂足为A,B,S△AOM=8cm2,OA=4cm,则MB=___.4cm【分析】根据求得AM的长度利用角平分线上的点到角两边的距离相等即可求解【详解】解:解得∵OM平分∠POQ∴故答案为:4cm 【点睛】本题考查角平分线的性质掌握角平分线上的点到角两边的距离相等是解解析:4cm【分析】根据12AOMS OA AM=⋅求得AM的长度,利用角平分线上的点到角两边的距离相等即可求解.【详解】解:114822AOMS OA AM AM=⋅=⨯=,解得4cmAM=,∵OM平分∠POQ,∴4cm MB AM==,故答案为:4cm .【点睛】本题考查角平分线的性质,掌握角平分线上的点到角两边的距离相等是解题的关键. 20.如图,//AD BC ,ABC ∠的角平分线BP 与BAD ∠的角平分线AP 相交于点P ,作PE AB ⊥于点E .若9PE =,则两平行线AD 与BC 间的距离为_______.;【分析】过点P 作MN ⊥AD 根据角平分线的性质以及平行线的性质即可得出PM=PE=2PE=PN=2即可得出答案【详解】过点P 作MN ⊥AD ∵AD ∥BC ∠ABC 的角平分线BP 与∠BAD 的角平分线AP 相交解析:18;【分析】过点P 作MN ⊥AD ,根据角平分线的性质以及平行线的性质即可得出PM=PE =2,PE=PN =2,即可得出答案.【详解】过点P 作MN ⊥AD∵AD ∥BC ,∠ABC 的角平分线BP 与∠BAD 的角平分线AP 相交于点P ,PE ⊥AB 于点E ∴AP ⊥BP ,PN ⊥B C∴PM=PE =9,PE=PN =9∴MN =9+9=18故答案为18.【点睛】此题主要考查了角平分线的性质以及平行线的性质,根据题意作出辅助线是解决问题的关键.三、解答题21.作图题:已知∠α,线段m 、n ,请按下列步骤完成作图(不需要写作法,保留作图痕迹)(1)作∠MON =∠α(2)在边OM上截取OA=m,在边ON上截取OB=n.(3)作直线AB.解析:(1)见解析;(2)见解析;(3)见解析【分析】(1)先画一条射线ON,以∠α的顶点为圆心,任意长度为半径画弧,交∠α的两个边于两个点,这两个点的距离记为a,接着以点O为圆心,同样的长度为半径画弧,交ON于一个点,以这个点为圆心,a为半径画弧,与刚刚画的弧有一个交点,连接这个点和点O,得到射线OM,即可得到∠MON=∠α;(2)以点O为圆心,m为半径画弧,交OM于点A,以点O为圆心,n为半径画弧,交ON于点B;(3)连接AB,线段AB所在的直线即直线AB.【详解】解:(1)如图所示,(2)如图所示,(3)如图所示,【点睛】本题考查尺规作图,解题的关键是掌握作已知角度的方法,截取线段和画直线的方法. 22.(阅读理解)课外兴趣小组活动时,老师提出了如下问题:如图1,ABC 中,若8AB =,6AC =,求BC 边上的中线AD 的取值范围.小明在组内经过合作交流,得到了如下的解决方法:延长AD 到点E ,使DE AD =,请根据小明的方法思考:(1)由已知和作图能得到ADC ≌EDB △的理由是______.(2)求得AD 的取值范围是______.(感悟)解题时,条件中若出现“中点”“中线”字样,可以考虑延长中线构造全等三角形,把分散的已知条件和所求证的结论集合到同一个三角形中.(问题解决)(3)如图2,在ABC 中,点D 是BC 的中点,点M 在AB 边上,点N 在AC 边上,若DM DN ⊥,求证:BM CN MN +>.解析:(1)SAS ;(2)17AD <<;(3)见解析【分析】(1)根据AD=DE ,∠ADC=∠BDE ,BD=DC 推出△ADC 和△EDB 全等即可;(2)根据全等得出BE=AC=6,AE=2AD ,由三角形三边关系定理得出8-6<2AD <8+6,求出即可;(3)延长ND 至点E ,使DE DN =,连接BE 、ME ,证明BED ≌()SAS CND △,得到BE CN =,根据三角形三边关系解答即可.【详解】(1)解:∵在△ADC 和△EDB 中,AD DE ADC BDE BD CD =⎧⎪∠=∠⎨⎪=⎩,∴△ADC ≌△EDB (SAS ),故答案为:SAS ;(2)解:∵由(1)知:△ADC ≌△EDB ,∴BE=AC=6,AE=2AD ,∵在△ABE 中,AB=8,由三角形三边关系定理得:8-6<2AD <8+6,∴1<AD <7,故答案为:1<AD <7.(3)证明:延长ND 至点E ,使DE DN =,连接BE 、ME ,如图所示:∵点D 是BC 的中点,∴BD CD =.在BED 和CND △中,DE DN BDE CDN BD CD =⎧⎪∠=∠⎨⎪=⎩, ∴BED ≌()SAS CND △,∴BE CN =,∵DM DN ⊥,DE DN =,∴ME MN =,在BEM △中,由三角形的三边关系得:BM BE ME +>,∴BM CN MN +>.【点睛】本题是三角形综合题,主要考查了三角形的中线,三角形的三边关系定理,全等三角形的性质和判定等知识点,主要考查学生运用定理进行推理的能力.23.如图,在ABC 和BCD △中,90BAC BCD ︒∠=∠=,AB AC =,CB CD =;延长CA 至点E ,使AE AC =;延长CB 至点F ,使BF BC =.连接AD ,AF ,DF ,EF .延长DB 交EF 于点N .(1)求证:AD AF =;(2)求证:BD EF =.解析:(1)证明见解析;(2)证明见解析【分析】(1)结合题意得:ABF BAC ACB ∠=∠+∠,ACD ACB BCD ∠=∠+∠,推导得ABF ACD ∠=∠;通过证明ABF ACD △≌△,即可完成证明;(2)根据(1)的结论ABF ACD △≌△得:BAF CAD ∠=∠;根据题意得90BAE ∠=;再通过证明AEF ABD △≌△,即可完成证明.【详解】(1) ∵ABF BAC ACB ∠=∠+∠,ACD ACB BCD ∠=∠+∠,90BAC BCD ︒∠=∠=∴ABF ACD ∠=∠∵BF BC =,CB CD =∴BF BC CD ==即AB AC ABF ACD BF CD =⎧⎪∠=∠⎨⎪=⎩∴ABF ACD △≌△∴AF AD =;(2)∵90BAC ︒∠=∴18090BAE BAC ∠=-∠=结合(1)的结论ABF ACD △≌△∴BAF CAD ∠=∠∵90EAF BAE BAF BAF ∠=∠-∠=-∠,90BAD BAC CAD CAD ∠=∠-∠=-∠ ∴EAF BAD ∠=∠∵AE AC =,AB AC =∴AE AC AB ==即AF AD EAF BAD AE AB =⎧⎪∠=∠⎨⎪=⎩∴AEF ABD △≌△∴BD EF =.【点睛】本题考查了三角形外角、全等三角形的知识;解题的关键是熟练掌握三角形外角、全等三角形的性质,从而完成求解.24.如图,已知在ABC 中,AB AC =,90BAC ∠=︒,别过B 、C 两点向过A 的直线作垂线,垂足分别为E 、F .求证:EF BE CF =+.解析:见解析【分析】证明△BEA ≌△AFC ,得到AE=CF ,BE=AF ,即可得到结论.【详解】证明:BE EA ⊥,CF AF ⊥,90BAC BEA AFC ∴∠=∠=∠=︒,90EAB CAF ∴∠+∠=︒,90EBA EAB ∠+∠=︒,CAF EBA ∴∠=∠,在ABE △和AFC △中,BEA AFC EBA CAF AB AC ∠=∠⎧⎪∠=∠⎨⎪=⎩,(AAS)BEA AFC ∴△≌△.AE CF ∴=,BE AF =.EF AF AE BE CF ∴=+=+..【点睛】此题考查全等三角形的判定及性质,熟记三角形的判定定理是解题的关键.25.如图,,AD BF 相交于点,//,O AB DF AB DF =,点E 与点C 在BF 上,且BE CF =.(1)求证:ABC DFE ∆≅∆;(2)求证:点О为BF 的中点.解析:(1)见解析;(2)见解析【分析】(1)由已知可证∠B=∠F ,BC=EF ,然后根据SAS 可以得到结论;(2)同(1)有∠B=∠F ,再结合已知条件和对顶角相等可以证得ΔABO ≅ΔDFO ,从而得到OB=OF ,所以点O 为BF 中点 .【详解】证明:(1)∵AB//DF ,∴∠B=∠F ,∵BE=CF ,∴BE+CE=CF+CE ,即BC=EF ,∴在ΔABC 和ΔDFE 中,AB DF B F BC EF =⎧⎪∠=∠⎨⎪=⎩,∴ΔABC ≅ΔDFE (SAS );(2)与(1)同理有∠B=∠F ,∴在ΔABO 和ΔDFO 中,AOB DOF B F AB DF ∠=∠⎧⎪∠=∠⎨⎪=⎩,∴ΔABO ≅ΔDFO (AAS ),∴OB=OF ,∴点O 为BF 中点 .【点睛】本题考查三角形全等的应用,熟练掌握三角形全等的判定与性质并灵活应用是解题关键. 26.在平面直角坐标系中,点A 坐标(5,0)-,点B 坐标(0,5),点 C 为x 轴正半轴上一动点,过点A 作AD BC ⊥交y 轴于点E .(1)如图①,若点C 的坐标为(3,0),求点E 的坐标;(2)如图②,若点C 在x 轴正半轴上运动,且5OC <,其它条件不变,连接DO ,求证:DO 平分ADC ∠;(3)若点C 在x 轴正半轴上运动,当OC CD AD +=时,则OBC ∠的度数为________. 解析:(1)(0,3)E ;(2)见解析;(3)30OBC ∠=︒.【分析】(1)先根据AAS 判定△AOE ≌△BOC ,得出OE=OC ,再根据点C 的坐标为(3,0),得到OC=OE=3,进而得到点E 的坐标;(2)先过点O 作OM ⊥AD 于点M ,作ON ⊥BC 于点N ,根据△AOE ≌△BOC ,得到S △AOE =S △BOC ,且AE=BC ,再根据OM ⊥AE ,ON ⊥BC ,得出OM=ON ,进而得到OD 平分∠ADC ;(3)在DA 上截取DP=DC ,连接OP ,根据SAS 判定△OPD ≌△OCD ,再根据三角形外角性质以及三角形内角和定理,求得∠PAO=30°,进而得到∠OBC=30°.【详解】证明:(1)AD BC ⊥,AO BO ⊥,90AOE BDE BOC ∠∠∠∴===︒.又AEO BED ∠=∠,OAE OBC ∴∠=∠.(5,0)A -,(0,5)B , 5OA OB ∴==.在AOE △和BOC 中OAE OBC OA OBAOE BOC ∠=∠⎧⎪=⎨⎪∠=∠⎩, (ASA)AOE BOC ∴≌,OE OC ∴=. C 点坐标(3,0),3OE OC ∴==,(0,3)E ∴.(2)过O 作OM AD ⊥于M ,ON BC ⊥于N ,AOE BOC ≌,AOE BOC S S ∴=,AE BC =, 1122AE OM BC ON ∴⨯⨯=⨯⨯, OM ON ∴=,OM AD ⊥,ON BC ⊥,DO ∴平分ADC ∠.(3)如所示,在DA 上截取DP=DC ,连接OP ,∵∠PDO=∠CDO ,OD=OD ,∴△OPD ≌△OCD ,∴OC=OP ,∠OPD=∠OCD ,∵OC CD AD +=,∴OC=AD-CD∴AD-DP=OP ,即AP=OP ,∴∠PAO=∠POA ,∴∠OPD=∠PAO+∠POA=2∠PAO=∠OCB ,又∵∠PAO+∠OCD=90°,∴3∠PAO=90°,∴∠PAO=30°,∵OAP OBC ∠=∠∴∠OBC=∠PAO =30°.【点睛】本题属于三角形综合题,主要考查了全等三角形的判定与性质,角平分线的判定定理以及等腰直角三角形的性质的综合应用,解决问题的关键是作辅助线构造全等三角形,运用全等三角形的性质进行求解.27.已知在ABC 中,90ACB ∠=︒,AC BC =,直线l 绕点C 旋转,过点A 作AD l ⊥于D ,过点B 作BE l ⊥于E ,若6AD =,3BE =,画图并直接写出DE 的长. 解析:图见解析,9DE =或3DE =【分析】分直线l 不经过线段AB 和直线l 经过线段AB 两种情况画图,证明△ACD ≌△CBE 即可求出DE 的长.【详解】解:如图1∵AD l ⊥于D , BE l ⊥于E ,∴∠ADC=∠CEB=90°,∴∠DAC+∠DCA=90°,∵90ACB ∠=︒,∴∠BCE+∠DCA=90°,∴∠DAC=∠ECB在△ACD 和△CBE 中,===ADC CEB DAC ECB AC CB ∠∠⎧⎪∠∠⎨⎪⎩,∴ △ACD ≌△CBE∴AD=CE=6,DC=EB=3,∴DE=DC+CE=9;如图2,∵AD l ⊥于D , BE l ⊥于E ,∴∠ADC=∠CEB=90°,∴∠DAC+∠DCA=90°,∵90ACB ∠=︒,∴∠BCE+∠DCA=90°,∴∠DAC=∠ECB在△ACD 和△CBE 中,===ADC CEB DAC ECB AC CB ∠∠⎧⎪∠∠⎨⎪⎩,∴ △ACD ≌△CBE∴AD=CE=6,DC=EB=3,∴DE=CE-CD=3;∴9DE =或3DE =.【点睛】本题考查了全等三角形的判定与性质,根据题意分类画图证明全等三角形是解题关键. 28.已知:AB BD ⊥,ED BD ⊥,AC CE =,BC DE =.(1)试猜想线段AC 与CE 的位置关系,并证明你的结论.(2)若将CD 沿CB 方向平移至图2情形,其余条件不变,结论12AC C E ⊥还成立吗?请说明理由.(3)若将CD 沿CB 方向平移至图3情形,其余条件不变,结论12AC C E ⊥还成立吗?请说明理由.解析:(1)AC CE ⊥,见解析;(2)成立,理由见解析;(3)成立,理由见解析【分析】(1)先用HL 判断出Rt Rt ABC CDE ≌△△,得出A DCE ∠=∠,进而判断出90DCE ACB ∠+∠=︒,即可得出结论;(2)同(1)的方法,即可得出结论;(3)同(1)的方法,即可得出结论.【详解】解:(1)AC CE ⊥理由如下:∵AB BD ⊥,ED BD ⊥,∴90B D ∠=∠=︒在Rt ABC △和Rt CDE △中AC CE BC DE =⎧⎨=⎩∴()Rt Rt HL ABC CDE △△≌, ∴A DCE ∠=∠∵90B ∠=︒,∴90A ACB ∠+∠=︒,∴()18090ACE DCE ACB ∠=︒-∠+∠=︒, ∴AC CE ⊥;(2)成立,理由如下:∵AB BD ⊥,ED BD ⊥,∴90B D ∠=∠=︒,在1Rt ABC 和2Rt C DE △中121AC C E BC DE =⎧⎨=⎩, ∴()12Rt Rt HL ABC C DE ≌△△, ∴2A C E D ∠=∠,∵90B ∠=︒,∴190B A AC ∠+∠=︒,∴2190DC E AC B ∠+∠=︒,在12C FC 中,()122118090C FC DC E AC B ∠=︒-∠+∠=︒, ∴12AC C E ⊥;(3)成立,理由如下:∵AB BD ⊥,ED BD ⊥,∴190ABC D ∠=∠=︒在1Rt ABC 和2Rt C DE △中121AC C E BC DE =⎧⎨=⎩, ∴()12Rt Rt HL ABC C DE ≌△△, ∴2A C E D ∠=∠,∵190ABC ∠=︒,∴190B A AC ∠+∠=︒,在12C FC 中,()2112180=90C FC DC E AC B ∠=︒-∠+∠︒, ∴12AC C E ⊥.【点睛】此题是几何变换综合题,主要考查了全等三角形的判定和性质,直角三角形的性质,判断出12Rt Rt ABC C DE ≌△△是解本题的关键.。
人教版八年级数学上册全等三角形的证明习题(大题)

全等三角形的证明1、如图,AB =AD ,∠BAD =∠CAE ,AC=AE ,求证:BC=DE2、如图,AF=DB ,BC=EF ,AC=DE ,求证:BC∠EF 。
3、已知:如图,∠ABC =∠DCB ,BD 、CA 分别是∠ABC 、∠DCB 的平分线. 求证:AB =DC .4、如图,∠DCE =90°,CD =CE ,AD∠AC ,BE∠AC ,垂足分别为A 、B . 求证:AD +AB =BE .ABCDE5、已知,AC∠CE ,AC=CE , ∠ABC=∠EDC=900,证明:BD=AB+ED 。
6、如图,在∠ABC 中,D 为BC 边的中点,过D 点分别作DE ∠AB 交AC 于点E , DF ∠AC 交AB 于点F .求证:BF=DE 。
7、如图,点E 在AB 上,AC=AD ,请你添加一个条件,使图中存在全等三角形,并给予证明。
所添条件为 ,你得到的一对全等三角形是∆ ∆≅ .证明:ABCDE8、如图,AD 平分∠BAC ,DE∠AB 于E ,DF∠AC 于F ,且DB=DC ,求证:EB=FC.9、如图,AE 是∠BAC 的平分线,AB=AC 。
若点D 是AE 上任意一点,请证明:∠ABD∠∠ACD ;10、(1)把一大一小两个等腰直角三角板(即EC=CD,AC=BC )如图1放置,点D 在BC上,连结BE ,AD ,AD 的延长线交BE 于点F . 求证:(1)ΔACD∠ΔBCE (2)AF∠BE .FE D CB AECDBABACDEFB DE A(2)把左边的小三角板逆时针旋转一定的角度如图2放置,问AF与BE是否垂直?并说明理由.图2。
八年级上册数学全等三角形证明题

八年级上册数学全等三角形证明题一、全等三角形证明题1 20题及解析。
(一)题目1。
1. 题目。
已知:如图,在△ABC中,AD是BC边上的中线,E是AD上一点,且BE = AC,延长BE交AC于F。
求证:AF = EF。
2. 解析。
证明:延长AD到G,使DG = AD,连接BG。
因为AD是BC边上的中线,所以BD = CD。
在△BDG和△CDA中,BD = CD,∠BDG = ∠CDA(对顶角相等),DG = DA。
根据SAS(边角边)全等判定定理,可得△BDG≌△CDA。
所以BG = AC,∠G = ∠CAD。
又因为BE = AC,所以BG = BE。
所以∠G = ∠BEG。
因为∠BEG = ∠AEF(对顶角相等),所以∠AEF = ∠CAD。
所以AF = EF。
(二)题目2。
1. 题目。
如图,在△ABC和△DEF中,AB = DE,BE = CF,∠B = ∠DEF。
求证:AC = DF。
2. 解析。
因为BE = CF,所以BE + EC = CF+EC,即BC = EF。
在△ABC和△DEF中,AB = DE,∠B = ∠DEF,BC = EF。
根据SAS全等判定定理,可得△ABC≌△DEF。
所以AC = DF。
(三)题目3。
1. 题目。
已知:如图,AB = CD,AE = DF,CE = FB。
求证:AF = DE。
2. 解析。
因为CE = FB,所以CE + EF = FB + EF,即CF = BE。
在△AEB和△DFC中,AB = CD,AE = DF,BE = CF。
根据SSS(边边边)全等判定定理,可得△AEB≌△DFC。
所以∠B = ∠C。
在△ABF和△DCE中,AB = CD,∠B = ∠C,BF = CE。
根据SAS全等判定定理,可得△ABF≌△DCE。
所以AF = DE。
(四)题目4。
1. 题目。
如图,在Rt△ABC中,∠ACB = 90°,CA = CB,D是AC上一点,E在BC的延长线上,且AE = BD,BD的延长线与AE交于点F。
新人教版八年级数学全等三角形基础证明题练习

全等三角形的判定班级:姓名:1.已知AD是⊿ABC的中线;BE⊥AD;CF⊥AD;求证BE=CF.. 2.已知AC=BD;AE=CF;BE=DF;求证AE∥CF3.已知AB=CD;BE=DF;AE=CF;求证AB∥CD4.已知在四边形ABCD中;AB=CD;AD=CB;求证AB∥CD 5.已知∠BAC=∠DAE;∠1=∠2;BD=CE;求证⊿ABD≌⊿ACE. 6.已知CD∥AB;DF∥EB;DF=EB;求证AF=CE7.已知BE=CF;AB=CD; ∠B=∠C;求证AF=DEAB CDFEA CB DE FDCFEA BADEB C1 2AD CEFB A D8.已知AD =CB ; ∠A =∠C ;AE =CF ;求证EB ∥DF9.已知M 是AB 的中点;∠1=∠2;MC =MD ;求证∠C =∠D ..10.已知;AE =DF ;BF =CE ;AE ∥DF ;求证AB =CD ..11.已知∠1=∠2;∠3=∠4;求证AC =AD12.已知∠E =∠F ;∠1=∠2;AB =CD ;求证AE =DF13.已知ED ⊥AB ;EF ⊥BC ;BD =EF ;求证BM =ME ..14.在⊿ABC 中;高AD 与BE 相交于点H;且AD =BD ;求证⊿BHD ≌⊿ACD .. A C D B 1 2 3 4A B C DEF 1 2A E H A C MEF B DB AD FEC MA B C D 1 2 D C F EA B15.已知∠A=∠D;AC∥FD;AC=FD;求证AB∥DE..16.已知AC=AB;AE=AD; ∠1=∠2;求证∠3=∠4..17.已知EF∥BC;AF=CD;AB⊥BC;DE⊥EF;求证⊿ABC≌⊿DEF.. 18.已知AD=AE;∠B=∠C;求证AC=AB..19.已知AD⊥BC;BD=CD;求证AB=AC20.已知∠1=∠2;BC=AD;求证⊿ABC≌⊿BAD..AB C EFDAB CEDFAD EBCAB CDADEB C1 23 421.已知AB=AC; ∠1=∠2;AD=AE;求证⊿ABD≌⊿ACE. 22.已知BE∥DF;AD∥BC;AE=CF;求证⊿AFD≌⊿CEB 23.已知AD=AE;BD=CE;∠1=∠2;求证⊿ABD≌⊿ACE 24.已知AB=AC;AD=AE;∠1=∠2;求证CE=BD.. 25.已知CE⊥AB;DF⊥AB;AC∥DB;AC=BD;求证CE=DF26.如图;AD=BC;AE=BE;求证∠C=∠D..CA EBFDBA DFECAB CD E1 2ACDBEFG12AC DEBADBEC1227.已知∠1=∠2;AC=BD;E;F;A;B在同一直线上;求证∠3=∠4 28.已知D O⊥BC;O C=O A;O B=O D;求证CD=AB29.已知CE=DF;AE=BF;AE⊥AD;FD⊥AD;求证⊿EAB≌⊿FDC 30.已知AB与CD相交于点E;EA=EC;ED=EB;求证⊿AED≌⊿CEB 31.已知AB=AC;D;E分别是AB;AC的中点..求证BE=CD..AEDCBOC DAE FB21 34ACBDECA EBFDACBED32.已知DE=FE;FC∥AB;求证AE=CE..33.已知CE⊥AB;DF⊥AB;CE=DF;AE=BF;求证⊿CEB≌⊿DFA..34.如图;D;E;F;B在一条直线上;AB=CD;∠B=∠D;BF=DE;求证1AE=CF2AE∥CF.. 35.已知;点C是AB的中点;CD∥BE;且CD=BE;求证∠D=∠E..36.已知;E、F是AB上的两点;AE=BF;又AC∥DB;AC=DB;求证CF=DE..37.已知;AC⊥CE;AC=CE; ∠ABC=∠DEC=900;求证BD=AB+ED.. BA C D E FCDEFA BAEDAECB12B ADFECAD BE FC38.⊿ABC ≌⊿A ′B ′C ′;AD 与A ′D ′分别是中线;求证AD =A ′D ′..39. 已知:如图 ; E; B; F; C 四点在同一直线上; ∠A=∠D=90° ; BE=FC; AB=DF .求证:∠E=∠C40.已知:如图 ; DN=EM ; 且DN AB 于 D ; EMAC 于E ; BM=CN .求证:∠B=∠C.41.已知:如图 ; AE ; FC 都垂直于BD ; 垂足为E 、F ; AD=BC ; BE=DF .求证:OA=OC.42. 已知:如图 ; AB=CD ; D 、B 到AC 的距离DE=BF .求证:AB ∥CD . AB C D A ′ B ′ C ′ D ′。
八年级全等三角形证明经典50题(含答案)

1. 已知:AB=4,AC=2,D 是BC 中点,AD 是整数,求AD解:延长AD 到E,使AD=DE∵D 是BC 中点∴BD=DC在△ACD 和△BDE 中AD=DE∠BDE=∠ADCBD=DC∴△ACD ≌△BDE∴AC=BE=2∵在△ABE 中AB-BE <AE <AB+BE∵AB=4即4-2<2AD <4+21<AD <3∴AD=22. 已知:D 是AB 中点,∠ACB=90°,求证:12CD AB延长CD 与P ,使D 为CP 中点。
连接AP,BP∵DP=DC,DA=DB∴ACBP 为平行四边形又∠ACB=90∴平行四边形ACBP 为矩形∴AB=CP=1/2AB3. 已知:BC=DE ,∠B=∠E ,∠C=∠D ,F 是CD 中点,求证:∠1=∠2AD BC证明:连接BF 和EF∵ BC=ED,CF=DF,∠BCF=∠EDF∴ 三角形BCF 全等于三角形EDF(边角边)∴ BF=EF,∠CBF=∠DEF连接BE在三角形BEF 中,BF=EF∴ ∠EBF=∠BEF 。
∵ ∠ABC=∠AED 。
∴ ∠ABE=∠AEB 。
∴ AB=AE 。
在三角形ABF 和三角形AEF 中AB=AE,BF=EF,∠ABF=∠ABE+∠EBF=∠AEB+∠BEF=∠AEF∴ 三角形ABF 和三角形AEF 全等。
∴ ∠BAF=∠EAF (∠1=∠2)。
4. 已知:∠1=∠2,CD=DE ,EF//AB ,求证:EF=AC过C 作CG ∥EF 交AD 的延长线于点GCG ∥EF ,可得,∠EFD =CGDDE =DC∠FDE =∠GDC (对顶角)∴△EFD ≌△CGDEF =CGB ACDF21E∠CGD=∠EFD又,EF∥AB∴,∠EFD=∠1∠1=∠2∴∠CGD=∠2∴△AGC为等腰三角形,AC=CG又EF=CG∴EF=AC5.已知:AD平分∠BAC,AC=AB+BD,求证:∠B=2∠CA证明:延长AB取点E,使AE=AC,连接DE∵AD平分∠BAC∴∠EAD=∠CAD∵AE=AC,AD=AD∴△AED≌△ACD (SAS)∴∠E=∠C∵AC=AB+BD∴AE=AB+BD∵AE=AB+BE∴BD=BE∴∠BDE=∠E∵∠ABC=∠E+∠BDE∴∠ABC=2∠E∴∠ABC=2∠C6.已知:AC平分∠BAD,CE⊥AB,∠B+∠D=180°,求证:AE=AD+BE证明:在AE 上取F ,使EF =EB ,连接CF∵CE ⊥AB∴∠CEB =∠CEF =90°∵EB =EF ,CE =CE ,∴△CEB ≌△CEF∴∠B =∠CFE∵∠B +∠D =180°,∠CFE +∠CFA =180°∴∠D =∠CFA∵AC 平分∠BAD∴∠DAC =∠FAC∵AC =AC∴△ADC ≌△AFC (SAS )∴AD =AF∴AE =AF +FE =AD +BE7. 已知:AB=4,AC=2,D 是BC 中点,AD 是整数,求AD解:延长AD 到E,使AD=DE ∵D 是BC 中点∴BD=DC在△ACD 和△BDE 中AD=DE∠BDE=∠ADCAD BCBD=DC∴△ACD≌△BDE∴AC=BE=2∵在△ABE中AB-BE<AE<AB+BE ∵AB=4即4-2<2AD<4+2 1<AD<3∴AD=28.已知:D是AB中点,∠ACB=90°,求证:12 CD AB9.已知:BC=DE,∠B=∠E,∠C=∠D,F是CD中点,求证:∠1=∠2证明:连接BF 和EF 。
人教版数学八年级上册第12章《全等三角形》复习测试题(配套练习附答案)

同理△DCB≌△C'DB,
∵∠A=∠C',∠AOB=∠C'OD,AB=C'D,
∴△AOB≌△C'OD (AAS) ,
所以共有四对全等三角形.
故答案为4.
【点睛】本题考查三角形全等的判定方法,判定两个三角形全等的一般方法有:SSS、SAS、SSA、HL.注意:AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.
故选D.
二.填空题(本大题共8小题,共24.0分)
9.如图,在 和 中, ,若利用“HL”证明 ≌ ,则需要加条件______.
【答案】 ,
【解析】
【分析】
添加∠C=∠D=90°,由HL证明△ABC≌△ABD即可.
【详解】添加∠C=∠D=90°,理由如下:
∵∠C=∠D=90°,
∴在Rt△ABC和Rt△ABD中,
A. AE=DFB. ∠A=∠DC. ∠B=∠CD. AB= CD
【答案】D
【解析】
【分析】
根据垂直定义求出∠CFD=∠AEB=90°,由已知 ,再根据全等三角形的判定定理推出即可.
【详解】添加的条件是AB=CD;理由如下:
∵AE⊥BC,DF⊥BC,
∴∠CFD=∠AEB=90°,
在Rt△ABE和Rt△DCF中,
【详解】①∵PR⊥AB,PS⊥AC,PR=PS,
∴点P在∠A的平分线上,∠ARP=∠ASP=90°,
∴∠SAP=∠RAP,
在Rt△ARP和Rt△ASP中,
,
∴Rt△ARP≌Rt△ASP(HL),
∴AR=AS,∴①正确;
第十二章全等三角形证明题变式训练(2)2021-2022学年八年级数学人教版上册

第十二章全等三角形证明题变式训练21.问题情境:已知,在等边△ABC中,∠BAC与∠ACB的角平分线交于点O,点M、N分别在直线AC,AB上,且∠MON=60°,猜想CM、MN、AN三者之间的数量关系.方法感悟:小芳的思考过程是在CM上取一点,构造全等三角形,从而解决问题;小丽的思考过程是在AB取一点,构造全等三角形,从而解决问题;问题解决:(1)如图1,M、N分别在边AC,AB上时,探索CM、MN、AN三者之间的数量关系,并证明;变式:(2)如图2,M在边AC上,点N在BA的延长线上时,请你在图2中补全图形,标出相应字母,探索CM、MN、AN三者之间的数量关系,并证明.2.在四边形ABDC中,AD平分∠BAC,并且∠B+∠C=180°.(1) 如图1,当∠C=90°时,求证:BD=CD;变式一:(2) 如图2,当∠C是钝角时,(1)中的结论是否仍然成立?请证明你的判断;变式二:(3) 如图3,在(2)的条件下,过点D作DE⊥AB于点E,若AC=2,BE=3,△ABD的面积为24,求DE的长.3.如图1,在△ABC中,∠A=120°,∠C=20°,BD平分∠ABC,交AC于点D.(1)求证:BD=CD.变式一:(2)如图2,若∠BAC的角平分线AE交BC于点E,求证:AB+BE=AC.变式二:(3)如图3,若∠BAC的外角平分线AE交CB的延长线于点E,则(2)中的结论是否成立?若成立,给出证明,若不成立,写出正确的结论.4.已知:▵ABC中,过B点作BE⊥AD,.(1)如图1,点D在BC的延长线上,连AD,作BE⊥AD于E,交AC于点F.求证:;变式一:(2)如图2,点D在线段BC上,连AD,过A作AE⊥AD,且,连BE交AC于F,连DE,问BD与CF有何数量关系,并加以证明;变式二:(3)如图3,点D在CB延长线上,且AE⊥AD,连接BE、AC的延长线交BE于点M,的值.若,请直接写出DBBC5.在△ABC中,∠ACB=2∠B,如图1,当∠C=90°,AD为∠BAC的角平分线时,在AB上截取AE=AC,连接DE,易证AB=AC+CD.(1)如图2,当∠C≠90°,AD为∠BAC的角平分线时,线段AB、AC、CD又有怎样的数量关系?请写出你的猜想,并对你的猜想给予证明.变式:(2)如图3,当AD为△ABC的外角平分线时,线段AB、AC、CD又有怎样的数量关系?请写出你的猜想,并对你的猜想给予证明.6.如图,△ABC中,CD⊥AB于点D,CD=BD,点E在CD上,DE=DA,连接BE.(1)求证:BE=CA;(2)延长BE交AC于点F,连接DF,求∠CFD的度数;变式:(3)过点C作CM⊥CA,CM=CA,连接BM交CD于点N,若BD=12,AD=5,直接写出△NBC的面积____.7.如图1,等腰直角三角形ABC中,O为斜边AC的中点,CD为∠ACB的平分线,过点B作BE⊥CD,垂足为D,交AC于点E,CD与BO交于点F.(1)求证:△BOE≌△COF;变式:(2)将∠DCB沿CB方向移动至P处,角的一边分别交BE,BO于点Q,H,如图2所示,试探究线段BQ和PH的数量关系,以及它们所在直线的位置关系.8.等边△ABC中,点H在边BC上,点K在边AC上,且满足AK=HC,连接AH,BK交于点F.(1)如图1,求∠AFB的度数;(2)如图2,连接FC,若∠BFC=90°,点G为边AC上一点,且满足∠GFC=30°,求证:AG⊥BG;变式:(3)如图3,在(2)条件下,在BF上取点D使得DF=AF,连接CD交AH于点E,若△DEF 面积为1,则△AHC的面积为__________.9.如图,在△ABC中,∠ABC为锐角,点D为直线BC上一动点,以AD为直角边且在AD的右侧作等腰直角三角形ADE,∠DAE=90°,AD=AE.(1)如果AB=AC,∠BAC=90°.①当点D在线段BC上时,如图1,线段CE,BD的位置关系为________,数量关系为________.变式一:②当点D在线段BC的延长线上时,如图2,①中的结论是否仍然成立,请说明理由.变式二:(2)如图3,如果AB≠AC,∠BAC≠90°,点D在线段BC上运动.探究:当∠ACB多少度时,CE⊥BC?请说明理由.10.如图,在△ABC中,∠ACB=90°,AC=BC,E为AC边的一点,F为AB边上一点,连接CF,交BE于点D且∠ACF=∠CBE,CG平分∠ACB交BD于点G,(1)求证:CF=BG;变式一:(2)延长CG交AB于H,连接AG,过点C作CP // AG交BE的延长线于点P,求证:PB=CP+CF;变式二:(3)在(2)问的条件下,当∠GAC=2∠FCH时,若S△AEG=3√3,BG=6,求AC的长.11.已知△ABC为等边三角形,点D为直线BC上一动点(点D不与点B,点C重合),以AD为边作等边三角形ADE,连接CE.(1)如图1,当点D在边BC上时,①求证:△ABD≌△ACE;②直接判断结论BC=DC+CE是否成立(不需证明).变式:(2)如图2,当点D在边BC的延长线上时,其他条件不变,请写出BC,DC,CE之间存在的数量关系,并写出证明过程.12.如图1,△ABC是等腰直角三角形,AC=BC=2√2,∠ACB=90°,点D是AB中点,在△ABC外取一点E,使DE=AD,连接DE,AE,BE.(1)求证:AE⊥BE.变式一:(2)如图2,若点E在直线AB下方,且∠AAA=30°,求CE的长.变式二:(3)若AE:AB=1:4,求△ACE的面积.13.将两个全等的直角三角形ABC和DBE按图(1)方式摆放,其中∠ACB=∠DEB=90°,∠A=∠D=30°,点E落在AB上,DE所在直线交AC所在直线于点F.(1)求证:CF=EF;变式一:(2)若将图(1)中的△DBE绕点B按顺时针方向旋转角a,且0°<a<60°,其他条件不变,如图(2).请你直接写出AF+EF与DE的大小关系:AF+EF________DE.(填“>”或“=”或“<”)变式二:(3)若将图(1)中△DBE的绕点B按顺时针方向旋转角B,且60°<β<180°,其他条件不变,如图(3).请你写出此时AF、EF与DE之间的关系,并加以证明.14.如图①,在△ABC中,∠ACB为锐角,点D为射线BC上一动点,连接AD,以AD为直角边且在AD的上方作等腰直角三角形ADF,连接CF.(1)若AB=AC,∠BAC=90°①当点D在线段BC上时(与点B不重合),试探究CF与BD的数量关系和位置关系,并说明理由.变式一:②当点D在线段BC的延长线上时,①中的结论是否仍然成立,请在图②中画出相应图形并直接写出你的猜想.变式二:(2)如图③,若AB≠AC,∠BAC≠90°,∠BCA=45°,点D在线段BC上运动,试探究CF 与BC的位置关系,并说明理由.15.(1)如图,已知在△ABC中,AD为中线,求证:AB+AC>2AD;变式:(2)如图,在△ABC中,D为BC的中点,DE⊥DF分别交AB,AC于点E,F.求证:BE+CF>EF.16.(1)问题发现:如图1,△ABC与△CDE均为等腰直角三角形,∠ACB=∠DCE=90°,则线段AE、BD的数量关系为_______,AE、BD所在直线的位置关系为________;变式:(2)深入探究:在(1)的条件下,若点A,E,D在同一直线上,CM为△DCE中DE边上的高,请判断∠ADB的度数及线段CM,AD,BD之间的数量关系,并说明理由.17.在△ABC中,AB=AC,点D是直线BC上一点(不与B、C重合),以AD为一边在AD的右侧作△ADE,使AD=AE,∠DAE=∠BAC,连接CE.(1)如图1,当点D在线段BC上,如果∠BAC=90°,求∠BCE的度数;变式:(2)设∠BAC=α,∠BCE=β.如图2,当点D在线段BC上移动,则α,β之间有怎样的数量关系?请直接写出你的结论.。
初二数学全等三角形证明题专题训练

初二数学全等三角形证明题专题训练1.如图,,,,A F E B 四点共线,AC CE ⊥,BD DF ⊥,AE BF =,AC BD =。
求证:ACF BDE ∆≅∆。
2.如图,在ABC ∆中,BE 是∠ABC 的平分线,AD BE ⊥,垂足为D 。
求证:21C ∠=∠+∠。
3.如图,在ABC ∆中,AB BC =,90ABC ∠=。
F 为AB 延长线上一点,点E 在BC 上,BE BF =,连接,AE EF 和CF 。
求证:AE CF =。
4.如图,AB //CD ,AD //BC ,求证:AB CD =。
5. 如图,,AP CP 分别是ABC ∆外角MAC ∠和NCA ∠的平分线,它们交于点P 。
求证:BP 为MBN ∠的平分线。
6.如图,D 是ABC ∆的边BC 上的点,且CD AB =,ADB BAD ∠=∠,AE 是ABD ∆的中线。
求证:2AC AE =。
7.如图,在ABC ∆中,AB AC >,12∠=∠,P 为AD 上任意一点。
求证:AB AC PB PC ->-。
8.直线CD 经过BCA ∠的顶点C ,CA=CB .E 、F 分别是直线CD 上两点,且BECCFA α∠=∠=∠.(1)若直线CD 经过BCA ∠的内部,且E 、F 在射线CD 上,请解决下面两个问题: ①如图1,若90,90BCA α∠=∠=,则EF BE AF -(填“>”,“<”或“=”号);②如图2,若0180BCA <∠<,若使①中的结论仍然成立,则α∠与BCA ∠ 应满足的关系是 ;(2)如图3,若直线CD 经过BCA ∠的外部,BCA α∠=∠,请探究EF 、与BE 、AF 三条线段的数量关系,并给予证明.9.已知:如图,△ABC 中,∠ABC =45°,CD ⊥AB 于D ,BE 平分∠ABC ,且BE ⊥AC 于E ,与CD 相交于点F ,H 是BC 边的中点,连结DH 与BE 相交于点G 。
最新人教版八年级数学上册全等三角形证明经典50题及答案解析-精品试题.do..

全等三角形证明50题1、已知:AB=4,AC=2,D 是BC 中点,111749AD 是整数,求AD 解:延长AD 到E,使AD=DE ∵D 是BC 中点∴BD=DC 在△ACD 和△BDE 中AD=DE ∠BDE=∠ADC BD=DC ∴△ACD ≌△BDE ∴AC=BE=2 ∵在△ABE 中AB-BE <AE <AB+BE ∵AB=4 即4-2<2AD <4+2 1<AD <3 A D B C ∴AD=2 1. 已知:D 是AB 中点,∠ACB=90°,求证:12CD AB =延长CD 与P ,使D 为CP 中点。
连接AP,BP ∵DP=DC,DA=DB ∴ACBP 为平行四边形又∠ACB=90 ∴平行四边形ACBP 为矩形∴AB=CP=1/2AB 2. 已知:BC=DE ,∠B=∠E ,∠C=∠D ,F 是CD 中点,求证:∠1=∠2 证明:连接BF 和EF A B C D E F 2 1 D A B C ∵ BC=ED,CF=DF,∠BCF=∠EDF ∴ 三角形BCF 全等于三角形EDF(边角边) ∴ BF=EF,∠CBF=∠DEF 连接BE 在三角形BEF 中,BF=EF ∴ ∠EBF=∠BEF 。
∵ ∠ABC=∠AED 。
∴ ∠ABE=∠AEB 。
∴ AB=AE 。
在三角形ABF 和三角形AEF 中AB=AE,BF=EF, ∠ABF=∠ABE+∠EBF=∠AEB+∠BEF=∠AEF ∴ 三角形ABF 和三角形AEF 全等。
∴ ∠BAF=∠EAF (∠1=∠2)。
3. 已知:∠1=∠2,CD=DE ,EF//AB ,求证:EF=AC 过C 作CG ∥EF 交AD 的延长线于点G B A C D F 2 1 E CG∥EF,可得,∠EFD=CGD DE=DC ∠FDE=∠GDC(对顶角)∴△EFD≌△CGD EF=CG ∠CGD=∠EFD 又,EF∥AB ∴,∠EFD=∠1 ∠1=∠2 ∴∠CGD=∠2 ∴△AGC为等腰三角形,AC=CG 又EF=CG ∴EF=AC 4.已知:AD平分∠BAC,AC=AB+BD,求证:∠B=2∠C 证明:延长AB 取点E ,使AE =AC ,连接DE ∵AD 平分∠BAC ∴∠EAD =∠CAD ∵AE =AC ,AD =AD ∴△AED ≌△ACD (SAS )∴∠E =∠C ∵AC =AB+BD ∴AE =AB+BD ∵AE =AB+BE ∴BD =BE ∴∠BDE =∠E ∵∠ABC =∠E+∠BDE ∴∠ABC =2∠E ∴∠ABC =2∠C 5. 已知:AC 平分∠BAD ,CE ⊥AB ,∠B+∠D=180°,求证:AE=AD+BE A 证明:在AE上取F,使EF=EB,连接CF ∵CE⊥AB ∴∠CEB=∠CEF=90°∵EB=EF,CE=CE,∴△CEB≌△CEF ∴∠B=∠CFE ∵∠B+∠D=180°,∠CFE+∠CFA=180°∴∠D=∠CFA ∵AC平分∠BAD ∴∠DAC=∠FAC ∵AC=AC ∴△ADC≌△AFC(SAS)∴AD=AF ∴AE=AF+FE=AD+BE 6. 已知:AB=4,AC=2,D 是BC 中点,AD 是整数,求AD 解:延长AD 到E,使AD=DE ∵D 是BC 中点∴BD=DC 在△ACD 和△BDE 中AD=DE ∠BDE=∠ADC BD=DC ∴△ACD ≌△BDE ∴AC=BE=2 ∵在△ABE 中AB-BE <AE <AB+BE ∵AB=4 即4-2<2AD <4+2 1<AD <3 ∴AD=2 A D B C 7. 已知:D 是AB 中点,∠ACB=90°,求证:12CD AB =解:延长AD 到E,使AD=DE ∵D 是BC 中点∴BD=DC 在△ACD 和△BDE 中AD=DE ∠BDE=∠ADC BD=DC ∴△ACD ≌△BDE ∴AC=BE=2 ∵在△ABE 中AB-BE <AE <AB+BE ∵AB=4 即4-2<2AD <4+2 1<AD <3 ∴AD=2 D A B C 8. 已知:BC=DE ,∠B=∠E ,∠C=∠D ,F 是CD 中点,求证:∠1=∠2 证明:连接BF 和EF 。
(完整word版)八年级全等三角形证明经典50题(含答案).doc

1.已知:AB=4 , AC=2 , D 是BC 中点,AD 是整数,求ADA 解:延长AD 至IJE,使AD=DE・・・D 是BC 中点BD=DC在厶ACD 和厶BDE 中AD=DEZBDE= ZADC BD=DCAA ACD A BDE•*. AC=BE=2・・•在△ ABE 中AB-BE < AE<AB+BE・・・AB=4即 4・2 <2AD < 4+21 < AD < 3・・・AD=2延长CD 与P,使D 为CP 中点。
连接VDP=DC,DA=DBA AC BP 为平行四边形又 Z ACB=90・・・平行四边形ACBP 为矩形AAB=CP=1/2AB 2.已知:D 是AB 中点,Z ACB=90 0,求证:CD [AB 2AAP,BP3.已知:BC=DE , Z B= ZE, Z C= ZD , F 是CD 中点,求证:Z 1= Z2证明:连接BF和EF・・・ BC=ED,CF=DF, Z BCF= Z EDF・・・三角形BCF全等于三角形EDF(边角边)・・・ BF=EF, ZCBF=Z DEF连接BE在三角形BEF中,BF=EF/. Z EBF=Z BEFo・・・ Z ABC= Z AED o・・・ Z ABE= Z AEBo/. AB=AE o在三角形ABF和三角形AEF屮AB=AE,BF=EF,ZABF= Z ABE+ Z EBF= ZAEB+ Z BEF= Z AEF・・・三角形ABF和三角形AEF全等。
・・・ Z BAF= Z EAF(Z 1= Z 2)o4. 己知:Z 1= Z 2 , CD=DE , EF//AB ,求证:EF=AC过C作CG〃EF交AD的延长线于点GCG// EF,可得,Z EFD= CGDDE= DCZFDE= Z GDC (对顶角)AA EFD^A CGDEF= CGZCGD = Z EFD又,EF// AB・・・,Z EFD= Z 1Z1= Z 2・・・Z CGD= Z 2・・・△ AGC为等腰三角形,AC= CG又EF=CG・・・EF= AC5.已知:AD 平分Z BAC, AC=AB+BD ,求证:Z B=2 Z C证明:延长AB取点E,使AE=AC,连接DEVAD 平分Z BACAZ EAD=Z CAD・・・AE=AC, AD = ADA A AED^A ACD ( SAS)AZ E=Z CVAC = AB+BD・・・AE= AB+BD・・・AE= AB+BEABD = BE・・・Z BDE=Z EVZ ABC=Z E+ Z BDEAZ ABC = 2 ZEAZ ABC = 2 ZC6.己知:AC 平分Z BAD , CE丄AB , Z B+ Z D=180 ° ,求证:AE=AD+BE・・・CE丄AB ・・・Z CEB=Z CEF= 90° ・・・EB=EF, CE = CE, AACEB^ACEF ・・・Z B=Z CFEVZ B+Z D= 180 ° , ZCFE+Z CFA= 180 0AZ D = Z CFAVAC 平分Z BAD・・・Z DAC = Z FACVAC = AC・・・△ ADC 竺△ AFC ( SAS)/.AD = AF ・・・AE= AF+ FE= AD + BE解:延长AD至IJE,使AD=DE・・・D是BC中点・・・BD=DC在厶ACD和厶BDE中AD=DEZBDE= Z ADCBD=DC7.已知:AB=4 , AC=2 , D是BC屮点, AD是整数,求ADA 证明:在AE上取F,使EF= EB,连接CFAAACD^ABDE•*. AC=BE=2・・•在△ ABE中AB-BE < AE<AB+BE・・・AB=4即4・2 < 2AD < 4+21 < AD < 3・・・AD=218.已知:D 是AB 中点,Z ACB=90 0,求证:CD -AB2解:延长AD到E,使AD=DE・・・D是BC屮点・・・BD=DC在厶ACD和厶BDE中AD=DEZBDE= Z ADCBD=DCAA ACD A BDE•*. AC=BE=2•・•在A ABE中9.已知:BC=DE , Z B= ZE, Z C= ZD , F 是CD 中点,求证:Z 1= Z2A证明:连接BF和EF。
人教版八年级上学期数学《全等三角形证明》专题练习
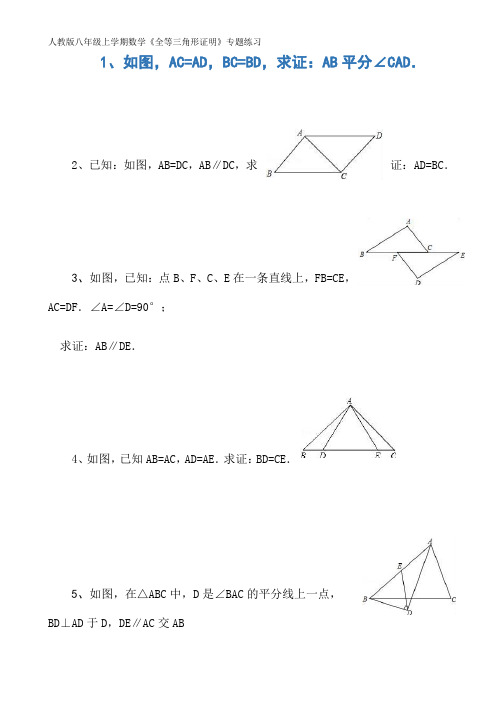
1、如图,AC=AD,BC=BD,求证:AB平分∠CAD.2、已知:如图,AB=DC,AB∥DC,求证:AD=BC.3、如图,已知:点B、F、C、E在一条直线上,FB=CE,AC=DF.∠A=∠D=90°;求证:AB∥DE.4、如图,已知AB=AC,AD=AE.求证:BD=CE.5、如图,在△ABC中,D是∠BAC的平分线上一点,BD⊥AD于D,DE∥AC交AB于E,请说明AE=BE.6、一个平分角的仪器如图所示,其中AB=AD,BC=DC.求证:∠BAC=∠DAC.7、如图:点C是AE的中点,∠A=∠ECD,AB=CD,求证:∠B=∠D.8、如图,BD⊥AC于点D,CE⊥AB于点E,AD=AE.求证:BE=CD.9、如图所示,已知AE⊥AB,AF⊥AC,AE=AB,AF=AC.求证:EC=BF.10、如图所示,已知AD是△ABC的角平分线,DE⊥AB,DF⊥AC,垂足分别为E,F.试说明:AD垂直平分EF.11、已知:如图,点E、F在AD上,且AF=DE,∠B=∠C,AB∥DC.求证:AB=DC.12、已知:如图,CB⊥AD,AE⊥DC,垂足分别B、E,AE、BC相交于点F,且AB=BC.求证:△ABF≌△CBD.13、如图所示,已知AD是△ABC的角平分线,DE⊥AB,DF⊥AC,垂足分别为E,F.试说明:AD垂直平分EF.14、如图,在四边形ABCD中,∠ABC=∠ADC=90°,M、N分别是AC、BD的中点,求证:(1)MD=MB;(2)MN平分∠DMB.15、如图,已知,△ABC和△ADE均为等边三角形,BD、CE交于点F.(1)求证:BD=CE;(2)求锐角∠BFC的度数.16、如图,在△ABC中,AB=AC,点D、E、F分别在BC、AB、AC边上,且BE=CF,BD=CE.(1)求证:△DEF是等腰三角形;(2)当∠A=40°时,求∠DEF的度数;(3)△DEF可能是等腰直角三角形吗?为什么?17、已知:如图,AB∥CD,AB=CD,点B、E、F、D在同一直线上,∠A=∠C.求证:(1)AE=CF;(2)AE∥CF.18、如图:在△ABC中,∠C=90°,AD是∠BAC的平分线,DE⊥AB于E,F在AC上,BD=DF;说明:(1)CF=EB.(2)AB=AF+2EB.19、如图所示,已知AE⊥AB,AF⊥AC,AE=AB,AF=AC.求证:(1)EC=BF;(2)EC⊥BF.20、如图1,将一块等腰直角三角板ABC的直角顶点C置于直线l上,图2是由图1抽象出的几何图形,过A、B两点分别作直线l的垂线,垂足分别为D、E.(1)求证:△ACD≌△CBE;(2)猜想线段AD、BE、DE之间的关系,并说明理由.21、在△ABC中,AB边的垂直平分线l1交BC于D,AC边的垂直平分线l2交BC于E,l1与l2相交于点O.△ADE的周长为6cm.(1)求BC的长;(2)分别连结OA、OB、OC,若△OBC的周长为16cm,求OA的长.22、(1)如图1,∠MAN=90°,射线AE在这个角的内部,点B、C分别在∠MAN 的边AM、AN上,且AB=AC,CF⊥AE于点F,BD⊥AE于点D.求证:△ABD≌△CAF;(2)如图2,点B、C分别在∠MAN的边AM、AN上,点E、F都在∠MAN内部的射线AD上,∠1、∠2分别是△ABE、△CAF的外角.已知AB=AC,且∠1=∠2=∠BAC.求证:△ABE≌△CAF;(3)如图3,在△ABC中,AB=AC,AB>BC.点D在边BC上,CD=2BD,点E、F 在线段AD上,∠1=∠2=∠BAC.若△ABC的面积为15,求△ACF与△BDE的面积之和.23、在△ABC中,∠ACB=90°,AC=BC,直线MN经过点C,且AD⊥MN于D,BE⊥MN 于E.(1)当直线MN绕点C旋转到图1的位置时,求证:①△ADC≌△CEB;②DE=AD+BE;(2)当直线MN绕点C旋转到图2的位置时,AD=5,BE=2,求线段DE的长.24、如图,已知△ABC中,AB=AC=6cm,∠B=∠C,BC=4cm,点D为AB的中点.(1)如果点P在线段BC上以1cm/s的速度由点B向点C运动,同时,点Q在线段CA上由点C向点A运动.①若点Q的运动速度与点P的运动速度相等,经过1秒后,△BPD与△CQP是否全等,请说明理由;②若点Q的运动速度与点P的运动速度不相等,当点Q的运动速度为多少时,能够使△BPD与△CQP全等?(2)若点Q以②中的运动速度从点C出发,点P以原来的运动速度从点B同时出发,都逆时针沿△ABC三边运动,则经过后,点P与点Q第一次在△ABC的边上相遇?(直接写出答案,不必书写解题过程)25、如图,在正方形ABCD中,AB=BC=CD=AD,∠BAD=∠B=∠C=∠D=90°,点E、F分别在正方形ABCD的边DC、BC上,AG⊥EF且 AG=AB,垂足为G,则:(1)△ABF与△AGF全等吗?说明理由;(2)求∠EAF的度数;(3)若AG=4,△AEF的面积是6,求△CEF的面积.26、已知Rt△ABC≌Rt△ADE,其中∠ACB=∠AED=90°.(1)将这两个三角形按图①方式摆放,使点E落在AB上,DE的延长线交BC 于点F.求证:BF+EF=DE;(2)改变△ADE的位置,使DE交BC的延长线于点F(如图②),则(1)中的结论还成立吗?若成立,加以证明;若不成立,写出此时BF、EF与DE之间的等量关系,并说明理由.。
八年级全等三角形简单证明题及解答(5道)

汇报人:XX
目 录
• 题目一:基本的全等三角形证明 • 题目二:利用角平分线性质证明 • 题目三:通过边边边条件证明 • 题目四:结合中线性质进行证明 • 题目五:综合应用多种性质证明 • 总结与拓展
01
题目一:基本的全等三角形证明
题目描述
• 已知三角形$ABC$和三角形$DEF$,其中$AB = DE$,$AC = DF$,$\angle BAC = \angle EDF$。求证:$\triangle ABC \cong \triangle DEF$。
由第二步可知,△BDE∽△CFD。
详细解答
4. 第四步,根据相似三角形的性质,对应边成比例,所以BD/CF=DE/DF。
5. 第五步,因为BD=AD(已知),所以AD/CF=DE/DF。又因为AE/EC=DE/EF(已知), 所以AD/CF=AE/EC。
6. 第六步,交叉相乘得AD*EC=AE*CF,即AE/AD=EC/CF。又因为∠A=∠ACF(对顶角相 等),所以△ADE∽△ACF。
第三步,根据相似三 角形的性质,有 AB/AC = BD/DC。
综上,我们证明了 AB/AC = BD/DC。
03
题目三:通过边边边条件证明
题目描述
已知
△ABC和△DEF中,AB = DE,BC = EF,AC = DF。
求证
△ABC ≌ △DEF。
题目描述
【分析】
本题主要考察全等三角形的判定方法——边边边条件。根据已知条件,我们可以 直接应用边边边定理来证明两个三角形全等。
题目描述
01
【解答】
02
证明
03
04
∵ 在△ABC和△DEF中,AB = DE,BC = EF,AC = DF(已
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
全等三角形的判定
令狐采学
班级: 姓名:
1.已知AD 是⊿ABC 的中线,BE⊥AD,CF⊥AD,求证2.已知AC=BD ,AE=CF ,BE=DF ,求证AE∥CF 3.已知AB=CD ,BE=DF ,AE=CF ,求证AB∥CD
4.已知在四边形ABCD 中,AB=CD ,AD=CB ,求证5.已知∠BAC=∠DAE,∠1=∠2,BD=CE 6.已知CD∥AB,DF∥EB,DF=EB ,求证AF=CE
7.已知BE=CF ,AB=CD ,∠B=∠C,求证AF=DE 8.已知AD=CB , ∠A=∠C,AE=CF ,求证EB∥DF 9.已知M 是AB
的中点,∠1=∠2,MC=MD ,求证∠C=∠D。
10.已知,AE=DF ,BF=CE ,AE∥DF,求证AB=CD 。
11.已知∠1=∠2,∠3=∠4,求证AC=AD
12.已知∠E=∠F,∠1=∠2,AB=CD ,求证AE=DF
13.已知ED⊥AB,EF⊥BC,BD=EF ,求证BM=ME 。
14.在⊿ABC 中,高AD 与BE 相交于点H ,且AD=BD ,求证⊿BHD≌⊿ACD。
15.已知∠A=∠D,A C∥FD,AC=FD ,求证AB∥DE。
16.已知AC=AB ,AE=AD ,∠1=∠2,求证∠3=∠4。
A
C
D B 1
2 3 4
A B C D E
F
1 2
A
B C
E
H
D
A C
M
E F B
D
A B
C
E F D
A D
E
1
2
B A D
E
B C 1 2
A D
C
E
F B
A
C
D B
E F
B
A D F E
C M
A
B
C D 1 2 D
C
F E A B
17.已知EF∥BC ,AF=CD ,AB⊥BC ,DE⊥EF ,求证⊿ABC≌⊿DEF。
18.已知AD=AE ,∠B=∠C,求证AC=AB 。
19.已知AD⊥BC,BD=CD ,求证AB=AC
20.已知∠1=∠2,BC=AD 21.已知AB=AC , ∠1=∠2,AD=AE 22.已知BE∥DF,AD∥BC,AE=CF 23.已知
AD=AE ,BD=CE
24.已知AB=AC ,AD=AE ,∠1=∠2,求证CE=BD 。
25.已知CE⊥AB,DF⊥AB,AC∥DB,AC=BD ,求证CE=DF 26.如图,AD=BC ,AE=BE ,求证∠C=∠D。
27.已知∠1=∠2,AC=BD ,E ,F ,A ,B 在同一直线上,求证∠3=∠4
28.已知DO⊥BC,OC=OA ,OB=OD ,求证CD=AB
29.已知CE=DF ,AE=BF ,AE⊥AD ,FD⊥AD ,求证
⊿EAB≌⊿FDC
30.已知AB 与CD 相交于点E ,EA=EC ,ED=EB ,求证⊿AED≌⊿CEB
31.已知AB=AC ,D ,E 分别是AB ,AC 的中点。
求证BE=CD 。
32.已知DE=FE ,FC∥AB,求证AE=CE 。
C A E B F D
A
C B C
D E 1 2
A C
D
B
E F G 1
2 A C D E
B A E
D
C B
O C
D
A E F
B 2
1 3
4
A
C B
D
E
C A
E
B
F
D A D B
E
F C A
C
B
E D
33.已知CE⊥AB ,DF⊥AB ,CE=DF ,AE=BF ,求证⊿CEB≌⊿DFA。
34.如图,D ,E ,F ,B 在一条直线上,AB=CD ,∠B=∠D,BF=DE ,求证(1)AE=CF(2)AE∥CF。
35.已知,点C 是AB 的中点,CD∥BE,且CD=BE ,求证∠D=∠E。
36.已知,E 、F 是AB 上的两点,AE=BF ,又AC∥DB,AC=DB ,求证CF=DE 。
37.已知,AC⊥CE ,AC=CE , ∠ABC=∠DEC=900,求证BD=AB+ED 。
38.⊿ABC≌⊿A′B′C′,AD 与A′D′分别是中线,求证AD=A′D′。
39. 已知:如图 , E, B, F, C 四点在同一直线上, ∠A=∠D=90° , BE=FC, AB=DF.求证:∠E=∠C
40.已知:如图 , DN=EM , 且DN AB 于D , EM AC 于E , BM=CN .求证:∠B=∠C.
41.已知:如图 , AE , FC 都垂直于BD , 垂足为E 、F , AD=BC , BE=DF .求证:OA=OC.
42. 已知:如图 , AB=CD , D 、B 到AC 的距离DE=BF .求证:AB∥CD.
B A
C
D
E F
C D
E F A B
A
B
C
D
E A
B
C
D
A ′
B ′
C ′
D ′
D A E
C
B 1
2
B A D F
E
C。
