控制图

合集下载

控制图控制图

控制图1、概念控制图又叫做管制图，是用于分析和判断工序是否处于稳定状态所使用的带有控制界限的一种工序管理图。

控制图是一种对过程质量加以测定、记录从而进行控制管理的一种用科学方法设计的图，图上有中心线（CL ）、上控制线（UCL ）、下控制线（LCL ），并有按时间顺序抽取的样本计量值的描点序列。

控制图主要用于：过程分析及过程控制。

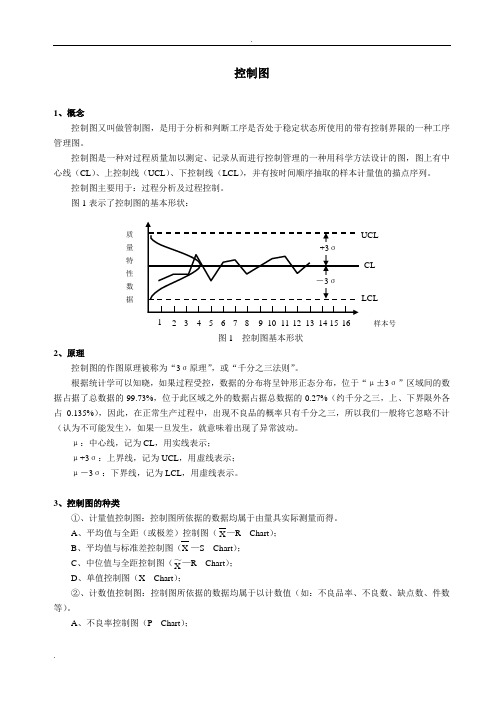
图1表示了控制图的基本形状：2、原理控制图的作图原理被称为“3σ原理”，或“千分之三法则”。

根据统计学可以知晓，如果过程受控，数据的分布将呈钟形正态分布，位于“μ±3σ”区域间的数据占据了总数据的99.73%，位于此区域之外的数据占据总数据的0.27%（约千分之三，上、下界限外各占0.135%），因此，在正常生产过程中，出现不良品的概率只有千分之三，所以我们一般将它忽略不计（认为不可能发生），如果一旦发生，就意味着出现了异常波动。

μ：中心线，记为CL ，用实线表示； μ+3σ：上界线，记为UCL ，用虚线表示； μ－3σ：下界线，记为LCL ，用虚线表示。

3、控制图的种类①、计量值控制图：控制图所依据的数据均属于由量具实际测量而得。

A R Chart ）； B S Chart ）；C Chart ）；D 、单值控制图（X Chart ）；②、计数值控制图：控制图所依据的数据均属于以计数值（如：不良品率、不良数、缺点数、件数等）。

A 、不良率控制图（P Chart ）；质量特性数据B、不良数控制图（Pn Chart）；C、缺点数控制图（C Chart）；D、单位缺点数控制图（U Chart）。

4、控制图的用途根据控制图在实际生产过程中的运用，可以将其分为分析用控制图、控制用控制图：①、分析用控制图（先有数据，后有控制界限）：用于制程品质分析用，如：决定方针、制程解析、制程能力研究、制程管制之准备。

分析用控制图的主要目的是：（1）分析生产过程是否处于稳态。

控制图

176 175 173 170 169 173 7
171 172 173 174 175 173 4
172 173 174 176 175 174 4
174 173 170 171 172 172 4
176 174 172 169 170 172 7
173 172 170 171 173 172 3
2-1
2-2 计算控制限计算控制限是为了显示仅存在变差的普通原因时子组的均值和极差的变化和范围。值和极差的变化和范围。控制限是由子组的样本容量以及反映在极差上的子组内的变差的量来决定的。映在极差上的子组内的变差的量来决定的。计算公式：计算公式： UCLR=D4 UCLx=X+ A2R UCLR=D4R LCLx=XLCLR=D3 LCLx=X- A2R LCLR=D3R
控制图（管制图）控制图（管制图）
什么是控制图
控制图是对过程质量加以测定、控制图是对过程质量加以测定、记录从而进行控制管理的一种用科学方法设计的图。制管理的一种用科学方法设计的图。图上有中心线 (CL)、上控制界限(UCL)和下控制界限(LCL) (UCL)和下控制界限(LCL)， (CL)、上控制界限(UCL)和下控制界限(LCL)，并有按时间顺序抽取的样本统计量数值的描点序列，时间顺序抽取的样本统计量数值的描点序列，参见控制图示例图。制图示例图。
的产品进行监测的子组频率可以是每班2 的产品进行监测的子组频率可以是每班2次，或一小时一次等。或一小时一次等。子组数：子组越多，变差越有机会出现。一般为25 25组 1-1-3 子组数：子组越多，变差越有机会出现。一般为25组，首次使用管制图选用35 组数据，以便调整。制图选用35 组数据，以便调整。见下图） 1-2 建立控制图及记录原始数据（见下图）

第六章控制图、过程能力和直方图

在工序控制中需要了解的三个方面，都能在控制图上得到。 (1) 在连续的生产监控中，有无变化的征兆； (2) 有无急剧的变化； (3) 有无越出控制范围的异常值。
－－控制图的作用：
在质量诊断方面，可以用来度量过程的稳定性，即过程是否处于统计控制状态；在质量控制方面，可以用来确定什么时候需要对过程加以调整，而什么时候则需使过程保持相应的稳定状态；在质量改进方面，可以用来确认某过程是否得到了改进。
1.864
1.816
1.777
E2
2.660
1.772
1.457
1.290
1.134
1.109
1.054
1.010
0.975
m3A2
1.880
1.187
0.796
0.691
0.549
0.509
0.430
0.410
0.360
D3
－
－
－
－
－
0.076
0.136
0.184
0.223
d2
1.128
1.693
P
－
n －
（1－）
Pn
－
Pn
－
3
u
－
3
n
u
－
＋
u
－
3
n
u -
c
－
3
c —
c
－
3
c ＋
控制系数选用表
n
2
3
4
5
6
7
8
9
10
A2
1.880
1.023
0.729
0.577
0.483

什么是控制图

什么是控制图控制图是根据假设检验的原理构造一种图，用于监测生产过程是否处于控制状态。

它是统计质量管理的一种重要手段和工具。

在生产过程中，产品质量由于受随机因素和系统因素的影响而产生变差；前者由大量微小的偶然因素叠加而成，后者则是由可辨识的、作用明显的原因所引起，经采取适当措施可以发现和排除。

当一生产过程仅受随机因素的影响，从而产品的质量特征的平均值和变差都基本保持稳定时,称之为处于控制状态。

此时,产品的质量特征是服从确定概率分布的随机变量，它的分布(或其中的未知参数)可依据较长时期在稳定状态下取得的观测数据用统计方法进行估计。

分布确定以后，质量特征的数学模型随之确定。

为检验其后的生产过程是否也处于控制状态，就需要检验上述质量特征是否符合这种数学模型。

为此，每隔一定时间，在生产线上抽取一个大小固定的样本，计算其质量特征，若其数值符合这种数学模型，就认为生产过程正常，否则，就认为生产中出现某种系统性变化，或者说过程失去控制。

这时，就需要考虑采取包括停产检查在内的各种措施，以期查明原因并将其排除，以恢复正常生产，不使失控状态延续而发展下去。

通常应用最广的控制图是W.A.休哈特在1925年提出的，一般称之为休哈特控制图。

它的基本结构是在直角坐标系中画三条平行于横轴的直线，中间一条实线为中线，上、下两条虚线分别为上、下控制界限。

横轴表示按一定时间间隔抽取样本的次序,纵轴表示根据样本计算的、表达某种质量特征的统计量的数值，由相继取得的样本算出的结果，在图上标为一连串的点子，它们可以用线段连接起来。

除了上述的休哈特控制图外，近年来出现了某些新形式的控制图,其基本思想与休哈特图相似,但作图根据的原理则各有不同。

其中较重要的是累积和控制图，这种控制图的对象，即标在图上的每一点，是在该点以前所有样本统计量的总和。

累积和图的提出，是考虑到在休哈特控制图中，判定过程是否处于控制状态全靠最新的一个或几个样本点，而忽略了较早的样本值中所包含的信息。

第二节-控制图原理

第二节-控制图原理什么是控制图控制图是一种用于监测和控制工程过程的可视化工具。

通常用于监测质量控制过程的统计数据，以便及时识别潜在问题并采取适当措施。

控制图也可以用于监测设备可靠性、生产进度等方面。

控制图的分类控制图可分为过程控制图和直方图。

过程控制图过程控制图是一种监测过程稳定性并指导改进的可视化工具。

它可以帮助我们在过程中及时发现不正常现象，以便采取适当措施，确保过程在稳定状态下运行。

过程控制图通常包括三种类型：一种是X-控制图，一种是S-控制图，另一种是R-控制图。

1.X控制图X控制图是一种数据类型控制图，用于监测均值是否稳定。

X控制图在原理上是比较简单的，是通过标准上下限范围内连续数据点的变化情况来判断过程是否稳定的。

2.S控制图S控制图用于监测数据分布的散布状况，通过这个散布情况来判断过程的稳定性。

如果散布过于广泛，则表明过程不稳定。

3.R控制图R控制图是一种可视的数据类型控制图，用于监测组内差异的大小和组间差异的大小。

如果组内差异很大，则表明过程不稳定。

直方图直方图是一种用于描述数据分布情况的图表。

它将数据进行分段，然后把每个分段的数据条数用柱状图表示出来，以便看出数据的分布规律。

直方图通常可以用于评估数据的分布形状，以便在研究中进行比较，并检测极端值/离群值。

如何制作控制图制作控制图的步骤如下:1.收集数据并进行分析首先我们需要收集数据，可以使用过程采样或过程监控系统，或手工记录过程数据。

然后对数据进行分析，计算出均值、标准差、极差等基本统计量。

2.设定控制限根据数据的均值、标准差和其他基本统计量，我们可以计算出控制限。

控制限是用来指导控制图的范围。

一般我们会选用3倍标准差作为上下控制限，即所谓的3σ控制图。

3.绘制控制图一旦确定了控制限，我们就可以开始绘制控制图了。

绘制控制图可以手动绘制，也可以使用计算机软件自动生成。

控制图的应用控制图的应用非常广泛，特别是在工业制造中。

经常使用控制图来监控生产过程，以及检测过程中的变化。

控制图PPT

03 控制图的结构
04 控制图的功能
05 控制图的作用
二、什么是控制图？
二、什么是控制图？
二、什么是控制图？
• 2.3控制图结构
中间一条实线为中心线；上、下两条虚线分别为上控制界限和下控制界限；并有按时间先后排列的统计数值的描点序列。
控制界限不能驾驭过程，仅仅反应当前过程的状态。
2.92
2.65
2.82
151107
2.83
2.88
2.78
2.73
六、控制图的制作示例
x
xR
计量控制图常数表
xR
x
当n=4时，A2=0.729；D4=2.282；D3=0
R
R
R
R
控制限 UCL CL LCL
极差UCL 极差CL 极差LCL
计算值 2.818 2.541 2.265 0.865 0.379
7
四、控制图的判稳与判异
①1个点落在A区外
②连续9点落在中心线同一侧
③连续6点递增或递减
④连续14点中相邻点交替上下
⑤连续3点中有2点落在中心线同一侧的B区以外
⑥连续5点中有4点落在中心线同一侧的C区以外
⑦连续15点落在中心线两侧C区内
⑧连续8点落在中心线两侧且无一在C区内
四、控制图的判稳与判异
二、什么是控制图？
二、什么是控制图？
三、控制图的分类
Contents
01 按数值质量特性分类
02 按控制图用途分类
三、控制图的分类
三、控制图的分类
x x ~x
三、控制图的分类
• 3.2按控制图的用途分类：
分析用控制图
控制用控制图

控制图(control charts)

控制图(control charts)又名：统计过程控制( statistical process control)方法演变：EQ \o(\s\up5(－),\s\do2(x))计量值控制图：⎺X－R控制图（又名均值极差控制图），⎺X－s控制图，单值控制图（又名X 控制图，X-R控制图，IX-MR控制图，XmR控制图，移动极差控制图），移动均值-移动极差控制图（又名MA-MR控制图），目标偏差控制图（又名差异控制图、偏差控制图、名义值偏差控制图），CUSUM（又名累计和控制图），EWMA（又名指数加权移动平均控制图），多元控制图（又名Hotelling T2控制图）。

计数值控制图：p控制图（又名不良品率控制图），np控制图，c控制图（又名缺陷数控制图），u控制图。

两种数据都适用的控制图：短期过程控制图（又名稳定控制图或者Z控制图），组控制图（又名多属性值控制图）。

概述控制图是一种对过程变异进行分析和控制的图形工具。

数据按时间顺序绘制在图上，控制图一般有一条代表均值的中心线，一条上控制限位于中心线上方，一条下控制限位于中心线下方，这些线是根据过程数据确定的。

通过当前数据和由历史数据计算所得的控制限的比较，我们可以判定当前过程变异是稳定的（受控制）还是不稳定的（不受控制，受到某个特定因素的干扰）。

控制图分为很多种，不同的过程、不同的数据，我们采用不同的控制图。

计量值数据的控制图经常是成对应用，其中常绘制在上方的一张控制图监测均值，或者说过程数据的分布中心，而绘制在下方的一张控制图监测极差，或者说分布的波动程度。

如果借助于练习打靶的例子来说明，那么均值就是靶子上射击集中的地方，极差是射击点的离散程度。

计量值数据要成对使用控制图，计数值数据则通常只使用一张控制图就足够了。

适用场合·当你希望控制当前过程，问题出现时能察觉并能对其采取补救措施时；·当你希望对过程输出的变化范围进行预测时：·当你判断一个过程是否稳定（处于统计受控状态）时；·当你分析过程变异来源是随机性（偶然事件）还是非随机性（过程本身固有）时；·当你决定怎样完成一个质量改进项目时——防止特殊问题的出现，或对过程进行基础性的改变。

控制图(control charts)

计数值控制图：p控制图（又名不良品率控制图），np控制图，c控制图（又名缺陷数控制图），u控制图。

两种数据都适用的控制图：短期过程控制图（又名稳定控制图或者Z控制图），组控制图（又名多属性值控制图）。

概述控制图是一种对过程变异进行分析和控制的图形工具。

控制图分为很多种，不同的过程、不同的数据，我们采用不同的控制图。

如果借助于练习打靶的例子来说明，那么均值就是靶子上射击集中的地方，极差是射击点的离散程度。

计量值数据要成对使用控制图，计数值数据则通常只使用一张控制图就足够了。

控制图又称管理图

控制上限
··········
1 2 3 4 5 6 7 8 9 10 11 12
中心线
控制下限
T
§10.3.6 工程项目质量控制方法(续34)
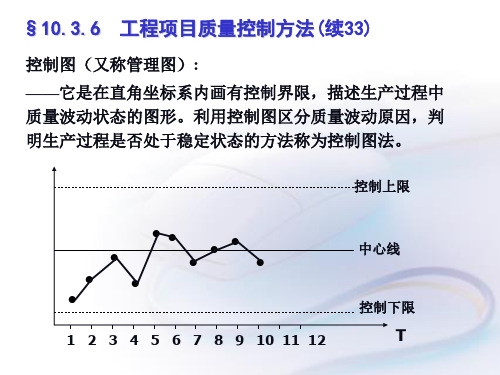
控制图的用途： 1、过程分析——分析生产过程是否稳定。 2、过程控制——控制生产过程质量状态。其原理：
衡量生产过程是否稳定，只需观察产品的分布情况，即：分布中心的位置μ和分布的离散程度σ。
§10.3.6 工程项目质量控制方法(续35)
当控制图同时满足以下两个条件：一是点子几乎全部落在控制界限之内；二是控制界限内的点子排列没有缺陷。我们就可以认为生产过程基本上处于稳定状态。如果点子的分布不满足其中任何一条，都应判断生产过程为异常。 1、点子几乎全部落在控制界线内，是指应符合下述三个要求： 1)连续25点以上处于控制界限内； 2)连续35点中仅有1点超出控制界限； 3)连续100点中不多于2点超出控制界限。
§10.3.6 工程项目质量控制方法(续39)
这里的异常现象是指点子排列出现了链多次同侧趋势或倾向周期性变动变动接近控制界限等பைடு நூலகம்况
§10.3.6 工程项目质量控制方法(续33)
控制图（又称管理图）: ——它是在直角坐标系内画有控制界限，描述生产过程中质量波动状态的图形。利用控制图区分质量波动原因，判明生产过程是否处于稳定状态的方法称为控制图法。
§10.3.6 工程项目质量控制方法(续36)
2、点子排列没有缺陷，是指点子的排列是随机的，而没有出现异常现象。这里的异常现象是指点子排列出现了“链”、“多次同侧”、“趋势或倾向”、“周期性变动”、“接近控制界限”等情况。 1)链:是指点子连续出现在中心线一侧的现象。出现五点链，应注意生产过程发展状况。出现六点链，应开始调查原因：出现七点链，应判定工序异常，需采取处理措施，如图7—12(a)所示。

控制图的原理作用应用范围

控制图的原理、作用及应用范围1. 控制图的原理控制图是一种用于分析和监测过程稳定性的统计工具，它基于统计学原理和概念，并结合实际数据将过程的表现可视化呈现出来。

控制图的原理主要包括以下几点： - 随机性原理：过程中的变化是由随机因素引起的，控制图通过测量样本数据并计算统计量，与过程的预期稳定性进行对比，从而判断变异是否超出预期范围。

- 稳态原理：在一个稳定的过程中，所测量的样本数据会围绕着一个中心值进行随机波动。

通过指定上下控制限，控制图可以帮助识别超出正常变异范围的异常情况。

- 规范化原理：控制图将过程数据标准化为无量纲形式，这样可以直观地比较不同过程的稳定性和性能。

2. 控制图的作用控制图在质量管理和过程改进中起到了重要的作用，主要体现在以下几个方面：- 监测过程稳定性：通过控制图的使用，可以对过程的稳定性进行实时监测。

当过程的变异超出控制限时，可以及时采取相应的纠正措施，确保过程能够持续稳定地运行。

- 识别特殊因子：控制图能够帮助识别过程中的特殊因子，如异常事件、材料变化等。

通过对控制图的分析，我们可以及时发现潜在问题并进行解决，以提高过程的品质和效率。

- 指导决策：控制图提供了过程数据的可视化展示，有助于决策者快速了解过程的状况并作出相应的决策。

例如，当控制图显示过程稳定时，可以进一步优化操作流程；当控制图显示过程异常时，可以立即采取措施进行调整。

3. 控制图的应用范围控制图可以应用于各种不同类型的过程，尤其在生产制造和服务行业中具有广泛的应用范围。

以下是一些常见的应用领域： - 制造业：控制图可以用于监测生产线上的产品质量，帮助找出生产过程中的异常情况，并及时调整以提高产品质量和生产效率。

- 服务业：控制图可以用于监测服务过程的性能指标，如平均等待时间、客户满意度等，帮助提高服务质量和客户体验。

- 医疗领域：控制图可以应用于医疗过程的监测和改进，如手术时间、治疗效果等，有助于提高医疗质量和安全性。

控制图

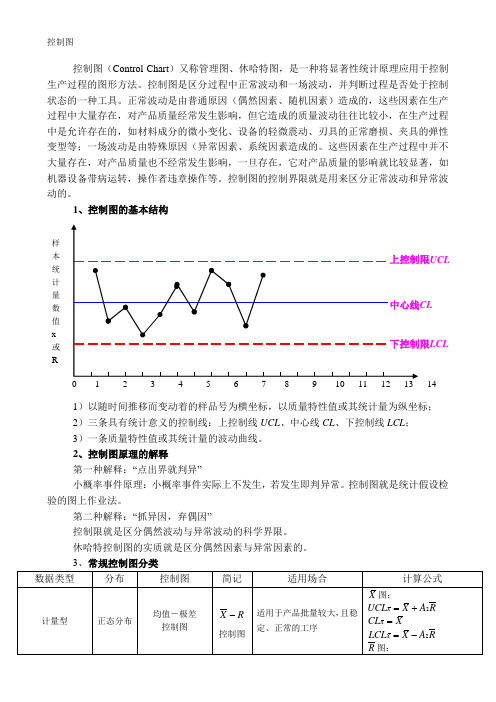
控制图控制图（Control Chart ）又称管理图、休哈特图，是一种将显著性统计原理应用于控制生产过程的图形方法。

控制图是区分过程中正常波动和一场波动，并判断过程是否处于控制状态的一种工具。

正常波动是由普通原因（偶然因素、随机因素）造成的，这些因素在生产过程中大量存在，对产品质量经常发生影响，但它造成的质量波动往往比较小，在生产过程中是允许存在的，如材料成分的微小变化、设备的轻微震动、刃具的正常磨损、夹具的弹性变型等；一场波动是由特殊原因（异常因素、系统因素造成的。

这些因素在生产过程中并不大量存在，对产品质量也不经常发生影响，一旦存在，它对产品质量的影响就比较显著，如机器设备带病运转，操作者违章操作等。

控制图的控制界限就是用来区分正常波动和异常波动的。

1、控制图的基本结构1）以随时间推移而变动着的样品号为横坐标，以质量特性值或其统计量为纵坐标； 2）三条具有统计意义的控制线：上控制线UCL 、中心线CL 、下控制线LCL ； 3）一条质量特性值或其统计量的波动曲线。

2、控制图原理的解释第一种解释：“点出界就判异”小概率事件原理：小概率事件实际上不发生，若发生即判异常。

控制图就是统计假设检验的图上作业法。

第二种解释：“抓异因，弃偶因”控制限就是区分偶然波动与异常波动的科学界限。

休哈特控制图的实质就是区分偶然因素与异常因素的。

UCLLCL样本统计量数值x 或R14 15 16 17 18按用途分类1）分析用控制图——用于质量和过程分析，研究工序或设备状态；或者确定某一“未知的”工序是否处于控制状态；2）控制用控制图——用于实际的生产质量控制，可及时的发现生产异常情况；或者确定某一“已知的”工序是否处于控制状态。

4、R X -图的绘制1）确定控制对象（统计量）一般应选择技术上最重要的、能以数字表示的、容易测定并对过程易采取措施的、大家理解并同意的关键质量特性进行控制。

2）选择控制图对于计量数据而言，R X -控制图是最常用最基本的。

控制图(Control chart)

Page-4
Page~4
一.管制图的概念:
2.管制图的定义(B):
基本上管制图功能有三:
1)决定制造工程所可能达到之目标或标准; 2)被用作为达到目标之工具; 3)可藉此判定是否已达到目标.
化专业为执行，使执行获收益
Page-5
Page~5
一.管制图的概念:
3.管制图的种类(A)
1)计量值管制图: 制作管制图所依据之数据,均属于由量具实际量测
Page-35
Page~35
三.管制图的看法:
2. 非管制状态的判断(C):
+ 3 b
c
a Ucl
+ 2
e
+1
d
CL
仅以单边管制界限(+3σ)示例
化专业为执行，使执行获收益
Page-36
Page~36
三.管制图的看法:
化专业为执行，使执行获收益
Page-2
Page~2
一.管制图的概念:
1.管制图的历史(B): 3)美国政府于二次大战期间(1941~1942),制定了三种强制性之战时规格,做为SQC的主要内涵;可以说美国能获得二次世界大战之胜利,SQC之贡献极大; 4)后续英国、日本、台湾等都将统计品质管制引进工厂生产过程中实施.
化专业为执行，使执行获收益
Page-26
Page~26
二.管制图的作法:
4.绘制管制图注意事项:
b. 双边规格 vs 单边规格(2/3): ※ 那么单边规格的产品特性如何使用管制图呢?在产品规格或客户可接受的范围内可适当实施以下的方法,将其转变为『双边对称』的规格,而后再使用管制图;
化专业为执行，使执行获收益

控制图介绍PPT

一般原因:由于随机的,偶然的波动所引起的变化; 异常原因:由于异常的,超出预想的波动所引起的变化.
控制图形式
控制图的基本格式
数据点
纵坐标
控制上限UCL
中心线
控制下限LCL 横坐标
4
控制图原理
5
控制图原理
从直方图看控制图
6
控制图原理
从直方图看控制图
7
控制图原理
控制界限的确定
1、两类错误和风险：控制图就是看点子是否越出控制界限或是否存在排列缺陷来判断过程是正常还是出现异常. 既然是判断,就有判断正确和判断错误的问题,会出现四种情况：
GB6.1 控制图
控制图概述
控制图又叫管理图,是用于区分由异常原因（系统原因）引起的波动或是由过程固有的随机原因引起的波动的一种工具方法;
主要用于对过程进行管控,以监控并保持过程的稳定运作;
控制图是对过程进行动态控制的工具; 是建立在数理统计学的基础上，运用有效数据建立控制界线。由美国贝尔电话公司休哈特工程师提出，他把统计学中的“发现异常”作为控制生产过程的一种工具。因此，“发现异常”就成为控制图的基础。这里所说的“异常”是指很少发生的事情发生了，也就是说“出现了小概率事件”。
±2σ
95.45%
4.55%
±3σ
99.73%
0.27%
±4σ 99.994%
0.006%
±5σ 99.99994% 0.00006%
9
控制图原理
3、控制界限的合理设置经过统计学家的统计大致在±3σ处，两种错误的总经济损失为最小。因此，以 ±3σ作为控制界限就被定了下来。也就是：上控制界限：UCL=CL+ 3σ 下控制界限：LCL=CL - 3σ

控制图的基本知识介绍

控制图的基本知识介绍一、控制图的定义：1、控制图是用来表示一个过程特性的图象，图上标有根据此特性收集到的一些统计数据，和一条中心线及一条或两条控制线（或者说是由折线图及三条控制线所构成）。

2、分析和监控过程的工具，它有两个用途：一是用来判定一个过程是否一直受统计控制；二是帮助过程保持受控状态。

3、控制图是由美国贝尔试验室休哈特博士（Walter）在二十世纪二十年代发明，从此，美国及世界上其它国家广泛运用，特别是在日本得到了发展。

4、控制图是分类：计量型和计数型：✧计量型控制图是指所采用的数据是定量的数据，可直接测量并用来分析；✧计数型控制图指所用数据是可以用来记录和分析的定性数据，不可测量，通常以不合格或不合格的形式收集。

5、使用控制图所需了解的几个术语：1)过程：共同工作以产生输出的供方、生产者、人、设备、输入材料、方法和环境以及使用输出的顾客之集合。

2)变差：没有两件产品或特性是完全相同的，亦即过程的单个输出之间存在不可避免的差别，这种差别就称之谓变差；它分为两类：一类是普通原因引起的变差，即固有变差，用节来估计。

3)普通原因指的是造成随着时间的推移具有稳定的且可重复的分布过程中的许多变差的原因。

4)特殊原因指是造成不是始终作用于过程的变差，即当它们出现时将造成（整个）过程的分布改变。

5)受控：当过程仅存在普通原因引起的变差且不改变时，普通原因表现为一个稳定系统的偶然原因，过程的输出是可预测的，我们称之为“处于统计控制”、或有时简称为“受控”。

二、使用控制图：1、使用控制图来改进过程是一个重复的程序，多次重复收集、控制及分析几个基本步骤组成；1)按计划收集数据；2)利用数据可计算控制限；3)当过程受控时，控制限可用来解释过程能力；4)为了使过程在受控和能力的基础上得以改进，就必须识别变差的普通及特殊原因，并据此加以改进；5)当所有的特殊原因被消除后，过程在统计控制状态下运行，可继续使用控制图作为监控工具，也可计算过程能力。

控制图

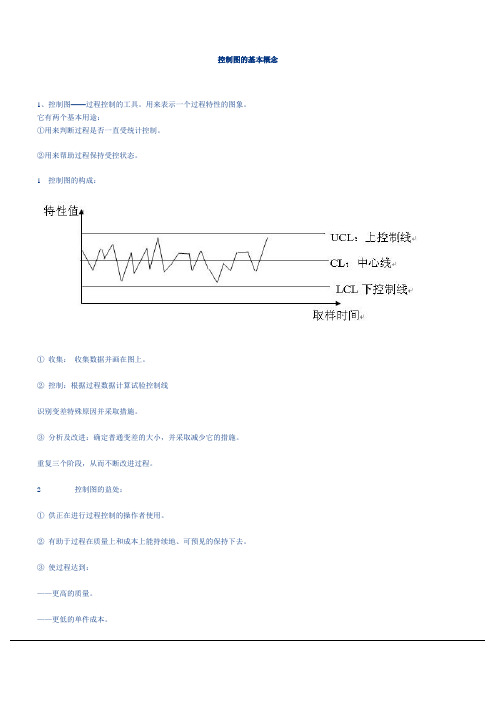
控制图的基本概念1、控制图——过程控制的工具。

用来表示一个过程特性的图象。

它有两个基本用途：①用来判断过程是否一直受统计控制。

②用来帮助过程保持受控状态。

1 控制图的构成：①收集：收集数据并画在图上。

②控制：根据过程数据计算试验控制线识别变差特殊原因并采取措施。

③分析及改进：确定普通变差的大小，并采取减少它的措施。

重复三个阶段，从而不断改进过程。

2 控制图的益处：①供正在进行过程控制的操作者使用。

②有助于过程在质量上和成本上能持续地、可预见的保持下去。

③使过程达到：——更高的质量。

——更低的单件成本。

——更高的有效能力。

④为讨论过程的性能提供共同的语言。

⑤区分变差的特殊原因和普通原因，作为采取局部措施或对系统采取措施的指南。

常用的控制图相关公式及表格SPC控制图应用详细介绍2.1什么是控制图控制图由正态分布演变而来。

正态分布可用两个参数即均值μ和标准差σ来决定。

正态分布有一个结论对质量管理很有用，即无论均值μ和标准差σ取何值，产品质量特性值落在μ±3σ之间的概率为99.73%，落在μ±3σ之外的概率为100%-99.73%= 0.27%，而超过一侧，即大于μ+3σ或小于μ-3σ的概率为0.27%/2=0.135%≈1‰,休哈特就根据这一事实提出了控制图。

由于上下的数值大小不合常规，再把分布图上下翻转180°，这样就得到一个单值控制图，称μ+3σ为上控制限，记为UCL，称μ为中心线，记为CL，称μ-3σ为下控制限，记为LCL,这三者统称为控制线。

规定中心线用实线绘制，上下控制限用虚线绘制。

综合上述，控制图是对过程质量数据测定、记录从而进行质量管理的一种用科学方法设计的图。

图上有中心线(CL)、上控制限(UCL)和下控制限(LCL)，并有按时间顺序抽取的样本统计量数值的描点序列。

2.2质量数据与控制图2.2.1计量型数所确定的控制对象即质量指标应能够定量。

所控制的过程必须具有重复性,即表现出统计规律性。

什么是控制图

控制图探究工作过程的变差什么是控制图控制图是通过分析某一工作过程的变差及其来源，判断此过程是否处于稳定状态，从而控制并改进某一时期工作表现的一种图形工具。

控制图的作用➢集中探询工作过程变差和变差来源；➢持续控制工作过程的质量；➢为过程质量改进提供依据。

怎么做1.选择工作过程控制图以前只应用于生产项目，用来控制产品的质量；在也用于研发项目、投资项目和服务项目等。

2.确定样本调查范围、规模、频率和方法A 选择样本时要综合考虑信息收集规模、时间和成本，一般需要收集25组左右数据。

具体可参考下面的树形图；B 尽可能获得同质本样，如同一批产品、同类工人等；C 样本调查的频率由能从数据中辨别出数据分布模式来确定。

可以是每班次、每天、每月或每年调查一次；D 样本必须随机抽取，抽样过程应按照工作的真实程序进行。

3.收集数据提示：按照工作过程真实进展收集样本数据，以出现的任何异常情况都要如实记录。

可使用检查表作为收集数据的工具。

4.选择控制图类型参照下面的树状图选择需要的控制图：见下页控制图—图15.计算“中心线”和控制极限A 如果是计量值，使用计量值表的“中心线”和“控制极限”公式；B 如果是计数值，使用计数值表的“中心线”和“控制极限”公式；C 如果是计量值控制图的下限(LCL)是负数，直接将它写为0；D 计数值表中的常数请查询常数表。

计量值表图详见书第149页。

(表一、表二)6.绘制控制图A 画出工作过程平均数，用实线“－”表示。

B 画出控制上限和控制下限，用虚线“------”表示。

C 对于计量值控制图，只画一个图，如控制图—图2的P图。

D 对于计数值控制衅，要画两个图――在上图中标出每个分组的均值或个体单位；在下图中标出每一分组的极差或标准差，如控制图－图3，4。

控制图3，4本档不能完成，请参照书第155页7.解释控制图A如果所有的数据点都处于控制极限范围之内，而且随机分散在均值线的周围，那么工作过程处于控制状态，没有受到特殊原因的影响。

质量管理工具“控制图”详解

控制图（Control Chart）又叫管制图，是对过程质量特性进行测定、记录、评估，从而监察过程是否处于控制状态的一种用统计方法设计的图。

有三条平行于横轴的直线：中心线（CL，Central Line）、上控制线（UCL，Upper Control Line）和下控制线（LCL，Lower Control Line），并有按时间顺序抽取的样本统计量数值的描点序列。

UCL、CL、LCL统称为控制线（Control Line），通常控制界限设定在±3标准差的位置。

根据控制图使用目的不同，控制图可分为：分析用控制图和控制用控制图。

根据统计数据的类型不同，控制图可分为：计量控制图和计数控制图（包括计件控制图和计点控制图）。

计量型控制图平均数与极差控制图( -X-R Chart )平均数与标准差控制图( -X-S Chart )中位数与极差控制图( ~X-R Chart )个別值与移动极差控制图( X-Rm Chart )计数值控制图不良率控制图(P chart)不良数控制图(nP chart，又称np chart 或d chart)缺点数控制图(C chart)单位缺点数控制图(U chart) 控制图种类及应用场合控制图的分析与判定应用控制图的目的，就是要及时发现过程中出现的异常，判断异常的原则就是出现了“小概率事件”，为此，判断的准则有两类。

第一类：点子越出界限的概率为0.27% 。

准则1属于第一类。

第二类：点子虽在控制界限内，但是排列的形状有缺陷。

准则2-8属于第二类。

控制图八大判异准则（口诀）2/3A （连续3点中有2点在中心线同一侧的B区外<即A区内>）4/5C （连续5点中有4点在中心线同一侧的C区以外）6连串（连续6点递增或递减，即连成一串）8缺C （连续8点在中心线两侧，但没有一点在C区中）9单侧（连续9点落在中心线同一侧）14交替（连续14点相邻点上下交替）15全C （连续15点在C区中心线上下，即全部在C区内1界外（1点落在A区以外）▶ 2/3A （连续3点中有2点在中心线同一侧的B区外<即A区内>）判读：1、控制过严；2、材料品质有差异；3、检验设备或方法之大不相同；4、不同制程之资料绘于同一控制图上；5、不同品质材料混合使用。

控制图培训课件

02
数据收集：收集数据，包括生产过程中的关键参数、质量指标等
03
数据分析：对收集到的数据进行分析，找出异常值和趋势
04
控制限设定：根据分析结果设定控制限，判断生产过程是否处于受控状态
05
控制图应用：根据控制图结果调整生产过程，确保产品质量稳定可靠
谢谢
U控制图：用于监控过程均值和标准差的同时变化
R控制图：用于监控过程均值和标准差的同时变化，但与U控制图不同，R控制图可以区分过程均值和标准差的变化。
2
控制图的制作方法
数据收集与整理
确定控制图的目的和范围
收集数据：包括原始数据、过程数据、结果数据等
整理数据：对数据进行分类、排序、筛选等处理
确定控制图的类型和参数：根据数据特点选择合适的控制图类型和参数
绘制控制图：将收集到的数据按照时间顺序绘制在控制图上，并在图上标注控制限
分析控制图：观察控制图上的数据点，判断是否存在异常情况，如数据点超出控制限、数据点分布不均匀等
采取措施：根据分析结果，采取相应的措施，如调整生产过程、改进质量管理等
2
3
4
控制图的分析
01
控制图类型：选择合适的控制图类型，如X-R控制图、P控制图等
监控生产过程：及时发现异常，确保产品质量
预测过程趋势：预测未来产品质量，提前采取措施
指导质量改进：确定改进方向，提高产品质量
控制图的类型
控制图类型：X-R控制图、P控制图、C控制图、U控制图、R控制图等
X-R控制图：用于监控过程均值和标准差的变化
P控制图：用于监控过程均值的变化
C控制图：用于监控过程标准差的变化
绘制控制图：根据控制图类型和参数绘制控制图