人教版数学九年级上册:24.1.2《垂直于弦的直径》 PPT课件(共21页)1
合集下载
人教版初中数学《垂直于弦的直径》免费课件

人教版初中数学《垂直于弦的直径》p pt精美 (PPT 优秀课 件)
小结:
解题方法: 在利用垂径定理解题时,通常需要作_弦__心__距_, 构造直__角__三__角__形__,把_垂__径_定理和勾__股__定理结合 起来,容易得到圆的半径r,弦心距d,和弦长 a之间的关系式_r_2___d_2___a___2 .
ห้องสมุดไป่ตู้
C
设 所在圆的圆心为O,
A
18.5 D
半径为R.
B
经过圆心O 作弦AB
R
R-7.23
的垂线OC,D为垂足. 由垂径定理可得,D 是
AB 的中点,C是 的中
O
在Rt△AOD中,
点,CD 就是拱高.
1
AD= 2
AB=18.5,OD=OC-CD=R-7.23
∵ OA2=AD2+OD2 ∴R2=18.52+(R-7.23)2
人教版初中数学《垂直于弦的直径》p pt精美 (PPT 优秀课 件)
练习4、如图是一个隧道横截面,它的形状是 以点O为圆心的圆的一部分.如果M是⊙O中弦 CD的中点,EM经过圆心O交⊙O于点E,并且 CD=4m,EM=6m. 求⊙O的半径.
人教版初中数学《垂直于弦的直径》p pt精美 (PPT 优秀课 件)
练习1、如图,在⊙O中,弦AB的长为8㎝,
圆心O到AB的距离为3㎝.
求⊙O的半径.
A
B
O.
人教版初中数学《垂直于弦的直径》p pt精美 (PPT 优秀课 件)
人教版初中数学《垂直于弦的直径》p pt精美 (PPT 优秀课 件)
练习2、如图,在⊙O中,AB、AC为互相垂直 且相等的两条弦,OD⊥AB,OE⊥AC,垂足 分别为D,E. 求证:四边形ADOE是正方形.
24.垂直于弦的直径PPT课件(人教版)

(√ ) (√ ) (×)
轴
经过圆心
中心
圆心
垂直于弦的 直径平分弦,并且平分弦所对的两条弧
垂直
弦所对的两条弧
问题:你知道赵州桥吗?它是1300多年前我国隋代建 造的石拱桥,是我国古代人民勤劳与智慧的结晶.它的主 桥拱是圆弧形,它的跨度(弧所对的弦的长)为37.4m, 拱高(弧的中点到弦的距离)为7.2m,你能求出赵州桥主 桥拱的半径吗?
∵AB∥CD,∴ON⊥CD于N
在RtAOM中,AM 5cm,OM OA2 AM2 12cm. 在RtOCN中,CN 12cm,ON OC2 CN 2 5cm.
∵MN=OM-ON,∴MN=7cm. (2)当AB、CD在O点异侧时,如图②所示,
由(1)可知OM=12cm,ON=5cm,MN=OM+ON,
(并2且)平A分M=A(BBM及,AA(DCB=.BC,AD=BD,即直径CD平分弦AB,
这样,我们就得到下面的定理:垂直于弦的直径平分弦, 并且平分弦所对的两条弧。进一步,我们还可以得到结论:平 分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧 。
知识点一 垂径定理及其推论
C
知识点一 垂径定理及其推论
通过本节课的学习,我们就会很容易解决这一问题.
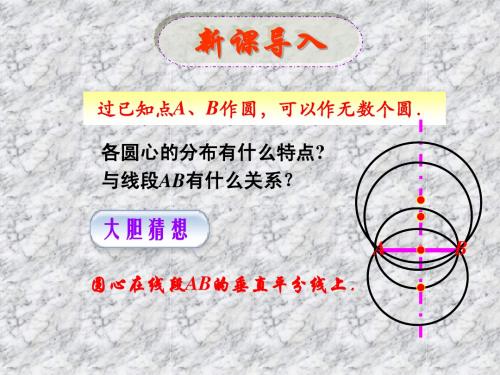
探究:1.圆是轴对称图形吗?如果是,它的对称轴是什 么?你能找到多少条对称轴?
分析讨论:圆是轴对称图形,它的对称轴是直径,我能找到 无数多条直径.
探究: 2.你是用什么方法解决上述问题的?与同伴进行 交流.
分析讨论我:是利用沿着圆的任意一条直径折叠的方法解决 圆的对称轴问题的.
.2垂直于弦的直径
判断:
(1)直径是弦.( √ )
(2)弦是直径. ( × )
人教版九年级数学上册《24.1.2 垂直于弦的直径》 PPT课件

A.4 2 B.8 2
C.2 5
D.4 5
练习巩固,综合应用
2.如图,将半径为2 cm 的圆形纸片折叠后,圆弧恰好 经过圆心O,则折痕AB的长为 __2__3__cm.
3.⊙O的直径为10,弦AB的长为8,P是弦AB 上的一个动点,则OP长的取值范围为 3≤OP≤5.
练习巩固,综合应用
4.已知⊙O中,若弦AB的长为
8 cm,圆心O到AB的距离为3 cm, A 求⊙O的半径.
解:连结OA,过O作OE⊥AB,
E
B
.
O
垂足为E,则OE=3 cm,AE=BE.
∵AB=8 cm,∴AE=4 cm.
在Rt△AOE中,根据勾股定理可得OA=5 cm.
∴⊙O的半径为5 cm.
练习巩固,综合应用
5.如图,AB是⊙O的直径,作半径OA的垂直平分 线,交⊙O于C,D两点,垂足为H,连接BC,BD.
——过圆心作垂直于弦的线段; ——连接半径.
再见
2
∴r=2 3.
故⊙O的半径长是2 3 .
练习巩固,综合应用
6.银川市某居民区一处圆形下水管道破裂,修 理人员准备更换一段新管道.如下图所示,污水水 面宽度为60 cm,水面至管道顶部距离为10 cm,问 修理人员应准备内径多大的管道?
练习巩固,综合应用
解:如图所示,连接OA,过点O作OE⊥AB,垂足为E,交圆于
2
2
在Rt△OAD中,由勾股定理,得
C
OA2=AD2+OD2,即R2=18.52+(R-7.23)2. 解得R≈27.3(m). 因此,赵州桥的主桥拱半径约为27.3 m.
D
A
B
R
O
练习巩固,综合应用
九年级上数学《24.1.2 垂直于弦的直径》课件
M
C A O 证明:作直径MN垂直于弦AB D ∵ AB∥CD B ∴ 直径MN也垂直于弦CD ⌒ ⌒ ∴AM=BM, ⌒ ⌒ CM=DM ⌒ ⌒ ⌒ ⌒ ∴AM-CM =BM-DM ⌒ ⌒ 即 AC=BD
N
两条弦在圆心的同侧
垂径定理的推论2 有这两种情况: O A C D A O C D B B
E
O
题设
③平分弦 ④平分弦所对的优弧 ⑤平分弦所对的劣弧 结论
垂径定理的推论1
① 直径过圆心 ③ 平分弦 C ② 垂直于弦 ④ 平分弦所对优弧 ⑤ 平分弦所对的劣弧
A
E
O B
已知:CD是直径,AB是弦,CD平分AB 求证:CD⊥AB,AD=BD,AC=BC
⌒ ⌒ ⌒ ⌒
D
(1)平分弦(不是直径)的直径垂直于弦, 并且平分弦所对的两条弧.
① 直径过圆心 ③ 平分弦 ⑤ 平分弦所对的劣弧
② 垂直于弦 ⑤ 平分弦所对的劣弧
① 直径过圆心 ③ 平分弦 ④ 平分弦所对优弧
(4)垂直于弦并且平分弦所对的一条弧的 直径过圆心,并且平分弦和所对的另一条弧.
③ 平分弦 ④ 平分弦所对优弧
① 直径过圆心 ② 垂直于弦 ⑤ 平分弦所对的劣弧
③ 平分弦 ⑤ 平分弦所对的劣弧
B
在 a , d , r, h中,已知其中任 意两个量,可以 求出其它两个量 .
B
⌒ 点O就是AB的圆心.
O
你 能 破 镜 重
m
n
A
C
圆
吗?
B O
作法: 作弦AB、AC及它们的垂直平分线m、n, 交于O点;以O为圆心,OA为半径作圆. 依据: 弦的垂直平分线经过圆心,并且平分弦 所对的两条弧.
垂径定理三角形
C A O 证明:作直径MN垂直于弦AB D ∵ AB∥CD B ∴ 直径MN也垂直于弦CD ⌒ ⌒ ∴AM=BM, ⌒ ⌒ CM=DM ⌒ ⌒ ⌒ ⌒ ∴AM-CM =BM-DM ⌒ ⌒ 即 AC=BD
N
两条弦在圆心的同侧
垂径定理的推论2 有这两种情况: O A C D A O C D B B
E
O
题设
③平分弦 ④平分弦所对的优弧 ⑤平分弦所对的劣弧 结论
垂径定理的推论1
① 直径过圆心 ③ 平分弦 C ② 垂直于弦 ④ 平分弦所对优弧 ⑤ 平分弦所对的劣弧
A
E
O B
已知:CD是直径,AB是弦,CD平分AB 求证:CD⊥AB,AD=BD,AC=BC
⌒ ⌒ ⌒ ⌒
D
(1)平分弦(不是直径)的直径垂直于弦, 并且平分弦所对的两条弧.
① 直径过圆心 ③ 平分弦 ⑤ 平分弦所对的劣弧
② 垂直于弦 ⑤ 平分弦所对的劣弧
① 直径过圆心 ③ 平分弦 ④ 平分弦所对优弧
(4)垂直于弦并且平分弦所对的一条弧的 直径过圆心,并且平分弦和所对的另一条弧.
③ 平分弦 ④ 平分弦所对优弧
① 直径过圆心 ② 垂直于弦 ⑤ 平分弦所对的劣弧
③ 平分弦 ⑤ 平分弦所对的劣弧
B
在 a , d , r, h中,已知其中任 意两个量,可以 求出其它两个量 .
B
⌒ 点O就是AB的圆心.
O
你 能 破 镜 重
m
n
A
C
圆
吗?
B O
作法: 作弦AB、AC及它们的垂直平分线m、n, 交于O点;以O为圆心,OA为半径作圆. 依据: 弦的垂直平分线经过圆心,并且平分弦 所对的两条弧.
垂径定理三角形
人教版九年级数学上册 24.1.2垂径定理(共21张PPT)

下课!
课堂作业:课本 家庭作业:练习册
O
A
B
E
D
∴ CD⊥弦AB ,A⌒D=
⌒
BD
,A⌒C=B⌒C
1.判断下列图形,能否满足垂径定理?
B
B
B
O
O
O
C A
(×)
DC A
DC E
(×)
(√)
注意:定理中的两个条件
(直径,垂直于弦)缺一不可!
DC
O D
A
(√)
2.如图,在圆O中,直径MN⊥AB,垂足
是C,则下列结论中错误的D是( )
A.A⌒N=⌒BN B. AC=BC
2
2
OD=OC-CD=R-7.2
在Rt△OAD中,由勾股定理,得A
C D B
OA2=AD2+OD2
R
即 R2=18.72+(R-7.2)2
O
解得:R≈27.9(m)
因此,赵州桥的主桥拱半径约为27.9m.
图一:AC、BD有什么关系? A C O D B
变式:图二AC=BD依然成立吗? (1)
AC
O
将圆心到弦的距离、半径、 弦长构成直角三角形,把问题 转化为直角三角形的问题。
B
A P
O
如图,A⌒B 所在圆的圆心是点O, 过O作OC⊥AB于点D,若CD=4 m, 弦AB=16 m,求此圆的半径.
课本例题
如图,1 400 多年前,我国隋代建造的赵州石拱桥 主桥拱是圆弧形,它的跨度(弧所对的弦长)是 37 m, 拱高(弧的中点到弦的距离)为 7.23 m,求赵州桥主桥 拱的半径(精确到 0.1 m).
M
C.A⌒M=⌒BM D.OC=CN
24.1.2垂直于弦的直径 课件人教版数学九年级上册

(1)证明:∵PG平分∠EPF,
∴∠DPO=∠APO. ∵AOIIPE,∴∠DPO=∠AOP, ∴∠APO=∠AOP,.∴AP=AO.
【综合拓展类作业】
(2)解:如图,过点O作OH⊥AB 于点H,
在Rt△AOH中, ∵AO=5,AH=4, ∴OH=√52-42=3. ∵AP=AO=5, ∴PH=AP+AH=9,
探究:剪一个圆形纸片,沿着它的任意一条直径对折,重复做几次,你发现了 什么?由此你能得出什么结论?
猜想:圆是轴对称图形,任何一条直径所在的直线都是圆的对称轴.
你能证明上述结论吗?
证明:如图,设CD是○O的任意一条直径, A为 0O上点C,D 以外的任意一点. 过点A作AA'⊥CD, 交00于点A', 垂足为M, 连接OA,OA'.
构造Rt△利用勾股定理计算或建立方程.
垂直于圆的直径 1.垂径定理:垂直于弦的直径平分弦,并且平分弦所对的两条弧 2.推论:平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧。
【知识技能类作业】必做题:
1.往直径为52cm 的圆柱形容器内装入一些水以后,截面如图所示,若水面 宽AB=48cm, 则水的最大深度为( C )
A.4cm
B.3cm
C.2cm
D.1cm
【知识技能类作业】必做题: 3.已知○ O 中,弦AB=8cm, 圆 心 到AB 的距离为3cm, 则此圆的半径为_5 cm.
4.如图,OE⊥AB 于E, 若○ O 的半径为10cm,OE=6cm, 则AB=16 .cm.
【知识技能类作业】选做题:
5.如图,在00中,弦AB的长为8cm, 圆心O到AB的距离为3cm.求 0 0 的半径.
∵OA=OB∴△OAB是等腰三角形
∴∠DPO=∠APO. ∵AOIIPE,∴∠DPO=∠AOP, ∴∠APO=∠AOP,.∴AP=AO.
【综合拓展类作业】
(2)解:如图,过点O作OH⊥AB 于点H,
在Rt△AOH中, ∵AO=5,AH=4, ∴OH=√52-42=3. ∵AP=AO=5, ∴PH=AP+AH=9,
探究:剪一个圆形纸片,沿着它的任意一条直径对折,重复做几次,你发现了 什么?由此你能得出什么结论?
猜想:圆是轴对称图形,任何一条直径所在的直线都是圆的对称轴.
你能证明上述结论吗?
证明:如图,设CD是○O的任意一条直径, A为 0O上点C,D 以外的任意一点. 过点A作AA'⊥CD, 交00于点A', 垂足为M, 连接OA,OA'.
构造Rt△利用勾股定理计算或建立方程.
垂直于圆的直径 1.垂径定理:垂直于弦的直径平分弦,并且平分弦所对的两条弧 2.推论:平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧。
【知识技能类作业】必做题:
1.往直径为52cm 的圆柱形容器内装入一些水以后,截面如图所示,若水面 宽AB=48cm, 则水的最大深度为( C )
A.4cm
B.3cm
C.2cm
D.1cm
【知识技能类作业】必做题: 3.已知○ O 中,弦AB=8cm, 圆 心 到AB 的距离为3cm, 则此圆的半径为_5 cm.
4.如图,OE⊥AB 于E, 若○ O 的半径为10cm,OE=6cm, 则AB=16 .cm.
【知识技能类作业】选做题:
5.如图,在00中,弦AB的长为8cm, 圆心O到AB的距离为3cm.求 0 0 的半径.
∵OA=OB∴△OAB是等腰三角形
人教版初中数学九年级上册 24.1.2垂直于弦的直径 教学课件PPT

谈谈本节课的收获
作业
1、必做题:
习题24.1 第10、 11、12题
2、思考题:
已知:在半径为5cm的圆O 中,两条平行弦AB,CD分别 长8cm,6cm.求两条平行弦间
的距离。
谢谢
想一想
AB是⊙O的一条弦,且AM=BM. 过点M作直径CD. 左图是轴对称图形吗?如果是,其对称轴是什么?
C
你能发现图中有哪些等量关系?与同伴说说你的
A
┗●
B
想法和理由.
M
●O
由 ① CD是直径 可推得
②CD⊥AB, ⌒⌒
④AC=BC,
③ AM=BM
⌒⌒ ⑤AD=BD.
D
C
推论:平分弦(不是直径)的直径垂 直于弦,并且平分弦所对的两条弧.
A
·O
M B
D
由①CD是直径 ③AM = BM
可推得
②CD⊥AB
⌒⌒ ④AC = BC
⌒⌒ ⑤AD = BD
辨一辨
下列哪些图形能直接满足垂径定理的题设条件?
O
O
O
(1)
(2)
(3)
O
O
(4)
(5)
(6)
垂径定理的应用 解决求赵州桥拱半径的问题
问题 :你知道赵州桥吗?它是1400多年前我国隋代建造的石 拱桥, 是我国古代人民勤劳与智慧的结晶.它的主桥拱是圆 弧形,它的跨度(弧所对的弦的长)为37.4m, 拱高(弧的中点到弦 的距离)为7.23m,你能求出赵洲桥主桥拱的半径吗?
4
1
8
.7
A
R
D
B
OD = OC-CD = R理,得
OA2 = AD2 +
人教版数学九年级上册 24.1.2垂直于弦的直径.ppt(共21张PPT)

通过本课时的学习,需要我们: 1.理解圆的轴对称性及垂径定理的推证过程; 能初步应用垂径定理进行计算和证明. 2.掌握垂径定理的推论,明确理解“知二推三” 的意义.利用垂径定理及其推论解决相应的数学问题.
六、家庭作业
• 1、必做 • 2、选作
p89页 2题 90页 9题 p89页 1题
• 学习难点:垂径定理及其推论。
自学指导
• 认真看书81-83页,独立完成以下问题,看 谁做得又对又快?
• 1、结合81探究,同学们动手操作,你发现 了什么?你得到什么结论?你会证明你的 结论吗?
• 2、什么是垂径定理?它的推论是什么? • 3、你知道解例2的每步依据吗?
一、 情境导入
问题:你知道赵州桥吗?它是1 300多年前我国隋代 建造的石拱桥,是我国古代人民勤劳与智慧的结晶, 它的主桥拱是圆弧形,它的跨度(弧所对的弦的长) 为37.4 m,拱高(弧的中点到弦的距离)为7.2 m, 你能求出赵州桥主桥拱的半径吗?
AD=BC AC【证明猜想】
垂径定理
已知:在⊙O中,CD是直径,AB是弦,CD⊥AB,垂足
为E.求证:AE=BE, AC=BC,AD=BD.
A
垂径定理 垂直于弦的直径平
分弦,并且平分弦所对的两条 C
O
ED
弧.
B
【定理辨析】
判断下列图形,能否使用垂径定理?
B
B
B
O
O
C
DC
DC
【跟踪训练】 如图,P为⊙O的弦BA延长线上一点,PA=AB=2,PO=5, 求⊙O的半径.
【解析】提示作OM 垂直
B
MA
P
于PB ,连接OA.
O
答案: 1 7
关于弦的问题,常常需要过圆心作弦的垂线段,这是一条
六、家庭作业
• 1、必做 • 2、选作
p89页 2题 90页 9题 p89页 1题
• 学习难点:垂径定理及其推论。
自学指导
• 认真看书81-83页,独立完成以下问题,看 谁做得又对又快?
• 1、结合81探究,同学们动手操作,你发现 了什么?你得到什么结论?你会证明你的 结论吗?
• 2、什么是垂径定理?它的推论是什么? • 3、你知道解例2的每步依据吗?
一、 情境导入
问题:你知道赵州桥吗?它是1 300多年前我国隋代 建造的石拱桥,是我国古代人民勤劳与智慧的结晶, 它的主桥拱是圆弧形,它的跨度(弧所对的弦的长) 为37.4 m,拱高(弧的中点到弦的距离)为7.2 m, 你能求出赵州桥主桥拱的半径吗?
AD=BC AC【证明猜想】
垂径定理
已知:在⊙O中,CD是直径,AB是弦,CD⊥AB,垂足
为E.求证:AE=BE, AC=BC,AD=BD.
A
垂径定理 垂直于弦的直径平
分弦,并且平分弦所对的两条 C
O
ED
弧.
B
【定理辨析】
判断下列图形,能否使用垂径定理?
B
B
B
O
O
C
DC
DC
【跟踪训练】 如图,P为⊙O的弦BA延长线上一点,PA=AB=2,PO=5, 求⊙O的半径.
【解析】提示作OM 垂直
B
MA
P
于PB ,连接OA.
O
答案: 1 7
关于弦的问题,常常需要过圆心作弦的垂线段,这是一条
人教版(2012)九年级数学上册24.1.2垂直于弦的直径 课件(29张ppt)

B D
在Rt△OAD中,由勾股定理,得OA2=AD2+OD2, ∴R2=18.52+(R-7.23)2,解得R≈27.3.
即赵州桥的主桥拱半径约为27.3m.
O
例题变式
如图,在⊙O中,弦AB的长为 6 cm,圆心O到AB的距离(弦心距)为 4 cm,
求⊙O的半径.
解: 过圆心O 作OE⊥AB于E, A
,(垂径定理)
3E B
4
O
在Rt △ AOE 中 ,
垂径定理 圆是轴对称图形
知识小结 内容
推论
垂直于弦的直径平分弦, 并且平分弦所对的两条弧
一条直线满足:①过圆心;②垂直于弦; ③平 分弦(不是直径); ④平分弦所对的优弧; ⑤平分弦所对的劣弧.满足其中两个条件就 可以推出其他三个结论(“知二推三”)
5)
y
.
C 3
A O 2M D
Hale Waihona Puke 5B x达标练习4.如图,⊙O 的直径CD⊥AB于E,AB=6cm,CE=9㎝.
求⊙O 的半径.
C
O
r 9-r
3E
A
B
D
角形全等. 要证 ⌒AC =A⌒D,⌒BC =⌒BD ,只需证明C点与D点
C
关于直径AB对称.
A
O ED B
同位讨论
CD是⊙O的一条弦,直径AB⊥CD,垂足为E. 求证:CE=DE,⌒AC = A⌒D, ⌒BC =⌒BD.
证明:连接OC,OD,则OC=OD 在Rt△OCE和Rt△ODE中:
A O
__O_E_=_O_E_____________
1.半径为4cm的⊙O 中,弦AB=2 cm,
那么圆心O 到弦AB 的距离是
人教版数学九年级上册24.1.2垂径定理同步课件(共23张PPT)

弦等于 2 5 c. m
B
O
D
P E
C
A
练习
6、将一个两边都带有刻度的直尺放在半圆形纸 片上,使其一边经过圆心O,另一边所在直线 与半圆交于点D、E, 量出半径 OC = 5cm,弦 DE=8cm。求直尺的宽度。
D
C
E
A
O
B
.
(2)如图,AB是⊙O的一条弦,做直径CD,使CD⊥AB,垂足为E.
(2)如图,AB是⊙O的一条弦,做直径CD,使CD⊥AB,垂足为E.
(1)圆是轴对称图形吗?如果是,它的对称轴是什么?
赵的州弦桥 的是长我)国为隋37代米建,O造拱的高石(拱弧桥的,中距点今到有弦1的4距00离年)的为历7史O. ,是我国古代人民勤劳和智慧的结O晶,它的主桥拱是圆形.它的跨度(弧所对
作业
• 课本90页:8 9
• 不经历风雨,怎么见彩虹 5、已知P为⊙ O内一点,且OP=2cm,如果
如图,用 表示主桥拱,设 所在圆的圆心为O,半径为R.经过圆心O 作弦AB 的垂线OC,D为垂足,OC与AB 相交于点D,根据前 面的结论,D是AB的中点,C是 的中点,CD就是拱高.
(2)线段:AE=BE
(1)是轴对称图形.直径CD所在
的直线是它的对称轴
C
(2)线段:AE=BE
弧: AC=BC
·O
把圆沿A着D直=径BCDD折叠时,CD两侧的两个半圆
E
重合,点A与点B重合,AE与BE重合,AC、AD A
B
分别与 B、C B重合。
D
D
2.垂径定理的内容是什么?画出适合题意的图形, 用符号语言表示出来. 垂直于弦的直径平分弦,且平分弦所对的两条弧.
所对的弦的长)为37.
B
O
D
P E
C
A
练习
6、将一个两边都带有刻度的直尺放在半圆形纸 片上,使其一边经过圆心O,另一边所在直线 与半圆交于点D、E, 量出半径 OC = 5cm,弦 DE=8cm。求直尺的宽度。
D
C
E
A
O
B
.
(2)如图,AB是⊙O的一条弦,做直径CD,使CD⊥AB,垂足为E.
(2)如图,AB是⊙O的一条弦,做直径CD,使CD⊥AB,垂足为E.
(1)圆是轴对称图形吗?如果是,它的对称轴是什么?
赵的州弦桥 的是长我)国为隋37代米建,O造拱的高石(拱弧桥的,中距点今到有弦1的4距00离年)的为历7史O. ,是我国古代人民勤劳和智慧的结O晶,它的主桥拱是圆形.它的跨度(弧所对
作业
• 课本90页:8 9
• 不经历风雨,怎么见彩虹 5、已知P为⊙ O内一点,且OP=2cm,如果
如图,用 表示主桥拱,设 所在圆的圆心为O,半径为R.经过圆心O 作弦AB 的垂线OC,D为垂足,OC与AB 相交于点D,根据前 面的结论,D是AB的中点,C是 的中点,CD就是拱高.
(2)线段:AE=BE
(1)是轴对称图形.直径CD所在
的直线是它的对称轴
C
(2)线段:AE=BE
弧: AC=BC
·O
把圆沿A着D直=径BCDD折叠时,CD两侧的两个半圆
E
重合,点A与点B重合,AE与BE重合,AC、AD A
B
分别与 B、C B重合。
D
D
2.垂径定理的内容是什么?画出适合题意的图形, 用符号语言表示出来. 垂直于弦的直径平分弦,且平分弦所对的两条弧.
所对的弦的长)为37.
人教版九年级上册第24章圆24.1.2垂直于弦的直径课件(共21张)

解决有关弦的问题,经常是过圆心作弦的弦心 距,或作垂直于弦的直径,连结半径等辅助线,为 应用垂径定理创造条件.
四 垂径定理的实际应用
例2 赵州桥(图24.1-7)是我国隋代建造白石拱桥,距今 约有1 400年的历史,是我国古代民勤劳与智慧的结晶.它的 主桥拱是圆弧形,它白跨度(弧所对的弦的长)为37 m,拱高(弧 的中点到弦的距离)为7.23 m,求赵州桥主桥拱的半径(结果保 留小数点后一位).
C u推导格式:
∵ CD是直径,CD⊥AB,
∴ AE=BE, A⌒C =⌒BC, A⌒D =B⌒D.
·O AE B
D
温馨提示:垂径定理是圆中一个重要的定理,三种
语言要相互转化,形成整体,才能运用自如.
想一想:下列图形是否具备垂径定理的条件?如果不 是,请说明为什么?
C
A O
A
EB
D
C B
O A
是
不是,因为
试一试:根据刚刚所学,你能利用垂径定理求出引入 中赵州桥主桥拱半径的问题吗?
解:如图,用AB表示主桥拱,设
AB所在圆的圆心为O,半径为R.
经过圆心O作弦AB的垂线OC
垂足为D,与弧AB交于点C,
则D是AB的中点,C是弧AB的 中点,CD就是拱高.
∴ AB=37m,CD=7.23m.
∴ AD= AB=18.5m,
如图,CD是⊙O的任意一条直
径,点A为⊙O上除点C、D外的 A 任意一点.过点A作AA΄⊥CD,交
·O
EM
A΄
D
⊙O于点A΄,垂足为M,连接OA,
OA΄.证明CD是AA΄的中垂线即
可问题:你能发现图中有那些相等的线段和弧?为什么?试用
文字语言表示
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
求证:AC=BD。
O.
E 证明:过O作OE⊥AB,垂足为E, A C
DB
则AE=BE,CE=DE。
AE-CE=BE-DE。
所以,AC=BD
实际上,往往只需从圆心作一条与弦垂直的 线段.就可以利用垂径定理来解决有关问题了.
3、在直径为650mm的圆柱形油槽内装入一些 油后,油面宽AB=600mm,求油的最大深度。
解: OE AB
A
AE 1 AB 1 8 4cm
2
2
在Rt △ AOE 中,由勾股
AO OE2 AE2 = 32 +42 =5cm
答:⊙O的半径为5cm.
在来!你行吗?
2、如图,OE⊥AB于E,若⊙O的半径为
10cm,OE=6cm,则A1B6= cm。
解:连接OA,∵ OE⊥AB
根据垂径定理与推论可知对于一个圆和 一条直线来说。如果具备
(1)过圆心 (2)垂直于弦 (3)平分弦(不是直径)
(4)平分弦所对的优弧 (5)平分弦所对的劣弧
上述五个条件中的任何两个条件都可以 推出其他三个结论
知二推三
随堂练习
1. 判断:
(1)垂直于弦的直线平分这条弦,并且平分弦所对
的两弧.
()
(2)平分弦所对的一条弧的直径一定平分这条弦所
2
2
B
设OA=x,则OE=x-1,由勾股定理得
x2=52+(x-1)2 解得:x=13
∴ OA=13 ∴
答:直径CDC的D长=为2O2A6=. 3*在13来=2!你还能行吗?
二、填空:
1.半径为4cm的⊙O中,弦AB=4cm,
那么圆心O到弦AB的距离是 2 3cm。
O AE B
2. ⊙O的直径为10cm,圆心O到弦AB的 距离为3cm,则弦AB的长是 8cm 。
平分A⌒B
及
⌒
ACB
CD⊥AB
AE=BE
⌒ ⌒⌒ ⌒
AD=BD,AC=BC A
C
·O
E B
D
垂径定理:垂直于弦的直径平分弦, 并且平分弦所对的两条弧.
思考:平分弦(不是直径)的直径有什么性质?
垂径定理的推论
如图: AB是⊙O的一条弦,直径CD交AB于M,AM=BM 连接OA,OB,则OA=OB.
在△OAM和△OBM中, ∵OA=OB,OM=OM,AM=BM
O AE B
3.半径为2cm的圆中,过半径中点且 垂直于这条半径的弦长是 2 3cm。
O
AE
B
圆是轴对称图形,经过圆心的每一条直线都是它的对称轴. 垂径定理: 垂直于弦的直径平分这条弦,并且平分弦所对的两条弧.
根据垂径定理与推论可知对于一个圆和一条直线来 说。如果具备
(1)过圆心 (2)垂直于弦 (3)平分弦 (4)平分弦所对的优弧 (5)平分弦所对的劣弧
1.两条弦在圆心的同侧
2.两条弦在圆心的两侧
A
●O
B
C
D
A C
B ●O
D
AEB
∴ 在Rt △ AOE 中,由勾股定理得:
AE OA2 OE 2
O·
102 62 8cm
∴ AB=2AE=16cm
3、如图,CD是⊙O的直径,弦AB⊥CD
于E,CE=1,AB=10,求直径CD的长。
解:连接OA,
A
∵ CD是直径,OE⊥AB
C E O·
D
AE 1 AB 1 10 5
1.理解圆的对称性; 2.理解掌握圆的垂径定理,并能灵活运用。
培养探索、推理、归纳、证明的能力及 用 数学语言表达数学问题的能力.
培养独立思考、敢于质疑、善于表达 的习惯;学会互助、合作、交流.
重点:理解掌握垂径定理 难点:灵活运用垂径定理解决有关圆问题
活动一
如图,AB是⊙O的一条弦,做直径CD,使CD⊥AB,垂足为E. (1)这个图形是轴对称图形吗?如果是,它的对称轴是什么? (2)你能发现图中有那些相等的线段和弧?为什么?
1、我们所学的圆是不是轴对称图形呢?
圆是轴对称图形,经过圆心的每一条直线都 是它们的对称轴
2、我们所学的圆是不是中心对称图形呢? 圆是中心对称图形,圆心是对称中心
.
3、填空:
(1)根据圆的定义,“圆”指的是“ 圆周”,是 线曲,而不是
“圆面”。
(2)圆心和半径是确定一个圆的两个必需条件,圆心决定圆
的 位置,半径决定圆的 大,小二者缺一不可。 (3)同一个圆的半径 处处 相等。
证明: OE AC OD AB AB AC
OEA 90 EAD 90 ODA 90
∴四边形ADOE为矩形, AE 1 AC,AD 1 AB
2
2
又 ∵AC=AB
C
∴ AE=AD
E
·O
∴ 四边形ADOE为正方形.
A
D
B
2、已知:如图,在以O为圆心的两 个同心圆中,大圆的弦AB交小圆于 C,D两点。
D
由 ① CD是直径 可推得 ② CD⊥AB
推论:平分弦(不是直径)的直径垂 直于弦,并且平分弦所对的两条弧.
③AM=BM,
④A⌒C=B⌒C, ⑤A⌒D=B⌒D.
由 ① CD是直径 可推得 ③ AM=BM
②CD⊥AB,
④A⌒C=B⌒C, ⑤A⌒D=B⌒D.
结论
垂径定理:垂直于弦的直径 平分弦,并且平分弦所对的 两条弧.
(1)是轴对称图形.直径CD所在的 直线是它的对称轴
(2弧):线A⌒段C:=BA⌒EC=BE,A⌒D=B⌒D
⌒ ⌒ 把圆沿着直径CD折叠时,CD两侧的两个半圆重合,
A
点A与点B重合,AE与BE重合,AC 和 BC
⌒ ⌒ 重合,AD和 BD重合.
C
·O
E B
D
CD⊥AB 时:
直径CD平分弦AB,并且
∴△OAM≌△OBM.
C
∴∠AMO= ∠BMO.
A
B ∴CD⊥AB
M
∵⊙O关于直径CD对称,
●O
∴当圆沿着直径CD对折时,点A与点B重合,
⌒⌒
⌒⌒
D
∴A⌒C =AB⌒CC和, AB⌒DC重=B⌒合D,. AD和BD重合.
平分弦(不是直径)的直径垂直于
弦,并且平分弦所对的两条弧.
C
O
A
M
B
垂径定理:垂直于弦的直径平分 弦,并且平分弦所对的两条弧.
解:
(1)
OB 650 (mm)
(2)
2
O
EB 600 (mm) 2
B
E
A
E A
B OE OB2 EB2
O
OE=125(mm)
D
D
油的最大深度ED=OD-OE=200(mm)
或者油的最大深度ED=OD + OE=450(mm).
4、⊙O的半径为10cm,弦AB∥CD, AB=16,CD=12,则AB、CD间的 距离是___2cm 或14cm.
上述五个条件中的任何两个条件都可以推出其他三个结论
在解决有关圆的问题时,可以利用垂径定理将其转化 为解直角三角形的问题 。
作业:
教材88页习题24.1 第 8、9题 ;
别忘记还有我哟!! 作业:
1、P82练习 1、2题 2、教材88页习题24.1
8、9 ; 3、练习册同步.
1.如图,在⊙O中,AB、AC为互相垂直且相等的 两条弦,OD⊥AB于D,OE⊥AC于E,求证四边形 ADOE是正方形.
对的另一弧.
(√ )
(3)经过弦的中点的直径一定垂直于弦( )
(4)平分弦的直径垂直于弦. ( )
(5)弦的垂直平分线一定平分这条弦所对的弧.
(√ )
垂径定理:垂直于弦的直径平分弦, 并且平分弦所对的两条弧.
重点强调:
A
E
B
·
O
1.如图,在⊙O中,弦AB的长为8cm,圆心O 到AB的距离为3cm,求⊙O的半径.
