菱形的性质与判定

合集下载

菱形的判定和性质

BCADO菱形的判定和性质一、基础知识（一）菱形的概念一组邻边相等的平行四边形叫做菱形。

（二）菱形的性质：1、具有平行四边形的一切性质；2、菱形四条边都相等；3、菱形的对角线互相垂直平分，每条对角线平分一组对角；4、菱形是轴对称图形；边角对角线对称性菱形对边平行；四边相等对角相等；邻角互补互相垂直平分且平分对角轴对称（三）菱形的判定：1、一组邻边相等的平行四边形是菱形；2、对角线互相垂直的平行四边形是菱形；3、四条边都相等的四边形是菱形；（四）菱形的面积1、可以用平行四边形的面积算（S=21底×高） 2、用对角线计算（面积的两对角线的积的一半 S=21ab)ABCDE二、例题讲解考点一：菱形的判定例1：下列命题正确的是（）（A ）一组对边相等，另一组对边平行的四边形一定是平行四边形（B ）对角线相等的四边形一定是矩形（C ）两条对角线互相垂直的四边形一定是菱形（D ）两条对角线相等且互相垂直平分的四边形一定是正方形练习1：菱形的对角线具有( ) A ．互相平分且不垂直 B ．互相平分且相等 C ．互相平分且垂直 D ．互相平分、垂直且相等练习2：如图，菱形ABCD 中，对角线AC 、BD 相交于点O ，M 、N 分别是边AB 、AD 的中点，连接OM 、ON 、MN ，则下列叙述正确的是（） A ．△AOM 和△AON 都是等边三角形B ．四边形AMON 与四边形ABCD 是位似图形C ．四边形MBON 和四边形MODN 都是菱形D ．四边形MBCO 和四边形NDCO 都是等腰梯形练习3：如图，在三角形ABC 中，AB ＞AC ，D 、E 分别是AB 、AC 上的点，△ADE 沿线段DE 翻折，使点A 落在边BC 上，记为A '．若四边形ADA E '是菱形，则下列说法正确的是( )A ．DE 是△ABC 的中位线B ．AA '是BC 边上的中线 C ．AA '是BC 边上的高D ．AA '是△ABC 的角平分线ABCDEA 'DBCA NM O练习4：如图，下列条件之一能使平行四边形ABCD 是菱形的为（） ①AC BD ⊥ ②90BAD ∠= ③AB BC = ④AC BD = A ．①③B ．②③C ．③④D ．①②③例2 ：已知AD 是△ABC 的平分线，DE ∥AC 交AB 于E ，DF ∥AB 交AC 于F ，则四边形AEDF 是什么四边形？请说明理由．变化：若D 是等腰三角形底边BC 的中点，DE ∥AC 交AB 于E ，DF ∥AB 交AC 于F ，则四边形AEDF 是什么四边形？请说明理由．练习1：如图，AD 是Rt △ABC 斜边上的高，BE 平分∠B 交AD 于G ，交AC 于E ，过E 作EF ⊥BC 于F ，试说明四边形AEFG 是菱形．练习2：如图，E 是菱形ABCD 边AD 的中点，EF ⊥AC 于点H ，交CB 延长线于点F ，交AB 于点G ，求证：AB 与EF 互相平分。

菱形的性质与判定

A
B
C
D
O
证明(1)∵四边形ABCD是菱形
∴DA=DC(菱形的定义)
∵DA=BC,AB=DC
∴AB=BC=DC=DA
(2)在△DAC中,又∵AO=CO
∴DB⊥AC， DB平分∠ADC（三线合一）
同理： DB平分∠ABC； AC平分∠DAB和∠DCB
(1)AB=BC=CD=DA
(2)AC⊥BD
A
B
C
D
E
F
你敢挑战吗？
交流反思
1.菱形概念
2.菱形特征
3.菱形与平行四边形的关系
①具有平行四边形的一切性质； ②菱形的四条边都相等； ③菱形的对角线互相垂直平分； ④菱形的对角线分别平分两组对角； ⑤菱形既是轴对称图形，又是中心对称图形。
有一组邻边相等的平行四边形叫做菱形
4.菱形的面积
方法总结:
01
02
03
单击此处添加正文。
平行四边形
菱形
四边形
单击此处添加正文。
对角线互相垂直
一组邻边相等菱形有四条边相等
判断下列说法是否正确？为什么？ (1)对角线互相垂直的四边形是菱形；（） (2)对角线互相垂直平分的四边形是菱形；（） (3)对角线互相垂直,且有一组邻边相等的四边形是菱形；（） (4)两条邻边相等，且一条对角线平分一组对角的四边形是菱形．（）
E
O
D
C
B
A
如图，矩形ABCD的对角线相交于点O，DE∥AC,AE∥DB，AE交DE于E。求证：四边形AODE是菱形。
D
C
B
A
M
N
2、将两张宽度相等的矩形纸片叠放在一起得到如图所示的四边形ABCD. 求证：四边形ABCD是菱形。

菱形的性质及判定

菱形得性质及判定中考要求知识点睛1、菱形得定义:有一组邻边相等得平行四边形叫做菱形.2.菱形得性质菱形就是特殊得平行四边形,它具有平行四边形得所有性质,•还具有自己独特得性质:①边得性质:对边平行且四边相等.②角得性质:邻角互补,对角相等、③对角线性质:对角线互相垂直平分且每条对角线平分一组对角.④对称性:菱形就是中心对称图形,也就是轴对称图形.菱形得面积等于底乘以高,等于对角线乘积得一半。

点评:其实只要四边形得对角线互相垂直,其面积就等于对角线乘积得一半、3。

菱形得判定判定①:一组邻边相等得平行四边形就是菱形、判定②:对角线互相垂直得平行四边形就是菱形。

判定③:四边相等得四边形就是菱形。

重、难点重点就是菱形得性质与判定定理。

菱形就是在平行四边形得前提下定义得,首先她就是平行四边形,但它就是特殊得平行四边形,特殊之处就就是“有一组邻边相等”,因而就增加了一些特殊得性质与不同于平行四边形得判定方法。

菱形得这些性质与判定定理即就是平行四边形性质与判定得延续,又就是以后要学习得正方形得基础、难点就是菱形性质得灵活应用。

由于菱形就是特殊得平行四边形,所以它不但具有平行四边形得性质,同时还具有自己独特得性质。

如果得到一个平行四边形就是菱形,就可以得到许多关于边、角、对角线得条件,在实际解题中,应该应用哪些条件,怎样应用这些条件,常常让许多学生手足无措,教师在教学过程中应给予足够重视。

例题精讲板块一、菱形得性质【例1】☆⑴菱形得两条对角线将菱形分成全等三角形得对数为⑵在平面上,一个菱形绕它得中心旋转,使它与原来得菱形重合,那么旋转得角度至少就是【例2】⑴如图2,一活动菱形衣架中,菱形得边长均为若墙上钉子间得距离,则度.⑵如图,在菱形中,,、分别就是、得中点,若,则菱形得边长就是______.【例3】如图,就是菱形得边得中点,于,交得延长线于,交于,证明:与互相平分.【例4】 ☆ 如图1所示,菱形中,对角线、相交于点,为边中点,菱形得周长为,则得长等于。

菱形的性质与判定

菱形的性质与判定菱形是一种具有特殊性质的四边形，它的对角线长度相等，且相交于垂直的交点。

在几何学中，我们可以通过一些准确的判定方法来确定一个四边形是否为菱形。

本文将介绍菱形的性质，并详细探讨判定菱形的几种方法。

一、菱形的性质1. 对角线相等：菱形的两条对角线长度相等，即AC=BD。

这是菱形的最基本特征。

2. 对角线相交垂直：菱形的两条对角线相交于一个垂直的交点。

换句话说，∠ACD和∠BCD是两条相交直线上的垂直角。

3. 对边平行：菱形的两对边互相平行，即AB║CD且AD║BC。

4. 具有四个等边角：菱形的四个内角均相等，每个角度为90度。

二、判定菱形的方法1. 利用对角线相等判定：如果一个四边形的两条对角线相等，那么它就是一个菱形。

例如：已知一个四边形ABCD，我们可以测量AC和BD的长度，如果AC=BD，那么我们可以确定该四边形是一个菱形。

2. 利用对边平行判定：如果一个四边形的两对边互相平行，那么它就是一个菱形。

例如：已知一个四边形ABCD，我们可以测量AB、BC、CD、DA的长度，并检查相邻边是否平行。

如果AB║CD且AD║BC，那么可以确认该四边形是一个菱形。

3. 利用角度特征判定：如果一个四边形的四个内角均为90度，那么它就是一个菱形。

例如：已知一个四边形ABCD，我们可以测量∠ABC、∠BCD、∠CDA和∠DAB的度数，如果每个角度都等于90度，那么可以断定该四边形是一个菱形。

以上三种方法可以独立或结合使用，来判定一个四边形是否为菱形。

在实际问题中，根据提供的信息，我们可以选择最适合的方法进行判定。

值得注意的是，只满足菱形的一些性质，比如对角线相等，不一定就能判定一个四边形是菱形。

必须满足菱形的所有性质才能确定。

三、菱形的应用菱形在几何学中有很多应用，以下列举几个常见的应用：1. 菱形判断：在解决几何问题时，判定一个四边形是否为菱形可以帮助我们简化推理过程，节省解题时间。

2. 菱形面积计算：菱形的面积计算公式为S=a×b/2，其中a和b分别表示菱形的对角线长度。

菱形的判定及知识点归纳

菱形的断定及知识点归纳
菱形的断定
① 四条边都相等的四边形是菱形。

② 对角线互相垂直且平分的平行四边形是菱形。

③ 一组邻边相等的平行四边形是菱形。

④对角线平分一组对角的平行四边形是菱形。

菱形知识点归纳
1、菱形的定义 :有一组邻边相等的平行四边形叫做菱形。

2、菱形的性质:⑴ 矩形具有平行四边形的一切性质;
⑵ 菱形的四条边都相等;
⑶ 菱形的两条对角线互相垂直，并且每一条对角线平分一组对角。

⑷ 菱形是轴对称图形。

提示:利用菱形的性质可证得线段相等、角相等，它的对角线互相垂直且把菱形分成四个全等的直角三角形，由此又可与勾股定理联络，
可得对角线与边之间的关系，即边长的平方等于对角线一半的平方和。

3、菱形的断定方法:
⑴ 定义:一组邻边相等的平行四边形是菱形。

⑵ 判断方法1:对角线互相垂直的平行四边形是菱形。

⑶ 判断方法2:四条边相等的四边形是菱形。

4、菱形面积的计算:
菱形面积 = 底×高 = 对角线长乘积的一半 S菱形
=1/2×ab(a、b为两条对角线)
归纳:对角线互相垂直的四边形的面积等于对角线长乘积的一半。

希望上面对菱形知识点的总结学习，同学们都能很好的掌握，相信同学们一定能很好的参加考试工作。

初中数学知识点总结:平面直角坐标系
下面是对平面直角坐标系的内容学习，希望同学们很好的掌握下面的内容。

菱形的性质与判定第一课时(菱形的性质)

B
D
(2)菱形ABCD的面积=△ABD的面积+△CBD的面积
=2×△ABD的面积
C
菱形的面积等于两条对角线乘积 1 2 BD AE 的一半 2 1 2 10 12 120 cm 2 . 2

D A
O
C
解得:
B
菱形的周长为20cm ,面积为24cm2
三、课堂小结
定理:菱形的四条边都相等. 定理:菱形的两条对角线互相垂直,并且每条对角线平分一组对角.
结论：菱形是轴对称图形，有2条对称轴，它们互相垂直。
首先它具有平行四边形的一切特征.
特殊的特征：
1、菱形的四条边相等.
思考：菱形的对角线有什么特征呢？
2、菱形的对角线互相垂直。
定理:菱形的四条边都相等.
已知:如图,四边形ABCD是菱形.
求证:AB=BC=CD=DA. 分析:由菱形的定义,利用平行四边形性质可使问题得证. 证明: ∵ 四边形ABCD是菱形, ∴AB=AD,四边形ABCD是平行四边形. ∴AB=CD,AD=BC. ∴ AB=BC=CD=AD. B A D C
O B
C
已知:如图,四边形ABCD是边长为13cm的菱形,其中对角线BD 长10cm. 求:(1).对角线AC的长度; (2).菱形ABCD的面积. 解:(1) ∵四边形ABCD是菱形, A E
∴∠AED=900,
AE
∴AC=2AE=2×12=24(cm).
1 1 DE BD 10 5cm . 2 2 AD 2 DE 2 132 52 12cm .
定理:菱形的两条对角线互相垂直。已知:如图,AC,BD是菱形ABCD的两条对角线,AC,BD相交于点O. 求证: AC⊥BD. 证明: ∵四边形ABCD是菱形, ∴AD=CD,AO=CO. ∵DO=DO, ∴△AOD≌△COD(SSS). ∴∠AOD=∠COD=900. ∴AC⊥BD. A D

九年级数学菱形的性质与判定

第一章特殊平行四边形第一节菱形的性质与判定一、什么是菱形菱形是一组邻边相等的平行四边形叫做菱形. 强调两部分：一是菱形是平行四边形二是菱形一组邻边相等二、菱形是特殊的平行四边形，它具有一般平行四边形的所有性质三、一般平行四边形的性质有：对边相等且互相平行，对角相等，对角线互相平分四、菱形的性质：菱形是轴对称图形，它有2条对称轴，两条对称轴互相垂直。

也就是他的两条对角线互相垂直。

五、菱形的两条定理：菱形的四条边相等菱形的对角线互相垂直。

六、定理：对角线互相垂直的平行四边形是菱形四边相等的四边形是菱形课后练习：1、四边形ABCD是菱形，对角线AC与BD相交于O，AB=5，AO=4，求BD的长。

解答：∵四边形ABCD 是菱形，对角线AC 与BD 相交于O ， ∴AC ⊥BD ，DO=BO ，∵AB=5，AO=4，∴BO=3452222=-=-AO AB∴BD=2BO=2×3=6.2、在菱形ABCD 中，∠BAD=2∠B ，试求出∠B 的度数，并说明△ABC 是等边三角形。

解答：在菱形ABCD 中，∠B+∠BAD=180∘.又∵∠BAD=2∠B ，∴∠B=60∘.∴△ABC 是等边三角形。

3、如图，在菱形ABCD 中，BD=6，AC=8，求菱形的周长。

解答：在菱形ABCD 中，BD=6，AC=8，∴OA=21AC=4,OB=21BD=3，AC ⊥BD ，∴AB=5342222=+=+OB OA∴菱形的周长为：4×5=20.4、已知，如图在菱形ABCD 中，对角线AC 与BD 相交于O ，求证：AC 平分∠BAD 和∠BCD ，BD 平分∠ABC 和∠ADC.解答：证明：∵四边形ABCD 是菱形，∴AD=AB=DC=BC ，∠ADC=∠ABC ，在△ADC 和△ABC 中，∵AD=DC∠ADC=∠ABCAB=BC ，∴△ADC≌△ABC，∴AC平分∠BAD和∠BCD，同理：△DAB≌△DCB，所以BD平分∠ABC和∠ADC.5、如图,在菱形ABCD中,对角线AC与BD交于点O,图中有多少个等腰三角形和直角三角形？解答：∵四边形ABCD是菱形∴AB=AD=BC=DC∴△ABD、△ABC、△ADC、△BCD均是等腰三角形，∵AC⊥BD∴△DOA、△AOB、△COB、△COD均是直角三角形故图中的等腰三角形有：△ABD、△ABC、△ADC、△BCD，共4个；直角三角形有：△DOA、△AOB、△COB、△COD，共4个。

第一讲菱形的性质与判定

第一讲菱形的性质与判定（一）菱形的定义与性质1.菱形的定义:有一组邻边相等的平行四边形叫做菱形.2.菱形的性质:（1）菱形的四条边都相等;（2）菱形的对角线互相垂直平分.并且平分一组对角。

（3）菱形既是中心对称图形，也是轴对称图形，对称轴是两条对角线所在的直线。

（4）菱形的面积计算：①菱形的面积等于底乘高②菱形的面积等于对角线乘积的一半；对角线互相垂直的四边形的面积都可以用两条对角线乘积的一半来进行计算3.菱形具有平行四边形的所有性质,应用菱形的性质可以进行计算和推理.典例分析：知识点1：利用菱形的性质求角的度数例1：如图，在菱形ABCD中，E，F分别是BC，CD上的点，∠B=∠EAF=60°，∠BAE=20°，求∠CEF的度数．知识点2：利用菱形的性质求线段长例2：（1）如图，已知菱形ABCD的对角线AC=8，BD=6，AC与BD相交于点O，求菱形ABCD 的周长与面积．（2）如图，P为菱形ABCD的对角线上一点，PE⊥AB于E，AP=5，AE=4，则点P到边AD 的距离等于_________．例2（2）图例2（3）图（3）如图，四边形ABCD是菱形，BE⊥AD、BF⊥CD，垂足分别为E、F．（1）求证：BE=BF；（2）当菱形ABCD的对角线AC=8，BD=6时，求BE的长．知识点3：利用菱形的对称性求最短距离例3：（1）如图，在周长为12的菱形ABCD中，AE=1，AF=2，若P为对角线BD 上一动点，则EP+FP的最小值为（）A．1B．2C．3D．4例3（1）图例3（2）图（2）如图，在菱形ABCD中，AB=6，∠B=60°，点G是边CD边的中点，点E、F 分别是AG、AD上的两个动点，则EF+ED的最小值是．知识点4：利用菱形的性质求面积例4：如图，菱形ABCD中，E是AB的中点，且DE丄AB，AE=2．求：（1）对角线AC，BD的长；（2）菱形ABCD的面积．知识点5：利用菱形的性质证明例5：（1）已知：如图，菱形ABCD中，E，F分别是CB，CD上的点，且BE=DF．①求证：AE=AF；②若∠B=60°，点E，F分别为BC和CD的中点，求证：△AEF为等边三角形．（2）如图，在菱形ABCD中，P是AB上的一个动点（不与A，B重合），连接DP交对角线AC于E，连接EB．求证：∠APD=∠EBC．（二）菱形的判定判定方法：1、定义法：有一组邻边相等的平行四边形叫做菱形2、对角线：①对角线互相垂直平分的四边形是菱形②对角线互相平分的平行四边形是菱形3、边：四条边都相等的四边形是菱形注：(1)菱形的判断可以从两个基本图形(四边形或平行四边形)考虑,进行证明.(2)菱形的性质定理和菱形的判定定理是互逆定理图文展示：典例分析：知识点6：利用定义判定菱形例6：已知：△ABC中，CD平分∠ACB交AB于D，DE∥AC交BC于E，DF∥BC 交AC于F．求证：四边形DECF是菱形．知识点7：利用“对角线互相垂直的平行四边形是菱形”判定菱形例7：如图:,在平行四边形ABCD中,对角线AC,BD相交于点O,过点O作直线EF⊥BD,分别交AD,BC于点E,F,求证四边形BEDF是菱形.知识点8：利用“四边相等的四边形是菱形”判定菱形例8：如图，在四边形ABCD中，AD=BC，点E、F、G、H分别是AB、CD、AC、BD的中点；求证：四边形EGFH是菱形．（三）菱形的性质与判定的综合应用例9：如图，在四边形ABCD中，AB=AD，CB=CD，E是CD上一点，BE交AC于F，连接DF．（1）证明：∠BAC=∠DAC，∠AFD=∠CFE．（2）若AB∥CD，试证明四边形ABCD是菱形；（3）在（2）的条件下，试确定E点的位置，使得∠EFD=∠BCD，并说明理由．例10：将平行四边形纸片ABCD按如图方式折叠，使点C与A重合，点D落到D′处，折痕为EF．（1）求证：△ABE≌△AD′F；（2）连接CF，判断四边形AECF是什么特殊四边形？证明你的结论．例11：如图，两张宽度相等的纸条叠放在一起，重叠部分构成四边形ABCD．（1）求证：四边形ABCD是菱形；（2）若纸条宽3cm，∠ABC=60°，求四边形ABCD的面积．例12：已知四边形ABCD是菱形，AB=4，∠ABC=60°，∠EAF的两边分别与射线CB，DC相交于点E，F，且∠EAF=60°．（1）如图1，当点E是线段CB的中点时，直接写出线段AE，EF，AF之间的数量关系；（2）如图2，当点E是线段CB上任意一点时（点E不与B、C重合），求证：BE=CF；（3）如图3，当点E在线段CB的延长线上，且∠EAB=15°时，求点F到BC的距离．夯实基础：1.下列性质中，菱形对角线不具有的是（）A．对角线互相垂直B．对角线所在直线是对称轴C．对角线相等D．对角线互相平分2.已知▱ABCD的对角线相交于点O,分别添加下列条件:①AC⊥BD;②AB＝BC;③AC平分∠BAD;④AO＝DO.使得▱ABCD是菱形的条件有()A.1个B.2个C.3个D.4个3.如图，菱形ABCD的周长为8，高AE长为，则AC：BD=（）A．1：2B．1：3C．1：D．1：第3题第4题4.菱形0BCD在平面直角坐标系中的位置如图所示，顶点B（2，0），∠DOB=60°，点P是对角线OC上一个动点，E（0，﹣1），当EP+BP最短时，点P的坐标为．5.在菱形ABCD中，E，F分别是BC，CD上的点，若△AEF是等边三角形，且EF=AB，则∠BAD的度数是（）A．100°B．105° C．110° D．120°6.已知菱形的周长为40cm，两条对角线之比3：4，则菱形面积为（）A．12B．24C．48D．967.菱形ABCD的对角线AC，BD相交于点O，E，F分别是AD，CD边上的中点，连接EF．若EF=，BD=2，则菱形ABCD的周长为．第7题第8题第9题8.如图，四边形ABCD是菱形，O是两条对角线的交点，过O点的三条直线将菱形分成阴影和空白部分．当菱形的两条对角线的长分别为6和8时，则阴影部分的面积为（）A．24 cm2B．20 cm2C．16 cm2D．12 cm29.如图，菱形ABCD中，∠DAB=60°，DF⊥AB于点E，且DF=DC，连结PC，则∠DCF的度数为度．10.如图，菱形ABCD的对角线AC与BD相交于点O，已知AB=13cm，AC=24cm．（1）求：菱形ABCD的面积；（2）如过点D作DE⊥BC，垂足为E，求DE的长．11.如图，已知菱形ABCD的对角线相交于点O，延长AB至点E，使BE=AB，连结CE，若∠E=50°，求∠BAO的大小．12.如图，已知点D在△ABC的BC边上，DE∥AC交AB于E，DF∥AB交AC于F．（1）求证：AE=DF；（2）若AD平分∠BAC，试判断四边形AEDF的形状，并说明理由．13.如图，在四边形ABCF中，∠ACB=90°，点E是AB边的中点，点F恰是点E关于AC所在直线的对称点．（1）证明：四边形CFAE为菱形；（2）连接EF交AC于点O，若BC=10，求线段OF的长．14.在Rt△ABC中，∠BAC=90°，D是BC的中点，E是AD的中点，过点A作AF ∥BC交BE的延长线于点F．（1）求证：△AEF≌△DEB；（2）证明四边形ADCF是菱形；（3）若AC=4，AB=5，求菱形ADCF的面积．15.如图，已知△ABC是等腰三角形，顶角∠BAC=α（α＜60°），D是BC边上的一点，连接AD，线段AD绕点A顺时针旋转α到AE，过点E作BC的平行线，交AB于点F，连接DE，BE，DF．（1）求证：BE=CD；（2）若AD⊥BC，试判断四边形BDFE的形状，并给出证明．16.已知四边形ABCD是边长为2的菱形，∠BAD=60°，对角线AC与BD交于点O，过点O的直线EF交AD于点E，交BC于点F．（1）求证：△AOE≌△COF；（2）若∠EOD=30°，求CE的长．。

菱形的判定与性质

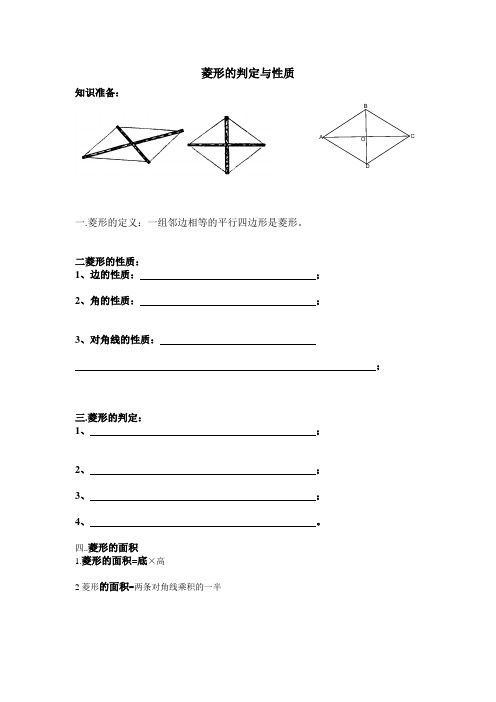
菱形的判定与性质知识准备：一.菱形的定义：一组邻边相等的平行四边形是菱形。

二菱形的性质：1、边的性质：；2、角的性质：；3、对角线的性质：；三.菱形的判定：1、；2、；3、；4、。

四..菱形的面积1.菱形的面积=底×高2菱形的面积=两条对角线乘积的一半ODCBA类别性质判定对称性平行四边形①两组对边分别平行②两组对边分别相等③两组对角分别相等邻角互补④两条对角线互相平分①两组对边分别平行的四边形是平行四边形。

（平行四边形的定义）②两组对边分别相等的四边形是平行四边形。

③一组对边平行且相等的四边形是平行四边形。

④两组对角分别相等的四边形是平行四边形。

⑤对角线互相平分的四边形是平行四边形。

中心对称一．选择题1．如图所示，在平面直角坐标系中，菱形MNPO 的顶点P 的坐标是（3，4），则顶点M 、N 的坐标分别是（） A ．M （5，0），N （8，4） B ．M （4，0），N （8，4） C ．M （5，0），N （7，4） D ．M （4，0），N （7，4）2．菱形的周长为4，一个内角为60°，则较短的对角线长为（）A ．2B ．C ．1D ．3．菱形的周长为8cm ，高为1cm ，则该菱形两邻角度数比为（） A ．3：1 B ．4：1 C ．5：1 D ．6：1 4．如图，菱形ABCD 中，AB=15，∠ADC=120°，则B 、D 两点之间的距离为（）A ．15B ．C ．7.5D ．二．填空题5．已知菱形的两条对角线长分别为2cm ，3cm ，则它的面积是 _________ cm 2．6．如图，菱形ABCD 的对角线AC 、BD 相交于点O ，且AC=8，BD=6，过点O 作OH 丄AB ，垂足为H ，则点0到边AB 的距离OH= _________ ．7．如图，菱形ABCD 的边长是2cm ，E 是AB 的中点，且DE 丄AB ，则菱形ABCD 的面积为 cm 2．矩形中心对称轴对称菱形中心对称轴对称8．如图，在菱形ABCD 中，对角线AC 与BD 相交于点O ，AB=13，AC=10，过点D 作DE ∥AC 交BC 的延长线于点E ，则△BDE 的周长为 _________ ．9.顺次连接矩形ABCD 各边的中点，得到四边形EFGH ，求证:四边形EFGH 是菱形。

菱形的性质与判定

如图，A’B’∥AB，B’C’∥BC， C’A’∥CA，图中有几个平行四边形？将它们表示出来，并说明理由。
解：图中共有3个平行四边形： □ABCB’、□C’BCA、□ABA’C。B ∵A’B’∥AB，B’C’∥BC
C’
A
B’
C A’
∴四边形ABCB’是平行四边形。（2组对边分别平行的四边形是平行四边形）同样可以得到：四边形C’BCA、四边形 ABA’C也是平行四边形。
菱形的判定
1.有一组邻边相等的平行四边形是菱形.
2.四条边相等的四边形是菱形. 3.对角线互相垂直的平行四边形是菱形.
明辨是非
1.对角线互相垂直的四边形是菱形 ⒉对角线互相垂直的平行四边形是菱形．
⒊对角线相等的平行四边形是菱形．
⒋对角线互相垂直平分的四边形是菱形．
检测练习
学校买了四棵树，准备栽在花园里，已经栽了三棵（如图），现在学校希望这四棵树能组成一个平行四边形，你觉得第四棵树应该栽理. 2.能熟练运用定理解题.
自学指导
认真看课本P16-18及P23-24 的内容,理解并熟记菱形的性质和判定. 6分钟后比谁能做对习题.
菱形的性质
菱形既是轴对称图形又是中心对称图形.
菱形的四条边相等
菱形的对角线互相垂直,并且每一条对角线平分一组对角.
如图，在四边形ABCD中， AB∥DC，∠A＝∠C，四边形ABCD是平行四边形吗？为什么？
A
D
B
C
课本P113习题3.4
第1、3题

菱形的性质与判定

菱形的性质菱形的定义：有一组邻边相等的平行四边形是菱形。

菱形的性质:1.对边平行，且四边都相等;2.对角相等;3.对角线互相平分且互相垂直4.菱形既是中心对称图形,又是轴对称图形5 菱形的面积: S 菱形=底×高=2对角线乘积习题 1.一个菱形的周长为8cm,一条对角线长为2 cm.则这个菱形的四个内角的度数＿＿2.菱形具有而平行四边形不一定具有的特征是（）A 、对角线互相平分B 、对边相等且平行C 、对角线平分一组对角D 、对角相等3.在菱形ABCD 中，∠BAD=2∠B ，则∠B= ,△ABC 是三角形，∠ABD 的度数为________ 。

4.已知：菱形ABCD 中，对角线AC 与BD 相交于点O ，且AC=12，BD=16，则菱形ABCD 的面积为，边长为，周长为。

5 如图，菱形ABC 中,AB=BD=2cm,OD CB A求①∠ABC的度数②菱形ABCD的周长6如图,在菱形ABCD中，∠BAD＝2∠B，试说明△ABC是等边三角形。

7如图，在菱形ABCD中，AC与BD相交于点O,AB＝5，OA ＝4，求这一菱形的周长与两条对角线的长度。

菱形的判定菱形的判定方法一组邻边相等的平行四边形是菱形对角线互相垂直的平行四边形是菱形四条边都相等的四边形是菱形习题判断下列说法是否正确：1.有一条对角线平分一组对角的四边形是菱形（）D2.对角线互相垂直，且一条对角线平分一组对角的四边形是菱形（）3.对角线相等且互相平分的四边形是菱形（）4.对角线互相垂直平分的四边形是菱形（）5、已知□ABCD的对角线AC、BD相交于点O,分别添加下列条件：（1）∠ABC=900 （2）AC ⊥BD （3）AB=BC （4）AC平分∠BAD （5）AO=DO 使得四边形ABCD是菱形的条件的序号有__________2 、下列条件中,不能判定四边形ＡＢＣＤ为菱形的是（）．Ａ、AC⊥BD ，AC与BD互相平分Ｂ、AB=BC=CD=DAＣ、AB=BC，AD=CD，且AC ⊥BDＤ、AB=CD，AD=BC，AC ⊥BD3、如图，在□ABCD中，对角线AC、BD相交于点O，AC=6厘米，BD=8厘米，AD=5厘米，则□ ABCD的周长=—————— , □ABCD的面积=————————4：如图，已知AD平分∠BAC，DE//AC，DF//AB，AE=5.（1）判断四边形AEDF的形状？（2）四边形AEDF的周长为多少？5：已知: ABCD的对角线AC的垂直平分线与边AD 、BC分别交于E、F求证:四边形AFCE是菱形。

菱形的判定和性质

菱形的判定和性质
一个菱形是一种四边形，判定一个图形是菱形首先要看它是否是四边形，如果是，再看其形状是否是对称的，即四条边是否是相等，如果都相等，则这个图形就是一个菱形。

菱形性质：菱形的外切圆的半径向内均等地分割菱形，菱形的四个角，每两条边相交形成的两个角都是相等的，所以菱形是一种正三角形；另外，菱形的对角线是一对平行线，并且对角线长度是菱形的四条边长度之和。

菱形所有边都相等，但是菱形是一种非凸多边形（concave polygon），也就是说，菱形边缘凹陷，两个邻接边之间角度大于180度，这是菱形与正多边形、凸多边形最大的区别。

还有一些性质：如果对菱形的对角线进行划分，那么菱形的四边形就会被划分为两个结构一致的三角形；菱形中外切圆的圆心在对角线的中点处，菱形最大内切圆以及最大外接圆的圆心也在对角线的中点处。

菱形具有很多有趣的性质，并且应用在许多方面。

比如，在绘画上，菱形用于定义简洁的对称元素，在棋盘游戏中使用菱形来实现多边形布局，也用于体育项目中的一些比赛线、标识圈范围等。

菱形的性质与判定

菱形性质与判定
一组邻边相等的平行四边形叫做菱形.
菱形有别于平行四边形性质有哪些？
B
A D C
A
B 边
菱形的两组对边分别平行. 菱形的四条边相等.
C
D
菱形的性质
角
菱形的两组对角分别相等,邻角互补. 菱形的两条对角线互相垂直平分. 菱形的每一条对角线都平分一组对角.
对角线
对称性
菱形是轴对称图形.
已知：如图所示的一张矩形纸片ABCD （AD>AB），将纸片折叠一次，使点A与点C重合，再展开，折痕EF交AD边于点E，交BC边于点F，分别连结AF和CE．（1）求证：四边形AFCE是菱形；
已知：如图所示的一张矩形纸片ABCD （AD>AB），将纸片折叠一次，使点A与点C重合，再展开，折痕EF交AD边于点E，交BC边于点F，分别连结AF和CE． 2 （2）若AE=10cm，△ABF的面积为24cm ，求 △ABF的周长；
菱形的面积等于两条对角线乘积的一半.
若用a、b表示菱形的两条对角线，那么菱形的面 A 积为： D
1 S a b 2
O C
B
有关菱形问题可转化为直角三角形或等腰三角形的问题来解决.
菱形的判定？
A
DBBiblioteka C有一组邻边相等的平行四边形是菱形.
菱形的判定
边
四条边都相等的四边形是菱形. 对角线互相垂直的平行四边形是菱形.
求证：四边形EGFC为菱形．
C F E A D G
B
如图，矩形ABCD中，点P是线段AD上一动点，O为BD的中点， PO的延长线交BC于Q. （1）求证： OP=OQ；
（2）若AD=8厘米，AB=6厘米，P从点A出发，以1厘米/秒的速度向D 运动（不与D重合）.设点P运动时间为t秒，请用t表示PD的长；并求t为何值时，四边形PBQD是菱形．

菱形的所有判定定理

菱形的所有判定定理菱形是一种几何形状，它有一些特殊的性质和定理。

在本文中，我们将讨论菱形的所有判定定理，并详细解释它们的意义和应用。

一、菱形的定义定理：菱形是一个四边形，它的所有边长相等。

在一个菱形中，对角线相互垂直且平分对方。

二、菱形的角定理：1. 菱形的内角和定理：菱形的内角和为360度。

2. 菱形的对角线交角定理：菱形的对角线交角为90度。

三、菱形的边定理：1. 菱形的边长定理：菱形的四条边长相等。

2. 菱形的边中点连线定理：菱形的边中点连线相互垂直且平分对角线。

四、菱形的对角线定理：1. 菱形的对角线长度定理：菱形的两条对角线长度相等。

2. 菱形的对角线垂直定理：菱形的对角线相互垂直。

五、菱形的面积定理：菱形的面积等于对角线长度的乘积再除以2。

六、菱形的高定理：菱形的高等于任意一边与对角线的乘积再除以对角线的长度。

七、菱形的中线定理：菱形的对角线中线相等且平行于边。

八、菱形的内切圆定理：菱形的内切圆与菱形的四条边相切。

九、菱形的外接圆定理：菱形的外接圆与菱形的四个顶点相切。

十、菱形的外接圆半径定理：菱形的外接圆半径等于对角线的一半。

以上是菱形的所有判定定理。

这些定理不仅可以帮助我们理解菱形的性质，还可以在解决各种几何问题时提供指导。

通过运用这些定理，我们可以计算菱形的边长、对角线长度、面积和高等参数，进一步推导出其他相关的几何性质。

菱形的判定定理是几何学中的重要内容，它们不仅在理论研究中有着广泛的应用，也在实际生活和工程中发挥着重要的作用。

比如，在建筑设计中，我们经常会遇到需要绘制或计算菱形的情况，而这些判定定理可以帮助我们准确地完成这些任务。

总结起来，菱形的判定定理是菱形几何学中的重要内容，它们描述了菱形的各种性质和特点。

通过运用这些定理，我们可以计算菱形的各种参数，解决各种几何问题。

同时，这些定理也在实际生活和工程中发挥着重要作用。

通过学习和理解这些定理，我们可以更好地理解和应用菱形几何学。

第七讲、菱形的性质和判定

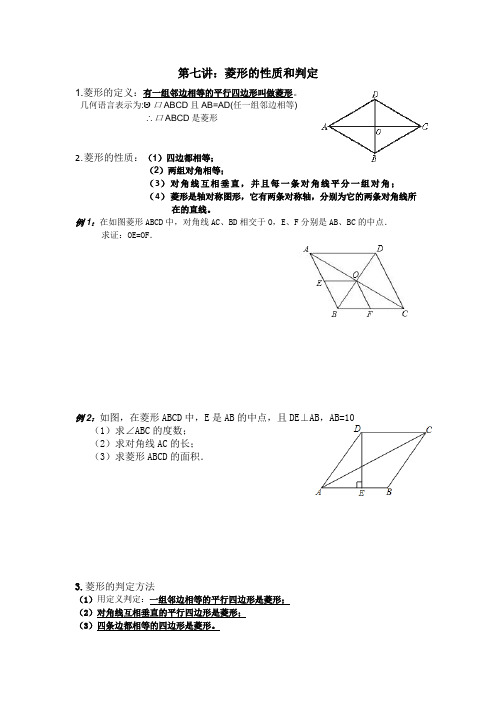
第七讲：菱形的性质和判定1.菱形的定义：有一组邻边相等的平行四边形叫做菱形。

几何语言表示为: 口ABCD且AB=AD(任一组邻边相等)口ABCD是菱形2.菱形的性质：（1）四边都相等；（2）两组对角相等；（3）对角线互相垂直，并且每一条对角线平分一组对角；（4）菱形是轴对称图形，它有两条对称轴，分别为它的两条对角线所在的直线。

例1：在如图菱形ABCD中，对角线AC、BD相交于O，E、F分别是AB、BC的中点．求证：OE=OF．例2：如图，在菱形ABCD中，E是AB的中点，且DE⊥AB，AB=10（1）求∠ABC的度数；（2）求对角线AC的长；（3）求菱形ABCD的面积．3.菱形的判定方法（1）用定义判定：一组邻边相等的平行四边形是菱形；（2）对角线互相垂直的平行四边形是菱形；（3）四条边都相等的四边形是菱形。

例3：如图所示，在△ABC中，∠ACB=90°，AD平分∠BAC交BC于D，CG⊥AB于 G，交AD 于F，DE⊥AB于E，求证：四边形CDEF是菱形。

例4：已知：如图，过平行四边形ABCD的对角线交点O作互相垂直的两条直线EG、FH与平行四边形ABCD各边分别相交于点E、F、G、H．求证：四边形EFGH是菱形例5：如图，在Rt△ABC中，∠ACB=90°，∠BAC=60°，DE垂直平分BC，垂足为D，交AB于点E．又点F在DE的延长线上，且AF=CE．求证：四边形ACEF是菱形．例6：如图所示，在矩形ABCD中，AB=4cm，BC=8cm、点P从点D出发向点A运动，同时点Q从点B出发向点C运动，点P、Q的速度都是1cm/s．（1）在运动过程中，四边形AQCP可能是菱形吗？如果可能，那么经过多少秒后，四边形AQCP是菱形？（2）分别求出菱形AQCP的周长、面积．例7（真题2014-2015期中）：如图,在菱形ABCD中,AB=4cm,∠ADC=120∘,点E. F同时由A. C两点出发,分别沿AB、CB方向向点B匀速移动(到点B为止)，点E的速度为1cm/s，点F的速度为2cm/s，经过t秒△DEF为等边三角形，求t的值例8（真题2014-2015期中）准备一张矩形纸片，按如图操作：将△ABE沿BE翻折，使点A落在对角线BD上的M点，将△CDF沿DF翻折，使点C落在对角线BD上的N点。

第1讲菱形的性质与判定(解析版)

第1讲菱形的性质与判定 1.理解掌握菱形的概念性质及判定定理2.会用菱形的有关知识进行证明，会计算菱形的面积知识点01 菱形的性质（1）菱形的定义：有一组邻边相等的平行四边形叫做菱形．（2）菱形的性质①菱形具有平行四边形的一切性质；②菱形的四条边都相等；③菱形的两条对角线互相垂直，并且每一条对角线平分一组对角；④菱形是轴对称图形，它有2条对称轴，分别是两条对角线所在直线．（3）菱形的面积计算①利用平行四边形的面积公式． ②菱形面积12ab ．（a 、b 是两条对角线的长度）【知识拓展1】菱形的两条对角线长的比是32，面积是cm 12，则它的对角线的长分别是 cm ， cm ． (★)解答方法：∵ 设菱形的两条对角线的长分别为厘米厘米x x 3,2，∴ 122132=⋅⋅=x x S 菱形，∴ 解得舍去）(2,221-==x x ， ∴ 对角线的长分别为cm cm 6,4。

答案：cm cm 6,4。

【总结方法】菱形的面积等于对角线乘积的一半。

【即学即练】两对角线分别是6cm 和8cm 的菱形面积是 _________ cm 2，周长是 _________ cm ． (★) 解答方法：菱形面积是224286cm =÷⨯；∵菱形的对角线互相垂直平分，根据勾股定理可得，边长为5cm ，则周长是20cm ．知识精讲目标导航故答案为24，20．解答：24,20【知识拓展2】菱形的周长是它的高的8倍，则菱形较小的一个角为（）(★★) A．60°B．45°C．30°D．15°解答方法：菱形的周长为边长的4倍，又∵菱形周长为高的8倍，∴AB=2AE，∵△ABE为直角三角形，∴∠ABC=30°．故选 C．答案：C【总结方法】本题考查了菱形各边长相等的性质，考查了直角三角形中的特殊角，本题中根据特殊角求得∠ABC=30°是解题的关键．【即学即练1】菱形的一条对角线与边长相等，则菱形中较小的内角是（）(★★) A．60°B．15°C．30°D．90°解答方法：因为菱形的一条对角线与边长相等，所以该对角线和菱形的两边组成的是等边三角形，可得该菱形较小内角的度数是60°．解答：A【即学即练2】如果菱形的周长等于一条对角线长的4倍，那么这个菱形较小的一个内角等于度．(★★)解答方法：∵菱形的周长等于一条对角线长的4倍，∴AB=BD=AD，∴△ABD是等边三角形，∴∠A=60°．即这个菱形较小的一个内角等于60°．解答：60【知识拓展3】已知：如图，四边形ABCD是菱形，F是AB上一点，DF交AC于E．求证：∠AFD=∠CBE． (★★)答案：证明：∵ 四边形ABCD 是菱形，∴ BCD CA CD CB ∠=平分,．∴ CE CE DCE BCE =∠=∠又.,∴ △BCE ≌△COB （SAS ）．∴ ∠CBE=∠CDE ．∵ 在菱形ABCD 中，AB ∥CD ， ∴∠AFD=∠FDC∴ ∠AFD=∠CBE ．【总结方法】通过菱形的基本性质可以得到三角形全等，进而推出对应角相等，然后利用平行内错角相等进行转化即可得到要证明的结论。

菱形的性质与判定.教师版

菱形的性质及判断中考要求知识点 A 要求B要求Ｃ要求菱形会辨别菱形掌握菱形的观点、性质和判断，会用菱形的性质及会用菱形的知识解决有关判断解决简单问题问题知识点睛1．菱形的定义：有一组邻边相等的平行四边形叫做菱形．2．菱形的性质菱形是特别的平行四边形，它拥有平行四边形的全部性质，?还拥有自己独到的性质：① 边的性质：对边平行且四边相等．② 角的性质：邻角互补，对角相等．③ 对角线性质：对角线相互垂直均分且每条对角线均分一组对角．④ 对称性：菱形是中心对称图形，也是轴对称图形．菱形的面积等于底乘以高，等于对角线乘积的一半．评论：其实只需四边形的对角线相互垂直，其面积就等于对角线乘积的一半．3．菱形的判断判断① ：一组邻边相等的平行四边形是菱形．判断② ：对角线相互垂直的平行四边形是菱形．判断③ ：四边相等的四边形是菱形．4．三角形的中位线中位线：连结三角形两边的中点所得的线段叫做三角形的中位线．也能够过三角形一边的中点作平行于三角形此外一边交于第三边所得的线段也是中位线．以上是中位线的两种作法，第一种能够直接用中位线的性质，第二种需要说明原因为何是中位线，再用中位线的性质．定理：三角形的中位线平行第三边且长度等于第三边的一半．重、难点要点是菱形的性质及判断定理。

菱形是在平行四边形的前提下定义的，第一她是平行四边形，但它是特别的平行四边形，特别之处就是“有一组邻边相等”，因此就增添了一些特别的性质和不一样于平行四边形的判断方法。

菱形的这些性质和判断定理即是平行四边形性质与判断的持续，又是此后要学习的正方形的基础。

难点是菱形性质的灵巧应用。

因为菱形是特别的平行四边形，所以它不只拥有平行四边形的性质，同时还拥有自己独到的性质。

假如获取一个平行四边形是菱形，就能够获取很多对于边、角、对角线的条件，在实质解题中，应当应用哪些条件，如何应用这些条件，经常让很多学生惊慌失措，教师在教课过程中应赐予足够重视。

例题精讲板块一、菱形的性质【例 1】菱形的两条对角线将菱形分红全等三角形的对数为【考点】菱形的性质及判断【题型】填空【难度】 2 星【要点词】【分析】依据菱形的性质可知：共有8对【答案】 8【例 2】在平面上，一个菱形绕它的中心旋转，使它和本来的菱形重合，那么旋转的角度起码是【考点】菱形的性质及判断【题型】填空【难度】 2 星【要点词】【分析】依据菱形的性质可知：应当旋转起码180【答案】 180【例 3】如图 2，一活动菱形衣架中，菱形的边长均为16cm 若墙上钉子间的距离AB BC 16cm ，则1度．【考点】菱形的性质及判断【题型】填空【难度】 2 星【要点词】 2009 年，中考【分析】由题意可知：组成三角形为等边三角形【答案】 120A 60，E、F分别是AB 、AD 的中点，若EF 2 ，则菱形ABCD 【例 4】如图，在菱形ABCD 中，的边长是 ______．AE FB DC【考点】菱形的性质及判断【要点词】 2009 年，中考【分析】省略【答案】 4【例 5】如图，E是菱形ABCD的边AD的中点，EF AC于 H ，交 CB的延伸线于 F ，交 AB于 P，证明： AB 与 EF 相互均分．DEHA CPBF【考点】菱形的性质及判断，平行四边形的性质和判断【题型】解答【难度】 3 星【要点词】【分析】省略【答案】连结 BD 、 AF 、 EB∵菱形 ABCD 中 BD AC，EF AC，∴BD∥EF∵ AD ∥ FC ，∴四边形 BDEF 是平行四边形，∴ ED FB∵AE ED，∴ AE FB又∵ AE ∥ FB ，∴四边形 AFBE 是平行四边形∴ AB 与 EF 相互均分【例 6】如图长为1 所示，菱形ABCD 中，对角线24 ，则 OH 的长等于AC 、．BD 订交于点O ，H为 AD 边中点，菱形ABCD 的周【考点】菱形的性质及判断【题型】填空【难度】 2 星【要点词】 2009 年，中考【分析】省略【答案】 3【例 7】如图，已知菱形ABCD 的对角线AC8cm ，BD4cm ，DE BC于点E ，则DE的长为【考点】菱形的性质及判断【题型】填空【难度】 2 星【要点词】【分析】省略【答案】8 5cm 5【例 8】菱形周长为52cm ，一条对角线长为10cm ，则其面积为．【考点】菱形的性质及判断【要点词】【分析】菱形的边长为52 4 13 cm ，由勾股数和菱形对角线的性质得另一对角线长为24 cm ，故面积为 120 cm2【答案】 120【例 9】菱形的周长为20cm ，两邻角度数之比为2:1 ，则菱形较短的对角线的长度为【考点】菱形的性质及判断【题型】填空【难度】 2 星【要点词】【分析】省略【答案】 5【例 10】如图 2，在菱形ABCD 中， AC 6 ， BD 8 ，则菱形的边长为（）A．5B．10C．6D．8【考点】菱形的性质及判断【题型】选择【难度】 2 星【要点词】 2009 年，江津中考【分析】由菱形的对角线相互垂直均分及勾股数可知选A【答案】 A【例 11】如图 3，在菱形ABCD中， A 110 ， E 、 F 分别是边 AB 和 BC 的中点， EP CD 于点 P ，则FPC（）A．35B．45C．50D．55【考点】菱形的性质及判断【题型】选择【难度】 2 星【要点词】 2009 年，市中考【分析】省略【答案】 D【例 12】如图，把一个长方形的纸片对折两次，而后剪下一个角，为了获取一个锐角为60 的菱形，剪口与折痕所成的角的度数应为（）A．15或30B．30或45C．45或60D．30或60【考点】菱形的性质及判断【题型】选择【难度】 2 星【要点词】 2009 年，市中考【分析】省略【答案】 D【例 13】菱形ABCD中，E、F分别是BC、CD的中点，且AE BC ，AF CD ，那么EAF 等于．【考点】菱形的性质及判断【题型】填空【难度】 2 星【要点词】【分析】省略【答案】 60【例 14】已知菱形的一个角为60 ，一条对角线的长为 2 3 ，则另一条对角线的长为________．【考点】菱形的性质及判断【题型】填空【难度】 2 星【要点词】 2009 年，中考【分析】省略【答案】 2或 6【例 15】如图，将一个长为10cm ，宽为 8cm 的矩形纸片对折两次后，沿所得矩形两邻边中点的连线（虚线）剪下，再翻开，获取的菱形的面积为（）A． 10cm2222B ． 20cm C． 40cm D． 80cm【考点】菱形的性质及判断【题型】选择【难度】 3 星【要点词】 2009 年，市中考【分析】省略【答案】 A【例 16】已知菱形ABCD的两条对角线AC ，BD 的乘积等于菱形的一条边长的平方，则菱形的一个钝角的大小是【考点】菱形的性质及判断【题型】填空【难度】 4 星【要点词】希望杯邀请赛【分析】如图，过点 A 作 AE BC于 E，则1AC BD BC AE ，又 AC BD AB2，得12 30 ，BAD 150AEAB， ABC2ABDEC【答案】 150【例 17】如图，菱形花坛ABCD 的周长为 20m ，ABC 60 ，?沿着菱形的对角线修筑了两条小道AC 和BD ，求两条小道的长和花坛的面积．【考点】菱形的性质及判断【题型】解答【难度】 3 星【要点词】【分析】∵四边形 ABCD 是菱形∴ABBCCDDA5∵ABC 60∴ABC 和 ADC 都是等边三角形∴AC 5又∵ AC BD在Rt ABO 和Rt ADO中可得5 3BO DO2∴BD 531253∴ S ABCD AC BD22评论：角为 60 和 120 的菱形学生一定掌握，这是考试的热门模型．【答案】看法析【例 18】如图，在菱形ABCD中， AB 4a ，E 在BC上， BE 2a ， BAD 120 ，P 点在BD上，则PE PC 的最小值为A DPB E C【考点】菱形的性质及判断【题型】填空【难度】 3 星【要点词】【分析】A，C 对于BD对称，连AE 交 BD 于 P ，且AE BC ， BAE2230 ，PE PC AE4a2a2 3a 为最小值【答案】 2 3a【例 19】已知，菱形ABCD中，E、F分别是BC、CD上的点，若AE AF EF AB ，求 C 的度数．【考点】菱形的性质及判断【题型】解答【难度】 4 星【要点词】【分析】∵ AE AB∴BAEB同理D AFD∵四边形 ABCD 是菱形∴ AD∥BC， B D， BAD C ，∴AEB AFD∵B D∴BAE DAF∵DE EF AF ，∴△AEF 是等边三角形，∴EAF 60设BAE x ，则BAD602x∵ABE ABE BAE180，∴ ABE90x2∵AD∥BC ，∴B BAD 180 ，∴90x60 2x1802∴ x 20 ∴ C BAD 60 2x 100【答案】 100【例 20】已知，菱形ABCD中，E、F分别是BC、CD上的点，且B EAF 60 ，BAE 18 ．求：CEF 的度数．【考点】菱形的性质及判断【题型】解答【难度】 4 星【要点词】【分析】连结AC ，∵四边形 ABCD 为菱形∴AB BC CD AD∴△ABC 和△ ACD 为等边三角形∴ AB AC， B ACD BAC 60∵EAF 60 ∴BAE CAF∴△ ABE ≌△ACF ∴AE AF∵EAF 60∴△AEF 为等边三角形∴AEF 60∵AEC B BAE AEF CEF∴CEF 18剖析：在矩形、菱形的定理题中，有时也常连对角线，把四边形问题转变为三角形问题．【答案】 18板块二、菱形的判断【例 21】如图，假如要使平行四边形是．ABCD 成为一个菱形，需要增添一个条件，那么你增添的条件【考点】菱形的性质及判断【题型】填空【难度】 2 星【要点词】 2007 年，【分析】 AB AD，AC 【答案】 AB AD，AC BD 等；BD【例 22】如图，在ABC 中， BD 均分ABC ， BD 的中垂线交AB 于点 E ，交 BC 于点 F ，求证：四边形BEDF 是菱形AE DB FC 【考点】菱形的性质及判断【题型】解答【难度】 3 星【要点词】【分析】省略【答案】∵EF 是 BD 的中垂线∴ BE DE ，BF DF ，∴DBE BDE∵EBD DBF∴DBF EDB ，所以BC∥DE同理 AB∥ DF所以四边形BEDF 是菱形【例 23】如图，在ABC中，AB AC ，D 是 BC 的中点，连结 AD ，在 AD 的延伸线上取一点E，连结 BE，CE ．当 AE 与 AD 知足什么数目关系时，四边形ABEC 是菱形？并说明原因．【考点】菱形的性质及判断【题型】解答【难度】 3 星【要点词】 2009 年，中考【分析】当 AE 2AD （或 AD DE或DE 1AE ）时，四边形ABEC是菱形2原因以下：∵ AE 2AD，∴ AD DE又点 D为 BC中点，∴ BD CD∴四边形 ABEC为平行四形边∵AB AC∴四边形 ABEC为菱形【答案】看法析【例 24】已知：如图，平行四边形ABCD 的对角线 AC 的垂直均分线与边AD 、 BC 分别订交于E、F.求证：四边形AFCE 是菱形.【考点】菱形的性质及判断【题型】解答【难度】 3 星【要点词】 2006 年，中考【分析】省略【答案】∵ EF 垂直均分 AC ，∴EF AC,AO CO .∴AOE COF90o .又∵ ABCD 平行四边形，∴EAO FCO .∴AOE ≌ COF .∴OE OF.∴四边形 AECF 是平行四边形.又由 AC EF 可知，四边形AECF 是菱形.【例 25】如图，在梯形纸片ABCD 中，AD 上的点 C 处，折痕 DE 交AD//BC， ADBC 于点 E ，连结CD ，将纸片沿过点C E .求证：四边形D的直线折叠，使点CDC E 是菱形．C 落在【考点】菱形的性质及判断【题型】解答【难度】 3 星【要点词】 2007 年，双柏【分析】省略【答案】依据题意可知CDE C'DE则 CDC'D，C'DECDE，CEC'E .∵AD//BC，∴ C DE CDE .∴CDE CED ，∴CD CE.∴CD CD CE CE，∴四边形 CDC E 为菱形.【例 26】如图，E是菱形ABCD的边AD的中点，EF AC于 H ，交CB的延伸线于 F ，交 AB于P，证明： AB 与 EF 相互均分A E D A E DP PF B C F B C【考点】菱形的性质及判断，平行四边形的性质和判断【题型】解答【难度】 3 星【要点词】【分析】省略【答案】连结BD ，AF ，EB ，因为菱形ABCD 中BD AC ，又因为EF AC，所以BD ∥ EF ，因为AD ∥ FC ，所以四边形从而 AE∥FB， AEBDEF 是平行四边形，可得ED FB ，因为FB ，所以四边形AFBE 是平行四边形，所以AE ED ，所以 AEAB 与 EF 相互均分FB ，【例 27】已知：如图，在平行四边形点 C 重合，得GFC ．若ABCD 中，B 60，当AE 是 BC 边上的高，将ABE 沿 BC 方向平移，使点 E 与AB 与 BC 知足什么数目关系时，四边形ABFG 是菱形？证明你的结论．【考点】菱形的性质及判断【题型】解答【难度】 3 星【要点词】 2009 年，市【分析】省略【答案】当BC 3 AB 时，四边形ABFC 是菱形．2∵AB∥GF ， AG∥BF∴四边形 ABFG 是平行四边形∵Rt ABE 中， B 60∴BAE 30∴ BE 1AB 2∵ BE CF，BC 3AB 2∴ EF 1AB 2∴ AB BF∴四边形 ABFG 是菱形．【例 28】如图，在ABC中，AB AC ，M 是 BC 的中点．分别作 MD AB于D，ME AC于 E ，DF AC 于 F ， EG AB于 G ． DF、EG 订交于点 P ．求证：四边形DMEP 是菱形．【考点】菱形的性质及判断【题型】解答【难度】 3 星【要点词】【分析】省略【答案】∵ MD AB， EG AB．∴ MD∥ EG ，同理 ME ∥ DF ，∴四边形 MFPD 是平行四边形∵ AB AC，∴B C∵ BM MC ，BDM CEM 90o，∴BDM≌CEM∴ DM EM ，∴四边形 DMEP 是菱形【例 29】如图，ABC中，ACB90，AD 是BAC 的均分线，交 BC 于 D ，CH 是 AB 边上的高，交 AD 于 F ， DE AB于 E ，求证：四边形CDEF 是菱形．【考点】菱形的性质及判断【题型】解答【难度】 3 星【要点词】【分析】省略【答案】∵ CH AB，∴ HAF AFH90∵ACB90 ，∴CAD ADC90∵AD 均分CAB ，∴CAD HAF ，∴ AFHCDF∵AFH CFD ，∴CDF CFD ，∴ CF CD∵AD均分CAB ， DC AC，DE AB∴ CD DE ，∴ CF DE又∵ CH AB， DE AB∴ CF ∥ DE ，故四边形ABCD 是平行四边形∵CD DE ，∴ 四边形 ABCD 是菱形【例 30】如图，M是矩形ABCD的随意一点，将MAB 沿 AD 方向平移，使AB 与 DC 重合，点 M 挪动到点 M '的地点⑴画出平移后的三角形；⑵连结 MD ，MC ，MM ' ，试说明四边形MDM 'C 的对角线相互垂直，且长度分别等于AB，AD 的长；⑶当 M 在矩形的什么地点时，在上述变换下，四边形MDM 'C 是菱形？为何？A DM'MB C【考点】菱形的性质及判断【题型】解答【难度】 3 星【要点词】【分析】省略【答案】⑴如图，DCM ' 就是所要作的三角形⑵因为 AM 平移到 DM ' ，所以 AM ∥ DM ' 且 AM DM ' ，四边形 DAMM ' 是平行四边形，所以AD ∥ MM ' ，矩形 ABCD 中， AD CD ，所以 MM ' CD ，又因为 AD MM ' ， CD AB ，所以四边形 MDM 'C 的对角线相互垂直，且长度分别等于AB，AD 的长⑶当点 M 是AC，BD的交点时，四边形MDM 'C 是菱形，原因：如图，矩形ABCD 中，AM BM MC MD ，又因为AM D 'M ，BM CM ' ，可得MD MC CM ' DM ' ，所以四边形 MDM 'C 是菱形【例 31】如图，ACD 、⑴按序连结 A、的条件．⑵当BAC为【考点】菱形的性质及判断【题型】解答【难度】 3 星ABE 、BCF 均为直线 BC 同侧的等边三角形．已知AB AC ．D 、 F 、E 四点所组成的图形有哪几类？直接写出组成图形的种类和相应度时，四边形ADFE 为正方形．【要点词】 2008 年，市中考改编【分析】省略【答案】⑴ 组成的图形有两类，一类是菱形，一类是线段．当图形为菱形时，∠ BAC≠60°（或 A 与 F 不重合、△ ABC 不为正三角形）（若写出图形为平行四边形时，不给分）当图形为线段时，∠ BAC = 60°（或A与F重合、△ ABC为正三角形）．⑵150 ．三、与菱形有关的几何综合题【例 32】已知等腰△ABC中，AB AC，AD均分BAC交BC于D点，在线段AD上任取一点P（A点除外），过 P 点作 EF∥ AB，分别交 AC 、 BC于 E 、 F 点，作 PM ∥ AC，交 AB于 M 点，连结ME.⑴求证四边形AEPM 为菱形⑵当 P 点在哪处时，菱形AEPM 的面积为四边形EFBM 面积的一半？【考点】菱形的性质及判断【题型】解答【难度】 3 星【要点词】【分析】省略【答案】⑴∵ PM ∥ AC ，EF ∥ AB∴四边形 AEPM 为平行四边形∵AB AC ， AD 均分 CAB ∴CAD BAD∵ AD BC ，BAD EPA∴CAD EPA∵EA EP∴四边形 AEPM 为菱形⑵当 P 为 EF 中点时，S菱形AEPM∵四边形 AEPM 为菱形，∴∵AD BC ∴EM∥BC1S四边形EFBM 2AD EM又 EF∥ AB∴四边形 EFBM 为平行四边形【例 33】问题：如图1，在菱形ABCD 和菱形BEFG 中，点A ，B ，E 在同一条直线上， P 是线段DF的中点，连结PG ，PC．若ABCBEF60，研究PG 与 PC 的地点关系及PG的值．小聪同学的思路是：延伸GP 交DC 于点HPC，结构全等三角形，经过推理使问题获取解决．请你参照小聪同学的思路，研究并解决以下问题： ⑴ 写出上边问题中线段PG 与 PC 的地点关系及PG的值； ⑵ 将图 1 中的菱形 BEFG 绕点 PC B 顺时针旋转，使菱形BEFG 的对角线 BF 恰巧与菱形ABCD 的边在同一条直线上，原问题中的其余条件不变（如图2）．你在⑴中获取的两个结论能否发生变化？写出你的猜想并加以证明．⑶若图1中 ABC BEF 2 090 ，将菱形 BEFG 绕点 B 顺时针旋转随意角度，原问题中的其余条件不变，求PG 的值（用含的式子表示）．PC【考点】菱形的性质及判断，全等三角形的性质和判断，旋转的性质【题型】解答【难度】 5 星【要点词】 2008 年，中考【分析】省略【答案】 ⑴ 线段PG 与 PC 的地点关系是PGPC ；PG3 ．PC⑵ 猜想： ⑴ 中的结论没有发生变化．证明：如图，延伸 GP 交 AD 于点 ∵ P 是线段 DF 的中点，∴ FP DP ．H，连结CH ，CG ．由题意可知 AD ∥ FG ． ∴ GFP HDP ．又∵ GPF HPD ，∴ GFP ≌ HDP ，∴ GP HP ， GF HD ． ∵ 四边形 ABCD 是菱形， ∴ CD CB ， HDC由 ABC BEF 60 ，且菱形 BEFG 的对角线ABC 60 ． BF 恰巧与菱形 ABCD 的边AB 在同一条直线上，可得 GBC 60 ． ∴ HDC GBC ．∵ 四边形 BEFG 是菱形， ∴ GF GB ，∴ HD GB ．∴ HDC ≌ GBC ，∴ CHCG ， DCH BCG ． ∴ DCHHCB BCG HCB 120 ，即 HCG 120 ． ∵ CH CG ， PH PG ， ∴ PG PC ， GCP HCP 60 ．∴PG3．PC⑶ PGtan 90．证明过程略． PC【评论】本题是一道研究性的几何综合题，本题的题干是以阅读资料的形式体现，从而降低了题目的难度，本题应当是在 05 年中考压轴题的基础上改良而来的．四、中位线与平行四边形【例 34】按序连结面积为20 的矩形四边中点获取一个四边形，再按序连结新四边形四边中点获取一个，其面积为．【考点】三角形的中位线【题型】填空【难度】 3 星【要点词】【分析】原因：由中位线得EF FG1GH HE AD 即可．【答案】 AD BC ．2【例 35】如图，在四边形ABCD 中， AB CD， E、F 、 G、H 分别是 AB、BD、CD、 AC的中点，要使四边形 EFGH 是菱形，四边形ABCD还知足的一个条件是，并说明原因．【考点】菱形的性质及判断，三角形的中位线【题型】填空【难度】 3 星【要点词】 2009 年，模拟【分析】原因：由中位线得EF FG GH 1HE AD 即可．2【答案】 AD BC ．【例 36】在四边形ABCD中，AB CD ， P ，Q分别是 AD 、 BC 的中点， M ， N 分别是对角线AC ， BD 中点，证明：PQ 与MN相互垂直．【考点】菱形的性质及判断，三角形的中位线【题型】解答【难度】 4 星【要点词】【分析】连结PN , NQ , MQ , PM ．证明PNQM为菱形．【答案】看法析【例 37】四边形ABCD中，R、P分别是BC、CD上的点，E、F分别是AP、RP的中点，当点P在CD 上从 C 向 D 挪动而点 R 不动时，那么以下结论建立的是（）A．线段B．线段C．线段D．线段EF 的长渐渐增大EF 的长渐渐减小EF 的长不变EF 的长与点 P 的地点有关【考点】三角形的中位线【题型】选择【难度】 4 星【要点词】【分析】连结AR ，利用三角形的中位线可得EF 1AR 与点P没关．2【答案】 C【例 38】如图，ABC 中， AD 是BAC 的均分线，CE AD 于 E ， M 为 BC 的中点，AB 14cm ，AC 10cm ，则 ME 的长为．AEB M D C【考点】三角形的中位线【题型】填空【难度】 3 星【要点词】【分析】延伸CE 交 AB 于点 N ．利用中位线的性质和直角三角形斜边中线可得14102 cm ．2【答案】 2【例 39】如图，四边形ABCD中，AB CD ，E，F分别是BC，AD的中点，连结 EF 并延伸，分别交BA，CD 的延伸线于点 G，H ，求证：BGE CHEH HG GDDA F A FPBE C BEC【考点】三角形的中位线【题型】解答【难度】 4 星【要点词】【分析】省略【答案】连结 BD ，取 BD 中点 P ，连结PE，PF，由条件易得PE，PF分别是BDC ， DBA 的中位线，所以 PE∥DC，PF∥BA ，且11，因为AB CD，所以PE PF ，所以PE DC ，PF BA22PEF PFE ，由 PE∥DC 可得： PEF CHE，同理可得 PFE BGE，所以BGE CHE【例 40】如图，已知BE、CF分别为ABC 中B、 C 的均分线， AM BE于M，AN CF于N，求证： MN ∥ BC．AFEN MB C【考点】三角形的中位线【题型】解答【难度】 4 星【要点词】【分析】延伸 AM 、 AN 交 BC 于点 Q 、 R ．由等腰三角形三线合一可得AMQM 、ANRN再由三角形中位线可得MN ∥BC ．【答案】看法析【例 41】如图，四边形ABCD 中， E ，F 分别是边 AB ，CD 的中点，则 AD ，BC 和 EF 的关系是（）A ． AD BC 2EFB ． AD BC ≥ 2EF C ． ADBC 2EFD ． ADBC ≤ 2EFFCFCDDPAEBA EB【考点】三角形的中位线【题型】选择【难度】 3 星【要点词】【分析】连结 BD ，取 BD 的中点 P ，连结 FP ，EP ，由三角形的中位线可知选 B 【答案】 B【例 42】已知以下图，E 、F 、G 、H 分别是四边形 ABCD 的四边的中点，求证：四边形 EFGH 是平行四边形．【考点】平行四边形的性质和判断，三角形的中位线【题型】解答【难度】 3 星【要点词】【分析】连结∵ HAC ．、G 分别为 AD 、 DC 中点∴ HG 1AC ，HG ∥ AC2 又∵ E 、 F 分别为 AB 、BC 中点∴ EF 1AC ，EF ∥AC ，∴ HGEF ，HG ∥EF2∴四边形 EFGH 为平行四边形【答案】看法析【例 43】如图，在四边形 ABCD 中， E 为 AB 上一点， ADE 和 BCE 都是等边三角形， AB 、 BC 、 CD 、DA 的中点分别为 P 、 Q 、 M 、 N ，证明四边形 PQMN 为平行四边形且PQ PN ．【考点】平行四边形的性质和判断，三角形的中位线【题型】解答【难度】 4 星【要点词】 2009 年，中考【分析】如图，连结AC、BD．∵ PQ为ABC 的中位线1∴PQ∥AC且PQ AC21同理 MN ∥ AC且MN AC2∴MN ∥PQ且 MN PQ∴四边形 PQMN 为平行四边形．在 AEC和 DEB中AE DE ， EC EB ,AED 60CEB即AEC DEB∴AEC ≌ DEB∴AC BD11∴PQ AC BD PN.22【答案】看法析【例 44】如图，四边形ABCD中， AB CD ，E ，F ，G ，H 分别是 AD ，BC ，BD，AC 的中点，求证： EF ，GH 相互垂直均分A ED A EDG H G HB FC B F C 【考点】菱形的性质及判断，三角形的中位线【题型】解答【难度】 3 星【要点词】【分析】连结 EG，GF，FH，HE ，依据题意， EG，HF分别是DAB，CAB 的中位线，所以1GF EH 1CD ，所以 EG HF GF EH，EG HF AB ，同理可证：CD ，因为AB22则四边形 EGFH 是菱形，所以EF ，GH 相互垂直【答案】看法析【例 45】ABC 的三条中线分别为AD 、 BE 、 CF ， H 为 BC 边外一点，且BHCF 为平行四边形，求证：AD∥EH ．【考点】平行四边形的性质和判断，三角形的中位线【题型】解答【难度】 4 星【要点词】【分析】本题解法好多，仅供两种解法参照．方法一：连结DE 、 DH ．（如图1）∵四边形 BHCF 为平行四边形∴CH BF AF且CH∥AF1由中位线可得DE AB AF2∴CH DE∴四边形 DECH 为平行四边形 ∴DH ∥CE 且 DH CE AE ∴四边形 DHEA 为平行四边形∴ AD ∥ EH方法二：连结 DE ．（如图 2）经过中位线和平行四边的性质可得 DE HC ，∴ AEDAB ∥DE ∥HCECH又∵AE EC明显 ADE ≌ EHC ∴ DAE HEC∴ AD ∥ EH【答案】看法析【例 46】在平行四边形 ABCD 的对角线 BD 上取一点 E ，使 BE1DE ，连结 AE 并延伸与 DC 的延伸线交于F ，则 CF 2AB ．3【考点】三角形的中位线【题型】解答【难度】 5 星【要点词】【分析】法 1：如图 2，取 BD 之中点 O ，由 O 引OM ∥AF 交 DF 于 M ，再由 C 引CG ∥FE 交BD 于 G ．∵ AB CD ， ABE CDG ， BAE DCG ， ∴ ABE ≌ CDG ， BE DG ，则 O 为 EG 的中点， ∴ EO OG ．又∵ DGBE1 ，DE3∴EO1DE ，OG3即G 、 O 是 DE 的三均分点． ∵ CG ∥OM ∥ AF ，∴ C 、 M 是 DF 的三均分点，有 CF 2CD ．而 CD AB ，∴ CF 2AB ．法 2：如图 3，连结 AC 交 BD 于 O ，则 O 为 AC 、 BD 的中点，取 AF 的中点 R ，连结 AC 交 BD于 O ，则 O 为 AC 、 BD 的中点，取 AF 的中点 R ，连结 OR ，则 OR ∥ 1CF ．2∵ OR ∥CD ∥ AB ，∴ ABE ROE ， BAE ORE ．又∵ BEOE OD ，BE11 DE(OE OD)，3 3由此可得 BE1 1OD ，OEDE ，23∴ BE OE ， ABE ≌ ROE ，∴ AB OR ．即 AB OR 12AB ． CF ，∴ CF 2法 3：如图1，∵ AB ∥ DF ，∴AB BE 1，DF DE3即 DF 3AB．又∵ AB CD，∴CF DF CD 3AB AB，即 CF2AB．【答案】看法析【例 47】如图，ABCFH 交于点 D 中， E、F 分别是 AB、BC的中点，．求证：四边形ABCD 是平行四边形．G 、 H是AC 的三均分点，连结并延伸EG 、A DGEHB F C【考点】平行四边形的性质和判断，三角形的中位线【题型】解答【难度】 4 星【要点词】【分析】连结BG 、 BH 、 BD ，设 BD 与 AC 订交与点 O∵ E、 F 分别是 AB、 BC的中点，∴ EG∥ BH ，同理 FH ∥ BG ∴四边形 BHDG 是平行四边形，∴ OB OD ， OG OH∵AG HC ，∴ OA OC∴四边形 ABCD 是平行四边形【答案】看法析【例 48】如图，在四边形ABCD 中，M 、N分别为AD 、 BC 的中点，BD AC，BD和AC 订交于点O ，MN分别与AC 、 BD 订交于 E 、F，求证：OE OF ．【考点】三角形的中位线【题型】解答【难度】 3 星【要点词】【分析】取AB 中点 P ，连结MP 、NP ．利用中位线可得MP 1 BDNP1AC 22∴PMN PNM∵MP∥ BD， NP∥ AC∴ OFE OEF∴OE OF【答案】看法析【例 49】如图，线段 AB，CD 订交于点O，且AB 分别交 AB，CD 于 M ，N ，求证：OMCD ，连结 ONAD ，BC，E，F分别是AD ，BC的中点，EFFBFBCMCMPONO NAEDAED【考点】三角形的中位线【题型】解答【难度】 4 星【要点词】【分析】连结 BD ，取 BD 中点 P ，连结 PE ，PF ，由条件易得 PE ，PF 分别是 DBA ， BDC 的中位线，所以 PE ∥BA ，PF ∥DC ，且 PE 1 BA ，PF2 PEF PFE ，由 PE ∥BA 可得 PEF OMN ONM ，所以 OM ON【答案】看法析1，所以PE PF ，所以 DC ，因为AB CD2 OMN ，同理可得 PFEONM ，所以【例 50】如图，梯形 ABCD 中， AD ∥ BC ，ABCD ，对角线 AC ，BD 订交于点 O ， AOD 60 ，E ，F ，G分别是 OA ，OB ，CD 的中点，求证：EFG 是等边三角形ADA DEEO GOGFFB C BC【考点】三角形的中位线，直角三角形斜边上的中线等于斜边的一半，等腰梯形的性质和判断【题型】解答【难度】 4 星【要点词】【分析】省略【答案】连结 DE ，由等腰梯形对角线相等，且AOD 60 ，可证点，所以 DEAC ，在 Rt DCE 中， G 是 DC 中点，所以为 E ，F 分别是 OA ，OB 的中点，所以 EF1 AB ，因为 AB2是等边三角形AOD 是等边三角形，因为 E 是OA中1 FG1 EG DC ，同理可证 DC ，因22DC ，所以 EG FG EF ，即 EFG【例 51】如图，求证：四边形两组对边中点连线与两对角线中点连结这三条线共点．LDAEMNOFB HC【考点】三角形的中位线【题型】解答【难度】 5 星【要点词】【分析】方法一：设 N ，H ，M ，L ，F ，E 分别为 AB ，BC ，CD ，DA ，AC ，BD 的中点，要证明 EF ，LH ，及 MN 三线共点．因为 LF ∥DC 且 LF 1DC ，2所以 EF ∥DC 且 EF1DC ，2LF ∥EH 且LF EH ，从而四边形 EHFL 为平行四边形，故 LH 与 EF 相互均分．设 LH 与 EF 的交点为 O ，则 LH 经过 EF 中点 O （自然也是 LH 中点）．同理， MN 也过 EF 中点 O ．所以， EF ， LH ， MN 三线共点于 O ．说明：本题证明的要点是平行四边形EHFL 的获取（它是经过三角形中位线定理来证明的）．因而可知，在某些四边形的问题中，经过结构平行四边形去解题是一种常用的技巧．请看下例．方法二：应用中点公式法可设 A x 1 ，y 1 ， B x 2 ，y 2 ，C x 3 ，y 3 ，D x 4 ，y 4那么 AC 线段的中点坐标为F x 1 x 3 ，y 1y 3， BD 线段的中点坐标为 E x 2x4，y2y 42 222那么 EF 线段的中点坐标为x 1 x 2 x 3x4，y1y 2 y 3y 422同理可得： MN ，LH 的中点坐标也为x 1 x 2 x 3 x 4 ，y 1y 2 y 3 y 422所以可知： EF ， LH ， MN 三线共点于 O【答案】看法析【例 52】如图，是平行四边形ABCD 随意一点， E ，F ， G ，H 分别是 OA ，OB ，OC ，OD 的中点．若 DE ，OCF 交于 P ， DG ，AF 交于 Q ， AH ，BG 交于 R ， BE ，CH 交于 S ，求证： PQ SR ．SADEOHPF GRBCQ【考点】平行四边形的性质和判断，三角形的中位线【题型】解答【难度】 6 星【要点词】【分析】想法证明四边形 PORS 为平行四边形．因为 F ， G 分别为 OB ， OC 的中点，所以FG ∥BC ，且 FG 1BC ，2FG ∥AD ，且 FG1AD ，2从而 F 是 AQ 中点．同理可证，F 是 PC 的中点（ EF 是 PCD 的中位线）．所以四边形 APQC 为平行四边形，PQ∥AC ，PA AC．同理， RS∥ AC，RS = AC ．所以PQ ∥ RS， PQ = RS，即四边形 PQRS 为平行四边形，故PQ RS ．说明本题证明显示了用平行四边形证题的技巧，平行四边形相连结的桥梁相同交流了条件与结论之间的道路．事实上，因为 PQRS 为平行四边形，我们还可获取PQ ∥ SR， PS∥ QR， PS QR ， SQ与为 DQ 的中点）的断言能够证明于下：取AD中点 M，连 MF，则 FG∥MD且FG MD，所以四边形 MFGD 为平行四边形，MF∥DG．所以 F 为【答案】看法析PQRS ， APQC ，ACRS像三座互F 为AQ的中点（相同G AQ 的中点．PR 相互均分等等一系列结论．。

菱形的性质与判定

菱形的判定和性质

菱形的性质与判定

菱形的性质及判定

菱形的性质与判定

菱形的判定及知识点归纳

菱形的性质与判定第一课时(菱形的性质)

九年级数学菱形的性质与判定

第一讲菱形的性质与判定

菱形的判定与性质

菱形的性质与判定

菱形的性质与判定

菱形的判定和性质

菱形的性质与判定

菱形的所有判定定理

第七讲、菱形的性质和判定

第1讲 菱形的性质与判定(解析版)

菱形的性质与判定.教师版

第1讲菱形的性质与判定(解析版)