自适应回波抵消器的算法与MATLAB仿真
自适应滤波器原理及matlab实现

自适应滤波器原理及matlab实现一、自适应滤波器概述自适应滤波器是一种特殊的滤波器,它能够根据信号的变化自动调整自身的特性,以更好地处理信号。
自适应滤波器在许多领域都有广泛的应用,例如通信、信号处理、语音识别等。
二、自适应滤波器原理自适应滤波器的原理基于最小均方误差(MMSE)准则。
它通过不断调整自身的系数,使得输出信号的误差最小,从而更好地匹配输入信号。
自适应滤波器的性能取决于其系数和输入信号的特点,因此需要根据不同的应用场景选择合适的滤波器。
三、MATLAB实现以下是一个简单的自适应滤波器的MATLAB实现示例:```matlab%定义系统参数n=100;%信号长度alpha=0.01;%学习率w=randn(1,n);%滤波器系数x=randn(n+1,1);%输入信号y=zeros(n+1,1);%输出信号e=zeros(n+1,1);%误差信号%自适应滤波器算法fori=1:ny(i)=w*x(i+1)+e(i);%输出信号e(i)=x(i+1)-y(i);%误差信号w=w+alpha*(x(i+1).^2-y(i).^2)*w-alpha*x(i+1)*e(i);%更新滤波器系数end%绘制滤波器系数随时间变化曲线plot(real(w),'b');holdon;plot([min(x),max(x)],[min(y)-3*std(y),max(y)+3*std(y)],'r');holdoff;xlabel('Time');ylabel( 'FilterCoefficient');legend('FilterCoefficient','SignalError' );gridon;```这段代码实现了一个简单的自适应滤波器,它根据输入信号不断调整自身的系数,以达到更好的匹配效果。
在代码中,我们使用了MATLAB的内置函数和矩阵运算来实现自适应滤波器的算法。
MATLAB语言编程实现回波信号的产生和消除

目录1·摘要⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯ 22.正文⋯⋯ (3)(1)设计目的和要求⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯.⋯ (3)(2)设计原理⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯.⋯⋯.3(3)设计内容⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯..3 3.总结与致谢⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯ (11)4·参考文献⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯12摘要回波是现代通信中影响通信质量的噪声干扰,也有测距估算等的使用价值。
MATLAB 语言具备高效、可及推理能力强等特点,在数值计算方法、图形功能、用户界面设计编程手段和工具等方面有着重要的应用,随着MATLAB 应用领域不断扩大,使其成为一种影响大、流行广的科学计算语言。
本文基于MATLAB 以回波这一最简单的线性模型进行分析,实现了回波的产生、消除、测量反射物的距离。
本设计方案用MATLAB 自带的函数功能读取语音信号,通过延迟叠加产生回波信号来模拟回声,通过计算分析输出信号的自相关函数利用基于自相关函数的方法来估计衰减系数和延迟,并利用快速傅里叶变换将回波信号滤除回声,得到原声音信号,同时根据延迟估计反射物的距离。
关键字:回波自相关函数MATLAB 延迟距离正文(1)设计目的和要求本课程设计要求用MATLAB 语言编程实现回波信号的产生和消除。
具体要求:(1)利用声音信号x 产生带有回声的声音文件y 。
(2)从带有回声的文件y 中消除回声。
(3)从y 中估计反射物的距离。
(2)设计原理1·根据设计要求分析系统功能,掌握设计中所需理论(采样频率、采样位数的概念,采样定理:回声信号,相关性分析;数字滤波器设计原理和方法) 。
采样频率:采样频率,也称为采样速度或者采样率,定义了每秒从连续信号中提取并成离散信号的采样个数。
采样位数:即采样值或取样值,用来衡量声音波动变化的参数,是指声卡在采集和播放声音文件时所使用数字声音信号的二进制位数。
回声抵消器的MATLAB设计与实现

回声抵消器的MATLAB设计与实现前言随着信息时代的到来,人们日渐依赖的通信方式正从早期的单一语言通信向多种业务、多种网络综合通信的方向发展,这也正是目前讨论比较多的多媒体通信的发展方向。
在各种各样的通信业务中,凡是需要同时使用扬声器和麦克风的场合,例如会议电视、免提电话等系统终端,都不可避免地会因本地扩声系统和麦克风之间电声祸合,产生回声问题。
为了增加系统稳定性,提到通信的质量,必须设置回声抵消器来排除回声的影响。
1回声抵消的原理回声抵消器(ACE)的基本原理是用一个自适应滤波器去辨识扬声器与麦克风之间的声回波路径,通过自适应滤波算法的调整,使其自适应权值与声回波房间的冲激响应逼近,从而得到声回波估计信号,再将估计信号从麦克风接收到的语言信号中减去,即可实现声回波抵消(如图1所示)。
其中,声回波抵消器产生的回波抵消预测信号为r(n),实际声回波信号为r(n),预测误差信号为e(n)。
则用公式表达声回波抵消的过程为:e(n)=r(n)-r(n) (1)(2)由图1可知,声回波抵消的核心是一个自适应滤波器。
自适应滤波器使用中要考虑的重要问题是优化调整滤波器参数的准则,该准则不仅要对滤波器性能提供有意义的度量,而且必须导出可实现的算法。
对自适应算法的要求是收敛速度快,计算复杂度低,稳定性好,失调误差小。
2回声抵消器的算法回声抵消器的算法都采用自适应算法,目前最受欢迎的自适应算法是LMS 算法,LMS 算法简单有效,易于实现,最小均方误差算法(LMS )是一种用瞬时值估计梯度矢量的方法,即2[()]()2()()()n e n e n n n ∂∇==-∂X h (3)按照自适应滤波器滤波系数矢量的变化与梯度矢量估计的方向之间的关系,可以写出LMS 算法调整滤波器系数的公式如下所示:1(1)()[()]2n n n μ+=+-∇h h()()()n e n n μ=+h X (4)上式中的μ为步长因子。
基于LMS的自适应干扰抵消算法的matlab实现

1自 适应 干扰抵 消算法 在通信系统 中,经常会遇到强 干扰 信号背 景下有用信 号的检测 问题 ,因此干扰抵 消是通 信 系统 的一 个很重要 的组成部分 。 自 应干扰 适 抵 消系统 , 包含有未知干扰 的原 始信 号作为 将 自 适应滤波器 的参 考信号 ,而同一干扰源 发出
法的迭代公式 如下 : e } i)Xn W( (- (- (T n n n  ̄ ) ) W( 1 w0 _u X( n ) 】 2 += n ) xI ln ( 一 ( L IF ( = ( 『 1 x) 1 ) 一 x — + ) 表示时 刻 n n J 的输入 信号矢量 ; Wn = 0 ) ㈤…WL 1 1 T [ (, w n w1 一 ( 表示 时刻 n的 自适 n 1 的干扰信号 为滤波器的输入 。通过 自 应滤波 应滤波器的权 系数 ; 中: 适 式 L为滤 波器的阶数 , d 器的权系数调整, 使得滤波器输出趋于干扰信 (为期 望输 出值 ,n n ) e】 (为误差 ,是 步长 因子 , U 为 号 。这样 , 通过相减器 , 考信号 中的干扰抵 控制稳定性和 收敛速度 的参 量。该 LMS 将参 算法 消掉 。如图 1 所示。 结构简单 、 计算量小且稳定性好. ( 频域块 L S 2 1 M 算法 块 L 算法 的基本 原理是 将输 人数 据序 MS 列 u ) 串, ( 通过 并变换将 其分成 长 为 L的块 , n 并 将 这样 的数据 数据块 逐块 的送 到阶 数为 M 的 自 适应 滤波器 。 在收集 到每个数 据块后 , 进行 自 适应 滤波抽头权值的更新 ,使滤波器 的 自适应 图 1为 典 型 自适 应 干 扰 抵 消 系统 的 原 理 框 图 过程逐块 的进行。其核心在于计算滤波器 抽头 图 1 原始 输入信 号 d 中, (是有 用信号 s ) r ( n 系数 和输 入信 号的线性卷积 ,以及输入 信号和 与噪声 干扰 v 1 (之和, 输入 信号是 与 v ) n 参考 (相 误 差信号 的线 性相关 。以 F T的 1 重叠保 留 n F 关 的噪声 un假设 s1(及(是零均值 的平稳 (, ) (' ) u nv n ) 法 的频域形式来实现 : 将输入信 号和期 望信号 随机过程且 满 足 与 v ) u ) (及 ( 互不相关, n n 由图 分成 N点 的数 据块 , 然后做 N点离散傅 里叶变 1 可见 , 整个 自 适应 干扰抵 消系统 的输 出为: 换, 权系数每 N个样点更新 一次 , 并且每次更新 e s )v1 , ) ( ( +O卜v( ( ) n n n 1 都是 由 N个误 差信 号样点 累加结果来控制 的。 对( 两边取平方 : 1 试 信普 域游辩 e ㈤ =2 ) v ) ,) 2( In v (对式 ( 2 s( 斗 (一 ( 】 8 ) (_ 侧 2 n { n v n2+ nv ) ) 2 ) 两边取数学期 望, 由于 s ) v (与 ㈤及 u n ㈤不相关 , s f与 vn n ,1 ) (也不相关, : 故 E2 【 【 ( 【 v n e s n - v ,) 2 )E o ( J 2 ( 3 )
自适应滤波器MATLAB仿真

自适应滤波器MATLAB仿真摘要:本文介绍了自适应滤波器的工作原理,以及推导了著名的LMS(Least mean squares)算法。
以一个例子演示了自适应滤波器的滤波效果。
实验结果表明,该滤波器滤波效果较好。
关键词:自适应滤波器 MATLAB7.0 LMS算法Simulate of adaptive filter based on MATLAB7.0Abstract:This article described the working principle of adaptive filter and deduced the well-known LMS algorithm. Take an example to demonstrate the adaptive filters filtering effects. The results show that the filter has an effective way to filter single.Key words:LMS algorithm Adaptive Filter Matlab7.01 引言由Widrow B等提出的自适应滤波理论,是在维纳滤波、卡尔曼滤波等线性滤波基础上发展起来的一种最佳滤波方法。
由于它具有更强的适应性和更优的滤波性能,从而广泛应用于通信、系统辨识、回波消除、自适应谱线增强、自适应信道均衡、语音线性预测和自适应天线阵等诸多领域[1]。
自适应滤波器最大的优点在于不需要知道信号和噪声的统计特性的先验知识就可以实现信号的最佳滤波处理。
本文通过一个具体例子和结果论证了自适应滤波器的滤波效果。
2 自适应滤波原理及LMS算法2.1 自适应滤波原理自适应滤波原理图[2],如图1所示。
图1自适应滤波原理图在自适应滤波器中,参数可调的数字滤波器一般为FIR数字滤波器,IIR数字滤波器或格型数字滤波器。
自适应滤波分2个过程。
第一,输入信号想x(n)通过参数可调的数字滤波器后得输出信号y(n),y(n)与参考信号d(n)进行比较得误差信号e(n);第二,通过一种自适应算法和x(n)和e(n)的值来调节参数可调的数字滤波器的参数,即加权系数,使之达到最佳滤波效果。
RLS自适应滤波器的Matlab设计与仿真概要

1引言目前,自适应滤波器技术在通信和雷达技术的信道均衡、回波抵消、噪声消除或抑制、语音编码、自适应跳频、天线旁瓣抑制、谱线增强、雷达杂波处理、雷达运动目标显示、窄带干扰抑制以及生物医学中的微弱电信号的处理等方面均获得了广泛的应用. 自适应滤波器是这样的处理器, 它在输入信号特性未知或者输入信号特性变化时,能够调整自己的参数, 以满足某种最佳滤波准则的要求.在设计滤波器时应该根据输入信号的特性,设计出最佳的滤波器. 那么, 什么样的滤波效果才算是最佳呢? 必须有一个判断的标准. 至今已研究出很多最佳滤波准则. 常见的有最小均方误差准则、最小二乘准则等. 最佳滤波准则和自适应滤波器关系密切,最佳滤波准则规定了与某种特性的信号对应的最佳参数,而这个最佳参数指出了自适应滤波器调整参数的方向. 以下主要介绍这两个准则.(1 最小均方误差准则 LM S(Least M ean Squar e 就是要使输出信号和理想信号的误差的平方的均值最小. 设 d(n 为滤波器输出要逼近的信号, y(n 为滤波器输出信号, 则误差为 e(n =d(n -y(n , 最小均方误差准则就是要使 E {e 2(n }达到最小.(2 最小二乘准则 LS(Least Squar e 就是要使一定范围内(从 k 到 k+m - 误差的平方和达到最小, 也就是要使 k+m -1i =k Σ达到最小.2最小二乘法 (RLS最小二乘算法(LS, Least -squar es 是一种批处理方法, 通过一个数据块接一个数据块的重复计算来适应非平稳数据, 因此它的计算量大. 推广最小二乘法将得到一种应用更广泛的算法, 即递推最小二乘法(R LS . 一般说来, R LS 算法具有较好的收敛性能和跟踪能力, 但是要求较多的计算量, 目前最快的 R LS 算法要比 LM S 算法多 2-3倍的计算量, 因此, R LS 自适应滤波一般用于要求较高的场合. 2. 1R LS 算法原理由于 LM S 算法的收敛速度很慢,为了得到较快的收敛速度, 有必要设计包含附加参数的更复杂的算法. 在快速收敛算法的推导中, 我们将采用最小二乘法. 因此, 将直接处理接收数据, 使二次性能指数最小, 而 LM S 是使平方误差的期望值最小. 这就意味着用时间平均而不是统计平均来表示性能指数.基于时间平均的最小平方误差被定义如下:J(n =ni =1Σλe 2(i (1式中, λ是接近 1, 但是小于 1的加权因子, 且误差 e(i 为:e(i =d(i -X T W (n (2 且 X (i =[x(i , x(i -1 , … , x(i -M +1 ]T(3 式中, X (i 是 i时刻的输入数据向量, W (n 是 n 时刻的新的抽头增益向量. 因而 e(i 是用 n 时刻的抽头增益向量测试时刻的旧数据所得的误差, J(n 是在所有旧数据上用新抽头增益所得的累计平方误差.要完成 R LS 算法就要找到均衡器的抽头增益向量 W (n , 使得累计平方误差J(n 最小. 为了测试新的抽头增益向量, 会用到那些先前的数据. 而因子λ会在计算时更依赖于新近的数据, 也就是说, J(n 会丢掉非稳定环境中的较旧的数据. 如果信道是稳定的, 那么λ可以设为 1.为了获得 J(n 的最小值, 可使 J(n 的梯度为 0, 即坠 J(n =0通过运算可知:R (nW 赞 (n =P(n (4式中, W 赞 (n 是 R LS 均衡器的最佳抽头增益向量. 方阵 R (n 是输入数据向量X (i 的确定相关矩阵, 向量 P(n 是输入向量 X (i 和期望输出 d(i 之间的确定互相关矩阵, 即:R (n =ni =1Σλn-1X *(i X T (i (5 P(n =n i =1Σλn-1d *(i X (i(6要用式(4 均衡器的抽头增益向量W 赞 (n , 就需要计算 R -1(n . 从式(5 中 R (n 的定义式, 我们可以得到关于 R (n-1 的递归公式:R (n =λR (n-1 +X (n X T (n (7同理得到 P(n 的递推表示式为:P(n =λP(n-1 +X (n d(n (8根据矩阵求逆定理, 若 A , B 是 M ×M 的正定矩阵,C 是一个 M ×N 矩阵,D 是一个 N ×N 矩阵, 当 A =B -1+CD -1C T 时, 有 A -=B-BC (D +C T BC -1C TB.现令 A =R (n , B -1=λR (n-1 , C=XR LS 自适应滤波器的 M at l ab 设计与仿真张立萍(赤峰学院物理与电子信息工程系,内蒙古赤峰024000摘要:自适应滤波技术已经被广泛应用于数字通信、雷达、生物医学和工业控制等领域 . 本文介绍了 R LS 算法, 并以随机干扰噪声信号为研究对象, 在 Matlab 上设计了 R LS 自适应滤波器的 M 文件,进行了仿真, 为硬件实现提供了有力的参考 . 关键词:自适应滤波器; R LS 算法; Matlab ; M 文件中图分类号:TN 273. 2文献标识码:A 文章编号 :1673-260X (2011 04-0025-02Vol. 27No. 4Apr. 2011第 27卷第 4期 2011年 4月赤峰学院学报(自然科学版 Journal of Chifeng University (Natural Science Edition 25--(n , D =J, 可以得到 R -1(n 递归公式:R -1(n =1R -1(n-1 - R -1(n-1 X (n X T (n R -1(n-1! " (9 令:K (n =R -1(n-1 X (n (10则(9 变为:R -1(n =λ-1[R -1(n-1 -K (n X T (n R -1(n-1 ](11 将式(10 中 K (n 的表示式重新安排:K (n =λ-1R -1(n-1 X (n -λ-1K (n X T (n R -1(n-1 X (n=λ-1[R -1(n-1 -K (n X T (n R -1(n-1 ]X (n=R -1(n X (n (12 由式(4 、 (8 、 (11 和式(12 可得W 赞 (n 的递推公式:W 赞 (n =R -1(n P(n =R -1(n [λP(n-1 +X (n d(n=λR -1(n P(n-1 +R -1(n-1 X (n d(n=λλ-1[R -1(n-1 -K (n X T (n R -1(n-1 ]P(n-1 +R -1(n-1 X (n d(n =R -1(n-1 P(n-1 -K (n X T (n R -1(n-1 P(n-1 +K (n d(n =W 赞 (n-1 -K (n X T (n W 赞 (n-1 +K (n d(n=W 赞 (n-1 +K (n [d(n -X T (n W 赞 (n-1 ]=W 赞 (n-1 +K (n α(n式中:α(n =d(n -X T (n W 赞 (n-1内积 X T (n W 赞 (n-1 表示利用 n-1时刻滤波器权系数对期望响应 d(n 作的一个估计, 所以称为先验估计误差.2. 2R LS 算法实现①初始化:W 赞 (0 =0, R -1(0 =δ-1I , δ是一个正常数②对于每一个时刻n=1, 2, … , 进行如下计算:y(n =W T(n-1 X (ne(n =d(n -y(nK (n =R -1(n-1 X (nα(n =d(n -X T (n W 赞 (n-1R -1(n =λ-1[R -1(n-1 -K (n X T (n R -1(n-1 ]W 赞 (n =W 赞 (n-1 +K (n α(n这样, 就用 R -1(n 的递归运算来取代了矩阵反演运算[X T (n X (n ]-1. 其中, δ是正则化参数, δ的设定与信噪比有关, 正则化参数δ与信噪比的关系己由 M oust a-ki des (1997 给出详细说明.3RLS 自适应滤波器 M 文件的设计与仿真根据前面介绍的 R LS 算法, 用 M A TLA B 设计 R LS 自适应滤波器. 下面将在M A TLA B 环境中编写 M 文件对 R LS 算法进行设计和仿真, 验证算法的可行性.在 M A TLA B 中编写 M 文件 R LS. m , 其中, 各参数的意义如下:s:标准正弦信号, 最大峰值为 m axV p=1. 00.sn:标准信号叠加标准白噪声(最大峰值为 m axV p=3. 94 . st ep:滤波器指数加权因子λ, 取值为 0. 99.W (n :滤波器的权向量序列.en:s(i 信号减去滤波器输出信号后得到的误差信号. N :时域抽头 R LS 算法滤波器阶数, 取值为 128.dl en:输入信号抽样点数, 取值为 1024.del t a:正则化参数δ, 取值为 0. 001.R LS 算法中各向量的更新表达式在 M 文件中的实现代码为:f or n=N :dl en;u=sn((n :-1:(n-N +1 ;v=p*u' ;k=v/(st ep+u*v ;y(n =u*w;e(n =s(n -y(n ;w=w+k*conj (e(n ;p=(1/st ep *(eye(N -k*u *p;end仿真时, 原始信号选为 si n((0. 05*pi *t , 其中 t =1:dl en, 噪声信号采用标准白噪声, 在 M A TLA B 环境中运行 R LS. m 文件, 调用绘图函数, 得到 R LS 算法的仿真结果如图 1. R LS 算法的均方误差曲线如图 2所示.4结束语R LS 算法具有良好的收敛速度,除收敛速度快于 LM S 算法以及稳定性强外, 而且具有更高的起始收敛速度、更小的权噪声和更大的抑噪能力.———————————————————参考文献 :〔 1〕么晖 . 基于 FPGA 的自适应滤波器设计 [D]. 硕士学位论文 . 北京 :航天科工集团第三研究院 , 2005.〔 2〕黄埔堪 , 陈建文 , 楼生强 . 现代数字信号处理 [M]. 北京 :电子工业出版社 , 2003.〔 3〕龚耀寰 . 自适应滤波器 [M]. 北京 :电子工业出版社 , 1989. 〔 4〕韩利竹 . MATLAB 电子仿真与应用 [M]. 北京 :国防工业出版社 , 2001.〔 5〕王立宁 , 乐光新 . MATLAB 与通信仿真 [M]. 北京 :人民邮电出版社 , 2000.〔 6〕 Simon Haykin . Adaptive Filter Thearo[M]. 北京 :电子工业出版社 , 2006.图 2R LS算法的均方误差曲线图 1R LS 算法的输入和输出曲线26 --。
基于LMS算法自适应回波抵消器的Simulink仿真分析

1 引言回波是原始声音或者信号经过延时和形变被反射回到源的一种现象,它在通信网络的许多地方出现,降低通信质量。
一般回波分为电学回波和声学回波,电学回波是由于混合变换器的阻抗不匹配,输入信号经过混合变换器后泄漏而产生的,声学回波是由于声波反射以及麦克风与扬声器间的声学耦合引起的,这种回波影响对话的自然性,严重时甚至会产生刺耳的啸叫声。
目前,声学回波消除的措施主要有移频技术、子带中心削波技术、话音控制开关技术、梳状滤波技术、话筒阵列技术、自适应回波消除技术。
前5种或者设施昂贵,或者会带来话音质量下降,或对用户进行限制,因此,自适应回波抵消技术是目前国际公认的主要技术。
Simulink是一个用来对动态系统进行建模、仿真和分析的软件包,它支持线性和非线性系统,连续和离散时间模型,或者是两者的混合,系统还可以是多采样率的。
对于建模,Simulink提供了一个图形化的用户界面(GUI),具有较高的交互性,还可以对最后得到的结果进行分析,并能够将仿真结果可视化显示。
本文即基于Simulink平台对回波抵消系统进行建模仿真,研究了该系统的消除性能。
2 回波抵消器的基本原理对于任何一种回波,回波抵消器都要先估计回波路径的特性,然后产生一个回波的副本,再利用该副本从接收信号中减去回波,以便得到期望接收的信号的估值。
由于在估计回波路径的特征参数时采用了自适应方法,因此可以跟踪回波路径的变化,这就是回波抵消器工作的基本原理。
图1给出了回波抵消器的结构框图。
图中A,B为通信的双方,A通过话筒发出的信号为x(n),该信号在传输过程中产生的回波信号为x'(n),即:B通过话筒发出的信号为s(n),传输过程中的噪声信号为v(n),两者叠加为:可见,由于回波路径是未知的,而且是时变的,因此用自适应滤波器来模拟回波,再从接收信号中减去这个回波的模拟值,从而达到抵消回波的目的。
根据具体的应用不同,自回波抵消器的算法和结构可有多种选择。
基于Matlab的自适应滤波器的设计及仿真

基于Matlab的自适应滤波器的设计及仿真赵夏爽物理与电子信息学院电子信息科学与技术专业学号:130522036指导教师:燕慧英摘要:自适应滤波器的研究是当今信号处理中最活跃的研究课题之一。
自适应滤波器因其具有很强的自学习、自跟踪能力和算法的简单易实现性等优越性能,已经在数字通信、工业控制和雷达等领域获得了广泛应用。
首先介绍了自适应滤波器的基本理论思想,具体阐述了自适应滤波器的基本原理、算法及设计方法。
接着对自适应滤波器的核心算法——最小均方误差(LMS)进行介绍和分析,最后基于LMS算法设计自适应滤波器并进行MatLab仿真,仿真结果表明设计的自适应滤波器具有良好的性能和较强的可操作性。
关键词:自适应滤波器;LMS算法;matlab仿真Design and Implemeutation of the Auto-adapted FilterZhao xia-shuangCollege of Physics and Electronic Information Electronic Information Science and TechnologyNo:130522036Tutor:YanHui-yingAbstract:The research of adaptive filter is one of the most active research topic in signal processing.Adaptive filter because of its strong self-learning,self tracking ability and simple algorithm of superior performance and easy to implement,has been widely used in digital communication,industrial control and other fields of radar.Firstly introduces the basic theory of adaptive filter,expounds the basic principle,algorithm and adaptive filter design method.The core algorithm of the adaptive filter--minimum mean square error(LMS)were introduced and analyzed,based on the design of adaptive LMS filter algorithm and MatLab simulation,the simulation results show that the design of adaptive filter has good performance and strong operability.Keywords:adaptive filter;LMS algorithm;MATLAB simulation目录1引言 (3)1.1国内外研究现状与前景 (3)1.2课题研究的意义和目的 (4)2自适应滤波器理论基础 (4)2.1滤波器的基本概念 (4)2.2自适应滤波器的结构 (5)2.3自适应滤波器原理 (5)2.4自适应滤波器的LMS算法 (6)3自适应滤波器设计及仿真 (7)3.1LMS算法参数分析 (7)3.2自适应滤波器的仿真 (7)3.2.1Matlab软件介绍 (7)3.2.2基于LMS算法实现的流程图 (8)3.2.3自适应滤波器的仿真结果及分析 (9)4总结 (12)参考文献 (12)1引言滤波技术是信号处理的一项重要技术,利用这种技术可以抑制信号中的干扰,获取需要的信息。
自适应噪声抵消LMS算法Matlab仿真

自适应噪声抵消LMS 算法Matlab 仿真传统的宽带信号中抑制正弦干扰的方法是采用陷波器(notch filter),为此我们需要精确知道干扰正弦的频率.然而当干扰正弦频率是缓慢变化时,且选频率特性要求十分尖锐时,则最好采用自适应噪声抵消的方法.下图是用一个二阶FIR 的LMS 自适应滤波器消除正弦干扰的一个方案。
1) 借助MATLAB 画出误差性能曲面和误差性能曲面的等值曲线; 2) 写出最陡下降法, LMS 算法的计算公式(δ=0.4);3) 用MATLAB 产生方差为0.05,均值为0白噪音S(n),并画出其中一次实现的波形据2)中的公式,并利用3)中产生的S(n),在1)中的误差性能曲面的等值曲n 的值曲线上叠加画出LMS 法时100情况确定,一般选取足够大以使算法达到基)(n y 宽带信号+正弦干扰0()()()y n S n N n =+图;4) 根线上叠加画出采用最陡下降法, LMS 法时H(n)的在叠代过程中的轨迹曲线。
5)用MATLAB 计算并画出LMS 法时 随时间变化曲线(对 应S(n)的某一次的一次实现)和e(n)波形;某一次实现的结果并不能从统计的角度反映实验的结果的正确性,为得到具有统计特性的实验结果,可用足够多次的实验结果的平均值作为实验的结果。
用MATLAB 计算并画出LMS 法时J(n)的100次实验结果的平均值随时间n 的变化曲线。
6)用MATLAB 计算并在1)中的误差性能曲面的等次实验中的H(n)的平均值的轨迹曲线;(在实验中n=1,,…..N,N 的取值根据实验本收敛)01(),(0)0.052()sin(16102()sin()16ss S n r N n n N n n πππ==+是均匀分布的白噪音不相关和)(),()(10n N n N n S)(n x x 1()())(n e n N n =1、用Matlab画误差性能曲面和误差性能曲面的等值曲线的程序如下:[h0,h1] = meshgrid(-2:0.1:4 , -4:0.1:2);J=0.55+h0.*h0+h1.*h1+2*cos(pi/8)*h1.*h0-sqrt(2)*h0*cos(pi/10)-sqrt(2)*h1*cos(9*pi/40);echo on;v=0:0.1:2;%axis([-4 4 -4 4 0 100]);figure(1);%误差曲面surf(h0,h1,J);xlabel('h0');ylabel('h1');title('误差性能曲面');figure(2);contour(h0,h1,J,v); %等值曲线xlabel('h0');ylabel('h1');title('误差性能曲面等值曲线');运行结果如下图示:2、①最陡下降法计算公式:)(n 21)()1(H G V n H n δ−=+ 其中δ取0.4,H(0)=[3 -4],T ⎟⎠⎞⎜⎝⎛+=⎟⎠⎞⎜⎝⎛−⎥⎦⎤⎢⎣⎡⎟⎠⎞⎜⎝⎛+==⎟⎠⎞⎜⎝⎛−⎟⎠⎞⎜⎝⎛=⎥⎦⎤⎢⎣⎡−⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡=−=∑∑==1016k 2cos 2116)(2sin 210162sin 2161)(r 16k2cos 16)(2sin 2162sin 2161)(r )1()0(2)()()0()1()1()0(22)(2)(V 15015010G ππππππππi yx i xx yx yx xx xx xx xx yxxx k i i k k i i k r r n h n h r r r r r n H R n 而故⎥⎦⎤⎢⎣⎡−−=⎥⎦⎤⎢⎣⎡−⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡=5320.37362.2)0(5377.06725.02)()(19239.09239.012)(10G G V n h n h n V②LMS 算法计算公式:,...2,1,0),1()1()()1()1()()1()1(e =+++=++−+=+n n X n e n H n H n X n H n y n T δ其中δ取0.4。
LMS和RLS算法应用及仿真分析

LMS 和RLS 算法应用及仿真分析摘要:本文采用MATLAB 软件对LMS 和RLS 两种自适应均衡算法在回波抵消器中的应用进行仿真,分析收敛步长μ、抽头w 、遗忘因子λ 等参数对回波抵消器性能的影响,并对两种算法下的性能做出比较。
关键词:LMS ;RLS ;自适应;回波抵消1 引言进入90 年代后期,通过网络拨打长途电话即IP 电话开始盛行,由于发话端到受话端的延迟达100ms 以上,而人耳对大于50ms 的回声就能辨别出来,因此IP 电话的回声严重影响通话效果。
如何消除回声成为非常重要的问题,回波抵消器就是一个自适应辨识系统,它通过特定的算法辨识未知的目标系统,即回声路径。
本文采用LMS 和RLS 算法实现回波抵消,并对收敛步长μ、抽头w 、遗忘因子λ 等相关参数对回波抵消性能的影响进行了仿真分析,从而为一种通用的回波抵消技术的实际应用提供理论参考。
回波抵消算法原理图如图1 所示。
图1 回波抵消算法原理图 2 LMS 和RLS 算法概述最陡下降法(LMS )和递归最小二乘算法(RLS )是自适应滤波最常用,也是最基本的两种算法。
下面分别对LMS 和RLS 两种算法原理做简单介绍。
2.1 LMS 算法设J(n)是n 时刻均方误差,J(n+1)是n+1 时刻的均方误差,W(n)、W(n+1)分别是n 、n+1时刻M 维抽头权向量011()[()()...()]T M W n w n w n w n -= (1)为使J(n+1)<J(n) (2)W(n)必须按J(n)的负方向变化即(1)()W n W n J μ→→→+=-∇ (μ>0) (3)最后以U (n )*e (n )瞬时值代替统计平均,得到抽头权向量迭代式 *(1)()()()W n W n U n e n μ→→+=- (4)式中U(n)式n 时刻的输入向量[u(n) u(n-1) u(n-2)···u(n-M+1)]。
自适应滤波器原理及matlab仿真应用 相关代码

自适应滤波器原理及matlab仿真应用相关代码文章标题:深度解析自适应滤波器原理及matlab仿真应用1. 引言自适应滤波器是数字信号处理中的重要概念,它可以根据输入信号的特性动态地调整滤波器的参数,从而更好地适应信号的变化。
本文将深入探讨自适应滤波器的原理以及在matlab中的仿真应用,帮助读者深入理解这一重要的概念。
2. 自适应滤波器原理自适应滤波器的原理基于最小均方误差准则,它通过不断调整权值参数,使得滤波器输出与期望输出的误差达到最小。
这一原理可以应用在很多领域,如通信系统、雷达系统以及生物医学工程中。
自适应滤波器能够有效地抑制噪声,提高信号的质量。
3. Matlab仿真应用在matlab中,我们可以利用现成的自适应滤波器函数来进行仿真实验。
通过编写相应的matlab代码,我们可以模拟各种不同的信号输入,并观察自适应滤波器的输出效果。
这对于理论学习和工程应用都具有重要意义。
4. 深入理解自适应滤波器我们可以通过探讨自适应滤波器的各种类型、参数选择以及性能评价指标,来深入理解这一概念。
LMS算法、RLS算法以及SVD方法都是自适应滤波器中常见的算法,它们各自适用于不同的场景,并且有着各自的优缺点。
了解这些算法的原理及应用可以帮助我们更好地理解自适应滤波器的工作机制。
5. 个人观点和总结个人观点:自适应滤波器在现代信号处理中具有极其重要的应用价值,通过对其原理的深入理解和matlab中的仿真实验,我们可以更好地掌握这一概念。
在实际工程中,合理地选择自适应滤波器的类型和参数,并结合matlab仿真,可以提高工程设计的效率和准确性。
总结:通过本文对自适应滤波器原理的深入解析和matlab的仿真应用,希望读者能够更好地理解这一重要概念,并且能够在工程实践中灵活应用。
自适应滤波器是数字信号处理中不可或缺的工具,深入掌握其原理和应用对于提高工程设计的水平具有重要意义。
6. 结束语自适应滤波器原理及matlab仿真应用是一个复杂而又精彩的领域,相信通过不断地学习和实践,我们能够更好地理解和应用这一概念。
基于LMS算法的自适应对消器的MATLAB实现
N = 5; w = ones(N,1); u = 0.0026; y = zeros(length(t),1); for k = N:length(t) y(k) = n1(k-N+1:k)'*w; e(k) = d(k) - y(k); w = w + 2*u*e(k).*n1(k-N+1:k); end
% 滤波器阶数 % 初始பைடு நூலகம்滤波器权值 % 步长因子
% 跟新权值
% 图像化仿真效果 subplot(211),plot(t,x);title('被噪声污染的正弦信号'); subplot(212),plot(t,s,'k',t,e,'g'); % 对消噪声后, 误差信号即为对原始信号的估计 legend('原始正弦信号','自适应滤波后的信号'); axis([0 1 -1 1]);title('滤波效果');
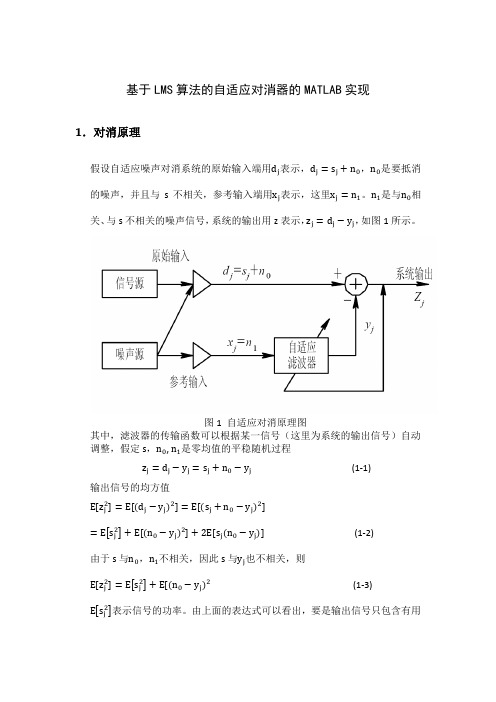
图 1 自适应对消原理图 其中,滤波器的传输函数可以根据某一信号(这里为系统的输出信号)自动 调整,假定 s,n0 , n1 是零均值的平稳随机过程 zj = dj − yj = sj + n0 − yj 输出信号的均方值 E[zj2 ] = E[(dj − yj )2 ] = E[(sj + n0 − yj )2 ] = E sj2 + E[(n0 − yj )2 ] + 2E[sj (n0 − yj )] 由于 s 与n0 ,n1 不相关,因此 s 与yj 也不相关,则 E[zj2 ] = E sj2 + E[(n0 − yj )2 (1-3) (1-2) (1-1)
E sj2 表示信号的功率。由上面的表达式可以看出,要是输出信号只包含有用
RLS算法实现自适应均衡器的Matlab仿真
基于RLS算法实现自适应均衡器的MATLAB仿真1. 实验目的用RLS算法实现自适应均衡器,画出一次实验的误差平方的收敛曲线,给出最后设计滤波器系数。
一次实验的训练序列长度为500。
进行20次独立实验,画出误差平方的收敛曲线。
2. 实验原理自适应均衡器的工作过程包含两个阶段,一是训练过程,二是跟踪过程。
在训练过程中,发送端向接收机发射一组已知的固定长度训练序列,接收机根据训练序列设定滤波器的参数,使检测误码率最小。
典型的训练序列是伪随机二进制信号或一个固定的波形信号序列,紧跟在训练序列后面的是用户消息码元序列。
接收机的自适应均衡器采用递归算法估计信道特性,调整滤波器参数,补偿信道特性失真,训练序列的选择应满足接收机均衡器在最恶劣的信道条件下也能实现滤波器参数调整图1自适应均衡试验框图如图1所示,系统中使用两个独立的随机数发生器,一个用xn来表示,用来测试信道。
另一个用v(n)来表示,用来模拟接收器中加性白噪声的影响。
序列xn是xn=1的Bernoulli2序列,随变量xn具有零均值和单位方差。
第二个序列v(n)具有零均值,其方差v由实验中需要的信噪比决定。
均衡器有11个抽头。
3. MATLAB仿真1. RLS法1次实验clear;N=500;db=25;sh1=sqrt(10^(-db/10));u=;m=*sh1^2;error_s=0;for loop=1:1w=zeros(1,11)';p=1/m*eye(11,11);V=sh1*randn(1,N );Z=randn(1,N);x=sign(Z);for n=3:N;M(n)=*x(n)+*x(n-1)+*x(n-2);endz=M+V;for n=8:N;d(n)=x(n-7);endfor n=11:N;z1=[z(n) z(n-1) z(n-2) z(n-3) z(n-4) z(n-5) z(n-6) z(n-7) z(n-8) z(n-9) z(n-10)]';k=u^(-1).*p*z1./(1+u^(-1).*z1'*p*z1);e(n)=d(n)-w'*z1;w=w+k.*conj(e(n));p=u^(-1).*p-u^(-1).*k*z1'*p;y(n)=w'*z1;e1(n)=d(n)-w'*z1;enderror_s=error_s+e.^2;endwerror_s=error_s./1;n=1:N;plot(n,error_s);xlabel('n (忘却因子u=1;DB=25时)');ylabel('误差');title('RLS法1次实验误差平方的均值曲线 ');2. RLS法20次实验clear;N=500;db=25;sh1=sqrt(10^(-db/10));u=;m=*sh1^2;error_s=0;for loop=1:20w=zeros(1,11)';p=1/m*eye(11,11);V=sh1*randn(1,N );Z=randn(1,N);x=sign(Z);for n=3:N;M(n)=*x(n)+*x(n-1)+*x(n-2);endz=M+V;for n=8:N;d(n)=x(n-7);endfor n=11:N;z1=[z(n) z(n-1) z(n-2) z(n-3) z(n-4) z(n-5) z(n-6) z(n-7) z(n-8) z(n-9) z(n-10)]';k=u^(-1).*p*z1./(1+u^(-1).*z1'*p*z1);e(n)=d(n)-w'*z1;w=w+k.*conj(e(n));p=u^(-1).*p-u^(-1).*k*z1'*p;y(n)=w'*z1;e1(n)=d(n)-w'*z1;enderror_s=error_s+e.^2;endwerror_s=error_s./20;n=1:N;plot(n,error_s);xlabel('n (忘却因子u=1;DB=25时)');ylabel('误差');title('RLS法20次实验误差平方的均值曲线 ');4. 实验结果图2图3。
lms算法自适应滤波器应用于自适应回声消除matlab基本步骤

lms算法自适应滤波器应用于自适应回声消除matlab基本步骤1.引言1.1 概述LMS算法自适应滤波器应用于自适应回声消除是一种有效的信号处理技术。
在通信系统、音频处理等领域,回声是一个常见的问题,它会导致信号质量下降和通信效果的恶化。
为了解决这个问题,自适应滤波器和LMS算法被广泛采用。
本文旨在介绍LMS算法自适应滤波器在自适应回声消除中的应用,并详细讲解其基本步骤。
首先,我们将对LMS算法和自适应滤波器进行介绍,包括其原理和基本概念。
然后,我们将探讨自适应回声消除的原理,并介绍LMS算法在回声消除中的具体应用。
通过研究本文,读者将了解到LMS算法自适应滤波器的基本原理和应用场景,以及如何利用该算法实现回声消除。
此外,我们还将对LMS算法自适应滤波器的性能进行分析和评价。
最后,我们将对本文进行总结,并展望其在未来的研究和应用中的发展前景。
通过本文的介绍,读者将具备一定的理论基础和实践经验,能够应用LMS算法自适应滤波器解决实际问题,提高信号处理的效果,从而为通信系统和音频处理领域的发展做出贡献。
文章结构部分应该包括对整篇文章的章节和内容进行简要介绍和概述。
以下是文章1.2文章结构部分的一个例子:1.2 文章结构本文主要介绍了LMS算法自适应滤波器在自适应回声消除中的应用,文章共分为以下几个部分:2. 正文2.1 LMS算法在本节中,我们将详细介绍LMS算法的原理和步骤。
我们将解释LMS算法是如何通过迭代过程来逼近系统的输入和输出之间的关系,从而实现滤波器的自适应调整。
2.2 自适应滤波器本节将重点介绍自适应滤波器的原理。
我们将分析自适应滤波器是如何通过反馈机制和参数调整来实现信号滤波的自适应性。
并探讨了自适应滤波器在实际应用中的一些典型场景。
2.3 自适应回声消除在本节中,我们将详细讨论回声消除的原理和技术。
我们将解释回声是如何产生的以及对通信信号产生的影响。
并介绍LMS算法在回声消除中的应用,以解决回声干扰带来的问题。
基于MATLAB的自适应声学回音抵消器优化设计

kn ( )=
,
h n Y n—m) () (
一
() 1
1
;
en ( )=sn ()一kn ( )=sn h n , n— ( )一 ( ), m) (
,
() 2
由此可知 , 回音抵消器 的核心部件是一 自 应滤波器 , 中主要 声学 适 其
维普资讯
第 6期
N 6 O.
宜宾学院学报
Ju l f ii nvri oma o bnU iesy Y t
Jn .0 8 u e2 0
61
基于 M TA A L B的 自适 应 声 学 回 音抵 消 器 优 化 设 计
肖尚辉 , 曾辉 , 邦 菊2, 启 忠 高 黄 周
化最小均方误差(N M )算法等 ‘ 。 SL S 。 J
1 声学 回音抵消器原理
差的均方值( en—SurdEr ) Ma qa rr 达到最小。 e o
Ⅳ 一1
声学回音抵消器的实质就是用一个自 适应横向滤波器( F A ate A , dpv i Ft) ie 对未知的声回授通道 L M Luesekr—R o lr R ( odr ae p om—Mc poe iohn ) r 进行系统辨识, 模拟回声路径 , 自 通过 适应滤波算法的调整, 使其时域冲
风被置于同一空间, 经本地扬声器放大的远端话音就可能被本地的麦克
风吸收并传回远端, 以致使远端用户仿佛听到了自己的回声。这种 回声
有一定的延时, 当延迟时间超过 5 m 并且没有衰减或只有很小衰减的 0s 时候, 人们就会感觉到清晰的回声, 这种回声是通过声学途径产生 的, 称之为声学回音(A osc co 。 cut h ) iE 为了增加系统的稳定性 , 提高通信的质量, 必须设置 回音抵消器来排
基于MATLAB的自适应噪声抵消器的设计与实现

基于MATLAB的自适应噪声抵消器的设计与实现
徐梅花;王福明
【期刊名称】《电子测试》
【年(卷),期】2009(000)011
【摘要】阐述了自适应噪声抵消(ANC)技术的基本原理,基于自适应滤波器的原理,设计了自适应噪声抵消器;在对自适应滤波器相关理论研究的基础上,重点研究了自适应噪声抵消器的核心--LMS自适应滤波算法.在MATLAB中的Simulink下,建立了自适应噪声抵消器的模型,并通过设置不同的参数进行仿真,结果表明系统能够有效地从噪声中恢复出原始信号.最后对系统进行了性能分析,给出了自适应噪声抵消系统在实际应用中选取参考信号的要求.
【总页数】4页(P43-46)
【作者】徐梅花;王福明
【作者单位】中北大学现代教育技术与信息中心,太原,030051;中北大学现代教育技术与信息中心,太原,030051
【正文语种】中文
【中图分类】TN911.4
【相关文献】
1.基于MATLAB的自适应噪声抵消器设计及应用研究 [J], 肖尚辉;高曾辉;黄邦菊
2.基于MATLAB的自适应噪声抵消器设计 [J], 马令坤;程林波
3.自适应噪声抵消器的MATLAB设计与实现 [J], 成利香;张桂新
4.基于机器视觉的智能手语识别翻译器设计与实现——评《机器人学、机器视觉与控制:MATLAB算法基础》 [J], 花有清
5.基于MATLAB和FPGA的DDS发生器的设计与实现 [J], 李奇;黄大胜;李倩;缪露露
因版权原因,仅展示原文概要,查看原文内容请购买。
基于MATLAB的自适应噪声抵消器的设计与实现

2009年11月第”期危子测斌ELECTRoNICTEsTNov.2009No.1/基于M棚,AB的自适应噪声抵消器的设计与实现徐梅花,王福明(中北大学现代教育技术与信息中心太原030051)摘要:阐述了自适应噪声抵消(ANC)技术的基本原理,基于自适应滤波器的原理,设计了自适应噪声抵消器;在对自适应滤波器相关理论研究的基础上,重点研究了自适应噪声抵消器的核心——I。
MS自适应滤波算法。
在MATLAB中的Simulink下,建立了自适应噪卢抵消器的模型,并通过设置不同的参数进行仿真,结果表明系统能够有效地从噪声中恢复出原始信号。
最后对系统进行了性能分析,给出了自适应噪声抵消系统在实际应用中选取参考信号的要求。
关键词:自适应滤波;噪声抵消;LMS;MATI。
AB仿真中图分类号:TN911.4文献标识码:ADesignandrealizationofadaptivenoisecancellerbasedonMATLABXuMeihua,WangFuming(ModernEducationTechnology&InformationCenterofNorthUniversityofChina。
Taiyuan030051.China)Abstract:ThispaperelaboratedthebasictheoryofAdaptivenoisecancellationtechnology(ANC),designedAdaptivenoisecancellerbasedonadaptivefilter;Afterstudyingtherelatedtheoryofadaptivefilter,thecoreofadaptivenoisecaneeller-LMSadaptivefilteringalgorithmisresearchedemphatically.UndertheSimulinkofMATI。
自适应滤波器原理及matlab仿真应用

自适应滤波器原理及matlab仿真应用自适应滤波器原理及MATLAB仿真应用一、引言自适应滤波器是一种能够自动调整参数以适应环境变化的滤波器。
它能够根据输入信号的特性和所需滤波效果,动态地调整滤波器的参数,从而实现对信号的优化处理。
自适应滤波器在许多领域都有广泛的应用,如通信系统、图像处理、声音处理等。
本文将介绍自适应滤波器的工作原理,并通过MATLAB仿真展示其在实际应用中的效果。
二、自适应滤波器原理自适应滤波器的核心思想是根据输入信号的统计特性以及期望输出信号的特性,通过调整滤波器的权值参数,使得滤波器输出信号尽可能接近期望输出信号。
其基本原理可以概括为以下几个步骤:1. 初始化滤波器的权值参数,一般可以设置为0或者随机值。
2. 输入信号通过滤波器后得到输出信号。
3. 根据输出信号与期望输出信号之间的误差,调整滤波器的权值参数。
4. 重复步骤2和步骤3,直到滤波器输出信号达到期望输出信号的要求。
自适应滤波器的关键在于如何调整滤波器的权值参数。
常用的调整算法有最小均方误差(LMS)算法、最小误差平方和(RLS)算法等。
这些算法通过不断迭代,逐渐调整权值参数,使得滤波器的输出信号与期望输出信号之间的误差逐渐减小,从而达到滤波的目的。
三、MATLAB仿真应用MATLAB是一种功能强大的数学计算和仿真软件,广泛应用于各个科学领域。
在自适应滤波器的仿真中,MATLAB提供了许多有用的函数和工具箱,可以方便地进行滤波器参数的计算和调整。
我们需要定义输入信号和期望输出信号。
可以使用MATLAB中的随机函数生成一组随机信号作为输入信号,然后根据需求定义期望输出信号。
在实际应用中,期望输出信号可以是某种理想信号或者已知的参考信号。
接下来,我们可以使用MATLAB中的自适应滤波器函数对输入信号进行滤波处理。
MATLAB提供了adapthfilt函数和nlms函数等用于自适应滤波的函数,可以根据需求选择合适的函数进行滤波处理。
一种自适应滤波器的设计与仿真

一种自适应滤波器的设计与仿真自适应滤波器(Adaptive Filter)是一种能够根据输入信号的特性自动调整滤波器参数的滤波器。
它可以应用于信号处理、通信系统、生物医学工程等领域,可以对信号进行降噪、回声消除、信道均衡等处理。
本文将介绍自适应滤波器的设计和仿真过程。
首先,自适应滤波器的设计需要确定滤波器的结构和选择合适的算法。
常见的自适应滤波器算法有最小均方误差(Least Mean Square, LMS)算法和递归最小二乘(Recursive Least Squares, RLS)算法等。
在这里,我们选择LMS算法,该算法简单易实现且具有较好的性能。
其次,自适应滤波器的设计需要明确滤波器的输入信号和输出信号。
输入信号可以是任意的实际信号,例如语音信号、音频信号等。
输出信号是通过滤波器进行处理后得到的估计信号。
接下来,通过仿真软件(如MATLAB)进行自适应滤波器的仿真。
具体步骤如下:1.定义输入信号。
可以通过载入实际的音频文件或者生成合成的信号作为输入信号,例如正弦信号、高斯白噪声等。
2. 设置滤波器的参数。
包括滤波器的阶数、步长(Step Size)等。
阶数决定了滤波器的复杂度,步长决定了滤波器的收敛速度和稳定性。
3.初始化滤波器的系数。
可以设置为全零向量,也可以设置为随机初始值。
4.开始滤波器的迭代计算。
在每次迭代中,计算滤波器对当前输入信号的输出估计,并根据与真实输出信号之间的误差,更新滤波器的系数。
5.重复步骤4,直到滤波器的系数收敛或达到事先设定的最大迭代次数。
6. 分析仿真结果。
通过比较滤波器的输出信号与真实信号之间的误差,评估滤波器的性能。
可以通过均方误差(Mean Square Error)等指标进行评估。
需要注意的是,自适应滤波器的设计和仿真需要具备一定的信号处理和数学基础。
了解LMS算法的原理和特点,熟练使用MATLAB等相关软件工具,能够正确理解和解释仿真结果是非常重要的。
自适应回声消除算法的仿真研究

・法 究 算研 ・
( 浙江大学 电气工程 学院 , 浙江
杭州
3 02 ) 10 7
【 摘
要 】介绍几种 自适应 回声消 除算法 :L SP L SP L S U I L SM N M , N M ,N M ,N M D , N M , P L S 并在 M tb环境 下进行 了 P aa l
【 e od】eh cneao; L S P L S P L S U IN M ; P L S K yw rs co acltn N M ; N M ; N M D ;P L S M N M li
1 引言
在语音传输 业务 中广泛 存在 回声 消除 问题 。 目
前, 自适应滤 波是 解决 回声 消除 问题 的最 有效 方 法 。
■ 一 技 一
u o n i #t0 Xi e n# r n
数 字 信 号 处 理
⑨6 舱囿 6 响匐0 翊 0 回 @@ s 响 @¥ 6
文章编号 :0 2 8 8 (0 2 0 - 0 7 0 10 - 64 2 1 )2 0 6— 5
自适应回声消 除算法 的仿真研 究
性 较大 时 , MS算 法 的 收 敛 性 很 差 , 定 性 不 如 L 稳
2 回声消除原理
回声 消 除的基 本 原理 如 图 1所 示 , ) 远 端 ( 为 输 入信号 , 过 未 知 的 回声 路径 产 生 回声 Y n , 经 ( )
NM L S算 法 _ 。 当 回 声 路 径 脉 冲 响 应 稀 疏 时 , N 4 J P. L MS算 法 的初 始收 敛 速度 快 于 N MS算 法 J N L 。P — L S算 法 的优 点是 初 始 阶段 的收敛 速 度较 快 , 是 M 但 经过 该 阶段后 , 敛速 度 明显 减 慢 , 至不 如 N MS 收 甚 L
