八年级数学几种证明图示
勾股定理种证明(有图)

勾股定理的9种证明(有图)【证法1】(邹元治证明)以a 、b 为直角边,以c 为斜边做四个全等的直角三角形,则每个直角三角形的面积等于ab21.把这四个直角三角形拼成如图所示形状,使A 、E 、B 三点在一条直线上,B 、F 、C 三点在一条直线上,C 、G 、D 三点在一条直线上.∵Rt ΔHAE ≌Rt ΔEBF, ∴∠AHE=∠BEF.∵∠AEH+∠AHE=90º,∴∠AEH+∠BEF=90º. ∴∠HEF=180º―90º=90º.∴四边形EFGH 是一个边长为c 的 正方形.它的面积等于c 2.∵Rt ΔGDH ≌Rt ΔHAE,∴∠HGD=∠EHA.∵∠HGD+∠GHD=90º, ∴∠EHA+∠GHD=90º. 又∵∠GHE=90º,∴∠DHA=90º+90º=180º.∴ABCD 是一个边长为a+b 的正方形,它的面积等于()2b a +.∴()22214c ab b a +⨯=+.∴222c b a =+.【证法2】(梅文鼎证明)做四个全等的直角三角形,设它们的两条直角边长分别为a 、b ,斜边长为c.把它们拼成如图那样的一个多边形,使D 、E 、F 在一条直线上.过C 作AC 的延长线交DF 于点P. ∵D 、E 、F 在一条直线上,且Rt ΔGEF ≌Rt Δ∴∠EGF=∠BED , ∵∠EGF+∠GEF=90°,∴∠BED+∠GEF=90°,∴∠BEG=180º―90º=90º. 又∵AB=BE=EG=GA=c ,∴ABEG 是一个边长为c 的正方形.∴∠ABC+∠CBE=90º.∵Rt ΔABC ≌Rt ΔEBD, ∴∠ABC=∠EBD.∴∠EBD+∠CBE=90º. 即∠CBD=90º.又∵∠BDE=90º,∠BCP=90º,BC=BD=a.∴BDPC 是一个边长为a 的正方形.同理,HPFG 是一个边长为b 的正方形. 设多边形GHCBE 的面积为S ,则abS c 2122⨯+=,∴222c b a =+. 【证法3】(项明达证明) 做两个全等的直角三角形,设它们的两条直角边长分别为a 、b (b>a ),斜边长为c.再做一个边长为c 的正方形.把它们拼成如图所示的多边形,使E 、A 、C 三点在一条直线上. 过点Q 作QP ∥BC ,交AC 于点P.过点B 作BM ⊥PQ ,垂足为M ;再过点F 作FN ⊥PQ ,垂足为N.∵∠BCA=90º,QP ∥BC ,∴∠MPC=90º,∵BM ⊥PQ , ∴∠BMP=90º,∴BCPM 是一个矩形,即∠MBC=90º.∵∠QBM+∠MBA=∠QBA=90º,∠ABC+∠MBA=∠MBC=90º, ∴∠QBM=∠ABC ,又∵∠BMP=90º,∠BCA=90º,BQ=BA=c , ∴Rt ΔBMQ ≌Rt ΔBCA.同理可证Rt ΔQNF ≌Rt ΔAEF. 从而将问题转化为【证法4】(梅文鼎证明). 【证法4】(欧几里得证明)做三个边长分别为a 、b 、c 的正方形,把它们拼成如图所示形状,使H 、C 、B 三点在一条直线上,连结 BF 、CD.过C 作CL ⊥DE , 交AB 于点M ,交DE 于点L.∵AF=AC ,AB=AD ,∠FAB=∠GAD , ∴ΔFAB ≌ΔGAD ,∵ΔFAB 的面积等于221a,ΔGAD 的面积等于矩形ADLM 的面积的一半,∴矩形ADLM 的面积=2a .同理可证,矩形MLEB 的面积=2b .∵正方形ADEB 的面积=矩形ADLM 的面积+矩形MLEB 的面积 ∴222b a c +=,即222c b a =+. 【证法5】(杨作玫证明) 做两个全等的直角三角形,设它们的两条直角边长分别为a 、b (b>a ),斜边长为c.再做一个边长为c 的正方形.把它们拼成如图所示的多边形.过A 作AF ⊥AC ,AF 交GT 于F ,AF 交DT 于R.过B 作BP ⊥AF ,垂足为P.过D 作DE 与CB 的延长线垂直,垂足为E ,DE 交AF 于H.∵∠BAD=90º,∠PAC=90º,∴∠DAH=∠BAC.又∵∠DHA=90º,∠BCA=90º, AD=AB=c , ∴Rt ΔDHA ≌Rt ΔBCA.∴DH=BC=a ,AH=AC=b.由作法可知,PBCA 是一个矩形, 所以Rt ΔAPB ≌Rt ΔBCA.即PB= CA=b ,AP=a ,从而PH=b ―a.∵Rt ΔDGT ≌Rt ΔBCA, Rt ΔDHA ≌Rt ΔBCA.∴Rt ΔDGT ≌Rt ΔDHA.∴DH=DG=a ,∠GDT=∠HDA. 又∵∠DGT=90º,∠DHF=90º,∠GDH=∠GDT+∠TDH=∠HDA+∠TDH=90º, ∴DGFH 是一个边长为a 的正方形. ∴GF=FH=a.TF ⊥AF ,TF=GT ―GF=b ―a. ∴TFPB 是一个直角梯形,上底TF=b ―a ,下底BP=b ,高FP=a+(b ―a ). 用数字表示面积的编号(如图),则以c 为边长的正方形的面积为543212S S S S S c ++++=①∵()[]()[]a b a a b b S S S -+∙-+=++21438=ab b 212-, 985S S S +=,∴824321S ab b S S --=+=812SS b --.② 把②代入①,得=922S S b ++=22a b +.∴222c b a =+.【证法6】(李锐证明)设直角三角形两直角边的长分别为a 、b (b>a ),斜边的长为c.做三个边长分别为a 、b 、c 的正方形,把它们拼成如图所示形状,使A 、E 、G 三点在一条直线上.用数字表示面积的编号(如图).∵∠TBE=∠ABH=90º, ∴∠TBH=∠ABE. 又∵∠BTH=∠BEA=90º,BT=BE=b , ∴Rt ΔHBT ≌Rt ΔABE. ∴HT=AE=a. ∴GH=GT ―HT=b ―a.又∵∠GHF+∠BHT=90º,∠DBC+∠BHT=∠TBH+∠BHT=90∴∠GHF=∠DBC.∵DB=EB ―ED=b ―a ,∠HGF=∠BDC=90º, ∴Rt ΔHGF ≌Rt ΔBDC.即27S S =.过Q 作QM ⊥AG ,垂足是M.由∠BAQ=∠BEA=90º,可知∠ABE =∠QAM ,而AB=AQ=c ,所以Rt ΔABE ≌Rt ΔQAM.又Rt ΔHBT ≌ Rt ΔABE.所以Rt ΔHBT ≌Rt ΔQAM.即58S S =.由Rt ΔABE ≌Rt ΔQAM ,又得QM=AE=a ,∠AQM=∠BAE. ∵∠AQM+∠FQM=90º,∠BAE+∠CAR=90º,∠AQM=∠BAE , ∴∠FQM=∠CAR.又∵∠QMF=∠ARC=90º,QM=AR=a ,∴Rt ΔQMF ≌Rt ΔARC.即64S S =.∵543212S S S S S c ++++=,612S S a +=,8732S S S b ++=,又∵27S S =,58S S =,64S S =,∴8736122S S S S S b a ++++=+=52341S S S S S ++++ =2c ,即222c b a =+. 【证法7】(利用多列米定理证明)在Rt ΔABC 中,设直角边BC=a ,AC=b ,斜边AB=c (如图).过点A 作AD ∥CB ,过点B 作BD ∥CA ,则ACBD 为矩形,矩形ACBD 内接于一个圆.根据多列米定理,圆内接四边形对角线的乘积等于两对边乘积之和,有BD AC BC AD DC AB ∙+∙=∙, ∵AB=DC=c ,AD=BC=a , AC=BD=b , ∴222AC BC AB +=,即222b a c +=, ∴222c b a =+.【证法8】(利用反证法证明)如图,在Rt ΔABC 中,设直角边AC 、BCb ,斜边AB 的长为c ,过点C 作CD ⊥AB ,垂足是D.假设222c b a ≠+,即假设222AB BC AC ≠+,则由AB AB AB ∙=2=()BD AD AB +=BD AB AD AB ∙+∙可知AD AB AC ∙≠2,或者BD AB BC ∙≠2.即AD :AC ≠AC :AB ,或者BD :BC ≠BC :AB.在ΔADC 和ΔACB 中,∵∠A=∠A ,∴若AD :AC ≠AC :AB ,则∠ADC ≠∠ACB. 在ΔCDB 和ΔACB 中, ∵∠B=∠B , ∴若BD :BC ≠BC :AB ,则 ∠CDB ≠∠ACB. 又∵∠ACB=90º,∴∠ADC ≠90º,∠CDB ≠90º.这与作法CD ⊥AB 矛盾.所以,222AB BC AC ≠+的假设不能成立.∴222c b a =+. 【证法9】(辛卜松证明)设直角三角形两直角边的长分别为a 、b ,斜边的长为c.作边长是a+b 的正方形ABCD.把正方形ABCD 划分成上方左图所示的几个部分,则正方形ABCD 的面积为()ab b a b a 2222++=+;把正方形ABCD 划分成上方右图所示的几个部分,则正方形ABCD 的面积为()22214c ab b a +⨯=+=22c ab +.∴22222c ab ab b a +=++,∴222c b a =+.。
人教版八年级数学上册专题复习证明三角形全等的常见题型

证明三角形全等的常见题型全等三角形是初中几何的重要内容之一,全等三角形的学习是几何入门最关键的一步,这部分内容学习的好坏直接影响着今后的学习。
而一些初学的同学,虽然学习了几种判定三角形全等的公理和推论,但往往仍不知如何根据已知条件证明两个三角形全等。
在辅导时可以抓住以下几种证明三角形全等的常见题型,进行分析。
一、已知一边与其一邻角对应相等1.证已知角的另一边对应相等,再用SAS证全等。
例1已知:如图1,点E、F在BC上,BE=CF,AB=DC,∠B=∠C .求证:AF=DE。
证明∵BE=CF(已知),∴BE+ EF=CF+EF,即 BF=CE。
在△ABF和△DCE中,∴△ABF≌△DCE(SAS)。
∴ AF=DE(全等三角形对应边相等)。
2.证已知边的另一邻角对应相等,再用ASA证全等。
例2已知:如图2,D是△ABC的边AB上一点,DF交AC于点E,DE=FE,FC∥AB。
求证:AE=CE。
证明∵ FC∥AB(已知),∴∠ADE=∠CFE(两直线平行,内错角相等)。
在△ADE和△CFE中,∴△ADE≌△CFE(ASA).∴ AE=CE(全等三角形对应边相等)3.证已知边的对角对应相等,再用AAS证全等。
例3(同例2).证明∵ FC∥AB(已知),∴∠A=∠ECF(两直线平行,内错角相等).在△ADE和△CFE中,∴△ADE≌△CFE(AAS).∴ AE=CE(全等三角形对应边相等)。
二、已知两边对应相等1.证两已知边的夹角对应相等,再用SAS证等。
例4已知:如图3,AD=AE,点D、E在BCBD=CE,∠1=∠2。
求证:△ABD≌△ACE.证明∵∠1=∠2(已知),∠ADB=180°-∠1,∠AEC=180°-∠2(邻补角定义),∴∠ADB = ∠AEC,在△ABD和△ACE中,∴△ABD≌△ACE(SAS).2.证第三边对应相等,再用SSS证全等。
例5已知:如图4,点A、C、B、D在同一直线AC=BD,AM=CN,BM=DN。
八年级数学 勾股定理证明方法
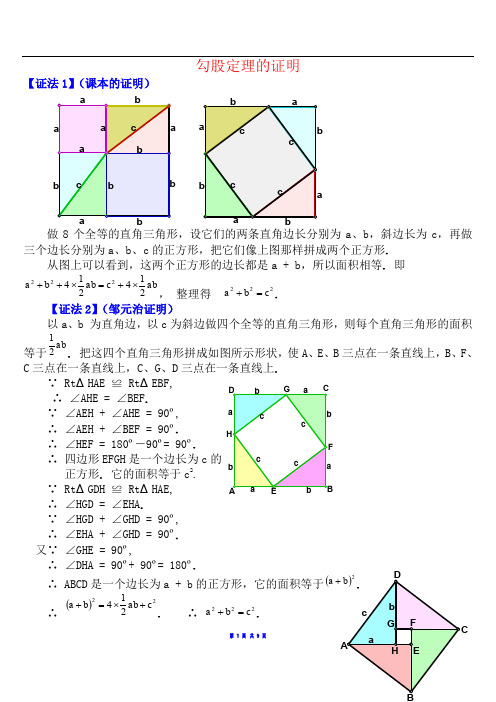
勾股定理的证明【证法1】(课本的证明)做8个全等的直角三角形,设它们的两条直角边长分别为a 、b ,斜边长为c ,再做三个边长分别为a 、b 、c 的正方形,把它们像上图那样拼成两个正方形.从图上可以看到,这两个正方形的边长都是a + b ,所以面积相等. 即abc ab b a 214214222⨯+=⨯++, 整理得 222c b a =+.【证法2】(邹元治证明)以a 、b 为直角边,以c 为斜边做四个全等的直角三角形,则每个直角三角形的面积等于ab21. 把这四个直角三角形拼成如图所示形状,使A 、E 、B 三点在一条直线上,B 、F 、C 三点在一条直线上,C 、G 、D 三点在一条直线上.∵ Rt ΔHAE ≌ Rt ΔEBF, ∴ ∠AHE = ∠BEF .∵ ∠AEH + ∠AHE = 90º, ∴ ∠AEH + ∠BEF = 90º. ∴ ∠HEF = 180º―90º= 90º.∴ 四边形EFGH 是一个边长为c 的 正方形. 它的面积等于c 2.∵ Rt ΔGDH ≌ Rt ΔHAE, ∴ ∠HGD = ∠EHA .∵ ∠HGD + ∠GHD = 90º, ∴ ∠EHA + ∠GHD = 90º. 又∵ ∠GHE = 90º,∴ ∠DHA = 90º+ 90º= 180º.∴ ABCD 是一个边长为a + b 的正方形,它的面积等于(a +∴()22214c ab b a +⨯=+. ∴ 222c b a =+.【证法3】(赵爽证明) 以a 、b 为直角边(b>a ), 以c 为斜 边作四个全等的直角三角形,则每个直角三角形的面积等于ab 21. 把这四个直角三角形拼成如图所示形状.∵ Rt ΔDAH ≌ Rt ΔABE, ∴ ∠HDA = ∠EAB .∵ ∠HAD + ∠HAD = 90º, ∴ ∠EAB + ∠HAD = 90º,∴ ABCD 是一个边长为c 的正方形,它的面积等于c 2. ∵ EF = FG =GH =HE = b ―a , ∠HEF = 90º.∴ EFGH 是一个边长为b ―a 的正方形,它的面积等于()2a b -.∴ ()22214c a b ab =-+⨯.∴ 222c b a =+. 【证法4】(1876年美国总统Garfield 证明)以a 、b 为直角边,以c 为斜边作两个全等的直角三角形,则每个直角三角形的面积等于ab 21. 把这两个直角三角形拼成如图所示形状,使A 、E 、B 三点在一条直线上.∵ Rt ΔEAD ≌ Rt ΔCBE, ∴ ∠ADE = ∠BEC .∵ ∠AED + ∠ADE = 90º,∴ ∠AED + ∠BEC = 90º.∴ ∠DEC = 180º―90º= 90º. ∴ ΔDEC 是一个等腰直角三角形,它的面积等于221c .又∵ ∠DAE = 90º, ∠EBC = 90º,∴ AD ∥BC .∴ ABCD 是一个直角梯形,它的面积等于()221b a +. ∴ ()222121221c ab b a +⨯=+. ∴ 222c b a =+.【证法5】(梅文鼎证明)做四个全等的直角三角形,设它们的两条直角边长分别为a 、b ,斜边长为c . 把它们拼成如图那样的一个多边形,使D 、E 、F 在一条直线上. 过C 作AC 的延长线交DF 于点P .∵ D 、E 、F 在一条直线上, 且Rt ΔGEF ≌ Rt ΔEBD, ∴ ∠EGF = ∠BED ,∵ ∠EGF + ∠GEF = 90°, ∴ ∠BED + ∠GEF = 90°, ∴ ∠BEG =180º―90º= 90º.又∵ AB = BE = EG = GA = c ,∴ ABEG 是一个边长为c 的正方形. ∴ ∠ABC + ∠CBE = 90º.∵ Rt ΔABC ≌ Rt ΔEBD, ∴ ∠ABC = ∠EBD .∴ ∠EBD + ∠CBE = 90º. 即 ∠CBD= 90º. 又∵ ∠BDE = 90º,∠BCP = 90º, BC = BD = a . ∴ BDPC 是一个边长为a 的正方形. 同理,HPFG 是一个边长为b 的正方形. 设多边形GHCBE 的面积为S ,则,21222ab S b a ⨯+=+ abS c 2122⨯+=,∴ 222c b a =+.【证法6】(项明达证明)做两个全等的直角三角形,设它们的两条直角边长分别为a 、b (b>a ) ,斜边长为c . 再做一个边长为c 的正方形. 把它们拼成如图所示的多边形,使E 、A 、C 三点在一条直线上.过点Q 作QP ∥BC ,交AC 于点P . 过点B 作BM ⊥PQ ,垂足为M ;再过点 F 作FN ⊥PQ ,垂足为N . ∵ ∠BCA = 90º,QP ∥BC , ∴ ∠MPC = 90º, ∵ BM ⊥PQ , ∴ ∠BMP = 90º, ∴ BCPM 是一个矩形,即∠MBC = 90∵ ∠QBM + ∠MBA = ∠QBA = 90º,∠ABC + ∠MBA = ∠MBC = 90º, ∴ ∠QBM = ∠ABC ,又∵ ∠BMP = 90º,∠BCA = 90º,BQ = BA = c , ∴ Rt ΔBMQ ≌ Rt ΔBCA .同理可证Rt ΔQNF ≌ Rt ΔAEF . 从而将问题转化为【证法4】(梅文鼎证明). 【证法7】(欧几里得证明)做三个边长分别为a 、b 、c 的正方形,把它们拼成如图所示形状,使H 、C 、B 三点在一条直线上,连结BF 、CD . 过C 作CL ⊥DE ,交AB 于点M ,交DE 于点L . ∵ AF = AC ,AB = AD , ∠FAB = ∠GAD , ∴ ΔFAB ≌ ΔGAD , ∵ ΔFAB 的面积等于221aΔGAD 的面积等于矩形ADLM的面积的一半,∴ 矩形ADLM 的面积 =2a 同理可证,矩形MLEB 的面积 =2b .∵ 正方形ADEB 的面积= 矩形ADLM 的面积 + 矩形MLEB 的面积 ∴ 222b a c += ,即 222c b a =+. 【证法8】(利用相似三角形性质证明)如图,在Rt ΔABC 中,设直角边AC 、BC 的长度分别为a 、b ,斜边AB 的长为c ,过点C 作CD ⊥AB ,垂足是D .在ΔADC 和ΔACB 中,∵ ∠ADC = ∠ACB = 90º,∠CAD = ∠BAC , ∴ ΔADC ∽ ΔACB .AD ∶AC = AC ∶AB , 即 AB AD AC ∙=2.同理可证,ΔCDB ∽ ΔACB ,从而有 AB BD BC ∙=2.∴ ()222AB AB DB AD BC AC =∙+=+,即 222c b a =+.【证法9】(杨作玫证明)做两个全等的直角三角形,设它们的两条直角边长分别为a 、b (b>a ),斜边长为c .再做一个边长为c 的正方形. 把它们拼成如图所示的多边形. 过A 作AF ⊥AC ,AF 交GT 于F ,AF 交DT 于R . 过B 作BP ⊥AF ,垂足为P . 过D 作DE 与CB 的延长线垂直,垂足为E ,DE 交AF 于H .∵ ∠BAD = 90º,∠PAC = 90º, ∴ ∠DAH = ∠BAC .又∵ ∠DHA = 90º,∠BCA = 90º,AD = AB = c ,∴ Rt ΔDHA ≌ Rt ΔBCA .∴ DH = BC = a ,AH = AC = b . 由作法可知, PBCA 是一个矩形, 所以 Rt ΔAPB ≌ Rt ΔBCA . 即PB = CA = b ,AP= a ,从而PH = b ―a .∵ Rt ΔDGT ≌ Rt ΔBCA , Rt ΔDHA ≌ Rt ΔBCA . ∴ Rt ΔDGT ≌ Rt ΔDHA .∴ DH = DG = a ,∠GDT = ∠HDA . 又∵ ∠DGT = 90º,∠DHF = 90º,∠GDH = ∠GDT + ∠TDH = ∠HDA+ ∠TDH = 90º, ∴ DGFH 是一个边长为a 的正方形.∴ GF = FH = a . TF ⊥AF ,TF = GT ―GF = b ―a .∴ TFPB 是一个直角梯形,上底TF=b ―a ,下底BP= b ,高FP=a +(b ―a ). 用数字表示面积的编号(如图),则以c 为边长的正方形的面积为543212S S S S S c ++++= ①∵()[]()[]a b a a b b S S S -+∙-+=++21438 =ab b 212-, 985S S S +=,∴ 824321S ab b S S --=+= 812S S b -- . ②把②代入①,得98812212S S S S b S S c ++--++== 922S S b ++ = 22a b +.∴ 222c b a =+.【证法10】(李锐证明)设直角三角形两直角边的长分别为a 、b (b>a ),斜边的长为c . 做三个边长分别为a 、b 、c 的正方形,把它们拼成如图所示形状,使A 、E 、G 三点在一条直线上. 用数字表示面积的编号(如图).∵ ∠TBE = ∠ABH = 90º, ∴ ∠TBH = ∠ABE . 又∵ ∠BTH = ∠BEA = 90º,BT = BE = b , ∴ Rt ΔHBT ≌ Rt ΔABE . ∴ HT = AE = a . ∴ GH = GT ―HT = b ―a .又∵ ∠GHF + ∠BHT = 90º,∠DBC + ∠BHT = ∠TBH + ∠∴ ∠GHF = ∠DBC .∵ DB = EB ―ED = b ―a , ∠HGF = ∠BDC = 90º,∴ Rt ΔHGF ≌ Rt ΔBDC . 即 27S S =.过Q 作QM ⊥AG ,垂足是M . 由∠BAQ = ∠BEA = 90º,可知 ∠ABE = ∠QAM ,而AB = AQ = c ,所以Rt ΔABE ≌ Rt ΔQAM . 又Rt ΔHBT ≌ Rt ΔABE . 所以Rt ΔHBT ≌ Rt ΔQAM . 即 58S S =.由Rt ΔABE ≌ Rt ΔQAM ,又得QM = AE = a ,∠AQM = ∠BAE .∵ ∠AQM + ∠FQM = 90º,∠BAE + ∠CAR = 90º,∠AQM = ∠BAE , ∴ ∠FQM = ∠CAR .又∵ ∠QMF = ∠ARC = 90º,QM = AR = a ,∴ Rt ΔQMF ≌ Rt ΔARC . 即64S S =.∵ 543212S S S S S c ++++=,612S S a +=,8732S S S b ++=,又∵ 27S S =,58S S =,64S S =,∴8736122S S S S S b a ++++=+ =52341S S S S S ++++=2c , 即 222c b a =+.【证法11】(利用切割线定理证明)在Rt ΔABC 中,设直角边BC = a ,AC = b ,斜边AB = c . 如图,以B 为圆心a 为半径作圆,交AB 及AB 的延长线分别于D 、E ,则BD = BE = BC = a . 因为∠BCA = 90º,点C 在⊙B 上,所以AC 是⊙B 的切线. 由切割线定理,得AD AE AC ∙=2=()()BD AB BE AB -+=()()a c a c -+= 22a c -,即222a c b -=,∴ 222c b a =+.【证法12】(利用多列米定理证明)在Rt ΔABC 中,设直角边BC = a ,AC = b ,斜边AB = c (如图). 过点A 作AD ∥CB ,过点B 作BD ∥CA ,则ACBD 为矩形,矩形ACBD 内接于一个圆. 根据多列米定理,圆内接四边形对角线的乘积等于两对边乘积之和,有BD AC BC AD DC AB ∙+∙=∙,∵ AB = DC = c ,AD = BC = a , AC = BD = b ,∴ 222AC BC AB +=,即 222b a c +=, ∴ 222c b a =+.【证法13】在Rt ΔABC 中,设直角边BC = a ,AC = b ,斜边AB = c . 作Rt ΔABC 的内切圆⊙O ,切点分别为D 、E 、F (如图),设⊙O 的半径为r .∵ AE = AF ,BF = BD ,CD = CE ,∴ ()()()BF AF CD BD CE AE AB BC AC +-+++=-+= CD CE += r + r = 2r,即 r c b a 2=-+, ∴ c r b a +=+2.∴ ()()222c r b a +=+,即 ()222242c rc r ab b a ++=++,∵ab S ABC 21=∆,∴ ABC S ab ∆=42, 又∵ AOC BOCAOB ABC S S S S ∆∆∆∆++= = br ar cr 212121++ = ()r c b a ++21= ()r c c r ++221= rc r +2,∴()ABC S rc r ∆=+442, ∴ ()ab rc r242=+,∴ 22222c ab ab b a +=++, ∴ 222c b a =+. 【证法14】(利用反证法证明)如图,在Rt ΔABC 中,设直角边AC 、BC 的长度分别为a 、b ,斜边AB 的长为c ,过点C 作CD ⊥AB ,垂足是D .假设222c b a ≠+,即假设 222AB BC AC ≠+,则由AB AB AB ∙=2=()BD AD AB +=BD AB AD AB ∙+∙可知 AD AB AC ∙≠2,或者 BD AB BC ∙≠2. 即 AD :AC ≠AC :AB ,或者 BD :BC ≠BC :AB .在ΔADC 和ΔACB 中,∵ ∠A = ∠A ,∴ 若 AD :AC ≠AC :AB ,则∠ADC ≠∠ACB . 在ΔCDB 和ΔACB 中, ∵ ∠B = ∠B , ∴ 若BD :BC ≠BC :AB ,则 ∠CDB ≠∠ACB . 又∵ ∠ACB = 90º,∴ ∠ADC ≠90º,∠CDB ≠90º.这与作法CD ⊥AB 矛盾. 所以,222AB BC AC ≠+的假设不能成立.∴ 222c b a =+.【证法15】(辛卜松证明)设直角三角形两直角边的长分别为a 、b ,斜边的长为c . 作边长是a+b 的正方形ABCD . 把正方形ABCD 划分成上方左图所示的几个部分,则正方形ABCD 的面积为()ab b a b a 2222++=+;把正方形ABCD划分成上方右图所示的几个部分,则正方形ABCD 的面积为 ()22214c ab b a +⨯=+ =22c ab +.∴ 22222c ab ab b a +=++,∴ 222c b a =+.【证法16】(陈杰证明)D设直角三角形两直角边的长分别为a 、b (b>a ),斜边的长为c . 做两个边长分别为a 、b 的正方形(b>a ),把它们拼成如图所示形状,使E 、H 、M 三点在一条直线上. 用数字表示面积的编号(如图). 在EH = b 上截取ED = a ,连结DA 、则 AD = c .∵ EM = EH + HM = b + a , ED = a ∴ DM = EM ―ED = ()a b +―a = b . 又∵ ∠CMD = 90º,CM = a , ∠AED = 90º, AE = b , ∴ Rt ΔAED ≌ Rt ΔDMC .∴ ∠EAD = ∠MDC ,DC = AD = c . ∵ ∠ADE + ∠ADC+ ∠MDC =180º,∠ADE + ∠MDC = ∠ADE + ∠EAD = 90º, ∴ ∠ADC = 90º.∴ 作AB ∥DC ,CB ∥DA ,则ABCD 是一个边长为c 的正方形. ∵ ∠BAF + ∠FAD = ∠DAE + ∠FAD = 90º, ∴ ∠BAF=∠DAE .连结FB ,在ΔABF 和ΔADE 中,∵ AB =AD = c ,AE = AF = b ,∠BAF=∠DAE , ∴ ΔABF ≌ ΔADE .∴ ∠AFB = ∠AED = 90º,BF = DE = a . ∴ 点B 、F 、G 、H 在一条直线上. 在Rt ΔABF 和Rt ΔBCG 中,∵ AB = BC = c ,BF = CG = a , ∴ Rt ΔABF ≌ Rt ΔBCG .∵ 54322S S S S c +++=, 6212S S S b ++=, 732S S a +=,76451S S S S S +===,∴6217322S S S S S b a ++++=+ =()76132S S S S S ++++=5432S S S S +++=2c ∴ 222c b a =+.。
人教版八年级数学下册17.1勾股定理的证明(比较全的证明方法)ppt课件
b
a
∵ S梯 形 AB CD = = 1
1 2
B
a+b 2
2 又 ∵S梯 形 AB CD =S AED +S EBC+S 1 1 1 1 = ab+ ba+ c2= (2ab+c2) 2 2 2 2 比 较上 面 二 式得 c2=a2+b2
(a2+2ab+b2)
CED
向常春的证明方法
S梯形ABCD 1 1 2 1 ( a b b )( a b ) a ab 2 2 2
那么:
朱实 中 黄实 b a
返回
( b- a) 2
ab c 4 ( b a )2 2
2
得: c2 =a2+ b2.
证明1:
该图2002年8月在北京召开的国际数学家大会的会标示意图,取材于我国古代数学著作《勾股圆方图》。
a c b
a
2 c 大正方形的面积可以表示为 ; 1 2 (b a ) 4 ab 也可以表示为 2 c 1 2 ∵ c2= (b a ) 4 ab 2 2 2 =b -2ab+a + 2ab b =a2+b2
G
已知:如图,以在Rt△ABC中, ∠ACB=90°,分别以a、b、c为边向外作 正方形.
K
H C b A c a B
F
求证:a2 +b2=c2.
D E
传说中毕达哥拉斯的证法
证明:从Rt△ABC的三边向外各作一个正方形(如图),作CN⊥DE交AB于M,那么正方形 ABED被分成两个矩形.连结CD和KB. ∵由于矩形ADNM和△ADC同底(AD),等高(即平行线AD和CN间的距离),
八年级数学下册第六章证明(一)定义与命题

小结 拓展
1、定义:对名称和术语的含义加以描述, 作出明确的规定,也就是给出它们的定 义.
2、命题的定义:判断一件事情的句子,叫 做命题.
3、命题的结构:每个命题都由条件和结论 两部分组成.条件是已知事项,结论是由 已事项推断出的事项.
1、原名: 某些数学名词称为原名. 2、公理: 公认的真命题称为公理.
3、证明: 除了公理外,其它真命题的正确性都通过
推理的方法证实.推理的过程称为证明.
4、定理: 经过证明的真命题称为定理.
经过证明的真
一些条件
推理的过程 叫证明
命题叫定理
+
推理
证实其它命 题的正确性
原名、公理 温馨提示:证明所需的定义、公理和其它定理都
语句.像这样判断一件事情的句子,叫做命题.
寻找命题的“共同的结构特征”
观察下列命题,试找出命题的共同的结构特征 (1)如果两个三角形的三条边对应相等,那么这两个三角形全等 (2)如果一个四边形的一组对边平行且相等,那么这个四边形是
平行四边形; (3)如果一个三角形是等腰三角形,那么这个三角形的两个底角
第六章 证明(一)
定义与命题
眼见未必为实!
a
线段a与线段b哪个 比较长?
b
a bc
谁与线段d在 一条直线上?
d
a
a bc
b
线段a与线段b哪个 比较长?
d
谁与线段d在 一条直线上?
a
b
a=b
a bc d
假如用一根比地球赤道长1 米的铁丝将 地球赤道围起来,那么铁丝与赤道之间的间 隙能有多大(把地球看成球形)?
勾股定理9种证明(有图)
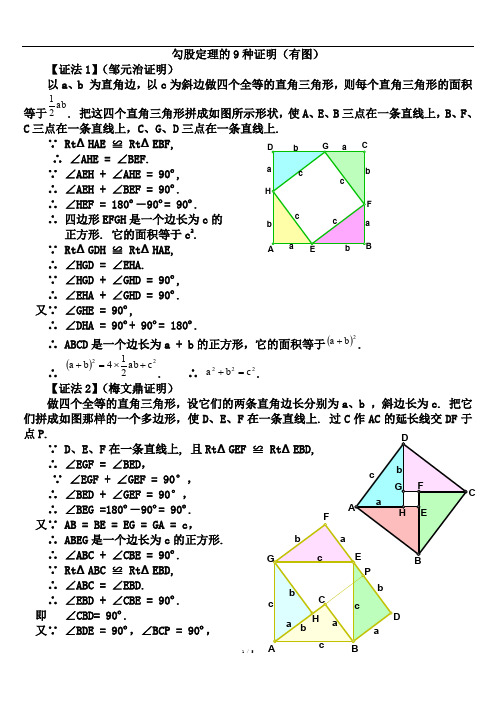
勾股定理的9种证明(有图)【证法1】(邹元治证明)以a 、b 为直角边,以c 为斜边做四个全等的直角三角形,则每个直角三角形的面积等于ab21. 把这四个直角三角形拼成如图所示形状,使A 、E 、B 三点在一条直线上,B 、F 、C 三点在一条直线上,C 、G 、D 三点在一条直线上.∵ Rt ΔHAE ≌ Rt ΔEBF, ∴ ∠AHE = ∠BEF.∵ ∠AEH + ∠AHE = 90º,∴ ∠AEH + ∠BEF = 90º. ∴ ∠HEF = 180º―90º= 90º.∴ 四边形EFGH 是一个边长为c 的 正方形. 它的面积等于c 2.∵ Rt ΔGDH ≌ Rt ΔHAE,∴ ∠HGD = ∠EHA.∵ ∠HGD + ∠GHD = 90º, ∴ ∠EHA + ∠GHD = 90º. 又∵ ∠GHE = 90º,∴ ∠DHA = 90º+ 90º= 180º.∴ ABCD 是一个边长为a + b 的正方形,它的面积等于()2b a +.∴ ()22214c ab b a +⨯=+. ∴ 222c b a =+.【证法2】(梅文鼎证明)做四个全等的直角三角形,设它们的两条直角边长分别为a 、b ,斜边长为c. 把它们拼成如图那样的一个多边形,使D 、E 、F 在一条直线上. 过C 作AC 的延长线交DF 于点P. ∵ D 、E 、F 在一条直线上, 且Rt ΔGEF ≌∴ ∠EGF = ∠BED , ∵ ∠EGF + ∠GEF = 90°,∴ ∠BED + ∠GEF = 90°,∴ ∠BEG =180º―90º= 90º. 又∵ AB = BE = EG = GA = c ,∴ ABEG 是一个边长为c 的正方形.∴ ∠ABC + ∠CBE = 90º. ∵ Rt ΔABC ≌ Rt ΔEBD, ∴ ∠ABC = ∠EBD. ∴ ∠EBD + ∠CBE = 90º. 即 ∠CBD= 90º. 又∵ ∠BDE = 90º,∠BCP = 90º,BC = BD = a.∴ BDPC 是一个边长为a 的正方形. 同理,HPFG 是一个边长为b 的正方形. 设多边形GHCBE 的面积为S ,则,21222ab S b a ⨯+=+ abS c 2122⨯+=,∴ 222c b a =+.【证法3】(项明达证明)做两个全等的直角三角形,设它们的两条直角边长分别为a 、b (b>a ) ,斜边长为c. 再做一个边长为c 的正方形. 把它们拼成如图所示的多边形,使E 、A 、C 三点在一条直线上. 过点Q 作QP ∥BC ,交AC 于点P.过点B 作BM ⊥PQ ,垂足为M ;再过点F 作FN ⊥PQ ,垂足为N.∵ ∠BCA = 90º,QP ∥BC ,∴ ∠MPC = 90º,∵ BM ⊥PQ , ∴ ∠BMP = 90º,∴ BCPM 是一个矩形,即∠MBC = 90º.∵ ∠QBM + ∠MBA = ∠QBA = 90º,∠ABC + ∠MBA = ∠MBC = 90º, ∴ ∠QBM = ∠ABC ,又∵ ∠BMP = 90º,∠BCA = 90º,BQ = BA = c , ∴ Rt ΔBMQ ≌ Rt ΔBCA.同理可证Rt ΔQNF ≌ Rt ΔAEF. 从而将问题转化为【证法4】(梅文鼎证明). 【证法4】(欧几里得证明)做三个边长分别为a 、b 、c 的正方形,把它们拼成如图所示形状,使H 、C 、B 三点在一条直线上,连结BF 、CD. 过C 作CL ⊥DE , 交AB 于点M ,交DE 于点L.∵ AF = AC ,AB = AD , ∠FAB = ∠GAD ,∴ ΔFAB ≌ ΔGAD , ∵ ΔFAB 的面积等于221a ,ΔGAD 的面积等于矩形ADLM 的面积的一半,∴ 矩形ADLM 的面积 =2a .同理可证,矩形MLEB 的面积 =2b .∵ 正方形ADEB 的面积= 矩形ADLM 的面积 + 矩形MLEB 的面积 ∴ 222b a c += ,即 222c b a =+. 【证法5】(杨作玫证明)做两个全等的直角三角形,设它们的两条直角边长分别为a 、b (b>a ),斜边长为c. 再做一个边长为c 的正方形. 把它们拼成如图所示的多边形. 过A 作AF ⊥AC ,AF 交GT 于F ,AF 交DT 于R. 过B 作BP ⊥AF ,垂足为P. 过D 作DE 与CB 的延长线垂直,垂足为E ,DE 交AF 于H.∵ ∠BAD = 90º,∠PAC = 90º,∴ ∠DAH = ∠BAC.又∵ ∠DHA = 90º,∠BCA = 90º, AD = AB = c , ∴ Rt ΔDHA ≌ Rt ΔBCA.∴ DH = BC = a ,AH = AC = b.由作法可知, PBCA 是一个矩形, 所以 Rt ΔAPB ≌ Rt ΔBCA. 即PB = CA = b ,AP= a ,从而PH = b ―a.∵ Rt ΔDGT ≌ Rt ΔBCA , Rt ΔDHA ≌ Rt ΔBCA.∴ Rt ΔDGT ≌ Rt ΔDHA .∴ DH = DG = a ,∠GDT = ∠HDA . 又∵ ∠DGT = 90º,∠DHF = 90º,∠GDH = ∠GDT + ∠TDH = ∠HDA+ ∠TDH = 90º, ∴ DGFH 是一个边长为a 的正方形.∴ GF = FH = a . TF ⊥AF ,TF = GT ―GF = b ―a .∴ TFPB 是一个直角梯形,上底TF=b ―a ,下底BP= b ,高FP=a +(b ―a ). 用数字表示面积的编号(如图),则以c 为边长的正方形的面积为543212S S S S S c ++++= ①∵()[]()[]a b a a b b S S S -+∙-+=++21438 =ab b 212-, 985S S S +=,∴ 824321S ab b S S --=+= 812S S b -- . ②把②代入①,得98812212S S S S b S S c ++--++== 922S S b ++ = 22a b +. ∴ 222c b a =+.【证法6】(李锐证明)设直角三角形两直角边的长分别为a 、b (b>a ),斜边的长为c. 做三个边长分别为a 、b 、c 的正方形,把它们拼成如图所示形状,使A 、E 、G 三点在一条直线上. 用数字表示面积的编号(如图).∵ ∠TBE = ∠ABH = 90º, ∴ ∠TBH = ∠ABE. 又∵ ∠BTH = ∠BEA = 90º,BT = BE = b , ∴ Rt ΔHBT ≌ Rt ΔABE. ∴ HT = AE = a. ∴ GH = GT ―HT = b ―a.又∵ ∠GHF + ∠BHT = 90º,∠DBC + ∠BHT = ∠TBH + ∠∴ ∠GHF = ∠DBC.∵ DB = EB ―ED = b ―a ,∠HGF = ∠BDC = 90º,∴ Rt ΔHGF ≌ Rt ΔBDC. 即 27S S =.过Q 作QM ⊥AG ,垂足是M. 由∠BAQ = ∠BEA = 90º,可知 ∠ABE = ∠QAM ,而AB = AQ = c ,所以Rt ΔABE ≌ Rt ΔQAM . 又Rt ΔHBT ≌ Rt ΔABE. 所以Rt ΔHBT ≌ Rt ΔQAM . 即 58S S =.由Rt ΔABE ≌ Rt ΔQAM ,又得QM = AE = a ,∠AQM = ∠BAE.∵ ∠AQM + ∠FQM = 90º,∠BAE + ∠CAR = 90º,∠AQM = ∠BAE , ∴ ∠FQM = ∠CAR.又∵ ∠QMF = ∠ARC = 90º,QM = AR = a ,∴ Rt ΔQMF ≌ Rt ΔARC. 即64S S =.∵ 543212S S S S S c ++++=,612S S a +=,8732S S S b ++=,又∵ 27S S =,58S S =,64S S =,∴8736122S S S S S b a ++++=+ =52341S S S S S ++++=2c , 即 222c b a =+.【证法7】(利用多列米定理证明)在Rt ΔABC 中,设直角边BC = a ,AC = b ,斜边AB = c (如图). 过点A 作AD ∥CB ,过点B 作BD ∥CA ,则ACBD 为矩形,矩形ACBD 内接于一个圆. 根据多列米定理,圆内接四边形对角线的乘积等于两对边乘积之和,有BD AC BC AD DC AB ∙+∙=∙,∵ AB = DC = c ,AD = BC = a , AC = BD = b ,∴ 222AC BC AB +=,即 222b a c +=, ∴ 222c b a =+.【证法8】(利用反证法证明)如图,在Rt ΔABC 中,设直角边AC 、BC 的长度分别为a 、b ,斜边AB 的长为c ,过点C 作CD ⊥AB ,垂足是D.假设222c b a ≠+,即假设 222AB BC AC ≠+,则由AB AB AB ∙=2=()BD AD AB +=BD AB AD AB ∙+∙可知 AD AB AC ∙≠2,或者 BD AB BC ∙≠2. 即 AD :AC ≠AC :AB ,或者 BD :BC ≠BC :AB.在ΔADC 和ΔACB 中,∵ ∠A = ∠A ,∴ 若 AD :AC ≠AC :AB ,则∠ADC ≠∠ACB. 在ΔCDB 和ΔACB 中, ∵ ∠B = ∠B , ∴ 若BD :BC ≠BC :AB ,则 ∠CDB ≠∠ACB. 又∵ ∠ACB = 90º,∴ ∠ADC ≠90º,∠CDB ≠90º.这与作法CD ⊥AB 矛盾. 所以,222AB BC AC ≠+的假设不能成立.∴ 222c b a =+. 【证法9】(辛卜松证明)设直角三角形两直角边的长分别为a 、b ,斜边的长为c. 作边长是a+b 的正方形ABCD. 把正方形ABCD 划分成上方左图所示的几个部分,则正方形ABCD 的面积为()ab b a b a 2222++=+;把正方形ABCD 划分成上方右图所示的几个部分,则正方形ABCD 的面积为 ()22214c ab b a +⨯=+ =22c ab +.∴ 22222c ab ab b a +=++,∴ 222c b a =+.。
2018秋人教版八年级数学上册课件:第三部分 专题探究 专题四 几何证明专题 (共20张PPT)

考点三中,AD⊥BC,垂 足为点D,E是线段AD上的点,且AD=BD,DE=DC. 求 证:∠BED=∠C.
证明:∵AD⊥BC,∴∠BDE=∠ADC=90°. 在△BDE和△ADC中,
∴△BDE≌△ADC (SAS). ∴∠BED=∠C.
考点四: 证明等边三角形 【例4】如图3-4-7,在Rt△ABC中,∠ACB=90°,BD 是△ABC的角平分线. (1)如图3-4-7①,若AD=BD,求∠A的度数; (2)如图3-4-7②,在(1)的条件下,作DE⊥AB于点 E,连接EC. 求证:△EBC是等边三角形.
(2)解:△ABE是等边三角形. 理由如下. ∵BC是线段AE的垂直平分线, ∴BA=BE,即△ABE是等腰三角形. 又∵∠CAB=60°, ∴△ABE是等边三角形.
5. 如图3-4-10,已知:在△ABC中,∠B,∠C的平分线 相交于点D,过点D作EF∥BC交AB于点E,交AC于点F, 求证:BE+CF=EF. 证明:∵BD平分∠ABC, ∴∠EBD=∠DBC. ∵EF∥BC,∴∠EDB=∠DBC. ∴∠EDB=∠EBD. ∴DE=BE. 同理,CF=DF. ∴EF=DE+DF=BE+CF, 即BE+CF=EF.
拓展提升
9. 如图3-4-14,在等边△ABC中,点P在△ABC内,点 Q在△ABC外,且∠ABP=∠ACQ,BP=CQ. 判断 △APQ的形状,并说明理由. 解:△APQ是等边三角形. 理由如下. ∵△ABC为等边三角形, ∴AB=AC.
在△ABP和△ACQ中,
∴△ABP≌△ACQ(SAS). ∴AP=AQ,∠BAP=∠CAQ. ∵∠BAC=∠BAP+∠PAC=60°, ∴∠PAQ=∠CAQ+∠PAC=60°. ∴△APQ是等边三角形.
八年级数学几种证明图示(共7张PPT)

法
我 国 清 代 数 学 家 华 蘅 芳 的 证 法
家 八年级数学几种证明图示
我国清代数学家梅文鼎的证法
梅 我国魏晋时期数学家刘徽的证法
八年级数学几种证明图示
文 我国清代数学家梅文鼎的证法
我国清代数学家梅文鼎的证法
鼎 我国清代数学家梅文鼎的证法
我国清代数学家梅文鼎的证法 我国魏晋时期数学家刘徽的证法
的 八年级数学几种证明图示
赵爽的弦图以及印度婆什伽罗的证法
八年级数学几种证明图示
毕达哥拉斯的十任总统伽菲尔德的证法 赵爽的弦图以及印度婆什伽罗的证法 赵爽的弦图以及印度婆什伽罗的证法 美国第二十任总统伽菲尔德的证法 我国清代数学家梅文鼎的证法 八年级数学几种证明图示 美国第二十任总统伽菲尔德的证法 我国魏晋时期数学家刘徽的证法 八年级数学几种证明图示 美国第二十任总统伽菲尔德的证法 八年级数学几种证明图示 我国清代数学家梅文鼎的证法 赵爽的弦图以及印度婆什伽罗的证法
赵爽的弦图以及印度婆什伽罗的证法 赵爽的弦图以及印度婆什伽罗的证法
美国第二十任总统伽菲尔德的证法 我国清代数学家梅文鼎的证法
我 国 魏 晋 时 期 数 学 家 刘 徽 的 证 法
我
国
清
代 数 八年级数学几种证明图示
美国第二十任总统伽菲尔德的证法
学 我国清代数学家梅文鼎的证法
八年级数学几种证明图示 美国第二十任总统伽菲尔德的证法
华师版初中数学八年级上册专训:三角形中的五种常见证明类型

专训一:三角形中的五种常见证明类型名师点金:学习了全等三角形及等腰三角形的性质和判定后,与此相关的几何证明题的类型非常丰富,常见的类型有:证明数量关系、位置关系,线段的和差关系、倍分关系、不等关系等.证明数量关系题型1证明线段相等1.如图,在△ABC中,AB=AC,D是BC的中点,E、F分别是AB、AC 上的点,且AE=AF,求证:DE=DF.(第1题)题型2证明角相等2.如图,在△ABC中,AB=AC,∠BAC=90°,D为AC的中点,AE⊥BD 于F交BC于E.求证:∠ADB=∠CDE.(第2题)证明位置关系3.如图,在△ABC中,AB=AC,点D,E,F分别在边BC,AB,AC上,且BD=CF,BE=CD,点G是EF的中点,求证:DG⊥EF.(第3题)4.如图,在△ABC中,AB=AC,AD,BE是△ABC的高,AD,BE相交于点H,且AE=BE,求证:AH=2BD.(第4题)5.如图,在△ABC中,∠ABC=2∠C,AD平分∠BAC.求证:AB+BD=AC.(第5题)6.如图,AD是△ABC中∠BAC的平分线,P是AD上的任意一点,且AB>AC,求证:AB-AC>PB-PC.(第6题)专训二:构造全等三角形的六种常用方法名师点金:在进行几何题的证明或计算时,需要在图形中添加一些辅助线,辅助线能使题目中的条件比较集中,能比较容易找到一些量之间的关系,使数学问题得以较轻松地解决.常见的辅助线作法有:构造法、平移法、旋转法、翻折法、加倍折半法和截长补短法,目的都是构造全等三角形.构造基本图形法1.如图,在Rt△ABC中,∠ACB=90°,AC=BC,点D为BC的中点,CE⊥AD于点E,其延长线交AB于点F,连接DF.求证:∠ADC=∠BDF.(第1题)翻折法2.如图,在△ABC中,BE是∠ABC的平分线,AD⊥BE,垂足为D.求证:∠2=∠1+∠C.(第2题)旋转法3.如图,在正方形ABCD中,E为BC上的一点,F为CD上的一点,BE +DF=EF,求∠EAF的度数.(第3题)平移法4.在△ABC中,∠BAC=60°,∠C=40°,AP平分∠BAC交BC于点P,BQ平分∠ABC交AC于点Q,且AP与BQ相交于点O.求证:AB+BP=BQ+AQ.(第4题)加倍折半法5.如图,在△ABC中,∠BAC=120°,AD⊥BC于D,且AB+BD=DC,求∠C的度数.(第5题)截长补短法6.如图所示,AB∥CD,BE、CE分别为∠ABC、∠BCD的平分线,点E 在AD上.求证:BC=AB+CD.(第6题)专训三:分类讨论思想在等腰三角形中的应用名师点金:分类讨论思想是解题的一种常用方法,在等腰三角形中,往往会遇到条件或结论不唯一的情况,此时就需要分类讨论.通过正确地分类讨论,可以使复杂的问题得到清晰、完整、严密的解答.其解题策略为:先分类,再画图,后计算.当顶角和底角不确定时,分类讨论1.若等腰三角形中有一个角等于40°,则这个等腰三角形的顶角度数为()A.40°B.100°C.40°或70°D.40°或100°2.已知等腰三角形ABC中,AD⊥BC于D,且AD=12BC,则等腰三角形ABC的底角的度数为()A.45°B.75°C.45°或75°D.65°3.若等腰三角形的一个外角为64°,则底角的度数为________.当底和腰不确定时,分类讨论4.(2015·荆门)已知一个等腰三角形的两边长分别是2和4,则该等腰三角形的周长为()A.8或10B.8C.10D.6或125.等腰三角形的两边长分别为7和9,则其周长为________.6.若实数x,y满足|x-5|+(10-y)2=0,则以x,y的值为边长的等腰三角形的周长为________.当高的位置关系不确定时,分类讨论7.等腰三角形一腰上的高与另一边的夹角为25°,求这个三角形的各个内角的度数.由腰的垂直平分线引起的分类讨论8.在三角形ABC中,AB=AC,AB边上的垂直平分线与AC所在的直线相交所得的锐角为40°,求∠B的度数.由腰上的中线引起的分类讨论9.等腰三角形ABC的底边BC长为5 cm,一腰上的中线BD把其分为周长差为3 cm的两部分.求腰长.点的位置不确定引起的分类讨论10.如图,在Rt△ABC中,∠ACB=90°,AB=2BC,在直线BC或AC上取一点P,使得△PAB为等腰三角形,则符合条件的点P共有()(第10题)A.7个B.6个C.5个D.4个11.如图,已知△ABC中,BC>AB>AC,∠ACB=40°,如果D,E是直线AB上的两点,且AD=AC,BE=BC,求∠DCE的度数.(第11题)专训四:三角形中常见的热门考点名师点金:本章主要学习了互逆命题与互逆定理,全等三角形的性质与判定,等腰三角形,线段垂直平分线与角平分线等常见的轴对称图形的性质与判定.本章的考点较多,也是中考的重点考查内容.互逆命题、基本事实、互逆定理1.下列命题是真命题的是()A.无限小数是无理数B.相反数等于它本身的数是0和1C.对顶角相等D.等边三角形既是轴对称图形,又是中心对称图形2.下列命题及其逆命题是互逆定理的是()A.全等三角形的对应角相等B.若两个角都是直角,则它们相等C.同位角相等,两直线平行D.若a=b,则|a|=|b|全等三角形的性质与判定3.如图所示,AB∥EF∥CD,∠ABC=90°,AB=DC,那么图中的全等三角形有()A.3对B.2对C.1对D.0对(第3题)(第4题)4.如图,在△ABC中,AC=5,F是高AD和BE的交点,AD=BD,则BF的长是()A.7 B.6 C.5 D.45.(2015·杭州)如图,在△ABC中,已知AB=AC,AD平分∠BAC,点M,N分别在AB,AC边上,AM=2MB,AN=2NC,求证:DM=DN.(第5题)等腰三角形的判定与性质6.如图,在△ABC中,AB=AC,AD平分∠BAC,DE⊥AB,DF⊥AC,E,F分别为垂足,则下列四个结论:(1)∠DEF=∠DFE;(2)AE=AF;(3)DA平分∠EDF;(4)AD垂直平分EF.其中正确的有()A.1个B.2个C.3个D.4个(第6题)(第7题)(第8题)7.如图,AD是△ABC的中线,∠ADC=60°,BC=6,把△ABC沿直线AD折叠,点C落在C′处,连接BC′,则BC′的长为________.8.如图所示,在△ABC中,∠ABC与∠ACB的平分线相交于点O,过点O作MN∥BC,分别交AB,AC于点M,N.若AB=6 cm,AC=9 cm,则△AMN 的周长为________.9.(中考·淄博)如图,AD∥BC,BD平分∠ABC.求证:AB=AD.(第9题)尺规作图10.如图,已知线段a,h,作等腰三角形ABC,使AB=AC,且BC=a,BC边上的高AD=h.张红的作法如下:(1)作线段BC=a;(2)作线段BC的垂直平分线MN,MN与BC相交于点D;(3)在直线MN上截取线段h;(4)连接AB,AC.△ABC即为所要求作的等腰三角形.上述作法的四个步骤中,你认为有错误的一步是()(第10题)A.(1) B.(2) C.(3) D.(4)线段垂直平分线与角平分线11.如图,在△ABC 中,AB =AC ,∠A =36°,AB 的垂直平分线DE 交AC 于点D ,交AB 于点E ,则下列结论错误的是( )A .BD 平分∠ABCB .△BCD 的周长等于AB +BCC .AD =BD =BCD .点D 是线段AC 的中点(第11题)(第12题)12.如图,已知在△ABC 中,AB =AC ,∠BAC 和∠ACB 的平分线相交于点D ,∠ADC =130°,那么∠CAB 的大小是( )A .80°B .50°C .40°D .20°13.如图,已知C 是∠MAN 的平分线上一点,CE ⊥AB 于 E ,点B ,D 分别在AM ,AN 上,且AE =12(AD +AB).问:∠1和∠2有何关系?并说明理由.(第13题)思想方法a .分类讨论思想14.等腰三角形的一个外角等于110°,则这个三角形的顶角度数为________.15.(2014·安顺)已知等腰三角形的两边长分别为a ,b ,且a ,b 满足2a -3b +5+(2a +3b -13)2=0,则此等腰三角形的周长为( )A .7或8B .6或10C .6或7D .7或10b .方程思想16.如图,在△ABC 中,AB =AC ,BC =BD ,AD =DE =EB ,求∠A 的度数.(第16题)c .转化思想17.如图,已知在△ABC 中,∠ABC =3∠C ,AD 是∠BAC 的平分线,BE ⊥AD于E ,求证:BE =12(AC -AB).(第17题)答案专训一1.证明:连接AD.∵AB =AC ,D 是BC 的中点,∴∠EAD =∠FAD.在△AED 和△AFD 中,⎩⎨⎧AE =AF ,∠EAD =∠FAD ,AD =AD ,∴△AED ≌△AFD(S .A .S .).∴DE =DF.2.证明:过点C 作CG ⊥AC 交AE 的延长线于G ,则CG ∥AB ,∴∠BAF =∠G .又∵AF ⊥BD ,AC ⊥CG ,∴∠BAF +∠ABF =90°,∠CAG +∠G =90°.∴∠ABF =∠CAG .在△ABD 和△CAG 中,⎩⎨⎧∠ABF =∠CAG ,AB =AC ,∠BAD =∠ACG =90°,∴△ABD ≌△CAG(A .S .A .).∴AD =CG ,∠ADB =∠G .又∵D 为AC 的中点,∴AD =CD ,∴CD =CG .∵AB =AC ,∴∠ABC =∠ACB.又∵AB ∥CG ,∴∠ABC =∠GCE.∴∠ACB =∠GCE.又∵CE =CE ,∴△CDE ≌△CGE(S .A .S .).∴∠G =∠CDE.∴∠ADB =∠CDE.(第3题)3.证明:如图,连接ED ,FD.∵AB =AC ,∴∠B =∠C.在△BDE 和△CFD 中,⎩⎨⎧BD =CF ,∠B =∠C ,BE =CD ,∴△BDE ≌△CFD(S .A .S .).∴DE =DF.又∵点G 是EF 的中点,∴DG ⊥EF.4.证明:∵AD ,BE 是△ABC 的高,∴∠ADB =∠AEB =90°,又∵∠BHD =∠AHE ,∴∠EBC =∠EAH.在△BCE 和△AHE 中,⎩⎨⎧∠EBC =∠EAH ,BE =AE ,∠BEC =∠AEH =90°,∴△BCE ≌△AHE(A .S .A .).∴AH =BC.又∵AB =AC ,AD ⊥BC ,∴BC =2BD ,∴AH =2BD.5.证明:如图,延长CB 至E ,使BE =BA ,则∠BAE =∠E.∵∠ABC =2∠C =2∠E ,∴∠E =∠C ,∴AE =AC.∵AD 平分∠BAC ,∴∠BAD =∠DAC.∵∠BAE =∠E ,∠E =∠C ,∴∠BAE =∠C.又∵∠EAD =∠BAE +∠BAD ,∠EDA =∠C +∠DAC ,∴∠EAD =∠EDA.∴AE =DE.∴AC =DE =BE +BD =AB +BD.(第5题)(第6题)6.证明:如图,在AB 上截取AE ,使AE =AC ,连接PE.∵AD 是∠BAC 的平分线,∴∠BAD =∠CAD.在△AEP 和△ACP 中,⎩⎨⎧AE =AC ,∠BAD =∠CAD ,AP =AP ,∴△AEP ≌△ACP(S .A .S .),∴PE =PC.在△PBE 中,BE >PB -PE ,∴AB -AC >PB -PC.专训二1.证明:如图,过点B 作BG ⊥BC 交CF 的延长线于点G .∵∠ACB =90°,∴∠2+∠ACF =90°.∵CE ⊥AD ,∴∠AEC =90°,∴∠1+∠ACF =180°-∠AEC =180°-90°=90°.∴∠1=∠2.在△ACD 和△CBG 中,⎩⎨⎧∠1=∠2,AC =CB ,∠ACD =∠CBG =90°,∴△ACD ≌△CBG(A .S .A .).∴∠ADC =∠G ,CD =BG .∵点D 为BC 的中点,∴CD =BD.∴BD =BG .又∵∠DBG =90°,∠DBF =45°,∴∠GBF =∠DBG -∠DBF =90°-45°=45°.∴∠DBF =∠GBF.在△BDF 和△BGF 中,⎩⎨⎧BD =BG ,∠DBF =∠GBF ,BF =BF ,∴△BDF ≌△BGF(S .A .S .).∴∠BDF =∠G .∴∠ADC =∠BDF.点拨:本题运用了构造基本图形法,通过作辅助线构造△CBG 、△BGF 是解题的关键.(第1题)(第2题)2.证明:如图,延长AD 交BC 于点F.(相当于将AB 边向下翻折,与BC 边重合,A 点落在F 点处,折痕为BE)∵BE 平分∠ABC ,∴∠ABE =∠CBE.∵BD ⊥AD ,∴∠ADB =∠BDF =90°.在△ABD 和△FBD 中,⎩⎨⎧∠ABD =∠FBD ,BD =BD ,∠ADB =∠FDB =90°,∴△ABD ≌△FBD(A .S .A .).∴∠2=∠DFB.又∵∠DFB =∠1+∠C ,∴∠2=∠1+∠C.(第3题)3.解:如图,延长CB 到点H ,使得BH =DF ,连接AH.∵∠ABE =90°,∠D =90°,∴∠ABH =∠D =90°.在△ABH 和△ADF 中,⎩⎨⎧AB =AD ,∠ABH =∠D =90°,BH =DF ,∴△ABH ≌△ADF.∴AH =AF ,∠BAH =∠DAF.∴∠BAH +∠BAF =∠DAF +∠BAF ,即∠HAF =∠BAD =90°.∵BE +DF =EF ,∴BE +BH =EF ,即HE =EF.在△AEH 和△AEF 中,⎩⎨⎧AH =AF ,AE =AE ,EH =EF ,∴△AEH ≌△AEF.∴∠EAH =∠EAF.∴∠EAF =12∠HAF =45°.点拨:图中所作辅助线,相当于将△ADF 绕点A 顺时针旋转90°,使AD 边与AB 边重合,得到△ABH.4.证明:过点O 作OD ∥BC 交AB 于点D ,∴∠ADO =∠ABC.∵∠BAC =60°,∠C =40°,∴∠ABC =80°.∴∠ADO =80°.∵BQ 平分∠ABC ,∴∠QBC =40°.∴∠AQB =∠C +∠QBC =80°.∴∠ADO =∠AQB.易知∠DAO =∠QAO ,OA =OA ,∴△ADO ≌△AQO.∴OD =OQ ,AD =AQ.∵OD ∥BP ,∴∠PBO =∠DOB ,又∵∠PBO =∠DBO ,∴∠DBO =∠DOB.∴BD =OD.∴BD =OQ.∵∠BAC =60°,∠ABC =80°,BQ 平分∠ABC ,AP 平分∠BAC ,∴∠BAP =30°,∠ABQ =40°,∴∠BOP =70°.∵∠BAP =30°,∠ABC =80°,∴∠APB =70°.∴∠BOP =∠APB ,∴BO =BP.∴AB +BP =AD +DB +BP =AQ +OQ +BO =BQ +AQ.5.解:在DC 上截取DE =BD ,连接AE ,∵AD ⊥BC ,BD =DE ,∴AD 是线段BE 的垂直平分线,∴AB =AE ,∠B =∠AEB.∵AB +BD =CD ,DE =BD ,∴AB +DE =CD.而CD =DE +EC ,∴AB =EC ,∴AE =EC.故设∠EAC =∠C =x ,∵∠AEB 为△AEC 的外角,∴∠AEB =∠EAC +∠C =2x ,∴∠B =2x ,∠BAE =180°-2x -2x =180°-4x.∵∠BAC =120°,∴∠BAE +∠EAC =120°,即180°-4x +x =120°,解得x =20°,则∠C =20°.6.证法一:用截长法,如图①所示,在BC 上截取BF =AB ,连接EF.(第6题)因为BE 平分∠ABC ,CE 平分∠BCD ,所以∠ABE =∠FBE ,∠FCE =∠DCE.在△ABE 和△FBE 中,因为⎩⎨⎧AB =FB ,∠ABE =∠FBE ,BE =BE ,所以△ABE ≌△FBE.所以∠A =∠EFB.因为AB ∥CD ,所以∠A +∠D =180°.因为∠BFE +∠EFC =180°,所以∠EFC =∠D.在△EFC 和△EDC 中,因为⎩⎨⎧∠FCE =∠DCE ,∠EFC =∠D ,EC =EC ,所以△EFC ≌△EDC.所以FC =DC.所以BC =BF +FC =AB +CD.证法二:用补短法,如图②所示,延长BE 交CD 的延长线于点G .因为AB ∥CD ,所以∠ABE =∠G .因为BE 平分∠ABC ,所以∠ABE =∠CBE.所以∠CBE =∠G .因为CE 平分∠BCD ,所以∠BCE =∠GCE.在△BEC 和△GEC 中,因为⎩⎨⎧∠CBE =∠G ,∠BCE =∠GCE ,CE =CE ,所以△BEC ≌△GEC.所以BC =GC ,BE =GE.在△ABE 和△DGE 中,因为⎩⎨⎧∠ABE =∠G ,∠AEB =∠DEG ,BE =GE ,所以△ABE ≌△DGE.所以AB =DG .所以BC =CG =GD +DC =AB +CD.专训三1.D 2.C 3.32°4.C 5.23或25 6.257.解:设等腰三角形ABC 中,AB =AC ,BD ⊥AC 于D.(1)当高与底边的夹角为25°时,高一定在△ABC 的内部,如图①,∵∠DBC =25°,∴∠C =90°-∠DBC =90°-25°=65°,∴∠ABC =∠C =65°,∠A =180°-2×65°=50°.(第7题)(2)当高与另一腰的夹角为25°时,如图②,高在△ABC 的内部时,∵∠ABD =25°,∴∠A =90°-∠ABD =65°,∴∠C =∠ABC =(180°-∠A)÷2=57.5°;如图③,高在△ABC 的外部时,∵∠ABD =25°,∴∠BAD =90°-∠ABD =90°-25°=65°,∴∠BAC =180°-65°=115°,∴∠ABC =∠C =(180°-115°)÷2=32.5°,故三角形各内角的度数为:65°,65°,50°或65°,57.5°,57.5°或115°,32.5°,32.5°.点拨:由于题目中的“另一边”没有指明是“腰”还是“底边”,因此必须进行分类讨论,另外,还要结合图形,分高在三角形内还是在三角形外.8.解:此题分两种情况:(1)如图①,AB边的垂直平分线与AC边交于点D,∠ADE=40°,则∠A=50°,∵AB=AC,∴∠B=(180°-50°)÷2=65°.(2)如图②,AB边的垂直平分线与CA的延长线交于点D,∠ADE=40°,则∠DAE=50°,∴∠BAC=130°.∵AB=AC,∴∠B=(180°-130°)÷2=25°.故∠B的大小为65°或25°.(第8题)9.解:∵BD为AC边上的中线,∴AD=CD.(1)当(AB+AD)-(BC+CD)=3 cm时,则AB-BC=3 cm,∵BC=5 cm,∴AB=8 cm;(2)当(BC+CD)-(AB+AD)=3 cm时,则BC-AB=3 cm,∵BC=5 cm,∴AB=2 cm;但是当AB=2 cm时,三边长为2 cm,2 cm,5 cm,而2+2<5,不符合三角形三边关系,故舍去,故腰长为8 cm.10.B11.解:(1)当点D,E在点A的同侧,且都在BA的延长线上时,如图①,(第11题)∵BE=BC,∴∠BEC=(180°-∠ABC)÷2,∵AD=AC,∴∠ADC=(180°-∠DAC)÷2=∠BAC÷2,∵∠DCE=∠BEC-∠ADC,∴∠DCE=(180°-∠ABC)÷2-∠BAC÷2=(180°-∠ABC-∠BAC)÷2=∠ACB÷2=40°÷2=20°.(2)当点D,E在点A的同侧,且点D在D′的位置,点E在E′的位置时,如图②,与(1)类似地可以求得∠D′CE′=∠ACB÷2=20°.(3)当点D,E在点A的两侧,且点E在E′的位置时,如图③,∵BE′=BC,∴∠BE′C=(180°-∠CBE′)÷2=∠ABC÷2,∵AD=AC,∴∠ADC=(180°-∠DAC)÷2=∠BAC÷2,又∵∠DCE′=180°-(∠BE′C+∠ADC),∴∠DCE′=180°-(∠ABC+∠BAC)÷2=180°-(180°-∠ACB)÷2=90°+∠ACB÷2=90°+40°÷2=110°.(4)当点D,E在点A的两侧,且点D在D′的位置时,如图④,∵AD′=AC,∴∠AD′C=(180°-∠BAC)÷2,∵BE=BC,∴∠BEC=(180°-∠ABC)÷2,∴∠D′CE=180°-(∠D′EC+∠ED′C)=180°-(∠BEC+∠AD′C)=180°-[(180°-∠ABC)÷2+(180°-∠BAC)÷2]=(∠BAC+∠ABC)÷2=(180°-∠ACB)÷2=(180°-40°)÷2=70°.综上所述,∠DCE的度数为20°或110°或70°.专训四1.C 2.C 3.A 4.C5.证明:∵AM=2MB,AN=2NC,∴AM=23AB,AN=23AC.又∵AB=AC,∴AM=AN.∵AD平分∠BAC,∴∠MAD=∠NAD.又∵AD=AD,∴△AMD≌△AND(S.A.S.).∴DM=DN.6.D7.38.15 cm9.证明:∵AD∥BC,∴∠DBC=∠ADB.又∵BD平分∠ABC,∴∠ABD=∠DBC,∴∠ABD=∠ADB,∴AB=AD.10.C11.D12.D(第13题)13.解:∠1与∠2互补.理由:作CF ⊥AN 于F(如图),∵AC 平分∠MAN ,∴∠3=∠4,又∵CE ⊥AM ,CF ⊥AN ,∴CF =CE ,∠CFA =∠CEA =90°,∴Rt △ACF ≌Rt △ACE ,∴AF =AE.∵AE =12(AD +AB)=12(AF -DF +AE +BE)=AE +12(BE -DF),∴BE -DF =0,∴BE =DF ,又CE =CF ,∠CEB =∠CFD ,∴△DFC ≌△BEC(S .A .S .),∴∠5=∠2,∵∠1+∠5=180°,∴∠1+∠2=180°.即∠1与∠2互补.14.70°或40° 点拨:本题运用了分类讨论思想,将已知条件外角等于110°分为底角处的外角和顶角处的外角两种情况进行讨论,解题时要防止漏解.15.A 点拨:∵2a -3b +5+(2a +3b -13)2=0,∴⎩⎨⎧2a -3b +5=0,2a +3b -13=0,解得⎩⎨⎧a =2,b =3.当a 为底边长时,三角形的三边长为2,3,3,则周长为8;当b 为底边长时,三角形的三边长为2,2,3,则周长为7.综上所述,此等腰三角形的周长为7或8.16.解:设∠ABD 的度数为x.∵AD =DE =EB ,∴∠A =∠AED =2∠ABD =2x.∵BC =BD ,∴∠C =∠BDC =∠ABD +∠A =3x.∵AB =AC ,∴∠ABC =∠C =3x.∴∠A +∠C +∠ABC =8x =180°.∴x =22.5°.∴∠A =2x =45°.17.证明:如图,延长BE 交AC 于F.∵AD 是∠BAC 的平分线,∴∠BAE =∠FAE.(第17题)在△ABE 和△AFE 中,⎩⎨⎧∠BAE =∠FAE ,AE =AE ,∠AEB =∠AEF =90°,∴△ABE ≌△AFE(A .S .A .).∴∠ABF=∠AFB,BE=FE,AB=AF.∴BE=12BF.∠ABC=∠ABF+∠FBC=∠AFB+∠FBC=∠C+∠FBC+∠FBC=∠C+2∠FBC,又∵∠ABC=3∠C,∴3∠C=∠C+2∠FBC.∴∠C=∠FBC.∴BF=CF.∴BE=12CF.∵CF=AC-AF=AC-AB,∴BE=12(AC-AB).点拨:本题运用了转化思想,通过添加辅助线构造等腰三角形,然后利用等腰三角形的性质将AC与AB的差转化为AC与AF的差是解题的关键.。
八年级数学几种证明图示

北师大版数学 八年级下册 第一章第3课时 等腰三角形的判定与反证法 优秀课件

由题得AB=15×2=30(海里)
N B 72° 36° C
∵ ∠A= ∠C
∴ BC=AB=30 (海里)
36°
A
2、如图, △ABC中, ∠A=36°,AB=AC, BD平分 ∠ABC, DE∥BC, EF平分∠AED,问在这个图形中,有 那几个等腰三角形?请分别写出来.
A
△ABC、 △BCD 、△EBD、 △EDF 、△FAE 、△ADE、 △ABD
的形式.而已知中的角平分线和平 行线告诉我们图形中有等腰三角形
M
D
出现,因此,找到问题的突破口. B
N C
4、已知五个正数的和等于1,用反证法证明:这五个数 中至少有一个大于或等于1/5.
证明: 设这五个正数为a1、a2、a3、a4、a5 假设这五个数中没有一个大于或等于1/5,即都小于1/5, 那么这五个数的和a1+a2+a3+a4+a5就小于1. 这与已知这五个数的和a1+a2+a3+a4+a5=1相矛盾. 因此, 假设不成立,即这五个数中至少有一个大于或等于 1/5成立.
36°
F
E 36°72°D
73263°°6°
B
72°
C
想一想
小明说, 在一个三角形中,如果两个角不相等, 那么这两个角所对的边也不相等.
即在△ABC中, 如果∠B≠∠C, 那么AB≠AC.
A
B
C
你认为这个结论成立吗? 如果成立, 你能证明它吗?
小明是这样想的:
如图, 在△ABC中, 已知∠B≠∠C, 此时, AB与AC要
B
C
在△ABD和 △ACD中
D
∵∠B=∠C. ∠ADB=∠ADC.AD=AD
八年级数学证明课件2(PPT)3-3

探索活动
❖ 让我们尝试从基本事实出发,证实我们曾探索、发 现的有关图形的许多性质的正确性。
❖ 本书选用下列真命题作为基本ห้องสมุดไป่ตู้实:
❖ 同位角相等,两直线平行
❖ 两直线平行,同位角相等。
❖ 两边和它们的夹角对应相等的两个三角形相 等
❖ 两角和它们的夹边对应相等的两个三角形全 等
❖ 三边对应相等的两个三角形全等
定后,注意水肥管理,产量才能提高;生育中期应注意水肥调控,要施缓肥,以保持根形的发育;此品种发芽后~8天长势茂盛,吸肥量剧增,第二时期肥料 应注意其延迟性,要后期起作用。 [] 改良新黑田五寸 生长势强,早期生育好,耐暑性、抗病性较强;肥大好,根部缩尾好,根形优秀;根色深红,根皮光 滑;夏季播种,秋、冬收; 微商货源 ; 获的丰产品种。 [] 超级红芯 属抽薹晚、收尾早、三红率高的超级品种。生长势强,耐 暑性、抗病性强;根部收尾好,长圆柱形,根长8~cm,单根重~g;着色好、肥大快商品率高,生育期天左右,亩产kg左右。 [] 汉城六寸 生长速度快, 根皮及芯部呈鲜红色;生长势强,不易抽 改良新黑田五寸、汉城六寸、超级红芯 改良新黑田五寸、汉城六寸、超级红芯(张) 薹,根形均匀一致,商品性好; 生育期约天,根型长圆筒型,根长8~cm,单根重g左右,根径.~.cm;抗病性强,高产品种,亩产kg以上。 [] 法国阿雅 属早熟性突出,根型好,心部颜 色佳的早熟品种。改良黑田五寸系列,大型高产品种;播种后天采收,根长~cm,肩宽.~cm;根形好,收尾渐细,根皮橘红色;耐热性好,抗萎缩病及叶 斑病。 [] 红映二号 引自日本的早熟杂交一代胡萝卜优种,播种后天即可收获。抗抽薹能力特强,适于早春覆膜播种。叶丛挺立,适于密植,产量高。生长 强健,肉质根肥大快,低温条件下成形、成色能力强;皮、肉、芯三红,颜色深,着色快,根形整齐,根皮光滑,收尾好,形状好看。 [] 宝冠 进口品种, 根形整齐,一般长~cm粗cm左右,尾部 宝冠 宝冠 收尖好,红心,红肉,红皮,中心轴细小,适于生产加工胡萝卜汁和胡萝卜粒原料,抗旱,耐暑,宜于 夏季播种,属高产增收型品种,播后天左右根重可达~g,播后天起可以开始上市,每亩(m)产成品可达kg。 [] 红芯六号 杂交种,地上部分长势强而不旺, 叶色浓绿生育期~天,抗抽薹性极强,适合中国大部分地区春季露地播种或南方地区小拱棚越冬栽培;肉质根光滑整齐,柱形;皮、肉、心浓鲜红色,心柱 细,口感好;肉质根长cm,粗约cm,单根重约g,m产量约kg;胡萝卜素含量为新黑田五寸的~倍,总胡萝卜素~mg/kg,其中β-胡萝卜素含量~mg/kg, 是适合鲜食与加工的理想品种。 [] 春红二号 生育期天左右,为早熟品种;根形为整齐的柱形,外表光滑 春红二号 春红二号 ,皮、肉、心均为鲜红色根长 8cm,直径~cm,是适合春夏栽培的早熟耐热品种,m产量~kg左右,适合中国
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
