第七节 自相关检验与修正
实验四--自相关性的检验及修正

实验四 -- 自相关性的检验及修正实验四自相关性的检验及修正一、实验目的掌握自相关性的检验与处理方法。
二、实验学时: 2三、实验内容及操作步骤建立我国城乡居民储蓄存款模型,并检验模型的自相关性。
1.回归模型的筛选2.自相关的检验3.自相关的调整四、实验要求利用表 5-1 资料,试建立我国城乡居民储蓄存款模型,并检验模型的自相关性。
我国城乡居民储蓄存款与GDP统计资料( 1978 年= 100)存款GDP 年份存款余额Y GDP指数X年份余额指数Y X19919241.6 199211759.4 199315203.5 199421518.8 199529662.3 199638520.8 199746279.8 199853407.5 199959621.8 200064332.4308.2200286910.6888.5 351.52003103617.7981.6 399.62004119555.41084.5 452.020051410511201.7 494.22006161587.31361.2 544.520071725341560.5 596.920082178851717.8 640.620092607721861.1 691.520103033022050.0 750.62011343635.92228.9 811.12410.3200173762.43995512012【实验步骤】(一)回归模型的筛选⒈相关图分析SCAT X Y相关图表明, GDP指数与居民储蓄存款二者的曲线相关关系较为明显。
现将函数初步设定为线性、双对数、对数、指数、二次多项式等不同形式,进而加以比较分析。
⒉估计模型,利用LS命令分别建立以下模型⑴线性模型: LS Y C Xy?62251.79175.4516 xt (-9.5629) (33.3308)R2= 0.9823 F=1110.940S.E=15601.32⑵双对数模型: GENR LNY=LOG(Y)GENR LNX=LOG(X)LS LNY C LNX?0.59996 1.7452 ln xln yt(-1.6069) (31.8572)R2= 0.9807 F= 1014.878 S.E=0.1567⑶对数模型: LS YCLNX?y1035947170915.4 ln xt(-10.2355)(11.5094)R2=0.8688 F =132.4672 S.E =42490.60⑷指数模型: LS LNY C Xln y? 9.5657 0.001581xt (55.0657) (11.2557)2R = 0.8637 F=126.6908 S.E=0.4163LS Y CXX2?16271.5477.8476x0.0378x2yt(-2.4325)(6.1317) (7.8569)R2= 0.9958F=2274.040 S.E= 7765.275⒊选择模型比较以上模型,可见各模型回归系数的符号及数值较为合理。
多重共线性、异方差及自相关的检验和修正

计量经济学实验报告多重共线性、异方差及自相关的检验和修正——以财政收入模型为例经济学 1班一、引言财政收入是一国政府实现政府职能的基本保障,对国民经济的运行及社会的发展起着非凡的作用。
首先,它是一个国家各项收入得以实现的物质保证。
一个国家财政收入规模的大小通常是衡量其经济实力的重要标志。
其次,财政收入是国家对经济实行宏观调控的重要经济杠杆。
财政收入的增长情况关系着一个国家的经济的发展和社会的进步。
因此,研究财政收入的增长显得尤为重要。
二、数据及模型说明研究财政收入的影响因素离不开一些基本的经济变量。
回归变量的选择是建立回归模型的一个极为重要的问题。
如果遗漏了某些重要变量,回归方程的效果肯定不会好;而考虑过多的变量,不仅计算量增大许多,而且得到的回归方程稳定性也很差,直接影响到回归方程的应用。
通过经济理论对财政收入的解释以及对实践的观察,对财政收入影响的因素主要有农业增加值、工业增加值、建筑业增加值、总人口数、最终消费、受灾面积等等。
全部数据均来源于中华人民共和国国家统计局网站/具体数据见附录一。
为分析被解释变量财政收入(Y)和解释变量农业增加值(X1)、工业增加值(X2)、建筑业增加值(X3)、总人口(X4)、最终消费(X5)、受灾面积(X6)的关系。
作如下线性图(图1)。
图1可以看出Y、X1、X2、X3、X5基本都呈逐年增长的趋势,仅增长速率有所变动,而X4和X6在多数年份呈现水平波动,可能这两个自变量和因变量间不一定是线性关系。
可以初步建立回归模型如下:Y=α+β1*X1+β2*X2+β3*X3+β4*X4 +β5*X5+β6*X6 +U i 其中,U i为随机干扰项。
三、模型的检验及验证(一)多重共线性检验及修正利用Eviews5.0,做Y对X1、X2、X3、X4、X5和X6的回归,Eviews的最小二乘估计的回归结果如下表(表1)所示:表1Dependent Variable: YMethod: Least SquaresDate: 11/16/13 Time: 20:54Sample: 1990 2011Included observations: 22Variable Coefficient Std. Error t-Statistic Prob.C 145188.0 26652.27 5.447488 0.0001X1 -0.972478 0.222703 -4.366701 0.0006X2 0.210089 0.068192 3.080851 0.0076X3 -0.100412 0.569465 -0.176327 0.8624X4 -1.268320 0.247725 -5.119870 0.0001X5 0.600205 0.130089 4.613794 0.0003X6 -0.007430 0.044233 -0.167964 0.8689R-squared 0.999306 Mean dependent var 27186.86Adjusted R-squared 0.999029 S.D. dependent var 28848.33S.E. of regression 899.0866 Akaike info criterion 16.69401Sum squared resid 12125351 Schwarz criterion 17.04116Log likelihood -176.6341 F-statistic 3600.848Durbin-Watson stat 1.825260 Prob(F-statistic) 0.000000 由上表的回归结果可见,,该模型可决系数R2=0.9993很高,F检验值3601,明显显著。
异方差、自相关检验及修正

异方差、自相关的检验与修正实验目的:通过对模型的检验掌握异方差性问题和自相关问题的检验方法及修正的原理,以及相关的Eviews 操作方法。
模型设定:εβββ+++=23121i i i X X YYi----人均消费支出X1--从事农业经营的纯收入X2--其他来源的纯收入 中国内地2006年各地区农村居民家庭人均纯收入与消费支出 单位:元 城市 y x1 x2 城市 y x1 x2 北京 5724.5 958.3 7317.2 湖北 2732.5 1934.6 1484.8 天津 3341.1 1738.9 4489 湖南 3013.3 1342.6 2047 河北 2495.3 1607.1 2194.7 广东 3886 1313.9 3765.9 山西 2253.3 1188.2 1992.7 广西 2413.9 1596.9 1173.6 内蒙古 2772 2560.8 781.1 海南 2232.2 2213.2 1042.3 辽宁 3066.9 2026.1 2064.3 重庆 2205.2 1234.1 1639.7 吉林 2700.7 2623.2 1017.9 四川 2395 1405 1597.4 黑龙江 2618.2 2622.9 929.5 贵州 1627.1 961.4 1023.2 上海 8006 532 8606.7 云南 2195.6 1570.3 680.2 江苏 4135.2 1497.9 4315.3 西藏 2002.2 1399.1 1035.9 浙江 6057.2 1403.1 5931.7 陕西 2181 1070.4 1189.8 安徽 2420.9 1472.8 1496.3 甘肃 1855.5 1167.9 966.2 福建 3591.4 1691.4 3143.4 青海 2179 1274.3 1084.1 江西 2676.6 1609.2 1850.3 宁夏 2247 1535.7 1224.4 山东 3143.8 1948.2 2420.1 新疆 2032.4 2267.4 469.9 河南 2229.3 1844.6 1416.4 数据来源:《中国农村住户调查年鉴(2007)》、《中国统计年鉴(2007)》参数估计:估计结果如下:2709030.01402097.01402.728X X Y ++=Λ(2.218) (2.438) (16.999) 922173.02=R D.W.=1.4289 F=165.8853 SE=395.2538实验步骤:一、检查模型是否存在异方差1.图形分析检验(1)散点相关图分析分别做出X1和Y 、X2和Y 的散点相关图,观察相关图可以看出,随着X1、X2的增加,Y 也增加,但离散程度逐步扩大,尤其表现在X1和Y .这说明变量之间可能存在递增的异方差性。
自相关的补救措施

自相关的补救措施引言在数据分析和时间序列预测中,自相关(Autocorrelation)是指时间序列数据中的各个观测值与其之前观测值之间的相关性。
自相关可以帮助我们理解时间序列数据中存在的模式和趋势,并用于预测未来观测值。
然而,自相关同时也可能引入一些问题,如误导性的相关性、不稳定的模型等。
为了解决这些问题,我们需要采取一些补救措施。
本文将介绍一些常见的自相关问题及其补救措施,包括合理选择滞后阶数、采用差分法、使用ARIMA模型等。
1. 合理选择滞后阶数自相关函数(ACF)和偏自相关函数(PACF)是衡量时间序列数据中自相关性的常用工具。
ACF显示了某个观测值与其滞后值之间的相关性,而PACF则显示了某个观测值与其滞后值之间的“直接”相关性,消除了中间的干扰。
通过分析ACF和PACF图,我们可以判断出最佳的滞后阶数。
当ACF和PACF图呈现出明显的减小趋势并在某个点后截尾时,我们可以选择该点之前的滞后阶数作为模型中的参数。
这样可以确保我们捕捉到了时间序列数据中的重要模式和趋势,避免了过多的冗余信息。
2. 采用差分法差分法(Differencing)是通过对时间序列数据进行差分运算来消除自相关性的一种方法。
差分法可以将非平稳的时间序列数据转化为平稳的时间序列数据,从而降低自相关性。
差分法的基本思想是对时间序列数据进行一阶或多阶的差分运算,计算相邻观测值之间的差异。
通过消除季节周期性和趋势等因素的干扰,我们可以得到平稳的时间序列数据,并减少自相关性的影响。
3. 使用ARIMA模型自回归移动平均模型(Autoregressive Integrated Moving Average, ARIMA)是一种常用的时间序列预测模型,它结合了自回归模型(AR)和移动平均模型(MA),并引入了差分运算。
ARIMA模型的基本原理是通过考虑时间序列的历史观测值和误差项来预测未来的观测值。
ARIMA模型的三个参数分别代表了自回归项、差分项和移动平均项的阶数。
多重共线性、异方差、自相关的检测与模型修正

多重共线性、异方差、自相关的检测与模型修正从《国家统计数据库》找到了自1978—2008年我国人均居民消费、人均国内生产总值、居民消费价格指数、前期人均居民消费、城镇居民人均可支配收入以及农村居民人均纯收入的官方数据。
以此来分析我国人均消费的影响因素以及它们具体是如何对消费产生影响的。
1978—2008年我国人均消费及其影响因素相关数据城镇居民农村居民人均居民人均国内居民消费前期人均年份人均可支人均纯收消费生产总值价格指数居民消费配收入入343 134 1978 184 381 100.7 165405 160 1979 208 419 101.9 184477 191 1980 238 463 107.5 208501 223 1981 264 492 102.5 238535 270 1982 288 528 102 264564 310 1983 316 583 102 288652 355 1984 361 695 102.7 316739 398 1985 446 858 109.3 361901 424 1986 497 963 106.5 4461002 463 1987 565 1112 107.3 4971180 545 1988 714 1366 111.8 5651373 602 1989 788 1519 118 7141510 686 1990 833 1644 103.1 7881701 709 1991 932 1893 103.4 8332027 784 1992 1116 2311 106.4 9322577 922 1993 1393 2998 114.7 11163496 1221 1994 1833 4044 124.1 13934283 1578 1995 2355 5046 117.1 18334839 1926 1996 2789 5846 108.3 23555160 2090 1997 3002 6420 102.8 27895425 2162 1998 3159 6796 99.2 30025854 2210 1999 3346 7159 98.6 31596280 2253 2000 3631 7858 100.4 33466859 2366 2001 3886 8622 100.7 36317703 2476 2002 4143 9398 99.2 38868472 2622 2003 4474 10542 101.2 41439422 2936 2004 5031 12336 103.9 447410493 3255 2005 5572 14053 101.8 503111759 3587 2006 6263 16165 101.5 557213786 4140 2007 7255 19524 104.8 626315781 4761 2008 8348 23648 105.9 7255来自《国家统计数据库》设定如下形式的计量经济模型1:=++++ Y,X,,,X,Xi33i24124其中,Y为人均居民消费 , X2为人均国内生产总值 , X3为居民消费价格指数 , X4为前期人均消费。
自相关的检验与修正

实验2自相关的检验与修正、实验目的:掌握自相关模型的检验方法与处理方法.。
、实验内容及要求:表1列出了1985—2007年中国农村居民人均纯收入与人均消费性支出的统计数据。
(1)利用OLS法建立中国农村居民人均消费性支出与人均纯收入的线性模型。
(2)检验模型是否存在自相关。
(3)如果存在自相关,试采用适当的方法加以消除。
表1 1985 —2007年中国农村居民人均纯收入与人均消费性支出(单位:元)年份全年人均纯收入(现价)全年人均消费性支出(现价)消费价格指数(1985=100)1985397.6317.42100 1986423.8357106.1 1987462.6398.3112.7 1988544.9476.7132.4 1989601.5535.4157.9 1990686.3584.63165.1 1991708.6619.8168.9 1992784659.8176.8 1993921.6769.7201 199412211016.81248 19951577.71310.36291.4 19961923.11572.1314.4 19972090.11617.15322.3 199821621590.33319.1 19992214.31577.42314.3 20002253.41670314 20012366.41741316.5 20022475.61834315.2 20032622.241943.3320.2 20042936.42185335.6 20053254.932555343 200635872829348.1实验如下:首先对数据进行调整,将全年人均纯收入和全年人均消费性支出相应调整为全年实际人均纯收入和全年实际人均消费性支出。
LIL I. .一.... U h ―................ H全年人沟地收入全年人均泊箜低立出J泊费桥特描旷全年人均实际地收/全年人枸实加寸抵性女出tMM1昭W7…6J17.4Z m35^.60 31X42恤(山妙1441斯石Mid JMJ m.T41M7ma«44J J-L7JJ2.44IL5636*05MU UU期M45W.A8州IMJ nus ltf.1Uf矽»ill14^1TlV.b他E I4B.9m到W:71417*4⑷話珊肿1W3Kl.«THL73D1 4SU1M1M喻i*ii toirn3JS49*14』I・M157TJ IJ1IU4^1.4:出紺阳阳J157!4314J«1.«750•巧2000J3t:J 5OL75[潮2U3159U331S,1491^8L9M2114J isn«314J■04J1S0LJB32WI22S3J L6TO314 71T..U531.852«1UWJ P4I JMJ卿AS1W2倔ud)m31SJ■SS.I1繩US:621.21ifl-jjj irsij UU4乂MU wn困口6.4sits»71.97izM.yj皿會埠HLN T I4.W 加?n«HU 1W負建tUMSW741 4055T43M 8iraj^171711用OLS 估计法估计参数<-□ Group; UN1TTUD Wcrldilft UNTTTLED;;UMtided\[UMr][fi&£|[Oto[jKt |ftjrtt£narrtfeJprMafe]匚][Sart|Eart£pflgj&]旦fc#^[Sapli4j 』T 程]色3y?.弓13S$ [1936 VT1937 1920 193919^?19931934 1935 1936 1037 1939 2»J0 2001 20 J 2 205J 20342035G3E?017397 5000 317.42M1399 43DO 330,«Q0 410 47DO 353.420C 411 56D0 36D.050C SSOEWDO333.0 30C416.690041^ 54J0443 44DU 375 190C 45S5100 382.340C 492.34 DO 410.0000 541 4200 443.680C 611.6700 501030C 648 50 DO 50L75M 677 53DO 4DL3SO0 704 52 DO 501 aaoo J17MOO 531 B500 747 68DO 550.080C 75541D0 M1.350C G10 94DO GO5.930C C74 97D0 esijD7oo 阳⑹0 71J.030C 1033.4S0 81Z7DOO 112R170 Q7B 71 nr也 E\ie\;&zi e Edit Object View Proc Qui:k Options Window Heipdaw Uy ciO Eq uatio n: U NTTTLED Worlcflvc UMTTTLEI>:U 般―、3. frx| JDEU |f i rure I UEUE ihstma 世 心已工竄 '曲ts KKdtCoefficientSU Error t SkteticProa.G 50.21B7S 14 548SB 3.E642100.(]0Q9KC 6969260.02134231 99373 C 0000R-gquan&10S7QQ34dep^nd&ntvarjqu Q013-etiusted R-squar?d C.978947&D, ciependeTitvar15E.3tZ3 3.El ofreer&ssion 22.97705 4<aike info cnteilori 9.1B9B13 Sun squared resic 1105B.87 Sshwa-irz. cnUnon9.2ft Log hka || hood -1026826 Hannar^Oiilrin cfit&r. 9214646 h-S^tlStlC1023.933 □urciin Batson sealU4 码rroa(r-statistic) 0.000030-i e Edit Otwect Viav Proc Quick Options 州nticm 卜口 dacg iy图2DeDerKfentA ;an3ti«: T LlEtnnd: LEastSqijarss Dats: 04/24^5 Tria: 12:32 fianph 1Q95200?ricuaec ooser/atcns 、u图4从图4中可以看出,中国农村居民人均消费性支出与人均纯收入存在着显著的正相关关系。
自相关检验方法

自相关检验方法自相关检验是一种时间序列分析方法,用于检测一个时间序列是否存在自相关关系。
自相关意味着一个时间序列中过去的值会对未来的值产生影响,因此这种检验在研究时间序列数据的影响因素时非常有用。
在进行自相关检验前,需要首先了解一些基本概念。
时间序列是指同一现象在不同时间点观测所得到的数据。
自相关是指一个时间序列中过去的值与现在值之间的关系。
自相关系数是用来衡量自相关强度的指标,其值范围在-1到1之间。
如果自相关系数为正,则表明时间序列中过去的值与现在值呈正相关关系;如果自相关系数为负,则表示它们呈负相关关系;若为0,表示它们之间无自相关关系。
对于自相关检验,经典的方法是使用Ljung-Box检验和Durbin-Watson检验。
Ljung-Box检验用来检验时间序列是否存在自相关关系。
它计算出一系列自相关系数,然后比较它们与随机分布的期望值,从而得出时间序列是否有显著的自相关关系。
这个检验需要提供用于计算的自相关滞后数(lags),通常建议在10~20之间选择适当的值。
如果Ljung-Box统计量的p值小于显著性水平(例如0.05),则可以推断该时间序列存在自相关关系。
Durbin-Watson检验也是一种常用的自相关检验方法,它特别适用于AR(1)模型。
该检验利用AR(1)模型的自相关系数的特性,基于残差的一阶自相关系数来判断时间序列的自相关性。
Durbin-Watson检验的检验统计量为DW,其范围为0到4。
一般DW值在2左右表明无自相关关系,小于2表明有正自相关关系,大于2表明有负自相关关系。
在进行自相关检验时,还需要注意以下几点:1. 时间序列的长度和样本容量要充分,否则结果会不够可靠。
2. 自相关检验只能检测线性自相关,其他形式的自相关关系无法检测。
3. 对于复杂的时间序列,可能需要采用其他更为复杂的自相关检验方法。
总之,自相关检验是一种重要的时间序列分析方法,可以用来检测时间序列中的自相关关系。
自相关性的检验和处理实验报告

ˆ 1
3.7831 13.9366 1 0.72855
由此,我们得到最终的收入-消费模型为
Yt 13.9366 0.9484 X t
二、根据北京市连续 19 年城镇居民家庭人均收入与人均支出的数据进行相关分析 1、建立居民收入-消费函数 以人均实际收入为 X,人均实际支出为 Y,创建工作文件,输入数据,命令如下: Create a 1 19 Data x y 建立居民收入-消费模型,输入命令 ls y c x,回归结果如下:
ˆ 0.72855 ,对原模型进行广义差分,得到差 ˆ 0.72855et 1 ,由回归方程可知 回归方程为 e
分方程: Yt 0.72855Yt 1 1 (1 0.72855) 2 ( X t 0.72855 X t 1 ) t 对 上 式 广 义 差 分 方 程 进 行 回 归 , 在 Eviews 命 令 栏 中 输 入 命 令 : ls Y -0.72855*Y(-1) c X-0.72855*X(-1),回归结果如下: 由回归结果可得回归方程为:
关进行相关检验。 (二)检验收入—消费模型的自相关情况 1、德宾-沃森检验(DW 检验)法 因为 n=36, k=1, 在 5%的显著水平下查表得 DL 1.411 , DU 1.525 , 而 0<0.5234=DW< D L , 因此此模型存在一阶正自相关。 2、偏相关系数检验法 由于 DW 法只能检验一阶自相关性,我们用偏相关系数检验法来检验是否存在高阶自相关性。 在模型回归结果中选择操作:View/Residual Test/Correlogram-Q-statistics ,默认滞后期为 16,得到偏 相关系数结果如下:
由偏相关系数分布图可知,该模型存在明显一阶自相关性,不存在显著高阶自相关性。 3、BG 检验法 在偏相关系数检验之后,我们运用 BG 检验对前面的检验结果进行进一步验证,选择操作 View/Residual Test/Serial Correlation LM Test ,选择滞后期为 5,得到结果如下:
自相关的检验与修正
实验2自相关的检验与修正一、实验目的:掌握自相关模型的检验方法与处理方法・。
二、实验内容及要求:表1列出了1985-2007年中国农村居民人均纯收入与人均消费性支岀的统讣数据。
(1)利用OLS法建立中国农村居民人均消费性支出与人均纯收入的线性模型。
(2)检验模型是否存在自相关。
(3)如果存在自相关,试采用适当的方法加以消除。
表1 1985-2007年中国农村居民人均纯收入与人均消费性支出弹位:元)实验如下:首先对数据进行调整,将全年人均纯收入和全年人均消费性支出相应调整为全年实际人均纯收入和全年实际人均消费性支出。
年份全年入丙纯收入飞年入改消转住支出F费价格抠數全年人均实际纯收〉全年人均实际消费性支出(现价〉(现价〉(1985=100)1985397.6317.42100397.60317.C 42X83571W.1399.43336.48 1987161.63983112.7410.47⑹上19S8544.9476.7132.4411.56360.05 60M535.415T.93S0.94339.03谢0686.3581.63145.1415.6P554.11 1991708.6619.8168.9419.54366.96 1W7M443.44373.19 1993921.6769.7201458.5138194 199412211016.812484X34410.00 19951577.7131036291.4541.42449.68 19961913A1572.1314.4611.67500.03 2090.11617.153X3648.50501.75 1998216215W33319.1677.53498.58 1好9211U1577.42314S704.52501.88 20M22SJ.41670314717.64531.E5 20012366.417413165747.68550.08 20022475.61834315J785.415S1.85 20032622.2419B3320.2818.94606.90 20042936 4218S335 6874.976S1.07 20053251. 932555343943.96744.20 20G635872329348 11030.45812.70 2W7414032243MJ 91128J7878.711>用OLS估计法估计参数data xy□ Group: UNTITLED Workfile: UNTITLED::Untitled\[v»ew][Proc][Cbjact |Print [Name [Freezej [pefaUt ^][Sort]|Tfanspose| ^It4-/-][Smpl47«|Title] Sample) 397.6ODS I X Y1985 | 397 6000 317.42001936 399 4330 335.48001937 4104700 353.42001988 411 5600 360.05001989 380 9430 333.08001990 415.6900 354.11001991 419 6400 36S96001992 •ICC o 443 4400ARO a H nA373 1900oo r c v cc1993 1994 458 01 JU492 34903oZ.94uU410.00001995 541.4200 449.68001996 611 6700 500.03001997 648.5000 501.75001998 677 5300 498.38001999 704 5200 501 88002000 717 6400 531 85002001 747 6890 550.08002002 785 4100 581.35002003 6189430 605.90002004 0749700 651.07002005 948 9600 744.90002006 103D.450 812.70002007 1128370 2787100® EViews-i e Edit Object View Proc Quick Options Window Help data xy Is ? ex□ Equation: UNTITLED Workfile: UNTnLED::Untitled\^e/v|[proc][obj2ct^ |pnnt.(Narre (Freeze] [estunate]f=ofecasi]|statsHResids] Dependent vanawe:YMethod: Least SquaresDate: 04/24M5 Timo: 12:32Sample 1985 2007inciudec oosefvaticns;23Cocffidcnt Std. Error t-Statistic Prob.C X 56.218780.6989281454858 3.8642100.021342 31 999730.00090.0000R-squaredAdjusted R-squared S.E. of regression Sum squared rcsid Log likelihood F-siatistlc Prob(F-statistic) 09799040.97894722 9770811086.87 -103 68281023.9830.000000fvlean deperdantx/zrs.D.aependentvar Akaikeinfo criterion Schwarz cri torio n Hannan-Quinn enterDuroin-watso n stat495.8012158.35739.1898139.2885519 2146450.409903费EViev/sFile Edit Object View Proc Quick Options Window Help图4从图4中可以看出,中国农村居民人均消费性支出与人均纯收入存在着显著的正相关 关系。
自相关 实验报告

**大学经济学院实验报告估计线性回归模型并计算残差。
用普通最小二乘法估计输出结果如下:20,73.0,086.0.,9988.0)02.122()79.6(18.045.1ˆ2====-+-=T DW e s R X Y tt所以,回归方程拟合得效果比较好,但是DW 值比较低。
(2)残差图见图2。
(3)自相关的检验(检验误差项t u 是否存在自相关)①DW 检验:已知DW=0.73,若给定05.0=α,查表得,得DW 检验临界值41.1,20.1==U L d d ,因为DW=0.73<1.20,认为误差项t u 存在严重的一阶正自相关。
②回归检验法:建立残差t u 与21,--t t e e 的回归模型,如表2和表3。
从表2可以看出,1-t e 的回归参数通过了显著性检验,而表3中,21,--t t e e 中只有1-t e 的回归参数通过显著性检验,故判断误差项具有一阶回归形式的自相关。
表2 残差回归相关结果(1)表3 残差回归结果(2)③LM(BG)检验:辅助回归估计输出结果如下表(1)。
表(1)由LM 检验结果可知,LM (1)=7.998,伴随概率p=0.0047<0.05.LM(2)=8.459,伴随概率p=0.0146,所以在α=0.05显著性水平显著,存在一阶,二阶自相关。
同时,由表一,可得LM(BG)自相关检验辅助回归式估计结果是:00.840.020,74.1,40.0)4.0()4.0()4.3(0004.00609.06388.0221=⨯====-+-+=-TR LM DW R v X e e tt t t因为84.3)1(205.0=χ,LM=8.00>3.84,所以LM 检验结果也说明随机误差项存在一阶正自相关。
(4)用差分法和广义差分法建立模型,消除自相关。
用广义最小二乘法估计回归参数。
估计自相关系数ρˆ,635.0273.0121ˆ=-=-=DW ρ 对原变量做广义差分变换。
第七节 自相关检验与修正

杜宾证明:当一阶自相关系数 0 时,h统计量 近似服从标准正态分布,所以利用正态分布可 以对一阶自相关性进行检验。
ˆ 显然,当 n var( b 2 ) 1 时,h统计量无法算出, 于是,杜宾建议采用渐进等价检验,即采用OLS估 计的残差et,建立如下线性回归模型 et=a0+a1xt+a2yt-1+a3et-1+vt 用t统计量检验 H:a3=0, 接受则无一阶自相关,否则存在一阶自相关。
u t 1u t 1 2 u t 2 p u t p v t
3、高阶自回归形式检验 Breusch-Godfrey(布罗斯-戈弗雷)检验 或拉格朗日乘数检验 对模型y=b1+b2x2i+…+bkxki+ut 设自相关形式为:
假设 H 0 : 1 2 p 0即不存在自相关 检验步骤: 1、用 OLS 估计模型,得残差 2、作辅助回归模型 计算样本决定系数 et
第七节 自相关检验与修正
一、自相关的检验方法 (一)图示法 1. 以t为横轴,et为纵轴作图,残差et随时间 的变化呈现有规律的变动,则et存在自相关, 即ut存在自相关。 2. 绘制et与et-1散点图 (二)解析法
1、Durbin-Watson检验(DW检验)。 适用于检验一阶自回归形式。 D-W检验内容: n 2 计算D-W统计量 (e e )
e (1 )e (1 ) e (1 )
t t 1 2 t-1
ˆ 3 .利 用 1 ) 进 行 广 义 差 分 变 换 : ( ˆ y * y t (1 ) y t 1 t * ˆ x t x t (1 ) x t 1 4 .用 O L S 法 估 计 广 义 差 分 模 型 :y t A b 2 x t v t,
序列自相关检验及修正

序列自相关检验及修正
三、G-B检验(拉格朗日乘数检验) 点击View\Residual Test\Serial Correlation LM Test,Lag取2,得到(见图三):
序列自相关检验及修正
含2阶滞后残差项的辅助回归为: et=6.593-0.0003*GDP+1.094*et-1-0.786et-2 (0.231)(-0.504)(6.231)(-3.692) R2=0.6614 LM=22*0.6614=14.55,该值大于显著性水平为 5%,自由度为2的x2分布的临界值x20.05(2) =5.991,由此判断原模型存在2阶序列自相关。
序列自相关检验及修正
序列自相关检验及修正
2阶广义差分的估计结果为: Mt=169.32+0.020GDPt+1.108AR(1)-0.801AR(2) D.W.=1.85>du=1.66,表明经广义差分变换后的 模型已不存在序列相关性。
序列自相关检验及修正
序列自相关检验及修正
序列自相关检验及修正
序列自相关检验及修正
Mnew=86.18+0.02GDPnew (2.76) (16.46) D.W.=1.583 ,在5%的显著性水平下, D.W.>du=1.43,已不存在自相关。
序列自相关检验及修正
2、科克伦-奥科特迭代法 将组m gdp打开,点Proc\Make Equations…在 specification中输入的变量:m gdp ar(1) ar(2) c,点确定得到结果(见图七)
序列自相关检验及修正
Mt=78.09+0.938Mt-1-0.469Mt-2+0.055GDPt0.096GDPt-1+0.054GDPt-2 R2=0.9913 D.W.=2.31
自相关的检验与修正
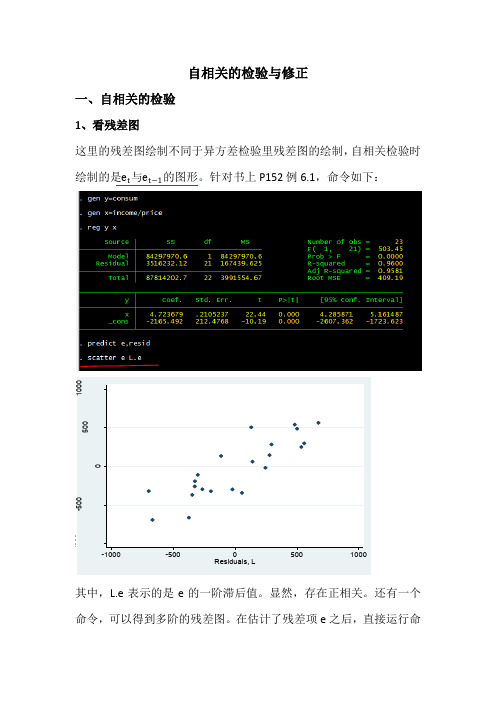
自相关的检验与修正一、自相关的检验1、看残差图这里的残差图绘制不同于异方差检验里残差图的绘制,自相关检验时绘制的是e t 与e t −1的图形。
针对书上P152例6.1,命令如下:其中,L.e 表示的是e 的一阶滞后值。
显然,存在正相关。
还有一个命令,可以得到多阶的残差图。
在估计了残差项e之后,直接运行命R e s i d u a l s令ac e 就可得到下图(ac 为autocorrelation 的缩写):横轴表示的是滞后阶数,阴影部分表示的是相应的置信区间,在上图中,显然一阶滞后是自相关的。
补充:滞后算子L 。
L.x 表示x 的一阶滞后值,L2.x 表示二阶滞后值。
差分算子D 。
D.x 表示x 的一阶差分,D2.x 表示二阶差分。
LD.x 表示一阶差分的一阶滞后值。
需要注意的是,在使用之后算子和差分算子时,一定要事先设定时间变量。
2、DW 检验该方法出现较早,现在已经过时,主要是因为该方法只能检验一阶自相关。
命令:estat dwatson 。
经验上DW 值在1.8---2.2之间接受原假设,不存在一阶自相关。
DW 值接近于0或者接近于4,拒绝原假设,存在一阶自相关。
3、LM检验(BG检验)命令:estat bgodfrey 一阶滞后自相关检验estat bgodfrey,lags(p) P阶滞后自相关检验滞后阶数P的选取最简单的方法就是看自相关图,阴影部分以外的自相关阶数为显著。
二、自相关的处理—广义最小二乘法FGLS命令:prais y x1 x2 x3 该命令对应的是书上P147的(6.33)方法prais y x1 x2 x3,corc 该命令对应的是书上P147的(6.32)方法在自相关检验及处理上,还有比较常用的稳健标准差命令newey以及Q-Test命令,感兴趣的同学可以去查阅相关书籍。
自相关的检验与修正

附件二:实验报告格式(首页)山东轻工业学院实验报告成绩课程名称计量经济学指导教师实验日期 2013-5-25 院(系)商学院专业班级实验地点二机房学生姓名学号同组人无实验项目名称自相关的检验与修正一、实验目的和要求掌握Eviews软件的操作和自相关的检验与修正二、实验原理Eviews软件的操作和自相关的检验与修正,图表法,DW检验,运用迭代法三、主要仪器设备、试剂或材料Eviews软件,计算机四、实验方法与步骤(1)准备工作:建立工作文件,并输入数据:CREATE EX-6-1 A 1978 2000;TATA CINSUM INCOME PRICE;(2)相关图分析:GENR Y=CONSUM/PRICE;GENR X=INCOME/PRICE;SCAT X Y;LS Y C X;(3)自相关检验1)图示法LINR RESID;SCAT RESID(-1) RESID;2)观察结果窗口,由DW统计量,查表,与DL,DU比较得出结论;3)LM检验在方程窗口中点击View—residual test –series correlation LM test;(4)自相关的修正GENR GDY=Y-0.7*Y(-1);GENR GDX=X-0.7*X(-1);LS GDY C GDX;(5)再次检验自相关是否存在,用1),2),3)之一检验;五、实验数据记录、处理及结果分析(1)建立工作组,输入数据如下:1978 344.88 388.32 11979 385.2 425.4 1.011980 474.72 526.92 1.0621982 496.56 576.72 1.0811983 520.84 604.31 1.0861984 599.64 728.17 1.0161985 770.64 875.52 1.251986 949.08 1069.61 1.3361987 1071.04 1187.49 1.4261988 1278.87 1329.7 1.6671989 1291.09 1477.77 1.9121990 1440.47 1638.92 1.971991 1585.71 1844.98 2.1711992 1907.17 2238.38 2.4181993 2322.19 2769.26 2.8441994 3301.37 3982.13 3.5261995 4064.1 4929.53 4.0661996 4679.61 5967.71 4.4321997 5204.29 6608.56 4.5691998 5471.01 7110.54 4.5461999 5851.53 7649.83 4.4962000 6121.07 8140.55 4.478(2)相关图分析Scat x y,得到关于X和Y的散点图如下:从上图可知,X和Y存在线性关系。
自相关的检验与修正

实验五自相关的检验与修正【实验目的】1、理解自相关的含义后果、2、学会自相关的检验与消除方法【实验内容】利用下表资料,试建立我国城乡居民储蓄存款模型,并检验模型的自相关性。
表3 我国城乡居民储蓄存款与GDP统计资料(1978年=100)要求:1)建立对数模型2)分别用图示法和DW检验法,判断双对数模型是否存在自相关3)用科-奥迭代法对双对数模型进行补救(1)Dependent Variable: LNYMethod: Least SquaresDate: 06/05/13 Time: 10:06Sample: 1978 1998Included observations: 21Variable Coefficient Std. Error t-Statistic Prob.C -8.075343 0.255516 -31.60412 0.0000LNX 2.958841 0.046096 64.18896 0.0000Adjusted R-squared 0.995168 S.D. dependent var 1.756767 S.E. of regression 0.122115 Akaike info criterion -1.277311 Sum squared resid 0.283330 Schwarz criterion -1.177832 Log likelihood 15.41176 F-statistic 4120.223 Durbin-Watson stat0.706200 Prob(F-statistic)0.000000ˆln-8.075343+2.958841lnX t Y (0.255516)(0.046096)t= (-31.60412) (64.18896)2R =0.995410 F=4120.223 DW=0.706200(2)对样本量为21,一个解释变量的模型,1%显著水平,差DW 统计表可知,l d =0.975,u d =1.161。
第七章(自相关)

第七章 自相关性一、自相关性及其产生的原因定义:对于模型01122...t t t k kt t y x x x u ββββ=+++++如果随机误差项的各期值之间存在着相关关系,即:(,)()0t t i t t i Cov u u E u u --=≠,1,2,3,....,i s =则称模型存在着自相关性。
原因:模型中遗漏了重要的解释变量,经济惯性,随机因素的影响、模型函数形式的设定误差。
自相关的类型:一阶自相关和高阶自相关。
一阶自相关指随机误差项只与它的前一期相关。
1t t t v ερε-=+,高阶自相关指随机误差项与它的前几期都相关。
1122...t t t p t p t v ερερερε---=++++称之为P 阶自回归形式,或称模型存在P 阶自相关。
二、自相关的影响将产生如下不利影响:(一) 最小二乘估计不再是有效估计OLS 估计仍然是无偏估计,但不再具备有效性。
和异方差对回归的影响相同吗?(二) 一般会低估OLS 估计的标准误差 会低估()i S β。
异方差对OLS 估计的标准误差是什么影响?(三) T 检验的可靠性降低 由于低估()i S β,使T 值偏大。
T 值偏大,会带来什么后果?和异方差带来的后果有何不同?(四) 降低模型的预测精度异方差会对模型的预测精度产生何种影响?三、自相关性的检验1. 残差图的分析如果随着时间的推移,残差分布呈现出周期性的变化,说明很可能存在自相关性。
2. 杜宾——瓦森检验检验范围:一阶自相关的检验。
步骤:(1)提出原假设:H 0:0ρ=,即不存在一阶自相关。
(2)构造检验统计量:21222()nt t nte eDW e--=∑∑可以推导出:2(1)DW ρ≈-(3)检验自相关性:DW=0,则,正自相关, DW=4,则,负自相关,DW=2,则,不存在一阶自相关。
0 d L d u 2 4- d U 4- d L 4(1)0,L DW d ≤≤拒绝原假设,认为存在正自相关性。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
接受则无一阶自相关,否则存在一阶自相关。
3、高阶自回归形式检验 Breusch-Godfrey(布罗斯-戈弗雷)检验
或拉格朗日乘数检验 对模型y=b1+b2x2i+…+bkxki+ut 设自相关形式为: ut 1ut1 2ut2 put p vt
逐步提高的近似估计精度.步骤如下:
1.利用OLS法估计模型yt b1 b2xt ut , 求出残差et (1);
2.根据残差计算的(第一轮)估计值:
(ˆ 1)
et (1)et1 (1)
e2 t-1
(1)
3.利用(ˆ 1)进行广义差分变换:
y
* t
yt
ˆ (1)yt1
即估计误差小于事先给定的精度 : ˆ (n 1) ˆ (n) ,
此时,以(ˆ n 1)作为的估计值并用广义差分变换,得
到回归系数的估计值。
对于模型中含有滞后的被解释变量的情况,上 述方法不适用。
例:yt=b0+b1xt+b2yt-1+ut
此时即使模型存在自相关,DW值也经常接近2,
因此不能用D-W检验。杜宾提出了Durbin-h统计
量:
h (1 DW ) 2
n 1 n var(bˆ2 )
其中,
var(bˆ2
)是y
t
系数估计方差。
4、给定显著水平,若nR 2
2(p), 则拒绝H
,即存在自相关
0
。
二、 自相关模型的修正方法
针对自相关产生的原因,可给出不同的处理方法。 如果是模型中省略了重要的解释变量,使随机项产生了 自相关,则应重新建立模型; 如果是模型建立不当,应重新建立模型; 如果是由于数据加工的原因,可增加样本容量、变换数 据处理形式等。 除了上述原因外还存在自相关,这就是真正的自相关。 如果模型存在真正自相关,其他假定都满足,则可采用广 义差分法、迭代法等估计参数。
yt a0 yt1 a1x t a 2x t1 vt 对上述模型应用OLS估计,得ˆ 再用的估计值ˆ进行广义差分变换,并估计广义差分模型。
此法也适用于多元线性回归模型。
(三)迭代估计或Cochranc-Orcutt
(科克伦-奥克特)估计
依据的近似估计公式, 进行一系列迭代,
第七节 自相关检验与修正
一、自相关的检验方法 (一)图示法
1. 以t为横轴,et为纵轴作图,残差et随时间 的变化呈现有规律的变动,则et存在自相关, 即ut存在自相关。
2. 绘制et与et-1散点图 (二)解析法
1、Durbin-Watson检验(DW检验)。
适用于检验一阶自回归形式。
D-W检验内容:
此外,ˆ
etet1 e2
t-1
或 ˆ
etet1 et2
(2)Durbin杜宾二步法 根据广义差分模型得
yt yt1 b0 (1 ) b1(x t x t1) vt 整理得 yt yt1 b0 (1 ) b1x t b1x t1 vt 令 a0 b0 (1 ),a1 b1 , a2 b1,则
(2)
令Yt*= Yt- Yt-1 Xt*=Xt- Xt-1 ,t=2, ,n
此种变换称为广义差分变换。这种变换损失了一个观测
值,为避免损失,K.R.凯迪雅勒提出做如下变换:
Y1*= Y1 1 2 (2)式写成:
X1*= X1 1 2
Y1*= b1(1- )+b2 Xt*+ t
(一)若自相关系数已知----广义差分法
以一元为例,设模型为
Yt=b1+b2Xt+ut , t=1,2,
, n (1)
随机项具有一阶自回归形式:
ut= ut-1+ t , t 是随机变量,满足前述假定。
将模型(1)减去(1)滞后一期并乘以 得:
Yt- Yt-1=b1(1- )+b2(Xt- Xt-1)+ t
计算D-W统计量
n
(et et1 )2
d t2 n
, et Yt Yˆt
et 2
t 1
可以证明此值约在0~4之间。根据样本容量n和解释变量数k查
D-W分布表,得到临界值dl和du,然后按照下列标准考察计算 得到的D-W值,以判断模型的自相关状态。
正不 自能 相确 关定
无一阶自 回归形式
x*t xt ˆ (1)xt1
4.用OLS法估计广义差分模型:y
* t
A
b2x*t
v
,
t
得到b1和b2的估计值,代入(1)中的一元线性回归模型,
求出残差et (2)和(ˆ 2)
et (2)et1 (2) et2 (2)
重复上述的3.和4.步骤,直至的前后两次估计值比较接近,
(3)
这样就可对(3)应用OLS进行参数估计。
如果是多元线性回归模型,处理方法类似。
(二)自相关系数未知
(1)若未知,可利用DW统计量求ˆ
大样本下,ˆ 1 (1 DW / 2) (k n2 (k 1)2
1)2
k为解释变量的个数,当n 时,ˆ 1 DW/2
不负 能自 确相 定关
0 dl du
2 4-du 4-dl 4
注意:
(1)D-W检验只能判断是否存在一阶自相关, 对于高阶自相关或非自相关皆不适用。
(2)不适用于联立方程组中的各方程随机项 的序列相关检验。
(3)不适用于不含截距项的线性回归模型。 (4)不适用模型中含有滞后的被解释变量的
情况
2.杜宾-h(Durbin-h)检验
假设H0 : 1 2 p 0即不存在自相关
检验步骤:
1、用OLS估计模型,得残差et
2、作辅助回归模型et 1et1 2et2 pet p vt
计算样本决定系数R 2
3、在大样本与假定成立条件下,布罗斯和戈弗雷证明了
nR2渐进服从(2 p)分布
1
杜宾证明:当一阶自相关系数 0 时,h统计量
近似服从标准正态分布,所以利用正态分布可 以对一阶自相关性进行检验。
显然,当 n var(bˆ2) 1 时,h统计量无法算出, 于是,杜宾建议采用渐进等价检验,即采用OLS估 计的残差et,建立如下线性回归模型
et=a0+a1xt+a2yt-1+a3et-1+vt
